Диагонали правильный шестиугольник: Диагональ правильного шестиугольника формула

Что такое правильный шестиугольник и какие задачи с ним могут быть связаны? :: SYL.ru

Самая известная фигура, у которой больше четырех углов — это правильный шестиугольник. В геометрии он часто используется в задачах. А в жизни именно такой вид имеют соты на срезе.

Чем он отличается от неправильного?

Во-первых, шестиугольником является фигура с 6 вершинами. Во-вторых, он может быть выпуклым или вогнутым. Первый отличается тем, что четыре вершины лежат по одну сторону от прямой, проведенной через две другие.

В-третьих, правильный шестиугольник характеризуется тем, что все его стороны равны. Причем каждый угол фигуры тоже имеет одинаковое значение. Чтобы определить сумму всех его углов, потребуется воспользоваться формулой: 180º * (n — 2). Здесь n — число вершин фигуры, то есть 6. Простой расчет дает значение в 720º. То есть каждый угол равен 120 градусам.

В повседневной деятельности правильный шестиугольник встречается в снежинке и гайке. Химики видят ее даже в молекуле бензола.

Какие свойства требуется знать при решении задач?

К тому, что указано выше, следует добавить:

• диагонали фигуры, проведенные через центр, делят ее на шесть треугольников, которые являются равносторонними;
• сторона правильного шестиугольника имеет значение, которое совпадает с радиусом описанной около него окружности;
• используя такую фигуру, есть возможность заполнить плоскость, причем между ними не получится пропусков и не будет наложений.

Введенные обозначения

Традиционно сторона правильной геометрической фигуры обозначается латинской буквой «а». Для решения задач требуются еще площадь и периметр, это S и P соответственно. В правильный шестиугольник бывает вписана окружность или описана около него. Тогда вводятся значения для их радиусов. Обозначаются они соответственно буквами r и R.

В некоторых формулах фигурируют внутренний угол, полупериметр и апофема (являющаяся перпендикуляром к середине любой стороны из центра многоугольника). Для них используются буквы: α, р, m.

Формулы, которые описывают фигуру

Для расчета радиуса вписанной окружности потребуется такая: r = (a * √3) / 2, причем r = m. То есть такая же формула будет и для апофемы.

Поскольку периметр шестиугольника — это сумма всех сторон, то он определится так: P = 6 * a. С учетом того, что сторона равна радиусу описанной окружности, для периметра существует такая формула правильного шестиугольника: P = 6 * R. Из той, что приведена для радиуса вписанной окружности, выводится зависимость между а и r. Тогда формула принимает такой вид: Р = 4 r * √3.

Для площади правильного шестиугольника может пригодиться такая: S = p * r = (a² * 3 √3) / 2.

Задачи

№ 1. Условие. Имеется правильная шестиугольная призма, каждое ребро которой равно 4 см. В нее вписан цилиндр, объем которого необходимо узнать.

Решение. Объем цилиндра определяется как произведение площади основания на высоту. Последняя совпадает с ребром призмы. А она равна стороне правильного шестиугольника. То есть высота цилиндра — тоже 4 см.

Чтобы узнать площадь его основания, потребуется вычислить радиус вписанной в шестиугольник окружности. Формула для этого указана выше. Значит, r = 2√3 (см). Тогда площадь круга: S = π * r² = 3,14 * (2√3 )² = 37,68 (см²).

Осталось сосчитать объем: V = 37, 68 * 4 = 150,72 (см³).

Ответ. V = 150,72 см³.

№ 2. Условие. Вычислить радиус окружности, которая вписана в правильный шестиугольник. Известно, что его сторона равна √3 см. Чему будет равен его периметр?

Решение. Эта задача требует использования двух из указанных формул. Причем их необходимо применять, даже не видоизменяя, просто подставить значение стороны и вычислить.

Таким образом, радиус вписанной окружности получается равным 1,5 см. Для периметра оказывается верным такое значение: 6√3 см.

Ответ. r = 1,5 см, Р = 6√3 см.

№ 3. Условие. Радиус описанной окружности равен 6 см. Какое значение в этом случае будет у стороны правильного шестиугольника?

Решение. Из формулы для радиуса вписанной в шестиугольник окружности легко получается та, по которой нужно вычислять сторону. Ясно, что радиус умножается на два и делится на корень из трех. Необходимо избавиться от иррациональности в знаменателе. Поэтому результат действий принимает такой вид: (12 √3) / (√3 * √3), то есть 4√3.

Ответ. а = 4√3 см.

Онлайн калькулятор: Длина стороны правильного многоугольника

От нашего нового пользователя поступил вот такой запрос:
«Калькулятор должен вычислять длину стороны правильного многоугольника (шестиугольник, пятигольник) по указанному диаметру (или радиусу) описанной окружности».

Удовлетворяем запрос оперативно. Заметим, что для решения задачи нужно найти длину третьей стороны треугольника, исходящего из центра описанной окружности и опирающегося на две соседние вершины правильного многоугольника. Про этот треугольник известно многое: длины двух сторон — это радиусы описанной окружности, и угол, как нетрудно заметить, — это 360, деленное на число вершин правильного многоугольника. Далее используется соотношение из теоремы синусов — две стороны относятся друг к другу также как и синусы противолежащих им углов. Поскольку треугольник равнобедренный и сумма углов в треугольнике равна 180 градусам, угол, противолежащий радиусу вычисляется тривиально. Результат — ниже.

Определение длины стороны правильного многоугольника по радиусу описанной окружности

Число сторон правильного многоугольника

Точность вычисления

Знаков после запятой: 2

Длина стороны правильного многоугольника

 

save Сохранить extension Виджет

P.S. В комментариях некто Александр поинтересовался, а как же найти длину стороны по радиусу вписанной окружности?

Отвечаю — с вписанной окружностью все гораздо проще. Надо рассмотреть треугольник, образованный перпендикуляром к точке касания окружности и многоугольника, половиной стороны многоугольника и линией от центра окружности до ближайшей к перпендикуляру вершины многоугольника. Этот треугольник перпендикулярный, и острый угол его равен 360, деленное на число вершин правильного многоугольника и еще пополам. Половина длины стороны находится легко — это радиус (прилежащий катет), умноженный на тангенс острого угла. Домножаем затем на два — получаем искомую длину стороны. Результат — ниже.

Определение длины стороны правильного многоугольника по радиусу вписанной окружности

Число сторон правильного многоугольника

Точность вычисления

Знаков после запятой: 2

Длина стороны правильного многоугольника

 

save Сохранить extension Виджет

Шестиугольник — Hexagon — qwe.wiki

Форма с несколькими сторонами

В геометрии , A шестиугольник (от греческой ЕЕ гекса , «шесть» и γωνία, Gonia , «угол, угол») представляет собой шестигранный многоугольник или 6-угольник. Сумма внутренних углов любого простого (несамопересекающегося) шестиугольника составляет 720 °.

Правильный шестиугольник

Регулярный шестиугольник

имеет символ шлефли {6} , а также может быть выполнен в виде усеченного равностороннего треугольника , т {3}, который чередует два типа ребер.

Когда задана длина стороны AB , вы рисуете вокруг точки A, а вокруг точки B — дугу окружности. Пересечение М является центром окружности . Перенесите отрезок AB четыре раза на описанную окружность и соедините угловые точки.

Правильный шестиугольник определяется как шестиугольник, который одновременно является равносторонним и равноугольным . Он бицентрический , что означает, что он является как циклическим (имеет описанную окружность), так и касательным (имеет вписанную окружность).

Общая длина сторон равна радиусу окружности или окружности , которая равна раз превышает апофемой (радиус вписанной окружности ). Все внутренние углы составляют 120 градусов . Правильный шестиугольник имеет шесть симметрий вращения (

вращательная симметрия шестого порядка ) и шесть симметрий отражения ( шесть линий симметрии ), составляющих группу диэдра D ₆ . Самые длинные диагонали правильного шестиугольника, соединяющие диаметрально противоположные вершины, вдвое превышают длину одной стороны. Из этого видно, что треугольник с вершиной в центре правильного шестиугольника и общей стороной с шестиугольником является равносторонним , и что правильный шестиугольник можно разделить на шесть равносторонних треугольников. 23{\ displaystyle {\ tfrac {2} {\ sqrt {3}}}}

Подобно квадратам и равносторонним треугольникам , правильные шестиугольники подходят друг к другу без каких-либо зазоров для мозаики плоскости (три шестиугольника, сходящиеся в каждой вершине), и поэтому полезны для построения мозаики . Ячейки сотового улья имеют шестиугольную форму по этой причине и потому, что форма позволяет эффективно использовать пространство и строительные материалы. Диаграмма Вороного регулярной треугольной решетки является сотовая тесселяция из шестиугольников. Обычно не считается триамбусом , хотя он равносторонний.

Параметры

Максимальный диаметр (который соответствует длинной диагонали шестиугольника),

D , в два раза превышает радиус максимальной или описанной окружности , R , которая равна длине боковой, т . Минимальный диаметр или диаметр вписанной окружности (разделение параллельных сторон, расстояние между плоскостями, короткая диагональ или высота при опоре на плоское основание), d , в два раза больше минимального радиуса или inradius , r . Максимумы и минимумы связаны одним и тем же фактором:

12dзнак равнорзнак равнопотому что⁡(30∘)рзнак равно32рзнак равно32т{\ displaystyle {\ frac {1} {2}} d = r = \ cos (30 ^ {\ circ}) R = {\ frac {\ sqrt {3}} {2}} R = {\ frac {\ sqrt {3}} {2}} t}     и аналогично dзнак равно32D.{\ displaystyle d = {\ frac {\ sqrt {3}} {2}} D.}

Площадь правильного шестиугольника

Азнак равно332р2знак равно3ррзнак равно23р2знак равно338D2знак равно34Ddзнак равно32d2≈2,598р2≈3,464р2≈0,6495D2≈0,866d2.{\ displaystyle {\ begin {align} A & = {\ frac {3 {\ sqrt {3}}} {2}} R ^ {2} = 3Rr = 2 {\ sqrt {3}} r ^ {2} \ \ & = {\ frac {3 {\ sqrt {3}}} {8}} D ^ {2} = {\ frac {3} {4}} Dd = {\ frac {\ sqrt {3}} {2 }} d ^ {2} \\ & \ приблизительно 2,598R ^ {2} \ приблизительно 3,464r ^ {2} \\ & \ приблизительно 0,6495D ^ {2} \ приблизительно 0,866d ^ {2}. \ end {выровнено }}}

Для любого правильного многоугольника площадь также может быть выражена через апофему a и периметр p . Для правильного шестиугольника они даются как a = r и p , поэтому знак равно6рзнак равно4р3{\ displaystyle {} = 6R = 4r {\ sqrt {3}}}

Азнак равноап2знак равнор⋅4р32знак равно2р23≈3,464р2.{\ displaystyle {\ begin {align} A & = {\ frac {ap} {2}} \\ & = {\ frac {r \ cdot 4r ​​{\ sqrt {3}}} {2}} = 2r ^ {2 } {\ sqrt {3}} \\ & \ приблизительно 3,464r ^ {2}. \ end {align}}}

Правильный шестиугольник заполняет часть его окружности . 332π≈0,8270{\ displaystyle {\ tfrac {3 {\ sqrt {3}}} {2 \ pi}} \ приблизительно 0,8270}

Если правильный шестиугольник имеет последовательные вершины A, B, C, D, E, F и если P — любая точка на описанной окружности между B и C, то PE + PF = PA + PB + PC + PD .

Из отношения радиуса описанной окружности к внутреннему радиусу следует, что отношение высоты к ширине правильного шестиугольника составляет 1: 1,1547005; то есть шестиугольник с длинной диагональю 1,0000000 будет иметь расстояние 0,8660254 между параллельными сторонами.

Симметрия

Шесть линий отражения правильного шестиугольника с симметрией Dih ₆ или r12 , порядок 12. Двугранные симметрии разделяются в зависимости от того, проходят ли они через вершины ( d для диагонали) или ребра ( p для перпендикуляров). Циклические симметрии в среднем столбце помечены как g для их центральных порядков вращения. Полная симметрия регулярной формы равна r12, а симметрия не помечена как a1 .

Правильный шестиугольник имеет DIH ₆ симметрии, порядок 12. Есть три подгруппы: двугранная DIH ₃ , DIH ₂ и DIH ₁ , и четыре циклических подгрупп: Z ₆ , Z ₃ , Z ₂ и Z ₁ .

Эти симметрии выражают девять различных симметрий правильного шестиугольника. Джон Конвей помечает их буквой и групповым порядком. r12 — полная симметрия, а a1 — несимметрия. p6 , изогональный шестиугольник, построенный из трех зеркал, может чередовать длинные и короткие края, и d6 , изотоксальный шестиугольник, построенный с равной длиной ребер, но вершинами, чередующимися с двумя разными внутренними углами. Эти две формы двойственны друг другу и имеют половину порядка симметрии правильного шестиугольника. В i4 формы правильные шестиугольники уплощены или растягиваются вдоль одного направления симметрии. Его можно рассматривать как удлиненный ромб , а d2 и p2 можно рассматривать как вытянутые по горизонтали и вертикали змеи . Шестиугольники g2 , противоположные стороны которых параллельны, также называются шестиугольными параллелогонами .

Симметрия каждой подгруппы допускает одну или несколько степеней свободы для неправильных форм. Только подгруппа g6 не имеет степеней свободы, но ее можно рассматривать как направленные ребра .

Пример шестиугольников по симметрии

Шестиугольники симметрии g2 , i4 и r12 , как параллелогоны, могут разбивать евклидову плоскость путем сдвига. Другие формы шестиугольника могут перекрывать плоскость с разной ориентацией.

Группы A2 и G2

Шесть корней простой группы Ли A2 , представленной диаграммой Дынкина , имеют правильный шестиугольный узор. Угол между двумя простыми корнями составляет 120 °.

12 корней исключительной группы Ли G2 , представленной диаграммой Дынкина также имеют шестиугольную форму. Два простых корня двух длин имеют угол между собой 150 °.

Рассечение

Кокстеровские гласит , что каждый зоногон (2 м -угольник которого противоположные стороны параллельны и равны по длине) можно разрезать на м ( м -1) / 2 параллелограммов. В частности, это верно для правильных многоугольников с равным числом сторон, и в этом случае все параллелограммы являются ромбическими. Это разложение правильного шестиугольника основано на многоугольной проекции куба Петри с 3 из 6 квадратных граней. Остальные параллелогоны и проективные направления куба рассекаются внутри прямоугольных кубоидов .

Связанные полигоны и мозаики

На правильном шестиугольнике есть символ Шлефли {6}. Правильный шестиугольник — это часть правильной шестиугольной мозаики {6,3} с тремя шестиугольными гранями вокруг каждой вершины.

Правильный шестиугольник можно также создать как усеченный равносторонний треугольник с символом Шлефли t {3}. При рассмотрении с двумя типами (цветами) кромок эта форма имеет только симметрию D ₃ .

Усеченный шестиугольник, т {6}, является двенадцатиугольник , {12}, чередуя два типа (цвета) ребер. Чередовались шестиугольник, ч {6}, представляет собой равносторонний треугольник , {3}. Правильный шестиугольник можно сделать звездообразным с равносторонними треугольниками по краям, образуя гексаграмму . Правильный шестиугольник можно разрезать на шесть равносторонних треугольников , добавив центральную точку. Этот узор повторяется внутри правильной треугольной плитки .

Правильный шестиугольник можно расширить до правильного двенадцатиугольника , добавив чередующиеся квадраты и равносторонние треугольники вокруг него. Этот узор повторяется внутри ромбогексагональной плитки .

Всего шесть самопересекающихся шестиугольников с расположением вершин правильного шестиугольника:

Гексагональные конструкции

Дорога гигантов крупным планом

От пчелиных сот до «Дороги гигантов» в природе преобладают шестиугольные узоры из-за их эффективности. В гексагональной сетке каждая линия настолько коротка, насколько это возможно, если большая область должна быть заполнена наименьшим количеством шестиугольников. Это означает, что для изготовления сот требуется меньше воска, и они приобретают большую прочность при сжатии .

Неправильные шестиугольники с параллельными противоположными краями называются параллелогонами и также могут перекрывать плоскость путем сдвига. В трех измерениях шестиугольные призмы с параллельными противоположными гранями называются параллелоэдрами, и они могут преобразовывать трехмерное пространство в мозаику путем перемещения.

Месселяция шестиугольниками

В дополнение к правильному шестиугольнику, который определяет уникальную мозаику плоскости, любой неправильный шестиугольник, который удовлетворяет критерию Конвея, будет мозаикой плоскости.

Шестиугольник, вписанный в коническое сечение

Теорема Паскаля (также известная как «Теорема Hexagrammum Mysticum») утверждает, что если произвольный шестиугольник вписан в какое-либо коническое сечение и пары противоположных сторон растянуты до тех пор, пока они не встретятся, три точки пересечения будут лежать на прямой линии, то » Линия Паскаля »этой конфигурации.

Циклический шестиугольник

Шестигранной Лемуан является циклическим шестиугольника (один вписан в окружность) с вершинами , заданных шести пересечений ребер треугольника и трех линий, которые параллельны краям , которые проходят через его симедиана точки .

Если последовательные стороны циклического шестиугольника — это a , b , c , d , e , f , то три главных диагонали пересекаются в одной точке тогда и только тогда, когда ace = bdf .

Если для каждой стороны циклического шестиугольника соседние стороны продолжаются до их пересечения, образуя треугольник, внешний по отношению к данной стороне, то сегменты, соединяющие центры описанных окружностей противоположных треугольников, совпадают .

Если шестиугольник имеет вершины на окружности в качестве острого треугольника в шести точках ( в том числе трех вершин треугольника) , где расширенные Высоты треугольника встречается окружности, то площадь шестиугольника в два раза превышает площадь треугольника.

Шестиугольник, касательный к коническому сечению

Пусть ABCDEF — шестиугольник, образованный шестью касательными конического сечения. Тогда теорема Брианшона утверждает, что три главных диагонали AD, BE и CF пересекаются в одной точке.

В шестиугольнике, который является касательным к окружности и имеет последовательные стороны a , b , c , d , e и f

,

а+c+езнак равноб+d+ж.{\ displaystyle a + c + e = b + d + f.}

Равносторонние треугольники по сторонам произвольного шестиугольника

Равносторонние треугольники по сторонам произвольного шестиугольника

Если равносторонний треугольник построен снаружи с каждой стороны любого шестиугольника, то середины отрезков, соединяющих центроиды противоположных треугольников, образуют другой равносторонний треугольник.

Наклоненный шестиугольник

Правильный косой шестиугольник, видимый как края (черные) треугольной антипризмы , симметрия D _3d , [2 ⁺ , 6], (2 * 3), порядок 12.

Перекос шестиугольник является перекос многоугольник с шестью вершинами и ребрами , но не существующие на одной и той же плоскости. Внутренняя часть такого шестиугольника обычно не определяется. У

косого зигзагообразного шестиугольника вершины чередуются между двумя параллельными плоскостями.

Регулярный перекос шестиугольник является вершина-симметрический с равными длинами ребер. В трех измерениях это будет зигзагообразный косой шестиугольник, который можно увидеть в вершинах и боковых гранях треугольной антипризмы с той же симметрией D _3d , [2 ⁺ , 6], порядок 12.

Куб и октаэдр (такой же , как трехстороннее антипризма) имеют регулярные косые шестиугольники как Питрите полигоны.

Полигоны Петри

Правильный косой шестиугольник — это многоугольник Петри для этих правильных , однородных и двойственных многогранников и многогранников более высокой размерности , показанных в этих косых ортогональных проекциях :

Выпуклый равносторонний шестиугольник

Главная диагональ шестиугольника является диагональной , который делит шестиугольник в четырехугольники. В любом выпуклом равностороннем шестиугольнике (все стороны равны) с общей стороной a существует главная диагональ d ₁ такая, что

d1а≤2{\ displaystyle {\ frac {d_ {1}} {a}} \ leq 2}

и главную диагональ d ₂ такую, что

d2а>3.{\ displaystyle {\ frac {d_ {2}} {a}}> {\ sqrt {3}}.}

Многогранники с шестиугольниками

Не существует Платонова твердого тела, состоящего только из правильных шестиугольников, потому что шестиугольники мозаичны , не позволяя результату «складываться». В архимедовых твердых частиц с некоторыми шестиугольными гранями являются усеченным тетраэдром , усеченный октаэдром , усеченный икосаэдром (из футбольного мяча и фуллерена известности), усеченный кубооктаэдра а усеченный икосододекаэдр . Эти шестиугольники можно рассматривать как усеченные треугольники, причем диаграммы Кокстера имеют вид а также .

Существуют и другие многогранники симметрии с вытянутыми или уплощенными шестиугольниками, например многогранник Гольдберга G (2,0):

Также есть 9 тел Джонсона с правильными шестиугольниками:

Галерея натуральных и искусственных шестиугольников

Смотрите также

Ссылки

внешняя ссылка

Правильная шестиугольная призма ℹ️ формула нахождения площади, объема, сторон и диагоналей, свойства и признаки, координаты фигуры

Общие сведения

Призма представляет собой многогранную объёмную фигуру. Две стороны её всегда конгруэнтные (равные) и расположены относительно друг друга в параллельных плоскостях. Остальные же грани являются параллелограммами и формируют общие боковые основания с параллельными поверхностями. Четырёхугольники состоят из попарно равноудалённых прямых. Называют их боковыми гранями призмы. Оставшиеся же 2 многоугольника — основанием. По сути, фигура — это частный случай некругового цилиндра.

Кроме основания и граней, в состав стереофигуры входит:

• высота — прямая, перпендикулярная плоскостям, лежащим у основания многогранника;
• боковые рёбра — стороны, являющиеся общими для боковых граней;
• вершины — точки, принадлежащие сразу двум отрезкам и формирующим периметр геометрического тела;
• диагонали — отрезки, проходящие через 2 вершины, но при этом несвойственные одной грани;
• диагональные плоскости — пересекающие боковые рёбра и диагональ у основания.

Кроме этого, используются такие понятия, как диагональное и ортогональное сечение. Первое представляет собой параллелограмм, полученный при пересечении призмы и диагональной плоскости. Второе же — пересечение многогранника с плоскостью, перпендикулярной боковому ребру.

В зависимости от расположения стенок и вида основания, призмы разделяют на 3 типа. Прямой называют ту, где все грани — прямоугольники. Если у фигуры в основании находится правильный многоугольник, стереофигура считается правильной. Частным случаем её является полуправильная призма. В ней боковые грани образуют квадраты. Когда же у многогранника основания непараллельные, призму называют усечённой.

Полуправильный многогранник, имеющий 2 параллельных основания в виде правильных n-угольников, равных между собой, чьи грани представляют собой ломаную линию, называют антипризмой. В качестве примера такой фигуры можно привести октаэдр, икосаэдр и восьмиугольный октагон.

Свойства шестигранника

Правильную шестиугольную призму принято обозначать большими латинскими буквами: ABCDEFA1B1C1D1E1F1. Длину основания подписывают маленьким символом a, а длину боковой стороны h. К характеристикам фигуры относят площади основания, боковые грани, полную поверхность, объём многогранника. Всего у геометрического тела 8 граней, 18 рёбер и 12 вершин.

Для успешного вычисления различных параметров фигуры понадобится знать следующие формулы:

1. Площадь основания. Так как в основе тела лежат правильные шестиугольники, то, используя их свойства, можно получить формулу: S = (3 * a ² * √ 3) / 2, где: а — сторона многоугольника.
2. Площадь полной поверхности. Определяется она из равенства: Sb = 6 * a * h + 2 * (3 * a ² * √ 3) / 2. Из-за того, что площадь плоскости можно получить путём сложения сторон призмы и двух поверхностей её основания, а грань — прямоугольник (S прямоугольника = a * h), то указанная формула будет верной.
3. Объём. Он равняется произведению площади основания на высоту. Роль последней может играть ребро любой стороны, например, BB1. Учитывая сказанное, формулу можно записать так: V = S * BB 1 = ((3 √ 3) / 2) * (a² * h).

Если рассмотреть правильный шестиугольник, лежащий в основе призмы ABCDEF, и провести отрезки AB, CD, EF, у них будет общая точка пересечения. Для удобства обозначить её можно буквой O. Так как, в соответствии со свойствами, треугольники AOB, BOC, COD, DOE, EOF, FOA будут правильными, можно составить равенство: AO = OD = EO = OB = CO = OF = a .

Через точку М можно провести прямую AC и CF. Образованный ранее треугольник AEO будет равнобедренным. В нём отрезок AO равняется по величине OE. Значит, угол EOA будет развёрнутым и равняться 120 градусам. Используя свойства равнобедренного треугольника, можно записать: AE = a * √2 * (1 — cos EOA). То есть: AE = AC = √3 * a.

По аналогии можно найти и стороны: EA1, FB1, AC1, BD1, CE1, DF1. Так как AA1 = h, а из свойств правильной призмы следует, что угол EAA1 — прямой, длины сторон будут равны между собой, и их можно найти, используя формулу: √(AA1² + AE²)= √(h² + 3 * a) = 2 * a. Грань EB1 = FC1 = AD1 = BE1 = CF1 = DA1 = √(BB1² + BE²) = √(h² + 4 *a) = √5 *a. Сторона FE1 = √(FE² + EE²) = √(h² + a²) = √2 *a.

Длины диагоналей призмы равняются сумме квадратов высоты и длины основания под корнем. Это легко доказать, если принять, что ЕЕ1 = h, а FE = a. Треугольник FEE1 прямоугольный, значит, FE = √(h² + a²), что и следовало доказать.

Решение простого примера

Такого вида задачи обычно даются в учебниках по геометрии для выпускных классов средней школы. Решить их самостоятельно несложно, нужно только знать формулы и представлять, как выглядит та или иная фигура. При этом часто приходится использовать дополнительные построения. Вот один из таких типовых примеров.

Пусть имеется девятиугольная фигура, в которую вписана правильная шестиугольная призма со стандартным обозначением вершин. Сторона основания в ней составляет 4 см, а длина бокового ребра меньше её в 2 раза, то есть равняется 2. Необходимо вычислить расстояние от точки C1 до прямой, соединяющей вершины EF. По условию задачи в основании лежит геометрическое тело, у которого все стороны и углы равны, то есть фигура правильная.

Чтобы понять, что будет представлять искомая прямая, нужно изобразить призму на рисунке и на нём же начертить отрезок. Фактически это будет перпендикуляр, который и является вычисляемым расстоянием. Проекцией точки С1 будет вершина С. Из неё можно построить перпендикуляр, который ограничится точкой E. Таким образом, поставленная задача сводится к поиску длины отрезка C1E.

Найти длину прямой можно как гипотенузу прямоугольного треугольника С1СE. Треугольная фигура будет с прямым углом C. Из условия задачи отрезок С1С в два раза меньше ребра основания, а значит равен 2. Теперь осталось найти, чему равняется длина CE. Геометрическое тело CDE является равнобедренным. По условию CD = ED. Сумму углов шестиугольника можно найти по формуле е = 180 * (n — 2) = 180 * 4 = 720. Получается, что на каждый угол приходится по 120 градусов.

С вершины D можно опустить перпендикуляр DN на CE. Принимая во внимание свойства равнобедренного треугольника, высота DN будет медианной и биссектрисой. Следовательно, угол C равняется 30 градусов, так как CDH — прямоугольный.

Теперь можно найти СH. Сделать это возможно через косинус угла C: cos 30 = CH / CD. Отсюда: CH = 4 * p/2 = 2 √ 3. Так как CH = HE, сторона CE = 2 * 2 √3. К треугольнику CC1E можно применить теорему Пифагора: C1E² = C1C² + CE = 2² + (4 c3) ². C1E² = √ 52. Таким образом, искомый ответ можно записать так: C1E = 2√13.

Задача высокого уровня

Решение примеров повышенного уровня сложности предполагает не только хорошее понимание изучаемого материала, но и знание предыдущих тем. Понадобится вспомнить формулы для нахождения площадей и объёмов плоских фигур и их свойства. Вот пример одной из таких задач.

Пусть имеется шестиугольная объёмная фигура, у которой баковая грань равняется 6, а площадь основания 12. Нужно найти объём геометрического тела с вершинами в точках A, B1, C1, D1, E1, F1.

В таких задачах перед тем как непосредственно приступить к вычислениям, желательно использовать вспомогательный рисунок. На нём нужно изобразить фигуру в трёхмерной системе координат и подписать все её вершины.

Согласно условию, площадь основания Sabcde1f1 = 12, отрезок AA1 = 6. Так как фигура правильная, то все ребра у призмы буду равны. Чтобы найти, сколько будет составлять объём, понадобится обозначить многогранник. Для этого следует построить отрезки F1B, F1A, B1, E1A, D1A, C1A. Получившаяся фигура представляет собой пирамиду.

Формула для нахождения объёма пирамиды записывается так: V = h * S / 3. Её можно привести к виду: V = (AA1 * Sb1c1d1e1f1) / 3. Теперь нужно определить, чему же будет равняться площадь шестиугольника. Так как в основании призмы лежит правильная фигура с шестью углами, радиус описанной окружности будет совпадать с боковой стороной.

Таким образом, искомая площадь будет равняться шести поверхностям правильного треугольника. В свою очередь, его занимаемый размер можно определить как Sтр = (a * b) * sin / 2. Значит, площадь основания призмы равна: S = (6 * R * R * sin 60) / 2. Подставив заданное условием значение из формулы, можно выразить радиус: R² = (12 * 2) / 3 √ 3 = 8 /√3.

Площадь треугольника A1B1F1 находится как произведение сторон, умноженное на синус угла и разделённое на 2: S = (a * a * sin120) / 2 = a² * sin60 / 2 = (R² * √ 3/3) / 2. Подставив значение R, можно получить: S = (½) * (8 / √ 3) * (√3 / 2) = 2. Тогда площадь пятиугольника будет равняться разнице поверхностей шестиугольника и треугольника A1B1F1, то есть S = 12 — 2 = 10. Теперь можно будет подсчитать и объём пирамиды: Vab1c1d1e1f1 = (1 / 3) * 6 * 10 = 20. Задача решена.

Свойства шестиугольника и калькулятора правильного шестиугольника

Теоретическая основа

Содержание

Определения

Шестиугольник — это многоугольник с шестью сторонами и шестью вершинами. Как и любой многоугольник, шестиугольник может быть выпуклым или вогнутым, как показано на следующем рисунке. В выпуклом состоянии шестиугольник (или многоугольник в целом) не имеет внутренних углов больше 180 °. Напротив, вогнутый шестиугольник (или многоугольник) имеет один или несколько внутренних углов больше 180 °. Шестиугольник называется правильным, если все его стороны и внутренние углы равны . В отличие от треугольника, наличие равных сторон не означает, что внутренние углы также равны, поскольку шестиугольник может быть вогнутым. Как показано на рисунке ниже, можно определить множество возможных вогнутых шестиугольников с равными сторонами, но с разными внутренними углами (они называются равносторонними). Неправильный шестиугольник называется неправильным.

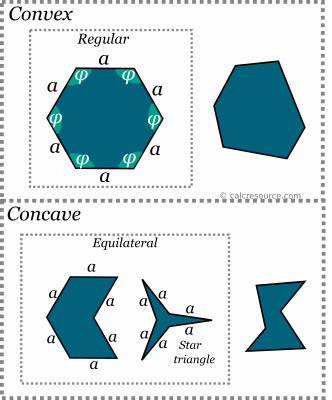Типы шестиугольников

Сумма внутренних углов любого шестиугольника, выпуклого или вогнутого, всегда равна 720 °.В этом легко заключить, посчитав количество треугольников, помещающихся внутри шестиугольника, соединив его вершины (избегая пересечений). Действительно, есть 4 треугольника. Так как сумма внутренних углов в одном треугольнике составляет 180 °, четыре треугольника, расположенные рядом, должны иметь размер 4×180 = 720 °.

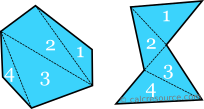Диагонали шестиугольника разделяют его внутреннюю часть на 4 треугольника

Свойства правильных шестиугольников

Симметрия

Правильный шестиугольник имеет шесть осей симметрии. Половина из них проходит через диагонально противоположные вершины, а оставшаяся — через середины противоположных ребер.\ circ

Остальные два угла в треугольнике также равны 60 °. На самом деле это \ varphi / 2, потому что диагонали шестиугольника (линии, соединяющие противоположные вершины) также являются осями симметрии, таким образом разделяя внутренний угол \ varphi пополам (который составляет 120 °). Следовательно, все шесть треугольников, у которых центр шестиугольника является одной из вершин, являются идентичными равносторонними треугольниками.

Внутренний и центральный углы также являются дополнительными, поскольку их сумма составляет 180 °:

\ varphi + \ theta = 120 ° + 60 ° = 180 °

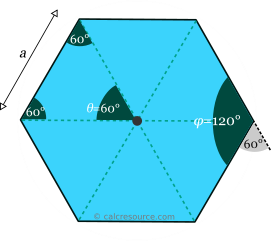
Правильный шестиугольник состоит из шести одинаковых равносторонних треугольников, имеющих общий вершина, центр многоугольника.

Окружность и вписанная окружность

Как и любой правильный многоугольник, можно нарисовать круг, проходящий через все шесть вершин шестиугольника. Это описанная окружность или описанная окружность многоугольника. Центр этого круга — центр шестиугольника. Точно так же диагонали шестиугольника — это диаметры описанной окружности. Радиус описанной окружности R_c обычно называют радиусом описанной окружности.

Можно нарисовать еще один круг, проходящий через середины сторон шестиугольника.Этот круг называется вписанным кругом или вписанным кругом. Он касается всех шести сторон, а его центр совпадает с центром описанной окружности. Радиус вписанной окружности R_i обычно называют внутренним радиусом.

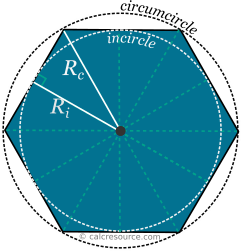Описанная и вписанная окружности правильного шестиугольника

Радиусы описанной окружности R_c и вписанной окружности R_i связаны с длиной стороны \ alpha, а также между собой. Эти отношения могут быть обнаружены с помощью свойств прямоугольного треугольника, стороны которого: радиус описанной окружности, внутренний радиус и половина стороны шестиугольника, как показано на рисунке ниже.Используя базовую тригонометрию, мы находим:

\ begin {split} R_c & = \ frac {a} {2 \ sin {\ frac {\ theta} {2}}} \\ R_i & = \ frac {a} {2 \ tan {\ frac {\ theta} {2}}} \\ R_i & = R_c \ cos {\ frac {\ theta} {2}} \ end {split}

, где \ theta — центральный угол, а \ alpha — сторона длина. Оказывается, эти выражения верны для любого правильного многоугольника, а не только для шестиугольника. Мы можем получить конкретное выражение для правильного шестиугольника, установив θ = 60 °. Это следующие выражения:

\ begin {split} R_c & = \ frac {a} {2 \ sin {30 ^ {\ circ}}} = a \\ R_i & = \ frac {a} {2 \ tan {30 ^ {\ circ}}} \ приблизительно 0.{\ circ}} \ приблизительно 0,866 R_c \ end {split}.

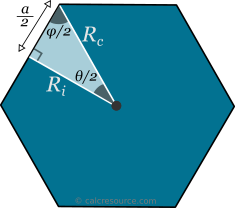
Радиус описанной окружности правильного шестиугольника равен его стороне.

Площадь и периметр

Площадь правильного шестиугольника может быть найдена, если учесть, что он состоит из 6 одинаковых равносторонних треугольников со сторонами \ alpha и высотой, равной радиусу шестиугольника (см. Рисунок ниже). Площадь каждого треугольника равна \ frac {1} {2} a R_i. Следовательно, общая площадь шести треугольников равна:

A = 6 \ frac {1} {2} a R_i = 3a \ frac {a} {2 \ tan {30 ^ {\ circ}}} \ Rightarrow

A = \ frac {3a ^ 2} {2 \ tan {30 ^ {\ circ}}}

Аппроксимация последнего уравнения:

A \ приблизительно 2.2

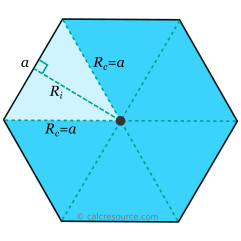
Периметр любого N-стороннего правильного многоугольника — это просто сумма длин всех сторон: P = N a. Следовательно, для правильного шестиугольника:

P = 6a

Ограничивающая рамка

Ограничивающая рамка плоской формы — это наименьший прямоугольник, который полностью охватывает форму. Размеры этого прямоугольника определяются высотой h и t шириной w правильного шестиугольника.

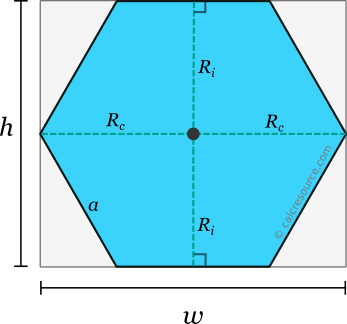
Высота

Высота h правильного шестиугольника — это расстояние между двумя противоположными краями.\ circ}

, что приблизительно равно:

h \ приблизительно 1,732 R_c

h \ приблизительно 1,732 a

Ширина

Ширина w — это расстояние между двумя противоположными вершинами правильного шестиугольника (длина его диагонали) . Это равно удвоенному радиусу описанной окружности R_c:

w = 2R_c

Поскольку R_c = a, мы могли бы также написать:

w = 2a

Как нарисовать правильный шестиугольник

Вы можете нарисовать правильный шестиугольник заданная длина стороны \ alpha, используя только линейку и циркуль.Выполните шаги, описанные ниже:

1. Сначала просто нарисуйте линейный сегмент, длина которого равна желаемой длине стороны шестиугольника \ alpha.
2. Затем постройте окружность с центром на одном конце линейного сегмента и радиусом, равным длине сегмента.
3. Не меняя радиуса, постройте вторую окружность, центр которой находится на другом конце линейного сегмента. Определены две точки, где этот круг пересекается с первым.
4. Используя тот же радиус, поместите кончик циркуля в любую из последних определенных точек и постройте новый круг.Новая точка определяется на пересечении с первым кругом.
5. Повторите ту же процедуру еще два раза. Поместите кончик циркуля в последнюю точку и постройте новый круг. Новая точка определяется на пересечении с первым кругом.
6. На данный момент определены шесть точек вокруг первого круга. Это вершины шестиугольника. Нарисуйте между ними линейные отрезки, и правильный шестиугольник теперь готов. Начальная окружность — это описанная окружность шестиугольника.

На следующем рисунке шаг за шагом показана процедура рисования.

Рисование правильного шестиугольника с помощью линейки и циркуля.

Примеры

Пример 1

Определите радиус описанной окружности, внутренний радиус и площадь правильного шестиугольника с длиной стороны a = 8 дюймов.

Радиус описанной окружности и внутренний радиус в единицах длины стороны a для правильного шестиугольника были получены в предыдущих разделах. Это:

\ begin {split} R_c & = a \\ R_i & = \ frac {a} {2 \ tan {30 ^ {\ circ}}} \ end {split}.2

Ключевой особенностью правильного шестиугольника является его способность размещать мозаику на плоскости, не оставляя зазоров. Это свойство позволяет предположить, что ни одно место в рамке улья не остается незанятым. Другими словами, мы можем найти количество ячеек в рамке улья, N, разделив общую площадь рамки на площадь ячейки:

N = \ frac {A_f} {A}

Путем подстановки и преобразования из квадратных дюймов до мм ² (т.е. 1 » = 25,4 мм) получаем:

N \ приблизительно \ frac {171 \ \ left (25.2} \ Rightarrow

N \ приблизительно 5825

Почти шесть тысяч ячеек. Но это число могло быть немного меньше, если учесть, что рядом с границами кадра формирование правильных шестиугольников невозможно. Если предположить, что один вертикальный и один горизонтальный столбцы ячеек потрачены впустую, по этой причине количество ячеек будет меньше примерно на 140 ячеек. Также имейте в виду, что размер ячеек может варьироваться. Данный размер в этом примере является обычным для имеющихся в продаже рамок ульев.Естественные клетки могут быть меньше.

Шпаргалка по правильному шестиугольнику

В следующей таблице приведен краткий список основных формул, относящихся к правильному шестиугольнику. Также перечислены некоторые приближения, которые могут оказаться полезными для практических задач.

Краткий справочник по правильному шестиграннику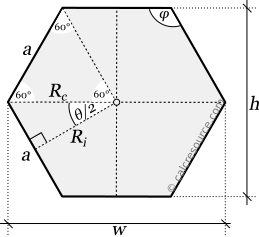
Окружной радиус:	R_c = a
Inradius:	R_i = \ 2 \ frac (a} } = \ frac {\ sqrt {3}} {2} a
Высота:	h = 2R_c = 2a
Ширина:	w = 2R_i
Площадь:	A = \ frac {3a ^ 2} {2 \ tan (30 ^ \ circ)} = \ frac {3 \ sqrt {3}} {2} a ^ 2
Внутренний угол:	\ varphi = 120 ^ \ circ
Центральный угол:	\ theta = 60 ^ \ circ
Приближение:	R_i = 0.2

См. Также

.

Введение в шестиугольную геометрию

Содержание

Введение

Ниже приводится краткий обзор некоторых элементарных свойств шестиугольников, и почему они могут быть полезны. Он не претендует на всестороннее рассмотрение данного предмета. Меня особенно интересуют математические свойства шестиугольников и, в некоторой степени, их роль в мире природы. Я избегал обсуждения шестиугольников, поскольку они имеют отношение к человеческой культуре, религии, истории и другим «местным» проблемам, хотя в этих областях есть много увлекательных примеров шестиугольника и шестиугольника, и они, несомненно, будут более подробно рассмотрены в другом месте в другое время. .

Эта статья находится в стадии разработки и на самом деле не «закончена» в каком-либо значимом смысле. Он актуален на момент последнего обновления. Я намерен в какой-то момент заменить или, по крайней мере, дополнить его более полным и красноречивым обзором гексагональных концепций. Имейте в виду, что в этой статье исследуется лишь очень небольшая часть интересных свойств шестиугольников, и есть надежда, что более полное представление об их качествах появится благодаря сумме разнообразного материала, доступного на этом сайте.

Замечание о терминологии: По моему обычаю, если не указано иное, «шестиугольник» относится только к правильным шестиугольникам. Кроме того, я склонен довольно свободно говорить о «шестиугольных» то и то. Описывая вещи как «шестиугольники», я часто имею в виду в очень широком смысле все шестиугольные и шестиугольные симметрии, и не обязательно правильные шестиугольники как таковые.

Некоторые наблюдения о шестиугольниках

Шестиугольник — это замкнутая плоская фигура с шестью ребрами и шестью вершинами.Правильный шестиугольник — это выпуклая фигура со сторонами одинаковой длины и внутренними углами 120 градусов. Он имеет шесть симметрий вращения и шесть симметрий отражения, составляющих двугранную группу D ₆ .

Свойства шестиугольников многочисленны и интересны. На первый взгляд выделяются несколько фактов о них:

• Шестиугольники — это один из трех правильных многоугольников, которые составляют мозаику евклидовой плоскости (наряду с квадратами и треугольниками).
• Гексагональная мозаика комбинаторно идентична плотной упаковке кругов на плоскости.
• Шестиугольники — единственный правильный многоугольник, который можно подразделить на другой правильный многоугольник. (Насколько мне известно, шестиугольники — единственный правильный многогранник любой размерности с этим конкретным свойством.)
• В связи с этим шестиугольники — это уникальный правильный многоугольник, такой, что расстояние между центром и каждой вершиной равно длине каждой стороны (разделяя это свойство с кубооктаэдром в 3-м пространстве).
• Шестиугольники — это первые многоугольники, возрастающие по количеству сторон, которые не образуют грани правильного выпуклого многогранника в евклидовом пространстве.Три многоугольника с меньшим количеством сторон составляют поверхности пяти платоновых тел, но для этой цели нельзя использовать многоугольник с шестью или более сторонами. Следствием этого является то, что ни один правильный многогранник ни в каком измерении не имеет шестиугольных граней, хотя многие из них имеют шестиугольные или шестиугольно-симметричные вершины или другие элементы.
• Шестиугольники — это пермутоэдры третьего порядка, что означает, что каждая вершина шестиугольника может быть описана декартовыми координатами с использованием одной из шести перестановок чисел 1, 2 и 3.Такой шестиугольник лежал бы на плоскости, состоящей из всех точек с координатами, которые в сумме дают 6, и делит пополам куб единичной длины 2 между координатами 1 и 3.

Еще одна интересная особенность шестиугольников — и, пожалуй, наиболее поразительный факт о них — это то, что они действительно имеют шесть сторон. А теперь позвольте нам перечислить некоторые интересные факты о числе шесть:

• Шесть — очень сложное число, второе по величине составное число и первое совершенное число.То есть 1 * 2 * 3 = 1 + 2 + 3 = 6.
• В смежном вопросе шесть — единственное число, которое является одновременно суммой и произведением трех последовательных натуральных чисел (1, 2 и 3).
• Шесть — наименьшее составное целое число без квадратов и, соответственно, первое натуральное число с двумя различными простыми множителями (2 и 3).
• Кубики имеют шесть сторон, и они тоже довольно полезны.

И так далее. Очевидно, что большинство уникальных и интересных свойств шестерки в конечном итоге проистекает из того факта, что это произведение и сумма первых трех натуральных чисел, и что, в более философском смысле, это можно рассматривать как сочетание архетипические ценности единства, двойственности и троичности в несколько уравновешенное целое.Единство разделяется на дуальность, которая примиряется в троице (один плюс два или два, объединяющихся в одно), которая затем рекомбинируется с двойственностью и единством — либо аддитивно, либо мультипликативно — для создания наших уважаемых шести.

Конечно, есть много других гексагональных и гексагональных чисел, и было бы ошибкой ассоциировать гексагональность только с шестью. Семерка, например, часто занимала видное место в человеческой культуре и, в частности, в некоторых религиозных традициях.Если вернуться назад и посмотреть на различные геометрические формы, связанные с такими семерками, часто становится очевидным, что они сконструированы так, чтобы образовывать шесть периферийных объектов вокруг одного центрального объекта — в виде шестиугольных окружностей или шестиугольной мозаики. Казалось бы, негексагональные числа, такие как восемь и десять, также имеют гексагональные коннотации, как и различные центрированные шестиугольные числа, правильные шестиугольные числа и так далее. Не говоря уже о числах, кратных шести, например, двенадцати, что также является действительно большим числом само по себе (добавление делимости на 4 к 1, 2, 3 ситуации).Но, безусловно, само собой разумеется, что шесть имеет отчетливую связь с гексагональностью, и в этом отношении стоит знать ее уникальные и интересные свойства.

В конечном итоге я считаю, что чем больше вы изучаете математические и физические основы Вселенной, тем более заметными и интересными становятся шестиугольники, шестерки и их различные аналоги в других математических системах. Постулирование какой-либо всеобъемлющей интерпретации этого выходит за рамки данной статьи, но это стоит отметить и учесть в наших интерпретациях реальности и во взаимоотношениях с ней.

Здесь я хотел бы подробнее остановиться на нескольких шестиугольных вопросах, поднятых выше.

Основная геометрия шестиугольников

Давайте сначала рассмотрим более внимательно основные пропорции и соотношения благородного шестиугольника:

Апофема правильного шестиугольника равна половине квадратного корня из 3. Это можно продемонстрировать с помощью единичного шестиугольника, где каждой стороне дана длина 1. Затем мы можем нарисовать прямоугольный треугольник, используя диаметр от вершины к вершине. шестиугольника как гипотенузы.Поскольку известно, что диаметр такого шестиугольника равен 2, у нас остается одно неопределенное ребро нашего треугольника, равное расстоянию между двумя противоположными сторонами шестиугольника (что в два раза больше апофемы). Назовем это ребро x . Теорема Пифагора говорит нам, что 1 ² + x ² = 2 ² . Отсюда следует, что 1 + x ² = 4, x ² = 3, и, следовательно, x = √3. Следовательно, «высота» «ширина» правильного шестиугольника равна √3 / 2. Quod erat manifestrandum.

Интересным следствием этого является то, что правильные шестиугольники и равносторонние треугольники имеют одинаковое отношение «ширины» к «высоте». То есть минимальный диаметр шестиугольника и треугольника равен √3 / 2 его максимального диаметра. В самом деле, √3 является повторяющимся значением во всей треугольной и шестиугольной геометрии — например, диагональное расстояние между двумя противоположными вершинами куба также равно √3 (сравните с диагональной шириной квадрата, которая равна √2, по причинам, аналогичным указанные выше).Как следствие, √3, конечно, занимает видное место в плоской тригонометрии, где она проявляется в выражении различных значений 60 и 30 градусов.

Площадь шестиугольника также может быть вычислена с помощью √3. Давайте сначала определим длину ребра нашего шестиугольника как s . Затем мы можем нарисовать прямоугольник между двумя противоположными краями шестиугольника с площадью s ² √3. Если мы затем посчитаем, что у нас осталось 4 правых треугольных сечения, и что сам шестиугольник можно считать состоящим из 12 таких треугольников, 8 из которых мы включили в наш прямоугольник, становится ясно, что общая площадь шестиугольника в полтора раза больше площади прямоугольника.Таким образом, s ² √3 (3/2). Quod erat faciendum.

(Это также пример более общего принципа, согласно которому площадь правильного выпуклого многоугольника равна произведению периметра и апофемы, деленных на 2 (в данном случае 6s√3 / 2/2). Это связано с к тому факту, что мы можем разделить правильный выпуклый многоугольник со сторонами n на 2 прямоугольных треугольника n , проведя отрезки линии от центра к каждой вершине, а также от центра к середине каждого ребра.Затем мы можем предположить, что каждые 2 сформированных таким образом прямоугольных треугольника можно объединить в прямоугольник с площадью апофемы, умноженной на половину длины ребра. Таким образом, просто разделив произведение апофемы на общий периметр пополам, мы приходим к общей площади многоугольника.)

Гексагональная мозаика

Как отмечалось ранее, шестиугольники можно выложить плиткой или мозаикой в ​​виде регулярного рисунка на плоской двумерной плоскости. То есть шестиугольник может быть ограничен шестью другими шестиугольниками, которые сами могут быть ограничены шестью шестиугольниками (включая друг друга), и так далее, бесконечно в любом направлении, без пустого пространства.Обратите внимание, что хотя существует любое количество потенциальных мозаик, состоящих из двух или более типов многоугольников, только шестиугольники, квадраты и треугольники могут сами по себе образовывать такие правильные мозаики. (Аналогично, в трех измерениях, среди однородных многогранников, только шестигранный куб и шестигранный аналог усеченного октаэдра могут сами по себе образовывать заполняющие пространство мозаики.)

Следовательно, шестиугольник — это, конечно, правильный многоугольник с высшей стороной в виде мозаики. Это делает его уникально важным во множестве областей, так как он имеет преимущество в том, что каждый составляющий шестиугольник более или менее равномерно отделен от его соседей.То есть любая заданная точка внутри шестиугольника (будь то мозаика из шестиугольников или нет) ближе к центру этого шестиугольника, чем любая заданная точка в квадрате или треугольнике равной площади. Поскольку квадраты и треугольники имеют более острые углы, точки около их углов находятся дальше от точек в другом месте их области, чем они были бы в аналогичных местах шестиугольника. То же самое будет верно и для любого многоугольника с более высокой стороной — идеальная эффективность для ограждения данной области, в конечном счете, является кругом.Но опять же, у шестиугольников есть преимущество тесселяции. Таким образом, для любой задачи, которая требует как регулярной сетки ячеек, так и элементов, и эффективного ограждения области этой ячейки, гексагональная тесселяция является логичным и необходимым выбором. Общие примеры такого использования гексагональных ячеек можно найти в таких разнообразных областях, как клеточные автоматы, статистическая выборка, настольные игры, компьютерные игры, соты уважаемой пчелы и т. Д.

Связанное с этим свойство гексагональной мозаики состоит в том, что она не создает диагональных краев.(Под «диагональю» здесь я подразумеваю соседей, которые имеют общую границу только вершины, а не границу ребра — я не знаю более точного математического термина для этого, хотя я знаю, что это не совсем то, что «диагональ» означает в самом строгом смысл этого термина.) Если вы посмотрите на мозаики из треугольников и квадратов, вы, конечно, увидите, что оба имеют диагональные связи между соседними элементами в их вершинах. В квадратной тесселяции каждый квадрат соединяется с одним квадратом непосредственно с каждой стороны и одним квадратом по диагонали в каждой вершине, всего восемь соседних квадратов, а в треугольной тесселяции каждый треугольник соединяется с одним треугольником с каждой стороны и с тремя треугольниками по диагонали на каждой. вершина, всего двенадцать соседних треугольников.Эти диагональные соединения, конечно же, являются ключом к способности квадратов и треугольников образовывать правильные многогранники — удалив диагональных соседей вокруг квадрата, можно легко загнуть оставшиеся соседние квадраты, пока они не соединятся друг с другом напрямую, чтобы сформировать куб, и аналогичным образом удаляя одного, двух или трех диагональных соседей из треугольника, можно сложить оставшиеся треугольники в икосаэдр, октаэдр или тетраэдр соответственно. (Хотя следует отметить, что, хотя оба диагонально-мозаичных правильных многоугольника образуют правильные многогранники при таком складывании, на поверхности нет особой причины, по которой этот должен иметь место .) Наоборот, поэтому шестиугольники не могут образовывать собственные правильные многогранники. Каждый внешний угол шестиугольника составляет 120 градусов, а единственная возможная конфигурация вершины — в евклидовом пространстве — с тремя соседними углами, составляющими в сумме 360 градусов (за исключением, конечно, «вырожденного» шестиугольного диэдра, который не особенно полезен для наши цели здесь).

Гексагональная тесселяция — это двойная треугольная тесселяция — вы можете превратить первую во вторую, заменив все вершины треугольниками, а все шестиугольники — вершинами.Точно так же в треугольной тесселяции, если вы замените все треугольники вершинами, а все вершины шестиугольниками, у вас снова останется шестиугольная мозаика. (Любой многогранник или мозаика с обратными количествами внешних элементов может быть перевернут по тому же принципу: октаэдр является обратным кубу, а икосаэдр — обратным додекаэдру — каждый представляет собой обращение вершины / грани своего аналога. Это могут быть представлены в виде записи путем изменения символа Шлефли конкретного объекта — в случае гексагональной и треугольной мозаики, путем изменения {6,3} на {3,6}, или наоборот.) Кроме того, поскольку шестиугольники можно разделить на равносторонние треугольники, а равносторонние треугольники можно объединить в шестиугольники, мозаику треугольников можно рассматривать как простое подразделение шестиугольника или наоборот.

Последнее преимущество гексагональной мозаики или гексагональной решетки, заслуживающее внимания, — это ее прочность на сжатие и растяжение, а также эффективность по сравнению с другими вариантами мозаики. Если мы рассмотрим абстрактную физическую «структуру», образованную линейными сегментами между вершинами правильной многоугольной мозаики (т.е.е. проволочная сетка), ясно, что такая структура, сформированная в виде шестиугольной решетки, обеспечит идеальное сочетание эффективности и прочности по сравнению с аналогичными треугольными или квадратными структурами. Либо треугольная, либо шестиугольная структура, построенная таким образом, будет явно сильнее, чем квадратная структура, и хотя треугольная структура, при прочих равных условиях, будет прочнее шестиугольной, она также будет использовать больше материала (с шестью линиями, соединяющимися через каждая вершина вместо трех) и, таким образом, будет менее «эффективным» — хотя для конкретных приложений, очевидно, это может быть предпочтительнее.

Тот факт, что квадратные решетки не имеют той же прочности, что и шестиугольные или треугольные решетки, становится очевидным, когда кто-то изучает иллюстрацию трех структур, представляя, что в каждой вершине линейные сегменты структуры сдвигаются или разрываются с той силой, с которой они будут действовать. физическая структура. Ясно, что с четырьмя сегментами, выходящими на точные углы 90 градусов в каждой вершине, квадратная структура легко срезается либо по горизонтали, либо по вертикали — у нее нет других углов, поддерживающих ее структуру, поэтому они просто как бы шатаются.И наоборот, в треугольной и шестиугольной конфигурации линейные сегменты, сходящиеся под углами 60 и 120 градусов, предотвращают любое срезание или сжатие — они уравновешивают друг друга и равномерно распределяют нагрузку (какой бы она ни была).

Например, если вы вообразите шестиугольную или треугольную решетку, «удерживающую» объект, ясно, что чередующиеся углы шестиугольной и треугольной решеток будут делать больше для распределения веса на нижние уровни, чем квадратная решетка с ортогональными ограничениями.Тот же принцип легко применим и к приложениям распределения силы в трех измерениях — таких, как мы видим, например, в замечательной прочности на разрыв углеродных нанотрубок, в распределении веса по геодезическим куполам и так далее.

Шестиугольники и круги

Гексагональная упаковка является наиболее эффективной системой для упаковки кругов на плоской плоскости. То есть, как и в случае с шестиугольной мозаикой, вы можете разместить шесть соседних кругов одинакового размера вокруг круга и шесть кругов вокруг каждого из них, и так до бесконечности, так что расположение кругов идентично расположению шестиугольников в гексагональная мозаика.Другими словами, можно вписать круги в каждый шестиугольник в шестиугольной мозаике, удалить шестиугольники, и в результате останутся идеально плотно упакованные круги. Это полезно и интересно по ряду причин, например, потому, что позволяет легко моделировать гексагонально упакованные круги с помощью шестиугольников или треугольников, когда это необходимо.

Интересное явление, связанное с этим пересечением круговой и гексагональной геометрии, заключается в том, что гексагональные узоры часто появляются спонтанно, когда силы природы пытаются приблизиться к окружностям.(Это, без сомнения, большая часть причины, по которой шестиугольники обычно считаются очень «естественной» формой.) Например, конвективные ячейки часто образуют шестиугольники. Поскольку каждая ячейка естественно стремится к наиболее эффективному замкнутому пространству, они имеют тенденцию к округлости, но поскольку каждая ячейка имеет любое количество соседних ячеек, прижимающихся к ней, результатом является своего рода квазигексагональная мозаика. Подходящим примером этого может быть Дорога гигантов в оккупированной Ирландии: когда базальтовая лава, которая сформировала структуру, первоначально остывала, она сжималась в примерно цилиндрические ячейки.Когда клетки охлаждались в твердую породу, они, естественно, приобретали шестиугольную геометрию упакованных кругов.

Также стоит отметить, что шестиугольники играют значительную роль в трехмерных сферах плотной упаковки, как в гексагональной плотной упаковке, так и в гранецентрированных кубических системах. И HCP, и FCC состоят из «листов» гексагонально упакованных сфер — они различаются только тем, как листы складываются вместе. Следует отметить, что, несмотря на их соответствующие названия, можно утверждать, что гранецентрированная кубическая упаковка на самом деле более «гексагональна», чем так называемая гексагональная упаковка — последняя получила свое название скорее из-за отсутствия кубичности, чем из-за преобладание гексагональности.Обратите внимание, что и HCP, и FCC значительно менее эффективны, чем гексагональная упаковка в двух измерениях: первая имеет плотность π / (3√2), а вторая — π / √12. Очевидно, что также известны регулярные плотные упаковки n-сфер до 8 измерений, которые могут включать или не включать гексагональные или гипергексагональные топологии.

Шестиугольники и треугольники

Во многих отношениях отношения между треугольниками и шестиугольниками являются продолжением отношений между шестиугольниками и кругами.Я считаю их частью одного неразрывного геометрического континуума (основанного, как я полагаю, на довольно очевидном факте, что самое близкое расположение трех кругов одинакового размера находится в вершинах равностороннего треугольника с длиной ребра, равной диаметру кругов) . Но пока давайте посмотрим конкретно на отношения между треугольниками и шестиугольниками:

Как уже отмечалось, правильный шестиугольник можно разделить на шесть равносторонних треугольников. Шестиугольник и треугольник — единственные два правильных многоугольника, и я считаю, что единственные два правильных многогранника обладают этим свойством.В дополнение к тому, что шестиугольник делится на равносторонние треугольники, треугольник, конечно, сам делится на подтреугольники, и поскольку группировка любых шести треугольников, расположенных вокруг вершины, дает шестиугольник, треугольники также могут делиться на шестиугольники, хотя с оставленными треугольными промежутками над. Треугольник, разделенный на 9 подтреугольников, можно представить как шестиугольник с тремя равносторонними треугольниками, образованными продолжением ребер чередующихся сторон шестиугольника до их встречи (как на рисунке Тетрактиса).

Топологически родственная концепция — это понятие треугольных чисел, которые можно визуализировать как гексагонально упакованные круги, шестиугольники или точки внутри треугольника. В частности, треугольные числа могут быть определены как сумма всех натуральных чисел от 1 до n , где n — количество единиц на каждой стороне рассматриваемого фигурного треугольника. То есть предположим, что вы взяли три точки и расположили их в виде треугольника. На каждой стороне треугольника две точки, и 1 + 2 = 3.Добавьте еще три точки к основанию этого треугольника, и у вас будет еще один треугольник, в данном случае с тремя точками на каждую сторону, и 1 + 2 + 3 = 6 (что также является произведением 1, 2 и 3, как упоминалось ранее). И так далее. Треугольное число с длиной стороны n также можно рассчитать как n * ( n +1) / 2 — таким образом, 3 * (3 + 1) / 2 = 3 + 2 + 1 = 6.

Та же фигуральная шестиугольная решетка также используется для центрированных шестиугольных чисел или шестнадцатеричных чисел, которые аналогичны треугольным числам, но, конечно, с шестиугольниками вместо треугольников.(По причинам, которые мне трудно понять, термин «шестиугольное число» зарезервирован для фигуры шестиугольного контура, которая на самом деле не очень похожа на то, что подразумевается под «треугольным числом» или «квадратным числом», по крайней мере, в некотором смысле что я нахожу особенно интересным.) Шестнадцатеричное число n ^th может быть выражено как шестикратное треугольное число ( n — 1) плюс один или как n * (n-1) * 3 + 1, который можно понимать как сумму трех прямоугольников плюс центральная точка.

Еще один интересный факт о шестнадцатеричных числах заключается в том, что сумма первых n шестнадцатеричных чисел равна кубу n . Например, 1 + 7 = 2 ³ = 8, 1 + 7 + 19 = 3 ³ = 27, 1 + 7 + 19 + 37 = 4 ³ = 64 и так далее. Чтобы понять это, представьте, что вы смотрите на угол куба таким образом, что куб выглядит как шестиугольник. Представьте, что куб на самом деле состоит из подкубиков, расположенных в виде числа в кубе. Первый кубик в углу можно рассматривать как первое шестнадцатеричное число, равное 1.Ниже и вокруг него расположены семь других кубиков, образующих слой кубиков вокруг углового куба, который можно рассматривать как второе шестнадцатеричное число, которое на самом деле равно 7, и так далее. Шестнадцатеричные числа можно рассматривать как последовательные «оболочки» кубиков, исходящие из углового куба. Таким образом, кубы и шестнадцатеричные числа — это просто разные образные способы описания одних и тех же значений — куб n может быть расположен либо как куб, либо как пирамида из шестиугольников с длиной основания n , и разница между любыми два последовательных куба — это шестиугольник.Мы снова видим взаимосвязь между шестигранным шестиугольником и шестигранным кубом — и, в более широком смысле, между шестиугольником и шестью «сторонами» самого трехмерного пространства.

Заключение

Опять же, эта статья лишь поверхностно коснулась многих интересных свойств шестиугольников и их аналогов. В самом деле, шестиугольники появляются в очень необычных местах в более абстрактных математических системах, и я в целом подозреваю, что если бы вы наметили все логические взаимосвязи математики, как их понимает и определило человечество, шестиугольник будет занимать видное место как повторяющаяся тема во всей структуре.

По мере развития человеческого общества мы, несомненно, будем находить все больше и больше приложений для универсального и эффективного шестиугольника. Будь то мозаика наших настольных игр, формирование наших эффективно замкнутых структур или помощь нам в лучшем понимании фундаментальных математических концепций, мы, несомненно, обнаружим, что живем во все более и более шестиугольном мире с течением времени. Является ли совпадением то, что научно-фантастические фильмы и телешоу — особенно те, которые происходят в открытом космосе — часто показывают шестиугольные двери, шестиугольные космические корабли, шестиугольную архитектуру и так далее? Думаю, нет.Провидцы и художники нашего общества уже видели, что грядет и что будет очевидно для наших потомков: что мы живем в шестиугольном мире, упорядоченном по шестиугольным принципам. Шестиугольники не могут быть решением всех мировых проблем. Они могут даже не быть решением очень многих проблем. Но они будут решением некоторых проблем, и это больше, чем вы можете сказать о многих вещах.

.

Шестиугольник

Шестиугольник — это 6-сторонний многоугольник (плоская форма с прямыми сторонами).

Мыльные пузыри имеют тенденцию образовывать шестиугольники
, когда они соединяются.

В сотах тоже есть шестиугольники!

Обычное или нестандартное

Когда все углы равны и все стороны равны, это обычный , в противном случае это неправильный :

Обычный шестигранник	Шестиугольники неправильной формы

вогнутая или выпуклая

Выпуклый шестигранник не имеет углов, направленных внутрь.Точнее, никакие внутренние углы не могут быть больше 180 °.

Если любой внутренний угол больше 180 °, это вогнутый . ( Подумайте: в вогнутой части есть «пещера» )

Выпуклый шестигранник	Вогнутый шестигранник

Это шестиугольник?

Без изогнутых сторон. И форма также должна быть замкнутой (все линии соединяются):

Шестигранник (прямые стороны)	Не Шестигранник (имеет изгиб)	Не a Шестигранник (открытый, не закрытый)

Недвижимость

Обычный шестигранник имеет:

• Внутренние углы 120 °
• Наружные углы 60 °
• Площадь = (1.5√3) × s ² , или приблизительно 2,5980762 × s ² (где s = длина стороны)
• Радиус равен длине стороны

Радиус — это длина стороны.
Он также состоит из 6 правильных треугольников!

Любой шестигранник имеет:

Другие изображения

Гайки и болты с шестигранной головкой легко захватываются гаечным ключом,
при необходимости можно переставлять через каждые 60 °.

На Сатурне находится огромный шестиугольник ,
шире Земли.

Еще одно изображение шестиугольника на Сатурне.

Снежинки имеют шестиугольные узоры, как это красивое изображение от НАСА.
Фотография НАСА / Алексей Клятов.

Тоже снежинка!
Фотография НАСА / Алексей Клятов.

.

Обычный восьмиугольник — Калькулятор геометрии

1D линия 2D правильных многоугольников: равносторонний треугольник, квадрат, пятиугольник, шестиугольник, семиугольник, восьмиугольник, нонагон, десятиугольник, шестиугольник, додекагон, шестиугольник, N-угольник, многоугольник кольцо другие многоугольники: треугольник, прямоугольный треугольник, равнобедренный треугольник ИК-треугольник, четырехугольник, прямоугольник, золотой прямоугольник, ромб, параллелограмм, полуквадратный воздушный змей, воздушный змей, воздушный змей, правая трапеция, равнобедренная трапеция, треугольная равносторонняя трапеция, трапеция, циклический четырехугольник, тангенциальный четырехугольник, стрелка, вогнутый четырехугольник, крест Антипараллелограмм, Форма дома, Симметричный пятиугольник, Вырезанный прямоугольник, Вогнутый пятиугольник, Вогнутый правильный пятиугольник, Параллелогон, Вытянутый шестиугольник, Вогнутый шестиугольник, Стрелка-шестиугольник, Прямоугольный шестиугольник, L-образная форма, Острый перегиб, T-образная форма, Усеченный квадрат, Рамка, Открытая рамка, сетка, крест, форма X, форма H, тройная звезда, четыре звезды, пентаграмма, гексаграмма, уникурсальная гексаграмма, октаграмма, звезда Лакшми, двойная звезда многоугольник, многоугольник, многоугольник 90 004 Круглые формы: Круг, Полукруг, Круговой сектор, Круговой сегмент, Круговой слой, Круговой центральный сегмент, Круглый угол, Круглый угол, Круговая касательная стрелка, Форма капли, Полумесяц, Остроконечный овал, Ланцетная арка, Бугорок, Кольцо, Кольцевой сектор , Изогнутый прямоугольник, закругленный многоугольник, закругленный прямоугольник, эллипс, полуэллипс, эллиптический сегмент, эллиптический сектор, эллиптическое кольцо, стадион, спираль, бревно.Спираль, Треугольник Рело, Циклоида, Двойная циклоида, Астроид, Гипоциклоида, Кардиоида, Эпициклоида, Параболический сегмент, Сердце, Треугольник, Межугловой треугольник, Круговой треугольник дуги, Четырехугольник Interarc, Межкруговый четырехугольник, Круговой четырехугольник дуги, Круговой многоугольник дуги, Коготь -Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Поликруг, Многоугольник с закругленными краями, Роза, Шестеренка, Овал, Профиль яйца, Лемниската, Сквикул, Круглый квадрат, Дигон, Сферический треугольник 3D Платоновых тел: тетраэдр, куб, октаэдр, додекаэдр, икосаэдр архимедова Solids: усеченный тетраэдр, кубооктаэдр, усеченный куб, усеченный октаэдр, ромбокубооктаэдр, усеченный кубооктаэдр, икосододекаэдр, усеченный додекаэдр, усеченный икосаэдр, Snub куб, ромбоикосододекаэдр , Усеченный икосододекаэдр, Snub Додекаэдр Каталонских Сухой остаток: триакистетраэдр, ромбический додекаэдр, триакисоктаэдр, тетракисгексаэдр, дельтоидальный икоситетраэдр, гексакис октаэдр, ромбический триаконтаэдр, триакисикосаэдр, пентакисдодекаэдр, Пятиугольные Icositetrahedron, дельтоидальный гексеконтаэдр, гексакис Икосаэдр, Пятиугольный гексеконтаэдр Твердые тела Джонсона: Пирамиды, купола, ротонда, удлиненные пирамиды, гиро-продолговатые пирамиды, бипирамиды, удлиненные бипирамиды, гиро-продолговатая квадратная дипирамида, гиробифастигедрон, дисфагениум Sphenocorona, Disphenocingulum Другие многогранники: Кубоид, квадратный столб, треугольная пирамида, квадратная пирамида, правильная пирамида, пирамида, правильная пирамида, створка, правильная бипирамида, бипирамида, пирамида, бифрустум, клин-фрустум, клин-фрустум Полутетраэдр, ромбоэдр, параллелепипед, правильная призма, призма, наклонная призма, антипризма, призматоид, трапецоэдр, дисфеноид, угол, общий тетраэдр, клин-кубоид, полукубоид, скошенный кубоид, слиток, скошенный трехгранный остриж, разрезанный кубоид Кубоид, кубоид с тупыми краями, обелиск, удлиненный додекаэдр, усеченный ромбоэдр, полый кубоид, полая пирамида, полый ствол, звездная пирамида, звездчатый октаэдр, малый звездчатый додекаэдр, большой звездчатый додекаэдр, большой додекаэдр 9000 9000 911 9000 9000 911 9000: большой икосаэдр Сфера, полусфера, сферический угол, цилиндр, отрезной цилиндр, наклонный цилиндр, изогнутый цилиндр, обобщенный цилиндр, конус, усеченный конус, наклонный C круговой конус, эллиптический конус, биконус, усеченный биконус, заостренный столб, закругленный конус, капля, сфероид, эллипсоид, полуэллипсоид, сферический сектор, сферический колпачок, сферический сегмент, сферический центральный сегмент, двойной калотт, сферический клин, полуцилиндр, диагональ Половинный цилиндр, цилиндрический клин, цилиндрический сектор, цилиндрический сегмент, цилиндр с плоским концом, полуконус, конический сектор, конический клин, сферическая оболочка, полусферическая оболочка, цилиндрическая оболочка, вырезанная цилиндрическая оболочка, наклонная цилиндрическая оболочка, полый конус, усеченный полый конус, Сферическое кольцо, Тор, Тороид шпинделя, Тороид, Сектор тора, Сектор тороида, Арка, Тетраэдр Рело, Капсула, Сегмент капсулы, Двойная точка, Линза, Вогнутая линза, Ствол, Форма яйца, Параболоид, Гиперболоид, Олоид, Тела Штейнмеца, Твердое тело Революции 4Д Тессеракт, Гиперсфера

Anzeige Расчеты на правильном восьмиугольнике, многоугольнике с 8 вершинами.Эта форма знакома по использованию в качестве знака остановки. Введите одно значение и выберите количество десятичных знаков. Затем нажмите Рассчитать. Формулы: d = a * √ 4 + 2 * √2 e = a * (1 + √2) f = a * √ 2 + √2 Высота = e = 2 * r i p = 8 * a A = 2 * a² * (1 + √2) r c = a / 2 * √ 4 + 2 * √2 r i = a / 2 * (1 + √2) Угол: 135 ° 20 диагоналей Длина кромки, диагонали, высота, периметр и радиус имеют одинаковые единицы измерения (например,г. метр), площадь имеет эту единицу квадрата (например, квадратный метр). Anzeige Поделиться: © Jumk.de Webprojects Anzeige

.