Правильный шестиугольник углы равны — Морской флот
Самая известная фигура, у которой больше четырех углов – это правильный шестиугольник. В геометрии он часто используется в задачах. А в жизни именно такой вид имеют соты на срезе.
Чем он отличается от неправильного?
Во-первых, шестиугольником является фигура с 6 вершинами. Во-вторых, он может быть выпуклым или вогнутым. Первый отличается тем, что четыре вершины лежат по одну сторону от прямой, проведенной через две другие.
В-третьих, правильный шестиугольник характеризуется тем, что все его стороны равны. Причем каждый угол фигуры тоже имеет одинаковое значение. Чтобы определить сумму всех его углов, потребуется воспользоваться формулой: 180º * (n — 2). Здесь n — число вершин фигуры, то есть 6. Простой расчет дает значение в 720º. То есть каждый угол равен 120 градусам.
В повседневной деятельности правильный шестиугольник встречается в снежинке и гайке. Химики видят ее даже в молекуле бензола.
Какие свойства требуется знать при решении задач?
К тому, что указано выше, следует добавить:
- диагонали фигуры, проведенные через центр, делят ее на шесть треугольников, которые являются равносторонними;
- сторона правильного шестиугольника имеет значение, которое совпадает с радиусом описанной около него окружности;
- используя такую фигуру, есть возможность заполнить плоскость, причем между ними не получится пропусков и не будет наложений.

Введенные обозначения
Традиционно сторона правильной геометрической фигуры обозначается латинской буквой «а». Для решения задач требуются еще площадь и периметр, это S и P соответственно. В правильный шестиугольник бывает вписана окружность или описана около него. Тогда вводятся значения для их радиусов. Обозначаются они соответственно буквами r и R.
В некоторых формулах фигурируют внутренний угол, полупериметр и апофема (являющаяся перпендикуляром к середине любой стороны из центра многоугольника). Для них используются буквы: α, р, m.
Формулы, которые описывают фигуру
Для расчета радиуса вписанной окружности потребуется такая: r = (a * √3) / 2, причем r = m. То есть такая же формула будет и для апофемы.
Поскольку периметр шестиугольника — это сумма всех сторон, то он определится так: P = 6 * a. С учетом того, что сторона равна радиусу описанной окружности, для периметра существует такая формула правильного шестиугольника: P = 6 * R. Из той, что приведена для радиуса вписанной окружности, выводится зависимость между а и r. Тогда формула принимает такой вид: Р = 4 r * √3.
Из той, что приведена для радиуса вписанной окружности, выводится зависимость между а и r. Тогда формула принимает такой вид: Р = 4 r * √3.
Для площади правильного шестиугольника может пригодиться такая: S = p * r = (a 2 * 3 √3) / 2.
Задачи
№ 1. Условие. Имеется правильная шестиугольная призма, каждое ребро которой равно 4 см. В нее вписан цилиндр, объем которого необходимо узнать.
Решение. Объем цилиндра определяется как произведение площади основания на высоту. Последняя совпадает с ребром призмы. А она равна стороне правильного шестиугольника. То есть высота цилиндра – тоже 4 см.
Чтобы узнать площадь его основания, потребуется вычислить радиус вписанной в шестиугольник окружности. Формула для этого указана выше. Значит, r = 2√3 (см). Тогда площадь круга: S = π * r 2 = 3,14 * (2√3 ) 2 = 37,68 (см 2 ).
Осталось сосчитать объем: V = 37, 68 * 4 = 150,72 (см 3 ).
Ответ. V = 150,72 см 3 .
№ 2. Условие. Вычислить радиус окружности, которая вписана в правильный шестиугольник. Известно, что его сторона равна √3 см. Чему будет равен его периметр?
Вычислить радиус окружности, которая вписана в правильный шестиугольник. Известно, что его сторона равна √3 см. Чему будет равен его периметр?
Решение. Эта задача требует использования двух из указанных формул. Причем их необходимо применять, даже не видоизменяя, просто подставить значение стороны и вычислить.
Таким образом, радиус вписанной окружности получается равным 1,5 см. Для периметра оказывается верным такое значение: 6√3 см.
Ответ. r = 1,5 см, Р = 6√3 см.
№ 3. Условие. Радиус описанной окружности равен 6 см. Какое значение в этом случае будет у стороны правильного шестиугольника?
Решение. Из формулы для радиуса вписанной в шестиугольник окружности легко получается та, по которой нужно вычислять сторону. Ясно, что радиус умножается на два и делится на корень из трех. Необходимо избавиться от иррациональности в знаменателе. Поэтому результат действий принимает такой вид: (12 √3) / (√3 * √3), то есть 4√3.
Правильным шестиугольником называется шестиугольник, у которого все стороны и углы равны.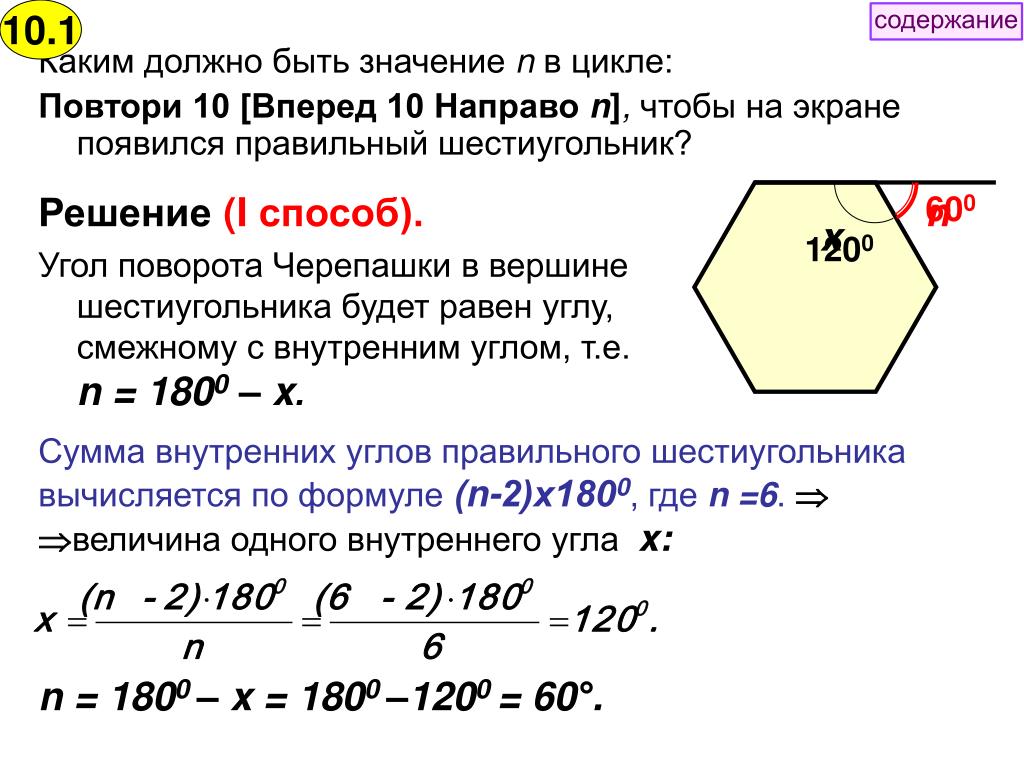 Правильный шестиугольник обладает следующими свойствами.
Правильный шестиугольник обладает следующими свойствами.
– Сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
– Большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам.
– Меньшая диагональ правильного шестиугольника в раз больше его стороны.
– Угол между сторонами правильного шестиугольника равен 120°.
– Меньшая диагональ правильного шестиугольника перпендикулярна его стороне.
– Треугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60°.
| Главная ≫ Инфотека ≫ Математика ≫ Правильный шестиугольник |
| Комментарии: 0 | Правильный шестиугольник (гексагон) — это правильный многоугольник с шестью сторонами. |
Особенность правильного шестиугольника — равенство его стороны и радиуса описанной окружности , поскольку Все углы равны 120°. Радиус вписанной окружности равен: Периметр правильного шестиугольника равен: Площадь правильного шестиугольника рассчитывается по формулам: Шестиугольники замощают плоскость, то есть могут заполнять плоскость без пробелов и наложений, образуя так называемый паркет. Шестиугольный паркет (шестиугольный паркетаж) — замощение плоскости равными правильными шестиугольниками, расположенными сторона к стороне. |
Шестиугольный паркет является двойственным треугольному паркету: если соединить центры смежных шестиугольников, то проведённые отрезки дадут треугольный паркетаж. Символ Шлефли шестиугольного паркета — <6,3>, что означает, что в каждой вершине паркета сходятся три шестиугольника.
Шестиугольный паркет является наиболее плотной упаковкой кругов на плоскости. В двумерном евклидовом пространстве наилучшим заполнением является размещение центров кругов в вершинах паркета, образованного правильными шестиугольниками, в котором каждый круг окружен шестью другими. Плотность данной упаковки равна . В 1940 году было доказано, что данная упаковка является самой плотной.
В двумерном евклидовом пространстве наилучшим заполнением является размещение центров кругов в вершинах паркета, образованного правильными шестиугольниками, в котором каждый круг окружен шестью другими. Плотность данной упаковки равна . В 1940 году было доказано, что данная упаковка является самой плотной.
Правильный шестиугольник со стороной является универсальной покрышкой, то есть всякое множество диаметра можно покрыть правильным шестиугольником со стороной (лемма Пала).
Правильный шестиугольник можно построить с помощью циркуля и линейки. Ниже приведён метод построения, предложенный Евклидом в «Началах», книга IV, теорема 15.
Пчелиные соты показывают разбиение плоскости на правильные шестиугольники. Шестиугольная форма больше остальных позволяет сэкономить на стенках, то есть на соты с такими ячейками уйдёт меньше воска.
Некоторые сложные кристаллы и молекулы , например графит, имеют гексагональную кристаллическую решётку.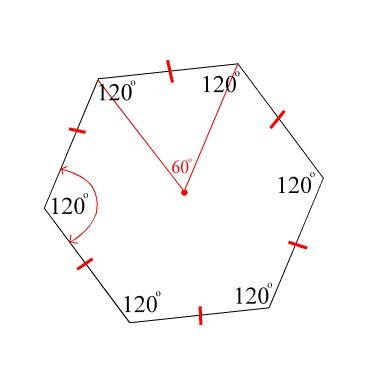
Снежинки образуется, когда микроскопические капли воды в облаках притягиваются к пылевым частицам и замерзают. Появляющиеся при этом кристаллы льда, не превышающие поначалу 0,1 мм в диаметре, падают вниз и растут в результате конденсации на них влаги из воздуха. При этом образуются шестиконечные кристаллические формы. Из-за структуры молекул воды между лучами кристалла возможны углы лишь в 60° и 120°. Основной кристалл воды имеет в плоскости форму правильного шестиугольника. На вершинах такого шестиугольника затем осаждаются новые кристаллы, на них — новые, и так получаются разнообразные формы звёздочек-снежинок.
Гигантский гексагон — атмосферное явление на Сатурне.
Учёные из Оксфордского университета смогли в лабораторных условиях смоделировать возникновение подобного гексагона. Чтобы выяснить, как возникает такое образование, исследователи поставили на вертящийся стол 30-литровый баллон с водой. Она моделировала атмосферу Сатурна и её обычное вращение. Внутри учёные поместили маленькие кольца, вращающиеся быстрее ёмкости. Это генерировало миниатюрные вихри и струи, которые экспериментаторы визуализировали при помощи зелёной краски. Чем быстрее вращалось кольцо, тем больше становились вихри, заставляя близлежащий поток отклоняться от круговой формы. Таким образом авторам опыта удалось получить различные фигуры — овалы, треугольники, квадраты и, конечно, искомый шестиугольник.
Она моделировала атмосферу Сатурна и её обычное вращение. Внутри учёные поместили маленькие кольца, вращающиеся быстрее ёмкости. Это генерировало миниатюрные вихри и струи, которые экспериментаторы визуализировали при помощи зелёной краски. Чем быстрее вращалось кольцо, тем больше становились вихри, заставляя близлежащий поток отклоняться от круговой формы. Таким образом авторам опыта удалось получить различные фигуры — овалы, треугольники, квадраты и, конечно, искомый шестиугольник.
Дорога гигантов — памятник природы из примерно 40 000 соединённых между собой базальтовых (реже андезитовых) колонн, образовавшихся в результате древнего извержения вулкана. Расположен на северо-востоке Северной Ирландии в 3 км к северу от города Бушмилса.
Верхушки колонн образуют подобие трамплина, который начинается у подножья скалы и исчезает под поверхностью моря. Большинство колонн шестиугольные, хотя у некоторых четыре, пять, семь и восемь углов. Самая высокая колонна высотой около 12 м.
Самая высокая колонна высотой около 12 м.
Около 50-60 миллионов лет назад, во время палеогенового периода, месторасположение Антрим подвергалось интенсивной вулканической активности, когда расплавленный базальт проникал через отложения, формируя обширные лавовые плато. По мере быстрого охлаждения происходило сокращение объёма вещества (подобное наблюдается при высыхании грязи). Горизонтальное сжатие приводило к характерной структуре шестигранных столбов.
Как доказать что шестиугольник правильный. Правильный шестиугольник и его свойства. Периметр и площадь
Математические свойства
Особенность правильного шестиугольника — равенство его стороны и радиуса описанной окружности , поскольку
Все углы равны 120°.
Радиус вписанной окружности равен:
Периметр правильного шестиугольника равен:
Площадь правильного шестиугольника рассчитывается по формулам:
Шестиугольники замощают плоскость, то есть могут заполнять плоскость без пробелов и наложений, образуя так называемый паркет.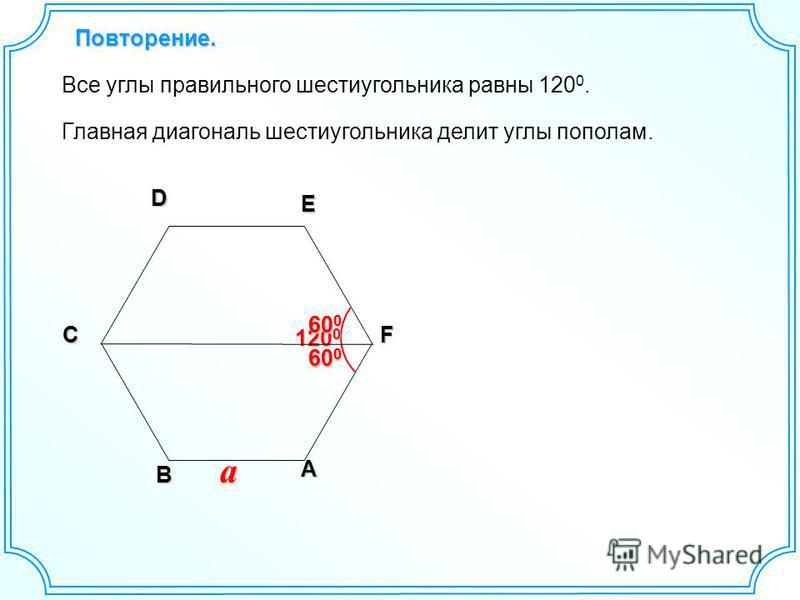
Шестиугольный паркет (шестиугольный паркетаж) — замощение плоскости равными правильными шестиугольниками, расположенными сторона к стороне.
Шестиугольный паркет является двойственным треугольному паркету: если соединить центры смежных шестиугольников, то проведённые отрезки дадут треугольный паркетаж. Символ Шлефли шестиугольного паркета — {6,3}, что означает, что в каждой вершине паркета сходятся три шестиугольника.
Шестиугольный паркет является наиболее плотной упаковкой кругов на плоскости. В двумерном евклидовом пространстве наилучшим заполнением является размещение центров кругов в вершинах паркета, образованного правильными шестиугольниками, в котором каждый круг окружен шестью другими. Плотность данной упаковки равна . В 1940 году было доказано, что данная упаковка является самой плотной.
Правильный шестиугольник со стороной является универсальной покрышкой, то есть всякое множество диаметра можно покрыть правильным шестиугольником со стороной
(лемма Пала).
Правильный шестиугольник можно построить с помощью циркуля и линейки. Ниже приведён метод построения, предложенный Евклидом в «Началах», книга IV, теорема 15.
Правильный шестиугольник в природе, технике и культуре
показывают разбиение плоскости на правильные шестиугольники. Шестиугольная форма больше остальных позволяет сэкономить на стенках, то есть на соты с такими ячейками уйдёт меньше воска.
Некоторые сложные кристаллы и молекулы , например графит, имеют гексагональную кристаллическую решётку.
Образуется, когда микроскопические капли воды в облаках притягиваются к пылевым частицам и замерзают. Появляющиеся при этом кристаллы льда, не превышающие поначалу 0,1 мм в диаметре, падают вниз и растут в результате конденсации на них влаги из воздуха. При этом образуются шестиконечные кристаллические формы. Из-за структуры молекул воды между лучами кристалла возможны углы лишь в 60° и 120°. Основной кристалл воды имеет в плоскости форму правильного шестиугольника.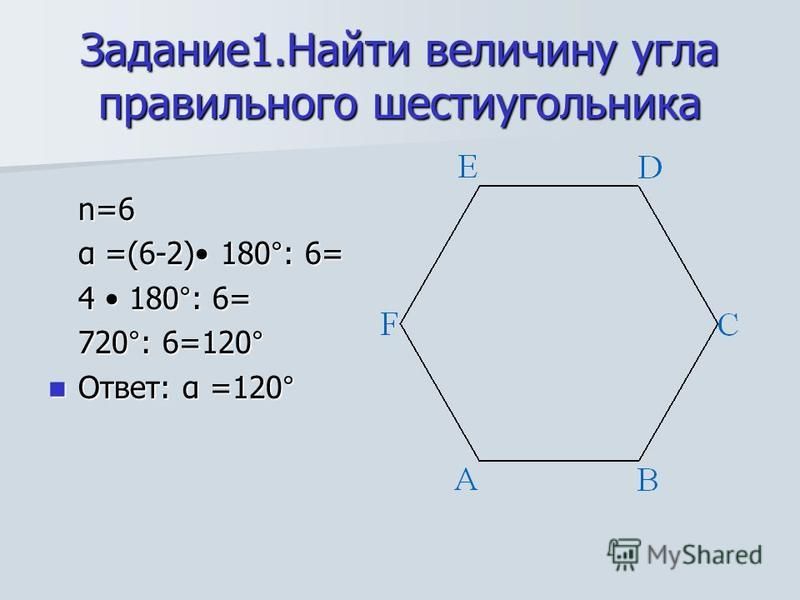
Учёные из Оксфордского университета смогли в лабораторных условиях смоделировать возникновение подобного гексагона. Чтобы выяснить, как возникает такое образование, исследователи поставили на вертящийся стол 30-литровый баллон с водой. Она моделировала атмосферу Сатурна и её обычное вращение. Внутри учёные поместили маленькие кольца, вращающиеся быстрее ёмкости. Это генерировало миниатюрные вихри и струи, которые экспериментаторы визуализировали при помощи зелёной краски. Чем быстрее вращалось кольцо, тем больше становились вихри, заставляя близлежащий поток отклоняться от круговой формы. Таким образом авторам опыта удалось получить различные фигуры — овалы, треугольники, квадраты и, конечно, искомый шестиугольник.
Памятник природы из примерно 40 000 соединённых между собой базальтовых (реже андезитовых) колонн, образовавшихся в результате древнего извержения вулкана.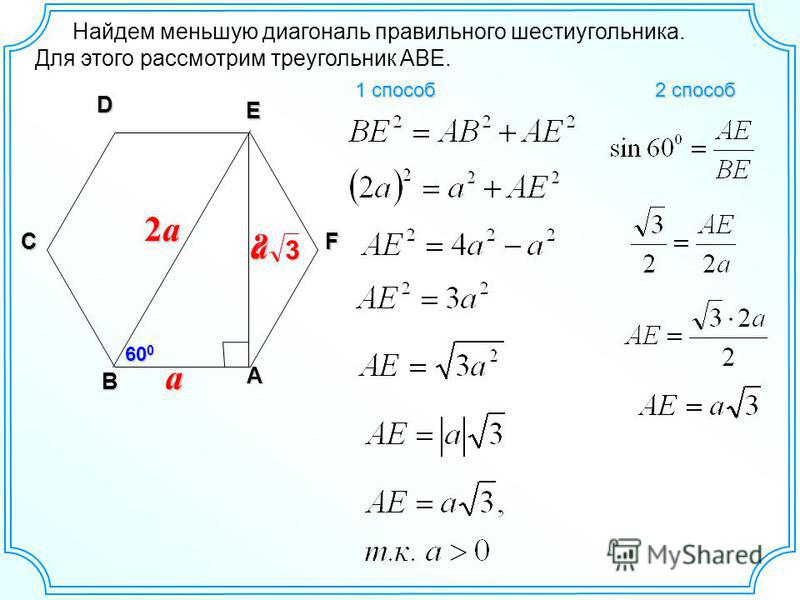
Верхушки колонн образуют подобие трамплина, который начинается у подножья скалы и исчезает под поверхностью моря. Большинство колонн шестиугольные, хотя у некоторых четыре, пять, семь и восемь углов. Самая высокая колонна высотой около 12 м.
Около 50-60 миллионов лет назад, во время палеогенового периода, месторасположение Антрим подвергалось интенсивной вулканической активности, когда расплавленный базальт проникал через отложения, формируя обширные лавовые плато. По мере быстрого охлаждения происходило сокращение объёма вещества (подобное наблюдается при высыхании грязи). Горизонтальное сжатие приводило к характерной структуре шестигранных столбов.
Сечение гайки имеет вид правильного шестиугольника.
Знаете ли вы, как выглядит правильный шестиугольник?
Этот вопрос задан не случайно. Большинство учащихся 11 класса не знают на него ответа.
Правильный шестиугольник — такой, у которого все стороны равны и все углы тоже равны .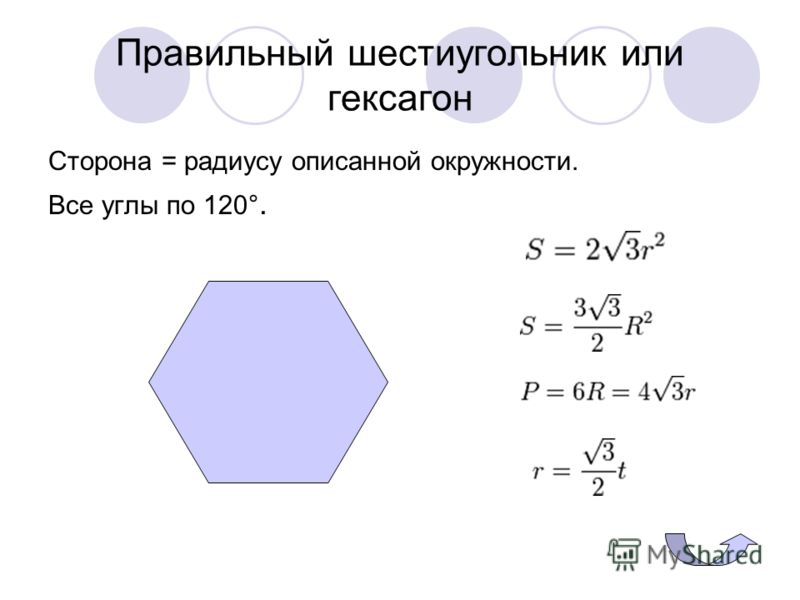
Железная гайка. Снежинка. Ячейка сот, в которых живут пчелы. Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.
Многие школьники теряются, видя задачи на правильный шестиугольник, и считают, что для их решения нужны какие-то особые формулы. Так ли это?
Проведем диагонали правильного шестиугольника. Мы получили шесть равносторонних треугольников.
Мы знаем, что площадь правильного треугольника: .
Тогда площадь правильного шестиугольника — в шесть раз больше.
Где — сторона правильного шестиугольника.
Обратите внимание, что в правильном шестиугольнике расстояние от его центра до любой из вершин одинаково и равно стороне правильного шестиугольник.
Значит, радиус окружности, описанной вокруг правильного шестиугольника, равен его стороне .
Радиус окружности, вписанной в правильный шестиугольник, нетрудно найти.
Теперь вы легко решите любые задачи ЕГЭ, в которых фигурирует правильный шестиугольник.

Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .
Радиус такой окружности равен .
Ответ: .
Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
Есть ли поблизости от Вас карандаш? Взгляните-ка на его сечение — оно представляет собой правильный шестиугольник или, как его еще называют, гексагон. Такую форму имеет также сечение гайки, поле гексагональных шахмат, некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты. Гигантский правильный шестиугольник был недавно обнаружен в Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим поподробнее.
Правильный шестиугольник представляет собой многоугольник с шестью одинаковыми сторонами и равными углами. Из школьного курса нам известно, что он обладает следующими свойствами:
Из школьного курса нам известно, что он обладает следующими свойствами:
- Длина его сторон соответствует радиусу описанной окружности. Из всех это свойство имеет лишь правильный шестиугольник.
- Углы равны между собой, и величина каждого составляет 120°.
- Периметр гексагона можно найти по формуле Р=6*R, если известен радиус описанной вокруг него окружности, или Р=4*√(3)*r, если окружность в него вписана. R и r — радиусы описанной и вписанной окружности.
- Площадь, которую занимает правильный шестиугольник, определяется следующим образом: S=(3*√(3)*R 2)/2. Если радиус неизвестен, вместо него подставляем длину одной из сторон — как известно, она соответствует длине радиуса описанной окружности.
У правильного шестиугольника есть одна интересная особенность, благодаря которой он получил в природе такое широкое распространение, — он способен заполнить любую поверхность плоскости без наложений и пробелов. Существует даже так называемая лемма Пала, согласно которой правильный гексагон, сторона которого равна 1/√(3), представляет собой универсальную покрышку, то есть может покрыть любое множество с диаметром в одну единицу.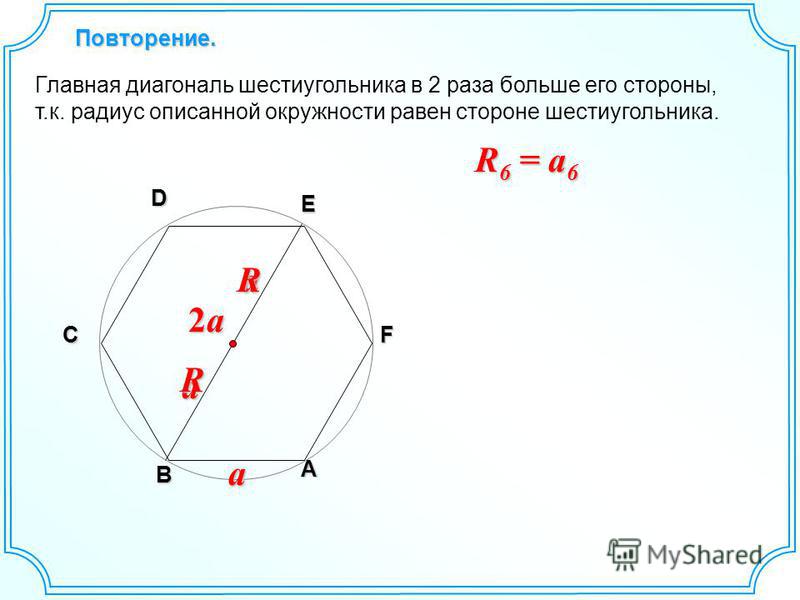
Теперь рассмотрим построение правильного шестиугольника. Есть несколько способов, самый простой из которых предполагает использование циркуля, карандаша и линейки. Вначале рисуем циркулем произвольную окружность, затем в произвольном месте на этой окружности делаем точку. Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек. Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.
На практике бывают случаи, когда требуется нарисовать шестиугольник большого размера. Например, на двухуровневом гипсокартонном потолке, вокруг места крепления центральной люстры, нужно установить на нижнем уровне шесть небольших светильников. Циркуль таких размеров найти будет очень и очень сложно. Как поступить в этом случае? Как вообще нарисовать большую окружность? Очень просто. Нужно взять крепкую нить нужной длины и обвязать один из ее концов напротив карандаша.
Самая известная фигура, у которой больше четырех углов — это правильный шестиугольник. В геометрии он часто используется в задачах. А в жизни именно такой вид имеют соты на срезе.
Чем он отличается от неправильного?
Во-первых, шестиугольником является фигура с 6 вершинами. Во-вторых, он может быть выпуклым или вогнутым. Первый отличается тем, что четыре вершины лежат по одну сторону от прямой, проведенной через две другие.
В-третьих, правильный шестиугольник характеризуется тем, что все его стороны равны. Причем каждый угол фигуры тоже имеет одинаковое значение. Чтобы определить сумму всех его углов, потребуется воспользоваться формулой: 180º * (n — 2). Здесь n — число вершин фигуры, то есть 6. Простой расчет дает значение в 720º. То есть каждый угол равен 120 градусам.
В повседневной деятельности правильный шестиугольник встречается в снежинке и гайке. Химики видят ее даже в молекуле бензола.
Какие свойства требуется знать при решении задач?
К тому, что указано выше, следует добавить:
- диагонали фигуры, проведенные через центр, делят ее на шесть треугольников, которые являются равносторонними;
- сторона правильного шестиугольника имеет значение, которое совпадает с радиусом описанной около него окружности;
- используя такую фигуру, есть возможность заполнить плоскость, причем между ними не получится пропусков и не будет наложений.
Введенные обозначения
Традиционно сторона правильной геометрической фигуры обозначается латинской буквой «а». Для решения задач требуются еще площадь и периметр, это S и P соответственно. В правильный шестиугольник бывает вписана окружность или описана около него. Тогда вводятся значения для их радиусов. Обозначаются они соответственно буквами r и R.
В некоторых формулах фигурируют внутренний угол, полупериметр и апофема (являющаяся перпендикуляром к середине любой стороны из центра многоугольника).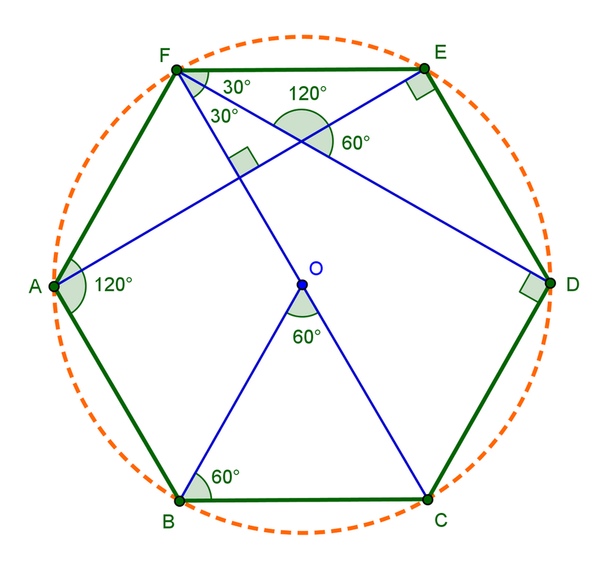 Для них используются буквы: α, р, m.
Для них используются буквы: α, р, m.
Формулы, которые описывают фигуру
Для расчета радиуса вписанной окружности потребуется такая: r = (a * √3) / 2, причем r = m. То есть такая же формула будет и для апофемы.
Поскольку периметр шестиугольника — это сумма всех сторон, то он определится так: P = 6 * a. С учетом того, что сторона равна радиусу описанной окружности, для периметра существует такая формула правильного шестиугольника: P = 6 * R. Из той, что приведена для радиуса вписанной окружности, выводится зависимость между а и r. Тогда формула принимает такой вид: Р = 4 r * √3.
Для площади правильного шестиугольника может пригодиться такая: S = p * r = (a 2 * 3 √3) / 2.
Задачи
№ 1. Условие. Имеется правильная шестиугольная призма, каждое ребро которой равно 4 см. В нее вписан цилиндр, объем которого необходимо узнать.
Решение. Объем цилиндра определяется как произведение площади основания на высоту. Последняя совпадает с ребром призмы. А она равна стороне правильного шестиугольника. То есть высота цилиндра — тоже 4 см.
А она равна стороне правильного шестиугольника. То есть высота цилиндра — тоже 4 см.
Чтобы узнать площадь его основания, потребуется вычислить радиус вписанной в шестиугольник окружности. Формула для этого указана выше. Значит, r = 2√3 (см). Тогда площадь круга: S = π * r 2 = 3,14 * (2√3) 2 = 37,68 (см 2).
Ответ . V = 150,72 см 3 .
№ 2. Условие. Вычислить радиус окружности, которая вписана в правильный шестиугольник. Известно, что его сторона равна √3 см. Чему будет равен его периметр?
Решение. Эта задача требует использования двух из указанных формул. Причем их необходимо применять, даже не видоизменяя, просто подставить значение стороны и вычислить.
Таким образом, радиус вписанной окружности получается равным 1,5 см. Для периметра оказывается верным такое значение: 6√3 см.
Ответ. r = 1,5 см, Р = 6√3 см.
№ 3. Условие. Радиус описанной окружности равен 6 см. Какое значение в этом случае будет у стороны правильного шестиугольника?
Решение.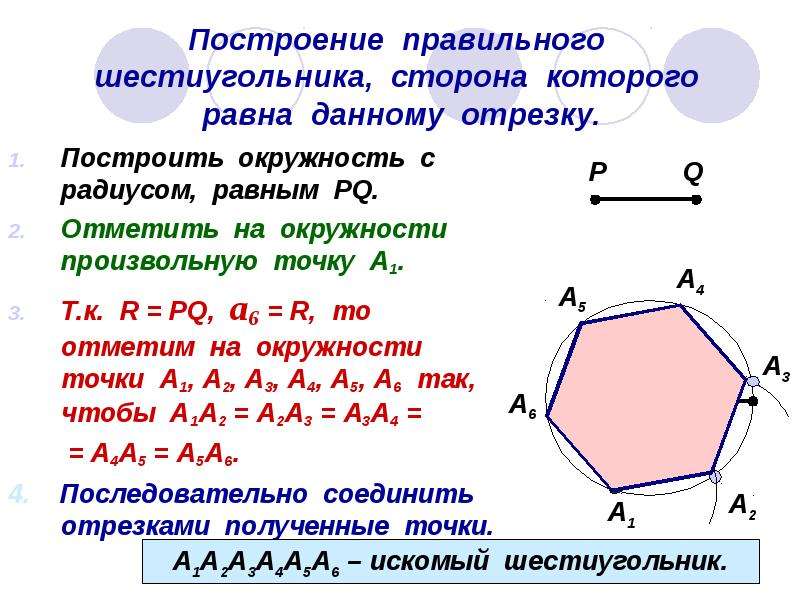 Из формулы для радиуса вписанной в шестиугольник окружности легко получается та, по которой нужно вычислять сторону. Ясно, что радиус умножается на два и делится на корень из трех. Необходимо избавиться от иррациональности в знаменателе. Поэтому результат действий принимает такой вид: (12 √3) / (√3 * √3), то есть 4√3.
Из формулы для радиуса вписанной в шестиугольник окружности легко получается та, по которой нужно вычислять сторону. Ясно, что радиус умножается на два и делится на корень из трех. Необходимо избавиться от иррациональности в знаменателе. Поэтому результат действий принимает такой вид: (12 √3) / (√3 * √3), то есть 4√3.
Ответ. а = 4√3 см.
Большая диагональ правильного шестиугольника
Правильным шестиугольником называется шестиугольник, у которого все стороны и углы равны. Правильный шестиугольник обладает следующими свойствами.
– Сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
– Большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам.
– Меньшая диагональ правильного шестиугольника в раз больше его стороны.
– Угол между сторонами правильного шестиугольника равен 120°.
– Меньшая диагональ правильного шестиугольника перпендикулярна его стороне.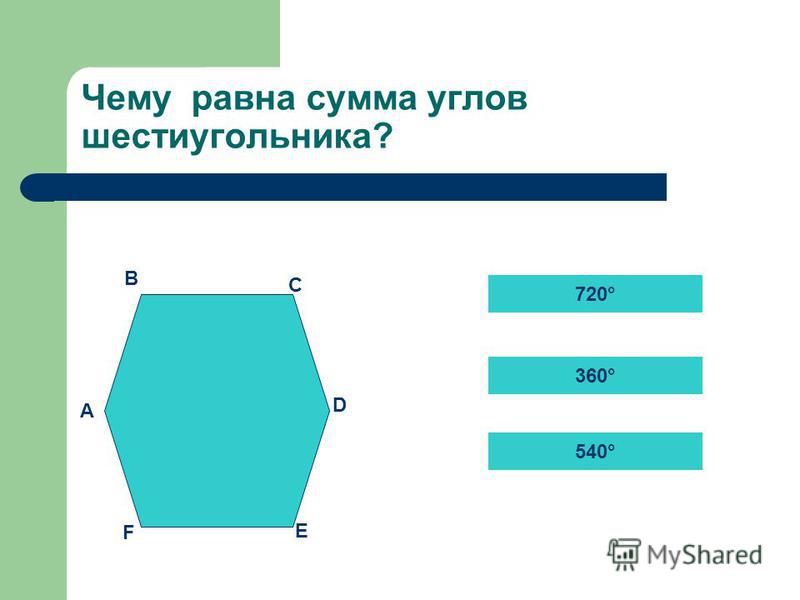
– Треугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60°.
Гексагон — правильный выпуклый многоугольник с шестью сторонами или шестиугольник.
Шестиугольник – это многоугольник, имеющий шесть сторон и шесть углов. В правильном шестиугольнике все стороны равны, а углы образуют шесть равносторонних треугольников.
Выпуклый шестиугольник – это многоугольник, с общим количеством вершин, равным шести, при этом все точки такого шестиугольника лежат по одну сторону от прямой, которая проведена между двумя любыми соседними его вершинами.
Правильный шестиугольник – это шестиугольник, все стороны которого равны между собой.
Сумма углов выпуклого шестиугольника определяется по общей формуле 180°(n-2) и равна 180 ( 6 – 2 ) = 720 градусов.
При решении задач для нахождения площади произвольного (неправильного) шестиугольника используют метод трапеций, который заключается в разбиении фигуры на отдельные трапеции, площадь каждой из которых можно найти по известным всем формулам.
Свойства правильного шестиугольника
- все внутренние углы равны между собой
- каждый внутренний угол правильного шестиугольника равен 120 градусам
- все стороны равны между собой
- сторона правильного шестиугольника равна радиусу описанной окружности
- большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам
- меньшая диагональ правильного шестиугольника в ( sqrt <3>) раз больше его стороны.
- vеньшая диагональ правильного шестиугольника перпендикулярна его стороне
- правильный шестиугольник заполняет плоскость без пробелов и наложений
- диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу вписанной в правильный шестиугольник окружности. 6.
- инвариантен относительно поворота плоскости на угол, кратный относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями)
- nреугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60° .
 circ) :
circ) :Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
Радиус вписанной окружности правильного шестиугольника равен апофеме:
(r = m = alargefrac<<sqrt 3 >><2>
ormalsize)Радиус описанной окружности равен стороне правильного шестиугольника:
Периметр правильного шестиугольника
Площадь правильного шестиугольника Формула площади правильного шестиугольника через длину стороны
(S = pr = largefrac<<3sqrt 3 >><2>
ormalsize),
где (p) − полупериметр шестиугольника.Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус вписанной окружности
Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус описанной окружности
Правильным шестиугольником называется выпуклый многоугольник с шестью одинаковыми сторонами и шестью углами.
 circ)
circ)Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
(m = alargefrac >
ormalsize)Радиус вписанной окружности правильного шестиугольника равен апофеме:
(r = m = alargefrac >
ormalsize)Радиус описанной окружности равен стороне правильного шестиугольника:
(R = a)Периметр правильного шестиугольника
(P = 6a)Площадь правильного шестиугольника
(S = pr = largefrac >
ormalsize),
где (p) − полупериметр шестиугольника.Самая известная фигура, у которой больше четырех углов — это правильный шестиугольник. В геометрии он часто используется в задачах. А в жизни именно такой вид имеют соты на срезе.
Чем он отличается от неправильного?
Во-первых, шестиугольником является фигура с 6 вершинами. Во-вторых, он может быть выпуклым или вогнутым. Первый отличается тем, что четыре вершины лежат по одну сторону от прямой, проведенной через две другие.

В-третьих, правильный шестиугольник характеризуется тем, что все его стороны равны. Причем каждый угол фигуры тоже имеет одинаковое значение. Чтобы определить сумму всех его углов, потребуется воспользоваться формулой: 180º * (n — 2). Здесь n — число вершин фигуры, то есть 6. Простой расчет дает значение в 720º. То есть каждый угол равен 120 градусам.
В повседневной деятельности правильный шестиугольник встречается в снежинке и гайке. Химики видят ее даже в молекуле бензола.
Какие свойства требуется знать при решении задач?
К тому, что указано выше, следует добавить:
- диагонали фигуры, проведенные через центр, делят ее на шесть треугольников, которые являются равносторонними;
- сторона правильного шестиугольника имеет значение, которое совпадает с радиусом описанной около него окружности;
- используя такую фигуру, есть возможность заполнить плоскость, причем между ними не получится пропусков и не будет наложений.
Введенные обозначения
Традиционно сторона правильной геометрической фигуры обозначается латинской буквой «а».
 Для решения задач требуются еще площадь и периметр, это S и P соответственно. В правильный шестиугольник бывает вписана окружность или описана около него. Тогда вводятся значения для их радиусов. Обозначаются они соответственно буквами r и R.
Для решения задач требуются еще площадь и периметр, это S и P соответственно. В правильный шестиугольник бывает вписана окружность или описана около него. Тогда вводятся значения для их радиусов. Обозначаются они соответственно буквами r и R.В некоторых формулах фигурируют внутренний угол, полупериметр и апофема (являющаяся перпендикуляром к середине любой стороны из центра многоугольника). Для них используются буквы: α, р, m.
Формулы, которые описывают фигуру
Для расчета радиуса вписанной окружности потребуется такая: r = (a * √3) / 2, причем r = m. То есть такая же формула будет и для апофемы.
Поскольку периметр шестиугольника — это сумма всех сторон, то он определится так: P = 6 * a. С учетом того, что сторона равна радиусу описанной окружности, для периметра существует такая формула правильного шестиугольника: P = 6 * R. Из той, что приведена для радиуса вписанной окружности, выводится зависимость между а и r. Тогда формула принимает такой вид: Р = 4 r * √3.

Для площади правильного шестиугольника может пригодиться такая: S = p * r = (a 2 * 3 √3) / 2.
Задачи
№ 1. Условие. Имеется правильная шестиугольная призма, каждое ребро которой равно 4 см. В нее вписан цилиндр, объем которого необходимо узнать.
Решение. Объем цилиндра определяется как произведение площади основания на высоту. Последняя совпадает с ребром призмы. А она равна стороне правильного шестиугольника. То есть высота цилиндра — тоже 4 см.
Чтобы узнать площадь его основания, потребуется вычислить радиус вписанной в шестиугольник окружности. Формула для этого указана выше. Значит, r = 2√3 (см). Тогда площадь круга: S = π * r 2 = 3,14 * (2√3 ) 2 = 37,68 (см 2 ).
Осталось сосчитать объем: V = 37, 68 * 4 = 150,72 (см 3 ).
Ответ. V = 150,72 см 3 .
№ 2. Условие. Вычислить радиус окружности, которая вписана в правильный шестиугольник. Известно, что его сторона равна √3 см. Чему будет равен его периметр?
Решение.
 Эта задача требует использования двух из указанных формул. Причем их необходимо применять, даже не видоизменяя, просто подставить значение стороны и вычислить.
Эта задача требует использования двух из указанных формул. Причем их необходимо применять, даже не видоизменяя, просто подставить значение стороны и вычислить.Таким образом, радиус вписанной окружности получается равным 1,5 см. Для периметра оказывается верным такое значение: 6√3 см.
Ответ. r = 1,5 см, Р = 6√3 см.
№ 3. Условие. Радиус описанной окружности равен 6 см. Какое значение в этом случае будет у стороны правильного шестиугольника?
Решение. Из формулы для радиуса вписанной в шестиугольник окружности легко получается та, по которой нужно вычислять сторону. Ясно, что радиус умножается на два и делится на корень из трех. Необходимо избавиться от иррациональности в знаменателе. Поэтому результат действий принимает такой вид: (12 √3) / (√3 * √3), то есть 4√3.
Правильный многоугольник
Правильный многоугольник — это многоугольник, все стороны и углы которого равны.
Вокруг правильного многоугольника можно описать окружность и в него можно вписать окружность.
 Центры этих окружностей совпадают.
Центры этих окружностей совпадают.Правильный шестиугольник
Правильный шестиугольник – это шестиугольник, все стороны и углы которого равны.
Описанный многоугольник
Если все стороны многоугольника касаются некоторой окружности , то он называется описанным многоугольником .
Сколько сторон имеет правильный многоугольник
ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ
Составила: Шатрабаева Тамара Захаровна
1 УРОВЕНЬ
Найдите углы правильного двенадцатиугольника.
Сколько сторон имеет правильный многоугольник, если каждый его угол равен 144°?
Найдите внешний угол правильного пятнадцатиугольника.
2 УРОВЕНЬ
Сколько сторон имеет правильный многоугольник, если его внешний угол в два раза меньше внутреннего?
Докажите, что четыре вершины правильного восьмиугольника, взятые через одну, служат вершинами квадрата.
Площадь правильного треугольника равна 4.
 Найдите его периметр.
Найдите его периметр.
3 УРОВЕНЬ
Докажите, что в правильном шестиугольнике ABCDEF диагональ AC делит его на две фигуры, площади которых пропорциональны числам 1 и 5.
Три вершины правильного шестиугольника, взятые через одну, служат вершинами треугольника. Найдите отношение периметров данного шестиугольника и получившегося треуголбника.
Можно ли покрыть плоскость правильными треугольниками и правильными шестиугольниками без просветов? Ответ обоснуйте.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ:
Найдите углы правильного шестнадцатиугольника.
Каждый угол правильного многоугольника равен 162°. Найдите число его сторон.
Чему равен внешний угол правильного восемнадцатиугольника?
Внешний угол правильного многоугольника равен 15°. Найдите число его сторон.
Является ли равнобедренный треугольник с углом при вершине в 60° правильным?
Ответ обоснуйте.
Является ли ромб с равными диагоналями правильным четырехугольником? Ответ обоснуйте.
Диагональ AD делит шестиугольник ABCDEF на две равновеликие трапеции. Является ли шестиугольник ABCDEF правильным? Ответ обоснуйте.
В правильном шестиугольнике ABCDEF проведены диагонали AC,AD,AE. Найдите площади получившихся треугольников, если площадь шестиугольника равна 42.
Угол в правильной шестиугольной призме
На сайте уже были рассмотрены некоторые типы задач по стереометрии, которые входят в единый банк заданий экзамена по математике. Например, задания про составные многогранники .
Призма называется правильной если её боковые перпендикулярны основаниям и в основаниях лежит правильный многоугольник. То есть правильная призма – это прямая призма, у которой в основании правильный многоугольник.
Правильная шестиугольная призма – в основании правильный шестиугольник, боковые грани – прямоугольники.

В этой статье для вас задачи на решение призмы, в основании которой лежит правильный шестиугольник . Особенностей и сложностей в решении нет никаких. В чём суть? Дана правильная шестиугольная призма, требуется вычислить расстояние между двумя вершинами или найти заданный угол. Задачи на самом деле простые, в итоге решение сводится к нахождению элемента в прямоугольном треугольнике.
Используется теорема Пифагора и теорема косинусов . Необходимо знание определений тригонометрических функций в прямоугольном треугольнике.
Обязательно посмотрите информацию о правильном шестиугольнике в этой статье (пункт 6) . Ещё вам пригодится навык извлечения квадратного корня их большого числа. Можете посмотреть статью на решение многогранников, там тоже вычисляли расстояние между вершинами и углы.
Кратко: что представляет собой правильный шестиугольник?
Известно, что в правильном шестиугольнике стороны равны. Кроме этого, углы между сторонами тоже равны .

*Противолежащие стороны параллельны.
Радиус окружности описанной около правильного шестиугольника равен его стороне. *Это подтверждается очень просто: если мы соединим противоположные вершины шестиугольника, то получим шесть равных равносторонних треугольников. Почему равносторонних?
У каждого треугольника угол при его вершине лежащей в центре равен 60 0 (360:6=60). Так как у треугольника две стороны имеющие общую вершину в центре равны (это радиусы описанной окружности), то каждый угол при основании такого равнобедренного треугольника так же равен 60 градусам.
То есть правильный шестиугольник, образно говоря, состоит как бы из шести равных равносторонних треугольников.
Какой полезный для решения задач факт ещё следует отметить? Угол при вершине шестиугольника (угол между его соседними сторонами) равен 120 градусам.
*Умышленно не коснулись формул правильного N-угольника. Данные формулы мы подробно рассмотрим в будущем, здесь они просто не нужны.

272533. В правильной шестиугольной призме ABCDEFA 1B 1C 1D 1E 1F 1 все ребра равны 48. Найдите расстояние между точками A и E1.
Рассмотрим прямоугольный треугольник AA 1 E 1 . По теореме Пифагора:
*Угол между сторонами правильного шестиугольника равен 120 градусам.
Отрезок АЕ 1 является гипотенузой, АА 1 и А 1 Е 1 катеты. Ребро АА 1 нам известно. Катет А 1 Е 1 мы можем найти используя используя теорему косинусов.
Теорема: Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними.
По теореме Пифагора:
*Обратите внимание, что 48 возводить в квадрат совсем не обязательно.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 35.
 Найдите расстояние между точками B и E.
Найдите расстояние между точками B и E.Рассмотрим правильный шестиугольник:
Сказано, что все рёбра равны 35, то есть сторона шестиугольника лежащего в основании равна 35. А так же, как уже сказано, радиус описанной около него окружности равен этому же числу.
273353. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны сорока корням из пяти. Найдите расстояние между точками B и E1.
Рассмотрим прямоугольный треугольник BB 1 E 1 . По теореме Пифагора:
Отрезок B 1 E 1 равен двум радиусам описанной около правильного шестиугольника окружности, а её радиус равен стороне шестиугольника, то есть
273683. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 45. Найдите тангенс угла AD1D.
Рассмотрим прямоугольный треугольник ADD1, в котором AD равно диаметру окружности, описанной вокруг основания.
 Известно, что радиус окружности, описанной вокруг правильного шестиугольника равен его стороне.
Известно, что радиус окружности, описанной вокруг правильного шестиугольника равен его стороне.В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 23. Найдите угол DAB. Ответ дайте в градусах.
Рассмотрим правильный шестиугольник:
В нём углы между сторонами равны 120°. Значит,
Сама длина ребра не имеет значения, на величину угла она не влияет.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 10. Найдите угол AC1C. Ответ дайте в градусах.
Рассмотрим прямоугольный треугольник AC1C:
Найдём AC . В правильном шестиугольнике углы между его сторонами равны 120 градусам, тогда по теореме косинусов для треугольника АВС :
Значит, угол AC 1 C равен 60 градусам.
274453.
 В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 10. Найдите угол AC1C. Ответ дайте в градусах.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 10. Найдите угол AC1C. Ответ дайте в градусах.Рассмотрим треугольник AС 1 С, он прямоугольный. Вычислим тангенс указанного в условии угла и определим угол. Известно, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему, то есть
Катет С1С = 10. Отрезок АС вычислим по теореме косинусов (это мы уже делали в первой задаче, запишем ещё раз):
В правильном шестиугольнике углы при вершинах равны 120 градусам, то есть
245364. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками А и Е1.
245365. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1.
 Найдите расстояние между точками В и Е.
Найдите расстояние между точками В и Е.245366. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1все ребра равны корню из пяти. Найдите расстояние между точками В и Е1.
245367. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите тангенс угла AD1D.
245368. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите угол DAB. Ответ дайте в градусах.
245369. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите угол AC1C. Ответ дайте в градусах.
На этом всё! Успеха Вам!
В состав ЕГЭ включены и другие задачи по стереометрии, и они довольно разнообразны.
 Обязательно будем их рассматривать, не пропустите! Успехов вам!
Обязательно будем их рассматривать, не пропустите! Успехов вам!Что ты хочешь узнать?
Ответ
Проверено экспертом
Найдите угол DAB – угол правильного шестиугольника ( основания призмы)
Сумма углов многоугольника находится по формуле
180(n-2)
180*(6-2)=720°
Величина одного угла правильного шестиугольника
720:6=120°Вопрос задан полностью? Иначе призма и ее ребра здесь как будто ни при чем.
Изучением призм занимается пространственная геометрия. Важными их характеристиками являются заключенный в них объем, площадь поверхности и число составляющих элементов. В статье рассмотрим все эти свойства для шестиугольной призмы.
О какой призме пойдет речь?
Призма шестиугольная – это фигура, образованная двумя многоугольниками, имеющими шесть сторон и шесть углов, и шестью параллелограммами, соединяющими отмеченные шестиугольники в единое геометрическое образование.
На рисунке изображен пример этой призмы.

Отмеченный красным цветом шестиугольник называется основанием фигуры. Очевидно, что число ее оснований равно двум, причем оба они идентичны. Желто-зеленоватые грани призмы называются ее боковыми сторонами. На рисунке они представлены квадратами, но в общем случае они являются параллелограммами.
Шестиугольная призма может быть наклонной и прямой. В первом случае углы между основанием и боковыми сторонами не являются прямыми, во втором они равны 90 o . Также эта призма может быть правильной и неправильной. Правильная шестиугольная призма обязательно должна быть прямой и иметь правильный шестиугольник в основании. Приведенная выше призма на рисунке этим требованиям удовлетворяет, поэтому она называется правильной. Далее в статье будем изучать только ее свойства, как общий случай.
Элементы
Для любой призмы главными ее элементами являются ребра, грани и вершины. Шестиугольная призма не является исключением. Приведенный выше рисунок позволяет посчитать количество этих элементов.
 Так, граней или сторон мы получаем 8 (два основания и шесть боковых параллелограммов), число вершин составляет 12 (по 6 вершин для каждого основания), количество ребер шестиугольной призмы равно 18 (шесть боковых и 12 для оснований).
Так, граней или сторон мы получаем 8 (два основания и шесть боковых параллелограммов), число вершин составляет 12 (по 6 вершин для каждого основания), количество ребер шестиугольной призмы равно 18 (шесть боковых и 12 для оснований).В 1750-е годы Леонард Эйлер (швейцарский математик) установил для всех полиэдров, к которым относится призма, математическую связь между числами указанных элементов. Эта связь имеет вид:
число ребер = число граней + число вершин – 2.
Указанные выше цифры удовлетворяют этой формуле.
Диагонали призмы
Все диагонали шестиугольной призмы можно разделить на два типа:
- те, которые лежат в плоскостях ее граней;
- те, которые принадлежат всему объему фигуры.
Рисунок ниже показывает все эти диагонали.
Видно, что D1 – это диагональ боковой стороны, D2 и D3 – диагонали всей призмы, D4 и D5 – диагонали основания.
Длины диагоналей боковых сторон между собой равны.
 Вычислить их легко, используя всем известную теорему Пифагора. Обозначим символом a длину стороны шестиугольника, символом b – длину бокового ребра. Тогда диагональ имеет длину:
Вычислить их легко, используя всем известную теорему Пифагора. Обозначим символом a длину стороны шестиугольника, символом b – длину бокового ребра. Тогда диагональ имеет длину:Диагональ D4 также легко определяется. Если вспомнить, что правильный шестиугольник вписывается в окружность радиусом a, то D4 является диаметром этой окружности, то есть получим следующую формулу:
Диагональ D5 основания найти несколько сложнее. Для этого следует рассмотреть равносторонний треугольник ABC (см. рис.). Для него AB = BC = a, угол ABC равен 120 o . Если из этого угла опустить высоту (она же будет биссектрисой и медианой), тогда половина основания AC будет равно:
Сторона AC является диагональю D5, поэтому получаем:
Теперь остается найти диагонали D2 и D3 правильной шестиугольной призмы. Для этого нужно увидеть, что они являются гипотенузами соответствующих прямоугольных треугольников. Воспользовавшись теоремой Пифагора, получаем:
Таким образом, самой большой диагональю для любых значений a и b является D2.

Площадь поверхности
Чтобы понять, о чем идет речь, проще всего рассмотреть развертку этой призмы. Она показана на рисунке.
Видно, что для определения площади всех сторон рассматриваемой фигуры необходимо рассчитать отдельно площадь четырехугольника и площадь шестиугольника, затем умножить их на соответствующие целые числа, равные количеству каждого n-угольника в призме, и сложить полученные результаты. Шестиугольников 2, прямоугольников 6.
Для площади прямоугольника получаем:
Тогда площадь боковой поверхности равна:
Для определения площади шестиугольника проще всего воспользоваться соответствующей формулой, которая имеет вид:
Подставляя в это выражение число n равное 6, получаем площадь одного шестиугольника:
Это выражение следует умножить на два, чтобы получить площадь оснований призмы:
Остается сложить Sos и S2, чтобы получить полную площадь поверхности фигуры:
Объем призмы
После того как была получена формула для площади шестиугольного основания, вычислить объем, заключенный в рассматриваемую призму, проще простого.
 Для этого следует лишь умножить площадь одного основания (шестиугольника) на высоту фигуры, длина которой равна длине бокового ребра. Получаем формулу:
Для этого следует лишь умножить площадь одного основания (шестиугольника) на высоту фигуры, длина которой равна длине бокового ребра. Получаем формулу:Отметим, что произведение основания на высоту дает значение объема абсолютно любой призмы, включая наклонную. Однако в последнем случае расчет высоты осложняется, поскольку она уже не будет равна длине бокового ребра. Что касается шестиугольной правильной призмы, то значение ее объема является функцией двух переменных: сторон a и b.
“>
Шестиугольник, виды, свойства и формулы
Шестиугольник, выпуклый и невыпуклый шестиугольник:
Шестиугольник – это многоугольник с шестью углами.
Шестиугольник – это многоугольник, общее количество углов (вершин) которого равно шести.
Шестиугольник может быть выпуклым и невыпуклым.
Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
 Невыпуклыми являются все остальные многоугольники.
Невыпуклыми являются все остальные многоугольники.Соответственно выпуклый шестиугольник – это шестиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
Рис. 1. Выпуклый шестиугольник
Рис. 2. Невыпуклый шестиугольник
Сумма внутренних углов любого выпуклого шестиугольника равна 720°.
.
Размеры
Чтобы отвертка прослужила долго, и не стерлась, важно выбрать правильный размер инструмент с нужным наконечником.

Для каждого вида разработаны специальные стандарты размеров, и присвоены им номерные обозначения.
Шлицевые отвертки с плоской формой наконечника могут иметь ширину от 2 до 18 мм, а крестообразные модели идут с нумерацией от 0 до 4.
Все номерные виды рассчитаны на определенный диаметр наружной резьбы:
• № 0 – до двух мм; • № 1 – от двух до трех мм; • № 2 – от трех до пяти мм; • № 3 – от пяти до семи мм и т.д.
Размеры стержня зависят от номера отвертки.
Так, например, нулевая отвертка имеет диаметр стержня 4 миллиметра при длине до 80 миллиметров.
По мере возрастания номера увеличивается диаметр и длина стержня.
Правильный шестиугольник (понятие и определение):
Правильный шестиугольник (гексагон) – это правильный многоугольник с шестью сторонами.
В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.
Правильный шестиугольник – это шестиугольник, у которого все стороны равны, а все внутренние углы равны 120°.

Рис. 3. Правильный шестиугольник
Правильный шестиугольник имеет 6 сторон, 6 углов и 6 вершин.
Углы правильного шестиугольника образуют шесть равносторонних треугольников.
Правильный шестиугольник можно построить с помощью циркуля и линейки.
Торцевые гаечные ключи
Этот вид ключей представляет собой полую трубку или цилиндр с углублениями на обоих концах. Торцевые ключи бывают двух типов:
Г-образные торцевые ключи
Они имеют одинаковый размер на обоих краях рабочих частей. Это сделано с тем расчетом, что гайка (или болт) могут находиться глубоко от поверхности и тогда используется длинная часть ключа, но при этом необходимо приложить больше усилий (из-за маленького рычага). Если деталь находится неглубоко, тогда используется короткая часть ключа, соответственно из-за большего рычага усилий прикладывается меньше.
I-образные гаечные ключи
Выглядят как полый цилиндр с рабочей частью разного размера на обоих концах.
 Работать таким ключом приходиться, используя рычаг (вороток) который вставляется в сквозное отверстие в корпусе ключа.
Работать таким ключом приходиться, используя рычаг (вороток) который вставляется в сквозное отверстие в корпусе ключа.Виды молотков и их назначение
Шестигранные ключи
Этот вид ключей имеет Г-образную форму и используется для работы с болтами (шурупами, винтами) имеющими не внешние грани, а внутренние. В основном применяются в основном при сборке мебели, ремонте бытовой технике и подобных работах.
Свойства правильного шестиугольника:
1. Все стороны правильного шестиугольника равны между собой.
a1 = a2 = a3 = a4= a5= a6.
2. Все углы равны между собой и составляют 120°.
α1 = α2 = α3 = α4 = α5 = α6 = 120°.
Рис. 4. Правильный шестиугольник
3. Сумма внутренних углов любого правильного шестиугольника равна 720°.
4. Все биссектрисы углов между сторонами равны и проходят через центр правильного шестиугольника O.
Рис. 5. Правильный шестиугольник
5.
 Количество диагоналей правильного шестиугольника равно 9.
Количество диагоналей правильного шестиугольника равно 9.Рис. 6. Правильный шестиугольник
6. Центр вписанной окружности O1 совпадает с центром описанной окружности O2, что и образуют центр многоугольника O.
Рис. 7. Правильный шестиугольник
7. Правильные шестиугольники замощают плоскость (то есть могут заполнять плоскость без пробелов и наложений).
8. Радиус описанной окружности правильного шестиугольника и его сторона равны.
Рис. 8. Правильный шестиугольник
R = a
Накидные ключи
У этих ключей рабочая часть имеет фору кольца с гранями на внутренней стороне. Его конструкция более надежна чем у рожковых ключей, так как деталь охватывается по всей поверхности (то есть как минимум в шести местах), что практически исключает деформацию углов. Накидные ключи существуют с двумя типами внутреннего профиля – с 6-и гранным профилем и 12-и гранным профилем. Профилем с 12-ю гранями работать в ограниченном пространстве удобней, так как ему достаточно поворота на 30 градусов, к ключу с 6-и гранным профилем необходимо 60 градусов поворота.

Чистый двор и дом — мойка высокого давления!
Более распространенны ключи с наклонной головкой, когда рабочая часть находится под небольшим углом к рукоятке. Накидные ключи выпускаются разного размера, как и рожковые ключи.
Правильный шестиугольник в природе, технике и культуре:
Пчелиные соты имеют форму правильного шестиугольника.
Графит, графен имеют гексагональную кристаллическую решетку.
Гигантский гексагон – атмосферное явление на Сатурне – имеет форму правильного шестиугольника.
Рис. 9. Гигантский гексагон на Сатурне
Сечение гайки и многих карандашей имеет вид правильного шестиугольника.
Игровое поле гексагональных шахмат составляют шестиугольники, в отличие от квадратов традиционной шахматной доски.
Панцирь черепахи состоит из шестиугольников.
Гексагоном иногда называют материковую часть Франции, потому что её географические очертания напоминают данную геометрическую фигуру.

Рис. 10. Материковая часть Франции
Виды отверток и их назначение
Универсальная отвертка слесарная – это инструмент, который есть практически в каждом доме.
Благодаря отвертке можно выполнять ремонтные работы разной степени сложности, главное знать, какой тип и диаметр подойдет в каждом конкретном случае.
О том, какие бывают отвертки можно узнать, если детальнее углубиться в тему.
Отличительной особенностью всех видов является разное толщина стержня.
Читать также: Как проверить акб без нагрузочной вилки
Наиболее популярными считают отвертки с круглым и квадратным сечением, с прямым или крестообразным шлицем.
Однако технический прогресс не стоит на месте и наряду с новыми видами крепежа появляются профессиональные отвертки для вкручивания болтов, шурупов и прочих элементов.
Все это делается для того, чтобы облегчить работу потребителям.
• На данный момент кроме универсальных моделей существует еще несколько модернизированных видов отверток для проведения разных работ.

Например, переставная отвертка отличается своей универсальностью, т.к. с одной стороны стержня она плоская, а с другой крестовая.
Некоторые переставные модели имеют несколько разных наконечников, что повышает универсальность инструмента.
• Точная или как ее еще называют, тонкая отвертка – подойдет для ремонта мобильных телефонов, ее маркировка соответствует нулевому обозначению.
Изделие производят с малым размером шлица, не более 2мм, что позволяет выполнить точную работу с мелкими деталями.
• Особые эргономичные свойства приобрела двухкомпонентная отвертка, ее отличительной особенностью стала прочная рукоять из комбинированных материалов.
Для покрытия рукояти использовали полипропилен и резину.
Двухкомпонентное покрытие способствует надежному захвату, чтобы изделие уже не могло выскользнуть из рук.
• Для работы с тонкими деталями используют часовые отвертки, с их помощью ремонтируют часовые механизмы.
Размер наконечника изделия – не более миллиметра.

На этом классификация профессиональных монтажных отверток не заканчивается, существует еще много разновидностей моделей, предназначенных для определенных целей.
Формулы правильного шестиугольника:
Пусть a – сторона шестиугольника, r – радиус окружности, вписанной в шестиугольник, R – радиус описанной окружности шестиугольника, P – периметр шестиугольника, S – площадь шестиугольника.
Формулы периметра правильного шестиугольника:
Формулы площади правильного шестиугольника:
Формула радиуса окружности, вписанной в правильный шестиугольник:
Формула радиуса окружности, описанной вокруг правильного шестиугольника:
R = a
Маркировка и размеры [ править | править код ]
Ключи и отвёртки имеют маркировку T
или
TX
с номером шлица — 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 15, 20, 25, 27, 30, 40, 45, 50, 55, 60, 70, 80, 90, 100.
Ключи и отвёртки со шлицом Torx Tamper Resistant
после основной маркировки дополнительно обозначаются
TR
.У ключей и отвёрток со шлицом Torx Plus
сначала указывается номер шлица, а после — вместо
T
или
TX
обозначается буквами
IP
.Ключи и отвёртки со шлицом Torx Plus Tamper Resistant
после основной маркировки дополнительно обозначаются
TS
.Размер определяется по диаметру окружности описанной по вершинам звездочки инструмента (для версии E — болта).
Приблизительные размеры и моменты затяжки [3]
Номер Размер Момент затяжки E Torx
дюймы мм Н•м T1 0,031″ 0,81 0,02 — 0,03 T2 0,036″ 0,93 0,07 — 0,09 T3 0,046″ 1,10 0,14 — 0,18 T4 0,050″ 1,28 0,22 — 0,28 T5 0,055″ 1,42 0,43 — 0,51 T5.  5 [4] [5] [6]
5 [4] [5] [6]T6 0,066″ 1,70 0,75 — 0,90 T7 0,078″ 1,99 1,4 — 1,7 T8 0,090″ 2,31 2,2 — 2,6 T9 0,098″ 2,50 2,8 — 3,4 T10 0,107″ 2,74 3,7 — 4,5 T15 0,128″ 3,27 6,4 — 7,7 T20 0,151″ 3,86 10,5 — 12,7 E4 T25 0,173″ 4,43 15,9 — 19 E5 T27 0,195″ 4,99 22,5 — 26,9 T30 0,216″ 5,52 31,1 — 37,4 E6 T35 [7] [8] [9] T40 0,260″ 6,65 54,1 — 65,1 E8 T45 0,306″ 7,82 86 — 103,2 T47 [10] [11] GM-Style T50 0,346″ 8,83 132 — 158 E10 T55 0,440″ 11,22 218 — 256 E12 T60 0,519″ 13,25 379 — 445 E16 T70 0,610″ 15,51 630 — 700 E18 T80 0,690″ 17,54 943 — 1048 E20 T90 0,784″ 19,92 1334 — 1483 T100 0,871″ 22,13 1843 — 2048 E24 Размеры внешних шлицов Torx
Номер Размер [12] Стандартный болт [13] дюймы мм SAE метрический E4 0,15″ 3,8 #6 M3 E5 0,18″ 4,7 #8 M4 E6 0,22″ 5,6 #10 M5 E7 0,24″ 6,1 E8 0,29″ 7,4 1/4″ M6 & M7 E10 0,36″ 9,3 5/16″ M8 E12 0,43″ 11,1 3/8″ M10 & M11 E14 0,50″ 12,8 7/16″ M12 E16 0,57″ 14,7 1/2″ E18 0,65″ 16,6 9/16″ M14 E20 0,72″ 18,4 5/8″ M16 E24 0,87″ 22,1 3/4″ M18 & M20 E28 7/8″ M22 E32 1″ M24 & M27 E36 1-1/8″ M30 E40 1-1/4″ M33 E44 1-3/8″ M36 Использование [ править | править код ]
Крепёж со шлицом Torx обычно используется в технике: автомобилях, велосипедах, тормозных системах, разнообразных сборных металлических конструкциях, жёстких дисках компьютеров, банкоматах, потребительской электронике и топливной аппаратуре.

Неизвестно, специально это было сделано или нет, но размеры Torx коррелируются с размерами инбусовых ключей и позволяют выкрутить сорванный шестигранный шлиц. При срыве шлица в образованное отверстие забивается инструмент Torx и практически со стопроцентным результатом позволяет выкрутить сорванный болт или винт.
Следует отметить, что при работе с Torx необходимо учитывать следующие особенности:
- Инструмент должен входить в крепёж достаточно плотно. Если инструмент болтается в шлице, то, скорее всего, он подобран неправильно. Особенно это касается не совсем стандартных размеров, например распространённый в автомобилях T47 практически всегда отсутствует в наборах ключей Torx и подбирается как T45.
- Инструмент должен входить в шлиц до конца. Учитывая изначально плотную посадку, для этого зачастую приходится прибегать к помощи ударного инструмента.
Несоблюдение этих правил зачастую ведёт к разрушению головки болта и, как следствие, к необоснованной критике Torx.

Правильные вписанные и описанные многоугольники
Правильный многоугольник. Правильным называется такой многоугольник, у которого все стороны и все углы равны.
Правильный треугольник есть равносторонний треугольник, каждый угол которого равен (2/3)d или 60°.
Правильный четырехугольник есть квадрат, каждый угол которого равен прямому углу или 90°.
Правильный многоугольник, имеющий n сторон, есть многоугольник, каждый угол которого равен .
Таким образом, полагая n = 3, 4, 5, 6, мы имеем для каждого угла величину (2/3)d, d, (6/5)d, (4/3)d и т. д.
Угол правильного пятиугольника равен (6/5)d = 108°, угол правильного шестиугольника равен (4/3)d = 120° и т. д.
Одноименные многоугольники. Все многоугольники, имеющие одинаковое число углов, называются одноименными многоугольниками.
Все правильные одноименные многоугольники имеют одинаковые углы и различаются только величиной сторон.
Подобие правильных многоугольников.
 Одноименные правильные многоугольники подобны, ибо у них углы равны и стороны пропорциональны.
Одноименные правильные многоугольники подобны, ибо у них углы равны и стороны пропорциональны.Из подобия их вытекает, что периметры одноименных правильных многоугольников относятся как стороны.
Теорема 117. Около правильного многоугольника всегда можно описать окружность.
Дан правильный многоугольник ABCDEF (черт. 192). Стороны его и углы равны между собой:
AB = BC = CD = DE = EF = AF и
A = B = C = D = E = FТребуется доказать, что существует точка, равноотстоящая от всех его вершин.
Доказательство. Проведем через три точки A, B, C окружность. Для этого из середины линий AB и BC восставляем перпендикуляры до взаимного их пересечения в точке O. Точка O есть центр круга, проходящего через три точки A, B, C. Докажем, что эта окружность пройдет и через точки D, E, F. Для этого соединим точку O с вершинами многоугольника отрезками AO, BO, CO, DO, EO, FO.
1. Все эти отрезки разделяют углы многоугольника пополам.

Из равнобедренных треугольников AOB и BOC видно, что
∠α = ∠β, ∠γ = ∠δ
Так как ΔABO = ΔBCO, то
∠β = ∠γ = ½B,
т. е. угол B делится пополам.
Из равенств
∠δ = ½B = ½C
следует, что угол C тоже делится пополам.
Точно также легко доказать, что угол D тоже делится пополам.
Треугольники BOC и COD равны, ибо OC сторона общая, BC = CD как стороны правильного многоугольника, ∠δ = ∠ε, следовательно, ∠γ = ∠η.
Так как ∠γ = ½B = ½C = ½D, то и угол η = ½D, т. е. угол D делится тоже пополам.
Подобным образом легко доказать, что все углы многоугольника делятся пополам отрезками, соединяющими точку O с вершинами многоугольника.
2. Все отрезки OA, OB, OC, OD, OE, OF равны.
Действительно, по построению следует, что
OA = OB = OC
Из равенства треугольников BOC и COD следует, что
OC = OD
Из равенства треугольников COD и DOE следует, что
OD = OE и т.
 д.
д.Таким образом точка O находится на равном расстоянии от всех вершин многоугольника, т. е. окружность, описанная радиусом OA, пройдет через все вершины многоугольника, и точка O будет центром описанного многоугольника (ЧТД).
Теорема 118. Центр описанного круга будет также центром круга, вписанного в правильный многоугольник.
Доказательство. Из точки O центра описанного многоугольника (черт. 192) опустим перпендикуляры Oa, Ob, Oc, Od, Oe, Of на стороны многоугольника. Так как треугольники ABO, BCO равнобедренные и многоугольники правильные, то
Aa = aB = Bb = bC = Cc = cD = …
Два прямоугольных треугольника aBO и BbO равны, ибо BO сторона общая
aB = Bb
следовательно, Oa = Ob.
Точно также легко доказать, что Ob = Oc и т. д.
Следовательно, вообще Oa = Ob = Oc = Od = Oe = Of.
Если мы радиусом Oa опишем окружность, то она коснется сторон правильного многоугольника в точках a, b, c, … т.
 е. она будет вписана в многоугольник.
е. она будет вписана в многоугольник.Точки a, b, c, … делят стороны многоугольника пополам.
Таким образом точка O, будучи центром описанного, есть в то же время и центр круга, вписанного в правильный многоугольник (ЧТД).
Апофема. Перпендикуляр, опущенный из центра на сторону правильного многоугольника, называется апофемой.
Теорема 119. Периметры одноименных правильных многоугольников относятся как радиусы описанных и вписанных кругов.
Даны два правильных одноименных многоугольника (черт. 193). Из центров O и O’ проведем радиусы кругов описанных и вписанных.
Требуется доказать, что
(AB + BC + CD + DE + EA) / (ab + bc + cd + de + ea) = OA/O’a = OG/O’g
Доказательство. Два треугольника GOB и gOb подобны, ибо они прямоугольны и ∠GBO = ∠gbO’, следовательно,
GB/gb = OB/O’b = GO/gO’
Так как GB = ½AB, gb = ½ab, то
AB/ab = OB/O’b = GO/gO’ (a)
Кроме того имеют место следующие равенства отношений:
AB/ab = BC/bc = CD/cd = DE/de = EA/ea
откуда по свойству пропорций имеем:
(AB + BC + CD + DE + EA) / (ab + bc + cd + de + ea) = AB/ab
Обозначим периметры этих многоугольников через P и p, имеем:
P/p = AB/ab (b)
Сравнивая пропорции (a) и (b), получаем равные отношения:
P/p = AB/ab = OB/O’b = GO/gO’ (ЧТД).

Теорема 120. Если углы описанного многоугольника равны, то и стороны равны, т. е. равноугольный описанный есть многоугольник правильный.
Дано. В описанном многоугольнике ABCDE углы равны (черт. 194):
A = B = C = D = E.
Требуется доказать, что AB = BC = CD = DE = EA.
Доказательство. Соединим вершины описанного многоугольника и точки прикосновения с центром круга O.
1. Два прямоугольных треугольника aBO и BbO равны, ибо у них BO сторона общая, aO = bO как радиусы, следовательно, ∠aOB = ∠Bob и ∠aBO = ∠bBO, т. е. отрезки, соединяющие вершины описанного многоугольника с центром, делят углы многоугольника пополам.
2. Треугольники AOB и BOC равны, ибо BO сторона общая, ∠ABO = ∠CBO по доказанному, ∠BAO = ∠BCO по условию, следовательно, AB = BC.
Таким образом можно доказать равенство остальных сторон описанного многоугольника, имеющего равные углы (ЧТД).
Теорема 121.
 По данному вписанному правильному многоугольнику можно описать правильный многоугольник того же числа сторон.
По данному вписанному правильному многоугольнику можно описать правильный многоугольник того же числа сторон.Дан правильный вписанный многоугольник (черт. 195) ABCDEF, следовательно, стороны и углы его равны.
AB = BC = CD = DE = EF = FA и
◡AB = ◡BC = ◡CD = ◡DE = ◡EF = ◡FAДля построения правильного описанного многоугольника по данному вписанному применяют два способа.
Первый способ. Нужно центр правильного вписанного многоугольника соединить с вершинами и в вершинах провести к этим отрезкам перпендикуляры, которые, пересекаясь, образуют правильный описанный многоугольник.
Проведем радиусы AO, BO, CO, и т. д. и в вершинах A, B, C, D, E, F проведем перпендикуляры к этим радиусам до взаимного их пересечения в точках a, b, c, d, e, f. Образуется многоугольник abcdef.
Требуется доказать, что многоугольник abcdef будет правильным описанным многоугольником.
Доказательство. Многоугольник abcdef будет описанным многоугольником, потому что ab, bc, … будут касательными к окружности, так как они проведены перпендикулярно к радиусам из их концов.

2. Треугольники AaB, BbC … равнобедренны, ибо
∠aAB = ∠aBA
∠bBC = ∠bCB и т. д.так как они измеряются половиной одной и той же дуги, следовательно, и соответствующие стороны равны
aA = aB, bB = bC, cC = Dc и т. д.
3. Треугольники AaB и BbC равны, ибо AB = BC как стороны правильного вписанного многоугольника
∠aAB = ∠bCB
∠aBA = ∠bBCибо они измеряются половиной равных дуг.
Из равенства треугольников AaB и BbC вытекает, что aB = Bb, т. е.
Каждая сторона таким образом описанного многоугольника делится в точке прикосновения пополам.
4. Кроме того,
aA = aB, или ½af = ½ab = ½bc и т. д.
следовательно,
af = ab = bc = cd и т. д.,
т. е. все стороны многоугольника равны.
5. Наконец, ∠a = ∠b, следовательно и все углы многоугольника abcdef равны. Поэтому этот многоугольник правильный (ЧТД).

Второй способ. Нужно из центра на стороне правильного вписанного многоугольника опустить перпендикуляры, продолжить их до пересечения с окружностью и в точках пересечения провести касательные прямые до взаимного их пересечения. Эти точки пересечения и будут вершинами правильного описанного многоугольника.
Дан правильный вписанный многоугольник ABCDEF (черт. 196).
Из центра O опустим перпендикуляр на стороны вписанного многоугольника и в точках m, n, p, q, r, s их встречи с окружностью проведем касательные до их взаимного пересечения в точках a, b, c, d, e, f.
Требуется доказать, что abcdef есть правильный описанный многоугольник.
Доказательство. 1. Стороны многоугольника abcdef касательны к окружности, следовательно, abcdef есть многоугольник описанный.
2. Его стороны параллельны сторонам правильного вписанного многоугольника, поэтому его углы равны
∠a = ∠b = ∠c = ∠d = ∠e = ∠f.

3. Соединим точки m, n, p, q … прямыми линиями.
Точки m, n, p, q … суть середины дуг AB, BC и т. д., следовательно, для дуг и хорд имеют место равенства:
sm = mn = np = pq = qr = rs.
4. Треугольники sam, mbn, ncp … равнобедренны, ибо
∠asm = ∠ams, ∠bmn = ∠bnm и т. д.
следовательно,
as = am, bm = bn, cn = cp и т. д.
5. Треугольники sam и mbn равны, ибо
∠ams = ∠bmn
∠asm = ∠bnmследовательно, am = bm, т. е. стороны описанного многоугольника делятся в точках прикосновения пополам.
6. Наконец из равенства as = am следует равенство
½af = ½ab или af = ab, т. е.
стороны описанного многоугольника равны.
Таким образом многоугольник abcdef есть правильный описанный многоугольник (ЧТД).
Теорема 122. По данному правильному описанному можно вписать правильный многоугольник того же числа сторон.

Здесь тоже имеют место два способа.
Первый способ. Чтобы по данному правильному описанному вписать правильный многоугольник, нужно соединить точки прикосновения описанного многоугольника между собой.
Дан описанный правильный многоугольник abcdef, следовательно,
ab = bc = cd = de = ef = fa и
∠a = ∠b = ∠c = ∠d = ∠e = ∠f.Стороны правильного описанного многоугольника (черт. 195) делятся в точках прикосновения пополам, следовательно,
aB = bB = bC = Cc = …
Соединим точки прикосновения A, B, C, D, E, F между собой.
Требуется доказать, что ABCDEF есть правильный вписанный многоугольник, т. е.
AB = BC = CD = DE = EF = FA и
∠A = ∠B = ∠C = ∠D = ∠E = ∠F.Доказательство. 1. Треугольники AaB и BbC равны, ибо они имеют по равному углу, содержащемуся между двумя равными сторонами. Действительно,
aA = bC
aB = bB
∠a = ∠bследовательно, AB = BC.

Точно также можно доказать, что
BC = CD = DE = EF = FA,
следовательно, и стороны и дуги AB, BC, CD … равны.
Таким образом стороны вписанного многоугольника равны.
2. Сравнивая две дуги BCDEF и CDEFA, мы находим, что
BCDEF = окружности — AB — AF
CDEFA = окружности — AB — BC.Так как ◡AF = ◡BC, то
◡BCDEF = ◡CDEFA
следовательно,
∠A = ∠B.
Подобным же образом можно доказать равенство других углов, следовательно,
∠A = ∠B = ∠C = ∠D = ∠E = ∠F
Таким образом углы вписанного многоугольника как и стороны тоже равны, следовательно, ABCDEF правильный вписанный многоугольник (ЧТД).
Второй способ. Чтобы по данному правильному описанному многоугольнику вписать правильный одноименный многоугольник, соединим его вершины с центром круга и точки пересечения этих отрезков с окружностью соединим между собой.
Дан правильный описанный многоугольник ABCDEFA (черт.
 197), следовательно,
197), следовательно,AB = BC = CD = DE = EF = FA
∠A = ∠B = ∠C = ∠D = ∠E = ∠Fи стороны его делятся в точках прикосновения пополам, т. е.
As = Bs = Cm = Cn = Dn = и т. д.
Соединим вершины его с центром и означим точки пересечения этих линий с окружностью через a, b, c, d, e, f.
Требуется доказать, что многоугольник abcdef правильный.
Доказательство. 1. Углы при центре AOB, BOC, COD и т. д. равны, а следовательно и дуги ab, bc, de, ef, fa равны.
Отсюда вытекает, что стороны тоже равны
ab = bc = cd = de = ef = fa
2. Углы многоугольника тоже равны, ибо измеряются дугами одинаковой величины.
Теорема 123. По данной стороне правильного вписанного многоугольника можно определить сторону описанного многоугольника того же числа сторон.
Означим длину стороны вписанного правильного многоугольника имеющего n сторон через an и одноименного описанного многоугольника через An, а радиус круга через r (черт.
 195)
195)AB = BC = CD = DE = … = an
ab = bc = cd = de = … AnСоединим точку a с O, тогда
aB = ½An, BQ = ½an
Из треугольника aBO имеем:
формулу, определяющую сторону правильного вписанного многоугольника по стороне одноименного правильного описанного многоугольника.
Удвоение числа сторон правильного вписанного многоугольника
Чтобы удвоить число сторон правильного вписанного многоугольника, опускают из центра перпендикуляры на его стороны, соединяют с вершинами данного многоугольника точки пересечения их с окружностью.
1. Полученный таким образом многоугольник будет правильным (черт. 198).
Доказательство. Стороны его равны, ибо перпендикуляры делят как хорды, так и дуги AB, BC, … пополам, следовательно,
Aa = aB = Bb = bC = Cc = …
Углы тогда равны, ибо измеряются одинаковыми дугами.

2. Периметр многоугольника при удвоении числа сторон увеличивается.
Действительно,
Aa + aB > AB
Bb + bC > BC и т. д.Складывая эти неравенства, получим
Aa + aB + Bb + bC + … > AB + BC + …
Обозначив периметр правильного многоугольника, имеющего n сторон, через pn, имеем:
p2n >pn
Теорема 124. Можно определить длину стороны вписанного многоугольника с удвоенным числом сторон по радиусу и стороне данного многоугольника.
Из треугольника AaO (черт. 198) длина стороны Aa, как стороны, лежащей против острого угла, выражается равенством:
Aa2 = AO2 + aO2 — 2aO · PO.
Из треугольника APO имеем:
Обозначив через r радиус круга, an длину стороны правильного вписанного многоугольника, имеющего n сторон, и через a2n сторону многоугольника с удвоенным числом сторон, мы имеем по формуле (a)
Удвоение числа сторон правильного описанного многоугольника
Чтобы удвоить число сторон правильного описанного многоугольника нужно разделить дуги ab, bc, cd, … пополам и провести через точки деления отрезки mn, pg, rs, … до пересечения их со сторонами данного многоугольника (черт.
 199).
199).В этом случае образуется многоугольник равноугольный, ибо его углы измеряются одинаковой мерой. В равноугольном же описанном многоугольнике стороны равны (теорема 120).
Периметр описанного многоугольника с удвоенным числом сторон уменьшается.
Действительно,
An > αn
Bp > βp, следовательно,
AB > αn + np + pβТакие же равенства имеют место и для сторон BC, CD, … и т. д. Сложив их, находим, что
AB + BC + CD + … > mn + np + pq + …
или Pn > P2nгде Pn и P2n означают периметры правильных описанных многоугольников, имеющих n и 2n сторон.
Теорема 125. Сторона правильного вписанного шестиугольника равна радиусу (a6 = r).
Дано. Пусть AB сторона правильного шестиугольника (черт. 200), вписанного в круг, радиус которого обозначим через r.
Требуется доказать, что AB = a6 = r.

Доказательство. Дуга AB равна 60°. Соединив A и B с центром O, имеем треугольник ABO, у которого угол AOB имеет 60° = (2/3)d.
Углы A и B равны, следовательно, из равенства A + B + O = 2d, имеем:
2A + (2/3)d = 2d, откуда A = B = (2/3)d
Таким образом треугольник ABO равносторонний и следовательно AB = AO = r.
Теорема 126. Сторона правильного вписанного треугольника равна радиусу, умноженному на √3 (a3 = r√3).
Дан правильный вписанный треугольник ABC (черт. 201).
Требуется доказать, что AB = r√3.
Доказательство. Из центра O опустим перпендикуляр OD к стороне AB и соединим D с вершинами A и B. Стороны AD и DB как стороны правильного вписанного шестиугольника равны радиусу. Четырехугольник ADBO есть ромб, ибо у него все стороны равны радиусу. Диагонали ромба перпендикулярны и делятся пополам, следовательно,
AE = EB = DE = EO и AB ⊥ DO.
Из треугольника AEO вытекает равенство
AE2 = AO2 — EO2
Так как AE = AB/2, EO = DO/2 = r/2, то это равенство дает
AB2/4 = r2 — r2/4 = (3/4)r2, откуда
AB = a3 = r√3 (ЧТД).
Теорема 127. Сторона вписанного квадрата равна радиусу, умноженному на √2.
Дан правильный вписанный четырехугольник или квадрат ABCD (черт. 202).
Требуется доказать, что AB = r√2.
Доказательство. Соединим B с D. Отрезок BD есть диаметр, ибо прямой угол B опирается на концы диаметра.
Из прямоугольного треугольника ABD вытекает равенство
AB2 + AD2 = BD2
Так как AB = AD, BD = 2r, то
2AB2 = 4r2, откуда AB = a4 = r√2 (ЧТД).
Теорема 128. Сторона правильного вписанного десятиугольника равна большей части радиуса, разделенного в крайнем и среднем отношении.
Дано. Положим AB есть сторона правильного вписанного десятиугольника (черт. 203), следовательно, дуга AB = 1/10 окружности и
∠AOB = (4d)/10 = (2/5)d.
Требуется доказать, что AB есть большая часть радиуса среднепропорциональная между целым радиусом и меньшей его частью.

Доказательство. Соединим точки A и B с центром и разделим угол BAO пополам.
∠AOB = (2/5)d
В равенстве ∠BAO + ∠ABO + ∠AOB = 2d
∠BAO = ∠ABO, следовательно, ∠BAO = ∠ABO = (4/5)d.
Так как ∠α = ∠β по построению, то из равенства
∠α + ∠β = (4/5)d следует, что ∠α = ∠β = (2/5)d
Треугольник ABC равнобедренный, ибо
∠α = (2/5)d, ∠B = (4/5)d,
следовательно, из равенства
∠α + ∠B + ∠ACB = 2d имеем:
(2/5)d + (4/5)d + ∠ACB = 2d и ∠ACB = (4/5)d.Таким образом
∠ACB = ∠ABC = (4/5)d
следовательно,
AB = AC
Треугольник ACO тоже равнобедренный, ибо
∠β = (2/5)d и ∠AOB = (2/5)d
следовательно, AC = CO и таким образом AB = AC = CO.
Так как отрезок AC делит угол треугольника пополам, то имеет место пропорция (теорема 98)
AO/AB = OC/CB
Так как AB = OC и AO = OB, то
OB/OC = OC/CB
откуда видно, что OC равно большей части радиуса OB, разделенного в крайнем и среднем отношении.
 Так как OC = AB, то и сторона десятиугольника обладает тем же свойством.
Так как OC = AB, то и сторона десятиугольника обладает тем же свойством.Обозначив ее через a10, а радиус через r, имеем пропорцию
r/a10 = a10/(r — a10)
откуда положительное решение квадратного уравнения, определяющее сторону правильного вписанного десятиугольника, будет:
a10 = ((√5 — 1)/2)r.
Как найти угол в шестиугольнике
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее то информацию, описанную ниже, назначенному ниже агенту. Если репетиторы вуза предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к адвокату.
Выполните следующие действия, чтобы отправить уведомление:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного расположения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т.
 д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении прав, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении прав, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105Или заполните форму ниже:
Шестиугольник
Шестиугольник — это многоугольник с 6 сторонами и 6 углами (шестиугольник означает шесть). На рисунке ниже представлены 3 различных типа шестиугольников.

Шестиугольник — это форма, которая обычно встречается в повседневной жизни.Формы, из которых состоят соты, гайка и болты, — все это примеры реальных объектов в форме шестиугольника.
Классификация шестиугольника
Как и другие многоугольники, шестиугольник можно классифицировать как правильный или неправильный. Если все стороны и внутренние углы шестиугольника равны, это правильный шестиугольник. В противном случае это неправильный шестиугольник.
Правильный шестигранник Неправильный шестигранник Все стороны и внутренние углы равны Не все стороны и углы равны Шестиугольники или другие многоугольники также могут быть классифицированы как выпуклые или вогнутые.Если все внутренние углы шестиугольника или многоугольника меньше 180 °, он выпуклый. Если один или несколько внутренних углов больше 180 °, он вогнутый.
 Правильный шестиугольник — это всегда выпуклый шестиугольник.
Правильный шестиугольник — это всегда выпуклый шестиугольник.Выпуклый шестигранник Вогнутый шестигранник Все внутренние углы <180 ° Один или несколько внутренних углов> 180 ° Диагонали шестигранника
Диагональ — это отрезок прямой, соединяющий две непоследовательные вершины.Из каждой вершины можно провести по три диагонали. Всего для шестиугольника можно нарисовать девять диагоналей. На следующем рисунке показан пример.
Внутренние углы шестигранника
Сумма внутренних углов шестиугольника равна 720 °.
Как показано на рисунке выше, можно нарисовать три диагонали, чтобы разделить шестиугольник на четыре треугольника. Синие линии выше показывают только один способ разделить шестиугольник на треугольники; есть и другие. Сумма внутренних углов четырех треугольников равна сумме внутренних углов шестиугольника.
 Так как сумма внутренних углов треугольника равна 180 °, сумма внутренних углов шестиугольника составляет 4 × 180 ° = 720 °.
Так как сумма внутренних углов треугольника равна 180 °, сумма внутренних углов шестиугольника составляет 4 × 180 ° = 720 °.Шестигранник правильный
Правильный шестиугольник — это шестиугольник, у которого все стороны имеют одинаковую длину и все внутренние углы имеют одинаковую меру.
Углы и стороны правильного шестиугольника
Поскольку каждый из шести внутренних углов в правильном шестиугольнике равны по размеру, каждый внутренний угол составляет 720 ° / 6 = 120 °, как показано ниже.
Каждый внешний угол правильного шестиугольника равен 60 °.
У правильного шестиугольника стороны равны по длине, а противоположные стороны параллельны.
AB = BC = CD = DE = EF = FA и AB // DE, BC // EF, CD // FA
Симметрия правильного шестиугольника
Правильный шестиугольник имеет 6 линий симметрии и вращательную симметрию порядка 6, что означает, что его можно повернуть таким образом, чтобы он 6 раз выглядел так же, как исходная форма на 360 °.

Линии симметрии Вращательная симметрия 6 линий симметрии Шесть углов поворота по 60 ° Площадь правильного шестиугольника
Площадь правильного шестиугольника со стороной s составляет:
От центра правильный шестиугольник можно разделить на шесть равносторонних треугольников, у каждого из которых длина стороны s, как показано ниже.
Площадь T одного из равносторонних треугольников, нарисованных синим цветом, может быть найдена с помощью, где апофема — это высота треугольника. Поскольку имеется шесть равносторонних треугольников, площадь правильного шестиугольника равна.
Пример:
Найдите площадь правильного шестиугольника с длиной стороны 8.
Использование:
Обычный шестиугольник | Справка по геометрии
В этом посте мы более подробно рассмотрим правильный шестиугольник — шестиугольник, все стороны которого равны.
 Мы посмотрим на его углы и найдем формулы для его периметра и площади, используя его сторону или радиус.
Мы посмотрим на его углы и найдем формулы для его периметра и площади, используя его сторону или радиус.Что такое правильный шестиугольник?
Правильный многоугольник — это двумерная выпуклая форма, стороны и внутренние углы которой равны. У правильного шестиугольника шесть равных сторон и шесть равных внутренних углов.
Внутренние углы правильного шестиугольника
Для любого многоугольника сумма внутренних углов равна S = (n-2) • 180 °, где n — количество сторон многоугольника.В шестиугольнике n = 6, поэтому сумма внутренних углов в шестиугольнике составляет (6-2) • 180 ° = 4 • 180 ° = 720 °. И поскольку все внутренние углы правильного шестиугольника равны, каждый из них имеет размер 720 ° / 6 = 120 °. Отсюда мы получаем много других интересных свойств, начиная с показа того, что правильный шестиугольник состоит из 6 равносторонних треугольников.
Правильный шестиугольник состоит из шести равносторонних треугольников
Многие из «доказательств», которые я видел, показывают, что правильный шестиугольник состоит из шести равносторонних треугольников, начинаются с таких вещей, как «Нарисуйте круг, проходящий через вершины правильного шестиугольника.
 «- но они не доказывают, что вы действительно можете нарисовать такой круг (это, конечно, можно, но это довольно сложно).Итак, давайте формально докажем этот интуитивный результат.
«- но они не доказывают, что вы действительно можете нарисовать такой круг (это, конечно, можно, но это довольно сложно).Итак, давайте формально докажем этот интуитивный результат.Нарисуем биссектрисы двух смежных внутренних углов и назовем их точку пересечения O:
. Легко видеть, что ΔOAB равносторонний — m∠BAF = m∠ABC = 120 °, как внутренние углы правильного шестиугольник. Биссектрисы образуют два полуугла размером 60 °: m∠OAB = m∠OBA = 60 °. И из суммы углов в треугольнике, ∠AOB также является углом 60 °, а ΔOAB — равносторонним треугольником.
Теперь давайте соединим O с вершиной C и сравним треугольники ΔOAB и ΔOCB
OB = OB как общую сторону
AB = BC как равные стороны правильного шестиугольника
m∠ABO = m∠CBO = 60 °, как BO. биссектриса угла
ABO≅∠CBO (определение конгруэнтных углов)
Таким образом, ΔOAB и ΔOCB являются конгруэнтными треугольниками согласно постулату стороны-угла-стороны, а ΔOCB — равносторонний треугольник, идентичный ΔOAB. Мы можем продолжить и сделать это для остальных сторон, соединив точку O с вершинами D, E и F, чтобы достичь желаемого результата — шесть одинаковых равносторонних треугольников составляют шестиугольник, все они встречаются в его центре, O.
Мы можем продолжить и сделать это для остальных сторон, соединив точку O с вершинами D, E и F, чтобы достичь желаемого результата — шесть одинаковых равносторонних треугольников составляют шестиугольник, все они встречаются в его центре, O.Площадь и периметр
Поскольку мы показали, что шесть равносторонних треугольников образуют правильный шестиугольник, легко придумать формулу для его площади — она в 6 раз больше площади одного из равносторонних треугольников. Мы показали, как получить формулу площади равностороннего треугольника, исходя из длины его стороны: Площадь ΔРавносторонний = (s 2 * √3) / 4, где s — длина стороны.
[Быстрое напоминание о том, как мы это сделали: если мы возьмем высоту за основание любого из этих треугольников, мы получим прямоугольный треугольник 30 ° -60 ° -90 ° с гипотенузой, равной s, катет, равный к s / 2, а другой катет равен s / 2 · √3. Площадь такого треугольника равна (ножка · ножка) / 2 или (s / 2 · s / 2 · √3) / 2.
 Два одинаковых треугольника 30-60-90 составляют равносторонний треугольник, поэтому его площадь равна 2 * (s / 2 * s / 2 · √3) / 2 = (s 2 * √3) / 4]
Два одинаковых треугольника 30-60-90 составляют равносторонний треугольник, поэтому его площадь равна 2 * (s / 2 * s / 2 · √3) / 2 = (s 2 * √3) / 4]Итак Площадь ⬡hex = 6 • (s 2 * √3) / 4 = 3 • √3 • s 2 /2.
Периметр любого многоугольника — это просто сумма его сторон. В правильном шестиугольнике все стороны равны, поэтому P ⬡hex = 6s.
Радиус
Радиус правильного многоугольника — это расстояние от его центра до любой из его вершин. По симметрии это расстояние одинаково для всех вершин. Итак, что это за радиус в правильном шестиугольнике? Мы уже видели, что центр правильного шестиугольника образует равносторонний треугольник со сторонами, поэтому его радиус (R) равен длине каждой из сторон.Это также показывает, что мы можем вписать правильный шестиугольник в круг с радиусом R
Шестиугольник
Шестиугольник
Геометрия — один из важнейших разделов математики, поскольку он занимается изучением различных форм, их размеров и их расчетами. В этом исследовании мы рассматриваем формы, образованные прямыми линиями, и формы с изогнутыми поверхностями. Двумерные фигуры с плоскими гранями, с прямыми линиями в качестве ребер и замкнутыми фигурами известны как многоугольники.Семейство многоугольников — это семейство, состоящее из разных форм с разным количеством сторон. Слово «поли» означает «много», а «гон» означает «угол». В зависимости от количества сторон многоугольника мы классифицируем их по следующим категориям. Например, многоугольники с 3 сторонами известны как треугольники, многоугольники с 4 сторонами известны как четырехугольники (прямоугольники, квадраты и т. Д.), А многоугольники с 5 сторонами известны как пятиугольники и так далее.
В этом исследовании мы рассматриваем формы, образованные прямыми линиями, и формы с изогнутыми поверхностями. Двумерные фигуры с плоскими гранями, с прямыми линиями в качестве ребер и замкнутыми фигурами известны как многоугольники.Семейство многоугольников — это семейство, состоящее из разных форм с разным количеством сторон. Слово «поли» означает «много», а «гон» означает «угол». В зависимости от количества сторон многоугольника мы классифицируем их по следующим категориям. Например, многоугольники с 3 сторонами известны как треугольники, многоугольники с 4 сторонами известны как четырехугольники (прямоугольники, квадраты и т. Д.), А многоугольники с 5 сторонами известны как пятиугольники и так далее.
Многоугольник, у которого 6 сторон, известен как шестиугольник. Слово «гекса» означает «шесть», а «гон» означает «угол».Поскольку у многоугольника 6 сторон, которые, следовательно, образуют 6 углов, он известен как шестиугольник.
Шестиугольник Определение:
Многоугольник, у которого 6 сторон (или ребер) и 6 углов, называется шестиугольником. Как показано на рисунке слева, шестиугольники имеют 6 вершин (или углов), 6 ребер (или сторон) и 6 углов.
Как показано на рисунке слева, шестиугольники имеют 6 вершин (или углов), 6 ребер (или сторон) и 6 углов.
Типы шестиугольников:
На основании размеров сторон шестиугольники подразделяются на 2 типа: правильные шестиугольники и неправильные шестиугольники.
1) Правильные шестиугольники: Шестиугольник, у которого все 6 сторон равны по размеру, известен как правильный шестиугольник. Поскольку у него 6 равных сторон, 6 внутренних углов шестиугольника также равны.
Недвижимость:
а) У правильного шестиугольника 6 равных сторон и 6 равных внутренних углов.
б) Поскольку у шестиугольника четное число сторон, значит, противоположные стороны правильного шестиугольника параллельны друг другу.
c) Линия, проведенная от центра правильного шестиугольника к любой из вершин, будет иметь ту же длину, что и длина стороны, как показано на рисунке ниже.
г) Все правильные шестиугольники выпуклые, что означает, что все его 6 вершин направлены наружу.
e) Отрезок, соединяющий любые две несмежные вершины многоугольника, называется «диагональю». Диагонали правильного шестиугольника делят шестиугольник на 6 равносторонних треугольников, как показано на рисунке справа.
2) Неправильный шестиугольник: Неправильный шестиугольник известен как неправильный шестиугольник. Это означает, что неправильный шестиугольник имеет 6 сторон, которые не все равны по размеру, или 6 внутренних углов, которые все не равны по мере.
Недвижимость:
а) Неправильные шестиугольники не имеют 6 равных сторон или 6 равных внутренних углов.
б) Противоположные стороны могут быть или не быть параллельны друг другу.
c) Неправильный шестиугольник может быть выпуклым или вогнутым. Выпуклый многоугольник — это многоугольник, все вершины которого направлены наружу. Но в вогнутом многоугольнике одна или несколько вершин указывают внутрь к центру многоугольника. По этой причине в вогнутом многоугольнике один или несколько внутренних углов больше 180 °.
г) Линия, проведенная через вогнутый шестиугольник (в зависимости от того, где проводится линия) может пересекать шестиугольник более чем в 2 точках. На рисунке ниже показана линия, пересекающая шестиугольник в 4 точках.
д) В вогнутом шестиугольнике не вся диагональ находится внутри шестиугольника. Одна или несколько диагоналей также лежат вне шестиугольника, как показано на рисунке ниже.
Углы шестиугольника:
1) Сумма всех внутренних углов правильного шестиугольника:
Сумма всех внутренних углов любого правильного многоугольника может быть вычислена по формуле, приведенной ниже:
Если правильный многоугольник имеет n сторон, то сумма всех его внутренних углов, S = (n — 2) * 180 °
Поскольку у шестиугольника 6 сторон, следовательно, n = 6.
Теперь Sum, S = (6-2) * 180 ° = 720 °
Следовательно, Сумма всех внутренних углов правильного шестиугольника, S = 720 °
2) Каждый внутренний угол правильного шестиугольника:
Измерение каждого внутреннего угла любого правильного многоугольника можно рассчитать по формуле, приведенной ниже:
Если правильный многоугольник имеет n сторон, то каждый внутренний угол = (n — 2) / n * 180 °
Так как шестиугольник имеет 6 сторон, то n = 6.
Итак, каждый внутренний угол = (6-2) / 6 * 180 ° = 120 °
Следовательно, каждый внутренний угол правильного шестиугольника = 120 °
3) Каждый внешний угол правильного шестиугольника:
Меру каждого внешнего угла любого правильного многоугольника можно рассчитать по формуле, приведенной ниже:
Если правильный многоугольник имеет n сторон, то Каждый внешний угол = 360 ° / n
Каждый внешний угол правильного выпуклого шестиугольника = 360 ° / 6 = 60 °
Следовательно, каждый внешний угол правильного шестиугольника = 60 °4) Диагонали шестиугольника:
Количество диагоналей в многоугольник с ‘n’ сторонами = n * (n — 3) / 2
Поскольку шестиугольник имеет 6 сторон, следовательно, n = 6.
Следовательно, количество диагоналей в шестиугольнике = 6 * (6 — 3) / 2 = 902 · 10 9 диагоналей.
Периметр шестиугольника:
Периметр — это общая длина, вычисленная при объединении всех длин сторон многоугольника. Периметр правильного или неправильного многоугольника можно рассчитать, сложив все стороны многоугольника. Периметр многоугольника = сумма длин всех его сторон.
Следовательно, периметр правильного шестиугольника с длиной стороны s (как показано на рисунке справа) будет записан как P = s + s + s + s + s + s = 6s
Пример: Вычислите периметр правильного шестиугольника с длиной стороны 7 м.
Периметр правильного шестиугольника, P = 6 * s ==> Периметр, P = 6 * 7 м = 42 мПример: вычислить периметр шестиугольника, показанного под .
Учитывая длины сторон шестиугольника на рисунке.
Периметр шестиугольника = Сумма всех длин сторон.
Следовательно, периметр, P = 4 м + 7 м + 3 м + 2 м + 8 м + 2 м = 26 мПлощадь шестиугольника:
Площадь любого многоугольника — это пространство, занимаемое в границах или краях многоугольника. Следовательно, площадь шестиугольника — это пространство, охватываемое его краями или сторонами. Площадь правильного шестиугольника отличается от площади неправильного шестиугольника. Для расчета его площади можно использовать различные процедуры. Давайте посмотрим на общие методы, используемые в процессе.
Следовательно, площадь шестиугольника — это пространство, охватываемое его краями или сторонами. Площадь правильного шестиугольника отличается от площади неправильного шестиугольника. Для расчета его площади можно использовать различные процедуры. Давайте посмотрим на общие методы, используемые в процессе.
1) Площадь правильного шестиугольника:
Как упоминалось выше, диагональ правильного шестиугольника делит шестиугольник на 6 равных треугольников, также известных как 6 равносторонних треугольников. Итак, если мы найдем площадь одного равностороннего треугольника, тогда будут известны площади всех 6 треугольников, а затем площадь шестиугольника будет складываться из площадей треугольника.
Дан правильный шестиугольник, как показано на рисунке выше, где точка «C» — центр шестиугольника.
Треугольник CPQ - это равносторонний треугольник, поскольку все углы внутри треугольника CPQ равны 60 ° (половина внутреннего угла 120 °). Следовательно, все его стороны также равны.
Следовательно, все его стороны также равны.
Следовательно, пусть длины сторон CP = PQ = CQ = s
CM — перпендикуляр, проведенный к стороне PQ. Пусть CM = h
Поскольку «M» становится средней точкой стороны PQ, следовательно, MQ = s / 2 (половина длины стороны PQ).
Теперь в треугольнике CMQ мы можем применить теорему Пифагора, чтобы получить взаимосвязь между высотой треугольника h и длиной стороны s.
Следовательно, h 2 + (s / 2) 2 = s 2 . Отсюда следует h 2 + s 2 /4 = s 2 . Это дает h 2 = s 2 — s 2 /4
Итак, h 2 = 3s 2 /4 ==> h = √ (3s 2 /4). Следовательно, высота треугольника CPQ, h = s * √3 / 2
Теперь площадь треугольника CPQ = 1/2 * основание * высота.
Это означает, что Область A = 1/2 * s * h ==> A = 1/2 * s * (s * √3 / 2) ==> A = s 2 * √3 / 4
Следовательно, Площадь треугольника CPQ = s 2 * √3 / 4.
Теперь правильный шестиугольник состоит из 6 таких равносторонних равносторонних треугольников.
Следовательно, площадь правильного шестиугольника = 6 * с 2 * √3 / 4, что может быть дополнительно упрощено как:
Площадь правильного шестиугольника = 3/2 * с 2 * √3
Пример 1: Какова площадь правильного шестиугольника с длиной стороны 5 м?
Учитывая, что длина стороны s = 5м
Площадь правильного шестиугольника, A = 3/2 * s 2 * √3
Следовательно, Площадь = 3/2 * 5 2 * √3 = √3, что равно 64.95м 2 (приблизительно)
2) Площадь неправильного шестиугольника:
Поскольку неправильный шестиугольник не имеет равных сторон или равных углов, мы не можем использовать метод или формулу правильного шестиугольника. Площадь неправильного шестиугольника можно вычислить с помощью различных методов. Давайте посмотрим на пример ниже:
Пример: Найдите площадь неправильного шестиугольника, показанного на рисунке ниже.
На данном рисунке мы видим, что указаны длины сторон и длины диагоналей.
Мы видим, что неправильный шестиугольник разделен на 4 треугольника A, B, C и D.
Поскольку длины сторон каждого треугольника указаны, мы можем использовать формулу Герона.
Формула Герона:
Если треугольник имеет длину сторон как ‘a’, ‘b’ и ‘c’, то s = (a + b + c) / 2
Тогда Площадь треугольника = √ [с * (са) * (сбн) * (сбн)]
Треугольник A:
s = (5 + 4 + 7) / 2 ==> s = 8
Теперь Площадь треугольника A = √ [s (s-a) (s-b) (s-c)] = √ [(8 * (8-5) * (8-4) * (8-7)]
Площадь треугольника A = √ (8 * 3 * 4 * 1) = 9.8м 2
Треугольник B:
s = (7 + 7 + 6) / 2 = 10
Площадь треугольника B = √ [(10 * (10 — 7) * (10 — 7) * (10 — 6)] = √ (10 * 3 * 3 * 4) = 18,9 м 2
Аналогично, используя формулу Герона, как показано выше, мы также получаем площади треугольников C и D.
Площадь треугольника C = 8,9 м 2 и площадь треугольника D = 7,9 м 2
Итак, площадь неправильного шестиугольника = площадь треугольника A + площадь треугольника B + площадь треугольника C + площадь треугольника D
. Площадь шестиугольника = 9.8 м 2 + 18,9 м 2 + 8,9 м 2 + 7,9 м 2 = 45,5 м 2 Шестиугольная мозаика: Когда плоская поверхность или плоскость покрыта формами, которые повторяются снова и снова, образуя периодический узор без каких-либо промежутков или перекрытий, это называется тесселяцией. Мы можем найти различные виды мозаики, такие как мозаика треугольников, квадратов, прямоугольников и т. Д. Регулярные многоугольники, которые конгруэнтны (то есть одинаковой формы и размера), образуют мозаику, известную как Обычная мозаика.Есть только 3 типа регулярных мозаик, и они состоят из треугольников, квадратов и шестиугольников.
Гексагональная мозаика — это мозаика, образованная, когда шестиугольники расположены на плоскости, как показано на рисунке ниже. Этот шаблон для регулярной шестиугольной мозаики идентичен. На рисунке ниже мы видим отмеченную вершину. В каждой вершине мы видим, что встречаются 3 шестиугольника. Так как каждый шестиугольник имеет 6 сторон, этот вид мозаики называется 6.6.6 Тесселяция.Шестиугольная призма:
Шестиугольная призма — это трехмерная фигура, состоящая из двух шестиугольных оснований и шести прямоугольных граней. Шестиугольная призма состоит из 8 граней, 18 ребер и 12 вершин. Из-за своих 8 граней он также известен как «Октаэдр».
Площадь поверхности правильной шестиугольной призмы:
Как показано на рисунке ниже, шестиугольная призма имеет 2 шестиугольных основания и 6 прямоугольных граней.
Боковая площадь шестиугольной призмы представляет собой сумму площадей шести прямоугольных граней.
Если высота призмы равна «h», а сторона правильного шестиугольника основания равна «s», то:
Площадь каждой прямоугольной грани = s * h
Боковая площадь = сумма площадей 6 прямоугольных граней
Следовательно, Боковая площадь = 6 * s * h
Площадь поверхности призмы = Площадь основания + боковая площадь
Перпендикуляр от центра шестиугольника к его основной стороне также известен как «Апофема» (обозначена буквой «d» на рисунке ниже).
Если длина стороны основания равна «s», то, как упомянуто выше, апофема или высота шестиугольника составляет s * √3 / 2
Тогда площадь шестиугольника = 3 * s * d = 3 * s * √3 / 2 * s = 3/2 * √3 * s 2
Так как таких базовых шестиугольников 2, следовательно, площадь основания = 2 * 3/2 * √3 * s 2 = 3√3 * s 2
Площадь поверхности = Площадь основания + Боковая площадь
Следовательно, площадь поверхности правильной шестиугольной призмы = (3√3 * s 2 ) + (6 * s * h)
( Где s — длина стороны основного правильного шестиугольника, а h ‘- высота призмы).
Пример: Какова площадь поверхности правильной шестиугольной призмы, если заданная длина стороны основного правильного шестиугольника составляет 4 дюйма, а высота призмы — 6 дюймов?
Учитывая, что длина стороны основания правильного шестиугольника, s = 4 дюйма
Высота призмы, h = 6 дюймов
Площадь поверхности правильной шестиугольной призмы = (3√3 * s 2 ) + (6 * s * h)
Следовательно, площадь поверхности = (3√3 * 4 2 ) + (6 * 4 * 6) = 48√3 + 144 = 227 квадратных дюймов (прибл. )
)
Объем шестиугольной призмы:
Объем призмы — это объем пространства, занимаемого в границах или краях призмы.
Объем шестиугольной призмы = площадь основания * высота призмы
Следовательно, Объем шестигранной призмы = 3/2 * √3 * s 2 * h
Пример: Рассчитайте объем шестиугольной призмы, длина стороны основания которой составляет 4 дюйма, а высота призмы — 6 дюймов. .
Учитывая, что длина стороны основания правильного шестиугольника, s = 4 дюйма
Высота призмы, h = 6 дюймов
Объем гексагональной призмы = 3/2 * √3 * с 2 * ч
Следовательно, Объем = 3/2 * √3 * 4 2 * 6 = 249.4 кубических дюйма.Внутренние углы многоугольника
Быстрые определения
Давайте пройдемся по нескольким ключевым словам, чтобы мы все оказались на одной странице. Помните, что многоугольник — это двухмерная форма, стороны которой нарисованы прямыми линиями (без кривых), которые вместе образуют замкнутую область.
 Каждая точка многоугольника, где встречаются две стороны, называется вершиной . В каждой вершине есть внутренний угол многоугольника. Квадрат, например, имеет четыре внутренних угла по 90 градусов каждый.Если квадрат представлял ваш класс, внутренние углы — это четыре угла комнаты.
Каждая точка многоугольника, где встречаются две стороны, называется вершиной . В каждой вершине есть внутренний угол многоугольника. Квадрат, например, имеет четыре внутренних угла по 90 градусов каждый.Если квадрат представлял ваш класс, внутренние углы — это четыре угла комнаты.Сумма внутренних углов
В целях дальнейшего расширения, если многоугольник имеет x сторон, сумма S мер степени этих x внутренних сторон определяется формулой S = (x — 2) (180) .
Например, у треугольника 3 угла, которые в сумме составляют 180 градусов. У квадрата 4 угла, которые в сумме составляют 360 градусов. Для каждой дополнительной стороны, которую вы добавляете, вы должны добавить еще 180 градусов к общей сумме.
{include ad_line.html%}Давайте поговорим о диагонали минутку. Что вообще такое диагональю ? Диагональ — это отрезок прямой, соединяющий две непоследовательных вершины многоугольника.
 Это все линии между точками многоугольника, если не считать те, которые также являются сторонами многоугольника. На картинке ниже BD — это диагональ. Как видите, отрезок BD делит четырехугольник ABCD на два треугольника. Сумма углов в этих треугольниках (180 + 180 = 360) равна сумме всех углов прямоугольника (360).
Это все линии между точками многоугольника, если не считать те, которые также являются сторонами многоугольника. На картинке ниже BD — это диагональ. Как видите, отрезок BD делит четырехугольник ABCD на два треугольника. Сумма углов в этих треугольниках (180 + 180 = 360) равна сумме всех углов прямоугольника (360).Пример 1
Четырехугольник ABCD, конечно, имеет четыре угла. Эти четыре угла находятся в соотношении 2: 3: 3: 4. Найдите градус наибольшего угла четырехугольника ABCD.
Что мы знаем?
У нас есть четыре неизвестных угла, но есть информация об их отношении друг к другу. Поскольку мы знаем, что сумма всех четырех углов должна составлять 360 градусов, нам просто нужно выражение, которое складывает наши четыре неизвестных угла и устанавливает их равными 360.Поскольку они находятся в соотношении, у них должен быть некий общий фактор, который нам нужно найти, называемый x.
Шагов:
- Добавьте условия 2x + 3x + 3x + 4x
- Приравнять сумму членов к 360
- Решить относительно x
- Определите угол в градусах.

Решить
2x + 3x + 3x + 4x = 360
12x = 360
x = 360/12
x = 30Несмотря на то, что мы знаем x = 30, мы еще не закончили. Умножаем 30 на 4, чтобы найти наибольший угол.Поскольку 30 умножить на 4 = 120, наибольший угол составляет 120 градусов. Аналогично, другие углы равны 3 * 30 = 90, 3 * 30 = 90 и 2 * 30 = 60.
Правильные многоугольники
Правильный многоугольник равносторонний. Все его углы имеют одинаковую меру. Он тоже равносторонний. Все его стороны имеют одинаковую длину. Квадрат — это правильный многоугольник, и хотя квадрат представляет собой тип прямоугольника, прямоугольники, которые составляют , а не квадратов, не будут правильными многоугольниками.
Пример 2
Найдите сумму углов шестиугольника в градусах.Предполагая, что шестиугольник — , правильный , найдите градус каждого внутреннего угла.
Что мы знаем?
Мы можем использовать формулу S = (x — 2) (180) для суммирования степени любого многоугольника.

У шестиугольника 6 сторон, поэтому x = 6.
Решить
Пусть x = 6 в формуле и упростит:
S = (6-2) (180)
S = 4 (180)
S = 720Правильный многоугольник — это равноугольный , что означает, что все углы имеют одинаковую величину.В случае правильного шестиугольника сумма в 720 градусов будет равномерно распределена между шестью сторонами.
Итак, 720/6 = 120. В правильном шестиугольнике шесть углов, каждый по 120 градусов.
Пример 3
Если сумма углов многоугольника равна 3600 градусам, найдите количество сторон многоугольника.
Обращение формулы
Опять же, мы можем использовать формулу S = (x — 2) (180), но на этот раз мы решаем для x вместо S. Ничего страшного!
Решить
В этой задаче положим S = 3600 и решим относительно x.
3600 = (x — 2) (180)
3600 = 180x — 360
3600 + 360 = 180x
3960 = 180x
3960/180 = x
22 = xМногоугольник с 22 сторонами имеет 22 угла, сумма которых равна 3600 градусам.

Внешние углы многоугольника
В каждой вершине многоугольника может быть образован внешний угол путем удлинения одной стороны многоугольника так, что внутренний и внешний углы в этой вершине являются дополнительными (в сумме 180). На рисунке ниже углы a, b, c и d являются внешними, а сумма их градусов равна 360.
Если правильный многоугольник имеет x сторон, то каждый внешний угол равен 360, деленному на x.
Давайте рассмотрим два типовых вопроса.
Пример 4
Найдите градус каждого внутреннего и внешнего угла правильного шестиугольника.
Помните, что формула суммы внутренних углов S = (x-2) * 180. У шестиугольника 6 сторон. Поскольку x = 6, сумму S можно найти, используя S = (x — 2) (180)
S = (10-6) (180)
S = 4 (180)
S = 720В шестиугольнике шесть углов, а в правильном шестиугольнике все они равны.Каждый составляет 720/6 или 120 градусов. Теперь мы знаем, что внутренние и внешние углы равны дополнительным (в сумме 180) в каждой вершине, поэтому размер каждого внешнего угла составляет 180 — 120 = 60.

Пример 5
Если размер каждого внутреннего угла правильного многоугольника равен 150, найдите количество сторон многоугольника.
Ранее мы определили количество сторон многоугольника, взяв сумму углов и используя формулу S = (x-2) * 180 для решения. Но на этот раз мы знаем только размер каждого внутреннего угла.Нам пришлось бы умножить на количество углов, чтобы найти сумму … но вся проблема в том, что мы еще не знаем количество сторон ИЛИ сумму!
Но, поскольку размер каждого внутреннего угла равен 150, мы, , также знаем, что размер внешнего угла, проведенного в любой вершине в терминах этого многоугольника, равен 180 — 150 = 30. Это потому, что они образуют дополнительные пары (внутренний + внешний = 180).
До примера 4 мы узнали, что мы можем также вычислить величину внешнего угла в правильном многоугольнике как 360 / x, где x — количество сторон.Теперь у нас есть способ найти ответ!
30 = 360 / x
30x = 360
x = 360/30
x = 12Наш многоугольник с внутренними углами 150 градусов (и внешними 30 градусами) имеет 12 сторон.

Кстати, геометрическая фигура с 12 сторонами называется двенадцатиугольником.
Урок, проводимый г-ном Фелизом
Иллюстративная математика
Задача
Типичный образец плитки с шестиугольниками показан ниже:
- Правильный шестиугольник — это шестиугольник с равными 6 $ сторонами и 6 $ конгруэнтными. внутренние углы.Найдите размеры внутренних углов правильного шестиугольника.
- Покажите, что можно расположить три правильных шестиугольника одинакового размера с общей вершиной. в конфигурации на картинке выше.
- Покажите, что один правильный шестиугольник можно окружить шестью правильными шестиугольниками. без пробелов и перекрытий, как на картинке ниже:
IM Комментарий
Образцы плитки будут знакомы учащимся как по работе с геометрическими плитками, так и по множеству плиток, с которыми они сталкиваются в мире.Здесь подробно исследуется один из наиболее важных примеров мозаики с правильными шестиугольниками.
 Это дает ученикам возможность использовать то, что они знают о сумме углов в треугольнике, а также о сумме углов, которые составляют
линия. Если доступны шестиугольные и равносторонние треугольные плитки, учитель может захотеть использовать их, чтобы помочь ученикам визуализировать.
Это дает ученикам возможность использовать то, что они знают о сумме углов в треугольнике, а также о сумме углов, которые составляют
линия. Если доступны шестиугольные и равносторонние треугольные плитки, учитель может захотеть использовать их, чтобы помочь ученикам визуализировать.Узор из правильных шестиугольников одинакового размера, соединяющихся вместе, самолет знаком не только по кафелю, но и в природе:
- молекулярная структура графена (тонкий «лист» графита в один атом) состоит из атомов углерода, расположенных в вершинах правильных шестиугольников,
- модели конвекции для тонких слоев нагретых жидкостей,
- Ульи часто строят по этой схеме из шестиугольников.
Эта задача идеально подходит для целей обучения, когда студенты могут не торопиться и разработать несколько стандартов математической практики, поскольку математическое содержание напрямую связано с содержанием стандарта 8.G.5, касающегося сумм углов в, но несколько превосходит его.
 \ circ $.\ circ $ » поворот »
— угол $ PBC $.
\ circ $.\ circ $ » поворот »
— угол $ PBC $. На рисунке ниже изображен второй шестиугольник, примыкающий к первому:
Мы знаем это $$ м (\ угол BCD) + м (\ угол BCF) + м (\ угол DCF) = 360. $$ Поскольку $ m (\ angle BCF) = m (\ angle DCF) = 120 $ из части (a), мы заключаем что $ m (\ angle BCD) = 120 $. Это означает, из части (а), что угол $ BCD $ образует внутренний угол правильного шестиугольника, совпадающего с двумя шестиугольниками изображено в части (а). Другими словами, третий шестиугольник можно разместить как в изображение:
Метод части (b) необходимо применить еще четыре раза, вставив новый шестиугольник в каждом открытом пространстве, одна сторона которого выходит из центрального шестиугольника и одна сторона выходит из одного из соседних шестиугольников.\ circ $.
Угловая сумма полигонов
Когда вы начинаете с многоугольника с четырьмя или более сторонами и рисуете все возможные диагонали из одной вершины, многоугольник затем делится на несколько неперекрывающихся треугольников.
 Рисунок иллюстрирует это деление с помощью семиугольника. Сумма внутренних углов этого многоугольника теперь может быть найдена путем умножения количества треугольников на 180 °. При исследовании обнаруживается, что количество треугольников всегда на два меньше, чем количество сторон.Этот факт утверждается в виде теоремы.
Рисунок иллюстрирует это деление с помощью семиугольника. Сумма внутренних углов этого многоугольника теперь может быть найдена путем умножения количества треугольников на 180 °. При исследовании обнаруживается, что количество треугольников всегда на два меньше, чем количество сторон.Этот факт утверждается в виде теоремы.Рис. 1 Триангуляция семистороннего многоугольника для определения суммы внутренних углов.
Теорема 39: Если у выпуклого многоугольника n сторон, то сумма его внутренних углов определяется следующим уравнением: S = ( n −2) × 180 °.
Многоугольник на рисунке 1 имеет семь сторон, поэтому, используя теорему , дает:
Внешний угол многоугольника образуется продолжением только одной из его сторон.Непрямым углом, примыкающим к внутреннему углу, является внешний угол. Рисунок может предложить следующую теорему:
Рисунок 2 (Непрямые) внешние углы многоугольника.

Теорема 40: Если многоугольник выпуклый, то сумма степеней внешних углов, по одному в каждой вершине, равна 360 °.
Пример 1: Найдите сумму внутренних углов десятиугольника.
У десятиугольника 10 сторон, поэтому:
Пример 2: Найдите сумму внешних углов, по одному внешнему углу в каждой вершине, выпуклого шестиугольника.
Сумма внешних углов любого выпуклого многоугольника равна 360 °.
Пример 3: Найдите размер каждого внутреннего угла правильного шестиугольника (рисунок 3).
Рисунок 3 Внутренний угол правильного шестиугольника.
Метод 1: Поскольку многоугольник правильный, все внутренние углы равны, поэтому вам нужно только найти сумму внутренних углов и разделить их на количество углов.
Есть шесть углов, поэтому 720 ÷ 6 = 120 °.
Каждый внутренний угол правильного шестиугольника имеет размер 120 °.


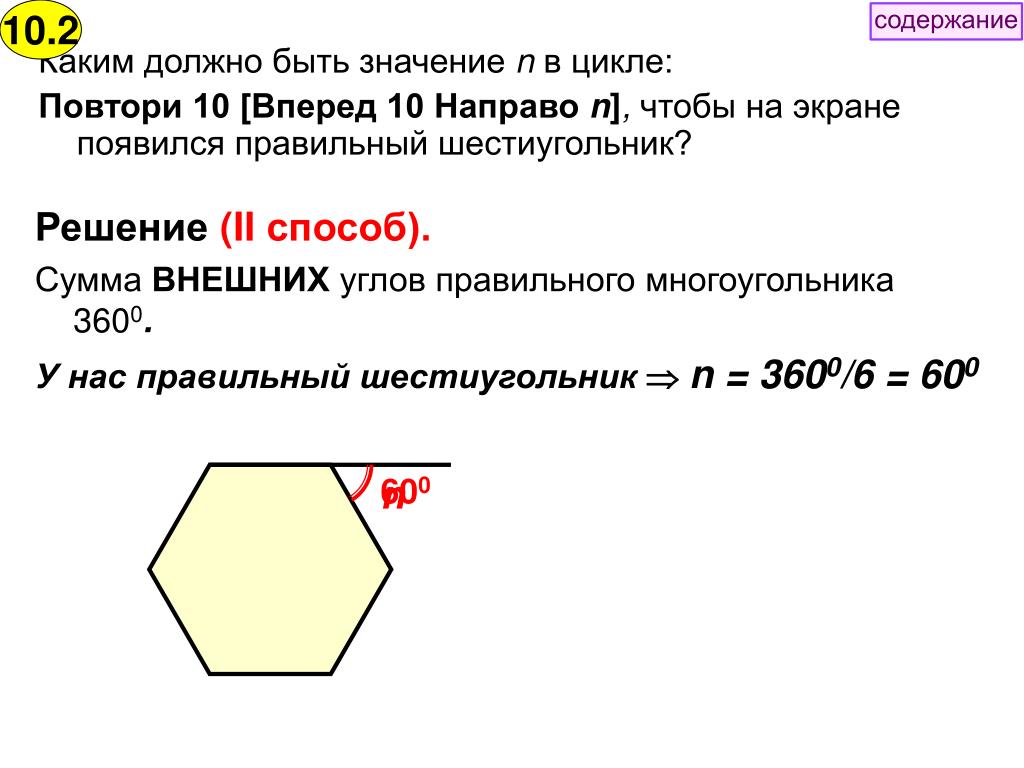
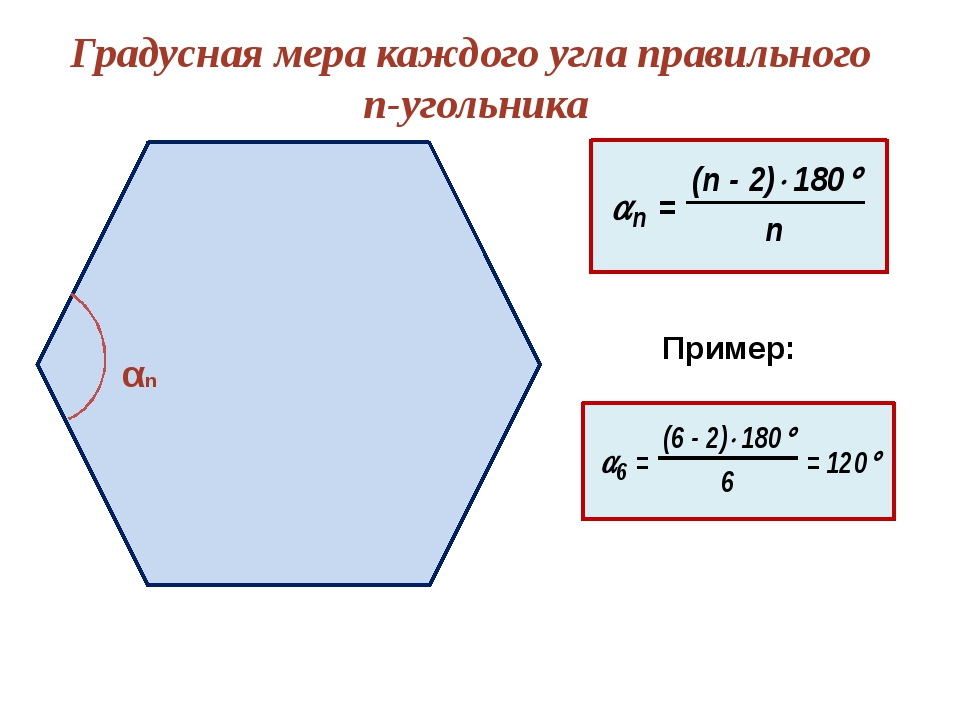
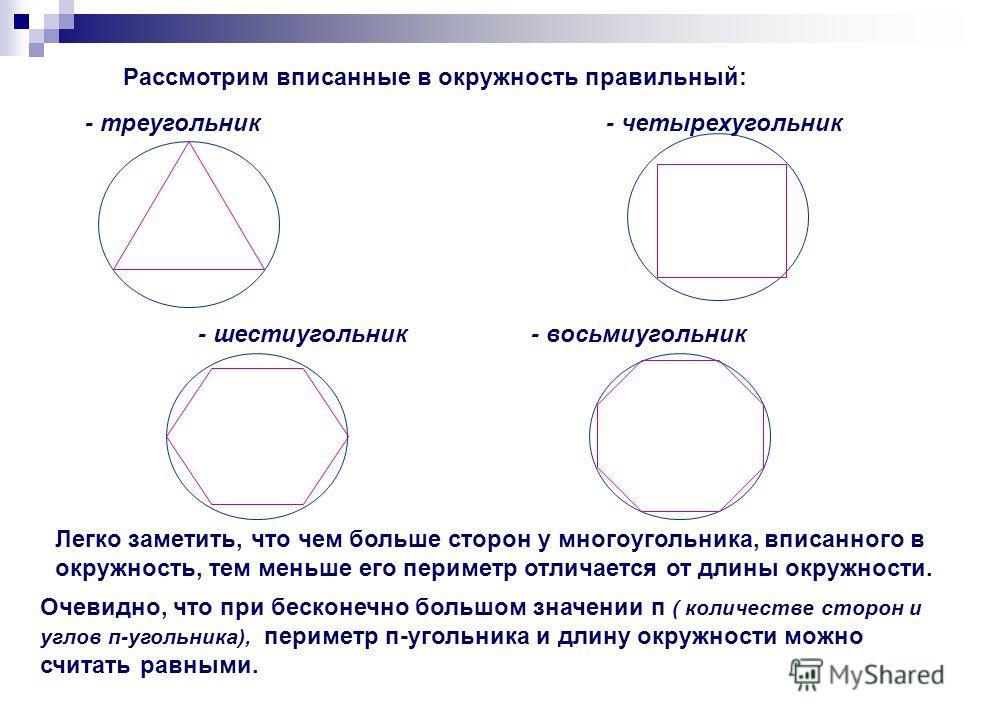 circ) :
circ) : circ)
circ)
 Для решения задач требуются еще площадь и периметр, это S и P соответственно. В правильный шестиугольник бывает вписана окружность или описана около него. Тогда вводятся значения для их радиусов. Обозначаются они соответственно буквами r и R.
Для решения задач требуются еще площадь и периметр, это S и P соответственно. В правильный шестиугольник бывает вписана окружность или описана около него. Тогда вводятся значения для их радиусов. Обозначаются они соответственно буквами r и R.
 Эта задача требует использования двух из указанных формул. Причем их необходимо применять, даже не видоизменяя, просто подставить значение стороны и вычислить.
Эта задача требует использования двух из указанных формул. Причем их необходимо применять, даже не видоизменяя, просто подставить значение стороны и вычислить. Центры этих окружностей совпадают.
Центры этих окружностей совпадают. Найдите его периметр.
Найдите его периметр.
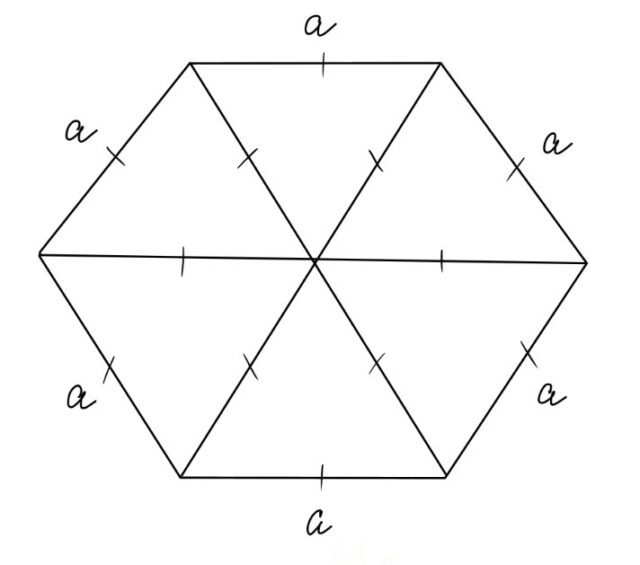

 Найдите расстояние между точками B и E.
Найдите расстояние между точками B и E. Известно, что радиус окружности, описанной вокруг правильного шестиугольника равен его стороне.
Известно, что радиус окружности, описанной вокруг правильного шестиугольника равен его стороне. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 10. Найдите угол AC1C. Ответ дайте в градусах.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 10. Найдите угол AC1C. Ответ дайте в градусах. Найдите расстояние между точками В и Е.
Найдите расстояние между точками В и Е.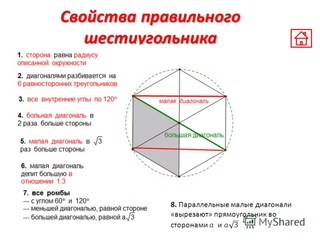 Обязательно будем их рассматривать, не пропустите! Успехов вам!
Обязательно будем их рассматривать, не пропустите! Успехов вам!
 Так, граней или сторон мы получаем 8 (два основания и шесть боковых параллелограммов), число вершин составляет 12 (по 6 вершин для каждого основания), количество ребер шестиугольной призмы равно 18 (шесть боковых и 12 для оснований).
Так, граней или сторон мы получаем 8 (два основания и шесть боковых параллелограммов), число вершин составляет 12 (по 6 вершин для каждого основания), количество ребер шестиугольной призмы равно 18 (шесть боковых и 12 для оснований).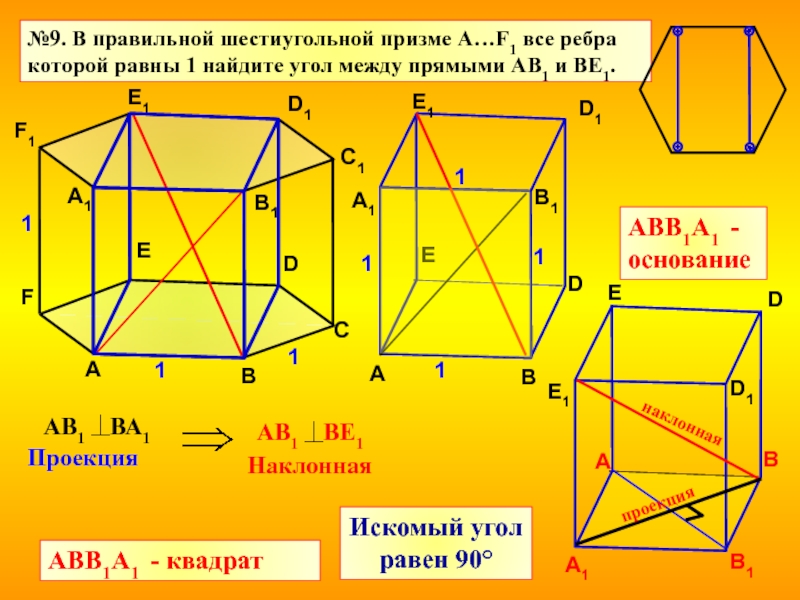 Вычислить их легко, используя всем известную теорему Пифагора. Обозначим символом a длину стороны шестиугольника, символом b – длину бокового ребра. Тогда диагональ имеет длину:
Вычислить их легко, используя всем известную теорему Пифагора. Обозначим символом a длину стороны шестиугольника, символом b – длину бокового ребра. Тогда диагональ имеет длину:
 Для этого следует лишь умножить площадь одного основания (шестиугольника) на высоту фигуры, длина которой равна длине бокового ребра. Получаем формулу:
Для этого следует лишь умножить площадь одного основания (шестиугольника) на высоту фигуры, длина которой равна длине бокового ребра. Получаем формулу: Невыпуклыми являются все остальные многоугольники.
Невыпуклыми являются все остальные многоугольники.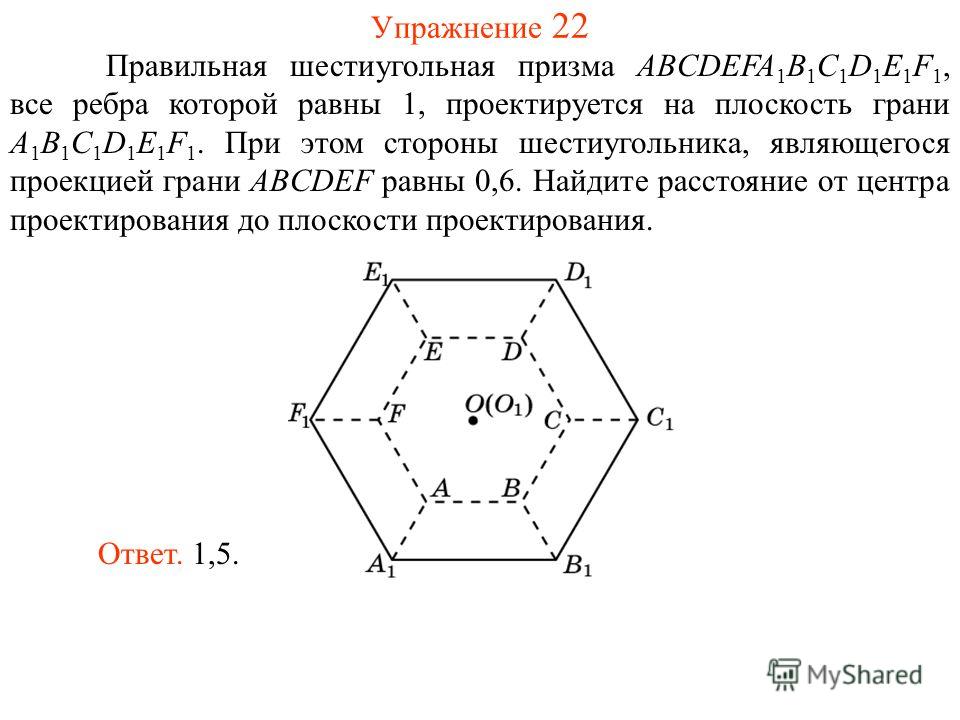
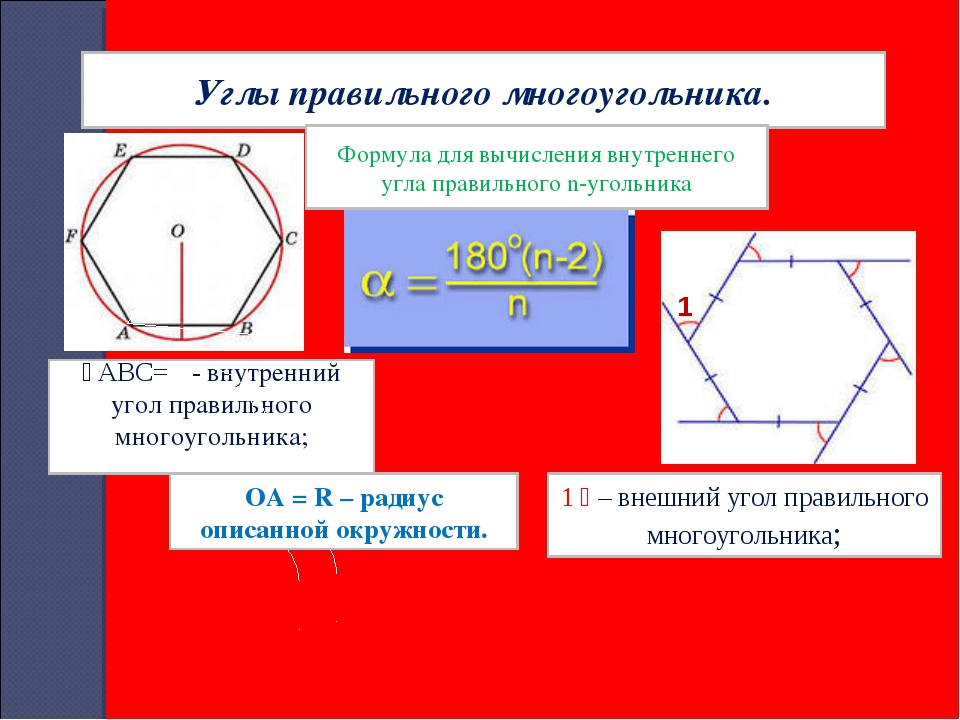
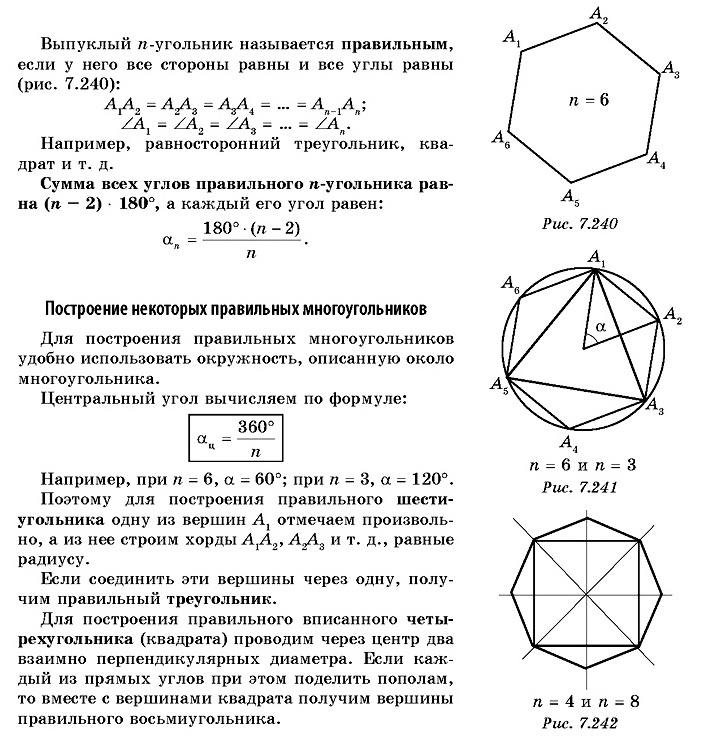 Работать таким ключом приходиться, используя рычаг (вороток) который вставляется в сквозное отверстие в корпусе ключа.
Работать таким ключом приходиться, используя рычаг (вороток) который вставляется в сквозное отверстие в корпусе ключа. Количество диагоналей правильного шестиугольника равно 9.
Количество диагоналей правильного шестиугольника равно 9.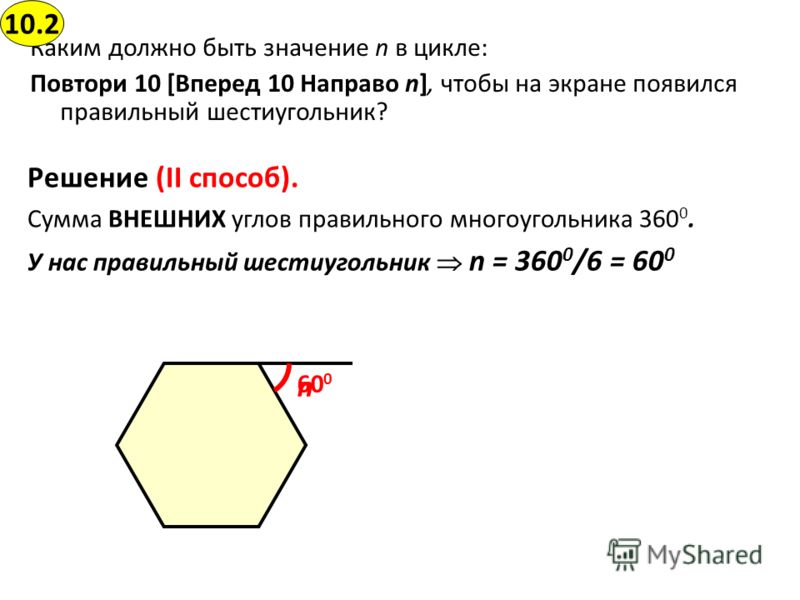
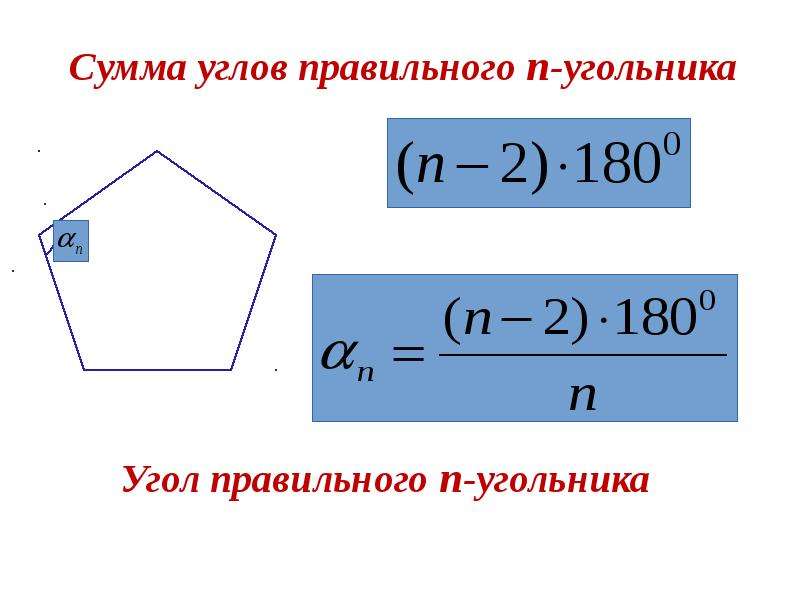

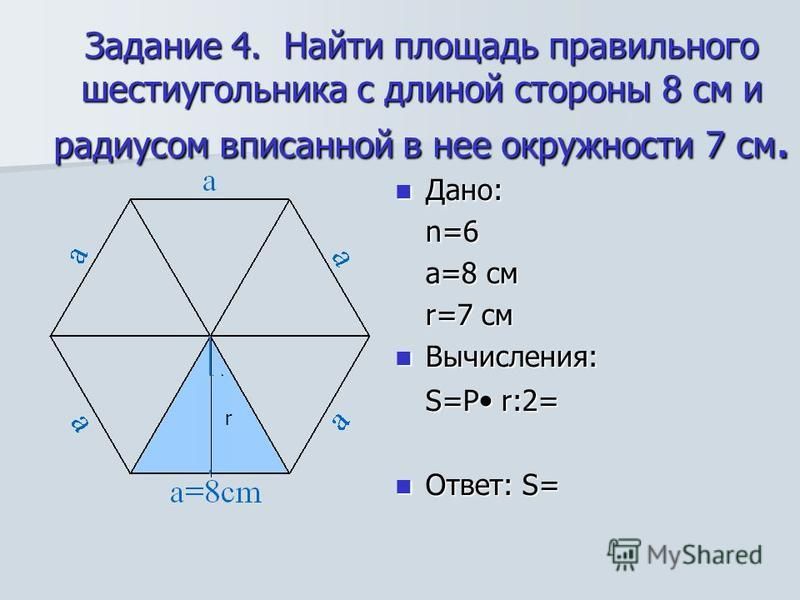

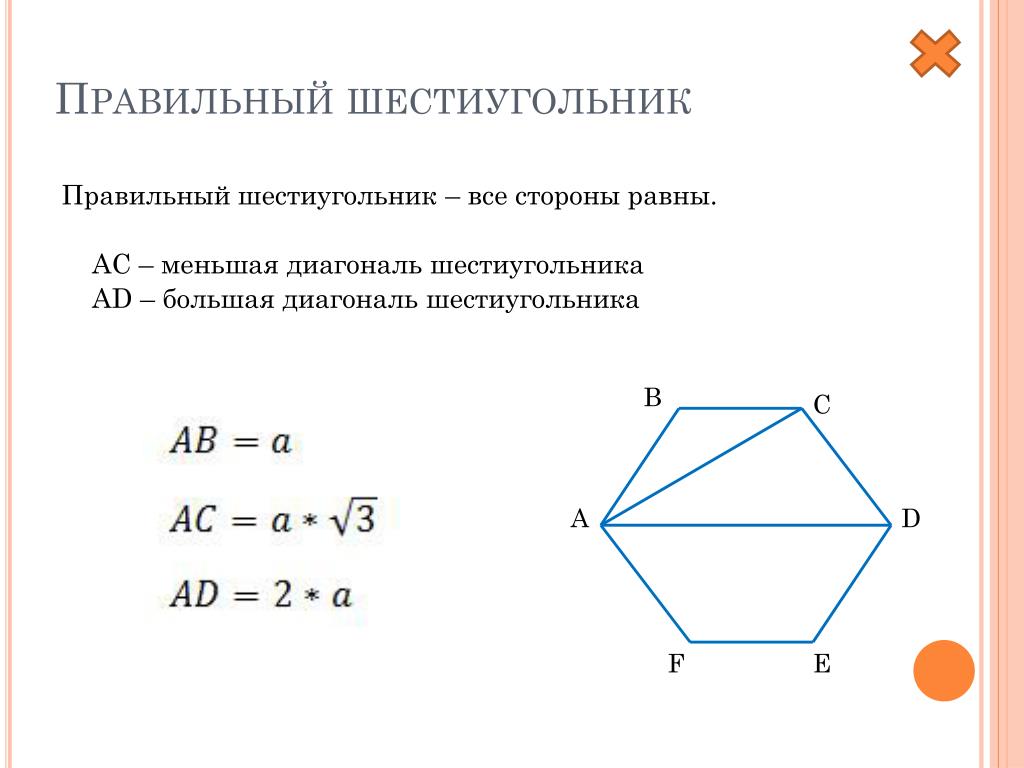 5 [4] [5] [6]
5 [4] [5] [6]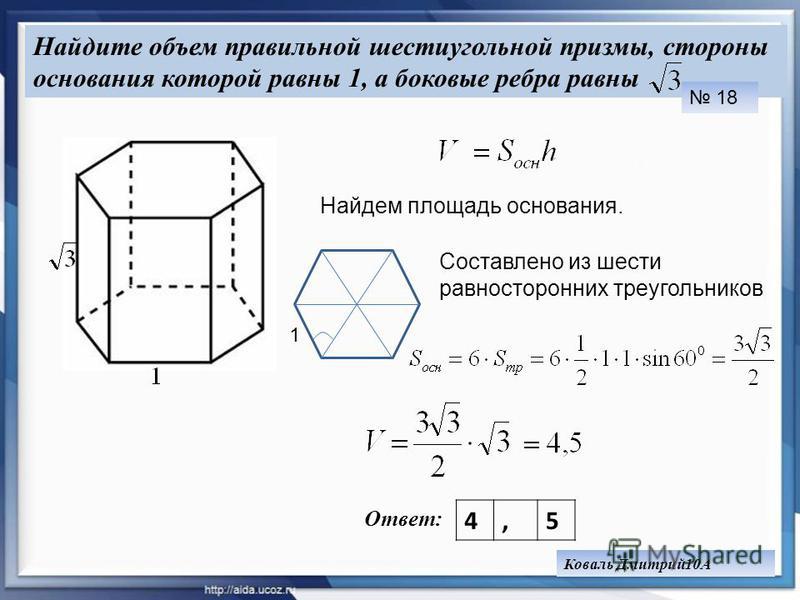
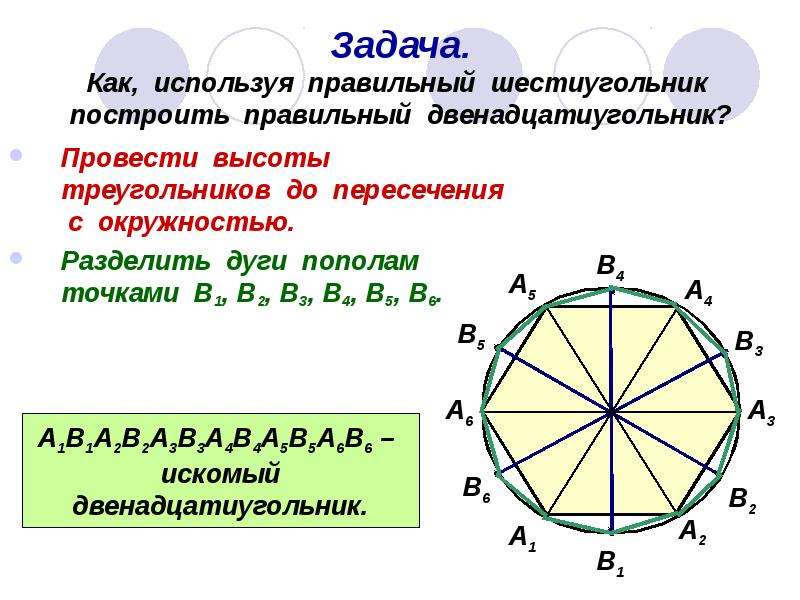
 Одноименные правильные многоугольники подобны, ибо у них углы равны и стороны пропорциональны.
Одноименные правильные многоугольники подобны, ибо у них углы равны и стороны пропорциональны.
 д.
д. е. она будет вписана в многоугольник.
е. она будет вписана в многоугольник.
 По данному вписанному правильному многоугольнику можно описать правильный многоугольник того же числа сторон.
По данному вписанному правильному многоугольнику можно описать правильный многоугольник того же числа сторон.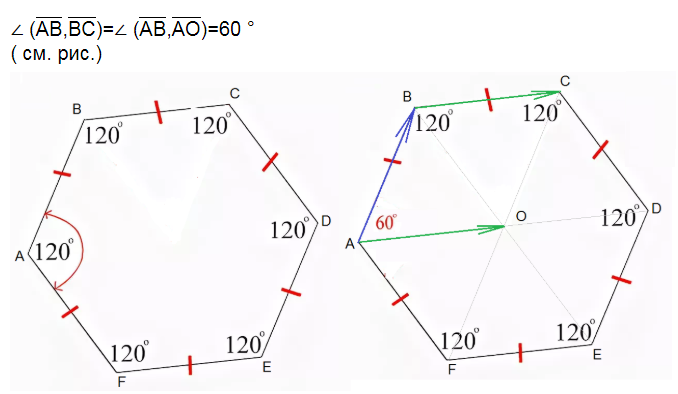
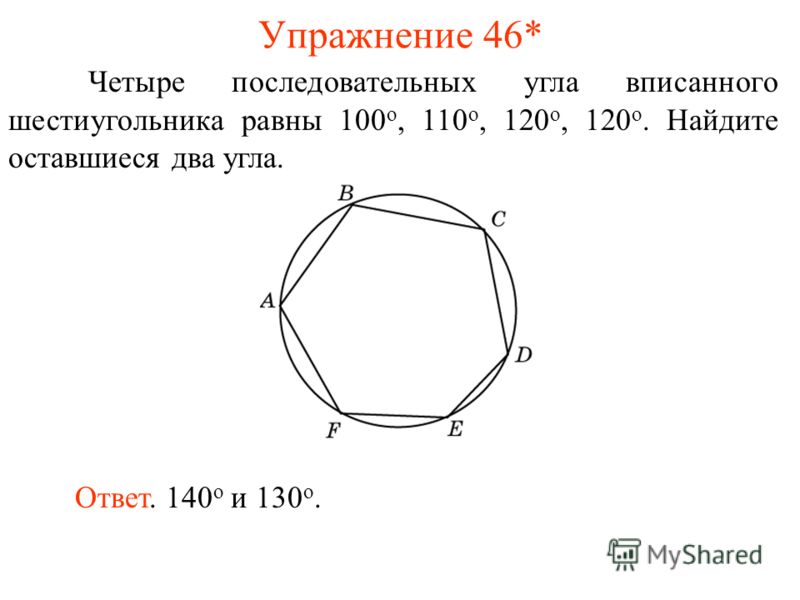


 197), следовательно,
197), следовательно,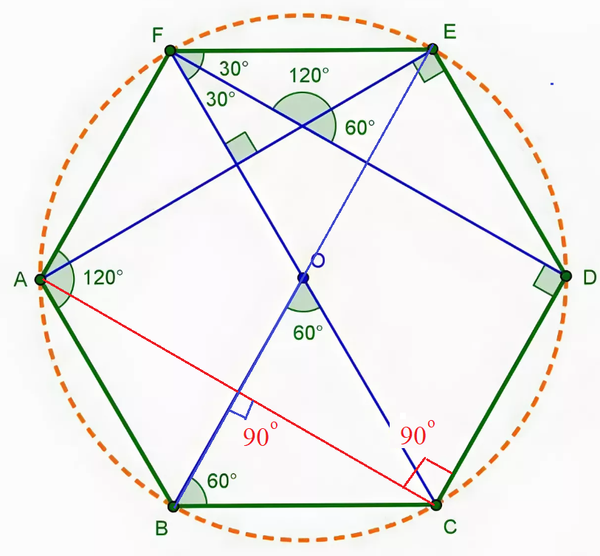 195)
195)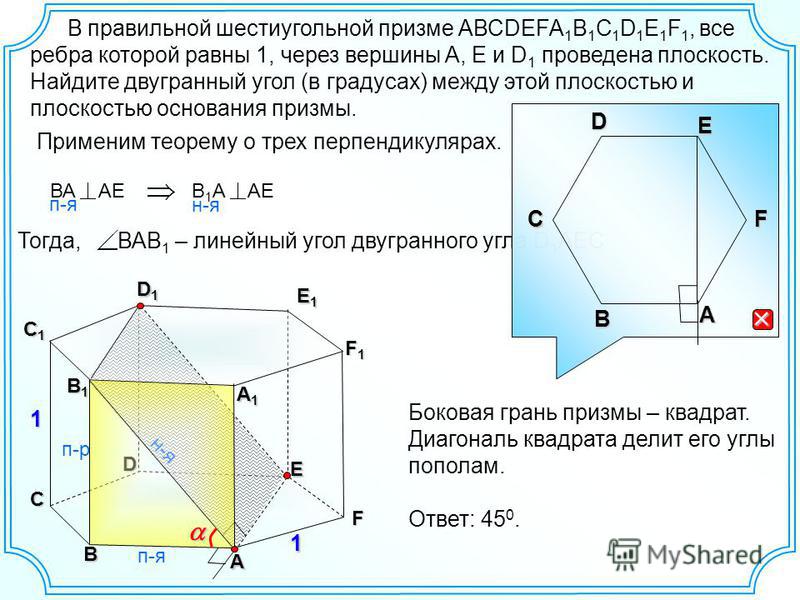
 199).
199).


 Так как OC = AB, то и сторона десятиугольника обладает тем же свойством.
Так как OC = AB, то и сторона десятиугольника обладает тем же свойством.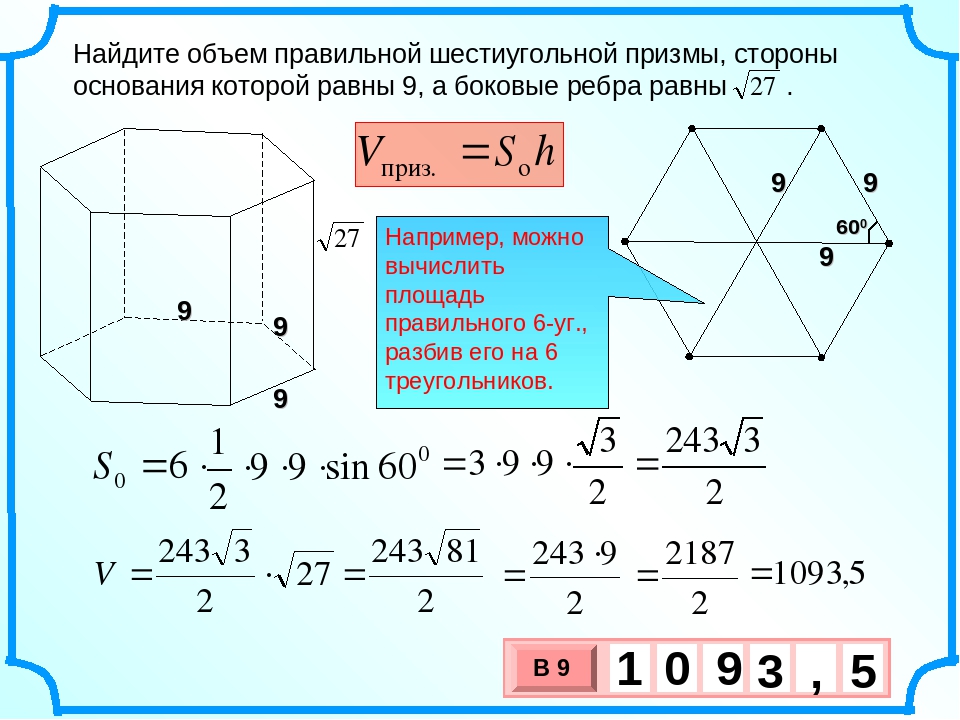
 д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении прав, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении прав, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.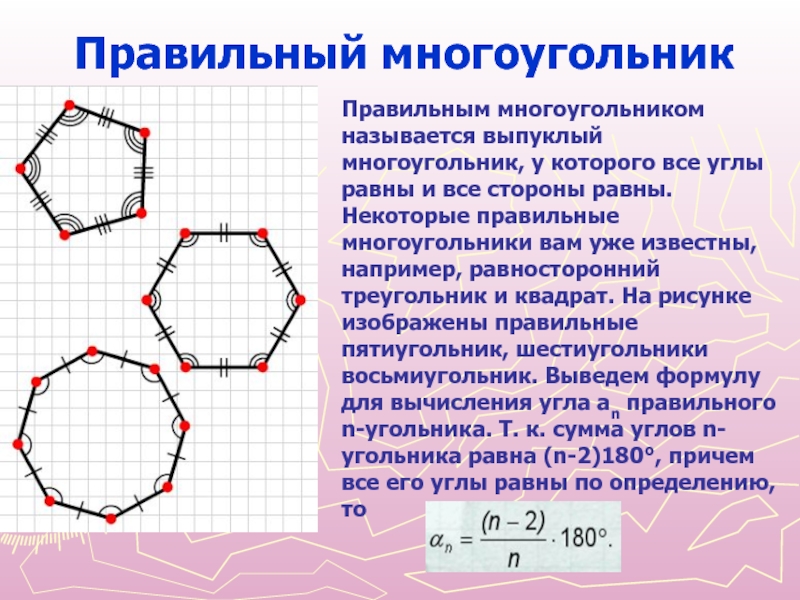
 Правильный шестиугольник — это всегда выпуклый шестиугольник.
Правильный шестиугольник — это всегда выпуклый шестиугольник. Так как сумма внутренних углов треугольника равна 180 °, сумма внутренних углов шестиугольника составляет 4 × 180 ° = 720 °.
Так как сумма внутренних углов треугольника равна 180 °, сумма внутренних углов шестиугольника составляет 4 × 180 ° = 720 °.
 Мы посмотрим на его углы и найдем формулы для его периметра и площади, используя его сторону или радиус.
Мы посмотрим на его углы и найдем формулы для его периметра и площади, используя его сторону или радиус. «- но они не доказывают, что вы действительно можете нарисовать такой круг (это, конечно, можно, но это довольно сложно).Итак, давайте формально докажем этот интуитивный результат.
«- но они не доказывают, что вы действительно можете нарисовать такой круг (это, конечно, можно, но это довольно сложно).Итак, давайте формально докажем этот интуитивный результат. Мы можем продолжить и сделать это для остальных сторон, соединив точку O с вершинами D, E и F, чтобы достичь желаемого результата — шесть одинаковых равносторонних треугольников составляют шестиугольник, все они встречаются в его центре, O.
Мы можем продолжить и сделать это для остальных сторон, соединив точку O с вершинами D, E и F, чтобы достичь желаемого результата — шесть одинаковых равносторонних треугольников составляют шестиугольник, все они встречаются в его центре, O. Два одинаковых треугольника 30-60-90 составляют равносторонний треугольник, поэтому его площадь равна 2 * (s / 2 * s / 2 · √3) / 2 = (s 2 * √3) / 4]
Два одинаковых треугольника 30-60-90 составляют равносторонний треугольник, поэтому его площадь равна 2 * (s / 2 * s / 2 · √3) / 2 = (s 2 * √3) / 4] В этом исследовании мы рассматриваем формы, образованные прямыми линиями, и формы с изогнутыми поверхностями. Двумерные фигуры с плоскими гранями, с прямыми линиями в качестве ребер и замкнутыми фигурами известны как многоугольники.Семейство многоугольников — это семейство, состоящее из разных форм с разным количеством сторон. Слово «поли» означает «много», а «гон» означает «угол». В зависимости от количества сторон многоугольника мы классифицируем их по следующим категориям. Например, многоугольники с 3 сторонами известны как треугольники, многоугольники с 4 сторонами известны как четырехугольники (прямоугольники, квадраты и т. Д.), А многоугольники с 5 сторонами известны как пятиугольники и так далее.
В этом исследовании мы рассматриваем формы, образованные прямыми линиями, и формы с изогнутыми поверхностями. Двумерные фигуры с плоскими гранями, с прямыми линиями в качестве ребер и замкнутыми фигурами известны как многоугольники.Семейство многоугольников — это семейство, состоящее из разных форм с разным количеством сторон. Слово «поли» означает «много», а «гон» означает «угол». В зависимости от количества сторон многоугольника мы классифицируем их по следующим категориям. Например, многоугольники с 3 сторонами известны как треугольники, многоугольники с 4 сторонами известны как четырехугольники (прямоугольники, квадраты и т. Д.), А многоугольники с 5 сторонами известны как пятиугольники и так далее.  Как показано на рисунке слева, шестиугольники имеют 6 вершин (или углов), 6 ребер (или сторон) и 6 углов.
Как показано на рисунке слева, шестиугольники имеют 6 вершин (или углов), 6 ребер (или сторон) и 6 углов. 
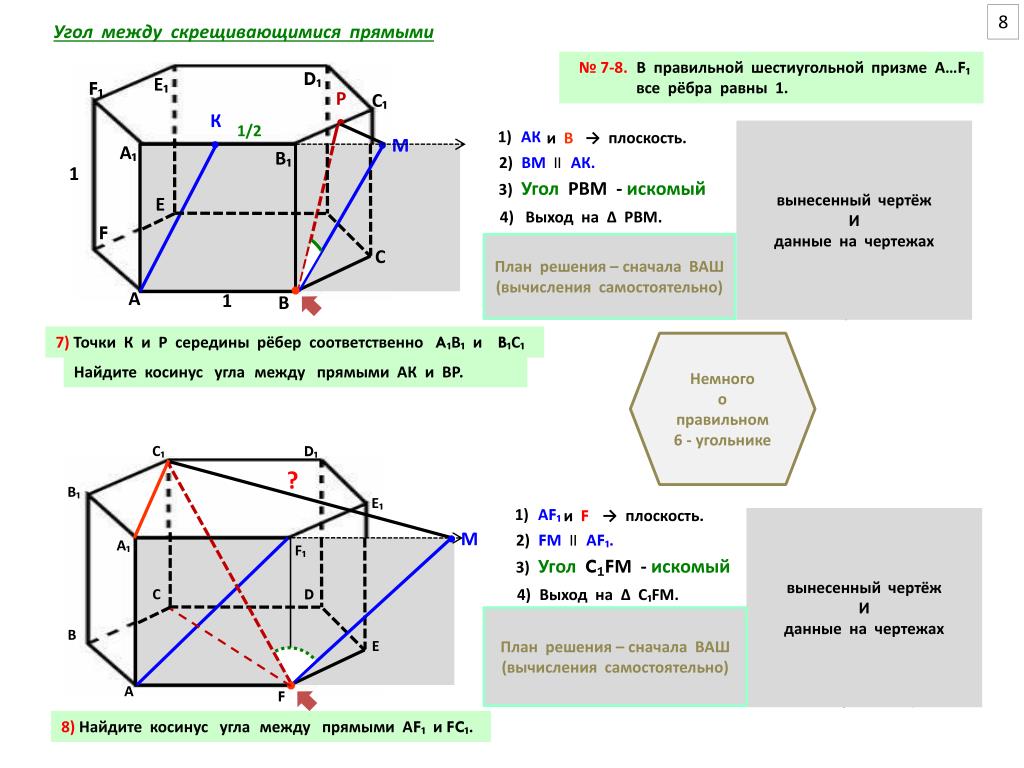

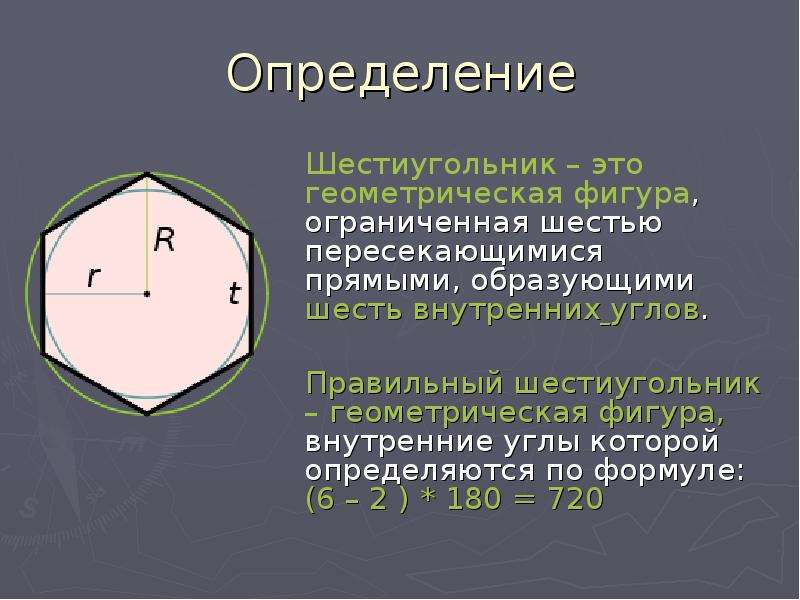
 Следовательно, площадь шестиугольника — это пространство, охватываемое его краями или сторонами. Площадь правильного шестиугольника отличается от площади неправильного шестиугольника. Для расчета его площади можно использовать различные процедуры. Давайте посмотрим на общие методы, используемые в процессе.
Следовательно, площадь шестиугольника — это пространство, охватываемое его краями или сторонами. Площадь правильного шестиугольника отличается от площади неправильного шестиугольника. Для расчета его площади можно использовать различные процедуры. Давайте посмотрим на общие методы, используемые в процессе.  Следовательно, все его стороны также равны.
Следовательно, все его стороны также равны. 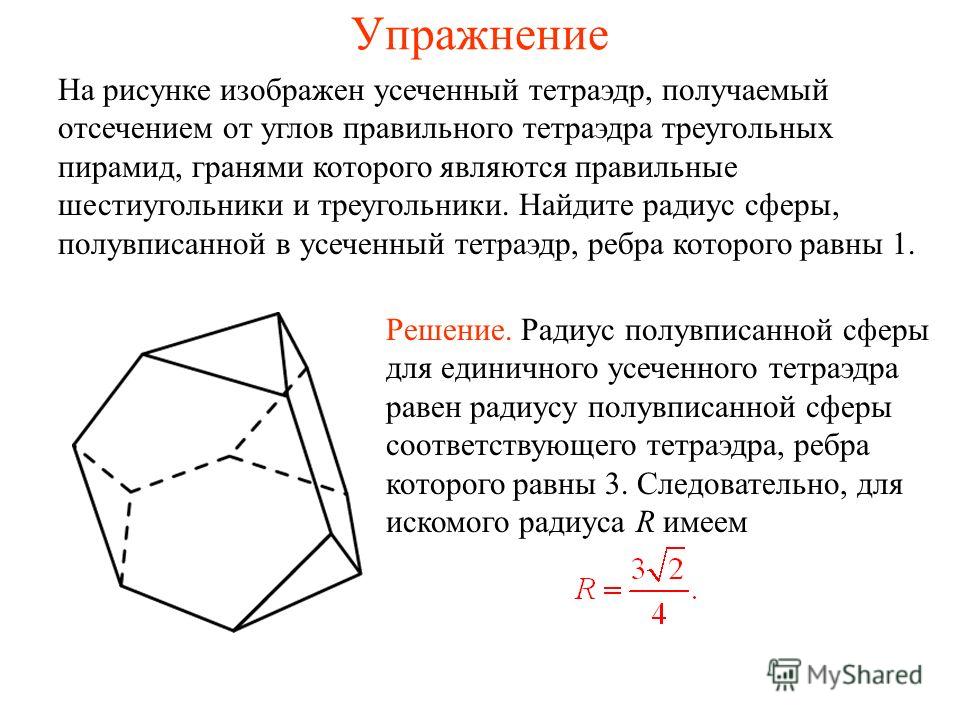



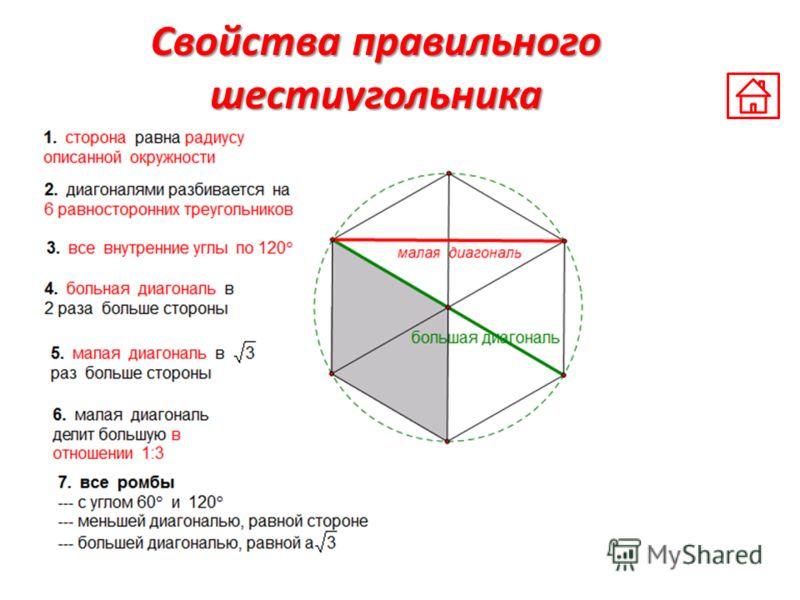
 )
)  Каждая точка многоугольника, где встречаются две стороны, называется вершиной . В каждой вершине есть внутренний угол многоугольника. Квадрат, например, имеет четыре внутренних угла по 90 градусов каждый.Если квадрат представлял ваш класс, внутренние углы — это четыре угла комнаты.
Каждая точка многоугольника, где встречаются две стороны, называется вершиной . В каждой вершине есть внутренний угол многоугольника. Квадрат, например, имеет четыре внутренних угла по 90 градусов каждый.Если квадрат представлял ваш класс, внутренние углы — это четыре угла комнаты. Это все линии между точками многоугольника, если не считать те, которые также являются сторонами многоугольника. На картинке ниже BD — это диагональ. Как видите, отрезок BD делит четырехугольник ABCD на два треугольника. Сумма углов в этих треугольниках (180 + 180 = 360) равна сумме всех углов прямоугольника (360).
Это все линии между точками многоугольника, если не считать те, которые также являются сторонами многоугольника. На картинке ниже BD — это диагональ. Как видите, отрезок BD делит четырехугольник ABCD на два треугольника. Сумма углов в этих треугольниках (180 + 180 = 360) равна сумме всех углов прямоугольника (360).

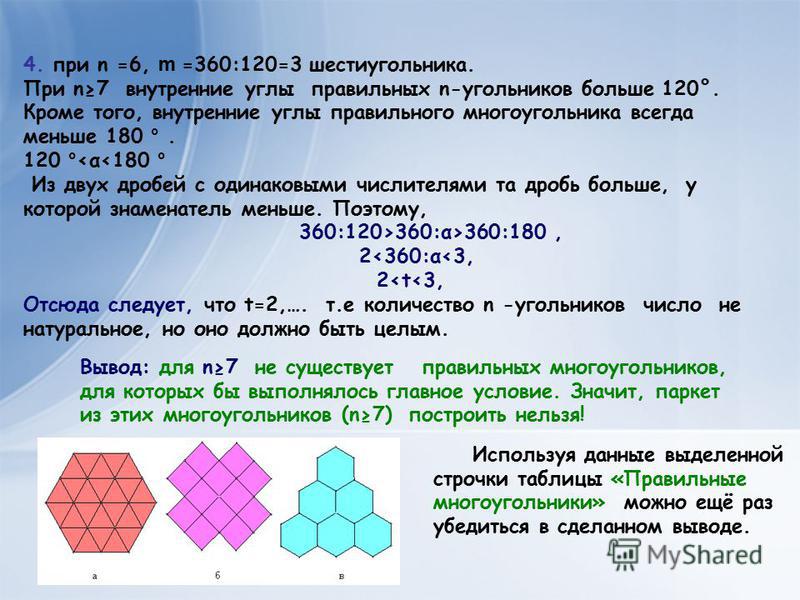

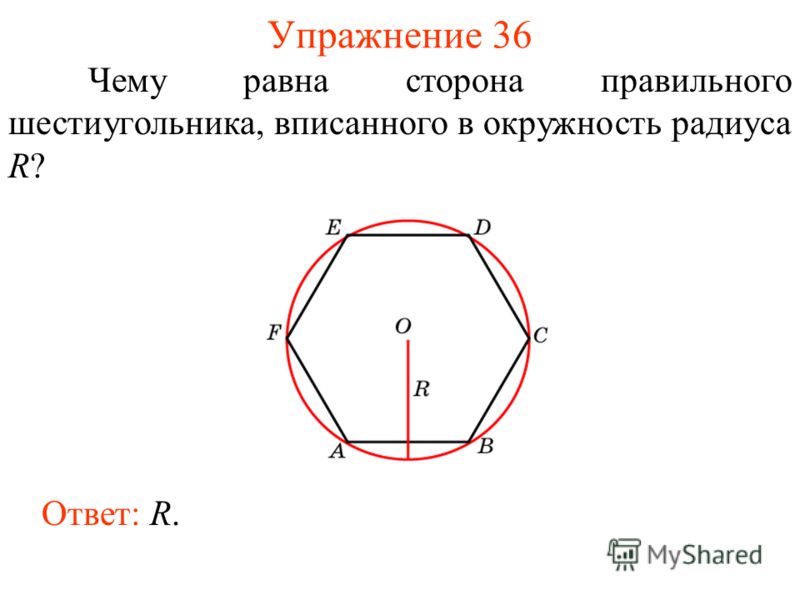
 Это дает ученикам возможность использовать то, что они знают о сумме углов в треугольнике, а также о сумме углов, которые составляют
линия. Если доступны шестиугольные и равносторонние треугольные плитки, учитель может захотеть использовать их, чтобы помочь ученикам визуализировать.
Это дает ученикам возможность использовать то, что они знают о сумме углов в треугольнике, а также о сумме углов, которые составляют
линия. Если доступны шестиугольные и равносторонние треугольные плитки, учитель может захотеть использовать их, чтобы помочь ученикам визуализировать. \ circ $.\ circ $ » поворот »
— угол $ PBC $.
\ circ $.\ circ $ » поворот »
— угол $ PBC $. Рисунок иллюстрирует это деление с помощью семиугольника. Сумма внутренних углов этого многоугольника теперь может быть найдена путем умножения количества треугольников на 180 °. При исследовании обнаруживается, что количество треугольников всегда на два меньше, чем количество сторон.Этот факт утверждается в виде теоремы.
Рисунок иллюстрирует это деление с помощью семиугольника. Сумма внутренних углов этого многоугольника теперь может быть найдена путем умножения количества треугольников на 180 °. При исследовании обнаруживается, что количество треугольников всегда на два меньше, чем количество сторон.Этот факт утверждается в виде теоремы.
