Как рассчитать периметр шестиугольника: формулы и способы вычислений
Иногда возникает необычная для учащегося задача по нахождению периметра шестиугольника. Не всегда на этот вопрос можно ответить сразу. В этой статье мы рассмотрим подробным образом, как найти периметр шестиугольника согласно формулам, а также вычислить и находить его другими способами.
Описание фигуры
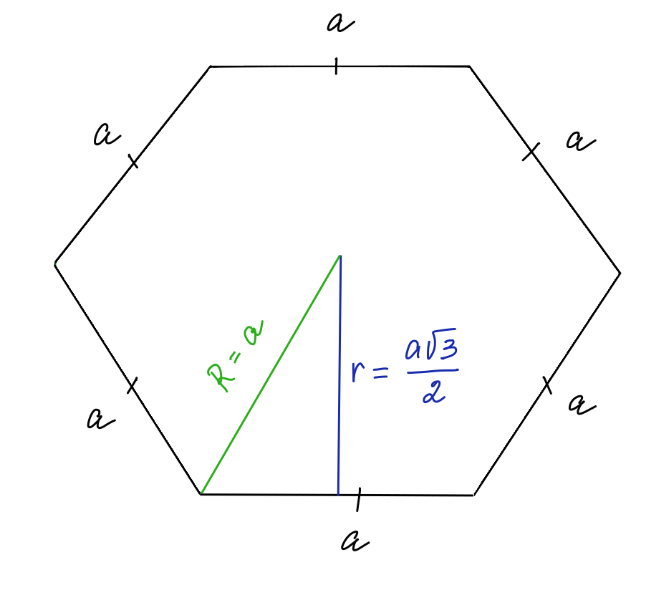
Непосредственно шестиугольник представляет собой плоскую фигуру, состоящую из шести отрезков, с расположением под углом 120 градусов относительно друг друга. Имеет научное название гексагон. Вокруг него или внутри можно вписать либо описать окружность. Между собой радиус и сторона многоугольника соотносятся по следующим формулам:
- R=2sin (pi/6)*a=a.
- r=0,866a.
- P=4*sqrt (3)*r или P=6*R.
Гексагон является очень популярной фигурой, ее имеют гайки, карандаши, соты, снежинки и многое другое. Является оптимальным вариантом для того, чтобы без пробелов замостить все пространство.
Поиски вышеописанного параметра гексагона являются простой, но в то же время довольно интересной задачей. Найдя периметр, можно убедиться в правильности замощенного пространства и отсутствии пробелов при составлении будущей документации.
До начала вычислений
Всем известно, что периметр плоской фигуры, к которой относится шестиугольник, является ничем иным, как длиной ограничивающей линии. Для нахождения периметра такой фигуры как гексагон, достаточно будет найти и сложить длины всех его сторон. Чтобы произвести эту процедуру, нужно измерить длины всех составляющих его отрезков. Значительно облегчается задача, если данная фигура имеет правильную форму. Разберем далее, как нужно искать периметр шестиугольника.
Первый вариант
Инструментарий достаточно простой. Понадобятся всего лишь циркуль и линейка. Вычислять периметр гексагона нужно следующим образом: измерить линейкой длину каждой из 6 сторон и сложить полученные значения. Все измерения длин сторон должны иметь единую систему единиц, тогда достаточно будет сложить числовые значения. То есть, единица измерения параметра шестиугольника совпадет с аналогичными параметрами длин отрезков.
Понадобятся всего лишь циркуль и линейка. Вычислять периметр гексагона нужно следующим образом: измерить линейкой длину каждой из 6 сторон и сложить полученные значения. Все измерения длин сторон должны иметь единую систему единиц, тогда достаточно будет сложить числовые значения. То есть, единица измерения параметра шестиугольника совпадет с аналогичными параметрами длин отрезков.
Например, имеются следующие отрезки: 2 сантиметра, 5,4,3,2 и 1 миллиметр. В этом случае нужно перевести 2 сантиметра в миллиметры из расчета 1 сантиметр равняется 10 миллиметрам и суммируете P=20+5+4+3+2+1=35 миллиметров. Таким образом рассчитывается периметр большинства видов шестиугольников.
Правильный шестиугольник
В случае, если шестиугольник имеет правильную форму, то расчет нужного параметра становится гораздо проще.
- Умножьте длину его стороны на 6 и вы получите нужное значение по формуле P=a*6, где a — сторона правильного шестиугольника.
- Например, у нас имеется фигура со стороной длиной 10 сантиметров, умножаем 10 на 6 и получаем в итоге 60 сантиметров в периметре.

- Также правильная фигура имеет уникальное свойство: радиус окружности, который описан вокруг такого шестиугольника, равен длине его стороны. Если вам известен радиус описанной окружности, то достаточно воспользоваться формулой в виде P=R*6, где R — радиус описанной окружности.
Например, известен прямоугольник, вписанный в окружность, имеющую диаметр 20 сантиметров. Тогда радиус будет в два раза меньше и составит 10 сантиметров. Полученную величину умножаем на 6 сторон и получаем периметр.
Иные варианты расчета
Если известен радиус вписанной в многоугольник окружности, рекомендуется использовать формулу P=4sqrt (3)*r, в которой r является радиусом вписанной окружности.
Можно высчитать периметр многоугольника, если в условии известна площадь. Площадь находится по формуле: S=3/2*sqrt (3)*a 2 , где S является площадью правильного шестиугольника. Далее находим из формулы a=sqrt (2/3*S/sqrt (3)). Найдя a, можно отыскать периметр, а именно P=6*a=6*sqrt (2/3*S/sqrt (3))=2*sqrt (2*s*sqrt (3)).
Другие способы измерения периметра шестиугольника можно найти в специализированной литературе и на особых порталах.
Шестиугольник относят к очень эффективной фигуре. Она встречается как в реальности, так и среди природных явлений. Если же вы боитесь, что не сможете правильно сами посчитать заданную величину, на помощь придут специальные онлайн-калькуляторы, в которых можно ввести необходимые данные для вычисления периметра. Удачной математической работы с поисками периметра для гексагона.
Видео
Посмотрите, как рассчитывается площадь правильного шестиугольника.
Площадь правильного многоугольника
Каким способом посчитать площадь многоугольника:
Через тангенс Через радиус вписанной окружности
Результат:
Решение
Теория
Правильный многоугольник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между смежными сторонами равны. 2}{4 \cdot \tg \lparen \dfrac{180\degree}{n} \rparen}
2}{4 \cdot \tg \lparen \dfrac{180\degree}{n} \rparen}
- S — площадь правильного многоугольника
- n — количество сторон
- a — длина стороны
Площадь правильного многоугольника через радиус вписанной окружности
rS = p \cdot r
S = \dfrac{1}{2} \cdot n \cdot a \cdot r
- S — площадь правильного многоугольника
- p — полупериметр правильного многоугольника
- r — радиус вписанной окружности правильного многоугольника
- n — количество сторон
- a — сторона правильного многоугольника
p = \dfrac{n \cdot a}{2}
Площадь правильного десятиугольника — Циклопедия
Площадь правильного десятиугольника
 2, \ r=\frac{\sqrt{10+2\sqrt{5}}}{4}R[/math]
2, \ r=\frac{\sqrt{10+2\sqrt{5}}}{4}R[/math],
где [math]\sin\frac{\pi}{10}=\frac{\sqrt{5}-1}{4}[/math], [math]\cos\frac{\pi}{10}=\frac{\sqrt{10+2\sqrt{5}}}{4}[/math], [math]tg\frac{\pi}{10}=\frac{\sqrt{25-10\sqrt{5}}}{5}[/math], [math]ctg\frac{\pi}{10}=\sqrt{5+2\sqrt{5}}[/math]
[править] Другие многоугольники
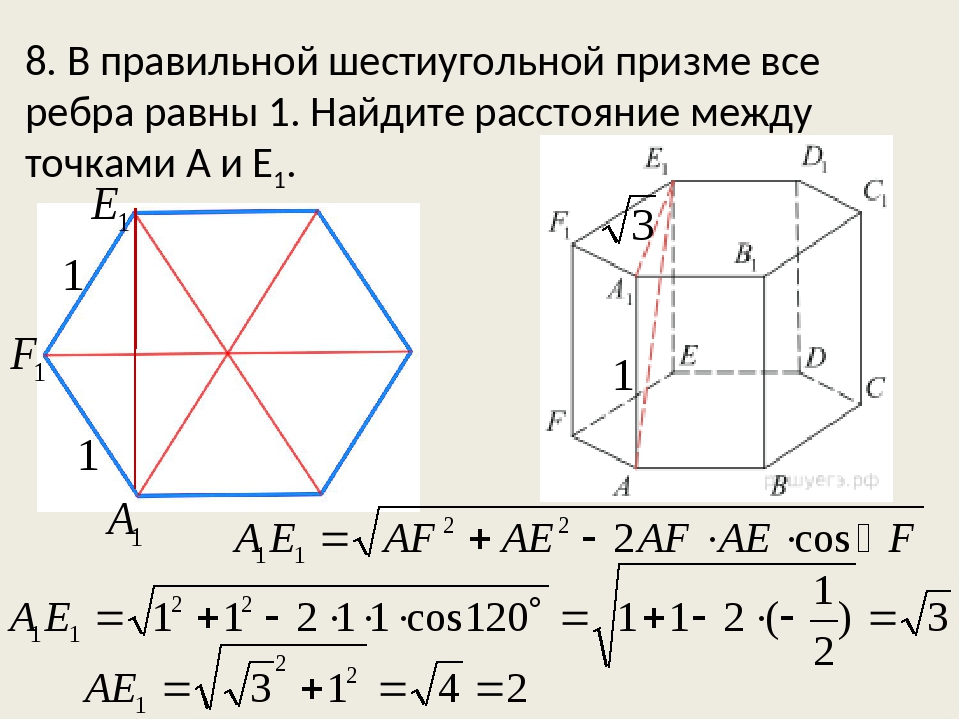
Как найти объем правильной шестиугольной призмы (формула)
Определение объемов геометрических тел является одной из важных задач пространственной геометрии. В данной статье рассматривается вопрос, что такое призма с шестиугольным основанием, а также приводится формула объема правильной шестиугольной призмы.
Определение призмы
С точки зрения геометрии призмой называется фигура в пространстве, которая образована двумя одинаковыми многоугольниками, расположенными в параллельных плоскостях. А также несколькими параллелограммами, которые эти многоугольники соединяют в единую фигуру.
В трехмерном пространстве призму произвольной формы можно получить, если взять любой многоугольник и отрезок. Причем последний плоскости многоугольника принадлежать не будет. Тогда, располагая этот отрезок от каждой вершины многоугольника, можно получить параллельный перенос последнего в другую плоскость. Образованная таким способом фигура будет призмой.
Причем последний плоскости многоугольника принадлежать не будет. Тогда, располагая этот отрезок от каждой вершины многоугольника, можно получить параллельный перенос последнего в другую плоскость. Образованная таким способом фигура будет призмой.
Чтобы иметь наглядное представление о рассматриваемом классе фигур, приведем рисунок четырехугольной призмы.
Многие знают эту фигуру под названием параллелепипеда. Видно, что два одинаковых многоугольника призмы представляют собой квадраты. Их называют основаниями фигуры. Остальные четыре ее стороны — прямоугольники, то есть это частный случай параллелограммов.
Прежде чем приводить формулу, как определяется объем шестиугольной правильной призмы, необходимо четко понять, о какой фигуре пойдет речь. Шестиугольная призма имеет в основаниях шестиугольник. То есть, плоский многоугольник с шестью сторонами, углов столько же. Боковые стороны фигуры так же, как и для любой призмы, в общем случае являются параллелограммами. Сразу отметим, что шестиугольное основание может быть представлено как правильным, так и неправильным шестиугольником.
Расстояние между основаниями фигуры — это ее высота. Далее мы будем обозначать ее буквой h. Геометрически высота h представляет собой отрезок, перпендикулярный обоим основаниям. Если этот перпендикуляр:
- опущен с геометрического центра одного из оснований;
- пересекает второе основание также в геометрическом центре.
Фигура в этом случае называется прямой. В любом другом случае призма будет косоугольной или наклонной. Разницу между этими видами шестиугольной призмы можно увидеть с первого взгляда.
Прямая шестиугольная призма — это фигура, имеющая в основании правильные шестиугольники. При этом она является прямой. Рассмотрим подробнее ее свойства.
Элементы правильной шестиугольной призмы
Чтобы понять, как вычислить объем правильной шестиугольной призмы (формула приведена ниже в статье), необходимо также разобраться, из каких элементов состоит фигура, а также какими свойствами она обладает. Чтобы было легче анализировать фигуру, покажем ее на рисунке.
Главными ее элементами являются грани, ребра и вершины. Количества этих элементов подчиняется теореме Эйлера. Если обозначить Р — число ребер, В — количество вершин и Г — граней, тогда можно записать равенство:
Р = Г + В — 2.
Проверим его. Число граней рассматриваемой фигуры равно 8. Две из них — это правильные шестиугольники. Шесть граней представляет собой прямоугольники, это видно из рисунка. Число вершин составляет 12. Действительно, 6 вершин принадлежат одному основанию, и 6 другому. Согласно формуле, число ребер должно равняться 18, что является справедливым. 12 ребер лежат в основаниях и 6 образуют параллельные друг другу стороны прямоугольников.
Переходя к получению формулы объема правильной шестиугольной призмы, следует остановить свое внимание на одном важном свойстве этой фигуры: прямоугольники, образующие боковую поверхность, равны между собой и перпендикулярны обоим основаниям. Это приводит к двум важным следствиям:
- Высота фигуры равна длине ее бокового ребра.

- Любое сечение боковой поверхности пирамиды, выполненное с помощью секущей плоскости, которая параллельна основаниям, является правильным шестиугольником, равным этим основаниям.
Площадь шестиугольника
Можно интуитивно догадаться, что эта площадь основания фигуры появится в формуле объема правильной призмы шестиугольной. Поэтому в данном пункте статьи найдем эту площадь. Правильный шестиугольник, разделенный на 6 одинаковых треугольников, вершины которых пересекаются в его геометрическом центре, показан ниже:
Каждый из этих треугольников является равносторонним. Доказать это не очень сложно. Поскольку вся окружность имеет 360o, то углы треугольников вблизи геометрического центра шестиугольника равны 360o/6=60o. Расстояния от геометрического центра до вершин шестиугольника являются одинаковыми.
Последнее означает, что все 6 треугольников будут равнобедренными. Поскольку один из углов равнобедренных треугольников равен 60o, значит, два остальных угла тоже равны по 60o. ((180o-60o)/2) — треугольники равносторонние.
((180o-60o)/2) — треугольники равносторонние.
Обозначим длину стороны шестиугольника буквой a. Тогда площадь одного треугольника будет равна:
S1 = 1/2*√3/2*a*a = √3/4*a2.
Формула получена на основании стандартного выражения для площади треугольника. Тогда площадь S6 для шестиугольника будет:
S6 = 6*S1 = 6*√3/4*a2 = 3*√3/2*a2.
Формула определения объема правильной шестиугольной призмы
Чтобы записать формулу для объема рассматриваемой фигуры, следует учесть приведенную выше информацию. Для произвольной призмы объем пространства, ограниченный ее гранями, вычисляется так:
V = h*So.
То есть, V равен произведению площади основания So на высоту h. Поскольку мы знаем, что высота h равна длине бокового ребра b для шестиугольной правильной призмы, а площадь ее основания соответствует S6, то формула объема правильной шестиугольной призмы примет вид:
V6 = 3*√3/2*a2*b.
Пример решения геометрической задачи
Дана шестиугольная правильная призма. Известно, что она вписана в цилиндр радиусом 10 см. Высота призмы в два раза больше стороны ее основания. Необходимо найти объем фигуры.
Чтобы найти требуемую величину, необходимо знать длину стороны и бокового ребра. При рассмотрении правильного шестиугольника было показано, что его геометрический центр расположен в середине описанной вокруг него окружности. Радиус последней равен расстоянию от центра до любой из вершин. То есть он равен длине стороны шестиугольника. Эти рассуждения приводят к следующим результатам:
a = r = 10 см;
b = h = 2*a = 20 см.
Подставляя эти данные в формулу объема правильной шестиугольной призмы, получим ответ: V6≈5196 см3 или около 5,2 литра.
Как найти площадь правильного и неправильного шестиугольника?
Оглавление:
- Площадь правильного шестиугольника
- Площадь неправильного шестиугольника
- Площадь равностороннего шестиугольника
Умение определять площадь различных фигур играет немалую
роль в жизни каждого человека.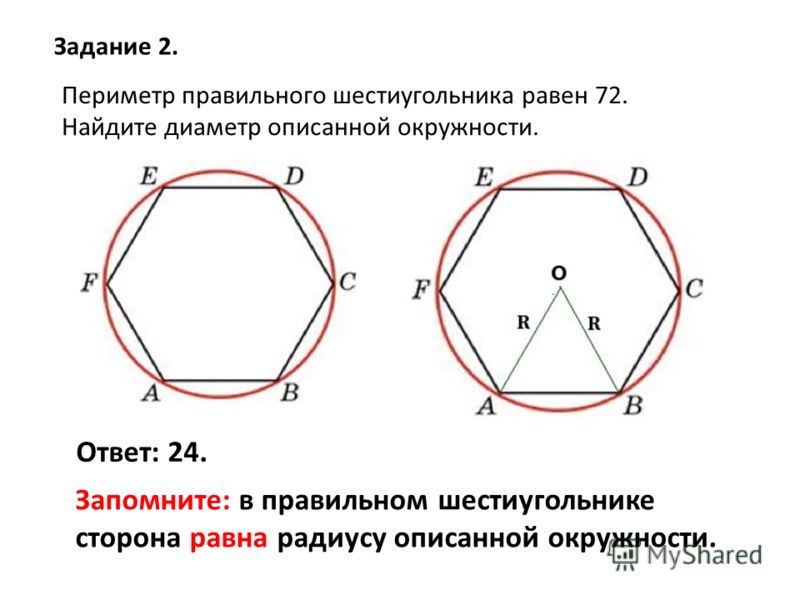
Знаниями в области геометрии пользовались еще в древнем Вавилоне и других странах. На первых шагах к культуре всегда возникала необходимость измерить участок, расстояние. При строительстве первых значительных сооружений требовались умения выдерживать вертикаль, спроектировать план.
Роль эстетических потребностей людей также имела немалое значение. Украшение жилища, одежды, рисование картин способствовало процессу формирования и накопления сведений в области геометрии, которые люди тех времён добывали опытным путем, по крупицам и передавали из поколения в поколение.
Сегодня знания геометрии необходимы и закройщику, и строителю, и архитектору и каждому простому человеку в быту.
Поэтому нужно учиться рассчитывать площадь различных фигур, и помнить, что каждая из формул может пригодиться впоследствии на практике, в том числе, и формула правильного шестиугольника. Шестиугольником называется такая многоугольная фигура, общее количество углов которой равно шести.
Площадь правильного шестиугольника
Правильным шестиугольником называют шестиугольную фигуру, которая имеет равные стороны. Углы у правильного шестиугольника также между собой равны.
В повседневной жизни мы часто можем встретить предметы, имеющие форму правильного шестиугольника. Это и металлическая гайка, и ячейки пчелиных сот, и структура снежинки. Шестиугольными фигурами отлично заполняются плоскости. Так, например, при мощении тротуарной плитки мы можем наблюдать, как плитка укладывается одна возле другой, не оставляя пустых мест.
Свойства правильного шестиугольника
- Правильный шестиугольник всегда будет иметь равные углы, каждый из которых составляет 120˚.
- Сторона фигуры равняется радиусу описанной окружности.
- Все стороны в правильном шестиугольнике равны.
- Правильный шестиугольник плотно заполняет плоскость.
Как посчитать площадь правильного шестиугольника?
Площадь правильного шестиугольника можно рассчитать, разбив его на шесть треугольников, каждый из которых будет иметь равные стороны.
Для расчета площади правильного треугольника используется следующая формула:Зная площадь одного из треугольников, можно легко рассчитать площадь шестиугольника. Формула для ее расчета проста: поскольку правильный шестиугольник — это шесть равных треугольников, следует площадь нашего треугольника умножить на 6.Если провести от центра фигуры к любой из ее сторон перпендикуляр, получим отрезок, который называется апофема. Рассмотрим, как найти площадь шестиугольника при известной апофеме:- Площадь = ½*периметр*апофему.
- Предположим, наша апофема равняется 5√3 см.
- Используя апофему, находим периметр: Поскольку апофема расположена перпендикулярно к стороне шестиугольника, то углы треугольника, созданного при помощи апофемы, будут равняться 30˚—60˚—90˚. Каждая сторона полученного треугольника будет соответствовать: x-x√3−2x, где короткая сторона, которая расположена напротив угла в 30˚— это x, длинная сторона, расположенная напротив угла в 60˚ — это x√3, а гипотенуза — 2x.
- Поскольку апофема представлена, ка
Правильная шестиугольная призма | Банк ЕГЭ
Правильная шестиугольная призма — призма, в основаниях которой лежат два правильных шестиугольника, а все боковые грани строго перпендикулярны этим основаниям.Обозначения
- $ABCDEFA_1B_1C_1D_1E_1F_1$ — правильная шестиугольная призма
- $a$ — длина стороны основания призмы
- $h$ — длина бокового ребра призмы
- $S_{\text{осн.}}$ — площадь основания призмы
- $S_{\text{бок.}}$ — площадь боковой грани призмы
- $S_{\text{полн.}}$ — площадь полной поверхности призмы
- $V_{\text{призмы}}$ — объем призмы
Площадь оснований призмы
В основаниях призмы находятся правильные шестиугольники со стороной $a$.2}$.Внутренние углы полигонов
Внутренний угол — это угол внутри формы
Другой пример:
Треугольники
Сумма внутренних углов треугольника составляет 180 °
Давайте попробуем треугольник:
90 ° + 60 ° + 30 ° = 180 °
Это работает для этого треугольника
Теперь наклоните линию на 10 °:
80 ° + 70 ° + 30 ° = 180 °
Еще работает!
Один угол пошел на вверх, на 10 °,
, а другой на вниз на 10 °
Четырехугольники (квадраты и т. Д.)
(У четырехугольника 4 прямые стороны)
Попробуем квадрат:
90 ° + 90 ° + 90 ° + 90 ° = 360 °
Квадрат в сумме дает 360 °
Теперь наклоните линию на 10 °:
80 ° + 100 ° + 90 ° + 90 ° = 360 °
В сумме все равно 360 °
Внутренние углы четырехугольника в сумме составляют 360 °
Потому что в квадрате 2 треугольника…
Сумма внутренних углов в треугольнике составляет 180 ° …
… а для квадрата они составляют 360 ° …
… потому что квадрат можно составить из двух треугольников!
Пентагон
У пятиугольника 5 сторон, и его можно составить из трех треугольников , так что вы знаете, что …
… его внутренние углы в сумме составляют 3 × 180 ° = 540 °
А когда это обычный (все углы одинаковые), то каждый угол будет 540 ° /5 = 108 °
(Упражнение: убедитесь, что каждый треугольник здесь составляет в сумме 180 °, и убедитесь, что внутренние углы пятиугольника составляют в сумме 540 °)
Суммарные внутренние углы пятиугольника составляют 540 °
Общие правила
Каждый раз, когда мы добавляем сторону (треугольник к четырехугольнику, четырехугольник к пятиугольнику и т. Д.), Мы добавляем еще на 180 °, к общей сумме:
Итак, общее правило:
Сумма внутренних углов = ( n −2) × 180 °
Каждый угол (правильного многоугольника) = ( n −2) × 180 ° / n
Возможно, поможет пример:
Пример: А как насчет правильного десятиугольника (10 сторон)?
Сумма внутренних углов = ( n −2) × 180 °
= ( 10 −2) × 180 °
= 8 × 180 °
= 1440 °
А для обычного десятиугольника:
Каждый внутренний угол = 1440 ° /10 = 144 °
Примечание: внутренние углы иногда называют «внутренними углами».
Площадь правильных многоугольников.Мы будем определять площадь правильных многоугольников по нотам.
Презентация на тему: «Площадь правильных многоугольников. Мы определим площадь правильных многоугольников с помощью нот.» — стенограмма презентации:
1 Площадь правильных многоугольников
2 Мы будем определять площадь правильных многоугольников по нотам.
3 Скопируйте в свои заметки:
4 Правильный многоугольник a = апофема P = периметр равные стороны равны углы * Используйте эту формулу для правильных пятиугольников, шестиугольников, восьмиугольников и т. Д. Скопируйте в свои заметки:
5 Apothem apothem — соединяет центр со средней точкой и образует прямой угол. Копируйте на ваши заметки:
6 Примеры Без примеров Скопируйте в свои заметки:
8 Пример 2: Найдите площадь правильного восьмиугольника.2,5 см 14 см Попробуйте сейчас…
9 Сначала разделите шестиугольник на шесть шести одинаковых фигур. Теперь разделите шестиугольник на 12 конгруэнтных фигур. Какие фигурки вы создали? Равносторонние треугольники Какие фигуры вы создали? 30 — 60 — 90 треугольников Обозначьте стороны одного из 30 — 60 — 90 треугольников. Как вы назвали апофему? x√3 Что обозначает длину стороны? 2x Щелкните анимацию и скопируйте важную информацию.
11 Пример 4: Найдите площадь правильного шестиугольника с периметром 42 см. (Округлите до ближайшей десятой.) Попробуйте это сейчас …
12 Пример 5: Площадь правильного шестиугольника составляет 54 см 2. Если периметр шестиугольника равен 48 см, какова длина апофемы? Продолжайте пытаться!
| 2020 | 6 ноября 2020 г.Hexagon Composites ASA: результаты за третий квартал 2020 годаВ третьем квартале 2020 года Hexagon Group получила выручку в размере 770 (770) миллионов норвежских крон и зафиксировала операционную прибыль до вычета износа ( EBITDA) 65 (49) миллионов норвежских крон.Результаты Hexagon Ragasco остались стабильными, а Agility пережила рекордно высокий квартал, оправившись от резкого воздействия глобальной пандемии в предыдущем квартале. Однако на Hexagon Mobile Pipeline по-прежнему повлияла пандемия и связанные с ней макроэкономические факторы, а также снижение активности на суше в Северной Америке. подробнее | Выпуск на фондовой бирже |
| 2020 | 6 ноября 2020 г. Компания Hino Trucks получила заказ на поставкуHexagon Purus в поддержку проекта Z — пути развития компании к автомобилям с нулевым уровнем выбросов (ZEV)Hexagon Purus, a дочерняя компания Hexagon Composites получила заказ на покупку трех грузовиков от Hino Trucks, входящей в группу Toyota, в рамках своего плана развития проекта Z. подробнее | Выпуск на фондовой бирже |
| 2020 | 6 ноября 2020 г.Hexagon Purus поставит композитные баллоны высокого давления для разработки первого пригородного поезда с водородным двигателем в СШАHexagon Purus подписал контракт вместе со Stadler Rail разработает систему хранения баллонов для первого водородного пригородного поезда в США подробнее | Выпуск на фондовой бирже |
| 2020 | 23 октября 2020 г. ДЛЯ ПЕРЕДАЧИ, ПУБЛИКАЦИИ ИЛИ РАСПРОСТРАНЕНИЯ, ПОЛНОСТЬЮ ИЛИ ЧАСТИЧНО, НАПРЯМУЮ ИЛИ КОСВЕННО, В АВСТРАЛИИ, КАНАДЕ, ЯПОНИИ, ГОНКОНГСКОМ ОСОБОМ АДМИНИСТРАТИВНОМ РЕГИОНЕ НАРОДНОЙ РЕСПУБЛИКИ КИТАЯ ИЛИ В СОЕДИНЕННЫХ ШТАТАХ ИЛИ В ГОСУДАРСТВО СОЕДИНЕННЫХ ШТАТОВ АМЕРИКИ И ОКРУГА КОЛУМБИИ) ИЛИ ЛЮБОЙ ДРУГОЙ ЮРИСДИКЦИИ, В КОТОРОЙ ВЫПУСК, PUBLICATI ПРИ РАСПРОСТРАНЕНИИ ИЛИ РАСПРОСТРАНЕНИЕМ БУДЕТ НЕЗАКОННЫМ.ДАННОЕ ОБЪЯВЛЕНИЕ НЕ ЯВЛЯЕТСЯ ПРЕДЛОЖЕНИЕМ НИКАКИХ ЦЕННЫХ БУМАГ, ОПИСАННЫХ ЗДЕСЬ. подробнее | Выпуск фондовой биржи |
| 2020 | 23 октября 2020 г.Hexagon Composites ASA: Уведомление о внеочередном общем собранииВнеочередное общее собрание Hexagon Composites ASA состоится 13 ноября 2020 года в 13:00 CET в офисах компании по адресу Korsegata 4B, Aalesund, Norway. подробнее | Выпуск фондовой биржи |
| 2020 | 21 октября 2020 г.Hexagon Composites ASA: Обновление предлагаемых поправок к соглашению об облигацияхHexagon Composites («Компания»), как сообщается в выпуске 8 для фондовой биржи В октябре 2020 года обратился к держателям облигаций по поводу выпуска приоритетных необеспеченных облигаций (HEX03 — ISIN NO NO0010846280), подробно изложив предложение о внесении поправок в условия Облигации, чтобы оградить Hexagon Purus от определения Hexagon Group и разрешить разовый безналичная передача до 25% акций Hexagon Purus существующим акционерам Hexagon Composites ASA. подробнее | Выпуск фондовой биржи |
| 2020 | 20 октября 2020 г.Hexagon Composites ASA: приглашение на презентацию результатов за третий квартал 2020 г.Результаты Hexagon Composites ASA за третий квартал 2020 г. будут опубликованы 6 ноября 2020 г., 07 : 00 CET. подробнее | Выпуск фондовой биржи |
| 2020 | 15 октября 2020 г.Hexagon Composites ASA: отзыв письменного решения Ссылка сделана на выпуск фондовой биржи, сделанный 8 октября 2020 года Hexagon Composites ASA («Hexagon »Или« Компания ») в отношении уведомления о письменном решении в отношении выпуска приоритетных необеспеченных облигаций, HEX03 — ISIN NO NO0010846280.Компания Nordic Trustee AS как Доверительный управляющий по облигациям уведомила Hexagon о том, что предложение получило достаточное количество голосов против, чтобы оно было отклонено до истечения периода голосования. Таким образом, предложенные поправки к условиям облигации отозваны. | Выпуск фондовой биржи |
| 2020 | 8 октября 2020 г.Hexagon Composites ASA: Уведомление о письменном решенииHexagon Composites ASA («Hexagon» или «Компания») запросил Nordic Trustee AS as Доверительный управляющий по Облигациям должен выпустить уведомление о письменном решении в отношении выпуска приоритетных необеспеченных облигаций в размере 1 100 000 000 норвежских крон, HEX03 — ISIN NO NO0010846280 («Облигация»), в контексте предложения определенных поправок к условиям Облигации, как изложено в прилагаемую копию уведомления и презентации, подготовленные в связи с письменным постановлением. подробнее | Выпуск фондовой биржи |
| 2020 | 1 октября 2020 г.Hexagon Composites ASA: Обязательное уведомление о передаче акций основным инсайдеромСиндре Ротеватн, старший финансовый менеджер и основной инсайдер Hexagon Composites, передал сегодня владение 7000 акций Hexagon Composites от его компании Bonsens AS лично ему. Компания на 100% контролируется Синдре Ротеватн. подробнее | Выпуск фондовой биржи |
| 2020 | 22 сентября 2020 г.Hexagon Composites ASA: Сохраните дату — День виртуальных рынков капитала 2020Hexagon Composites проведет День виртуальных рынков капитала во вторник, 17 ноября 2020 г., с 09: 00-12: 00 CET. подробнее | Выпуск на фондовой бирже |
| 2020 | 15 сентября 2020 г.Консорциум h3Bus и Wrightbus объединили усилия для преобразования общественного транспорта с первыми электрическими автобусами на топливных элементах с истинным нулевым уровнем выбросов поставка электробусов на водородных топливных элементах в Европу. Консорциум h3Bus в настоящее время планирует развернуть 1000 электрических автобусов на водородных топливных элементах вместе со вспомогательной инфраструктурой в европейских городах по конкурентоспособным ценам. подробнее | Пресс-релиз |
| 2020 | 31 августа 2020 г.Hexagon Composites ASA: Обязательное уведомление о торговле первичным инсайдеромКарен Ромер, старший вице-президент по коммуникациям в Hexagon Composites ASA, 31 августа 2020 г. приобрела 1800 акции Hexagon Composites ASA по средней цене 52,75 норвежских крон. После этой сделки г-жа Ромер владеет в общей сложности 1 800 акциями Hexagon Composites ASA. подробнее | Выпуск фондовой биржи |
| 2020 | 31 августа 2020 г.Hexagon Composites ASA: Регистрация увеличения уставного капиталаСсылка сделана на уведомление фондовой биржи, опубликованное Hexagon Composites ASA («Компания») 24 августа 2020 года в отношении частного размещения 18 329 064 новых акций в рамках частного размещения («Частное размещение»).Увеличение акционерного капитала, связанное с новыми акциями, выпущенными при частном размещении, теперь зарегистрировано в Норвежском регистре коммерческих предприятий. Новый зарегистрированный акционерный капитал компании составляет 20 161 971,20 норвежских крон, разделенный на 201 619 712 акций каждая с номинальной стоимостью 0,10 норвежских крон. подробнее | Выпуск фондовой биржи |
| 2020 | 27 августа 2020 г.Обязательное уведомление о сделках — опционыСсылка сделана на объявление от 5 апреля 2017 г., в котором Hexagon Composites ASA («Компания» ) объявила о предоставлении сотрудникам 1 640 000 опционов на акции в рамках своей опционной программы для сотрудников, каждый по цене исполнения 27 норвежских крон за акцию.Из 1 640 000 опционов 1 175 000 опционов были предоставлены высшим руководителям и менеджерам, указанным в качестве основных инсайдеров. подробнее | Выпуск фондовой биржи |
| 2020 | 26 августа 2020 г.Hexagon Composites ASA: обязательное уведомление о сделке первичным инсайдеромГанс Питер Хавдал, член совета директоров Hexagon Composites ASA, 25 августа 2020 г. приобрел 3900 акций Hexagon Composites ASA по средней цене 51 норвежскую крону. После этой сделки г-н.Havdal владеет 3 900 акциями Hexagon Composites ASA. подробнее | Выпуск фондовой биржи |
| 2020 | 25 августа 2020 г.Hexagon Composites ASA: Приглашение на презентацию Hexagon и его планов Spin Off для Hexagon Purus Ссылка на объявление фондовой биржи от 24 августа 2020, в отношении планируемого выделения и листинга Hexagon Purus. | Выпуск на фондовой бирже |
| 2020 | 24 августа 2020 годаHexagon Composites ASA: частное размещение успешно завершеноНЕ ДЛЯ ВЫПУСКА, ПУБЛИКАЦИИ ИЛИ РАСПРОСТРАНЕНИЯ, ПОЛНОСТЬЮ ИЛИ ЧАСТИЧНО ПРЯМО ИЛИ КОСВЕННО, ЧАСТЬ , КАНАДА, ЯПОНИЯ ИЛИ СОЕДИНЕННЫЕ ШТАТЫ НАПРЯМУЮ ИЛИ КОСВЕННО, В АВСТРАЛИИ, КАНАДЕ, ЯПОНИИ ИЛИ СОЕДИНЕННЫХ ШТАТАХ ИЛИ В ЛЮБОМ ДРУГИХ ЮРИСДИКЦИЯХ, В КОТОРЫХ РАСПРОСТРАНЕНИЕ, ПУБЛИКАЦИЯ ИЛИ РАСПРОСТРАНЕНИЕ БЫЛИ НЕЗАКОННЫМИ.ДАННОЕ ОБЪЯВЛЕНИЕ НЕ ЯВЛЯЕТСЯ ПРЕДЛОЖЕНИЕМ НИКАКИХ ЦЕННЫХ БУМАГ, ОПИСАННЫХ ЗДЕСЬ. подробнее | Выпуск фондовой биржи |
| 2020 | 24 августа 2020 г.Hexagon Composites ASA: Предполагается частное размещение и намерение выделить и разместить Hexagon PurusНЕ ДЛЯ ВЫПУСКА, ПУБЛИКАЦИИ ИЛИ РАСПРОСТРАНЕНИЯ ИЛИ В ЦЕЛОМ ИЛИ ЧАСТЬ НАПРЯМУЮ ИЛИ КОСВЕННО, В АВСТРАЛИИ, КАНАДЕ, ЯПОНИИ ИЛИ СОЕДИНЕННЫХ ШТАТАХ НАПРЯМУЮ ИЛИ КОСВЕННО, В АВСТРАЛИИ, КАНАДЕ, ЯПОНИИ ИЛИ СОЕДИНЕННЫХ ШТАТАХ ИЛИ ЛЮБОЙ ЮРИСДИКЦИИ, В КОТОРОЙ БЫЛО РАЗРЕШЕНО, ПУБЛИКАЦИЯ ИЛИ РАСПРОСТРАНЕНИЕ.ДАННОЕ ОБЪЯВЛЕНИЕ НЕ ЯВЛЯЕТСЯ ПРЕДЛОЖЕНИЕМ НИКАКИХ ЦЕННЫХ БУМАГ, ОПИСАННЫХ ЗДЕСЬ. подробнее | Выпуск фондовой биржи |
| 2020 | 21 августа 2020 г.Обязательное уведомление о сделках — опционыСсылка сделана на объявление от 5 апреля 2017 г., в котором Hexagon Composites ASA («Компания» ) объявила о предоставлении сотрудникам 1 640 000 опционов на акции в рамках своей опционной программы для сотрудников, каждый по цене исполнения 27 норвежских крон за акцию.Из 1 640 000 опционов 1 175 000 опционов были предоставлены высшим руководителям и менеджерам, указанным в качестве основных инсайдеров. подробнее | Выпуск фондовой биржи |
Шестиугольник: шестигранный многоугольник.
Произношение: /ˈhɛk.səˌgɒn/ Объясните
| Шестиугольник — это шестигранник. многоугольник.Стороны шестиугольника — это отрезки прямых линий. Шестиугольник — это плоский фигура, фигура, существующая в самолет. Шестиугольник может быть вогнутый или выпуклый. Если выпуклый шестиугольник равносторонний (стороны одинаковой длины), то шестиугольник — правильный шестиугольник. |
Указатель статей
ШестиугольникПравильный шестиугольник
Части правильного шестиугольника
Формулы правильного шестиугольника
Как построить правильный шестиугольник из его окружности
Как построить центр, вписанную и окружную окружность правильного шестиугольника
Тесселяции естественного шестиугольника
и изготовленные шестиугольники
Правильный шестигранник
Правильный шестиугольник — это шестигранник, равносторонний, выпуклый многоугольник.У равностороннего многоугольника все стороны одинаковой длины. Между любые две точки выпуклой фигуры покидают фигуру.
| Нажмите на синие точки и перетащите их, чтобы изменить фигуру. Когда длина стороны отличается от радиуса описанной окружности? |
| Манипулятор 1 — правильный шестиугольник, созданный с помощью GeoGebra. |
Детали правильного шестигранника
- сторона или край : один из отрезок что составляет шестиугольник.Длина стороны правильного шестиугольника в этой статье мы будем обозначать s .
- вершина: Где встречаются две стороны шестиугольника.
- интерьер: Площадь внутри шестиугольника.
- Внешний вид: Площадь за пределами шестиугольника.
- граница: Стороны и вершины шестиугольника.
- центр: Точка в середине шестиугольника.Центр правильного шестиугольника можно найти на пересечении серединных перпендикуляров любого две стороны. См. Как построить центр, Вписанная и окружность правильного шестиугольника. Центр правильный шестиугольник — это также его центр тяжести .
- вписанной окружности: Круг, центр которого находится в центре правильного шестиугольника, который касается каждую сторону шестиугольника один раз.В этой статье радиус Вписанный круг обозначим r 1 .
- описанной окружности: Круг, центр которого находится в центре правильного шестиугольника, который пересекает каждую из вершин правильного шестиугольника. В этой статье, Радиус описанной окружности обозначим r 2 .
- апофема: Отрезок от центра правильного шестиугольника до середины одной из сторон.Длина апофемы такая же, как и радиус вписанной окружности и обозначается ( r 1 ).
- сагитта: Отрезок от центра стороны до края описанная окружность правильного шестиугольника, лежащего на одной прямой с апофемой.
- центральный угол: : угол между двумя отрезками прямой от центра правильного шестиугольника до двух соседних вершин.В центральный угол правильного шестиугольника всегда 72 °.
- внутренний угол: Угол между двумя соседними сторонами. Внутренние углы обычного шестиугольник всегда измеряйте 120 °. Сумма мер внутренних углов любого выпуклого шестиугольника составляет 720 °.
- внешний угол: Угол между удлиненной стороной правильного шестиугольника и соседняя сторона. Внешние углы правильного шестиугольника всегда Измерьте 60 °.
Формулы правильного шестиугольника
Как построить правильный шестиугольник из его окружности
| Шаг | Рисунок | Описание и обоснование |
|---|---|---|
| 1 | Нарисуйте круг. Обозначьте центр круга a . Это дано. | |
| 2 | Нарисуйте круг с центром на окружности круга a это тот же радиус, что и у окружности a .Обозначьте центр этого круга б . | |
| 3 | Обозначьте точки пересечения окружностей c и d . | |
| 4 | Нарисуйте отрезки линии ab , ac , ad , bc и bd . Обратите внимание, что все эти отрезки являются радиусами конгруэнтных круги.Это означает, что все они одинаковой длины. Итак, треугольники Δabc и Δabd — равносторонние треугольники, треугольники, стороны которых имеют одинаковую меру. Углы равносторонних треугольников тоже есть такая же мера. Следовательно, треугольники Δabc и Δabd конгруэнтны Теорема сравнения SAS. | |
| 5 | Нарисуйте еще один круг с тем же радиусом, что и , с центром в с .Обозначьте новое пересечение круга c и круга a как e . | |
| 6 | Нарисуйте еще один круг с тем же радиусом, что и , с центром в и . Обозначьте новое пересечение круга e и круга a как f . Обратите внимание, что с помощью тех же аргументов, которые использовались в шаг 5, треугольники Δabc и Δace составляют конгруэнтные равносторонние треугольники. | |
| 7 | Продолжайте узор до окружностей с центрами b , c ,
Нарисованы d , e , f и g . Мы знаем это
правильный шестиугольник, потому что
| |
| Таблица 2: Как построить правильный шестиугольник от его описанной окружности. | ||
Как построить центр, окружность и окружность правильного шестиугольника
Мозаика шестиугольника
Тесселяция одного или нескольких многоугольников — это расположение тех многоугольников, которые заполняет самолет. Это ряд мозаик, в которых используются шестиугольники. В большинстве представленных здесь мозаик используются правильные шестиугольники.
| Правильная мозаика шестиугольника.Вокруг три шестиугольника каждая вершина. | Трехгранник. Каждая вершина имеет правильный шестиугольник, равносторонний треугольник, правильный шестиугольник и равносторонний треугольник. |
| Таблица 4: мозаика шестиугольника | |
Естественные и промышленные шестиугольники
Список литературы
- МакАдамс, Дэвид Э .. Словарь всех математических слов, шестиугольник . 2-е классное издание 20150108-4799968.стр. 90. ООО «Жизнь — это история проблемы». 8 января 2015 года. Купить книгу
Дополнительная информация
- Макадамс, Дэвид Э .. Многоугольник . allmathwords.org. ООО «Жизнь — это история проблемы». 22.10.2010.
Цитируйте эту статью как:
Макадамс, Дэвид Э. Шестиугольник . 22.04.2019. Энциклопедия всех математических слов. ООО «Жизнь — это история проблемы». http://www.allmathwords.org/en/h/hexagon.html.Изображение кредита
История изменений
22.04.2019: Обновите уравнения и выражения в новом формате.(Макадамс, Дэвид Э.)21.12.2018: Проверено и исправлено произношение IPA. (Макадамс, Дэвид Э.)
16.07.2018: Удалены неработающие ссылки, обновлена лицензия, добавлена новая разметка, реализован новый протокол Geogebra. (Макадамс, Дэвид Э.)
22.10.2010: Начальная версия. (Макадамс, Дэвид Э.)
правильных многоугольников
Обзор
Многоугольник (от греческих слов poly, означающих «много» и «gon», что означает «угол») — это замкнутая двумерная фигура с множеством (т.е.е. три и более) прямых сторон. Правильный многоугольник — это такой многоугольник, у которого все стороны имеют одинаковую длину (т.е. фигура равносторонняя ), и все внутренние углы (и, следовательно, все внешние углы) имеют одинаковую величину (т.е. фигура равносторонний ). Когда мы говорим, что фигура замкнута , мы имеем в виду, что ровно две стороны встречаются в каждой вершине фигуры. Правильный многоугольник может быть простым или сложным .Простой правильный многоугольник — это выпуклая фигура, в которой стороны образуют границу вокруг единого замкнутого пространства, а внутренний угол не превышает ста восьмидесяти градусов. сложный правильный многоугольник будет иметь форму звезды, и стороны будут пересекаться друг с другом в разных точках. Ниже мы приводим некоторые из наиболее часто встречающихся выпуклых правильных многоугольников.
- Равносторонний треугольник — трехсторонняя фигура с внутренними углами шестьдесят градусов (60 °)
Равносторонний треугольник
- Квадрат — четырехсторонняя фигура, у которой все внутренние углы прямые (90 °)
Площадь
- Пентагон — пятиугольная фигура с внутренними углами сто восемь градусов (108 °)
Пятиугольник
- Hexagon — шестигранная фигура с внутренними углами сто двадцать градусов (120 °)
Шестиугольник
По мере увеличения количества сторон ему соответствует количество вершин.Величина внутреннего угла в каждой вершине будет одинаковой и будет увеличиваться по мере увеличения количества сторон. Сумма внутренних углов будет просто внутренним углом в любой вершине, умноженным на количество сторон. Если у многоугольника n сторон, соотношение между количеством сторон и внутренним углом в любой вершине (в градусах) можно найти по следующей формуле:
| Внутренний угол = ( n -2) × | 180 ° |
| n |
В качестве альтернативы мы можем выразить внутренний угол в радианах:
| Внутренний угол = ( n -2) × | π |
| n |
Внешний угол в каждой вершине выпуклого правильного многоугольника будет одинаковым и будет разницей между внутренним углом в этой вершине и ста восемьюдесятью градусами, поскольку внутренний и внешний углы выпуклого многоугольника всегда равны дополнительный (в сумме дает сто восемьдесят градусов).Чем больше сторон имеет выпуклый правильный многоугольник, тем меньше будет внешний угол в каждой вершине, потому что внутренний угол будет больше. Сумма внешних углов выпуклого многоугольника всегда будет составлять триста шестьдесят градусов (360 °), поэтому, если многоугольник имеет n сторон, соотношение между количеством сторон и внешним углом в любой вершине ( в градусах) можно выразить следующей формулой:
| Внешний угол = | 360 ° |
| n |
Мы также можем выразить внешний угол в радианах:
| Внешний угол = | 2π радиан |
| n |
На схеме ниже показано соотношение между внутренними и внешними углами выпуклого многоугольника.Показанная здесь фигура представляет собой шестиугольник, что означает, что у него шесть сторон, что дает внутренний угол в сто двадцать градусов (120 °) и внешний угол в шестьдесят градусов (60 °) в каждой вершине.
Внутренний и внешний углы выпуклого правильного многоугольника являются дополнительными.
Выше мы упоминали, что сумму внутренних углов можно вычислить, умножив внутренний угол в любой вершине на количество сторон.Следующая формула также работает для выпуклого правильного многоугольника со сторонами n и не требует, чтобы вы сначала находили внутренний угол в одной вершине:
Сумма внутренних углов = ( n — 2) × 180 °
Детали других выпуклых правильных многоугольников приведены в таблице ниже. Обратите внимание, что теоретически нет ограничений на количество возможных выпуклых правильных многоугольников, хотя по мере увеличения количества сторон и вершин форма будет все больше и больше походить на круг.
Анатомия выпуклого правильного многоугольника
Внутри любого выпуклого правильного многоугольника есть точка, которая равноудалена от вершин многоугольника. Эта точка, которая называется центром многоугольника, также находится на одинаковом расстоянии от середин сторон многоугольника. Отрезок линии, проведенный от центра к любой вершине выпуклого правильного многоугольника, известен как радиус многоугольника.Это также радиус круга, который полностью охватывает многоугольник и проходит через все вершины. Этот круг называется описанным кругом или описанным кругом . Второй отрезок линии, проведенный от центра к середине любой стороны выпуклого правильного многоугольника, известен как апофема многоугольника. Он также образует радиус круга, в данном случае тот, который полностью заключен в многоугольник и касается каждой стороны многоугольника в его средней точке.Этот круг известен как вписанный круг или вписанный круг .
Связь между радиусом ( r ), апофемой ( a ) и стороной ( s ) восьмиугольника
Восьмиугольник с описанной и вписанной окружностями
Из рисунка выше вы должны увидеть, что размер области восьмиугольника будет где-то между размером вписанной и описанной окружностей.По мере увеличения числа сторон выпуклого правильного многоугольника он будет становиться все более и более похожим на круг, а разница в длине между радиусом и апофемой будет становиться все менее и менее значительной. Области многоугольника, вписанной и описанной окружности также сойдутся.
Вращательная симметрия
Линия симметрии , проведенная через двумерную фигуру, — это линия, которая делит фигуру на две половины, являющиеся зеркальным отображением друг друга.У правильных многоугольников может быть много линий симметрии, что позволяет им поворачиваться вокруг своего центра на некоторый угол (кроме трехсот шестидесяти градусов) без изменения их внешнего вида. Количество линий симметрии напрямую связано с количеством сторон многоугольника, так что равносторонний треугольник имеет три линии симметрии , пятиугольник имеет пять линий симметрии , восьмиугольник имеет восемь линий симметрии , и так далее. Линии симметрии этих форм показаны ниже.Обратите внимание, что для правильных многоугольников с числом сторон и вершин и даже линии симметрии будут проходить через обе пары противоположных вершин и середины противоположных сторон. Для правильных многоугольников с нечетным числом сторон и вершин каждая линия симметрии будет проходить через одну вершину и среднюю точку стороны, противоположной этой вершине.
Правильный многоугольник с n сторонами имеет n линий симметрии.
Диагонали
Диагональ в правильном многоугольнике — это любой линейный сегмент , кроме стороны , которая соединяет одну вершину с другой.Другими словами, это любой отрезок линии, соединяющий две непоследовательных вершины . Любой правильный многоугольник с более чем тремя сторонами имеет две или более диагоналей. Количество диагоналей увеличивается с количеством сторон n и связано с n по следующей формуле:
| Количество диагоналей = | n ( n — 3) |
| 2 |
Давайте рассмотрим те же самые правильные многоугольники, которые мы использовали для демонстрации вращательной симметрии, но на этот раз со ссылкой на их диагонали.Равносторонний треугольник имеет нулевые диагонали, потому что все три отрезка, соединяющие вершины, являются сторонами треугольника. Пентагон имеет пять сторон и вершин, и из рисунка ниже видно, что он также имеет пять диагоналей (использование приведенной выше формулы для определения количества диагоналей для пятиугольника также даст результат пять). Последний правильный многоугольник, показанный здесь, — это восьмиугольник, восьмиугольная фигура. Теперь вы можете начать испытывать некоторые трудности с подсчетом количества диагоналей, но формула говорит нам, что на самом деле существует двадцать (20).Квадрат в формуле говорит нам, что количество диагоналей увеличивается на экспоненциально на с увеличением количества сторон.
Количество диагоналей увеличивается экспоненциально с n
Помимо количества диагоналей, принадлежащих конкретному правильному многоугольнику, математиков также интересует количество пересечений между диагоналями (включая вершины многоугольника), количество отрезков линии , которые они пересекают друг друга. в (это включает стороны многоугольника) и количество областей (замкнутых областей), которые создают пересечения внутри многоугольника.Взяв в качестве примера пятиугольник, у нас есть десять (10) пересечений, двадцать (20) отрезков прямых и одиннадцать (11) областей. В восемнадцатом веке нашей эры швейцарский математик Леонард Эйлер разработал формулу, связывающую количество пересечений, отрезков прямых и областей. Формула Эйлера представляет особый интерес в связи с изучением теории графов . Обратите внимание, кстати, что рисование всех диагоналей из одной вершины только правильного многоугольника разделит многоугольник на n — 2 треугольника, где n — количество сторон.
Диагонали одной вершины образуют n — 2 треугольника
Нахождение площади выпуклого правильного многоугольника
Определение периметра правильного многоугольника — относительно тривиальное упражнение. Как только вы знаете длину одной стороны, вы просто умножаете ее на количество сторон, чтобы получить периметр.Найти площадь правильного многоугольника не так-то просто. Самый простой правильный многоугольник — это равносторонний треугольник. Если мы знаем длину каждой стороны, мы можем относительно легко найти площадь, потому что площадь треугольника определяется путем умножения длины основания треугольника на его высоту и деления на два. Если мы возьмем одну сторону в качестве основания треугольника, мы сможем использовать теорему Пифагора, чтобы найти высоту. Рассмотрим следующий равносторонний треугольник:
Треугольник ABC — равносторонний треугольник
В равностороннем треугольнике ABC длина каждой стороны треугольника представлена как s .Высота h треугольника — это длина перпендикуляра от средней точки D основания треугольника до вершины B. Поскольку треугольник ABD является прямоугольным, теорема Пифагора говорит нам, что длина перпендикуляра BD , а значит, и высоту h треугольника, можно найти по следующей формуле:
ч = √ ( с 2 — ( 1 / 2 с ) 2 )
Следовательно, если мы знаем значение s , мы можем найти высоту ( BD ) треугольника и, следовательно, площадь треугольника (площадь равна половине длины основания, умноженной на высоту).Если у нас есть значение для s из шесть (6), мы получим следующее:
ч = √ (6 2 — 3 2 ) = √ (36-9) = √27 = 5,196
Теперь мы можем вычислить площадь треугольника:
| Площадь треугольника = | 6 × 5,196 | = 15,588 |
| 2 |
В качестве альтернативы мы могли бы использовать следующую формулу, которая позволяет нам найти площадь равностороннего треугольника без предварительного определения высоты треугольника, при условии, что мы знаем длину s каждой стороны:
| Площадь треугольника = | с 2 × √3 |
| 4 |
С помощью этой формулы, если мы снова используем значение для s из шести, мы получим следующее:
| Площадь треугольника = | 36 × 1.732 | = 15.588 |
| 4 |
Нахождение площади квадрата — тривиальное упражнение, так как площадь будет просто длиной одной стороны, умноженной на себя (то есть в квадрате). Найти площадь правильного выпуклого многоугольника с более чем четырьмя сторонами не так просто, хотя есть простая формула, которую можно применить, если мы знаем длину каждой стороны и длину апофемы (отрезок линии соединяет центр многоугольника со средней точкой любой стороны).Длину апофемы для данного правильного многоугольника с n сторонами и длиной s можно найти с помощью ряда различных формул, но поскольку все эти формулы используют тригонометрические функции, мы не будем их здесь обсуждать. Предположим вместо этого, что для целей этого упражнения мы нашли апофему путем измерения. Мы можем использовать следующую формулу, чтобы найти площадь:
| Площадь выпуклого правильного многоугольника = | ap |
| 2 |
где:
- a = длина апофемы
- p = длина периметра
Рассмотрим следующий восьмиугольник:
У восьмиугольника длина стороны 6 и апофема 7.243
Показанный выше восьмиугольник имеет длину стороны шесть (6) и апофему семь запятая два четыре три (7,243). Периметр p восьмиугольника будет равен длине одной стороны ( шесть ), умноженной на общее количество сторон ( восемь ), что дает значение p из сорок восемь (48) . Теперь мы можем вычислить площадь восьмиугольника следующим образом:
| Площадь = | 7.243 × 48 | = 173,832 |
| 2 |
Чтобы дважды проверить этот результат, мы можем подойти к проблеме поиска площади восьмиугольника с другой точки зрения, чтобы увидеть, получим ли мы тот же результат. Рассмотрим следующую схему, на которой показан тот же восьмиугольник, но с некоторой дополнительной конструкцией:
Восьмиугольник имеет внутренние углы 135 ° и внешние углы 45 °.
Мы уже знаем, что восьмиугольник имеет внутренние углы, равные ста тридцати пяти градусам (135 °), а поскольку внутренний и внешний углы выпуклого многоугольника равны дополнительным (т.е.е. в сумме они составляют сто восемьдесят градусов) тогда внешние углы должны составлять сорок пять градусов (45 °). Таким образом, треугольник ABC имеет два угла, каждый из которых составляет сорок пять градусов, поэтому оставшийся угол должен составлять девяносто градусов (90 °), что делает его прямоугольным. Кроме того, с двумя углами, имеющими одинаковое значение, треугольник ABC должен быть равнобедренным прямоугольным треугольником , что означает, что отрезок AB такой же длины, как отрезок BC . Следовательно, мы можем использовать теорему Пифагора, чтобы найти длину отрезков AB, и BC, :
| AB = BC = √ | s 2 | = √18 = 4.243 |
| 2 |
Фактически, мы можем построить четыре прямоугольных треугольника, как показано на рисунке ниже, чтобы преобразовать восьмиугольник в квадрат. Площадь квадрата можно рассчитать, умножив общую длину одной стороны на себя (т.е. на , возведя в квадрат ее).
Можно построить четыре равных треугольника, чтобы превратить восьмиугольник в квадрат.
Площадь восьмиугольника можно найти, вычтя площадь четырех прямоугольных треугольников из площади квадрата.Расчет будет следующим:
| Площадь восьмиугольника = (4,243 × 2 + 6) 2 — 4 × | 4,243 2 |
| 2 |
Площадь восьмиугольника = 14,486 2 — 4 × 9,001 = 209,844 — 36,004 = 173,84
Ответ, который мы получаем здесь, по сути тот же, что и ранее, с (очень небольшой) разницей из-за ошибки округления.Хотя этот подход работает для пятиугольника, однако он не работает так хорошо для других правильных многоугольников, поэтому формула апофемы является более универсальным решением. Посмотрим, как это работает.
Угол, образованный в центре выпуклого правильного многоугольника двумя смежными радиусными линиями, известен как центральный угол . Для многоугольника со сторонами n центральный угол будет равен триста шестидесяти градусам, разделенным на n (360 ° ÷ n ).Две радиальные прямые вместе со стороной многоугольника, к которой они примыкают, образуют равнобедренный треугольник. На диаграмме ниже одна сторона s пятиугольника образует основание равнобедренного треугольника ABC, а прилегающие радиусы образуют боковые стороны треугольника. Поскольку апофема a образует перпендикуляр, который соединяет основание треугольника с вершиной B , то высота треугольника будет равна длине апофемы.
Равнобедренный треугольник образован одной стороной и двумя смежными радиусными линиями.
Каждая сторона многоугольника образует основу равнобедренного треугольника, а площадь многоугольника может быть найдена путем сложения площадей всех образованных таким образом треугольников.Площадь треугольника определяется по следующей формуле:
| Площадь треугольника = | основание × высота |
| 2 |
Таким образом, площадь многоугольника с n сторонами может быть выражена следующим образом:
| Площадь выпуклого правильного многоугольника = | n × основание × высота |
| 2 |
Мы уже установили, что длина основания треугольника равна длине s одной из сторон многоугольника.Мы также установили, что длина p периметра многоугольника равна количеству сторон n , умноженному на длину s каждой стороны. Учитывая, что высота треугольника равна длине a апофемы, мы можем переписать формулу как:
| Площадь выпуклого правильного многоугольника = | ap |
| 2 |
Правильные звездчатые многоугольники
Правильные многоугольники, которые являются , а не выпуклыми , образуют различные типы звездообразных форм в зависимости от общего количества вершин.Как и в случае с выпуклым правильным многоугольником, вершины равномерно распределены вокруг некоторой центральной точки, от которой они равноудалены. В отличие от выпуклого многоугольника, стороны не соединяют вершины последовательно. Например, они могут соединять каждую вторую вершину или каждую третью вершину. Чтобы кратко классифицировать эти невыпуклые (звездообразные) правильные многоугольники, мы можем использовать нечто, называемое символом Шафли . Символ Шлефли назван в честь швейцарского математика девятнадцатого века Людвига Шлефли и используется в геометрии для обозначения конфигурации двух и трехмерных геометрических фигур.В своей наиболее тривиальной форме он обозначает количество сторон выпуклого правильного многоугольника и принимает форму { n }, где n представляет количество сторон. Например, пятиугольник, который является простейшим примером выпуклого правильного многоугольника, будет иметь символ Шлефли {5}.
Когда мы начинаем рассматривать невыпуклые многоугольники, символ Шлефли становится немного более полезным, так как он также сообщает нам «расстояние» (в терминах вершин) между двумя вершинами, которые соединены одной стороной многоугольника.Взяв в качестве примера пентаграмму , вершины находятся в точно таком же положении, как и у пятиугольника, но «стороны» многоугольника соединяют альтернативных вершин . Таким образом, символ Шлефли для пентаграммы будет записан как {5/2}, где пять представляет количество сторон, а два представляет расстояние между соседними вершинами (то есть вершинами, которые соединены одним отрезком линии. ). Поскольку мы говорим о невыпуклых (по сути, звездообразных) многоугольниках, это может помочь избежать путаницы, если вы перестанете думать в терминах «сторон» и вместо этого будете думать в терминах «краев».На схеме ниже изображена пентаграмма. Мы наложили пятиугольник, который будет образован из тех же вершин.
Пентаграмма и пятиугольник с общим набором вершин
Таким образом, модифицированный символ Шлефли принимает форму { n / m }, где n представляет количество сторон (или ребер ), а m представляет расстояние между соседними вершинами.Значение м. приблизительно представляет, сколько раз граница многоугольника обвивается вокруг центра. Отношение между n и m определяет еще одну особенность невыпуклого правильного многоугольника, а именно, будет ли он вырожденным . Чтобы многоугольник был невырожденным , значения n и m должны быть взаимно простыми. Другими словами, единственное целое число, которое разделит их оба и даст результат целого числа, будет один .Пентаграмма со значениями для n и m , равными пяти и двум соответственно, является невырожденной (единственное число, на которое можно разделить пять и два, чтобы получить результат целого числа, является единица).
Ребра пентаграммы пересекаются друг с другом в пяти точках пересечения, которые сами образуют вершины небольшого внутреннего пятиугольника. Однако эти точки пересечения не считаются вершинами, а отрезки линии, соединяющие точки пересечения друг с другом, не считаются сторонами или ребрами сами по себе.Интересно, что пентаграмму можно создать из пятиугольника, расширив стороны пятиугольника до пересечения. Затем можно построить более крупный пятиугольник, последовательно соединив вершины вновь созданной пентаграммы. Теоретически этот процесс можно повторять бесконечно, создавая пентаграммы и пятиугольники все большего размера. Вот типичный вырожденный невыпуклый правильный многоугольник, октаграмма (число Шефли {8/2}):
Октаграмма имеет число Склефли {8/2}.
Одно ощутимое различие между вырожденным невыпуклым правильным многоугольником и невырожденным состоит в том, что невырожденный невыпуклый правильный многоугольник можно нарисовать вручную, не отрывая ручки (или карандаша) от бумаги или проходя по нему. линия дважды.В области компьютерной векторной графики невырожденность является довольно важным фактором, определяющим легкость, с которой рисунок может быть отрисован на компьютере.