Модуль Юнга
Модуль Юнга (упругости I рода, продольной упругости) – механическая характеристика материалов, определяющая их способность сопротивляться продольным деформациям. Показывает степень жесткости материала.
Назван в честь английского ученого Томаса Юнга.
Обозначается латинской прописной буквой E
Единица измерения – Паскаль [Па].
В сопротивлении материалов модуль продольной упругости участвует в расчетах на жесткость при растяжении-сжатии и изгибе, а также в расчетах на устойчивость.
Учитывая то, что практически все конструкционные материалы имеют значение E высокого порядка (как правило 109 Па), его размерность часто записывают с помощью кратной приставки «гига» (гигапаскаль [ГПа])
Для всех материалов его величину можно определить в ходе эксперимента по определению модуля упругости I рода.
Приближенно значение модуля можно определить по диаграмме напряжений получаемой при испытаниях на растяжение.
Рис. 1 Начальный фрагмент диаграммы напряжений
В этом случае модуль Юнга равен отношению нормальных напряжений к соответствующим относительным деформациям, на участке диаграммы (рис. 1) до предела пропорциональности σпц (тангенсу угла α наклона участка пропорциональности к оси деформаций ε).
E=σ/ε=tgα
В таблице 1 приведены сравнительные значения модуля для некоторых наиболее часто используемых материалов
Таблица 1
Материал | Модуль Юнга |
Сталь | 200 |
Чугун | 120 |
Серый чугун | 110 |
Алюминий | 70 |
Дюралюминий | 74 |
Титан | 120 |
Бронза | 100 |
Латунь | 95 |
Медь | 110 |
Олово | 35 |
Хром | 300 |
Никель | 210 |
Кремний | 110 |
Свинец | 18 |
Бетон | 20 |
Дерево | 10 |
Стекло | 70 |
Модуль упругости I рода служит коэффициентом пропорциональности в формуле описывающей закон Гука:
σ=Eε
Связка модуля Юнга с геометрическими характеристиками поперечных сечений бруса показывает их жесткость:
EA – жесткость поперечного сечения при растяжении-сжатии,
где A – площадь поперечного сечения стержня;
EI – жесткость поперечного сечения при изгибе,
где I – осевой момент инерции сечения балки.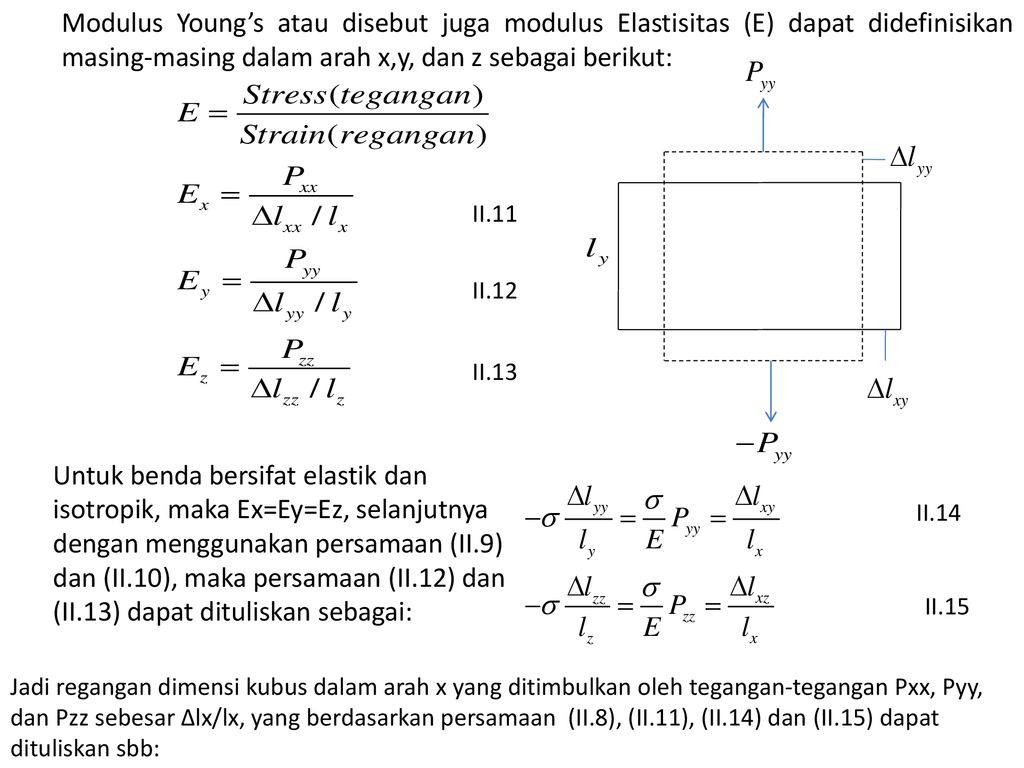
Модуль упругости II рода (модуль сдвига) >
Примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Подробнее
Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.
НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ
На нашем сайте можно бесплатно скачать:
— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку
Сохранить или поделиться с друзьями
Помощь с решением
ВЫБЕРИТЕ РАЗДЕЛ МЕХАНИКИ
- Техническая механика (техмех)
- Теоретическая механика (теормех)
- Сопротивление материалов (сопромат)
- Строительная механика (строймех)
- Детали машин и ОК (ДМ)
Поддержать сайт
Модуль упругости Юнга и сдвига, коэффициент Пуассона значения (Таблица)
Упругие свойства тел
Ниже приводятся справочные таблицы общеупотребительных констант; если известны две их них, то этого вполне достаточно для определения упругих свойств однородного изотропного твердого тела.
Модуль Юнга или модуль продольной упругости в дин/см2.
Модуль сдвига или модуль кручения G в дин/см2.
Модуль всестороннего сжатия или модуль объемной упругости К в дин/см2.
Объем сжимаемости k=1/K/.
Коэффициент Пуассона µ равен отношению поперечного относительного сжатия к продольному относительному растяжению.
Для однородного изотропного твердого материала имеют место следующие соотношения между этими константами:
G = E / 2(1 + μ) — (α)
μ = (E / 2G) — 1 — (b)
K = E / 3(1 — 2μ) — (c)
Коэффициент Пуассона имеет положительный знак, и его значение обычно заключено в пределах от 0,25 до 0,5, но в некоторых случаях он может выходить за указанные пределы. Степень совпадения наблюдаемых значений µ и вычисленных по формуле (b) является показателем изотропности материала.
Таблицы значений Модуля упругости Юнга, Модуля сдвига и коэффициента Пуассона
Курсивом даны значения, вычисленные из соотношений (a), (b), (c).
|
Материал при 18°С |
Модуль Юнга E, 1011 дин/см2. |
Модуль сдвига G, 1011 дин/см2. |
Коэффициент Пуассона µ |
|
|
Алюминий |
7,05 |
2,62 |
0,345 |
7,58 |
|
Висмут |
3,19 |
1,20 |
0,330 |
3,13 |
|
Железо |
|
8,2 |
0,29 |
16,9 |
|
Золото |
7,8 |
2,7 |
0,44 |
21,7 |
|
Кадмий |
4,99 |
1,92 |
0,300 |
4,16 |
|
Медь |
12,98 |
4,833 |
0,343 |
13,76 |
|
Никель |
20,4 |
7,9 |
0,280 |
16,1 |
|
Платина |
16,8 |
6,1 |
0,377 |
|
|
Свинец |
1,62 |
0,562 |
0,441 |
4,6 |
|
Серебро |
8,27 |
3,03 |
0,367 |
10,4 |
|
Титан |
11,6 |
4,38 |
|
10,7 |
|
Цинк |
9,0 |
3,6 |
0,25 |
6,0 |
|
Сталь (1% С) 1) |
21,0 |
8,10 |
0,293 |
16,88 |
|
(мягкая) |
21,0 |
8,12 |
0,291 |
16,78 |
|
Константан 2) |
16,3 |
6,11 |
0,327 |
15,7 |
|
Манганин |
12,4 |
4,65 |
0,334 |
12,4 |
|
1) Для стали, содержащий около 1% С, упругие константы, как известно , меняются при термообработке. 2) 60% Cu, 40% Ni. |
||||
Экспериментальные результаты, приводимые ниже, относятся к обычным лабораторным материалам, главным образом проволокам.
|
Вещество |
Модуль Юнга E, 1011 дин/см2. |
Модуль сдвига G, 1011 дин/см2. |
Коэффициент Пуассона µ |
Модуль объемной упругости К, 1011 дин/см2. |
|
Бронза (66% Cu) |
-9,7-10,2 |
3,3-3,7 |
0,34-0,40 |
11,2 |
|
Медь |
10,5-13,0 |
3,5-4,9 |
0,34 |
13,8 |
|
Нейзильбер1) |
11,6 |
4,3-4,7 |
0,37 |
— |
|
Стекло |
5,1-7,1 |
3,1 |
0,17-0,32 |
3,75 |
|
Стекло иенское крон |
6,5-7,8 |
2,6-3,2 |
0,20-0,27 |
4,0-5,9 |
|
Стекло иенское флинт |
5,0-6,0 |
2,0-2,5 |
0,22-0,26 |
3,6-3,8 |
|
Железо сварочное |
19-20 |
7,7-8,3 |
0,29 |
16,9 |
|
Чугун |
10-13 |
3,5-5,3 |
0,23-0,31 |
9,6 |
|
Магний |
4,25 |
1,63 |
0,30 |
— |
|
Бронза фосфористая2) |
12,0 |
4,36 |
0,38 |
— |
|
Платиноид3) |
13,6 |
3,6 |
0,37 |
— |
|
Кварцевые нити (плав. |
7,3 |
3,1 |
0,17 |
3,7 |
|
Резина мягкая вулканизированная |
0,00015-0,0005 |
0,00005-0,00015 |
0,46-0,49 |
— |
|
Сталь |
20-21 |
7,9-8,9 |
0,25-0,33 |
16,8 |
|
Цинк |
8,7 |
3,8 |
0,21 |
— |
|
1) 60% Cu, 15% Ni, 25% Zn 2) 92,5% Cu, 7% Sn, 0,5% P 3) Нейзильбер с небольшим количеством вольфрама. |
||||
)
|
Вещество |
Модуль Юнга E, 1011 дин/см2. |
Вещество |
Модуль Юнга E, 1011 дин/см2. |
|
Цинк (чистый) |
9,0 |
Дуб |
1,3 |
|
Иридий |
52,0 |
Сосна |
0,9 |
|
Родий |
29,0 |
Красное дерево |
0,88 |
|
Тантал |
18,6 |
Цирконий |
7,4 |
|
Инвар |
17,6 |
Титан |
10,5-11,0 |
|
Сплав 90% Pt, 10% Ir |
21,0 |
Кальций |
2,0-2,5 |
|
Дюралюминий |
7,1 |
Свинец |
0,7-1,6 |
|
Шелковые нити1 |
0,65 |
Тиковое дерево |
1,66 |
|
Паутина2 |
0,3 |
Серебро |
7,1-8,3 |
|
Кетгут |
0,32 |
Пластмассы: |
|
|
Лед (-20С) |
0,28 |
Термопластичные |
0,14-0,28 |
|
Кварц |
7,3 |
Термореактивные |
0,35-1,1 |
|
Мрамор |
3,0-4,0 |
Вольфрам |
41,1 |
|
1) Быстро уменьшается с увеличением нагрузки 2) Обнаруживает заметную упругую усталость |
|||
|
Температурный коэффициент (при 150С) Et=E11 (1-ɑ (t-15)), Gt=G11 (1-ɑ (t-15)) |
Сжимаемость k, бар-1 |
|||
|
|
ɑ, для Е |
ɑ, для G |
|
|
|
Алюминий |
4,8*10-4 |
5,2*10-4 |
Алюминий |
1,36*10-6 |
|
Латунь |
3,7*10-4 |
4,6*10-4 |
Медь |
0,73*10-6 |
|
Золото |
4,8*10-4 |
3,3*10-4 |
Золото |
0,61*10-6 |
|
Железо |
2,3*10-4 |
2,8*10-4 |
Свинец |
2,1*10-6 |
|
Сталь |
2,4*10-4 |
2,6*10-4 |
Магний |
2,8*10-6 |
|
Платина |
0,98*10-4 |
1,0*10-4 |
Платина |
0,36*10-6 |
|
Серебро |
7,5*10-4 |
4,5*10-4 |
Стекло флинт |
3,0*10-6 |
|
Олово |
— |
5,9*10-4 |
Стекло немецкое |
2,57*10-6 |
|
Медь |
3,0*10-4 |
3,1*10-4 |
Сталь |
0,59*10-6 |
|
Нейзильбер |
— |
6,5*10-4 |
|
|
|
Фосфористая бронза |
— |
3,0*10-4 |
|
|
|
Кварцевые нити |
-1,5*10-4 |
-1,1*10-4 |
|
|
Справочник CRC по материаловедению и инженерии, стр.
46
http://www.memsnet.org/material/aluminumalbulk/
Янга модуль
70 ГПа
Тонкие твердые пленки, 270 (1995), стр. 263
http://www.memsnet.org/material/aluminumalbulk/
Коэффициент Пуассона
0,33
Микрозондовое измерение модуля Юнга и Пуассона коэффициент с помощью определения глубины вдавливания и акустической микроскопии, Comte, C. von Stebut, J. Surface & Coatings Technology, v 154, n 1, 1 May 2002, p. 42-8
Жесткость Константы
Растяжение или прочность на излом
Чистый алюминий: 47 МПа
Пленка в артикуле: 70 МПа
Алюминий
осаждение с использованием MOCVD на углеродных волокнах на основе пека, Suzuki, T.
, Materials
Общество служения науке и технике. Материалы Третьего Окинагского симпозиума по материаловедению и инженерии
Общество служения, 1998, стр. 210-13
Остаток нагрузка на кремний
от -20 до -30 МПа неотожженный от 120 до 140 МПа отожженный при 450С
Рентген определение остаточных напряжений в тонких алюминиевых пленках, нанесенных на кремниевые подложки, Корхонен, М.А., Пашкиет, К.А., Scripta Metallurgica, т. 23, № 8, август 1989 г., стр. 1449-53
Удельная теплоемкость
898,7 Дж/кг/К
Справочник CRC по материаловедению и инженерии, стр. 260
http://www.memsnet.org/material/aluminumalbulk/
Термальный проводимость
237 Вт/м/К
Справочник CRC по материаловедению и инженерии, стр.
270-274
http://www.memsnet.org/material/aluminumalbulk/
Диэлектрик константа
Алюминиевый порошок 1,6–1,8
Справочное руководство по диэлектрической проницаемости
http://www.asiinstr.com/dc1.html#Список
Индекс преломление
1,44
Справочник по химическим свойствам
Под редакцией Yaws, C.L. 1999 г.; Макгроу-Хилл
Электрика проводимость
3,538×10 7 Ш/м
ResourceCenter по неразрушающему контролю
http://www.ndt-ed.org/GeneralResources/MaterialProperties/ET/ET_matlprop_Aluminum.htm
Магнитный проходимость
мк r =1
Восприимчивость = 6×10-7 сгс
Базовый анализ металлоискателя Yamazaki, S.
; Накане,
ЧАС.; Танака, А., IEEE
Сделки по инструментам
и измерения, Том: 51, Выпуск: 4, Год: август 2002 г., Страниц: 810-
814
Восприимчивость с http://www.matweb.com/search/SpecificMaterial.asp?bassnum=MEAl00
Пьезосопротивление
2×10-5 Ом-см
Определение
коэффициент пьезосопротивления в алюминии
межблочные конструкции из сплава
Reilly,
CJ, Санчес,
Дж. Э., младший, материалы
Надежность в микроэлектронике IX. Симпозиум, 1999, стр. 213-18
Пьезоэлектричество
Мокрое травление метод
85 мас.% раствор фосфорной кислоты
Механизмы жидкостного травления алюминия
электроды под низким давлением-ширина линии
явления сужения
Утияма,
М.
; Накамура,
М. Денки Кагаку, v
56, № 7, июль 1988 г., стр. 563-8
Плазменное травление метод
Cl 2 , BCl 3 /Cl 2
Ленгмюровские зондовые исследования плазмы с трансформаторной связью,
травитель алюминия
Малышев М.В.; Доннелли,
В.М.; Корнблит, А .; Чиампа, Н.А.; Полковник, JI; Ли, JTC
Источник: Journal of Vacuum Science & Technology A (Вакуум, поверхности и
Фильмы), т. 17, № 2, 19 марта99, стр. 480-92
Адгезия к диоксид кремния
хорошо
Реакция Al
со стекловидным кварцем
Черный, J.R., 15th
Ежегодные труды по физике надежности, 1977 г., стр. 257-61
Биосовместимость
№
Зависимость биосовместимости иономерных цементов in vitro от высвобождения ионов, A.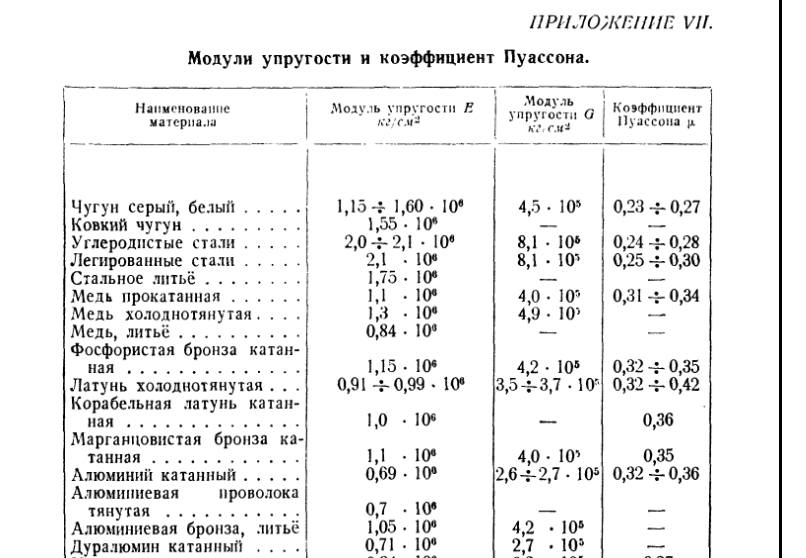
J. Devlin,
Journal of Materials Science: Materials in Medicine 9(12): 737-741; декабрь 1998 г.
Ссылка на медицинское устройство — MDDI, июль 2002 г.
Металлообработка: будущее завтра, сегодня Медицинское устройство…
Гидрофобность
90 градусов ниже 120°C
Угол контакта
температурная зависимость капель воды на практических алюминиевых поверхностях
Bernardin, J.D.; Мудавар, И.; Уолш, CB;
Франсес, E.I.International Journal of Heat and Mass Transfer,
т. 40, № 5, март 1997 г., стр. 1017-33
Значения модуля Юнга, предела прочности при растяжении и предела текучести для некоторых материалов
Модуль упругости или модуль Юнга альт.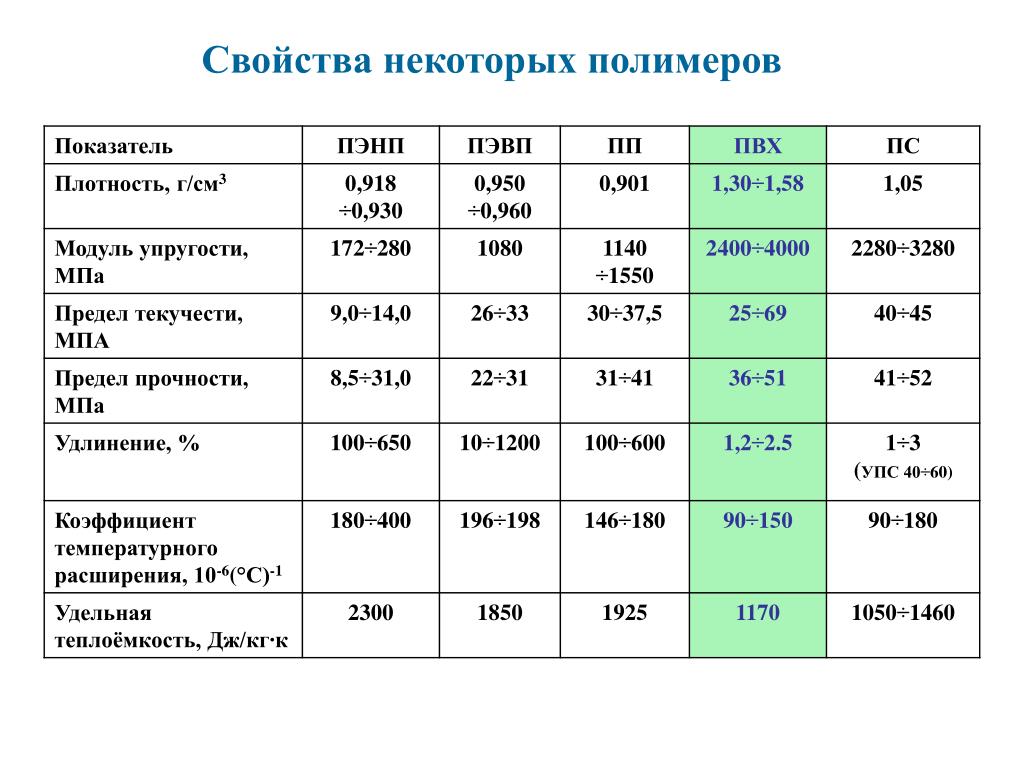
Модуль упругости — это мера жесткости упругого материала. Он используется для описания упругих свойств таких объектов, как провода, стержни или колонны, когда они растягиваются или сжимаются.
Модуль упругости при растяжении определяется как
«отношение напряжения (силы на единицу площади) вдоль оси к деформации (отношение деформации к начальной длине) вдоль этой оси»
Его можно использовать для прогнозирования удлинения или сжатие объекта до тех пор, пока напряжение меньше, чем предел текучести материала. Подробнее об определениях ниже таблицы.
| АБС-пластик | 1,4 — 3,1 | 40 | ||
| A53 Seamless and Welded Standard Steel Pipe — Grade A | 331 | 207 | ||
| A53 Seamless and Welded Standard Steel Pipe — Grade B | 414 | 241 | ||
| A106 Бесшовные трубы из углеродистой стали класса A | 330 | 205 | ||
| A106 Бесшовные трубы из углеродистой стали класса B | 415 | 240 | ||
| A106 Безумительная углеродистая стальная труба — класс C | 485 | 275 | ||
| A252 Стальная труба — класс 1 | 345 | 2079999 | A255 | 9000 9000 | A255 | 900099000 9000. 414 | 241 |
| A252 Стальная труба для свай — класс 3 | 455 | 310 | ||
| A501 Горячеформованная труба из углеродистой стали класса | 400 | 248 | ||
| A501 Горячая конструкционная трубка из углеродистой стали — класс B | 483 | 345 | ||
| A523 Кабельная контура. | A523 Стальной трубопровод кабельной цепи — класс B | 414 | 241 | |
| A618 Горячеформованные высокопрочные низколегированные конструкционные трубы — класс Ia и Ib | 483 | 345 | ||
| A618 Горячие формированные высокопрочные конструкционные трубки-класс II | 414 | 345 | ||
| A618 HOR-FORMED HIGH-LUSTER LOW-All-All-All-All-Allytying Tub Уровень III | 448 | 345 | ||
| API 5L Line Pipe | 310 — 1145 | 175 — 1048 | ||
| Acetals | 2,8 | 5 | ||
| Acrylic | 3. 2 | 70 | ||
| Aluminum Bronze | 120 | |||
| Aluminum | 69 | 110 | 95 | |
| Aluminum Alloys | 70 | |||
| Сурьма | 78 | |||
| Арамид | 70 — 112 | |||
| Beryllium (Be) | 287 | |||
| Beryllium Copper | 124 | |||
| Bismuth | 32 | |||
| Bone, compact | 18 | 170 (сжатие) | ||
| Кость губчатая | 76 | |||
| Бор | ||||
| 0003 | Brass | 102 — 125 | 250 | |
| Brass, Naval | 100 | |||
| Bronze | 96 — 120 | |||
| CAB | 0. 8 | |||
| Кадмий | 32 | |||
| Пластик, армированный углеродным волокном | 150 | 39 | 1000 | |
| Cast Iron 4.5% C, ASTM A-48 | 170 | |||
| Cellulose, cotton, wood pulp and regenerated | 80 — 240 | |||
| Cellulose acetate, Формованная | 12 — 58 | |||
| Ацетат целлюлозы, лист | 30 — 52 | |||
| Нитрат целлюлозы, Celluloid | 50 | |||
| .0009 | ||||
| Chlorinated polyether | 1.1 | 39 | ||
| Chlorinated PVC (CPVC) | 2.9 | |||
| Chromium | 248 | |||
| Cobalt | 207 | |||
| Бетон | 17 | |||
| Бетон, высокопрочный (сжатие) | 30 | 40 (compression) | ||
| Copper | 117 | 220 | 70 | |
| Diamond (C) | 1220 | |||
| Douglas fir Wood | 13 | 50 (сжатие) | ||
| Epoxy Resins | 3-2 | 26 — 85 | ||
. 0028 | ||||
| Flax fiber | 58 | |||
| Glass | 50 — 90 | 50 (compression) | ||
| Glass reinforced polyester matrix | 17 | |||
| Gold | 74 | |||
| Гранит | 52 | |||
| Графен | 1000 | |||
| 130 | ||||
| Hemp fiber | 35 | |||
| Inconel | 214 | |||
| Iridium | 517 | |||
| Iron | 210 | |||
| Свинец | 13,8 | |||
| Магний металлический | 45 | |||
| Manganese | 159 | |||
| Marble | 15 | |||
| MDF — Medium-density fiberboard | 4 | |||
| Mercury | ||||
| Молибден (Mo) | 329 | |||
| Монель-металл | 179 | |||
| Nickel | 170 | |||
| Nickel Silver | 128 | |||
| Nickel Steel | 200 | |||
| Niobium (Columbium) | 103 | |||
| Нейлон-6 | 2 — 4 | 45 — 90 | 45 | 9 500903 | 4 Нейлон0004 60 — 80 |
| Oak Wood (along grain) | 11 | |||
| Osmium (Os) | 550 | |||
| Phenolic cast resins | 33 — 59 | |||
| Феноло -формальдегидные формовочные соединения | 45 — 52 | |||
| Фосфор Бронз | 116 | |||
| СРЕДНЯ СРЕДНА (ВОЛЛЕДОЙ МЕРНА0009 | 9 | 40 | ||
| Platinum | 147 | |||
| Plutonium | 97 | |||
| Polyacrylonitrile, fibers | 200 | |||
| Polybenzoxazole | 3. 5 | |||
| Поликарбонаты | 2.6 | 52 — 62 | ||
| Полиэтилен HDPE (высокой плотности) | 0.8 | 15 | ||
| Polyethylene Terephthalate, PET | 2 — 2.7 | 55 | ||
| Polyamide | 2.5 | 85 | ||
| Polyisoprene, hard rubber | 39 | |||
| Полиметилметакрилат (ПММА) | 2,4–3,4 | |||
| Полиимидные ароматические соединения | 3,1 | 68 | ||
| Полипропилен, стр. | 1,5 — 2 | 28 — 36 | ||
| Полистирол, PS | 3 — 3,5 | 30 — 100 | . — 0,45 | |
| Политетрафлюоруэтилен (PTFE) | 0,4 | |||
| Полиуретан лик0003 | Polyurethane elastomer | 29 — 55 | ||
| Polyvinylchloride (PVC) | 2. 4 — 4.1 | |||
| Potassium | ||||
| Rhodium | 290 | |||
| Резина, малая деформация | 0,01 — 0,1 | |||
| Сапфир | 435 | |||
| Selenium | 58 | |||
| Silicon | 130 — 185 | |||
| Silicon Carbide | 450 | 3440 | ||
| Silver | 72 | |||
| Натрий | ||||
| Сталь, высокопрочный сплав ASTM A-514 | 760 | 690 | ||
| Steel, stainless AISI 302 | 180 | 860 | 502 | |
| Steel, Structural ASTM-A36 | 200 | 400 | 250 | |
| Tantalum | 186 | |||
| Thorium | 59 | |||
| 47 | ||||
| Titanium | ||||
| Titanium Alloy | 105 — 120 | 900 | 730 | |
| Tooth enamel | 83 | |||
| Tungsten (W) | 400 — 410 | |||
| В вольвательский карбид (WC) | 450 — 650 | |||
| Уран | 170 | |||
| Vanadium | 131 | |||
| Wrought Iron | 190 — 210 | |||
| Wood | ||||
| Zinc | 83 |
- 1 Па (Н/м 2 ) = 1×10 -6 Н/мм 2 = 1,4504×10 -4 фунтов на кв.
дюйм - 19 16 МПа0234 6 Pa (N/m 2 ) = 0.145×10 3 psi (lb f /in 2 ) = 0.145 ksi
- 1 GPa = 10 9 Н/м 2 = 10 6 Н/см 2 = 10 3 Н/мм 2 = 0,145534 3 н/мм 2 = 0,145534 3 н/мм 2 = 0,145534 3 н/мм 2 = 0,14534 3 н/мм 2 . )
- 1 МПа = 10 6 пси = 10 3 ksi
- 1 psi (lb/in 2 ) = 0.001 ksi = 144 psf (lb f /ft 2 ) = 6,894.8 Pa (N/m 2 ) = 6.895 x10 -3 Н/мм 2
дюйм
Скачать и схема преобразования 9108 8888888888 88 888 888 88 888 88 888 88 888 88 88 88 88 88 88 88 88 88 88 88 888 88 88 88 888 88 88 888 88 888 888 888 88 888 88 888 88 888 88 888 888 888 888 888 888 88 888 88 88 888 8888.
10 тысяч фунтов на квадратный дюйм , как указано в таблице ниже:
Внимание! — этот онлайн-конвертер давления также можно использовать для преобразования единиц модуля упругости при растяжении.
Деформация —
εДеформация — это «деформация твердого тела из-за напряжения» — изменение размера, деленное на исходное значение размера — и может быть выражена как
ε = / L (1)
, где
ε = strain (m/m, in/in)
dL = elongation or compression (offset) of object (m, in)
L = length of object (m, in)
Stress —
σStress is force per unit area and can be expressed as
σ = F / A (2)
where
σ = стресс (N/M 2 , LB/в 2 , PSI)
F = приложенный силу (N, LB) F = приложенный силу (N, LB) F = Applied (N, LB) F (N, LB)
F (N, LB)
F (N, LB)
F .
площадь напряжения объекта (м 2 , в 2 ) - растягивающее напряжение — напряжение, которое стремится растянуть или удлинить материал — действует нормально к напряженной области
- сжимающее напряжение, которое имеет тенденцию к сжатию или укорачиванию материала — действует нормально к напряженной зоне
- напряжение сдвига — напряжение, стремящееся к сдвигу материала — действует в плоскости напряженной области под прямым углом к сжимаемому или растягивающему напряжению
- Расчет напряжения в балках Упругость — E
Модуль Юнга может быть выражен как
E = напряжение/деформация
= σ ε 93 961640
= (f / a) / (DL / L) (3)
, где
E = Модлель of ELALCTION 9164
- 9024 9. 9024 9. 9024 9024 9.9130 9024 9.
9130 9024 9.9164 9.9134 9024 9.9130 9024 9.9134E = of ELALTU , фунт/дюйм 2 , psi)
- назван в честь английского врача и физика XVIII века Томаса Янга первоначальная форма после искажения.
Примером упругого объекта является пружина: при растяжении она создает восстанавливающую силу, которая стремится вернуть ее к исходной длине. Эта возвращающая сила в целом пропорциональна растяжению, описываемому законом Гука.
Закон Гука
Чтобы растянуть пружину вдвое больше, требуется примерно вдвое больше силы. Эта линейная зависимость смещения от силы растяжения называется законом Гука и может быть выражена как
F с = -K DL (4)
, где
F S = сила в весне (N)
= FIRCE в весне)
K 8888.
dL = удлинение пружины (м)
Обратите внимание, что закон Гука также может применяться к материалам, подвергающимся трехмерному напряжению (трехосное нагружение).
- 9024 9. 9024 9. 9024 9024 9.9130 9024 9.
9130 9024 9.9164 9.9134 9024 9.9130 9024 9.9134