стороны, вершины, диагонали. Периметр многоугольника
Многоугольник — это геометрическая фигура, ограниченная замкнутой ломаной линией, не имеющей самопересечений.
Звенья ломаной называются сторонами многоугольника, а её вершины — вершинами многоугольника.
Углами многоугольника называются внутренние углы, образованные соседними сторонами. Число углов многоугольника равно числу его вершин и сторон.
Многоугольникам даются названия по количеству сторон. Многоугольник с наименьшим количеством сторон называется треугольником, он имеет всего три стороны. Многоугольник с четырьмя сторонами называется четырёхугольником, с пятью — пятиугольником и т. д.
Обозначение многоугольника составляют из букв, стоящих при его вершинах, называя их по порядку (по часовой или против часовой стрелки). Например, говорят или пишут: пятиугольник ABCDE
:
В пятиугольнике

Выпуклые и вогнутые
Многоугольник называется выпуклым, если ни одна из его сторон, продолженная до прямой линии, его не пересекает. В обратном случае многоугольник называется вогнутым:
Периметр
Сумма длин всех сторон многоугольника называется его периметром.
Периметр многоугольника
AB + BC + CD + DE + EA.
Если у многоугольника равны все стороны и все углы, то его называют правильным. Правильными многоугольниками могут быть только выпуклые многоугольники.
Диагональ
Диагональ многоугольника — это отрезок, соединяющий вершины двух углов, не имеющих общей стороны. Например, отрезок AD является диагональю:
Единственным многоугольником, который не имеет ни одной диагонали, является треугольник, так как в нём нет углов, не имеющих общих сторон.
Если из какой-нибудь вершины многоугольника провести все возможные диагонали, то они разделят многоугольник на треугольники:
Треугольников будет ровно на два меньше, чем сторон:
t = n — 2,
где t — это количество треугольников, а n — количество сторон.
Разделение многоугольника на треугольники с помощью диагоналей используется для нахождения площади многоугольника, так как чтобы найти площадь какого-нибудь многоугольника, нужно разбить его на треугольники, найти площадь этих треугольников и полученные результаты сложить.
Пентагон — Pentagon — qaz.wiki
| Пентагон | |
|---|---|
Равносторонний пятиугольник, то есть пятиугольник, все пять сторон которого имеют одинаковую длину. | |
| Ребра и вершины | 5 |
| Внутренний угол ( градусы ) | 108 ° (при равноугловом, включая обычный) |
В геометрии , A пятиугольник
Пентагон может быть простым или самопересекающимся . Самопересекающийся правильный пятиугольник (или звездный пятиугольник ) называется пентаграммой .
Правильные пятиугольники
Регулярный пятиугольник имеет Шлефли символ {5} и внутренние углы 108 °.
Регулярный пятиугольник имеет пять линий reflectional симметрии , и поворотную симметрию порядка 5 (через 72 °, 144 °, 216 ° и 288 °). В диагоналях из более выпуклого правильного пятиугольника находятся в золотая пропорция к его сторонам.
- Высотазнак равно5+252⋅Боковая сторона≈1,539⋅Боковая сторона,{\ displaystyle {\ text {Height}} = {\ frac {\ sqrt {5 + 2 {\ sqrt {5}}}} {2}} \ cdot {\ text {Side}} \ примерно 1,539 \ cdot {\ текст {Side}},}
- Шириназнак равноДиагональзнак равно1+52⋅Боковая сторона≈1,618⋅Боковая сторона,{\ displaystyle {\ text {Width}} = {\ text {Diagonal}} = {\ frac {1 + {\ sqrt {5}}} {2}} \ cdot {\ text {Side}} \ приблизительно 1,618 \ cdot {\ text {Side}},}
- Шириназнак равно2-25⋅Высота≈1.051⋅Высота,{\ displaystyle {\ text {Width}} = {\ sqrt {2 — {\ frac {2} {\ sqrt {5}}}}} \ cdot {\ text {Height}} \ приблизительно 1.051 \ cdot {\ text {Высота}},}
- Диагональзнак равнор 5+52знак равно2рпотому что18∘знак равно2рпотому чтоπ10≈1,902р,{\ displaystyle {\ text {Diagonal}} = R \ {\ sqrt {\ frac {5 + {\ sqrt {5}}} {2}}} = 2R \ cos 18 ^ {\ circ} = 2R \ cos { \ frac {\ pi} {10}} \ приблизительно 1,902R,}
где R — радиус описанной окружности .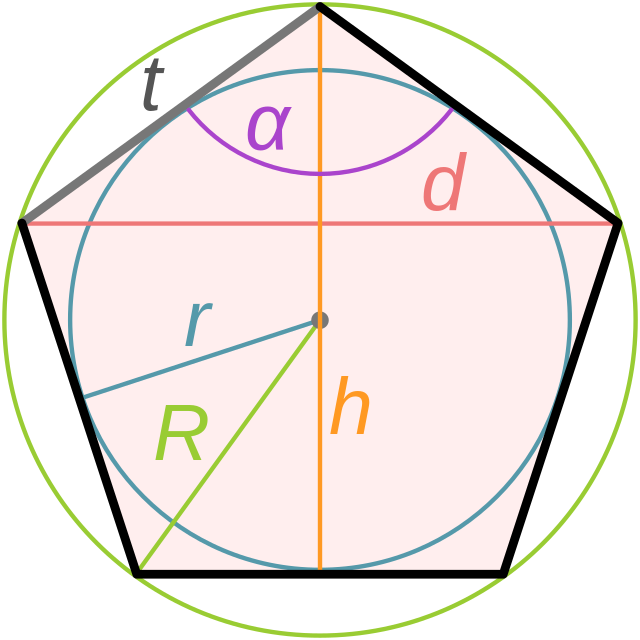 {\ circ})} {4}}}
{\ circ})} {4}}}
с длиной стороны t .
Inradius
Как и в любой правильный выпуклый многоугольник, в правильный выпуклый пятиугольник вписан круг . Апофема , что радиус г вписанной окружности, правильный пятиугольник связана с длиной стороны т путем
- рзнак равнот2загар(π/5)знак равнот25-20≈0,6882⋅т.{\ displaystyle r = {\ frac {t} {2 \ tan (\ pi / 5)}} = {\ frac {t} {2 {\ sqrt {5 — {\ sqrt {20}}}}}} \ примерно 0,6882 \ cdot т.}
Хорды от описанной окружности к вершинам
Как и любой правильный выпуклый многоугольник, правильный выпуклый пятиугольник имеет описанную окружность . Для правильного пятиугольника с последовательными вершинами A, B, C, D, E, если P — любая точка на описанной окружности между точками B и C, то PA + PD = PB + PC + PE.
Точка в плоскости
Для произвольной точки на плоскости правильного пятиугольника с описанным радиусом , расстояния до центра тяжести правильного пятиугольника и его пяти вершин равны и соответственно, имеем р{\ displaystyle R}L{\ displaystyle L}dя{\ displaystyle d_ {i}}
- ∑язнак равно15dя2знак равно5(р2+L2),{\ displaystyle \ textstyle \ sum _ {i = 1} ^ {5} d_ {i} ^ {2} = 5 (R ^ {2} + L ^ {2}),}
- ∑язнак равно15dя4знак равно5((р2+L2)2+2р2L2),{\ displaystyle \ textstyle \ sum _ {i = 1} ^ {5} d_ {i} ^ {4} = 5 ((R ^ {2} + L ^ {2}) ^ {2} + 2R ^ {2 } L ^ {2}),}
- ∑язнак равно15dя6знак равно5((р2+L2)3+6р2L2(р2+L2)),{\ displaystyle \ textstyle \ sum _ {i = 1} ^ {5} d_ {i} ^ {6} = 5 ((R ^ {2} + L ^ {2}) ^ {3} + 6R ^ {2 } L ^ {2} (R ^ {2} + L ^ {2})),}
- ∑язнак равно15dя8знак равно5((р2+L2)4+12р2L2(р2+L2)2+6р4L4).
 {4}.}
{4}.}
Построение правильного пятиугольника
Правильный пятиугольник можно построить с помощью циркуля и линейки , так как 5 — простое число Ферма . Известно множество методов построения правильного пятиугольника. Некоторые обсуждаются ниже.
Метод Ричмонда
Один из методов построения правильного пятиугольника в данном круге описан Ричмондом и далее обсуждается в Многогранниках Кромвеля .
На верхней панели показана конструкция, использованная в методе Ричмонда для создания стороны вписанного пятиугольника. Окружность, определяющая пятиугольник, имеет единичный радиус. Его центр расположен в точке C, а средняя точка M отмечена на полпути по его радиусу. Эта точка соединена с периферией вертикально над центром в точке D . Угол ЦМД пополам, а биссектриса пересекает вертикальную ось в точке Q . Горизонтальная линия, проходящая через Q, пересекает окружность в точке P , а хорда PD — это искомая сторона вписанного пятиугольника. {2} = 2-2h = 2-2 \ left ({\ frac {{\ sqrt {5}} — 1} {4}} \ right) \}
{2} = 2-2h = 2-2 \ left ({\ frac {{\ sqrt {5}} — 1} {4}} \ right) \}
- знак равно5-52 .{\ displaystyle = {\ frac {5 — {\ sqrt {5}}} {2}} \.}
Таким образом, сторона s :
- sзнак равно5-52 ,{\ displaystyle s = {\ sqrt {\ frac {5 — {\ sqrt {5}}} {2}}} \,}
хорошо зарекомендовавший себя результат. Следовательно, такая конструкция пятиугольника верна.
Карлайл круги
Метод с использованием кругов КарлайлаКруг Карлайла был изобретен как геометрический метод поиска корней квадратного уравнения . Эта методика приводит к процедуре построения правильного пятиугольника. Шаги следующие:
- Нарисуйте круг , в котором , чтобы вписать пятиугольник и пометить центральную точку O .
- Проведите горизонтальную линию через центр круга. Отметить левое пересечение с кругом в качестве точки B .
- Проведите вертикальную линию через центр. Отметьте одно пересечение с кругом в качестве точки А .

- Построить точку М как средняя точка O и B .
- Нарисуйте круг с центром в точке М через точку А . Отметьте ее пересечения с горизонтальной линией (внутри исходной окружности) в точке W и ее пересечение вне окружности в качестве точки V .
- Нарисуйте окружность радиуса ОА и центра W . Он пересекает исходный круг в двух вершинах пятиугольника.
- Нарисуйте окружность радиуса ОА и центр V . Он пересекает исходный круг в двух вершинах пятиугольника.
- Пятая вершина — это крайнее правое пересечение горизонтальной линии с исходной окружностью.
Шаги 6–8 эквивалентны следующей версии, показанной на анимации:
- 6а. Постройте точку F как середину точек O и W.
- 7а. Постройте вертикальную линию через F. Она пересекает исходную окружность в двух вершинах пятиугольника. Третья вершина — это крайнее правое пересечение горизонтальной линии с исходной окружностью.

- 8а. Постройте две другие вершины, используя циркуль и длину вершины, найденную на шаге 7a.
Использование тригонометрии и теоремы Пифагора
Использование тригонометрии и теоремы Пифагора для построения правильного пятиугольника.Конструкция
- Сначала отметим, что правильный пятиугольник можно разделить на 10 равных треугольников, как показано в наблюдении . Кроме того, cos 36 ° = . †1+54{\ displaystyle {\ tfrac {1 + {\ sqrt {5}}} {4}}}
- На шаге 1 мы используем четыре единицы (показаны синим цветом) и прямой угол, чтобы построить отрезок длиной 1+ √ 5 , в частности, создав прямоугольный треугольник 1-2- √ 5 и затем расширив гипотенузу √ 5 на длина 1. Затем мы делим этот сегмент пополам, а затем снова делим пополам, чтобы создать сегмент длины (показан красным).1+54{\ displaystyle {\ tfrac {1 + {\ sqrt {5}}} {4}}}
- На шаге 2 мы строим две концентрические окружности с центром в точке O радиусом 1 и длиной .
 {2} -4 (4) (- 1)}}} {2 (4)}} \\ u & {} = {\ frac {1+ {\ sqrt {5}}} {4}} \ end {align}}}
{2} -4 (4) (- 1)}}} {2 (4)}} \\ u & {} = {\ frac {1+ {\ sqrt {5}}} {4}} \ end {align}}}Это быстро следует из знания, что удвоение синуса 18 градусов является обратным золотым сечением, которое мы знаем геометрически из треугольника с углами 72,72,36 градусов. Из тригонометрии мы знаем, что косинус дважды 18 градусов равен 1 минус два квадрата синуса 18 градусов, и это сводится к желаемому результату с помощью простой квадратичной арифметики.
Длина стороны указана
Правильный пятиугольник согласно золотому сечению , делящий отрезок линии внешним делением
Пентагон с заданной длиной стороны- Нарисуйте отрезок AB , длина которого равна заданной стороне пятиугольника.
- Вытяните отрезок BA от точки A примерно на три четверти отрезка BA .
- Нарисуйте дугу окружности с центром в точке B и радиусом AB .
- Нарисуйте дугу окружности с центром A и радиусом AB ; возникает пересечение F .

- Постройте перпендикуляр к отрезку AB через точку F ; возникает пересечение G .
- Проведите линию, параллельную отрезку FG, от точки A до дуги окружности вокруг точки A ; возникает пересечение Н .
- Нарисуйте дугу окружности, центральную точку G с радиусом GH до продолжения отрезка AB ; возникает пересечение J .
- Нарисуйте дугу окружности, центральную точку B с радиусом BJ до перпендикуляра в точке G ; возникают пересечение D на перпендикуляре, и пересечение Е с дугой окружности , которая была создана вокруг точки А .
- Нарисуйте дугу окружности с центром в точке D с радиусом BA, пока эта дуга окружности не пересечет другую дугу окружности вокруг точки B ; возникает пересечение С .
- Соедините точки BCDEA . Получается пятиугольник.
Золотое сечение
- BJ¯АB¯знак равноАB¯АJ¯знак равно1+52знак равноφ≈1,618{\ displaystyle {\ frac {\ overline {BJ}} {\ overline {AB}}} = {\ frac {\ overline {AB}} {\ overline {AJ}}} = {\ frac {1 + {\ sqrt {5}}} {2}} = \ varphi \ приблизительно 1,618}
Метод Евклида
Метод Евклида для пятиугольника на заданной окружности, с использованием золотого треугольника , анимация 1 мин 39 сПравильный пятиугольник можно построить с помощью циркуля и линейки , вписав один в заданный круг или построив один на заданном крае.
 Этот процесс был описан Евклидом в его « Элементах» около 300 г. до н. Э.
Этот процесс был описан Евклидом в его « Элементах» около 300 г. до н. Э.Просто с помощью транспортира (не классическая конструкция)
Ниже приводится прямой метод с использованием степеней:
- Нарисуйте круг и выберите точку пятиугольника (например, центр вверху)
- Выберите точку A на окружности, которая будет одной из вершин пятиугольника. Нарисуйте линию через O и A .
- Проведите через него направляющую линию и центр круга.
- Нарисуйте линии под углом 54 ° (от направляющей), пересекающие точку пятиугольника.
- Там, где они пересекают круг, нарисуйте линии под углом 18 ° (от параллели к направляющей).
- Присоединяйтесь к тому месту, где они пересекают круг
После формирования правильного выпуклого пятиугольника, если соединить несмежные углы (нарисовать диагонали пятиугольника), получится пентаграмма с меньшим правильным пятиугольником в центре. Или, если расширить стороны, пока не встретятся несмежные стороны, получится пентаграмма большего размера.

Физические методы
Узел сверху бумажной полосы- Правильный пятиугольник можно создать просто из полоски бумаги, завязав на полоску узел сверху и аккуратно расплющивая узел, потянув за концы полоски бумаги. Если загнуть один из концов над пятиугольником, то при заднем освещении будет открыта пентаграмма .
- Постройте правильный шестиугольник на плотной бумаге или картоне. Сделайте складку по трем диаметрам между противоположными вершинами. Вырежьте от одной вершины к центру, чтобы получился равносторонний треугольный лоскут. Закрепите этот клапан под его соседом, чтобы получилась пятиугольная пирамида . Основание пирамиды — правильный пятиугольник.
Симметрия
Симметрии правильного пятиугольника. Вершины окрашены в соответствии с их положением симметрии. Синие зеркальные линии проводятся через вершины и ребра. В центре даны приказы гирации.Правильный пятиугольник имеет DIH 5 симметрии , порядка 10.

Эти 4 симметрии можно увидеть в 4 различных симметриях на пятиугольнике. Джон Конвей помечает их буквой и групповым порядком. Полная симметрия регулярной формы равна r10, а симметрия не помечена как a1 . Двугранные симметрии разделяются в зависимости от того, проходят ли они через вершины ( d для диагонали) или ребра ( p для перпендикуляров), и i, когда линии отражения проходят через оба ребра и вершины. Циклические симметрии в среднем столбце обозначены буквой
Симметрия каждой подгруппы допускает одну или несколько степеней свободы для неправильных форм. Только подгруппа g5 не имеет степеней свободы, но ее можно рассматривать как направленные ребра .
Равносторонние пятиугольники
Равносторонний пятиугольник, состоящий из четырех равных кругов, расположенных в виде цепочки.
Равносторонний пятиугольник — это многоугольник с пятью сторонами равной длины. Однако его пять внутренних углов могут принимать ряд наборов значений, что позволяет ему образовывать семейство пятиугольников. Напротив, правильный пятиугольник уникален до подобия, потому что он равносторонний и равносторонний (его пять углов равны).
Циклические пятиугольники
Циклический пятиугольник один , для которых окружность называется окружность проходит через все пять вершин. Правильный пятиугольник — это пример циклического пятиугольника. Площадь циклического пятиугольника, правильного или неправильного, может быть выражена как одна четвертая квадратного корня одного из корней септического уравнения , коэффициенты которого являются функциями сторон пятиугольника.
Существуют циклические пятиугольники с рациональными сторонами и рациональной площадью; они называются пятиугольниками Роббинса . В пятиугольнике Роббинса либо все диагонали рациональны, либо все иррациональны, и предполагается, что все диагонали должны быть рациональными.

Общие выпуклые пятиугольники
Для всех выпуклых пятиугольников сумма квадратов диагоналей меньше, чем в 3 раза больше суммы квадратов сторон.
Графики
Полный граф K 5 часто рисуется в виде правильного пятиугольника со всеми 10 связными ребрами. Этот граф также представляет собой ортогональную проекцию 5 вершин и 10 ребер 5-ячейки . Выпрямляется 5-элементный , с вершинами в середине ребер 5-клетки проецируются внутри пятиугольника.
Примеры пятиугольников
Растения
Животные
Минералы
Pyritohedral кристалл пирита . Пиритоэдр имеет 12 одинаковых пятиугольных граней, которые не обязательно должны быть правильными.
Искусственный
Пентагоны в плитке
Правильный пятиугольник не может появляться ни в одной мозаике из правильных многоугольников. Во- первых, чтобы доказать , пятиугольник не может сформировать регулярную черепицу (один , в котором все грани конгруэнтны, таким образом , требует , чтобы все многоугольники быть пятиугольников), заметим , что 360 ° / 108 ° = 3 1 / 3 (где 108 ° Принимают внутрь угол), который не является целым числом; следовательно, не существует целого числа пятиугольников, разделяющих одну вершину и не оставляющих промежутков между ними.
 Сложнее доказать, что пятиугольник не может входить ни в одну мозаику от края до края, образованную правильными многоугольниками:
Сложнее доказать, что пятиугольник не может входить ни в одну мозаику от края до края, образованную правильными многоугольниками:Максимальная известная плотность упаковки правильного пятиугольника составляет приблизительно 0,921, что достигается показанной двойной решетчатой упаковкой. В препринте, выпущенном в 2016 году, Томас Хейлз и Воден Куснер объявили о доказательстве того, что двойная решетчатая упаковка обычного пятиугольника (которую они называют «пятиугольной упаковкой ледяного луча» и которая восходит к работе китайских мастеров в 1900 году) имеет оптимальную плотность среди всех упаковок правильных пятиугольников на плоскости. По состоянию на 2020 год их доказательства еще не рецензировались и не публиковались.
Не существует комбинаций правильных многоугольников с 4 или более, пересекающимися в вершине, содержащими пятиугольник. Для комбинаций с 3, если 3 многоугольника встречаются в вершине и один имеет нечетное число сторон, другие 2 должны быть конгруэнтными.
 Причина этого в том, что многоугольники, соприкасающиеся с краями пятиугольника, должны чередоваться вокруг пятиугольника, что невозможно из-за нечетного количества сторон пятиугольника. Для пятиугольника это дает многоугольник, все углы которого равны (360-108) / 2 = 126 ° . Для того, чтобы найти число сторон этого многоугольника, результат равен 360 / (180 — 126) = 6 2 / 3 , которое не является целым числом. Следовательно, пятиугольник не может появиться ни в одной мозаике из правильных многоугольников.
Причина этого в том, что многоугольники, соприкасающиеся с краями пятиугольника, должны чередоваться вокруг пятиугольника, что невозможно из-за нечетного количества сторон пятиугольника. Для пятиугольника это дает многоугольник, все углы которого равны (360-108) / 2 = 126 ° . Для того, чтобы найти число сторон этого многоугольника, результат равен 360 / (180 — 126) = 6 2 / 3 , которое не является целым числом. Следовательно, пятиугольник не может появиться ни в одной мозаике из правильных многоугольников.Существует 15 классов пятиугольников, которые могут моноэдрально замостить плоскость . Ни один из пятиугольников не обладает какой-либо симметрией в целом, хотя у некоторых есть особые случаи с зеркальной симметрией.
Пентагоны в многогранниках
Смотрите также
Встроенные заметки и ссылки
внешние ссылки
Равносторонний пятиугольник — Equilateral pentagon
Равносторонний пятиугольник, состоящий из четырех равных кругов, расположенных в виде цепочки.
В геометрии равносторонний пятиугольник является многоугольник с пятью сторонами одинаковой длины. Его пять внутренних углов, в свою очередь, могут принимать ряд наборов значений, что позволяет ему образовывать семейство пятиугольников. Требуется, чтобы все углы в сумме составляли 540 градусов и составляли от 0 до 360 градусов, но не равнялись 180 градусам. Напротив, правильный пятиугольник уникален, потому что он равносторонний и, кроме того, равноугольный (его пять углов равны; мера составляет 108 градусов).
Четырех пересекающихся равных окружностей, образующих замкнутую цепочку, достаточно, чтобы образовался выпуклый равносторонний пятиугольник. Центр каждого круга — одна из четырех вершин пятиугольника. Оставшаяся вершина определяется одной из точек пересечения первой и последней окружностей цепочки.
Пять углов любого выпуклого равностороннего пятиугольника можно описать только двумя углами α и β, при условии, что α ≥ β и δ — наименьший из других углов. Таким образом, общий равносторонний пятиугольник можно рассматривать как функцию двух переменных f (α, β), где остальные углы могут быть получены с помощью тригонометрических соотношений.
 {2}} {2 (1) (1)}} \.}
{2}} {2 (1) (1)}} \.}Упрощая, получаем δ как функцию от α и β:
- δзнак равноarccos[потому что(α)+потому что(β)-потому что(α+β)-12].{\ displaystyle \ delta = \ arccos \ left [\ cos (\ alpha) + \ cos (\ beta) — \ cos (\ alpha + \ beta) — {\ frac {1} {2}} \ right].}
Остальные углы пятиугольника можно найти геометрически: оставшиеся углы оранжевого и синего треугольников легко найти, заметив, что два угла равнобедренного треугольника равны, а сумма всех трех углов равна 180 °. Тогда и два оставшихся угла зеленого треугольника можно найти из четырех уравнений, утверждающих, что сумма углов пятиугольника составляет 540 °, сумма углов зеленого треугольника равна 180 °, угол — это сумма его углов. три составляющих, а угол — это сумма двух составляющих. ϵ,γ,{\ displaystyle \ epsilon, \ gamma,}γ{\ displaystyle \ gamma}ϵ{\ displaystyle \ epsilon}
Циклический пятиугольник равноугольные тогда и только тогда , когда оно имеет равную стороны и , таким образом , является регулярным.
 Точно так же тангенциальный пятиугольник является равносторонним тогда и только тогда, когда он имеет равные углы и, следовательно, правильный.
Точно так же тангенциальный пятиугольник является равносторонним тогда и только тогда, когда он имеет равные углы и, следовательно, правильный.Двумерное отображение
Все равносторонние пятиугольники нанесены на область, ограниченную условием α ≥ β ≥ δ. Показаны три области для каждого из трех типов пятиугольников: звездчатый, вогнутый и выпуклый.Равносторонний пятиугольник как функцию двух переменных можно изобразить на двумерной плоскости . Каждая пара значений (α, β) отображается в одну точку плоскости, а также в один пятиугольник.
Периодичность значений α и β и условие α ≥ β ≥ δ позволяют ограничить размер отображения. В плоскости с осями координат α и β, α = β — линия, разделяющая плоскость на две части (южная граница показана на чертеже оранжевым цветом). δ = β, поскольку кривая делит плоскость на разные участки (северная граница показана синим цветом).
Обе границы охватывают непрерывную область плоскости, точки которой соответствуют уникальным равносторонним пятиугольникам.
 Точки за пределами региона просто соответствуют повторяющимся пятиугольникам, то есть пятиугольникам, которые при повороте или отражении могут совпадать с другими уже описанными. Пентагоны, которые точно совпадают с этими границами, имеют линию симметрии .
Точки за пределами региона просто соответствуют повторяющимся пятиугольникам, то есть пятиугольникам, которые при повороте или отражении могут совпадать с другими уже описанными. Пентагоны, которые точно совпадают с этими границами, имеют линию симметрии .Внутри области уникальных отображений есть три типа пятиугольников: звездчатые, вогнутые и выпуклые, разделенные новыми границами.
Звездчатый
У звездчатых пятиугольников есть стороны, пересекаемые другими. Типичный пример этого типа пятиугольника — пентаграмма . Условие для того, чтобы пятиугольник был звездообразным или самопересекающимся, должен иметь 2α + β ≤ 180 °. Итак, на карте линия 2α + β = 180 ° (показанная оранжевым на севере) является границей между областями звездчатых и незвездных пятиугольников. Пентагоны, которые сопоставляются точно с этой границей, имеют вершину, касающуюся другой стороны.
Вогнутый
В вогнутых пятиугольниках не являются звездообразными пятиугольниками , имеющими по меньшей мере один углом , большим , чем 180 °.
 Первый угол, который открывается больше 180 °, — это γ, поэтому γ = 180 ° (граница, показанная зеленым справа) — это кривая, которая является границей областей вогнутых пятиугольников и других, называемых выпуклыми. Пентагоны, которые сопоставляются точно с этой границей, имеют по крайней мере две последовательные стороны, которые выглядят как сторона двойной длины, которая напоминает пятиугольник, вырожденный в четырехугольник.
Первый угол, который открывается больше 180 °, — это γ, поэтому γ = 180 ° (граница, показанная зеленым справа) — это кривая, которая является границей областей вогнутых пятиугольников и других, называемых выпуклыми. Пентагоны, которые сопоставляются точно с этой границей, имеют по крайней мере две последовательные стороны, которые выглядят как сторона двойной длины, которая напоминает пятиугольник, вырожденный в четырехугольник.Выпуклый
В выпуклых пятиугольников есть все свои пять углов меньше 180 ° , а не сторон , пересекающих другие. Типичный пример этого типа пятиугольника — правильный пятиугольник .
Ссылки
Пентагон (фигура) — это… Что такое Пентагон (фигура)?
- Пентагон (фигура)
Правильный пятиугольник
Правильный пятиугольник или пентагон (греч. πενταγωνον) — геометрическая фигура, правильный многоугольник с пятью сторонами.

Свойства
Поэтому радиус вписанной окружности, радиус описанной окружности, высоту и площадь правильного пятиугольника можно вычислить и без использования тригонометрических функций:
- Высота правильного пятиугольника:
- Площадь правильного пятиугольника:
- Радиус вписанной окружности правильного пятиугольника:
- Радиус описанной окружности правильного пятиугольника:
Построение
Правильный пятиугольник может быть построен с помощью циркуля и линейки, или вписыванием его в заданную окружность, или построением на основе заданной стороны. Этот процесс описан Евклидом в его «Началах» около 300 года до н. э.
Вот один из методов построения правильного пятиугольника в заданной окружности:
- Постройте окружность, в которую будет вписан пятиугольник и обозначьте её центр как O. (Это зелёная окружность на схеме справа).

- Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
- Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью как точку B.
- Постройте точку C посередине между O и B.
- Проведите окружность с центром в C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
- Проведите окружность с центром в A через точку D. Обозначьте её пересечения с оригинальной (зелёной окружностью) как точки E и F.
- Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.
- Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.

- Постройте правильный пятиугольник AEGHF.
Альтернативный метод построения правильного многоугольника с помощью линейки и циркуля
Получение с помощью полоски бумаги
Правильный пятиугольник можно получить, завязав узлом полоску бумаги.
Интересные факты
Пентагон
- Пентагон — здание Министерства обороны США имеет форму правильного пятиугольника.
- Правильный пятиугольник — правильный многоугольник с наименьшим количеством углов из тех, которыми нельзя замостить плоскость.
См. также
Wikimedia Foundation. 2010.
- Пентагон (многоугольник)
- Пентадеканолид
Смотреть что такое «Пентагон (фигура)» в других словарях:
ПЕНТАГОН — (греч., от pente пять, и gonia угол). Геометрическая фигура, окруженная 5 ю сторонами и 5 ю углами: пятиугольник.
 Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ПЕНТАГОН греч., от pente, пять, и gonia, угол.… … Словарь иностранных слов русского языка
Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ПЕНТАГОН греч., от pente, пять, и gonia, угол.… … Словарь иностранных слов русского языкаПентагон — (Греч.) От pente пять , и gonia угол ; в геометрии плоская фигура с пятью углами. Источник: Теософский словарь … Религиозные термины
Пентагон-додекаэдр — Пентагондодекаэдр Индексы граней {2 1 0} Тип Неправильный многогранник Грань Неправильный пятиугольник Граней 12 Рёбер 30 Вершин 20 Граней при вершине … Википедия
Пентагон (многоугольник) — Пятиугольник многоугольник с пятью углами. Также пятиугольником называют всякий предмет такой формы. Сумма внутренних углов выпуклого пятиугольника равна 540°. См.также Правильный пятиугольник Звезда (геометрическая фигура) Многоугольники … Википедия
ПЕНТАГОН — (Греч.) От pente пять , и gonia угол ; в геометрии плоская фигура с пятью углами … Теософский словарь
Пентаграмма — Пентаграмма … Википедия
Пентакль — Пентаграмма Пентаграмма (пентальфа, пентакл, пентагерон; греч.
 πεντάγραμμον от πέντε «пять» и γράμμα «черта, линия») правильный … Википедия
πεντάγραμμον от πέντε «пять» и γράμμα «черта, линия») правильный … ВикипедияПентакл — Пентаграмма Пентаграмма (пентальфа, пентакл, пентагерон; греч. πεντάγραμμον от πέντε «пять» и γράμμα «черта, линия») правильный … Википедия
Пифагорейский пентакл — Пентаграмма Пентаграмма (пентальфа, пентакл, пентагерон; греч. πεντάγραμμον от πέντε «пять» и γράμμα «черта, линия») правильный … Википедия
Сатанинская звезда — Пентаграмма Пентаграмма (пентальфа, пентакл, пентагерон; греч. πεντάγραμμον от πέντε «пять» и γράμμα «черта, линия») правильный … Википедия
Пятиугольник — Карта знаний
- Пятиугольник — многоугольник с пятью углами.
 Также пятиугольником называют всякий предмет такой формы.
Также пятиугольником называют всякий предмет такой формы.
Источник: Википедия
Связанные понятия
Шестиугольник — многоугольник с шестью углами. Также шестиугольником называют всякий предмет такой формы. Пятиугольник Роббинса — это вписанный пятиугольник, стороны которого и площадь являются рациональными числами. Звёздчатый многоугольник — многоугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного многоугольника. Стороны звёздчатого многоугольника могут пересекаться между собой. Существует множество звёздчатых многоугольников или звёзд, среди них пентаграмма, гексаграмма, две гептаграммы, октограмма, декаграмма, додекаграмма. Звёздчатые многоугольники можно получить, продолжая одновременно все стороны правильного многоугольника после их пересечения в его вершинах до их. ..
Шестиугольник Лемуана представляет собой шестиугольник, около которого можно описать окружность. Его вершинами являются шесть точек пересечениями сторон треугольника с тремя линиями, которые параллельны сторонам и которые проходят через его точку Лемуана. В любом треугольнике шестиугольник Лемуана находится внутри треугольника с тремя парами вершин, лежащих попарно на каждой стороне треугольника.
Правильный восьмиугольник (октагон) — геометрическая фигура из группы правильных многоугольников. У него восемь сторон и восемь углов, все углы и стороны равны между собой.
..
Шестиугольник Лемуана представляет собой шестиугольник, около которого можно описать окружность. Его вершинами являются шесть точек пересечениями сторон треугольника с тремя линиями, которые параллельны сторонам и которые проходят через его точку Лемуана. В любом треугольнике шестиугольник Лемуана находится внутри треугольника с тремя парами вершин, лежащих попарно на каждой стороне треугольника.
Правильный восьмиугольник (октагон) — геометрическая фигура из группы правильных многоугольников. У него восемь сторон и восемь углов, все углы и стороны равны между собой.Упоминания в литературе
Действительно, семь из 13 Архимедовых тел могут быть получены отрезанием кусочков от Платоновых тел – среди этих многогранников и классический футбольный мяч из пятиугольников и шестиугольников. Но более примечательным было открытие некоторых других форм. Оказывается, возможно объединение 30 квадратов, 20 правильных шестиугольников и 12 правильных десятиугольников в симметричную форму, которая называется ромбоусеченный икосододекаэдр (рис. 2.06).
Рис. 18. Геометрические построения, в основе которых лежат гармоничные пропорции: а – «золотое сечение»; б – квадрат; в – равносторонний треугольник; г – пятиугольник; д – прямоугольники, построенные на соответствующих гармоничных отрезках
Вот, например, по стороне вазы, от горлышка, но не доходя до низу, сбегает круговая линия, почти (но не вполне!) совпадающая с правильным кругом; внутри круга вписаны другие кривые, неполными спиралями касающиеся окружности, выходящие из одной точки и направленные под разными уклонами; низ вазы украшен параллельными поперечными полосами; свободное пространство в круге оживлено звездочками и пальметками. Или вот со дна шаровидной вазы дерзко вскидываются к ее середине лучевые линии, заканчивающиеся широким, вытянуто-округлым пятном, подобием огромного вопросительного знака, а сверху вазы из сплетения круговых линий получаются, идущие навстречу, секирообразные полушария.
Оказывается, возможно объединение 30 квадратов, 20 правильных шестиугольников и 12 правильных десятиугольников в симметричную форму, которая называется ромбоусеченный икосододекаэдр (рис. 2.06).
Рис. 18. Геометрические построения, в основе которых лежат гармоничные пропорции: а – «золотое сечение»; б – квадрат; в – равносторонний треугольник; г – пятиугольник; д – прямоугольники, построенные на соответствующих гармоничных отрезках
Вот, например, по стороне вазы, от горлышка, но не доходя до низу, сбегает круговая линия, почти (но не вполне!) совпадающая с правильным кругом; внутри круга вписаны другие кривые, неполными спиралями касающиеся окружности, выходящие из одной точки и направленные под разными уклонами; низ вазы украшен параллельными поперечными полосами; свободное пространство в круге оживлено звездочками и пальметками. Или вот со дна шаровидной вазы дерзко вскидываются к ее середине лучевые линии, заканчивающиеся широким, вытянуто-округлым пятном, подобием огромного вопросительного знака, а сверху вазы из сплетения круговых линий получаются, идущие навстречу, секирообразные полушария. Или вот из резко-стилизованных листьев и цветов получается сложный узор, заполняющий всю поверхность вазы, образующий вогнутые ромбы, ограниченные вытянутыми кругами, причем внутренность и кругов и ромбов, в свою очередь, заполнена комбинацией из пяти звездочек, составляющих пятиугольник. Во всех этих линейных орнаментах поражает умение заполнить пространство, дать впечатление сложности при помощи самых простых, в сущности, элементов. Глаз сначала видит определенный узор, потом, пытаясь вникнуть в его систему, запутывается безнадежно; лишь после, усилием мысли, удается восстановить сложно простое построение.
Пятиугольная звезда, используемая как область отсечения формы, создается с помощью описанной в листинге 1.15 процедуры Make5Angle. После ее создания изменяется порядок следования вершин пятиугольника, чтобы их обход при построении региона выполнялся в той же последовательности, как рисуется звезда карандашом на бумаге (например, 1-3-5-2-4) (листинг 1.
Или вот из резко-стилизованных листьев и цветов получается сложный узор, заполняющий всю поверхность вазы, образующий вогнутые ромбы, ограниченные вытянутыми кругами, причем внутренность и кругов и ромбов, в свою очередь, заполнена комбинацией из пяти звездочек, составляющих пятиугольник. Во всех этих линейных орнаментах поражает умение заполнить пространство, дать впечатление сложности при помощи самых простых, в сущности, элементов. Глаз сначала видит определенный узор, потом, пытаясь вникнуть в его систему, запутывается безнадежно; лишь после, усилием мысли, удается восстановить сложно простое построение.
Пятиугольная звезда, используемая как область отсечения формы, создается с помощью описанной в листинге 1.15 процедуры Make5Angle. После ее создания изменяется порядок следования вершин пятиугольника, чтобы их обход при построении региона выполнялся в той же последовательности, как рисуется звезда карандашом на бумаге (например, 1-3-5-2-4) (листинг 1. 16).
А потом Владимир Авинский приложил свой магический пятиугольник к плану марсианских пирамид. Увиденное повергло его в шок. Угол альфа использовался везде… Марсианские пирамиды явно старше земных. Если отбросить древние тексты, останется беспристрастная геометрия и математика. Она доказывает – сооружения на Земле и на другой планете построены по единому инженерному замыслу… На это же обратил внимание и доктор геолого-минералогических наук Александр ПОРТНОВ:
16).
А потом Владимир Авинский приложил свой магический пятиугольник к плану марсианских пирамид. Увиденное повергло его в шок. Угол альфа использовался везде… Марсианские пирамиды явно старше земных. Если отбросить древние тексты, останется беспристрастная геометрия и математика. Она доказывает – сооружения на Земле и на другой планете построены по единому инженерному замыслу… На это же обратил внимание и доктор геолого-минералогических наук Александр ПОРТНОВ:Связанные понятия (продолжение)
Равносторонний многоугольник — многоугольник, у которого все стороны равны. Например, равносторонний треугольник — это треугольник, у которого все три стороны одинаковы; все равносторонние треугольники подобны и имеют внутренние углы 60 градусов. Равносторонний четырёхугольник — это ромб, и квадрат является частным случаем ромба. Пра́вильный икоса́эдр (от др. -греч. εἴκοσι «двадцать»; ἕδρον «сиденье», «основание») — правильный выпуклый многогранник, двадцатигранник, одно из Платоновых тел. Каждая из 20 граней представляет собой равносторонний треугольник. Число ребер равно 30, число вершин — 12.
Купол можно рассматривать как призму, где один из многоугольников наполовину стянут путём объединения вершин попарно.
В геометрии гиробифастигиум или двускатный повёрнутый бикупол является 26-м многогранником Джонсона (J26). Его можно построить объединением двух треугольных призм с правильными гранями по соответствующим квадратным граням с поворотом одной призмы на 90º . Это единственное тело Джонсона, которым можно заполнить трёхмерное пространство.
Звезда — определённый вид плоских невыпуклых многоугольников, не имеющий, однако, однозначного математического определения.
-греч. εἴκοσι «двадцать»; ἕδρον «сиденье», «основание») — правильный выпуклый многогранник, двадцатигранник, одно из Платоновых тел. Каждая из 20 граней представляет собой равносторонний треугольник. Число ребер равно 30, число вершин — 12.
Купол можно рассматривать как призму, где один из многоугольников наполовину стянут путём объединения вершин попарно.
В геометрии гиробифастигиум или двускатный повёрнутый бикупол является 26-м многогранником Джонсона (J26). Его можно построить объединением двух треугольных призм с правильными гранями по соответствующим квадратным граням с поворотом одной призмы на 90º . Это единственное тело Джонсона, которым можно заполнить трёхмерное пространство.
Звезда — определённый вид плоских невыпуклых многоугольников, не имеющий, однако, однозначного математического определения. Семиуго́льник, называемый иногда гептагон — многоугольник с семью углами. Семиугольником также называют всякий предмет такой формы.
Пра́вильный многоуго́льник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между смежными сторонами равны.
Равнобедренный треугольник — это треугольник, в котором две стороны равны между собой по длине. Боковыми называются равные стороны, а последняя неравная им сторона — основанием. По определению, каждый правильный треугольник также является равнобедренным, но обратное утверждение неверно.
В геометрии плосконосый двуклиноид или сиамский додекаэдр — это трёхмерный выпуклый многогранник с двенадцатью правильными треугольниками в качестве граней. Многогранник не является правильным, поскольку в некоторых вершинах сходятся четыре грани, а в остальных — пять граней.
Семиуго́льник, называемый иногда гептагон — многоугольник с семью углами. Семиугольником также называют всякий предмет такой формы.
Пра́вильный многоуго́льник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между смежными сторонами равны.
Равнобедренный треугольник — это треугольник, в котором две стороны равны между собой по длине. Боковыми называются равные стороны, а последняя неравная им сторона — основанием. По определению, каждый правильный треугольник также является равнобедренным, но обратное утверждение неверно.
В геометрии плосконосый двуклиноид или сиамский додекаэдр — это трёхмерный выпуклый многогранник с двенадцатью правильными треугольниками в качестве граней. Многогранник не является правильным, поскольку в некоторых вершинах сходятся четыре грани, а в остальных — пять граней. Многогранник является двенадцатигранником, одним из восьми дельтаэдров (выпуклых многогранников с гранями в виде правильных треугольников) и одним из 92 многогранников Джонсона (неоднородные выпуклые многогранники с правильными…
Правильный пятиугольник (или пентагон от греч. πενταγωνον) — геометрическая фигура, правильный многоугольник с пятью сторонами.
Бикуполы более высоких порядков можно построить, если допускается растяжение боковых граней в прямоугольники и равнобедренные треугольники.
Одиннадцатиуго́льник, называемый иногда Гендекаго́н — многоугольник с одиннадцатью углами. Одиннадцатиугольником также называют всякий предмет, имеющий такую форму.
Площадь круга с радиусом r равна πr2. Здесь символ π (греческая буква пи) обозначает константу, выражающую отношение длины окружности к её диаметру или площади круга к квадрату его радиуса.
Многогранник является двенадцатигранником, одним из восьми дельтаэдров (выпуклых многогранников с гранями в виде правильных треугольников) и одним из 92 многогранников Джонсона (неоднородные выпуклые многогранники с правильными…
Правильный пятиугольник (или пентагон от греч. πενταγωνον) — геометрическая фигура, правильный многоугольник с пятью сторонами.
Бикуполы более высоких порядков можно построить, если допускается растяжение боковых граней в прямоугольники и равнобедренные треугольники.
Одиннадцатиуго́льник, называемый иногда Гендекаго́н — многоугольник с одиннадцатью углами. Одиннадцатиугольником также называют всякий предмет, имеющий такую форму.
Площадь круга с радиусом r равна πr2. Здесь символ π (греческая буква пи) обозначает константу, выражающую отношение длины окружности к её диаметру или площади круга к квадрату его радиуса. Поскольку площадь правильного многоугольника равна половине его периметра, умноженного на апофему (высоту), а правильные многоугольники стремятся к окружности при росте числа сторон, площадь круга равна половине длины окружности, умноженной на радиус (то есть 1⁄2 × 2πr × r).
В геометрии ротонда — любой член семейства диэдрально-симметричных многогранников. Они похожи на куполы, но вместо перемежающихся квадратов и треугольников перемежаются пятиугольники и треугольники (по отношению к оси). Пятискатная ротонда является телом Джонсона (J6).
Треуго́льный парке́т (треугольный паркета́ж) или треугольная мозаика — это замощение плоскости равными правильными треугольниками, расположенными сторона к стороне.
В геометрии удлинённый квадратный гиробикупол или псевдоромбокубооктаэдр (по Залгаллеру — удлинённый четырёхскатный повёрнутый бикупол) — это один из многогранников Джонсона (J37 = (по Залгаллеру) М5+П8+М5).
Поскольку площадь правильного многоугольника равна половине его периметра, умноженного на апофему (высоту), а правильные многоугольники стремятся к окружности при росте числа сторон, площадь круга равна половине длины окружности, умноженной на радиус (то есть 1⁄2 × 2πr × r).
В геометрии ротонда — любой член семейства диэдрально-симметричных многогранников. Они похожи на куполы, но вместо перемежающихся квадратов и треугольников перемежаются пятиугольники и треугольники (по отношению к оси). Пятискатная ротонда является телом Джонсона (J6).
Треуго́льный парке́т (треугольный паркета́ж) или треугольная мозаика — это замощение плоскости равными правильными треугольниками, расположенными сторона к стороне.
В геометрии удлинённый квадратный гиробикупол или псевдоромбокубооктаэдр (по Залгаллеру — удлинённый четырёхскатный повёрнутый бикупол) — это один из многогранников Джонсона (J37 = (по Залгаллеру) М5+П8+М5). Тело, обычно, не считается архимедовым телом, хотя его грани и являются правильными многоугольниками и многоугольники вокруг каждой вершины те же самые, но, в отличие от 13 архимедовых тел, многогранник не обладает глобальной симметрией, переводящей любую вершину в любую другую (хотя Грюнбаум…
В евклидовой геометрии равнодиагональный четырёхугольник — это выпуклый четырёхугольник, две диагонали которого имеют равные длины. Равнодиагональные четырёхугольники имели важное значение в древней индийской математике, где в классификации в первую очередь выделялись равнодиагональные четырёхугольники, и только потом четырёхугольники подразделялись на другие типы .
В геометрии вершина — это вид точки, в которой две кривые, две прямые либо два ребра сходятся. Из этого определения следует, что точка, в которой сходятся два луча, образуя угол, является вершиной, а также ею являются угловые точки многоугольников и многогранников.
Тело, обычно, не считается архимедовым телом, хотя его грани и являются правильными многоугольниками и многоугольники вокруг каждой вершины те же самые, но, в отличие от 13 архимедовых тел, многогранник не обладает глобальной симметрией, переводящей любую вершину в любую другую (хотя Грюнбаум…
В евклидовой геометрии равнодиагональный четырёхугольник — это выпуклый четырёхугольник, две диагонали которого имеют равные длины. Равнодиагональные четырёхугольники имели важное значение в древней индийской математике, где в классификации в первую очередь выделялись равнодиагональные четырёхугольники, и только потом четырёхугольники подразделялись на другие типы .
В геометрии вершина — это вид точки, в которой две кривые, две прямые либо два ребра сходятся. Из этого определения следует, что точка, в которой сходятся два луча, образуя угол, является вершиной, а также ею являются угловые точки многоугольников и многогранников. Вписанный четырёхугольник — это четырёхугольник, вершины которого лежат на одной окружности. Эта окружность называется описанной. Обычно предполагается, что четырёхугольник выпуклый, но бывают и самопересекающиеся вписанные четырёхугольники. Формулы и свойства, данные ниже, верны только для выпуклых четырёхугольников.
Девятиуго́льник — многоугольник с девятью углами. Девятиугольником также называют всякий предмет, имеющий такую форму.
Окта́эдр (греч. οκτάεδρον от οκτώ «восемь» + έδρα «основание») — многогранник с восемью гранями.
Десятиуго́льник (правильный десятиугольник — декагон) — многоугольник с десятью углами и десятью сторонами.
Описанный многоугольник, известный также как тангенциальный многоугольник — это выпуклый многоугольник, который содержит вписанную окружность. Это окружность, которая касательна каждой стороны многоугольника. Двойственный многоугольник описанного многоугольника — это многоугольник, который имеет описанную окружность, проходящую через все его вершины.
Апейрогон (от др.-греч. ἄπειρος — бесконечный или безграничный и др.-греч. γωνία — угол) — обобщённый многоугольник со счётно-бесконечным числом сторон.
В евклидовой геометрии описанный четырёхугольник — это выпуклый четырёхугольник, стороны которого являются касательными к одной окружности внутри четырёхугольника. Эта окружность называется вписанной в четырёхугольник. Описанные четырёхугольники являются частным случаем описанных многоугольников.
Сглаженный восьмиугольник — это область плоскости, предположительно, имеющая самую малую наибольшую плотность упаковки плоскости из всех центрально симметричных выпуклых фигур. Фигура получается заменой углов правильного восьмиугольника секцией гиперболы, которая касается двух сторон угла и асимптотически приближается к продолжениям сторон восьмиугольника, смежным сторонам угла.
Звезда Лакшми — октаграмма, составной правильный звездчатый многоугольник, представленный символом Шлефли a{8}, {8/2} или 2{4}, составленный из двух квадратов с общим центром, повёрнутых друг относительно друга на 45°. В индуизме является символом Ашталакшми, восьми форм богини Лакшми.
Наибольший многоугольник единичного диаметра — многоугольник с n сторонами (для заданного числа n), диаметр которого равен единице (то есть любые две его точки находятся друг от друга на расстоянии, не превосходящем единицы), и имеющий наибольшую площадь среди других n-угольников диаметра единица. Решением (не уникальным) для n = 4 является квадрат, решением для нечётных n является правильный многоугольник, при этом для остальных чётных n правильный многоугольник наибольшим не будет.
Двенадцатиуго́льник, додекаго́н (греч. δώδεκα — двенадцать и греч. γωνία — угол) — многоугольник с 12 углами и 12 сторонами. Как правило, додекагоном называют правильный многоугольник, то есть такой, у которого все стороны и все углы равны (в случае додекагона углы равны 150°). Правильный двенадцатиугольник используется в некоторых странах в качестве формы для монет.
В геометрии конциклическими (или гомоциклическими) точками называют точки, находящиеся на одной окружности. Три точки на плоскости, не лежащие на одной прямой, всегда лежат на одной окружности, поэтому иногда термин «конциклические» прилагают только к наборам из 4 или более точек.
Вписанный четырёхугольник — это четырёхугольник, вершины которого лежат на одной окружности. Эта окружность называется описанной. Обычно предполагается, что четырёхугольник выпуклый, но бывают и самопересекающиеся вписанные четырёхугольники. Формулы и свойства, данные ниже, верны только для выпуклых четырёхугольников.
Девятиуго́льник — многоугольник с девятью углами. Девятиугольником также называют всякий предмет, имеющий такую форму.
Окта́эдр (греч. οκτάεδρον от οκτώ «восемь» + έδρα «основание») — многогранник с восемью гранями.
Десятиуго́льник (правильный десятиугольник — декагон) — многоугольник с десятью углами и десятью сторонами.
Описанный многоугольник, известный также как тангенциальный многоугольник — это выпуклый многоугольник, который содержит вписанную окружность. Это окружность, которая касательна каждой стороны многоугольника. Двойственный многоугольник описанного многоугольника — это многоугольник, который имеет описанную окружность, проходящую через все его вершины.
Апейрогон (от др.-греч. ἄπειρος — бесконечный или безграничный и др.-греч. γωνία — угол) — обобщённый многоугольник со счётно-бесконечным числом сторон.
В евклидовой геометрии описанный четырёхугольник — это выпуклый четырёхугольник, стороны которого являются касательными к одной окружности внутри четырёхугольника. Эта окружность называется вписанной в четырёхугольник. Описанные четырёхугольники являются частным случаем описанных многоугольников.
Сглаженный восьмиугольник — это область плоскости, предположительно, имеющая самую малую наибольшую плотность упаковки плоскости из всех центрально симметричных выпуклых фигур. Фигура получается заменой углов правильного восьмиугольника секцией гиперболы, которая касается двух сторон угла и асимптотически приближается к продолжениям сторон восьмиугольника, смежным сторонам угла.
Звезда Лакшми — октаграмма, составной правильный звездчатый многоугольник, представленный символом Шлефли a{8}, {8/2} или 2{4}, составленный из двух квадратов с общим центром, повёрнутых друг относительно друга на 45°. В индуизме является символом Ашталакшми, восьми форм богини Лакшми.
Наибольший многоугольник единичного диаметра — многоугольник с n сторонами (для заданного числа n), диаметр которого равен единице (то есть любые две его точки находятся друг от друга на расстоянии, не превосходящем единицы), и имеющий наибольшую площадь среди других n-угольников диаметра единица. Решением (не уникальным) для n = 4 является квадрат, решением для нечётных n является правильный многоугольник, при этом для остальных чётных n правильный многоугольник наибольшим не будет.
Двенадцатиуго́льник, додекаго́н (греч. δώδεκα — двенадцать и греч. γωνία — угол) — многоугольник с 12 углами и 12 сторонами. Как правило, додекагоном называют правильный многоугольник, то есть такой, у которого все стороны и все углы равны (в случае додекагона углы равны 150°). Правильный двенадцатиугольник используется в некоторых странах в качестве формы для монет.
В геометрии конциклическими (или гомоциклическими) точками называют точки, находящиеся на одной окружности. Три точки на плоскости, не лежащие на одной прямой, всегда лежат на одной окружности, поэтому иногда термин «конциклические» прилагают только к наборам из 4 или более точек.Подробнее: Конциклические точки
Девятигранник (иногда используется название эннеаэдр) — это многогранник с девятью гранями. Существует 2606 видов выпуклых девятигранников, каждый из которых имеет свою отличную конфигурацию вершин, рёбер и граней. Ни один из этих многогранников не является правильным. Ромбокубооктаэдр или ромбокубоктаэдр — полуправильный многогранник, гранями которого являются 18 квадратов и 8 треугольников. Также называется малым ромбокубооктаэдром. В геометрии пространственный многоугольник — это многоугольник, вершины которого не компланарны. Пространственные многоугольники должны иметь по меньшей мере 4 вершины. Внутренняя поверхность таких многоугольников однозначно не определяется. Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Шестиуго́льный парке́т (шестиугольный паркета́ж) или шестиугольная мозаика — замощение плоскости равными правильными шестиугольниками, расположенными сторона к стороне. Вписанная в треугольник окружность — окружность внутри треугольника, касающаяся всех его сторон; наибольшая окружность, которая может находиться внутри треугольника. Центр этой окружности является точкой пересечения биссектрис треугольника и называется инцентром треугольника. Ромботриаконтáэдр( от греч. τριάκοντα (греч. τριάντα) — «тридцать» и εδρον — «грань») — выпуклый тридцатигранник с одинаковыми ромбическими гранями. Относится к каталановым телам. Является двойственным по отношению к икосододекаэдру и зоноэдром.Подробнее: Ромботриаконтаэдр
Правильный многогранник или плато́ново тело — это выпуклый многогранник, состоящий из одинаковых правильных многоугольников и обладающий пространственной симметрией. Внеописанный четырёхугольник — это выпуклый четырёхугольник, продолжения всех четырёх сторон которого являются касательными к окружности (вне четырёхугольника). Окружность называется вневписанной. Центр вневписанной окружности лежит на пересечении шести биссектрис. Это биссектрисы двух внутренних углов противоположных углов четырёхугольника, биссектрисы внешних углов двух других вершин, и биссектрисы внешних углов в точках пересечения продолжений противоположных сторон (смотрите рисунок справа, указанные… Звёздчатый многогра́нник (звёздчатое тело) — это невыпуклый многогранник, грани которого пересекаются между собой. Как и у незвёздчатых многогранников, грани попарно соединяются в рёбрах (при этом внутренние линии пересечения не считаются рёбрами). Сферический треугольник — геометрическая фигура на поверхности сферы, состоящая из трёх точек и трёх дуг больших кругов, соединяющих попарно эти точки. Три больших круга на поверхности сферы, не пересекающихся в одной точке, образуют восемь сферических треугольников. Соотношения между элементами сферических треугольников изучает сферическая тригонометрия.Значение слова ПЯТИУГОЛЬНИК. Что такое ПЯТИУГОЛЬНИК?
ПЯТИУГО́ЛЬНИК, -а, м. Геометрическая фигура, ограниченная замкнутой ломаной линией, звенья которой образуют пять углов.
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
- Пятиугольник — многоугольник с пятью углами. Также пятиугольником называют всякий предмет такой формы.
Источник: Википедия
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова оглаживать (глагол), оглаживая:
Кристально
понятноПонятно
в общих чертахМогу только
догадыватьсяПонятия не имею,
что этоДругое
ПропуститьНекоторые ответы о пятиугольниках
Некоторые ответы о пятиугольникахНекоторые отношения в правильных пятиугольниках
Сумма углов -> Угол при вершине
Сумма углов пятиугольника = 3 * 180 = 540 градусов. Таким образом, каждый угол при вершине = 540/5 = 108 градусов.
Равнобедренные треугольники <-> Углы
Две стороны и вершина образуют тупой равнобедренный треугольник, две такие заштрихованные. Вот.
Так как угол при тупой вершине EAB = 108 и два равных угла при основании имеют сумму = 180 108 = 72, острые углы основания, такие как CAB = 36 градусов.
Кроме того, угол CAD = угол EAB — 2 * 36 = 36 градусов, поэтому 2 диагонали от вершина, такая как A, делит угол при вершине пополам; то есть они делят угол при вершине на 3 равных угла по 36 градусов.
Наконец, треугольник DAC равнобедренный, поскольку каждый из углов основания ACD и ADC равны 108 36 = 72 градусам.
Пентаграмма (5 звезд)
Если все 5 диагоналей нарисованы в правильном пятиугольнике, эти 5 сегментов образуют звезду, называемую правильной пентаграммой.
Объединив то, что сейчас известно о равных углах при вершинах, получим Легко видеть, что пятиугольник ABCDE разделен на 5 равнобедренных треугольников, похожих на к треугольнику ABC 36-108-36 градусов, 5 равнобедренных треугольников, подобных 72-36-72 треугольник DAC градусов и один правильный пятиугольник в центре.
Равнобедренная трапеция и параллельные линии
Есть несколько способов увидеть, что диагональ BE параллельна CD и что CDEB — это равнобедренная трапеция.Если предположить, что знания об углах разработано выше, есть несколько быстрых способов увидеть это.
Метод поперечного и дополнительного угла: Линия BC является поперечной CD и BE. Угол DCB = 3 * 36 и угол CBE = 2 * 36, поэтому сумма углов = 5 * 36 = 180. Поскольку углы дополнительные, прямые CD и BE параллельны.
Метод поперечных и равных углов: Линия BD является поперечной CD и BE.Угол BDC = 36 и угол DBE = 36. Эти совпадающие чередующиеся внутренние Углы означают, что прямые CD и BE параллельны.
Метод симметрии линии равнобедренного треугольника: Поскольку треугольник EAB равнобедренный, биссектриса угла EAB является серединным перпендикуляром отрезка БЫТЬ. Поскольку треугольник DAC равнобедренный, биссектриса угла DAC — серединный перпендикуляр к CD. Но биссектрисы углов двух углы — это одна и та же линия (так как биссектриса DAC делит угол EAB на два углы размером 18 + 36 градусов).Но это значит, что у CD и BE одинаковые перпендикулярная биссектриса. Таким образом, эти линии параллельны. Кроме того, поскольку BC является При отражении DE отрезки имеют одинаковую длину.
Ромбики одинаковой длины
Теперь мы знаем, что каждая диагональ параллельна одной из сторон. Итак, если мы нарисуем две диагонали, они образуют параллелограмм параллелограммом. Но с тех пор стороны правильного пятиугольника равны, параллелограмм — ромб.(В любом параллелограмме противоположные стороны равны; если две соседние стороны равны, тогда все четыре стороны равны.)
Это означает, что определенные длины внутри звездообразной формы равны сторонам пятиугольника.
Золотое сечение в регулярном пентагоне
Теперь у нас есть много способов найти вложенные похожие равнобедренные треугольники в пентаграмме. 2 d 1 = 0.
Положительный корень этого квадратного уравнения равен (1/2) * (1 + sqrt 5). Это называется золотым сечением .
Для любого правильного пятиугольника со стороной s и длиной диагонали d отношение d / s = золотое сечение.
Построение правильного пятиугольника со стороны
Мы узнали, как по единице длины s построить длину sqrt 5, так что это можно использовать для построения длины d, которая является золотым сечением * s.
Затем с помощью s и d можно начать с отрезка AB и построить все треугольники ABC, ABD, ABE и таким образом построить правильный пятиугольник со стороной AB.
Этот метод также создает случайные углы, равные 36 градусам и целым числам. кратные 36 градусам.
Построение правильного пятиугольника из центра и вершины
Учитывая центр O и точку A, можно построить правильный пятиугольник ABCDE нарисовав круг с центром О через А, а затем построив углы необходимы (либо центральные углы, такие как AOB, либо углы при вершинах).
Но построение золотого сечения также дает необходимые углы, как было отмечено в предыдущем разделе.
Итак, вы хотите знать о пятиугольниках?
В геометрии учащиеся работают с множеством различных форм. Один из самых важных полигонов, с которым нужно познакомиться, — это пятиугольник.
7 фактов о пятиугольниках, которых вы могли не знать
- Все пятиугольники имеют пять прямых сторон, но стороны не должны быть одинаковой длины.
- У правильного пятиугольника пять равных сторон и пять равных углов. В базовой геометрии большинство проблем связано с правильными многоугольниками.
- Каждый внутренний угол правильного пятиугольника = 108 градусов.
- Каждый внешний угол правильного пятиугольника = 72 градуса.
- Сумма внутренних углов правильного пятиугольника = 540 градусов.
- Рисование диагональных линий между точками пятиугольника приведет к идеальной форме звезды или пентаграммы.
- Если пять сторон фигуры НЕ соединены или у фигуры есть изогнутые стороны, это НЕ пятиугольник.
Типы пятиугольников
- Правильный или равносторонний пятиугольник: пять равных сторон и углов
- Неправильный пятиугольник: пять неравных сторон и неравные углы
- Выпуклый пятиугольник: внутренний угол не может превышать 180 градусов
- Вогнутый пятиугольник: имеет внутренний угол более 180 градусов, из-за чего две стороны «погружаются», как «пещера»
Части Пентагона
- Сторона: один из пяти линейных сегментов
- Вершина: две стороны встречаются в точке, называемой вершиной
- Диагональ: линия, соединяющая две вершины, не являющиеся одной из пяти сторон
- Внутренний угол : внутренний угол, образованный двумя сторонами пятиугольника
- Внешний угол : угол снаружи пятиугольника, образованный двумя соседними сторонами
Как рассчитать площадь пятиугольника
- Начало с одной стороны и апофемы *
- Разделите пятиугольник на 5 треугольников, проведя 5 линий из центра пятиугольника
- Вычислить площадь треугольника **
- Умножьте на 5, чтобы найти общую площадь
* Апофема — это линия от центра пятиугольника к стороне, пересекающая сторону под прямым углом 90º.
** Запомните формулу для вычисления площади треугольника: ½ x основание x высота
Пентагоны — несколько забавных фактов
Почему Пентагон — это пятиугольник: Штаб-квартира Министерства обороны США в Вашингтоне, округ Колумбия, называется Пентагоном. Это массивное здание из бетона и стали имеет общую площадь почти 7 миллионов квадратных футов и 17,5 миль коридоров. В начале Второй мировой войны в 1941 году президент Рузвельт решил, что для Военного департамента необходимо новое здание.
Архитектор решил воспользоваться свойствами симметричного пятиугольника. Это сократило расстояние, которое люди должны были бы пройти от одного офиса до другого в этом огромном здании по сравнению с традиционным прямоугольным зданием. Круглое здание также должно было включать более короткие пешеходные расстояния, но построить здание с прямыми сторонами, такими как пятиугольник, было намного проще и быстрее.
Бамия: В следующий раз, когда вы будете есть жареную бамию или гамбо, взгляните на ломтик бамии.Он имеет форму пятиугольника.
Морская звезда: Почти все морские звезды имеют пятикратную радиальную симметрию или имеют форму пятиугольника.
Поэзия: На самом деле существует так называемая поэзия пятиугольника.
Музыкальные пятиугольники: Если вам нравится музыка 1980-х годов, обратите внимание на группу Pentagon Band Рича Клэра. Для чего-то другого, в Южной Корее есть бойз-бэнд под названием Pentagon.
Как видите, пятиугольник — очень полезная форма. Мало того, что пятиугольник часто используется в базовой геометрии, это форма, полезная в архитектуре и встречающаяся во всем мире природы.
Что такое Пентагон? | Определение, свойства и типы
Определение Пентагона
В геометрии пятиугольник — это пятиугольник с пятью прямыми сторонами и пятью внутренними углами, которые в сумме составляют 540 °. Пятиугольник — это плоская фигура или плоская (двумерная) 5-гранная геометрическая форма.
Свойства Пентагона
Пентагоны могут быть простыми или самопересекающимися. Свойства простого пятиугольника (5-угольника) заключаются в том, что он должен иметь пять прямых сторон, которые пересекаются, чтобы образовать пять вершин, но не пересекаются друг с другом:
- Пентагоны имеют пять прямых сторон
- Пентагоны имеют пять внутренних углов, которые в сумме составляют 540 °
- Пять сторон не пересекаются
Самопересекающийся правильный пятиугольник называется пентаграммой .
Содержание
- Определение формы пятиугольника
- Свойства Пентагона
- Типы пятиугольников
- Примеры пятиугольников
- Периметр и площадь пятиугольника
Типы пятиугольников
Пятиугольники двух типов — правильные пятиугольники и неправильные пятиугольники.
Обычные пятиугольники
Правильный пятиугольник должен иметь пять конгруэнтных сторон, пять конгруэнтных внутренних углов и конгруэнтные внешние углы:
- пять равных сторон (стороны равной длины)
- пять одинаковых внутренних углов (каждый по 108 °)
- пять конгруэнтных внешних углов 72 °
У правильных пятиугольников нет параллельных сторон.
Как и любой правильный многоугольник, пятиугольник завершает полный круг, поэтому внешние углы находятся путем деления 360 ° на количество сторон, в данном случае 360 ° 5 = 72 °.
Неправильные пятиугольники
Неправильные пятиугольники могут быть выпуклым пятиугольником или вогнутым пятиугольником, но у них должно быть пять сторон разной длины.
- Выпуклый пятиугольник — Внутренний угол не может превышать 180 °
- Вогнутый пятиугольник — Один внутренний угол больше 180 °
Распространенный пример выпуклого неправильного пятиугольника — домашняя пластина на бейсбольном поле.
Все пятиугольники (правильные и неправильные) имеют пятиугольную форму с пятью внутренними углами и пятью внешними углами.
Примеры пятиугольников
Если вы будете искать вокруг себя пятиугольник, вы обязательно его найдете. Будь то неправильный пятиугольник с различной длиной сторон или правильный пятиугольник с равными сторонами и равными углами, существует множество реальных примеров пятиугольников:
- Знаменитое здание Министерства обороны США в Вашингтоне, округ Колумбия.(Здание Пентагона)
- Домашняя тарелка на бейсбольном поле
- Знаки школьного перехода
- Участки на футбольном мяче
пятиугольник Википедия
форма с пятью сторонами
Пентагон Равносторонний пятиугольник, то есть пятиугольник, все пять сторон которого имеют одинаковую длину
Кромки и вершины 5 18 Внутренний угол (градусов) 90 если равноугловой, включая правильный) В геометрии пятиугольник (от греческого πέντε pente и γωνία gonia , что означает пять и угол [1] ) — это любая пять многоугольник или 5-угольник.Сумма внутренних углов в простом пятиугольнике составляет 540 °.
Пятиугольник может быть простым или самопересекающимся. Самопересекающийся правильный пятиугольник (или пятиугольник звезды ) называется пентаграммой.
Правильные пятиугольники []
Правильный пятиугольник имеет символ Шлефли {5}, а внутренние углы составляют 108 °.
Правильный пятиугольник имеет пять линий отражательной симметрии и вращательную симметрию 5-го порядка (72 °, 144 °, 216 ° и 288 °).Диагонали выпуклого правильного пятиугольника находятся в золотой пропорции к его сторонам. Его высота (расстояние от одной стороны до противоположной вершины) и ширина (расстояние между двумя наиболее удаленными друг от друга точками, равное длине диагонали) задаются выражением
- Высота = 5 + 252⋅ Сторона≈1,539⋅ Сторона, {\ displaystyle {\ text {Height}} = {\ frac {\ sqrt {5 + 2 {\ sqrt {5}}}} {2}} \ cdot {\ text {Side}} \ приблизительно 1,539 \ cdot {\ text {Side}},}
- Ширина = Диагональ = 1 + 52⋅ Сторона ≈ 1,618⋅ Сторона, {\ displaystyle {\ text {Width}} = {\ text {Diagonal}} = {\ frac {1 + {\ sqrt {5}}} {2 }} \ cdot {\ text {Side}} \ приблизительно 1.{2}.}
Пентаграмма или пятиугольник — правильный пятиугольник. {\ circ})} {4}}}
с длиной стороны t .
Inradius []
Как и любой правильный выпуклый многоугольник, правильный выпуклый пятиугольник имеет вписанную окружность. Апофема, которая представляет собой радиус r вписанной окружности, правильного пятиугольника связана с длиной стороны t соотношением
- r = t2tan (π / 5) = t25−20≈0,6882⋅t. {\ Displaystyle r = {\ frac {t} {2 \ tan (\ pi / 5)}} = {\ frac {t} {2 {\ sqrt {5 — {\ sqrt {20}}}}}} \ приблизительно 0,6882 \ cdot t.}
Хорды от описанной окружности до вершин []
Как и любой правильный выпуклый многоугольник, правильный выпуклый пятиугольник имеет описанную окружность.Для правильного пятиугольника с последовательными вершинами A, B, C, D, E, если P — любая точка на описанной окружности между точками B и C, то PA + PD = PB + PC + PE.
Точка на плоскости []
Для произвольной точки на плоскости правильного пятиугольника с радиусом описанной окружности R {\ displaystyle R}, расстояния до центра тяжести правильного пятиугольника и его пяти вершин равны L {\ displaystyle L} и di {\ displaystyle d_ {i} } соответственно имеем [2]
- ∑i = 15di2 = 5 (R2 + L2), {\ displaystyle \ textstyle \ sum _ {i = 1} ^ {5} d_ {i} ^ {2} = 5 (R ^ {2} + L ^ {2}),}
- ∑i = 15di4 = 5 ((R2 + L2) 2 + 2R2L2), {\ displaystyle \ textstyle \ sum _ {i = 1} ^ {5} d_ {i} ^ { 4} = 5 ((R ^ {2} + L ^ {2}) ^ {2} + 2R ^ {2} L ^ {2}),}
- ∑i = 15di6 = 5 ((R2 + L2) 3 + 6R2L2 (R2 + L2)), {\ displaystyle \ textstyle \ sum _ {i = 1} ^ {5} d_ {i} ^ {6} = 5 ((R ^ {2} + L ^ { 2}) ^ {3} + 6R ^ {2} L ^ {2} (R ^ {2} + L ^ {2})),}
- ∑i = 15di8 = 5 ((R2 + L2) 4 + 12R2L2 (R2 + L2) 2 + 6R4L4).{4}.}
Строительство правильного пятиугольника []
Правильный пятиугольник можно построить с помощью циркуля и линейки, так как 5 — простое число Ферма. Известно множество методов построения правильного пятиугольника. Некоторые обсуждаются ниже.
Метод Ричмонда []
Один из методов построения правильного пятиугольника в данном круге описан Ричмондом [3] и далее обсуждается в книге Кромвеля Многогранники . [4]
На верхней панели показана конструкция, использованная в методе Ричмонда для создания стороны вписанного пятиугольника.Окружность, определяющая пятиугольник, имеет единичный радиус. Его центр расположен в точке C , а средняя точка M отмечена на полпути по его радиусу. Эта точка соединяется с периферией вертикально над центром в точке D . Угол CMD делится пополам, а биссектриса пересекает вертикальную ось в точке Q . Горизонтальная линия, проходящая через Q , пересекает окружность в точке P , а хорда PD является необходимой стороной вписанного пятиугольника.
Для определения длины этой стороны под кружком изображены два прямоугольных треугольника DCM и QCM . Используя теорему Пифагора и две стороны, гипотенуза большего треугольника находится как 5/2 {\ displaystyle \ scriptstyle {\ sqrt {5}} / 2}. Сторона h меньшего треугольника определяется по формуле половинного угла:
- загар (ϕ / 2) знак равно 1 − cos (ϕ) sin (ϕ), {\ Displaystyle \ загар (\ phi / 2) = {\ гидроразрыва {1- \ cos (\ phi)} {\ sin (\ phi)}} \,}
где косинус и синус ϕ известны из большего треугольника.{2} = 2-2h = 2-2 \ left ({\ frac {{\ sqrt {5}} — 1} {4}} \ right) \}
- = 5−52. {\ Displaystyle = {\ frac {5 — {\ sqrt {5}}} {2}} \.}
Таким образом, сторона s :
- s = 5−52, {\ displaystyle s = {\ sqrt {\ frac {5 — {\ sqrt {5}}} {2}}} \,}
хорошо зарекомендовавший себя результат. [5] Следовательно, эта конструкция пятиугольника верна.
Круги Карлайла []
Метод с использованием кругов КарлайлаКруг Карлайла был изобретен как геометрический метод нахождения корней квадратного уравнения. [6] Эта методология приводит к процедуре построения правильного пятиугольника. Шаги следующие: [7]
- Нарисуйте круг, в который нужно вписать пятиугольник, и отметьте центральную точку O .
- Проведите горизонтальную линию через центр круга. Отметьте левое пересечение с кругом как точку B .
- Постройте вертикальную линию через центр. Отметьте одно пересечение с окружностью как точку A .
- Постройте точку M как среднюю точку O и B .
- Нарисуйте круг с центром M через точку A . Отметьте его пересечение с горизонтальной линией (внутри исходного круга) как точку W и его пересечение вне круга как точку V .
- Нарисуйте окружность с радиусом OA и центром W . Он пересекает исходный круг в двух вершинах пятиугольника.
- Нарисуйте окружность радиуса OA и центра V . Он пересекает исходный круг в двух вершинах пятиугольника.
- Пятая вершина — это крайнее правое пересечение горизонтальной линии с исходной окружностью.
Шаги 6–8 эквивалентны следующей версии, показанной на анимации:
- 6а. Постройте точку F как среднюю точку O и W.
- 7a. Проведите вертикальную линию через F.Он пересекает исходный круг в двух вершинах пятиугольника. Третья вершина — это крайнее правое пересечение горизонтальной линии с исходной окружностью.
- 8а. Постройте две другие вершины, используя циркуль и длину вершины, найденную на шаге 7a.
Использование тригонометрии и теоремы Пифагора []
Использование тригонометрии и теоремы Пифагора для построения правильного пятиугольника.Строительство []
- Сначала отметим, что правильный пятиугольник можно разделить на 10 равных треугольников, как показано в наблюдении Наблюдения .Кроме того, cos 36 ° = 1 + 54 {\ displaystyle {\ tfrac {1 + {\ sqrt {5}}} {4}}}. †
- В шаге 1 мы используем четыре единицы (показаны синим) и прямой угол, чтобы построить отрезок длиной 1 + √5, в частности, создав прямоугольный треугольник 1-2-√5 и затем расширив гипотенузу √ 5 на длину 1. Затем мы делим этот сегмент пополам, а затем снова делим пополам, чтобы создать сегмент длиной 1 + 54 {\ displaystyle {\ tfrac {1 + {\ sqrt {5}}} {4}}} ( показан красным.)
- На шаге 2 мы строим две концентрические окружности с центром O с радиусами длины 1 и длины 1 + 54 {\ displaystyle {\ tfrac {1 + {\ sqrt {5}}} {4}}}.Затем мы помещаем P произвольно на меньший круг, как показано. Строя прямую, перпендикулярную OP, проходящую через P , мы строим первую сторону пятиугольника, используя точки, созданные на пересечении касательной и единичной окружности. Копирование этой длины четыре раза по внешнему краю единичных кругов дает нам правильный пятиугольник. {\ circ}} {2}}}} (используя формулы двойного и половинного угла)
- Пусть u = cos 36 °.{2} -4 (4) (- 1)}}} {2 (4)}} \\ u & {} = {\ frac {1 + {\ sqrt {5}}} {4}} \ end {выровнено }}}
Это быстро следует из знания, что удвоение синуса 18 градусов является обратным золотым сечением, которое мы знаем геометрически из треугольника с углами 72,72,36 градусов. Из тригонометрии мы знаем, что косинус дважды 18 градусов равен 1 минус два квадрата синуса 18 градусов, и это сводится к желаемому результату с помощью простой квадратичной арифметики.
Указана длина стороны []
Правильный пятиугольник согласно золотому сечению, делящий отрезок линии внешним делением.
Пентагон при заданной длине стороны- Нарисуйте отрезок AB , длина которого равна заданной стороне пятиугольника.
- Удлините сегмент BA от точки A примерно на три четверти сегмента BA .
- Нарисуйте дугу окружности с центром B и радиусом AB .
- Нарисуйте дугу окружности с центром A с радиусом AB ; возникает перекресток F .
- Постройте перпендикуляр к отрезку AB через точку F ; возникает перекресток G .
- Проведите линию, параллельную отрезку FG , от точки A до дуги окружности вокруг точки A ; возникает перекресток H .
- Нарисуйте дугу окружности, центр G с радиусом GH до продолжения сегмента AB ; возникает перекресток J .
- Нарисуйте дугу окружности, центральная точка B с радиусом BJ до перпендикуляра в точке G ; возникает пересечение D на перпендикуляре и пересечение E с дугой окружности, созданной вокруг точки A .
- Нарисуйте дугу окружности с центром D с радиусом BA , пока эта дуга окружности не пересечет другую дугу окружности вокруг точки B ; возникает перекресток C .
- Соедините точки BCDEA . Получается пятиугольник.
Золотое сечение []
- BJ¯AB¯ = AB¯AJ¯ = 1 + 52 = φ≈1.618 {\ displaystyle {\ frac {\ overline {BJ}} {\ overline {AB}}} = {\ frac {\ overline { AB}} {\ overline {AJ}}} = {\ frac {1 + {\ sqrt {5}}} {2}} = \ varphi \ приблизительно 1.618}
Метод Евклида []
Метод Евклида для пятиугольника в заданной окружности, с использованием золотого треугольника, анимация 1 мин 39 сПравильный пятиугольник можно построить с помощью циркуля и линейки, вписав один в заданный круг или построив один на заданном крае. Этот процесс был описан Евклидом в его Elements около 300 г. до н.э. [8] [9]
Просто используя транспортир (не классическая конструкция) []
Прямой метод с использованием градусов:
- Нарисуйте круг и выберите точку, которая будет пятиугольником (например,грамм. вверху в центре)
- Выберите точку A на окружности, которая будет одной вершиной пятиугольника. Проведите линию через O и A .
- Проведите через него направляющую и центр круга
- Нарисуйте линии под углом 54 ° (от направляющей), пересекающие точку пятиугольника
- Там, где они пересекают круг, нарисуйте линии под углом 18 ° (от параллелей к направляющей)
- Соединитесь там, где они пересекают окружность
После образования правильного выпуклого пятиугольника, если соединить несмежные углы (рисуя диагонали пятиугольника), получится пентаграмма с меньшим правильным пятиугольником в центре.Или, если расширить стороны, пока не встретятся несмежные стороны, получится пентаграмма большего размера. Точность этого метода зависит от точности транспортира, используемого для измерения углов.
Физические методы []
Узел на бумажной полоске сверху- Правильный пятиугольник можно создать из полоски бумаги, завязав на ней узел сверху и осторожно расправив узел, потянув за концы полоски. Если загнуть один из концов над пятиугольником, то при заднем освещении будет открыта пентаграмма.
- Постройте правильный шестиугольник на плотной бумаге или картоне. Сделайте складку по трем диаметрам между противоположными вершинами. Вырежьте от одной вершины к центру, чтобы получился равносторонний треугольный лоскут. Закрепите этот клапан под его соседом, чтобы получилась пятиугольная пирамида. Основание пирамиды — правильный пятиугольник.
Симметрия []
Симметрии правильного пятиугольника. Вершины окрашены в соответствии с их положением симметрии. Синие зеркальные линии проводятся через вершины и ребра. В центре даны приказы гирации.Правильный пятиугольник имеет симметрию Dih 5 , порядок 10. Поскольку 5 — простое число, имеется одна подгруппа с двугранной симметрией: Dih 1 и 2 симметрии циклических групп: Z 5 и Z 1 .
Эти 4 симметрии можно увидеть в 4 различных симметриях на пятиугольнике. Джон Конвей помечает их буквой и групповым порядком. [10] Полная симметрия правильной формы — r10 , и никакая симметрия не помечена как a1 .Двугранные симметрии разделяются в зависимости от того, проходят ли они через вершины ( d для диагонали) или ребра ( p для перпендикуляров) и i , когда линии отражения проходят через ребра и вершины. Циклические симметрии в среднем столбце обозначены как g для их центральных порядков вращения.
Симметрия каждой подгруппы допускает одну или несколько степеней свободы для неправильных форм. Только подгруппа g5 не имеет степеней свободы, но ее можно рассматривать как направленные грани.
Равносторонние пятиугольники []
Равносторонний пятиугольник, состоящий из четырех равных кругов, расположенных в виде цепочки.Равносторонний пятиугольник — это многоугольник с пятью сторонами одинаковой длины. Однако его пять внутренних углов могут принимать различные наборы значений, что позволяет ему образовывать семейство пятиугольников. Напротив, правильный пятиугольник уникален с точностью до подобия, потому что он равносторонний и равноугольный (его пять углов равны).
Циклические пятиугольники []
Циклический пятиугольник — это пятиугольник, у которого окружность, называемая описанной окружностью, проходит через все пять вершин.Правильный пятиугольник — это пример циклического пятиугольника. Площадь циклического пятиугольника, правильного или неправильного, может быть выражена как одна четвертая квадратного корня одного из корней септического уравнения, коэффициенты которого являются функциями сторон пятиугольника. [11] [12] [13]
Существуют циклические пятиугольники с рациональными сторонами и рациональной площадью; они называются пятиугольниками Роббинса. В пятиугольнике Роббинса либо все диагонали рациональны, либо все иррациональны, и предполагается, что все диагонали должны быть рациональными. [14]
Общие выпуклые пятиугольники []
Для всех выпуклых пятиугольников сумма квадратов диагоналей меньше трехкратной суммы квадратов сторон. [15] : стр.75, № 1854
Графики []
Полный граф K 5 часто изображается в виде правильного пятиугольника со всеми 10 соединенными ребрами. Этот граф также представляет собой ортогональную проекцию 5 вершин и 10 ребер 5-ячейки. Выпрямленная 5-ячеечная с вершинами на средних краях 5-ячеечной проекции проецируется внутри пятиугольника.
Примеры пятиугольников []
Растения []
Животные []
Минералы []
Пиритоэдрический кристалл пирита. Пиритоэдр имеет 12 одинаковых пятиугольных граней, которые не обязательно должны быть правильными.
Искусственный []
Пентагоны в мозаике []
Правильный пятиугольник не может появиться ни в одной мозаике из правильных многоугольников. Во-первых, чтобы доказать, что пятиугольник не может образовывать правильную мозаику (в которой все грани совпадают, что требует, чтобы все многоугольники были пятиугольниками), заметьте, что 360 ° / 108 ° = 3 1 ⁄ 3 (где 108 ° внутренний угол), который не является целым числом; следовательно, не существует целого числа пятиугольников, разделяющих одну вершину и не оставляющих промежутков между ними.Сложнее доказать, что пятиугольник не может входить ни в одну мозаику от края до края, образованную правильными многоугольниками:
Максимальная известная плотность упаковки правильного пятиугольника составляет приблизительно 0,921, что достигается показанной двойной решетчатой упаковкой. В препринте, выпущенном в 2016 году, Томас Хейлз и Воден Куснер объявили о доказательстве того, что двойная решетчатая упаковка обычного пятиугольника (которую они называют упаковкой «пятиугольного ледяного луча» и которая восходит к работам китайских мастеров в 1900 году) имеет оптимальную плотность среди всех упаковок правильных пятиугольников на плоскости. [16] По состоянию на 2020 год [обновление] , их доказательство еще не рецензировалось и не публиковалось.
Не существует комбинаций правильных многоугольников с 4 или более пересекающимися вершинами, содержащими пятиугольник. Для комбинаций с 3, если 3 многоугольника встречаются в вершине и один имеет нечетное число сторон, другие 2 должны быть конгруэнтными. Причина этого в том, что многоугольники, соприкасающиеся с краями пятиугольника, должны чередоваться вокруг пятиугольника, что невозможно из-за нечетного количества сторон пятиугольника.Для пятиугольника это дает многоугольник, все углы которого равны (360-108) / 2 = 126 °. Чтобы найти количество сторон этого многоугольника, результат: 360 / (180 — 126) = 6 2 ⁄ 3 , что не является целым числом. Следовательно, пятиугольник не может появиться ни в одной мозаике из правильных многоугольников.
Существует 15 классов пятиугольников, которые могут моноэдрально замостить плоскость. Ни один из пятиугольников не обладает какой-либо симметрией в целом, хотя у некоторых есть особые случаи с зеркальной симметрией. Хейлз, Томас; Kusner, Wöden (сентябрь 2016 г.), Уплотнения правильных пятиугольников в плоскости , arXiv: 1602.07220
Внешние ссылки []
Найдите пятиугольник в Wiktionary, бесплатном словаре. Мы Пентагон | Ускорьте свой онлайн-рост
«Пентагон помог сформировать нашу стратегию выхода на рынок, и когда они были готовы, они были гибкими и действовали быстро, чтобы это произошло.С момента запуска они были как продолжение моей команды, всегда готовы ответить на наши вопросы и даже предвидеть наши потребности. Они продолжают сотрудничать с нами, чтобы бросить вызов рынку, чтобы мы могли расти вместе, понимая коммерческое влияние на нас ».
— Чарльз Оудс, директор по новым бизнес-моделям в Coty«Коммерческая модель Пентагона — это разделенный риск, что означает, что они верят в себя и всегда стремятся вывести Sports Direct на новые рынки.”
— Найл Сазерленд, руководитель отдела электронной торговли в Sports Direct«Пентагон является чрезвычайно ценным дополнением к нашей команде по электронной коммерции. С самого первого дня они активно разрабатывали наши предложения на рынке, начиная с создания новых запасов и заканчивая их оптимизацией. Пентагон помог нам получить максимальную отдачу от нашей рыночной стратегии, и имели решающее значение во времена достижения целей роста и управления торговой политикой рынка, чтобы минимизировать торговые и сбытовые риски.«
— Марк Барклай, менеджер группы по электронной торговле в The Parts Alliance«У Пентагона есть культура обучения в рамках своего бизнеса, что означает, что они постоянно улучшают услуги, которые предлагают нам, гарантируя постоянный рост доходов и удовлетворенность клиентов. Мы полностью доверяем их знаниям и опыту, чтобы добиться успеха в Интернете на мировых рынках ».
— Пол Херст, руководитель отдела онлайн-оптимизации и оптимизации сайта Cotton Traders«Команда Пентагона чрезвычайно хорошо осведомлена, оперативна и всегда в курсе всех последних рыночных тенденций, что позволяет нам опережать тенденции и соответствовать любым новым изменениям.Сейчас мы стремимся к расширению за пределами Великобритании и полностью намерены максимально использовать огромный опыт Пентагона по выходу на новые рынки ».
— Крис Хиам, руководитель отдела продаж на Kitbag.comБарнсли
Пентагон предлагает 3 франшизы, включая Nissan, Jeep и Peugeot. Пожалуйста, выберите желаемого производителя ниже:
Барнсли, Клейклифф-роуд, Барух Грин, Барнсли, Южный Йоркшир, S75 1LR.
Бертон-он-Трент
Выберите Vauxhall или Peugeot в Бертон-он-Трент, нажав на логотип ниже:
Бертон-он-Трент, Дерби-роуд, Стреттон, Бертон-он-Трент, Стаффордшир, DE13 0DF.
Дерби
Пентагон — это название Воксхолла в Дерби, Дербишир.
Дерби, Остров Пентагон, Ноттингем-роуд, Дерби, Дербишир, DE21 6HB.
Хаддерсфилд
Выберите SEAT или CUPRA в Хаддерсфилде, щелкнув логотип ниже:
Хаддерсфилд, 1 Fartown Green Road, Брэдфорд-роуд, Хаддерсфилд, Западный Йоркшир, HD2 1AA.
Lincoln (Outer Circle Rd)
Пентагон предлагает 3 франшизы, включая Renault, Dacia и Mitsubishi. Пожалуйста, выберите желаемого производителя ниже:
Lincoln (Outer Circle Rd), Внешняя кольцевая дорога, Линкольн, Линкольншир, LN2 4LD.
Линкольн
Пентагон предлагает 5 франшиз, включая Vauxhall, Citroen, Jeep, Mazda и Peugeot.Пожалуйста, выберите желаемого производителя ниже:
Линкольн, 8 Tritton Road, Линкольн, Линкольншир, LN6 7QY.
Лафборо
Пентагон предлагает 4 франшизы, включая Vauxhall, Citroen, Peugeot и Renault. Пожалуйста, выберите желаемого производителя ниже:
Лафборо, Белтон-роуд, 52, Лафборо, Лестершир, LE11 1NE.
Мэнсфилд
Пентагон — это название Воксхолла в Мэнсфилде, Ноттингемшир.
Мэнсфилд, Саттон-роуд, Мэнсфилд, Ноттингемшир, NG18 5HX.
Миддлтон
Пентагон — это название компании Vauxhall в Манчестере, Ланкашир.
Миддлтон, Гринсайд Уэй, Миддлтон, Манчестер, Ланкашир, M24 1SW.
Ноттингем (Арнольд)
Пентагон — это название Vauxhall в Ноттингеме, Ноттингемшир.


 {4}.}
{4}.}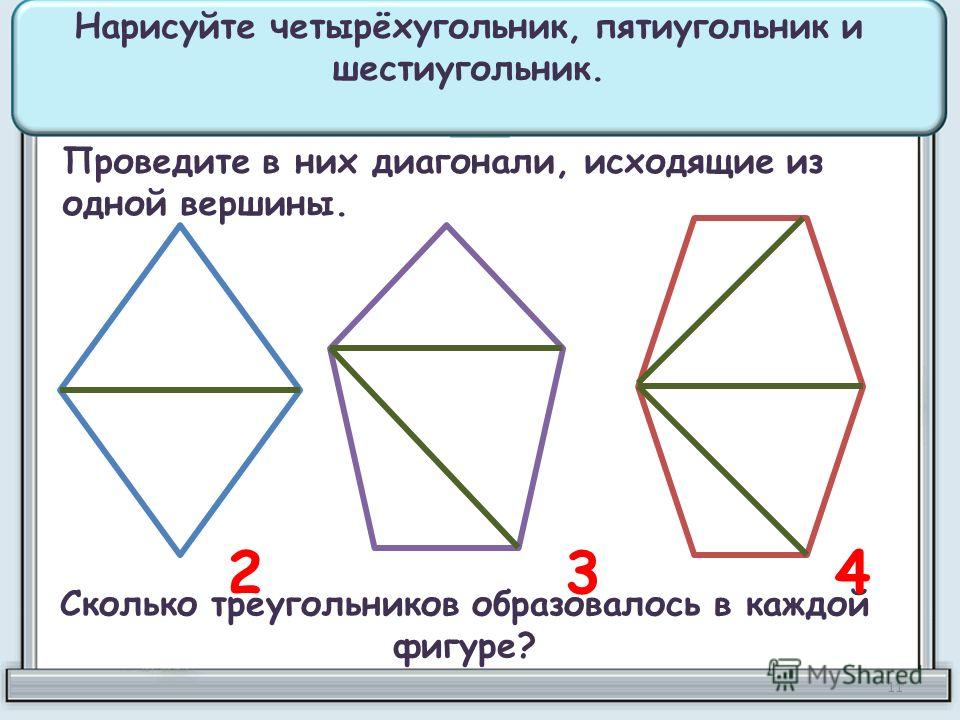

 {2} -4 (4) (- 1)}}} {2 (4)}} \\ u & {} = {\ frac {1+ {\ sqrt {5}}} {4}} \ end {align}}}
{2} -4 (4) (- 1)}}} {2 (4)}} \\ u & {} = {\ frac {1+ {\ sqrt {5}}} {4}} \ end {align}}}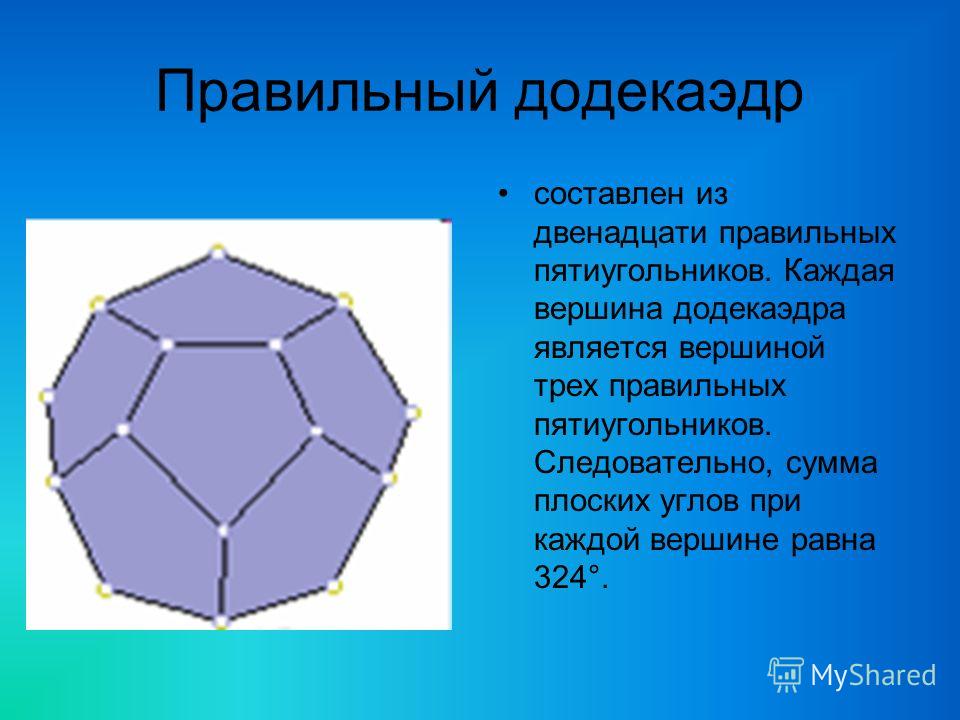
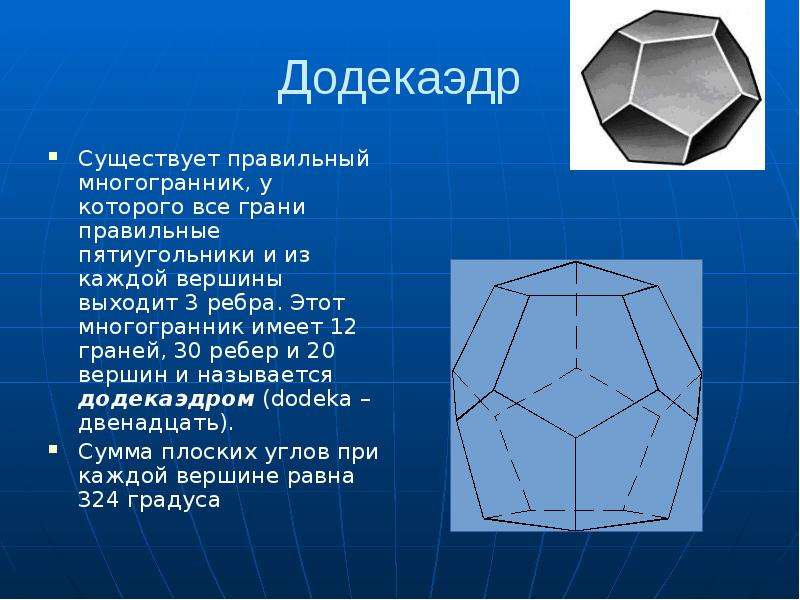 Этот процесс был описан Евклидом в его « Элементах» около 300 г. до н. Э.
Этот процесс был описан Евклидом в его « Элементах» около 300 г. до н. Э.


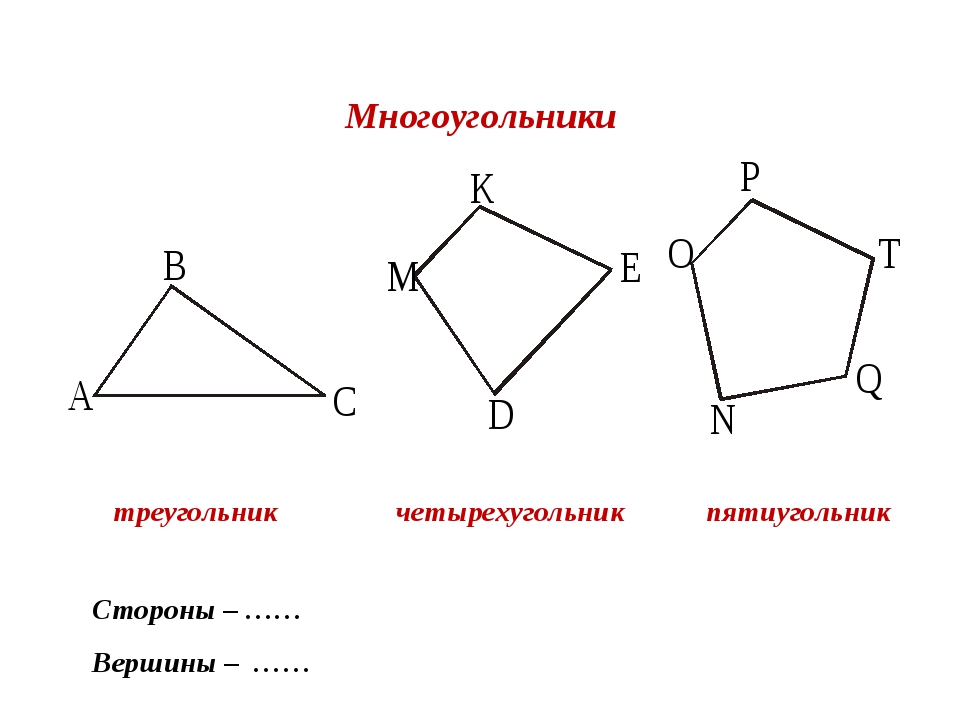
 Сложнее доказать, что пятиугольник не может входить ни в одну мозаику от края до края, образованную правильными многоугольниками:
Сложнее доказать, что пятиугольник не может входить ни в одну мозаику от края до края, образованную правильными многоугольниками: Причина этого в том, что многоугольники, соприкасающиеся с краями пятиугольника, должны чередоваться вокруг пятиугольника, что невозможно из-за нечетного количества сторон пятиугольника. Для пятиугольника это дает многоугольник, все углы которого равны (360-108) / 2 = 126 ° . Для того, чтобы найти число сторон этого многоугольника, результат равен 360 / (180 — 126) = 6 2 / 3 , которое не является целым числом. Следовательно, пятиугольник не может появиться ни в одной мозаике из правильных многоугольников.
Причина этого в том, что многоугольники, соприкасающиеся с краями пятиугольника, должны чередоваться вокруг пятиугольника, что невозможно из-за нечетного количества сторон пятиугольника. Для пятиугольника это дает многоугольник, все углы которого равны (360-108) / 2 = 126 ° . Для того, чтобы найти число сторон этого многоугольника, результат равен 360 / (180 — 126) = 6 2 / 3 , которое не является целым числом. Следовательно, пятиугольник не может появиться ни в одной мозаике из правильных многоугольников.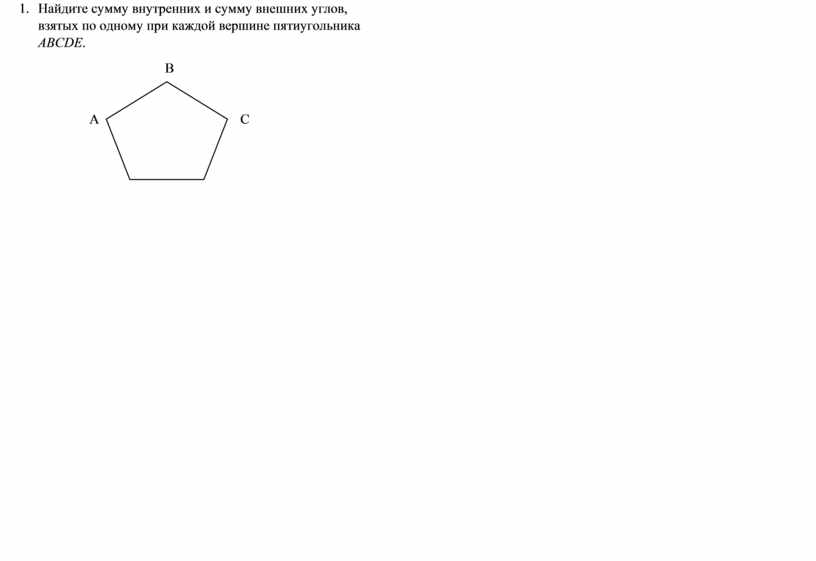
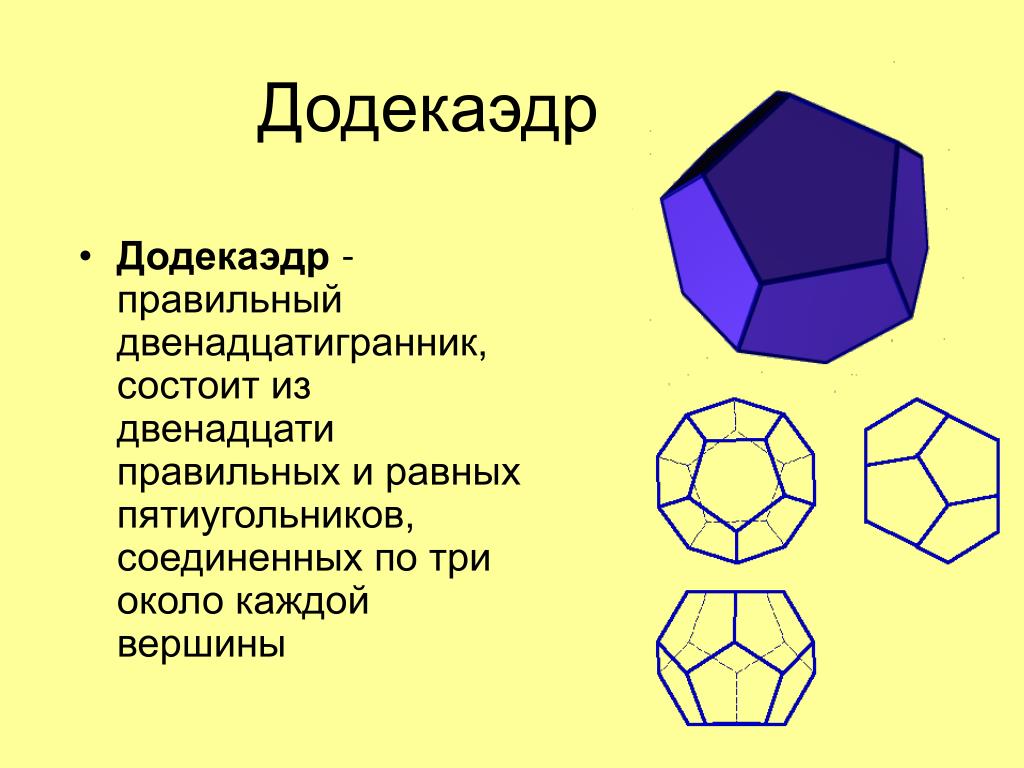 {2}} {2 (1) (1)}} \.}
{2}} {2 (1) (1)}} \.} Точно так же тангенциальный пятиугольник является равносторонним тогда и только тогда, когда он имеет равные углы и, следовательно, правильный.
Точно так же тангенциальный пятиугольник является равносторонним тогда и только тогда, когда он имеет равные углы и, следовательно, правильный.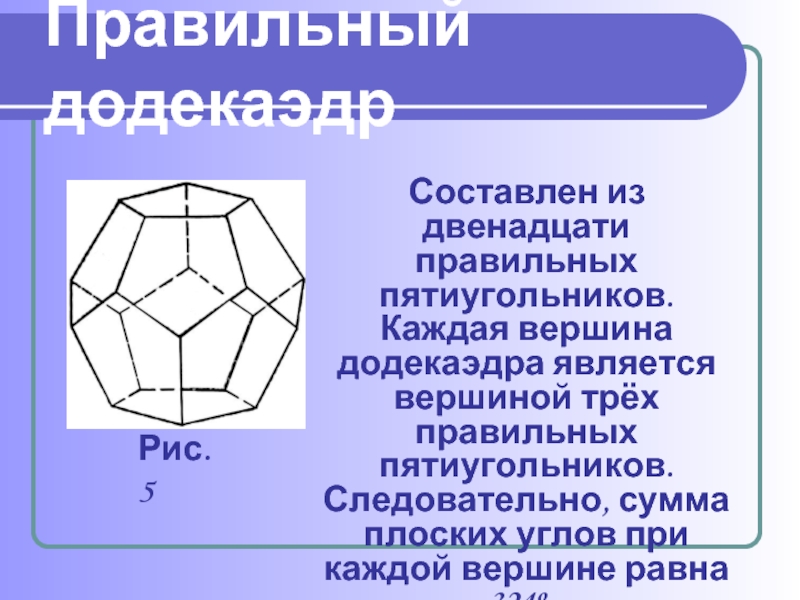 Точки за пределами региона просто соответствуют повторяющимся пятиугольникам, то есть пятиугольникам, которые при повороте или отражении могут совпадать с другими уже описанными. Пентагоны, которые точно совпадают с этими границами, имеют линию симметрии .
Точки за пределами региона просто соответствуют повторяющимся пятиугольникам, то есть пятиугольникам, которые при повороте или отражении могут совпадать с другими уже описанными. Пентагоны, которые точно совпадают с этими границами, имеют линию симметрии . Первый угол, который открывается больше 180 °, — это γ, поэтому γ = 180 ° (граница, показанная зеленым справа) — это кривая, которая является границей областей вогнутых пятиугольников и других, называемых выпуклыми. Пентагоны, которые сопоставляются точно с этой границей, имеют по крайней мере две последовательные стороны, которые выглядят как сторона двойной длины, которая напоминает пятиугольник, вырожденный в четырехугольник.
Первый угол, который открывается больше 180 °, — это γ, поэтому γ = 180 ° (граница, показанная зеленым справа) — это кривая, которая является границей областей вогнутых пятиугольников и других, называемых выпуклыми. Пентагоны, которые сопоставляются точно с этой границей, имеют по крайней мере две последовательные стороны, которые выглядят как сторона двойной длины, которая напоминает пятиугольник, вырожденный в четырехугольник.


 Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ПЕНТАГОН греч., от pente, пять, и gonia, угол.… … Словарь иностранных слов русского языка
Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ПЕНТАГОН греч., от pente, пять, и gonia, угол.… … Словарь иностранных слов русского языка πεντάγραμμον от πέντε «пять» и γράμμα «черта, линия») правильный … Википедия
πεντάγραμμον от πέντε «пять» и γράμμα «черта, линия») правильный … Википедия Также пятиугольником называют всякий предмет такой формы.
Также пятиугольником называют всякий предмет такой формы. ..
Шестиугольник Лемуана представляет собой шестиугольник, около которого можно описать окружность. Его вершинами являются шесть точек пересечениями сторон треугольника с тремя линиями, которые параллельны сторонам и которые проходят через его точку Лемуана. В любом треугольнике шестиугольник Лемуана находится внутри треугольника с тремя парами вершин, лежащих попарно на каждой стороне треугольника.
Правильный восьмиугольник (октагон) — геометрическая фигура из группы правильных многоугольников. У него восемь сторон и восемь углов, все углы и стороны равны между собой.
..
Шестиугольник Лемуана представляет собой шестиугольник, около которого можно описать окружность. Его вершинами являются шесть точек пересечениями сторон треугольника с тремя линиями, которые параллельны сторонам и которые проходят через его точку Лемуана. В любом треугольнике шестиугольник Лемуана находится внутри треугольника с тремя парами вершин, лежащих попарно на каждой стороне треугольника.
Правильный восьмиугольник (октагон) — геометрическая фигура из группы правильных многоугольников. У него восемь сторон и восемь углов, все углы и стороны равны между собой. Оказывается, возможно объединение 30 квадратов, 20 правильных шестиугольников и 12 правильных десятиугольников в симметричную форму, которая называется ромбоусеченный икосододекаэдр (рис. 2.06).
Рис. 18. Геометрические построения, в основе которых лежат гармоничные пропорции: а – «золотое сечение»; б – квадрат; в – равносторонний треугольник; г – пятиугольник; д – прямоугольники, построенные на соответствующих гармоничных отрезках
Вот, например, по стороне вазы, от горлышка, но не доходя до низу, сбегает круговая линия, почти (но не вполне!) совпадающая с правильным кругом; внутри круга вписаны другие кривые, неполными спиралями касающиеся окружности, выходящие из одной точки и направленные под разными уклонами; низ вазы украшен параллельными поперечными полосами; свободное пространство в круге оживлено звездочками и пальметками. Или вот со дна шаровидной вазы дерзко вскидываются к ее середине лучевые линии, заканчивающиеся широким, вытянуто-округлым пятном, подобием огромного вопросительного знака, а сверху вазы из сплетения круговых линий получаются, идущие навстречу, секирообразные полушария.
Оказывается, возможно объединение 30 квадратов, 20 правильных шестиугольников и 12 правильных десятиугольников в симметричную форму, которая называется ромбоусеченный икосододекаэдр (рис. 2.06).
Рис. 18. Геометрические построения, в основе которых лежат гармоничные пропорции: а – «золотое сечение»; б – квадрат; в – равносторонний треугольник; г – пятиугольник; д – прямоугольники, построенные на соответствующих гармоничных отрезках
Вот, например, по стороне вазы, от горлышка, но не доходя до низу, сбегает круговая линия, почти (но не вполне!) совпадающая с правильным кругом; внутри круга вписаны другие кривые, неполными спиралями касающиеся окружности, выходящие из одной точки и направленные под разными уклонами; низ вазы украшен параллельными поперечными полосами; свободное пространство в круге оживлено звездочками и пальметками. Или вот со дна шаровидной вазы дерзко вскидываются к ее середине лучевые линии, заканчивающиеся широким, вытянуто-округлым пятном, подобием огромного вопросительного знака, а сверху вазы из сплетения круговых линий получаются, идущие навстречу, секирообразные полушария. Или вот из резко-стилизованных листьев и цветов получается сложный узор, заполняющий всю поверхность вазы, образующий вогнутые ромбы, ограниченные вытянутыми кругами, причем внутренность и кругов и ромбов, в свою очередь, заполнена комбинацией из пяти звездочек, составляющих пятиугольник. Во всех этих линейных орнаментах поражает умение заполнить пространство, дать впечатление сложности при помощи самых простых, в сущности, элементов. Глаз сначала видит определенный узор, потом, пытаясь вникнуть в его систему, запутывается безнадежно; лишь после, усилием мысли, удается восстановить сложно простое построение.
Пятиугольная звезда, используемая как область отсечения формы, создается с помощью описанной в листинге 1.15 процедуры Make5Angle. После ее создания изменяется порядок следования вершин пятиугольника, чтобы их обход при построении региона выполнялся в той же последовательности, как рисуется звезда карандашом на бумаге (например, 1-3-5-2-4) (листинг 1.
Или вот из резко-стилизованных листьев и цветов получается сложный узор, заполняющий всю поверхность вазы, образующий вогнутые ромбы, ограниченные вытянутыми кругами, причем внутренность и кругов и ромбов, в свою очередь, заполнена комбинацией из пяти звездочек, составляющих пятиугольник. Во всех этих линейных орнаментах поражает умение заполнить пространство, дать впечатление сложности при помощи самых простых, в сущности, элементов. Глаз сначала видит определенный узор, потом, пытаясь вникнуть в его систему, запутывается безнадежно; лишь после, усилием мысли, удается восстановить сложно простое построение.
Пятиугольная звезда, используемая как область отсечения формы, создается с помощью описанной в листинге 1.15 процедуры Make5Angle. После ее создания изменяется порядок следования вершин пятиугольника, чтобы их обход при построении региона выполнялся в той же последовательности, как рисуется звезда карандашом на бумаге (например, 1-3-5-2-4) (листинг 1. 16).
А потом Владимир Авинский приложил свой магический пятиугольник к плану марсианских пирамид. Увиденное повергло его в шок. Угол альфа использовался везде… Марсианские пирамиды явно старше земных. Если отбросить древние тексты, останется беспристрастная геометрия и математика. Она доказывает – сооружения на Земле и на другой планете построены по единому инженерному замыслу… На это же обратил внимание и доктор геолого-минералогических наук Александр ПОРТНОВ:
16).
А потом Владимир Авинский приложил свой магический пятиугольник к плану марсианских пирамид. Увиденное повергло его в шок. Угол альфа использовался везде… Марсианские пирамиды явно старше земных. Если отбросить древние тексты, останется беспристрастная геометрия и математика. Она доказывает – сооружения на Земле и на другой планете построены по единому инженерному замыслу… На это же обратил внимание и доктор геолого-минералогических наук Александр ПОРТНОВ: -греч. εἴκοσι «двадцать»; ἕδρον «сиденье», «основание») — правильный выпуклый многогранник, двадцатигранник, одно из Платоновых тел. Каждая из 20 граней представляет собой равносторонний треугольник. Число ребер равно 30, число вершин — 12.
Купол можно рассматривать как призму, где один из многоугольников наполовину стянут путём объединения вершин попарно.
В геометрии гиробифастигиум или двускатный повёрнутый бикупол является 26-м многогранником Джонсона (J26). Его можно построить объединением двух треугольных призм с правильными гранями по соответствующим квадратным граням с поворотом одной призмы на 90º . Это единственное тело Джонсона, которым можно заполнить трёхмерное пространство.
Звезда — определённый вид плоских невыпуклых многоугольников, не имеющий, однако, однозначного математического определения.
-греч. εἴκοσι «двадцать»; ἕδρον «сиденье», «основание») — правильный выпуклый многогранник, двадцатигранник, одно из Платоновых тел. Каждая из 20 граней представляет собой равносторонний треугольник. Число ребер равно 30, число вершин — 12.
Купол можно рассматривать как призму, где один из многоугольников наполовину стянут путём объединения вершин попарно.
В геометрии гиробифастигиум или двускатный повёрнутый бикупол является 26-м многогранником Джонсона (J26). Его можно построить объединением двух треугольных призм с правильными гранями по соответствующим квадратным граням с поворотом одной призмы на 90º . Это единственное тело Джонсона, которым можно заполнить трёхмерное пространство.
Звезда — определённый вид плоских невыпуклых многоугольников, не имеющий, однако, однозначного математического определения.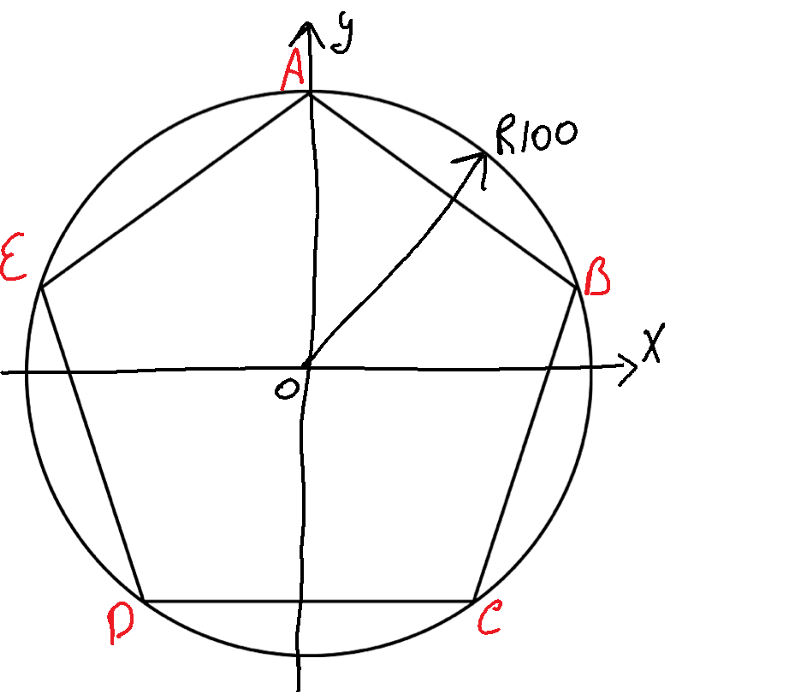 Семиуго́льник, называемый иногда гептагон — многоугольник с семью углами. Семиугольником также называют всякий предмет такой формы.
Пра́вильный многоуго́льник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между смежными сторонами равны.
Равнобедренный треугольник — это треугольник, в котором две стороны равны между собой по длине. Боковыми называются равные стороны, а последняя неравная им сторона — основанием. По определению, каждый правильный треугольник также является равнобедренным, но обратное утверждение неверно.
В геометрии плосконосый двуклиноид или сиамский додекаэдр — это трёхмерный выпуклый многогранник с двенадцатью правильными треугольниками в качестве граней. Многогранник не является правильным, поскольку в некоторых вершинах сходятся четыре грани, а в остальных — пять граней.
Семиуго́льник, называемый иногда гептагон — многоугольник с семью углами. Семиугольником также называют всякий предмет такой формы.
Пра́вильный многоуго́льник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между смежными сторонами равны.
Равнобедренный треугольник — это треугольник, в котором две стороны равны между собой по длине. Боковыми называются равные стороны, а последняя неравная им сторона — основанием. По определению, каждый правильный треугольник также является равнобедренным, но обратное утверждение неверно.
В геометрии плосконосый двуклиноид или сиамский додекаэдр — это трёхмерный выпуклый многогранник с двенадцатью правильными треугольниками в качестве граней. Многогранник не является правильным, поскольку в некоторых вершинах сходятся четыре грани, а в остальных — пять граней. Многогранник является двенадцатигранником, одним из восьми дельтаэдров (выпуклых многогранников с гранями в виде правильных треугольников) и одним из 92 многогранников Джонсона (неоднородные выпуклые многогранники с правильными…
Правильный пятиугольник (или пентагон от греч. πενταγωνον) — геометрическая фигура, правильный многоугольник с пятью сторонами.
Бикуполы более высоких порядков можно построить, если допускается растяжение боковых граней в прямоугольники и равнобедренные треугольники.
Одиннадцатиуго́льник, называемый иногда Гендекаго́н — многоугольник с одиннадцатью углами. Одиннадцатиугольником также называют всякий предмет, имеющий такую форму.
Площадь круга с радиусом r равна πr2. Здесь символ π (греческая буква пи) обозначает константу, выражающую отношение длины окружности к её диаметру или площади круга к квадрату его радиуса.
Многогранник является двенадцатигранником, одним из восьми дельтаэдров (выпуклых многогранников с гранями в виде правильных треугольников) и одним из 92 многогранников Джонсона (неоднородные выпуклые многогранники с правильными…
Правильный пятиугольник (или пентагон от греч. πενταγωνον) — геометрическая фигура, правильный многоугольник с пятью сторонами.
Бикуполы более высоких порядков можно построить, если допускается растяжение боковых граней в прямоугольники и равнобедренные треугольники.
Одиннадцатиуго́льник, называемый иногда Гендекаго́н — многоугольник с одиннадцатью углами. Одиннадцатиугольником также называют всякий предмет, имеющий такую форму.
Площадь круга с радиусом r равна πr2. Здесь символ π (греческая буква пи) обозначает константу, выражающую отношение длины окружности к её диаметру или площади круга к квадрату его радиуса. Поскольку площадь правильного многоугольника равна половине его периметра, умноженного на апофему (высоту), а правильные многоугольники стремятся к окружности при росте числа сторон, площадь круга равна половине длины окружности, умноженной на радиус (то есть 1⁄2 × 2πr × r).
В геометрии ротонда — любой член семейства диэдрально-симметричных многогранников. Они похожи на куполы, но вместо перемежающихся квадратов и треугольников перемежаются пятиугольники и треугольники (по отношению к оси). Пятискатная ротонда является телом Джонсона (J6).
Треуго́льный парке́т (треугольный паркета́ж) или треугольная мозаика — это замощение плоскости равными правильными треугольниками, расположенными сторона к стороне.
В геометрии удлинённый квадратный гиробикупол или псевдоромбокубооктаэдр (по Залгаллеру — удлинённый четырёхскатный повёрнутый бикупол) — это один из многогранников Джонсона (J37 = (по Залгаллеру) М5+П8+М5).
Поскольку площадь правильного многоугольника равна половине его периметра, умноженного на апофему (высоту), а правильные многоугольники стремятся к окружности при росте числа сторон, площадь круга равна половине длины окружности, умноженной на радиус (то есть 1⁄2 × 2πr × r).
В геометрии ротонда — любой член семейства диэдрально-симметричных многогранников. Они похожи на куполы, но вместо перемежающихся квадратов и треугольников перемежаются пятиугольники и треугольники (по отношению к оси). Пятискатная ротонда является телом Джонсона (J6).
Треуго́льный парке́т (треугольный паркета́ж) или треугольная мозаика — это замощение плоскости равными правильными треугольниками, расположенными сторона к стороне.
В геометрии удлинённый квадратный гиробикупол или псевдоромбокубооктаэдр (по Залгаллеру — удлинённый четырёхскатный повёрнутый бикупол) — это один из многогранников Джонсона (J37 = (по Залгаллеру) М5+П8+М5). Тело, обычно, не считается архимедовым телом, хотя его грани и являются правильными многоугольниками и многоугольники вокруг каждой вершины те же самые, но, в отличие от 13 архимедовых тел, многогранник не обладает глобальной симметрией, переводящей любую вершину в любую другую (хотя Грюнбаум…
В евклидовой геометрии равнодиагональный четырёхугольник — это выпуклый четырёхугольник, две диагонали которого имеют равные длины. Равнодиагональные четырёхугольники имели важное значение в древней индийской математике, где в классификации в первую очередь выделялись равнодиагональные четырёхугольники, и только потом четырёхугольники подразделялись на другие типы .
В геометрии вершина — это вид точки, в которой две кривые, две прямые либо два ребра сходятся. Из этого определения следует, что точка, в которой сходятся два луча, образуя угол, является вершиной, а также ею являются угловые точки многоугольников и многогранников.
Тело, обычно, не считается архимедовым телом, хотя его грани и являются правильными многоугольниками и многоугольники вокруг каждой вершины те же самые, но, в отличие от 13 архимедовых тел, многогранник не обладает глобальной симметрией, переводящей любую вершину в любую другую (хотя Грюнбаум…
В евклидовой геометрии равнодиагональный четырёхугольник — это выпуклый четырёхугольник, две диагонали которого имеют равные длины. Равнодиагональные четырёхугольники имели важное значение в древней индийской математике, где в классификации в первую очередь выделялись равнодиагональные четырёхугольники, и только потом четырёхугольники подразделялись на другие типы .
В геометрии вершина — это вид точки, в которой две кривые, две прямые либо два ребра сходятся. Из этого определения следует, что точка, в которой сходятся два луча, образуя угол, является вершиной, а также ею являются угловые точки многоугольников и многогранников. Вписанный четырёхугольник — это четырёхугольник, вершины которого лежат на одной окружности. Эта окружность называется описанной. Обычно предполагается, что четырёхугольник выпуклый, но бывают и самопересекающиеся вписанные четырёхугольники. Формулы и свойства, данные ниже, верны только для выпуклых четырёхугольников.
Девятиуго́льник — многоугольник с девятью углами. Девятиугольником также называют всякий предмет, имеющий такую форму.
Окта́эдр (греч. οκτάεδρον от οκτώ «восемь» + έδρα «основание») — многогранник с восемью гранями.
Десятиуго́льник (правильный десятиугольник — декагон) — многоугольник с десятью углами и десятью сторонами.
Описанный многоугольник, известный также как тангенциальный многоугольник — это выпуклый многоугольник, который содержит вписанную окружность. Это окружность, которая касательна каждой стороны многоугольника. Двойственный многоугольник описанного многоугольника — это многоугольник, который имеет описанную окружность, проходящую через все его вершины.
Апейрогон (от др.-греч. ἄπειρος — бесконечный или безграничный и др.-греч. γωνία — угол) — обобщённый многоугольник со счётно-бесконечным числом сторон.
В евклидовой геометрии описанный четырёхугольник — это выпуклый четырёхугольник, стороны которого являются касательными к одной окружности внутри четырёхугольника. Эта окружность называется вписанной в четырёхугольник. Описанные четырёхугольники являются частным случаем описанных многоугольников.
Сглаженный восьмиугольник — это область плоскости, предположительно, имеющая самую малую наибольшую плотность упаковки плоскости из всех центрально симметричных выпуклых фигур. Фигура получается заменой углов правильного восьмиугольника секцией гиперболы, которая касается двух сторон угла и асимптотически приближается к продолжениям сторон восьмиугольника, смежным сторонам угла.
Звезда Лакшми — октаграмма, составной правильный звездчатый многоугольник, представленный символом Шлефли a{8}, {8/2} или 2{4}, составленный из двух квадратов с общим центром, повёрнутых друг относительно друга на 45°. В индуизме является символом Ашталакшми, восьми форм богини Лакшми.
Наибольший многоугольник единичного диаметра — многоугольник с n сторонами (для заданного числа n), диаметр которого равен единице (то есть любые две его точки находятся друг от друга на расстоянии, не превосходящем единицы), и имеющий наибольшую площадь среди других n-угольников диаметра единица. Решением (не уникальным) для n = 4 является квадрат, решением для нечётных n является правильный многоугольник, при этом для остальных чётных n правильный многоугольник наибольшим не будет.
Двенадцатиуго́льник, додекаго́н (греч. δώδεκα — двенадцать и греч. γωνία — угол) — многоугольник с 12 углами и 12 сторонами. Как правило, додекагоном называют правильный многоугольник, то есть такой, у которого все стороны и все углы равны (в случае додекагона углы равны 150°). Правильный двенадцатиугольник используется в некоторых странах в качестве формы для монет.
В геометрии конциклическими (или гомоциклическими) точками называют точки, находящиеся на одной окружности. Три точки на плоскости, не лежащие на одной прямой, всегда лежат на одной окружности, поэтому иногда термин «конциклические» прилагают только к наборам из 4 или более точек.
Вписанный четырёхугольник — это четырёхугольник, вершины которого лежат на одной окружности. Эта окружность называется описанной. Обычно предполагается, что четырёхугольник выпуклый, но бывают и самопересекающиеся вписанные четырёхугольники. Формулы и свойства, данные ниже, верны только для выпуклых четырёхугольников.
Девятиуго́льник — многоугольник с девятью углами. Девятиугольником также называют всякий предмет, имеющий такую форму.
Окта́эдр (греч. οκτάεδρον от οκτώ «восемь» + έδρα «основание») — многогранник с восемью гранями.
Десятиуго́льник (правильный десятиугольник — декагон) — многоугольник с десятью углами и десятью сторонами.
Описанный многоугольник, известный также как тангенциальный многоугольник — это выпуклый многоугольник, который содержит вписанную окружность. Это окружность, которая касательна каждой стороны многоугольника. Двойственный многоугольник описанного многоугольника — это многоугольник, который имеет описанную окружность, проходящую через все его вершины.
Апейрогон (от др.-греч. ἄπειρος — бесконечный или безграничный и др.-греч. γωνία — угол) — обобщённый многоугольник со счётно-бесконечным числом сторон.
В евклидовой геометрии описанный четырёхугольник — это выпуклый четырёхугольник, стороны которого являются касательными к одной окружности внутри четырёхугольника. Эта окружность называется вписанной в четырёхугольник. Описанные четырёхугольники являются частным случаем описанных многоугольников.
Сглаженный восьмиугольник — это область плоскости, предположительно, имеющая самую малую наибольшую плотность упаковки плоскости из всех центрально симметричных выпуклых фигур. Фигура получается заменой углов правильного восьмиугольника секцией гиперболы, которая касается двух сторон угла и асимптотически приближается к продолжениям сторон восьмиугольника, смежным сторонам угла.
Звезда Лакшми — октаграмма, составной правильный звездчатый многоугольник, представленный символом Шлефли a{8}, {8/2} или 2{4}, составленный из двух квадратов с общим центром, повёрнутых друг относительно друга на 45°. В индуизме является символом Ашталакшми, восьми форм богини Лакшми.
Наибольший многоугольник единичного диаметра — многоугольник с n сторонами (для заданного числа n), диаметр которого равен единице (то есть любые две его точки находятся друг от друга на расстоянии, не превосходящем единицы), и имеющий наибольшую площадь среди других n-угольников диаметра единица. Решением (не уникальным) для n = 4 является квадрат, решением для нечётных n является правильный многоугольник, при этом для остальных чётных n правильный многоугольник наибольшим не будет.
Двенадцатиуго́льник, додекаго́н (греч. δώδεκα — двенадцать и греч. γωνία — угол) — многоугольник с 12 углами и 12 сторонами. Как правило, додекагоном называют правильный многоугольник, то есть такой, у которого все стороны и все углы равны (в случае додекагона углы равны 150°). Правильный двенадцатиугольник используется в некоторых странах в качестве формы для монет.
В геометрии конциклическими (или гомоциклическими) точками называют точки, находящиеся на одной окружности. Три точки на плоскости, не лежащие на одной прямой, всегда лежат на одной окружности, поэтому иногда термин «конциклические» прилагают только к наборам из 4 или более точек.