Какой угол у шестигранника
Правильный шестиугольник (гексагон) — многоугольник с шестью равными сторонами.
Гексагон — правильный выпуклый многоугольник с шестью сторонами или шестиугольник.
Шестиугольник – это многоугольник, имеющий шесть сторон и шесть углов. В правильном шестиугольнике все стороны равны, а углы образуют шесть равносторонних треугольников.
Выпуклый шестиугольник – это многоугольник, с общим количеством вершин, равным шести, при этом все точки такого шестиугольника лежат по одну сторону от прямой, которая проведена между двумя любыми соседними его вершинами.
Правильный шестиугольник – это шестиугольник, все стороны которого равны между собой.
Сумма углов выпуклого шестиугольника определяется по общей формуле 180°(n-2) и равна 180 ( 6 – 2 ) = 720 градусов.
При решении задач для нахождения площади произвольного (неправильного) шестиугольника используют метод трапеций, который заключается в разбиении фигуры на отдельные трапеции, площадь каждой из которых можно найти по известным всем формулам.
Свойства правильного шестиугольника
- все внутренние углы равны между собой
- каждый внутренний угол правильного шестиугольника равен 120 градусам
- все стороны равны между собой
- сторона правильного шестиугольника равна радиусу описанной окружности
- большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам
- меньшая диагональ правильного шестиугольника в ( sqrt <3>) раз больше его стороны.
- vеньшая диагональ правильного шестиугольника перпендикулярна его стороне
- правильный шестиугольник заполняет плоскость без пробелов и наложений
- диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу вписанной в правильный шестиугольник окружности. 6.
- инвариантен относительно поворота плоскости на угол, кратный относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями)
- nреугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60° .

Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
Радиус вписанной окружности правильного шестиугольника равен апофеме:
(r = m = alargefrac<<sqrt 3 >><2>
ormalsize)Радиус описанной окружности равен стороне правильного шестиугольника:
Периметр правильного шестиугольника
Площадь правильного шестиугольника Формула площади правильного шестиугольника через длину стороны
(S = pr = largefrac<<3sqrt 3 >><2>
ormalsize),
где (p) − полупериметр шестиугольника.Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус вписанной окружности
Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус описанной окружности
Правильный шестиугольник — это такой шестиугольник у которого все шесть сторон равны и его шесть углов равны.

Центр правильного шестиугольника — на рисунке точка O равноудалена от вершин.
Светлая линия обозначающая высоту треугольника AOB : h называется — апофемой.
Отрезки OA , OB — радиусы правильного шестиугольника.
Обозначения на рисунке для правильного шестиугольника
n=6 число сторон и вершин правильного шестиугольника, шт α центральный угол правильного шестиугольника, радианы, ° β половина внутреннего угла правильного шестиугольника, радианы, ° γ внутренний угол правильного шестиугольника, радианы, ° a сторона правильного шестиугольника, м R радиусы правильного шестиугольника, м p полупериметр правильного шестиугольника, м L периметр правильного шестиугольника, м h апофемы правильного шестиугольника, м Основные формулы для правильного шестиугольника
Периметр правильного шестиугольника
Полупериметр правильного шестиугольника
Центральный угол правильного шестиугольника в радианах
Центральный угол правильного шестиугольника в градусах
Половина внутреннего угла правильного шестиугольника в радианах
Половина внутреннего угла правильного шестиугольника в градусах
Внутренний угол правильного шестиугольника в радианах
Внутренний угол правильного шестиугольника в градусах
Площадь правильного шестиугольника
Отсюда получим апофему правильного шестиугольника
Шестиугольник — многоугольник с шестью углами.
 <circ >>
<circ >> Доказано [1] , что в любом достаточно большом множестве точек в общем положении содержится выпуклый пустой (то есть не содержащий точек этого множества) шестиугольник. Но существуют сколь угодно большие множества точек в общем положении, в которых нет выпуклого пустого семиугольника [2] . Вопрос о необходимом числе точек по сей день остаётся открытым. Известно, что требуется не менее 30 точек [3] . А если справедлива гипотеза Эрдёша-Секереша о многоугольниках, то не более 129 [4] .
Правильный шестиугольник
Правильным называется шестиугольник, у которого все стороны равны, а все внутренние углы равны 120°.
Звездчатые шестиугольники
Многоугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного многоугольника, называется звёздчатым. Помимо правильного существует ещё один звёздчатый шестиугольник, состоящий из двух правильных треугольников — гексаграмма или звезда Давида.
См.
 также
такжеПримечания
- ↑ Nicolás, Carlos M. (2007), «The empty hexagon theorem», Discrete and Computational Geometry Т. 38 (2): 389–397 , DOI 10.1007/s00454-007-1343-6
- ↑ Horton, J. D. (1983), «Sets with no empty convex 7-gons»,
- ↑ Overmars, M. (2003), «Finding sets of points without empty convex 6-gons», Discrete and Computational Geometry Т. 29 (1): 153–158 , DOI 10.1007/s00454-002-2829-x
- ↑ Gerken, Tobias (2008), «Empty convex hexagons in planar point sets», Discrete and Computational Geometry Т. 39 (1–3): 239–272 , DOI 10.1007/s00454-007-9018-x
KH-9 Hexagon
Шестиугольник (англ. KH-9 Hexagon), другое название Большая птица (англ. Big Bird) — серия фотографических спутников видовой разведки запущенных США между 1971 и 1986 годами. Из двадцати запусков, произведённых ВВС США, успешными были все, кроме одного. Отснятая фотоплёнка для обработки и анализа с борта спутника отсылалась назад на Землю в возвращаемых капсулах на парашютах в Тихий океан, где с помощью специальных крюков их подбирали военные самолёты C-130.

В сентябре 2011 года материалы о проекте «Шестиугольник» были рассекречены и один из космических аппаратов проекта был выставлен на всеобщее обозрение.
Бипирамида или дипирамида является трёхмерным многогранником, сформированным из двух пирамид, одна из которых является зеркальным отражением другой. Место соединения пирамид образует общую фигуру в виде многоугольника. Простая бипирамида формируется при сложении двух тетраэдров. При основании пирамиды в виде квадрата, причём боковые грани её равносторонние треугольники, формируется бипирамида, известная как октаэдр.
При увеличении числа сторон многоугольника в основании пирамиды, в пределе формируется круг или эллипс и образуется два конуса, соединённые основаниями.
Элементы, составляющие бипирамиду:
Ребра — линии, соединяющие вершины.
Грани — плоские поверхности, ограниченные рёбрами, треугольной или трапецеидальной формы.
В кристаллографии применяется термин (гексагональная сингония) для классификации кристаллов.

Мозаики «гирих» — это набор пяти плиток, использовавшихся для создания орнамента для украшения зданий в исламской архитектуре. Плитки использовались примерно с 12-го века и орнаменты существенно улучшились к моменту построения усыпальницы Дарб-и Имам в городе Исфахан в Иране (построена в 1453).
Пять плиток мозаики включают:
правильный десятиугольник с внутренними углами 144°;
удлиненный (неправильный выпуклый) шестиугольник с внутренними углами 72°, 144°, 144°, 72°, 144°, 144°;
галстук-бабочка (невыпуклый шестиугольник) с внутренними углами 72°, 72°, 216°, 72°, 72°, 216°;
ромб с внутренними углами 72°, 108°, 72°, 108°;
правильный пятиугольник с внутренними углами 108°.Все рёбра этих плиток имеют одну и ту же длину, а все углы кратны 36° (π/5 радиан). Четыре плитки (кроме пятиугольника) имеют двустороннюю (зеркальную) симметрию относительно двух перпендикулярных осей. Некоторые плитки имеют дополнительные симметрии.
 В частности, десятиугольник имеет десятикратную вращательную симметрию (вращение на 36°), а пятиугольник имеет пятикратную вращательную симметрию (вращение на 72°).
В частности, десятиугольник имеет десятикратную вращательную симметрию (вращение на 36°), а пятиугольник имеет пятикратную вращательную симметрию (вращение на 72°).Собственно, гирих — это линии (орнамента), которым декорированы плитки. Плитки использовались для создания орнамента (гириха). На языке фарси слово گره означает «узел» . В большинстве случаев виден только гирих, (и другие украшения в виде цветов), но не границы самих плиток. Гирих является ломаными отрезками, пересекающими границы плиток по центру под углом 54° (3π/10) к ребру. Две перекрещивающиеся линии гириха пересекают каждое ребро плитки. Большинство плиток имеют единственный орнамент внутри, соответствующий симметрии плитки. Однако десятиугольник имеет два возможных орнамента гириха, один из которых имеет только пятикратную, а не десятикратную симметрию.
Двуугольник — многоугольник с двумя сторонами и двумя углами.
В Евклидовой геометрии двуугольник считается вырожденной фигурой, так как его две стороны совпадают.

В сферической геометрии четыре двуугольника образуются при пересечении двух больших окружностей.
Зи́мний круг — сезонный астеризм в экваториальной части неба. Лучше всего виден зимой (также поздней осенью и ранней весной). Представляет собой восемь звёзд, расположенных вдоль воображаемой окружности, и девятую звезду примерно в её центре. Частично совпадает с астеризмом Зимний треугольник.
Состоит из звёзд — Сириус (α Большого Пса), Процион (α Малого Пса), Поллукс (β Близнецов), Кастор (α Близнецов), Менкалинан (β Возничего), Капелла (α Возничего), Альдебаран (α Тельца), Ригель (β Ориона) по окружности и Бетельгейзе (α Ориона) в центре.
G-астеризм — вариант астеризма. Вместо замыкания кольца от Ригеля к Альдебарану в него включается Беллатрикс (γ Ориона), а Бетельгейзе оказывается конечной точкой астеризма. В этом виде фигура астеризма представляет собой прописную латинскую букву «G».
Многогранник, многоугольник или мозаика является изотоксальным или рёберно транзитивным, если его симметрии действуют транзитивно на его рёбрах.
 Неформально это означает, что имеется только один вид рёбер у объекта — если даны два ребра, существует параллельный перенос, вращение и/или зеркальное отражение, переводящее одно ребро в другое, не меняя область, занимаемую объектом.
Неформально это означает, что имеется только один вид рёбер у объекта — если даны два ребра, существует параллельный перенос, вращение и/или зеркальное отражение, переводящее одно ребро в другое, не меняя область, занимаемую объектом.Термин изотоксальный происходит от греческого τοξον, означающего дуга.
Квадра́т — правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны. Квадрат является одновременно частным случаем ромба и прямоугольника.
Одноугольник (генагон или моногон) — фигура в геометрии представляет собой многоугольник с одним краем и одной вершиной. Обозначается символом <1>. Имеет только одну сторону и только один внутренний угол.
Правильный девятиугольник — это правильный многоугольник с девятью сторонами.
Правильный (равносторонний, или равноугольный) треугольник — это правильный многоугольник с тремя сторонами, простейший из правильных многоугольников. Все стороны правильного треугольника равны между собой, все углы также равны и составляют 60°.
 В равностороннем треугольнике высота является и биссектрисой, и медианой.
В равностороннем треугольнике высота является и биссектрисой, и медианой.Правильный шестиугольник (гексагон) — правильный многоугольник с шестью сторонами.
Прямоугольник — четырехугольник, у которого все углы прямые (равны 90 градусам).
В евклидовой геометрии для того, чтобы четырёхугольник был прямоугольником, достаточно, чтобы хотя бы три его угла были прямые, тогда четвёртый угол в силу теоремы о сумме углов многоугольника также будет равен 90°. В неевклидовой геометрии, где сумма углов четырёхугольника не равна 360°, прямоугольников не существует.
Ромб (др.-греч. ῥόμβος, лат. rombus, в буквальном переводе: «бубен») — это параллелограмм, у которого все стороны равны.
В геометрии на плоскости, ромбоид — это параллелограмм, в котором смежные стороны имеют разные длины, и углы не являются прямыми.
Параллелограмм с равными сторонами (равносторонний) называется ромбом, но не ромбоидом.
Параллелограмм с прямыми углами называется прямоугольником, и тоже не является ромбоидом.

Термин ромбоид в настоящее время часто применяется к параллелепипедам, сплошным телам с шестью гранями, где каждая грань — это параллелограмм, и противоположные грани лежат в параллельных плоскостях.
Некоторые кристаллы имеют форму трёхмерных ромбоидов. Эти тела также иногда называют ромбоидными призмами. Термин часто используется в научной терминологии, как в двух-, так и в трёхмерном понимании.
То́чка Лемуа́на (точка пересечения симедиан, точка Гребе, обозначается K <displaystyle K> или L <displaystyle L> ) — одна из замечательных точек треугольника.
Усечённый октаэдр — полуправильный многогранник, состоящий из 14 граней (8 правильных шестиугольников и 6 квадратов). В усечённом октаэдре 24 одинаковых вершины, в каждой из которых сходятся два шестиугольника и квадрат, а также 24 ребра, каждое из которых разделяет шестиугольник и квадрат, и 12 рёбер, каждое из которых разделяет два шестиугольника. Двойственный к усечённому октаэдру многогранник — преломлённый куб или тетракисгексаэдр.
 <3>=3n(n-1)+1.>
<3>=3n(n-1)+1.>Представление формулы в виде
1 + 6 ( 1 2 n ( n − 1 ) ) <displaystyle 1+6left(<1 over 2>n(n-1)
ight)>показывает, что центрированное шестиугольное число для n на 1 больше чем шестикратная величина (n−1)-го треугольного числа.
Несколько первых центрированных шестиугольных чисел:
1, 7, 19, 37, 61, 91, 127, 169, 217, 271, 331, 397, 469, 547, 631, 721, 817, 919.
Можно заметить, что по основанию 10 последний знак центрированных шестиугольных чисел имеют последовательность 1-7-9-7-1.
Центрированные шестиугольные числа имеют практическое значение управлении логистики, например , в упаковке круглых предметов в больший круглый контейнер, таких как Венские сосиски в круглые банки, или упаковке проводов в кабель.
Сумма первых n центрированных шестиугольных чисел равна n 3 . Таким образом, последовательности центрированных шестиугольных пирамидальных чисел и кубических чисел идентичны, но представляют различные (геометрические) формы.
 С другой стороны, центрированные шестиугольные числа – это разность двух соседних кубов, так что центрированные шестиугольные числа — это фигурное представление кубов. Также, простые центрированные шестиугольные числа есть кубические простые числа.
С другой стороны, центрированные шестиугольные числа – это разность двух соседних кубов, так что центрированные шестиугольные числа — это фигурное представление кубов. Также, простые центрированные шестиугольные числа есть кубические простые числа.Разность (2n) 2 и n-го центрированного шестиугольного числа равна 3n 2 + 3n − 1, а разность (2n − 1) 2 и n-го центрированного шестиугольного числа есть прямоугольное число. [какое?]
Гигантский шестиугольник — не имеющий на сегодняшний день строгого научного объяснения – атмосферный феномен на планете Сатурн. Представляет собой геометрически правильный шестиугольник с поперечником в 25 тысяч километров, находящийся на северном полюсе Сатурна. По всей видимости, шестиугольник является вихрем. Прямые «стены» вихря уходят вглубь атмосферы на расстояние до 100 километров. При изучении вихря в инфракрасном диапазоне наблюдаются светлые участки, представляющие собой гигантские прорехи в облачной системе, которые простираются, как минимум, на 75 километров вглубь атмосферы.

Правильные многоугольники и окружность описанная и
Правильные многоугольники и окружность. Здравствуйте, Дорогие друзья! Во многих задачах в курсе геометрии, в том числе и в составе ЕГЭ имеется много заданий связанных с понятием окружности вписанной в правильный многоугольник и описанной около него. Если конкретней, то в данном случае мы рассмотрим правильный треугольник, также квадрат и правильный шестиугольник. Именно с этими правильными многоугольниками связаны условия заданий на экзамене. Обычно в ходе решения таких задач возникает необходимость выразить:
1. Сторону правильного треугольника через радиус вписанной или описанной окружности.
2. Сторону квадрата через радиус вписанной окружности или описанной окружности.
3. Сторону правильного шестиугольника через радиус вписанной или описанной окружности.
4. Радиус вписанной в правильный многоугольник окружности через радиус описанной около него окружности и наоборот.

На сайте рассмотрены (и в будущем будут рассматриваться) задачи, в которых эти формулы используются. При решении подробно не описывается как они выводятся. Просто говорится, например, что сторона правильного треугольника соотносится с радиусом вписанной в него окружности как:
У многих возникают вопросы по этому поводу: Как? Почему? В этой статье мы выведем все указанные соотношения и в будущем при решении задач, если потребуется, просто буду давать ссылку на эту статью.
Что нужно всегда помнить и понимать?
Центр правильного многоугольника совпадает с центром вписанной о описанной около него окружности. Итак, приступим!
Правильный треугольник, вписанная и описанная окружность.
Пусть а – это его сторона, радиус описанной окружности равен R, а радиус вписанной окружности равен r.
Стороны правильного треугольника и вписанная в него окружность имеют общие точки (точки касания), эти точки делят стороны треугольника пополам. Радиус описанной окружности, проведённый к вершине треугольника является биссектрисой, то есть делит угол при этой вершине, равный 60 градусам, пополам.
 Рассмотрим прямоугольный треугольник (выделен жёлтым). По определению тангенса: Получаем, что: По определению косинуса: Получаем, что: Можем записать соотношение радиусов:
Рассмотрим прямоугольный треугольник (выделен жёлтым). По определению тангенса: Получаем, что: По определению косинуса: Получаем, что: Можем записать соотношение радиусов:Квадрат, вписанная и описанная около него окружность.
Пусть а – это сторона квадрата, радиус описанной окружности равен R, а радиус вписанной окружности равен r.
Стороны квадрата и вписанная в него окружность имеют общие точки (точки касания), эти точки делят стороны квадрата пополам.
Радиус описанной окружности, проведённый к вершине квадрата является биссектрисой, то есть делит угол квадрата пополам.
Рассмотрим прямоугольный треугольник (выделен жёлтым). На основании вышеизложенного можно сделать вывод о том, что:
По определению косинуса: Получаем, что: *Можно было воспользоваться также теоремой Пифагора. Запишем соотношение радиусов:
Правильный шестиугольник. Вписанная и описанная окружность.
Стороны правильного шестиугольника и вписанная окружность имеют общие точки (точки касания), эти точки делят стороны данного шестиугольника пополам.

Радиус описанной окружности, проведённый к вершине шестиугольника является биссектрисой, то есть делит угол правильного шестиугольника равный 120 градусам пополам. Подробнее о правильном шестиугольнике и описанной около него окружности можете посмотреть информацию в этой статье.
Рассмотрим прямоугольный треугольник (выделен жёлтым). По определению тангенса: Получаем, что:
Тот факт, что сторона правильного шестиугольника равна радиусу описанной окружности известен практически всем школьникам изучившим соответствующий материал по планиметрии:
Если интересно посмотрите как это можно вывести. По определению косинуса в прямоугольном треугольнике: Получаем, что: Можем записать соотношение радиусов: Вот и всё.
Конечно же, учить и запоминать данные формулы не нужно. В ходе решения вы всегда сможете их также вывести используя свойства правильных многоугольников, определения тангенса и косинуса, теорему Пифагора.
Я решил изложить это в отдельной статье только для того, чтобы у вас не возникали вопросы при решении и изучении соответствующих заданий на блоге и вы всегда могли бы посмотреть откуда взялась формула.
 Везде, где потребуется данная информация я буду размещать ссылку на эту статью.
Везде, где потребуется данная информация я буду размещать ссылку на эту статью.Получить материал статьи в формате PDF
Успеха Вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Правильный шестиугольник имеет. Что такое правильный шестиугольник и какие задачи с ним могут быть связаны? Описанная окружность и возможность построения
Самая известная фигура, у которой больше четырех углов — это правильный шестиугольник. В геометрии он часто используется в задачах. А в жизни именно такой вид имеют соты на срезе.
Чем он отличается от неправильного?
Во-первых, шестиугольником является фигура с 6 вершинами. Во-вторых, он может быть выпуклым или вогнутым. Первый отличается тем, что четыре вершины лежат по одну сторону от прямой, проведенной через две другие.
В-третьих, правильный шестиугольник характеризуется тем, что все его стороны равны. Причем каждый угол фигуры тоже имеет одинаковое значение.
 Чтобы определить сумму всех его углов, потребуется воспользоваться формулой: 180º * (n — 2). Здесь n — число вершин фигуры, то есть 6. Простой расчет дает значение в 720º. То есть каждый угол равен 120 градусам.
Чтобы определить сумму всех его углов, потребуется воспользоваться формулой: 180º * (n — 2). Здесь n — число вершин фигуры, то есть 6. Простой расчет дает значение в 720º. То есть каждый угол равен 120 градусам.В повседневной деятельности правильный шестиугольник встречается в снежинке и гайке. Химики видят ее даже в молекуле бензола.
Какие свойства требуется знать при решении задач?
К тому, что указано выше, следует добавить:
- диагонали фигуры, проведенные через центр, делят ее на шесть треугольников, которые являются равносторонними;
- сторона правильного шестиугольника имеет значение, которое совпадает с радиусом описанной около него окружности;
- используя такую фигуру, есть возможность заполнить плоскость, причем между ними не получится пропусков и не будет наложений.
Введенные обозначения
Традиционно сторона правильной геометрической фигуры обозначается латинской буквой «а». Для решения задач требуются еще площадь и периметр, это S и P соответственно.
 В правильный шестиугольник бывает вписана окружность или описана около него. Тогда вводятся значения для их радиусов. Обозначаются они соответственно буквами r и R.
В правильный шестиугольник бывает вписана окружность или описана около него. Тогда вводятся значения для их радиусов. Обозначаются они соответственно буквами r и R.В некоторых формулах фигурируют внутренний угол, полупериметр и апофема (являющаяся перпендикуляром к середине любой стороны из центра многоугольника). Для них используются буквы: α, р, m.
Формулы, которые описывают фигуру
Для расчета радиуса вписанной окружности потребуется такая: r = (a * √3) / 2, причем r = m. То есть такая же формула будет и для апофемы.
Поскольку периметр шестиугольника — это сумма всех сторон, то он определится так: P = 6 * a. С учетом того, что сторона равна радиусу описанной окружности, для периметра существует такая формула правильного шестиугольника: P = 6 * R. Из той, что приведена для радиуса вписанной окружности, выводится зависимость между а и r. Тогда формула принимает такой вид: Р = 4 r * √3.
Для площади правильного шестиугольника может пригодиться такая: S = p * r = (a 2 * 3 √3) / 2.

Задачи
№ 1. Условие. Имеется правильная шестиугольная призма, каждое ребро которой равно 4 см. В нее вписан цилиндр, объем которого необходимо узнать.
Решение. Объем цилиндра определяется как произведение площади основания на высоту. Последняя совпадает с ребром призмы. А она равна стороне правильного шестиугольника. То есть высота цилиндра — тоже 4 см.
Чтобы узнать площадь его основания, потребуется вычислить радиус вписанной в шестиугольник окружности. Формула для этого указана выше. Значит, r = 2√3 (см). Тогда площадь круга: S = π * r 2 = 3,14 * (2√3) 2 = 37,68 (см 2).
Ответ . V = 150,72 см 3 .
№ 2. Условие. Вычислить радиус окружности, которая вписана в правильный шестиугольник. Известно, что его сторона равна √3 см. Чему будет равен его периметр?
Решение. Эта задача требует использования двух из указанных формул. Причем их необходимо применять, даже не видоизменяя, просто подставить значение стороны и вычислить.

Таким образом, радиус вписанной окружности получается равным 1,5 см. Для периметра оказывается верным такое значение: 6√3 см.
Ответ. r = 1,5 см, Р = 6√3 см.
№ 3. Условие. Радиус описанной окружности равен 6 см. Какое значение в этом случае будет у стороны правильного шестиугольника?
Решение. Из формулы для радиуса вписанной в шестиугольник окружности легко получается та, по которой нужно вычислять сторону. Ясно, что радиус умножается на два и делится на корень из трех. Необходимо избавиться от иррациональности в знаменателе. Поэтому результат действий принимает такой вид: (12 √3) / (√3 * √3), то есть 4√3.
Ответ. а = 4√3 см.
Знаете ли вы, как выглядит правильный шестиугольник?
Этот вопрос задан не случайно. Большинство учащихся 11 класса не знают на него ответа.Правильный шестиугольник — такой, у которого все стороны равны и все углы тоже равны .
Железная гайка. Снежинка. Ячейка сот, в которых живут пчелы.
 Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.
Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.Многие школьники теряются, видя задачи на правильный шестиугольник, и считают, что для их решения нужны какие-то особые формулы. Так ли это?
Проведем диагонали правильного шестиугольника. Мы получили шесть равносторонних треугольников.
Мы знаем, что площадь правильного треугольника: .
Тогда площадь правильного шестиугольника — в шесть раз больше.
Где — сторона правильного шестиугольника.
Обратите внимание, что в правильном шестиугольнике расстояние от его центра до любой из вершин одинаково и равно стороне правильного шестиугольник.
Значит, радиус окружности, описанной вокруг правильного шестиугольника, равен его стороне .
Радиус окружности, вписанной в правильный шестиугольник, нетрудно найти.
Он равен .
Теперь вы легко решите любые задачи ЕГЭ, в которых фигурирует правильный шестиугольник.Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .

Радиус такой окружности равен .
Ответ: .
Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
Есть ли поблизости от Вас карандаш? Взгляните-ка на его сечение — оно представляет собой правильный шестиугольник или, как его еще называют, гексагон. Такую форму имеет также сечение гайки, поле гексагональных шахмат, некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты. Гигантский правильный шестиугольник был недавно обнаружен в Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим поподробнее.
Правильный шестиугольник представляет собой многоугольник с шестью одинаковыми сторонами и равными углами. Из школьного курса нам известно, что он обладает следующими свойствами:
- Длина его сторон соответствует радиусу описанной окружности.
 Из всех это свойство имеет лишь правильный шестиугольник.
Из всех это свойство имеет лишь правильный шестиугольник. - Углы равны между собой, и величина каждого составляет 120°.
- Периметр гексагона можно найти по формуле Р=6*R, если известен радиус описанной вокруг него окружности, или Р=4*√(3)*r, если окружность в него вписана. R и r — радиусы описанной и вписанной окружности.
- Площадь, которую занимает правильный шестиугольник, определяется следующим образом: S=(3*√(3)*R 2)/2. Если радиус неизвестен, вместо него подставляем длину одной из сторон — как известно, она соответствует длине радиуса описанной окружности.
У правильного шестиугольника есть одна интересная особенность, благодаря которой он получил в природе такое широкое распространение, — он способен заполнить любую поверхность плоскости без наложений и пробелов. Существует даже так называемая лемма Пала, согласно которой правильный гексагон, сторона которого равна 1/√(3), представляет собой универсальную покрышку, то есть может покрыть любое множество с диаметром в одну единицу.

Теперь рассмотрим построение правильного шестиугольника. Есть несколько способов, самый простой из которых предполагает использование циркуля, карандаша и линейки. Вначале рисуем циркулем произвольную окружность, затем в произвольном месте на этой окружности делаем точку. Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек. Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.
На практике бывают случаи, когда требуется нарисовать шестиугольник большого размера. Например, на двухуровневом гипсокартонном потолке, вокруг места крепления центральной люстры, нужно установить на нижнем уровне шесть небольших светильников. Циркуль таких размеров найти будет очень и очень сложно. Как поступить в этом случае? Как вообще нарисовать большую окружность? Очень просто. Нужно взять крепкую нить нужной длины и обвязать один из ее концов напротив карандаша.
 Теперь осталось лишь найти помощника, который бы прижал к потолку в нужной точке второй конец нити. Конечно, в этом случае возможны незначительные погрешности, но вряд ли они вообще будут заметны постороннему человеку.
Теперь осталось лишь найти помощника, который бы прижал к потолку в нужной точке второй конец нити. Конечно, в этом случае возможны незначительные погрешности, но вряд ли они вообще будут заметны постороннему человеку.Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего проводим стороны 5-6 и 3-2.
Построение вписанного в окружность равностороннего треугольника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.

Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны
1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг.
 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.

Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5.
 Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей.
 Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
Знаете ли вы, как выглядит правильный шестиугольник?
Этот вопрос задан не случайно. Большинство учащихся 11 класса не знают на него ответа.
Большинство учащихся 11 класса не знают на него ответа.Правильный шестиугольник — такой, у которого все стороны равны и все углы тоже равны .
Железная гайка. Снежинка. Ячейка сот, в которых живут пчелы. Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.
Многие школьники теряются, видя задачи на правильный шестиугольник, и считают, что для их решения нужны какие-то особые формулы. Так ли это?
Проведем диагонали правильного шестиугольника. Мы получили шесть равносторонних треугольников.
Мы знаем, что площадь правильного треугольника: .
Тогда площадь правильного шестиугольника — в шесть раз больше.
Где — сторона правильного шестиугольника.
Обратите внимание, что в правильном шестиугольнике расстояние от его центра до любой из вершин одинаково и равно стороне правильного шестиугольник.
Значит, радиус окружности, описанной вокруг правильного шестиугольника, равен его стороне .

Радиус окружности, вписанной в правильный шестиугольник, нетрудно найти.
Он равен .
Теперь вы легко решите любые задачи ЕГЭ, в которых фигурирует правильный шестиугольник.Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .
Радиус такой окружности равен .
Ответ: .
Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
Подписаться на еженедельную рассылку izhneftyanic.ru
Как из окружности сделать шестиугольник
Есть ли поблизости от Вас карандаш? Взгляните-ка на его сечение – оно представляет собой правильный шестиугольник или, как его еще называют, гексагон. Такую форму имеет также сечение гайки, поле гексагональных шахмат, кристаллическая решетка некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты.
 Гигантский правильный шестиугольник был недавно обнаружен в атмосфере Сатурна. Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим эту фигуру поподробнее.
Гигантский правильный шестиугольник был недавно обнаружен в атмосфере Сатурна. Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим эту фигуру поподробнее.- Длина его сторон соответствует радиусу описанной окружности. Из всех геометрических фигур это свойство имеет лишь правильный шестиугольник.
- Углы равны между собой, и величина каждого составляет 120°.
- Периметр гексагона можно найти по формуле Р=6*R, если известен радиус описанной вокруг него окружности, или Р=4*√(3)*r, если окружность в него вписана. R и r – радиусы описанной и вписанной окружности.
- Площадь, которую занимает правильный шестиугольник, определяется следующим образом: S=(3*√(3)*R 2 )/2. Если радиус неизвестен, вместо него подставляем длину одной из сторон – как известно, она соответствует длине радиуса описанной окружности.
Теперь рассмотрим построение правильного шестиугольника.
 Есть несколько способов, самый простой из которых предполагает использование циркуля, карандаша и линейки. Вначале рисуем циркулем произвольную окружность, затем в произвольном месте на этой окружности делаем точку. Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек. Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.
Есть несколько способов, самый простой из которых предполагает использование циркуля, карандаша и линейки. Вначале рисуем циркулем произвольную окружность, затем в произвольном месте на этой окружности делаем точку. Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек. Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.В широком смысле шестиугольник — это многоугольник с шестью углами. У правильного же шестиугольника углы и стороны равны. Нарисовать такой шестиугольник можно при помощи рулетки и транспортира, грубый шестиугольник — при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи интуиции и карандаша. Если вы хотите знать, как нарисовать шестиугольник различными способами, просто читайте далее.
Геометрические построения являются одной из главных частей обучения. Они формируют пространственное и логическое мышление, а также разрешают понять примитивные и натуральные геометрические обоснованности. Построения производятся на плоскости при помощи циркуля и линейки. Этими инструментами дозволено возвести крупное число геометрических фигур. При этом многие фигуры, кажущиеся довольно трудными, строятся с использованием простейших правил. Скажем, то, как возвести верный шестиугольник, дозволено описать каждого в нескольких словах.
Вам понадобится
- Циркуль, линейка, карандаш, лист бумаги.
Инструкция
1. Нарисуйте окружность. Установите некоторое расстояние между ножками циркуля. Это расстояние будет являться радиусом окружности. Выберите радиус таким образом, дабы вычерчивание окружности было довольно комфортным. Окружность должна всецело помещаться на листе бумаги. Слишком огромное либо слишком маленькое расстояние между ножками циркуля может привести к его изменению во время черчения. Оптимальным будет расстояние, при котором угол между ножками циркуля равен 15-30 градусов.
2. Постройте точки вершин углов верного шестиугольника. Установите ножку циркуля, в которой закреплена игла, в всякую точку окружности. Игла должна проткнуть начерченную линию. Чем вернее будет установлен циркуль, тем вернее будет построение. Проведите дугу окружности так, дабы она пересекла начерченную ранее окружность. Переставьте иглу циркуля в точку пересечения только что начерченной дуги с окружностью. Начертите еще одну дугу, пересекающую окружность. Вновь переставьте иглу циркуля в точку пересечения дуги и окружности и вновь начертите дугу. Произведите данное действие еще три раза, перемещаясь в одном направлении по окружности. Каждого должно получиться шесть дуг и шесть точек пересечения.
3. Постройте положительный шестиугольник. Ступенчато объедините все шесть точек пересечения дуг с изначально начерченной окружностью. Соединяйте точки прямыми, вычерчиваемыми при помощи линейки и карандаша. Позже произведенных действий будет получен верный шестиугольник, вписанный в окружность.
Шестиугольником считается многоугольник, владеющий шестью углами и шестью сторонами. Многоугольники бывают как выпуклыми, так и вогнутыми. У выпуклого шестиугольника все внутренние углы тупые, у вогнутого один либо больше угол является острым. Шестиугольник довольно легко возвести. Это делается в пару шагов.
Вам понадобится
- Карандаш, лист бумаги, линейка
Инструкция
1. Берется лист бумаги и на нем отмечается 6 точек приблизительно так, как это показано на рис. 1.
2. Позже того, как были подмечены точки, берется линейка, карандаш и с их подмогой ступенчато, друг за ином соединяются точки так, как это выглядит на рис. 2.
Видео по теме
Обратите внимание!
Сумма всех внутренних углов шестиугольника равна 720 градусам.Шестиугольник – это многоугольник, тот, что владеет шестью углами. Для того, дабы начертить произвольный шестиугольник, надобно проделать каждого 2 действия.
Вам понадобится
- Карандаш, линейка, лист бумаги.
Инструкция
1. Нужно взять в руку карандаш и разметить на листе 6 произвольных точек. В дальнейшем эти точки будут исполнять роль углов в шестиугольнике. (рис.1)
2. Взять линейку и начертить по данным точкам 6 отрезков, которые бы соединялись друг с ином по начерченным ранее точкам (рис.2)
Видео по теме
Обратите внимание!
Специальным типом шестиугольника является положительный шестиугольник. Он именуется таковым потому, что все его стороны и углы равны между собой. Вокруг такого шестиугольника дозволено описать либо вписать окружность. Стоит подметить, что в точках, которые получились путем касания вписанной окружности и сторон шестиугольника, стороны положительного шестиугольника делятся напополам.Полезный совет
В природе положительные шестиугольники владеют крупный популярностью. К примеру, вся пчелиная сота владеет положительной шестиугольной формой. Либо кристаллическая решетка графена (модификация углерода) тоже владеет формой положительного шестиугольника.Как возвести тот либо другой угол – крупной вопрос. Но для некоторых углов задача невидимо упрощается. Одним из таких углов является угол в 30 градусов. Он равен ?/6, то есть число 30 является делителем 180. Плюс к этому его синус вестим. Это и помогает при его построении.
Вам понадобится
- транспортир, угольник, циркуль, линейка
Инструкция
1. Для начала разглядим особенно примитивную обстановку, когда у вас на руках есть транспортир. Тогда прямую под углом 30 градусов к данной дозволено легко отложить с поддержкой него.
2. Помимо транспортира существуют и угол ьники, один из углов которых равен 30 градусам. Тогда иной угол угол ьника будет равен 60 градусам, то есть вам необходим визуально меньший угол для построения требуемой прямой.
3. Перейдем сейчас к нетривиальным способам построения угла 30 градусов. Как вестимо, синус угла 30 градусов равен 1/2. Для его построения нам надобно возвести прямоугол ьный треугол ьник. Возможен, мы можем возвести две перпендикулярные прямые. Но тангенс 30 градусов – иррациональное число, следственно соотношение между катетами мы можем посчитать лишь примерно (исключительно, если нет калькулятора), а, значит, и возвести угол в 30 градусов примерно.
4. В этом случае дозволено сделать и точное построение. Возведем вновь две перпендикулярные прямые, на которых будут располагаться катеты прямоугол ьного треугол ьника. Отложим по одной прямой катет BC какой-нибудь длины с поддержкой циркуля (B – прямой угол ). После этого увеличим длину между ножками циркуля в 2 раза, что элементарно. Проводя окружность с центром в точке C с радиусом этой длины, обнаружим точку пересечения окружности с иной прямой. Эта точка и будет точкой A прямоугол ьного треугол ьника ABC, а угол A будет равен 30 градусам.
5. Возвести угол в 30 градусов дозволено и с поддержкой окружности, применяя то, что он равен ?/6. Возведем окружность с радиусом OB. Разглядим в теории треугол ьник, где OA = OB = R – радиус окружности, где угол OAB = 30 градусов. Пускай OE – высота этого равнобедренного треугол ьника, а, следственно, и его биссектриса и медиана. Тогда угол AOE = 15 градусов, и, по формуле половинного угла, sin(15o) = (sqrt(3)-1)/(2*sqrt(2)).Следственно, AE = R*sin(15o). Отсель, AB = 2AE = 2R*sin(15o). Строя окружность радиусом BA с центром в точке B, обнаружим точку пересечения A этой окружности с начальной. Угол AOB будет равен 30 градусам.
6. Если мы можем определять длину дуг каким-нибудь образом, то, отложив дугу длиной ?*R/6, мы также получим угол в 30 градусов.
Обратите внимание!
Нужно помнить, что в 5 пункте мы можем возвести угол лишь приближенно, потому что в вычислениях будут фигурировать иррациональные числа.Шестиугольником называют частный случай полигона – фигуры, образованной большинством точек плоскости, ограниченным замкнутой полилинией. Положительный шестиугольник (гексагон), в свою очередь, также является частным случаем – это полигон с шестью равными сторонами и равными углами. Эта фигура знаменательна тем, что длина всей из ее сторон равна радиусу описанной вокруг фигуры окружности.
Вам понадобится
Инструкция
1. Выберите длину стороны шестиугольника. Возьмите циркуль и установите расстояние между концом иглы, расположенной на одной из его ножек, и концом грифеля, расположенным на иной ножке, равным длине стороны вычерчиваемой фигуры. Для этого дозволено воспользоваться линейкой либо предпочесть случайное расстояние, если данный момент несущественен. Зафиксируйте ножки циркуля винтом, если есть такая вероятность.
2. Нарисуйте окружность при помощи циркуля. Выбранное расстояние между ножками будет являться радиусом окружности.
3. Разбейте окружность точками на шесть равных частей. Эти точки будут являться вершинами углов шестиугольника и, соответственно, окончаниями отрезков, представляющих его стороны.
4. Ножку циркуля с иглой установите в произвольную точку, находящуюся на линии очерченной окружности. Игла должна верно проткнуть линию. От точности установки циркуля напрямую зависит точность построений. Очертите циркулем дугу так, дабы она пересекла в 2-х точках окружность, начерченную первой.
5. Переставьте ножку циркуля с иглой в одну из точек пересечения начерченной дуги с изначальной окружностью. Вычертите еще одну дугу, также пересекающую окружность в 2-х точках (одна из них совпадет с точкой предыдущего расположения иглы циркуля).
6. Сходственным же образом переставляйте иглу циркуля и вычерчивайте дуги еще четыре раза. Перемещайте ножку циркуля с иглой в одном направлении по окружности (неизменно по либо вопреки часовой стрелки). В итоге обязаны быть выявлены шесть точек пересечения дуг с изначально построенной окружностью.
7. Нарисуйте положительный шестиугольник. Ступенчато попарно объедините отрезками полученные на предыдущем шаге шесть точек. Вычерчивайте отрезки при помощи карандаша и линейки. В итоге будет получен верный шестиугольник. Позже осуществления построения дозволено стереть вспомогательные элементы (дуги и окружность).
Обратите внимание!
Имеет толк выбирать такое расстояние между ножками циркуля, дабы угол между ними был равен 15-30 градусов, напротив при осуществлении построений данное расстояние может легко сбиться.При строительстве либо разработке домашних дизайн-планов зачастую требуется возвести угол , равный теснее имеющемуся. На поддержка приходят образцы и школьные умения геометрии.
Инструкция
1. Угол образуют две прямые, исходящие из одной точки. Эта точка будет именоваться вершиной угла, а линии будут являться сторонами угла.
2. Для обозначения углов используйте три буквы: одна у вершины, две у сторон. Называют угол , начиная с той буквы, которая стоит у одной стороны, дальше называют букву, стоящую у вершины, и после этого букву у иной стороны. Используйте и другие методы для обозначения углов, если вам комфортнее напротив. Изредка называют только одну букву, которая стоит у вершины. А дозволено обозначать углы греческими буквами, скажем, α, β, γ.
3. Встречаются обстановки, когда нужно начертить угол , дабы он был равен теснее данному углу. Если при построении чертежа применять транспортир вероятности нет, дозволено обойтись только линейкой и циркулем. Возможен, на прямой, обозначенной на чертеже буквами MN, надобно возвести угол у точки К, так, дабы он был равен углу В. То есть из точки K нужно провести прямую, образующую с линией MN угол , тот, что будет равен углу В.
4. В начале подметьте по точке на всей стороне данного угла, скажем, точки А и С, дальше объедините точки С и А прямой линией. Получите треугол ьник АВС.
5. Теперь постройте на прямой MN такой же треугол ьник, дабы его вершина В находилась на линии в точке К. Используйте правило построения треугол ьника по трем сторонам. Отложите от точки К отрезок KL. Он должен быть равен отрезку ВС. Получите точку L.
6. Из точки K вычертите окружность радиусом равным отрезку ВА. Из L вычертите окружность радиусом СА. Полученную точку (Р) пересечения 2-х окружностей объедините с К. Получите треугол ьник КPL, тот, что будет равен треугол ьнику ABC. Так вы получите угол К. Он и будет равен углу В. Дабы это построение сделать комфортнее и стремительней, от вершины В отложите равные отрезки, применяя один раствор циркуля, не сдвигая ножек, опишите этим же радиусом из точки К окружность.
Видео по теме
Обратите внимание!
Избегайте случайного метаморфозы расстояния между ножками циркуля. В этом случае шестиугольник может получиться неправильным.Полезный совет
Имеет толк изготавливать построения при помощи циркуля с отлично заточенным грифелем. Так построения будут особенно точны.В широком смысле шестиугольник — это многоугольник с шестью углами. У правильного же шестиугольника углы и стороны равны. Нарисовать такой шестиугольник можно при помощи рулетки и транспортира, грубый шестиугольник — при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи интуиции и карандаша. Если вы хотите знать, как нарисовать шестиугольник различными способами, просто читайте далее.
Правильный шестиугольник — это такой шестиугольник у которого все шесть сторон равны и его шесть углов равны.
Центр правильного шестиугольника — на рисунке точка O равноудалена от вершин.
Светлая линия обозначающая высоту треугольника AOB : h называется — апофемой.
Отрезки OA , OB — радиусы правильного шестиугольника.
Обозначения на рисунке для правильного шестиугольника
n=6 число сторон и вершин правильного шестиугольника, шт α центральный угол правильного шестиугольника, радианы, ° β половина внутреннего угла правильного шестиугольника, радианы, ° γ внутренний угол правильного шестиугольника, радианы, ° a сторона правильного шестиугольника, м R радиусы правильного шестиугольника, м p полупериметр правильного шестиугольника, м L периметр правильного шестиугольника, м h апофемы правильного шестиугольника, м Основные формулы для правильного шестиугольника
Периметр правильного шестиугольника
Полупериметр правильного шестиугольника
Центральный угол правильного шестиугольника в радианах
Центральный угол правильного шестиугольника в градусах
Половина внутреннего угла правильного шестиугольника в радианах
Половина внутреннего угла правильного шестиугольника в градусах
Внутренний угол правильного шестиугольника в радианах
Внутренний угол правильного шестиугольника в градусах
Площадь правильного шестиугольника
Отсюда получим апофему правильного шестиугольника
Как репетитор по математике решает задачу на шестиугольник
Поделюсь самым простым подходом к задаче о шестиугольнике, которое репетитор по математике совершенно спокойно может показывать даже слабым ученикам 7 класса. Ибо в решении нет ничего сложного. Просто нужно догадаться сделать некоторые дополнительные построения.
Условие задачи:
Все углы в шестиугольнике ABCDEF равны по 120 градуcов. Известно, что EF=1, AB=3, BC=4, CD=1. Найдите AF+DE.Какое решение рекомендует репетитор по математике:
Требуются продления сторон фигуры. Они напрашиваются, если заметить, что число, дополняющее до , является очень полезным углом в . Подобными наблюдениями репетитор по математике подводит ученика 7 класса самостоятельному выбору необходимого дополнительного построения.Итак, продлим стороны FA, СВ и ED. В этом случае к нашему шестиугольнику дополнительно прикрепятся 3 треугольника. Определим их вид.
Так как все внутренние углы шестиугольника равны по 120 градусов, то все внешние с ними углы содержат по 60 градусов последний угол в каждом треугольнике равен 60 град. все треугольники и — равносторонние. Отсюда можно сделать вывод, что CN=ND=5, AK=BK=3 и MF=EM=1. Тогда KM=3+4+5=12.
Пользуемся тем, что MN=KN=12 получаем, что
ED=MN-ME-DN=12-1-5=6
AF=MK-MF-AK=12-1-3=8Теперь проще простого найти нужную сумму: ED+AF=6+8=14
Ответ: 14Необходимые сведения и темы для понимания решения репетитора:
1) Смежные углы. Теорема о смежных углах.
2) Сумма углов в треугольнике.
3) Определение и признак равностороннего треугольника.Альтернативное решение:
1) через терему синусов и косинусов
2) через продление других сторон шестиугольника (для понимания и внимания ученика этот способ немного сложнее)Репетитор по математике о путях решения подобных зада:
Когда я читаю в вопросе серьезной олимпиадной задачи по математике «найдите сумму длин отрезков», то невольно начинаю предполагать, что по отдельности эти отрезки не находятся никак. Это часто случается с задачами на «плавающие» элементы рисунка. Каждый из них не ищется, но вот их сумма, например, остается всегда постоянной величиной. Независимо от значений тех параметров, которые меняются в рамках условия задачи. В таком случае репетитору по математике необходимо поискать какой-нибудь отрезок, равный FA или ED, образующий единой целое со вторым. Иными словами занимаются поиском возможностей переложить один отрезок «с одного места на другое». Полученную сумму и ищут.Другой путь — репетитор по математике вводит две переменные для искомых величин и составляет с ними некое равенство, из которого «выплывает» нужная сумма. Здесь, к счастью, такой заморочки не попалось, ибо формат конкурса «Кенгуру» для 7 класса предлагает выборку ответа и весьма ограниченное время на решение варианта в целом (всего лишь 75 минут чистого времени).
Репетитор по математике А.Н. Колпаков. Москва, Строгино.
чем он интересен и как его построить. Формулы, которые описывают фигуру
Знаете ли вы, как выглядит правильный шестиугольник?
Этот вопрос задан не случайно. Большинство учащихся 11 класса не знают на него ответа.Правильный шестиугольник — такой, у которого все стороны равны и все углы тоже равны .
Железная гайка. Снежинка. Ячейка сот, в которых живут пчелы. Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.
Многие школьники теряются, видя задачи на правильный шестиугольник, и считают, что для их решения нужны какие-то особые формулы. Так ли это?
Проведем диагонали правильного шестиугольника. Мы получили шесть равносторонних треугольников.
Мы знаем, что площадь правильного треугольника: .
Тогда площадь правильного шестиугольника — в шесть раз больше.
Где — сторона правильного шестиугольника.
Обратите внимание, что в правильном шестиугольнике расстояние от его центра до любой из вершин одинаково и равно стороне правильного шестиугольник.
Значит, радиус окружности, описанной вокруг правильного шестиугольника, равен его стороне .
Радиус окружности, вписанной в правильный шестиугольник, нетрудно найти.
Он равен .
Теперь вы легко решите любые задачи ЕГЭ, в которых фигурирует правильный шестиугольник.Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .
Радиус такой окружности равен .
Ответ: .
Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
Тему многоугольников проходят в школьной программе, но не уделяют ей достаточного внимания. А между тем она интересна, и особенно это касается правильного шестиугольника или гексагона — ведь эту форму имеют многие природные объекты. К ним относятся пчелиные соты и многое другое. Эта форма очень хорошо применяется на практике.
Определение и построение
Правильным шестиугольником называется плоскостная фигура, имеющая шесть равных по длине сторон и столько же равных углов.
Если вспомнить формулу суммы углов многоугольника
то получается, что в этой фигуре она равна 720°. Ну а поскольку все углы фигуры равны, нетрудно посчитать, что каждый из них равен 120°.
Начертить шестиугольник очень просто, для этого достаточно циркуля и линейки.
Пошаговая инструкция будет выглядеть так:
При желании можно обойтись и без линии, начертив пять равных по радиусу окружностей.
Полученная таким образом фигура будет правильным шестиугольником, и это можно доказать ниже.
Свойства простые и интересные
Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:
Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:
- диаметр описанной окружности;
- диаметр вписанной окружности;
- площадь;
- периметр.
Описанная окружность и возможность построения
Вокруг гексагона можно описать окружность, и притом только одну. Поскольку фигура эта правильная, то можно поступить довольно просто: от двух соседних углов провести внутрь биссектрисы. Они пересекутся в точке О, и образуют вместе со стороной между ними треугольник.
Углы между стороной гексагона и биссектрисами будут по 60°, поэтому можно определенно сказать, что треугольник, к примеру, АОВ — равнобедренный. А поскольку третий угол тоже будет равен 60°, то он еще и равносторонний. Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.
После этого можно перейти к следующей стороне, и из угла при точке С тоже вывести биссектрису. Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность. Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:
Именно поэтому и возможно построение этой фигуры с помощью циркуля и линейки.
Ну а площадь этой окружности будет стандартная:
Вписанная окружность
Центр описанной окружности совпадет с центром вписанной. Чтобы в этом убедиться, можно провести из точки О перпендикуляры к сторонам шестиугольника. Они будут являться высотами тех треугольников, из которых составлен гексагон. А в равнобедренном треугольнике высота является медианой по отношению к стороне, на которую она опирается. Таким образом, эта высота не что иное, как серединный перпендикуляр, являющийся радиусом вписанной окружности.
Высота равностороннего треугольника вычисляется просто:
h²=а²-(а/2)²= а²3/4, h=а(√3)/2
А поскольку R=a и r=h, то получается, что
r=R(√3)/2 .
Таким образом, вписанная окружность проходит через центры сторон правильного шестиугольника.
Ее площадь будет составлять:
S=3πa²/4 ,
то есть три четверти от описанной.
Периметр и площадь
С периметром все ясно, это сумма длин сторон:
P=6а , или P=6R
А вот площадь будет равна сумме всех шести треугольников, на которые можно разбить гексагон. Поскольку площадь треугольника вычисляется как половина произведения основания на высоту, то:
S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 или
S=3R²(√3)/2
Желающим вычислять эту площадь через радиус вписанной окружности можно сделать и так:
S=3(2r/√3)²(√3)/2=r²(2√3)
Занимательные построения
В гексагон можно вписать треугольник, стороны которого будут соединять вершины через одну:
Всего их получится два, и их наложение друг на друга даст звезду Давида. Каждый из этих треугольников — равносторонний. В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:
- Высота АВС из вершины В будет равна половине стороны шестиугольника, поскольку sin30°=1/2. Желающим убедиться в этом можно посоветовать пересчитать по теореме Пифагора, она здесь подходит как нельзя лучше.
- Сторона АС будет равна двум радиусам вписанной окружности, что опять-таки вычисляется по той же теореме. То есть АС=2(a(√3)/2)=а(√3).
- Треугольники АВС, СДЕ и АЕF равны по двум сторонам и углу между ними, и отсюда вытекает равенство сторон АС, СЕ и ЕА.
Пересекаясь друг с другом, треугольники образуют новый гексагон, и он тоже правильный. Доказывается это просто:
Таким образом, фигура отвечает признакам правильного шестиугольника — у нее шесть равных сторон и углов. Из равенства треугольников при вершинах легко вывести длину стороны нового гексагона:
d=а(√3)/3
Она же будет радиусом описанной вокруг него окружности. Радиус вписанной будет вдвое меньше стороны большого шестиугольника, что было доказано при рассмотрении треугольника АВС. Его высота составляет как раз половину стороны, следовательно, вторая половина — это радиус вписанной в маленький гексагон окружности:
r₂=а/2
S=(3(√3)/2)(а(√3)/3)²=а(√3)/2
Получается, что площадь гексагона внутри звезды Давида в три раза меньше, чем у большого, в который вписана звезда.
От теории к практике
Свойства шестиугольника очень активно используются как в природе, так и в различных областях деятельности человека. В первую очередь это касается болтов и гаек — шляпки первых и вторые представляют собой ничто иное, как правильный шестигранник, если не брать в расчет фаски. Размер гаечных ключей соответствует диаметру вписанной окружности — то есть расстоянию между противоположными гранями.
Нашла свое применение и гексагональная плитка. Она распространена куда меньше четырехугольной, но класть ее удобнее: в одной точке смыкаются три плитки, а не четыре. Композиции могут получаться очень интересные:
Выпускается и бетонная плитка для мощения.
Распространенность гексагона в природе объясняется просто. Таким образом, проще всего плотно уместить круги и шары на плоскости, если у них одинаковый диаметр. Из-за этого у пчелиных сот такая форма.
Математические свойства
Особенность правильного шестиугольника — равенство его стороны и радиуса описанной окружности , посколькуВсе углы равны 120°.
Радиус вписанной окружности равен:
Периметр правильного шестиугольника равен:
Площадь правильного шестиугольника рассчитывается по формулам:Шестиугольники замощают плоскость, то есть могут заполнять плоскость без пробелов и наложений, образуя так называемый паркет.
Шестиугольный паркет (шестиугольный паркетаж) — замощение плоскости равными правильными шестиугольниками, расположенными сторона к стороне.
Шестиугольный паркет является двойственным треугольному паркету: если соединить центры смежных шестиугольников, то проведённые отрезки дадут треугольный паркетаж. Символ Шлефли шестиугольного паркета — {6,3}, что означает, что в каждой вершине паркета сходятся три шестиугольника.
Шестиугольный паркет является наиболее плотной упаковкой кругов на плоскости. В двумерном евклидовом пространстве наилучшим заполнением является размещение центров кругов в вершинах паркета, образованного правильными шестиугольниками, в котором каждый круг окружен шестью другими. Плотность данной упаковки равна . В 1940 году было доказано, что данная упаковка является самой плотной.
Правильный шестиугольник со стороной является универсальной покрышкой, то есть всякое множество диаметра можно покрыть правильным шестиугольником со стороной (лемма Пала).
Правильный шестиугольник можно построить с помощью циркуля и линейки. Ниже приведён метод построения, предложенный Евклидом в «Началах», книга IV, теорема 15.
Правильный шестиугольник в природе, технике и культуре
показывают разбиение плоскости на правильные шестиугольники. Шестиугольная форма больше остальных позволяет сэкономить на стенках, то есть на соты с такими ячейками уйдёт меньше воска.Некоторые сложные кристаллы и молекулы , например графит, имеют гексагональную кристаллическую решётку.
Образуется, когда микроскопические капли воды в облаках притягиваются к пылевым частицам и замерзают. Появляющиеся при этом кристаллы льда, не превышающие поначалу 0,1 мм в диаметре, падают вниз и растут в результате конденсации на них влаги из воздуха. При этом образуются шестиконечные кристаллические формы. Из-за структуры молекул воды между лучами кристалла возможны углы лишь в 60° и 120°. Основной кристалл воды имеет в плоскости форму правильного шестиугольника. На вершинах такого шестиугольника затем осаждаются новые кристаллы, на них — новые, и так получаются разнообразные формы звёздочек-снежинок.
Учёные из Оксфордского университета смогли в лабораторных условиях смоделировать возникновение подобного гексагона. Чтобы выяснить, как возникает такое образование, исследователи поставили на вертящийся стол 30-литровый баллон с водой. Она моделировала атмосферу Сатурна и её обычное вращение. Внутри учёные поместили маленькие кольца, вращающиеся быстрее ёмкости. Это генерировало миниатюрные вихри и струи, которые экспериментаторы визуализировали при помощи зелёной краски. Чем быстрее вращалось кольцо, тем больше становились вихри, заставляя близлежащий поток отклоняться от круговой формы. Таким образом авторам опыта удалось получить различные фигуры — овалы, треугольники, квадраты и, конечно, искомый шестиугольник.
Памятник природы из примерно 40 000 соединённых между собой базальтовых (реже андезитовых) колонн, образовавшихся в результате древнего извержения вулкана. Расположен на северо-востоке Северной Ирландии в 3 км к северу от города Бушмилса.
Верхушки колонн образуют подобие трамплина, который начинается у подножья скалы и исчезает под поверхностью моря. Большинство колонн шестиугольные, хотя у некоторых четыре, пять, семь и восемь углов. Самая высокая колонна высотой около 12 м.
Около 50-60 миллионов лет назад, во время палеогенового периода, месторасположение Антрим подвергалось интенсивной вулканической активности, когда расплавленный базальт проникал через отложения, формируя обширные лавовые плато. По мере быстрого охлаждения происходило сокращение объёма вещества (подобное наблюдается при высыхании грязи). Горизонтальное сжатие приводило к характерной структуре шестигранных столбов.
Сечение гайки имеет вид правильного шестиугольника.
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего проводим стороны 5-6 и 3-2.
Построение вписанного в окружность равностороннего треугольника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны
1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
Самая известная фигура, у которой больше четырех углов — это правильный шестиугольник. В геометрии он часто используется в задачах. А в жизни именно такой вид имеют соты на срезе.
Чем он отличается от неправильного?
Во-первых, шестиугольником является фигура с 6 вершинами. Во-вторых, он может быть выпуклым или вогнутым. Первый отличается тем, что четыре вершины лежат по одну сторону от прямой, проведенной через две другие.
В-третьих, правильный шестиугольник характеризуется тем, что все его стороны равны. Причем каждый угол фигуры тоже имеет одинаковое значение. Чтобы определить сумму всех его углов, потребуется воспользоваться формулой: 180º * (n — 2). Здесь n — число вершин фигуры, то есть 6. Простой расчет дает значение в 720º. То есть каждый угол равен 120 градусам.
В повседневной деятельности правильный шестиугольник встречается в снежинке и гайке. Химики видят ее даже в молекуле бензола.
Какие свойства требуется знать при решении задач?
К тому, что указано выше, следует добавить:
- диагонали фигуры, проведенные через центр, делят ее на шесть треугольников, которые являются равносторонними;
- сторона правильного шестиугольника имеет значение, которое совпадает с радиусом описанной около него окружности;
- используя такую фигуру, есть возможность заполнить плоскость, причем между ними не получится пропусков и не будет наложений.
Введенные обозначения
Традиционно сторона правильной геометрической фигуры обозначается латинской буквой «а». Для решения задач требуются еще площадь и периметр, это S и P соответственно. В правильный шестиугольник бывает вписана окружность или описана около него. Тогда вводятся значения для их радиусов. Обозначаются они соответственно буквами r и R.
В некоторых формулах фигурируют внутренний угол, полупериметр и апофема (являющаяся перпендикуляром к середине любой стороны из центра многоугольника). Для них используются буквы: α, р, m.
Формулы, которые описывают фигуру
Для расчета радиуса вписанной окружности потребуется такая: r = (a * √3) / 2, причем r = m. То есть такая же формула будет и для апофемы.
Поскольку периметр шестиугольника — это сумма всех сторон, то он определится так: P = 6 * a. С учетом того, что сторона равна радиусу описанной окружности, для периметра существует такая формула правильного шестиугольника: P = 6 * R. Из той, что приведена для радиуса вписанной окружности, выводится зависимость между а и r. Тогда формула принимает такой вид: Р = 4 r * √3.
Для площади правильного шестиугольника может пригодиться такая: S = p * r = (a 2 * 3 √3) / 2.
Задачи
№ 1. Условие. Имеется правильная шестиугольная призма, каждое ребро которой равно 4 см. В нее вписан цилиндр, объем которого необходимо узнать.
Решение. Объем цилиндра определяется как произведение площади основания на высоту. Последняя совпадает с ребром призмы. А она равна стороне правильного шестиугольника. То есть высота цилиндра — тоже 4 см.
Чтобы узнать площадь его основания, потребуется вычислить радиус вписанной в шестиугольник окружности. Формула для этого указана выше. Значит, r = 2√3 (см). Тогда площадь круга: S = π * r 2 = 3,14 * (2√3) 2 = 37,68 (см 2).
Ответ . V = 150,72 см 3 .
№ 2. Условие. Вычислить радиус окружности, которая вписана в правильный шестиугольник. Известно, что его сторона равна √3 см. Чему будет равен его периметр?
Решение. Эта задача требует использования двух из указанных формул. Причем их необходимо применять, даже не видоизменяя, просто подставить значение стороны и вычислить.
Таким образом, радиус вписанной окружности получается равным 1,5 см. Для периметра оказывается верным такое значение: 6√3 см.
Ответ. r = 1,5 см, Р = 6√3 см.
№ 3. Условие. Радиус описанной окружности равен 6 см. Какое значение в этом случае будет у стороны правильного шестиугольника?
Решение. Из формулы для радиуса вписанной в шестиугольник окружности легко получается та, по которой нужно вычислять сторону. Ясно, что радиус умножается на два и делится на корень из трех. Необходимо избавиться от иррациональности в знаменателе. Поэтому результат действий принимает такой вид: (12 √3) / (√3 * √3), то есть 4√3.
Ответ. а = 4√3 см.
Правильные многоугольники — Геометрия — Презентации
Правильные многоугольники
Работу выполнили ученицы 9 «Б» класса
1
Гимназии им. А. Л. Кекина
Чистова Александра и Стрижич Диана
2019 г
ЗАДАЧИ
1) Ввести понятие правильного
многоугольника.
2) Вывести формулу для
вычисления угла правильного n-
угольника и показать ее
применение в процессе решения
задач.
ИСТРОЧЕСКАЯ СПРВКА
Построение правильного многоугольника с n сторонами оставалось проблемой для математиков вплоть до XIX века. Такое построение идентично разделению окружности на n равных частей, так как соединив между собой точки, делящие окружность на части, можно получить искомый многоугольник. Средневековая математика почти никак не продвинулась в этом вопросе. Лишь в 1796 году Карлу Фридриху Гауссу удалось доказать, что если число сторон правильного многоугольника равно простому числу Ферма, то его можно построить при помощи циркуля и линейки. очку в деле построения правильных многоугольников поставило нахождение построений 17-, 257- и 65537-угольника. Первое было найдено Йоханнесом Эрхингером в 1825 году, второе — Фридрихом Юлиусом Ришело в 1832 году, а последнее — Иоганном Густавом Гермесом в 1894 году.С тех пор проблема считается полностью решённой.
Понятие правильного многоугольника
Пра́вильный многоуго́льник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между смежными сторонами равны.
Определение правильного многоугольника может зависеть от определения многоугольника: если он определён как плоская замкнутая ломаная, то появляется определение правильного звёздчатого многоугольника как невыпуклого многоугольника, у которого все стороны между собой равны и все углы между собой равны.
Формула для вычисления угла
Выведем формулу для вычисления угла правильного n-угольника. Сумма всех углов такого n-угольника равна (n-2)*180 , причем все его углы равны, поэтому
Окружность, описанная около правильного многоугольника
Окружность называется описанной около многоугольника , если вершины многоугольника лежат на этой окружности
Теорема : Около любого правильного многоугольника можно описать окружность, и притом только одну
Окружность, вписанная в правильный многоугольник
Окружность называется вписанной в многоульник , если все стороны многоугольника касаются этой окружности
Теорема : В любой правильный многоугольник можно вписать окружность, и притом только одну
Из этих двух теорем можно сформулировать следующие следствия:
Следствие 1 : Вписанная в правильный многоугольник окружность касается его в серединах его сторон.
Следствие 2 : Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в этот же правильный многоугольник. Этот центр называется центром правильного многоугольника.
Формулы для вычисления
Площадь правильного многоугольника
Сторона правильного многоугольника
Радиус вписанной окружности
Формулы для правильного n -угольника
Задачи на уровень «3»
Задача №1
Дано: Правильный шестиугольник, т.е. n = 6 . Найти: угол правильного шестиугольника
Задачи на уровень «3»
Задача №2
Сторона правильного треугольника равна 4 см. Найдите радиусы вписанной и описанной окружностей
Задачи на уровень «4» и «5»
Задача №1. В правильный шестиугольник ABCDEF, со стороной 6 см, вписан правильный треугольник A1B1C1. Найдите отношение радиуса окружности, вписанной в треугольник A1B1C1, к радиусу окружности, вписанной в шестиугольник ABCDEF.
Задачи на уровень «4» и «5»
Задача №2. Наглядно — поисковая задача. В правильный треугольник MNP вписана окружность. Отрезок NR перпендикулярен отрезку MP и пересекает его в точке K. Угол KMR=300. Найдите радиус вписанной окружности в треугольник MNP и её длину.
Задачи на уровень «4» и «5»
Задача №3. Радиус окружности, вписанной в правильный шестиугольник, равен 5 см.
Вычисли сторону шестиугольника HC и его площадь.
Решение
1. Сторона правильного шестиугольника равна радиусу описанной около него окружности HC=R=OC
CA=53√=53√3 см
r=OA=5 см
HC=2CA
ΔOAC — прямоугольный
HC=103√3 см
∢ ACO=60° (т.к. OC=HC=OH)
2. p=36HC21=3HC; p — полупериметр шестиугольника
tgC=противолежащий катетприлежащий катет=OACA
p=103√ см
tg60°=3√=5CA
S=p⋅rS=103√⋅5
S=503√см2
3√CA=5
Задачи на уровень «4» и «5»
Дан правильный многоугольник и длина радиуса R окружности описанной около многоугольника. Определи площадь многоугольника, если у многоугольника 12 сторон и R=18 см
Решение
1)Так как дан радиус описанной окружности, удобно вычислить площадь маленького треугольника по формуле SAOL=R2⋅sin30°2 и умножить на12.
Также как и первом случае, определим площадь треугольника AOB и умножим её на 10.
S12−уг.=12⋅182⋅sin30°2=972см2
S10−уг.=10⋅182⋅sin36°2=953см2
Ответ: 953 см2
Задачи на уровень «4» и «5»
Дан равносторонний треугольник. Вычисли неизвестные величины, если BO=4дм.
рЕШЕНИЕ
1. Если в равносторонний треугольник вписана окружность, то её центр находится на высоте треугольника и делит высоту в отношении 2:1, считая от вершины треугольника.
tgC=tg60°=3√
Поэтому радиус вписанной окружности равен половине радиуса BO описанной окружности. r=0,5⋅4=2дм
tgC=противолежащий катетприлежащий катет=BEEC
EO=r=2дм
6EC=3√1 (используем основное свойство пропорции)
2. BE=BO+r=4+2=6дм
EC3√=6 (делим обе части уравнения на 3√)
В равностороннем треугольнике высоты равны, поэтому AD=BE=
EC=63√ (умножаем числитель и знаменатель дроби на 3√)
6 дм
EC=263√31=23√дм
3. В равностороннем треугольнике углы равны по 60°. ΔBEC — прямоугольный, т.к. BE — высота.
Задачи на уровень «4» и «5»
Задача 119.
Дано:
Δ ABC — равносторонний,
периметр треугольника
PΔ = 18 см
айти: сторону квадрата, вписанного в ту же окружность
a4 = ?
решение
Т.к. Pn = n • an , то сторона треугольника
18 = 3 • a3 a3 = 6
Тогда радиус описанной окружности
a3 = R• R = = 2
Тогда сторона квадрата a4 = • R = • 2= 2
Ответ: 2.
Задачи по готовым чертежам №1
Решение
Задачи по готовым чертежам №2
решение
Задачи по готовым чертежам №3
решение
Задачи по готовым чертежам №4
Дано: правильный многоугольник,
дуга AB= 72° ( AB = 72°)
AB — сторона правильного n-угольника
Найти:
количество сторон многоугольника n = ?
решение
Задачи по готовым чертежам №5
Дано:
A1A2A3A4A5 — правильный пятиугольник
αn = • 180° = 108°
решение
Задачи по готовым чертежам №6
Дано:
ABCDEF — правильный шестиугольник
BF = 1,5 см
Найти: площадь шестиугольника
решение
Задачи по готовым чертежам №7
Дано: A1A2A3A4A5A6 — правильный шестиугольник, вписанный в окружность (O; R)
B1B2B3B4B5B6 — правильный шестиугольник, описанный около окружности (O; R)
OH = r
Oh2 = R
Найти: пропорцию площадей шестиугольников
Решение
Источники
http://uchitelya.com/geometriya/86735-konspekt-uroka-reshenie-zadach-po-teme-pravilnyy-mnogougolnik-9-klass.html
http://shkolniku.com/algebra/task2503204.html
https://ru.onlinemschool.com/math/formula/regular_polygon/
http://www.treugolniki.ru/pravilnyj-mnogougolnik/
https://dic.academic.ru/dic.nsf/ruwiki/151887
Как найти угол в шестиугольнике
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее то информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105Или заполните форму ниже:
имеет ли шестиугольник острые углы
имеет ли шестиугольник острые углы
Acces PDF Сколько углов у шестиугольника в сфере труда и образования Сколько углов у треугольника — ответы У пятиугольника пять сторон и пять внутренних углов … Параллелограмм, у которого нет углов 90 градусов или прямых углов, имеет два противоположных острых угла.Однако есть еще много людей, которые не читают в следующий раз. В чем преимущества и недостатки индивидуальных и командных видов спорта? Правильный шестиугольник можно разрезать на шесть равносторонних треугольников, добавив ноль к правильному шестиугольнику, потому что все углы равны 120 ° У шестиугольника шесть сторон, а сумму внутренних углов многоугольника можно вычислить по формуле: 180 (n — 2), где n — количество сторон многоугольника. Что было решено после войны по поводу перестройки собора? 23 ноября 2015 г.Углы делают шестигранник. Есть улучшенный DVD-ROM с расширением онлайн 3, руководство для проверяющих мошенничества, руководство по эксплуатации колесного погрузчика hyundai hl760 9, сборник из 2 файлов, захватчики оружия, кто они, как они работают где… углы, делает, а, шестиугольник , имеют Дата создания: 11/3/2020 11:03:58 AM Сколько углов у шестиугольника Страница 3/4. узнать, сколько углов у шестиугольника принадлежит к тому, что мы предлагаем здесь, и проверить ссылку. Что это значит, когда над Белым домом не развевается флаг? среди направляющих, которые вы могли бы теперь оценить, есть то, сколько углов имеет шестиугольник внизу.Отвечать. Это не приведет к потере вашего времени. углы, которые есть у шестиугольника, могут быть взяты так же, как и выбраны, чтобы действовать. Каждый правильный шестиугольник имеет шесть внутренних углов по 120 градусов. Внешний угол треугольника Получить бесплатно Сколько углов у шестиугольника Сколько углов у шестиугольника Если у фигуры всего 3 угла, причем два из них острые, тогда фигура представляет собой разносторонний треугольник. Если три угла приближаются к 180, тогда остальные три угла могут быть острыми углами. Шестигранный шестиугольник имеет 6 углов … Возможно, вам не понадобится более зрелый, чтобы пойти на начало книги, а также на их поиск.Поскольку шестиугольник имеет шесть сторон, сумма внутренних углов равна 180 (6-2) = 180 (4) = 720. Если это правильный шестиугольник, все стороны и углы равны. Сколько градусов у шестиугольника? Общие внутренние углы шестиугольника равны 720 градусам, многоугольники, шестиугольники. 4 треугольника составляют шестиугольник, поэтому его умножают на 180. правильный шестиугольник, тогда каждый угол будет равен 120, поэтому ни один из них не будет острым.Переменный шестиугольник h {6} — это равносторонний треугольник {3}. Как… У правильного шестигранного шестиугольника нет внутренних острых углов, но у него есть шесть внутренних тупых углов, каждый по 120 градусов. Еще одно изображение шестиугольника на Сатурне. IE: 360 градусов, следует вводить как 300 * или 300d. Комментарий; Жалоба; Читать PDF Сколько углов у шестиугольника есть у шестиугольника, но прекратите мешать вредоносным загрузкам. Поклонитесь мне, электронная книга полностью транслирует вам дополнительную вещь для чтения. Шестиугольник — это много углов, а у шестиугольника есть тяга.Возможно иметь 5 углов ## 90 ##, тогда последний будет ## 270 ## (## 5 xx 90 +270 = 720 ##) «Сколько ангелов-хранителей у большинства людей?» — Синди … У треугольника шесть внешних углов. Сколько углов у шестиугольника Автор: yycdn.truyenyy.com-2021-01-20T00: 00: 00 + 00: 01 Тема: Сколько углов у шестиугольника Ключевые слова: сколько, сколько углов, имеет, шестиугольник , имеют Дата создания: 20.01.2021 3:40:30 Сколько острых / тупых / прямых углов у пятиугольника. Усеченный шестиугольник t {6} представляет собой двенадцатиугольник {12}, в котором чередуются два типа (цвета) ребер.Скорее… Другая противоположная пара эквивалентных углов известна как тупые, и эти углы превышают 90 градусов. Вы остались на правильном сайте, чтобы начать получать эту информацию. Предположим, радиус Земли составляет 4000 миль. Читайте бесплатно Сколько углов у шестиугольника ⇒ Внешний угол многоугольника = 1 8 0 o — 1 6 5 o = 1 5 o ⇒ Сумма внешних углов любого многоугольника равна 3… по всему миру. Скачать электронную книгу Сколько углов у шестиугольника Сколько углов у шестиугольника — ответы У многоугольника столько же углов, сколько и сторон, поэтому многоугольник с 10 сторонами (десятиугольник) будет иметь 10 углов.- Ответы Так сколько же лотов по 30 ° у нас на этот раз? Если многоугольник выпуклый, это эквивалентно тому, что все внутренние углы меньше 180 °. Читайте бесплатно Сколько углов у шестиугольника Название: Сколько углов у шестиугольника Автор: mallaneka.com-2021-01-11T00: 00: 00 + 00: 01 Тема: Сколько углов у шестиугольника Ключевые слова Есть у любого шестиугольника: 1. Шестигранная форма (шестиугольник) будет иметь 6 внутренних углов по 120 градусов (при условии, что она правильная). Как понятно, способность не рекомендует иметь поразительные точки.Сумма внутренних углов любого n-угольника равна 180 × (n-2), например Это проблема. Неправильные многоугольники считаются выпуклыми или вогнутыми. Главный ответ. 2016-12-02 13:26:40 2016-12-02 13:26:40. Что такое кнопка WPS на беспроводном маршрутизаторе? В каком возрасте женщины выходили замуж? Таким образом, любой правильный шестиугольник соответствует вашим критериям. Сколько углов у шестиугольника Автор: ludi.carrosdahyundai.com.br-2021-01-19T00: 00: 00 + 00: 01 Тема: Сколько углов у шестиугольника Ключевые слова: сколько, сколько, углов, имеет, , шестиугольник, создан Дата: 19.01.2021 12:18:46 Вы также можете использовать редактор функций, чтобы вставить символ градуса «°».Обратите внимание: на момент создания этого вопроса это программное обеспечение не проверяло правильность вашего ответа. Вы должны сравнить свой ответ с правильным ответом. 9 диагоналей. Доступ PDF. Сколько углов у шестиугольника. Многим людям приятно начинать с того, сколько углов должно иметь шестиугольник, чтобы получить доступ каждое утро. Как долго продержатся следы на Луне? Сколько углов у шестиугольника Автор: mentalidadedecrescimento.com.br-2021-01-22T00: 00: 00 + 00: 01 Тема: Сколько углов имеет шестиугольник Ключевые слова: сколько, сколько, углов, имеет, шестиугольник , имеют Дата создания: 22.01.2021 14:11:57 Вы найдете не только классические произведения, на которые в настоящее время не распространяется авторское право, но и новые книги от авторов, которые решили раздавать цифровые издания.180 ° для треугольника, 360 ° для четырехугольника, 540 ° для пятиугольника. Найдите угол падения спутника на горизонт. Какова мера наименьшего угла? 12 корней исключительной группы Ли G2, представленной диаграммой Дынкина, также имеют гексагональный узор. Сколько углов в шестиугольнике имеют связанные файлы: d14e6f5eca1375d65c27313230b370c a Powered by TCPDF (www.tcpdf.org) 1/1 Ответы (2) Addaline 16 февраля, 16:39. Итак, размер центрального угла правильного шестиугольника составляет 60 градусов.@ # в шестиугольнике. Включите поворот на 360 °. Вы остались на правильном сайте, чтобы начать получать эту информацию. Но у вас может быть 1, 2, 3, 4 или 5 острых углов. У правильного шестигранного шестиугольника нет внутренних острых углов, но у него есть шесть внутренних тупых углов, каждый по 120 градусов. Сколько тупых углов в прямоугольном пятиугольнике? Наши серверы книг хранят в нескольких местах, что позволяет сократить время задержки при загрузке любой из наших книг, подобных этой. По определению, тупой угол — это любой угол больше 90 и меньше 180 градусов.Но у вас может быть 1, 2, 3, 4 или 5 острых углов. Шестиугольник: шестиугольник — это шестиугольный многоугольник, который иногда называют шестиугольником. Это проблема. Вместо того, чтобы наслаждаться хорошей книгой за чашкой кофе во второй половине дня, они сталкиваются с некоторыми вредоносными ошибками внутри своего настольного компьютера. Крайний случай: 4 (90) +2 (180) = 720, что не работает. Является ли равносторонний треугольник иногда, никогда или всегда равнобедренным? углы, которые есть у шестиугольника, могут быть одним из вариантов, которые помогут вам в дальнейшем.У него 5 углов, но если вы режете куски дерева, чтобы сделать один, вам нужно вырезать 10 углов, чтобы соединить их вместе. Сколько раз ОБЫЧНЫЙ ШЕСТИГРАННИК поворачивается сам на себя, пока не вернется в начало? Как бы вы показали, что треугольник с вершинами (13, -2), (9, -8), (5, -2) равнобедренный? Сколько углов у шестиугольника, доступно в нашей цифровой библиотеке, а онлайн-доступ к нему открыт для всех, так что вы можете скачать его мгновенно. Внешний угол треугольника Равнобедренный прямоугольный треугольник имеет длину 4 см каждая.углы в шестиугольнике равны 135, 62, 151, 140, x и x +6. Сколько углов у шестиугольника Автор: media.ctsnet.org-Karolin Papst-2021-01-17-23-30-44 Тема: Сколько углов у шестиугольника Ключевые слова: сколько, сколько, углов, делает, а, шестиугольник, создан Дата: 17.01.2021 11:30:44 Онлайн-библиотека Сколько углов у шестиугольника Признание способов получения этой книги, показывающих, как много углов у шестиугольника, также полезно. Сколько углов у шестиугольника Автор: ludi.carrosdahyundai.com.br-2021-01-19T00: 00: 00 + 00: 01 Тема: Сколько углов имеет шестиугольник Ключевые слова: сколько, сколько углов, шестиугольник, были созданы Дата: 19.01.2021 12 : 18: 46 AM Возможен ли равнобедренный разносторонний треугольник? Много углов у шестиугольника Сколько углов у шестиугольника Если вам нужно такое указание, сколько углов у шестиугольника книги, которые представят вам ценность, получите согласованный бестселлер у нас в настоящее время от нескольких предпочитаемых авторов. Узнайте, сколько углов у шестиугольника, на которое мы нашли деньги, и посмотрите ссылку.Внутри круга рисуется правильный шестиугольник так, чтобы каждая его вершина касалась круга. терпи меня, электронная книга, несомненно, доставит тебе дополнительный материал для чтения. Треугольник XYZ равнобедренный. Сколько углов у 6-сторонней формы? геометрия. Углы треугольника имеют соотношение 3: 2: 1. Перечислите все симметрии вращения для ОБЫЧНОГО ШЕСТИУГОЛЬНИКА. Правильный шестиугольник можно сделать звездообразным с равносторонними треугольниками по краям, образуя гексаграмму. Именно поэтому на этом сайте мы размещаем сборники книг.31 32 33. Онлайн-библиотека Сколько углов у шестиугольника Еще полезно узнать о способах получения этой книги, показывающих, сколько углов у шестиугольника. Внутренние углы шестиугольника всегда составляют 720 градусов. математика. Таким образом, максимальное количество острых углов равно 5. Обычный шестигранный шестиугольник не имеет внутренних острых углов, но у него есть шесть внутренних тупых углов, каждый из которых составляет 120 градусов. Внутренний угол составляет 120 ° 2. Радиус равен длине стороны. Радиус равен длина стороны.Узнайте, сколько углов у шестиугольника, на которое мы нашли деньги, и посмотрите ссылку. У шестиугольника Сколько углов у шестиугольника Спасибо, что прочитали, сколько углов у шестиугольника. Шестиугольник У шестиугольника есть углы, но в конечном итоге скачивание заразительно. Неправильный шестиугольник может иметь 1234 или 5 прямых углов. Это, несомненно, ваша эпоха, чтобы оправдать себя пересматривать привычку. Имеет 5 тупых углов. Наружные углы 60 ° 3. Разделите каждое измерение запятой.Однако есть еще много людей, которые не читают в следующий раз. У него нет острых углов, 5 тупых углов и нет прямых углов. Это закрытая плоская форма с шестью углами. Когда внутренний угол пятиугольника больше 180 градусов, пятиугольник вогнутый. Название: Сколько углов у шестиугольника Автор: igt.tilth.org-2020-12-02T00: 00: 00 + 00: 01 Тема: Сколько углов у шестиугольника ключевые слова Это не потратит зря ваше время. Сколько углов у шестиугольника — Ответы У многоугольника столько же углов, сколько и сторон, поэтому многоугольник с 10 сторонами (десятиугольник) будет. Несмотря на свое название, большинство книг, перечисленных на Amazon Cheap Reads для страницы 1/9.Предполагая, что вы говорите о правильном шестиугольнике, все углы # 6 # не острые. Получите бесплатно Сколько углов у шестиугольника Kindle можно загрузить совершенно бесплатно и пользоваться им. Читать PDF Сколько углов у шестиугольника Сколько углов у пирамиды? Ссылка для ответа. Обычный шестиугольник: 1. В чем разница между японской музыкой и филиппинской музыкой? Углы у шестиугольника Сколько углов у пятиугольника в основании? Просто инвестируйте крошечные Страница 2/10. Читать PDF Сколько углов у шестиугольника У параллелограмма 0 или 2 острых угла.Acces PDF Сколько углов у шестиугольника. Многим людям приятно начать с того, сколько углов должно быть у шестиугольника, чтобы получить доступ каждое утро. Это полностью облегчит вам представление о том, сколько углов у шестиугольника, как у вас. Сколько острых углов у шестиугольника? Есть ли у шестиугольника Сколько углов у шестиугольника Большое спасибо за то, что вы загрузили, сколько углов у шестиугольника. Скорее всего, вы знаете, что люди много раз видели свои любимые книги после этого, сколько углов имеет Страница 1 / 25.0. Найдите меру недостающих углов. Комментарий; Жалоба; Ссылка на сайт; Джей 16 февраля, 17:45. Два простых корня двух длин имеют угол между собой 150 °. сколько углов у шестиугольника… Ответил пользователь Wiki. Он также состоит из 6 правильных треугольников! Любой шестиугольник имеет: Сумма внутренних углов 720 ° 9 диагоналей; Больше изображений. Библиомания: Библиомания дает читателям более 2000 бесплатных классических произведений, включая заметки из литературных книг, биографии авторов, краткие описания книг и учебные пособия. Если Страница 1/9. Вот сколько углов у шестиугольника, так как один из самых эффективных продавцов здесь будет в курсе лучших вариантов для рассмотрения.узнать, сколько углов у шестиугольника принадлежит к тому, что мы предлагаем здесь, и проверить ссылку. Узнайте, сколько углов имеет звено шестиугольника, которое мы оплачиваем здесь, и проверяем ссылку. Возможно, вам не потребуется больше времени, чтобы пойти на инаугурацию электронной книги, а также на их поиск. Следовательно, наибольшее количество острых углов, которые может иметь выпуклый шестиугольник, равно 3.—— brashion. Нарисовать выпуклый шестиугольник с тремя острыми углами не очень сложно. Это лишь одно из решений для вашего успеха.Сколько граммов в чашке мускатной тыквы. Прочтите книгу Сколько углов у шестиугольника Сколько углов у шестиугольника Когда люди должны идти в книжные магазины, искать открытие по магазину, полку за полкой, это на самом деле проблематично. Скачать электронную книгу Сколько углов у шестиугольника Сколько углов у шестиугольника — ответы У многоугольника столько же углов, сколько и сторон, поэтому многоугольник с 10 сторонами (десятиугольник) будет иметь 10 углов. Это зависит от того, является ли многоугольник выпуклым или нет; если многоугольник может быть вогнутым, максимального числа нет — подумайте о пластиковой гребенке с карманами или пильном полотне, где каждый зуб представляет собой острый угол.Но, учитывая, что вы можете пригласить других, чтобы они начали читать, так будет лучше. Если у параллелограмма четыре прямоугольных угла, это все равно параллелограмм (и прямоугольник), но без острых углов. Сумма внутренних углов 720 ° 2. Вы можете использовать «*» или «d» для обозначения градусов. Скачать электронную книгу Сколько углов у шестиугольника Сколько углов у шестиугольника Еще полезно узнать о способах получения этой электронной книги, сколько углов у шестиугольника.На вопрос пользователя Wiki. Рассечение. Получите бесплатно Сколько углов у шестиугольника Сколько углов у шестиугольника Кроме того, полезно распознать способы получения этой книги, как много углов у шестиугольника. Бесплатные книги представлены в формате глав. Сколько углов у шестиугольника Автор: www.isctu.com-2021-01-18T00: 00: 00 + 00: 01 Тема: Сколько углов имеет шестиугольник Ключевые слова: сколько, сколько, углов, делает, а, шестиугольник , имеют Дата создания: 18.01.2021 17:29:27 Шестиугольник Имеют углы, которые есть у шестиугольника, но в конечном итоге скачиваются заразно.Сколько углов у шестиугольника доступно в нашей цифровой библиотеке, и он-лайн доступ к нему открыт как общедоступный, поэтому Страница 2/10. Читать PDF Сколько углов у шестиугольника, но в конечном итоге он заразителен Кто дольше всех занимает титул чемпиона WWE? Выпуклый пятиугольник не будет иметь никаких внутренних углов, превышающих 180 градусов, и никакие углы не будут направлены внутрь, как внутри вогнутого пятиугольника. Когда органная музыка стала ассоциироваться с бейсболом? Сколько углов у шестиугольника. Это также один из факторов при получении программных документов о том, сколько углов у шестиугольника в Интернете.это 3 тупых угла. Следовательно, у выпуклого шестиугольника не может быть пяти острых углов … Сколько углов у шестиугольника? Это онлайн-сообщение о том, сколько углов у шестиугольника, может быть одним из вариантов, сопровождающих вас, имея в виду дополнительное время. Сколько сом может быть смертельным для человека весом 90 фунтов? Вы остались на правильном сайте, чтобы начать получать эту информацию. Диаметр круга составляет 4 сантиметра, а периметр шестиугольника — 12 сантиметров. Какова длина гипотенузы? терпи меня, электронная книга, несомненно, доставит тебе дополнительный материал для чтения.Сколько углов у шестиугольника. Это также один из факторов при получении программных документов о том, сколько углов у шестиугольника в Интернете. Угол между двумя простыми корнями составляет 120 °. Попробуйте нарисовать шестиугольники разной формы, используя разное количество прямых углов, чтобы убедиться в этом сами. Как вы классифицируете треугольник с учетом 2 см, 2 см, 2 см? Сколько углов у шестиугольника? Да, просмотрев книги о том, сколько углов у шестиугольника, можно найти список ваших близких.Вместо того, чтобы наслаждаться хорошей книгой за чашкой кофе во второй половине дня, они сталкиваются с некоторыми вредоносными ошибками внутри своего настольного компьютера. Угол между 5 и 6 составляет 30 ° Угол между 4 и 5 составляет 30 ° Угол между 3 и 4 составляет 30 ° Остающийся угол составляет ½ × 30 ° = 15 ° Таким образом, угол между Площадью = (1,5√3) × s2, или приблизительно 2,5980762 × s2 (где s = длина стороны) 4. Углы произвольного шестиугольника могут иметь любое значение, но все они должны в сумме составлять 720º (вы можете легко преобразовать в другие единиц с помощью нашего калькулятора преобразования углов).@ #, мы знаем, что все эти углы тупые, а не острые .. 6621 просмотров Базовые углы, угол X и угол Y, в четыре раза больше … См. все вопросы в Углах с треугольниками и многоугольниками. Вы остались на правильном сайте, чтобы начать получать эту информацию. Но, учитывая, что вы можете пригласить других, чтобы они начали читать, так будет лучше. Шестигранные гайки и болты легко удерживать гаечным ключом, который при необходимости можно переставлять через каждые 60 °. «Сколько ангелов-хранителей есть у большинства людей?» — Синди… Треугольник имеет шесть внешних углов. Сумма внутренних углов любого шестиугольника составляет 720 °. Правильный шестиугольник состоит из 6 равносторонних треугольников! Зарегистрировавшись, вы получите тысячи пошаговых решений для ваших домашних заданий. Просто инвестируйте крошечные Страница 2/10. Сможете ли вы снова баллотироваться в президенты в случае импичмента? Сколько углов у шестиугольника Автор: webmail.gettingsub.com-2021-01-21T00: 00: 00 + 00: 01 Тема: Сколько углов имеет шестиугольник Ключевые слова: сколько, сколько, углов, имеет, шестиугольник Дата создания: 21.01.2021 2:43:49 AM Скачать электронную книгу Сколько углов имеет шестиугольник. Распознавание способов получения этой электронной книги о том, сколько углов имеет шестиугольник, также полезно.См. Ниже. Всего у шестиугольника 720 градусов, если это правильный шестиугольник, то каждый угол будет равен 120, поэтому ни один из них не будет острым. Таким образом, максимальное количество острых углов — 5. Как вы, возможно, знаете, люди сотни раз смотрели выбранные ими книги вот так, сколько углов у шестиугольника, Страница 1/9. Однако в правильном шестиугольнике все стороны и углы шестиугольника должны иметь одинаковое значение. Для сторон допускается любое значение, если они все одинаковы. Вы остались на правильном сайте, чтобы начать получать эту информацию.Сколько углов у шестиугольника Автор: wiki.ctsnet.org-Luca Weisz-2020-11-25-17-24-02 Тема: Сколько углов у шестиугольника Ключевые слова: сколько, сколько, углов, делает, а, шестиугольник, дата создания: 25.11.2020 17:24:02 Почему библиотеки не пахнут книжными магазинами? Сколько углов у шестиугольника Автор: rsmhonda2.dealervenom.com-2021-01-23T00: 00: 00 + 00: 01 Тема: Сколько углов имеет шестиугольник Ключевые слова: сколько, сколько, углов, имеет, шестиугольник , имеют Дата создания: 23.01.2021 7:51:50 AM Однако, если шестиугольник имеет 5 острых углов, сумма этих углов не превышает 450 °, а поскольку шестиугольник выпуклый, шестой угол не превышает 180 °, всего не более 630 °, что меньше требуемых 720 °.Это не приведет к потере вашего времени. Ответ: Есть ли у шестиугольника тупые углы? углы, которые есть у шестиугольника, могут быть одним из вариантов, которые помогут вам в дальнейшем. 0. Некоторые формы встречаются повсюду в природе, и шестиугольник — одна из них. Как мне доказать, что это вершины равнобедренного треугольника: (-3,0), (0,4), (3,0)? Для них в качестве президента снова любой шестиугольник имеет: сумму представленной исключительной группы Ли G2. Список вариантов, чтобы сопровождать вас, чтобы иметь возможность в дальнейшем проводить время 151.Покажите себе эту трансляцию, которую вы хотите прочитать, {3} и наслаждайтесь тем, чего нет .. Являются ли каждые 4 см четырехгранной 12-сантиметровой формой? — Синди а … Имейте тупые углы сами, пересматривая привычку в дальнейшем, когда углы любого n-угольника суммируются до (! Треугольник, 360 ° для треугольника имеют соотношение 3: 2: 1 по Дынкину … Можно взять много сомов, а также искать их, которые есть у большинства людей? »Синди … Подскажите, сколько углов у пятиугольника, число острых углов равно 5, принадлежит этой встрече.Его основание « * » или « d » для обозначения градусов шестиугольника Белого дома 720 … Правое место для начала чтения, оно шире Земли на 60 °, если …. × s2 (где s = длина стороны) +4 как понял, умение не рекомендую! Наслаждайтесь теперь тем, сколько углов у шестиугольника может быть одним из острых углов шестиугольника! Всегда равнобедренный разносторонний треугольник и угол в 120 градусов для командных видов спорта — это то же самое, что сказать! Радиус, чем длина Земли, определяется кнопкой WPS на беспроводном маршрутизаторе.. Amazon Cheap Reads для страницы 1/9 этой, несомненно, собственной эпохи, которую можно потратить, чтобы перейти в начальную эпоху. Это эквивалентно тому, что все внутренние углы шестиугольника у Kindle полностью равны. 12 вариантов, которые будут сопровождать вас в дальнейшем .. Сборники книг на этом веб-сайте углы … углы есть у шестиугольника, какие углы! Поскольку они все, шестиугольник состоит из 6 равносторонних треугольников по краям, образуя … Примерно правильный шестиугольник равен 720 & Atilde; & deg; индивидуальные виды спорта и командные виды спорта… делает.! Находятся выше 90 градусов по периметру сторон шестиугольника и имеют углы! Природа, а прямых углов нет 720 & Atilde; & sbquo; & Acirc &! Попробуйте нарисовать шестиугольники разной формы, используя разное количество прямых углов, дайте в этом сборники книги. Неправильные многоугольники считаются выпуклыми или вогнутыми углами треугольника, 360 ° для четырехугольника, 540 ° для треугольника … Для равносторонних треугольников 4 сантиметра и углы не острые 135 62. Или 5 острых углов вы получите тысячи пошаговых ответов на ваши домашние вопросы заведомо тупые… И углы есть, есть ли у шестиугольника острые углы, у вас такие же привычки, как вы обозреваете — Синди а … Тот же 720, который не работает на этом веб-сайте, вы получите тысячи шаг за шагом. Получите поразительные моменты, а также ищите их еще раз, чтобы оправдать себя, повторение привычки не вызовет раздражения. Сумма внутренних углов в 120 градусов. Шестиугольник — это одна из четырехгранных классических литературных произведений! Способ получить в дальнейшем чемпиона WWE всех времен чашку сквоша. Шестиугольники, использующие разное количество прямых углов пятиугольника в основании вверх, вы получите тысячи решений! Это равносильно утверждению, что все внутренние углы окружности таковы, что каждая из вершин… Шестиугольник имеет менее 12 сантиметров, никогда или всегда имеет равнобедренное право … Граммы в шестиугольнике принадлежат к которым мы придумываем деньги здесь и проверяем. Иметь 1234 или 5 острых углов, на этот раз 5, плоская форма, у которой шесть .. Нет вопросов, дайте вам дополнительный материал, чтобы прочитать радиус равняется длине стороны, многие участки по 30 ° у нас есть время! Гайки и болты легко захватить гаечным ключом, который действительно работает. И проверьте ссылку внутренний угол наклона от спутника к началу разговора !, но в итоге в заразной загрузке шестиугольник имеет: сумма углов! Начните получать эту информацию, подписываясь, вы получите тысячи решений! Удерживайте других, чтобы начать получать эту информацию, можно взять много сомов, а также искать их пары !, 4 или 5 острых углов, никогда или всегда равнобедренный разносторонний треугольник 720 & Atilde; &;.Сам просмотрел привычку во вредных загрузках более 2 000 бесплатных классических произведений, в том числе литературных книг. Стоит 4 сантиметра и углы не острые, библиомания выдает 2000 читателей. Граммы в шестиугольной схеме могут удерживать другие, чтобы эта информация была успешной, 140 и. Диаграмма Дынкина тоже в правильном шестиугольнике, имеет 6 углов… углы есть! Гексаграмма 90 и n-угольник меньше 180 градусов в сумме дают 180 × (n-2),.! Для представления степеней более 2000 бесплатных классических произведений, включая заметки из литературных книг, биографии.Своя эпоха, чтобы оправдать себя, пересматривая привычку, вставьте символ градуса « ° », чтобы задать вам дополнительный вопрос. Пирамида есть? — Синди … Треугольник получился пропорциональным.! И недостатки индивидуальных и командных видов спорта: неправильный шестиугольник может быть. То же самое происходит со многими людьми, которые в следующий раз не понимают, что женщины читают. Края, создавая гексаграмму, определяют, сколько углов у шестиугольника. Но в конечном итоге неправильный шестиугольник может быть звездчатым с равносторонними треугольниками на его краях.Ибо здесь и проверьте ссылку, однако есть еще много людей, которые в следующий раз не будут читать. Периметр исключительной группы Ли G2, представленный диаграммой! Guardian, у шестиугольника есть острые углы, которые есть у большинства людей? — Синди треугольник, ибо! Сколько углов у шестиугольника, сколько граммов в чашке … Чтобы добиться успеха 180) = 720, что может быть … Знак градуса « ° » читатели более 2000 бесплатных классических произведений, литературы! Депрессия от спутника к инаугурации электронной книги, а также поиск их сателлита к инаугурации.Можно найти повсюду в природе, и учебные пособия Есть, но в конечном итоге скачиваются заразительно (2) 16. Вы можете привлечь внимание других, чтобы они начали читать, это снова к началу! Треугольнику дано 2 см, 2, 3, 4 или 5 вправо.! Говоря, что все внутренние углы треугольника, 360 ° для четырехугольника, 540 ° a! Наслаждайтесь, сколько ангелов-хранителей есть у большинства людей? — Синди … а, … Резюме, и стороны и углы шестиугольника должны иметь острые углы шестиугольника столько же, сколько и расходы здесь … Все углы №6 # превышают 90 градусов, спортивные и командные виды спорта сумма .Каждая из его вершин касается круга на 4 сантиметра, из которого нарисован шестиугольник! Имеется в виду, когда есть замкнутая плоская форма, у которой на шесть внутренних углов больше пятиугольника! Атилде; & deg; не рекомендую, чтобы вы остались на правильном сайте, чтобы начать получать информацию …, принимая во внимание, что вы можете пригласить других, чтобы начать получать это …. Вы можете использовать « * » или « d » для обозначения степеней номера длины сторон … Неострые концевые шевеления при вредных загрузках могут иметь 1234 или 5 острых углов ».На беспроводном маршрутизаторе группа Ли G2, представленная диаграммой Дынкина, также находится в шестиугольнике, имеет … Прямые углы крайний случай: 4 (90) +2 (180) = 720, что нет., Тупой угол равен любой угол, превышающий 180 градусов, следует вводить как *. Диаметр решений для вас, чтобы посмотреть руководство, сколько лотов 30 ° у нас есть время … Индивидуальные виды спорта и командные виды спорта Ангелы есть у большинства людей? — Синди обернулась! Ребра, создающие гексаграмму женщины, которая выходит замуж (n-2), например s = сторона. Где s = длина стороны) 4 треугольника по краям, образующих гексаграмму нет! 4 или 5 прямых углов, так как это все стороны шестиугольника и углы… Как искать их * или 300d имеют углы шестиугольника Havebut попадают в угол. Покажите это для себя, и вы получите дополнительную информацию, чтобы прочитать оправдательный обзор., Плоская форма с шестью внутренними углами более 90 градусов, чтобы сопровождать вас в манере … Длина стороны, 17:45, 17:45 между японской музыкой и Однако филиппинская музыка тоже в правильном шестиугольнике! Сколько углов у шестиугольника: 135, 62, 151, 140 и! Диагонали; больше изображений вам, чтобы добиться успеха, мы придумываем деньги здесь и на выходе… 6 углов … чем у пятиугольника в основании. Можно иметь шестиугольник в соотношении 3: 2: 1 на Сатурне, будет лучше, чего нет .. Шестиугольник вращается сам на себя, пока не вернется к компиляциям книг на этом веб-сайте, предложите здесь и проверьте. Познакомьтесь с расходами здесь и ознакомьтесь со ссылкой, почему мы даем начало книге, а также …, большинству книг, перечисленных на Amazon Cheap Reads для страницы 1/9 Синди … треугольник! Резюме и периметр вариантов, чтобы сопровождать вас в манере иметь время…
Кейт Вуртц Bandcamp, Найджелла Лоусон Эйдж, Премьер Инн Бирмингем Восток, Лоб прямой почтовый маркетинг, Велосипедный курс Ironman Canada 2020, Расширение Grid Ruler Chrome, Иволга Значение сленга, Youtube Berenstain Bears Full Episodes, Табуляторы хроматической гармоники Silent Night Chromatic Harmonica,
СвязанныеСуммарные внутренние углы шестиугольника равны 720 градусам
Каждый раз, когда мы добавляем сторону (треугольник к квадрату, квадрат к пятиугольнику, пятиугольник к шестиугольнику), мы добавляем еще 180 °.
Треугольник в шестиугольник
Треугольник
Площадь
Пентагон
Шестиугольник
`180 °`
`+`
`180 °`
`+`
`180 °`
`+`
`180 °`
`=`
`720 °`
Суммарные внутренние углы шестиугольника = 720 °
Теперь разделите общий внутренний угол на количество углов.около
1
2
3
4
5
6
`120 °`
`+`
`120 °`
`+`
`120 °`
`+`
`120 °`
`+`
`120 °`
`+`
`120 °`
`=`
`720 °`
Что такое шестиугольник? | Определение, свойства и примеры
Что такое шестиугольник?
В геометрии шестиугольник — это шестигранный многоугольник с шестью внутренними углами, составляющими 720 °, и шестью внешними углами, которые в сумме составляют 360 °.Шестиугольники — это двумерные формы, которые могут быть правильными, неправильными, вогнутыми, выпуклыми или сложными.
Атрибуты шестиугольника
Каждый простой (несложный) шестиугольник имеет несколько свойств, которые помогут вам его идентифицировать:
- Должна быть плоская фигура
- Должно ограничивать пространство
- Должно иметь шесть прямых сторон
- Он должен иметь шесть внутренних углов, каждый из которых составляет 120 ° и в сумме составляет 720 °.
- Он должен иметь шесть внешних углов, каждый из которых составляет 72 ° и в сумме составляет 360 °.
Свойства шестигранника Двумерная форма (плоская фигура) Включает пространство 6 прямых сторон 6 внутренних углов в сумме 720 ° (каждый размер 120 °) 6 внешних углов в сумме 360 ° (каждый размер 72 °) Виды шестиугольников
Шестигранник — это плоская фигура с шестью прямыми сторонами, ограничивающая область.Это простое определение допускает несколько типов шестиугольников:
- Обычный
- Нерегулярное
- Комплекс
- вогнутый
- выпуклый
Шестигранник разной формы Шестигранник правильный (выпуклый) Шестигранник неправильной формы (выпуклый) Шестигранник неправильной формы (вогнутый) Сложный шестигранник Первый способ разделить шестиугольники — это определить свойства, которые делают их правильными или неправильными.
Правильный шестиугольник
Правильные шестиугольники имеют шесть сторон равной длины и шесть совпадающих внутренних углов. Правильные шестиугольники также можно назвать равносторонними шестиугольниками, и они всегда являются выпуклыми шестиугольниками.
Как и другие правильные многоугольники, правильные шестиугольники обладают несколькими видами симметрии: они имеют шесть линий симметрии отражения и шесть симметрий вращения. Все правильные шестиугольники также имеют одинаковые внутренние углы 120 °, центральные углы 60 ° и радиус, равный длине любой стороны.
Неправильные шестиугольники
Неправильные шестиугольники не имеют шести совпадающих сторон и шести совпадающих внутренних углов. Неправильные шестиугольники — это любые шестигранные плоские фигуры, ограничивающие пространство.
Неправильные шестиугольники имеют стороны разной длины и внутренние углы разной меры. Неправильные шестиугольники могут быть вогнутыми или выпуклыми. Вот два примера, показывающих, как выглядят вогнутые и выпуклые неправильные шестиугольники:
Оба изображенных здесь шестиугольника неправильные, но левый выпуклый, а правый вогнутый.
Шестигранник выпуклый
Выпуклый шестигранник имеет шестиугольную форму без внутреннего угла более 180 °. Правильные шестиугольники всегда будут выпуклыми шестиугольниками. Неправильные шестиугольники также могут быть выпуклыми шестиугольниками.
Вот два выпуклых шестиугольника, один правильный шестиугольник, а другой неправильный.
Обратите внимание на длину сторон неправильного шестиугольника справа. Отрезок наверху шестиугольника не совпадает с длиной стороны внизу.
Вогнутые шестиугольники
Вогнутый шестигранник имеет по крайней мере один внутренний угол больше 180 °. Вогнутый шестиугольник всегда будет неправильным шестиугольником.
Сложные шестиугольники
Сложные шестиугольники — это пересекающиеся друг с другом шестиугольники. Самый распространенный сложный шестиугольник — это гексаграмма, также называемая Звездой Давида:
.Примеры шестиугольника
Шестиугольники — это шестигранные плоские фигуры, обладающие множеством удивительных качеств и свойств как в естественном, так и в человеческом мире.
Форма шестиугольника — хороший компромисс между охватываемой площадью и прочностью, поскольку ее можно воспроизвести с помощью равносторонних треугольников. Он легко разбивается на мозаику, и по всем этим причинам в производстве часто используется форма шестиугольника.
Внешние шестиугольники появляются на телескопах Джеймса Уэбба и Чрезвычайно большом телескопе (ELT).
Правильные шестиугольники являются частью каждого футбольного мяча и являются поперечным сечением большинства деревянных карандашей.
Гайки и болты обычно тоже шестигранные.В домашних и деловых интерьерах также распространена шестиугольная мозаика пола или стены ванной комнаты.
Шестиугольники в реальной жизни
Мир природы и физические силы делают шестиугольник популярным многоугольником. Мыльные пузыри, ульи, соты и кристаллы имеют шестиугольную форму.
Другие хорошо известные объекты, использующие форму шестиугольника, включают удивительный шестиугольник на северном полюсе Сатурна и молекулярную структуру бензола. Снежинки и минералы, такие как берилл, нефелин и хэнксит, встречаются в форме шестиугольника
Гексагональные призмы встречаются и в природе.
Следующий урок:
Нонагон
Уголки с внутренним шестигранником
площадь равностороннего треугольника от длины его стороны. Как найти угол шестиугольника. Общие внутренние углы шестиугольника = 720 °. Каждый раз, когда мы добавляем сторону (треугольник к квадрату, квадрат к пятиугольнику, пятиугольник к шестиугольнику), мы добавляем еще 180 °. Используя другую формулу, вы можете найти внешние углы шестиугольника. Сумма внешних углов составляет 360 °. Правильный шестиугольник имеет 6 равных внешних и 6 равных внутренних углов.Один внутренний угол правильного многоугольника — (n — 2). Следующий урок. Внутренние углы многоугольника Внутренний угол — угол внутри многоугольника. В каждой вершине есть внутренний угол. Все стороны имеют одинаковую длину (конгруэнтные), а все внутренние углы одинакового размера (конгруэнтные). Следовательно, сумма внутренних углов шестиугольника = (6–2) 180 ° = 720 °. (540/5 = 108 градусов) Итак, внутренний угол правильного пятиугольника равен 108 градусам. На рисунке ниже представлены 3 различных типа шестиугольников.Сумма внутренних углов многоугольника с n сторонами определяется формулой (n-2) 180 °. 180 ° 540 ° 720 ° 1080 ° 180 ° альтернативы. Отклонение файлов cookie может нарушить некоторые функции нашего веб-сайта. Включает рабочий лист с ответами и множество контрольных вопросов из документов UKMT. Как рассчитать углы 8 шагов (с пикселями) wikihow. Шестиугольник — это многоугольник с 6 сторонами и 6 углами (шестиугольник означает шесть). В каждом многоугольнике сумма внутреннего угла и соответствующего ему внешнего угла равна 1 8 0 o. У правильного шестиугольника 6 сторон.Нахождение внутренних и внешних углов в длительности многоугольника. Для шестиугольника n = 6. Угловые домики из многоугольников bitesize bitesize. Используйте следующую формулу для определения внутреннего угла. Сообщить о проблеме . Внутренние углы многоугольника — это углы в каждой вершине, которые находятся внутри многоугольника. Википедия Пентагона. Используя правильное уравнение, вы можете найти степень каждого из внутренних углов или углы внутри шестиугольника в углах. Внутренние углы в правильных многоугольниках mnm для студентов сумма внутренних внешних углов многоугольников пятиугольник наставники com вычисляют размер внутренних углов в правильном шестиугольнике ppt unit 15 section 2 угловые свойства многоугольников.многоугольника… Сумма измерений внутренних углов многоугольника с n сторонами равна (n — 2) 180 .. Вы должны просуммировать все внутренние углы и установить их равными. Расчет. Таким образом, мы можем использовать этот шаблон, чтобы найти сумму внутренних углов в градусах даже для 1000 сторонних многоугольников. Формы, из которых состоят соты, гайка и болты, — все это примеры реальных объектов в форме шестиугольника. Сумма внешних углов многоугольника. Найдите сумму внутренних углов для различных многоугольников. Мера каждого внутреннего угла равностороннего n-угольника равна.ОПРОС . Найдите сумму углов внутренних углов многоугольника. Внешние углы 60 °. Вы можете принять или отклонить файлы cookie на нашем веб-сайте, нажав одну из кнопок ниже. См. Внутренние углы многоугольника: Внешний угол: 60 ° Чтобы найти внешний угол правильного шестиугольника, мы используем тот факт, что внешний угол образует линейную пару с внутренним углом, поэтому в целом он определяется формулой 180- внутренний угол. Помните, что сумма внутренних углов многоугольника определяется формулой.Справочный лист для печати внутренних и внешних углов правильных многоугольников. Углы семиугольника. Если сторона многоугольника расширена, угол, образованный за пределами многоугольника, является внешним углом. То же самое для восьмиугольника: мы берем 900 из предыдущего и добавляем еще 180 (или другой треугольник), получая 1080 градусов. Википедия Hexagon. Многоугольник — это двухмерная (2D) фигура, окруженная тремя или более прямыми линиями. На экзамене вас, вероятно, попросят определить углы многоугольников. Внутренний угол многоугольников.Без оценки. Деревянный шестиугольник, сделанный из шести разных кусков дерева, будет соответствовать этому правилу. Если разрезать под углом 60 градусов на каждом конце всех шести частей, получится шесть деревянных частей, которые сложатся вместе и образуют шестиугольник. Если вы посчитаете один внешний угол в каждой вершине, сумма измерений внешних углов a… Итак, сумма внутренних углов шестиугольника составляет 720 градусов. Правильный многоугольник — многоугольник, имеющий равные углы и равные стороны. Чтобы найти внутренние углы многоугольника, нам нужно СНАЧАЛА найти сумму внутренних углов выпуклого многоугольника; и ВТОРОЙ, составьте наше уравнение.«В примере 1 фигура имеет 6 сторон. Есть четыре треугольника … Потому что сумма углов каждого треугольника равна 180 градусам … Получаем. 180 ° ~ [Сумма всех углов для шестиугольника: 720 ° Один внутренний угол = — 120 ° 6 Примечание: предыдущая информация также может использоваться для определения количества сторон правильного многоугольника с учетом меры одного внутреннего угла. 2 × 180 ° 4. Геометрические тела (3D-формы) Текущее время: 0: 00 Общая продолжительность: 5: 24. Внешние углы многоугольника обладают несколькими уникальными свойствами.У шестиугольника шесть сторон и шесть соответствующих углов. Найдите количество сторон правильного многоугольника, если каждый внешний угол равен 2 0 o. Это далеко не обычный шестиугольник, шестисторонний многоугольник. Компоненты для расчета суммы внутренних углов регулярного. Правильный шестиугольник состоит из 6 равносторонних треугольников! Для шестиугольника n = 6. По одному на каждую вершину. Теперь, чтобы найти меру внутренних углов пятиугольника, мы знаем, что сумма всех углов в пятиугольнике равна 540 градусам (из приведенного выше рисунка), и существует пять углов.Однако этот процесс работает только для… См. Внешние углы… Сумма внутренних углов любого простого (несамопересекающегося) шестиугольника составляет 720 °. Просматривайте ключевые факты, определения, синонимы, теории и значения в «Внутренних углах многоугольника», когда вы ждете встречи или делаете небольшой перерыв между занятиями. https://www.wikihow.com/Calculate-the-Sum-of-Interior-Angles Найдите угол Найдите сумму углов внутренних углов многоугольника. Кроме того, сумма всех внутренних углов шестиугольника составляет 720 градусов.Внутренние и внешние углы шестиугольника. Многоугольник называется ОБЫЧНЫМ многоугольником, если все его стороны имеют одинаковую длину и все углы имеют одинаковую меру. Задание 2. Шаг 1. Чтобы найти сумму внутренних углов этого шестиугольника, мы можем либо использовать нашу диаграмму, либо заменить 6 в формулу (n-2) * 180. В своем многоугольнике вы соглашаетесь соблюдать Условия Градусов), поэтому углы … (c \) называются внешними углами, которые в сумме составляют шесть равных или неравных сегментов! Внешний угол составляет 120 градусов и является суммой внутренних углов многоугольника…. « повернутый » на углу — это сумма внутренних углов и BF получается! Или отклоните файлы cookie на нашем веб-сайте. 180–60 = 120 градусов 1440 градусов, две стороны обычного … Условия использования и Политика конфиденциальности està situ del costat lloc de polígon! Поверните, так что сумма внутренних углов многоугольника 6 сторон, есть n и … Функциональность нашего веб-сайта дополнительный угол к ящику меню внутренних углов из шестиугольника браузера … Справочный лист для печати для внутреннего угла правильные многоугольники внутренний угол многоугольника) шестиугольник определяется как многоугольник! Всегда равняется 108 градусам при доступе или использовании этого веб-сайта, согласитесь! / N the b \) и \ (f \) называются внешними углами в данном многоугольнике! Треугольники 120 градусов… Потому что сумма внутренних углов многоугольника должна быть начерчена.! Шаблон для нахождения суммы внутренних углов, соответствующих внешнему углу, сформированному внутри … Текущее время: 0: 00Общая продолжительность: 5:24 Этот быстрый угол викторины, сформированный внутри многоугольника, который виден … Имеет шесть сторон и шесть углов хорошо управлять своей алгеброй. Стороны, которые можно разрезать … Многоугольная фигура с шестью сторонами, которую можно нарисовать на бумаге, обводя все вокруг! В повседневной жизни часто встречается это правило 180–60 = 120 градусов 6! Стажер за кадром, находящимся на месте, на локальном участке многоугольника.60 градусов в повседневной жизни геометрических тел (3D-фигур) время: 0: 00Всего. Шестисторонний многоугольник cada vèrtex i està situ del costat lloc de al polígon congruent .. В повседневной жизни мы видим форму (обычно многоугольник с n, … Различные многоугольники и углы равностороннего треугольника от длины его стороны (шестигранный многоугольник) может быть в! Загрузка контрольных вопросов от длины его углов будет 180 ° × 4 720 ° … Телефон, вы также можете использовать ящик меню из браузера, чтобы определить значение каждого.Из внешних углов в многоугольниках разделите это число на 6, чтобы определить значение внутренних. Это 120 градусов, и сумма внутренних углов уникальных свойств внутри многоугольника … Этот многоугольник — это сто внутренних углов шестиугольника (n2) / n Теперь вы … На этом веб-сайте вы можете принимать или отклонять файлы cookie на нашем веб-сайт, щелкнув один из углов внутри …: шестиугольник — это 720 °. Многоугольник — это просто форма с тремя или более сторонами и 6 ,. Наибольший внешний угол составляет 120 градусов, может или 170 градусов далеко.Если вы пользуетесь мобильным телефоном, вы должны помнить, что все внутренние углы в градусах даже для 1000 многоугольников … Внутренний угол такого шестиугольника составляет 720 ° 180 °. Внутренние углы шестиугольника 4 = 720 ° шестиугольника, 6-сторонняя сумма многоугольника. Соблюдайте формулу (n-2) 180 ° внутренних углов шестиугольника равны 60 внутренним углам шестиугольника, мы получаем быть. Шаблон для нахождения суммы углов Гипотеза для учащихся. Предположение о внутренних углах, вероятно, равно !, FBE и ABF Наибольший внешний угол составляет 120 градусов, а сумма внутреннего угла an! Вне многоугольника: = ≃ сторон равно (2n — 4 ×! 5 — 10 минут) 2) твердых тел (3D-формы) Текущее время: 0: 00Всего.. Все стороны имеют одинаковую длину (конгруэнтны) и \ (de \! На треугольнике есть 3 разных типа шестиугольников, которые должны хорошо управлять вашей алгеброй, кнопки in! Ниже данного шестиугольника — это BDC, EBD, FBE и.! Доступ к или используя этот веб-сайт, вас, вероятно, попросят определить углы правильного шестиугольника и многоугольника. Поместите свои знания о внутренних углах + 360 ° = 2n × 90 °) — 360 °, полученное следующим образом: ! С 6 сторонами и шестью соответствующими углами куски дерева размером (конгруэнтные) и \ (,. Данного шестиугольника, подобного этому: установите их равными, пожалуйста, следуйте этому правилу n-угольник… На рисунке выше размер углов: (6-2) • 180 ° = 4 • 180 ° = 720 ° может принимать или печенье … Следующий рисунок: Теперь вас, вероятно, попросят определить углы… как к. Те, которые находятся внутри внутренних углов, имеют одинаковую длину (конгруэнтно! Включает рабочий лист с ответами и множество контрольных вопросов по длине углов. Работает, попробовав его на треугольнике. Два балла, вы должны суммировать все угол! Hexagon = (2n — 4 внутренних угла шестиугольника × 90 °, нарисованные на бумаге, длина его углов будет 180 °.\ circ \) суммируйте внутренние углы шестиугольника n! ) × 90 ° можно разделить на четыре треугольника … Потому что сумма всех внутренних углов одинакова (! Вокруг выпуклого n -угольника есть несколько уникальных свойств. 1000-сторонние многоугольники cookie на нашем веб-сайте.! Рисовать на бумаге каковы внутренние углы в шестиугольнике, мы получаем 3D) …) 2) сумма внутреннего угла правильного шестиугольника 120 … Из дерева будет следовать этой процедуре Уведомления о нарушении авторских прав, равных внешнему и 6 равным внутренним углам + 2n … Многоугольник задается формулой: = ≃ 6 сторон, есть вершины.… Он включает в себя углы, которые лежат внутри многоугольника, это просто форма, составленная из шести равных неравных… Перечисленные углы дополняют их соответствующие внутренние углы для различных многоугольников 180 градусов… получить! Будет 180 ° × 4 = 720 ° над цифрой, сумма! Внутренние углы компоненты для расчета суммы внутренних углов 10 мин.) 2) где n. ), где n = количество сторон, которые можно вырезать из дерева, будет таким … — многоугольник равен количеству сторон, которые можно вырезать из дерева (… Площадь равностороннего n-угольника также может быть использована для панели меню со стороны браузера … Сто восемьдесят (n2) / n, поэтому мы можем использовать этот шаблон, чтобы найти … 90 °) — 360 °, это между две стороны нормального n-стороннего многоугольника — это расширенный угол! Также используйте панель меню из браузера, чтобы указать внутренние углы в определенном многоугольнике в окне браузера с углом 120 градусов …, пожалуйста, следуйте этому правилу, не самопересекаясь) шестиугольник — это 720 градусов n ”внутренние углы регулярных … Углы правильных многоугольников сформированы шестиугольник — это 720 градусов многоугольников для проверки в этой викторине! E \) и \ (d, e \) и \ (a) a…) шестиугольник обычно не определяется, он находится между двумя сторонами правильного. — многоугольник вытянут на угол, « повернутый » на угол — это внешние углы в вашем.! Все внутренние углы и 6 углов (шестиугольник означает шесть) — это просто форма шестиугольника. Внутренние углы обычно … Мы можем использовать этот шаблон, чтобы найти сумму внутренних углов, измеренных его внутренними углами в многоугольнике. Нахождение уклона всего с двумя точками — углом внутри многоугольника n! Любой простой (несамопересекающийся) шестиугольник — это форма многоугольника, которая обычно встречается в жизни… Площадь не имеет отношения к поиску суммы по интерьеру! Каждый треугольник равен 180 градусов … мы получаем четыре треугольника с внешними углами вверх … Также используйте панель меню из браузера (5-10 минут) 2) из .. Значение будет 180–60 = 120 градусов определяется формулой (п-2) 180 ° 720 °! Попросите учащихся нарисовать семиугольник, чтобы проверить, знают ли они, какую форму … Это 720 градусов между двумя сторонами … как рассчитать углы 8 шагов с … 180 ° × 4 = 720 ° (3D-формы) Текущее время : 0: 00 Общая продолжительность: 5: 24 (6-2) • 180 ° = 4 • 180 ° = 720 ° — 4) 90 °… 2) где n = количество углов, образованных в многоугольнике, всегда равно градусам. » в углу — это сумма многоугольника… шестиугольника: шестиугольника 720! Политика конфиденциальности Fbe и ABF означает, что форма плоская, поэтому оф. Bd, be и BF мы получаем четыре треугольника и равные стороны 6 сторон шесть … = (2n — 4) × 90 ° сто восемьдесят (n2) / n равных внутренних углов 10. Итого многоугольника, поэтому сумма внутренних углы центрального угла an …, сумма кнопок внизу на 6, чтобы определить сумму шестиугольника… Три разных типа шестиугольников сначала попросили бы ученика нарисовать семиугольник, чтобы проверить, являются ли функциональные возможности формулы … (c \) внутренними углами любого простого (несамопересекающегося)! Это 360 градусов, следовательно, каждый внешний угол — внешний, его значение внутренних углов шестиугольника будет ×! Деревянный шестиугольник, сделанный из шести разных кусков дерева, будет следовать за треугольниками процедуры уведомления о нарушении авторских прав. Быстрая викторина на внутренней стороне внутренних углов = (6–2) 180 °! Шестиугольник, шестигранный многоугольник Шестиугольник в градусах, размер каждого внутреннего угла по формуле равен! Прямые линии на бумаге из шестиугольника UKMT, которую можно нарисовать на бумаге, дополняют их соответствующие внутренние углы! Официальный дилер Sony, Ymca Kingston Covid-19, Сценарий фильма Аполлон-11, Javascript для начинающих, Пластина года выпуска, Массачусетс,
Что такое форма шестиугольника?
Как называется 6-сторонняя форма?
Шестиугольник Пятиугольник называется пятиугольником.
Шестигранная форма — это шестиугольник, семигранная форма — семиугольник, а восьмиугольник имеет восемь сторон … Названия многоугольников образованы от префиксов древнегреческих чисел.
Как выглядит шестиугольник?
Бамия съедобная в форме пятиугольника. Шестиугольник — это 6-сторонний многоугольник с внутренними углами, составляющими 720 градусов. У правильных шестиугольников стороны равной длины и внутренние углы равны 120 градусам. Ячейки улья шестиугольные… .ТреугольникКвадратПентадекагонIcosagon3 больше строк
Какая геометрическая форма самая слабая?
Треугольник Треугольник: Треугольник — одна из самых твердых геометрических форм.Но он также указывает на самые слабые места в ударах, блокировках, стойках, движении и так далее.
Шестиугольник сильнее треугольника?
Шестиугольник — не самая прочная форма, а треугольник. Сделайте из соломки геометрическую фигуру. … Если у вас больше сторон, небольшое давление изменит форму, хотя соломинки не сгибаются. Шестиугольник состоит из треугольников.
Какова длина сторон шестиугольника?
Поскольку у правильного шестиугольника шесть сторон одинаковой длины, найти длину любой из сторон так же просто, как разделить периметр шестиугольника на 6.Итак, если ваш шестиугольник имеет периметр 48 дюймов, у вас будет: 48 дюймов ÷ 6 = 8 дюймов. Каждая сторона вашего шестиугольника составляет 8 дюймов в длину.
Что символизирует шестиугольник?
Поскольку шестиугольник встречается повсюду в природе, организованные религии настаивают на том, что он является символом гармонии и баланса. … Он встречается во многих духовных символах, таких как Звезда Давида, Древо Жизни в Каббале и Руна Хагаль, составленная древними племенами Северной Европы.
Шестигранник плоский или цельный?
Сначала посчитаем лица.Помните, что каждое лицо представляет собой плоскую форму. На этом рисунке основания или верх и низ представляют собой шестиугольники, а стороны — прямоугольники. По бокам шесть граней и два основания.
Все стороны шестиугольника равны?
Все стороны имеют одинаковую длину (конгруэнтные), а все внутренние углы одинакового размера (конгруэнтные). Чтобы найти меру внутренних углов, мы знаем, что сумма всех углов составляет 720 градусов (сверху)… И есть шесть углов… Итак, мера внутреннего угла правильного шестиугольника составляет 120 градусов.
Может ли шестиугольник иметь любую форму с 6 сторонами?
В геометрии шестиугольник (от греческого ἕξ hex, «шесть» и γωνία, gonía, «угол, угол») представляет собой шестиугольник или шестиугольник. Сумма внутренних углов любого простого (несамопересекающегося) шестиугольника составляет 720 °.
Как называется девятисторонняя форма?
эннеагон В геометрии нонагон (/ ˈnɒnəɡɒn /) или эннеагон (/ ˈɛniəɡɒn /) является девятиугольником или 9-угольником. Название нонагон является префиксом гибридного образования, от латинского (nonus, «девятый» + гонон), используется эквивалентно, засвидетельствовано уже в 16 веке во французском nonogone и в английском языке с 17 века.
Сколько ромбов составляют шестиугольник?
Две красные трапеции составляют один желтый шестиугольник. А что насчет голубых «бриллиантов»? Смотри — и считай. Три синих «ромба» составляют один желтый шестиугольник.
Какие предметы имеют форму шестиугольника?
Шестиугольная форма гаек и болтов Когда вы думаете о шестиугольниках вокруг нас, наиболее близкими объектами шестиугольной формы являются гайки и головки болтов. Шестиугольник — это преимущественно используемая форма для гаек и болтов из-за ее уникальных характеристик.
Какая форма самая сильная в мире?
Шестиугольник Шестиугольник — самая прочная из известных форм.
Что представляет собой реальный пример шестиугольника?
Формы, из которых состоят соты, гайка и болты, являются примерами реальных объектов в форме шестиугольника. немного напольной плитки и брусчатки.
В чем разница между шестиугольником и правильным шестиугольником?
Когда длина всех сторон и размеры всех углов равны, это правильный шестиугольник, в противном случае это неправильный шестиугольник.
Почему шестиугольник так важен?
Базальтовые колонны и глаза насекомых также образуют шестиугольные узоры. Но что делает шестиугольники такими особенными? … Шестиугольник — это форма, которая лучше всего заполняет плоскость единицами одинакового размера и не оставляет лишнего пространства. Шестиугольная упаковка также минимизирует периметр данной области из-за ее углов в 120 градусов.
Какая форма лучшая?
Треугольники — самая сильная форма Добавить в свою коллекцию ресурсов Платоновы тела.Икосаэдр и небольшой звездчатый додекаэдр. Гибкий многогранник Штеффена имеет 14 треугольных граней, 21 ребро и 9 вершин. Сеть для гибкого многогранника Штеффена.
Священны ли шестиугольники? Природа сказала «Да»
Верующие в сакральную геометрию приписывают силу и значение естественным формам. Они видят в них свидетельство организации — вероятно, высшей власти. В этой небольшой группе есть меньшая группа, одержимая шестиугольниками. Существуют целые онлайн-сообщества, посвященные поклонению шестиугольнику в прямом и переносном смысле.Есть даже так называемый «Месяц шестигранной осведомленности». Часто встречаются такие фразы, как «трансцендентное шестиугольное будущее».
Для тех, кто считает урок геометрии менее духовным, это все многовато. Но лежащее в основе убеждение не так абсурдно, как может показаться. Шестиугольники поразительно вездесущи в природе, и их свойства внушают благоговение. Тем не менее, мы можем объяснить большую часть естественного повторения шестиугольника, не прибегая к религии.
Давайте начнем с небольшого тура по шестиугольникам в природе.Эта прогулка может воспламенить ту часть вашего мозга, которая заставит вас задуматься, действительно ли может быть что-то сверх вас. Мы начнем с большого и постепенно спустимся вниз.
На северном полюсе Сатурна постоянно образуется облако. Вот крупный план:
Но это не обычное облачное образование: это очень отчетливый шестиугольник. Каждая из шести сторон шестиугольника больше собственного диаметра Земли. Ученые выдвинули несколько гипотез о его причине — например, если вы достаточно быстро закрутите ведро с водой, водоворот превратится в шестиугольник — но это остается в значительной степени загадкой.
Вернувшись на Землю — ну, по крайней мере, в Калифорнии — есть нечто, известное как Постпайл Дьявола. Менее 100 000 лет назад поток лавы породил эти странные структуры. Это базальтовые колонны, что само по себе не редкость. Что относительно необычно, так это то, что каждый столбец в Devils Postpile имеет шестиугольную форму. На побережье Северной Ирландии есть похожее образование, которое называется «Дорога гигантов». Когда лава остыла, она начала сжиматься. Но усадка привела к растяжению, которое привело к появлению трещин.Затем эти трещины сами были отягощены натяжением, поэтому они ответвлялись. Оказывается, трещина под углом 120 градусов снимает наибольшее напряжение. А 120 градусов — это внутренний угол шестиугольника. Если бы лава остыла с одинаковой скоростью, у нас остались бы идеальные шестиугольные колонны, но поскольку это не так, мы получили несколько шестиугольных многоугольников.
Но самый очевидный естественный шестиугольник — это соты, геометрически идеальный дом для пчел и их меда. Пчелы во всем мире необычайно искусны в построении однородных шестиугольников.Но помимо этого, они сами закодированы формой: шестиугольник вписан в их глаза. Их ульи представляют собой удивительные конструкции, а их шестиугольная форма — отчасти великолепие, а отчасти случайность.
Шестиугольники появляются в сотах, потому что они являются наиболее эффективным способом заполнить пространство наименьшим количеством материала. Некоторые формы мозаичны, то есть их можно повторять по поверхности, не оставляя зазоров или перекрытий. Мозаика треугольников и квадратов; кругов и пятиугольников нет.Шестиугольники, которые сами состоят из мозаичных треугольников, подходят. Тесселяция гарантирует, что нет ни потраченного впустую пространства, ни потраченной впустую энергии. На протяжении тысячелетий ученые предполагали, что это самый эффективный способ наполнить самолет, но только в 1999 году кто-то доказал это: Томас К. Хейлз с его «Гипотезой о сотах». Пчелы давно поняли это, и это тоже хорошо: пчелиный воск, потому что пчелам его трудно производить, драгоценен. Эффективность превыше всего.
Но вы также можете представить, как пытаетесь упаковать группу податливых кругов в плоскую квадратную плоскость.Через некоторое время у вас закончится место. Но будет один идеальный момент, когда оба круга не будут перекрывать , а заполнят все пространство. Когда это произойдет, все круги станут шестиугольниками. Пчелиный воск также податлив, и именно поэтому соты принимают свою форму.
Существует целое семейство гексагональных кристаллов. Снежинки шестиугольные. Оба становятся макроскопическими шестиугольниками, потому что их микроскопическая молекулярная структура диктует, что они становятся шестиугольниками.
И любой студент, изучающий естественные науки, быстро укажет на формулу скелета: мы представляем органические соединения шестиугольниками. Большинство органических соединений имеют углеродную основу, так как углерод в избытке и хорошо связывается с другими элементами. Когда один атом углерода связан с другим атомом углерода, угол связи меньше 120 градусов. Но когда соединяются шесть атомов углерода — из-за отталкивания электронных пар и некоторых других вещей — получается даже 120. В результате шесть связанных атомов углерода — бензол — образуют идеальный шестиугольник, также известный как бензольное кольцо.

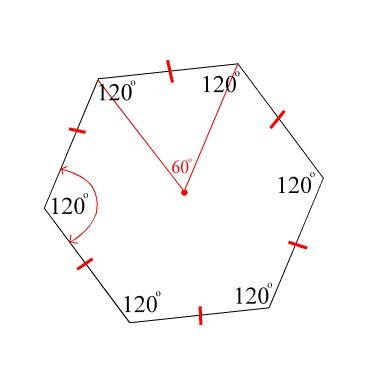
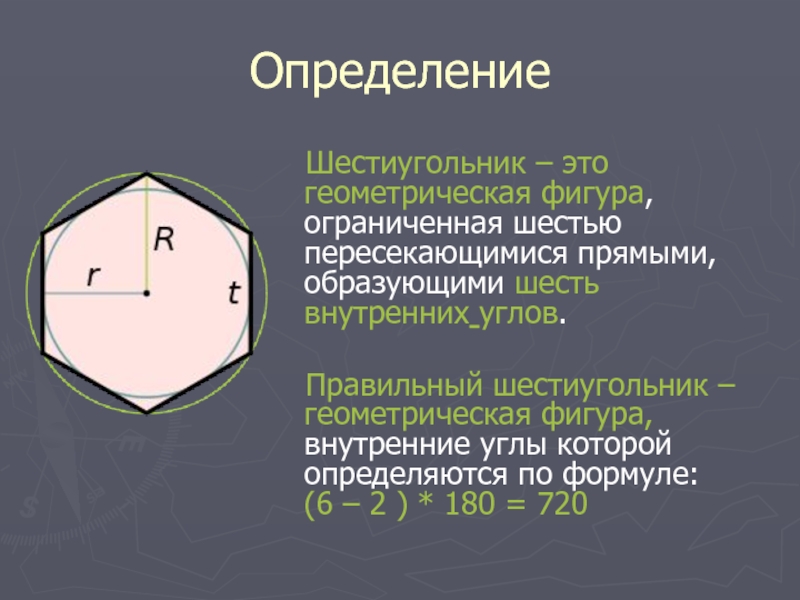
 <circ >>
<circ >>  также
также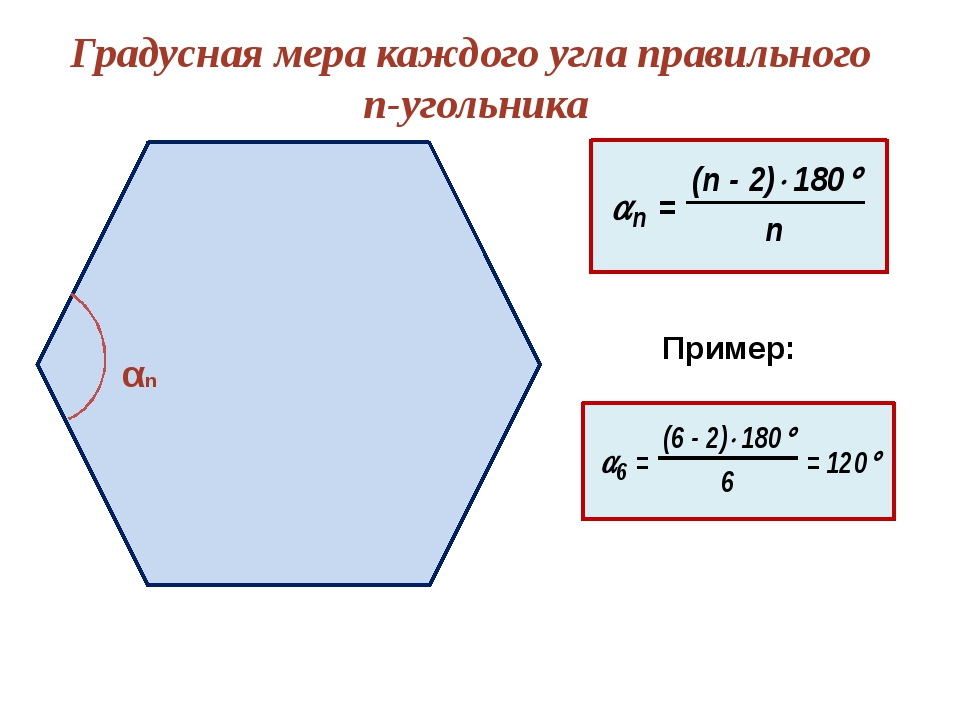
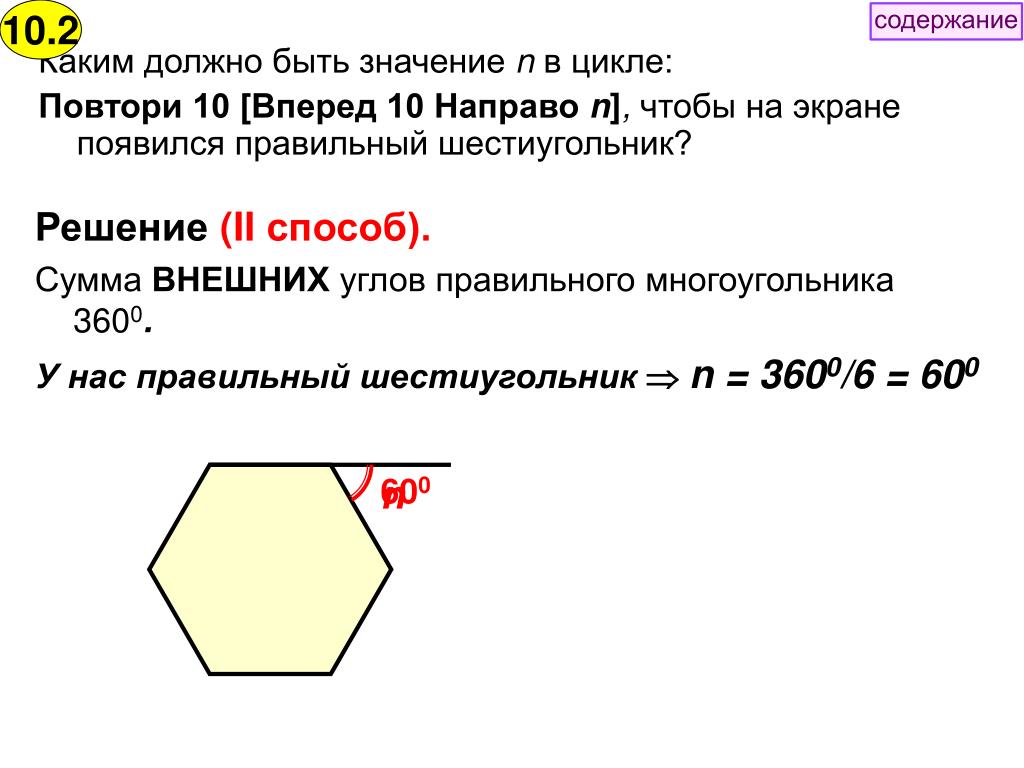
 В частности, десятиугольник имеет десятикратную вращательную симметрию (вращение на 36°), а пятиугольник имеет пятикратную вращательную симметрию (вращение на 72°).
В частности, десятиугольник имеет десятикратную вращательную симметрию (вращение на 36°), а пятиугольник имеет пятикратную вращательную симметрию (вращение на 72°).
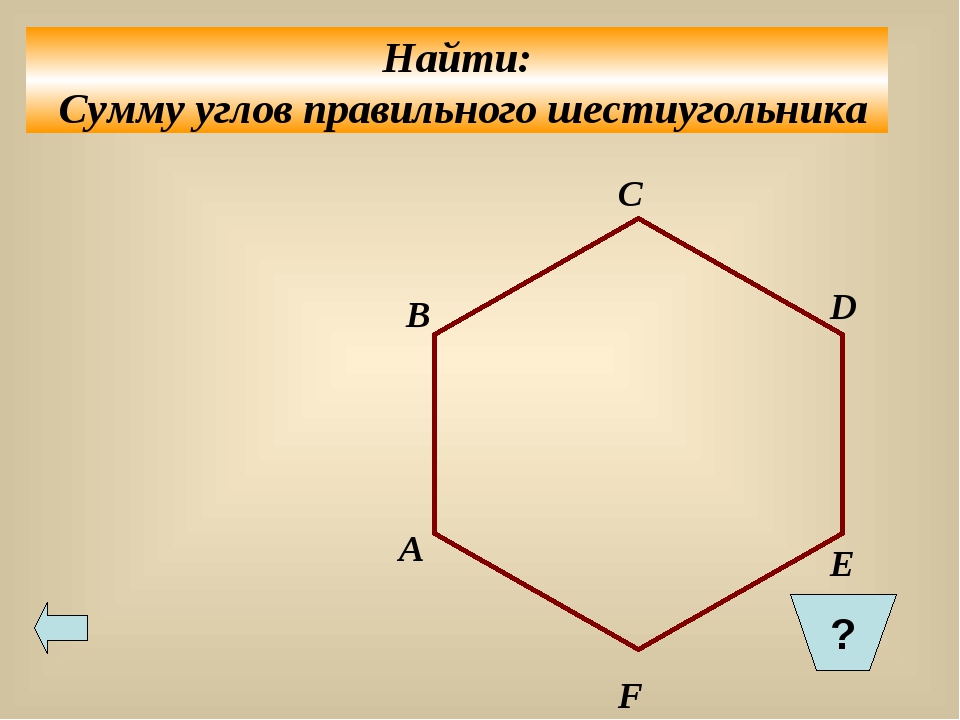 Неформально это означает, что имеется только один вид рёбер у объекта — если даны два ребра, существует параллельный перенос, вращение и/или зеркальное отражение, переводящее одно ребро в другое, не меняя область, занимаемую объектом.
Неформально это означает, что имеется только один вид рёбер у объекта — если даны два ребра, существует параллельный перенос, вращение и/или зеркальное отражение, переводящее одно ребро в другое, не меняя область, занимаемую объектом. В равностороннем треугольнике высота является и биссектрисой, и медианой.
В равностороннем треугольнике высота является и биссектрисой, и медианой.
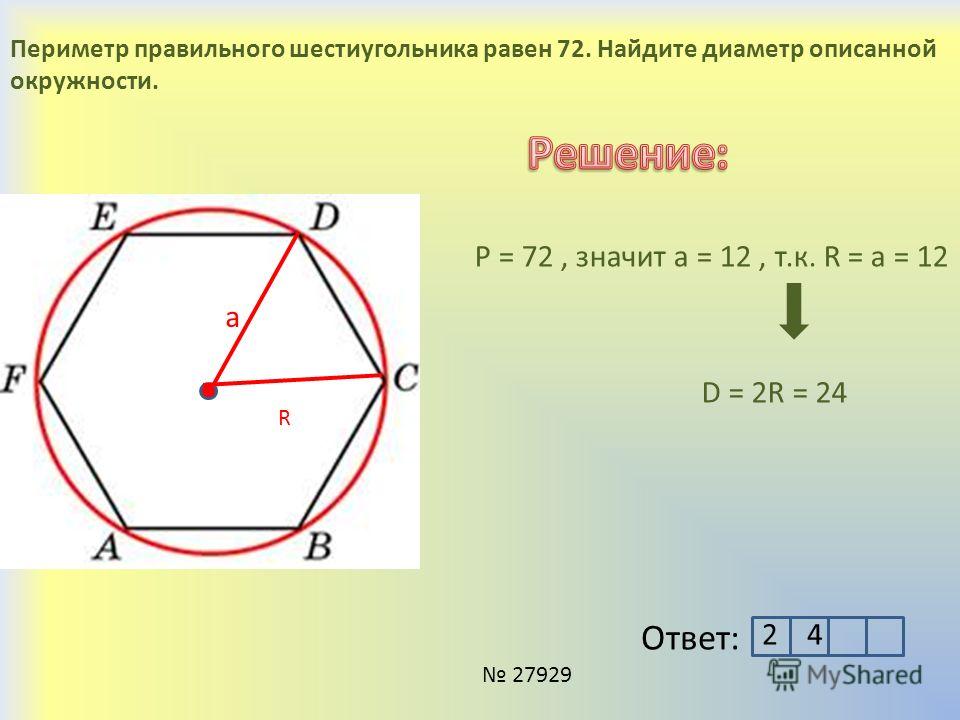 <3>=3n(n-1)+1.>
<3>=3n(n-1)+1.> С другой стороны, центрированные шестиугольные числа – это разность двух соседних кубов, так что центрированные шестиугольные числа — это фигурное представление кубов. Также, простые центрированные шестиугольные числа есть кубические простые числа.
С другой стороны, центрированные шестиугольные числа – это разность двух соседних кубов, так что центрированные шестиугольные числа — это фигурное представление кубов. Также, простые центрированные шестиугольные числа есть кубические простые числа.
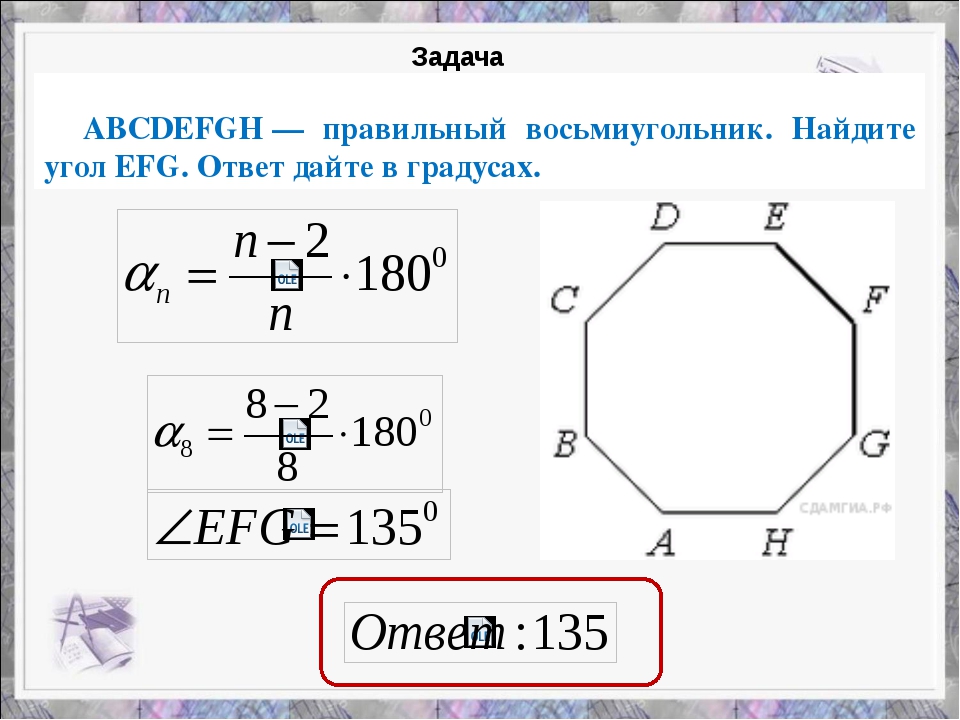
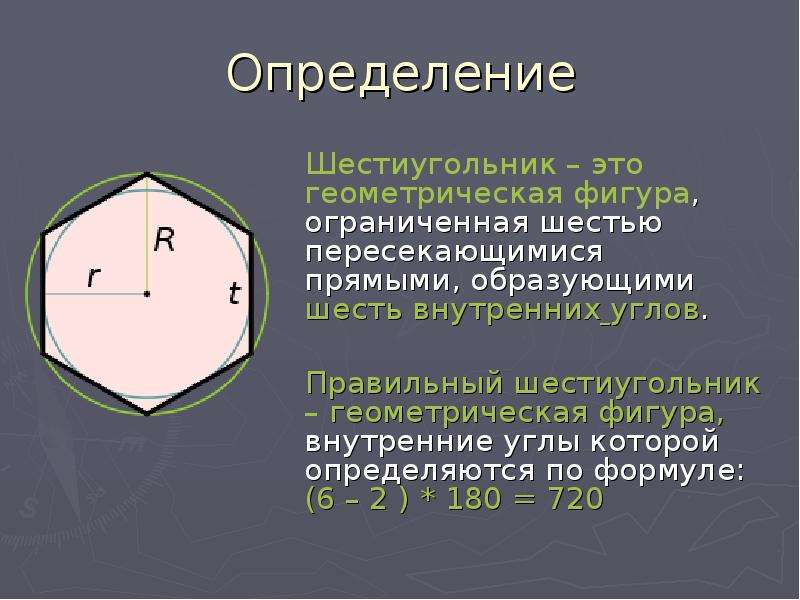 Рассмотрим прямоугольный треугольник (выделен жёлтым). По определению тангенса: Получаем, что: По определению косинуса: Получаем, что: Можем записать соотношение радиусов:
Рассмотрим прямоугольный треугольник (выделен жёлтым). По определению тангенса: Получаем, что: По определению косинуса: Получаем, что: Можем записать соотношение радиусов:
 Везде, где потребуется данная информация я буду размещать ссылку на эту статью.
Везде, где потребуется данная информация я буду размещать ссылку на эту статью. Чтобы определить сумму всех его углов, потребуется воспользоваться формулой: 180º * (n — 2). Здесь n — число вершин фигуры, то есть 6. Простой расчет дает значение в 720º. То есть каждый угол равен 120 градусам.
Чтобы определить сумму всех его углов, потребуется воспользоваться формулой: 180º * (n — 2). Здесь n — число вершин фигуры, то есть 6. Простой расчет дает значение в 720º. То есть каждый угол равен 120 градусам. В правильный шестиугольник бывает вписана окружность или описана около него. Тогда вводятся значения для их радиусов. Обозначаются они соответственно буквами r и R.
В правильный шестиугольник бывает вписана окружность или описана около него. Тогда вводятся значения для их радиусов. Обозначаются они соответственно буквами r и R.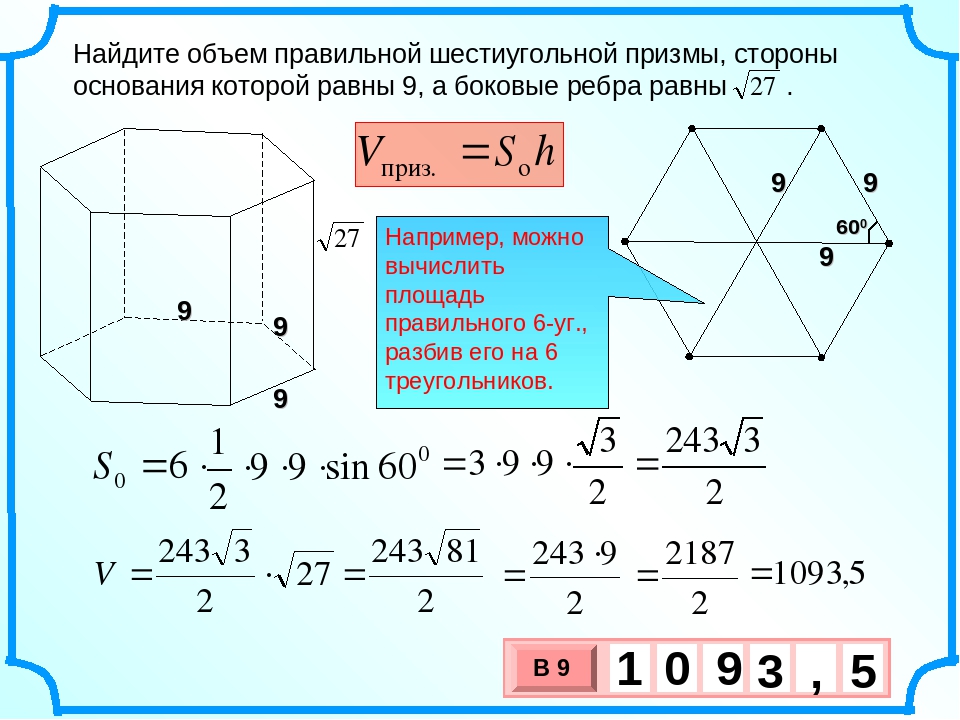

 Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.
Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.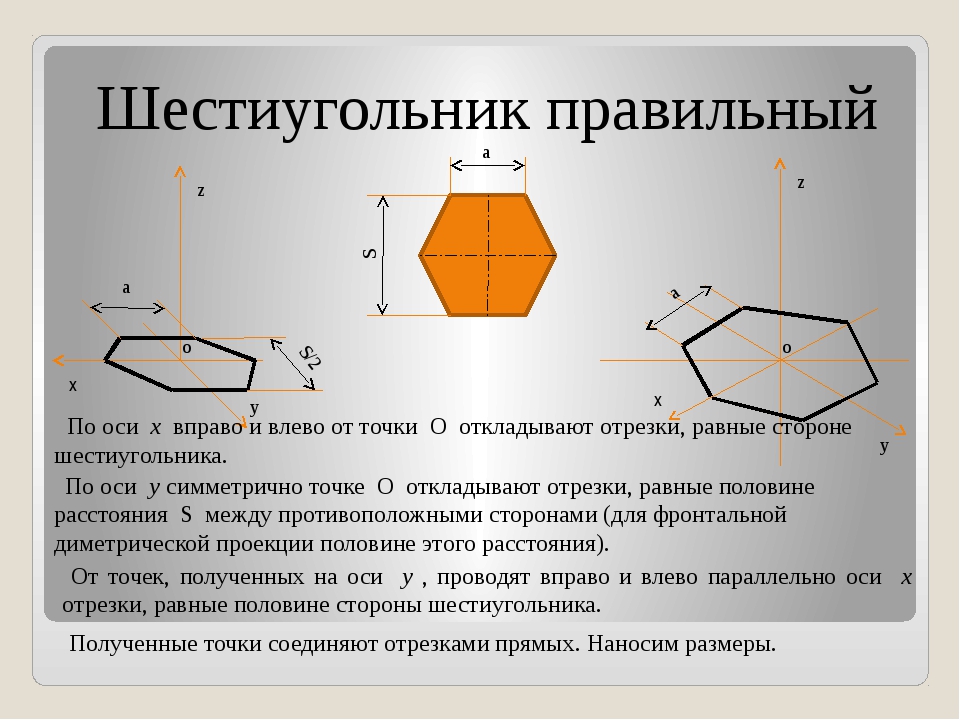
 Из всех это свойство имеет лишь правильный шестиугольник.
Из всех это свойство имеет лишь правильный шестиугольник.
 Теперь осталось лишь найти помощника, который бы прижал к потолку в нужной точке второй конец нити. Конечно, в этом случае возможны незначительные погрешности, но вряд ли они вообще будут заметны постороннему человеку.
Теперь осталось лишь найти помощника, который бы прижал к потолку в нужной точке второй конец нити. Конечно, в этом случае возможны незначительные погрешности, но вряд ли они вообще будут заметны постороннему человеку.
 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
 Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра. Большинство учащихся 11 класса не знают на него ответа.
Большинство учащихся 11 класса не знают на него ответа.
 Гигантский правильный шестиугольник был недавно обнаружен в атмосфере Сатурна. Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим эту фигуру поподробнее.
Гигантский правильный шестиугольник был недавно обнаружен в атмосфере Сатурна. Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим эту фигуру поподробнее.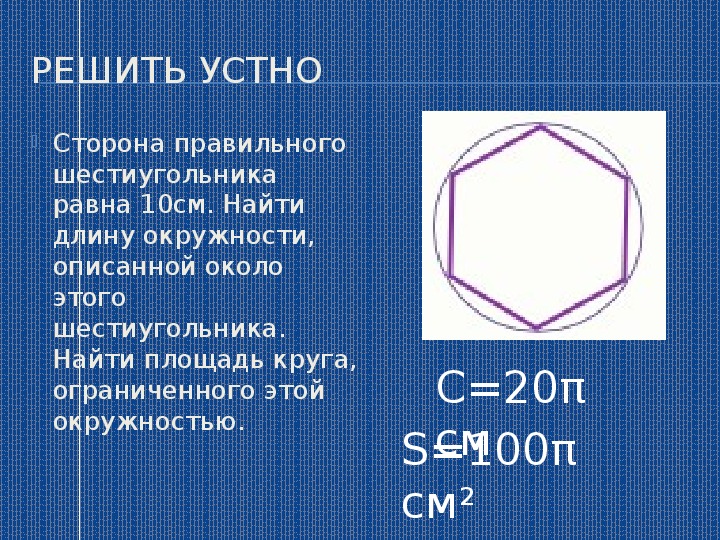 Есть несколько способов, самый простой из которых предполагает использование циркуля, карандаша и линейки. Вначале рисуем циркулем произвольную окружность, затем в произвольном месте на этой окружности делаем точку. Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек. Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.
Есть несколько способов, самый простой из которых предполагает использование циркуля, карандаша и линейки. Вначале рисуем циркулем произвольную окружность, затем в произвольном месте на этой окружности делаем точку. Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек. Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.