Периметр пятиугольника: онлайн калькулятор, формулы, примеры решений
Пятиугольник — это многоугольник с пятью углами. Если углы и стороны такого многоугольника равны, то он считается правильным и называется пентагон. Это оригинальная фигура, которую большинство людей встречает только в учебнике по геометрии.
Геометрия пятиугольника
Пятиугольник — геометрическая фигура, ограниченная пятью отрезками. Произвольный пятиугольник может иметь разные стороны, разные углы и строиться с самопересечениями, однако такая форма многоугольника крайне редко встречается в реальности. Самой распространенной формой пятиугольника считается пентагон — выпуклый многоугольник с равными сторонами и углами. Геометрическая фигура считается выпуклой, если все точки фигуры лежат с одной стороны от любой прямой, проведенной через две соседние вершины.
В отличие от треугольника, изучение которого не прерывалось на протяжении веков, все тайны пятиугольника были открыты еще в Древней Греции.
В третьем веке до нашей эры Евклид описал метод построения пентагона с помощью линейки и циркуля. Пифагор изучал диагонали пентагона, которые образуют отдельную фигуру — пентаграмму, идеальную по мнению античного ученого, так как отношение сторон пентаграммы и пентагона демонстрирует золотое сечение.
Пятиугольник в реальности
В человеческой повседневности пятиугольник встречается редко, так как пентагоном невозможно замостить плоскость без пробелов, а пентагональные призмы неудобно хранить. Форма пентагона используется обычно в архитектуре, и наиболее известным объектом, имеющим форму правильного пятиугольника, является здание министерства обороны США.
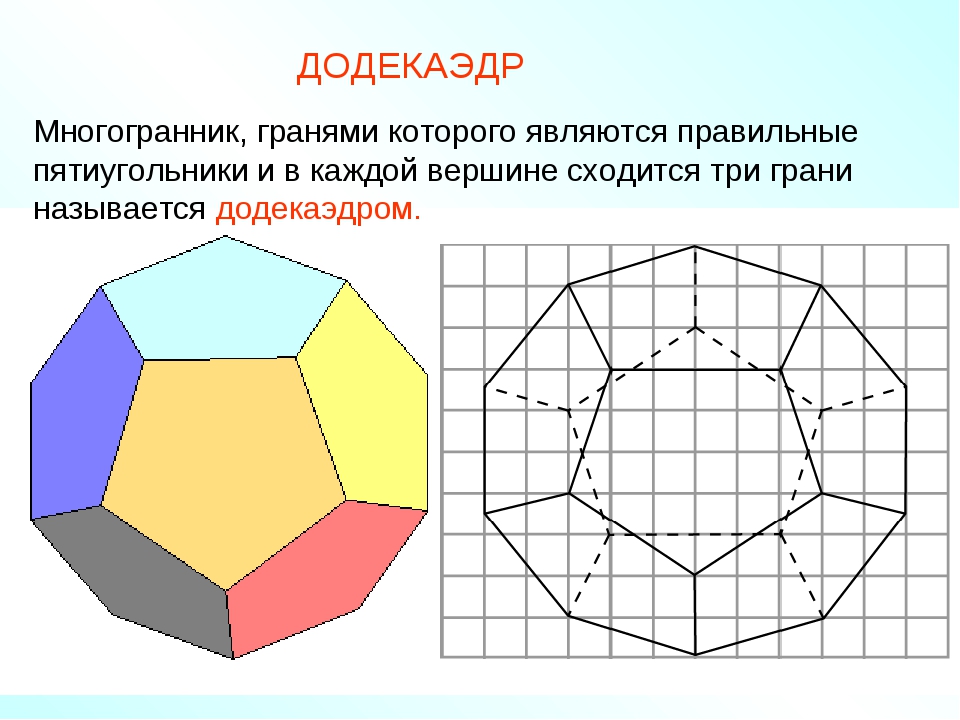
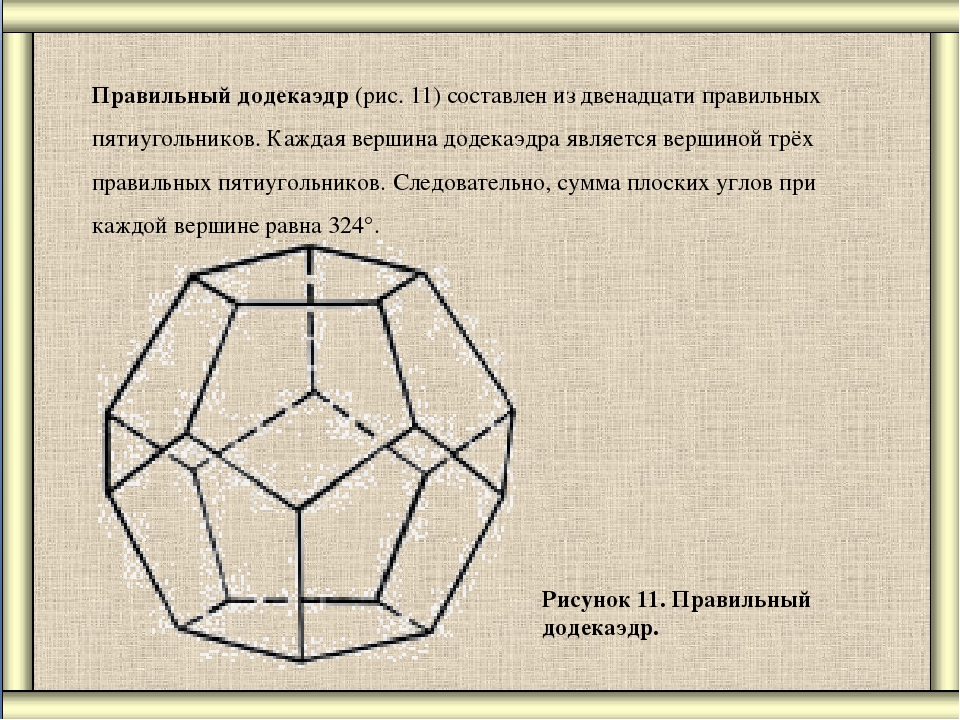
Додекаэдр – трехмерное воплощение пятиугольника, является правильным многогранником, каждая сторона которого — пентагон. В древности были распространены римские додекаэдры — бронзовые объекты, составленные из 12 пятиугольников, однако истинное назначение предметов до сих пор не выяснено. Сегодня наиболее очевидным реальным додекаэдром является игральная кость, которая выступает в качестве генератора случайных чисел для настольных ролевых игр.
В природе форма пятиугольника не встречается, однако некоторые организмы, например иглокожие, обладают пентасимметрией. Кроме того, в природе не существует кристаллов, грани которых были бы пятиугольными.
Периметр пентагона
Периметр любой геометрической фигуры — это сумма длин всех сторон. Пентагон имеет пять равных сторон, поэтому его периметр находится по простой формуле:
P = 5 a,
где a – длина одной стороны.
Сторона пятиугольника и радиусы вписанной r и описанной R окружностей приблизительно соотносятся как:
- a = 1,1756 R
- a = 1,4131 r
Таким образом, алгоритм нашего калькулятора позволяет рассчитать периметр пентагона, зная только один из трех параметров на выбор:
- сторона;
- радиус описанной окружности;
- радиус вписанной окружности.
Рассмотрим пару примеров на определение периметра правильного пятиугольника.
Примеры из жизни
Пентагон
Пентагон — всемирно известное здание, в котором располагается штаб министерства обороны США.
Объект получил название благодаря своей форме, так как здание геометрически является правильным пятиугольником. Давайте посчитаем периметр Пентагона. Согласно данным из Википедии, каждая сторона здания равна 281,05 м. Зная сторону, мы можем легко вычислить периметр штаба:
P = 1 405,25
Таким образом, суммарная длина сторон Пентагона составляет практически полтора километра.
Школьная задача
Допустим, вам нужно определить периметр правильного пятиугольника, зная, что радиус описанной вокруг него окружности равен 5 см. Вы можете последовательно использовать приведенные выше соотношения для вычисления стороны пентагона, а затем и его периметра. Давайте сэкономим время и просто введем значение в форму калькулятора «Радиус описанной окружности R».
P = 29,38
Помимо периметра, калькулятор определил значения стороны пентагона, а также радиус вписанной в него окружности.
Заключение
Правильный пятиугольник — достаточно редкая в человеческой повседневности и природе фигура.
Впрочем, вычисление параметров пентагона может понадобиться вам при решении школьных задач или рабочих вопросов. Используйте для этих целей наш онлайн-калькулятор, который определяет периметр пятиугольника, зная только один параметр фигуры.
Описание и примеры стандартных функций SVG
Доминирующей причиной появления этого блога стало незаслуженное забвение на целых десять лет языка разметки масштабируемой векторной графики – SVG (Scalable Vector Graphics), входящего в подмножество расширяемого языка разметки XML.
Стандарт SVG 1.0 был принят в качестве спецификации Консорциумом Всемирной паутины (W3C) в сентябре 2001 г. Стандарт SVG 1.1 и его версии SVG mobile profiles (SVG Basic and SVG Tiny) были приняты консорциумом в качестве рекомендации в январе 2003 г.
Сейчас ведутся работы по созданию стандарта SVG 2.0
Основные преимущества формата SVG.
Я не буду долго распространяться о преимуществах векторной графики перед растровой в вебдизайне, замечу лишь, что, однажды созданный, файл в формате SVG одинаково хорошо выглядит без потери качества и на мобильном устройстве и на станционарном мониторе домашнего ПК.
Шапка данного сайта выполнена в формате SVG, попробуйте уменьшить окно браузера до минимальных размеров, картинка на “лету” будет также пропорционально уменьшаться.
Бесконечное полотно документа svg.
Итак, как происходит формирование векторного изображения.
Документ формата SVG – это двухмерный объект, который может иметь бесконечные координаты, как в положительном, так и в отрицательном направлении по осям X и Y. Также документ SVG имеет две области просмотра: viewport – системная область просмотра и viewBox – пользовательская область просмотра, положение которой относительно начала системных координат viewport, может задаваться собственной, пользовательской системой координат. Другими словами окно просмотра viewBox, может быть перемещёно в любое место документа SVG, при этом берется фрагмент изображения под ним, который после процесса согласования между viewBox и viewport, возвращается обратно в системную область просмотра viewport, которую видит пользователь.
При уменьшении размера пользовательского окна просмотра viewbox можно пропорционально увеличивать фрагмент изображения в системной области просмотра или уменьшать его при увеличении размера viewbox.
Взаимодействие SVG, XML с HTML, CSS, Jscript
В SVG, как и в HTML можно добавлять ссылки на внешние ресурсы. Но если в HTML одна картинка может служить только для одной внешней ссылки, то в SVG документ можно добавлять сколько угодно внешних ссылок . Картинка кликабельна.
Внутрь HTML страницы легко встраивается код SVG документа или целиком подключается внешний SVG файл. Можно наоборот, внутри SVG файла разместить код HTML внутри тегов 
Получаются интересные эффекты: Внутри SVG файла находится работающий внешний HTML сайт. К SVG формату можно подключать внешние таблицы стилей CSS 2.0, что позволяет управлять сразу несколькими файлами *.svg. Также вполне допустимо подключение стилей внутри файла *.svg внутри тегов style или использовать внутренние стили непосредственно внутри командных строк фигур и путей.
SVG, как любой основанный на XML формат, позволяет использовать для его обработки таблицы трансформации (XSLT).
Преобразуя XML-данные в SVG с помощью простого XSL, можно получить графическое представление текстовых данных, например визуализировать графики, круговые диаграммы, гистограммы и т.д.
Анимация и интерактивность SVG.
Анимация в SVG осуществляется при помощи языка SMIL (Synchronized Multimedia Integration Language). Также поддерживаются скриптовые языки на основе спецификации ECMAScript — это встраиваемый расширяемый язык программирования.
То есть всё находится в одном месте, внутри документа SVG, поэтому нет необходимости для подключения внешних библиотек.
На каждую отдельную фигуру или на целое изображение можно установить обработчик событий (клик, наведение мышки, нажатие клавиши и т.д), таким образом, пользователь может управлять рисунком. Наведите курсор мышки на кнопку“Start” на примере слева.
Следующий пример анимации – плавная отрисовка картинки с нуля до полного изображения.
Уже встроенные в SVG языки программирования позволяют реализовать довольно сложные сценарии анимации.
Но, в дополнение к этому есть еще более мощные средства для реализации интерактивности графики и ее анимации – это внешние библиотеки сторонних разработчиков: D3.js, BonsaiJS, Svg.js, Snapsvg.jsЕще примеры анимации ⇛
Недостатки SVG формата
- С увеличением количества мелких деталей в изображении, быстрее растёт размер файла SVG-данных. Предельный случай — когда изображение представляет собой белый шум. В этом случае SVG не только не даёт никаких преимуществ в размере файла, но даже имеет проигрыш по отношению к растровому формату. На практике, SVG становится невыгоден уже задолго до того, как изображение дойдёт до стадии белого шума.
- Трудность использования в крупных картографических приложениях из-за того, что для правильного отображения маленькой части изображения документ необходимо прочитать целиком.
- В настоящее время SVG формат применяется в Интернете сравнительно мало, из-за недостаточной кроссбраузерности. Лучше всего обстоят дела у Mozilla Firefox со встроенным просмотрщиком SVG, так как ее разработчики находятся в рабочей группе Консорциума Всемирной паутины (W3C) по разработке и внедрению стандарта SVG.
Браузеры Apple Safari, Google Chrome намного лучше поддерживают SVG, но не полностью, так как SVG – это большая спецификация (вдвое больше HTML 4.01), именно поэтому разработчики браузеров внедряют функции постепенно, от версии к версии. Но абсолютно все разработчики современных браузеров заявляют, что за форматом SVG будущее в области графики вебдизайна.
UPD.
следующая: Структура SVG документа ⇛
Задание 1. Правильный многоугольник | Уроки математики и физики для школьников и родителей
Прежде чем приступить к решению примеров и задач, обязательно ознакомьтесь с теоретической частью урока
1. Укажите номера верных утверждений.
1) Вписанный
угол равен половине центрального, опирающегося на ту же дугу.
2) Сумма углов треугольника равна 360°.
3) Катет всегда больше гипотенузы.
4) Все равнобедренные треугольники равны.
5) Все углы правильного шестиугольника равны 135°.
а) 2, 5;в) 1, 3;
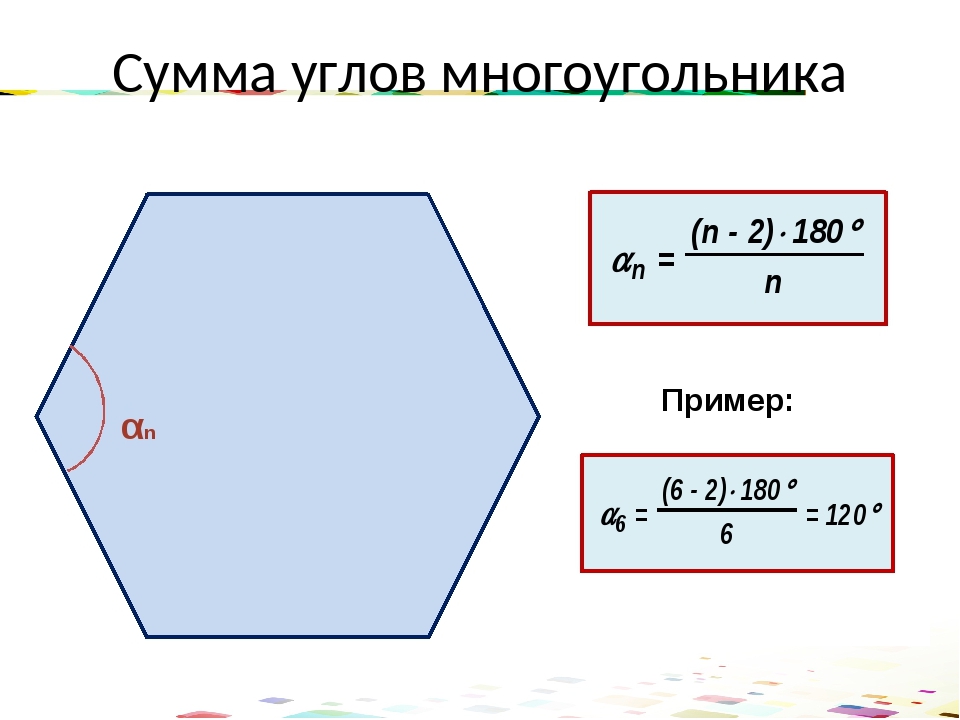
г) 1. 2. Найдите сумму внутренних углов правильного пятиугольника. а) 540°;
б) 360°;
в) 450°;
г) 720°. 3. Найдите количество сторон правильного многоугольника, если сумма его внутренних углов равна 1080°. а) 6;
б) 9;
в) 8;
г) 7. 4. Выразите через радиус R описанной окружности апофему правильного треугольника. а) 0,25R;
б) 0,5R;
в) 2R;
г) R. 5. Найдите количество сторон правильного многоугольника, внешний угол которого равен 60°
а) 5; б) 8;
в) 6;
г) 7. 6. Центральный угол правильного многоугольника равен 30°. Определите количество сторон многоугольника. а) 12;
б) 18;
в) 6;
г) 10. 7. Найдите градусную меру внутреннего угла правильного шестиугольника. а) 150°;
б) 90°;
в) 100°;
г) 120°. 8. Шаблон для гаек имеет углы, равные
90°, 120° и 135°.
Для каких правильных многоугольников можно использовать этот шаблон ? а) 4, 5, 8;
б) 5, 6, 8;
в) 4, 6, 8;
г) 3, 6, 9. 9. Сколько сторон имеет правильный многоугольник, угол которого равен 140° ? а) 9;
б) 8;
в) 7;
г) 10. 10. Укажите неправильное утверждение.
а) если стороны четырёхугольника равны, то его углы равны; б) если вокруг четырёхугольника можно описать
окружность, то суммы его противоположных углов равны;
в) любой правильный п – угольник имеет ось
симметрии;
г) в любой правильный п – угольник можно вписать окружность.
11. Найдите углы треугольника, вершины которого находятся на серединах сторон правильного шестиугольника. а) 40°, 60°, 80⁰;б) 45⁰, 45°, 90°;
в) 60°, 90°, 30°;
г) 60°, 60°, 60°.
а) 36°;
б) 144°;
в)
90°;
г) 120°.
Как найти угол в пятиугольнике
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту.
Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Найдите внутренние углы правильного многоугольника — Уроки домашнего обучения по средней математике 9-й год
3.$blocks-article-row-5.1:$z69fxbk-5=10.1.1.$0″> Пример 1 — Правильный пятиугольник Пятиугольник (5-сторонняя форма) выше можно разделить на 3 треугольника.Чтобы найти сумму внутренних углов, умножьте 3 на 180 °.
Сумма внутренних углов пятиугольника = 3 x 180 ° = 540 °
Если многоугольник правильный — все его внутренние углы равны — вы можете использовать результат суммы углов выше, чтобы вычислить размер каждый угол.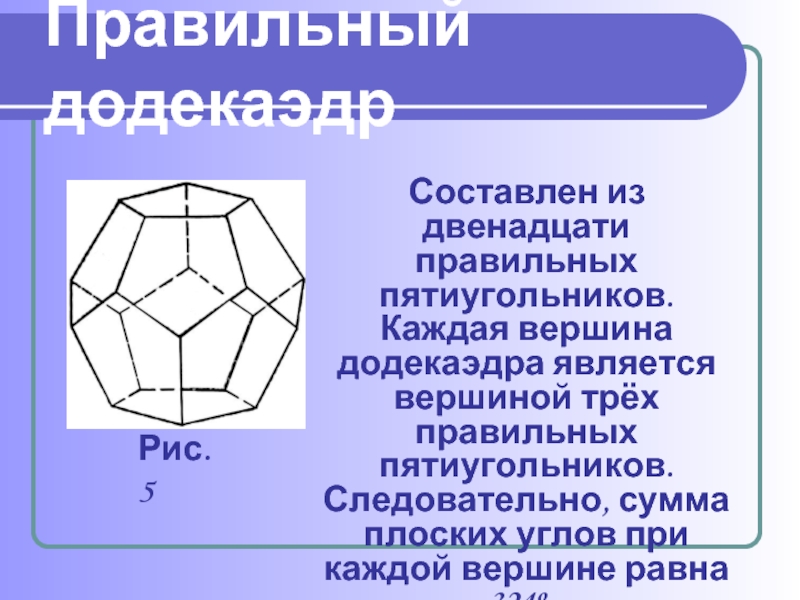
Для этого нужно разделить сумму внутренних углов на количество внутренних углов .
В приведенном выше примере вы разделите 540 ° на 5 , потому что в правильном пятиугольнике есть 5 внутренних углов одинакового размера.
Следовательно, размер внутреннего угла правильного пятиугольника = 540 ° ÷ 5 = 108 °
Десятиугольник
ДесятиугольникМатематика 150
Проектов
Доктор Уилсон
Построение правильного десятиугольника путем обрезания углов Обычный Пентагон
Чтобы построить правильный десятиугольник, срезав углы правильный пятиугольник,
вопрос в том, что такое х? Если десятиугольник правильный, то имеем
Где
— это пропорция золотой середины.
Переставьте 2x в другое
сторона уравнения
Рационализируйте знаменатель.
, что сокращается до
или
или
Хотя этот формат не имеет рационализированных знаменателей, это конструктивный номер. Один из способов построить правильный десятиугольник: срезание углов правильного пятиугольника происходит следующим образом.
На рисунке ABC представляет собой квадрат. E — середина BC. Как В результате мы можем использовать теорему Пифагора
, чтобы найти, что
F — это место, где единичный круг с центром в точке A пересекает AE. G — стопа F в AB.
По простому соотношению
получаем, что
Теперь вернемся к нашей предыдущей цифре
., чтобы увидеть, что
Если мы позволим мне быть серединой ВЧ, то
— это количество, которое мы должны снять с углов пятиугольник, чтобы получился правильный десятиугольник.
Если сравнить постройку штатного
восьмиугольник из квадрата и правильного
двенадцатиугольник из правильного шестиугольника, это
один намного сложнее.
Неясно, есть ли вообще
метод проверки этой конструкции геометрически, как для
восьмиугольник и
двенадцатигранник. Это также ставит под сомнение наши
поискать общий метод, который будет работать для всех обычных
полигоны. Однако есть общий метод, который будет работать для всех
правильные многоугольники, которые хоть и не так интересны, как наши методы
для восьмиугольника и
dodecagon, проще в случае
десятиугольник.
| 1D линия, круговая дуга, парабола, спираль, кривая Коха
2D Правильные многоугольники: Равносторонний треугольник, квадрат, пятиугольник, шестиугольник, семиугольник, восьмиугольник, девятиугольник, десятиугольник, шестиугольник, додекагон, шестиугольник, N-угольник, кольцо многоугольника Другие многоугольники: 90 117 круглых форм: тетраэдр, куб, октаэдр, додекаэдр, икосаэдр архимедова Solids: Каталонских Сухой остаток: Твердые тела Джонсона: Другие многогранники: | Anzeige Расчеты в правильном пятиугольнике, многоугольнике с 5 вершинами. Формулы: Длина кромки, диагонали , высота, периметр и радиус имеют одинаковые единицы измерения (например,грамм. метр), площадь равна этой единице в квадрате (например, квадратный метр). Anzeige Высоты, биссектрисы и срединные линии совпадают, они пересекаются в центре тяжести, который также является центром описанной и вписанной окружности. К этому моменту правильный пятиугольник осесимметричен при вращении на 72 ° или кратное этому. Кроме того, правильный пятиугольник аксиально симметричен средним линиям.
© Jumk. Anzeige |
Спираль, Треугольник Рело, Циклоида, Двойная циклоида, Астроид, Гипоциклоида, Кардиоида, Эпициклоида, Параболический сегмент, Сердце, Треугольник, Межугловой треугольник, Круговой треугольник дуги, Четырехугольник Interarc, Межкруговый четырехугольник, Круговой четырехугольник дуги, Круговой дуговый многоугольник, Коготь, Коготь — Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Поликруг, Многоугольник с закругленными краями, Роза, Шестеренка, Овал, Профиль яйца, Лемниската, Сквикул, Круглый квадрат, Дигон, Сферический треугольник 
Эта форма часто используется в архитектуре. Введите одно значение и выберите количество десятичных знаков. Затем нажмите Рассчитать.
de WebprojectsПентагон — Academic Kids
От академических детей
Шаблон: Альтернативы
Изображение отсутствуетRegular_pentagon.png
Правильный пятиугольник
В геометрии пятиугольник — это любой пятиугольник.
Однако этот термин обычно используется для обозначения правильного пятиугольника , у которого все стороны равны и все углы равны (108).2 <математика>
Regular_pentagram.png
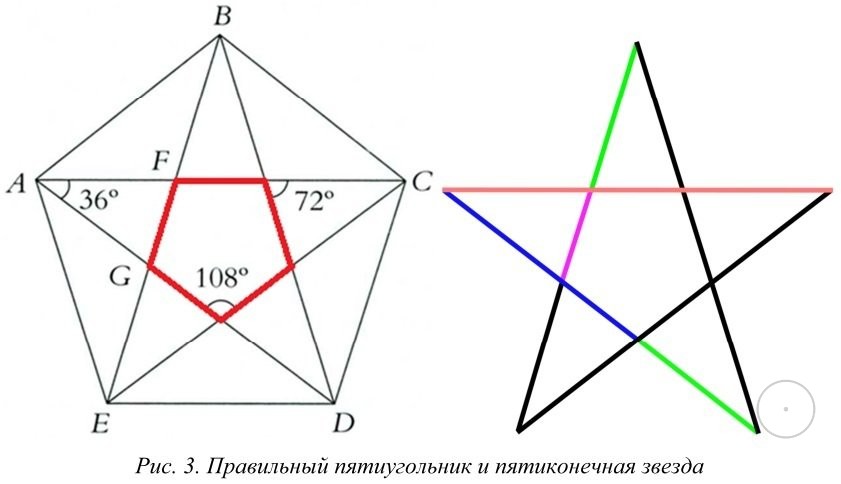
Пентаграмма, заключенная в пятиугольник
Пентаграмма может быть образована из правильного пятиугольника, либо вытягивая его стороны, либо вычерчивая его диагонали, и получившаяся фигура содержит различные длины, связанные золотым сечением, φ = (1 + √5) / 2.
Построение пятиугольника
Правильный пятиугольник можно построить с помощью линейки и циркуля. Этот процесс был описан Евклидом в его Elements около 300 г.
до н.э.К. Карл Фридрих Гаусс сделал некоторые теоретические доказательства теории многоугольников.
- Нарисуйте горизонтальную линию с кругом размером с желаемый пятиугольник, центр которого находится на этой линии.
- Поместите стрелку циркуля в то место, где окружность круга пересекает горизонтальную линию, и проведите полукруг через центр вашего первого круга, пересекая окружность первого круга в двух местах. Проведите вертикальную линию через точки, где полукруг пересекает первый круг.Эта линия пройдет через точку, которую мы называем (а).
- Раскройте циркули, чтобы вы могли, поместив стрелку в два пересечения между горизонтальной линией и первым кругом, нарисовать небольшой крест над и под горизонтальной линией, за пределами первого круга, с одной линией креста от каждая точка. Если вы соедините эти кресты, вы получите линию, перпендикулярную горизонтальной линии, также проходящую через центр первого круга. Точку, где эта линия пересекает окружность первого круга сверху, мы называем (b). Это первый угол пятиугольника.
- Поместите стрелку циркуля в (a) и проведите отрезок круга, проходящий через (b) и вниз через горизонтальную линию, получив точку на этой линии, которую мы называем (c).
- Вставьте иглу в (b) и проведите отрезок круга через (c) и первый круг. Эти точки на первом круге являются вторым и третьим углами пятиугольника.
- Не вытягивая циркуль, введите его стрелку во второй и третий углы и нарисуйте сегменты круга, проходящие через первый круг, чтобы найти два оставшихся угла.
- Соедините каждый угол с соседними, и у вас получится пятиугольник.
- Если вы соедините несмежные углы (рисуя диагонали пятиугольника), вы получите пентаграмму с меньшим правильным пятиугольником в центре. Или, если вы вытянете стороны, пока не встретятся несмежные, вы получите пентаграмму большего размера.
Это первый угол пятиугольника.Внешние ссылки
- Пентагоны и пентаграммы ( http://agutie.homestead.com/files/pentagram_menelaus1.htm ) новые факты о пятиугольниках и пентаграммах Антонио Гутьерреса из книги «Геометрия шаг за шагом из страны инков». Ключевое понятие: теорема Менелая. Шаблон: многоугольники
Ключевое понятие: теорема Менелая. Шаблон: многоугольникиda: Фемкант de: Fnfeck fr: Пентагон он: מחומש это: Fimmhyrningur это: Пентагоно (геометрия) ja: 五角形 nl: Vijfhoek нет: Пентагон pl: Pięciokąt pt: Пентгоно sv: Пентагон ж: 正 五边形
Базовая геометрия — Многоугольники | Shmoop
Многоугольники
Многоугольник — это любая замкнутая фигура с тремя или более прямыми сторонами . «Закрыто» означает, что в нем нет зияющих отверстий и что все стороны соединяются вместе.
Это многоугольники:
Это не многоугольники:
Первая фигура — это линия, которая определенно не является фигурой с более чем тремя сторонами. Извини, брат, тебя нет. У следующей формы более трех сторон, но не все они соединяются. Плохие новости, чувак, тебя тоже нет. Правильно, круг — это тоже не многоугольник . Хотя это замкнутая фигура, очень сложно подсчитать количество сторон у круга, потому что у него их нет.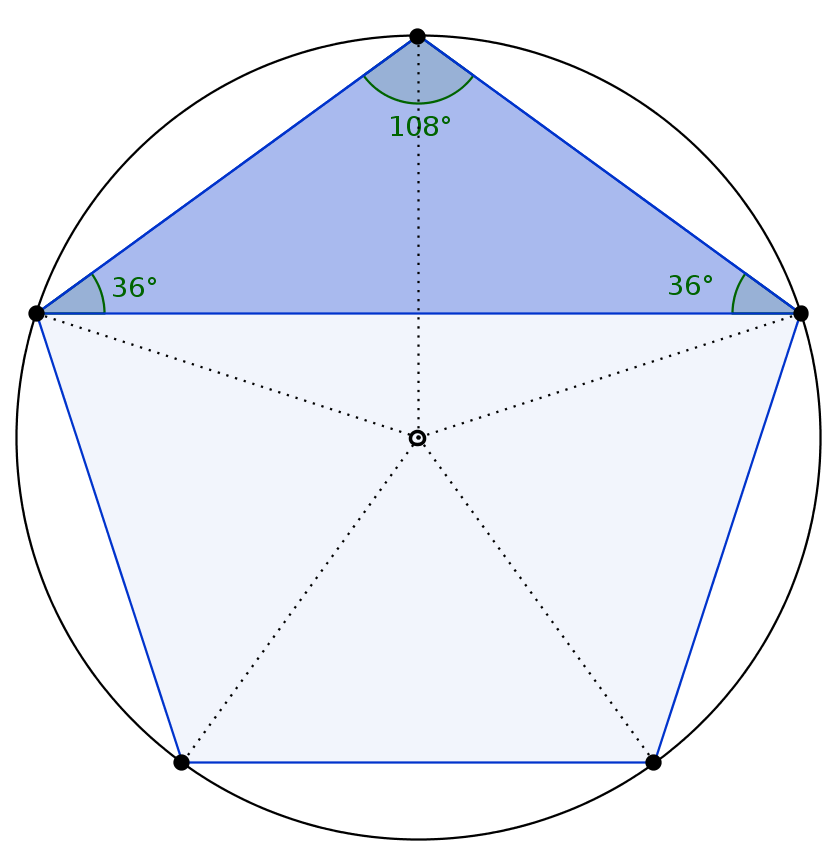
Окончательная форма замкнута, и у нее более трех сторон, но две из них изогнуты.Это не прямые линии, так что еще раз извините, Чарли.
АКА «уголок».
Это примеры выпуклых многоугольников.
Такие многоугольники называются равноугольными. Прямоугольники равноугольные, потому что все четыре угла равны 90 °. Чтобы многоугольник был равноугольным, стороны не должны быть равной длины.
76 см, а площадь 688 см.
