Удельное сопротивление — проводник — Большая Энциклопедия Нефти и Газа, статья, страница 1
Удельное сопротивление — проводник
Cтраница 1
Удельное сопротивление проводника зависит от температуры, давления, материала и др., вследствие чего от этих же факторов зависит и сопротивление проводника. Наибольшее практическое значение имеет зависимость удельного сопротивления, а следовательно, и сопротивления проводника, от температуры. В общем случае эта зависимость достаточно сложна. [1]
Удельное сопротивление проводников является величиной не постоянной, а зависящей от температуры. Для всех металлов сопротивление увеличивается с увеличением температуры. При небольших колебаниях температуры зависимость удельного сопротивления от температуры следует линейному закону. Для каждого металла существует определенный температурный коэффициент сопротивления а, который определяет собой изменение удельного сопротивления проводника, отнесенное к одному ому при повышении температуры на ГС.
Удельное сопротивление проводников лежит в пределах от 10 — 6 до 10 — 2 ом-см, а технических диэлектриков от 109 до 1020 ом-см. Эти пределы в известной мере условны, но приближенно отражают установившиеся в технике представления. [3]
Удельное сопротивление проводника представляет собой сопротивление провода длиной I м и площадью поперечного сечения 1 мм2 при температуре 20 С. [4]
Удельное сопротивление проводников и непроводников зависит от температуры. [5]
Удельное сопротивление проводников первого рода зависит от температуры. Как правило, с ростом температуры оно повышается. Исключение составляют графит и уголь. [6]
Чем меньше удельное сопротивление проводника, тем меньшее количество тепла ( при том же токе) в нем выделяется.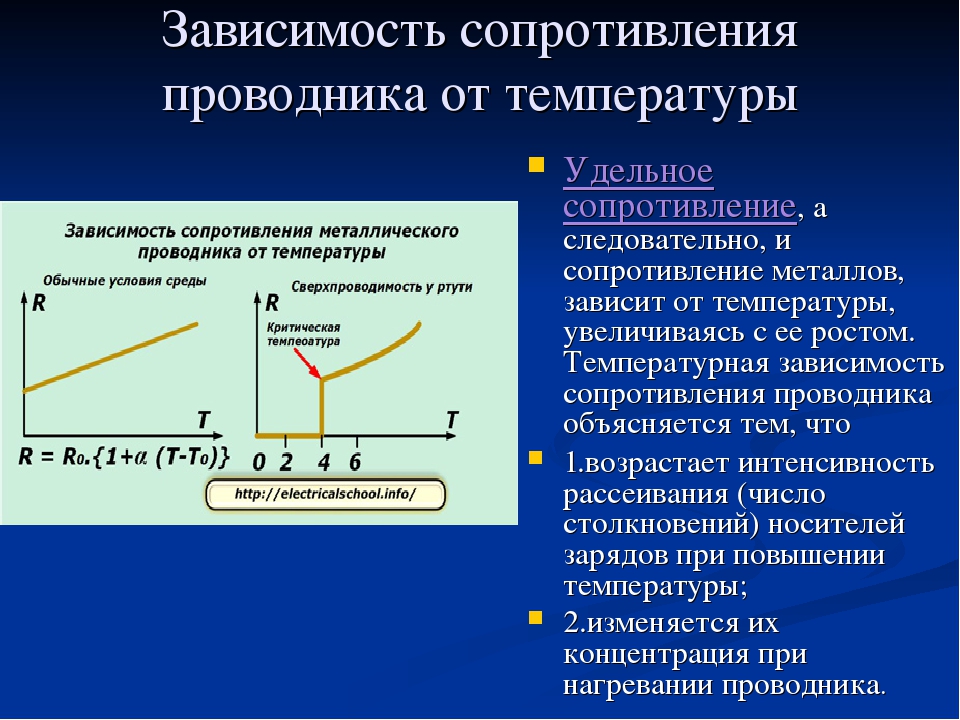 При состоянии сверхпроводимости, когда удельное сопротивление становится неизмерим э малым, в проводнике при прохождении тока не выделяется сколько-нибудь заметного количества тепла. Так как при этом энергия тока никуда не тратится, то раз возбужденный в замкнутом сверхпроводнике то; поддерживается в нем неопределенно долго без затраты энергии извне.
[7]
При состоянии сверхпроводимости, когда удельное сопротивление становится неизмерим э малым, в проводнике при прохождении тока не выделяется сколько-нибудь заметного количества тепла. Так как при этом энергия тока никуда не тратится, то раз возбужденный в замкнутом сверхпроводнике то; поддерживается в нем неопределенно долго без затраты энергии извне.
[7]
Изменение удельного сопротивления проводника под действием растягивающих или сжимающих усилий называют тензорезистивным эффектом. Он характеризуется тензочувст-вительностью, устанавливающей связь между относительным изменением сопротивления и относительной деформацией. [8]
Здесь р — удельное сопротивление проводника, остальные обозначения расшифрованы в предыдущей задаче. [9]
От чего зависит удельное сопротивление проводника. [10]
[10]
Если бы величина удельного сопротивления проводника р не зависела от его температуры, соотношение между допустимой плотностью тока / 1ДОп и допустимым превышением температуры проводника при коротком замыкании было бы относительно простым. В действительности удельное сопротивление р изменяется с нагревом проводника, и соотношение между плотностью тока и превышением температуры получается более сложным. [11]
Чтобы повысить величину удельного сопротивления проводников, применяют сплавы нескольких металлов. Установлено, что только сплавы с неупорядоченной структурой обладают повышенными значениями удельного сопротивления и малыми значениями температурного коэффициента сопротивления. Сплавами с неупорядоченной структурой называются такие, в кристаллической решетке которых нет правильного чередования атомов металлов, составляющих сплав. Эти сплавы составляют группу проводниковых материалов с большим удельным сопротивлением и малыми значениями температурного коэффициента удельного сопротивления.
Величина р называется удельным сопротивлением проводника. [13]
Ом; Р — удельное сопротивление проводника. [14]
При этом учитывается возрастание удельного сопротивления проводника при его нагреве. [15]
Страницы: 1 2 3 4
Как изменяется сопротивление проводника при повышении температуры
Зависимость сопротивления проводника от температуры
Удельное сопротивление, а следовательно, и сопротивление металлов, зависит от температуры, увеличиваясь с ее ростом. Температурная зависимость сопротивления проводника объясняется тем, что
- возрастает интенсивность рассеивания (число столкновений) носителей зарядов при повышении температуры;
- изменяется их концентрация при нагревании проводника.

Опыт показывает, что при не слишком высоких и не слишком низких температурах зависимости удельного сопротивления и сопротивления проводника от температуры выражаются формулами:
ho_t =
ho_0 (1 + alpha t) ,) (
R_t = R_0 (1 + alpha t) ,)
где ρ0, ρt — удельные сопротивления вещества проводника соответственно при 0 °С и t °C; R0, Rt — сопротивления проводника при 0 °С и t °С, α — температурный коэффициент сопротивления: измеряемый в СИ в Кельвинах в минус первой степени (К -1 ). Для металлических проводников эти формулы применимы начиная с температуры 140 К и выше.
Температурный коэффициент сопротивления вещества характеризует зависимость изменения сопротивления при нагревании от рода вещества. Он численно равен относительному изменению сопротивления (удельного сопротивления) проводника при нагревании на 1 К.
mathcal h alpha mathcal i) — среднее значение температурного коэффициента сопротивления в интервале ΔΤ.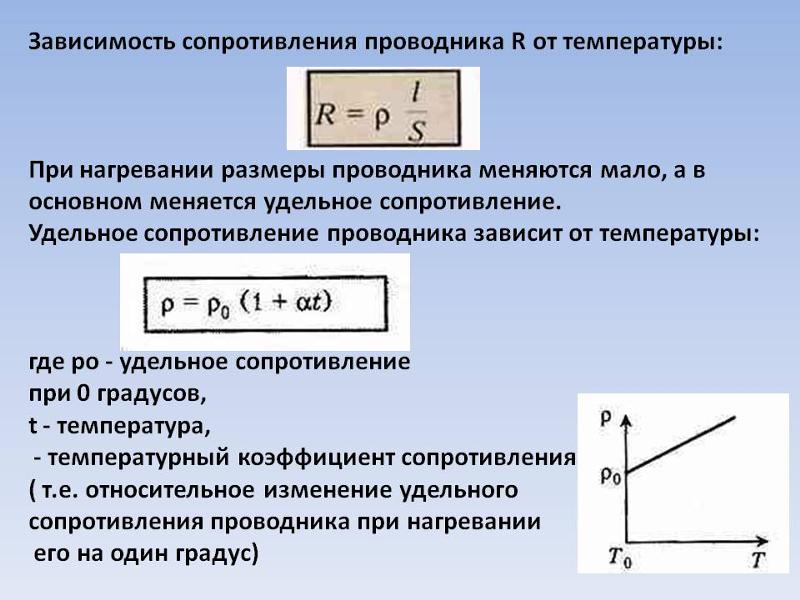
Для всех металлических проводников α > 0 и слабо изменяется с изменением температуры. У чистых металлов α = 1/273 К -1 . У металлов концентрация свободных носителей зарядов (электронов) n = const и увеличение ρ происходит благодаря росту интенсивности рассеивания свободных электронов на ионах кристаллической решетки.
Для растворов электролитов α -1 . Сопротивление электролитов с ростом температуры уменьшается, так как увеличение числа свободных ионов из-за диссоциации молекул превышает рост рассеивания ионов при столкновениях с молекулами растворителя.
Формулы зависимости ρ и R от температуры для электролитов аналогичны приведенным выше формулам для металлических проводников. Необходимо отметить, что эта линейная зависимость сохраняется лишь в небольшом диапазоне изменения температур, в котором α = const. При больших же интервалах изменения температур зависимость сопротивления электролитов от температуры становится нелинейной.
Графически зависимости сопротивления металлических проводников и электролитов от температуры изображены на рисунках 1, а, б.
При очень низких температурах, близких к абсолютному нулю (-273 °С), сопротивление многих металлов скачком падает до нуля. Это явление получило название сверхпроводимости. Металл переходит в сверхпроводящее состояние.
Зависимость сопротивления металлов от температуры используют в термометрах сопротивления. Обычно в качестве термометрического тела такого термометра берут платиновую проволоку, зависимость сопротивления которой от температуры достаточно изучена.
Об изменениях температуры судят по изменению сопротивления проволоки, которое можно измерить. Такие термометры позволяют измерять очень низкие и очень высокие температуры, когда обычные жидкостные термометры непригодны.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 256-257.
сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 256-257.
Зависимость сопротивления проводника от температуры
Удельное сопротивление, а следовательно, и сопротивление металлов, зависит от температуры, увеличиваясь с ее ростом. Температурная зависимость сопротивления проводника объясняется тем, что
- возрастает интенсивность рассеивания (число столкновений) носителей зарядов при повышении температуры;
- изменяется их концентрация при нагревании проводника.
Опыт показывает, что при не слишком высоких и не слишком низких температурах зависимости удельного сопротивления и сопротивления проводника от температуры выражаются формулами:
ho_t =
ho_0 (1 + alpha t) ,) (
R_t = R_0 (1 + alpha t) ,)
где ρ0, ρt — удельные сопротивления вещества проводника соответственно при 0 °С и t °C; R0, Rt — сопротивления проводника при 0 °С и t °С, α — температурный коэффициент сопротивления: измеряемый в СИ в Кельвинах в минус первой степени (К -1 ). Для металлических проводников эти формулы применимы начиная с температуры 140 К и выше.
Для металлических проводников эти формулы применимы начиная с температуры 140 К и выше.
Температурный коэффициент сопротивления вещества характеризует зависимость изменения сопротивления при нагревании от рода вещества. Он численно равен относительному изменению сопротивления (удельного сопротивления) проводника при нагревании на 1 К.
mathcal h alpha mathcal i) — среднее значение температурного коэффициента сопротивления в интервале ΔΤ.
Для всех металлических проводников α > 0 и слабо изменяется с изменением температуры. У чистых металлов α = 1/273 К -1 . У металлов концентрация свободных носителей зарядов (электронов) n = const и увеличение ρ происходит благодаря росту интенсивности рассеивания свободных электронов на ионах кристаллической решетки.
Для растворов электролитов α -1 . Сопротивление электролитов с ростом температуры уменьшается, так как увеличение числа свободных ионов из-за диссоциации молекул превышает рост рассеивания ионов при столкновениях с молекулами растворителя.
Формулы зависимости ρ и R от температуры для электролитов аналогичны приведенным выше формулам для металлических проводников. Необходимо отметить, что эта линейная зависимость сохраняется лишь в небольшом диапазоне изменения температур, в котором α = const. При больших же интервалах изменения температур зависимость сопротивления электролитов от температуры становится нелинейной.
Графически зависимости сопротивления металлических проводников и электролитов от температуры изображены на рисунках 1, а, б.
При очень низких температурах, близких к абсолютному нулю (-273 °С), сопротивление многих металлов скачком падает до нуля. Это явление получило название сверхпроводимости. Металл переходит в сверхпроводящее состояние.
Зависимость сопротивления металлов от температуры используют в термометрах сопротивления. Обычно в качестве термометрического тела такого термометра берут платиновую проволоку, зависимость сопротивления которой от температуры достаточно изучена.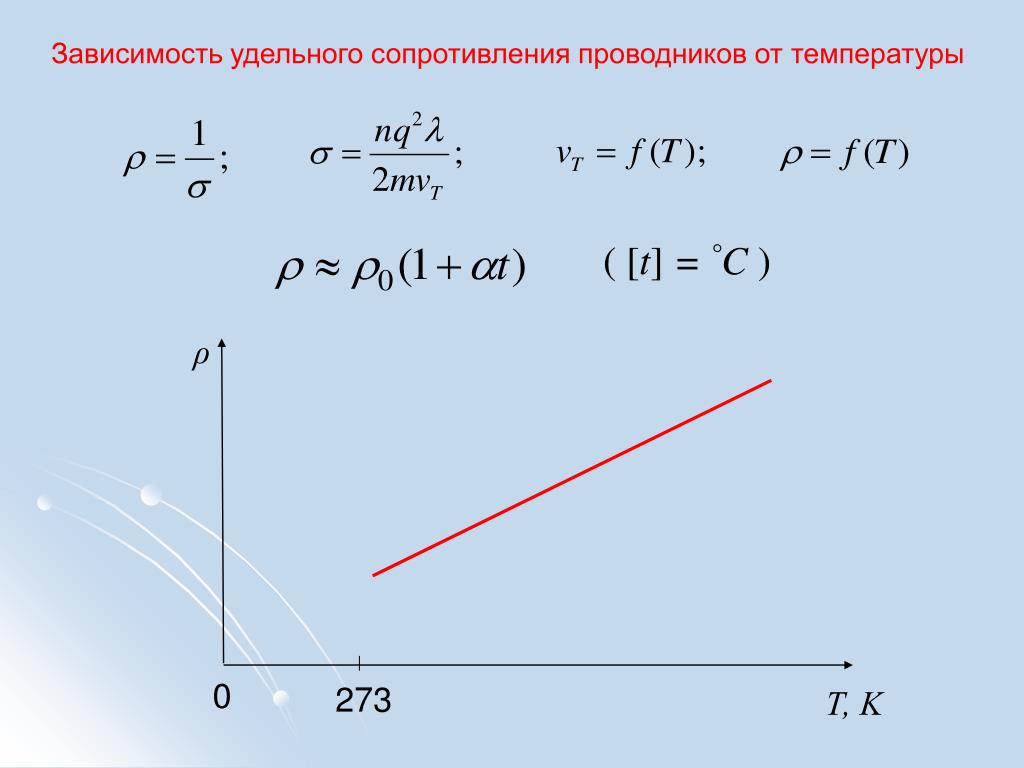
Об изменениях температуры судят по изменению сопротивления проволоки, которое можно измерить. Такие термометры позволяют измерять очень низкие и очень высокие температуры, когда обычные жидкостные термометры непригодны.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 256-257.
В своей практической деятельности каждый электрик встречается с разными условиями прохождения носителей зарядов в металлах, полупроводниках, газах и жидкостях. На величину тока влияет электрическое сопротивление, которое различным образом изменяется под влиянием окружающей среды.
Одним из таких факторов является температурное воздействие. Поскольку оно значительно изменяет условия протекания тока, то учитывается конструкторами в производстве электрооборудования. Электротехнический персонал, участвующий в обслуживании и эксплуатации электроустановок, обязан грамотно использовать эти особенности в практической работе.
Влияние температуры на электрическое сопротивление металлов
В школьном курсе физики предлагается провести такой опыт: взять амперметр, батарейку, отрезок проволоки, соединительные провода и горелку. Вместо амперметра с батарейкой можно подключить омметр или использовать его режим в мультиметре.
Далее необходимо собрать электрическую схему, показанную на картинке и замерить величину тока в цепи. Его значение показано на шкале миллиамперметра стрелкой черного цвета.
Теперь поднесем пламя горелки к проволоке и станем ее нагревать. Если смотреть на амперметр, то будет видно, что стрелка станет перемещаться влево и достигнет положения, отмеченного красным цветом.
Результат опыта демонстрирует, что при нагревании металлов их проводимость уменьшается, а сопротивление возрастает.
Математическое обоснование этого явления приведено формулами прямо на картинке. В нижнем выражении хорошо видно, что электрическое сопротивление «R» металлического проводника прямо пропорционально его температуре «Т» и зависит еще от нескольких параметров.
Как нагрев металлов ограничивает электрический ток на практике
Ежедневно при включении освещения мы встречаемся с проявлением этого свойства у ламп накаливания. Проведем несложные измерения на лампочке с мощностью 60 ватт.
Самым простым омметром, питающемся от низковольтной батарейки 4,5 V, замерим сопротивление между контактами цоколя и увидим значение 59 Ом. Этой величиной обладает нить накала в холодном состоянии.
Вкрутим лампочку в патрон и через амперметр подключим к ней напряжение домашней сети 220 вольт. Стрелка амперметра покажет 0,273 ампера. По закону Ома для участка цепи определим сопротивление нити в нагретом состоянии. Оно составит 896 Ом и превысит предыдущее показание омметра в 15,2 раза.
Такое превышение предохраняет металл тела накала от перегорания и разрушения, обеспечивая его длительную работоспособность под напряжением.
Переходные процессы при включении
При работе нити накала на ней создается тепловой баланс между нагревом от проходящего электрического тока и отводом части тепла в окружающую среду.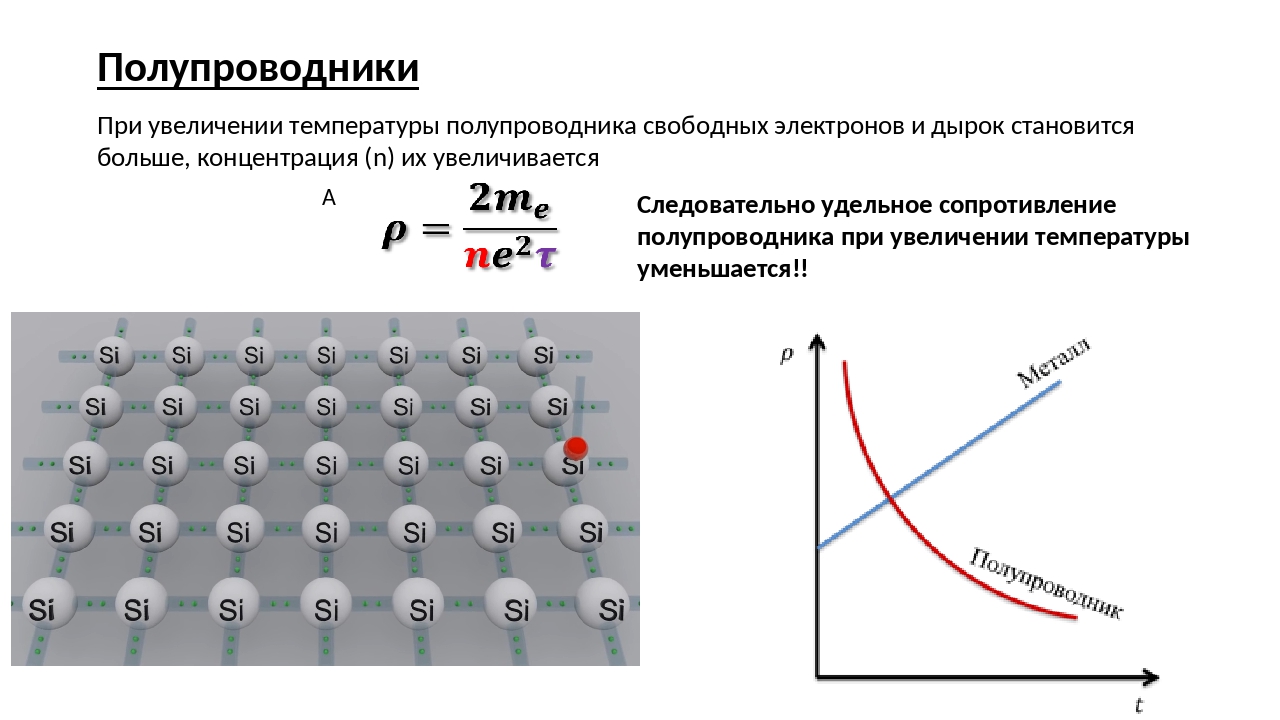 Но, на первоначальном этапе включения при подаче напряжения возникают переходные процессы, создающие бросок тока, который может привести к перегоранию нити.
Но, на первоначальном этапе включения при подаче напряжения возникают переходные процессы, создающие бросок тока, который может привести к перегоранию нити.
Переходные процессы протекают за короткое время и вызваны тем, что скорость возрастания электрического сопротивления от нагрева металла не успевает за увеличением тока. После их окончания устанавливается рабочий режим.
Во время длительного свечения лампы постепенно толщина ее нити доходит до критического состояния, которое приводит к перегоранию. Чаще всего этот момент возникает при очередном новом включении.
Для продления ресурса лампы различными способами уменьшают этот бросок тока, используя:
1. устройства, обеспечивающие плавную подачу и снятие напряжения;
2. схемы последовательного подключения к нити накала резисторов, полупроводников или терморезисторов (термисторов).
Пример одного из способов ограничения пускового тока для автомобильных светильников показан на картинке ниже.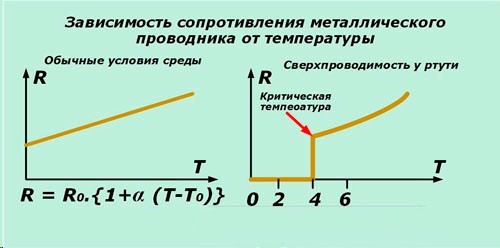
Здесь ток на лампочку подается после включения тумблера SA через предохранитель FU и ограничивается резистором R, у которого номинал подбирается так, чтобы бросок тока во время переходных процессов не превышал номинальное значение.
При нагреве нити накала ее сопротивление возрастает, что ведет к увеличению разности потенциалов на ее контактах и параллельно подключенной обмотке реле KL1. Когда напряжение достигнет величины уставки реле, то нормально открытый контакт KL1 замкнется и зашунтирует резистор. Через лампочку начнет протекать рабочий ток уже установившегося режима.
Влияние температуры металла на его электрическое сопротивление используется в работе измерительных приборов. Их называют термометрами сопротивления.
Их чувствительный элемент выполняют тонкой проволочкой из металла, сопротивление которой тщательно замерено при определенных температурах. Эту нить монтируют в корпусе со стабильными термическими свойствами и закрывают защитным чехлом. Созданная конструкция помещается в среду, температуру которой необходимо постоянно контролировать.
Созданная конструкция помещается в среду, температуру которой необходимо постоянно контролировать.
На выводы чувствительного элемента монтируются провода электрической схемы, которыми подключается цепь замера сопротивления. Его величина пересчитывается в значения температуры на основе ранее произведенной калибровки прибора.
Бареттер — стабилизатор тока
Так называют прибор, состоящий из стеклянного герметичного баллона с газообразным водородом и металлической проволочной спиралью из железа, вольфрама или платины. Эта конструкция по внешнему виду напоминает лампочку накаливания, но она обладает специфической вольт-амперной нелинейной характеристикой.
На ВАХ в определенном ее диапазоне образуется рабочая зона, которая не зависит от колебаний приложенного на тело накала напряжения. На этом участке бареттер хорошо компенсирует пульсации питания и работает в качестве стабилизатора тока на подключенной последовательно к нему нагрузке.
Работа бареттера основана на свойстве тепловой инерции тела накала, которая обеспечивается маленьким сечением нити и высокой теплопроводностью окружающего ее водорода. За счет этого при снижении напряжения на приборе ускоряется отвод тепла с его нити.
За счет этого при снижении напряжения на приборе ускоряется отвод тепла с его нити.
Это основное отличие бареттера от осветительных ламп накаливания, в которых для поддержания яркости свечения стремятся уменьшить конвективные потери тепла с нити.
В обычных условиях среды при охлаждении металлического проводника происходит уменьшение его электрического сопротивления.
При достижении критической температуры, близкой к нулю градусов по системе измерения Кельвина, происходит резкое падение сопротивления до нулевого значения. На правой картинке показана такая зависимость для ртути.
Это явление, названное сверхпроводимостью, считается перспективной областью для исследований с целью создания материалов, способных значительно снизить потери электроэнергии при ее передаче на огромные расстояния.
Однако, продолжающиеся изучения сверхпроводимости выявили ряд закономерностей, когда на электрическое сопротивление металла, находящегося в области критических температур, влияют другие факторы.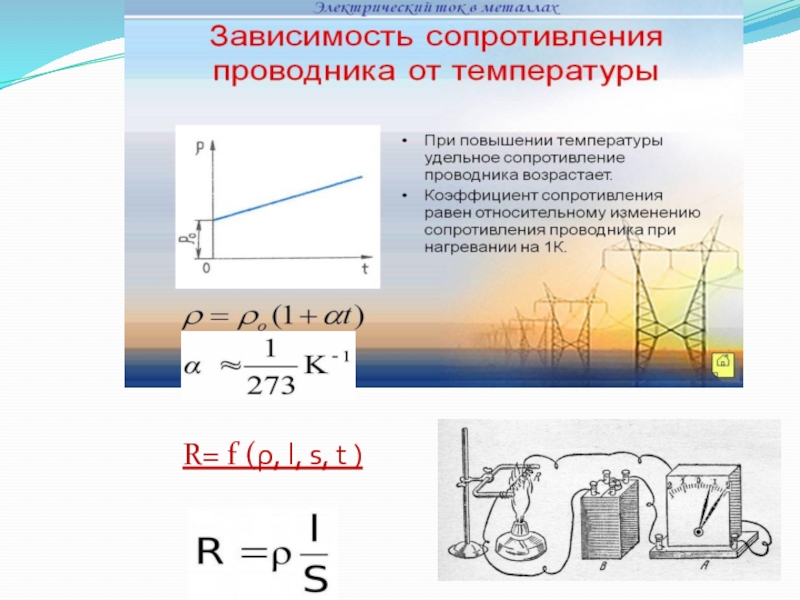 В частности, при прохождении переменного тока с повышением частоты его колебаний возникает сопротивление, величина которого доходит до диапазона обычных значений у гармоник с периодом световых волн.
В частности, при прохождении переменного тока с повышением частоты его колебаний возникает сопротивление, величина которого доходит до диапазона обычных значений у гармоник с периодом световых волн.
Влияние температуры на электрическое сопротивление/проводимость газов
Газы и обычный воздух являются диэлектриками и не проводят электрический ток. Для его образования нужны носители зарядов, которыми выступают ионы, образующиеся в результате воздействия внешних факторов.
Нагрев способен вызвать ионизацию и движение ионов от одного полюса среды к другому. Убедиться в этом можно на примере простого опыта. Возьмем то же оборудование, которым пользовались для определения влияния нагрева на сопротивление металлического проводника, только вместо проволоки к проводам подключим две металлические пластины, разделенные воздушным пространством.
Подсоединенный к схеме амперметр покажет отсутствие тока. Если между пластинами поместить пламя горелки, то стрелка прибора отклонится от нулевого значения и покажет величину проходящего через газовую среду тока.
Таким образом установили, что в газах при нагревании происходит ионизация, приводящая к движению электрически заряженных частиц и снижению сопротивления среды.
На значении тока сказывается мощность внешнего приложенного источника напряжения и разность потенциалов между его контактами. Она способна при больших значениях пробить изоляционный слой газов. Характерным проявлением подобного случая в природе является естественный разряд молнии во время грозы.
Примерный вид вольт-амперной характеристики протекания тока в газах показан на графике.
На начальном этапе под действие температуры и разности потенциалов наблюдается рост ионизации и прохождение тока примерно по линейному закону. Затем кривая приобретает горизонтальное направление, когда увеличение напряжения не вызывает рост тока.
Третий этап пробоя наступает тогда, когда высокая энергия приложенного поля так разгоняет ионы, что они начинают соударяться с нейтральными молекулами, массово образуя из них новые носители зарядов. В результате ток резко возрастает, образуя пробой диэлектрического слоя.
В результате ток резко возрастает, образуя пробой диэлектрического слоя.
Практическое использование проводимости газов
Явление протекания тока через газы используется в радиоэлектронных лампах и люминесцентных светильниках.
Для этого внутри герметичного стеклянного баллона с инертным газом располагают два электрода:
У люминесцентной лампы они выполнены в виде нитей накала, которые разогреваются при включении для создания термоэлектронной эмиссии. Внутренняя поверхность колбы покрыта слоем люминофора. Он излучает видимый нами спектр света, образующийся при инфракрасном облучении, исходящем от паров ртути, бомбардируемых потоком электронов.
Ток газового разряда возникает при приложении напряжения определенной величины между электродами, расположенными по разным концам колбы.
Когда одна из нитей накала перегорит, то на этом электроде нарушится электронная эмиссия и лампа гореть не будет. Однако, если увеличить разность потенциалов между катодом и анодом, то снова возникнет газовый разряд внутри колбы и свечение люминофора возобновится.
Это позволяет использовать светодиодные колбы с нарушенными нитями накала и продлять их ресурс работы. Только следует учитывать, что при этом в несколько раз надо поднять на ней напряжение, А это значительно повышает потребляемую мощность и риски безопасного использования.
Влияние температуры на электрическое сопротивление жидкостей
Прохождение тока в жидкостях создается в основном за счет движения катионов и анионов под действием приложенного извне электрического поля. Лишь незначительную часть проводимости обеспечивают электроны.
Влияние температуры на величину электрического сопротивления жидкого электролита описывается формулой, приведенной на картинке. Поскольку в ней значение температурного коэффициента α всегда отрицательно, то с увеличением нагрева проводимость возрастает, а сопротивление падает так, как показано на графике.
Это явление необходимо учитывать при зарядке жидкостных автомобильных (и не только) аккумуляторных батарей.
Влияние температуры на электрическое сопротивление полупроводников
Изменение свойств полупроводниковых материалов под воздействием температуры позволило использовать их в качестве:
Таким названием обозначают полупроводниковые приборы, изменяющие свое электрическое сопротивление под влиянием тепла. Их температурный коэффициент сопротивления (ТКС) значительно выше, чем у металлов.
Их температурный коэффициент сопротивления (ТКС) значительно выше, чем у металлов.
Величина ТКС у полупроводников может иметь положительное или отрицательное значение. По этому параметру их разделяют на позитивные «РТС» и негативные «NTC» термисторы. Они обладают различными характеристиками.
Для работы терморезистора выбирают одну из точек на его вольт-амперной характеристике:
линейный участок применяют для контроля температуры либо компенсации изменяющихся токов или напряжений;
нисходящая ветвь ВАХ у элементов с ТКС
Применение релейного терморезистора удобно при контроле или измерениях процессов электромагнитных излучений, происходящих на сверхвысоких частотах. Это обеспечило их использование в системах:
1. контроля тепла;
2. пожарной сигнализации;
3. регулирования расхода сыпучих сред и жидкостей.
Кремниевые терморезисторы с маленьким ТКС>0 используют в системах охлаждения и стабилизации температуры транзисторов.
Эти полупроводники работают на основе явления Зеебека: при нагреве спаянного места двух разрозненных металлов на стыке замкнутой цепи возникает ЭДС. Таким способом они превращают тепловую энергию в электричество.
Конструкцию из двух таких элементов называют термопарой. Ее КПД лежит в пределах 7÷10%.
Термоэлементы используют в измерителях температур цифровых вычислительных устройств, требующих миниатюрные габариты и высокую точность показаний, а также в качестве маломощных источников тока.
Полупроводниковые нагреватели и холодильники
Они работают за счет обратного использования термоэлементов, через которые пропускают электрический ток. При этом на одном месте спая происходит его нагрев, а на противоположном — охлаждение.
Полупроводниковые спаи на основе селена, висмута, сурьмы, теллура позволяют обеспечить разность температур в термоэлементе до 60 градусов. Это позволило создать конструкцию холодильного шкафа из полупроводников с температурой в камере охлаждения до -16 градусов.
Зависимость сопротивления проводника от температуры: почему увеличивается
Каждое вещество имеет свое удельное сопротивление. Причем сопротивление будет зависеть от температуры проводника. Убедимся в этом, проведя следующий опыт.
Пропустим ток через стальную спираль. В цепи со спиралью подключим последовательно амперметр. Он покажет некоторое значение. Теперь будем нагревать спираль в пламени газовой горелки. Значение силы тока, которое покажет амперметр, уменьшится. То есть, сила тока будет зависеть от температуры проводника.
Изменение сопротивления в зависимости от температуры
Пусть при температуре 0 градусов, сопротивление проводника равняется R0, а при температуре t сопротивление равно R, тогда относительное изменение сопротивления будет прямо пропорционально изменению температуры t:
В данной формуле а – коэффициент пропорциональности, который называют еще температурным коэффициентом. Он характеризует зависимость сопротивления, которым обладает вещество, от температуры.
Температурный коэффициент сопротивления численно равен относительному изменению сопротивления проводника при нагревании его на 1 Кельвин.
Для всех металлов температурный коэффициент больше нуля. При изменениях температуры он будет незначительно меняться. Поэтому, если изменение температуры невелико, то температурный коэффициент можно считать постоянным, и равным среднему значению из этого интервала температур.
Растворы электролитов с ростом температуры сопротивление уменьшается. То есть для них температурный коэффициент будет меньше нуля.
Сопротивление проводника зависит от удельного сопротивления проводника и от размеров проводника. Так как размеры проводника при нагревании меняются незначительно, то основной составляющей изменения сопротивления проводника является удельное сопротивление.
Зависимость удельного сопротивления проводника от температуры
Попытаемся найти зависимость удельного сопротивления проводника от температуры.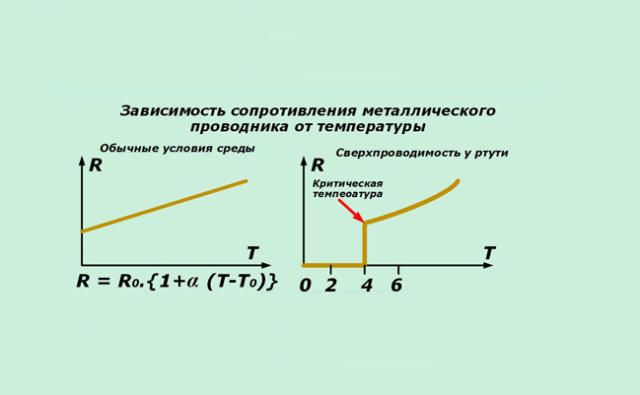
Подставим в полученную выше формулу значения сопротивлений R=p*l/S R0=p0*l/S.
Получим следующую формулу:
Температурный коэффициент можно считать постоянным, следовательно, удельное сопротивление проводника будет прямо пропорционально температуре проводника.
Данная зависимость представлена на следующем рисунке.
Попробуем разобраться, почему увеличивается сопротивление
Когда мы повышаем температуру, то увеличивается амплитуда колебаний ионов в узлах кристаллической решетки. Следовательно, свободные электроны будут чаще с ними сталкиваться. При столкновении они будет терять направленность своего движения. Следовательно, сила тока будет уменьшаться.
Зависимость сопротивления проводника от температуры, широко используется в технике и физике. Например, в изготовлении термометров сопротивления.
Нужна помощь в учебе?
Предыдущая тема: Опыт Милликена и Иоффе: суть эксперимента и как это было
Следующая тема:   Сверхпроводимость: определение, история открытия, свойства и перспективы
лабораторная работа 32
Рассмотрим классическую теорию.
Под действием внешнего электрического поля электроны будут совершать упорядоченное движение (см. рис. 3), т.к. на них действует электрическая сила Fе = еЕ , кроме того, на электрон со стороны поля кристаллической решетки действует сила сопротивления Fс = -. Поэтому общая сила, действующая на электрон, равна
F = еЕ –. (2)
По второму закону Ньютона
mа = еЕ –. (3)
Дрейфовая скорость будет увеличиваться до тех пор, пока Fе = Fс, а = 0, т.е. еЕ = , отсюда
u =. (4).
Величина, равная b = , называется подвижностью электрона.
Смысл коэффициента следующий. Пусть Е = 0, тогда (3) запишется в
Пусть Е = 0, тогда (3) запишется в
виде mа = –.Так как ускорение электрона определяется по формуле:
, то
, или . (5)
Из (5) следует, что u=. Если , то t = τ и это время, за ко-
торое электрон уменьшает дрейфовую скорость в раз. За это время он пробегает расстояние, которое называется транспортным:
L = , (6)
где γ – число столкновений (рассеяния) электронов с дефектами; – средняя длина свободного пробега электрона между двумя последовательными столкновениями. За время τ электрон испытывает γ число столкновений с дефектами кристаллической решетки и пробегает транспортное расстояние L.
С другой стороны, транспортное
расстояние равно L=, так как электрон движется со средней скоростью.
С учетом (6) получим
или . (7)
Подставляя (7) в (4), найдем
u = . (8)
Плотность тока равна
j = nеu, (9)
где n – концентрация электронов.
Подставляя (8) в (9), получим
j =. (10)
Закон Ома в дифференциальной форме
j =. (11)
Тогда с учетом (10) и (11) имеем
и . (12)
Полученная, с точки зрения квантовой
теории, формула удельного сопротивления
ρ имеет такой же вид, что и формулы (12).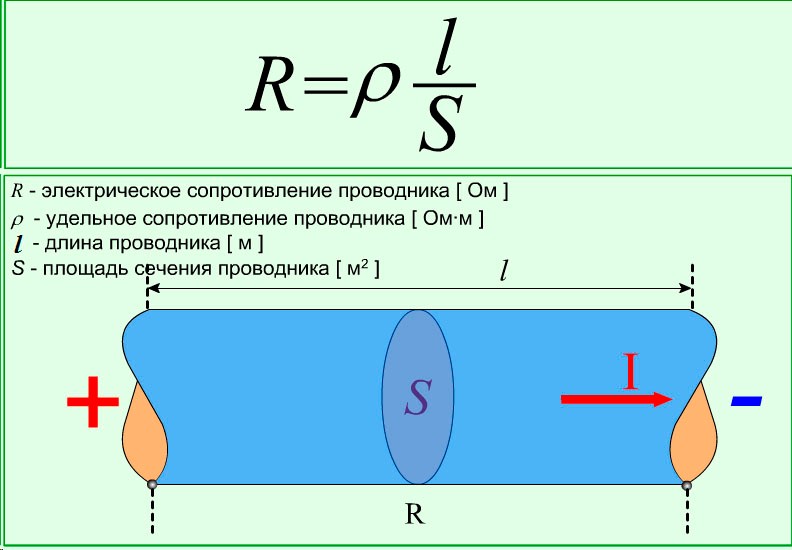 Но вместо m, , , рассмотренные в классической теории, в квантовой
теории вводятся: эффективная масса , фермиевская скорость и длина свободного
пробега . Учитывая эти изменения, формула (12) приобретет следующий
вид (13):
Но вместо m, , , рассмотренные в классической теории, в квантовой
теории вводятся: эффективная масса , фермиевская скорость и длина свободного
пробега . Учитывая эти изменения, формула (12) приобретет следующий
вид (13):
. (13)
Квантово-механические расчеты показывают, что при низких температурах число столкновений , а . Тогда удельное сопротивление ρ пропорционально и сопротивление металлов обусловлено рассеянием электронов проводимости на дефектах и ионах кристаллической решетки.
При высоких температурах сопротивление в основном обусловлено рассеянием электронов на тепловых ионах кристаллической решетки (фононах), а сопротивление, обусловленное рассеянием электронов на дефектах, пренебрежимо мало. Поэтому при высоких температурах не зависит от Т, а . Тогда .
Расчет показывает, что при высоких температурах удельное сопротивление зависит от температуры:
, (14)
где α – температурный
коэффициент сопротивления; – удельное сопротивление
при температуре 0 °С;
t – температура по шкале Цельсия.
Температурный коэффициент α равен относительному изменению удельного сопротивления при изменении температуры проводника на 1 градус:
, .
Для металлических изотропных проводников коэффициент почти не зависит от температуры и примерно равен . Так как сопротивление металлических проводников зависит от [см. формулу (1)], т.е. R~, то с учетом (14) сопротивление можно представить в виде
R = R0(1+). (15)
Откуда можно найти :
, (16)
где R0 – сопротивление проводника при t = 0°С.
Для металлических проводников , т.е. с увеличением температуры сопротивление
увеличивается. Поэтому эти проводники называются проводниками I рода. Для
электролитов, графита и других , т.е. с увеличением температуры сопротивление
проводника уменьшается. Они называются проводниками
II рода.
Поэтому эти проводники называются проводниками I рода. Для
электролитов, графита и других , т.е. с увеличением температуры сопротивление
проводника уменьшается. Они называются проводниками
II рода.
Ход работы
Схема установки приведена на рис. 4. Исследуемый проводник помещается в колбу, заполненную непроводящей жидкостью (масло, глицерин, дистиллированная вода). Температура измеряется термометром.
Для равномерного нагревания жидкость перемешивается мешалкой. Исследуемый проводник R подключается в качестве неизвестного сопротивления к клеммам измерительного моста. Измеряют сопротивление исследуемого проводника при комнатной температуре.
Включают нагреватель и непрерывно перемешивают жидкость мешалкой.
Зависимость удельного объемного сопротивления от температуры.
 Зависимость электрического сопротивления от температуры
Зависимость электрического сопротивления от температурыУдельное сопротивление, а следовательно, и сопротивление металлов, зависит от температуры, увеличиваясь с ее ростом. Температурная зависимость сопротивления проводника объясняется тем, что
- возрастает интенсивность рассеивания (число столкновений) носителей зарядов при повышении температуры;
- изменяется их концентрация при нагревании проводника.
Опыт показывает, что при не слишком высоких и не слишком низких температурах зависимости удельного сопротивления и сопротивления проводника от температуры выражаются формулами:
\(~\rho_t = \rho_0 (1 + \alpha t) ,\) \(~R_t = R_0 (1 + \alpha t) ,\)
где ρ 0 , ρ t — удельные сопротивления вещества проводника соответственно при 0 °С и t °C; R 0 , R t — сопротивления проводника при 0 °С и t °С, α — температурный коэффициент сопротивления: измеряемый в СИ в Кельвинах в минус первой степени (К -1). Для металлических проводников эти формулы применимы начиная с температуры 140 К и выше.
Для металлических проводников эти формулы применимы начиная с температуры 140 К и выше.
Температурный коэффициент сопротивления вещества характеризует зависимость изменения сопротивления при нагревании от рода вещества. Он численно равен относительному изменению сопротивления (удельного сопротивления) проводника при нагревании на 1 К.
\(~\mathcal h \alpha \mathcal i = \frac{1 \cdot \Delta \rho}{\rho \Delta T} ,\)
где \(~\mathcal h \alpha \mathcal i\) — среднее значение температурного коэффициента сопротивления в интервале ΔΤ .
Для всех металлических проводников α > 0 и слабо изменяется с изменением температуры. У чистых металлов α = 1/273 К -1 . У металлов концентрация свободных носителей зарядов (электронов) n = const и увеличение ρ происходит благодаря росту интенсивности рассеивания свободных электронов на ионах кристаллической решетки.
Для растворов электролитов α α
= -0,02 К -1 . Сопротивление электролитов с ростом температуры уменьшается, так как увеличение числа свободных ионов из-за диссоциации молекул превышает рост рассеивания ионов при столкновениях с молекулами растворителя.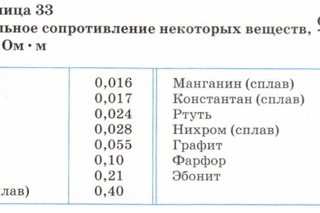
Формулы зависимости ρ и R от температуры для электролитов аналогичны приведенным выше формулам для металлических проводников. Необходимо отметить, что эта линейная зависимость сохраняется лишь в небольшом диапазоне изменения температур, в котором α = const. При больших же интервалах изменения температур зависимость сопротивления электролитов от температуры становится нелинейной.
Графически зависимости сопротивления металлических проводников и электролитов от температуры изображены на рисунках 1, а, б.
При очень низких температурах, близких к абсолютному нулю (-273 °С), сопротивление многих металлов скачком падает до нуля. Это явление получило название сверхпроводимости . Металл переходит в сверхпроводящее состояние.
Зависимость сопротивления металлов от температуры используют в термометрах сопротивления. Обычно в качестве термометрического тела такого термометра берут платиновую проволоку, зависимость сопротивления которой от температуры достаточно изучена.
Об изменениях температуры судят по изменению сопротивления проволоки, которое можно измерить. Такие термометры позволяют измерять очень низкие и очень высокие температуры, когда обычные жидкостные термометры непригодны.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 256-257.
Удельное сопротивление зависит не только от рода вещества, но и от его состояния, в частности, от температуры. Зависимость удельного сопротивления от температуры можно охарактеризовать, задавая температурный коэффициент сопротивления данного вещества:
Он даёт относительное приращение сопротивления при увеличении температуры на один градус.
Температурный коэффициент сопротивления для данного вещества различен при разных температурах. Это показывает, что удельное сопротивление изменяется с температурой не по линейному закону, а зависит от неё более сложным образом.
ρ=ρ 0 (1+αt) (14.12)
где ρ 0 – удельное сопротивление при 0ºС, ρ – его значение при температуре tºС.
Температурный коэффициент сопротивления может быть как положительным, так и отрицательным. У всех металлов сопротивление увеличивается с увеличением температуры, а следовательно для металлов
α >0. У всех электролитов в отличии от металлов сопротивление при нагревании всегда уменьшается. Сопротивление графита с повышением температуры также уменьшается. Для таких веществ α
На основании электронной теории электропроводности металлов можно объяснить зависимость сопротивления проводника от температуры. С повышением температуры его удельное сопротивление увеличивается, а электропроводимость уменьшается. Анализируя выражение (14.7), видим, что электропроводимость пропорциональна концентрации электронов проводимости и средней длине свободного пробега , т.е. чем больше , тем меньшую помеху для упорядоченного движения электронов представляют соударения.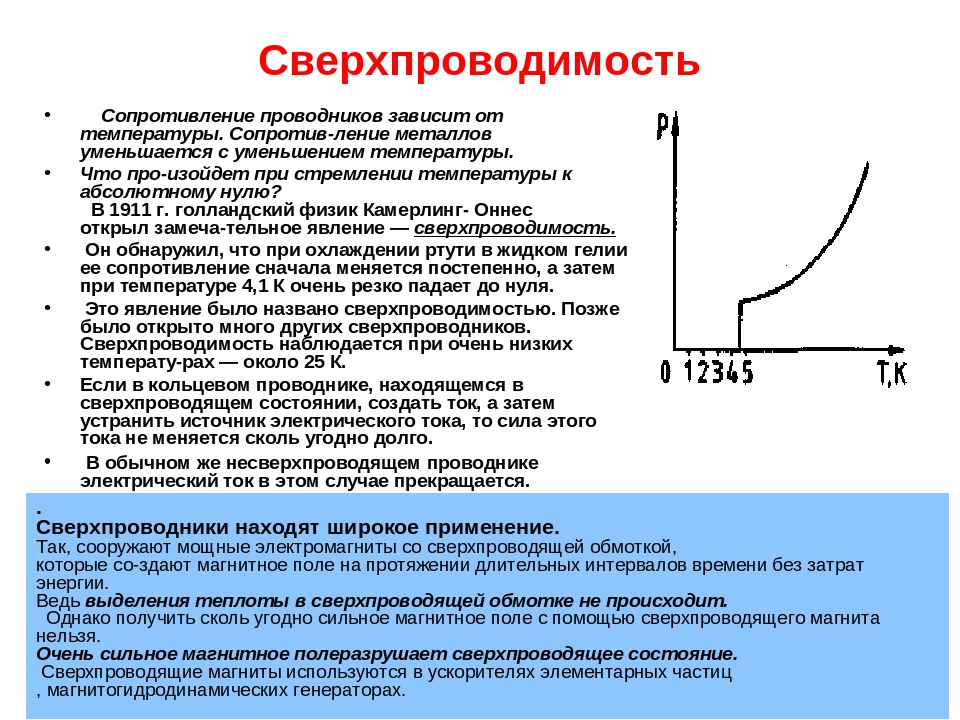 Электропроводимость обратно пропорциональна средней тепловой скорости . Тепловая скорость при повышении температуры возрастает пропорционально , что приводит к уменьшению электропроводимости и увеличению удельного сопротивления проводников. Анализируя формулу (14.7), можно, кроме того, объяснить зависимость γ и ρ от рода проводника.
Электропроводимость обратно пропорциональна средней тепловой скорости . Тепловая скорость при повышении температуры возрастает пропорционально , что приводит к уменьшению электропроводимости и увеличению удельного сопротивления проводников. Анализируя формулу (14.7), можно, кроме того, объяснить зависимость γ и ρ от рода проводника.
При очень низких температурах порядка 1-8ºК сопротивление некоторых веществ резко падает в миллиарды раз и практически становится равным нулю.
Это явление, впервые открыто голландским физиком Г.Камерлинг-Оннесом в 1911 г.. называется сверхпроводимостью . В настоящее время сверхпроводимость установлена у целого ряда чистых элементов (свинца, олова, цинка, ртути, алюминия и др), а также у большого числа сплавов этих элементов друг с другом и с другими элементами. На рис. 14.3 схематически показана зависимость сопротивления сверхпроводников от температуры.
Теория сверхпроводимости была создана в 1958 г. Н. Н. Боголюбовым. Согласно этой теории, сверхпроводимость – это движение электронов в кристаллической решётке без соударений друг с другом и с атомами решётки. Все электроны проводимости движутся как один поток невязкой идеальной жидкости, не взаимодействуя между собой и с решёткой, т.е. не испытывая трения. Поэтому сопротивление сверхпроводников равно нулю. Сильное магнитное поле, проникая в сверхпроводник, отклоняет электроны, и, нарушая «ламинарное течение» электронного потока, вызывает соударение электронов с решёткой, т.е. возникает сопротивление.
Н. Боголюбовым. Согласно этой теории, сверхпроводимость – это движение электронов в кристаллической решётке без соударений друг с другом и с атомами решётки. Все электроны проводимости движутся как один поток невязкой идеальной жидкости, не взаимодействуя между собой и с решёткой, т.е. не испытывая трения. Поэтому сопротивление сверхпроводников равно нулю. Сильное магнитное поле, проникая в сверхпроводник, отклоняет электроны, и, нарушая «ламинарное течение» электронного потока, вызывает соударение электронов с решёткой, т.е. возникает сопротивление.
В сверхпроводящем состоянии между электронами происходит обмен квантами энергии, что приводит к созданию между электронами сил притяжения, которые больше кулоновских сил отталкивания. При этом образуются пары электронов (куперовские пары) с взаимно скомпенсированными магнитными и механическими моментами. Такие пары электронов движутся в кристаллической решётке без сопротивления.
Одним из важнейших практических применений сверхпроводимости является применение её в электромагнитах со сверхпроводящей обмоткой. Если бы не существовало критического магнитного поля, разрушающего сверхпроводимость, то с помощью таких электромагнитов можно было бы получать магнитные поля в десятки и сотни миллионов ампер на сантиметр. Получать такие большие постоянные поля с помощью обычных электромагнитов невозможно, так как для этого потребовались бы колоссальные мощности, и был бы практически невозможен отвод тепла, выделяемого при поглощении обмоткой столь больших мощностей. В сверхпроводящем электромагните расход мощности источника тока ничтожен, а расход мощности на охлаждение обмотки до гелиевой температуре (4,2ºК) на четыре порядка ниже, чем в обычном электромагните, создающем такие же поля. Сверхпроводимость применяется и для создания систем памяти электронных математических машин (криотронные элементы памяти).
Если бы не существовало критического магнитного поля, разрушающего сверхпроводимость, то с помощью таких электромагнитов можно было бы получать магнитные поля в десятки и сотни миллионов ампер на сантиметр. Получать такие большие постоянные поля с помощью обычных электромагнитов невозможно, так как для этого потребовались бы колоссальные мощности, и был бы практически невозможен отвод тепла, выделяемого при поглощении обмоткой столь больших мощностей. В сверхпроводящем электромагните расход мощности источника тока ничтожен, а расход мощности на охлаждение обмотки до гелиевой температуре (4,2ºК) на четыре порядка ниже, чем в обычном электромагните, создающем такие же поля. Сверхпроводимость применяется и для создания систем памяти электронных математических машин (криотронные элементы памяти).
В 1853 г. Видеман и Франц опытным путём установили, что отношение теплопроводности λ к электропроводности γ для всех метал лов при одной и той же температуре одинаково и пропорционально их термодинамической температуре.
Это заставляет предполагать, что теплопроводность в металлах, так же как и электропроводность, обусловлена движением свободных электронов. Будем считать, что электроны подобны одноатомному газу, коэффициент теплопроводности которого, согласно кинетической теории газов, равен
У металлов, не обладающих сверхпроводимостью, при низких температурах из-за наличия примесей наблюдается область 1 – область остаточного сопротивления, почти не зависящая от температуры (рис. 10.5). Остаточное сопротивление — r ост тем меньше, чем чище металл.
Рис. 10.5. Зависимость удельного сопротивления металла от температуры
Быстрый рост удельного сопротивления при низких температурах до температуры Дебая Q д может быть объяснен возбуждением новых частот тепловых колебаний решетки, при которых происходит рассеяние носителей заряда — область 2 .
При Т >
Q
д , когда спектр колебаний возбужден полностью,
увеличение амплитуды колебаний с ростом температуры приводит к линейному росту
сопротивления примерно до Т пл — область 3 . При нарушении
периодичности структуры электрон испытывает рассеяние, приводящее к
изменению направления движения, конечным длинам свободного пробега и
проводимости металла. Энергия электронов проводимости в
металлах составляет 3–15 эВ, что соответствует длинам волн 3–7 Å. Поэтому
любые нарушения периодичности, обусловленные примесями, дефектами, поверхностью
кристалла или тепловыми колебаниями атомов (фононами) вызывают рост удельного
сопротивления металла.
При нарушении
периодичности структуры электрон испытывает рассеяние, приводящее к
изменению направления движения, конечным длинам свободного пробега и
проводимости металла. Энергия электронов проводимости в
металлах составляет 3–15 эВ, что соответствует длинам волн 3–7 Å. Поэтому
любые нарушения периодичности, обусловленные примесями, дефектами, поверхностью
кристалла или тепловыми колебаниями атомов (фононами) вызывают рост удельного
сопротивления металла.
Проведем качественный анализ температурной зависимости удельного сопротивления металлов. Электронный газ в металлах является вырожденным и основным механизмом рассеяния электронов в области высоких температур является рассеяние на фононах.
При понижения температуры до абсолютного нуля сопротивление
нормальных металлов стремится к постоянному значению
— остаточному сопротивлению . Исключением из этого правила
являются сверхпроводящие металлы и сплавы, в которых сопротивление
исчезает ниже некоторой критической температуры Т св
(температура перехода в сверхпроводящее состояние).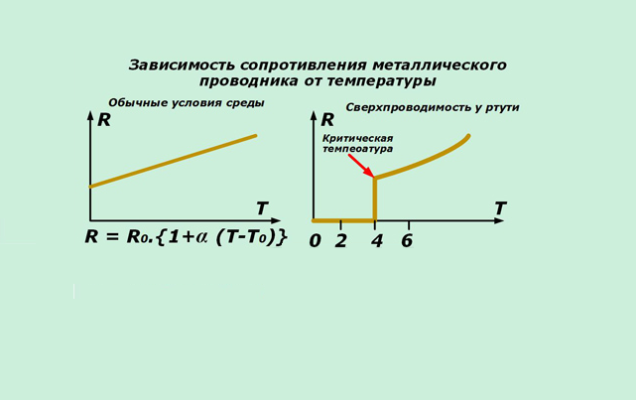
При увеличении температуры, отклонение удельного сопротивления от линейной зависимости у большинства металлов наступает вблизи температуры плавления Т пл . Некоторое отступление от линейной зависимости может наблюдаться у ферромагнитных металлов, в которых происходит дополнительное рассеяние электронов на нарушениях спинового порядка.
При достижении температуры плавления и переходе в жидкое состояние у большинства металлов наблюдается резкое увеличение удельного сопротивления и у некоторых его уменьшение. Если плавление металла или сплава сопровождается увеличением объема, то удельноесопротивление повышается в два–четыре раза (например, у ртути в 4 раза).
У металлов, объем которых
при плавлении уменьшается, наоборот, происходит понижение удельного
сопротивления (у галлия на 53%, у сурьмы –29% и у висмута –54%) .
Подобная аномалия может быть объяснена возрастанием плотности и модуля
сжимаемости при переходе этих металлов из
твердого в
жидкое состояние. У некоторых расплавленных (жидких) металлов удельное
сопротивление с ростом температуры при постоянном объеме перестает расти, у
других оно растет более медленно, чем в твердом состоянии. Такие аномалии,
по-видимому, можно связать с явлениями разупорядочения решетки, которые
неодинаково происходят в различных металлах при переходе их из одного
агрегатного состояния в другое.
У некоторых расплавленных (жидких) металлов удельное
сопротивление с ростом температуры при постоянном объеме перестает расти, у
других оно растет более медленно, чем в твердом состоянии. Такие аномалии,
по-видимому, можно связать с явлениями разупорядочения решетки, которые
неодинаково происходят в различных металлах при переходе их из одного
агрегатного состояния в другое.
Важной характеристикой металлов является температурный коэффициент удельного электрического сопротивления , показывающий относительное изменение удельного сопротивления при изменении температуры на один Кельвин (градус)
a r — положительно, когда удельное сопротивление возрастает при повышении температуры. Очевидно, что величина a r также является функцией температуры. В области 3 линейной зависимости r (T ) (см. рисунок 10.3) выполняется соотношение:
r=r 0 [ 1 +a r (T —T 0)] | (10. |
где r 0 и a r — удельное сопротивление и температурный коэффициент удельного сопротивления при температуре T 0 , а r — удельное сопротивление при температуре T . Экспериментальные данные показывают, что у большинства металлов a r при комнатной температуре примерно 0,004 К -1 .У ферромагнитных металлов значение a r несколько выше.
Остаточное удельное сопротивление металлов. Как говорилось выше, сопротивление нормальных металлов стремится к постоянному значению — остаточному сопротивлению, по мере снижения температуры до абсолютного нуля. У нормальных металлов (не сверхпроводников) остаточное сопротивление возникает из-за рассеяния электронов проводимости статическими дефектами
Общую чистоту и совершенство
металлического проводника можно определять отношением сопротивлений
r
=R 273 /R 4,2 K . Для стандартной меди чистоты 99,999 это
отношение составляет 1000. Б
óльших значений
r
можно достигнуть путем дополнительных зонных
переплавок и приготовлением образцов в виде монокристаллов.
Обширный экспериментальный материал содержит многочисленные данные по измерению сопротивления вметаллах, вызванному наличием в них примесей. Можно отметить следующие наиболее характерные изменения в металлах, вызываемые легированием. Во-первых, не считая фононных возмущений, примесь является локальным нарушением идеальности решетки совершенное во всех других отношениях. Во-вторых, легирование влияет на зонную структуру, сдвигая энергию Ферми и изменяя плотность состоянии и эффективную массу, т.е. параметры, частично определяющие идеальное сопротивление металла. В-третьих, легирование может менять упругие константы и, соответственно, колебательный спектр решетки, оказывая влияние на идеальное сопротивление.
Общее удельное сопротивление проводника при температурах выше 0К складывается из остаточного сопротивления r ост и удельного сопротивления, обусловленного рассеянием на тепловых колебаниях решетки — r Т
r=r ост + r Т | (10. |
Это соотношение известно как правило Матиссена об аддитивности удельного сопротивления. Часто, однако, наблюдаются значительные отклонения от правила Матиссена , причем некоторые их этих отклонений могут говорить не в пользу применимости основных факторов, влияющих на сопротивление металлов при введении в них примесей. Однако второй и третий факторы, отмеченные в начале этого раздела, также дают заметный вклад. Но, все же более сильное воздействие на сопротивление разбавленных твердых растворов оказывает первый фактор.
Изменение остаточного сопротивления на 1 ат . % примеси для одновалентных металлов можно найти по правилу Линде, согласно которому
Δρ ост = а + b (ΔΖ ) | (10.14) |
где a и b —
константы, зависящие от природы металла и периода,
который занимает в Периодической системе элементов примесный атом;
ΔΖ —
разность валентностей металла-растворителя и примесного атома.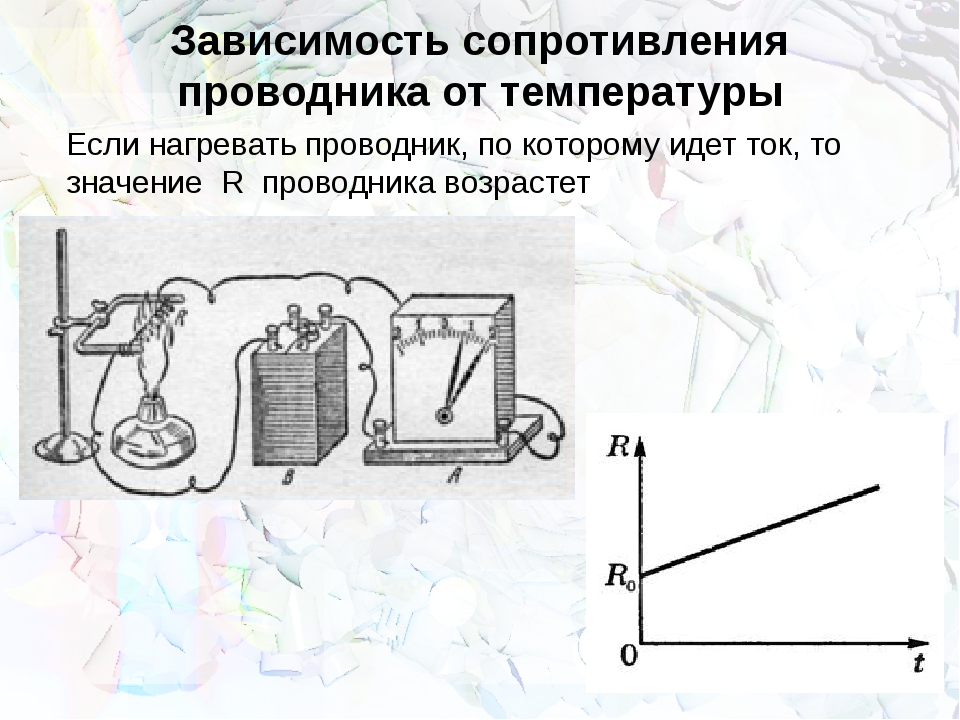 Значительный практический интерес представляют расчеты сопротивления,
обусловленные вакансиями и внедренными атомами. Такие дефекты легко возникает
при облучении образца частицами высоких энергий, например нейтронами из
реактора или ионами из ускорителя.
Значительный практический интерес представляют расчеты сопротивления,
обусловленные вакансиями и внедренными атомами. Такие дефекты легко возникает
при облучении образца частицами высоких энергий, например нейтронами из
реактора или ионами из ускорителя.
На основании классической электронной теории проводимости металлов можно объяснить закон Джоуля-Ленца.
Упорядоченное движение электронов происходит под действием сил поля. Как и выше, будем считать, что в момент соударения с положительными ионами кристаллической решётки электроны полностью передают ей свою кинетическую энергию. К концу свободного пробега скорость электрона , а кинетическая энергия
(14.9)
Мощность, выделяемая единицей объёма металла (плотность мощности), равна произведению энергии одного электрона на число соударений в секундуи на концентрациюn электронов:
(14.10)
Учитывая (14.7), имеем
— закон Джоуля-Ленца в дифференциальной форме.
Если нас
интересует энергия, выделяемая проводником
длиной ℓ, площадью поперечного сечения
S
за промежуток времени dt,
то выражение (14. 10) нужно умножить на
объём проводника V=St
и время dt:
10) нужно умножить на
объём проводника V=St
и время dt:
Учитывая, что
(гдеR–
сопротивление проводника), получаем
закон Джоуля-Ленца в виде
§ 14.3 Зависимость сопротивления металлов от температуры. Сверхпроводимость. Закон Видемана-Франца
Удельное сопротивление зависит не только от рода вещества, но и от его состояния, в частности, от температуры. Зависимость удельного сопротивления от температуры можно охарактеризовать, задавая температурный коэффициент сопротивления данного вещества:
(14.11)
Он даёт относительное приращение сопротивления при увеличении температуры на один градус.
Рисунок 14.3
Температурный коэффициент сопротивления для данного вещества различен при разных температурах. Это показывает, что удельное сопротивление изменяется с температурой не по линейному закону, а зависит от неё более сложным образом.ρ=ρ 0 (1+αt) (14.12)
где ρ 0 – удельное сопротивление при 0ºС, ρ – его значение при температуре tºС.
Температурный
коэффициент сопротивления может быть
как положительным, так и отрицательным.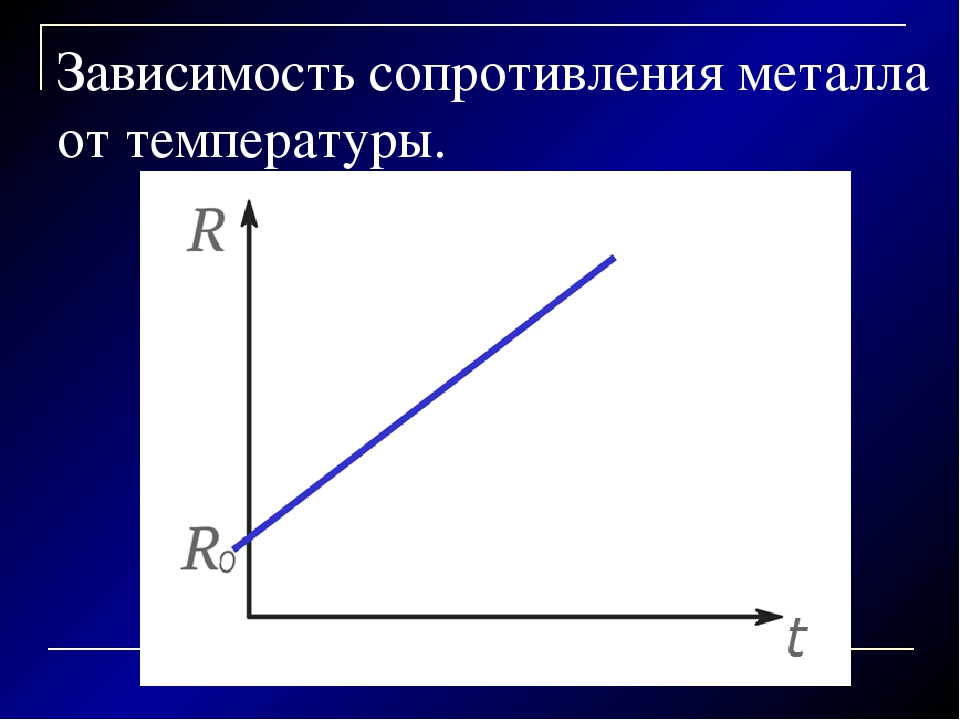 У всех металлов сопротивление увеличивается
с увеличением температуры, а следовательно
для металлов
У всех металлов сопротивление увеличивается
с увеличением температуры, а следовательно
для металлов
α >0. У всех электролитов в отличии от металлов сопротивление при нагревании всегда уменьшается. Сопротивление графита с повышением температуры также уменьшается. Для таких веществ α
На основании
электронной теории электропроводности
металлов можно объяснить зависимость
сопротивления проводника от температуры.
С повышением температуры его удельное
сопротивление увеличивается, а
электропроводимость уменьшается.
Анализируя выражение (14.7), видим, что
электропроводимость пропорциональна
концентрации электронов проводимости
и средней длине свободного пробега ,
т.е. чем больше ,
тем меньшую помеху для упорядоченного
движения электронов представляют
соударения. Электропроводимость обратно
пропорциональна средней тепловой
скорости υ τ > .
Тепловая
скорость при повышении температуры
возрастает пропорционально
,
что приводит к уменьшению электропроводимости
и увеличению удельного сопротивления
проводников. Анализируя формулу (14.7),
можно, кроме того, объяснить зависимость
γ и
ρ
от рода
проводника.
Анализируя формулу (14.7),
можно, кроме того, объяснить зависимость
γ и
ρ
от рода
проводника.
При очень низких температурах порядка 1-8ºК сопротивление некоторых веществ резко падает в миллиарды раз и практически становится равным нулю.
Это явление, впервые открыто голландским физиком Г.Камерлинг-Оннесом в 1911 г.. называется сверхпроводимостью . В настоящее время сверхпроводимость установлена у целого ряда чистых элементов (свинца, олова, цинка, ртути, алюминия и др), а также у большого числа сплавов этих элементов друг с другом и с другими элементами. На рис. 14.3 схематически показана зависимость сопротивления сверхпроводников от температуры.
Теория сверхпроводимости
была создана в 1958 г. Н.Н. Боголюбовым.
Согласно этой теории, сверхпроводимость
– это движение электронов в кристаллической
решётке без соударений друг с другом и
с атомами решётки. Все электроны
проводимости движутся как один поток
невязкой идеальной жидкости, не
взаимодействуя между собой и с решёткой,
т. е. не испытывая трения. Поэтому
сопротивление сверхпроводников равно
нулю. Сильное магнитное поле, проникая
в сверхпроводник, отклоняет электроны,
и, нарушая «ламинарное течение»
электронного потока, вызывает соударение
электронов с решёткой, т.е. возникает
сопротивление.
е. не испытывая трения. Поэтому
сопротивление сверхпроводников равно
нулю. Сильное магнитное поле, проникая
в сверхпроводник, отклоняет электроны,
и, нарушая «ламинарное течение»
электронного потока, вызывает соударение
электронов с решёткой, т.е. возникает
сопротивление.
В сверхпроводящем состоянии между электронами происходит обмен квантами энергии, что приводит к созданию между электронами сил притяжения, которые больше кулоновских сил отталкивания. При этом образуются пары электронов (куперовские пары) с взаимно скомпенсированными магнитными и механическими моментами. Такие пары электронов движутся в кристаллической решётке без сопротивления.
Одним из важнейших
практических применений сверхпроводимости
является применение её в электромагнитах
со сверхпроводящей обмоткой. Если бы
не существовало критического магнитного
поля, разрушающего сверхпроводимость,
то с помощью таких электромагнитов
можно было бы получать магнитные поля
в десятки и сотни миллионов ампер на
сантиметр. Получать такие большие
постоянные поля с помощью обычных
электромагнитов невозможно, так как
для этого потребовались бы колоссальные
мощности, и был бы практически невозможен
отвод тепла, выделяемого при поглощении
обмоткой столь больших мощностей. В
сверхпроводящем электромагните расход
мощности источника тока ничтожен, а
расход мощности на охлаждение обмотки
до гелиевой температуре (4,2ºК) на четыре
порядка ниже, чем в обычном электромагните,
создающем такие же поля. Сверхпроводимость
применяется и для создания систем памяти
электронных математических машин
(криотронные элементы памяти).
Получать такие большие
постоянные поля с помощью обычных
электромагнитов невозможно, так как
для этого потребовались бы колоссальные
мощности, и был бы практически невозможен
отвод тепла, выделяемого при поглощении
обмоткой столь больших мощностей. В
сверхпроводящем электромагните расход
мощности источника тока ничтожен, а
расход мощности на охлаждение обмотки
до гелиевой температуре (4,2ºК) на четыре
порядка ниже, чем в обычном электромагните,
создающем такие же поля. Сверхпроводимость
применяется и для создания систем памяти
электронных математических машин
(криотронные элементы памяти).
В 1853 г. Видеман и Франц опытным путём установили, что отношение теплопроводности λ к электропроводности γ для всех метал лов при одной и той же температуре одинаково и пропорционально их термодинамической температуре.
Это заставляет предполагать, что теплопроводность в металлах, так же как и электропроводность, обусловлена движением свободных электронов. Будем считать, что электроны подобны одноатомному газу, коэффициент теплопроводности которого, согласно кинетической теории газов, равен
(14. 13)
13)
(n – концентрация атомов, m -масса атома, -средняя длина свободного пробега электрона, c V -удельная теплоёмкость).
Для одноатомного газа
(k -постоянная Больцмана, М –молярная масса).
(14.14)
Из уравнений (14.7) и (14.14) находим отношение теплопроводности и электропроводности металла:
(14.15)
Из кинетической
теории газов известно, что
,
тогда
(14.16)
(k и е – постоянные величины).
Поэтому отношение теплопроводности и электропроводности металла пропорционально термодинамической температуре, что и было установлено законом Видемана-Франца. Так как k =1,38∙10 -23 Дж/К; е = 1,6∙10 -19 Кл, то
(14.17)
Закон Видемана-Франца
для большинства металлов выполняется
при температуре 100-400 К, но при низкой
температуре закон существенно нарушается.
Имеются металлы (бериллий, марганец)
которые совсем не подчиняются закону
Видемана-Франца. Выход из непреодолимых
противоречий был найден в квантовой
электронной теории металлов.
Одна из характеристик любого проводящего электрический ток материала — это зависимость сопротивления от температуры. Если ее изобразить в виде графика на где по горизонтальной оси отмечаются промежутки времени (t), а по вертикальной — значение омического сопротивления (R), то получится ломаная линия. Зависимость сопротивления от температуры схематично состоит из трех участков. Первый соответствует небольшому нагреву — в этом время сопротивление изменяется очень незначительно. Так происходит до определенного момента, после которого линия на графике резко идет вверх — это второй участок. Третья, последняя составляющая — это прямая, уходящая вверх от точки, на которой остановился рост R, под относительно небольшим углом к горизонтальной оси.
Физический смысл данного графика следующий: зависимость сопротивления от температуры у проводника описывается простым до тех пор, пока величина нагрева не превысит какое-то значение, характерное именно для данного материала. Приведем абстрактный пример: если при температуре +10°C сопротивление вещества составляет 10 Ом, то до 40°C значение R практически не изменится, оставаясь в пределах погрешности измерений. Но уже при 41°C возникнет скачок сопротивления до 70 Ом. Если же дальнейший рост температуры не прекратится, то на каждый последующий градус придутся дополнительные 5 Ом.
Но уже при 41°C возникнет скачок сопротивления до 70 Ом. Если же дальнейший рост температуры не прекратится, то на каждый последующий градус придутся дополнительные 5 Ом.
Данное свойство широко используется в различных электротехнических устройствах, поэтому закономерно привести данные по меди как одному из самых распространенных материалов в Так, для медного проводника нагрев на каждый дополнительный градус приводит к росту сопротивления на полпроцента от удельного значения (можно найти в справочных таблицах, приводится для 20°C, 1 м длины сечением 1 кв.мм).
При возникновении в металлическом проводнике появляется электрический ток — направленное перемещение элементарных частиц, обладающих зарядом. Ионы, находящиеся в узлах металла, не в состоянии долго удерживать электроны на своих внешних орбитах, поэтому они свободно перемещаются по всему объему материала от одного узла к другому. Это хаотичное движение обусловлено внешней энергией — теплом.
Хотя факт перемещения налицо, оно не является направленным, поэтому не рассматривается в качестве тока. При появлении электрического поля электроны ориентируются в соответствии с его конфигурацией, формируя направленное движение. Но так как тепловое воздействие никуда не исчезло, то хаотично перемещающиеся частицы сталкиваются с направленными полем. Зависимость сопротивления металлов от температуры показывает величину помех прохождению тока. Чем больше температура, тем выше R проводника.
При появлении электрического поля электроны ориентируются в соответствии с его конфигурацией, формируя направленное движение. Но так как тепловое воздействие никуда не исчезло, то хаотично перемещающиеся частицы сталкиваются с направленными полем. Зависимость сопротивления металлов от температуры показывает величину помех прохождению тока. Чем больше температура, тем выше R проводника.
Очевидный вывод: снижая степень нагрева, можно уменьшить и сопротивление. (около 20°K) как раз и характеризуется существенным снижением теплового хаотичного движения частиц в структуре вещества.
Рассматриваемое свойство проводящих материалов нашло широкое применение в электротехнике. Например, зависимость сопротивления проводника от температуры используется в электронных датчиках. Зная ее значение для какого-либо материала, можно изготовить терморезистор, подключить его к цифровому или аналоговому считывающему устройству, выполнить соответствующую градуировку шкалы и использовать в качестве альтернативы В основе большинства современных термодатчиков заложен именно такой принцип, ведь надежность выше, а конструкция проще.
Кроме того, зависимость сопротивления от температуры дает возможность рассчитывать нагрев обмоток электродвигателей.
Зависимость сопротивления от длины. Как зависит сопротивление проводника от температуры
Удельное сопротивление, а следовательно, и сопротивление металлов, зависит от температуры, увеличиваясь с ее ростом. Температурная зависимость сопротивления проводника объясняется тем, что
- возрастает интенсивность рассеивания (число столкновений) носителей зарядов при повышении температуры;
- изменяется их концентрация при нагревании проводника.
Опыт показывает, что при не слишком высоких и не слишком низких температурах зависимости удельного сопротивления и сопротивления проводника от температуры выражаются формулами:
где — удельные сопротивления вещества проводника соответственно при 0°С и t°C; R 0 , R t — сопротивления проводника при 0°С и t°С, — температурный коэффициент сопротивления: измеряемый в СИ в Кельвинах в минус первой степени (К -1). Для металлических проводников эти формулы применимы начиная с температуры 140 К и выше.
Для металлических проводников эти формулы применимы начиная с температуры 140 К и выше.
Вещества характеризует зависимость изменения сопротивления при нагревании от рода вещества. Он численно равен относительному изменению сопротивления (удельного сопротивления) проводника при нагревании на 1 К.
где — среднее значение температурного коэффициента сопротивления в интервале .
Для всех металлических проводников > 0 и слабо изменяется с изменением температуры. У чистых металлов = 1/273 К -1 . У металлов концентрация свободных носителей зарядов (электронов) n = const и увеличение происходит благодаря росту интенсивности рассеивания свободных электронов на ионах кристаллической решетки.
Для растворов электролитов 0, например, для 10%-ного раствора поваренной соли = -0,02 К -1 . Сопротивление электролитов с ростом температуры уменьшается, так как увеличение числа свободных ионов из-за диссоциации молекул превышает рост рассеивания ионов при столкновениях с молекулами растворителя.
Формулы зависимости и R от температуры для электролитов аналогичны приведенным выше формулам для металлических проводников. Необходимо отметить, что эта линейная зависимость сохраняется лишь в небольшом диапазоне изменения температур, в котором = const. При больших же интервалах изменения температур зависимость сопротивления электролитов от температуры становится нелинейной.
Графически зависимости сопротивления металлических проводников и электролитов от температуры изображены на рисунках 1, а, б.
При очень низких температурах, близких к абсолютному нулю (-273 °С), сопротивление многих металлов скачком падает до нуля. Это явление получило название сверхпроводимости. Металл переходит в сверхпроводящее состояние.
Зависимость сопротивления металлов от температуры используют в термометрах сопротивления. Обычно в качестве термометрического тела такого термометра берут платиновую проволоку, зависимость сопротивления которой от температуры достаточно изучена.
Об изменениях температуры судят по изменению сопротивления проволоки, которое можно измерить. Такие термометры позволяют измерять очень низкие и очень высокие температуры, когда обычные жидкостные термометры непригодны.
Такие термометры позволяют измерять очень низкие и очень высокие температуры, когда обычные жидкостные термометры непригодны.
>>Физика: Зависимость сопротивления проводника от температуры
Различные вещества имеют разные удельные сопротивления (см. § 104). Зависит ли сопротивление от состояния проводника? от его температуры ? Ответ должен дать опыт.
Если пропустить ток от аккумулятора через стальную спираль, а затем начать нагревать ее в пламени горелки, то амперметр покажет уменьшение силы тока. Это означает, что с изменением температуры сопротивление проводника меняется.
Если при температуре, равной 0°С, сопротивление проводника равно R 0 , а при температуре t оно равно R , то относительное изменение сопротивления, как показывает опыт, прямо пропорционально изменению температуры t :
Коэффициент пропорциональности α называют температурным коэффициентом сопротивления . Он характеризует зависимость сопротивления вещества от температуры. Температурный коэффициент сопротивления численно равен относительному изменению сопротивления проводника при нагревании на 1 К.
Для всех металлических проводников коэффициент α > 0 и незначительно меняется с изменением температуры. Если интервал изменения температуры невелик, то температурный коэффициент можно считать постоянным и равным его среднему значению на этом интервале температур. У чистых металлов α ≈ 1/273 K -1 . У растворов электролитов сопротивление с ростом температуры не увеличивается, а уменьшается . Для них α α ≈
-0,02 K -1 .
Температурный коэффициент сопротивления численно равен относительному изменению сопротивления проводника при нагревании на 1 К.
Для всех металлических проводников коэффициент α > 0 и незначительно меняется с изменением температуры. Если интервал изменения температуры невелик, то температурный коэффициент можно считать постоянным и равным его среднему значению на этом интервале температур. У чистых металлов α ≈ 1/273 K -1 . У растворов электролитов сопротивление с ростом температуры не увеличивается, а уменьшается . Для них α α ≈
-0,02 K -1 .
При нагревании проводника его геометрические размеры меняются незначительно. Сопротивление проводника меняется в основном за счет изменения его удельного сопротивления. Можно найти зависимость этого удельного сопротивления от температуры, если в формулу (16.1) подставить значения
. Вычисления приводят к следующему результату:
Так как α мало меняется при изменении температуры проводника, то можно считать, что удельное сопротивление проводника линейно зависит от температуры (рис.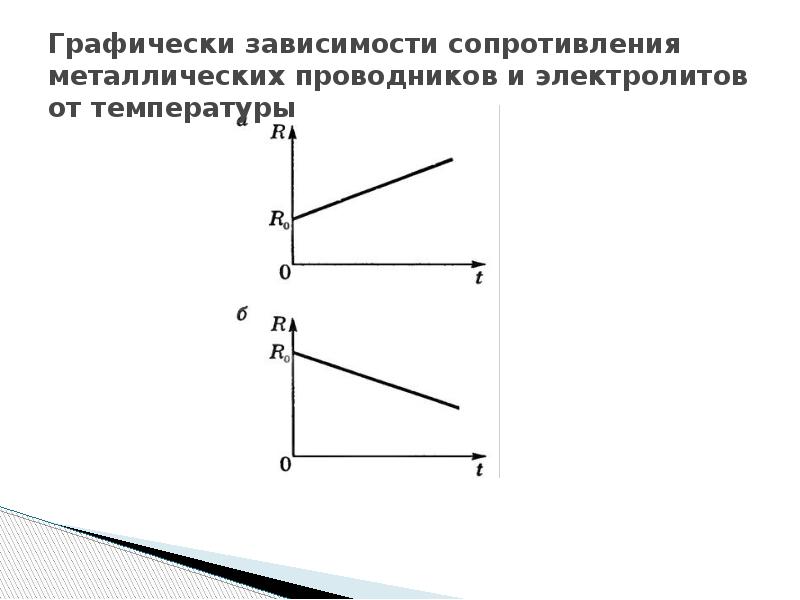 16.2 ).
16.2 ).
Увеличение сопротивления можно объяснить тем, что при повышении температуры увеличивается амплитуда колебаний ионов в узлах кристаллической решетки, поэтому свободные электроны сталкиваются с ними чаще, теряя при этом направленность движения. Хотя коэффициент α довольно мал, учет зависимости сопротивления от температуры при расчете нагревательных приборов совершенно необходим. Так, сопротивление вольфрамовой нити лампы накаливания увеличивается при прохождении по ней тока более чем в 10 раз.
У некоторых сплавов, например у сплава меди с никелем (константан), температурный коэффициент сопротивления очень мал: α ≈ 10 -5 K -1 ; удельное сопротивление константана велико: ρ ≈ 10 -6 Ом м. Такие сплавы используют для изготовления эталонных сопротивлений и добавочных сопротивлений к измерительным приборам, т. е. в тех случаях, когда требуется, чтобы сопротивление заметно не менялось при колебаниях температуры.
Зависимость сопротивления металлов от температуры используют в термометрах сопротивления . Обычно в качестве основного рабочего элемента такого термометра берут платиновую проволоку, зависимость сопротивления которой от температуры хорошо известна. Об изменениях температуры судят по изменению сопротивления проволоки, которое можно измерить.
Обычно в качестве основного рабочего элемента такого термометра берут платиновую проволоку, зависимость сопротивления которой от температуры хорошо известна. Об изменениях температуры судят по изменению сопротивления проволоки, которое можно измерить.
Такие термометры позволяют измерять очень низкие и очень высокие температуры, когда обычные жидкостные термометры непригодны.
Удельное сопротивление металлов растет линейно с увеличением температуры. У растворов электролитов оно уменьшается при увеличении температуры.
???
1. Когда электрическая лампочка потребляет большую мощность: сразу после включения ее в сеть или спустя несколько минут?
2. Если бы сопротивление спирали электроплитки не менялось с температурой, то ее длина при номинальной мощности должна быть большей или меньшей?
Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс
Содержание урока конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологии Практика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учеников Иллюстрации аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочие Совершенствование учебников и уроков исправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей идеальные уроки календарный план на год методические рекомендации программы обсуждения Интегрированные урокиЕсли у вас есть исправления или предложения к данному уроку,
Вспомните, какую физическую величину называют сопротивлением.
От чего и как зависит сопротивление металлического проводника?
Различные вещества имеют разные удельные сопротивления (см. § 101). Зависит ли сопротивление от состояния проводника? от его температуры? Ответ должен дать опыт.
Если пропустить ток от аккумулятора через стальную спираль, а затем начать нагревать её в пламени горелки, то амперметр покажет уменьшение силы тока. Это означает, что с изменением температуры сопротивление проводника меняется.
Если при температуре, равной 0 °С, сопротивление проводника равно R 0 , а при температуре t оно равно R, то относительное изменение сопротивления, как показывает опыт, прямо пропорционально изменению температуры t:
Коэффициент пропорциональности α называют температурным коэффициентом сопротивления.
Он характеризует зависимость сопротивления вещества от температуры.
Для всех металлических проводников коэффициент α > 0 и незначительно меняется с изменением температуры. Если интервал изменения температуры невелик, то температурный коэффициент можно считать постоянным и равным его среднему значению на этом интервале температур. У чистых металлов
У чистых металлов
При нагревании проводника его геометрические размеры меняются незначительно. Сопротивление проводника меняется в основном за счёт изменения его удельного сопротивления. Можно найти зависимость этого удельного сопротивления от температуры, если в формулу (16.1) подставить значения Вычисления приводят к следующему результату:
ρ = ρ 0 (1 + αt), или ρ = ρ 0 (1 + αΔТ), (16.2)
где ΔТ — изменение абсолютной температуры.
Увеличение сопротивления можно объяснить тем, что при повышении температуры увеличивается амплитуда колебаний ионов в узлах кристаллической решётки, поэтому свободные электроны сталкиваются с ними чаще, теряя при этом направленность движения. Хотя коэффициент а довольно мал, учёт зависимости сопротивления от температуры при расчёте параметров нагревательных приборов совершенно необходим. Так, сопротивление вольфрамовой нити лампы накаливания увеличивается при прохождении по ней тока за счёт нагревания более чем в 10 раз.
У некоторых сплавов, например у сплава меди с никелем (Константин), температурный коэффициент сопротивления очень мал: α ≈ 10 -5 К -1 ; удельное сопротивление Константина велико: ρ ≈ 10 -6 Ом м. Такие сплавы используют для изготовления эталонных резисторов и добавочных резисторов к измерительным приборам, т. е. в тех случаях, когда требуется, чтобы сопротивление заметно не менялось при колебаниях температуры.
Такие сплавы используют для изготовления эталонных резисторов и добавочных резисторов к измерительным приборам, т. е. в тех случаях, когда требуется, чтобы сопротивление заметно не менялось при колебаниях температуры.
Существуют и такие металлы, например никель, олово, платина и др., температурный коэффициент которых существенно больше: α ≈ 10 -3 К -1 . Зависимость их сопротивления от температуры можно использовать для измерения самой температуры, что и осуществляется в термометрах сопротивления .
На зависимости сопротивления от температуры основаны и приборы, изготовленные из полупроводниковых материалов, — термисторы . Для них характерны большой температурный коэффициент сопротивления (в десятки раз превышающий этот коэффициент у металлов), стабильность характеристик во времени. Номинальное сопротивление термисторов значительно выше, чем у металлических термометров сопротивления, оно обычно составляет 1, 2, 5, 10, 15 и 30 кОм.
Каждое вещество имеет свое удельное сопротивление. Причем сопротивление будет зависеть от температуры проводника. Убедимся в этом, проведя следующий опыт.
Пропустим ток через стальную спираль. В цепи со спиралью подключим последовательно амперметр . Он покажет некоторое значение. Теперь будем нагревать спираль в пламени газовой горелки. Значение силы тока, которое покажет амперметр, уменьшится. То есть, сила тока будет зависеть от температуры проводника.
Изменение сопротивления в зависимости от температуры
Пусть при температуре 0 градусов, сопротивление проводника равняется R0, а при температуре t сопротивление равно R, тогда относительное изменение сопротивления будет прямо пропорционально изменению температуры t:
В данной формуле а — коэффициент пропорциональности, который называют еще температурным коэффициентом. Он характеризует зависимость сопротивления, которым обладает вещество, от температуры.
Температурный коэффициент сопротивления численно равен относительному изменению сопротивления проводника при нагревании его на 1 Кельвин.
Для всех металлов температурный коэффициент больше нуля. При изменениях температуры он будет незначительно меняться. Поэтому, если изменение температуры невелико, то температурный коэффициент можно считать постоянным, и равным среднему значению из этого интервала температур.
Растворы электролитов с ростом температуры сопротивление уменьшается. То есть для них температурный коэффициент будет меньше нуля.
Сопротивление проводника зависит от удельного сопротивления проводника и от размеров проводника. Так как размеры проводника при нагревании меняются незначительно, то основной составляющей изменения сопротивления проводника является удельное сопротивление.
Зависимость удельного сопротивления проводника от температуры
Попытаемся найти зависимость удельного сопротивления проводника от температуры.
Подставим в полученную выше формулу значения сопротивлений R=p*l/S R0=p0*l/S.
Получим следующую формулу:
Данная зависимость представлена на следующем рисунке.
Попробуем разобраться, почему увеличивается сопротивление
Когда мы повышаем температуру, то увеличивается амплитуда колебаний ионов в узлах кристаллической решетки. Следовательно, свободные электроны будут чаще с ними сталкиваться. При столкновении они будет терять направленность своего движения. Следовательно, сила тока будет уменьшаться.
В своей практической деятельности каждый электрик встречается с разными условиями прохождения носителей зарядов в металлах, полупроводниках, газах и жидкостях. На величину тока влияет электрическое сопротивление, которое различным образом изменяется под влиянием окружающей среды.
Одним из таких факторов является температурное воздействие. Поскольку оно значительно изменяет условия протекания тока, то учитывается конструкторами в производстве электрооборудования. Электротехнический персонал, участвующий в обслуживании и эксплуатации электроустановок, обязан грамотно использовать эти особенности в практической работе.
Влияние температуры на электрическое сопротивление металлов
В школьном курсе физики предлагается провести такой опыт: взять амперметр, батарейку, отрезок проволоки, соединительные провода и горелку. Вместо амперметра с батарейкой можно подключить омметр или использовать его режим в мультиметре.
Теперь поднесем пламя горелки к проволоке и станем ее нагревать. Если смотреть на амперметр, то будет видно, что стрелка станет перемещаться влево и достигнет положения, отмеченного красным цветом.
Результат опыта демонстрирует, что при нагревании металлов их проводимость уменьшается, а сопротивление возрастает.
Математическое обоснование этого явления приведено формулами прямо на картинке. В нижнем выражении хорошо видно, что электрическое сопротивление «R» металлического проводника прямо пропорционально его температуре «Т» и зависит еще от нескольких параметров.
Как нагрев металлов ограничивает электрический ток на практике
Лампы накаливания
Ежедневно при включении освещения мы встречаемся с проявлением этого свойства у ламп накаливания. Проведем несложные измерения на лампочке с мощностью 60 ватт.
Самым простым омметром, питающемся от низковольтной батарейки 4,5 V, замерим сопротивление между контактами цоколя и увидим значение 59 Ом. Этой величиной обладает нить накала в холодном состоянии.
Вкрутим лампочку в патрон и через амперметр подключим к ней напряжение домашней сети 220 вольт. Стрелка амперметра покажет 0,273 ампера. По определим сопротивление нити в нагретом состоянии. Оно составит 896 Ом и превысит предыдущее показание омметра в 15,2 раза.
Такое превышение предохраняет металл тела накала от перегорания и разрушения, обеспечивая его длительную работоспособность под напряжением.
Переходные процессы при включении
При работе нити накала на ней создается тепловой баланс между нагревом от проходящего электрического тока и отводом части тепла в окружающую среду. Но, на первоначальном этапе включения при подаче напряжения возникают переходные процессы, создающие бросок тока, который может привести к перегоранию нити.
Переходные процессы протекают за короткое время и вызваны тем, что скорость возрастания электрического сопротивления от нагрева металла не успевает за увеличением тока. После их окончания устанавливается рабочий режим.
Во время длительного свечения лампы постепенно толщина ее нити доходит до критического состояния, которое приводит к перегоранию. Чаще всего этот момент возникает при очередном новом включении.
Для продления ресурса лампы различными способами уменьшают этот бросок тока, используя:
1. устройства, обеспечивающие плавную подачу и снятие напряжения;
2. схемы последовательного подключения к нити накала резисторов, полупроводников или терморезисторов (термисторов).
Пример одного из способов ограничения пускового тока для автомобильных светильников показан на картинке ниже.
Здесь ток на лампочку подается после включения тумблера SA через предохранитель FU и ограничивается резистором R, у которого номинал подбирается так, чтобы бросок тока во время переходных процессов не превышал номинальное значение.
При нагреве нити накала ее сопротивление возрастает, что ведет к увеличению разности потенциалов на ее контактах и параллельно подключенной обмотке реле KL1. Когда напряжение достигнет величины уставки реле, то нормально открытый контакт KL1 замкнется и зашунтирует резистор. Через лампочку начнет протекать рабочий ток уже установившегося режима.
Влияние температуры металла на его электрическое сопротивление используется в работе измерительных приборов. Их называют .
Их чувствительный элемент выполняют тонкой проволочкой из металла, сопротивление которой тщательно замерено при определенных температурах. Эту нить монтируют в корпусе со стабильными термическими свойствами и закрывают защитным чехлом. Созданная конструкция помещается в среду, температуру которой необходимо постоянно контролировать.
На выводы чувствительного элемента монтируются провода электрической схемы, которыми подключается цепь замера сопротивления. Его величина пересчитывается в значения температуры на основе ранее произведенной калибровки прибора.
Бареттер — стабилизатор тока
Так называют прибор, состоящий из стеклянного герметичного баллона с газообразным водородом и металлической проволочной спиралью из железа, вольфрама или платины. Эта конструкция по внешнему виду напоминает лампочку накаливания, но она обладает специфической вольт-амперной нелинейной характеристикой.
На ВАХ в определенном ее диапазоне образуется рабочая зона, которая не зависит от колебаний приложенного на тело накала напряжения. На этом участке бареттер хорошо компенсирует пульсации питания и работает в качестве стабилизатора тока на подключенной последовательно к нему нагрузке.
Работа бареттера основана на свойстве тепловой инерции тела накала, которая обеспечивается маленьким сечением нити и высокой теплопроводностью окружающего ее водорода. За счет этого при снижении напряжения на приборе ускоряется отвод тепла с его нити.
Это основное отличие бареттера от осветительных ламп накаливания, в которых для поддержания яркости свечения стремятся уменьшить конвективные потери тепла с нити.
Сверхпроводимость
В обычных условиях среды при охлаждении металлического проводника происходит уменьшение его электрического сопротивления.
При достижении критической температуры, близкой к нулю градусов по системе измерения Кельвина, происходит резкое падение сопротивления до нулевого значения. На правой картинке показана такая зависимость для ртути.
Это явление, названное сверхпроводимостью, считается перспективной областью для исследований с целью создания материалов, способных значительно снизить потери электроэнергии при ее передаче на огромные расстояния.
Однако, продолжающиеся изучения сверхпроводимости выявили ряд закономерностей, когда на электрическое сопротивление металла, находящегося в области критических температур, влияют другие факторы. В частности, при прохождении переменного тока с повышением частоты его колебаний возникает сопротивление, величина которого доходит до диапазона обычных значений у гармоник с периодом световых волн.
Влияние температуры на электрическое сопротивление/проводимость газов
Газы и обычный воздух являются диэлектриками и не проводят электрический ток. Для его образования нужны носители зарядов, которыми выступают ионы, образующиеся в результате воздействия внешних факторов.
Нагрев способен вызвать ионизацию и движение ионов от одного полюса среды к другому. Убедиться в этом можно на примере простого опыта. Возьмем то же оборудование, которым пользовались для определения влияния нагрева на сопротивление металлического проводника, только вместо проволоки к проводам подключим две металлические пластины, разделенные воздушным пространством.
Подсоединенный к схеме амперметр покажет отсутствие тока. Если между пластинами поместить пламя горелки, то стрелка прибора отклонится от нулевого значения и покажет величину проходящего через газовую среду тока.
Таким образом установили, что в газах при нагревании происходит ионизация, приводящая к движению электрически заряженных частиц и снижению сопротивления среды.
На значении тока сказывается мощность внешнего приложенного источника напряжения и разность потенциалов между его контактами. Она способна при больших значениях пробить изоляционный слой газов. Характерным проявлением подобного случая в природе является естественный разряд молнии во время грозы.
Примерный вид вольт-амперной характеристики протекания тока в газах показан на графике.
На начальном этапе под действие температуры и разности потенциалов наблюдается рост ионизации и прохождение тока примерно по линейному закону. Затем кривая приобретает горизонтальное направление, когда увеличение напряжения не вызывает рост тока.
Третий этап пробоя наступает тогда, когда высокая энергия приложенного поля так разгоняет ионы, что они начинают соударяться с нейтральными молекулами, массово образуя из них новые носители зарядов. В результате ток резко возрастает, образуя пробой диэлектрического слоя.
Практическое использование проводимости газов
Явление протекания тока через газы используется в радиоэлектронных лампах и люминесцентных светильниках.
Для этого внутри герметичного стеклянного баллона с инертным газом располагают два электрода:
1. анод;
2. катод.
У люминесцентной лампы они выполнены в виде нитей накала, которые разогреваются при включении для создания термоэлектронной эмиссии. Внутренняя поверхность колбы покрыта слоем люминофора. Он излучает видимый нами спектр света, образующийся при инфракрасном облучении, исходящем от паров ртути, бомбардируемых потоком электронов.
Ток газового разряда возникает при приложении напряжения определенной величины между электродами, расположенными по разным концам колбы.
Когда одна из нитей накала перегорит, то на этом электроде нарушится электронная эмиссия и лампа гореть не будет. Однако, если увеличить разность потенциалов между катодом и анодом, то снова возникнет газовый разряд внутри колбы и свечение люминофора возобновится.
Это позволяет использовать светодиодные колбы с нарушенными нитями накала и продлять их ресурс работы. Только следует учитывать, что при этом в несколько раз надо поднять на ней напряжение, А это значительно повышает потребляемую мощность и риски безопасного использования.
Влияние температуры на электрическое сопротивление жидкостей
Прохождение тока в жидкостях создается в основном за счет движения катионов и анионов под действием приложенного извне электрического поля. Лишь незначительную часть проводимости обеспечивают электроны.
Влияние температуры на величину электрического сопротивления жидкого электролита описывается формулой, приведенной на картинке. Поскольку в ней значение температурного коэффициента α всегда отрицательно, то с увеличением нагрева проводимость возрастает, а сопротивление падает так, как показано на графике.
Это явление необходимо учитывать при зарядке жидкостных автомобильных (и не только) аккумуляторных батарей.
Влияние температуры на электрическое сопротивление полупроводников
Изменение свойств полупроводниковых материалов под воздействием температуры позволило использовать их в качестве:
термических сопротивлений;
термоэлементов;
холодильников;
нагревателей.
Терморезисторы
Таким названием обозначают полупроводниковые приборы, изменяющие свое электрическое сопротивление под влиянием тепла. Их значительно выше, чем у металлов.
Величина ТКС у полупроводников может иметь положительное или отрицательное значение. По этому параметру их разделяют на позитивные «РТС» и негативные «NTC» термисторы. Они обладают различными характеристиками.
Для работы терморезистора выбирают одну из точек на его вольт-амперной характеристике:
линейный участок применяют для контроля температуры либо компенсации изменяющихся токов или напряжений;
нисходящая ветвь ВАХ у элементов с ТКС
Применение релейного терморезистора удобно при контроле или измерениях процессов электромагнитных излучений, происходящих на сверхвысоких частотах. Это обеспечило их использование в системах:
1. контроля тепла;
2. пожарной сигнализации;
3. регулирования расхода сыпучих сред и жидкостей.
Кремниевые терморезисторы с маленьким ТКС>0 используют в системах охлаждения и стабилизации температуры транзисторов.
Термоэлементы
Эти полупроводники работают на основе явления Зеебека: при нагреве спаянного места двух разрозненных металлов на стыке замкнутой цепи возникает ЭДС. Таким способом они превращают тепловую энергию в электричество.
Конструкцию из двух таких элементов называют термопарой. Ее КПД лежит в пределах 7÷10%.
Термоэлементы используют в измерителях температур цифровых вычислительных устройств, требующих миниатюрные габариты и высокую точность показаний, а также в качестве маломощных источников тока.
Полупроводниковые нагреватели и холодильники
Они работают за счет обратного использования термоэлементов, через которые пропускают электрический ток. При этом на одном месте спая происходит его нагрев, а на противоположном — охлаждение.
Полупроводниковые спаи на основе селена, висмута, сурьмы, теллура позволяют обеспечить разность температур в термоэлементе до 60 градусов. Это позволило создать конструкцию холодильного шкафа из полупроводников с температурой в камере охлаждения до -16 градусов.
Зависимость сопротивления металлических проводников от температуры. Температурный коэффициент сопротивления
Зависимость сопротивления проводника от температуры
Удельное сопротивление, а следовательно, и сопротивление металлов, зависит от температуры, увеличиваясь с ее ростом. Температурная зависимость сопротивления проводника объясняется тем, что
- возрастает интенсивность рассеивания (число столкновений) носителей зарядов при повышении температуры;
- изменяется их концентрация при нагревании проводника.
Опыт показывает, что при не слишком высоких и не слишком низких температурах зависимости удельного сопротивления и сопротивления проводника от температуры выражаются формулами:
\(~\rho_t = \rho_0 (1 + \alpha t) ,\) \(~R_t = R_0 (1 + \alpha t) ,\)
где ρ
0,
ρ
t — удельные сопротивления вещества проводника соответственно при 0 °С и
t
°C;
R
0,
R
t — сопротивления проводника при 0 °С и
t
°С,
α
— температурный коэффициент сопротивления: измеряемый в СИ в Кельвинах в минус первой степени (К-1). Для металлических проводников эти формулы применимы начиная с температуры 140 К и выше.
Температурный коэффициент
сопротивления вещества характеризует зависимость изменения сопротивления при нагревании от рода вещества. Он численно равен относительному изменению сопротивления (удельного сопротивления) проводника при нагревании на 1 К.
\(~\mathcal h \alpha \mathcal i = \frac{1 \cdot \Delta \rho}{\rho \Delta T} ,\)
где \(~\mathcal h \alpha \mathcal i\) — среднее значение температурного коэффициента сопротивления в интервале ΔΤ
.
Для всех металлических проводников α
> 0 и слабо изменяется с изменением температуры. У чистых металлов
α
= 1/273 К-1. У металлов концентрация свободных носителей зарядов (электронов)
n
= const и увеличение
ρ
происходит благодаря росту интенсивности рассеивания свободных электронов на ионах кристаллической решетки.
Для растворов электролитов α
< 0, например, для 10%-ного раствора поваренной соли
α
= -0,02 К-1. Сопротивление электролитов с ростом температуры уменьшается, так как увеличение числа свободных ионов из-за диссоциации молекул превышает рост рассеивания ионов при столкновениях с молекулами растворителя.
Формулы зависимости ρ
и
R
от температуры для электролитов аналогичны приведенным выше формулам для металлических проводников. Необходимо отметить, что эта линейная зависимость сохраняется лишь в небольшом диапазоне изменения температур, в котором
α
= const. При больших же интервалах изменения температур зависимость сопротивления электролитов от температуры становится нелинейной.
Графически зависимости сопротивления металлических проводников и электролитов от температуры изображены на рисунках 1, а, б.
Рис. 1
При очень низких температурах, близких к абсолютному нулю (-273 °С), сопротивление многих металлов скачком падает до нуля. Это явление получило название сверхпроводимости
. Металл переходит в сверхпроводящее состояние.
Зависимость сопротивления металлов от температуры используют в термометрах сопротивления. Обычно в качестве термометрического тела такого термометра берут платиновую проволоку, зависимость сопротивления которой от температуры достаточно изучена.
Об изменениях температуры судят по изменению сопротивления проволоки, которое можно измерить. Такие термометры позволяют измерять очень низкие и очень высокие температуры, когда обычные жидкостные термометры непригодны.
Электронная проводимость металлов. Зависимость сопротивления от температуры
Как вы знаете, электрический ток могут проводить и твердые, и жидкие, и газообразные тела. На практике, чаще всего применяются металлические проводники. Можно привести много примеров: линии электропередач, обеспечивающие передачу энергии от различных источников тока к потребителям.
Генераторы, электронагревательные приборы и так далее. Как мы уже говорили ранее, хорошими проводниками являются некоторые растворы. Наиболее распространенный пример — это батарейка, в которой используется электролит. Примеров использования батарей и аккумуляторов тоже достаточно: они используются в автомобилях, ноутбуках, мобильных телефонах, планшетах и так далее.
Напомним, что помимо проводников, существуют такие тела, как полупроводники и диэлектрики. Как вы знаете, диэлектрики используются для изоляции проводки или электроприборов. Полупроводники представляют довольно большой интерес, поскольку их проводимостью достаточно легко управлять, а это открывает большие возможности.
Со всем выше перечисленным мы познакомимся по окончании курса физики десятого класса, и начнем с проводимости металлов.
Мы уже много раз говорили, что электрический ток — это упорядоченное движение заряженных частиц
, и всегда утверждали, что
в металлах носителями свободных зарядов являются электроны.
Дело в том, что за этим утверждением стоят многочисленные опыты разных ученых. Мы рассмотрим несколько таких опытов.
В 1901 году, Эдуард Рикке провел следующий эксперимент: он подключил к электрической цепи металлические цилиндры, плотно прилегающие друг к другу. В центре находился алюминиевый цилиндр, а по краям — медные.
В течение приблизительно одного года через эти цилиндры протекал электрический ток. После окончания эксперимента, все три цилиндра были исследованы на предмет изменения химического состава. Выяснилось, что никаких изменений не произошло, за исключением очень незначительной диффузии. Это послужило доказательством того, что ток в металлах обусловлен именно движением электронов. Если бы в движении участвовали какие-то другие частицы (например, ионы кристаллической решетки), то это, неизбежно привело бы к изменению химического состава.
Другой опыт, был проведен в 1912 году учеными Леонидом Мандельштамом и Николаем Папалекси. К катушке, которая могла вращаться вокруг своей оси, был подключен гальванометр при помощи скользящих контактов.
При резкой остановке катушки, гальванометр регистрировал кратковременные токи. Дело в том, что при резкой остановке заряженные частицы какое-то время могли двигаться по инерции относительно проводника (то есть проволоки катушки). Поскольку сила тока характеризуется зарядом, а инерция — массой частиц, переносимый при торможении заряд пропорционален отношению заряда частиц к их массе. Из этого эксперимента было определено это соотношение, которое совпало с найденным до этого из других опытов отношением модуля заряда электрона к его массе:
Таким образом, эксперимент Мандельштама и Папалекси еще раз подтвердил, что ток в металлах обусловлен движением электронов. Поэтому, проводимость металлов называют электронной проводимостью.
Вы уже знаете, что электроны в металлах двигаются с постоянной скоростью из-за того, что взаимодействуют с ионами кристаллической решетки. Это приводит к тому, что скорость движения электронов пропорциональна напряженности электрического поля:
В свою очередь, напряженность пропорциональна напряжению. Из чего мы можем заключить, что скорость электронов в проводнике пропорциональна напряжению на концах этого проводника:
Напомним, что не так давно мы выяснили, что скорость также пропорциональна и силе тока:
Из этого мы можем сделать вывод, что
Влияние температуры на сопротивление
- Изучив этот раздел, вы сможете:
- • Опишите влияние температуры на сопротивление проводника.
- • Опишите влияние температуры на сопротивление изолятора.
- • Определите отрицательные и положительные температурные коэффициенты.
Как температура изменяет сопротивление
Хотя сопротивление проводника изменяется в зависимости от его размера (например,грамм. более толстые провода имеют меньшее сопротивление току, чем более тонкие), сопротивление проводника также изменяется при изменении температуры. Этого можно ожидать, потому что при изменении температуры размеры проводника будут изменяться при его расширении или сжатии.
Однако материалы, которые классифицируются как ПРОВОДНИКИ, имеют тенденцию ПОВЫШАТЬ свое сопротивление с повышением температуры. Однако ИЗОЛЯТОРЫ могут УМЕНЬШИТЬ свое сопротивление с повышением температуры.Материалы, используемые для изготовления изоляторов (стекло, пластик и т. Д.), Демонстрируют заметное падение сопротивления только при очень высоких температурах. Они остаются хорошими изоляторами при любых температурах, с которыми они могут столкнуться при использовании.
Следовательно, эти изменения сопротивления нельзя объяснить изменением размеров из-за теплового расширения или сжатия. Фактически, для проводника данного размера изменение сопротивления в основном связано с изменением удельного сопротивления материала и вызвано изменением активности атомов, составляющих материал.
Температура и атомная структура
Причины этих изменений удельного сопротивления можно объяснить, рассмотрев протекание тока через материал. Поток тока — это фактически движение электронов от одного атома к другому под действием электрического поля. Электроны — это очень маленькие отрицательно заряженные частицы, которые отталкиваются отрицательным электрическим зарядом и притягиваются положительным электрическим зарядом. Следовательно, если к проводнику приложен электрический потенциал (положительный на одном конце, отрицательный на другом), электроны будут «мигрировать» от атома к атому к положительному полюсу.
Однако только некоторые электроны могут свободно перемещаться. Остальные внутри каждого атома так сильно привязаны к своему конкретному атому, что даже электрическое поле не сместит их. Следовательно, ток, протекающий в материале, обусловлен движением «свободных электронов», и количество свободных электронов в любом материале по сравнению с теми, которые тесно связаны с их атомами, определяет, является ли материал хорошим проводником (много свободных электронов) или хороший изолятор (почти нет свободных электронов).
Воздействие тепла на атомную структуру материала заставляет атомы колебаться, и чем выше температура, тем сильнее колеблются атомы.
В проводнике, по которому уже протекает большое количество свободных электронов, колебания атомов вызывают множество столкновений между свободными электронами и захваченными электронами. Каждое столкновение использует некоторую энергию свободного электрона и является основной причиной сопротивления. Чем больше атомы толкаются в материале, тем больше возникает столкновений и, следовательно, больше сопротивление току.
Однако в изоляторе ситуация несколько иная. Свободных электронов так мало, что ток почти не протекает. Почти все электроны прочно связаны внутри своего атома. Нагрев изолирующего материала вызывает вибрацию атомов, и при достаточном нагреве атомы вибрируют достаточно сильно, чтобы фактически освободить часть своих захваченных электронов, создавая свободные электроны, которые становятся носителями тока. Поэтому при высоких температурах сопротивление изолятора может упасть, а в некоторых изоляционных материалах — довольно резко.
В материале, сопротивление которого УВЕЛИЧИВАЕТСЯ с повышением температуры, считается, что материал имеет ПОЛОЖИТЕЛЬНЫЙ ТЕМПЕРАТУРНЫЙ КОЭФФИЦИЕНТ.
Когда сопротивление ПАДАЕТ с повышением температуры, считается, что материал имеет ОТРИЦАТЕЛЬНЫЙ ТЕМПЕРАТУРНЫЙ КОЭФФИЦИЕНТ.
Как правило, проводники имеют ПОЛОЖИТЕЛЬНЫЙ температурный коэффициент, в то время как (при высоких температурах) изоляторы имеют ОТРИЦАТЕЛЬНЫЙ температурный коэффициент.
Различные материалы в пределах каждой группы имеют разные температурные коэффициенты.Материалы, выбранные для изготовления резисторов, используемых в электронных схемах, представляют собой тщательно отобранные проводники с очень низким положительным температурным коэффициентом. При использовании резисторы, изготовленные из таких материалов, будут иметь лишь очень небольшое увеличение удельного сопротивления и, следовательно, их сопротивления. Использование таких материалов для изготовления резисторов создает компоненты, значение которых незначительно изменяется в заданном диапазоне температур.
Материалы, выбранные в качестве изоляторов, будут иметь очень низкий ОТРИЦАТЕЛЬНЫЙ ТЕМПЕРАТУРНЫЙ КОЭФФИЦИЕНТ во всем рабочем диапазоне температур.
Сопротивление и удельное сопротивление | Физика II
Цели обучения
К концу этого раздела вы сможете:
- Объясните понятие удельного сопротивления.
- Используйте удельное сопротивление для расчета сопротивления материалов указанной конфигурации.
- Используйте термический коэффициент удельного сопротивления для расчета изменения сопротивления в зависимости от температуры.
Зависимость сопротивления от материала и формы
Сопротивление объекта зависит от его формы и материала, из которого он сделан.Цилиндрический резистор на Рисунке 1 легко анализировать, и таким образом мы можем получить представление о сопротивлении более сложных форм. Как и следовало ожидать, электрическое сопротивление цилиндра R прямо пропорционально его длине L , подобно сопротивлению трубы потоку жидкости. Чем длиннее цилиндр, тем больше зарядов соударяется с его атомами. Чем больше диаметр цилиндра, тем больше тока он может пропускать (аналогично потоку жидкости по трубе).Фактически, R обратно пропорционален площади поперечного сечения цилиндра A .
Рис. 1. Однородный цилиндр длиной L и площадью поперечного сечения A. Его сопротивление потоку тока аналогично сопротивлению, которое труба оказывает потоку жидкости. Чем длиннее цилиндр, тем больше его сопротивление. Чем больше площадь его поперечного сечения A, тем меньше его сопротивление.
Для данной формы сопротивление зависит от материала, из которого состоит объект.Различные материалы обладают разным сопротивлением потоку заряда. Мы определяем удельное сопротивление ρ вещества так, чтобы сопротивление R объекта было прямо пропорционально ρ . Удельное сопротивление ρ — это внутреннее свойство материала, независимо от его формы или размера. Сопротивление R однородного цилиндра длиной L , площадью поперечного сечения A и изготовленного из материала с удельным сопротивлением ρ составляет
[латекс] R = \ frac {\ rho L} {A} \\ [/ латекс].
В таблице 1 приведены репрезентативные значения ρ . Материалы, перечисленные в таблице, разделены на категории проводников, полупроводников и изоляторов на основе широких групп удельных сопротивлений. У проводников наименьшее удельное сопротивление, а у изоляторов наибольшее; полупроводники имеют промежуточное удельное сопротивление. Проводники имеют различную, но большую плотность свободных зарядов, тогда как большинство зарядов в изоляторах связаны с атомами и не могут двигаться. Полупроводники являются промежуточными, имеют гораздо меньше свободных зарядов, чем проводники, но обладают свойствами, из-за которых количество свободных зарядов сильно зависит от типа и количества примесей в полупроводнике.Эти уникальные свойства полупроводников находят применение в современной электронике, о чем мы поговорим в следующих главах.
| Материал | Удельное сопротивление ρ ( Ом м ) |
|---|---|
| Проводники | |
| Серебро | 1. 59 × 10 −8 |
| Медь | 1.72 × 10 −8 |
| Золото | 2. 44 × 10 −8 |
| Алюминий | 2. 65 × 10 −8 |
| Вольфрам | 5. 6 × 10 −8 |
| Утюг | 9. 71 × 10 −8 |
| Платина | 10. 6 × 10 −8 |
| Сталь | 20 × 10 −8 |
| Свинец | 22 × 10 −8 |
| Манганин (сплав Cu, Mn, Ni) | 44 × 10 −8 |
| Константан (сплав Cu, Ni) | 49 × 10 −8 |
| Меркурий | 96 × 10 −8 |
| Нихром (сплав Ni, Fe, Cr) | 100 × 10 −8 |
| Полупроводники | |
| Углерод (чистый) | 3.5 × 10 5 |
| Углерод | (3,5 — 60) × 10 5 |
| Германий (чистый) | 600 × 10 −3 |
| Германий | (1−600) × 10 −3 |
| Кремний (чистый) | 2300 |
| Кремний | 0,1–2300 |
| Изоляторы | |
| Янтарь | 5 × 10 14 |
| Стекло | 10 9 -10 14 |
| Люцит | > 10 13 |
| Слюда | 10 11 -10 15 |
| Кварц (плавленый) | 75 × 10 16 |
| Резина (твердая) | 10 13 -10 16 |
| сера | 10 15 |
| тефлон | > 10 13 |
| Дерево | 10 8 -10 11 |
Пример 1.Расчет диаметра резистора: нить накала фары
Нить накала автомобильной фары изготовлена из вольфрама и имеет сопротивление холоду 0,350 Ом. Если нить представляет собой цилиндр длиной 4,00 см (ее можно свернуть в бухту для экономии места), каков ее диаметр?
СтратегияМы можем переписать уравнение [латекс] R = \ frac {\ rho L} {A} \\ [/ latex], чтобы найти площадь поперечного сечения A нити на основе данной информации. Тогда его диаметр можно определить, предположив, что он имеет круглое поперечное сечение.{-5} \ text {m} \ end {array} \\ [/ latex].
ОбсуждениеДиаметр чуть меньше десятой миллиметра. Он состоит только из двух цифр, потому что ρ известен только из двух цифр.
Температурное изменение сопротивления
Удельное сопротивление всех материалов зависит от температуры. Некоторые даже становятся сверхпроводниками (нулевое сопротивление) при очень низких температурах. (См. Рисунок 2.)
Рис. 2. Сопротивление образца ртути равно нулю при очень низких температурах — это сверхпроводник примерно до 4.2 К. Выше этой критической температуры его сопротивление делает резкий скачок, а затем почти линейно увеличивается с температурой.
И наоборот, удельное сопротивление проводников увеличивается с повышением температуры. Поскольку атомы колеблются быстрее и на больших расстояниях при более высоких температурах, электроны, движущиеся через металл, совершают больше столкновений, эффективно увеличивая удельное сопротивление. При относительно небольших изменениях температуры (около 100 ° C или меньше) удельное сопротивление ρ изменяется с изменением температуры Δ T , как выражается в следующем уравнении
ρ = ρ 0 (1 + α Δ T ),
, где ρ 0 — исходное удельное сопротивление, а α — температурный коэффициент удельного сопротивления .(См. Значения α в Таблице 2 ниже.) Для более значительных изменений температуры α может изменяться, или может потребоваться нелинейное уравнение, чтобы найти ρ . Обратите внимание, что α является положительным для металлов, что означает, что их удельное сопротивление увеличивается с температурой. Некоторые сплавы были разработаны специально, чтобы иметь небольшую температурную зависимость. Например, у манганина (который состоит из меди, марганца и никеля) α близко к нулю (до трех знаков на шкале в Таблице 2), и поэтому его удельное сопротивление незначительно меняется с температурой.Это полезно, например, для создания не зависящего от температуры эталона сопротивления.
| Материал | Коэффициент (1 / ° C) |
|---|---|
| Проводники | |
| Серебро | 3,8 × 10 −3 |
| Медь | 3,9 × 10 −3 |
| Золото | 3.4 × 10 −3 |
| Алюминий | 3,9 × 10 −3 |
| Вольфрам | 4,5 × 10 −3 |
| Утюг | 5,0 × 10 −3 |
| Платина | 3,93 × 10 −3 |
| Свинец | 3,9 × 10 −3 |
| Манганин (сплав Cu, Mn, Ni) | 0,000 × 10 −3 |
| Константан (сплав Cu, Ni) | 0.002 × 10 −3 |
| Меркурий | 0,89 × 10 −3 |
| Нихром (сплав Ni, Fe, Cr) | 0,4 × 10 −3 |
| Полупроводники | |
| Углерод (чистый) | −0,5 × 10 −3 |
| Германий (чистый) | −50 × 10 −3 |
| Кремний (чистый) | −70 × 10 −3 |
Также обратите внимание, что α отрицательно для полупроводников, перечисленных в Таблице 2, что означает, что их удельное сопротивление уменьшается с повышением температуры.Они становятся лучшими проводниками при более высоких температурах, потому что повышенное тепловое перемешивание увеличивает количество свободных зарядов, доступных для переноса тока. Это свойство уменьшения ρ с температурой также связано с типом и количеством примесей, присутствующих в полупроводниках. Сопротивление объекта также зависит от температуры, поскольку R 0 прямо пропорционально ρ . Для цилиндра мы знаем R = ρL / A , и поэтому, если L и A не сильно изменяются с температурой, R будет иметь такую же температурную зависимость, как ρ .(Исследование коэффициентов линейного расширения показывает, что они примерно на два порядка меньше, чем типичные температурные коэффициенты удельного сопротивления, поэтому влияние температуры на L и A примерно на два порядка меньше, чем на ρ .) Таким образом,
R = R 0 (1 + α Δ T )
— это температурная зависимость сопротивления объекта, где R 0 — исходное сопротивление, а R — сопротивление после изменения температуры Δ T .Многие термометры основаны на влиянии температуры на сопротивление. (См. Рис. 3.) Одним из наиболее распространенных является термистор, полупроводниковый кристалл с сильной температурной зависимостью, сопротивление которого измеряется для определения его температуры. Устройство небольшое, поэтому быстро приходит в тепловое равновесие с той частью человека, к которой прикасается.
Рис. 3. Эти знакомые термометры основаны на автоматическом измерении сопротивления термистора в зависимости от температуры.(Источник: Biol, Wikimedia Commons)
Пример 2. Расчет сопротивления: сопротивление горячей нити
Хотя следует соблюдать осторожность при применении ρ = ρ 0 (1 + α Δ T ) и R = R 0 (1 + α Δ T ) для изменений температуры более 100 ° C, для вольфрама уравнения достаточно хорошо работают при очень больших изменениях температуры. Каково же сопротивление вольфрамовой нити в предыдущем примере, если ее температура повышается с комнатной температуры (20ºC) до типичной рабочей температуры 2850ºC?
СтратегияЭто прямое применение R = R 0 (1 + α Δ T ), поскольку исходное сопротивление нити было задано равным R 0 = 0.{-3} / º \ text {C} \ right) \ left (2830º \ text {C} \ right) \ right] \\ & = & {4.8 \ Omega} \ end {array} \\ [/ latex] .
ОбсуждениеЭто значение соответствует примеру сопротивления фары в Законе Ома: сопротивление и простые цепи.
Исследования PhET: сопротивление в проводеУзнайте о физике сопротивления в проводе. Измените его удельное сопротивление, длину и площадь, чтобы увидеть, как они влияют на сопротивление провода. Размеры символов в уравнении меняются вместе со схемой провода.
Щелкните, чтобы запустить моделирование.
Краткое содержание раздела
- Сопротивление R цилиндра длиной L и площадью поперечного сечения A составляет [латекс] R = \ frac {\ rho L} {A} \ [/ латекс], где ρ — удельное сопротивление материала.
- Значения ρ в таблице 1 показывают, что материалы делятся на три группы — проводники, полупроводники и изоляторы .
- Температура влияет на удельное сопротивление; для относительно небольших изменений температуры Δ T удельное сопротивление равно [латекс] \ rho = {\ rho} _ {0} \ left (\ text {1} + \ alpha \ Delta T \ right) \\ [/ latex], где ρ 0 — исходное удельное сопротивление, а [латекс] \ text {\ alpha} [/ latex] — температурный коэффициент удельного сопротивления.
- В таблице 2 приведены значения для α , температурного коэффициента удельного сопротивления.
- Сопротивление R объекта также зависит от температуры: [латекс] R = {R} _ {0} \ left (\ text {1} + \ alpha \ Delta T \ right) \\ [/ latex], где R 0 — исходное сопротивление, а R — сопротивление после изменения температуры.
Концептуальные вопросы
1. В каком из трех полупроводниковых материалов, перечисленных в Таблице 1, примеси дают свободные заряды? (Подсказка: изучите диапазон удельного сопротивления для каждого из них и определите, имеет ли чистый полупроводник большую или меньшую проводимость.)
2. Зависит ли сопротивление объекта от пути, по которому проходит ток? Рассмотрим, например, прямоугольный стержень — одинаково ли его сопротивление по длине и по ширине? (См. Рисунок 5.)
Рис. 5. Встречается ли ток, проходящий по двум разным путям через один и тот же объект, с разным сопротивлением?
3. Если алюминиевый и медный провода одинаковой длины имеют одинаковое сопротивление, какой из них имеет больший диаметр? Почему?
4. Объясните, почему [латекс] R = {R} _ {0} \ left (1+ \ alpha \ Delta T \ right) \\ [/ latex] для температурного изменения сопротивления R объекта равен не так точен, как [латекс] \ rho = {\ rho} _ {0} \ left ({1} + \ alpha \ Delta T \ right) \\ [/ latex], что дает температурное изменение удельного сопротивления ρ .
Задачи и упражнения
1. Каково сопротивление отрезка медного провода 12-го калибра длиной 20,0 м и диаметром 2,053 мм?
2. Диаметр медного провода нулевого калибра — 8,252 мм. Найдите сопротивление такого провода длиной 1,00 км, используемого для передачи энергии.
3. Если вольфрамовая нить диаметром 0,100 мм в лампочке должна иметь сопротивление 0,200 Ом при 20 ° C, какой длины она должна быть?
4. Найдите отношение диаметра алюминиевого провода к медному, если они имеют одинаковое сопротивление на единицу длины (как в бытовой электропроводке).
5. Какой ток протекает через стержень из чистого кремния диаметром 2,54 см и длиной 20,0 см при приложении к нему 1,00 × 10 3 В? (Такой стержень может быть использован, например, для изготовления детекторов ядерных частиц.)
6. (a) До какой температуры нужно нагреть медный провод, изначально равный 20,0 ° C, чтобы удвоить его сопротивление, не обращая внимания на любые изменения в размерах? (б) Происходит ли это в бытовой электропроводке при обычных обстоятельствах?
7. Резистор из нихромовой проволоки используется там, где его сопротивление не может изменяться более чем на 1.00% от его значения при 20,0ºC. В каком температурном диапазоне его можно использовать?
8. Из какого материала изготовлен резистор, если его сопротивление на 40,0% больше при 100 ° C, чем при 20,0 ° C?
9. Электронное устройство, предназначенное для работы при любой температуре в диапазоне от –10,0 ° C до 55,0 ° C, содержит резисторы из чистого углерода. В какой степени их сопротивление увеличивается в этом диапазоне?
10. (a) Из какого материала сделана проволока, если она имеет длину 25,0 м, диаметр 0,100 мм и сопротивление 77.7 Ом при 20,0 ° C? (б) Каково его сопротивление при 150 ° C?
11. При условии постоянного температурного коэффициента удельного сопротивления, каков максимальный процент уменьшения сопротивления константановой проволоки, начиная с 20,0 ° C?
12. Через матрицу протягивают проволоку, растягивая ее в четыре раза по сравнению с исходной длиной. По какому фактору увеличивается его сопротивляемость?
13. Медный провод имеет сопротивление 0,500 Ом при 20,0 ° C, а железный провод имеет сопротивление 0,525 Ом при той же температуре.При какой температуре их сопротивления равны?
14. (a) Цифровые медицинские термометры определяют температуру путем измерения сопротивления полупроводникового устройства, называемого термистором (который имеет α, = –0,0600 / ºC), когда он находится при той же температуре, что и пациент. Какова температура пациента, если сопротивление термистора при этой температуре составляет 82,0% от его значения при 37,0 ° C (нормальная температура тела)? (b) Отрицательное значение для α не может поддерживаться при очень низких температурах.Обсудите, почему и так ли здесь. (Подсказка: сопротивление не может стать отрицательным.)
15. Integrated Concepts (a) Повторите упражнение 2 с учетом теплового расширения вольфрамовой нити. Вы можете принять коэффициент теплового расширения 12 × 10 −6 / ºC. б) На какой процент ваш ответ отличается от приведенного в примере?
16. Необоснованные результаты (a) До какой температуры нужно нагреть резистор из константана, чтобы удвоить его сопротивление, при условии постоянного температурного коэффициента удельного сопротивления? б) разрезать пополам? (c) Что необоснованного в этих результатах? (d) Какие предположения необоснованны или какие посылки несовместимы?
Сноски
- 1 Значения сильно зависят от количества и типа примесей
- 2 значения при 20 ° C.
Глоссарий
- удельное сопротивление:
- внутреннее свойство материала, независимо от его формы или размера, прямо пропорциональное сопротивлению, обозначаемое как ρ
- температурный коэффициент удельного сопротивления:
- эмпирическая величина, обозначаемая α , которая описывает изменение сопротивления или удельного сопротивления материала при температуре
Избранные решения проблем и упражнения
1.0,104 Ом
3. 2,8 × 10 −2 м
5. 1,10 × 10 −3 A
7. от −5ºC до 45ºC
9. 1.03
11. 0,06%
13. −17ºC
15. (а) 4,7 Ом (всего) (б) уменьшение на 3,0%
Температурный коэффициент сопротивления | Физика проводников и изоляторов
Вы могли заметить в таблице удельных сопротивлений, что все значения указаны для температуры 20 ° C. Если вы подозревали, что это означает, что удельное сопротивление материала может изменяться с температурой, вы были правы!
Значения сопротивления для проводников при любой температуре, отличной от стандартной (обычно указываемой на уровне 20 Цельсия) в таблице удельного сопротивления, должны определяться по еще одной формуле:
Константа «альфа» (α) известна как температурный коэффициент сопротивления и символизирует коэффициент изменения сопротивления на градус изменения температуры.Так же, как все материалы обладают определенным удельным сопротивлением (при 20 ° C), они также изменяют сопротивление в зависимости от температуры на определенную величину. Для чистых металлов этот коэффициент является положительным числом, что означает, что сопротивление увеличивается на с повышением температуры. Для элементов углерода, кремния и германия этот коэффициент является отрицательным числом, что означает, что сопротивление уменьшается на с повышением температуры. Для некоторых металлических сплавов температурный коэффициент сопротивления очень близок к нулю, что означает, что сопротивление практически не изменяется при изменении температуры (хорошее свойство, если вы хотите построить прецизионный резистор из металлической проволоки!).В следующей таблице приведены температурные коэффициенты сопротивления для нескольких распространенных металлов, как чистых, так и легированных:
Температурные коэффициенты сопротивления при 20 градусах Цельсия
| Материал | Элемент / Сплав | «альфа» на градус Цельсия |
|---|---|---|
| Никель | Элемент | 0,005866 |
| Утюг | Элемент | 0,005671 |
| молибден | Элемент | 0.004579 |
| Вольфрам | Элемент | 0,004403 |
| Алюминий | Элемент | 0,004308 |
| Медь | Элемент | 0,004041 |
| Серебро | Элемент | 0,003819 |
| Платина | Элемент | 0,003729 |
| Золото | Элемент | 0,003715 |
| цинк | Элемент | 0.003847 |
| Сталь * | Сплав | 0,003 |
| нихром | Сплав | 0,00017 |
| Нихром В | Сплав | 0,00013 |
| Манганин | Сплав | +/- 0,000015 |
| Константан | Сплав | -0,000074 |
* = Стальной сплав с содержанием железа 99,5%, углерода 0,5% тыс
Давайте посмотрим на пример схемы, чтобы увидеть, как температура может повлиять на сопротивление провода и, следовательно, на характеристики схемы:
Эта цепь имеет полное сопротивление проводов (провод 1 + провод 2) 30 Ом при стандартной температуре.Составив таблицу значений напряжения, тока и сопротивления получаем:
При 20 ° C мы получаем 12,5 В на нагрузке и всего 1,5 В (0,75 + 0,75) падаем на сопротивление провода. Если бы температура поднялась до 35 ° по Цельсию, мы могли бы легко определить изменение сопротивления для каждого отрезка провода. Предполагая использование медной проволоки (α = 0,004041), получаем:
Пересчитав значения нашей схемы, мы увидим, какие изменения принесет это повышение температуры:
Как видите, на нагрузке снизилось напряжение (с 12.От 5 до 12,42 вольт), а падение напряжения на проводах выросло (с 0,75 до 0,79 вольт) в результате повышения температуры. Хотя изменения могут показаться незначительными, они могут быть значительными для линий электропередач, протянувшихся на несколько километров между электростанциями и подстанциями, подстанциями и нагрузками. Фактически, электроэнергетические компании часто должны учитывать изменения сопротивления линии в результате сезонных колебаний температуры при расчете допустимой нагрузки системы.
ОБЗОР:
- Большинство проводящих материалов изменяют удельное сопротивление при изменении температуры.Вот почему значения удельного сопротивления всегда указываются для стандартной температуры (обычно 20 или 25 ° C).
- Коэффициент изменения сопротивления на градус Цельсия при изменении температуры называется температурным коэффициентом сопротивления . Этот коэффициент представлен греческой строчной буквой «альфа» (α).
- Положительный коэффициент для материала означает, что его сопротивление увеличивается с повышением температуры. Чистые металлы обычно имеют положительный температурный коэффициент сопротивления.Коэффициенты, приближающиеся к нулю, могут быть получены путем легирования некоторых металлов.
- Отрицательный коэффициент для материала означает, что его сопротивление уменьшается с повышением температуры. Полупроводниковые материалы (углерод, кремний, германий) обычно имеют отрицательные температурные коэффициенты сопротивления.
- Формула, используемая для определения сопротивления проводника при температуре, отличной от указанной в таблице сопротивлений, выглядит следующим образом:
СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:
Температурный коэффициент сопротивления | Electrical4U
Как мы обсуждали на странице под заголовком «Изменение сопротивления в зависимости от температуры», электрическое сопротивление каждого вещества изменяется с изменением его температуры.
Температурный коэффициент сопротивления — это мера изменения электрического сопротивления любого вещества на градус изменения температуры.
Возьмем проводник с сопротивлением R 0 при 0 o C и R t при t o C соответственно.
Из уравнения изменения сопротивления в зависимости от температуры получаем
Этот α o называется температурным коэффициентом сопротивления этого вещества при 0 o C.
Из приведенного выше уравнения ясно, что изменение электрического сопротивления любого вещества из-за температуры в основном зависит от трех факторов:
- значение сопротивления при начальной температуре,
- повышение температуры и
- температурный коэффициент. сопротивления α o .
Эти α o различаются для разных материалов, поэтому влияние на сопротивление при разной температуре у разных материалов разное.
Таким образом, температурный коэффициент сопротивления при 0 o C любого вещества является обратной величиной предполагаемой температуры нулевого сопротивления этого вещества. До сих пор мы обсуждали материалы, сопротивление которых увеличивается с повышением температуры, но есть много материалов, электрическое сопротивление которых уменьшается с понижением температуры. На самом деле в металле при повышении температуры случайное движение свободных электронов и межатомные колебания внутри металла увеличиваются, что приводит к большему количеству столкновений.Больше столкновений препятствует плавному потоку электронов через металл, следовательно, сопротивление металла увеличивается с повышением температуры. Итак, температурный коэффициент сопротивления считаем положительным для металла.
Но в случае полупроводника или другого неметалла количество свободных электронов увеличивается с повышением температуры. Поскольку при более высокой температуре из-за достаточной тепловой энергии, подводимой к кристаллу, значительное количество ковалентных связей разрывается, и, следовательно, создается больше свободных электронов.Это означает, что при повышении температуры значительное количество электронов попадает в зоны проводимости из валентных зон, пересекая запрещенную запрещенную зону. По мере увеличения количества свободных электронов сопротивление этого типа неметаллических веществ уменьшается с увеличением температуры. Следовательно, температурный коэффициент сопротивления отрицателен для неметаллических веществ и полупроводников.
Если сопротивление приблизительно не изменяется с температурой, мы можем считать значение этого коэффициента равным нулю.Сплав константана и манганина имеет температурный коэффициент сопротивления, близкий к нулю.
Значение этого коэффициента не является постоянным, оно зависит от начальной температуры, на которой основано приращение сопротивления. Когда приращение основано на начальной температуре 0 o C, значение этого коэффициента составляет α o , что является не чем иным, как обратной величиной соответствующей предполагаемой температуры нулевого сопротивления вещества. Но при любой другой температуре температурный коэффициент электрического сопротивления не такой, как у этого α o .Фактически для любого материала значение этого коэффициента максимально при температуре 0 o ° C. Скажем, значение этого коэффициента для любого материала при любом t o C равно α t , тогда его значение можно определить по следующему уравнению:
Значение этого коэффициента при температуре t 2 o C в терминах того же самого при t 1 o C определяется как,
Обзор концепции температурного коэффициента сопротивления
Электрическое сопротивление проводников, таких как серебро, медь, золото, алюминий и т. Д. ., зависит от процесса столкновения электронов внутри материала. По мере увеличения температуры этот процесс столкновения электронов ускоряется, что приводит к увеличению сопротивления с повышением температуры проводника. Сопротивление проводов обычно повышается с повышением температуры.
Если проводник имеет сопротивление R 1 при t 1 o C и после повышения температуры его сопротивление становится R 2 при t 2 o C.Это повышение сопротивления (R 2 — R 1 ) при повышении температуры (t 2 — t 1 ) зависит от следующих факторов —
Путем объединения вышеуказанных эффектов,
Где α — это температурный коэффициент сопротивления материала при t 1 o C.
Из уравнения (1)
Если при определенной температуре мы знаем сопротивление и температурный коэффициент сопротивления материала , мы можем узнать сопротивление материала при других температурах с помощью уравнения (2).
Температурный коэффициент сопротивления некоторых материалов или веществ
Температурный коэффициент сопротивления некоторых материалов / веществ при 20 o C приведен ниже:
| Sl. № | Материал / Вещества | Химический символ / Химический состав | Температурный коэффициент сопротивления / o C (при 20 o C) | |||||||||||||||||||||||||||||||||||||||||||
| 1 | Серебро | Ag | 0.0038 | |||||||||||||||||||||||||||||||||||||||||||
| 2 | Медь | Медь | 0,00386 | |||||||||||||||||||||||||||||||||||||||||||
| 3 | Золото | Au | 0,0034 | |||||||||||||||||||||||||||||||||||||||||||
| 4 | 9012 9012 9012 9012 9012 9012 9012 909 Алюминий 9012 Вольфрам | W | 0,0045 | |||||||||||||||||||||||||||||||||||||||||||
| 6 | Железо | Fe | 0,00651 | |||||||||||||||||||||||||||||||||||||||||||
| 7 | Платина | Pt | 0.003927 | |||||||||||||||||||||||||||||||||||||||||||
| 8 | Манганин | Cu = 84% + Mn = 12% + Ni = 4% | 0,000002 | |||||||||||||||||||||||||||||||||||||||||||
| 9 | Ртуть | Hg | 0,00092| 0,00092 Hg | 0,0009 | Ni = 60% + Cr = 15% + Fe = 25% | 0,0004 | 11 | Константин | Cu = 55% + Ni = 45% | 0,00003 | 12 | Углерод | С | — 0.0005 | 13 | Германий | Ge | — 0,05 | 14 | Кремний | Si | — 0,07 | 15 | 901 65129% Латунь + | 50-35% | 0,0015 | 16 | Никель | Ni | 0,00641 | 17 | Олово | Sn | 0,0042 | 19 | Марганец | Mn | 0,00001 | 20 | Тантал | Ta | 0,0033 | 9012 Температурный коэффициент5 |
Температурный коэффициент сопротивления материала 911 Влияние температуры 911 Сопротивление материала также изменяется в зависимости от температуры.
Если α o — температурный коэффициент сопротивления материала при 0 o C, то из уравнения (2) сопротивление материала при t o C,
Где, R 0 — сопротивление материала при 0 o C
Аналогично, если температурный коэффициент сопротивления материала при t o C равен αt, тогда сопротивление материала при 0 o C, из уравнения (2)
Где, R t — сопротивление материала при t o C
Из уравнений (3) и (4)
Где α 1 и α 2 температурный коэффициент сопротивления материала при t 1 o C и t 2 o C соответственно.
Следовательно, если мы знаем температурный коэффициент сопротивления материала при определенной температуре, мы можем узнать температурный коэффициент материала при любой другой температуре, используя уравнение (6).
Проводящие материалы имеют большой положительный температурный коэффициент сопротивления. Следовательно, сопротивление проводящих материалов (металлов) повышается с повышением температуры.
Полупроводники и изоляционный материал имеют отрицательный температурный коэффициент сопротивления.Следовательно, сопротивление полупроводников и изоляторов уменьшается с повышением температуры.
Сплавы, такие как манганин, константан и т. Д., Имеют очень низкий и положительный температурный коэффициент сопротивления . Следовательно, сопротивление сплавов увеличивается с повышением температуры, но это повышение сопротивления очень низкое (почти незначительное) по сравнению с другими металлами, что делает эти сплавы пригодными для использования в измерительных приборах.
Температурный коэффициент сопротивления | Примечания по электронике
Подробная информация о температурном коэффициенте сопротивления, формула и расчеты, а также таблица распространенных материалов.
Resistance Tutorial:
Что такое сопротивление
Закон Ома
Омические и неомические проводники
Удельное сопротивление
Таблица удельного сопротивления для распространенных материалов
Температурный коэффициент сопротивления
Электрическая проводимость
Последовательные и параллельные резисторы
Таблица параллельных резисторов
Сопротивление и удельное электрическое сопротивление всех материалов зависит от температуры.
Изменение электрического сопротивления влияет на электрические и электронные цепи.В некоторых это может привести к значительным изменениям. В результате температурный коэффициент сопротивления является важным параметром для многих приложений.
Температурный коэффициент сопротивления указан для материалов ввиду его важности, при этом обычно используемые материалы широко доступны.
Внизу страницы находится таблица температурных коэффициентов сопротивления для многих распространенных материалов, используемых в электротехнической и электронной промышленности.
Температурный коэффициент сопротивления: основы
Есть две основные причины, по которым сопротивление материалов зависит от температуры.
Один эффект возникает из-за количества столкновений, которые происходят между носителями заряда и атомами в материале. По мере увеличения температуры увеличивается количество столкновений, и поэтому можно представить себе, что будет незначительное увеличение сопротивления с температурой.
Это может быть не всегда, потому что некоторые материалы имеют отрицательный температурный коэффициент сопротивления. Это может быть вызвано тем фактом, что с повышением температуры высвобождаются дополнительные носители заряда, что приводит к снижению сопротивления с температурой.Как и следовало ожидать, этот эффект часто наблюдается в полупроводниковых материалах.
При рассмотрении температурной зависимости сопротивления обычно предполагается, что температурный коэффициент сопротивления подчиняется линейному закону. Это имеет место при комнатной температуре, а также для металлов и многих других материалов. Однако было обнаружено, что эффекты сопротивления, возникающие в результате количества столкновений, не всегда постоянны, особенно при очень низких температурах для этих материалов.
Было показано, что удельное сопротивление обратно пропорционально длине свободного пробега между столкновениями, то есть это приводит к увеличению удельного сопротивления / сопротивления с увеличением температуры. Для температур выше примерно 15 ° К (то есть выше абсолютного нуля) это ограничено тепловыми колебаниями атомов, и это дает линейную область, которая нам знакома. Ниже этой температуры сопротивление ограничено примесями и доступными носителями.
График сопротивленияТемпературный коэффициент формулы сопротивления
Сопротивление проводника при любой заданной температуре можно рассчитать, зная температуру, температурный коэффициент сопротивления, сопротивление при стандартной температуре и рабочую температуру.Формулу этой зависимости сопротивления от температуры в общих чертах можно выразить как:
Где
R = сопротивление при температуре, T
R ref = сопротивление при температуре Tref
α = температурный коэффициент сопротивления материала
T = температура материала в ° C
T ref = — эталонная температура, для которой указан температурный коэффициент.
Температурный коэффициент сопротивления обычно стандартизирован для температуры 20 ° C.Эта температура обычно считается нормальной «комнатной температурой». В результате это обычно учитывается в формуле для температурного коэффициента сопротивления:
Где
R 20 = сопротивление при 20 ° C
α 20 — температурный коэффициент сопротивления при 20 ° C
Температурный коэффициент сопротивления таблица
В таблице ниже приведены температурные коэффициенты сопротивления для различных веществ, включая температурный коэффициент сопротивления меди, а также температурный коэффициент сопротивления алюминия и многих других материалов.
| Таблица температурных коэффициентов сопротивления для различных веществ | ||
|---|---|---|
| Вещество | Температурный коэффициент ° C -1 | |
| Алюминий | 43 x 10 -4 | |
| Сурьма | 40 x 10 -4 | |
| Висмут | 42 x 10 -4 | |
| Латунь | ~ 10 x 10 -4 | |
| Кадмий | 40 x 10 -4 | |
| Кобальт | 7 x 10 -5 | |
| константан (сплав) | 33 x 10 -4 | |
| Медь | 40 x 10 -4 | |
| Золото | 34 x 10 -4 | |
| Углерод (графит) | -5.6 х 10 -4 | |
| Германий | -4,8 х 10 -2 | |
| Утюг | 56 x 10 -4 | |
| Свинец | 39 x 10 -4 | |
| Манганин | ~ 2 x 10 -5 | |
| молибден | 46 x 10 -4 | |
| нихром | 1.7 х 10 -4 | |
| Никель | 59 x 10 -4 | |
| Платина | 38 x 10 -4 | |
| Кремний | -7,5 x 10 24 | |
| Серебро | 40 x 10 -4 | |
| Тантал | 33 x 10 -4 | |
| Олово | 45 x 10 -4 | |
| Вольфрам | 45 x 10 -4 | |
| цинк | 36 x 10 -4 | |
Видно, что большинство материалов, но не широко используемых в электротехнической и электронной промышленности, имеют температурный коэффициент сопротивления примерно от 30 до 50 x 10 -4 , за исключением полупроводников, которые сильно различаются.
Дополнительные основные понятия:
Напряжение
Текущий
Сопротивление
Емкость
Мощность
Трансформеры
Радиочастотный шум
Децибел, дБ
Q, добротность
Вернуться в меню «Основные понятия». . .
Физика — электрические свойства — Бирмингемский университет
Электрическое сопротивление ( R ) компонента схемы согласно закону Ома — это отношение напряжения ( В, ) к току ( I ), обычно выражаемое как В, = IR .Его не следует путать с удельным сопротивлением ( ρ ) — внутренним свойством материала, которое указывает, насколько сильно он противостоит электрическому току.
Сопротивление или удельное сопротивление?
Компоненты схемы имеют характерное поведение сопротивления, как это видно из графика зависимости их тока от напряжения. Резистор имеет постоянное значение сопротивления, лампа накаливания имеет сопротивление, которое увеличивается с температурой, а диод имеет очень высокое сопротивление в одном направлении.
Для провода сопротивление ( R ) зависит от его длины, площади поперечного сечения и материала, из которого он сделан. Интуитивно понятно, что ток, протекающий по проводу, представляет собой воду, протекающую по трубе — провод большей длины ( l ) будет иметь более высокое сопротивление, чем более короткий провод, а провод с меньшей площадью поперечного сечения ( A ). ) будет иметь более высокое сопротивление, чем устройство с большей площадью поперечного сечения. Удельное сопротивление ( ρ ) — постоянная, которая связывает все эти вещи вместе, определяемая уравнением:
Мы можем измерить удельное сопротивление металла в лаборатории, измерив напряжение и ток на проводе известной длины и площади поперечного сечения, следуя принципиальной схеме ниже
Как мы исследуем удельное сопротивление в лаборатории?
Как измерить удельное сопротивление провода?
Каковы реальные приложения?
Электричество стало частью нашей повседневной жизни, поэтому полезно хотя бы знать основные символы схем.Вот несколько распространенных примеров:
Температура — это переменная, которая не фигурирует в нашем уравнении для удельного сопротивления, однако удельное сопротивление (и, следовательно, сопротивление) зависит от температуры и обычно задается при определенной температуре. Как правило, чем выше температура, тем больше удельное сопротивление. Один из способов представить это: чем горячее компонент, тем сильнее колеблются молекулы, затрудняя прохождение тока. Термисторы — это особый тип резистора, который особенно чувствителен к температуре.Термисторы с отрицательным температурным коэффициентом (или NTC) имеют уменьшающееся сопротивление с повышением температуры, поэтому обычно используются в качестве датчиков температуры для предотвращения условий перенапряжения в большинстве электронных устройств.
Лабораторные признания
В подкасте «Лаборатория исповеди» исследователи рассказывают о своем лабораторном опыте в контексте практических экзаменов A Level. В этом выпуске мы рассмотрим приборы для измерения малых расстояний и принципиальные схемы.
Какая связь между удельным сопротивлением и проводимостью?
Сопротивление, обратное сопротивлению, равно , проводимость ( σ ).Это показатель того, насколько хорошо материал действует как проводник. Сверхпроводники — это особый тип материала, который при охлаждении ниже характеристической температуры имеет сопротивление, близкое к нулю. Поскольку они не имеют сопротивления, постоянный электрический ток течет по поверхности сверхпроводника, что также исключает его внутренние силовые линии магнитного поля.
Сопротивление традиционных проводников, таких как медь, не будет равным нулю, даже при охлаждении почти до абсолютного нуля, однако такие материалы, как оксид висмута, стронция, кальция, меди (BSCOO), имеют критические температуры для сверхпроводимости, такие как 77 градусов Кельвина, поэтому известны как высокотемпературные сверхпроводники.Их намного легче охладить до критических температур, чем традиционные сверхпроводники, которые часто имеют критические температуры около 30K, и для охлаждения требуется жидкий гелий, а не жидкий азот. Сверхпроводники находят широкое применение — от исследований, в которых условия требуют небольшого сопротивления или его отсутствие (например, ускорители частиц), до разработки новых технологий (например, плавающих магнитных поездов) и сканеров МРТ.
Следующие шаги
Эти ссылки предоставляются только для удобства и в информационных целях; они не означают одобрения или одобрения Бирмингемским университетом какой-либо информации, содержащейся на внешнем веб-сайте.Бирмингемский университет не несет ответственности за точность, законность или содержание внешнего сайта или последующих ссылок. Пожалуйста, свяжитесь с внешним сайтом для получения ответов на вопросы относительно его содержания.
Горячие и холодные
Горячие и холодныеГорячие и холодные
Температура и сопротивление электронных материалов
Цель: цель этой лаборатории — показать, как температура влияет на проводимость (сопротивление) в различных электротехнических материалах и устройств.
Обзор научных принципов:
Тепло: когда тепло применяется к кристаллическому твердому телу, мы говорим «оно становится горячее »; это означает повышение температуры. На атомном уровне кинетическая энергия количество атомов увеличилось, что означает, что атомы движутся быстрее. Однако в кристаллическое твердое тело, атомное движение ограничено вибрацией вокруг конюшни позиции решетки. При повышении температуры атомы колеблются. в большей амплитуды и отдаляются от своей устойчивой решетки позиции.Этот движение отрицательно влияет на способность материала провести электрический ток, в результате чего он имеет большую электрическую сопротивление.
Металлы: в металле валентные электроны считаются разделяется всеми положительными ионами. Следовательно, электроны могут свободно двигаться. двигаться повсюду кристаллическая решетка. Электроны движутся беспорядочно кристалл до тех пор, пока к материалу не будет приложено электрическое поле.Тогда электрическое поле заставляет электроны двигаться в направлении, противоположном полю. Фактически, электроны по-прежнему движутся несколько беспорядочно, но с наложением «дрейф». Это производит ток. При повышении температуры положительный ионы в кристалл вибрирует больше, и происходит больше столкновений между валентными электроны и колеблющиеся ионы. Эти столкновения препятствуют «дрейфующему» движению. из валентные электроны, тем самым уменьшая ток.Таким образом, для металл, повышение температуры вызывает повышение сопротивления.
Полупроводники: в полупроводнике при 0 К валентность электроны в заполненных энергетических уровнях (связи образуются электронными парами, заполняющими энергия уровней). Они не реагируют на приложенное электрическое поле к производить ток поток. В присутствии электрического поля движение электрона имеет вид Все еще случайный; нет чистого движения в одном направлении (ток не течет).Эти заполненные уровни энергии, которые занимают валентные электроны, образуют валентные группа. В для протекания тока электроны должны перемещаться из заполненного валентная зона пустая зона проводимости. Чтобы сделать этот ход, требуется энергия, которая может быть в форма тепла. (Важно: электроны не движутся из «место» в кристалл назвал валентную полосу в другое «место», названное зона проводимости. Электроны обладают энергией, связанной с валентной зоной, и приобретать достаточно энергии, чтобы иметь энергию, связанную с проводимостью группа.Энергия происходит изменение, а не изменение положения.) При комнатной температуре многие электроны будет иметь энергию, необходимую для перехода в зону проводимости. Как один электрон выходит из валентной зоны в зону проводимости, дыра (вакансия) производится в валентной зоне. Оба электрона в проводимости группа и соответствующие дырки в валентной зоне считаются заряженными перевозчики. Когда к материалу приложено электрическое поле, эти электроны и дыры «дрейф».Электроны в зоне проводимости дрейфуют в направление противоположное к приложенному полю, и отверстия дрейфуют в том же направлении, что и прикладной поле. Таким образом производится ток. Поскольку температура материал увеличивается, большее количество валентных электронов приобретает энергию, достаточную для движения к зона проводимости (образующая дыры), поэтому течет больше тока. это все еще верно что с повышением температуры атомы вибрируют сильнее и вызвать больше столкновения с дрейфующими электронами.Однако эта противоположная эффект незначительно по сравнению с увеличением носителей заряда.
Приложения:
Различные типы материалов по-разному реагируют на температуру изменения. А компьютерный инженер, проектирующий схему, должен уметь предсказать, в проводимость каждого материала в устройстве будет в пределах приемлемый диапазон в ожидаемом температурном диапазоне работы устройства.
Время: один час
Материалы и принадлежности:
источник тепла для кипящей воды (предпочтительно плита)
5 стаканов для водных бань
термометр
дроссельные катушки или катушки сопротивления
германиевые диоды
термисторы
светодиоды (LED)
резисторы угольные
стеклянный стержень (5 см)
2 цифровых мультиметра или вольтметр и миллиамперметр
соединители проводов с зажимами типа «крокодил»
источник питания (от 0 до 12 В постоянного тока)
Общие правила техники безопасности:
* Источник тепла может вызвать ожоги.Соблюдайте осторожность.
* Остерегайтесь поражения электрическим током.
* Осторожно обращайтесь с приборами и образцами.
* Носите защитные очки.
Процедура:
1. Установите пять водяных бань с примерно 100-200 мл воды в мензурки на следующие
температуры: кипения, 75 C, 50 C, 25 C и лед воды.
2. Измерьте температуру каждой ванны термометром. термистор, или
термопара.
3. Для измерения сопротивления устройства (дросселя или сопротивления катушка) настроить
мультиметр для считывания значений сопротивления и подключения, как показано ниже. диаграмма.
4. Осторожно держитесь за выводные провода, чтобы не пережечь пальцы, погрузить
катиться в кипящую водяную баню, пока не установится стабильное значение. получил (для около одного
минуту) и запишите сопротивление в таблице данных.
5. Выполните ту же процедуру для 75, 50, 25 и лед воды.
6. Снимите катушку и присоедините к счетчику другое устройство, следуя тому же
порядок измерения сопротивления.
Данные и анализ:

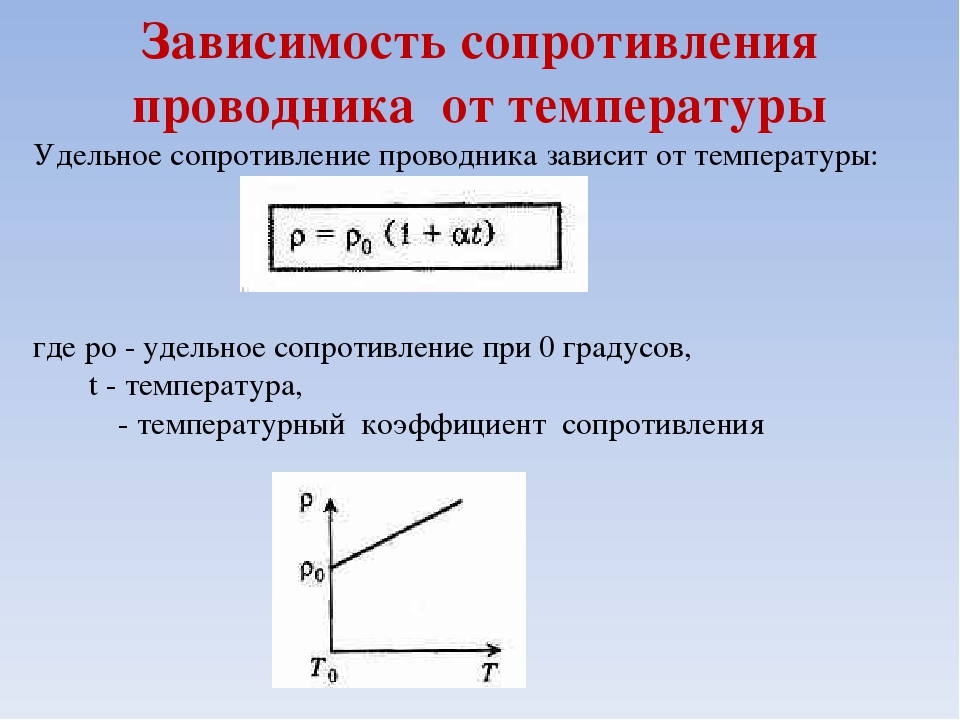
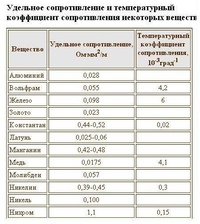 12)
12) 13)
13)