| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Физический справочник / / Электрические и магнитные величины / / Электрическое сопротивление и проводимость проводников, растворов, почв…. / / Электрическое сопротивление r (Ом) 1м проволоки (провода…) в зависимости от ее диаметра d и материала. Поделиться:
| |||||||||||||||||||||||||||||||||||||
Электрическая проводимость металлов таблица — booktube. ru
ru
Электрическое сопротивление 1 метра провода (в Ом), сечением 1 мм², при температуре 20 С°. Формула: ρ = Ом · мм²/м.
| Материал проводника | Удельное сопротивление ρ в Ом |
|---|---|
| Серебро | 0.015 |
| Медь | 0.0175 |
| Золото | 0.023 |
| Латунь | 0,025. 0,108 |
| Хром | 0,027 |
| Алюминий | 0.028 |
| Натрий | 0.047 |
| Иридий | 0.0474 |
| Вольфрам | 0.05 |
| Цинк | 0.054 |
| Молибден | 0.059 |
| Никель | 0.087 |
| Бронза | 0,095. 0,1 |
| Железо | 0.1 |
| 0,103. 0,137 | |
| Олово | 0.12 |
| Свинец | 0.22 |
| Никелин (сплав меди, никеля и цинка) | 0.42 |
| Манганин (сплав меди, никеля и марганца) | 0,43.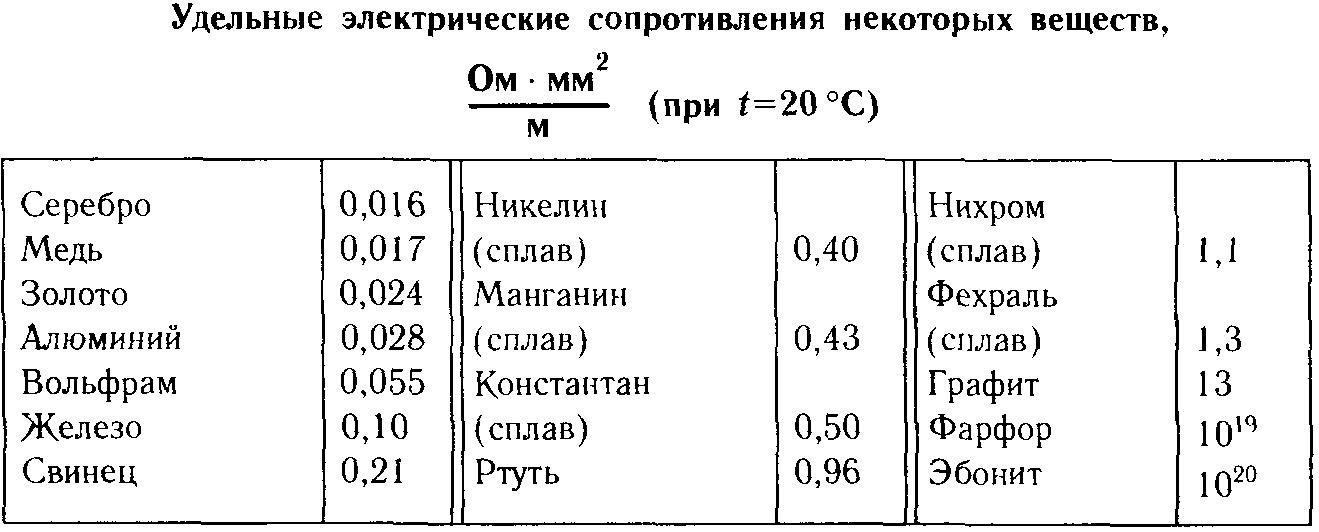 0,51 0,51 |
| Константан (сплав меди, никеля и алюминия) | 0,44-0,52 |
| Копель ( медно-никелевый сплав с 43% никеля и 0,5% марганца) | 0.5 |
| Титан | 0.6 |
| Ртуть | 0.94 |
| Хромель (хром 8,7—10 %; никель 89—91 %; кремний, медь, марганец, кобальт — примеси) | 1.01 |
| Нихром (сплав никеля, хрома, железа и марганца) | 1,05. 1,4 |
| Фехраль | 1,15. 1,35 |
| Висмут | 1.2 |
| Хромаль (Сплав 4.5 – 6% алюминия, 17%-30% хрома, остальное железо) | 1,3. 1,5 |
Наименьшим удельным сопротивлением обладает серебро. 1 Ом сопротивления можно получить, если взять 62,5 м серебряной проволоки сечением 1 мм². Серебро — лучший проводник, но стоимость серебра исключает возможность его массового применения. После серебра в таблице идет медь: 1 м медной проволоки сечением 1 мм² обладает сопротивлением 0,0175 Ом. Чтобы получить сопротивление в 1 Ом, нужно взять 57 м такой проволоки.
Чтобы получить сопротивление в 1 Ом, нужно взять 57 м такой проволоки.
Химически чистая, полученная путем рафинирования, медь нашла себе повсеместное применение в электротехнике для изготовления проводов, кабелей, обмоток электрических машин и аппаратов. Широко применяют также в качестве проводников алюминий и железо.
Сопротивление проводника можно определить по формуле:
где r — сопротивление проводника в омах; ρ — удельное сопротивление проводника; l — длина проводника в м; S — сечение проводника в мм².
В связи с тем, что существует два типа электрических сопротивлений –
В связи с электромагнитными явлениями, возникающими в проводниках при прохождении через него переменного тока в них возникает два важных для их электротехнических свойств физических явления.
Два последних явления делают неэффективным применение проводников радиусом больше характерной глубины проникновения электрического тока в проводник. Эффективный диаметр проводников (2RБхар): 50Гц -7 Ом. Используя микроомметры, можно определить качество электрических контактов, сопротивление электрических шин, обмоток трансформаторов, электродвигателей и генераторов, наличие дефектов и инородного металла в слитках (например, сопротивление слитка чистого золота вдвое ниже позолоченного слитка вольфрама).
Эффективный диаметр проводников (2RБхар): 50Гц -7 Ом. Используя микроомметры, можно определить качество электрических контактов, сопротивление электрических шин, обмоток трансформаторов, электродвигателей и генераторов, наличие дефектов и инородного металла в слитках (например, сопротивление слитка чистого золота вдвое ниже позолоченного слитка вольфрама).
Для расчета длины провода, его диаметра и необходимого электрического сопротивления, необходимо знать удельное сопротивление проводников ρ.
В международной системе единиц удельное сопротивление ρ выражается формулой:
Оно означает: электрическое сопротивление 1 метра провода (в Омах), сечением 1 мм 2 , при температуре 20 градусов по Цельсию.
Таблица удельных сопротивлений проводников
| Материал проводника | Удельное сопротивление ρ в |
| Серебро Медь Золото Латунь Алюминий Натрий Иридий Вольфрам Цинк Молибден Никель Бронза Железо Олово Свинец Никелин (сплав меди, никеля и цинка) Манганин (сплав меди, никеля и марганца) Константан (сплав меди, никеля и алюминия) Титан Ртуть Нихром (сплав никеля, хрома, железа и марганца) Фехраль Висмут Хромаль | 0,015 0,0175 0,023 0,025.  0,108 0,108 0,028 0,047 0,0474 0,05 0,054 0,059 0,087 0,095. 0,1 0,1 0,103. 0,137 0,12 0,22 0,42 0,43. 0,51 0,5 0,6 0,94 1,05. 1,4 1,15. 1,35 1,2 1,3. 1,5 |
Из таблицы видно, что железная проволока длиной 1 м и сечением 1 мм 2 обладает сопротивлением 0,13 Ом. Чтобы получить 1 Ом сопротивления нужно взять 7,7 м такой проволоки. Наименьшим удельным сопротивлением обладает серебро. 1 Ом сопротивления можно получить, если взять 62,5 м серебряной проволоки сечением 1 мм 2 . Серебро – лучший проводник, но стоимость серебра исключает возможность его массового применения. После серебра в таблице идет медь: 1 м медной проволоки сечением 1 мм 2 обладает сопротивлением 0,0175 Ом. Чтобы получить сопротивление в 1 Ом, нужно взять 57 м такой проволоки.
Химически чистая, полученная путем рафинирования, медь нашла себе повсеместное применение в электротехнике для изготовления проводов, кабелей, обмоток электрических машин и аппаратов.
Сопротивление проводника можно определить по формуле:
где r – сопротивление проводника в омах; ρ – удельное сопротивление проводника; l – длина проводника в м; S – сечение проводника в мм 2 .
Пример 1. Определить сопротивление 200 м железной проволоки сечением 5 мм 2 .
Пример 2. Вычислить сопротивление 2 км алюминиевой проволоки сечением 2,5 мм 2 .
Из формулы сопротивления легко можно определить длину, удельное сопротивление и сечение проводника.
Пример 3. Для радиоприемника необходимо намотать сопротивление в 30 Ом из никелиновой проволоки сечением 0,21 мм 2 . Определить необходимую длину проволоки.
Пример 4. Определить сечение 20 м нихромовой проволоки, если сопротивление ее равно 25 Ом.
Пример 5. Проволока сечением 0,5 мм 2 и длиной 40 м имеет сопротивление 16 Ом. Определить материал проволоки.
Определить материал проволоки.
Материал проводника характеризует его удельное сопротивление.
По таблице удельных сопротивлений находим, что таким сопротивлением обладает свинец.
Выше было указано, что сопротивление проводников зависит от температуры. Проделаем следующий опыт. Намотаем в виде спирали несколько метров тонкой металлической проволоки и включим эту спираль в цепь аккумулятора. Для измерения тока в цепь включаем амперметр. При нагревании спирали в пламени горелки можно заметить, что показания амперметра будут уменьшаться. Это показывает, что с нагревом сопротивление металлической проволоки увеличивается.
У некоторых металлов при нагревании на 100° сопротивление увеличивается на 40 – 50 %. Имеются сплавы, которые незначительно меняют свое сопротивление с нагревом. Некоторые специальные сплавы практически не меняют сопротивления при изменении температуры. Сопротивление металлических проводников при повышении температуры увеличивается, сопротивление электролитов (жидких проводников), угля и некоторых твердых веществ, наоборот, уменьшается.
Способность металлов менять свое сопротивление с изменением температуры используется для устройства термометров сопротивления. Такой термометр представляет собой платиновую проволоку, намотанную на слюдяной каркас. Помещая термометр, например, в печь и измеряя сопротивление платиновой проволоки до и после нагрева, можно определить температуру в печи.
Если при температуре t сопротивление проводника равно r, а при температуре t равно rt, то температурный коэффициент сопротивления
Примечание. Расчет по этой формуле можно производить лишь в определенном интервале температур (примерно до 200°C).
Приводим значения температурного коэффициента сопротивления α для некоторых металлов (таблица 2).
Значения температурного коэффициента для некоторых металлов
| Металл | α | ||
| Серебро Медь Железо Вольфрам Платина | 0,0035 0,0040 0,0066 0,0045 0,0032 | Ртуть Никелин Константан Нихром Манганин | 0,0090 0,0003 0,000005 0,00016 0,00005 |
Из формулы температурного коэффициента сопротивления определим rt:
Пример 6. Определить сопротивление железной проволоки, нагретой до 200°C, если сопротивление ее при 0°C было 100 Ом.
Определить сопротивление железной проволоки, нагретой до 200°C, если сопротивление ее при 0°C было 100 Ом.
Удельное сопротивление металлов и сплавов таблица
Электрическое сопротивление 1 метра провода (в Ом), сечением 1 мм², при температуре 20 С°. Формула: ρ = Ом · мм²/м.
| Материал проводника | Удельное сопротивление ρ в Ом |
|---|---|
| Серебро | 0.015 |
| Медь | 0.0175 |
| Золото | 0.023 |
| Латунь | 0,025. 0,108 |
| Хром | 0,027 |
| Алюминий | 0.028 |
| Натрий | 0.047 |
| Иридий | 0.0474 |
| Вольфрам | 0.05 |
| Цинк | 0.054 |
| Молибден | 0.059 |
| Никель | 0.087 |
| Бронза | 0,095. 0,1 |
| Железо | 0.1 |
| Сталь | 0,103. 0,137 0,137 |
| Олово | 0.12 |
| Свинец | 0.22 |
| Никелин (сплав меди, никеля и цинка) | 0.42 |
| Манганин (сплав меди, никеля и марганца) | 0,43. 0,51 |
| Константан (сплав меди, никеля и алюминия) | 0,44-0,52 |
| Копель ( медно-никелевый сплав с 43% никеля и 0,5% марганца) | 0.5 |
| Титан | 0.6 |
| Ртуть | 0.94 |
| Хромель (хром 8,7—10 %; никель 89—91 %; кремний, медь, марганец, кобальт — примеси) | 1.01 |
| Нихром (сплав никеля, хрома, железа и марганца) | 1,05. 1,4 |
| Фехраль | 1,15. 1,35 |
| Висмут | 1.2 |
| Хромаль (Сплав 4.5 – 6% алюминия, 17%-30% хрома, остальное железо) | 1,3. 1,5 |
Наименьшим удельным сопротивлением обладает серебро. 1 Ом сопротивления можно получить, если взять 62,5 м серебряной проволоки сечением 1 мм².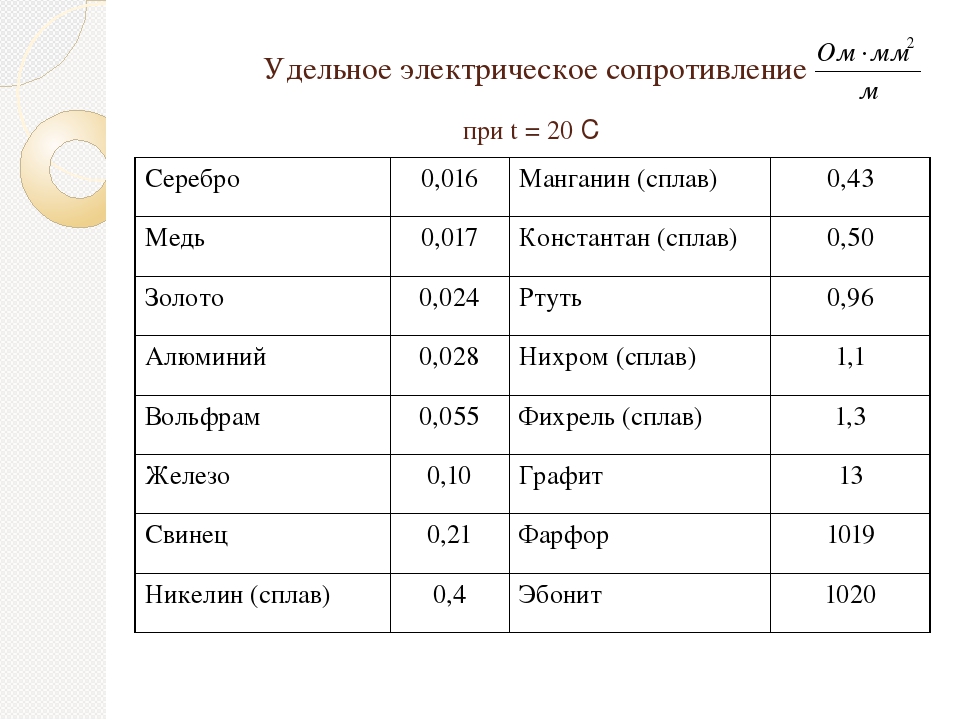 Серебро — лучший проводник, но стоимость серебра исключает возможность его массового применения. После серебра в таблице идет медь: 1 м медной проволоки сечением 1 мм² обладает сопротивлением 0,0175 Ом. Чтобы получить сопротивление в 1 Ом, нужно взять 57 м такой проволоки.
Серебро — лучший проводник, но стоимость серебра исключает возможность его массового применения. После серебра в таблице идет медь: 1 м медной проволоки сечением 1 мм² обладает сопротивлением 0,0175 Ом. Чтобы получить сопротивление в 1 Ом, нужно взять 57 м такой проволоки.
Химически чистая, полученная путем рафинирования, медь нашла себе повсеместное применение в электротехнике для изготовления проводов, кабелей, обмоток электрических машин и аппаратов. Широко применяют также в качестве проводников алюминий и железо.
Сопротивление проводника можно определить по формуле:
где r — сопротивление проводника в омах; ρ — удельное сопротивление проводника; l — длина проводника в м; S — сечение проводника в мм².
Представлены таблицы значений удельного электрического сопротивления сталей различных типов и марок в зависимости от температуры — в диапазоне от 0 до 1350°С.
В общем случае, удельное сопротивление определяется только составом вещества и его температурой, оно численно равно полному сопротивлению изотропного проводника, имеющего длину 1 м и площадь поперечного сечения 1 м 2 .
Удельное электрическое сопротивление стали существенно зависит от состава и температуры. При повышении температуры этого металла увеличивается частота и амплитуда колебаний атомов кристаллической решетки, что создает дополнительное сопротивление прохождению электрического тока через толщу сплава. Поэтому, с ростом температуры сопротивление стали увеличивается.
Изменение состава стали и процента содержания в ней легирующих добавок значительно сказывается на величине электросопротивления. Например, углеродистые и низколегированные стали в несколько раз лучше проводят электрический ток, чем высоколегированные и жаропрочные, которые имеют высокое содержание никеля и хрома.
Углеродистые стали
Углеродистые стали при комнатной температуре, как уже было сказано, имеют низкое удельное электросопротивление за счет высокого содержания железа. При 20°С значение их удельного сопротивления находится в диапазоне от 13·10 -8 (для стали 08КП) до 20·10 -8 Ом·м (для У12).
При нагревании до температур более 1000°С способность углеродистых сталей проводить электрический ток сильно снижается. Величина сопротивления возрастает на порядок и может достигать значения 130·10 -8 Ом·м.
| Температура, °С | Сталь 08КП | Сталь 08 | Сталь 20 | Сталь 40 | Сталь У8 | Сталь У12 |
|---|---|---|---|---|---|---|
| 12 | 13,2 | 15,9 | 16 | 17 | 18,4 | |
| 20 | 13 | 14,2 | 16,9 | 17,1 | 18 | 19,6 |
| 50 | 14,7 | 15,9 | 18,7 | 18,9 | 19,8 | 21,6 |
| 100 | 17,8 | 19 | 21,9 | 22,1 | 23,2 | 25,2 |
| 150 | 21,3 | 22,4 | 25,4 | 25,7 | 26,8 | 29 |
| 200 | 25,2 | 26,3 | 29,2 | 29,6 | 30,8 | 33,3 |
| 250 | 29,5 | 30,5 | 33,4 | 33,9 | 35,1 | 37,9 |
| 300 | 34,1 | 35,2 | 38,1 | 38,7 | 39,8 | 43 |
| 350 | 39,3 | 40,2 | 43,2 | 43,8 | 45 | 48,3 |
| 400 | 44,8 | 45,8 | 48,7 | 49,3 | 50,5 | 54 |
| 450 | 50,9 | 51,8 | 54,6 | 55,3 | 56,5 | 60 |
| 500 | 57,5 | 58,4 | 60,1 | 61,9 | 62,8 | 66,5 |
| 550 | 64,8 | 65,7 | 68,2 | 68,9 | 69,9 | 73,4 |
| 600 | 72,5 | 73,4 | 75,8 | 76,6 | 77,2 | 80,2 |
| 650 | 80,7 | 81,6 | 83,7 | 84,4 | 85,2 | 87,8 |
| 700 | 89,8 | 90,5 | 92,5 | 93,2 | 93,5 | 96,4 |
| 750 | 100,3 | 101,1 | 105 | 107,9 | 110,5 | 113 |
| 800 | 107,3 | 108,1 | 109,4 | 111,1 | 112,9 | 115 |
| 850 | 110,4 | 111,1 | 111,8 | 113,1 | 114,8 | 117,6 |
| 900 | 112,4 | 113 | 113,6 | 114,9 | 116,4 | 119,6 |
| 950 | 114,2 | 114,8 | 115,2 | 116,6 | 117,8 | 121,2 |
| 1000 | 116 | 116,5 | 116,7 | 117,9 | 119,1 | 122,6 |
| 1050 | 117,5 | 117,9 | 118,1 | 119,3 | 120,4 | 123,8 |
| 1100 | 118,9 | 119,3 | 119,4 | 120,7 | 121,4 | 124,9 |
| 1150 | 120,3 | 120,7 | 120,7 | 122 | 122,3 | 126 |
| 1200 | 121,7 | 122 | 121,9 | 123 | 123,1 | 127,1 |
| 1250 | 123 | 123,3 | 122,9 | 124 | 123,8 | 128,2 |
| 1300 | 124,1 | 124,4 | 123,9 | — | 124,6 | 128,7 |
| 1350 | 125,2 | 125,3 | 125,1 | — | 125 | 129,5 |
Низколегированные стали
Низколегированные стали способны чуть более сильно сопротивляться прохождению электричества, чем углеродистые.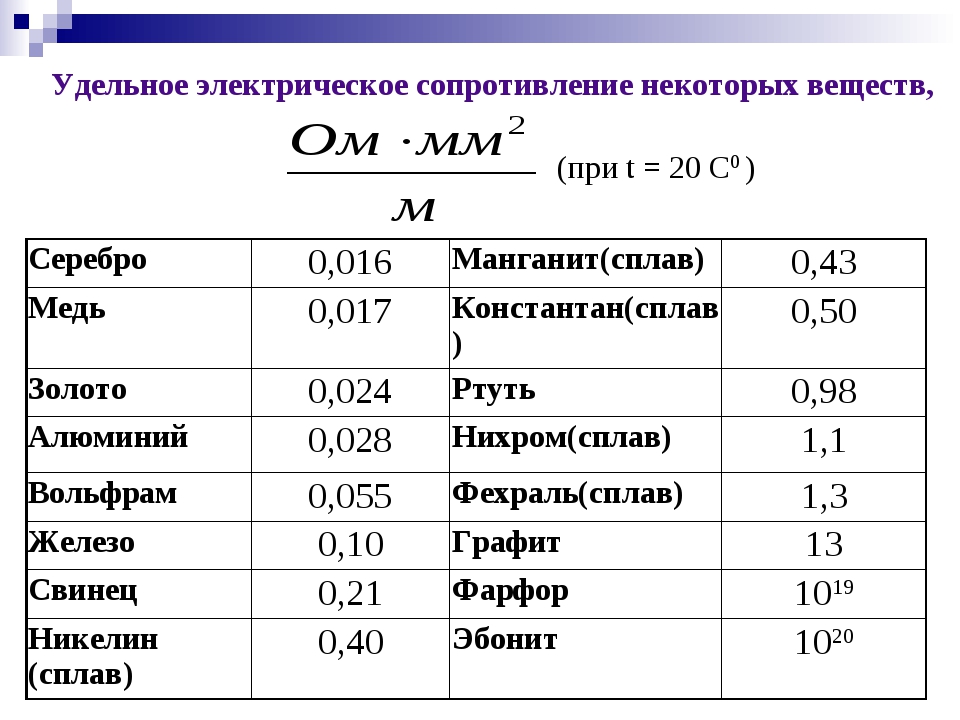 Их удельное электросопротивление составляет (20…43)·10 -8 Ом·м при комнатной температуре.
Их удельное электросопротивление составляет (20…43)·10 -8 Ом·м при комнатной температуре.
Следует отметить марки стали этого типа, которые наиболее плохо проводят электрический ток — это 18Х2Н4ВА и 50С2Г. Однако при высоких температурах, способность проводить электрический ток у сталей, приведенных в таблице, практически не различается.
| Марка стали | 20 | 100 | 300 | 500 | 700 | 900 | 1100 | 1300 |
|---|---|---|---|---|---|---|---|---|
| 15ХФ | — | 28,1 | 42,1 | 60,6 | 83,3 | — | — | — |
| 30Х | 21 | 25,9 | 41,7 | 63,6 | 93,4 | 114,5 | 120,5 | 125,1 |
| 12ХН2 | 33 | 36 | 52 | 67 | — | 112 | — | — |
| 12ХН3 | 29,6 | — | — | 67 | — | 116 | — | — |
| 20ХН3 | 24 | 29 | 46 | 66 | — | 123 | — | — |
| 30ХН3 | 26,8 | 31,7 | 46,9 | 68,1 | 98,1 | 114,8 | 120,1 | 124,6 |
| 20ХН4Ф | 36 | 41 | 56 | 72 | 102 | 118 | — | — |
| 18Х2Н4ВА | 41 | 44 | 58 | 73 | 97 | 115 | — | — |
| 30Г2 | 20,8 | 25,9 | 42,1 | 64,5 | 94,6 | 114,3 | 120,2 | 125 |
| 12МХ | 24,6 | 27,4 | 40,6 | 59,8 | — | — | — | — |
| 40Х3М | — | 33,1 | 48,2 | 69,5 | 96,2 | — | — | — |
| 20Х3ФВМ | — | 39,8 | 54,4 | 74,3 | 98,2 | — | — | — |
| 50С2Г | 42,9 | 47 | 60,1 | 78,8 | 105,7 | 119,7 | 124,9 | 128,9 |
| 30Н3 | 27,1 | 32 | 47 | 67,9 | 99,2 | 114,9 | 120,4 | 124,8 |
Высоколегированные стали
Высоколегированные стали имеют удельное электрическое сопротивление в несколько раз выше чем углеродистые и низколегированные.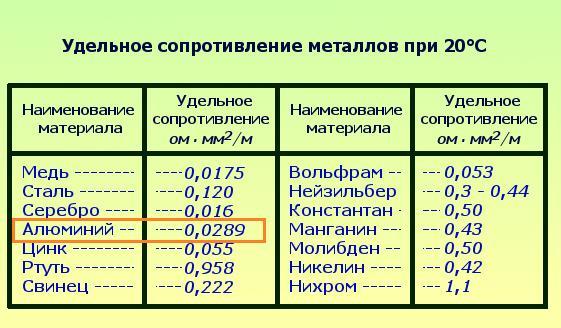 По данным таблицы видно, что при температуре 20°С его величина составляет (30…86)·10 -8 Ом·м.
По данным таблицы видно, что при температуре 20°С его величина составляет (30…86)·10 -8 Ом·м.
При температуре 1300°С сопр
Удельное электрическое сопротивление — ООО «Эстив»
|
Алюминий |
0,028 |
|
Вольфрам |
0,055 |
|
Графит |
13 |
|
Железо |
0,1 |
|
Золото |
0,024 |
|
Латунь |
0,07-0,08 |
|
Магний |
0,045 |
|
Медь |
0,017 |
|
Никель |
0,073 |
|
Олово |
0,12 |
|
Платина |
0,1 |
|
Ртуть |
0,96 |
|
Свинец |
0,21 |
|
Серебро |
0,016 |
|
Сталь |
0,10-0,14 |
|
Цинк |
0,061 |
|
Чугун |
0,5-0,8 |
|
Антимонид индия |
0,23 x 104 |
|
Бор |
0,17 x 105 |
|
Германий |
0,47 |
|
Кремний |
0,58 x 10-4 |
|
Селенид свинца |
9,1 x 10-6 |
|
Сульфид свинца |
1,7 x 10-5 |
|
Воздух |
1015-1018 |
|
Кварц |
109 |
|
Резина |
1011-1012 |
|
Слюда |
1011-1015 |
|
Стекло |
109-1013 |
|
Сухое дерево |
109-1010 |
|
Трансформаторное масло |
1010-1013 |
|
Гетинакс |
109-1012 |
|
Капрон |
1010-1011 |
|
Лавсан |
1014-1016 |
|
Органическое стекло |
1011-1013 |
|
Пенопласт |
1011 |
|
Поливинилхлорид |
1010-1012 |
|
Полистирол |
1013-1015 |
|
Полиэтилен |
1015 |
|
Стеклотекстолит |
1011-1012 |
|
Текстолит |
107-1010 |
|
Целлулоид |
109 |
|
Эбонит |
1012-1014 |
| 0,05 | 0,07 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,7 | 1 | 1,5 | 2 | 2,5 | 4 | 6 | 11 | |
| Наибольший допустимый ток, А | 0,7 | 1 | 1,3 | 2,5 | 3,5 | 4 | 5 | 7 | 10 | 14 | 17 | 20 | 25 | 30 | 54 |
| Температура, °С | Сталь 08КП | Сталь 08 | Сталь 20 | Сталь 40 | Сталь У8 | Сталь У12 |
|---|---|---|---|---|---|---|
| 12 | 13,2 | 15,9 | 16 | 17 | 18,4 | |
| 20 | 13 | 14,2 | 16,9 | 17,1 | 18 | 19,6 |
| 50 | 14,7 | 15,9 | 18,7 | 18,9 | 19,8 | 21,6 |
| 100 | 17,8 | 19 | 21,9 | 22,1 | 23,2 | 25,2 |
| 150 | 21,3 | 22,4 | 25,4 | 25,7 | 26,8 | 29 |
| 200 | 25,2 | 26,3 | 29,2 | 29,6 | 30,8 | 33,3 |
| 250 | 29,5 | 30,5 | 33,4 | 33,9 | 35,1 | 37,9 |
| 300 | 34,1 | 35,2 | 38,1 | 38,7 | 39,8 | 43 |
| 350 | 39,3 | 40,2 | 43,2 | 43,8 | 45 | 48,3 |
| 400 | 44,8 | 45,8 | 48,7 | 49,3 | 50,5 | 54 |
| 450 | 50,9 | 51,8 | 54,6 | 55,3 | 56,5 | 60 |
| 500 | 57,5 | 58,4 | 60,1 | 61,9 | 62,8 | 66,5 |
| 550 | 64,8 | 65,7 | 68,2 | 68,9 | 69,9 | 73,4 |
| 600 | 72,5 | 73,4 | 75,8 | 76,6 | 77,2 | 80,2 |
| 650 | 80,7 | 81,6 | 83,7 | 84,4 | 85,2 | 87,8 |
| 700 | 89,8 | 90,5 | 92,5 | 93,2 | 93,5 | 96,4 |
| 750 | 100,3 | 101,1 | 105 | 107,9 | 110,5 | 113 |
| 800 | 107,3 | 108,1 | 109,4 | 111,1 | 112,9 | 115 |
| 850 | 110,4 | 111,1 | 111,8 | 113,1 | 114,8 | 117,6 |
| 900 | 112,4 | 113 | 113,6 | 114,9 | 116,4 | 119,6 |
| 950 | 114,2 | 114,8 | 115,2 | 116,6 | 117,8 | 121,2 |
| 1000 | 116 | 116,5 | 116,7 | 117,9 | 119,1 | 122,6 |
| 1050 | 117,5 | 117,9 | 118,1 | 119,3 | 120,4 | 123,8 |
| 1100 | 118,9 | 119,3 | 119,4 | 120,7 | 121,4 | 124,9 |
| 1150 | 120,3 | 120,7 | 120,7 | 122 | 122,3 | 126 |
| 1200 | 121,7 | 122 | 121,9 | 123 | 123,1 | 127,1 |
| 1250 | 123 | 123,3 | 122,9 | 124 | 123,8 | 128,2 |
| 1300 | 124,1 | 124,4 | 123,9 | — | 124,6 | 128,7 |
| 1350 | 125,2 | 125,3 | 125,1 | — | 125 | 129,5 |
Низколегированные стали
Низколегированные стали способны чуть более сильно сопротивляться прохождению электричества, чем углеродистые.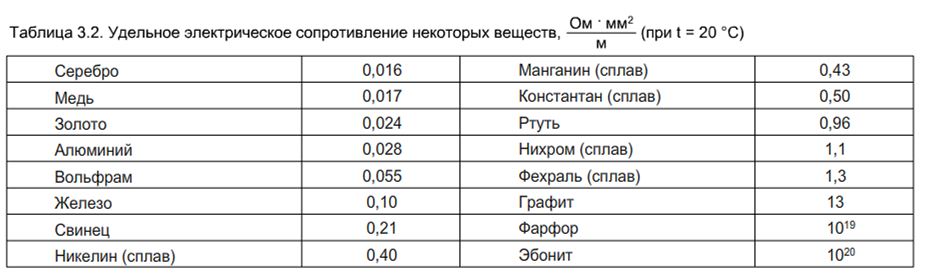 Их удельное электросопротивление составляет (20…43)·10 -8 Ом·м при комнатной температуре.
Их удельное электросопротивление составляет (20…43)·10 -8 Ом·м при комнатной температуре.
Следует отметить марки стали этого типа, которые наиболее плохо проводят электрический ток — это 18Х2Н4ВА и 50С2Г. Однако при высоких температурах, способность проводить электрический ток у сталей, приведенных в таблице, практически не различается.
| Марка стали | 20 | 100 | 300 | 500 | 700 | 900 | 1100 | 1300 |
|---|---|---|---|---|---|---|---|---|
| 15ХФ | — | 28,1 | 42,1 | 60,6 | 83,3 | — | — | — |
| 30Х | 21 | 25,9 | 41,7 | 63,6 | 93,4 | 114,5 | 120,5 | 125,1 |
| 12ХН2 | 33 | 36 | 52 | 67 | — | 112 | — | — |
| 12ХН3 | 29,6 | — | — | 67 | — | 116 | — | — |
| 20ХН3 | 24 | 29 | 46 | 66 | — | 123 | — | — |
| 30ХН3 | 26,8 | 31,7 | 46,9 | 68,1 | 98,1 | 114,8 | 120,1 | 124,6 |
| 20ХН4Ф | 36 | 41 | 56 | 72 | 102 | 118 | — | — |
| 18Х2Н4ВА | 41 | 44 | 58 | 73 | 97 | 115 | — | — |
| 30Г2 | 20,8 | 25,9 | 42,1 | 64,5 | 94,6 | 114,3 | 120,2 | 125 |
| 12МХ | 24,6 | 27,4 | 40,6 | 59,8 | — | — | — | — |
| 40Х3М | — | 33,1 | 48,2 | 69,5 | 96,2 | — | — | — |
| 20Х3ФВМ | — | 39,8 | 54,4 | 74,3 | 98,2 | — | — | — |
| 50С2Г | 42,9 | 47 | 60,1 | 78,8 | 105,7 | 119,7 | 124,9 | 128,9 |
| 30Н3 | 27,1 | 32 | 47 | 67,9 | 99,2 | 114,9 | 120,4 | 124,8 |
Высоколегированные стали
Высоколегированные стали имеют удельное электрическое сопротивление в несколько раз выше чем углеродистые и низколегированные. По данным таблицы видно, что при температуре 20°С его величина составляет (30…86)·10 -8 Ом·м.
По данным таблицы видно, что при температуре 20°С его величина составляет (30…86)·10 -8 Ом·м.
При температуре 1300°С сопротивление высоко- и низко- легированных сталей становится почти одинаковым и не превышает 131·10 -8 Ом·м.
| Марка стали | 20 | 100 | 300 | 500 | 700 | 900 | 1100 | 1300 |
|---|---|---|---|---|---|---|---|---|
| Г13 | 68,3 | 75,6 | 93,1 | 95,2 | 114,7 | 123,8 | 127 | 130,8 |
| Г20Х12Ф | 72,3 | 79,2 | 91,2 | 101,5 | 109,2 | — | — | — |
| Г21Х15Т | — | 82,4 | 95,6 | 104,5 | 112 | 119,2 | — | — |
| Х13Н13К10 | — | 90 | 100,8 | 109,6 | 115,4 | 119,6 | — | — |
| Х19Н10К47 | — | 90,5 | 98,6 | 105,2 | 110,8 | — | — | — |
| Р18 | 41,9 | 47,2 | 62,7 | 81,5 | 103,7 | 117,3 | 123,6 | 128,1 |
| ЭХ12 | 31 | 36 | 53 | 75 | 97 | 119 | — | — |
| 40Х10С2М (ЭИ107) | 86 | 91 | 101 | 112 | 122 | — | — | — |
Хромистые нержавеющие стали
Хромистые нержавеющие стали имеют высокую концентрацию атомов хрома, что увеличивает их удельное сопротивление — электропроводность такой нержавеющей стали не высока. При обычных температурах ее сопротивление составляет (50…60)·10 -8 Ом·м.
При обычных температурах ее сопротивление составляет (50…60)·10 -8 Ом·м.
| Марка стали | 20 | 100 | 300 | 500 | 700 | 900 | 1100 | 1300 |
|---|---|---|---|---|---|---|---|---|
| Х13 | 50,6 | 58,4 | 76,9 | 93,8 | 110,3 | 115 | 119 | 125,3 |
| 2Х13 | 58,8 | 65,3 | 80 | 95,2 | 110,2 | — | — | — |
| 3Х13 | 52,2 | 59,5 | 76,9 | 93,5 | 109,9 | 114,6 | 120,9 | 125 |
| 4Х13 | 59,1 | 64,6 | 78,8 | 94 | 108 | — | — | — |
Хромоникелевые аустенитные стали
Хромоникелевые аустенитные стали также являются нержавеющими, но за счет добавки никеля имеют удельное сопротивление почти в полтора раза выше, чем у хромистых — оно достигает величины (70…90)·10 -8 Ом·м.
| Марка стали | 20 | 100 | 300 | 500 | 700 | 900 | 1100 |
|---|---|---|---|---|---|---|---|
| 12Х18Н9 | — | 74,3 | 89,1 | 100,1 | 109,4 | 114 | — |
| 12Х18Н9Т | 72,3 | 79,2 | 91,2 | 101,5 | 109,2 | — | — |
| 17Х18Н9 | 72 | 73,5 | 92,5 | 103 | 111,5 | 118,5 | — |
| Х18Н11Б | — | 84,6 | 97,6 | 107,8 | 115 | — | — |
| Х18Н9В | 71 | 77,6 | 91,6 | 102,6 | 111,1 | 117,1 | 122 |
| 4Х14НВ2М (ЭИ69) | 81,5 | 87,5 | 100 | 110 | 117,5 | — | — |
| 1Х14Н14В2М (ЭИ257) | — | 82,4 | 95,6 | 104,5 | 112 | 119,2 | — |
| 1х14Н18М3Т | — | 89 | 100 | 107,5 | 115 | — | — |
| 36Х18Н25С2 (ЭЯ3С) | — | 98,5 | 105,5 | 110 | 117,5 | — | — |
| Х13Н25М2В2 | — | 103 | 112,1 | 118,1 | 121 | — | — |
| Х7Н25 (ЭИ25) | — | — | 109 | 115 | 121 | 127 | — |
| Х2Н35 (ЭИ36) | 87,5 | 92,5 | 103 | 110 | 116 | 120,5 | — |
| Н28 | 84,2 | 89,1 | 99,6 | 107,7 | 114,2 | 118,4 | 122,5 |
Жаропрочные и жаростойкие стали
По своим электропроводящим свойствам жаропрочные и жаростойкие стали близки к хромоникелевым.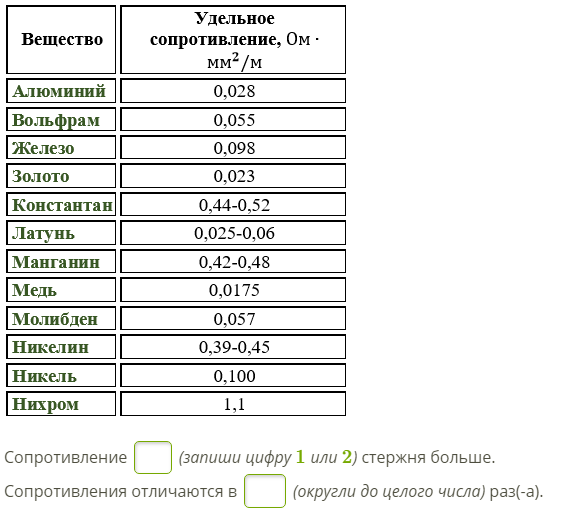 Высокое содержание в этих сплавах хрома и никеля не позволяет им проводить электрический ток, подобно обычным углеродистым с высокой концентрацией железа.
Высокое содержание в этих сплавах хрома и никеля не позволяет им проводить электрический ток, подобно обычным углеродистым с высокой концентрацией железа.
Значительное удельное электросопротивление и высокая рабочая температура таких сталей делают возможным их применение в качестве рабочих элементов электрических нагревателей. В частности, сталь 20Х23Н18 по своему сопротивлению и жаростойкости в некоторых случаях способна заменить такой популярный сплав для нагревателей, как нихром Х20Н80.
В данной статье мы подробно разберем что такое удельное сопротивление и электропроводность, ясно опишем все формулы с помощью примеров задач, а так же дадим вам таблицу удельных сопротивлений некоторых проводников.
Описание
Закон Ома гласит, что, когда источник напряжения (V) подается между двумя точками в цепи, между ними будет протекать электрический ток (I), вызванный наличием разности потенциалов между этими двумя точками. Количество протекающего электрического тока ограничено величиной присутствующего сопротивления (R).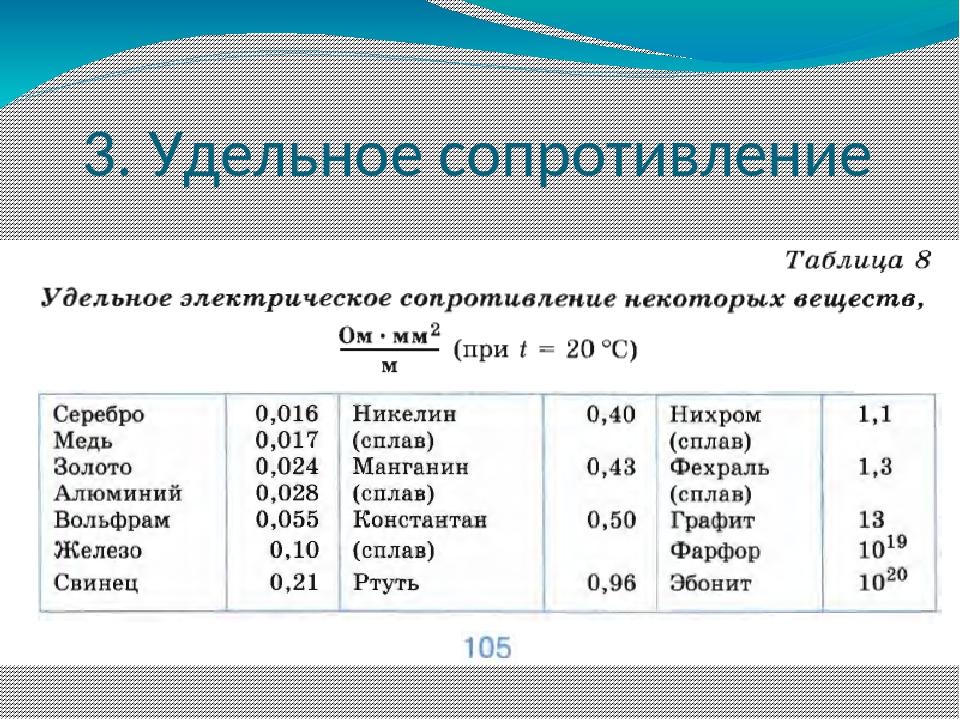 Другими словами, напряжение стимулирует протекание тока (движение заряда), но это сопротивление препятствует этому.
Другими словами, напряжение стимулирует протекание тока (движение заряда), но это сопротивление препятствует этому.
Мы всегда измеряем электрическое сопротивление в Омах, где Ом обозначается греческой буквой Омега, Ω. Так, например: 50 Ом, 10 кОм или 4,7 МОм и т.д. Проводники (например, провода и кабели) обычно имеют очень низкие значения сопротивления (менее 0,1 Ом), и, таким образом, мы можем пренебречь ими, как мы предполагаем в расчетах анализа цепи, что провода имеют ноль сопротивление. С другой стороны, изоляторы (например, пластиковые или воздушные), как правило, имеют очень высокие значения сопротивления (более 50 МОм), поэтому мы можем их игнорировать и для анализа цепи, поскольку их значение слишком велико.
Но электрическое сопротивление между двумя точками может зависеть от многих факторов, таких как длина проводников, площадь их поперечного сечения, температура, а также фактический материал, из которого он изготовлен. Например, давайте предположим, что у нас есть кусок провода (проводник), который имеет длину L, площадь поперечного сечения A и сопротивление R, как показано ниже.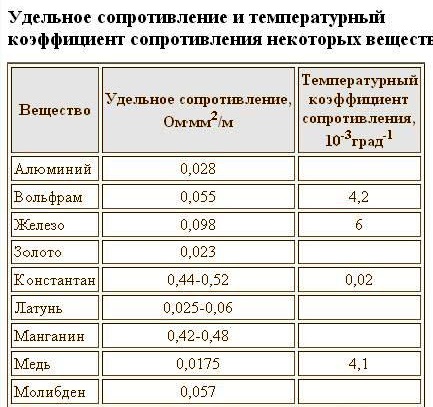
Электрическое сопротивление R этого простого проводника является функцией его длины, L и площади поперечного сечения A. Закон Ома говорит нам, что для данного сопротивления R ток, протекающий через проводник, пропорционален приложенному напряжению, поскольку I = V / R. Теперь предположим, что мы соединяем два одинаковых проводника вместе в последовательной комбинации, как показано на рисунке.
Здесь, соединив два проводника вместе в последовательной комбинации, то есть, к концу, мы фактически удвоили общую длину проводника (2L), в то время как площадь поперечного сечения A остается точно такой же, как и раньше. Но помимо удвоения длины, мы также удвоили общее сопротивление проводника, дав 2R как: 1R + 1R = 2R.
Таким образом , мы можем видеть , что сопротивление проводника пропорционально его длину, то есть: R ∝ L. Другими словами, мы ожидаем, что электрическое сопротивление проводника (или провода) будет пропорционально больше, чем оно длиннее.
Отметим также, что, удваивая длину и, следовательно, сопротивление проводника (2R), чтобы заставить тот же ток I, чтобы течь через проводник, как и раньше, нам нужно удвоить (увеличить) приложенное напряжение I = (2 В) / (2R). Далее предположим, что мы соединяем два идентичных проводника вместе в параллельной комбинации, как показано.
Здесь, соединяя два проводника в параллельную комбинацию, мы фактически удвоили общую площадь, дающую 2А, в то время как длина проводников L остается такой же, как у исходного одиночного проводника. Но помимо удвоения площади, путем параллельного соединения двух проводников мы фактически вдвое сократили общее сопротивление проводника, получив 1 / 2R, поскольку теперь каждая половина тока протекает через каждую ветвь проводника.
Таким образом, сопротивление проводника обратно пропорционально его площади, то есть: R 1 / ∝ A или R ∝ 1 / A. Другими словами, мы ожидаем, что электрическое сопротивление проводника (или провода) будет пропорционально меньше, чем больше его площадь поперечного сечения.
Кроме того, удваивая площадь и, следовательно, вдвое увеличивая суммарное сопротивление ветви проводника (1 / 2R), для того же тока, чтобы I протекал через параллельную ветвь провода, как раньше, нам нужно только наполовину уменьшить приложенное напряжение I = (1 / 2V) / (1 / 2R).
Надеемся, мы увидим, что сопротивление проводника прямо пропорционально длине (L) проводника, то есть: R ∝ L, и обратно пропорционально его площади (A), R ∝ 1 / A. Таким образом, мы можем правильно сказать, что сопротивление это:
Пропорциональность сопротивления
Но помимо длины и площади проводника, мы также ожидаем, что электрическое сопротивление проводника будет зависеть от фактического материала, из которого он изготовлен, потому что разные проводящие материалы, медь, серебро, алюминий и т.д., имеют разные физические и электрические свойства. Таким образом, мы можем преобразовать знак пропорциональности (∝) вышеприведенного уравнения в знак равенства, просто добавив «пропорциональную константу» в вышеприведенное уравнение, давая:
Уравнение удельного электрического сопротивления
Где: R — сопротивление в омах (Ω), L — длина в метрах (м), A — площадь в квадратных метрах (м 2 ), и где известна пропорциональная постоянная ρ (греческая буква «rho») — удельное сопротивление .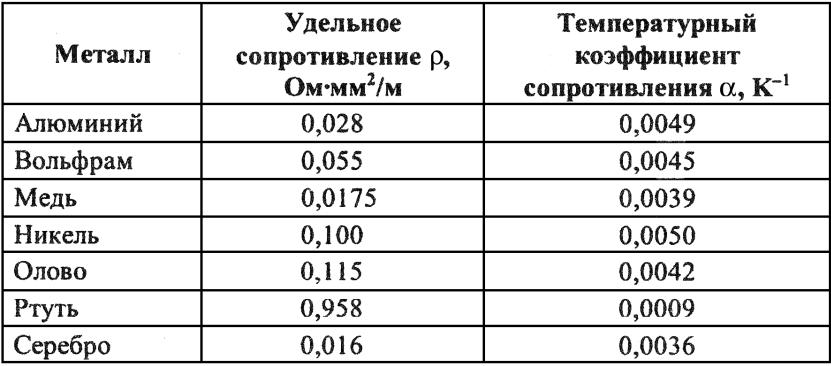
Удельное электрическое сопротивление
Удельное электрическое сопротивление конкретного материала проводника является мерой того, насколько сильно материал противостоит потоку электрического тока через него. Этот коэффициент удельного сопротивления, иногда называемый его «удельным электрическим сопротивлением», позволяет сравнивать сопротивление различных типов проводников друг с другом при определенной температуре в соответствии с их физическими свойствами без учета их длины или площади поперечного сечения. Таким образом, чем выше значение удельного сопротивления ρ, тем больше сопротивление, и наоборот.
Например, удельное сопротивление хорошего проводника, такого как медь, составляет порядка 1,72 х 10 -8 Ом (или 17,2 нОм), тогда как удельное сопротивление плохого проводника (изолятора), такого как воздух, может быть значительно выше 1,5 х 10 14 или 150 трлн.
Такие материалы, как медь и алюминий, известны низким уровнем удельного сопротивления, благодаря чему электрический ток легко проходит через них, что делает эти материалы идеальными для изготовления электрических проводов и кабелей. Серебро и золото имеют очень низкие значения удельного сопротивления, но по понятным причинам дороже делать из них электрические провода.
Серебро и золото имеют очень низкие значения удельного сопротивления, но по понятным причинам дороже делать из них электрические провода.
Тогда факторы, которые влияют на сопротивление (R) проводника в омах, могут быть перечислены как:
- Удельное сопротивление (ρ) материала, из которого сделан проводник.
- Общая длина (L) проводника.
- Площадь поперечного сечения (А) проводника.
- Температура проводника.
Пример удельного сопротивления № 1
Рассчитайте общее сопротивление постоянному току 100-метрового рулона медного провода 2,5 мм 2 , если удельное сопротивление меди при 20 o C составляет 1,72 x 10 -8 Ом метр.
Приведенные данные: удельное сопротивление меди при 20 o C составляет 1,72 x 10 -8 , длина катушки L = 100 м, площадь поперечного сечения проводника составляет 2,5 мм 2 , что дает площадь: A = 2,5 x 10 -6 м 2 .
Ответ: 688 МОм или 0,688 Ом.
Удельное электрическое сопротивление материала
Ранее мы говорили, что удельное сопротивление — это электрическое сопротивление на единицу длины и на единицу площади поперечного сечения проводника, таким образом, показывая, что удельное сопротивление ρ имеет размеры в Ом-метрах или Ом · м, как это обычно пишется. Таким образом, для конкретного материала при определенной температуре его удельное электрическое сопротивление определяется как.
Таким образом, для конкретного материала при определенной температуре его удельное электрическое сопротивление определяется как.
Электрическая проводимость
Хотя как электрическое сопротивление (R), так и удельное сопротивление ρ, являются функцией физической природы используемого материала, а также его физической формы и размера, выраженных его длиной (L) и площадью его сечения ( А), Проводимость или удельная проводимость относится к легкости, с которой электрический ток проходит через материал.
Проводимость (G) является обратной величиной сопротивления (1 / R) с единицей проводимости, являющейся сименсом (S), и ей дается перевернутый символ омов mho, ℧. Таким образом, когда проводник имеет проводимость 1 сименс (1S), он имеет сопротивление 1 Ом (1 Ом). Таким образом, если его сопротивление удваивается, проводимость уменьшается вдвое, и наоборот, как: Сименс = 1 / Ом, или Ом = 1 / Ом.
В то время как сопротивление проводников дает степень сопротивления потоку электрического тока, проводимость проводника указывает на легкость, с которой он пропускает электрический ток.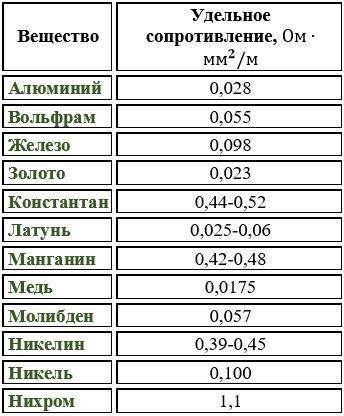 Таким образом, металлы, такие как медь, алюминий или серебро, имеют очень большие значения проводимости, что означает, что они являются хорошими проводниками.
Таким образом, металлы, такие как медь, алюминий или серебро, имеют очень большие значения проводимости, что означает, что они являются хорошими проводниками.
Проводимость, σ (греческая буква сигма), является обратной величиной удельного сопротивления. Это 1 / ρ и измеряется в сименах на метр (S / m). Поскольку электропроводность σ = 1 / ρ, предыдущее выражение для электрического сопротивления R можно переписать в виде:
Электрическое сопротивление как функция проводимости
Тогда мы можем сказать, что проводимость — это эффективность, посредством которой проводник пропускает электрический ток или сигнал без потери сопротивления. Поэтому материал или проводник, который имеет высокую проводимость, будет иметь низкое удельное сопротивление, и наоборот, поскольку 1 сименс (S) равен 1 Ом -1 . Таким образом, медь, которая является хорошим проводником электрического тока, имеет проводимость 58,14 x 10 6 Симен на метр.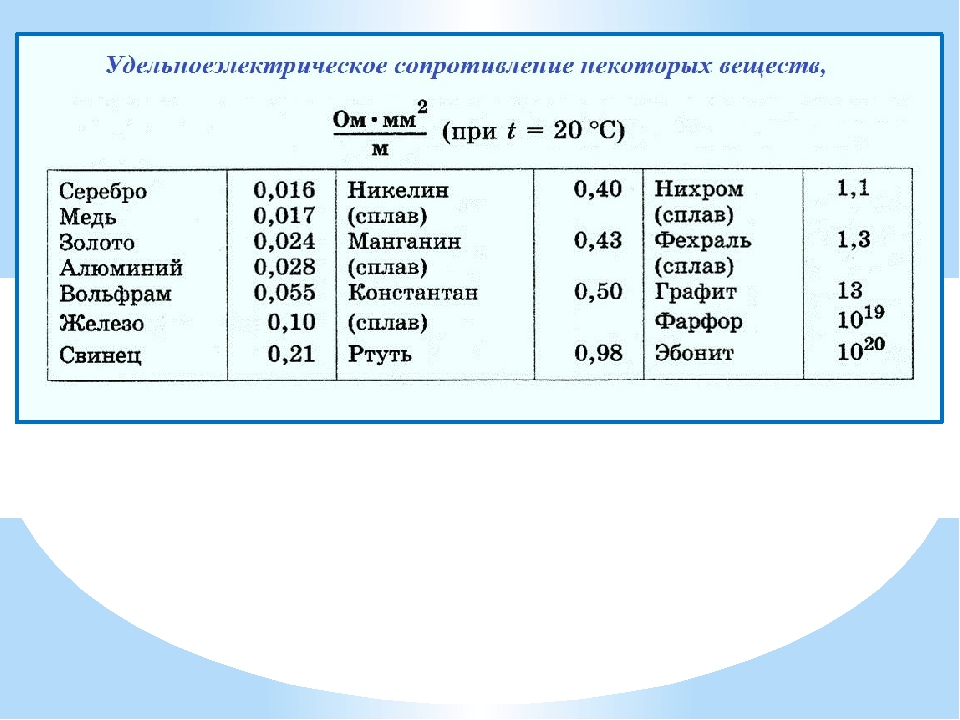
Пример удельного сопротивления №2
Кабель длиной 20 метров имеет площадь поперечного сечения 1 мм 2 и сопротивление 5 Ом. Рассчитать проводимость кабеля.
Приведенные данные: сопротивление постоянному току, R = 5 Ом, длина кабеля, L = 20 м, а площадь поперечного сечения проводника составляет 1 мм 2, что дает площадь: A = 1 x 10 -6 м 2 .
Ответ: 4 мега-симена на метр длины.
Таблица удельных сопротивлений проводников
| Проводник | Удельное сопротивление ρ | Температурный коэффициент α |
| Алюминий | 0,028 | 4,2 |
| Бронза | 0,095 — 0,1 | — |
| Висмут | 1,2 | — |
| Вольфрам | 0,05 | 5 |
| Железо | 0,1 | 6 |
| Золото | 0,023 | 4 |
| Иридий | 0,0474 | — |
| Константан | 0,5 | 0,05 |
| Латунь | 0,025 — 0,108 | 0,1-0,4 |
| Магний | 0,045 | 3,9 |
| Манганин | 0,43 — 0,51 | 0,01 |
| Медь | 0,0175 | 4,3 |
| Молибден | 0,059 | — |
| Нейзильбер | 0,2 | 0,25 |
| Натрий | 0,047 | — |
| Никелин | 0,42 | 0,1 |
| Никель | 0,087 | 6,5 |
| Нихром | 1,05 — 1,4 | 0,1 |
| Олово | 0,12 | 4,4 |
| Платина | 0. 107 107 | 3,9 |
| Ртуть | 0,94 | 1,0 |
| Свинец | 0,22 | 3,7 |
| Серебро | 0,015 | 4,1 |
| Сталь | 0,103 — 0,137 | 1-4 |
| Титан | 0,6 | — |
| Фехраль | 1,15 — 1,35 | 0,1 |
| Хромаль | 1,3 — 1,5 | — |
| Цинк | 0,054 | 4,2 |
| Чугун | 0,5-1,0 | 1,0 |
Где: удельное сопротивление ρ измеряется в Ом*мм 2 /м и температурный коэффициент электрического сопротивления металлов α измеряется в 10 -3 *C -1 (или K -1 ) .
Краткое описание удельного сопротивления
Мы поговорили в этой статье об удельном сопротивлении, что удельное сопротивление — это свойство материала или проводника, которое указывает, насколько хорошо материал проводит электрический ток. Мы также видели, что электрическое сопротивление (R) проводника зависит не только от материала, из которого сделан проводник, меди, серебра, алюминия и т.д., но также от его физических размеров.
Мы также видели, что электрическое сопротивление (R) проводника зависит не только от материала, из которого сделан проводник, меди, серебра, алюминия и т.д., но также от его физических размеров.
Сопротивление проводника прямо пропорционально его длине (L) как R ∝ L. Таким образом, удвоение его длины удвоит его сопротивление, в то время как последовательное удвоение проводника уменьшит вдвое его сопротивление. Также сопротивление проводника обратно пропорционально его площади поперечного сечения (A) как R ∝ 1 / A. Таким образом, удвоение его площади поперечного сечения уменьшило бы его сопротивление вдвое, тогда как удвоение его площади поперечного сечения удвоило бы его сопротивление.
Мы также узнали, что удельное сопротивление (символ: ρ) проводника (или материала) связано с физическим свойством, из которого он изготовлен, и варьируется от материала к материалу. Например, удельное сопротивление меди обычно дается как: 1,72 х 10 -8 Ом · м. Удельное сопротивление конкретного материала измеряется в единицах Ом-метров (Ом), которое также зависит от температуры.
В зависимости от значения удельного электрического сопротивления конкретного материала его можно классифицировать как «проводник», «изолятор» или «полупроводник». Обратите внимание, что полупроводники — это материалы, в которых их проводимость зависит от примесей, добавляемых в материал.
Удельное сопротивление также важно в системах распределения электроэнергии, так как эффективность системы заземления для системы электропитания и распределения сильно зависит от удельного сопротивления земли и материала почвы в месте расположения системы.
Проводимость — это имя, данное движению свободных электронов в форме электрического тока. Проводимость, σ является обратной величиной удельного сопротивления. Это 1 / ρ и имеет единицу измерения сименс на метр, S / m. Проводимость варьируется от нуля (для идеального изолятора) до бесконечности (для идеального проводника). Таким образом, сверхпроводник имеет бесконечную проводимость и практически нулевое омическое сопротивление.
Тимеркаев Борис — 68-летний доктор физико-математических наук, профессор из России. Он является заведующим кафедрой общей физики в Казанском национальном исследовательском техническом университете имени А. Н. ТУПОЛЕВА — КАИ
Удельное сопротивление алюминия ом мм2 м
В связи с тем, что существует два типа электрических сопротивлений –
В связи с электромагнитными явлениями, возникающими в проводниках при прохождении через него переменного тока в них возникает два важных для их электротехнических свойств физических явления.
Два последних явления делают неэффективным применение проводников радиусом больше характерной глубины проникновения электрического тока в проводник. Эффективный диаметр проводников (2RБхар): 50Гц -7 Ом. Используя микроомметры, можно определить качество электрических контактов, сопротивление электрических шин, обмоток трансформаторов, электродвигателей и генераторов, наличие дефектов и инородного металла в слитках (например, сопротивление слитка чистого золота вдвое ниже позолоченного слитка вольфрама).
Для расчета длины провода, его диаметра и необходимого электрического сопротивления, необходимо знать удельное сопротивление проводников ρ.
В международной системе единиц удельное сопротивление ρ выражается формулой:
Оно означает: электрическое сопротивление 1 метра провода (в Омах), сечением 1 мм 2 , при температуре 20 градусов по Цельсию.
Таблица удельных сопротивлений проводников
| Материал проводника | Удельное сопротивление ρ в |
| Серебро Медь Золото Латунь Алюминий Натрий Иридий Вольфрам Цинк Молибден Никель Бронза Железо Сталь Олово Свинец Никелин (сплав меди, никеля и цинка) Манганин (сплав меди, никеля и марганца) Константан (сплав меди, никеля и алюминия) Титан Ртуть Нихром (сплав никеля, хрома, железа и марганца) Фехраль Висмут Хромаль | 0,015 0,0175 0,023 0,025. 0,108 0,028 0,047 0,0474 0,05 0,054 0,059 0,087 0,095. 0,1 0,1 0,103. 0,137 0,12 0,22 0,42 0,43. 0,51 0,5 0,6 0,94 1,05. 1,4 1,15. 1,35 1,2 1,3. 1,5 |
Из таблицы видно, что железная проволока длиной 1 м и сечением 1 мм 2 обладает сопротивлением 0,13 Ом. Чтобы получить 1 Ом сопротивления нужно взять 7,7 м такой проволоки. Наименьшим удельным сопротивлением обладает серебро. 1 Ом сопротивления можно получить, если взять 62,5 м серебряной проволоки сечением 1 мм 2 . Серебро – лучший проводник, но стоимость серебра исключает возможность его массового применения. После серебра в таблице идет медь: 1 м медной проволоки сечением 1 мм 2 обладает сопротивлением 0,0175 Ом. Чтобы получить сопротивление в 1 Ом, нужно взять 57 м такой проволоки.
Химически чистая, полученная путем рафинирования, медь нашла себе повсеместное применение в электротехнике для изготовления проводов, кабелей, обмоток электрических машин и аппаратов. Широко применяют также в качестве проводников алюминий и железо.
Сопротивление проводника можно определить по формуле:
где r – сопротивление проводника в омах; ρ – удельное сопротивление проводника; l – длина проводника в м; S – сечение проводника в мм 2 .
Пример 1. Определить сопротивление 200 м железной проволоки сечением 5 мм 2 .
Пример 2. Вычислить сопротивление 2 км алюминиевой проволоки сечением 2,5 мм 2 .
Из формулы сопротивления легко можно определить длину, удельное сопротивление и сечение проводника.
Пример 3. Для радиоприемника необходимо намотать сопротивление в 30 Ом из никелиновой проволоки сечением 0,21 мм 2 . Определить необходимую длину проволоки.
Пример 4. Определить сечение 20 м нихромовой проволоки, если сопротивление ее равно 25 Ом.
Пример 5. Проволока сечением 0,5 мм 2 и длиной 40 м имеет сопротивление 16 Ом. Определить материал проволоки.
Материал проводника характеризует его удельное сопротивление.
По таблице удельных сопротивлений находим, что таким сопротивлением обладает свинец.
Выше было указано, что сопротивление проводников зависит от температуры. Проделаем следующий опыт. Намотаем в виде спирали несколько метров тонкой металлической проволоки и включим эту спираль в цепь аккумулятора. Для измерения тока в цепь включаем амперметр. При нагревании спирали в пламени горелки можно заметить, что показания амперметра будут уменьшаться. Это показывает, что с нагревом сопротивление металлической проволоки увеличивается.
У некоторых металлов при нагревании на 100° сопротивление увеличивается на 40 – 50 %. Имеются сплавы, которые незначительно меняют свое сопротивление с нагревом. Некоторые специальные сплавы практически не меняют сопротивления при изменении температуры. Сопротивление металлических проводников при повышении температуры увеличивается, сопротивление электролитов (жидких проводников), угля и некоторых твердых веществ, наоборот, уменьшается.
Способность металлов менять свое сопротивление с изменением температуры используется для устройства термометров сопротивления. Такой термометр представляет собой платиновую проволоку, намотанную на слюдяной каркас. Помещая термометр, например, в печь и измеряя сопротивление платиновой проволоки до и после нагрева, можно определить температуру в печи.
Если при температуре t сопротивление проводника равно r, а при температуре t равно rt, то температурный коэффициент сопротивления
Примечание. Расчет по этой формуле можно производить лишь в определенном интервале температур (примерно до 200°C).
Приводим значения температурного коэффициента сопротивления α для некоторых металлов (таблица 2).
Значения температурного коэффициента для некоторых металлов
| Металл | α | ||
| Серебро Медь Железо Вольфрам Платина | 0,0035 0,0040 0,0066 0,0045 0,0032 | Ртуть Никелин Константан Нихром Манганин | 0,0090 0,0003 0,000005 0,00016 0,00005 |
Из формулы температурного коэффициента сопротивления определим rt:
Пример 6. Определить сопротивление железной проволоки, нагретой до 200°C, если сопротивление ее при 0°C было 100 Ом.
Пример 7. Термометр сопротивления, изготовленный из платиновой проволоки, в помещении с температурой 15°C имел сопротивление 20 Ом. Термометр поместили в печь и через некоторое время было измерено его сопротивление. Оно оказалось равным 29,6 Ом. Определить температуру в печи.
Электрическая проводимость
До сих пор мы рассматривали сопротивление проводника как препятствие, которое оказывает проводник электрическому току. Но все же ток по проводнику проходит. Следовательно, кроме сопротивления (препятствия), проводник обладает также способностью проводить электрический ток, то есть проводимостью.
Чем большим сопротивлением обладает проводник, тем меньшую он имеет проводимость, тем хуже он проводит электрический ток, и, наоборот, чем меньше сопротивление проводника, тем большей проводимостью он обладает, тем легче току пройти по проводнику. Поэтому сопротивление и проводимость проводника есть величины обратные.
Из математики известно, что число, обратное 5, есть 1/5 и, наоборот, число, обратное 1/7, есть 7. Следовательно, если сопротивление проводника обозначается буквой r, то проводимость определяется как 1/r. Обычно проводимость обозначается буквой g.
Электрическая проводимость измеряется в (1/Ом) или в сименсах.
Пример 8. Сопротивление проводника равно 20 Ом. Определить его проводимость.
Если r = 20 Ом, то
Пример 9. Проводимость проводника равна 0,1 (1/Ом). Определить его сопротивление,
Если g = 0,1 (1/Ом), то r = 1 / 0,1 = 10 (Ом)
Материалы высокой проводимости
К наиболее широкораспрстраненным материалам высокой проводимости следует отнести медь и алюминий (Сверхпроводящие материалы, имеющие типичное сопротивление в 10 -20 раз ниже обычных проводящих материалов (металлов) рассматриваются в разделе Сверхпроводимость).
Преимущества меди, обеспечивающие ей широкое применение в качестве проводникового материала, следующие:
- малое удельное сопротивление;
- достаточно высокая механическая прочность;
- удовлетворительная в большинстве случаев применения стойкость по отношению к коррозии;
- хорошая обрабатываемость: медь прокатывается в листы, ленты и протягивается в проволоку, толщина которой может быть доведена до тысячных долей миллиметра;
- относительная легкость пайки и сварки.
Медь получают чаще всего путем переработки сульфидных руд. После ряда плавок руды и обжигов с интенсивным дутьем медь, предназначенная для электротехнических целей, обязательно проход
Что такое единицы удельной проводимости и удельного сопротивления?
Электропроводность измеряет способность раствора проводить электрический ток между двумя электродами. В растворе ток протекает за счет переноса ионов. Следовательно, с увеличением количества ионов, присутствующих в жидкости, жидкость будет иметь более высокую проводимость. Если количество ионов в жидкости очень мало, раствор будет «сопротивляться» току. Переменный ток используется для предотвращения полной миграции ионов к двум электродам.
Электропроводность измеряет способность раствора проводить электрический ток между двумя электродами. В растворе ток протекает за счет переноса ионов. Следовательно, с увеличением количества ионов, присутствующих в жидкости, жидкость будет иметь более высокую проводимость. Если количество ионов в жидкости очень мало, раствор будет «сопротивляться» току. Переменный ток используется для предотвращения полной миграции ионов к двум электродам.Введение в измерения и единицы измерения
Проводимость измеряет способность раствора проводить электрический ток между двумя электродами.В растворе ток протекает за счет переноса ионов. Следовательно, с увеличением количества ионов, присутствующих в жидкости, жидкость будет иметь более высокую проводимость. Если количество ионов в жидкости очень мало, раствор будет «сопротивляться» току. Переменный ток используется для предотвращения полной миграции ионов к двум электродам.
Проводимость = 1 / сопротивление
Единица проводимости: mho = Siemen
Нормальная единица измерения электропроводности:
1 микромо (мкСм) = 1 микросименс (мкСм)
1 миллимхо (ммхо) = 1 миллиСименс (мСм) = 1000 микросименс (мкСм)
Единица сопротивления: Ом
Нормальная единица измерения удельного сопротивления:
МОм = 1000000 Ом
Преобразование единиц проводимости.
20 микросименс (мкСм)
= 20 х 10-6 S
= 2 х 10-5 S
= 2 x 10-5 мхо>
Преобразование единиц удельного сопротивления
1 Ом / 2 x 10-5
= 1 / проводимость
= 1/2 x 10-5 Ом
= 0,5 х 10-5 Ом
= 5 x 10 4 Ом
Электропроводность и удельное сопротивление (растворы NaCl и CaCO 3 при 25 ° C)
| ppm как CaCO 3 | частей на миллион NaCl | Электропроводность мкмос / см | Удельное сопротивление, МОм / см |
| 1700 | 2000 | 3860 | 0.00026 |
| 1275 | 1500 | 2930 | 0,00034 |
| 850 | 1000 | 1990 | 0,00050 |
| 425 | 500 | 1020 | 0,00099 |
| 170 | 200 | 415 | 0.0024 |
| 127,5 | 150 | 315 | 0,0032 |
| 85,0 | 100 | 210 | 0,0048 |
| 42,5 | 50 | 105 | 0,0095 |
| 17,0 | 20 | 42.7 | 0,023 |
| 12,7 | 15 | 32,1 | 0,031 |
| 8,5 | 10 | 21,4 | 0,047 |
| 4,25 | 5,0 | 10,8 | 0,093 |
| 1,70 | 2.0 | 4,35 | 0,23 |
| 1,27 | 1,5 | 3,28 | 0,30 |
| 0,85 | 1,00 | 2,21 | 0,45 |
| 0,42 | 0,50 | 1,18 | 0,88 |
| 0.17 | 0,20 | 0,49 | 2,05 |
| 0,13 | 0. |
Единицы электропроводности и удельного сопротивления и теория измерений.
Введение в измерения и единицы измерения
Электропроводность измеряет способность раствора проводить электрический ток. между двумя электродами.В растворе ток течет по ионам транспорт. Следовательно, с увеличением количества присутствующих ионов в жидкости жидкость будет иметь более высокую проводимость. Если количество ионов в жидкости очень мало, раствор будет быть «резистентным» к току. Переменный ток используется для предотвращения полная миграция ионов к двум электродам.В этой статье более подробно объясняется, как измеряется проводимость.
Проводимость = 1 / сопротивление
Единица проводимости: mho = Siemen
Нормальная единица измерения проводимости:
1 микромо (мкСм) = 1 микросименс (мкСм),
1 миллимхо (ммхо) = 1 миллиСименс (мСм) = 1000 микросименс (мкСм)
Единица измерения сопротивления: Ом
Нормальная единица измерения удельного сопротивления:
мегом = 1000000 Ом
Преобразование единиц проводимости:
20 микросименс (мкСм)= 20 х 10-6 S
= 2 х 10-5 S
= 2 x 10-5 мхо >
Преобразование единиц удельного сопротивления:
1 Ом / 2 x 10-5 = 1 / проводимость= 1/2 x 10-5 Ом
= 0.5 x 10-5 Ом
= 5 x 10 4 Ом
Электропроводность и удельное сопротивление (растворы NaCl и CaCO3 при 25 ° C)
частей на миллион как CaCO 3 | частей на миллион NaCl | Электропроводность микромос / см | Удельное сопротивление мегом-см |
1700 | 2000 | 3860 | 0.00026 |
1275 | 1500 | 2930 | 0,00034 |
850 | 1000 | 1990 | 0.00050 |
425 | 500 | 1020 | 0,00099 |
170 | 200 | 415 | 0.0024 |
127,5 | 150 | 315 | 0,0032 |
85.0 | 100 | 210 | 0,0048 |
42,5 | 50 | 105 | 0.0095 |
17,0 | 20 | 42,7 | 0,023 |
12.7 | 15 | 32,1 | 0,031 |
8,5 | 10 | 21.4 | 0,047 |
4,25 | 5,0 | 10,8 | 0.093 |
1,70 | 2,0 | 4,35 | 0,23 |
1.27 | 1,5 | 3,28 | 0,30 |
0,85 | 1.00 | 2,21 | 0,45 |
0,42 | 0,50 | 1.18 | 0,88 |
0,17 | 0,20 | 0,49 | 2.05 |
0,13 | 0,15 | 0,38 | 2,65 |
.085 | 0,10 | 0,27 | 3,70 |
0,042 | 0.05 | 0,16 | 6,15 |
0,017 | 0,02 | 0.098 | 10,2 |
0,012 | 0,015 | 0,087 | 11.5 |
0,008 | 0,010 | 0,076 | 13,1 |
0.004 | 0,005 | 0,066 | 15,2 |
0,002 | 0.002 | 0,059 | 16,9 |
0,001 | 0,001 | 0.057 | 17,6 |
нет | нет | 0,055 | 18.3 |
Константы датчика
Постоянная зонда определяет объем между электродами. Решения с чрезвычайно высокой проводимостью требуется датчик с зондом константа больше 1.0. Решения с чрезвычайно низкой проводимостью требуется датчик с константой зонда менее 1.0. Чем больше чем расстояние между электродами, тем меньше токовый сигнал. Электропроводность | Удельное сопротивление | Растворенный
Твердые вещества |
.056 | 18 000 000 | . 0277 |
.084 | 12 000 000 | 0.417 |
. 167 | 6 000 000 | 0,833 |
1,00 | 1 000 000 | .500 |
2,50 | 400 000 | 1,25 |
20,0 | 50 000 | 10.0 |
200 | 5000 | 100 |
2000 | 500 | 1 000 |
20 000 | 50 | 10 000 |
Электропроводность | Сопутствующие товары
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ВЫСОКОКАЧЕСТВЕННЫЕ АЛЮМИНИЕВЫЕ ПРУТКИ
Riyadh Cables предлагает высококачественные алюминиевые стержни 9.Катушки 5 мм.
Типичные свойства алюминиевого прутка
Диаметр 9,5 мм ± 0,5 мм Чистота 99,5% Алюминий Плотность 2,7 г / см³ Удельное сопротивление 0,02801 Ом мм² / м при 20 ° C. Проводимость 61.5% IACS при 20 ° C. Предел прочности 8,3 кг / мм² (типичное значение). Удлинение 4% (мин.) При длине колеи 250 мм Упаковка
Пруток алюминиевый поставляется в бухтах по 2000 кг. Бухты упакованы на прочные деревянные поддоны, надежно закреплены четырьмя стальными ремнями и покрыты толстым листом полиэтилена.
Артикул
Каждая катушка должна иметь следующую заметную маркировку:
- Производитель / Торговая марка
- Оценка
- Вес нетто / брутто
- Заводской номер катушки
- Заводской номер
Контроль качества
Все важные параметры постоянно проверяются для обеспечения контроля качества.Следующие ниже тесты гарантируют, что произведенная удочка неизменно высокого качества.
- Вес одного метра (г / м)
- Анализ химического состава — измерение% Fe, B, Mg, Si, V, Zn, Ti, Cr, Na, Mn, Cu, Ga, Al.
- Объемное сопротивление при 20 ° C.
- Проводимость — прецизионный прибор для измерения проводимости алюминия.
- Испытание на удлинение и растяжение — стержень испытывают на удлинение при разрыве и прочность на разрыв.
- Проверка диаметра — это гарантия того, что стержень имеет правильную круглую форму и необходимый диаметр.
Закон Ома
- Ресурс исследования
- Исследовать
- Искусство и гуманитарные науки
- Бизнес
- Инженерная технология
- Иностранный язык
- История
- Математика
- Наука
- Социальная наука
Лучшие подкатегории
- Высшая математика
- Алгебра
- Базовая математика
- Исчисление
- Геометрия
- Линейная алгебра
- Предалгебра
- Предварительный расчет
- Статистика и вероятность
- Тригонометрия
- другое →
Лучшие подкатегории
- Астрономия
- Астрофизика
- Биология
- Химия
- Науки о Земле
- Наука об окружающей среде
- Здравоохранение
- Физика
- другое →
Лучшие подкатегории
- Антропология
- Закон
- Политология
- Психология
- Социология
- другое →
Лучшие подкатегории
- Бухгалтерский учет
- Экономика
- Финансы
- Менеджмент
- другое →
Лучшие подкатегории
- Аэрокосмическая техника
- Биоинженерия
- Химическая инженерия
- Гражданское строительство
- Компьютерные науки
- Электротехника
- Промышленное проектирование
- Машиностроение
- Веб-дизайн
- другое →
Лучшие подкатегории
- Архитектура
Состав манганина, свойства, удельное сопротивление, использование, шунт
Манганин — это торговая марка сплава, состоящего из трех металлических элементов — меди, никеля и марганца.Этот сплав используется в различных отраслях промышленности. Читайте дальше, чтобы узнать больше о составе, свойствах и использовании этого материала.
История Манганина
Эдвард Уэстон, американский химик, был первым, кто открыл «манганин» в 1892 году, работая над улучшением другого металлического сплава. Этот сплав, ранее известный как «Сплав № 2», был обнаружен Уэстоном, который переименовал его в «Константин».
Состав манганина
Этот металлический сплав состоит из следующих металлов в следующих пропорциях:
- Медь (Cu): 86%
- Марганец (Mn): 12%
- Никель (Ni): 2%
Химическая формула манганина
Химическая формула этого вещества — CuMnNi.Он состоит из формул всех составляющих металлов, а именно CU для меди, Mn для марганца и Ni для никеля.
Рисунок 1 — Манганин
Источник — o-digital.com
Свойства манганина
Ниже приведены некоторые из основных свойств этого сплава:
- Его вес по формуле (сумма молекулярных масс атомов в формуле) составляет 177,18 г / моль.
- Этот сплав имеет низкий температурный коэффициент сопротивления (относительное изменение физических свойств вещества при изменении температуры на 1 К).
- Удельное сопротивление этого сплава сопротивления составляет 4,55 × 10 9 10 21 -5 9 10 22 Ом сантиметр.
- Он электропроводен.
- Он имеет температуру плавления 960 ° C.
- Предел прочности на разрыв этого вещества составляет 300-600 МПа.
- Удельное электрическое сопротивление этого сплава варьируется от 43 до 48 мкОм · см.
- Плотность этого сплава 8,4 г / см 3 .
- Он имеет удельный вес 8,5.
- Его электрическое сопротивление остается постоянным в диапазоне температур.
Использование манганина
Манганин с момента открытия использовался в различных промышленных целях. Свойства этого материала делают его наиболее эффективным для определенных применений. Он широко используется в промышленности для производства различных веществ, таких как:
Шунты
Проволока и фольга из этого материала в основном используются для изготовления различных резисторов, в основном амперметрических шунтов. Шунт — это устройство, контролирующее прохождение электрического тока в разных точках цепи.Этот металлический сплав имеет очень низкий температурный коэффициент сопротивления. Он также имеет долгосрочную стабильность. Эти свойства делают его очень полезным для изготовления шунтов.
Катушка этого вещества обычно имеет ширину 150 мм и толщину 0,025 мм.
Калибры
Это вещество имеет низкую чувствительность к деформации (деформация вещества из-за приложенного к нему напряжения или деформации) и высокую чувствительность к гидростатическому давлению (давление, прикладываемое жидкостью в состоянии равновесия в результате действия силы тяжести). .По этой причине он очень полезен в манометрах для изучения ударных волн высокого давления (волна, несущая энергию, возникает из различных сред, таких как газ, жидкость, твердое тело, а также через различные поля под высоким давлением).
Манометрышироко используются в исследованиях ударных волн высокого давления в диапазоне от 1 до 400 килобар (1 бар = 100 000 Н / м2 или 14,5 фунтов на квадратный дюйм). В обычных применениях датчик крепится между двумя плоскими полимерными пластинами или металлическими пластинами.
Манганин-константановые термопарыболее эффективны, чем медно-константановые термопары в блоках термометрии (измерения температуры) коммерческих ультразвуковых гипертермических систем.
Манганиновая проволока также может использоваться в качестве электрического проводника в криогенных системах. Его использование сводит к минимуму передачу тепла между точками, требующими электрических соединений.
Артикул:
http://www.ncbi.nlm.nih.gov/pubmed/7714367
.

 ru
ru Формулировка для участка электрической цепи (проводника), не содержащего источников электродвижущей силы (ЭДС): сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению проводника. Законы Ома для замкнутой неразветвлённой цепи: сила тока прямо пропорциональна электродвижущей силе и обратно пропорциональна полному сопротивлению цепи. Закон Ома справедлив для постоянных и квазистационарных токов. Был открыт немецким физиком Георгом Омом в 1826 году. * Современная энциклопедия
Формулировка для участка электрической цепи (проводника), не содержащего источников электродвижущей силы (ЭДС): сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению проводника. Законы Ома для замкнутой неразветвлённой цепи: сила тока прямо пропорциональна электродвижущей силе и обратно пропорциональна полному сопротивлению цепи. Закон Ома справедлив для постоянных и квазистационарных токов. Был открыт немецким физиком Георгом Омом в 1826 году. * Современная энциклопедия 2/м] (SI – Ω·m, рус. – Ом-метр, англ. – ohm-meter). Для измерения проводниковых материалов разрешается использовать внесистемную единицу –
2/м] (SI – Ω·m, рус. – Ом-метр, англ. – ohm-meter). Для измерения проводниковых материалов разрешается использовать внесистемную единицу – 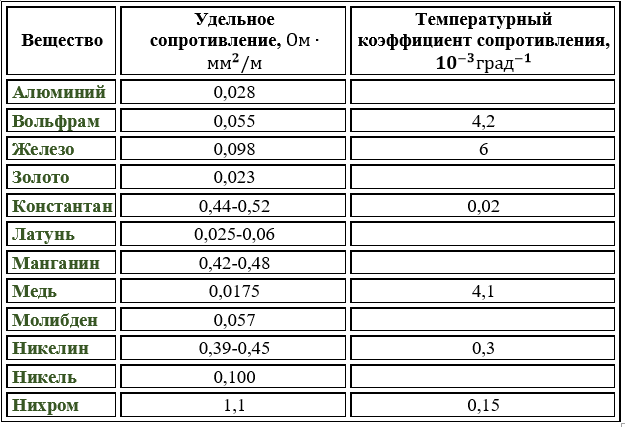 -9 Ом•м)
-9 Ом•м) Таким образом, считается желательным, увеличение напряжения до величин в десятки (внутригородские воздушные и кабельные сети электропередач на 380 вольт, 6, 10, 20, 35, 110, 220 и 330 кВ) и сотни киловольт (магистральные электросети сверхвысокого – ЛЭП500-750 кВ и ультравысокого напряжения, 1150кВ и выше) на линиях переменного и постоянного (150, 400, 800 кВ) тока. Но, при таких параметрах эксплуатации, постоянно растущем потреблении электрической энергии и частых пиковых перегрузках, износ оборудования, отсутствие резервных мощностей, погодные аномалии, локальные несоответствия требованиям безопасности, непрофессионализм и элементарное разгильдяйство – могут стать причиной нештатных ситуаций и системных аварий (называемых теперь, на английский манер – блэкаут). По этой причине, муниципальные власти любого посёлка и города – имеют постоянную головную боль по обеспечению резервными источниками питания (аккумуляторами и дизель-генераторами) для бесперебойного электроснабжения социальных объектов по резервной схеме.
Таким образом, считается желательным, увеличение напряжения до величин в десятки (внутригородские воздушные и кабельные сети электропередач на 380 вольт, 6, 10, 20, 35, 110, 220 и 330 кВ) и сотни киловольт (магистральные электросети сверхвысокого – ЛЭП500-750 кВ и ультравысокого напряжения, 1150кВ и выше) на линиях переменного и постоянного (150, 400, 800 кВ) тока. Но, при таких параметрах эксплуатации, постоянно растущем потреблении электрической энергии и частых пиковых перегрузках, износ оборудования, отсутствие резервных мощностей, погодные аномалии, локальные несоответствия требованиям безопасности, непрофессионализм и элементарное разгильдяйство – могут стать причиной нештатных ситуаций и системных аварий (называемых теперь, на английский манер – блэкаут). По этой причине, муниципальные власти любого посёлка и города – имеют постоянную головную боль по обеспечению резервными источниками питания (аккумуляторами и дизель-генераторами) для бесперебойного электроснабжения социальных объектов по резервной схеме.
 -9 Ом – наноом нОм nΩ
-9 Ом – наноом нОм nΩ Так как значения ТКС очень малы, то в справочниках их указывают в единицах тысячных или миллионных долей (ppm/°С – Parts Per Million) относительного изменения сопротивления на градус.
Так как значения ТКС очень малы, то в справочниках их указывают в единицах тысячных или миллионных долей (ppm/°С – Parts Per Million) относительного изменения сопротивления на градус.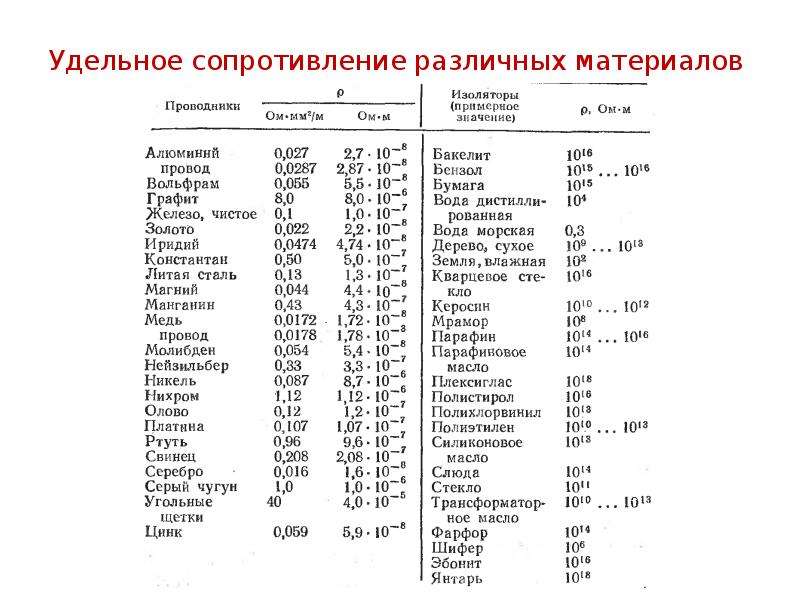
 2)/4
2)/4 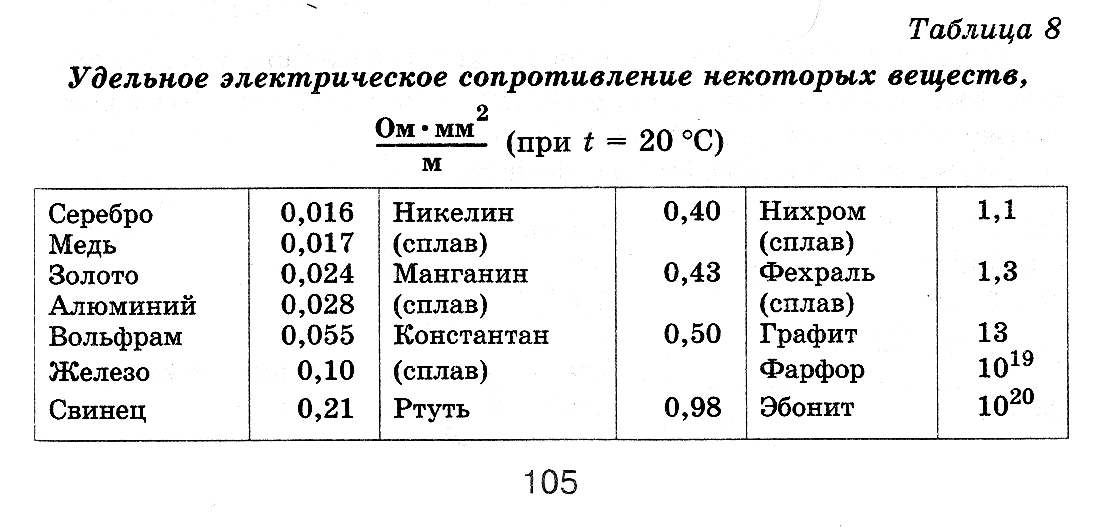 При повышении температуры этого металла увеличивается частота и амплитуда колебаний атомов кристаллической решетки, что создает дополнительное сопротивление прохождению электрического тока через толщу сплава. Поэтому, с ростом температуры сопротивление стали увеличивается.
При повышении температуры этого металла увеличивается частота и амплитуда колебаний атомов кристаллической решетки, что создает дополнительное сопротивление прохождению электрического тока через толщу сплава. Поэтому, с ростом температуры сопротивление стали увеличивается. Величина сопротивления возрастает на порядок и может достигать значения 130·10 -8 Ом·м.
Величина сопротивления возрастает на порядок и может достигать значения 130·10 -8 Ом·м.