Формула суммы углов правильного многоугольника. Площадь правильного многоугольника формула. Формула радиуса правильного многоугольника.
- Альфашкола
- Статьи
- Формулы правильного многоугольника
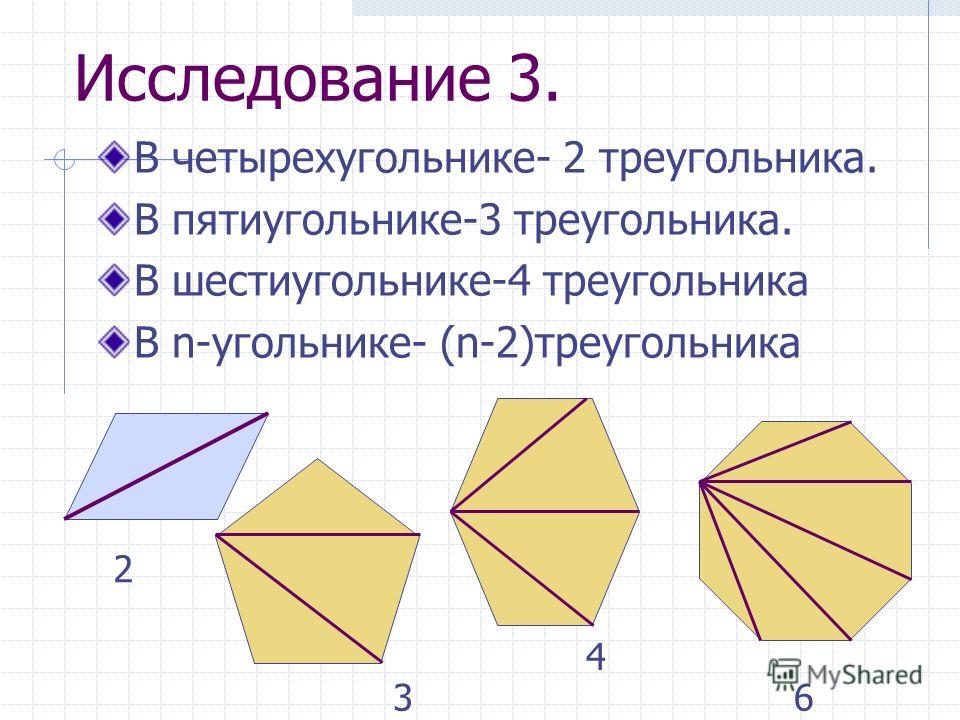
Многоугольник — это плоская замкнутая фигура с множеством углов. Правильный многоугольник — это равноугольный и равносторонний многоугольник. Центр правильного многоугольника является общим центром его вписанных и описанных окружностей. Центральный угол правильного многоугольника — это угол, вершиной которого является центр многоугольника. \( N\) сторонний многоугольник будет иметь \(n\) центральных углов. Сумма внешних углов многоугольника \(360°\).
Сумма внутренних углов правильного многоугольника с n сторонами равна:
\((n — 2)180°\)
Радиус описанной окружности равен:
\(R = \frac{a}{{2\sin \frac{{{{180}^o}}}{n}}}\)
\(a-\)сторона многоугольника
Вписанный радиус:
\(r = \frac{a}{{2tg\frac{{{{180}^o}}}{n}}}\)
\(a-\)сторона многоугольника
Площадь правильного многоугольника
\(S = p \cdot r\)
\(S = {r^2} \cdot n \cdot tg\frac{{{{180}^o}}}{n}\)
\(S = \frac{1}{2}{R^2} \cdot n \cdot \sin \frac{{{{360}^o}}}{n}\)
\(S = \frac{{{a^2} \cdot n}}{{4tg\frac{{{{180}^o}}}{n}}}\)
\(a-\)сторона многоугольника ,\(n\)- число сторон , \(p\)-полупериметр,
\(r-\) радиус вписанной окружности , \(R-\)радиус описанной окружности
Для нахождения стороны в многоугольнике используют фрмулы:
\(a = 2r \cdot tg\frac{{{{180}^o}}}{n}\)
\(a = 2R \cdot \sin \frac{{{{180}^o}}}{n}\)
\(a-\)сторона многоугольника, \(r-\) радиус вписанной окружности , \(R-\)радиус описанной окружности
Если задан радиус правильного многоугольника:
\(S = \frac{R^2n}{2} sin (\frac{2π}{n})\)
Периметр многоугольника:
\(Р = an \)
\(n\)- число углов, \(a\)-длина стороны
Сторона многоугольника:
\(a =\frac{ 2rsinα }{ 2}\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Всеволод Константинович Добровольский
Репетитор по математике
Стаж (лет)
Образование:
РГПУ им. А.И. Герцена
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-11 кл.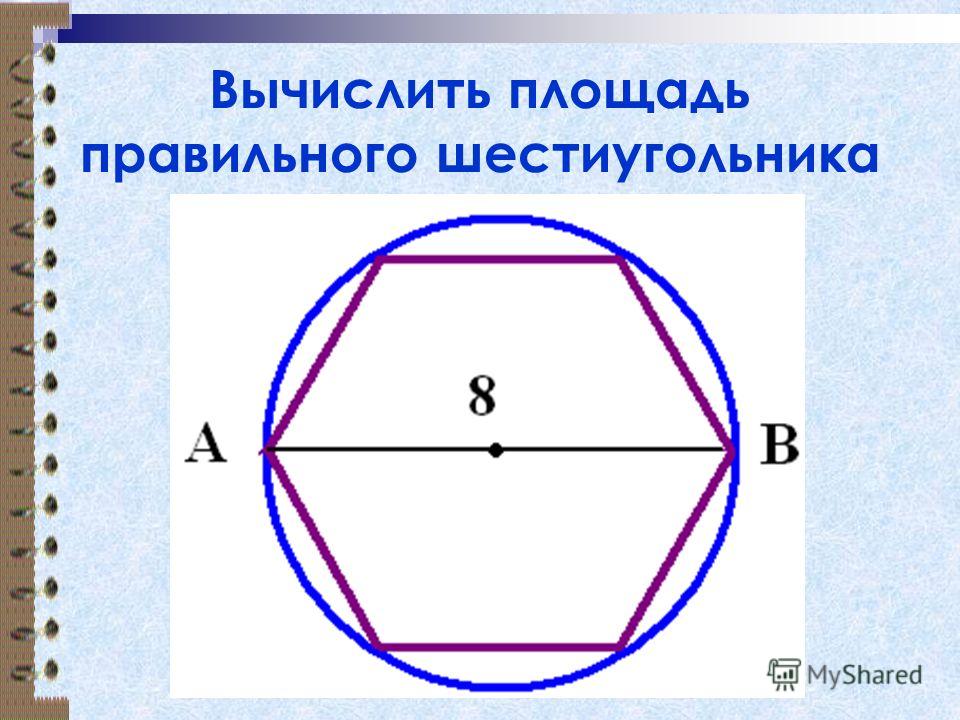 Подготовка к ОГЭ/ЕГЭ/олимпиады. География — удивительная наука. Через понимание географии можно понять процессы, которые происходят вокруг нас в природе и в обществе. Я люблю свой предмет и делюсь этим с учениками. Работа с ребятами строится на взаимоуважении и равных требованиях.
Подготовка к ОГЭ/ЕГЭ/олимпиады. География — удивительная наука. Через понимание географии можно понять процессы, которые происходят вокруг нас в природе и в обществе. Я люблю свой предмет и делюсь этим с учениками. Работа с ребятами строится на взаимоуважении и равных требованиях.
Наталья Анатольевна Люфт
Репетитор по математике
Стаж (лет)
Образование:
Новосибирскй педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по химии 8-9 классов. Подготовка к ОГЭ. Учитель высшей категории. Стаж работы 30 лет.
Мои занятия будут способствовать качественному усвоению знаний, привитию интереса к науке. На своих уроках совмещаю традиционные и инновационные методы обучения. Большое внимание уделяю выработке практических навыков и умений.
Учащиеся, сдававшие ОГЭ по химии, показали хорошие и отличные результаты.
Регулярно повышаю свой уровень образования, занимаясь на курсах переподготовки. Принимала участие в обсуждении следующих вопросов:
1. «Формирование профессиональной компетентности учителя»
2. «Реализация требований обновлённых ФГОС в работе учителя химии и биологии»
3. «Методология и технологии цифровых образовательных технологий в образовательном процессе»
Подготовка к ОГЭ. Учитель высшей категории. Стаж работы 30 лет.
Мои занятия будут способствовать качественному усвоению знаний, привитию интереса к науке. На своих уроках совмещаю традиционные и инновационные методы обучения. Большое внимание уделяю выработке практических навыков и умений.
Учащиеся, сдававшие ОГЭ по химии, показали хорошие и отличные результаты.
Регулярно повышаю свой уровень образования, занимаясь на курсах переподготовки. Принимала участие в обсуждении следующих вопросов:
1. «Формирование профессиональной компетентности учителя»
2. «Реализация требований обновлённых ФГОС в работе учителя химии и биологии»
3. «Методология и технологии цифровых образовательных технологий в образовательном процессе»
Денис Валерьевич Кочнев
Репетитор по математике
Стаж (лет)
Образование:
Омский государственный педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 7-11 классов.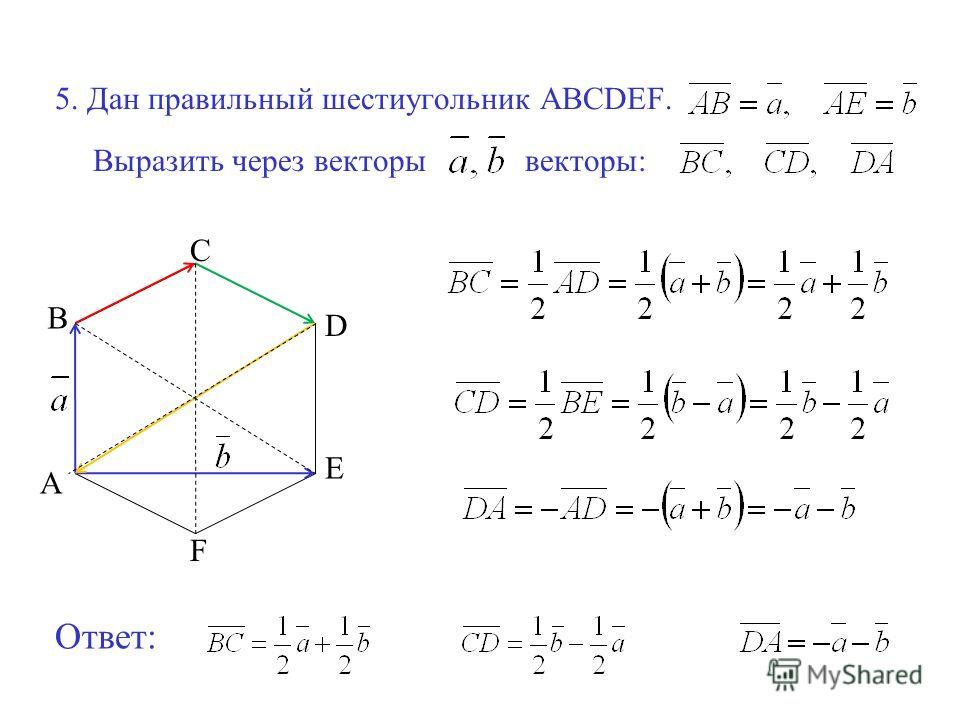
Похожие статьи
- Формулы по алгебре
- 10 фактов о треугольнике
- ИВТ (НИУ ВШЭ) | Информатика и вычислительная техника
- МИФИ: Инновационный менеджмент
- МИФИ (Экономическая Безопасность): Проходной балл, учебный план
- Как сделать первый шаг и пригласить объект симпатии на свидание
- Я внучка (внук): взаимоотношения с бабушками и дедушками
- Что такое конформизм или влияние чужого мнения на собственное поведение и мышление
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
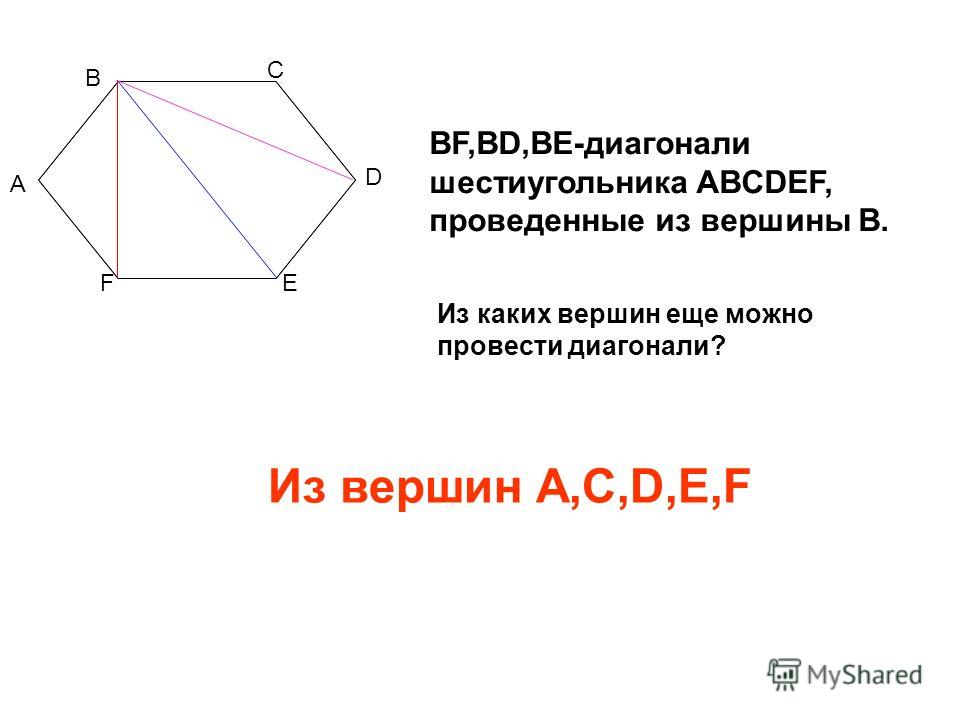
Правильный шестиугольник.
 Правильный шестиугольник свойства.
Правильный шестиугольник свойства.- Альфашкола
- Статьи
- Правильный шестиугольник
В этой статье мы дадим определение правильного шестиугольника, также опишем его свойства.
Если шесть равносторонних треугольников расположены бок о бок, то образуется правильный шестиугольник. Поэтому площадь правильного шестиугольника равна шести равносторонним треугольникам.
- Правильный шестиугольник имеет \(6\) сторон, \(6\) углов и 6 вершин.
- Сумма внутренних углов шестиугольника \(-(6 − 2) · 180° = 720°\).
- Значение внутреннего угла правильного шестиугольника равно \(720º / 6 = 120º\).
 2-\frac{l}{2}}\)
2-\frac{l}{2}}\)Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Алла Александровна Коледа
Репетитор по математике
Стаж (лет)
Образование:
Барановичский высший педагогический колледж
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике и русскому языку 1-4 классов.

Денис Владимирович Нестюк
Репетитор по математике
Стаж (лет)
Образование:
Брестский государственный университет им А.С. Пушкина
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике 5-9 классы, подготовка к олимпиадам. Математика всегда держит наш мозг в тонусе, помогает разобраться во многих вопросах техники, финансовых операциях.
 Всегда есть область в которой можно улучшать свои навыки. На своих уроках привожу практические примеры. Ищу точки соприкосновения с учениками.
Всегда есть область в которой можно улучшать свои навыки. На своих уроках привожу практические примеры. Ищу точки соприкосновения с учениками.Юлия Игоревна Ярош
Репетитор по математике
Стаж (лет)
Образование:
Брестский государственный университет имени А. С. Пушкина
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по русскому языку для 5-11 классов. Мне очень нравится преподавать русский язык, использовать индивидуальный подход на своих уроках, все мои уроки проходит в очень динамичной обстановки.
 Руководствуюсь комплексный подходов, всесторонним анализом текста, ученик осознает, что русский язык -это неразрывная система, понимает, как его разделы связаны между собой и функционируют друг с другом. Всегда нахожу подход к каждому ученику, выстраиваю доверительные отношения. На уроке партнеры, у нас общая цель!
Руководствуюсь комплексный подходов, всесторонним анализом текста, ученик осознает, что русский язык -это неразрывная система, понимает, как его разделы связаны между собой и функционируют друг с другом. Всегда нахожу подход к каждому ученику, выстраиваю доверительные отношения. На уроке партнеры, у нас общая цель!Похожие статьи
- Особенности решения текстовых задач
- Умножения и деление отрицательных чисел
- Диаграммы
- Пирамида и ее свойства
- Как быстро умножить число на 1,5
- Сезон аллергии: как распознать и как спасаться
- Основы мейкапа: как научить дочь пользоваться косметикой
- Отпусти меня, мама, я уже взрослый
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Как найти угол в шестиугольнике
Все математические ресурсы PSAT
10 диагностических тестов 421 практический тест Вопрос дня Карточки Learn by Concept
PSAT Math Help » Геометрия » Плоская геометрия » Шестиугольники » Как найти угол в шестиугольнике?0004 170
Правильный ответ:
190
Пояснение:
Сообщить об ошибке
Если треугольник имеет 180 градусов, какова сумма внутренних углов правильного восьмиугольника?
Возможные ответы:
Правильный ответ:
Объяснение:
Сумма внутренних углов многоугольника определяется как где = количество сторон многоугольника.
 У восьмиугольника 8 сторон, поэтому формула становится
У восьмиугольника 8 сторон, поэтому формула становитсяСообщить об ошибке
Какова величина каждого внутреннего угла в прямоугольном шестиугольнике?
Возможные ответы:
150 градусов
90 градусов
105 градусов
72 градусов
120 градусов
Правильный ответ:
120 градусов
. Пояснение:
Сумма внутренних углов шестиугольника должна равняться 720 градусам. Поскольку шестиугольник правильный, все внутренние углы будут иметь одинаковую величину. Шестиугольник имеет шесть сторон и шесть внутренних углов. Следовательно, каждый угол измеряет.
Сообщить об ошибке
Примечание. Рисунок выполнен НЕ в масштабе.
См. рисунок выше. Оценивать .
Возможные ответы:
Правильный ответ:
Объяснение:
Сумма градусных мер углов (шестистороннего) шестиугольника равна
.
 Мы можем решить в уравнении
Мы можем решить в уравненииСообщить об ошибке
Примечание: Рисунок выполнен НЕ в масштабе.
См. рисунок выше. Оценивать .
Возможные ответы:
Правильный ответ:
Объяснение:
Сумма показателей степени углов гексагона (шестисторонний) составляет
Мы можем решить в уравнении
. Сообщение о ошибке
40005
Три угла шестиугольника. Остальные три угла равны между собой. Какова мера каждого из последних трех углов?
Возможные ответы:
Этот шестиугольник не может существовать.
Правильный ответ:
Объяснение:
Сумма градусных мер углов (шестистороннего) шестиугольника равна
Позвольте быть общей мерой трех рассматриваемых конгруэнтных углов.
 Мы можем найти в уравнении
Мы можем найти в уравненииСообщить об ошибке
Какова величина одного из внутренних углов правильного шестиугольника?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти сумму внутренних углов любого правильного многоугольника, используйте формулу , где представляет количество сторон правильного многоугольника.
Сумма внутренних углов правильного шестиугольника равна 720 градусов. Чтобы найти величину одного угла, разделите его на количество внутренних углов (или сторон):
Размер одного угла в правильном шестиугольнике равен 120 градусам.
Сообщить об ошибке
Уведомление об авторских правах
Все математические ресурсы PSAT
10 диагностических тестов 421 практический тест Вопрос дня Карточки Учитесь по концепции
Сумма внутренних углов шестиугольника
Сумма всех внутренних углов шестиугольника равна 720°.
 Сумма всегда выполняется независимо от того, является ли шестиугольник правильным или неправильным. Меру каждого отдельного угла в правильном шестиугольнике можно определить, разделив сумму на 6. Однако для неправильных шестиугольников мы должны использовать меры других углов, чтобы определить меру отсутствующего угла.
Сумма всегда выполняется независимо от того, является ли шестиугольник правильным или неправильным. Меру каждого отдельного угла в правильном шестиугольнике можно определить, разделив сумму на 6. Однако для неправильных шестиугольников мы должны использовать меры других углов, чтобы определить меру отсутствующего угла.Здесь мы узнаем больше о внутренних углах шестиугольников.
ГЕОМЕТРИЯ
Актуально для …
Изучение суммы внутренних углов шестиугольников.
См. углы
Содержание
ГЕОМЕТРИЯ
Актуально для …
Изучение суммы внутренних углов шестиугольников.
См. углы
Сумма внутренних углов шестиугольника
Сумма всех внутренних углов шестиугольника всегда равна 720°. Это верно независимо от того, является ли шестиугольник правильным или неправильным. Сумма углов получается по формуле суммы углов многоугольников:
$латекс (n-2)\times 180$° где n — количество сторон многоугольника.
 Для шестиугольника мы используем $латекс n = 6$. Таким образом, мы имеем:
Для шестиугольника мы используем $латекс n = 6$. Таким образом, мы имеем:$латекс (n-2)\times 180$°
$латекс =(6-2)\times 180$°
$латекс =(4)\times 180$°
$ латекс =720$°
Формулу суммы внутренних углов можно получить, разделив любой многоугольник на треугольники, как показано на следующей диаграмме:
Мы знаем, что сумма внутренних углов любого треугольника равна 180°. Кроме того, мы можем составить в общей сложности 90 275 n 90 276 -2 треугольников в любом многоугольнике, где 90 275 n 90 276 — количество сторон многоугольника. Это означает, что $latex (n-2) \times 180$° соответствует сумме всех внутренних углов многоугольника.
Как определить размеры всех внутренних углов шестиугольников?
Если у нас есть правильный шестиугольник, мы можем определить меры каждого внутреннего угла, разделив общую сумму углов на 6. Это возможно, потому что все внутренние углы в правильном многоугольнике имеют одинаковую меру. Поэтому имеем:
720°÷6 = 120°
Каждый внутренний угол правильного шестиугольника имеет размер, равный 120°.

Чтобы определить размеры любого отсутствующего угла в неправильных шестиугольниках, нам нужно знать размеры других углов, поскольку эти шестиугольники имеют внутренние углы, отличные друг от друга.
Например, если у нас есть шестиугольник с внутренними углами 100°, 110°, 120°, 130°, 150°, мы можем определить величину шестого угла, сложив известные углы и вычтя из 720°:
100°+110°+120°+130°+150° = 610°
⇒ 720°-610° = 110°
Недостающий угол равен 110°.
Примеры внутренних углов шестиугольников
ПРИМЕР 1
Найдите недостающие углы в шестиугольнике ниже.
Решение: У нас есть размеры пяти из шести внутренних углов неправильного шестиугольника. Мы знаем, что общая сумма равна 720°, поэтому мы можем сложить известные углы и вычесть из 720°:
110°+140°+100°+120°+150° = 620°
⇒ 720°-620° = 100°
Недостающий угол равен 100°.
ПРИМЕР 2
Найдите недостающие углы в неправильном шестиугольнике ниже.


 2-\frac{l}{2}}\)
2-\frac{l}{2}}\)
 Всегда есть область в которой можно улучшать свои навыки. На своих уроках привожу практические примеры. Ищу точки соприкосновения с учениками.
Всегда есть область в которой можно улучшать свои навыки. На своих уроках привожу практические примеры. Ищу точки соприкосновения с учениками.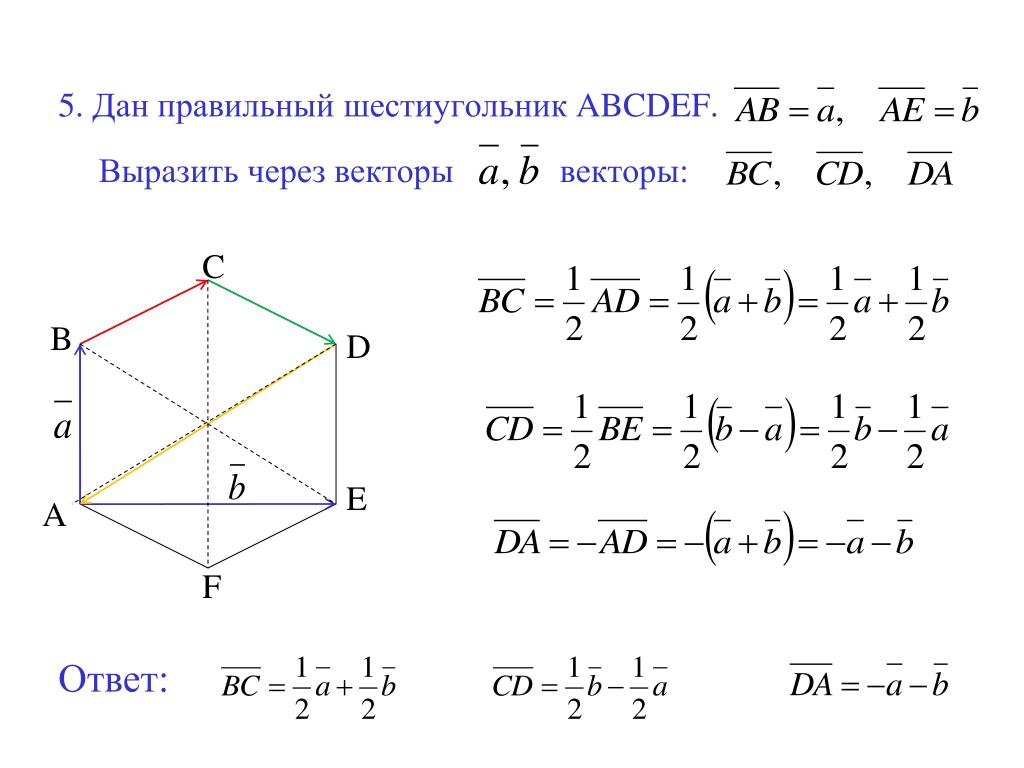 Руководствуюсь комплексный подходов, всесторонним анализом текста, ученик осознает, что русский язык -это неразрывная система, понимает, как его разделы связаны между собой и функционируют друг с другом. Всегда нахожу подход к каждому ученику, выстраиваю доверительные отношения. На уроке партнеры, у нас общая цель!
Руководствуюсь комплексный подходов, всесторонним анализом текста, ученик осознает, что русский язык -это неразрывная система, понимает, как его разделы связаны между собой и функционируют друг с другом. Всегда нахожу подход к каждому ученику, выстраиваю доверительные отношения. На уроке партнеры, у нас общая цель! У восьмиугольника 8 сторон, поэтому формула становится
У восьмиугольника 8 сторон, поэтому формула становится Мы можем решить в уравнении
Мы можем решить в уравнении Мы можем найти в уравнении
Мы можем найти в уравнении Сумма всегда выполняется независимо от того, является ли шестиугольник правильным или неправильным. Меру каждого отдельного угла в правильном шестиугольнике можно определить, разделив сумму на 6. Однако для неправильных шестиугольников мы должны использовать меры других углов, чтобы определить меру отсутствующего угла.
Сумма всегда выполняется независимо от того, является ли шестиугольник правильным или неправильным. Меру каждого отдельного угла в правильном шестиугольнике можно определить, разделив сумму на 6. Однако для неправильных шестиугольников мы должны использовать меры других углов, чтобы определить меру отсутствующего угла. Для шестиугольника мы используем $латекс n = 6$. Таким образом, мы имеем:
Для шестиугольника мы используем $латекс n = 6$. Таким образом, мы имеем: