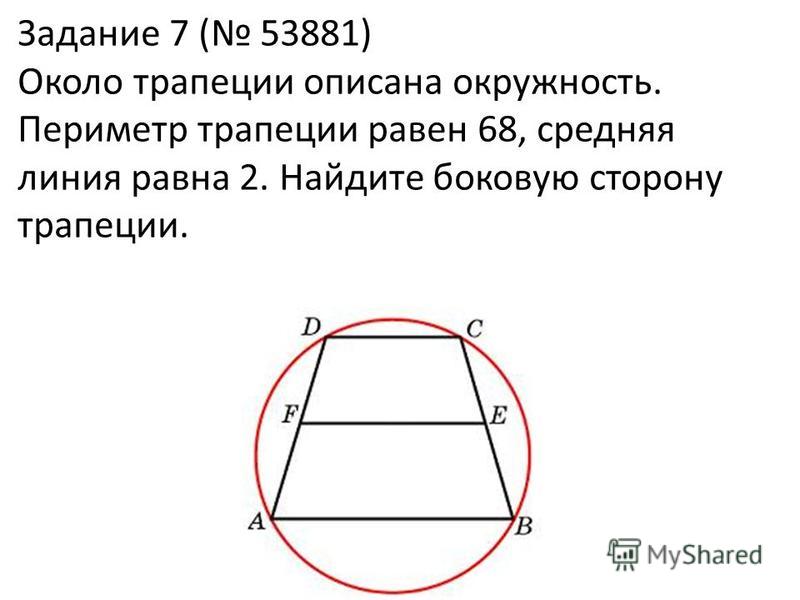
Описанная окружность и трапеция
Описанная окружность и трапеция. Здравствуйте! Для вас ещё одна публикация, в которой рассмотрим задачи с трапециями. Задания входят в состав экзамена по математике. Здесь они объединены в группу, дана не просто одна трапеция, а комбинация тел – трапеция и окружность. Большинство из таких задачек решаются устно. Но есть и такие на которые нужно обратить особое внимание, например, задача 27926.
Какую теорию необходимо помнить? Это:
1. Свойство сторон четырёхугольника описанного около окружности.
2. Теорему Пифагора. *Куда мы без неё )
3. Понятие средней линии трапеции.
Задачи с трапециями, которые имеются на блоге можно посмотреть здесь.
27924. Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции.
Отметим, что описать окружность можно только около равнобедренной трапеции. Нам дана средняя линия, значит можем определить сумму оснований, то есть:
Значит сумма боковых сторон будет равна 22–10=12 (периметр минус основания). Так как боковые стороны равнобедренной трапеции равны, то одна сторона будет равна шести.
Так как боковые стороны равнобедренной трапеции равны, то одна сторона будет равна шести.
Ответ: 6
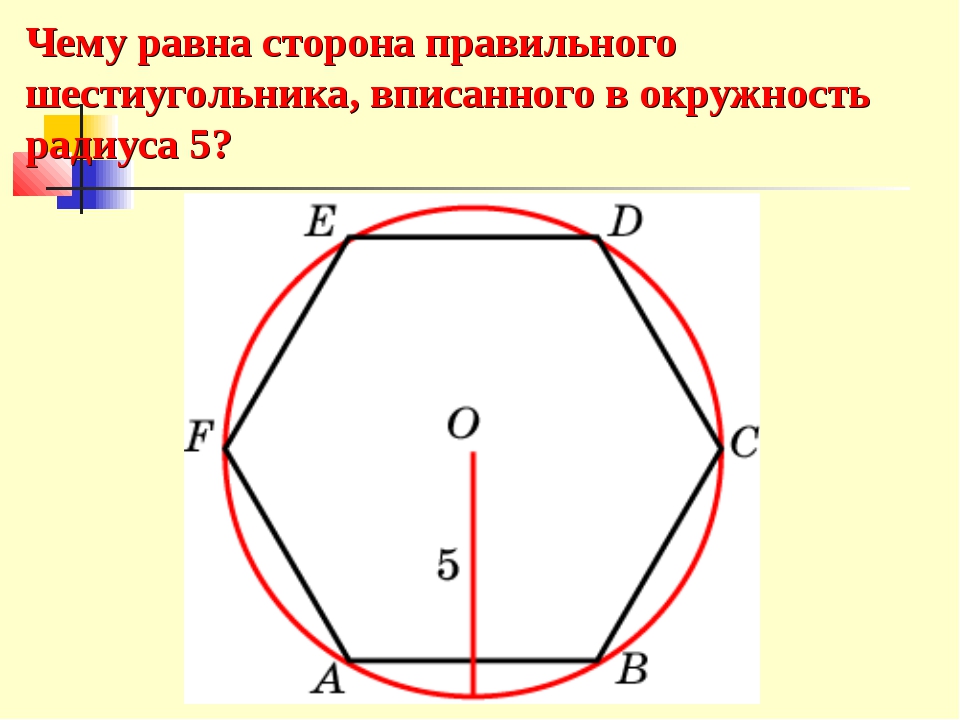
27925. Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 600, большее основание равно 12. Найдите радиус описанной окружности этой трапеции.
Если вы решали задачи с окружностью и вписанным в неё шестиугольником, то сразу озвучите ответ – радиус равен 6. Почему?
Посмотрите: равнобедренная трапеция с углом при основании равным 600 и равными сторонами AD, DC и CB, представляет собой половину правильного шестиугольника:
В таком шестиугольнике отрезок соединяющий противоположные вершины проходит через центр окружности. *Центр шестиугольника и центр окружности совпадают, подробнее здесь п.6
То есть большее основание этой трапеции совпадает с диаметром описанной окружности. Таким образом радиус равен шести.
*Конечно, можно рассмотреть равенство треугольников ADO, DOС и OCB. Доказать что они равносторонние. Далее сделать вывод о том, что угол AOB равен 1800 и точка О равноудалена от вершин A, D, C и B, а и значит АО=ОВ=12/2=6.
Доказать что они равносторонние. Далее сделать вывод о том, что угол AOB равен 1800 и точка О равноудалена от вершин A, D, C и B, а и значит АО=ОВ=12/2=6.
Ответ: 6
27926. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.
Отметим, что центр описанной окружности лежит на оси симметрии, при чём если построить высоту трапеции проходящую через этот центр, то она при пересечении с основаниями разделит их пополам. Покажем это на эскизе, также соединим центр с вершинами:
Отрезок EF является высотой трапеции, его нам нужно найти.
В прямоугольном треугольнике OFC нам известна гипотенуза (это радиус окружности), FC=3 (так как DF=FC). По теореме Пифагора можем вычислить OF:
В прямоугольном треугольнике OEB нам известна гипотенуза (это радиус окружности), EB=4 (так как AE=EB). По теореме Пифагора можем вычислить OE:
Таким образом EF=FO+OE=4+3=7.
Ответ: 7
Теперь важный нюанс!
В этой задаче на рисунке чётко показано, что основания лежат по разные стороны от центра окружности, поэтому задача решается именно так.
А если бы в условии не было дано эскиза?
Тогда у задачи было бы два ответа. Почему? Посмотрите внимательно – в любую окружность можно вписать две трапеции с заданными основаниями:
*То есть при данных основаниях трапеции и радиусе окружности существует две трапеции.
И решение будет «второго варианта» будет следующим.
По теореме Пифагора вычисляем OF:
Также вычислим OE:
Таким образом EF=FO–OE=4–3=1.
Конечно, в задаче с кратким ответом на ЕГЭ двух ответов быть не может, и подобная задача без эскиза дана не будет. Поэтому обратите особое внимание на эскиз! А именно: как расположены основания трапеции. А вот в заданиях с развёрнутым ответом такая в прошлые годы присутствовала (немного с усложнённым условием). Тот, кто рассматривал только один вариант расположения трапеции теряли балл на этом задании.
27937. Около окружности описана трапеция, периметр которой равен 40. Найдите ее среднюю линию.
Здесь сразу следует вспомнить свойство четырёхугольника описанного около окружности:
Суммы противоположных сторон любого четырёхугольника описанного около окружности равны.
Значит
А средняя линия равна половине суммы оснований, то есть 10.
Ответ: 10
27938. Периметр прямоугольной трапеции, описанной около окружности, равен 22, ее большая боковая сторона равна 7. Найдите радиус окружности.
Радиус окружности равен половине высоты. Используя свойство указанное в предыдущей задаче получим:
Большая сторона у нас это СВ, следовательно можем вычислить AD=11–CB=11–7=4. Таким образом, радиус будет равен 2.
Ответ: 2
27915. Найдите высоту трапеции, в которую вписана окружность радиуса 1.
Посмотреть решение
27936. Боковые стороны трапеции, описанной около окружности, равны 3 и 5. Найдите среднюю линию трапеции.
Посмотреть решение
На этом всё, успеха вам!
С уважением, Александр Крутицких.
*Расскажите о сайте в социальных сетях.
Как найти Среднюю Линию Треугольника? Свойства, Теорема
Понятие треугольника
Треугольник — это геометрическая фигура, которая получилось из трех отрезков. Их соединили тремя точками, которые не лежат на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
Их соединили тремя точками, которые не лежат на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
Виды треугольника:
- Прямой. Один угол прямой, два других меньше 90 градусов.
- Острый. Градус угла больше 0, но меньше 90 градусов.
- Тупой. Один угол тупой, два других — острые.
Треугольник считают равнобедренным, если две его стороны равны. Эти стороны называют боковыми сторонами, а третью — основанием.
Треугольник, у которого все стороны равны, называется равносторонним или правильным.
Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, которая лежит напротив прямого угла —
Правильный (равносторонний или равноугольный) треугольник — это правильный многоугольник, в котором все стороны равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.
В равностороннем треугольнике высота является и биссектрисой, и медианой.
Свойства треугольников:
- В треугольнике против большего угла лежит большая сторона — и наоборот.
- Сумма углов треугольника равна 180 градусов.
- Все углы равностороннего треугольника равны 60 градусам.
Понятие средней линии треугольника
Определение средней линии треугольника подходит для любого вида этой фигуры.
Средняя линия треугольника — отрезок, который соединяет середины двух сторон. В любом треугольнике можно провести три средних линии.
Основанием считается сторона, с которой средняя линия не пересекается.
Как найти среднюю линию треугольника расскажем дальше, а для начала еще немного разберемся со всеми определениями.
Запоминаем
Средняя линия параллельна третьей стороне, а ее длина равна половине длины этой стороны.
Понятие средней линии прямоугольного треугольника
Математики говорят: в любом треугольнике можно провести три средних линии. В прямоугольном треугольнике этот отрезок будет равен половине основания — это и есть формула средней линии прямоугольного треугольника. Основанием считается сторона, с которой средняя линия не пересекается.
Прямой угол помогает нам применить другие признаки равенства и подобия. Для углов в прямоугольном треугольнике можно использовать геометрические тождества без дополнительных построений, а любую из сторон можно найти по теореме Пифагора.
В прямоугольном треугольнике две средние линии перпендикулярны катетам, а третья равна медиане, проведённой к гипотенузе. Средние линии острого и разностороннего треугольника не обладают подобными свойствами.
Важное свойство
Средняя линия прямоугольного треугольника делит его на четыре прямоугольные фигуры.
Свойства средней линии треугольника
Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.
Свойства:
- Средняя линия отсекает треугольник, подобный данному с коэффициентом 1/2; его площадь равна четверти площади данного.
- Три средние линии разделяют исходную фигуру на четыре равных треугольника. Центральный из них называют дополнительным.
- Три средние линии разделяют исходный прямоугольный треугольник на четыре равных прямоугольных треугольника.
Теорема о средней линии треугольника
Теорема о средней линии треугольника звучит так:
Средняя линия треугольника параллельна основанию и равна его половине. А так выглядит формула нахождения средней линии треугольника:
Докажем теорему:
- По условию нам дано, что MA = MB, NA = NC
- Рассмотрим два образовавшихся треугольника ΔAMN и ΔABC.
По второму признаку подобия треугольников:
- Поэтому ∠1 = ∠2 , как соответственные, а по признаку параллельности прямых: MN || BC.

Параллельность средней линии и соответствующего ей основания доказана.
- Еще из подобия треугольников △AMN~△ABC можно выписать и отношение их третьих сторон
То, что средняя линия равна половине соответствующего основания, доказано.
Теорема доказана.
Пример 1. В треугольнике ΔABC AB = 8, BC = 7, CA = 5, точки M, N, K — середины сторон AB, BC, CA. Найти периметр ΔMNK.
Как найти периметр треугольника:
- Сначала проверим существует ли указанный в условии треугольник ΔABC. Проверим это при помощи неравенства для его наибольшей стороны:
7 + 5 > 8.
Неравенство выполнено, значит, такой треугольник действительно есть.
- Соединим середины сторон треугольника ΔABC и получим его средние линии. Найдем их длины по теореме о средней линии:
Ответ: периметр треугольника равен 10.
Пример 2. В прямоугольном треугольнике АВС есть три средние линии: MN, NP, MP.
Как решаем:
- В прямоугольнике две диагонали между собой равны. Одна из диагоналей MP — это гипотенуза прямоугольного треугольника MNP. Катеты треугольника известны, значит можно найти гипотенузу через теорему Пифагора:
- Найдем площадь прямоугольника, как произведение диагоналей на синус угла между ними:
S = 5 * 5 * 0,5 = 12,5
- В большом треугольнике четыре малых, а в прямоугольнике два малых треугольника. Все малые треугольники между собой равны, значит, чтобы найти площадь прямоугольного треугольнику, нужно умножить площадь прямоугольника на 2.
Ответ: площадь большого прямоугольного треугольника равна 25.
Приходите решать увлекательные задачки в современную школу Skysmart. Ребенка ждет интерактивный формат, примеры разной сложности и онлайн-доска, на которой можно чертить вместе с учителем.
Запишитесь на бесплатный вводный урок математики и начните заниматься с удовольствием уже завтра!
Сканави. Планиметрия. Задачи 151 – 190 с ответами и решениями
Задачи по планиметрии с ответами и решениями
перейти к содержанию
Группа А. Задачи 151 — 190 (с ответами и решениями)
Вычислить площадь трапеции по разности оснований, равной 14 см, и двум непараллельным сторонам, равным 13 и 15 см, если известно, что в трапецию можно вписать окружность. Ответ: Решение
В трапеции, площадь которой равна 594 м2, высота 22 м, а разность параллельных сторон равна 6 м, найти длину каждой из параллельных сторон. Ответ: Решение
- Доказать, что площадь трапеции равна произведению длины одной из непараллельных сторон и длины перпендикуляра, проведенного через середину другой боковой стороны к первой.
- Трапеция разбита диагоналями на четыре треугольника.
 Найти отношение площадей треугольников, прилегающих к боковым сторонам трапеции. Ответ: Решение
Найти отношение площадей треугольников, прилегающих к боковым сторонам трапеции. Ответ: Решение - Диагональ прямоугольной трапеции и ее боковая сторона равны. Найти длину средней линии, если высота трапеции равна 2 см, а боковая сторона 4 см. Ответ: Решение
- Вычислить площадь прямоугольной трапеции, если ее острый угол равен 60°, меньшее основание равно , а большая боковая сторона равна . Ответ: Решение
- Прямые, содержащие боковые стороны равнобедренной трапеции, пересекаются под прямым углом. Найти длины сторон трапеции, если ее площадь равна 12 см
- Определить боковые стороны равнобедренной трапеции, если ее основания и площадь равны соответственно 8 см, 14 см и 44 см2. Ответ: Решение
- Диагональ равнобедренной трапеции делит ее тупой угол пополам. Меньшее основание трапеции равно 3 см, периметр равен 42 см. Найти площадь трапеции. Ответ: Решение
- В равнобедренной трапеции одно основание равно 40 см, а другое 24 см.
 Диагонали трапеции взаимно перпендикулярны. Найти ее площадь. Ответ: Решение
Диагонали трапеции взаимно перпендикулярны. Найти ее площадь. Ответ: Решение - В равнобедренной трапеции длина средней линии равна 5, а диагонали взаимно перпендикулярны. Найти площадь трапеции. Ответ: Решение
- Большее основание’трапеции в 2 раза больше ее меньшего основания. Через точку пересечения диагоналей проведена прямая, параллельная основаниям. Найти отношение высоты каждой из двух полученных трапеций к высоте трапеции. Ответ: Решение
- Основания равнобедренной трапеции и , боковая сторона ее равна , а диагональ равна . Доказать, что .
- Найти диагональ и боковую сторону равнобедренной трапеции с основаниями 20 и 12 см, если известно, что центр описанной окружности лежит на большем основании трапеции. Ответ: Решение
- В равнобедренной трапеции даны основания =21 см, = 9 см и высота = 9 см. Найти радиус описанного круга. Ответ: Решение
- В окружность радиуса вписана трапеция, у которой нижнее основание вдвое больше каждой из остальных сторон.
 Найти площадь трапеции. Ответ: Решение
Найти площадь трапеции. Ответ: Решение - Длины оснований равнобедренной трапеции относятся как 5:12, а длина ее высоты равна 17 см. Вычислить радиус окружности, описанной около трапеции, если известно, что ее средняя линия равна высоте. Ответ: Решение
- Найти площадь равнобедренной трапеции, если ее высота равна , а боковая сторона видна из центра описанной окружности под углом 60°. Ответ: Решение
- Около окружности с диаметром 15 см описана равнобедренная трапеция с боковой стороной, равной 17 см. Найти основания трапеции. Ответ: Решение
- Площадь равнобедренной трапеции, описанной около круга, равна , а высота трапеции в 2 раза меньше ее боковой стороны. Определить радиус вписанного круга. Ответ: Решение
- Площадь равнобедренной трапеции, описанной около круга, равна см2. Определить боковую сторону трапеции, если известно, что острый угол при основании равен . Ответ: Решение
- Площадь равнобедренной трапеции, описанной около круга, равна 8 см2.
 Определить стороны трапеции, если угол при основании содержит 30°. Ответ: Решение
Определить стороны трапеции, если угол при основании содержит 30°. Ответ: Решение - Площадь равнобедренной трапеции, описанной около круга, равна . Определить боковую сторону трапеции, если известно, что острый угол при основании равен . Ответ: Решение
- Площадь равнобедренной трапеции, описанной около круга, равна . Определить радиус круга, если угол при основании трапеции равен 30°. Ответ: Решение
- В равнобедренную трапецию вписана окружность радиуса . Верхнее основание трапеции в 2 раза меньше ее высоты. Найти площадь трапеции. Ответ: Решение
- Найти площадь круга, вписанного в равнобедренную трапецию, если ее большее основание равно , а угол при меньшем основании равен 120°. Ответ: Решение
- В равнобедренную трапецию вписан круг. Одна из боковых сторон делится точкой касания на отрезки длиной n и m. Определить площадь трапеции. Ответ: Решение
- В равнобедренную трапецию вписан круг. Доказать, что отношение площади круга к площади трапеции равно отношению длины окружности к периметру трапеции.

- Равносторонний шестиугольник ABCDEF состоит из двух трапеций, имеющих общее основание CF. Известно, что АС = 13 см, АЕ = 10 см. Найти площадь шестиугольника. Ответ: Решение
- Найти сторону правильного шестиугольника, равновеликого равнобедренной трапеции с основаниями 20 и 12 см, если известно, что центр описанной окружности лежит на большем основании трапеции. Ответ: Решение
- Вычислить отношение площадей квадрата, правильного треугольника и правильного шестиугольника, вписанных в одну и ту же окружность. Ответ: Решение
- Найти отношение площадей равностороннего треугольника, квадрата и правильного шестиугольника, длины сторон которых равны. Ответ: Решение
- В правильный треугольник со стороной, равной , вписана окружность, в которую вписан правильный шестиугольник. Найти площадь шестиугольника. Ответ: Решение
- Около квадрата, сторона которого равна , описана окружность, а около окружности — правильный шестиугольник. Определить площадь шестиугольника.
 Ответ: Решение
Ответ: Решение - Из точки М, находящейся на расстоянии от окружности, приведена к этой окружности касательная длиной . Найти площадь правильного шестиугольника, вписанного в окружность. Ответ: Решение
- В правильный треугольник вписана окружность, а в нее — правильный шестиугольник. Найти отношение площадей треугольника и шестиугольника. Ответ: Решение
- На сторонах равностороннего треугольника вне его построены квадраты. Их вершины, лежащие вне треугольника, последовательно соединены. Определить площадь полученного шестиугольника, если сторона данного треугольника равна . Ответ: Решение
- В правильный шестиугольник, сторона которого равна , вписана окружность, и около него же описана окружность. Определить площадь кругового кольца, заключенного между этими окружностями. Ответ: Решение
- Данный квадрат со стороной срезан по углам так, что образовался правильный восьмиугольник. Определить площадь этого восьмиугольника. Ответ: Решение
- Доказать, что сумма расстояний от любой точки, взятой внутри правильного шестиугольника, до всех прямых, содержащих его стороны, есть величина постоянная.

Метки Сканави. Смотреть запись.
Средняя линия выпуклого четырехугольника: свойства, определение
В данной публикации мы рассмотрим определение и основные свойства средних линий выпуклого четырехугольника касательно точки их пересечения, соотношения с диагоналями и т.д.
Примечание: далее мы будем рассматривать только выпуклую фигуру.
Определение средней линии четырехугольника
Отрезок, соединяющий середины противоположных сторон четырехугольника (т.е. не пересекающий их), называется его средней линией.
- EF – средняя линия, соединяющая середины AB и CD; AE=EB, CF=FD.
- GH – средняя линия, сеодиняющая середины BC и AD; BG=GC, AH=HD.
Свойства средней линии четырехугольника
Свойство 1
Средние линии четырехугольника пересекаются и в точке пересечения делятся пополам.
- EF и GH (средние линии) пересекаются в точке O;
- EO=OF, GO=OH.
Примечание: Точка O является центроидом (или барицентром) четырехугольника.
Свойство 2
Точка пересечения средних линий четырехугольника является серединой отрезка, соединяющего середины его диагоналей.
- K – середина диагонали AC;
- L – середина диагонали BD;
- KL проходит через точку O, соединяя K и L.
Свойство 3
Середины сторон четырехугольника являются вершинами параллелограмма, который называется параллелограммом Вариньона.
Центром образованного таким образом параллелограмма и точкой пересечения его диагоналей является середина средних линий исходного четырехугольника, т.е. точка их пересечения – O.
Примечание: Площадь параллелограмма равняется половине площади четырехугольника.
Свойство 4
Если углы между диагоналями четырехугольника и его средней линией равны, значит диагонали имеют одинаковую длину.
- EF – средняя линия;
- AC и BD – диагонали;
- ∠ELC = ∠BMF = α, следовательно AC=BD.
Свойство 5
Средняя линия четырехугольника меньше или равна полусумме непересекающих ее сторон (при условии, что данные стороны параллельны).
EF – средняя линия, не пересекающаяся со сторонами AD и BC.
Иначе говоря, средняя линия четырехугольника равняется половине суммы не пересекающих ее сторон тогда и только тогда, когда данный четырехугольник является трапецией. В этом случае рассматриваемые стороны являются основаниями фигуры.
Свойство 6
Для вектора средней линии произвольного четырехугольника выполняется следующее равенство:
B4 (№ 54789) Около окружности радиус которой равен описан правильный шестиугольник Найдите радиус окружности описанной около этого шестиугольника B4 (№ 54719) Около окружности радиус которой равен описан квадрат Найдите радиус окружности
B4 (№ 54789) Около окружности, радиус которой равен , описан правильный шестиугольник.
 Найдите радиус окружности, описанной около этого шестиугольника.
Найдите радиус окружности, описанной около этого шестиугольника.B4 (№ 54719) Около окружности, радиус которой равен , описан квадрат. Найдите радиус окружности, описанной около этого квадрата.
B4 (№ 54689) К окружности, вписанной в треугольник
ABC, проведены три касательные. Периметры отсеченных треугольников равны 8, 29, 53. Найдите периметр данного треугольника.В4 (№ 54639) Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как . Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 150.
B4 (№ 54599) В четырехугольник
ABCD вписана окружность, , и . Найдите четвертую сторону четырехугольника.В4 (№ 54429) Периметр прямоугольной трапеции, описанной около окружности, равен 100, ее большая боковая сторона равна 31. Найдите радиус окружности.
В4.(№54529)Около окружности описана трапеция, периметр которой равен 172. Найдите ее среднюю линию.
Найдите ее среднюю линию.
B4 (№ 54359) Боковые стороны трапеции, описанной около окружности, равны 21 и 3. Найдите среднюю линию трапеции.
B4 (№ 54309) Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 21 и 2, считая от вершины, противолежащей основанию. Найдите периметр треугольника
.
B4 (№ 54249) Боковые стороны равнобедренного треугольника равны 181, основание равно 38. Найдите радиус вписанной окружности.
B4 (№ 54159) Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 22. Найдите гипотенузу
c этого треугольника. В ответе укажите .B4 (№ 54009) Два угла вписанного в окружность четырехугольника равны и . Найдите больший из оставшихся углов. Ответ дайте в градусах.
B4 (№ 53809) Сторона AB треугольника ABC равна 26. Противолежащий ей угол C равен . Найдите радиус окружности, описанной около этого треугольника.
B4 (№ 53859) Около трапеции описана окружность. Периметр трапеции равен 34, средняя линия равна 7. Найдите боковую сторону трапеции.
B4 (№ 53759) Угол
C треугольника ABC, вписанного в окружность радиуса 18, равен . Найдите сторону AB этого треугольника.B4 (№ 53659) Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .
B4 (№ 53559) Найдите высоту трапеции, в которую вписана окружность радиуса 36.
B4 (№ 53499) Острый угол ромба равен . Радиус вписанной в этот ромб окружности равен 6,5.Найдите сторону ромба.
B4 (№ 52509)Высота правильного треугольника равна 18. Найдите радиус окружности, описанной около этого треугольника.
B4 (№ 27279) В треугольнике
ABC угол C равен , CH — высота, , . Найдите AH.B4 (№ 27379) В треугольнике
ABC угол C равен , , . Найдите тангенс внешнего угла при вершине A.
B4 (№ 54109) Угол между стороной правильного
n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен . Найдите n.Геометрия Калькулятор | Геометрия Расчет
Inradius ромба, когда заданы одна диагональ и половина угла Inradius ромба, когда указаны диагонали и сторона Более длинная диагональ ромба при заданных боковых и половинных углах Внутренний радиус ромба, если указаны площадь и длина стороны Внутренний радиус ромба, когда указаны площадь и угол Внутренний радиус ромба, когда указаны сторона и угол Вписанный угол, если указаны радиус и длина малой дуги Вписанный угол, когда указаны радиус и длина большой дуги Высота прямоугольной пирамиды с учетом высоты наклона и длины стороны Высота прямоугольной пирамиды с учетом объема и длины стороны Высота равнобедренной трапеции Высота равносторонней квадратной пирамиды Высота трапеции при задании площади и суммы параллельных сторон Высота треугольной призмы с учетом площади боковой поверхности Высота треугольной призмы, если даны основание и объем Диагональ 1 трапеции Диагональ 2 трапеции Диагональ равнобедренной трапеции Диагональ ромба при задании боковой и другой диагонали Диагональ ромба при задании стороны и угла Диагональ ромба при заданных радиусе и половинном угле Диагональ ромба, когда заданы другие диагональ и половина угла Диагональ ромба, когда заданы площадь и другая диагональ Диаметр круга при заданной окружности Диаметр круга при заданной площади Диаметр круга при заданном радиусе Длина бокового края прямоугольной пирамиды с указанием длины стороны и высоты наклона Длина бокового ребра пирамиды правильного квадрата Длина боковой грани прямоугольной пирамиды, если заданы объем и длина стороны Длина дуги при указании центрального угла и радиуса Длина стороны прямоугольной пирамиды с указанием объема и высоты Длина стороны прямоугольной пирамиды, если заданы наклонная высота и высота Длина хорды при задании радиуса и центрального угла Длина хорды, если заданы радиус и вписанный угол Значение вписанного угла при задании центрального угла Измерение внешнего угла правильного многоугольника Меньшая диагональ ромба при заданных боковых и половинных углах Наклонная высота конуса Наклонная высота прямоугольной пирамиды Наклонная высота прямоугольной пирамиды, если заданы объем и длина стороны Наклонная высота ствола Объем правой квадратной пирамиды, если заданы длина стороны и высота наклона Объем прямоугольной пирамиды Объем равносторонней квадратной пирамиды Объем треугольной призмы при задании двух длин сторон и угла Объем треугольной призмы при задании двух углов и стороны между ними Объем треугольной призмы при заданных длинах сторон Объем треугольной призмы, если указаны площадь основания и высота Окружность круга Окружность эллипса Периметр трапеции Площадь боковой поверхности правой квадратной пирамиды Площадь боковой поверхности прямоугольной пирамиды с указанием длины стороны и высоты наклона Площадь боковой поверхности треугольной призмы Площадь верхней поверхности треугольной призмы Площадь верхней поверхности треугольной призмы, если заданы объем и высота Площадь нижней поверхности треугольной призмы Площадь нижней поверхности треугольной призмы, если заданы объем и высота Площадь основания прямоугольной пирамиды Площадь поверхности прямоугольной пирамиды с указанием длины стороны и высоты наклона Площадь правильного многоугольника с периметром и внутренним радиусом Площадь правильного многоугольника с периметром и радиусом описанной области Площадь правой квадратной пирамиды Площадь равносторонней квадратной пирамиды Площадь ромба по одной диагонали и полууглу Площадь ромба при указании радиуса и угла Площадь ромба, если указаны сторона и внутренний радиус Площадь ромба, если указаны сторона и высота Площадь ромба, когда указаны сторона и угол Площадь сектора, если указаны радиус и центральный угол Площадь трапеции при заданной средней линии Площадь эллипса Радиус вписанного круга в трапецию Радиус круга при заданной окружности Радиус круга при заданной площади Радиус круга при заданном диаметре Радиус окружности, описанной вокруг равнобедренной трапеции Радиус ромба при заданной высоте Радиус ромба при заданных диагоналях Расстояние между линиями Сглаживание эллипса Средняя линия трапеции при заданной длине оснований Сторона воздушного змея, когда указаны другая сторона и периметр Сторона воздушного змея, когда указаны другая сторона и площадь Сторона восьмиугольника при задании площади Сторона правильного семиугольника Сторона ромба при задании диагонали и полуугла Сторона ромба при задании диагонали и угла Сторона ромба при заданном периметре Сторона ромба при заданных диагоналях Сторона ромба при указании площади и внутреннего радиуса Сторона ромба, если указаны площадь и высота Сторона ромба, когда указаны площадь и угол Сторона шестиугольника при заданной площади Сумма внутренних углов правильного многоугольника Сумма параллельных сторон трапеции, когда указаны площадь и высота Третий угол треугольника, когда заданы два угла Фокальный параметр эллипса Центральный угол, когда указаны радиус и длина большой дуги Центральный угол, когда указаны радиус и длина малой дуги Центроид трапеции Экрадиус эллипса| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Геометрические фигуры. Свойства, формулы: периметры, площади, объемы, длины. Треугольники, Прямоугольники и т.д. Градусы в радианы. / / Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. / / Замечательные линии треугольника. Медиана, средняя линия, биссектриса, высота, серединный перпендикуляр, взаимное расположение линий треугольника. Поделиться:
 д. д. | ||||||
| Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста. | |||||||
| Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | ||||||
Как найти длину стороны шестиугольника
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Как рассчитать длину сторон в правильных шестиугольниках
Обновлено 1 декабря 2020 г.
Лиза Мэлони
Шестигранная форма шестиугольника появляется в самых неожиданных местах: сотах, формах, которые образуют мыльные пузыри, когда они » были разбиты вместе, внешний край болтов и даже шестиугольные базальтовые колонны Дороги гигантов, естественного горного образования на северном побережье Ирландии. Предполагая, что вы имеете дело с правильным шестиугольником, что означает, что все его стороны имеют одинаковую длину, вы можете использовать периметр шестиугольника или его площадь, чтобы найти длину его сторон.
Предполагая, что вы имеете дело с правильным шестиугольником, что означает, что все его стороны имеют одинаковую длину, вы можете использовать периметр шестиугольника или его площадь, чтобы найти длину его сторон.
TL; DR (слишком длинный; не читал)
Самый простой и наиболее распространенный способ определения длины сторон правильного шестиугольника — использовать следующую формулу:
s = P ÷ 6, где P — периметр шестиугольника, а s — длина любой из его сторон.
Расчет сторон шестиугольника по периметру
Поскольку у правильного шестиугольника шесть сторон одинаковой длины, найти длину любой из сторон так же просто, как разделить периметр шестиугольника на 6. Итак, если периметр вашего шестиугольника равен 48 дюймов, у вас есть:
\ frac {48 \ text {дюймы}} {6} = 8 \ text {дюймы}
Длина каждой стороны вашего шестиугольника составляет 8 дюймов. 2
2
Первый Шаг в решении для s — выделить его на одной стороне уравнения.2} = \ sqrt {49.269}
s = 7.019 \ text {дюймы}
2 февраля 2012 г.
Возьмем любой четырехугольник, например этот
затем отметьте средние точки и соедините их.
Похоже, мы построили параллелограмм, не так ли? Удивительный факт здесь заключается в том, что , независимо от того, с какого четырехугольника вы начинаете, вы всегда получаете параллелограмм, когда соединяете средние точки .
Это результат, который кажется случайным и удивительным. Вам нужно нарисовать несколько четырехугольников, чтобы убедить себя, что это даже кажется правильным. Как вы в целом собираетесь это доказать?
На днях некоторые студенты спросили меня, почему это так. Я совершенно забыл, как подойти к проблеме, поэтому у меня появился шанс поиграть с ней по-новому. У меня было две идеи, как начать. Первый заключался в том, чтобы провести еще одну линию на чертеже и посмотреть, поможет ли это.
Первый заключался в том, чтобы провести еще одну линию на чертеже и посмотреть, поможет ли это.
Разве синяя линия не параллельна оранжевым линиям над и под ней? Если бы это было правдой, это дало бы нам мощный путь вперед.Это также предвещает мою вторую идею: попробуйте соединить середины треугольника, а не четырехугольника.
Вот как выглядит произвольный треугольник.
Похоже, соединение этих средних точек создает четыре конгруэнтных треугольника, не так ли? На самом деле это не так уж сложно доказать. Узнав это, мы увидим, что любая пара соприкасающихся треугольников образует параллелограмм. Это означает, что две синие линии ниже параллельны.
Таким образом, можно заключить:
Лемма.Синие линии выше параллельны.
Теорема. Оранжевая фигура выше представляет собой параллелограмм.
Доказательство. Снова нарисуйте эту синюю линию.
У нас такая же ситуация, как на картинке треугольника сверху! Видишь?
Сотрем нижнюю половину рисунка и нарисуем параллельные линии одного цвета:
Видите, что синие линии параллельны? Верхняя линия соединяет середины треугольника, поэтому мы можем применить нашу лемму!
Но то же самое верно и для нижней, и для средней линии! Таким образом, все синие линии внизу должны быть параллельны.
То же самое верно и для оранжевых линий по тому же аргументу.
Значит, четырехугольник в конце концов — параллелограмм!
Я нашел это довольно неплохим аргументом: рисование линий из противоположных углов превращает непостижимое в (надеюсь) очевидное. Переход от путаницы к ясности для меня — одна из величайших радостей математических вычислений.
Следующий вопрос заключается в том, можем ли мы изменить результат, отказавшись от первоначальной настройки.Верен ли наш результат, например, когда четырехугольник не выпуклый?
Похоже, он еще будет держаться. Я оставлю это вам.
Вот еще несколько вопросов, на которые стоит обратить внимание:
- Как площадь параллелограмма, полученная при соединении середин четырехугольника, соотносится с исходным четырехугольником?
- Есть шестиугольник, у которого, когда вы соединяете середины его сторон, вы получаете шестиугольник с большей площадью, чем вы начали.
 Сможете ли вы найти шестиугольник с этим свойством?
Сможете ли вы найти шестиугольник с этим свойством? - Сможете ли вы найти такой шестиугольник, что, соединив середины его сторон, получится четырехугольник?
Дэйв Турецки
|
⋯ — Горизонтальное многоточие по средней линии: U + 22EF ctdot
Значение символа
Горизонтальное многоточие по средней линии.Математические операторы.
Срединное горизонтальное многоточие было одобрено как часть Unicode 1.1 в 1993 году.
Недвижимость
| Возраст | 1.1 |
| Блок | Математические операторы |
| Тип парного кронштейна Bidi | Нет |
| Исключение состава | № |
| Футляр складной | 22EF |
| Простой складной футляр | 22EF |
Кодировка
| Кодировка | шестигранник | дека (байты) | дек | двоичный |
|---|---|---|---|---|
| UTF-8 | E2 8B AF | 226 139 175 | 14846895 | 11100010 10001011 10101111 |
| UTF-16BE | 22 EF | 34 239 | 8943 | 00100010 11101111 |
| UTF-16LE | EF 22 | 239 34 | 61218 | 11101111 00100010 |
| UTF-32BE | 00 00 22 EF | 0 0 34 239 | 8943 | 00000000 00000000 00100010 11101111 |
| UTF-32LE | EF 22 00 00 | 239 34 0 0 | 4011982848 | 11101111 00100010 00000000 00000000 |
| 1D линия, круговая дуга, парабола, спираль, кривая Коха
2D Правильные многоугольники: Равносторонний треугольник, квадрат, пятиугольник, шестиугольник, семиугольник, восьмиугольник, девятиугольник, десятиугольник, шестиугольник, додекагон, шестиугольник, N-угольник, кольцо многоугольника Другие многоугольники: 90 599 круглых форм: тетраэдр, куб, октаэдр, додекаэдр, икосаэдр архимедова Solids: Каталонских Сухой остаток: Твердые тела Джонсона: Другие многогранники: 99 Круглые формы: | Anzeige Расчеты на трапеции.Трапеция (или трапеция) — это четырехугольник с двумя параллельными сторонами. Введите три длины стороны и один угол между двумя из этих сторон. Выберите количество десятичных знаков и нажмите Рассчитать. Пожалуйста, введите углы в градусах, здесь вы можете конвертировать угловые единицы. Здесь можно рассчитать только те трапеции, где c не перекрывает a (g1, g2 ≥ 0; α, β ≤ 90 °). Форма трапеции: Формулы: Длина сторон, высота, диагонали и периметр указаны в одинаковых единицах измерения (например,грамм. метр), площадь равна этой единице в квадрате (например, квадратный метр). Anzeige
© Jumk.de Webprojects Anzeige |
Площадь трапеции с медианой
В дополнение к стандартной формуле для площади трапеции с использованием ее оснований, мы также можем вычислить площадь трапеции с ее серединой и ее высотой.Медиана — это линия, соединяющая две средние точки ног трапеции — непараллельные стороны трапеции. Медиана также называется срединным сегментом или средней линией.
Задача
BCD — трапеция, AB || CD . EF — линия, соединяющая середины отрезков AD, и BC , AE = ED и BF = FC . h — высота трапеции. Найдите формулу для его площади, используя h и | EF |
Стратегия
Давайте посмотрим, как мы можем связать то, что мы знаем о медиане трапеции, с формулой, которая у нас уже есть для площади трапеции.Площадь трапеции составляет (короткое основание + длинное основание) · высота / 2, или A = ½ ( AB + DC ) · h.
В этой задаче у нас есть высота и средний или средний сегмент. Из теоремы о срединном сегменте трапеции мы получаем связь между средним сегментом и основаниями: | EF | = ½ ( AB + DC ). Глядя на две формулы, мы видим, что можем просто заменить EF на ½ ( AB + DC ) в формуле для площади и получить A = | EF | · h
Решение
(1) A = ½ ( AB + DC ) · h // Площадь трапеции
(2) AE = ED , BF = FC // задано
(3) EF — средний сегмент // (2), Определение среднего сегмента
(4) | EF | = ½ ( AB + DC ) // (3), теорема о среднем сегменте трапеции
(5) A = | EF | · H // (1), (4), подстановка
Другой способ решения этой проблемы
В предыдущем разделе мы полагались на признание того, что формула для площади трапеции — A = ½ ( AB + DC ) · h очень похожа на формулу для длины среднего сегмента — | EF | = ½ ( AB + DC ), и произведена замена, которая привела к очень компактному и элегантному решению.
Но что, если мы не сразу узнаем, что формулы похожи, или не вспомним, что средний сегмент равен половине суммы оснований? Давайте посмотрим на другой способ решить эту проблему, не полагаясь на это.
Поскольку EF — это линия, соединяющая середины сторон, мы могли бы использовать теорему о треугольнике середины отрезка, но для этого нам нужен треугольник. Итак, давайте нарисуем один, используя диагональ AC:
Решение, используя теорему о среднем сегменте треугольника
В треугольнике ΔACD, | EG | — это линия, параллельная основанию CD, которая начинается от середины стороны AD, поэтому согласно обратной теореме о среднем сегменте треугольника, это средний сегмент, равный половине основания.Положим | EG | = x. Если x равен половине базы, то CD базы должен быть равен 2x.
Теперь посмотрим на другой треугольник ΔACB. Используя те же рассуждения, что и выше, | GF | начинается от середины стороны BC и параллельна AB — так что, согласно обратной теореме о среднем сегменте треугольника, это средний сегмент, равный половине основания.



 Найти отношение площадей треугольников, прилегающих к боковым сторонам трапеции. Ответ: Решение
Найти отношение площадей треугольников, прилегающих к боковым сторонам трапеции. Ответ: Решение Диагонали трапеции взаимно перпендикулярны. Найти ее площадь. Ответ: Решение
Диагонали трапеции взаимно перпендикулярны. Найти ее площадь. Ответ: Решение Найти площадь трапеции. Ответ: Решение
Найти площадь трапеции. Ответ: Решение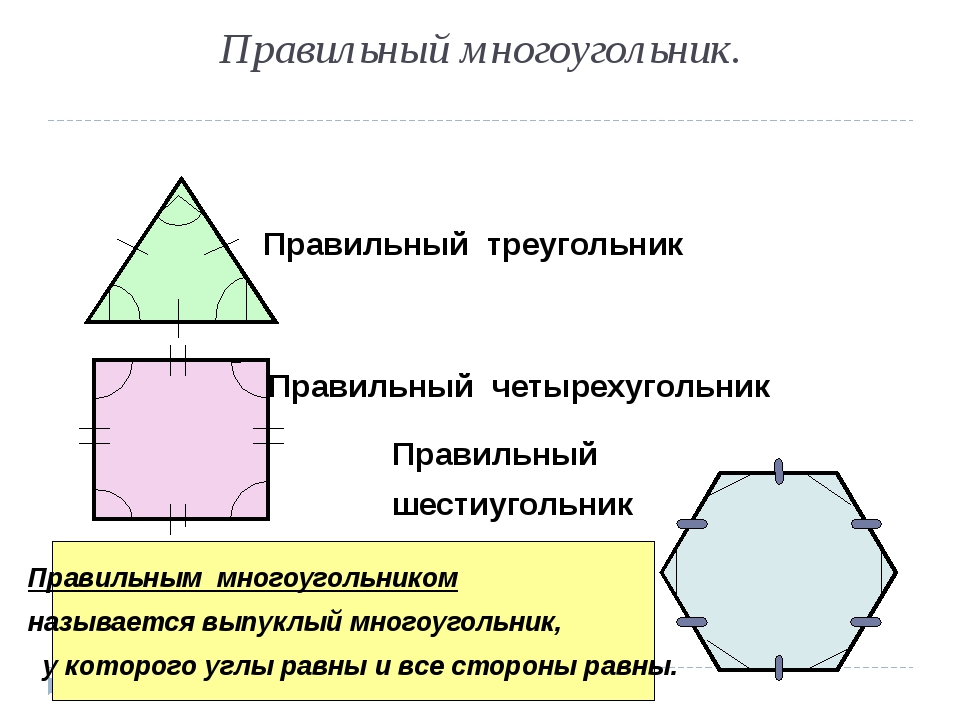 Определить стороны трапеции, если угол при основании содержит 30°. Ответ: Решение
Определить стороны трапеции, если угол при основании содержит 30°. Ответ: Решение
 Ответ: Решение
Ответ: Решение
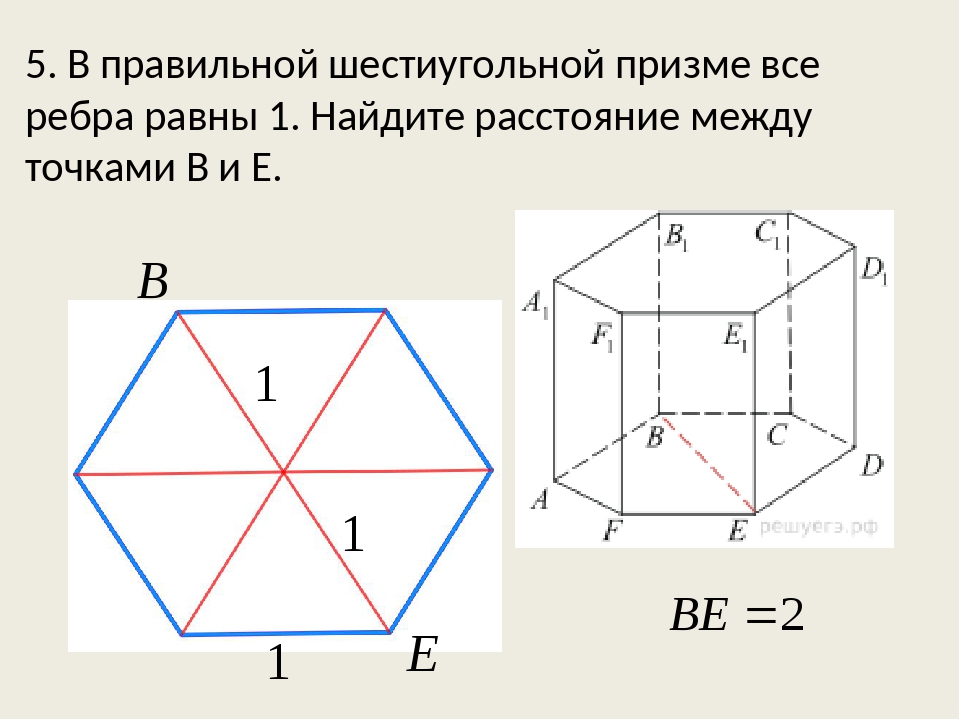
 Медиана, средняя линия, биссектриса, высота, серединный перпендикуляр, взаимное расположение линий треугольника.
Медиана, средняя линия, биссектриса, высота, серединный перпендикуляр, взаимное расположение линий треугольника. Медиана, средняя линия, биссектриса (длина биссектрисы+ центр вписанной окружности), высота (ортоцентр треугольника), серединный перпендикуляр (+центр описанной окружности), взаимное расположение линий треугольника. Точки пересечения медиан, биссектрис, высот и срединных перпендикуляров треугольника.
Медиана, средняя линия, биссектриса (длина биссектрисы+ центр вписанной окружности), высота (ортоцентр треугольника), серединный перпендикуляр (+центр описанной окружности), взаимное расположение линий треугольника. Точки пересечения медиан, биссектрис, высот и срединных перпендикуляров треугольника.
 Сможете ли вы найти шестиугольник с этим свойством?
Сможете ли вы найти шестиугольник с этим свойством?