Шестиугольник вписанный: Радиус вписанной окружности в шестиугольник | Формулы и расчеты онлайн

Значение слова ШЕСТИУГОЛЬНИК. Что такое ШЕСТИУГОЛЬНИК?

• ШЕСТИУГО́ЛЬНИК, -а, м. Геометрическая фигура, ограниченная замкнутой ломаной линией, звенья которой образуют шесть углов.

Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека

• Шестиугольник — многоугольник с шестью углами. Также шестиугольником называют всякий предмет такой формы.

Источник: Википедия

• шестиуго́льник

  1. геометр. многоугольник с шестью углами

  2. предмет такой формы

  Фразеологизмы и устойчивые сочетания

Источник: Викисловарь

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.

Насколько понятно значение слова социалистка (существительное):

Кристально
понятно

Понятно
в общих чертах

Могу только
догадываться

Понятия не имею,
что это

Другое
Пропустить

Вписанный шестиугольник — Большая Энциклопедия Нефти и Газа, статья, страница 1

Вписанный шестиугольник

Cтраница 1

Вписанный шестиугольник учащемуся предлагается построить самостоятельно.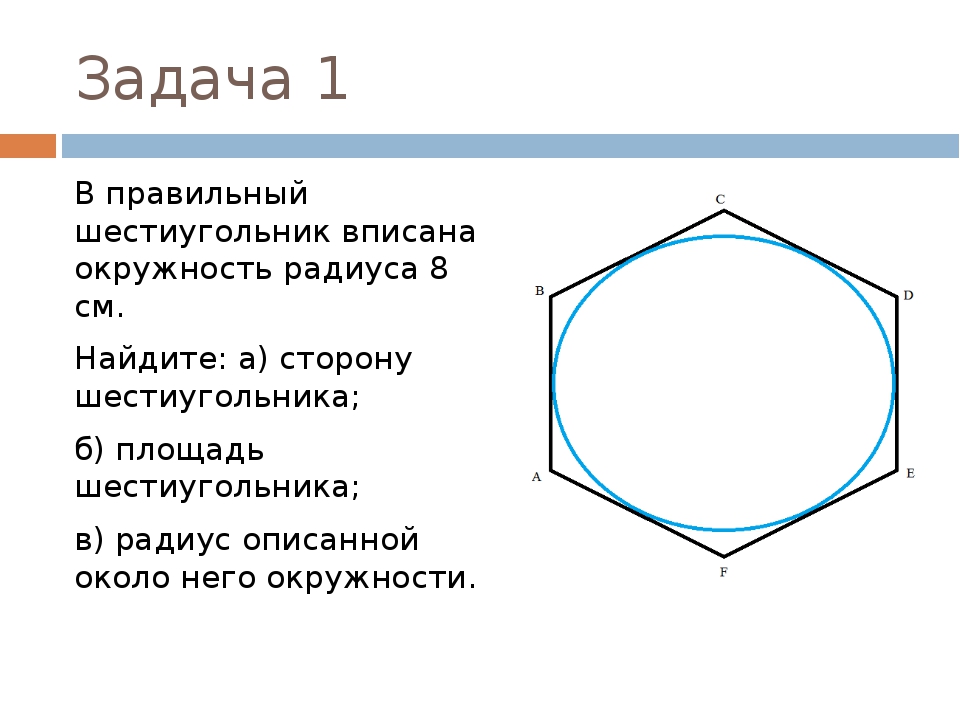

 [1]

Рассмотрим вписанный шестиугольник, вершинами которого являются точки касания описанного шестисторонника. Спроектируем плоскость чертежа на другую плоскость так, чтобы круг перешел в круг и у этого шестиугольника противоположные стороны были параллельны ( см. указание к задаче 810), тогда искомые прямые пройдут через центр окружности — одну точку.  [2]

Если позволить вершинам вписанного шестиугольника сливаться, при этом внимательно следя за тем, чтобы сохранились их обозначения, то мы сможем вывести несколько интересных теорем о вписанных пятиугольниках и четырехугольниках. В таких случаях сторона, конечные точки которой сливаются, превращается в точку, а прямая, содержащая ее, переходит в касательную к этой окружности ( или коническому сечению) в этой точке.  [3]

Благодаря этому все шесть вершин вписанного шестиугольника оказываются налицо, и теорема Паскаля может быть применена.  [4]

Диагонали AD, BE и CF вписанного шестиугольника ABCDEF пересекаются в одной точке.  [5]

Таким образом, трапеция образована тремя сторонами и диагональю

вписанного шестиугольника.  [6]

Аналогично тому, как из теоремы Паскаля можно вывести ряд новых предложений, считая, что те или иные вершины вписанного шестиугольника совпадают между собой ( см. примечание к предыдущей задаче), так из теоремы Брианшона можно вывести новые теоремы, если считать отдельные стороны описанного шестиугольника совпадающими.  [7]

ⓘ Правильный шестиугольник. Все углы равны 120°. Радиус вписан

Пользователи также искали:

найти радиус окружности, вписанной в правильный шестиугольник, правильный шестиугольник площадь, правильный шестиугольник свойства, правильный шестиугольник углы, в правильный шестиугольник вписана окружность, шестиугольника, шестиугольник, Правильный, правильный, Правильный шестиугольник, окружность, правильный шестиугольник свойства, правильный шестиугольник углы, неправильный шестиугольник, формулы, площадь, правильный шестиугольник площадь, свойства, неправильный, сторона, правильного, вписанного, вписана, найти, радиус, окружности, вписанной, углы, правильный шестиугольник формулы, 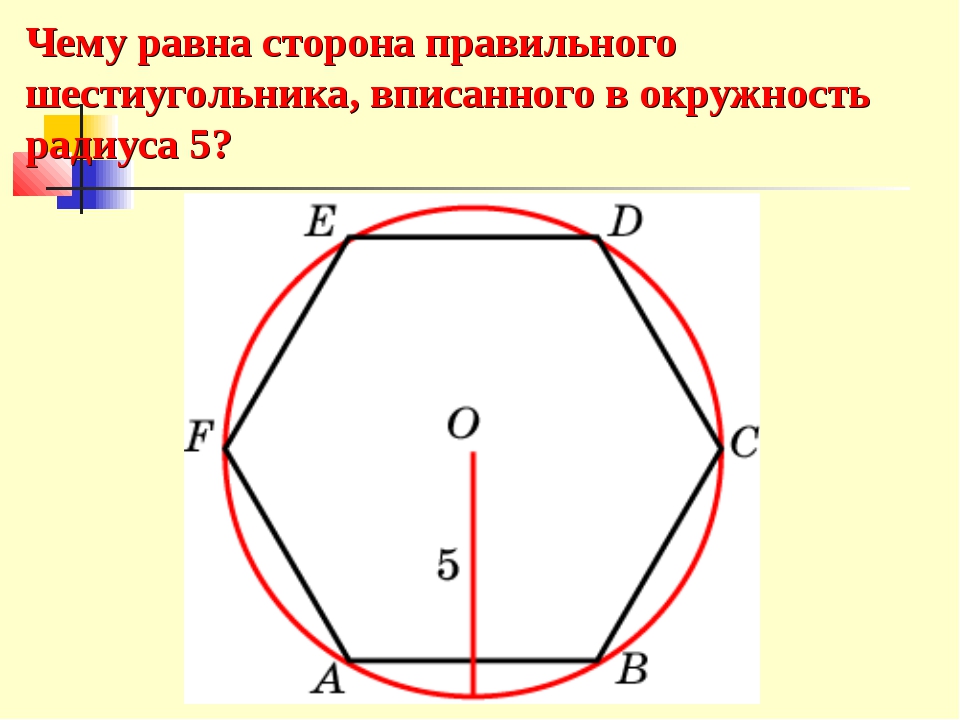сторона правильного шестиугольника вписанного в окружность, в правильный шестиугольник вписана окружность, найти радиус окружности вписанной в правильный шестиугольник, правильный шестиугольник, cтатьи по геометрии.

правильный шестиугольник,

…

Евклид IV.15: Чтобы вписать правильный шестиугольник в данный круг

ПРИМЕЧАНИЕ: Я переписал и отредактировал это из различных древних переводов Евклида, дополненных и умеренных, где это необходимо, по крайней мере структурой более современных версий. Я почти уверен, что в нем нет ошибок. Это, конечно, только одно из многих интересных евклидовых предложений, касающихся шестиугольников, и всем, кто читает это, у кого фактически нет копии Евклида, я настоятельно рекомендую купить ее прямо сейчас.Спасибо.

Пусть ABCDEF — данная окружность. Требуется вписать в окружность ABCDEF равносторонний и равносторонний шестиугольник.

Найдите центр G окружности ABCDEF и начертите диаметр AGD; а от центра D на расстоянии DG описать окружность EGCH. Соедините EG и CG и проведите их через них к точкам B и F. Соедините AB, BC, CD, DE, EF и FA.

Я говорю, что шестиугольник ABCDEF равносторонний и равносторонний.

Поскольку, поскольку точка G является центром окружности ABCDEF, GE равняется GD.

Поскольку точка D является центром окружности GCH, DE равно DG

Следовательно, GE равно GD, следовательно, GE также равно ED. Следовательно, треугольник EGD равносторонний, и, следовательно, его три угла EGD, GDE, DEG равны друг другу, потому что углы в основании равнобедренного треугольника равны.

И сумма трех углов треугольника равна двум прямым углам, поэтому угол EGD является третьей частью двух прямых углов.

Таким же образом можно продемонстрировать, что угол DGC также является третьей частью двух прямых углов.

И поскольку прямая линия CG, стоящая на EB, делает сумму смежных углов EGC и CGB равной двум прямым углам, следовательно, оставшийся угол CGB является третьей частью двух прямых углов.

Следовательно, углы EGD, DGC и CGB равны друг другу. И им равны вертикальные противоположные углы BGA, AGF и FGE.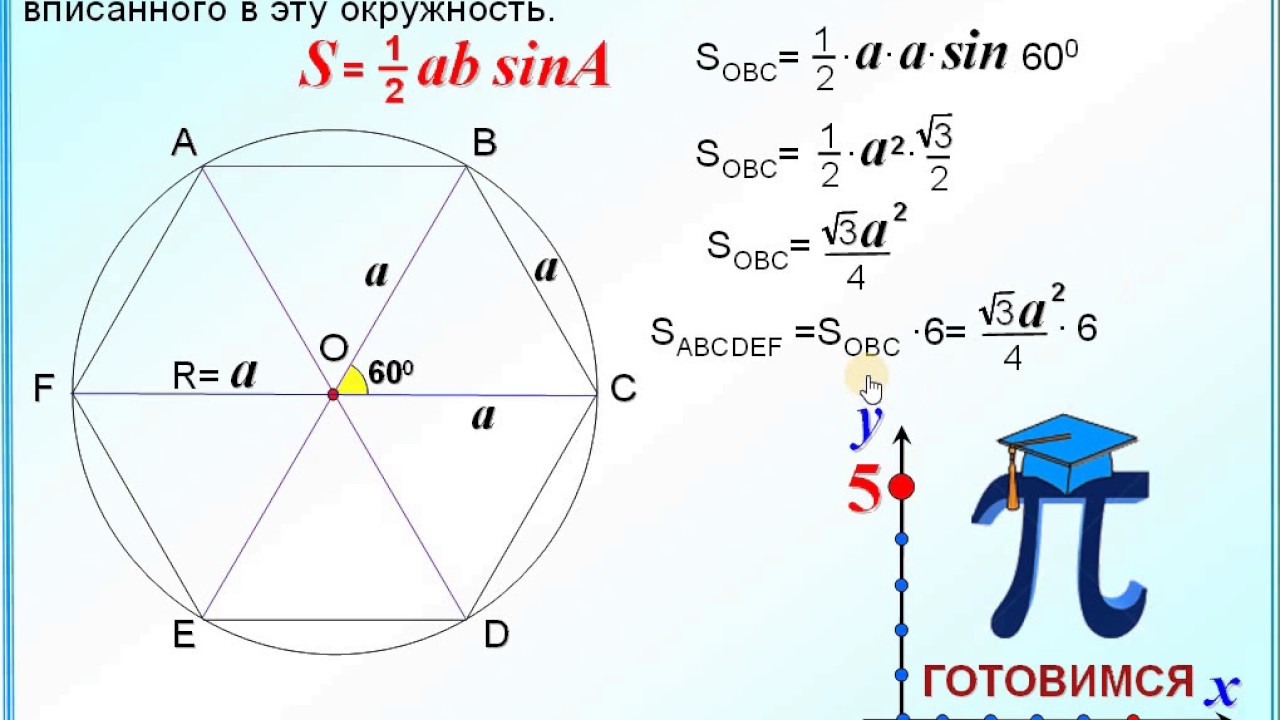

Следовательно, шесть углов EGD, DGC, CGB, BGA, AGF и FGE равны друг другу.

Но равные углы в центре стоят на равных окружностях, поэтому шесть окружностей AB, BC, CD, DE, EF и FA равны друг другу.

И равные окружности обозначены равными прямыми линиями; Следовательно, шесть прямых равны друг другу, а шестиугольник ABCDEF равносторонний.

Далее я говорю, что он равносторонний.

Поскольку, поскольку окружность AF равна окружности ED, к каждому из них добавляют окружность ABCD, поэтому вся окружность FABCD равна всей EDCBA.

Угол FED лежит на окружности FABCD, а угол AFE — на окружности EDCBA; следовательно, угол AFE равен DEF.

Таким же образом можно продемонстрировать, что каждый из других углов шестиугольника ABCDEF равен углам AFE и FED.

Следовательно, шестиугольник равноугольный.Он также равносторонний, как было показано, и вписан в данную окружность ABCDEF.

Quod erat faciendum.

Следствие: Отсюда видно, что сторона шестиугольника равна радиусу круга.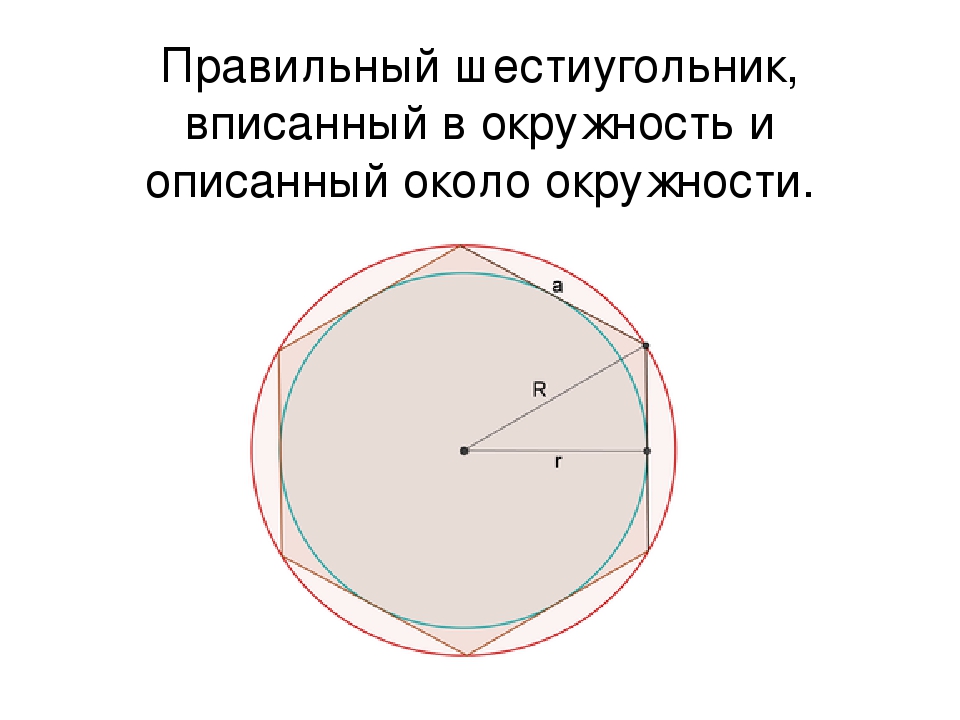

И если через точки A, B, C, D, E и F будут проведены прямые линии, касающиеся круга, вокруг него будет описан равносторонний и равносторонний шестиугольник, что может быть продемонстрировано из того, что было сказано о пятиугольнике.Кроме того, круг можно вписать в данный равносторонний и равносторонний шестиугольник и описать вокруг него способом, подобным тому, который используется для пятиугольника.

FTVW.

Начертание правильного пятиугольника в круг и доказательство

Скотт Э. Броди

Построения по линейке и циркулю из нескольких правильных многоугольников — равностороннего треугольника, квадрата, шестиугольника и восьмиугольника — знакомы. Действительно, построение равностороннего треугольника — самое первое предложение в «Элементах» Евклида (I.1). Менее известно удивительно простое построение правильного пятиугольника теми же методами. Построение и его проверка дают еще одну иллюстрацию того, как теорема Пифагора вплетается в структуру геометрии, хотя в пятиугольнике нет прямых углов.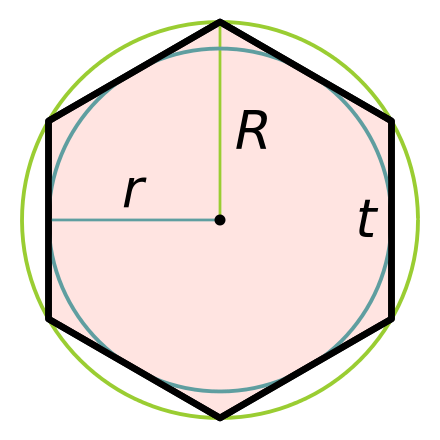 (Правильный пятиугольник также можно смоделировать, расплющивая узел сверху, завязанный из полосы одинаковой ширины.)

Начните с круга радиусом $ 1 $ (рис. 1).

Постройте перпендикулярные диаметры $ AB $ и $ CD.$ Разделите пополам радиус $ OB $ в точке $ M. $ С центром $ M $ и радиусом $ MC $ начертите дугу, пересекающую радиус $ OA $ в точке $ N. $ Я утверждаю, что $ CN $ — это сторона вписанного правильного пятиугольника. по кругу.

Чтобы проверить конструкцию, сначала посмотрите на «звездную пентаграмму», правильный пятиугольник, на котором вписана пятиконечная звезда (рис. 2). Рассмотрим две диагонали, исходящие из одной вершины. Эти две диагонали охватывают одну сторону пятиугольника, образуя равнобедренный треугольник (например, $ CPQ $ на рисунке 2).{2} = 5/2 — \ sqrt {5} /2.$

С другой стороны, пусть $ s $ — длина стороны вписанного пятиугольника, $ d $ — длина диагонали и $ t $ — длина отрезка $ DQ $ на рисунке (сторона правильный десятиугольник вписан в тот же круг). {2} = 4.{2}} = \ sqrt {5 / 2- \ sqrt {5} / 2}, $ QED.

Несмотря на элегантность этой конструкции, она не такая, как в Euclid Elements . Это сооружение обычно приписывают другому греческому математику Птолемею, жившему примерно 400 лет спустя. Процедура Евклида (IV.11) заключается в следующем: начните с отрезка прямой, разделенного точкой на два отрезка, отношение которых равно \ phi (II.11). (Обратите внимание, как эта конструкция очень похожа на построение пятиугольника, приведенного выше.) Затем постройте равнобедренный треугольник со сторонами, пропорциональными $ \ phi, $ $ \ phi, $ и $ 1 $ (IV.10). Евклид отмечает, что в таком треугольнике углы основания в два раза больше угла при вершине. Впишите в круг (IV.2) похожий на этот треугольник. Теперь разделите пополам основные углы вписанного треугольника. Пересечения биссектрисы с кругом вместе с вершинами вписанного треугольника определяют желаемый пятиугольник.

(Эта конструкция легко реализуется складыванием бумаги. Также есть элегантная японская конструкция XIX века в виде правильного пятиугольника.)

Hexagonmc.eu Форум

Wir beginnen mit der Stabilität des Servers im Allgemeinen. Insgesamt sind wir mit diesem Ergebnis zufrieden, sehen aber noch deutlich Luft nach oben und haben uns der Sache angenommen. In der Vergangenheit haben wir viele neue Spieler grüßen dürfen und ein Wachstum der Community war deutlich spürbar. Damit wir euch weiterhin einen stabilen Server bieten können, wird Pixelmon in naher Zukunft auf einen leistungsstärkeren Server umziehen.
Der Spawn wurde sehr unterschiedlich bewertet, doch die Gründe waren zu 90% dieselben.Es wurden sehr of die Lags am Spawn bemängelt, besonders bei den Lootkisten. Wir haben unstensiv mit den möglichen Ursachen auseinander gesetzt, den Fehler gefunden und beseitigt.

Der Großteil von euch ist mit den Lootkisten zufrieden. Da diese erst vor kurzem ein Update bekommen haben, freut uns das besonders. Auch hier gab es einige Vorschläge, die wir gut fanden und auch umsetzen wollen. Ab sofort erwarten euch regelmäßige Änderungen und Anpassungen. Einige eurer vielen Vorschläge werden da natürlich berücksichtigt.

Der Großteil von euch ist auch hier zufrieden mit unserem Voteshop, Allerdings nur mit dem Design. Niemand fand unsere Preise aktuell und pasnd, wir auch nicht. Deswegen arbeiten wir gerade an einer neuen Version des Voteshops und wollen diesen auch zeitnah veröffentlichen. Спарт также использует неткойны.

Kommen wir nun zu den Dungeons. Grundsätzlich war die Aufteilung in leicht und schwer eine sehr gute Idee und diese wollen wir auch weiter behavior. Kritisiert wurden öfters die Belohnungen und der Schwierigkeitsgrad normal wurde sich des Öfteren gewünscht.Neben vielen anderen Projekten, nehmen wir uns dem hier auch zeitnah an.
Mit unserem Arenasystem seid ihr insgesamt sehr zufrieden. Die Arenaorga wurde verstärkt und sind schon fleißig am Ideen sammeln und umsetzen.

Zum Schluss haben wir euch gefragt, был gefällt, был euch nicht gefällt, был ihr euch für die Zukunft wünscht und wir bekamen sehr viele ausführliche Antworten. Wir haben uns durch eure Antworten gearbeitet und haben jetzt eine riesige Liste voller Projekte. Wir haben sehr viel tolles Обратная связь bekommen.Zum Beispiel wurdet ihr als Community unglaublich of sehr positiv hervorgehoben.

Seid gespannt auf Hexagons Zukunft, den wir haben viel vor!

Гексагона

Черная пятница: скидка до 50% на отдельные статьи. Купить сейчас!

Поиск

• НОВИНКА
  • • НОВИНКА

      • Новое в мужчинах
      • Новое в женщинах

  • • Новое для женщин

  • • Новое для мужчин

• женщины

  • • Сумки

      • Наплечные сумки
      • Ручные сумки
      • Сумки через плечо
      • A4 и сумки для ноутбуков
      • Рюкзаки
      • Сумки Tote
      • Дорожные сумки и аксессуары
      • Сумки-клатчи

  • • Мелкие изделия из кожи

      • Кошельки
      • Кошельки
      • Чехлы и чехлы
      • Чековые книжки
      • Открытка

    • • Электронная подарочная карта

  • • Строки

      • Альва
      • Аппалуза
      • Артистический
      • Калипсо
      • Карнаби
      • Цитадин
      • Cosmo
      • Двойной
      • Дюна
      • Стрекоза
      • Эклатс
      • Эдем
      • Eden Business
      • Эйлин
      • Esma
      • Экзотика
      • Фортис
      • Gracieuse
      • Графика
      • Ледяной
      • Мадрид
      • Малибу
      • Матча
      • Nomade
      • Ода
      • Пайпер
      • Поэма
      • Поп
      • Портофино
      • Позитано
      • Психея
      • Королева
      • République
      • Sauvage
      • Серена
      • Подпись
      • Неясно
      • Бархат
      • Рейсы
      • Дикий

  • • Женщины

.