Рисуем шестиугольный геометрический узор в Adobe Illustrator
Геометрические узоры весьма популярны в последнее время. В сегодняшнем уроке мы научимся создавать один из таких узоров. Используя переход, оформление и модные цвета мы создадим паттерн, который вы сможете использовать в веб и полиграфическом дизайне.
Результат
1. Рисуем шестиугольники
Шаг 1
Первый шаг прост: нарисуйте шестиугольник. Для этого выберите инструмент Polygon/Многоугольник и создайте фигуру с шестью сторонами (sided) и радиусом (Radius) в 100pt.
Шаг 2
Нарисуйте еще один шестиугольник, на этот раз меньше — выберите радиус в 20pt.
2. Переход между шестиугольниками
Шаг 1
Выделите оба шестиугольника и выровняйте их по центру (вертикально и горизонтально). Используя инструмент Blend/Переход (W), выделите оба шестиугольника и укажите им переход в 6 шагов (Steps).
Шаг 2
Выделите только что получившуюся группу и в меню выберите Object > Expand/Объект>Разобрать. Затем разберите и группу, чтобы у вас получилось восемь разных и отдельных друг от друга фигур.
3. Делим на секции
Шаг 1
Инструментом Line Segment/Отрезок линии (\) нарисуйте линию, пересекающую шестиугольники по центру от самого левого угла к самому правому. Нарисуйте еще две линии, пересекающие шестиугольники по центру от противоположных углов.
Выделите все шестиугольники и линии и в палитре Pathfinder/Обработка контура кликните по иконке Divide/Разделить. Каждый из ваших восьми шестиугольников должен оказаться в результате разделенным на шесть равных секций.
4. Закрашиваем секции
Шаг 1
Перед тем как начать закрашивать секции, давайте определимся с палитрой.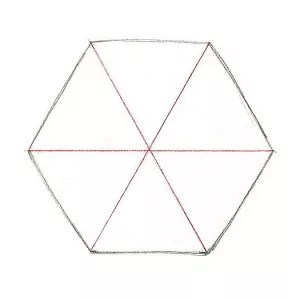 Вот какова палитра из примера:
Вот какова палитра из примера:
- Синий: C65 M23 Y35 K0
- Бежевый: C13 M13
- Персиковый: C0 M32 Y54 K0
- Светло-розовый: C0 M64 Y42 K0
- Темно-розовый: C30 M79 Y36 K4
В примере сразу использовался режим CMYK, чтобы можно было распечатать узор без изменений.
Шаг 2
Разгруппируйте секции, составляющие шестиугольники и секции. Выделите три первые секции и укажите им синий цвет. Выделите следующие три секции и укажите им бежевый цвет. Продолжайте окрашивать узор, выделяя по три секции одного шестиугольника.
Шаг 3
Продолжайте окрашивать фигуру. Можете отступить от четкой последовательности цветов и поэкспериментировать.
Можете отступить от четкой последовательности цветов и поэкспериментировать.
Шаг 4
Чем больше секций, тем разнообразнее может быть ваш узор. Если вы используете приглушенные цвета, как в примере, вы можете сделать узор более пестрым. Если вы хотите использовать более яркие цвета, сократите их количество и даже количество секций.
5. Последние штрихи и узор
Шаг 1
Сгруппируйте (Control-G) все секции и шестиугольники, после того как закончите с их окраской.
Шаг 2
Примените Linear Gradient/Линейный градиент к группе Hexagon B. В палитре Gradient/Градиент укажите заливку от фиолетового (C60 M86 Y45 K42) к кремовому цвету (C0 M13 Y57 K0).
Шаг 3
В палитре Transparency/Прозрачность
Шаг 4
Выделите получившуюся группу и в палитре Pattern Options/Настройки узора найдите Options/Настройки и выберите Make Pattern/Создать узор. Назовите ваш новый паттерн и настройте параметры как показано ниже. Сохраните узор.
Результат
Автор урока Mary Winkler
Перевод — Дежурка
Смотрите также:
Как нарисовать шестиугольник с помощью циркуля
Есть ли поблизости от Вас карандаш? Взгляните-ка на его сечение – оно представляет собой правильный шестиугольник или, как его еще называют, гексагон. Такую форму имеет также сечение гайки, поле гексагональных шахмат, кристаллическая решетка некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты. Гигантский правильный шестиугольник был недавно обнаружен в атмосфере Сатурна. Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим эту фигуру поподробнее.
Такую форму имеет также сечение гайки, поле гексагональных шахмат, кристаллическая решетка некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты. Гигантский правильный шестиугольник был недавно обнаружен в атмосфере Сатурна. Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим эту фигуру поподробнее.
- Длина его сторон соответствует радиусу описанной окружности. Из всех геометрических фигур это свойство имеет лишь правильный шестиугольник.
- Углы равны между собой, и величина каждого составляет 120°.
- Периметр гексагона можно найти по формуле Р=6*R, если известен радиус описанной вокруг него окружности, или Р=4*√(3)*r, если окружность в него вписана. R и r – радиусы описанной и вписанной окружности.
- Площадь, которую занимает правильный шестиугольник, определяется следующим образом: S=(3*√(3)*R 2 )/2. Если радиус неизвестен, вместо него подставляем длину одной из сторон – как известно, она соответствует длине радиуса описанной окружности.

Теперь рассмотрим построение правильного шестиугольника. Есть несколько способов, самый простой из которых предполагает использование циркуля, карандаша и линейки. Вначале рисуем циркулем произвольную окружность, затем в произвольном месте на этой окружности делаем точку. Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек. Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.
Наверняка каждому из нас приходилось сталкиваться с тем, что нужно срочно что-то начертить, точный угол или многоугольник, а транспортира как нарочно под рукой нет, или Вы вообще никогда раньше ничего не чертили. Сегодня я хочу поделиться с Вами простыми схемами построения фигур на плоскости. Думаю, этот навык пригодится всем. Продолжение статьи:
http://www.livemaster.ru/topic/383001-postroenie-na-ploskosti-chast-2?ins >
Нам понадобятся: карандаш, линейка, циркуль.
Построение угла в 60
1. Проведём прямую и отметим на ней точку А.
2. Из точки А проведём дугу произвольного радиуса и получим точку В.
3. Из точки В проведём дугу радиуса АВ, чтобы она пересекла ранее начерченную дугу.
4. Проведённая через точку пересечения (С) и точку А прямая будет второй стороной требуемого угла.
Построение угла в 45
1. Построим угол 60, кака описано выше.
2. Разделим полученный угол пополам.
3. Угол между лучами 60 и 30 разделим пополам. В результате получим угол в 45.
Построение угла в 75
1. Построим угол в 60, как описано выше, и разделим его пополам.
2. В ходе дальнейшего деления надвое получим угол в 15.
3. Отразим угол в 15 через луч 60 и так получим угол в 75.
Построение угла в 90
1. Построим угол в 60, как описано выше, и разделим его пополам.
2. Получившийся угол в 30 через луч 60 и так получим угол точно в 90.
Разделение отрезка на равные части.
1. Проведём прямую и отметим на ней отрезок АВ.
2. Из точки А проведём вспомогательную прямую и разделим её на столько одинаковых частей, на сколько требуется разделить отрезок АВ. Делить будем при помощи циркуля. Последнюю точку обозначим буквой С.
3. Последнюю точка (С) соединим с концом отрезка АВ. Построим рад параллельных отрезку СВ прямых по всей длине отрезка АВ. Точки пересечения параллельных прямых с отрезком АВ и будут точками раздела отрезка на несколько равных частей.
Построение правильного пятиугольника.
1. Проведём окружность радиусом 50 мм. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.
2. Разделим пополам расстояние ОВ. Разведём ножки циркуля на расстояние FC . Из точки F проведём дугу через С. Дуга пересечёт горизонтальную линию в точке G .
Дуга пересечёт горизонтальную линию в точке G .
3. Расстояние CG будет длиной стороны пятиугольника. Из вершины С отложим пять раз расстояние CG .
Построение правильного шестиугольника.
1. Проведём окружность радиусом 50 мм.
2. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.
3. Из точки А на линии окружности отложим шесть раз радиус нашей окружности. Соединив прямыми точки пересечения, получим шестиугольник.
Построение правильного семиугольника.
1. Проведём окружность заданного радиуса. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.
2. Из точки D проведём дугу радиусом равным радиусу окружности.
3. Дуга пересечёт окружность в точках E и G .
4. Длина отрезка EF на хорде EG равна длине стороны семиугольника. Из вершины С семь раз отложим расстояние EF .
Общий метод построения многоугольников.
1. Проведём окружность радиусом 50 мм. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии. Продолжим горизонтальную лини. За точки А и В.
2. Из точки D проведём дугу радиусом, равным радиусу окружности так, чтобы дуга пересекла горизонтальную линию.
3. При помощи вспомогательной прямой разделим вертикальную линию на столько равных частей, сколько сторон многоугольника требуется получить. Для примера показано построение одиннадцатиугольника.
4. Из точки Е проведём прямые через нечётные точки раздела вертикальной линии так, чтобы эти прямые пересекли окружность. Такую же операцию проведём из точки G . Полученные лучи пересекают окружность в точках, соединив которые прямыми получаем одиннадцатиугольник.
Первый способ — по данной стороне S с помощью транспортира.
Проводим прямую и откладываем на ней AB = S; принимаем эту линию за радиус и этим радиусом из точек A и В описываем дуги: далее с помощью транспортира строим в этих точках углы в 108°, стороны которых пересекутся с дугами в точках С и D; из этих точек радиусом АВ = 5 описываем дуги, которые пересекутся в Е, и прямыми линиями соединяем точки Л, С, Е, D, В.
Полученный пятиугольник — искомый.
Первый способ построения пятиугольника
Второй способ. Проведем окружность радиусом r. Из точки А циркулем проводим дугу радиуса AM до пересечения в точках В и С с окружностью. Соединяем В и С линией, которая пересечет горизонтальную ось в точке Е.
Затем из точки Е проводим дугу, которая пересечет горизонтальную линию в точке О. Описываем, наконец, из точки F дугу, которая пересечет окружность в точках Н и К. Отложив по окружности расстояние FO = FH = FK пять раз и соединив точки деления линиями, получим правильный пятиугольник.
Второй способ построения пятиугольника
Третий способ. В данный круг вписать правильный пятиугольник. Проводим два взаимно перпендикулярных диаметра АВ и МС. Делим радиус АО точкой Е пополам. Из точки Е, как из центра, проводим дугу окружности радиуса ЕМ и засекаем ею диаметр АВ в точке F. Отрезок MF равен стороне искомого правильного пятиугольника. Раствором циркуля, равным MF, делаем засечки N1, Р1, Q1, К1 и соединяем их прямыми.
Отрезок MF равен стороне искомого правильного пятиугольника. Раствором циркуля, равным MF, делаем засечки N1, Р1, Q1, К1 и соединяем их прямыми.
Третий способ построения пятиугольника
На рисунке построен шестиугольник по данной стороне.
Построение шестиугольника
Прямой АВ = 5, как радиусом, из точек А и В описываем дуги, которые пересекутся в С; из этой точки тем же радиусом описываем окружность, на которой сторона А В отложится 6 раз.
Шестиугольник ADEFGB — искомый.
«Отделка комнат при ремонте»,
Н.П.Краснов
Маляру часто приходится иметь дело с правильными многоугольниками, а также треугольниками и четырехугольниками, т. е. такими фигурами, у которых все стороны и, соответственно, углы равны между собой. Может встретиться необходимость построить правильный многоугольник по данной стороне, или вписать правильный многоугольник в окружность данного радиуса, или описать его вокруг окружности.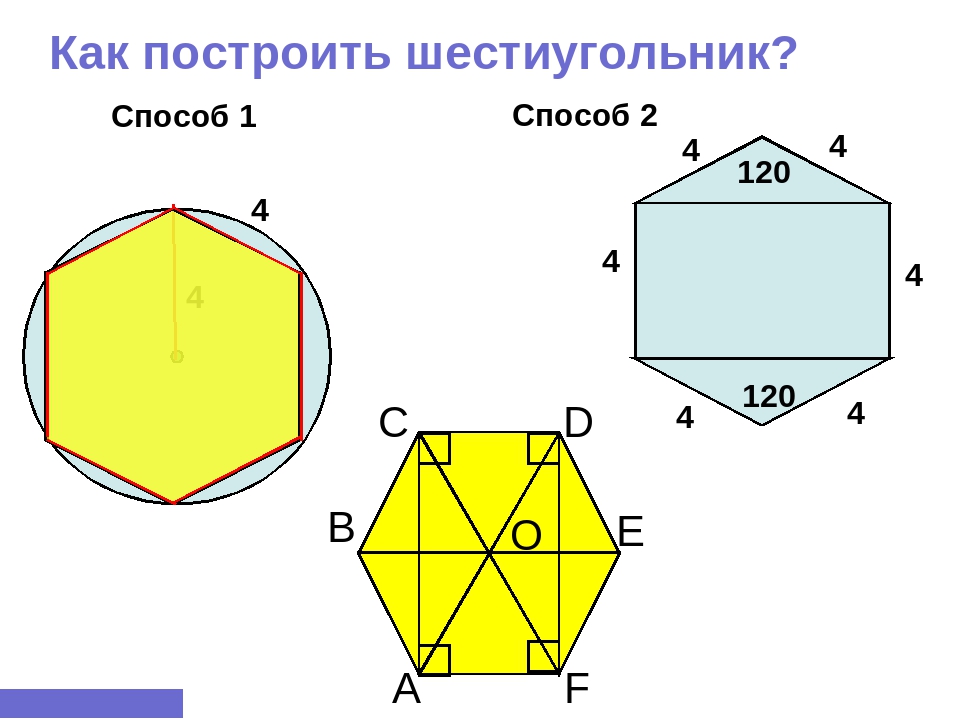 Первый вопрос сводится к нахождению внутреннего…
Первый вопрос сводится к нахождению внутреннего…
Построение вписанных и описанных правильных многоугольников сводится, как уже было сказано, к делению окружности на столько равных частей, сколько в многоугольнике сторон. Однако точное деление окружности путем геометрического построения возможно лишь на 3, 4, 5 и 15 равных частей, а также при делении на число частей, получаемое последовательным удвоением этих чисел. В остальных случаях приходится…
Построение овала (коробовой кривой) по данной длине АВ. Делим длину ЛВ на 3 равные части и из D и Е радиусом DF описываем дуги которые пересекутся в F и G; соединяем D и E c F и G и продолжаем эти прямые, как на фигуре; далее радиусом AD = BE из точек D и Е…
Первый способ построения. Проводим горизонтальную (АВ) и вертикальную (CD) оси и из точки их пересечения М откладываем в соответствующем масштабе полуоси. Наносим малую полуось от точки М на большой оси до точки Е. Эллипс, первый способ построения Делим BE на 2 части и одну наносим от точки М на большой оси (до F или H)…
Основанием для нанесения росписи служат полностью законченные окраской поверхности стен, потолков и других конструкций; роспись делается по высококачественным клеевым и масляным окраскам, сделанным под торцовку или флейц.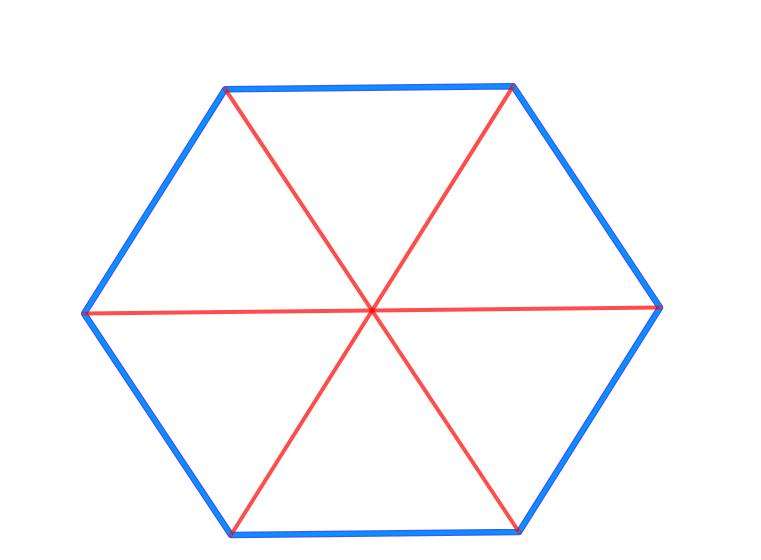 Приступая к разработке эскиза отделки, мастер должен ясно представить себе всю композицию в бытовой обстановке и отчетливо осознать творческий замысел. Только при соблюдении этого основного условия можно правильно…
Приступая к разработке эскиза отделки, мастер должен ясно представить себе всю композицию в бытовой обстановке и отчетливо осознать творческий замысел. Только при соблюдении этого основного условия можно правильно…
3 методика:Рисуем идеальный шестиугольник при помощи циркуляРисуем грубый шестиугольник при помощи круглого предмета и линейкиРисуем грубый шестиугольник при помощи одного карандаша Обычный шестиугольник, также называемый идеальным шестиугольником, имеет шесть равных сторон и шесть равных углов. Вы можете нарисовать шестиугольник при помощи рулетки и транспортира, грубый шестиугольник – при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи только карандаша и немного интуиции. Если вы хотите знать, как нарисовать шестиугольник различными способами – просто читайте далее. ШагиМетод 1 из 3: Рисуем идеальный шестиугольник при помощи циркуля
Метод 2 из 3: Рисуем грубый шестиугольник при помощи круглого предмета и линейки
Метод 3 из 3: Рисуем грубый шестиугольник при помощи одного карандаша
Советы
Предупреждения
Принцип работы
Что вам понадобится
|
Построение правильного шестигранника — Лед совет
Построение правильных многоугольников – Техническое черчение
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего проводим стороны 5—6 и 3—2.
Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего проводим стороны 5—6 и 3—2.
Построение вписанного в окружность равностороннего треугольника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны
1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Обратите внимание
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°.
Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4—1 и 3—2.
Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1.
Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1.
Важно
Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5.
Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.
Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей.
Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника.
Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника.
Совет
Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой.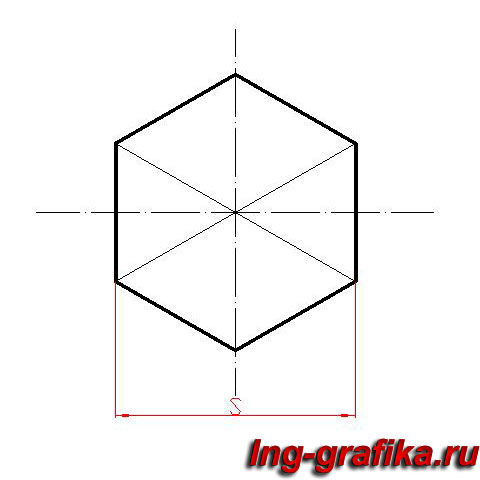 Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты.Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.
Как построить правильный шестиугольник
Есть ли поблизости от Вас карандаш? Взгляните-ка на его сечение – оно представляет собой правильный шестиугольник или, как его еще называют, гексагон.
Такую форму имеет также сечение гайки, поле гексагональных шахмат, кристаллическая решетка некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты. Гигантский правильный шестиугольник был недавно обнаружен в атмосфере Сатурна.
Важно Важно Важно
Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим эту фигуру поподробнее.
Правильный шестиугольник (гексагон) — правильный многоугольник с шестью сторонами. Правильный шестиугольник можно построить с помощью циркуля и линейки. Ниже приведён метод построения, предложенный Евклидом в «Началах», книга IV, теорема 15.
С помощью циркуля, равным радиусу круга, делаем на окружности засечки в точках А, В, С, D, E, F. Соединяя точки А, В, С, D, Е, F подряд, получим правильный шестиугольник. Соединяя их через одну, можем получить правильный (равносторонний) треугольник. Таким образом, для того чтобы построить правильный шестиугольник, вписанный в окружность, мы можем построить два правильных треугольника.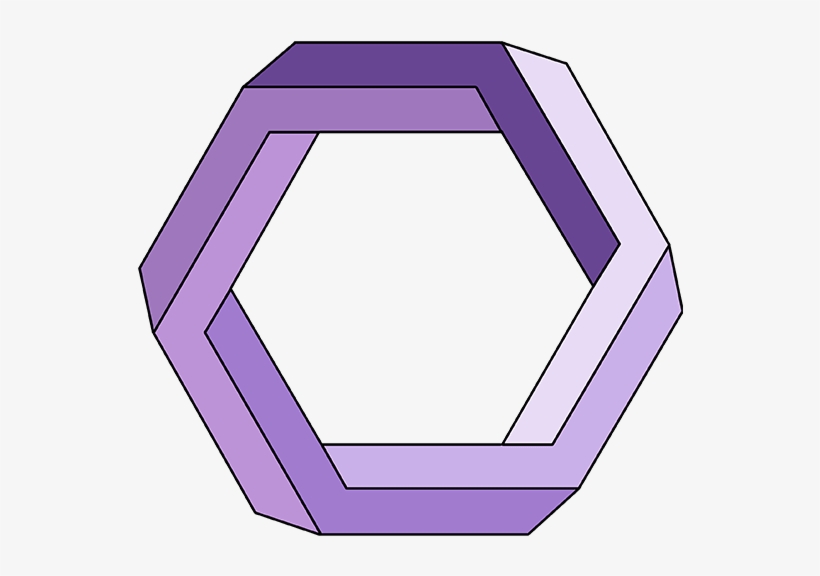
Построение вписанного в окружность правильного шестиугольника. Построение правильного пятиугольника по данной его стороне.
Переставьте иглу циркуля в точку пересечения только что начерченной дуги с окружностью. Это построение можно выполнить при помощи угольника и циркуля.
Обратите внимание
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Постройте точки вершин углов правильного шестиугольника.
Построение шестигранника может производиться несколькими способами. Удобнее всего использовать стандартный набор чертежных инструментов: циркуль, линейку. Однако, в отсутствие циркуля, фигура этого типа может быть начерчена с помощью рейсшины, угольника заводского изготовления с углами 90/60/30°.
Подробнее: MoiInstrumenty.ru
Есть ли поблизости от Вас карандаш? Взгляните-ка на его сечение – оно представляет собой правильный шестиугольник или, как его еще называют, гексагон.
Такую форму имеет также сечение гайки, поле гексагональных шахмат, кристаллическая решетка некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты.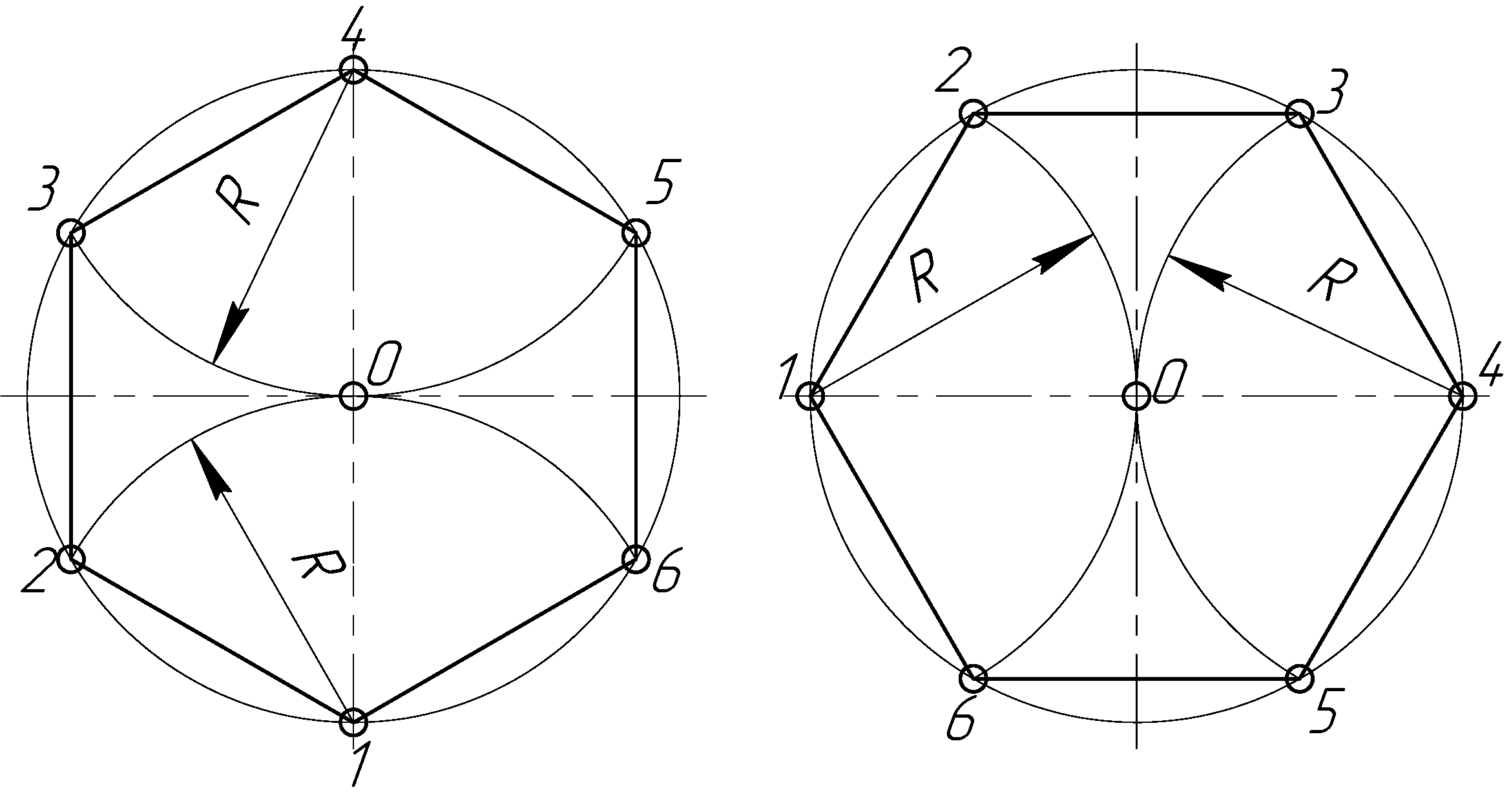 Гигантский правильный шестиугольник был недавно обнаружен в атмосфере Сатурна.
Гигантский правильный шестиугольник был недавно обнаружен в атмосфере Сатурна.
Важно Важно Важно
Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим эту фигуру поподробнее.
Здравствуйте коллеги. В этом уроке узнаем, как нарисовать шестиугольник в перспективе. Как вписать его фронтально в окружность мы смотрели в прошлом уроке. Заметьте ничего сложного нет. Нам удалось малыми средствами начертить равнобедренный предмет с шестью вершинами.
Правильный описанный треугольник строят следующим образом (рисунок 38). Из центра заданной окружности радиуса R1 проводят окружность радиусом R2 = 2R1 и делят ее на три равные части. Точки деления А, В, С являются вершинами правильного треугольника, описанного около окружности радиуса R1.
Подробнее: studopedia.org
Понимая самые простые закономерности в геометрии, можно научиться строить на плоскости более сложные фигуры. Так, большинство геометрических фигур имеют достаточно сложный вид, однако, зная определённые правила, можно понять, как построить шестиугольник с помощью только лишь циркуля и линейки.
Так, большинство геометрических фигур имеют достаточно сложный вид, однако, зная определённые правила, можно понять, как построить шестиугольник с помощью только лишь циркуля и линейки.
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Подробнее: www.nacherchy.ru
Есть ли поблизости от Вас карандаш? Взгляните-ка на его сечение — оно представляет собой правильный шестиугольник или, как его еще называют, гексагон.
Важно
Такую форму имеет также сечение гайки, поле гексагональных шахмат, кристаллическая решетка некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты. Гигантский правильный шестиугольник был недавно обнаружен в атмосфере Сатурна.
Важно Важно Важно
Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим эту фигуру поподробнее.
Геометрические построения являются одной из главных частей обучения. Они формируют пространственное и логическое мышление, а также разрешают понять примитивные и натуральные геометрические обоснованности. Построения производятся на плоскости при помощи циркуля и линейки.
Этими инструментами дозволено возвести крупное число геометрических фигур. При этом многие фигуры, кажущиеся довольно трудными, строятся с использованием простейших правил. Скажем, то, как возвести верный шестиугольник, дозволено описать каждого в нескольких словах.
Вам понадобится
Есть ли поблизости от Вас карандаш? Взгляните-ка на его сечение — оно представляет собой правильный шестиугольник или, как его еще называют, гексагон.
Такую форму имеет также сечение гайки, поле гексагональных шахмат, кристаллическая решетка некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты. Гигантский правильный шестиугольник был недавно обнаружен в атмосфере Сатурна.
Гигантский правильный шестиугольник был недавно обнаружен в атмосфере Сатурна.
Важно Важно Важно
Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим эту фигуру поподробнее.
Некоторые геометрические фигуры нарисовать непросто. К примеру, множество людей может столкнуться с немалыми трудностями при выполнении такого задания, как начертить шестиугольник правильной формы: на создание подобной фигуры, обладающей одинаковыми сторонами, с помощью линейки уйдет немало времени.
Еще по теме: YouTube последние новости, Atac последние новости
Метод 1 из 3: Рисуем идеальный шестиугольник при помощи циркуля
По оси х вправо и влево от точки О откладывают отрезки, равные стороне шестиугольника. Построение вписанного в окружность правильного шестиугольника. Переставьте иглу циркуля в точку пересечения только что начерченной дуги с окружностью. Нарисуйте еще две горизонтальные линии, исходящие из первых горизонтальных прямых, нарисованных вовнутрь.
Шесть мест, где ваши отметки пересекаются с краем круга, — это шесть вершин шестиугольника. Сотрите все вспомогательные линии. К вспомогательным линиям относятся ваш круг, три линии, которые разделили ваш круг на секции и другие отметки, которые вы делали в процессе.
В идеале эта линия должна быть параллельной к верхней горизонтальной линии. Вот вы и завершили свой шестиугольник. Каждый метод поможет нарисовать шестиугольник, образованный шестью равносторонними треугольниками с радиусом, равным длине всех сторон.
Совет
Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые.
Начертите еще одну дугу, пересекающую окружность. Всего должно получиться шесть дуг и шесть точек пересечения. В этом случае шестиугольник может получиться неправильным. Какой бы метод создания фигуры вы ни выбрали, дабы начертить шестиугольник, потребуются циркуль и линейка. Собираясь начертить шестиугольник, нарисуйте сперва при помощи циркуля круг любого диаметра.
Как нарисовать (начертить) шестиугольник в автокаде — урок
По завершении таких действий начертить шестиугольник будет совсем несложно. Полученные шесть точек на окружности будут вершинами искомого шестиугольника. Поэтому, чтобы начертить шестиугольник, вам останется лишь соединить эти точки, а затем, при необходимости, стереть все вспомогательные линии, включая обе окружности. Впрочем, начертить шестиугольник возможно и иными способами.
Подобные засечки и станут вершинами будущего шестиугольника. Шестиугольник AutoCAD будет создан относительно этого центра. Свойства шестиугольника AutoCAD можно вызвать при помощи выделения левой кнопкой, затем правой кнопкой мыши, выпадающий список — Свойства.
При помощи циркуля рисуем круг. Вставьте карандаш в циркуль. Передвиньте иглу циркуля к краю круга. Поставьте его на вершину круга. Не меняйте угол и расположение циркуля.
Если нет, тогда, скорее всего, угол, под которым вы держали циркуль и делали отметки, изменился. Нарисуйте «Х» над половиной круга, разделяя его на шесть равных секций.
Чтобы это сделать, при помощи линейки нарисуйте прямую линию под изогнутой частью каждой секции, соединяя ее с другими двумя линиями, образовывая треугольник.
Диагональная линия с левой стороны должна быть направлена наружу так же, как и диагональная линия справа. Карандаш и циркуль должны быть острыми, чтобы минимизировать ошибки от слишком широких отметок.
Обратите внимание
Если при использовании метода с циркулем вы соединили каждую отметку вместо всех шести, то получите равносторонний треугольник.
Шесть нарисованных радиусов одинаковой длины и все линии для создания шестиугольника тоже одной длины, так как ширина циркуля не менялась.
В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты
Построение вписанного в окружность равностороннего треугольника.
Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей.
Для начала надо провести при помощи линейки прямые, проходящие через центр первой окружности и точки ее пересечения со второй
Приведённый способ годен для построения правильных многоугольников с любым числом сторон. Нарисуйте окружность. Это расстояние будет являться радиусом окружности. Оптимальным будет расстояние, при котором угол между ножками циркуля равен 15-30 градусов.
Игла должна проткнуть начерченную линию. Чем точнее будет установлен циркуль, тем точнее будет построение. Имеет смысл производить построения при помощи циркуля с хорошо заточенным грифелем.
Обязательно отметьте его центр — ту точку, куда при вычерчивании окружности встанет центральная нога инструмента. Эта точка потребуется вам для последующего шага.
Вновь возьмите циркуль и раздвиньте его ножки на расстояние радиуса только что нарисованной окружности.
Постройте точки вершин углов правильного шестиугольника. Это построение можно выполнить при помощи угольника и циркуля. Построение правильного пятиугольника по данной его стороне.
Например, то, как построить правильный шестиугольник, можно описать всего в нескольких словах. При помощи линейки и карандаша нарисуйте прямые линии, соединяя соседние отметки.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Также интересно:
Раствор
Построение аксонометрической проекции правильного шестиугольника, расположенного в разных плоскостях проекций
Сначала строим правильный шестиугольник в прямоугольной системе координат (рисунок 54), обозначаем все точки шестиугольника и точки пересечения вертикального диаметра со сторонами фигуры 3-4 и 5-6, получив точки 7 и 8.
Рисунок 54 – Построение правильного шестиугольника в прямоугольной системе координат
Затем строим аксонометрические оси прямоугольной изометрии (рисунок 55а).
а) б) в) г)
Рисунок 55 – Построения аксонометрических проекций правильного шестиугольника в разных плоскостях, проекций
В плоскости Н, имеющей оси Х и Y, строим вспомогательные оси, на которых и произведём построения шестиугольника (рисунок 55б).
На оси Х1О1 по обе стороны от центра О1 откладываем точки 1 и 2, по оси О1Y1 откладываем точки 7 и 8 от центра О1и проводим прямые, параллельные оси О1Х1.
Важно
На этих прямых откладываем точки 3, 4 и 5, 6. Соединив последовательно точки между собой прямыми линиями, получим изометрическую проекцию шестиугольника в плоскости Н (горизонтальной плоскости).
Для построения изометрии шестиугольника в плоскости V (фронтальной), строим вспомогательные оси О1Х1 и О1Z1 (рисунок 55в). Затем все построения повторяются.
Изометрия шестиугольника в плоскости W (профильной) строится со вспомогательных осей О1Y1 и О1Z1и повторения построений точек (вершин) шестиугольника (рисунок 55г).
Материал для закрепления:
1 Дать определение понятия аксонометрия.
2 Сформулировать определение аксонометрической проекции.
3 Определить понятие коэффициента искажения.
4 Назвать виды аксонометрических проекций и указать коэффициенты искажения.
5 Объяснить различие видов аксонометрических проекций.
6 Объяснить, с чего начинается построение аксонометрических проекций.
7 Показать обозначение коэффициентов искажения по осям Х, Y, Z.
8 Назвать виды прямоугольной аксонометрической проекции.
9 Указать угол расположения аксонометрических осей в прямоугольной изометрической проекции (изометрии).
10 Указать коэффициенты искажения по осям для изометрии.
11 Указать расположение аксонометрических осей в прямоугольной диметрической проекции (диметрии).
12 Указать коэффициенты искажения по осям для диметрии.
13 Указать расположение аксонометрических осей в косоугольной фронтальной диметрической проекции.
14 Указать коэффициенты искажения по осям в косоугольной фронтальной диметрической проекции.
Проверка степени усвоения материала:
Для подтверждения компетенции по теме «Аксонометрические проекции» обучающиеся должны выполнить индивидуальные практические задания на построение аксонометрических проекций плоских деталей (рисунок 56) и моделей (рисунки 57; 58). Задание выполняется на формате А4, в масштабе 1:1, с соблюдением линий чертежа.
Название задания – «Графическая работа №5а. Аксонометрические проекции».
Задание №5а
«Аксонометрические проекции»
Рисунок 56 – Задание для выполнения аксонометрических проекций плоской детали Рисунок 57 – Задание для выполнения изометрической проекции модели Рисунок 58 – Задание для выполнения диметрической проекции модели
Построение правильного пятиугольника – Сведения, необходимые при выполнении росписи – Отделка комнат при ремонте
Главная / Отделка комнат при ремонте / Сведения, необходимые при выполнении росписи / Построение правильного пятиугольника
Первый способ — по данной стороне S с помощью транспортира.
Проводим прямую и откладываем на ней AB = S; принимаем эту линию за радиус и этим радиусом из точек A и В описываем дуги: далее с помощью транспортира строим в этих точках углы в 108°, стороны которых пересекутся с дугами в точках С и D; из этих точек радиусом АВ = 5 описываем дуги, которые пересекутся в Е, и прямыми линиями соединяем точки Л, С, Е, D, В.
Полученный пятиугольник — искомый.
Первый способ построения пятиугольника
Второй способ. Проведем окружность радиусом r. Из точки А циркулем проводим дугу радиуса AM до пересечения в точках В и С с окружностью. Соединяем В и С линией, которая пересечет горизонтальную ось в точке Е.
Затем из точки Е проводим дугу, которая пересечет горизонтальную линию в точке О. Описываем, наконец, из точки F дугу, которая пересечет окружность в точках Н и К. Отложив по окружности расстояние FO = FH = FK пять раз и соединив точки деления линиями, получим правильный пятиугольник.
Второй способ построения пятиугольника
Третий способ. В данный круг вписать правильный пятиугольник. Проводим два взаимно перпендикулярных диаметра АВ и МС. Делим радиус АО точкой Е пополам.
Совет
Из точки Е, как из центра, проводим дугу окружности радиуса ЕМ и засекаем ею диаметр АВ в точке F. Отрезок MF равен стороне искомого правильного пятиугольника.
Раствором циркуля, равным MF, делаем засечки N1, Р1, Q1, К1 и соединяем их прямыми.
Третий способ построения пятиугольника
На рисунке построен шестиугольник по данной стороне.
Построение шестиугольника
Прямой АВ = 5, как радиусом, из точек А и В описываем дуги, которые пересекутся в С; из этой точки тем же радиусом описываем окружность, на которой сторона А В отложится 6 раз.
Шестиугольник ADEFGB — искомый.
«Отделка комнат при ремонте»,
Н.П.Краснов
Расчерчивание потолков и стен
Основанием для нанесения росписи служат полностью законченные окраской поверхности стен, потолков и других конструкций; роспись делается по высококачественным клеевым и масляным окраскам, сделанным под торцовку или флейц. Приступая к разработке эскиза отделки, мастер должен ясно представить себе всю композицию в бытовой обстановке и отчетливо осознать творческий замысел. Только при соблюдении этого основного условия можно правильно…
Обмер выполненных работ, за исключением особо оговоренных случаев, производится по площади действительно обработанной поверхности с учетом ее рельефа и за вычетом необработанных мест.
Для определения действительно обработанных поверхностей при малярных работах следует пользоваться переводными коэффициентами, приведенными в таблицах. А.
Деревянные оконные устройства (обмер производится по площади проемов по наружному обводу коробок) Наименование устройств Коэффициент при…
Геометрические построения
Мы уже говорили, что для исполнения некоторых видов малярных работ необходимо уметь рисовать.
А умение рисовать, в свою очередь, предполагает знание правил построения геометрических фигур.
Эскизы на бумаге вычерчивают при помощи треугольников, рейсшин, транспортаpa и циркуля, а на плоскости стен и потолков построения выполняются при помощи веска, линейки, деревянного циркуля и шнура. При этом надо…
Обратите внимание
Прямой угол, т. е. равный 90°, образуется двумя взаимно перпендикулярными линиями. Перпендикуляр строится следующим образом. Опустить перпендикуляр. Из данной точки С (лежащей вне прямой), как из центра, произвольным радиусом описываем дугу так, чтобы она пересекла данную прямую в двух точках D и Е из этих точек, как из центров, одинаковыми радиусами описываем дуги, чтобы они…
Построение угла, равного данному и параллельные линии
Построение угла, равного данному Угол, равный данному, строится следующим образом.
Из вершины А данного угла произвольным радиусом проводим дугу тем же радиусом из точки D на данной прямой описываем дугу EF; величину дуги ВС откладываем по дуге EF до точки F и проводим DE.
Угол EDF — искомый. Построение угла, равного данному Параллельные линии Линии,…
Как нарисовать невозможный шестиугольник – Невозможные фигуры
Понравились мои уроки рисования? Получите больше на YouTube:
Нажмите ЗДЕСЬ, чтобы сохранить учебник в Pinterest!
Что такое невозможный объект? Также называемые невозможными фигурами или неразрешимыми фигурами, эти рисунки являются разновидностью оптического обмана. Двумерная фигура кажется трехмерной, но геометрия не похожа ни на что, что могло бы существовать в реальном мире. Невозможные предметы использовались в интригующих произведениях искусства на протяжении всего двадцатого века.
Невозможный шестиугольник в этом руководстве по рисованию основан на треугольнике Пенроуза, который был создан художником в 1934 году. Полигоны Пенроуза, такие как этот шестиугольник, строятся путем добавления дополнительных сторон к треугольнику Пенроуза.
Тем не менее, оптическая иллюзия становится менее яркой, поскольку добавляется больше сторон. Таким образом, шестиугольник может казаться искривленным, заплетенным или искривленным, а не «невозможным».
Шестиугольники являются общими структурами как в искусстве, так и в природе. Вы знали? Соты сделаны из маленьких шестиугольников пчелиного воска. Интересно, что шестиугольник позволяет покрывать большое пространство как можно меньшим количеством воска.
Хотите нарисовать невозможный шестиугольник? Сделать это легко и весело с помощью этого простого, пошагового руководства по рисованию фигур. Все, что вам нужно, это карандаш, ручка или маркер и лист бумаги. Вы также можете покрасить свой законченный рисунок.
Пошаговая инструкция по рисованию – Невозможный шестиугольник
1. Начните с рисования шестиугольника. Шестиугольник — это правильная шестигранная фигура, в которой все стороны имеют одинаковую длину.
2. Нарисуйте короткую линию, идущую от верхнего угла шестиугольника. От этой линии вытяните более длинную линию, параллельную стороне шестиугольника. Затем от конца этой линии протяните прямую линию, параллельную следующей стороне шестиугольника. Обратите внимание, что расстояние между линией и второй стороной больше, чем между линией и первой стороной.
3. Нарисуйте короткую прямую линию, идущую от следующего угла шестиугольника. Протяните от него прямую линию, параллельную стороне шестиугольника.
4. Протяните короткую прямую линию от нижнего угла шестиугольника. Из этой линии нарисуйте прямую линию, параллельную нижней части шестиугольника. Затем продлите еще одну линию вверх, параллельно следующей стороне шестиугольника.
5. Проведите короткую линию от оставшегося нижнего угла шестиугольника. Отсюда нарисуйте прямую линию, параллельную стороне шестиугольника. Затем проведите еще одну линию параллельно следующей стороне шестиугольника.
6. Нарисуйте короткую прямую линию, выходящую из следующего угла шестиугольника. Затем протяните прямую линию, параллельную стороне шестиугольника.
7. Проведите короткую прямую линию от последнего угла шестиугольника. Отсюда вытяните прямую линию, параллельную вершине шестиугольника.
8. Начните соединять внешние края невозможного шестиугольника. Расширьте короткие линии от верхнего угла и стороны формы. Затем соедините эти линии с существующими линиями, заключив верхнюю и верхнюю часть рисунка.
9. Проведите короткую линию, идущую от нижнего угла шестиугольника. Затем соедините все открытые линии, пока фигура не будет полностью заключена.
Цвет и тень вашего невозможного шестиугольника. Обратите внимание, как затенение в нашем примере делает трехмерную иллюзию более яркой.
Инструменты «Многоугольник» и «Линия», построение звёзд и стрелок
Установка числа сторон 3 в панели параметров дает нам простой способ создания треугольника:
Равносторонний треугольник, построенный с помощью инструмента «Многоугольник» (Polygon Tool).
А вот пример фигуры многоугольника с количеством сторон 12
Двенадцатиугольник, отображение контура отключено
Как и в случае с радиусом скруглений для инструмента «Прямоугольник со скруглёнными углами», Photoshop не позволяет изменить число сторон после создания фигуры, так что если перед началом построения фигуры вы неправильно указали количество сторон, остаётся только нажать Ctrl+Z для отмены шага по построению фигуры, а затем ввести другое значение в опцию «Стороны» (Sides) и начать рисовать многоугольник заново:
Рисование звезды с помощью «Многоугольника» (Polygon Tool)
Чтобы нарисовать звезду при помощи этого инструмента, нажмите на значок шестеренки в панели параметров, а затем выберите опцию «Звезда» (Star):
Нажатие на значок шестеренки и выбор опции «Звезда» (Star).
Затем просто нажмите внутри документа и создайте фигуру звезды методом перетаскивания курсора. При активной опции «Звезда» (Star), опция «Стороны» (Sides) в панели параметров задаёт количество лучей звезды. Так, при его значении 5 у нас получится пятиконечная звезда:
Пятиконечная звезда, начерченная с помощью инструмента «Многоугольник», параметры фигуры заданы по умолчанию.(Polygon Tool).
Изменение значения сторон на 8 дает нам восьмиконечную звезду:
Управление количеством лучей звезды.
Мы можем изменять у звездообразной фигуры не только количество лучей, но и положение внутренних вершин между центром звезды и внешними вершинами. По умолчанию, внутренние вершины находятся посередине, за это отвечает параметр «Глубина лучей» (Indent Sides By), по умолчанию он равен 50%:
Изменение параметра «Глубина лучей» (Indent Sides By) с 50 процентов, заданных по умолчанию, до 90%.
Посмотрите, что получилось:
Та же восьмиконечная звезда, но со значением параметра «Глубина лучей» (Indent Sides By) 90%. Контур скрыт.
По умолчанию, звезды имеют острые углы на вершинах, но мы можем сделать их закруглёнными, выбрав опцию «Сгладить внешние углы» (Smooth Corners):
Включение скругления углов при помощи опции «Сгладить внешние углы» (Smooth Corners).
Во как будет выглядеть стандартная пятиконечная звезда со сглаженными вершинами лучей при включенной опции «Сгладить внешние углы» (Smooth Corners):
Опция сглаживания углов придает звезде веселый, дружелюбный вид.
Мы можем сгладить не только вершины лучей, но и вершины впадин с помощью опции «Сгладить внутренние углы» (Smooth Indents):
Включение опции «Сгладить внутренние углы» (Smooth Indents).
При включении обеих этих опций мы получаем форму, похожую на морскую звезду:
Звезда с сглаженными углами и впадинами получена при одновременном включении опций «Сгладить внешние углы» (Smooth Corners) и «Сгладить внутренние углы» (Smooth Indents).
Инструмент Линия (Line Tool)
Последним из основных геометрических инструментов формы Photoshop является инструмент «Линия» (Line Tool). Я выберу его на панели инструментов:
Выбор инструмента «Линия» (Line Tool).
Инструмент «Линия» позволяет создавать простые прямые линии, но кроме этого мы можем использовать его для рисования фигур в виде стрелки. Чтобы нарисовать прямую линию, во-первых, установите толщину линии, которую следует задать в пикселях в поле ввода «Толщина» (Weight) в панели параметров. Значение по умолчанию задано в 1 пиксель. Я увеличу его до 16-ти пикселей:
Опция «Толщина» (Weight) задаёт толщину (ширину) линии.
Также, как и при работе другими инструментами векторных форм, для создания линии, нажмите левой клавишей мыши внутри документа и перетащите вашу линию. Чтобы проще было построить горизонтальную, вертикальную или линию под углом 45 градусов, зажмите клавишу Shift в процессе перетаскивания курсора, и отпустите клавишу Shift после отпускания клавиши мыши:
Держите клавишу Shift при перетаскивании курсора для создания горизонтальных или вертикальных линий.
Рисование указательных стрелок (стрелок направления)
Чтобы из линии получить стрелку, нажмите на значок шестеренки на панели параметров, чтобы открыть окно опции «Стрелки» (Arrowhead) с вариантами изменения наконечника (острия) стрелки. Выберите, чтобы наконечник отобразился в начале линии, в конце линии или же с обоих сторон сразу:
Нажмите на значок шестеренки для доступа к опции «Стрелки» (Arrowhead).
Вот линия, начерченная, как и ранее, но на этот раз со стрелкой на конце:
Инструмент «Линия» позволяет легко рисовать указательные стрелки, размеры наконечника стрелки заданы Photoshop по умолчанию.
Если размеры по умолчанию наконечника стрелки вам не подходят, вы можете настроить их, изменив параметры «Ширина» (Width) и «Длина» (Length).
«Ширина» и «Длина» наконечника задаются в процентах от толщины линии, значит, на данный момент ширина моего наконечника стрелки 80 пикселей, а длина -160.
Вы также можете заострить хвостовик наконечника путем увеличения параметра «Кривизна» (Concavity). Я повышу его значение с 0% по умолчанию до 50%:
Опция «Кривизна» (Concavity) для изменения формы наконечника стрелы методом заострения его краев.
Вот так стрелка выглядит теперь. Перед тем, как начать рисовать фигуру, убедитесь, что вы правильно задали параметры инструмента «Линия», так как они не могут быть скорректированы после (если вам необходимо внести изменения, вам нужно отменить форму и рисовать новую).
Гексагональный иерархический пространственный индекс Uber
Грид-системыимеют решающее значение для анализа больших наборов пространственных данных, разделяя области Земли на идентифицируемые ячейки сетки.
Помня об этом, Uber разработал h4, нашу сеточную систему для эффективной оптимизации цен на поездки и диспетчеризации, для визуализации и изучения пространственных данных. h4 позволяет нам анализировать географическую информацию, чтобы устанавливать динамические цены и принимать другие решения на уровне города. Мы используем h4 как сетку для анализа и оптимизации на наших торговых площадках.h4 был разработан для этой цели и заставил нас сделать выбор, например использовать гексагональные иерархические индексы.
Ранее в этом году мы открыли исходный код h4 на Github, предоставив другим доступ к этому мощному решению, а на прошлой неделе мы открыли исходный код наших привязок JavaScript для h4. В этой статье мы обсудим, почему мы используем систему сеток, некоторые уникальные свойства h4 и как вы можете начать использовать h4.
Рис. 1. h4 позволяет пользователям разделить земной шар на шестиугольники для более точного анализа.Расчет с использованием сеток
Ежедневно на торговой площадке Uber происходят миллионы событий. Каждую минуту райдеры запрашивают поездки, водители-партнеры начинают поездки, а голодные пользователи запрашивают еду среди других действий на платформе. Каждое событие происходит в определенном месте, например, гонщик запрашивает поездку из дома, а водитель принимает этот запрос в своей машине всего в нескольких километрах от него.
Эти события позволяют Uber лучше понять и оптимизировать рынок для пользователей наших сервисов.Например, эти события могут сообщить нам, что в определенной части города спрос больше, чем предложение, и скорректировать цены в ответ, или сообщить платформе, что есть два запроса на поездку в непосредственной близости от конкретного водителя на uberPOOL.
Для получения информации и анализа данных на рынке Uber требуется анализ данных по всему городу. Поскольку города географически разнообразны, этот анализ необходимо проводить с высокой степенью детализации. Анализ с высочайшей степенью детализации, точного места, где происходит событие, очень сложно и дорого.Анализ по областям, таким как кварталы в городе, намного практичнее.
| Рис. 2. На картах выше показан процесс выделения точек с h4: автомобили в городе; автомобили в шестиугольниках; и шестиугольники заштрихованы числами автомобилей. |
Мы используем систему сеток для группирования событий в шестиугольные области, другими словами, ячейки. Точки данных разделены на шестиугольники и могут быть записаны с использованием данных с шестигранными разделениями. Например, мы рассчитываем всплеск цен, измеряя спрос и предложение в шестиугольниках в каждом городе, который мы обслуживаем.Эти шестиугольники составляют основу нашего анализа рынка Uber.
Шестиугольники были важным выбором, потому что люди в городе часто находятся в движении, а шестиугольники минимизируют ошибку квантования, возникающую при перемещении пользователей по городу. Шестиугольники также позволяют легко аппроксимировать радиусы, как в этом примере с помощью Elasticsearch.
Рисунок 3. Карта почтовых индексов Нью-Йорка (Манхэттен).Есть и другие варианты, которые мы могли бы использовать для разделения событий на области, например, многоугольные зоны вокруг областей.Это могут быть области почтового индекса, но такие области имеют необычные формы и размеры, которые бесполезны для анализа и могут быть изменены по причинам, совершенно не связанным с тем, для чего мы будем их использовать. Зоны также могут быть нанесены операционными группами Uber на основе их знаний о городе, но такие зоны требуют частого обновления, поскольку города меняются, и часто произвольно определяют границы областей.
Рис. 4. Случайно сгенерированные гексагональные кластеры покрывают город Сан-Франциско. Сетевые системымогут иметь сопоставимые формы и размеры в городах, в которых работает Uber, и не подлежат произвольным изменениям.Хотя сеточные системы не выравниваются по улицам и районам в городах, их можно использовать для эффективного представления кварталов путем кластеризации ячеек сетки. Кластеризация может быть выполнена с использованием целевых функций, создавая формы, гораздо более полезные для анализа. Определение членства в кластере так же эффективно, как и операция поиска набора.
ч4
Мы решили создать h4, чтобы объединить преимущества гексагональной глобальной сеточной системы с иерархической системой индексации.
Глобальная сеточная система обычно требует как минимум двух вещей: проекции карты и сетки, накладываемой поверх карты.Картографическая проекция необходима для перехода от трехмерного места на Земле к двумерной точке на карте. Затем на карту накладывается сетка, образуя глобальную сеточную систему.
Этот процесс может быть выполнен бесчисленными способами путем комбинирования различных картографических проекций и сеток, например широко известной проекции Меркатора и квадратной сетки. Хотя этот простой метод сработает, у него есть ряд недостатков. Начнем с того, что проекция Меркатора имеет значительное искажение размера, поэтому некоторые ячейки будут иметь совершенно разные площади.Квадратные сетки также имеют недостатки, требующие нескольких наборов коэффициентов при использовании для анализа. Этот недостаток является результатом того, что квадраты имеют два разных типа соседей: один тип, с которым они имеют общее ребро (в четырех основных направлениях), и другой тип, с которым они имеют общую вершину (в четырех диагональных направлениях).
| Рис. 5. Мы решили использовать гномонические проекции с центром на гранях икосаэдра (слева) для проекции карты h4, проецируя Землю как сферический икосаэдр (справа). |
Для проекции карты мы решили использовать гномонические проекции с центром на гранях икосаэдра. Он проецируется от Земли в виде сферы к икосаэдру, двадцатигранному платоническому телу. Проекция карты на основе икосаэдра дает двадцать отдельных двухмерных плоскостей, а не одну плоскость. Икосаэдр можно развернуть разными способами, каждый раз создавая двумерную карту. h4, однако, не разворачивает икосаэдр для построения своей системы сеток, а вместо этого кладет свою сетку на сами грани икосаэдра, образуя геодезическую дискретную глобальную систему сеток.
| Рисунок 6. Расстояния от треугольника до его соседей (слева), от квадрата до его соседей (в центре) и от шестиугольника до его соседей (справа). |
Использование шестиугольника в качестве формы ячейки критично для h4. Как показано на рисунке 6, шестиугольники имеют только одно расстояние между центром шестиугольника и его соседями, по сравнению с двумя расстояниями для квадратов или тремя расстояниями для треугольников. Это свойство значительно упрощает выполнение анализа и сглаживания градиентов.
Рис. 7. h4 используется для создания сетки на одной грани икосаэдра.Сетка h4 построена путем размещения 122 базовых ячеек над Землей, по десять ячеек на грань. Некоторые ячейки содержат более одного лица. Поскольку невозможно замостить икосаэдр только шестиугольниками, мы решили ввести двенадцать пятиугольников, по одному в каждой вершине икосаэдра. Эти вершины были расположены с использованием сферической ориентации икосаэдра Р. Бакминстера Фуллера, которая помещает все вершины в воду.Это помогает избежать всплытия пятиугольников в нашей работе.
| Рис. 8. h4 позволяет пользователю разделить области на все меньшие и меньшие шестиугольники. |
h4 поддерживает шестнадцать разрешений. Каждое более высокое разрешение имеет ячейки с одной седьмой областью более грубого разрешения. Шестиугольники нельзя полностью разделить на семь шестиугольников, поэтому более мелкие ячейки лишь приблизительно содержатся в родительской ячейке.
Идентификаторы для этих дочерних ячеек можно легко усечь, чтобы найти их предковую ячейку с более грубым разрешением, что позволяет эффективно индексировать.Поскольку дочерние ячейки содержатся только приблизительно, процесс усечения приводит к фиксированному искажению формы. Это искажение присутствует только при выполнении усечения идентификатора ячейки; при индексировании местоположений с определенным разрешением границы ячеек являются точными.
Начало работы с h4
Система индексирования h4 имеет открытый исходный код и доступна на GitHub. Сама библиотека h4 написана на C, и привязки доступны для ряда языков.Использование привязок — это рекомендуемый способ начать использовать h4. Uber опубликовал привязки для Java и JavaScript, а сообщество внесло привязки для других языков. Скоро появятся привязки для Python и Go.
| Рис. 9. Точка (синяя, слева) и содержащий ее шестиугольник, центроид (светло-синий, середина) содержащего шестиугольника, а также точка и центроид содержащего шестиугольника (справа) изображают возможную разницу между двумя. |
Код: https: // github.com / uber / h4 / blob / master / examples / index.c
Основные функции библиотеки h4 предназначены для индексации местоположений, которая преобразует пары широты и долготы в 64-битный индекс h4, идентифицируя ячейку сетки. Функция geoToh4 принимает широту, долготу и разрешение (от 0 до 15, где 0 — самое грубое, а 15 — самое точное) и возвращает индекс. h4ToGeo и h4ToGeoBoundary являются инверсией этой функции, обеспечивая координаты центра и контур ячейки сетки, заданной индексом h4, соответственно.
После того, как вы проиндексировали данные с помощью h4, в h4 API появятся функции для работы с индексами.
| Рис. 10. Шестиугольники, соседствующие с индексом, с расстоянием 0 (слева; только исходный индекс), 1 (посередине; с соседями исходного индекса) и 2 (справа; с соседями соседей). |
Код: https://github.com/uber/h4/blob/master/examples/neighbors.c
Соседние шестиугольники обладают полезным свойством аппроксимации окружностей с использованием системы сеток.Функция kRing предоставляет ячейки сетки в пределах расстояния k сетки от исходного индекса.
| Рис. 11. Плотные шестиугольники, представляющие Калифорнию, резко контрастируют с компактными шестиугольниками, представляющими штат, требуя гораздо меньшего количества шестиугольников для представления той же площади. |
Код: https://github.com/uber/h4/blob/master/examples/compact.c
Иерархический характер h4 позволяет эффективно сокращать точность (или разрешение) индекса и восстанавливать исходные индексы. Выше показаны некомпактные и компактные представления набора шестиугольников. В некомпактном представлении имеется 10 633 шестиугольника с разрешением 6, а в компактном представлении — 901 шестиугольник с разрешением до 6. В обоих случаях шестигранный индекс является 64-битным целым числом.
Точность одного индекса также может быть эффективно усечена с помощью побитовой операции или расширена до набора индексов более высокой точности.
Рисунок 12. h4 может представлять движение из одной ячейки в другую, здесь показано стрелкой от исходной ячейки к целевой.Код: https://github.com/uber/h4/blob/master/examples/edge.c
h4 имеет функции для направленных краев ячеек сетки, которые могут представлять движение от одной ячейки к другой. Направленные ребра могут быть сохранены как 64-битные целые числа и могут быть получены из двух соседних ячеек или путем нахождения всех ребер ячейки. При необходимости ребро можно преобразовать обратно в исходный или целевой индексы.
Движение вперед
h4 используется в Uber для количественного анализа нашего рынка, и теперь, когда его исходный код открыт, вы тоже можете гексагонизировать мир! Мы с нетерпением ждем, когда вы присоединитесь к сообществу h4, подписавшись на наш репозиторий на Github и написав твит с хэштегом # uberh4.
Карты, созданные с помощью MapboxGL.
Узнайте больше о наших поставщиках картографических данных.
Основными участниками библиотеки h4 являются Кевин Сар (Университет Южного Орегона), Джозеф Гилли (Uber), Ник Рабиновиц (Uber) и Дэвид Эллис (CarDash).
Подпишитесь на нашу рассылку новостей , чтобы быть в курсе последних инноваций от Uber Engineering.
1. Заголовок:2. Введение / Инструкции для студентовHEXAGON ESSAY-PLANNING TOOL. ПЕРЕТАСКИВАЙТЕ эти шестиугольники по категориям по вашему выбору. Вы можете присвоить цветовой код шестиугольникам и создать новые шестиугольники (например, в качестве заголовков для каждой группы), дважды щелкнув в любом месте холста.Когда вы закончите, вы можете использовать свою работу как основу для плана сочинения, презентации или проекта! 3. Текст шестиугольника: разделяйте каждый символ новой строкой | Причины победы Союза в гражданской войнеЗеленый = первоисточники добавлены в конце в соответствующие категории Последствия черной смертиОранжевый = рукописные шестиугольники на основе видеозаметок Причины прихода Сталина к властиКонфеты вручаются каждой команде за определение факторов, не указанных в исходных шестиугольниках Генератор шестиугольника — СловоРаспечатайте свой собственный рабочий лист версии Генератор шестиугольников — HTML5Используйте свои шестиугольники прямо на интерактивной доске Историография Первой мировой войны«Устрой историкам званый обед: никаких аргументов!» Последствия черной смертиОтличная командная работа учеников 7 класса Узнать большеИспользование Hexagon Learning для категоризации, связывания и определения приоритетов Пустые шестиугольники: загружаемый шаблон Word HTML5 Hexagons: The Black Death (из ActiveHistory ). Загружаемые шестиугольники: Историография Первой мировой войны (из ActiveHistory ). |
Как нарисовать шестиугольник с помощью HTML5 и тега холста
Как нарисовать шестиугольник с помощью HTML5 и тега холстаЕсли вы хотите нарисовать шестиугольную форму на веб-странице, HTML5 предоставляет удобный способ сделать это. используя тег холста и javascript.
Построение шестиугольника на основе предыдущего примера. мы находим, что этот процесс значительно проще, если использовать векторы и линии как часть холста HTML 5.Вот пример, показывающий, как нарисовать шестиугольную форму с помощью HTML5 и тега холста.
В этом примере не представлены параметры стиля CSS из предыдущего примера рисования шестиугольника, но его легче использовать в отношении других операций программирования, которые вам нужно будет выполнить, если вы пишете сценарии это для игры. Например, логично предположить, что что-то должно быть помещено «внутри» форма, которая демонстрируется здесь.
Пример тега и кода
Код, использованный для создания примера, можно увидеть ниже.Тег холста сначала создается в DOM. Здесь применяются некоторые правила стиля CSS с использованием класса my_canvas просто для того, чтобы сопоставьте цветовую схему здесь, а также чтобы показать, что вы можете применить стили CSS к холсту с помощью атрибутов html класса или стиля. Пример кода javascript запускается кнопкой рядом с холстом. Кнопка использует состояние переключения, чтобы отслеживать, должен ли щелчок «очищать» холст или «рисовать» на холсте. Я подумал, что может быть полезно увидеть здесь контекст, но, оглядываясь назад, я не большой поклонник переключения здесь, потому что это загрязняет взаимодействие с холстом — ваш пример, вероятно, не нужно рисовать или очищать с помощью кнопки.Приношу свои извинения за любую путаницу, я надеюсь пересмотреть это в будущем, чтобы лучше изолировать эти два аспекта.Вот что делает этот пример
- Создать тег холста
- Получите ссылку на тег холста с помощью javascript
- Настройка контекста чертежа («2D» означает двухмерный)
- Установить переменные x и y
- Перемещайтесь по изменениям x и y, необходимым для отслеживания формы шестиугольника.
- Нарисуйте линии для любой из ног, которые нам нужно показать
- Установка характеристик стиля рисования, таких как цвет и толщина линии
- Запуск рисования
- Добавить текст
Canvas Tag
Пример кода
См. Также
Hexagon — Переиздание Википедии // WIKI 2
Форма с шестью сторонами
В геометрии шестиугольник (от греческого ἕξ hex , «шестерка» и γωνία, gonía , «угол, угол») представляет собой шестиугольник или 6-угольник.Сумма внутренних углов любого простого (несамопересекающегося) шестиугольника составляет 720 °.
Энциклопедия YouTube
1/5
Просмотры:1824 496
1954715
456202
2206038
714849
Шестиугольники — это Бестагоны
Почему природа любит шестиугольники
Песня HEXAGON | Пение и формы заклинаний HeidiSongs!
Почему пчелы любят шестиугольники? — Зак Паттерсон и Энди Петерсон
Как нарисовать правильный шестиугольник, зная длину одной стороны
Содержание
Шестигранник правильный
Правильный шестиугольник имеет символ Шлефли {6} [1] и также может быть построен как усеченный равносторонний треугольник t {3}, в котором чередуются два типа ребер.
Когда задана длина стороны AB, вы рисуете вокруг точки A и вокруг точки B дугу окружности. Пересечение M является центром описанной окружности. Перенесите отрезок AB четыре раза на описанную окружность и соедините угловые точки.Правильный шестиугольник — это шестиугольник, который одновременно является равносторонним и равноугольным. Он бицентрический, что означает, что он является одновременно циклическим (имеет описанную окружность) и касательным (имеет вписанную окружность).
Общая длина сторон равна радиусу описанной окружности или описанной окружности, который равен 23 {\ displaystyle {\ tfrac {2} {\ sqrt {3}}}}, умноженным на апофему (радиус вписанной окружности).Все внутренние углы составляют 120 градусов. Правильный шестиугольник имеет шесть симметрий вращения ( вращательная симметрия шестого порядка ) и шесть симметрий отражения ( шесть линий симметрии ), составляя двугранную группу D 6 . Самые длинные диагонали правильного шестиугольника, соединяющие диаметрально противоположные вершины, вдвое превышают длину одной стороны. Из этого видно, что треугольник с вершиной в центре правильного шестиугольника и общей стороной с шестиугольником является равносторонним, и что правильный шестиугольник можно разделить на шесть равносторонних треугольников.
Подобно квадратам и равносторонним треугольникам, правильные шестиугольники подходят друг к другу без каких-либо зазоров, так что соединяет плоскость (три шестиугольника, пересекающиеся в каждой вершине), и поэтому полезны для построения мозаики. Ячейки соты улья шестиугольные по этой причине, а также потому, что форма позволяет эффективно использовать пространство и строительные материалы. Диаграмма Вороного правильной треугольной решетки — это сотовая мозаика шестиугольников. Обычно не считается триамбусом, хотя он равносторонний.
Параметры
Максимальный диаметр (который соответствует длинной диагонали шестиугольника), D , в два раза больше максимального радиуса или радиуса описанной окружности, R , что равняется длине стороны, t . {\ circ}) R = {\ frac { \ sqrt {3}} {2}} R = {\ frac {\ sqrt {3}} {2}} t} и аналогично d = 32D.{\ displaystyle d = {\ frac {\ sqrt {3}} {2}} D.}
Площадь правильного шестиугольника
- A = 332R2 = 3Rr = 23r2 = 338D2 = 34Dd = 32d2≈2,598R2≈3,464
Hexagon Game — играть в Hexagon Online
Играйте в Hexagon против компьютера или с другом.
Прочтите ниже инструкции, если вы не знакомы с тем, как играть в Hexagon.
Hexagon — это настольная игра, в которую играют два человека. Доска состоит из нескольких небольших шестиугольных коробок, расположенных в форме ромба.Цель игры — завершить линию одного цвета от одного края до другого.
Общая форма доски может иногда отличаться, и даже более того — два цвета, используемые для фишек обоих игроков.
Как играть в Hexagon
У каждого игрока есть несколько фигур одного цвета. Они по очереди помещают фишку в исходное положение с любой стороны доски, сверху или снизу. Каждый последующий ход должен включать размещение новой фигуры на доске так, чтобы она находилась на шестиугольнике, касающемся хотя бы одной другой фигуры этого игрока.
Игрок, который выстраивает линию своих фигур от одного края до другого, объявляется победителем, и игра завершается.
Блокбастеры
Формат этой игры был популяризирован благодаря популярному сериалу Blockbusters, где на каждом шестиугольнике была буква алфавита. Применялись те же правила, однако игрок не мог просто заявить шестиугольник как свой собственный. Вместо этого после выбора шестиугольника задавался вопрос, ответ на который должен начинаться с буквы, найденной в этом месте.
Если игрок ответил правильно, он выиграет позицию, в противном случае она останется открытой для другого оппонента.
Этот формат, пожалуй, самая известная и популярная версия игры. Он часто используется на уроках языка и других предметов, чтобы помочь студентам выучить новые слова, идеи и другие вещи.
Цифровые версии
Поскольку Hexagon все чаще используется для компьютерной игры (будь то онлайн или просто настольный компьютер), строгое соблюдение стилей доски, цветовых схем и количества игроков сильно колебалось.
При игре на компьютере обычно доступны два варианта. Во-первых, игра против компьютерной программы или, во-вторых, подключение к Интернету и игра с противником в другом месте в мире. Там, где компьютерные программы часто имеют тенденцию двигаться намного быстрее и позволяют быстро разворачивать игру, они могут стать довольно предсказуемыми и не будут создавать особых проблем по прошествии определенного периода времени. С другой стороны, люди могут дольше обдумывать каждое движение.
Они могут отвлекаться и растягивать время, затрачиваемое на каждое движение.Это жертва, которую нужно принимать, играя с реальным человеком, но положительным моментом, конечно же, является то, что ходы будут намного более непредсказуемыми, они также будут изучать ваши техники так же, как вы изучаете их.
Этот органичный прогресс двух игроков друг против друга лежит в основе стратегических игр, и Hexagon ничем не отличается. Такой подход принесет огромное удовольствие и вызовет от игры, а также постоянно улучшит стратегические навыки каждого игрока.
Hexagonads Launcher 2.0 от YGKtech на DeviantArt
Я рад, что вам понравилосьПохоже, вы на правильном пути, но, вероятно, вам просто не хватает нескольких файлов. Я сформулирую свой ответ как обобщенное руководство на случай, если у кого-то еще возникнут проблемы с дублированием скина.
Файл Hexagonads.ini — это просто набор инструкций, рассказывающих Rainmeter, как отображать шестиугольники и что делать при щелчке по ним, сами шестиугольники представляют собой файлы изображений, которые Rainmeter должен найти, прежде чем он сможет отобразить скин; Если Rainmeter не знает, где найти файлы изображений, он ничего не может сделать.На изображения и файлы ресурсов на самом деле не обращают внимания пользователи, плохо знакомые с Rainmeter, потому что окно управления, в котором вы загружаете скины, отображает папки и файлы .ini, но скрывает все остальное, поэтому с этой точки зрения не очевидно, нужно ли скину что-то еще. чем файл .ini для работы (некоторым скинам на самом деле не нужны файлы изображений, потому что Rainmeter может создавать простые формы самостоятельно).
Есть несколько различных способов включения ресурсов (файлов изображений, цветовых кодов и т. Д.) В Rainmeter, но Hexagonads использует очень простой подход: он ожидает, что все файлы изображений, которые он использует, будут находиться в той же папке, что и.ini файл.
Итак, чтобы сделать вторую рабочую копию этого скина, вам нужно скопировать всю папку. Откройте браузер файлов и перейдите в папку «Скины» (расположение по умолчанию — «C: \ Users \ YourName \ My Documents \ Rainmeter \ Skins»), найдите папку Hexagonads Launcher, затем просто скопируйте и вставьте всю папку. (Windows автоматически создаст новую папку с именем «Hexagonads Launcher — Copy», вы можете переименовать ее как угодно).
Откройте окно управления Rainmeter и нажмите «Обновить все», это заставит Rainmeter повторно загрузить все ваши активные скины и повторно просканировать папку на предмет новых скинов.Вы должны увидеть новую папку, которую вы создали, в списке доступных скинов, разверните папку, щелкните Hexagonads.ini, а затем нажмите «Загрузить». Вы должны увидеть копию своей первой пусковой установки со всеми теми же кнопками и цветами, за исключением того, что она будет застрять в верхнем левом углу экрана, просто отключите настройку «держать на экране», как при первой настройке этот лаунчер.
Некоторые скины могут включать ресурсы из другого места, документация Rainmeter на самом деле предлагает хранить их в папке «@ Resources», чтобы улучшить время загрузки, но я сделал этот скин незадолго до того, как эта функция была добавлена в Rainmeter, просто помните, что Rainmeter нуждается в чтобы знать, где найти файлы, и вы должны понять, что делать.Эти инструкции должны работать для большинства скинов, но некоторые скины, особенно те, которые используются в наборах / макетах с несколькими скинами, могут совместно использовать ресурсы с другими скинами, включая общий файл, дублирование этих скинов может потребовать некоторых дополнительных шагов в зависимости от того, как они помещены вместе, и хотите ли вы, чтобы копия разделяла эти ресурсы или была полностью отдельной.


 Вставьте карандаш в циркуль. Расширьте циркуль на желаемую ширину радиуса вашего круга. Радиус может быть от пары до десятка сантиметров шириной. Далее поставьте циркуль с карандашом на бумагу и нарисуйте круг.
Вставьте карандаш в циркуль. Расширьте циркуль на желаемую ширину радиуса вашего круга. Радиус может быть от пары до десятка сантиметров шириной. Далее поставьте циркуль с карандашом на бумагу и нарисуйте круг. Вы должны вернуться назад на первоначальную отметку. Если нет, тогда, скорее всего, угол, под которым вы держали циркуль и делали отметки, изменился. Возможно, это случилось из-за того, что вы сжали его слишком сильно или наоборот, немного ослабили.
Вы должны вернуться назад на первоначальную отметку. Если нет, тогда, скорее всего, угол, под которым вы держали циркуль и делали отметки, изменился. Возможно, это случилось из-за того, что вы сжали его слишком сильно или наоборот, немного ослабили.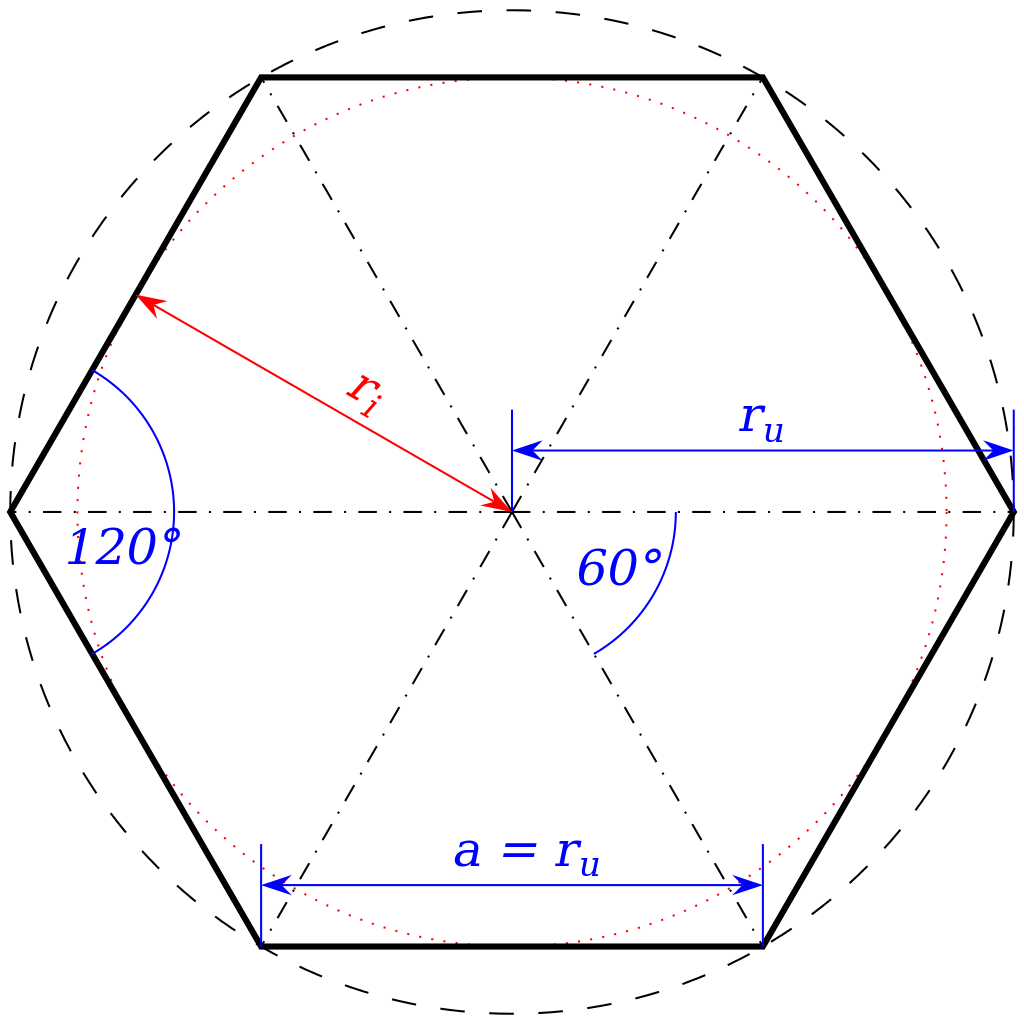 Вы также можете обвести перевернутый стакан, банку или что-то еще, что имеет круглую основу.
Вы также можете обвести перевернутый стакан, банку или что-то еще, что имеет круглую основу. Нижняя левая линия должна быть отражением верхней левой линии, а нижняя правая — отражением верхней правой линии. В то время как верхние горизонтальные линии должны смотреть наружу, нижние должны смотреть вовнутрь основания.
Нижняя левая линия должна быть отражением верхней левой линии, а нижняя правая — отражением верхней правой линии. В то время как верхние горизонтальные линии должны смотреть наружу, нижние должны смотреть вовнутрь основания. Шесть нарисованных радиусов одинаковой длины и все линии для создания шестиугольника тоже одной длины, так как ширина циркуля не менялась. Благодаря тому, что шесть треугольников равносторонние, углы между их вершинами равны 60 градусов.
Шесть нарисованных радиусов одинаковой длины и все линии для создания шестиугольника тоже одной длины, так как ширина циркуля не менялась. Благодаря тому, что шесть треугольников равносторонние, углы между их вершинами равны 60 градусов.