Гексагон
- Главная
- Справочник
- Геометрия
- Фигуры
- Гексагон
- Свойства правильного шестиугольника
фывафыва
Гексагон — правильный выпуклый многоугольник с шестью сторонами или шестиугольник.
Шестиугольник — это многоугольник, имеющий шесть сторон и шесть углов. В правильном шестиугольнике все стороны равны, а углы образуют шесть равносторонних треугольников.
Выпуклый шестиугольник — это многоугольник, с общим количеством вершин, равным шести, при этом все точки такого шестиугольника лежат по одну сторону от прямой, которая проведена между двумя любыми соседними его вершинами.
Правильный шестиугольник — это шестиугольник, все стороны которого равны между собой.
Сумма углов выпуклого шестиугольника определяется по общей формуле 180°(n-2) и равна 180 ( 6 — 2 ) = 720 градусов.
При решении задач для нахождения площади произвольного (неправильного) шестиугольника используют метод трапеций, который заключается в разбиении фигуры на отдельные трапеции, площадь каждой из которых можно найти по известным всем формулам.
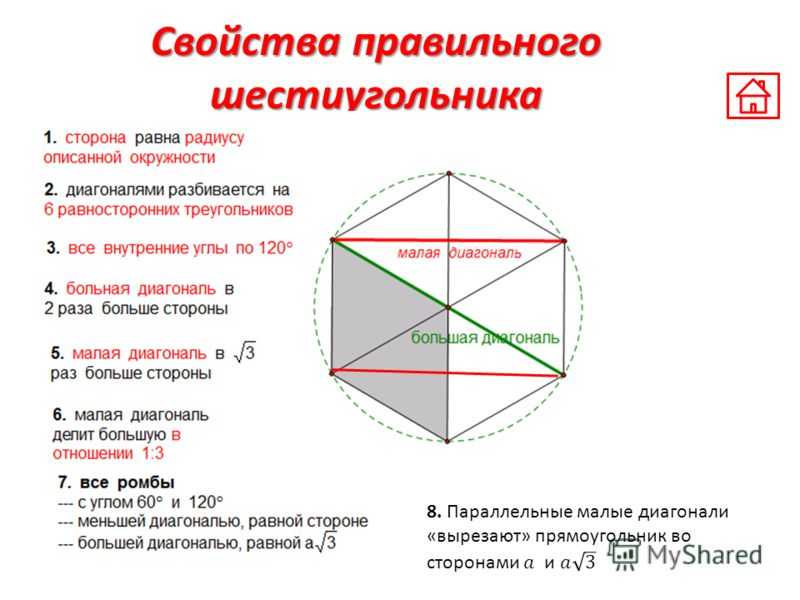
Свойства правильного шестиугольника
- все внутренние углы равны между собой
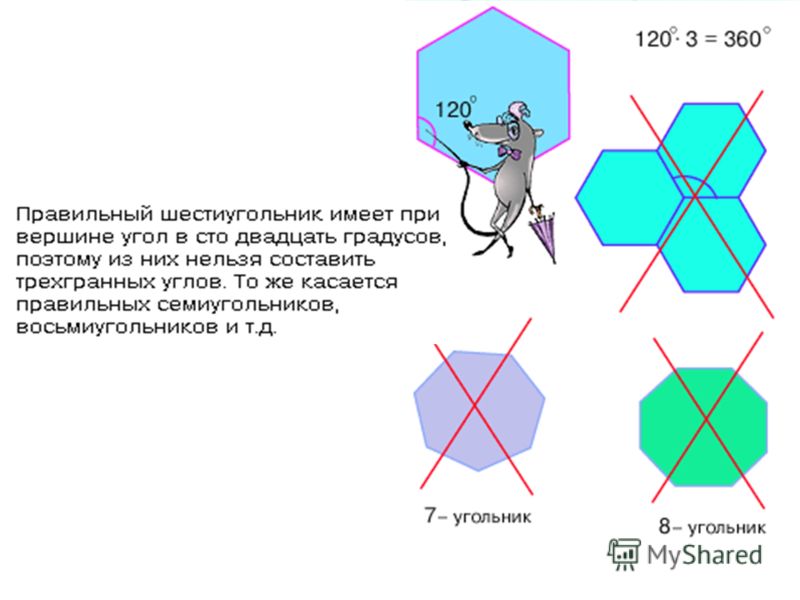
- каждый внутренний угол правильного шестиугольника равен 120 градусам
- все стороны равны между собой
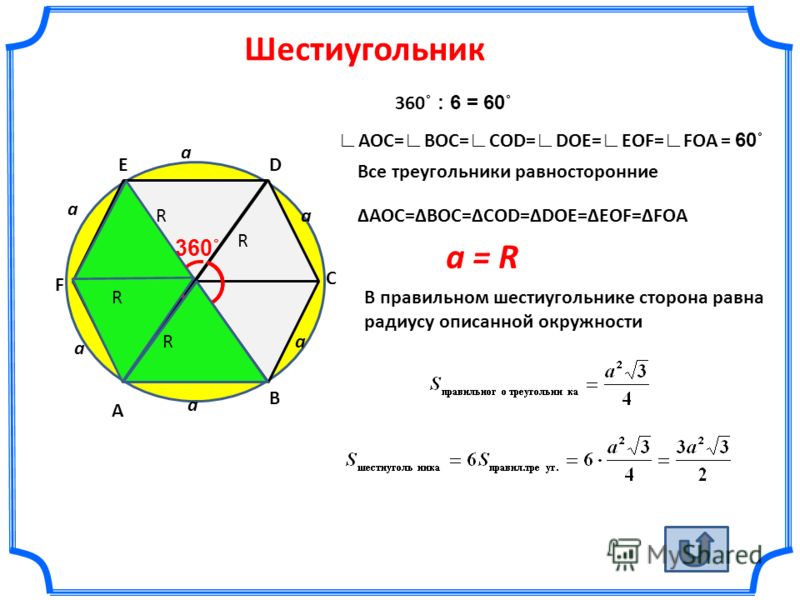
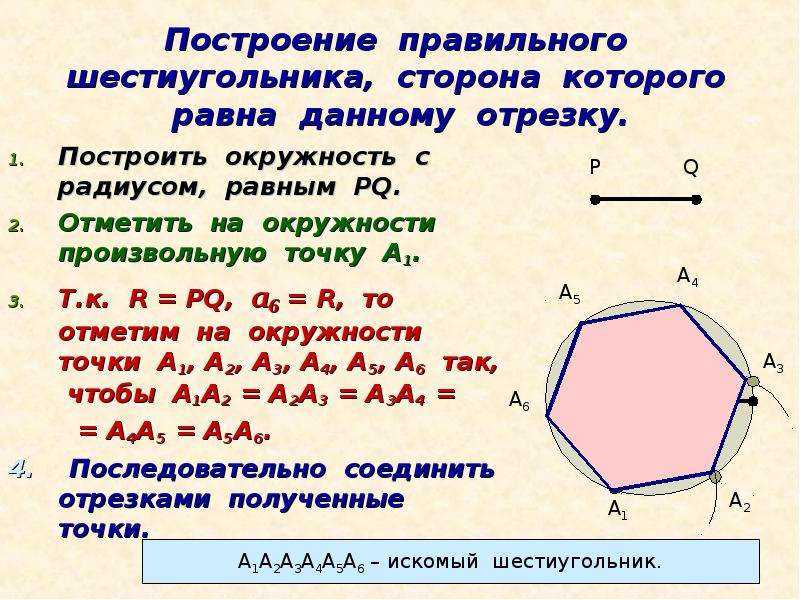
- сторона правильного шестиугольника равна радиусу описанной окружности
- большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам
- меньшая диагональ правильного шестиугольника в раз больше его стороны.
- vеньшая диагональ правильного шестиугольника перпендикулярна его стороне
- правильный шестиугольник заполняет плоскость без пробелов и наложений
- диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу вписанной в правильный шестиугольник окружности.
 6.
6. - инвариантен относительно поворота плоскости на угол, кратный относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями)
- nреугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60°.
Внутренние углы Внутренние углы в правильном шестиугольнике равны :
Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
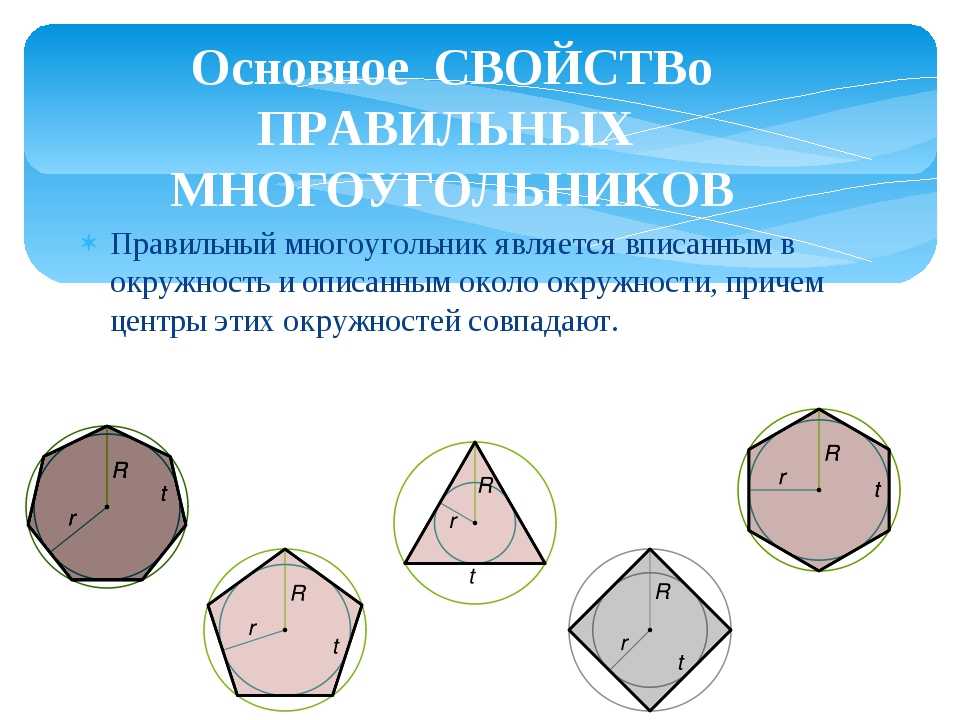
Радиус вписанной окружности правильного шестиугольника равен апофеме:
Радиус описанной окружности равен стороне правильного шестиугольника:
Периметр правильного шестиугольника
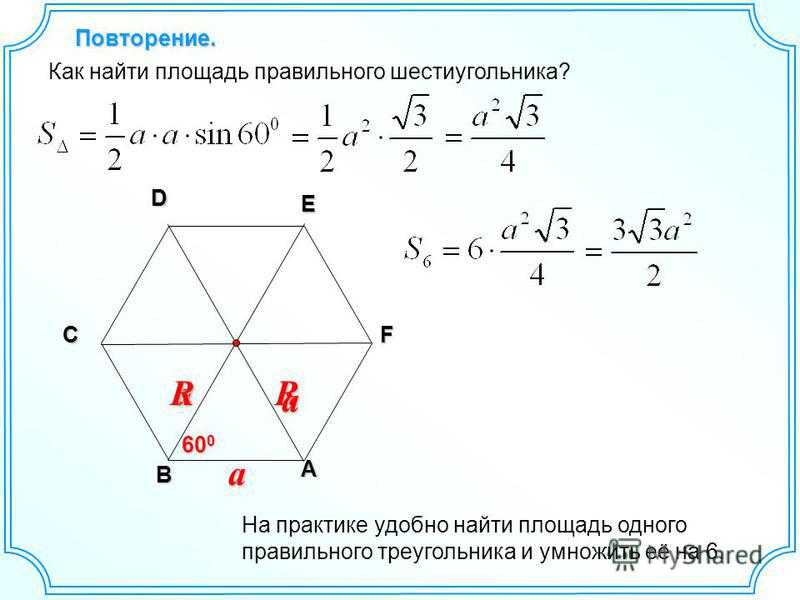
Площадь правильного шестиугольника Формула площади правильного шестиугольника через длину стороны
,
где − полупериметр шестиугольника.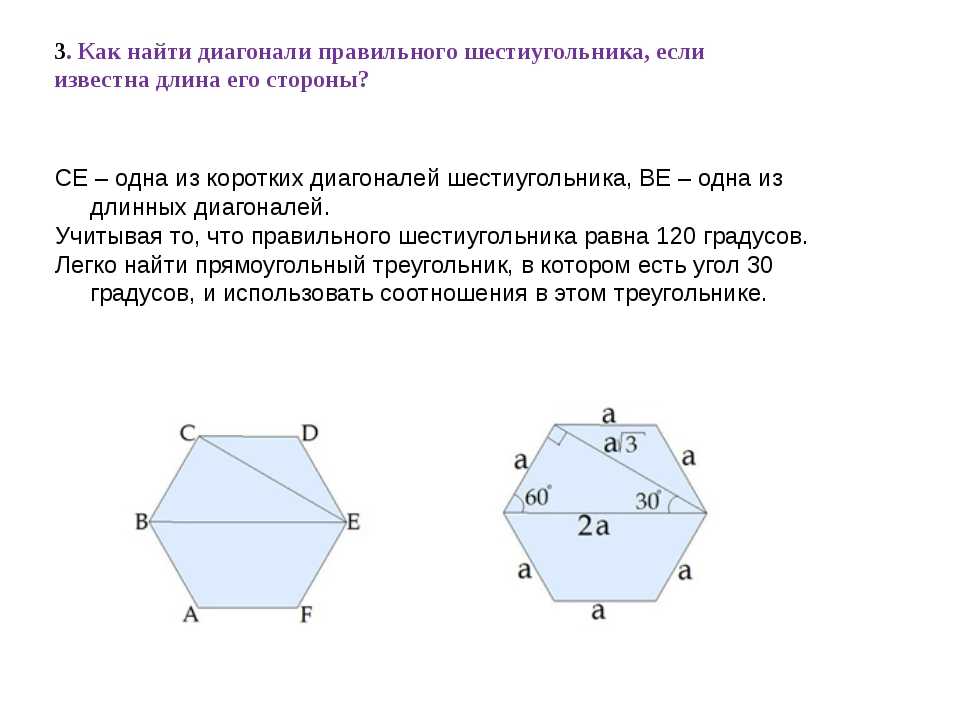
Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус вписанной окружности
Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус описанной окружности
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Фигуры Математика Формулы Геометрия Теория Фигуры 27588
Как известно, пчелы строят соты правильной шестиугольной формы. Дело в том, что шестиугольник – самая оптимальная геометрическая форма для максимально полезного использования единицы площади. Шестиугольник близок к кругу – идеальной естественной фигуре, – но у него есть преимущество: вплотную примыкая друг к другу, шестиугольники позволяют использовать всю полезную площадь сот, максимально заполняя ее медом.

Панцирь черепахи состоит из шестиугольников. Благодаря ячейкам такой формы он проще всего наращивается. Черепахи растут, и их панцирь должен увеличиваться вместе с ними, причем равномерно по всей площади. Поэтому черепаший панцирь формируется из отдельных пластинок, плотно пригнанных друг к другу, как дощечки паркета, но сохраняющих способность прирастать по краям. Если бы пластинки могли равномерно расти во все стороны, они имели бы форму кругов. Однако круги не могут плотно прилегать друг к другу, между ними неизбежно будут оставаться просветы.
Некоторые сложные молекулы углерода (напр., графит) имеют гексагональную кристаллическую решётку.
Гигантский гексагон — атмосферное явление на Сатурне.
Сечение гайки и многих карандашей имеет вид правильного шестиугольника.

Игровое поле гексагональных шахмат составляют шестиугольники, в отличие от квадратов традиционной шахматной доски.
Гексаграмма — шестиконечная звезда, образованная двумя равносторонними треугольниками. Является, в частности, символом иудаизма.
Контур Франции напоминает правильный шестиугольник, поэтому он является символом страны.
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Треугольник
Треугольник — многоугольник, образованный тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.
Фигуры Математика Формулы Геометрия Теория Фигуры
Квадрат
Квадрат — это правильный четырёхугольник. У него все стороны и углы равны между собой.
Фигуры Математика Формулы Геометрия Теория Фигуры
Прямоугольник
Прямоугольник — параллелограмм, у которого все углы прямые (равны 90 градусам).

Фигуры Математика Формулы Геометрия Теория Фигуры
Параллелограмм
Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны.
Фигуры Математика Формулы Геометрия Теория Фигуры
Ромб
Ромб — это параллелограмм, у которого все стороны равны.
Фигуры Математика Формулы Геометрия Теория Фигуры
Четырёхугольник
Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки.
Фигуры Математика Формулы Геометрия Теория Фигуры
Круг и окружность
Круг — геометрическое место точек плоскости, равноудаленных от одной заданной точки, называемой центром круга.
Фигуры Математика Формулы Геометрия Теория Фигуры
Прямоугольный треугольник
Треугольник называют прямоугольным, если у него есть прямой угол, который равен 90 градусов.
Фигуры Математика Формулы Геометрия Теория Фигуры
Русский алфавит
Современный русский алфавит состоит из 33 букв.

Литература 1 класс Литература Алфавит Азбука
ЕГЭ: обязательные предметы для сдачи экзамена
ЕГЭ Экзамены
Бесплатный генератор паролей онлайн
Создать бесплатно пароль любой длины и уровня сложности для ваших приложений, аккаунтов, соц. сетей, паролей к Windows, зашифрованным архивам и т.д.
Работа с текстом Генератор Инструмент Текст Пароли
Таблица мер измерения
Таблицы
Что такое баррель. Чему равен 1 баррель в литрах?
Американский нефтяной баррель равен 42 галлонам в английской системе мер или 158,988 л в метрической системе.
Масса и вес Масса Физика Теория Единицы измерения
Узнать знак зодиака по дате рождения
Калькуляторы времени и даты Калькулятор Расчёт Время
Таблица перевода сухопутных миль в километры (mi в км)
1 сухопутная миля (США и Британия) = 1,60934 км
Размеры и расстояния Теория Расстояния
Калькулятор размеров колец на пальцы
Выбор обручальных колец — один из самых волнующих моментов для молодоженов.

Калькуляторы размеров одежды Калькулятор Расчёт Конвертер Преобразовать Размеры
Геометрия многоугольника: пятиугольники, шестиугольники и додекагоны
Автор Глеб Захаров На чтение 6 мин. Просмотров 4.7k. Опубликовано
Содержание
- Двумерные правильные многоугольники везде
- О полигонах
- Как называются полигоны
- N-угольники
- Предел полигона
- Классификация полигонов
- Регулярные и неправильные полигоны
- Выпуклые против вогнутых полигонов
- Простые и сложные полигоны
- Правило суммы внутренних углов
- Сколько треугольников в этом многоугольнике?
- Размер угла для правильных многоугольников
- Некоторые известные полигоны
- Фермы
- Пентагон
- Главная пластина
- Поддельный Пентагон
- Снежинки
- Пчелы и осы
- Тротуар гиганта
- Восьмиугольник
- Стоп Знаки
Немногие геометрические фигуры столь же разнообразны, как многоугольники. Они включают в себя знакомый треугольник, квадрат и пятиугольник, но это только начало.
Они включают в себя знакомый треугольник, квадрат и пятиугольник, но это только начало.
В геометрии многоугольник – это любая двумерная форма, которая удовлетворяет следующим условиям:
- Состоит из трех или более прямых
- Закрыто без отверстий или разрывов в форме
- Имеет пары линий, которые соединяются в углах или вершинах, где они образуют углы
- Имеет равное количество сторон и внутренних углов
Двумерный означает плоский, как лист бумаги. Кубы не являются полигонами, потому что они трехмерны. Круги не являются полигонами, потому что они не содержат прямых линий.
Специальный вид многоугольника может иметь углы, которые не все равны. В этом случае он называется неправильным многоугольником.
О полигонах
Название многоугольник происходит от двух греческих слов:
- Poly , , что означает много .
- Гон , что означает угол
Формы, которые являются полигонами
- Треугольник (треугольник): 3 стороны
- Тетрагон (квадрат): 4 стороны
- Пентагоны: 5 сторон
- Шестиугольник: 6 сторон
- Семиугольник: 7 сторон
- Восьмиугольники: 8 сторон
- Нонагон: 9 сторон
- Декагон: 10 граней
- Undecagon: 11 сторон
- Додекагоны: 12 сторон
Как называются полигоны
Названия отдельных многоугольников получаются из числа сторон или углов, которыми обладает форма. Полигоны имеют одинаковое количество сторон и углов.
Полигоны имеют одинаковое количество сторон и углов.
Общим названием для большинства полигонов является греческий префикс «сторон», прикрепленный к греческому слову «угол» (gon).
Примеры этого для пяти- и шестигранных правильных многоугольников:
- Пента (по-гречески означает пять) + гон = Пентагон
- Гекса (по-гречески означает шесть) + гон = шестиугольник
Есть исключения из этой схемы именования. В частности, со словами, которые чаще всего используются для некоторых полигонов:
- Треугольник . Использует греческий префикс Tri , но вместо греческого гона используется латинский угол . Trigon – правильное геометрическое имя, но оно используется редко.
- Четырехсторонний. Производный от латинского префикса quadri, , означающего четыре, прилагается к слову боковой, , которое является еще одним латинским словом, означающим сторона .

- Квадрат . Иногда четырехсторонний многоугольник (квадрат) называется четырехугольником или четырехугольником .
N-угольники
Полигоны с более чем 10 сторонами встречаются нечасто, но следуют тому же греческому соглашению об именовании Таким образом, 100-сторонний многоугольник называется гектогоном .
Однако в математике пятиугольники иногда удобнее называть n-гонами :
- 11-гонник: гендекагон
- 12-Гон: Додекагон
- 20-угольник: Icosagon
- 50-гонник: пятиконечный
- 1000-гон: чилиагон
- 1000000-гон: мегагон
В математике н-гоны и их греческие аналоги взаимозаменяемы.
Предел полигона
Теоретически, нет ограничения на количество сторон, которые может иметь многоугольник.
По мере того, как размер внутренних углов многоугольника увеличивается, а длина его сторон становится короче, многоугольник приближается к кругу, но никогда не достигает его.
Классификация полигонов
Регулярные и неправильные полигоны
Полигоны классифицируются на основании того, равны ли все углы или стороны.
- Обычный многоугольник . Все углы имеют одинаковый размер, а все стороны равны по длине.
- Нерегулярный многоугольник . Углы или стороны одинакового размера не имеют одинаковой длины.
Выпуклые против вогнутых полигонов
Второй способ классификации полигонов – по размеру их внутренних углов.
- Выпуклые многоугольники : Внутренние углы не превышают 180 °.
- Вогнутые многоугольники . Как минимум, один внутренний угол превышает 180 °.
Простые и сложные полигоны
Еще один способ классификации полигонов – это то, как линии, образующие многоугольник, пересекаются.
- Простые полигоны : линии соединяются или пересекаются только один раз – в вершинах.

- Сложные полигоны : линии пересекаются более одного раза.
Названия сложных многоугольников иногда отличаются от названий простых многоугольников с одинаковым числом сторон.
Например:
- шестиугольник правильной формы – это шестигранный простой многоугольник.
- Звездообразная гексаграмма – это шестигранный сложный многоугольник, созданный наложением двух равносторонних треугольников.
Правило суммы внутренних углов
Как правило, каждый раз, когда сторона добавляется в многоугольник, например:
- От треугольника до четырехугольника (три-четыре стороны)
- От пятиугольника до шестиугольника (пять-шесть сторон)
еще 180 ° добавляется к сумме внутренних углов.
Это правило можно записать в виде формулы:
(n – 2) × 180 °
где n равно числу сторон многоугольника.
Таким образом, сумма внутренних углов для шестиугольника может быть найдена с помощью формулы:
(6 – 2) × 180 ° = 720 °
Сколько треугольников в этом многоугольнике?
Приведенная выше формула внутреннего угла получается путем деления многоугольника на треугольники, и это число можно найти с помощью вычисления:
n – 2
В этой формуле n равно числу сторон многоугольника.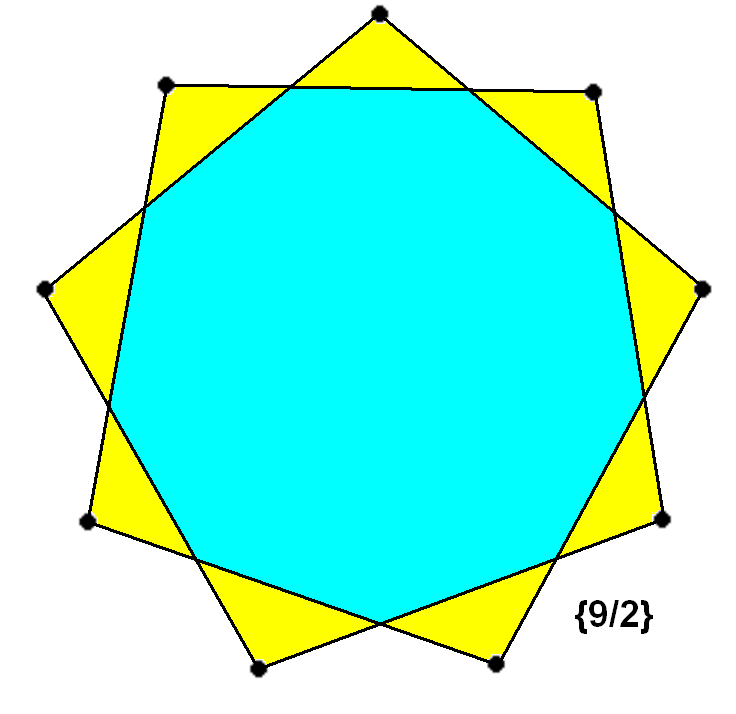
Шестиугольник (шесть сторон) можно разделить на четыре треугольника (6 – 2) и додекагон на 10 треугольников (12 – 2).
Размер угла для правильных многоугольников
Для правильных многоугольников, у которых все углы одинакового размера, а стороны одинаковой длины, размер каждого угла в многоугольнике можно рассчитать путем деления общего размера углов (в градусах) на общее количество сторон.
Для правильного шестигранного шестигранника каждый угол равен:
720 ° ÷ 6 = 120 °
Некоторые известные полигоны
Фермы
Фермы часто имеют треугольную форму. В зависимости от ширины и уклона крыши ферма может включать равносторонние или равнобедренные треугольники. Из-за их большой прочности, треугольники используются в строительстве мостов и велосипедных рам, и видны в Эйфелевой башне.
Пентагон
Пентагон – штаб-квартира Министерства обороны США – берет свое название от его формы. Здание представляет собой пятисторонний, правильный пятиугольник.
Здание представляет собой пятисторонний, правильный пятиугольник.
Главная пластина
Другой известный пятисторонний правильный пятиугольник – домашняя тарелка на бейсбольном алмазе.
Поддельный Пентагон
Гигантский торговый центр недалеко от Шанхая, Китай, построен в форме правильного пятиугольника и его иногда называют поддельным пятиугольником.
Снежинки
Каждая снежинка начинается с шестиугольника, но температура и уровень влажности добавляют ветви и усики, так что каждая из них выглядит по-разному.
Пчелы и осы
Естественные шестиугольники также включают ульи, где каждая клетка в соте, которую пчелы строят для содержания меда, является шестиугольной. Гнезда бумажных ос также содержат гексагональные клетки, в которых они растут.
Тротуар гиганта
Шестиугольники также найдены на мощёной дорожке Гиганта, расположенной на северо-востоке Ирландии. Это естественная горная порода, состоящая из около 40000 взаимосвязанных базальтовых колонн, которые были созданы в виде лавы из-за медленно остывающего древнего вулканического извержения.
Восьмиугольник
Восьмиугольник – имя, данное кольцу или клетке, используемому в боях Ultimate Fighting Championship (UFC) – берет свое название от своей формы. Это восьмигранный правильный восьмиугольник.
Стоп Знаки
Стоп знак – один из самых знакомых дорожных знаков – еще один восьмигранный правильный восьмиугольник. Хотя цвет, формулировка или символы на знаке могут различаться, восьмиугольная форма знака остановки используется во многих странах мира.
Объяснениешестиугольников! Полное руководство по шестиугольникам — Mashup Math
Что такое шестиугольник? — Определение, факты, примеры и многое другое!Добро пожаловать в это полное руководство по шестиугольникам, где вы узнаете все, что вам нужно знать об этом красивом шестиугольнике!
Шестиугольник Определение: В математике и геометрии шестиугольник определяется как многоугольник (замкнутая двумерная фигура с прямыми сторонами) с 6 сторонами.
Обратите внимание, что шестиугольники имеют 6 сторон и 6 углов.
Существует два типа шестиугольников: правильные шестиугольники и неправильные шестиугольники.
Что такое правильный шестиугольник?Правильный шестиугольник определяется как 6-сторонний многоугольник, который является одновременно равносторонним и равноугольным, что означает, что все стороны имеют одинаковую длину и все углы имеют одинаковую меру.
Что такое неправильный шестиугольник?Неправильный шестиугольник определяется как 6-сторонний многоугольник, который не является правильным — это означает, что все стороны и углы не имеют одинаковой меры.
Каковы свойства правильного шестиугольника?В геометрии вы чаще всего будете иметь дело с правильными шестиугольниками. Важно знать три их основных свойства:
Все стороны правильного шестиугольника имеют одинаковую длину.

Все внутренние углы правильного шестиугольника равны 120° каждый.
Сумма внутренних углов равна 720°.
Изображение с сайта www.wikipedia.org
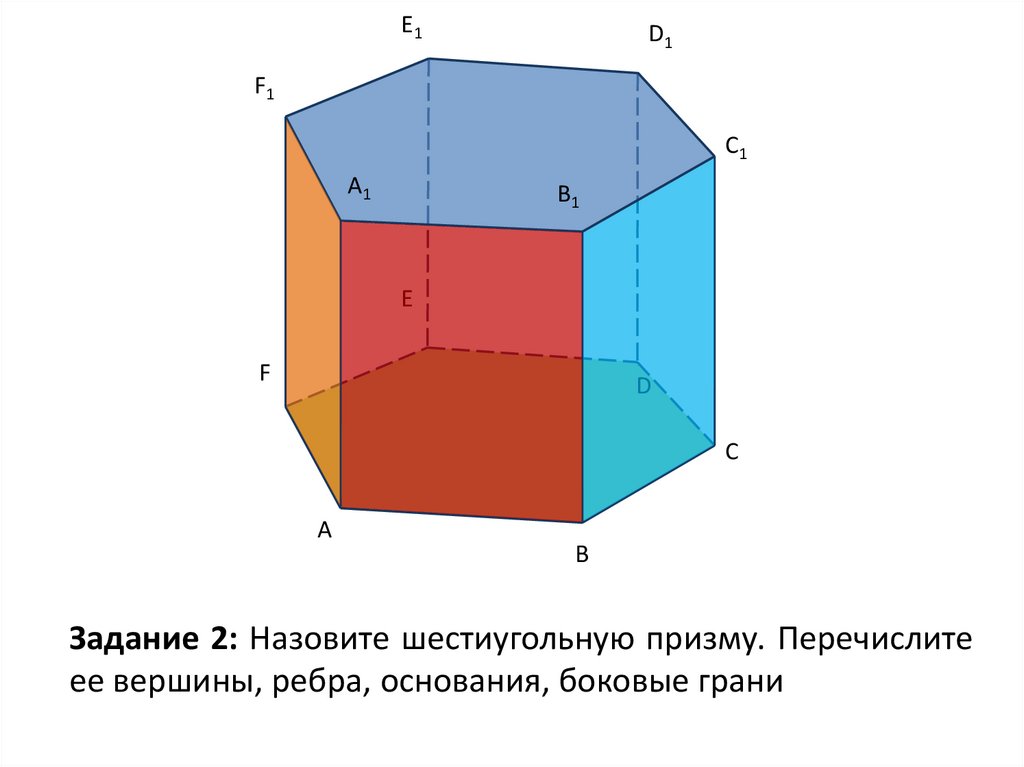
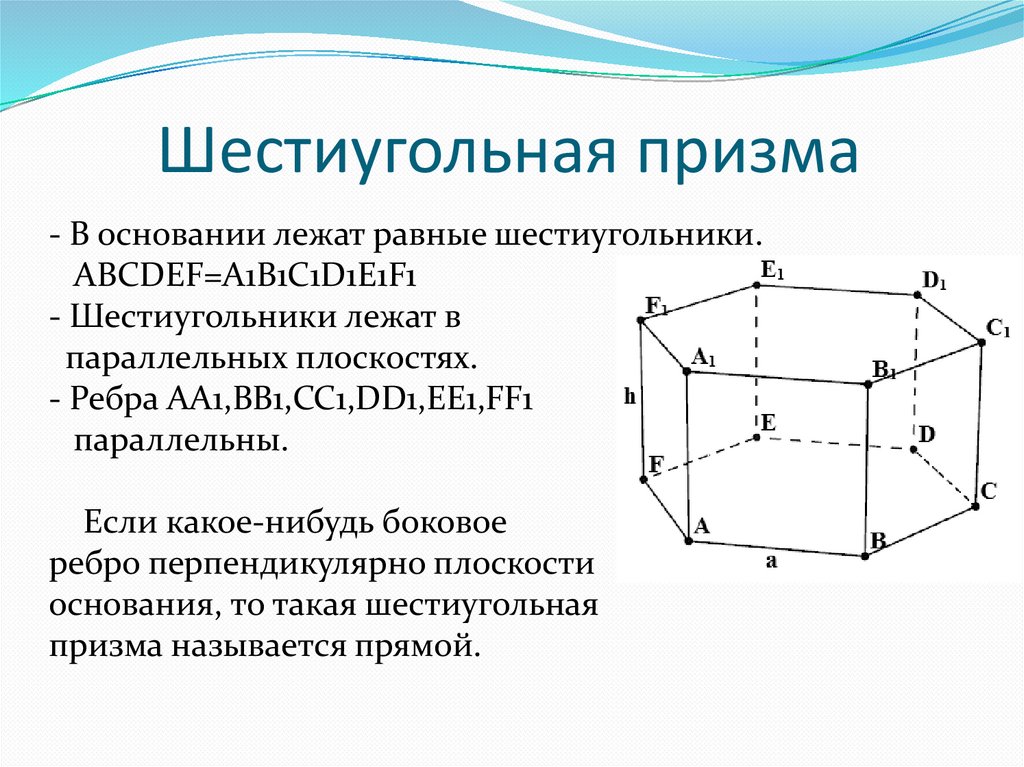
В геометрии трехмерный шестиугольник называется шестиугольником призмой — это призма с шестиугольным основанием .
В случае трехмерных шестиугольников шестиугольное основание обычно представляет собой правильный шестиугольник.
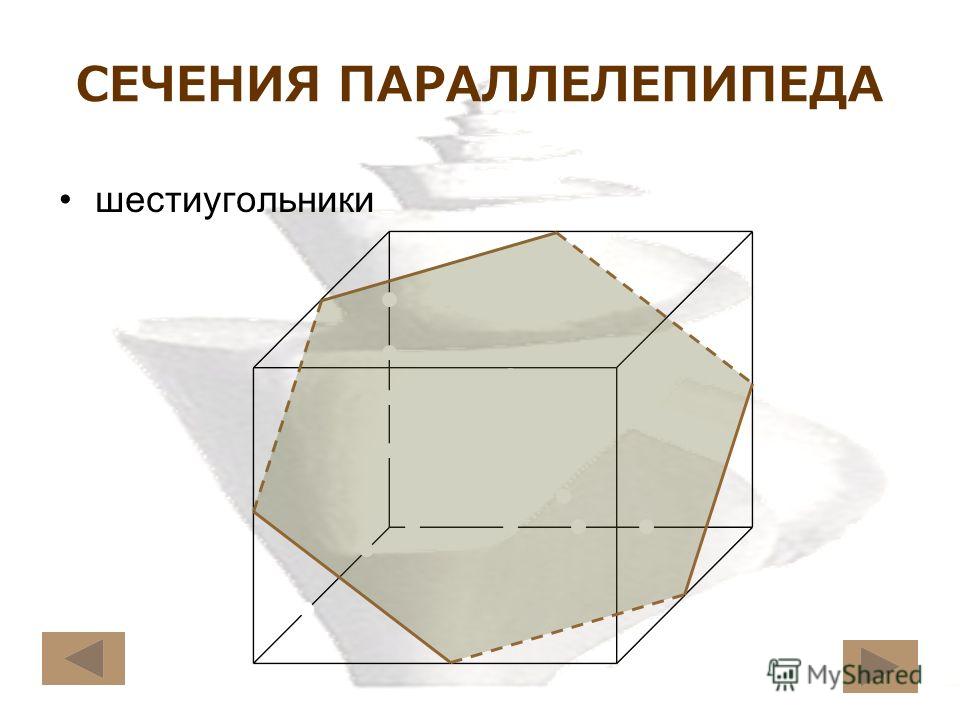
Например, усеченный октаэдр можно считать трехмерным шестиугольником, поскольку он имеет шестиугольное основание.
Вот еще несколько примеров трехмерных шестиугольников:
Выпуклые шестиугольники и вогнутые шестиугольники В геометрии многоугольник может быть выпуклым или вогнутый.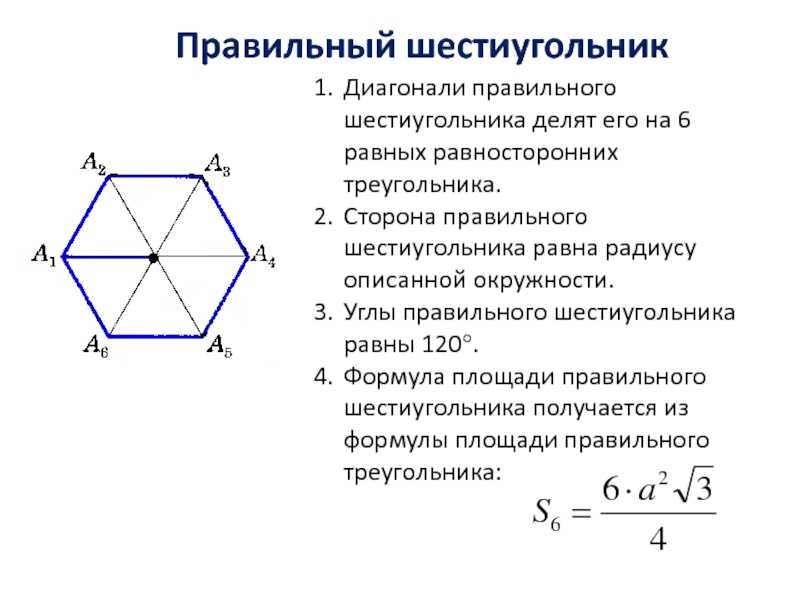
Чтобы шестиугольник был выпуклым, все его внутренние углы должны быть меньше 180°.
Чтобы шестиугольник был вогнутым, хотя бы один из его внутренних углов должен быть больше 180°.
Например, правильный шестиугольник также является выпуклым многоугольником, поскольку все его внутренние углы равны 120°, что меньше 180°.
Градусы шестиугольников: Почему 720 °?Как было сказано ранее, размер каждого внутреннего угла шестиугольника равен 120°, а общая сумма всех внутренних углов равна 720°.
Но почему? Так как в правильном шестиугольнике 6 углов и каждый угол равен 120°, общая сумма будет: , вы можете использовать формулу внутренней суммы многоугольников, чтобы найти сумму внутренних углов для любого правильного многоугольника.
Применяя формулу внутренней суммы многоугольника к шестиугольнику, вы заменяете n на 6 (поскольку у шестиугольника 6 сторон) следующим образом:
(n — 2) x 180° ➞ ( 6 — 2) x 180 ° = 4 x 180° = 720°
Шестиугольники в реальной жизни Шестиугольник — это простая, но замечательная форма, которую можно найти повсюду и где угодно — от искусства до архитектуры и природы. Вот несколько замечательных примеров шестиугольников в реальной жизни:
Вот несколько замечательных примеров шестиугольников в реальной жизни:
Шестиугольники в реальной жизни: Снежинки
Знаете ли вы, что все снежинки — шестиугольники? Когда образуются кристаллы льда, молекулы объединяются в гексагональную структуру . Мать-природа определила, что этот тип формирования является наиболее эффективным способом образования снежинок.
Шестиугольники в реальной жизни: соты
Правильные шестиугольники — это один из трех многоугольников, которые образуют мозаику на плоскости — это означает, что их можно бесконечно дублировать, чтобы заполнить пространство без пробелов. И когда пчелы строят соты, они выбирают шестиугольники. Всегда!
Шестиугольники в реальной жизни: Архитектура
Пчелы не единственные, кто понимает силу и эффективность шестиугольников.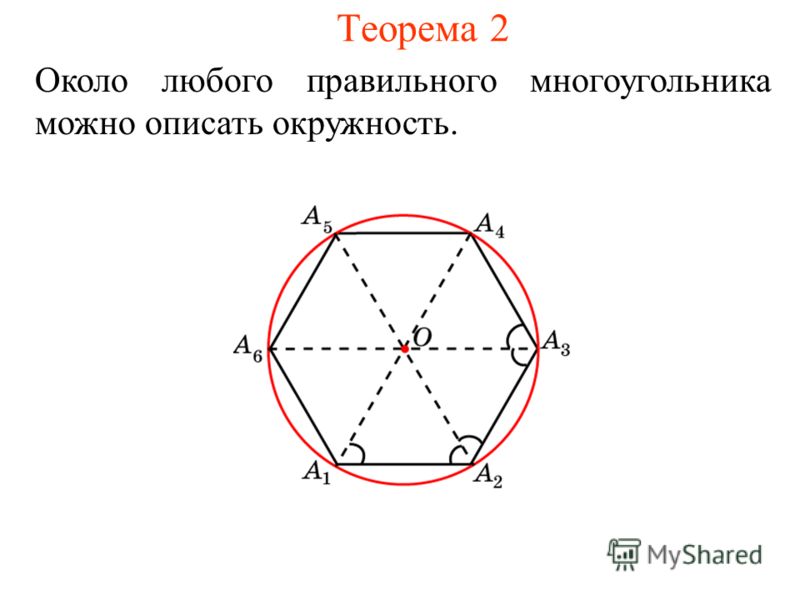 Древняя и современная архитектура постоянно использует эту форму от напольной плитки до окон и богато украшенных потолков. Шестиугольники повсюду!
Древняя и современная архитектура постоянно использует эту форму от напольной плитки до окон и богато украшенных потолков. Шестиугольники повсюду!
Шестиугольники в реальной жизни: Искусство
Благодаря своей красивой форме и способности создавать мозаику, шестиугольники постоянно используются в искусстве и графическом дизайне для создания узоров, мозаик, логотипов и многого другого!
На самом деле, многие компании выбирают для логотипа шестиугольную форму, поскольку она символизирует силу и безопасность.
Шестиугольники в реальной жизни: религия
Поскольку правильные шестиугольники часто встречаются в природе (например, снежинки и соты), они часто включаются в сакральную геометрию, которая придает более высокое значение и духовность определенным формам и пропорциям. На самом деле, некоторые считают шестиугольник самой интересной формой во Вселенной.
2 комментария
Введение в гексагональную геометрию
Содержание
- Введение
- Некоторые наблюдения о шестиугольниках
- Базовая геометрия шестиугольников
- Шестиугольная мозаика
- Шестиугольники и круги
- Шестиугольники и треугольники
- Заключение
Введение
Ниже приводится краткий обзор некоторых элементарных свойств шестиугольников и того, почему они могут быть полезны. Он не предназначен для всестороннего рассмотрения предмета. Меня особенно интересуют математические свойства шестиугольников и, в некоторой степени, их роль в мире природы. Я избегал обсуждения шестиугольников в связи с человеческой культурой, религией, историей и другими «местными» интересами, хотя в этих областях есть много интересных примеров шестиугольника и шестиугольника, и они, несомненно, будут более подробно рассмотрены в другом месте в другой раз. .
.
Эта статья в значительной степени находится в стадии разработки и на самом деле не «готова» в каком-либо осмысленном смысле. Он актуален на момент последнего обновления. В какой-то момент я намерен заменить или, по крайней мере, дополнить его более полным и красноречивым обзором гексагональных концепций. Имейте в виду, что в этой статье исследуется лишь очень небольшая часть интересных свойств шестиугольников, и есть надежда, что более полное представление об их качествах появится благодаря сумме разнообразного материала, доступного на этом сайте.
Примечание о терминологии: По моему обычному правилу, если не указано иное, «шестиугольник» относится только к правильным шестиугольникам. Кроме того, я склонен довольно расплывчато говорить о «гексагональности» того или иного. Описывая вещи как «шестиугольные», я часто имею в виду в очень широком смысле все шестиугольные и подобные шестиугольникам симметрии, а не обязательно правильные шестиугольники как таковые.
Некоторые наблюдения о шестиугольниках
Шестиугольник — это замкнутая плоская фигура с шестью ребрами и шестью вершинами. Правильный шестиугольник — выпуклая фигура со сторонами одинаковой длины и внутренними углами 120 градусов. Он имеет шесть вращательных симметрий и шесть отражательных симметрий, образуя группу диэдра D 6 .
Свойства шестиугольников многочисленны и интересны. На первый взгляд выделяются несколько фактов о них:
- Шестиугольники являются одним из трех правильных многоугольников, образующих мозаику на евклидовой плоскости (наряду с квадратами и треугольниками).
- Шестиугольная мозаика комбинаторно идентична плотной упаковке кругов на плоскости.
- Шестиугольники — это единственные правильные многоугольники, которые можно разделить на другие правильные многоугольники. (Насколько мне известно, шестиугольники — единственные правильные многогранники любой размерности, обладающие этим особым свойством.
 )
) - В родственном факте шестиугольники являются единственным правильным многоугольником, расстояние между центром и каждой вершиной которого равно длине каждой стороны (разделяя это свойство с кубооктаэдром в 3-пространстве).
- Шестиугольники — это первые многоугольники — при возрастании числа сторон — которые не образуют граней правильного выпуклого многогранника в евклидовом пространстве. Три многоугольника с меньшим количеством сторон составляют поверхности пяти платоновых тел, но ни один многоугольник с шестью или более сторонами не может быть использован для этой цели. Следствием этого является то, что ни один правильный многогранник ни в каком измерении не имеет шестиугольных граней, хотя многие из них имеют шестиугольные или шестиугольно-симметричные вершины или другие элементы.
- Шестиугольники — это перестановочные эдра третьего порядка, что означает, что каждая вершина шестиугольника может быть описана в декартовых координатах с использованием одной из шести перестановок чисел 1, 2 и 3.
 Такой шестиугольник будет лежать на плоскости, состоящей из всех точек с координатами, в сумме дает 6 и делит пополам куб единичной длины 2 между координатами 1 и 3.
Такой шестиугольник будет лежать на плоскости, состоящей из всех точек с координатами, в сумме дает 6 и делит пополам куб единичной длины 2 между координатами 1 и 3.
Еще одна интересная вещь о шестиугольниках — и, возможно, самый поразительный факт о них — это то, что они действительно имеют шесть сторон. Давайте на минутку перечислим некоторые интересные факты о числе шесть:
- Шесть — очень составное число, второе по величине составное число и первое совершенное число. То есть 1*2*3 = 1+2+3 = 6.
- В связи с этим шесть — единственное число, которое одновременно является суммой и произведением трех последовательных натуральных чисел (1, 2 и 3).
- Шесть — наименьшее составное целое число без квадратов и, соответственно, первое натуральное число с двумя различными простыми множителями (2 и 3).
- У кубов шесть сторон, и они тоже очень полезны.
И так далее. Очевидно, что большинство уникальных и интересных свойств числа шесть в конечном счете проистекает из того факта, что оно является произведением 90 249 и суммы 90 250 первых трех натуральных чисел и что в более философском смысле его можно рассматривать как сочетание архетипические ценности единства, двойственности и троичности в несколько сбалансированное целое. Единство разделяется на двойственность, которая примиряется в троице (один плюс два, или два, соединяющиеся в одно), которая затем воссоединяется с двойственностью и единством — либо аддитивно, либо мультипликативно — чтобы получить нашу уважаемую шестерку.
Единство разделяется на двойственность, которая примиряется в троице (один плюс два, или два, соединяющиеся в одно), которая затем воссоединяется с двойственностью и единством — либо аддитивно, либо мультипликативно — чтобы получить нашу уважаемую шестерку.
Конечно, есть много других шестиугольных и соответствующих шестиугольнику чисел, и было бы ошибкой связывать шестиугольник только с шестью. Семерка, например, часто занимала видное место в человеческой культуре и, в частности, в некоторых религиозных традициях. Если вернуться назад и посмотреть на различные геометрические формы, связанные с такими семерками, часто становится очевидным, что они представляют собой шесть периферийных сущностей вокруг одной центральной сущности — наподобие шестиугольно упакованных кругов или шестиугольной мозаики. По-видимому, не шестиугольные числа, такие как восемь и десять, также имеют шестиугольные коннотации, как и различные центрированные шестиугольные числа, правильные шестиугольные числа и так далее. Не говоря уже о числах, кратных шести, таких как двенадцать, которые сами по себе тоже являются действительно большим числом (добавляя делимость на 4 к ситуации 1, 2, 3). Но, конечно же, само собой разумеется, что шесть имеет четкую связь с шестиугольником, и стоит знать о его уникальных и интересных свойствах в этом отношении.
Не говоря уже о числах, кратных шести, таких как двенадцать, которые сами по себе тоже являются действительно большим числом (добавляя делимость на 4 к ситуации 1, 2, 3). Но, конечно же, само собой разумеется, что шесть имеет четкую связь с шестиугольником, и стоит знать о его уникальных и интересных свойствах в этом отношении.
В конечном счете я утверждаю, что чем больше вы изучаете математические и физические основы Вселенной, тем более заметными и интересными становятся шестиугольники, шестерки и их различные аналоги в других математических системах. В задачу данной статьи не входит формулирование какой-либо всеобъемлющей интерпретации этого, но это стоит отметить и учесть в наших интерпретациях реальности и отношениях с ней.
На этом этапе я хотел бы остановиться на нескольких шестиугольных вопросах, поднятых выше.
Базовая геометрия шестиугольников
Давайте сначала рассмотрим более внимательно основные пропорции и отношения благородного шестиугольника:
Апофема правильного шестиугольника равна половине квадратного корня из 3. Это можно продемонстрировать с помощью единичного шестиугольника, где длина каждой стороны равна 1. Затем мы можем нарисовать прямоугольный треугольник, используя диаметр вершины к вершине. шестиугольника в качестве гипотенузы. Поскольку известно, что диаметр такого шестиугольника равен 2, у нас остается одно неопределенное ребро нашего треугольника, равное расстоянию между двумя противоположными ребрами шестиугольника (которое вдвое больше апофемы). Назовем это ребро х . Тогда теорема Пифагора говорит нам, что 1 2 + x 2 = 2 2 . Отсюда следует, что 1 + x 2 = 4, x 2 = 3, и, таким образом, x = √3. Следовательно, отношение «высоты» к «ширине» правильного шестиугольника равно √3/2. Quod Erat demstrandum.
Это можно продемонстрировать с помощью единичного шестиугольника, где длина каждой стороны равна 1. Затем мы можем нарисовать прямоугольный треугольник, используя диаметр вершины к вершине. шестиугольника в качестве гипотенузы. Поскольку известно, что диаметр такого шестиугольника равен 2, у нас остается одно неопределенное ребро нашего треугольника, равное расстоянию между двумя противоположными ребрами шестиугольника (которое вдвое больше апофемы). Назовем это ребро х . Тогда теорема Пифагора говорит нам, что 1 2 + x 2 = 2 2 . Отсюда следует, что 1 + x 2 = 4, x 2 = 3, и, таким образом, x = √3. Следовательно, отношение «высоты» к «ширине» правильного шестиугольника равно √3/2. Quod Erat demstrandum.
Интересным следствием этого является то, что правильные шестиугольники и равносторонние треугольники имеют точно такое же отношение «ширины» к «высоте». То есть минимальный диаметр шестиугольника и треугольника составляет √3/2 его максимального диаметра. Действительно, √3 является повторяющимся значением в треугольной и шестиугольной геометрии — например, расстояние по диагонали между двумя противоположными вершинами куба также равно √3 (сравните ширину диагонали квадрата, которая равна √2, по причинам, аналогичным изложенные выше). Как следствие, конечно, √3 занимает видное место в плоской тригонометрии, где оно заметно в выражении различных значений 60 и 30 градусов.
Действительно, √3 является повторяющимся значением в треугольной и шестиугольной геометрии — например, расстояние по диагонали между двумя противоположными вершинами куба также равно √3 (сравните ширину диагонали квадрата, которая равна √2, по причинам, аналогичным изложенные выше). Как следствие, конечно, √3 занимает видное место в плоской тригонометрии, где оно заметно в выражении различных значений 60 и 30 градусов.
Площадь шестиугольника также можно рассчитать с помощью √3. Давайте сначала определим длину ребра нашего шестиугольника как s . Затем мы можем нарисовать прямоугольник между двумя противоположными сторонами шестиугольника с площадью s 2 √3. Если мы тогда учтем, что у нас осталось 4 прямоугольных сечения, и что сам шестиугольник можно считать состоящим из 12 таких треугольников, 8 из которых мы включили в наш прямоугольник, ясно, что общая площадь шестиугольника в полтора раза больше площади прямоугольника. Таким образом, с 2 √3(3/2). Quod erat faciendum.
Quod erat faciendum.
(Это также пример более общего принципа, согласно которому площадь правильного выпуклого многоугольника равна произведению периметра и апофемы, деленному на 2 (в данном случае 6s√3/2/2). Это связано с к тому факту, что мы можем разделить n -сторонний правильный выпуклый многоугольник на 2 n прямоугольных треугольников, проведя отрезки от центра к каждой вершине, а также от центра к середине каждого ребра. предположим, что каждые 2 образованных таким образом прямоугольных треугольника могут быть объединены в прямоугольник с площадью апофемы, умноженной на половину длины ребра Таким образом, просто разделив произведение апофемы на общий периметр пополам, мы придем к общему площадь полигона).
Шестиугольная мозаика
Как отмечалось ранее, шестиугольники могут быть мозаичными или мозаичными по регулярному шаблону на плоской двумерной плоскости. То есть шестиугольник может быть окаймлен шестью другими шестиугольниками, которые сами могут быть окаймлены шестью шестиугольниками (включая друг друга) и так далее до бесконечности в любом направлении, не оставляя пустого места. Обратите внимание, что хотя существует любое количество потенциальных мозаик, состоящих из двух или более типов многоугольников, только шестиугольники, квадраты и треугольники могут образовывать такие правильные мозаики сами по себе. (Точно так же и в трех измерениях среди однородных многогранников только шестигранный куб и шестиугольно-аналогичный усеченный октаэдр могут сами по себе образовывать заполняющие пространство мозаики.)
Обратите внимание, что хотя существует любое количество потенциальных мозаик, состоящих из двух или более типов многоугольников, только шестиугольники, квадраты и треугольники могут образовывать такие правильные мозаики сами по себе. (Точно так же и в трех измерениях среди однородных многогранников только шестигранный куб и шестиугольно-аналогичный усеченный октаэдр могут сами по себе образовывать заполняющие пространство мозаики.)
Таким образом, шестиугольник, конечно, является правильным многоугольником, допускающим тесселяцию с самой высокой стороной. Это делает его уникально важным в различных областях, поскольку он имеет то преимущество, что каждый составляющий шестиугольник более или менее равномерно отделен от его соседей. То есть любая заданная точка внутри шестиугольника (будь то мозаика шестиугольников или нет) ближе к центру этого шестиугольника, чем любая заданная точка равновеликого квадрата или треугольника. Поскольку квадраты и треугольники имеют более острые углы, точки возле их углов находятся дальше от точек в других местах их площади, чем они были бы в аналогичных местах в шестиугольнике. Теперь то же самое верно и для любого многоугольника с более высокими сторонами — идеальной эффективностью для ограждения данной области является, в конечном счете, круг. Но опять же, у шестиугольников есть преимущество тесселяции. Таким образом, для любой задачи, требующей как регулярной сетки ячеек, так и элементов, и эффективное ограждение площади этой ячейки, шестиугольная мозаика является логичным и необходимым выбором. Общие примеры такого использования шестиугольных ячеек можно найти в таких различных областях, как клеточные автоматы, статистическая выборка, настольные игры, компьютерные игры, соты уважаемой медоносной пчелы и так далее.
Теперь то же самое верно и для любого многоугольника с более высокими сторонами — идеальной эффективностью для ограждения данной области является, в конечном счете, круг. Но опять же, у шестиугольников есть преимущество тесселяции. Таким образом, для любой задачи, требующей как регулярной сетки ячеек, так и элементов, и эффективное ограждение площади этой ячейки, шестиугольная мозаика является логичным и необходимым выбором. Общие примеры такого использования шестиугольных ячеек можно найти в таких различных областях, как клеточные автоматы, статистическая выборка, настольные игры, компьютерные игры, соты уважаемой медоносной пчелы и так далее.
Родственным свойством шестиугольной мозаики является то, что она не создает диагональных ребер. (Под «диагональю» здесь я подразумеваю соседей, у которых общая граница только вершины, а не границы ребра — я не знаю более точного математического термина для этого, хотя я знаю, что это не совсем то, что означает «диагональ» в самом строгом смысле. смысл этого термина.) Если вы посмотрите на замощение треугольников и квадратов, вы, конечно, увидите, что оба имеют диагональные связи между соседними элементами в своих вершинах. В квадратной мозаике каждый квадрат соединяется с одним квадратом непосредственно на каждой стороне и с одним квадратом по диагонали на каждой вершине, всего восемь соседних квадратов, а в треугольной мозаике каждый треугольник соединяется с одним треугольником на каждой стороне и с тремя треугольниками по диагонали на каждой вершине. вершина, всего двенадцать соседних треугольников. Эти диагональные соединения, конечно же, являются ключом к способности квадратов и треугольников образовывать правильные многогранники — удаляя диагональные соседи вокруг квадрата, можно легко свернуть оставшиеся соседние квадраты, пока они не соединятся друг с другом напрямую, образуя многогранник. куб, и, аналогичным образом удаляя из треугольника одного, двух или трех соседей по диагонали, можно сложить оставшиеся треугольники в икосаэдр, октаэдр или тетраэдр соответственно.
смысл этого термина.) Если вы посмотрите на замощение треугольников и квадратов, вы, конечно, увидите, что оба имеют диагональные связи между соседними элементами в своих вершинах. В квадратной мозаике каждый квадрат соединяется с одним квадратом непосредственно на каждой стороне и с одним квадратом по диагонали на каждой вершине, всего восемь соседних квадратов, а в треугольной мозаике каждый треугольник соединяется с одним треугольником на каждой стороне и с тремя треугольниками по диагонали на каждой вершине. вершина, всего двенадцать соседних треугольников. Эти диагональные соединения, конечно же, являются ключом к способности квадратов и треугольников образовывать правильные многогранники — удаляя диагональные соседи вокруг квадрата, можно легко свернуть оставшиеся соседние квадраты, пока они не соединятся друг с другом напрямую, образуя многогранник. куб, и, аналогичным образом удаляя из треугольника одного, двух или трех соседей по диагонали, можно сложить оставшиеся треугольники в икосаэдр, октаэдр или тетраэдр соответственно. (Хотя следует отметить, что, хотя оба диагонально-мозаичных правильных многоугольника образуют правильные многогранники, если сложить их таким образом, на первый взгляд нет особой причины, по которой это должно быть .) И наоборот, именно поэтому шестиугольники не могут образовывать собственные правильные многогранники. Каждый внешний угол шестиугольника равен 120 градусам, а единственная возможная конфигурация вершин — в евклидовом пространстве — с тремя соседними углами, составляющими в сумме 360 градусов (конечно, за исключением «вырожденного» шестиугольного двугранника, который не особенно полезен для наши цели здесь).
(Хотя следует отметить, что, хотя оба диагонально-мозаичных правильных многоугольника образуют правильные многогранники, если сложить их таким образом, на первый взгляд нет особой причины, по которой это должно быть .) И наоборот, именно поэтому шестиугольники не могут образовывать собственные правильные многогранники. Каждый внешний угол шестиугольника равен 120 градусам, а единственная возможная конфигурация вершин — в евклидовом пространстве — с тремя соседними углами, составляющими в сумме 360 градусов (конечно, за исключением «вырожденного» шестиугольного двугранника, который не особенно полезен для наши цели здесь).
Шестиугольная мозаика двойственна треугольной мозаике: первую можно превратить во вторую, заменив все вершины треугольниками, а все шестиугольники вершинами. Точно так же в треугольной мозаике, если вы замените все треугольники вершинами, а все вершины шестиугольниками, вы снова получите шестиугольную мозаику. (Любой многогранник или мозаику с обратными количествами внешних элементов можно обратить по тому же принципу: октаэдр — это обратная сторона куба, а икосаэдр — обратная сторона додекаэдра — каждый представляет собой перестановку вершины/грани своего аналога. Это может быть представлено нотно путем обращения символа Шлефли определенного объекта — в случае шестиугольной и треугольной мозаики, заменяя {6,3} на {3,6} или наоборот.) Кроме того, поскольку шестиугольники могут быть разделены на равносторонние треугольники , а равносторонние треугольники могут быть объединены в шестиугольники, треугольная мозаика может рассматриваться как простое подразделение шестиугольной или наоборот.
Это может быть представлено нотно путем обращения символа Шлефли определенного объекта — в случае шестиугольной и треугольной мозаики, заменяя {6,3} на {3,6} или наоборот.) Кроме того, поскольку шестиугольники могут быть разделены на равносторонние треугольники , а равносторонние треугольники могут быть объединены в шестиугольники, треугольная мозаика может рассматриваться как простое подразделение шестиугольной или наоборот.
Последним преимуществом шестиугольной мозаики или шестиугольных решеток, заслуживающим внимания, является ее прочность на сжатие и растяжение и эффективность по сравнению с другими вариантами мозаики. Если мы рассмотрим абстрактную физическую «структуру», состоящую из отрезков линий между вершинами правильной многоугольной мозаики (т. подобные треугольные или квадратные конструкции. Либо треугольная, либо шестиугольная конструкция, построенная таким образом, будет явно прочнее квадратной конструкции, и хотя треугольная конструкция, при прочих равных условиях, будет прочнее шестиугольной, она также потребует больше материала (с шестью линиями, соединяющимися в одной точке). каждую вершину вместо трех) и, таким образом, быть менее «эффективным» — хотя для конкретных приложений, очевидно, это может быть предпочтительнее.
каждую вершину вместо трех) и, таким образом, быть менее «эффективным» — хотя для конкретных приложений, очевидно, это может быть предпочтительнее.
Тот факт, что квадратные решетки не обладают силой шестиугольных или треугольных решеток, становится очевидным, если рассмотреть изображение трех структур, представив, что в каждой вершине линейные сегменты структуры сближаются или расходятся с той силой, с которой они должны были бы физическая структура. Ясно, что с четырьмя сегментами, отходящими точно под углом 90 градусов в каждой вершине, квадратная структура легко срезается как по горизонтали, так и по вертикали — у нее нет других углов, поддерживающих ее структуру, поэтому они просто переворачиваются. И наоборот, в треугольной и шестиугольной конфигурации отрезки линии, сходящиеся под углами 60 и 120 градусов, предотвращают сдвиг или разрушение — они уравновешивают друг друга и равномерно распределяют нагрузку (какой бы она ни была).
Например, если вы представляете шестиугольную или треугольную решетку, «удерживающую» объект, становится ясно, что чередующиеся углы шестиугольной и треугольной решеток сделают больше для распределения веса на нижние уровни, чем ортогонально ограниченная квадратная решетка. Тот же принцип легко применим и к приложениям распределения силы в трех измерениях — как мы видим, например, в замечательной прочности на растяжение углеродных нанотрубок, в распределении веса геодезическими куполами и так далее.
Тот же принцип легко применим и к приложениям распределения силы в трех измерениях — как мы видим, например, в замечательной прочности на растяжение углеродных нанотрубок, в распределении веса геодезическими куполами и так далее.
Шестиугольники и круги
Шестиугольная упаковка является наиболее эффективной системой упаковки кругов на плоской поверхности. То есть, как и в случае шестиугольной мозаики, вы можете расположить шесть соседних кругов одинакового размера вокруг круга, и шесть кругов вокруг каждого из них, и так до бесконечности, так что расположение кругов идентично расположению шестиугольников в шестиугольная мозаика. Иными словами, можно вписать круги в каждый шестиугольник в шестиугольной мозаике, удалить шестиугольники, и останутся идеально плотно упакованные круги. Это полезно и интересно по ряду причин, например, позволяет легко моделировать гексагонально упакованные круги с помощью шестиугольников или треугольников, когда это необходимо.
Интересное явление, связанное с этим пересечением круговой и шестиугольной геометрии, заключается в том, что шестиугольные узоры часто появляются спонтанно, когда естественные силы пытаются аппроксимировать круги. (Это, без сомнения, большая часть причины, по которой шестиугольники обычно считаются очень «естественной» формой.) Например, конвекционные ячейки часто образуют шестиугольники. Поскольку каждая ячейка естественным образом стремится к наиболее эффективному ограждению своего пространства, они стремятся к округлости, но поскольку каждая ячейка имеет любое количество соседних ячеек, прижимающихся к ней, результатом является своего рода квазигексагональная мозаика. Подходящим примером этого может быть Дорога гигантов в оккупированной Ирландии: когда базальтовая лава, сформировавшая структуру, первоначально охлаждалась, она сжалась в примерно цилиндрические ячейки. По мере того как клетки превращались в твердую породу, они естественным образом приобретали шестиугольную геометрию упакованных кругов.
(Это, без сомнения, большая часть причины, по которой шестиугольники обычно считаются очень «естественной» формой.) Например, конвекционные ячейки часто образуют шестиугольники. Поскольку каждая ячейка естественным образом стремится к наиболее эффективному ограждению своего пространства, они стремятся к округлости, но поскольку каждая ячейка имеет любое количество соседних ячеек, прижимающихся к ней, результатом является своего рода квазигексагональная мозаика. Подходящим примером этого может быть Дорога гигантов в оккупированной Ирландии: когда базальтовая лава, сформировавшая структуру, первоначально охлаждалась, она сжалась в примерно цилиндрические ячейки. По мере того как клетки превращались в твердую породу, они естественным образом приобретали шестиугольную геометрию упакованных кругов.
Стоит также отметить, что шестиугольники играют значительную роль в трехмерных плотноупакованных сферах, как в гексагональной плотной упаковке, так и в гранецентрированных кубических системах. И HCP, и FCC состоят из «листов» шестиугольно упакованных сфер — они отличаются только тем, как листы уложены вместе. Следует отметить, что, несмотря на их соответствующие названия, можно привести аргумент, что гранецентрированная кубическая упаковка на самом деле более «гексагональна», чем так называемая гексагональная упаковка — последняя получила свое название скорее из-за отсутствия кубичности, чем из-за Преобладание шестиугольника. Обратите внимание, что и HCP, и FCC значительно менее эффективны, чем гексагональная упаковка в двух измерениях: первая имеет плотность π/(3√2), а вторая имеет плотность π/√12. Очевидно, также известны регулярные плотные упаковки n-сфер до 8 измерений, и они могут включать или не включать гексагональные или гипергексагональные топологии.
И HCP, и FCC состоят из «листов» шестиугольно упакованных сфер — они отличаются только тем, как листы уложены вместе. Следует отметить, что, несмотря на их соответствующие названия, можно привести аргумент, что гранецентрированная кубическая упаковка на самом деле более «гексагональна», чем так называемая гексагональная упаковка — последняя получила свое название скорее из-за отсутствия кубичности, чем из-за Преобладание шестиугольника. Обратите внимание, что и HCP, и FCC значительно менее эффективны, чем гексагональная упаковка в двух измерениях: первая имеет плотность π/(3√2), а вторая имеет плотность π/√12. Очевидно, также известны регулярные плотные упаковки n-сфер до 8 измерений, и они могут включать или не включать гексагональные или гипергексагональные топологии.
Шестиугольники и треугольники
Во многом отношения между треугольниками и шестиугольниками являются продолжением отношений между шестиугольниками и кругами. Я считаю их частью одного непрерывного геометрического континуума (коренящегося в довольно очевидном факте, я полагаю, что самое близкое расположение трех кругов одинакового размера находится в вершинах равностороннего треугольника с длиной ребра, равной диаметру кругов) . Но на данный момент давайте посмотрим конкретно на отношения между треугольниками и шестиугольниками:
Но на данный момент давайте посмотрим конкретно на отношения между треугольниками и шестиугольниками:
Как уже отмечалось, правильный шестиугольник можно разделить на шесть равносторонних треугольников. Шестиугольник и треугольник — единственные два правильных многоугольника, и я полагаю, что единственные два правильных многогранника обладают этим свойством. Вдобавок к тому, что шестиугольник делится на равносторонние треугольники, треугольник, конечно же, сам делится на подтреугольники, а поскольку объединение любых шести треугольников, расположенных вокруг вершины, дает шестиугольник, треугольники также можно разделить на шестиугольники, хотя и с оставленными треугольными промежутками. над. Треугольник, разделенный на 9подтреугольники можно рассматривать как шестиугольник с тремя равносторонними треугольниками, образованными путем расширения краев чередующихся сторон шестиугольника до их встречи (например, на фигуре Тетрактис).
Топологически связанная концепция — это концепция треугольных чисел, которые можно визуализировать в виде шестиугольной упаковки кругов, шестиугольников или точек внутри треугольника. В частности, треугольные числа могут быть определены как сумма всех натуральных целых чисел от 1 до n , где n — количество единиц на сторону рассматриваемого фигурного треугольника. То есть, предположим, вы берете три точки и расставляете их треугольником. На каждой стороне треугольника две точки, и 1+2 = 3. Добавьте еще три точки к основанию этого треугольника, и вы получите еще один треугольник, в данном случае с тремя точками на стороне, и 1+2+3 = 6 (которое также является произведением 1, 2 и 3, как упоминалось ранее). И так далее. Треугольное число длины стороны n также можно рассчитать как n *( n +1)/2 — таким образом, 3*(3+1)/2 = 3+2+1 = 6.
В частности, треугольные числа могут быть определены как сумма всех натуральных целых чисел от 1 до n , где n — количество единиц на сторону рассматриваемого фигурного треугольника. То есть, предположим, вы берете три точки и расставляете их треугольником. На каждой стороне треугольника две точки, и 1+2 = 3. Добавьте еще три точки к основанию этого треугольника, и вы получите еще один треугольник, в данном случае с тремя точками на стороне, и 1+2+3 = 6 (которое также является произведением 1, 2 и 3, как упоминалось ранее). И так далее. Треугольное число длины стороны n также можно рассчитать как n *( n +1)/2 — таким образом, 3*(3+1)/2 = 3+2+1 = 6.
Та же фигурная шестиугольная решетка также используется центрированными шестиугольными числами или шестнадцатеричными числами, которые аналогичны треугольным числам, но, конечно, с шестиугольниками вместо треугольников. (По причинам, которые мне трудно понять, термин «шестиугольное число» зарезервирован для шестиугольной контурной фигуры, которая на самом деле не похожа на то, что подразумевается под «треугольным числом» или «квадратным числом», по крайней мере, в некотором роде. что я нахожу особенно интересным.) n th шестнадцатеричное число может быть выражено как шестикратное треугольное число ( n – 1) плюс один, или как n *(n-1)*3+1, что можно понимать как сумма трех прямоугольников плюс центральная точка.
что я нахожу особенно интересным.) n th шестнадцатеричное число может быть выражено как шестикратное треугольное число ( n – 1) плюс один, или как n *(n-1)*3+1, что можно понимать как сумма трех прямоугольников плюс центральная точка.
Еще один интересный факт о шестнадцатеричных числах заключается в том, что сумма первых n шестнадцатеричных чисел равна кубу n . Например, 1+7 = 2 3 = 8, 1+7+19 = 3 3 = 27, 1+7+19+37 = 4 3 = 64 и так далее. Чтобы понять это, представьте, что вы смотрите на угол куба таким образом, что куб выглядит как шестиугольник. Представьте, что куб на самом деле состоит из подкубов, расположенных в виде числа в кубе. Первый куб в углу можно рассматривать как первое шестнадцатеричное число, равное 1. Ниже и вокруг него находятся семь других кубов, образующих слой кубов вокруг углового куба, который можно рассматривать как второе шестнадцатеричное число, которое на самом деле 7, и так далее. Шестнадцатеричные числа можно рассматривать как последовательные «оболочки» кубов, исходящие из углового куба. Таким образом, кубы и шестнадцатеричные числа — это просто разные образные способы описания одних и тех же значений — куб 9.0249 n можно расположить либо в виде куба, либо в виде пирамиды из шестиугольников с длиной основания n , а разность между любыми двумя последовательными кубами сама по себе является шестиугольником. Мы снова видим связь между шестиугольником с шестью сторонами и кубом с шестью сторонами — и, в более широком смысле, между шестиугольником и шестью «сторонами» самого трехмерного пространства.
Шестнадцатеричные числа можно рассматривать как последовательные «оболочки» кубов, исходящие из углового куба. Таким образом, кубы и шестнадцатеричные числа — это просто разные образные способы описания одних и тех же значений — куб 9.0249 n можно расположить либо в виде куба, либо в виде пирамиды из шестиугольников с длиной основания n , а разность между любыми двумя последовательными кубами сама по себе является шестиугольником. Мы снова видим связь между шестиугольником с шестью сторонами и кубом с шестью сторонами — и, в более широком смысле, между шестиугольником и шестью «сторонами» самого трехмерного пространства.
Заключение
Опять же, эта статья только поверхностно коснулась многих интересных свойств шестиугольников и их аналогов. Действительно, шестиугольники появляются в очень необычных местах в более абстрактных математических системах, и у меня есть общее подозрение, что если вы наметите все логические отношения математики, как их понимает и определяет человечество, шестиугольник будет занимать видное место в качестве повторяющаяся тема во всей структуре.
По мере развития человеческого общества мы, несомненно, будем находить все больше и больше применений для универсального и эффективного шестиугольника. Будь то тесселяция наших настольных игр, формирование наших эффективно закрытых структур или помощь нам в лучшем понимании фундаментальных математических концепций, мы, безусловно, с течением времени обнаружим, что живем во все более и более шестиугольном мире. Является ли совпадением то, что в научно-фантастических фильмах и телевизионных шоу, особенно в космическом пространстве, часто фигурируют шестиугольные двери, шестиугольные космические корабли, шестиугольная архитектура и так далее? Думаю, нет. Провидцы и художники нашего общества уже видели, что грядет, и то, что будет очевидно нашим потомкам: что мы живем в шестиугольном мире, упорядоченном по шестиугольным принципам. Шестиугольники не могут быть решением всех мировых проблем. Они могут даже не быть решением очень многих проблем. Но они будут решением некоторых проблем, а этого нельзя сказать о многих вещах.

 6.
6.

 )
) Такой шестиугольник будет лежать на плоскости, состоящей из всех точек с координатами, в сумме дает 6 и делит пополам куб единичной длины 2 между координатами 1 и 3.
Такой шестиугольник будет лежать на плоскости, состоящей из всех точек с координатами, в сумме дает 6 и делит пополам куб единичной длины 2 между координатами 1 и 3.