Определение шестиугольник общее значение и понятие. Что это такое шестиугольник
Этимология шестиугольника относится к латинскому слову hexagōnum, которое в свою очередь происходит от греческого шестиугольника . Концепция намекает на многоугольник, который имеет шесть сторон и шесть углов .
Напомним, что идея многоугольника используется в геометрии для обозначения фрагмента плоскости, которая ограничена прямыми линиями . Следовательно, это плоская геометрическая фигура . Линии, составляющие многоугольники, называются сторонами .
В конкретном случае шестиугольника это фигура, которая ограничена шестью сторонами (то есть шестью отрезками линии). Из-за своей конфигурации он также имеет шесть внутренних углов и шесть вершин .
Сумма мер внутренних углов этого типа многоугольника равна 720º
Когда шестиугольник имеет шесть равных сторон, а также шесть равных внутренних углов, он называется правильным шестиугольником . В этих случаях внутренние углы являются конгруэнтными : все они измеряют 120º (120º x 6 = 720º).
Если, с другой стороны, стороны и внутренние углы шестиугольника не равны друг другу, фигура называется неправильным шестиугольником .
Можно найти шестиугольники в разных областях природы . Например, соты пчел состоят из восковых клеток, которые имеют гексагональную структуру. С другой стороны, шестиугольник Сатурна представляет собой облачную модель, расположенную вокруг северного полюса этой планеты, с шестью сторонами около 13 800 километров каждая.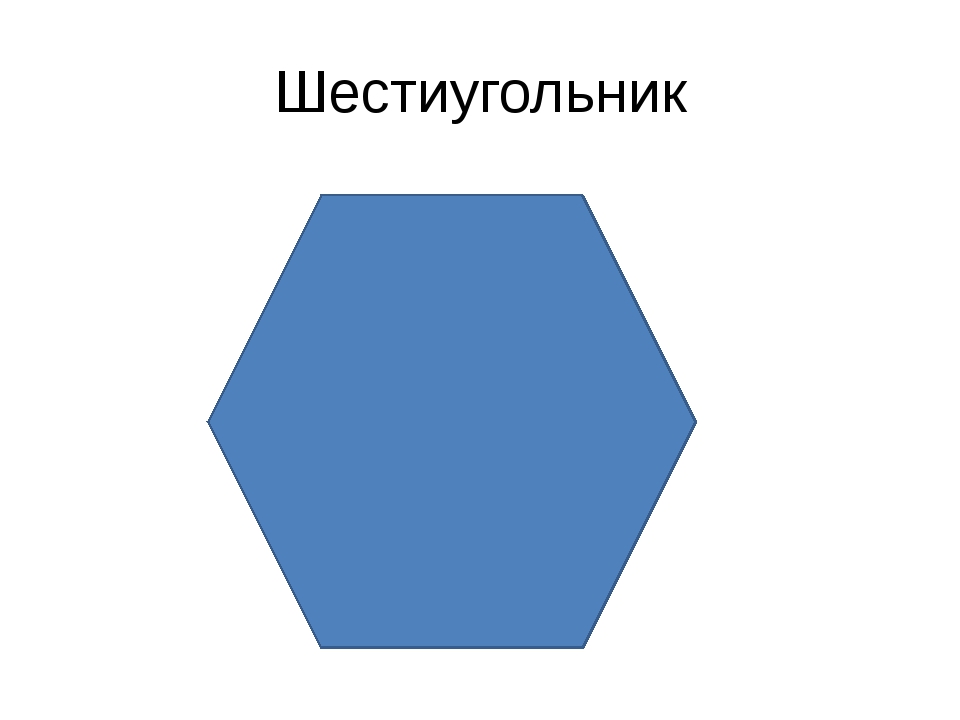
На что похож шестиугольник
Правильный шестиугольник (гексагон) — многоугольник с шестью равными сторонами.
Гексагон — правильный выпуклый многоугольник с шестью сторонами или шестиугольник.
Шестиугольник – это многоугольник, имеющий шесть сторон и шесть углов. В правильном шестиугольнике все стороны равны, а углы образуют шесть равносторонних треугольников.
Выпуклый шестиугольник – это многоугольник, с общим количеством вершин, равным шести, при этом все точки такого шестиугольника лежат по одну сторону от прямой, которая проведена между двумя любыми соседними его вершинами.
Правильный шестиугольник – это шестиугольник, все стороны которого равны между собой.
Сумма углов выпуклого шестиугольника определяется по общей формуле 180°(n-2) и равна 180 ( 6 – 2 ) = 720 градусов.
При решении задач для нахождения площади произвольного (неправильного) шестиугольника используют метод трапеций, который заключается в разбиении фигуры на отдельные трапеции, площадь каждой из которых можно найти по известным всем формулам.
Свойства правильного шестиугольника
- все внутренние углы равны между собой
- каждый внутренний угол правильного шестиугольника равен 120 градусам
- все стороны равны между собой
- сторона правильного шестиугольника равна радиусу описанной окружности
- большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам
- меньшая диагональ правильного шестиугольника в ( sqrt <3>) раз больше его стороны.
- vеньшая диагональ правильного шестиугольника перпендикулярна его стороне
- правильный шестиугольник заполняет плоскость без пробелов и наложений
- диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу вписанной в правильный шестиугольник окружности.
 circ) :
circ) :Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
Радиус вписанной окружности правильного шестиугольника равен апофеме:
(r = m = alargefrac<<sqrt 3 >><2>
ormalsize)Радиус описанной окружности равен стороне правильного шестиугольника:
Периметр правильного шестиугольника
Площадь правильного шестиугольника Формула площади правильного шестиугольника через длину стороны
(S = pr = largefrac<<3sqrt 3 >><2>
ormalsize),
где (p) − полупериметр шестиугольника.Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус вписанной окружности
Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус описанной окружности
Ksenia Donskaya
При достаточной наблюдательности в живой природе легко обнаружить строгую геометрию. В особом почете оказываются гексагоны — правильные шестиугольники. Почему их так любят пчелы и архитекторы и какие у них преимущества с точки зрения физики, рассказал английский ученый и научный журналист Филип Болл. «Теории и практики» перевели отрывок из книги «Закономерности в природе: Почему живой мир выглядит так, как выглядит», опубликованный на сайте Nautilus.
Как пчелам это удается? Соты, в которых они хранят золотистый нектар, — это чудеса инженерного искусства, набор ячеек в форме призмы с правильным шестиугольником в основании. Толщина восковых стенок строго определена, ячейки немного отклоняются от горизонтали, чтобы вязкий мед не вытекал, и соты находятся в равновесии с учетом влияния магнитного поля Земли. А ведь эту конструкцию без чертежей и прогнозов строят множество пчел, которые одновременно работают и координируют свои попытки сделать соты одинаковыми.

Древнегреческий философ Папп Александрийский думал, что пчелы, должно быть, наделены «геометрическим предвидением». И кто, если не Господь, мог одарить их такой мудростью? Как писал английский энтомолог Уильям Керби в середине XIX века, пчелы — «математики от Бога». Чарльз Дарвин не был в этом уверен и проводил эксперименты, чтобы установить, могут ли пчелы строить идеальные соты, используя лишь приобретенные и врожденные способности, как предполагалось в его теории эволюции. Но все же почему шестиугольник? Это чисто геометрический вопрос. Если вы хотите сложить вместе несколько одинаковых по форме и размерам ячеек таким образом, чтобы они заполняли всю плоскость, подойдут только три правильные фигуры (с равными сторонами и углами): равносторонние треугольники, квадраты и гексагоны. Если выбирать из этих вариантов, то шестиугольные соты потребуют наименьшей общей длины перегородок, в отличие от треугольников и квадратов той же площади. Поэтому в пчелиной любви к гексагонам есть смысл: на изготовление воска тратится энергия, и они стараются минимизировать расходы — точно так же, как строители пытаются сэкономить на стоимости кирпичей. К такому выводу пришли в XVIII веке, и Дарвин объявил, что соты из правильных шестиугольников «идеальны для экономии труда и воска».
Дарвин думал, что естественный отбор наделил пчел инстинктами для строительства восковых ячеек, у которых есть весомое преимущество: на них нужно тратить меньше времени и энергии, чем на соты других форм. И хотя кажется, что пчелы действительно обладают особыми способностями в том, что касается измерения углов и толщины стен, мнения ученых по поводу того, насколько активно насекомые их используют, расходятся, поскольку скопления шестиугольников встречаются в природе довольно часто.
Если вы подуете на пузырьки на поверхности воды, чтобы согнать их вместе, то они приобретут форму шестиугольников — или, по крайней мере, приблизятся к ней. Вы никогда не увидите скопище квадратных пузырей: если даже четыре стенки соприкоснутся, они немедленно перестроятся в конструкцию с тремя сторонами, между которыми будут примерно равные углы в 120 градусов — что-то вроде центра эмблемы «Мерседеса».

Очевидно, нет никаких организмов, которые работали бы над этими склеенными пузырями, как пчелы над сотами. Рисунок образуется исключительно благодаря законам физики. Так же очевидно, что у этих законов есть определенные предпочтения: например, склонность к трехстороннему соединению стенок пузырей. Аналогичная вещь происходит и с пеной, которая сложнее по строению. Если вы дуете через соломинку в мыльную воду и создаете «гору» пузырей в трехмерном пространстве, вы видите, что их стенки при соприкосновении всегда создают четырехсторонний союз и пересекающиеся мембраны находятся под углом около 109 градусов — это угол, который имеет непосредственное отношение к тетраэдру.
Что определяет форму пузырей и закономерности образования «развилок» мыльных стенок? Природа еще более озабочена экономией, чем пчелы. Пузыри и мыльная пленка состоят из воды (и слоя мыльных молекул), и поверхностное натяжение сжимает поверхность жидкости таким образом, чтобы она занимала наименьшую площадь. Поэтому капли дождя при падении принимают форму, близкую к сферической: у сферы наименьшая площадь поверхности по сравнению с другими фигурами того же объема. На восковом листке капли воды сжимаются в маленькие бусинки по той же причине.
Поверхностное натяжение объясняет и тот узор, который образуют пузыри или пена. Пена стремится к такой конструкции, при которой общее поверхностное натяжение будет минимальным, а значит, минимальной должна быть и площадь мыльной мембраны. Но конфигурация стенок пузырей должна быть прочной и с точки зрения механики: натяжение в разных направлениях на «перекрестке» должно быть идеально сбалансировано (по тому же принципу нужен баланс при строительстве стен собора). Трехстороннее соединение в пленке из пузырьков и четырехстороннее — в пене — комбинации, которые достигают этого баланса.
Но тем, кто думает (а такие имеются), что соты — это просто застывшее обилие пузырей из теплого воска, трудно будет объяснить, как такие же множества шестиугольных ячеек получаются у бумажных ос, которые при строительстве используют не воск, а комки жеваных волокон древесины и стеблей, из которых они изготавливают подобие бумаги.
 Мало того, что поверхностное натяжение тут не играет особой роли, но к тому же ясно, что у разных видов ос разные врожденные инстинкты с точки зрения архитектурных решений: они могут значительно различаться.
Мало того, что поверхностное натяжение тут не играет особой роли, но к тому же ясно, что у разных видов ос разные врожденные инстинкты с точки зрения архитектурных решений: они могут значительно различаться.Хотя геометрия стыков стенок пузырей диктуется взаимодействием механических сил, в ней бессмысленно искать намек на то, какую форму должна принять пена. Обычная пена содержит многогранные элементы различной формы и размера. Присмотритесь — и вы увидите, что их стенки не идеально прямые: они немного изогнуты. Поскольку чем меньше пузырь, тем выше в нем давление газа, стенка маленького пузыря рядом с большим будет слегка выпирать вперед. Более того, у некоторых элементов пять граней, у других — шесть, а у только четыре или всего три. При небольшой гибкости стенок все эти формы могут образовать четырехстороннее соединение, близкое по композиции к тетраэдру, что необходимо для механической устойчивости. Так что форма пузырей может изменяться. И хотя пену можно изучать с помощью правил геометрии, по своей сути она довольно хаотична.
Предположим, что вы могли бы сделать «идеальную» пену, в которой все пузыри одного размера. Какой тогда должна быть их идеальная форма, чтобы общая площадь стенок была наименьшей, но требование для углов на стыке выполнялось? Этот вопрос обсуждался много лет, и долгое время считалось, что идеальной формой будет четырнадцатигранник c квадратными и шестиугольными гранями. Но в 1993 году была открыта немного более экономичная, хотя и менее упорядоченная структура, состоящая из повторяющейся группы из восьми разных форм. Этот более сложный рисунок был использован в качестве вдохновения для пеноподобного дизайна водного стадиона для Олимпиады 2008 года в Пекине.
Здание Национального плавательного комплекса в Пекине © Ben McMillan
Правила, работающие для пузырей в пене, также можно отнести и к другим узорам, которые обнаруживаются в живых организмах. Не только фасеточные глаза мухи состоят из групп шестиугольных ячеек, которые напоминают группы пузырей; еще и светочувствительные клетки в каждой из этих ячеек собираются в гроздья по четыре, что опять же напоминает мыльные пузыри.
 Даже в случае мух-мутантов, у которых таких клеток больше, можно говорить о том, что их организация более-менее идентична поведению пузырей.
Даже в случае мух-мутантов, у которых таких клеток больше, можно говорить о том, что их организация более-менее идентична поведению пузырей.Из-за поверхностного натяжения мыльная пленка, охватывающая проволочную петлю, натянута ровно, как упругая сетка батута. Но если проволочный каркас погнут, то пленка также будет выгибаться элегантным контуром, который автоматически подсказывает вам наиболее экономичный с точки зрения использования материала способ покрытия пространства, огороженного каркасом. Таким образом, архитектор может увидеть, как построить крышу для здания со сложной архитектурой и потратить минимум стройматериалов. Как бы то ни было, дело не только в экономичности этих так называемых минимальных поверхностей, но и в их красоте и элегантности; вот почему такие архитекторы, как Фрай Отто, использовали их в качестве вдохновения для своих работ.
Эти поверхности минимизируют не только площадь, но и кривизну. Чем круче изгиб, тем больше кривизна. Она может быть положительной (выпуклости) или отрицательной (углубление, впадина или прогиб). Средняя кривизна изогнутой поверхности будет нулевой, если положительная и отрицательная кривизна друг друга уравновешивают. Поэтому лист может быть весь покрыт искривлениями, а средняя кривизна окажется наименьшей. Такая минимально искривленная поверхность разрезает пространство аккуратным лабиринтом коридоров и каналов — сетью.
Фрай Отто, Олимпийский стадион в Мюнхене © Atelier Frei Otto Warmbronn
Это явление называют периодической минимальной поверхностью («периодическая» лишь означает, что эта структура повторяется вновь и вновь; другими словами, это постоянная последовательность). Когда такие последовательности были обнаружены в XIX веке, они казались просто математическим курьезом. Но теперь мы знаем, что природа извлекает из них пользу.
Клетки организмов различных видов, от растений до миног или крыс, обладают мембранами с подобными микроскопическими структурами. Никто не знает, зачем они нужны, но они встречаются настолько часто, что логично предположить, что они выполняют какую-то полезную функцию.
 Может быть, они отделяют один биохимический процесс от другого, упраздняя их взаимное влияние друг на друга. Или, возможно, они просто эффективны в качестве «рабочей поверхности», поскольку многие биохимические процессы протекают на мембранах, где могут находиться ферменты и другие активные молекулы. Каковы бы ни были функции таких лабиринтов, вам не понадобятся сложные генетические инструкции для их строительства: законы физики сделают все за вас.
Может быть, они отделяют один биохимический процесс от другого, упраздняя их взаимное влияние друг на друга. Или, возможно, они просто эффективны в качестве «рабочей поверхности», поскольку многие биохимические процессы протекают на мембранах, где могут находиться ферменты и другие активные молекулы. Каковы бы ни были функции таких лабиринтов, вам не понадобятся сложные генетические инструкции для их строительства: законы физики сделают все за вас.У некоторых бабочек, таких как голубянка малинная, на крыльях есть чешуйки, в которых располагается аккуратный лабиринт из жесткого материала — хитина, — сформированный в виде определенной периодической минимальной поверхности под названием гироид. Взаимодействие между неровностями на чешуйчатой поверхности крыльев приводит к тому, что волны определенной длины — то есть определенные цвета — исчезают, в то время как другие усиливают друг друга. Этот механизм влияет на окраску насекомого.
Скелет морского ежа Cidaris rugosa — пористая совокупность ячеек в форме другого вида периодической минимальной поверхности. Это экзоскелет, который расположен снаружи мягких тканей организма, защитная раковина, на которой растут кажущиеся опасными колючки из того же минерала, который входит в состав мела и мрамора. Открытая решетчатая структура указывает на то, что материал прочный, но при этом нетяжелый, — как пенометалл, который используется в авиастроительстве.
Читайте также: Электроды для сварки виды маркировка и выбор
Но давайте вначале рассмотрим психогеометрическую сущность самого шестиугольника. Его изображение представлено на рис. 8.1. У фигуры отчетливо выражен центр. В этом аспекте шестиугольник чем-то сродни кругу. Однозначно есть своя идеология, единство и целостность. Шестиугольник обладает ярко выраженной самостью. Поэтому во внешних «варягах» совершенно не нуждается. Управление из центра идет по стратегическим радиальным каналам по направлению к углам. Административная иерархия четко прослеживается.
 Проще говоря, шестиугольник знает, что нужно делать, и умеет эффективно выстроить свой менеджмент.
Проще говоря, шестиугольник знает, что нужно делать, и умеет эффективно выстроить свой менеджмент.Есть два ударных угла. Что весьма немаловажно. Можно концентрировать силы на главных направлениях. А в общем-то, в наличии еще четыре дополнительных угла по круговой обороне, потому-то и шестиугольник. Попробуй подкатись без тщательной рекогносцировки. Шестиугольник умеет очень хорошо защищать свою территорию и свои интересы вовне ее. Своего рода скрытая агрессия, неумолимая и весьма беспощадная. Железно работает правило: «кто не с нами – тот против нас». Однако авантюрного риска в этой фигуре совершенно нет. Исключено.
Обратим также внимание на внутренние производственные возможности, на рисунке зона производства заштрихована (рис. 8.2). Шестиугольник особенно удачно сочетает логику и иррациональность в своей тактике и стратегии. Где надо – работать, где надо – атаковать (углы-то выступающие). Добавьте к этому единство идеологии и диктат центра. Поистине неотразимое сочетание. И все как-то целостно объединено.
Но главная фишка все же в другом. Шестиугольник может. производить себе подобных! Скажем, для круга, треугольника либо овала это просто физически невозможно, да и немыслимо. Зато шестиугольник очень легко объединяется с себе подобными в некую ячеистую сеть, которая непрерывно множится (рис. 8.3). Такова уж его конфигурация. Она позволяет устанавливать связи в самых различных направлениях. Создавая, например, сеть однотипных филиалов. Что и есть отличительным признаком корпорации (от позднелатинского corporatio – объединение, сообщество). Впрочем, можно применять термин «множение» либо «клонирование». Наверное, это так увлекательно – бесконечно расширяться и строить мир по своему плану и подобию. Идея, многократно воспроизведенная, становится очевидным материальным и духовным могуществом. Применительно к шестиугольнику мы можем говорить об уникальной способности к самовоспроизводству. Своего рода матричная система. В естественной природе идеально применяемая некоторыми видами насекомых.
 Муравьи, термиты, осы, пчелы, шершни расширяют свой ареал по одному и тому же «строительному генплану». И если вы встанете у них на пути, то, скорее всего, вас заставят ретироваться. Либо придется принять вызов и приступить к активным контрмерам. Третьего, увы, не дано. Правда, в бизнесе и политике есть еще третий вариант, а именно – инкорпорироваться в множащуюся структуру. Стать ее частью, филиалом и безоговорочно принять правила игры корпорации. Тем самым получив надежную «крышу» и гарантию того, что тонуть в случае чего придется всем «титаником». У шестиугольника неважно с адаптацией к внешней среде. Это уж точно не ромб. Изменять свою структуру он никак не желает. Приходится применять иную глобальную стратегию выживания. Чтобы предвидеть будущее, его надо создать однотипным и сделать управляемым. Что шестиугольник активно и претворяет в жизнь. Зачастую в нашей цивилизации это очень даже неплохо получается. Хотя все же бывают досадные сбои. Даже идеальный план не может учесть все факторы. И уж тем более, когда имеешь дело со временем, пространством и бытием в его сущности. Хотя, все мировые религии довольно устойчиво процветают многие и многие века. Чем не удачное клонирование некой парадигмы? Современный бизнес таким устойчивым долголетием похвастаться не может. Другие темпы и другие правила эволюции. Для мощных корпоративных структур в том числе.
Муравьи, термиты, осы, пчелы, шершни расширяют свой ареал по одному и тому же «строительному генплану». И если вы встанете у них на пути, то, скорее всего, вас заставят ретироваться. Либо придется принять вызов и приступить к активным контрмерам. Третьего, увы, не дано. Правда, в бизнесе и политике есть еще третий вариант, а именно – инкорпорироваться в множащуюся структуру. Стать ее частью, филиалом и безоговорочно принять правила игры корпорации. Тем самым получив надежную «крышу» и гарантию того, что тонуть в случае чего придется всем «титаником». У шестиугольника неважно с адаптацией к внешней среде. Это уж точно не ромб. Изменять свою структуру он никак не желает. Приходится применять иную глобальную стратегию выживания. Чтобы предвидеть будущее, его надо создать однотипным и сделать управляемым. Что шестиугольник активно и претворяет в жизнь. Зачастую в нашей цивилизации это очень даже неплохо получается. Хотя все же бывают досадные сбои. Даже идеальный план не может учесть все факторы. И уж тем более, когда имеешь дело со временем, пространством и бытием в его сущности. Хотя, все мировые религии довольно устойчиво процветают многие и многие века. Чем не удачное клонирование некой парадигмы? Современный бизнес таким устойчивым долголетием похвастаться не может. Другие темпы и другие правила эволюции. Для мощных корпоративных структур в том числе.Да, еще несколько слов о пространственном положении фигуры. Шестиугольник весьма самодостаточен, автономен, идеологичен, он обладает собственной базой воспроизводства, и потому ему, как и ромбу, больше всего подходит вертикальное положение, когда ударные углы смотрят вверх и вниз (рис. 8.1). Но бывают ситуации, когда шестиугольник вынужден ложиться на бок (рис. 8.5). Скорее всего, из-за чисто прагматических интересов. Приоритеты экспансии оказались несколько более заземленными, нежели ожидалось. Здесь уже не до мегаломании. Приходится ближе на более понятном языке контактировать со средой обитания и как-то с ней сосуществовать. Пусть даже получая далеко не ту прибыль, которая предполагалась. В реальной жизни корпорации слишком запоздало прибегают к стратегии «перемен на понижение». Комплекс успеха не позволяет поступить иначе. Тем более что управленческий механизм корпорации-шестиугольника отлажен безупречно для исполнения единой миссии. Для отдаленных географически и этнически филиалов тоже. Хотя там могли бы действовать гораздо более продуктивно, что называется, по обстановке. Однако указания из штаб-квартиры не оспариваются. Безусловно, можно упорствовать до бесконечности, надеясь на непобедимую силу корпоративного духа. Вот только где теперь мамонты и динозавры?
ЛЮДИ И ФИРМЫ КОРПОРАТИВНОГО ДУХА. Здесь ответ однозначен – им это очень нравится. Достигать высот можно различными путями. В данном случае лучше под надежной и могущественной крышей. Сопричастность к великому делу порой захватывает дух не хуже любого индивидуального экстрима. И при этом есть масса плюсов. Прежде всего не надо терзаться со смыслом жизни, личной миссией, вечными «гамлетовскими» вопросами и прочими неврозами выбора и принятия решения. Корпоративная религия в прямом смысле даст покой душе. Что в наше время очень даже немало. Стимул к успеху также налицо. Финансовое поощрение, атрибуты власти, чувство собственной значимости мало кого оставят равнодушными. Остается лишь денно и нощно стараться не выпасть из генерального русла. Люди корпоративного духа всегда исполнительные и превосходные работники. Им нравится по утрам облачаться в «деловую униформу» и с наслаждением приступать к порученным делам. Соты множатся, и это приятно. Причитающееся вознаграждение – тем более. И после затяжных праздничных выходных опять тянет обрести привычный смысл «времяпрожития» в офисе, с которым уже почти сроднился. Тем более что преданность и деловой энтузиазм (а если он еще и сверхактивный) корпорацией только поощряются.
Никаких сомнений и только сплошной позитив в работе, общении и, безусловно, настроении. Пожалуй, по психологической атмосфере коммунистические субботники эпохи начала строительства советского социализма здесь могут и проигрывать. Для корпоративного духа важна исключительно добровольная мотивация быть сопричастным. Снова подчеркнем – не безвозмездно. Особенно для адептов (фр. adepte – сторонник, приверженец, лат. adeptus – достигший) от бизнеса.
Для фирмы, правда, очень бурный корпоративный рост может сыграть плохую шутку. Все оборотные и наличные активы окажутся втянутыми в дело. Свободные деньги иссякнут, и может возникнуть угроза локального дефолта по неотложным платежам. А если еще незаметно подкрадется более глобальный кризис мирового сообщества, тогда станет совсем плохо. Корпорации, в отличие от фирм, гораздо легче идут с молотка по столь низкой цене, о которой даже никогда и не мечталось. Работники будут несказанно шокированы. Как же так? Незыблемый дотоле муравейник вдруг разорен! Подобный суперстресс корпоративному человеку весьма трудно будет пережить. Придется стремглав подыскивать новую ячейку. А в общем-то, корпорации и их работники очень боятся любых перемен. И уж тем более непредсказуемых, а то и угрожающих вызовов внешней среды и эпохи. Как, впрочем, и любая другая империя. Но здесь стабильность и величие именно в создании сети по единому образу и подобию, исходя из первоначального эскиза. Шестиугольники (человек и фирма) терпеливы и могут долго ждать своего часа для успешного клонирования. Сотовая сеть сразу и просто так не возникает. Ей предшествует скрытый от посторонних глаз латентный период. Поэтому до конца всю правду вы так и не узнаете. Публичность и откровенность все же разные вещи.
СОТОВЫЙ КОНТАКТ, или ДЕЛОВАЯ КОММУНИКАЦИЯ ШЕСТИУГОЛЬНИКА. Уже сама постановка вопроса слегка проблематична. Шестиугольнику, который сам себя воспроизводит, союзники и партнеры не особенно-то и нужны. По идее. На практике все несколько иначе. Сотовое клонирование имеет как своих союзников, так и врагов. Нейтралитет, впрочем, тоже возможен, но лишь до поры до времени. Экспансия – она и есть экспансия, даже если существует лишь в одиночном проекте.
С квадратом и прямоугольником может наблюдаться нечто вроде симбиоза. Все-таки нужда в производственном аспекте требует системности, рационального подхода и отлаженного хода воспроизводства. Главное, чтобы квадрат ни в коем случае не мешал корпоративному расширению. Сравните рис. 8.6 и 8.7. В первом случае с гармонией несколько не сложилось. Квадрат не позволяет ему вовсю клонироваться. Да и сама рациональная система квадрата серьезно подменена чужеродным корпоративным духом. Рано или поздно шестиугольник сбросит оболочку квадрата, использовав ее лишь как мимикрию. На рис. 8.7 ситуация гораздо благоприятнее. Вместо иррациональной корпоративной харизмы шестиугольника – исключительно голый расчет и строго системный подход во всех делах. Штаб-квартира в виде квадрата диктует свою волю будущему клонированию и созданию сети.
Вариант наиболее удачного симбиоза с прямоугольником уже показан на рис. 8.2. Только полное слияние и тотальное растворение прямоугольника в структуре шестиугольника. Другие варианты не рассматриваются.
С кругом у шестиугольника общая склонность к идеологическому центру. Ну а два идеолога, да еще «центровых», далеко не всегда находят общий язык. Тем более что круг иррационален и мистичен, а шестиугольник скорее рационалист и руководствуется сугубо прагматичным подходом в своих делах. Поэтому представить шестиугольник внутри круга можно (рис. 8.8), но, как и в случае с наружным квадратом, гармонии здесь нет. Круг уж больно не любит что-либо впускать внутрь себя, да еще в зоне сакральной идеи. Все, ей теперь конец. Там уже диктат идеологии шестиугольника. Хотя и шестиугольнику не совсем уютно. Из круга как-то надо будет вырваться. А круги не склонны просто за так кого-либо из своих объятий выпускать. А вдруг удастся переделать шестиугольник под себя? Все-таки некое тождество наличествует.
Но вот если круг окажется внутри шестиугольника (рис. 8.9), то можно смело предположить, что внутри корпорации имеется еще один, более закрытый идеологический центр. Корпоративный дух служит некой наружной оболочкой, что, однако, не мешает корпорации развиваться. До тех пор пока круг не начнет ради своих идей отбирать слишком много оборотных средств. А так, скорее всего, и будет. Если босс со своим ближайшим окружением вдруг увлекся религией, то менеджеры-практики начнут подыскивать другое рабочее место. Тандем «корпорация + религия» – это все же не «корпоративная религия». Но тем не менее в наше время подобное слияние только набирает обороты.
Но вот с треугольником и ромбом никакого глубокого идейного слияния у шестиугольника не предвидится. Для объяснения почему, здесь даже рисунков не требуется. Эти фигуры по своей жесткой и независимой природе не склонны куда-либо инкорпорироваться. Корпорация их может использовать только методом аутсорсинга, т. е. временные контракты для оказания определенной услуги. Шестиугольник, тем более в сотовом варианте, не любит идти на слишком большой риск. Есть, что терять. Треугольнику и ромбу это как раз не страшно, ибо они для такой работы и предназначены. Но вот с корпоративным духом будет посложней. Строптивость, видите ли. Да и нежелание годами высиживать карьеру.
С овалом, овоидом и каплей тоже судьба не сложится. Уж больно разный стиль жизни и решаемые задачи. Миссия тоже совершенно разная. Тем более что названные фигуры динамичны, а шестиугольник таковым не является. Опять же, тот же овоид имеет свою идеологию и знает, куда двигаться. Биполярный овал внесет только ненужную полярность для центричного шестиугольника. А у капли слишком короткий срок жизни. Стабильной корпорации такой сценарий и даром не нужен. Сеть должна в своем существовании стремиться к вечности.
МОНОЦВЕТИЕ КОРПОРАТИВНОЙ СТРУКТУРЫ. Пожалуй, начнем с того, что для логотипов шестиугольник очень даже подходит. Особенно если будет красиво выложен фрагмент ячеистой структуры (см. рис. 8.3). Все хотят быть стабильными и развивающимися. Да еще и согласно своему стратегическому бизнес-плану. Осталось лишь удачно выбрать корпоративный стиль. И цветовое решение логотипа, в котором шестиугольник – ключевая фигура.
Белый шестиугольник динамично стремится в будущее, легко находит альтернативы своего клонирования, привлекает партнеров и работников. Но у него «забелены» истоки и, собственно, сама корпоративная миссия. Такое ощущение, что корпорация непрерывно находится в поиске чего-то нового. Может быть, в этом и суть миссии? В любом случае сочетание цвета и формы здесь неожиданно, но может сработать.
Желтый, равно как и оранжевый, добавит позитивной активности, но внесет легкомыслие и повышенную трату ресурсов. Для корпорации не совсем подходящий вариант. Разве что она специализируется на дорожно-строительных работах. Там действительно много тратят и почти всегда не укладываются в смету.
Зато отлично подойдет глубокий золотистый цвет. Лучше без полировки, т. е. не зеркальный. Престижность и уверенность. И никаких сомнений. Успех корпорации будет всегда обеспечен!
Алый шестиугольник активный и весьма импульсивно атакующий среду. Корпоративный дух едва ли не приравнен к духу боевому. Чем-то напоминает самурайство в бизнесе. Можно и так развивать сеть. Хотя темновато-красный шестиугольник уже более глубокий и уравновешенный, при сохранении корпоративной «боевитости». Но еще лучше – вишневый и пурпурный. Поистине императорские цвета, а корпорации именно это и нужно. Глубина развертывания сотовой сети только усилится за счет чувствования внутренних и внешних процессов без ослабления мощи экспансии. Только теперь она будет более взвешенной. Малиновый еще больше усилит коммуникативные качества корпоративного духа как внутри структуры, так и с внешней средой, но слабым малиновый шестиугольник казаться не будет.
Соты черного цвета покажутся уж очень мрачными и, следовательно, потерявшими вкус к жизни. Черный сжимает и уходит вглубь, а здесь как раз и нужны активная внешняя экспансия и позитивный имидж развертывания сети. Не подойдет черный цвет для корпоративных задач.
Серый в любых оттенках, кроме очень бледного, а также серебристо-серый очень даже ничего. Хорошая динамика, отлично разработанные стратегия и тактика продвижения, внимания к внешней среде и мощная аналитика собственных проблем и задач. Полная толерантность и внимание ко всему. В сером цвете корпорацию точно лихорадить не будет. Все будет происходить без эксцессов, что для шестиугольника немаловажно.
Цвет металла шестиугольникам надо также избегать. Внешняя среда начнет более активно сопротивляться политике экспансии. И тогда сотовая сеть начнет восприниматься агрессивно. Зачем это делать?
Намного лучше темно-синий, а также фиолетовый цвет. У структуры появляется внутренняя глубина процессов и собственно самого корпоративного духа. Чувство внешней среды также усилится. Главное, чтобы корпоративный дух постепенно не подменился духом религиозным. Тогда уже будет не до дальнейшего развертывания. Зато комфортно в слитном единстве.
Хотите, чтобы в коллективах корпорации сохранялись дружелюбные отношения между коллегами и работа не воспринималась как трудовая повинность? Тогда выбирайте приятный голубой, т. е. более интенсивный и не бледный.
ПОПУТНОЕ ДОПОЛНЕНИЕ К ТЕМЕ. ВОСЬМИУГОЛЬНИКИ по своей форме начинают «округляться» и являются переходным звеном к кругу. Нет доминирующих ударных углов, а центр, в сравнении с шестиугольником, выражен еще более. Правда, внешний контур фигуры пока рациональный, хотя совершенно лишен жесткости. Так что дорожный знак «Движение без остановки запрещено» хоть и в алом цвете, но водителей не раздражает. Тем более что команда «STOP» написана белым, а значит, еще облегчает команду приоритета, психологически снимая агрессивные установки водителей, которые вынуждены остановиться. Как говорится, «стали, подождали, а дальше все опять будет». И еще один очень важный момент относительно восьмиугольника. У этой фигуры резко ослаблена тенденция создавать ячеистые структуры. Это, скорее всего, будет монофирма со своей внутренней идеологией и уравновешенной деловой коммуникацией с партнерами. Удачно для логотипа, если бы только не прочно сложившаяся ассоциация с упомянутым дорожным знаком.
“>
Почему шестиугольники?—Справка | Документация
Агрегация случайных точечных данных в регулярные сетки используется по многим причинам, в частности для нормирования географии для нанесения на карту или для уменьшения неоднородности при использовании полигонов неправильной формы, созданных произвольно (например, границы избирательных округов или блоков, созданных в результате политических процессов). Регулярные сетки могут состоять только из равносторонних треугольников, квадратов или шестиугольников, т.к. только такая геометрия полигонов позволяет создавать мозаичное замощение (совокупность одинаковых фигур, охватывающую всю область без пробелов и перекрытий), чтобы получить равномерную сетку.
Хотя сетка квадратов является основным типом геометрии в ГИС-анализе и тематической картографии, бывают ситуации, когда шестиугольники лучше подходят для анализа, в зависимости от сути вопроса.
Агрегация по гексагональной сетке может применять по следующим причинам:
- Шестиугольники позволяют уменьшить смещение выборки из-за краевых эффектов, вызванных геометрией сетки, что связано с низким значением соотношения периметра к площади шестиугольника. Наименьшее соотношение имеет окружность, но окружности не могут создать замощение в виде непрерывной сетки. Шестиугольники обладают наиболее близкой к окружности геометрией и могут складываться в мозаику, формируя равномерную сетку.
- Такая приближенность гексагональной сетки к окружности позволяет более естественно представлять кривые в распределении данных, чем квадратная сетка.
- При сравнении полигонов с равными площадями, чем ближе форма полигона к окружности, тем ближе к центроиду оказываются точки у границ (особенно рядом с вершинами). Это означает, что любая точка внутри шестиугольника находится ближе к его центроиду, чем любая точка в квадрате или треугольнике равной площади (из-за более острых углов квадрата и треугольника по сравнению с шестиугольником).
- Шестиугольники более предпочтительны, когда в анализ включаются аспекты связности или пути перемещения.
- Из-за линейной природы прямоугольников, регулярные сетки формируют прямые параллельные линии, что может скрывать от наблюдателя закономерности, имеющиеся в данных. Шестиугольники позволяют разбить эти линии и позволяют легче наблюдать закономерности в данных, имеющие криволинейную форму. Это позволяет прервать искусственные прямолинейные закономерности и снизить смещение по расположению, которое может проявляться в регулярных сетках.
- Если вы работаете с большой областью, гексагональная сетка вносит меньше искажений, вызванных кривизной земной поверхности, чем регулярная сетка.
- Поиск соседств с помощью гексагональной сетки является более эффективным. Поскольку ребро или длина контакта каждой стороны одинаковы, центроид каждого соседства является равноудаленным. Однако с регулярной сеткой центроиды соседства Queen’s Case (над/под/справа/слева) находятся на удалении N единиц, а центроиды диагонального (Rook) соседства – несколько дальше (точнее, на расстоянии квадратного корня из 2N единиц).
- Поскольку в гексагональной сетке расстояние между центроидами во всех шести направлениях одинаково, если вы используете для поиска соседей полосу расстояний или инструменты Оптимизированный анализ горячих точек, Оптимизированный анализ выбросов или Создать куб Пространство-Время по агрегации точек, в гексагональной сетке для каждого объекта в вычисления войдет большее число соседей, чем при использовании регулярной сетки.
Дополнительные источники:
Birch, Colin P.D., Oom, Sander P., and Beecham, Jonathan A. Rectangular and hexagonal grids used for observation, experiment, and simulation in ecology. Ecological Modelling, Vol. 206, No. 3–4. (August 2007), pp. 347–359.
Гексагональные сетки, как вы находите, в каком шестиугольнике находится точка?
EDIT: этот вопрос сложнее, чем я думал сначала, я перепишу свой ответ с некоторой работой, однако я не уверен, является ли путь решения каким-либо улучшением по сравнению с другими ответами.
Вопрос можно перефразировать: для любого x, y найдите шестиугольник, центр которого ближе всего к x, y
т. е. минимизировать dist_squared( Hex[n]. center, (x, y)) над n (квадрат означает, что вам не нужно беспокоиться о квадратных корнях, что экономит некоторые CPU)
Однако сначала мы должны сузить число шестиугольников для проверки-мы можем сузить его максимум до 5 следующим методом:
Итак, первый шаг-оставьте свой точке (x,y) в UV-пространство т. е. (х,г) = lambda у + му V, поэтому = (lambda, му) в UV-пространство
Это просто матричное преобразование 2D( http://playtechs.blogspot.co.uk/2007/04/hex-grids.html может быть полезно, если вы не понимаете линейных преобразований).
Теперь, учитывая точку (lambda, mu), если мы округлим оба до ближайшего целого числа, то получим следующее:
Везде в пределах зеленого квадрата карты возвращаются к (2,1)
Таким образом, большинство точек внутри этого зеленого квадрата будут правильными, то есть они находятся в шестиугольнике (2,1).
Но некоторые точки должны возвращать шестиугольник # (2,2), т. е.:
Точно так же некоторые должны возвращать шестиугольник # (3,1). А затем на противоположном углу этого зеленого параллелограмма появятся еще 2 области.
Итак, подводя итог, если int (lambda, mu) = (p, q), то мы, вероятно, находимся внутри шестиугольника (p, q), но мы также можем быть внутри шестиугольников (p+1, q), (p, q+1), (p-1, q) или (p, q-1)
Несколько способов определить, какой из них имеет место. Проще всего было бы преобразовать центры всех этих 5 шестиугольников обратно в исходную систему координат и найти, какая из них ближе всего к нашей точке.
Но оказывается, что вы можете сузить это до ~50% времени, не делая никаких проверок расстояния, ~25% времени, делая одну проверку расстояния, а остальные ~25% времени, делая 2 проверки расстояния (я угадываю цифры, глядя На области, на которых работает каждая проверка):
p,q = int(lambda,mu) if lambda * mu < 0.2: // inside circle, so guaranteed inside hexagon (p,q) outPQ = p,qelse: if lambda > 0.0: candHex = (lambda>mu) ? (p+1,q): (p,q+1) else: candHex = (lambda<mu) ? (p-1,q) : (p,q-1)И этот последний тест можно привести в порядок:
else: // same sign, but which end of the parallelogram are we? sign = (lambda<0) ? -1 : +1 candHex = ( abs(lambda) > abs(mu) ) ? (p+sign,q) : (p,q+sign)Теперь мы сузили его до одного другого возможного шестиугольника, нам просто нужно найти, который ближе:
dist2_cand = dist2( Hex2Rect(lambda, mu), Hex2Rect(candHex) ) outPQ = ( distSquared < dist2_cand ) ? (p,q) : candHexФункция Dist2_hexSpace(A,B) привела бы все в порядок еще больше.
Шестиугольник Сатурна — Мастерок.жж.рф — LiveJournal
На Северном полюсе Сатурна существует уникальный феномен — в атмосфере висит гигантское облако правильной шестиугольной формы. Каждая из сторон шестиугольника (его еще называют Гексагоном Сатурна) имеет в длину 13 800 километров и сравнима с размерами Земли.
Давайте узнаем о нем подробнее …
Шестиугольник вращается — каждые 10 часов 39 минут он совершает полный оборот вокруг своей оси. В отличие от остальных облаков в атмосфере Сатурна, шестиугольник не смещается и все время находится на одном и том же месте.
На Южном полюсе Сатурна никаких шестиугольников нет — зато там есть огромная воронка в атмосфере. В центре шестиугольника на Северном полюсе тоже есть такая воронка. Впервые этот феномен обнаружили космические аппараты проекта «Вояджер» в начале 1980-х годов. Когда в 2006 году к Сатурну подлетел аппарат «Кассини», он снял на видео вращение шестиугольника.
На сегодняшний день нет определенного научного определения для шестиугольника Сатурна, которое бы объясняло этот атмосферный феномен. Геометрически правильный шестиугольник в 25 тыс. километров в поперечнике находится на северном полюсе планеты. Его «стены» уходят вглубь атмосферы на расстояние до 100 километров.
Сатурн – шестая планета от Солнца и вторая по размерам в Солнечной системе, состоит из водорода, с примесями гелия, следами воды, метана, аммиака и тяжелых элементов.
Фотография выше была сделана 27 ноября 2012 года с расстояния 376 171 км. за северным полюсом Сатурна с помощью орбитального аппарата Кассини, принадлежащего НАСА. На фото запечатлено очень интересное атмосферное явление, которое ранее нигде не встречалось.
А вот приближенное изображение вихря в центре шестиугольника:
Фото сделано также 27 ноября 2012 года с помощью специальных фильтров P0 и CB2. Камера Кассини была направлена в сторону Сатурна примерно на расстоянии 400 048 километров.
Другой вид шестиугольника Сатурна:
Учёные из Оксфордского университета смогли в лабораторных условиях смоделировать возникновение подобного гексагона. Чтобы выяснить, как возникает такое образование, исследователи поставили на вертящийся стол 30-литровый баллон с водой. Она моделировала атмосферу Сатурна и её обычное вращение. Внутри учёные поместили маленькие кольца, вращающиеся быстрее ёмкости. Это генерировало миниатюрные вихри и струи, которые экспериментаторы визуализировали при помощи зелёной краски. Чем быстрее вращалось кольцо, тем больше становились вихри, заставляя близлежащий поток отклоняться от круговой формы. Таким образом авторам опыта удалось получить различные фигуры — овалы, треугольники, квадраты и, конечно, искомый шестиугольник.
Учёные сопоставили данные опыта с происходящим на Сатурне и выдвинули предположение, что в его высоких северных широтах отдельные струйные течения разогнаны как раз до той скорости, при которой формируется нечто вроде устойчивой волны — планетарный гексагон. И хотя «расследование» не раскрывает происхождения подобных течений, оно показывает, почему вся система столь красива и, главное, столь долго живёт
«Чем быстрее вращается кольцо, тем меньше становится круговое движение зеленой струи. Малые вихри образуются по краям, медленно становятся все больше и больше, и заставляют жидкость меняться из формы кольца в многоугольник. Изменяя скорость вращения кольца, ученые могут создавать различные формы. «Мы могли бы создавать овалы, треугольники, квадраты и почти все, что угодно», говорит физик Оксфордского Университета Питер Рид (Peter Read). Чем больше разница в скорости вращения планеты и струйного течения – в опыте это цилиндр и кольцо – тем меньше сторон будет у многоугольника. Физики университета предполагают, что струйное течение северного полюса Сатурна вращается с определенной скоростью по отношению к остальной части атмосферы, что способствует созданию формы шестиугольника».
А вот снимок, сделанный ранее в 2006 году инфракрасной камерой:
Это было первое изображение, содержащее в одном кадре всю фигуру и область, прилегающую к северному полюсу Сатурна.
И хотя ученые не пришли к единогласному выводу о происхождении этого вихря, нам остается любоваться поистине завораживающей красотой планеты.
Давайте еще вспомним про Загадочный Япет и где можно наблюдать Мощнейший ураган в Солнечной системе
Шестиугольная плитка — раздел Статьи на сайте АРГО СТ
Шестиугольная плитка
Шестиугольная плитка-гексагон сейчас на пике моды. Мы узнали, почему шестиугольная плитка действительно достойна того, чтобы появиться в вашем жилище
Правильный шестиугольник или гексагон – в древности символ изобилия, красоты, гармонии симметрии, образа человека (две руки, две ноги, голова и туловище). Если говорить о шестиугольнике в архитектуре, то первопроходцами тут были пчелы. Идеально ровные соты, выстроенные по принципу золотого сечения, завораживают наблюдателей до сих пор. Что уж говорить о древних философах и математиках, ведь в те времена к символам привязывался каждый шаг из жизни человека.
Долгое время в архитектуре шестиугольник использовался как защита от врагов или символ поклонения. Одно из древних упоминаний шестиугольника в архитектуре – это храм Юпитера Гилиополитанского, созданный римлянами еще в 200-ых годах нашей эры. Перед святилищем был выстроен шестиугольный двор – явная попытка сообщить богу Юпитеру, как сильно его почитают.
Еще одно, более позднее появление гексагона – это шестиугольная башня замка, построенного в Англии около 1400 года. Она стояла на возвышении, была окружена рвом и была призвана вселять ужас в неприятеля и обращать его в бегство.
Шестиугольные крепости строились в Европе и в средние века. Примером может служить город Карловац в Хорватии, построенный в 1579 г. Он состоял из укреплений, образующих шестиугольную звезду с бастионами по углам. Известный на весь мир город Пальманова – это уже усовершенствованный девятиугольник, но идея в нем читается все та же.
Плитка- гексагон уверенно держит лидирующее место в линейке форматов фабрик-производителей. Заказчики и дизайнеры полюбили соты, а теперь еще вытянутые соты и их интерпретации за необычность формы даже в самом простом исполнении, за широкую линейку декоративных возможностей при использовании бюджетных серий.
Самые трендовые – это гексагоны бетонной, асфальтовой текстуры, с оттисками чугунных водосточных люков. А еще сейчас появляются фактуры крупноувеличенного плетения ткани, что дает прекрасную декоративную игру светотени на форме. Какой только не бывает шестиугольная плитка! Матовой и глянцевой, мелкой и крупноформатной, с растительным орнаментом, с имитацией под старинный английский кирпич, мрамор, дерево.
Все это даже в несколько безумном сочетании друг с другом легко сделает интерьер сложным и оригинальным. А еще, благодаря форме и тому, что гексагоны – это в основном керамограниты, они дают прекрасную возможность сделать перетекающее, разлетающееся на модули пространство.
И только в 17-18 веках сакральное значение шестиугольника и его мистический смысл отошли на второй план. Эта форма в новом кокетливом и изысканном виде стала модным украшением роскошных особняков – шестиугольная форма здания, двора, мебели.
А плитка-гексагон начала появляться в Италии и Испании – там, где рождаются лучшие интерьерные тенденции. Венцом ее существования стала знаменитая рельефная плитка с морскими узорами, которую в начале 20 века создал Антонио Гауди. Ею выложены тротуары в Барселоне.
В наше время шестиугольная плитка получила новое прочтение в архитектуре. Например, «чешуйчатая» корона из рельефной черной керамической плитки венчает базельский Музей культур в Швейцарии, созданный архитекторами Херцогом и де Мёроном.
Что касается жилых интерьеров, то создать «пчелиное» жилище, то есть идеально продуманное и уютное – это мечта любого архитектора или дизайнера. Форма шестиугольника активно используется при создании мебели, декора и отделки помещения, но плитка – это классика.
Гексагональную плитку используют в оформлении не только ванной и кухни, но и гостиной, прихожей или придомового участка. При помощи такой плитки можно оригинально зонировать пространство в помещении, отделив, например, кухню от столовой: граница получится неровной и переход из одной зоны в другую будет плавным и ненавязчивым.
Современные коллекции шестиугольной плитки могут быть миниатюрными почти как мозайка или наоборот очень большими и достигать более 50 сантиметров в ширину. Эта плитка без труда впишется и в классический, и в современный интерьер, но главное правило – расцветка должна быть сдержанной и монохромной. Мы подготовили подборку самых популярных у российских дизайнеров вариантов. Наверняка и вы найдете тот, что придется вам по душе.
Если правильная форма гексагона вам не близка, но все равно хочется геометрических мотивов, то можно выбрать один из таких вариантов
Ну и конечно, классическая квадратная или прямоугольная плитка с геометрическим узором – еще один тренд, который ничем не хуже гексагона
ТАИНСТВЕННЫЙ ШЕСТИУГОЛЬНИК | Наука и жизнь
Громовой знак на изделиях древних мастериц.
Фасад дома в городе Богородицке (Ногинске) украшен древними символическими изображениями.
‹
›
У нас в деревне на водокачке (у колодца) вырезан шестиугольный знак, напоминающий так называемую звезду Давида. Деревня наша глухая, и, насколько известно, люди, исповедующие иудаизм, там не селились. Хотелось бы получить разъяснение специалистов.
Л. Деева (г. Тверь).Подобные изображения часто встречаются в наружном декоре дореволюционных зданий и на многих предметах старинной утвари.
Первоначальный смысл этого знака на Руси, во времена язычества, был связан с богом-громовержцем Перуном: его святилище представляло собой в плане шестилучевую розетку. У этнографов такая розетка получила название «громовой знак». Наши предки изображали его на верхних частях домов под крышей в качестве защиты от грома. Но и у колодца это изображение неслучайно: Перун был не только метателем огненных стрел, но и подателем живительной влаги.
Нужно отметить, что «громовой знак» по своему внешнему виду все же отличается от «звезды Давида», в конструкции которой четко просматриваются два наложенных друг на друга треугольника. Общими остаются только шесть обязательных лучей.
Как это часто случается, по прошествии времени многие символы утрачивают свой первоначальный смысл и приобретают новый. Так, со второй половины XVIII столетия многие архитекторы применяли в декоре как светских, так и церковных зданий изображение шестиконечной Вифлеемской звезды, как правило, располагая его на верхних частях строений. Этот символ быстро прижился в дореволюционной России. Подобными звездами, сделанными из деревянных планок и обвитых светящимися гирляндами, украшали дома во время пасхальных и рождественских праздников.
Таким образом, и «громовой знак», и Вифлеемская звезда остаются доброжелательными, оберегающими знаками.
Определение шестиугольника по Merriam-Webster
гекса · гон | \ ˈHek-sə-ˌgän \: многоугольник с шестью углами и шестью сторонами.
Почему в мире природы изобилует шестиугольник
От сот до снежинок и мозаичных узоров на кожуре фруктов — шестиугольник изобилует в мире природы.Джон Райт исследует, почему лучше всего иметь шесть сторон.
Мы ожидаем, что Природа будет беспорядочным делом, избегающим прямых линий и простой геометрии и состоящим только из органических комков и выпуклостей, случайных расположений или простого хаоса, тем не менее, строго евклидов шестиугольник появляется в мире природы с удивительной частотой. От гигантских до субмикроскопических — шестиугольники есть повсюду. Возникает вопрос, почему.
Все дело в эффективности, полезности и случайной способности формироваться почти случайно.Шестиугольник симметричен, прост и обладает редким навыком мозаики (мозаики). Более того, что касается мозаичных форм, они превосходны, поскольку могут ограничить наибольшую площадь по заданному периметру.
Самый известный природный шестиугольник — это соты. Как пчелы могут построить такое сложное хранилище, на протяжении веков занимали умы естествоиспытателей. Британская энциклопедия 1797 года отмечает, что из трех правильных мозаичных форм — равностороннего треугольника, квадрата и шестиугольника — шестиугольник является наиболее подходящим как с точки зрения удобства, так и прочности.Пчелы, как будто знали это, делают свои клетки правильными шестиугольниками.
Однако, как подразумевает автор, пчелы — не те геометрические фигуры, которыми их считают — скорее, соты — это естественный результат следования некоторым простым правилам. Сделайте трубки из воска большого диаметра, расположив их как можно ближе друг к другу. По завершении залезьте внутрь и поднимите температуру тела. Тепло размягчает клетки, которые затем расслабляются относительно своих соседей, принимая шестиугольную форму. Вот и все, мощная и эффективно вместительная кладовая-магазин, созданная по простым правилам.
Аналогичный эффект наблюдается в трубных домах сотового червя Sabellaria alveolata. Эти поистине отвратительные существа строят свои жилища из склеенных песчинок. В малонаселенных популяциях они образуют круглые трубки. Однако, если недвижимость в цене, они становятся плотно упакованными, образуя шестиугольники, создавая рассыпчатые песчаные рифы, которые можно увидеть на берегу моря во время отлива.
Этот мозаичный узор также иногда встречается на кожуре фруктов. Самая яркая принадлежит тому обитателю фойе отелей, швейцарскому сырному комбинату (восхитительно, Monstera deliciosa).
Он имеет форму кукурузного початка и покрыт отчетливыми зелеными шестиугольными чешуйками. Кстати, часть его латинского названия deliciosa применяется только тогда, когда плод созревает и чешуя начинает отпадать, так как до этого момента он довольно токсичен. Хлебные фрукты имеют такую же маркировку.
Животные также имеют шестиугольную структуру. Поверхность вымершего коралла Cyathophyllum hexagonum целиком состоит из шестиугольников, как и скелеты многих диатомовых водорослей. Последние изящно сконструированы, иногда образуют сплющенную сферу, иногда крошечный треугольник, казалось бы, все из тончайшего кружева.
Затем есть глаза стрекоз, состоящие из 30 000 шестиугольников, которые создают систему настолько сложную и мощную, что New Scientist назвал их видения «ультра-многоцветными», добавив, что они «лучше, чем что-либо, что когда-либо видели у животных. Мир.»
Мы можем быть немного удивлены, увидев так много шестиугольников в живых существах, но в неорганических структурах их ожидаемо больше. Кристаллы бывают разных форм, отражающих формы составляющих их атомов или молекул и то, как они соединяются за руки.
Кристаллы — это большие молекулы. Наиболее известное кристаллическое вещество — кварц. Эта форма диоксида кремния очень серьезно относится к своей форме — она не только гексагональна в поперечном сечении, но и концы образуют шестигранные пирамиды.
Тогда есть снежинка. Ни один другой кристалл не обладает таким чутьем, таким воображением. Как известно, нет двух одинаковых людей, и это очевидная гипербола, и это правда. Тем не менее, все они, по сути, шестиугольные.
Действительно, существует более дюжины расположений молекул воды, которые образуют различные льды (включая, для читателей Курта Воннегута-младшего, апокалиптическую «Ледяную девятку»), но шестиугольник доминирует.Молекулы воды имеют положительный и отрицательный заряды, расположенные под прямым углом, шесть из которых образуют шестиугольник.
Остаточные заряды позволяют шестиугольникам соединяться с другими шестиугольниками ребром. Они также могут соединяться лицом к лицу, идеально выровненные, образуя кристалл. Я сильно упрощаю здесь, но поверьте мне, это к лучшему.
Одиночные снежинки обычно симметричны и всегда имеют шесть углов. У них такая же симметрия, как у шестиугольника, но снегопад не оставляет тысячи шестиугольников на лужайке.Маленькие молодые снежинки представляют собой идеальные шестиугольники, но вскоре более электрически заряженные точки притягивают молекулы воды, создавая украшения Фаберже, которые придают им полную красоту.
Снежинка завораживает своей нежной красотой; базальтовые колонны, такие как Дорога гигантов в Северной Ирландии (изображенная в верхней части экрана), внушают трепет. Они также озадачивали естествоиспытателей на протяжении веков — идея о том, что это огромные кристаллы, быстро отвергается, поскольку они содержат мелкие кристаллы нескольких минералов.
На самом деле, ответ прост — они образуются при усадке горячего базальта, когда он охлаждается из расплавленного состояния, очень похоже на примерно шестиугольные трещины, которые возникают на вашем (когда-то заснеженном) газоне после летней засухи. Массивная и однородная природа базальта гарантирует, что задействованные силы распределяются равномерно, а трещины происходят с большой регулярностью и имеют наиболее экономичную форму: шестиугольник.
Если вы думаете, что сами свободны от шестиугольников, то я должен вам сказать, что вы на самом деле в значительной степени построены из них.Боюсь, без шестиугольников вы были бы неприятной лужей слизи на ковре. Все дело в необычайно талантливом атоме углерода.
Шесть из них соединяются в шестиугольные «кольца», иногда с атомом углерода, замещенным атомом другого элемента. Они содержатся во многих известных биохимических веществах, таких как ванилин (ваниль), бензол, сахара, аминокислоты и даже ДНК. Некоторые сахара имеют одно кольцо, некоторые — два, и поэтому называются моно и дисахаридами соответственно. Некоторые из них находятся в «базах», несущих генетическую информацию.
Общее у этих колец то, что они действуют как держатели так называемых «функциональных групп», которые представляют собой молекулярные структуры, прикрепленные к углероду и другим атомам кольца, которые выполняют работу всей молекулы.
Начиная с наименьшего известного шестиугольника, мы заканчиваем наибольшим. Обнаруженный только в 1982 году миссией «Вояджер», «шестиугольник», как его разумно называют, представляет собой облачный узор вокруг северного полюса Сатурна.
Как был создан и поддерживается такой чудовищный и безошибочный шестиугольник — новая проблема для ученых, но не вызывает сомнений его размер: он вдвое больше диаметра Земли.
Шестиугольник в северной стратосфере Сатурна, окружающий возникающий летний полярный вихрь
Гексагональная граница NPSV
В данном исследовании используется спектроскопия зондирования надиром CIRS 27,35 Cassini, спектрометр с преобразованием Фурье 10–1400 см. с программируемым спектральным разрешением от 0,5 до 15,5 см −1 . Мы использовали интерферометр Майкельсона среднего инфракрасного диапазона (600–1400 см, –1 ), который включал две решетки из детекторов HdCdTe размером 1 × 10, каждый с мгновенным полем зрения 0.27 × 0,27 мрад. Спектры инвертируются с использованием алгоритма поиска оптимальной оценки 36,37 для характеристики верхней тропосферы (80–300 мбар) и стратосферы (0,5–5,0 мбар) и состава 38 как функции времени (см. Методы). Прежде чем выполнять спектральные инверсии, мы начнем с исследования полярной морфологии, наблюдаемой в необработанных яркостных температурах.
На рисунке 1 показаны карты яркостных температур CIRS с пространственным разрешением с 2013 по 2017 гг.Это яркостные температуры, усредненные по излучению полосы Q CH 4 между 1280 и 1320 см, −1 , и представляют собой кинетические температуры в широком диапазоне высот от 0,5 до 5,0 мбар 38 . Для этих наблюдений фокальная плоскость CIRS медленно сканировалась с севера на юг, когда планета вращалась под ней за один или два оборота (10–20 ч).
Рис.1Карты яркостной температуры северной полярной стратосферы с 2013 по 2017 гг.Яркостные температуры были усреднены по диапазону 1280–1320 см, –1 , чувствительность 0,5–5,0 мбар, и каждая карта имеет одинаковую шкалу температур. На рисунке показана гексагональная граница полярного стратосферного колпака. На панелях представлены карты для a 17 августа 2013 г., b 18 октября 2014 г., c 9 июня 2016 г., d 20 сентября 2016 г., e 8 ноября 2016 г., f 12 февраля , 2017, г 17 апреля 2017 г. и ч 26 августа 2017 г.Здесь использовались карты со спектральным разрешением 2,5 см -1 (REGMAP) и 15,0 см -1 (FIRMAP), охватывающие миссию Кассини во время солнцестояния и проксимальные орбиты. Эти данные были получены при относительно высоком наклонении орбиты, чтобы облегчить обзор северного полюса. Спектры были усреднены на проекции равной площади для уменьшения шума. Области темно-синего цвета представляют собой недостающие данные и дефекты — в частности, центральный полярный циклон был частично скрыт в окончательной FIRMAP миссии, полученной в августе 2017 года ( h ).Гексагональная граница в районе 78–80 ° широты наиболее четко видна в данных за октябрь 2014 г. ( b ), ноябрь 2016 г. ( e ) и февраль 2017 г. ( f ). Синусоидальное изменение температуры показано на рис. 2e – f для двух дат
Четыре особенности сразу видны на картах. Во-первых, яркостная температура увеличилась примерно на 10 К за 4 года, показанные на этом рисунке. Во-вторых, компактный полярный циклон 5 виден в центре каждого изображения, связанный с сильным отрицательным вертикальным сдвигом на зональной струе на 87 ± 1 ° с.ш. (см. Ниже).В-третьих, на более поздних изображениях можно увидеть границу около 78 ° с.ш., отделяющую более низкие температуры в низких широтах от более теплых полярных температур и предполагающую усиление там температурного градиента. И, наконец, что наиболее удивительно, на многих из этих изображений граница выглядит гексагональной. Кассини продемонстрировал, что знаменитая гексагональная волна Сатурна 28 , наблюдаемая на вершинах облаков ( p ~ 500 мбар) со времен «Вояджера», была связана с гексагональными температурными контрастами, достигающими уровня тропопаузы Сатурна ( p ~ 80–100 мбар). ) 5 .Однако, согласно заключению исследования 12 за 2004–2014 гг., В северной полярной стратосфере не наблюдалось достаточного широтного температурного градиента (∂ T / ∂ y , где y — расстояние с севера на юг) наблюдать любой контраст, связанный со струей на 78 ° с.ш. Таким образом, это первое свидетельство того, что шестиугольник Сатурна простирается намного выше, чем считалось ранее, в стабильно стратифицированную среднюю атмосферу до уровня 0,5–5,0 мбар.
Есть ограничения на то, что нам могут сказать наблюдения CIRS.Попытка обеспечить восстановление температуры стратосферного шестиугольника с пространственным разрешением не увенчалась успехом, поскольку объединенные спектры не имели достаточного отношения сигнал / шум, чтобы ограничить гексагональную форму температурного поля как функцию высоты. Поэтому мы не можем сказать, присутствует ли шестиугольник при 5 мбар или 0,5 мбар или их комбинации. Однако данные, представленные в следующем разделе, показывают, что полосчатая структура Сатурна более четкая при 5 мбар, чем при более низких давлениях, что повышает вероятность того, что шестиугольник можно обнаружить только в нижней стратосфере ( p > 1 мбар).Кроме того, низкий сигнал в данных до 2014 года означает, что мы не можем различить сценарии, в которых шестиугольник всегда присутствует в стратосфере независимо от времени года или шестиугольник может расширяться вверх из-за сезонного изменения температуры по мере приближения летнего солнцестояния (до обсуждается ниже).
На рисунке 2 показан анализ периодограммы и попытка подогнать простую синусоидальную форму к яркостным температурам шестиугольника в 2014 и 2017 годах. Волновое число 6 четко обнаруживается как в тропосфере, так и в стратосфере, и мы обнаруживаем, что вершины шестиугольника отличаются по положению не более чем на 4 ° долготы между двумя высотами, поэтому, похоже, нет продольного смещения в схеме с высотой.Используя карты тропосферы, мы находим движение шестиугольника по часовой стрелке (на запад) со временем, равное ((9.9 ± 1.3) × 10 −3 ) ° день −1 (с использованием системы западной долготы Системы III). . Выполнение того же расчета в стратосфере дает ((7,6 ± 1,9) × 10 −3 ) ° сутки −1 , так что скорости вращения эквивалентны с точностью до неопределенностей. Учитывая, что точное определение долготы вершин ограничено низким пространственным разрешением и шумом тепловых карт, эта скорость дрейфа, вероятно, согласуется с ((12.8 ± 1,3) × 10 −3 ) ° день −1 оценка 29 по отслеживанию шестиугольника на вершине облаков в период с 2008 по 2014 год. Следовательно, шестиугольник присутствует как минимум в трех диапазонах высот, разделенных тремя декадами давление, от глубокой тропосферы 8 до тропопаузы 5 и в стратосферу, расстояние по вертикали ~ 300 км. Наконец, отметим, что вершины тропосферного шестиугольника не перемещаются со скоростью ~ 120 мс — 1 на восток верхней границы облаков струи на 78 ° с.ш., поэтому, несмотря на сильный сдвиг ветра из тропосферы в стратосферу (следующий раздел), наличие когерентной волны в обеих высотных областях, с сопряженным и очень медленным вращением, вероятно независимо от ветра.Долгосрочные изменения температуры, которые позволили шестиугольнику быть видимым в стратосфере после 2014 года, будут исследованы в следующем разделе.
Рис. 2Обнаружение шестиугольника в тропосфере и стратосфере. c — f показывают яркостные температуры и их неопределенности в тропосфере ( c , d , усредненные по 600–620 см, −1 ) и стратосфере ( e , f , усредненные по 1280 –1320 см −1 ), извлеченные из 77–79 ° с.ш. в наблюдениях REGMAP 25 июня 2014 г. и 12 февраля 2017 г., а также в наблюдении FIRMAP 18 октября 2014 г.В качестве ориентира для каждого наблюдения была подобрана синусоида волнового числа 6 (красная кривая), хотя стратосферная карта в 2014 году очень зашумлена. a , b , g , h показывают соответствующие периодограммы Ломба-Скаргла 5 , отображаемые как функцию широты, показывающие спектральную мощность, содержащуюся в каждом сканировании яркостной температуры с продольным разрешением. Черные линии на цветных полосах представляют вероятность ложного срабатывания (сверху вниз) равную 0.001, 0,01 и 0,1. Особенность волнового числа-6 отчетливо видна в каждом наборе данных около 78 ° с.ш. (вертикальная красная пунктирная линия), хотя стратосферный шестиугольник 2014 г. довольно зашумлен (рис. 1b). Используя синусоидальную аппроксимацию, мы обнаруживаем смещение на запад вершин тропосферного шестиугольника на 8,5 ± 1,1 ° за 963 дня (неопределенность зависит от качества синусоидальной аппроксимации). Смещения между вершинами тропосферы и стратосферы были <4 ° в феврале 2017 г.
Долгосрочные тренды температуры
На рисунке 3 показаны температуры, полученные для каждой широты (усреднение спектров по долготе, см. Методы) для выбора стратосферного давления в качестве функции времени.Они интерполированы на рис. 4 для отображения восстановленных температур для Северного полюса и Южного полюса для трех высот (0,5, 1,0 и 5,0 мбар) в стратосфере. Предполагая геострофический баланс (допустимое предположение для полярных широт с числами Россби <0,2 29 ), меридиональные градиенты температуры (∂ T / ∂ y , где y — расстояние с севера на юг) находятся в тепловом ветровом балансе. с вертикальным сдвигом на зональных ветрах 39 (∂ u / ∂ z , где u — зональный ветер, а z — высота).Это позволяет нам оценить сдвиг ветра ∂ u / ∂ z = — ( g / fT ) ∂ T / ∂ y , где g — ускорение свободного падения для каждой широты и высоты. и f — параметр Кориолиса. Это дает нам возможность выразить изменяющиеся меридиональные градиенты как функцию времени, где сдвиг ветра можно интерпретировать как усиление ветров восточного направления (положительный сдвиг) или западных ветров (отрицательный сдвиг), если где-то существует уровень нулевого движения. в нижней стратосфере.Тропосферные температуры и сдвиг ветра показаны на дополнительном рисунке 1.
Рис. 3Полученные значения температуры в верхней тропосфере и стратосфере из всей миссии Кассини. Температуры отображаются на пяти уровнях давления: a 0,5 мбар, b 1,1 мбар, c 2,5 мбар, d 5,0 мбар и e 110 мбар. Цвета относятся к датам, указанным в легенде. Экваториальные колебания Сатурна наблюдаются на низких широтах 58 , эффекты Великой северной бури видны на северных средних широтах 61 , а изменение стратосферной асимметрии температуры наиболее очевидно на полюсах (эта работа)
Рис. .4Градиенты температуры стратосферы северного и южного полюсов как функция времени на протяжении всей миссии Кассини, 2004–2017 гг. Мы отображаем северные полярные температуры ( a — c ), северные полярные сдвиги ветра ( d — f ), южные полярные сдвиги ветра ( g, — и ) и южные полярные температуры ( j — ). l ) при трех различных уровнях давления (0,5, 1,0 и 5,0 мбар). Они были получены из средних значений спектров CIRS низкого разрешения на месячной временной сетке и интерполированы с использованием натянутых сплайнов 43 для восстановления сглаженного температурного поля.Горизонтальные пунктирные линии обозначают пик зональных джетов восточного направления в тропосфере 9 . Данные отображаются как функция времени (годы), но вторая горизонтальная ось показывает планетоцентрическую долготу Солнца ( L с ) в градусах
Рисунок 4 позволяет нам сравнить исчезновение теплого SPSV с началом НПСВ. Теплые стратосферные полярные вихри становятся очевидными, когда с течением времени развиваются сильные градиенты температуры, усиливая отрицательный сдвиг ветра, способствуя возникновению западных ветров.Средние зональные температуры показывают широтные градиенты, которые наиболее сильны при 5 мбар, напоминающие полосчатую структуру, преобладающую в тропосфере. Эти контрасты не так очевидны при 0,5–1,0 мбар, где температуры меняются более плавно с широтой и преобладают за счет отрицательного сдвига к полюсу прогрессивных зональных струй на 78 ° северной широты и 74 ° южной широты. В начале временного ряда Кассини SPSV имел две первичные структуры: отрицательную d T / d y около 88 ° ю.ш., которая определяет край компактного полярного циклона 4 и отрицательную d T / d y в районе 74 ° ю.ш., который представляет край SPSV 5 (рис.4j – l). В 2006 г. ( L с = 320 °) температура увеличилась к Южному полюсу на всех высотах, но в 2007–2008 гг. Начала формироваться полоса холода при 5 мбар с центром на 84 ° ю. положительный сдвиг ветра на рис. 4g – j. К 2013–2014 гг. ( L с ≈ 40 °) отрицательный сдвиг на границе SPSV (74 ° ю.ш.) значительно ослаб, и начала формироваться холодная полоса около 80–85 ° ю.ш. при давлении 1 мбар, что означает кончина СПСВ. Охлаждение и рассеяние SPSV началось до равноденствия ( L с ≈ 340 °), как измерено по времени наиболее отрицательного сдвига ветра на 74 ° ю.
Широтная структура вертикального сдвига ветра в северном полушарии (рис. 4d – f) очень похожа на таковую на юге: более высокие давления демонстрируют полосчатую структуру температуры, а более низкие давления демонстрируют плавные широтные градиенты. Отрицательный сдвиг ветра преобладает к полюсу 78 ° с.ш. и p <1 мбар на протяжении всего временного ряда, поскольку температура всегда повышалась до 90 ° с.ш., несмотря на последовательность, начинающуюся полярной зимой, вопреки ожиданиям радиационных моделей климата 12,13 40 .Область положительного сдвига ветра в 5 мбар (рис. 4c, f, т. Е. Холодная полоса, отражающая полосу, образовавшуюся в SPSV) была сосредоточена на 83 ° с.ш. до 2017 г., когда она ослабла и сменилась более высокими температурами (т. Е. К концу миссии температура на уровне 5 мбар повысилась повсюду к полюсу до ~ 75 ° с.ш.). Подобные полосы положительного сдвига ветра, сосредоточенные над широкими тропосферными струями, направленными на запад, существовали на 73 ± 1 ° с.ш. и 63 ± 1 ° с.ш., но все они ослабевали по мере приближения Сатурна к солнцестоянию, что указывает на положительный градиент d T / d y на всем протяжении. северный полярный регион.В частности, температуры около 78 ° с.ш., направленной на восток струи на рис. 4a, демонстрируют усиление градиента ∂ T / ∂ y со временем, что означает развитие границы NPSV. Сдвиг ветра на этой струе изменился со слабоположительного на отрицательный при 5 мбар в 2012–2013 гг. ( L s ≈ 40 °), что могло способствовать развитию западных ветров, окружающих летний вихрь.
Однако к концу миссии около точки летнего солнцестояния ( L s = 93 °) сдвиг ветра на границе NPSV был менее половины от того, что на границе SPSV в 2006–2008 гг., И 5 мбар. температурный максимум (~ 140 К при 90 ° с.ш. на рис.4в) была все еще ниже максимальной температуры на южном полюсе (~ 150 К при 90 ° ю.ш. на рис. 4l). Таким образом, хотя NPSV развивал сильный температурный градиент с момента окончания последнего исследования CIRS северной весной 12 и зоны положительного сдвига ветра исчезли к северному лету, ему все еще не хватало контрастов, демонстрируемых SPSV во время более поздних частей южное лето. Поскольку тепловой максимум отстает от сезонного максимума инсоляции 12 , мы ожидаем, что NPSV продолжит нагреваться после северного летнего солнцестояния и окончания наблюдений Кассини.
Состав NPSV и SPSV
Хотя NPSV формировался в последние годы миссии «Кассини», температурные градиенты (и отрицательный сдвиг ветра) еще не достигли степени наблюдаемых в южном полушарии, окружающем SPSV. Это не может быть неожиданностью — северное лето произошло около афелия (17 апреля 2018 г.), тогда как южное лето было ближе к перигелию (26 июля 2003 г.), что подразумевает разницу в скорости депонирования энергии в верхних слоях атмосферы.Однако CIRS предлагает другой метод оценки сходства и различий между NPSV и SPSV путем изучения относительного усиления различных химических веществ в каждом вихре. Это требует подгонки наблюдений CIRS с высоким спектральным разрешением, которые смотрели непосредственно на каждый вихрь (см. Методы), как показано для NPSV на рис. 5.
Рис. Наблюдение NPSV с разрешением 27 марта 2017 г. (охват 84–87 ° с.ш.).На рисунке показано соответствие модели (красный цвет) данным (черные точки с серыми неопределенностями). Рисунок разделен на два спектральных диапазона, используемых в инверсиях: a 600–870 см −1 и b 1120–1370 см −1 . Обозначены ключевые газообразные компоненты. Данные между 870 и 1120 см -1 не были включены в инверсию. Неопределенности измерения (серые столбцы) зависят от количества закодированных спектров CIRS и количества эталонных спектров дальнего космоса, используемых в калибровке.Вертикальные профили температуры, этана и ацетилена были получены на основе широкого набора априорных значений (см. Методы) и показаны на рис.6 как для NPSV ( L с = 88 °), так и для SPSV ( L с = 346 °). Профили температуры сравниваются с прогнозами радиационной модели климата 13 для того же сезона, в которой предполагается неизменное во времени низкоширотное среднее значение стратосферных охладителей этана и ацетилена, полученное из наблюдений за конечностями CIRS в период с 2005 по 2008 год . В то время как северный T ( p ) согласуется с этими прогнозами для 2–100 мбар, южный T ( p ) всегда теплее, даже несмотря на максимальные стратосферные температуры ( T ~ 160 K при атмосферном давлении). 0.3–0,5 мбар) на обоих полюсах одинаковы. Это намекает на отсутствующий источник тепла в радиационной модели для нижней стратосферы в течение южного лета, который не требовался на севере на L s = 88 °, возможно, из-за стратосферных аэрозолей (радиационных) или более сильного полярного оседания ( адиабатический нагрев) 12,13,25 , причем последнее поддерживается избытком C 2 H 2 , наблюдаемым в SPSV по сравнению с NPSV в таблице 1, обсуждаемым ниже. При более низких давлениях инверсии как NPSV, так и SPSV предполагают слабую стратопаузу с понижением температуры со 160 К при 0.От 3 мбар до ~ 150 К при 0,01 мбар, что снова согласуется с радиационной моделью с присутствием полярных аэрозолей и без них 25 . Хотя это зависит от предшествующего положения и затруднено геометрией наблюдения в надире, стоит отметить, что это снижение температуры происходит даже при изотермическом предварительном 170-K. Интересно, что присутствие мезосферы над более теплой стратосферой было также выведено из наземных наблюдений IRTF южного полушария Сатурна 41 на L s = 268 °, до прибытия Кассини.
Рис. 6Вертикальные распределения температуры, ацетилена и этана, полученные по данным спектрального разрешения 0,5 см –1 для обоих полюсов. На панелях показаны COMPSIT, нацеленные на северный полюс в марте 2017 г. ( a — c , 84–87 ° с.ш.) и южный полюс в июле 2008 г. ( d — f , 83–88 ° S). В качестве отправной точки использовалась сетка из 2000 априорных атмосфер (с изменением температуры и распределения углеводородов). Красные линии указывают на профили, соответствующие спектру в пределах 1σ от наилучшего соответствия, синие линии — для 2σ, бирюзовые линии — для 3σ, а серые линии — для оптимальных оценок, которые не укладываются в конверт 3σ.Мы уверены в восстановленных профилях в диапазонах высот, где профили сходятся, независимо от априорных начальных точек. Углеводородные профили сравниваются с результатами диффузионной фотохимической модели 19 на широте ± 72 ° для L с = 88 ° (пунктирная черная линия) и L с = 346 ° (сплошная черная линия ). Профили температуры сравниваются с прогнозами или радиационной моделью климата 13 в отсутствие стратосферных аэрозолей для широты ± 85 ° и для L с = 88 ° (пунктирная черная линия) и L с = 346 ° (сплошная черная линия)
Таблица 1 Содержание газов в NPSV и SPSV при 1 мбар (ppbv) по сравнению с ожидаемым соотношением из фотохимической модели 19 для того же сезонаВертикальные профили углеводородов на рис.6, менее жестко ограничены, чем температуры, но они показывают, что данные спектрального разрешения CIRS 0,5 см -1 могут ограничивать градиент ацетилена между 0,05 и 5 мбар и градиент этана между 0,5 и 5 мбар. За пределами этих диапазонов профили расходятся и возвращаются к своим предыдущим значениям. По этой причине к содержанию при низких давлениях ( p <0,1 мбар) следует относиться с осторожностью, но есть тенденция к тому, что данные для южных полярных областей показывают хорошо перемешанные углеводороды с высотой (т.е.е. нет отклонений от однородного предшествующего уровня при низких давлениях), в то время как этан северного полюса показывает небольшое снижение с высотой, а ацетилен северного полюса показывает высотный пик около 0,01 мбар. Этан увеличивается в диапазоне 0,5–5 мбар по сравнению с ожиданиями фотохимических моделей 19,40,42 для обоих полюсов и демонстрирует несколько меньший вертикальный градиент, чем прогнозировалось. Это качественно согласуется с идеей долгоживущего фотохимического продукта, переносимого вниз через полюс.Напротив, градиент ацетилена круче, чем ожидалось из фотохимической модели, что предполагает фотохимическое истощение со скоростью, которая выше, чем адвекция вниз. Содержание ацетилена в 1 мбар хорошо согласуется на южном полюсе, но несколько снижается на северном полюсе по сравнению с прогнозами.
Минорные углеводороды
Приняв наиболее подходящие (т.е. минимальные χ 2 ) профили температуры, этана и ацетилена из рис. 6, спектры 0,5 см –1 были использованы для поиска свидетельств второстепенных видов как в NPSV, так и в SPSV путем масштабирования модельных профилей 19 каждого вида во время спектральной инверсии.На рисунке 7 показано влияние на спектры удаления частиц газа или удвоения его наиболее подходящего содержания по сравнению с неопределенностью в кодированном спектре CIRS. Изменение χ 2 , оцененное в спектральном диапазоне, показанном на каждом рисунке, дано под каждым спектром яркостной температуры. Метилацетилен и диацетилен четко обнаруживаются на обоих полюсах, тогда как обнаружение пропана, CO 2 и бензола является более незначительным, особенно в NPSV.
Рис. 7Обнаружение второстепенных видов в северных и южных полярных вихрях Сатурна. NPSV наблюдалась в марте 2017 г. ( a — e ), SPSV наблюдалась в июле 2008 г. ( f — j ) с использованием тех же данных, что и на рис. 6. Показаны пять второстепенных видов: пропан ( a , f ), диацетилен ( b , г ), метилацетилен ( c , h ), диоксид углерода ( d , i ) и бензол ( e , j ).После того, как были установлены наиболее подходящие атмосферные профили (температуры и углеводороды), мы масштабировали численность пяти второстепенных видов в 0,0 (черный), 1,0 (красный) и 2,0 (синий) раз, чтобы показать их обнаруживаемость в спектре. Для каждой панели и газообразных веществ мы показываем спектр яркостной температуры и его неопределенность, а также разностный спектр между данными и моделью. Степень согласия сообщается для каждой модели, где Δ χ 2 > 1 означает обнаружение 1σ
Полученные значения численности записаны в Таблице 1 и показывают, что соотношение численностей NPSV и SPSV всегда равно <1, вопреки ожиданиям фотохимической модели 19 для того же сезона.Это является еще одним свидетельством того, что NPSV не был таким зрелым, как SPSV, если рассматривать его в период летнего солнцестояния в северной части страны. Только этан и бензол имеют содержание, которое соответствует обоим полюсам (хотя и с наибольшей неопределенностью), тогда как все другие виды менее многочисленны на 20–60% на севере по сравнению с югом. Неопределенности мольных долей в Таблице 1 представляют собой неопределенности масштабного фактора для предшествующего содержания — пропан и диацетилен превышают ожидания фотохимической модели 19 , метилацетилен близок к ожиданиям, а CO 2 и бензола меньше чем ожидания.То, что бензол составляет 0,6–0,8 × <1 мбар по фотохимическим предсказаниям на полюсах, согласуется с предыдущими выводами, полученными с использованием зондирования конечностей спектров CIRS 25 . Тем не менее, измеренное соотношение отклоняется от модельного отношения 19 практически для всех, кроме этана и бензола.
Может быть слабая тенденция с продолжительностью жизни фотохимических частиц 18 , причем более долгоживущие этан и пропан демонстрируют наибольшее сходство между полюсами (отношения 0,7–1,0) и более короткоживущие ацетилен, диацетилен и метил. ацетилен показывает большие контрасты (0.2–0,6). Это имеет смысл, если более короткоживущие виды более чувствительны к динамическим и химическим изменениям, связанным с образованием полярных вихрей, хотя этот качественный взгляд игнорирует любые потенциальные обратные связи между динамикой, химией и радиационным охлаждением в вихрях. Задача будущих сезонных фотохимических моделей состоит в том, чтобы воспроизвести наблюдаемые градиенты путем лучшего ограничения скорости вертикального и горизонтального смешивания.
Распределение химикатов в пределах NPSV
Несмотря на строгие ограничения на численность, обеспечиваемые 0.5-см −1 CIRS, им не хватает пространственного покрытия для отслеживания широтных изменений этих видов. Компромисс заключается в рассмотрении изменений только температуры, этана и ацетилена с использованием наблюдений REGMAP с разрешением 2,5 см –1 . Априорные значения северных полярностей (рис. 6a – c) использовались в качестве отправной точки для извлечения данных с разрешением по широте в период с 2013 по 2017 г., показанных на рис. 8. Эти цифры подтверждают тенденции потепления, описанные выше, и показывают разницу между p <1 мбар. , где градиенты ∂ T / ∂ y относительно плавные с широтой, а p > 2 мбар, где видна полосатая структура, которая типична для тропосферы.Северный полярный циклон легко наблюдается во все даты, поскольку резкий рост температуры в пределах 3 ° от полюса для p > 1 мбар, но не очевиден для p <1 мбар. Градиенты температуры 2,5, 5 и 10 мбар особенно сильны на широте гексагональной струи на 78 ° с.ш., поэтому стратосферный шестиугольник легко появляется на рис. 1.
Рис. 8Зональное среднее. северные полярные температуры для трех наборов данных REGMAP, показывающих потепление полярной стратосферы.Температуры отображаются на шести уровнях давления: a 0,5 мбар, b 1,1 мбар, c 2,5 мбар, d 5,0 мбар, e 11 мбар и f 110 мбар. В каждую панель включены три даты: 17 августа 2013 г. (черный, REGMAP 196 — 001), 25 июня 2014 г. (синий, REGMAP 205 — 001) и 12 февраля 2017 г. (красный, REGMAP 261 — 003) . Вертикальные пунктирные линии показывают положение пиков прямой струи 9 для сравнения с меридиональными градиентами температуры.Планки погрешностей представляют формальную неопределенность поиска. Обратите внимание, что набор данных за июнь 2014 г. использовал спектры разрешения 15 см –1 , тогда как наборы данных 2013 и 2017 гг. Лучше ограничены спектрами разрешения –1 2,5 см
Распределение ацетилена и этана на уровне 1 мбар при Северный полюс для тех же трех дат показан на рис. 9a, b и был получен путем масштабирования наиболее подходящих вертикальных профилей на рис. 6. Мы предупреждаем читателя, что эти простые вычисления априорных содержаний газа пропустят любые изменения в вертикальных градиентах углеводородов, которые в настоящем исследовании считаются неизменными.Они сравниваются с содержаниями 1 мбар на обоих полюсах, полученными из инверсий низкого разрешения, которые были сглажены и интерполированы с помощью натянутого сплайна 12,43 . C 2 H 2 показывает минимум около 75 ° с.ш. и увеличивается по направлению к полюсам в ~ 2 раза (рис. 9c), аналогично тому, что видно к полюсу от 75 ° ю.ш., когда присутствовала SPSV (рис. 9e. ). Однако, хотя в период с 2013 по 2014 год изменений не было, к 2017 году произошло неожиданное падение C 2 H 2 , что противоречит тенденции до 2014 года: 12 .Это уменьшение видно в инверсиях на 2,5 см –1 и 15 см –1 , предполагая, что численность C 2 H 2 достигла пика перед летним солнцестоянием. Однако сравнение с SPSV предполагает, что NPSV не достигла такой же повышенной численности в течение этого временного ряда, как показано в Таблице 1.
Рис. 9Временная эволюция полярных этана и ацетилена. Широтные распределения ацетилена a и этана b при 1 мбар, полученные из спектров 17 августа 2013 г. (черный, REGMAP 196 — 001), 25 июня 2014 г. (синий, REGMAP 205 — 001) и 12 февраля 2017 г. (красный, REGMAP 261 — 003).Эти результаты получены в результате масштабирования профилей углеводородов, полученных для северного полюса из наблюдений с разрешением 0,5 см –1 , одновременно с восстановлением профилей температуры на рис. 8. Неопределенности этих восстановленных масштабных коэффициентов показаны для каждого из них. точка данных. Четыре контурных графика показывают сплайн-интерполированные результаты для c севернополярного ацетилена, d северного полярного этана, e южнополярного ацетилена и f южнополярного этана из временного ряда низкого разрешения на рис.4. Пунктирными / пунктирными линиями показаны положения прямых пиков струи 9 на всех шести панелях
Распределение C 2 H 6 отличается, показывая общий рост в северном полушарии и потенциальный всплеск в численность к полюсу 86 ° с.ш. (рис. 9b), хотя это не видно во временных рядах с низким разрешением (рис. 9d). Подобный высокоширотный пик этана мог присутствовать в центре SPSV в начале миссии Кассини (рис. 9f). Таким образом, как C 2 H 2 , так и C 2 H 6 увеличиваются к полюсу от границы NPSV на 78 ° с.ш., аналогично химическому усилению, наблюдаемому в SPSV в начале миссии Кассини.Такое увеличение не наблюдается в фотохимических моделях, в которых отсутствуют меридиональные движения 19,42 , и является дополнительным свидетельством того, что проседание происходит по всему NPSV, вызывая потепление и повышенное содержание химических веществ 30 . Основываясь на записях SPSV, мы ожидаем, что эти полярные усиления начнут снижаться после летнего солнцестояния ( L s = 90 °). Однако мы предупреждаем, что химия ионов в авроральных областях, которая также может модулировать содержание углеводородов, еще требует детального изучения.
Определение шестиугольника на Dictionary.com
[hek-suh-gon, -guhn] SHOW IPA
/ ˈhɛk səˌgɒn, -gən / PHONETIC RESPELLING
существительное
многоугольник, имеющий шесть углов и шесть сторон.
ВОПРОСЫ
ДУМАЕТЕ, ЧТО У ВАС ПОЛУЧИТСЯ РУКОВОДСТВО ПО ЭТОЙ ВИКТОРИНЕ НА ИМЕНИ ДЛЯ ГОСУДАРСТВЕННЫХ СРЕДСТВ США?
Вы когда-нибудь собирали все эти государственные кварталы? Используйте их с пользой в этой викторине, посвященной любопытным государственным прозвищам и фактам, которые их окружают.
Вопрос 1 из 8
Прозвище Миссисипи происходит от великолепных деревьев, которые там растут.Что это?
Происхождение шестиугольника
От греческого слова hexágōnon, восходящего к 1560–1570 годам. См. Гекса-, -гонСлова рядом с шестиугольником
гексадекановая кислота, шестнадцатеричный, гексаэмерон, гексаэтилтетрафосфат, гексафторид, гексагон, гексагональ, гексаграмма, гексаэдр, гексагидрат, гексагидрическийDictionary.com Unabridged На основе Несокращенного словаря Random House, © Random House, Inc. 2021
Примеры предложений из Интернета для шестиугольника
.expandable-content {display: none;}.css-12x6sdt.expandable.content-extended> .expandable-content {display: block;}]]> СМОТРЕТЬ БОЛЬШЕ ПРИМЕРОВ СМОТРЕТЬ МЕНЬШЕ ПРИМЕРОВ
Изучить Dictionary.com
li {-webkit-flex- основа: 49%; — ms-flex-предпочтительный размер: 49%; гибкая основа: 49%;} @ media only screen и (max-width: 769px) {. css-2jtp0r> li {-webkit-flex- основа: 49%; — ms-flex-предпочтительный-размер: 49%; гибкая-основа: 49%;}} @ media only screen и (max-width: 480px) {. css-2jtp0r> li {-webkit-flex -basis: 100%; — ms-flex-предпочтительный-размер: 100%; flex-base: 100%;}}]]>Определения шестиугольника в Британском словаре
существительное
многоугольник с шестью сторонами
Коллинза Английский словарь — полное и несокращенное цифровое издание 2012 г. © William Collins Sons & Co.Ltd. 1979, 1986 © HarperCollins Издатели 1998, 2000, 2003, 2005, 2006, 2007, 2009, 2012
Научные определения шестиугольника
Многоугольник, имеющий шесть сторон.
Научный словарь американского наследия® Авторские права © 2011. Издано издательской компанией Houghton Mifflin Harcourt Publishing Company. Все права защищены.
Культурные определения шестиугольника
Новый словарь культурной грамотности, третье издание Авторские права © 2005 издательской компании Houghton Mifflin Harcourt.Опубликовано Houghton Mifflin Harcourt Publishing Company. Все права защищены.
Прочие — это Readingli {-webkit-flex-base: 100%; — ms-flex-предпочтительный размер: 100%; flex-base: 100%;} @ media only screen и (max-width: 769px) {. Css -1uttx60> li {-webkit-flex-base: 100%; — ms-flex-предпочтительный-размер: 100%; flex-base: 100%;}} @ экран только мультимедиа и (max-width: 480px) {. css-1uttx60> li {-webkit-flex-base: 100%; — ms-flex-предпочтительный-размер: 100%; flex-base: 100%;}}]]>правильный шестиугольник — это шестигранная фигура со всеми сторонами равными и всеми шестью углами.
Ты С.
задано • 04.09.18правильный шестиугольник — это шестигранная фигура, у которой все стороны равны и все шесть углов равны. найти длину сторон, если периметр правильного шестиугольника составляет 360 дюймов.
Более
Привет, Тай.
Поскольку все 6 сторон имеют одинаковую длину, назовем длину сторон X
P = 6X = 360
X = 60 дюймов
Все еще ищете помощь? Получите правильный ответ быстро.
ИЛИ
Найдите онлайн-репетитора сейчасВыберите эксперта и познакомьтесь онлайн.Никаких пакетов или подписок, платите только за необходимое время.
¢ € £ ¥ ‰ µ · • § ¶ SS ‹ › « » < > ≤ ≥ — — ¯ ‾ ¤ ¦ ¨ ¡ ¿ ˆ ˜ ° — ± ÷ ⁄ × ƒ ∫ ∑ ∞ √ ∼ ≅ ≈ ≠ ≡ ∈ ∉ ∋ ∏ ∧ ∨ ¬ ∩ ∪ ∂ ∀ ∃ ∅ ∇ * ∝ ∠ ´ ¸ ª º † ‡ А Á Â Ã Ä Å Æ Ç È É Ê Ë Я Я Я Я Ð Ñ Ò Ó Ô Õ Ö Ø Œ Š Ù Ú Û Ü Ý Ÿ Þ à á â ã ä å æ ç è é ê ë я я я я ð ñ ò ó ô х ö ø œ š ù ú û ü ý þ ÿ Α Β Γ Δ Ε Ζ Η Θ Ι Κ Λ Μ Ν Ξ Ο Π Ρ Σ Τ Υ Φ Χ Ψ Ω α β γ δ ε ζ η θ ι κ λ μ ν ξ ο π ρ ς σ τ υ φ χ ψ ω ℵ ϖ ℜ ϒ ℘ ℑ ← ↑ → ↓ ↔ ↵ ⇐ ⇑ ⇒ ⇓ ⇔ ∴ ⊂ ⊃ ⊄ ⊆ ⊇ ⊕ ⊗ ⊥ ⋅ ⌈ ⌉ ⌊ ⌋ 〈 〉 ◊Шестиугольник Сатурна в движении | Сатурн — НАСА Исследование солнечной системы
Этот красочный вид из миссии НАСА «Кассини» представляет собой снимок с высочайшим разрешением уникального шестигранного реактивного потока на северном полюсе Сатурна, известного как «шестиугольник».«Этот фильм, созданный из изображений, полученных с помощью фотоаппаратов« Кассини », является первым фильмом, в котором показан шестиугольник в цветных фильтрах, и первым фильмом, в котором показан полный вид от северного полюса до примерно 70 градусов северной широты.
В этом фильме ученые могут увидеть движение множества облачных структур, находящихся внутри шестиугольника. На северном полюсе находится мощный ураган с глазом примерно в 50 раз больше, чем средний ураган на Земле. (Более подробная информация об урагане Сатурн находится на PIA14947.) Также присутствуют многочисленные маленькие вихри, которые выглядят как красноватые овалы. Некоторые из этих вихрей вращаются по часовой стрелке, в то время как шестиугольник и ураган вращаются против часовой стрелки. Некоторые из этих мелких деталей уносятся струей шестиугольника, как на гоночной трассе. Самый большой из этих вихрей, видимый около правого нижнего угла шестиугольника и кажущийся беловатым, охватывает около 2200 миль (3500 километров), что примерно вдвое превышает размер самого большого урагана на Земле.
Шестиугольник — это просто поток воздуха, и погодные условия, которые имеют с ним сходство, заведомо турбулентны и нестабильны.Ураган на Земле обычно длится неделю, но он длится десятилетия — и кто знает — может быть, столетия.
— Эндрю Ингерсолл, группа обработки изображений CassiniРазличия в этой версии фильма, в которой разные длины волн света от ультрафиолетового до видимого и инфракрасного были присвоены цвета, показывают отчетливый контраст между типами атмосферных частиц внутри и вне шестиугольника. Внутри шестиугольника меньше крупных частиц дымки и концентрация мелких частиц дымки, а за пределами шестиугольника все наоборот.Реактивная струя, составляющая шестиугольник, кажется, действует как преграда, что приводит к чему-то вроде «озоновой дыры» в Антарктике.
В этом фильме показан вид прямо над северным полюсом, идущий в ногу с вращением планеты, так что все движения, видимые на экране, являются движением шестиугольного реактивного потока или штормов внутри него, без каких-либо дополнительных движений от вращение самой планеты. Исходные изображения были повторно спроецированы, чтобы показать этот полярный вид.
Виды шестиугольника с высоким разрешением стали возможны только недавно из-за смены времен года на Сатурне и изменений орбиты космического корабля Кассини.Когда «Кассини» впервые прибыл в июле 2004 года, на северный полюс было темно. Солнце действительно начало освещать всю внутреннюю часть шестиугольника только в августе 2009 года, с началом северной весны. В конце 2012 года «Кассини» начал совершать колебания над полюсами Сатурна, улучшая вид на шестиугольник.
Восемь кадров фильма были сняты за 10 часов 10 декабря 2012 года. Каждый из восьми кадров состоит из 16 проецируемых на карту изображений (четыре на каждый цветовой фильтр и четыре фильтра на кадр), поэтому фильм объединяет данные из 128 всего изображений.
В этой цветовой схеме ученые отнесли красный к 0,750-микронной части светового спектра (ближний инфракрасный). Эта часть спектра проникает через слой высокогорной дымки, чтобы ощутить верхнюю часть слоя тропосферных облаков. Они приписали зеленый цвет 0,727-микронной части светового спектра, которая воспринимает верхнюю тропосферную дымку (длина волны в ближнем инфракрасном диапазоне, соответствующая полосе поглощения метана). Они присвоили синий цвет сумме синего и ультрафиолетового широкополосных фильтров — вместе взятых, этот синий канал покрывает между 0.400 и 0,500 микрон (покрытие от очень близкого ультрафиолета до синего в видимом свете). Эта часть спектра чувствительна к мелким аэрозолям.
Человеческому глазу шестиугольник и северный полюс кажутся золотыми и синими. См. PIA14945 для неподвижного изображения области в естественных цветах.
Черно-белая версия фильма Кассини «Гексагон».Почему шестиугольники? —ArcGIS Pro | Документация
Агрегирование данных точек инцидента в сетки правильной формы используется по многим причинам, например, для нормализации географии для картирования или для смягчения проблем, связанных с использованием неправильной формы. произвольно созданные полигоны (например, границы округов или группы блоков, которые были созданы в результате политического процесса).Сетки правильной формы могут состоять только из равносторонних треугольники, квадраты или шестиугольники, так как эти три формы многоугольника — единственные три, которые могут быть мозаичными (повторение одной и той же формы снова и снова, край к краю, чтобы покрыть область без промежутков или перекрытий), чтобы создать равномерно распределенная сетка.
Хотя квадратная сетка (сетка-сетка) является преимущественно используемым типом формы в ГИС-анализе и тематическом картировании, существуют способы, которыми шестиугольники могут быть лучше подходят для вашего анализа в зависимости от характера вашего вопроса.
Причины, по которым следует рассмотреть возможность объединения в шестиугольную сетку, следующие:
- Шестиугольники уменьшают смещение выборки из-за краевых эффектов формы сетки, это связано с низким отношением периметра к площади формы шестиугольника. У круга самый низкий коэффициент, но он не может разбиваться на мозаику, чтобы сформировать непрерывную сетку. Шестиугольники — это многоугольники наиболее круглой формы, которые можно разбить на мозаику, чтобы сформировать равномерно распределенную сетку.
- Эта округлость шестиугольной сетки позволяет отображать кривые в шаблонах ваших данных более естественно, чем квадратные сетки.
- При сравнении многоугольников с равными площадями, чем больше похож на круг многоугольник, тем ближе к центроиду точки около границы (особенно точки около вершин). Это означает, что любая точка внутри шестиугольника ближе к центроиду шестиугольника, чем любая заданная точка в квадрате или треугольнике равной площади (это связано с более острыми углами квадрата и треугольника по сравнению с шестиугольником).
- Шестиугольники предпочтительнее, если ваш анализ включает аспекты связности или путей движения.

 circ) :
circ) :

 Мало того, что поверхностное натяжение тут не играет особой роли, но к тому же ясно, что у разных видов ос разные врожденные инстинкты с точки зрения архитектурных решений: они могут значительно различаться.
Мало того, что поверхностное натяжение тут не играет особой роли, но к тому же ясно, что у разных видов ос разные врожденные инстинкты с точки зрения архитектурных решений: они могут значительно различаться.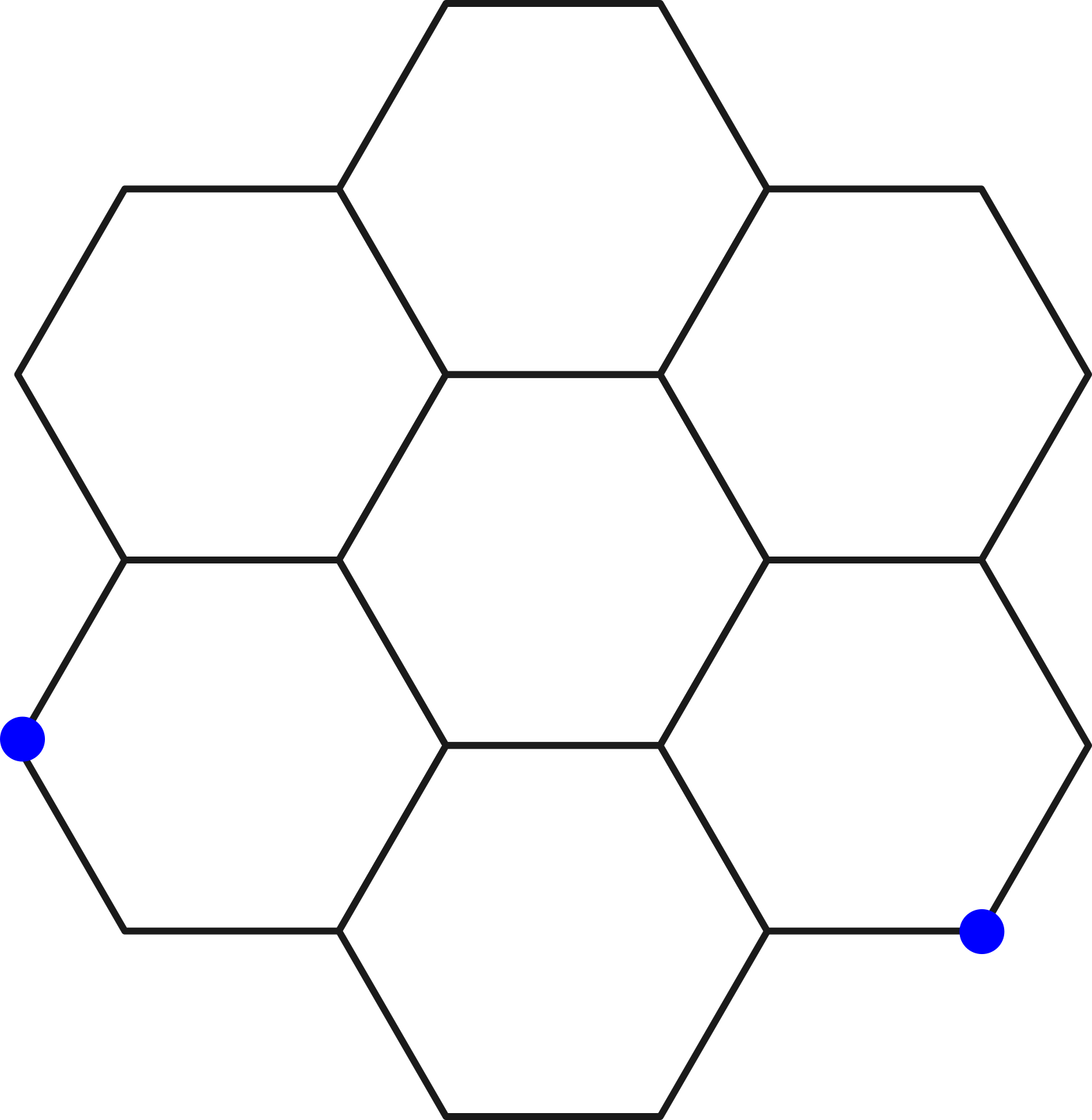 Даже в случае мух-мутантов, у которых таких клеток больше, можно говорить о том, что их организация более-менее идентична поведению пузырей.
Даже в случае мух-мутантов, у которых таких клеток больше, можно говорить о том, что их организация более-менее идентична поведению пузырей. Может быть, они отделяют один биохимический процесс от другого, упраздняя их взаимное влияние друг на друга. Или, возможно, они просто эффективны в качестве «рабочей поверхности», поскольку многие биохимические процессы протекают на мембранах, где могут находиться ферменты и другие активные молекулы. Каковы бы ни были функции таких лабиринтов, вам не понадобятся сложные генетические инструкции для их строительства: законы физики сделают все за вас.
Может быть, они отделяют один биохимический процесс от другого, упраздняя их взаимное влияние друг на друга. Или, возможно, они просто эффективны в качестве «рабочей поверхности», поскольку многие биохимические процессы протекают на мембранах, где могут находиться ферменты и другие активные молекулы. Каковы бы ни были функции таких лабиринтов, вам не понадобятся сложные генетические инструкции для их строительства: законы физики сделают все за вас. Проще говоря, шестиугольник знает, что нужно делать, и умеет эффективно выстроить свой менеджмент.
Проще говоря, шестиугольник знает, что нужно делать, и умеет эффективно выстроить свой менеджмент. Муравьи, термиты, осы, пчелы, шершни расширяют свой ареал по одному и тому же «строительному генплану». И если вы встанете у них на пути, то, скорее всего, вас заставят ретироваться. Либо придется принять вызов и приступить к активным контрмерам. Третьего, увы, не дано. Правда, в бизнесе и политике есть еще третий вариант, а именно – инкорпорироваться в множащуюся структуру. Стать ее частью, филиалом и безоговорочно принять правила игры корпорации. Тем самым получив надежную «крышу» и гарантию того, что тонуть в случае чего придется всем «титаником». У шестиугольника неважно с адаптацией к внешней среде. Это уж точно не ромб. Изменять свою структуру он никак не желает. Приходится применять иную глобальную стратегию выживания. Чтобы предвидеть будущее, его надо создать однотипным и сделать управляемым. Что шестиугольник активно и претворяет в жизнь. Зачастую в нашей цивилизации это очень даже неплохо получается. Хотя все же бывают досадные сбои. Даже идеальный план не может учесть все факторы. И уж тем более, когда имеешь дело со временем, пространством и бытием в его сущности. Хотя, все мировые религии довольно устойчиво процветают многие и многие века. Чем не удачное клонирование некой парадигмы? Современный бизнес таким устойчивым долголетием похвастаться не может. Другие темпы и другие правила эволюции. Для мощных корпоративных структур в том числе.
Муравьи, термиты, осы, пчелы, шершни расширяют свой ареал по одному и тому же «строительному генплану». И если вы встанете у них на пути, то, скорее всего, вас заставят ретироваться. Либо придется принять вызов и приступить к активным контрмерам. Третьего, увы, не дано. Правда, в бизнесе и политике есть еще третий вариант, а именно – инкорпорироваться в множащуюся структуру. Стать ее частью, филиалом и безоговорочно принять правила игры корпорации. Тем самым получив надежную «крышу» и гарантию того, что тонуть в случае чего придется всем «титаником». У шестиугольника неважно с адаптацией к внешней среде. Это уж точно не ромб. Изменять свою структуру он никак не желает. Приходится применять иную глобальную стратегию выживания. Чтобы предвидеть будущее, его надо создать однотипным и сделать управляемым. Что шестиугольник активно и претворяет в жизнь. Зачастую в нашей цивилизации это очень даже неплохо получается. Хотя все же бывают досадные сбои. Даже идеальный план не может учесть все факторы. И уж тем более, когда имеешь дело со временем, пространством и бытием в его сущности. Хотя, все мировые религии довольно устойчиво процветают многие и многие века. Чем не удачное клонирование некой парадигмы? Современный бизнес таким устойчивым долголетием похвастаться не может. Другие темпы и другие правила эволюции. Для мощных корпоративных структур в том числе.