Расчет уголка на изгиб онлайн: Строительные калькуляторы

Расчет балки на прогиб

Однопролетные балки на двух шарнирных опорах
1	Расчет балки на двух шарнирных опорах при одной сосредоточенной нагрузке	Смотреть расчет
2	Расчет балки на двух шарнирных опорах при двух сосредоточенных нагрузках	Смотреть расчет
3	Расчет балки на двух шарнирных опорах при одной равномерно-распределенной нагрузке	Смотреть расчет
4	Расчет балки на двух шарнирных опорах при одной неравномерно-распределенной нагрузке	Смотреть расчет
5	Расчет балки на двух шарнирных опорах при действии изгибающего момента	Смотреть расчет
Балки с жестким защемлением на двух опорах
6	Расчет балки с жестким защемлением на опорах при одной сосредоточенной нагрузке	Смотреть расчет
7	Расчет балки с жестким защемлением на опорах при двух сосредоточенных нагрузках	Смотреть расчет
8	Расчет балки с жестким защемлением на опорах при одной равномерно-распределенной нагрузке	Смотреть расчет
9	Расчет балки с жестким защемлением на опорах при одной неравномерно-распределенной нагрузке	Смотреть расчет
10	Расчет балки с жестким защемлением на опорах при действии изгибающего момента	Смотреть расчет
Балки с жестким защемлением на одной опоре (консольные)
11	Расчет однопролетной балки с жестким защемлением на одной опоре при одной сосредоточенной нагрузке	Смотреть расчет
12	Расчет однопролетной балки с жестким защемлением на одной опоре при одной равномерно-распределенной нагрузке	Смотреть расчет
13	Расчет однопролетной балки с жестким защемлением на одной опоре при одной неравномерно-распределенной нагрузке	Смотреть расчет
14	Расчет однопролетной балки с жестким защемлением на одной опоре при действии изгибающего момента	Смотреть расчет
Балки двухпролетные
15	Расчет двухпролетной с шарнирными опорами при одной сосредоточенной нагрузке	Смотреть
16	Расчет двухпролетной с шарнирными опорами при двух сосредоточенных нагрузках	Смотреть
17	Расчет двухпролетной с шарнирными опорами при одной равномерно-распределенной нагрузке	Смотреть
18	Расчет двухпролетной с шарнирными опорами при одной неравномерно-распределенной нагрузке	Смотреть
19	Расчет двухпролетной с шарнирными опорами при одной неравномерно-распределенной нагрузке	Смотреть

Вес уголка – калькулятор, таблицы

Как рассчитать вес уголка по его размерам?

Формула для расчета одного погонного метра металлического уголка:

P = ((A + B — t) × t + (1 — π4) × (r_внутр.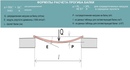 ² — 2 × r_внеш.²)) × ρ

А – ширина большей полки, мм;
B – ширина меньшей полки, мм;
t – толщина полки, мм;
r_внутр. – радиус внутреннего закругления, мм;

r_внеш. – радиус внешнего закругления, мм;
ρ – плотность металла;

Для упрощения расчетов внешним и внутренним радиусами можно пренебречь, тогда формула примет вид:

P = ((A + B — t) × t + (1 — π4)) × ρ

Таблицы размеров и веса стальных уголков

Уголки стальные горячекатаные равнополочные (ГОСТ 8509-93)

Наименование уголка	Сторона 1, a	Сторона 2, b	Толщина полки, t	Вес метра, кг	Метров в тонне
20×3	20	20	3	0. 89	1123.6
20×4	20	20	4	1.15	869.57
25×3	25	25	3	1.12	892.86
25×4	25	25	4	1.46	684.93
25×5	25	25	5	1.78	561.8
28×3	28	28	3	1. 27	787.4
30×3	30	30	3	1.36	735.29
30×4	30	30	4	1.78	561.8
30×5	30	30	5	2.18	458.72
32×3	32	32	3	1.46	684.93
32×4	32	32	4	1. 91	523.56
35×3	35	35	3	1.6	625
35×4	35	35	4	2.1	476.19
35×5	35	35	5	2.58	387.6
40×3	40	40	3	1.85	540.54
40×4	40	40	4	2. 42	413.22
40×5	40	40	5	2.98	335.57
40×6	40	40	6	3.52	284.09
45×3	45	45	3	2.08	480.77
45×4	45	45	4	2.73	366.3
45×5	45	45	5	3. 37	296.74
45×6	45	45	6	3.99	250.63
50×3	50	50	3	2.32	431.03
50×4	50	50	4	3.05	327.87
50×5	50	50	5	3.77	265.25
50×6	50	50	6	4. 47	223.71
50×7	50	50	7	5.15	194.17
50×8	50	50	8	5.82	171.82
56×4	56	56	4	3.44	290.7
56×5	56	56	5	4.25	235.29
60×4	60	60	4	3. 71	269.54
60×5	60	60	5	4.58	218.34
60×6	60	60	6	5.43	184.16
60×8	60	60	8	7.1	140.85
60×0	60	60	10	8.7	114.94
63×4	63	63	4	3. 9	256.41
63×5	63	63	5	4.81	207.9
63×6	63	63	6	5.72	174.83
65×6	65	65	6	5.91	169.2
65×8	65	65	8	7.73	129.37
70×4	70	70	4	4. 87	205.34
70×5	70	70	5	5.38	185.87
70×6	70	70	6	6.39	156.49
70×7	70	70	7	7.39	135.32
70×8	70	70	8	8.37	119.47
70×0	70	70	10	10. 29	97.18
75×5	75	75	5	5.8	172.41
75×6	75	75	6	6.89	145.14
75×7	75	75	7	7.96	125.63
75×8	75	75	8	9.02	110.86
75×9	75	75	9	10. 07	99.3
80×5	80	80	5	6.78	147.49
80×6	80	80	6	7.36	135.87
80×7	80	80	7	8.51	117.51
80×8	80	80	8	9.65	103.63
80×10	80	80	10	11. 88	84.18
80×12	80	80	12	14.05	71.17
90×6	90	90	6	8.33	120.05
90×7	90	90	7	9.64	103.73
90×8	90	90	8	10.93	91.49
90×9	90	90	9	12. 2	81.97
90×10	90	90	10	13.48	74.18
90×12	90	90	12	15.96	62.66
100×6.5	100	100	6	10.06	99.4
100×7	100	100	7	10.79	92.68
100×8	100	100	8	12. 25	81.63
100×10	100	100	10	15.1	66.23
100×12	100	100	12	17.9	55.87
100×14	100	100	14	20.63	48.47
100×15	100	100	15	21.97	45.52
100×16	100	100	16	23. 3	42.92
110×7	110	110	7	11.89	84.1
110×8	110	110	8	13.5	74.07
120×8	120	120	8	14.76	67.75
120×10	120	120	10	18.24	54.82
120×12	120	120	12	21. 67	46.15
120×15	120	120	15	26.68	37.48
125×8	125	125	8	15.46	64.68
125×9	125	125	9	17.3	57.8
125×10	125	125	10	19.1	52.36
125×12	125	125	12	22. 68	44.09
125×14	125	125	14	26.2	38.17
125×16	125	125	16	29.65	33.73
140×9	140	140	9	19.41	51.52
140×10	140	140	10	21.45	46.62
140×12	140	140	12	25. 5	39.22
150×10	150	150	10	23.02	43.44
150×12	150	150	12	27.39	36.51
150×15	150	150	15	33.82	29.57
150×18	150	150	18	40.11	24.93
160×10	160	160	10	24. 67	40.54
160×11	160	160	11	27.02	37.01
160×12	160	160	12	28.35	35.27
160×14	160	160	14	33.97	29.44
160×16	160	160	16	38.52	25.96
160×18	160	160	18	43.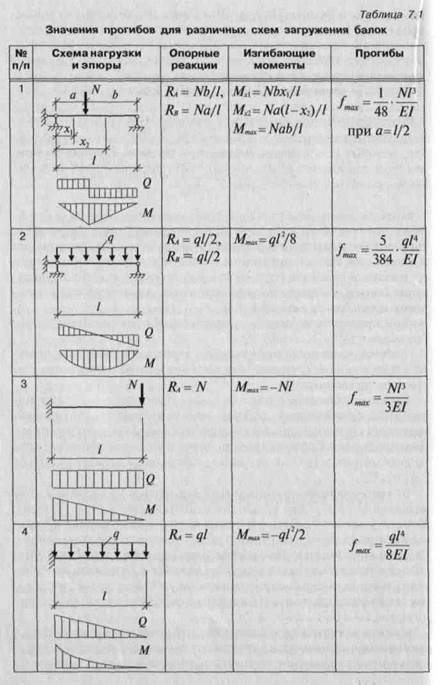 01	23.25
160×20	160	160	20	47.44	21.08
180×11	180	180	11	30.47	32.82
180×12	180	180	12	33.12	30.19
180×15	180	180	15	40.96	24.41
180×18	180	180	18	48. 66	20.55
180×20	180	180	20	53.72	18.62
200×12	200	200	12	36.97	27.05
200×13	200	200	13	39.92	25.05
200×14	200	200	14	42.8	23.36
200×16	200	200	16	48. 65	20.55
200×18	200	200	18	54.4	18.38
200×20	200	200	20	60.08	16.64
200×24	200	200	24	71.26	14.03
200×25	200	200	25	74.02	13.51
200×30	200	200	30	87. 56	11.42
220×14	220	220	14	47.4	21.1
220×16	220	220	16	53.83	18.58
250×16	250	250	16	61.55	16.25
250×18	250	250	18	68.86	14.52
250×20	250	250	20	76. 11	13.14
250×22	250	250	22	83.31	12
250×25	250	250	25	93.97	10.64
250×28	250	250	28	104.5	9.57
250×30	250	250	30	111.44	8.97
250×35	250	250	35	128. 51	7.78

Уголки стальные горячекатаные неравнополочные (ГОСТ 8510-86)

Наименование уголка	Сторона 1, a	Сторона 2, b	Толщина полки, t	Вес метра, кг	Метров в тонне
25×16×3	25	16	3	0.91	1098.9
30×20×3	30	20	3	1.12	892.86
30×20×4	30	20	4	1.45	689. 66
32×20×3	32	20	3	1.17	854.7
32×20×4	32	20	4	1.52	657.89
40×25×3	40	25	3	1.48	675.68
40×25×4	40	25	4	1.94	515.46
40×25×5	40	25	5	2.37	421. 94
40×30×4	40	30	4	2.26	442.48
40×30×5	40	30	5	2.46	406.5
45×28×3	45	28	3	1.68	595.24
45×28×4	45	28	4	2.2	454.55
50×32×3	50	32	3	1.9	526.32
50×32×4	50	32	4	2.4	416.67
56×36×4	56	36	4	2.81	355.87
56×36×5	56	36	5	3.46	289.02
63×40×4	63	40	4	3.17	315.46
63×40×5	63	40	5	3.91	255.75
63×40×6	63	40	6	4.63	215.98
63×40×8	63	40	8	6.03	165.84
65×50×5	65	50	5	4.36	229.36
65×50×6	65	50	6	5.18	193.05
65×50×7	65	50	7	5.93	168.63
65×50×8	65	50	8	6.77	147.71
70×45×5	70	45	5	4.3	232.56
75×60×5	75	60	5	4.79	208.77
75×60×6	75	60	6	5.69	175.75
75×60×7	75	60	7	6.57	152.21
75×60×8	75	60	8	7.43	134.59
80×50×5	80	50	5	4.49	222.72
80×50×6	80	50	6	5.92	168.92
80×60×6	80	60	6	6.39	156.49
80×60×7	80	60	7	7.39	135.32
80×60×8	80	60	8	8.37	119.47
90×56×5	90	56	5	6.17	162.07
90×56×6	90	56	6	6.7	149.25
90×56×8	90	56	8	8.77	114.03
100×63×6	100	63	6	7.53	132.8
100×63×7	100	63	7	8.7	114.94
100×63×8	100	63	8	9.87	101.32
100×63×10	100	63	10	12.14	82.37
100×65×7	100	65	7	8.81	113.51
100×65×8	100	65	8	9.99	100.1
100×65×10	100	65	10	12.3	81.3
110×70×6	110	70	6	8.98	111.36
110×70×8	110	70	8	10.93	91.49
125×80×7	125	80	7	11.04	90.58
125×80×8	125	80	8	12.58	79.49
125×80×10	125	80	10	15.47	64.64
125×80×12	125	80	12	18.34	54.53
140×90×8	140	90	8	14.13	70.77
140×90×10	140	90	10	17.46	57.27
160×100×9	160	100	9	17.96	55.68
160×100×10	160	100	10	19.85	50.38
160×100×12	160	100	12	23.58	42.41
160×100×14	160	100	14	27.26	36.68
180×110×10	180	110	10	22.2	45.05
180×110×12	180	110	12	26.4	37.88
200×125×11	200	125	11	27.37	36.54
200×125×12	200	125	12	29.74	33.62
200×125×14	200	125	14	34.43	29.04
200×125×16	200	125	16	39.07	25.6

Стальной уголок представляет собой изделие, выполненное из металла. Относится к фасонному металлопрокату. При этом есть несколько видов классификации, включая тип сечения, класс точности, длину изделия. Производят горячекатанным и холодногнутым способом.

Состав сталей определяет условия применения уголков. Они имеют различные характеристики изгиба, растяжения, кручения. При стандартных требованиях часто применяются уголки, выполненные из углеродистой стали. При наличии дополнительных требований выбираются конструкционные стали.

Сфера, где используются стальные уголки очень широка. Их используют повсеместно в возведении металлических конструкций, в гражданском и промышленном строительстве. Также применяется в монтажных и крепежных работах, когда необходима прокладка трубопроводов и т.д.

Чтобы рассчитать вес уголка, используйте представленный на странице калькулятор. Для расчетов мы предоставляем таблицы ГОСТ. Подбирайте значения, исходя из размеров и материала изготовления.

Беляева_Расчет и проектирование.indd

%PDF-1.3 % 1 0 obj >]/Pages 3 0 R/Type/Catalog/ViewerPreferences>>> endobj 2 0 obj >stream 2019-11-11T15:20:54+05:002019-11-11T15:21:31+05:002019-11-11T15:21:31+05:00Adobe InDesign CS6 (Windows)uuid:3226a5ca-cfbf-4075-b9b5-93cb6424310cxmp.did:A3EFBA1FB752E4118BF5AA137F15CC0Cxmp.id:212888606C04EA119267D73F75A3E5C0proof:pdf1xmp.iid:1F2888606C04EA119267D73F75A3E5C0xmp.did:A7EFBA1FB752E4118BF5AA137F15CC0Cxmp.did:A3EFBA1FB752E4118BF5AA137F15CC0Cdefault

convertedfrom application/x-indesign to application/pdfAdobe InDesign CS6 (Windows)/2019-11-11T15:20:54+05:00

application/pdf

Беляева_Расчет и проектирование.indd

Adobe PDF Library 10.0.1FalsePDF/X-1:2001PDF/X-1:2001PDF/X-1a:2001 endstream endobj 3 0 obj > endobj 6 0 obj > endobj 7 0 obj > endobj 8 0 obj > endobj 9 0 obj > endobj 10 0 obj > endobj 31 0 obj > endobj 32 0 obj > endobj 33 0 obj > endobj 34 0 obj > endobj 35 0 obj > endobj 36 0 obj > endobj 37 0 obj > endobj 68 0 obj >/Font>/ProcSet[/PDF/Text]>>/TrimBox[0.0 0.0 481.89 680.315]/Type/Page>> endobj 69 0 obj >/Font>/ProcSet[/PDF/Text]>>/TrimBox[0.0 0.0 481.89 680.315]/Type/Page>> endobj 70 0 obj >/Font>/ProcSet[/PDF/Text]>>/TrimBox[0.0 0.0 481.89 680.315]/Type/Page>> endobj 71 0 obj >/Font>/ProcSet[/PDF/Text]>>/TrimBox[0.0 0.0 481.89 680.315]/Type/Page>> endobj 72 0 obj >/Font>/ProcSet[/PDF/Text]>>/TrimBox[0.0 0.0 481.89 680.315]/Type/Page>> endobj 73 0 obj >/Font>/ProcSet[/PDF/Text]>>/TrimBox[0.0 0.0 481.89 680.315]/Type/Page>> endobj 86 0 obj >stream HTMo10V3c{?q%

Калькулятор треугольников

Укажите 3 значения, включая хотя бы одну сторону в следующих 6 полях, и нажмите кнопку «Рассчитать». Если в качестве единицы измерения угла выбраны радианы, он может принимать такие значения, как пи / 2, пи / 4 и т. Д.

Треугольник — это многоугольник с тремя вершинами. Вершина — это точка, где встречаются две или более кривых, линий или ребер; в случае треугольника три вершины соединены тремя отрезками, называемыми ребрами. Треугольник обычно называют его вершинами.Следовательно, треугольник с вершинами a, b и c обычно обозначается как Δabc. Кроме того, треугольники, как правило, описываются на основе длины их сторон, а также их внутренних углов. Например, треугольник, в котором все три стороны имеют равную длину, называется равносторонним треугольником, а треугольник, в котором две стороны имеют равную длину, называется равнобедренным. Когда ни одна из сторон треугольника не имеет одинаковой длины, он называется разносторонним, как показано ниже.

Отметки на краю треугольника — это обычное обозначение, которое отражает длину стороны, где одинаковое количество отметок означает одинаковую длину.Аналогичные обозначения существуют для внутренних углов треугольника, которые обозначаются разным количеством концентрических дуг, расположенных в вершинах треугольника. Как видно из треугольников выше, длина и внутренние углы треугольника напрямую связаны, поэтому логично, что равносторонний треугольник имеет три равных внутренних угла и три стороны равной длины. Обратите внимание, что треугольник, представленный в калькуляторе, не показан в масштабе; хотя он выглядит равносторонним (и имеет отметки угла, которые обычно воспринимаются как равные), он не обязательно является равносторонним и представляет собой просто представление треугольника.Когда введены фактические значения, выходные данные калькулятора будут отражать форму входного треугольника.

Треугольники, классифицируемые на основе их внутренних углов, делятся на две категории: прямые и наклонные. Прямоугольный треугольник — это треугольник, в котором один из углов равен 90 °, и обозначается двумя отрезками прямой, образующими квадрат в вершине, составляющей прямой угол. Самый длинный край прямоугольного треугольника, противоположный прямому углу, называется гипотенузой.Любой треугольник, который не является прямоугольным, классифицируется как наклонный треугольник и может быть тупым или острым. В тупоугольном треугольнике один из углов больше 90 °, а в остром треугольнике все углы меньше 90 °, как показано ниже.

Факты, теоремы и законы о треугольнике

• Учитывая длины всех трех сторон любого треугольника, каждый угол можно рассчитать с помощью следующего уравнения. Обратитесь к треугольнику выше, предполагая, что a, b и c — известные значения.

Площадь треугольника

Существует несколько различных уравнений для вычисления площади треугольника в зависимости от того, какая информация известна. Вероятно, наиболее известное уравнение для вычисления площади треугольника включает его основание b и высоту h . «Основание» относится к любой стороне треугольника, где высота представлена ​​длиной отрезка линии, проведенного от вершины, противоположной основанию, до точки на основании, образующей перпендикуляр.

Учитывая длину двух сторон и угол между ними, следующую формулу можно использовать для определения площади треугольника. Обратите внимание, что используемые переменные относятся к треугольнику, показанному на калькуляторе выше. Для a = 9, b = 7 и C = 30 °:

Другой метод вычисления площади треугольника основан на формуле Герона. В отличие от предыдущих уравнений, формула Герона не требует произвольного выбора стороны в качестве основания или вершины в качестве начала координат.Однако для этого требуется, чтобы длина трех сторон была известна. Опять же, со ссылкой на треугольник, представленный в калькуляторе, если a = 3, b = 4 и c = 5:

Медиана, внутренний и окружной радиус

Медиана

Медиана треугольника определяется как длина линейного сегмента, который проходит от вершины треугольника до середины противоположной стороны. Треугольник может иметь три медианы, каждая из которых будет пересекаться в центре тяжести (среднее арифметическое положение всех точек в треугольнике) треугольника.См. Рисунок ниже для пояснения.

Медианы треугольника представлены отрезками m _a , m _b и m _c . Длину каждой медианы можно рассчитать следующим образом:

Где a, b и c обозначают длину стороны треугольника, как показано на рисунке выше.

В качестве примера, учитывая, что a = 2, b = 3 и c = 4, медиана m _a может быть рассчитана следующим образом:

Inradius

Inradius — это радиус наибольшего круга, который может поместиться внутри данного многоугольника, в данном случае треугольника.Внутренний радиус перпендикулярен каждой стороне многоугольника. В треугольнике внутренний радиус можно определить, построив две биссектрисы угла, чтобы определить центр треугольника. Inradius — это перпендикулярное расстояние между центром тяжести и одной из сторон треугольника. Можно использовать любую сторону треугольника, если определено перпендикулярное расстояние между стороной и центром, поскольку центр, по определению, находится на равном расстоянии от каждой стороны треугольника.

В данном калькуляторе внутренний радиус рассчитывается с использованием площади (Area) и полупериметра (ов) треугольника по следующим формулам:

, где a, b и c — стороны треугольника

Круговой радиус

Радиус описанной окружности определяется как радиус окружности, проходящей через все вершины многоугольника, в данном случае треугольника.Центр этой окружности, где пересекаются все срединные перпендикуляры каждой стороны треугольника, является центром описанной окружности и точкой, от которой измеряется радиус описанной окружности. Центр описанной окружности треугольника не обязательно должен находиться внутри треугольника. Стоит отметить, что у всех треугольников есть описанная окружность (окружность, проходящая через каждую вершину) и, следовательно, радиус описанной окружности.

В данном калькуляторе радиус описанной окружности рассчитывается по следующей формуле:

Где a — сторона треугольника, а A — угол, противоположный стороне a

Хотя используются сторона a и угол A, в формуле можно использовать любую из сторон и их соответствующие противоположные углы.

Калькулятор уклона

По определению, уклон или уклон линии описывает ее крутизну, уклон или уклон. Где м — уклон θ — угол наклона

Если известны 2 точки

Если известны 1 точка и наклон

Уклон, иногда называемый в математике градиентом, — это число, которое измеряет крутизну и направление линии или участка линии, соединяющей две точки, и обычно обозначается м .Как правило, крутизна линии измеряется по абсолютной величине ее уклона, м . Чем больше значение, тем круче линия. Учитывая м , можно определить направление линии, которую описывает м , на основе ее знака и значения:

• Линия возрастает и идет вверх слева направо, когда m> 0
• Линия убывает и идет вниз слева направо, когда m <0
• Линия имеет постоянный наклон и является горизонтальной при m = 0
• Вертикальная линия имеет неопределенный наклон, так как это приведет к дроби с 0 в знаменателе.См. Приведенное ниже уравнение.

Наклон — это, по сути, изменение высоты при изменении горизонтального расстояния, и его часто называют «подъем через пробег». Он применяется в градиентах в географии, а также в гражданском строительстве, например, в строительстве дорог. В случае дороги «подъем» — это изменение высоты, а «пробег» — это разница расстояний между двумя фиксированными точками, если расстояние для измерения недостаточно велико, чтобы учитывать кривизну земли. как фактор.Наклон математически представлен как:

В приведенном выше уравнении y ₂ — y ₁ = Δy или вертикальное изменение, а x ₂ — x ₁ = Δx или горизонтальное изменение, как показано на представленном графике. Также видно, что Δx и Δy — это отрезки прямых, которые образуют прямоугольный треугольник с гипотенузой d , причем d — это расстояние между точками (x ₁ , y ₁ ) и (x ₂ , y ₂ ) .Поскольку Δx и Δy образуют прямоугольный треугольник, можно вычислить d , используя теорему Пифагора. Обратитесь к калькулятору треугольника для получения более подробной информации о теореме Пифагора, а также о том, как вычислить угол наклона θ , указанный в калькуляторе выше. Кратко:

d = √ (x ₂ — x ₁ ) ² + (y ₂ — y ₁ ) ²

Вышеприведенное уравнение является теоремой Пифагора в своем корне, где гипотенуза d уже решена, а две другие стороны треугольника определяются вычитанием двух значений x и y , заданных двумя точками. .Учитывая две точки, можно найти θ , используя следующее уравнение:

м = загар (θ)

По точкам (3,4) и (6,8) найдите наклон прямой, расстояние между двумя точками и угол наклона:

d = √ (6 — 3) ² + (8 — 4) ² = 5

Хотя это выходит за рамки данного калькулятора, помимо его основного линейного использования, концепция наклона важна в дифференциальном исчислении. Для нелинейных функций скорость изменения кривой меняется, и производная функции в данной точке — это скорость изменения функции, представленная наклоном линии, касательной к кривой в этой точке.

Калькулятор

для инженеров — Неподвижная балка: изгибающий момент и поперечное усилие

Отличные калькуляторы

Калькулятор преобразования напряжения
Расчет главного напряжения, максимального напряжения сдвига и их плоскостей

Калькулятор для анализа подвижной нагрузки
Для определения абсолютного макс. Б.М. из-за движущихся грузов.

Калькулятор изгибающего момента
Расчет изгибающего момента и поперечной силы для балки с прямой опорой

Калькулятор момента инерции
Расчет момента инерции плоских секций e.грамм. швеллер, уголок, тройник и др.

Калькулятор железобетона
Расчет прочности железобетонной балки

Калькулятор распределения моментов
Решение неопределенных балок

Калькулятор прогиба и уклона
Расчет прогиба и уклона свободно опертой балки для многих случаев нагружения

Калькулятор фиксированной балки
Инструмент для расчета изгибающего момента и поперечной силы для фиксированной балки для многих случаев нагружения

Калькулятор BM и SF для консоли
Расчет SF и BM для консоли

Калькулятор прогиба и наклона консоли
Для многих случаев нагружения консоли

Вычислитель нависающей балки
Для SF и BM многих случаев нагружения нависающей балки

Дополнительные ссылки

Викторина по гражданскому строительству
Проверьте свои знания по различным темам гражданского строительства

Научные статьи
Научные статьи, диссертации и диссертации

Небоскребы мира
Высокие здания мира

Предстоящие конференции
Список конференций, семинаров и практикумов по гражданскому строительству

Профиль инженеров-строителей
Познакомьтесь с выдающимися инженерами-строителями

Профессиональные общества
Международные профессиональные сообщества инженеров-строителей

Продолжайте посещать, чтобы получать обновления, или присоединяйтесь к нашему списку рассылки, чтобы получать обновления

Поищите на нашем сайте больше…

Расскажите о нас друзьям

Другие полезные ссылки

Калькулятор изгибающего момента и поперечного усилия

Bendingmomentdiagram.com — это бесплатный онлайн-калькулятор, который создает диаграммы изгибающего момента (BMD) и диаграммы поперечного усилия (SFD) для большинства простых балок. Калькулятор полностью настраивается для работы с большинством балок; эта функция недоступна в большинстве других калькуляторов. Программное обеспечение работает на базе SkyCiv, предлагая мощное программное обеспечение для структурного анализа и проектирования в облаке.

Инструмент полностью функциональный, поэтому посетите наше Бесплатное программное обеспечение Beam, чтобы начать работу! Он будет работать со всеми опорными определяющими балками и способен воспринимать точечные нагрузки, сосредоточенные моменты и распределенные нагрузки. Кроме того, он чрезвычайно регулируется и настраивается, чтобы вы могли создавать свои собственные лучи. Это чрезвычайно точный инструмент и, в отличие от современных калькуляторов, очень удобный. Это чрезвычайно полезный инструмент для студентов университетов, колледжей и старших классов, которым утомительно приходится перерисовывать BMD и SFD для заданий и практических / учебных вопросов.

У нас также есть учебная страница, которая поможет студентам университетов с расчетами, ожидаемыми в их инженерной степени, а также студентам старших классов. Эти студенты могут научиться рассчитывать и создавать диаграммы поперечной силы и изгибающего момента, и мы понимаем, что процесс расчета балки иногда может быть трудным, поэтому мы предоставили простое пошаговое руководство по расчету диаграмм изгибающего момента и поперечной силы. Включены простые уравнения и формулы изгибающего момента, которые хорошо помогают в ваших расчетах.Существуют также примеры и генераторы случайных балок, которые позволят вам поэкспериментировать с тем, как различные нагрузки влияют на расчет балки, а также на поперечную силу и изгибающий момент балки.

Схема

Bending Moment Diagram разработана командой SkyCiv Engineering, которая предлагает студенческие и профессиональные пакеты, которые предоставляют пользователям доступ к разнообразному программному обеспечению для проектирования конструкций для выполнения работы. Все учетные записи основаны на подписке, поэтому вы можете ежемесячно оплачивать программное обеспечение по мере необходимости! Больше никаких проблем с установкой, загрузкой или лицензированием!

Калькулятор тангенса онлайн — Расчет тангенса — производная — первообразная

Резюме:

Тригонометрическая функция tan для вычисления тангенса угла в радианах, градусы или градианы.

загар

---

Описание:

Калькулятор позволяет использовать большинство тригонометрических функций , есть возможность вычислить загар , синус и косинус угла через одноименные функции ..

Тангенс тригонометрической функции отмечен tan , позволяет вычислить тангенс угла онлайн , можно использовать разные угловые единицы:

• радиан — угловая единица по умолчанию,
• градусов или
• градов.

Расчет тангенса

Тангенс для вычисления угла в радианах

Калькулятор тангенса позволяет с помощью функции загара рассчитать онлайн тангенс угла в радианах, сначала необходимо выберите желаемую единицу измерения, нажав кнопку параметров модуля расчета. После этого можно приступать к расчетам.

Чтобы вычислить касательную онлайн числа «пи / 6», введите tan (`pi / 6`), после вычисления результат sqrt (3) / 3 возвращается.

Обратите внимание, что функция тангенса может распознавать некоторые особые углы и расчеты со специальными связанными значениями в точной форме.

Вычислить тангенс угла в градусах

Чтобы вычислить тангенс угла в градусах, необходимо сначала выбрать нужную единицу нажав кнопку опций модуля расчета.После этого вы можете приступить к расчету.

Чтобы вычислить тангенс 60, введите tan (60), после расчета restults возвращается `sqrt (3)`.

Вычислить тангенс угла в градусах

Для вычисления тангенса угла в градусах необходимо сначала выбрать желаемую единицу измерения. нажав кнопку опций модуля расчета. После этого вы можете приступить к расчету.

Чтобы вычислить тангенс 50, введите tan (50), после вычисления возвращается результат «1».

Обратите внимание, что функция тангенса может распознавать некоторые особые углы и выполнять исчисление со специальными связанными точными значениями.

Особые значения тангенса

Касательная допускает некоторые особые значения, которые калькулятор может определять в точном виде.2`.

Первообразная касательной

Первообразная касательной равна `-ln (cos (x))`.

Свойства касательной функции

Функция тангенса является нечетной функцией, для любого действительного x: tan (-x) = — tan (x). Следствием для кривой, представляющей касательную функцию, является то, что она допускает начало отсчета как точку симметрии.


Тригонометрическая функция tan для вычисления тангенса угла в радианах, градусы или градианы. 2`

---

Касательная к первообразным:

Калькулятор первообразной позволяет вычислить первообразную касательной функции.

Первообразное для tan (x) — это первообразное_производное (`tan (x)`) = `-ln (cos (x))`

---

Предельный тангенс:

Калькулятор пределов позволяет вычислять пределы касательной функции.

Предел для tan (x) — limit_calculator (`tan (x)`)

---

Тангенс обратной функции:

Функция , обратная касательной , является функцией арктангенса, отмеченной как arctan.

---

---

Тангенс графика:

Графический калькулятор может строить касательную функцию в интервале ее определения.

---

---

Свойство тангенса функции:

Касательная функция — нечетная функция.

---

Рассчитать онлайн с тангенсом тангенса (тангенс)

Калькулятор прямоугольного треугольника — Расчет высокой точности

[1] 2020/11/10 12:43 Мужчина / 40-летний уровень / Офисный работник / Государственный служащий / Очень /

Цель использования

Для расчета пиявки грот для изготовления.

[2] 2020/11/07 02:53 Мужской / возраст 50 лет / Другое / Очень /

Цель использования

Для расчета угла фаски на стальной детали на основе двух фиксированных измерений

[3] 2020/11/02 19:27 Мужчина / Уровень 40 лет / Другое / Полезно /

Цель использования

Рассчитайте угол наклона кресла-коляски с 2-дюймовым углом наклона сиденья.

[4] 2020/10/21 09:42 Мужчина / 40 лет / Другое / Очень /

Цель использования

Используется для определения длины растяжек для вышки радиоантенны

[5 ] 2020/10/09 12:07 Мужчина / 60 лет и старше / Пенсионер / Очень /

Цель использования

рассчитать высоту вышки сотовой связи без авиационного освещения.

[6] 2020/10/08 13:00 Мужской / 30-летний уровень / Самозанятые лица / Очень /

Цель использования

Рассчитать угол наклона сетки прицела относительно регулировочных турелей.

Комментарий / запрос

Спасли меня от просмотра SohCahToa 🙂

[7] 2020/10/06 02:38 Мужчина / 50 лет уровень / Другое / Очень /

Цель использования

Рассчитать угол крестовины в воротах

[8] 2020/09/15 02:55 Женщина / 60 лет и старше / Старшая школа / Вуз / Аспирант / Полезно /

Цель использования

Рассчитать угол изголовья

[9] 2020/08/27 00:40 Мужчина / 60 лет и старше / Пенсионер / Очень /

Цель использования

Вычислить количество зерна, оставшегося в бункере, который опорожняется.

No related posts.