Расчет на изгиб балки: Расчет балки онлайн — Калькулятор балок перекрытия из дерева

alexxlab

Содержание

Построение эпюр при изгибе для балки

Привет! Вы находитесь на сайте – sopromats.ru, проекте о сопромате и не только! Это новая статья из серии – «сопромат для чайников», в которой я расскажу о построении эпюр при изгибе для балки. Как обычно, буду писать просто и по делу. Здесь я не буду спамить специфическими фразами из сопромата и рассматривать сложные примеры. Будем учиться на простейшей балке. Ну что же давайте начнем учиться!

Сколько можно нарисовать эпюр при изгибе для балок?

Для простого изгиба, который будем рассматривать в этой статье, можно нарисовать всего две эпюры. Одна именуется как эпюра поперечных сил, другая зовется эпюрой изгибающих моментов. Одна показывает распределение внутренних сил внутри элемента, работающего на изгиб, другая моментов. Если хотите, можете изучить больше информации по этим силовым факторам в следующих материалах:

  • Как построить эпюру поперечных сил? Здесь вы можете найти полное досье на поперечную силу: кто такая, зачем нужна и как обозначается.
    Тут же можно почитать подробную инструкцию по построению эпюры этой величины. В статье рассказано про 3 методики расчета и построения.
  • Как построить эпюру изгибающих моментов? В этом материале можно узнать много всего об изгибающем моменте. Например, зачем он нужен и как определяется, как обозначается и в чем измеряется. А также подробнейшим образом изучить методики построения эпюры этой величины, 3-мя способами.

Если Вам лень читать эти статьи, то ничего. Это нормально 🙂 Просто хотел пропиарить немного эти материалы, не зря же я их писал…В этой статье, для чайников, мы, итак, научимся строить эти эпюры, но только одним методом.

Подготовительные работы

Для того, чтобы построить эпюры, первым делом вычертите расчетную схему, с указанием всех нагрузок и размеров:

После этого нужно определить реакции опор. Без них дальше никуда. Если Вы не умеет этого делать, обязательно прочтите этот урок про расчет реакций опор для чайников. Здесь же сразу приведу результат вычислений:

Расчет и построение эпюр

Для расчета эпюр сначала нужно наметить участки, на которых эпюра будет либо постоянна, либо меняться по одному закону. Опознать эти участки достаточно просто. Границами участков служат те места, где прикладываются нагрузки (сосредоточенные силы и моменты, в том числе реакции опор). Если на балку действует распределенная нагрузка, то границы – это ее начало и конец. В нашем случае, как видите, 2 участка, каждый по 2 метра:

Рассматриваем произвольное сечение первого участка, которое обзовем буквой – С. Оно будет находится на расстоянии z1 от левого торца балки. И относительного него будем записывать законы, по которым меняются поперечные силы и изгибающие моменты на этом участке:

Записываем уравнение для поперечной силы

Поперечная сила будет равняться сумме всех сосредоточенных сил, находящихся слева от сечения (или справа). Мы будем подсчитывать все, что находится слева, т.к. там меньше нагрузки. В уравнении поперечной силы, все внешние нагрузки нужно учитывать с учетом правила знаков: если сила, относительно рассматриваемого сечения, поворачивает ПО часовой стрелке, то в уравнение она пойдет с ПЛЮСОМ (и наоборот).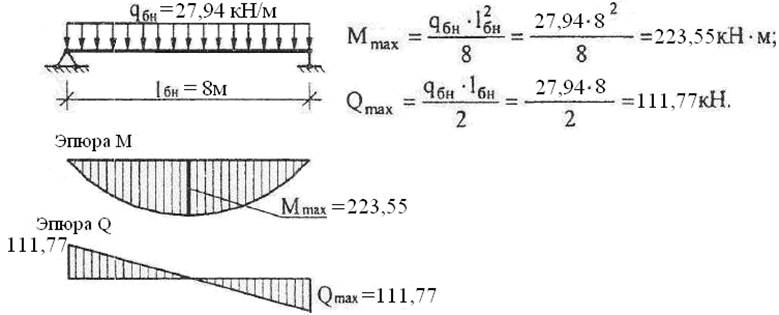

В рассматриваемом примере, реакция RA поворачивает ПО часовой стрелке, и уравнение получится такое:

Причем, как видно, эта зависимость справедлива для любого сечения на первом участке, тем самым поперечная сила в пределах этого участка постоянна и равна – 5 кН. Откладываем это значение на графике:

Эпюры заштриховываются перпендикулярно нулевой линии и на каждом участке проставляются знаки поперечной силы.

Записываем уравнение для изгибающего момента

Что касается изгибающего момента, то тут в уравнении нужно учесть сумму моментов, находящихся по одну сторону от сечения. Реакция RA, относительно сечения С создает момент RA·z1. Напомню, что момент – это сила, умноженная на плечо. Где плечо – это расстояние от силы до центра момента (в этом случае, центр – это рассматриваемое сечение). В уравнении моментов, все моменты нужно учитывать с учетом правила знаков: если момент силы, стремится растянуть нижние волокна, то в уравнении будем записывать его со знаком «+». И наоборот.

Придерживаясь этого правила, будем откладывать эпюры изгибающих моментов со стороны РАСТЯНУТЫХ волокон. Что практикуется у инженеров-строителей. У механиков, другие правила, они рисуют эти эпюры со стороны сжатых волокон. Кстати, что такое растянутое и сжатое волокно? Покажу на нашем же примере:

Как видно, сила RA, при повороте, стремится растянуть нижние волокна, поэтому в уравнение будем записывать момент этой силы со знаком плюс:

Анализируя это уравнение, видим, что изгибающий момент будет меняться по линейному закону и зависеть от координаты z1. И чтобы рассчитать и построить эпюру на этом участке достаточно подставить в уравнение координаты начала участка z1=0 и конца z1=2 м. После чего отложить эти точки на графике и соединить прямой линией:

Эпюры для второго участка балки

С учетом всех вышеописанных рекомендаций, я думаю Вы сами теперь сможете построить эпюры для второго участка. Подробно комментировать уже не буду, приведу сразу решение и окончательные эпюры для этой балки:

Сегодня мы рассмотрели урок по построению эпюр для простой балки. Однако, много нюансов по расчету и построению я не рассказал, т.к. все это уместить в одном уроке, довольно сложно и не всем это нужно, статья ведь для чайников! Если Вы хотите прокачать свой знания, в этих вопросах, обязательно прочитайте эти материалы о эпюрах. Здесь можно найти подробные статьи о поперечной силе, о изгибающем моменте. Где я рассказывал о 3-х методиках расчета, причем один из них, даже проще, чем мы рассматривали в данной статье. С помощью которого можно устно рисовать эти эпюры. Также там можно посмотреть, как учитывать моменты и распределенные нагрузки при расчете эпюр и какие особенности есть по построению при действии данных видов нагрузок.

Спасибо за внимание! Если Вам понравилась статья, да и сайт в целом, добавляйте его в свои закладки, чтобы иметь быстрый доступ к нему, а также подписывайтесь на наши соц. сети, делитесь этой статьей с друзьями и т.д. Буду благодарен 🙂

Расчёт балок на прочность при изгибе

Задача 1

В некотором сечении балки прямоугольного сечения 20×30см М=28 кНм, Q=19 кН.

Требуется:

а) определить нормальное и касательное напряжения в заданной точке К, отстоящей от нейтральной оси на расстоянии 11 см,

б) проверить прочность деревянной балки, если [σ]=10 МПа, [τ]=3 МПа.

Решение

а) Для определения σ(К), τ(К)

и maxσ,maxτ потребуется знать величины осевого момента инерции всего сечения IН.О., осевого момента сопротивления WН.О., статического момента отсечённой части  и статического момента половины сечения Smax:

Тогда:

б) Проверка прочности:

— по условию прочности нормальных напряжений:

— по условию прочности касательных напряжений:

Задача 2

В некотором сечении балки М=10кНм, Q=40кН.

Поперечное сечение – треугольное. Найти нормальное и касательное напряжения в точке, отстоящей от нейтральной оси на расстоянии 15 см.

где 

Тогда

где:

Тогда

Задача 3

Подобрать сечение деревянной балки в двух вариантах: круглое и прямоугольное (при h/b=2), если [σ]=10 МПа, [τ]=3 МПа, и сравнить их по расходу материала.

Задаёмся направлениями опорных реакций А и В и составляем уравнения статики:

(1)          ∑М(В) = F·8 – М – А·6 + (q·6)·3 =0,

откуда 

(2)          ∑М(А

) = F·2 – М + В·6 — (q·6)·3 =0,

откуда 

Iучасток   

∑М(С) = М(z1) +F·z1=0,

ММ(z1) = —F·z1= — 30 ·z1 —

– уравнение прямой.

При z1 = 0:      М = 0,

z1 = 2:      М =- 60 кНм.

∑у= — F — Q(z1) = 0,

Q(z

1) = — F = -30 кН – постоянная функция.

II участок     

откуда

— уравнение параболы.

При z2=0:     М = 0,

z2=3м:  М = 30 · 3 – 5 · 32 = 90 — 45 = 45кНм,

z2=6м:  М = 30 · 6 – 5 · 62 = 180 — 180 = 0.

∑у= Q(z2) — q·z2 + B= 0,

Q(z2) = q·z2 — B= 10·z2 – 30 – уравнение прямой,

при  z2 = 0:     Q = -30,

        z2 = 6м:     Q = 10·6 – 30 = 30.

Определение аналитического максимума изгибающего момента второго участка:

из условиянаходим :

И тогда

Заметим, что скачок в эп.М расположен там, где приложен сосредоточенный момент М = 60кНм и равен этому моменту, а скачок в эп.Q – под сосредоточенной силой А = 60 кН.

Подбор сечения балок производится из условия прочности по нормальным напряжениям, куда следует подставлять наибольший по абсолютной величине изгибающий момент из эпюры М.

В данном случае максимальный момент по модулю М = 60кНм

откуда: :

а) сечение круглой формы d=?

б) сечение прямоугольной формы при h/b = 2:

тогда

Размеры сечения, определенные из условия прочности по нормальным напряжениям, должны удовлетворять также условию прочности по касательным напряжениям:

Для простых форм сечений известны компактные выражения наибольшего касательного напряжения:

— для круглого сечения 

— для прямоугольного сечения 

Воспользуемся этими формулами. Тогда

— для балки круглого сечения при :

— для балки прямоугольного сечения

Чтобы выяснить, какое сечение требует меньшего расхода материала, достаточно сравнить величины площадей поперечных сечений:

Апрямоугольного = 865,3см2 < Акруглого = 1218,6см2, следовательно, балка прямоугольного сечения в этом смысле выгоднее, чем круглого.

 

Задача 4

Подобрать двутавровое сечение стальной балки, если [σ]=160МПа, [τ]=80МПа. 

Задаёмся направлениями опорных реакций А и В и составляем два уравнения статики для их определения:

(1)              ∑М(А) = – М1– F  ·2 — (q·8)·4 + М2 + В·6 =0,

откуда 

(2)      ∑М(В) = – М1– А · 6 + F · 4 + (q·8)·2 + М2 =0,

откуда 

Проверка:

∑у = А – F – q · 8 + В = 104 – 80 – 20 · 8 +136 = 240 – 240 ≡ 0.

∑М(С) = М(z1) — М1=0,

М(z1) = М1= 40 кНм – постоянная функция.   

∑у= — Q(z1) = 0,

Q(z1) = 0.

II участок 

— парабола.

Приz2=0:       М = 40 кНм,

z2=1м:    М = 40 + 104 – 10=134кНм,

z2=2м:    М = 40+ 104 · 2 – 10 · 22 = 208 кНм.

∑у=А — q·z2 — Q(z2) = 0,

Q(z2) =А— q·z2 = 104 –  20·z2  – уравнение прямой,

при  z2 = 0:       Q = 104кН,

        z2 = 6м:    Q = 104 – 40 = 64кН.

III участок

— парабола.

Приz3=0:       М = 24+40=-16 кНм,

z3=2м:    М = 24 + 136·2 — 10 (2+2)2 = 24 + 272 – 160 = 136кНм,

z3=4м:    М = 24 + 136·4 – 10 (2+4)2 = 24 + 544 – 360 = 208 кНм.

∑у=В — q(2+z3 ) + Q(z3) = 0,

Q(z3) =- В + q(2+z3 ) = -136 + 20 (2+z3 )   – уравнение прямой,

при  z3 = 0:        Q = -136 + 40 = — 94кН,

        z3 = 4м:     Q = — 136 + 20 (2+4) = — 136 + 120 = — 16кН.

IV участок

— парабола.

z4=0:       М = 0кНм,

z4=1м:    М = – 10кНм,

z4=2м:    М = — 40кНм.

∑у=- q·z4 + Q(z4) = 0,

Q(z4) =q·z4 = 20·z4  – уравнение прямой.

Приz4 = 0:       Q = 0,

        z4 = 2м:     Q = 40кН.

Проверяем скачки в эпюрах:

а) В эпюре М скачок на правой опоре величиной 24кНм (от 16 до 40) равен сосредоточенному моменту М2=24, приложенному в этом месте.

б) В эпюре Q три скачка:

первый из них на левой опоре соответствует сосредоточенной реакции А=104кН,

второй – под силой F=80кН и равен ей (64+16=80кН),

третий – на правой опоре и соответствует правой опорной реакции 136кН (94+40=136 кН)

Наконец, проектируем двутавровое сечение.

Подбор его размеров производится из условия прочности по нормальным напряжениям :

 

В сортаменте двутавровых профилей профиля с точно таким моментом сопротивления Wх нет. Есть № 40а с Wх=1190 см3 и № 45а с Wх=1430 см3

Попробуем  меньший из них. Если принять двутавр № 40а, у которого Wх=1190 см3 , то наибольшее напряжение в опасном сечении будет:

и перенапряжение составитчто превышает рекомендуемую величину отклонения, равную 5%.

Поэтому приходится принимать ближайший больший размер двутавра, а именно №45а, у которого Wх=1430 см3. В этом случае балка будет работать с недонапряжением:

что меньше [σ]=160МПа на  

Итак, принимается двутавр №45а, у которого: Wх=1430 см3, Iх=32240см4, Iх: Sх=38,6см, d=11,5мм.

Далее необходима проверка прочности по касательным напряжениям с помощью условия прочности :

 

Это условие прочности выполняется, даже с избыточным запасом.

 

Задача 5

Подобрать сечение балки, рассмотрев шесть вариантов форм и три вида материалов (древесина, чугун, сталь).

Решение 

1.Определение опорных реакций 

∑М(А) = F · 2 + М1 — М2— q·6·7 + В · 8 =0,∑М(В) = F · 10 + М1— М2 – А · 8 + q·6·1 =0,Проверка:

∑у = – 20 – 40 ·6 +50+210 = — 260 + 260 ≡ 0.

2.Построение эпюр изгибающих моментов и поперечных сил.

I участок

∑М(С) = М(z1) + F·z1=0,

М(z1) = — F·z1= -20·z1.

При z1=0:     М = 0,

        z1=2м:  М = – 40кНм,

∑у= — F— Q(z1) = 0,

Q(z1) = — 20кН.

II участок

        z2=0:      М = — 20 – 40 = -60 кНм,

z2=4м:   М = 200 — 20 – 120 = 200 — 140 = 60кНм.

∑у=- F + А — Q(z2) = 0,

Q =- F + А= -20+50=30кН.

III участок

— парабола.

Приz3=0:      М = — 20·4= — 80 кНм,

z3=2м:   М = 210·2 — 20·(2+2)2 = 420 – 320 = 100кНм,

z3=4м:   М = 210·4 – 20 · (2+4)2 = 840 – 720 = 120кНм.

∑у= Q(z3) + В — q·(2+z3) = 0,

Q(z3) = — В + q·(2+z3) = — 210 + 40·(2+z3) – уравнение прямой.

Приz3 = 0:       Q = -130кН,

        z3 = 4м:     Q = 30кН.

Q(z0) = — 210 + 40·(2+z0) = 0,

— 210 + 80 + 40·z0 = 0,

40·z0 = 130,

z0 =3,25м,

IV участок

парабола.

Приz4=0:      М = 0 кНм,

z4=1м:   М = – 20кНм,

z4=2м:   М = — 80кНм.

∑у=- q·z4 + Q(z4) = 0,

Q(z4) =q·z4 = 40·z4  – уравнение прямой,

        z4 = 0:        Q = 0,

        z4 = 2м:     Q = 80кН.

3. Подбор сечений (опасное сечение по σ: |maxМ|=131,25кНм,

опасное сечение по τ: |maxQ|=130кН).

Вариант 1. Деревянное прямоугольное ([σ]=15МПа, [τ]=3МПа)

Принимаем: В=0,24м,

                         Н=0,48м.

Проверяем по τ:

Вариант 2. Деревянное круглое

Принимаем d=0,45м,

Проверяем по τ:

Вариант 3. Чугун : ([σР]=30МПа, [σс]=120МПа, [τ]=15МПа)

Принимаем b=0,19м, тогда h=0,38м, d=0,076м.

Проверка по τ:

b(у)= b — d= 0,19 — 0,076 = 0,114м

Вариант 4. Сталь, двутавр : ([σ]=160МПа, [τ]=80МПа).

по сортаменту Wх=953см3. Это №40: Ix=19062см4, Sх=545см3, d=0,83см.

Проверка по τ:

Вариант 5. Сталь, круглая труба

Принимаем D=0,22м   →  d = 0,6·D =0,132м.

Проверка по τ:

Вариант 6. Сталь, прямоугольная труба  

b1= b — 2t = b — 2·0,1b = 0,8b,

h1= h — 2t  = 0,8h,

Принимаем b=0,13м, h=0,26м.

Проверка по τ:

Кстати: какое из сечений стальной балки выгодней по расходу материала?

Двутавр —  А = 72,6см2 = 72,6·10-4 = 0,00726м2,

круглая труба –

прямоугольная труба — 

Самый лёгкий: двутавр → самый выгодный с точки зрения изгиба.

 

Задачи на изгиб | ПроСопромат.ру

Для балки определить  опорные реакции и построить эпюры изгибающих моментов (М) и поперечных сил (Q).

  1. Обозначаем опоры буквами А и В и направляем опорные реакции RА и RВ.

Составляем уравнения равновесия.

Проверка

Записываем значения RА и RВ на расчетную схему.

2. Построение эпюры поперечных сил методом сечений. Сечения расставляем на характерных участках (между изменениями). По размерной нитке – 4 участка, 4 сечения.

сеч. 1-1   ход слева.

Сечение проходит по участку с равномерно распределенной нагрузкой, отмечаем размер z1 влево от сечения до начала участка. Длина участка 2 м. Правило знаков для Q — см. здесь.

Строим по найденным значением эпюру Q.

сеч. 2-2   ход справа.

Сечение вновь проходит по участку равномерно распределенной нагрузкой, отмечаем размер z2  вправо от сечения до начала участка. Длина участка 6 м.

Строим эпюру Q.

сеч. 3-3   ход справа.

сеч. 4-4   ход справа.

Строим эпюру Q.

3. Построение эпюры М методом характерных точек.

Характерная точка – точка, сколь-либо заметная на балке. Это точки А, В, С, D, а также точка К, в которой Q=0 и изгибающий момент имеет экстремум. Также в середине консоли поставим дополнительную точку Е, поскольку на этом участке под равномерно распределенной нагрузкой эпюра М описывается кривой линией, а она строится, как минимум, по 3 точкам.

Итак, точки расставлены, приступаем к определению в них  значений изгибающих моментов. Правило знаков — см. здесь.

Участки NA, AD – параболическая кривая (правило «зонтика» у механических специальностей или «правило паруса» у строительных ), участки DС, СВ – прямые наклонные линии.

Момент в точке D следует определять как слева, так и справа от точки D. Сам момент в эти выражения не входит. В точке D получим два значения с разницей на величину m – скачок на его величину.

Теперь следует определить момент в точке К (Q=0). Однако сначала определим положение точки К, обозначив расстояние от нее до начала участка неизвестным х.

Т. К принадлежит второму характерному участку, его уравнение для поперечной силы (см. выше)

Но поперечная сила в т. К равна 0, а z2 равняется неизвестному х.

Получаем уравнение:

Теперь, зная х, определим  момент в точке К с правой стороны.

Строим эпюру М. Построение выполним для механических специальностей, откладывая положительные значения вверх от нулевой линии и используя правило «зонтика».

Основы сопромата, расчет прогиба балки

Cодержание:

Основы сопромата кратко.

1. Виды опор.

1.1. Шарнирные опоры.

Расчетная длина (пролет) балки.

1.2. Опорные связи шарнирно закрепленной балки.

1.3 Жесткое защемление на опорах.

1.4. Скользящие заделки.

2. Нагрузки (внешние силы).

3. Напряжения (внутренние силы).

4. Реакции опор.

5. Уравнения статического равновесия.

4.1. Определение опорных реакций.

6. Уравнения изгибающего момента.

7. Балка на двух шарнирных опорах.

8. Консольная балка.

9. Метод сечений.

10. Определение момента сопротивления.

11. Определение угла поворота.

12. Определение прогиба.

13. Определение угла поворота через прогиб.

14. Список использованной литературы.

Расчет прогиба балки не то, чтобы такой уж сложный, но для того, чтобы каждый раз не повторять одни и те же операции при расчете и этим максимально сократить время расчета, специалисты по сопромату уже давно вывели формулы для наиболее вероятных вариантов опор балок и нагрузок, действующих на балки. Достаточно только определиться с расчетной моделью балки и формула для расчета прогиба к Вашим услугам. Но аксиомы: «если хочешь, чтобы работа была сделана хорошо, сделай это сам» пока никто не отменял. Дело в том, что в разного рода справочниках и пособиях иногда бывают опечатки или ошибки, поэтому использовать готовые формулы не всегда есть хорошо.

11. Определение угла поворота.

(вернуться к основному содержанию)

Прогиб строительной конструкции, а в нашем случае балки — единственная величина, которую проще всего определить опытным путем и сложнее всего теоретическим. Когда мы прикладывали к линейке нагрузку (давили на нее пальцем или мощью своего интеллекта), то невооруженным глазом видели, что линейка прогибалась:

Рисунок 11.1. Перемещение центра тяжести поперечного сечения балки в центре балки и угол поворота продольной оси, проходящей через центр тяжести поперечного сечения, на одной из опор.

Если бы мы хотели определить величину прогиба опытным путем, то достаточно было бы измерить расстояние от стола, на котором лежат книги (на рисунке не показан) до верха или низа линейки, затем приложить нагрузку и измерить расстояние от стола до верха или низа линейки. Разница в расстояниях — это и есть искомый прогиб (на фотографии величина прогиба обозначена оранжевой линией):

Фотография 1.

Но попробуем прийти к тому же результату, следуя по тернистому пути теории сопромата.

Так как балка прогнулась (в хорошем значении этого слова), получается, что и продольная ось, проходящая через центры тяжести поперечных сечений всех точек балки, и до приложения нагрузки совпадавшая с осью х, сместилась. Это смещение центра тяжести поперечного сечения по оси у называется прогибом балки f. Кроме того, очевидно, что на опоре эта самая продольная ось теперь находится под некоторым углом θ к оси х, а в точке действия сосредоточенной нагрузки угол поворота = 0, так как нагрузка у нас приложена посредине и балка прогнулась симметрично. Угол поворота принято обозначать «θ«, а прогиб «f» (во многих справочниках по сопромату прогиб обозначается как «ν«, «w» или любыми другими литерами, но нам, как практикам, удобнее использовать обозначение «f«, принятое в СНиПах).

Как определить этот самый прогиб мы пока не знаем, но зато мы знаем, что нагрузка, действуя на балку, создает изгибающий момент. А изгибающий момент создает внутренние нормальные сжимающие и растягивающие напряжения в поперечных сечениях балки. Эти самые внутренние напряжения приводят к тому, что в верхней части балка сжимается, а в нижней растягивается, при этом длина балки по оси, проходящей через центры тяжести поперечных сечений остается такой же, в верхней части длина балки уменьшается, а в нижней части увеличивается, причем чем дальше расположены точки поперечных сечений от продольной оси, тем больше будет деформация. Определить эту самую деформацию мы можем используя еще одну характеристику материала — модуль упругости.

Если мы возьмем кусок бинтовой резины и попробуем его растянуть, то обнаружим, что резина растягивается очень легко, а выражаясь по научному деформируется на значительную величину при воздействии даже небольшой нагрузки. Если мы попробуем проделать то же самое с нашей линейкой, то растянуть ее даже на десятые доли миллиметра руками вряд ли получится, даже если прилагать к линейке нагрузку в десятки раз большую, чем к бинтовой резине. Это свойство любого материала описывается модулем Юнга, который часто называется просто модулем упругости. Физический смысл модуля Юнга при максимально допустимом загружении рассчитываемой конструкции примерно следующий: модуль Юнга показывает отношение нормальных напряжений, (которые при максимально допустимом загружении равны расчетному сопротивлению материала к относительной деформации при таком загружении:

E = R/Δ (11.1.1)

а это значит, что для работы материала в области упругих деформаций значение внутренних нормальных напряжений, действующих не абстрактно, а на вполне определенную площадь сечения, с учетом относительной деформации не должно превышать значения модуля упругости:

E ≥ N/ΔS (11.1.2)

в нашем случае балка имеет прямоугольное сечение, поэтому S = b·h, где b — ширина балки, h — высота балки.

Измеряется модуль Юнга в Паскалях или кгс/м2. Для абсолютного большинства строительных материалов модули упругости определены эмпирическим путем, узнать значение модуля для того или иного материала можно по справочнику или сводной таблице.

Определить величину деформации для поперечного сечения, к которому приложена равномерно распределенная нагрузка или сосредоточенная сила в центре тяжести поперечного сечения, очень просто. В таком сечении возникают нормальные сжимающие или растягивающие напряжения, равные по значению действующей силе, направленные противоположно и постоянные по всей высоте балки (согласно одной из аксиом теоретической механики):

Рисунок 507.10.1

и тогда определить относительную деформацию, если известны геометрические параметры балки (длина, ширина и высота) несложно, простейшие математические преобразования формулы (11.1.2) дают следующий результат:

Δ = Q/(S·Е) (11.2.1) или Δ = q·h/(S·Е) (11.2.2)

Так как расчетное сопротивление показывает какую максимальную нагрузку можно приложить к определенной площади, то в данном случае мы можем рассматривать действие сосредоточенной нагрузки на всю площадь сечения нашей конструкции. В некоторых случаях важно определить деформации именно в точке приложения сосредоточенной нагрузки, но сейчас мы эти случаи не рассматриваем. Чтобы определить суммарную деформацию, нужно обе части уравнения умножить на длину балки:

Δl = Q·l/(b·h·Е) (11.2.3) или Δl = q·h·l/(b·h·Е) (11.2.4)

Но в рассматриваемом нами случае на поперечные сечения балки действует не сосредоточенная сила, приложенная к центру тяжести поперечного сечения, а изгибающий момент, который можно представить в виде следующей нагрузки:

Рисунок 149.8.3 

При такой нагрузке максимальные внутренние напряжения и соответственно максимальные деформации будут происходить в самой верхней и в самой нижней части балки, а посредине никаких деформаций не будет. Равнодействующую для такой распределенной нагрузки и плечо действия сосредоточенной силы мы находили в предыдущей части (2), когда определяли момент сопротивления балки. Поэтому теперь без особого труда можем определить суммарную деформацию в самой верхней и в самой нижней части балки:

Δх = M·х/((h/3)·b·(h/2)·Е) (11.3.1)

или

Δх = M·х/(W·Е) (11.3.2)

так как W = b·h2/6 (10.6)

Эту же формулу мы можем получить и другим способом. Как мы знаем, момент сопротивления поперечного сечения балки должен удовлетворять следующему условию:

W ≥ М / R (10.3)

Если мы будем рассматривать эту зависимость как уравнение и заменим в этом уравнении значение R на ΔЕ, получим следующее уравнение:

W = М / ΔЕ (11.4.1)

И тогда:

М = WΔЕ (11.4.2) a Δ = M/(W·Е) (11.4.5) и соответственно Δх = M·х/(W·Е) (11.3.2)

В результате деформации, которую мы только что определили, наша балка могла была бы выглядеть так:

Рисунок 11.2. Предполагаемая (для наглядности) деформация балки

то есть в результате деформаций самая верхняя и самая нижняя точки поперечного сечения сместятся на величину Δх. А это значит, что зная величину деформации и высоту балки, мы можем определить угол поворота θ поперечного сечения на опоре балки. Из школьного курса геометрии мы знаем, что отношение катетов прямоугольного треугольника (в нашем случае катеты Δх и h/2) равно тангенсу угла θ:

tgφ = Δх/(h/2) (11.5.1)

и тогда

tgφ = 2 M·х/(h·W·Е) (11.5.3)

Если вспомнить, что момент инерции — это момент сопротивления поперечного сечения, умноженный на расстояние от центра тяжести до крайней точки сечения или наоборот, момент сопротивления — это момент инерции, разделенный на расстояние от центра тяжести до крайней точки сечения:

W = I/(h/2) (10.7) или I = W·h/2 (10.7.2)

то мы можем заменить момент сопротивления на момент инерции:

tgφ = M·х/(I·Е) (11.5.4)

хотя делать это было не обязательно, но таким образом мы получили формулу угла поворота почти такой, как она дается во всех учебниках и справочниках по сопромату. Главное отличие в том, что обычно речь идет о угле поворота, а не о тангенсе угла. И хотя при малых деформациях значения тангенса угла и угол сопоставимы, но тем не менее угол и тангенс угла — это разные вещи (впрочем в некоторых справочниках, например: Фесик С.П. «Справочник по сопротивлению материалов» Киев: Будiвельник. — 1982 переход от тангенса к углу упоминается, хотя и без достаточных на мой взгляд объяснений). Более того, если быть совсем уж точным, то таким способом мы определяем отношение продольной деформации к высоте балки

Рассчитываемые элементы далеко не всегда имеют прямоугольное сечение, как наша рассматриваемая линейка. В качестве балок и перемычек могут использоваться различные горячекатаные профили, тесанные и не тесанные бревна и вообще все, что угодно. Тем не менее понимание принципов расчета момента инерции позволяет определить момент инерции для поперечного сечения любой, даже очень сложной геометрической формы. В абсолютном большинстве случаев вычислять самому момент инерции нет необходимости, для металлических профилей сложного сечения (уголки, швеллера, двутавры и др.) момент инерции, как впрочем и момент сопротивления определяется по сортаменту. Для элементов круглого овального, треугольного сечения и некоторых других видов сечения определить момент инерции можно по соответствующей таблице.

Если рассматривать суммарную деформацию всей балки, т.е. по всей длине l, то очевидно, что суммарная деформация при наших нагрузках не может быть только с одной стороны балки, как показано на рисунке 11.3.а:

Рисунок 11.3.

Так как к нашей балке нагрузка приложена посредине, в результате чего реакции на опорах, возникающие в результате действия нагрузки равны между собой и каждая равна половине приложенной нагрузки, то скорее при этих условиях суммарная деформация будет выглядеть так, как показано на рисунке 11.3.b и тогда в нашем конкретном случае угол наклона поперечного сечения на каждой из опор будет:

tgθ = M·х/(2IЕ) (11.5.5)

Пока мы определяли тангенс угла поворота простым графоаналитическим методом и в случае, когда нагрузка к балке приложена посредине, это у нас неплохо получилось. Но варианты приложения нагрузок к балке бывают всякие и хотя суммарная деформация всегда будет равна Δl, но угол наклона поперечных сечений на опорах может быть разным. Если мы присмотримся к формулам (11.5.4) и (11.5.5) повнимательнее, то увидим, что мы умножаем значение момента в некоторой точке на величину х, которая с точки зрения теоретической механики ни чем не отличается от понятия — «плечо действия силы». Получается, что для определения тангенса угла поворота мы должны умножить значение момента на плечо действия момента, и значит, понятие «плечо» можно применить не только к силе, но и к моменту. Когда мы использовали понятие плеча действия силы, открытое еще Архимедом, то мы и предполагали как далеко это может нас завести. Метод, показанный на рисунке 5.3, дал нам значение плеча момента = х/2. Теперь попробуем определить плечо момента другим способом (графоаналитический метод). Тут нам пригодятся эпюры, построенные для балки на шарнирных опорах:

               

          Рисунок 149.7.1                                                             Рисунок 149.7.2

Теория сопротивления материалов позволяет рассматривать внутренние нормальные напряжения, характеризуемые эпюрой «М» рисунка 149.7.1 для балки с постоянной жесткостью, как некую внешнюю фиктивную нагрузку. Тогда площадь эпюры «М» от начала балки до середины пролета — это фиктивная опорная реакция материала балки на равномерно изменяющуюся нагрузку. А фиктивный изгибающий момент — это площадь эпюры «М», умноженная на расстояние от центра тяжести эпюры «М» до рассматриваемой точки. Так как значение изгибающего момента посредине пролета составляет Ql/4, то площадь такой фигуры составит Ql/4(l/2)(1/2) = Ql2/16. А если это значение разделить на жесткость ЕI, то мы получим значение тангенса угла поворота.

Забегая наперед, определим значение прогиба. Расстояние от центра тяжести треугольной эпюры «М» до середины пролета равно l/6, тогда фиктивный изгибающий момент составит (Ql2/16)l/2 — (Ql2/16)l/6 = Ql3/48. Тогда прогиб f = Ql3/48EI. А так как эпюра моментов у нас расположена снизу балки, то такая фиктивная нагрузка будет в итоге давать отрицательное значение угла поворота и прогиба, что в общем-то логично, так как при таком действии нагрузки прогиб — смещение центра тяжести поперечного сечения будет происходить вниз по оси у.

Характерная особенность графоаналитического метода состоит в том, что количество вычислений можно еще сократить. Для этого нужно умножить площадь эпюры фиктивной нагрузки на расстояние от центра тяжести эпюры до начала координат, а не до рассматриваемой точки на оси. Например, для вышеприведенного случая (Ql2/16)l/3 = Ql3/48

При равномерно распределенной нагрузке эпюра моментов описывается квадратичной параболой, определить площадь такой фигуры и расстояние до центра тяжести сложнее, но для того нам и нужны знания по геометрии, чтобы можно было определить площадь любой фигуры и положение центра тяжести такой фигуры.

Таким образом получается, что для балки, на которую действует сосредоточенная нагрузка в середине балки при х=l/2:

tgθ = М·(x/2)/(ЕI) = ((Ql/4)·(l/4))/(ЕI) = Ql2/(16EI) (11.6.1)

То, что мы только что делали называется интегрированием, ведь если умножить значение значение эпюры «Q» (рисунок 149.7.1) на длину действия нагрузки, мы тем самым определим площадь прямоугольника со сторонами «Q» и х, при этом площадь данного прямоугольника равняется значению эпюры «М» в точке х.

Теоретически получается, что мы можем определить значение тангенса угла поворота, интегрируя одно из уравнений моментов, составленных для нашей балки. Максимальное значение тангенса угла поворота для балки на двух шарнирных опорах, на которую действует сосредоточенная нагрузка посредине (рисунок 149.7.1), будет при х=l/2

tgθ = ∫Mdx/(EI) = ∫Axdx/(EI)= Ax2/(2EI) = (Q/2)·(l/2)2/(2ЕI) = Ql2/(16EI) (11.6.2)

где А — это реакция опоры = Q/2

При распределенной нагрузке интегрирование уравнения моментов: q(l/2)·x — qx2/2 для левой части балки дает следующий результат:

tgθ = ∫Mdx/(EI) = q·(l/2)·(l/2)2/(2ЕI) -q·(l/2)3/(6ЕI) = ql3/(24EI) (11.6.3)

Тот же результат мы получим и при использовании графо-аналитического метода.

Когда мы определяли угол поворота, то для наглядности предположили, что балка деформировалась так, как показано на рисунке 5.2, потом так, как показано на рисунке 11.3.b, потом мы выяснили, что если бы второй опоры не было, то балка повернулась вокруг первой опоры, но в действительности вторая опора есть и потому так балка деформироваться (при нашей нагрузке на балку) не может. Так как на опоре нет никакого вращающего момента и соответственно никаких внутренних напряжений, способных изменить геометрическую форму балки, то геометрическая форма балки на опоре остается неизменной, а внутренние напряжения, увеличивающиеся по ходу балки, деформируют балку все сильнее и это приводит к тому, что балка поворачивается вокруг шарнирных опор и этот угол поворота равен углу наклона поперечного сечения θ (так как мы рассматриваем балку-параллелепипед):

Рисунок 11.4. Реальная деформация балки.

 

Если мы просто постоим эпюру углов поворота для балки со сосредоточенной нагрузкой посредине по уравнениям для левой и для правой части балки, то эпюра будет выглядеть так:

Рисунок 11.5.

Данная эпюра была бы правильной только для балки, изображенной на рисунке 5.3.а. Очевидно, что в нашем случае эпюра так выглядеть не может и для построения правильной эпюры нужно учесть, что поперечные сечения балки имеют наклон на обоих опорах, причем наклон этот одинаковый по значению, но разный по направлению а наклон поперечного сечения балки посредине =0. Если мы опустим эпюру на Ql2/16EI, которое мы получаем при интегрировании уравнения моментов для левой части балки и которое показывает угол наклона поперечного сечения именно на опоре, то получим эпюру следующего вида:

Рисунок 11.6.

Данная эпюра абсолютно точно показывает, изменение угла поворота поперечных сечений, вдоль всей балки, а значение тангенса угла поворота на левой опоре балки не что иное, как некая постоянная С1, которую мы получаем, если интегрирование выполнять корректно. И тогда уравнение угла поворота для балки при данной нагрузке на участке 0<x<0.5l будет выглядеть так:

tgθх = — tgθA + Ax2/(2EI) (11.6.5)

Эпюра углов поворота для балки с распределенной нагрузкой визуально ни чем не отличается от эпюры углов поворота для балки со сосредоточенной нагрузкой, разница только в том, что эпюра углов поворота для балки с распределенной нагрузкой — это кубическая парабола. Уравнение угла поворота для балки с равномерно распределенной нагрузкой будет выглядеть так:

tgθх = — tgθA + Ax2/(2EI) — qx3/(6ЕI) (11.6.6)

По поводу знаков в данном уравнении. «-» означает, что рассматриваемый член уравнения как бы пытается повернуть балку против часовой стрелки относительно рассматриваемого поперечного сечения, а «+» — по часовой стрелке. Впрочем и по эпюре углов поворота видно, что значение tgθА должно быть отрицательным. Таким образом, если сечение имеет наклон по часовой стрелке относительно оси х, то оно будет отрицательным, а если против часовой стрелки — то положительным.

 

Ну и теперь самое главное, все эти разборки с углом поворота поперечного сечения нужны нам были для того, чтобы определить прогиб балки.

12. Определение прогиба.

(вернуться к основному содержанию)

Как мы видим из рисунка 11.4, треугольник с катетами h/2 и Δх является подобным треугольнику с катетом Х и вторым катетом, равным f+у, а это значит, что теперь мы можем определить значение прогиба:

tgθ = (f + y)/Х (12.1)

тогда

f + y = tgθ·X (12.2.1) или f + y = М·x·Х/(2ЕI) (12.2)

при малых значениях х значение у близко к 0, но в более дальних точках сечения значение у увеличивается. Значение у — это и есть влияние на величину прогиба наличия второй опоры. Отметим, что это значение у показывает разницу между реальным наклоном продольной оси балки и наклоном продольной оси балки, если бы балка просто поворачивалась вокруг опоры, и получается, что значение у зависит от изменения угла поворота. Кроме того, мы опять получили уравнение, в котором значение прогиба в некоторой точке зависит от тангенса угла поворота (12.2.1) и таким образом получается, что у угла поворота тоже есть «плечо действия». Например при у=f/2 (если присмотреться к левой части фотографии 1, то посредине балки это где-то так и будет) мы бы получили следующую формулу для определения прогиба:

f = М·x2/(3ЕI) (12.3.1)

Но мы не будем ничего предполагать, а воспользуемся интегрированием. Если мы проинтегрируем уравнение моментов для левой части балки, то получим значение у (эпюра для у показана бирюзовым цветом на фотографии 1):

у =∫∫∫(Q/2)dх = (Q/2)·(l/2)3/6EI = Ql3/(96EI) (12.3.2)

или площадь фиолетовой эпюры для левой части балки(рисунок 5.5), но нам нужна площадь голубой эпюры на левом участке балки (рисунок 5.6), которая в 2 раза больше площади фиолетовой эпюры. Таким образом:

f =2∫∫∫(Q/2)dх =2 (Q/2)·(l/2)3/6EI = Ql3/(48EI) (12.3.3)

Почему площадь голубой эпюры в 2 раза больше площади фиолетовой эпюры, объяснить очень легко. Площадь треугольника равна 1/2 от площади прямоугольника с теми же сторонами, площадь фигуры, описанной квадратной параболой, составляет 1/3 от площади прямоугольника с теми же сторонами. Если бы мы развернули фиолетовую эпюру, то получили бы прямоугольник, образованный голубой и фиолетовой эпюрами. Соответственно, если из площади прямоугольника вычесть 1/3, то мы получим 2/3. У этого логического ряда есть продолжение — площадь фигуры, описанной кубической параболой, составляет 1/4 от площади прямоугольника с теми же сторонами и так далее.

Мы можем найти значение прогиба и другим способом. Из рисунка 11.4 и формул (12.2) следует, что:

fх = — tgθx + ∫tgθdx (12.3.4)

fl/2 = — (Ql2/16EI) l/2 + (Ql3/96EI) = -(Ql3/48EI) (12.3.5)

В данном случае знак «-» показывает, что центр поперечного сечения балки переместится вниз по оси у относительно оси х. А теперь вернемся к фотографии 1. Под продольной осью балки изображена эпюра у, именно это значение в точке l/2 мы и вычли, решая уравнение (12.3.3).  Кроме того получается, что соотношение между f и у зависит от коэффициента предыдущего интегрирования, т.е. у = kf или f = y/k. Когда мы интегрировали уравнение сил, то получили коэффициент 1/2. Впрочем, такое же значение мы получили и тогда, когда определяли плечо действия момента. Если продолжить этот логический ряд, то получается, что при определении прогиба от распределенной нагрузки мы должны использовать коэффициент 1/3, то есть прогиб в середине балки мы можем вычислить по следующей формуле:

f= 2∫∫∫(ql/2)dx — 3∫∫∫∫qdх = (2(qlx3/6) — 3(qx4/24))/EI = 5ql4/(384EI) (12.4.4)

или

fх= — ∫tgθdx + ∫∫∫(ql/2)dx -∫∫∫∫qdх (12.4.5)

fl/2 = (- ql3x/24 + (qlx3/6) — (qx4/24))/EI = — 5ql4/(384EI) (12.4.6)

В данном случае знак «-» означает, что центр тяжести поперечного сечения перемещается вниз по оси у.

Примечание: Предложенный метод определения прогиба несколько отличается от общепринятых, так как я старался сделать основной упор на наглядность.

Если определять прогиб графоаналитическим методом, то площадь фиктивной нагрузки — эпюры моментов, описываемой квадратной параболой, будет составлять (согласно таблице 378.1) (2ql2/(8·3))l/2 = ql3/24. А расстояние от центра тяжести эпюры до начала координат составляет 5/8, Тогда фиктивный момент равен (ql3/24)(5l/(8·2)) = 5ql4/384.

Конечно же, сосредоточенная нагрузка к балке может быть приложена и не посредине, распределенная нагрузка может быть не только равномерно распределенной и действовать не по всей длине балки, да и варианты крепления балки на опорах бывают разные. Но для того и существуют готовые формулы, чтобы ими пользоваться.

-Позвольте! — Скажете вы, — Все это хорошо, но как быть с касательными напряжениями? Ведь они действуют вдоль оси у и потому должны как-то влиять на прогиб!

Все верно. Касательные напряжения действительно влияют на прогиб, однако для балок с соотношением l/h > 10 это влияние очень незначительно и потому допустимо для определения прогиба пользоваться изложенным в данной статье методом.

Но это еще не все, как мы уже говорили, определить значение прогиба опытным путем достаточно просто по методу, описанному в самом начале статьи. Так так ничего лучшего под рукой не было, то я взял деревянную линейку, прообраз которой я так долго описывал (см. фотографию 1). Деревянная линейка имела размеры около 91.5 см, ширину b=4.96 см и высоту h=0.32 cм (высоту и ширину определял штангенциркулем). Затем я положил линейку на опоры, при этом расстояние между опорами составило около 90 см и таким образом получил балку с пролетом l=90 см. Под воздействием собственного веса линейка конечно же немного прогнулась, но столь малый прогиб меня не интересовал. Я измерил рулеткой (точность до 1 мм) расстояние от пола до низа линейки (77.65 см), затем приложил посредине условно сосредоточенную нагрузку (поместил посредине мерный стакан весом около 52 грамм с 250 граммами воды) и измерил расстояние от пола до низа линейки при нагрузке (75.5 см). Разница этих двух измерений и составила искомый прогиб. Таким образом величина прогиба определенного опытным путем составила 77.65 — 75.5 = 2.15 см. Осталось только найти модуль упругости для древесины, определить момент инерции для данного сечения и точно посчитать нагрузку. Модуль упругости Е для древесины = 105 кгс/см2, момент инерции прямоугольного сечения Iz = bh3/12 = 4.98·0.323/12 = 0.01359872 см4, полная нагрузка — 0.302 кг.

Расчет прогиба по формуле дал: f = Ql3/(48EI) = 0.302·903/(48·105·0.0136) = 3.37 см. Напомню, что прогиб, определенный опытным путем, составил: f = 2.15 см. Возможно следовало учесть влияние на прогиб первой производной функции — тангенса угла поворота? Ведь угол наклона, судя по фотографии, достаточно большой.

Проверяем: tgθ = Ql2/(16EI) = 0.302·902/(16·105·0.0136) = 0.11233. Тогда согласно формулы (542.12) f = 3.37/((1 + 0.1122)3/2) = 3.307 см. Т.е. влияние конечно есть, но оно не превышает 2% или 0.63 мм. 

Результат меня сначала удивил, но потом объяснений для такого расхождения нашлось несколько, в частности в середине поперечное сечение линейки было не прямоугольным, так как линейка была деформирована от времени и воздействия воды, соответственно момент инерции для такого сечения больше чем, для прямоугольного, кроме того, линейка изготовлена не из сосны, а из более твердой породы древесины, для которой и модуль упругости следует принимать больше. Да и с научной точки зрения одного результата совершенно недостаточно, чтобы говорить о каких-либо закономерностях. После этого я проверил величину прогиба для деревянного бруска с моментом инерции I=2.02 см4, длиной более 2 м при пролете 2 м под нагрузкой 2 кг, приложенной посредине бруска и тогда значение прогиба, определенного теоретическим путем и опытным путем, совпало до десятых долей миллиметра. Конечно, можно было бы и дальше продолжать эксперименты, но так уж получилось, что до меня это уже сделали сотни других людей и получили на практике результаты, очень близкие к теоретическим. А если еще учесть, что идеально изотропные материалы бывают только в теории, то это очень хорошие результаты.

13. Определение угла поворота через прогиб.

(вернуться к основному содержанию)

Определить значение угла поворота для шарнирно опертой балки, на которую действует только изгибающий момент M на одной из опор, например на опоре А, казалось бы, проще простого:

tgθх = — tgθA + Мx/(EI) — Аx2/(2ЕI) (13.1.1)

где А = М/l, (B = — M/l), но для этого нужно знать угол поворота на опоре А, а мы его не знаем, однако вычислить его помогает понимание того, что прогиб на опорах будет равен нулю и тогда:

fA = tgθBl — Bl3/(6EI) = 0; tgθB = — Ml3/(6l2EI) = — Ml/(6EI) (13.1.2)

fB = tgθAl + Ml2/(2EI)- Al3/(6EI) = 0; tgθA = — Ml/(3EI) (13.1.3)

Как видим, угол поворота на опоре к которой приложен изгибающий момент, в два раза больше угла поворота на противоположной опоре, это очень важная закономерность, которая в дальнейшем нам очень пригодится.

Когда сосредоточенная нагрузка к балке приложена не по центру тяжести или распределенная нагрузка является неравномерной, то углы поворота на опорах определяются через прогиб, как в вышеприведенном примере. Другими словами — значения начальных параметров определяются в ходе решения дифференциальных уравнений.

Расчет прогиба балки методом начальных параметров

В этой статье будут рассмотрены основные нюансы расчета прогибов, методом начальных параметров, на примере консольной балки, работающей на изгиб. А также рассмотрим пример, где с помощью универсального уравнения, определим прогиб балки и угол поворота.

Теория по методу начальных параметров

Возьмем консольную балку, нагруженную сосредоточенной силой, моментом, а также распределенной нагрузкой. Таким образом, зададимся такой расчетной схемой, где присутствуют все виды нагрузок, тем самым, охватим всю теоретическую часть по максимуму. Обозначим опорные реакции в жесткой заделке, возникающие под действием внешней нагрузки:

Выбор базы и обозначение системы координат

Для балки выберем базу с левой стороны, от которой будем отсчитывать расстояния до приложения сил, моментов, начала и конца распределенной нагрузки. Базу обозначим буквой O и проведем через нее систему координат:

Базу традиционно выбирают с левого краю балки, но можно выбрать ее и справа. Тогда в уравнении будут противоположные знаки, это может пригодиться в некоторых случаях, упростит  немного решение. Понимание, когда принимать базу слева или справа, придет с опытом решения задач на метод начальных параметров.

Универсальное уравнение прогибов для балки

После введения базы, системы координат и обозначении расстояний а, б, в, г записываем универсальную формулу, с помощью которой, будем рассчитывать прогиб балки (вертикальное перемещение сечения K, находящегося на свободном торце балки): Теперь поговорим об этой формуле, проанализируем так сказать:

  • E – модуль упругости;
  • I – момент инерции;
  • Vk – прогиб сечения K;
  • VO – прогиб сечения O;
  • θO – угол поворота сечения О.

Не буду приводить вывод этой формулы, не хочу отпугивать читателей, продвинутые студенты могут ознакомиться с выводом самостоятельно в учебнике по сопромату. Я только расскажу об основных закономерностях этого уравнения и как записать его для любой балки постоянного сечения.

Итак, изучаем эту формулу с лева направо. В левой части уравнения обознается искомый прогиб, в нашем случае Vk, который дополнительно умножается на жесткость балки — EI:В уравнении всегда учитывается прогиб сечения балки, совпадающего с нашей базой EIVO:

Также всегда учитывается угол поворота сечения совпадающего с выбранной базой. Причем, произведение EIθO всегда умножается на расстояние от базы до сечения, прогиб которого рассчитывается, в нашем примере — это расстояние г.

Следующие компоненты этого уравнения учитывают всю нагрузку находящуюся слева от рассматриваемого сечения. В скобках расстояния от базы до сечения отнимаются расстояния от базы до соответствующей силы или момента, начала или конца распределенной нагрузки.

Скобка, в случае с сосредоточенными силами, возводится в 3 степень и делится на 6. Если сила смотрит вверх, то считаем ее положительной, если вниз, то в уравнении она записывается с минусом:

В случае с моментами, скоба возводится во 2 степень и делится на 2. Знак у момента будет положительный, когда он направлен почасовой стрелке и отрицательным, соответственно, когда против часовой стрелки.

Учет распределенной нагрузки

Теперь поговорим о распределенной нагрузке. Как уже говорилось, в уравнении метода начальных параметров должно учитываться начало и конец распределенной нагрузки, но конец ее совпадает с сечением, прогиб которого мы хотим вычислить, поэтому в уравнение попадает только ее начало.

Причем важно, даже если бы в этом сечении была бы сила или момент, их бы так же не учитывали. Нас интересует все, что находится слева от рассматриваемого сечения.

Для распределенной нагрузки скобочка возводится в 4 степень и делится на 24. Правило знаков такое же, как и для сосредоточенных сил:

Граничные условия

Чтобы решить уравнение нам понадобятся еще кое-какие данные. С первого взгляда в уравнении у нас наблюдается три неизвестных: VK, VO и θO. Но кое-что мы можем почерпнуть из самой схемы. Мы знаем, в жесткой заделке не может быть никаких прогибов, и ни каких поворотов, то есть VO=0 и θO=0, это и есть так называемые начальные параметры или их еще называют граничными условиями. Теперь, если бы у нас была реальная задача, мы бы подставили все численные данные и нашли перемещение сечения K.

Если бы балка была закреплена с помощью шарнирно подвижной и неподвижной опоры, тогда мы бы приняли прогибы в опорах равными нулю, но угол поворота в опорах был бы уже отличен от нуля. Более подробно об этом рассказано в другой моей статье, посвященной методу начальных параметров на примере балки на двух опорах.

Чуть не забыл про еще одну величину, которую часто требуется определять методом начальных параметров.  Как известно, при изгибе, поперечные сечения балок помимо того, что перемещаются вертикально (прогибаются) так еще и поворачиваются на какой-то угол. Углы поворота и прогибы поперечных сечений связаны дифференциальной зависимостью.

Если продифференцировать уравнение, которое мы получили для прогиба поперечного сечения K, то получим уравнение угла поворота этого сечения:

Пример расчета прогиба балки

Для закрепления пройденного материала, предлагаю рассмотреть пример с заданными численными значениями всех параметров балки и нагрузок. Возьмем также консольную балку, которая жестко закреплена с правого торца. Будем считать, что балка изготовлена из стали (модуль упругости E = 2·105 МПа), в сечении у нее двутавр №16 (момент инерции по сортаменту I = 873 см4). Рассчитывать будем прогиб свободного торца, находящегося слева.

Подготовительный этап

Проводим подготовительные действия, перед расчетом прогиба: помечаем базу O, с левого торца балки, проводим координатные оси и показываем реакции, возникающие в заделке, под действием заданной нагрузки:

В методе начальных параметров, есть еще одна особенность, которая касается распределенной нагрузки. Если на балку действует распределенная нагрузка, то ее конец, обязательно должен находиться на краю балки (в точке наиболее удаленной от заданной базы). Только в таком случае, рассматриваемый метод будет работать. В нашем примере, нагрузка, как видно, начинается на расстоянии 2 м. от базы и заканчивается на 4 м. В таком случае, нагрузка продлевается до конца балки, а искусственное продление компенсируется дополнительной, противоположно-направленной нагрузкой. Тем самым, в расчете прогибов будет уже учитываться 2 распределенные нагрузки:

Расчет прогиба

Записываем граничные условия для заданной расчетной схемы:

VA = 0 при x = 6м

θA = 0 при x = 6м

Напомню, что нас, в этом примере, интересует прогиб сечения O (VO). Для его нахождения составим уравнение, для сечения A, в которое будет входить искомая величина:

В полученном уравнении, у нас содержится две неизвестные величины: искомый прогиб VO и угол поворота этого сечения — θO:

Таким образом, чтобы решить поставленную задачу, составим дополнительное уравнение, но только теперь, не прогибов, а углов поворотов, для сечения A:Из второго уравнения, найдем угол поворота:После чего, рассчитываем искомый прогиб:

Таким образом, свободный торец такой балки, прогнется практически на 6 см. Данную задачу, можно решить несколько проще, если ввести базу с правого торца. В таком случае, для решения потребовалось бы лишь одно уравнение, однако, оно было бы немного объемнее, т.к. включало реакции в заделке.

Расчет балок онлайн. Примеры расчета

Расчет балки различается в зависимости от того, является она статически определимой, либо статически неопределимой. На сайте производится расчет любых балок, но подробное решение расписывается только для статически определимых балок, не имеющих промежуточных шарниров.

Балка на двух опорах. Построение эпюр

Для этого типа балок сервис позволяет определить и подробно расписывает:

  • реакции опор
  • эпюры поперечных сил и изгибающих моментов (эпюры Q и M)
  • подбор сечений — двутавр, прямоугольник, круг, квадрат, труба
  • строятся эпюры нормальных и касательных напряжений
  • по уравнениям метода начальных параметров вычисляются прогибы и углы поворота. Записываются и сами уравнения метода начальных параметров по участкам.

Посмотреть пример »

Консольная балка. Построение эпюр.

Для этого типа балок сервис позволяет определить и подробно расписывает:

  • построение эпюр поперечных сил и изгибающих моментов
  • подбор сечений — двутавр, прямоугольник, круг, квадрат, труба
  • строятся эпюры нормальных и касательных напряжений
  • вычисляются прогибы и углы поворота.

Посмотреть пример »

Статически неопределимая балка. Подбор сечения.

Для такого типа балок Вы можете получить

  • только результаты расчета — (эпюры Q и M).

Естественно, по этим эпюрам можно легко найти реакции опор. Подробный ход расчета не расписывается, но, имея результаты, Вы легко можете проверить все промежуточные итоги своего расчета.

Посмотреть пример »

Балка с промежуточными шарнирами

Расчет балки с промежуточными шарнирами Вы должны производить, скорее всего, методом построения поэтажной схемы. Сервис, опять же, дает только конечный результат, но его наличие, естественно, очень упрощает проверку промежуточных этапов решения заданий.

 

Посмотреть пример »

Формулы для расчета изгибов труб и коробов

Создано в Sketch. Создано в Sketch. Переключить меню

800-767-1576

Поиск Сбросить поиск ×
  • Войдите или зарегистрируйтесь
  • 0
Поиск Сбросить поиск × Поиск Сбросить поиск × Поиск Сбросить поиск ×
    Поиск Сбросить поиск ×

      Главное меню

    • Бренды
    • Труба и трубопровод
    • Подземные инструменты и принадлежности
    • Ящики для тяги
    • Электрооборудование и HVAC
    • Инструменты и оборудование
    • Ресурсы
      • Выбор подходящей трубы для подземных коммуникаций
      • Выбор корпусов и подкладок для электрических и подземных коммуникаций
      • Определение надлежащей грузоподъемности по ANSI для подземных тяговых ящиков
      • Как согнуть трубопровод и трубу с помощью гибочного станка
      • Как рассчитать размер подземной вытяжной коробки
      • Как запрограммировать таймер Tork серии 1100
      • Что такое элементы управления фотографиями? Статья
      • Формулы для расчета изгибов трубопроводов и труб
      • Действительно ли стоят более дорогие светодиоды?
      • Сварка и соединение труб из ПНД
      • Таблицы и схемы заполнения кабелепровода
      • Таблица замены балласта
      • Формулы электрических расчетов
    • Насчет нас
    • Свяжитесь с нами

      • Сортировать по категориям

    • Подземные трубы и трубопроводы
      • Труба HDPE
      • Муфты HDPE
      • Трубы и воздуховоды из ПВХ
        • Воздуховод из ПВХ Multi-Gard
        • P&C Воздуховод
        • Трубопровод из ПВХ 40 и 80
        • Телефонный канал
        • Разделенный трубопровод из ПВХ
        • Труба из ПВХ Bore-Gard
    • Подземные инструменты и принадлежности
      • Нагреватели трубопроводов и труб
      • Клеи для подземных трубопроводов
      • Поддержка стойки и рамы
      • Блок и захват
      • Крючки
      • Носители / Ракеты
      • Линии рук
      • Заглушки для воздуховодов
      • Шкивы
      • Блоки и захваты
      • Канальные стержни: стержни Tuf и стержни Ruf
      • Шашки
      • Блокирующие и захватывающие ролики
      • Палатки
      • Инструменты и расходные материалы
        • Смазка для протяжки кабеля
        • Лента / веревка
        • Притягивая глаза
        • Съемники
        • Потянуть за ручки
        • Вертлюги HDPE
      • Комплекты уплотнений
      • Трассирующий провод
      • Подземный кабель
      • Другие подземные утилиты
    • Подземные корпуса и крышки
      • Электрические тяговые ящики / ручки
      • Крышки корпуса
      • Удлинители для тяговых ящиков
      • Ящики для полива
        • Ящики для травы для орошения Jumbo
        • Ящики для орошения дерна LUB / XLUB
        • Круглые ящики для травы для орошения
        • Стандартные ящики для орошения дерна
    • Электрооборудование и HVAC
      • Защита от перегрузки
      • Органы управления и переключатели
        • Жилые таймеры
        • Автоматические выключатели
        • Панели управления
        • Переключатели
        • Диммеры
        • Управление бассейном / спа
        • Контроль энергии / времени
        • Элементы управления фотографиями — элементы управления и переключатели
        • Центры нагрузки
        • Разъединители — органы управления и переключатели
        • Дверные и оконные переключатели
      • Электрооборудование
        • Маркеры проводов
        • провод
        • Поставка и электрические кабели
        • Аксессуары для протягивания проволоки
        • Всепогодные уличные чехлы
        • Булавки
        • Рыба — Электрооборудование
        • Будильники
        • Выключатели
        • Отключение — Электроснабжение
        • Контакторы
        • Панели аварийного генератора
      • Принадлежности для ОВК
        • Циркуляторы воздуха
      • Промышленное и коммерческое освещение
        • Промышленные и коммерческие светодиодные фонари
        • Светодиодная модернизация
        • Балласт
        • Промышленное аварийное освещение
    • Инструменты
      • Аккумуляторные инструменты
      • Ручные инструменты
        • Бары
        • Кабельные, трубопроводные и трубогибы
        • Кабельные ножницы
        • Обжимные инструменты
        • Резаки
        • Молотки
        • Шестигранные ключи
        • Кольцевые пилы
        • Изолированные ручные инструменты
        • Нокаут-наборы
        • Многоцелевые инструменты
        • Драйверы для гаек
        • Плоскогубцы
        • Пилы и ножи
        • Отвертки
        • Инструменты для зачистки
        • Смесители и швы
        • Наборы инструментов
        • Гаечные ключи
        • Прочие ручные инструменты
      • Измерительные инструменты
        • Датчики измерения
        • Тестеры
        • Метры
        • Трейсеры
        • Измерительные аксессуары
      • Склад для инструментов
        • Ящики для хранения
        • Ящики для инструментов
        • Сумки для инструментов
        • Ковши для хранения
        • Ремни для хранения
        • Сумки для хранения инструментов
        • Принадлежности для хранения
      • Принадлежности для инструментов
        • Полотна для сабельной пилы
        • Принадлежности для дрели / шуруповерта
        • Кольцевые пилы
        • Сверла
      • Рабочее место и оборудование для обеспечения безопасности
        • Фонари и освещение на рабочем месте
        • Шлемы
        • Подставки и шпиндели
        • Перчатки — Безопасность на рабочем месте
        • Локауты
        • Защитное оборудование для очков
        • Предупреждающая лента: электрическая и предупреждающая лента
        • Аксессуары для рабочих мест
        • Другое защитное оборудование
      • Электрооборудование и запчасти Chapman

      • Сортировать по марке

    • Klein Tools
    • Молоток Eaton / Cutler
    • NSI Tork
    • Текущие инструменты
    • Квазитовые своды и люки
    • Легкий эффективный дизайн
    • Дизайн и производство DCD
    • Интерматик
    • Condux
    • Атлас Освещение
    • Продукция Highline
    • Rack-A-Tiers
    • Dura-Line
    • Lutron
    • Prime Conduit
    • Инструменты Nebo
    • Специальные продукты Etco
    • Универсальный балласт
    • Keystone Technologies
    • Вентиляционные изделия Air King
    • Copperhead Industries
    • Centennial Plastics, Inc.
    • Blue Diamond Industries
    • Houston Wire
    • Milbank
    • Карлон
    • Эрин Веревка
    • Посмотреть все бренды
      • Подарочные сертификаты
      • Войдите или зарегистрируйтесь
    Поиск Сбросить поиск ×

      Главное меню

    • Бренды
    • Труба и трубопровод
    • Подземные инструменты и принадлежности
    • Ящики для тяги
    • Электрооборудование и HVAC
    • Инструменты и оборудование
    • Ресурсы
      • Выбор подходящей трубы для подземных коммуникаций
      • Выбор корпусов и подкладок для электрических и подземных коммуникаций
      • Определение надлежащей грузоподъемности по ANSI для подземных тяговых ящиков
      • Как согнуть трубопровод и трубу с помощью гибочного станка
      • Как рассчитать размер подземной вытяжной коробки
      • Как запрограммировать таймер Tork серии 1100
      • Что такое элементы управления фотографиями? Статья
      • Формулы для расчета изгибов трубопроводов и труб
      • Действительно ли стоят более дорогие светодиоды?
      • Сварка и соединение труб из ПНД
      • Таблицы и схемы заполнения кабелепровода
      • Таблица замены балласта
      • Формулы электрических расчетов
    • Насчет нас
    • Свяжитесь с нами

      • Сортировать по категориям

    • Подземные трубы и трубопроводы
      • Труба HDPE
      • Муфты HDPE
      • Трубы и воздуховоды из ПВХ
        • Воздуховод из ПВХ Multi-Gard
        • P&C Воздуховод
        • Трубопровод из ПВХ 40 и 80
        • Телефонный канал
        • Разделенный трубопровод из ПВХ
        • Труба из ПВХ Bore-Gard
    • Подземные инструменты и принадлежности
      • Нагреватели трубопроводов и труб
      • Клеи для подземных трубопроводов
      • Поддержка стойки и рамы
      • Блок и захват
      • Крючки
      • Носители / Ракеты
      • Линии рук
      • Заглушки для воздуховодов
      • Шкивы
      • Блоки и захваты
      • Канальные стержни: стержни Tuf и стержни Ruf
      • Шашки
      • Блокирующие и захватывающие ролики
      • Палатки
      • Инструменты и расходные материалы
        • Смазка для протяжки кабеля
        • Лента / веревка
        • Притягивая глаза
        • Съемники
        • Потянуть за ручки
        • Вертлюги HDPE
      • Комплекты уплотнений
      • Трассирующий провод
      • Подземный кабель
      • Другие подземные утилиты
    • Подземные корпуса и крышки
      • Электрические тяговые ящики / ручки
      • Крышки корпуса
      • Удлинители для тяговых ящиков
      • Ящики для полива
        • Ящики для травы для орошения Jumbo
        • Ящики для орошения дерна LUB / XLUB
        • Круглые ящики для травы для орошения
        • Стандартные ящики для орошения дерна
    • Электрооборудование и HVAC
      • Защита от перегрузки
      • Органы управления и переключатели
        • Жилые таймеры
        • Автоматические выключатели
        • Панели управления
        • Переключатели
        • Диммеры
        • Управление бассейном / спа
        • Контроль энергии / времени
        • Элементы управления фотографиями — элементы управления и переключатели
        • Центры нагрузки
        • Разъединители — органы управления и переключатели
        • Дверные и оконные переключатели
      • Электрооборудование
        • Маркеры проводов
        • провод
        • Поставка и электрические кабели
        • Аксессуары для протягивания проволоки
        • Всепогодные уличные чехлы
        • Булавки
        • Рыба — Электрооборудование
        • Будильники
        • Выключатели
        • Отключение — Электроснабжение
        • Контакторы
        • Панели аварийного генератора
      • Принадлежности для ОВК
        • Циркуляторы воздуха
      • Промышленное и коммерческое освещение
        • Промышленные и коммерческие светодиодные фонари
        • Светодиодная модернизация
        • Балласт
        • Промышленное аварийное освещение
    • Инструменты
      • Аккумуляторные инструменты
      • Ручные инструменты
        • Бары
        • Кабельные, трубопроводные и трубогибы
        • Кабельные ножницы
        • Обжимные инструменты
        • Резаки
        • Молотки
        • Шестигранные ключи
        • Кольцевые пилы
        • Изолированные ручные инструменты
        • Нокаут-наборы
        • Многоцелевые инструменты
        • Драйверы для гаек
        • Плоскогубцы
        • Пилы и ножи
        • Отвертки
        • Инструменты для зачистки
        • Смесители и швы
        • Наборы инструментов
        • Гаечные ключи
        • Прочие ручные инструменты
      • Измерительные инструменты
        • Датчики измерения
        • Тестеры
        • Метры
        • Трейсеры
        • Измерительные аксессуары
      • Склад для инструментов
        • Ящики для хранения
        • Ящики для инструментов
        • Сумки для инструментов
        • Ковши для хранения
        • Ремни для хранения
        • Сумки для хранения инструментов
        • Принадлежности для хранения
      • Принадлежности для инструментов
        • Полотна для сабельной пилы
        • Принадлежности для дрели / шуруповерта
        • Кольцевые пилы
        • Сверла
      • Рабочее место и оборудование для обеспечения безопасности
        • Фонари и освещение на рабочем месте
        • Шлемы
        • Подставки и шпиндели

    Балки, изгиб и граничные условия: опора балки

    Балки, изгиб и граничные условия: опора балки В этом модуле мы рассмотрим два разных метода поддержки балки.В Первый метод называется консолью , которая получается жестко зажим или привинчивание балки на одном из ее концов, и позволяя балке свободно висеть на другом конце. Второй метод называется балка без опоры. В этом случае балка размещается на двух несущие конструкции и балка закреплена так, чтобы она могла гнуться, но не переводить.

    В модели статических балок, которую мы используем в этой лаборатории, отклонение балки описывается функцией отклонения w (x) .Значение w ( x ) — это величина вертикального смещения. в позиции на балке x единиц с левого конца.

    Способ опоры балки приводит к условиям на функция w ( x ) и ее производные. Эти условия вместе именуемые граничными условиями .

    Граничные условия и опоры балки

    В дальнейшем изложении мы примем L как общий длины балки и пусть x измеряют положение вдоль балка (где x = 0 — левая конечная точка луч.)

    Значения w ( x ) и его производная имеют физические интерпретации, связанные с опорой балки. Вот «словарь», помогающий переводить граничные условия и поддерживает:

    • w ( x ) — это просто высота балки.
    • w ‘ ( x ) — Как мы знаем из расчетов, w’ обозначает наклон балки x . Ничего загадочного Вот.
    • w « ( x ) — в терминах исчисления w» измеряет кривизна графика w ( x ). Интуитивно чем больше w « ( x ), тем более искривлен график. условия, w « ( x ) измеряет изгибающий момент луч при x . Это крутящий момент, который нагрузка оказывает на балку. при x . Один из способов подумать об этом — представить балку с очень жесткий шарнир, как показано ниже.

      Нагрузка на балку справа от петли будет оказывать крутящий момент на шарнир, стремящийся его повернуть. Даже в сплошной балке без петель балка будет иметь тенденцию гнуться. Насколько он гнется, зависит от величина изгибающего момента и модуль упругости балочный материал.

    • w » ( x ) — Третья производная имеет менее интуитивный имеется в виду геометрия кривой, чем w ‘ и w «. Однако у него есть довольно прямая физическая интерпретация.Так же, как w « ( x ) измеряет изгибающий момент при x , w » ( x ) измеряет силу сдвига на балку при x . Если мы подумаем о нашей балке с соединением в виде ласточкина хвоста вместо петли, то разница сил сразу вправо и слева от совместной воли стремятся раздвинуть его вертикально. (На самом деле это разница в изгибающий момент, поскольку w » ‘ является производной от w «.) Этот усилие сдвига измеряется как w » ( x ).

    Консольные балки

    Для консольной балки граничные условия следующие:

    • w (0) = 0 . Это граничное условие говорит о том, что база балка (у стены) не прогибается.
    • w ‘(0) = 0 . Также предполагаем, что балка у стены горизонтально, так что производная функции прогиба равен нулю в этой точке.
    • w » (L) = 0 . Это граничное условие моделирует предположение что на свободном конце кантилевера отсутствует изгибающий момент.
    • w » ‘(L) = 0 . Это граничное условие моделирует предположение, что на свободном конце луч.
    Если к свободному концу балки приложить сосредоточенную силу (для Например, на свободный конец подвешен груз массой м ), то это вызывает сдвиг на конце балки. 2 ). Отметим, что на самом деле мы могли бы использовать это граничное условие все время, поскольку если m = 0 , сводится к предыдущему случаю.

    Балки с простой опорой

    Для балки с опорой мы используем следующие граничные условия:

    • w (0) = 0 . Поскольку балка прикреплена к опоре, балка не может прогибаться на левой опоре.
    • w (L) = 0 . Балка также прикреплена к правой опоре.
    • w » (0) = 0 . Что касается консольной балки, то эта граница состояние говорит о том, что луч может свободно вращаться и не испытывает никаких крутящий момент. В реальной жизни обычно бывает небольшой крутящий момент из-за трения. между балкой и ее штифтом, но если штифт хорошо смазан, этим крутящим моментом можно пренебречь.
    • w » (L) = 0 . Точно так же луч не испытывает и изгибающие моменты на его правом креплении.

    Другие опоры балки

    Есть много других механизмов поддержки балок.Например, оба конца балки можно прикрепить к стене. Или один конец может быть закреплен болтами, а другой конец может свободно вращаться. Или луч может быть зажимается с одного конца, но «нависает» над опорой, размещенной в некоторой точке вдоль его длина.

    Каждый из этих опорных механизмов имеет связанные граничные условия, но мы не будем рассматривать эти механизмы здесь.

    Вернуться к: Основные идеи лаборатории
    Команда разработчиков расчетов Geometry Center

    Авторское право 1996 г. — Центр геометрии.Последнее изменение: 12 апреля, пятница, 15:54:29 1996 г.

    Калькулятор для инженеров | Калькулятор изгибающего момента

    НОВОСТИ | ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ | ЛИСТ

    Этим бесплатным калькулятором строительства можно управлять онлайн. Он представляет собой практический программный инструмент для расчета изгибающего момента и поперечной силы в любой период балки с простой опорой (без выступов) на основе точечной нагрузки, равнозначно заданной нагрузки, изменяемой нагрузки и функциональных моментов в диапазоне или опорах.

    Этот строительный калькулятор работает с расчетами стационарного равновесия для вычисления откликов на опорах, а также для вычисления величины поперечной силы и изгибающего момента на предпочтительной стадии. Он также вычисляет максимальное значение изгибающего момента и положение наивысшего изгибающего момента, которые являются случайными при расчете изгибающего момента для экземпляра нагрузки.

    Как пользоваться калькулятором изгибающего момента:

    Соглашение о знаках — Нагрузки, работающие ввысь, считаются оптимистичными, а в идентичном случае нисходящие нагрузки считаются неконструктивными.Проходящий изгибающий момент считается конструктивным, а монополизирующий — неконструктивным. Моменты по часовой стрелке / правой руке отрицательны, а против часовой стрелки — положительны.

    Все расстояния определены относительно источника осей, полученного в самой крайней левой последней части луча. Значения для всех расстояний должны быть в метрах, а нагрузка в килограммах Ньютона. Он предлагает количество пучка в килограмм-ньютон-метрах и силу сдвига в килоньютонах. При использовании нагрузки убедитесь, что нагрузки не должны продолжаться за пределами диапазона балки.

    Вы можете быстро найти значения изгибающего момента на разных фазах балки, просто изменив положение сегмента «x». Однако убедитесь, что количество «x» не должно превышать расстояние луча.

    Чтобы управлять более чем одной нагрузкой, выберите сложение результатов всех экземпляров (с законом суперпозиции). Рассчитанные значения используются для создания эскиза изгибающего момента.

    Калькулятор также идеально подходит для определения точек влияния линии рисунка на конструкции.

    Чтобы выполнить онлайн-расчет, перейдите по следующей ссылке на Калькулятор изгибающего момента

    .

    No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *