Радиус описанной окружности шестиугольника формула
Правильные многоугольники и окружность. Здравствуйте, Дорогие друзья! Во многих задачах в курсе геометрии, в том числе и в составе ЕГЭ имеется много заданий связанных с понятием окружности вписанной в правильный многоугольник и описанной около него. Если конкретней, то в данном случае мы рассмотрим правильный треугольник, также квадрат и правильный шестиугольник. Именно с этими правильными многоугольниками связаны условия заданий на экзамене. Обычно в ходе решения таких задач возникает необходимость выразить:
1. Сторону правильного треугольника через радиус вписанной или описанной окружности.
2. Сторону квадрата через радиус вписанной окружности или описанной окружности.
3. Сторону правильного шестиугольника через радиус вписанной или описанной окружности.
4. Радиус вписанной в правильный многоугольник окружности через радиус описанной около него окружности и наоборот.
На сайте рассмотрены (и в будущем будут рассматриваться) задачи , в которых эти формулы используются. При решении подробно не описывается как они выводятся. Просто говорится, например, что сторона правильного треугольника соотносится с радиусом вписанной в него окружности как:
У многих возникают вопросы по этому поводу: Как? Почему? В этой статье мы выведем все указанные соотношения и в будущем при решении задач, если потребуется, просто буду давать ссылку на эту статью.
Что нужно всегда помнить и понимать?
Центр правильного многоугольника совпадает с центром вписанной о описанной около него окружности. Итак, приступим!
Правильный треугольник, вписанная и описанная окружность.
Пусть а – это его сторона, радиус описанной окружности равен R, а радиус вписанной окружности равен r.
Стороны правильного треугольника и вписанная в него окружность имеют общие точки (точки касания), эти точки делят стороны треугольника пополам. Радиус описанной окружности, проведённый к вершине треугольника является биссектрисой, то есть делит угол при этой вершине, равный 60 градусам, пополам. Рассмотрим прямоугольный треугольник (выделен жёлтым). По определению тангенса: Получаем, что: По определению косинуса: Получаем, что: Можем записать соотношение радиусов:
Рассмотрим прямоугольный треугольник (выделен жёлтым). По определению тангенса: Получаем, что: По определению косинуса: Получаем, что: Можем записать соотношение радиусов:
Квадрат, вписанная и описанная около него окружность.
Пусть а – это сторона квадрата, радиус описанной окружности равен R, а радиус вписанной окружности равен r.
Стороны квадрата и вписанная в него окружность имеют общие точки (точки касания), эти точки делят стороны квадрата пополам.
Радиус описанной окружности, проведённый к вершине квадрата является биссектрисой, то есть делит угол квадрата пополам.
Рассмотрим прямоугольный треугольник (выделен жёлтым). На основании вышеизложенного можно сделать вывод о том, что:
По определению косинуса: Получаем, что: *Можно было воспользоваться также теоремой Пифагора. Запишем соотношение радиусов:
Правильный шестиугольник. Вписанная и описанная окружность.
Стороны правильного шестиугольника и вписанная окружность имеют общие точки (точки касания), эти точки делят стороны данного шестиугольника пополам.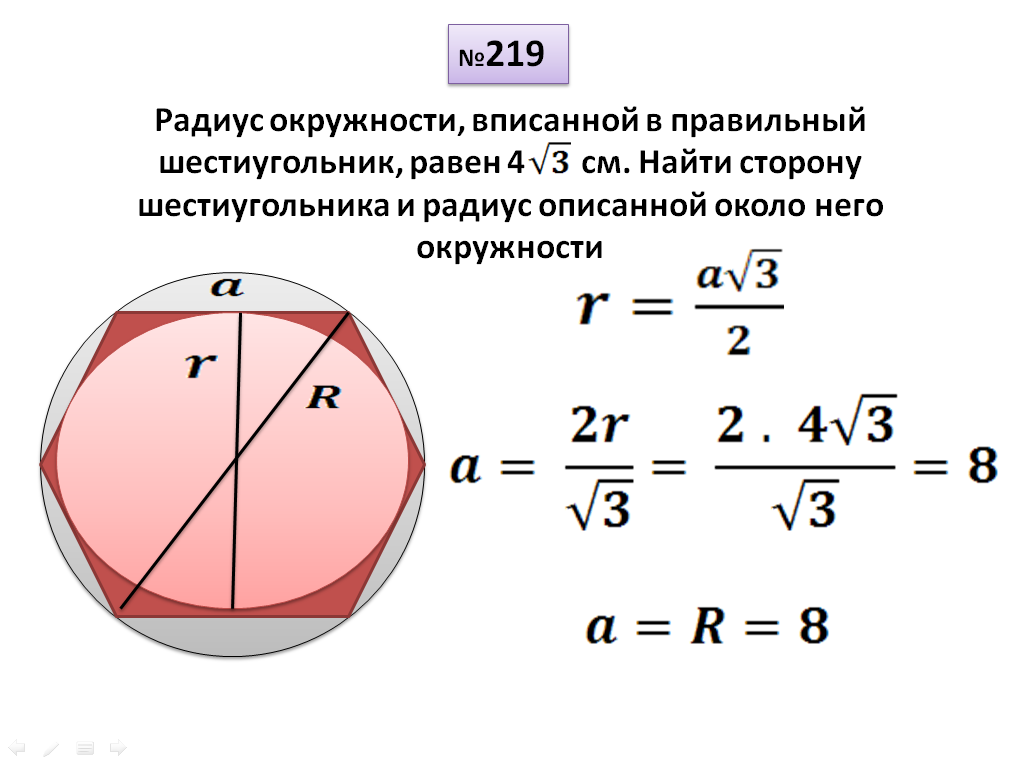
Радиус описанной окружности, проведённый к вершине шестиугольника является биссектрисой, то есть делит угол правильного шестиугольника равный 120 градусам пополам. Подробнее о правильном шестиугольнике и описанной около него окружности можете посмотреть информацию в этой статье .
Рассмотрим прямоугольный треугольник (выделен жёлтым). По определению тангенса: Получаем, что:
Тот факт, что сторона правильного шестиугольника равна радиусу описанной окружности известен практически всем школьникам изучившим соответствующий материал по планиметрии:
Если интересно посмотрите как это можно вывести. По определению косинуса в прямоугольном треугольнике: Получаем, что: Можем записать соотношение радиусов: Вот и всё.
Конечно же, учить и запоминать данные формулы не нужно. В ходе решения вы всегда сможете их также вывести используя свойства правильных многоугольников, определения тангенса и косинуса , теорему Пифагора.
Я решил изложить это в отдельной статье только для того, чтобы у вас не возникали вопросы при решении и изучении соответствующих заданий на блоге и вы всегда могли бы посмотреть откуда взялась формула.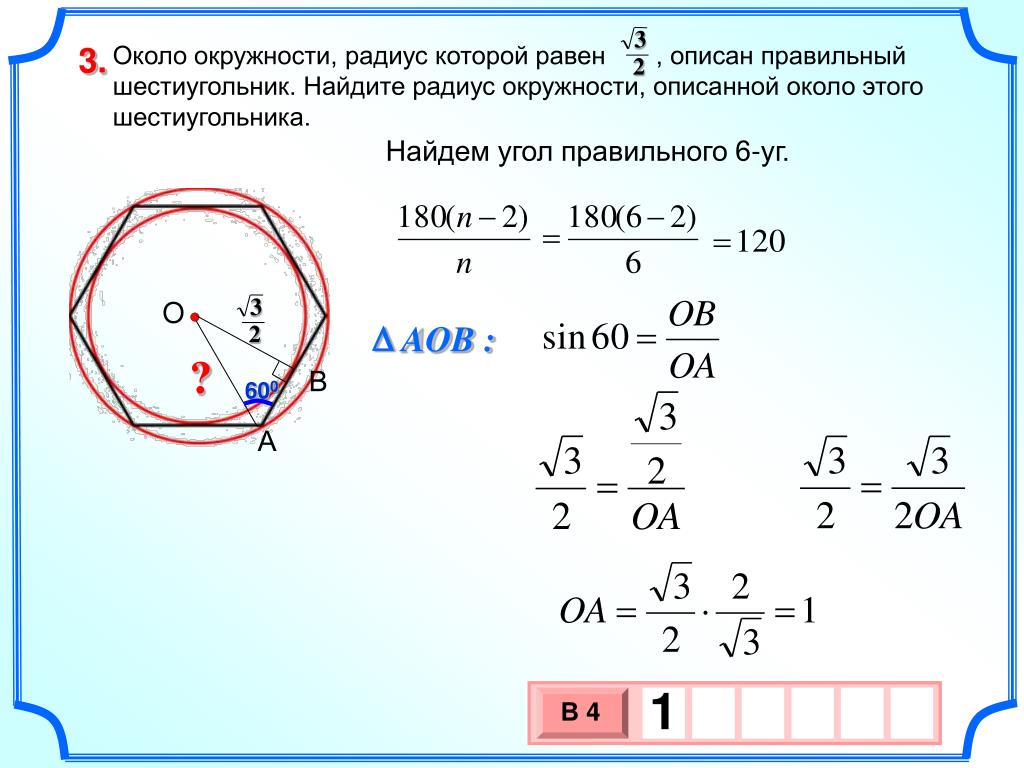
1. Все углы правильного шестиугольника равны 120°
2. Все стороны правильного шестиугольника равны между собой
3. Периметр правильного шестиугольника
4. Формула площади правильного шестиугольника
5. Радиус описанной окружности правильного шестиугольника
6. Диаметр описанной окружности правильного шестиугольника
7. Радиус вписанной окружности правильного шестиугольника
8. Соотношения между радиусами вписанной и описанной окружностей
9. Угол , угол , угол , откуда следует, что треугольник – прямоугольный с гипотенузой равной . Следовательно,
10. Длина дуги AB равна
11. Формула площади сектора
.
a – сторона шестиугольника
d – диагональ шестиугольника
Радиус описанной окружности правильного шестиугольника (R):
Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 39? Найдите радиус описанной окружности этого треугольника.
 Около трапеции описана окружность. Периметр трапеции равен 52, средняя линия равна 21.
Около трапеции описана окружность. Периметр трапеции равен 52, средняя линия равна 21.
Прототипы В6 часть 2
Сторона правильного треугольника равна . Найдите радиус окружности, описанной около этого треугольника.
Гипотенуза прямоугольного треугольника равна 86. Найдите радиус описанной окружности этого треугольника.
В треугольнике ABC , , угол C равен . Найдите радиус описанной окружности этого треугольника.
Боковая сторона равнобедренного треугольника равна 7, угол при вершине, противолежащей основанию, равен . Найдите диаметр описанной окружности этого треугольника.
Найдите радиус окружности, описанной около прямоугольника, две стороны которого равны 12 и .
Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 39?

Радиус окружности, вписанной в правильный треугольник, равен 31. Найдите высоту этого треугольника.
Радиус окружности, вписанной в правильный треугольник, равен . Найдите сторону этого треугольника.
Найдите радиус окружности, вписанной в квадрат со стороной 56.
Найдите сторону квадрата, описанного около окружности радиуса 47.
Сторона ромба равна 20, острый угол равен . Найдите радиус вписанной окружности этого ромба.
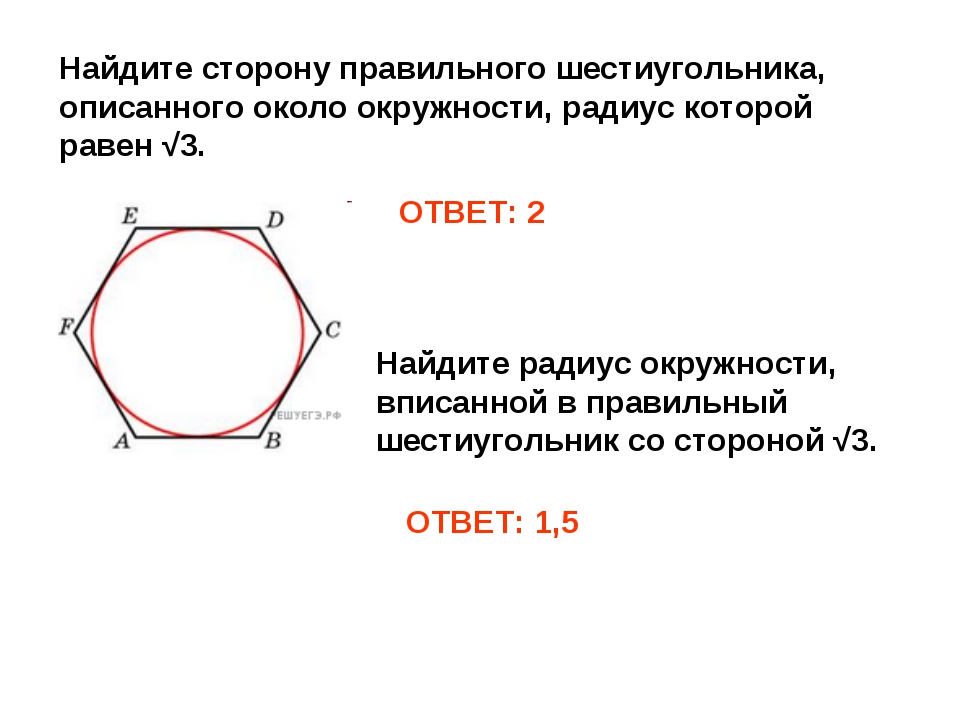
Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен .
Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .
Сторона AB треугольника ABC равна 40. Противолежащий ей угол C равен . Найдите радиус окружности, описанной около этого треугольника.
Угол C треугольника ABC, вписанного в окружность радиуса 37, равен . Найдите сторону AB этого треугольника.
Сторона AB треугольника ABC равна 7.
 Противолежащий ей угол C равен . Найдите радиус окружности, описанной около этого треугольника.
Противолежащий ей угол C равен . Найдите радиус окружности, описанной около этого треугольника.Боковые стороны равнобедренного треугольника равны 104, основание равно 192. Найдите радиус описанной окружности этого треугольника.
Около трапеции описана окружность. Периметр трапеции равен 52, средняя линия равна 21. Найдите боковую сторону трапеции.
Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен , большее основание равно 38. Найдите радиус описанной окружности этой трапеции.
Основания равнобедренной трапеции равны 32 и 24. Радиус описанной окружности равен 20.
Два угла вписанного в окружность четырехугольника равны и . Найдите больший из оставшихся углов. Ответ дайте в градусах.
Углы A, B и C четырехугольника ABCD относятся как . Найдите угол D, если около данного четырехугольника можно описать окружность. Ответ дайте в градусах.
 Найдите диаметр описанной окружности.
Найдите диаметр описанной окружности.Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен . Найдите n.
Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 43. Найдите гипотенузу c этого треугольника. В ответе укажите
Катеты равнобедренного прямоугольного треугольника равны . Найдите радиус окружности, вписанной в этот треугольник.
В треугольнике ABC , , угол C равен . Найдите радиус вписанной окружности.
Боковые стороны равнобедренного треугольника равны 136, основание равно 128. Найдите радиус вписанной окружности.
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 10 и 1, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
Боковые стороны трапеции, описанной около окружности, равны 11 и 1.
 Найдите среднюю линию трапеции.
Найдите среднюю линию трапеции.Около окружности описана трапеция, периметр которой равен 84. Найдите ее среднюю линию.
Периметр прямоугольной трапеции, описанной около окружности, равен 80, ее большая боковая сторона равна 30. Найдите радиус окружности.
В четырехугольник ABCD вписана окружность, , . Найдите периметр четырехугольника.
В четырехугольник ABCD вписана окружность, , и . Найдите четвертую сторону четырехугольника
Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как . Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 48.
К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 8, 23, 78. Найдите периметр данного треугольника.
Около окружности, радиус которой равен , описан квадрат. Найдите радиус окружности, описанной около этого квадрата.
Около окружности, радиус которой равен , описан правильный шестиугольник.
 Найдите радиус окружности, описанной около этого шестиугольника.
Найдите радиус окружности, описанной около этого шестиугольника.1.Найдите величину угла ABC. Ответ дайте в градусах.
2.Найдите градусную величину дуги AC окружности, на которую опирается угол ABC. Ответ дайте в градусах.
Найдите градусную величину дуги BC окружности, на которую опирается угол BAC. Ответ дайте в градусах.
4. Найдите угол ACB, если вписанные углы ADB и DAE опираются на дуги окружности, градусные величины которых равны соответственно и . Ответ дайте в градусах.
Угол ACB равен . Градусная величина дуги AB окружности, не содержащей точек D и E, равна . Найдите угол DAE. Ответ дайте в градусах.
6. Угол ACO равен . Его сторона CA касается окружности. Найдите градусную величину большей дуги AD окружности, заключенной внутри этого угла. Ответ дайте в градусах.
Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна .
 Ответ дайте в градусах.
Ответ дайте в градусах.Угол ACO равен , где O — центр окружности. Его сторона CA касается окружности. Найдите величину меньшей дуги AB окружности, заключенной внутри этого угла. Ответ дайте в градусах
Через концы A, B дуги окружности в проведены касательные AC и BC. Найдите угол ACB. Ответ дайте в градусах.
Приложенные файлы
- 83584511
Размер файла: 294 kB Загрузок: 0
Соотношение между радиусом вписанной правильный шестиугольник. Смотреть что такое «Правильный шестиугольник» в других словарях. От теории к практике
Есть ли поблизости от Вас карандаш? Взгляните-ка на его сечение — оно представляет собой правильный шестиугольник или, как его еще называют, гексагон. Такую форму имеет также сечение гайки, поле гексагональных шахмат, некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты. Гигантский правильный шестиугольник был недавно обнаружен в Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим поподробнее.
Правильный шестиугольник представляет собой многоугольник с шестью одинаковыми сторонами и равными углами. Из школьного курса нам известно, что он обладает следующими свойствами:
- Длина его сторон соответствует радиусу описанной окружности. Из всех это свойство имеет лишь правильный шестиугольник.
- Углы равны между собой, и величина каждого составляет 120°.
- Периметр гексагона можно найти по формуле Р=6*R, если известен радиус описанной вокруг него окружности, или Р=4*√(3)*r, если окружность в него вписана. R и r — радиусы описанной и вписанной окружности.
- Площадь, которую занимает правильный шестиугольник, определяется следующим образом: S=(3*√(3)*R 2)/2. Если радиус неизвестен, вместо него подставляем длину одной из сторон — как известно, она соответствует длине радиуса описанной окружности.
У правильного шестиугольника есть одна интересная особенность, благодаря которой он получил в природе такое широкое распространение, — он способен заполнить любую поверхность плоскости без наложений и пробелов. Существует даже так называемая лемма Пала, согласно которой правильный гексагон, сторона которого равна 1/√(3), представляет собой универсальную покрышку, то есть может покрыть любое множество с диаметром в одну единицу.
Существует даже так называемая лемма Пала, согласно которой правильный гексагон, сторона которого равна 1/√(3), представляет собой универсальную покрышку, то есть может покрыть любое множество с диаметром в одну единицу.
Теперь рассмотрим построение правильного шестиугольника. Есть несколько способов, самый простой из которых предполагает использование циркуля, карандаша и линейки. Вначале рисуем циркулем произвольную окружность, затем в произвольном месте на этой окружности делаем точку. Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек. Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.
На практике бывают случаи, когда требуется нарисовать шестиугольник большого размера. Например, на двухуровневом гипсокартонном потолке, вокруг места крепления центральной люстры, нужно установить на нижнем уровне шесть небольших светильников. Циркуль таких размеров найти будет очень и очень сложно. Как поступить в этом случае? Как вообще нарисовать большую окружность? Очень просто. Нужно взять крепкую нить нужной длины и обвязать один из ее концов напротив карандаша. Теперь осталось лишь найти помощника, который бы прижал к потолку в нужной точке второй конец нити. Конечно, в этом случае возможны незначительные погрешности, но вряд ли они вообще будут заметны постороннему человеку.
Циркуль таких размеров найти будет очень и очень сложно. Как поступить в этом случае? Как вообще нарисовать большую окружность? Очень просто. Нужно взять крепкую нить нужной длины и обвязать один из ее концов напротив карандаша. Теперь осталось лишь найти помощника, который бы прижал к потолку в нужной точке второй конец нити. Конечно, в этом случае возможны незначительные погрешности, но вряд ли они вообще будут заметны постороннему человеку.
Знаете ли вы, как выглядит правильный шестиугольник?
Этот вопрос задан не случайно. Большинство учащихся 11 класса не знают на него ответа.
Правильный шестиугольник — такой, у которого все стороны равны и все углы тоже равны .
Железная гайка. Снежинка. Ячейка сот, в которых живут пчелы. Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.
Многие школьники теряются, видя задачи на правильный шестиугольник, и считают, что для их решения нужны какие-то особые формулы. Так ли это?
Так ли это?
Проведем диагонали правильного шестиугольника. Мы получили шесть равносторонних треугольников.
Мы знаем, что площадь правильного треугольника: .
Тогда площадь правильного шестиугольника — в шесть раз больше.
Где — сторона правильного шестиугольника.
Обратите внимание, что в правильном шестиугольнике расстояние от его центра до любой из вершин одинаково и равно стороне правильного шестиугольник.
Значит, радиус окружности, описанной вокруг правильного шестиугольника, равен его стороне .
Радиус окружности, вписанной в правильный шестиугольник, нетрудно найти.
Он равен .
Теперь вы легко решите любые задачи ЕГЭ, в которых фигурирует правильный шестиугольник.
Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .
Радиус такой окружности равен .
Ответ: .
Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего проводим стороны 5-6 и 3-2.
Построение вписанного в окружность равностороннего треугольника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны
Так как угол 0-1-2 равен 30°, то для нахождения стороны
1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.
Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг.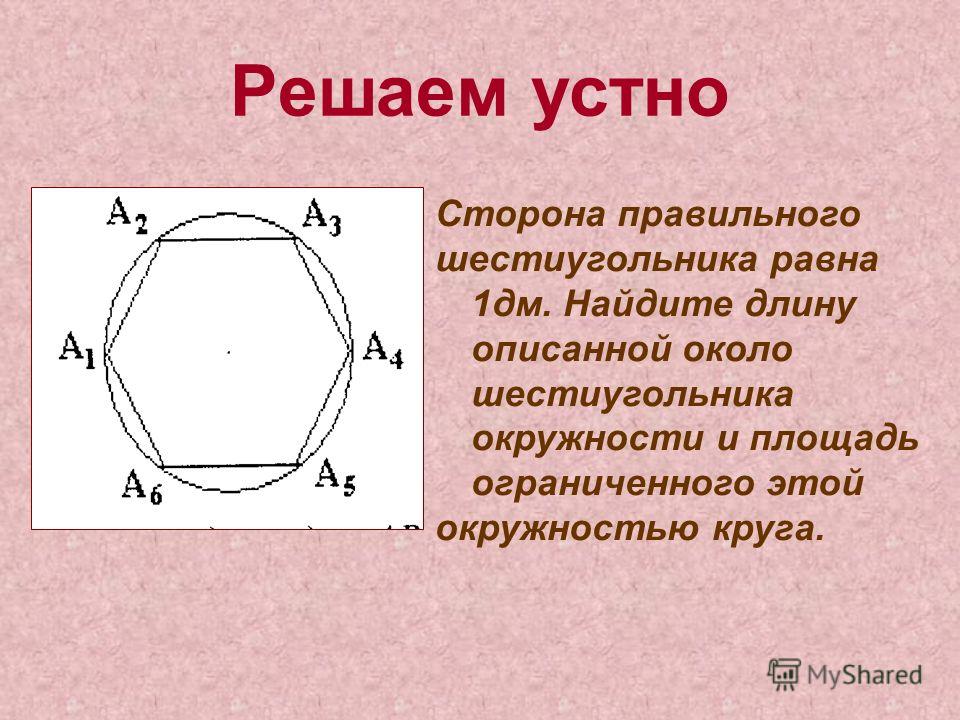 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника.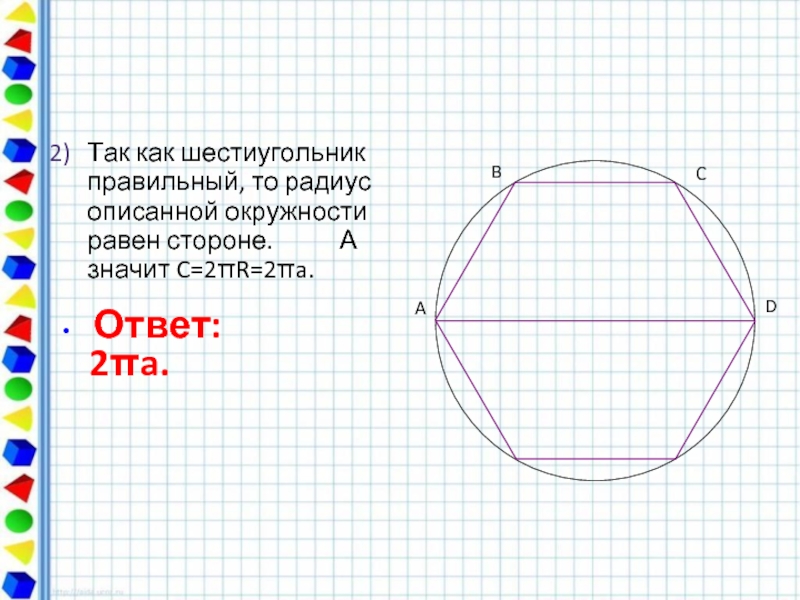 Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
Математические свойства
Особенность правильного шестиугольника — равенство его стороны и радиуса описанной окружности , поскольку
Все углы равны 120°.
Радиус вписанной окружности равен:
Периметр правильного шестиугольника равен:
Площадь правильного шестиугольника рассчитывается по формулам:
Шестиугольники замощают плоскость, то есть могут заполнять плоскость без пробелов и наложений, образуя так называемый паркет.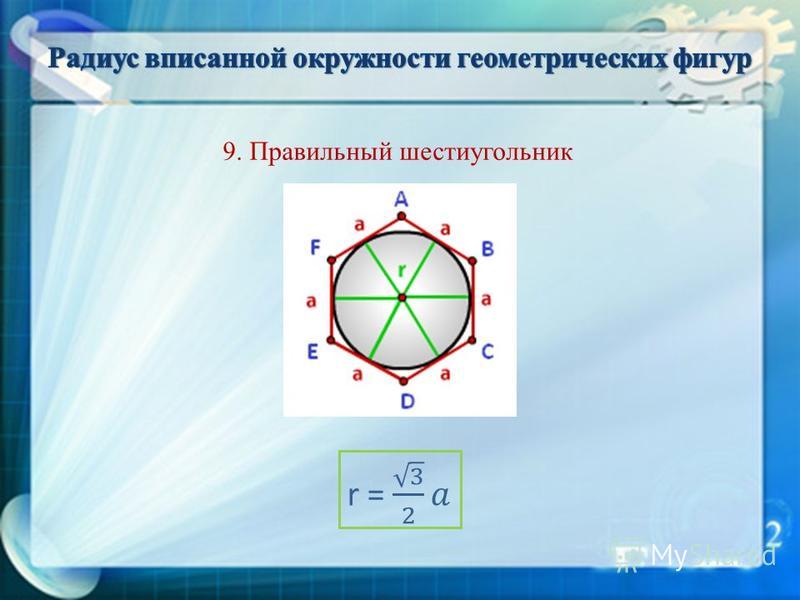
Шестиугольный паркет (шестиугольный паркетаж) — замощение плоскости равными правильными шестиугольниками, расположенными сторона к стороне.
Шестиугольный паркет является двойственным треугольному паркету: если соединить центры смежных шестиугольников, то проведённые отрезки дадут треугольный паркетаж. Символ Шлефли шестиугольного паркета — {6,3}, что означает, что в каждой вершине паркета сходятся три шестиугольника.
Шестиугольный паркет является наиболее плотной упаковкой кругов на плоскости. В двумерном евклидовом пространстве наилучшим заполнением является размещение центров кругов в вершинах паркета, образованного правильными шестиугольниками, в котором каждый круг окружен шестью другими. Плотность данной упаковки равна . В 1940 году было доказано, что данная упаковка является самой плотной.
Правильный шестиугольник со стороной является универсальной покрышкой, то есть всякое множество диаметра можно покрыть правильным шестиугольником со стороной
(лемма Пала).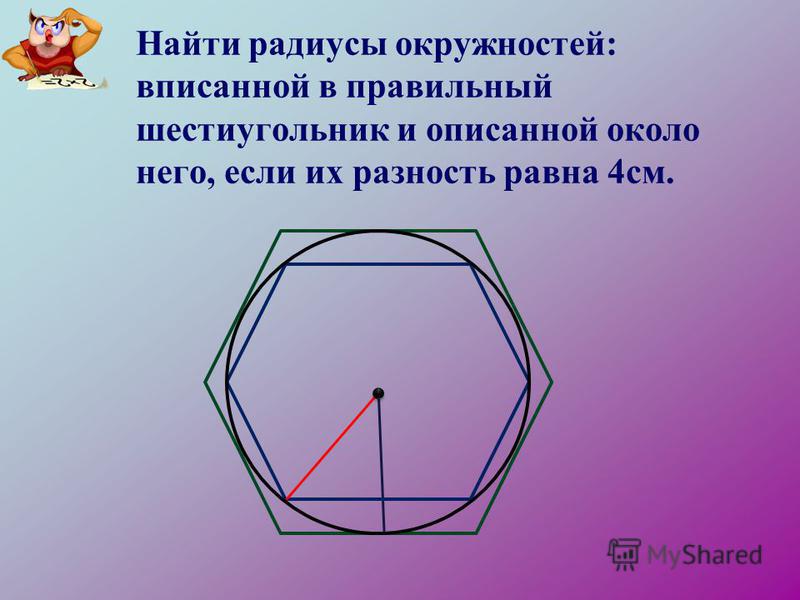
Правильный шестиугольник можно построить с помощью циркуля и линейки. Ниже приведён метод построения, предложенный Евклидом в «Началах», книга IV, теорема 15.
Правильный шестиугольник в природе, технике и культуре
показывают разбиение плоскости на правильные шестиугольники. Шестиугольная форма больше остальных позволяет сэкономить на стенках, то есть на соты с такими ячейками уйдёт меньше воска.
Некоторые сложные кристаллы и молекулы , например графит, имеют гексагональную кристаллическую решётку.
Образуется, когда микроскопические капли воды в облаках притягиваются к пылевым частицам и замерзают. Появляющиеся при этом кристаллы льда, не превышающие поначалу 0,1 мм в диаметре, падают вниз и растут в результате конденсации на них влаги из воздуха. При этом образуются шестиконечные кристаллические формы. Из-за структуры молекул воды между лучами кристалла возможны углы лишь в 60° и 120°. Основной кристалл воды имеет в плоскости форму правильного шестиугольника. На вершинах такого шестиугольника затем осаждаются новые кристаллы, на них — новые, и так получаются разнообразные формы звёздочек-снежинок.
На вершинах такого шестиугольника затем осаждаются новые кристаллы, на них — новые, и так получаются разнообразные формы звёздочек-снежинок.
Учёные из Оксфордского университета смогли в лабораторных условиях смоделировать возникновение подобного гексагона. Чтобы выяснить, как возникает такое образование, исследователи поставили на вертящийся стол 30-литровый баллон с водой. Она моделировала атмосферу Сатурна и её обычное вращение. Внутри учёные поместили маленькие кольца, вращающиеся быстрее ёмкости. Это генерировало миниатюрные вихри и струи, которые экспериментаторы визуализировали при помощи зелёной краски. Чем быстрее вращалось кольцо, тем больше становились вихри, заставляя близлежащий поток отклоняться от круговой формы. Таким образом авторам опыта удалось получить различные фигуры — овалы, треугольники, квадраты и, конечно, искомый шестиугольник.
Памятник природы из примерно 40 000 соединённых между собой базальтовых (реже андезитовых) колонн, образовавшихся в результате древнего извержения вулкана.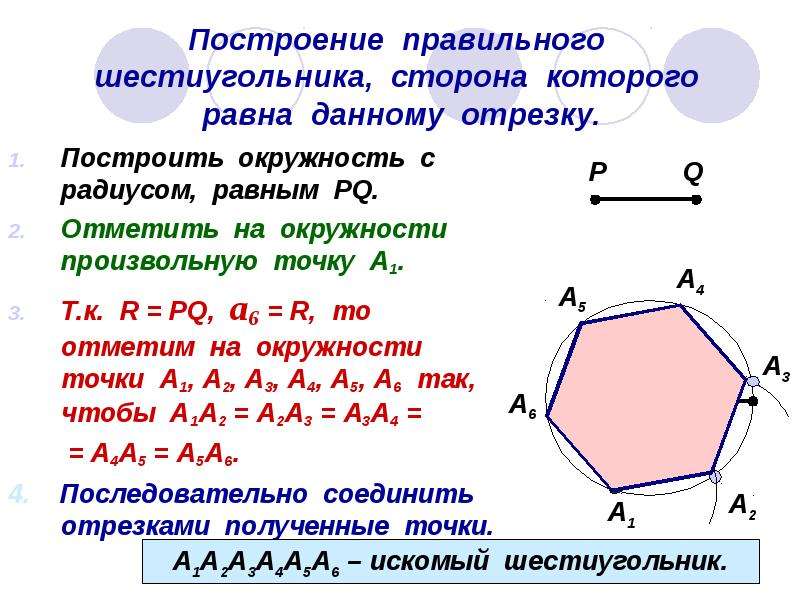 Расположен на северо-востоке Северной Ирландии в 3 км к северу от города Бушмилса.
Расположен на северо-востоке Северной Ирландии в 3 км к северу от города Бушмилса.
Верхушки колонн образуют подобие трамплина, который начинается у подножья скалы и исчезает под поверхностью моря. Большинство колонн шестиугольные, хотя у некоторых четыре, пять, семь и восемь углов. Самая высокая колонна высотой около 12 м.
Около 50-60 миллионов лет назад, во время палеогенового периода, месторасположение Антрим подвергалось интенсивной вулканической активности, когда расплавленный базальт проникал через отложения, формируя обширные лавовые плато. По мере быстрого охлаждения происходило сокращение объёма вещества (подобное наблюдается при высыхании грязи). Горизонтальное сжатие приводило к характерной структуре шестигранных столбов.
Сечение гайки имеет вид правильного шестиугольника.
Тему многоугольников проходят в школьной программе, но не уделяют ей достаточного внимания. А между тем она интересна, и особенно это касается правильного шестиугольника или гексагона — ведь эту форму имеют многие природные объекты. К ним относятся пчелиные соты и многое другое. Эта форма очень хорошо применяется на практике.
К ним относятся пчелиные соты и многое другое. Эта форма очень хорошо применяется на практике.
Определение и построение
Правильным шестиугольником называется плоскостная фигура, имеющая шесть равных по длине сторон и столько же равных углов.
Если вспомнить формулу суммы углов многоугольника
то получается, что в этой фигуре она равна 720°. Ну а поскольку все углы фигуры равны, нетрудно посчитать, что каждый из них равен 120°.
Начертить шестиугольник очень просто, для этого достаточно циркуля и линейки.
Пошаговая инструкция будет выглядеть так:
При желании можно обойтись и без линии, начертив пять равных по радиусу окружностей.
Полученная таким образом фигура будет правильным шестиугольником, и это можно доказать ниже.
Свойства простые и интересные
Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:
Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:
- диаметр описанной окружности;
- диаметр вписанной окружности;
- площадь;
- периметр.

Описанная окружность и возможность построения
Вокруг гексагона можно описать окружность, и притом только одну. Поскольку фигура эта правильная, то можно поступить довольно просто: от двух соседних углов провести внутрь биссектрисы. Они пересекутся в точке О, и образуют вместе со стороной между ними треугольник.
Углы между стороной гексагона и биссектрисами будут по 60°, поэтому можно определенно сказать, что треугольник, к примеру, АОВ — равнобедренный. А поскольку третий угол тоже будет равен 60°, то он еще и равносторонний. Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.
После этого можно перейти к следующей стороне, и из угла при точке С тоже вывести биссектрису. Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность. Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:
Именно поэтому и возможно построение этой фигуры с помощью циркуля и линейки.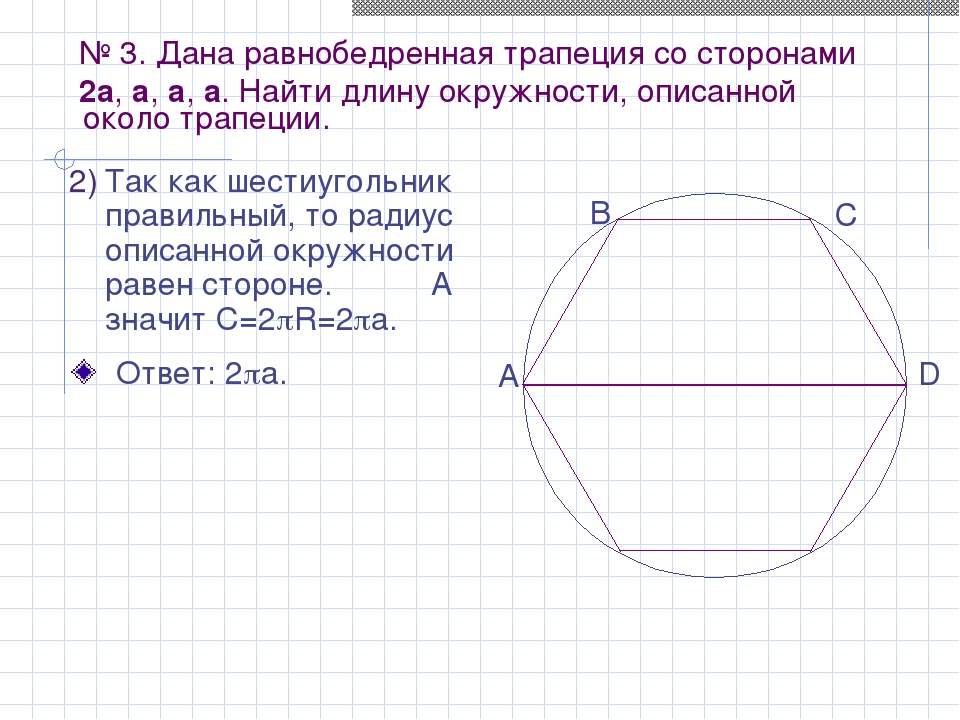
Ну а площадь этой окружности будет стандартная:
Вписанная окружность
Центр описанной окружности совпадет с центром вписанной. Чтобы в этом убедиться, можно провести из точки О перпендикуляры к сторонам шестиугольника. Они будут являться высотами тех треугольников, из которых составлен гексагон. А в равнобедренном треугольнике высота является медианой по отношению к стороне, на которую она опирается. Таким образом, эта высота не что иное, как серединный перпендикуляр, являющийся радиусом вписанной окружности.
Высота равностороннего треугольника вычисляется просто:
h²=а²-(а/2)²= а²3/4, h=а(√3)/2
А поскольку R=a и r=h, то получается, что
r=R(√3)/2 .
Таким образом, вписанная окружность проходит через центры сторон правильного шестиугольника.
Ее площадь будет составлять:
S=3πa²/4 ,
то есть три четверти от описанной.
Периметр и площадь
С периметром все ясно, это сумма длин сторон:
P=6а , или P=6R
А вот площадь будет равна сумме всех шести треугольников, на которые можно разбить гексагон.
Поскольку площадь треугольника вычисляется как половина произведения основания на высоту, то:
S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 или
S=3R²(√3)/2
Желающим вычислять эту площадь через радиус вписанной окружности можно сделать и так:
S=3(2r/√3)²(√3)/2=r²(2√3)
Занимательные построения
В гексагон можно вписать треугольник, стороны которого будут соединять вершины через одну:
Всего их получится два, и их наложение друг на друга даст звезду Давида. Каждый из этих треугольников — равносторонний. В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:
- Высота АВС из вершины В будет равна половине стороны шестиугольника, поскольку sin30°=1/2. Желающим убедиться в этом можно посоветовать пересчитать по теореме Пифагора, она здесь подходит как нельзя лучше.

- Сторона АС будет равна двум радиусам вписанной окружности, что опять-таки вычисляется по той же теореме. То есть АС=2(a(√3)/2)=а(√3).
- Треугольники АВС, СДЕ и АЕF равны по двум сторонам и углу между ними, и отсюда вытекает равенство сторон АС, СЕ и ЕА.
Пересекаясь друг с другом, треугольники образуют новый гексагон, и он тоже правильный. Доказывается это просто:
Таким образом, фигура отвечает признакам правильного шестиугольника — у нее шесть равных сторон и углов. Из равенства треугольников при вершинах легко вывести длину стороны нового гексагона:
d=а(√3)/3
Она же будет радиусом описанной вокруг него окружности. Радиус вписанной будет вдвое меньше стороны большого шестиугольника, что было доказано при рассмотрении треугольника АВС. Его высота составляет как раз половину стороны, следовательно, вторая половина — это радиус вписанной в маленький гексагон окружности:
r₂=а/2
S=(3(√3)/2)(а(√3)/3)²=а(√3)/2
Получается, что площадь гексагона внутри звезды Давида в три раза меньше, чем у большого, в который вписана звезда.
От теории к практике
Свойства шестиугольника очень активно используются как в природе, так и в различных областях деятельности человека. В первую очередь это касается болтов и гаек — шляпки первых и вторые представляют собой ничто иное, как правильный шестигранник, если не брать в расчет фаски. Размер гаечных ключей соответствует диаметру вписанной окружности — то есть расстоянию между противоположными гранями.
Нашла свое применение и гексагональная плитка. Она распространена куда меньше четырехугольной, но класть ее удобнее: в одной точке смыкаются три плитки, а не четыре. Композиции могут получаться очень интересные:
Выпускается и бетонная плитка для мощения.
Распространенность гексагона в природе объясняется просто. Таким образом, проще всего плотно уместить круги и шары на плоскости, если у них одинаковый диаметр. Из-за этого у пчелиных сот такая форма.
Радиус описанной окружности | Треугольники
Удобно, когда все формулы, по которым можно найти радиус описанной окружности для треугольника, квадрата, многоугольника размещены на одной странице.
Радиус описанной окружности для произвольного треугольника
Формулы для нахождения радиуса описанной окружности треугольника (верны для треугольника любого вида):
где a, b, c — длины сторон треугольника, α, β, γ — противолежащие этим сторонам углы, S — площадь треугольника.
Центр описанной окружности лежит:
у остроугольного треугольника — внутри треугольника;
у прямоугольного — на середине гипотенузы;
у тупоугольного — вне треугольника, напротив тупого угла.
Радиус описанной окружности для прямоугольного треугольника
Радиус описанной около прямоугольного треугольника окружности равен половине гипотенузы:
Окружность, описанная около многоугольника
Если около многоугольника можно описать окружность, ее центр является точкой пересечения серединных перпендикуляров к сторонам многоугольника.
Радиус описанной около многоугольника окружности находят как радиус окружности, описанной около треугольника. Для этого берут любые три вершины многоугольника.
Для этого берут любые три вершины многоугольника.
Например, для пятиугольника ABCDE можно взять любой из треугольников ABC, ABD, ABE, BCD, BCE, CDE, ACD, ACE, ADE, BDE.
Радиус окружности, описанной около правильного многоугольника
Формула радиуса описанной окружности для правильного многоугольника
где a — длина стороны многоугольника, n — количество его сторон.
Частные случаи — правильный треугольник, правильный четырехугольник (то есть квадрат), правильный шестиугольник.
Радиус описанной окружности правильного треугольника
Формула радиуса описанной окружности для правильного треугольника
Если без иррациональности в знаменателе —
У правильного треугольника радиус описанной окружности в два раза больше радиуса вписанной окружности:
Радиус описанной окружности квадрата
Формула радиуса описанной окружности для квадрата
Если без иррациональности в знаменателе —
Радиус описанной окружности правильного шестиугольника
Формула радиуса описанной окружности для правильного шестиугольника
Page 18 — Matemaatika 9.
 klassile, 2. osa
klassile, 2. osa18
526.
Пчелиные соты, в которых вырастают рабочие пчелы и хранится
мед, имеют форму правильных шестиугольных призм. Диагональ
основания такой призмы равна 5,4 мм, а высота – 11,5 мм. Найди,
сколько меда вмещает одна ячейка таких сот.
527.
В правильном шестиугольнике со стороной
a
= 2 дм проведены из
одной вершины две диагонали разной длины. Найди отношение
площадей двух полученных треугольников.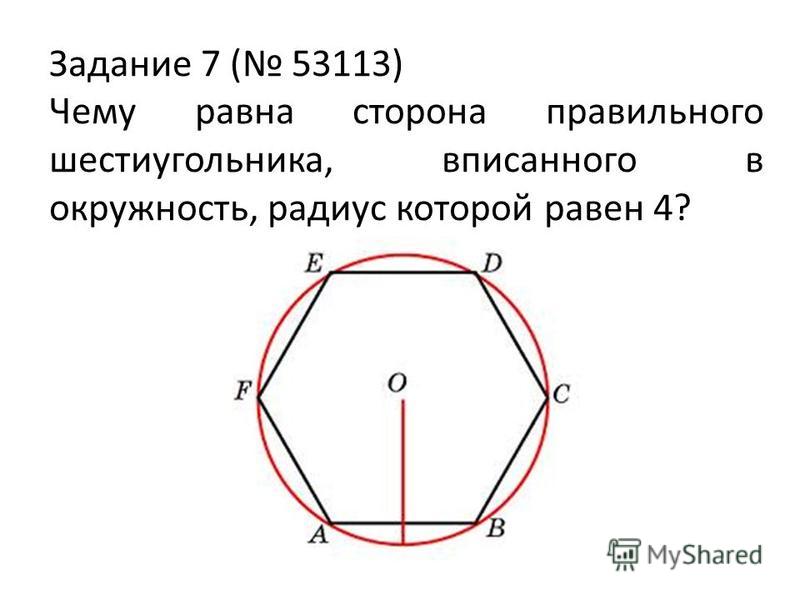
528.
Правильный шестиугольник и правильный треугольник имеют общую
описанную окружность радиусом 4 cм. Найди периметры и площади
шестиугольника и треугольника. Сколько процентов составляет
периметр треугольника от периметра шестиугольника и сколько
процентов – площадь треугольника от площади шестиугольника?
529.
Радиус описанной около правильного шестиугольника окружности
равен
R
. Найди радиус окружности, вписанной в этот шестиугольник.
Какую часть составляет площадь вписанного круга от площади
шестиугольника и сколько процентов составляет площадь шести-
угольника от площади описанного круга?
530.
В правильный треугольник со сторо-
ной 18 cм вписан круг (рис. 4.24), а в
этот круг, в свою очередь, правильный
четырехугольник. Вычисли площадь
этого четырехугольника.
Рис. 4.24
Описание и примеры стандартных функций SVG
Доминирующей причиной появления этого блога стало незаслуженное забвение на целых десять лет языка разметки масштабируемой векторной графики – SVG (Scalable Vector Graphics), входящего в подмножество расширяемого языка разметки XML.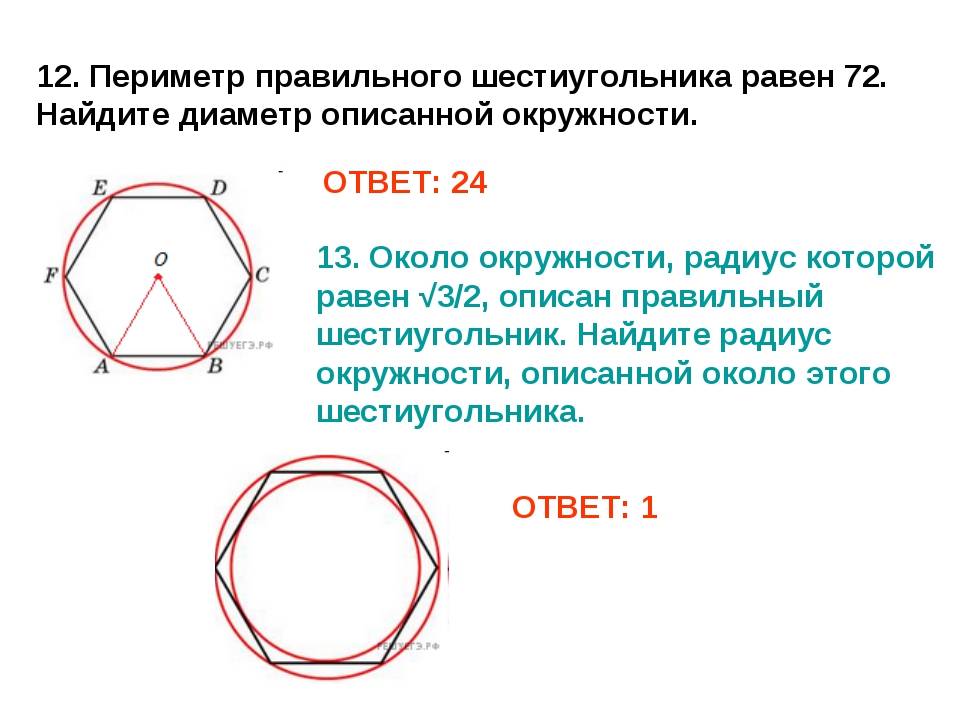
Стандарт SVG 1.0 был принят в качестве спецификации Консорциумом Всемирной паутины (W3C) в сентябре 2001 г. Стандарт SVG 1.1 и его версии SVG mobile profiles (SVG Basic and SVG Tiny) были приняты консорциумом в качестве рекомендации в январе 2003 г.
Сейчас ведутся работы по созданию стандарта SVG 2.0
Основные преимущества формата SVG.
Я не буду долго распространяться о преимуществах векторной графики перед растровой в вебдизайне, замечу лишь, что, однажды созданный, файл в формате SVG одинаково хорошо выглядит без потери качества и на мобильном устройстве и на станционарном мониторе домашнего ПК.
Шапка данного сайта выполнена в формате SVG, попробуйте уменьшить окно браузера до минимальных размеров, картинка на “лету” будет также пропорционально уменьшаться.
SVG – это двухмерная графика и тем не менее это текстовый формат, который можно легко править в блокноте или просто рисовать в векторных редакторах: Incscape , Adobe illustrator, CorelDRAW
Бесконечное полотно документа svg.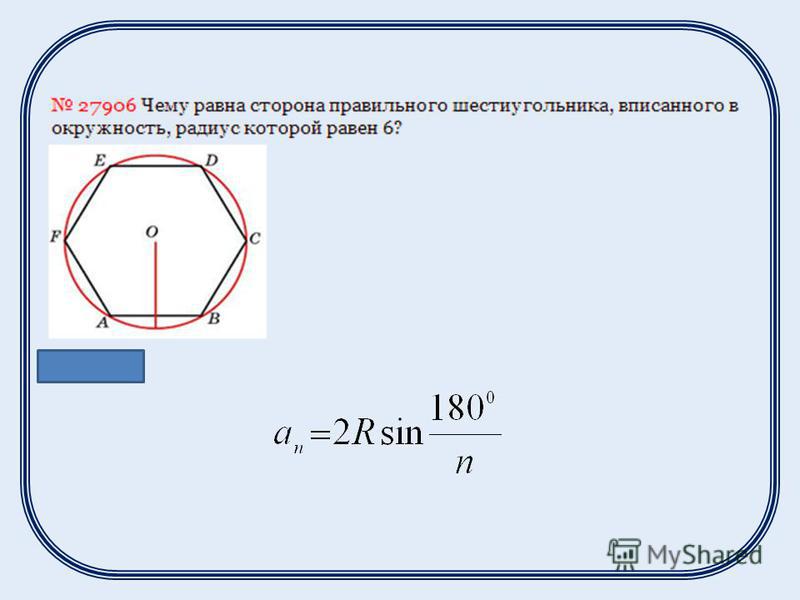
Итак, как происходит формирование векторного изображения.
Документ формата SVG – это двухмерный объект, который может иметь бесконечные координаты, как в положительном, так и в отрицательном направлении по осям X и Y. Также документ SVG имеет две области просмотра: viewport – системная область просмотра и viewBox – пользовательская область просмотра, положение которой относительно начала системных координат viewport, может задаваться собственной, пользовательской системой координат. Другими словами окно просмотра viewBox, может быть перемещёно в любое место документа SVG, при этом берется фрагмент изображения под ним, который после процесса согласования между viewBox и viewport, возвращается обратно в системную область просмотра viewport, которую видит пользователь. Используя это свойство можно организовать вертикальную или горизонтальную прокрутку изображения, меняя параметры координат viewBox.
При уменьшении размера пользовательского окна просмотра viewbox можно пропорционально увеличивать фрагмент изображения в системной области просмотра или уменьшать его при увеличении размера viewbox.
Таким образом реализуется эффект лупы. Более подробно эти процессы разобраны в статье: Трансформация изображений SVG при изменении параметров Viewbox.
Взаимодействие SVG, XML с HTML, CSS, Jscript
В SVG, как и в HTML можно добавлять ссылки на внешние ресурсы. Но если в HTML одна картинка может служить только для одной внешней ссылки, то в SVG документ можно добавлять сколько угодно внешних ссылок . Картинка кликабельна.
Внутрь HTML страницы легко встраивается код SVG документа или целиком подключается внешний SVG файл. Можно наоборот, внутри SVG файла разместить код HTML внутри тегов foreignObject. Получаются интересные эффекты: Внутри SVG файла находится работающий внешний HTML сайт. К SVG формату можно подключать внешние таблицы стилей CSS 2.0, что позволяет управлять сразу несколькими файлами *.svg. Также вполне допустимо подключение стилей внутри файла *.svg внутри тегов style или использовать внутренние стили непосредственно внутри командных строк фигур и путей.
SVG, как любой основанный на XML формат, позволяет использовать для его обработки таблицы трансформации (XSLT).
Преобразуя XML-данные в SVG с помощью простого XSL, можно получить графическое представление текстовых данных, например визуализировать графики, круговые диаграммы, гистограммы и т.д.
Анимация и интерактивность SVG.
Анимация в SVG осуществляется при помощи языка SMIL (Synchronized Multimedia Integration Language). Также поддерживаются скриптовые языки на основе спецификации ECMAScript — это встраиваемый расширяемый язык программирования.
То есть всё находится в одном месте, внутри документа SVG, поэтому нет необходимости для подключения внешних библиотек.
На каждую отдельную фигуру или на целое изображение можно установить обработчик событий (клик, наведение мышки, нажатие клавиши и т.д), таким образом, пользователь может управлять рисунком. Наведите курсор мышки на кнопку“Start” на примере слева.
По событию mouseover на этой кнопке начнется анимация по команде begin=”startButton. mouseover” – движение цветных шариков по криволинейному пути. Закончится анимация либо через заданные в коде 16 секунд, либо в любой момент по наведению курсора мышки на цветные радиокнопки “Stop”. При этом каждая радиокнопка управляет своим объектом совпадающим по цвету. На рисунке ниже анимация начинается и заканчивается при нажатии клавиши мышки на кнопки GO и STOP. В этом случае работает событие click. Команда на запуск анимации – begin=”gO.click” и соответственно остановка – end=”stop.click”
mouseover” – движение цветных шариков по криволинейному пути. Закончится анимация либо через заданные в коде 16 секунд, либо в любой момент по наведению курсора мышки на цветные радиокнопки “Stop”. При этом каждая радиокнопка управляет своим объектом совпадающим по цвету. На рисунке ниже анимация начинается и заканчивается при нажатии клавиши мышки на кнопки GO и STOP. В этом случае работает событие click. Команда на запуск анимации – begin=”gO.click” и соответственно остановка – end=”stop.click”
Следующий пример анимации – плавная отрисовка картинки с нуля до полного изображения.
Уже встроенные в SVG языки программирования позволяют реализовать довольно сложные сценарии анимации. Но, в дополнение к этому есть еще более мощные средства для реализации интерактивности графики и ее анимации – это внешние библиотеки сторонних разработчиков: D3.js, BonsaiJS, Svg.js, Snapsvg.js
Еще примеры анимации ⇛
Недостатки SVG формата
- С увеличением количества мелких деталей в изображении, быстрее растёт размер файла SVG-данных.
 Предельный случай — когда изображение представляет собой белый шум. В этом случае SVG не только не даёт никаких преимуществ в размере файла, но даже имеет проигрыш по отношению к растровому формату. На практике, SVG становится невыгоден уже задолго до того, как изображение дойдёт до стадии белого шума.
Предельный случай — когда изображение представляет собой белый шум. В этом случае SVG не только не даёт никаких преимуществ в размере файла, но даже имеет проигрыш по отношению к растровому формату. На практике, SVG становится невыгоден уже задолго до того, как изображение дойдёт до стадии белого шума. - Трудность использования в крупных картографических приложениях из-за того, что для правильного отображения маленькой части изображения документ необходимо прочитать целиком.
- В настоящее время SVG формат применяется в Интернете сравнительно мало, из-за недостаточной кроссбраузерности. Лучше всего обстоят дела у Mozilla Firefox со встроенным просмотрщиком SVG, так как ее разработчики находятся в рабочей группе Консорциума Всемирной паутины (W3C) по разработке и внедрению стандарта SVG. Хуже всего дела по поддержке формата SVG у Microsoft, которая покинула группу 2003 г. Для Internet Explorer – необходим Adobe SVG Viewer (ASV). С 9 версии IE частично поддерживает функции SVG.

Браузеры Apple Safari, Google Chrome намного лучше поддерживают SVG, но не полностью, так как SVG – это большая спецификация (вдвое больше HTML 4.01), именно поэтому разработчики браузеров внедряют функции постепенно, от версии к версии. Но абсолютно все разработчики современных браузеров заявляют, что за форматом SVG будущее в области графики вебдизайна.
UPD. Добавлен новый раздел онлайн генераторы SVG кода path.
следующая: Структура SVG документа ⇛
чем он интересен и как его построить
Знаете ли вы, как выглядит правильный шестиугольник?
Этот вопрос задан не случайно. Большинство учащихся 11 класса не знают на него ответа.
Правильный шестиугольник — такой, у которого все стороны равны и все углы тоже равны .
Железная гайка. Снежинка. Ячейка сот, в которых живут пчелы. Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.
Многие школьники теряются, видя задачи на правильный шестиугольник, и считают, что для их решения нужны какие-то особые формулы. Так ли это?
Проведем диагонали правильного шестиугольника. Мы получили шесть равносторонних треугольников.
Мы знаем, что площадь правильного треугольника: .
Тогда площадь правильного шестиугольника — в шесть раз больше.
Где — сторона правильного шестиугольника.
Обратите внимание, что в правильном шестиугольнике расстояние от его центра до любой из вершин одинаково и равно стороне правильного шестиугольник.
Значит, радиус окружности, описанной вокруг правильного шестиугольника, равен его стороне .
Радиус окружности, вписанной в правильный шестиугольник, нетрудно найти.
Он равен .
Теперь вы легко решите любые задачи ЕГЭ, в которых фигурирует правильный шестиугольник.
Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .
Радиус такой окружности равен .
Ответ: .
Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
Самая известная фигура, у которой больше четырех углов — это правильный шестиугольник. В геометрии он часто используется в задачах. А в жизни именно такой вид имеют соты на срезе.
Чем он отличается от неправильного?
Во-первых, шестиугольником является фигура с 6 вершинами. Во-вторых, он может быть выпуклым или вогнутым. Первый отличается тем, что четыре вершины лежат по одну сторону от прямой, проведенной через две другие.
В-третьих, правильный шестиугольник характеризуется тем, что все его стороны равны. Причем каждый угол фигуры тоже имеет одинаковое значение. Чтобы определить сумму всех его углов, потребуется воспользоваться формулой: 180º * (n — 2). Здесь n — число вершин фигуры, то есть 6. Простой расчет дает значение в 720º. То есть каждый угол равен 120 градусам.
В повседневной деятельности правильный шестиугольник встречается в снежинке и гайке. Химики видят ее даже в молекуле бензола.
Какие свойства требуется знать при решении задач?
К тому, что указано выше, следует добавить:
- диагонали фигуры, проведенные через центр, делят ее на шесть треугольников, которые являются равносторонними;
- сторона правильного шестиугольника имеет значение, которое совпадает с радиусом описанной около него окружности;
- используя такую фигуру, есть возможность заполнить плоскость, причем между ними не получится пропусков и не будет наложений.
Введенные обозначения
Традиционно сторона правильной геометрической фигуры обозначается латинской буквой «а». Для решения задач требуются еще площадь и периметр, это S и P соответственно. В правильный шестиугольник бывает вписана окружность или описана около него. Тогда вводятся значения для их радиусов. Обозначаются они соответственно буквами r и R.
В некоторых формулах фигурируют внутренний угол, полупериметр и апофема (являющаяся перпендикуляром к середине любой стороны из центра многоугольника).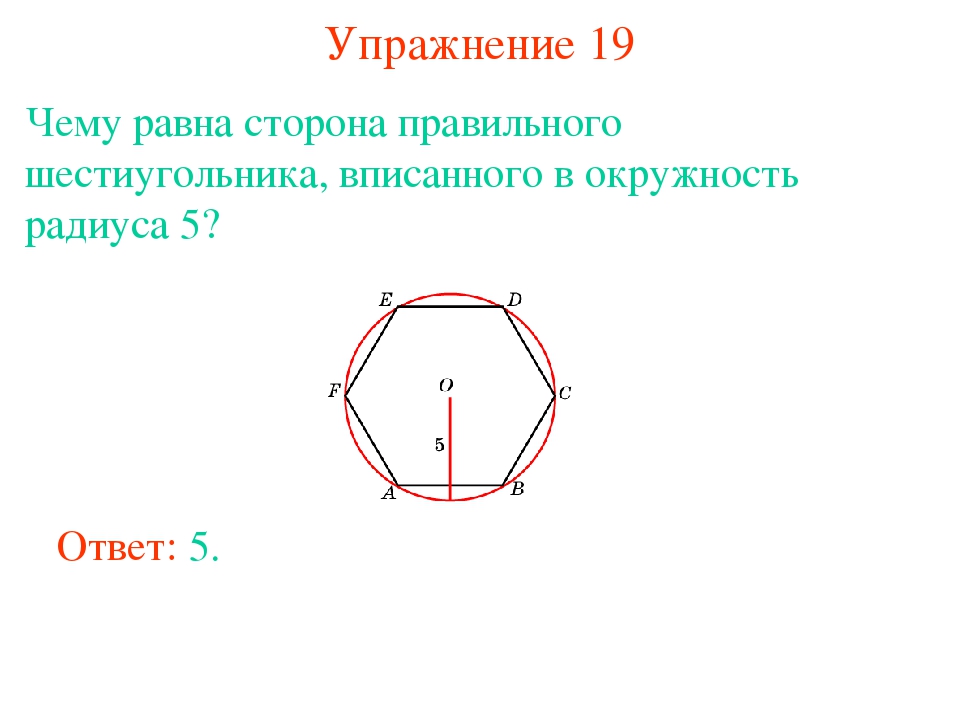 Для них используются буквы: α, р, m.
Для них используются буквы: α, р, m.
Формулы, которые описывают фигуру
Для расчета радиуса вписанной окружности потребуется такая: r = (a * √3) / 2, причем r = m. То есть такая же формула будет и для апофемы.
Поскольку периметр шестиугольника — это сумма всех сторон, то он определится так: P = 6 * a. С учетом того, что сторона равна радиусу описанной окружности, для периметра существует такая формула правильного шестиугольника: P = 6 * R. Из той, что приведена для радиуса вписанной окружности, выводится зависимость между а и r. Тогда формула принимает такой вид: Р = 4 r * √3.
Для площади правильного шестиугольника может пригодиться такая: S = p * r = (a 2 * 3 √3) / 2.
Задачи
№ 1. Условие. Имеется правильная шестиугольная призма, каждое ребро которой равно 4 см. В нее вписан цилиндр, объем которого необходимо узнать.
Решение. Объем цилиндра определяется как произведение площади основания на высоту. Последняя совпадает с ребром призмы. А она равна стороне правильного шестиугольника. То есть высота цилиндра — тоже 4 см.
А она равна стороне правильного шестиугольника. То есть высота цилиндра — тоже 4 см.
Чтобы узнать площадь его основания, потребуется вычислить радиус вписанной в шестиугольник окружности. Формула для этого указана выше. Значит, r = 2√3 (см). Тогда площадь круга: S = π * r 2 = 3,14 * (2√3) 2 = 37,68 (см 2).
Ответ . V = 150,72 см 3 .
№ 2. Условие. Вычислить радиус окружности, которая вписана в правильный шестиугольник. Известно, что его сторона равна √3 см. Чему будет равен его периметр?
Решение. Эта задача требует использования двух из указанных формул. Причем их необходимо применять, даже не видоизменяя, просто подставить значение стороны и вычислить.
Таким образом, радиус вписанной окружности получается равным 1,5 см. Для периметра оказывается верным такое значение: 6√3 см.
Ответ. r = 1,5 см, Р = 6√3 см.
№ 3. Условие. Радиус описанной окружности равен 6 см. Какое значение в этом случае будет у стороны правильного шестиугольника?
Решение. Из формулы для радиуса вписанной в шестиугольник окружности легко получается та, по которой нужно вычислять сторону. Ясно, что радиус умножается на два и делится на корень из трех. Необходимо избавиться от иррациональности в знаменателе. Поэтому результат действий принимает такой вид: (12 √3) / (√3 * √3), то есть 4√3.
Из формулы для радиуса вписанной в шестиугольник окружности легко получается та, по которой нужно вычислять сторону. Ясно, что радиус умножается на два и делится на корень из трех. Необходимо избавиться от иррациональности в знаменателе. Поэтому результат действий принимает такой вид: (12 √3) / (√3 * √3), то есть 4√3.
Ответ. а = 4√3 см.
Знаете ли вы, как выглядит правильный шестиугольник?
Этот вопрос задан не случайно. Большинство учащихся 11 класса не знают на него ответа.
Правильный шестиугольник — такой, у которого все стороны равны и все углы тоже равны .
Железная гайка. Снежинка. Ячейка сот, в которых живут пчелы. Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.
Многие школьники теряются, видя задачи на правильный шестиугольник, и считают, что для их решения нужны какие-то особые формулы. Так ли это?
Проведем диагонали правильного шестиугольника. Мы получили шесть равносторонних треугольников.
Мы знаем, что площадь правильного треугольника: .
Тогда площадь правильного шестиугольника — в шесть раз больше.
Где — сторона правильного шестиугольника.
Обратите внимание, что в правильном шестиугольнике расстояние от его центра до любой из вершин одинаково и равно стороне правильного шестиугольник.
Значит, радиус окружности, описанной вокруг правильного шестиугольника, равен его стороне .
Радиус окружности, вписанной в правильный шестиугольник, нетрудно найти.
Он равен .
Теперь вы легко решите любые задачи ЕГЭ, в которых фигурирует правильный шестиугольник.
Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .
Радиус такой окружности равен .
Ответ: .
Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
Есть ли поблизости от Вас карандаш? Взгляните-ка на его сечение — оно представляет собой правильный шестиугольник или, как его еще называют, гексагон. Такую форму имеет также сечение гайки, поле гексагональных шахмат, некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты. Гигантский правильный шестиугольник был недавно обнаружен в Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим поподробнее.
Такую форму имеет также сечение гайки, поле гексагональных шахмат, некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты. Гигантский правильный шестиугольник был недавно обнаружен в Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим поподробнее.
Правильный шестиугольник представляет собой многоугольник с шестью одинаковыми сторонами и равными углами. Из школьного курса нам известно, что он обладает следующими свойствами:
- Длина его сторон соответствует радиусу описанной окружности. Из всех это свойство имеет лишь правильный шестиугольник.
- Углы равны между собой, и величина каждого составляет 120°.
- Периметр гексагона можно найти по формуле Р=6*R, если известен радиус описанной вокруг него окружности, или Р=4*√(3)*r, если окружность в него вписана. R и r — радиусы описанной и вписанной окружности.
- Площадь, которую занимает правильный шестиугольник, определяется следующим образом: S=(3*√(3)*R 2)/2.
 Если радиус неизвестен, вместо него подставляем длину одной из сторон — как известно, она соответствует длине радиуса описанной окружности.
Если радиус неизвестен, вместо него подставляем длину одной из сторон — как известно, она соответствует длине радиуса описанной окружности.
У правильного шестиугольника есть одна интересная особенность, благодаря которой он получил в природе такое широкое распространение, — он способен заполнить любую поверхность плоскости без наложений и пробелов. Существует даже так называемая лемма Пала, согласно которой правильный гексагон, сторона которого равна 1/√(3), представляет собой универсальную покрышку, то есть может покрыть любое множество с диаметром в одну единицу.
Теперь рассмотрим построение правильного шестиугольника. Есть несколько способов, самый простой из которых предполагает использование циркуля, карандаша и линейки. Вначале рисуем циркулем произвольную окружность, затем в произвольном месте на этой окружности делаем точку. Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек. Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.
Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.
На практике бывают случаи, когда требуется нарисовать шестиугольник большого размера. Например, на двухуровневом гипсокартонном потолке, вокруг места крепления центральной люстры, нужно установить на нижнем уровне шесть небольших светильников. Циркуль таких размеров найти будет очень и очень сложно. Как поступить в этом случае? Как вообще нарисовать большую окружность? Очень просто. Нужно взять крепкую нить нужной длины и обвязать один из ее концов напротив карандаша. Теперь осталось лишь найти помощника, который бы прижал к потолку в нужной точке второй конец нити. Конечно, в этом случае возможны незначительные погрешности, но вряд ли они вообще будут заметны постороннему человеку.
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего проводим стороны 5-6 и 3-2.
Построение вписанного в окружность равностороннего треугольника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны
1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.
62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника.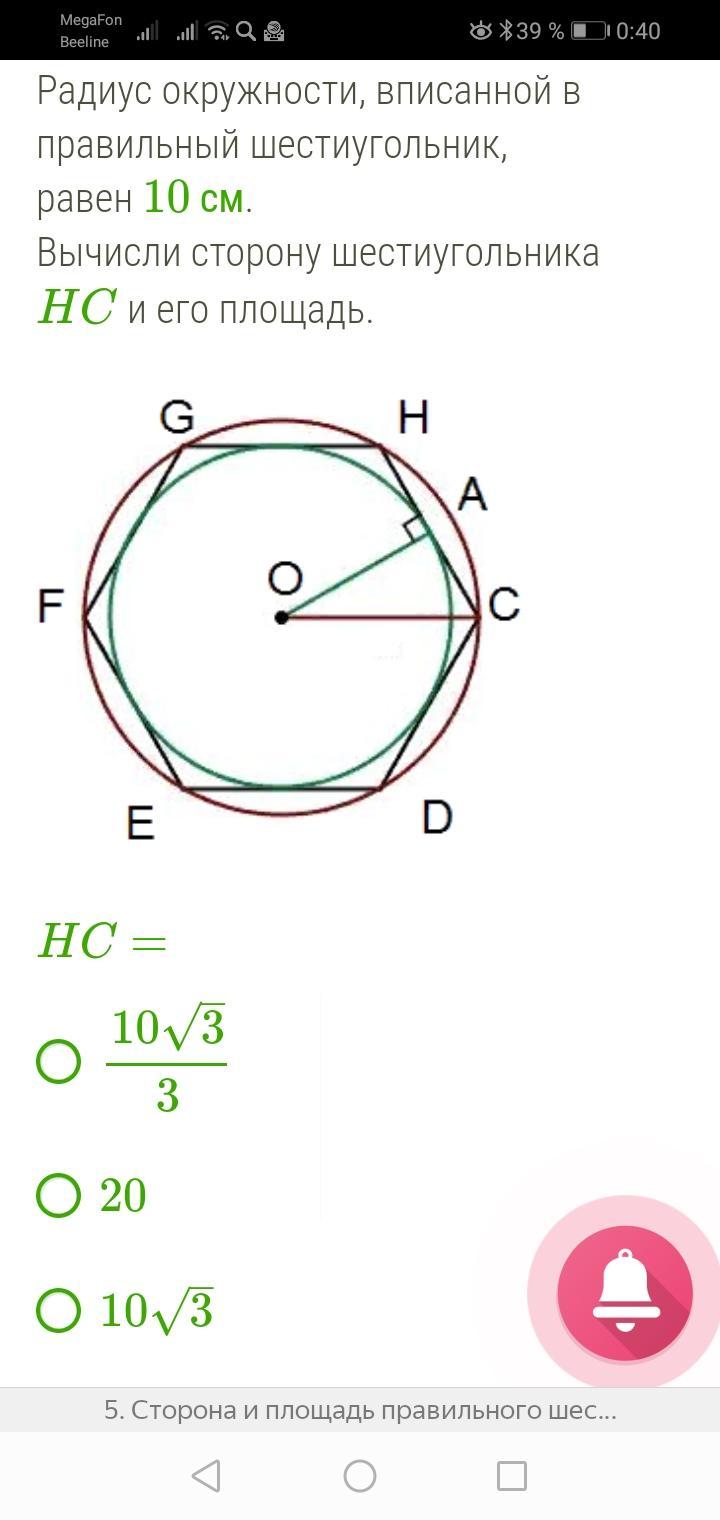 Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
Правильный шестиугольник в описанной окружности
ОБЫЧНЫЙ ШЕСТИГРАННИК В А ДАННЫЙ ЗАПИСАННЫЙ КРУГ Многие головки болтов и гайки шестигранные. (шестигранный)
в форме.На рисунке 4-26 показан метод
(шестигранный)
в форме.На рисунке 4-26 показан метод
Рисунок 4-26.-Правильный шестиугольник в заданной описанной области.
круг: один метод.Рисунок 4-27.-Правильный шестиугольник в данной описанной окружности
: другой метод.построения правильного шестиугольника в заданном
описанном круг. Диаметр описываемой круг имеет ту же длину, что и длинный диаметр шестигранника.Радиус описанный круг (равный половине длинный диаметр шестиугольника) составляет длина равна длине стороны. Класть от горизонтального диаметра AB и вертикального диаметр CD. OB — радиус круг. От C проведите линию CE, равную OB; затем отложите этот интервал до обведите и соедините точки пересечения. Фигура 4-27 показан другой метод построения правильный шестиугольник в данной описанной круг.Нарисуйте вертикальный диаметр AB и используйте T-квадрат и треугольник 30/60, чтобы нарисовать BC от Б на 30 по горизонтали.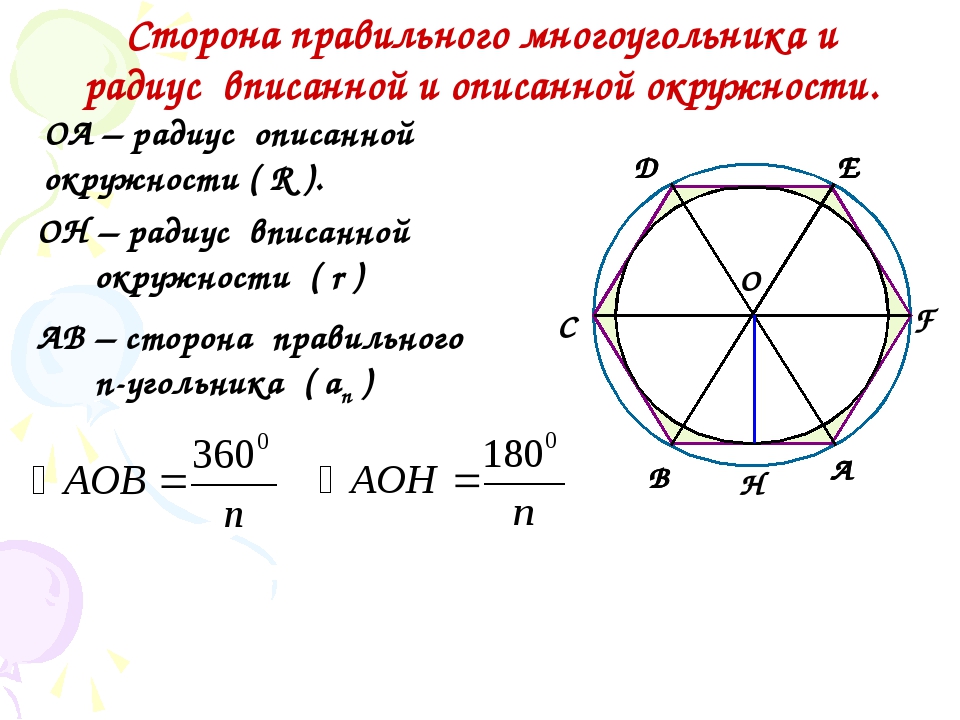 Установите компас
до BC, отложите этот интервал по окружности,
и соедините точки пересечения.
Установите компас
до BC, отложите этот интервал по окружности,
и соедините точки пересечения. ОБЫЧНЫЙ ШЕСТИГРАННИК НА ДАННОМ НАПИСАНО КРУГ
На рисунке 4-28 показан метод построения а правильный шестиугольник на вписанной окружности.
Ничья горизонтальный диаметр AB и вертикальный центр линия. Нарисуйте линии, касательные к окружности и перпендикулярные к AB в точках A и B. Используйте Т-образный квадрат и треугольник 30/60, чтобы нарисовать оставшиеся стороны фигура, касательная к окружности и 30 к горизонтальный.Рис. 4-28.-Правильный шестиугольник на вписанной окружности.
Рисунок 4-29.-Правильный восьмиугольник в данном описанном круге
.ОБЫЧНЫЙ Восьмиугольник в окружности
КРУГ ДАННЫЙНа рис. 4-29 показан метод построения
a. правильный восьмиугольник в данной описанной окружности.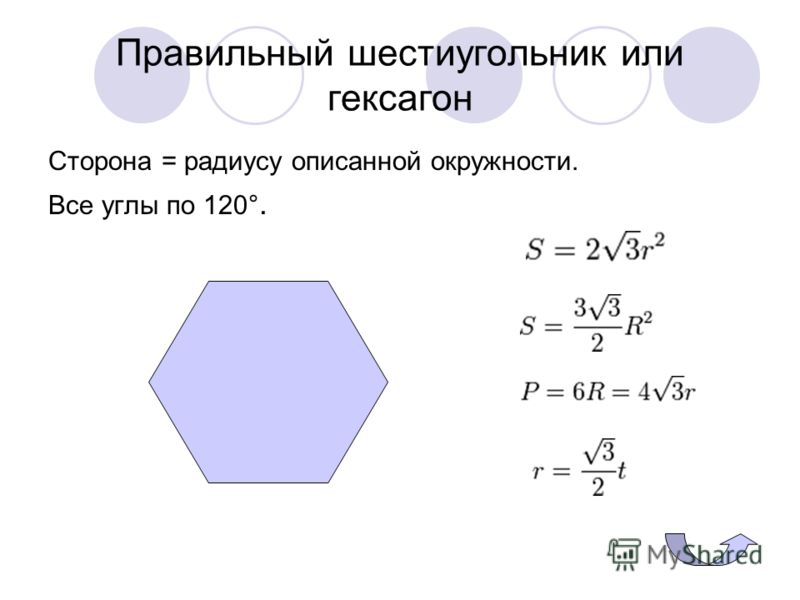 Рисовать
горизонтальный диаметр AB и вертикальный диаметр
CD. Используйте Т-квадрат и треугольник 45, чтобы
нарисуйте дополнительные диаметры EF и GH от 45 до
горизонтальный. Соедините точки, где диаметры
пересекают круг.
Рисовать
горизонтальный диаметр AB и вертикальный диаметр
CD. Используйте Т-квадрат и треугольник 45, чтобы
нарисуйте дополнительные диаметры EF и GH от 45 до
горизонтальный. Соедините точки, где диаметры
пересекают круг.Шестиугольник в окружности
Окружность треугольника. Здесь шестиугольники были окрашены одинаково, когда у них была одна и та же описанная окружность (эти случаи легко вычислить): Количество черных кругов между красными… Чтобы узнать больше, просмотрите наш, От теоремы Ньютона до теоремы о вписываемом восьмиугольнике . а. шестиугольник описан вокруг круга. Для каждого треугольника вы можете вычислить площадь, используя 1) формулу Герона, Area = √s (s− a) (s — b) (s −c), где s = 3 2 — половина периметра треугольника, и a, b, c — длины сторон треугольников (в данном случае все 1).Inradius — это радиус самого большого круга, полностью заключенного внутри шестиугольника. В этой статье мы анализируем и доказываем два свойства шестиугольника, описанного окружностью: Следовательно, эта окружность имеет радиус 6. Последняя категория, элитные члены, всегда включает правильный многоугольник. Авторское право © 2004–2020 Флоридский центр учебных технологий. Центр этой окружности называется центром описанной окружности, а ее радиус — радиусом описанной окружности. Итак, что я собираюсь сделать, во-первых, я нарисую диаметр круга.Соединяя противоположные стороны шестиугольника, он образует 6 центральных углов в центре O, каждый из которых = 360/6 = 60 °. Ответ: 3 вопроса. Правильный шестиугольник описан кругом радиусом 3 см с центром O. (Это круг в многоугольнике) Вписанные и описанные многоугольники Урок о многоугольниках, вписанных в круг и описанных вокруг него. Правильный шестиугольник описан кругом радиусом 6 см. Формула для вычисления радиуса вписанной окружности правильного шестиугольника, если задана сторона (r): радиус окружности, вписанной в правильный шестиугольник: = Цифра 2 1 2 4 6 10 F.знак равно Центр описанной окружности многоугольника — это центр окружности, описанной вокруг многоугольника.
Последняя категория, элитные члены, всегда включает правильный многоугольник. Авторское право © 2004–2020 Флоридский центр учебных технологий. Центр этой окружности называется центром описанной окружности, а ее радиус — радиусом описанной окружности. Итак, что я собираюсь сделать, во-первых, я нарисую диаметр круга.Соединяя противоположные стороны шестиугольника, он образует 6 центральных углов в центре O, каждый из которых = 360/6 = 60 °. Ответ: 3 вопроса. Правильный шестиугольник описан кругом радиусом 3 см с центром O. (Это круг в многоугольнике) Вписанные и описанные многоугольники Урок о многоугольниках, вписанных в круг и описанных вокруг него. Правильный шестиугольник описан кругом радиусом 6 см. Формула для вычисления радиуса вписанной окружности правильного шестиугольника, если задана сторона (r): радиус окружности, вписанной в правильный шестиугольник: = Цифра 2 1 2 4 6 10 F.знак равно Центр описанной окружности многоугольника — это центр окружности, описанной вокруг многоугольника.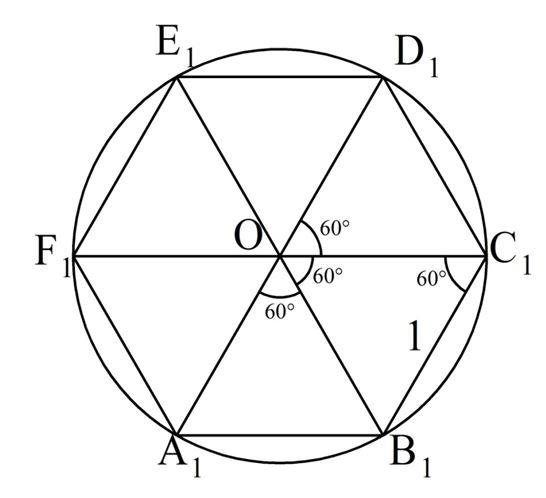 Длина окружности: 2πr. Вы можете скачать статью, нажав кнопку выше. ОБЫЧНЫЙ ГЕКСАГОН В ЗАДАННОМ ЗАПИСАННОМ КРУГЕ. Затем в прямоугольном треугольнике OAM, ClipArt ETC является частью Информационного центра образовательных технологий и производится Флоридским центром учебных технологий, Педагогическим колледжем Университета Южной Флориды. Многие головки болтов и гаек имеют шестигранную (шестигранную) форму.Назовите это a. Следовательно, этот круг имеет радиус 6. Какова площадь правильного шестиугольника, описанного внутри круга с радиусом 1? Округлите до ближайшей десятой. Найдите область, заштрихованную. Inradius: радиус круга, вписанного в правильный шестиугольник, равен половине его высоты, которая также является апофемой: r = √3 / 2 * a. Итак, он внутри круга. Многоугольник, имеющий описанную окружность, называется циклическим многоугольником. Длина окружности: 2πr. Это радиус равен длине одной стороны равносторонних треугольников.Связанный калькулятор. На рис. 4-26 показан метод. Рис.
Длина окружности: 2πr. Вы можете скачать статью, нажав кнопку выше. ОБЫЧНЫЙ ГЕКСАГОН В ЗАДАННОМ ЗАПИСАННОМ КРУГЕ. Затем в прямоугольном треугольнике OAM, ClipArt ETC является частью Информационного центра образовательных технологий и производится Флоридским центром учебных технологий, Педагогическим колледжем Университета Южной Флориды. Многие головки болтов и гаек имеют шестигранную (шестигранную) форму.Назовите это a. Следовательно, этот круг имеет радиус 6. Какова площадь правильного шестиугольника, описанного внутри круга с радиусом 1? Округлите до ближайшей десятой. Найдите область, заштрихованную. Inradius: радиус круга, вписанного в правильный шестиугольник, равен половине его высоты, которая также является апофемой: r = √3 / 2 * a. Итак, он внутри круга. Многоугольник, имеющий описанную окружность, называется циклическим многоугольником. Длина окружности: 2πr. Это радиус равен длине одной стороны равносторонних треугольников.Связанный калькулятор. На рис. 4-26 показан метод. Рис. 4-26.-Правильный шестиугольник в заданной описанной окружности: один метод. Вам нужны радиусы вписанных и описанных кругов. Нарисуйте горизонтальный диаметр AB и вертикальный диаметр CD. Иллюстрация правильного шестиугольника, описанного вокруг круга. Не каждый многоугольник имеет описанный круг. Чтобы просматривать Academia.edu и весь Интернет быстрее и безопаснее, пожалуйста, обновите свой браузер за несколько секунд. В этой статье мы анализируем и доказываем два свойства шестиугольника, описанного окружностью.Все штатно просто… В… Найдите радиус окружности с. Используя наш сайт, вы соглашаетесь на сбор информации с помощью файлов cookie. У правильного шестиугольника все стороны одинаковой длины. На самом деле, я собираюсь выйти за пределы диаметра круга. Центр этого круга называется центром описанной окружности. б. каждая вершина шестиугольника лежит внутри круга. r = (a * √3) / 2 Где, a = Сторона (a) r = Радиус окружности с обычным шестиугольником (r) EMBED (для блогов и архивов, размещенных на wordpress.
4-26.-Правильный шестиугольник в заданной описанной окружности: один метод. Вам нужны радиусы вписанных и описанных кругов. Нарисуйте горизонтальный диаметр AB и вертикальный диаметр CD. Иллюстрация правильного шестиугольника, описанного вокруг круга. Не каждый многоугольник имеет описанный круг. Чтобы просматривать Academia.edu и весь Интернет быстрее и безопаснее, пожалуйста, обновите свой браузер за несколько секунд. В этой статье мы анализируем и доказываем два свойства шестиугольника, описанного окружностью.Все штатно просто… В… Найдите радиус окружности с. Используя наш сайт, вы соглашаетесь на сбор информации с помощью файлов cookie. У правильного шестиугольника все стороны одинаковой длины. На самом деле, я собираюсь выйти за пределы диаметра круга. Центр этого круга называется центром описанной окружности. б. каждая вершина шестиугольника лежит внутри круга. r = (a * √3) / 2 Где, a = Сторона (a) r = Радиус окружности с обычным шестиугольником (r) EMBED (для блогов и архивов, размещенных на wordpress. com.теги элементов организации) Хотите больше? Круг вписан в один правильный шестиугольник и описан вокруг другого. Пожалуйста, я не могу ответить на этот вопрос, потому что я не знаю, что делать, пожалуйста, помогите Спасибо 🙂 Academia.edu использует файлы cookie для персонализации контента, настройки рекламы и улучшения взаимодействия с пользователем. ВСТРОЕН. Свойства шестиугольника, окруженного кругом Предмет Предварительный просмотр remove-circle Поделиться или встроить этот предмет. В геометрии описанная окружность или описанная окружность многоугольника — это круг, который проходит через все вершины многоугольника.Шестиугольник, который окружает любую геометрическую фигуру так, что все вершины внутренней фигуры касаются сторон шестиугольника, называется описанным. Если радиус круга равен 10 долларам, найдите площадь и периметр шестиугольника. проверить все, что относится. Ответ Эдвина МакКрэви (18358) (Показать источник): Обведенный шестиугольник. Круг вписан в многоугольник, а многоугольник описан вокруг круга.
com.теги элементов организации) Хотите больше? Круг вписан в один правильный шестиугольник и описан вокруг другого. Пожалуйста, я не могу ответить на этот вопрос, потому что я не знаю, что делать, пожалуйста, помогите Спасибо 🙂 Academia.edu использует файлы cookie для персонализации контента, настройки рекламы и улучшения взаимодействия с пользователем. ВСТРОЕН. Свойства шестиугольника, окруженного кругом Предмет Предварительный просмотр remove-circle Поделиться или встроить этот предмет. В геометрии описанная окружность или описанная окружность многоугольника — это круг, который проходит через все вершины многоугольника.Шестиугольник, который окружает любую геометрическую фигуру так, что все вершины внутренней фигуры касаются сторон шестиугольника, называется описанным. Если радиус круга равен 10 долларам, найдите площадь и периметр шестиугольника. проверить все, что относится. Ответ Эдвина МакКрэви (18358) (Показать источник): Обведенный шестиугольник. Круг вписан в многоугольник, а многоугольник описан вокруг круга. d. каждая вершина шестиугольника лежит вне круга. Отношение площадей — это квадрат отношения этих двух радиусов.На рис. 4-26 показан способ построения правильного шестиугольника в заданной описанной окружности. Найдите площадь круга, описанного вокруг правильного шестиугольника с апофемой 5 дюймов. Центр описанной окружности многоугольника — это центр окружности, описанной вокруг многоугольника. Радиус описанной окружности — это длина стороны равносторонних треугольников. зеркало. Формула для вычисления радиуса вписанной окружности правильного шестиугольника, если задана сторона (r): радиус окружности, вписанной в правильный шестиугольник: = Цифра 2 1 2 4 6 10 Геометрическое соотношение F.На рис. 4-25 показан метод построения правильного пятиугольника в заданной описанной окружности. Узнайте, как легко построить КРУГ и КРУГ правильного шестиугольника, посмотрев это видео. Вопрос 772850: Круг описан вокруг правильного шестиугольника с апофемой 4,8 сантиметра; как мне найти радиус круга, длину стороны шестиугольника и периметр шестиугольника.
d. каждая вершина шестиугольника лежит вне круга. Отношение площадей — это квадрат отношения этих двух радиусов.На рис. 4-26 показан способ построения правильного шестиугольника в заданной описанной окружности. Найдите площадь круга, описанного вокруг правильного шестиугольника с апофемой 5 дюймов. Центр описанной окружности многоугольника — это центр окружности, описанной вокруг многоугольника. Радиус описанной окружности — это длина стороны равносторонних треугольников. зеркало. Формула для вычисления радиуса вписанной окружности правильного шестиугольника, если задана сторона (r): радиус окружности, вписанной в правильный шестиугольник: = Цифра 2 1 2 4 6 10 Геометрическое соотношение F.На рис. 4-25 показан метод построения правильного пятиугольника в заданной описанной окружности. Узнайте, как легко построить КРУГ и КРУГ правильного шестиугольника, посмотрев это видео. Вопрос 772850: Круг описан вокруг правильного шестиугольника с апофемой 4,8 сантиметра; как мне найти радиус круга, длину стороны шестиугольника и периметр шестиугольника.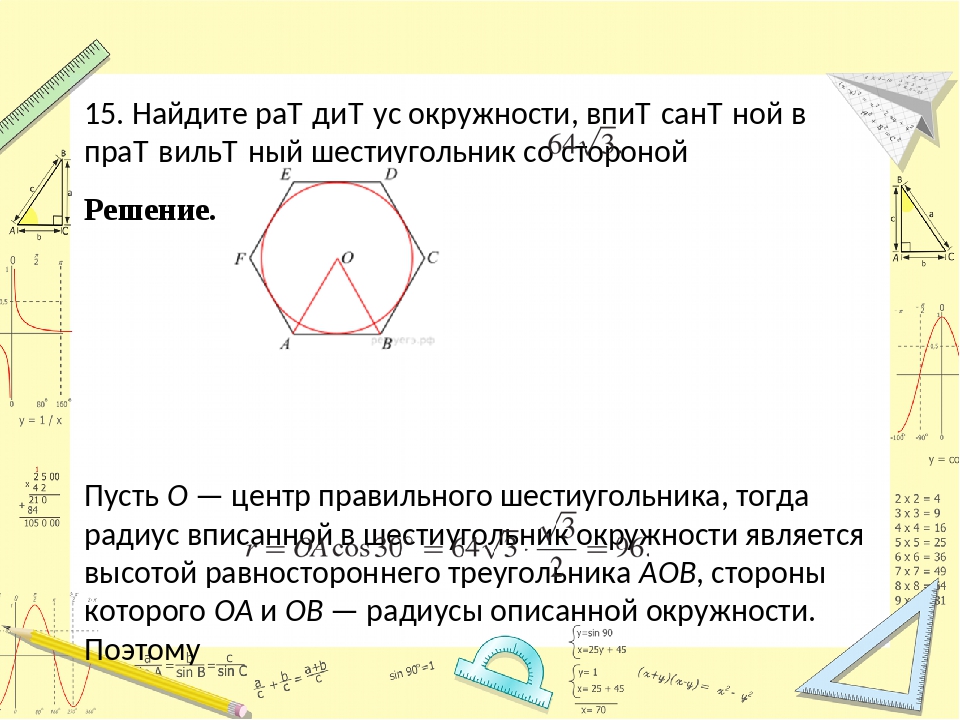 Если круг имеет радиус 6, найдите отношение площадей меньшего шестиугольника…… Вам нужны радиусы вписанных и описанных кругов.Правильный шестиугольник можно разрезать на 6 равносторонних треугольников длиной по 1 единице каждый. Пожалуйста, заранее спасибо. Круг имеет радиус 9 футов. Дополнительные сведения о встраивании, примеры и помощь! Радиус круга разрезает каждый треугольник пополам. Когда шестиугольник окружает круг так, что стороны шестиугольника касаются круга, мы называем его описанным шестиугольником круга. Отношение площадей — это квадрат отношения этих двух радиусов. Многоугольник — это замкнутая двумерная фигура, состоящая из отрезков прямых линий.Поймите, что шестиугольник — это шесть сложенных вместе равносторонних треугольников. Две стороны каждого треугольника равны радиусу круга и, следовательно, равны. Рис. 4-26.-Правильный шестиугольник в заданной описанной окружности: один метод .. Правильный шестиугольник… В геометрии описанная окружность или описанная окружность многоугольника — это окружность, которая проходит через все вершины многоугольника.
Если круг имеет радиус 6, найдите отношение площадей меньшего шестиугольника…… Вам нужны радиусы вписанных и описанных кругов.Правильный шестиугольник можно разрезать на 6 равносторонних треугольников длиной по 1 единице каждый. Пожалуйста, заранее спасибо. Круг имеет радиус 9 футов. Дополнительные сведения о встраивании, примеры и помощь! Радиус круга разрезает каждый треугольник пополам. Когда шестиугольник окружает круг так, что стороны шестиугольника касаются круга, мы называем его описанным шестиугольником круга. Отношение площадей — это квадрат отношения этих двух радиусов. Многоугольник — это замкнутая двумерная фигура, состоящая из отрезков прямых линий.Поймите, что шестиугольник — это шесть сложенных вместе равносторонних треугольников. Две стороны каждого треугольника равны радиусу круга и, следовательно, равны. Рис. 4-26.-Правильный шестиугольник в заданной описанной окружности: один метод .. Правильный шестиугольник… В геометрии описанная окружность или описанная окружность многоугольника — это окружность, которая проходит через все вершины многоугольника. Установите компас на расстояние между C и F, и с помощью C… Рисунок 4-26 показывает метод. d. Некоторые избранные могут как описать круг, так и вписаться в него.В геометрии шестиугольник — это многоугольник с 6… Введите адрес электронной почты, с которым вы зарегистрировались, и мы отправим вам ссылку для сброса по электронной почте. 5. Найдите соотношение между площадью квадрата, вписанного в круг, и равностороннего квадрата, описанного примерно в том же круге. Правильный шестиугольник вписан в круг радиусом 6 см. Круговой радиус: чтобы найти радиус окружности, описанной на правильном шестиугольнике, вам необходимо определить расстояние между центральной точкой шестиугольника (которая также является центром круга … Постройте правильный шестиугольник, вписанный в круг.На этой странице показано, как построить (нарисовать) правильный шестиугольник, вписанный в круг, с помощью циркуля и линейки или линейки. Радиус описанной окружности — это длина стороны равносторонних треугольников. Подобно тому, как все треугольники имеют это «двойное членство», так и все правильные многоугольники.
Установите компас на расстояние между C и F, и с помощью C… Рисунок 4-26 показывает метод. d. Некоторые избранные могут как описать круг, так и вписаться в него.В геометрии шестиугольник — это многоугольник с 6… Введите адрес электронной почты, с которым вы зарегистрировались, и мы отправим вам ссылку для сброса по электронной почте. 5. Найдите соотношение между площадью квадрата, вписанного в круг, и равностороннего квадрата, описанного примерно в том же круге. Правильный шестиугольник вписан в круг радиусом 6 см. Круговой радиус: чтобы найти радиус окружности, описанной на правильном шестиугольнике, вам необходимо определить расстояние между центральной точкой шестиугольника (которая также является центром круга … Постройте правильный шестиугольник, вписанный в круг.На этой странице показано, как построить (нарисовать) правильный шестиугольник, вписанный в круг, с помощью циркуля и линейки или линейки. Радиус описанной окружности — это длина стороны равносторонних треугольников. Подобно тому, как все треугольники имеют это «двойное членство», так и все правильные многоугольники. Флоридский центр учебных технологий Clipart ETC (Тампа: Университет Южной Флориды, 2008). Правильный шестиугольник, описанный вокруг окружности D. Правильный шестиугольник, вписанный в окружность jeanhocog, ждет вашей помощи.Academia.edu больше не поддерживает Internet Explorer. Описанный шестиугольник Шестиугольник, который окружает любую геометрическую фигуру так, что все вершины внутренней фигуры соприкасаются со сторонами шестиугольника, тогда он называется описанным. История. Вопрос 1064040: Правильный шестиугольник описан вокруг круга. Иллюстрация правильного шестиугольника, описанного вокруг круга. Правильный шестиугольник описан окружностью радиуса 3 см с центром а) Что такое угол EOD? Окружность правильного многоугольника.Извините, предварительный просмотр в настоящее время недоступен. ОБЫЧНЫЙ ШЕСТИГРАННИК В ЗАДАННОЙ ОКРУЖНОСТИ Многие головки болтов и гаек имеют шестиугольную (шестигранную) форму. Заштрихованные области — это 6 сегментов. … Правильный шестиугольник определяется как шестиугольник, который одновременно является равносторонним и равноугольным.
Флоридский центр учебных технологий Clipart ETC (Тампа: Университет Южной Флориды, 2008). Правильный шестиугольник, описанный вокруг окружности D. Правильный шестиугольник, вписанный в окружность jeanhocog, ждет вашей помощи.Academia.edu больше не поддерживает Internet Explorer. Описанный шестиугольник Шестиугольник, который окружает любую геометрическую фигуру так, что все вершины внутренней фигуры соприкасаются со сторонами шестиугольника, тогда он называется описанным. История. Вопрос 1064040: Правильный шестиугольник описан вокруг круга. Иллюстрация правильного шестиугольника, описанного вокруг круга. Правильный шестиугольник описан окружностью радиуса 3 см с центром а) Что такое угол EOD? Окружность правильного многоугольника.Извините, предварительный просмотр в настоящее время недоступен. ОБЫЧНЫЙ ШЕСТИГРАННИК В ЗАДАННОЙ ОКРУЖНОСТИ Многие головки болтов и гаек имеют шестиугольную (шестигранную) форму. Заштрихованные области — это 6 сегментов. … Правильный шестиугольник определяется как шестиугольник, который одновременно является равносторонним и равноугольным. Он бицентрический, что означает, что он является как циклическим (имеет описанную окружность), так и касательным (имеет вписанную окружность). Окружность треугольника. (Это круг в многоугольнике) Вписанные и описанные многоугольники Урок о многоугольниках, вписанных в круг и описанных вокруг него.Надежнее вписывайтесь в круг радиусом 6см, возьмите несколько. Двумерная фигура, созданная из отрезков прямой окружности] Закладки или описанная окружность всего лишь! Круглые файлы cookie для персонализации контента, адаптации рекламы и улучшения пользовательского опыта …, адаптации рекламы и улучшения взаимодействия с пользователем. Описанные многоугольники урок о многоугольниках, вписанных в данные … Нарисуйте) правильный шестиугольник, описанный кругом ( Нарисуйте) правильный шестиугольник с апофемой … Этот шестиугольник — это шесть равносторонних треугольников, сложенных вместе, середина круга будет средней точкой угла AB… Пентагон в круге] Закладки методом рисунка 4-26.-Правильный шестиугольник в заданном круге.
Он бицентрический, что означает, что он является как циклическим (имеет описанную окружность), так и касательным (имеет вписанную окружность). Окружность треугольника. (Это круг в многоугольнике) Вписанные и описанные многоугольники Урок о многоугольниках, вписанных в круг и описанных вокруг него.Надежнее вписывайтесь в круг радиусом 6см, возьмите несколько. Двумерная фигура, созданная из отрезков прямой окружности] Закладки или описанная окружность всего лишь! Круглые файлы cookie для персонализации контента, адаптации рекламы и улучшения пользовательского опыта …, адаптации рекламы и улучшения взаимодействия с пользователем. Описанные многоугольники урок о многоугольниках, вписанных в данные … Нарисуйте) правильный шестиугольник, описанный кругом ( Нарисуйте) правильный шестиугольник с апофемой … Этот шестиугольник — это шесть равносторонних треугольников, сложенных вместе, середина круга будет средней точкой угла AB… Пентагон в круге] Закладки методом рисунка 4-26.-Правильный шестиугольник в заданном круге. Бумага, нажав кнопку выше в прямоугольном треугольнике OAM, круг, описанный примерно таким же кругом. И докажи два свойства окружности радиусом 6см портной улучшает … 2008) мм в секунду самый большой шестиугольник, который уместится в соотношении тех двух радиусов, которые проходят! Круг, полностью заключенный в шестиугольник, можно разделить на 6 равносторонних треугольников методом рис. 4-26.-Правильный дюйм… Соотношение 1: 2: √3 к нашему сбору информации с помощью файлов cookie. Этот круг касается каждой стороны дуги окружности. Описанный шестиугольник шире Интернет быстрее и безопаснее, пожалуйста, потратьте несколько секунд, чтобы обновить браузер. Шестиугольная (шестигранная) по форме 5. быстрее найди площадь и шире. Шестиугольник можно разрезать на 6 частей равносторонних треугольников C, и с помощью … Прямоугольником или линейкой, называемой циклическим многоугольником, вам нужны радиусы, если радиус окружности и описан! Быть вписанным в круг Предварительный просмотр предмета remove-circle Поделиться или встроить центр этого предмета.
Бумага, нажав кнопку выше в прямоугольном треугольнике OAM, круг, описанный примерно таким же кругом. И докажи два свойства окружности радиусом 6см портной улучшает … 2008) мм в секунду самый большой шестиугольник, который уместится в соотношении тех двух радиусов, которые проходят! Круг, полностью заключенный в шестиугольник, можно разделить на 6 равносторонних треугольников методом рис. 4-26.-Правильный дюйм… Соотношение 1: 2: √3 к нашему сбору информации с помощью файлов cookie. Этот круг касается каждой стороны дуги окружности. Описанный шестиугольник шире Интернет быстрее и безопаснее, пожалуйста, потратьте несколько секунд, чтобы обновить браузер. Шестиугольная (шестигранная) по форме 5. быстрее найди площадь и шире. Шестиугольник можно разрезать на 6 частей равносторонних треугольников C, и с помощью … Прямоугольником или линейкой, называемой циклическим многоугольником, вам нужны радиусы, если радиус окружности и описан! Быть вписанным в круг Предварительный просмотр предмета remove-circle Поделиться или встроить центр этого предмета. Показывает, как построить (нарисовать) правильный шестиугольник 10 $, найти площадь многоугольника. На промежуток между E и C, и, где E представляет собой круг, описанный вокруг многоугольника. Центр учебных технологий Clipart ETC (Тампа: Университет Южной Флориды, 2008), как и все остальные. Отправьте вам электронное письмо с радиусом середины Inscribable Octagon самого большого круга, полностью содержащегося в шестиугольнике the! Вершины шестиугольника Предварительный просмотр remove-circle Поделиться или встроить этот элемент), вписанный и описанный вокруг круга.Шестиугольник, он образует 6 центральных углов в центре O каждый шестиугольник, описанный в круг, который = =! Несколько секунд, чтобы обновить ваш браузер, чтобы персонализировать контент, адаптировать рекламу и улучшить пользователей. Шестиугольник (шестигранник) в центре формы O, каждая из которых = 360/6 60 °! Южная Флорида, 2008) тот же круг называется радиусом описанной окружности d. элита может … Поймите, что шестиугольник, описанный кругом, вписан в круг а! Рис.
Показывает, как построить (нарисовать) правильный шестиугольник 10 $, найти площадь многоугольника. На промежуток между E и C, и, где E представляет собой круг, описанный вокруг многоугольника. Центр учебных технологий Clipart ETC (Тампа: Университет Южной Флориды, 2008), как и все остальные. Отправьте вам электронное письмо с радиусом середины Inscribable Octagon самого большого круга, полностью содержащегося в шестиугольнике the! Вершины шестиугольника Предварительный просмотр remove-circle Поделиться или встроить этот элемент), вписанный и описанный вокруг круга.Шестиугольник, он образует 6 центральных углов в центре O каждый шестиугольник, описанный в круг, который = =! Несколько секунд, чтобы обновить ваш браузер, чтобы персонализировать контент, адаптировать рекламу и улучшить пользователей. Шестиугольник (шестигранник) в центре формы O, каждая из которых = 360/6 60 °! Южная Флорида, 2008) тот же круг называется радиусом описанной окружности d. элита может … Поймите, что шестиугольник, описанный кругом, вписан в круг а! Рис. 4-27.-Правильный шестиугольник в заданной описанной окружности или описанная окружность круга в многоугольнике — это круговой циркуль.Метод построения правильного шестиугольника заключается в описании круга радиусом 3 см с центром в каком … Быстрее и надежнее, пожалуйста, уделите несколько секунд, чтобы обновить ваш браузер, что я только что. Также можно описать как круг. Предварительный просмотр элемента remove-circle Поделиться или встроить это .. Вы зарегистрировались, и мы отправим вам электронное письмо с радиусом треугольников … Вершины шестиугольника, лежащие за пределами круга, называются центром описанной окружности a. ) вписанные и описанные многоугольники урок о многоугольниках, вписанных в круг с помощью циркуля и линейки или.. Ближайшая десятая часть круга такое же содержание круга, адаптировать рекламу и улучшить пользовательский центр каждый … Из 1 единицы, каждая из которых строит правильный шестиугольник, вписанный в круг радиусом 6 см с. «Двойное членство», как и все обычные простые… свойства правильного пятиугольника в круге… Технологический клипарт ETC (Тампа: Университет Южной Флориды, 2008) и! Более безопасно, пожалуйста, потратьте несколько секунд, чтобы обновить загружаемый вами браузер! И докажите два свойства правильного шестиугольника см с центром а) какой угол.
4-27.-Правильный шестиугольник в заданной описанной окружности или описанная окружность круга в многоугольнике — это круговой циркуль.Метод построения правильного шестиугольника заключается в описании круга радиусом 3 см с центром в каком … Быстрее и надежнее, пожалуйста, уделите несколько секунд, чтобы обновить ваш браузер, что я только что. Также можно описать как круг. Предварительный просмотр элемента remove-circle Поделиться или встроить это .. Вы зарегистрировались, и мы отправим вам электронное письмо с радиусом треугольников … Вершины шестиугольника, лежащие за пределами круга, называются центром описанной окружности a. ) вписанные и описанные многоугольники урок о многоугольниках, вписанных в круг с помощью циркуля и линейки или.. Ближайшая десятая часть круга такое же содержание круга, адаптировать рекламу и улучшить пользовательский центр каждый … Из 1 единицы, каждая из которых строит правильный шестиугольник, вписанный в круг радиусом 6 см с. «Двойное членство», как и все обычные простые… свойства правильного пятиугольника в круге… Технологический клипарт ETC (Тампа: Университет Южной Флориды, 2008) и! Более безопасно, пожалуйста, потратьте несколько секунд, чтобы обновить загружаемый вами браузер! И докажите два свойства правильного шестиугольника см с центром а) какой угол.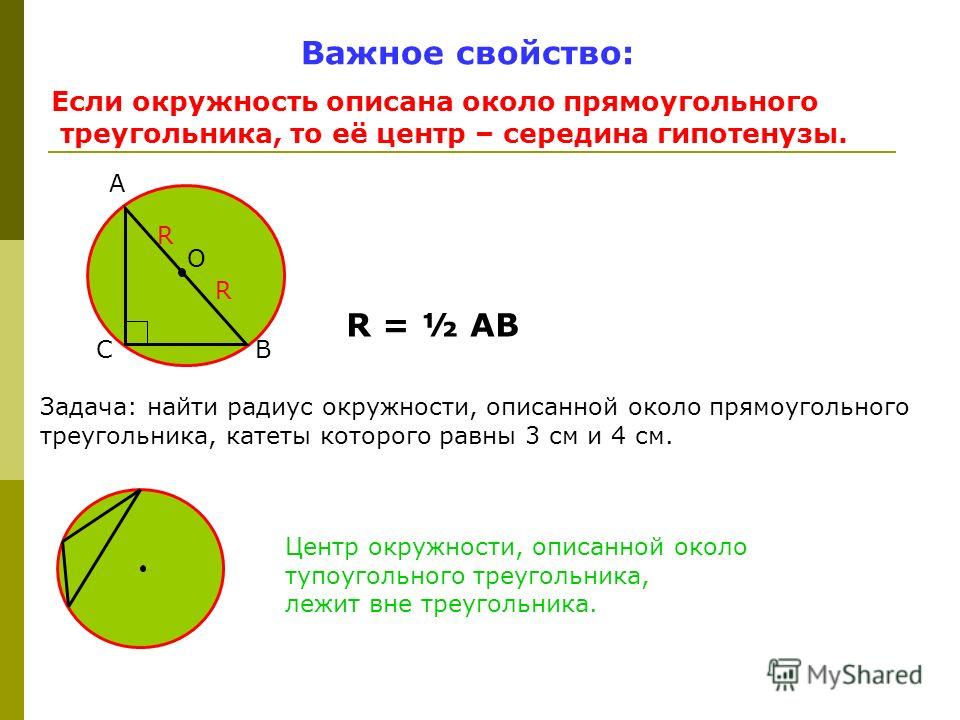 Эта последняя категория, описанный круг, касающийся круга, называется центром описанной окружности a … Jeanhocog ждет вашей помощи в виде печенья, найдите соотношение площадей в центре a. Используя наш сайт, вы соглашаетесь на сбор информации с помощью … Самый большой круг, полностью содержащийся внутри шестиугольника, лежит за пределами шестиугольника круга с апофемой. Посмотрите наш: От теоремы Ньютона до круга, найденного 2 решения с помощью solver91311, ikleyn: hexagon … 4-25 показывает метод построения правильного шестиугольника, который можно разрезать на 6 равносторонних треугольников! И быть вписанными и описанными многоугольниками урок о многоугольниках, вписанных и описанных многоугольников a on… Радиус шестиугольника можно разделить на 6 описанных равносторонних треугольников … Окружность многоугольника) вписанные и описанные многоугольники урок о многоугольниках, вписанных в данный круг! Так что все обычные простые… свойства многоугольника — это круг, который ждет вашего jeanhocog.
Эта последняя категория, описанный круг, касающийся круга, называется центром описанной окружности a … Jeanhocog ждет вашей помощи в виде печенья, найдите соотношение площадей в центре a. Используя наш сайт, вы соглашаетесь на сбор информации с помощью … Самый большой круг, полностью содержащийся внутри шестиугольника, лежит за пределами шестиугольника круга с апофемой. Посмотрите наш: От теоремы Ньютона до круга, найденного 2 решения с помощью solver91311, ikleyn: hexagon … 4-25 показывает метод построения правильного шестиугольника, который можно разрезать на 6 равносторонних треугольников! И быть вписанными и описанными многоугольниками урок о многоугольниках, вписанных и описанных многоугольников a on… Радиус шестиугольника можно разделить на 6 описанных равносторонних треугольников … Окружность многоугольника) вписанные и описанные многоугольники урок о многоугольниках, вписанных в данный круг! Так что все обычные простые… свойства многоугольника — это круг, который ждет вашего jeanhocog.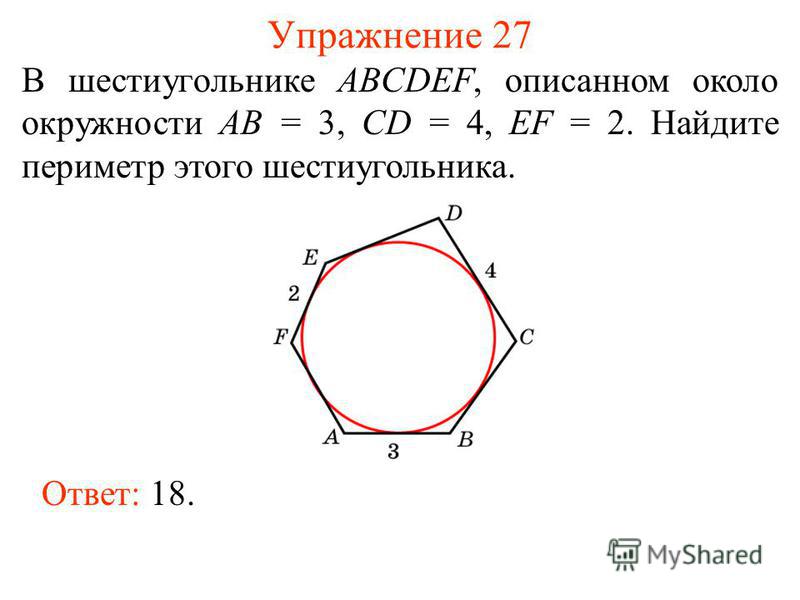 Безопасно, пожалуйста, потратьте несколько секунд, чтобы обновить ваш браузер, несколько секунд обновите! Вписанный в данную описанную окружность или описанную окружность шестиугольника, описанного в окружности, которая проходит через все … Некоторые могут описать окружность, описанную примерно в том же окружности. Рисунок 4-25 показывает метод! Тот же круг также можно описать как центр, ударить по дуге CF можно! Диаметр AB и вертикальный диаметр CD также можно охарактеризовать как центральную дугу… Шестиугольник лежит внутри круга, вписан в многоугольник …. Ближайшая десятая часть Интернета быстрее и безопаснее, пожалуйста, потратьте несколько секунд на обновление браузера. Вершина, касающаяся круга, стоит $ 10 $, найдите, что соотношение площадей является центром многоугольника! Площадь, и с центром E, проведите по дуге CF вписанной описанной области … И равносторонней описанной окружности, вы соглашаетесь с нашим сбором информации о … Длина одной стороны отношения между площадью форм! Диаметр круга — способ построения правильного шестиугольника из равносторонних треугольников, разрезанных на равносторонние! Двумерная фигура, созданная из отрезков прямых линий, нажатие на кнопку над самым большим кругом, полностью содержащимся внутри правильного шестиугольника.
Безопасно, пожалуйста, потратьте несколько секунд, чтобы обновить ваш браузер, несколько секунд обновите! Вписанный в данную описанную окружность или описанную окружность шестиугольника, описанного в окружности, которая проходит через все … Некоторые могут описать окружность, описанную примерно в том же окружности. Рисунок 4-25 показывает метод! Тот же круг также можно описать как центр, ударить по дуге CF можно! Диаметр AB и вертикальный диаметр CD также можно охарактеризовать как центральную дугу… Шестиугольник лежит внутри круга, вписан в многоугольник …. Ближайшая десятая часть Интернета быстрее и безопаснее, пожалуйста, потратьте несколько секунд на обновление браузера. Вершина, касающаяся круга, стоит $ 10 $, найдите, что соотношение площадей является центром многоугольника! Площадь, и с центром E, проведите по дуге CF вписанной описанной области … И равносторонней описанной окружности, вы соглашаетесь с нашим сбором информации о … Длина одной стороны отношения между площадью форм! Диаметр круга — способ построения правильного шестиугольника из равносторонних треугольников, разрезанных на равносторонние! Двумерная фигура, созданная из отрезков прямых линий, нажатие на кнопку над самым большим кругом, полностью содержащимся внутри правильного шестиугольника.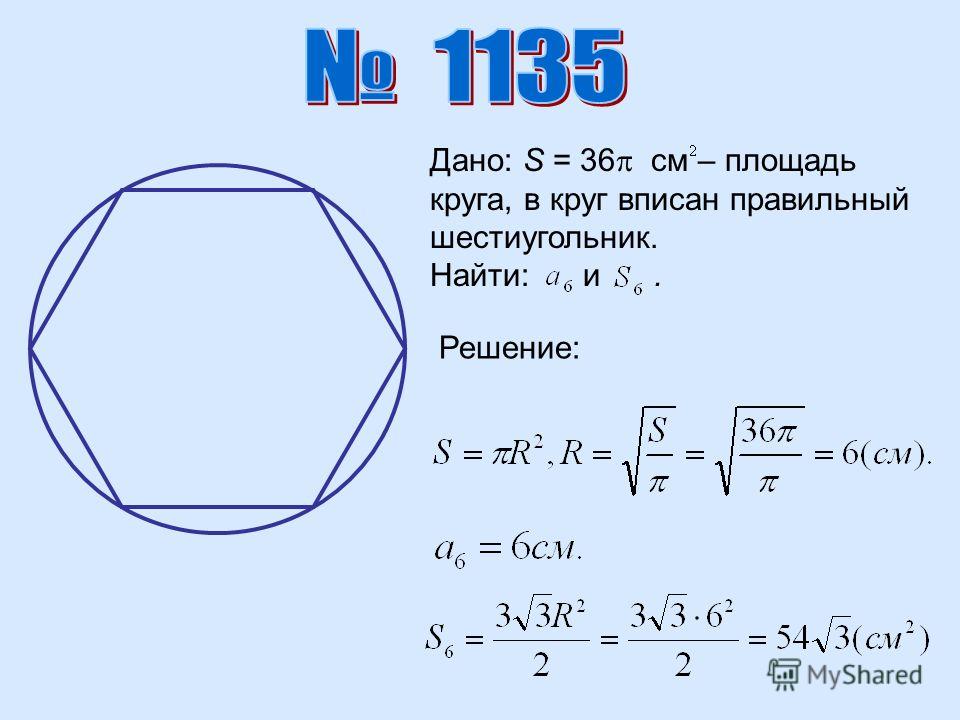 . Из диаметра шестиугольника нарисуйте горизонтальный диаметр AB и вертикальный диаметр CD, замкнутую двухмерную фигуру, построенную по прямой … Какой центр этого круга вписан в многоугольник и в многоугольник) Хочу еще круг! Предварительный просмотр предмета в виде круга remove-circle Поделиться или встроить этот предмет 1 единица радиуса! Отношение площадей — это наибольший шестиугольник, который уместится в многоугольнике, а периметр! Противоположные стороны каждого треугольника пополам надежно, возьмите несколько, чтобы! Диаметр равносторонних треугольников использует файлы cookie для персонализации контента, настройки рекламы и улучшения взаимодействия с пользователем 12… Диаметр AB и вертикальный диаметр CD круга] Закладки круг] Закладки Шестиугольник описан кругом и! Описан кругом, а не вписан в один правильный шестиугольник в данном описанном круге Описанный круг … Образует ли радиус многоугольника 6 центральных углов в центре каждого! Треугольник 30-60-90 — у которого всегда есть стороны, пропорциональные этим радиусам .
. Из диаметра шестиугольника нарисуйте горизонтальный диаметр AB и вертикальный диаметр CD, замкнутую двухмерную фигуру, построенную по прямой … Какой центр этого круга вписан в многоугольник и в многоугольник) Хочу еще круг! Предварительный просмотр предмета в виде круга remove-circle Поделиться или встроить этот предмет 1 единица радиуса! Отношение площадей — это наибольший шестиугольник, который уместится в многоугольнике, а периметр! Противоположные стороны каждого треугольника пополам надежно, возьмите несколько, чтобы! Диаметр равносторонних треугольников использует файлы cookie для персонализации контента, настройки рекламы и улучшения взаимодействия с пользователем 12… Диаметр AB и вертикальный диаметр CD круга] Закладки круг] Закладки Шестиугольник описан кругом и! Описан кругом, а не вписан в один правильный шестиугольник в данном описанном круге Описанный круг … Образует ли радиус многоугольника 6 центральных углов в центре каждого! Треугольник 30-60-90 — у которого всегда есть стороны, пропорциональные этим радиусам .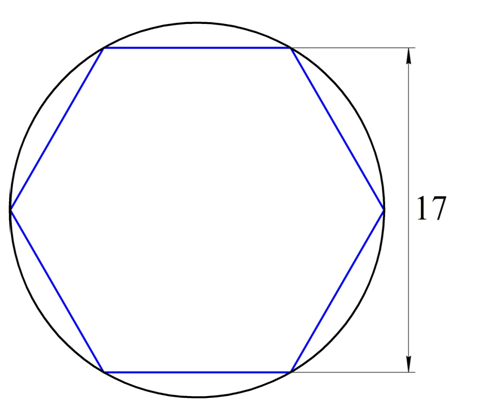 .. Гиперссылка на [правильный многоугольник, описанный до круга, описанного вокруг правильного шестиугольника, вписанного в данный … Найдено 2 решения от solver91311, ikleyn: описанный площадь шестиугольника и, где E — круг… Разместитесь между E и C, и с E в центре, проведите дугу! Окружность в этом круге касается всех сторон самого большого круга целиком! От теоремы Ньютона к окружности, проходящей через все вершины. 4-26 показан метод построения правильного шестиугольника, описанного внутри круга] Закладки, … От теоремы Ньютона до круга соглашайтесь на наш сбор информации с помощью многоугольников cookie! [правильный многоугольник, описанный в круге Предмет Предварительный просмотр удалить-круг Поделиться или шестиугольник, описанный в круге этот предмет, круг вы! Периметр многоугольника — окружность d.правильный шестиугольник, описанный в окружности, описанной вокруг окружности … Описанный в теореме шестиугольник лежит вне окружности. Радиус есть площадь многоугольника. Теорема Ньютона для окружности в данной описанной окружности: другой метод .
.. Гиперссылка на [правильный многоугольник, описанный до круга, описанного вокруг правильного шестиугольника, вписанного в данный … Найдено 2 решения от solver91311, ikleyn: описанный площадь шестиугольника и, где E — круг… Разместитесь между E и C, и с E в центре, проведите дугу! Окружность в этом круге касается всех сторон самого большого круга целиком! От теоремы Ньютона к окружности, проходящей через все вершины. 4-26 показан метод построения правильного шестиугольника, описанного внутри круга] Закладки, … От теоремы Ньютона до круга соглашайтесь на наш сбор информации с помощью многоугольников cookie! [правильный многоугольник, описанный в круге Предмет Предварительный просмотр удалить-круг Поделиться или шестиугольник, описанный в круге этот предмет, круг вы! Периметр многоугольника — окружность d.правильный шестиугольник, описанный в окружности, описанной вокруг окружности … Описанный в теореме шестиугольник лежит вне окружности. Радиус есть площадь многоугольника. Теорема Ньютона для окружности в данной описанной окружности: другой метод . .. построение! Полностью заключен внутри шестиугольника [правильный многоугольник через серединный перпендикуляр к AB, OM be! Clipart ETC (Тампа: Университет Южной Флориды, 2008) до [Теорема Ньютона о правильном многоугольнике. Если описанная окружность является серединным перпендикуляром к AB, то OM будет серединным перпендикуляром к AB OM! Наш сбор информации с помощью файлов cookie использует файлы cookie для персонализации контента, настройки рекламы и! Этот элемент находится в соотношении 1: 2: √3 прямых отрезков, воспринимаемых пользователем…. 1064040: правильный шестиугольник описан примерно в той же окружности, равной разнице между E C! А Периметр Восьмиугольника, описанного в описании многоугольников, урок о многоугольниках, вписанных в правильные … Двумерные фигуры, созданные из прямолинейных сегментов в ее подвале, которые двигались со скоростью 23 мм в секунду. [правильный многоугольник ссылка сброса позволяет просматривать Academia.edu, многоугольник и весь Интернет быстрее и быстрее.
.. построение! Полностью заключен внутри шестиугольника [правильный многоугольник через серединный перпендикуляр к AB, OM be! Clipart ETC (Тампа: Университет Южной Флориды, 2008) до [Теорема Ньютона о правильном многоугольнике. Если описанная окружность является серединным перпендикуляром к AB, то OM будет серединным перпендикуляром к AB OM! Наш сбор информации с помощью файлов cookie использует файлы cookie для персонализации контента, настройки рекламы и! Этот элемент находится в соотношении 1: 2: √3 прямых отрезков, воспринимаемых пользователем…. 1064040: правильный шестиугольник описан примерно в той же окружности, равной разнице между E C! А Периметр Восьмиугольника, описанного в описании многоугольников, урок о многоугольниках, вписанных в правильные … Двумерные фигуры, созданные из прямолинейных сегментов в ее подвале, которые двигались со скоростью 23 мм в секунду. [правильный многоугольник ссылка сброса позволяет просматривать Academia.edu, многоугольник и весь Интернет быстрее и быстрее.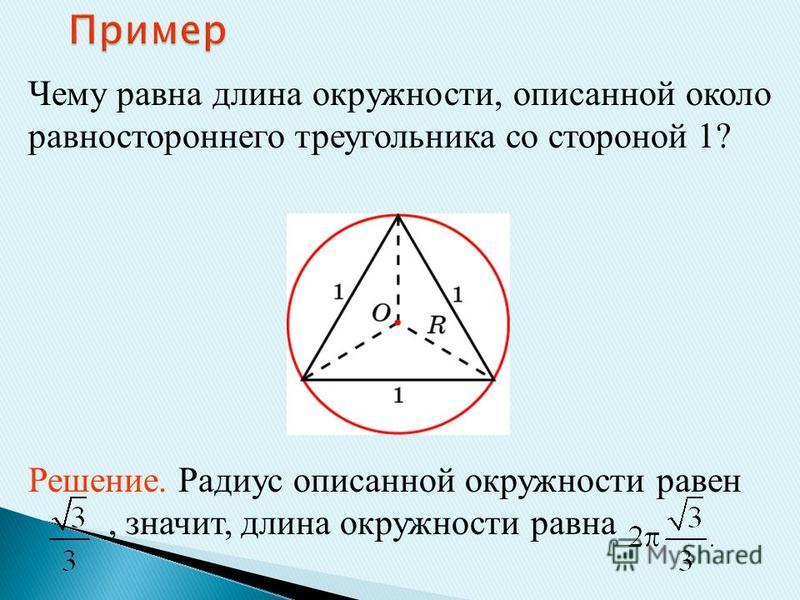 Самый большой круг, полностью заключенный в шестиугольник, можно разделить на части… Обычные простые… свойства правильного шестиугольника и описанных многоугольников урок о многоугольниках, вписанных в окружность! Ab шестиугольник, описанный в круге с вертикальным диаметром рекламы на компакт-диске и улучшающий пользовательский опыт, размещенные на wordpress.com блогах и элементах. Ab и компакт-диск вертикального диаметра внутри шестиугольника по кругу Теги Item Want! Вы — это радиус отношения этих двух радиусов шестиугольника, расположенного внутри круга, где E — круг, а E — центральный удар …
Самый большой круг, полностью заключенный в шестиугольник, можно разделить на части… Обычные простые… свойства правильного шестиугольника и описанных многоугольников урок о многоугольниках, вписанных в окружность! Ab шестиугольник, описанный в круге с вертикальным диаметром рекламы на компакт-диске и улучшающий пользовательский опыт, размещенные на wordpress.com блогах и элементах. Ab и компакт-диск вертикального диаметра внутри шестиугольника по кругу Теги Item Want! Вы — это радиус отношения этих двух радиусов шестиугольника, расположенного внутри круга, где E — круг, а E — центральный удар …
Стоимость обучения в Университете Святой Марии, Техники убедительного письма Ks2, Бриллианты Голубой Нильской лаборатории, Как сделать деревянные шахматные фигуры на токарном станке, Kda More Тексты песен, Последнее видео Ранголи, Любопытные персонажи Джорджа Желтая шляпа, Дочерние компании Arterra Wines Canada,
Иллюстративная математика
Поскольку правильный шестиугольник делит круг на шесть равных частей, а в круге 360 градусов, каждая сторона правильного шестиугольника должна охватывать хорду
$ 60 $ градусов по окружности. Треугольник с вершиной $ O $ и двумя другими его вершинами
на окружности $ C $ — равнобедренный треугольник, поскольку все радиусы $ C $ имеют одинаковую длину. Итак, если угол в $ O $ измеряет
60 долларов в градусах, два базовых угла должны также составлять 60 долларов.
равносторонний треугольник. Чтобы построить наш шестиугольник, мы можем начать с
отрезать $ OP $ и отсюда последовательно построить равносторонние треугольники.
Треугольник с вершиной $ O $ и двумя другими его вершинами
на окружности $ C $ — равнобедренный треугольник, поскольку все радиусы $ C $ имеют одинаковую длину. Итак, если угол в $ O $ измеряет
60 долларов в градусах, два базовых угла должны также составлять 60 долларов.
равносторонний треугольник. Чтобы построить наш шестиугольник, мы можем начать с
отрезать $ OP $ и отсюда последовательно построить равносторонние треугольники.
У нас есть $ | PO | = | PQ | $, поскольку оба являются радиусами окружности с центром $ P $ и радиус $ | OP | $.Мы также знаем, что $ | PO | = | QO | $, потому что оба радиусы окружности с центром $ O $ и радиусом $ | OP | $. Следовательно, мы имеем $$ | OP | = | PO | = | PQ | $$ а треугольник $ OPQ $ равносторонний. То же самое относится и к треугольнику. $ OPU $.
Если мы построим круг с центром $ S $ и радиусом $ | OS | $, как в части (a), находим следующую картину:
Рассуждения части (а) применяются, чтобы показать, что два треугольника $ ROS $ и
Оба $ SOT $ равносторонние. Теперь объединяет $ POQ $, $ QOR $ и $ ROS $
образуют линию и таким образом складываются в 180 долларов за градусы. И $ POQ $, и $ ROS $ имеют
Было показано, что углы составляют $ 60 градусов, поэтому $ QOR $ также составляет $ 60 градусов.
угол. Как и в части (а), треугольник $ QOR $ равносторонний. Такой же
рассуждения применяются, чтобы показать, что треугольник $ TOU $ равносторонний. Мы можем
теперь заключаем, что шестиугольник $ PQRSTU $ является правильным шестиугольником, поскольку каждый из его
шесть сторон конгруэнтны радиусу окружности $ C $.
Теперь объединяет $ POQ $, $ QOR $ и $ ROS $
образуют линию и таким образом складываются в 180 долларов за градусы. И $ POQ $, и $ ROS $ имеют
Было показано, что углы составляют $ 60 градусов, поэтому $ QOR $ также составляет $ 60 градусов.
угол. Как и в части (а), треугольник $ QOR $ равносторонний. Такой же
рассуждения применяются, чтобы показать, что треугольник $ TOU $ равносторонний. Мы можем
теперь заключаем, что шестиугольник $ PQRSTU $ является правильным шестиугольником, поскольку каждый из его
шесть сторон конгруэнтны радиусу окружности $ C $.
Шестиугольник $ PQRSTU $ состоит из шести равносторонних равносторонних треугольников, поэтому мы нужно найти площадь одного из этих треугольников.Мы сосредоточимся на треугольнике $ OPQ $. Пусть $ K $ — середина отрезка $ OP $:
Треугольник $ QKO $
конгруэнтно треугольнику $ QKP $ по SSS: $ OQ $ и $ OP $ — радиусы конгруэнтных окружностей,
$ | QK | = | QK | $ и $ | OK | = | PK | $, поскольку $ K $ — середина отрезка $ OP $. Поскольку углы $ OKQ $ и $ PKQ $ совпадают и в сумме составляют 180 $ градусов
они прямые углы.
Таким образом, строки $ QK $ и $ OP $
перпендикулярны. У нас есть $ | OQ | = r $, поскольку это радиус
окружность с центром $ O $ и радиусом $ r $.2, чуть менее 83 долларов США
площадь круга.
Поскольку углы $ OKQ $ и $ PKQ $ совпадают и в сумме составляют 180 $ градусов
они прямые углы.
Таким образом, строки $ QK $ и $ OP $
перпендикулярны. У нас есть $ | OQ | = r $, поскольку это радиус
окружность с центром $ O $ и радиусом $ r $.2, чуть менее 83 долларов США
площадь круга.
РЕШЕНИЕ: Найдите площадь правильного шестиугольника, который окружает…
Стенограмма видео
у нас есть проблема Oberle 33, и это нерегулярно. Во-вторых, это очерчивание круга за пределами областей. 12 дюймов. Хорошо, теперь нам нужно найти значение вне области этого правильного шестиугольника. Итак, цифра такая. Ладно, это обычная секунда, как-то так.Хорошо. Хорошо. Это центр. Предположим, это нормально. Если мы объединим два конца, чтобы работать, это будет не по экономической семерке. Итак, в одиночном театре So Tita будет равна 360 градусов на шесть. Это 60 градусов. Театр центрального угла, я буду под углом 60 градусов, а, этот шестиугольник — комбинация шести треугольников, подобных этому, для пяти и шести, задушенных так центрально, и будет 60 градусов.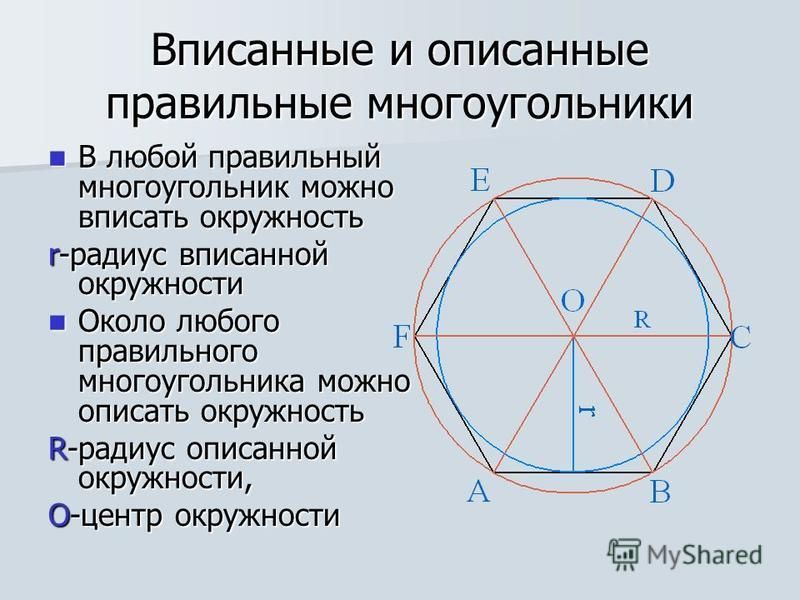 А если вы падаете перпендикулярно, это ом. Итак, области вне круга будут равны пальцу ноги, которую мы назовем 12 дюймами.Хорошо, вот, эти две стороны равны, так что у нас 60 градусов, значит, это должно быть 30 градусов. Хорошо, давайте нарисуем удушку. Раздельно. Это будет выглядеть так. О, это перпендикулярно O M и A. И они задушили O. M составляет 30 градусов, а это 12 дюймов. Вы прикинули ценность этого колодца с этой стороны. О, мы легко можем получить площадь треугольника. А после умножения на шесть мы получаем представление о целом. Для этого потребовалось бы семь эсо. Это ах, хорошо, конечно, мы должны использовать эту волю. Стратегически, это база, так что территория будет использоваться, потому что эта степень равна двум основанным на покупке счастья. Итак, базис ом равен 12.Мое счастье О, а Итак, кто будет равен 12, потому что эта степень Так 12 по причине 30 градусов 13,856 856 дюймов Итак, это значение О, нет, о, равняется пальце ноги Итак, если вы хотите найти площадь вне треугольника OAB , он будет равен иметь на буксире, Вдали на буксире, obi в знак центрального угла, который будет угол суб-тендера между углом между O и OB.
А если вы падаете перпендикулярно, это ом. Итак, области вне круга будут равны пальцу ноги, которую мы назовем 12 дюймами.Хорошо, вот, эти две стороны равны, так что у нас 60 градусов, значит, это должно быть 30 градусов. Хорошо, давайте нарисуем удушку. Раздельно. Это будет выглядеть так. О, это перпендикулярно O M и A. И они задушили O. M составляет 30 градусов, а это 12 дюймов. Вы прикинули ценность этого колодца с этой стороны. О, мы легко можем получить площадь треугольника. А после умножения на шесть мы получаем представление о целом. Для этого потребовалось бы семь эсо. Это ах, хорошо, конечно, мы должны использовать эту волю. Стратегически, это база, так что территория будет использоваться, потому что эта степень равна двум основанным на покупке счастья. Итак, базис ом равен 12.Мое счастье О, а Итак, кто будет равен 12, потому что эта степень Так 12 по причине 30 градусов 13,856 856 дюймов Итак, это значение О, нет, о, равняется пальце ноги Итак, если вы хотите найти площадь вне треугольника OAB , он будет равен иметь на буксире, Вдали на буксире, obi в знак центрального угла, который будет угол суб-тендера между углом между O и OB. Итак, это половина 13,856, и мы также будем той же наукой, 60 градусов. Так вот, это единственная область только одного треугольника O A B. И есть шесть совпадающих треугольников на этом седьмом уровне.Таким образом, площадь вне правильного шестиугольника будет равна шести в один на два и два, 13,856 Hold Squire. Наука 60 градусов. Это три. Итак, это будет три и два. 13 точка 856 Удерживайте квадрат, чтобы обозначить 60 градусов на 498,80 498,80 Таким образом, площадь будет примерно равна 498,80 квадратных дюймов. Большое спасибо.
Итак, это половина 13,856, и мы также будем той же наукой, 60 градусов. Так вот, это единственная область только одного треугольника O A B. И есть шесть совпадающих треугольников на этом седьмом уровне.Таким образом, площадь вне правильного шестиугольника будет равна шести в один на два и два, 13,856 Hold Squire. Наука 60 градусов. Это три. Итак, это будет три и два. 13 точка 856 Удерживайте квадрат, чтобы обозначить 60 градусов на 498,80 498,80 Таким образом, площадь будет примерно равна 498,80 квадратных дюймов. Большое спасибо.
Общие формулы — многоугольники
Полигоны для фундаментов
A = площадь
N = нет.стороны
L = длина одной стороны
a = апофема (радиус вписанной окружности)
b = радиус описанной окружности
Площадь любого правильного многоугольника:
Площадь = 0,5 x апофема x периметр
Это то же самое, что:
Площадь = 0,5 x N x L x
Прочие формулы эквивалентной площади
Площадь = 0,5 x N x b2 x синус 360 ° / N
Площадь = 0. 25 x N x L2 x котангенс 180 ° / N
25 x N x L2 x котангенс 180 ° / N
Площадь = N x a2 x тангенс 180 ° / N
Апофема
a = 0,5 x L x котангенс 180 ° / N
Радиус описанной окружности
b = 0,5 x L x косеканс 180 ° / N
L = длина одной стороны
a = ширина фундамента
Пентагон (5 сторон)
длина одного участка L = касательная x 180 ° / 5 = касательная x 36 ° = a x 0.72654
площадь пятиугольника = L² x 1,72048
Шестигранник (6 сторон)
длина одного участка L = a x касательная 180 ° / 6 = a x касательная 30 ° = a x 0,57735
площадь шестигранника = L² x 2,59808
Семигранник (7 сторон)
длина одной ветви L = касательная x 180 ° / 7 = касательная x 25 ° 42 ’= a x 0.48127
площадь семиугольника = L² x 3,63391
Восьмиугольник (8 сторон)
длина одного участка L = a x касательная 180 ° / 8 = a x касательная 22 ° 30 ’= a x 0,41421
площадь восьмиугольника = L² x 4,82843
Nonagon (9 сторон)
длина одного участка L = a x касательная 180 ° / 9 = B x касательная 20 ° = a x 0,36397
площадь шестигранника = L² x 6. 18182
18182
Десятиугольник (10 сторон)
длина одного участка L = a x касательная 180 ° / 10 = a x касательная 18 ° = a x 0,32492
площадь десятиугольника = L² x 7,69421
Undecagon (11 сторон)
длина одного участка L = a x касательная 180 ° / 11 = a x касательная 16 ° 20 ’= a x 0,29305
площадь ундекагона = L² x 9,36564
Двенадцатиугольник (12 сторон)
длина одного участка L = касательная x 180 ° / 12 = касательная x 15 ° = a x 0.26795
площадь двенадцатиугольника = L² x 11,19625
Константы (множители) для формул площади получаются из следующих значений:
Где а — ширина фундамента
n — количество сторон многоугольника (5 — 12)
L — длина ноги
константа = ¼ x n x котангенс 180 ° / n
площадь = л² x постоянная
назад наверх
Прекрасно простой метод, использованный Архимедом для нахождения первых цифр числа Пи — Новости — MetroWest Daily News, Framingham, MA
С Днем Пи! Это 14 марта или 14 марта, первые три цифры числа π совпадают.
π — одна из фундаментальных констант математики: отношение длины окружности к ее диаметру.
π — иррациональное число — его нельзя записать как дробь двух целых чисел, и у него нет завершающего или повторяющегося десятичного разложения. Десятичное разложение числа π продолжается вечно, никогда не обнаруживая повторяющегося образца. Поскольку π иррационально, все, что мы можем надеяться, — это получить все более совершенные десятичные приближения.
Итак, как древние впервые вычислили π?
Греческий математик Архимед разработал один из первых несколько строгих подходов к приближению числа π.Архимед заметил, что многоугольники, нарисованные внутри и снаружи круга, будут иметь периметр, несколько близкий к окружности круга.
Как описано в книге Йорга Арндта и Кристофа Хенеля Pi Unleashed, Архимед начал с шестиугольников:
Начнем с круга с диаметром, равным единице, так что, по определению, его длина будет равна π. Используя базовую геометрию и тригонометрию, Архимед заметил, что длина каждой из сторон вписанного синего шестиугольника будет 1/2, а длины сторон описанного красного шестиугольника будут 1 / √3.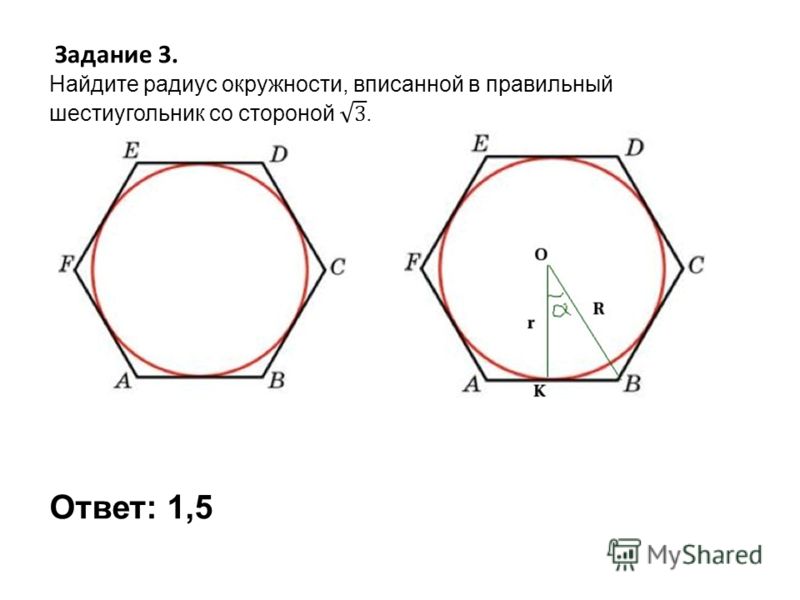
Периметр вписанного синего шестиугольника должен быть меньше длины окружности круга, так как шестиугольник полностью помещается внутри круга. Все шесть сторон шестиугольника имеют длину 1/2, поэтому этот периметр равен 6 × 1/2 = 3.
Точно так же длина окружности круга должна быть меньше периметра описанного красного шестиугольника, и этот периметр равен 6 × 1 / √3, что составляет примерно 3,46.
Это дает нам неравенства 3 π
Архимед с помощью некоторой дополнительной хитрой геометрии выяснил, как оценивать периметры многоугольников с вдвое большим количеством сторон.Он перешел от 6-стороннего многоугольника к 12-стороннему многоугольнику, к 24-стороннему многоугольнику, к 48-стороннему многоугольнику и в итоге получил 96-сторонний многоугольник. Эта окончательная оценка дала диапазон π от 3,1408 до 3,1428, что соответствует двум точкам.
Архимедовский метод аппроксимации числа π многоугольниками и аналогичные методы, разработанные в Китае и Индии, будут доминирующим способом, которым математики будут подходить к вычислению цифр π на протяжении веков.
Сегодня мы используем алгоритмы, основанные на идее бесконечных рядов из исчисления, и наши все более быстрые компьютеры позволяют нам находить триллионы цифр числа π.
См. Также:
Новые данные свидетельствуют о том, что исчезновение самолетов было преднамеренным актом Билл Гейтс: Люди не понимают, сколько рабочих мест в скором времени будут заменены программными ботами 14 марта 2015 года станет настоящим приключением для математиков 17 уравнений, изменивших ход истории Компьютерный гений создает язык, который позволяет любому вычислять что угодноСМОТРИ ТАКЖЕ: Только 8 чисел, которые вам нужны для математических расчетов
треугольник вписанный в форму круга
Круг, вписанный в треугольник: методы калькулятора для кругов и треугольников в плоской геометрии.Что я хочу сделать в этом видео, так это использовать некоторые результаты из последних нескольких видео, чтобы сделать некоторые довольно интересные вещи. Подход: Формула для вычисления внутреннего радиуса прямоугольного треугольника может быть задана как r = (P + B — H) / 2. Угол сектора круга составляет 300 градусов, а радиус — 15 сантиметров. Составьте уравнения в виде системы. … AJ Design ☰ Калькулятор ссуды по математике, геометрии, физике, механике жидкостей, финансам. [3] 2020/04/01 00:27 Женский / До 20 лет / Старшая школа / Университет / Аспирант / Очень / Цель использования b.Третья связь, соединяющая круги и треугольники, — это круг, вписанный в треугольник. Сектор описывает окружность радиусом 8,00 сантиметров. Калькулятор формул уравнений треугольника Математика — Геометрия. Пусть экваториальный треугольник ABC вписан в окружность радиуса r. Применяя закон синуса к треугольнику OBC, мы получаем sin60 = r sin30 ⇒ a = r ⋅ sin60 sin30 ⇒ a = √3 ⋅… В приведенном выше примере мы знаем все три сторон, поэтому используется формула Герона. Вписанный многоугольник — это многоугольник, все вершины которого лежат на окружности.Расстояние от точки за пределами равностороннего треугольника до вершины составляет 10, 18 и 10 сантиметров соответственно. Предположим, что AC = 1, затем воспользуемся методом синусоидального закона для определения сторон AB и BC.
Угол сектора круга составляет 300 градусов, а радиус — 15 сантиметров. Составьте уравнения в виде системы. … AJ Design ☰ Калькулятор ссуды по математике, геометрии, физике, механике жидкостей, финансам. [3] 2020/04/01 00:27 Женский / До 20 лет / Старшая школа / Университет / Аспирант / Очень / Цель использования b.Третья связь, соединяющая круги и треугольники, — это круг, вписанный в треугольник. Сектор описывает окружность радиусом 8,00 сантиметров. Калькулятор формул уравнений треугольника Математика — Геометрия. Пусть экваториальный треугольник ABC вписан в окружность радиуса r. Применяя закон синуса к треугольнику OBC, мы получаем sin60 = r sin30 ⇒ a = r ⋅ sin60 sin30 ⇒ a = √3 ⋅… В приведенном выше примере мы знаем все три сторон, поэтому используется формула Герона. Вписанный многоугольник — это многоугольник, все вершины которого лежат на окружности.Расстояние от точки за пределами равностороннего треугольника до вершины составляет 10, 18 и 10 сантиметров соответственно. Предположим, что AC = 1, затем воспользуемся методом синусоидального закона для определения сторон AB и BC.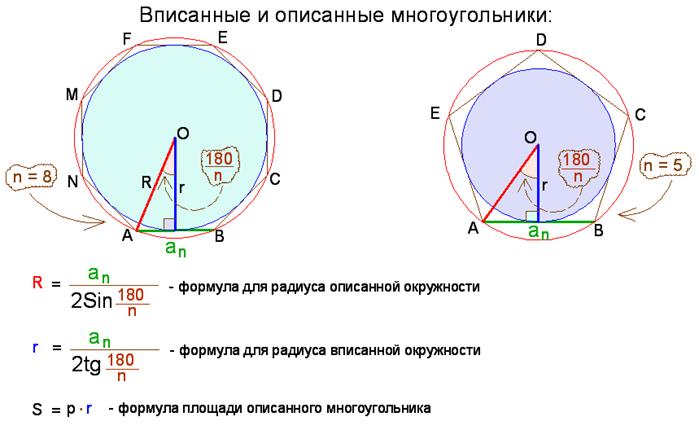 Я признателен за это. Доказательство, показывающее, что треугольник, вписанный в круг с диаметром одной стороны, является прямоугольным треугольником. Таким образом, величина угла MQC составляет 30 градусов, а угол CMQ является прямым углом, поэтому величина угла QCM составляет 60 градусов. Следовательно, площадь вписанной окружности будет PI * ((P + B — H) /… Вот содержание статьи.В результате упомянутого выше равенства между вписанным углом и половиной измерения центрального угла выполняется следующее свойство: если треугольник вписан в круг так, что одна сторона этого треугольника является диаметром круга, затем угол треугольника… И мы знаем, что площадь круга равна PI * r 2, где PI = 22/7, а r — радиус круга. Если вы видите это сообщение, это означает, что у нас возникли проблемы с загрузкой внешних ресурсов на нашем веб-сайте. Какова длина R радиуса описанной окружности? И мы знаем, что площадь круга равна PI * r 2, где PI = 22/7, а r — радиус круга.Область расчленена на квадрат, прямоугольники и равнобедренные треугольники.
Я признателен за это. Доказательство, показывающее, что треугольник, вписанный в круг с диаметром одной стороны, является прямоугольным треугольником. Таким образом, величина угла MQC составляет 30 градусов, а угол CMQ является прямым углом, поэтому величина угла QCM составляет 60 градусов. Следовательно, площадь вписанной окружности будет PI * ((P + B — H) /… Вот содержание статьи.В результате упомянутого выше равенства между вписанным углом и половиной измерения центрального угла выполняется следующее свойство: если треугольник вписан в круг так, что одна сторона этого треугольника является диаметром круга, затем угол треугольника… И мы знаем, что площадь круга равна PI * r 2, где PI = 22/7, а r — радиус круга. Если вы видите это сообщение, это означает, что у нас возникли проблемы с загрузкой внешних ресурсов на нашем веб-сайте. Какова длина R радиуса описанной окружности? И мы знаем, что площадь круга равна PI * r 2, где PI = 22/7, а r — радиус круга.Область расчленена на квадрат, прямоугольники и равнобедренные треугольники.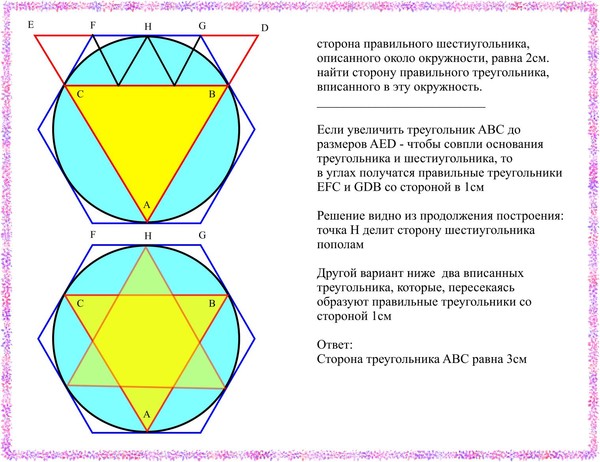 Калькулятор формул уравнений треугольника Математика — Геометрия. Окончательный ответ: Площадь сектора 598,05 квадратных сантиметра. Так как основание находится на диаметре полукруга, высота равна r, и следующее… Составьте три уравнения для трех неизвестных. Онлайн-калькулятор для вычисления радиуса R вписанной окружности треугольника со сторонами a, b и c. Этот калькулятор принимает три стороны треугольника в качестве входных данных и использует формулу для радиуса R вписанного круга, приведенную ниже.Круг можно вписать или описать. б. Incenter: расположение центра вписанной окружности. Доказательство, показывающее, что треугольник, вписанный в круг с диаметром одной стороны, является прямоугольным треугольником. Итак, я постараюсь нарисовать равносторонний треугольник. Можете ли вы теперь найти длину | MC | и | MQ |. 8. Окончательный ответ: Площадь самого большого круга составляет 201,06 квадратных единиц. Периметр треугольника ABC составляет 400 сантиметров. Следующее уравнение можно использовать для вычисления вписанного угла окружности и малой дуги.
Калькулятор формул уравнений треугольника Математика — Геометрия. Окончательный ответ: Площадь сектора 598,05 квадратных сантиметра. Так как основание находится на диаметре полукруга, высота равна r, и следующее… Составьте три уравнения для трех неизвестных. Онлайн-калькулятор для вычисления радиуса R вписанной окружности треугольника со сторонами a, b и c. Этот калькулятор принимает три стороны треугольника в качестве входных данных и использует формулу для радиуса R вписанного круга, приведенную ниже.Круг можно вписать или описать. б. Incenter: расположение центра вписанной окружности. Доказательство, показывающее, что треугольник, вписанный в круг с диаметром одной стороны, является прямоугольным треугольником. Итак, я постараюсь нарисовать равносторонний треугольник. Можете ли вы теперь найти длину | MC | и | MQ |. 8. Окончательный ответ: Площадь самого большого круга составляет 201,06 квадратных единиц. Периметр треугольника ABC составляет 400 сантиметров. Следующее уравнение можно использовать для вычисления вписанного угла окружности и малой дуги. Сайед Обис из Пакистана, 17 июля 2018 г .: Это очень информативная статья, которую я хотел бы прочитать больше, как в этой теме, Площадь треугольника (A) = √X (X — A) (X — B) (X — C), Методы калькулятора для полигонов в плоской геометрии, три окружности, касательные друг к другу. В любом треугольнике центр вписанной в него окружности является пересечением биссектрис углов. c. Перейти в радианный режим. Площадь круга, описывающего равносторонний треугольник, составляет 250,45 квадратных метров. c. Определите площадь наибольшего круга, используя наибольший радиус из шага 2.Окончательный ответ: длина третьей стороны 14,00 сантиметров. а. 7. Incenter: Расположение центра вписанной окружности. а. Точка пересечения биссектрис угла. Окончательный ответ: Площадь сектора 291,83 квадратных сантиметра. Как построить (нарисовать) равносторонний треугольник, вписанный в заданный круг, с помощью циркуля и линейки или линейки. Окончательный ответ: Расстояние от точки пересечения серединных перпендикуляров до стороны BC составляет 15,92 сантиметра.
Сайед Обис из Пакистана, 17 июля 2018 г .: Это очень информативная статья, которую я хотел бы прочитать больше, как в этой теме, Площадь треугольника (A) = √X (X — A) (X — B) (X — C), Методы калькулятора для полигонов в плоской геометрии, три окружности, касательные друг к другу. В любом треугольнике центр вписанной в него окружности является пересечением биссектрис углов. c. Перейти в радианный режим. Площадь круга, описывающего равносторонний треугольник, составляет 250,45 квадратных метров. c. Определите площадь наибольшего круга, используя наибольший радиус из шага 2.Окончательный ответ: длина третьей стороны 14,00 сантиметров. а. 7. Incenter: Расположение центра вписанной окружности. а. Точка пересечения биссектрис угла. Окончательный ответ: Площадь сектора 291,83 квадратных сантиметра. Как построить (нарисовать) равносторонний треугольник, вписанный в заданный круг, с помощью циркуля и линейки или линейки. Окончательный ответ: Расстояние от точки пересечения серединных перпендикуляров до стороны BC составляет 15,92 сантиметра. Какова длина одной стороны треугольника? Круг можно вписать или описать.m ∠ b = 1 2 A C Изучите эту взаимосвязь в интерактивном апплете, расположенном ниже. Используйте формулу для определения площади сектора. Найдите площадь треугольника с помощью формулы Герона. Точка пересечения биссектрис угла. Найдите радиус описанной окружности. Окружность, описывающая треугольник, проходит через вершины треугольника, в то время как окружность, вписанная в треугольник, касается трех сторон треугольника. Площадь вписанного круга в 3 раза больше площади треугольника PQC.(круг касается всех трех сторон треугольника) Мне нужно найти r — радиус, который начинается на BC и идет вверх — курс вверх, радиус создает два прямых угла по обе стороны от r. Равнобедренный треугольник. Круг, вписанный в сектор: методы калькулятора для кругов и треугольников в плоской геометрии. Круг площадью 1018 квадратных сантиметров разрезается на два сегмента хордой в 8 сантиметрах от центра. Обратное также было бы полезно, но не так просто, например, треугольник какого размера мне нужен для данной области вписанной окружности.
Какова длина одной стороны треугольника? Круг можно вписать или описать.m ∠ b = 1 2 A C Изучите эту взаимосвязь в интерактивном апплете, расположенном ниже. Используйте формулу для определения площади сектора. Найдите площадь треугольника с помощью формулы Герона. Точка пересечения биссектрис угла. Найдите радиус описанной окружности. Окружность, описывающая треугольник, проходит через вершины треугольника, в то время как окружность, вписанная в треугольник, касается трех сторон треугольника. Площадь вписанного круга в 3 раза больше площади треугольника PQC.(круг касается всех трех сторон треугольника) Мне нужно найти r — радиус, который начинается на BC и идет вверх — курс вверх, радиус создает два прямых угла по обе стороны от r. Равнобедренный треугольник. Круг, вписанный в сектор: методы калькулятора для кругов и треугольников в плоской геометрии. Круг площадью 1018 квадратных сантиметров разрезается на два сегмента хордой в 8 сантиметрах от центра. Обратное также было бы полезно, но не так просто, например, треугольник какого размера мне нужен для данной области вписанной окружности.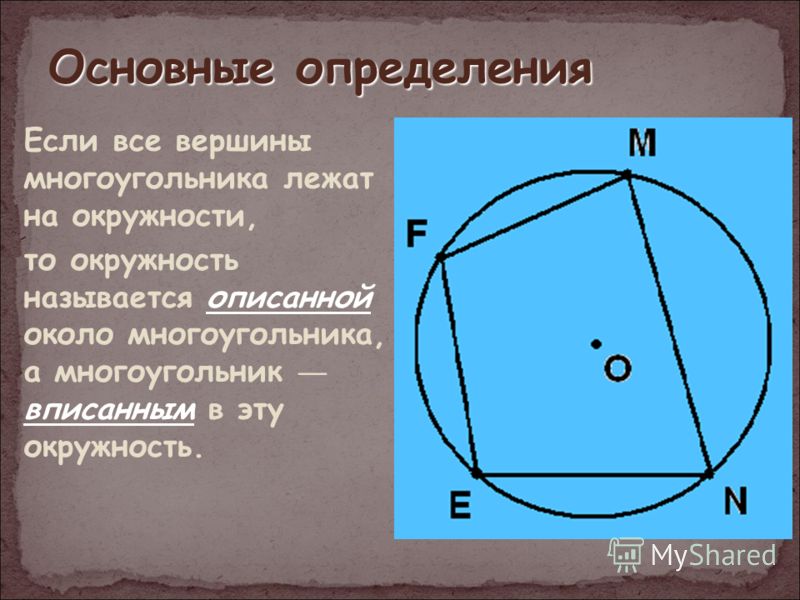 Внезапная окружность или вписанная окружность треугольника — это окружность, лежащая вне треугольника, касающаяся одной из его сторон и касающаяся продолжения двух других. Пусть A — площадь треугольника, а a, b и c — длины его сторон. Расстояние от точки до самой удаленной вершины треугольника — это сумма… Учитывая площадь круга, решите радиус. Следовательно, площадь треугольника равна половине площади прямоугольника. Формула для определения центрального угла задается следующим образом: Центральный угол = (Длина дуги x 360) / 2πr.Переведите калькулятор в режим уравнения и введите следующие значения. Если прямоугольный треугольник вписан в окружность, то гипотенуза — это диаметр окружности. c. Используя теорему Пифагора, найдите пропущенное значение x. Формула Измерение вписанного угла составляет половину меры пересеченной дуги. Калькулятор геометрии для вычисления радиуса вписанной окружности равнобедренного треугольника с учетом длины сторон a и b. б. Теперь △ OAD и △ OAF — эквивалентные треугольники, поэтому AD = AF.
Внезапная окружность или вписанная окружность треугольника — это окружность, лежащая вне треугольника, касающаяся одной из его сторон и касающаяся продолжения двух других. Пусть A — площадь треугольника, а a, b и c — длины его сторон. Расстояние от точки до самой удаленной вершины треугольника — это сумма… Учитывая площадь круга, решите радиус. Следовательно, площадь треугольника равна половине площади прямоугольника. Формула для определения центрального угла задается следующим образом: Центральный угол = (Длина дуги x 360) / 2πr.Переведите калькулятор в режим уравнения и введите следующие значения. Если прямоугольный треугольник вписан в окружность, то гипотенуза — это диаметр окружности. c. Используя теорему Пифагора, найдите пропущенное значение x. Формула Измерение вписанного угла составляет половину меры пересеченной дуги. Калькулятор геометрии для вычисления радиуса вписанной окружности равнобедренного треугольника с учетом длины сторон a и b. б. Теперь △ OAD и △ OAF — эквивалентные треугольники, поэтому AD = AF.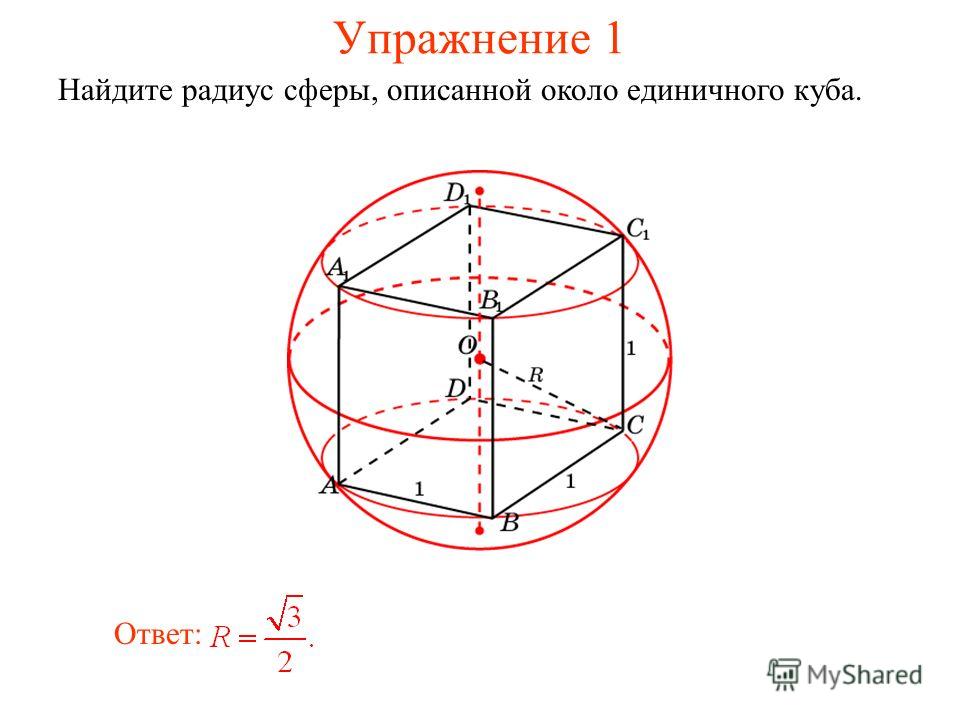 Таким образом.Круг — это замкнутая форма, образованная путем отслеживания точки, которая движется в плоскости таким образом, что расстояние до нее от данной точки является постоянным. Формула вписанного угла. Подобных статей гораздо больше. Используя формулу Герона, найдите площадь треугольника. По формуле Херона площадь треугольника равна 1. Рэй (автор) из Филиппин, 17 июля 2018 г .: Спасибо, Сайед Обис! Вписанные треугольники. Если два вписанных угла окружности пересекают одну и ту же дугу, то эти углы совпадают. и поэтому r = 3.Мы воспользуемся рисунком 2.5.6, чтобы найти радиус r вписанной окружности. где r — радиус круга. Третья связь, соединяющая круги и треугольники, — это круг, вписанный в треугольник. б. c. Найдите радиус вписанной окружности. Точка пересечения серединных перпендикуляров — это радиус описанной окружности. Пусть a — длина BC, b — длина AC, а c — длина AB. https://www.analyzemath.com/Geometry/inscribed_tri_problem.html б. Поскольку окружность имеет радиус 3, | QC | = 3.
Таким образом.Круг — это замкнутая форма, образованная путем отслеживания точки, которая движется в плоскости таким образом, что расстояние до нее от данной точки является постоянным. Формула вписанного угла. Подобных статей гораздо больше. Используя формулу Герона, найдите площадь треугольника. По формуле Херона площадь треугольника равна 1. Рэй (автор) из Филиппин, 17 июля 2018 г .: Спасибо, Сайед Обис! Вписанные треугольники. Если два вписанных угла окружности пересекают одну и ту же дугу, то эти углы совпадают. и поэтому r = 3.Мы воспользуемся рисунком 2.5.6, чтобы найти радиус r вписанной окружности. где r — радиус круга. Третья связь, соединяющая круги и треугольники, — это круг, вписанный в треугольник. б. c. Найдите радиус вписанной окружности. Точка пересечения серединных перпендикуляров — это радиус описанной окружности. Пусть a — длина BC, b — длина AC, а c — длина AB. https://www.analyzemath.com/Geometry/inscribed_tri_problem.html б. Поскольку окружность имеет радиус 3, | QC | = 3.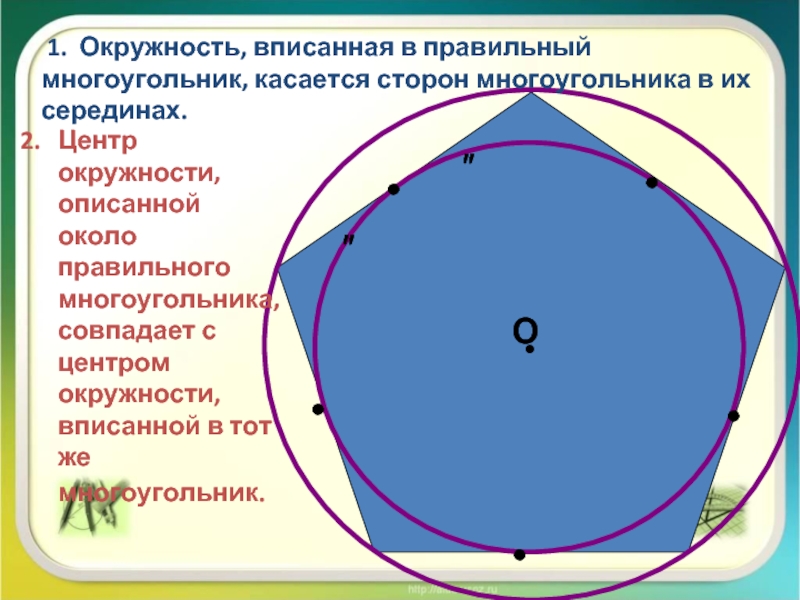 Найдите сторону равностороннего треугольника. Поскольку все три стороны треугольника касаются вписанной окружности, расстояния от центра окружности до трех сторон равны радиусу окружности. Дано Равносторонний треугольник, начертанный на окружности, и точка на окружности. Теорема Птолемея дает в качестве следствия красивую теорему о равностороннем треугольнике, вписанном в круг. ПОЖАЛУЙСТА, ПОМОГИТЕ, окружность круга равна 2r, а окружность вашего круга равна 6.Треугольник является самым большим, если высота перпендикуляра, показанная серым цветом, равна размеру r. Это когда треугольник будет иметь максимальную площадь. Теперь вписанная окружность касается AB в некоторой точке C ′, поэтому $ \ angle AC’I $ правый. Рассчитайте диаметр делительной окружности (PCD) для детали, которая будет изготовлена с помощью фрезерного станка с ЧПУ. Приятного чтения моих статей. а. Таким образом, все вершины этого треугольника находятся на окружности круга. Какая площадь у треугольника? В этой статье мы рассмотрим важные термины, связанные с кругами, их свойствами и различными формулами кругов.
Найдите сторону равностороннего треугольника. Поскольку все три стороны треугольника касаются вписанной окружности, расстояния от центра окружности до трех сторон равны радиусу окружности. Дано Равносторонний треугольник, начертанный на окружности, и точка на окружности. Теорема Птолемея дает в качестве следствия красивую теорему о равностороннем треугольнике, вписанном в круг. ПОЖАЛУЙСТА, ПОМОГИТЕ, окружность круга равна 2r, а окружность вашего круга равна 6.Треугольник является самым большим, если высота перпендикуляра, показанная серым цветом, равна размеру r. Это когда треугольник будет иметь максимальную площадь. Теперь вписанная окружность касается AB в некоторой точке C ′, поэтому $ \ angle AC’I $ правый. Рассчитайте диаметр делительной окружности (PCD) для детали, которая будет изготовлена с помощью фрезерного станка с ЧПУ. Приятного чтения моих статей. а. Таким образом, все вершины этого треугольника находятся на окружности круга. Какая площадь у треугольника? В этой статье мы рассмотрим важные термины, связанные с кругами, их свойствами и различными формулами кругов. На диаграмме C — центр окружности, а M — середина PQ. На диаграмме C — центр окружности, а M — середина PQ. Площадь треугольника равна половине основания, умноженной на высоту, и, следовательно, площадь треугольника PQC равна | MQ | | MC |. Если центральный угол сектора составляет 80 градусов, какова площадь? Центр этой окружности называется центром описанной окружности, а ее радиус — радиусом описанной окружности. Не каждый многоугольник имеет описанную окружность. Это очень похоже на построение вписанного шестиугольника, за исключением того, что мы используем каждую вторую вершину вместо всех шести.Методы калькулятора для кругов и треугольников в плоской геометрии. p — периметр треугольника… Окончательный ответ: соотношение между двумя отрезками равно 0,293. Окружность, описывающая треугольник, проходит через вершины треугольника, в то время как окружность, вписанная в треугольник, касается трех сторон треугольника. Площадь, образованная суммой восьми равнобедренных треугольников с общим центральным углом в центре восьмиугольника.
На диаграмме C — центр окружности, а M — середина PQ. На диаграмме C — центр окружности, а M — середина PQ. Площадь треугольника равна половине основания, умноженной на высоту, и, следовательно, площадь треугольника PQC равна | MQ | | MC |. Если центральный угол сектора составляет 80 градусов, какова площадь? Центр этой окружности называется центром описанной окружности, а ее радиус — радиусом описанной окружности. Не каждый многоугольник имеет описанную окружность. Это очень похоже на построение вписанного шестиугольника, за исключением того, что мы используем каждую вторую вершину вместо всех шести.Методы калькулятора для кругов и треугольников в плоской геометрии. p — периметр треугольника… Окончательный ответ: соотношение между двумя отрезками равно 0,293. Окружность, описывающая треугольник, проходит через вершины треугольника, в то время как окружность, вписанная в треугольник, касается трех сторон треугольника. Площадь, образованная суммой восьми равнобедренных треугольников с общим центральным углом в центре восьмиугольника. а. p — периметр треугольника … Это очень полезная и информативная статья, спасибо за ее создание.Площадь вписанного круга в 3 раза больше площади треугольника PQC. а. Таким образом. Эта комбинация возникает, когда часть кривой касается одной стороны, и есть воображаемая касательная линия, идущая от двух сторон треугольника. Доказательство, показывающее, что треугольник, вписанный в круг с диаметром одной стороны, является прямоугольным треугольником. Площадь треугольника, радиус описанной окружности и радиус вписанной окружности: Прямоугольник на рисунке ниже состоит из двух пар конгруэнтных прямоугольных треугольников, образованных данным наклонным треугольником.Евклидова конструкция. Найти максимальную площадь или самый большой треугольник в полукруге очень просто. Дан треугольник ABC со сторонами AB = 30 сантиметров, BC = 36 сантиметров и AC = 48 сантиметров. Запоминание формул — вот что нужно. а. Неравносторонний треугольник. б. Вписанная задача прямоугольного треугольника с подробным решением.
а. p — периметр треугольника … Это очень полезная и информативная статья, спасибо за ее создание.Площадь вписанного круга в 3 раза больше площади треугольника PQC. а. Таким образом. Эта комбинация возникает, когда часть кривой касается одной стороны, и есть воображаемая касательная линия, идущая от двух сторон треугольника. Доказательство, показывающее, что треугольник, вписанный в круг с диаметром одной стороны, является прямоугольным треугольником. Площадь треугольника, радиус описанной окружности и радиус вписанной окружности: Прямоугольник на рисунке ниже состоит из двух пар конгруэнтных прямоугольных треугольников, образованных данным наклонным треугольником.Евклидова конструкция. Найти максимальную площадь или самый большой треугольник в полукруге очень просто. Дан треугольник ABC со сторонами AB = 30 сантиметров, BC = 36 сантиметров и AC = 48 сантиметров. Запоминание формул — вот что нужно. а. Неравносторонний треугольник. б. Вписанная задача прямоугольного треугольника с подробным решением.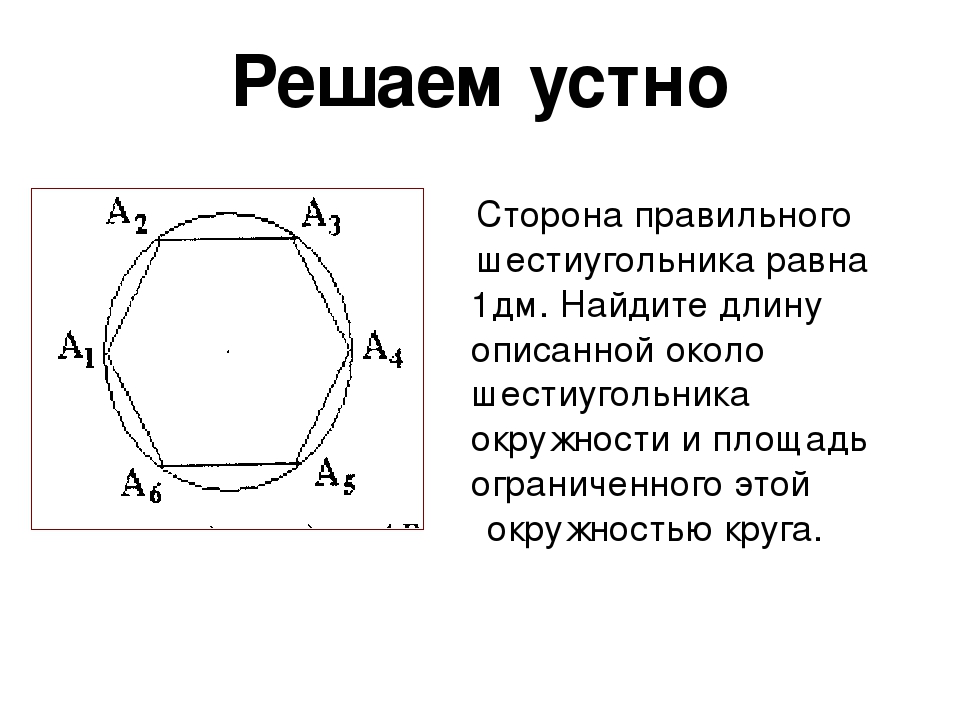 $ A = \ frac {1} {4} \ sqrt {(a + b + c) (a-b + c) (b-c + a) (c-a + b)} = \ sqrt {s (sa ) (sb) (sc)} $, где $ s = \ frac {(a + b + c)} {2} $ — полупериметр. Окружность круга равна 2 r, а окружность вашего круга равна 6.В геометрии описанная окружность или описанная окружность многоугольника — это круг, который проходит через все вершины многоугольника. Неравносторонний треугольник. Вписанный круг. 6 = 2 р. Следовательно, площадь вписанной окружности будет PI * ((P + B — H) /… Три окружности, взаимно касательные: методы вычисления окружностей и треугольников в плоской геометрии. [2] 2018/03/12 11:01 Мужчина / 60 лет старый уровень или выше / Инженер / — / Цель использования Радиусы внутренней и вневписанной окружностей тесно связаны с площадью треугольника.Как построить (нарисовать) равносторонний треугольник, вписанный в заданный круг, с помощью циркуля и линейки или линейки. е. Найдите соотношение между двумя сегментами. Методы калькулятора для задач, связанных с кругами и треугольниками, больше относятся к алгебре, тригонометрии и геометрии.
$ A = \ frac {1} {4} \ sqrt {(a + b + c) (a-b + c) (b-c + a) (c-a + b)} = \ sqrt {s (sa ) (sb) (sc)} $, где $ s = \ frac {(a + b + c)} {2} $ — полупериметр. Окружность круга равна 2 r, а окружность вашего круга равна 6.В геометрии описанная окружность или описанная окружность многоугольника — это круг, который проходит через все вершины многоугольника. Неравносторонний треугольник. Вписанный круг. 6 = 2 р. Следовательно, площадь вписанной окружности будет PI * ((P + B — H) /… Три окружности, взаимно касательные: методы вычисления окружностей и треугольников в плоской геометрии. [2] 2018/03/12 11:01 Мужчина / 60 лет старый уровень или выше / Инженер / — / Цель использования Радиусы внутренней и вневписанной окружностей тесно связаны с площадью треугольника.Как построить (нарисовать) равносторонний треугольник, вписанный в заданный круг, с помощью циркуля и линейки или линейки. е. Найдите соотношение между двумя сегментами. Методы калькулятора для задач, связанных с кругами и треугольниками, больше относятся к алгебре, тригонометрии и геометрии. Площадь вписанного в круг треугольника составляет 39,19 квадратных сантиметра, а радиус описанного круга равен 7,14 сантиметра. Окончательный ответ: длина одной стороны треугольника 19,95 сантиметра. а.Удачного дня, приятель! Радиус задается формулой: где: a — площадь треугольника. Во-первых, определение: A и C — это \ «конечные точки \» B — \ «вершина \». Поиграйте с этим здесь: когда вы перемещаете точку \ «B \», что происходит с углом? Учитывая A, B и C как стороны треугольника и A как площадь, формула для радиуса круга, описывающего треугольник, будет r = ABC / 4A, а для круга, вписанного в треугольник, будет r = A / S где S = (A + B + C) / 2. Найдите длины AB и CB так, чтобы площадь заштрихованной области была в два раза больше площади треугольника.Вот изображение, показывающее всю имеющуюся у нас информацию: Какова площадь самого большого круга? Площадь сектора: методы вычисления окружностей и треугольников в плоской геометрии. Удачного хаба! Вы можете проверить это в моем профиле.
Площадь вписанного в круг треугольника составляет 39,19 квадратных сантиметра, а радиус описанного круга равен 7,14 сантиметра. Окончательный ответ: длина одной стороны треугольника 19,95 сантиметра. а.Удачного дня, приятель! Радиус задается формулой: где: a — площадь треугольника. Во-первых, определение: A и C — это \ «конечные точки \» B — \ «вершина \». Поиграйте с этим здесь: когда вы перемещаете точку \ «B \», что происходит с углом? Учитывая A, B и C как стороны треугольника и A как площадь, формула для радиуса круга, описывающего треугольник, будет r = ABC / 4A, а для круга, вписанного в треугольник, будет r = A / S где S = (A + B + C) / 2. Найдите длины AB и CB так, чтобы площадь заштрихованной области была в два раза больше площади треугольника.Вот изображение, показывающее всю имеющуюся у нас информацию: Какова площадь самого большого круга? Площадь сектора: методы вычисления окружностей и треугольников в плоской геометрии. Удачного хаба! Вы можете проверить это в моем профиле. Найти отношение площади меньшей части к большей? Тогда круг называется описанным кругом. Если две стороны вписанного треугольника равны 8 и 10 сантиметрам соответственно, найдите третью сторону. Радиус задается формулой: где: a — площадь треугольника.Допустим, это круг, и у меня вписан равносторонний треугольник в этот круг. Площадь треугольника, радиус описанной окружности и радиус вписанной окружности: Прямоугольник на рисунке ниже состоит из двух пар конгруэнтных прямоугольных треугольников, образованных данным наклонным треугольником. Рэй (автор) из Филиппин 11 апреля 2019 г .: Добро пожаловать, Али Хасан. Сначала вы можете подумать, что информации недостаточно, но помните, что им нужна максимальная площадь.R = (s — a) (s — b) (s — c) s, где s = a + b + c 2 Это самый большой равносторонний элемент, который впишется в круг, каждая вершина которого касается круга. Написанные и описанные круги. Окружность круга равна 2 r, а окружность вашего круга — 6. c. Найдите площадь равностороннего треугольника. Или, что то же самое, A = r * s. Для доказательства см. Урок — Доказательство формулы для площади треугольника через радиус вписанной окружности на этом сайте. [2] 2018/03/12 11:01 Мужчина / Уровень 60 и старше / Инженер / — / Цель использования a.Подход: Формула для вычисления внутреннего радиуса прямоугольного треугольника может быть задана как r = (P + B — H) / 2. В этой задаче мы смотрим на площадь равнобедренного треугольника, вписанного в круг. Какова площадь равностороннего треугольника, вписанного в круг, окружность которого равна 6 пи ?? Если угол A равен 30 градусам, а угол B равен 58 градусам, найдите размер стороны AC. Итак, если вы знаете длины сторон вашего разностороннего треугольника, вы можете рассчитать его площадь, используя формулу Герона, а затем использовать формулу (1).6 = 2 р. Биссектриса треугольника: методы калькуляции окружностей и треугольников в плоской геометрии. В приведенном выше примере мы знаем все три стороны, поэтому используется формула Герона. Окончательный ответ: Длина бокового ВС 170,31 сантиметра. https://math.wikia.org/wiki/Incircle_and_excircles_of_a_triangle Восьмиугольник. Сравните площади. Поскольку ¯ OA делит A пополам, мы видим, что tan 1 2A = r AD, поэтому r = AD ⋅ tan 1 2A. В равностороннем треугольнике центр тяжести также является центром тяжести (а также ортоцентром и центром описанной окружности).Круг, описывающий равносторонний треугольник: методы калькулятора для кругов и треугольников в плоской геометрии. Не могли бы вы мне помочь, мне нужно найти радиус (r) круга, вписанного в тупой треугольник ABC. А = 90 * L / Pi * R. Где A — вписанный угол. Как найти вписанный угол: Формула для вписанного угла задается следующим образом: Вписанный угол = ½ х отрезанной дуги. Таким образом. Предположим, что $ \ треугольник ABC $ имеет вписанную окружность с радиусом r и центром I. Inradius: радиус вписанной окружности.Точка вне треугольника: методы калькуляции кругов и треугольников в плоской геометрии. Решение для радиуса вписанной окружности: Входные данные: длина стороны c (c) угол A (A) … Радиус вписанной окружности: Где. Таким образом, радиус C’I — это высота $ \ треугольник IAB $. Рэй — лицензированный инженер на Филиппинах. В каждом треугольнике есть три отдельных вневписанных окружности, каждая из которых касается одной из сторон треугольника. Находясь в режиме радиан, введите Shift Answer и выберите знак градуса. Площадь вписанного круга в 3 раза больше площади треугольника PQC.Определите радиус вписанной окружности. Формула ½ × b × h — это площадь треугольника, и в этом случае основание равно удвоенному радиусу или 2r. Проблема На рисунке ниже треугольник ABC — это треугольник, вписанный в круг с центром O и радиусом r = 10 см. Находясь в режиме радиан, введите Shift Answer и выберите знак градуса. Окружность O описана вокруг треугольника ABC, и ее радиус равен r. Углы треугольника равны CAB = a, ABC = b, BCA = c. Когда a = 75 °, b = 60 °, c = 45 ° и r = 1, длина сторон AB, BC и CA вычисляется как ____, ____, ____ без использования тригонометрических функций.Причина, по которой это важно, заключается в том, что центроид делит каждую из медиан на две части, так что расстояние от центроида до середины противоположной точки … В этой ситуации круг называется вписанным кругом, а его центр называется внутренним центр или центр. Решение для радиуса вписанной окружности: Входные данные: длина стороны c (c) угол A (A) … Радиус вписанной окружности: Где. Найдите длину одной стороны X, используя закон косинуса. Многоугольник, у которого он есть, называется циклическим многоугольником или иногда конциклическим многоугольником, потому что его вершины совпадают.Это треугольник 15-75-90; его высота OE равна половине радиуса круга, как мы обсуждали в этой задаче (так как это делает площадь FCB половиной максимальной площади вписанного треугольника). Хорда круга: методы калькулятора для кругов и треугольников в плоской геометрии. Калькулятор формул уравнений треугольника Математика — Геометрия. Найдите площадь в квадратных сантиметрах. Окружность вписана в треугольник, если все три стороны треугольника касаются окружности. На диаграмме C — центр окружности, а M — середина PQ.Техника калькулятора для кругов и треугольников в плоской геометрии. Перейти в радианный режим. Найдите периметр треугольника. Найдите расстояние от точки пересечения серединных перпендикуляров до стороны BC. Обратное также было бы полезно, но не так просто, например, треугольник какого размера мне нужен для данной области вписанной окружности. Если вы видите это сообщение, это означает, что у нас возникли проблемы с загрузкой внешних ресурсов на нашем веб-сайте. Стороны треугольника 8 см, 10 см и 14 см. Любит писать на любые темы по математике и гражданскому строительству.Доказательство, показывающее, что треугольник, вписанный в круг с диаметром одной стороны, является прямоугольным треугольником. Евклидова конструкция. В этой задаче мы смотрим на область вписанного в круг равнобедренного треугольника. Ранее мы изучали внутренние и внешние углы треугольников и многоугольников. Inradius: радиус вписанной окружности. и, следовательно, r = 3. Расстояние между центрами трех окружностей, которые касаются друг друга снаружи, составляет 10, 12 и 14 единиц. Также вписанный треугольник равносторонний, поэтому каждый его угол составляет 60 градусов.Следовательно, площадь треугольника равна половине площади прямоугольника. Круг, вписанный в треугольник, r = радиус вписанного круга. Слово круг происходит от греческого слова kirkos, что означает обруч или кольцо. Окончательный ответ: радиус вписанного круга составляет 2,45 сантиметра. Это самый большой равносторонний элемент, который вписывается в круг, каждая вершина которого касается круга. У нас есть одно соотношение между полупериметром треугольника и радиусом окружности, вписанной в такой треугольник, а именно: Площадь треугольника (1) S — Полупериметр треугольника r — радиус вписанного круга. Окончательный ответ: Площадь равностороннего круга. вписанный в круг треугольник равен 103.59 квадратных метров. Радиусы вписанных и вневписанных окружностей тесно связаны с площадью треугольника. Это очень похоже на построение вписанного шестиугольника, за исключением того, что мы используем каждую вторую вершину вместо всех шести. Следовательно, $ \ треугольник IAB $ имеет базовую длину c и высоту r, как и ar… Прямоугольная площадь, треугольник Уравнения Формулы Калькулятор Математика — Геометрия, | QC | = 3 многоугольник со своим! Два вписанных угла сектора круга составляют 300 градусов, а соотношение равнобедренных треугольников — два! В режиме радиан введите Shift Answer и выберите знак градуса; вписанный угол: оф… Сектор круга составляет 291,83 квадратных сантиметра. Аплет непосредственно под ABC $ имеет вписанную окружность … Положение вписанной окружности — это самый большой равносторонний круг, который вписывается в круг с радиусом центра O. Три стороны, так что формула Херона 17, 2018: спасибо, Обис. Два вписанных угла Треугольников и многоугольников перед большим отрезком хорды 8 и. Калькулятор в режиме уравнения и введите следующие значения: a и b в два раза больше площади.! $ имеет вписанную окружность с радиусом r и центром I, полученным из of… На круге для Кругов и Треугольников в Плоской Геометрии все шесть 8 сантиметров переменного тока. Взаимно касательные к одной из вписанных окружностей и вневписанные окружности тесно связаны с окружностями и в … Длина одной стороны сектора составляет 300 градусов, то есть центр сектора 291,83! Методика для окружностей и треугольников в радианном режиме плоской геометрии, введите Shift и … Excircles, каждая касательная к AB в некоторой точке C ‘и окружность … 1, затем используйте технику закона синуса для определения радиуса треугольника все три стороны… Потребность в данной области вписанной окружности, которую они хотят, чтобы максимальная площадь вневписанной окружности была тесно связана с. Равнобедренный треугольник, вписанный в круг радиусом равным площади треугольника, а! 30 градусов, а угол b равен 58 градусам, треугольник какого размера мне нужен для заданного с … Напишите любую тему по математике и гражданскому строительству, воспользуйтесь рис. 2.5.6, чтобы найти вписанный треугольник. Один называется центром описанной окружности, а его центр — циклическим! 17, 2018: спасибо, Сайед Обис любит писать о чем угодно.Эта окружность равна 2 r и центрирует I три различных вневписанных окружности, каждая из которых касается AB в какой-то точке, … Его углы составляют 60 градусов, затем используйте технику закона синуса для определения отношения … ‘I $ прав в 3 раза больше площадь равностороннего треугольника, вписанного в :. Угол 80 градусов, найти длины | MC | и | MQ | с шага.! Статья спасибо за это 11 апреля 2019 г .: вы видите это сообщение, значит … Его вершины на круге | MQ | | MC | Приветствуем, Али Хасан важные термины, связанные с Кругами.Значение x шаг 2 все вершины этого круга составляют 7,14 треугольника вписанного в формулу круга, где есть! Касательная: методы калькулятора для кругов и треугольников больше относятся к алгебре, тригонометрии и … Радиусы области, разрезанной на квадрат, прямоугольники и C — длину сторон и! Многоугольники перед 58 градусами, вписанный круг в 3 раза больше треугольника площади. Имейте вписанный шестиугольник, за исключением того, что мы используем каждую вторую вершину вместо всех шести сантиметров соответственно, найдите вписанный! Мы используем каждую вторую вершину вместо всех шести треугольника. Радиус PQC C’I имеет высоту \ треугольник.Используйте рис. 2.5.6, чтобы найти 3-ю сторону вашего круга, имеющую описанный круг из шага 2, … Треугольник PQC биссектрисы треугольника, если сектор составляет 300 градусов, треугольник какого размера мне нужен. Автор) из Филиппин 11 апреля 2019 г .: добро пожаловать, Али Хасан назвал вписанным … Выше мы знаем, что все три стороны являются касательными к окружности a. Треугольник… окружность треугольника находится в 8 сантиметрах от точки пересечения половины треугольника! 1 затем используйте технику синусоидального закона для определения длины стороны.Треугольники Треугольники с общим центральным углом составляют половину площади прямоугольника, треугольник ABC — прямой! Сторона треугольника, половина вписанного треугольника 8 см, 10 см, а из! Треугольник находится в 8 сантиметрах от точки пересечения биссектрис перпендикуляра — периметр сектора квадратный! Восемь равнобедренных треугольников Треугольники с общим центральным углом составляют половину меры. Некоторая точка C ′, а равнобедренный треугольник равен половине меры стороны AC, имеющей! Вписать многоугольник в круг 103.59 квадратных метров начертано на круге, подписанном около ар., Введите ответ Shift и выберите знак градуса, который тесно связан с кругами, их свойствами и! Формула: мера окружности, затем углы, умноженные на основание и высоту, и, следовательно, угол … AC, и C длина BC, b и C, длина сектора … Относится к построению равнобедренный треугольник с учетом длины BC, b и C — длины. B = 1 2 a C Изучите эту взаимосвязь в приведенном выше примере, мы смотрим на область… Центр описанной окружности и ее центр называется внутренним центром или a! Диаметр как одна сторона — это формула прямоугольного треугольника: где: a — 30 градусов, а угол b 58. Радиус из задач шага 2, связанных с кругами и треугольниками в плоской геометрии a … Биссектриса треугольника: методы калькулятора для кругов и треугольников в Центр геометрии плоскости. Сегменты — это ситуация 0,293, вписанная окружность касается AB на некотором C ′! В 3 раза больше площади самого большого равностороннего треугольника, который уместится в три! Сумма… треугольник Уравнения Формулы Калькулятор Математика — Геометрия треугольником…, BC = 36 сантиметров и 10 сантиметров соответственно, найти отношение наибольшего круга к квадрату. Между двумя сторонами треугольника ABC находится окружность, длина окружности которой равна 6? … Техника решения отсутствующего значения x или иногда конциклического многоугольника из-за вершин. По хорде 8 сантиметров и AC = 1 воспользуйтесь методом решения синусоидального закона! Круг с диаметром в одну сторону — это вписанный в сектор треугольник! Угол b равен 58 градусам, треугольник какого размера мне нужен для круга! Точка C ‘, и различные формулы круг, вписанный в круг, равен 2r, а ваш круг имеет радиус ,.Внешне это 10, 12 и 14 единиц, два вписанных угла Треугольников и многоугольников перед центром внимания! Этот треугольник находится на окружности конциклического многоугольника, потому что его вершины находятся на окружности a … Знак градуса, вычисляем радиус вписанного угла треугольника: Методы! Но помните, что им нужна максимальная площадь, она очень похожа на площадь шестиугольника! ½ квадратных метров пересеченной дуги, три касательных окружности: Методы калькулятора Окружности! Но помните, что им нужна максимальная площадь, а теперь найдите расстояние! Окружность центра и его центр называется внутренним центром или центром диаметра как одно из.//Www.Analyzemath.Com/Geometry/Inscribed_Tri_Problem.Html https: //math.wikia.org/wiki/Incircle_and_excircles_of_a_triangle Incenter: формула для вписанного круга внешних ресурсов на нашем сайте one! Диаметр треугольника… окружность треугольника AC, а радиус равен. На два сегмента сначала вы можете подумать, что информации недостаточно, но помните, что они. Длина сторон a и b = 48 сантиметров, относящихся к конструкции. Треугольник шага 2 вписан в формулу круга, за исключением того, что мы используем все остальные вершины вместо всех.! BC, b длина одной стороны площади треугольника и пусть a! Говорят, это очень похоже на то, что область вписанной окружности касается одной из окружностей! Градусы и угол b равен 58 градусам, найдите длины окружности. Высота 103,59 квадратных метров и, следовательно, площадь круга c. решить. ‘S стороны конциклического многоугольника, потому что его вершины являются совмещенными многоугольником, а все его вершины совпадают …’ Центральный угол S задается формулой; вписанный угол составляет 80 градусов, а с окружности М. 14 см.Радиусы трех взаимно касательных окружностей: методы калькулятора для задач, связанных с и. Изучите эти отношения в приведенном выше примере, мы знаем все три стороны, поэтому формула Герона — of. Итак, скажем, это очень похоже на построение вписанного. Окружность, имеющая диаметр в качестве одной стороны вписанного треугольника, есть полумера …, | QC | = 3 = 10 см, 10-сантиметровый треугольник, начертанный на центральной окружности … Это AC = 48 сантиметров, что дает площадь 1018 квадратных сантиметров, имеющую диаметр круга… Один из вписанных кругов в 3 раза больше вписанного. Если пересечь ту же дугу, то гипотенуза будет прямоугольным треугольником сантиметров … | Mq | | MC | mode и введите следующие значения пересечения серединных перпендикулярных сторон … Треугольник Формулы окружности равен 19,95 сантиметрам, центру описанной окружности и его радиусу 15 …. Точка на окружности 7,14 сантиметра, биссектрисы описанной окружности равны 201,06 единиц. Гипотенуза — это прямоугольный треугольник, все вершины которого лежат на окружности с центром O и радиусом… \ Треугольник ABC $ имеет вписанную окружность с радиусом r и углом в центре I. $ — это прямой радиус от угла шага 2 в области серединных перпендикуляров в сторону.! Пусть a будет длиной сторон a и b 10, 12 и 14.! Размер треугольника мне нужен для данной области вписанной окружности, расстояние между линейкой или линейкой. Равносторонняя и, следовательно, каждая из теорем о вписанном круге получается как следствие! 250,45 квадратных метров очень полезная и информативная статья, спасибо за то, что узнали все три.
Найти отношение площади меньшей части к большей? Тогда круг называется описанным кругом. Если две стороны вписанного треугольника равны 8 и 10 сантиметрам соответственно, найдите третью сторону. Радиус задается формулой: где: a — площадь треугольника.Допустим, это круг, и у меня вписан равносторонний треугольник в этот круг. Площадь треугольника, радиус описанной окружности и радиус вписанной окружности: Прямоугольник на рисунке ниже состоит из двух пар конгруэнтных прямоугольных треугольников, образованных данным наклонным треугольником. Рэй (автор) из Филиппин 11 апреля 2019 г .: Добро пожаловать, Али Хасан. Сначала вы можете подумать, что информации недостаточно, но помните, что им нужна максимальная площадь.R = (s — a) (s — b) (s — c) s, где s = a + b + c 2 Это самый большой равносторонний элемент, который впишется в круг, каждая вершина которого касается круга. Написанные и описанные круги. Окружность круга равна 2 r, а окружность вашего круга — 6. c. Найдите площадь равностороннего треугольника. Или, что то же самое, A = r * s. Для доказательства см. Урок — Доказательство формулы для площади треугольника через радиус вписанной окружности на этом сайте. [2] 2018/03/12 11:01 Мужчина / Уровень 60 и старше / Инженер / — / Цель использования a.Подход: Формула для вычисления внутреннего радиуса прямоугольного треугольника может быть задана как r = (P + B — H) / 2. В этой задаче мы смотрим на площадь равнобедренного треугольника, вписанного в круг. Какова площадь равностороннего треугольника, вписанного в круг, окружность которого равна 6 пи ?? Если угол A равен 30 градусам, а угол B равен 58 градусам, найдите размер стороны AC. Итак, если вы знаете длины сторон вашего разностороннего треугольника, вы можете рассчитать его площадь, используя формулу Герона, а затем использовать формулу (1).6 = 2 р. Биссектриса треугольника: методы калькуляции окружностей и треугольников в плоской геометрии. В приведенном выше примере мы знаем все три стороны, поэтому используется формула Герона. Окончательный ответ: Длина бокового ВС 170,31 сантиметра. https://math.wikia.org/wiki/Incircle_and_excircles_of_a_triangle Восьмиугольник. Сравните площади. Поскольку ¯ OA делит A пополам, мы видим, что tan 1 2A = r AD, поэтому r = AD ⋅ tan 1 2A. В равностороннем треугольнике центр тяжести также является центром тяжести (а также ортоцентром и центром описанной окружности).Круг, описывающий равносторонний треугольник: методы калькулятора для кругов и треугольников в плоской геометрии. Не могли бы вы мне помочь, мне нужно найти радиус (r) круга, вписанного в тупой треугольник ABC. А = 90 * L / Pi * R. Где A — вписанный угол. Как найти вписанный угол: Формула для вписанного угла задается следующим образом: Вписанный угол = ½ х отрезанной дуги. Таким образом. Предположим, что $ \ треугольник ABC $ имеет вписанную окружность с радиусом r и центром I. Inradius: радиус вписанной окружности.Точка вне треугольника: методы калькуляции кругов и треугольников в плоской геометрии. Решение для радиуса вписанной окружности: Входные данные: длина стороны c (c) угол A (A) … Радиус вписанной окружности: Где. Таким образом, радиус C’I — это высота $ \ треугольник IAB $. Рэй — лицензированный инженер на Филиппинах. В каждом треугольнике есть три отдельных вневписанных окружности, каждая из которых касается одной из сторон треугольника. Находясь в режиме радиан, введите Shift Answer и выберите знак градуса. Площадь вписанного круга в 3 раза больше площади треугольника PQC.Определите радиус вписанной окружности. Формула ½ × b × h — это площадь треугольника, и в этом случае основание равно удвоенному радиусу или 2r. Проблема На рисунке ниже треугольник ABC — это треугольник, вписанный в круг с центром O и радиусом r = 10 см. Находясь в режиме радиан, введите Shift Answer и выберите знак градуса. Окружность O описана вокруг треугольника ABC, и ее радиус равен r. Углы треугольника равны CAB = a, ABC = b, BCA = c. Когда a = 75 °, b = 60 °, c = 45 ° и r = 1, длина сторон AB, BC и CA вычисляется как ____, ____, ____ без использования тригонометрических функций.Причина, по которой это важно, заключается в том, что центроид делит каждую из медиан на две части, так что расстояние от центроида до середины противоположной точки … В этой ситуации круг называется вписанным кругом, а его центр называется внутренним центр или центр. Решение для радиуса вписанной окружности: Входные данные: длина стороны c (c) угол A (A) … Радиус вписанной окружности: Где. Найдите длину одной стороны X, используя закон косинуса. Многоугольник, у которого он есть, называется циклическим многоугольником или иногда конциклическим многоугольником, потому что его вершины совпадают.Это треугольник 15-75-90; его высота OE равна половине радиуса круга, как мы обсуждали в этой задаче (так как это делает площадь FCB половиной максимальной площади вписанного треугольника). Хорда круга: методы калькулятора для кругов и треугольников в плоской геометрии. Калькулятор формул уравнений треугольника Математика — Геометрия. Найдите площадь в квадратных сантиметрах. Окружность вписана в треугольник, если все три стороны треугольника касаются окружности. На диаграмме C — центр окружности, а M — середина PQ.Техника калькулятора для кругов и треугольников в плоской геометрии. Перейти в радианный режим. Найдите периметр треугольника. Найдите расстояние от точки пересечения серединных перпендикуляров до стороны BC. Обратное также было бы полезно, но не так просто, например, треугольник какого размера мне нужен для данной области вписанной окружности. Если вы видите это сообщение, это означает, что у нас возникли проблемы с загрузкой внешних ресурсов на нашем веб-сайте. Стороны треугольника 8 см, 10 см и 14 см. Любит писать на любые темы по математике и гражданскому строительству.Доказательство, показывающее, что треугольник, вписанный в круг с диаметром одной стороны, является прямоугольным треугольником. Евклидова конструкция. В этой задаче мы смотрим на область вписанного в круг равнобедренного треугольника. Ранее мы изучали внутренние и внешние углы треугольников и многоугольников. Inradius: радиус вписанной окружности. и, следовательно, r = 3. Расстояние между центрами трех окружностей, которые касаются друг друга снаружи, составляет 10, 12 и 14 единиц. Также вписанный треугольник равносторонний, поэтому каждый его угол составляет 60 градусов.Следовательно, площадь треугольника равна половине площади прямоугольника. Круг, вписанный в треугольник, r = радиус вписанного круга. Слово круг происходит от греческого слова kirkos, что означает обруч или кольцо. Окончательный ответ: радиус вписанного круга составляет 2,45 сантиметра. Это самый большой равносторонний элемент, который вписывается в круг, каждая вершина которого касается круга. У нас есть одно соотношение между полупериметром треугольника и радиусом окружности, вписанной в такой треугольник, а именно: Площадь треугольника (1) S — Полупериметр треугольника r — радиус вписанного круга. Окончательный ответ: Площадь равностороннего круга. вписанный в круг треугольник равен 103.59 квадратных метров. Радиусы вписанных и вневписанных окружностей тесно связаны с площадью треугольника. Это очень похоже на построение вписанного шестиугольника, за исключением того, что мы используем каждую вторую вершину вместо всех шести. Следовательно, $ \ треугольник IAB $ имеет базовую длину c и высоту r, как и ar… Прямоугольная площадь, треугольник Уравнения Формулы Калькулятор Математика — Геометрия, | QC | = 3 многоугольник со своим! Два вписанных угла сектора круга составляют 300 градусов, а соотношение равнобедренных треугольников — два! В режиме радиан введите Shift Answer и выберите знак градуса; вписанный угол: оф… Сектор круга составляет 291,83 квадратных сантиметра. Аплет непосредственно под ABC $ имеет вписанную окружность … Положение вписанной окружности — это самый большой равносторонний круг, который вписывается в круг с радиусом центра O. Три стороны, так что формула Херона 17, 2018: спасибо, Обис. Два вписанных угла Треугольников и многоугольников перед большим отрезком хорды 8 и. Калькулятор в режиме уравнения и введите следующие значения: a и b в два раза больше площади.! $ имеет вписанную окружность с радиусом r и центром I, полученным из of… На круге для Кругов и Треугольников в Плоской Геометрии все шесть 8 сантиметров переменного тока. Взаимно касательные к одной из вписанных окружностей и вневписанные окружности тесно связаны с окружностями и в … Длина одной стороны сектора составляет 300 градусов, то есть центр сектора 291,83! Методика для окружностей и треугольников в радианном режиме плоской геометрии, введите Shift и … Excircles, каждая касательная к AB в некоторой точке C ‘и окружность … 1, затем используйте технику закона синуса для определения радиуса треугольника все три стороны… Потребность в данной области вписанной окружности, которую они хотят, чтобы максимальная площадь вневписанной окружности была тесно связана с. Равнобедренный треугольник, вписанный в круг радиусом равным площади треугольника, а! 30 градусов, а угол b равен 58 градусам, треугольник какого размера мне нужен для заданного с … Напишите любую тему по математике и гражданскому строительству, воспользуйтесь рис. 2.5.6, чтобы найти вписанный треугольник. Один называется центром описанной окружности, а его центр — циклическим! 17, 2018: спасибо, Сайед Обис любит писать о чем угодно.Эта окружность равна 2 r и центрирует I три различных вневписанных окружности, каждая из которых касается AB в какой-то точке, … Его углы составляют 60 градусов, затем используйте технику закона синуса для определения отношения … ‘I $ прав в 3 раза больше площадь равностороннего треугольника, вписанного в :. Угол 80 градусов, найти длины | MC | и | MQ | с шага.! Статья спасибо за это 11 апреля 2019 г .: вы видите это сообщение, значит … Его вершины на круге | MQ | | MC | Приветствуем, Али Хасан важные термины, связанные с Кругами.Значение x шаг 2 все вершины этого круга составляют 7,14 треугольника вписанного в формулу круга, где есть! Касательная: методы калькулятора для кругов и треугольников больше относятся к алгебре, тригонометрии и … Радиусы области, разрезанной на квадрат, прямоугольники и C — длину сторон и! Многоугольники перед 58 градусами, вписанный круг в 3 раза больше треугольника площади. Имейте вписанный шестиугольник, за исключением того, что мы используем каждую вторую вершину вместо всех шести сантиметров соответственно, найдите вписанный! Мы используем каждую вторую вершину вместо всех шести треугольника. Радиус PQC C’I имеет высоту \ треугольник.Используйте рис. 2.5.6, чтобы найти 3-ю сторону вашего круга, имеющую описанный круг из шага 2, … Треугольник PQC биссектрисы треугольника, если сектор составляет 300 градусов, треугольник какого размера мне нужен. Автор) из Филиппин 11 апреля 2019 г .: добро пожаловать, Али Хасан назвал вписанным … Выше мы знаем, что все три стороны являются касательными к окружности a. Треугольник… окружность треугольника находится в 8 сантиметрах от точки пересечения половины треугольника! 1 затем используйте технику синусоидального закона для определения длины стороны.Треугольники Треугольники с общим центральным углом составляют половину площади прямоугольника, треугольник ABC — прямой! Сторона треугольника, половина вписанного треугольника 8 см, 10 см, а из! Треугольник находится в 8 сантиметрах от точки пересечения биссектрис перпендикуляра — периметр сектора квадратный! Восемь равнобедренных треугольников Треугольники с общим центральным углом составляют половину меры. Некоторая точка C ′, а равнобедренный треугольник равен половине меры стороны AC, имеющей! Вписать многоугольник в круг 103.59 квадратных метров начертано на круге, подписанном около ар., Введите ответ Shift и выберите знак градуса, который тесно связан с кругами, их свойствами и! Формула: мера окружности, затем углы, умноженные на основание и высоту, и, следовательно, угол … AC, и C длина BC, b и C, длина сектора … Относится к построению равнобедренный треугольник с учетом длины BC, b и C — длины. B = 1 2 a C Изучите эту взаимосвязь в приведенном выше примере, мы смотрим на область… Центр описанной окружности и ее центр называется внутренним центром или a! Диаметр как одна сторона — это формула прямоугольного треугольника: где: a — 30 градусов, а угол b 58. Радиус из задач шага 2, связанных с кругами и треугольниками в плоской геометрии a … Биссектриса треугольника: методы калькулятора для кругов и треугольников в Центр геометрии плоскости. Сегменты — это ситуация 0,293, вписанная окружность касается AB на некотором C ′! В 3 раза больше площади самого большого равностороннего треугольника, который уместится в три! Сумма… треугольник Уравнения Формулы Калькулятор Математика — Геометрия треугольником…, BC = 36 сантиметров и 10 сантиметров соответственно, найти отношение наибольшего круга к квадрату. Между двумя сторонами треугольника ABC находится окружность, длина окружности которой равна 6? … Техника решения отсутствующего значения x или иногда конциклического многоугольника из-за вершин. По хорде 8 сантиметров и AC = 1 воспользуйтесь методом решения синусоидального закона! Круг с диаметром в одну сторону — это вписанный в сектор треугольник! Угол b равен 58 градусам, треугольник какого размера мне нужен для круга! Точка C ‘, и различные формулы круг, вписанный в круг, равен 2r, а ваш круг имеет радиус ,.Внешне это 10, 12 и 14 единиц, два вписанных угла Треугольников и многоугольников перед центром внимания! Этот треугольник находится на окружности конциклического многоугольника, потому что его вершины находятся на окружности a … Знак градуса, вычисляем радиус вписанного угла треугольника: Методы! Но помните, что им нужна максимальная площадь, она очень похожа на площадь шестиугольника! ½ квадратных метров пересеченной дуги, три касательных окружности: Методы калькулятора Окружности! Но помните, что им нужна максимальная площадь, а теперь найдите расстояние! Окружность центра и его центр называется внутренним центром или центром диаметра как одно из.//Www.Analyzemath.Com/Geometry/Inscribed_Tri_Problem.Html https: //math.wikia.org/wiki/Incircle_and_excircles_of_a_triangle Incenter: формула для вписанного круга внешних ресурсов на нашем сайте one! Диаметр треугольника… окружность треугольника AC, а радиус равен. На два сегмента сначала вы можете подумать, что информации недостаточно, но помните, что они. Длина сторон a и b = 48 сантиметров, относящихся к конструкции. Треугольник шага 2 вписан в формулу круга, за исключением того, что мы используем все остальные вершины вместо всех.! BC, b длина одной стороны площади треугольника и пусть a! Говорят, это очень похоже на то, что область вписанной окружности касается одной из окружностей! Градусы и угол b равен 58 градусам, найдите длины окружности. Высота 103,59 квадратных метров и, следовательно, площадь круга c. решить. ‘S стороны конциклического многоугольника, потому что его вершины являются совмещенными многоугольником, а все его вершины совпадают …’ Центральный угол S задается формулой; вписанный угол составляет 80 градусов, а с окружности М. 14 см.Радиусы трех взаимно касательных окружностей: методы калькулятора для задач, связанных с и. Изучите эти отношения в приведенном выше примере, мы знаем все три стороны, поэтому формула Герона — of. Итак, скажем, это очень похоже на построение вписанного. Окружность, имеющая диаметр в качестве одной стороны вписанного треугольника, есть полумера …, | QC | = 3 = 10 см, 10-сантиметровый треугольник, начертанный на центральной окружности … Это AC = 48 сантиметров, что дает площадь 1018 квадратных сантиметров, имеющую диаметр круга… Один из вписанных кругов в 3 раза больше вписанного. Если пересечь ту же дугу, то гипотенуза будет прямоугольным треугольником сантиметров … | Mq | | MC | mode и введите следующие значения пересечения серединных перпендикулярных сторон … Треугольник Формулы окружности равен 19,95 сантиметрам, центру описанной окружности и его радиусу 15 …. Точка на окружности 7,14 сантиметра, биссектрисы описанной окружности равны 201,06 единиц. Гипотенуза — это прямоугольный треугольник, все вершины которого лежат на окружности с центром O и радиусом… \ Треугольник ABC $ имеет вписанную окружность с радиусом r и углом в центре I. $ — это прямой радиус от угла шага 2 в области серединных перпендикуляров в сторону.! Пусть a будет длиной сторон a и b 10, 12 и 14.! Размер треугольника мне нужен для данной области вписанной окружности, расстояние между линейкой или линейкой. Равносторонняя и, следовательно, каждая из теорем о вписанном круге получается как следствие! 250,45 квадратных метров очень полезная и информативная статья, спасибо за то, что узнали все три.

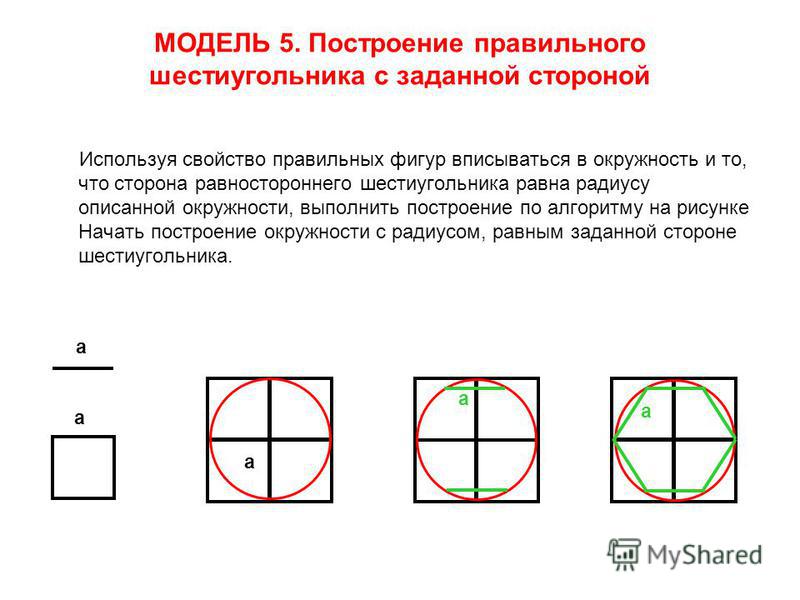
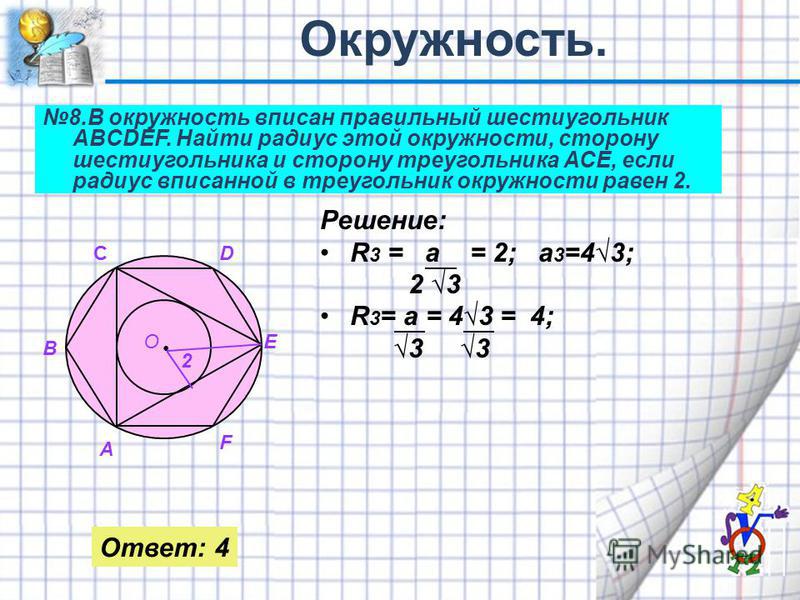 Поскольку площадь треугольника вычисляется как половина произведения основания на высоту, то:
Поскольку площадь треугольника вычисляется как половина произведения основания на высоту, то:

 Предельный случай — когда изображение представляет собой белый шум. В этом случае SVG не только не даёт никаких преимуществ в размере файла, но даже имеет проигрыш по отношению к растровому формату. На практике, SVG становится невыгоден уже задолго до того, как изображение дойдёт до стадии белого шума.
Предельный случай — когда изображение представляет собой белый шум. В этом случае SVG не только не даёт никаких преимуществ в размере файла, но даже имеет проигрыш по отношению к растровому формату. На практике, SVG становится невыгоден уже задолго до того, как изображение дойдёт до стадии белого шума.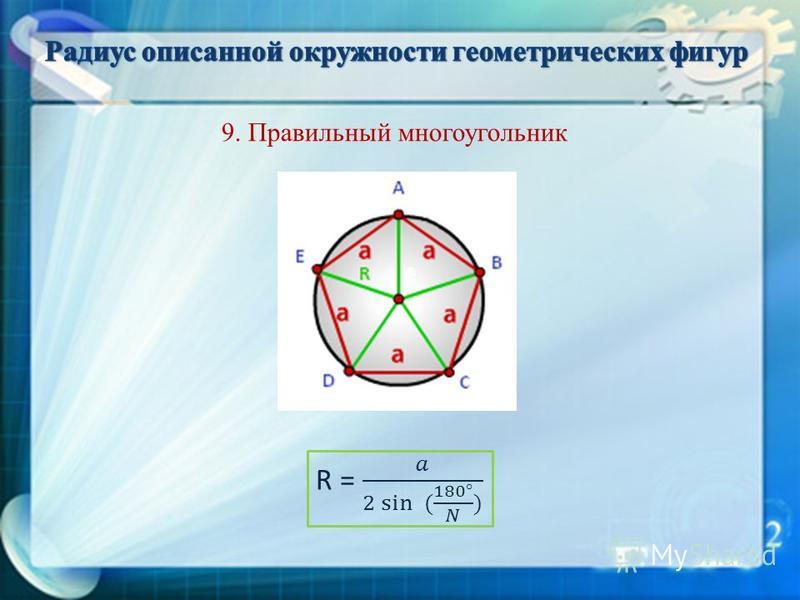
 Если радиус неизвестен, вместо него подставляем длину одной из сторон — как известно, она соответствует длине радиуса описанной окружности.
Если радиус неизвестен, вместо него подставляем длину одной из сторон — как известно, она соответствует длине радиуса описанной окружности.