Прогиб балки онлайн: Балка-онлайн SOPROMATu.NET

alexxlab

Содержание

Онлайн расчет статически неопределенной балки

Расчет выполняется методом сил

Канонические уравнения метода сил:

Где коэффициенты системы определяются:

Принцип ввода данных, рассмотрим с помощью следующего примера:

1. Задание длины (12м) и условий закрепления стержня. Левый конец стержня свободен, а правый — жестко закрепленный. Задаем координаты опор (отсчет ведется от левого конца стержння). Первая опора имеет координату 2м, вторая — 7м.

2.

Задаем нагрузки, использовав соответствующие правила знаков:

3. В случае, если жесткость балки переменная, задайте необходимые пропорции (нажмите на кнопку «Изменить жесткость»):

4. Для начала расчета нажмите на кнопку «Построить эпюры».

Для расчета балок используется следующая основная система (ОС). Выбрать ОС невозможно.

Решение системы уравнений:

Опорные реакции:

Прокатная балка онлайн

Інструкція.

Программа позволяет определить опорные реакции, построить эпюры внутренних усилий (поперечных сил, изгибающих моментов) и эпюры перемещений (угла поворота, прогиб балки) для двухопорном и консольной балки.

Дальнейшие инструкции будут приведены на примере балки на двух опорах.

1. Выберите условия крепления концов балки. Возможны варианты — свободный, шарнир и жесткое. В нашем примере левый — «шарнир», а правый — «свободный».

Если по ошибке был выбран другой вариант, нажимаем на кнопку «Новая схема».

2. Указываем длину балки, координаты опор и допускаемые напряжения. Длина балки равна «16» (м), а координаты опор от левого конца балки, соответственно к опоре A — «0» (не нужно указывать) и к опоре B — «11» (м). Допустимые нормальные напряжения σadm = 160 МПа, допустимые касательные напряжения τadm = 100 МПа.

3. Указываем нагрузки.
Выбираем количество сосредоточенных моментов — «1». В таблице вводим значения моментов и их координаты от левого конца балки. M1=18 (кН·м), a1=9 (м)(момент который вращается против часовой стрелки — положительный, по — отрицательный).
Выбираем количество сосредоточенных сил — «1». В таблице вводим значение сил и их координаты. F1=-20 (кН), b1=4 (м) (сила направленная вниз — положительная, вверх — отрицательная).
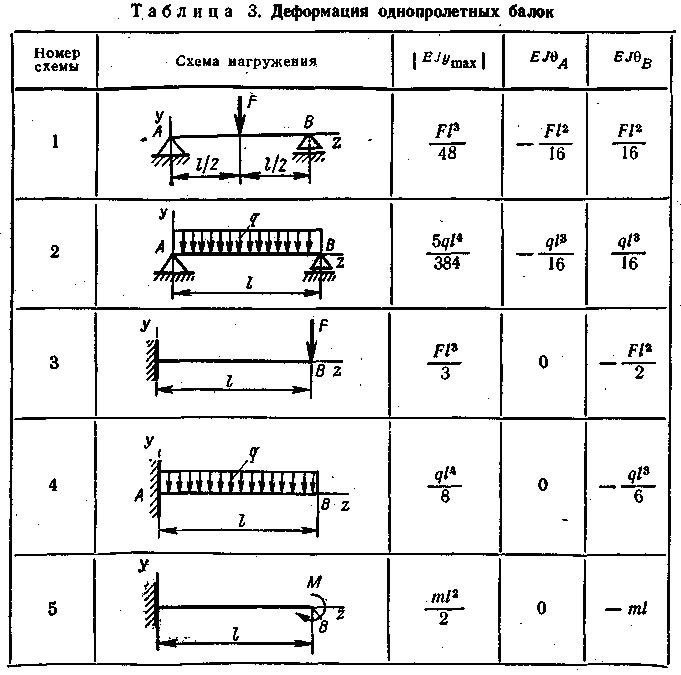
Выбираем количество равномерно распределенной нагрузки — «1». В таблице вводим значение РРН, координаты начала и конца РРН. q
1=4 (кН/м), c1=11 (м) та d1=16 (м) (РРН направлено вниз — положительное, вверх — отрицательное).

4. Нажимаем на кнопку «Посчитать прокатную балку». После нажатия определяются опорные реакции, строятся эпюры усилий, перемещений и подбирается двутавровое сечение. Если нужно определить усилия и перемещения в произвольном сечении, введите координату в форму. Если нужно, задайте точность расчета и выберите правое или левое сечение.

Скриншот к примеру:

Скриншот к примеру (эпюра поперечных сил):

Скриншот к примеру (эпюра изгибающих моментов):

Скриншот к примеру (эпюра углов поворота):

Скриншот к примеру (эпюра прогибов):

Калькуляторы для расчета теплопотерь прямоугольного помещения и основных характеристик прямоугольной отопительной печи

Расчет несущей способности и прогиба деревянных балок

При проектировании любой постройки требуется проводить расчеты несущей способности балок. В индивидуальном строительстве в подавляющем большинстве случаев используются однопролетные деревянные балки в виде досок, брусьев или бревен различной длины. Предлагаемый калькулятор поможет Вам быстро подобрать оптимальное сечение и шаг балок в зависимости от длины пролета и предполагаемых нагрузок.

Онлайн-калькулятор для расчета балок находится здесь >>>


Версию калькулятора для работы в офлайне можно скачать здесь >>> (zip-файл, 566 Кб)

Расчет теплопотерь помещения

С помощью предлагаемого калькулятора Вы можете самостоятельно определить потребности любого жилого помещения в тепле.


Под термином «жилое» подразумевается помещение, в котором проживают постоянно в течение отопительного сезона. Дачные строения, в которых отопление в холодное время года работает периодически, как правило, в выходные дни, в данную категорию не попадают. Для выхода на оптимальный тепловой режим в них потребуется значительное время, зависящее от конструктивных особенностей здания, и увеличенная мощность системы отопления.


Для расчета теплопотерь в соответствующие поля и раскрывающиеся списки калькулятора требуется ввести данные конкретного помещения. Перерасчет значений производится автоматически. Результирующее значение суммарных теплопотерь помещения выводится в левой нижней части калькулятора в пункте «Суммарные теплопотери помещения, Вт».


Онлайн-калькулятор для расчета теплопотерь помещения находится здесь >>>

Версию калькулятора для работы в офлайне можно скачать здесь >>> (zip-файл, 576 Кб)

Расчет теплоотдачи прямоугольной отопительной печи

После определения теплопотерь помещения можно подобрать отопительную печь с требуемыми характеристиками по теплоотдаче и габаритам. Одновременно определяются основные характеристики топливника, расчитанного на применение определенного вида топлива.


Калькулятор для расчета теплоотдачи печи находится здесь >>>

Версию калькулятора для работы в офлайне можно скачать здесь >>> (zip-файл, 563 Кб)

Расчет деревянных балок перекрытий: онлайн калькулятор

Деревянные брусья для перекрытий в частном строительстве используют часто. Легкость, доступность по цене и возможность самостоятельного монтажа компенсируют способность к возгоранию, поражению грибком и гниению. В любом случае при возведению второго и более этажей просто необходимо произвести расчет деревянных балок перекрытия. Онлайн-калькулятор, который мы представляем в этом обзоре, поможет справиться с этой задачей просто и быстро.

Деревянные брусья для перекрытия – только качественная древесина

Читайте в статье

Польза онлайн-калькулятора для расчета деревянных перекрытий

Самостоятельные расчеты утомительны и чреваты риском не учесть какой-либо важный параметр. Так, деревянные балки для перекрытий должны обладать определенным сечением, учитывающим возможную нагрузку на них от мебели и техники, находящихся в помещении людей. При таких расчетах крайне важно знать возможный прогиб балки и максимальное напряжение в опасном сечении.

Разное сечение бруса

Преимущества калькулятора в следующем:

  • Точность. Формулы расчета учитывают множество параметров. В специальных полях задаются: тип поперечного сечения (круглое или прямоугольное), длину балки между опорами и шаг, параметры используемой древесины, предполагаемую постоянную нагрузку.
  • Сроки. Ввести готовые параметры и получить результат выйдет значительно быстрее, чем рассчитывать вручную требуемые значения.
  • Удобство. Онлайн-калькулятор расчета деревянных балок составлен таким образом, что после введения всех постоянных величин, вам остается просто подбирать сечение балки до тех пор, пока не будет обеспечена необходимая прочность.

Расчет деревянного бруса для перекрытия: на что обратить внимание

До расчетов и покупки рекомендовано обратить внимание на типы перекрытий. Брус для надежной связки строительных конструкций, бывает следующих видов:

  • Балки. Массив квадратного или прямоугольного сечения, уложенный с шагом от 60 см до 1 м. Стандартная длина – 6 м, на заказ изготавливаются балки до 15 м.
  • Ребра. Балки, напоминающие широкую (20 см) и толстую доску (7 см). Шаг укладки на ребро не более 60 см. Стандартная длина – 5 м, под заказ – 12 м.
Ребра перекрытия для одноэтажных построек
  • Комбинация двух типов бруса. Наиболее надежные перекрытия, служащие опорой для пролетов, до 15 м.

Сначала определяется прогиб балки, максимальное напряжение в опасном сечении и коэффициент запаса прочности. Если значение коэффициента получается меньше 1, то это значит, что прочность не обеспечена. В этом случае необходимо изменить условия расчета (изменить сечение балки, увеличить или уменьшить шаг, выбрать другую породу древесины и т.д.)

Длина балок, м
Шаг укладки, м2,03,04,05,0
0,675*10075*200100*200150*225
175*150100*175150*200175*250

Когда нужное сечение найдено требуется рассчитать его кубатуру. Это произведение длины, ширины и высоты. Далее по проекту находим количество балок перекрытия и умножаем на полученный результат.

Брус

Итог

Важно! Для строительства многоэтажных домов не рекомендовано приобретать балки недостаточной длины. Сращивание, даже качественное, снижает надежность конструкций.

Сращивание двух балок перекрытия = снижение надежности

Для наглядности пользователю предоставлено видео расчета древесины для перекрытий.

ПОНРАВИЛАСЬ СТАТЬЯ? Поддержите нас и поделитесь с друзьями

Рассчитать балку на прогиб калькулятор

Одним из самых популярных решений при устройстве межэтажных перекрытий в частных домах является использование несущей конструкции из деревянных балок. Она должна выдерживать расчетные нагрузки, не изгибаясь и, тем более, не разрушаясь. Прежде чем приступить к возведению перекрытия рекомендуем воспользоваться нашим онлайн-калькулятором и рассчитать основные параметры балочной конструкции.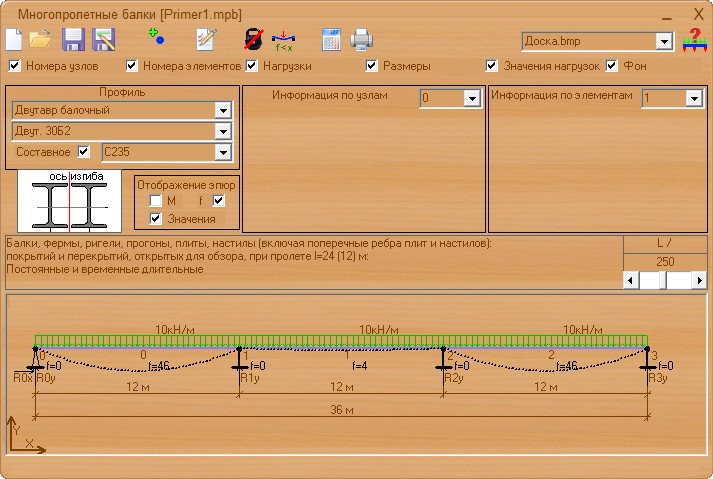

Необходимые пояснения к расчетам

  • Высота и ширина определяют площадь сечения и механическую прочность балки.
  • Материал древесины: сосна, ель или лиственница – характеризует прочность балок, их стойкость к прогибам и излому, другие особые эксплуатационные свойства. Обычно отдают предпочтение сосновым балкам. Изделия из лиственницы применяют для помещений с влажной средой (бань, саун и т.п.), а балки из ели используют при строительстве недорогих дачных домов.
  • Сорт древесины влияет на качество балок (по мере увеличения сорта качество ухудшается).
  • 1 сорт. На каждом однометровом участке бруса с любой стороны могут быть здоровые сучки размером 1/4 ширины (пластевые и ребровые), размером 1/3 ширины (кромочные). Могут быть и загнившие сучки, но их количество не должно превышать половины здоровых. Также нужно учитывать, что суммарные размеры всех сучков на участке в 0,2 м должны быть меньше предельного размера по ширине. Последнее касается всех сортов, когда речь идет о несущей балочной конструкции. Возможно наличие пластевых трещин размером 1/4 ширины (1/6, если они выходят на торец). Длина сквозных трещин ограничивается 150 мм, брус первого сорта может иметь торцевые трещины размером до 1/4 ширины. Из пороков древесины допускаются: наклон волокон, крень (не более 1/5 площади стороны бруса), не более 2 кармашков, односторонняя прорость (не более 1/30 по длине или 1/10 — по толщине или ширине). Брус 1 сорта может быть поражен грибком, но не более 10% площади пиломатериала, гниль не допускается. Может быть неглубокая червоточина на обзольных частях. Обобщая вышесказанное: внешний вид такого бруса не должен вызывать какие-либо подозрения.
  • 2 сорт. Такой брус может иметь здоровые сучки размером 1/3 ширины(пластевые и ребровые), размером 1/2 ширины (кромочные). По загнившим сучкам требования, как и для 1 сорта. Материал может иметь глубокие трещины длиной 1/3 длины бруса. Максимальная длина сквозных трещин не должна превышать 200 мм, могут быть трещины на торцах размером до 1/3 от ширины. Допускается: наклон волокон, крень, 4 кармашка на 1 м., прорость (не более 1/10 по длине или 1/5 – по толщине или ширине), рак (протяжением до 1/5 от длины, но не больше 1 м). Древесина может быть поражена грибком, но не более 20% площади материала. Гниль не допускается, но может быть до двух червоточин на 1 м. участке. Обобщим: сорт 2 имеет пограничные свойства между 1 и 3, в целом оставляет положительные впечатления при визуальном осмотре.
  • 3 сорт. Тут допуски по порокам больше: брус может иметь сучки размером 1/2 ширины. Пластевые трещины могут достигать 1/2 длины пиломатериала, допускаются торцевые трещины размером 1/2 от ширины. Для 3 сорта допускается наклон волокон, крень, кармашки, сердцевина и двойная сердцевинаы, прорость (не более 1/10 по длине или 1/4 — по толщине или ширине), 1/3 длины может быть поражена раком, грибком, но гнили не допускаются. Максимальное количество червоточин — 3 шт. на метр. Обобщая: 3 сорт даже невооруженным глазом выделяется не самым лучшим качеством. Но это не делает его непригодным для изготовления перекрытий по балкам.Подробнее про сорта читайте ГОСТ 8486-86 Пиломатериалы хвойных пород. Технические условия;
  • Пролет – расстояние между стенами, поперек которых укладываются балки. Чем он больше, тем выше требования к несущей конструкции;
  • Шаг балок определяет частоту их укладки и во многом влияет на жесткость перекрытия;
  • Коэффициент надежности вводится для обеспечения гарантированного запаса прочности перекрытия. Чем он больше, тем выше запас прочности

    • Наш онлайн-калькулятор позволит вам рассчитать параметры деревянных балок и подобрать оптимальную конфигурацию перекрытия.

    Для расчета балок первым делом необходимо определить усилия, возникающие в конструкциях. В данном разделе показано, как находить усилия, опорные реакции, прогибы и углы поворота в различных изгибаемых конструкциях. Для самых распространенных из них вы можете воспользоваться онлайн расчетом. Для редких – приведены все формулы определения необходимых значений.

    Онлайн расчет балки на двух опорах (калькулятор).

    Приведен расчет на момент, прогиб и опорные реакции от сосредоточенной и распределнной силы.

    Синие ячейки – ввод данных. (Белые ячейки – ввод координаты для определения промежуточного итога).

    Зеленые ячейки – расчетные, промежуточный итог.

    Оранжевые ячейки – максимальные значения.

    >>> Перейти к расчету балки на двух опорах

    Онлайн расчет консольной балки (калькулятор).

    Приведен расчет на момент, прогиб и опорные реакции от сосредоточенной и распределнной силы.

    Синие ячейки – ввод данных. (Белые ячейки – ввод координаты для определения промежуточного итога).

    Зеленые ячейки – расчетные, промежуточный итог.

    Оранжевые ячейки – максимальные значения.

    >>> Перейти к расчету консольной балки

    Расчет однопролетной балки на двух шарнирных опорах.

    Рис.1 Расчет балки на двух шарнирных опорах при одной сосредоточенной нагрузке

    Рис.2 Расчет балки на двух шарнирных опорах при двух сосредоточенных нагрузках

    Рис.3 Расчет балки на двух шарнирных опорах при одной равномерно-распределенной нагрузке

    Рис4. Расчет балки на двух шарнирных опорах при одной неравномерно-распределенной нагрузке

    Рис5. Расчет балки на двух шарнирных опорах при действии изгибающего момента

    Расчет балок с жестким защемлением на двух опорах

    Рис6. Расчет балки с жестким защемлением на опорах при одной сосредоточенной нагрузке

    Рис7. Расчет балки с жестким защемлением на опорах при двух сосредоточенных нагрузках

    Рис8. Расчет балки с жестким защемлением на опорах при одной равномерно-распределенной нагрузке

    Рис9. Расчет балки с жестким защемлением на опорах при одной неравномерно-распределенной нагрузке

    Рис10.Расчет балки с жестким защемлением на опорах при действии изгибающего момента

    Расчет консольных балок

    Рис11. Расчет однопролетной балки с жестким защемлением на одной опоре при одной сосредоточенной нагрузке

    Рис12. Расчет однопролетной балки с жестким защемлением на одной опоре при одной равномерно-распределенной нагрузке

    Рис13. Расчет однопролетной балки с жестким защемлением на одной опоре при одной неравномерно-распределенной нагрузке

    Рис14. Расчет однопролетной балки с жестким защемлением на одной опоре при действии изгибающего момента

    Расчет двухпролетных балок

    Рис15. Расчет двухпролетной балки с шарнирными опорами при одной сосредоточенной нагрузке

    Рис16. Расчет двухпролетной балки с шарнирными опорами при одной равномерно-распределенной нагрузке

    Рис17. Расчет двухпролетной балки с шарнирными опорами при одной неравномерно-распределенной нагрузке

    Чтобы построить деревянный дом необходимо провести расчёт несущей способности деревянной балки. Также особое значение в строительной терминологии имеет определение прогиба.

    Без качественного математического анализа всех параметров просто невозможно построить дом из бруса. Именно поэтому перед тем как начать строительство крайне важно правильно рассчитать прогиб деревянных балок. Данные расчёты послужат залогом вашей уверенности в качестве и надёжности постройки.

    Что нужно для того чтобы сделать правильный расчёт

    Расчёт несущей способности и прогиба деревянных балок не такая простая задача, как может показаться на первый взгляд. Чтобы определить, сколько досок вам нужно, а также, какой у них должен быть размер необходимо потратить немало времени, или же вы просто можете воспользоваться нашим калькулятором.

    Во-первых, нужно замерить пролёт, который вы собираетесь перекрыть деревянными балками. Во-вторых, уделите повышенное внимание методу крепления. Крайне важно, насколько глубоко фиксирующие элементы будут заходить в стену. Только после этого вы сможете сделать расчёт несущей способности вместе с прогибом и ряда других не менее важных параметров.

    Длина

    Перед тем как рассчитать несущую способность и прогиб, нужно узнать длину каждой деревянной доски. Данный параметр определяется длиной пролёта. Тем не менее это не всё. Вы должны провести расчёт с некоторым запасом.

    При подсчёте особое значение имеет материал, из которого сделан дом. Если это кирпич, доски будут монтироваться внутрь гнёзд. Приблизительная глубина около 100—150 мм.

    Когда речь идёт о деревянных постройках параметры согласно СНиПам сильно меняются. Теперь достаточно глубины в 70—90 мм. Естественно, что из-за этого также изменится конечная несущая способность.

    Если в процессе монтажа применяются хомуты или кронштейны, то длина брёвен или досок соответствует проёму. Проще говоря, высчитайте расстояние от стены до стены и в итоге сможете узнать несущую способность всей конструкции.

    К сожалению, далеко не всё зависит от фантазии архитектора, когда дело касается исключительно математики. Для обрезной доски максимальная длина шесть метров. В противном случае несущая способность уменьшается, а прогиб становится больше.

    Само собой, что сейчас не редкость дома, у которых пролёт достигает 10—12 метров. В таком случае используется клееный брус. Он может быть двутавровым или же прямоугольным. Также для большей надёжности можно использовать опоры. В их качестве идеально подходят дополнительные стены или колоны.

    Общая информация по методологии расчёта

    В большинстве случаев в малоэтажном строительстве применяются однопролётные балки. Они могут быть в виде брёвен, досок или брусьев. Длина элементов может варьироваться в большом диапазоне. В большинстве случаев она напрямую зависит от параметров строения, которые вы собираетесь возвести.

    Роль несущих элементов в конструкции выполняют деревянные бруски, высота сечения которых составляет от 140 до 250 мм, толщина лежит в диапазоне 55—155 мм. Это наиболее часто используемые параметры при расчёте несущей способности деревянных балок.

    Очень часто профессиональные строители для того чтобы усилить конструкцию используют перекрёстную схему монтажа балок. Именно эта методика даёт наилучший результат при минимальных затратах времени и материалов.

    Если рассматривать длину оптимального пролёта при расчёте несущей способности деревянных балок, то лучше всего ограничить фантазию архитектора в диапазоне от двух с половиной до четырёх метров.

    Как рассчитать несущую способность и прогиб

    Стоит признать, что за множество лет практики в строительном ремесле был выработан некий канон, который чаще всего используют для того, чтобы провести расчёт несущей способности:

    Расчёт прогиба деревянной балки является частью, представленной выше формулы. Буква М указывает нам на данный показатель. Чтобы узнать параметр применяется следующая формула:

    M=(ql 2 )/8

    В формуле расчёта прогиба есть всего две переменных, но именно они в наибольшей степени определяют, какой в конечном итоге будет несущая способность деревянной балки:

    • Символ q показывает нагрузку, которую способна выдержать доска.
    • В свою очередь буква l — это длина одной деревянной балки.

    Насколько важно правильно рассчитать прогиб

    Этот параметр крайне важен для прочности всей конструкции. Дело в том, что одной стойкости бруса недостаточно для долгой и надёжной службы, ведь со временем его прогиб под нагрузкой может увеличиваться.

    Прогиб не просто портит эстетичный вид перекрытия. Если данный параметр превысит показатель в 1/250 от общей длины элемента перекрытия, то вероятность возникновения аварийной ситуации возрастёт в десятки раз.

    Так зачем нужен калькулятор

    Представленный ниже калькулятор позволит вам моментально просчитать прогиб, несущую способность и многие другие параметры без использования формул и подсчётов. Всего несколько секунд и данные по вашему будущему дому будут готовы.

    Как посчитать прогиб балки

    При проектировании и изготовлении конструкций из металла и других материалов очень важно соблюдать и выполнять физико-механические расчеты на прочность, одним из которых является расчет балок на изгиб (прогиб). Выполнять расчет прогиба балки онлайн – очень удобно и быстро. Поэтому специалисты нашего предприятия подготовили онлайн калькулятор для расчетов.

    Расчет прогиба балки онлайн

    Площадь поперечного сечения профиля:

    Расчетный вес профиля (балки):

    Описание

    При выборе схемы с распределенной нагрузкой, приложенная «Нагрузка Q» указывается как относительная «килограмм на метр». Определяется она по формуле Q = [общяя нагрузка, кг]/[общая длина, м].

    Использование калькулятора «Расчет прогиба балки онлайн» значительно сократит время и послужит залогом надежных инженерных конструкций.

    Калькулятор разработан исключительно по формулам Сопромата и справочным данным для каждого типа материала и сечения балки. Расчет прогиба сечения является теоретическим, следовательно практические значения могут быть отличными от расчетных и зависеть от множества условий.
    Однако значения полученные в данном калькуляторе будут невероятно полезными и послужат основой для расчета необходимой конструкции.

    Для быстрого доступа к расчетам необходимого профиля добавьте калькулятор в избранное (CTRL+D на ПК или значек «звездочка» справа вверху браузера)

    Балка является основным элементом несущей конструкции сооружения. При строительстве важно провести расчет прогиба балки. В реальном строительстве на данный элемент действует сила ветра, нагружение и вибрации. Однако при выполнении расчетов принято принимать во внимание только поперечную нагрузку или проведенную нагрузку, которая эквивалентна поперечной.

    При расчете балка воспринимается как жесткозакрепленный стержень, который устанавливается на двух опорах. Если она устанавливается на трех и более опорах, расчет ее прогиба является более сложным, и провести его самостоятельно практически невозможно. Основное нагружение рассчитывается как сумма сил, которые действуют в направлении перпендикулярного сечения конструкции. Расчетная схема требуется для определения максимальной деформации, которая не должна быть выше предельных значений. Это позволит определить оптимальный материал необходимого размера, сечения, гибкости и других показателей.

    Виды балок

    Для строительства различных сооружений применяются балки из прочных и долговечных материалов. Такие конструкции могут отличаться по длине, форме и сечению. Чаще всего используются деревянные и металлические конструкции. Для расчетной схемы прогиба большое значение имеет материал элемента. Особенность расчета прогиба балки в данном случае будет зависеть от однородности и структуры ее материала.

    Деревянные

    Для постройки частных домов, дач и другого индивидуального строительства чаще всего используются деревянные балки. Деревянные конструкции, работающие на изгиб, могут использоваться для потолочных и напольных перекрытий.

    Для расчета максимального прогиба следует учитывать:

    1. Материал. Различные породы дерева обладают разным показателем прочности, твердости и гибкости.
    2. Форма поперечного сечения и другие геометрические характеристики.
    3. Различные виды нагрузки на материал.

    Допустимый прогиб балки учитывает максимальный реальный прогиб, а также возможные дополнительные эксплуатационные нагрузки.

    Стальные

    Металлические балки отличаются сложным или даже составным сечением и чаще всего изготавливаются из нескольких видов металла. При расчете таких конструкций требуется учитывать не только их жесткость, но и прочность соединений.

    Металлические конструкции изготавливаются путем соединения нескольких видов металлопроката, используя при этом такие виды соединений:

    • электросварка;
    • заклепки;
    • болты, винты и другие виды резьбовых соединений.

    Стальные балки чаще всего применяются для многоэтажных домов и других видов строительства, где требуется высокая прочность конструкции. В данном случае при использовании качественных соединений гарантируется равномерно распределенная нагрузка на балку.

    Для проведения расчета балки на прогиб может помочь видео:

    Прочность и жесткость балки

    Чтобы обеспечить прочность, долговечность и безопасность конструкции, необходимо выполнять вычисление величины прогиба балок еще на этапе проектирования сооружения. Поэтому крайне важно знать максимальный прогиб балки, формула которого поможет составить заключение о вероятности применения определенной строительной конструкции.

    Использование расчетной схемы жесткости позволяет определить максимальные изменения геометрия детали. Расчет конструкции по опытным формулам не всегда эффективен. Рекомендуется использовать дополнительные коэффициенты, позволяющие добавить необходимый запас прочности. Не оставлять дополнительный запас прочности – одна из основных ошибок строительства, которая приводит к невозможности эксплуатации здания или даже тяжелым последствиям.

    Существует два основных метода расчета прочности и жесткости:

    1. Простой. При использовании данного метода применяется увеличительный коэффициент.
    2. Точный. Данный метод включает в себя использование не только коэффициентов для запаса прочности, но и дополнительные вычисления пограничного состояния.

    Последний метод является наиболее точным и достоверным, ведь именно он помогает определить, какую именно нагрузку сможет выдержать балка.

    Расчет на жесткость

    Для расчета прочности балки на изгиб применяется формула:

    M – максимальный момент, который возникает в балке;

    Wn,min – момент сопротивления сечения, который является табличной величиной или определяется отдельно для каждого вида профиля.

    Ry является расчетным сопротивлением стали при изгибе. Зависит от вида стали.

    γc представляет собой коэффициент условий работы, который является табличной величиной.

    Расчет жесткости или величины прогиба балки является достаточно простым, поэтому расчеты может выполнить даже неопытный строитель. Однако для точного определения максимального прогиба необходимо выполнить следующие действия:

    1. Составление расчетной схемы объекта.
    2. Расчет размеров балки и ее сечения.
    3. Вычисление максимальной нагрузки, которая воздействует на балку.
    4. Определение точки приложения максимальной нагрузки.
    5. Дополнительно балка может быть проверена на прочность по максимальному изгибающему моменту.
    6. Вычисление значения жесткости или максимально прогиба балки.

    Чтобы составить расчетную схему, потребуются такие данные:

    • размеры балки, длину консолей и пролет между ними;
    • размер и форму поперечного сечения;
    • особенности нагрузки на конструкцию и точно ее приложения;
    • материал и его свойства.

    Если производится расчет двухопорной балки, то одна опора считается жесткой, а вторая – шарнирной.

    Расчет моментов инерции и сопротивления сечения

    Для выполнения расчетов жесткости потребуется значение момент инерции сечения (J) и момента сопротивления (W). Для расчета момента сопротивления сечения лучше всего воспользоваться формулой:

    Важной характеристикой при определении момента инерции и сопротивления сечения является ориентация сечения в плоскости разреза. При увеличении момента инерции увеличивается и показатель жесткости.

    Определение максимальной нагрузки и прогиба

    Для точного определения прогиба балки, лучше всего применять данную формулу:

    q является равномерно-распределенной нагрузкой;

    E – модуль упругости, который является табличной величиной;

    I – момент инерции сечения.

    Чтобы рассчитать максимальную нагрузку, следует учитывать статические и периодические нагрузки. К примеру, если речь идет о двухэтажном сооружении, то на деревянную балку будет постоянно действовать нагрузка от ее веса, техники, людей.

    Особенности расчета на прогиб

    Расчет на прогиб проводится обязательно для любых перекрытий. Крайне важен точный расчет данного показателя при значительных внешних нагрузках. Сложные формулы в данном случае использовать необязательно. Если использовать соответствующие коэффициенты, то вычисления можно свести к простым схемам:

    1. Стержень, который опирается на одну жесткую и одну шарнирную опору, и воспринимает сосредоточенную нагрузку.
    2. Стержень, который опирается на жесткую и шарнирную опору, и при этом на него действует распределенное нагружение.
    3. Варианты нагружения консольного стержня, который закреплен жестко.
    4. Действие на конструкцию сложной нагрузки.

    Применение этого метода вычисления прогиба позволяет не учитывать материал. Поэтому на расчеты не влияют значения его основных характеристик.

    Пример подсчета прогиба

    Чтобы понять процесс расчета жесткости балки и ее максимального прогиба, можно использовать простой пример проведения расчетов. Данный расчет проводится для балки с такими характеристиками:

    • материал изготовления – древесина;
    • плотность составляет 600 кг/м3;
    • длина составляет 4 м;
    • сечение материала составляет 150*200 мм;
    • масса перекрывающих элементов составляет 60 кг/м²;
    • максимальная нагрузка конструкции составляет 249 кг/м;
    • упругость материала составляет 100 000 кгс/ м²;
    • J равно 10 кг*м².

    Для вычисления максимальной допустимой нагрузки учитывается вес балки, перекрытий и опор. Рекомендуется также учесть вес мебели, приборов, отделки, людей и других тяжелых вещей, который также будут оказывать воздействие на конструкцию. Для расчета потребуются такие данные:

    • вес одного метра балки;
    • вес м2 перекрытия;
    • расстояние, которое оставляется между балками;
    • временная нагрузка;
    • нагрузка от перегородок на перекрытие.

    Чтобы упросить расчет данного примера, можно принять массу перекрытия за 60 кг/м², нагрузку на каждое перекрытие за 250 кг/м², нагрузки на перегородки 75 кг/м², а вес метра балки равным 18 кг. При расстоянии между балками в 60 см, коэффициент k будет равен 0,6.

    Если подставить все эти значения в формулу, то получится:

    q = ( 60 + 250 + 75 ) * 0,6 + 18 = 249 кг/м.

    Для расчета изгибающего момента следует воспользоваться формулой f = (5 / 384) * [(qn * L4) / (E * J)] £ [¦].

    Подставив в нее данные, получается f = (5 / 384) * [(qn * L4) / (E * J)] = (5 / 384) * [(249 * 44) / (100 000 * 10)] = 0,13020833 * [(249 * 256) / (100 000 * 10)] = 0,13020833 * (6 3744 / 10 000 000) = 0,13020833 * 0,0000063744 = 0,00083 м = 0,83 см.

    Именно это и является показателем прогиба при воздействии на балку максимальной нагрузки. Данные расчеты показывают, что при действии на нее максимальной нагрузки, она прогнется на 0,83 см. Если данный показатель меньше 1, то ее использование при указанных нагрузках допускается.

    Использование таких вычислений является универсальным способом вычисления жесткости конструкции и величины их прогибания. Самостоятельно вычислить данные величины достаточно легко. Достаточно знать необходимые формулы, а также высчитать величины. Некоторые данные необходимо взять в таблице. При проведении вычислений крайне важно уделять внимание единицам измерения. Если в формуле величина стоит в метрах, то ее нужно перевести в такой вид. Такие простые ошибки могут сделать расчеты бесполезными. Для вычисления жесткости и максимального прогиба балки достаточно знать основные характеристики и размеры материала. Эти данные следует подставить в несколько простых формул.

    В качестве примера, возьмем металлическую балку на двух опорах. Запишем для нее формулу для вычисления прогиба, посчитаем его численное значение. И также в конце этой статьи дам ссылки на другие полезные статьи с примерами определения прогибов для различных расчетных схем.

    Что такое прогиб балки?

    Под действием внешней нагрузки, поперечные сечения балки перемещаются вертикально (вверх или вниз), эти перемещения называются прогибами. Сопромат позволяет нам определить прогиб балки, зная ее геометрические параметры: длину, размеры поперечного сечения. И также нужно знать материал, из которого изготовлена балка (модуль упругости).

    Кстати! Помимо вертикальных перемещений, поперечные сечения балки, поворачиваются на определенный угол. И эти величины также можно определить методом начальных параметров.

    ν-прогиб сечения C; θ-угол поворота сечения C.

    Прогибы балки необходимо рассчитывать, при расчете на жесткость. Расчётные значения прогибов не должны превышать допустимых значений. Если расчетное значение меньше, чем допустимое, то считают, что условие жесткости элемента конструкции соблюдается. Если же нет, то принимаются меры по повышению жесткости. Например, задаются другим материалом, у которого модуль упругости БОЛЬШЕ. Либо же меняют геометрические параметры балки, чаще всего, поперечное сечение. Например, если балка двутаврового профиля №12, не подходит по жесткости, принимают двутавр №14 и делают перерасчет. Если потребуется, повторяют подбор, до того момента пока не найдут тот самый – двутавр.

    Метод начальных параметров

    Метод начальных параметров, является довольно универсальным и простым методом. Используя этот метод можно записывать формулу для вычисления прогиба и угла поворота любого сечения балки постоянной жесткости (с одинаковым поперечным сечением по длине.)

    Под начальными параметрами понимаются уже известные перемещения:

    • в опорах прогибы равны нулю;
    • в жесткой заделке прогиб и угол поворота сечения равен нулю.

    Расчет прогибов балки

    Посмотрим, как пользоваться методом начальных параметров на примере простой балки, которая загружена всевозможными типами нагрузок, чтобы максимально охватить все тонкости этого метода:

    Реакции опор

    Для расчета нужно знать все внешние нагрузки, действующие на балку, в том числе и реакции, возникающие в опорах.

    Система координат

    Далее вводим систему координат, с началом в левой части балки (точка А):

    Распределенная нагрузка

    Метод начальных параметров, который будем использовать чуть позднее, работает только в том случае, когда распределенная нагрузка доходит до крайнего правого сечения, наиболее удаленного от начала системы координат. Конкретно, в нашем случае, нагрузка обрывается и такая расчетная схема неприемлема для дальнейшего расчета.

    Если бы нагрузка была приложена вот таким способом:

    То можно было бы сразу приступать к расчету перемещений. Нам же потребуется использовать один хитрый прием – ввести дополнительные нагрузки, одна из которых будет продолжать действующую нагрузку q, другая будет компенсировать это искусственное продолжение. Таким образом, получим эквивалентную расчетную схему, которую уже можно использовать в расчете методом начальных параметров:

    Вот, собственно, и все подготовительные этапы, которые нужно сделать перед расчетом.

    Приступим непосредственно к самому расчету прогиба балки. Рассмотрим наиболее интересное сечение в середине пролета, очевидно, что это сечение прогнется больше всех и при расчете на жесткость такой балки, рассчитывалось бы именно это сечение. Обзовем его буквой – C:

    Относительно системы координат записываем граничные условия. Учитывая способ закрепления балки, фиксируем, что прогибы в точках А и В равны нулю, причем важны расстояния от начала координат до опор:

    Записываем уравнение метода начальных параметров для сечения C:

    Произведение жесткости балки EI и прогиба сечения C будет складываться из произведения EI и прогиба сечения в начале системы координат, то есть сечения A:

    Напомню, E – это модуль упругости первого рода, зависящий от материала из которого изготовлена балка, I – это момент инерции, который зависит от формы и размеров поперечного сечения балки. Также учитывается угол поворота поперечного сечения в начале системы координат, причем угол поворота дополнительно умножается на расстояние от рассматриваемого сечения до начала координат:

    Учет внешней нагрузки

    И, наконец, нужно учесть внешнюю нагрузку, но только ту, которая находится левее рассматриваемого сечения C. >]

    • Начало и конец распределенных нагрузок нужно умножать на дробь:

    Формулы прогибов

    С учетом всех вышеописанных правил запишем окончательное уравнение для сечения C:

    В этом уравнении содержится 2 неизвестные величины – искомый прогиб сечения C и угол поворота сечения A.

    Поэтому, чтобы найти прогиб, составим второе уравнение для сечения B, из которого можно определить угол поворота сечения A. Заодно закрепим пройденный материал:

    Выражаем угол поворота:

    Подставляем это значение в наше первое уравнение и находим искомое перемещение:

    Вычисление прогиба

    Значение получили в общем виде, так как изначально не задавались тем, какое поперечное сечение имеет рассчитываемая балка. Представим, что металлическая балка имеет двутавровое поперечное сечение №30. Тогда:

    Таким образом, такая балка прогнется максимально на 2 см. Знак «минус» указывает на то, что сечение переместится вниз.

    Формула для расчета прогиба и напряжения балки конструкции и калькулятор прогиба балки

    2D Statics Load Modeler и Calculator Создайте 2D статическую модель и решите для сил реакции.
    Инжиниринг, проектирование, производство и связанные с ними электронные таблицы Excel для загрузки — требуется членство Premium
    Калькулятор электронных таблиц 2D конечно-элементного анализа Требуется премиум-членство
    Уравнения и калькулятор розетки тензодатчика, применяемые к образцу из линейного изотропного материала.
    Трехэлементные уравнения и калькулятор тензорезистора с дельта-розеткой, применяемые к образцу из линейного изотропного материала.
    Коэффициенты концентрации напряжений
    Расчет напряжения-деформации и аппроксимация построенной кривой с использованием уравнения Рамберга-Осгуда
    Vector Mechanics for Engineers, Statics and Dynamics Требуется членство Premium.Механику можно определить как науку, которая описывает и предсказывает условия покоя или движения тел под действием сил. Это делится на три части: механика твердого тела, механика твердого тела. деформируемые тела и механика жидкостей.
    Сложение сил по параллелограмму, полученному из уравнения двух сил и калькулятора

    Сложение сил по параллелограмму, полученному из уравнения двух сил и калькулятора

    Закон косинусов, «правило косинусов» для параллограммы (треугольник с непрямым углом) для вычисления вектора результирующей силы

    Калькулятор для подключения консольных труб
    Калькулятор расчета напряжений и прогибов изогнутой балки
    Постоянное поперечное сечение балки Сдвиг, уравнения напряжения и калькулятор Прогиб несущей балки, уравнения сдвига и напряжения и калькулятор для балки с опорой на один конец, консольный с частичной распределенной нагрузкой
    Напряжение, дефект и наклон балки с опорой на консоль с одной стороны с обратной конической нагрузкой. Уравнения прогиба, сдвига, наклона и напряжения балки и калькулятор для балки с опорой на один конец, консольный с наклонной нагрузкой.
    Уравнения прогиба, сдвига и напряжения и калькулятор Консольная балка w

    Прогиб балок

    Расс Эллиот

    Благодарности : Существует ряд стандартных работ, касающихся принципов отклонения балки. Особенно хорошее описание, на котором основаны приведенные здесь уравнения, содержится в книге Mechanics of Materials (четвертое издание SI) Дж. М. Гира и С. П. Тимошенко, Стэнли Торнса, ISBN 0 7487 3998 X.Для вывода уравнений следует обращаться к этой работе.

    Введение

    Прогиб пружинной балки зависит от ее длины, формы поперечного сечения, материала, к которому приложена отклоняющая сила, и от того, как балка поддерживается.

    Уравнения, приведенные здесь, относятся к однородным, линейно упругим материалам и в которых вращение балки невелико.

    В следующих примерах рассматриваются только нагрузки, действующие в одной точке или отдельных точках — точка приложения силы F на диаграммах предназначена для обозначения рожкового блока модели локомотива (или буксы транспортного средства), способного перемещаться вертикально. в hornguide, и действуя против силы пружины, закрепленной на балке или переносимого локомотива или транспортного средства ЭВМ.Доля общего веса, действующего на каждую ось локомотива или транспортного средства, будет зависеть от положения его центра тяжести по отношению к оси (или точек крепления уравновешивающих балок шасси, если они используются).

    Приложение для моделирования рожковых блоков локомотивов

    Как видно из уравнений, толщина материала ( h или d ) очень важна, и, следовательно, увеличивающиеся размеры в диапазоне доступных гитарных струн делают их очень привлекательными для использования в качестве пружинные балки.Существует также значительная разница в прогибе балки при заданной силе в зависимости от того, как она поддерживается и фиксируется, а также от того, поддерживается ли она только на одном конце или на обоих концах.

    Предполагается, что конструкция должна быть основана на заданном прогибе рогового блока, а затем определить, какая длина, толщина и стиль балки наиболее подходят для конкретной силы, которая должна поддерживаться каждой осью.

    Для локомотивов, вес которых составляет от 4 до 6 граммов на тонну прототипа, массы, поддерживаемые каждым отдельным роговым блоком локомотива, вероятно, будут находиться в диапазоне от 30 до 60 граммов (что соответствует нагрузке прототипа от 14 до 20 тонн на тонну). ось).

    Выбор значения отклонения

    Для гусеницы с мелким размером 4 мм рекомендуемое значение прогиба рогового блока δ при конечной нагрузке локомотива составляет 0,5 мм.

    Приведенная выше рекомендация, как известно, является чрезмерно упрощенным и, возможно, неправильным предположением о том, каким должно быть расчетное значение прогиба, и вызвала серьезные споры. Любой опыт применения этой рекомендации в реальной практике моделирования шасси приветствуется — цель этой статьи — начало обсуждения, а не его заключение.Щелкните здесь, чтобы ознакомиться с вопросами по этому поводу.

    Момент инерции, I

    Момент инерции прямоугольного сечения

    I = bh 3 ∕ 12

    где h — размер в плоскости изгиба, т. Е. По оси, по которой действует изгибающий момент


    Момент инерции круглого сечения

    I = π r 4 ∕ 4 = π d 4 ∕ 64

    , где r и d — радиус и диаметр соответственно

    Все приведенные ниже уравнения содержат I , момент инерции балки, который является константой, определяемой формой и толщиной поперечного сечения балки.Момент инерции не зависит от длины или материала балки. Здесь рассматриваются только прямоугольные и круглые цельные сечения.

    Пояснения к схемам прогиба и обозначениям

    На схемах показаны два типа опор: фиксированная и простая. На неподвижной опоре балка удерживается жестко, а угловой прогиб в точке крепления равен нулю. На простой опоре балка может скользить по опоре и вращаться в соответствии с силой, прилагаемой к балке.

    L = длина балки
    a = промежуточная длина балки
    δ = прогиб балки
    F = сила (т. Е. Пропорция веса локомотива, которому оказывает сопротивление букса)
    E = модуль Юнга
    I = момент инерции балки

    Уравнения и диаграммы прогиба

    Примечание к схемам и уравнениям .Приведенные здесь диаграммы были перевернуты по сравнению с их обычным описанием в учебниках, чтобы отразить их применение для моделей локомотивов и букс транспортных средств. Однако, хотя уравнения для отклонения были согласованы с их описанием в учебниках, нормальное соглашение о знаках (+ или -, чтобы указать отклонения по вертикальной оси y от базовой линии балки) было проигнорировано, поскольку мы здесь обеспокоены только с абсолютной величиной прогиба балки.

    Концевая нагрузка на консольную балку с одинарной неподвижной опорой

    δ = FL 3 ∕ 3 EI

    Это уравнение также следует использовать для отклонения уравнительной балки, вращающейся вокруг фиксированной оси и опирающейся на два рупорных блока по обе стороны от оси поворота.

    Двойные нагрузки на балку с двумя простыми опорами
    (примеры применения этой конфигурации)

    Это может быть применено для двух роговых блоков, прижимающихся к одной балке. Прогиб на расстоянии a от соседней опоры составляет:

    δ = Fa 2 (3 L — 4 a ) ∕ 6 EI

    Свисающая нагрузка на балку, ограниченная двумя простыми опорами

    δ = Fa 2 ( L + a ) ∕ 3 EI

    Промежуточная / центральная нагрузка на балку с одной фиксированной и одной простой опорой

    Прогиб по длине a от неподвижной опоры составляет:

    δ = Fa 3 ( L — a ) 2 (4 L — a ) ∕ 12 EIL 3

    Для нагрузки в центре балки, подставив в приведенное выше уравнение a = L the 2 , прогиб составит:

    δ = 3.5 FL 3 ∕ 384 EI

    Центровка нагрузки на балку с двумя неподвижными опорами

    δ = FL 3 ∕ 192 EI

    При нагрузке в центре отклонение на расстоянии a от фиксированной опоры
    (где a меньше чем или равно L ∕ 2 ):

    δ = Fa 2 (3 L — 4 a ) ∕ 48 EI

    Промежуточная нагрузка на балку с двумя неподвижными опорами

    Прогиб на расстоянии a от неподвижной опоры составляет:

    δ = 2 Fa 3 ( L — a ) 2 ∕ 3 EI (2 а + Д ) 2

    Значения модуля Юнга, E

    Бериллий медный 124 ГПа 1
    Латунь, твердость 70/30 117.2 ГПа
    Латунь неуточненная от 96 до 110 ГПа
    Нейзильбер 132,5 ГПа (127 ГПа 1 )
    Бронза фосфористая, 5%, твердая 131,8 ГПа
    Фосфорно-бронзовая (92% Cu / 8% Sn или CuSn8)111 ГПа 1
    Сталь мягкая или инструментальная 212 ГПа
    Сталь мягкая, низкоуглеродистая 210 ГПа
    Сталь мягкая (закаленная) 201.4 ГПа
    Сталь нержавеющая 215,2 ГПа (190 ГПа 1 )
    Сталь инструментальная (закаленная) 203,2 ГПа

    Следует отметить, что это теоретические значения.

    Типичное значение для стальной гитарной струны можно принять как 205 ГПа.

    Значения, указанные для фосфористой бронзы, различаются: кажется, что они будут зависеть от того, является ли материал «пружинным» или «экстрапружинным» типом фосфористой бронзы 92% Cu / 8% Sn. обычно используется в переключателях с защелкой.

    1 Шигли, отдел машиностроения, 1980, McGraw Hill

    Примечания к единицам и размерам

    1 Па = 1 Н · м -2 = 10 -6 Н · мм -2 = 10 -6 кг · м · с -2 · мм -2 = 1 г · мм -1 · с -2

    Чтобы получить силу F в приведенных выше уравнениях, массу нужно умножить на гравитационную постоянную г (9.81 м · с -2 , или, что нам удобнее, 9810 мм · с -2 )

    Размеры модуля Юнга E составляют ML -1 T -2
    Размеры усилия F составляют L 2 ML -1 T -2 = MLT -2
    Размеры момента инерции I L 4

    © Расс Эллиотт

    , впервые опубликовано 19 апреля 2000 г .;
    небольшая редакционная правка, август 2001 г .;
    уравнение для промежуточной нагрузки на балку с двумя фиксированными опорами исправлено, и уравнение прогиба для промежуточной / центральной нагрузки на балку с одной фиксированной и одной простой опорой повторно выражено, январь 2005 г .; Диаграмма
    для свисающей нагрузки на балку, ограниченную двумя простыми опорами, пересмотрена 8 октября 2009 г .;
    Уравнение промежуточной нагрузки на балку с двумя неподвижными опорами исправлено, 30 декабря 2010 г.

    Колебания консольных балок:

    Колебания консольных балок:







    Колебания консольных балок:

    Отклонение, частота и использование в исследованиях



    Для: Dr.Негахбан

    EngrM 325H





    Скотт Уитни

    23 апреля 1999 г.

    Введение

    Измерение свойств тонкой пленки затруднено по сравнению с сыпучие материалы. Один из методов определения модуля упругости тонкого фильм взят из частотного анализа консольной балки. Прямая, горизонтальная консольная балка под действием вертикальной нагрузки деформируется в кривую.Когда это сила снимается, балка вернется в первоначальную форму; Однако, его инерция будет удерживать луч в движении. Таким образом, балка будет вибрировать на его характерные частоты. Если на луч напыляется тонкая пленка, будет изменена жесткость на изгиб. Это изменение вызывает частоту колебаний сдвинуть. Если сдвиг частоты измерен, пленки модуль упругости можно рассчитать.

    Установка тонкой консольной балки

    Балки, изучаемые в этой статье, представляют собой длинные, тонкие консольные балки.Рисунок 1 ниже показана такая балка. Один конец балки закреплен, а другой конец свободен. Начало координатной оси находится на фиксированном конце, точка А . Типичная балка, использованная в этом исследовании, имеет длину L, = 30 мм, Вт = Шириной 5 мм и т = толщиной 0,5 мм. Материал балки необходимо выбрать так что его жесткость отличается от жесткости тонких пленок, так что частотный сдвиг значительный. В данном исследовании использовались пленки оксида цинка (около Толщиной 5м), поэтому хорошая подложка — алюминий.

    Рисунок 1: Изученная типичная консольная балка

    Прогиб консольной балки

    Если свободный конец консольной балки подвергается точечной нагрузке, P , луч отклонится в кривую. См. Рисунок 2 ниже. Чем больше нагрузка, тем больше прогиб, (x) .

    Рисунок 2: Прогиб консольной балки под нагрузкой на неподвижном конце

    Предполагая, что балка претерпевает небольшие отклонения, находится в линейно-упругой области и имеет однородное поперечное сечение, следующие уравнения могут быть использовал (Гир, стр.602).

    Кривизна балки ,, равна второй производной прогиба

    Кривизна также может быть связана с изгибающим моментом, M , и жесткость на изгиб, EI, где E — модуль упругости балки, а I — момент инерции. Изгибающий момент в балке может быть связан с поперечной силой, В , и боковая нагрузка на балку q .Таким образом, (1а, б, в) Для нагрузки, показанной на рисунке 2, распределенная нагрузка, поперечная сила и изгибающий момент составляет: Таким образом, решение уравнения (1a) есть

    (2а)

    На свободном конце балки смещение составляет: (2b) Колебания балок

    -Определение уравнений

    Когда сила P снимается со смещенной балки, балка вернется к своей первоначальной форме.Однако инерция балки вызовет луч вибрирует вокруг этого исходного местоположения. Предполагая, что эластичный модуль, инерция и площадь поперечного сечения ( A ) постоянны вдоль длина балки, уравнение для этой вибрации (Volterra, стр. 310)

    (3) где линейная массовая плотность балки. Уравнение (3) лучше всего решается разделением переменных (Аткинс, стр. A29). Предположим, что перемещение можно разделить на две части, одна зависит от положения, а другая от времени. (х, t) = X (x) f (t) (4) где X не зависит от времени, а f не зависит от положения. Тогда уравнение (3) принимает вид

    Разделив уравнение (3) на X (x) f (t) : (5) Поскольку левая часть уравнения (5) не меняется при изменении t , правая часть должна быть постоянной. Аналогично, поскольку правая половина уравнения (5) не меняется при изменении x , левая половина должна быть постоянной.Поскольку каждая сторона постоянна, уравнение (4) действительно и метод может использоваться разделение переменных. Обозначим эту постоянную. Можно показать, что это реальная величина, и что — собственные частоты балки.

    Уравнение (5) теперь можно записать в виде двух дифференциальных уравнений (Вольтерра, п. 311),

    (6а, б) где (6c) Чтобы решить уравнение (6a), следующие граничные условия для консольная балка необходима

    Эти граничные условия исходят от опор консольной балки.Фиксированный конец должен иметь нулевое смещение и нулевой наклон из-за зажима. Свободный конец не может иметь изгибающий момент или усилие сдвига.

    Общее решение уравнения (6a) представляет собой линейную комбинацию тригонометрических уравнения (Вольтерра, стр.312)

    (7) Используя первое граничное условие, можно найти C 1 => Взяв первую производную уравнения (7) и используя вторую границу состояние, C 3 можно найти

    => Старшие производные уравнения (7) и остальные граничные условия дать (8а) (8b)

    Уравнения (8a) и (8b) можно объединить, чтобы получить

    (9) Таким образом, для консольной балки уравнение (7) сводится к

    (10)

    Согласно Volterra, p.312, константы C n равны произвольно. Однако для динамического решения смещения быть равным статическому решению (в момент времени t = 0), C 2 должно быть равно ½. С этим значением для C 2 , X n (0) = 0 и X n (L) = 1 .

    Подстановка уравнения (9) в (8a) или (8b) приведет к уравнение для консольной балки,

    (11) Частотное уравнение может быть решено для постоянных: k n L ; первые шесть показаны ниже на рисунке 3 (примечание, k n = 0 игнорируется, так как это означает, что стержень находится в состоянии покоя, поскольку = 0).Эти константы вместе с уравнением (6c) могут использоваться для нахождения естественного частоты консольной балки.

    Рис. 3. Константы колебаний консольной балки. Обратите внимание, поскольку cosh ( x ) большой, когда x большой, k n L требуется быть найденным с высокой точностью.

    Для каждой частоты существует характерная вибрация (Вольтерра, п. 319)

    (12) где A n зависит от начального положения в момент времени t = 0, и B n зависит от начальной скорости.В этом исследовании, балка начинает вибрировать при смещении и в состоянии покоя. Таким образом, B n = 0 а также (13) Начальное смещение, (x, 0) , было найдено выше, уравнение (2a). Уравнение (13) можно решить аналитически с помощью компьютерной математической программы,

    -Примеры режимов вибрации

    Типичные значения A n и частоты (для используемых лучей в этом исследовании) показаны на рисунке 3 выше.Обратите внимание, что только первый несколько видов колебаний имеют существенно большие значения для константы А № . Таким образом, колебательными модами более высокого порядка можно пренебречь. Чтобы получить полное смещение консольной балки, просто сложите все смещения, найденные в уравнении (12) для каждой моды. Ниже на рисунке 4 показано смещение, вызванное каждой модой при т = 0; также включен полное начальное смещение балки. Из этих смещений очевидно, что даже третья характеристическая мода мало влияет на полное перемещение балки.

    Рис. 4: Начальное смещение, вызванное каждой модой.

    Со временем каждая мода будет колебаться вокруг нулевого смещения. линии с частотой, указанной на рисунке 3 выше. На рисунке 5 ниже показано эта вибрация для первых двух режимов, более высокие моды действуют аналогично. В общее движение луча сложное; каждая характерная мода колеблется с разного размера, формы и частоты.

    Следующие файлы можно загрузить, чтобы просмотреть анимацию первого несколько режимов и полная вибрация консольной балки.Чтобы просмотреть их, необходимо загрузить Lotus Screencam Player: Scplayer.exe

    Общее движение: 325Htot.exe
    1-й режим: 325h2st.exe
    2-й режим: 325h3nd.exe
    3-й режим: 325h4rd.exe
    4-й режим: 325h5th.exe

    На рисунке 6 ниже показаны показания пьезоэлектрического датчика, расположенного возле закрепленного конца балки; этот датчик показывает взаимодействие каждого режим вибрации.Также показана вибрация, предсказанная из уравнения (12). в этом месте. Фактические и прогнозируемые сигналы почти идентичны; основное различие между ними — демпфирование (вязкое и по Кельвину-Фойгту) колебаний высших порядков в реальном сигнале.

    Рисунок 5: Колебания первых двух характерных мод; другие режимы вибрировать аналогично. Время, t , в микросекундах.

    Рисунок 6: Сигнал ZnO от вибрирующей консольной балки по сравнению с теоретические колебания.

    Измерение модуля упругости для тонких пленок

    -Причина использования частотного анализа

    Если консольная балка покрыта напылением тонкой пленки, то изгиб изменится жесткость. Изменение жесткости напрямую повлияет на частоту колебаний балок. Таким образом, модуль упругости пленки может быть определяется из этого сдвига частоты. См. Рисунок 7 для схематического изображения. напыленного пучка; индекс s относится к подложке, а f относится к фильму.Обратите внимание, высота пленки сильно преувеличена, поскольку .

    Рис.7: Распылитель консольной балки, покрытый тонкой пленкой

    Теоретически жесткость можно определить по неподвижной балке. под нагрузкой, P , см. уравнения (2a, b). Предположим, что жесткость на изгиб был увеличен добавлением тонкой пленки к лучу. Тогда, предполагая, что нагрузка была постоянной, прогиб на свободном конце уменьшится.Для Типичная балка, описанная выше, это изменение смещения чрезвычайно мало. Например, алюминиевая балка с начальным смещением (на свободном конце) 0,55 мм будет иметь начальное смещение 0,49 мм при относительно толстый (8 м) ZnO фильм. Изменение 0,06 мм слишком мало, чтобы его можно было измерить обычным инструменты и более тонкая пленка ZnO (1 м) даст неизмеримую разницу в смещении. Таким образом, стационарный измерения модуля упругости пленок затруднены, если не невозможно.

    Однако тот же луч, покрытый ZnO, будет иметь основную частоту сдвиг с 329,7 Гц на 342,0 Гц. Любой осциллограф можно использовать для измерения колебания балок, см. рисунок 6 выше. Если берется достаточно точек данных, преобразование Фурье сигнала может измерять частотные сдвиги даже при малая как 0,2 Гц. Следовательно, частотный сдвиг может быть известен с помощью высокая точность, и модуль упругости пленок может быть рассчитан.

    -Определение уравнений

    Все уравнения, полученные в предыдущих разделах (1-13), все еще могут применяется к двухкомпонентной балке при изменении нескольких постоянных: EI заменяется на E s I s + E f I f и исправлено как показано ниже.Заявленные ранее предположения все еще должны выполняться: малые прогибы, линейно-упругие и однородное поперечное сечение. Последний Из этого предположения следует, что толщина пленки не может меняться вдоль луча (затруднительно делать при напылении покрытия длинных балок).

    Линейная массовая плотность балки с покрытием теперь равна

    Центр масс, а также инерция балки с покрытием сместятся

    Уравнение (6c) используется для измерения модуля упругости пленки. от сдвига частоты.(14)

    (15)

    Поскольку амплитуды более высоких мод колебаний настолько малы, см. Рис. 4 уравнение (15) решается с использованием основной частоты n = 1.

    Заключение

    Из-за небольшого размера тонких пленок обычные методы измерения их свойства часто не работают. Эти свойства тонкой пленки могут отличаться от свойств сыпучего материала. Поэтому альтернативные методы измерения должны быть развиты.Вибрация консольных балок — один из таких методов. Это не ограничивается только определением модуля упругости; Другие полезная информация, такая как пьезоэлектрические постоянные, может быть определена из консольных балок.

    Цитируемые работы

    Аткинс, П. У. Физическая химия . 5 -е изд. Нью-Йорк: У. Х. Фриман и компания, 1994.

    Гир Дж. М., Тимошенко С. П. Механика материалов .4 -й изд. Бостон: Издательство PWS, 1997.

    Вольтера Э., Захманоглу Э. К. Динамика колебаний . Колумбус, Charles E. Merrill Books, Inc., 1965.



    PPT — Прогиб балок Презентация PowerPoint, скачать бесплатно

  • 9 Прогиб балок

  • Прогиб балок Деформация балки под действием поперечного нагружения Уравнение упругой кривой Прямое определение упругой кривой по Нагрузка Di… Пример задачи о статически неопределенных балках 9.1 Пример задачи 9.3 Метод наложения Пример задачи 9.7 Применение суперпозиции к статически неопределенным … Пример задачи 9.8 Применение теорем о моменте и площади к консольным балкам и балкам с симметричными … Образцами диаграмм моментов изгиба по частям Проблема 9.11 Применение теорем момент-площадь к балкам с несимметрией … Максимальное отклонение Использование теорем момент-площадь со статически неопределенным …

  • Связь между изгибающим моментом и кривизной для чистого изгиба остается в силе для общих поперечных нагрузок .• Консольная балка, подверженная сосредоточенной нагрузке на свободном конце, • На свободном конце A, • На опоре B, деформация балки при поперечной нагрузке • Кривизна изменяется линейно в зависимости от x

  • Реакции на A и C • Диаграмма изгибающего момента • Кривизна равна нулю в точках, где изгибающий момент равен нулю, т. Е. На каждом конце и в точке E. Деформация балки при поперечной нагрузке • Свисающая балка • Балка вогнута вверх, где изгибающий момент положительный, и вогнута вниз, где это отрицательно.• Максимальная кривизна возникает там, где величина момента максимальна. • Уравнение формы балки или упругой кривой требуется для определения максимального прогиба и наклона.

  • Из элементарного расчета, упрощенного для параметров балки, • Подстановка и интегрирование, Уравнение упругой кривой

  • Константы определяются из граничных условий • Три случая для статически определяемых балок, • Балка с простой опорой • Свисающая балка • Консольная балка Уравнение упругой кривой • Более сложные нагрузки требуют нескольких интегралов и применения требования непрерывности смещения и наклона.

  • Для балки, подверженной распределенной нагрузке, • Уравнение для смещения балки принимает вид • Четырехкратное интегрирование дает прямое определение упругой кривой из распределения нагрузки • Константы определяются из граничных условий.

  • Рассмотрим балку с фиксированной опорой в точке A и роликовой опорой в точке B. • На диаграмме свободного тела обратите внимание на четыре неизвестных компонента реакции. • Условия статического равновесия текучести. Балка статически неопределима.• Также имеется уравнение отклонения балки, которое вводит два неизвестных, но дает три дополнительных уравнения из граничных условий: Статически неопределенные балки

  • Для части AB нависающей балки (a) выведите уравнение для упругой кривой, (б) определить максимальный прогиб, (в) оценить ymax. Пример задачи 9.1 • РЕШЕНИЕ: • Разработайте выражение для M (x) и выведите дифференциальное уравнение для упругой кривой. • Дважды интегрировать дифференциальное уравнение и применить граничные условия, чтобы получить упругую кривую.• Найдите точку нулевого наклона или точку максимального отклонения. • Оцените соответствующий максимальный прогиб.

  • РЕШЕНИЕ: • Разработайте выражение для M (x) и выведите дифференциальное уравнение для упругой кривой. • Реакции: • Из диаграммы свободного тела для раздела AD, • Дифференциальное уравнение для упругой кривой, Пример задачи 9.1

  • Проинтегрируйте дифференциальное уравнение дважды и примените граничные условия для получения упругой кривой.Подстановка, пример задачи 9.1

  • Найдите точку нулевого наклона или точку максимального отклонения. • Оцените соответствующий максимальный прогиб. Пример задачи 9.1

  • Для однородной балки определите реакцию в точке A, выведите уравнение для упругой кривой и определите наклон в точке A. (Обратите внимание, что балка является статически неопределимой в первой степени). 9.3 • РЕШЕНИЕ: • Составьте дифференциальное уравнение для упругой кривой (будет функционально зависеть от реакции в точке A).• Проинтегрируйте дважды и примените граничные условия, чтобы найти реакцию в точке A и получить кривую упругости. • Оцените наклон в A.

  • Рассмотрите момент, действующий на участке D, • Дифференциальное уравнение для упругой кривой, Пример задачи 9.3

  • Интегрируйте дважды • Примените граничные условия: Пример задачи 9.3

  • Замените C1, C2 и RA в уравнении упругой кривой, • Продифференцируйте один раз, чтобы найти наклон, при x = 0, Пример задачи 9.3

  • Метод наложения • Принцип наложения: • Деформации балок, подвергнутых комбинациям нагрузок, могут быть получены как линейная комбинация деформаций от отдельных нагрузок. • Процедура упрощена таблицами решений для общих типов нагрузки и опоры.

  • Для показанной балки и нагрузки определите наклон и прогиб в точке B. РЕШЕНИЕ: S

    • Анализ долгосрочного прогиба с использованием программы SAFE |