Правильный восьмиугольник как построить: Как начертить восьмиугольник с помощью циркуля

Как начертить восьмиугольник с помощью циркуля

Деление окружности на равные части и по­строение правильных вписанных многоуголь­ников можно выполнить как циркулем, так и с помощью угольников и рейсшины.

Деление окружности на четыре равные части и построение пра­вильного вписанного четырех­угольника. Две взаимно перпендикулярные центровые линии делят окружность на четыре равные части (рис. 115, а). Соединив точки пе­ресечения этих линий с окружностью прямы­ми, получают правильный вписанный четырех­угольник.

Деление окружности на восемь равных частей и построение пра­вильного вписанного восьмиуголь­ника. Две взаимно перпендикулярные линии, проведенные под углом 45° к центровым ли­ниям с помощью угольника с углами 45, 45 и 90° и рейсшины (рис. 115, б), вместе с центро­выми линиями разделят окружность на восемь равных частей.

Деление окружности на восемь равных час­тей можно выполнить циркулем. Для этого из точек 1 и 3 (точки пересечения центровых линий с окружностью) произвольным радиусом делаются засечки до взаимного пересечения, тем же радиусом делают две засечки из точек 3 и 5 (рис.

115, в). Через точки пересечения засечек и центр окружности проводят прямые линии до пересечения с окружностью в точках 2, 4, 6, 8.

Если полученные восемь точек соединить последовательно прямыми линиями, то полу­чится правильный вписанный восьмиугольник (рис. 115, в).

Деление окружности на три рав­ные части и построение правиль­ного вписанного треугольника вы­полняют с помощью циркуля или угольника с углами 30, 60 и 90° и рейсшины.

При делении окружности циркулем на три равные части из любой точки окружности, на­пример из точки Л пересечения центровых ли­ний с окружностью (рис. 116, а и б), проводят дугу радиусом R, равным радиусу данной ок­ружности, получают точки 1 и 2. Третья точка деления (точка 3) будет находиться на про­тивоположном конце диаметра, проходящего через точку Л. Последовательно соединив точ­ки 1, 2 и 3, получают правильный вписанный треугольник. При построении правильного впи­санного треугольника, если задана одна из его вершин, например точка 1, находят точку А.

Для этого через заданную точку 1 проводят диаметр (рис. 116, в). Точка А будет находить­ся на противоположном конце этого диаметра. Затем проводят дугу радиусом R равным ра­диусу данной окружности, получают точки 2 и 3.

При делении окружности на три равные час­ти с помощью угольника и рейсшины через точку 1 под углом 60° проводят две прямые линии до пересечения с окружностью в точках 2 и 3 (рис. 117, а, б), точки 2 и 3 соединяют и получают правильный вписанный треугольник (рис. 117, в).

Деление окружности на шесть равных частей и построение пра­вильного вписанного шестиуголь­ника выполняют с помощью угольника с уг­лами 30, 60 и 90° и рейсшины или циркуля. При делении окружности на шесть равных частей циркулем из двух концов одного диа­метра радиусом, равным радиусу данной окруж­ности, проводят дуги до пересечения с окруж­ностью в точках 2, 6 и 3, 5 (рис. 118). Последовательно соединив полученные точки, полу­чают правильный вписанный шестиугольник. Деление окружности на шесть равных час-1ен и построение правильного вписанного шестиугольника с помощью угольника и рейс­шины показано на рис.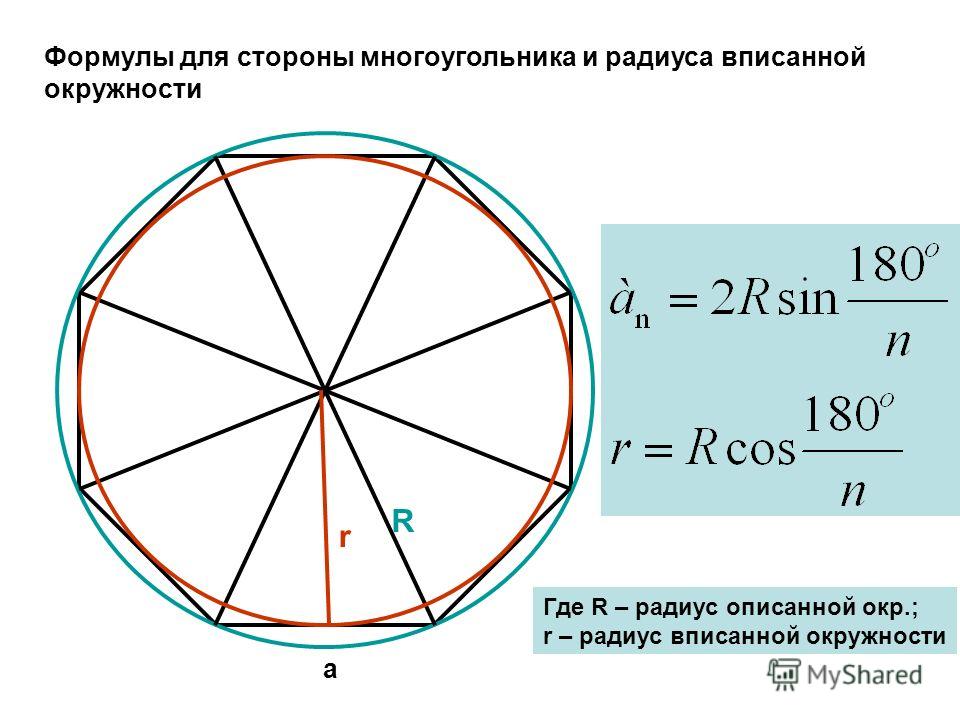

119 и 120. Деление окружности на двенад­цать равных частей и построение правильного вписанного двенад­цатиугольника выполняют с помощью угольника с углами 30, 60 и 90° и рейсшины или циркуля.

При делении окружности циркулем из четы­рех концов двух взаимно перпендикулярных диаметров окружности проводят радиусом, рав­ным радиусу данной окружности, дуги до пере­сечения с окружностью (рис. 121). Соединив по­лученные точки, получают двенадцатиугольник.

При построении двенадцатиугольника с по­мощью угольника и рейсшины точки деления строят, как показано на рис. 119 и 120.

Деление окружности на пять и десять равных частей и построе­ние правильного вписанного пяти­угольника и десятиугольника пока­зано на рис. 122.

Половину любого диаметра (радиус) делят пополам (рис. 122, а), получают точку А. Из точки А, как из центра, проводят дугу радиу­сом, равным расстоянию от точки А до точки

1, до пересечения со второй половиной этого диаметра, в точке В (рис. 122, б). Отрезок 1В равен хорде, стягивающей дугу, длина которой равна 1 /₅ длины окружности. Делая засечки на окружности (рис. 122, в) радиусом R, равным отрезку 1В, делят окруж­ность на пять равных частей. Начальную точку 1 выбирают в зависимости от расположения пятиугольника. Из точки / строят точки 2 и 5 (рис. 122, в), затем из точки 2 строят точку 3, а из точки 5 строят точку 4. Расстояние от точки 3 до точки 4 проверяют циркулем; если расстояние между точками 3 и 4 равно отрезку 1В, то построения были выполнены точно. Нельзя выполнять засечки последовательно, в одну сторону, так как происходит набегание ошибок и последняя сторона пятиугольника получается перекошенной. Последовательно соединив найденные точки, получают пяти­угольник (рис. 122, г).

Деление окружности на десять равных час­тей выполняют аналогично делению окруж­ности на пять равных частей (рис. 122), но сначала делят окружность на пять частей, на­чиная построение из точки /, а затем из точ­ки 6, находящейся на противоположном конце диаметра (рис. 123, а). Соединив последова­тельно все точки, получают правильный впи­санный десятиугольник (рис. 123, б).

Деление окружности на семь и четырнадцать равных частей и по­строение правильного вписанного семиугольника и четырнадцатиугольника показано на рис. 124 и 125.

Из любой точки окружности, например точ­ки Л, радиусом заданной окружности проводят дугу (рис. 124, а) до пересечения с окруж­ностью в точках В и D. Соединим точки В и D прямой. Половина полученного отрезка (в данном случае отрезок ВС) будет равна хорде, которая стягивает дугу, составляющую 1 /₇ дли­ны окружности. Радиусом, равным отрезку ВС, делают засечки на окружности в последова­тельности, показанной на рис. 124, б. Соединив последовательно все точки, получают правиль­ный вписанный семиугольник (рис.

124, в).

Деление окружности на четырнадцать рав­ных частей выполняется делением окружности на семь равных частей два раза от двух точек (рис. 125, а).

Сначала окружность делится на семь рав­ных частей от точки /, затем то же построение выполняется от точки 8. Построенные точки соединяют последовательно прямыми линиями и получают правильный вписанный четырна-дцатиугольник (рис. 125, б).

СОПРЯЖЕНИЯ

Рассматривая детали, видим, что в их конст­рукции часто одна поверхность переходит в другую. Обычно эти переходы делают плав­ными, что повышает прочность деталей и де­лает их более удобными в работе. На чертеже поверхности изображаются линиями, которые также плавно переходят одна в другую.

На рис. 126, а изображена деталь, в которой плавные переходы одних плоскостей в другие представляют собой цилиндрические поверхнос­ти. На чертеже (рис. 126, б) эти плоскости изо­бражены прямыми линиями, а цилиндрические поверхности — дугами окружностей. Плавные переходы от одной прямой к другой в этих случаях выполняются дугой заданного радиуса.

Плавный переход одной цилиндрической поверхности в другую может являться цилинд­рической поверхностью (рис. 127, а). На черте­же эти цилиндрические поверхности изобра­жены дугами окружностей, (рис. 127, б). В этом случае плавный переход одной дуги окруж­ности в другую осуществляется дугой окруж­ности заданного радиуса.

На рис. 126, а и 127, а рассмотрены простей­шие примеры плавных переходов поверхностей. В чертежах более сложных деталей плавные переходы между поверхностями изображают­ся различными сочетаниями прямых, окруж­ностей и их дуг. Вариантов таких сочетаний может быть много, но их объединяет од­но — плавность перехода. Такой плавный пе­реход одной линии (поверхности) в другую ли­нию (поверхность) называют сопряжени­ем. При построении сопряжения необходимо определить границу, где кончается одна линия и начинается другая, т. е. найти на чертеже точку перехода, которая называется точкой сопряжения или точкой касания.

Задачи на сопряжения условно можно раз­делить на три группы.

Первая группа задачвключает в себя зада­чи на построение сопряжений, где участвуют прямые линии. Это может быть непосредствен­ное касание прямой и окружности, сопряжение двух прямых дугой заданного радиуса, а также проведение касательной прямой к двум окружностям.

Построение окружности, каса­тельной к прямой, связано с нахождени­ем точки касания и центра окружности.

Задана горизонтальная прямая АВ, требует­ся построить окружность радиусом R, касательную к данной прямой (рис. 128). Точка касания выбирается произвольно. Так как точка касания не задана, то окружность ра­диуса R может коснуться данной прямой в любой точке. Таких окружностей можно про­вести множество. Центры этих окружностей (O₁, О₂и т. д.) будут находиться на одина­ковом расстоянии от заданной прямой, т. е. на линии, расположенной параллельно заданной прямой АВ на расстоянии, равном радиусу заданной окружности (рис. 128). Назовем эту линию линией центров. Проведем линию центров параллельно прямой АВ на расстоя­нии R. Так как центр касательной окруж­ности не задан, возьмем любую точку на линии центров, например точку О. Прежде чем про­водить касательную окружность, следует опре­делить точку касания. Точка касания будет лежать на перпендикуляре, опущенном из точ­ки О на прямую АВ. В пересечении перпендику­ляра с прямой АВ получим точку К, которая будет точкой касания. Из центра О радиусом R от точки К проведем окружность. Задача решена.

В детали, которая изображена на рис. 129, а, пластина плавно переходит в цилиндр. При выполнении чертежа этой детали необходимо построить плавный переход прямой в окруж­ность.

Задача аналогична предыдущей, но до­полнена условием, что точка касания задана, так как задан размер А (рис. 129, б), который определяет величину прямолинейного участка.

Отложив размер Л, находят точку касания (точку /С), затем из точки К восставляют пер­пендикуляр, на котором откладывают радиус R заданной окружности, и находят центр ок­ружности (точку О). При обводке сначала от точки касания проводится дуга заданного ра­диуса, а потом — прямая.

Из сказанного следует:

1) центр окружности, касательной к прямой, лежит на прямой (линия центров), проведенной параллельно заданной прямой, на расстоянии, равном радиусу данной окружности;

Не нашли то, что искали? Воспользуйтесь поиском:

Ответ

Проверено экспертом

Вспомогательная задача:
Разделить данный отрезок АВ пополам или провести серединный перпендикуляр к отрезку (рис. 1 внизу)
Из концов отрезка АВ одним и тем же радиусом, большим половины отрезка АВ провести две дуги. Через точки их пересечения проводим прямую. Это серединный перпендикуляр к отрезку АВ.

Построение правильного восьмиугольника:
Проводим диаметр АВ. Строим CD — серединный перпендикуляр к АВ.
Хорду СВ делим пополам — прямая KL.
Хорду АС делим пополам — прямая MN.
Соединяем точки A, M, C, K, B, N, D и L. Получили правильный восьмиугольник.

Построение правильного пятиугольника.
Строим два перпендикулярных диаметра АВ и CD.
Делим пополам отрезок ОА — точка Е.
Из Е радиусом ЕС проводим дугу, которая пересекает ОВ в точке F.
Из С радиусом CF проводим дугу, которая пересекает окружность в точке G. CG — сторона правильного пятиугольника.
Проводим радиусом CG из точки G как из центра дугу, которая пересекает окружность в точке K. GK — вторая сторона.
И т.д.
Получаем правильный пятиугольник CGKLM.

Есть ли поблизости от Вас карандаш? Взгляните-ка на его сечение – оно представляет собой правильный шестиугольник или, как его еще называют, гексагон. Такую форму имеет также сечение гайки, поле гексагональных шахмат, кристаллическая решетка некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты. Гигантский правильный шестиугольник был недавно обнаружен в атмосфере Сатурна. Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим эту фигуру поподробнее.

• Длина его сторон соответствует радиусу описанной окружности. Из всех геометрических фигур это свойство имеет лишь правильный шестиугольник.
• Углы равны между собой, и величина каждого составляет 120°.
• Периметр гексагона можно найти по формуле Р=6*R, если известен радиус описанной вокруг него окружности, или Р=4*√(3)*r, если окружность в него вписана. R и r – радиусы описанной и вписанной окружности.
• Площадь, которую занимает правильный шестиугольник, определяется следующим образом: S=(3*√(3)*R 2 )/2. Если радиус неизвестен, вместо него подставляем длину одной из сторон – как известно, она соответствует длине радиуса описанной окружности.

Теперь рассмотрим построение правильного шестиугольника. Есть несколько способов, самый простой из которых предполагает использование циркуля, карандаша и линейки. Вначале рисуем циркулем произвольную окружность, затем в произвольном месте на этой окружности делаем точку. Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек. Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.

Наверняка каждому из нас приходилось сталкиваться с тем, что нужно срочно что-то начертить, точный угол или многоугольник, а транспортира как нарочно под рукой нет, или Вы вообще никогда раньше ничего не чертили. Сегодня я хочу поделиться с Вами простыми схемами построения фигур на плоскости. Думаю, этот навык пригодится всем. Продолжение статьи:
http://www.livemaster.ru/topic/383001-postroenie-na-ploskosti-chast-2?ins >

Нам понадобятся: карандаш, линейка, циркуль.

Построение угла в 60

1. Проведём прямую и отметим на ней точку А.

2. Из точки А проведём дугу произвольного радиуса и получим точку В.

3. Из точки В проведём дугу радиуса АВ, чтобы она пересекла ранее начерченную дугу.

4. Проведённая через точку пересечения (С) и точку А прямая будет второй стороной требуемого угла.

Построение угла в 45

1. Построим угол 60, кака описано выше.

2. Разделим полученный угол пополам.

3. Угол между лучами 60 и 30 разделим пополам. В результате получим угол в 45.

Построение угла в 75

1. Построим угол в 60, как описано выше, и разделим его пополам.

2. В ходе дальнейшего деления надвое получим угол в 15.

3. Отразим угол в 15 через луч 60 и так получим угол в 75.

Построение угла в 90

1. Построим угол в 60, как описано выше, и разделим его пополам.

2. Получившийся угол в 30 через луч 60 и так получим угол точно в 90.

Разделение отрезка на равные части.

1. Проведём прямую и отметим на ней отрезок АВ.

2. Из точки А проведём вспомогательную прямую и разделим её на столько одинаковых частей, на сколько требуется разделить отрезок АВ. Делить будем при помощи циркуля. Последнюю точку обозначим буквой С.

3. Последнюю точка (С) соединим с концом отрезка АВ. Построим рад параллельных отрезку СВ прямых по всей длине отрезка АВ. Точки пересечения параллельных прямых с отрезком АВ и будут точками раздела отрезка на несколько равных частей.

Построение правильного пятиугольника.

1. Проведём окружность радиусом 50 мм. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.

2. Разделим пополам расстояние ОВ. Разведём ножки циркуля на расстояние FC . Из точки F проведём дугу через С. Дуга пересечёт горизонтальную линию в точке G .

3. Расстояние CG будет длиной стороны пятиугольника. Из вершины С отложим пять раз расстояние CG .

Построение правильного шестиугольника.

1. Проведём окружность радиусом 50 мм.

2. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.

3. Из точки А на линии окружности отложим шесть раз радиус нашей окружности. Соединив прямыми точки пересечения, получим шестиугольник.

Построение правильного семиугольника.

1. Проведём окружность заданного радиуса. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.

2. Из точки D проведём дугу радиусом равным радиусу окружности.

3. Дуга пересечёт окружность в точках E и G .

4. Длина отрезка EF на хорде EG равна длине стороны семиугольника. Из вершины С семь раз отложим расстояние EF .

Общий метод построения многоугольников.

1. Проведём окружность радиусом 50 мм. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии. Продолжим горизонтальную лини. За точки А и В.

2. Из точки D проведём дугу радиусом, равным радиусу окружности так, чтобы дуга пересекла горизонтальную линию.

3. При помощи вспомогательной прямой разделим вертикальную линию на столько равных частей, сколько сторон многоугольника требуется получить. Для примера показано построение одиннадцатиугольника.

4. Из точки Е проведём прямые через нечётные точки раздела вертикальной линии так, чтобы эти прямые пересекли окружность. Такую же операцию проведём из точки G . Полученные лучи пересекают окружность в точках, соединив которые прямыми получаем одиннадцатиугольник.

Первый способ — по данной стороне S с помощью транспортира.

Проводим прямую и откладываем на ней AB = S; принимаем эту линию за радиус и этим радиусом из точек A и В описываем дуги: далее с помощью транспортира строим в этих точках углы в 108°, стороны которых пересекутся с дугами в точках С и D; из этих точек радиусом АВ = 5 описываем дуги, которые пересекутся в Е, и прямыми линиями соединяем точки Л, С, Е, D, В.

Полученный пятиугольник — искомый.

Первый способ построения пятиугольника

Второй способ. Проведем окружность радиусом r. Из точки А циркулем проводим дугу радиуса AM до пересечения в точках В и С с окружностью. Соединяем В и С линией, которая пересечет горизонтальную ось в точке Е.

Затем из точки Е проводим дугу, которая пересечет горизонтальную линию в точке О. Описываем, наконец, из точки F дугу, которая пересечет окружность в точках Н и К. Отложив по окружности расстояние FO = FH = FK пять раз и соединив точки деления линиями, получим правильный пятиугольник.

Второй способ построения пятиугольника

Третий способ. В данный круг вписать правильный пятиугольник. Проводим два взаимно перпендикулярных диаметра АВ и МС. Делим радиус АО точкой Е пополам. Из точки Е, как из центра, проводим дугу окружности радиуса ЕМ и засекаем ею диаметр АВ в точке F. Отрезок MF равен стороне искомого правильного пятиугольника. Раствором циркуля, равным MF, делаем засечки N₁, Р₁, Q₁, К₁ и соединяем их прямыми.

Третий способ построения пятиугольника

На рисунке построен шестиугольник по данной стороне.

Построение шестиугольника

Прямой АВ = 5, как радиусом, из точек А и В описываем дуги, которые пересекутся в С; из этой точки тем же радиусом описываем окружность, на которой сторона А В отложится 6 раз.

Шестиугольник ADEFGB — искомый.

«Отделка комнат при ремонте»,
Н.П.Краснов

Маляру часто приходится иметь дело с правильными многоугольниками, а также треугольниками и четырехугольниками, т. е. такими фигурами, у которых все стороны и, соответственно, углы равны между собой. Может встретиться необходимость построить правильный многоугольник по данной стороне, или вписать правильный многоугольник в окружность данного радиуса, или описать его вокруг окружности. Первый вопрос сводится к нахождению внутреннего…

Построение вписанных и описанных правильных многоугольников сводится, как уже было сказано, к делению окружности на столько равных частей, сколько в многоугольнике сторон. Однако точное деление окружности путем геометрического построения возможно лишь на 3, 4, 5 и 15 равных частей, а также при делении на число частей, получаемое последовательным удвоением этих чисел. В остальных случаях приходится…

Построение овала (коробовой кривой) по данной длине АВ. Делим длину ЛВ на 3 равные части и из D и Е радиусом DF описываем дуги которые пересекутся в F и G; соединяем D и E c F и G и продолжаем эти прямые, как на фигуре; далее радиусом AD = BE из точек D и Е…

Первый способ построения. Проводим горизонтальную (АВ) и вертикальную (CD) оси и из точки их пересечения М откладываем в соответствующем масштабе полуоси. Наносим малую полуось от точки М на большой оси до точки Е. Эллипс, первый способ построения Делим BE на 2 части и одну наносим от точки М на большой оси (до F или H)…

Основанием для нанесения росписи служат полностью законченные окраской поверхности стен, потолков и других конструкций; роспись делается по высококачественным клеевым и масляным окраскам, сделанным под торцовку или флейц. Приступая к разработке эскиза отделки, мастер должен ясно представить себе всю композицию в бытовой обстановке и отчетливо осознать творческий замысел. Только при соблюдении этого основного условия можно правильно…

«>

Что-то я туплю.. Как начертить правильный восьмиугольник по стороне? — Спрашивалка

АН

Александр Наумов

Что-то я туплю.. Как начертить правильный восьмиугольник по стороне?

А по стороне то как? Вот сторона 2,5 см. Какой диаметр окружности будет тогда?

• сторона

МТ

Марина Толстикова

Умеете построить угол 45 градусов?
Для этого надо от конца первой стороны построить угол -90 и в нём построить биссектрису продлите биссектрису в противоположную сторону и отложите туда длину стороны.

Всё повторить ещё 5 раз и замкнуть 8-угольник.

Если не нравится,
1. нарисуйте перекрестье двух перпендикулярных линий
2. постройте биссектрисы всех четырёх прямых углов
3. получили 8 лучей, надо к каждому лучу построить по две параллельные линии,
отстоящие на половину стороны 8-угольника, Длина этой стороны должна быть задана в начале задания.
4. Не принимая во внимание 8 первоначальных лучей, найдите точки пересечения всех остальных шестнадцати линий, соедините 8 точек, лежащих дальше всего от центра, ломаной линией, поочерёдно переходя к следующей ближайшей точке. Получится правильный 8-угольник.

Зу

Зульфия

Ув. Джойстик. В вопросе автора длина стороны считается заданной.

А можно так.

1) Продолжить данный отрезок А1 в одну из сторон.
2) Провести перпендикуляр к отрезку А1.
3) Построить биссектрису полученного прямого угла.
4) На биссектрисе отложить новый отрезок А2 такой же длины,
как у А1.
5) Повторить 7 раз операции 1-4, начиная с отрезка А2.

Алексей 10

Только циркулем и линейкой? ! —не знаю.
А так — угол вычислить, и порядок.

АП

Анастасия Плотникова

При помощи циркуля проведите окружность. Отметьте ее центр.

2

Сделайте отметки на концах любого диаметра окружности. Это первые две вершины будущего восьмиугольника.

3

Установите раствор циркуля, равный диаметру окружности. Поставив иглу циркуля в одну из отмеченных на предыдущем этапе точек, сделайте засечки выше и ниже окружности. Старайтесь делать их не слишком короткими, поскольку они должны будут пересекаться с засечками, которые вы сделаете на следующем этапе.

4

Поставьте иглу циркуля в другую отмеченную точку и точно так же сделайте засечки выше и ниже окружности. Если провести прямую линию между точками пересечения засечек, то она пройдет через центр окружности, разделив первоначальный диаметр точно пополам, и будет к нему перпендикулярна.

5

Приложите линейку к двум найденным точкам и сделайте отметки на окружности там, где ее пересекает построенный перпендикуляр. Вы разделили окружность на четыре равные части, и найденные вами точки являются вершинами квадрата, вписанного в окружность. Первоначальный диаметр и его перпендикуляр, найденный на предыдущем этапе, служат диагоналями этого квадрата.

6

Чтобы завершить построение правильного восьмиугольника, нужно найти перпендикуляры к сторонам квадрата.

7

Установите раствор циркуля, равный стороне квадрата. Поместите иглу циркуля в любую вершину квадрата и сделайте засечки по обеим ее сторонам вне окружности.

8

Повторите процедуру с двумя вершинами квадрата, смежными с первой. У вас должны получиться две точки в местах пересечения засечек.

9

Приложите линейку так, чтобы она проходила через любую из найденных точек и центр окружности. Сделайте две отметки на окружности там, где ее пересекает полученная прямая. Повторите то же самое со второй найденной точкой. Теперь у вас есть восемь точек, делящих окружность на восемь равных частей. Это и есть вершины правильного восьмиугольника.

10

При помощи линейки соедините последовательно все восемь найденных точек. Построение завершено.

ЕС

Екатерина Скокова

Построить равнобедренный треугольник (любого размера) с углом при вершине 45.

На основании треугольника отложить отрезок с длиной, равной длине стороны восьмиугольника, который следует построить.

Из конца отрезка провести прямую, параллельную боковой стороне треугольника, примыкающей к началу отрезка, до пересечения её с второй боковой стороной треугольника.

Отрезок от вершины треугольника до найденной точки и будет являться радиусом окружности, описанной вокруг искомого 8-угольника.

Далее легко…

Похожие вопросы

кто может доступно объяснить как начертить правильный пятиугольник со сторонами 10 см?

Как найти сумму углов восьмиугольника?

чему равна площадь круга, вписанного в правильный восьмиугольник со стороной 1.

Можно ли начертить треугольник со сторонами 1,2,3 см

Вычесление площадь восьмиугольника.

Как начертить правильный, вписанный в окружность четырехугольник? Если можно, киньте ссылку с изображением.

сколько различных диагоналей можно провести в восьмиугольнике?

помогите решить задачу: Начерти два квадрата: сторона одного 3 см, сторона другого в 3 раза больше

Как начертить четырёхугольник с двумя смежными сторонами? Что для этого нужно сделать?

вычислите синус внутреннего угла правильного восьмиугольника Геометрия

25 способов построить восьмиугольник с помощью компаса #quiz_container»),$(‘

‘).insertBefore( «#newsletter_block_main»), ha(!0),b=document.getElementsByClassName(«scrolltomarker»),a=0;a

Скачать статью

Изучите эту статью

Скачать статью

Если вы хотите нарисовать восьмиугольник с помощью циркуля, вы попали по адресу. В этой статье мы объясним, как легко нарисовать ряд линий и точек, которые в конечном итоге образуют восьмиугольник. Если вы готовы начать, прокрутите вниз!

Шаги

1. Соберите материалы и обустройте рабочее место. Вам понадобится:

   • Механический компас с карандашом
   • Ластик для карандашей
   • Линейка
   • Запасной карандаш (рекомендуется)

Реклама

1. Сделайте линию длиной 9 дюймов. Для достижения наилучших результатов используйте маркировку светлым карандашом.

1. Отметьте среднюю точку и назовите ее «А». Это будет центр вашего восьмиугольника.

Реклама

1. Измерьте ширину кончика карандаша и стрелки компаса. Установите его на 3 дюйма.

1. Поверните ручку компаса, чтобы создать круг, как показано на рисунке. Будьте осторожны, стрелка компаса острая.

Реклама

1. Пометьте первую точку на левом конце буквой «B». Обозначьте вторую точку справа буквой «С».

1. Назовите самую верхнюю точку пересечения «D» и самую нижнюю точку «E».

Реклама

1. С помощью карандаша и линейки начертите вертикальную линию.

1. Назовите эту точку «F».

Реклама

1. Должен пересекаться в 2-х точках.

1. Обозначьте точку пересечения F и E буквой «H». Затем поместите линейку по кругу, выровняв ее рядом с точками A и H.

Реклама

1. Сделайте так, чтобы диаметр пересекал окружность в двух разных точках.

1. Нарисуйте диаметр, содержащий точки A и G. Убедитесь, что линия пересекает окружность еще в 2 точках. Пометьте 2 новых перекрестка следующим образом:

   • Самый верхний правый перекресток должен называться точкой K.
   • Крайний левый нижний перекресток должен называться точкой L.

Реклама

1. Назовите эту новую точку М.

1. Назовите эту новую точку N.

Реклама

1. Эти точки находятся в верхнем левом углу круга.

1. Повторите этот шаг со следующими точками:

   • Точки I и M, создающие отрезок IM
   • Точки M и K, образующие отрезок MK
   • Точки K и C, образующие отрезок KC
   • Точки C и J, образующие отрезок линии CJ
   • Точки J и N, образующие отрезок JN
   • Точки N и L, образующие отрезок линии NL
   • Наконец, точки L и B, образующие отрезок LB

Реклама

1. Теперь ваш восьмиугольник должен выглядеть так. Вы успешно построили восьмиугольник с помощью циркуля и линейки.

   • Как видите, поэтому лучше использовать светлые метки. В противном случае на вашем рисунке могут остаться трудно стираемые следы.

Поиск

Добавить новый вопрос

• Вопрос

  Должен ли он быть 6 дюймов?

  Нет, но где-то это должно быть пропорционально. Например, вы также можете сделать диаметр 3 дюйма, а это означает, что вам придется уменьшить другие размеры на 50%.

• Вопрос

  Мне нужно построить ту, у которой стороны 5см. Сколько дюймов я буду использовать для параметра?

  1 дюйм равен примерно 2 с половиной сантиметрам, поэтому 5 сантиметров составляют примерно 4 с половиной дюйма.

• Вопрос

  Как получить восемь равных сторон?

  Используйте линейку! Линейки полезны во многих отношениях. Вы также можете найти фигуры с 8 равными сторонами и скопировать их.

Посмотреть больше ответов

Задать вопрос

Осталось 200 символов

Укажите свой адрес электронной почты, чтобы получить сообщение, когда на этот вопрос будет дан ответ.

Отправить

Реклама

• Ознакомьтесь с тем, что такое дуга, отрезок и компас и как ими пользоваться.

  Спасибо! Мы рады, что это было полезно.
  Ищете более интересные способы обучения на wikiHow?
  Узнайте о себе с помощью тестов > или попробуйте нашу новую игру в слова Train Your Brain.

  Полезный 0 Не полезно 0

• Используйте светлые метки для облегчения последующего стирания.

  Спасибо! Мы рады, что это было полезно.
  Ищете более интересные способы обучения на wikiHow?
  Узнайте о себе с помощью тестов > или попробуйте нашу новую игру в слова Train Your Brain.

  Полезный 0 Не полезно 0

• Подобные формы можно найти в другом месте на wikiHow.

  Спасибо! Мы рады, что это было полезно.
  Ищете более интересные способы обучения на wikiHow?
  Узнайте о себе с помощью тестов > или попробуйте нашу новую игру в слова Train Your Brain.

  Полезный 0 Не полезно 0

Показать больше советов

Отправить

Спасибо, что отправили совет на рассмотрение!

Реклама

Реклама

Вещи, которые вам понадобятся

• Механический компас с карандашом
• Ластик для карандашей
• Линейка
• Запасной карандаш (рекомендуется)

Об этом изделии

• Печать
• Отправить фанатскую почту авторам

Спасибо всем авторам за создание страницы, прочитано 30,943 раза.

Реклама

Что такое Octagon? Определение, формула, свойства, примеры

Что такое форма восьмиугольника?

Эй! Я ВОСЬМИУГОЛЬНИК . Я принадлежу к семье ПОЛИГОН. Итак, что такое многоугольник? Очень простой. Это замкнутая плоская фигура с как минимум тремя прямыми сторонами и углами, обычно пятью или более. Вы уже знакомы с некоторыми членами моей семьи, такими как треугольник и квадрат.

Уверен, вы все видели восьмиугольный знак «Стоп»; он красный, и автомобили останавливаются, когда видят этот знак. Знак остановки обычно находится в форма восьмиугольника — замкнутая двумерная фигура с восемью сторонами и восемью вершинами.

Свойства восьмиугольника

• Это многоугольник с восемью сторонами и восемью углами.
• Всего в нем 20 диагоналей.

• Все его внутренние углы в сумме составляют 1080°.
• Сумма всех внешних углов равна 360°.

Типы восьмиугольников

В зависимости от размера сторон и углов восьмиугольники можно разделить на следующие типы:

• Регулярные и нерегулярные октагоны
• Выпуклый и вогнутые октагоны

Регулярные и нерегулярные Octagons

Регулярный Octagon

A Retural Octagon octagon и восьми 7016 a Retural Octagon Octagon

A Retural Octagon octagon и равный Angles . Все стороны имеют одинаковую длину, и все углы равны. Сумма внутренних углов равна 1080°, а сумма внешних углов равна 360°. В правильном восьмиугольнике внутренний угол при каждой вершине равен 135°.

Неправильный восьмиугольник

В неправильном восьмиугольнике восемь сторон и восемь углов не равны. Все стороны не равны по длине, и все углы не равны по размеру. Хотя внутренние углы имеют разную величину, в сумме они все равно составляют 1080°.

Выпуклые и вогнутые восьмиугольники

Выпуклые восьмиугольники

Восьмиугольник, у которого все углы направлены наружу или нет углов, направленных внутрь, является выпуклым восьмиугольником. Выпуклые восьмиугольники выпирают наружу. В выпуклом восьмиугольнике ни один из внутренних углов не больше 180°.

Вогнутый восьмиугольник

Восьмиугольник, в котором хотя бы один из углов направлен внутрь, имеет форму вогнутого восьмиугольника. Вогнутый восьмиугольник имеет по крайней мере один край, направленный внутрь. Это означает, что по крайней мере один из внутренних углов вогнутого восьмиугольника больше 180°.

Интересные факты

• Слово «восьмиугольник» произошло от греческого слова ὀκτάγωνον ( oktágōnon ), что означает восемь углов. Вот так фигура с восемью углами была названа восьмиугольником.
• В 1850-х и 1900-х годах многие люди начали строить свои дома в форме восьмиугольника, поскольку это символ, олицетворяющий возрождение, бесконечность, возрождение и переход.
• Зонты часто имеют восьмиугольную форму.

Периметр восьмиугольника

Периметр двумерной формы представляет собой общую длину границы. Это сумма длин всех сторон.

Периметр правильного восьмиугольника

Формула для расчета периметра правильного восьмиугольника = 8 ✕ стороны. Здесь «сторона» относится к длине равных сторон правильного восьмиугольника.

Периметр неправильного восьмиугольника

Для неправильного восьмиугольника периметр вычисляется путем сложения длин отдельных сторон. Таким образом, периметр будет равен сумме длин всех 8 сторон.

Решенные примеры

Пример 1. Если длина стороны правильного восьмиугольника равна 10 см, найдите его периметр.

Решение :

Длина стороны данного правильного восьмиугольника равна 10 см.

Формула для вычисления периметра правильного восьмиугольника: сторона 8 ✕.

Следовательно, периметр данного правильного восьмиугольника = 8 ✕ 10 = 80 см.

Пример 2. Если периметр правильного восьмиугольника равен 200 см, найдите длину его стороны.

Решение:

Периметр правильного восьмиугольника равен 200 см (дан).

Формула для вычисления периметра правильного восьмиугольника: сторона 8 ✕.

Следовательно,

8 ✕ сторона = 200

Сторона = $\frac{200}{8}$  = 25 см.

Пример 3. Найдите периметр неправильного восьмиугольника, стороны которого равны 6 см, 16 см, 14 см, 20 см, 12 см, 8 см, 10 см и 18 см.

Решение:

Длины сторон данного неправильного восьмиугольника равны 6 см, 16 см, 14 см, 20 см, 12 см, 8 см, 10 см и 18 см (данные).

Периметр неправильного восьмиугольника равен сумме длин всех 8 сторон.

Периметр = (6 + 16 + 14 + 20 + 12 + 8 + 10 + 18) см

Следовательно, периметр данного неправильного восьмиугольника = 104 см.

Практические задачи

Правильный восьмиугольник

Неправильный восьмиугольник

Вогнутый восьмиугольник

Ничего из вышеперечисленного

Правильный ответ: Неправильный восьмиугольник
Это потому, что стороны не имеют одинаковой длины.

200 см

100 см

180 см

160 см

Правильный ответ: 160 см
Формула для периметра правильного восьмиугольника = $8$ ✕ $сторона$.
Следовательно, периметр данного правильного восьмиугольника = $8$ ✕ $20$ = $160$ см.

135°

160°

1080°

360°

Правильный ответ: 135°
Размер каждого внутреннего угла правильного восьмиугольника равен 135°.

50 см

72 см

52 см

34 см

Правильный ответ: 52 см
Периметр неправильного восьмиугольника равен сумме длин всех 8 сторон.
Периметр $= (3 + 7 + 8 + 5 + 4 + 6 + 10 + 9)$ см
Периметр $= 52$ см.

Часто задаваемые вопросы

Все ли восьмиугольники называются восьмиугольниками?

Восьмиугольник является восьмиугольником только в том случае, если он замкнут и состоит из прямых линий.

Чему равна сумма углов неправильного восьмиугольника?

Углы неправильного восьмиугольника не равны.

No related posts.