Правильный семиугольник
Пользователи также искали:
правильный семиугольник оси симметрии,
правильный семиугольник углы,
семиугольник периметр,
сколько осей симметрии имеет правильный семиугольник,
семиугольник,
Правильный,
правильный,
Правильный семиугольник,
симметрии,
сколько,
семиугольник выпуклый,
семиугольник как начертить,
семиугольник периметр,
осей,
семиугольник по клеточкам,
имеет,
углы,
клеточкам,
выпуклый,
начертить,
периметр,
правильный семиугольник оси симметрии,
правильный семиугольник углы,
неправильный,
неправильный семиугольник,
сколько осей симметрии имеет правильный семиугольник,
правильный семиугольник,
cтатьи по геометрии.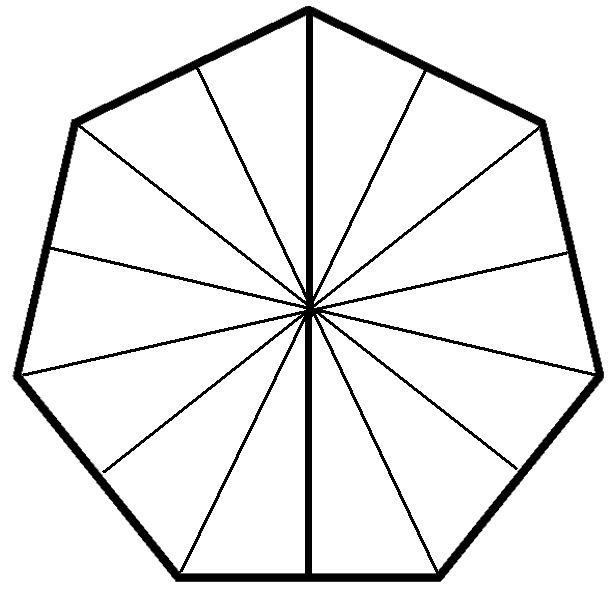
Как начертить правильный семиугольник
Сколько занимательных заданий порой получают школьники по геометрии. И очень часто решение геометрических задач на построение различных фигур находит свое отражение в черчении. К примеру, построить правильный семиугольник с помощью транспортира не составит школьнику труда, а вот выполнить задачу только с линейкой и циркулем сможет не каждый.Вам понадобитсяНачертите по линейке две перпендикулярные прямые (оси координат Х и Y). Это легко сделать на тетрадном листе в клетку. Точка пересечения прямых послужит центром будущего правильного а. Теперь нарисуйте окружность диаметром кратным семи, для удобства построения фигуры. Соответственно радиус окружности должен быть кратным трем с половиной. Используйте радиус, равный семи клеткам или семи сантиметрам. Точки пересечения окружности и вертикального диаметра обозначьте буквами А и В.
Используйте радиус, равный семи клеткам или семи сантиметрам. Точки пересечения окружности и вертикального диаметра обозначьте буквами А и В.
Разделите вертикальный диаметр полученной окружности на семь равных частей. Если вы использовали при построении радиус в семь клеток – седьмая часть диаметра будет равна двум клеткам. Если радиус вашей окружности равен семи сантиметрам – одна седьмая часть диаметра будет равна двум сантиметрам (четырем клеткам). Пронумеруйте точки деления по вертикали сверху вниз.
Из точки В (точка №7) проведите дугу радиусом, равным диаметру построенной окружности (равным АВ). Точку пересечения дуги с горизонтальной осью Х обозначьте буквой С. Теперьиз точки С через четные деления вертикального диаметра (точки №№2, 4 и 6) проведите лучи. Пересекая окружность, лучи образуют вершины семиугольника E, F, D.
При помощи линейки через вершины E, F, D проведите параллельные оси Х прямые. Обозначьте точки пересечения прямых с противоположной частью окружности буквами K, L, M. По линейке соедините поочередно друг с другом вершины D, F, E, А, K, L, M. Правильный семиугольник готов!
По линейке соедините поочередно друг с другом вершины D, F, E, А, K, L, M. Правильный семиугольник готов!
Помощь студенту — практические примеры, задачи, теория: Правильный семиугольник
Разберём олимпиадную задачу по планиметрии.Дан правильный семиугольник A₁A₂A₃A₄A₅A₆A₇. Доказать , что 1/A₁A₅ + 1/A₁A₃ = 1/A₁A₇.
Домножим обе части равенства на A₁A₅·A₁A₃·A₁A₇ ≠ 0 и перепишем его в виде:
A₁A₇·A₁A₅ = A₁A₃·(A₁A₅ − A₁A₇)
Известно,что вокруг правильного многоугольника можно описать окружность. Обозначим через O центр центр описанной окружности, R — её радиус.
Правильный семиугольник. Рисунок из Bикипeдии.
Треугольники A₁OA₇, A₁OA₅, A₁OA₃ — равнобедренные с боковыми сторонами
A₁O = A₃O = A₅O = A₇O = R и углами ∠A₁OA₇ = 2·π/7, ∠A₁OA₅ = 6·π/7, ∠A₁OA₃ = 4·π/7.
Основания треугольников равны соответственно: A₁A₇ = 2·R·sin(π/7), A₁A₅ = 2·R·sin(3·π/7),
A₁A₃ = 2·R·sin(2·π/7).
Подставим найденные значения оснований треугольников в равенство:
4·R²·sin(π/7)·sin(3·π/7) = 4·R²·sin(2·π/7)·(sin(3·π/7) − sin(π/7))
Сократим обе части равенства на 4·R² ≠ 0:
sin(π/7)·sin(3·π/7) = sin(2·π/7)·(sin(3·π/7) − sin(π/7))
Теперь мы можем либо преобразовать произведение синусов в разность косинусов, либо наоборот — разность синусов в произведение тригонометрических функций.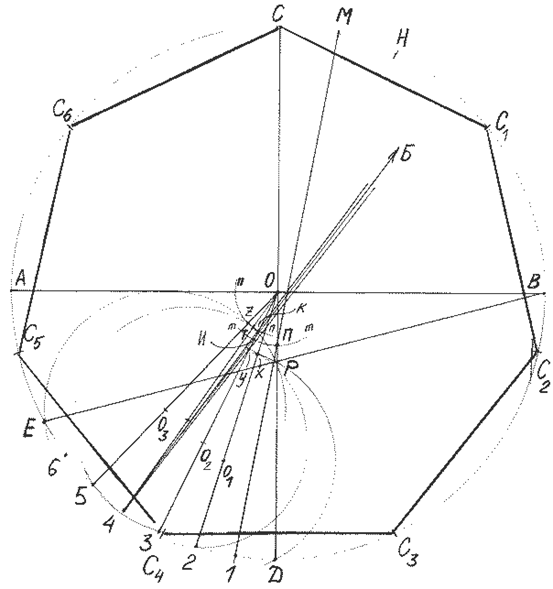 Выберем второй вариант. Формула преобразования разности синусов в произведение тригонометрических функций имеет вид:
Выберем второй вариант. Формула преобразования разности синусов в произведение тригонометрических функций имеет вид:
sin α − sin β = 2·sin(½ (α − β))·cos(½ (α + β))
Получаем: sin(π/7)·sin(3·π/7) = 2·sin(π/7)·sin(2·π/7)·cos(2·π/7)
Сократим теперь обе части равенства на sin(π/7) ≠ 0 и применим к правой части формулу синуса двойного аргумента: 2·sin α·cos α = sin(2·α).
Получим: sin(3·π/7) = 2·sin(2·π/7)·cos(2·π/7) = sin(4·π/7).
И наконец, применим к правой части формулу приведения: sin(π − α) = sin α.
sin(3·π/7) = sin(4·π/7) = sin(π − 4·π/7) = sin(3·π/7) ⇒ sin(3·π/7) ≡ sin(3·π/7)
Равенство обратилось в тождество. Исходное утверждение доказано, и Золотой ключик у нас в кармане:)
%d0%bf%d1%80%d0%b0%d0%b2%d0%b8%d0%bb%d1%8c%d0%bd%d1%8b%d0%b9%20%d1%81%d0%b5%d0%bc%d0%b8%d1%83%d0%b3%d0%be%d0%bb%d1%8c%d0%bd%d0%b8%d0%ba на итальянский — Русский-Итальянский
Я знала, как высоко Бог ценит человека и его тело, но даже это не останавливало меня. Дженнифер, 20 лет
Дженнифер, 20 лет
So che per Dio il corpo umano è prezioso, ma ciò non mi ha impedito di farlo”. — Jennifer, 20 anni.
jw2019
Спорим на 20
Scommetto venti dollari che non riuscirai a stare tutto il giorno da sola.
OpenSubtitles2018.v3
Когда мы помогаем другим, мы и сами в какой-то мере испытываем счастье и удовлетворение, и наше собственное бремя становится легче (Деяния 20:35).
Quando ci prodighiamo per i nostri simili non solo aiutiamo loro, ma noi stessi proviamo una certa felicità e soddisfazione, e questo rende più sopportabili i nostri pesi. — Atti 20:35.
jw2019
Речь и обсуждение со слушателями, основанные на «Сторожевой башне» от 15 июля 2003 года, с. 20.
Discorso con partecipazione dell’uditorio basato sulla Torre di Guardia del 15 luglio 2003, pagina 20.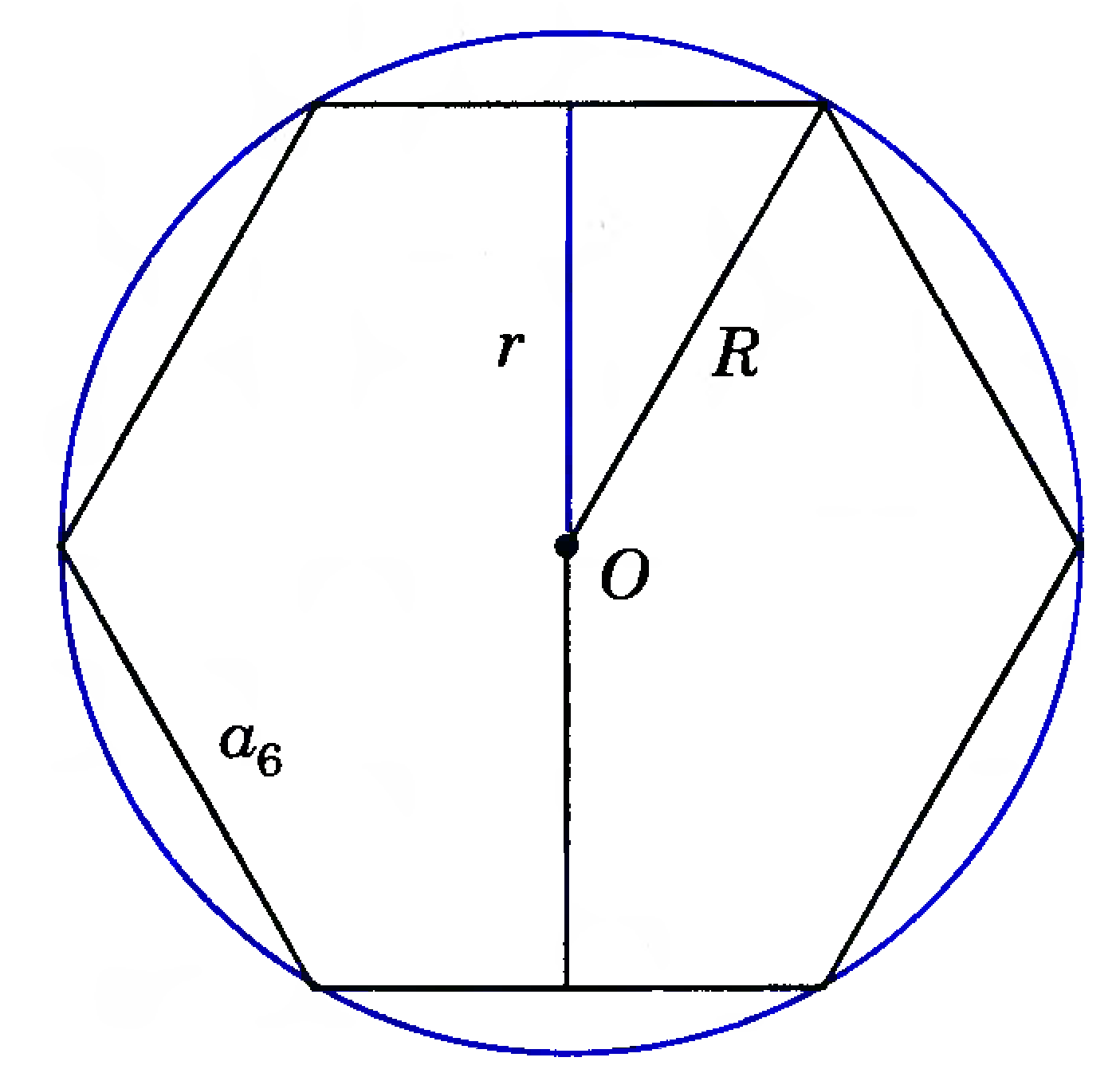
jw2019
Ну, в то время, мы говорим о 80-х, в то время это было модно.
Beh, all’epoca, parliamo degli anni’80, erano molto di moda.
OpenSubtitles2018.v3
Он уехал 20 минут назад.
Se ne e’andato 20 minuti fa.
OpenSubtitles2018.v3
В 1996 году Ланге вступился за противоречивую работу исследователя ВИЧ/СПИДА Дэвида Хо, который лечил инфицированных пациентов, прописывая им по
Nel 1996, Lange ha difeso il lavoro di David Ho, controverso ricercatore sull’HIV e l’AIDS, che trattava i pazienti infetti facendogli assumere 20 pillole al giorno all’interno di un regime terapeutico costituito da un «cocktail» di molti farmaci.
WikiMatrix
Предполагая, что такие вкладчики находят держателей FE желающих приобрести их BE, то вырисовывается значительный курс BE к FE, который зависит от размера сделки, относительного нетерпения держателей 
Supponendo che tali depositanti trovano dei possessori di euro liberi disposti ad acquistare i loro euro bancari, emerge un sostanziale tasso di cambio euro libero-euro bancario, che varia con le dimensioni dell’operazione, l’impazienza dei titolari di euro bancari e la durata prevista dei controlli sui capitali.
ProjectSyndicate
Я был женат 20 лет.
Sono stato sposato per vent’anni.
OpenSubtitles2018.v3
Их высота варьирует от 2 до
Comprende palme generalmente di dimensioni piccole o medie, alte da 2 a 20 m e con foglie lunghe da 2 a 12 m. Comprende le seguenti specie: Arenga australasica (H.Wendl. & Drude) S.T.Blake ex H.E.Moore Arenga brevipes Becc.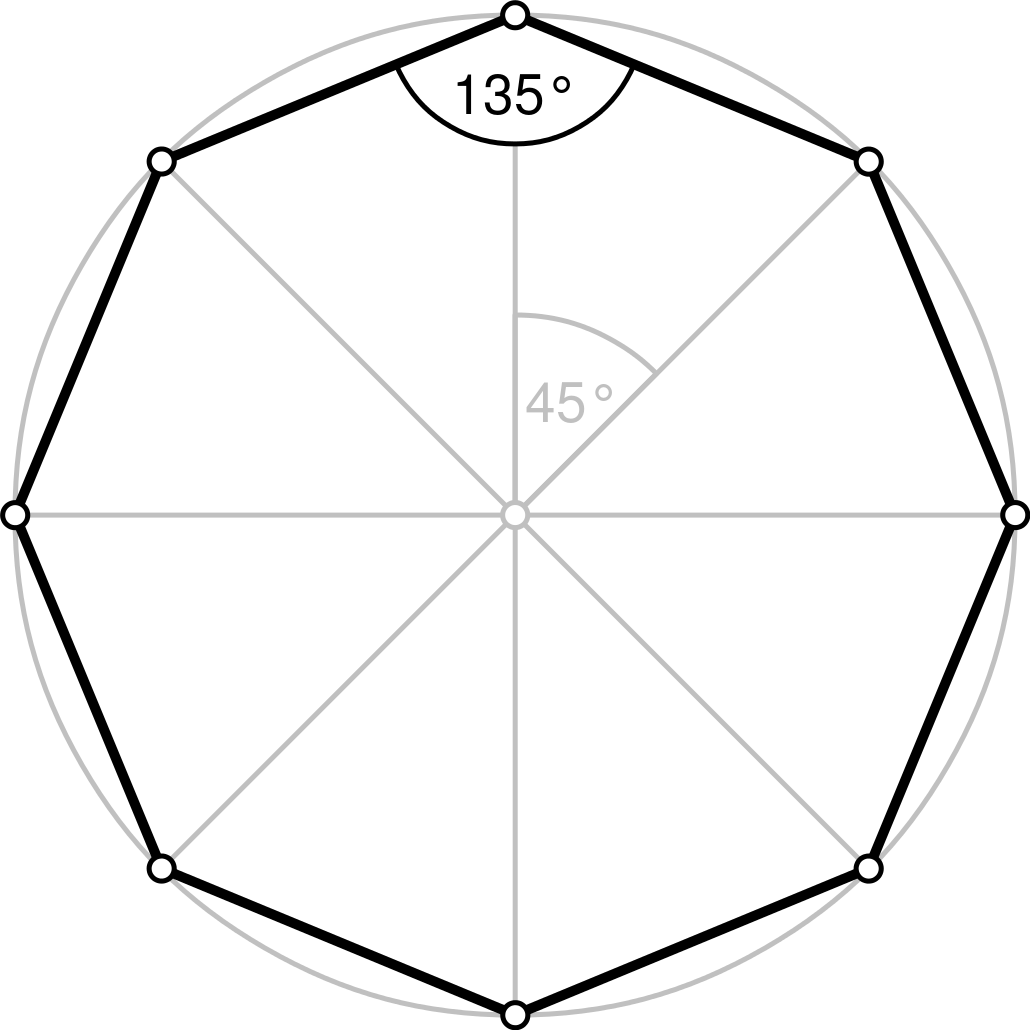
WikiMatrix
20 Оставлена родителями, но любима Богом
20 Abbandonata dai genitori, amata da Dio
jw2019
Когда в 80-х годах люди якудзы увидели, как легко брать ссуды и «делать» деньги, они создали компании и занялись операциями с недвижимым имуществом и куплей-продажей акций.
Quando la Yakuza vide quanto era facile ottenere prestiti e far soldi negli anni ’80, costituì delle società e si tuffò nelle operazioni immobiliari e nelle speculazioni in borsa.
jw2019
Вот что пророчествовал Алма жителям Гидеона около 83 года до Р. Х.:
Attorno all’83 a.C.Alma profetizzò quanto segue al popolo di Gedeone:
LDS
Обычно проводят связь между этим древним городом и современной Газой (Газза, Азза), расположенной примерно в
In genere l’antica città viene identificata con l’odierna Gaza (Ghazzeh; ʽAzza), circa 80 km a OSO di Gerusalemme.
jw2019
20 Даже преследование или заключение в тюрьму не может закрыть уста преданных Свидетелей Иеговы.
20 Neanche la persecuzione o la prigionia possono chiudere la bocca ai testimoni di Geova devoti.
jw2019
Ты был в отключке минут 20.
Sei stato privo di sensi per quasi 20 minuti.
OpenSubtitles2018.v3
Есть ещё кое- что в начале 20— го века, что усложняло вещи ещё сильнее.
Ora c’è qualcos ́altro all’inizio del 20° secolo che rendeva le cose ancora più complicate.
QED
Она не опускается глубже 10 м в летний период и 20 м зимой.
In estate non si inoltra in acque più profonde di 10 metri, in inverno di 20 metri.
WikiMatrix
«К одинадцати Апостолам» был причислен Матфий, чтобы служить с ними (Деяния 1:20, 24—26).
Fu nominato Mattia perché prestasse servizio “con gli undici apostoli”. — Atti 1:20, 24-26.
— Atti 1:20, 24-26.
jw2019
Роберт Коэмс, доцент Торонтского университета, обобщает их взгляды: «Рак легких — через 20 лет.
Robert Coambs, assistente universitario presso l’Università di Toronto, ha riassunto così il loro modo di ragionare: “Il cancro del polmone mi verrà tra 20 anni.
jw2019
Большинство местных органов при планировании развития на следующие 5, 10, 15, 20 лет начинают с предпосылки, что можно ожидать больше энергии, больше автомобилей, больше домов, больше рабочих мест, больше роста и т.д.
La maggior parte delle autorità locali, quando decidono di pianificare per i successivi 10, 15, 20 anni la propria comunità ancora partono dall’assunto che ci sarà maggiore disponibilità di energia, più auto, più edifici, più lavoro, più crescita e così via.
ted2019
Именно это приводит к счастью, как было сказано царем Соломоном: «Кто надеется на Господа, тот блажен [счастлив, НМ]» (Притчи 16:20).
Questo contribuisce alla felicità, come spiegò il re Salomone: “Felice è chi confida in Geova”. — Proverbi 16:20.
jw2019
Будьте щедрыми и заботьтесь о благополучии других (Деяния 20:35).
Essere generosi e impegnarsi per la felicità degli altri. — Atti 20:35.
jw2019
Два важнейших события 20 века:
Due dei piu’importanti eventi del 20esimo secolo:
OpenSubtitles2018.v3
Последние 20 лет — я.
OpenSubtitles2018.v3
%d0%bf%d1%80%d0%b0%d0%b2%d0%b8%d0%bb%d1%8c%d0%bd%d1%8b%d0%b9%20%d1%81%d0%b5%d0%bc%d0%b8%d1%83%d0%b3%d0%be%d0%bb%d1%8c%d0%bd%d0%b8%d0%ba на сербский — Русский-Сербский
Я знала, как высоко Бог ценит человека и его тело, но даже это не останавливало меня. Дженнифер, 20 лет
Znala sam koje je Božje gledište o ljudskom telu, ali čak me ni to nije sprečavalo“ (Dženifer, 20 godina).
jw2019
Когда мы помогаем другим, мы и сами в какой-то мере испытываем счастье и удовлетворение, и наше собственное бремя становится легче (Деяния 20:35).
Kada se trudimo oko drugih, mi ne pomažemo samo njima već i sami doživljavamo izvesnu meru sreće i zadovoljstva što čini da breme koje nosimo bude podnošljivije (Dela apostolska 20:35).
jw2019
Речь и обсуждение со слушателями, основанные на «Сторожевой башне» от 15 июля 2003 года, с. 20.
Govor i razmatranje s publikom na temelju Stražarske kule od 15. jula 2003, strana 20.
jw2019
Ну, в то время, мы говорим о 80-х, в то время это было модно.
Pa, u to vreme, a pričamo o 80-im to je bilo moderno.
OpenSubtitles2018.v3
20 Я приведу их в землю, о которой клялся их предкам+, в землю, где течёт молоко и мёд+, и они будут есть+ досыта, разжиреют+ и повернутся к другим богам+.
+ 20 Jer ću ih dovesti u zemlju koju sam pod zakletvom obećao njihovim praočevima,+ u zemlju u kojoj teče med i mleko.
jw2019
Я был женат 20 лет.
Bio sam u braku 20 godina.
OpenSubtitles2018.v3
20 Оставлена родителями, но любима Богом
20 Roditelji su me napustili — ali me je Bog voleo
jw2019
Когда в 80-х годах люди якудзы увидели, как легко брать ссуды и «делать» деньги, они создали компании и занялись операциями с недвижимым имуществом и куплей-продажей акций.
Kada su jakuze tokom ’80-ih videle kako je lako pozajmiti i zaraditi novac, oni su osnovali kompanije i uleteli u špekulacije s nekretninama i akcijama.
jw2019
20 Даже преследование или заключение в тюрьму не может закрыть уста преданных Свидетелей Иеговы.
20 Čak ni progonstvo ili zatvor ne može zatvoriti usta predanim Svedocima Jehove.
jw2019
Ты был в отключке минут 20.
Bio si vani otprilike 20 minuta.
OpenSubtitles2018.v3
Есть ещё кое- что в начале 20— го века, что усложняло вещи ещё сильнее.
Međutim, početkom 20. veka još nešto je dodatno zakomplikovalo stvari.
QED
б) Чему мы учимся из слов, записанных в Деяниях 4:18—20 и Деяниях 5:29?
(b) Šta možemo naučiti iz Dela apostolskih 4:18-20 i 5:29?
jw2019
Да что ты понимаешь, в 80-ых это движение было пределом мечтаний любого мужика.
To je bio strava pokret 80-ih.
OpenSubtitles2018.v3
Именно это приводит к счастью, как было сказано царем Соломоном: «Кто надеется на Господа, тот блажен [счастлив, НМ]» (Притчи 16:20).
To doprinosi sreći, kao što je kralj Solomon objasnio: „Srećan je ko se u Gospoda uzda“ (Poslovice 16:20).
jw2019
20 Тогда Ио́в встал, разорвал+ на себе верхнюю одежду, остриг свою голову+, упал на землю+, поклонился+ 21 и сказал:
20 Tada je Jov ustao i razderao+ svoj ogrtač, odsekao kosu+ na svojoj glavi pa je pao na zemlju,+ poklonio se+ 21 i rekao:
jw2019
Будьте щедрыми и заботьтесь о благополучии других (Деяния 20:35).
Biti velikodušan i nastojati da se usreće drugi (Dela apostolska 20:35).
jw2019
Два важнейших события 20 века:
Dva najznačajnija događaja 20. veka:
OpenSubtitles2018.v3
Это забавно, когда тебе 20 лет.
Čudno je koliko možeš naivan da budeš sa 20.
OpenSubtitles2018.v3
Через 4 года предполагаемая капитализация достигнет 80 миллиардов долларов.
Procenjuje se da će za četiri godine vredeti preko 80 milijardi dolara.
ted2019
Он хочет 20 кусков и Иксбокс
Kaže… 20 hiljada i jedan Xbox.
OpenSubtitles2018.v3
Исследователи провели эксперимент с учащимися колледжа — юношами и девушками. В течение 20 минут одна группа играла в жестокие видеоигры, а другая — в обычные.
Istraživači su nasumično izabrali studente i studentkinje, koje su podelili u dve grupe — jedni su 20 minuta igrali nasilne, a drugi nenasilne video-igrice.
jw2019
Итак, в США с появлением лечения в середине 1990- х годов число ВИЧ- инфицированных детей снизилось на 80%.
Дакле, у Сједињеним Државама је, од појаве лечења средином деведесетих, за 80% опао број деце заражене ХИВ- ом.
QED
Он мертв уже 20 лет.
OpenSubtitles2018.v3
Но оно оценено всего в 20 долларов.
Ovo vrijedi samo 20 dolara.
OpenSubtitles2018.v3
20:24). Павел был готов пожертвовать всем, в том числе жизнью, чтобы успешно завершить забег.
Bio je spreman da žrtvuje sve, pa i svoj život, samo da bi dovršio svoju trku.
jw2019
%d0%bf%d1%80%d0%b0%d0%b2%d0%b8%d0%bb%d1%8c%d0%bd%d1%8b%d0%b9 %d1%81%d0%b5%d0%bc%d0%b8%d1%83%d0%b3%d0%be%d0%bb%d1%8c%d0%bd%d0%b8%d0%ba PNG, векторы, PSD и пнг для бесплатной загрузки
Мемфис дизайн геометрические фигуры узоры мода 80 90 х годов
4167*4167
естественный цвет bb крем цвета
1200*1200
схема бд электронный компонент технологии принципиальная схема технологическая линия
2000*2000
поп арт 80 х патч стикер
3508*2480
аудиокассета изолированные вектор старая музыка ретро плеер ретро музыка аудиокассета 80 х пустой микс
5000*5000
поп арт 80 х патч стикер
3508*2480
green environmental protection pattern garbage can be recycled green clean
2000*2000
Мемфис бесшовные модели 80 х 90 х стилей
4167*4167
поп арт 80 х патч стикер
2292*2293
80 основных форм силуэта
5000*5000
поп арт 80 х патч стикер
3508*2480
дизайн плаката премьера фильма кино с белым вектором экрана ба
1200*1200
диско дизайн в стиле ретро 80 х неон
5556*5556
80 летний юбилей дизайн шаблона векторные иллюстрации
4083*4083
Векторная иллюстрация мультфильм различных овощей на деревянном ба
800*800
поп арт 80 х патч стикер
2292*2293
be careful to slip fall warning sign carefully
2500*2775
поп арт 80 х патч стикер
3508*2480
мемфис бесшовной схеме 80s 90 все стили
4167*4167
Мемфис шаблон 80 х 90 х годов стилей фона векторные иллюстрации
4167*4167
но логотип компании вектор дизайн шаблона иллюстрация
4083*4083
ценю хорошо как плоская цвет значок векторная icon замечания
5556*5556
поп арт 80 х патч стикер
3508*2480
Дизайн персонажей моды 80 х годов может быть коммерческими элементами
2000*2000
скейтборд в неоновых цветах 80 х
1200*1200
Красивая розовая и безупречная воздушная подушка bb крем косметика постер розовый красивый розовый Нет времени На воздушной
3240*4320
Мемфис бесшовные модели 80 х 90 х стилей
4167*4167
поп арт 80 х патч стикер
3508*2480
в первоначальном письме bd логотипа
1200*1200
ретро стиль 80 х годов диско дизайн неон плакат
5556*5556
дизайн логотипа bc значок буквы b
8333*8333
поп арт 80 х патч стикер
3508*2480
крем крем вв вв на воздушной подушке иллюстрация
2000*2000
поп арт 80 х патч стикер
3508*2480
Золотая буква b логотип bc письмо дизайн вектор с золотыми цветами
8334*8334
в первоначальном письме вв логотипа
1200*1200
happy singing mai ba sing self indulgence happy singing
2000*2000
три группы 3d реалистичное декоративное яйцо с золотым цветом на гнезде bd с золотым всплеском текстовый баннер
5000*5000
мега распродажа 80
1200*1200
bb крем cc крем пудра Порошок торт фонд
2000*2000
буква bc 3d логотип круг
1200*1200
в первоначальном письме вв логотип шаблон векторный дизайн
1200*1200
розовый бб крем красивый бб крем ручная роспись бб крем мультфильм бб крем
2000*3000
Ретро мода 80 х градиент цвета художественного слова
1200*1200
элегантный серебряный золотой bb позже логотип значок символа
1200*1200
bd письмо 3d круг логотип
1200*1200
80 основных форм гранж
1200*1200
логотип bc
1200*1200
ма дурга лицо индуистский праздник карта
5000*5000
в первоначальном письме bd шаблон векторный дизайн логотипа
1200*1200
Построение правильных многоугольников / Длина окружности и площадь круга / Справочник по геометрии 7-9 класс
Задача 1Построить правильный шестиугольник, сторона которого равна данному отрезку.
Дано: отрезок DC.
Построить: правильный шестиугольник, сторона которого равна DC.
Решение:
Для решения задачи воспользуемся тем, что сторона шестиугольника равна радиусу описанной около него окружности, т.е. (смотри формулу для вычисления стороны правильного многоугольника), где — радиус окружности описанной около правильного многоугольника. Нам нужно построить правильный шестиугольник со стороной DC, поэтому с помощью циркуля измеряем отрезок DC и строим окружность радиуса DC, и отмечаем на ней произвольную точку А1, центр окружности обозначаем буквой О.
Затем не меняя раствора циркуля, построим на этой окружности точки А2, А3, А4, А5, А6, так, чтобы выполнялись равенства
А1А2 = А2А3 = А3А4 = А4А5 = А5А6 = DC (т. е. сначала строим окружность радиуса DC с центром в точке А1(всю окружность строить необязательно, смотри выделенное красным), данная окружность пересечет окружность с центром О в точке А2, далее аналогично строим окружность радиуса DC с центром в точке А2, она пересечет окружность с центром О в точке А3 и т.д.).
е. сначала строим окружность радиуса DC с центром в точке А1(всю окружность строить необязательно, смотри выделенное красным), данная окружность пересечет окружность с центром О в точке А2, далее аналогично строим окружность радиуса DC с центром в точке А2, она пересечет окружность с центром О в точке А3 и т.д.).
Теперь соединяя последовательно построенные точки отрезками, получим искомый правильный шестиугольник А1А2А3А4А5А6.
Задача 2
Дан правильный -угольник. Построить правильный 2-угольник.
Дано: правильный -угольник А1А2А3. ..Аn.
..Аn.
Построить: правильный 2-угольник.
Решение:
Пусть, например, нам дан шестиугольник А1А2А3А4А5А6, значит, построить нужно двенадцатиугольник.
Сначала опишем около данного шестиугольника А1А2А3А4А5А6 окружность. Для этого построим биссектрисы углов А1и А2. Чтобы построить биссектрису угла А1, строим окружность произвольного радиуса с центром в точке А1 (полностью окружность строить необязательно, смотри выделенное красным цветом), данная окружность пересечет стороны А1А2 и А1А6 угла А1 в точках Е и К. Затем строим две окружности с центрами в точках Е и К радиуса ЕК (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом), данные окружности пересекутся в точке Р. Далее проводим луч А1Р, который и будет биссектрисой угла А1.
Затем строим две окружности с центрами в точках Е и К радиуса ЕК (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом), данные окружности пересекутся в точке Р. Далее проводим луч А1Р, который и будет биссектрисой угла А1.
Аналогично строим биссектрису угла А2.
Точку пересечения биссектрис углов А1 и А2 обозначаем буквой О и строим окружность радиуса ОА1 с центром О (окружность описанная около А1А2А3А4А5А6).
Далее нужно каждую из дуг А1А2, А2А3, А3А4, А4А5, А5А6, А6А1 разделить пополам. Чтобы разделить дугу А1А2пополам, построим серединный перпендикуляр к отрезку А1А2. Для этого строим две окружности с центрами в точках А1 и А2 радиуса А1А2 (полностью окружность строить необязательно, смотри выделенное красным цветом). Данные окружности пересекутся в двух точках, одну обозначим буквой М, а другая совпадет с точкой О, т.к. у шестиугольника сторона равна радиусу (с другими многоугольниками совпадения с точкой О не будет) . Затем проводим прямую МО, данная прямая пересечет дугу А1А2 в точке В1, которая и разделит дугу А1А2пополам.
Чтобы разделить дугу А1А2пополам, построим серединный перпендикуляр к отрезку А1А2. Для этого строим две окружности с центрами в точках А1 и А2 радиуса А1А2 (полностью окружность строить необязательно, смотри выделенное красным цветом). Данные окружности пересекутся в двух точках, одну обозначим буквой М, а другая совпадет с точкой О, т.к. у шестиугольника сторона равна радиусу (с другими многоугольниками совпадения с точкой О не будет) . Затем проводим прямую МО, данная прямая пересечет дугу А1А2 в точке В1, которая и разделит дугу А1А2пополам. Далее точку В1 соединяем с концами А1и А2 дуги А1А2.
Далее точку В1 соединяем с концами А1и А2 дуги А1А2.
Аналогично находим точки В2, В3. Точки В4, В5, В6 в данном случае строить необязательно, они получаются автоматически при построении точек В1, В2, В3, т.к. шестиугольник симметричная фигура.
Получили двенадцатиугольник А1В1А2В2А3В3А4В4А5В5А6В6 (смотри выделенное красным).
Мы выполняли построения на примере правильного шестиугольника, если мы имеем произвольный правильный -угольник, то все построения выполняются аналогично.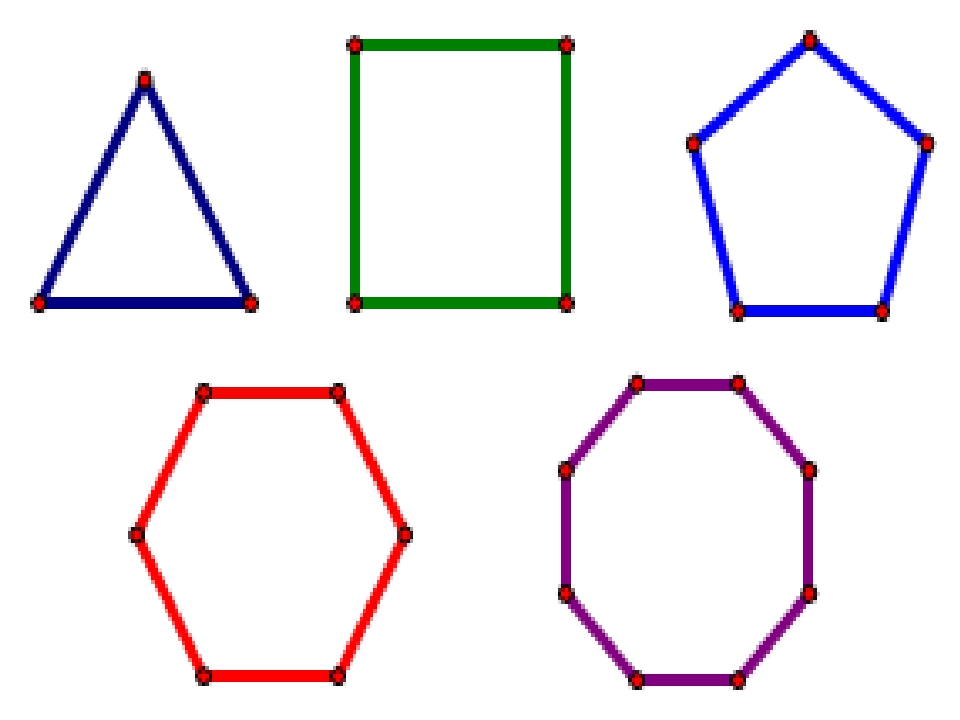
Применяя указанный способ, можно с помощью циркуля и линейки построить целый ряд правильных многоугольников, если построен один из них. Например, построив правильный треугольник и пользуясь результатом задачи 2, можно построить правильный шестиугольник, затем правильный двенадцатиугольник и вообще 2k-угольник, где — любое целое число, больше двух.
Замечание
Не все правильные многоугольники можно построить с помощью циркуля и линейки. Доказано, например, что правильный семиугольник не может быть построен при помощи циркуля и линейки.
Полигоны — семиугольники
Свойства семиугольников, внутренние углы семиугольников
| Полигоны: свойства семиугольников | |||
шестиугольника: | |||
| |||
| Обычные семиугольники: | |||
| Свойства правильных семиугольников: | |||
| |||
| длина всех сторон одинаковая. ) и все внутренние углы одинакового размера (совпадают). | |||
| Измерение центральных углов правильного семиугольника: | |
| Чтобы найти меру центрального угла правильного семиугольника , сделайте круг посередине… Окружность составляет 360 градусов вокруг … Разделите это на семь углов … Итак, центральный угол правильного семиугольника составляет 51,43 градуса. | |
Шестиугольник | Блог по математике ∞
Семиугольник — это тип многоугольника с семью сторонами. Бывают правильные и неправильные семиугольники. У правильного семиугольника все стороны равны по длине и углы будут одинаковыми. Когда длина сторон правильного семиугольника задана, можно определить периметр, апофему и площадь семиугольника.
Уголки для семиугольника
В правильном семиугольнике все стороны имеют одинаковую длину, поэтому все углы тоже будут одинаковыми. Внутренние углы в сумме составляют 900 градусов, а каждый составляет 128,57 градусов. Центральные углы (те, что находятся в центре семиугольника) составляют 51,43 градуса. Они оба верны для семиугольника любого размера, если это правильный семиугольник. Неправильные семиугольники могут иметь различную длину сторон и углы.
Внутренние углы в сумме составляют 900 градусов, а каждый составляет 128,57 градусов. Центральные углы (те, что находятся в центре семиугольника) составляют 51,43 градуса. Они оба верны для семиугольника любого размера, если это правильный семиугольник. Неправильные семиугольники могут иметь различную длину сторон и углы.
Определение периметра семиугольника
Если задана длина сторон, периметр определяется путем умножения 7 (количества сторон) на длину стороны.Если сторона 11, периметр равен 77.
Определите апофему семиугольника
Если смотреть на правильный семиугольник, линия, идущая от центральной точки к середине одной из сторон, является апофемой. Это нужно для определения площади семиугольника. Если длина сторон известна, апофему можно определить по формуле: апофема = s / 2 tan (180 / n). В этой формуле «s» — длина сторон, а «n» — количество сторон. Например, если стороны семиугольника равны 7, формула будет заполнена как апофема = 7/2 тангенса (180/7). В итоге мы получим апофему 7,268.
В итоге мы получим апофему 7,268.
Определение площади семиугольника
Изучение того, как найти площадь семиугольника, включает изучение предыдущей формулы, а также формулы для определения площади. Апофема семиугольника должна быть найдена до того, как будет найдена площадь семиугольника. Формула для этого: Площадь = (1/2) nsr. В этом случае «n» — это количество сторон, «s» — это длина сторон, а «r» — это апофема. Используя тот же пример выше, со стороной 7, формула площади будет работать следующим образом: Площадь = (1/2) (7) (7) (7.268). Таким образом, площадь для этого примера будет 178,066.
Когда семиугольник не правильный
У правильных семиугольников одинаковые углы и стороны. Это означает, что можно найти центральную точку. У неправильных семиугольников, поскольку углы и стороны могут быть разными, обычно нет центральной точки.
В целом, чтобы научиться определять площадь семиугольника, нужно выполнить несколько шагов, но это возможно, если человек знает длину сторон. Если семиугольник является правильным семиугольником, предыдущие шаги могут позволить человеку найти периметр, апофему и площадь.
Если семиугольник является правильным семиугольником, предыдущие шаги могут позволить человеку найти периметр, апофему и площадь.
Видео с вопросом: Определение площади правильного семиугольника по длине его стороны
Стенограмма видеозаписи
У правильного семиугольника длина стороны 36 сантиметров. Найдите область, дающую ответ с двумя десятичными знаками.
В этом вопросе нам нужно найти площадь правильного семиугольника, длина стороны которого составляет 36 сантиметров.И нам нужно дать ответ с двумя десятичными знаками. Поскольку этот вопрос просит нас найти площадь правильного многоугольника, мы можем сделать это, используя нашу формулу для определения площади правильных многоугольников. Напомним, что площадь правильного многоугольника с-сторонами и длиной стороны задается следующей формулой. Его площадь равна в квадрате четырех, умноженном на 180, разделенное на.
И есть несколько моментов, на которые стоит обратить внимание в связи с этой формулой. Во-первых, мы измеряем угол в градусах.А во-вторых, единицы нашей площади будут квадратом тех единиц, которые мы используем для нашей длины. Итак, в нашем вопросе, поскольку мы берем длину в сантиметрах, наша площадь будет в сантиметрах в квадрате. Итак, чтобы найти площадь любого правильного многоугольника, нам нужно знать только две вещи. Нам нужно знать, сколько сторон у нашего многоугольника, и нам нужно знать одну из длин сторон.
Во-первых, мы измеряем угол в градусах.А во-вторых, единицы нашей площади будут квадратом тех единиц, которые мы используем для нашей длины. Итак, в нашем вопросе, поскольку мы берем длину в сантиметрах, наша площадь будет в сантиметрах в квадрате. Итак, чтобы найти площадь любого правильного многоугольника, нам нужно знать только две вещи. Нам нужно знать, сколько сторон у нашего многоугольника, и нам нужно знать одну из длин сторон.
Во-первых, в вопросе нам сказали, что мы работаем с обычным семиугольником. А семиугольник — это любой многоугольник с семью сторонами, поэтому наше значение 𝑛 будет равно семи.В этом вопросе также сказано, что длина стороны нашего правильного семиугольника равна 36. Поэтому мы устанавливаем значение our равным 36 сантиметрам. Теперь все, что нам нужно сделать, это подставить эти значения в нашу формулу. Подставив 𝑛 равно семи и 𝑥 равно 36 сантиметрам в нашу формулу, мы получим, что площадь нашего правильного семиугольника равна семи умноженным на 36 сантиметров, все в квадрате на четыре, умноженные на раскладушку 180 градусов, разделенную на семь.
Теперь мы можем приступить к вычислению этого выражения. Во-первых, конечно, поскольку это площадь, и мы возводим в квадрат значение сантиметра, наши единицы измерения будут сантиметрами в квадрате.Далее мы оценим наш коэффициент. Семь, умноженное на 36 в квадрате на четыре, равно 2268.
Наконец, мы напоминаем, что котангенс угла равен котангенсу, деленному на тангенс этого угла. Таким образом, мы можем упростить раскладку 180, разделенную на семь градусов, до единицы, разделенной на загар 180, разделенный на семь градусов. Следовательно, площадь нашего правильного семиугольника равна 2268, умноженному на единицу, деленную на загар 180, деленную на семь градусов сантиметров в квадрате. И теперь мы можем вычислить это выражение.Что ж, мы помним, что нам нужно установить наш калькулятор в режим градусов. Получаем, что это равно 4709,550, и это расширение продолжается в сантиметрах в квадрате.
Но помните, вопрос требует, чтобы мы дали ответ с двумя десятичными знаками. Итак, мы смотрим на третий десятичный знак в нашем расширении и видим, что он равен нулю. Поскольку это меньше пяти, это означает, что нам нужно округлить в меньшую сторону. И это дает нам окончательный ответ. В этом вопросе нам удалось найти площадь правильного семиугольника с длиной стороны 36 сантиметров.Нам удалось показать его площадь с точностью до двух знаков после запятой — 4709,55 сантиметра в квадрате.
Итак, мы смотрим на третий десятичный знак в нашем расширении и видим, что он равен нулю. Поскольку это меньше пяти, это означает, что нам нужно округлить в меньшую сторону. И это дает нам окончательный ответ. В этом вопросе нам удалось найти площадь правильного семиугольника с длиной стороны 36 сантиметров.Нам удалось показать его площадь с точностью до двух знаков после запятой — 4709,55 сантиметра в квадрате.
Гептагон
Гептагон — это многоугольник с семью сторонами (Гепта- означает семь). На рисунке ниже представлены несколько типов семиугольников.
Классификация семиугольников
Как и другие многоугольники, семиугольник можно разделить на правильный и неправильный. Если все стороны и внутренние углы семиугольника равны, это правильный семиугольник. В противном случае это неправильный семиугольник.
| Правильный семиугольник | Неправильный семиугольник |
|---|---|
| Все стороны и внутренние углы равны | Не все стороны и углы равны |
Гептагоны и другие многоугольники также можно разделить на выпуклые и вогнутые. Если все внутренние углы семиугольника меньше 180 °, он выпуклый. Если один или несколько внутренних углов больше 180 °, он вогнутый.Правильный семиугольник — это выпуклый семиугольник. Вогнутый семиугольник — это неправильный семиугольник.
Если все внутренние углы семиугольника меньше 180 °, он выпуклый. Если один или несколько внутренних углов больше 180 °, он вогнутый.Правильный семиугольник — это выпуклый семиугольник. Вогнутый семиугольник — это неправильный семиугольник.
| Выпуклый семиугольник | Вогнутый семиугольник |
|---|---|
| Все внутренние углы <180 ° | Один или несколько внутренних углов> 180 ° |
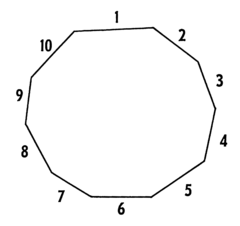
Диагонали семиугольника
Диагональ — это отрезок прямой, соединяющий две непоследовательные вершины. Всего можно нарисовать четырнадцать различных диагоналей семиугольника.Следующий рисунок является примером.
Есть 4 диагонали, отходящие от каждой из 7 вершин семиугольника выше, образуя в общей сложности 14 диагоналей.
Внутренние углы семиугольника
Сумма внутренних углов семиугольника равна 900 °.
Как показано на рисунке выше, можно провести четыре диагонали, чтобы разделить семиугольник на пять треугольников.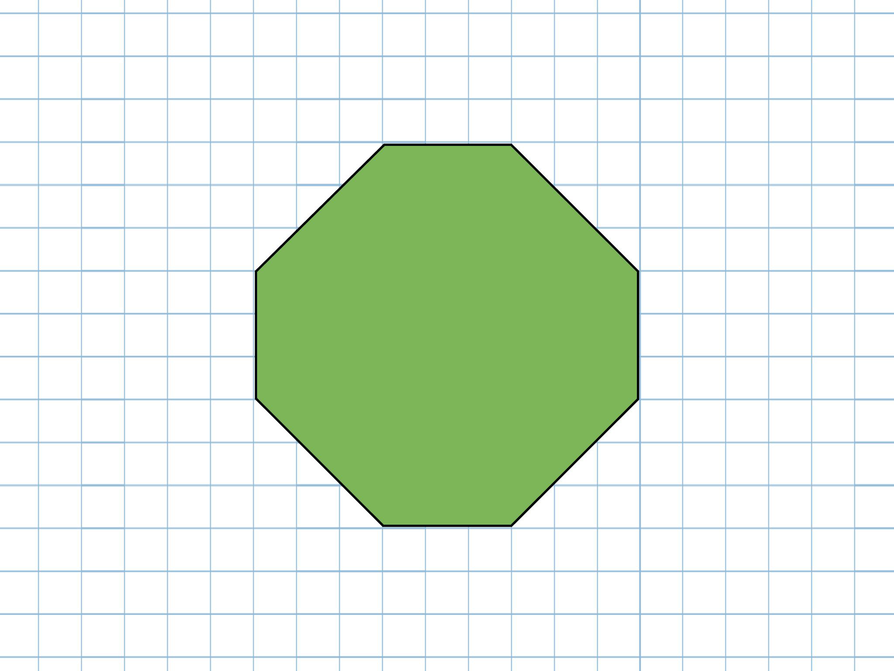 Синие линии выше показывают только один способ разделить семиугольник на треугольники; есть и другие. Сумма внутренних углов пяти треугольников равна сумме внутренних углов семиугольника.Поскольку сумма внутренних углов треугольника равна 180 °, сумма внутренних углов семиугольника составляет 5 × 180 ° = 900 °.
Синие линии выше показывают только один способ разделить семиугольник на треугольники; есть и другие. Сумма внутренних углов пяти треугольников равна сумме внутренних углов семиугольника.Поскольку сумма внутренних углов треугольника равна 180 °, сумма внутренних углов семиугольника составляет 5 × 180 ° = 900 °.
Правильный семиугольник
Правильный семиугольник — это семиугольник, в котором все стороны имеют одинаковую длину и все внутренние углы имеют одинаковую длину.
Углы правильного семиугольника
Поскольку каждый из семи внутренних углов в правильном семиугольнике равны по размеру, каждый внутренний угол составляет 900 ° ÷ 7 ≈ 128,57 °, как показано ниже.
Каждый внешний угол правильного семиугольника имеет одинаковую величину, равную примерно 51.43 °.
Симметрия правильного семиугольника
Правильный семиугольник имеет 7 линий симметрии и вращательную симметрию 7-го порядка, что означает, что его можно повернуть таким образом, чтобы он выглядел так же, как исходная форма 7 раз на 360 °.
| Линии симметрии | Вращательная симметрия |
|---|---|
| 7 линий симметрии | Семь углов поворота по 51,43 градуса вокруг центра |
геометрия — Можно ли построить правильный семиугольник, используя только циркуль и линейку? Геометрия
— Можно ли построить правильный семиугольник с помощью циркуля и линейки? — Обмен математическим стекомСеть обмена стеков
Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
- 0
- +0
- Авторизоваться Зарегистрироваться
Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществуКто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено 4к раз
$ \ begingroup $Можно ли построить правильный семиугольник (фигуру с семью сторонами) с помощью циркуля и линейки? Если да, не могли бы вы дать мне указания, как это сделать?
Создан 19 янв.
Нет, это невозможно; Фактически, правильный семиугольник — это правильный многоугольник с наименьшим числом сторон, который невозможно построить с помощью только циркуля и линейки.Однако его можно построить с помощью линейки neusis. Здесь был задан связанный с этим вопрос (и дан ответ).
Создан 19 янв.
Анонимный5,51844 золотых знака1414 серебряных знаков4343 бронзовых знака
$ \ endgroup $ Высокоактивный вопрос . Заработайте 10 репутации, чтобы ответить на этот вопрос. Требование репутации помогает защитить этот вопрос от спама и отсутствия ответов. Mathematics Stack Exchange лучше всего работает с включенным JavaScript
Заработайте 10 репутации, чтобы ответить на этот вопрос. Требование репутации помогает защитить этот вопрос от спама и отсутствия ответов. Mathematics Stack Exchange лучше всего работает с включенным JavaScriptВаша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Принимать все файлы cookie Настроить параметры
Геометрия— Можно ли построить правильный семиугольник с помощью циркуля, линейки и трехугольника?
Хотя есть хороший ответ с явным геометрическим построением, есть альтернативный (алгебраический) подход к нему.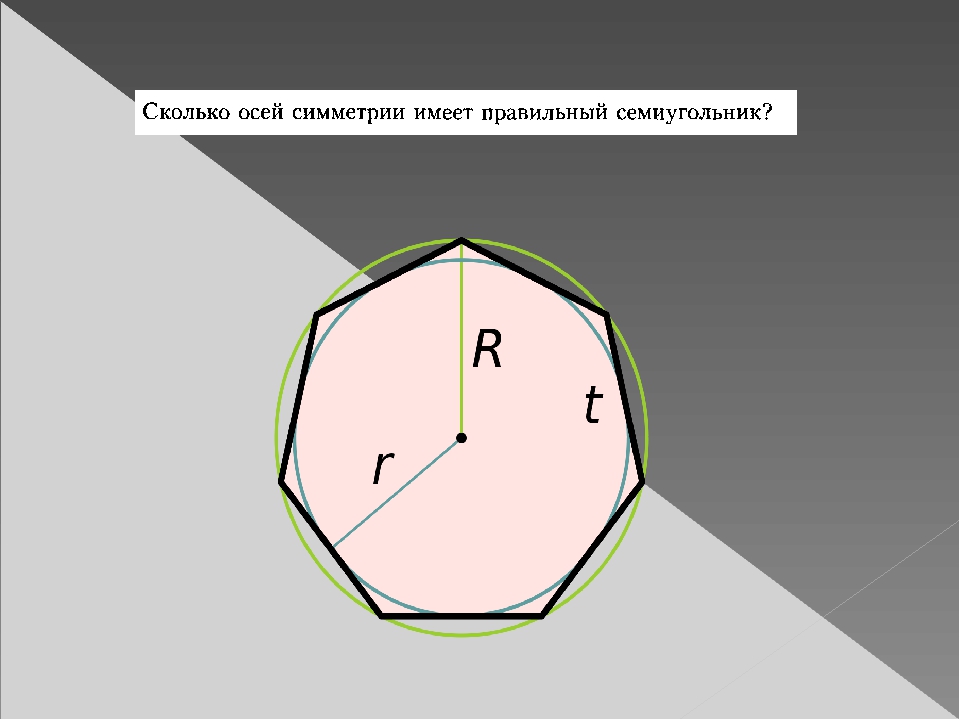 2 = 4p / 3 $.2-4c ‘}} {2} $$
2 = 4p / 3 $.2-4c ‘}} {2} $$
$ y_1 $ также можно построить. В конце концов, $ \ cos (2 \ pi / 7) = (y_1-a) / 3 $ можно построить, поэтому семиугольник можно построить с помощью линейки, циркуля и трисектора.
PS : Есть альтернативный, но действительный аргумент в знаменитой книге Galois Theory от Яна Стюарта; проверьте теорему $ 7.16 $.
Heptagon | Math Wiki | Фэндом
В геометрии семиугольник — это многоугольник с семью сторонами и семью углами.В правильном семиугольнике, в котором все стороны и все углы равны, стороны встречаются под углом в радиан, 128,5714286 градусов. Его символ Шлефли — {7}. Площадь правильного семиугольника с длиной стороны определяется выражением
Гептагон также иногда называют септагоном , используя «септ-» (исключение septua-, числового префикса латинского происхождения, а не гепта-, числового префикса греческого происхождения). В OED термин «септагон» обозначается как «семиугольник».
Строительство
Правильный семиугольник нельзя построить с помощью циркуля и линейки, но можно построить с помощью линейки и циркуля с отметками.Такой тип конструкции называется конструкцией Нойсиса. Его также можно построить с помощью циркуля, линейки и трисектора. Невозможность построения линейки и циркуля следует из наблюдения, которое является нулем неприводимой кубики.
Следовательно, этот многочлен является минимальным многочленом от, тогда как степень минимального многочлена для конструктивного числа должна быть степенью двойки.
A Neusis конструкция внутреннего угла правильного семиугольника.
Приблизительное значение
Приближение шестиугольника
На рисунке показано подходящее приближение для практического использования с точностью 0,2%. Пусть A лежит на окружности описанной окружности. Нарисуйте дугу BOC. Затем дает приближение для края семиугольника.
Гептаграммы
Два вида гептаграммы могут быть построены из правильных семиугольников, обозначенных символами Шлефли {7/2} и {7/3}, с делителем, являющимся интервалом соединения.
Синий, {7/2} и зеленый {7/3} гептаграммы внутри красного семиугольника.
использует
В настоящее время (2008 г.) Соединенное Королевство имеет две семиугольные монеты, 50 пенсов и 20 пенсов, и Барбадосский доллар также семиугольный. Монета 20 евроцентов имеет аналогичные углубления. Строго говоря, форма монет представляет собой криволинейный семиугольник, что делает их кривыми постоянной ширины: стороны изогнуты наружу, так что монета будет плавно катиться в торговых автоматах. На бразильской монете в 25 центов вписан семиугольник.
Графики
Полный граф K 7 часто изображается как правильный семиугольник со всеми 21 ребром, соединенным. Этот граф также представляет собой ортогональную проекцию 7 вершин и 21 ребра 6-симплекса. 21 и 35 вершин выпрямленного и двунаправленного 6-симплекса также ортогонально выступают в правильные семиугольники.
См. Также
Шаблон: Wiktionarypar
Внешние ссылки
ar: سباعي (مضلع) ast: Heptágonu az: Düzgün yeddibucaqlı ca: Heptàgon cs: Sedmiúhelník gl: Heptágono это: Эттагоно ка: ჰეპტაგონი hu: Hétszög nl: Zevenhoek нет: семиугольник nn: семиугольник pl: Siedmiokąt foremny pt: Heptágono sl: Седемкотник sr: Седмоугао sv: семиугольник th: รูป เจ็ด เหลี่ยม
.

 ..
.. 