Персональный сайт учителя Низамутдиновой З.И.
Правильный пятиугольник
Правилый пятиугольник
Правильный пятиугольник или пентагон — геометрическая фигура, правильный многоугольник с пятью сторонами.
Свойства
Построение правильного пятиугольника
У правильного пятиугольника угол равен
Площадь правильного пятиугольника с длиной стороны t рассчитывается по формуле:
или
,
где R — радиус описанной окружности, r — радиус вписанной окружности.
Отношение диагонали правильного пятиугольника к стороне равно золотому сечению, то есть числу.
Поэтому радиус вписанной окружности, радиус описанной окружности, высоту и площадь правильного пятиугольника можно вычислить и без использования тригонометрических функций:
Сторона правильного пятиугольника:
Высота правильного пятиугольника:
Площадь правильного пятиугольника:
Радиус вписанной окружности правильного пятиугольника:
Радиус описанной окружности правильного пятиугольника:
Пятиугольником невозможно заполнить плоскость без промежутков.

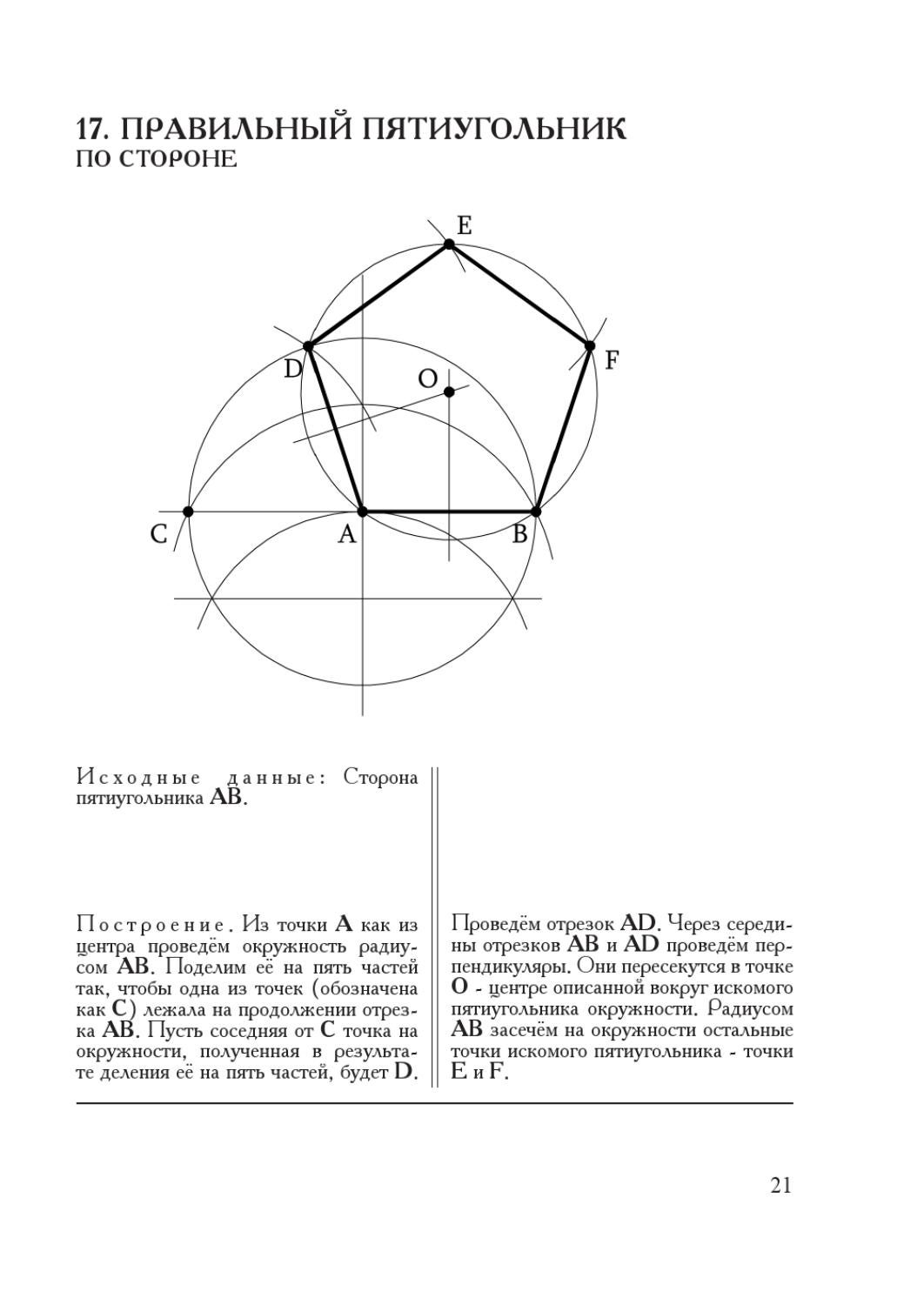
Построение
Правильный пятиугольник может быть построен с помощью циркуля и линейки, или вписыванием его в заданную окружность, или построением на основе заданной стороны. Этот процесс описан Евклидом в его «Началах» около 300 года до н. э.
Вот один из методов построения правильного пятиугольника в заданной окружности:
By Aldoaldoz — Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=10023658
- Постройте окружность, в которую будет вписан пятиугольник и обозначьте её центр как O. (Это зелёная окружность на схеме справа).
- Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
- Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью как точку B.
- Постройте точку C посередине между O и B.

- Проведите окружность с центром в C через точку A. Обозначьте её пересечение с прямой
- Проведите окружность с центром в A через точку D. Обозначьте её пересечения с оригинальной (зелёной окружностью) как точки E и F.
- Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.
- Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.
- Постройте правильный пятиугольник AEGHF.
Альтернативный метод построения правильного многоугольника с помощью линейки и циркуля
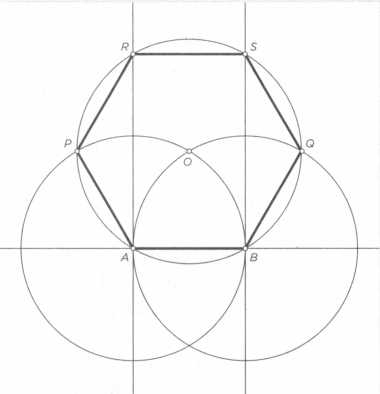
Правильный шестиугольник
Правильный шестиугольник
Правильный шестиугольник (гексагон) — это правильный многоугольник с шестью сторонами.
Свойства
Особенность правильного шестиугольника — равенство его стороны и радиуса описанной окружности .
Все углы равны 120°.
Радиус вписанной окружности равен:
Периметр правильного шестиугольника равен:
Площадь правильного шестиугольника рассчитывается по формулам:
Шестиугольники замощают плоскость (то есть могут заполнять плоскость без пробелов и наложений).
Правильный шестиугольник со стороной является универсальной покрышкой, то есть всякое множество диаметра 1 можно покрыть правильным шестиугольником со стороной (лемма Пала).
Построение
Правильный шестиугольник можно построить с помощью циркуля и линейки. Ниже приведён метод построения, предложенный Евклидом в «Началах», книга IV, теорема 15.
Правильный семиугольник
Правильный семиугольник
Правильный семиугольник — это правильный многоугольник с семью сторонами.
Свойства
Пусть t — сторона семиугольника, R — радиус описанной окружности, r — радиус вписанной окружности.
Периметр правильного семиугольника равен
Площадь правильного семиугольника рассчитывается по формулам:
Построение
Приближённое построение правильного семиугольника
Точное
Согласно теореме Гаусса — Ванцеля, правильный семиугольник невозможно построить с помощью циркуля и линейки, но можно построить с помощью циркуля и размеченной линейки то есть линейки, на которой можно делать отметки и с помощью которой можно проводить прямые, проходящие через какую-нибудь точку, причём отмеченные на линейке точки будут принадлежать данным линиям (прямым или окружностям).
Приближённое
Приближённое (но с достаточной для практики точностью — 0,2 %) построение семиугольника показано на рисунке. Из точки A на окружности радиусом, равным радиусу окружности, проводим дугу BOC. Отрезок и даст искомое приближение.
Отрезок и даст искомое приближение.
Семиугольные звезды
Семиугольная звезда 7/2
Семиугольная звезда 7/3
Существует два звёздчатых семиугольника (гептаграммы): 7/2 и 7/3. Методы их построения аналогичны построению обычного семиугольника, только вершины нужно соединять через одну (7/2) или через две (7/3).
Правильный восьмиугольник
Правильный восьмиугольник
Правильный восьмиугольник (октагон) — геометрическая фигура из группы правильных многоугольников. У него восемь сторон и восемь углов и все углы и стороны равны между собой.
Свойства
Построение правильного восьмиугольника
Восьмиугольник можно построить, проведя к сторонам квадрата серединные перпендикуляры и соединив точки их пересечения с описанной окружностью квадрата с его сторонами.
Угол правильного восьмиугольника составляет 135°
Формулы расчёта параметров правильного восьмиугольника
Примем:
* t — длина стороны восьмиугольника
* r — радиус вписанной окружности
* R — радиус описанной окружности
* S — площадь восьмиугольника
Так как правильный восьмиугольник можно получить соответствующим отсечением углов квадрата со стороной , радиус вписанной окружности, радиус описанной окружности и площадь правильного восьмиугольника можно вычислить и без использования тригонометрических функций:
* Радиус описанной окружности правильного восьмиугольника:
* Площадь правильного восьмиугольника:
Правильный девятиугольник
Правильный девятиугольник
Правильный девятиугольник — это правильный многоугольник с девятью сторонами.
Свойства
Правильный девятиугольник имеет внутренние углы, равные 140°.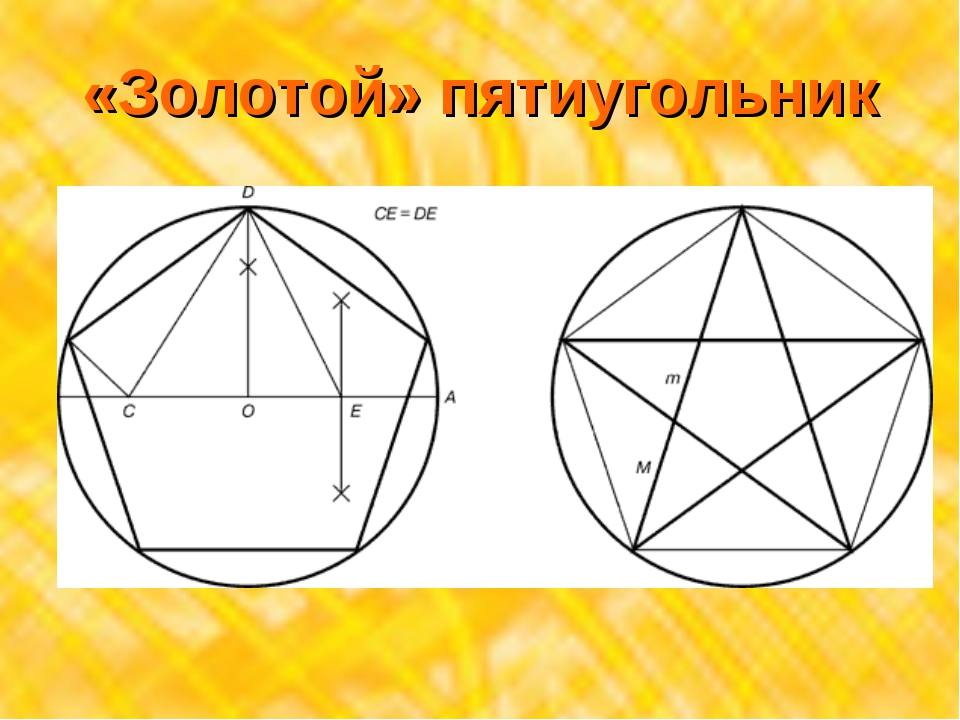
Построение
Хотя правильный девятиугольник и невозможно построить с помощью циркуля и линейки, существуют методы построения достаточно точных приближений.
Девятиугольные звёзды
Существует три звёздчатых девятиугольника: {9/2}, {9/3} и {9/4}, причём звезда {9/3} состоит из трёх равносторонних треугольников:
Правильный семнадцатиугольник
Правильный семнадцатиугольник
Правильный семнадцатиугольник — геометрическая фигура, принадлежащая к группе правильных многоугольников. Он имеет семнадцать сторон и семнадцать углов, все его углы и стороны равны между собой, все вершины лежат на одной окружности.
Центральный угол a равен
Отношение длины стороны к радиусу описанной окружности составляет
Правильный семнадцатиугольник можно построить при помощи циркуля и линейки, что было доказано Гауссом в 1796 году.
Факты
* Гаусс был настолько воодушевлён своим открытием, что в конце жизни завещал, чтобы правильный семнадцатиугольник высекли на его могиле. Скульптор отказался это сделать, утверждая, что построение будет настолько сложным, что результат нельзя будет отличить от окружности.
Примерное построение
1. Ставим на плоскости точку M, строим вокруг неё окружность k и проводим её диаметр AB;
2. Делим пополам радиус AM три раза по очереди по направлению к центру (точки C, D и E).
3. Делим пополам отрезок EB (точка F).
4. строим перпендикуляр к AB в точке F.
* Вкратце: строим перпендикуляр к диаметру на расстоянии 9/16 диаметра от B.
Точки пересечения последнего перпендикуляра с окружностью являются хорошим приближением для точек P3 и P14.
При этом построении получается относительная ошибка в 0,83%. Углы и стороны получаются таким образом немного больше, чем нужно. При радиусе 332,4 мм сторона получается длиннее на 1 мм.
Построение семнадцатиугольника циркулем и линейкой в 64 шага по Йоханнесу Эрхингеру
Урок 26. построение правильных многоугольников — Геометрия — 9 класс
Для построения правильных n-угольников при n>4 обычно используется окружность, описанная около многоугольника.
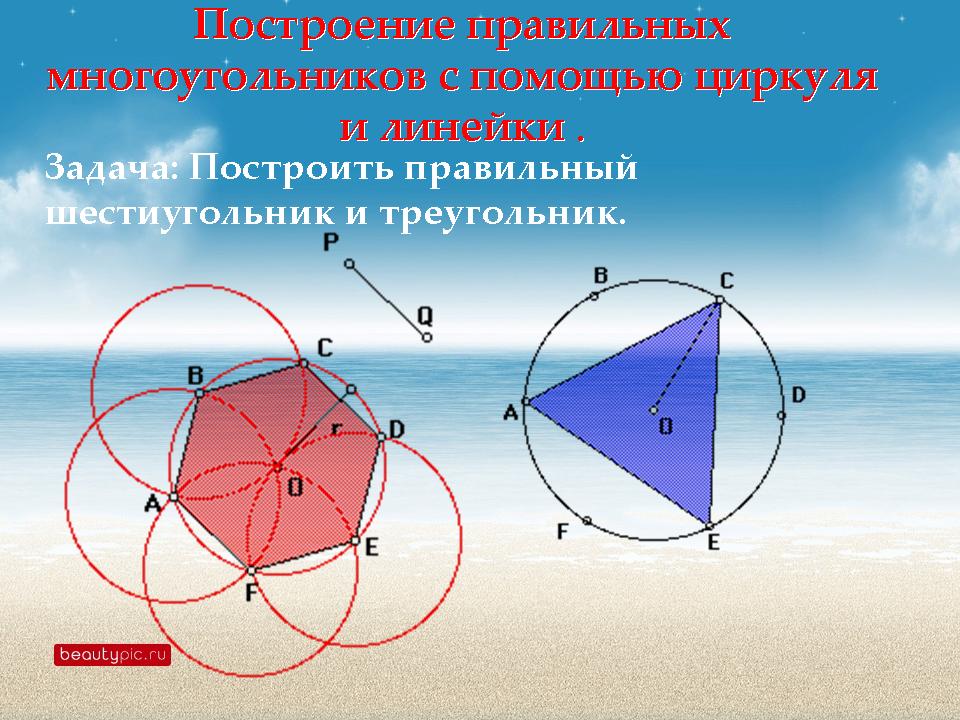
Задача 1. Построим правильный шестиугольник, сторона которого равна данному отрезку
Воспользуемся формулой для стороны правильного шестиугольника:
a6 = 2Rsin (180°)/6 = 2R sin30° = 2R ∙ 1/2 = R, т.е. сторона шестиугольника равна радиусу описанной окружности.
Построим с помощью отрезка PQ окружность, радиусом которой будет являться данный отрезок.
Отметим на окружности точку А1 в произвольном месте. Для построения остальных точек возьмем циркуль. Зафиксируем его раствор размером с выбранный нами отрезок. Не меняя раствора циркуля, построим на окружности точки А2, А3, А4, А5, А6, таким образом, чтобы выполнялись равенства отрезков A1A2 = A2A3 = A3A4 = A4A5 = A5A6.
Соединим точки отрезками. Получим искомый правильный шестиугольник
Задача 2. Дан правильный n-угольник. Построить правильный 2n-угольник.
Пусть А1А2А3Аn правильный n-угольник. Начертим описанную окружность. Для этого построим биссектрисы углов А1 и А2.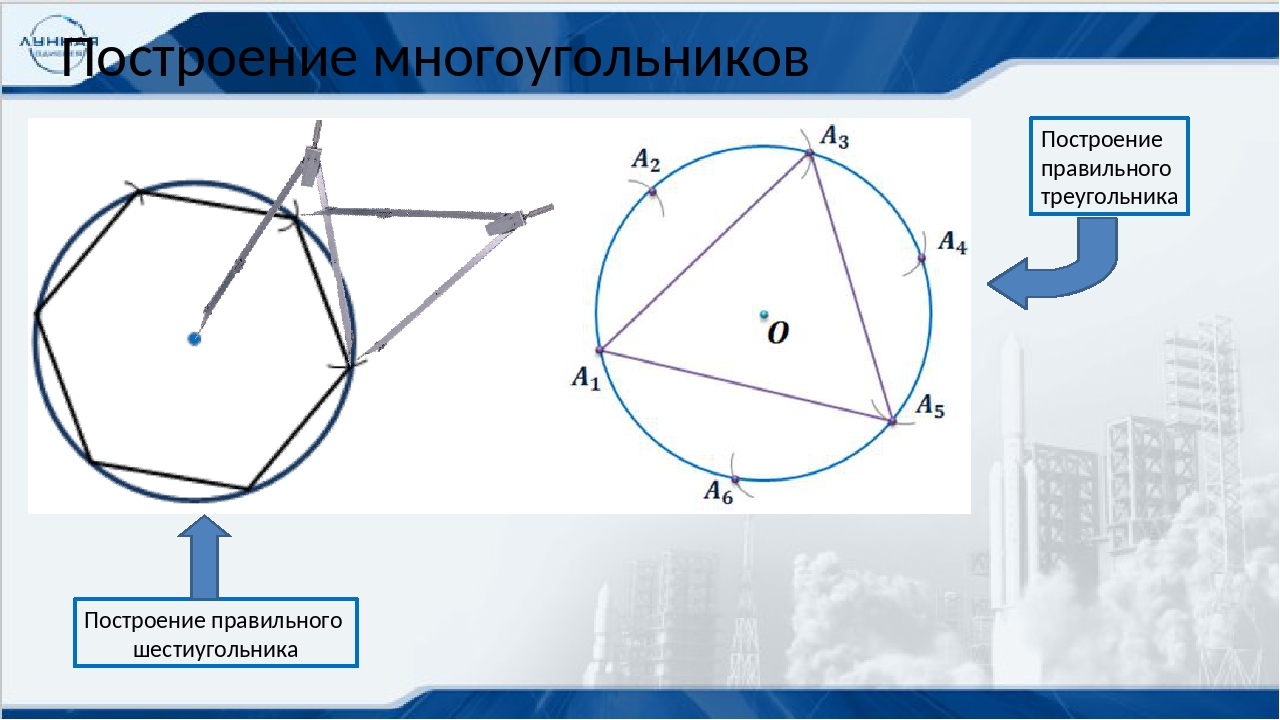 Точку пересечения биссектрис, а это центр окружности, обозначим буквой О. Из точки пересечения биссектрис проведем окружность радиуса ОА1. Разделим дуги А1А2, А2А3 и так до Аn пополам. Точки деления дуг обозначим как В1, В2 и так до Вn. Для построения точек В1, В2 до Вn можно воспользоваться серединными перпендикулярами к сторонам рассматриваемого нами многоугольника.
Точку пересечения биссектрис, а это центр окружности, обозначим буквой О. Из точки пересечения биссектрис проведем окружность радиуса ОА1. Разделим дуги А1А2, А2А3 и так до Аn пополам. Точки деления дуг обозначим как В1, В2 и так до Вn. Для построения точек В1, В2 до Вn можно воспользоваться серединными перпендикулярами к сторонам рассматриваемого нами многоугольника.
Соединим эти точки с концами соответствующей дуги, т.е. с вершинами многоугольника.
Таким образом, построен правильный двенадцатиугольник из шестиугольника.
С помощью данного способа, применяя простые инструменты циркуль и линейку, можно построить целый ряд правильных многоугольников, если построен один из них.
Правило. С помощью циркуля и линейки можно построить любой правильный 2k-угольник, где k любое целое число, большее двух.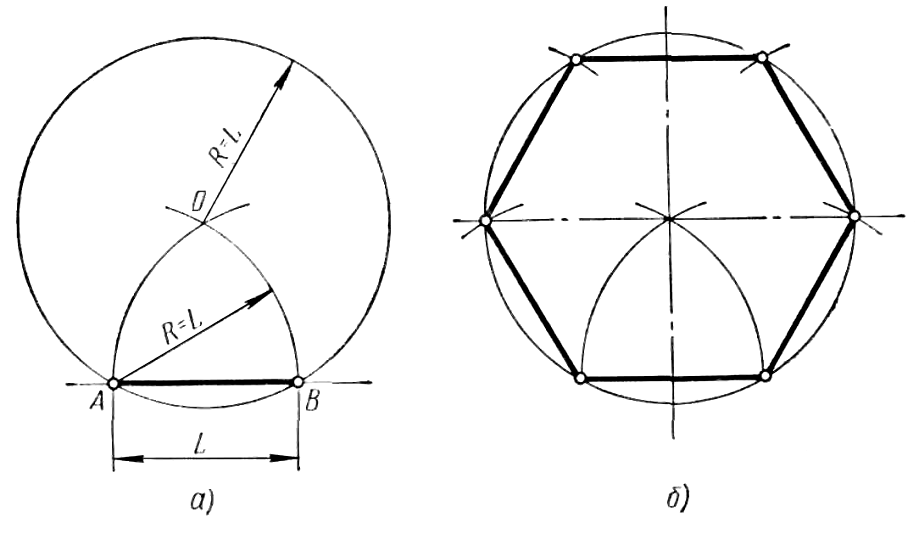
Интересные факты.
Семиугольник не может быть построен при помощи циркуля и линейки.
Семнадцатиугольник может быть построен с помощью циркуля и линейки.
Все прекрасно знают что математика используется в самых разных профессиях и жизненных ситуациях
Введение.
Все прекрасно знают, что математика используется в самых разных профессиях и жизненных ситуациях. Математика – предмет непростой. И геометрию большинство учащихся называет «трудной». Задачи на построение отличаются от традиционных геометрических задач. Программа по геометрии предполагает изучение учащимися лишь простейших приемов и методов построений. Но применение этих приемов часто вызывает затруднения. Цикл задач на построение правильных многоугольников вызывает интерес и восхищение красотой построений, но и забывается достаточно быстро. При этом слабо формируются умения абстрагировать, моделировать, работать с литературой, не происходит развитие интереса к предмету.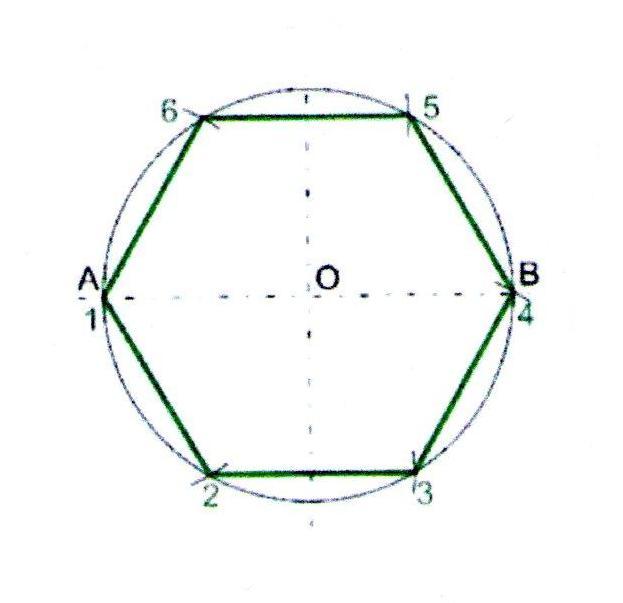
Многие не привыкли замечать знакомые геометрические отношения в окружающем нас мире, применять знания, полученные в геометрии в черчении, физике и практической жизни.
Объектом моего исследования являются правильные многоугольники, построенные с помощью циркуля и линейки.
Цель моей работы: рассмотреть различные способы построений, как точные, так и приближенные. При использовании приближенных способов построений вычислить погрешности и оценить возможность применения.
Методы исследования:
Анализ уже существующих способов построений.
Поиск новых, более точных способов приближенных построений и способов простых в применении.
Задачи:
— получить более полное представление о различных способах построений;
— проследить за развитием этого фрагмента геометрии в истории математики;
— показать связь геометрии с другими науками;
— показать применение задач на построение в практической жизни;
— продолжить развитие исследовательских умений
1. О построениях циркулем и линейкой
О построениях циркулем и линейкой
Каждый ученик, изучающий геометрию в школе, знает, как построить с помощью циркуля и линейки отрезок равный данному, угол равный данному, биссектрису угла. Сможет провести перпендикуляр к прямой и найти середину отрезка. При помощи циркуля и линейки можно строить новые отрезки, длины которых получаются из длин уже имеющихся отрезков при помощи следующих операций: сложения рис1 а), вычитания б), умножения в), деления г)и извлечения квадратного корня д). Последовательно проводя эти операции, при помощи циркуля и линейки можно построить любой отрезок, длина которого выражается через единицу конечным числом операций сложения, вычитания, умножения, деления и извлечения квадратного корня. Такие числа называются квадратичными иррациональностями. Можно доказать, что никакие другие отрезки построить при помощи циркуля и линейки нельзя.
.
2. Из истории геометрического построения циркулем и линейкой.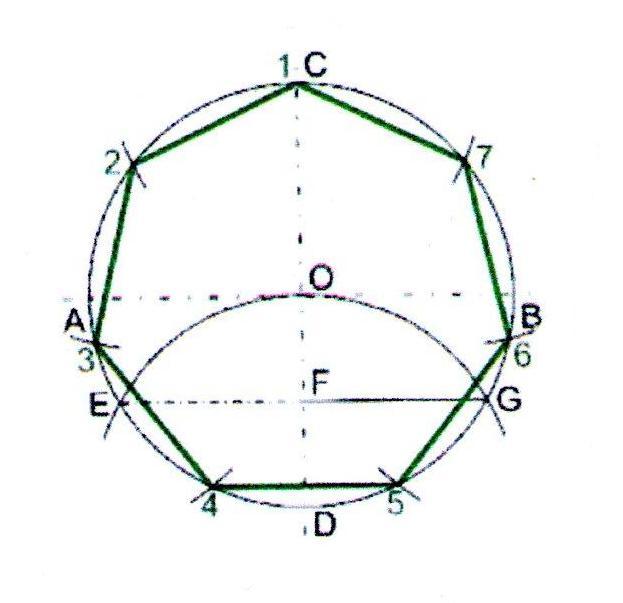
Традиционное ограничение орудий геометрических построений восходит к глубокой древности. В своей книге «;Начала»; Евклид (III век до н. э.) строго придерживается геометрических построений, выполняемых циркулем и линейкой, хотя названий инструментов он нигде не упоминает. Ограничения, по-видимому, были связаны с тем, что эти инструменты заменили собой веревку, первоначально служившую как для проведения прямых, так и для описания окружностей. Но многие историки математики объясняют произведенный Евклидом отбор материала тем, что он, следуя Платону и пифагорейцам, считал только прямую и круг «;совершенными»; линиями.
Искусство построения геометрических фигур было в высокой степени развито в Древней Греции. Древнегреческие математики еще 3000 лет назад проводили свои построения с помощью двух приборов: гладкой дощечки с ровным краем (это линейка) и двух заостренных палок, связанных на одном конце (это циркуль). Однако этих простейших инструментов оказалось достаточно для выполнения огромного множества различных построений.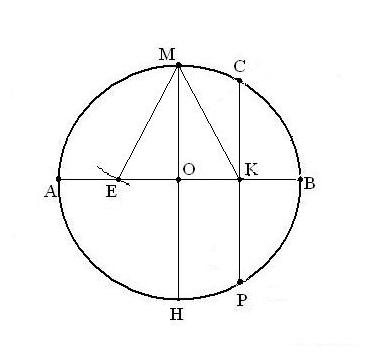 Древним грекам даже казалось, что любое разумное построение можно совершить этими инструментами, пока они не столкнулись с тремя знаменитыми впоследствии задачами.
Древним грекам даже казалось, что любое разумное построение можно совершить этими инструментами, пока они не столкнулись с тремя знаменитыми впоследствии задачами.
Они издавна преобразовывали любую прямолинейную фигуру с помощью циркуля и линейки в произвольную прямолинейную фигуру, равновеликую ей. В частности, всякая прямолинейная фигура преобразовывалась в равновеликий ей квадрат. Поэтому понятно, что появилась мысль обобщить эту задачу: построить с помощью циркуля и линейки такой квадрат, площадь которого была бы равна площади данного круга. Это задача получила название квадратуры круга. Следы этой задачи можно усмотреть еще в древнегреческих и вавилонских памятниках второго тысячелетия до н.э. Однако ее непосредственная постановка встречается в греческих сочинениях V века до н.э.
Еще две задачи древности привлекали внимание выдающихся ученых на протяжении многих веков. Это задача об удвоении куба. Она состоит в построении циркулем и линейкой куба, имеющего объем вдвое больший, чем объем данного куба.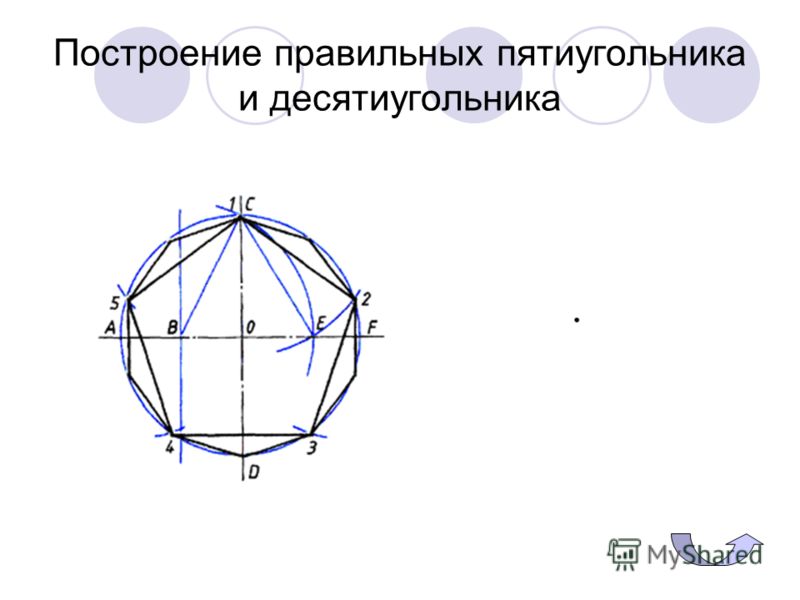 Ее появление связывают с легендой, что на острове Делос в Эгейском море оракул, чтобы избавить жителей от эпидемии чумы, повелел удвоить алтарь, имевший форму куба. И третья задача трисекции угла о делении угла на три равные части с помощью циркуля и линейки.
Ее появление связывают с легендой, что на острове Делос в Эгейском море оракул, чтобы избавить жителей от эпидемии чумы, повелел удвоить алтарь, имевший форму куба. И третья задача трисекции угла о делении угла на три равные части с помощью циркуля и линейки.
Эти три задачи, так называемые 3 знаменитые классические задачи древности привлекали внимание выдающихся математиков на протяжении двух тысячелетий. И лишь в середине XIX века была доказана их неразрешимость, то есть невозможность указанных построений лишь с использованием только циркуля и линейки. В математике это были первые результаты о неразрешимости задач, когда средства решения указаны. Они были получены средствами не геометрии, а алгебры (с помощью перевода этих задач на язык уравнений), что еще раз подчеркнуло единство математики. Не поддаваясь решению, эти проблемы обогатили математику значительными результатами, привели к созданию новых направлений математической мысли.
Еще одной интереснейшей задачей на построение с помощью циркуля и линейки является задача построения правильного многоугольника с заданным числом сторон.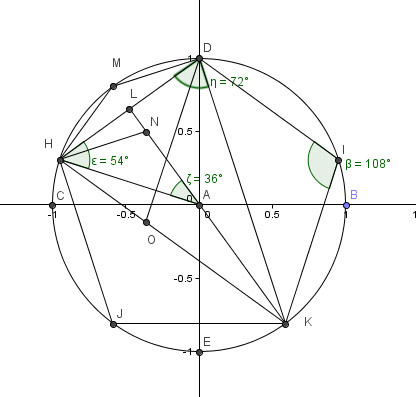 Древние греки умели строить правильный треугольник, квадрат, правильные пятиугольник и 15-угольник, а также все многоугольники, которые получаются из них путем удвоения сторон, и только их. Лишь в 1796 году великий немецкий математик К.Ф.Гаусс открыл способ построения правильного 17-угольника при помощи циркуля и линейки и указал все значения N, при которых возможно построение правильного N-угольника указанными средствами. Первокурсник Геттингенского университета Карл Гаусс решил задачу, перед которой математическая наука пасовала более 2 с лишним тысяч лет. Таким образом, была доказана невозможность построения с помощью циркуля и линейки правильных 7, 9, 11, 13, 18, 21, 22, 23 и т.д. угольников.
Древние греки умели строить правильный треугольник, квадрат, правильные пятиугольник и 15-угольник, а также все многоугольники, которые получаются из них путем удвоения сторон, и только их. Лишь в 1796 году великий немецкий математик К.Ф.Гаусс открыл способ построения правильного 17-угольника при помощи циркуля и линейки и указал все значения N, при которых возможно построение правильного N-угольника указанными средствами. Первокурсник Геттингенского университета Карл Гаусс решил задачу, перед которой математическая наука пасовала более 2 с лишним тысяч лет. Таким образом, была доказана невозможность построения с помощью циркуля и линейки правильных 7, 9, 11, 13, 18, 21, 22, 23 и т.д. угольников.
Теория построения при помощи циркуля и линейки получила свое дальнейшее развитие. Был получен ответ на вопрос: можно ли решить задачу с помощью только одного из двух рассматриваемых инструментов, и достаточно неожиданный. Независимо друг от друга, датчанин Г.Мор в 1672 году и итальянец Л.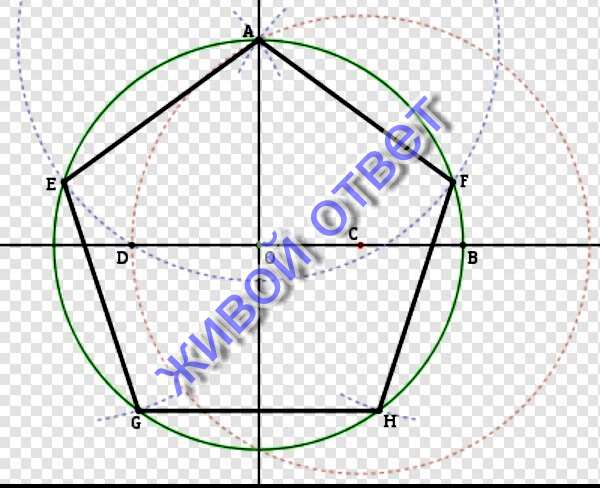 Маскерони в 1797 году доказали, что любая задача на построение, разрешаемая циркулем и линейкой, может быть точно решена с помощью только одного циркуля. Это кажется невероятным, но это так. А в XIX веке было доказано, что любое построение, выполняемое с помощью циркуля и линейки можно провести лишь с помощью одной линейки, при условии, что в плоскости построения задана некоторая окружность и указан ее центр.
Маскерони в 1797 году доказали, что любая задача на построение, разрешаемая циркулем и линейкой, может быть точно решена с помощью только одного циркуля. Это кажется невероятным, но это так. А в XIX веке было доказано, что любое построение, выполняемое с помощью циркуля и линейки можно провести лишь с помощью одной линейки, при условии, что в плоскости построения задана некоторая окружность и указан ее центр.
3. Правильные многоугольники.
Выпуклый многоугольник называется правильным, если все его углы равны и все стороны равны. Квадрат и равносторонний треугольник являются примерами правильных многоугольников. Около любого правильного многоугольника можно описать окружность, и притом только одну, и также в любой правильный многоугольник можно вписать окружность, и притом только одну. Центры описанной около правильного многоугольника и вписанной в него окружностей совпадают.
Так же существует и другое определение:
Правильным многоугольникомназывается многоугольник, вершины которого лежат на некоторой окружности на одинаковых расстояниях друг от друга. Если у правильного многоугольника n вершин, то мы называем его правильным n-угольником. Если мы проведем п радиусов, соединяющих центр окружности с вершинами, то получим п центральных углов величиной— каждый. Если можно построить угол, имеющий эту величину, то можно построить и сам многоугольник.
Если у правильного многоугольника n вершин, то мы называем его правильным n-угольником. Если мы проведем п радиусов, соединяющих центр окружности с вершинами, то получим п центральных углов величиной— каждый. Если можно построить угол, имеющий эту величину, то можно построить и сам многоугольник.
Теорема: Многоугольник, вписанный в окружность, является выпуклым. Если все стороны вписанного многоугольника равны, то он является правильным.
Доказательство. Рассмотрим многоугольник вписанный в окружность с центром О. Докажем сначала что этот многоугольник выпуклый. Для этого нужно доказать, что он лежит по одну сторону от любой прямой, содержащей сторону многоугольника. Докажем, например, что он лежит по одну сторону от прямой. Для этого достаточно убедиться в том, что вершины принадлежат одной и той же полуплоскости с границей . Рассмотрим полуплоскость с границей , в которой лежит точка . Точка принадлежит этой же полуплоскости, так как в противном случае прямая пересекает дугу окружности и, следовательно, имеет с окружностью больше двух общих точек, что невозможно. Точно так же вершина А5 и все остальные вершины принадлежат этой же полуплоскости. Аналогично доказывается, что многоугольник лежит по одну сторону от каждой из прямых .
Точка принадлежит этой же полуплоскости, так как в противном случае прямая пересекает дугу окружности и, следовательно, имеет с окружностью больше двух общих точек, что невозможно. Точно так же вершина А5 и все остальные вершины принадлежат этой же полуплоскости. Аналогично доказывается, что многоугольник лежит по одну сторону от каждой из прямых .
Рис.2
Пусть все стороны вписанного многоугольника равны: . Докажем, что углы многоугольника также равны:. Если п = 3, то это утверждение очевидно. Допустим, что n > 3, и рассмотрим вершины (Рис.2). Треугольники равны друг другу по трем сторонам, а так как эти треугольники равнобедренные, то . Поэтому . Точно так же доказывается равенство других углов многоугольника. Следовательно, многоугольник правильный.
Используя эту теорему, докажем следующее утверждение:
каково бы ни было натуральное число n, большее двух, существует правильный n-угольник.
Возьмем какую-нибудь окружность с центром О и разделим ее на п равных дуг. Для этого проведем радиусы этой окружности так, чтобы
(Рис.3, на этом рисунке п = 8).
Если теперь провести отрезки , то получим n-угольник . Треугольники равны друг другу (по двум сторонам и углу между ними), поэтому . Отсюда согласно доказанной теореме следует, — правильный n-угольник.
Итак, каково бы ни было натуральное число n, больше двух, существует правильный n-угольник. Отсюда, однако, еще не следует, что с помощью циркуля и линейки такой многоугольник можно построить. Возникает вопрос, какие правильные многоугольники можно построить циркулем и линейкой? Частично ответ на этот вопрос дает следующая лемма:
Если построен какой-нибудь правильный n-угольник, то с помощью циркуля и линейки можно построить правильный 2n-угольник. Опишем около данного многоугольника А1, А2… Аn oкружность. Для этого построим серединные перпендикуляры a и b к oтрезкам А1 А2 и А2 А3 (на рисунке n= 4). Они пересекаются в некоторой точке О. Окружность с центром О радиуса ОА1 является описанной около многоугольника А1 А2…Аn. Построим теперь середины В1,В2, …, Bn соответственно дуг А1А2, А2 А3,…, Аn А1 следующим образом. Точки В1и В2 получаются как точки пересечения прямых а и b с дугами А1 А2 и А2 А3. Для построения точки B3 проведём oкружность с центром А3 радиуса А3 В2. Одна из точек пересечения этой oкружности с описанной окружностью есть точка В2, а другая — искомая точка B3. Аналогично строятся точки B4,…, Bn. Соединив каждую из точек В1, В2,…, Bn отрезками с концами соответствующей дуги, получим 2n-угольник А1 В1 А2 В2 А3… Аn Bn, который является правильным в силу теоремы о вписанном в окружность многоугольнике
Для этого построим серединные перпендикуляры a и b к oтрезкам А1 А2 и А2 А3 (на рисунке n= 4). Они пересекаются в некоторой точке О. Окружность с центром О радиуса ОА1 является описанной около многоугольника А1 А2…Аn. Построим теперь середины В1,В2, …, Bn соответственно дуг А1А2, А2 А3,…, Аn А1 следующим образом. Точки В1и В2 получаются как точки пересечения прямых а и b с дугами А1 А2 и А2 А3. Для построения точки B3 проведём oкружность с центром А3 радиуса А3 В2. Одна из точек пересечения этой oкружности с описанной окружностью есть точка В2, а другая — искомая точка B3. Аналогично строятся точки B4,…, Bn. Соединив каждую из точек В1, В2,…, Bn отрезками с концами соответствующей дуги, получим 2n-угольник А1 В1 А2 В2 А3… Аn Bn, который является правильным в силу теоремы о вписанном в окружность многоугольнике
Рис.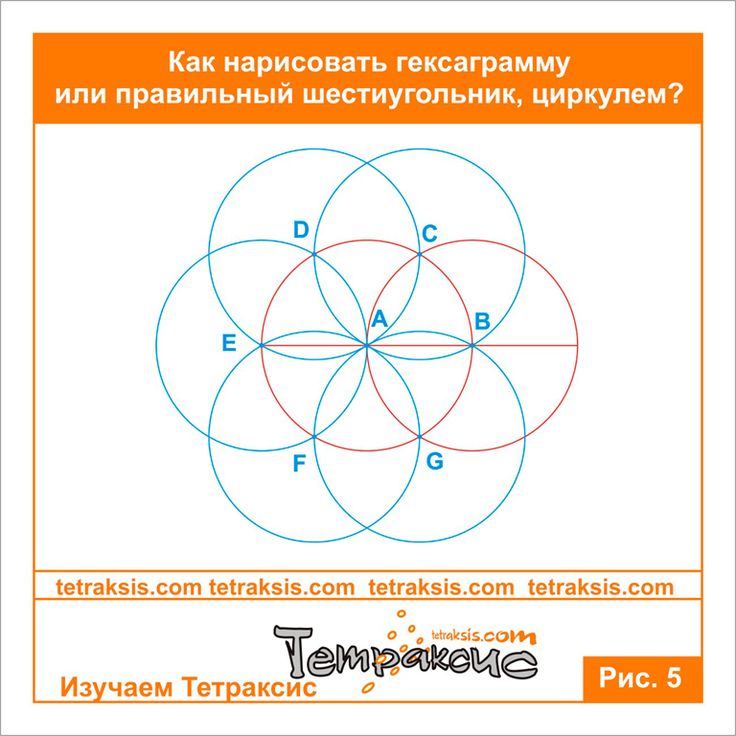 4
4
На рис.4 по данному правильному четырёхугольнику А1А2А3А4 построен правильный восьмиугольник А1 В1 А2 В2 А3 В3 А4 В4.
Итак, если мы можем построить циркулем и линейкой правильный n-угольник, где n — данное натуральное число, то можно построить правильные 2n-угольник, 4n-угольник и, вообще, 2∙n -угольник, где k — любое натуральное число. Знаменитый немецкий математик К. Ф. Гаусс (1777- 1855) доказал следующую интересную теорему:
Построение правильного n-угольника с помощью линейки и циркуля возможно тогда и только тогда, когда число n имеет следующее разложение на множители:n=2р
1∙р2…ps,где m-целое неотрицательное число, а р1, р2,…,ps-различные между собой простые числа вида 2+1.
Рассмотрим примеры применения этой теоремы.
При m=0, s=1 число n имеет вид n=2+1. Для значений k, равных 0, 1, 2, 3, 4, получаем n=3, n=5, n=17, n=257, n=65 537.
При m=0, s=2 имеем n= р1∙р 2 . Если, например, р1=3, р2=5, то n=15.
Значит, согласно теореме Гаусса, можно построить циркулем и линейкой правильный 15-угольник, в чём мы убедимся позже (см. задачу 5 раздела»; Построение правильных многоугольников»;)
Число 7 простое, но оно не является числом вида 2+1, поэтому с помощью циркуля и линейки нельзя построить правильный семиугольник. Точно так же нельзя построить правильный девятиугольник. Отметим, наконец, что число 360=2∙32∙5 не удовлетворяет теореме Гаусса, поскольку простое число 3 входит сомножителем два раза.
Следовательно, циркулем и линейкой нельзя построить правильный 360-угольник. Другими словами, нельзя разделить окружность на 360 равных частей и поэтому циркулем и линейкой нельзя построить угол в 1°.
Гаусс показал, что правильный многоугольник с нечетным числом вершин может быть построен с помощью циркуля и линейки тогда и только тогда, когда число п является простым числом Ферма или произведением нескольких различных простых чисел Ферма.
Что это нам дает для небольших значений n? Очевидно, треугольник и пятиугольник могут быть построены, в то время как семиугольник не может быть построен, так как 7 не является простым числом Ферма. Не может быть построен и девяти угольник, так как 9=3∙3 является произведением двух равных простых чисел Ферма. Для n=11 и n=13 соответствующий п-угольник не может быть построен, но он может быть построен для n=15=и n=17.
Открытие Гаусса, естественно, возродило интерес к числам Ферма. За последнее столетие были предприняты поистине героические поиски «вручную», без помощи машин, новых простых чисел Ферма. В настоящее время эти вычисления ведутся со все возрастающей скоростью при помощи ЭВМ, однако до сих пор результаты были отрицательными. Ни одного нового простого числа Ферма пока не найдено. И сейчас многие математики склонны считать, что их больше нет.
Ни одного нового простого числа Ферма пока не найдено. И сейчас многие математики склонны считать, что их больше нет.
3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,…
4.Примеры построения n-угольников.
4.1 Построение правильного треугольника, квадрата и правильного шестиугольника.
Построение правильного шестиугольника.
Анализ. Пусть АВ (рис.) — сторона правильного шестиугольника, вписанного в окружность радиуса OA = R. Сторона АВ является хордой, стягивающей дугу в 60°. Треугольник АОВ — равнобедренный, поэтому АВО==60°. Рассматриваемый треугольник АОВ равноугольный и, следовательно, равносторонний. Отсюда вытекает, что AB = R, т. е.
Построение: Так как сторона правильного шестиугольника вписанного в данную окружность, равна радиусу этой окружности, то построение такого шестиугольника в том, что из любой точки окружности радиусом, равным радиусу окружности, на ней делают последовательно шесть засечек.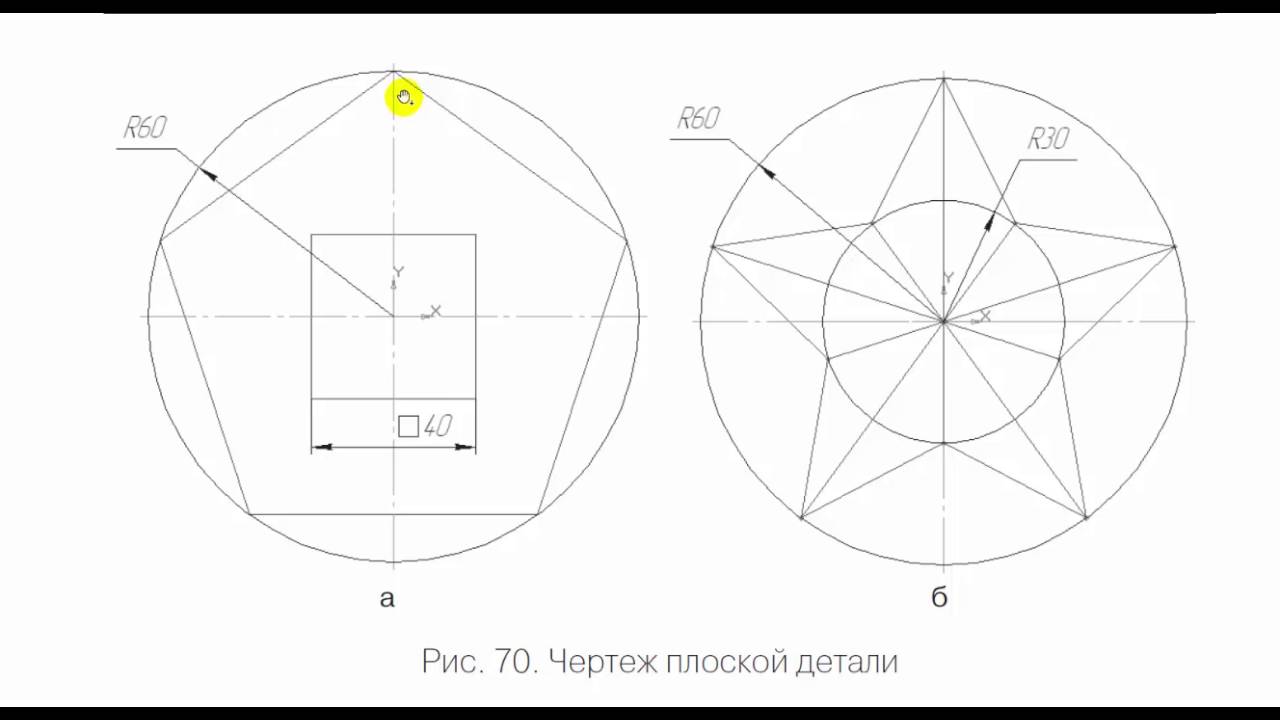 Окружность окажется разделённой на шесть равных частей. Соединив последовательно точки деления хордами, впишем тем самым в окружность правильный шестиугольник.
Окружность окажется разделённой на шесть равных частей. Соединив последовательно точки деления хордами, впишем тем самым в окружность правильный шестиугольник.
Построение правильного треугольника.
Построение. Разделим окружность на шесть равных частей и соединим хордами точки деления через одну. Полученный вписанный треугольник ABCбудет правильным, так как АВ = ВС = AC(черт. 68).
По формуле находим, что а3= 2Rsin 60°. но sin 60° = , следовательно,
Построение квадрата.
1. Разделим окружность на четыре равные части.
Решение. Из произвольной точки А1засекаем окружность радиусом, равным радиусу окружности (рис.7) в точке В, потом из точки В тем же радиусом засекаем окружность в точке С и из С — в точке A3. Точки и A3 —противоположные вершины квадрата. Для отыскания двух других вершин квадрата проводим из точек А1и A3 дуги радиусом, равным А1С, до пересечения в точке D. Из точки А1 радиусом, равным OD, засекаем окружность в точках А2и A4. Точки А2и A4искомые.
Точки и A3 —противоположные вершины квадрата. Для отыскания двух других вершин квадрата проводим из точек А1и A3 дуги радиусом, равным А1С, до пересечения в точке D. Из точки А1 радиусом, равным OD, засекаем окружность в точках А2и A4. Точки А2и A4искомые.
Доказательство.
Рис.7
2. Впишем в окружность данного радиуса квадрат и выразим его сторону через радиус.
Построение. Проводим в данной окружности два взаимно перпендикулярных диаметра АС и BD (рис.8). Точками А, В, С и D окружность разделилась на 4 равные части. Соединив последовательно отрезками точки А, В, С и D, получим квадрат.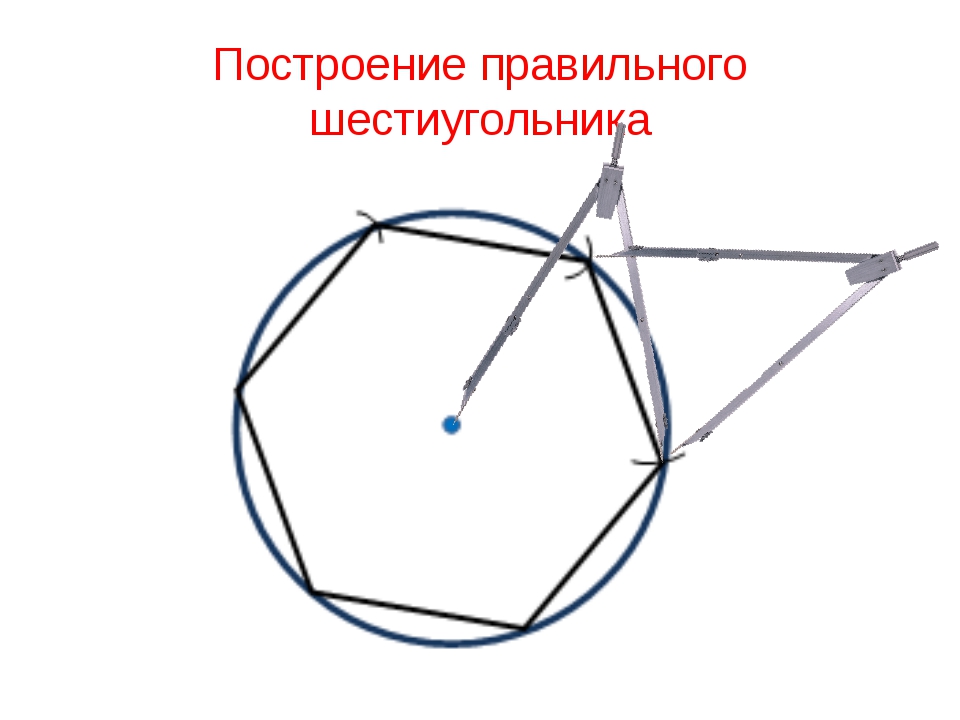
По формуле находим, что а4=2R sin 45°, но sin 45°, следовательно, a4 =2R или т.е. сторона квадрата, вписанного в круг, равна радиусу квадрата умноженному на.
4.2. Построение правильного десятиугольника, пятиугольника, пятнадцатиугольника.
Построение правильного десятиугольника.
1. Разделим окружность на десять равных частей.
Решение. Строим последовательно пять вершинА1A2, А3, A4 и A5 правильного шестиугольника (рис.9).
Рис.9
Из точек А1и A4 радиусами, равными и, проводим дуги до пересечения в точке В. . Из точек A3 и A5 — радиусами, Равными , проводим дуги до пересечения в точке С. Докажем, что ОС = а10.
Докажем, что ОС = а10.
Доказательство. Точка С лежит на прямой. D —точка пересечения прямых A1CA4и А3А5; (апофема правильного треугольника). Из прямоугольного треугольника A3DС имеем:
Деление окружности на десять равных частей при помощи одного циркуля было известно ещё Птолемею.
2. По данной стороне построить правильный десятиугольник.
Решение. Из формулы а10 = выражающей сторону правильного вписанного десятиугольника через радиус rокружности, находим, что
Итак, зная сторону правильного десятиугольника, вписанного в круг, можно определить радиус круга и построить круг. Пусть АгВ = а10. Из точки В как из центра радиусом, равным— стороне десятиугольника, проводим окружность (рис. 10). Строим последовательно пять вершин А1,A2,А3,A4,A5 правильного вписанного шестиугольника. Из точек A1 и A4 радиусами AtA3и A2A4соответственно проводим дуги до их пересечения и в точке К; , где .
10). Строим последовательно пять вершин А1,A2,А3,A4,A5 правильного вписанного шестиугольника. Из точек A1 и A4 радиусами AtA3и A2A4соответственно проводим дуги до их пересечения и в точке К; , где .
Из точек A3 и A5 радиусом, равным , проводим дуги до их пересечения в точке С.
Отрезок CA4 = а10 = —радиус круга, описанного около десятиугольника, сторона которого А1В дана.
Действительно, точка С лежит на А1В .Точка Dлежит в середине отрезка А3А5; DA4 — апофема правильного треугольника, вписанного в круг радиуса а10,
а потому DAf— Из прямоугольного треугольника
имеем:
Рис. 10
10
.
Итак,
Т.е. равно радиусу круга, описанного около десятиугольника.
Для отыскания центра круга из точек Atи В радиусом равным СА4, проводим дуги до их пересечения в точке О. Из центра О радиусом ОА1проводим окружность. Откладывая последовательно от точки А1десять раз дуги радиусом, равным At В , построим искомый десятиугольник.
Построение правильного пятиугольника.
1. Разделим окружность на пять равных частей.
Разделив окружность на десять равных частей, отмечаем точки деления через одну. Эти точки — вершины правильного пятиугольника.
2.По данной стороне ABпостроить правильный пятиугольник
Описываем из центра А окружностьрадиусом АВ.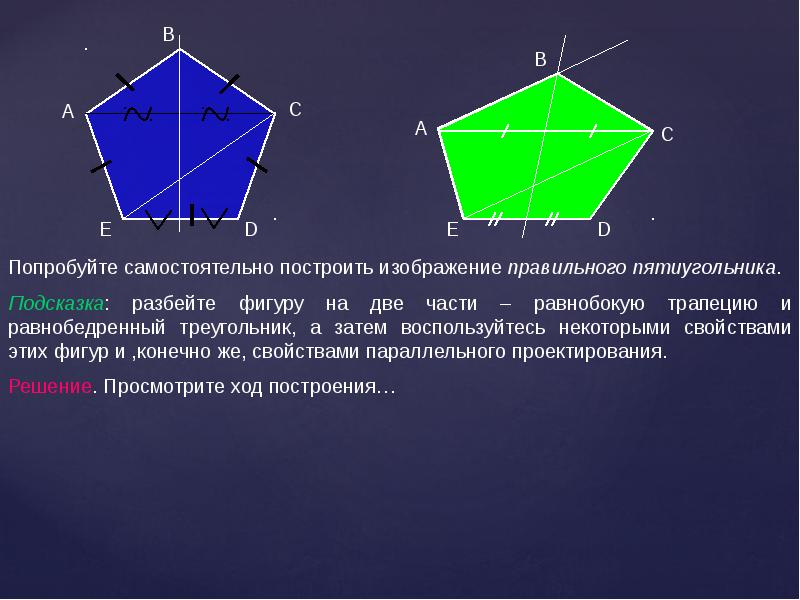 Строим АН=а10=(-1). От Bпоследовательно три раза засекаем окружность дугой, радиус которой равен АН; получаем точку С —вершину пятиугольника. Действительно, = 108° (по построению). Итак, мы имеем три вершины искомого пятиугольника. Для получения двух других поступаем следующим образом: из точки В проводим дугу радиусом АВ и из вершины А —дугу радиусом, равным ВС, до их пересечения в точке D. Точка D —четвёртая вершина пятиугольника (диагональ ВС равна диагонали BD). Для получения пятой вершины Е из точек С и Dпроводим дуги радиусом, равным АВ.
Строим АН=а10=(-1). От Bпоследовательно три раза засекаем окружность дугой, радиус которой равен АН; получаем точку С —вершину пятиугольника. Действительно, = 108° (по построению). Итак, мы имеем три вершины искомого пятиугольника. Для получения двух других поступаем следующим образом: из точки В проводим дугу радиусом АВ и из вершины А —дугу радиусом, равным ВС, до их пересечения в точке D. Точка D —четвёртая вершина пятиугольника (диагональ ВС равна диагонали BD). Для получения пятой вершины Е из точек С и Dпроводим дуги радиусом, равным АВ.
Рис.11
Построение правильного пятнадцатиугольника.
Способ построения заключается в этом: центральный угол в правильном 15-угольнике равени он может быть получен с помощью , угла в, соответствующего правильному пятиугольнику, и угла в соответствующего правильному треугольнику, если удвоить первый угол и вычесть из него второй.
Если мы можем построить циркулем и линейкой правильный n-угольник, где n — данное натуральное число, то можно построить правильные 2n-угольник, 4n-угольник и, вообще, 2∙n -угольник, где k — любое натуральное число. С другой стороны, из 2n- угольника можно получить n-угольник, используя лишь каждую вторую вершину. Это показывает, что достаточно провести поиск многоугольников, которые могут быть построены с помощью циркуля и линейки, только среди многоугольников с нечетным числом вершин.
5. История построения правильного 17-угольника.
«;Математическая деятельность Гаусса, — пишет Феликс Клейн,- началась одним крупным открытием, которое привело его к твёрдому убеждению навсегда посвятить себя науке… 30 марта 1796 года ему – девятнадцатилетнему — удалось показать, что правильный семнадцатиугольник может быть построен с помошью циркуля и линейки»;, т. е. совершить прорыв в проблеме, где не было никакого прогресса в течение свыше 2000 лет.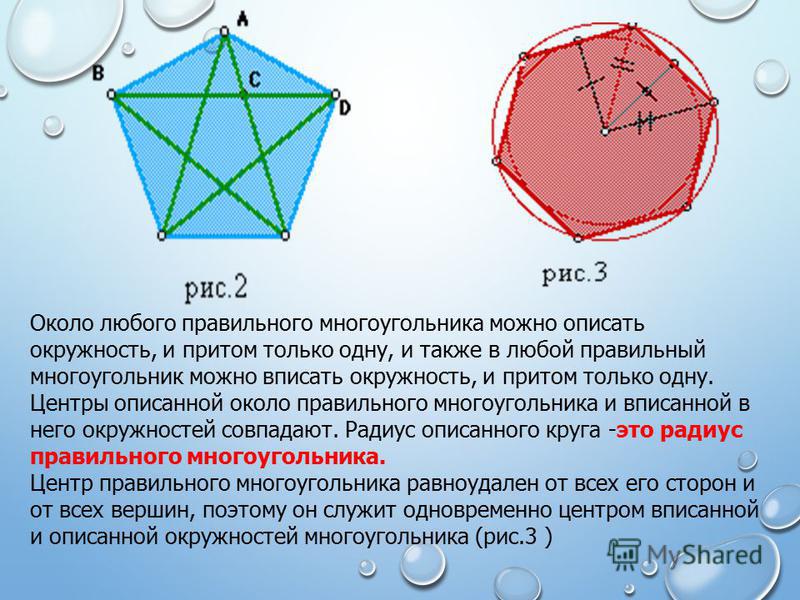 Подобно Архимеду Гаусс выразил желание, чтобы на его могиле был увековечен семнадцатиугольник. Потомки постарались выполнить завещание великого учёного. Они воздвигли ему памятник (на родине, в Брауншвейге), который стоит на постаменте, являющемся правильным семнадцатиугольником. Но если не знать этого, то и не заметишь: правильный семнадцатиугольник почти неотличим от круга.
Подобно Архимеду Гаусс выразил желание, чтобы на его могиле был увековечен семнадцатиугольник. Потомки постарались выполнить завещание великого учёного. Они воздвигли ему памятник (на родине, в Брауншвейге), который стоит на постаменте, являющемся правильным семнадцатиугольником. Но если не знать этого, то и не заметишь: правильный семнадцатиугольник почти неотличим от круга.
Угадать способ построения правильного семнадцатиугольника в рамках традиционных геометрических методов времени Евклида (подобие треугольников и т. п.) было практически невозможно; это открытие по существу принадлежит другой эпохе в математике
Для построения правильного семнадцатиугольника, вписанного в окружность радиуса 1, достаточно построить отрезок длины cos ( рис.12). Однако для этого построения Гауссу потребовались некоторые соотношения в комплексных числах, он получил следующее выражение для cos:
cos=-1+++ .
.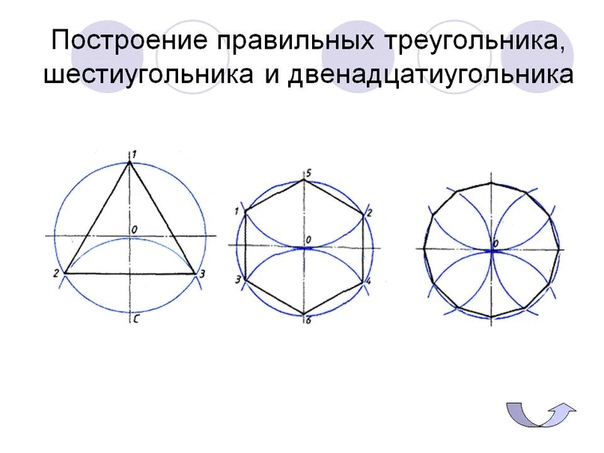
Рис.12
6.Приближённые построения.
6.1Приближённое построение правильного пятиугольника.
Приближенное построение правильного пятиугольника способом А. Дюрера. Приближенное построение правильного пятиугольника представляет собой интерес. А.Дюрером оно проводится при условии неизменности раствора циркуля, что повышает точность построения. Способ построения описан Дюрером так:»;Однако пятиугольник, построенный неизменным раствором циркуля, делай так. Проведи две окружности так, чтобы каждая из них проходила через центр другой. Два центра А и В соедини прямой линией. Это и будет стороной пятиугольника. Точки пересечения окружностей обозначь сверху С, снизу D и проведи прямую линию CD. После этого возьми циркуль с неизменным раствором и, установив одну его ножку в точку D, другой проведи через оба центра А и В дугу до пересечения её с обеими окружностями. Точки пересечения обозначь через E и F, а точку пересечения с прямой CD обозначь буквой G.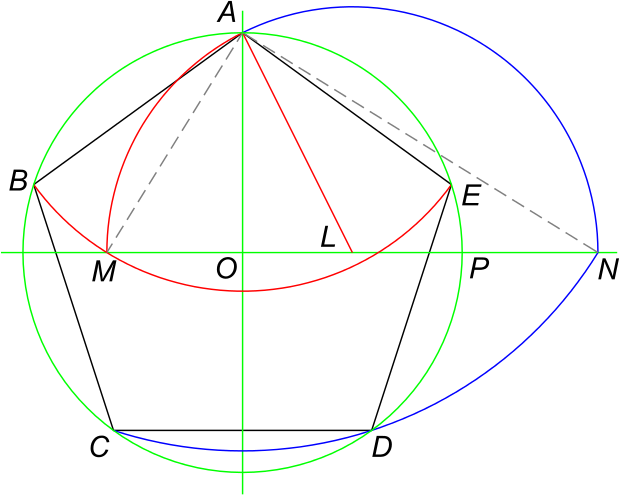 Теперь проведи прямую линию через Е и G до пересечения с линией окружности. Эту точку обозначь Н. Затем проведи другую линию через F и G до пересечения с линией окружности и поставь здесь J. Соединив J,A и H,B прямыми, получим три стороны пятиугольника. Дав возможность двум сторонам такой длины достигнуть совпадения в точке K из точек J и H, получим некоторый пятиугольник.»;
Теперь проведи прямую линию через Е и G до пересечения с линией окружности. Эту точку обозначь Н. Затем проведи другую линию через F и G до пересечения с линией окружности и поставь здесь J. Соединив J,A и H,B прямыми, получим три стороны пятиугольника. Дав возможность двум сторонам такой длины достигнуть совпадения в точке K из точек J и H, получим некоторый пятиугольник.»;
Рис. 13
6.2 Приближённое построение девятиугольника.
Сторона правильного девятиугольника, выраженная через радиус Rописанной окружности, имеет длину, равную R.
Способ Герона.
Еще в I в. Герон Александрийский указал приближенное значение длины стороны этой фигуры, приняв ее равной двум третьим радиуса. Нетрудно подсчитать, что сторона правильного девяти угольника окажется 0,(6). Таким образом, абсолютная погрешность составляет 0,0174. Для практических нужд это приближение вполне удовлетворительно, поскольку его погрешность соответствует возможностям обычных чертежных инструментов.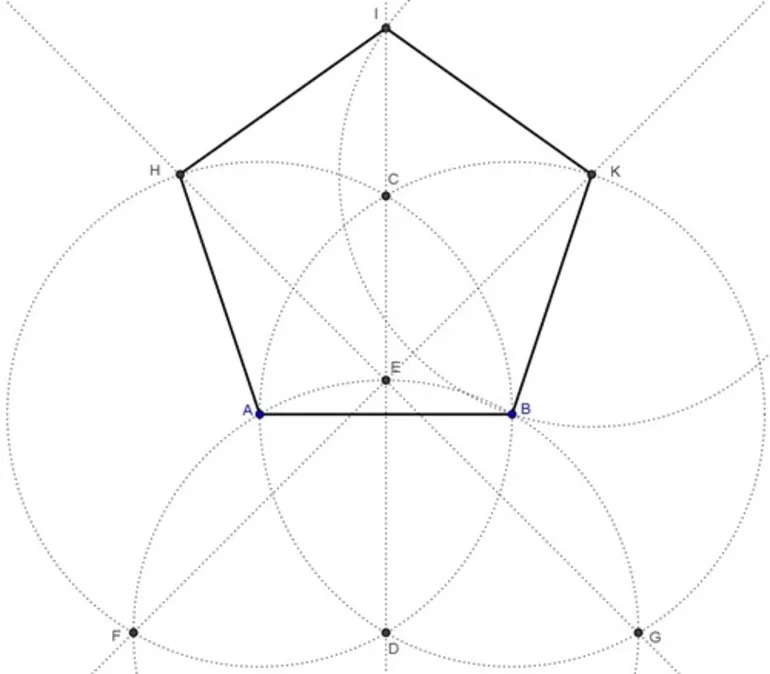
Дюрер же предложил другой способ построения. Пусть А, В и С-вершины треугольника, вписанного в окружность единичного радиуса (рис.15). Проведем дуги АОВ, ВОС, СОА окружностей того же радиуса с центрами в точках центрально-симметричных вершинам треугольника относительно центра О. Построенную фигуру называют «рыбьим пузырем».
Радиус ОВ разделим на три равные части (точки Dи E). Проведем окружность радиуса ODс тем же центром в точке О и построим в ней хорду FG, как показано на рис. 1. Проведя затем через точки Fи Gрадиусы исходной окружности, получим на ней точкии . Хорда , приближенно равна стороне правильного девяти угольника. Подчеркнем, что построение выполнено в строгом соответствии с классическими требованиями, т.е. только с помощью циркуля и линейки.
Докажем, что оно приводит к поставленной цели (рис.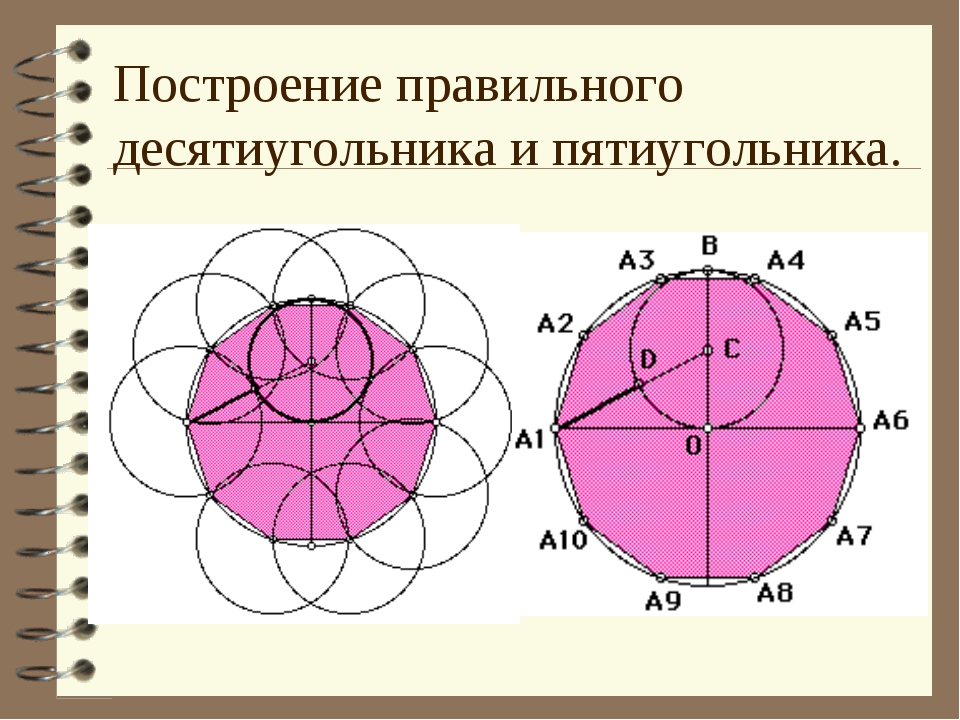 16). Так как секторы, и FOGподобны и коэффициент подобия равен трем по построению, то
16). Так как секторы, и FOGподобны и коэффициент подобия равен трем по построению, то
Рис.16
Хорда FG = 2FH=. Но значит, . Остается найти угол FOH.
Проведем касательную OYк дуге СОВ в точке О. Угол YOB равен 30° (в
этом нетрудно убедиться, зная, что отрезки ,OB и равны и =9О°), а искомый угол F0Hсоставляет 30° — а, где а — угол между хордой OFи касательной. Как известно, такие углы измеряются половиной дуги, отсекаемой хордой. Но на эту же дугу опирается и угол FA1O— центральный для окружности с центром в точке А1 ,который равен 2а. В равнобедренном треугольнике биссектриса А1Кделит основание OFпополам, т.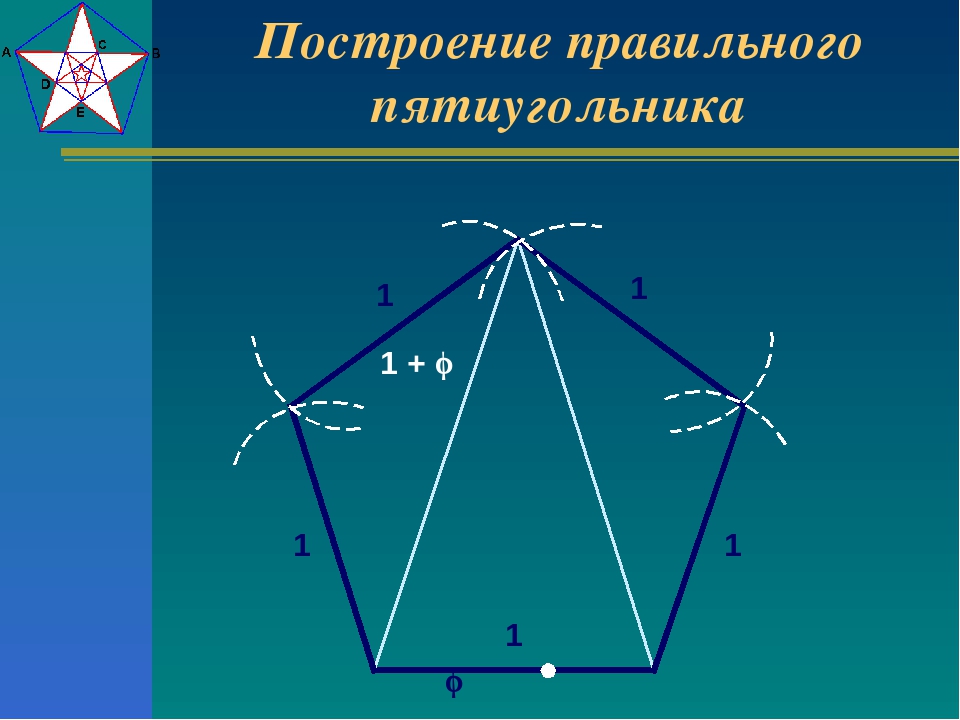 е.. По построению ОА1 = 1, отсюда sin=.
е.. По построению ОА1 = 1, отсюда sin=.
Найдем sin(30°—). Теперь нетрудно определить, чему равен отрезок, что действительно близко к 0,6840.
Результат Дюрера отличается от дроби, предложенной Героном, причем абсолютная погрешность у Дюрера оказывается меньшей 0,0133, относительная 1,9%.
Современный способ построения (автор Р.И.Сарбаш)
Произвольным раствором циркуля описываем окружность с центром О, через который проводим диаметр АВ (рис.14). Тем же раствором циркуля, ставя его ножку в точку А, описываем дугу, пересекающую окружность в двух точках — С и D. Через эти точки проводим прямую, делящую радиус AOпополам в точке Е. Отрезок СЕ, представляющий собой высоту равностороннего треугольника со стороной R, также делим пополам с помощью циркуля и линейки.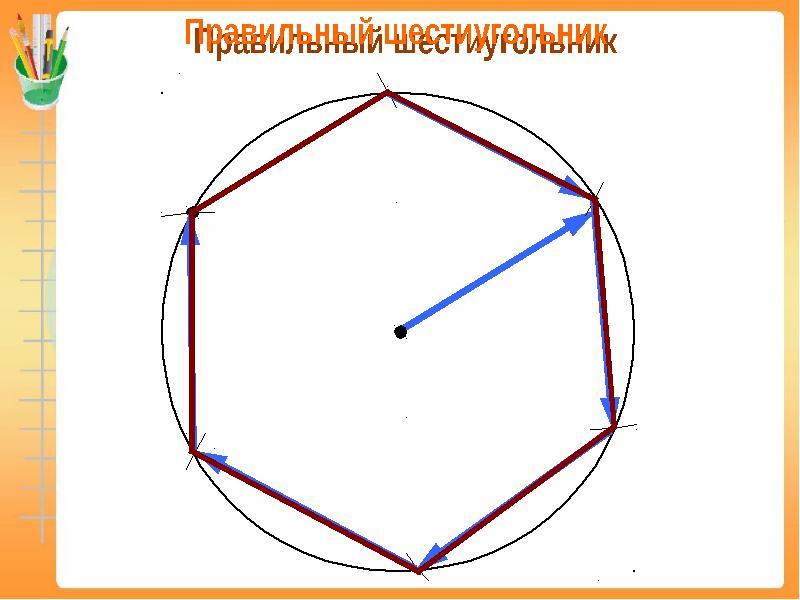 Затем половину отрезка CE, равную , с помощью циркуля откладываем на диаметре АВ от точки В к центру окружности, получив при этом точку F. Далее раствором циркуля, равным AF, поставив его ножку в точку F, делаем засечку на окружности, обозначив на ней точку KПрямая, соединяющая точки A и K, пересечёт проведённую ранее дугу радиуса R в точке L. Теперь выразим длину отрезка EL через элементы треугольников AEL и AOK , для чего используем теорему косинусов:
Затем половину отрезка CE, равную , с помощью циркуля откладываем на диаметре АВ от точки В к центру окружности, получив при этом точку F. Далее раствором циркуля, равным AF, поставив его ножку в точку F, делаем засечку на окружности, обозначив на ней точку KПрямая, соединяющая точки A и K, пересечёт проведённую ранее дугу радиуса R в точке L. Теперь выразим длину отрезка EL через элементы треугольников AEL и AOK , для чего используем теорему косинусов:
Величину угла определим с помощью все той же теоремы косинусов:
После соответствующей подстановки значения, а и вынесения Rза знак радикала найдем длину EL:
Как видим, длина отрезка ELочень незначительно отличается от приведенной выше величины 0,68404 R, что позволяет с достаточно большой степенью обоснованности считать ее равной длине стороны правильного девяти угольника.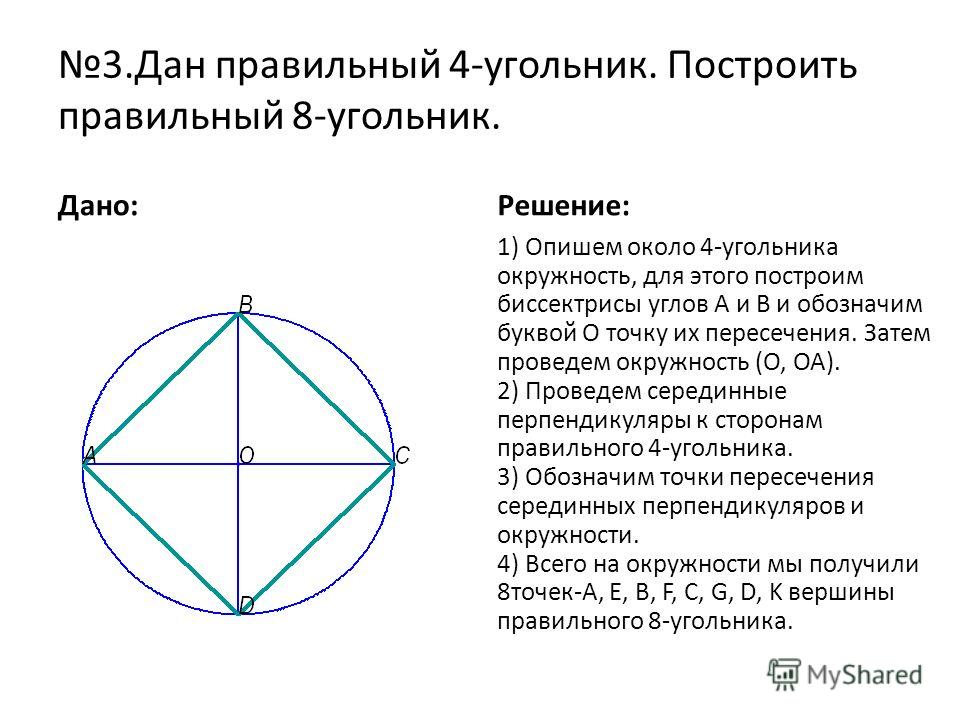 Относительная погрешность предложенного построения составляет примерно 0,15%, что для практических целей вполне приемлемо.
Относительная погрешность предложенного построения составляет примерно 0,15%, что для практических целей вполне приемлемо.
Рис.14
7. Построение правильных вписанных в окружность многоугольников с любым числом сторон.
Один из практических методов, позволяющий построить правильный вписанный в окружность многоугольник с любым числом сторон известен как приём
Биона .Пусть дана окружность и АВ — её диаметр. Построим правильный треугольник АВС и разделим АВ‚ точкой D в отношении AD : AB =2 : n. Пусть продолжение CD пересечёт окружность в точке E. Тогда АЕ представляет сторону правильного вписанного n-угольника.(На рис.17 приведено построение стороны правильного семиугольника.) При n=5,7,9,10 погрешность построения не превышает 1%. С возрастанием n погрешность приближения растёт, но остаётся меньше 10,3%.
Рис.17
Ещё в XV в. великий художник Леонардо да Винчи (1452-1519), установил соотношение
между стороной многоугольника и апофемой:
Рис.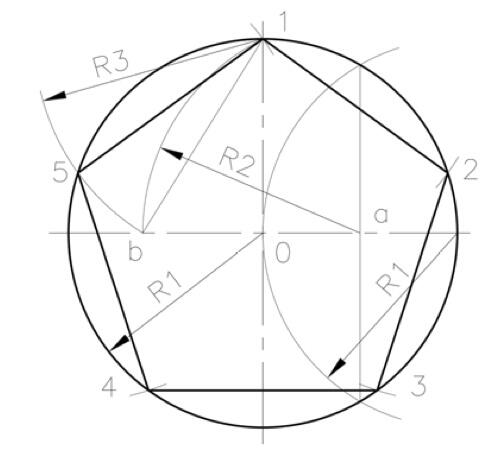 18
18
аn/2 : ha =3/n-1(рис.18), которое можно выразить так: tg180°/n =3/n-1.
В 1888 г. в журнале «; Вестник опытной физики и элементарной математики»; появилась статья Ф. Коваржика, где он предложил общий способ построения правильных многоугольников по данной стороне (рис.19).
Пусть АВ- сторона правильного n-угольника, который требуется построить. На АВ строим равносторонний треугольник АВС, из точки С опускаем перпендикуляр CD на АВ и продолжаем его. Затем делим АВ на 6 равных частей и такие откладываем на СD по обе стороны от С. Точки деления являются центрами окружностей, описанных около искомых многоугольников. Перенумеровав эти точки, как показано на рисунке, получим, что, например, А7 — радиус окружности, описанной около семиугольника, сторона которого равна АВ.
Рис.19
Для шестиугольника и двенадцатиугольника такое построение даёт точный результат. Докажем, что для других значений n предложенное построение обладает достаточно высокой точностью. Пусть величина центрального угла ANB некоторого n-угольника равна х. Обозначим АВ через а. Тогда
Пусть величина центрального угла ANB некоторого n-угольника равна х. Обозначим АВ через а. Тогда
tgx/2=AD/ND=AD/(NC+CD)=a/2((n-6)∙a/2+(a∙)/2)=
=3/n-6+3 = 3/(n-1)+0,19615.
n | tgх/2= 3/(n-1+0.196) | Центральный угол х | Точное значение угла α = |
7 | 0,4841 | 51,68 | 51,42 |
8 | 0,4169 | 45,26 | 45 |
9 | 0,3660 | 40,2 | 40 |
10 | 0,3262 | 36,14 | 36 |
11 | 0,2942 | 32,78 | 32,72 |
15 | 0,2113 | 23,9 | 24 |
18 | 0,1745 | 19,8 | 20 |
20 | 0,1565 | 17,8 | 18 |
30 | 0,1028 | 11,74 | 12 |
40 | 0,0765 | 8,78 | 9 |
Приближённые способы построения правильных многоугольников просты и удобны на практике.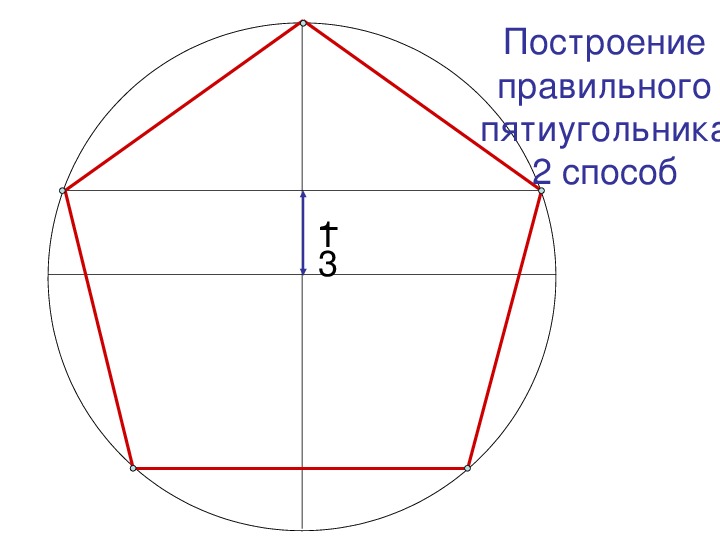
7.1 Пример построения правильного 59- угольника.
Построим правильный 59-угольник с использованием всего лишь простейших инструментов — циркуля и линейки без делений.
При этом выполняют следующие построения (рис.20):
1. В заданной окружности АВ с центром в точке Р проводят два перпендикулярных диаметра ОВ и АК;
2. Откладывают на заданной окружности вниз от точки О произвольным размером 59 равных дуг. При этом отмечают точкой 4 окончание четвертой отложенной дуги, а точкой 59 — окончание 59-й дуги;
3. Точки А и 59 соединяют отрезком, который пересечет диаметр ОВ в точке М;
4. Проводят луч из точки М через точку 4;
5. Из точки М проводят циркулем полуокружность радиусом АМ, которая пересечет диаметр ОВ в точке Е, его продолжение за точкой О — в точке Н, и луч из точки М через точку 4 — в точке Т;
6.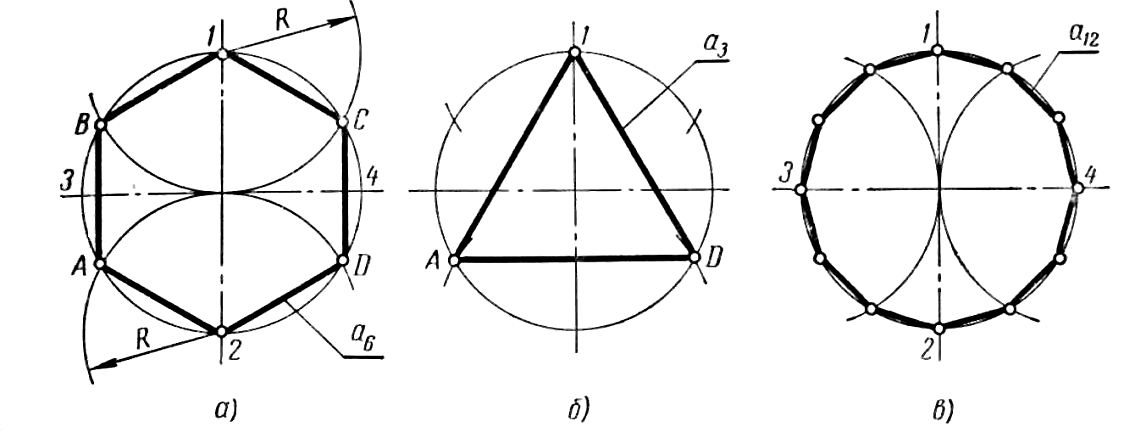 Откладывают на дуге АЕ от точки А дугу АС, равную дуге НТ;
Откладывают на дуге АЕ от точки А дугу АС, равную дуге НТ;
7. Проводят луч из точки Р через точку С, который пересечет заданную окружность в точке Д. При этом величина дуги АД на заданной окружности составит точно 1/59 длины заданной окружности с центром в точке Р;
8. Откладывают на заданной окружности от точки Д вниз следующие дуги: ДД1 , Д1 Д2 и т.д. до дуги Д57 А, все равные дуге АД;
9. Соединяют отрезками точки А и Д, Д1 и Д2 и т.д. до точек Д 57 с точкой А, получают при этом правильный 59-угольник, вписанный в заданную окружность с центром в точке Р.
Точность геометрических построений по данному способу, в основном, зависит от точности применяемых инструментов и тщательности выполняемых построений.
Особенность описанного построения правильного 59-угольника в том, что он выполняется методом засечек с использованием всего лишь простейших инструментов — циркуля и линейки без делений.
7.2 Приспособление для построения правильных n- угольников.
Если построение правильных многоугольников с четным количеством сторон с применением простых инструментов — циркуля и линейки без делений — не вызывает особых затруднений, то построение правильных многоугольников с нечетным количеством сторон (например, 7 или 9 и более сторон) без специальных сложных устройств весьма затруднено.
Предложено простое устройство для графического построения правильных многоугольников как с четным, так и нечетным количеством сторон.
Устройство (рис.21) представляет собой тонкую прозрачную или непрозрачную полимерную пластинку в виде полукруга с центром в точке Р. Основание полукруга представляет собой ровную линейку без делений. По внешней стороне полукруга с левой стороны нанесены риски с одним и тем же интервалом. Каждая риска обозначена цифрами от 1 до 35 (или кратными последней цифре, например 5, 10, 15 и т.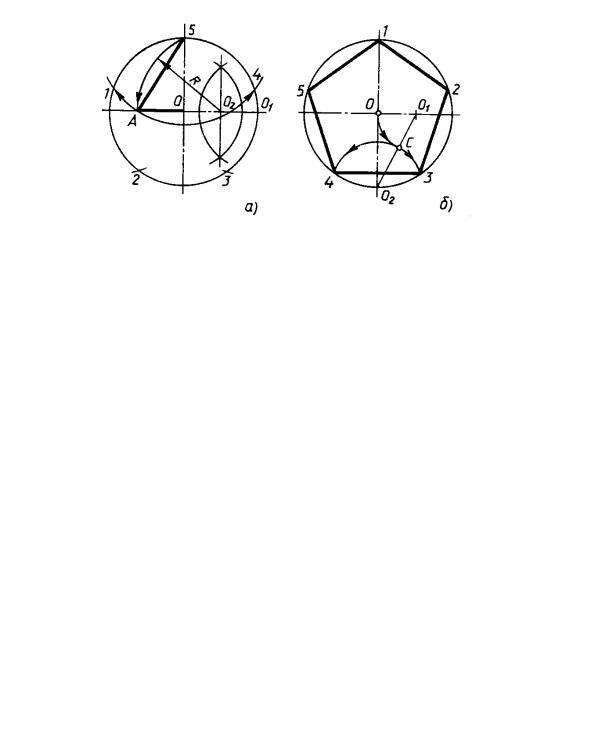 д.). Расстояние между рисками выбрано по величине произвольно. Количество рисок на устройстве определяет максимальное количество сторон для построения правильного многоугольника.
д.). Расстояние между рисками выбрано по величине произвольно. Количество рисок на устройстве определяет максимальное количество сторон для построения правильного многоугольника.
С уменьшением расстояния между рисками возможно расположить по контуру полукруга большее количество рисок, что позволит строить правильные многоугольники с большим количеством сторон.
На правой стороне полукруга от точки В риской А отделена дуга величиной 60 градусов.
Графическое построение правильных многоугольников при помощи данного устройства производится следующим образом. Например, необходимо построить правильный 9-угольник. Для этого делают следующие шаги:
1. Проводят на листе бумаги горизонтальную линию.
2. Прикладывают полукруг сверху на проведенную линию и обводят по контуру полностью полукруг. После этого точками обозначают на листе бумаги риски с буквами Р, О, В, А, а также точки напротив рисок с цифрами 6 и 9.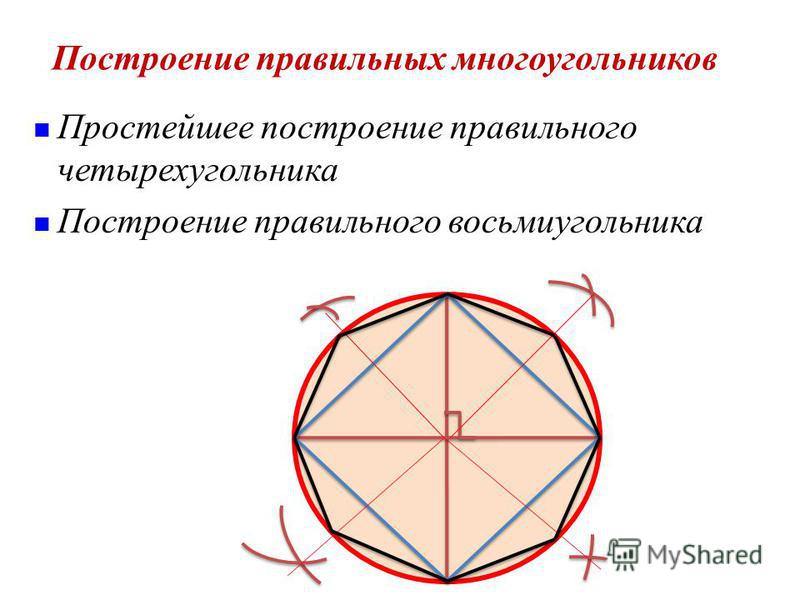
3. Проводят линию между точками 6 и В.
4. Проводят два луча: один из точки Р через точку А, а второй — из точки 9 параллельно линии ОВ. Эти два луча пересекутся в точке, которую необходимо обозначить, например, буквой К.
5. Циркулем проводят полуокружность из точки М на линии ОВ так, чтобы эта полуокружность проходила через точки 9 и К. В этом случае точка М является точкой пересечения диаметра ОВ с перпендикуляром к середине отрезка, соединяющего точки 9 и К.
6. Проведенная циркулем полуокружность пересечет линию ОВ в точке Е, а ее продолжение за точку В — в точке Д, и, кроме того, она пересечет луч из точки В через точку 6 в точке С.
7. Циркулем откладывают на дуге КД дугу НД, равную дуге СЕ.
8. Проводят луч из точки Р через точку Н, который пересечет дугу АВ в точке Т. Величина дуги ВТ составит точно 1/9 часть окружности с центром в точке Р и радиусом РВ.
9. Откладывая на данной окружности девять размеров дуги ВТ и соединив соседние засечки отрезками, получают правильный 9-угольник, вписанный в окружность с центром в точке Р.
Точность графических построений зависит только от точности применяемых инструментов и тщательности выполняемых графических работ.
Литература:
1. Атанасян Л.С. и др. Геометрия: Учебник для 7-9 классов общеобразовательных учреждений. – М: «Просвещение». 1998.
2. Атанасян Л.С. и др. Дополнительные главы к школьному учебнику 9 класса – М.: «Просвещение»,1997.
3. Перельман Я.И. Занимательная геометрия. – М.: АО «Столетие» 1994.
5. Прасолов В.В. Задачи по планиметрии. Части 1 и 2.- М.: «Наука» 1991.
7. Дорофеев Г.В. и др. Избранные вопросы математики. Журнал «Математика в школе» № 10 2003г.
8. Ботвинников А.Д. Справочник по техническому черчению. – М.: «Просвещение» 1974.
9.
Б. И. Аргунов, М Б Балк. Геометрические построения на плоскости, Пособие для студентов педагогических институтов. Издание второе. М., Учпедгиз, 1957 — 268 с.
Ю. И. Манин, О разрешимости задач на построение с помощью циркуля и линейки, Энциклопедия элементарной математики книга четвёртая (геометрия), М., Физматгиз, 1963. — 568с.
Выступление.
Тема моей работы «Построение правильных многоугольников с помощью циркуля и линейки».В школе на уроках геометрии рассматривается задача о построении правильных многоугольников при помощи циркуля и линейки. Легко построить правильный четырехугольник-квадрат. Совсем просто строится правильный треугольник и почти так же правильный шестиугольник (его сторона равна радиусу описанной около него окружности). Более хитрое дело — построение правильного пятиугольника. Научившись строить указанные многоугольники, легко построить и многие другие. И у меня возник вопрос : « А любой ли многоугольник можно построить циркулем и линейкой?»
Оказалось, что еще в древней Греции никому из самых замечательных геометров, не удалось построить ни правильного семиугольника, ни правильного девяти угольника; не удавалось осуществить построения правильного р-угольника ни для какого простого р, отличного от 3 и 5. Две тысячи лет никто не мог продвинуться в решении этой проблемы. И лишь совсем недавно 210 лет назад в 1796 году 19-ти летний Карл Фридрих Гаусс доказал возможность построения правильного 17-угольника при помощи циркуля и линейки.
В течение нескольких последующих лет Гаусс полностью решил проблему построения
правильных n-угольников циркулем и линейкой, выяснив, в частности, что такое построение невозможно при p = 7, 9, и 13, и что правильный n-угольник можно построить, только если n=2р
1∙р2…ps, где m-целое неотрицательное число, а р1, р2,…,ps-различные между собой простые числа вида 2+1.Но как же тогда построить 7- или 9- угольник? Существуют ли приближенные способы построения правильных многоугольников? Какова их точность? Существуют ли какие- либо компьютерные программы, позволяющие строить многоугольники? На эти вопросы я и постарался ответить в своей работе. Для каждого из приближенных способов я нашел погрешность построения Так например еще в I в. Герон Александрийский указал приближенное значение длины стороны 9 угольника, приняв ее равной двум третьим радиуса. Абсолютная погрешность его способа составляет около 2%. Чем сложнее способ построения, тем он точнее. Так ,например приём Биона: при n=5,7,9,10 погрешность построения не превышает 1%. С возрастанием n погрешность приближения растёт, но остаётся меньше 10,3%. Способ заключается в следующем:
Пусть дана окружность и АВ — её диаметр. Построим правильный треугольник АВС и разделим АВ‚ точкой D в отношении AD : AB =2 : n. Пусть продолжение CD пересечёт окружность в точке E. Тогда АЕ представляет сторону правильного вписанного n-угольника.
Также в своей работе я рассмотрел способ построения 59 угольника,(рассказать о способе)
Считаю, что материал моей работы может быть использован на уроках геометрии, черчения (особенно простые универсальные способы построений), ОИВТ или как факультатив, на котором учащиеся смогут научиться выполнять построения с помощью циркуля и линейки правильных многоугольников, смогут изготовить шаблоны для построения правильных многоугольников, а также использовать компьютерные программы для выполнения построений
Приближенное построение правильных многоугольников с помощью циркуля и линейки. Учебно-методические пособие
1. Любимова Виктория Сергеевна, учитель математики ГБОУ СОШ 454 Колпинского района Санкт-Петербурга
ПРИБЛИЖЕННОЕ ПОСТРОЕНИЕправильных многоугольников
с помощью циркуля и линейки
Учебно-методические пособие
2. Пояснительная записка
• В геометрии нередко для различных целей требуетсяпостроить правильный n-угольник, но, как известно,
не все правильные n-угольники могут быть
построены с помощью циркуля и линейки абсолютно
точно.
• Тем не менее, для практических целей часто бывает
достаточно приближенного построения.
• В пособии рассматриваются некоторые способы
построения правильных n-угольников, которые без
особого труда могут освоить учащиеся.
3. Приближенное построение правильного семиугольника
Шаг 1. Построим окружность, в которую будет вписансемиугольник, и из произвольной точки этой окружности
проведем дугу тем же радиусом до пересечения с окружностью
в точках M и N:
M
N
4. Приближенное построение правильного семиугольника
Шаг 2. Половина хорды MN приблизительно равна стороневписанного семиугольника (разделить хорду пополам можно,
построив серединный перпендикуляр к отрезку MN)
M
N
5. Приближенное построение правильного семиугольника
Шаг 3. Строим дугу с центром в точке М радиуса, равногополовине хорды MN, находим точки A и B пересечения с
окружностью.
А
N
M
В
6. Приближенное построение правильного семиугольника
Шаг 4. Аналогично находим положение остальных вершинсемиугольника:
А
В
7. Приближенное построение правильного семиугольника
Шаг 5. Соединяя найденные точки на окружности, получаемискомый правильный семиугольник
8. Деление окружности на n равных частей
Задача о делении данной окружности на n равныхчастей равносильна задаче о построении правильного
n-угольника, вписанного в эту окружность.
Универсальный способ приблизительного построения
любого правильного n-угольника, вписанного в
окружность, особенно удобен при нечетном числе
сторон.
Величина погрешности при точном построении
не превышает 0,02d (где d – диаметр данной
окружности, описанной около многоугольника).
9. Последовательность действий
• Строим окружность заданного диаметра (если диаметр не задан,то выбираем такой, чтобы его удобно было разделить на
нужное число частей).
• Проводим два взаимно перпендикулярных диаметра.
• Вертикальный диаметр делим на нужное число частей.
• Из какого-либо конца вертикального диаметра, как из центра,
проводим дугу окружности радиусом, равным выбранному
диаметру, до пересечения с прямой, содержащей
горизонтальный диаметр, в двух точках справа и слева от
окружности.
• Из левой точки проводим лучи через четные деления
вертикального диаметра до пересечения с окружностью.
Аналогично проводим лучи через правую точку и те же деления
на вертикальном диаметре. В точках пересечения лучей с
окружностью получаем искомые вершины многоугольника.
• Соединяя полученные точки отрезками, строим многоугольник.
10. Приближенное построение правильного пятиугольника
Шаг 1. Строим окружность заданного диаметра, проводим двавзаимно перпендикулярных диаметра и один из диаметров
делим на нужное число частей (в данном случае – на пять
равных частей).
11. Приближенное построение правильного пятиугольника
Шаг 2. Из какого-либо конца вертикального диаметра, как изцентра, проводим дугу окружности радиусом, равным
выбранному диаметру, до пересечения с прямой, содержащей
горизонтальный диаметр, в двух точках справа и слева от
окружности.
12. Приближенное построение правильного пятиугольника
Шаг 3. Из левой точки проводим лучи через четные делениявертикального диаметра до пересечения с окружностью.
Аналогично проводим лучи через правую точку и те же
деления на вертикальном диаметре.
13. Приближенное построение правильного пятиугольника
Шаг 4. В точках пересечения лучей с окружностью (дальние отначала луча точки) получаем искомые вершины
многоугольника. Соединяя полученные точки отрезками,
строим многоугольник.
14. Построение правильного восьмиугольника
15. Литература
• Годик Е. И., Хаскин А. М. Справочноеруководство по черчению. Изд. 4-е,
перераб. и доп. М., «Машиностроение»,
1974.
• Или в электронном виде
http://biblioteka.cc/index.php?newsid=86302
Построение правильных десяти- и пятиугольников с помощью циркуля и линейки. И2
Данный информационный модуль представляет собой анимированный ролик со звуком. Состоит из логически законченных частей, которые можно проигрывать как последовательно, так и в любом порядке по желанию учащегося. Каждая часть состоит из двух блоков: видеоряд и сопровождающий текст. Видеоряд может быть увеличен на весь экран (щелчок мышкой по пиктограмме «лупа с плюсом»). В этом режиме видеоряд проигрывается без сопровождающего текста. В любом режиме воспроизведения учащийся может включить/выключить звуковое сопровождение видеоряда (щелчок мышкой по пиктограмме «громкоговоритель»). Целью данного информационного модуля является: изучение учащимися методов построения правильных вписанных в окружность десяти- и пятиугольников с помощью циркуля и линейки.
Категория пользователей
Обучаемый, Преподаватель
Дисциплины
Математика
/ Правильные многоугольники
Уровень образования
Профессионально-техническая подготовка, повышение квалификации
Статус
Завершенный вариант (готовый, окончательный)
Тип ИР сферы образования
информационный модуль
Ключевые слова
правильный
Издатель
ООО «Кирилл и Мефодий»
ООО «Кирилл и Мефодий»
Россия, 127549, Москва, стр.1, ул. Пришвина, 8
Тел. — +7-495- 787-2610, +7-495- 787-2610
Сайт —
http://www.nmg.ru
Правообладатель
ООО «Кирилл и Мефодий»
ООО «Кирилл и Мефодий»
Россия, 127549, Москва, стр.1, ул. Пришвина, 8
Тел. — +7-495- 787-2610, +7-495- 787-2610
Сайт —
http://www.nmg.ru
Внимание! Для воспроизведения модуля необходимо установить на компьютере проигрыватель ресурсов.
Характеристики информационного ресурса
Тип используемых данных:
text/plain, text/html, image/jpeg
Объем цифрового ИР
844 131 байт
Проигрыватель
Категория модифицируемости компьютерного ИР
Признак платности
бесплатный
Наличие ограничений по использованию
нет ограничений
Рубрикация
Ступени образования
Основное общее образование
Целевое назначение
Учебное
Тип ресурса
Открытая образовательная модульная мультимедийная система (ОМС)
Классы общеобразовательной школы
9
Уровень образовательного стандарта
Федеральный
Характер обучения
Базовое
Построение треугольника по трем элементам и правильного пятиугольника
Построение треугольника по трем элементам и правильного пятиугольника
Гнатко И.В. 11МБОУ «Лицей №159»
Бутакова В.И. 11МБОУ «Лицей №159»
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
Гипотеза исследования построена на предположении о том, что задачи на построение правильного пятиугольника имеют достаточно широкое распространение в архитектуре, живописи и других, смежных с математикой, науках.
Методы исследования:
Поисковый;
Анализ;
Дедуктивный метод.
Объект исследования — задачи на построение с помощью циркуля и линейки.
Предмет исследования — решение задач повышенной сложности на построение треугольников по трем элементам, построение правильного пятиугольника различными способами.
Проблема — задачи на построение правильного пятиугольника и задачи повышенной сложности на построение треугольника по трем элементам почти не изучаются в школьном курсе математики.
Цель исследования — поиск решения задач на построение правильного пятиугольника, на построение треугольников по трем элементам.
Задачи исследования:
1. Определить в математике понятие задачи на построение с помощью циркуля и линейки, изучить основную литературу по данной теме;
2. Решение задач повышенной сложности на построение треугольников по трем элементам;
3.Исследовать архитектурные сооружения, при проектировании которых использовались правильные пятиугольники;
4.Рассмотреть наиболее интересные способы построения правильных пятиугольников;
5. Создание творческих проектов.
Актуальность исследования — данная тема очень актуальна, так как, выбирая профессию инженера, ученик сталкивается с множеством вопросов, например одним из них: «Где мы можем применить знания математики?» Исследования в данной области приводят к выводу о том, что математика имеет большое практическое применение, как в архитектуре, живописи, дизайне так и в других науках.
История возникновения
Первые задачи на построение возникли в глубокой древности. Уже древними архитекторами и землемерами приходилось решать простейшие задачи на построение, связанные с их профессией.
Самые первые задачи на построение, по-видимому, решались непосредственно на местности и заключались в проведении прямых линий и построения прямого угла.
Древнегреческие математики еще 3000 лет назад проводили свои построения с помощью двух приборов: гладкой дощечки с ровным краем и двух заостренных палок, связанных на одном конце.
К задачам на построение прибегали древние инженеры, когда составляли рабочий чертеж того или иного сооружения. Задачи на построение помогали людям в их хозяйственной жизни, их решения формулировались в виде «практических правил», исходя из наглядных соображений.
Первым греческим ученым, который рассматривал геометрические задачи на построение, был Фалес Милетский. Это он, пользуясь построением треугольника, определил расстояние, недоступное для непосредственного измерения. Это он вычислил и высоту египетской пирамиды по отбрасываемой ею тени.
Задачи на построение интересовали и Пифагора. Пифагор и его ученики потратили много сил, чтобы отдельным геометрическим сведениям, состоящим до того времени из набора интуитивных правил, придать характер настоящей науки. Задачи на построение интересовали Платона. Платон и его ученики считали построение геометрическим, если оно выполнялось при помощи циркуля и линейки. Если же в процессе построения использовались другие чертежные инструменты, то построение не считалось геометрическим. Уже в древности греческие математики встретились с тремя задачами на построение, которые не поддавались решению.
Первая задача. Задача об удвоении куба. Требуется построить ребро куба, который по объему был бы в два раза больше данного куба.
Вторая задача. Задача о трисекции угла. Требуется произвольный угол разделить на три равные части.
Третья задача. Задача о квадратуре круга. Требуется построить квадрат, площадь которого равнялась бы данному кругу. Эти три задачи на построение и носят название «знаменитых геометрических задач древности». Большую роль задачи на построение играют в «Началах» Эвклида , где существование фигур доказывается их построением при помощи циркуля и линейки. В «Началах» Эвклида находятся почти все задачи на построение, которые изучаются в настоящее время в школе.
Теоретическая часть
Что такое задачи на построение?
Задача на построение — это задача, в которой требуется построить геометрический объект, пользуясь только двумя инструментами: циркулем и линейкой (односторонней и без делений). Решение задач на построение состоит не в том, чтобы проделать «руками» соответствующие построения, а в том, чтобы найти алгоритм решения, то есть описать решение задачи в виде последовательности уже известных стандартных построений, а также рассмотреть различные способы построения правильного пятиугольника. В этом и состоит цель моей работы.
К элементарным задачам на построение, которые рассматривают на начальных этапах изучения в школьном курсе геометрии, как правило, относят следующие:
1. Отложение на прямой отрезка, равного данному.
2. Отложение от заданной полупрямой в заданную полуплоскость угла, равного данному.
3. Построение прямой, проходящей через данную точку и параллельную данной прямой.
4. Построение прямой, проходящей через данную точку и перпендикулярную к данной прямой.
5. Деление отрезка на две равные части.
6. Деление отрезка в заданном отношении.
7. Построение биссектрисы угла.
8. Построение угла, равного данному.
9. Построение треугольника по трём сторонам, по двум сторонам и углу между ними, по стороне и прилежащим к ней углам.
10. Построение прямоугольного треугольника по гипотенузе и катету, по гипотенузе и острому углу, по двум катетам.
11. Нахождение центра построенной окружности.
12. Построение касательной к окружности через заданную на ней точку. Заметим, что представленный перечень элементарных задач является условным, его можно дополнить.
Сколько бывает решений для задач на построение?
Решить задачу на построение — найти все её решения. Покажем на простейших примерах возможные случаи.
З адача имеет одно решение.
Рисунок 1
Пусть требуется построить прямоугольный треугольник по катету и гипотенузе. Таких треугольников на плоскости можно построить множество, и они могут располагаться как угодно, но у всех равны соответственно две стороны два данных отрезка: гипотенуза и катет, а значит, эти треугольники равны. В этом случае говорят, что задача имеет одно решение «с точностью до равенства». Поэтому достаточно построить один треугольник.
Задача имеет конечное число решений.
Рисунок 2
Пусть требуется построить прямоугольный треугольник, катетом которого служит данный отрезок AC, а гипотенуза равна другому данному отрезку L. В этом случае условие задачи требует определённого расположения искомого треугольника относительно катета AC. Треугольник может оказаться в верхней полуплоскости и в нижней полуплоскости относительно отрезка AC. Поэтому задача имеет два решения: Δ и Δ (рис. 2), причём Δ = Δ . Важно отметить, что хотя здесь треугольники и равны, мы считаем их разными решениями (поскольку они расположены по-разному относительно отрезка AC).
Задача имеет бесконечно много решений.
Такого рода задачи называют неопределёнными. Конечно, мы не можем построить все решения неопределённой задачи. Когда же считают неопределённую задачу решённой? В том случае, когда указаны:
1) приём построения одной из искомых фигур задачи;
2) приём получения других искомых фигур.
Пример. Построить окружность данного радиуса и касающуюся данной прямой.
Рисунок 3
Р ешение. Через произвольную точку B прямой L проведём прямую L1⊥L. Отложим на прямой L1 от точки B, например, в верхнюю полуплоскость отрезок BO = r. Проведём окружность ω(O;OB=r). Через точку O проведём прямую L2 параллельную L. Заметим, что при всевозможных положениях точки O на прямой L2 возникают все решения данной задачи. Задача решена.
Задача не имеет решений.
Такие задачи называют переопределёнными.
Пример. Построить окружность, проходящую через три данные точки, лежащие на одной прямой. Если точки лежат на одной прямой, то провести через них окружность нельзя. Следовательно, задача не имеет решения.
О расположении данных в задаче ничего не сказано. В таких случаях задачу считают решённой, если рассмотрены всевозможные случаи расположения данных.
Пример. Провести через данную точку касательную к данной окружности.
Решение. Возможны три случая расположения данных (точки и окружности).
Случай 1. Точка находится вне окружности, но не принадлежит кругу. Здесь можно провести две касательные к окружности (рис. 4).
Случай 2. Точка находится на окружности. Здесь можно провести одну касательную (рис. 5).
Рисунок 4
Рисунок 5
Рисунок 6
С лучай 3. Точка находится вне окружности, но принадлежит кругу. Здесь касательную к окружности провести нельзя (рис. 6).
Что такое правильный пятиугольник? Правильный пятиугольник, или пентагон (от греческого πενταγωνον-пятиугольник) — выпуклая фигура, имеющая пять вершин, все стороны которой равны между собой (рис 7).
Также, можно заметить, что данная фигура делится в золотом сечении.
Рисунок 7. Правильный пятиугольник
Рисунок 8. Деление правильного пятиугольника в золотом сечении
Архитектурные сооружения, при проектировании которых использовались правильные пятиугольники
Пятиугольный храм (1475-1554) (рис. 10)
Дворец в крепости (1475-1554) (рис. 11)
Театр Советской армии (1934-1940) (рис. 12)
Цитадель в Кортрейке ( III-IV вв.) (рис. 13)
Укреплённая крепость Пиллау (начало XVIIв.) (рис. 14)
Схема типовой крепости из руководства по военному искусству(рис. 15)
Здание министерства обороны США (окончание строительства — январь 1943) (рис. 16)
Дом Советов в Махачкале (1927) (рис. 17)
План типового этажа( 2-9 этаж) 9-этажного дома башенного типа жилого комплекса Слоттсбергет в Гётеборге
Рисунок 9
Рисунок 10
Рисунок 11 Рисунок 12
Рисунок 13 Рисунок 14
Рисунок 15 Рисунок 16
Практическая часть. Приложение А
Заключение
Своеобразие геометрии,
выделяющее её среди
других разделов математики,
да и всех наук вообще,
заключается в неразрывном
органическом соединении живого
воображения со строгой логикой.
Геометрия в своей сути и есть
пространственное воображение,
пронизанное и организованное
строгой логикой.
В ходе моей работы цель исследования – поиск решений задач на построение треугольника по трем элементам и правильного пятиугольника была достигнута. В своей работе я рассмотрел архитектурные сооружения различных стилей, построенные в разные эпохи, и выявил, что при проектировании данных сооружений использовались правильные пятиугольники. Памятники архитектуры, получившие широкую известность как образцы пропорциональности и гармонии, буквально пронизаны математикой, численными расчетами и геометрией.
Практическая часть моей работы включает в себя различные задачи повышенной сложности на построение с помощью циркуля и линейки треугольника по трем элементам и правильного пятиугольника.
Я выбрал эту тему, так как она имеет большое практическое применение в нашей жизни, например, в архитектуре, геометрии, инженерной графике, проектировании.
Список использованной литературы
1.http://www.psciences.net/main/sciences/mathematics/articles/article-1.html
2.http://poisk-ru.ru/s5188t3.html
3.https://ru.wikipedia.org/wiki/Правильный_пятиугольник
4. В. Н. Литвинов «Правильный пятиугольник» 2012г.
5. Александров И.И. «Сборник геометрических задач на построение», 1950 г
Просмотров работы: 48
Что нарисовать из шестиугольника ребенку. Построение пятиугольника подробно
8 июня 2011Первый способ — по данной стороне S с помощью транспортира.
Проводим прямую и откладываем на ней AB = S; принимаем эту линию за радиус и этим радиусом из точек A и В описываем дуги: далее с помощью транспортира строим в этих точках углы в 108°, стороны которых пересекутся с дугами в точках С и D; из этих точек радиусом АВ = 5 описываем дуги, которые пересекутся в Е, и прямыми линиями соединяем точки Л, С, Е, D, В.
Полученный пятиугольник — искомый.
Второй способ. Проведем окружность радиусом r. Из точки А циркулем проводим дугу радиуса AM до пересечения в точках В и С с окружностью. Соединяем В и С линией, которая пересечет горизонтальную ось в точке Е.
Затем из точки Е проводим дугу, которая пересечет горизонтальную линию в точке О. Описываем, наконец, из точки F дугу, которая пересечет окружность в точках Н и К. Отложив по окружности расстояние FO = FH = FK пять раз и соединив точки деления линиями, получим правильный пятиугольник.
Третий способ. В данный круг вписать правильный пятиугольник. Проводим два взаимно перпендикулярных диаметра АВ и МС. Делим радиус АО точкой Е пополам. Из точки Е, как из центра, проводим дугу окружности радиуса ЕМ и засекаем ею диаметр АВ в точке F. Отрезок MF равен стороне искомого правильного пятиугольника. Раствором циркуля, равным MF, делаем засечки N 1 , Р 1 , Q 1 , К 1 и соединяем их прямыми.
На рисунке построен шестиугольник по данной стороне.
Прямой АВ = 5, как радиусом, из точек А и В описываем дуги, которые пересекутся в С; из этой точки тем же радиусом описываем окружность, на которой сторона А В отложится 6 раз.
Шестиугольник ADEFGB — искомый.
«Отделка комнат при ремонте»,
Н.П.Краснов
Основанием для нанесения росписи служат полностью законченные окраской поверхности стен, потолков и других конструкций; роспись делается по высококачественным клеевым и масляным окраскам, сделанным под торцовку или флейц. Приступая к разработке эскиза отделки, мастер должен ясно представить себе всю композицию в бытовой обстановке и отчетливо осознать творческий замысел. Только при соблюдении этого основного условия можно правильно…
Обмер выполненных работ, за исключением особо оговоренных случаев, производится по площади действительно обработанной поверхности с учетом ее рельефа и за вычетом необработанных мест. Для определения действительно обработанных поверхностей при малярных работах следует пользоваться переводными коэффициентами, приведенными в таблицах. А. Деревянные оконные устройства (обмер производится по площади проемов по наружному обводу коробок) Наименование устройств Коэффициент при…
Мы уже говорили, что для исполнения некоторых видов малярных работ необходимо уметь рисовать. А умение рисовать, в свою очередь, предполагает знание правил построения геометрических фигур. Эскизы на бумаге вычерчивают при помощи треугольников, рейсшин, транспортаpa и циркуля, а на плоскости стен и потолков построения выполняются при помощи веска, линейки, деревянного циркуля и шнура. При этом надо…
Вы находитесь в категории раскраски пятиугольник. Раскраска которую вы рассматриваете описана нашими посетителями следующим образом «» Тут вы найдете множество раскрасок онлайн. Вы можете скачать раскраски пятиугольник и так же распечатать их бесплатно. Как известно творческие занятия играют огромную роль в развитии ребенка. Они активизируют умственную деятельность, формируют эстетический вкус и прививают любовь к искусству. Процесс раскрашивания картинок на тему пятиугольник развивает мелкую моторику, усидчивость и аккуратность, помогает узнать больше об окружающем мире, знакомит со всем разнообразием цветов и оттенков. Мы ежедневно добавляем на наш сайт новые бесплатные раскраски для мальчиков и девочек, которые можно раскрашивать онлайн или скачать и распечатать. Удобный каталог, составленный по категориям, облегчит поиск нужной картинки, а большой выбор раскрасок позволит каждый день находить новую интересную тему для раскрашивания.Эта фигура является многоугольником с минимальным количеством углов, которым невозможно замостить площадь. Только у пятиугольника количество диагоналей совпадает с количеством его сторон. Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон. Например, вписать его в окружность с заданным радиусом либо построить на базе заданной боковой стороны.
Как правильно начертить луч и какие принадлежности для черчения вам понадобятся? Возьмите листок бумаги и отметьте в произвольном месте точку. Затем приложите линейку и проведите линию, начиная с указанной точки и до бесконечности. Чтобы начертить ровную линию, нажмите клавишу «Shift»и проведите линию нужной длины. Сразу после начертания откроется вкладка «Формат». Уберите выделение с линии и увидите, что в начале линии появилась точка. Для создания надписи нажмите кнопку «Нарисовать надпись» и создайте поле, где будет находиться надпись.
Первый способ построения пятиугольника считается более «классическим». Получившаяся в результате построения фигура будет правильным пятиугольником. Двенадцатиугольник не является исключением, поэтому его построение будет невозможным без применения циркуля. Задача построения правильного пятиугольника сводится к задаче деления окружности на пять равных частей. Начертить пентаграмму можно с использованием простейших инструментов.
Я долго бился пытаясь этого добиться и самостоятельно найти пропорции и зависимости, но мне этого не удалось. Оказалось, что есть несколько различных вариантов построения правильного пятиугольника, разработанных известными математиками. Инересным моментов является то, что арифметически эту задачу решить только приблизительно точно, поскольку придется использовать иррациональные числа. Зато ее можно решить геометрически.
Деление окружностей. Точки пересечения этих линий с окружностью и являются вершинами квадрата. В окружности радиуса R (Шаг 1) следует провести вертикальный диаметр. В точке сопряжения N прямой и окружности прямая является касательной к окружности.
Получение с помощью полоски бумаги
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника. Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
А на другой конец нитки устанавливаемые карандаш и одержим. Если умеете чертить звезду, но не умеете пятиугольник, начертите звезду карандашом, затем соедините между собой соседние концы звезды, а саму звезду потом сотрите. Затем положите лист бумаги (лучше его закрепить на столе при помощи четырёх кнопок или иголочек). Приколите эти 5 полосочек к листку бумаги кнопками или иголочками, чтобы они оставались неподвижными. Затем обведите полученный пятиугольник и снимите эти полосочки с листка.
Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь.
С центра опусти на окружность 2 луча, чтоб угол между ними был 72 градуса (транспортиром). Деление круга на пять частей осуществляется с помощью обычного циркуля или транспортира. Поскольку правильный пятиугольник — это одна из фигур, содержащая в себе пропорции золотого сечения, его построением издавна интересовались живописцы и математики. Эти принципы построения с применением циркуля и линейки были изложены еще в эвклидовых «Началах».
Математических изображений | Рисование правильного пятиугольника с линейкой и циркулем
Если мы начнем с сегмента, мы можем нарисовать правильный пятиугольник, только используя линейку и циркуль, у которого этот сегмент является одной стороной.
Мы уже знаем, что диагональ правильного пятиугольника находится в золотом сечении по отношению к его сторонам и что золотое сечение обозначается как и его значение:
Это основной шаг:
Тогда значение a равно:
Затем мы можем нарисовать отрезок длиной диагональ правильного пятиугольника:
А можно закончить работу и получить правильный пятиугольник:
Нарисовав двенадцать пятиугольников, мы получим сетку додекаэдра:
БОЛЬШЕ ССЫЛКИ
Демонстрация теоремы Пифагора, вдохновленная Евклидом.
В своей книге «Underweysung der Messung» Дюрер нарисовал неправильный пятиугольник с линейкой и неподвижным циркулем. Это простая конструкция, очень хорошо напоминающая правильный пятиугольник.
Золотой прямоугольник состоит из квадрата и другого золотого прямоугольника.
Золотой прямоугольник состоит из квадрата и другого золотого прямоугольника. Эти прямоугольники связаны расширяющимся вращением.
Золотая спираль — хорошее приближение к равноугольной спирали.
Две равноугольные спирали содержат все вершины золотых прямоугольников.
Двенадцать вершин икосаэдра лежат в трех золотых прямоугольниках. Тогда мы можем вычислить объем икосаэдра
Из трех золотых прямоугольников можно построить икосаэдр.
Некоторые свойства этого платонического тела и его отношение к золотому сечению. Построение додекаэдров разными методами.
Он изучал трансформации образов, например, лиц.
Дюрер первым опубликовал на немецком языке метод рисования эллипсов в виде конических сечений.
Дюрер ошибся, объясняя, как рисовать эллипсы. Мы можем доказать, используя только основные свойства, что эллипс не имеет формы яйца.
Первый рисунок плоской сети правильного додекаэдра был опубликован Дрером в его книге «Underweysung der Messung» («Четыре книги измерений»), опубликованной в 1525 году.
Два преобразования равносторонней спирали с одинаковым общим эффектом.
В равноугольной спирали угол между вектором положения и касательной постоянен.
Леонардо да Винчи сделал несколько рисунков многогранников для книги Луки Пачоли «De divina пропорционально». Здесь мы видим адаптацию додекаэдра.
Расширяющее вращение — это комбинация вращения и растяжения от одной и той же точки.
Эссе 2: Построение правильных многоугольников
, Шон Д. Бродерик
Правильные многоугольники — это замкнутые плоские фигуры, состоящие из ребер равной длины и вершин равного размера.Самый простой правильный многоугольник — это равносторонний треугольник, который состоит из трех ребер равной длины и трех углов между каждой парой ребер, составляющих 60 градусов. Три ребра — это наименьшее количество ребер для построения многоугольника, поскольку два ребра образуют угол, а одно ребро — сегмент. Полигоны — это замкнутые фигуры. Правильный многоугольник с четырьмя ребрами и есть квадрат. Пять ребер составляют пятиугольник, а шесть — шестиугольник.
Мы исследуем, как построить правильные многоугольники, используя циркуль и линейку, в сравнении с программой динамической геометрии, такой как Sketchpad Geometer.
Сначала рассмотрим построение равностороннего треугольника с помощью линейки и циркуля. Это простейший правильный многоугольник на плоскости. Он состоит из трех сторон.
1. Мы начинаем с рисования произвольной точки A.
2. Затем мы открываем наш компас на фиксированное расстояние и делаем небольшую отметку справа от нашей точки A. Это то место, где в конечном итоге будет наша точка B.
3. Не отрывая циркуль от бумаги, перемещаем конец карандаша вверх и к середине и делаем еще одну отметку.Это будет то место, куда в конечном итоге попадет точка C.
4. Теперь мы помечаем нашу точку B в любом месте отметки. (Почему мы можем отметить его где-нибудь на линии и при этом сохранить определенную длину?)
5. Теперь поместите конец циркуля в точку B и сделайте отметку вверх и до середины, пересекая место, куда пойдет точка C.
6. Отметьте пересечение как точку C.
7. Используя линейку, проведите первую сторону треугольника от A до B.
8. Снова, используя линейку, проведите вторую сторону треугольника от B. к С.
9. Нарисуйте последнюю сторону. На этом мы закончили построение равностороннего треугольника.
Теперь мы сравним этот процесс с процессом, который можно использовать для построения равностороннего треугольника в GSP:
1. Начнем с рисования отрезка произвольной длины. Это будет одна из сторон нашего треугольника.
2. Обозначим точки A для левой точки и B для правой точки.
3. Теперь мы построим круг, используя точку B в качестве центра и точку A в качестве края.
4. Затем мы делаем еще один круг, используя точку A как центр и точку B как край.
5. Строим их пересечение и маркируем его точкой C.
6. Строим отрезок AC.
7. Строим отрезок ВС.
8. Если мы скроем наши круги, у нас теперь есть равносторонний треугольник.
1. Почему эти конструкции работают?
2. Что делает этот треугольник равносторонним в любой среде?
3. Теряем ли мы что-нибудь или получаем что-нибудь, если мы учим студентов делать это, используя один, другой или оба средства?
1 (и часть 2).В классе мы обсуждали, что эти равносторонние треугольники работают, потому что две окружности, которые построены, или отметки из двух окружностей, мы увидим, что сегменты треугольника являются радиусами окружностей. Если круги одинакового размера, то радиусы одинакового размера и их положение таково, что они встречаются в трех точках (центры кругов и их пересечение). Вот диаграмма, которая может помочь:
Мы начали с одного круга и построили два радиуса. Затем мы отразили круг поперек линии, чтобы получилось два круга.
Мы выберем один круг и объединим его с другим, чтобы показать, как радиусы образуют равносторонний треугольник.
По мере приближения мы видим, что радиусы образуют треугольник.
Поскольку круги слились и теперь имеют общий радиус, образующий основание, мы можем видеть, что поскольку все радиусы равны, если они перекрываются, образуя основание, а два других соединяются наверху, мы должны иметь равносторонний треугольник.
Остальные части 2. Мы видели, что составляет равносторонний треугольник в GSP, но что касается конструкции из карандаша и бумаги, мы видим, что они такие же, но вместо того, чтобы использовать круги, чтобы показать конгруэнтность радиусов, компас (открытость которого остается постоянной) используется для создания конгруэнтных радиусов.
3. Мы можем немного потерять конструкцию карандаша и бумаги, потому что круги полностью проиллюстрированы в GSP, а с карандашом и бумагой мы видим только дуги окружностей, а равномерное расстояние, созданное компасом, скрыто. Однако я считаю, что оба типа конструкций полезны для того, чтобы у студентов было более полное представление о конструкциях.
Давайте посмотрим, как построить квадрат. Снова начнем с построения по циркулю и линейке:
1.Мы отмечаем точку А, выставляем циркуль на определенную длину и делаем отметку. Нам нужно сохранить эту длину, поэтому не теряйте ее.
2. Мы отмечаем точку на отметке компаса, B.
3. Затем мы проводим прямую линию через точку A и точку B.
4. Используя компас при текущих настройках, отметьте отметку слева от точки A и справа от точки B.
5. Если мы хотим сделать квадрат, нам нужно построить перпендикулярные линии, идущие вверх от точек A и B. Итак, чтобы сделать это, нам нужно продлить компас от нашей произвольной длины чуть-чуть.Затем мы размещаем точку на самом левом пересечении и делаем дугу, как показано выше. Затем мы помещаем конец циркуля в точку B и делаем еще одну дугу вокруг точки A, чтобы они пересекались, как показано на рисунке. Повторите этот процесс, чтобы сделать аналогичные дуги вокруг точки B. Начните с точки циркуля на точке A и сделайте дугу вокруг точки B. Затем поместите точку циркуля на крайнее правое пересечение и сделайте дугу, соединяющуюся с другой точкой. , охватывающую точку B.
6. Сначала сделайте две отметки над точками A и B, используя исходный циркуль произвольной длины.Это будет означать высоту квадрата. Он будет точно такой же длины, как и от A до B, поэтому он будет квадратным. Далее нам нужно выяснить, где будет вершина квадрата. Поэтому мы сделали дуги. Используя линейку, проведите линию от A вверх через две дуги вокруг A и пересеките ее с отметкой сверху. На иллюстрации показано, как это могло теперь выглядеть.
7. Теперь мы закончим построение, проведя перпендикулярную линию вверх от B до отметки и обозначив эту точку пересечения C.Наконец, мы соединяем точку D и точку C, чтобы закончить квадрат.
Теперь проиллюстрируем, как можно построить квадрат, используя GSP:
1. Постройте отрезок произвольной длины.
2. Постройте круг, используя A как центр и B как край. В верхней части круга мы отметили расстояние, такое же, как и от A до B.
3.Итак, теперь мы строим перпендикулярную линию через A к отрезку AB. Пересечение этой линии через вершину круга обозначим точкой D.
4. Построим перпендикулярную линию через точку D к прямой AD.
5. Затем мы строим еще одну перпендикулярную линию, на этот раз через точку B к прямой AB.
6.Мы обозначаем эту точку C.
.7. Если мы скроем объекты, которые помогли нам в строительстве, мы получим построенный квадрат ABCD.
Комментарий:
Кажется, что причина, по которой это работает, похожа на объяснение равностороннего треугольника. Вот несколько эскизов:
Здесь мы имеем тот же тип конструкции, что и у треугольника.Теперь наши радиусы перпендикулярны и одинаковой длины. Это похоже на атрибуты квадрата.
Теперь мы выделяем две точки на одном круге и объединяем их с другим.
Как только они объединятся, мы увидим квадрат. Просто соединяем верхние точки и у нас будет наш квадрат.
Теперь обратим наше внимание на построение пятиугольника с помощью циркуля и линейки. Сначала я понятия не имел, как это сделать, поэтому мне понадобился Интернет.Есть много разных способов построить пятиугольник. В центре внимания этого эссе — показать, как это сделать, и обсудить, почему этот подход работает. Что за математика стоит за этим?
1. Пятиугольник состоит из круга. Каждая из вершин будет пересекаться с краем круга. Итак, сначала строим круг с помощью циркуля. Далее мы проводим линию по центру круга, разделяя его пополам.
2.Нам нужно построить еще одну линию, разделяющую левую половину круга пополам. На рисунке мы сделали это, разделив пополам угол 180 градусов, идущий вниз по середине круга. Для этого выставляем компас на определенную точку открытия. Мы помещаем конец циркуля в центр круга и делаем отметки на обоих лучах на произвольном расстоянии. Затем мы помещаем кончик циркуля на сделанные отметки и делаем еще одну отметку в области, где будет идти деление угла пополам.Создает X, пересечение которого является местом, где должен пройти луч круга. Проведите линейкой биссектрису угла.
3. Следующая цель — построить середину отрезка, который мы только что нарисовали. Для этого мы открываем компас на произвольное расстояние, которое чуть больше, чем приблизительная средняя точка сегмента. Помещаем конец циркуля в центр круга и делаем отметку дуги как на картинке.Затем мы сохраняем измерение компаса как есть и помещаем точку компаса на пересечение сегмента и края круга и делаем аналогичную отметку. Если компас открыт достаточно далеко, дуги должны пересекаться, как показано. Если эти новые пересечения соединены, пересечение обоих сегментов является средней точкой сегмента.
4. Затем соедините середину найденного сегмента с вершиной круга и с точкой пересечения разделительной линии и края круга.Наша следующая цель — разделить пополам угол, образованный отрезком, от центра к краю и средней точки к краю, как показано на рисунке. Мы используем те же методы, что и в начале. Раскрываем циркуль на произвольную длину, которая меньше длины отрезков угла. Поместив острие циркуля в вершину угла, делаем отметки на отрезках угла. Затем мы немного закрываем циркуль и помещаем его конец на сделанные нами отметки и делаем новые отметки в направлении центра угла.Эти отметки должны пересекаться под биссектрисой угла. Проведена линия биссектрисы угла от вершины угла через точку X до линии, разделяющей круг на две равные части. (На самом деле, как показано на следующем рисунке, вам нужно продлить биссектрису угла за вертикальную линию.)
5. Следующая цель — построить прямую, параллельную горизонтальному сегменту, в точке пересечения вертикального сегмента и биссектрисы угла.Это делается путем размещения острия циркуля в вершине угла, разделенного пополам, и разметки угла дугой, как показано. Там, где биссектриса угла пересекает вертикальный сегмент, поместите точку циркуля и нарисуйте еще одну дугу, как и раньше. Затем мы открываем компас ровно настолько, чтобы переходить от углового сегмента к угловому сегменту на сделанной вами отметке. Затем сделайте еще одну отметку вниз от дуги, которую вы проводите выше, и это пересечение является точкой, где параллельная линия может быть проведена через пересечение биссектрисы угла и вертикальной линии.Давай, сделай это.
6. Соедините пересечение нового сегмента и края круга с верхним пересечением вертикальной линии и края круга, и мы построили первую сторону нашего пятиугольника.
7. Теперь нам нужно повторить весь этот процесс, чтобы построить еще три стороны. Четвертую сторону мы можем соединить с пятой, не делая конструкции.Однако мы все равно делаем его, чтобы убедиться, что фигура построена правильно. Теперь нам просто нужно определиться, с чего начать. Поскольку мы построили сторону, начинающуюся сверху и наклоненную вниз влево, мы делаем наш сегмент, проходящий через центр круга, начиная с последней точки, которую мы только что построили.
8. Повторим этот процесс в другой раз.
9.Повторяем этот процесс еще раз.
10. Теперь мы закончим построением последней стороны, хотя в этом нет необходимости. Теперь у нас есть пятиугольник ABCDE.
Мне также любопытно, что есть математические побочные продукты построения пятиугольника, которые можно наблюдать. Это большой круг на внешней стороне конструкции, прежде чем мы его скроем.Кроме того, внутри пятиугольника есть небольшой кружок, если дуги, определяющие середину сегмента, были немного более согласованными. Внутри большого тоже есть маленький пятиугольник. Однако регулярно ли это? Это пропорционально большому пятиугольнику? Если бы конструкция была нарисована идеально, был бы маленький пятиугольник правильным? Означает ли это, что большой пятиугольник не совсем правильный?
Теперь мы покажем этот же процесс с помощью GSP:
1.Строим круг произвольной длины. Затем мы проводим линию по центру круга.
2. Затем мы строим перпендикулярную линию к вертикальной линии, проходящей через центр круга. Мы делаем отрезок из только что созданной линии от центра к левому краю. Затем мы строим середину этого отрезка.
3. Оттуда мы проводим линию, соединяющую среднюю точку с вершиной круга.Это создает угол, а затем мы строим биссектрису угла.
4. Мы строим параллельную линию предыдущей горизонтальной линии, и пересечение новой линии с краем круга является точкой для создания первой стороны нашего пятиугольника. Теперь рисуем эту сторону. Этот процесс будет повторяться с разными цветами, начиная с боковой точки, которую мы только что построили.
5.Теперь мы повторяем этот процесс для второй стороны бордового цвета.
6. Повторяем этот процесс еще раз с оранжевым.
7. Мы повторяем этот процесс с розовым или темно-синим цветом, каким бы он ни был. На этом этапе мы можем просто соединить две последние стороны, но поскольку меня интересовала внутренняя геометрия, я повторил процесс еще раз, чтобы посмотреть, поможет ли точность GSP.
8. Похоже, что в середине этого сооружения происходит много всего. Однако пятиугольник, который, как я думал, находится прямо внутри, не так идеально расположен, как я думал.
9. Если мы скроем все тонкие линии, мы увидим наш пятиугольник.
Вопрос:
Почему это работает?
Ответ:
В классе мы обсуждали использование золотого сечения.В пятиугольнике,
отношение длины красной диагонали к длине стороны равно специальному числу.
Мы будем использовать эту демонстрацию, чтобы показать, как конструкция выше представляет собой пятиугольник. Теперь сделаем круг радиуса с одной стороной единицы длины:
.Затем мы наклеили несколько ярлыков для облегчения обсуждения:
Во-первых, мы замечаем, что треугольник ABF похож на треугольник AEB .Из этого можно сделать вывод, что:
Тогда через подстановку получаем:
Что дает:
Мы знаем, что фи — это золотое сечение. Таким образом, мы имеем утверждение, что отношение длины диагонали правильного пятиугольника к длине его стороны есть золотое сечение. Теперь посмотрим на нашу конструкцию:
Чтобы обсудить причину, по которой эта конструкция представляет собой пятиугольник, мы используем вышеуказанные метки.Наша цель — доказать, что отношение диагонали пятиугольника (EF) к стороне (AE) равно фи или золотому сечению, тогда фигура оказывается пятиугольником. Показанная выше конструкция является той же конструкцией, которую мы использовали, за исключением того, что я построил сегмент EO, чтобы облегчить вычисление EF.
Начну с того, что нам дано, что отрезки AO, BO и EO имеют длину 2 единицы. Сегменты BC и CO имеют длину одну единицу, потому что C является средней точкой BO. Если AO равно 2, а CO равно 1, то AC:
Теперь мы можем найти угол ACO с помощью тригонометрии.Следовательно, угол ACO равен:
Таким образом, угол DCO составляет половину этого, по определению:
Сегмент DO / 1 равен:
Поскольку мы знаем, что EO равно 2, мы используем теорему Пифагора, чтобы найти ED. Таким образом, ED 2 + DO 2 = EO 2 . Итак, имеем:
Следовательно, ED =
Мы умножаем это выражение на 2, чтобы получить длину EF.Итак, EF =
Мы на полпути к нашей цели. Помните, что мы рассчитываем соотношение длины стороны нашей фигуры к длине диагонали. У нас есть диагональ EF. Теперь мы ищем длину стороны, скажем AE. Мы планируем использовать теорему Пифагора, чтобы найти AE. Мы будем использовать уравнение AE 2 = ED 2 + AD 2 . Мы знаем ED и можем найти AD с выражением 2 — DO. Следовательно, решаем:
Когда мы находим AE и используем наш калькулятор для получения десятичного приближения, мы получаем AE = 2.35114100917. Десятичное приближение для EF = 3,80422606518. Тогда EF / AE = 1,61803398875. Десятичное приближение для золотого сечения — это то же самое, что и мое приближение для EF / AE. Следовательно, эта конструкция дает правильный многоугольник.
Теперь перейдем к разделу построения шестиугольника с линейкой и циркулем:
1. Начнем с построения круга произвольного размера.
2. Делаем отметку на краю круга с правой стороны.Сохраняя исходный произвольный размер компаса, мы помещаем точку циркуля на эту отметку и отмечаем пересечения круга сверху и снизу.
3. Теперь мы рисуем диаметр круга от верхнего пересечения кругов через центр и продолжаем через противоположный край внизу с помощью нашей линейки.
4. Проделаем то же самое на противоположном перекрестке.
5.Теперь мы можем приступить к построению сторон шестиугольника. Наша первая сторона идет от отмеченной нами правой точки до верхнего пересечения круга.
6. Наша вторая сторона соединяет верхние перекрестки. Но подождите, куда пойдет наша третья сторона?
7. Делаем нашу третью сторону, строя линию, соединяющую отметки центров двух наших кругов. Если мы продолжим эту линию через другую сторону, у нас будет пересечение слева, которое отмечает точку, где наша третья сторона закончится.Теперь мы можем построить эту третью сторону.
8. Рисуем четвертую сторону, начиная с только что сделанного пересечения и заканчивая левым нижним пересечением.
9. Наша пятая сторона построена путем соединения нижних перекрестков.
10. Мы закончили конструирование сторон шестиугольника, соединив точки пересечения от правого нижнего до крайней правой отметки.
11.У нас есть шестиугольник!
Хм … Похоже, верх немного криво … Не знаю, почему так получилось. Снова мы спрашиваем, как эта конструкция дает шестиугольник. Связано ли это с умением создавать внутренние или дополнительные углы?
Мы выполняем этот процесс в GSP:
1. Сначала построим круг произвольного размера.
2. Затем мы строим горизонтальную линию от центра круга до края.
3. Затем мы строим еще один круг, используя край первого в качестве центра и центр первого в качестве края.
4. Затем мы проводим линию через центр первого круга и верхнее пересечение обоих кругов.
5. Затем мы строим еще одну линию через центр первого круга, которая проходит через нижнее пересечение кругов.
6.Теперь мы готовы нарисовать стороны нашего шестиугольника. Первая сторона начинается от нижнего пересечения обоих кругов и идет к центру второго круга.
7. Вторая сторона идет от нижнего пересечения двух кругов до нижнего пересечения первой нарисованной линии и первого круга.
8. Третья сторона идет от нижнего пересечения первой окружности и первой линии до левого пересечения горизонтальной линии и первой окружности.
9. Четвертая сторона идет от пересечения первой окружности и горизонтальной линии до верхнего пересечения первой окружности и второй линии.
10. Пятая сторона идет от верхнего пересечения первого круга и второй линии до верхнего пересечения обоих кругов.
11. Шестая сторона соединяет пятую сторону с первой стороной, и у нас есть шестиугольник.
12.Когда мы скрываем линии и помечаем вершины, мы получаем чистое изображение нашего построенного шестиугольника.
Теперь мы подошли к вопросу о том, как построить семиугольник. Невозможно построить идеально правильный семиугольник, используя только линейку и циркуль, как мы делали раньше. Итак, мой вопрос, почему это так?
Поскольку это невозможно, я считаю, что сейчас хорошее время, чтобы закончить это эссе.
Построение пятиугольника можно выполнить с помощью компаса и…
Контекст 1
… построения линейки и циркуля состоят из многократного применения пяти основных построений, основанных на аксиомах Евклида [39], с использованием точек, линий и окружностей, которые уже были построены. Основанные на этих геометрических примитивах и фиксированном наборе операций конструкции линейки и циркуля, такие как показано на рисунке 1, являются первыми алгоритмическими описаниями генеративных моделей. 3. Пусть D — середина BO. …
Контекст 2
… Элементарные структуры данных обычно используются в компьютерной графике (см. рисунок 10). Увеличивая количество примитивов, можно создать лучшее приближение цилиндра. …
Context 3
… качество аппроксимации поверхности объекта полигонами сильно зависит от количества примитивов и используемых операций моделирования. Как только приближение найдено, вся информация об аппроксимируемой поверхности часто теряется, см. Рисунок 11. …
Контекст 4
… Поверхности Подразделения поверхностей определяются рекурсивно, начиная с заданной многоугольной сетки (обычно четырехугольной или треугольной), как показано на рисунке 10 (в центре). Схема уточнения применяется к этой сетке, создавая новые вершины и грани, сходящиеся к поверхности предельного подразделения (которая является поверхностью, полученной путем применения схемы уточнения бесконечное количество раз). …
Контекст 5
… к тому факту, что положение и размер вокселя предопределены заранее, воксели хороши для представления регулярно выбираемых пространств.Аппроксимация форм произвольной формы страдает от этого врожденного свойства, как видно на рисунке 10 (справа). Тем не менее, представления вокселей не страдают от числовой нестабильности, поскольку они обычно определяются на целочисленной сетке. …
Контекст 6
… таким образом можно выполнить деформированное разделение, деформацию можно запечь в любой точке, чтобы учесть прямые разрезы в деформированной геометрии. Пример показан на рисунке 13. …
Контекст 7
… Первым шагом процесса является регистрация генеративной модели (включая ее свободные параметры) для лазерного сканирования. Затем разница между генеративной моделью и лазерным сканированием сохраняется в текстуре, которую можно применить ко всем экземплярам одного и того же семейства форм, как показано на рисунке 14. …
Контекст 8
… Платформа моделирования позволяет разработчикам оптимизировать компромисс перекодирования для создания интерактивных трехмерных визуализаций. Пример приложения дополненной реальности, показанный на Рисунке 15, отображает подземную инфраструктуру, созданную из данных географических информационных систем (ГИС)….
Контекст 9
… Чтобы уменьшить пространство поиска, из классификаций выводится нерегулярная сетка, а алгоритм синтаксического анализа применяется для получения наиболее вероятного применения правил, которое дает классификационную метку для каждого ячейка сетки. Такое дерево синтаксического анализа может быть легко преобразовано в процедурную модель, как показано на рисунке 16. …
Контекст 10
… система завершает работу, если каждой вершине присвоено состояние. Этот процесс показан на рисунке 17.На основе этих классификаций получается неправильная сетка (c) и анализируется двумерная разбитая грамматика (d). …
Контекст 11
… авторы предлагают меру сходства между статистической моделью и заданной входной сеткой, которая состоит из трех частей: расстояние формы, которое измеряет общее несоответствие формы, геометрическое расстояние, которое отражает статистика геометрии его ветвей и структурное расстояние, которое кодирует стоимость преобразования графического представления модели статистического дерева в графическое представление входной модели дерева.Некоторые примеры см. На рисунке 18. Метод MCMC также применялся другими методами для нахождения параметров статистической генеративной модели: [101], [119], [127]. …
Контекст 12
… примерный набор данных, показанный на рисунке 19, состоит из отсканированных лазером чашек и описания генеративных чашек. Алгоритм способен обнаружить экземпляр генеративной чаши. …
Контекст 13
… можно комбинировать, вызывая последовательность различных преобразований.На рисунке 21a показан пример многоугольника профиля, копии которого расположены радиально вокруг начала координат (рисунок 21b). Эти многоугольники сначала преобразуются в двухсторонние грани. …
Контекст 14
… можно комбинировать, вызывая последовательность различных преобразований. На рисунке 21a показан пример многоугольника профиля, копии которого расположены радиально вокруг начала координат (рисунок 21b). Эти многоугольники сначала преобразуются в двухсторонние грани. …
Контекст 15
… полигоны сначала преобразуются в двусторонние грани. Затем соответствующие задняя и передняя стороны соединяются (рисунок 21c) и создается поверхность разделения (рисунок 21d). Многоугольник профиля, угол поворота и набор пользовательских параметров являются входными данными для этой функции преобразования (рисунок 21f). …
Контекст 16
… сначала многоугольники преобразуются в двусторонние грани. Затем соответствующие задняя и передняя стороны соединяются (рисунок 21c) и создается поверхность разделения (рисунок 21d).Многоугольник профиля, угол поворота и набор пользовательских параметров являются входными данными для этой функции преобразования (рисунок 21f). …
Контекст 17
… соответствующие задняя и передняя стороны соединяются (рисунок 21c), и создается поверхность разделения (рисунок 21d). Многоугольник профиля, угол поворота и набор пользовательских параметров являются входными данными для этой функции преобразования (рисунок 21f). На этапе постобработки выбранные грани можно раскрасить по-разному (Рисунок 21h)….
Контекст 18
… многоугольник профиля, угол поворота и набор настраиваемых параметров являются входными данными для этой функции преобразования (рисунок 21f). На этапе постобработки выбранные грани можно раскрасить по-разному (Рисунок 21h). Создание базовой формы отделено от дополнительных шагов по созданию гравюр, изменению материалов или добавлению драгоценных камней. …
Как сделать правильный пятиугольник с помощью циркуля. Как построить и нарисовать правильный пятиугольник по кругу.Построение правильных многоугольников по заданной стороне
Правильный пятиугольник — это многоугольник, в котором все пять сторон и все пять углов равны друг другу. Вокруг него легко описать круг. Постройте пятиугольник , и этот круг вам поможет.
Инструкция по эксплуатации
Прежде всего, необходимо построить круг с помощью циркуля. Пусть центр окружности совпадает с точкой О. Нарисуйте оси симметрии перпендикулярно друг другу.На пересечении одной из этих осей с окружностью поставьте точку V. Эта точка будет вершиной будущего пятиугольника и . На пересечении другой оси с окружностью, позиция D.
На отрезке OD найдите середину и отметьте на ней точку A. После этого нужно циркулем начертить круг с центром в этой точке. Кроме того, он должен проходить через точку V, то есть с радиусом CV. Точку пересечения оси симметрии и этого круга обозначьте B.
После этого с помощью циркуля нарисуйте круг такого же радиуса, поместив стрелку в точку V. Обозначьте пересечение этого круга с оригиналом точкой F. Эта точка станет второй вершиной будущего правильного пятиугольника и.
Теперь вам нужно провести ту же окружность через точку E, но с центром в F. Обозначьте пересечение только что нарисованной окружности с исходной как G. Эта точка также станет одной из вершин пятиугольника и.Аналогичным образом нужно построить еще один круг. Его центр находится в G. Пусть это будет точка пересечения с исходной окружностью. Это последняя вершина правильного многоугольника.
У вас должно получиться пять вершин. Осталось просто соединить их по линейке. В результате всех этих операций у вас получится правильный, вписанный в круг пятиугольник .
Построение правильных пятиугольников возможно с помощью циркуля и линейки. Правда, процесс довольно длительный, как, впрочем, и построение любого правильного многоугольника с нечетным числом сторон.Современные компьютерные программы позволяют сделать это за несколько секунд.
Вам понадобится
- — компьютер с AutoCAD.
Руководство по эксплуатации
Найдите в AutoCAD верхнее меню и вкладку «Главная» в нем. Щелкните по нему левой кнопкой мыши. Появится панель рисования. Появятся разные типы линий. Выберите замкнутую полилинию. Это многоугольник, осталось только ввести параметры. AutoCAD позволяет рисовать множество различных правильных многоугольников.Количество сторон может достигать 1024. Вы можете использовать командную строку, в зависимости от версии, набрав «_polygon» или «multi-angle».
Независимо от того, используете ли вы командную строку или контекстное меню, на экране появится окно с просьбой ввести количество сторон. Введите туда цифру «5» и нажмите Enter. Вам будет предложено определить центр пятиугольника. Вбейте в появившееся окно координаты. Вы можете обозначить их как (0,0), но могут быть и любые другие данные.
Выберите предпочтительный метод строительства.. AutoCAD предлагает три варианта. Пятиугольник можно описать или вписать в круг, но вы также можете построить его в соответствии с заданным размером стороны. Выберите нужный вариант и нажмите Enter. При необходимости укажите радиус окружности и также нажмите Enter.
Пятиугольник на данной стороне сначала строится точно таким же образом. Выберите «Нарисовать» замкнутую полилинию и введите количество сторон. Щелкните правой кнопкой мыши, чтобы открыть контекстное меню. Нажмите ребро или боковую команду. В командной строке введите координаты начальной и конечной точек одной из сторон пятиугольника.После этого на экране появится пятиугольник.
Все операции можно выполнять из командной строки. Например, чтобы построить пятиугольник сбоку в русскоязычной версии программы, введите букву «с». В английской версии это будет «_e». Чтобы построить вписанный или описанный пятиугольник, после определения количества сторон введите буквы «o» или «b» (или английские «_c» или «_i»).
Таким простым способом можно построить не только пятиугольник. Для того, чтобы построить треугольник, необходимо развести ножки циркуля на расстояние, равное радиусу круга.Затем поместите иглу в любую точку. Нарисуйте тонкий опорный круг. Две точки пересечения кругов, а также точка, в которой была ножка циркуля, образуют три вершины правильного треугольника.
Построение правильного шестиугольника, вписанного в круг.
Построение шестиугольника основано на том, что его сторона равна радиусу описанной окружности. Поэтому для построения достаточно разделить круг на шесть равных частей и соединить найденные точки между собой.
Правильный шестиугольник можно построить с помощью подъемника и угла 30X60 °. Для выполнения этой конструкции возьмем горизонтальный диаметр окружности за биссектрису углов 1 и 4, построим стороны 1 — 6, 4 — 3, 4 — 5 и 7 — 2, после чего проведем стороны 5 — 6 и 3. — 2.
Вершины такого треугольника можно построить с помощью циркуля и квадрата с углами 30 и 60 ° или всего одного циркуля. Рассмотрим два способа построить равносторонний треугольник, вписанный в круг.
Первый способ (рис. 61, а) основан на том, что все три угла треугольника 7, 2, 3 содержат 60 °, а вертикальная линия, проведенная через точку 7, является одновременно высотой и биссектрисой угла 1. .Так как угол 0 — 1 — 2 равен 30 °, то для нахождения стороны 1 — 2 достаточно построить угол 30 ° в точке 1 и стороне 0 — 1. Для этого установите подъемник и угольник. как показано на рисунке, проведите линию 1-2, которая будет одной из сторон желаемого треугольника. Чтобы построить сторону 2–3, мы устанавливаем траншею в положение, показанное пунктирными линиями, и через точку 2 проводим прямую линию, определяющую третью вершину треугольника.
Второй способ основан на том, что если вы построите правильный шестиугольник, вписанный в круг, а затем соедините его вершины через одну, то получится равносторонний треугольник.
Чтобы построить треугольник, отметьте вершину 1 на диаметре и проведите диаметральную линию 1 — 4. Далее из точки 4 с радиусом, равным D / 2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами желаемого треугольника.
Это построение можно сделать с помощью квадрата и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описываемой окружности и наклонены к ее осям под углом 45 °. Исходя из этого, устанавливаем подъемник и угольник с углами 45 °, как показано на фиг. 62, а, отметьте точки 1 и 3. Затем через эти точки проведите горизонтальные стороны квадрата 4 — 1 и 3 — 2 с помощью рейки. Затем с помощью подъемника по ножке квадрата проводим вертикальные стороны квадрата 1-2 и 4-3.
Второй способ основан на том, что вершины квадрата делятся пополам дугами окружности, заключенными между концами диаметра. Мы отмечаем на концах двух взаимно перпендикулярных диаметров точки A, B и C, и из них радиусом y описываем дуги до их взаимного пересечения.
Далее через точки пересечения дуг проведите вспомогательные линии, отмеченные на рисунке сплошными линиями. Точки их пересечения с окружностью определяют вершины 1 и 3; 4 и 2.Полученные таким образом вершины искомого квадрата соединяются последовательно между собой.
Построение правильного пятиугольника, вписанного в круг.
Чтобы вписать правильный пятиугольник в круг, сделаем следующие конструкции. Отметим на окружности точку 1 и примем ее за одну из вершин пятиугольника. Разделите отрезок АО пополам. Для этого радиусом AO от точки A описываем дугу до пересечения с окружностью в точках M и B.Соединяя эти точки прямой, получаем точку K, которую затем соединяем с точкой 1. Радиусом, равным отрезку A7, описываем дугу от точки K до пересечения с линией AO в точке H. Соединяя точку 1 с точкой H, получаем сторону пятиугольника. Затем с помощью циркуля, равного отрезку 1H, описав дугу от вершины 1 до пересечения с окружностью, найдем вершины 2 и 5. Сделав такой же циркуль решения выемки из вершин 2 и 5, мы получим оставшиеся вершины 3 и 4.Находим соединенные точки последовательно друг с другом.
Построение правильного пятиугольника на заданной стороне.
Чтобы построить правильный пятиугольник с этой стороны (рис. 64), разделим отрезок AB на шесть равных частей. Из точек A и B с радиусом AB мы описываем дуги, пересечение которых даст точку K. Через эту точку и разделив 3 линией AB, проведите вертикальную линию. Далее от точки K на этой прямой откладываем отрезок равный 4/6 AB.Получаем точку 1 — вершину пятиугольника. Затем с радиусом, равным AB, от точки 1 описываем дугу до пересечения с дугами, предварительно проведенными из точек A и B. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Находим вершины соединяем последовательно друг с другом.
Построение правильного семиугольника, вписанного в круг.
Пусть дан круг диаметром D; в него нужно ввести правильный семиугольник (рис.65). Разделите вертикальный диаметр круга на семь равных частей. От точки 7 с радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точка F называется полюсом многоугольника. Взяв точку VII за одну из вершин семиугольника, проведите лучи от полюса F через четные части вертикального диаметра, пересечение которых с окружностью определит вершины VI, V и IV семиугольника.Чтобы получить вершины / — // — /// из точек IV, V и VI, проведем горизонтальные линии до пересечения с окружностью. Найденные вершины соединяются последовательно друг с другом. Семиугольник можно построить, проведя лучи от полюса F через нечетные части вертикального диаметра.
Приведенный выше метод подходит для построения правильных многоугольников с любым количеством сторон.
Разделение круга на любое количество равных частей также можно выполнить, используя данные в таблице.2, где приведены коэффициенты, позволяющие определять размеры сторон правильных вписанных многоугольников.
Длины сторон правильных вписанных многоугольников.
В первом столбце этой таблицы указано количество сторон правильного вписанного многоугольника, а во втором — коэффициенты. Длина стороны данного многоугольника будет получена путем умножения радиуса данного круга на коэффициент, соответствующий количеству сторон этого многоугольника.2) (4) \ sqrt (\ frac (5+ \ sqrt (5
{2}};Правильный пятиугольник (греч. Πενταγωνον ) — геометрическая фигура, правильный многоугольник с пятью сторонами.
Недвижимость
- Додекаэдр — единственный правильный многогранник, грани которого являются правильными пятиугольниками.
- Пентагон — Здание Министерства обороны США имеет форму правильного пятиугольника.
- Правильный пятиугольник — это правильный многоугольник с наименьшим числом углов из тех, которые нельзя расположить на плоскости.
- В природе не бывает кристаллов с гранями в форме правильного пятиугольника.
- Пятиугольник со всеми его диагоналями — это проекция 4-симплекса.
см. Также
Написать отзыв на статью «Регулярный Пентагон»
Заметки
| ||||||||||||||||||||||
| ||||||||||||||||||||||||||||||
Отрывок о регулярном Пентагоне
Петя не знал, как долго это продолжалось: он наслаждался, все время удивлялся своему удовольствию и хотел, чтобы некому было ему рассказать.Его разбудил ласковый голос Лихачева.— Готово, ваш благородный, пополам, держите хранителя равнодушным.
Петя проснулся.
— Ой, уже светло, верно, светло! Он закричал.
Лошади, ранее невидимые, стали видны хвостам, а водянистый свет был виден сквозь голые ветви. Петя встряхнулся, вскочил, вынул из кармана девственницу и отдал ее Лихачеву, размахивая ею, попробовал саблю и засунул ее в ножны. Казаки развязали лошадей и подтянули подпруги.
«Вот командир, — сказал Лихачев. Денисов вышел из гауптвахты и, позвав Петю, приказал собраться.
В темноте быстро разобрали лошадей, натянули подпруги и разобрали команды. Денисов стоял у караулки, отдавая последние приказы. Пехота отряда, прыгнув на сотни футов, двинулась вперед по дороге и быстро скрылась между деревьями в предрассветном тумане. Есаул что-то заказал казакам. Петя при случае держал свою лошадь, с нетерпением ожидая приказа сесть.Омытое холодной водой, его лицо, особенно глаза, горело огнем, по спине пробежал озноб, и что-то быстро и равномерно тряслось по всему телу.
«Ну что, все готово?» — сказал Денисов. — Давай на лошадях.
Лошадей накормили. Денисов рассердился на казака за то, что кушак слабый, и, разорвав его, сел. Петя взялся за стремя. Конь по привычке хотел укусить его за ногу, но Петя, не чувствуя его веса, быстро вскочил в седло и, оглянувшись на гусара, двигавшегося сзади в темноте, подъехал к Денисову.
— Василий Федорович, вы мне что-нибудь доверите? Пожалуйста … ради бога … — сказал он. Денисов как будто забыл о существовании Пети. Он снова посмотрел на него.
«Про тебя г о у о о, — сказал он строго, — чтобы меня слушались и никуда не лезли.
За все время переезда Денисов больше ни слова с Петей не говорил и ехал молча. Когда мы приехали. на опушке леса поле уже стало заметно светлее, Денисов шепотом заговорил с есаулом, и казаки стали проходить мимо Пети и Денисова.Когда все ехали, Денисов тронул лошадь и поехал под гору. Сидя на спине и скользя, лошади со всадниками спустились в лощину. Петя ехал рядом с Денисовым. Дрожь во всем теле усилилась. Становилось все светлее и ярче, только туман скрывал далекие объекты. Спустившись и оглянувшись, Денисов кивнул стоявшему рядом казаку.
— Сигнал! Он сказал.
Казак поднял руку, раздался выстрел. И в это же мгновение перед скачущими лошадьми раздался стук, крики со всех сторон и еще выстрелы.
В тот момент, когда послышались первые звуки грома и крика, Петя, ударив свою лошадь и отпустив поводья, не слушая крика Денисова, поскакал вперед. Пете показалось, что вдруг, как посреди дня, ярко осенило в ту минуту, когда раздался выстрел. Он прыгнул на мост. Казаки неслись вперед по дороге. На мосту он наткнулся на отсталого казака и поскакал дальше. Впереди некоторые люди — должно быть, французы — сбежали с правой стороны дороги на левую.Один упал в грязь под ноги Петиной лошади.
Казаки толпились в одной избе, что-то делают. Из толпы раздался жуткий крик. Петя подскочил к этой толпе, и первое, что он увидел, было лицо француза, бледного с дрожащей нижней челюстью, державшегося за направленные на него пики.
«Ура! .. Ребята … наши … — крикнул Петя и, отдав поводья пылающему коню, поскакал вперед по улице.
Впереди раздались выстрелы. Казаки, гусары и русские оборванные пленные, бежавшие с двух сторон дороги, громко и неловко кричали.Молодой, без шляпы, с красным нахмуренным лицом француз в синем пальто отбивался штыком от гусар. Когда Петя прыгнул, француз уже упал. Опять опоздал, промелькнуло в голове Пети, и он поскакал обратно туда, где слышались частые выстрелы. Стрельба велась во дворе того дворянского дома, где он был с Долоховым вчера вечером. Французы поселились там за плетенкой в густом заросшем кустарником саду и стреляли в теснившихся у ворот казаков.Подойдя к воротам, Петя в пороховом дыму увидел Долохова с бледным зеленоватым лицом, который что-то кричал людям. «В объезд! Ждите пехоту! — крикнул он, пока Петя подъезжал к нему.
«Подождите? .. Ураааа! … »- крикнул Петя и, не медля ни секунды, поскакал к тому месту, откуда слышались выстрелы и где пороховой дым был гуще. Раздался залп, визг пустых и во что-то шлепались пули. Казаки и Долохов последовали за Петей в ворота дома. Французы в качающемся густом дыму одни бросили оружие и выбегали из кустов навстречу казакам, другие бежали под гору к пруду.Петя ехал на коне по двору усадьбы и, вместо того чтобы держать поводья, странно и быстро махнул обеими руками и все дальше и дальше от седла уходил в сторону. Лошадь, наткнувшись на тлеющий в утреннем свете костер, отдохнула, а Петя тяжело упал на мокрую землю. Казаки видели, как быстро его руки и ноги дергались, несмотря на то, что голова не двигалась. Пуля пробила ему голову.
После разговора со старшим французским офицером, который подошел к нему из-за дома с шарфом на шпаге и объявил, что они сдаются, Долохов слез с лошади и подошел к Пете, который раскинул руки. протянутый.
«Готово», — сказал он, нахмурившись, и прошел через ворота к Денисову, который шел к нему.
— Убито ?! Денисов вскрикнул, увидев издали знакомое, несомненно, безжизненное положение, в котором лежало тело Пети.
«Готово», — повторил Долохов, как будто ему понравилось произношение, и быстро пошел к пленным, окруженным спешившимися казаками. — Не возьмемся! Он крикнул Денисову.
Первый способ — на этой стороне S с помощью транспортира.
Проведите линию и установите на ней AB = S; возьмем эту прямую за радиус и этим радиусом из точек A и B опишем дуги: Далее с помощью транспортира построим в этих точках углы 108 °, стороны которых пересекаются с дугами в точках C и D; из этих точек с радиусом AB = 5 описываем дуги, которые пересекаются в E, и соединяем точки A, C, E, D, B прямыми линиями.
Получившийся пятиугольник — желаемый.
Способ второй. Нарисуйте круг радиуса r. Из точки A проводим циркуль дугой радиуса AM до пересечения в точках B и C круга. Соединяем B и C линией, пересекающей горизонтальную ось в точке E.
Затем из точки E проводим дугу, которая пересекает горизонтальную линию в точке O. Наконец, из точки F описываем дугу, пересекающую окружность в точках H и K. Кладем окружность FO = FH = FK пять раз по кругу и соединяя точки деления линиями, получаем правильный пятиугольник.
Способ третий. Введите правильный пятиугольник в этот круг. Рисуем два взаимно перпендикулярных диаметра AB и MS. Разделите радиус AO точкой E пополам. Из точки E, как и из центра, проведите дугу окружности радиуса EM и разрежьте ее диаметром AB в точке F. Отрезок MF равен стороне искомого правильного пятиугольника. Раствором циркуля равным MF делаем засечки N 1, P 1, Q 1, K 1 и соединяем их прямыми линиями.
На рисунке с этой стороны построен шестиугольник.
Линия AB = 5, как радиус, из точек A и B описывают дуги, пересекающиеся в C; отсюда тем же радиусом описываем окружность, на которую нанесена сторона A B 6 раз.
Hexagon ADEFGB — желательно.
«Отделка помещений под ремонт»,
Н.П. Краснов
Первый способ сборки. Проведем горизонтальную (AB) и вертикальную (CD) оси и от точки их пересечения M отложим соответствующую ось на соответствующей оси.Применяем малую ось от точки M на большой оси к точке E. Эллипс, первый метод построения. Разделите BE на 2 части и примените одну из точки M на большой оси (к F или H) …
Основанием для нанесения краски является полностью законченная окраска поверхности стен, потолка и других конструкций; покраска выполняется по качественным клеевым и масляным морилкам для обрезки или флейца. Приступая к разработке эскиза декора, мастер должен четко представить всю композицию в домашней обстановке и четко понять творческую идею.Только при соблюдении этого основного условия оно может быть правильным …
Замер выполненных работ, за исключением особых случаев, проводится по площади фактически обработанной поверхности с учетом ее рельефа и за вычетом необработанных мест. Для определения реально обработанных поверхностей во время покраски следует использовать коэффициенты пересчета, приведенные в таблицах. A. Деревянные оконные устройства (замер производится по площади проемов по внешнему контуру ящиков) Наименование устройств Коэффициент…
Положительный пятиугольник Многоугольник, в котором все пять сторон и все пять углов равны друг другу. Вокруг него легко описать круг. Возведите пятиугольник , и этот круг поможет.
Инструкция по эксплуатации
1. Прежде всего, нужно построить круг с помощью циркуля. Пусть центр окружности совпадает с точкой О. Нарисуйте оси симметрии перпендикулярно друг другу. На пересечении одной из этих осей с окружностью поставьте точку V.Эта точка будет вершиной будущего пятиугольника и . На пересечении другой оси с окружностью расположите D.
2. Найдите середину отрезка OD и отметьте на нем точку A. Позже вам нужно будет нарисовать круг с центром в этой точке. Кроме того, он должен проходить через точку V, то есть с радиусом CV. Точку пересечения оси симметрии и этого круга обозначьте B.
3. Позже с помощью циркуля нарисуйте круг того же радиуса, поместив стрелку в точку V.Обозначим пересечение этой окружности с оригиналом точкой F. Эта точка будет второй вершиной будущего точного пятиугольника и .
4. Теперь вам нужно провести тот же круг через точку E, но с центром в F. Обозначьте пересечение только что нарисованного круга с исходным как G. Эта точка также станет одной из вершин пятиугольника и. Аналогичным образом нужно построить еще один круг. Его центр находится в G. Пусть это будет точка пересечения с исходной окружностью.Это последняя вершина правильного многоугольника.
5. У вас должно получиться пять вершин. Осталось легко совместить их в линию. В результате всех этих операций у вас получится вписанный в круг пятиугольник .
Построение положительного элемента пятиугольника Допускается использование компаса и линейки. Правда, процесс довольно долгий, как, впрочем, и построение любого положительного многоугольника с нечетным числом сторон. Современные компьютерные программы позволяют сделать это за несколько секунд.
Вам понадобится
- — Компьютер с AutoCAD.
Инструкция по эксплуатации
1. Найдите верхнее меню в AutoCAD и вкладку «Главное» в нем. Щелкните по нему левой кнопкой мыши. Появится панель рисования. Появятся различные типы линий. Выберите замкнутую полилинию. Это многоугольник, осталось только ввести параметры. AutoCAD позволяет правильно рисовать различные многоугольники. Количество сторон может достигать 1024.Разрешено использовать командную строку, в зависимости от версии, набрав «_polygon» или «multi-angle».
2. Независимо от того, используете ли вы командную строку или контекстное меню, на экране появится окно с просьбой ввести количество сторон. Введите туда цифру «5» и нажмите Enter. Вам будет предложено определить центр пятиугольника. Вбейте в появившееся окно координаты. Их можно обозначать как (0,0), но могут быть и другие данные любого рода.
3. Выберите желаемый метод строительства. . AutoCAD предлагает три варианта. Пятиугольник можно описать вокруг круга или вписать в него, но можно построить его в соответствии с заданным размером стороны. Выберите нужный вариант и нажмите Enter. При необходимости укажите радиус окружности и также нажмите Enter.
4. Пятиугольник на данной стороне изначально строится правильно таким же образом. Выберите «Нарисовать» замкнутую полилинию и введите количество сторон.Щелкните правой кнопкой мыши, чтобы открыть контекстное меню. Нажмите ребро или боковую команду. В командной строке введите координаты исходной и конечной точек одной из сторон пятиугольника. Позже этот пятиугольник появится на экране.
5. Все операции можно выполнять с поддержкой командной строки. Скажем, чтобы построить пятиугольник сбоку в русской версии программы, введите букву «с». В английской версии это будет «_e». Чтобы построить вписанный или описанный пятиугольник, введите позже количество сторон буквы «o» или «b» (или английского «_c» или «_i»)
Видео по теме
Видео по теме
Полезный совет
Этот простой способ позволяет построить не только пятиугольник.Для того чтобы построить треугольник, нужно развести ножки циркуля на расстояние, равное радиусу круга. После этого установите иглу в любую точку. Нарисуйте тонкий опорный круг. Две точки пересечения окружностей, а также точка, в которой была ножка циркуля, образуют три вершины положительного треугольника.
Построение правильных многоугольников
Построение правильных многоугольников
«ВОЗВРАЩАТЬСЯ» Copyright 2001 & nbsp & nbsp & nbsp 1728 Software Systems |
Приблизительное построение правильных многоугольников: два художника эпохи Возрождения
Альбрехт Дюрер (1471-1528), которого считают отцом современной немецкой живописи, также был большим математическим любителем. Он написал книгу под названием Unterweysung der Messung …, в которой рассматриваются всевозможные геометрические задачи. В этой книге он дает точное построение правильного пятиугольника, но он также дает приблизительное построение, которое быстро может быть выполнено на практике.(Его книга была адресована ремесленникам, каменщикам и т. Д., Которые больше заботились о простых процедурах, чем о геометрической точности.)
Эта конструкция показана ниже:
Возьмем фиксированное отверстие компаса: AB = . Нарисуйте окружности радиуса a с центрами A и B ; пусть эти круги пересекаются в точках C и D . Тогда, как мы знаем, AB = AD = BD . Нарисуйте окружность с центром D и радиусом DA .Этот круг будет проходить через B ; пусть E будет точкой, где он пересекает CD , и пусть F и G будут точками, где он пересекает круги с центрами A и B , соответственно. Произведите FE , пока он не пересечется в точке H с кругом с центром в точке B ; производите GE , пока он не пересечет в точке I круг с центром в точке A . Тогда пересечение K окружностей радиуса a с центрами H и I дает пятую вершину пятиугольника.
Насколько правильный пятиугольник? Если бы он был точно правильным, все стороны должны были бы составлять угол 360 ° / 5 = 72 ° в центре пятиугольника. Следовательно, все углы при вершинах пятиугольника должны быть равны 180 ° -72 ° = 108 ° (поскольку каждый из них является суммой двух равных углов [180 ° -72 °] / 2). Фактически, мы увидим, что угол ABH = 108 ° 21’58 ”- чуть больше 108 °, так что какой-то другой угол должен быть немного меньше 108 °. Сначала отметим, что угол FBG = 90 °; тогда, поскольку FG = 2 a и GB = a , мы имеем FB = a √3.Кроме того, угол DFE = 45 ° и угол DFC = угол DFA = 60 ° ( F , A , C коллинеарны, а также C , B , G и F , D , G ), следовательно, угол AFE = 15 °. Поскольку угол BFE образует дугу окружности FABG , равную дуге, образуемой углом AFE , мы также имеем угол BFE = 15 °.
Теперь воспользуемся законом синусов для треугольника FBH ; это дает sin (угол BHF ) = √3 sin15 ° (обратите внимание, что, поскольку угол BHF можно найти, можно найти угол BHF , а затем угол HBF ; затем угол вычитания ABF = 30 ° от угла HBF , мы находим, что угол ABH составляет примерно 108 ° 22 ‘, значение, близкое к значению Педо [2].
Поскольку угол BAI равен углу ABH , он тоже немного больше 108 °. Кроме того, каждый из углов BHK и AIK немного больше 107 °, а угол HKI немного больше 109 ° … и все же на нашем чертеже это будет едва заметно.
Дюрер не предупреждает читателя своей книги, что эта конструкция приблизительна. (Он также выполняется с помощью «ржавого» компаса, то есть компаса с фиксированным отверстием.Фактически, он также цитирует, как мы уже сказали, точное построение пятиугольника.
«Интерес Дюрера к построению правильных многоугольников объясняется применением геометрии в средние века в исламском и готическом декоративном дизайне, а после изобретения оружия — в строительстве укрепленных городов. (Любопытно, что очень мало зданий в истории было построено на основе пятиугольной формы. Пентагон, расположенный недалеко от Вашингтона, округ Колумбия, является заметным исключением.) »[2]
Обобщая этот обзор многоугольных построек эпохи Возрождения, мы можем сказать, что и Леонардо да Винчи, и Альбрехт Дюрер были большими любителями математики.«Леонардо много писал о многоугольниках; но именно Дюрер, а не Леонардо, передал нам популярные средневековые постройки ». [2]
Построение правильного пятиугольника
Сегодня мы рассмотрим построение правильного пятиугольника с помощью циркуля и линейки на основе следующей тригонометрической формулы $$ \ cos {\ frac {\ pi} {5}} = \ frac {1 + \ sqrt {5} } {4}. $$
Построения равносторонних треугольников , квадратов , правильных шестиугольников и правильных восьмиугольников (8 сторон) довольно просты.Мы не можем не задать вопрос, можно ли с помощью циркуля и линейки построить правильных пятиугольника , правильных семиугольника (7 сторон) и правильных неугольника (9 сторон) или нет.
Оказывается, есть много способов построить правильные пятиугольники, но невозможно построить правильные семиугольники или правильные неугольники, используя только циркуль и линейку. Сегодня мы рассмотрим конструкцию обычного пятиугольника. Мы оставляем обсуждение конструкции семиугольника и неугольника для наших последующих публикаций.
Давайте теперь проведем небольшой анализ. На следующем рисунке мы видим, что если мы можем построить точку $ H $, то из $ H $ мы можем построить точки $ N_3 $ и $ N_4 $, и, таким образом, мы можем легко получить правильный пятиугольник $ N_1 N_2 N_3 N_4 N_5 $.
Итак, чтобы найти способ построить точку $ H $, во-первых, нам нужно определить значение $ \ cos {\ frac {\ pi} {5}} $.2 — 2t-1 = 0 $$ получаем два корня противоположных знаков $$ t_ {1,2} = \ frac {1 \ pm \ sqrt {5}} {4} $$
Таким образом, наш $ \ cos {\ frac {\ pi} {5}} $ является положительным корнем, и мы завершаем вычисление $$ \ cos {\ frac {\ pi} {5}} = \ frac {1 + \ sqrt {5}} {4}. $$
Использование теоремы Пифагора
Возвращаясь к приведенному выше рисунку, мы имеем $$ OH = r \ cos {\ frac {\ pi} {5}} = \ frac {(1 + \ sqrt {5}) r} {4} $$
Чтобы построить отрезок $ OH $, нам нужно построить отрезок длины $ (1 + \ sqrt {5}) r $, а затем разделить его на четыре равные части.2 $$
Построение правильного пятиугольника
На основании приведенного выше анализа получаем следующую конструкцию:
- Постройте две перпендикулярные координатные линии $ x’Ox $, $ y’Oy $;
- Возьмите $ O $ в качестве центра и постройте произвольную окружность, которая пересекает $ Ox $, $ Ox ‘$, $ Oy $ в точках $ X $, $ N_1 $, $ Y $ соответственно;
- Постройте точку $ A $ на $ Oy $ так, чтобы $ YA = YO $;
- Постройте точку $ B $ на $ Ox $ так, чтобы $ XB = XA $;
- Постройте среднюю точку $ C $ для $ OB $ и среднюю точку $ H $ для $ OC $;
- Через $ H $ постройте прямую, перпендикулярную к $ Ox $, которая пересекает окружность $ (O) $ в точках $ N_3 $, $ N_4 $;
- Постройте круг с центром в точке $ N_1 $ и радиусом, равным $ N_3N_4 $, который пересекает круг $ (O) $ в точках $ N_2 $, $ N_5 $;
- Тогда $ N_1N_2N_3N_4N_5 $ — правильный пятиугольник.
В этой конструкции мы видим, что $$ OA = 2r, ~~ XA = \ sqrt {5} r, ~~ XB = \ sqrt {5} r, ~~ OB = (1+ \ sqrt {5}) r , ~~ OH = (1+ \ sqrt {5}) r / 4 $$
Итак, мы завершили построение правильного пятиугольника с помощью циркуля и линейки!
Сразу возникает вопрос, для каких значений $ n $ мы можем построить правильный многоугольник с $ n $ сторонами. Несмотря на простоту формулировки, на самом деле это очень сложная математическая задача. Эта проблема оставалась нерешенной более тысячи лет.Гаусс был человеком, который сделал первый прорыв в решении проблемы. Мы продолжим эту увлекательную историю в наших будущих публикациях. Надеюсь увидеть тебя тогда.
.