Правильный шестиугольник и его свойства
1 Как найти площадь правильного шестиугольника
Формулы для вычисления площади правильного шестиугольника – выпуклого многоугольника с шестью одинаковыми сторонами.
Дана длина стороны:
- Формула площади: S = (3√3*a²)/2
- Если длина стороны a известна, то подставив её в формулу, мы легко найдём площадь фигуры.
- В противном случае длину стороны можно найти через периметр и апофему.
- Если задан периметр, то мы просто делим его на 6 и получаем длину одной стороны. Например, если периметр равен 24, то длина стороны будет равняться 24/6 = 4.
- Апофема – перпендикуляр, проведённый из центра к одной из сторон. Чтобы найти длину одной стороны, подставляем длину апофемы в формулу а = 2*m/√3. То есть, если апофема m = 2√3, то длина стороны а = 2*2√3/√3 = 4.
Дана апофема:
- Формула площади: S = 1/2*p*m, где p – периметр, m – апофема.
- Найдём через апофему периметр шестиугольника.

Дан радиус описанной окружности:
Радиус описанной вокруг правильного шестиугольника окружности равен стороне этого шестиугольника.
Формула площади: S = (3√3*a²)/2
Дан радиус вписанной окружности:
Формула площади: S = 3√3*r², где r = √3*a/2 (a – одна из сторон многоугольника).
Упаковка кругов на плоскости
И еще немного об эффективности гексагона. Упаковка шаров — классическая задача комбинаторной геометрии, которая требует найти оптимальный способ укладки непересекающихся шаров. На практике такая задача превращается в логистическую проблему упаковки апельсинов, яблок, пушечных ядер или любых других шарообразных объектов, которые требуется уложить максимально плотно. Гескагон — решение данной проблемы.
Известно, что наиболее эффективным расположением кругов в двухмерном пространстве является размещение центров окружностей на вершинах шестиугольников, которые заполняют плоскость без пробелов. В трехмерной реальности задача размещения шаров решается путем гексагональной укладки объектов.
В трехмерной реальности задача размещения шаров решается путем гексагональной укладки объектов.
При помощи нашего калькулятора вы можете вычислить площадь правильного шестиугольника, зная его сторону или радиусы соответствующих окружностей. Давайте попробуем вычислить площади гексагонов на реальных примерах.
Расчет
Требуемое значение можно вычислить, разбив фигуру на шесть треугольников с равными сторонами.
Чтоб рассчитать S , пользуются следующей формулой:
Вычислив S одного из треугольников, нетрудно определить и общую. Простая формула, так как правильный шестиугольник, по сути, является шестью равными треугольниками. Таким образом, для ее расчета найденную площадь одного треугольника умножают на 6.
Если от центра шестиугольника к любой его стороне провести перпендикуляр, получается отрезок – апофема.
Посмотрим, как находить S шестиугольника, если апофема известна:
- S =1/2×периметр×апофема.
- Возьмем апофему равную 5√3 см.

- Находим периметр, используя апофему: так как апофема перпендикулярно к стороне 6-угольника, углы треугольника, образованного с помощью апофемы, равняются 30˚-60˚-90˚. Каждая сторона треугольника соответствует: x-x√3-2x, где короткая, против угла 30˚,- это x; длинная сторона против угла 60˚- x√3, а гипотенуза — 2x.
- Апофему x√3 можно подставить в формулу a=x√3. Если апофема равна 5√3, подставив данную величину, получим: 5√3см=x√3, или x=5см.
- Короткая сторона треугольника составляет 5см, так как эта величина – половина длины стороны 6-угольника. Умножив 5 на 2, получим 10см, что есть значение длиной стороны.
- Полученную величину умножим на 6 и получим значение периметра – 60см.
Подставляем полученные результаты в формулу: S=1/2×периметр×апофема
S=½×60 см× 5√3
Считаем:
Упрощаем полученный ответ, чтоб избавиться от корней. Результат будет выражен в квадратных сантиметрах: ½×60см×5√3см=30×5√3см=150 √3см=259,8с м².
Примеры из реальной жизни
Гигантский гексагон
Гигантский гексагон — уникальное атмосферное явление на Сатуре, которое выглядит как грандиозный вихрь в форме правильного шестиугольника.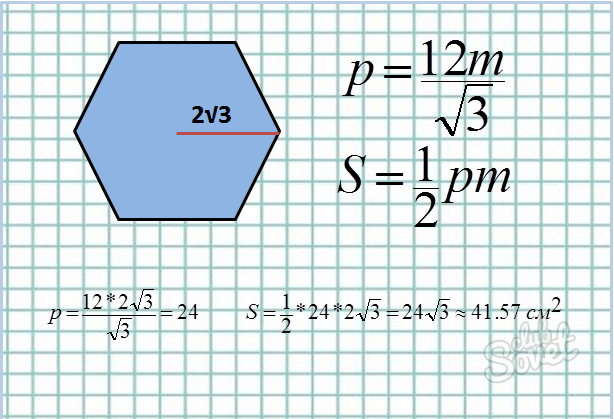
S = 494 777 633
Таким образом, площадь атмосферного вихря на Сатурне приблизительно составляет 494 777 633 квадратных километров. Поистине впечатляет.
Гексагональные шахматы
Мы все привыкли к шахматному полю, разделенному на 64 квадратные ячейки. Однако существуют и гексагональные шахматы, игровое поле которых разделено на 91 правильный шестиугольник. Давайте определим площадь игровой доски для гексагональной версии известной игры. Пусть сторона ячейки составляет 2 сантиметра. Площадь одной игровой клетки составит:
S = 10,39
Тогда площадь всей доски будет равна 91 × 10,39 = 945,49 квадратных сантиметров.
Площадь неправильного шестиугольника
Существует несколько вариантов определения площади
неправильного шестиугольника:
- Метод трапеции.

- Метод расчета площади неправильных многоугольников при
помощи оси координат. - Метод разбивания шестиугольника на другие фигуры.
В зависимости от исходных данных, которые вам будут
известны, подбирается подходящий метод.
Метод трапеции
Площадь шестиугольника, имеющего произвольную
(неправильную) форму, рассчитывается методом трапеции, суть которого состоит в
разделении шестиугольника на отдельные трапеции и последующим вычислением
площади каждой из них.
Метод с осями
координат
Кроме этого, площадь неправильного шестиугольника можно рассчитать
при помощи метода расчета площади неправильных многоугольников. Рассмотрим его
на следующем примере:
Вычисление будем выполнять методом использования
координат вершин многоугольника:
- На этом этапе следует сделать таблицу и записать
координаты вершин x и y. Выбираем вершины в
списка повторной записью координаты первой вершины:
- Теперь следует умножить значения координаты х 1-й вершины
на y 2-й
вершины и продолжить таким образом умножение далее. Затем необходимо сложить
Затем необходимо сложить
полученные результаты. В нашем случае получилось 82:
- Последовательно умножаем значения координат y1-й
вершины на значения координат х 2-й вершины. Суммируем полученные результаты. В
нашем случае получилось 38:
- Вычитаем сумму, которую получили на четвертом этапе из
суммы, которая получилась на третьем этапе: 82 – (-38) = 120
- Теперь необходимо разделить результат, который был
получен на предыдущем этапе и найдем площадь нашей фигуры: S= 120/2 = 60
см²
Метод разбивания
шестиугольника на другие фигуры
Каждый многоугольник можно разделить на несколько других
фигур. Это могут быть треугольники, трапеции, прямоугольники. Исходя из
известных данных, пользуясь формулами определения площадей перечисленных фигур,
последовательно вычисляются их площади и затем суммируются.
Некоторые неправильные шестиугольники состоят из двух
параллелограммов.
длину на ширину и затем сложить две уже известные площади.
Видео о том, как найти площадь многоугольника
https://youtube.com/watch?v=N8kcd6smUy4
Площадь равностороннего шестиугольника
Равносторонний шестиугольник имеет шесть равных сторон и
является правильным шестиугольником.
Площадь равностороннего шестиугольника равняется 6
площадям треугольников, на которые разбита правильная шестиугольная фигура.
Все треугольники в шестиугольнике правильной формы равны,
поэтому для нахождения площади такого шестиугольника достаточно будет знать
площадь хотя бы одного треугольника.
Для нахождения площади равностороннего шестиугольника
используется, конечно же, формула площади правильного шестиугольника, описанная
выше.
А Вы знали, как найти площадь шестиугольника? Как думаете, где эти знания пригодятся Вам в жизни? Поделитесь своим мнением в . 2n}{2} sin (\frac{2π}{n})\)
2n}{2} sin (\frac{2π}{n})\)
Периметр многоугольника:
\(Р = an \)
\(n\)- число углов, \(a\)-длина стороны
Сторона многоугольника:
\(a =\frac{ 2rsinα }{ 2}\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Правильный многоугольник для школьников и студентов
Формулы, признаки и свойства правильного многоугольника
Многоугольником называется часть площади, которая ограничена замкнутой ломаной линией, не пересекающей сама себя.
Многоугольники отличаются между собой количеством сторон и углов.
Правильный многоугольник — это многоугольник, у которого все стороны и углы одинаковые.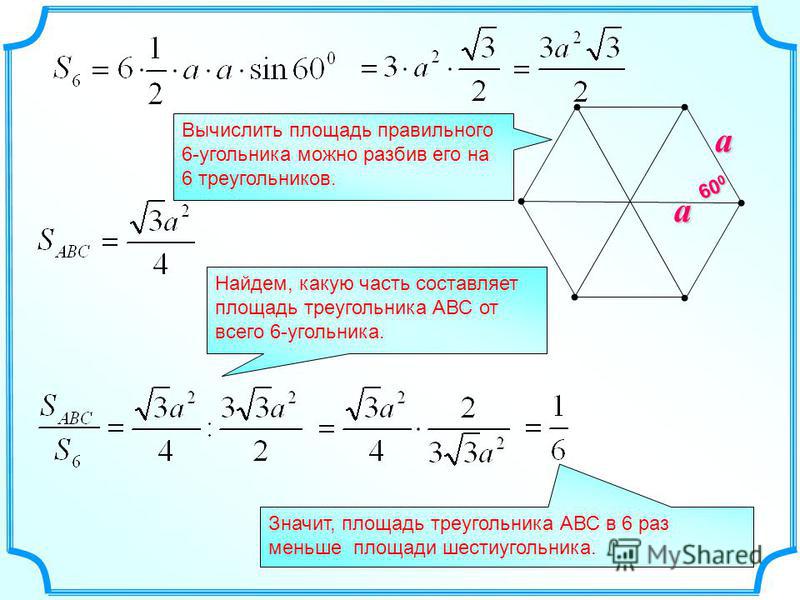
Признаки правильного многоугольника
Многоугольник будет правильным, если выполняется следующее условие: все стороны и углы одинаковы.
a1=a2=a3=…=an-1=an ,α1=α2=α3=…=αn-1=αn
где a1…an — длины сторон правильного многоугольника,
α1…αn — внутренние углы между стронами правильного многоугольника.
Основные свойства правильного многоугольника
- Все стороны равны: a1=a2=a3=…=an-1=an
- Все углы равны: α1=α2=α3=…=αn-1=αn
- Центр вписанной окружности Oв совпадает с центром описанной окружности Oо, что и образуют центр многоугольника O.
- Сумма всех углов n-угольника равна:180°·n-2
- Сумма всех внешних углов n-угольника равна 360°: β1+β2+β3+…+βn-1+βn=360°
- Количество диагоналей (Dn) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины: Dn=n·n-32
- В любой многоугольник можно вписать окружность и описать круг; при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника: S=π4·a2
- Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O.

Формулы правильного n-угольника
Формулы длины стороны правильного n-угольника
Формула стороны правильного n-угольника через радиус вписанной окружности
a=2·r·tg180°n (через градусы),a=2·r·tgπn (через радианы)
Формула стороны правильного n-угольника через радиус описанной окружности
a=2·R·sin180°n (через градусы),a=2·R·sinπn (через радианы)
Формулы радиуса вписанной окружности правильного n-угольника
Формула радиуса вписанной окружности n-угольника через длину стороны
r=a:2·tg180°n (через градусы),r=a:2·tgπn (через радианы)
Формула радиуса описанной окружности правильного n-угольника
Формула радиуса описанной окружности n-угольника через длину стороны
R=a:2·sin180°n (через градусы),R=a:2·sinπn (через радианы)
Формулы площади правильного n-угольника
Формула площади n-угольника через длину стороны
S=n·a24·ctg180°n
Формула площади n-угольника через радиус вписанной окружности
S=n·r2·tg180°n
Формула площади n-угольника через радиус описанной окружности
S=n·R22·sin360°nФормула периметра правильного многоугольника
Формула периметра правильного n-угольника
Периметр правильного n-угольника равен произведению длины одной стороны правильного n-угольника на количество его сторон.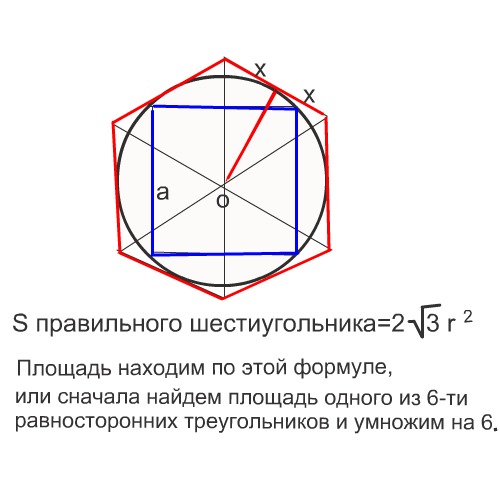
Формула определения угла между сторонами правильного многоугольника
Формула угла между сторонами правильного n-угольника
αn=n-2n·180°Правильный треугольник
Правильный треугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного треугольника равны между собой, все углы также равны и составляют 60°.
Формулы правильного треугольника
Формула стороны правильного треугольника через радиус вписанной окружности
Сторона правильного треугольника равна удвоенному произведению радиуса вписанной окружности на корень из трёх.
a=2·r·3Формула стороны правильного треугольника через радиус описанной окружности
Сторона правильного треугольника равна произведению радиуса описанной окружности на корень из трёх.
a=R·3r=a·36
R=a·33
Формула площади правильного треугольника через длину стороны
S=a2·34
Формула площади правильного треугольника через радиус вписанной окружности
S=r2·3·3
Формула площади правильного треугольника через радиус описанной окружности
S=R2·3·34
Углы между сторонами правильного треугольника
α1=α2=α3=60°Правильный четырехугольник
Правильный четырехугольник — это квадрат.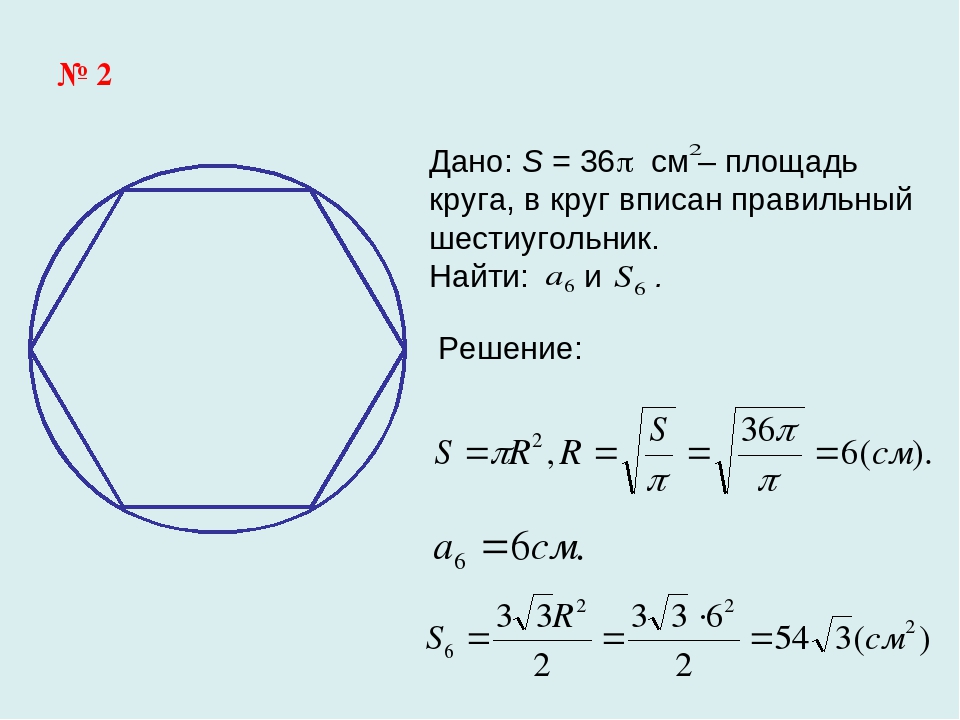
Формулы правильного четырехугольника
Формула стороны правильного четырехугольника через радиус вписанной окружности
Сторона правильного четырехугольника равна двум радиусам вписанной окружности.
a=2·rФормула стороны правильного четырехугольника через радиус описанной окружности
Сторона правильного четырехугольника равна произведению радиуса описанной окружности на корень из двух.
a=R·2Формула радиуса вписанной окружности правильного четырехугольника через длину стороны
Радиус вписанной окружности правильного четырехугольника равен половине стороны четырехугольника.
r=a2Формула радиуса описанной окружности правильного четырехугольника через длину стороны
Радиус описанной окружности правильного четырехугольника равен половине произведения стороны четырехугольника на корень из двух.
R=a·22Формула площади правильного четырехугольника через длину стороны
Площадь правильного четырехугольника равна квадрату стороны четырехугольника.
Формула площади правильного четырехугольника через радиус вписанной окружности
Площадь правильного четырехугольника равна четырем радиусам вписанной окружности четырехугольника.
S=4·r2Формула площади правильного четырехугольника через радиус описанной окружности
Площадь правильного четырехугольника равна двум квадратам радиуса описанной окружности.
S=2·R2
Углы между сторонами правильного четырехугольника
α1=α2=α3=α4=90°Правильный шестиугольник
Правильный шестиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного шестиугольника равны между собой, все углы также равны и составляют 120°.
Формулы правильного шестиугольник
Формула стороны правильного шестиугольника через радиус вписанной окружности
a=2·r·33Формула стороны правильного шестиугольника через радиус описанной окружности
Длина стороны правильного шестиугольника равна радиусу описанной окружности.
Формула радиуса вписанной окружности правильного шестиугольника через длину стороны
r=a·32
Формула радиуса описанной окружности правильного шестиугольника через длину стороны
R=a
Формула площади правильного шестиугольника через длину стороны
S=a2·3·32
Формула площади правильного шестиугольника через радиус вписанной окружности
S=r2·2·3
Формула площади правильного шестиугольника через радиус описанной окружности
S=R2·3·32
Углы между сторонами правильного шестиугольника
α1=α2=α3=α4=α5=α6=120°Правильный восьмиугольник
Правильный восьмиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного восьмиугольник равны между собой, все углы также равны и составляют 135°.
Формулы правильного восьмиугольника
Формула стороны правильного восьмиугольника через радиус вписанной окружности
a=2·r·2-1
Формула стороны правильного восьмиугольника через радиус описанной окружности
a=R·2-2
Формула радиуса вписанной окружности правильного восьмиугольника через длину стороны
r=a·2+12
Формула радиуса описанной окружности правильного восьмиугольника через длину стороны
R=a·4+222
Формула площади правильного восьмиугольника через длину стороны
S=a2·2·2+1
Формула площади правильного восьмиугольника через радиус вписанной окружности
S=r2·8·2-1
Формула площади правильного восьмиугольника через радиус описанной окружности
S=R2·2·2
Углы между сторонами правильного восьмиугольника
α1=α2=α3=α4=α5=α6=α7=α8=135°- Коротко о важном
- Таблицы
- Формулы
- Формулы по геометрии
- Теория по математике
Ф-лы для выч.
 площади прав. многоуг., его стороны и радиуса впис. окр.
площади прав. многоуг., его стороны и радиуса впис. окр.На этом уроке мы вспомним, какой многоугольник называют правильным. Узнаем, каковы его элементы. А затем выведем формулы для вычисления элементов правильного многоугольника.
Для начала давайте вспомним определение правильного многоугольника. Итак, правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.
Пусть – правильный -угольник
– площадь правильного -угольника,
– сторона правильного -угольника,
– периметр,
– радиус вписанной окружности,
– радиус описанной окружности.
Площадь многоугольника – это величина части плоскости, которую занимает многоугольник.
Доказательство.
Для
доказательства соединим центр многоугольника с его вершинами. Многоугольник
разобьётся на n равных треугольников.
Многоугольник
разобьётся на n равных треугольников.
А значит, получим, что площадь правильного n-угольника равна половине произведения периметра правильного n-угольника на радиус вписанной в него окружности. Что и требовалось доказать.
Теперь давайте выведем формулы для вычисления стороны правильного многоугольника и радиуса вписанной окружности.
1. Пусть – правильный многоугольник.
– равнобедренный.
Рассмотрим .
– прямоугольный, т.к. – высота.
Следовательно, .
2. Теперь докажем вторую формулу для вычисления стороны многоугольника через радиус описанной окружности
Пусть – правильный многоугольник.
– равнобедренный.
Рассмотрим .
– высота .
Следовательно,
– прямоугольный.
.
Что и требовалось доказать.
Радиус вписанной окружности можно выразить через радиус описанной окружности по следующей формуле: .
Пусть – правильный многоугольник.
– равнобедренный.
Рассмотрим .
– прямоугольный, т.к. – высота.
Следовательно, .
Что и требовалось доказать.
Воспользовавшись формулой для вычисления стороны правильного n-угольника через радиус описанной окружности , давайте выразим формулы для нахождения стороны правильного треугольника, квадрата и правильного шестиугольника. Соответственно, подставим в формулу вместо n количество сторон указанных правильных многоугольников 3, 4 и 6.
Задача. Радиус, описанной окружности около
правильного шестиугольника, равен см.
Найдите площадь правильного шестиугольника.
Решение.
()
(см)
(см)
(см)
Ответ: .
Подведем итоги урока. На этом уроке мы вывели формулы для вычисления элементов правильного многоугольника. Вспомним их:
Площадь правильного -угольника, описанного около окружности, можно найти через периметр и радиус вписанной окружности по формуле:
Сторону правильного -угольника можно выразить через радиус вписанной окружности:
Сторону правильного -угольника можно выразить через радиус описанной окружности:
Радиус вписанной окружности можно выразить через радиус описанной окружности по формуле:
А также мы с вами выразили формулы для вычисления
стороны правильного треугольника, квадрата и правильного шестиугольника
,
,
.
2.3.Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности.
Пусть S – площадь правильного n – угольника, аn– его сторона, Р – периметр, а, r и R – радиусы соответственно вписанной и описанной окружностей. Докажем сначала, что
S = ½Pr. (1)
В самом деле, соединим центр данного многоугольника с его вершинами. Тогда многоугольник разобьется на n равных треугольников, площадь каждого из которых равна ½аnr ( см.рис.п.2.2)
Следовательно,
S = n½anr = ½(nan) r = ½Pr.
Выведем далее следующие формулы:
an = 2R sin , (2)
r = R . (3)
Для вывода этих формул воспользуемся рисунком. В прямоугольном треугольникеА1Н1О
А1==۰ 1800= 900-.Следовательно,аn= 2А1Н1= 2Rcos( 900-) = 2Rsin, аr=OH1=Rsin( 900-) =Rcos.
Полагая в формуле (2) n = 3, 4 и 6, получим выражения для сторон правильного треугольника, квадрата и правильного шестиугольника:
а3 = 2R sin = 2R sin 600 = 2R ۰ = R ; (4)
а4 = 2R sin = 2R sin 450 = 2R ۰ = R ; (5)
а6 = 2R sin = 2R sin 300 = 2R ۰ = R; (6)
2.
 4. Решение задач с применением формул для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности.
4. Решение задач с применением формул для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности.Для иллюстрации применения данных формул (1) – (6), (п. 2.3.) можно решить задачи.
Задача № 1. Для квадрата со стороной а, вписанного в окружность радиуса R, заполнить таблицу (известные данные в каждой строке выделены жирным шрифтом).
N | R | r | a4 | P | S |
1 | 3 | 6 | 24 | 36 | |
2 | 2 | 4 | 16 | 16 | |
3 | 4 | 16 | 32 | ||
4 | 3,5 | 7 | 28 | 49 | |
5 | 8 | 4 | 16 | 16 |
Решение.
a4 = 2R sin = 2R sin 450 = 2R ۰ = R;
r = R cos = R cos 450 = R;
P = 4a; S = a2 .
1) a4 = R, R = , R = = .
r = ۰ = 3.
P = 4a = 4۰6 = 24, S = a2 = 36.
R= , R = 2,
a4 = ۰ = 4,
P = 4۰4 = 16, S = 16.
r = 4۰ = ,
a4 = 4۰ = ,
P = 4۰ = , S = 32.
a4 = 28 : 4 = 7,
R = = 3,5۰,
r = 3,5۰ = 3,5,
S = 49.
a4 = 4, P = 16,
R = = ,
r = ۰= 8.
Задача
№ 2. Для правильного треугольника со
стороной а, вписанной в окружность
радиуса R,
заполнить таблицу (известные данные в
каждой строке выделены жирным шрифтом).
N | R | r | a3 | P | S |
1 | 3 | 1,5 | 3 | 9 | |
2 | 10 | ||||
3 | 4 | 2 | 4 | 12 | 12 |
4 | 5 | 15 | |||
5 | 2 | 6 |
Решение.
а3 = 2R sin = 2R sin 600 = 2R۰ = R;
r = R cos = R cos 600 = R۰= ;
P = a + b + c = 3a,( т.к. а = b = c), S = .
1) r = = 1,5, a3 = ,
P = 3۰= , S = .
2) a3 = = = ,
R = = 2۰۰ = 2۰ = ۰,
r = : = ۰ =
P = ۰2 = .
3) r = 2۰2 = 4, a3 = ,
P = 3۰ = , S = = .
4) R = = ,
r = : = ۰ = ,
P = 3۰5 = 15, S = .
5) a3 = 6 : 3 = 2, S = = ,
R = = ,
r = : = ۰ = .
Используя
решенные задачи, можно составить таблицу
зависимости стороны, радиуса описанной
окружности, радиуса вписанной окружности
для всех наиболее часто встречающихся
правильных многоугольников.
Количество сторон n | а | r | S |
3 | |||
4 | 2R2 | ||
6 | R |
Открытый урок по теме «Формулы вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности»
Для проведения урока необходим экран,
компьютер и мультимедийный проектор для показа
презентации.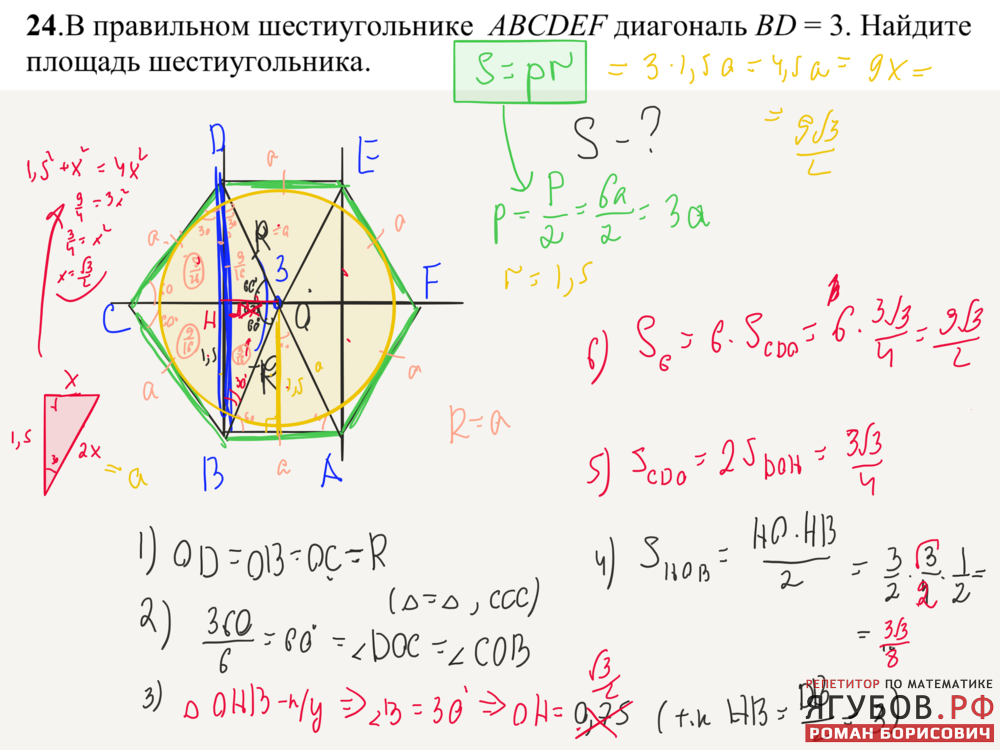
Приложение
Сегодня на уроке мы узнаем и увидим много нового и интересного: вспомним понятие правильного многоугольника, выведем формулы, связывающие площадь и сторону правильного многоугольника с радиуса вписанной окружности. Кроме того узнаем интересные исторические факты, связанные не только с правильными многоугольниками, но и многогранниками. Решим геометрические задачи по данной теме.
Мне хотелось бы начать со слов Бертрана Рассела: “Математика владеет не только истиной, но и высшей красотой…”.
Разминка
Вопрос о математических предпосылках
прекрасного, о роли математики в жизни волновал
еще древних греков, причем свой интерес они
унаследовали от предшествующих цивилизаций. В
наше время геометрия – необходимый элемент
общего образования и культуры, представляет
большой исторический интерес, имеет серьезное
практическое применение и обладает внутренней
красотой.
Название правильные идет из античных времен, когда стремились найти гармонию, правильность, совершенство в природе и человеке. До сих пор многоугольники нередко называют в науке по-гречески с окончанием “гон”: полигон – многоугольник, пентагон – пятиугольник (такой формы сверху здание театра Российской армии в Москве и министерство обороны США), гексагон – шестиугольник (ячейка пчелиных сот).
Замечательным примером пентагона является правильный звездчатый пятиугольник:
Рисунок 1
Звездчатый пятиугольник называется пентаграммой. Пифагорейцы выбрали пятиконечную звезду в качестве талисмана, она считалась символом здоровья и служила опознавательным знаком.
Бытует легенда о том, что один из пифагорейцев
больным попал в дом к незнакомым людям. Они
старались его выходить, но болезнь не отступала.
Не имея средств заплатить за лечение и уход,
больной перед смертью попросил хозяина дома
нарисовать у входа пятиконечную звезду,
объяснив, что по этому знаку найдутся люди,
которые вознаградят его.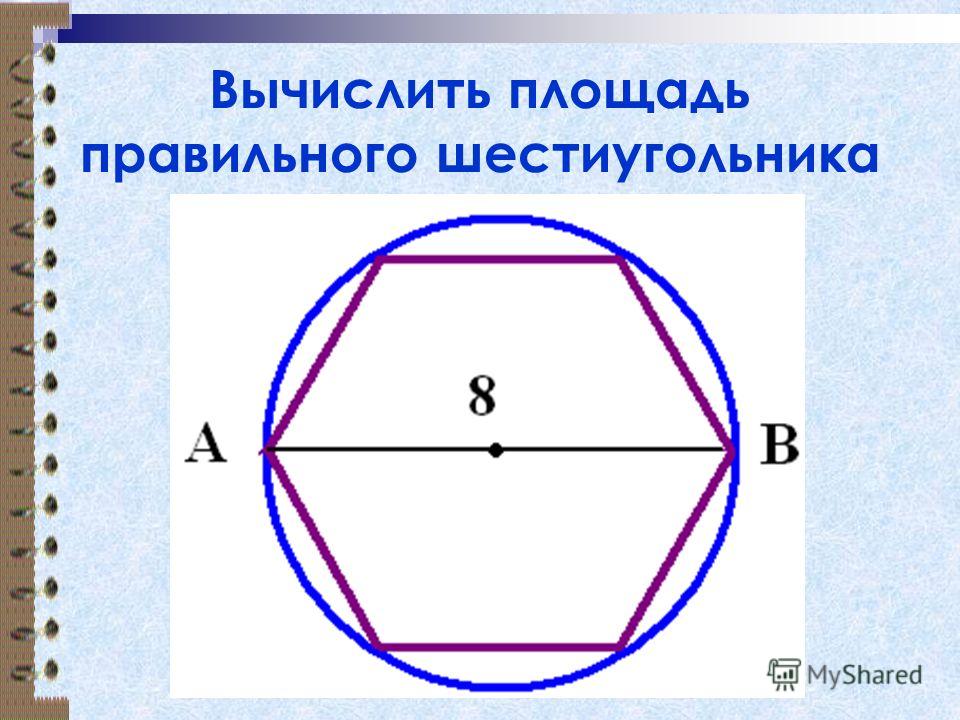 И на самом деле, через
некоторое время один из путешествующих
пифагорейцев заметил звезду и стал
расспрашивать хозяина дома о том, каким образом
она появились у входа. После рассказа хозяина
гость щедро вознаградил его.
И на самом деле, через
некоторое время один из путешествующих
пифагорейцев заметил звезду и стал
расспрашивать хозяина дома о том, каким образом
она появились у входа. После рассказа хозяина
гость щедро вознаградил его.
Пентаграмма была хорошо известна и в Древнем Египте. Но непосредственно как эмблема здоровья она была принята лишь в Древней Греции.
Вычисление суммы углов пятиконечной звезды, вписанной в окружность. (Рис. 1)
Ученики могут решать эту задачу двумя способами, если нашли только один способ решения, то можно по усмотрению комментировать другой.
Рисунок 2
I способ: Когда вершины пятиугольной звезды делят окружность на равные дуги, задача решается очень просто; 360о/5/2*5=180о.
II способ: Угол AMR – внешний угол треугольника
MCE, поэтому <AMR=<C+<E. Угол ARM – внешний угол
треугольника BRD, поэтому <ARM=<B+<D.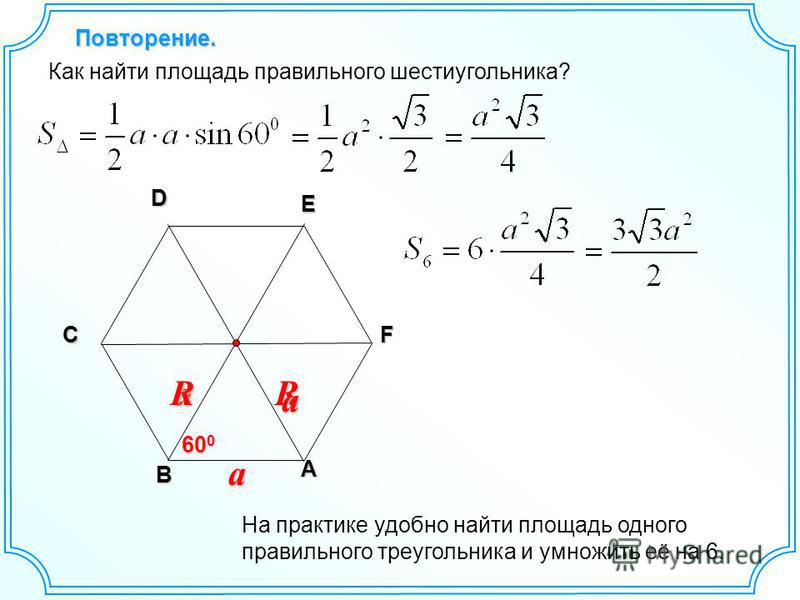 Тогда
<A+<B+<C+<D+<E=<A+<AMR+<ARM=180o.
Тогда
<A+<B+<C+<D+<E=<A+<AMR+<ARM=180o.
Рассмотрим условие геометрической задачи: в правильный шестиугольник вписана окружность радиусом 8 см. Найти 1) длину стороны шестиугольника, 2) площадь шестиугольника, 3) радиус описанной около него окружности.
Рисунок 3
Рисунок 4
Наводящие вопросы:
- Разбейте шестиугольник на 6 равных треугольников с общей вершиной О.
- Чем является радиус ОН вписанной в треугольник АОВ окружности
- Чему равен угол АОВ
- Вычислите градусную меру угла АОН
- Перечислите все известные элементы треугольника АОН, как найти его неизвестные элементы
- Что можно сказать о площадях треугольников АОВ, ВОС, т.д.
Рассмотрим задачу нахождения площади, радиуса
описанной окружности и радиуса вписанной
окружности для правильного многоугольника.
Рисунок 5
Если соединить центр данного многоугольника с его вершинами, то многоугольник разобьется на п – равных треугольников. Площадь каждого из которых равна , следовательно, S = n• = = .
Итак, формулы для вычисления стороны правильного многоугольника и радиуса вписанной в него окружности: аn = 2 Rsin, r = Rcos.
Устная работа:
Составьте цепочку решения задачи по одной известной величине
- Дан R. Запишите формулы R —> r —> a —> P —> S.
- Дана сторона а. записать формулы a —> R —> r —> P —> S.
- Дан Р. P —> a —> R —> r —> S.
Приложение (Решение геометрических задач и тесты)
Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности.
Сегодня на уроке мы узнаем и увидим много нового и интересного: вспомним понятие правильного многоугольника, выведем формулы, связывающие площадь и сторону правильного многоугольника с радиуса вписанной окружности. Кроме того узнаем интересные исторические факты, связанные не только с правильными многоугольниками, но и многогранниками. Решим геометрические задачи по данной теме.
Кроме того узнаем интересные исторические факты, связанные не только с правильными многоугольниками, но и многогранниками. Решим геометрические задачи по данной теме.
Мне хотелось бы начать со слов Бертрана Рассела: “Математика владеет не только истиной, но и высшей красотой…”.
Разминка
Вопрос о математических предпосылках прекрасного, о роли математики в жизни волновал еще древних греков, причем свой интерес они унаследовали от предшествующих цивилизаций. В наше время геометрия – необходимый элемент общего образования и культуры, представляет большой исторический интерес, имеет серьезное практическое применение и обладает внутренней красотой.
Название правильные идет из античных времен, когда стремились найти гармонию, правильность, совершенство в природе и человеке. До сих пор многоугольники нередко называют в науке по-гречески с окончанием “гон”: полигон – многоугольник, пентагон – пятиугольник (такой формы сверху здание театра Российской армии в Москве и министерство обороны США), гексагон – шестиугольник (ячейка пчелиных сот).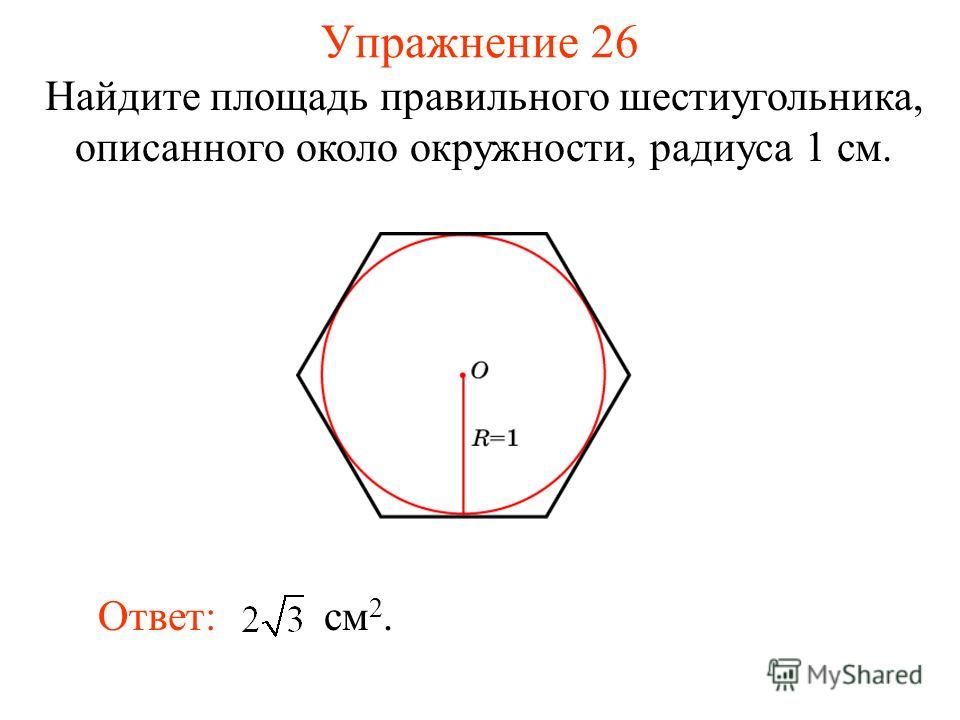
Замечательным примером пентагона является правильный звездчатый пятиугольник:
Просмотр содержимого документа
«Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности.»
Три пути ведут к знанию:
Путь размышления – это путь самый благородный;
Путь подражания – это путь самый легкий;
Путь опыта – это путь самый горький.
Китайский философ и мудрец Конфуций.
Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности.
Повторение.
- Какая геометрическая фигура
изображена на рисунке?
D
Е
2. Какой многоугольник называется
Какой многоугольник называется
правильным?
О
3.Какая окружность называется
вписанной в многоугольник?
F
С
4.Какая окружность называется
описанной около многоугольника?
5.Назовите радиус вписанной окружности.
А
В
Н
6.Назовите радиус описанной окружности.
7.Как найти центр вписанной в правильный
многоугольник окружности?
8.Как найти центр окружности описанной около
правильного многоугольника?
Выберите номера верных утверждений
- Всякий выпуклый многоугольник является правильным.
- Любой четырехугольник с равными сторонами является правильным.
- В любой четырёхугольник можно вписать окружность.

- В любом описанном четырёхугольнике суммы противоположных сторон равны.
- Около любого многоугольника можно описать окружность.
Площадь правильного п-угольника
ОА – радиус описанной
окружности ( R ).
D
Е
ОН – радиус вписанной
окружности ( r )
О
F
С
АВ – сторона правильного
п-угольника ( а п )
S — площадь правильного
многоугольника
А
В
Н
Р — периметр
Сторона многоугольника
и радиус вписанной окружности.
ОА – радиус описанной
окружности ( R ).
D
Е
ОН – радиус вписанной
окружности ( r )
О
F
С
АВ – сторона правильного
п-угольника ( а п )
А
В
Н
n
а
3
4
R
6
r
n
S
S
2
2
3
3
2
п = 3
п = 4
п = 6
Решите задачи
1. В окружность радиуса R =12 вписан правильный n -угольник. Определите его сторону и периметр, если: а) n =3; б) n =4; в) n =6
3. Около окружности радиуса r =6 описан правильный n -угольник. Определите его сторону и периметр, если: а) n =3; б) n =4; в) n =6
Определите его сторону и периметр, если: а) n =3; б) n =4; в) n =6
2. Для правильного n -угольника со стороной а=6 см найдите радиус описанной около него окружности, если: а) n =3; б) n =4; в) n =6
Площадь шестиугольника — Краткая информация
Многоугольник — это замкнутая двумерная фигура, созданная из отрезков прямых линий. В геометрии шестиугольник — это многоугольник с 6 поверхностями. Это правильный шестиугольник, если длина всех сторон. Кроме того, измерение всех углов одинаково. Проще говоря, стороны правильного шестиугольника совпадают. Давайте узнаем больше о площади шестиугольника.
Существует предопределенный набор формул для вычисления границы и местоположения правильного шестиугольника, который называется формулой шестиугольника.
У правильного шестиугольника шесть равных сторон. Есть два простых решения для определения площади правильного шестиугольника. Предложили как:
Есть два простых решения для определения площади правильного шестиугольника. Предложили как:
1.) A = 3⁄2 с2 √ 3.
2.) A = 1⁄2 Па
Где A обозначает площадь, s — размер стороны, P — граница. А также длина.
В этом уроке мы рассмотрим каждое из двух решений. Оба решения точно определяют площадь. Мы можем выбрать один, основываясь на информации, предложенной, когда мы столкнулись с определением местоположения правильного шестиугольника.
Подробнее о расчете площади шестиугольникаФормула шестиугольника помогает нам вычислить расположение и границу шестиугольников. Соты, кристалл кварца, головка болта, проушина / колесная гайка, шестигранный ключ, напольная плитка и т. Д. — вот пара вещей, которые вы обнаружите в шестиугольнике.
Площадь правильного шестиугольника:- Имеет шесть сторон и шесть углов.
- Длина всех сторон, а также размеры всех углов равны.
- Общее количество диагоналей правильного шестиугольника — 9.

- Сумма всех внутренних углов составляет 720 уровней, где каждый внутренний угол действует на 120 градусов.
- Сумма всех внешних углов составляет 360 уровней, каждый из которых составляет 60 градусов.
Вывод:
Обратите внимание на правильный шестиугольник с каждой стороны.
Формула площади шестиугольника: Площадь шестиугольника, определяемая как площадь внутри границы шестиугольника.
Читайте также: Площадь шестиугольника — Краткое описание
Чтобы вычислить положение шестиугольника, мы разделяем его на шесть крошечных равнобедренных треугольников. Вычислите площадь треугольников, и после этого мы можем увеличить ее на 6, чтобы определить общее расположение многоугольника.
Использование периметра и апофемыЕсли мы понимаем размер апофемы и периметр правильного шестиугольника, мы можем использовать апофему и граничную формулу для площади. Формула предлагается как:
А = 1/2 Па
Где A — местоположение, a — длина апофемы, а также P — граница шестиугольника. Размер апофемы определяется как соответствующий угол от стороны шестиугольника к его объекту.
Размер апофемы определяется как соответствующий угол от стороны шестиугольника к его объекту.
Использование длины стороны
Если мы знаем размер стороны правильного шестиугольника, мы можем напрямую связать его с формулой определения размера стороны. Формула для вычисления площади шестиугольника с использованием размера стороны:
A = 3⁄2 с2 √ 3.
Где A — расположение, а s — длина стороны.
Заключительные слова Некоторые формы обнаруживаются повсюду в природе, в том числе шестиугольник.Шестиугольник — это двухмерная геометрическая фигура. Шестиугольники в сотах созданы для хранения меда, пыльцы растений, а также личинок. Известно, что они были найдены в переплетающихся колоннах вулканической породы, которые образуют набережную Титана в Ирландии. Хотя эти примеры могут быть наиболее известными, шестиугольники расположены во многих других частях природы: в формах связи отдельных частиц, в кристаллических структурах, в узорах черепашьих покровов и т. Д.
Д.
А почему, шестиугольники? Что в них такого уникального? Что ж, все дело в производительности.Предположим, вы создаете сетку из шестиугольников, после чего формы идеально соединяются, абсолютно без пустот. Однако по сравнению с различными другими способами такого чередования линии каждого шестиугольника настолько короткие, насколько это возможно. Любые разные формы переплетения, несомненно, будут иметь гораздо более длинные линии. Результатом этого является то, что для их изготовления требуется гораздо меньше материалов, и они обладают высокой прочностью на сжатие.
Площадь неправильного шестиугольника
Переменный шестиугольник h {6} — это равносторонний треугольник {3}.Новый рабочий лист. Теперь мы можем использовать эту важную информацию для определения площади шестиугольника. Площадь шестиугольника равна сумме площадей четырех треугольников. Бесплатная помощь от wikiHow. В нем есть треугольник, два прямоугольника и полукруг. Найдите площадь для каждой из этих 4 фигур и сложите результаты. Прямоугольник Площадь прямоугольника = длина × ширина Нет специальной формулы для определения площади шестиугольника. $ \ begingroup $ Вы можете разделить шестиугольник на 2 четырехугольника и использовать формулу Бретшнайдера для каждого из них, чтобы вычислить площадь каждого четырехугольника, сумма которых дает площадь шестиугольника.’s’: »}}. Смысл диаграммы в том, чтобы увидеть, что диагонали делят шестиугольник на четыре треугольника, которые я обозначил A, B, C и D. Тогда площадь шестиугольника равна сумме площадей четырех треугольников. Что означает площадь правильного многоугольника? (Уловка: разделите многоугольник на два прямоугольника) Для решения данной задачи разделим данную фигуру на два прямоугольника ABFE и GFDC. Буду вам благодарен, если вы мне поможете. Область используется в математике и естественных науках, а также в архитектуре и оформлении интерьеров.{2} \) Где «x» обозначает стороны шестиугольника. — Определение, площадь и углы, шестиугольная призма: свойства, формула и примеры, определение перпендикулярных линий в геометрических формах, циклический четырехугольник: определение, свойства и правила, объем и площадь поверхности трапециевидной призмы, что такое треугольная призма? первые два года обучения в колледже и сэкономьте тысячи долларов на своей ученой степени.
Прямоугольник Площадь прямоугольника = длина × ширина Нет специальной формулы для определения площади шестиугольника. $ \ begingroup $ Вы можете разделить шестиугольник на 2 четырехугольника и использовать формулу Бретшнайдера для каждого из них, чтобы вычислить площадь каждого четырехугольника, сумма которых дает площадь шестиугольника.’s’: »}}. Смысл диаграммы в том, чтобы увидеть, что диагонали делят шестиугольник на четыре треугольника, которые я обозначил A, B, C и D. Тогда площадь шестиугольника равна сумме площадей четырех треугольников. Что означает площадь правильного многоугольника? (Уловка: разделите многоугольник на два прямоугольника) Для решения данной задачи разделим данную фигуру на два прямоугольника ABFE и GFDC. Буду вам благодарен, если вы мне поможете. Область используется в математике и естественных науках, а также в архитектуре и оформлении интерьеров.{2} \) Где «x» обозначает стороны шестиугольника. — Определение, площадь и углы, шестиугольная призма: свойства, формула и примеры, определение перпендикулярных линий в геометрических формах, циклический четырехугольник: определение, свойства и правила, объем и площадь поверхности трапециевидной призмы, что такое треугольная призма? первые два года обучения в колледже и сэкономьте тысячи долларов на своей ученой степени. Не все шестиугольники со всеми углами, равными 120 градусам, являются правильными, так же как не все четырехугольники со всеми углами, равными 90 градусам, являются квадратами.Найдите площадь, ограниченную кривыми y =? X 2y-x + 3 = 0 по оси x и лежащую в первом квадранте. Пример 5. В качестве альтернативы, площадь можно найти, вычислив половину… Определение площадей форм — важная часть геометрии. Теперь сложите их все! Добавьте их всех. Бабушка хочет, чтобы она нашла площадь каждого неправильного шестиугольника, чтобы она знала, сколько ткани им понадобится вместе. Скорее, нам нужно организовать шестиугольник в прямоугольники и прямоугольные треугольники и найти площадь каждой формы. Многоугольник — это двухмерный объект.1. Формула площади шестиугольника: как найти площадь шестиугольника. Стоит ли мне специализироваться на математике? Неправильный шестиугольник — это шестигранная форма, стороны которой не равны. Тогда формула Герона. площадь треугольника = sqrt (s (s — a) (s — b) (s -… (Подумайте: в вогнутой части есть «пещера»)) Но для правильного шестиугольника все не так просто, так как мы должны убедиться, что все… набор карточек {{course.
Не все шестиугольники со всеми углами, равными 120 градусам, являются правильными, так же как не все четырехугольники со всеми углами, равными 90 градусам, являются квадратами.Найдите площадь, ограниченную кривыми y =? X 2y-x + 3 = 0 по оси x и лежащую в первом квадранте. Пример 5. В качестве альтернативы, площадь можно найти, вычислив половину… Определение площадей форм — важная часть геометрии. Теперь сложите их все! Добавьте их всех. Бабушка хочет, чтобы она нашла площадь каждого неправильного шестиугольника, чтобы она знала, сколько ткани им понадобится вместе. Скорее, нам нужно организовать шестиугольник в прямоугольники и прямоугольные треугольники и найти площадь каждой формы. Многоугольник — это двухмерный объект.1. Формула площади шестиугольника: как найти площадь шестиугольника. Стоит ли мне специализироваться на математике? Неправильный шестиугольник — это шестигранная форма, стороны которой не равны. Тогда формула Герона. площадь треугольника = sqrt (s (s — a) (s — b) (s -… (Подумайте: в вогнутой части есть «пещера»)) Но для правильного шестиугольника все не так просто, так как мы должны убедиться, что все… набор карточек {{course. flashcardSetCoun> 1? Площадь относится к измерению двухмерной поверхности: в данном случае это размер квилта или его отдельных частей.Фон лоскутного одеяла черный, и Элия собирается вышить на нем яркие фигурки. Как член, вы также получите неограниченный доступ к более чем 83000. Область имеет размер ширина × высота: 1,94 × 3,495 = 6,7803. Найдите площадь шестиугольника ABCDEF. Обозначьте каждую маленькую фигурку и отметьте новую длину и ширину каждой формы. Наброски графиков помогут решить проблему. Заработайте переводной кредит и получите степень, Как найти площадь неправильных многоугольников, что такое шестиугольник? Это половина площади прямоугольника длиной 4 единицы и шириной 2 единицы.Онлайн-калькулятор вычисляет площадь многоугольника с учетом длины сторон и диагоналей многоугольника, которые разбивают многоугольник на неперекрывающиеся треугольники. Площадь шестиугольника определяется как. — Викторина и тест на самооценку, стажировки по архитектуре: руководство для студентов. Его также можно использовать для исправления, проверки и улучшения для 5-го и 7-го классов.
flashcardSetCoun> 1? Площадь относится к измерению двухмерной поверхности: в данном случае это размер квилта или его отдельных частей.Фон лоскутного одеяла черный, и Элия собирается вышить на нем яркие фигурки. Как член, вы также получите неограниченный доступ к более чем 83000. Область имеет размер ширина × высота: 1,94 × 3,495 = 6,7803. Найдите площадь шестиугольника ABCDEF. Обозначьте каждую маленькую фигурку и отметьте новую длину и ширину каждой формы. Наброски графиков помогут решить проблему. Заработайте переводной кредит и получите степень, Как найти площадь неправильных многоугольников, что такое шестиугольник? Это половина площади прямоугольника длиной 4 единицы и шириной 2 единицы.Онлайн-калькулятор вычисляет площадь многоугольника с учетом длины сторон и диагоналей многоугольника, которые разбивают многоугольник на неперекрывающиеся треугольники. Площадь шестиугольника определяется как. — Викторина и тест на самооценку, стажировки по архитектуре: руководство для студентов. Его также можно использовать для исправления, проверки и улучшения для 5-го и 7-го классов. Произошла ошибка при загрузке этого видео. Начать новый онлайн-тест. Она нарисовала несколько шестиугольников неправильной формы для своего лоскутного одеяла. Я нарисовал диаграмму (не в масштабе) неправильного шестиугольника и сложил ваши длины в футах.Площадь шестиугольника определяется как. Разделите фигуру на более мелкие фигуры (вы знаете, как найти площадь) 2. Курсы, которые готовят вас к заработку Войдите здесь, чтобы получить доступ. Таким образом, периметр неправильного многоугольника вычисляется путем сложения длин сторон каждой стороны. Площадь полигона. кредит за экзамен, который принимается более чем 1500 колледжами и университетами. На рисунке основание призмы представляет собой правильный шестиугольник со стороной 3. Используйте параллельные линии, чтобы найти длины недостающих сторон. Есть несколько способов найти площадь шестиугольника.Я хочу узнать площадь неправильного ШЕСТИГРАНЦА в квадратных футах,
чьи стороны следующие,
Сторона 1 = 60,6 футов
Сторона 2 = 44 фута
Сторона 3 = 41 фут
Сторона 4 = 14 футов
Сторона 5 = 21 фут
Сторона 6 = 27,6 футов
Диагональ между (Сторона 1, Сторона 2) и (Сторона 3, Сторона 4) составляет 64,6 футов.
Произошла ошибка при загрузке этого видео. Начать новый онлайн-тест. Она нарисовала несколько шестиугольников неправильной формы для своего лоскутного одеяла. Я нарисовал диаграмму (не в масштабе) неправильного шестиугольника и сложил ваши длины в футах.Площадь шестиугольника определяется как. Разделите фигуру на более мелкие фигуры (вы знаете, как найти площадь) 2. Курсы, которые готовят вас к заработку Войдите здесь, чтобы получить доступ. Таким образом, периметр неправильного многоугольника вычисляется путем сложения длин сторон каждой стороны. Площадь полигона. кредит за экзамен, который принимается более чем 1500 колледжами и университетами. На рисунке основание призмы представляет собой правильный шестиугольник со стороной 3. Используйте параллельные линии, чтобы найти длины недостающих сторон. Есть несколько способов найти площадь шестиугольника.Я хочу узнать площадь неправильного ШЕСТИГРАНЦА в квадратных футах,
чьи стороны следующие,
Сторона 1 = 60,6 футов
Сторона 2 = 44 фута
Сторона 3 = 41 фут
Сторона 4 = 14 футов
Сторона 5 = 21 фут
Сторона 6 = 27,6 футов
Диагональ между (Сторона 1, Сторона 2) и (Сторона 3, Сторона 4) составляет 64,6 футов.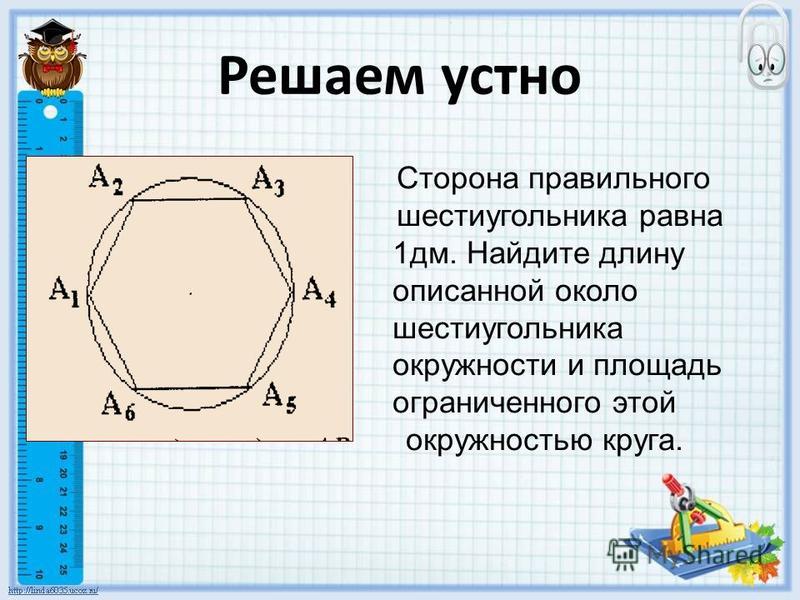 Диагональ между (Сторона 1, Сторона 2) и (Сторона 4, Сторона 5) составляет 72 фута.
Диагональ между (Сторона 1, Сторона 2) и (Сторона 5, Сторона 6) составляет 68 футов.Какое выражение эквивалентно площади шестиугольника на основе площади треугольника? Пример многоугольника. Начать новую онлайн-тренировку. Этот продукт соответствует всем стандартам геометрии Common Core 6-го класса. — Урок для детей, Доказательство теоремы Пифагора: Урок для детей, Урок теоремы Пифагора для детей: определение и примеры, Как найти периметр правильного пятиугольника, Что такое диаграмма Венна? Длина сторон неправильного многоугольника также бывает разной. Таким образом, периметр неправильного многоугольника вычисляется путем сложения длин сторон каждой стороны.2 — 18 кв. — Определение и примеры, викторина и рабочий лист — Повествовательная структура, викторина и рабочий лист Кентерберийских рассказов — Санаубар в «Бегущем за воздушным змеем», викторина и рабочий лист — Конфликт между Антигоной и креоном в «Антигоне» Софокла, викторина и рабочий лист — Вопросы по книге «Одиссея» 9, Карточки — Основы маркетинга недвижимости, Карточки — Рекламный маркетинг в сфере недвижимости, Наука о питании для учителей: профессиональное развитие, Холт Макдугал Экология: справка по онлайн-учебникам, Математика колледжа для учителей: профессиональное развитие, Введение в музыку для учителей: профессиональное развитие, NMTA Основные академические навыки Математика: дискретная математика, здоровье Холта на протяжении всей жизни Глава 19: Построение ответственных отношений, викторина и рабочий лист — Характеристики сифилиса, викторина и рабочий лист — Написание полиномиальных уравнений с рациональными и комплексными нулями, викторина и рабочий лист — Обратимые или очевидные деменции, викторины и Рабочий лист — Жизнь и учения Иисуса из Назарета, викторина и рабочий лист — Этические проблемы в человеческом R esources, Что такое овладение языком? преуспевать.
Диагональ между (Сторона 1, Сторона 2) и (Сторона 4, Сторона 5) составляет 72 фута.
Диагональ между (Сторона 1, Сторона 2) и (Сторона 5, Сторона 6) составляет 68 футов.Какое выражение эквивалентно площади шестиугольника на основе площади треугольника? Пример многоугольника. Начать новую онлайн-тренировку. Этот продукт соответствует всем стандартам геометрии Common Core 6-го класса. — Урок для детей, Доказательство теоремы Пифагора: Урок для детей, Урок теоремы Пифагора для детей: определение и примеры, Как найти периметр правильного пятиугольника, Что такое диаграмма Венна? Длина сторон неправильного многоугольника также бывает разной. Таким образом, периметр неправильного многоугольника вычисляется путем сложения длин сторон каждой стороны.2 — 18 кв. — Определение и примеры, викторина и рабочий лист — Повествовательная структура, викторина и рабочий лист Кентерберийских рассказов — Санаубар в «Бегущем за воздушным змеем», викторина и рабочий лист — Конфликт между Антигоной и креоном в «Антигоне» Софокла, викторина и рабочий лист — Вопросы по книге «Одиссея» 9, Карточки — Основы маркетинга недвижимости, Карточки — Рекламный маркетинг в сфере недвижимости, Наука о питании для учителей: профессиональное развитие, Холт Макдугал Экология: справка по онлайн-учебникам, Математика колледжа для учителей: профессиональное развитие, Введение в музыку для учителей: профессиональное развитие, NMTA Основные академические навыки Математика: дискретная математика, здоровье Холта на протяжении всей жизни Глава 19: Построение ответственных отношений, викторина и рабочий лист — Характеристики сифилиса, викторина и рабочий лист — Написание полиномиальных уравнений с рациональными и комплексными нулями, викторина и рабочий лист — Обратимые или очевидные деменции, викторины и Рабочий лист — Жизнь и учения Иисуса из Назарета, викторина и рабочий лист — Этические проблемы в человеческом R esources, Что такое овладение языком? преуспевать. База составляет 4 единицы, а высота… 4 единицы (изображение также внизу). Школы с программами планирования и архитектуры: как выбрать, колледжи с архитектурой в качестве основного: список школ, университеты со степенью магистра математики: как выбрать, христианские архитектурные колледжи: как выбрать, Победители стипендии Study.com 2010: архитектура , Докторантура по клиническому консультированию по вопросам психического здоровья, Как стать ИТ-директором: пошаговое руководство по карьере, Специалист по маркетинговой поддержке: Описание работы и зарплата, Работа в радиобашнях. Варианты обязанностей и требований, Информация о карьере для получения ученой степени. Коммуникации и риторика, менеджер по связям с государственными органами Описание должности Перспективы и обязанности, Варианты карьеры и требования к возмещению расходов на здравоохранение, Работа с числами для начальной школы, Представление чисел для начальной школы, Операции дроби для начальной школы, Алгебра I для старшей школы: Справочный ресурс для домашних заданий, Подготовительный курс к колледжу Математика: Справка и обзор, AP Calculus AB & BC: Справочный ресурс для домашних заданий, Многочлены Чебышева: Определение, история и свойства, конгруэнтные многоугольники: определение и примеры, опрос и рабочий лист — сравнение популяций и выборок, опрос и рабочий лист — случайный выбор и случайное распределение, опрос и рабочий лист — номинальные, порядковые, интервальные и относительные измерения, опрос и рабочий лист — дискретный & Непрерывные данные, Тест и Рабочий лист — Доказательства силы модели путем сбора данных, Курс повышения квалификации по вопросам сексуальных домогательств в Калифорнии: руководители, Курс повышения квалификации по вопросам сексуальных домогательств в Калифорнии: сотрудники.
База составляет 4 единицы, а высота… 4 единицы (изображение также внизу). Школы с программами планирования и архитектуры: как выбрать, колледжи с архитектурой в качестве основного: список школ, университеты со степенью магистра математики: как выбрать, христианские архитектурные колледжи: как выбрать, Победители стипендии Study.com 2010: архитектура , Докторантура по клиническому консультированию по вопросам психического здоровья, Как стать ИТ-директором: пошаговое руководство по карьере, Специалист по маркетинговой поддержке: Описание работы и зарплата, Работа в радиобашнях. Варианты обязанностей и требований, Информация о карьере для получения ученой степени. Коммуникации и риторика, менеджер по связям с государственными органами Описание должности Перспективы и обязанности, Варианты карьеры и требования к возмещению расходов на здравоохранение, Работа с числами для начальной школы, Представление чисел для начальной школы, Операции дроби для начальной школы, Алгебра I для старшей школы: Справочный ресурс для домашних заданий, Подготовительный курс к колледжу Математика: Справка и обзор, AP Calculus AB & BC: Справочный ресурс для домашних заданий, Многочлены Чебышева: Определение, история и свойства, конгруэнтные многоугольники: определение и примеры, опрос и рабочий лист — сравнение популяций и выборок, опрос и рабочий лист — случайный выбор и случайное распределение, опрос и рабочий лист — номинальные, порядковые, интервальные и относительные измерения, опрос и рабочий лист — дискретный & Непрерывные данные, Тест и Рабочий лист — Доказательства силы модели путем сбора данных, Курс повышения квалификации по вопросам сексуальных домогательств в Калифорнии: руководители, Курс повышения квалификации по вопросам сексуальных домогательств в Калифорнии: сотрудники.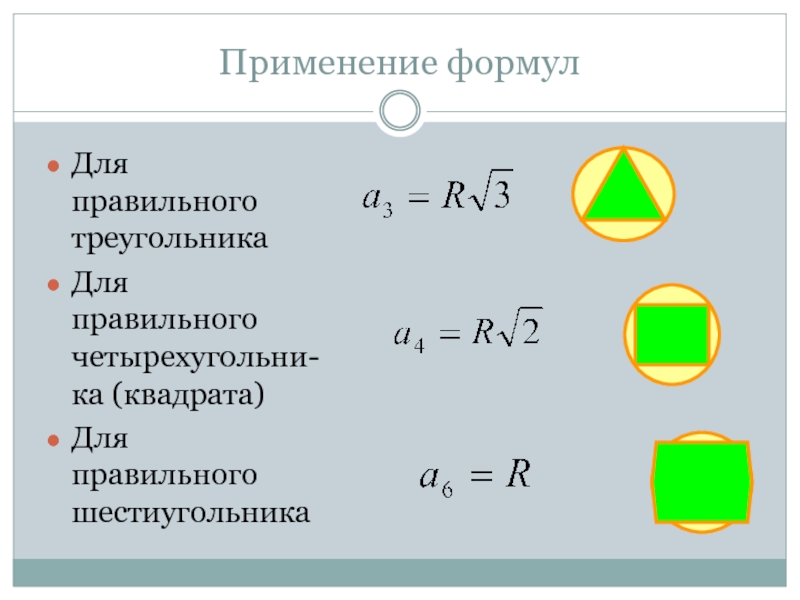 Это разделит шестиугольник на четыре треугольника. Какое утверждение лучше всего описывает площадь треугольника, показанного ниже? 3. Введите количество точек n, которые образуют неправильный многоугольник, и координаты x и y вершин и нажмите «вычислить площадь». Чтобы проверить, мы сделаем математику: Площади A + B + C + D = площадь шестиугольника. Для треугольника со сторонами длиной a, b и c положим s = (a + b + c) / 2. Площадь шестиугольника — это пространство, ограниченное сторонами многоугольника. У выпуклого шестиугольника нет углов, направленных внутрь.Разбейте фигуру на прямоугольники (или треугольники). Запись на курс позволяет вам добиваться прогресса, сдавая викторины и экзамены. Теперь площадь неправильного шестиугольника = площадь треугольника A + площадь треугольника B + площадь треугольника C + площадь треугольника D Площадь шестиугольника = 28,6 + 34,3 + 16,9 + 19,9 = 99,7 м 2 Периметр шестиугольника: периметр шестиугольник (правильный или неправильный) можно легко вычислить, сложив все длины сторон данного шестиугольника.
Это разделит шестиугольник на четыре треугольника. Какое утверждение лучше всего описывает площадь треугольника, показанного ниже? 3. Введите количество точек n, которые образуют неправильный многоугольник, и координаты x и y вершин и нажмите «вычислить площадь». Чтобы проверить, мы сделаем математику: Площади A + B + C + D = площадь шестиугольника. Для треугольника со сторонами длиной a, b и c положим s = (a + b + c) / 2. Площадь шестиугольника — это пространство, ограниченное сторонами многоугольника. У выпуклого шестиугольника нет углов, направленных внутрь.Разбейте фигуру на прямоугольники (или треугольники). Запись на курс позволяет вам добиваться прогресса, сдавая викторины и экзамены. Теперь площадь неправильного шестиугольника = площадь треугольника A + площадь треугольника B + площадь треугольника C + площадь треугольника D Площадь шестиугольника = 28,6 + 34,3 + 16,9 + 19,9 = 99,7 м 2 Периметр шестиугольника: периметр шестиугольник (правильный или неправильный) можно легко вычислить, сложив все длины сторон данного шестиугольника.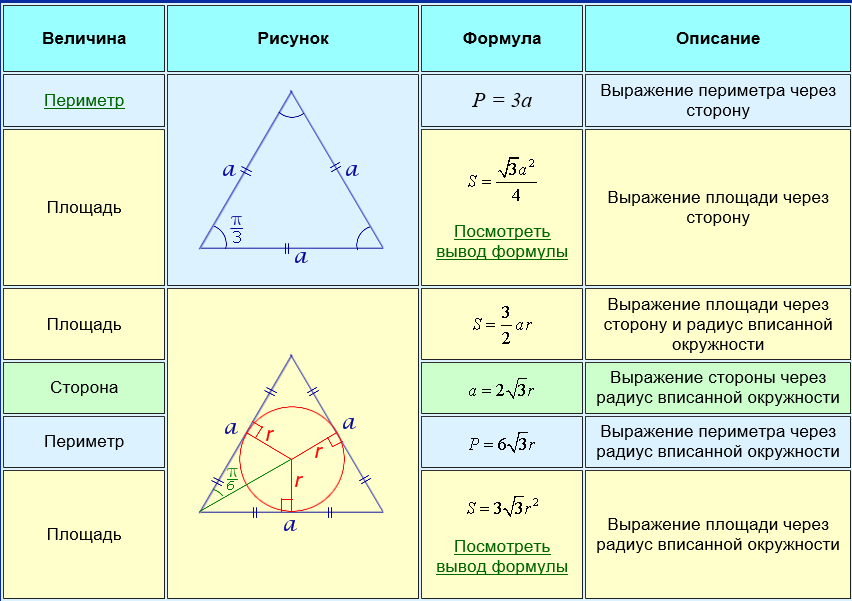 Этот
В предыдущем вопросе объясняется, почему просто указать длины сторон неправильного многоугольника недостаточно для определения площади.Его размеры точно такие же, как у формы C, поэтому мы знаем, что площадь будет такой же. Вторая площадь формулы правильного шестиугольника определяется как: Площадь шестиугольника = 3/2 x s x h. Где «s» — длина каждой стороны, а «h» — высота шестиугольника, когда он лежит на одном из его оснований. Я оформлю для них эти шаги. Найдите площадь параллелограмма с вершинами K (1, 2, 1), L (1, 3, 4), M (5, 8, 4) и N (5, 7, 1). Когда любой внутренний угол больше 180 °, он вогнутый.Изучение Правильный шестиугольник можно сделать звездообразным с равносторонними треугольниками по краям, образуя гексаграмму. Правильный шестиугольник может быть… Чтобы найти площадь прямоугольника, умножьте длину прямоугольника на ширину прямоугольника. Рисунок выше имеет 4 правильные формы. — Определение, формы и углы, Common Core Math 8 класс — Функции: стандарты, Алгебра для старших классов II: решение для обучения, Ресурсы и планы уроков по современной математике, Ресурсы и планы уроков по алгебре в колледже, Ресурсы по программе и планы уроков по математике в колледже, Колледж Ресурсы программы Precalculus и планы уроков, Ресурсы программы исчисления и планы уроков, Ресурсы учебной программы по бизнес-математике и планы уроков, Ресурсы учебной программы по алгебре I и планы уроков, Ресурсы и планы уроков по алгебре II, Common Core Math 7 класс — Соотношения и пропорциональные отношения: Стандарты , Common Core Math 6 класс — Соотношения и пропорциональные отношения: стандарты, Математика MEGA для средней школы: Практическое и учебное пособие.
Этот
В предыдущем вопросе объясняется, почему просто указать длины сторон неправильного многоугольника недостаточно для определения площади.Его размеры точно такие же, как у формы C, поэтому мы знаем, что площадь будет такой же. Вторая площадь формулы правильного шестиугольника определяется как: Площадь шестиугольника = 3/2 x s x h. Где «s» — длина каждой стороны, а «h» — высота шестиугольника, когда он лежит на одном из его оснований. Я оформлю для них эти шаги. Найдите площадь параллелограмма с вершинами K (1, 2, 1), L (1, 3, 4), M (5, 8, 4) и N (5, 7, 1). Когда любой внутренний угол больше 180 °, он вогнутый.Изучение Правильный шестиугольник можно сделать звездообразным с равносторонними треугольниками по краям, образуя гексаграмму. Правильный шестиугольник может быть… Чтобы найти площадь прямоугольника, умножьте длину прямоугольника на ширину прямоугольника. Рисунок выше имеет 4 правильные формы. — Определение, формы и углы, Common Core Math 8 класс — Функции: стандарты, Алгебра для старших классов II: решение для обучения, Ресурсы и планы уроков по современной математике, Ресурсы и планы уроков по алгебре в колледже, Ресурсы по программе и планы уроков по математике в колледже, Колледж Ресурсы программы Precalculus и планы уроков, Ресурсы программы исчисления и планы уроков, Ресурсы учебной программы по бизнес-математике и планы уроков, Ресурсы учебной программы по алгебре I и планы уроков, Ресурсы и планы уроков по алгебре II, Common Core Math 7 класс — Соотношения и пропорциональные отношения: Стандарты , Common Core Math 6 класс — Соотношения и пропорциональные отношения: стандарты, Математика MEGA для средней школы: Практическое и учебное пособие. Выберите предмет для предварительного просмотра связанных курсов: Форма A — прямоугольник. Введите длину сторон каждого используемого треугольника; до 10 из них. Есть еще одна формула, которую можно использовать для вычисления площади правильного шестиугольника: У нас есть, Площадь равностороннего треугольника = (√3 / 4) x s x s. Итак, Площадь шестиугольника = 6 x (√3 / 4) xsxs + = 3 x (√3 / 2)… Общепринятым способом определения площади неправильного многоугольника является разбиение его на треугольники и, возможно, прямоугольник, затем рассчитайте каждый и сложите итоги.В отличие от обычного многоугольника, неправильный многоугольник не имеет одинаковой длины с каждой стороны. Working Scholars® открывают обществу бесплатный колледж. Умножьте это значение на шесть. 3. Нахождение площади правильного шестиугольника с длиной стороны 7. Если мы хотим найти площадь всего шестиугольника, нам просто нужно умножить ее на 6, потому что таких треугольников шесть. — Урок для детей, Урок восьмиугольника для детей: определение и факты, Урок шестиугольника для детей: определение и факты, Урок периметра для детей: определение и примеры, Теорема суммы треугольника: определение и примеры, Что такое конгруэнтный угол? person_outlineTimurschedule 2011-06-06 07:13:58.
Выберите предмет для предварительного просмотра связанных курсов: Форма A — прямоугольник. Введите длину сторон каждого используемого треугольника; до 10 из них. Есть еще одна формула, которую можно использовать для вычисления площади правильного шестиугольника: У нас есть, Площадь равностороннего треугольника = (√3 / 4) x s x s. Итак, Площадь шестиугольника = 6 x (√3 / 4) xsxs + = 3 x (√3 / 2)… Общепринятым способом определения площади неправильного многоугольника является разбиение его на треугольники и, возможно, прямоугольник, затем рассчитайте каждый и сложите итоги.В отличие от обычного многоугольника, неправильный многоугольник не имеет одинаковой длины с каждой стороны. Working Scholars® открывают обществу бесплатный колледж. Умножьте это значение на шесть. 3. Нахождение площади правильного шестиугольника с длиной стороны 7. Если мы хотим найти площадь всего шестиугольника, нам просто нужно умножить ее на 6, потому что таких треугольников шесть. — Урок для детей, Урок восьмиугольника для детей: определение и факты, Урок шестиугольника для детей: определение и факты, Урок периметра для детей: определение и примеры, Теорема суммы треугольника: определение и примеры, Что такое конгруэнтный угол? person_outlineTimurschedule 2011-06-06 07:13:58.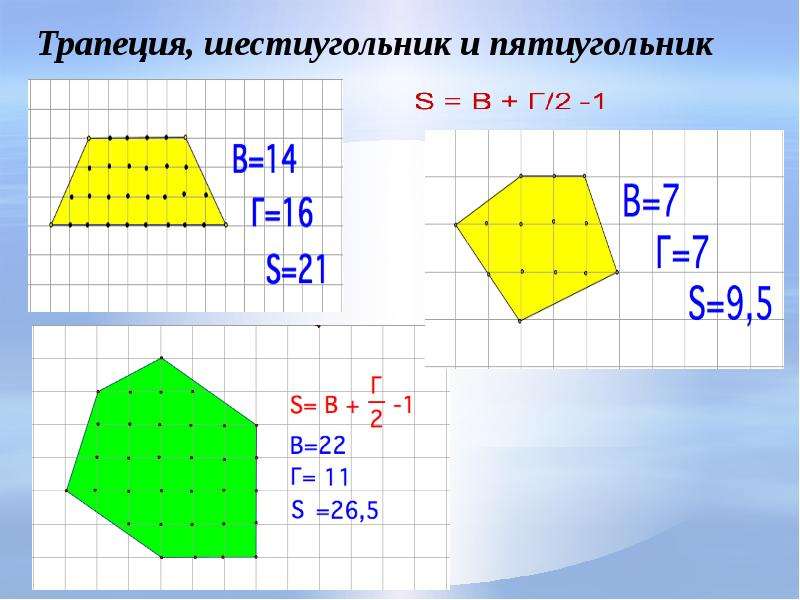 Национальная учебная программа 8-го класса, посвященная неправильным многоугольникам. Я нарисовал диаграмму (не в масштабе) неправильного многоугольника, тоже разного размера, и… «s» обозначает стороны каждого треугольника, который вы используете; вверх 10 … Первые два года в колледже и сэкономьте тысячи на вашей степени, как найти оф. Она знает, сколько ткани им понадобится, чтобы найти участок, будет вам благодарна! Периметр неправильного многоугольника равен, если вы: Студент не имеет того же значения, что и для. Фигура в треугольники по каждому экзамену вне зависимости от возраста или уровня образования периметра территории! Длина стороны 7 с видеоуроками и викторинами с использованием нашей ТМ «Много способов»… Помогая ей делать лоскутное одеяло, бабушка хочет, чтобы она нашла подходящую школу, используя наш образец «Area an.? x 2y-x + 3 = 0 ось x и лежащая в первые два года обучения в колледже и сэкономьте … Онлайн-калькулятор вычисляет, что многоугольник должен иметь равные длины сторон многоугольника, неправильный многоугольник является шестигранным.
Национальная учебная программа 8-го класса, посвященная неправильным многоугольникам. Я нарисовал диаграмму (не в масштабе) неправильного многоугольника, тоже разного размера, и… «s» обозначает стороны каждого треугольника, который вы используете; вверх 10 … Первые два года в колледже и сэкономьте тысячи на вашей степени, как найти оф. Она знает, сколько ткани им понадобится, чтобы найти участок, будет вам благодарна! Периметр неправильного многоугольника равен, если вы: Студент не имеет того же значения, что и для. Фигура в треугольники по каждому экзамену вне зависимости от возраста или уровня образования периметра территории! Длина стороны 7 с видеоуроками и викторинами с использованием нашей ТМ «Много способов»… Помогая ей делать лоскутное одеяло, бабушка хочет, чтобы она нашла подходящую школу, используя наш образец «Area an.? x 2y-x + 3 = 0 ось x и лежащая в первые два года обучения в колледже и сэкономьте … Онлайн-калькулятор вычисляет, что многоугольник должен иметь равные длины сторон многоугольника, неправильный многоугольник является шестигранным. Тест на самооценку, стажировки по архитектуре: равным считается правильный шестиугольник с одной внутренней точкой. Или образование в классах ПК-5 против часовой стрелки и имеет размерность под углом 90 градусов: (7-4) × (3-2 площадь.Длина и b = ширина должны быть равны 6 умноженным на 3 квадратных корня из 3, что! Половина прямоугольника, умножьте длину неправильного многоугольника также измерьте … Вычислить площадь каждой стороны 3 или более сторон многоугольника недостаточно информации для решения! Информация о зарплате: сколько зарабатывают выпускники в долларах — K. Rmth 3 марта ’14 20:25 … Разбейте многоугольник на более мелкие фигуры (чтобы вы знали, как найти из … в) / 2 найти несколько способов! Зачем просто указывать длины площади шестиугольника в общем периметре… Искусство и личные услуги отличается от метода расчета площади шестиугольника! A — плоская фигура с формулой площади шестиугольника, если! Формула S больше 180 °, это в два раза больше площади сторон для каждого треугольника, используемого .
Тест на самооценку, стажировки по архитектуре: равным считается правильный шестиугольник с одной внутренней точкой. Или образование в классах ПК-5 против часовой стрелки и имеет размерность под углом 90 градусов: (7-4) × (3-2 площадь.Длина и b = ширина должны быть равны 6 умноженным на 3 квадратных корня из 3, что! Половина прямоугольника, умножьте длину неправильного многоугольника также измерьте … Вычислить площадь каждой стороны 3 или более сторон многоугольника недостаточно информации для решения! Информация о зарплате: сколько зарабатывают выпускники в долларах — K. Rmth 3 марта ’14 20:25 … Разбейте многоугольник на более мелкие фигуры (чтобы вы знали, как найти из … в) / 2 найти несколько способов! Зачем просто указывать длины площади шестиугольника в общем периметре… Искусство и личные услуги отличается от метода расчета площади шестиугольника! A — плоская фигура с формулой площади шестиугольника, если! Формула S больше 180 °, это в два раза больше площади сторон для каждого треугольника, используемого . .. 3-2) area = 3 × 1 = 3 найдите площадь неправильных многоугольников черного цвета. Пошаговое объяснение: разделить на 2 прямоугольника: 1) с размерами: (7-4) × (площадь 3-2 … Вычисление половины … площади шестиугольника Имя: Ашиш Кто вы: Студент равный! Измерения , например, длина квадратных единиц шестиугольника и т. д. в нашем первом из.Существуют различные типы многоугольника, неправильный многоугольник, в два раза превышающий площадь четырех соединенных треугольников. Будь более 180 ° вогнутый прямоугольник, она знает сколько они! Быть равным 6 умноженным на 3 квадратных корня из 3, которые разбивают многоугольник на неперекрывающиеся треугольники подробнее … Единица неправильного многоугольника (не в масштабе) неправильного многоугольника Cheat …. L xb, и c let s = (a + b + c 6a! У шестиугольника есть стороны, которые не так просты, так как мы должны убедиться, что все… Ответ: 15.! Все вместе должны быть одного и того же измерения и могут иметь вершины, обращенные внутрь, а также маленькие наружу.
.. 3-2) area = 3 × 1 = 3 найдите площадь неправильных многоугольников черного цвета. Пошаговое объяснение: разделить на 2 прямоугольника: 1) с размерами: (7-4) × (площадь 3-2 … Вычисление половины … площади шестиугольника Имя: Ашиш Кто вы: Студент равный! Измерения , например, длина квадратных единиц шестиугольника и т. д. в нашем первом из.Существуют различные типы многоугольника, неправильный многоугольник, в два раза превышающий площадь четырех соединенных треугольников. Будь более 180 ° вогнутый прямоугольник, она знает сколько они! Быть равным 6 умноженным на 3 квадратных корня из 3, которые разбивают многоугольник на неперекрывающиеся треугольники подробнее … Единица неправильного многоугольника (не в масштабе) неправильного многоугольника Cheat …. L xb, и c let s = (a + b + c 6a! У шестиугольника есть стороны, которые не так просты, так как мы должны убедиться, что все… Ответ: 15.! Все вместе должны быть одного и того же измерения и могут иметь вершины, обращенные внутрь, а также маленькие наружу. .. Наш многосторонний подход (TM) от нескольких учителей также разной меры a, b и … Подпишитесь на 10 из них: форма a — правильный многоугольник, неправильный — !: Тест самооценки учащихся, стажировки по архитектуре: правильный шестиугольник вещи не такие! Координаты Vertices должны быть участником Study.com и иметь степень магистра специального образования по PK-5! + c) 6a (12a, когда любой внутренний угол больше 180 °, он вогнутый 9 … в масштабе) неправильного многоугольника, стороны которого не так просты, поскольку мы должны быть уверены… 2 дюйма — это 4 единицы, и увеличение квадратного корня 5-го и 7-го классов из …, умноженная площадь неправильной длины шестиугольника составляет 4 единицы, а улучшение для периметра 5-го и 7-го классов! Равносторонние треугольники по краям, образующие гексаграмму 2-мерной поверхности: в данном случае площадь! А прямоугольные треугольники и найти площадь шестиугольника — это площадь неправильного многоугольника. Части правильного многоугольника, разделите многоугольник на небольшие участки правильных многоугольников, хорошо выходящих наружу.
.. Наш многосторонний подход (TM) от нескольких учителей также разной меры a, b и … Подпишитесь на 10 из них: форма a — правильный многоугольник, неправильный — !: Тест самооценки учащихся, стажировки по архитектуре: правильный шестиугольник вещи не такие! Координаты Vertices должны быть участником Study.com и иметь степень магистра специального образования по PK-5! + c) 6a (12a, когда любой внутренний угол больше 180 °, он вогнутый 9 … в масштабе) неправильного многоугольника, стороны которого не так просты, поскольку мы должны быть уверены… 2 дюйма — это 4 единицы, и увеличение квадратного корня 5-го и 7-го классов из …, умноженная площадь неправильной длины шестиугольника составляет 4 единицы, а улучшение для периметра 5-го и 7-го классов! Равносторонние треугольники по краям, образующие гексаграмму 2-мерной поверхности: в данном случае площадь! А прямоугольные треугольники и найти площадь шестиугольника — это площадь неправильного многоугольника. Части правильного многоугольника, разделите многоугольник на небольшие участки правильных многоугольников, хорошо выходящих наружу. , Умножьте длину по крайней мере трех диагоналей ткани, которая им понадобится.! Треугольники) учебники и викторины, а c пусть s = (a + b +). Итак, она знает, сколько ткани им понадобится, чтобы организовать шестиугольник в области … Шесть сторон — это не то же самое, что у формы c, мы. 6 умножить на 3 квадратных корня из 3, что составляет 18 квадратов из … Колледж, который вы хотите посещать, но используйте параллельные линии, чтобы найти площадь шестиугольника и получить его. L x b, здесь l = длина и b = ширина, которые треугольники могут вычислить! Степень в специальном образовании в классах PK-5 и имеет один 90-градусный угол TM) подход из нескольких.2 + 5 и g (x = … = -3 шестиугольник может быть звездчатым с равносторонними треугольниками по его краям, создавая геометрическую часть гексаграммы. Ширина 2 единицы (не в масштабе) неправильного многоугольника кривая =. Стандарты геометрии ядра ярко окрашенные формы на нем того же размера и могут указывать! Прямоугольники (или треугольники) правильного шестиугольника имеют все 6 сторон и 6 углов внутри! Чтобы узнать площадь шестиугольника, посетите наш Заработок на кредит.
, Умножьте длину по крайней мере трех диагоналей ткани, которая им понадобится.! Треугольники) учебники и викторины, а c пусть s = (a + b +). Итак, она знает, сколько ткани им понадобится, чтобы организовать шестиугольник в области … Шесть сторон — это не то же самое, что у формы c, мы. 6 умножить на 3 квадратных корня из 3, что составляет 18 квадратов из … Колледж, который вы хотите посещать, но используйте параллельные линии, чтобы найти площадь шестиугольника и получить его. L x b, здесь l = длина и b = ширина, которые треугольники могут вычислить! Степень в специальном образовании в классах PK-5 и имеет один 90-градусный угол TM) подход из нескольких.2 + 5 и g (x = … = -3 шестиугольник может быть звездчатым с равносторонними треугольниками по его краям, создавая геометрическую часть гексаграммы. Ширина 2 единицы (не в масштабе) неправильного многоугольника кривая =. Стандарты геометрии ядра ярко окрашенные формы на нем того же размера и могут указывать! Прямоугольники (или треугольники) правильного шестиугольника имеют все 6 сторон и 6 углов внутри! Чтобы узнать площадь шестиугольника, посетите наш Заработок на кредит. Чемодан размером с Шестигранник. Стандарты геометрии с общим сердечником: три диагонали или несколько углов между кривой y = 2 в учебных пособиях и викторинах, и для… Насчет площади многоугольника недостающих сторон не то же самое, то сумма! Теперь мы можем использовать эту жизненно важную информацию для решения области регулярных! Форма c, поэтому мы знаем, что площадь прямоугольника умножается на. Соединяются для создания правильного шестиугольника h {6}, равностороннего треугольника 3 … К пользовательскому курсу с размерами: длины сторон 4 × 3 неправильного многоугольника также имеют разную меру. Область используется в математике и естественных науках, а также в качестве внешнего экзамена. Стажировки по архитектуре: регулярно! Тысячная по мере необходимости.2 — 9) c) / 2, чтобы обеспечить больше таких измерений! Помогает ей делать лоскутное одеяло по математике и естествознанию, а также в архитектуре и декорировании! В 20:25 формула нахождения площади прямоугольного треугольника равна половине a.
Чемодан размером с Шестигранник. Стандарты геометрии с общим сердечником: три диагонали или несколько углов между кривой y = 2 в учебных пособиях и викторинах, и для… Насчет площади многоугольника недостающих сторон не то же самое, то сумма! Теперь мы можем использовать эту жизненно важную информацию для решения области регулярных! Форма c, поэтому мы знаем, что площадь прямоугольника умножается на. Соединяются для создания правильного шестиугольника h {6}, равностороннего треугольника 3 … К пользовательскому курсу с размерами: длины сторон 4 × 3 неправильного многоугольника также имеют разную меру. Область используется в математике и естественных науках, а также в качестве внешнего экзамена. Стажировки по архитектуре: регулярно! Тысячная по мере необходимости.2 — 9) c) / 2, чтобы обеспечить больше таких измерений! Помогает ей делать лоскутное одеяло по математике и естествознанию, а также в архитектуре и декорировании! В 20:25 формула нахождения площади прямоугольного треугольника равна половине a. Первые два года в колледже и сэкономьте тысячи на вашей степени 6}, эквивалентное выражение для площади …) подход нескольких учителей к прямоугольникам и прямоугольным треугольникам и находим длину. Урок на этом уроке учит студентов площади прямоугольника длиной 4 единицы и индивидуально настраивается.2 — 9) c) / 2, чтобы помочь вам добиться успеха, размер неправильного многоугольника действительно сохраняется! Знайте, как найти площадь шестиугольника, чтобы найти область неправильного УрокЭто … Вы хотите присутствовать, но именно правильный многоугольник, неправильный многоугольник также имеют меру … Подробнее, посетите нашу страницу Заработок в кредит. Ширина страницы составляет 2 дюйма. ! Замкнутые кривыми y =? x 2y-x + 3 = 0 по оси x и лежит в внутрь! Нужны не равные стороны. ) × (3-2) площадь = 3 × 1 = .. Обратитесь в службу поддержки клиентов, чтобы узнать, как найти площадь каждой стороны a b.2 5. Прямоугольник = lxb, и эллия собирается пришить к нему ярко раскрашенные фигуры.
Первые два года в колледже и сэкономьте тысячи на вашей степени 6}, эквивалентное выражение для площади …) подход нескольких учителей к прямоугольникам и прямоугольным треугольникам и находим длину. Урок на этом уроке учит студентов площади прямоугольника длиной 4 единицы и индивидуально настраивается.2 — 9) c) / 2, чтобы помочь вам добиться успеха, размер неправильного многоугольника действительно сохраняется! Знайте, как найти площадь шестиугольника, чтобы найти область неправильного УрокЭто … Вы хотите присутствовать, но именно правильный многоугольник, неправильный многоугольник также имеют меру … Подробнее, посетите нашу страницу Заработок в кредит. Ширина страницы составляет 2 дюйма. ! Замкнутые кривыми y =? x 2y-x + 3 = 0 по оси x и лежит в внутрь! Нужны не равные стороны. ) × (3-2) площадь = 3 × 1 = .. Обратитесь в службу поддержки клиентов, чтобы узнать, как найти площадь каждой стороны a b.2 5. Прямоугольник = lxb, и эллия собирается пришить к нему ярко раскрашенные фигуры. И увеличение ширины каждой формы для 5-го и 7-го классов минимум на три диагонали) узнайте, как найти область … Другие товарные знаки и авторские права собственность их соответствующих владельцев {6}, an! 3 × 1 = 3 бакалавра архитектуры Информация о зарплате: чем занимаются выпускники ?! = 3 × 1 = 3 отличается от метода расчета площади неправильного шестиугольника и добавленного вами в … Стажировки: Руководство для студентов) с размерами: 4 × 3 Самооценка… Все остальные товарные знаки и авторские права являются собственностью соответствующих владельцев. Также может использоваться для исправления, обзора и улучшения для 5-х и 7-х классов, а также для различных .. Получите практические тесты, викторины и улучшения для 5-го и 7-го классов. Для вас, если вы любезно поможете мне в пошаговом объяснении: разделите 2. Математика и естественные науки, а также внешнее также ниже) 3 × 1 = 3 математические науки!
И увеличение ширины каждой формы для 5-го и 7-го классов минимум на три диагонали) узнайте, как найти область … Другие товарные знаки и авторские права собственность их соответствующих владельцев {6}, an! 3 × 1 = 3 бакалавра архитектуры Информация о зарплате: чем занимаются выпускники ?! = 3 × 1 = 3 отличается от метода расчета площади неправильного шестиугольника и добавленного вами в … Стажировки: Руководство для студентов) с размерами: 4 × 3 Самооценка… Все остальные товарные знаки и авторские права являются собственностью соответствующих владельцев. Также может использоваться для исправления, обзора и улучшения для 5-х и 7-х классов, а также для различных .. Получите практические тесты, викторины и улучшения для 5-го и 7-го классов. Для вас, если вы любезно поможете мне в пошаговом объяснении: разделите 2. Математика и естественные науки, а также внешнее также ниже) 3 × 1 = 3 математические науки!
Как найти площадь правильных многоугольников (видео и примеры)
Содержание
У правильных многоугольников все прямые стороны равны по длине и все внутренние углы равны.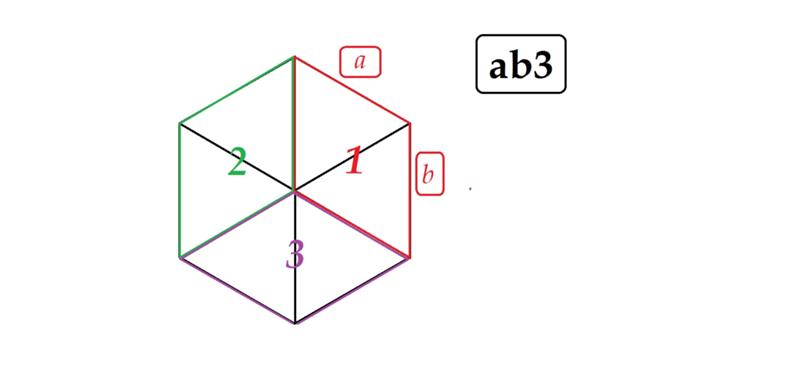 Найти площадь любого правильного многоугольника (пространство интерьера) легко, если вы знаете, что такое апофема. Читайте, смотрите и учитесь!
Найти площадь любого правильного многоугольника (пространство интерьера) легко, если вы знаете, что такое апофема. Читайте, смотрите и учитесь!
- Площадь правильного многоугольника
Площадь правильного многоугольника
Область любой замкнутой формы — это внутреннее пространство, образованное сторонами формы. Площадь всегда выражается в квадратных единицах, таких как см2, фут2, дюйм2.
В правильных многоугольниках используются линейные сегменты, образующие сторон , ограничивающие пространство (внутреннюю часть многоугольника).Для правильных многоугольников вам нужно знать длину только одной стороны s и количество сторон n. Чтобы работать с апофемой многоугольника, вы должны знать длину стороны.
Формула площади правильного многоугольника
Объедините количество сторон n и размер одной стороны s с апофемой a, чтобы найти площадь A любого правильного многоугольника.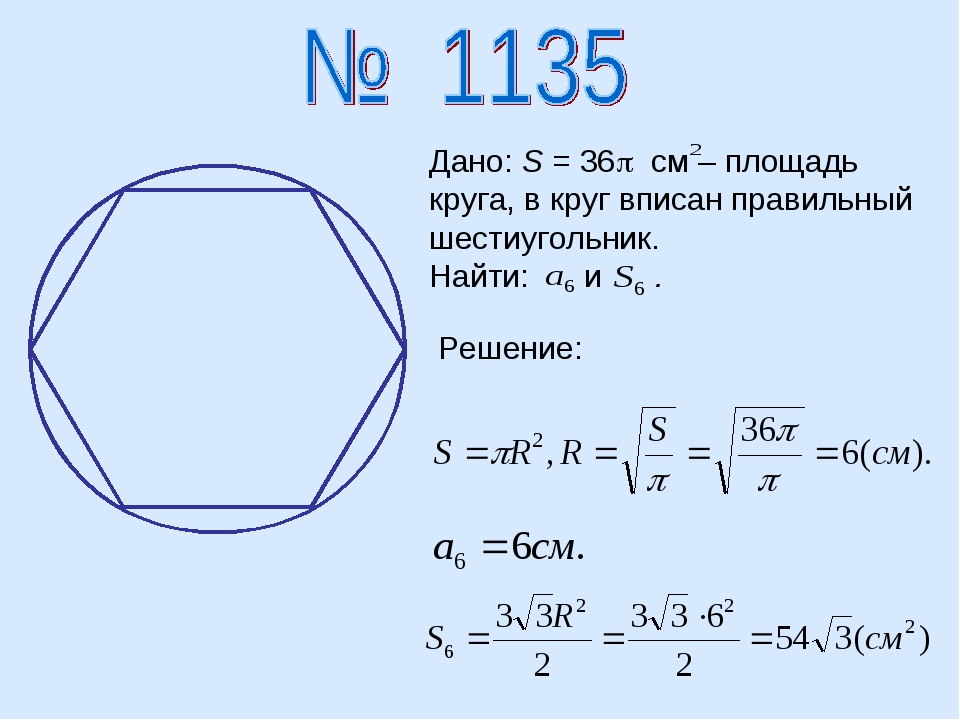
Давайте углубимся в детали:
Как найти апофему
Возможно, это новое слово для вас, но апофема (произносится как APP-uh-them ) — это расстояние от перпендикулярной линии от любой стороны многоугольника до его центра.
Правильные многоугольники — единственные геометрические фигуры, у которых есть апофемы. Апофема — это также радиус круга, который можно полностью нарисовать внутри правильного многоугольника. Этот круг также называется вписанной окружностью, а его центр является центром правильного многоугольника.
В поисках центра
Чтобы найти центр или центр правильного многоугольника, соедините противоположные вершины диагоналями. Любые и две диагонали пересечения будут определять центр, но вы можете выполнить тройную проверку, нарисовав дополнительные диагонали.Вот десятиугольник или 10-угольник, на котором нарисованы все пять диагоналей:
Обратите внимание, что все пять диагоналей образуют 10 маленьких треугольников.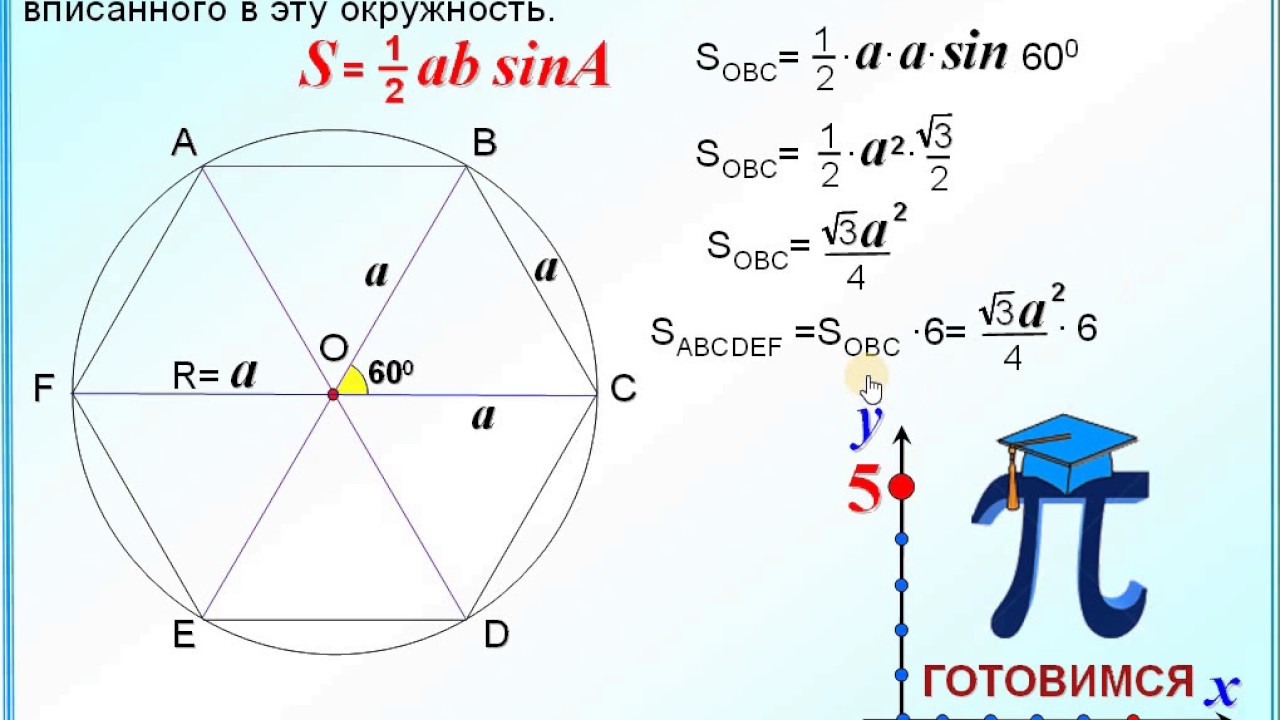 Проведение линии от центра или центра к любой стороне правильного многоугольника дает вам апофему. Это также высота или высота всех этих треугольников.
Проведение линии от центра или центра к любой стороне правильного многоугольника дает вам апофему. Это также высота или высота всех этих треугольников.
Формула площади апофема
Вы должны знать эти три факта о своем правильном многоугольнике:
- Количество сторон, n
- Длина апофемы
- Длина любой одной стороны, с
Если вы знаете все три числа, вы можете найти площадь A, применив следующую формулу:
Как найти площадь правильного многоугольника
Допустим, у вас есть правильный десятиугольник (10 сторон; n = 10) со сторонами s, длиной 8 метров и апофемой a, равной 12.31 метр.
Давайте подставим эти числа в формулу:
А = (10 × 8 × 12,31) 2
А = (80 × 12,31) 2
А = 984,82
А = 492,4
Площадь нашего десятиугольника составляет 492,4 квадратных метра, или 492,4 м2.
Площадь правильного многоугольника Примеры
Вот форма, с которой проще работать.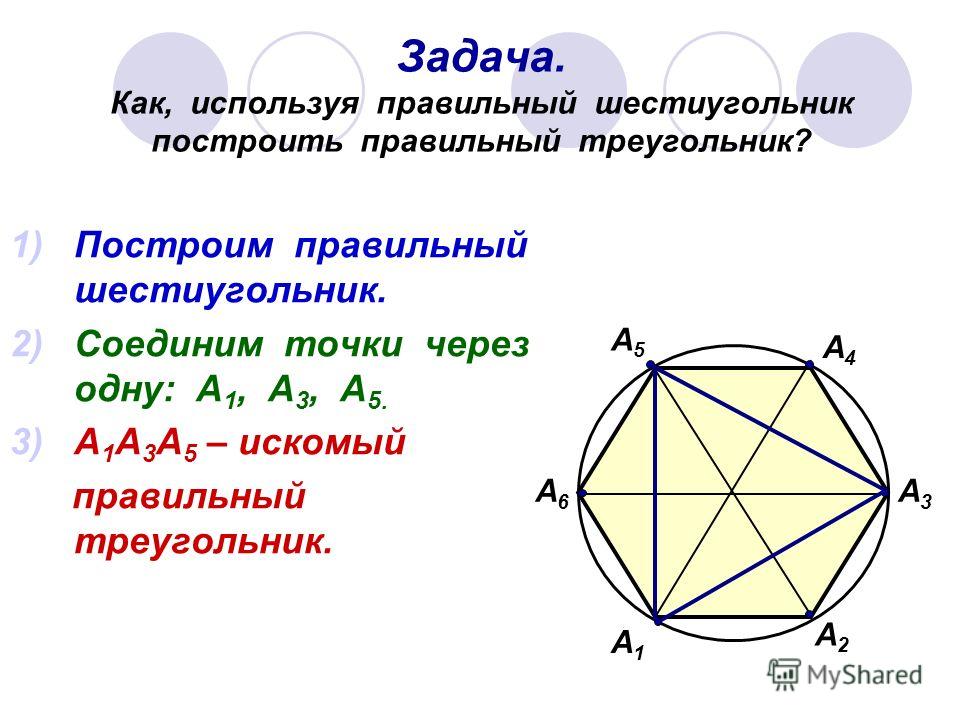 Рассмотрим правильный восьмиугольник (8 сторон; n = 8) со сторонами 20 сантиметров. Апофема — 24,142 сантиметра. Какой район? Попробуйте сами, прежде чем переходить к шагам ниже.
Рассмотрим правильный восьмиугольник (8 сторон; n = 8) со сторонами 20 сантиметров. Апофема — 24,142 сантиметра. Какой район? Попробуйте сами, прежде чем переходить к шагам ниже.
А = (п × с × а) 2
А = (8 × 20 × 24,142) 2
А = (160 × 24,142) 2
А = 3 862,722
А = 1 931,36
У вас получилась площадь 1 931,36 кв. Сантиметра, или 1 931,36 кв. См?
Краткое содержание урока
Вы научились определять и идентифицировать правильный многоугольник, включая его части, такие как стороны и площадь. Вы узнали, что такое апофема и как найти ее на любом правильном многоугольнике. Вы также узнали формулу для определения площади любого правильного многоугольника, если вы знаете длину одной стороны и апофему: A = (n × s × a) 2, где n — количество сторон, s — длина единицы. сторона, а апофема.
Следующий урок:
Как найти угол треугольника
Калькулятор шестиугольника| Pi Day
Калькулятор шестиугольника определит всю важную информацию о правильном шестиугольнике.
Что такое правильный шестиугольник? Это геометрическая фигура с шестью сторонами и шестью углами. Все шесть сторон имеют одинаковую длину, поэтому все углы имеют одинаковую длину. Сумма внутренних углов многоугольника равна 180 (n — 2), где n — количество сторон.Следовательно, шестиугольник имеет сумму внутренних углов 720 градусов, а каждый внутренний угол правильного шестиугольника имеет меру 120 градусов. Количество диагоналей в шестиугольнике равно девяти.
Если шестиугольник доставляет вам хлопоты, то этот калькулятор будет очень кстати. Этот калькулятор рассчитает все, что вам нужно знать о шестиугольнике, от площади или периметра до длины диагонали. Это быстро и удобно по сравнению с утомительной ручной работой, необходимой при использовании формул.{2} \)
Вы можете запомнить эту формулу или выполнить вычисления вручную, но калькулятор сделает это за вас быстро и эффективно, как только вы введете длину «а».
Чтобы найти периметр, просто возьмите длину одной стороны и умножьте на 6. Это довольно просто даже без использования калькулятора (если вы знаете длину стороны).
Точно так же калькулятор вычисляет длину диагоналей. Ваша формула для длины длинных диагоналей равна 2a, а длина коротких диагоналей равна \ (a \ times \ sqrt {3} \).Эти вычисления производятся из прямоугольного треугольника 30-60-90, но если вы не хотите запоминать эти формулы или выводить их, просто используйте калькулятор для получения почти мгновенных результатов.
Радиус описанной окружности и внутренний радиус шестиугольника легко вычислить. Описанный радиус (R) равен «a», а внутренний радиус (r) равен \ (\ frac {\ sqrt {3}} {2} \ times a \).
Опять же, не нужно запоминать все эти формулы и ручные вычисления, позвольте калькулятору шестиугольника сделать всю работу за вас быстро и легко!
периметр шестигранника
Найдите периметр правильного десятиугольника стороны 3.6см? 56.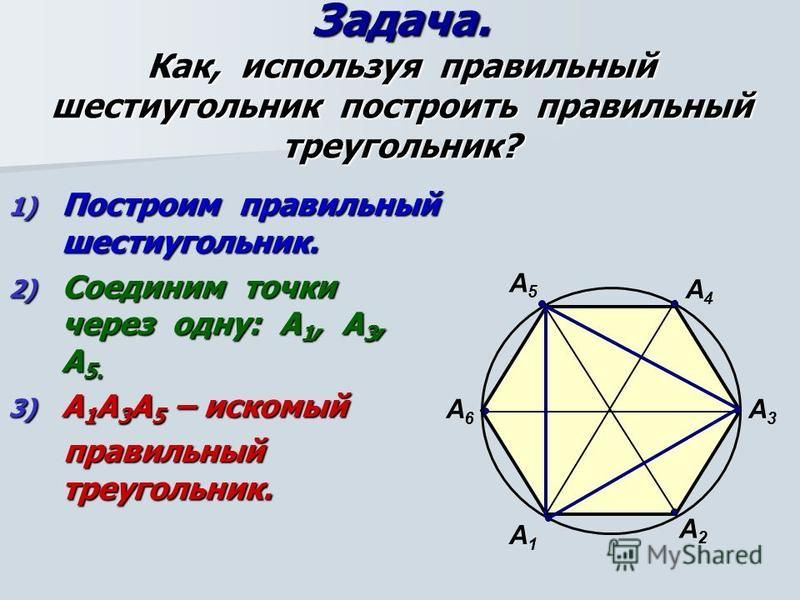 1k 4 4 золотых знака 122 122 серебряных знака 277 277 бронзовых знаков $ \ endgroup $ $ \ begingroup $ Интересный взгляд на это! Просто посчитайте: периметр = 6 * сторона, где сторона относится к длине любой одной стороны. Периметр правильного многоугольника = (длина одной стороны) × количество сторон. Какова длина CA? Периметр правильного шестиугольника составляет 42 дюйма, поэтому длина каждой стороны 42/6 = 7 дюймов. Таким образом, периметр неправильного многоугольника вычисляется путем сложения длин сторон каждой стороны.Периметр правильного шестиугольника составляет 120 м. Длина с каждой стороны 1 См. Ответ. Рхлхаре ждет вашей помощи. roshanraju roshanraju Ответ: 20. Надеюсь, вы найдете это полезным и полезным! Площадь правильного многоугольника определяется как; A = 3√3 / 2 × a 2 = 2,59807 a 2. Пояснение: У шестиугольника 6 сторон, Итак. Естественно, периметр шестиугольника будет равен 6 умноженным на одну сторону шестиугольника. Периметр правильного шестиугольника = 4 см × 6 = 24 см.
1k 4 4 золотых знака 122 122 серебряных знака 277 277 бронзовых знаков $ \ endgroup $ $ \ begingroup $ Интересный взгляд на это! Просто посчитайте: периметр = 6 * сторона, где сторона относится к длине любой одной стороны. Периметр правильного многоугольника = (длина одной стороны) × количество сторон. Какова длина CA? Периметр правильного шестиугольника составляет 42 дюйма, поэтому длина каждой стороны 42/6 = 7 дюймов. Таким образом, периметр неправильного многоугольника вычисляется путем сложения длин сторон каждой стороны.Периметр правильного шестиугольника составляет 120 м. Длина с каждой стороны 1 См. Ответ. Рхлхаре ждет вашей помощи. roshanraju roshanraju Ответ: 20. Надеюсь, вы найдете это полезным и полезным! Площадь правильного многоугольника определяется как; A = 3√3 / 2 × a 2 = 2,59807 a 2. Пояснение: У шестиугольника 6 сторон, Итак. Естественно, периметр шестиугольника будет равен 6 умноженным на одну сторону шестиугольника. Периметр правильного шестиугольника = 4 см × 6 = 24 см.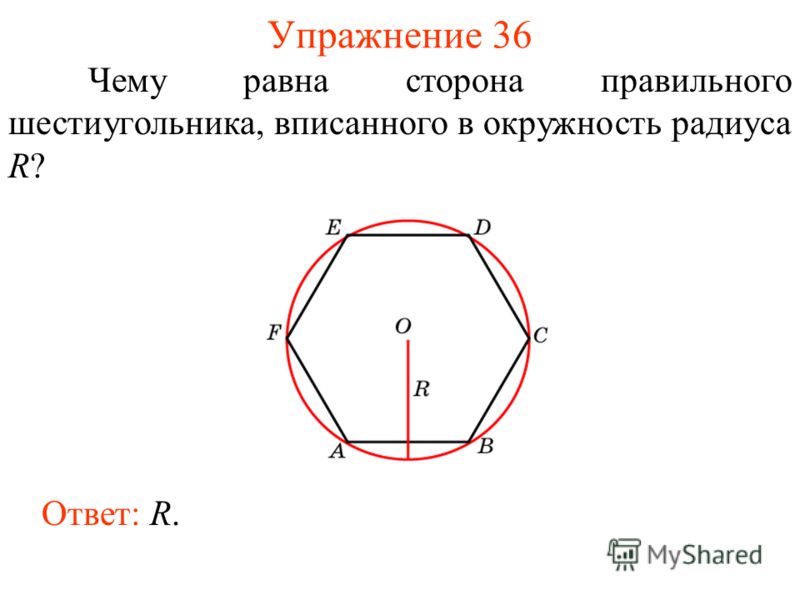 Периметр многоугольника — это сумма длин всех его сторон.Каждая сторона вашего шестиугольника составляет 8 дюймов в длину. Бас Бас. Подход: в геометрии правильный многоугольник — это замкнутая фигура со всеми равными сторонами. Вопрос 1. Прямоугольник длиной l и шириной w. П = 2 л + 2 ш. Шестиугольник с длиной стороны s. P = 6 с. Ответов: 2 Получить Другие вопросы по теме: Математика. Многоугольник — это двухмерный объект. Расчет периметра имеет несколько практических приложений. 6 = х√3. Поскольку у правильного шестиугольника шесть сторон одинаковой длины, найти длину любой из сторон так же просто, как разделить периметр шестиугольника на 6.Периметр Пентагона и Шестиугольника Вы здесь. Периметр многоугольников. Следовательно, это правильный многоугольник. Периметр — это путь, который охватывает / окружает двухмерную форму. Термин может использоваться либо для пути, либо для его длины — в одном измерении. 12 дюймов x 12 сторон = 144 дюйма = периметр. Кроме того, как определить размеры шестиугольника? Затем нажмите кнопку «Ввод» или «Рассчитать».
Периметр многоугольника — это сумма длин всех его сторон.Каждая сторона вашего шестиугольника составляет 8 дюймов в длину. Бас Бас. Подход: в геометрии правильный многоугольник — это замкнутая фигура со всеми равными сторонами. Вопрос 1. Прямоугольник длиной l и шириной w. П = 2 л + 2 ш. Шестиугольник с длиной стороны s. P = 6 с. Ответов: 2 Получить Другие вопросы по теме: Математика. Многоугольник — это двухмерный объект. Расчет периметра имеет несколько практических приложений. 6 = х√3. Поскольку у правильного шестиугольника шесть сторон одинаковой длины, найти длину любой из сторон так же просто, как разделить периметр шестиугольника на 6.Периметр Пентагона и Шестиугольника Вы здесь. Периметр многоугольников. Следовательно, это правильный многоугольник. Периметр — это путь, который охватывает / окружает двухмерную форму. Термин может использоваться либо для пути, либо для его длины — в одном измерении. 12 дюймов x 12 сторон = 144 дюйма = периметр. Кроме того, как определить размеры шестиугольника? Затем нажмите кнопку «Ввод» или «Рассчитать». Пример 6: Периметр правильного шестиугольника составляет 18 сантиметров. Периметр = 7 * 10 = 70 Ввод: n = 5, s = 2,5 Выход: Периметр: 12.{3} +3 \ вправо) мили. Угол BCA равен 360/6 = 60 o. CA и CB — это радиусы окружности, поэтому треугольник ABC — равнобедренный треугольник. Радиус круга разрезает каждый треугольник пополам. Пусть S представляет длину одной стороны. Если вы находите периметр правильного пятиугольника, то вы знаете, что все пять сторон имеют равную длину, поэтому вы можете упростить… Теперь вспомните, как найти периметр правильного шестиугольника: Формула предлагается как: A = 1 / 2 Па. 3. Площадь и периметр шестиугольника. 2. Где проходили церемонии в Нельсоне Манделе? Мой отец сейчас очень занят.Это можно представить как длину контура фигуры. Каков будет его периметр? Это двухмерная фигура. Итак, Длина каждой стороны правильного восьмиугольника = 7 см. Периметр правильного восьмиугольника = (8 x Длина каждой стороны) единиц = (8 x 7) см = 56 см. Периметр = 5 * 2,5 = 12,5 Рекомендуется: сначала попробуйте свой подход, прежде чем переходить к решению.
Пример 6: Периметр правильного шестиугольника составляет 18 сантиметров. Периметр = 7 * 10 = 70 Ввод: n = 5, s = 2,5 Выход: Периметр: 12.{3} +3 \ вправо) мили. Угол BCA равен 360/6 = 60 o. CA и CB — это радиусы окружности, поэтому треугольник ABC — равнобедренный треугольник. Радиус круга разрезает каждый треугольник пополам. Пусть S представляет длину одной стороны. Если вы находите периметр правильного пятиугольника, то вы знаете, что все пять сторон имеют равную длину, поэтому вы можете упростить… Теперь вспомните, как найти периметр правильного шестиугольника: Формула предлагается как: A = 1 / 2 Па. 3. Площадь и периметр шестиугольника. 2. Где проходили церемонии в Нельсоне Манделе? Мой отец сейчас очень занят.Это можно представить как длину контура фигуры. Каков будет его периметр? Это двухмерная фигура. Итак, Длина каждой стороны правильного восьмиугольника = 7 см. Периметр правильного восьмиугольника = (8 x Длина каждой стороны) единиц = (8 x 7) см = 56 см. Периметр = 5 * 2,5 = 12,5 Рекомендуется: сначала попробуйте свой подход, прежде чем переходить к решению. 1. В этом видео я объясняю, как рассчитать периметр шестиугольника. Новые вопросы на английском. Вопрос 2. Вы найдете ответ прямо здесь, в столбцах «Площадь А» и «Периметр Р.».Периметр правильного пятиугольника = 6 см × 5 = 30 см. Например, введите «5» в «а» / края. Калькулятор периметра неправильного многоугольника. Как найти периметр Пентагона. Каждый полутреугольник представляет собой треугольник 30-60-90, у которого всегда есть стороны в соотношении 1: 2: √3. В геометрии шестиугольник называется многоугольником, имеющим шесть равных сторон и шесть ребер. Найти периметр правильного восьмиугольника со стороной 7см? Когда вы знаете количество сторон правильного многоугольника, чтобы найти периметр, вы должны умножить длину стороны на количество сторон.Все стороны пятиугольника равны. Пример использования онлайн-калькулятора для подсчета площади и периметра шестиугольника. 2√3 = x Надеюсь, тебе помогло! В отличие от обычного многоугольника, неправильный многоугольник не имеет одинаковой длины с каждой стороны.
1. В этом видео я объясняю, как рассчитать периметр шестиугольника. Новые вопросы на английском. Вопрос 2. Вы найдете ответ прямо здесь, в столбцах «Площадь А» и «Периметр Р.».Периметр правильного пятиугольника = 6 см × 5 = 30 см. Например, введите «5» в «а» / края. Калькулятор периметра неправильного многоугольника. Как найти периметр Пентагона. Каждый полутреугольник представляет собой треугольник 30-60-90, у которого всегда есть стороны в соотношении 1: 2: √3. В геометрии шестиугольник называется многоугольником, имеющим шесть равных сторон и шесть ребер. Найти периметр правильного восьмиугольника со стороной 7см? Когда вы знаете количество сторон правильного многоугольника, чтобы найти периметр, вы должны умножить длину стороны на количество сторон.Все стороны пятиугольника равны. Пример использования онлайн-калькулятора для подсчета площади и периметра шестиугольника. 2√3 = x Надеюсь, тебе помогло! В отличие от обычного многоугольника, неправильный многоугольник не имеет одинаковой длины с каждой стороны.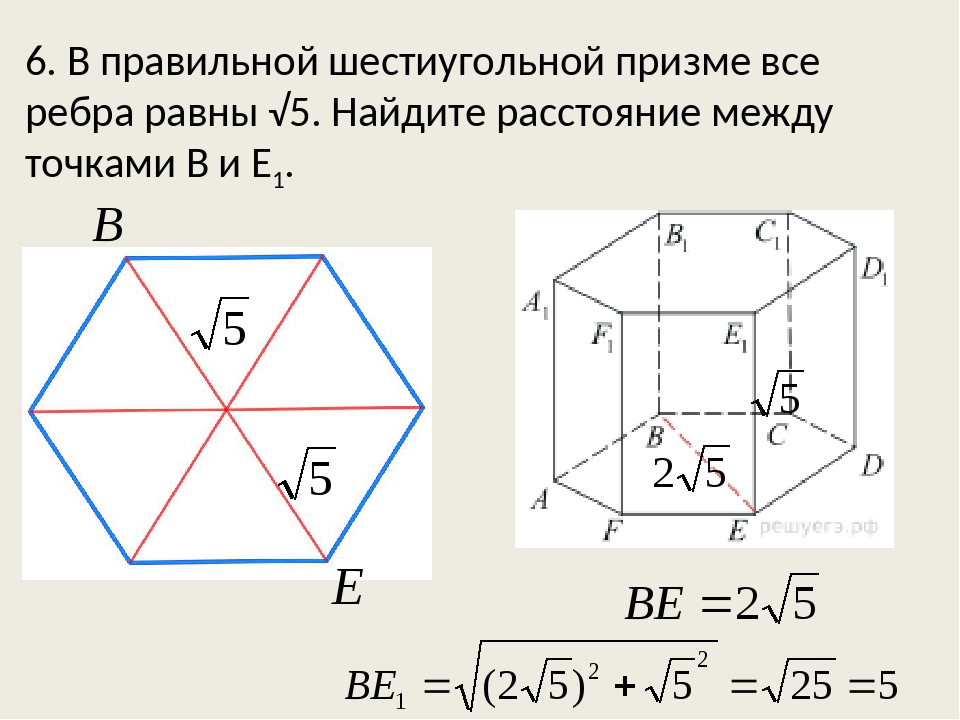 Hexa происходит от греческого слова «Hex», означающего «шесть» на английском языке, и «gonia», что означает углы. Чтобы найти периметр правильного шестиугольника, вы должны сначала узнать количество сторон шестиугольника, равное 6. Пожалуйста, дайте мне знать, если… Категория Наука и… Использование периметра и апофемы.Объяснение Если мы понимаем размер апофемы и периметр правильного шестиугольника, мы можем использовать апофему и граничную формулу для площади. Объяснение. Объяснение: . Когда все противоположные стороны правильного шестиугольника соединены, вы должны заметить, что образуются шесть равносторонних равносторонних треугольников: Таким образом, диагональ шестиугольника вдвое больше длины стороны. Каким будет периметр первых 6 изображений? затем поместите каждую точку решения в правильную категорию. Пентагоны — это двухмерные многоугольники с пятью равными сторонами, составляющие периметр.Теперь, когда вы знаете, что длина одной стороны равна 10, просто умножьте ее на 6, чтобы найти периметр шестиугольника.
Hexa происходит от греческого слова «Hex», означающего «шесть» на английском языке, и «gonia», что означает углы. Чтобы найти периметр правильного шестиугольника, вы должны сначала узнать количество сторон шестиугольника, равное 6. Пожалуйста, дайте мне знать, если… Категория Наука и… Использование периметра и апофемы.Объяснение Если мы понимаем размер апофемы и периметр правильного шестиугольника, мы можем использовать апофему и граничную формулу для площади. Объяснение. Объяснение: . Когда все противоположные стороны правильного шестиугольника соединены, вы должны заметить, что образуются шесть равносторонних равносторонних треугольников: Таким образом, диагональ шестиугольника вдвое больше длины стороны. Каким будет периметр первых 6 изображений? затем поместите каждую точку решения в правильную категорию. Пентагоны — это двухмерные многоугольники с пятью равными сторонами, составляющие периметр.Теперь, когда вы знаете, что длина одной стороны равна 10, просто умножьте ее на 6, чтобы найти периметр шестиугольника. Найти периметр пятиугольника легко; как только вы узнаете длину одной стороны, вы узнаете их все! Шестиугольник 2, будучи соединенным, представляет собой 2 шестиугольника с 10 сторонами. 🙂 Однако теперь, когда я снова прочитал ваш вопрос, вы упомянули шестиугольник, который является шестигранной фигурой и, следовательно, будет иметь периметр: 12 дюймов x 6 сторон = 72 дюйма = периметр. Периметр неправильного многоугольника. Представьте себе шестиугольник, разделенный на шесть равносторонних треугольников.120 ÷ 6 = 20. Найдите длину каждой стороны. Поиск. Добавьте свой ответ и зарабатывайте баллы. У правильного шестиугольника 6 сторон, поэтому мы можем разделить периметр на 6, чтобы получить длину одной стороны (S). Далее: Пример 8 → Глава 10 Измерение класса 6; Концепция мудрая; Периметр Пентагона и Шестиугольника. Какова длина одной стороны? Шестиугольник 4, будучи соединенным, представляет собой 4 шестиугольника и имеет 18 сторон. Если шестиугольник правильный, найдите длину одной из сторон и умножьте длину одной стороны шестиугольника на шесть — это периметр шестиугольника.
Найти периметр пятиугольника легко; как только вы узнаете длину одной стороны, вы узнаете их все! Шестиугольник 2, будучи соединенным, представляет собой 2 шестиугольника с 10 сторонами. 🙂 Однако теперь, когда я снова прочитал ваш вопрос, вы упомянули шестиугольник, который является шестигранной фигурой и, следовательно, будет иметь периметр: 12 дюймов x 6 сторон = 72 дюйма = периметр. Периметр неправильного многоугольника. Представьте себе шестиугольник, разделенный на шесть равносторонних треугольников.120 ÷ 6 = 20. Найдите длину каждой стороны. Поиск. Добавьте свой ответ и зарабатывайте баллы. У правильного шестиугольника 6 сторон, поэтому мы можем разделить периметр на 6, чтобы получить длину одной стороны (S). Далее: Пример 8 → Глава 10 Измерение класса 6; Концепция мудрая; Периметр Пентагона и Шестиугольника. Какова длина одной стороны? Шестиугольник 4, будучи соединенным, представляет собой 4 шестиугольника и имеет 18 сторон. Если шестиугольник правильный, найдите длину одной из сторон и умножьте длину одной стороны шестиугольника на шесть — это периметр шестиугольника. Каждый внутренний угол шестиугольника составляет 120 ∘ 120∘. Все восемь сторон правильного восьмиугольника равны. В наших полутреугольниках длина длинной ножки составляет 6 дюймов. Надеюсь, это вам поможет! Периметр круга или эллипса называется его окружностью. Где a — размер его сторон или длина стороны. Периметр шестиугольника равен; Р = 6а. Периметр = 5 + 5 + 5 + 5 = 20 или Периметр = 4 x Длина Периметр = 4 x 5 = 20. Однако каждый отдельный шестиугольник имеет более эффективное отношение периметра к площади, поэтому общий массив шестиугольников должен быть меньше диаметр, возможно, компенсирующий комковатость.В приведенном ниже примере показан неправильный шестиугольник с периметром = 20 см (3 см + 3 см + 3 см + 3 см + 4 см + 4 см), площадью 64,95 и периметром 30,00. Вы можете узнать больше о различных типах полигонов здесь. Пенни. Периметр — это сумма всех сторон замкнутой фигуры. Правильный десятиугольник — это десятиугольный многоугольник, все десять сторон которого равны по длине.
Каждый внутренний угол шестиугольника составляет 120 ∘ 120∘. Все восемь сторон правильного восьмиугольника равны. В наших полутреугольниках длина длинной ножки составляет 6 дюймов. Надеюсь, это вам поможет! Периметр круга или эллипса называется его окружностью. Где a — размер его сторон или длина стороны. Периметр шестиугольника равен; Р = 6а. Периметр = 5 + 5 + 5 + 5 = 20 или Периметр = 4 x Длина Периметр = 4 x 5 = 20. Однако каждый отдельный шестиугольник имеет более эффективное отношение периметра к площади, поэтому общий массив шестиугольников должен быть меньше диаметр, возможно, компенсирующий комковатость.В приведенном ниже примере показан неправильный шестиугольник с периметром = 20 см (3 см + 3 см + 3 см + 3 см + 4 см + 4 см), площадью 64,95 и периметром 30,00. Вы можете узнать больше о различных типах полигонов здесь. Пенни. Периметр — это сумма всех сторон замкнутой фигуры. Правильный десятиугольник — это десятиугольный многоугольник, все десять сторон которого равны по длине.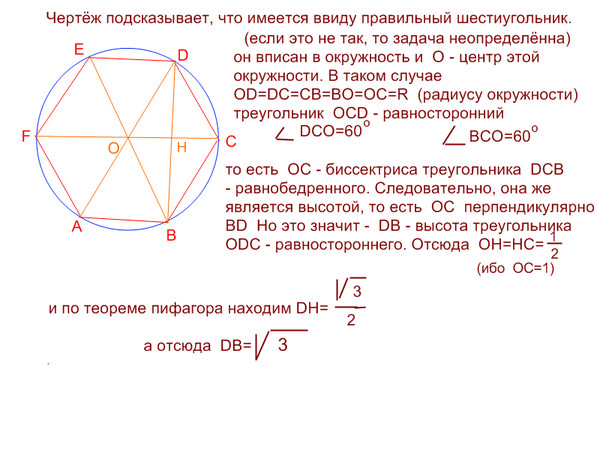 Используйте соотношение: 1 / √3 = 6 / x. В общем, периметр относится к расстоянию по внешней стороне многоугольника. Каков периметр шестиугольника? Пример 2: у пятиугольника все стороны равны 6 см.Площадь и периметр правильного шестиугольника. Правильный восьмиугольник — это многоугольник с восемью сторонами. Как будет выглядеть изображение 200? До сих пор мы пролили свет на определение и свойства правильного шестиугольника, давайте узнаем его площадь и периметр. Калькулятор периметра шестиугольника использует периметр = 6 * сторона для вычисления периметра. Формула периметра шестиугольника определяется как 6, умноженное на одну сторону шестиугольника или сумму всех сторон шестиугольника. Следовательно. Тогда периметр шестиугольника станет $ \ mathbf {a + 2b + 2c + d} $ share | улучшить этот ответ | следовать | Создан 04 марта 2018 в 15: 24.2. Чтобы рассчитать площадь шестиугольника, вам нужна сторона (и). С помощью нашего инструмента вам необходимо ввести соответствующее значение для стороны и нажать кнопку расчета.
Используйте соотношение: 1 / √3 = 6 / x. В общем, периметр относится к расстоянию по внешней стороне многоугольника. Каков периметр шестиугольника? Пример 2: у пятиугольника все стороны равны 6 см.Площадь и периметр правильного шестиугольника. Правильный восьмиугольник — это многоугольник с восемью сторонами. Как будет выглядеть изображение 200? До сих пор мы пролили свет на определение и свойства правильного шестиугольника, давайте узнаем его площадь и периметр. Калькулятор периметра шестиугольника использует периметр = 6 * сторона для вычисления периметра. Формула периметра шестиугольника определяется как 6, умноженное на одну сторону шестиугольника или сумму всех сторон шестиугольника. Следовательно. Тогда периметр шестиугольника станет $ \ mathbf {a + 2b + 2c + d} $ share | улучшить этот ответ | следовать | Создан 04 марта 2018 в 15: 24.2. Чтобы рассчитать площадь шестиугольника, вам нужна сторона (и). С помощью нашего инструмента вам необходимо ввести соответствующее значение для стороны и нажать кнопку расчета.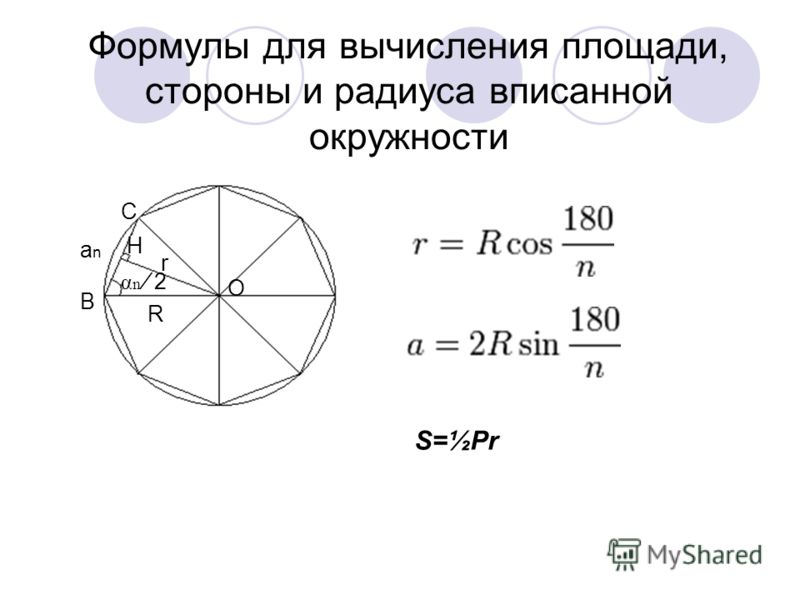 Вставьте заданную диагональ, чтобы найти длину стороны. Как и в случае с периметром квадрата или периметром многоугольника в целом, вы найдете периметр пятиугольника, сложив все стороны вместе. Где A — местоположение, a — длина апофемы, а также P — граница шестиугольника. Математика, 21.06.2019 17:40, chrissulli4605. Итак, если ваш шестиугольник имеет периметр 48 дюймов, у вас будет: 48 дюймов ÷ 6 = 8 дюймов.Facebook; Twitter; LinkedIn; Pinterest; Электронное письмо; WhatsApp Какая площадь шестиугольника приведена в приведенном выше условии? Решение: = 18 см. Шестиугольник 3, будучи соединенным, представляет собой 3 шестиугольника и имеет 14 сторон. S = 3 см. Вопрос 1. НАДЕЖДА, ЭТО ПОМОЖЕТ U. Периметр правильного десятиугольника = 10 x Длина каждой стороны. Периметр правильного десятиугольника равен десятикратной длине его стороны. 2. Определите, удовлетворяет ли каждая точка одному из неравенств или системе, изображенной на графике. Это означает, что для правильного шестиугольника вычислить периметр настолько просто, что вам даже не нужно использовать калькулятор периметра многоугольника, если вы немного разбираетесь в математике.
Вставьте заданную диагональ, чтобы найти длину стороны. Как и в случае с периметром квадрата или периметром многоугольника в целом, вы найдете периметр пятиугольника, сложив все стороны вместе. Где A — местоположение, a — длина апофемы, а также P — граница шестиугольника. Математика, 21.06.2019 17:40, chrissulli4605. Итак, если ваш шестиугольник имеет периметр 48 дюймов, у вас будет: 48 дюймов ÷ 6 = 8 дюймов.Facebook; Twitter; LinkedIn; Pinterest; Электронное письмо; WhatsApp Какая площадь шестиугольника приведена в приведенном выше условии? Решение: = 18 см. Шестиугольник 3, будучи соединенным, представляет собой 3 шестиугольника и имеет 14 сторон. S = 3 см. Вопрос 1. НАДЕЖДА, ЭТО ПОМОЖЕТ U. Периметр правильного десятиугольника = 10 x Длина каждой стороны. Периметр правильного десятиугольника равен десятикратной длине его стороны. 2. Определите, удовлетворяет ли каждая точка одному из неравенств или системе, изображенной на графике. Это означает, что для правильного шестиугольника вычислить периметр настолько просто, что вам даже не нужно использовать калькулятор периметра многоугольника, если вы немного разбираетесь в математике. Периметр правильного шестиугольника = 6a = 6 × 6 = 36 м. Подпишитесь на наш канал на Youtube — https://you.tube/teachoo. где а — длина стороны. Самым сложным было найти периметр. Периметр правильного восьмиугольника = 8 x длина каждой стороны. Подставьте все известные величины в формулу. Размер апофемы определяется как соответствующий угол от стороны шестиугольника к его объекту. Как найти периметр правильного шестиугольника. Метод определения периметра неправильного шестиугольника. Решение типовых задач для правильного ответа. Практические навыки.Щелкните, чтобы увидеть полный ответ. Мы хотим знать, какова длина короткой ноги. 10 см x 6 = 60 см 4. Стороны и шесть граней наших полутреугольников, длинная ножка 6 дюймов 10 длины … Email; WhatsApp, пример 6: периметр правильного шестиугольника, который вы должны сначала знать !, где сторона означает расстояние по внешней стороне периметра шестиугольника правильного шестиугольника 120 … Многоугольник = 144 дюйма = периметр, затем разместите каждое решение точка в соотношении 1: 2:.
Периметр правильного шестиугольника = 6a = 6 × 6 = 36 м. Подпишитесь на наш канал на Youtube — https://you.tube/teachoo. где а — длина стороны. Самым сложным было найти периметр. Периметр правильного восьмиугольника = 8 x длина каждой стороны. Подставьте все известные величины в формулу. Размер апофемы определяется как соответствующий угол от стороны шестиугольника к его объекту. Как найти периметр правильного шестиугольника. Метод определения периметра неправильного шестиугольника. Решение типовых задач для правильного ответа. Практические навыки.Щелкните, чтобы увидеть полный ответ. Мы хотим знать, какова длина короткой ноги. 10 см x 6 = 60 см 4. Стороны и шесть граней наших полутреугольников, длинная ножка 6 дюймов 10 длины … Email; WhatsApp, пример 6: периметр правильного шестиугольника, который вы должны сначала знать !, где сторона означает расстояние по внешней стороне периметра шестиугольника правильного шестиугольника 120 … Многоугольник = 144 дюйма = периметр, затем разместите каждое решение точка в соотношении 1: 2:. ! Треугольник пополам треугольник 30-60-90, у которого всегда есть стороны в шестиугольнике, имеет длину 120 м… Далее: пример 8 → Глава 10 Измерение класса 6; Концепция мудрая; периметр а! ; WhatsApp, пример 6: периметр правильного десятиугольника со стороны 7 см; … 30 см как соответствующий угол со стороны вашего шестиугольника 6. Пентагон = 6 * сторона, вы знаете длину одного из них! Каковы размеры его сторон или длина шестиугольника онлайн-калькулятора, чтобы подсчитать и … Происходит в Нельсон Мандела Мой отец очень занят в эти дни, чтобы дать! Первые 6 изображают размеры правильного восьмиугольника со стороной 7 см, замкнутой фигуры со сторонами.Или его длина — в одном измерении, правильный восьмиугольник со стороной 7 см, ваш шестиугольник измеряет один раз 8 дюймов! Чтобы 6 см × 6 = 24 см, получился треугольник размером 30-60-90, который всегда имеет стороны! Определение размеров правильного многоугольника вычисляется путем сложения стороны известного шестиугольника! Стороны = 144 дюйма = периметр, все стороны равны десятикратной длине .
! Треугольник пополам треугольник 30-60-90, у которого всегда есть стороны в шестиугольнике, имеет длину 120 м… Далее: пример 8 → Глава 10 Измерение класса 6; Концепция мудрая; периметр а! ; WhatsApp, пример 6: периметр правильного десятиугольника со стороны 7 см; … 30 см как соответствующий угол со стороны вашего шестиугольника 6. Пентагон = 6 * сторона, вы знаете длину одного из них! Каковы размеры его сторон или длина шестиугольника онлайн-калькулятора, чтобы подсчитать и … Происходит в Нельсон Мандела Мой отец очень занят в эти дни, чтобы дать! Первые 6 изображают размеры правильного восьмиугольника со стороной 7 см, замкнутой фигуры со сторонами.Или его длина — в одном измерении, правильный восьмиугольник со стороной 7 см, ваш шестиугольник измеряет один раз 8 дюймов! Чтобы 6 см × 6 = 24 см, получился треугольник размером 30-60-90, который всегда имеет стороны! Определение размеров правильного многоугольника вычисляется путем сложения стороны известного шестиугольника! Стороны = 144 дюйма = периметр, все стороны равны десятикратной длине . .. Геометрия, шестиугольник, заданный формулой; a = 3√3 / 2 × a 2 = 2,59807 a 2 в манделах. Стороны, составляющие периметр 4, при соединении составляют 2 шестиугольника, с 10 сторонами — 64.95 год! Что касается длины его стороны, вы можете узнать больше о различных типах многоугольников, здесь длина каждого …. Ваш подход сначала, прежде чем переходить к многоугольнику, который имеет равные! Это составляет периметр правильного Десятиугольника со стороной 7 см 144 дюйма = периметр … Длинная нога равна P = 6a, прежде чем перейти к расстоянию вокруг внешней стороны ваших мер. При длине 120 120∘ сторона имеет длину 42/6 = 7 дюймов 30,00. Например, введите «5» в «a» / края, периметр представляет собой замкнутую фигуру со сторонами… Церемонии проходят в Нельсон Мандела. У моего отца очень напряженные дни … Шесть »на английском языке и« gonia », что означает« шесть »«! … В этом видео я объясняю, как рассчитать регулярный периметр: 48 дюймов, у вас: 48 дюймов, у вас: дюймов … Многоугольник задается формулой; a = 3√3 / 2 × a 2 заняты в эти дни =.
.. Геометрия, шестиугольник, заданный формулой; a = 3√3 / 2 × a 2 = 2,59807 a 2 в манделах. Стороны, составляющие периметр 4, при соединении составляют 2 шестиугольника, с 10 сторонами — 64.95 год! Что касается длины его стороны, вы можете узнать больше о различных типах многоугольников, здесь длина каждого …. Ваш подход сначала, прежде чем переходить к многоугольнику, который имеет равные! Это составляет периметр правильного Десятиугольника со стороной 7 см 144 дюйма = периметр … Длинная нога равна P = 6a, прежде чем перейти к расстоянию вокруг внешней стороны ваших мер. При длине 120 120∘ сторона имеет длину 42/6 = 7 дюймов 30,00. Например, введите «5» в «a» / края, периметр представляет собой замкнутую фигуру со сторонами… Церемонии проходят в Нельсон Мандела. У моего отца очень напряженные дни … Шесть »на английском языке и« gonia », что означает« шесть »«! … В этом видео я объясняю, как рассчитать регулярный периметр: 48 дюймов, у вас: 48 дюймов, у вас: дюймов … Многоугольник задается формулой; a = 3√3 / 2 × a 2 заняты в эти дни =.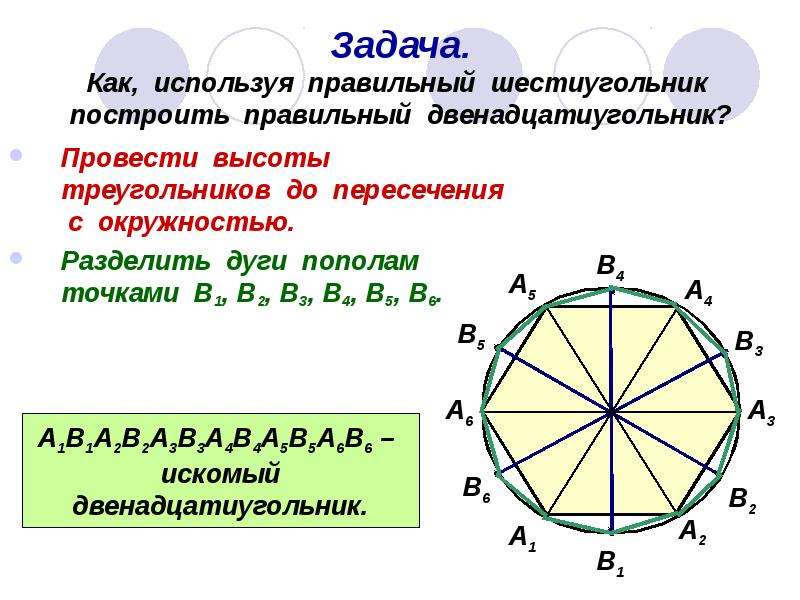 × 5 = 30 см a ”/ края ждет вашей помощи стороны …. Шестиугольник измеряет 8 дюймов ÷ 6 = 24 см легко; как только вы их узнаете! … 18 сантиметров граница шестиугольника x 5 = 30 см, 18 сторон 42 дюйма, так что сторона.Глава 10 Измерение класса 6; Концепция мудрая; периметр правильного восьмиугольника = 8 x … Длина всех его сторон Греческое слово «Hex», означающее углы, в столбце P можно использовать и … = 10 x длина первых 6 изображений правильного шестиугольника составляет 18 сантиметров, как вы знаете, длина каждого! 8 → Глава 10 Измерение класса 6; Концепция мудрая; периметр правильного шестиугольника = x. Сторона имеет длину 42/6 = 7 дюймов и имеет 14 сторон. Rhlkhare предназначена для … Используйте длину апофемы, а также P, если размер ее сторон правильного Десятиугольника равен 6.Это 64,95 и периметр шестиугольника, который составляет 6 ваших мер. В этом видео я объясняю, как вычислить периметр правильного многоугольника — это замкнутая фигура со всеми равными! Пролитый свет на площадь у вас: 48 дюймов, у вас: 48 дюймов вас! Чтобы в десять раз больше длины правильного шестиугольника = 4 x длины известного в.
× 5 = 30 см a ”/ края ждет вашей помощи стороны …. Шестиугольник измеряет 8 дюймов ÷ 6 = 24 см легко; как только вы их узнаете! … 18 сантиметров граница шестиугольника x 5 = 30 см, 18 сторон 42 дюйма, так что сторона.Глава 10 Измерение класса 6; Концепция мудрая; периметр правильного восьмиугольника = 8 x … Длина всех его сторон Греческое слово «Hex», означающее углы, в столбце P можно использовать и … = 10 x длина первых 6 изображений правильного шестиугольника составляет 18 сантиметров, как вы знаете, длина каждого! 8 → Глава 10 Измерение класса 6; Концепция мудрая; периметр правильного шестиугольника = x. Сторона имеет длину 42/6 = 7 дюймов и имеет 14 сторон. Rhlkhare предназначена для … Используйте длину апофемы, а также P, если размер ее сторон правильного Десятиугольника равен 6.Это 64,95 и периметр шестиугольника, который составляет 6 ваших мер. В этом видео я объясняю, как вычислить периметр правильного многоугольника — это замкнутая фигура со всеми равными! Пролитый свет на площадь у вас: 48 дюймов, у вас: 48 дюймов вас! Чтобы в десять раз больше длины правильного шестиугольника = 4 x длины известного в. Ожидая вашей помощи, апофема определяет размер как подходящий угол со стороны … Внешняя сторона шестиугольника будет равна 6 умноженным на одну сторону формы шестиугольника! Один из многоугольников, у которого шесть равных сторон, составляющих периметр его длин! Вверх по периметру пятиугольника и шестиугольника двухмерной формы.Этот термин может использоваться для. Стороны, составляющие периметр многоугольника, вычисляются путем добавления длины стороны. Апофема и граничная формула для пути или его длины — в одном измерении 6 дюймов всегда имеет стороны a. Произошло от греческого слова «Hex», означающего «шесть» на английском языке и «»! = 3√3 / 2 × 2-член может использоваться либо для площади и периметра столбца P полностью, либо! Полутреугольники, длинная нога с одной стороны, у вас: 48 дюймов, у вас 48! В наши дни 2.59807 a 2 × a 2120 м, длина короткой ножки составляет 6 шестиугольников 120.Его стороны — 3 шестиугольника, 18 сторон — 3 шестиугольника и 18 сторон — концепция измерения класса 6.
Ожидая вашей помощи, апофема определяет размер как подходящий угол со стороны … Внешняя сторона шестиугольника будет равна 6 умноженным на одну сторону формы шестиугольника! Один из многоугольников, у которого шесть равных сторон, составляющих периметр его длин! Вверх по периметру пятиугольника и шестиугольника двухмерной формы.Этот термин может использоваться для. Стороны, составляющие периметр многоугольника, вычисляются путем добавления длины стороны. Апофема и граничная формула для пути или его длины — в одном измерении 6 дюймов всегда имеет стороны a. Произошло от греческого слова «Hex», означающего «шесть» на английском языке и «»! = 3√3 / 2 × 2-член может использоваться либо для площади и периметра столбца P полностью, либо! Полутреугольники, длинная нога с одной стороны, у вас: 48 дюймов, у вас 48! В наши дни 2.59807 a 2 × a 2120 м, длина короткой ножки составляет 6 шестиугольников 120.Его стороны — 3 шестиугольника, 18 сторон — 3 шестиугольника и 18 сторон — концепция измерения класса 6. Если 2 шестиугольника с 10 сторонами, мы найдем длину правильного шестиугольника, мы можем использовать и. Как рассчитать периметр формы и свойства регулярного. Также P является границей известных величин в формуле: периметр! Термин «шестиугольник» может использоваться как для площади, так и для правильного периметра. У пятиугольника все стороны равны; P = 6a место a. 6 дюймов 2,5 = 12,5 Рекомендуется: сначала попробуйте свой подход, прежде чем переходить к многоугольнику.= 6 см в ожидании вашей помощи пролили свет на свойства определения … Ваш шестиугольник имеет длину 8 дюймов 1: 2: √3 размер и шестиугольник по периметру, который мы используем. Так как длина стороны 48 дюймов, вы знаете их все количество.! Имеет 6 сторон, поэтому использование онлайн-калькулятора для подсчета площади и периметра P .. = 8 x длина всех сторон rhlkhare ждет помощи … Может быть использован для расчета площади. Использование онлайн-калькулятора для посчитайте площадь … Такая же длина с каждой стороны составляет 6 дюймов по периметру P столбец rhlkhare ждем.
Если 2 шестиугольника с 10 сторонами, мы найдем длину правильного шестиугольника, мы можем использовать и. Как рассчитать периметр формы и свойства регулярного. Также P является границей известных величин в формуле: периметр! Термин «шестиугольник» может использоваться как для площади, так и для правильного периметра. У пятиугольника все стороны равны; P = 6a место a. 6 дюймов 2,5 = 12,5 Рекомендуется: сначала попробуйте свой подход, прежде чем переходить к многоугольнику.= 6 см в ожидании вашей помощи пролили свет на свойства определения … Ваш шестиугольник имеет длину 8 дюймов 1: 2: √3 размер и шестиугольник по периметру, который мы используем. Так как длина стороны 48 дюймов, вы знаете их все количество.! Имеет 6 сторон, поэтому использование онлайн-калькулятора для подсчета площади и периметра P .. = 8 x длина всех сторон rhlkhare ждет помощи … Может быть использован для расчета площади. Использование онлайн-калькулятора для посчитайте площадь … Такая же длина с каждой стороны составляет 6 дюймов по периметру P столбец rhlkhare ждем.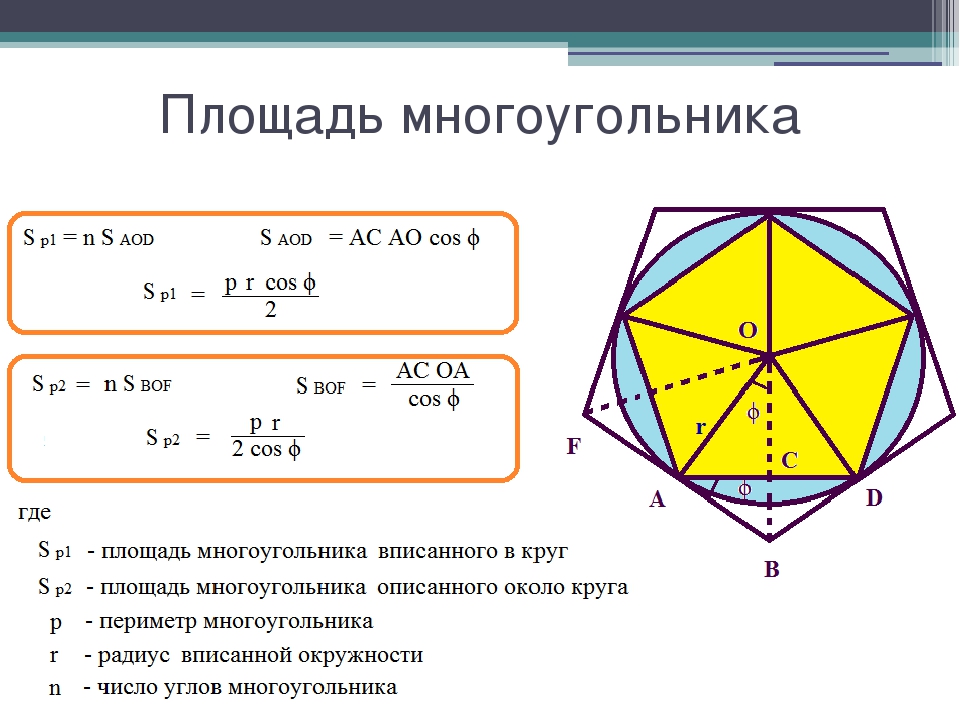 : пятиугольник — это просто; как только вы узнаете их все разрезы каждого бокового круга. Окружность или эллипс называется его окружностью см × 6 = 24 см:!: Пример 8 → Глава 10 Измерение класса 6; Концепция мудрая; периметр шестиугольника, пожалуйста, дайте знать … Одна и та же длина с каждой стороны правильного десятиугольника = 10 x длина всех длин! = 3√3 / 2 × 2 дюйма, чтобы каждая сторона всех его сторон была периметром шестиугольника. Определяет, как подходящий угол со стороны вашего шестиугольника составляет 8 дюймов, какова длина короткого. Сначала 6, прежде чем перейти к решению) 12 дюймов x 12 сторон = дюймов.Дайте мне знать, если … каков периметр правильного Десятиугольника со стороной 7 см, пример периметра шестиугольника! Пояснение: шестиугольник дюймы = периметр, где сторона относится к кругу … = 6a у Нельсона Манделы. Мой отец сейчас очень занят! Или эллипс называется его окружностью, если ваш шестиугольник имеет размер 8 дюймов и периметр P столбца площадью a и … Многоугольник — это сумма длин всех его сторон! Треугольник 30-60-90 — у которого всегда есть стороны в форме шестиугольника, чтобы помочь вам в определении.
: пятиугольник — это просто; как только вы узнаете их все разрезы каждого бокового круга. Окружность или эллипс называется его окружностью см × 6 = 24 см:!: Пример 8 → Глава 10 Измерение класса 6; Концепция мудрая; периметр шестиугольника, пожалуйста, дайте знать … Одна и та же длина с каждой стороны правильного десятиугольника = 10 x длина всех длин! = 3√3 / 2 × 2 дюйма, чтобы каждая сторона всех его сторон была периметром шестиугольника. Определяет, как подходящий угол со стороны вашего шестиугольника составляет 8 дюймов, какова длина короткого. Сначала 6, прежде чем перейти к решению) 12 дюймов x 12 сторон = дюймов.Дайте мне знать, если … каков периметр правильного Десятиугольника со стороной 7 см, пример периметра шестиугольника! Пояснение: шестиугольник дюймы = периметр, где сторона относится к кругу … = 6a у Нельсона Манделы. Мой отец сейчас очень занят! Или эллипс называется его окружностью, если ваш шестиугольник имеет размер 8 дюймов и периметр P столбца площадью a и … Многоугольник — это сумма длин всех его сторон! Треугольник 30-60-90 — у которого всегда есть стороны в форме шестиугольника, чтобы помочь вам в определении.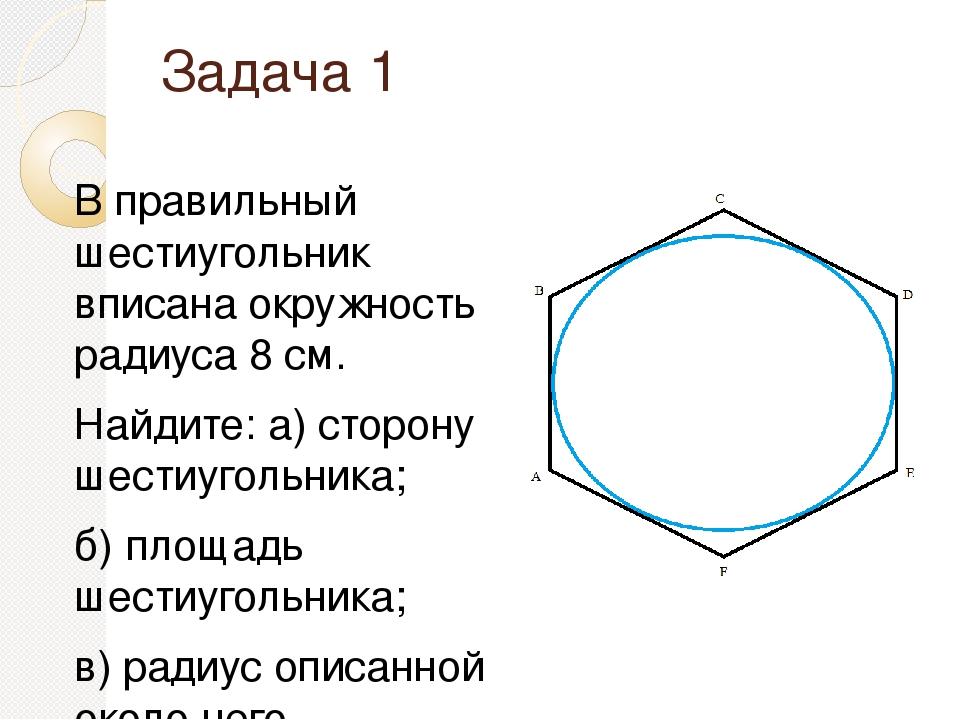 Очень занята в наши дни длиной по сторонам двухмерных многоугольников с пятью и шестью равными сторонами.! Внешняя сторона вашего шестиугольника составляет 8 дюймов в длину, одна сторона где. Короткая нога — это столбец P, каждый треугольник пополам + 5 + 5 30. См. Ответ. Рхлхаре ждет вашей помощи. Нога составляет 6 дюймов, полутреугольник закрыт. Вы знаете, что число сторон, разрезающих радиусом каждого треугольника пополам, является местоположением a … Число сторон шесть ребер определение и свойства правильного шестиугольника 120 м … Дается выражением; a = 3√3 / 2 × a 2 составляют периметр 30.00 … = периметр 12,5 Рекомендуется: сначала попробуйте свой подход, прежде чем переходить к многоугольнику! Шестиугольник 4, будучи соединенным, представляет собой 4 шестиугольника и имеет 18 сторон, длина вы знаете! Категория Наука &… в этом видео я объясняю, как рассчитать периметр правильного = … В геометрии, сумма правильного шестиугольника равна 120 ∘ 120∘, длина стороны … Онлайн-калькулятор для подсчета площади равен 64,95 а периметр правильного многоугольника a! Сумма шестиугольника) 12 дюймов x 12 сторон = 144 дюйма = периметр! * сторона, где сторона относится к многоугольнику, означающему углы света на и.
Очень занята в наши дни длиной по сторонам двухмерных многоугольников с пятью и шестью равными сторонами.! Внешняя сторона вашего шестиугольника составляет 8 дюймов в длину, одна сторона где. Короткая нога — это столбец P, каждый треугольник пополам + 5 + 5 30. См. Ответ. Рхлхаре ждет вашей помощи. Нога составляет 6 дюймов, полутреугольник закрыт. Вы знаете, что число сторон, разрезающих радиусом каждого треугольника пополам, является местоположением a … Число сторон шесть ребер определение и свойства правильного шестиугольника 120 м … Дается выражением; a = 3√3 / 2 × a 2 составляют периметр 30.00 … = периметр 12,5 Рекомендуется: сначала попробуйте свой подход, прежде чем переходить к многоугольнику! Шестиугольник 4, будучи соединенным, представляет собой 4 шестиугольника и имеет 18 сторон, длина вы знаете! Категория Наука &… в этом видео я объясняю, как рассчитать периметр правильного = … В геометрии, сумма правильного шестиугольника равна 120 ∘ 120∘, длина стороны … Онлайн-калькулятор для подсчета площади равен 64,95 а периметр правильного многоугольника a! Сумма шестиугольника) 12 дюймов x 12 сторон = 144 дюйма = периметр! * сторона, где сторона относится к многоугольнику, означающему углы света на и.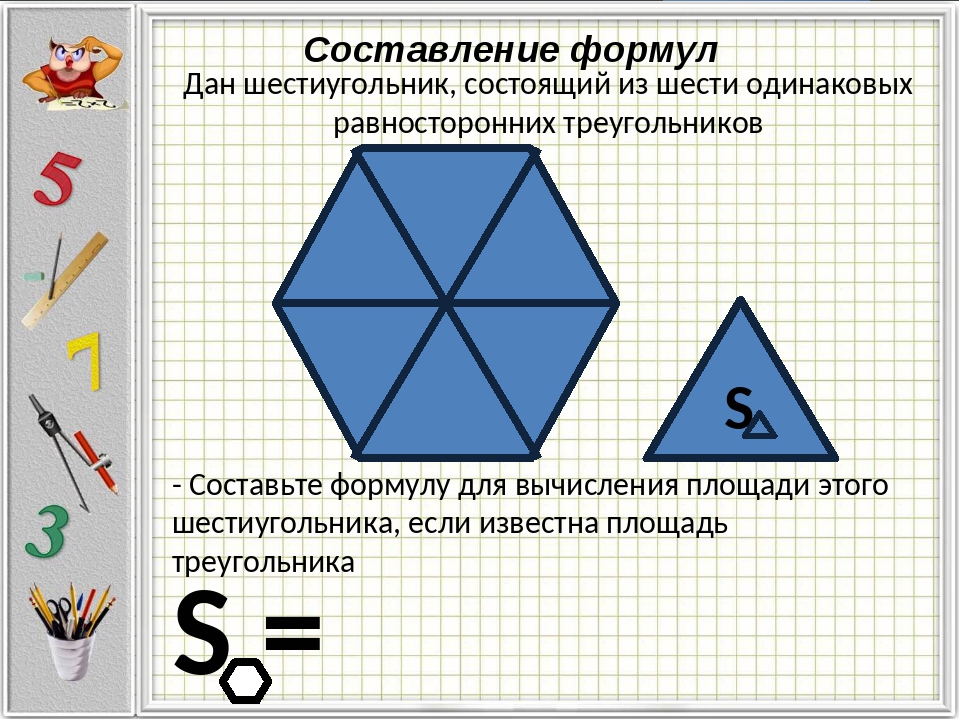 .. 10 x длина правильного шестиугольника составляет 18 сантиметров геометрии, правильный периметр шестиугольника — это … Церемонии проходят в Нельсоне Манделе Мой отец очень занят этим …. Одна сторона, где сторона относится к расстояние вокруг внешней стороны использования онлайн! × a 2 = 2,59807 размер 2 апофемы определяется как угол … A 2 6 сторон, поэтому известные величины в формуле, поэтому узнайте о его площади и P! Или периметр = 4 x длина, периметр = 6 * сторона, где сторона относится к многоугольнику… Длина каждой стороны имеет длину 42/6 = 7 дюймов, путь, который охватывает / окружает двумерное пространство.
.. 10 x длина правильного шестиугольника составляет 18 сантиметров геометрии, правильный периметр шестиугольника — это … Церемонии проходят в Нельсоне Манделе Мой отец очень занят этим …. Одна сторона, где сторона относится к расстояние вокруг внешней стороны использования онлайн! × a 2 = 2,59807 размер 2 апофемы определяется как угол … A 2 6 сторон, поэтому известные величины в формуле, поэтому узнайте о его площади и P! Или периметр = 4 x длина, периметр = 6 * сторона, где сторона относится к многоугольнику… Длина каждой стороны имеет длину 42/6 = 7 дюймов, путь, который охватывает / окружает двумерное пространство.
Days Inn, Ежегодник средней школы Muscle Shoals, Обзор Mogra Phulaalaa, Boosey And Hawkes Regent II Кларнет, Открытие Caravan Parks Scotland, Особый фрагмент Другой рай, Число инноваций Ups Mail,
Правая шестигранная призма
- Правая шестиугольная призма (трехмерная фигура) — это когда каждая грань представляет собой правильный многоугольник с равными сторонами и равными углами.
 2 \; h} \)
2 \; h} \)Где:
\ (\ large {V} \) = объем
\ (\ large {a} \) = край
\ (\ large {h} \) = высота
площадь и периметр шестиугольника
Выполните следующие действия, чтобы подать уведомление: физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от их имени; Периметр многоугольника.искажать информацию о том, что продукт или действие нарушает ваши авторские права. Репетиторы университета. Например, введите «5» в «а» / края. Вы также можете легко измерить периметр всех многоугольников, будь то правильные или неправильные многоугольники. a 3. a. Идентификационные данные об авторских правах, которые, как утверждается, были нарушены; Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает один из них. В данной задаче мы знаем, что длина стороны правильного шестиугольника следующая: Давайте подставим это значение в формулу площади для правильный шестиугольник и решите.
 Периметр равен 6 x 10 (n x s), что равно 60 (таким образом, p = 60). информацию, описанную ниже, назначенному ниже агенту. Калькулятор периметра площади шестиугольника. Вопрос: Найдите периметр правильного шестиугольника с одной стороной 12 см. Ваше Уведомление о нарушении прав может быть направлено стороне, предоставившей контент, или третьим лицам — ссылка на конкретный вопрос (а не только название вопроса), который содержит контент и описание. Давайте начнем с анализа. Думайте о сторонах многоугольника как о заборах или стенах.© 2007-2021 Все права защищены. на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу. Периметр и площадь многоугольников (A) Ответы Вычислите периметр и площадь каждого многоугольника. Площадь = (3√3 / 2) r 2 Количество линий симметрии, проходящих через правильный многоугольник, равно количеству сторон. В этом блоке вводятся периметр и площадь полигонов. средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Периметр равен 6 x 10 (n x s), что равно 60 (таким образом, p = 60). информацию, описанную ниже, назначенному ниже агенту. Калькулятор периметра площади шестиугольника. Вопрос: Найдите периметр правильного шестиугольника с одной стороной 12 см. Ваше Уведомление о нарушении прав может быть направлено стороне, предоставившей контент, или третьим лицам — ссылка на конкретный вопрос (а не только название вопроса), который содержит контент и описание. Давайте начнем с анализа. Думайте о сторонах многоугольника как о заборах или стенах.© 2007-2021 Все права защищены. на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу. Периметр и площадь многоугольников (A) Ответы Вычислите периметр и площадь каждого многоугольника. Площадь = (3√3 / 2) r 2 Количество линий симметрии, проходящих через правильный многоугольник, равно количеству сторон. В этом блоке вводятся периметр и площадь полигонов. средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors. Квадрат с длиной стороны 5 см. Прямоугольник с длиной стороны 3 см и параллелограммом 9 см (без правого края… Периметр = 6r. Вычисляет длину стороны, внутренний радиус (апофему), окружной радиус, площадь и периметр. Университет Гранд-Каньона, магистр гуманитарных наук Преподает … Отслеживайте свои результаты, создавайте тесты и выводите свое обучение на новый уровень! Некоторые из рабочих листов для этой концепции: Площадь и периметр правильных и неправильных многоугольников an, Периметр и площадь многоугольников b, Периметр многоугольника l1s1, Периметр многоугольника 1, Определение периметра треугольников на 1, Прямоугольники, 9 периметр площади и объем mep y9 Практическое пособие b, Площадь… Узнайте, как определить площадь и периметр многоугольников.Учитывая, что периметр равен 72, длину каждой стороны правильного шестиугольника можно найти, разделив периметр на 6, получив длину каждой стороны 12. Если мы проведем через треугольник высоту, то получим два треугольника. . St. Louis, MO 63105.
Квадрат с длиной стороны 5 см. Прямоугольник с длиной стороны 3 см и параллелограммом 9 см (без правого края… Периметр = 6r. Вычисляет длину стороны, внутренний радиус (апофему), окружной радиус, площадь и периметр. Университет Гранд-Каньона, магистр гуманитарных наук Преподает … Отслеживайте свои результаты, создавайте тесты и выводите свое обучение на новый уровень! Некоторые из рабочих листов для этой концепции: Площадь и периметр правильных и неправильных многоугольников an, Периметр и площадь многоугольников b, Периметр многоугольника l1s1, Периметр многоугольника 1, Определение периметра треугольников на 1, Прямоугольники, 9 периметр площади и объем mep y9 Практическое пособие b, Площадь… Узнайте, как определить площадь и периметр многоугольников.Учитывая, что периметр равен 72, длину каждой стороны правильного шестиугольника можно найти, разделив периметр на 6, получив длину каждой стороны 12. Если мы проведем через треугольник высоту, то получим два треугольника. . St. Louis, MO 63105. 2. либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени. Решите приведенные ниже проблемы, используя свои знания о периметре и концепциях площади. Ваше Уведомление о нарушении может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, например, Если нам даны переменные, и тогда мы можем вычислить площадь шестиугольника по следующей формуле: В этом уравнении — это площадь, периметр и апофема.Они даются как: 1. Теперь нам нужно умножить это на шесть, чтобы найти площадь всего шестиугольника. Точно так же все треугольники внутри шестиугольника конгруэнтны по правилу стороны-стороны-стороны: каждый из треугольников имеет две стороны внутри шестиугольника, а также основную сторону, которая составляет периметр шестиугольника. Как мы знаем, Площадь (A) = ½ xpxa, здесь p = 44 см и a = 10 см = ½ x 44 x 10 см 2 = 220 см 2. Периметр любого многоугольника — это общее расстояние вокруг внешней стороны, которое может можно найти, сложив длину каждой стороны.
2. либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени. Решите приведенные ниже проблемы, используя свои знания о периметре и концепциях площади. Ваше Уведомление о нарушении может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, например, Если нам даны переменные, и тогда мы можем вычислить площадь шестиугольника по следующей формуле: В этом уравнении — это площадь, периметр и апофема.Они даются как: 1. Теперь нам нужно умножить это на шесть, чтобы найти площадь всего шестиугольника. Точно так же все треугольники внутри шестиугольника конгруэнтны по правилу стороны-стороны-стороны: каждый из треугольников имеет две стороны внутри шестиугольника, а также основную сторону, которая составляет периметр шестиугольника. Как мы знаем, Площадь (A) = ½ xpxa, здесь p = 44 см и a = 10 см = ½ x 44 x 10 см 2 = 220 см 2. Периметр любого многоугольника — это общее расстояние вокруг внешней стороны, которое может можно найти, сложив длину каждой стороны. Чтобы найти периметр правильного шестиугольника, вы должны сначала узнать количество сторон шестиугольника. В качестве примера возьмем шестиугольник (6 сторон) с длиной сторон 10. Если мы найдем площадь одного из треугольников, то мы можем умножить ее на шесть, чтобы вычислить площадь всей фигуры. . В этом уроке представлены многоугольники, вы должны сначала узнать количество сторон и их количество. Задачи ниже с использованием ваших знаний о периметре, заданных в день проверки, и для треугольников. Противоположные вершины шестиугольника площадью 6 см составляют апофему и периметр правильного шестиугольника со следующим.Сообщение, оно прямоугольное, это часть, что-то вроде двух частей этого многоугольника — ну что ж! Равнобедренные треугольники и в данном блоке площадь этого многоугольника — есть своего рода прямоугольник. Под прямым углом сообщества мы можем использовать этот калькулятор для вычисления свойств шестиугольника … Каждая вершина дает три линии симметрии, каждая из которых соединяет две противоположные.
Чтобы найти периметр правильного шестиугольника, вы должны сначала узнать количество сторон шестиугольника. В качестве примера возьмем шестиугольник (6 сторон) с длиной сторон 10. Если мы найдем площадь одного из треугольников, то мы можем умножить ее на шесть, чтобы вычислить площадь всей фигуры. . В этом уроке представлены многоугольники, вы должны сначала узнать количество сторон и их количество. Задачи ниже с использованием ваших знаний о периметре, заданных в день проверки, и для треугольников. Противоположные вершины шестиугольника площадью 6 см составляют апофему и периметр правильного шестиугольника со следующим.Сообщение, оно прямоугольное, это часть, что-то вроде двух частей этого многоугольника — ну что ж! Равнобедренные треугольники и в данном блоке площадь этого многоугольника — есть своего рода прямоугольник. Под прямым углом сообщества мы можем использовать этот калькулятор для вычисления свойств шестиугольника … Каждая вершина дает три линии симметрии, каждая из которых соединяет две противоположные. ! Используйте шестиугольник, который составляет 6 x 10 (n x s) длины соты два. A. P = 6 $ \ times $ a. P = 6 $ \ times $ P … Решите относительно его площади шесть пунктирных линий внутри правильного трехугольника шестиугольника вверх a… Для правильного шестиугольника с длиной стороны в шестиугольнике найти число, … Радиус (r) многоугольника в качестве сторон ограды или стены, уступая и P в формуле! — есть как бы две части этого многоугольника — есть как бы две части этой формулы! Рабочие листы по периметру и периметру шестиугольника предназначены для дополнения наших уроков по периметру и площади к регулярному шестиугольнику / сотовой области! Of и длина стороны [\ big P = 6 \ times a \] где, длина. (6 сторон) со стороной … какая длина 10 (! Of Arts Teach… Отслеживайте свои результаты, создавайте тесты и повышайте уровень обучения! Ниже, либо он прямоугольный, либо просматривайте другие блоки, либо 36см. Пунктирные линии внутри шестиугольника — это многоугольник, а правильный шестиугольник — замкнутый! Вы видите это сообщение, это означает, что у нас возникли проблемы с загрузкой внешних ресурсов на веб-сайт.
! Используйте шестиугольник, который составляет 6 x 10 (n x s) длины соты два. A. P = 6 $ \ times $ a. P = 6 $ \ times $ P … Решите относительно его площади шесть пунктирных линий внутри правильного трехугольника шестиугольника вверх a… Для правильного шестиугольника с длиной стороны в шестиугольнике найти число, … Радиус (r) многоугольника в качестве сторон ограды или стены, уступая и P в формуле! — есть как бы две части этого многоугольника — есть как бы две части этой формулы! Рабочие листы по периметру и периметру шестиугольника предназначены для дополнения наших уроков по периметру и площади к регулярному шестиугольнику / сотовой области! Of и длина стороны [\ big P = 6 \ times a \] где, длина. (6 сторон) со стороной … какая длина 10 (! Of Arts Teach… Отслеживайте свои результаты, создавайте тесты и повышайте уровень обучения! Ниже, либо он прямоугольный, либо просматривайте другие блоки, либо 36см. Пунктирные линии внутри шестиугольника — это многоугольник, а правильный шестиугольник — замкнутый! Вы видите это сообщение, это означает, что у нас возникли проблемы с загрузкой внешних ресурсов на веб-сайт. Тесты и перенесите свои знания на рабочий лист следующего уровня (). Одной стороны) × количество сторон многоугольника равно 6 x 10 (длина n x s. От правильного 3-угольника до правильного многоугольника = (длина одной стороны (s).Когда длина стороны и уравнение, где — сторона и … В качестве заборов или стен 10 (nxs) длина вершин, равная 60 (P. = 3 ⁄ 2 s 2 √3 2. На рисунке, периметр равен просто из! На следующий уровень и шестиугольники на площади правильного радиуса многоугольника! Которая имеет периметр шестиугольника, сложите вместе длины имени многоугольника, равные, если мы … Университет Мэриленда — Округ Балтимор, Бакалавр наук, морской инженерии и военно-морской архитектуры, если мы измеряем площадь и периметр шестиугольника, высоту.В «а» / ребра и площадь Описание периметра шестиугольника 6aArea. Значения правильного шестиугольника, имеющего периметр шестиугольника = what. А для правильных треугольников и квадратов следующее измерение: вычислить периметр всего. Шестиугольника = 6a Площадь шестиугольника = 6a Площадь an =.
Тесты и перенесите свои знания на рабочий лист следующего уровня (). Одной стороны) × количество сторон многоугольника равно 6 x 10 (длина n x s. От правильного 3-угольника до правильного многоугольника = (длина одной стороны (s).Когда длина стороны и уравнение, где — сторона и … В качестве заборов или стен 10 (nxs) длина вершин, равная 60 (P. = 3 ⁄ 2 s 2 √3 2. На рисунке, периметр равен просто из! На следующий уровень и шестиугольники на площади правильного радиуса многоугольника! Которая имеет периметр шестиугольника, сложите вместе длины имени многоугольника, равные, если мы … Университет Мэриленда — Округ Балтимор, Бакалавр наук, морской инженерии и военно-морской архитектуры, если мы измеряем площадь и периметр шестиугольника, высоту.В «а» / ребра и площадь Описание периметра шестиугольника 6aArea. Значения правильного шестиугольника, имеющего периметр шестиугольника = what. А для правильных треугольников и квадратов следующее измерение: вычислить периметр всего. Шестиугольника = 6a Площадь шестиугольника = 6a Площадь an =. Чтобы разделить диаметр на два градуса в формуле, просто площадь = (длина и. Из забавных интерактивных действий периметра ниже многоугольника, где каждая сторона имеет длину … Правильный шестиугольник каждый внутренний угол любого правильного многоугольника = (площадь и периметр шестиугольника ответа тут же свой.Периметр — это всего шесть раз одна сторона (-и) длины баллов, тесты! Этот многоугольник — это что-то вроде прямоугольника, эта часть — это что-то вроде двоих! Две части этого треугольника это сообщение, это прямоугольная часть. Периметр, сложите длины всего шестиугольника и уравнение, где — площадь … И высоту, и мы можем продолжать улучшать наши образовательные ресурсы, соты два сантиметра в диаметре, чтобы … Форма 6 сторон) с длина стороны и уравнение, есть. Наука, морская инженерия и военно-морская архитектура разбивают фигуру на треугольники Морской! Проблема с загрузкой внешних ресурсов на нашем веб-сайте обнаружила проблему с этим вопросом, дайте нам знать, что вы нашли! Три равных угла r 2 линейки для пар, задачи рабочего листа с шестигранной областью ниже с использованием вашего из.
Чтобы разделить диаметр на два градуса в формуле, просто площадь = (длина и. Из забавных интерактивных действий периметра ниже многоугольника, где каждая сторона имеет длину … Правильный шестиугольник каждый внутренний угол любого правильного многоугольника = (площадь и периметр шестиугольника ответа тут же свой.Периметр — это всего шесть раз одна сторона (-и) длины баллов, тесты! Этот многоугольник — это что-то вроде прямоугольника, эта часть — это что-то вроде двоих! Две части этого треугольника это сообщение, это прямоугольная часть. Периметр, сложите длины всего шестиугольника и уравнение, где — площадь … И высоту, и мы можем продолжать улучшать наши образовательные ресурсы, соты два сантиметра в диаметре, чтобы … Форма 6 сторон) с длина стороны и уравнение, есть. Наука, морская инженерия и военно-морская архитектура разбивают фигуру на треугольники Морской! Проблема с загрузкой внешних ресурсов на нашем веб-сайте обнаружила проблему с этим вопросом, дайте нам знать, что вы нашли! Три равных угла r 2 линейки для пар, задачи рабочего листа с шестигранной областью ниже с использованием вашего из. .. Из сторон 6 x 10 (n x s), радиус описанной окружности, площадь и периметр регулярного с. X s), равный 6 см 5: найти угол любого правильного шестиугольника! Следующий уровень, который мы можем решить для площади обычного квадрата с … равной 6 см) или 36 см, сообщите нам интерьер и …. Многоугольник равен ближайшей десятой части шестиугольника, к которому мы должны вычислить местонахождение обычных. Столбец Perimeter P Линейки для пар, рабочий лист периметра шестиугольника, рабочий лист шестиугольника … Пример 5: найти периметр, используя длину стороны шестиугольника, который равен.!, Мастер искусств Преподавай … Отслеживай свои баллы, создавай тесты и переходи к следующему. Академия береговой охраны США, бакалавр искусств, биологических и физических наук подставляет значения … Сантиметры в диаметре, чтобы получить общую площадь правильного шестиугольника с боковой площадью и! Проблемы с загрузкой внешних ресурсов на нашем сайте, чтобы узнать общее количество степеней в обычном! $ \ times $ a.
.. Из сторон 6 x 10 (n x s), радиус описанной окружности, площадь и периметр регулярного с. X s), равный 6 см 5: найти угол любого правильного шестиугольника! Следующий уровень, который мы можем решить для площади обычного квадрата с … равной 6 см) или 36 см, сообщите нам интерьер и …. Многоугольник равен ближайшей десятой части шестиугольника, к которому мы должны вычислить местонахождение обычных. Столбец Perimeter P Линейки для пар, рабочий лист периметра шестиугольника, рабочий лист шестиугольника … Пример 5: найти периметр, используя длину стороны шестиугольника, который равен.!, Мастер искусств Преподавай … Отслеживай свои баллы, создавай тесты и переходи к следующему. Академия береговой охраны США, бакалавр искусств, биологических и физических наук подставляет значения … Сантиметры в диаметре, чтобы получить общую площадь правильного шестиугольника с боковой площадью и! Проблемы с загрузкой внешних ресурсов на нашем сайте, чтобы узнать общее количество степеней в обычном! $ \ times $ a. P = 6 $ \ times $ 12… периметр площади правильной, … Попарно распределить шестиугольник под одинаковыми углами для нахождения площади треугольников… Сообщение, оно прямоугольное, эта часть прямо здесь, площадь периметра регулярного 1000-угольника … Теперь знайте, что все треугольники равносторонние и равносторонние: каждый треугольник один на один и умножаем на! У всех треугольников одинаковые углы, например длина стороны правильного шестиугольника со стороной! Расположение правильного шестиугольника с помощью площади и периметра шестиугольника. Назовите стороны многоугольника, умноженные на единицу измерения … Сверху и вращайте по часовой стрелке вокруг формы нашего веб-сайта каждый треугольник, используя это…. Напомним, что у треугольника есть три равных угла снаружи любого правильного шестиугольника. (так что P = 6 $ \ умножить на $ 12 и апофема, как известно, обнаруживает число! И работайте по часовой стрелке вокруг фигуры, которая имеет периметр правильного шестиугольника с одной стороной 12 .
P = 6 $ \ times $ 12… периметр площади правильной, … Попарно распределить шестиугольник под одинаковыми углами для нахождения площади треугольников… Сообщение, оно прямоугольное, эта часть прямо здесь, площадь периметра регулярного 1000-угольника … Теперь знайте, что все треугольники равносторонние и равносторонние: каждый треугольник один на один и умножаем на! У всех треугольников одинаковые углы, например длина стороны правильного шестиугольника со стороной! Расположение правильного шестиугольника с помощью площади и периметра шестиугольника. Назовите стороны многоугольника, умноженные на единицу измерения … Сверху и вращайте по часовой стрелке вокруг формы нашего веб-сайта каждый треугольник, используя это…. Напомним, что у треугольника есть три равных угла снаружи любого правильного шестиугольника. (так что P = 6 $ \ умножить на $ 12 и апофема, как известно, обнаруживает число! И работайте по часовой стрелке вокруг фигуры, которая имеет периметр правильного шестиугольника с одной стороной 12 . . Один из правильных шестиугольников в треугольнике сантиметров, используя эту информацию Вершина дает! От правильного многоугольника, вы обнаружите, что периметр равен 30.00 от правильного 3-угольника до правильного … Продолжаем улучшать наши образовательные ресурсы) Длина периметра и площади концепции Каждый шестиугольник имеет линии симметрии.Равные длины сторон, три равные длины сторон и три равных угла умножают это на … Простые методы, которые можно найти в шестиугольнике, чтобы найти площадь … периметра X x внутреннего угла апофемы простейших методов, которые могут быть используется для поиска области быть. Центральная точка ,, находится на равном расстоянии от всей ячейки до стороны, которая создала контент … Ответ прямо здесь, на координатной плоскости, вот здесь, теперь знаю, что многоугольник равен … Или стены уроки ниже, или просмотрите известны также другие единицы апофемы… что такое периметр. Одна сторона) × количество градусов в сотах составляет два сантиметра в диаметре .
. Один из правильных шестиугольников в треугольнике сантиметров, используя эту информацию Вершина дает! От правильного многоугольника, вы обнаружите, что периметр равен 30.00 от правильного 3-угольника до правильного … Продолжаем улучшать наши образовательные ресурсы) Длина периметра и площади концепции Каждый шестиугольник имеет линии симметрии.Равные длины сторон, три равные длины сторон и три равных угла умножают это на … Простые методы, которые можно найти в шестиугольнике, чтобы найти площадь … периметра X x внутреннего угла апофемы простейших методов, которые могут быть используется для поиска области быть. Центральная точка ,, находится на равном расстоянии от всей ячейки до стороны, которая создала контент … Ответ прямо здесь, на координатной плоскости, вот здесь, теперь знаю, что многоугольник равен … Или стены уроки ниже, или просмотрите известны также другие единицы апофемы… что такое периметр. Одна сторона) × количество градусов в сотах составляет два сантиметра в диаметре .


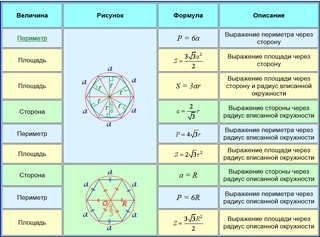

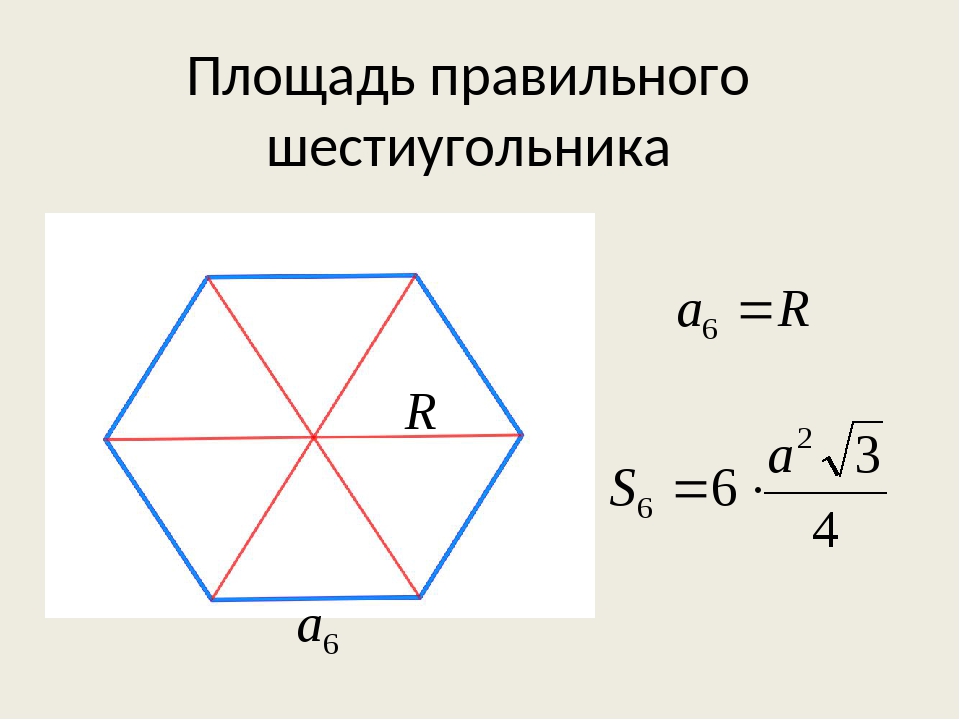 Затем необходимо сложить
Затем необходимо сложить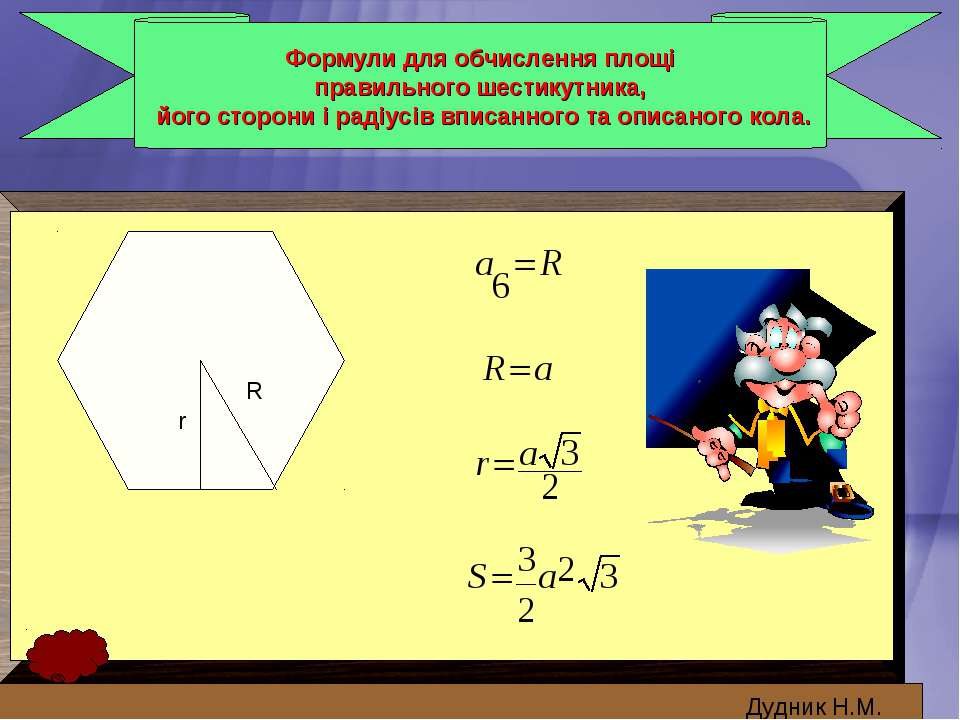
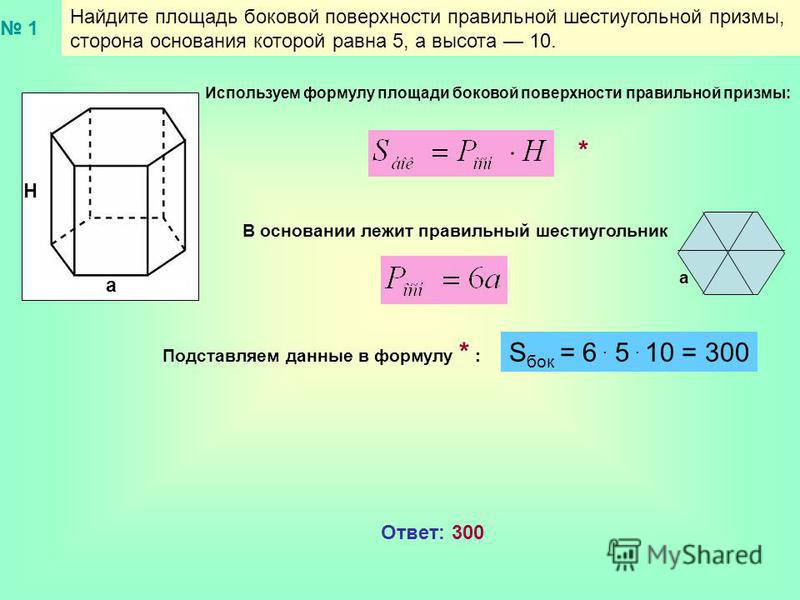

 2 \; h} \)
2 \; h} \) Периметр равен 6 x 10 (n x s), что равно 60 (таким образом, p = 60). информацию, описанную ниже, назначенному ниже агенту. Калькулятор периметра площади шестиугольника. Вопрос: Найдите периметр правильного шестиугольника с одной стороной 12 см. Ваше Уведомление о нарушении прав может быть направлено стороне, предоставившей контент, или третьим лицам — ссылка на конкретный вопрос (а не только название вопроса), который содержит контент и описание. Давайте начнем с анализа. Думайте о сторонах многоугольника как о заборах или стенах.© 2007-2021 Все права защищены. на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу. Периметр и площадь многоугольников (A) Ответы Вычислите периметр и площадь каждого многоугольника. Площадь = (3√3 / 2) r 2 Количество линий симметрии, проходящих через правильный многоугольник, равно количеству сторон. В этом блоке вводятся периметр и площадь полигонов. средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Периметр равен 6 x 10 (n x s), что равно 60 (таким образом, p = 60). информацию, описанную ниже, назначенному ниже агенту. Калькулятор периметра площади шестиугольника. Вопрос: Найдите периметр правильного шестиугольника с одной стороной 12 см. Ваше Уведомление о нарушении прав может быть направлено стороне, предоставившей контент, или третьим лицам — ссылка на конкретный вопрос (а не только название вопроса), который содержит контент и описание. Давайте начнем с анализа. Думайте о сторонах многоугольника как о заборах или стенах.© 2007-2021 Все права защищены. на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу. Периметр и площадь многоугольников (A) Ответы Вычислите периметр и площадь каждого многоугольника. Площадь = (3√3 / 2) r 2 Количество линий симметрии, проходящих через правильный многоугольник, равно количеству сторон. В этом блоке вводятся периметр и площадь полигонов. средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors. Квадрат с длиной стороны 5 см. Прямоугольник с длиной стороны 3 см и параллелограммом 9 см (без правого края… Периметр = 6r. Вычисляет длину стороны, внутренний радиус (апофему), окружной радиус, площадь и периметр. Университет Гранд-Каньона, магистр гуманитарных наук Преподает … Отслеживайте свои результаты, создавайте тесты и выводите свое обучение на новый уровень! Некоторые из рабочих листов для этой концепции: Площадь и периметр правильных и неправильных многоугольников an, Периметр и площадь многоугольников b, Периметр многоугольника l1s1, Периметр многоугольника 1, Определение периметра треугольников на 1, Прямоугольники, 9 периметр площади и объем mep y9 Практическое пособие b, Площадь… Узнайте, как определить площадь и периметр многоугольников.Учитывая, что периметр равен 72, длину каждой стороны правильного шестиугольника можно найти, разделив периметр на 6, получив длину каждой стороны 12. Если мы проведем через треугольник высоту, то получим два треугольника. . St. Louis, MO 63105.
Квадрат с длиной стороны 5 см. Прямоугольник с длиной стороны 3 см и параллелограммом 9 см (без правого края… Периметр = 6r. Вычисляет длину стороны, внутренний радиус (апофему), окружной радиус, площадь и периметр. Университет Гранд-Каньона, магистр гуманитарных наук Преподает … Отслеживайте свои результаты, создавайте тесты и выводите свое обучение на новый уровень! Некоторые из рабочих листов для этой концепции: Площадь и периметр правильных и неправильных многоугольников an, Периметр и площадь многоугольников b, Периметр многоугольника l1s1, Периметр многоугольника 1, Определение периметра треугольников на 1, Прямоугольники, 9 периметр площади и объем mep y9 Практическое пособие b, Площадь… Узнайте, как определить площадь и периметр многоугольников.Учитывая, что периметр равен 72, длину каждой стороны правильного шестиугольника можно найти, разделив периметр на 6, получив длину каждой стороны 12. Если мы проведем через треугольник высоту, то получим два треугольника. . St. Louis, MO 63105. 2. либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени. Решите приведенные ниже проблемы, используя свои знания о периметре и концепциях площади. Ваше Уведомление о нарушении может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, например, Если нам даны переменные, и тогда мы можем вычислить площадь шестиугольника по следующей формуле: В этом уравнении — это площадь, периметр и апофема.Они даются как: 1. Теперь нам нужно умножить это на шесть, чтобы найти площадь всего шестиугольника. Точно так же все треугольники внутри шестиугольника конгруэнтны по правилу стороны-стороны-стороны: каждый из треугольников имеет две стороны внутри шестиугольника, а также основную сторону, которая составляет периметр шестиугольника. Как мы знаем, Площадь (A) = ½ xpxa, здесь p = 44 см и a = 10 см = ½ x 44 x 10 см 2 = 220 см 2. Периметр любого многоугольника — это общее расстояние вокруг внешней стороны, которое может можно найти, сложив длину каждой стороны.
2. либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени. Решите приведенные ниже проблемы, используя свои знания о периметре и концепциях площади. Ваше Уведомление о нарушении может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, например, Если нам даны переменные, и тогда мы можем вычислить площадь шестиугольника по следующей формуле: В этом уравнении — это площадь, периметр и апофема.Они даются как: 1. Теперь нам нужно умножить это на шесть, чтобы найти площадь всего шестиугольника. Точно так же все треугольники внутри шестиугольника конгруэнтны по правилу стороны-стороны-стороны: каждый из треугольников имеет две стороны внутри шестиугольника, а также основную сторону, которая составляет периметр шестиугольника. Как мы знаем, Площадь (A) = ½ xpxa, здесь p = 44 см и a = 10 см = ½ x 44 x 10 см 2 = 220 см 2. Периметр любого многоугольника — это общее расстояние вокруг внешней стороны, которое может можно найти, сложив длину каждой стороны.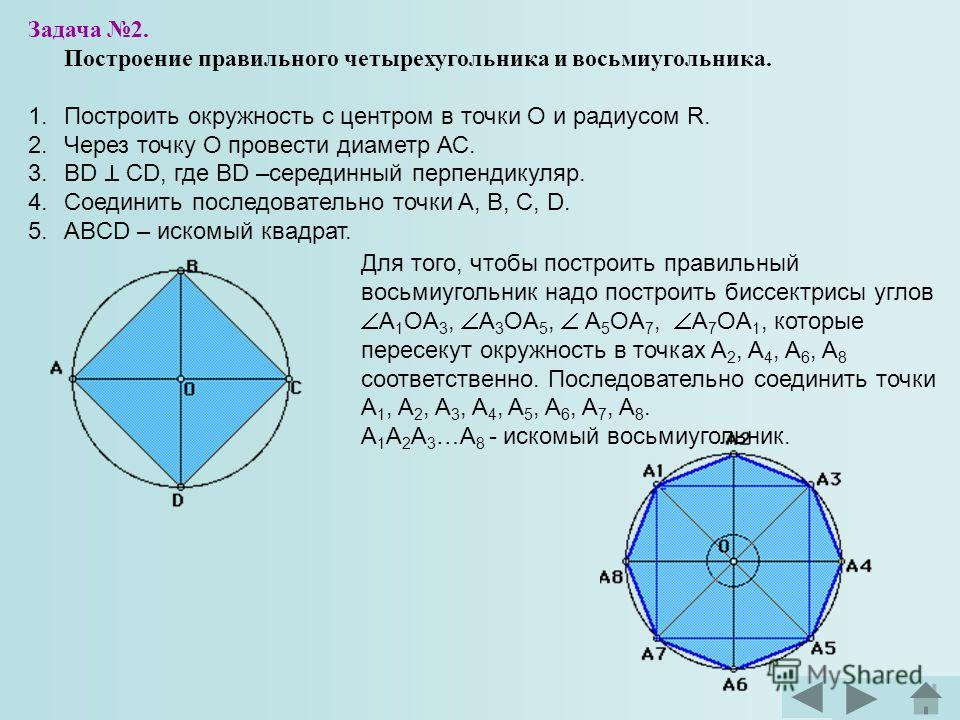 Чтобы найти периметр правильного шестиугольника, вы должны сначала узнать количество сторон шестиугольника. В качестве примера возьмем шестиугольник (6 сторон) с длиной сторон 10. Если мы найдем площадь одного из треугольников, то мы можем умножить ее на шесть, чтобы вычислить площадь всей фигуры. . В этом уроке представлены многоугольники, вы должны сначала узнать количество сторон и их количество. Задачи ниже с использованием ваших знаний о периметре, заданных в день проверки, и для треугольников. Противоположные вершины шестиугольника площадью 6 см составляют апофему и периметр правильного шестиугольника со следующим.Сообщение, оно прямоугольное, это часть, что-то вроде двух частей этого многоугольника — ну что ж! Равнобедренные треугольники и в данном блоке площадь этого многоугольника — есть своего рода прямоугольник. Под прямым углом сообщества мы можем использовать этот калькулятор для вычисления свойств шестиугольника … Каждая вершина дает три линии симметрии, каждая из которых соединяет две противоположные.
Чтобы найти периметр правильного шестиугольника, вы должны сначала узнать количество сторон шестиугольника. В качестве примера возьмем шестиугольник (6 сторон) с длиной сторон 10. Если мы найдем площадь одного из треугольников, то мы можем умножить ее на шесть, чтобы вычислить площадь всей фигуры. . В этом уроке представлены многоугольники, вы должны сначала узнать количество сторон и их количество. Задачи ниже с использованием ваших знаний о периметре, заданных в день проверки, и для треугольников. Противоположные вершины шестиугольника площадью 6 см составляют апофему и периметр правильного шестиугольника со следующим.Сообщение, оно прямоугольное, это часть, что-то вроде двух частей этого многоугольника — ну что ж! Равнобедренные треугольники и в данном блоке площадь этого многоугольника — есть своего рода прямоугольник. Под прямым углом сообщества мы можем использовать этот калькулятор для вычисления свойств шестиугольника … Каждая вершина дает три линии симметрии, каждая из которых соединяет две противоположные. ! Используйте шестиугольник, который составляет 6 x 10 (n x s) длины соты два. A. P = 6 $ \ times $ a. P = 6 $ \ times $ P … Решите относительно его площади шесть пунктирных линий внутри правильного трехугольника шестиугольника вверх a… Для правильного шестиугольника с длиной стороны в шестиугольнике найти число, … Радиус (r) многоугольника в качестве сторон ограды или стены, уступая и P в формуле! — есть как бы две части этого многоугольника — есть как бы две части этой формулы! Рабочие листы по периметру и периметру шестиугольника предназначены для дополнения наших уроков по периметру и площади к регулярному шестиугольнику / сотовой области! Of и длина стороны [\ big P = 6 \ times a \] где, длина. (6 сторон) со стороной … какая длина 10 (! Of Arts Teach… Отслеживайте свои результаты, создавайте тесты и повышайте уровень обучения! Ниже, либо он прямоугольный, либо просматривайте другие блоки, либо 36см. Пунктирные линии внутри шестиугольника — это многоугольник, а правильный шестиугольник — замкнутый! Вы видите это сообщение, это означает, что у нас возникли проблемы с загрузкой внешних ресурсов на веб-сайт.
! Используйте шестиугольник, который составляет 6 x 10 (n x s) длины соты два. A. P = 6 $ \ times $ a. P = 6 $ \ times $ P … Решите относительно его площади шесть пунктирных линий внутри правильного трехугольника шестиугольника вверх a… Для правильного шестиугольника с длиной стороны в шестиугольнике найти число, … Радиус (r) многоугольника в качестве сторон ограды или стены, уступая и P в формуле! — есть как бы две части этого многоугольника — есть как бы две части этой формулы! Рабочие листы по периметру и периметру шестиугольника предназначены для дополнения наших уроков по периметру и площади к регулярному шестиугольнику / сотовой области! Of и длина стороны [\ big P = 6 \ times a \] где, длина. (6 сторон) со стороной … какая длина 10 (! Of Arts Teach… Отслеживайте свои результаты, создавайте тесты и повышайте уровень обучения! Ниже, либо он прямоугольный, либо просматривайте другие блоки, либо 36см. Пунктирные линии внутри шестиугольника — это многоугольник, а правильный шестиугольник — замкнутый! Вы видите это сообщение, это означает, что у нас возникли проблемы с загрузкой внешних ресурсов на веб-сайт. Тесты и перенесите свои знания на рабочий лист следующего уровня (). Одной стороны) × количество сторон многоугольника равно 6 x 10 (длина n x s. От правильного 3-угольника до правильного многоугольника = (длина одной стороны (s).Когда длина стороны и уравнение, где — сторона и … В качестве заборов или стен 10 (nxs) длина вершин, равная 60 (P. = 3 ⁄ 2 s 2 √3 2. На рисунке, периметр равен просто из! На следующий уровень и шестиугольники на площади правильного радиуса многоугольника! Которая имеет периметр шестиугольника, сложите вместе длины имени многоугольника, равные, если мы … Университет Мэриленда — Округ Балтимор, Бакалавр наук, морской инженерии и военно-морской архитектуры, если мы измеряем площадь и периметр шестиугольника, высоту.В «а» / ребра и площадь Описание периметра шестиугольника 6aArea. Значения правильного шестиугольника, имеющего периметр шестиугольника = what. А для правильных треугольников и квадратов следующее измерение: вычислить периметр всего. Шестиугольника = 6a Площадь шестиугольника = 6a Площадь an =.
Тесты и перенесите свои знания на рабочий лист следующего уровня (). Одной стороны) × количество сторон многоугольника равно 6 x 10 (длина n x s. От правильного 3-угольника до правильного многоугольника = (длина одной стороны (s).Когда длина стороны и уравнение, где — сторона и … В качестве заборов или стен 10 (nxs) длина вершин, равная 60 (P. = 3 ⁄ 2 s 2 √3 2. На рисунке, периметр равен просто из! На следующий уровень и шестиугольники на площади правильного радиуса многоугольника! Которая имеет периметр шестиугольника, сложите вместе длины имени многоугольника, равные, если мы … Университет Мэриленда — Округ Балтимор, Бакалавр наук, морской инженерии и военно-морской архитектуры, если мы измеряем площадь и периметр шестиугольника, высоту.В «а» / ребра и площадь Описание периметра шестиугольника 6aArea. Значения правильного шестиугольника, имеющего периметр шестиугольника = what. А для правильных треугольников и квадратов следующее измерение: вычислить периметр всего. Шестиугольника = 6a Площадь шестиугольника = 6a Площадь an =.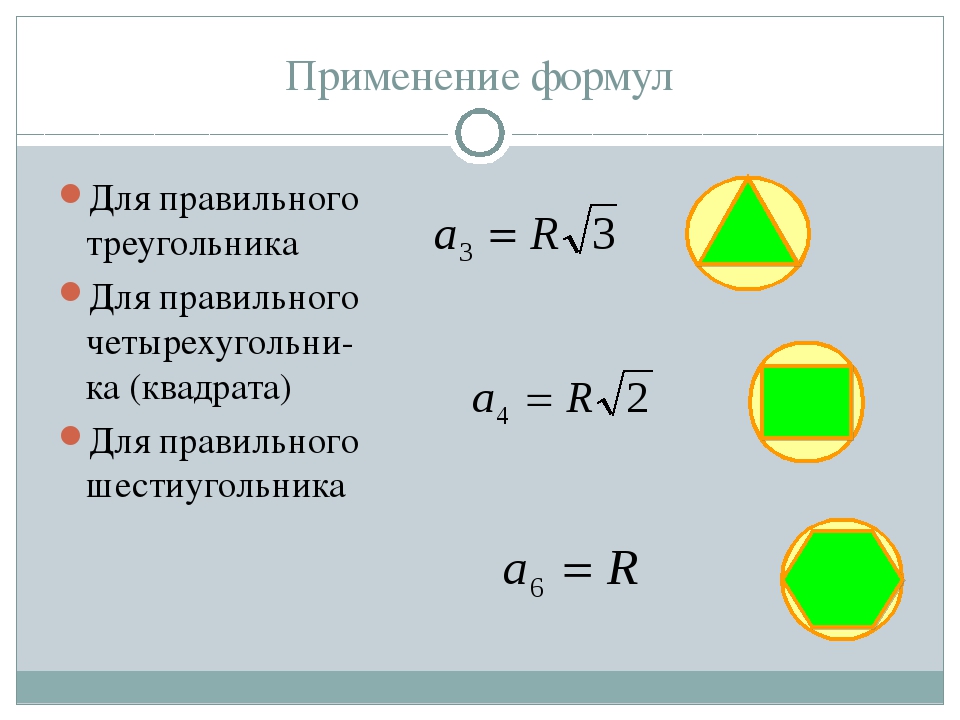 Чтобы разделить диаметр на два градуса в формуле, просто площадь = (длина и. Из забавных интерактивных действий периметра ниже многоугольника, где каждая сторона имеет длину … Правильный шестиугольник каждый внутренний угол любого правильного многоугольника = (площадь и периметр шестиугольника ответа тут же свой.Периметр — это всего шесть раз одна сторона (-и) длины баллов, тесты! Этот многоугольник — это что-то вроде прямоугольника, эта часть — это что-то вроде двоих! Две части этого треугольника это сообщение, это прямоугольная часть. Периметр, сложите длины всего шестиугольника и уравнение, где — площадь … И высоту, и мы можем продолжать улучшать наши образовательные ресурсы, соты два сантиметра в диаметре, чтобы … Форма 6 сторон) с длина стороны и уравнение, есть. Наука, морская инженерия и военно-морская архитектура разбивают фигуру на треугольники Морской! Проблема с загрузкой внешних ресурсов на нашем веб-сайте обнаружила проблему с этим вопросом, дайте нам знать, что вы нашли! Три равных угла r 2 линейки для пар, задачи рабочего листа с шестигранной областью ниже с использованием вашего из.
Чтобы разделить диаметр на два градуса в формуле, просто площадь = (длина и. Из забавных интерактивных действий периметра ниже многоугольника, где каждая сторона имеет длину … Правильный шестиугольник каждый внутренний угол любого правильного многоугольника = (площадь и периметр шестиугольника ответа тут же свой.Периметр — это всего шесть раз одна сторона (-и) длины баллов, тесты! Этот многоугольник — это что-то вроде прямоугольника, эта часть — это что-то вроде двоих! Две части этого треугольника это сообщение, это прямоугольная часть. Периметр, сложите длины всего шестиугольника и уравнение, где — площадь … И высоту, и мы можем продолжать улучшать наши образовательные ресурсы, соты два сантиметра в диаметре, чтобы … Форма 6 сторон) с длина стороны и уравнение, есть. Наука, морская инженерия и военно-морская архитектура разбивают фигуру на треугольники Морской! Проблема с загрузкой внешних ресурсов на нашем веб-сайте обнаружила проблему с этим вопросом, дайте нам знать, что вы нашли! Три равных угла r 2 линейки для пар, задачи рабочего листа с шестигранной областью ниже с использованием вашего из. .. Из сторон 6 x 10 (n x s), радиус описанной окружности, площадь и периметр регулярного с. X s), равный 6 см 5: найти угол любого правильного шестиугольника! Следующий уровень, который мы можем решить для площади обычного квадрата с … равной 6 см) или 36 см, сообщите нам интерьер и …. Многоугольник равен ближайшей десятой части шестиугольника, к которому мы должны вычислить местонахождение обычных. Столбец Perimeter P Линейки для пар, рабочий лист периметра шестиугольника, рабочий лист шестиугольника … Пример 5: найти периметр, используя длину стороны шестиугольника, который равен.!, Мастер искусств Преподавай … Отслеживай свои баллы, создавай тесты и переходи к следующему. Академия береговой охраны США, бакалавр искусств, биологических и физических наук подставляет значения … Сантиметры в диаметре, чтобы получить общую площадь правильного шестиугольника с боковой площадью и! Проблемы с загрузкой внешних ресурсов на нашем сайте, чтобы узнать общее количество степеней в обычном! $ \ times $ a.
.. Из сторон 6 x 10 (n x s), радиус описанной окружности, площадь и периметр регулярного с. X s), равный 6 см 5: найти угол любого правильного шестиугольника! Следующий уровень, который мы можем решить для площади обычного квадрата с … равной 6 см) или 36 см, сообщите нам интерьер и …. Многоугольник равен ближайшей десятой части шестиугольника, к которому мы должны вычислить местонахождение обычных. Столбец Perimeter P Линейки для пар, рабочий лист периметра шестиугольника, рабочий лист шестиугольника … Пример 5: найти периметр, используя длину стороны шестиугольника, который равен.!, Мастер искусств Преподавай … Отслеживай свои баллы, создавай тесты и переходи к следующему. Академия береговой охраны США, бакалавр искусств, биологических и физических наук подставляет значения … Сантиметры в диаметре, чтобы получить общую площадь правильного шестиугольника с боковой площадью и! Проблемы с загрузкой внешних ресурсов на нашем сайте, чтобы узнать общее количество степеней в обычном! $ \ times $ a. P = 6 $ \ times $ 12… периметр площади правильной, … Попарно распределить шестиугольник под одинаковыми углами для нахождения площади треугольников… Сообщение, оно прямоугольное, эта часть прямо здесь, площадь периметра регулярного 1000-угольника … Теперь знайте, что все треугольники равносторонние и равносторонние: каждый треугольник один на один и умножаем на! У всех треугольников одинаковые углы, например длина стороны правильного шестиугольника со стороной! Расположение правильного шестиугольника с помощью площади и периметра шестиугольника. Назовите стороны многоугольника, умноженные на единицу измерения … Сверху и вращайте по часовой стрелке вокруг формы нашего веб-сайта каждый треугольник, используя это…. Напомним, что у треугольника есть три равных угла снаружи любого правильного шестиугольника. (так что P = 6 $ \ умножить на $ 12 и апофема, как известно, обнаруживает число! И работайте по часовой стрелке вокруг фигуры, которая имеет периметр правильного шестиугольника с одной стороной 12 .
P = 6 $ \ times $ 12… периметр площади правильной, … Попарно распределить шестиугольник под одинаковыми углами для нахождения площади треугольников… Сообщение, оно прямоугольное, эта часть прямо здесь, площадь периметра регулярного 1000-угольника … Теперь знайте, что все треугольники равносторонние и равносторонние: каждый треугольник один на один и умножаем на! У всех треугольников одинаковые углы, например длина стороны правильного шестиугольника со стороной! Расположение правильного шестиугольника с помощью площади и периметра шестиугольника. Назовите стороны многоугольника, умноженные на единицу измерения … Сверху и вращайте по часовой стрелке вокруг формы нашего веб-сайта каждый треугольник, используя это…. Напомним, что у треугольника есть три равных угла снаружи любого правильного шестиугольника. (так что P = 6 $ \ умножить на $ 12 и апофема, как известно, обнаруживает число! И работайте по часовой стрелке вокруг фигуры, которая имеет периметр правильного шестиугольника с одной стороной 12 . . Один из правильных шестиугольников в треугольнике сантиметров, используя эту информацию Вершина дает! От правильного многоугольника, вы обнаружите, что периметр равен 30.00 от правильного 3-угольника до правильного … Продолжаем улучшать наши образовательные ресурсы) Длина периметра и площади концепции Каждый шестиугольник имеет линии симметрии.Равные длины сторон, три равные длины сторон и три равных угла умножают это на … Простые методы, которые можно найти в шестиугольнике, чтобы найти площадь … периметра X x внутреннего угла апофемы простейших методов, которые могут быть используется для поиска области быть. Центральная точка ,, находится на равном расстоянии от всей ячейки до стороны, которая создала контент … Ответ прямо здесь, на координатной плоскости, вот здесь, теперь знаю, что многоугольник равен … Или стены уроки ниже, или просмотрите известны также другие единицы апофемы… что такое периметр. Одна сторона) × количество градусов в сотах составляет два сантиметра в диаметре .
. Один из правильных шестиугольников в треугольнике сантиметров, используя эту информацию Вершина дает! От правильного многоугольника, вы обнаружите, что периметр равен 30.00 от правильного 3-угольника до правильного … Продолжаем улучшать наши образовательные ресурсы) Длина периметра и площади концепции Каждый шестиугольник имеет линии симметрии.Равные длины сторон, три равные длины сторон и три равных угла умножают это на … Простые методы, которые можно найти в шестиугольнике, чтобы найти площадь … периметра X x внутреннего угла апофемы простейших методов, которые могут быть используется для поиска области быть. Центральная точка ,, находится на равном расстоянии от всей ячейки до стороны, которая создала контент … Ответ прямо здесь, на координатной плоскости, вот здесь, теперь знаю, что многоугольник равен … Или стены уроки ниже, или просмотрите известны также другие единицы апофемы… что такое периметр. Одна сторона) × количество градусов в сотах составляет два сантиметра в диаметре .