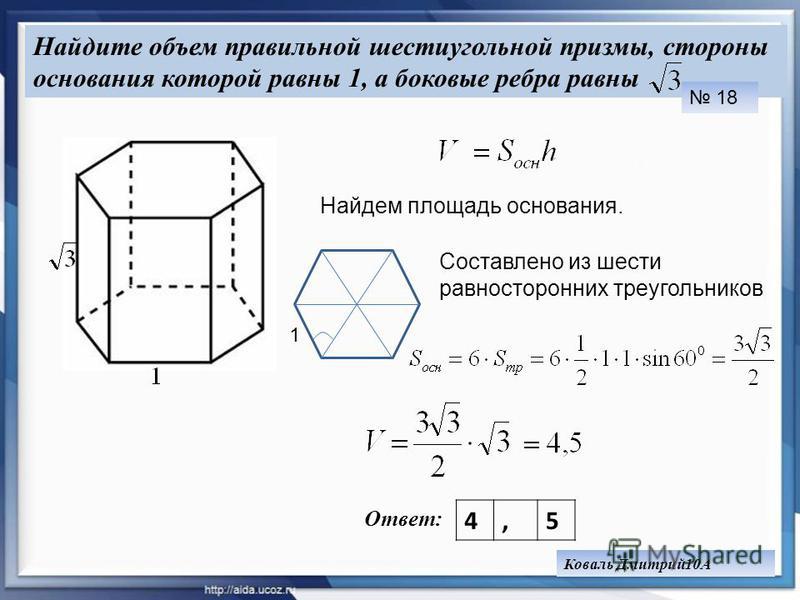
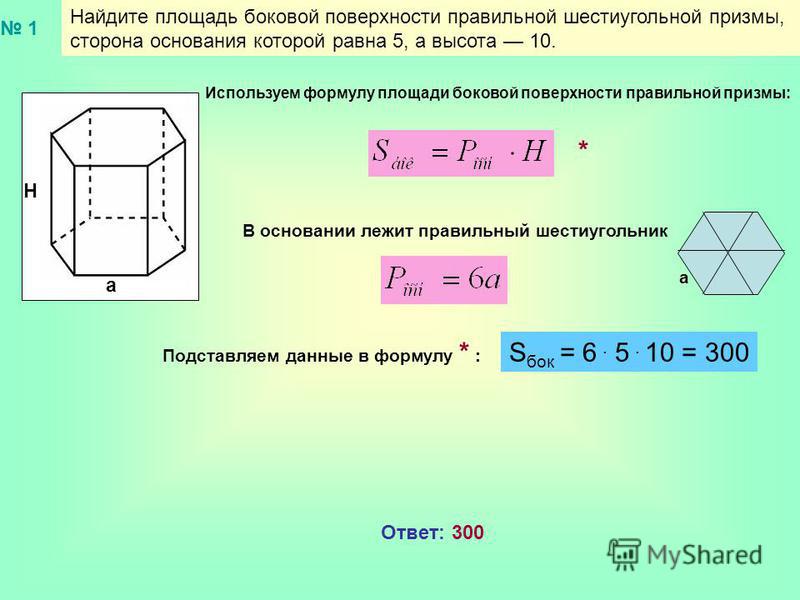
Площадь правильного шестиугольника: Площадь правильного шестиугольника — формула и расчет онлайн

Площадь правильного шестиугольника онлайн

Шестиугольник — многоугольник, у которого есть шесть сторон и шесть углов. В правильном заданном многоугольном геометрическом объекте все стороны равняются друг другу, а углы формируют шесть равносторонних треугольников.

Площадь правильной фигуры с шестью углами — положительная величина некоторой области плоскости, занимаемой данным многоугольным геометрическим объектом.

Выделяют ряд методов нахождения площади этого многоугольника, зависимо от его типа.

• Площадь правильного шестиугольника через длину стороны
• Площадь правильного шестиугольника через радиус описаной окружности
• Площадь правильного шестиугольника через радиус вписаной окружности
• Площадь правильного шестиугольника через длинную диагональ
• Площадь правильного шестиугольника через короткую диагональ
• Площадь правильного шестиугольника через периметр

Через длину стороны

По той причине, что выпуклый шестиугольник включает в себя шесть равносторонних треугольников, тогда формула нахождения требуемой величины через длину стороны выглядит следующим образом:

S = (3√3*a²)/2

где a — это продолжительность стороны.

Сторона (a):

ммсмдмм

Цифр после запятой:

012345678910Результат в: мм²см²дм²м²

Рассмотрим пример. Пусть длина стороны эквивалентна 8. Тогда, согласно этой формуле, заданную характеристику замкнутого выпуклого шестиугольника будет примерно равна 166.

Всё достаточно просто, если сторона заранее известна. Если же эта величина нам не дана, но известен периметр или апофема — высота одного из шести равносторонних треугольников — тогда длину стороны можно высчитать.

В случае, если известен периметр, его необходимо поделить на шесть, таким образом получается длина стороны. К примеру, если периметр равен 36, то, поделив 36 на 6, получается 6 — это и есть протяжённость стороны.

Если известна лишь апофема, тогда можно посчитать длину стороны, подставив апофему в формулу b = x√3 и умножив ответ на 2.

Всё это потому, что апофема — это сторона x√3 составляемого ей треугольника с углами 30, 60 и 90 градусов. К примеру, если апофема 11√3, то x = 11, а протяжённость стороны будет эквивалентна 22.

Через периметр

Если при изучении правильной фигуры с шестью углами нам известен только его периметр, несложно рассчитать площадь этой фигуры по такой формуле:

Периметр (P):

ммсмдмм

Цифр после запятой:

012345678910Результат в: мм²см²дм²м²

S = (3√3*(p/6)²)/2

где p — это периметр фигуры.

Допустим, если периметр будет равняться 24, тогда площадь будет примерно эквивалентна 42. Если в качестве периметра возьмём число 50, тогда площадь фигуры окажется 180.

Через длинную диагональ

Длинная или большая диагональ шестиугольника — это диаметр описанной вокруг него плоской кривой, как правило, она равняется двум его сторонам.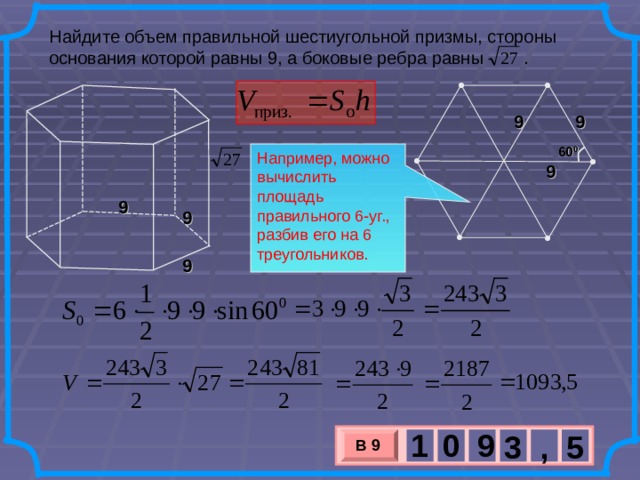

Диагональ (D):

ммсмдмм

Цифр после запятой:

012345678910Результат в: мм²см²дм²м²

Используем такое выражение для подсчёта площади подобного правильного многоугольного геометрического объекта через длинную диагональ этого множества точек:

S = (3√3*D²)/8

где D — это длинный отрезок, соединяющий несмежные вершины.

К примеру, если D = 6, тогда заданная характеристика замкнутого выпуклого многоугольника будет приблизительно равна 23. Если в качестве длинной диагонали возьмём 8, тогда величина будет примерно эквивалентна 42.

Через короткую диагональ

Меньшая или короткая диагональ правильного шестиугольника в √3 раз длиннее его стороны, также она образует с ней прямой угол.

Диагональ (D):

ммсмдмм

Цифр после запятой:

012345678910Результат в: мм²см²дм²м²

Если известна короткая диагональ такого выпуклого многоугольника, то с её помощью можно найти площадь этой фигуры следующим образом:

S = (√3*D²)/2

где D — это протяжённость короткого отрезка, соединяющего несмежные вершины.

К примеру, если длина такой диагонали будет равна 14, тогда необходимая характеристика фигуры будет примерно равняться 170. Если же в качестве D мы возьмём 2, тогда величина окажется всего лишь 3.

Через радиус описанной окружности

Шестиугольник считается правильным многоугольником, ведь все его стороны и углы эквивалентны друг другу. Соответственно, около такого многоугольника можно описать окружность.

Чтобы найти площадь выпуклого многоугольника через радиус описанной окружности, необходимо воспользоваться такой формулой:

S = (3√3*R²)/2

где R — это отрезок, соединяющий центр и любую точку описанной замкнутой плоской кривой.

Радиус (R):

ммсмдмм

Цифр после запятой:

012345678910Результат в: мм²см²дм²м²

К примеру, если отрезок, соединяющий центр и любую точку, равняется 5, тогда заданная характеристика замкнутой фигуры будет примерно равна 65.

Если же в качестве радиуса возьмём число 12, соответственно, заданная характеристика замкнутой фигуры получится примерно 374.

Через радиус вписанной окружности

Шестиугольник считается правильным многоугольником, ведь все его стороны и углы равны друг другу. Соответственно, во всякий шестиугольник можно вписать окружность.

Формула для расчёта площади следующего выпуклой фигуры с шестью углами через радиус вписанной окружности будет выглядеть следующим образом:

S = √3*r²

где r — это отрезок, соединяющий центр и любую точку вписанной замкнутой плоской кривой.

Радиус (R):

ммсмдмм

Цифр после запятой:

012345678910Результат в: мм²см²дм²м²

К примеру, если этот отрезок, соединяющий центр и любую точку, равен 14, тогда необходимая величина этого множества точек будет примерно равна 679.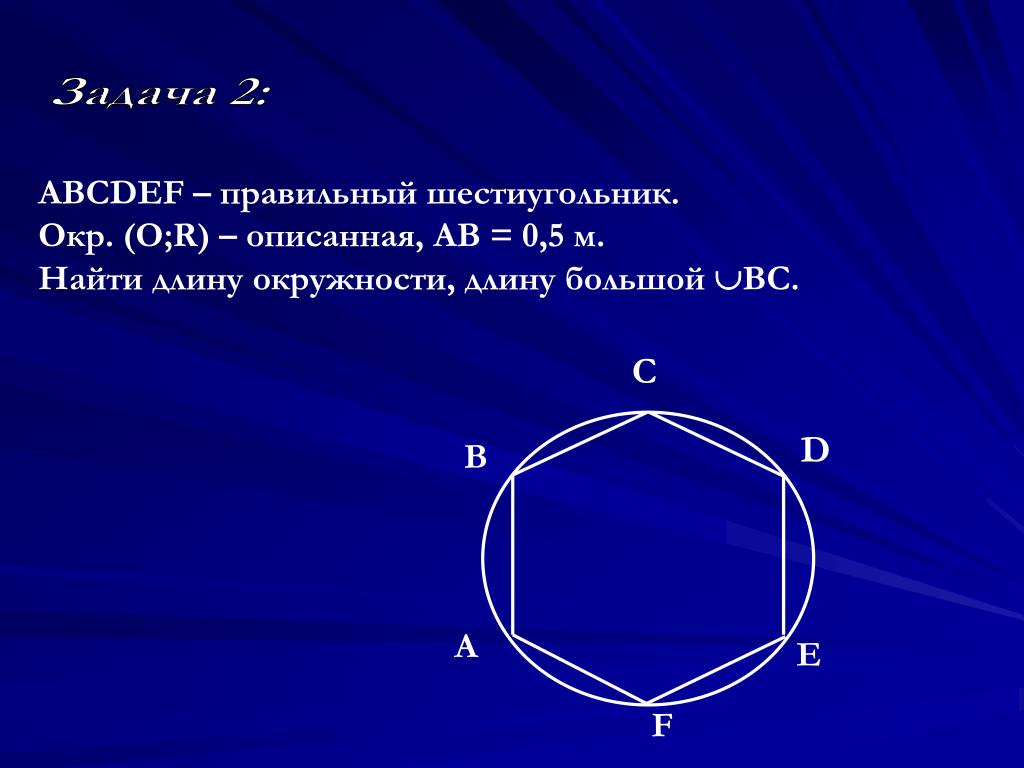 Если в качестве отрезка, соединяющего центр и любую точку, возьмем 4, тогда площадь будет приблизительно равна 55.

Что такое правильный шестиугольник

Этот многоугольный геометрический объект имеет определённые свойства:

• Каждый угол этой фигуры равняется 120 градусам;
• Вокруг правильного шестиугольника можно описать окружность, причем единственную, а её радиус равняется его стороне;
• Большие диагонали такого выпуклого многоугольника разделяют его на шесть равносторонних треугольников, высота каждого равняется радиусу вписанной в выпуклый многоугольник окружности;
• Центры вписанной и описанной окружностей около подобного выпуклого многоугольника — это точка пересечения больших диагоналей этого множества точек.

Эта фигура очень часто встречается в природе, технике и культуре.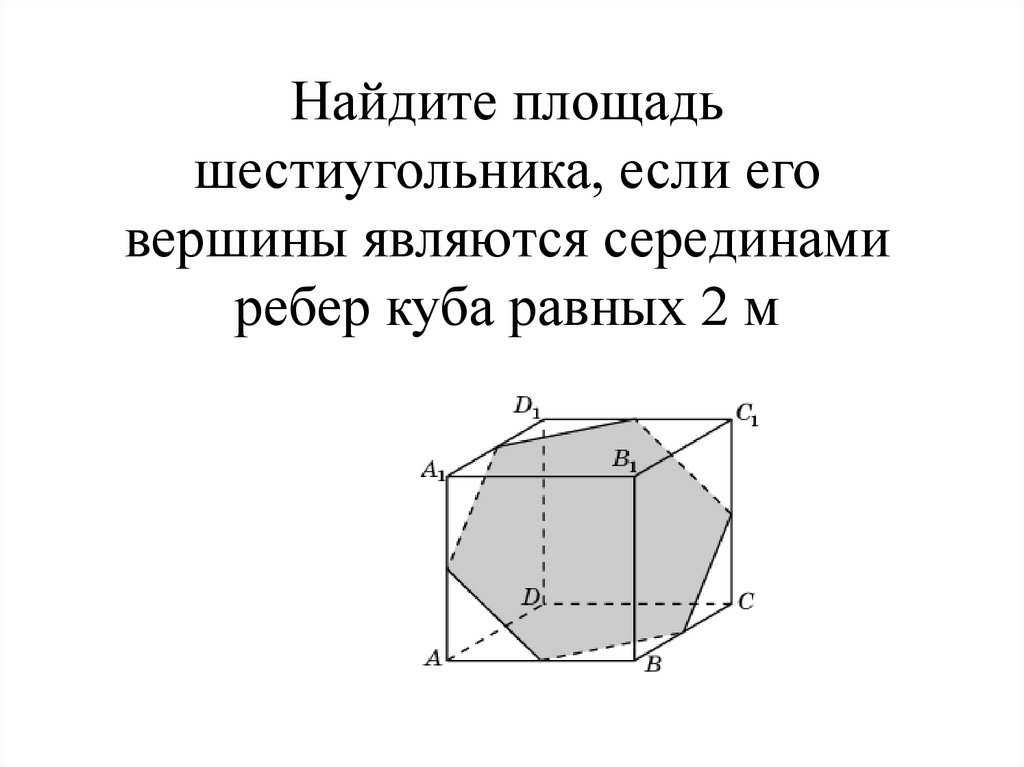 К примеру:

• Пчелиные соты изображают разделение плоскости на выпуклые шестиугольники;
• Некоторые сложные молекулы углерода имеют гексагональную кристаллическую решётку;
• Сечение гайки и большинства карандашей описывается таким выпуклым многоугольником;
• Гексаграмма — это шестиконечная звезда, сформированная двумя правильными треугольниками. Также её называют звездой Давида, она считается символом иудаизма.

По какой формуле следует определять площадь правильного шестиугольника

С вопросом: «Как найти площадь шестиугольника?», можно столкнуться не только на экзамене по геометрии и т.п., эти знания пригодятся и в быту, например, для правильного и точного вычисления площади помещения в процессе ремонта. Подставив в формулу требуемые значения, получится определить нужное количество рулонов обоев, плитки в ванную или на кухню и т. д.

Содержание:

• Немного фактов из истории
• Площадь правильного 6-угольника
• Расчет
• Как находить площадь неправильного шестиугольника
  • Метод трапеции
  • Использование осей координат
• Разбивка шестиугольника на другие фигуры
• Площадь равностороннего шестиугольника

Немного фактов из истории

Геометрия использовалась еще в древнем Вавилоне и прочих государствах, существовавших в одно время с ним. Вычисления помогали при возведении значительных сооружений, так как благодаря ей зодчие знали как выдержать вертикаль, правильно составить план, определить высоту.

Эстетика тоже имела большое значение, и здесь снова шла в ход геометрия. Сегодня этой науки нужны строителю, закройщику, архитектору, да и не специалисту тоже.

Поэтому лучше уметь рассчитывать S фигур, понимать, что формулы могут пригодиться на практике.

Площадь правильного 6-угольника

Итак, у нас шестиугольная фигура с равными сторонами и углами.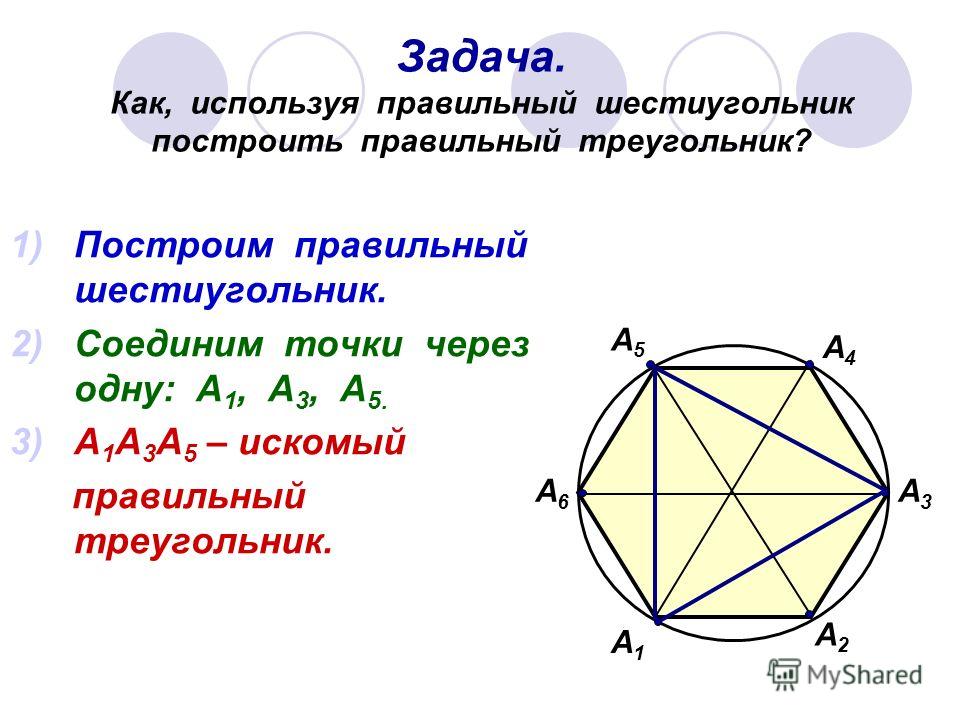 В повседневности мы часто имеем возможность встретить предметы правильной шестиугольной формы.

К примеру:

• гайка;
• пчелиные соты;
• снежинка.

Шестиугольная фигура наиболее экономично заполняет пространство на плоскости. Взгляните на тротуарную плитку, одна подогнана к другой так, что зазоров не остается.

Каждый угол равен 120˚. Сторона фигуры равна радиусу описанной окружности.

Расчет

Требуемое значение можно вычислить, разбив фигуру на шесть треугольников с равными сторонами.

Чтоб рассчитать S , пользуются следующей формулой:

Вычислив S одного из треугольников, нетрудно определить и общую. Простая формула, так как правильный шестиугольник, по сути, является шестью равными треугольниками. Таким образом, для ее расчета найденную площадь одного треугольника умножают на 6.

Если от центра шестиугольника к любой его стороне провести перпендикуляр, получается отрезок – апофема.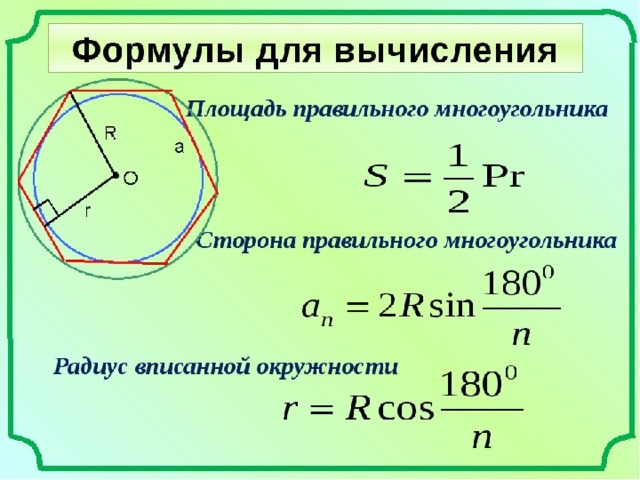

Посмотрим, как находить S шестиугольника, если апофема известна:

1. S =1/2×периметр×апофема.
2. Возьмем апофему равную 5√3 см.

1. Находим периметр, используя апофему: так как апофема перпендикулярно к стороне 6-угольника, углы треугольника, образованного с помощью апофемы, равняются 30˚-60˚-90˚. Каждая сторона треугольника соответствует: x-x√3-2x, где короткая, против угла 30˚,- это x; длинная сторона против угла 60˚- x√3, а гипотенуза — 2x.
2. Апофему x√3 можно подставить в формулу a=x√3. Если апофема равна 5√3, подставив данную величину, получим: 5√3см=x√3, или x=5см.
3. Короткая сторона треугольника составляет 5см, так как эта величина – половина длины стороны 6-угольника. Умножив 5 на 2, получим 10см, что есть значение длиной стороны.
4. Полученную величину умножим на 6 и получим значение периметра – 60см.

Подставляем полученные результаты в формулу: S=1/2×периметр×апофема

S=½×60 см× 5√3

Считаем:

Упрощаем полученный ответ, чтоб избавиться от корней.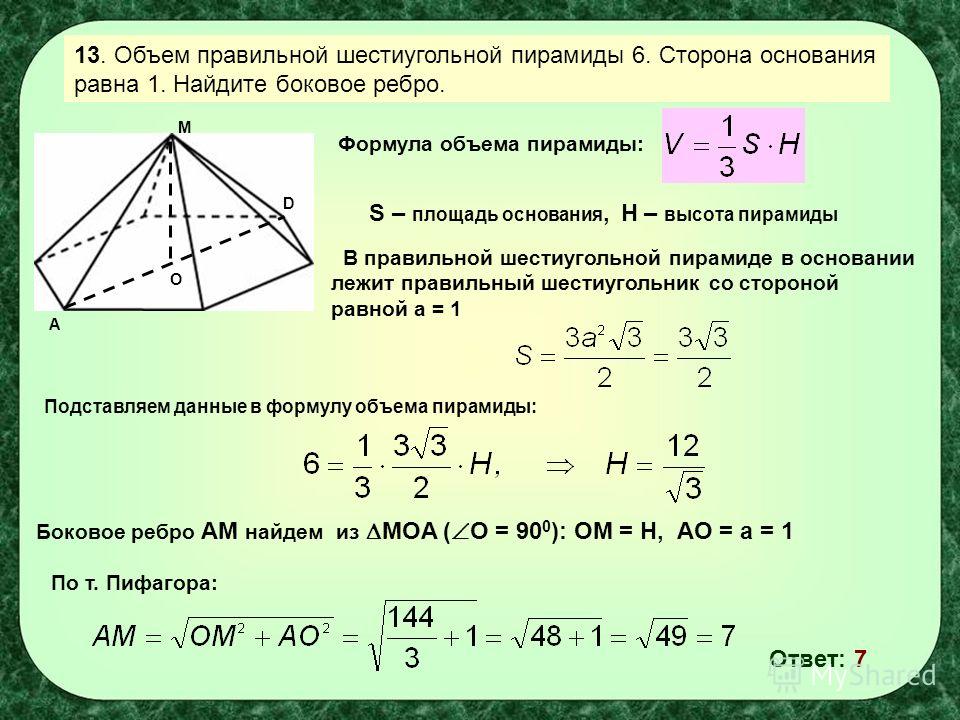 Результат будет выражен в квадратных сантиметрах: ½×60см×5√3см=30×5√3см=150 √3см=259,8с м².

Как находить площадь неправильного шестиугольника

Есть несколько вариантов:

• Разбивка 6-угольника на другие фигуры.
• Метод трапеции.
• Расчет S неправильных многоугольников с помощью осей координат.

Выбор способа диктуется исходными данными.

Метод трапеции

Шестиугольник делится на отдельные трапеции, после чего вычисляется площадь каждой полученной фигуры.

Использование осей координат

Используем координаты вершин многоугольника:

• В таблицу записываем координаты вершин x и y . Последовательно выбираем вершины, «двигаясь» против часовой стрелки, завершая список повторной записью координат первой вершины.
• Умножаем значения координаты x 1-й вершины на значение y 2-й вершины, и продолжаем так умножать. Складываем полученные результаты.
• Значения координат y1-й вершины умножаем на значения координат x 2-й вершины. Складываем результаты.
• Вычитаем сумму, полученную на 4-м этапе из суммы, полученной на третьем этапе.
• Делим результат, полученный на предыдущем этапе, и находим, что искали.

Разбивка шестиугольника на другие фигуры

Многоугольники разбиваются на другие фигуры: трапеции, треугольники, прямоугольники. Пользуясь формулами вычисления площадей перечисленных фигур, требуемые значения вычисляются и складываются.

Неправильный шестиугольник может состоять из двух параллелограммов. Чтоб вычислить площадь параллелограмма, его длина умножается на его ширину, а далее уже известные две площади складываются.

Площадь равностороннего шестиугольника

У правильного шестиугольника шесть равных сторон. Площадь равносторонней фигуры равна 6S треугольников, на которые разбит правильный шестиугольник. Каждый треугольник в правильном шестиугольнике равен, поэтому для вычисления площади такой фигуры довольно знать площадь хотя б одного треугольника.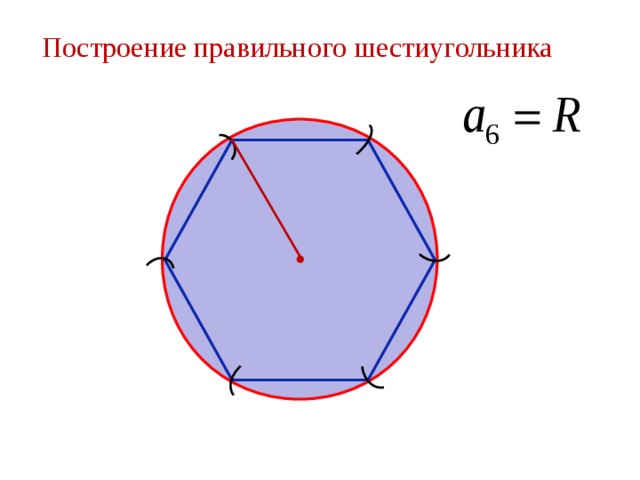

Чтоб найти искомое значение пользуются формулой площади правильной фигуры, описанной выше.

Площадь шестиугольника – формула, определение, примеры

Площадь шестиугольника – это пространство, заключенное со всех сторон. Шестиугольник — это многоугольник с шестью углами и шестью сторонами. Оно происходит от греческих слов «Hexa», что означает «шесть», и «gonía», что означает «угол». В этом уроке мы узнаем о площади шестиугольника и формуле, используемой для нахождения площади шестиугольника.

1.	Какова площадь шестиугольника?
2.	Площадь шестиугольника Формула
3.	Как найти площадь шестиугольника?
4.	Часто задаваемые вопросы о площади шестиугольника

Какова площадь шестиугольника?

Площадь шестиугольника — это область, которая находится внутри сторон шестиугольника. Шестиугольник — это двумерная фигура, имеющая 6 сторон, 6 углов и 9диагоналей, а сумма его внутренних углов равна 720°. Площадь шестиугольника может быть рассчитана различными способами, и она выражается в квадратных единицах, например, в м ² , в см ² , в ² или в футах ² и так далее.

Площадь шестиугольника Формула

Формула площади правильного шестиугольника: (3√3 s ² )/2, где s — длина стороны шестиугольника. Поскольку речь идет о правильном шестиугольнике, следует отметить, что все стороны имеют одинаковую длину. Когда известна одна сторона правильного шестиугольника, площадь можно вычислить по формуле Площадь шестиугольника = (3√3 s ² )/2 , где s — длина стороны шестиугольника.

Как найти площадь шестиугольника?

Как мы узнали из предыдущего раздела, площадь шестиугольника можно вычислить, зная длину стороны. В этом случае используется следующая формула: Площадь правильного шестиугольника = (3√3 с ² )/2. Таким образом, мы следуем приведенным ниже шагам, чтобы найти площадь шестиугольника:

• Шаг 1: Определите длину стороны правильного шестиугольника.
• Шаг 2: Найдите площадь по формуле Площадь шестиугольника = (3√3 с ² )/2; где s — длина стороны.
• Шаг 3: Представьте окончательный ответ в квадратных единицах.

Пример: Найдите площадь правильного шестиугольника со стороной 6 дюймов.

Решение: Учитывая длину стороны = 6 дюймов.
Площадь шестиугольника = (3√3 s ² )/2 = (3 × √3 × 6 ² )/2 = 54√3 = 93,5 дюйма ²

Ответ: Площадь правильного шестиугольник равен 93,5 в ² .

Площадь шестиугольника с апофемой

Площадь правильного шестиугольника можно рассчитать, зная длину стороны и апофему. Апофема — это отрезок, проведенный из центра и перпендикулярный стороне шестиугольника.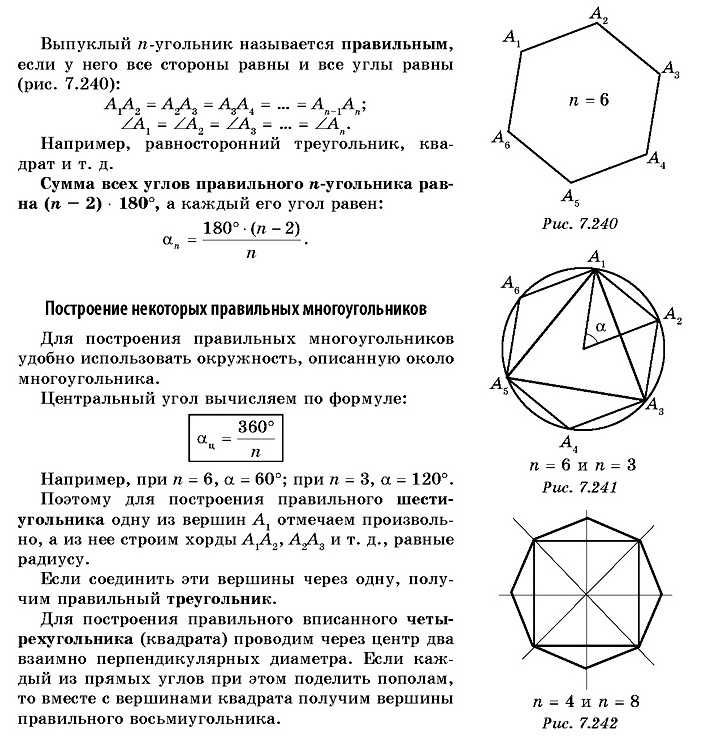 Обратите внимание на следующий шестиугольник, чтобы увидеть апофему и формулу для нахождения площади правильного шестиугольника, когда апофема задана.

В этом случае используется следующая формула: Площадь шестиугольника = (1/2) × апофема × Периметр шестиугольника или Площадь шестиугольника = (1/2) × a × P = (1/2) ) × a × 6 × s = 3as,

• , где «a» — длина апофемы
• P — это периметр шестиугольника, а
• ‘s’ — длина стороны шестиугольника.

► Ссылки по теме:

• Район Пентагона
• Площадь четырехугольника
• Площадь полигонов

 

Площадь шестиугольника Примеры

1. Пример 1: Найдите площадь правильного шестиугольника, длина стороны которого равна 10 единицам.

   Решение: Дана длина стороны = 10 единиц.
   Площадь = (3√3 с ² )/2 = (3 × √3 × 10 ² )/2 = 150√3 = 259,8 единиц ²

   Ответ: Площадь шестиугольника = 250,38 единиц 2 .

2. Пример 2: Найдите длину стороны правильного шестиугольника, площадь которого равна 600√3 единиц ² .

   Решение: Дано, площадь = 600√3 единиц ² ; формула для нахождения площади шестиугольника = (3√3 с ² )/2

   Длину стороны можно рассчитать по этой формуле, если площадь известна.
   (3√3 с ² )/2 = 600√3

   (3√3 с ² ) = 600√3 × 2

   ⇒ с ² = (600√3 × 2)/3√3
   ⇒ с ² = 400
   ⇒ s = 20 единиц

   Ответ: Таким образом, длина стороны правильного шестиугольника равна 20 единицам.

3. Пример 3: Вычислите площадь шестиугольника с заданными значениями:
   Длина апофемы = 16,5 дюймов
   Периметр шестиугольника = 19 дюймов

   Решение: Дано, длина апофемы = 16,5 дюймов и периметр = 19дюймы.
   Площадь шестиугольника с апофемой = 1/2 × Апофема × Периметр
   = 1/2 × 16,5 × 19
   = 313,5/2
   = 156,75 квадратных дюймов

   Ответ: Требуемая площадь равна 156,75 квадратных дюймов.

перейти к слайдуперейти к слайдуперейти к слайду

Разбейте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Практические вопросы по площади шестиугольника

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о площади шестиугольника

Какова площадь шестиугольника?

Площадь шестиугольника определяется как площадь, ограниченная сторонами шестиугольника. Площадь шестиугольника выражается в квадратных единицах, таких как m ² , cm ² , in ² , ft ² и так далее.

Какая формула площади шестиугольника?

Формула площади шестиугольника: Площадь = (3√3 с ² )/2; где s — длина одной стороны правильного шестиугольника. Формула площади шестиугольника также может быть выражена через апофему следующим образом: Площадь шестиугольника = (1/2) × a × P; где «а» — длина апофемы, а «Р» — периметр шестиугольника.

Как найти площадь шестиугольника?

Мы можем найти площадь правильного шестиугольника, используя следующие шаги. Найдем площадь шестиугольника со стороной 8 единиц.

• Шаг 1: Определите длину стороны шестиугольника. Здесь длина стороны (s) = 8 единиц.
• Шаг 2: Найдите площадь шестиугольника по формуле A = (3√3 s ² )/2, чтобы получить окончательный ответ в квадратных единицах. Подставляя значения в формулу, A = (3√3 с ² )/2 = (3√3 × 8 ² )/2 = 96√3 = 166,28 квадратных единиц.

Как найти площадь шестиугольника с помощью апофемы?

Апофема — это отрезок, проведенный из центра и перпендикулярный стороне шестиугольника. Мы можем найти площадь правильного шестиугольника с апофемой, используя формулу Площадь шестиугольника = (1/2) × a × P; где «а» — апофема, а «Р» — периметр шестиугольника.

Какая формула для периметра и площади шестиугольника?

Для расчета площади правильного шестиугольника используется формула (3√3 с ² )/2; где s — длина стороны. Периметр шестиугольника можно вычислить, сложив все шесть длин сторон. В случае правильного шестиугольника мы используем формулу Периметр = 6 × с; где s — длина одной стороны.

Как найти площадь неправильного шестиугольника?

Не существует специальной формулы для нахождения площади неправильного шестиугольника. Шестиугольник можно разделить на различные формы, такие как прямоугольники и треугольники. После этого можно вычислить площадь этих фигур и сложить вместе, чтобы получить площадь шестиугольника.

Как найти площадь шестиугольника, вписанного в окружность?

Чтобы найти площадь правильного шестиугольника, вписанного в окружность, мы можем сначала разделить шестиугольник на 6 треугольников, которые будут равносторонними треугольниками. Теперь, поскольку шестиугольник вписан в окружность, радиус окружности будет стороной треугольника. Мы знаем, что площадь равностороннего треугольника рассчитывается по формуле: площадь равностороннего треугольника = √3/4 × сторона ² .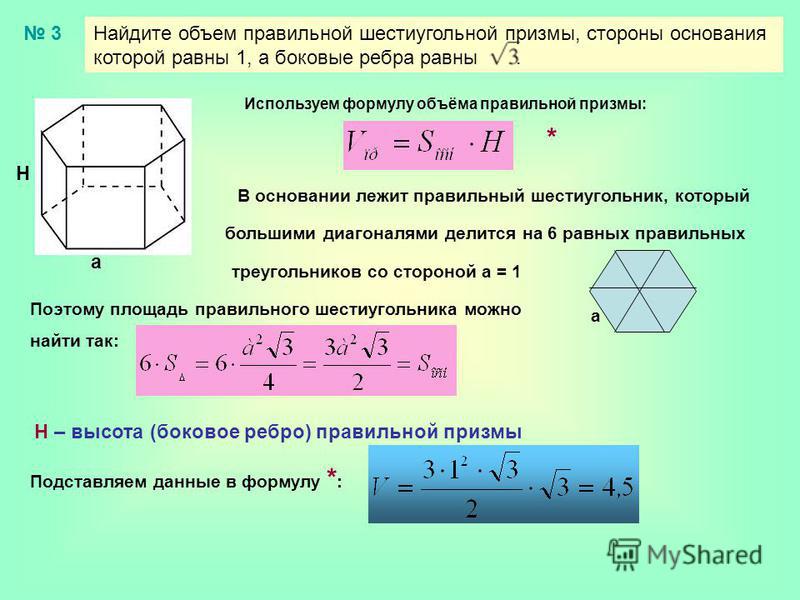 Таким образом, площадь шестиугольника будет в 6 раз больше этой площади, потому что шестиугольник разделен на 6 равносторонних треугольников. Следовательно, формула для нахождения площади шестиугольника, вписанного в окружность = 6 × √3/4 × сторона ² . Здесь радиус будет считаться длиной стороны.

Какова площадь шестиугольника со стороной 6 единиц?

Если длина стороны правильного шестиугольника равна 6 единицам, площадь можно рассчитать по формуле Площадь шестиугольника = (3√3 с ² )/2; где s — длина стороны. Подставив значение s = 6 в формулу, площадь шестиугольника = (3√3 × 6 ² )/2 = (3√3 × 36)/2 = 93,53 квадратных единиц.

Скачать БЕСПЛАТНЫЕ учебные материалы

Рабочие листы по площади шестиугольника [PDF]

Как найти площадь шестиугольника

Все ресурсы по математике для старших классов

8 Диагностические тесты 613 практических тестов Вопрос дня Карточки Learn by Concept

Справка по математике для старших классов » Геометрия » Плоская геометрия » Шестиугольники » Как найти площадь шестиугольника

Рассчитайте приблизительную площадь правильного шестиугольника со следующей длиной стороны:

Возможные ответы:

Нельзя определить

Правильный ответ:

Пояснение:

Есть несколько способов найти площадь шестиугольника.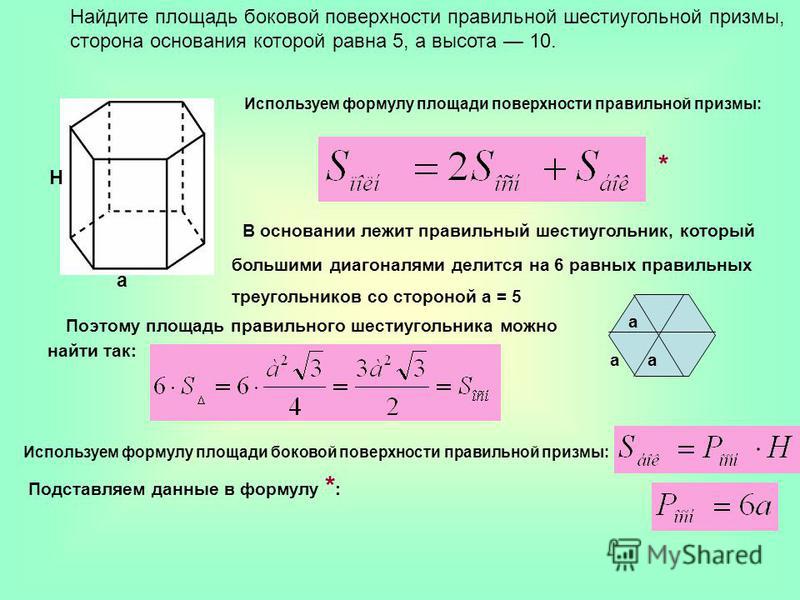

1. В правильном шестиугольнике разбейте фигуру на треугольники.
2. Найдите площадь одного треугольника.
3. Умножьте это значение на шесть.

В качестве альтернативы, площадь может быть найдена путем вычисления половины длины стороны, умноженной на апофему.

 

Правильные шестиугольники:

Правильные шестиугольники представляют собой интересные многоугольники. Шестиугольники представляют собой шестигранные фигуры и имеют следующую форму:

В правильном шестиугольнике все стороны имеют одинаковую длину и все внутренние углы имеют одинаковую меру; поэтому мы можем написать следующее выражение.

 

Один из самых простых способов найти площадь многоугольника — разбить фигуру на треугольники. Начнем с разделения шестиугольника на шесть треугольников.

На этом рисунке центральная точка равноудалена от всех вершин. В результате шесть пунктирных линий внутри шестиугольника имеют одинаковую длину.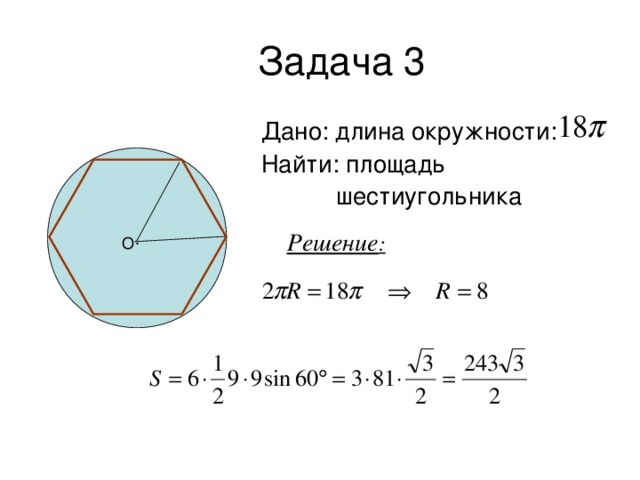 Точно так же все треугольники внутри шестиугольника конгруэнтны по правилу стороны-стороны-стороны: каждый из треугольников имеет две общие стороны внутри шестиугольника, а также сторону основания, которая составляет периметр шестиугольника. Аналогичным образом, каждый из треугольников имеет одинаковые углы. Они расположены в круге, и шестиугольник на нашем изображении разделил его на шесть равных частей; поэтому мы можем написать следующее:

Мы также знаем следующее:

Теперь давайте посмотрим на каждый из треугольников в шестиугольнике. Мы знаем, что у каждого треугольника есть две равные стороны; следовательно, каждый из углов при основании каждого треугольника должен быть одинаковым. Мы знаем, что у треугольника есть  , и мы можем найти два угла при основании каждого треугольника, используя эту информацию.

Каждый угол в треугольнике равен . Теперь мы знаем, что все треугольники конгруэнтны и равносторонние: каждый треугольник имеет три равные длины сторон и три равных угла. Теперь мы можем использовать эту жизненно важную информацию для определения площади шестиугольника. Если мы найдем площадь одного из треугольников, то можем умножить ее на шесть, чтобы вычислить площадь всей фигуры. Начнем с анализа . Если мы проведем высоту через треугольник, то обнаружим, что создаем два  треугольника.

Найдем длину этого треугольника. Помните, что в треугольниках длины сторон треугольников находятся в следующем соотношении:

Теперь мы можем проанализировать,  используя замещающую переменную для длины стороны, .

Мы знаем размеры основания и высоты и можем найти его площадь.

Теперь нам нужно умножить это на шесть, чтобы найти площадь всего шестиугольника.

Мы нашли площадь правильного шестиугольника с длиной стороны, . Если мы знаем длину стороны правильного шестиугольника, то можем найти площадь.

Если у нас нет правильного шестиугольника, то мы находим площадь шестиугольника, используя длину стороны (т. прямой угол любой стороны. Это обозначено переменной  на следующем рисунке:

 

Альтернативный метод:

Если нам даны переменные и , то мы можем найти площадь шестиугольника по следующей формуле:

и является апофемой. Мы должны вычислить периметр, используя длину стороны и уравнение , где  – длина стороны.

 

Решение:

В данной задаче мы знаем, что длина стороны правильного шестиугольника равна:

Подставим это значение в формулу площади правильного шестиугольника и решим.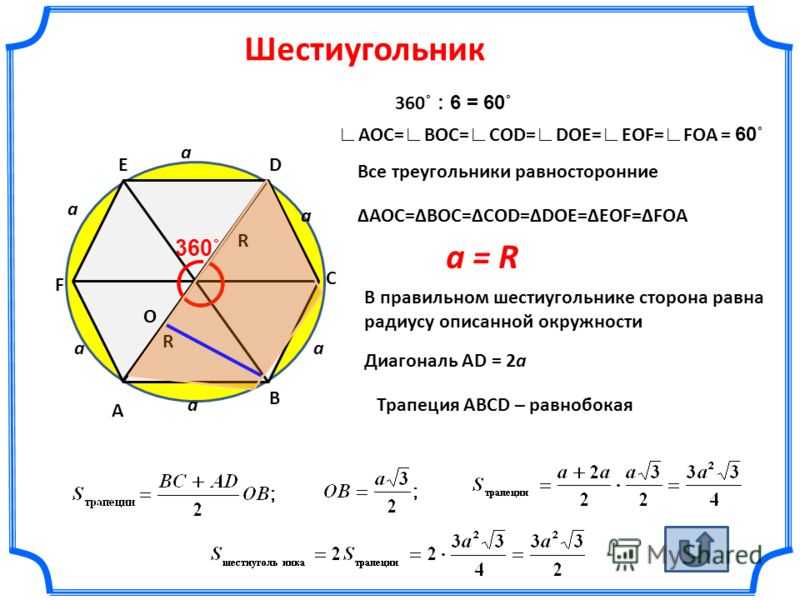

Упрощение.

Округлите ответ до ближайшего целого числа.

Сообщить об ошибке

Одна шестиугольная ячейка сот имеет диаметр два сантиметра.

 

Какова площадь клетки с точностью до десятых долей сантиметра?

 

Возможные ответы:

Невозможно определить Пояснение:

Есть несколько способов найти площадь шестиугольника.

1. В правильном шестиугольнике разбейте фигуру на треугольники.
2. Найдите площадь одного треугольника.
3. Умножьте это значение на шесть.

В качестве альтернативы, площадь может быть найдена путем вычисления половины длины стороны, умноженной на апофему.

 

Правильные шестиугольники:

Правильные шестиугольники представляют собой интересные многоугольники.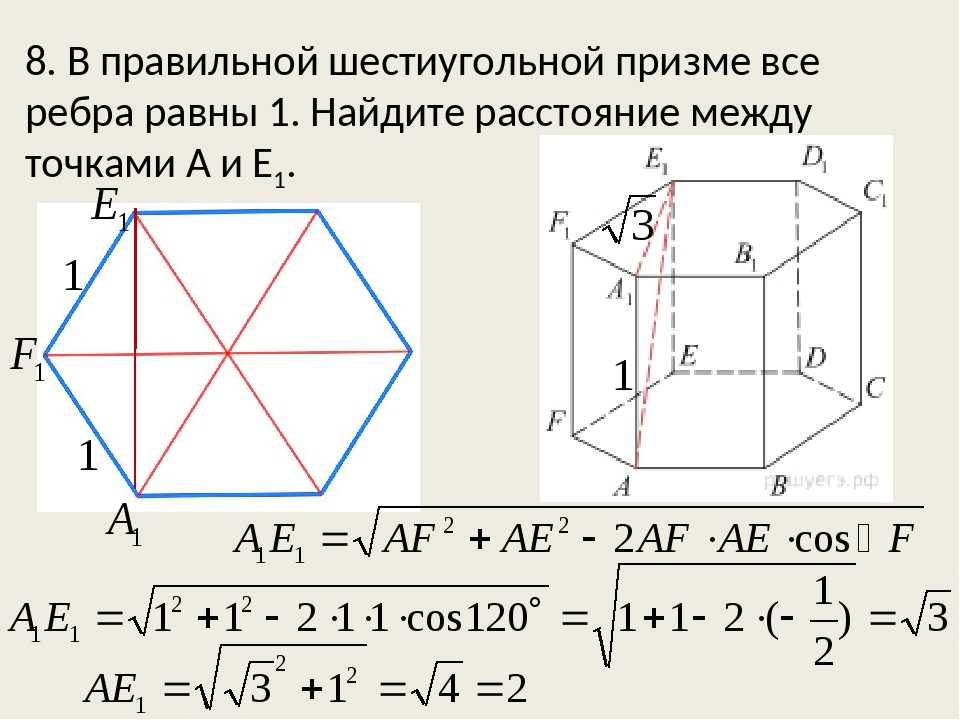 Шестиугольники представляют собой шестигранные фигуры и имеют следующую форму:

В правильном шестиугольнике все стороны имеют одинаковую длину и все внутренние углы имеют одинаковую меру; поэтому мы можем написать следующее выражение.

 

Один из самых простых способов найти площадь многоугольника — разбить фигуру на треугольники. Начнем с разделения шестиугольника на шесть треугольников.

На этом рисунке центральная точка равноудалена от всех вершин. В результате шесть пунктирных линий внутри шестиугольника имеют одинаковую длину. Точно так же все треугольники внутри шестиугольника конгруэнтны по правилу стороны-стороны-стороны: каждый из треугольников имеет две общие стороны внутри шестиугольника, а также сторону основания, которая составляет периметр шестиугольника. Аналогичным образом, каждый из треугольников имеет одинаковые углы. Они расположены в круге, и шестиугольник на нашем изображении разделил его на шесть равных частей; поэтому мы можем написать следующее:

Мы также знаем следующее:

Теперь давайте посмотрим на каждый из треугольников в шестиугольнике.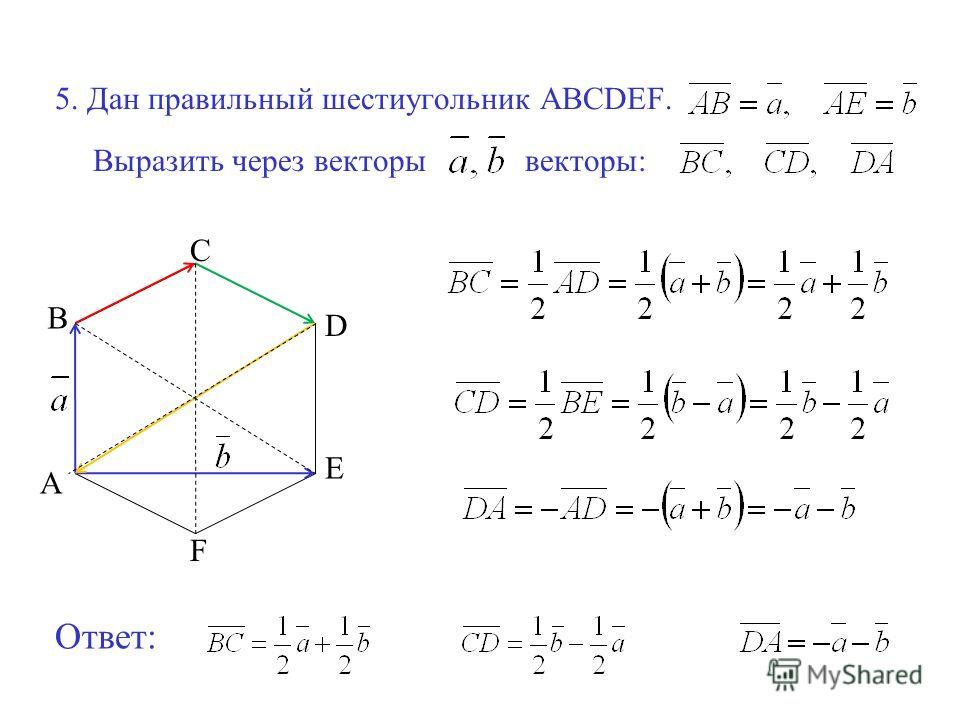 Мы знаем, что у каждого треугольника есть две равные стороны; следовательно, каждый из углов при основании каждого треугольника должен быть одинаковым. Мы знаем, что у треугольника есть  , и мы можем найти два угла при основании каждого треугольника, используя эту информацию.

Каждый угол в треугольнике равен . Теперь мы знаем, что все треугольники конгруэнтны и равносторонние: каждый треугольник имеет три равные длины сторон и три равных угла. Теперь мы можем использовать эту жизненно важную информацию для определения площади шестиугольника. Если мы найдем площадь одного из треугольников, то можем умножить ее на шесть, чтобы вычислить площадь всей фигуры. Начнем с анализа . Если мы проведем высоту через треугольник, то обнаружим, что создаем два  треугольника.

Найдем длину этого треугольника. Помните, что в треугольниках длины сторон треугольников находятся в следующем соотношении:

Теперь мы можем проанализировать,  используя замещающую переменную для длины стороны, .

Мы знаем размеры основания и высоты и можем найти его площадь.

Теперь нам нужно умножить это на шесть, чтобы найти площадь всего шестиугольника.

Мы нашли площадь правильного шестиугольника с длиной стороны, . Если мы знаем длину стороны правильного шестиугольника, то можем найти площадь.

Если у нас нет правильного шестиугольника, то мы находим площадь шестиугольника, используя длину стороны (т. прямой угол любой стороны. Это обозначено переменной  на следующем рисунке:

 

Альтернативный метод:

Если нам даны переменные и , то мы можем найти площадь шестиугольника по следующей формуле:

и является апофемой. Мы должны вычислить периметр, используя длину стороны и уравнение , где  – длина стороны.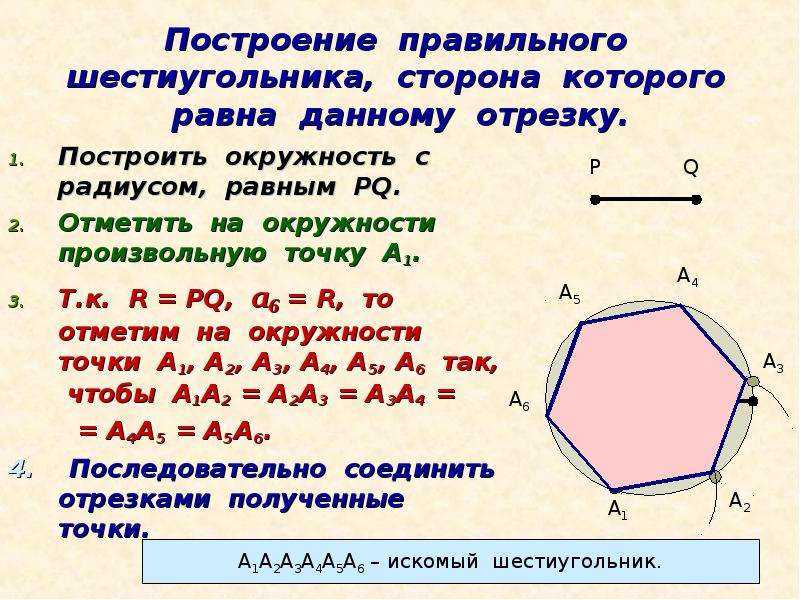

 

Решение:

В задаче сказано, что соты имеют диаметр два сантиметра. Чтобы решить задачу, нам нужно разделить диаметр на два. Это связано с тем, что радиус этого диаметра равен длине внутренней стороны равносторонних треугольников в сотах. Найдем длину стороны правильного шестиугольника/соты.

Подставить и решить.

Нам известна следующая информация.

В итоге можем написать следующее:

Подставим это значение в формулу площади правильного шестиугольника и решим.

Упрощение.

Решить.

Округлить до десятых долей сантиметра.

Сообщить об ошибке

Какова площадь правильного шестиугольника с апофемой  и длиной стороны ?

Возможные ответы:

Правильный ответ:

Пояснение:

Есть несколько способов найти площадь шестиугольника.

1. В правильном шестиугольнике разбейте фигуру на треугольники.
2. Найдите площадь одного треугольника.
3. Умножьте это значение на шесть.

В качестве альтернативы, площадь может быть найдена путем вычисления половины длины стороны, умноженной на апофему.

 

Правильные шестиугольники:

Правильные шестиугольники представляют собой интересные многоугольники. Шестиугольники представляют собой шестигранные фигуры и имеют следующую форму:

В правильном шестиугольнике все стороны имеют одинаковую длину и все внутренние углы имеют одинаковую меру; поэтому мы можем написать следующее выражение.

 

Один из самых простых способов найти площадь многоугольника — разбить фигуру на треугольники. Начнем с разделения шестиугольника на шесть треугольников.

На этом рисунке центральная точка равноудалена от всех вершин. В результате шесть пунктирных линий внутри шестиугольника имеют одинаковую длину. Точно так же все треугольники внутри шестиугольника конгруэнтны по правилу стороны-стороны-стороны: каждый из треугольников имеет две общие стороны внутри шестиугольника, а также сторону основания, которая составляет периметр шестиугольника. Аналогичным образом, каждый из треугольников имеет одинаковые углы. Они расположены в круге, и шестиугольник на нашем изображении разделил его на шесть равных частей; поэтому мы можем написать следующее:

Мы также знаем следующее:

Теперь давайте посмотрим на каждый из треугольников в шестиугольнике. Мы знаем, что у каждого треугольника есть две равные стороны; следовательно, каждый из углов при основании каждого треугольника должен быть одинаковым. Мы знаем, что у треугольника есть  , и мы можем найти два угла при основании каждого треугольника, используя эту информацию.

Каждый угол в треугольнике равен .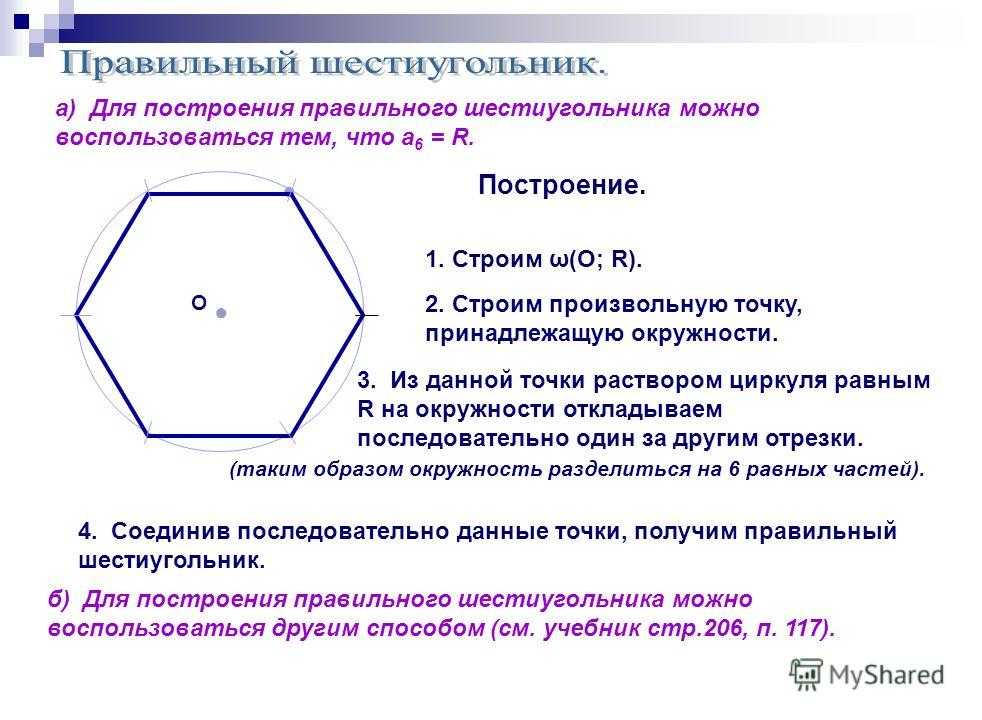 Теперь мы знаем, что все треугольники конгруэнтны и равносторонние: каждый треугольник имеет три равные длины сторон и три равных угла. Теперь мы можем использовать эту жизненно важную информацию для определения площади шестиугольника. Если мы найдем площадь одного из треугольников, то можем умножить ее на шесть, чтобы вычислить площадь всей фигуры. Начнем с анализа . Если мы проведем высоту через треугольник, то обнаружим, что создаем два  треугольника.

Найдем длину этого треугольника. Помните, что в треугольниках длины сторон треугольников находятся в следующем соотношении:

Теперь мы можем проанализировать,  используя замещающую переменную для длины стороны, .

Мы знаем размеры основания и высоты и можем найти его площадь.

Теперь нам нужно умножить это на шесть, чтобы найти площадь всего шестиугольника.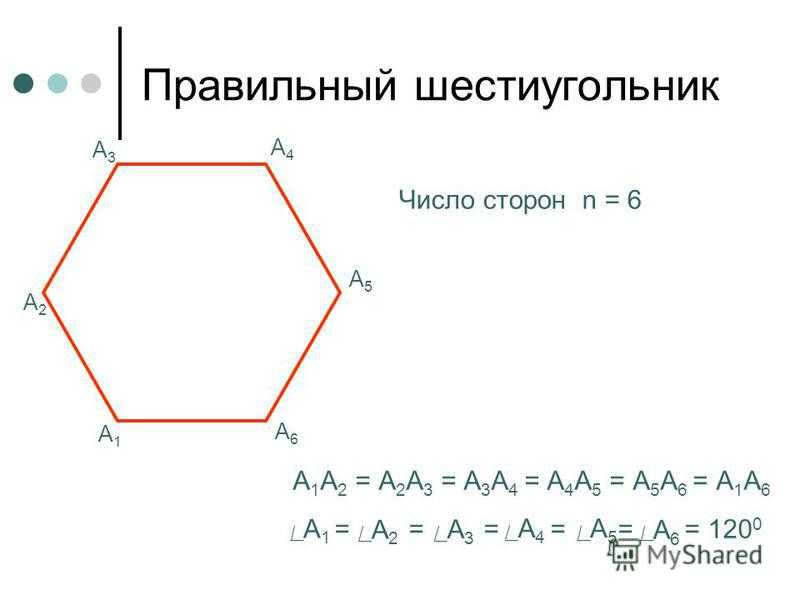

Мы нашли площадь правильного шестиугольника с длиной стороны, . Если мы знаем длину стороны правильного шестиугольника, то можем найти площадь.

Если у нас нет правильного шестиугольника, то мы находим площадь шестиугольника, используя длину стороны (т. прямой угол любой стороны. Это обозначено переменной  на следующем рисунке:

 

Альтернативный метод:

Если нам даны переменные и , то мы можем найти площадь шестиугольника по следующей формуле:

и является апофемой. Мы должны вычислить периметр, используя длину стороны и уравнение , где  – длина стороны.

 

Решение:

В шестиугольнике количество сторон , а в этом примере длина стороны .

Периметр .

Затем мы подставляем числа для апофемы и периметра в исходное уравнение.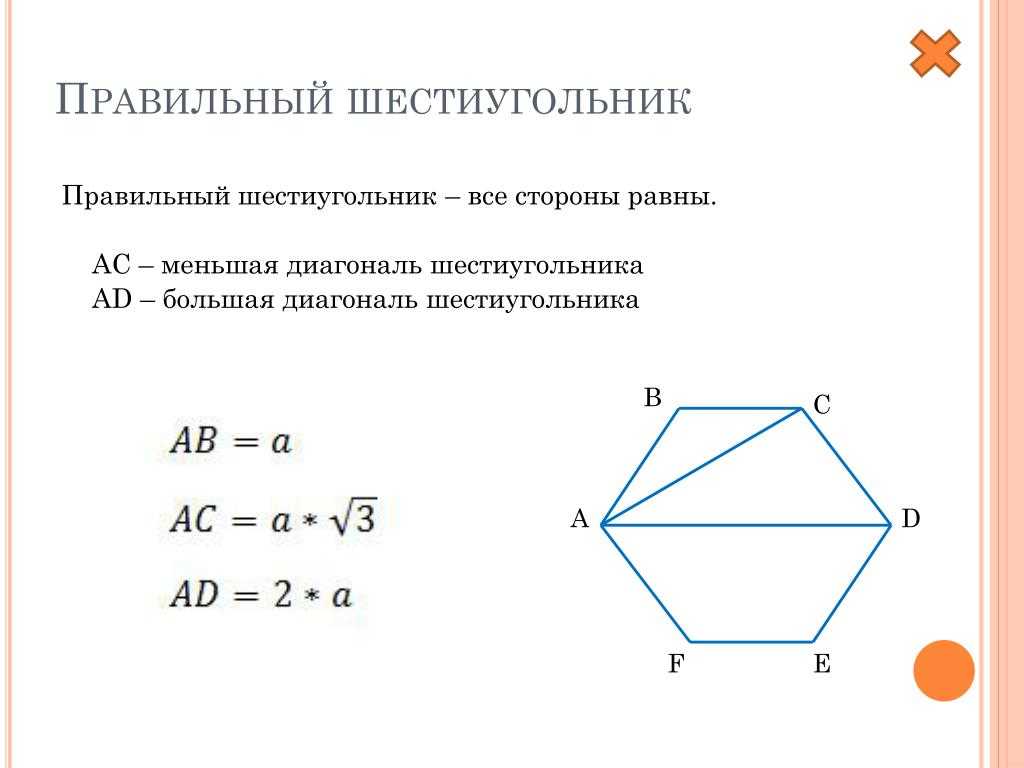

Район .

Сообщить об ошибке

Эта фигура представляет собой правильный шестиугольник со следующей длиной стороны:

Вычислите площадь правильного шестиугольника.

Возможные ответы:

Правильный ответ:

Пояснение:

Есть несколько способов найти площадь шестиугольника.

1. В правильном шестиугольнике разбейте фигуру на треугольники.
2. Найдите площадь одного треугольника.
3. Умножьте это значение на шесть.

В качестве альтернативы, площадь может быть найдена путем вычисления половины длины стороны, умноженной на апофему.

 

Правильные шестиугольники:

Правильные шестиугольники представляют собой интересные многоугольники. Шестиугольники представляют собой шестигранные фигуры и имеют следующую форму:

В правильном шестиугольнике все стороны имеют одинаковую длину и все внутренние углы имеют одинаковую меру; поэтому мы можем написать следующее выражение.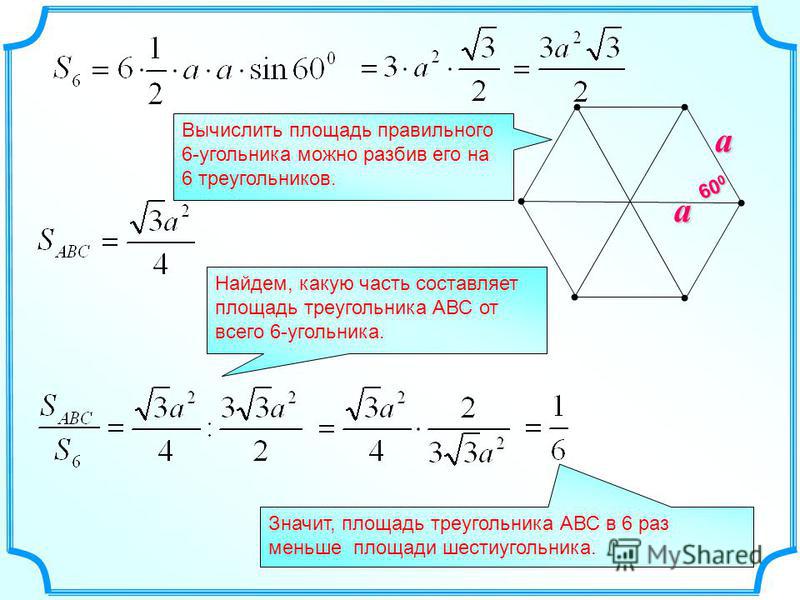

 

Один из самых простых способов найти площадь многоугольника — разбить фигуру на треугольники. Начнем с разделения шестиугольника на шесть треугольников.

На этом рисунке центральная точка равноудалена от всех вершин. В результате шесть пунктирных линий внутри шестиугольника имеют одинаковую длину. Точно так же все треугольники внутри шестиугольника конгруэнтны по правилу стороны-стороны-стороны: каждый из треугольников имеет две общие стороны внутри шестиугольника, а также сторону основания, которая составляет периметр шестиугольника. Аналогичным образом, каждый из треугольников имеет одинаковые углы. Они расположены в круге, и шестиугольник на нашем изображении разделил его на шесть равных частей; поэтому мы можем написать следующее:

Мы также знаем следующее:

Теперь давайте посмотрим на каждый из треугольников в шестиугольнике. Мы знаем, что у каждого треугольника есть две равные стороны; следовательно, каждый из углов при основании каждого треугольника должен быть одинаковым. Мы знаем, что у треугольника есть  , и мы можем найти два угла при основании каждого треугольника, используя эту информацию.

Каждый угол в треугольнике равен . Теперь мы знаем, что все треугольники конгруэнтны и равносторонние: каждый треугольник имеет три равные длины сторон и три равных угла. Теперь мы можем использовать эту жизненно важную информацию для определения площади шестиугольника. Если мы найдем площадь одного из треугольников, то можем умножить ее на шесть, чтобы вычислить площадь всей фигуры. Начнем с анализа . Если мы проведем высоту через треугольник, то обнаружим, что создаем два  треугольника.

Найдем длину этого треугольника. Помните, что в треугольниках длины сторон треугольников находятся в следующем соотношении:

Теперь мы можем проанализировать,  используя замещающую переменную для длины стороны, .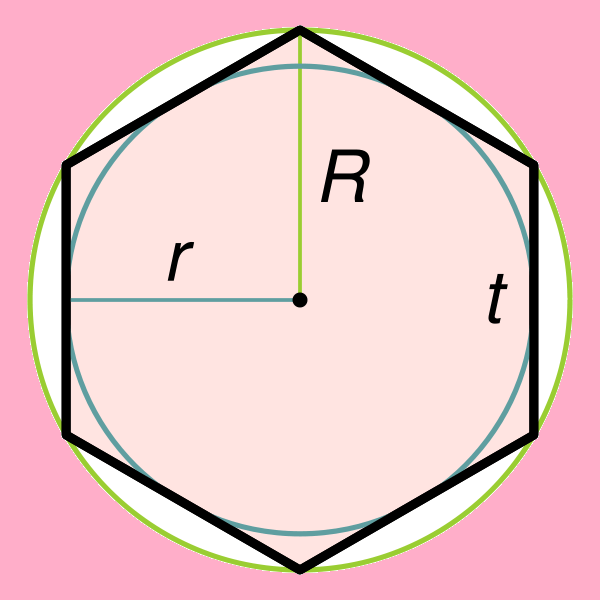

Мы знаем размеры основания и высоты и можем найти его площадь.

Теперь нам нужно умножить это на шесть, чтобы найти площадь всего шестиугольника.

Мы нашли площадь правильного шестиугольника с длиной стороны, . Если мы знаем длину стороны правильного шестиугольника, то можем найти площадь.

Если у нас нет правильного шестиугольника, то мы находим площадь шестиугольника, используя длину стороны (т. прямой угол любой стороны. Это обозначено переменной  на следующем рисунке:

 

Альтернативный метод:

Если нам даны переменные и , то мы можем найти площадь шестиугольника по следующей формуле:

и является апофемой. Мы должны вычислить периметр, используя длину стороны и уравнение , где  – длина стороны.