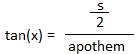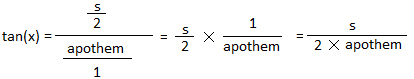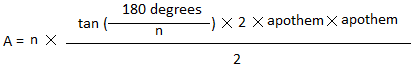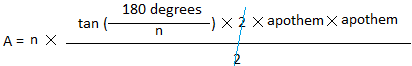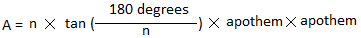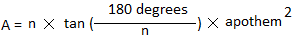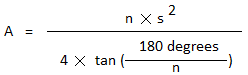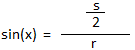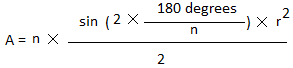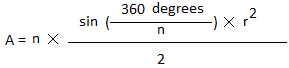Правильный пятиугольник ☑️ как построить, сколько осей симметрии имеет, свойства, какой угол у равностороннего пятиугольника, формула площади и периметра
Точное построение фигуры
Специалисты рекомендуют некоторую последовательность действий, по которым построить правильный пятиугольник очень просто. Для операции необходимы обыкновенная тетрадь в клеточку, циркуль, карандаш, резинка и линейка. Следует выполнить некоторые шаги:
- Построить окружность с центром в некоторой точке О.
- Провести два диаметра. Они должны пересекаться под прямым углом.
- Поставить точку V (пересечение окружности с одним из диаметров), которая является вершиной фигуры.
- По левой стороне поставить точку D. Это пересечение диаметра (оси симметрии) с окружностью.
- Отметить на отрезке OD точку А, которая делит его пополам.
- Выполнить построение вспомогательной окружности, центром которой является точка, полученная в 5 пункте. Кроме того, круг с радиусом CV должен проходить через V.
- Точку, полученную при пересечении диаметра и окружности, нужно обозначить литерой B.
- Нарисовать окружность с радиусом, равным CV, из точки V.
- Отметить пересечение круга с первой окружностью, центром которой является точка О. Искомое место пересечения обозначить литерой F (вторая вершина пентагона).
- Поставить иглу циркуля в точку F и провести окружность через Е.
- Обозначить пересечение окружностей с центрами в F и O точкой G, которая будет вершиной пентагона.
- Аналогичным образом проделать шаг 11, только центр выбрать не в F, а в G. Полученную точку следует обозначить литерой H (последняя вершина фигуры).
- Соединить пять точек (СVEFG) между собой с помощью линейки.
Если все пункты алгоритма выполнены правильно, то должен получиться пентагон, изображенный на рисунке 1:
Этот способ следует применять для точных построений и чертежей деталей. Однако для решения задач, в которых необходимо схематически изобразить пятиугольник, этот вариант не подойдет.
Алгоритм Биона
Прием Биона является менее точным методом, чем первый. Он позволяет построить любой правильный многоугольник, вписанный в произвольный круг. Для операции необходимо воспользоваться алгоритмом (шаблоном) Биона, имеющим такой вид:
- Начертить окружность с центром в точке О и радиусом R.
- Провести в ней диаметр АD.
- Построить правильный (равносторонний) треугольник с одной из сторон, равной диаметру.
- Поделить диаметр на несколько равных частей (АС = СE = ED), количество которых вычисляется по формуле: (n — 2). Переменная «n» эквивалентна количеству граней правильного многоугольника, то есть n = 3. Соотношение можно записать следующей зависимостью: АС = [1 / (n — 2)] * AD = AD / 3.
- Провести из точек С и Е прямые, перпендикулярные диаметру.
- Точки пересечения прямых с окружностью обозначить F и G.
- Если соединить точки, то получится пентагон ABDFG.
Погрешность построения многоугольника с 5, 7, 9 и 10 сторонами при использовании алгоритма довольно маленькая. Ее значения равно 3,2%. Однако при n>10 погрешность составляет не более 11%.
Приближенные методы
Существует несколько методов, позволяющих приближенно изобразить фигуру. Однако оптимальным является построение пентагона (рис. 2), используя две окружности (описанную и вписанную).
Метод известного математика А. Дюрера является оптимальным среди остальных, поскольку на построение затрачивается минимальное количество времени. Для его реализации следует выполнить определенные шаги алгоритма Дюрера:
- Начертить произвольную окружность с центром в точке О.
- Не вынимая иглу циркуля из точки О, выполнить построение другой окружности. Ее радиус нужно уменьшить таким образом, чтобы общий радиус R был равен стороне пятиугольника.
- Отметить на окружности с большим радиусом две произвольные точки. При этом следует руководствоваться правилом: прямая, проходящая через них, должна касаться малой окружности в одной точке (касательная).
- Отметить следующую точку, чтобы можно было соединить ее с предыдущей. Правило при этом должно соблюдаться.
- Аналогично проделать операции с другими сторонами пентагона.
Существует еще один метод — построение пятиугольника из десятиугольника, который вписан в окружность. Для этого следует соединить его вершины через одну. Однако способ рекомендуется применять только в том случае, когда исходная фигура уже имеется. Кстати, его следует строить также методом А. Дюрера.
Математики рекомендуют еще один простой способ. Для его реализации необходимо начертить окружность с диаметром АD. После этого его нужно поделить на 3 равные части, то есть AB = BC = CD. Затем из точки С следует опустить перпендикуляры на окружность. Обозначить места пересечения точками E и F. Проделать такую же процедуру с точкой B, обозначив пересечения точками G и H. Остается лишь соединить все точки отрезками.
Признаки и свойства
Не всегда получается верно идентифицировать пятиугольник. Для этого математики предлагают признаки, которые применимы только к правильной фигуре. К ним можно отнести следующие:
- Стороны равны между собой.
- Любой угол правильного пятиугольника равен остальным его углам.
Следует отметить, что признаки справедливы для любого правильного многогранника. Пять осей симметрии имеет правильный пятиугольник (сколько сторон, столько и осей). Пентагон обладает некоторыми свойствами, которые будут очень полезны при решении задач. К ним можно отнести следующие:
- Равенство сторон.
- Центры вписанной и описанной окружностей совпадают.
- Сумма внутренних углов равна 180 * (5 — 2) = 540 (градусов), а внешних — 360.
- Количество диагоналей соответствует 5.
- Значение площади кольца, которое образуется между вписанным и описанным кругами, эквивалентно произведению квадрата длины стороны на константу Pi / 4.
- Биссектрисы, проведенные через центр, равны.
- Диагонали — трисектрисы внутренних углов. Одна диагональ делит его на 1/3 и 2/3 части.
- Отношение диагонали к стороне эквивалентно «золотому сечению» и равно [1 + 5^(1/2)] / 2.
Однако свойств недостаточно при решении задач, поскольку существуют некоторые формулы и соотношения для нахождения основных параметров пентагона.
Расчет параметров
С помощью соотношений можно легко найти необходимые характеристики любой фигуры. Однако в некоторых источниках не указаны условные обозначения известного параметра пентагона. Это существенно затрудняет понимание формулы, а также ее дальнейшее использование. Перед изучением следует нарисовать фигуру и обозначить некоторые величины, которыми могут быть диагонали, стороны, апофемы и радиусы.
Рекомендуется использовать различные литеры или буквенные обозначения. Недопустимо пронумеровывать вершины, поскольку при вычислениях можно ошибиться. Нельзя использовать вместо букв цифры при обозначениях. Например, пентагон ABCDE является правильной записью. Допускается применение чисел в индексах, а именно, в пятиугольнике правильного типа ABCDE при пересечении его диагоналей образовался пентагон A1B1C1D1E1.
Математики рекомендуют обозначать только промежуточные фигуры или их проекции литерами с индексами. Для каждой новой фигуры следует вводить другие обозначения. Не следует использовать зарезервированные переменные. Например, центр окружности в точке P является недопустимой записью, поскольку такой буквой обозначается периметр.
Условные обозначения
Для нахождения основных величин пентагона следует обозначить некоторые его параметры. Фигура имеет следующие обозначения:
- Сторона: a.
- Радиус вписанной и описанной окружностей: r и R соответственно.
- Площадь: S.
- Периметр и полупериметр: P и p соответственно.
- Диагональ: d.
- Отношение золотого сечения: Ф.
Значения сторон равны между собой. Площадь правильного пятиугольника — характеристика двумерной фигуры, которая показывает ее размерность. Периметром называется сумма всех 5 сторон. Полупериметр вычисляется по следующему соотношению: p = P / 2. Диагонали — отрезки, проведенные из одной вершины к противоположной (несмежной).
Соотношения и формулы
После обозначений следует переходить к рассмотрению основных формул, при помощи которых можно вычислять параметры фигуры. Сторону можно найти, воспользовавшись такими соотношениями:
- a = 2r * tg(36).
- a = 2R * sin(36).
- a = R * [(5 — (5)^(1/2)) / 2]^(1/2).
Радиус вписанной окружности в пентагон можно найти, используя тригонометрические функции. Однако существует также формула, позволяющая вычислить приближенное значение. Это необходимо в том случае, когда под рукой нет специального онлайн-калькулятора, компьютера или таблиц Брадиса. Формулы для нахождения радиуса вписанной окружности:
- r = a / (2tg(36)).
- r = a * [5^(1/2) * [5 + 2 * 5^(1/2)]^(1/2) / 10].
Математики также рекомендуют описать вокруг пентагона окружность. Это расширит возможности по поиску его основных характеристик. Однако ее радиус следует вычислить. Формулы для его нахождения выглядят таким образом:
- R = a / (2sin(36)).
- R = a * [10^(1/2) * [5 + 5^(1/2)]^(1/2) / 10] = (5^(1/2) — 1) * r.
Периметр определяется просто: Р = 5а. Значение полупериметра эквивалентно половине периметра, то есть p = P / 2 = 5a / 2 = 2,5a. Площадь можно найти, используя такие формулы:
- S = (5a^2 / 4) * ctg(36).
- S = 5r^2 * tg(36).
- S = 2,5 * R^2 * sin(72).
- S = (5/12) * R * d.
Высота правильного пятиугольника (h) — отрезок, проведенный из центра на любую из сторон. Она делит ее на две равные части, поскольку является биссектрисой и медианой равнобедренного треугольника. У последнего две стороны — радиусы описанной окружности, а третья — сторона пентагона. Высота называется также апофемой и проекцией на «а». Вычисляется ее значение по формуле h = a * tg(72) / 2.
Величина Ф является отношением площади пентагона (S) к площади (S1) правильного пятиугольника, полученного при пересечении диагоналей первого: S / S1 = Ф^4 = 3Ф + 2 = (3 * 5^(1/2) + 7) / 2. Длина диагонали находится по такому соотношению: d = [Ф * 5^(1/2) * R]^(1/2).
Таким образом, при решении задач необходимо знать основные признаки, свойства, соотношения и формулы для нахождения основных характеристик пентагона. Практика обязательна, поскольку теоретические знания без практического применения бесполезны.
Правильный пятиугольник | Формулы и расчеты онлайн
Правильный пятиугольник — это такой пятиугольник у которого все пять сторон равны и его пять углов равны.
Правильный пятиугольник
Центр правильного пятиугольника — на рисунке точка O равноудалена от вершин.
Светлая линия обозначающая высоту треугольника AOB : h называется — апофемой.
Отрезки OA, OB — радиусы правильного пятиугольника.
Обозначения на рисунке для правильного пятиугольника
| n=5 | число сторон и вершин правильного пятиугольника, | шт |
|---|---|---|
| α | центральный угол правильного пятиугольника, | радианы, ° |
| β | половина внутреннего угла правильного пятиугольника, | радианы, ° |
| γ | внутренний угол правильного пятиугольника, | радианы, ° |
| a | сторона правильного пятиугольника, | м |
| R | радиусы правильного пятиугольника, | м |
| p | полупериметр правильного пятиугольника, | м |
| L | периметр правильного пятиугольника, | м |
| h | апофемы правильного пятиугольника, | м |
Основные формулы для правильного пятиугольника
Периметр правильного пятиугольника
\[ L = 5a \]
Полупериметр правильного пятиугольника
\[ p = \frac{5}{2}a \]
Центральный угол правильного пятиугольника в радианах
\[ α = \frac{2}{5}π \]
Центральный угол правильного пятиугольника в градусах
\[ α = \frac{360°}{5} = 72° \]
Половина внутреннего угла правильного пятиугольника в радианах
\[ β = \frac{3}{10}π \]
Половина внутреннего угла правильного пятиугольника в градусах
\[ β = \frac{3}{10}180° = 54° \]
Внутренний угол правильного пятиугольника в радианах
\[ γ = 2β = \frac{3}{5}π \]
Внутренний угол правильного пятиугольника в градусах
\[ γ = \frac{3}{5}180° = 108° \]
Площадь правильного пятиугольника
\[ S = ph = \frac{5}{2}ha \]
Или учитывая формулу Площади правильного пятиугольника получим
\[ S = \frac{5}{2} · a · \sqrt[-1.0]{(\frac{a}{2 sin(π/5)})^2-\frac{a^2}{4}} \]
Отсюда получим апофему правильного пятиугольника
\[ h = \sqrt[-1.0]{(\frac{a}{2 sin(π/5)})^2-\frac{a^2}{4}} \]
Правильный пятиугольник | стр. 268 |
|---|
Площадь пятиугольника: онлайн калькулятор, формулы, примеры решений
Пятиугольник представляет собой геометрическую фигуру с пятью углами. Существует множество разных пятиугольников, однако если стороны равны, а каждый угол фигуры равен 108 градусам, то многоугольник называется правильным и носит название «пентагон».
Геометрия пятиугольника
Пятиугольник — это фигура, которая состоит из пяти соединенных отрезков. Стороны произвольного многоугольника могут соединяться под разными углами, в результате чего фигура может быть невыпуклой. Наиболее ярким примером невыпуклого многоугольника является звезда, а пятиугольника — проекция зубчатой короны, когда два «зубца» выступают над прямоугольным основанием. Выпуклый многоугольник — это фигура, продолжение отрезков которого не пересекает других сторон. Если же мы продлим отрезки зубцов или лучей звезды, они пересекут другие стороны фигуры.
Пятиугольник в реальности
Невыпуклые геометрические фигуры редко встречаются в человеческой повседневности и обычно представляют собой основания для нестандартных призм. Наиболее распространенным пятиугольником в реальности считается пентагон — правильный многоугольник. Пентагон нашел применение в архитектуре и дизайне, и тезкой фигуры является одно из самых известных зданий Америки — штаб министерства обороны США.
Додекаэдр — платоново тело, каждая из 12 сторон которого является правильным пятиугольником. Додекаэдр используется в различных сферах, но наиболее известным представлением многогранника считается игральная кость d12, которая используется как генератор случайных чисел для настольных ролевых игр.
Несмотря на то, что многие организмы обладают пентасимметрией, например, морские звезды или плоды мушмулы, природные пятиугольные объекты практически не встречаются в природе.
Площадь пентагона
Площадь любой геометрической фигуры — это количественная оценка того, какую часть плоскости ограничивают ее стороны. Площадь правильного пятиугольника рассчитывается по общей для всех правильных многоугольников формуле:
S = n/4 × a2 × ctg(pi/n),
где n – количество сторон фигуры, a – длина стороны.
Таким образом, если подставить n = 5 и выразить получившееся выражение десятичной дробью, мы получим простую формулу для вычисления площади пентагона:
S = 1,72 a2
где a — длина одной стороны.
Сторона пентагона и радиусы вписанной r и описанной окружности R приблизительно соотносятся как:
- a = 1,4131 r
- a = 1,1756 R
Программный код калькулятора использует эти соотношения, что позволяет вам найти площадь правильного пятиугольника, зная только один параметр из перечисленных:
- радиус вписанной окружности;
- радиус описанной окружности;
- длина стороны.
Рассмотрим на примерах, как вычислить площадь правильного пятиугольника.
Примеры из жизни
Пентагон
Штаб министерства обороны США — это всемирно известное здание, которое имеет форму правильного пятиугольника. Каждая сторона штаба имеет длину 281 м и мы без проблем можем узнать, какую площадь занимает здание. Для более удобного представления выразим длину в километрах, введем эти данные в форму калькулятора a = 0,281 и получим результат:
S = 0,1359
Площадь Пентагона составит 0,136 квадратных километров.
Школьная задача
К примеру, необходимо вычислить площадь пентагона, зная, что радиус вписанной окружности составляет 15 см. Мы можем выразить сторону многоугольника через простое соотношение радиуса вписанной окружности и длины стороны a = 1,4131 r, после чего посчитать по формуле его площадь. Проще всего ввести значение радиуса в ячейку «Радиус вписанной окружности r» и получить мгновенный результат:
S = 817,36
Кроме непосредственно площади фигуры, калькулятор автоматически подсчитал остальные атрибуты пятиугольника.
Заключение
Пентагон нечасто встречается в реальной жизни, однако при решении производственных вопросов или школьных задач вам может понадобиться рассчитать площадь или периметр правильных многоугольников. Наш каталог калькуляторов к вашим услугам.
Правильный пятиугольник — Википедия
Материал из Википедии — свободной энциклопедии
Правильный пятиугольник (или пентагон от греч. πενταγωνον) — геометрическая фигура, правильный многоугольник с пятью сторонами.
Свойства
Построение правильного пятиугольника- α=(n−2)n⋅180∘=35⋅180∘=108∘{\displaystyle \alpha ={\frac {(n-2)}{n}}\cdot 180^{\circ }={\frac {3}{5}}\cdot 180^{\circ }=108^{\circ }}
- Площадь правильного пятиугольника рассчитывается по любой из формул:
- S=54t2ctgπ5=55+254t2=512Rd=52R2sin2π5=5r2tgπ5{\displaystyle S={\frac {5}{4}}t^{2}\mathop {\mathrm {ctg} } \,{\frac {\pi }{5}}={\frac {{\sqrt {5}}{\sqrt {5+2{\sqrt {5}}}}}{4}}t^{2}={\frac {5}{12}}Rd={\frac {5}{2}}R^{2}\sin {\frac {2\pi }{5}}=5r^{2}\mathop {\mathrm {tg} } \,{\frac {\pi }{5}}},
- где R{\displaystyle R} — радиус описанной окружности, r{\displaystyle r} — радиус вписанной окружности, d{\displaystyle d} — диагональ, t{\displaystyle t} — сторона.
- Высота правильного пятиугольника:
- h=tg72∘2t=5+252t≈1,539t{\displaystyle h={\frac {\operatorname {tg} \,72^{\circ }}{2}}t={\frac {\sqrt {5+2{\sqrt {5}}}}{2}}t\approx 1,539t}
- Диагонали правильного пятиугольника являются трисектрисами его внутренних углов.
- Отношение диагонали правильного пятиугольника к стороне равно золотому сечению, то есть числу 1+52{\displaystyle {\frac {1+{\sqrt {5}}}{2}}}.
Поэтому радиус вписанной окружности, радиус описанной окружности, высоту и площадь правильного пятиугольника можно вычислить и без использования тригонометрических функций:
- t=R5−52≈1,17557 R{\displaystyle t=R{\sqrt {\frac {5-{\sqrt {5}}}{2}}}\approx 1{,}17557~R}
- Радиус вписанной окружности:
- r=55+2510t≈0,688191 t{\displaystyle r={\frac {{\sqrt {5}}{\sqrt {5+2{\sqrt {5}}}}}{10}}t\approx 0{,}688191~t}
- Радиус описанной окружности:
- R=105+510t=(5−1) r≈0,850651 t≈1,23607 r{\displaystyle R={\frac {{\sqrt {1}}0{\sqrt {5+{\sqrt {5}}}}}{10}}t=({\sqrt {5}}-1)~r\approx 0{,}850651~t\approx 1{,}23607~r}
- d=Φ5R=5+12t≈1,902 R≈1,618 t{\displaystyle d={\sqrt {\Phi {\sqrt {5}}}}R={\frac {{\sqrt {5}}+1}{2}}t\approx 1{,}902~R\approx 1{,}618~t}
- S=55+254t2≈1,72048 t2{\displaystyle S={\frac {{\sqrt {5}}{\sqrt {5+2{\sqrt {5}}}}}{4}}t^{2}\approx 1{,}72048~t^{2}}
- Правильным пятиугольником невозможно заполнить плоскость без промежутков (см. также Паркет)
- Отношение площадей правильного пятиугольника и другого правильного пятиугольника, образованного пересечением диагоналей исходного (середина пятиугольной звезды)
- Ss=Φ4=3Φ+2=35+72≈6,8541{\displaystyle {\frac {S}{s}}=\Phi ^{4}=3\Phi +2={\frac {3{\sqrt {5}}+7}{2}}\approx 6{,}8541}
- где Φ{\displaystyle \Phi } — отношение золотого сечения.
Построение
Построение правильного пятиугольникаПостроение правильного пятиугольника
Правильный пятиугольник может быть построен с помощью циркуля и линейки или вписыванием его в заданную окружность, или построением на основе заданной стороны. Этот процесс описан Евклидом в его «Началах» около 300 года до н. э.
Альтернативный метод построения правильного многоугольника с помощью линейки и циркуля
Вот один из методов построения правильного пятиугольника в заданной окружности:
- Постройте окружность, в которую будет вписан пятиугольник, и обозначьте её центр как O. (Это зелёная окружность на схеме справа).
- Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
- Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью как точку B.
- Постройте точку C посередине между O и B.
- Проведите окружность с центром в точке C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
- Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F.
- Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.
- Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.
- Постройте правильный пятиугольник AEGHF.
Получение с помощью полоски бумаги
Правильный пятиугольник можно получить, завязав узлом полоску бумаги.
В природе
Исследования формирования водяного льда на ровной поверхности меди при температурах 100—140 K показали, что сначала на поверхности возникают цепочки молекул шириной около 1 нм не гексагональной, а пентагональной структуры.[1] Пентасимметрию можно увидеть во многих цветах и некоторых фруктах, например в таких как эта мушмула германская.
Пентасимметрией обладают иглокожие (например морские звёзды) и некоторые растения. См. также Закономерности в природе.
Интересные факты
- Додекаэдр — единственный из правильных многогранников, грани которого представляют собой правильные пятиугольники.
- Пентагон — здание Министерства обороны США — имеет форму правильного пятиугольника.
- Правильный пятиугольник — правильный многоугольник с наименьшим количеством углов из тех, которыми нельзя замостить плоскость.
- В природе не существует кристаллов с гранями в форме правильного пятиугольника.
- Пятиугольник со всеми его диагоналями является проекцией 4-симплекса.
См. также
Примечания
| Многоугольники | |
|---|---|
| Звёздчатые многоугольники | |
| Паркеты на плоскости | |
| Правильные многогранники и сферические паркеты | |
| Многогранники Кеплера — Пуансо | |
| Соты | |
| Четырёхмерные многогранники |
|
Как отыскать площадь правильного пятиугольника?

Верный пятиугольник либо пентагон (англ. regular pentagon) — это пятиугольник, все стороны и все углы которого равны меж собой.
Формулы для правильного пятиугольника:
α = (n — 2)/n · 180° = (3/5) · 180° = 108°.
S = (5/4) a2 ctg(π/5) = (1/4) √5 √(5 + 2√5) a2 ≈ 1,720 a2.
S = (5/2) R2 sin(2π/5) = (5√2/8) √(5 + √5) R2 ≈ 2,378 R2.
S = 5 r2 tg(π/5) = 5 √(5 — 2√5) r2 ≈ 3,633 r2.
h = (1/2) a tg 72° = (1/2) √(5 + 2√5) a2 = 1,539 a.
d/a = (1 + √5) / 2 ≈ 1,618.
r = (1/10) √5 √(5 + 2√5) a ≈ 0,688 a.
R = (1/10) √10 √(5 + √5) a ≈ 0,851 a.
Факты о правильном пятиугольнике:
Источники:
Дополнительно на New-Best.com:
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
-
Как отыскать площадь правильного пятиугольника?
Верный пятиугольник либо пентагон (англ. regular pentagon) — это пятиугольник, все стороны и все углы которого равны меж собой. Формулы для правильного пятиугольника: Величина α внутренних углов правильного пятиугольника (n=5) составляет:α = (n — 2)/n · 180° = (3/5) · 180° = 108°. Площадь правильного пятиугольника со стороной a рассчитывается по формуле: S = (5/4)…
- ВКонтакте
- Одноклассники
- Mail.ru
- Google+
- Livejournal
Правильный пятиугольник — Википедия
Материал из Википедии — свободной энциклопедии
Правильный пятиугольник (или пентагон от греч. πενταγωνον) — геометрическая фигура, правильный многоугольник с пятью сторонами.
Свойства
Построение правильного пятиугольника- α=(n−2)n⋅180∘=35⋅180∘=108∘{\displaystyle \alpha ={\frac {(n-2)}{n}}\cdot 180^{\circ }={\frac {3}{5}}\cdot 180^{\circ }=108^{\circ }}
- Площадь правильного пятиугольника рассчитывается по любой из формул:
- S=54t2ctgπ5=55+254t2=512Rd=52R2sin2π5=5r2tgπ5{\displaystyle S={\frac {5}{4}}t^{2}\mathop {\mathrm {ctg} } \,{\frac {\pi }{5}}={\frac {{\sqrt {5}}{\sqrt {5+2{\sqrt {5}}}}}{4}}t^{2}={\frac {5}{12}}Rd={\frac {5}{2}}R^{2}\sin {\frac {2\pi }{5}}=5r^{2}\mathop {\mathrm {tg} } \,{\frac {\pi }{5}}},
- где R{\displaystyle R} — радиус описанной окружности, r{\displaystyle r} — радиус вписанной окружности, d{\displaystyle d} — диагональ, t{\displaystyle t} — сторона.
- Высота правильного пятиугольника:
- h=tg72∘2t=5+252t≈1,539t{\displaystyle h={\frac {\operatorname {tg} \,72^{\circ }}{2}}t={\frac {\sqrt {5+2{\sqrt {5}}}}{2}}t\approx 1,539t}
- Диагонали правильного пятиугольника являются трисектрисами его внутренних углов.
- Отношение диагонали правильного пятиугольника к стороне равно золотому сечению, то есть числу 1+52{\displaystyle {\frac {1+{\sqrt {5}}}{2}}}.
Поэтому радиус вписанной окружности, радиус описанной окружности, высоту и площадь правильного пятиугольника можно вычислить и без использования тригонометрических функций:
- t=R5−52≈1,17557 R{\displaystyle t=R{\sqrt {\frac {5-{\sqrt {5}}}{2}}}\approx 1{,}17557~R}
- Радиус вписанной окружности:
- r=55+2510t≈0,688191 t{\displaystyle r={\frac {{\sqrt {5}}{\sqrt {5+2{\sqrt {5}}}}}{10}}t\approx 0{,}688191~t}
- Радиус описанной окружности:
- R=105+510t=(5−1) r≈0,850651 t≈1,23607 r{\displaystyle R={\frac {{\sqrt {1}}0{\sqrt {5+{\sqrt {5}}}}}{10}}t=({\sqrt {5}}-1)~r\approx 0{,}850651~t\approx 1{,}23607~r}
- d=Φ5R=5+12t≈1,902 R≈1,618 t{\displaystyle d={\sqrt {\Phi {\sqrt {5}}}}R={\frac {{\sqrt {5}}+1}{2}}t\approx 1{,}902~R\approx 1{,}618~t}
- S=55+254t2≈1,72048 t2{\displaystyle S={\frac {{\sqrt {5}}{\sqrt {5+2{\sqrt {5}}}}}{4}}t^{2}\approx 1{,}72048~t^{2}}
- Правильным пятиугольником невозможно заполнить плоскость без промежутков (см. также Паркет)
- Отношение площадей правильного пятиугольника и другого правильного пятиугольника, образованного пересечением диагоналей исходного (середина пятиугольной звезды)
- Ss=Φ4=3Φ+2=35+72≈6,8541{\displaystyle {\frac {S}{s}}=\Phi ^{4}=3\Phi +2={\frac {3{\sqrt {5}}+7}{2}}\approx 6{,}8541}
- где Φ{\displaystyle \Phi } — отношение золотого сечения.
Построение
Построение правильного пятиугольникаПостроение правильного пятиугольника
Правильный пятиугольник может быть построен с помощью циркуля и линейки или вписыванием его в заданную окружность, или построением на основе заданной стороны. Этот процесс описан Евклидом в его «Началах» около 300 года до н. э.
Альтернативный метод построения правильного многоугольника с помощью линейки и циркуля
Вот один из методов построения правильного пятиугольника в заданной окружности:
- Постройте окружность, в которую будет вписан пятиугольник, и обозначьте её центр как O. (Это зелёная окружность на схеме справа).
- Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
- Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью как точку B.
- Постройте точку C посередине между O и B.
- Проведите окружность с центром в точке C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
- Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F.
- Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.
- Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.
- Постройте правильный пятиугольник AEGHF.
Получение с помощью полоски бумаги
Правильный пятиугольник можно получить, завязав узлом полоску бумаги.
В природе
Исследования формирования водяного льда на ровной поверхности меди при температурах 100—140 K показали, что сначала на поверхности возникают цепочки молекул шириной около 1 нм не гексагональной, а пентагональной структуры.[1] Пентасимметрию можно увидеть во многих цветах и некоторых фруктах, например в таких как эта мушмула германская.
Пентасимметрией обладают иглокожие (например морские звёзды) и некоторые растения. См. также Закономерности в природе.
Интересные факты
- Додекаэдр — единственный из правильных многогранников, грани которого представляют собой правильные пятиугольники.
- Пентагон — здание Министерства обороны США — имеет форму правильного пятиугольника.
- Правильный пятиугольник — правильный многоугольник с наименьшим количеством углов из тех, которыми нельзя замостить плоскость.
- В природе не существует кристаллов с гранями в форме правильного пятиугольника.
- Пятиугольник со всеми его диагоналями является проекцией 4-симплекса.
См. также
Примечания
| Многоугольники | |
|---|---|
| Звёздчатые многоугольники | |
| Паркеты на плоскости | |
| Правильные многогранники и сферические паркеты | |
| Многогранники Кеплера — Пуансо | |
| Соты | |
| Четырёхмерные многогранники |
|
Правильный пятиугольник — Википедия. Что такое Правильный пятиугольник
Материал из Википедии — свободной энциклопедии
Правильный пятиугольник (или пентагон от греч. πενταγωνον) — геометрическая фигура, правильный многоугольник с пятью сторонами.
Свойства
Построение правильного пятиугольника- α=(n−2)n⋅180∘=35⋅180∘=108∘{\displaystyle \alpha ={\frac {(n-2)}{n}}\cdot 180^{\circ }={\frac {3}{5}}\cdot 180^{\circ }=108^{\circ }}
- Площадь правильного пятиугольника рассчитывается по любой из формул:
- S=54t2ctgπ5=55+254t2=512Rd=52R2sin2π5=5r2tgπ5{\displaystyle S={\frac {5}{4}}t^{2}\mathop {\mathrm {ctg} } \,{\frac {\pi }{5}}={\frac {{\sqrt {5}}{\sqrt {5+2{\sqrt {5}}}}}{4}}t^{2}={\frac {5}{12}}Rd={\frac {5}{2}}R^{2}\sin {\frac {2\pi }{5}}=5r^{2}\mathop {\mathrm {tg} } \,{\frac {\pi }{5}}},
- где R{\displaystyle R} — радиус описанной окружности, r{\displaystyle r} — радиус вписанной окружности, d{\displaystyle d} — диагональ, t{\displaystyle t} — сторона.
- Высота правильного пятиугольника:
- h=tg72∘2t=5+252t≈1,539t{\displaystyle h={\frac {\operatorname {tg} \,72^{\circ }}{2}}t={\frac {\sqrt {5+2{\sqrt {5}}}}{2}}t\approx 1,539t}
- Диагонали правильного пятиугольника являются трисектрисами его внутренних углов.
- Отношение диагонали правильного пятиугольника к стороне равно золотому сечению, то есть числу 1+52{\displaystyle {\frac {1+{\sqrt {5}}}{2}}}.
Поэтому радиус вписанной окружности, радиус описанной окружности, высоту и площадь правильного пятиугольника можно вычислить и без использования тригонометрических функций:
- t=R5−52≈1,17557 R{\displaystyle t=R{\sqrt {\frac {5-{\sqrt {5}}}{2}}}\approx 1{,}17557~R}
- Радиус вписанной окружности:
- r=55+2510t≈0,688191 t{\displaystyle r={\frac {{\sqrt {5}}{\sqrt {5+2{\sqrt {5}}}}}{10}}t\approx 0{,}688191~t}
- Радиус описанной окружности:
- R=105+510t=(5−1) r≈0,850651 t≈1,23607 r{\displaystyle R={\frac {{\sqrt {1}}0{\sqrt {5+{\sqrt {5}}}}}{10}}t=({\sqrt {5}}-1)~r\approx 0{,}850651~t\approx 1{,}23607~r}
- d=Φ5R=5+12t≈1,902 R≈1,618 t{\displaystyle d={\sqrt {\Phi {\sqrt {5}}}}R={\frac {{\sqrt {5}}+1}{2}}t\approx 1{,}902~R\approx 1{,}618~t}
- S=55+254t2≈1,72048 t2{\displaystyle S={\frac {{\sqrt {5}}{\sqrt {5+2{\sqrt {5}}}}}{4}}t^{2}\approx 1{,}72048~t^{2}}
- Правильным пятиугольником невозможно заполнить плоскость без промежутков (см. также Паркет)
- Отношение площадей правильного пятиугольника и другого правильного пятиугольника, образованного пересечением диагоналей исходного (середина пятиугольной звезды)
- Ss=Φ4=3Φ+2=35+72≈6,8541{\displaystyle {\frac {S}{s}}=\Phi ^{4}=3\Phi +2={\frac {3{\sqrt {5}}+7}{2}}\approx 6{,}8541}
- где Φ{\displaystyle \Phi } — отношение золотого сечения.
Построение
Построение правильного пятиугольникаПостроение правильного пятиугольника
Правильный пятиугольник может быть построен с помощью циркуля и линейки или вписыванием его в заданную окружность, или построением на основе заданной стороны. Этот процесс описан Евклидом в его «Началах» около 300 года до н. э.
Альтернативный метод построения правильного многоугольника с помощью линейки и циркуля
Вот один из методов построения правильного пятиугольника в заданной окружности:
- Постройте окружность, в которую будет вписан пятиугольник, и обозначьте её центр как O. (Это зелёная окружность на схеме справа).
- Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
- Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью как точку B.
- Постройте точку C посередине между O и B.
- Проведите окружность с центром в точке C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
- Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F.
- Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.
- Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.
- Постройте правильный пятиугольник AEGHF.
Получение с помощью полоски бумаги
Правильный пятиугольник можно получить, завязав узлом полоску бумаги.
В природе
Исследования формирования водяного льда на ровной поверхности меди при температурах 100—140 K показали, что сначала на поверхности возникают цепочки молекул шириной около 1 нм не гексагональной, а пентагональной структуры.[1] Пентасимметрию можно увидеть во многих цветах и некоторых фруктах, например в таких как эта мушмула германская.
Пентасимметрией обладают иглокожие (например морские звёзды) и некоторые растения. См. также Закономерности в природе.
Интересные факты
- Додекаэдр — единственный из правильных многогранников, грани которого представляют собой правильные пятиугольники.
- Пентагон — здание Министерства обороны США — имеет форму правильного пятиугольника.
- Правильный пятиугольник — правильный многоугольник с наименьшим количеством углов из тех, которыми нельзя замостить плоскость.
- В природе не существует кристаллов с гранями в форме правильного пятиугольника.
- Пятиугольник со всеми его диагоналями является проекцией 4-симплекса.
См. также
Примечания
| Многоугольники | |
|---|---|
| Звёздчатые многоугольники | |
| Паркеты на плоскости | |
| Правильные многогранники и сферические паркеты | |
| Многогранники Кеплера — Пуансо | |
| Соты | |
| Четырёхмерные многогранники |
|
Площадь Формулы Пентагона
- БЕСПЛАТНАЯ ЗАПИСЬ КЛАСС
- КОНКУРСНЫЕ ЭКЗАМЕНА
- BNAT
- Классы
- Класс 1 — 3
- Класс 4-5
- Класс 6-10
- Класс 110003 CBSE
- Книги NCERT
- Книги NCERT для класса 5
- Книги NCERT, класс 6
- Книги NCERT для класса 7
- Книги NCERT для класса 8
- Книги NCERT для класса 9
- Книги NCERT для класса 10
- NCERT Книги для класса 11
- NCERT Книги для класса 12
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11 9plar
- RS Aggarwal
- RS Aggarwal Решения класса 12
- RS Aggarwal Class 11 Solutions
- RS Aggarwal Решения класса 10
- Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Решения RS Aggarwal класса 6
- RD Sharma
- RD Sharma Class 6 Решения
- RD Sharma Class 7 Решения
- Решения RD Sharma класса 8
- Решения RD Sharma класса 9
- Решения RD Sharma класса 10
- Решения RD Sharma класса 11
- Решения RD Sharma Class 12
- PHYSICS
- Механика
- Оптика
- Термодинамика
- Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- MATHS
- Статистика
- 9000 Pro Числа
- Числа
- 9000 Pro Числа Тр Игонометрические функции
- Взаимосвязи и функции
- Последовательности и серии
- Таблицы умножения
- Детерминанты и матрицы
- Прибыль и убытки
- Полиномиальные уравнения
- Деление фракций
- Microology
- 0003000
- Книги NCERT
- FORMULAS
- Математические формулы
- Алгебраические формулы
- Тригонометрические формулы
- Геометрические формулы
- КАЛЬКУЛЯТОРЫ
- Математические калькуляторы
- 0003000
- 000 Калькуляторы
- 000 Физические модели 900 Образцы документов для класса 6
- Образцы документов CBSE для класса 7
- Образцы документов CBSE для класса 8
- Образцы документов CBSE для класса 9
- Образцы документов CBSE для класса 10
- Образцы документов CBSE для класса 1 1
- Образцы документов CBSE для класса 12
- Вопросники предыдущего года CBSE
- Вопросники предыдущего года CBSE, класс 10
- Вопросники предыдущего года CBSE, класс 12
- HC Verma Solutions
- HC Verma Solutions Класс 11 Физика
- HC Verma Solutions Класс 12 Физика
- Решения Лакмира Сингха
- Решения Лакмира Сингха класса 9
- Решения Лахмира Сингха класса 10
- Решения Лакмира Сингха класса 8
9000 Класс
- Примечания CBSE класса 7 Примечания
- Примечания CBSE класса 8
- Примечания CBSE класса 9
- Примечания CBSE класса 10
- Примечания CBSE класса 11
- Примечания 12 CBSE
- Дополнительные вопросы по математике класса 8 CBSE
- Дополнительные вопросы по науке 8 класса CBSE
- Дополнительные вопросы по математике класса 9 CBSE
- Дополнительные вопросы по математике класса 9 CBSE Вопросы
- CBSE Class 10 Дополнительные вопросы по математике
- CBSE Class 10 Science Extra questions
- Class 3
- Class 4
- Class 5
- Class 6
- Class 7
- Class 8 Класс 9
- Класс 10
- Класс 11
- Класс 12
- Решения NCERT для класса 11
- Решения NCERT для класса 11 по физике
- Решения NCERT для класса 11 Химия
- Решения NCERT для биологии класса 11
- Решение NCERT s Для класса 11 по математике
- NCERT Solutions Class 11 Accountancy
- NCERT Solutions Class 11 Business Studies
- NCERT Solutions Class 11 Economics
- NCERT Solutions Class 11 Statistics
- NCERT Solutions Class 11 Commerce
- NCERT Solutions for Class 12
- Решения NCERT для физики класса 12
- Решения NCERT для химии класса 12
- Решения NCERT для биологии класса 12
- Решения NCERT для математики класса 12
- Решения NCERT, класс 12, бухгалтерия
- Решения NCERT, класс 12, бизнес-исследования
- NCERT Solutions Class 12 Economics
- NCERT Solutions Class 12 Accountancy Part 1
- NCERT Solutions Class 12 Accountancy Part 2
- NCERT Solutions Class 12 Micro-Economics
- NCERT Solutions Class 12 Commerce
- NCERT Solutions Class 12 Macro-Economics
- NCERT Solut Ионы Для класса 4
- Решения NCERT для математики класса 4
- Решения NCERT для класса 4 EVS
- Решения NCERT для класса 5
- Решения NCERT для математики класса 5
- Решения NCERT для класса 5 EVS
- Решения NCERT для класса 6
- Решения NCERT для математики класса 6
- Решения NCERT для науки класса 6
- Решения NCERT для класса 6 по социальным наукам
- Решения NCERT для класса 6 Английский язык
- Решения NCERT для класса 7
- Решения NCERT для математики класса 7
- Решения NCERT для науки класса 7
- Решения NCERT для социальных наук класса 7
- Решения NCERT для класса 7 Английский язык
- Решения NCERT для класса 8
- Решения NCERT для математики класса 8
- Решения NCERT для науки 8 класса
- Решения NCERT для социальных наук 8 класса ce
- Решения NCERT для класса 8 Английский
- Решения NCERT для класса 9
- Решения NCERT для класса 9 по социальным наукам
- Решения NCERT для математики класса 9
- Решения NCERT для математики класса 9 Глава 1
- Решения NCERT для математики класса 9, глава 2 Решения NCERT
- для математики класса 9, глава 3
- Решения NCERT для математики класса 9, глава 4
- Решения NCERT для математики класса 9, глава 5 Решения NCERT
- для математики класса 9, глава 6
- Решения NCERT для математики класса 9, глава 7 Решения NCERT
- для математики класса 9, глава 8
- Решения NCERT для математики класса 9, глава 9
- Решения NCERT для математики класса 9, глава 10 Решения NCERT
- для математики класса 9, глава 11
- NCERT для математики класса 9 Глава 12 Решения NCERT
- для математики класса 9 Глава 13
- NCER Решения T для математики класса 9 Глава 14
- Решения NCERT для математики класса 9 Глава 15
- Решения NCERT для науки класса 9
- Решения NCERT для науки класса 9 Глава 1
- Решения NCERT для науки класса 9 Глава 2
- Решения NCERT для науки класса 9 Глава 3
- Решения NCERT для науки класса 9 Глава 4
- Решения NCERT для науки класса 9 Глава 5
- Решения NCERT для науки класса 9 Глава 6
- Решения NCERT для науки класса 9 Глава 7
- Решения NCERT для науки класса 9 Глава 8
- Решения NCERT для науки класса 9 Глава 10
- Решения NCERT для науки класса 9 Глава 12
- Решения NCERT для науки класса 9 Глава 11
- Решения NCERT для науки класса 9 Глава 13 Решения NCERT
- для науки класса 9 Глава 14
- Решения NCERT для класса 9 по науке Глава 15
- Решения NCERT для класса 10
- Решения NCERT для класса 10 по социальным наукам
- Решения NCERT для математики класса 10
- Решения NCERT для математики класса 10 Глава 1
- Решения NCERT для математики класса 10, глава 2
- Решения NCERT для математики класса 10, глава 3
- Решения NCERT для математики класса 10, глава 4
- Решения NCERT для математики класса 10, глава 5
- Решения NCERT для математики класса 10, глава 6
- Решения NCERT для математики класса 10, глава 7
- Решения NCERT для математики класса 10, глава 8
- Решения NCERT для математики класса 10, глава 9
- Решения NCERT для математики класса 10, глава 10
- Решения NCERT для математики класса 10 Глава 11
- Решения NCERT для математики класса 10 Глава 12
- Решения NCERT для математики класса 10 Глава ter 13
- Решения NCERT для математики класса 10 Глава 14
- Решения NCERT для математики класса 10 Глава 15
- Решения NCERT для науки класса 10
- Решения NCERT для класса 10 науки Глава 1
- Решения NCERT для класса 10 Наука, глава 2
- Решения NCERT для класса 10, глава 3
- Решения NCERT для класса 10, глава 4
- Решения NCERT для класса 10, глава 5
- Решения NCERT для класса 10, глава 6
- Решения NCERT для класса 10 Наука, глава 7
- Решения NCERT для класса 10, глава 8,
- Решения NCERT для класса 10, глава 9
- Решения NCERT для класса 10, глава 10
- Решения NCERT для класса 10, глава 11
- Решения NCERT для класса 10 Наука Глава 12
- Решения NCERT для класса 10 Наука Глава 13
- NCERT S Решения для класса 10 по науке Глава 14
- Решения NCERT для класса 10 по науке Глава 15
- Решения NCERT для класса 10 по науке Глава 16
- Программа NCERT
- NCERT
- Class 11 Commerce Syllabus
- Учебный план класса 11
- Учебный план бизнес-класса 11 класса
- Учебный план экономического факультета 11
- Учебный план по коммерции 12 класса
- Учебный план класса 12
- Учебный план бизнес-класса 12 Учебный план
- Класс 12 Образцы документов для торговли
- Образцы документов для предприятий класса 11
- Образцы документов для коммерческих предприятий класса 12
- TS Grewal Solutions
- TS Grewal Solutions Class 12 Accountancy
- TS Grewal Solutions Class 11 Accountancy
- Отчет о движении денежных средств 9 0004
- Что такое предпринимательство
- Защита прав потребителей
- Что такое основные средства
- Что такое баланс
- Что такое фискальный дефицит
- Что такое акции
- Разница между продажами и маркетингом
- ICC
- Образцы документов ICSE
- Вопросы ICSE
- ML Aggarwal Solutions
- ML Aggarwal Solutions Class 10 Maths
- ML Aggarwal Solutions Class 9 Maths
- ML Aggarwal Solutions Class 8 Maths
- ML Aggarwal Solutions Class 7 Maths Решения Математика класса 6
- Решения Селины
- Решения Селины для класса 8
- Решения Селины для класса 10
- Решение Селины для класса 9
- Решения Фрэнка
- Решения Фрэнка для математики класса 10
- Франк Решения для математики 9 класса
- ICSE Class
- ICSE Class 6
- ICSE Class 7
- ICSE Class 8
- ICSE Class 9
- ICSE Class 10
- ISC Class 11
- ISC Class 12
- 900 Экзамен по IAS
- Мок-тест IAS 2019 1
- Мок-тест IAS4
- Экзамен KPSC KAS
- Экзамен UPPSC PCS
- Экзамен MPSC
- Экзамен RPSC RAS
- TNPSC Group 1
- APPSC Group 1
- Экзамен BPSC
- Экзамен WPSC
- Экзамен JPSC
- Экзамен GPSC
- Ответный ключ UPSC 2019
- Коучинг IAS Бангалор
- Коучинг IAS Дели
- Коучинг IAS Ченнаи
- Коучинг IAS Хайдарабад
- Коучинг IAS Мумбаи
- Программа BYJU NEET
- NEET 2020
- NEET Eligibility
- NEET Eligibility
- NEET Eligibility 2020 Подготовка
- NEET Syllabus
- Support
- Разрешение жалоб
- Служба поддержки
- Центр поддержки
- GSEB
- GSEB Syllabus GSEB
Образец статьи
- MSBSHSE Syllabus
- MSBSHSE Учебники
- MSBSHSE Образцы статей
- MSBSHSE Вопросы
- 9000
- AP 2 Year Syllabus
- MP Board Syllabus
- MP Board Образцы документов
- Учебники MP Board
- Assam Board Syllabus
- Assam Board
- Assam Board
- Assam Board Документы
- Bihar Board Syllabus
- Bihar Board Учебники
- Bihar Board Question Papers
- Bihar Board Model Papers
- Odisha Board
- Odisha Board
- Odisha Board 9000
- ПСЕБ 9 0002
- PSEB Syllabus
- PSEB Учебники
- PSEB Вопросы и ответы
- RBSE
- Rajasthan Board Syllabus
- RBSE Учебники
- RBSE
- 000 RBSE 000 HPOSE
- 000 HPOSE
- 000 000 HPOSE
- 000 HPOSE
- 000 000
000 HPOSE - 000 HPOSE 000
- JKBOSE Syllabus
- JKBOSE Образцы документов
- Экзаменационные образцы JKBOSE
- TN Board
- 5
- 5 .
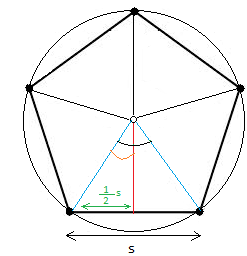
Разделим пятиугольник на 5 равных треугольников, проведя линию от центра к каждой из вершин (радиус).
Затем мы проводим линию от центра до основания одного из треугольников так, чтобы он касался основания под углом 90 °. Это тоже апофема треугольника.
Теперь, поскольку Пентагон — это правильный пятиугольник, угол, который апофема составляет с радиусом в центре, всегда равен 36 °.
В итоге мы получаем прямоугольный треугольник, противоположный треугольник которого равен половине длины стороны, а прилегающий — апофеме.\ circ} \]
Единственный способ найти площадь неправильного пятиугольника — разделить его на несколько меньших фигур, соединив вершины, средние точки и т. д., а затем найти все площади меньших частей, а затем продолжаем добавлять их все.
.Пентагон — определение математического слова
Пентагон — определение математического слова — Math Open ReferenceОпределение: многоугольник с 5 сторонами.
Попробуй это Отрегулируйте пятиугольник ниже, перетащив любую оранжевую точку. Нажав на верхнюю левую командную строку, вы можете переключать его между регулярные и неправильный пятиугольник.Свойства правильных пятиугольников
Внутренний угол 108 ° Как и любой правильный многоугольник, чтобы найти внутренний угол, мы используем формулу (180н – 360) / л.Для пятиугольника n = 5. См. Внутренние углы многоугольника Внешний угол 72 ° Чтобы найти внешний угол правильного пятиугольника, мы используем тот факт, что внешний угол образует линейную пару с внутренним углом, поэтому в целом он определяется формулой 180-внутренний угол. См. Внешние углы многоугольника Площадь 1,72 S 2
(приблизительно)Где S — длина стороны.Чтобы найти точную площадь правильного пятиугольника или любого правильного многоугольника, используя различные методы, см. Площадь правильного многоугольника и Площадь неправильного многоугольника Свойства всех пятиугольников
Количество диагоналей 5 Количество различных диагоналей, возможных для всех вершин. (Обычно ½n (n – 3)). На рисунке выше нажмите «показать диагонали», чтобы увидеть их. См. Диагонали многоугольника Количество треугольников 3 Количество треугольников, созданных путем рисования диагоналей из заданной вершины.(В общем n – 2). На рисунке выше нажмите «показать треугольники», чтобы увидеть их. Увидеть треугольники многоугольника Сумма внутренних углов 540 ° Обычно 180 (n – 2) градусов. См. Внутренние углы многоугольника Пентагон
Выше хорошо известное здание штаб-квартиры Министерства обороны США — широко известный как «Пентагон» из-за своей формы.
Как видите, внутри несколько контор.В геометрических терминах их можно было бы назвать концентрическими правильными пятиугольниками, поскольку они имеют общую центральную точку. и симметричны, как и правильный многоугольник.
Он был построен в 1943 году, имеет 17,5 миль (28 км) коридоров, и общей площадью 6 500 000 квадратных футов (604 000 м 2 2 ). В 1992 году Пентагон стал национальным историческим памятником.
Другие полигоны
Общие
Типы многоугольника
Площадь различных типов полигонов
Периметр различных типов полигонов
Углы, связанные с многоугольниками
Именованные полигоны
(C) Открытый справочник по математике, 2011 г.
.
Все права защищены.Площадь правильного многоугольника
Мы покажем вам, как вывести 3 формулы, которые можно использовать для определения площади правильного многоугольника, также называемого n-угольником: Нарисовать n-угольник непросто, поэтому давайте изобразим правильный многоугольник или n-угольник с помощью пятиугольника.
Наша стратегия до того, как мы выведем формулу площади правильного многоугольника, будет состоять в том, чтобы показать вам, как получить площадь пятиугольника, а затем обобщить подход для n-угольника.
Чтобы получить площадь пятиугольника выше, выполните следующие действия. следующие шаги:
1.Разбейте пятиугольник на 5 равных треугольников
2. Получите площадь одного треугольника
3. Умножьте на 5, чтобы получить площадь для всех 5 треугольников или всего пятиугольника
Обратите внимание, что у пятиугольника 5 сторон, и вы можете сделать 5 треугольники. Точно так же у n-угольника n сторон, и вы можете составить n треугольников.
Формула для вычисления площади треугольника: A =основание × высота / 2
Глядя на треугольник выше, вы можете видеть, что основание равно s, а длина s также равна длине одной стороны пятиугольника.Красная линия — это высота, она называется апофемой в n-угольнике
Скажем, s = 4 и апофема = 8
Поскольку в пятиугольнике 5 треугольников, A = 5 ×4 × 8 / 2
Первое обобщение площади правильного многоугольникаbase = s и height = apothem. У n-угольника n треугольников
Поскольку в n-угольнике n треугольников, A = n ×s × апофема / 2
Иногда s не указывается, но вы знаете апофему и количество сторон.Итак, в этом случае вам нужно найти s. Вам понадобятся базовые тригонометрические отождествления.
Вам также нужно знать, как получить центральный угол. Взгляните еще раз на рисунок, центральный угол — это черный.
Найдите площадь, когда n = 5 и апофема = 8
Назовите угол оранжевым x и используйте тригонометрическую идентичность.

Если 4 =
8 / 2
тогда 8 = 4 × 2 Аналогично, если tan (x) =s / 16
тогда s = tan (x) × 16Теперь нам нужно найти x.x — половина угла в черном цвете. Угол, отмеченный черным, — это центральный угол.
Центральный угол можно найти по формуле: Центральный угол =360 градусов / п
n — количество сторон.
Центральный угол =360 градусов / 5
= 72 градусаУгол, обозначенный оранжевым или x, равен 72, деленному на 2 или 36 градусов. Таким образом, s = tan (36 °) × 16
Собирая все вместе, A = 5 ×загар (36 °) × 16 × 8 / 2
Эту математику можно выполнить довольно легко, но мы не будем этого делать, чтобы вы могли лучше понять, как мы можем обобщить и придумать формулу для n-угольника
Второе обобщение площади правильного многоугольника
base = s, height = apothem и n-угольник имеет n сторон
А = п ×s × апофема / 2
Используя tan (x) =s / 2 × апофема
, получаем s = tan (x) × 2 × апофемаНайдите x для n-угольника.
Центральный угол =360 градусов / п
Напомним, что x — это оранжевый угол, поэтому360 градусов / п
делится на 2 Это дает x =180 градусов / п
s = загар (180 градусов / п
) × 2 × апофема
Распространенная ошибка: думать, что апофему нужно писать только один раз! Взгляните еще раз. Апофема появляется в s, а также появляется в A



Определение площади правильного многоугольника, когда s и n заданы, но апофема неизвестна
Поскольку апофема отсутствует, мы можем использовать формулу s = tan (x) × 2 × апофема и найти апофему.
Замените апофему в формуле для площади и упростите. Вы получите уравнение в терминах s и угла
s = 2 × tan (x) × apothem
Если мы перепишем A = n ×s × апофема / 2
будет легче управлять А =п × с / 2
× апофема
А =п × с 2 / 4 × загар (х)
x — все тот же угол, поэтому x =180 градусов / п

Определение площади правильного многоугольника, когда радиус задан, но апофема и s неизвестны
Радиус — синяя линия или гипотенуза.Если x — это угол, обозначенный оранжевым, и пусть радиус будет равен r, мы получим:

s = 2 × r sin (x)
апофема = cos (x) × r
Замените значение апофемы и s в формуле A = n ×s × апофема / 2
А = п ×2 × r sin (x) × cos (x) × r / 2
А = п ×2 × sin (x) × cos (x) × r 2 / 2
Полезная тригонометрическая формула: sin (2x) = 2 sin (x) cos (x)
А = п ×грех (2x) × r 2 / 2


Новые уроки математики
Ваша электронная почта в безопасности.Мы будем использовать его только для информирования вас о новых уроках математики.
.
Площадь Пентагона | Площадь Пентагона с Апофемой и радиусом
Пятиугольник — это многоугольник с 5 сторонами. Это может быть выпуклый пятиугольник или вогнутый пятиугольник, который представляет собой самопересекающуюся пятиугольную замкнутую фигуру. В первом случае, если 5 сторон имеют равную длину, то он называется правильным пятиугольником с внутренним и внешним углами, равными 108 ° и 72 ° соответственно. В неправильном пятиугольнике одна или несколько сторон и углов могут не совпадать с другими. В выпуклом пятиугольнике 5 диагоналей.
В вогнутом пятиугольнике один или несколько углов больше 180 °, то есть угол отражения. В выпуклом пятиугольнике все внутренние углы меньше 180 °. Это означает, что все вершины многоугольника направлены наружу от центра фигуры.
Расчет площади пятиугольника
Площадь плоского пространства, занимаемого пятиугольником, называется площадью пятиугольника. Прежде чем мы начнем изучать, как вычислить площадь пятиугольника, давайте разберемся с несколькими терминами.
Апофема пятиугольника — это отрезок прямой, проведенный из центра пятиугольника перпендикулярно одной из его сторон.
Радиус пятиугольника — это длина, которая проходит от центра до вершины пятиугольника.
Сторона — это длина стороны, а периметр — это сумма длин всех сторон пятиугольника.
Даны правильные пятиугольники с длиной стороны и апофемой.
Для правильного пятиугольника с известной длиной стороны и апофемы простейший способ найти площадь — использовать эту формулу.2} \]
Примечание. В этом методе мы умножаем апофему на периметр многоугольника, а затем делим ее пополам, чтобы найти площадь. Это, в свою очередь, упрощает умножение апофемы на 5-кратное значение стороны и последующее определение площади.
Это также можно понимать как деление пятиугольника на 5 составляющих треугольников, имеющих равную площадь. Теперь апофема становится высотой, а длина стороны — основанием. Площадь треугольника находится по формуле:
\ [\ text {Площадь треугольника} = \ frac {1} {2} \ times {\ text {base}} \ times {\ text {height}} \]
Это даст нам площадь треугольников.Таких треугольников 5. Умножение площади на 5 дает нам общую площадь пятиугольника, до которой упрощается формула.
Но все проблемы, с которыми мы можем столкнуться, могут быть не такими простыми, как эта. Итак, давайте исследуем некоторые способы определения площади пятиугольника.
Правильный пятиугольник с заданной только длиной стороны
Когда задана только длина стороны правильного пятиугольника, мы используем этот метод.