О массе, силе, весе, рычаге и не только
- Участник: Вавилина Екатерина Анатольевна
- Руководитель: Завершинская Ирина Андреевна
В учебнике физики Перышкина А.В. за 7 класс в §19 мы найдем определение массы. Масса тела – это физическая величина, которая характеризует его инертность.
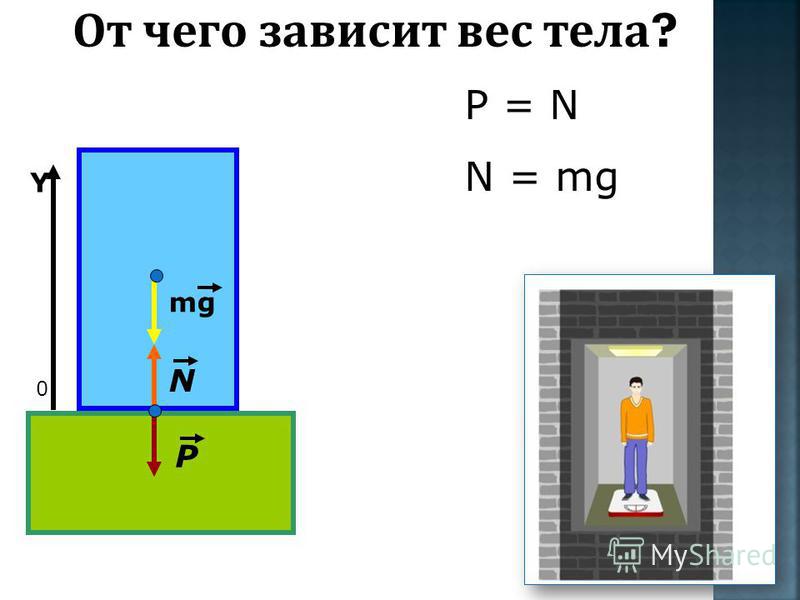
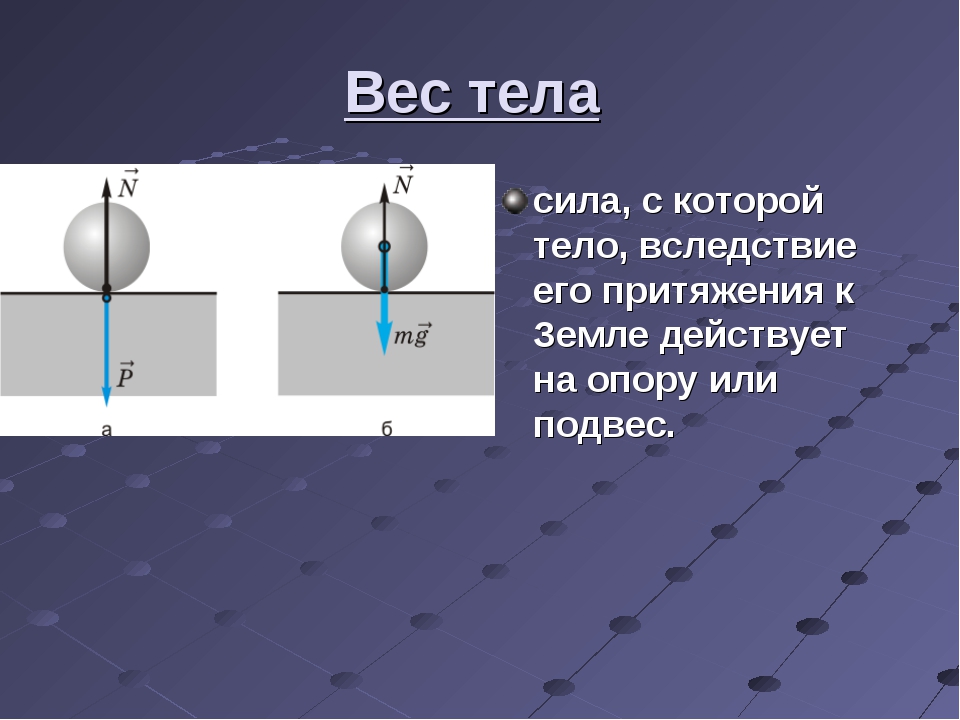
А в § 26 найдем определение веса. Вес тела – это сила, с которой тело вследствие притяжения к Земле действует на опору или подвес.
Масса измеряется в килограммах, а вес в ньютонах.
В 7 классе мы начали изучать физику по УМК Перышкина А.В.
Я спешила познакомиться с этой наукой, потому, что моя мама закончила физический факультет Куйбышевского государственного университета. Она всегда говорит, что физика – это очень интересно и очень увлекательно!
Сейчас я учусь в 9 классе, скоро экзамены. На ОГЭ, кроме математики и русского языка, я выбрала физику. Физика, действительно, очень интересная, увлекательная наука, но и сложная.
В повседневной жизни многие физические понятия используются неверно. Например, очень часто можно услышать: «Мой вес 40 килограмм» или «Этот тортик весит полкило». Но, вес и масса – это два разных понятия! Их нельзя путать.
В учебнике физики Перышкина А.В. за 7 класс в §19 мы найдем определение массы. Масса тела – это физическая величина, которая характеризует его инертность.
А в § 26 найдем определение веса. Вес тела – это сила, с которой тело вследствие притяжения к Земле действует на опору или подвес.
Масса измеряется в килограммах, а вес в ньютонах.
Масса – это вещь постоянная. Массу можно изменить, если от тела, например, отломать кусочек. С весом все гораздо сложнее…
В 7 классе, до изучения второго закона Ньютона, в учебнике говорилось, что если тело и опора покоятся или движутся равномерно и прямолинейно, то вес тела равен силе тяжести и определяется по той же формуле:
P = Fт = mg
Но следовало учитывать, что «сила тяжести действует на тело, а значит, приложена к самому телу, а вес действует на опору или подвес, т. е. приложен к опоре».
е. приложен к опоре».
А в § 2 для дополнительного чтения, мы впервые узнали, что такое невесомость. В состоянии невесомости вес тела равен нулю, а сила тяжести, как и масса тела, нулю не равны.
Удивительно, но в момент прыжка, когда на нас действует только сила тяжести, а сопротивлением воздуха можно пренебречь, то наш вес равен нулю. Можно считать, что мы находимся в невесомости.
А вот в 9 классе в § 11 был введен второй закон Ньютона: ускорение тела прямо пропорционально равнодействующей сил, приложенных к телу, и обратно пропорционально его массе.
=
И поэтому, вес тела – это результат совместного решения двух уравнений, составленных в соответствии со вторым и третьим законами Ньютона.
Если тело лежит на неподвижной опоре относительно Земли, то на тело действуют сила тяжести направленная вертикально вниз, и сила нормального давления или сила реакции опоры. Силы, действующие на тело, уравновешивают друг друга. В соответствии с третьим законом Ньютона тело действует на опору с некоторой силой – весом, равной по модулю силе реакции опоры и направленной в противоположную сторону. Т.е. вес численно равен силе тяжести, это как раз то, о чем мы говорили в 7 классе.
Если же наше тело, будет находиться в лифте, который движется с ускорением, то вес тела может быть больше или меньше силы тяжести. Результат зависит от направления ускорения.
Таким образом, в физике принято строгое различие понятий веса, силы тяжести и массы. С точки зрения физики, приходя на рынок и обращаясь к продавцу, следовало бы говорить: «Дайте, пожалуйста, десять ньютон клубники». Но все уже привыкли к слову вес, как синониму термина «масса».
Но очень важно понимать, что это вовсе не одно и то же!
Однако, массы некоторых тел очень большие. А человеку часто приходится поднимать, двигать тяжелые предметы. С давних пор человек применяет различные вспомогательные приспособления для облегчения своего труда.
С давних пор человек применяет различные вспомогательные приспособления для облегчения своего труда.
В § 55-56 учебника физики для 7 класса мы познакомились с простыми механизмами и в частности – рычагом.
В нашем современном мире рычаги находят широкое применение как в природе, так и в повседневной жизни, созданной человеком. Практически любой механизм, преобразующий механическое движение, в том или ином виде использует рычаги.
С помощью рычагов три тысячи лет назад при строительстве пирамид в Древнем Египте передвигали и поднимали на большую высоту тяжелые каменные плиты.
Рычаги позволяю получить выигрыш в силе!
Рычаги встречаются в разных частях тела человека и животных. Это, например, конечности, челюсти. Много рычагов можно увидеть в теле насекомых и птиц.
Рычаги так же распространены и в быту. Это и водопроводный кран, и дверь, и различные кухонные приборы
Правило рычага лежит в основе действия рычажных весов, различного рода инструментов и устройств, применяемых там, где требуется выигрыш в силе или в расстоянии.
Рычаг – это твёрдое тело, которое может вращаться вокруг точки опоры. Рычаг находится в равновесии, если сумма моментов сил равна нулю. Момент силы – это величина, равная произведению силы на плечо этой силы. M = Fl. Плечо – это кратчайшее расстояние от точки опоры, до линии, вдоль которой действует сила (перпендикуляр).
Различают рычаги 1 рода, в которых точка опоры располагается между точками приложения сил, и рычаги 2 рода, в которых точки приложения сил располагаются по одну сторону от опоры.
Среди рычагов 2 рода выделяют рычаги 3 рода, с точкой приложения «входящей» силы ближе к точке опоры, чем нагрузки, что даёт выигрыш в скорости и пути
Примеры: рычаги первого рода — детские качели (перекладина), ножницы; рычаги второго рода — тачка (точка опоры — колесо), приподнимание предмета ломом движением вверх; рычаги 
Рычаги очень часто встречаются в живой природе.
В скелете животных и человека все кости, имеющие некоторую свободу движения, являются рычагами.
- у человека – кости рук и ног, нижняя челюсть, череп, фаланги пальцев,
- у кошек рычагами являются подвижные когти;
- у многих рыб – шипы спинного плавника;
- у членистоногих – большинство сегментов их наружного скелета.
Рычажные механизмы скелета в основном рассчитаны на выигрыш в скорости при потере в силе. Особенно большие выигрыши в скорости получаются у насекомых.
Для осуществления полета крылья должны иметь особое расположение и возможность свободно двигаться. Крыло насекомых можно сравнить с двуплечим рычагом. Короткое плечо представлено его внутренней частью (основанием), которая скрыта под мембраной, а длинное располагается снаружи: собственно, эту видимую часть и принято считать крылом. На внутренней поверхности экзоскелета, сразу под местом сочленения крыла с телом, находится плотный выступ, который называют плейральным столбиком; данная структура играет роль точки опоры при взмахе крыльев.
Также рычажный механизм есть у цветка шалфея. От оси у тычинок шалфейного цветка отходят два плеча: длинное и короткое. На конце длинного, изогнутого, как у коромысла, плеча висит пыльцевой мешочек. А короткое плечо сплющено, оно-то и закрывает вход в глубину цветка. Потянется шмель своим хоботком к нектару и обязательно толкнет короткое плечо. А оно тотчас приведет в движение длинное плечо — коромысло. То в свою очередь ударяет по спине шмеля своими пыльниками — вот и сработал рычаг.
В скелете животных и человека все кости, имеющие некоторую свободу движения, являются рычагами, например, у человека – кости конечностей, нижняя челюсть, череп, фаланги пальцев.
Однажды я увидела в журнале рисунок, который захотелось использовать для оформления стенгазеты. Но рисунок был очень маленьким, а мне хотелось сохранить масштаб при увеличении его размеров. Я задумалась, как можно увеличить рисунок до нужных размеров. Оказывается, это можно сделать либо вручную «методом клеток», либо с помощью приборов: эпидиаскопа, или пантографа.
Но рисунок был очень маленьким, а мне хотелось сохранить масштаб при увеличении его размеров. Я задумалась, как можно увеличить рисунок до нужных размеров. Оказывается, это можно сделать либо вручную «методом клеток», либо с помощью приборов: эпидиаскопа, или пантографа.
Пантограф (название происходит от двух греческих слов (pantos) – все и qrapho – пишу) – прибор в виде раздвижного шарнирного параллелограмма для перерисовки рисунков, чертежей, схем в другом (увеличенном или уменьшенном масштабе). В основе работы этого прибора тоже лежит рычаг. Важной особенностью пантографа является простота его конструкции и очень высокая «точность» скопированного изображения. Но купить пантограф в магазине оказалось делом не простым. Тогда я решила его изготовить самостоятельно.
Пантографы широко используются в технике.
Так одним из основных видов городского транспорта является трамвай. Большинство трамваев используют электротягу с подачей электроэнергии через воздушную контактную сеть с помощью токоприёмников, чаще всего токоприёмник изготовлен в виде пантографов.
Очень часто пантографы используют в мебели. В этом случае пантограф по представляет собой штангу с подъемным механизмом. Обеспечивая легкий доступ к верхнему ярусу, пантограф способствует более эффективному использованию внутреннего пространства шкафа и лучшей организации хранения вещей.
Практическая часть
Прежде чем изготовить пантограф, я изготовила качели – рычаги.
Качели с перемещаемым сиденьем
Всем известны обычные детские качели рычажного типа, когда 2 ребёнка садятся по разным концам качелей и качаются, поочерёдно отталкиваясь от земли ногами. Но дети бывают разного веса. И обычно лёгкий ребёнок сидит наверху, а тяжёлый перевешивает его. Последний должен больше работать ногами, чтобы качели хоть как-то качались. Чтобы уравнять работу обоих, можно сделать перемещаемое сиденье на конструкции качелей. Тогда в зависимости от веса ребёнка подбирается длина рычага и у обоих детей уравниваются возможности и количество отталкиваний от земли в единицу времени.
Тогда в зависимости от веса ребёнка подбирается длина рычага и у обоих детей уравниваются возможности и количество отталкиваний от земли в единицу времени.
|
1 модель качелей из конструктора «ЛЕГО»:
|
2 модель:
|
3 модель: При перемещении сидения равновесие снова устанавливается
Изготовление пантографа
Воспользовавшись описанием изготовления пантографа с сайта «Мир самоделок»[5] я купила пластмассовые линейки, болты и гайки и изготовила свой пантограф.
Я изготовила анимационный материал, ссылка на который представлена: https://cloud.mail.ru/home/ВавилинаЕА.mkv
Работая над этим материалом, я не только повторила основные законы, определения. Я узнала много нового о рычагах. Изготовила пантограф и научилась его использовать. Изготовила небольшой анимационный материал.
Пожалуй, самое удивительное, это то, что когда я начала свою работу над проектом для участия во Всероссийском заочном конкурсе для обучающихся «Я учу физику», посвящённого 115-летию А.В. Пёрышкина, я не знала что получится. Оказывается, физические явления вокруг нас словно цепляются друг за друга. Так и хочется сказать: «Все взаимосвязано! А физика самая интересная и увлекательная наука!»
Сила тяжести и вес тела
В § 2-а мы начали знакомство с явлением гравитации вообще и земным тяготением в частности.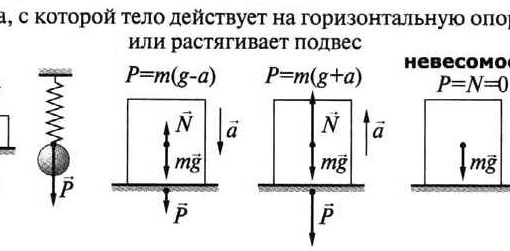 Теперь настало время более подробного изучения силы тяжести на Земле и других планетах.
Теперь настало время более подробного изучения силы тяжести на Земле и других планетах.
На рисунке изображён опыт с двумя гирями и динамометрами. Вы видите, что при массе гири 200 г (то есть 0,2 кг) на неё действует сила тяжести 2 Н, а при массе 500 г (то есть 0,5 кг) – сила тяжести 5 Н. Обратим внимание на закономерность:
| = 10 Н/кг | и | = 10 Н/кг |
Проделав опыты с многими телами, мы обнаружим ту же самую закономерность: отношение силы тяжести, действующей на тело, к массе этого тела является постоянной величиной, не зависящей ни от силы тяжести, ни от массы тела. Эту величину называют коэффициентом силы тяжести:
Формулу для вычисления коэффициента «g» можно преобразовать, поместив слева силу тяжести:
| Fтяж – сила тяжести, Н m – масса тела, кг g – коэффициент, Н/кг |
В опыте с двумя гирями мы выяснили, что вблизи поверхности Земли коэффициент «g» имеет значение 10 Н/кг (более точные значения 9,78 Н/кг и 9,83 Н/кг – см. далее в таблице).
Опыты показывают, что по мере удаления от Земли сила тяжести ослабевает. Например, на высоте 300 км значение коэффициента «g» уменьшается приблизительно до 9 Н/кг.
Повторяя опыт с гирями и динамометрами в различных местах Земли, а также на поверхности Луны, Марса и так далее, можно выяснить, что коэффициент «g» зависит от места наблюдения:
Коэффициенты силы тяжести, Н/кг
| Луна | 1,7 | Земля: | » 10 | |
| Марс | 3,8 | а) полюс | 9,83 | |
| Юпитер | 24 | б) экватор | 9,78 |
В обыденной жизни под словом «вес» мы зачастую подразумеваем массу тела, не делая различия между этими терминами. Однако это неверно.
Однако это неверно.
Весом тела называют силу, с которой тело давит на опору или тянет подвес. Например, на рисунке медведь действует на опору – прогнувшуюся доску. Согласно определению, сила давления медведя на доску – вес медведя. На рисунке правее медведь действует на подвес – канат. Эта сила тоже является весом, но уже медведя вместе с доской.
Часто вес тела равен действующей на него силе тяжести. В виде формулы это записывается так:
| W – вес тела, Н Fтяж – сила тяжести, Н |
Однако эта формула верна не всегда. Например, если тело погружено в жидкость или газ. В этом случае возникает выталкивающая сила, обычно приводящая к уменьшению веса. Многочисленные опыты показывают, что вес тела равен действующей на него силе тяжести, когда тело и его опора (подвес) покоятся или движутся вместе равномерно и прямолинейно, и не действуют другие силы, кроме силы тяжести. Это – границы применимости формулы W = Fтяж
Забегая вперед, скажем, что когда тело или его опора (подвес) движутся непрямолинейно или неравномерно, вес тела никогда не равен силе тяжести. Он может быть как больше, так и меньше неё, а также направлен в другую сторону.
Академия занимательных наук. Физика — Масса и вес тела. Видеоуроки физики
Масса и вес тела. Видеоуроки физики
Выпуск 15Пятнадцатая серия передачи посвящена новым физическим величинам — массе тела и его весу. Эти понятия часто путают и измеряют вес в килограммах. Но это является грубой ошибкой и профессор Даниил Эдисонович Кварк объяснит, почему это так. Можно ли изменить свой вес тела или даже сделать его совершенно невесомым? Физика отвечает утвердительно. Хотите узнать, как это сделать? Тогда смотрите видеоурок физики от Академии занимательных наук, посвящённый массе и весу тела.
Масса и вес тела
В чём заключается отличие между массой и весом тела? Вроде бы это одно и то же. Но почему тогда, стоя на весах, мы можем изменять их показания, выполняя те или иные действия (поднимая руки или сгибая туловище)? Видеоурок физики — это то, что нужно для выяснения этих вопросов. Да, разница есть. С точки зрения физики, неправильно интересоваться у продавца, сколько весит тот или иной продукт. А правильно — спросить, какова его масса! Вес это векторная величина, сила. Она всегда имеет направление. При неизменной массе тела, его вес можно изменить. Например, положив на весы банан и надавив на него рукой мы получим больший вес, в то время, как масса банана останется прежней. Вес тела — это сила, с которой это тело, притягиваясь к земле, давит на опору или растягивает подвес. Если масса тела измеряется в килограммах, то вес, как и любая сила — ньютонами. Теперь понятно, почему неверно говорить, что вес тела равен столько-то килограммам? Итак, вес тела всегда измеряется в ньютонах, в то время как масса тела может измерять в граммах, килограммах и т.д. В отличие от массы тела, вес тела не является постоянной величиной. Он может увеличиваться или уменьшаться, при этом масса тела останется прежней. Масса тела представляет собой скалярную величину. Почему если сильно раскачаться на качелях, начинает «захватывать дух»? Профессор Кварк считает, что это ощущение невесомости, похожее на то, которое бывает в космосе. Как же получается, что вес тела становится равным нулю, пусть даже на какое-то мгновение? А получается так потому, что в момент падения тело ни на что не давит и ничего не оттягивает, следовательно, не имеет веса. Вот ещё один пример, доказывающий, что вес тела может меняться при неизменной массе. В воде все тела весят меньше, чем на суше. Иначе мы не могли бы плавать, а шли прямиком ко дну. Слон с массой тела в 1 тонну весит на суше больше, чем в воде. Киты с массой более 30 тонн способны в воде парить как птицы.
Динамометр. Вес тела | Физика
Динамометр (от греческого слова «динамис» — сила) — это прибор для измерения силы.
Существуют различные конструкции динамометров. Силу тяги тракторов, тягачей, буксиров и т. д. измеряют с помощью тяговых динамометров (рис. 35). Для измерения мышечной силы руки используют медицинский динамометр — силомер (рис. 36).
На рисунке 37 изображен учебный пружинный динамометр, рассчитанный на измерение сил до 4 Н. Он состоит из стальной пружины с указателем и крючком, прикрепленном к пластмассовому (в старых конструкциях к деревянному) основанию, на которое нанесена шкала (буква «N» на шкале динамометра — это международное обозначение ньютона).
Действие пружинного динамометра основано на уравновешивании измеряемой силы силой упругости пружины.
Градуирование пружины динамометра (т. е. создание шкалы с делениями) можно осуществить следующим образом. К основанию динамометра (под пружиной) прикрепляют полоску белой бумаги. Затем отмечают положение указателя при нерастянутой пружине — это нулевое деление (рис. 38, а). После этого к крючку подвешивают груз массой 102 г. На этот груз действует сила тяжести 1 Н. Под действием этого груза пружина растягивается и указатель перемещается вниз. В положении равновесия сила тяжести, действующая на груз, уравновешивается противоположно направленной силой упругости. Следовательно, растяжение пружины при этом будет соответствовать силе упругости, также равной 1 Н. Поэтому новое положение указателя отмечают на бумаге цифрой 1 (рис. 38, б).Затем к первому грузу подвешивают еще один такой же, увеличивая тем самым общую массу до 204 г, а силу тяжести — до 2 Н. Соответствующее положение указателя отмечают цифрой 2. После этого прикрепляют третий, а затем четвертый груз, каждый раз отмечая положение указателя соответствующей цифрой.
Для того чтобы можно было измерять десятые доли ньютона, каждое из расстояний между отметками 0 и 1, 1 и 2, 2 и 3, 3 и 4 делят на десять равных частей. Такое построение шкалы возможно благодаря закону Гука, из которого следует, что сила упругости пружины увеличивается во столько же раз, во сколько раз увеличивается ее удлинение.
Динамометр можно применять и для измерения веса тела. Весом тела называют силу, с которой оно давит на горизонтальную опору или растягивает вертикальный подвес.
Р — вес тела.
Если к вертикально расположенному пружинному динамометру прикрепить груз, то после того, как груз растянет пружину и остановится, на крючок динамометра будут действовать две силы: сила упругости пружины Fупр и вес груза Р. Эти силы будут противоположны по направлению, но равны по величине. Поэтому динамометр позволяет измерить не только силу упругости (и равную ей силу тяжести груза), но и вес тела Р.
Вес покоящегося, а также равномерно и прямолинейно движущегося (относительно Земли) тела равен действующей на него силе тяжести:
P = mg.
Несмотря на совпадение формул, между силой тяжести и весом тела есть существенное различие. Сила тяжести приложена к телу, на которое действует Земля, а вес тела приложен к подвесу или опоре, на которую это тело давит. Если обе эти силы изобразить в виде стрелок, указывающих их направление (а направлены эти силы вертикально вниз), то это будет выглядеть так, как показано на рисунке 39.Вес тела не следует путать с его массой. Масса тела измеряется в килограммах, а вес тела (как и любая другая сила) — в ньютонах. Вес тела имеет направление, а масса никакого направления не имеет.
1. Что такое динамометр? 2. На чем основано действие пружинного динамометра? 3. Что называют весом тела? 4. По какой формуле находится вес покоящегося тела? 5. Чем отличается вес тела от силы тяжести и массы тела?
Физика. Вес тела. Невесомость | 7 класс Онлайн
Конспект по физике для 7 класса «Вес тела. Невесомость». ВЫ УЗНАЕТЕ: Что такое вес тела. Чем отличается вес тела от силы тяжести. Чем отличается вес тела от массы. Что такое невесомость. ВСПОМНИТЕ:
Конспекты по физике Учебник физики Тесты по физике
Вес тела. Невесомость
В повседневной жизни мы очень часто используем слово «вес». Мы говорим: вес продуктов, вес нашего тела. При этом зачастую под словом «вес» подразумевается масса тела. В физике используют термины «вес», «масса» и «сила тяжести», и все они обозначают совершенно разные понятия.
Мы говорим: вес продуктов, вес нашего тела. При этом зачастую под словом «вес» подразумевается масса тела. В физике используют термины «вес», «масса» и «сила тяжести», и все они обозначают совершенно разные понятия.
ВЕС ТЕЛА
Рассмотрим тело, подвешенное к динамометру. На само тело действуют сила тяжести и сила упругости пружины. Именно поэтому тело находится в равновесии. Но и растянутая пружина также находится в равновесии, хотя сила упругости, возникающая в ней, стремится вернуть её в первоначальное состояние. То есть не только пружина действует на тело, но и тело действует на пружину с некоторой силой.
Силу, с которой тело, находящееся под действием силы тяжести, действует на опору или подвес, называют весом тела. Таким образом, на крючок динамометра действуют две силы: сила упругости пружины и вес тела.
Вес тела, как и любая сила, — векторная величина. Вес тела обозначают буквой Р. Сила упругости и вес тела имеют противоположные направления: сила упругости направлена вверх, а вес тела вниз. При этом модули этих сил равны: Р = Fупр.
Именно поэтому говорят, что динамометром можно измерять не только силу упругости, но и вес тела. Динамометр также называют пружинными весами.
ВЕС ТЕЛА И СИЛА ТЯЖЕСТИ
Вес возникает в результате притяжения Земли и зависит от состояния движения тела.
Если тело и опора находятся в покое или движутся равномерно и прямолинейно, то вес тела по своему числовому значению равен силе тяжести, действующей на тело: Р = Fтяж или Р = mg.
При этом важно помнить, что сила тяжести и вес тела не одно и то же, они имеют различную физическую природу: сила тяжести возникает вследствие взаимодействия тела и Земли, а вес — в результате взаимодействия тела и опоры. Именно поэтому сила тяжести приложена к телу, а вес приложен к опоре или подвесу.
ВЕС ТЕЛА И МАССА
Единицей веса тела, как и любой силы, является ньютон. Вес имеет числовое значение, направление и точку приложения.
Вес имеет числовое значение, направление и точку приложения.
Вес тела не следует путать с массой тела, которая измеряется в килограммах и является скалярной величиной, т. е. величиной, не имеющей направления и точки приложения. Так, ребёнок, имеющий массу 30 кг, имеет вес, равный 300 Н, если считать, что g = 10 Н/кг.
ЗАВИСИМОСТЬ ВЕСА ОТ УСЛОВИЙ, В КОТОРЫХ НАХОДИТСЯ ТЕЛО
Вес тела равен по своему числовому значению силе тяжести, если тело находится на неподвижной опоре или опора движется равномерно и прямолинейно. Если же опора вместе с телом движется неравномерно по линии действия силы, т. е. вверх или вниз, то тело действует на опору сильнее или слабее, чем при равномерном движении. В этом случае вес тела может быть больше силы тяжести, меньше се или равным нулю.
Поднимаясь на скоростном лифте, в самом начале движения мы ощущаем, как нас слегка прижимает к полу. А при спуске нас как будто слегка приподнимает. Дело в том, что при движении лифта вверх вес тела увеличивается, а при движении вниз — уменьшается. Этот факт можно проверить, если подняться или опуститься в лифте стоя на весах.
НЕВЕСОМОСТЬ
Проведем следующий опыт. Подвесим за нитку пружину, а к ней прикрепим груз. В результате пружина растянется. Теперь перережем нить и понаблюдаем за процессом падения пружины вместе с грузом. В течение всего времени падения пружина будет оставаться нерастянутой. Получается, что при падении груз не действует на пружину и, следовательно, его вес в этот момент равен нулю.
Таким образом, свободно падающее тело не действует на свободно падающую вместе с нам пружину. В этом случае вес тела равен нулю.
Про такое тело говорят, что оно находится в состоянии невесомости. При этом сила тяжести по-прежнему действует на тело и заставляет его падать.
Подобные явления наблюдаются и на спутнике, обращающемся вокруг Земли.
Сам спутник и все находящиеся в нем тела, включая космонавта, обращаясь вокруг Земли, как бы непрерывно свободно падают на Землю. Вследствие этот, все находящиеся на спутнике тела не действуют на опоры, а подвешенные к пружине не растягивают её. Все предметы находятся в состоянии невесомости. Однако при разгоне космического корабля, когда он выходит на орбиту, или при торможении во время посадки вес космонавта оказывается больше силы тяжести и он испытывает сильные перегрузки.
Вы смотрели Конспект по физике для 7 класса «Вес тела. Невесомость»: Что такое вес тела. Чем отличается вес тела от силы тяжести. Чем отличается вес тела от массы. Что такое невесомость.
Вернуться к Списку конспектов по физике (В оглавление).
Каган И.Е. «Вес тела» (IX класс)
Цель урока: изучить вес тела в различных условиях.
Приборы и принадлежности: динамометры демонстрационный и Бакушинского, связка прямоугольных брусков, наклонная плоскость, прямолинейная планка (в качестве подставки), деревянный куб массой 200 г, деревянная полированная доска длиной 1,5 м, метровая линейка, два набора грузов с шестью грузиками в каждом, жестяная банка с водой, штатив с муфтой, шар для демонстрации невесомости, диск с подшипниками на оси, укрепленный на массивной подставке, стакан с водой, прозрачный скотч.
I. Методическое обоснование темы
Тема «Вес тела» является одной из важных и серьезных тем механики, имеет много нюансов, требующих внимания и размышления. Некоторые осложнения связаны с целым рядом расхождений в формулировках и определениях веса тела, а также в описаниях функции весов (особенно рычажных), имеющих место во многих учебниках и пособиях по физике и механике.
Для формирования логического мышления и способности рассуждать учащимся в принципе полезно знать о множестве таких разночтений, но сразу это сделать довольно трудно. Однако для того, чтобы опыты на таком уроке были понятны учащимся, а результаты разбора разных случаев логически доступны, они должны быть предварительно подготовлены по трем вопросам.
1. Что такое вес тела (т.е. нужно определить предмет обсуждения)?
2. Как изобразить вес тела?
3. Что измеряют весы?
1. Прохождение темы имеет смысл начинать с формулировки «веса тела», тем более, что учащиеся с ней сталкиваются уже в VII классе, изучая курс механики либо по учебнику А.В.Перышкина, Н.А.Родиной, либо по учебнику Л.А.Исаченковой, Ю.Д.Лещинского.
Необходимо отметить, что понятие «вес тела» неодинаково формулируется в различных учебниках и пособиях разных лет. Одна из самых популярных и, вероятно, точных формулировок выглядит так: «Вес – это сила, с которой тело действует на опору или подвес под действием притяжения к Земле (или силы тяжести)».
В целом ряде учебников по физике дается чуть-чуть другая формулировка веса: «Вес тела – это сила, с которой тело действует на горизонтальную (!) опору или подвес и т.д.».
А где взять «идеально горизонтальную» опору? Значит, на других, не горизонтальных, опорах вес будет уже другим? Более или менее приближенным? А, может, покоящееся тело сохраняет вес неизменным на любой опоре? И как быть с весом тела, движущегося равномерно прямолинейно?
В некоторых изданиях можно прочесть и другие формулировки веса.
В учебнике «Физика, 9» (авт. Л.А.Исаченкова, И.И.Жолнеревич, И.Н.Медведь, 2000) в § 32 (с. 129) в определении «силы веса» горизонтальная опора не упоминается, но на с. 131 «сила веса» численно приравнивается к нормальной силе реакции, что подтверждается рис. 133 на с. 131. Значит, величина веса зависит от угла наклона плоскости? Каким же будет вес покоящегося тела на вертикальной плоскости? Тем более, что на рис. 133 показана и сила трения.
133 на с. 131. Значит, величина веса зависит от угла наклона плоскости? Каким же будет вес покоящегося тела на вертикальной плоскости? Тем более, что на рис. 133 показана и сила трения.
В учебнике П.Г.Саенко «Физика, 9» (1992), § 25, с. 83 в определении веса «горизонтальная» опора не указывается, но на с. 84 автор все-таки к ней возвращается и, таким образом, себе противоречит.
То же самое можно прочитать в учебнике Ю.А.Селезнева «Основы элементарной физики» (1966, с. 46), где на одной и той же этой странице напечатаны два разных суждения.
Целый ряд авторов, переиздавая свои издания, сами себе противоречат. В одних своих работах они формулируют понятие веса покоящегося тела для любой опоры, в других – для горизонтальной опоры. Таковы учебники физики для 6-7 кл. А.В.Перышкина, Н.А.Родиной, «Методика преподавания физики в 6-7 кл.» под редакцией В.П.Орехова, А.В.Усовой, «Пособие по физике для поступающих в вузы» М.С.Цедрика, Ф.Г.Китуновича, А.С.Микулича, А.М.Качинского, задачники Н.Е.Савченко.
В некоторых изданиях встречаются и другие формулировки веса.
1. В учебнике Б.Б.Буховцева, Ю.Л.Климонтовича, Г.Я.Мякишева «Физика, механика» (1971, § 49) на с. 102 читаем: «…вес тела определяется всей совокупностью действующих на тело сил, а не только силой тяготения (так, вес тела в жидкости или воздухе меньше, чем в вакууме из-за появления выталкивающей силы)». Что же это такое – вес в воздухе, жидкости, вакууме?
2. «Курс физики» (Б.М.Яворский, А.А.Детлаф, Л.Б.Милковская, Г.П.Сергеев, 1965, т. 1), § 6.1, с. 98: «Сила Р,называемая весом тела или силой тяжести, вызывает падение незакрепленного тела к земле».
3. «Повторим физику» (Л.Б.Милковская, 72), § 3.5, с. 73: «Так как тела падают на землю под действием силы тяжести, т.е. своего веса, то P = m∙g».
4. «Законы природы» (Р.Е.Пайернс, 1962), гл. 1, с. 23: «Тот факт, что сила тяготения, действующая на тело, т.е. вес тела, точно пропорциональна его массе или инерции, пока является для нас неожиданным совпадением».
«Законы природы» (Р.Е.Пайернс, 1962), гл. 1, с. 23: «Тот факт, что сила тяготения, действующая на тело, т.е. вес тела, точно пропорциональна его массе или инерции, пока является для нас неожиданным совпадением».
5. «Большой энциклопедический словарь. Физика» (гл. ред. А.М.Прохоров, 1999), с. 70, определяет, что «…вес – это численная величина силы тяжести, действующей на тело, находящееся вблизи земной поверхности».
6. «Физика. Ответы на вопросы для абитуриентов и учащихся 11 кл.» (2000), гл. 2, с. 27 (коллектив авторов), определяет, что «весом тела называют силу нормального давления, действующую на подставку со стороны тела».
7. И даже такие авторы, как Л.Д.Ландау, А.И.Китайгородский в книге «Физика для всех» (1974), с. 9, пишут, что «Вес – это сила, с которой тело притягивается к земле. Эту силу можно измерить пружинными весами».
1. Изображение веса на рисунках
Исходя из имеющихся формулировок веса и третьего закона Ньютона, учащиеся должны понять, что весу тела по модулю равна сила реакции опоры N, и какой она будет, таким будет по величине и вес тела (рис. 1) (m∙g = Fтяжести).
Рис. 1
Учащиеся должны изображать вес тела как силу, приложенную к опоре. Здесь мы имеет несколько вариантов.
а) Если покоящееся тело – материальная точка, а горизонтальная опора – нет (рис. 2).
Рис. 2
б) Если покоящееся тело и горизонтальная опора – не материальные точки (рис. 3). Элементарные силы реакции действуют на всю опору (рис. 3, а), мы учитываем действие результирующей силы реакции опоры. Следует заметить, что сила реакции опоры N может смещаться, если к телу, например, приложить дополнительную силу F по горизонтали (рис. 3, б).
Рис. 3
3
а б
Рис. 3
в) Если покоящееся тело и горизонтальная опора – материальные точки (рис. 4). M·g – сила тяжести самой опоры, Р –- вес покоящегося на опоре тела, Nо6 – общая сила реакции нижней опоры. Иногда такие случаи нужно учитывать в задачах.
Рис. 4
г) Если покоящееся тело – материальная точка, а наклонная опора – не материальная точка (рис. 5, а или 5, б).
а б
Рис. 5
У покоящегося тела на любой опоре вес сохраняется (в инерциональной системе) и численно равен силе тяжести, т.е. |P| = |m∙g| = |Npез|. Результирующая сила реакции N является векторной суммой силы нормальной реакции Nнорм и силы трения покоя Fтр. пок.Вес тела Рприложен к опоре.
д) Покоящееся тело висит на вертикальном подвесе (рис. 6, а и 6, б).
а б
Рис. 6
Составляющие F1и F2,образующие при векторном сложении результирующую силу реакции N,численно равную весу Р,сами по себе могут быть по величине больше веса (или одна из них или обе одновременно).
Это бывает на тросах, растянутых под большим углом (рис. 7), или на кронштейнах (рис. 8, а, 8, б).
Рис. 7
а б
Рис. 8
8
2. Что измеряют весы?
Многие скажут – «смотря какой конструкции это будут весы».
Обратимся к словарям.
Толковые словари С.И.Ожегова (с. 62) и Д.Н.Ушакова (т. 1, с. 262) утверждают, что весы – это прибор для измерения веса. При этом на с. 64 в первом словаре и т. 1, с. 273 во втором глагол «взвесить» означает – определить вес.
Энциклопедический словарь (1953), т. 1, с. 296, Физический энциклопедический словарь (1960), т. 1, с. 220, Малая Советская Энциклопедия (1958), т. 2, с. 343 (все под редакцией Б.А.Введенского) и Большая Советская Энциклопедия, под редакцией А.М.Прохорова (1971), т. 4, с. 568 указывают, что весы – это прибор для определения массы тела.
Все издания утверждают, что пружинные весы измеряют вес. В то же время многие издания утверждают, что рычажные (равноплечие) весы измеряют массу. Только в учебнике Б.М.Яворского, А.А.Пинского «Основы физики», т. 1, и Г.С.Ландсберга «Элементарный учебник физики», т. 1, указывается, что рычажные весы измеряют вес. Чему должен верить читатель?
Действительно, с пружинными весами все ясно. В их «весовой» функции даже невозможно усомниться.
А на рычажных весах вроде бы очень удобно измерять массу тела. Ведь при балансе чашек (в случае равенства весов тел) мы тут же можем судить о равенстве масс исследуемого тела и уравновешенных гирь.
Кроме того, рычажные весы имеют еще одно неоспоримое удобство. Равновесие чашек с грузами не нарушается, если их перевести на полюс, экватор, с Земли на Луну и т.д. (вес тела при этом меняется, а масса нет!).
Думается, равновесие рычажных весов здесь не нарушается не столько из-за постоянства масс тел, сколько из-за одинаковой кратности изменения весов тел на обеих чашках.
И почему ни одни весы ничего не показывают в состоянии полной невесомости (ведь масса тела остается неизменной и сила тяжести также!)?
Да потому, что в состоянии полной невесомости вес тела равен нулю, вот весы и фиксируют нулевой вес!
А как быть тогда, когда мы на рычажных весах взвешиваем пуховое тело или хлопок (вату)? Ведь это объемное тело, испытывающее ощутимое действие выталкивающей силы воздуха, которая в большинстве случаев незначительная и на гири, стоящие на второй чашке весов, почти не действует. При балансе чашек можно еще говорить о равенстве весов тел на чашках, но именно масса пухового тела при балансе чашек будет обязательно большей, чем совокупная масса гирь. И здесь уже рычажные весы не могут дать точный ответ о массе пухового тела!
При балансе чашек можно еще говорить о равенстве весов тел на чашках, но именно масса пухового тела при балансе чашек будет обязательно большей, чем совокупная масса гирь. И здесь уже рычажные весы не могут дать точный ответ о массе пухового тела!
А если в состоянии полной невесомости пытаться определить массу тела, то неизбежно нужно будет создать какое-то силовое взаимодействие этого тела с другим телом. Иначе говоря, весы все-таки в принципе созданы для определения силы, и «лишить» их своей весовой функции практически невозможно. Поэтому останавливаемся на точке зрения, что весы любой конструкции измеряют вес, но иногда позволяют оценить и массу. Разговоры о том, что весы градуируются в граммах, килограммах, тоннах и каратах, сути весовой функции весов не меняют.
В интересах доказательства назначения весов для определения массы предлагают даже ввести термин «массометр» («Толковый словарь школьника по физике», 1999, авторы К.К.Гомоюнов, М.Ф.Кесаманлы, Т.Г.Кесаманлы, с 39). Думается, что это не получится. Ведь с древних времен человека интересовала масса как мера тяжести (т.е. проблема веса) гораздо в большей степени, чем масса инертная.
И ссылки на то, что в седьмом классе мы учим детей определять массу на весах, ничего не меняют. Мы видим, какое сложное понятие – «вес тела», и не усложняем жизнь маленьким учащимся. А научить их практически пользоваться весами нужно еще с малых лет.
II. Ход урока
Такое множество формулировок и точек зрения запутывает и дезинформирует учащихся. Тем более, что противоречат друг другу, а иногда и самим себе довольно авторитетные авторы учебных и методических изданий.
К данному уроку учащиеся были подведены проблемно. Они ознакомились с разными формулировками веса, способами изображения веса и различными точками зрения на назначение весов как измерительного прибора (особенно рычажных равноплечих).
Исходя из такой преамбулы, можно более конкретно нацелить урок: на самых простых и доступных опытах убедиться в неизменности веса тела в инерциальных системах и его «изменчивости» в системах неинерциальных, т. е. когда тело будет иметь ускорение.
е. когда тело будет иметь ускорение.
Предполагается определить вес покоящегося тела на разных опорах, выяснить, меняется ли вес при погружении тела в жидкость, и пронаблюдать, каким будет вес при наличии у тела ускорения.
Дополнительно к вышеперечисленному оборудованию были специально изготовлены два небольших приспособления. Из двух фанерок была сбита наклонная плоскость с приступочкой В внизу (рис. 9, а) и сделана связка из трех деревянных брусков (рис. 9, б).
а б
Рис. 9
Средний брусок был несколько поднят, чтобы он не мог касаться опоры при вертикальном положении всей связки.
Первая часть урока. Вес покоящегося тела на различных плоскостях
а) Повторяем формулировку «веса» тела (без слова «горизонтальна»).
б) Устанавливаем стрелку демонстрационного динамометра (пружинных весов) на нуль, на верхнюю подставку динамометра помещаем горизонтальную планку, на которую кладем отдельно связку брусков и наклонную плоскость (как совокупность тел). Связка на планке лежит (рис. 10). Фиксируем показание весов.
Рис. 10
в) Связку брусков кладем на наклонную плоскость (бруски покоятся) (рис. 11). Снова фиксируем показание весов и убеждаемся в его неизменности.
Рис. 11
г) Ничего не меняется в показании весов, если бруски стопорить о приступку В (рис. 12). Приступка В играет роль второй наклонной плоскости, заменяющей силу трения покоя. Как видим, на наклонной плоскости покоящееся тело весит столько же, сколько и на горизонтальной опоре. И это потому, что вес тела численно равен по величине не нормальной реакции тела на наклонной плоскости, а общей реакции, включающей и силу трения покоя и численно равной силе тяжести |m∙g|.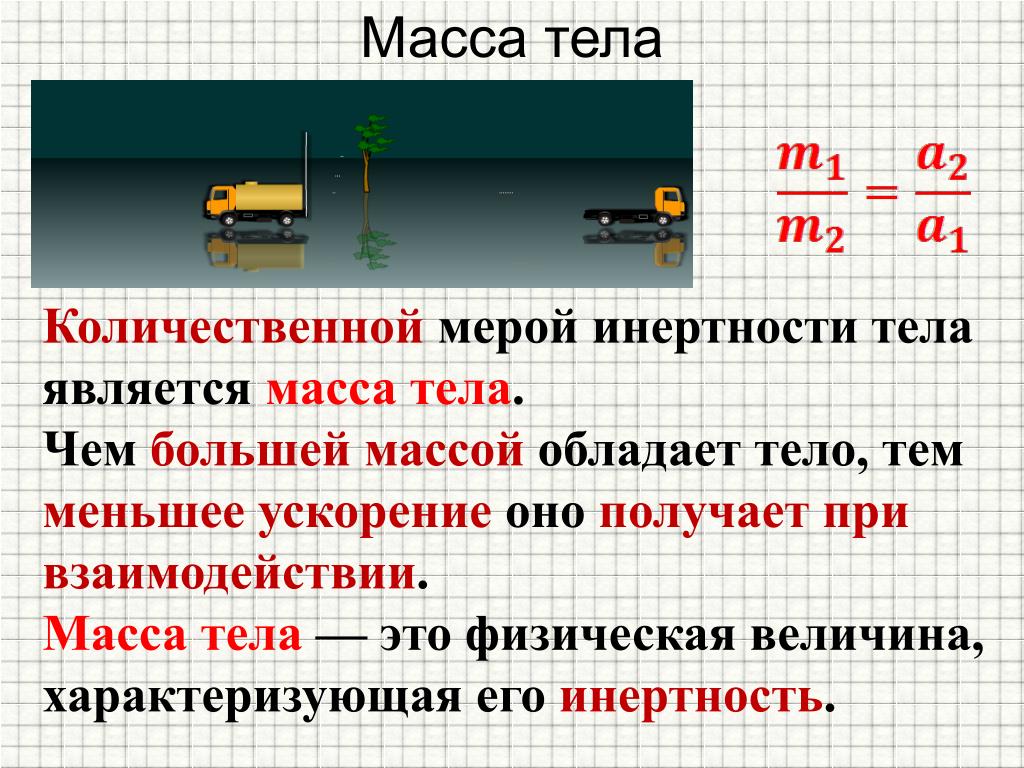
Рис. 12
д) А чему равен вес покоящегося тела на вертикальной плоскости? Если верить некоторым изданиям (например, учебнику «Физика, 9» (2000), авторы Л.А.Исаченкова, И.И.Жолнеревич, И.Н.Медведь, с. 131, рис. 133), утверждающим, что величина веса определяется величиной силы нормальной реакции тела на наклонной плоскости, то на вертикальной плоскости у тела вообще веса не будет, так как при этом Nнорм = 0.
В таком случае наглядно и убедительно используется связка трех брусков. Средний брусок не касается опоры, когда связка стоит (рис. 13).
Рис. 13
Весы показывают совершенно одинаковый вес, стоит связка на двух брусках или на одном, будучи перевернутой (рис. 14). И не имеет абсолютно никакого значения, стоит связка брусков или лежит. Но когда связка лежит, давят на опору все три бруска, а если связка стоит? Весы подтверждают, что на опору все равно давят те же три бруска! Те бруски, которые не касаются опоры в каждом случае, весят или давят на нее благодаря силе трения покоя между вертикальными соприкасающимися стенками брусков.
Рис. 14
Если бы тело, прижатое к вертикальной стенке и покоящееся на ней, не весило, уже давно был бы придуман способ укладки вещевого мешка или другой паковки, которые бы при одинаковом количестве упакованных предметов весили меньше. Но этот фокус не получается! Как бы ни был упакован вещевой мешок или чемодан, все предметы в нем будут весомы. И ни одни весы в мире не покажут уменьшения веса покоящегося тела на наклонной плоскости из-за увеличения угла наклонной плоскости.
Учащимся задаем итоговый вопрос: «Играет ли роль для определения веса покоящегося тела угол наклонной плоскости?» И получаем ответ: «Нет, не играет».
Учащимся было продемонстрировано уменьшение веса тела на наклонной плоскости, когда тело движется вниз практически без трения.
Был поставлен следующий эксперимент.
На рычаге длиной 1 м на одном конце была установлена почти вертикально доска высотой 1,5 м с подвешенным на нити кубом массой 200 г, а на другом – две коробки с грузиками по 1 Н (12 грузиков) (рис. 15).
Рис. 15
Все уравновешивается и балансирует.
Нить пережигается, куб начинает падать, и в это время противоположное плечо рычага с грузиками опускается, что свидетельствует об уменьшении веса тела на наклонной плоскости. Но в это время тело на ней не покоилось, а летело вниз практически без трения.
На первую часть урока уходит 14 минут.
Вторая часть урока. «Вес тела в жидкости или газе»Во многих изданиях, особенно выпущенных в прежние годы, мы часто сталкиваемся с терминологией «вес тела в воде», «вес тела в воздухе» и др. Например, в «Сборнике вопросов и задач» различных лет (авторы П.А.Знаменский и др.) на с. 52 в задачах № 397 и № 400 – «вес в керосине», «вес в воздухе» – в № 403, «истинный вес хлопка в кипе» – с. 53, № 409.
Был поставлен следующий эксперимент. Взвешиваем на крюке демонстрационного динамометра деревянный куб (рис. 16) и начинаем подводить под него банку с водой. По мере погружения куба в воду стрелка динамометра показывает уменьшение нагрузки на динамометр, создавая иллюзию уменьшения веса. Когда куб начинает плавать в воде, стрелка динамометра устанавливается на нуле. Так что – плавающее тело вообще не имеет веса?
Рис. 16
Снова взвешиваем куб на крюке, снимаем его и взвешиваем банку с водой без куба. Затем в подвешенную на крюк банку с водой кладем плавать куб. И что же? Весы показывают суммарный вес банки с водой и куба.
Это значит, что тело в воде или другой жидкости сохраняет свой вес, т. е. понятия «вес в воде», «вес в воздухе» или «вес в вакууме» и т.д. не имеют смысла.
е. понятия «вес в воде», «вес в воздухе» или «вес в вакууме» и т.д. не имеют смысла.
Есть одно понятие – вес тела, неизменный в инерциальных системах.
Уменьшение показаний динамометра при погружении тела в жидкость связано с появлением еще одной опоры – жидкости, которая «берет на себя» часть веса. То есть вес тела распределяется на две опоры точно так же, как вес рычага, лежащего на двух опорах. В случае плавающего тела жидкость «берет на себя» весь вес тела, вследствие чего динамометр, к которому привязана нить с таким телом, ничего и не показывает.
С помощью учащихся делаем вывод о постоянстве веса тела в инерциальных системах на любой опоре. Выясняем, что вес тела сохраняется у пассажира в равномерно движущемся лифте и у парашютиста, спускающегося равномерно на парашюте.
На эту часть урока уходит еще 12 минут.
Третья часть урока. Вес тела в пеинерциальных системах или вес тела, имеющего ускорение (пока по вертикали)Начинаем с демонстрации подвешенных грузиков на динамометре Бакушинского (рис. 17).
Рис. 17
Показываем динамометр с двумя грузиками в состоянии покоя или равномерного прямолинейного движения по вертикали в любую сторону. Динамометр показывает вес, равный 2H = m∙g,т.е. вес тела численно равен силе тяжести. Начинаем поднимать динамометр с грузиками вверх с ускорением. И пока сохраняется ускорение при подъеме, учащиеся ясно видят увеличение растяжения пружины (рис. 18). Объясняем, что увеличение веса – это перегрузка. Напоминаем, что она ощущается в самом начале подъема лифта и в конце его спуска при торможении.
Рис. 18
До этого учащиеся уже решали задачи на расчет силы реакции при подъеме тела вверх с ускорением и знают, что она равна: , где Р’ – искусственный вес тела в данных условиях.
Приводим пример взвешивания с «походом», когда тело швыряют на весы и последние показывают «завышенный» вес. Выясняем, почему нас не устраивает, когда тело швыряют на весы (ведь не только из-за невежливости!), обращаем внимание учащихся на наличие торможения тела. Далее выясняем, чего мы ждем. Учащиеся отвечают, что мы ждем, когда весы уравновесятся и покажут в состоянии покоя вес тела, равный его силе тяжести.
Объясняем, что перегрузка не означает только увеличение воздействия на опору, а предполагает увеличение веса всего, что находится в такой системе. Увеличивается вес всех частей тела человека. Тяжелеет голова, руки, ноги, туловище, сердце, веки глаз, кровь и т.д. Нетренированный человек выдерживает троекратную перегрузку нормально. Особенно большие перегрузки бывают на тренировках космонавтов на больших скоростях (до 11-12 Р0)и при выходе самолета из состояния пикирования. Поясняем всю тяжесть и опасность таких ситуаций.
Показываем уменьшение веса при спуске тела с ускорением вниз (рис. 19). Получаем «недогрузку» или частичную невесомость, которая ощущается в начале спуска лифта (пока есть ускорение вниз) или в конце его подъема с торможением. В этом случае
Рис. 19.
Поясняем, что именно тогда, когда ускорение исчезает, сила реакции N будет компенсировать силу тяжести. Только тогда |N| = m∙g = |P0|,т.е. весу тела в состоянии покоя или равномерного прямолинейного движения.
Выясняем с учащимися, что с увеличением ускорения а по вертикали вниз «недогрузка» тела увеличивается, и при ускорении, равном g,вес становится равным нулю, т.е. наступает полная невесомость.
Обязательно обращаем внимание учащихся на то, что полная невесомость бывает только тогда, когда на тело действует одна-единственная сила – сила тяжести и тело находится в свободном падении.
Очень важно отметить, что если не учитывать сопротивление воздуха, полная невесомость имеет место при любых бросках.
Учащимся демонстрируется шар с подсветкой, которая зажигается внутри шара только в состоянии невесомости в любом броске. Шар можно бросать вертикально вверх, под углом к горизонту, горизонтально, ронять или подталкивать отвесно вниз. Шар светится только в полете, а учащиеся подтверждают, что при этом на тело действует только сила тяжести.
Подробно изучить явление полной невесомости на этом уроке невозможно. Эта тема достойна отдельного урока, который проводится после темы «Вес тела».
На эту часть урока уходит 10 минут.
Четвертая часть урока. Перегрузка при наличии ускорения тела по горизонталиБыл поставлен вопрос – каков вес тела при горизонтальном разгоне? Рассуждения проводятся на примере сосуда с водой.
В состоянии инерции (т.е. покоя или равномерного прямолинейного движения) на жидкость действуют сила тяжести m∙g и сила нормальной реакции N0компенсирующие друг друга.
Для того, чтобы сообщить жидкости горизонтальное ускорение а,на нее необходимо подействовать горизонтальной силой т∙а (рис. 20).
Рис. 20
При этом возникает результирующая сила реакции N’,по модулю большая, чем N0(как гипотенуза прямоугольного треугольника). Так как искусственный вес Р’ жидкости по третьему закону Ньютона численно равен силе реакции N’,то и он возрастает, вследствие чего и возникает перегрузка.
Рассчитаем угол α.
и не зависит от массы.
Тогда
Следует обратить внимание учащихся на то, что на рис. 20 точка приложения веса Р’ не должна совпадать с центром масс жидкости.
20 точка приложения веса Р’ не должна совпадать с центром масс жидкости.
Опыт с водой или другой не очень вязкой жидкостью очень нагляден из-за наклона свободной поверхности жидкости на угол α и ее «наплыва» на заднюю стенку (рис. 20).
Объясняем учащимся причину появления этого угла наклона. На угол α от вертикали отклоняется линия ответа, по которой направлен вес Р’. Плоскость свободной поверхности жидкости всегда перпендикулярна линии отвеса.
Как и углы с взаимно перпендикулярными сторонами, угол наклона жидкости также равен α. Если ускорение а постоянно, постоянным будет и угол α. При торможении ускорение тела отрицательное и жидкость «наплывает» на переднюю стенку (угол α отрицательный, a tg α – функция нечетная).
Практически бывает трудно сохранить долго ускорение по горизонтали постоянным. Тогда меняется угол наклона плоскости свободной поверхности жидкости и жидкость начинает плескаться. А если жидкость равномерно вращать? Ведь тогда центростремительное ускорение жидкости а будет постоянным и угол наклона α будет также постоянным. Учащимся демонстрируется установка с гироскопическим колесом (рис. 21). На краю колеса с помощью прозрачного скотча укрепляется стакан с водой. Колесо раскручивается вокруг своей оси и благодаря подшипникам на оси и большой инертности долго сохраняет скорость вращения практически постоянной.
Рис. 21
При большой скорости вращения колеса учащиеся хорошо видят большой угол α наклона плоскости свободной поверхности воды к горизонту.
Постепенно скорость вращение колеса убывает и уменьшается угол a наклона воды.
На эту часть урока уходит 6 минут.
Итак, третья и четвертая части урока были посвящены изучению веса тела, имеющего ускорение. Учащиеся выяснили, что при наличии ускорения вес тела может быть различным – от больших перегрузок до полной невесомости.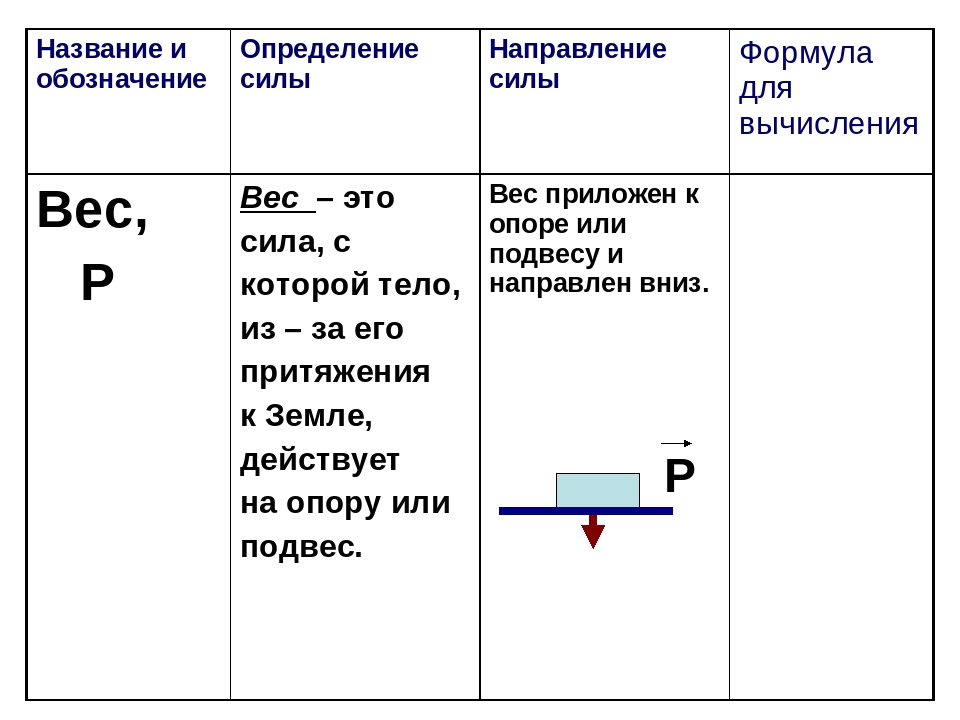
Учащимся уместно задать «провокационный» вопрос: «Почему у покоящегося тела на экваторе вес меньший, чем на полюсе?» И находятся ребята, которые подмечают, что на экваторе тело имеет линейную скорость, как следствие этого у него есть центростремительное ускорение, и вес на экваторе должен отличаться от веса на полюсе.
III. Итоги урока
Учащиеся получили полное экспериментальное подтверждение, что:
1) в инерциальных системах отсчета тело, покоящееся или движущееся равномерно прямолинейно, неизменно сохраняет свой вес на любой опоре независимо от того, каков угол наклона опоры, а также жидкая это опора или твердая;
2) в неинерциальных системах отсчета вес тела может изменяться в зависимости от ускорения тела.
Урок вызвал живой интерес у учащихся класса. Они приняли активное участие в обсуждении опытов и их результатов.
На уроке пришлось обратить внимание учащихся на то, что на с. 131 учебника «Физики-9» (авторы Л.А.Исаченкова, И.И.Жолнеревич, И.Н.Медведь) приведен неверный рис. 133. Он был опровергнут экспериментами, проведенными на уроке. Там же имеются ошибки в описании невесомости тела в самолете.
Вес тела
ВЕС ТЕЛАОткрытый урок в 7 классе: «Вес тела»
Цель урока:
1.Образовательная: формировать понятие веса тела, рассмотреть вес тела, находящегося на неподвижной или равномерно движущейся опоре. Выяснить физический смысл веса тела.
2.Развивающая: совершенствовать интеллектуальные умения (наблюдать, сравнивать, размышлять, применять знания, делать выводы), активизировать познавательную деятельность учащихся через решение проблем, выдвинутых перед ними.
3.Воспитательная: прививать культуру умственного труда, аккуратность, учить видеть практическую пользу знаний, продолжить формирование коммуникативных умений.
Тип урока: комбинированный.
Оборудование и ТСО:
набор грузов, штатив, пружина, сосуд с водой, динамометр, интерактивная доска, компьютерная презентация с использованием материалов «Класс!ной физики» (http://class-fizika.narod.ru).
План урока
1. Организационный момент (1 мин.)
2. Проверка домашнего задания (5 мин.)
3. Изучение нового материала (20 мин.)
4. Обобщение и систематизация знаний (5 мин.)
5. Первичный контроль знаний (10 мин.)
6. Запись домашнего задания (2 мин.)
7. Подведение итогов урока (рефлексия) (2 мин.)
Ход урока
1. Организационный момент.
Начнём урок. Всем здравствуйте, прошу садиться.
Отметим отсутствующих.
2. Проверка домашнего задания.
Прежде чем приступить к изучению нового материала, проверим выполнение домашнего задания.(слайд 2)
Опыт 1: У меня в руках грузик. Я выпускаем его из рук. Что с ним происходит? (ЛК – щелчок левой клавишей мыши) Почему? (Грузик падает вниз под действием силы тяжести (притяжения земли)) Что такое сила тяжести? По какой формуле определяется? (ЛК) Как направлена сила тяжести? (ЛК)
Опыт 2: Этот же самый грузик подвешиваем к пружине, закреплённой в штативе. Скажите, сейчас на грузик действует сила тяжести? (Да.)
А почему тогда грузик не падает? (Потому, что на него действует сила упругости пружины.) А что такое сила упругости? (ЛК) По какой формуле рассчитывается? Куда она направлена? (слайд 3)
3. Изучение нового материала
Сегодня на уроке мы поговорим о силе, под действием которой произошло растяжение этой пружины.
Скажите, в какой момент пружина, закреплённая в штативе, начала растягиваться? (Когда мы прикрепили к ней груз) Сила, с которой груз действует на пружину, вы давите на стул, я действую на пол и так далее, называется весом тела (слайд 4).
Итак, тема нашего урока «Вес тела». Запишем в тетрадь.
Сегодня на уроке мы с вами должны познакомиться с новой силой, выяснить, от чего она зависит, как направлена, по какой формуле рассчитывается.
Представьте себя космонавтом. Скажите, а в космосе вы с такой же силой действовали бы на кресло космического корабля? А груз с такой же силой растягивал бы пружину? Правильно, нет. Так в чём же причина, что на Земле груз растягивает пружину, а в космосе нет? Нет притяжения Земли, поэтому в космосе тело не имеет веса, т.е. находится в состоянии невесомости (слайд 5).
Запишем определение:
Вес тела – это сила, с которой тело вследствие притяжения к Земле действует на опору или подвес.
Давайте подумаем, от чего зависит вес тела? (слайд 6)
К первому грузу подвесим второй такой же груз.
Пружина растянулась сильней (слайд 7),
значит, вес двух грузов больше, чем вес одного груза (слайд 8).
Какой из этого можно сделать вывод?(Вес зависит от массы тела.) Чем больше масса тела, тем больше его вес. От чего ещё зависит вес? (слайд 9)
Внимание на экран. (Ролик про вес тела на Земле и на Луне).
Какой вывод можно сделать? (Вес тела зависит от того, на какой планете находится тело). Но вес на других планетах вы будете изучать позже.
Оказывается, что и на Земле вес одного и того же тела, в отличие от массы, может быть различным (слайд 10)(Ролик про вес тела на экваторе и на полюсе).
Какой вывод можно сделать? (слайд 11)
Представим себе такую ситуацию: Проводится чемпионат мира по тяжёлой атлетике сразу в двух точках Земли на полюсе и на экваторе. Два спортсмена подняли штангу одной и той же массы (400 кг). Кому бы из спортсменов вы присудили первое место? Оказывается, что первое место нужно присудить спортсмену с полюса, потому что на полюсе ускорение свободного падения больше, притяжение Земли сильней и Вес тела на полюсе больше, чем на экваторе.

Если вы поднимитесь высоко в горы, то ваш вес тоже станет меньше, потому что расстояние до центра Земли в горах больше, чем у подножия горы, ускорение свободного падения меньше и вес уменьшается (слайд 12).
Итак, вес тела зависит от массы и ускорения свободного падения. Поэтому вес неподвижного тела или тела, движущегося с постоянной скоростью, определяется по формуле Р = mg (записывают в тетрадь). Вес направлен из центра соприкосновения тела и опоры или подвеса вертикально вниз.
(Демонстрация опыта с водой). Вес тела в воде или в другой жидкости меньше, чем в воздухе (слайд 13).
Давайте подумаем, где это может использоваться? (Для тренировки космонавтов).
Оказывается, что каждый из вас здесь и сейчас может побыть в состоянии невесомости. (Ученик подпрыгивает как можно выше). Во время прыжка у тебя была под ногами опора? Нет. А был какой-нибудь подвес? Нет. Значит, ты не действовал ни на опору, ни на подвес и ты был в состоянии невесомости.
4. Обобщение и систематизация знаний
• Вес тела – это…
• Формула для веса – …
• Вес направлен…
• Вес зависит от…
(слайд 14)
5. Первичный контроль знаний (работа в группах) (слайд 15).
Сказка: В одном сказочном физическом городе жила прекрасная девушка Масса. Всю свою сознательную жизнь она мечтала о прекрасном принце на белом коне, а влюбилась в обычного мальчишку с обычным физическим именем Вес. С утра до ночи мальчик Вес со своими друзьями гонял мяч во дворе. Так и пролетало бы его беззаботное детство, если бы его взгляд не привлекла эта очаровательная девушка Масса. Мальчик Вес собрал в себе все силы, подошёл к Массе и сказал: «Ты мне очень понравилась, давай с тобой дружить?» «Никакой дружбы у вас не получится!»- вдруг воскликнул мальчик по – имени Ж. Масса всегда постоянная, а ты, то больше, то меньше, а то тебя вообще нет.
 Я ей больше подхожу, я – ускорение свободного падения, практически не изменяюсь!
Я ей больше подхожу, я – ускорение свободного падения, практически не изменяюсь!Очень сильно обиделся Вес на слова своего друга и пошёл он прочь со слезами на глазах. «Безвыходных ситуаций не бывает» — воскликнул самый умный
ученик 7-го класса и посоветовал Весу, что нужно делать, чтобы не изменяться (слайд 16).
Задание 1-й группе: Придумать продолжение сказки. Что посоветовал семиклассник мальчику Весу, чтобы всегда оставаться постоянным? (Переселиться на планету шарообразной формы, у которой поверхность ровная, нет гор и морей. Жить на этой планете спокойно, без резких движений.) (слайд 17)
Задание 2-й группе: Решить задачи из «Физики» Григория Остера №104, №106 (слайд 18).
Задание 3-й группе: Подписать название сил, показанных на рисунке (слайд 19).
6. Запись домашнего задания (слайд 20)
7. Подведение итогов урока.
5.4 Масса и вес | Университетская физика, том 1,
Цели обучения
К концу раздела вы сможете:
- Объясните разницу между массой и весом
- Объясните, почему падающие на Земле объекты никогда не падают в свободном падении
- Опишите понятие невесомости
В повседневной беседе масса и вес часто используются как синонимы. Например, в наших медицинских записях наш вес часто указывается в килограммах, но никогда в правильных единицах — ньютонах.Однако в физике есть важное различие. Вес — это сила притяжения Земли к объекту. Это зависит от расстояния от центра Земли. В отличие от веса, масса не зависит от местоположения. Масса объекта одинакова на Земле, на орбите или на поверхности Луны.
Единицы силы
Уравнение [латекс] {F} _ {\ text {net}} = ma [/ latex] используется для определения чистой силы в терминах массы, длины и времени. Как объяснялось ранее, единицей силы в системе СИ является ньютон.{2}. [/ латекс]
Хотя почти весь мир использует ньютон в качестве единицы силы, в Соединенных Штатах наиболее известной единицей силы является фунт (фунт), где 1 Н = 0,225 фунта. Таким образом, человек весом 225 фунтов весит 1000 Н.
Таким образом, человек весом 225 фунтов весит 1000 Н.
Вес и сила тяжести
Когда объект падает, он ускоряется к центру Земли. Второй закон Ньютона гласит, что общая сила, действующая на объект, отвечает за его ускорение. Если сопротивление воздуха незначительно, результирующая сила, действующая на падающий объект, — это сила тяжести, обычно называемая его весом [латекс] \ overset {\ to} {w} [/ latex], или его сила, вызванная гравитацией, действующей на объект объект массой м .Вес можно обозначить как вектор, потому что он имеет направление; вниз , по определению, является направлением силы тяжести, и, следовательно, вес — это сила, направленная вниз. Величина веса обозначается как w . Галилей сыграл важную роль в демонстрации того, что при отсутствии сопротивления воздуха все объекты падают с одинаковым ускорением g . Используя результат Галилея и второй закон Ньютона, мы можем вывести уравнение для веса.
Рассмотрим объект массой м , падающий на Землю.Он испытывает только направленную вниз силу тяжести, то есть вес [латекс] \ overset {\ to} {w} [/ latex]. Второй закон Ньютона гласит, что величина чистой внешней силы, действующей на объект, равна [латекс] {\ overset {\ to} {F}} _ {\ text {net}} = m \ overset {\ to} {a}. [/ latex] Мы знаем, что ускорение объекта под действием силы тяжести равно [latex] \ overset {\ to} {g}, [/ latex] или [latex] \ overset {\ to} {a} = \ overset { \ to} {g} [/ латекс]. Подставляя их во второй закон Ньютона, мы получаем следующие уравнения.{2}) = 9.80 \, \ text {N}. [/ латекс]
Когда чистая внешняя сила, действующая на объект, — это его вес, мы говорим, что он находится в состоянии свободного падения , то есть единственной силой, действующей на объект, является гравитация. Однако, когда объекты на Земле падают вниз, они никогда не находятся в состоянии свободного падения, потому что всегда существует некоторая восходящая сила сопротивления со стороны воздуха, действующая на объект.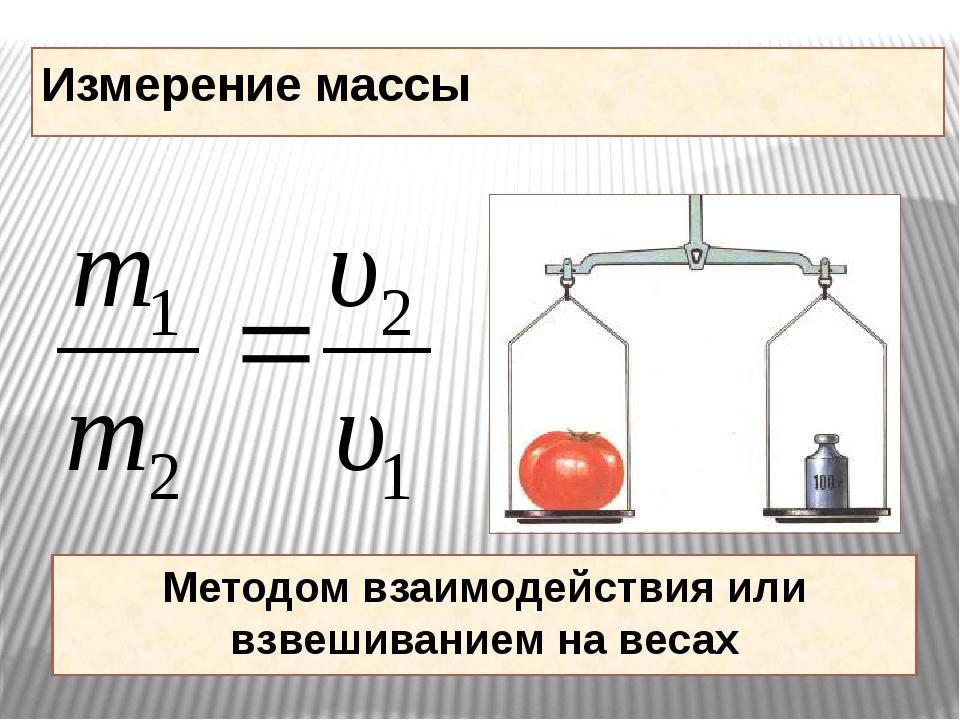
Ускорение свободного падения г незначительно меняется по поверхности Земли, поэтому вес объекта зависит от его местоположения и не является внутренним свойством объекта.{2} [/ латекс]. Таким образом, масса в 1,0 кг имеет вес 9,8 Н на Земле и всего около 1,7 Н на Луне.
Самое широкое определение веса в этом смысле состоит в том, что вес объекта — это сила тяжести, действующая на него со стороны ближайшего крупного тела, такого как Земля, Луна или Солнце. Это наиболее распространенное и полезное определение веса в физике. Однако оно кардинально отличается от определения веса, используемого НАСА и популярными СМИ в отношении космических путешествий и исследований.Когда они говорят о «невесомости» и «микрогравитации», они имеют в виду явление, которое в физике мы называем «свободным падением». Мы используем предыдущее определение веса, силы [латекс] \ overset {\ to} {w} [/ latex], возникающей из-за силы тяжести, действующей на объект массой м , и мы тщательно различаем свободное падение и фактическую невесомость.
Имейте в виду, что вес и масса — это разные физические величины, хотя они тесно связаны. Масса — это внутреннее свойство объекта: это количество материи.Количество или количество вещества объекта определяется количеством атомов и молекул различных типов, которые он содержит. Поскольку эти числа не меняются, в физике Ньютона масса не меняется; поэтому его реакция на приложенную силу не меняется. Напротив, вес — это сила тяжести, действующая на объект, поэтому она зависит от силы тяжести. Например, человек, находящийся ближе к центру Земли, на небольшой высоте, такой как Новый Орлеан, весит немного больше, чем человек, находящийся на более высокой высоте в Денвере, даже если у них может быть такая же масса.
Заманчиво приравнять массу к весу, потому что большинство наших примеров имеет место на Земле, где вес объекта лишь немного зависит от его местоположения. Кроме того, трудно подсчитать и идентифицировать все атомы и молекулы в объекте, поэтому масса редко определяется таким способом.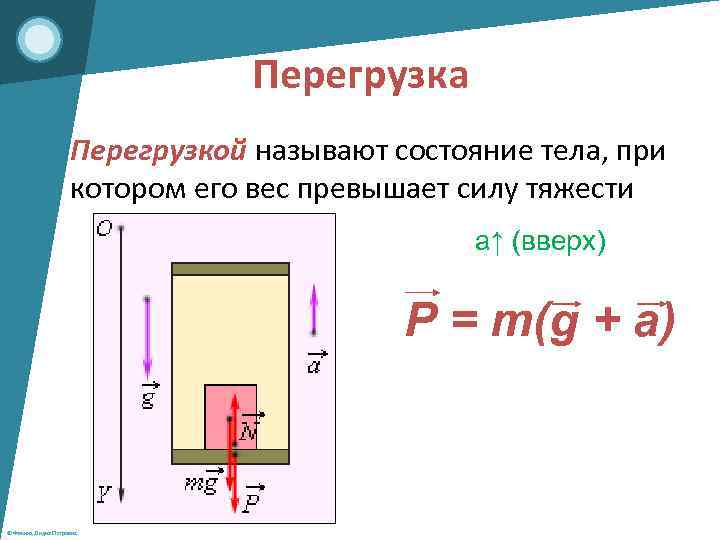 Если мы рассмотрим ситуации, в которых [latex] \ overset {\ to} {g} [/ latex] является постоянной на Земле, мы увидим, что вес [latex] \ overset {\ to} {w} [/ latex] напрямую пропорционально массе м , поскольку [latex] \ overset {\ to} {w} = m \ overset {\ to} {g}, [/ latex] то есть чем массивнее объект, тем больше он весит .{2}? [/ латекс]
Если мы рассмотрим ситуации, в которых [latex] \ overset {\ to} {g} [/ latex] является постоянной на Земле, мы увидим, что вес [latex] \ overset {\ to} {w} [/ latex] напрямую пропорционально массе м , поскольку [latex] \ overset {\ to} {w} = m \ overset {\ to} {g}, [/ latex] то есть чем массивнее объект, тем больше он весит .{2}? [/ латекс]
Стратегия
Нам дали вес камня, который мы используем при нахождении чистой силы на камне. Однако нам также необходимо знать его массу, чтобы применить второй закон Ньютона, поэтому мы должны применить уравнение для веса, [латекс] w = мг [/ латекс], чтобы определить массу.
Решение
Никакие силы не действуют в горизонтальном направлении, поэтому мы можем сосредоточиться на вертикальных силах, как показано на следующей диаграмме свободного тела. Размечаем ускорение в сторону; технически это не часть диаграммы свободного тела, но помогает напомнить нам, что объект ускоряется вверх (так что результирующая сила направлена вверх).{2}) \ hfill \\ \ hfill F-180 \, \ text {N} & = \ hfill & 27 \, \ text {N} \ hfill \\ \ hfill F & = \ hfill & 207 \, \ text { N} = 210 \, \ text {N до двух значащих цифр} \ hfill \ end {array} [/ latex]
Значение
Чтобы применить второй закон Ньютона в качестве основного уравнения при решении задачи, нам иногда приходится полагаться на другие уравнения, такие как уравнение для веса или одно из кинематических уравнений, чтобы завершить решение.
Проверьте свое понимание
Для (Пример) найдите ускорение, когда сила, приложенная фермером, равна 230.{2} [/ латекс]
5.5: Масса и вес — Физика LibreTexts
В повседневной беседе масса и вес часто используются как синонимы. Например, в наших медицинских записях наш вес часто указывается в килограммах, но никогда в правильных единицах — ньютонах. Однако в физике есть важное различие. Вес — это сила притяжения Земли к объекту. Это зависит от расстояния от центра Земли. В отличие от веса, масса не зависит от местоположения. Масса объекта одинакова на Земле, на орбите или на поверхности Луны.{2} \ ldotp \ nonumber \]
В отличие от веса, масса не зависит от местоположения. Масса объекта одинакова на Земле, на орбите или на поверхности Луны.{2} \ ldotp \ nonumber \]
Хотя почти весь мир использует ньютон в качестве единицы силы, в Соединенных Штатах наиболее известной единицей силы является фунт (фунт), где 1 Н = 0,225 фунта. Таким образом, человек весом 225 фунтов весит 1000 Н.
Вес и гравитационная сила
Когда объект падает, он ускоряется к центру Земли. Второй закон Ньютона гласит, что общая сила, действующая на объект, отвечает за его ускорение. Если сопротивление воздуха незначительно, результирующая сила, действующая на падающий объект, — это сила тяжести, обычно называемая его весом \ (\ vec {w} \), или его сила, обусловленная гравитацией, действующей на объект массой m.Вес можно обозначить как вектор, потому что он имеет направление; вниз по определению является направлением силы тяжести, и, следовательно, вес — это сила, направленная вниз. Величина веса обозначается как w. Галилей сыграл важную роль в демонстрации того, что при отсутствии сопротивления воздуха все объекты падают с одинаковым ускорением g. Используя результат Галилея и второй закон Ньютона, мы можем вывести уравнение для веса.
Рассмотрим объект с массой m, падающий на Землю. Он испытывает только силу тяжести, направленную вниз, то есть вес \ (\ vec {w} \).Второй закон Ньютона гласит, что величина чистой внешней силы, действующей на объект, равна \ (\ vec {F} _ {net} = m \ vec {a} \). Мы знаем, что ускорение объекта под действием силы тяжести равно \ (\ vec {g} \) или \ (\ vec {a} = \ vec {g} \). Подставляя их во второй закон Ньютона, мы получаем следующие уравнения.
Определение: Вес
Сила тяжести на массу — это ее вес. Мы можем записать это в векторной форме, где \ (\ vec {w} \) — вес, а m — масса, так как
\ [\ vec {w} = m \ vec {g} \ ldotp \ label {5.{2}) = 9.80 \; N \ ldotp \]
Когда чистая внешняя сила, действующая на объект, — это его вес, мы говорим, что он находится в состоянии свободного падения , то есть единственной силой, действующей на объект, является гравитация. Однако, когда объекты на Земле падают вниз, они никогда не находятся в состоянии свободного падения, потому что всегда существует некоторая восходящая сила сопротивления со стороны воздуха, действующая на объект.
Однако, когда объекты на Земле падают вниз, они никогда не находятся в состоянии свободного падения, потому что всегда существует некоторая восходящая сила сопротивления со стороны воздуха, действующая на объект.
Ускорение силы тяжести g незначительно меняется по поверхности Земли, поэтому вес объекта зависит от его местоположения и не является внутренним свойством объекта.Вес резко меняется, если мы покидаем поверхность Земли. На Луне, например, ускорение свободного падения составляет всего 1,67 м / с 2 . Таким образом, масса в 1,0 кг имеет вес 9,8 Н на Земле и всего около 1,7 Н на Луне.
Самое широкое определение веса в этом смысле состоит в том, что вес объекта — это сила тяжести, действующая на него со стороны ближайшего крупного тела, такого как Земля, Луна или Солнце. Это наиболее распространенное и полезное определение веса в физике. Однако оно кардинально отличается от определения веса, используемого НАСА и популярными СМИ в отношении космических путешествий и исследований.Когда они говорят о «невесомости» и «микрогравитации», они имеют в виду явление, которое в физике мы называем «свободным падением». Мы используем предыдущее определение веса, силы \ (\ vec {w} \), возникающей из-за силы тяжести, действующей на объект массы m, и проводим тщательное различие между свободным падением и фактической невесомостью.
Имейте в виду, что вес и масса — это разные физические величины, хотя они тесно связаны. Масса — это внутреннее свойство объекта: это количество материи. Количество или количество вещества объекта определяется количеством атомов и молекул различных типов, которые он содержит.Поскольку эти числа не меняются, в физике Ньютона масса не меняется; поэтому его реакция на приложенную силу не меняется. Напротив, вес — это сила тяжести, действующая на объект, поэтому она зависит от силы тяжести. Например, человек, находящийся ближе к центру Земли, на небольшой высоте, такой как Новый Орлеан, весит немного больше, чем человек, находящийся на более высокой высоте в Денвере, даже если у них может быть такая же масса.
Заманчиво приравнять массу к весу, потому что большинство наших примеров имеет место на Земле, где вес объекта лишь немного зависит от его местоположения.Кроме того, трудно подсчитать и идентифицировать все атомы и молекулы в объекте, поэтому масса редко определяется таким способом. Если мы рассмотрим ситуации, в которых \ (\ vec {g} \) является постоянной на Земле, мы увидим, что вес \ (\ vec {w} \) прямо пропорционален массе m, поскольку \ (\ vec {w} = m \ vec {g} \), то есть чем массивнее объект, тем больше он весит. На практике массы объектов определяются путем сравнения со стандартным килограммом, как мы обсуждали в разделе «Единицы измерения и измерение».Но сравнивая объект на Земле с объектом на Луне, мы легко можем увидеть изменение веса, но не массы. Например, на Земле объект массой 5,0 кг весит 49 Н; на Луне, где g составляет 1,67 м / с 2 , объект весит 8,4 Н. Однако масса объекта все еще составляет 5,0 кг на Луне.
Пример \ (\ PageIndex {1} \): очистка поля
Фермер поднимает с поля несколько камней средней тяжести, чтобы посадить урожай. Он поднимает камень весом 40 фунтов (около 180 Н).Какую силу он применяет, если камень ускоряется со скоростью 1,5 м / с 2 ?
Стратегия
Нам дали вес камня, который мы используем при нахождении чистой силы на камне. Однако нам также необходимо знать его массу, чтобы применить второй закон Ньютона, поэтому мы должны применить уравнение для веса, w = mg, для определения массы.
Решение
Никакие силы не действуют в горизонтальном направлении, поэтому мы можем сосредоточиться на вертикальных силах, как показано на следующей диаграмме свободного тела.{2}) \ nonumber \]
\ [F — 180 \; N = 27 \; N \ nonumber \]
\ [F = 207 \; N = 210 \; N \; \ text {до двух значащих цифр} \ nonumber \]
Значение
Чтобы применить второй закон Ньютона в качестве основного уравнения при решении задачи, нам иногда приходится полагаться на другие уравнения, такие как уравнение для веса или одно из кинематических уравнений, чтобы завершить решение.
Упражнение \ (\ PageIndex {1} \)
Для \ (\ PageIndex {1} \) найдите ускорение, когда сила, приложенная фермером, равна 230.0 N
Моделирование
Сможете ли вы избежать поля валунов и безопасно приземлиться непосредственно перед тем, как у вас закончится топливо, как это сделал Нил Армстронг в 1969 году? Эта версия классической видеоигры точно имитирует реальное движение лунного посадочного модуля с правильной массой, тягой, расходом топлива и лунной гравитацией. Настоящий лунный аппарат сложно контролировать.
Определение веса | определить Вес
Определение веса
«Сила, с которой тело притягивается к земле.«
Вес — это еще одно название силы гравитации Земли на объект.
Пружинные весы используются для измерения веса объекта.
Подробнее о весе:
Вес объекта равен произведению массы и напряженности гравитационного поля в данном конкретном месте.
Сила гравитационного поля (g) меняется от одного места к другому.
На поверхности земли объект массой 1 кг имеет вес 9,8 Н (для удобства мы рассматриваем 10 Н для целей расчета).
Рабочий пример:
В точке на поверхности Земли напряженность гравитационного поля составляет 10 Н / кг.
Какие пары значений массы и веса верны для объекта, помещенного в эту позицию?
Масса / кг | вес / Н | |
А | 10 | 10 |
Б | 20 | 2 |
К | 50 | 100 |
Д | 2 | 20 |
Правильный ответ: C.
Решения
Шаг 1: Напряженность гравитационного поля 10 Н / кг (дано).
Шаг 2: Вес = масса x напряженность гравитационного поля: напряженность гравитационного поля = Вес / масса.
Шаг 3: A- 10/10 = 1, но ≠ 10
B- 2/20 = 0,2, но ≠ 10
C- 100/50 = 2, но ≠ 10;
D- 20/2 = 10 = напряженность гравитационного поля (дано). Следовательно, D — правильный ответ.
Рабочий пример
Каков вес человека на поверхности Луны, если его масса на Земле составляет 100 кг?
Напряженность гравитационного поля на Луне равна 1.6N / кг.
А. 100 Н
Б. 200 N
С. 160 N
D. 16 N
Правильный ответ — D.
Решение
Шаг 1: Масса Луны и Земли равна.
Масса объекта на Земле = 100 кг.
Масса объекта на Луне = 100 кг.
Шаг 2: Напряженность гравитационного поля на Луне = 1,6 Н / кг.
Шаг 3: Вес = мг = 100 x 1,6 = 160 Н.
Связанные термины: масса | сила
Разница между массой и весом с примерами
Масса против весаОсновное различие между массой и весом состоит в том, что масса — это количество вещества в объекте, а вес — это сила тяжести, с помощью которой земля притягивается к нему.Масса — это скалярная величина, а вес — это векторная величина. Единица массы — кг, а единица веса — N. Массу нельзя изменить, поменяв место, вес можно изменить, поменяв место.
К сожалению, вес и масса часто считаются одинаковыми величинами и неправильно используются в повседневных разговорах. Поэтому вам важно различать эти две физические величины.
Продолжайте читать…
Что такое масса?
Масса — это количество вещества, которое имеет объект.Это количественная мера сопротивления тела ускорению. Мы видим это как сопротивление посуды, когда скатерть выдергивают.
Независимо от того, где находится тело, масса всегда будет одинаковой, то есть это внутреннее количество материи.
Масса — это обширное свойство материи , оно зависит от количества и размера исследуемой системы. Это означает, что если у объекта масса равна 1 кг, мы отбираем 0,1 кг, так как масса не будет равна исходному объекту.
Как измеряется масса?
Масса обычно измеряется на весах, сравнивая с известным эталоном. В Международной системе единиц (СИ) масса выражается в килограммах (кг). По состоянию на 20 мая 2019 года килограмм определяется в терминах постоянной Планка h , фундаментальной постоянной квантовой физики, которая является универсальной:
Это новое измерение килограмма заменяет старое определение килограмма, основанное на прототипе международного килограмма , цилиндра из платины и иридия, который охраняется Международным бюро мер и весов в Севре, Франция, в 1889 году.
Что такое вес?
Вес — это сила тяжести, прилагаемая Землей или любым другим небесным телом к объекту, которая равна произведению массы объекта и значения местного ускорения свободного падения:
Значение постоянной ускорения на Земле 9,8 м / с 2 . Формула может интерпретировать, что вес пропорционален массе объекта.
Вес — это векторная величина, поскольку у нее есть интенсивность, направление и смысл.Таким образом, вес является мерой, возникающей в результате действия земной гравитации на тело, и, следовательно, вес является переменной величиной.
Массовые свойства
- Масса — это количество вещества, которым обладает тело.
- Это скалярная величина, имеющая только величину.
- Единица измерения — килограмм (кг).
- Не меняется при смене позиции.
- Рассчитывается по формуле: m = w / g
- Измеряется с помощью физических весов, весов лучей, электронных весов и т.
 Д.
Д.
Весовые характеристики
- Вес — это сила тяжести, с помощью которой Земля притягивает ее.
- Это векторная величина, что означает, что она имеет величину и направление.
- Единица измерения — ньютон (Н).
- Меняется изменением позиции.
- Рассчитывается по формуле: w = мг
- Измеряется с помощью пружинных весов.
Разница между массой и весом в табличной форме
Масса | Масса |
| Это скалярная величина. | Количество векторов. |
| Значение массы остается постоянным. | Значение веса зависит от положения объекта. |
| Обозначается буквой «м». | Обозначается буквой «W». |
| Его единица СИ — кг. | Его единица СИ — Ньютон. |
| Измеряется такими приборами, как балансир. | Это мерные инструменты, такие как пружинные весы. |
| Его формула: m = w / g | Его формула: W = мг |
Предлагаемое видео: масса против веса
Соотношение веса и массы
Вес и масса взаимосвязаны, тела, имеющие большую массу, также имеют большой вес.Например, большой предмет трудно бросить из-за большого веса.
Чтобы понять взаимосвязь между весом и массой, обратите внимание, что свободно падающее тело имеет ускорение величиной «g». Из второго закона Ньютона мы узнаем, что сила должна действовать, чтобы вызвать ускорение свободного падения.
Например, если тело массой 1 кг падает с ускорением 9,8 квадратных метра в секунду, требуемая сила имеет величину, которая определяется как:
F = ma
= (1 кг) (9.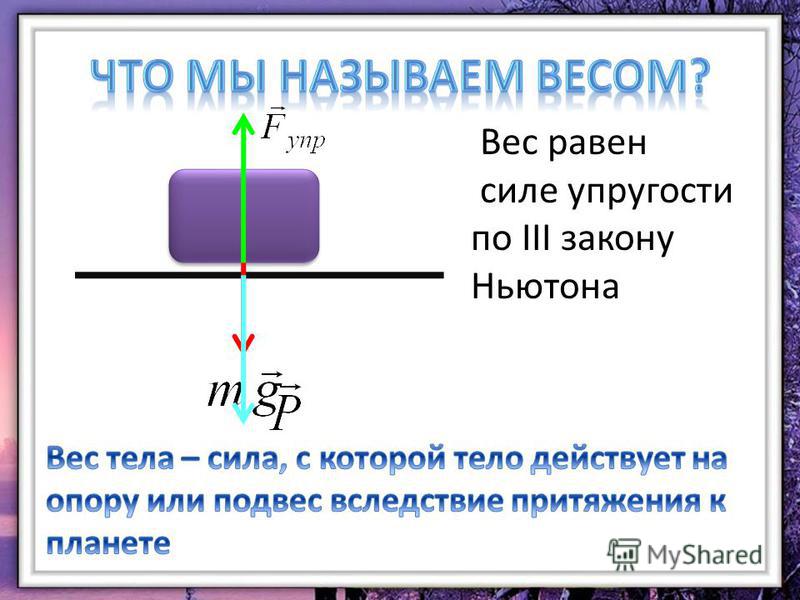 8 м / с²)
8 м / с²)
= 9,8 кгм / с²
= 9,8N
Сила, которая заставляет тело ускоряться вниз, известна его весом. Любой, кто находится у поверхности земли и имеет массу 1 кг, должен иметь вес 9,8 Н, чтобы дать ему ускорение.
Как измеряется вес?
Тело массы m должно иметь вес с величиной «w», которая измеряется по следующей формуле:
Вт =
мг Следовательно, вес тела прямо пропорционален его массе m.Чем больше масса объекта, тем больше будет его вес.
Поскольку вес является векторной величиной, мы можем записать отношение для нахождения веса в векторной форме как:
w = m г
Где g — величина g, — ускорение свободного падения.
Для любопытства:
Знаете ли вы, что, измеряя свой вес, мы фактически измеряем нашу массу?
Когда мы ставим себя на весы, чтобы взвесить себя, мы обычно называем наш вес, на самом деле, который мы измеряем, это наша масса, то есть количество вещества в нашем теле.Существуют и другие машины, которые действительно могут измерять наш вес, они не используются и работают, стоя на них на мгновение, и, в конце концов, они дают истинное значение веса, также выраженное в Ньютонах.
Вес меняется в зависимости от того, где мы находимся?
Мы не весим одинаково на Луне, и даже в космосе, где нет гравитации, масса остается постоянной, но вес равен нулю.
Масса основана на объеме, который занимает тело, вес показывает энергию этого объекта по отношению к притяжению, которое гравитация оказывает на другой объект.Вес на земле определяется силой, с которой земля притягивает нас к земле. Точнее, на вершине горы мы не весим столько же, сколько на уровне моря, поэтому во избежание ошибок были установлены мировые стандарты, поскольку разница очень мала.
С другой стороны, стоит отметить, что наше тело в воде весит меньше из-за плавучести, создаваемой силой, противоположной силе тяжести.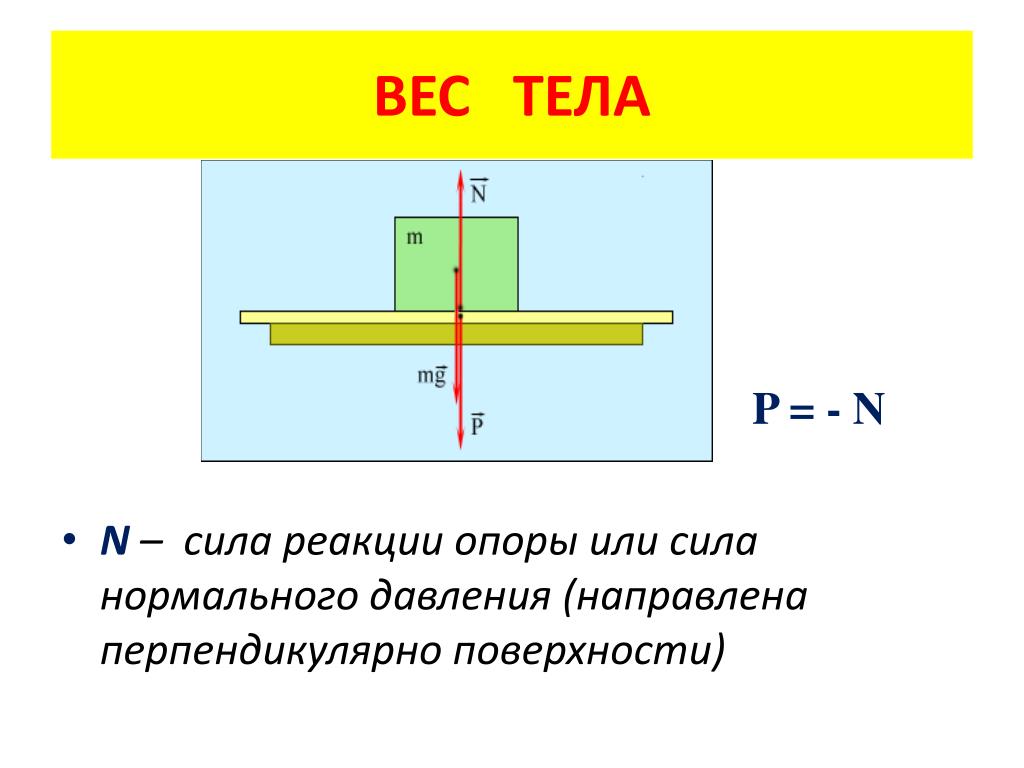
Типы массы и веса
С научной точки зрения, если понимать, что масса и масса являются величинами, с помощью которых соответственно измеряется материя, содержащаяся в теле, и сила, действующая на него под действием силы тяжести, наиболее известны и используются их типы:
- Атомная масса: масса атома.
- Молярная масса: Масса одного моля вещества.
- Молекулярная масса: масса молекулы вещества.
- Инерционная масса: Физическая величина, которая указывает сопротивление тела изменению скорости.
- Масса тела: это масса тела человека.
- Атомный вес: это средняя масса атомов элемента.
- Молекулярный вес: это результат суммы атомных весов элементов, составляющих соединение.
На наших веб-сайтах есть следующие темы:
Определение веса по физике.
Примеры веса в следующих темах:
Масса
- В физике важно отличать вес объекта от его массы.
- С другой стороны, вес объекта является внешней величиной.
- В обычных единицах США вес объекта может быть выражен в фунтах.
- В этом случае вес объекта изменяется из-за силы плавучести.
- Весы с пружинами измеряют вес , определяя степень сжатия пружины. Это пропорционально силе, которую груз оказывает на весы из-за своего веса .
Масса
- На заседании 2011 года Генеральная конференция по вопросу о весах , и мерах (CGPM) согласилась с тем, что килограмм следует пересмотреть в терминах постоянной Планка.
- В повседневном использовании массу объекта в килограммах часто называют его весом .
- С научной точки зрения, «вес » относится к гравитационной силе, действующей на данное тело.
- Например, вес человека на Земле отличается от веса человека на Луне из-за различий в гравитационном притяжении каждого тела.

- Соответственно, космонавты в условиях микрогравитации должны приложить в 10 раз больше силы, чтобы разогнать объект весом 10 кг с той же скоростью, что и объект весом 1 кг, даже если разница в весе незаметна.
Флотация
- Итак, для плавающего объекта на жидкости вес вытесненной жидкости равен весу объекта.
- Когда любая лодка перемещает вес воды, равный ее собственному весу , она плывет.
- Это часто называют «принципом плавучести», когда плавучий объект вытесняет вес жидкости, равный его собственному весу .
- Каждый корабль, подводная лодка и дирижабль должны быть спроектированы так, чтобы вытеснять вес жидкости, равный его собственному весу .
- Выталкивающая сила, равная весу вытесненной жидкости, таким образом, больше веса объекта.
Нормальные силы
- Боб имеет вес 800 Н.
- Согласно третьему закону Ньютона, земля оказывает на человека силу, равную по величине весу человека.
- В этом простом случае вес человека и противодействующая нормальная сила — единственные две силы, принимаемые во внимание на человека.
- Человек остается неподвижным, потому что силы из-за веса и нормальной силы создают нулевую чистую силу на человека.
- В этом случае нормальная сила не находится в прямо противоположном направлении, как сила, обусловленная весом массы.
Плавучесть и принцип Архимеда
- Если выталкивающая сила больше веса объекта , объект поднимется на поверхность и будет плавать.
- Если подъемная сила меньше веса объекта , объект утонет.
- Если выталкивающая сила равна весу объекта , объект останется подвешенным на этой глубине.
- Однако мы также знаем, что выталкивающая сила, действующая на жидкость, должна быть равна ее весу , поскольку жидкость не тонет сама по себе.

- Выталкивающая сила на судне (a) равна весу воды, вытесняемой судном — показано пунктирной областью на (b).
Масса
- Термины масса и вес часто меняют местами, однако это неверно.
- Вес — это другое свойство материи, которое, хотя и связано с массой, является не массой, а скорее величиной гравитационной силы, действующей на данное тело материи.
Определение центра масс
- Положение COM — это массовое взвешенное средних положений частиц.
- Это означает, что позиция COM является массой взвешенных средних положений частиц.
- В трех измерениях: поддерживая объект в трех точках и измеряя силы, которые сопротивляются весу объекта, можно определить COM трехмерных координат центра масс.
Трансляционное равновесие
- Книга, лежащая на столе, толкает его вниз с силой своего веса .
- Обратите внимание, что величина силы, которую стол толкает вверх к объекту (вектор N), равна направленной вниз силе веса объекта (показано здесь как мг, поскольку вес равен массе объекта, умноженной на ускорением свободного падения): поскольку эти силы равны, объект находится в состоянии равновесия (все силы, действующие на него, уравновешиваются до нуля).
Свободно падающие предметы
- Свободное падение — это движение тела, при котором его вес является единственной силой, действующей на объект.
- Свободное падение — это движение тела, при котором его вес является единственной силой, действующей на объект.
Дозиметрия
- Были установлены весовой коэффициент (wr) и весовой фактор ткани / органа (WT).
- Весовой коэффициент для всего тела равен 1, так что 1 Гр излучения, доставляемого на все тело, равен одному зиверту.

Вес и масса — Силы — GCSE Physics (Single Science) Revision — Other
Вес — это не то же самое, что масса.Масса — это мера количества вещества в объекте. Вес — это сила, действующая на этот вопрос. Масса сопротивляется любому изменению движения предметов.
В физике термин «вес» имеет особое значение — силу, действующую на массу под действием силы тяжести. Вес измеряется в ньютонах. Масса измеряется в килограммах.
Масса данного объекта везде одинакова, но его вес может меняться. Мы используем весы для измерения веса и массы.
Напряженность гравитационного поля
Вес — результат действия силы тяжести.Напряженность гравитационного поля Земли составляет 10 Н / кг (десять ньютонов на килограмм). Это означает, что объект массой 1 кг будет притягиваться к центру Земли силой 10 Н. Мы ощущаем такие силы как вес.
Вы бы весили меньше на Луне, потому что сила гравитационного поля Луны составляет одну шестую от земного ( 1,6 Н / кг ). Но учтите, что ваша масса останется прежней.
Вес
На Земле, если вы уроните объект, он ускорится к центру планеты.Вес объекта рассчитывается по следующему уравнению:
вес (Н) = масса (кг) × напряженность гравитационного поля (Н / кг)
- 0.0.1:0.1.0.$0.$4.$0.0″> Вопрос
Масса человека составляет 60 кг. Сколько они весят на Земле, если напряженность гравитационного поля составляет 10 Н / кг?
- Показать ответ
вес = масса × напряженность гравитационного поля
вес = 60 кг × 10 Н / кг
вес = 600 Н
- Вопрос
Сколько весит тот же человек на Луне, если напряженность гравитационного поля равна 1.6 Н / кг?
- Выявить ответ
вес = масса × напряженность гравитационного поля
вес = 60 кг × 1,6 Н / кг
Вес = 96 Н
Разница между массой и весом
Масса — это количество вещества, присутствующего в теле, а масса — это мера того, насколько сильно гравитация воздействует на это вещество. Масса — внутреннее свойство тела и остается неизменной, где бы оно ни находилось.Вес — это сила, а сила — (Масса * Ускорение). Вес объекта — это его масса, умноженная на ускорение свободного падения. Вес тела зависит от места. Например, объекты весят меньше на Луне, где сила тяжести ниже, чем на Земле.
Вес объекта — это его масса, умноженная на ускорение свободного падения. Вес тела зависит от места. Например, объекты весят меньше на Луне, где сила тяжести ниже, чем на Земле.
Таблица сравнения
| Масса | Масса | |
|---|---|---|
| Определение | Масса — это количество вещества в теле независимо от его объема или любых сил, действующих на него. | Вес — это величина силы тяжести, действующей на объект. |
| Влияние силы тяжести | Масса всегда постоянна в любом месте и в любое время | Вес объекта зависит от силы тяжести в этом месте |
| Единица измерения | Масса выражается в килограммах (кг), граммах (г) и миллиграммах (мг). | Вес выражен в Ньютонах (Н) |
| Весы, используемые для измерения | Масса измеряется с помощью балансировочных весов, трехлучевых весов, рычажных весов или электронных весов. | Вес измеряется с помощью пружинных весов. |
| Тип величины | Скалярная и базовая величина | Вектор и производная величина |
Измерение массы vs.вес
Вес измеряется с помощью весов, которые эффективно измеряют силу тяжести земли. Масса тела измеряется путем уравновешивания его с другим известным количеством массы. Масса может быть измерена с помощью весов с чашкой, а вес может быть измерен с помощью пружинных весов. Методы можно менять, если гравитация известна и постоянна, как на Земле.
Влияние силы тяжести массы и веса
Вес объекта зависит от силы тяжести в этом месте, в то время как Масса всегда постоянна в любом месте и в любое время. Например, если масса объекта составляет 60 кг, то его вес будет 600 ньютонов, но когда его доставят на Луну, этот объект будет иметь вес 100 ньютонов, поскольку гравитация Луны составляет 1/6 гравитации Земли. Но масса этого объекта останется прежней.
Например, если масса объекта составляет 60 кг, то его вес будет 600 ньютонов, но когда его доставят на Луну, этот объект будет иметь вес 100 ньютонов, поскольку гравитация Луны составляет 1/6 гравитации Земли. Но масса этого объекта останется прежней.
Масса может быть постоянной, в то время как Вес варьируется.
Внешние факторы, влияющие на вес
Масса — это внутренняя мера объекта и, следовательно, не зависит от каких-либо внешних факторов. Вес, с другой стороны, зависит от массы, которая его привлекает, и силы, с которой он притягивается.
Преобразование массы в вес
Второй закон Ньютона используется для преобразования веса (силы) в массу:
Уравнение силы: F = ma (сила = масса × ускорение).
Здесь F — сила тяжести (т. Е. Вес), м, — масса рассматриваемого объекта, и a — ускорение свободного падения, на Земле примерно 9,8 м / с² или 32.2 фут / с²).
В этом контексте то же уравнение часто записывается как W = mg , где W обозначает вес, а g — ускорение свободного падения.
Относительный вес на Земле, Луне и других планетах
Ниже приводится список веса массы на поверхности некоторых тел в Солнечной системе по отношению к ее весу на Земле:
Использование веса по сравнению с массой
В физических науках термины «масса» и «вес» жестко определены как отдельные меры для обеспечения ясности и точности.В повседневном использовании, учитывая, что все массы на Земле имеют вес, и это соотношение обычно очень пропорционально, вес часто служит для описания обоих свойств, его значение зависит от контекста. Например, в торговле чистый вес розничных товаров фактически относится к массе и правильно выражается в фунтах (США) или килограммах.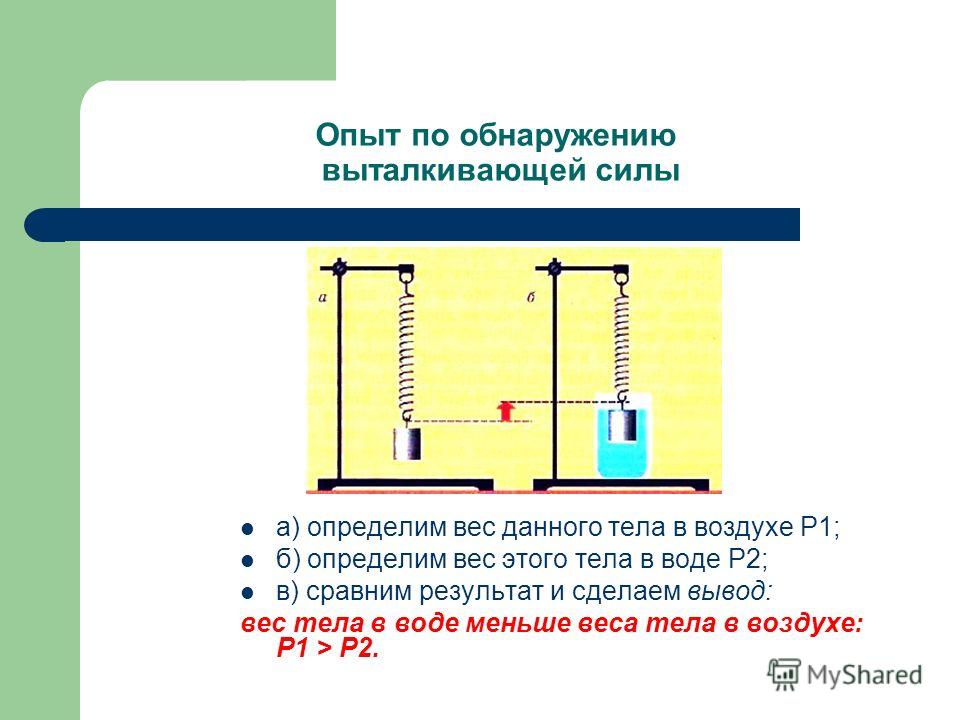

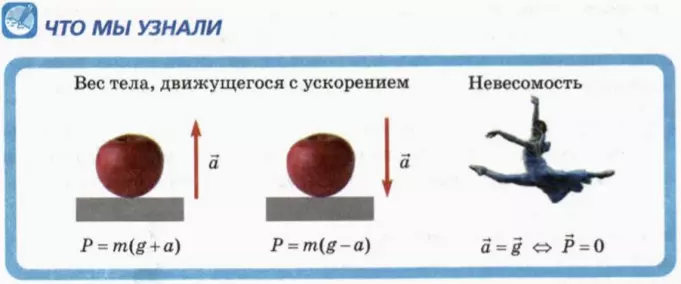 Д.
Д.