ЧЕРЧЕНИЕ. Школьный интернет-учебник — Сечения и разрезы 4-1
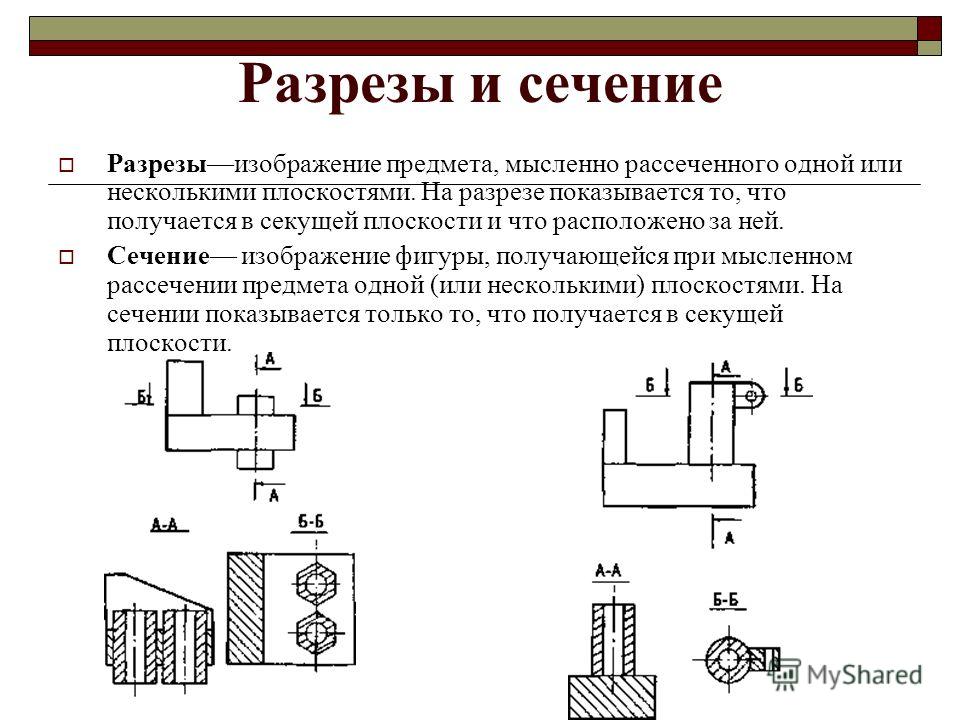
Производственные чертежи содержат различные типы изображений — виды, сечения и разрезы. С видами на чертеже мы уже познакомились…
Сечения и разрезы позволяют выявить внешнюю и внутреннюю форму детали (рис.1, а, б). Названные изображения получают в результате мысленного рассечения детали секущей плоскостью, положение которой выбирают в зависимости от формы изображаемой детали.
Рис. 1. Сечение (а) и разрез (б)
Сечения и разрезы дополняют и уточняют геометрическую информацию о предмете и тем самым увеличивают возможности выявления формы изображаемого объекта на чертеже. В некоторых случаях они имеют большую информационную емкость, чем виды. Разрезы и сечения являются проекционными изображениями и выполняются по правилам прямоугольного проецирования.
Сечение — изображение фигуры, получающейся при мысленном рассечении предмета секущей плоскостью.
Образование сечения
Деталь мысленно рассекают секущей плоскостью в том месте, где необходимо уточнить форму изделия. В секущей плоскости получают фигуру сечения (рис.2).
Рис. 2. Образование сечения
Изображение сечения
После этого секущую плоскость (вместе с фигурой сечения) мысленно вынимают, поворачивают вокруг вертикальной оси, перемещают параллельно плоскости проекций и совмещают с фронтальной плоскостью так, чтобы изображения вида спереди и фигуры сечения не заслоняли друг друга. В сечении показывается только то, что находится в секущей плоскости.
Расположение сечений
В зависимости от расположения на чертеже сечения разделяют на:
а) вынесенные, когда сечения располагают в любом месте чертежа;
б) наложенные, когда их располагают непосредственно на виде предмета;
в) в разрыве — располагают в разрыве изображения.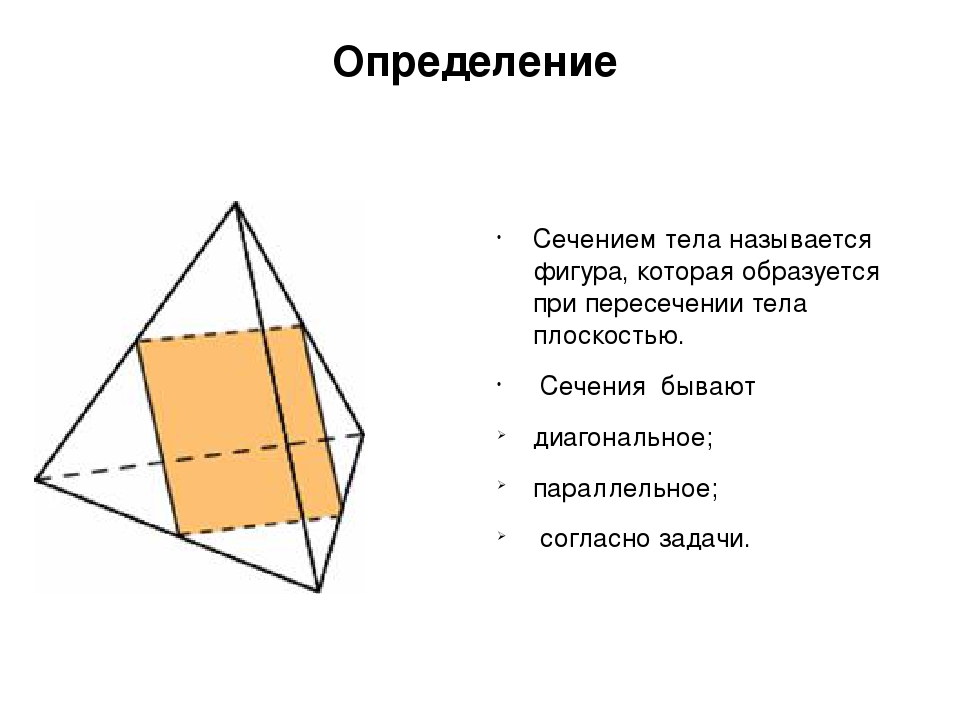
Вынесенное и наложенное сечение показано на рис.3.
Рис.3. Построение сечений
Вынесенное сечение можно выполнять двумя способами:
1. если вид спереди находится в проекционной связи с сечением, то полученное изображение фигуры сечения называют сечением, выполненным в проекционной связи (рис.4).
Рис. 4. Сечение, выполненное в проекционной связи.
2. секущую плоскость с фигурой сечения допускается перемещать в произвольном направлении, совмещая ее с плоскостью проекций, без учета проекционной связи. Такое сечение называется сечением, выполненным на свободном месте чертежа (рис. 5).
Рис. 5. Сечение, выполненное на свободном месте чертежа.
ГОСТ 2.305–68 устанавливает правила изображения и обозначения сечений.
При вынесенном сечении положение секущей плоскости указывают на чертеже линией сечения – разомкнутой линией, которая проводится в виде отдельных штрихов, не пересекающих контур соответствующего изображения. Толщина штрихов берётся в пределах от S до 1,5 S, а длина их от 8 до 20 мм. На начальном и конечном штрихах перпендикулярно им, на расстоянии 2–3 мм от конца штриха, ставят стрелки, указывающие направление взгляда (рис. 6).
У начала и конца линии сечения ставят одну и ту же прописную букву русского алфавита. Буквенные обозначения присваиваются в алфавитном порядке без повторений и без пропусков, за исключением букв И, О, X, Ъ, Ы, Ь (рис. 4). Если для выявления формы деталей требуется выполнить несколько сечений, тогда проводят несколько разомкнутых линий, которые на чертеже продолжают обозначать следующими буквами русского алфавита (Б, В, Г и т.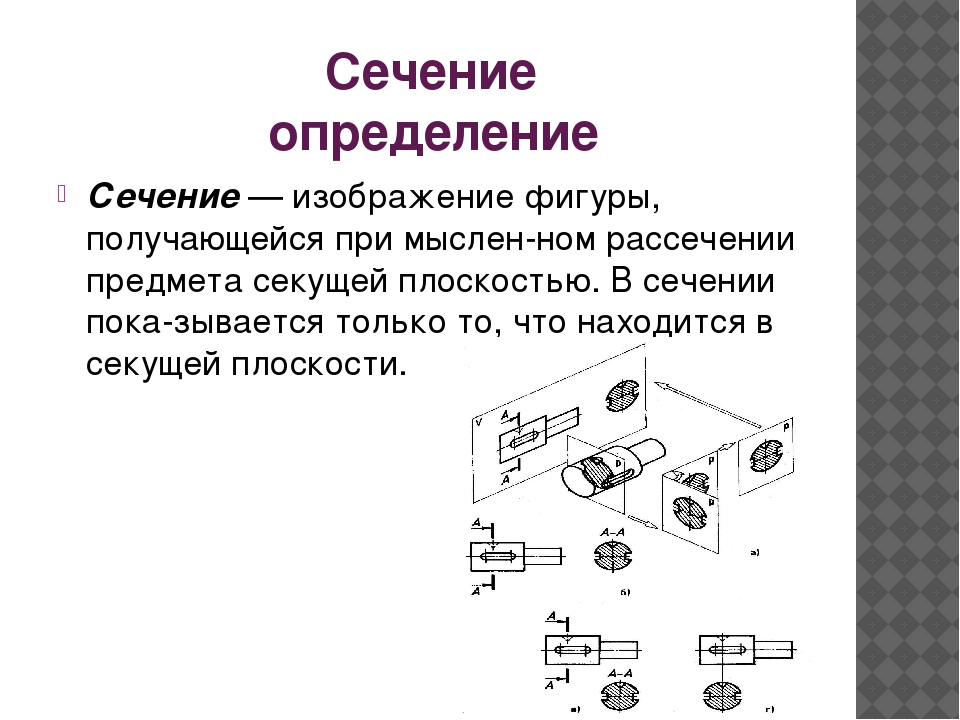
д.) (рис. 7).
Рис. 7. Обозначение нескольких сечений
Контур вынесенного сечения обводится сплошной основной линией такой же толщины S, как видимый контур изображения. Фигуру сечения на чертеже выделяют
Если сечение представляет собой симметричную фигуру и располагается на продолжении линии сечения (штрихпунктирной), то стрелок и букв не наносят (см. рис. 5).
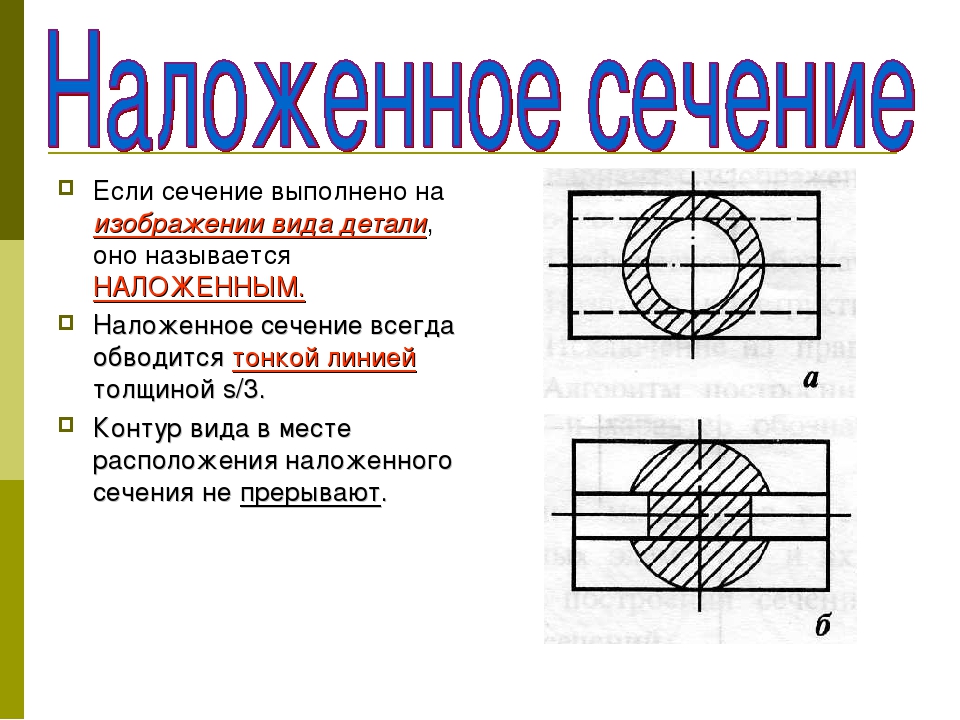
Наложенным называют сечение, которое располагают непосредственно на виде предмета в том месте, где проходила секущая плоскость, то есть, как бы накладывают на изображение. Наложенное сечение выполняется в том случае, когда форма детали на всём протяжении одинакова.
Наложенное сечение тоже бывает двух видов:
1. если наложенное сечение симметрично относительно секущей плоскости, то на сечении указывается только ось штрихпунктирной линией без обозначения буквами и стрелками (рис. 8, а).
2. если наложенное сечение представляет собой
Рис. 8. Наложенное сечение: а) симметричное; б) несимметричное.
Если сечение находится в разрыве между частями одного и того же вида, то его выполняют сплошной основной линией (рис. 9). Правила обозначения сечений, расположенных в разрыве, аналогичны правилам обозначений наложенных сечений: у симметричных сечений указывается только ось (рис.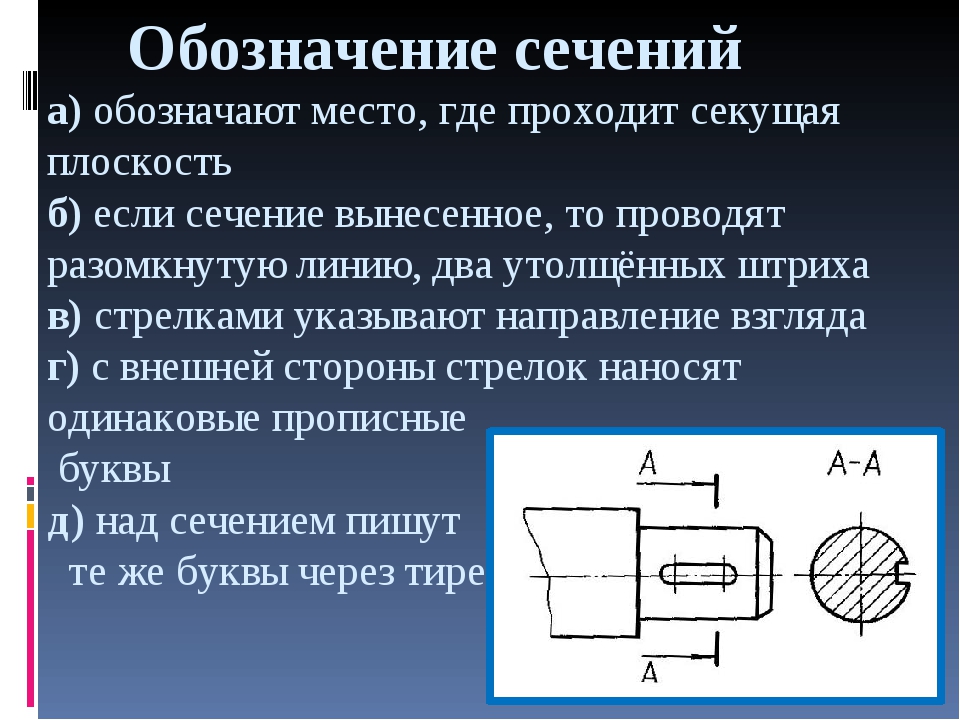
9,а), а несимметричные сечения сопровождают указанием разомкнутой линии и стрелками, указывающими направление взгляда (рис. 9,б).
Рис. 9. Сечения в разрыве: а) симметричное; б) несимметричное
Особенности выполнения
При выполнении сечений применяют следующие условности:
1. Вынесенным сечениям следует отдавать предпочтение перед наложенным, так как последние затемняют чертеж и неудобны для нанесения размеров.
2. При прохождении секущей плоскости через ось поверхности вращения, ограничивающей отверстие или углубление, контур отверстия или углубления в сечении показывают полностью (рис. 10).
Рис. 10. Сечение, проходящее через оси поверхностей вращения
3. Если секущая плоскость проходит через призматическое сквозное отверстие и фигура сечения распадается на несколько частей, сечение не выполняется (рис.
11).
Рис. 11. Сечение, проходящее через призматическое сквозное отверстие.
4. Сечение, распадающееся на отдельные части, заменяют разрезом (рис. 12).
Рис. 12. Замена сечения разрезом
5. Сечения с линией контура под углом 45° штрихуются под углом
Рис. 13. Штриховка под углом 60°.
6. Для нескольких одинаковых сечений, относящихся к одному предмету, линию сечения обозначают одинаковыми буквами и вычерчивают одно сечение (рис. 14).
Рис. 14. Выполнение нескольких одинаковых сечений
7. Сечение можно располагать с поворотом, тогда к надписи А – А должен быть добавлен символ повёрнуто , то есть А – А . Если секущие плоскости нескольких одинаковых сечений не параллельны друг другу, то значок не наносится.
Значение слова «сечение»
Лексическое значение: определение
Общий запас лексики (от греч. Lexikos) — это комплекс всех основных смысловых единиц одного языка. Лексическое значение слова раскрывает общепринятое представление о предмете, свойстве, действии, чувстве, абстрактном явлении, воздействии, событии и тому подобное. Иначе говоря, определяет, что обозначает данное понятие в массовом сознании. Как только неизвестное явление обретает ясность, конкретные признаки, либо возникает осознание объекта, люди присваивают ему название (звуко-буквенную оболочку), а точнее, лексическое значение. После этого оно попадает в словарь определений с трактовкой содержания.
Словари онлайн бесплатно — открывать для себя новое
Словечек и узкоспециализированных терминов в каждом языке так много, что знать все их интерпретации попросту нереально. В современном мире существует масса тематических справочников, энциклопедий, тезаурусов, глоссариев.
Пробежимся по их разновидностям:
- Толковые Найти значение слова вы сможете в толковом словаре русского языка. Каждая пояснительная «статья» толкователя трактует искомое понятие на родном языке, и рассматривает его употребление в контенте. (PS: Еще больше случаев словоупотребления, но без пояснений, вы прочитаете в Национальном корпусе русского языка. Это самая объемная база письменных и устных текстов родной речи.) Под авторством Даля В.И., Ожегова С.И., Ушакова Д.Н. выпущены наиболее известные в нашей стране тезаурусы с истолкованием семантики. Единственный их недостаток — издания старые, поэтому лексический состав не пополняется.
- Энциклопедические
В отличии от толковых, академические и энциклопедические онлайн-словари дают более полное, развернутое разъяснение смысла. Большие энциклопедические издания содержат информацию об исторических событиях, личностях, культурных аспектах, артефактах. Статьи энциклопедий повествуют о реалиях прошлого и расширяют кругозор.
Они могут быть универсальными, либо тематичными, рассчитанными на конкретную аудиторию пользователей. К примеру, «Лексикон финансовых терминов», «Энциклопедия домоводства», «Философия. Энциклопедический глоссарий», «Энциклопедия моды и одежды», мультиязычная универсальная онлайн-энциклопедия «Википедия». - Отраслевые Эти глоссарии предназначены для специалистов конкретного профиля. Их цель объяснить профессиональные термины, толковое значение специфических понятий узкой сферы, отраслей науки, бизнеса, промышленности. Они издаются в формате словарика, терминологического справочника или научно-справочного пособия («Тезаурус по рекламе, маркетингу и PR», «Юридический справочник», «Терминология МЧС»).
- Этимологические и заимствований
Этимологический словарик — это лингвистическая энциклопедия. В нем вы прочитаете версии происхождения лексических значений, от чего образовалось слово (исконное, заимствованное), его морфемный состав, семасиология, время появления, исторические изменения, анализ. Лексикограф установит откуда лексика была заимствована, рассмотрит последующие семантические обогащения в группе родственных словоформ, а так же сферу функционирования. Даст варианты использования в разговоре. В качестве образца, этимологический и лексический разбор понятия «фамилия»: заимствованно из латинского (familia), где означало родовое гнездо, семью, домочадцев. С XVIII века используется в качестве второго личного имени (наследуемого). Входит в активный лексикон.
Этимологический словарик также объясняет происхождение подтекста крылатых фраз, фразеологизмов. Давайте прокомментируем устойчивое выражение «подлинная правда». Оно трактуется как сущая правда, абсолютная истина. Не поверите, при этимологическом анализе выяснилось, эта идиома берет начало от способа средневековых пыток. Подсудимого били кнутом с завязанными на конце узлом, который назывался «линь». Под линью человек выдавал все начистоту, под-линную правду.
- Глоссарии устаревшей лексики
Чем отличаются архаизмы от историзмов?
Какие-то предметы последовательно выпадают из обихода. А следом выходят из употребления лексические определения единиц. Словечки, которые описывают исчезнувшие из жизни явления и предметы, относят к историзмам. Примеры историзмов: камзол, мушкет, царь, хан, баклуши, политрук, приказчик, мошна, кокошник, халдей, волость и прочие. Узнать какое значение имеют слова, которые больше не употребляется в устной речи, вам удастся из сборников устаревших фраз.
Архаизмамы — это словечки, которые сохранили суть, изменив терминологию: пиит — поэт, чело — лоб, целковый — рубль, заморский — иностранный, фортеция — крепость, земский — общегосударственный, цвибак — бисквитный коржик, печенье. Иначе говоря их заместили синонимы, более актуальные в современной действительности. В эту категорию попали старославянизмы — лексика из старославянского, близкая к русскому: град (старосл.) — город (рус.), чадо — дитя, врата — ворота, персты — пальцы, уста — губы, влачиться — волочить ноги. Архаизмы встречаются в обороте писателей, поэтов, в псевдоисторических и фэнтези фильмах.
- Переводческие, иностранные Двуязычные словари для перевода текстов и слов с одного языка на другой. Англо-русский, испанский, немецкий, французский и прочие.
- Фразеологический сборник
Фразеологизмы — это лексически устойчивые обороты, с нечленимой структурой и определенным подтекстом. К ним относятся поговорки, пословицы, идиомы, крылатые выражения, афоризмы. Некоторые словосочетания перекочевали из легенд и мифов. Они придают литературному слогу художественную выразительность. Фразеологические обороты обычно употребляют в переносном смысле. Замена какого-либо компонента, перестановка или разрыв словосочетания приводят к речевой ошибке, нераспознанному подтексту фразы, искажению сути при переводе на другие языки. Найдите переносное значение подобных выражений в фразеологическом словарике.
Примеры фразеологизмов: «На седьмом небе», «Комар носа не подточит», «Голубая кровь», «Адвокат Дьявола», «Сжечь мосты», «Секрет Полишинеля», «Как в воду глядел», «Пыль в глаза пускать», «Работать спустя рукава», «Дамоклов меч», «Дары данайцев», «Палка о двух концах», «Яблоко раздора», «Нагреть руки», «Сизифов труд», «Лезть на стенку», «Держать ухо востро», «Метать бисер перед свиньями», «С гулькин нос», «Стреляный воробей», «Авгиевы конюшни», «Калиф на час», «Ломать голову», «Души не чаять», «Ушами хлопать», «Ахиллесова пята», «Собаку съел», «Как с гуся вода», «Ухватиться за соломинку», «Строить воздушные замки», «Быть в тренде», «Жить как сыр в масле».
- Определение неологизмов
Языковые изменения стимулирует динамичная жизнь. Человечество стремятся к развитию, упрощению быта, инновациям, а это способствует появлению новых вещей, техники. Неологизмы — лексические выражения незнакомых предметов, новых реалий в жизни людей, появившихся понятий, явлений. К примеру, что означает «бариста» — это профессия кофевара; профессионала по приготовлению кофе, который разбирается в сортах кофейных зерен, умеет красиво оформить дымящиеся чашечки с напитком перед подачей клиенту. Каждое словцо когда-то было неологизмом, пока не стало общеупотребительным, и не вошло в активный словарный состав общелитературного языка. Многие из них исчезают, даже не попав в активное употребление. Неологизмы бывают словообразовательными, то есть абсолютно новообразованными (в том числе от англицизмов), и семантическими. К семантическим неологизмам относятся уже известные лексические понятия, наделенные свежим содержанием, например «пират» — не только морской корсар, но и нарушитель авторских прав, пользователь торрент-ресурсов. Вот лишь некоторые случаи словообразовательных неологизмов: лайфхак, мем, загуглить, флэшмоб, кастинг-директор, пре-продакшн, копирайтинг, френдить, пропиарить, манимейкер, скринить, фрилансинг, хедлайнер, блогер, дауншифтинг, фейковый, брендализм. Еще вариант, «копираст» — владелец контента или ярый сторонник интеллектуальных прав.
- Прочие 177+
Кроме перечисленных, есть тезаурусы: лингвистические, по различным областям языкознания; диалектные; лингвострановедческие; грамматические; лингвистических терминов; эпонимов; расшифровки сокращений; лексикон туриста; сленга. Школьникам пригодятся лексические словарники с синонимами, антонимами, омонимами, паронимами и учебные: орфографический, по пунктуации, словообразовательный, морфемный. Орфоэпический справочник для постановки ударений и правильного литературного произношения (фонетика). В топонимических словарях-справочниках содержатся географические сведения по регионам и названия. В антропонимических — данные о собственных именах, фамилиях, прозвищах.
Они могут быть универсальными, либо тематичными, рассчитанными на конкретную аудиторию пользователей. К примеру, «Лексикон финансовых терминов», «Энциклопедия домоводства», «Философия. Энциклопедический глоссарий», «Энциклопедия моды и одежды», мультиязычная универсальная онлайн-энциклопедия «Википедия».
Лексикограф установит откуда лексика была заимствована, рассмотрит последующие семантические обогащения в группе родственных словоформ, а так же сферу функционирования. Даст варианты использования в разговоре. В качестве образца, этимологический и лексический разбор понятия «фамилия»: заимствованно из латинского (familia), где означало родовое гнездо, семью, домочадцев. С XVIII века используется в качестве второго личного имени (наследуемого). Входит в активный лексикон.
Этимологический словарик также объясняет происхождение подтекста крылатых фраз, фразеологизмов. Давайте прокомментируем устойчивое выражение «подлинная правда». Оно трактуется как сущая правда, абсолютная истина. Не поверите, при этимологическом анализе выяснилось, эта идиома берет начало от способа средневековых пыток. Подсудимого били кнутом с завязанными на конце узлом, который назывался «линь». Под линью человек выдавал все начистоту, под-линную правду.
А следом выходят из употребления лексические определения единиц. Словечки, которые описывают исчезнувшие из жизни явления и предметы, относят к историзмам. Примеры историзмов: камзол, мушкет, царь, хан, баклуши, политрук, приказчик, мошна, кокошник, халдей, волость и прочие. Узнать какое значение имеют слова, которые больше не употребляется в устной речи, вам удастся из сборников устаревших фраз.
Архаизмамы — это словечки, которые сохранили суть, изменив терминологию: пиит — поэт, чело — лоб, целковый — рубль, заморский — иностранный, фортеция — крепость, земский — общегосударственный, цвибак — бисквитный коржик, печенье. Иначе говоря их заместили синонимы, более актуальные в современной действительности. В эту категорию попали старославянизмы — лексика из старославянского, близкая к русскому: град (старосл.) — город (рус.), чадо — дитя, врата — ворота, персты — пальцы, уста — губы, влачиться — волочить ноги. Архаизмы встречаются в обороте писателей, поэтов, в псевдоисторических и фэнтези фильмах.
Вот лишь некоторые случаи словообразовательных неологизмов: лайфхак, мем, загуглить, флэшмоб, кастинг-директор, пре-продакшн, копирайтинг, френдить, пропиарить, манимейкер, скринить, фрилансинг, хедлайнер, блогер, дауншифтинг, фейковый, брендализм. Еще вариант, «копираст» — владелец контента или ярый сторонник интеллектуальных прав.
Толкование слов онлайн: кратчайший путь к знаниям
Проще изъясняться, конкретно и более ёмко выражать мысли, оживить свою речь, — все это осуществимо с расширенным словарным запасом. С помощью ресурса How to all вы определите значение слов онлайн, подберете родственные синонимы и пополните свою лексику. Последний пункт легко восполнить чтением художественной литературы. Вы станете более эрудированным интересным собеседником и поддержите разговор на разнообразные темы. Литераторам и писателям для разогрева внутреннего генератора идей полезно будет узнать, что означают слова, предположим, эпохи Средневековья или из философского глоссария.
Глобализация берет свое. Это сказывается на письменной речи. Стало модным смешанное написание кириллицей и латиницей, без транслитерации: SPA-салон, fashion-индустрия, GPS-навигатор, Hi-Fi или High End акустика, Hi-Tech электроника. Чтобы корректно интерпретировать содержание слов-гибридов, переключайтесь между языковыми раскладками клавиатуры.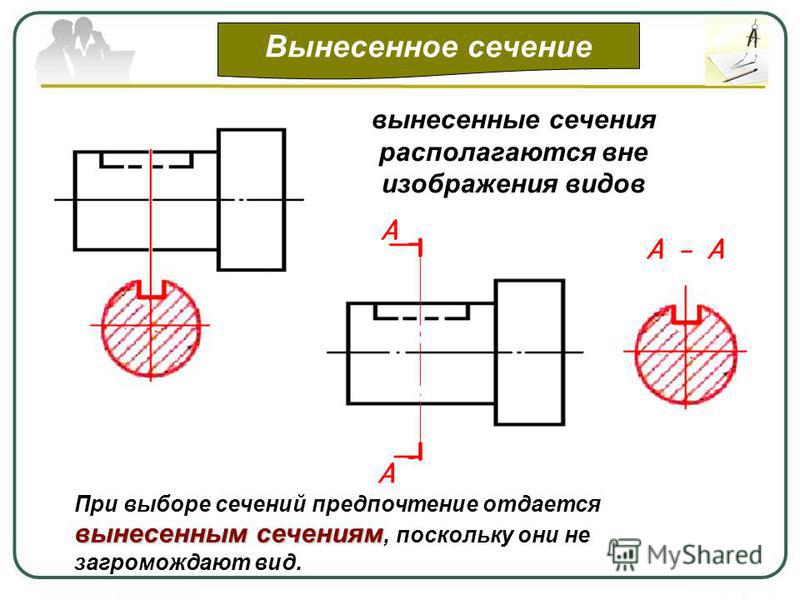
Пусть ваша речь ломает стереотипы. Тексты волнуют чувства, проливаются эликсиром на душу и не имеют срока давности. Удачи в творческих экспериментах!
Проект how-to-all.com развивается и пополняется современными словарями с лексикой реального времени. Следите за обновлениями. Этот сайт помогает говорить и писать по-русски правильно. Расскажите о нас всем, кто учится в универе, школе, готовится к сдаче ЕГЭ, пишет тексты, изучает русский язык.
Расчет прямоугольного сечения балки — Лекции и примеры решения задач технической механики
Задача
Для заданной стальной балки подобрать размеры прямоугольного поперечного сечения по условию прочности.
Соотношение сторон сечения h=2b (h – высота, b – ширина).
Полученные размеры принять согласно ГОСТ 6636.
Допустимые напряжения для материала балки [σ]=160МПа.
Решение
Предыдущие пункты решения задачи:
- Определение опорных реакций
- Построение эпюр внутренних поперечных сил и изгибающих моментов
- Расчет момента сопротивления сечения балки по условию прочности
Минимально необходимый расчетный момент сопротивления сечения балки составил
В случаях, когда система изгибающих нагрузок действующих на балку расположена в вертикальной плоскости сечение тоже следует располагать вертикально.
По справочнику находим формулу осевого момента сопротивления прямоугольного сечения
Используя заданное соотношение сторон (h=2b), уменьшим количество переменных в выражении
и запишем необходимое неравенство
откуда находим расчетную высоту прямоугольного сечения
Из заданного соотношения сторон определяем расчетную ширину сечения
Отметим, что полученные размеры являются минимально необходимыми для обеспечения прочности заданной балки.
При отсутствии дополнительных условий расчетные размеры можно округлить до целого значения в миллиметрах исключительно в большую сторону (h=153мм, b=77мм).
По ГОСТ 6636 нормальных линейных размеров выбираются ближайшие значения в сторону увеличения.
Следовательно, за окончательные размеры прямоугольного сечения балки принимаем: h=155мм, b=80мм.
После принятия размеров согласно ГОСТ заданное соотношение сторон может несколько измениться. Это нормально.
Оценка экономичности сечений >
Построение эпюры нормальных напряжений >
Другие примеры решения задач >
Свойства поперечного сечения | MechaniCalc
ПРИМЕЧАНИЕ.
Эта страница использует JavaScript для форматирования уравнений для правильного отображения. Пожалуйста, включите JavaScript.
Поведение конструктивного элемента определяется его материалом и геометрией. Поперечное сечение и длина элемента конструкции влияют на то, насколько этот элемент прогибается под нагрузкой, а поперечное сечение определяет напряжения, которые существуют в элементе при заданной нагрузке.
Недвижимость участков
Центроид
Центроид формы представляет собой точку, вокруг которой равномерно распределена площадь сечения.Если область является дважды симметричной относительно двух ортогональных осей, центр тяжести лежит на пересечении этих осей. Если область симметрична только относительно одной оси, то центр тяжести лежит где-то вдоль этой оси (необходимо вычислить другую координату). Если точное местоположение центроида не может быть определено путем осмотра, его можно рассчитать следующим образом:
где dA представляет собой площадь бесконечно малого элемента, A представляет собой общую площадь поперечного сечения, а x и y являются координатами элемента dA относительно интересующей оси.
Центроидальные положения общих поперечных сечений хорошо задокументированы, поэтому обычно нет необходимости рассчитывать местоположение с помощью приведенных выше уравнений.
Если поперечное сечение состоит из набора основных форм, центроидальное положение которых известно относительно некоторой контрольной точки, то центральное положение составного поперечного сечения можно рассчитать как:
где х с, я и у с, я являются прямоугольные координаты центра тяжести расположения я -й сечения относительно опорной точки, и А я является площадь я -й раздел.
Центроидное расстояние
Центроидное расстояние , c — это расстояние от центра тяжести поперечного сечения до крайнего волокна. Центроидное расстояние в направлении y для прямоугольного поперечного сечения показано на рисунке ниже:
Обычно центроидное расстояние используется:
Первый момент области
Первый момент области относительно интересующей оси рассчитывается как:
| Q x = ∫ y dA | Q y = ∫ x dA |
где Q x — это первый момент вокруг оси x, а Q y — это первый момент вокруг оси y.
Если область состоит из набора основных форм, чьи центроидные положения известны относительно интересующей оси, то первый момент составной области может быть рассчитан как:
Обратите внимание, что первый момент площади используется при вычислении центра тяжести поперечного сечения относительно некоторого начала координат (как обсуждалось ранее). Первый момент также используется при расчете значения напряжения сдвига в определенной точке поперечного сечения. В этом случае первый момент рассчитывается для области, которая составляет меньшую часть поперечного сечения, где область ограничена интересующей точкой и крайним волокном (верхним или нижним) поперечного сечения.Первый момент рассчитывается относительно оси, проходящей через центр тяжести поперечного сечения.
На рисунке выше заштрихованная синяя область представляет собой интересующую область в общем поперечном сечении. Первый момент этой области относительно оси x (которая проходит через центр тяжести поперечного сечения, точку O на рисунке выше) рассчитывается как:
Если центральное положение интересующей области известно, то первый момент области относительно оси может быть вычислен как (см.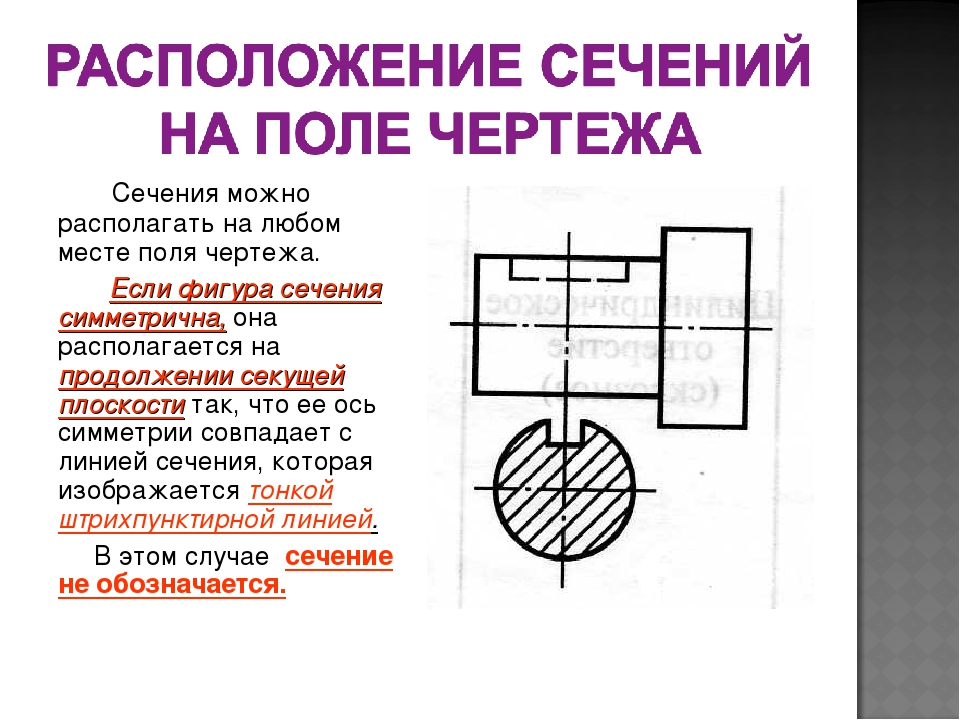
Рисунок выше):
Q cx = y c1 A 1
Следует отметить, что первый момент области будет положительным или отрицательным в зависимости от положения положения области относительно оси интереса.Следовательно, первый момент всей площади поперечного сечения относительно его собственного центроида будет равен нулю.
Момент инерции площади
Второй момент площади, более известный как момент инерции , I, поперечного сечения, является показателем способности конструктивного элемента сопротивляться изгибу. (Примечание 1) I x и I y — моменты инерции относительно осей x и y, соответственно, и рассчитываются по формуле:
| I x = ∫ y 2 dA | I y = ∫ x 2 dA |
где x и y — координаты элемента dA относительно интересующей оси.
Чаще всего моменты инерции рассчитываются относительно центра тяжести сечения.
В этом случае они упоминаются как центроидных моментов инерции и обозначаются как I cx для инерции относительно оси x и I cy для инерции относительно оси y.
Моменты инерции обычных поперечных сечений хорошо задокументированы, поэтому обычно нет необходимости рассчитывать их с помощью приведенных выше уравнений. Свойства нескольких распространенных поперечных сечений приведены в конце этой страницы.
Если поперечное сечение состоит из набора основных форм, все центроиды которых совпадают, то момент инерции составного сечения является просто суммой отдельных моментов инерции. Примером этого является балка коробчатого сечения, состоящая из двух прямоугольных секций, как показано ниже. В этом случае внешняя часть имеет «положительную площадь», а внутренняя часть имеет «отрицательную площадь», поэтому составной момент инерции представляет собой вычитание момента инерции внутренней части из внешней части.
В случае более сложного составного поперечного сечения, в котором центральные положения не совпадают, момент инерции может быть вычислен с использованием теоремы о параллельных осях .
Важно не путать момент инерции площади с массой момента инерции твердого тела. Момент инерции площади указывает на сопротивление поперечного сечения изгибу, тогда как момент инерции массы указывает на сопротивление тела вращению.
Теорема о параллельной оси
Если известен момент инерции поперечного сечения относительно центральной оси, то для вычисления момента инерции относительно любой параллельной оси можно использовать теорему о параллельных осях :
I параллельная ось = I c & plus; А д 2
где I c — момент инерции относительно центральной оси, d — расстояние между центральной осью и параллельной осью, а A — площадь поперечного сечения.
Если поперечное сечение состоит из набора основных форм, центроидные моменты инерции которых известны вместе с расстояниями центроидов до некоторой контрольной точки, то теорема о параллельных осях может использоваться для вычисления момента инерции составного поперечного сечения.
Например, двутавровая балка может быть аппроксимирована 3 прямоугольниками, как показано ниже. Поскольку это составное сечение симметрично относительно осей x и y, центр тяжести сечения можно определить путем осмотра на пересечении этих осей.Центроид расположен в начале координат O на рисунке.
Момент инерции составной секции можно рассчитать с помощью теоремы о параллельности осей. Центроидный момент инерции секции относительно оси x, I cx , рассчитывается как:
I cx.IBeam = I cx.W & plus; (I cx.F1 & plus; A F1 d 1 2 ) & plus; (I cx.F2 & plus; A F2 d 2 2 )
где члены I cx представляют собой моменты инерции отдельных секций относительно их собственных центроидов в ориентации оси x, члены d представляют собой расстояния между центрами тяжести отдельных секций до центроида составной секции, а Термины — это площади отдельных разделов.
Поскольку центроид сечения W и центр тяжести составного сечения совпадают, d для этого сечения равно нулю, поэтому член Ad 2 отсутствует.
Важно отметить, что из теоремы о параллельных осях следует, что по мере того, как отдельная секция перемещается дальше от центра тяжести составной секции, вклад этой секции в момент инерции составной секции увеличивается в d 2 . Следовательно, если намерение состоит в том, чтобы увеличить момент инерции секции относительно определенной оси, наиболее эффективно расположить область как можно дальше от этой оси.Это объясняет форму двутавровой балки. Фланцы вносят основной вклад в момент инерции, а перегородка служит для отделения фланцев от оси изгиба. Однако полотно должно сохранять некоторую толщину, чтобы избежать коробления и потому, что полотно принимает на себя значительную часть напряжения сдвига в сечении.
Полярный момент инерции
Полярный момент инерции , I, поперечного сечения является показателем способности конструктивного элемента противостоять скручиванию вокруг оси, перпендикулярной сечению.
Полярный момент инерции для сечения относительно оси можно рассчитать следующим образом:
J = ∫ r 2 dA = ∫ (x 2 & plus; y 2 ) dA
где x и y — координаты элемента dA относительно интересующей оси, а r — расстояние между элементом dA и интересующей осью.
Хотя полярный момент инерции может быть вычислен с использованием приведенного выше уравнения, обычно удобнее рассчитывать его, используя теорему о перпендикулярной оси , которая утверждает, что полярный момент инерции области является суммой моментов инерции относительно любые две ортогональные оси, проходящие через интересующую ось:
J = I x и плюс; Я y
Чаще всего интересующая ось проходит через центр тяжести поперечного сечения.
Модуль упругости сечения
Максимальное изгибающее напряжение в балке рассчитывается как σ b = Mc / I c , где c — расстояние от нейтральной оси до крайнего волокна, I c — центроидный момент инерции, а M — изгибающий момент.
Модуль сечения объединяет члены c и I c в уравнении напряжения изгиба:
S = I c / c
Используя модуль упругости сечения, напряжение изгиба рассчитывается как σ b = M / S.Полезность модуля сечения заключается в том, что он характеризует сопротивление сечения изгибу одним членом. Это позволяет оптимизировать поперечное сечение балки, чтобы противостоять изгибу, за счет максимального увеличения одного параметра.
Радиус вращения
Радиус вращения представляет собой расстояние от центра тяжести секции, на котором вся площадь может быть сосредоточена без какого-либо влияния на момент инерции. Радиус вращения формы относительно каждой оси определяется как:
Полярный радиус инерции также может быть вычислен для задач, связанных с кручением вокруг центральной оси:
Прямоугольные радиусы вращения также можно использовать для вычисления полярного радиуса вращения:
r p 2 = r x 2 и плюс; г г 2
Свойства общих сечений
В таблице ниже приведены свойства общих сечений.
Более подробные таблицы можно найти в перечисленных ссылках.
Свойства, вычисленные в таблице, включают площадь, центроидный момент инерции, модуль упругости сечения и радиус вращения.
| Форма | Представительство | Недвижимость |
|---|---|---|
| Прямоугольник |
сечение рассеяния Википедия
Вероятность того, что данный процесс происходит при столкновении частиц
В физике сечение является мерой вероятности того, что определенный процесс будет иметь место, когда какое-то излучение возбуждения (например,грамм. пучок частиц, звуковая волна, свет или рентгеновское излучение) пересекает локализованное явление (например, частицу или флуктуацию плотности). Например, сечение Резерфорда является мерой вероятности того, что альфа-частица будет отклонена на заданный угол во время столкновения с атомным ядром. Поперечное сечение обычно обозначается σ (сигма) и выражается в единицах поперечной площади.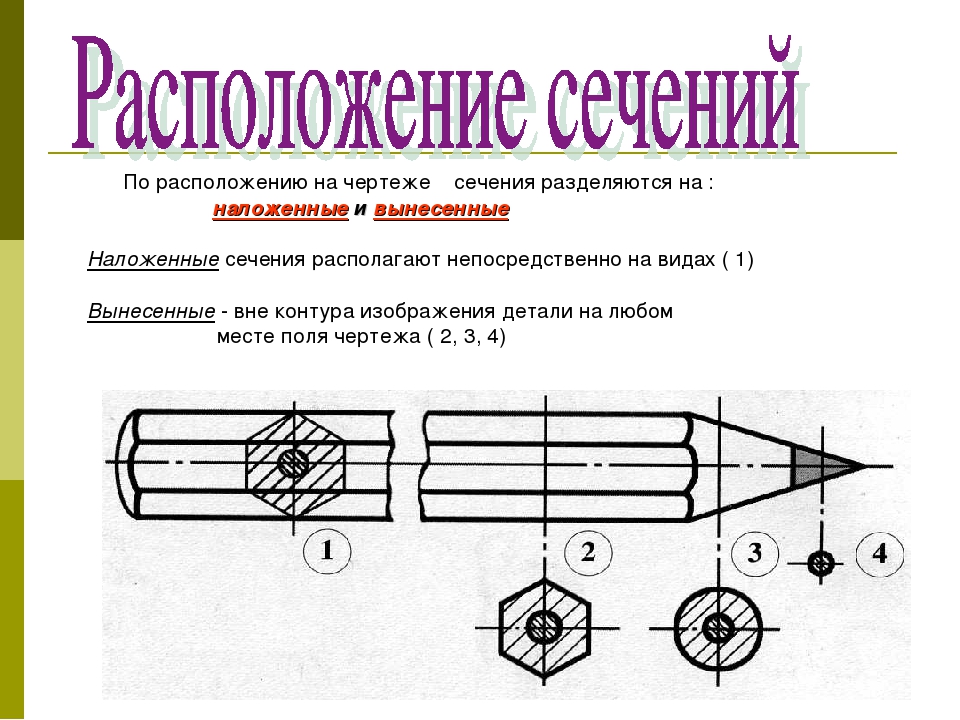
В некотором смысле его можно рассматривать как размер объекта, в который должно попасть возбуждение, чтобы процесс произошел, но точнее, это параметр случайного процесса.
В классической физике эта вероятность часто сходится к детерминированной пропорции энергии возбуждения, участвующей в процессе, так что, например, при рассеянии света частицей сечение определяет количество оптической мощности, рассеянной светом. заданной освещенности (мощность на площадь). Важно отметить, что хотя поперечное сечение имеет те же единицы измерения, что и площадь, поперечное сечение не обязательно может соответствовать фактическому физическому размеру цели, полученному с помощью других форм измерения.Нередко фактическая площадь поперечного сечения рассеивающего объекта намного больше или меньше поперечного сечения какого-либо физического процесса. Например, плазмонные наночастицы могут иметь сечения рассеяния света для определенных частот, которые намного превышают их фактические площади поперечного сечения.
Когда две дискретные частицы взаимодействуют в классической физике, их взаимное поперечное сечение — это область, поперечная их относительному движению, внутри которой они должны встретиться, чтобы разойтись друг от друга.Если частицы представляют собой твердые неупругие сферы, которые взаимодействуют только при контакте, их сечение рассеяния связано с их геометрическими размерами. Если частицы взаимодействуют посредством некоторой силы, действующей на расстоянии, такой как электромагнетизм или гравитация, их сечение рассеяния обычно больше, чем их геометрический размер.
Когда поперечное сечение задается как дифференциальный предел функции некоторой переменной конечного состояния, такой как угол или энергия частицы, оно называется дифференциальным поперечным сечением (см. Подробное обсуждение ниже).Когда сечение интегрируется по всем углам рассеяния (и, возможно, другим переменным), оно называется общим сечением или интегральным полным сечением .
Например, в рэлеевском рассеянии интенсивность, рассеянная под прямым и обратным углами, больше, чем интенсивность, рассеянная вбок, поэтому прямое дифференциальное сечение рассеяния больше, чем перпендикулярное дифференциальное сечение, и при сложении всех бесконечно малых сечений по весь диапазон углов с помощью интегрального исчисления можно найти полное сечение.
Сечения рассеяния могут быть определены в ядерной, атомной физике и физике частиц для столкновений ускоренных пучков частиц одного типа с мишенями (неподвижными или движущимися) частиц второго типа. Вероятность возникновения любой данной реакции пропорциональна ее поперечному сечению. Таким образом, указание сечения для данной реакции является показателем вероятности того, что данный процесс рассеяния произойдет.
Измеренная скорость реакции данного процесса сильно зависит от экспериментальных переменных, таких как плотность материала мишени, интенсивность луча, эффективность обнаружения устройства или установка угла устройства обнаружения.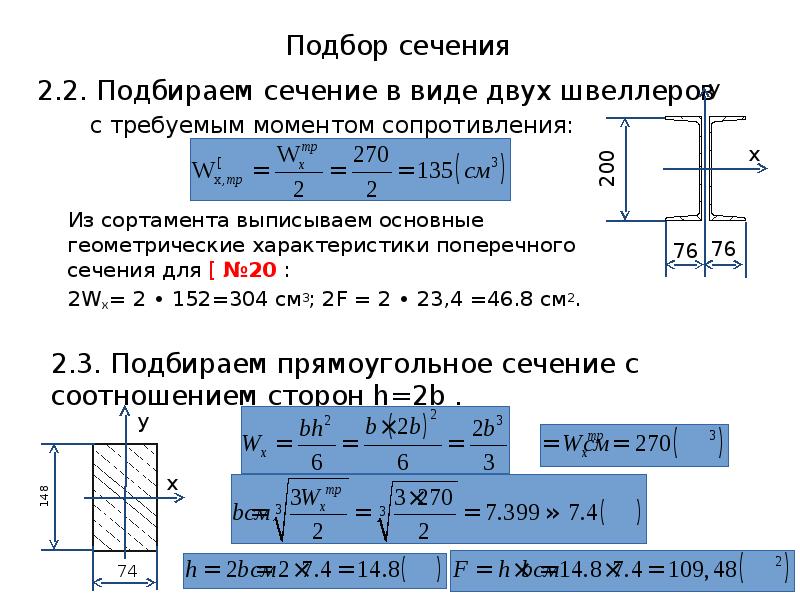
Однако эти величины можно учесть, что позволяет измерить основное сечение столкновения двух частиц.
Дифференциальные и полные сечения рассеяния являются одними из наиболее важных измеряемых величин в ядерной, атомной физике и физике элементарных частиц.
Столкновение частиц газа []
Рис. 1. В газе частиц с индивидуальным диаметром 2 r , поперечное сечение σ для столкновений связано с плотностью числа частиц n и средней длиной свободного пробега между столкновениями λ .В газе частиц конечного размера происходят столкновения между частицами, которые зависят от их размера в поперечном сечении. Среднее расстояние, которое проходит частица между столкновениями, зависит от плотности частиц газа. Эти количества связаны соотношением
- σ = 1nλ, {\ displaystyle \ sigma = {\ frac {1} {n \ lambda}},}
где
- σ — сечение столкновения двух частиц (единицы СИ: м 2 ),
- λ — длина свободного пробега между столкновениями (единицы СИ: м),
- n — это числовая плотность частиц мишени (единицы СИ: м −3 ). {2}}
{2}}Если частицы в газе взаимодействуют посредством силы, диапазон которой превышает их физический размер, то поперечное сечение представляет собой большую эффективную площадь, которая может зависеть от множества переменных, таких как энергия частиц. .
Поперечные сечения могут быть вычислены для атомных столкновений, но также используются в субатомной области. Например, в ядерной физике «газ» нейтронов низкой энергии сталкивается с ядрами в реакторе или другом ядерном устройстве, с поперечным сечением, зависящим от энергии, и, следовательно, также с четко определенной длиной свободного пробега между столкновениями.
Затухание пучка частиц []
Если пучок частиц входит в тонкий слой материала толщиной d z , поток Φ пучка будет уменьшаться на d Φ согласно
- dΦdz = −nσΦ, {\ displaystyle {\ frac {\ mathrm {d} \ Phi} {\ mathrm {d} z}} = — n \ sigma \ Phi,}
, где σ — общее сечение всех событий , включая рассеяние, поглощение или преобразование в другой вид.
{-n \ sigma z},}
, где Φ 0 — начальный поток, а z — общая толщина материала. Для света это называется законом Бера – Ламберта.
Дифференциальное сечение []
Рассмотрим классическое измерение, в котором отдельная частица рассеивается от одной неподвижной частицы-мишени. Обычно используется сферическая система координат, при этом цель размещается в начале координат, а ось z этой системы координат совмещена с падающим лучом.Угол θ — это угол рассеяния , измеренный между падающим лучом и рассеянным лучом, а θ — азимутальный угол.
Прицельный параметр b представляет собой перпендикулярное смещение траектории падающей частицы, а выходящая частица выходит под углом θ . Для данного взаимодействия (кулоновского, магнитного, гравитационного, контактного и т. Д.) Прицельный параметр и угол рассеяния имеют определенную взаимно однозначную функциональную зависимость друг от друга.
Как правило, прицельный параметр нельзя ни контролировать, ни измерять от события к событию, и предполагается, что он принимает все возможные значения при усреднении по множеству событий рассеяния. Дифференциальный размер поперечного сечения — это элемент площади в плоскости прицельного параметра, т.е. d σ = b d φ d b . Дифференциальный угловой диапазон рассеянной частицы под углом θ представляет собой элемент телесного угла d Ω = sin θ d θ d φ .Дифференциальное сечение является частным этих величин, d σ / d Ω .
Это функция угла рассеяния (и, следовательно, также прицельного параметра), а также других наблюдаемых, таких как импульс падающей частицы. Дифференциальное поперечное сечение всегда считается положительным, даже если более высокие параметры удара обычно вызывают меньший прогиб. В цилиндрически симметричных ситуациях (относительно оси луча) азимутальный угол φ не изменяется в процессе рассеяния, и дифференциальное сечение можно записать как
- dσd (cosθ) = ∫02πdσdΩdφ {\ displaystyle {\ frac {\ mathrm {d} \ sigma} {\ mathrm {d} (\ cos \ theta)}} = \ int _ {0} ^ {2 \ pi} {\ frac {\ mathrm {d} \ sigma} {\ mathrm {d} \ Omega}} \, \ mathrm {d} \ varphi}.
В ситуациях, когда процесс рассеяния не является азимутально-симметричным, например, когда луч или частицы мишени обладают магнитными моментами, ориентированными перпендикулярно оси луча, дифференциальное сечение также должно быть выражено как функция от азимутального угла.
Для рассеяния частиц падающего потока F inc от неподвижной мишени, состоящей из множества частиц, дифференциальное сечение d σ / d Ω под углом ( θ , φ ) равно связанный с потоком детектирования рассеянных частиц F out ( θ , φ ) в частицах в единицу времени на
- dσdΩ (θ, φ) = 1ntΔΩFout (θ, φ) Finc.{\ displaystyle {\ frac {\ mathrm {d} \ sigma} {\ mathrm {d} \ Omega}} (\ theta, \ varphi) = {\ frac {1} {nt \ Delta \ Omega}} {\ frac {F _ {\ text {out}} (\ theta, \ varphi)} {F _ {\ text {inc}}}}.}
Здесь Δ Ом — конечный угловой размер детектора (единица СИ: ср), n — это плотность частиц мишени (единицы СИ: м −3 ), а t — толщина неподвижной мишени (единицы СИ: м).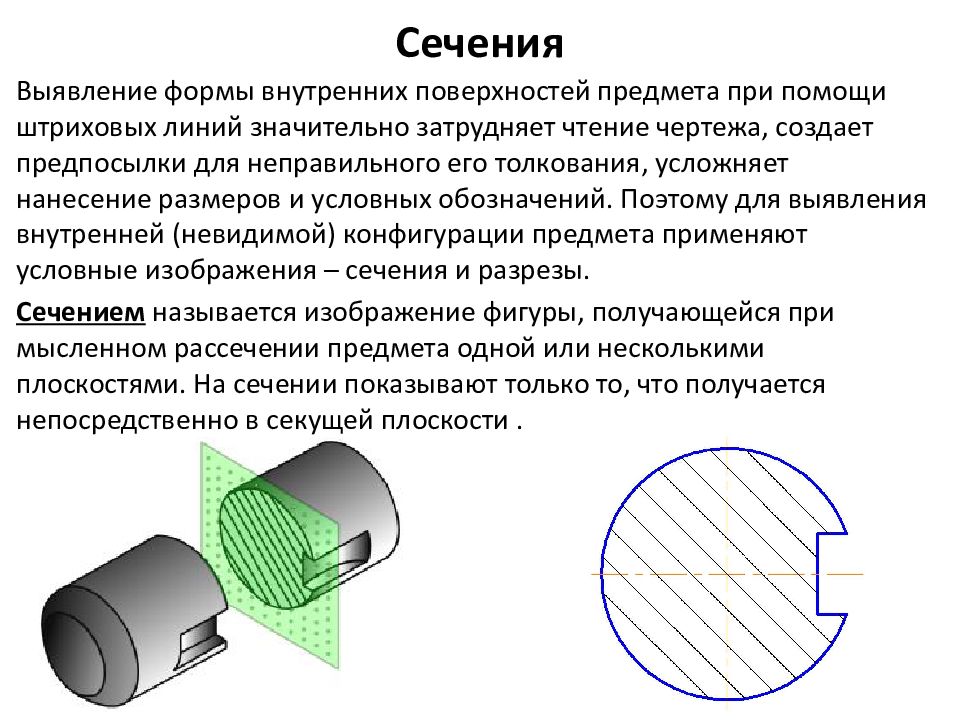
Эта формула предполагает, что цель достаточно тонкая, чтобы каждая частица луча взаимодействовала не более чем с одной частицей цели.{\ pi} {\ frac {\ mathrm {d} \ sigma} {\ mathrm {d} \ Omega}} \ sin \ theta \, \ mathrm {d} \ theta \, \ mathrm {d} \ varphi.}
Обычно опускают квалификатор «дифференциал», когда тип поперечного сечения может быть выведен из контекста. В этом случае σ может называться интегральным сечением или полным сечением . Последний термин может сбивать с толку в контекстах, где задействовано несколько событий, поскольку «общее» также может относиться к сумме поперечных сечений по всем событиям.
Дифференциальное сечение — чрезвычайно полезная величина во многих областях физики, поскольку его измерение может выявить большой объем информации о внутренней структуре частиц мишени. Например, дифференциальное сечение резерфордского рассеяния явилось убедительным доказательством существования атомного ядра.
Вместо телесного угла в качестве независимой переменной дифференциальных сечений можно использовать переданный импульс.
{ikr}} {r}},}
где f — некоторая функция угловых координат, известная как амплитуда рассеяния.Эта общая форма действительна для любого короткодействующего энергосберегающего взаимодействия. Это неверно для дальнодействующих взаимодействий, поэтому при работе с электромагнитными взаимодействиями возникают дополнительные сложности.
Полная волновая функция системы ведет себя асимптотически как сумма
- ϕ (r) ⟶r → ∞ϕ− (r) + ϕ + (r). {\ Displaystyle \ phi (\ mathbf {r}) \; {\ stackrel {r \ to \ infty} {\ longrightarrow} } \; \ phi _ {-} (\ mathbf {r}) + \ phi _ {+} (\ mathbf {r}).}
Дифференциальное сечение связано с амплитудой рассеяния:
- dσdΩ (θ, ϕ) = | f (θ, ϕ) | 2.{2}.}
Это имеет простую интерпретацию как плотность вероятности обнаружения рассеянного снаряда под заданным углом.
Таким образом, поперечное сечение является мерой эффективной площади поверхности, видимой падающими частицами, и поэтому выражается в единицах площади.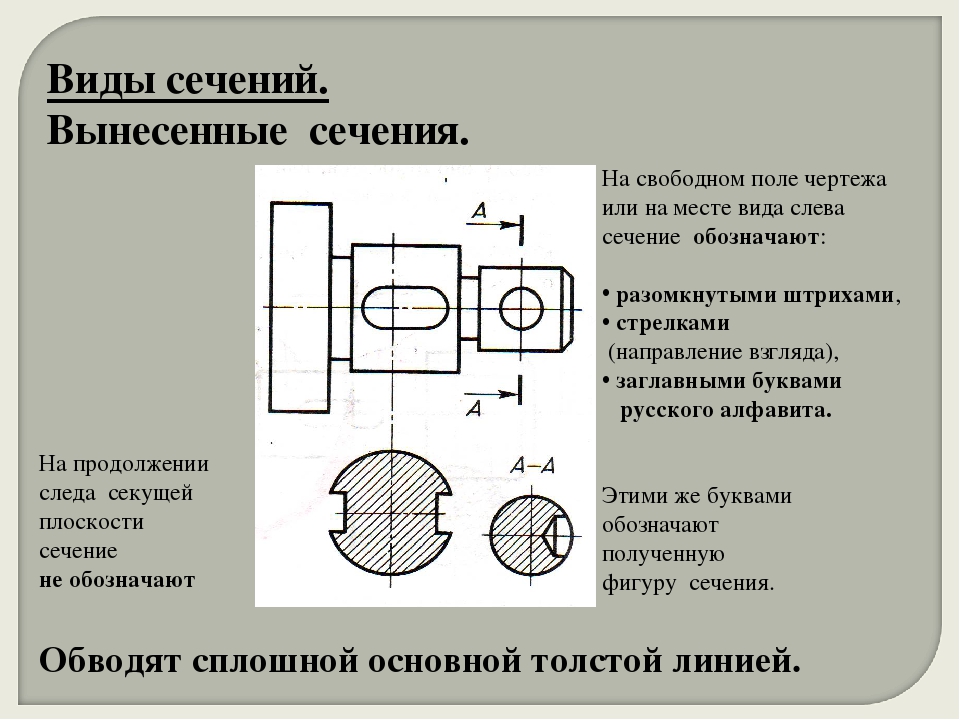
Поперечное сечение двух частиц (т.е. наблюдаемое, когда две частицы сталкиваются друг с другом) является мерой события взаимодействия между двумя частицами. Сечение пропорционально вероятности того, что взаимодействие произойдет; например, в простом эксперименте по рассеянию количество частиц, рассеянных в единицу времени (ток рассеянных частиц I r ) зависит только от числа падающих частиц в единицу времени (ток падающих частиц I i ), характеристики цели (например, количество частиц на единицу поверхности N ) и тип взаимодействия.Для Nσ ≪ 1 имеем
- Ir = IiNσ, σ = IrIi1N = вероятность взаимодействия × 1N. {\ Displaystyle {\ begin {align} I _ {\ text {r}} & = I _ {\ text {i}} N \ sigma, \\\ sigma & = {\ frac {I _ {\ text {r}}} {I _ {\ text {i}}}} {\ frac {1} {N}} \\ & = {\ text {вероятность взаимодействия}} \ times {\ frac {1} {N}}. \ end {align}}}
Связь с S-матрицей []
Если приведенные массы и импульсы сталкивающейся системы равны m i , p i и m f , p f до и после столкновения соответственно, дифференциальное сечение дается как [требуется уточнение ]
- dσdΩ = (2π) 4mimfpfpi | Tfi | 2, {\ displaystyle {\ frac {\ mathrm {d} \ sigma} {\ mathrm {d} \ Omega}} = \ left (2 \ pi \ right) ^ { 4} m_ {i} m_ {f} {\ frac {p_ {f}} {p_ {i}}} {\ bigl |} T_ {fi} {\ bigr |} ^ {2},}
где Встроенная матрица T определяется как
- Sfi = δfi − 2πiδ (Ef − Ei) δ (pi − pf) Tfi {\ displaystyle S_ {fi} = \ delta _ {fi} -2 \ pi i \ delta \ left (E_ {f} -E_ { i} \ right) \ delta \ left (\ mathbf {p} _ {i} — \ mathbf {p} _ {f} \ right) T_ {fi}}
в терминах S-матрицы.
Здесь δ — дельта-функция Дирака. Вычисление S-матрицы — основная цель теории рассеяния.
единиц []
Хотя в системе СИ для общих сечений используется м 2 , на практике обычно используются меньшие единицы.
В ядерной физике и физике элементарных частиц условной единицей является сарай b, где 1 b = 10 −28 м 2 = 100 фм 2 . [1] Также широко используются меньшие единицы с префиксом, такие как mb и μb.Соответственно, дифференциальное сечение может быть измерено в таких единицах, как мб / ср.
Когда рассеянное излучение представляет собой видимый свет, принято измерять длину пути в сантиметрах. Чтобы избежать необходимости в коэффициентах преобразования, сечение рассеяния выражается в см 2 , а числовая концентрация — в см −3 . Измерение рассеяния видимого света, известное как нефелометрия, эффективно для частиц диаметром 2–50 мкм: как таковое, оно широко используется в метеорологии и при измерении загрязнения атмосферы.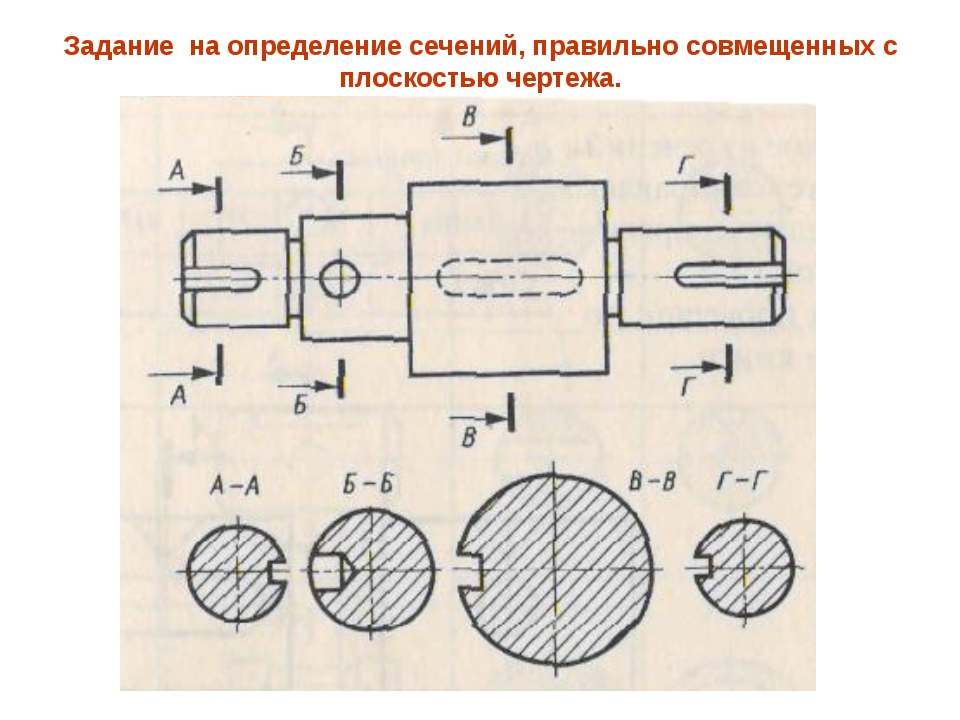
Рассеяние рентгеновских лучей также можно описать в терминах сечений рассеяния, и в этом случае квадрат Ангстрема является удобной единицей: 1 Å 2 = 10 −20 м 2 = 10000 пм 2 = 10 8 б. Сумма сечений рассеяния, фотоэлектрического излучения и образования пар (в амбарах) отображается как «атомный коэффициент ослабления» (узкий луч) в амбарах. [2]
Рассеяние света []
Для света, как и в других параметрах настройки, сечение рассеяния для частиц обычно отличается от геометрического сечения частицы и зависит от длины волны света и диэлектрической проницаемости, формы и размера частицы.Общее количество рассеяния в разреженной среде пропорционально произведению поперечного сечения рассеяния на количество присутствующих частиц.
При взаимодействии света с частицами происходит множество процессов, каждый со своим сечением, включая поглощение, рассеяние и фотолюминесценцию. Сумму сечений поглощения и рассеяния иногда называют сечением затухания или экстинкции.
- σ знак равно σa + σs + σl. {\ Displaystyle \ sigma = \ sigma _ {\ text {a}} + \ sigma _ {\ text {s}} + \ sigma _ {\ text {l}}.}
Полное сечение экстинкции связано с ослаблением интенсивности света через закон Бера – Ламберта, который гласит, что ослабление пропорционально концентрации частиц:
- Aλ = Clσ, {\ displaystyle A _ {\ lambda} = Cl \ sigma,}
, где A λ — затухание на заданной длине волны λ , C — концентрация частиц в виде числовая плотность, а l — длина пути.Поглощение излучения представляет собой логарифм (десятичный или, чаще, естественный) обратной величины коэффициента пропускания T: [3]
- Aλ = −logT. {\ Displaystyle A _ {\ lambda} = — \ log {\ mathcal {T}}.}
Такое объединение сечений рассеяния и поглощения часто бывает необходимо из-за невозможности различить их экспериментально, и много исследовательских усилий было вложено в разработку моделей, позволяющих их различать, причем теория Кубелки-Мунка является одной из самых важных в этой области.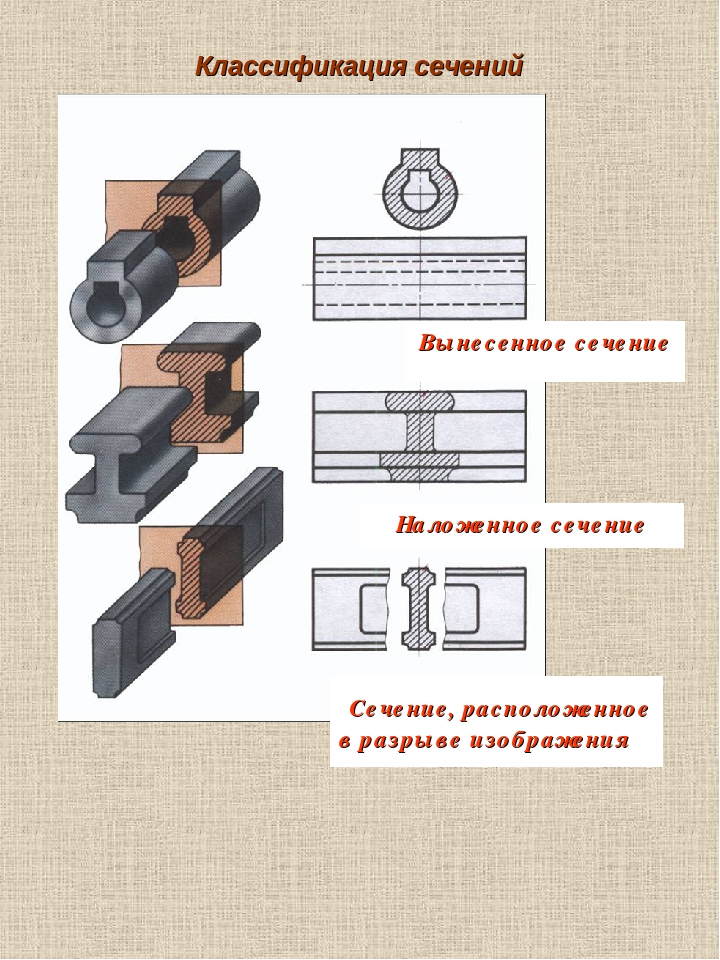
Рассеяние света на протяженных телах []
В контексте рассеяния света на протяженных телах сечение рассеяния, σ scat , описывает вероятность рассеяния света макроскопической частицей. Как правило, поперечное сечение рассеяния отличается от геометрического поперечного сечения частицы, поскольку оно зависит от длины волны света и диэлектрической проницаемости в дополнение к форме и размеру частицы. Общее количество рассеяния в разреженной среде определяется произведением поперечного сечения рассеяния и количества присутствующих частиц.Что касается площади, полное сечение ( σ ) представляет собой сумму сечений, обусловленных поглощением, рассеянием и люминесценцией:
- σ = σa + σs + σl. {\ Displaystyle \ sigma = \ sigma _ {\ text {a}} + \ sigma _ {\ text {s}} + \ sigma _ {\ text {l}}.}
Полное сечение связано с поглощением интенсивности света через закон Бера-Ламберта, который гласит, что поглощение пропорционально концентрации: A λ = Clσ , где A λ — поглощение на данной длине волны λ , C — концентрация в виде числовой плотности, а l — длина пути.
Ослабление или поглощение излучения — это логарифм (десятичный или, чаще, естественный) обратной величины коэффициента пропускания T: [3]
- Aλ = −logT. {\ Displaystyle A _ {\ lambda} = — \ log {\ mathcal {T}}.}
Отношение к физическому размеру []
Нет простой зависимости между сечением рассеяния и физическим размером частиц, так как сечение рассеяния зависит от длины волны используемого излучения. Это можно увидеть, глядя на ореол, окружающий Луну, в прилично туманный вечер: фотоны красного света испытывают большую площадь поперечного сечения капель воды, чем фотоны более высокой энергии.Таким образом, ореол вокруг Луны имеет периметр красного света из-за того, что фотоны с более низкой энергией рассеиваются дальше от центра Луны. Фотоны из остальной части видимого спектра остаются в центре ореола и воспринимаются как белый свет.
Метеорологическая дальность []
Сечение рассеяния связано с метеорологическим диапазоном L V :
- LV = 3. 9Cσscat. {\ Displaystyle L _ {\ text {V}} = {\ frac {3.9} {C \ sigma _ {\ text {scat}}}}.}
9Cσscat. {\ Displaystyle L _ {\ text {V}} = {\ frac {3.9} {C \ sigma _ {\ text {scat}}}}.}Величина Cσ scat иногда обозначается как b scat , коэффициент рассеяния на единицу длины. [4]
Примеры []
Пример 1: упругое столкновение двух твердых сфер []
Упругое столкновение двух твердых сфер — поучительный пример, демонстрирующий смысл называть эту величину поперечным сечением. R и r — соответственно радиусы рассеивающего центра и рассеянной сферы.{2}.}
Таким образом, в этом случае полное сечение рассеяния равно площади круга (радиусом r + R ), в пределах которого должен находиться центр масс падающей сферы. он отклоняется, а за его пределами проходит неподвижный рассеивающий центр.
Пример 2: рассеяние света от двумерного круглого зеркала []
Другой пример иллюстрирует детали расчета простой модели светорассеяния, полученной путем уменьшения размера.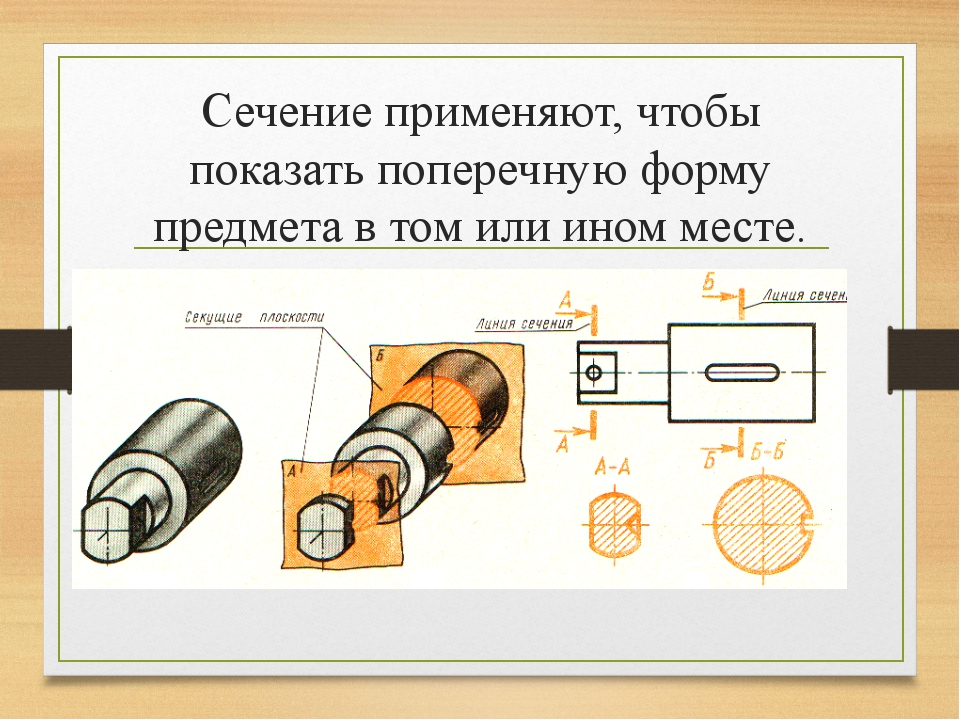
Для простоты рассмотрим рассеяние луча света на плоскости, рассматриваемой как однородная плотность параллельных лучей, и в рамках геометрической оптики от круга радиусом r с идеально отражающей границей. Поэтому его трехмерный эквивалент представляет собой более сложную проблему рассеяния света лазера или фонарика от зеркальной сферы, например, от шарика механического подшипника. [5] Единицей измерения поперечного сечения в одном измерении является длина, например 1 м.Пусть α будет углом между световым лучом и радиусом, соединяющим точку отражения светового луча с центральной точкой круглого зеркала. Тогда увеличение длины элемента, перпендикулярного лучу света, выражается этим углом как
- dx = rcosαdα, {\ displaystyle \ mathrm {d} x = r \ cos \ alpha \, \ mathrm {d} \ alpha,}
угол отражения этого луча относительно входящего луча равен то 2 α , а угол рассеяния равен
- θ = π − 2α.{\ displaystyle \ theta = \ pi -2 \ alpha. }
}Энергия или количество фотонов, отраженных от светового луча с интенсивностью или плотностью фотонов I на длине d x , равно
- Idσ = Idx (x) = Ircosαdα = Ir2sin (θ2) dθ = Idσdθdθ. {\ Displaystyle I \, \ mathrm {d} \ sigma = I \, \ mathrm {d} x (x) = Ir \ cos \ alpha \, \ mathrm {d} \ alpha = I {\ frac {r} {2}} \ sin \ left ({\ frac {\ theta} {2}} \ right) \, \ mathrm {d } \ theta = I {\ frac {\ mathrm {d} \ sigma} {\ mathrm {d} \ theta}} \, \ mathrm {d} \ theta.}
Следовательно, дифференциальное сечение (d Ом = d θ )
- dσdθ = r2sin (θ2). {\ Displaystyle {\ frac {\ mathrm {d} \ sigma} {\ mathrm {d} \ theta}} = {\ frac {r} {2}} \ sin \ left ({\ frac {\ theta} {2}} \ right).}
Как видно из поведения синусоидальной функции, эта величина имеет максимум для обратного рассеяния ( θ = π; свет отражается перпендикулярно и возвращается), и нулевой минимум для рассеяния от края круга прямо вперед ( θ = 0).{2 \ pi} = 2r,}
, поэтому оно равно тому, насколько круглое зеркало полностью экранирует двумерное пространство для луча света. Таким образом, в трех измерениях для зеркального шара с радиусом r он равен σ = π r 2 .
Пример 3: рассеяние света от сферического 3D-зеркала []
Теперь мы можем использовать результат из примера 2 для вычисления дифференциального сечения рассеяния света от идеально отражающей сферы в трех измерениях.Обозначим теперь радиус сферы как a . Параметризуем плоскость, перпендикулярную падающему световому лучу, цилиндрическими координатами r и φ . В любой плоскости входящего и отраженного луча мы можем теперь написать из предыдущего примера:
- r = asinα, dr = acosαdα, {\ displaystyle {\ begin {выровнено} r & = a \ sin \ alpha, \\\ mathrm {d} r & = a \ cos \ alpha \, \ mathrm { d} \ alpha, \ end {align}}}
, а элемент области удара
- dσ = dr (r) × rdφ = a22sin (θ2) cos (θ2) dθdφ. {2}} {4}},}
, а полное сечение, как мы и ожидали, равно
- σ = ∮4πdσdΩdΩ = πa2. М. Сюй, Р. Р. Альфано (2003). «Подробнее о закономерностях в рассеянии Ми». Оптика связи . 226 (1–6): 1–5. Bibcode: 2003OptCo.226 …. 1X. DOI: 10.1016 / j.optcom.2003.08.019.
Источники
- Дж. Д. Бьоркен, С. Д. Дрелл, Релятивистская квантовая механика , 1964
- П. Роман, Введение в квантовую теорию , 1969
- W. Greiner, J. Reinhardt, Quantum Electrodynamics , 1994
- Р.Г. Ньютон. Теория рассеяния волн и частиц . Макгроу Хилл, 1966.
- Р. К. Ферноу (1989). Введение в экспериментальную физику элементарных частиц . Издательство Кембриджского университета. ISBN 978-0-521-379-403 .
Внешние ссылки []
Еврокод 3. Пример 6.6: Сопротивление поперечного сечения при комбинированном изгибе и сжатии
В этой статье мы сравниваем сопротивление при комбинированном изгибе и сжатии в соответствии с SDC Verifier и Руководством проектировщика по Еврокоду 3: Проектирование стальных зданий EN 1993-1-1.
Все результаты генерируются с помощью SDC Verifier 4.5 и рассчитываются с помощью FEMAP v11.3.1
Задача:
Элемент должен быть спроектирован так, чтобы выдерживать комбинированный изгибающий момент по главной оси и осевую силу. В этом примере выполняется проверка поперечного сечения для определения максимального изгибающего момента, который может выдержать UKB 457 x 191 x 98 из стали марки S275 при наличии осевого усилия 1400 кН.
Рисунок 6.15. Свойства сечения для 457 × 191 × 98 UKB