Бесплатный Калькулятор Луча | Изгибающий момент, Калькулятор поперечной силы и прогиба
Добро пожаловать в наш бесплатный онлайн калькулятор изгибающего момента и диаграммы силы сдвига, который может генерировать реакции, Диаграммы силы сдвига (SFD) и диаграммы изгибающих моментов (BMD) консольной балки или опертой балки. Используйте этот калькулятор балок, чтобы определить реакции на опорах, нарисуйте диаграмму сдвига и момента для балки и рассчитайте прогиб стали или дерево луч. Бесплатный онлайн лучевой калькулятор для генерации реакций, расчет прогиба стальной или деревянной балки, составление диаграмм сдвига и момента для балки. Это бесплатная версия нашей полной SkyCiv. Beam Software. Доступ к нему можно получить в любом из наших Платные аккаунты, который также включает программное обеспечение для полного структурного анализа.
Используйте интерактивную рамку выше для просмотра и удаления длины луча, поддерживает и добавляет нагрузки. Любые сделанные изменения автоматически перерисовывают диаграмму свободного тела любым простым или консольным лучом.
Калькулятор пролета луча легко рассчитает реакции на опорах. Умеет рассчитывать реакции на опорах для консольных или простых балок.. Это включает в себя расчет реакций для балки кантилевера, который имеет реакцию изгибающего момента, а также х,у сил реакции.
Вышеуказанный калькулятор балок со стальной балкой — это универсальный инструмент для расчета конструкций, используемый для расчета изгибающего момента в алюминии., деревянная или стальная балка. Его также можно использовать в качестве калькулятора грузоподъемности балки, используя его в качестве калькулятора напряжения изгиба или напряжения сдвига. Может вместить до 2 различные сосредоточенные точечные нагрузки, 2 распределенные нагрузки и 2 моменты. Распределенные нагрузки могут быть расположены так, чтобы они были равномерно распределенными нагрузками.
Одна из самых мощных функций использует его в качестве калькулятора отклонения луча (или калькулятор смещения луча). Это может быть использовано для наблюдения расчетного отклонения балки с простой опорой или балки кантилевера. Возможность добавлять формы и материалы раздела, это делает его полезным в качестве калькулятора для деревянных балок или в качестве калькулятора для стальных балок для LVL-лучей или I-лучевой конструкции. На данный момент, эта функциональность доступна в SkyCiv Beam который имеет гораздо больше функциональных возможностей для древесины, конструкция из бетона и стальных балок.
SkyCiv предлагает широкий спектр программного обеспечения для анализа и проектирования облачных вычислений для инженеров. Как постоянно развивающаяся технологическая компания, мы стремимся к инновациям и стимулированию существующих рабочих процессов, чтобы сэкономить время инженеров в их рабочих процессах и проектах.
Расчет деревянной балки Онлайн, расчет несущей способности и прогиба деревянных балок
Распределенная нагрузка (перекрытия)
Шаг балок,мм
Нагрузка по площади, кг/кв.м
Распределенная нагрузка, кг/кв.м 150
При относительном прогибе 1/2501/2001/150
максимально допустимый прогиб для междуэтажных перекрытий, мм 16
Расчетный прогиб, мм 12
Расчетный относительный прогиб 1/333
Запас по прогибу в 1.
Разрушающая нагрузка, кг 2475
Сосредоточенная нагрузка (ригели)
Сосредоточенная нагрузка, кг
Расчетный прогиб, мм 16
Запас по прогибу в 1.33 раза
Разрушающая нагрузка, кг 1238
применение, расчет на прогиб, характеристики
Швеллер – разновидность фасонного металлопроката, получаемая путем горячей прокатки или гибки, имеет поперечное сечение П-образной формы.
Горячекатаный стальной швеллер: нормативы, сортамент, характеристики
Сортамент этой продукции определяется ГОСТом 8240-89. Размер профиля характеризуется номером, который равен (примерно) высоте стенки, взятой в сантиметрах. В соответствии со стандартом выпускают продукцию:
- С уклоном внутренних граней полок.
 В маркировке после номера присутствует буква «У». Норматив предусматривает производство изделий с высотой стенки 50-400 мм, шириной полки 32-115 мм, толщиной стенки 4,4-8,0 мм, толщиной полки 7,0-13,5 мм. Если в обозначении между номером профиля и буквой «У» присутствует буква «а», это означает, что изделие имеет увеличенную ширину и толщину полок. Основная область применения этого вида швеллера – строительство. Благодаря некоторому утолщению во внутренних углах, профиль обладает повышенными прочностными характеристиками. Такая металлопродукция используется в каркасном строительстве, для устройства перекрытий, сооружения ферм, лестниц, малых архитектурных форм, металлических конструкций различного назначения.
В маркировке после номера присутствует буква «У». Норматив предусматривает производство изделий с высотой стенки 50-400 мм, шириной полки 32-115 мм, толщиной стенки 4,4-8,0 мм, толщиной полки 7,0-13,5 мм. Если в обозначении между номером профиля и буквой «У» присутствует буква «а», это означает, что изделие имеет увеличенную ширину и толщину полок. Основная область применения этого вида швеллера – строительство. Благодаря некоторому утолщению во внутренних углах, профиль обладает повышенными прочностными характеристиками. Такая металлопродукция используется в каркасном строительстве, для устройства перекрытий, сооружения ферм, лестниц, малых архитектурных форм, металлических конструкций различного назначения. - С параллельными внутренними гранями полок. В маркировке после номера указывается буква «П». Индекс «а» свидетельствует о наличии усиленных полок. В соответствии с нормативом, высота стенки изделий находится в диапазоне 50-400 мм, ширина полки – 32-115 мм, толщина стенки – 4,4-8,0 мм, толщина полки – 7,0-13,5 мм.

Таблица геометрических характеристик горячекатаного швеллера
| Номер швеллера | Высота профиля, см | Ширина полки, мм | Толщина стенки, мм | Толщина полки, мм | Масса 1 м, кг |
| С уклоном внутренних граней полок | |||||
| 5У | 5 | 32 | 4,4 | 7,0 | 4,84 |
| 6,5У | 6,5 | 36 | 4,4 | 7,2 | 5,9 |
| 8У | 8 | 40 | 4,5 | 7,4 | 7,05 |
| 10У | 10 | 46 | 4,5 | 7,6 | 8,59 |
| 12У | 12 | 52 | 4,8 | 7,8 | 10,4 |
| 14У | 14 | 58 | 4,9 | 8,1 | 12,3 |
| 16У | 16 | 64 | 5,0 | 8,4 | 14,2 |
| 16аУ | 16 | 68 | 5,0 | 9,0 | 15,3 |
| 18У | 18 | 70 | 5,1 | 8,7 | 16,3 |
| 18аУ | 18 | 74 | 5,1 | 9,3 | 17,4 |
| 20У | 20 | 76 | 5,2 | 9,0 | 18,4 |
| 22У | 22 | 82 | 5,4 | 9,5 | 21,0 |
| 24У | 24 | 90 | 5,6 | 10,0 | 24,0 |
| 27У | 27 | 95 | 6,0 | 10,5 | 27,7 |
| 30У | 30 | 100 | 6,5 | 11,0 | 31,8 |
| 33У | 33 | 105 | 7,0 | 11,7 | 36,5 |
| 36У | 36 | 110 | 7,5 | 12,6 | 41,9 |
| 40У | 40 | 115 | 8,0 | 13,5 | 48,3 |
| С параллельными гранями полок | |||||
| 5П | 5 | 32 | 4,4 | 7,0 | 4,84 |
| 6,5П | 6,5 | 36 | 4,4 | 7,2 | 5,9 |
| 8П | 8 | 40 | 4,5 | 7,4 | 7,5 |
| 10П | 10 | 46 | 4,5 | 7,6 | 8,59 |
| 12П | 12 | 52 | 4,8 | 7,8 | 10,4 |
| 14П | 14 | 58 | 4,9 | 8,1 | 12,3 |
| 16П | 16 | 64 | 5,0 | 8,4 | 14,2 |
| 16аП | 16 | 68 | 5,0 | 9,0 | 15,3 |
| 18П | 18 | 70 | 5,1 | 8,7 | 16,3 |
| 18аП | 18 | 74 | 5,1 | 9,3 | 17,4 |
| 20П | 20 | 76 | 5,2 | 9,0 | 18,4 |
| 22П | 22 | 82 | 5,4 | 9,5 | 21,0 |
| 24П | 24 | 90 | 5,6 | 10,0 | 24,0 |
| 27П | 27 | 95 | 6,0 | 10,5 | 27,7 |
| 30П | 30 | 100 | 6,5 | 11,0 | 31,8 |
| 33П | 33 | 105 | 7,0 | 11,7 | 36,5 |
| 36П | 36 | 110 | 7,5 | 12,6 | 41,9 |
| 40П | 40 | 115 | 8,0 | 13,5 | 48,3 |
Расчет табличного веса швеллера осуществляется с использованием среднего значения плотности различных марок стали – 7,85 г/см3.
Гнутый стальной швеллер: ГОСТ, сортамент, технические характеристики
Исходной заготовкой при производстве гнутого профиля является стальная горяче- или холоднокатаная полоса. Процесс изготовления проходит на профилегибочных агрегатах. Гнутый металлопрофиль можно отличить от горячекатаного по скругленным наружным углам и одинаковой толщине стенки и полок, которая не превышает 8 мм. При гибке устраняются некоторые поверхностные дефекты. В отличие от горячекатаной металлопродукции, которая выпускается только равнополочной, гнутая производится как равно-, так и неравнополочной. Сортамент равнополочных изделий определяется ГОСТом 8278-83, неравнополочных – ГОСТом 8281-80. Их ассортимент гораздо шире перечня горячекатаного проката П-образного профиля. Высота стенки равнополочного профиля – 25-410 мм, ширина полки – 26-65 мм, толщина стенки – 2-8 мм.
Из-за прочности, уступающей аналогичной характеристике горячекатаных металлоизделий, различные марки гнутого швеллера применяются в качестве дополнительных усиливающих элементов в металлоконструкциях, при проведении отделочных работ, мероприятий по реконструкции ветхих строений, в которых невысокая масса металла имеет решающую роль.
Расчет швеллера на нагрузки
Стальной прокат с П-образным поперечным сечением – популярный тип металлопроката, востребованный в строительстве. При использовании швеллера для создания перекрытий и других ответственных строительных конструкций производят расчеты на изгиб и прогиб с помощью формул, таблиц, онлайн-калькуляторов. Для упрощения расчетов условия работы профильных изделий приводят к стандартным схемам. Основные из них:
- Швеллер работает как однопролетная шарнирно-опертая балка, на которую оказывает воздействие распределенная нагрузка, такой тип расчета применяется при использовании металлопроката в межэтажных перекрытиях.
- Консольная балка, жестко закрепленная с одного конца, нагрузка равномерно распределена. Такая схема характерна для козырьков, изготовленных путем приварки проката с одной стороны к выпускам из вертикальной ограждающей конструкции.
- Шарнирно-опертая балка с двумя опорами и консолью. Этот вариант применяется в случае организации пролета с выпуском металлопроката за пределы стены для опирания балконной плиты.

- Однопролетная балка с шарнирной опорой, на которую действуют одна или две сосредоточенные силы. Такая схема применяется для расчета несущей способности швеллера, выполняющего функцию перемычки, на которую опираются одна или две балки перекрытия.
Для онлайн-калькулятора, кроме схемы расчета, понадобятся: длина пролета, расчетная и нормативная нагрузка, расчетное сопротивление, тип швеллера (его площадь калькулятор определит самостоятельно). Результат – расчеты по прочности.
При покупке швеллера в компании ООО «РМК» вычисления для корректного подбора металлопроката вам поможет произвести менеджер.
Расчет нагрузки на профильную трубу калькулятор
Используя профильную трубу для создания несущих конструкций, в обязательном порядке должны выполняться расчеты на изгиб. Такой вид трубного проката применяется в промышленном, коммерческом и частном строительстве. Из него изготавливают навесы, всевозможные каркасные и лестничные конструкции, фермы, стеллажи, козырьки, тепличные сооружения, элементы кровельной системы, беседки.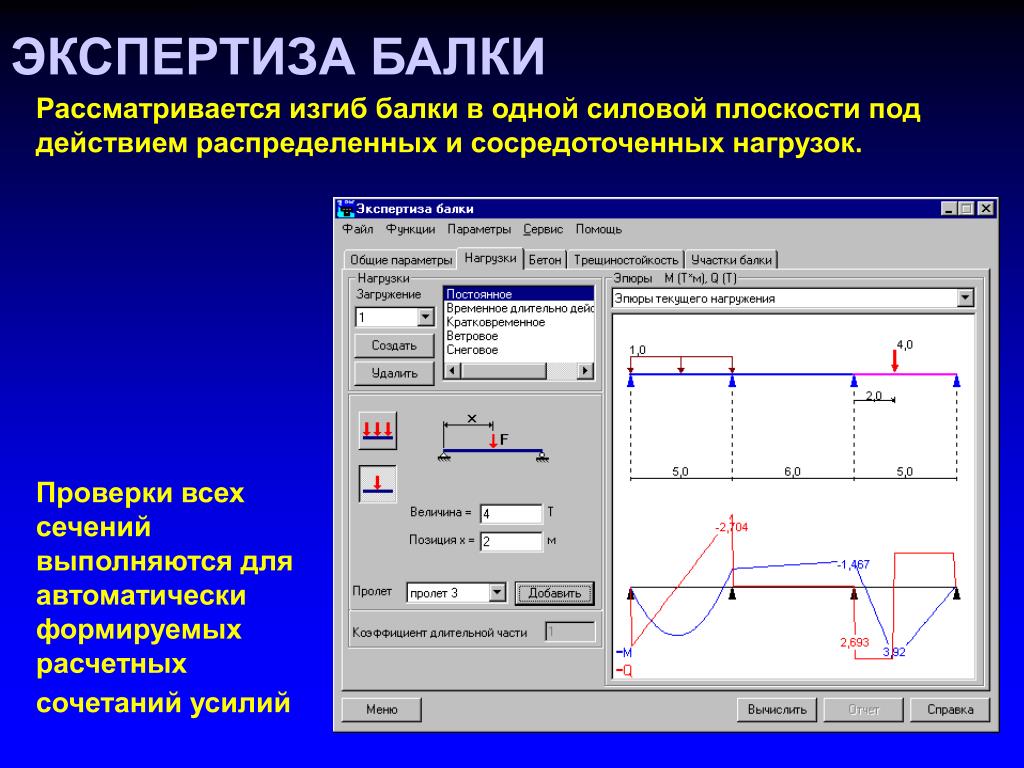 Поэтому без правильных и тщательных расчетов никак не обойтись. Превышение допустимого давления приведет к деформации или разрыву изделия в месте сгибания профтрубы.
Поэтому без правильных и тщательных расчетов никак не обойтись. Превышение допустимого давления приведет к деформации или разрыву изделия в месте сгибания профтрубы.
Схема 1
Используя методы расчета нагрузок на профильную трубу, можно:
- сохранить первоначальную форму изделий;
- придать конструкции повышенной прочности;
- увеличить период эксплуатации;
- минимизировать расходы на материале;
- избежать негативных разрушительных последствий.
Какая нагрузка действует на профтрубу?
Важным критерием, который учитывается при подсчетах, является время воздействия и тип нагрузок. Данные показатели регламентированы СП 20.13330.2011 «Нагрузки и воздействия». Различают силу давления:
- Постоянные, когда масса и воздействующая сила не меняются на протяжении длительного временного периода. Воздействия создаются элементами здания (несущими и ограждающими конструкциями), грунтами, гидростатическим давлением.
- Длительные.
 Временные перегородки из ГКЛ, стационарное оборудование, складируемые материалы, а также как результат изменения влажности или усадки.
Временные перегородки из ГКЛ, стационарное оборудование, складируемые материалы, а также как результат изменения влажности или усадки. - Кратковременные. Оборудование, вес людей и транспортных средств, климатические, создаваемые снегом, ветром, перепадами температур, обледенением.
- Особые. Сейсмические и взрывные воздействия, влекущие изменения структуры грунта, результат столкновения транспортных средств и обусловленные пожаром.
В Своде правил представлены формулы для подсчета, таблицы и схемы по каждому типу нагрузок. Также берется в учет реалистичное сочетание все типов давления.
Показатели массы и нагрузки на изгиб
При расчете профильной трубы: масса и изгиб являются основными показателями. Знать вес погонного метра проката нужно, чтобы не ошибиться в прочностных значениях создаваемой конструкции. Метод определения направлен на подбор оптимального сечения трубного проката при разной его длине. Наглядный пример соотношений этих двух показателей представлен в таблицах ниже.
Табл.№1. Значения для изделий квадратного сечения:
Табл. №2. Значения для изделий прямоугольного сечения:
Методы и формулы для вычисления
Чтобы рассчитать прочность трубы профильной на изгиб необходимо определить максимальное напряжение на ту либо иную точку конструкции. Каждый вид материала, из которого изготавливается прокатная продукция, обладает индивидуальным показателем напряжения и точкой сопротивления. В учет берутся следующие параметры: вид проката, сечение, толщина стенки, общие характеристики. Владея такими данными, можно предположить, какие будут последствия от воздействия различных факторов, в том числе окружающей среды. При давлении на поперечную часть профтрубы напряжение создается даже в точках, которые удалены от нейтральной оси.
Получить данные можно разными способами:
- Берутся готовые показатели из строительных справочников и подставляются в формулу. Такие действия предусматривают выбор трубного проката в соответствии с указанными характеристиками, что позволяет делать самые точные подсчеты прогиба.
 ГОСТ 8639-82 (для изделий квадратного сечения) и ГОСТ 8645-68 (прямоугольного) регламентированы: момент инерции трубы (I), длину пролета (L), нагрузку (Q), модуль упругости в соответствии СНиП. Схемы вычислений индивидуальные и для каждого случая подбирается формула.
ГОСТ 8639-82 (для изделий квадратного сечения) и ГОСТ 8645-68 (прямоугольного) регламентированы: момент инерции трубы (I), длину пролета (L), нагрузку (Q), модуль упругости в соответствии СНиП. Схемы вычислений индивидуальные и для каждого случая подбирается формула. - Самостоятельно рассчитывается прочность на изгиб. В данном случае применим Закон Гука, который выражается формулой: Pизг = M/W, где Pизг — величина прочностного предела, M — изгибающий момент; W — сопротивление. Такие вычисления требуют дополнений: учитываются характеристики исходного материала, давления и т.д.
- При помощи калькулятора. В специальную расчетную таблицу вносятся исходные данные — длина пролета, нормативная и расчетная нагрузка, Fmax,количество изделий, расчетное сопротивление, параметры. После нажатия на клавишу «Рассчитать» выдается готовый результат.
Не стоит выполнять расчеты самостоятельно. Нужно уметь пользоваться ГОСТами, СНиПами и владеть сложной специфической техникой — сопроматом. При малейших неточностях в подсчетах не избежать серьезных последствий.
При малейших неточностях в подсчетах не избежать серьезных последствий.
Проще применить один из калькуляторов для расчета нагрузки на профильную трубу:
http://www.rsi-llc.ru/calculator/
http://svoydomtoday.ru/building-onlayn-calculators/336-rschet-kvadratnoy-trubi-na-progib-i-izgib.html
https://trubanet.ru/onlajjn-kalkulyatory/raschet-balok-iz-trub-na-izgib.html
Также полезно будет просмотреть видео:
Расчет прогиба пластины в Excel
Опубликовано 26 Мар 2016
Рубрика: Механика | 105 комментариев
При выполнении расчетов стенок емкостей, стенок конструкций или различных покрытий возникает задача определения напряжений и прогибов. Хочется ответа на простые вопросы — на сколько и как выгнется пластина под нагрузкой, и не разрушится ли она? Теория предлагает. ..
..
…по заданной известной функции нагрузки найти функцию прогибов. Для этого нужно решить неоднородное бигармоническое дифференциальное уравнение четвертого порядка в частных производных. От одного прочтения предыдущего предложения, я думаю, многим читателям стало грустно и тоскливо. А если добавить, что для практической реализации одного из методов предстоит решить систему из 15-и уравнений и найти 15 неизвестных, то большинство на этом просто прекратят чтение и потеряют всякий интерес к теме, либо продолжат поиск программ, выполняющих автоматически подобные расчеты. Эти программы, выполняющие расчет прогиба пластин, чаще всего реализуют приближенные численные методы конечных элементов и конечных разностей и стоят приличных денег.
Но есть и другой путь… (Как известно, выходов всегда не меньше двух…) Эта дорога старая, заросшая лесом новых теорий, но не до конца забытая!
Этот путь является достаточно узким и индивидуальным для различных форм пластин, способов закрепления контуров и относительных величин прогибов. Для каждой расчетной схемы – свои таблицы коэффициентов к расчетным формулам! Расчет прогиба пластины по старым методикам прост – это несомненный плюс, но не универсален – это существенный минус.
Для каждой расчетной схемы – свои таблицы коэффициентов к расчетным формулам! Расчет прогиба пластины по старым методикам прост – это несомненный плюс, но не универсален – это существенный минус.
Цель данной статьи – рассказать, как наши деды — инженеры прошлого века — решали такие практические вопросы, и показать простой пример модернизированного расчета в Excel задачи об изгибе пластины для одного из наиболее распространенных случаев в практике.
Из-за отсутствия каких-либо машин для выполнения рутинных сложных расчетов (кроме светлой головы, листка бумаги, карандаша, таблиц функций и логарифмической линейки ничего не было) ученые в начале и в середине 20-ого века стремились вооружить простого инженера короткими и понятными алгоритмами, «привязанными» к рассчитанным в НИИ номограммам и таблицам. Такой подход обеспечивал значительное упрощение и ускорение работы инженеров, хотя и не давал им полного понимания теории.
Расчет прогиба пластины изучается в общей теории оболочек, которая является сложным самостоятельным разделом механики, давно выделившимся из недр классического сопромата.
Теория тонких пластин распространяется на листы и плиты, у которых толщина h менее 20% от наименьшего габаритного размера в плане a.
Тонкие пластины делят на 3 класса в зависимости от величины максимального прогиба w:
жесткие — w<0,25h
гибкие — 0,25h<w<5h
абсолютно гибкие — w>5h
Попадание конкретной пластины в тот или иной класс, как видите, зависит от прогиба, а значит — от величины нагрузки. Важно отметить, что одна и та же пластина при разных нагрузках может быть отнесена к разным классам, и расчет её будет производиться по различным формулам.
Далее в примере рассматривается тонкая жесткая пластина.
Расчет в Excel прогиба пластины. Пример.
Прямоугольная пластина из изотропного материала (Сталь Ст3) жестко закреплена по всему контуру. В перпендикулярном направлении к плоскости пластины приложена равномерно распределенная по всей площади нагрузка.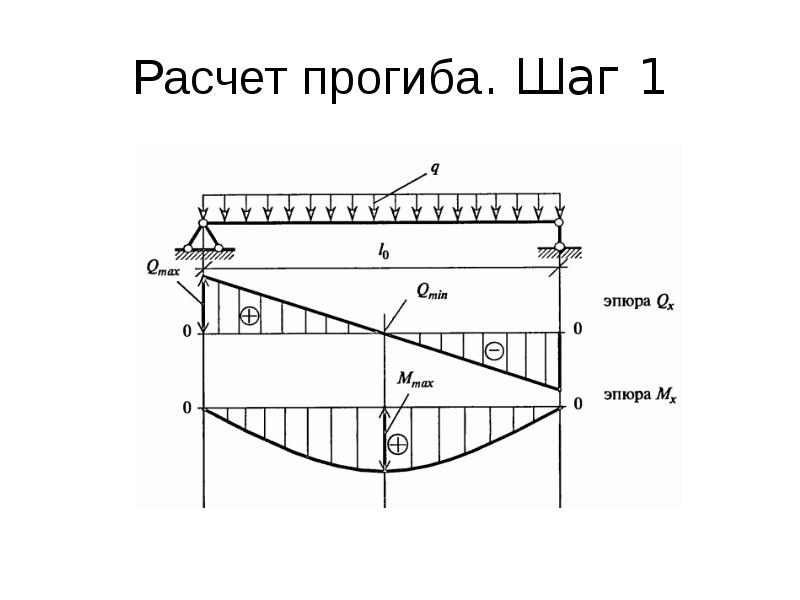
Требуется вычислить наибольший прогиб пластины от действия нагрузки и найти максимальные возникающие в теле листа напряжения.
Исходные данные:
Первые три параметра являются справочными характеристиками свойств материала пластины.
1. Предел текучести для пластичных материалов или прочности для хрупких материалов [σ] в Н/мм2 записываем
в ячейку D3: 245
Этот параметр не участвует в расчетах и нужен лишь для сравнения с полученными в результате расчета напряжениями. Правильнее вместо него использовать допускаемые напряжения материала с учетом всех запасов для конкретного случая применения.
2. Модуль упругости или модуль Юнга E в Н/мм2 заносим
в D4: 210000
3. Коэффициент Пуассона μ вписываем
в D5: 0,28
В примечаниях к ячейкам D4 и D5 приведены значения модулей упругости и коэффициентов Пуассона для некоторых материалов.
4.,5.,6. Далее вводим в таблицу размеры пластины h, a и b в мм
в ячейку D6: 5,0
в D7: 500
в D8: 1000
В примечаниях к ячейкам D6, D7 и D8 записаны ограничения, которые должны соблюдаться. В случае их нарушения цифры окрашиваются инверсным белым цветом, а поле ячейки – красным, сообщая пользователю об ошибке ввода данных.
7. Значение распределенной равномерно по всей площади нагрузки q в Н/мм2 вносим
в D9: 0,016
Прошу УВАЖАЮЩИХ труд автора скачать файл ПОСЛЕ ПОДПИСКИ на анонсы статей.
Ссылка на скачивание файла с программой: raschet-progiba-plastiny (xls 90,5KB).
Результаты расчета:
8. Цилиндрическую жесткость пластины D в Н*мм (аналог EI – линейной жесткости для стержней) вычисляем
в ячейке D11: D=(E*h3)/(12*(1- μ2)=2373589
9. ,11. Безразмерные коэффициенты k1 и k2, зависящие от формы и размеров пластины, а также от способов закрепления контурных сторон, можно найти в таблицах старых справочников (Тимошенко С.П., Войновский-Кригер С. Пластины и оболочки; Вайнберг Д.В, Вайнберг Е.Д. Расчет пластин). Правда, k2 зависит еще и от μ, а в таблицах приведены значения только для стали μ≈0,3 и бетона μ≈1/6, но, проанализировав ряд таблиц, можно увидеть, что эта зависимость не очень значительная…
,11. Безразмерные коэффициенты k1 и k2, зависящие от формы и размеров пластины, а также от способов закрепления контурных сторон, можно найти в таблицах старых справочников (Тимошенко С.П., Войновский-Кригер С. Пластины и оболочки; Вайнберг Д.В, Вайнберг Е.Д. Расчет пластин). Правда, k2 зависит еще и от μ, а в таблицах приведены значения только для стали μ≈0,3 и бетона μ≈1/6, но, проанализировав ряд таблиц, можно увидеть, что эта зависимость не очень значительная…
Выполнив аппроксимацию в Excel табличных данных, получим аналитические выражения для расчетов коэффициентов
в ячейке D12: при 0,5<a/b<1
k1=0,16747*(a/b)6-0,766*(a/b)5+1,4455*(a/b)4-1,4342*(a/b)3+0,78433*(a/b)2-0,22506*(a/b)+0,029239=0,0254
при 0<a/b<0,5
k1=-0,00012*(a/b)+0,0026=0,0254
в D14: при 0,5<a/b<1
k2=0,71922*(a/b)6-3,1489*(a/b)5+5,6353*(a/b)4-5,1372*(a/b)3+2,3658*(a/b)2-0,50294*(a/b)+0,12003=0,0829
при 0<a/b<0,5
k1=-0,0008*(a/b)+0,0833=0,0829
Точность аппроксимации очень и очень высокая.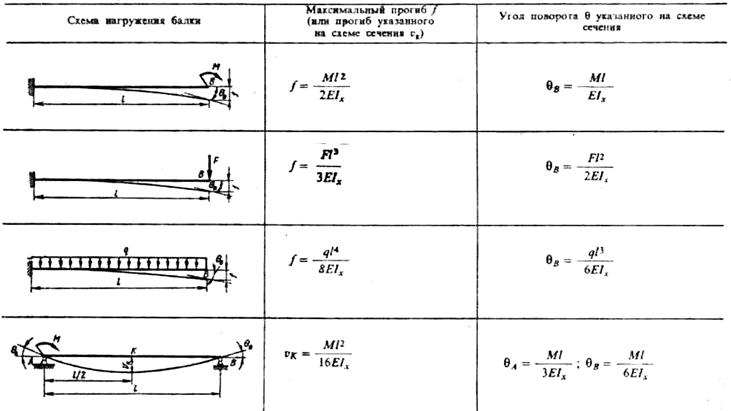 Об этом можно судить как по абсолютным Δабс и относительным Δотн погрешностям, так и по величине достоверности R2.
Об этом можно судить как по абсолютным Δабс и относительным Δотн погрешностям, так и по величине достоверности R2.
10. Максимальный прогиб пластины w в мм будет в рассматриваемой схеме в центре пластины в точке O; вычисляем его
в ячейке D13: w=k1*q*a4/D=1,07
Расчет прогиба в MS Excel выполнен. Величина прогиба не превышает четверти толщины листа, следовательно применение использованных формул правомерно.
12. Наибольшие моменты на единицу длины сечения пластины Mmax возникают в рассматриваемой схеме по серединам больших сторон контура в точках A и A’. Вычисляем их в Н*мм/мм
Вычисляем их в Н*мм/мм
в ячейке D15: Mmax=k2*q*a2=332
13. Наибольшие напряжения в пластине σmax в точках действия максимального момента вычисляем в Н/мм2
в ячейке D16: σmax=6* Mmax/h2=80
Напряжения не превышают предела текучести. Деформации листа являются упругими, после снятия нагрузки пластина вернется в исходное плоское состояние.
Заключение.
По предложенной программе в Excel можно выполнять расчет прогиба тонкой жесткой прямоугольной пластины из любого изотропного материала – стекла, пластмассы, бетона, любого металла при жестком закреплении контура.
Прогиб вычисляется точно для любых материалов. Напряжения рассчитываются точно только для стали. Чем значительней коэффициент Пуассона материала отличается от коэффициента Пуассона стали, тем больше будет ошибка в определении действующих напряжений.
Так как способов закрепления контура пластины, видов форм пластины, сочетаний нагрузок — очень много, то задача расчета прогибов при рассмотренном подходе к решению распадается на сотни индивидуальных задач, в которых значения коэффициентов k1 и k2 также индивидуальны!
Возможно развитие программы для решения других вариантов задач по вашим, уважаемые читатели, индивидуальным запросам.
В продолжение темы «Расчет прогиба пластины» может быть в одной из будущих публикаций попробую рассмотреть более универсальный подход – метод конечных разностей с использованием MS Excel.
Напишите ваше мнение о статье или возникшие вопросы в комментариях.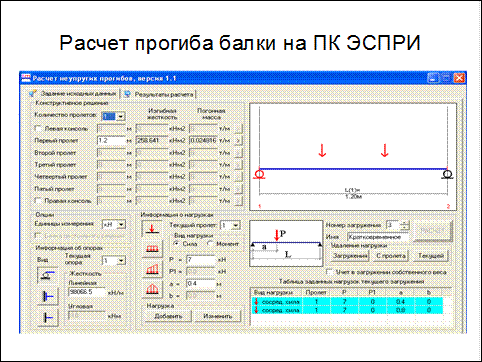
Статьи с близкой тематикой
Отзывы
Таблица нагрузки на двутавровую балку: расчет нагрузки на прогиб
Двутавр – вид фасонного металлопроката, способный принимать большие нагрузки, по сравнению с уголком и швеллером. В частном строительстве металлопрокат с сечением Н-образного профиля используется только при создании крупногабаритных строений. Для выбора подходящего номера двутавровой балки производят профессиональные расчеты на прочность и прогиб с помощью формул или с использованием онлайн-калькулятора. Исходными данными являются: длина пролета, тип закрепления балки, характер нагрузки, планируемый шаг размещения профильного проката, наличие или отсутствие дополнительных опор, марку стали.
Выбор типа балки, в зависимости от запланированных нагрузок
Производители предлагают металлические двутавры с несколькими типами поперечного сечения, предназначенные для различных эксплуатационных условий. Такая продукция, в зависимости от типа сечения, может применяться в крупногабаритном жилищном строительстве, при возведении зданий промышленного и гражданского назначения, в мостостроении. Для каждого из них в соответствующем стандарте имеется таблица, в которой указаны размерные параметры, масса 1 м, момент и радиус инерции, момент сопротивления. Эти характеристики используются в расчетах на прогиб и прочность.
Такая продукция, в зависимости от типа сечения, может применяться в крупногабаритном жилищном строительстве, при возведении зданий промышленного и гражданского назначения, в мостостроении. Для каждого из них в соответствующем стандарте имеется таблица, в которой указаны размерные параметры, масса 1 м, момент и радиус инерции, момент сопротивления. Эти характеристики используются в расчетах на прогиб и прочность.
С уклоном внутренних граней полок 6-12 %
Производство этого металлопроката регламентируется ГОСТом 8239-89. Благодаря скруглению внутренних граней около стенки, обладают высокой прочностью и устойчивостью к прилагаемым усилиям.
С параллельными внутренними гранями полок
Эта продукция выпускается в соответствии с ГОСТом 26020-83, выделяют следующие типы:
- Б – нормальный. Применяется для эксплуатации под средними нагрузками.
- Ш – широкополочный. Может использоваться для разрезки по продольной оси для получения таврового профиля.
 Тавр укладывается на один пролет. Целый двутавровый профиль – на один или несколько пролетов. Эти металлоизделия очень массивны. Плюсом их использования является возможность использования в качестве самостоятельного элемента без применения усиливающих деталей.
Тавр укладывается на один пролет. Целый двутавровый профиль – на один или несколько пролетов. Эти металлоизделия очень массивны. Плюсом их использования является возможность использования в качестве самостоятельного элемента без применения усиливающих деталей. - К – колонный. Это наиболее массивные профили. Имеют широкие, утолщенные полки и стенки. Применяются при устройстве большепролетных конструкций.
Типовые схемы расположения двутавра
Один из исходных параметров, учитываемых в расчетах, – схема закрепления балки и вид прилагаемой нагрузки. Большинство вариантов сводится к основным схемам:
Сбор нагрузок
Перед началом расчета производят сбор сил, действующих на двутавровую балку. В зависимости от продолжительности воздействия,их разделяют на временные и постоянные.
Таблица нагрузок на двутавровые балки
| Постоянные | Собственная масса балки и перекрытия. В упрощенном варианте вес межэтажного перекрытия без цементной стяжки с учетом массы балки принимают равным 350 кг/м2, с цементной стяжкой – 500 кг/м2 В упрощенном варианте вес межэтажного перекрытия без цементной стяжки с учетом массы балки принимают равным 350 кг/м2, с цементной стяжкой – 500 кг/м2 | |
| Длительные | Полезные | Зависят от назначения здания |
| Кратковременные | Снеговые, зависят от климатических условий региона | |
| Особые | Взрывные, сейсмические. Для балок, работающих в стандартных эксплуатационных условиях, не учитываются. В онлайн-калькуляторах обычно не учитываются | |
Нагрузки разделяют на нормативные и расчетные. Нормативные устанавливаются строительными нормами и правилами. Расчетные равны нормативной величине, умноженной на коэффициент надежности. При усилии менее 200 кг/м2 коэффициент обычно принимают равным 1,3, при более 200 кг/м2 – 1,2. Шаг между балками принимают равным 1 м. В некоторых случаях, если это допустимо в конкретных эксплуатационных условиях, в целях экономии материалов его принимают равным 1,1 или 1,2 м.
При расчетах принимают во внимание марку стали. Для использования в условиях высоких нагрузок и при минусовых температурах востребованы двутавровые балки, изготовленные из низколегированных сталей.
Способы выбора оптимального размера сечения профиля
Наиболее точным вариантом подбора номера и типа двутаврового профиля является проведение профессиональных расчетов. Именно этот способ применяется при проектировании ответственных крупногабаритных объектов. При строительстве небольших зданий можно воспользоваться онлайн-калькулятором.
Совет! По результатам расчетов онлайн-калькуляторы обычно предлагают два или более вариантов профиля. Для обеспечения надежности строения рекомендуется отдавать предпочтение профилю с большим номером.
Для примерного определения размера профиля можно воспользоваться таблицей соответствия номера двутавровой балки максимально допустимой нагрузке:
| Общая нагрузка, кг/м2 | Длина пролета | ||||||||
| 3 м при шаге, м | 4 м при шаге, м | 6 м при шаге, м | |||||||
| 1,0 | 1,1 | 1,2 | 1,0 | 1,1 | 1,2 | 1,0 | 1,1 | 1,2 | |
| 300 | 10 | 10 | 10 | 10 | 12 | 12 | 16 | 16 | 16 |
| 400 | 10 | 10 | 10 | 12 | 12 | 12 | 20 | 20 | 20 |
| 500 | 10 | 12 | 12 | 12 | 12 | 12 | 20 | 20 | 20 |
Из этой таблицы видно, что для двутавровой балки номер 10 максимальная длина пролета составляет 4 м при шаге 1,2 м, нагрузка – 400 кг/м2, для номера 16 длина пролета может достигать 6 м, нагрузка, которую он может выдержать, – 300 кг/м2, для профиля 20 – 6 м и нагрузка 400 кг/м2.
пошаговая инструкция онлайн – калькулятора
Расчет стойки на прочность и устойчивость: онлайн – калькулятор.
С помощью онлайн – калькулятора можно рассчитать параметры стойки из металла, по — другому колонны с центрально – нагруженным типом, которая имеет форму круга, прямоугольника, квадрата либо шестигранника.
Расчет стойки на прочность и устойчивость, также гибкость можно выполнить легко, введя необходимые параметры, программа выдаст через несколько минут верные цифры. Таким образом, можно рассчитать значение прочности, также гибкости или устойчивости колонн из Двутавра, либо Тавра, либо Швеллера, либо Уголка.
Общие сведения
Во время проведения проектировочных действий всех конструкций строительства разрабатывают схемы, которые дают гарантию на устойчивость, прочность, также имеют высокий показатель неизменяемости в пространстве всего строения и индивидуальных частей во время монтажа с эксплуатацией.
Важно! Стойки должны обеспечивать устойчивость и прочность всей строительной конструкции, поэтому ее подвергают тщательной проверке, когда она находится под сжимающим воздействием нагрузки.
Колонны подвергаются проверке на:
1.уровень прочности.
2.на уровень устойчивости.
3.на уровень гибкости, которая может быть допустима.
Для проведения расчетов свойств стойки можно воспользоваться онлайн – калькулятором.
Программа рассчитана на вычисление стоек, выполненных из трех материалов:
1.из дерева трех сортов.
2.из стали десяти классов.
3.из бетона девяти классов.
Программа различает такие виды сечения, как:
1.труба,
2.круг.
3.двутавр.
4.швеллер.
5.уголка.
6.сечение в виде квадрата.
7.сечение в виде прямоугольника.
8.труба с квадратным профилем.
Чтобы рассчитать стойку, необходимо ввести в специальные поля размеры диаметров фигур по их геометрии, они показаны на рисунке, также нужно знать значение длины изделия, показатель расчетной крепежной схемы, задают нагрузочный параметр для колонны.
После того, как пустые поля заполнены, нажимают «считать», программой выводится на экран показатели на прочностные свойства колонны и ее устойчивость. Если надо получить расширенную информацию, нажимают «подробнее», тогда на экране появляются значения площади внутри стойки, показатель расчетного сопротивления материла, значение напряжения, значение инерционного радиуса по Х-У оси, значение гибкости по оси, показатель расчетного значения длины изделия, параметры изгибов продольного типа.
Пошаговая инструкция проведения расчета
1.Вводят тип проката: круглый, квадратный, в форме полосы, шестигранника и т.д.
2.Указывают разновидность схемы, по которой крепится стойка: в виде заделки консоли, в виде заделки заделки, в виде заделка шарнир, либо шарнир шарнир.
3.Выбирают материал проката, к примеру: из Стали С235 — Ст3кп2, из Стали С245 — Ст3пс5 либо Ст3сп5.
4.Устанавливают разновидность стойки, ее назначение, к примеру: стойки передающие, служащие для опоры, основные либо второстепенные.
Важно! При отсутствии типа материала в таблице, а показатель его расчетного сопротивления (кг /см 2) известен, значит, следует ввести значение в специальное поле.
Чтобы произвести расчет вводят:
1.Длину стойки — L, выражают в метрах.
2.Размер D либо Dv, либо A, выражают в миллиметрах.
3.Размер B, выражают в миллиметрах.
4.Нагрузку на колонну — P, выражают в килограммах.
По последней версии СНиПа II – 23 – 81 проводя расчет прочности стальных деталей, оснащенных центральным растяжением либо сжатием посредством силы Р вычисляют при помощи следующей формулы:
P : Fp Х Ry Х Yc<=1
Формула состоит из:
1.P – показатель актуальной нагрузки.
2.Fp – значение диаметральной площади, рассчитанный поперек стержня.
3.Ry – параметр подсчетного сопротивления стоечного материла, определяется согласно таблице В5, в приложении СНиП.
4.Yc – значение коэффициента условий функционирования, согласно данным таблицы No1 по СНиПу. Согласно примечаниям, данной таблица калькулятора в пункте No5 имеет показатель Yc равный 1.
Расчет на устойчивость детали, имеющей сплошное сечение с центральным сжатием силой Р вычисляют согласно формуле:
P : Fi х Fp х Ry х Yс<=1
В формуле:
1.Fi – значение коэффициента, указывающий на продольный изгиб, элементов центрально – сжатого типа.
Данный коэффициент компенсирует небольшую не прямолинейность стойки, нехватку крепежной жесткости, также неточность определения нагрузки вдоль двух осей колонны.
Параметр Fi отличается в зависимости от марки стального материла его гибкости, как правило, значение определяют по таблице No 72 из СНиПа II-23-81 за 1990 год, зависит также от показателя сопротивления материала, сжатию при расчете, изгиба и растяжения.
Данное условие делает расчет более простым, но более грубым, потому что в СНиП указаны инженерные формулы, по которым рассчитывают Fi.
Физическая величина – гибкость стойки, по-другому Lambda, определяющая параметры стойки, которые значение длины, поперечное сечение, в том числе значение инерционного радиуса.
LAMBDA = Lr : i
В формуле:
Lr – значение расчётной стержневой длины.
i – значение инерционного радиуса стержневого диаметра поперечного типа.
Данная величина, обозначаемая i вычисляется, как корень квадратный из значения I : Fp, в котором I равен моменту инерции, а Fp равно площади сечения.
Lr=Mu * L,
В формуле:
Mu – коэффициент, определяемый крепежной схемой колонны.
L – значение длины стойки.
Различают следующие виды схем для крепления колонны, у каждой схемы свой коэффициент:
1.тип заделка — консоль со свободным концом, Mu = 2.
2.тип заделка — заделка, Mu = 0.
5.
3.тип заделки – шарнир, Mu = 0.7.
4.тип шарнир – шарнир, Mu = 1.
Важно! Если у прямоугольника, имеющего два радиуса инерции сечения, вычисляют Lambda, использовать следует наименьший из них.
Гибкость стойки, которую рассчитывают по вышеуказанной схеме, не может быть выше значения 220 согласно таблице No 19 по СНиПу II – 23 – 81, в нем указаны максимальные показатели предельной гибкости стоек центрально-сжатого типа.
Чтобы их правильно применять, следует в калькуляторе выбрать таблицу с названием Вид и назначение стоек, далее определить подвид.
Значение предельной гибкости определяется параметрами геометрических фигур, на величину влияет изгиб продольный, нагрузка, расчетное сопротивление материала изделия, рабочие условия.
Перед тем, как начать работать в калькуляторе онлайн, следует тщательно изучить инструкцию.
Изменения, внесенные в работу калькулятора
Исправления, внесенные от 20 июня 2018 года, стали:
1.
включили проверку стоек по значению гибкости.
2.включили возможность расчета уголков спаренного и крестообразного типа.
3.включили функцию расчета швеллера, который имеет форму короба или двутавра.
4.включили проверку уголка согласно главным осям.
Исправления, внесенные от 8 сентября 2018 года включают:
1.добавление проверки локальной устойчивости стенок либо полок в двутавре, или швеллере, или уголке, также металлического профиля.
Исправления, внесенные от 2 декабря 2018 года, включают:
1.исправление расчетного параметра сопротивления деревянного материала на сжатие в разделе СП под названием ”Деревянные конструкции».
2.исправление коэффициентов расчетного значения по длине, применяемые для материала из дерева.
3.исправление замечаний, отображающих итоговые расчеты.
youtube.com/embed/Wa_C7cz4sAc?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
Онлайн-калькулятор вычета изгибов | Микроформа Precision
Пример формулы изгиба
Нейтральная ось {{lineOD2Angle}} ° Уменьшение изгибаОбъяснение расчета изгиба
Белая пунктирная линия на показанной выше части представляет нейтральную ось , которая является теоретической точкой в материале, которая не изменяется в процессе формования.Материал внутри этой линии должен сжиматься, тогда как материал снаружи должен расширяться. Расстояние между внутренней поверхностью детали и нейтральной осью известно как смещение нейтральной оси . Коэффициент K , в данном случае {{kFactor}}, выражает это расстояние в процентах от толщины материала. Другими словами, нейтральная ось для этой детали проходит {{kFactor * 100}}% пути через толщину материала. Учитывая толщину {{толщину}}, это расстояние вычисляется как {{kFactor * толщина}} «({{толщина}} x {{kFactor}}).
Другими словами, нейтральная ось для этой детали проходит {{kFactor * 100}}% пути через толщину материала. Учитывая толщину {{толщину}}, это расстояние вычисляется как {{kFactor * толщина}} «({{толщина}} x {{kFactor}}).
Вычет изгиба означает, что материал, как ожидается, будет растягиваться на эту величину в ходе изгиба. Это моделируется на части, показанной выше секцией, показанной красным. «Следует вычесть из развертки, чтобы формованная деталь достигает желаемых размеров. Поскольку уменьшение изгиба можно измерить в физической детали, это наиболее точный способ рассчитать растяжение материала.
Допуск на изгиб — это величина изгиба нейтральной оси.В приведенном выше примере это обозначено синей пунктирной линией. Хотя это вариант для расчета изгиба в некоторых программах САПР, таких как Solid Works, на него не часто ссылаются в реальном производственном процессе, поскольку это теоретическое число и не может быть проверено в физической части.
Бесплатный калькулятор луча | ClearCalcs
Как использовать калькулятор свободного луча
Калькулятор луча ClearCalcs позволяет пользователю ввести геометрию и нагрузку луча для анализа за несколько простых шагов.Затем он определяет изгибающий момент, диаграммы сдвига и прогиба, а также максимальные требования, используя мощный механизм анализа методом конечных элементов.
Регистрация учетной записи ClearCalcs откроет дополнительные расширенные функции для проектирования и анализа балок и множества других структурных элементов. ClearCalcs позволяет проектировать из стали, бетона и дерева в соответствии со стандартами Австралии, США и ЕС.
Лист разделен на три основных раздела:
- «Ключевые свойства», где пользователь вводит геометрию выбранного сечения и опор балки.

- «Нагрузки», где можно ввести распределенные, точечные и приложенные моментные нагрузки,
- «Сводка», в котором отображаются основные выходные данные и диаграммы.
Раздел «Комментарии» также включен для того, чтобы пользователь мог оставить какие-либо конкретные примечания по дизайну. Щелчок по любой из меток ввода / свойства дает описательное справочное объяснение.
1. Свойства входного ключа
Свойства балки и сечения задаются путем ввода непосредственно в поля ввода.
Длина балки — это общая длина балки, включая все пролеты балки, в мм или футах.
Модуль Юнга установлен на значение по умолчанию 200000 МПа или 29000 тысяч фунтов на квадратный дюйм для конструкционной стали, но может быть изменен пользователем.
Площадь поперечного сечения зависит от выбранного сечения балки и по умолчанию соответствует значениям для обычной стальной балки.
Второй момент площади (или момент инерции) также зависит от выбранного сечения балки и снова по умолчанию соответствует свойствам обычной стальной балки.
Свойства E, A и Ix для других секций балки можно получить из библиотеки свойств секций ClearCalcs.Кроме того, вы можете создать свой собственный раздел, используя наш бесплатный калькулятор момента инерции.
Положение опор слева позволяет пользователю ввести любое количество опор и указать их положение по длине балки. Тип опоры может быть закрепленным (фиксированный в перемещении, свободный поворот) или фиксированным (фиксированный как при перемещении, так и при повороте) и выбирается из раскрывающегося меню. Требуется минимум одна фиксированная опора или две штифтовые опоры.
Вычислитель балки также позволяет использовать пролет консолей на каждом конце, поскольку положение первой опоры не обязательно должно быть равно 0 мм, а положение последней опоры не обязательно должно быть равно длине балки.
Реакции на каждой из опор автоматически обновляются при добавлении, изменении или удалении опор в зависимости от указанной нагрузки.
2. Входные нагрузки
Калькулятор поддерживает различные типы нагрузок, которые можно применять в комбинации. Каждой загрузке пользователь может присвоить имя.
Каждой загрузке пользователь может присвоить имя.
Знаковое обозначение, используемое для нагружения (показаны положительные значения):
Распределенные нагрузки указываются в единицах силы на единицу длины, кН / м или PLF, вдоль балки и могут применяться между любыми двумя точками.В калькуляторе можно использовать два разных типа:
Равномерная нагрузка имеет постоянную величину по всей длине приложения. Следовательно, начальная и конечная величины, указанные пользователем, должны быть одинаковыми.
Линейные нагрузки имеют разную величину по длине приложения. Различные начальные и конечные величины должны быть указаны пользователем, и они могут использоваться для представления треугольных или трапециевидных нагрузок.
Точечные нагрузки указываются в единицах силы, кН или тысячах фунтов, и площади, приложенной в дискретных точках вдоль балки.Например, они могут представлять реакции других элементов, подключенных к балке. Пользователь вводит имя, величину и местоположение слева от луча.
Пользователь вводит имя, величину и местоположение слева от луча.
На приведенной ниже диаграмме из сводного раздела показана двухпролетная неразрезная балка с линейно распределенной нагрузкой на заплату и точечной нагрузкой.
3. Итоговые результаты вычислений
После задания нагрузки и геометрии калькулятор автоматически использует механизм конечно-элементного анализа ClearCalcs для определения моментов, поперечных сил и прогибов.Максимальные значения каждого из них выводятся как «Требуемый момент» , «Требуемый сдвиг» и «Прогиб» вместе с диаграммами по длине балки.
Положительные значения означают отклонение вниз, а отрицательные значения — отклонение вверх. Знаковое соглашение, используемое в диаграммах силы сдвига и изгибающего момента, следующее (показаны положительные значения):
Использование курсора для наведения курсора на любую точку на диаграммах изгибающего момента, силы сдвига или прогиба дает конкретные значения в этом месте вдоль балки. В приведенном ниже примере показаны выходные параметры для двухпролетной неразрезной балки с линейно распределенной коммутационной нагрузкой и точечной нагрузкой.
В приведенном ниже примере показаны выходные параметры для двухпролетной неразрезной балки с линейно распределенной коммутационной нагрузкой и точечной нагрузкой.
Холодная гибка труб. Глубина изгиба с основным валом.
Статья написана по заказу пользователей, которые хотели рассчитать глубину изгиба секции с основным валом для получения гнутой трубы с заданными параметрами.
До запроса я не знала о существовании станков для холодной гибки. Кроме того, существуют промышленные гибочные станки и ручные гидравлические гибочные станки.
Они работают так же, как вы можете видеть на картинке.
.
Секция (труба) помещается между роликами, затем основной ролик сгибает секцию, а оставшаяся часть скользит через гибочную машину.
С моей любительской точки зрения этот процесс выглядит так
Размещение секции
- Гибка
или, если объединить
Итак, вопрос в том, насколько сильно мы должны гнуть трубку i.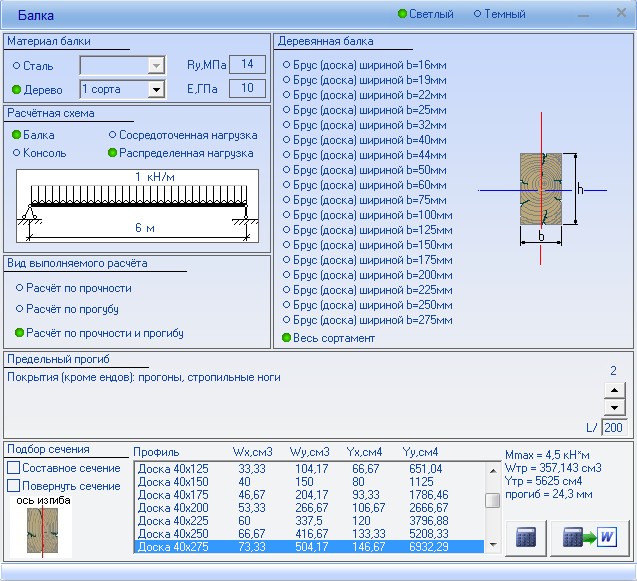 е. опустить главный вал, чтобы после прохождения секции мы имели необходимый изгиб? Кривая задается радиусом. Но, как показал запрос пользователя, параметры можно задавать не только по радиусу, но и по длине и высоте хорды, если вам нужна дуга. Калькулятор, вычисляющий длину секции (L) и радиус окружности (R) по заданной длине (C) и высоте хорды (h) — см. Рисунок.
е. опустить главный вал, чтобы после прохождения секции мы имели необходимый изгиб? Кривая задается радиусом. Но, как показал запрос пользователя, параметры можно задавать не только по радиусу, но и по длине и высоте хорды, если вам нужна дуга. Калькулятор, вычисляющий длину секции (L) и радиус окружности (R) по заданной длине (C) и высоте хорды (h) — см. Рисунок.
Сегмент, определяемый хордой и высотой
Точность вычисленияЦифры после десятичной точки: 2
content_copy Ссылка сохранить Сохранить расширение Виджет
Подробнее и формулы здесь — Круговой сегмент
Идем дальше.
Итак, если нам нужно иметь глубину изгиба, зная радиус, расстояние между ведомыми роликами, радиус роликов и размер сечения.
Перепишем комбинированный рисунок, добавив несколько необходимых строк и убрав все лишнее.
Точка B — центр нашего круга. Обратите внимание, что расчет производится по внешнему краю профиля относительно кривой.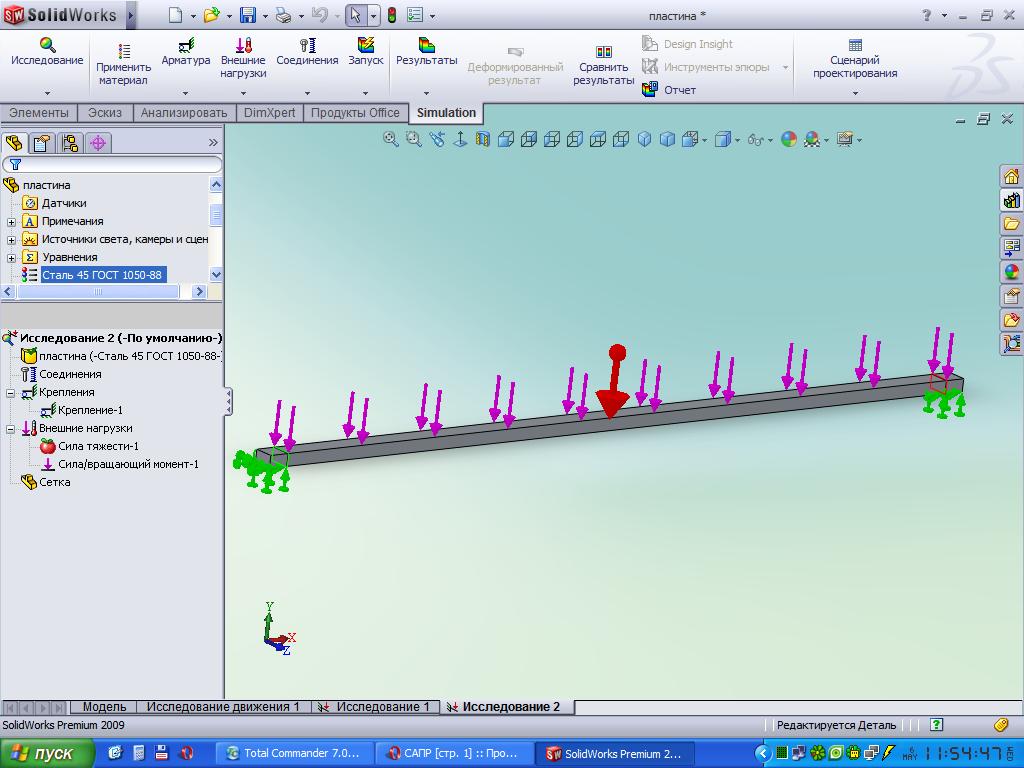 Поскольку радиус высоты и ширины хорды, вероятно, будет рассчитываться в соответствии с осью профиля, радиус профиля должен быть добавлен к полученному радиусу, чтобы у вас был радиус внешнего края профиля.
Поскольку радиус высоты и ширины хорды, вероятно, будет рассчитываться в соответствии с осью профиля, радиус профиля должен быть добавлен к полученному радиусу, чтобы у вас был радиус внешнего края профиля.
Затем используется геометрия.
На расстоянии AC и AB находим треугольник ABD
Отсюда
А вот и калькулятор
Труба холодная гибка. Глубина изгиба с основным валом.
Радиус по внешнему краю секции
Расстояние между осями ведомых роликов
Точность расчетаЦифры после десятичной точки: 3
content_copy Ссылка сохранить Сохранить расширение Виджет
Расчет допуска на изгиб, вычета изгиба и коэффициента К
В моем предыдущем посте я говорил о К-факторе, допуске на изгиб и уменьшении изгиба и о том, что они означают при проектировании листового металла.Теперь давайте посмотрим, как мы можем получить эти значения для конкретного листа.
Как я уже упоминал в своем последнем посте, вам нужно провести несколько тестов, чтобы вычислить эти значения для конкретного листа.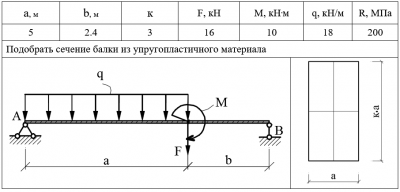 Эти испытания включают в себя изгиб некоторых образцов, а затем выполнение некоторых измерений и расчетов.
Эти испытания включают в себя изгиб некоторых образцов, а затем выполнение некоторых измерений и расчетов.
Рассмотрим лист толщиной 20 мм и длиной 300 мм, как показано на рисунке 1. Мы собираемся рассмотреть три сценария изгиба с тремя разными углами изгиба; 60, 90 и 120, и мы рассчитаем для них К-фактор, допуск на изгиб и вычет изгиба.Инструмент для гибки имеет радиус 30 мм, что означает, что наш внутренний радиус изгиба (R) составляет 30 мм. Начнем с изгиба на 90 градусов, что является наиболее простым сценарием.
Рисунок 1: Плоский лист
Угол изгиба 90 градусов
На рис. 2 показан лист, согнутый с углом сгиба 90 градусов. Начнем с расчета допуска на изгиб. Отсюда мы можем рассчитать K-фактор и вычет изгиба. После сгибания листа нам нужно провести некоторые измерения, как показано на рисунке 2.
Рисунок 2: изгиб на 90 градусов
Мы можем рассчитать длину ноги 1 и 2 следующим образом:
На нейтральной оси имеем:
В этой формуле начальная длина равна 300 мм.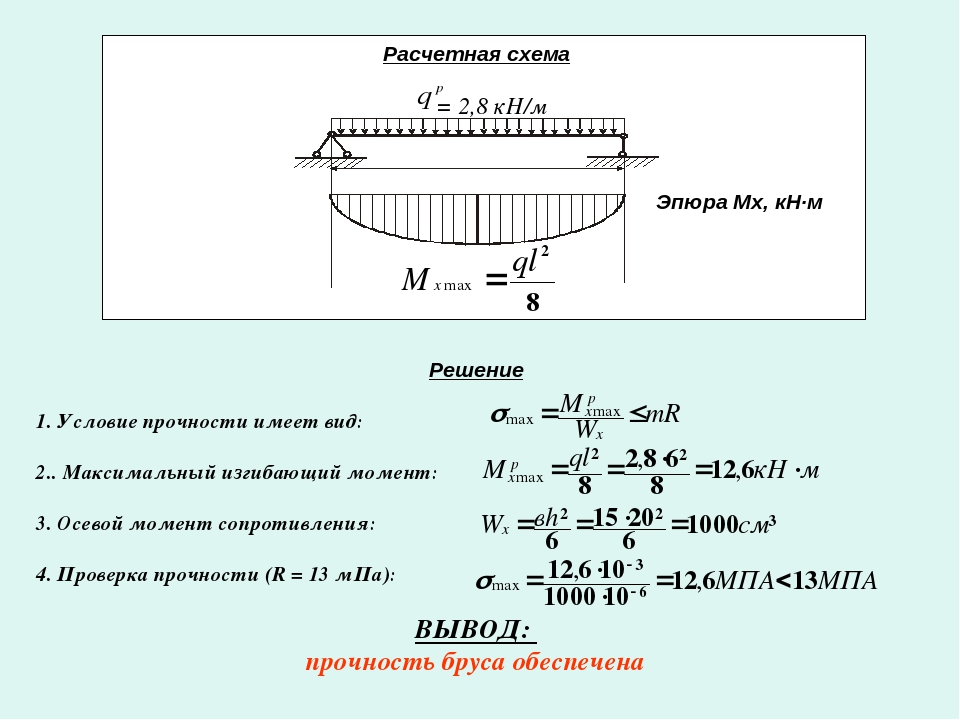 Заменив исходную длину, длину ноги 1 и 2 в приведенном выше уравнении, мы можем рассчитать допуск на изгиб следующим образом:
Заменив исходную длину, длину ноги 1 и 2 в приведенном выше уравнении, мы можем рассчитать допуск на изгиб следующим образом:
Мы знаем, что BA — это длина дуги на нейтральной оси. Длина дуги для этого сценария может быть рассчитана как:
Где R ’- радиус дуги на нейтральной оси.Подставляя значение допуска на изгиб в приведенное выше уравнение, мы получаем:
Теперь, если мы вычтем R из R ’, мы сможем найти расстояние от нейтральной оси (t) до внутренней поверхности:
Из уравнения K-фактора имеем:
Объявление службы Javelin SOLIDWORKS
Наши специалисты SOLIDWORKS могут настроить вашу среду так, чтобы ваша команда использовала полный набор из шаблонов , таблиц и библиотеки инструментов формования
Углы изгиба менее 90 градусов
Для нашего второго сценария мы собираемся обсудить расчеты для углов изгиба менее 90 градусов. В качестве примера мы будем использовать угол изгиба 60 градусов. Мы снова должны выполнить некоторые измерения, как показано на рисунке 3. Затем мы должны вычислить длину ноги 1 и длину ноги 2.
В качестве примера мы будем использовать угол изгиба 60 градусов. Мы снова должны выполнить некоторые измерения, как показано на рисунке 3. Затем мы должны вычислить длину ноги 1 и длину ноги 2.
Рисунок 3: изгиб 60 градусов
Начнем с вычисления длины ноги 1. Из рисунка 3 мы знаем, что
Где R — внутренний радиус изгиба, который в этом примере равен 30 мм. Мы можем рассчитать длину ноги 1 с помощью нескольких простых уравнений, как показано ниже:
Теперь посчитаем длину ноги 2:
Теперь, когда у нас есть длина опоры 1 и 2, мы можем снова использовать следующее уравнение для расчета допуска на изгиб:
Чтобы вычислить R ’, который является радиусом дуги на нейтральной оси, мы можем использовать следующее уравнение:
A — это угол изгиба в приведенном выше уравнении, поэтому
Для расчета расстояния нейтральной оси от внутренней поверхности (t) мы можем вычесть внутренний радиус изгиба из R ’:
Имея t и толщину листа (T), мы можем вычислить K-фактор следующим образом:
Углы изгиба более 90 градусов
Как и в предыдущих сценариях, давайте начнем с вычисления длины ноги 1.
Рисунок 4: изгиб 120 градусов
На основании рисунка 4 имеем:
Далее рассчитываем длину ноги 2:
Теперь мы можем рассчитать допуск на изгиб:
Имея BA, мы можем рассчитать K-фактор:
Расчет вычета изгиба
Как объяснялось в моем первом посте, уменьшение изгиба можно рассчитать с помощью следующего уравнения:
Где OSSB — внешняя неудача.OSSB определяется, как показано на рисунке 5, для различных углов изгиба и может быть рассчитан с использованием следующего уравнения:
Где A — угол изгиба, T — толщина листа, а R — радиус изгиба.
Рисунок 5: Внешнее понижение (OSSB) при разных углах изгиба
В следующем посте мы поговорим о таблицах сгибов и размеров в SOLIDWORKS и о том, как мы можем использовать вычисленные здесь числа для создания наших собственных таблиц сгибов и размеров.
Просто поддерживаемый калькулятор пучка | calcresource
Предпосылки
Оглавление
Введение
Балка с простой опорой — одна из самых простых конструкций.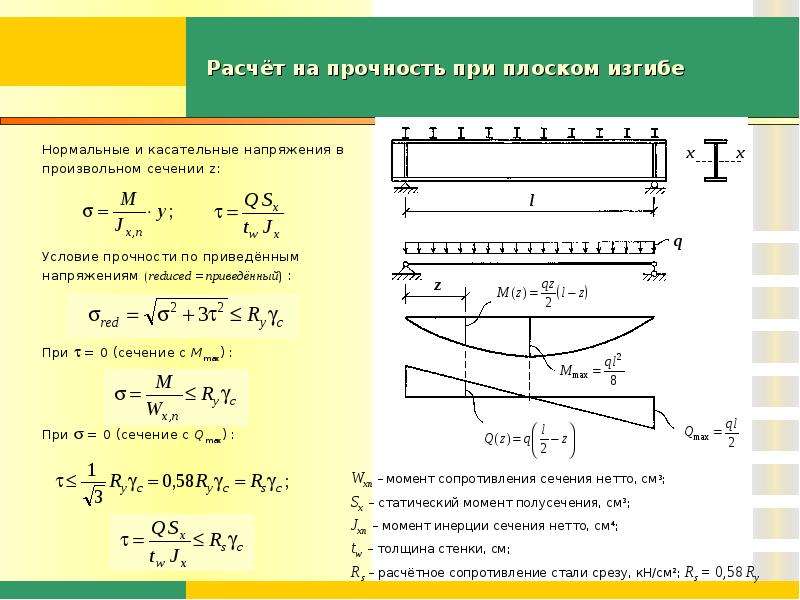 У него всего две опоры, по одной с каждой стороны. Одна штифтовая опора и роликовая опора. Оба они запрещают любое вертикальное движение, позволяя, с другой стороны, свободно вращаться вокруг них. Роликовая опора также позволяет балке расширяться или сжиматься в осевом направлении, хотя свободному горизонтальному перемещению препятствует другая опора.
У него всего две опоры, по одной с каждой стороны. Одна штифтовая опора и роликовая опора. Оба они запрещают любое вертикальное движение, позволяя, с другой стороны, свободно вращаться вокруг них. Роликовая опора также позволяет балке расширяться или сжиматься в осевом направлении, хотя свободному горизонтальному перемещению препятствует другая опора.
Удаление любой из опор или установка внутреннего шарнира приведет к тому, что балка с простой опорой перейдет в механизм, то есть тело перемещается без ограничений в одном или нескольких направлениях.Очевидно, это нежелательно для несущей конструкции. Следовательно, балка с простой опорой не обеспечивает избыточности с точки зрения опор. Если произойдет локальный сбой, вся конструкция рухнет. Эти типы структур, которые не предлагают избыточности, называются структурами критических или определителей . Напротив, конструкция, которая имеет больше опор, чем требуется для ограничения ее свободного движения, называется избыточной или неопределенной конструкцией .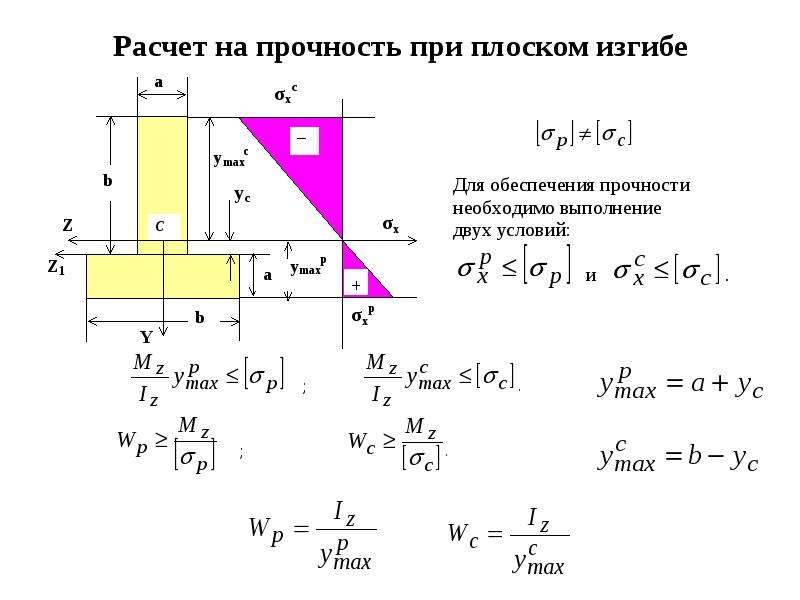
Допущения
Статический анализ любой несущей конструкции включает оценку ее внутренних сил и моментов, а также ее прогибов. Как правило, для плоской конструкции с плоской нагрузкой интересующими внутренними воздействиями являются осевая сила N, поперечная поперечная сила V и изгибающий момент M. Для балки с простой опорой, которая несет только поперечные нагрузки, осевая сила всегда равна ноль, поэтому им часто пренебрегают. Результаты расчетов на странице основаны на следующих предположениях:
- Материал однороден и изотропен (другими словами, его характеристики одинаковы во всех точках и в любом направлении)
- Материал линейно эластичный
- Нагрузки применяются статически (они не меняются со временем)
- Поперечное сечение одинаково по всей длине балки
- Прогибы небольшие
- Каждое поперечное сечение, которое изначально является плоским, а также перпендикулярно продольной оси, остается плоской и перпендикулярно отклоненной оси.
 Это тот случай, когда высота поперечного сечения значительно меньше длины балки (в 10 и более раз), а также поперечное сечение не является многослойным (не сечение сэндвич-типа).
Это тот случай, когда высота поперечного сечения значительно меньше длины балки (в 10 и более раз), а также поперечное сечение не является многослойным (не сечение сэндвич-типа).
Последние два предположения удовлетворяют кинематическим требованиям теории пучка Эйлера-Бернулли, которая здесь также принята.
Условные обозначения
Для расчета внутренних сил и моментов при любом разрезе сечения балки необходимо условное обозначение. Здесь приняты следующие значения:
- Осевая сила считается положительной, когда она вызывает растяжение детали.
- Сила сдвига положительна, когда она вызывает вращение детали по часовой стрелке.
- Изгибающий момент является положительным, когда он вызывает растяжение нижнего волокна балки и сжатие верхнего волокна.
Эти правила хотя и не являются обязательными, но достаточно универсальны. Другой набор правил, если следовать им последовательно, также даст те же физические результаты.
Символы
- E: модуль упругости материала (модуль Юнга)
- I: момент инерции поперечного сечения вокруг упругой нейтральной оси изгиба
- L: общий пролет балки
- R: опора реакция
- d: прогиб
- M: изгибающий момент
- V: поперечная поперечная сила
- \ theta: slope
Балка с простой опорой и равномерно распределенной нагрузкой
Нагрузка w распределяется по всему пролету балки с постоянной величиной и направление.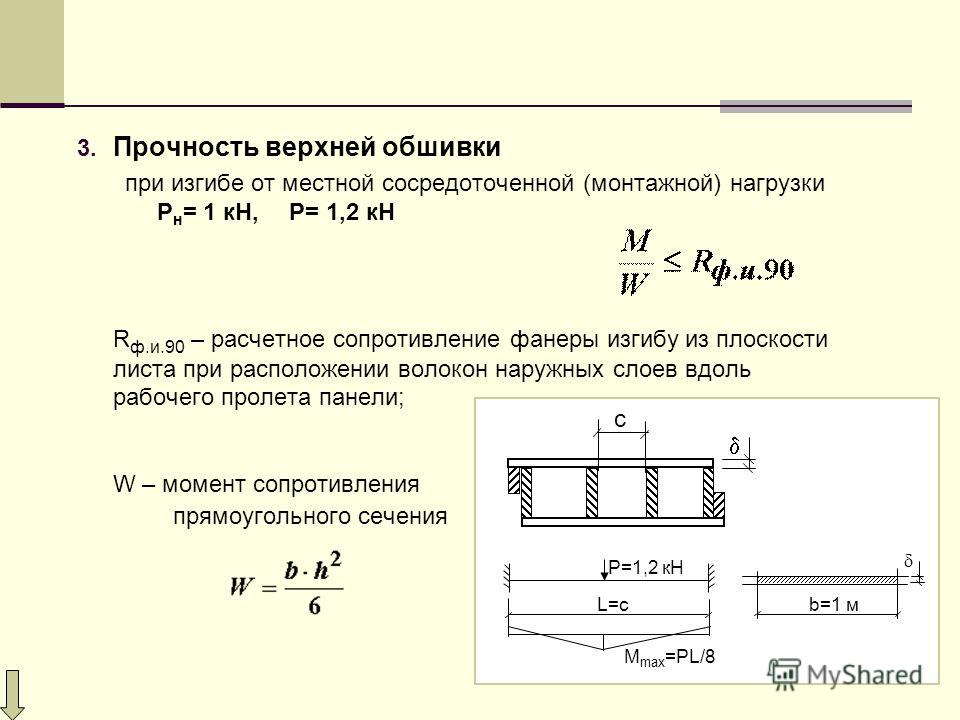 3)} {24 EI} 90 473
3)} {24 EI} 90 473
Балка с простой опорой и точечной силой в середине
Сила сосредоточена в одной точке, расположенной в середине балки.Однако на практике сила может распространяться на небольшую площадь, хотя размеры этой области должны быть существенно меньше длины пролета балки. В непосредственной близости от приложения силы ожидаются концентрации напряжений, и в результате отклик, предсказываемый классической теорией балки, может быть неточным. Однако это только местное явление. По мере удаления от места расположения силы результаты становятся действительными в силу принципа Сен-Венана.
В следующей таблице представлены формулы, описывающие статический отклик простой балки под действием сосредоточенной точечной силы P, приложенной в середине.2)} {16 E I} &, x> L / 2 \ end {align} \ right.
где:
\ строго {x} = L-x
Балка с простой опорой и точечной силой в произвольном положении
Сила сосредоточена в одной точке в любом месте пролета балки. Однако на практике сила может распространяться на небольшую площадь. Однако, чтобы считать силу сосредоточенной, размеры области приложения должны быть существенно меньше длины пролета балки.В непосредственной близости от силы ожидаются концентрации напряжений, и в результате отклик, предсказываемый классической теорией пучка, может быть неточным. Однако это только локальное явление, и по мере удаления от места расположения силы расхождение результатов становится незначительным.
Однако на практике сила может распространяться на небольшую площадь. Однако, чтобы считать силу сосредоточенной, размеры области приложения должны быть существенно меньше длины пролета балки.В непосредственной близости от силы ожидаются концентрации напряжений, и в результате отклик, предсказываемый классической теорией пучка, может быть неточным. Однако это только локальное явление, и по мере удаления от места расположения силы расхождение результатов становится незначительным.
В следующей таблице представлены формулы, описывающие статический отклик простой балки под действием сосредоточенной точечной силы P, приложенной на случайном расстоянии a от левого конца.
Балка с точечной нагрузкой в случайном положении | |
|---|---|
| Количество | Формула |
| Реакции: | R_A = {Pb \ over L} R_A = {Pb \ over L} над L} |
| Концевые уклоны: | \ theta_A = — \ frac {P b (L ^ 2-b ^ 2)} {6E IL} \ theta_B = \ frac {P a (L ^ 2-a ^ 2)} {6E IL} |
| Предельный изгибающий момент: | M_u = {Pab \ over L} |
| Предельное усилие сдвига: | V_u = \ left \ {\ begin {выровнено } & {Pb \ over L} &, \ textrm {if:} a \ le L / 2 \\ — & {Pa \ over L} &, \ textrm {if:} a> L / 2 \ end {выровнено} \правильно. 3} {6EI} &, x> a \ end {align} \ right.2} {2 E I} &, x> a \ end {align} \ right. 3} {6EI} &, x> a \ end {align} \ right.2} {2 E I} &, x> a \ end {align} \ right. |
где: b = La \ строго {x} = Lx | |
Балка без опоры с точечным моментом
В этом случае момент накладывается на одну точку балки в любом месте пролета балки. На практике это может быть силовая пара или элемент на кручение, соединенный не в плоскости и перпендикулярно балке.
В любом случае область приложения момента должна распространяться на небольшую длину луча, чтобы ее можно было успешно идеализировать как сосредоточенный момент в точке.Хотя в непосредственной близости от области применения ожидается, что результаты, предсказанные с помощью классической теории пучков, будут неточными (из-за концентраций напряжений и других локализованных эффектов), по мере того, как мы удаляемся, предсказанные результаты полностью верны, как заявил Святой -Венантный принцип.
В следующей таблице представлены формулы, описывающие статический отклик простой балки под действием сосредоточенного момента M точки, приложенного на расстоянии a от левого конца.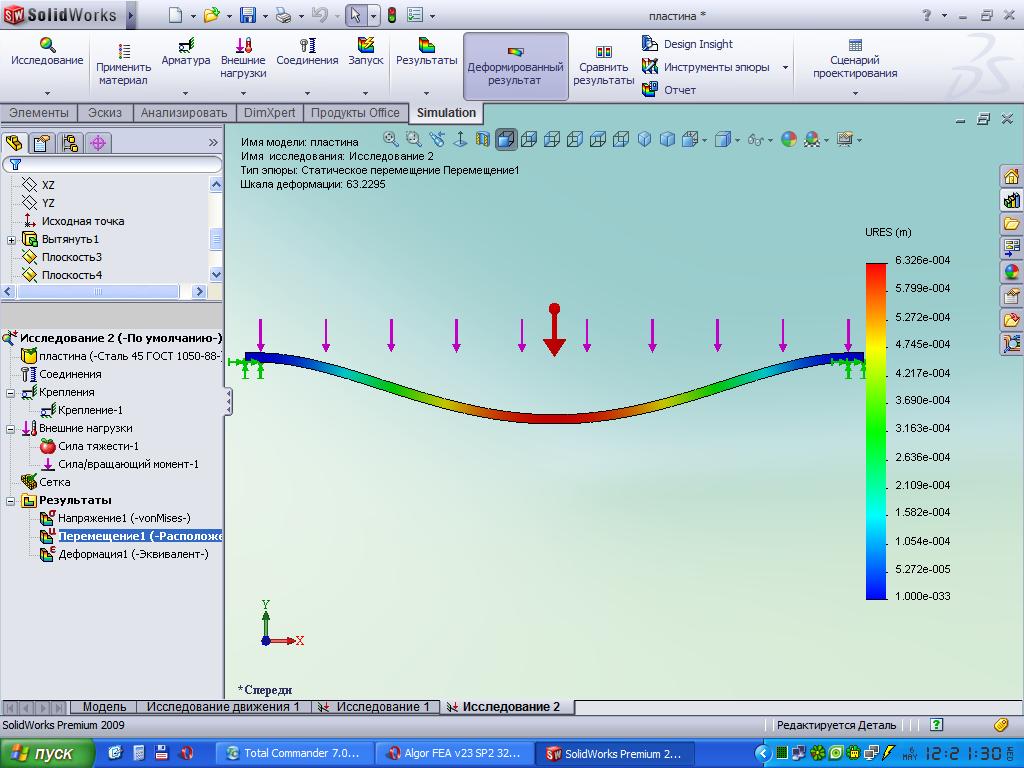 2 )} {6E IL}
2 )} {6E IL}
где:
b = La
\ строго {x} = Lx
Балка без опоры с треугольной нагрузкой
Нагрузка распределяется по всему пролету балки, однако ее величина не константа, но изменяется линейно, начиная от нуля на левом конце до максимального значения w_1 на правом конце. Размеры w_1 — сила на длину. Общее количество силы, приложенной к балке, равно W = {1 \ over2} w L, где L — длина пролета.
Ориентация треугольной нагрузки важна! Формулы, представленные в этом разделе, были подготовлены для случая восходящей нагрузки (слева направо), как показано на схеме. Для нисходящей нагрузки вы можете отразить балку так, чтобы ее левый конец (точка A) был наименее загруженным.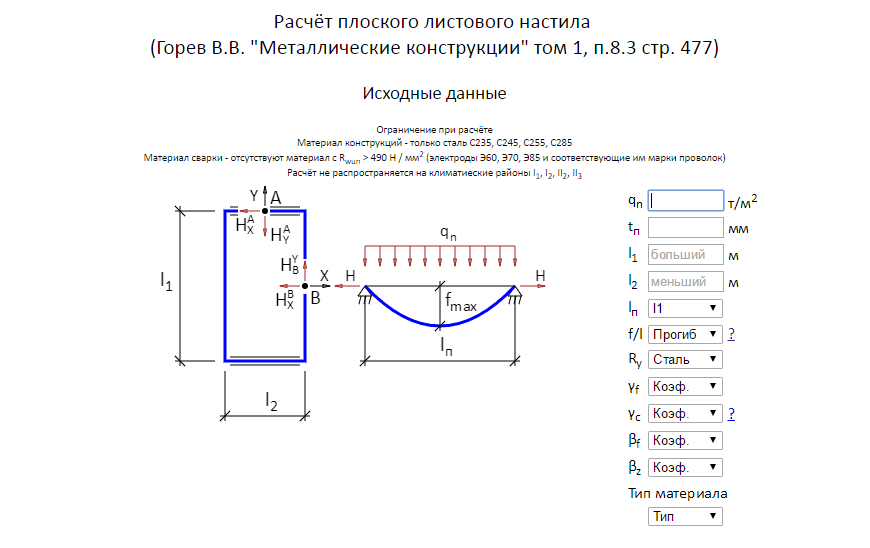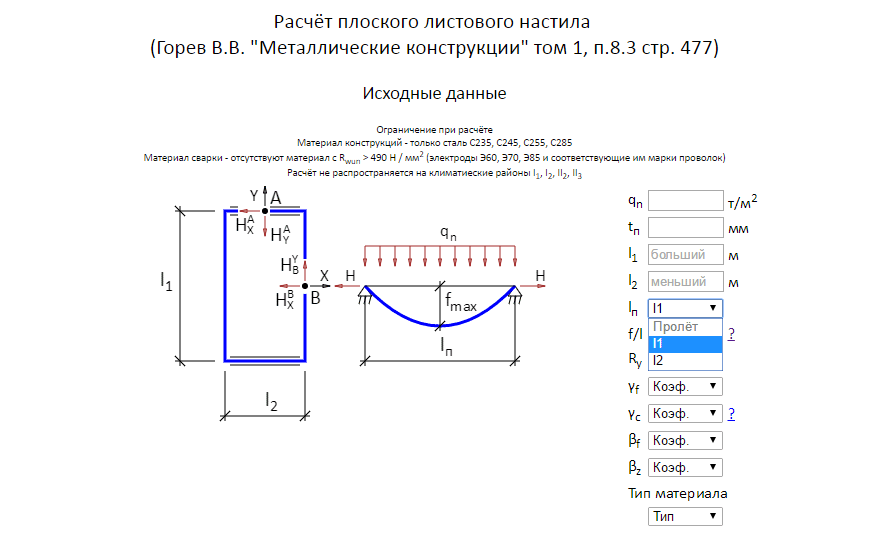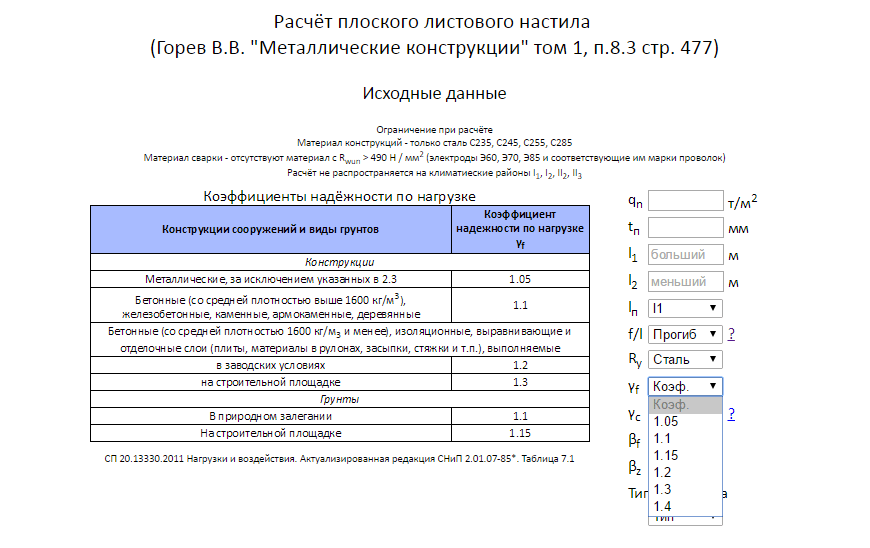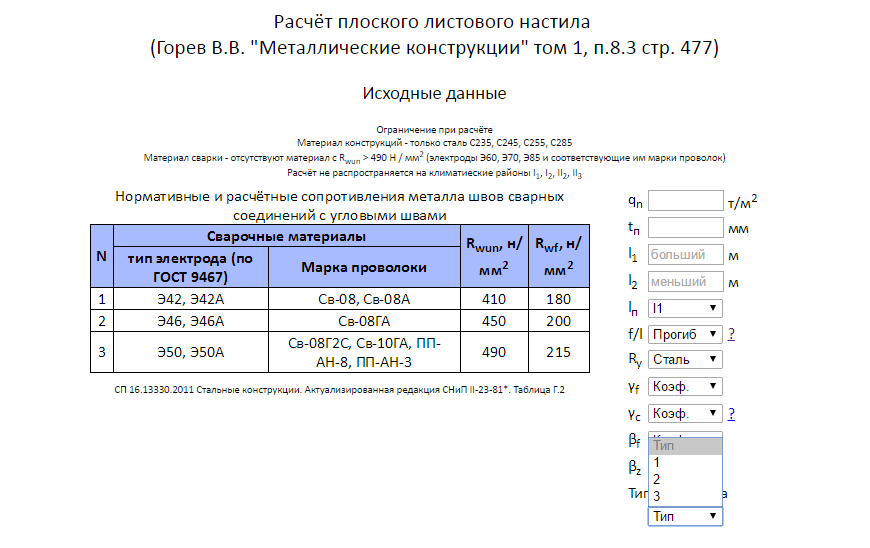 Ось x и все результаты также будут отражены.
Ось x и все результаты также будут отражены.
В следующей таблице представлены формулы, описывающие статический отклик простой балки при линейно изменяющейся (треугольной) распределенной нагрузке, восходящей слева направо.4} {24EIL}
где:
C = \ sqrt {15- \ sqrt {120}} \ left (\ sqrt {15} + \ sqrt {50} \ right) \ приблизительно 22.01237
Балка с простой опорой и трапецеидальной нагрузкой
Нагрузка распределяется по всему пролету балки и имеет линейно изменяющуюся величину, начиная с w_1 на левом конце и заканчивая w_2 на правом конце. Размеры w_1 и w_2 — сила на длину. Общее количество силы, приложенной к балке, равно W = {L \ over2} (w_1 + w_2), где L — длина пролета.
Значения w_1 и w_2 могут быть присвоены произвольно. Первое не обязательно должно быть меньше второго. Они могут принимать даже отрицательные значения (одно или оба).
В следующей таблице представлены формулы, описывающие статический отклик простой балки при переменной распределенной нагрузке трапециевидной формы.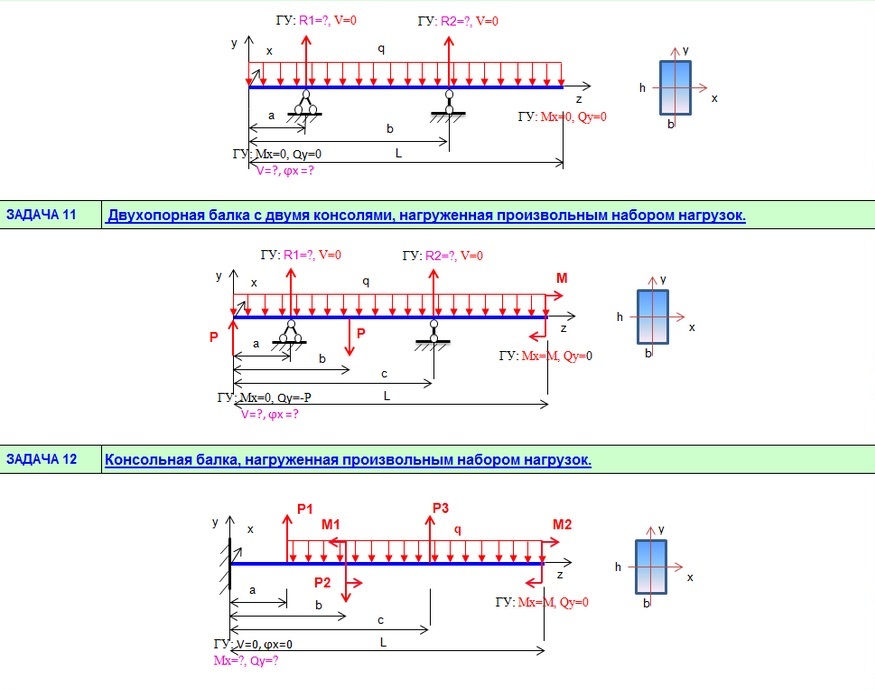 3} {24EI}
3} {24EI}
где:
w_x = w_1 + {(w_2-w_1) x \ over L}
904 21Балка с простой опорой и трапециевидным распределением нагрузки в виде плиты
Такое распределение нагрузки типично для балок по периметру плиты.Распределение имеет трапециевидную форму с максимальной величиной w внутри балки, а на двух ее концах становится равной нулю. Размеры (\ w \) — это сила на длину. Общее количество силы, приложенной к балке, равно W = w (La / 2-b / 2), где L — длина пролета, а a, b — длины с левой и правой стороны балки соответственно, где распределение нагрузки равно разная (треугольная).
В следующей таблице представлены формулы, описывающие статический отклик простой балки при трапецеидальном распределении нагрузки, как показано на схеме выше.3
Балка с простой опорой и частично распределенной равномерной нагрузкой
Нагрузка распределяется на часть пролета балки с постоянной величиной w, в то время как оставшийся пролет разгружен. Размеры w — сила на длину. Общее количество силы, приложенной к балке, равно W = \ left (L-a-b \ right) w, где L — длина пролета, а a, b — длины без нагрузки с левой и правой стороны балки, соответственно.
Размеры w — сила на длину. Общее количество силы, приложенной к балке, равно W = \ left (L-a-b \ right) w, где L — длина пролета, а a, b — длины без нагрузки с левой и правой стороны балки, соответственно.
В следующей таблице представлены формулы, описывающие статический отклик простой балки при частично распределенной равномерной нагрузке.2} {2 E I} &, x \ ge L-b \ end {align} \ right.
где:
\ острый {x} = Lx
x_a = xa
L_w = Lab
Балка с простой опорой и частично распределенной трапециевидной нагрузкой
Часть нагрузки распределяется на часть пролет балки, имеющий линейно изменяющуюся величину от w_1 до w_2, а оставшийся пролет разгружен. Размеры w_1 и w_2 — сила на длину. Общее количество силы, приложенной к балке, равно W = {L-a-b \ over2} (w_1 + w_2), где L — длина пролета, а a, b — длины без нагрузки с левой и правой стороны балки соответственно.
Значения w_1 и w_2 могут быть присвоены произвольно.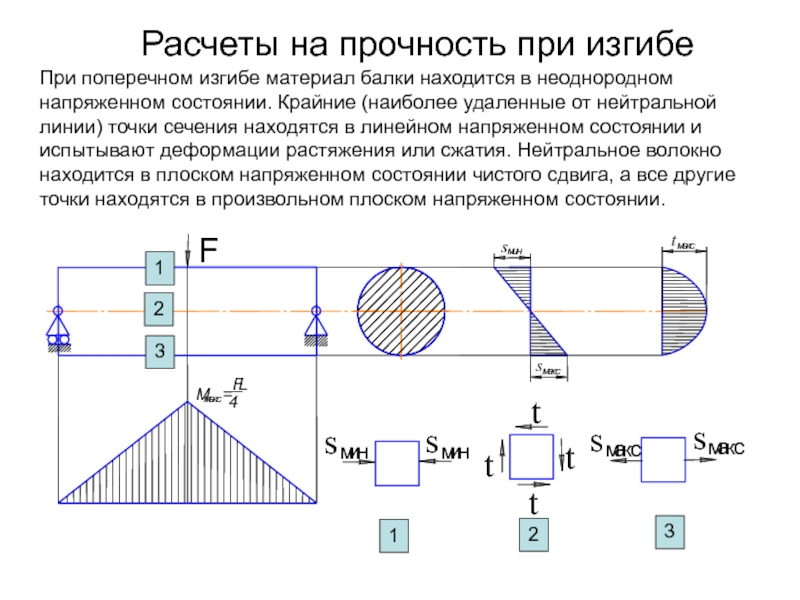 Первое не обязательно должно быть меньше второго. Они могут принимать даже отрицательные значения (одно или оба).
Первое не обязательно должно быть меньше второго. Они могут принимать даже отрицательные значения (одно или оба).
Это самый общий случай. Формулы для частично распределенных равномерных и треугольных нагрузок можно получить, соответствующим образом задав значения w_1 и w_2. Более того, соответствующие случаи для полностью нагруженного пролета можно получить, установив a и b равными нулю.
В следующей таблице представлены формулы, описывающие статический отклик простой балки при частично распределенной трапециевидной нагрузке.3
Статьи по теме
Понравилась эта страница? Поделись с друзьями!
Прогнозирование внутреннего радиуса при гибке листогибочным прессом
Рисунок 1
Много раз во время формирования мы не формируем истинный радиус,
но вместо этого парабола.
Если вы в последние месяцы следили за нашим обсуждением радиуса изгиба и его происхождения, добро пожаловать обратно. В любом случае, давайте посмотрим, насколько глубока эта кроличья нора радиуса.
В любом случае, давайте посмотрим, насколько глубока эта кроличья нора радиуса.
В предыдущих статьях я обсуждал различные практические правила, которые операторы используют в цехах для выполнения работы. Эти правила могут приблизить прогноз внутреннего радиуса изгиба, но вы можете приблизиться к нему.
Какая разница?
Рассмотрим типичную ситуацию, когда вы используете правило 20 процентов, которое гласит, что радиус изгиба воздухом формируется в процентах от отверстия матрицы, от 20 до 22 процентов для нержавеющей стали и около 16 процентов для холоднокатаной стали 60-KSI. , наш базовый материал.
Допустим, вы изгибаете мягкий алюминий толщиной 13 KSI с помощью инструмента 0,984 дюйма. ширину матрицы и пуансон с радиусом 0,032 дюйма. В качестве отправной точки вы рассчитываете, что внутренний радиус изгиба на 16% отверстия матрицы составляет 0,157 дюйма, хотя это для материала 60-KSI, поэтому вам нужно будет адаптироваться к типу материала. Между тем, когда вы рассчитываете, станет ли изгиб резким, вы обнаружите, что минимальный радиус перед вашим 0,032 дюйма. пуансон начинает сгибать, линия сгиба составляет 0,172 дюйма. Наконец, вы запускаете тестовый сгиб, только чтобы обнаружить, что фактический радиус равен 0.170 дюймов
пуансон начинает сгибать, линия сгиба составляет 0,172 дюйма. Наконец, вы запускаете тестовый сгиб, только чтобы обнаружить, что фактический радиус равен 0.170 дюймов
У вас есть 0,157 дюйма. радиус, рассчитанный по правилу 20 процентов, тогда у вас есть 0,172 дюйма. радиус из ваших расчетов крутого изгиба. Это разница в радиусе 0,015 дюйма. Вы не так много говорите? В этом случае разница при применении к вычету изгиба может достигать 0,009 дюйма за изгиб.
Создавали ли вы когда-нибудь деталь с четырьмя боковыми фланцами с четырьмя дополнительными фланцами вверху, только чтобы обнаружить, что один угол выходит идеально, два угла почти удовлетворительны, а один выглядит просто ужасно? Почему так происходит? Небольшая ошибка в вычислении изгиба, вызванная расхождениями в расчетах внутреннего радиуса изгиба, имеет большое значение, если вы хотите получить идеальные детали с первого раза.
В основе любой операции гибки лежит внутренний радиус гибки. Если вы можете рассчитать уменьшение изгиба на основе фактических результатов, точность гарантирована. Единственный недостаток этой теории состоит в том, что во многих случаях во время формования мы не формируем истинный радиус. Форма, которую вы формируете, может быть параболой, симметричной зеркальной кривой, обычно U-образной при ориентации, как показано на рис. 1 . И конечный радиус, который вы получите, является результатом упругого возврата.
Единственный недостаток этой теории состоит в том, что во многих случаях во время формования мы не формируем истинный радиус. Форма, которую вы формируете, может быть параболой, симметричной зеркальной кривой, обычно U-образной при ориентации, как показано на рис. 1 . И конечный радиус, который вы получите, является результатом упругого возврата.
Эффекты пружинения
Итак, как нам предсказать наиболее точный внутренний радиус и правильный вычет изгиба? Чтобы сделать это вручную, математика глубоко вникает в сорняки, поэтому я не буду туда идти.Скорее, мы просто будем использовать два разных веб-калькулятора.
Первый находится на www.handymath.com. Нажмите Полный калькулятор круговой дуги . Обратите внимание, что метка «Ширина дуги» в калькуляторе совпадает с шириной штампа, а угол , дополненный дугой совпадает с включенным углом изгиба.
Убедитесь, что настройки размеров калькулятора соответствуют используемым вами данным — дюймы, футы, миллиметры и т. Д. Обратите внимание, что когда мы нажимаем Enter, ответы, которые мы получаем, являются чисто математическими и не учитываются для прочности материала на разрыв. .
Д. Обратите внимание, что когда мы нажимаем Enter, ответы, которые мы получаем, являются чисто математическими и не учитываются для прочности материала на разрыв. .
Рисунок 2
Как показано в этом расчете из The Complete Circular Arc Calculator на сайте www.handymath.com, с увеличением угла изгиба увеличивается и радиус (высота дуги).
Информация, которую мы ищем на калькуляторе, — это Высота дуги , что соответствует внешнему радиусу изгиба. Давайте найдем значение для нашей базовой линии, холоднокатаной стали 60-KSI, толщиной 0,125 дюйма, используя диаметр 0,984 дюйма.ширина матрицы. Обратите внимание, что мы обсуждаем воздушное формование, поэтому угол матрицы не имеет значения; это может быть канал, острый или V-образный штамп. Важна ширина.
Во-первых, давайте введем ослабленный угол — 90 градусов, которые мы хотим достичь.
Введенные значения Угол, образованный дугой (включая угол изгиба): 90 градусов Ширина дуги (ширина матрицы): 0,984 дюйма Расчетное значение Высота дуги (внешний радиус изгиба): 0,20379 дюйма Эти расчеты не учитывают для пружинящего возврата. В нашем примере мы будем использовать значение 1 градус для упругого возврата, которое возникает, когда у нас есть примерное отношение толщины материала к внутреннему радиусу изгиба 1: 1. После того, как пуансон снимает давление формования, материал отжимается на 1 градус, поэтому для компенсации теперь мы используем угол изгиба 89 градусов. Снова используя The Complete Circular Arc Calculator на handymath.com, мы вводим следующее:
В нашем примере мы будем использовать значение 1 градус для упругого возврата, которое возникает, когда у нас есть примерное отношение толщины материала к внутреннему радиусу изгиба 1: 1. После того, как пуансон снимает давление формования, материал отжимается на 1 градус, поэтому для компенсации теперь мы используем угол изгиба 89 градусов. Снова используя The Complete Circular Arc Calculator на handymath.com, мы вводим следующее:
Теперь мы берем значение высоты дуги для нашего нового угла изгиба и подставляем его в следующую формулу:
Высота дуги — (2 × толщина материала 2 ) = внутренний радиус 0,201 — (2 × 0,01562) = внутренний радиус изгиба 0,201 — 0,031 = 0,170 дюйма Внутренний радиус изгиба Обратите внимание, что этот подход к высоте дуги отличается от подхода, использованного в прошлой колонке «Основы гибки», когда мы использовали , длина дуги . В прошлом месяце мы рассчитали внутренний радиус на основе ширины отверстия матрицы; на этот раз мы используем определенный радиус.
В прошлом месяце мы рассчитали внутренний радиус на основе ширины отверстия матрицы; на этот раз мы используем определенный радиус.
В прошлом месяце мы рассчитали радиус 0,136 дюйма, а сейчас мы вычислили внутренний радиус другим методом и получили 0,170 дюйма — разницу 0,034 дюйма. Вдобавок к этому, если бы мы использовали 20 По правилу процентов (опять же, для холоднокатаной стали 60-KSI радиус рассчитан как примерно 16 процентов ширины матрицы), мы бы вычислили внутренний радиус 0,157 дюйма — на полпути между этими двумя предыдущими измерениями. Все это разные способы вычисления радиуса с немного разными результатами.Но да, кроличья нора действительно становится глубже!
Парабола и острые изгибы
Если вы используете значение радиуса штампа, равное или меньшее минимального радиуса острого изгиба для воздуха, образующего деталь, вы больше не будете создавать радиус в детали (подробнее о крутых изгибах, см. «Как сделать изгиб воздуха резким» на сайте thefabricator.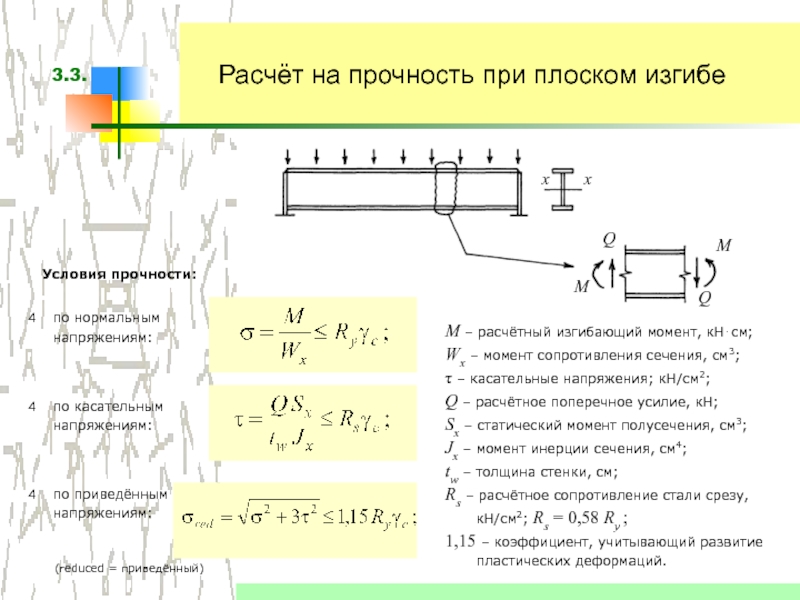 com). Вместо этого вы создадите параболу. Фактически вы протягиваете дугу другой длины в отверстие матрицы.
com). Вместо этого вы создадите параболу. Фактически вы протягиваете дугу другой длины в отверстие матрицы.
http: // wwwhad2know.ru / academics / parabola-segment-arc-length-area.html. Используя калькулятор параболического сегмента , мы вводим внешний радиус и ширину матрицы, чтобы найти длину дуги параболы. Значение Высота в этом онлайн-калькуляторе эквивалентно внешнему радиусу изгиба, а значение Ширина эквивалентно ширине матрицы:
Введенные значения Высота : (внешний радиус): 0,201 дюйма Ширина (ширина матрицы) : 0,984 дюйма Расчетное значение Длина дуги: 1,0845 дюйма Здесь глубина параболы (или высота дуги) составляет 0,201 дюйма, а длина дуги параболы составляет 1,0845 дюйма. Запомните эти значения. Вернувшись теперь к полному калькулятору круговой дуги на сайте www.handymath.com, мы вводим длину дуги равную 1,0845 дюйма и ширину штампа в 0,984 дюйма.
Когда вы это сделаете, вы увидите, что высота дуги (то есть внешний радиус) составляет 0,195 дюйма, что немного меньше, чем 0,201 дюйма. внешний радиус из предыдущего калькулятора, который не учитывал эффект параболы. Зная это, мы можем с уверенностью сказать, что внутренний радиус уменьшается, когда образуется парабола, что происходит при использовании пуансона с радиусом меньше минимального радиуса острого изгиба. Обратите внимание, что парабола также требует большего угла изгиба, чтобы получить желаемый ослабленный угол изгиба; мы перешли с 89 на 86.Угол изгиба 68 градусов, дополнительный упругий ход на 2,32 градуса. Также обратите внимание, что внутренний радиус детали будет не меньше радиуса вершины пуансона.
Угол и радиусы изгиба
Помните, что любое изменение радиуса приводит к изменению угла изгиба. Если мы введем ширину матрицы и угол изгиба на сайте www.handymath.com, мы получим результаты, показанные на , рис. 2, .
Если мы введем ширину матрицы и угол изгиба на сайте www.handymath.com, мы получим результаты, показанные на , рис. 2, .
Результаты показывают, что при воздушной формовке радиус уменьшается с учетом угла изгиба (за исключением острых изгибов).
Эта взаимосвязь угла изгиба / радиуса прекращается при включенных углах менее 28 градусов (152 градуса дополнительных), хотя минимальный включенный угол может быть больше в материале со значительной упругостью.
Отчасти это верно, потому что минимальный угол пуансона листогибочного пресса составляет 28 градусов. При этом, если продолжать закрывать изгиб выше 28 градусов, это приведет к некоторой форме сглаживания. Радиус будет раздавлен до тех пор, пока не будет достигнут желаемый угол изгиба или не будет завершена операция подгиба кромки.(Вкратце, для закрытой кромки радиус равен нулю, а уменьшение изгиба рассчитывается как процент от толщины материала — 43 процента в идеальных условиях, хотя это очень зависит от оператора. )
)
Факторинг для растяжения. Прочность
В предыдущем примере для расчетов мы использовали упругую отдачу в 1 градус. Для мягкой холоднокатаной стали 60-KSI средняя степень упругости составляет 1 градус или меньше. А как насчет других материалов?
Для этого мы можем предсказать возвратное движение с разумной степенью точности, используя следующую формулу, которая требует, чтобы мы преобразовали все значения в метрики.Обратите внимание, что прогнозирование упругого возврата никогда не бывает точным. Однако эти формулы довольно хорошо справляются со своей задачей.
[(Внутренний радиус в миллиметрах / 2) / Толщина материала в миллиметрах] × Фактор растяжения Фактор растяжения = Прочность материала на растяжение в PSI / 60,000Во-первых, давайте рассчитаем упругую отдачу, как если бы мы работали с нашим 60 -KSI базовый материал с внутренним радиусом изгиба 0,170 дюйма:
[(Внутренний радиус в миллиметрах / 2) / Толщина материала в миллиметрах] × Фактор растяжения Толщина материала: 0. 125 дюймов × 25,4 = 3,175 мм Внутренний радиус изгиба: 0,170 дюйма × 25,4 = 4,318 мм (4,318 / 2) / 3,175 2,159 мм / 3,175 мм = 0,68 градуса упругого возврата
125 дюймов × 25,4 = 3,175 мм Внутренний радиус изгиба: 0,170 дюйма × 25,4 = 4,318 мм (4,318 / 2) / 3,175 2,159 мм / 3,175 мм = 0,68 градуса упругого возврата В этом примере мы Округлим до 1 градуса. Затем мы можем применить коэффициент растяжения для нержавеющей стали 88-KSI 304.
Фактор растяжения = предел прочности материала на растяжение в фунтах на квадратный дюйм / 60 000 88 000/60 000 = 1,466666 1,0 градус × 1,466666Это дает 1,46 градуса для нержавеющей стали 88-KSI 304.В результате получается 1,5 градуса предполагаемого упругого возврата с соотношением 1: 1 между внутренним радиусом и толщиной материала.
Назад к калькулятору
Теперь, когда вы можете оценить упругое восстановление с некоторой приемлемой степенью точности, теперь вы можете его компенсировать. Чтобы определить угол, необходимый для компенсации упругого возврата, вы просто вычтите значение упругого возврата, если вы работаете с включенными углами изгиба, или добавьте это значение, если вы используете дополнительные углы изгиба.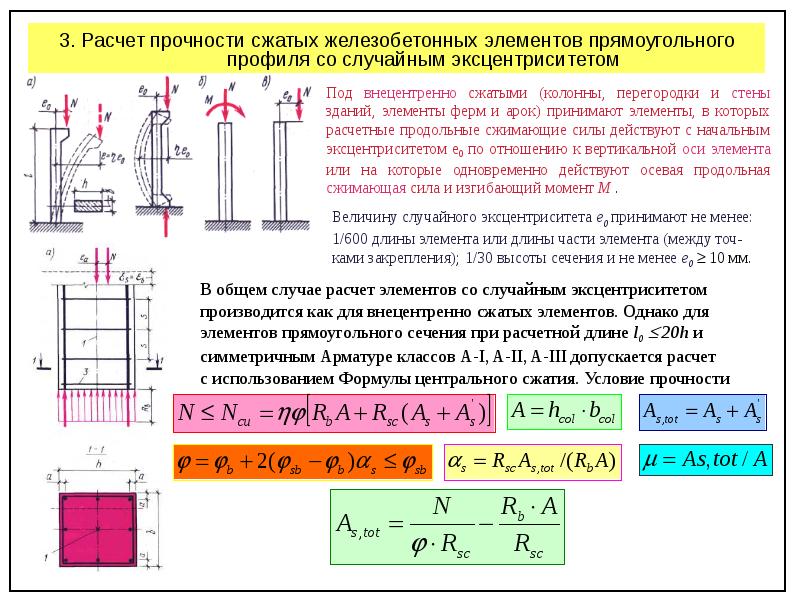 Калькулятор дуги окружности на сайте www.handymath.com работает с включенными углами изгиба (опять же, обозначенными как Subtended Angle of Arc).
Калькулятор дуги окружности на сайте www.handymath.com работает с включенными углами изгиба (опять же, обозначенными как Subtended Angle of Arc).
Как только вы узнаете внутренний радиус, то есть фактический внутренний радиус, который будет отображаться в готовой детали, вы можете вставить это значение радиуса в свои формулы гибки (см. Врезку).
Заключение, на данный момент
Правильно спрогнозировав внутренний радиус, мы можем точно рассчитать вычеты изгиба. Из нескольких различных способов предсказания внутреннего радиуса ни один не идеален, но этот примерно так же хорош, как и получается.Тем не менее, у гибки слишком много переменных, чтобы добиться стопроцентной точности.
При формовании воздухом обязательно, чтобы инженер или программист проинформировал техника о наборах инструментов, для которых был разработан любой изгиб. Более того, технический специалист должен осознавать абсолютную важность использования этих инструментов для получения качественных деталей.
В следующем месяце мы расскажем, как рассчитать внутренний радиус изгиба, когда связь между внутренним радиусом и толщиной материала становится очень большой — изгиб с большим радиусом.Изгибы с большим радиусом имеют проблемы с углом матрицы, шириной матрицы, множественным поломкой и, конечно же, очень большим упругим возвратом.
В кроличью нору еще есть куда пойти, но это того стоит.
Обзор формул изгиба
Эти формулы для допуска на изгиб, внешнего отступа и вычета изгиба хорошо известны, и каждое значение можно использовать по-разному для расчета компоновки плоской заготовки детали.
Формулы BA = [(0,017453 × Rp) + (0.0078 × Mt)] × Дополнительные степени изгиба OSSB = [Касательная (угол изгиба / 2)] × (Mt + Rp) BD = (OSSB × 2) — BA Позиция Rp = радиус вершины пуансона (нижняя часть) или плавающий внутренний радиус (воздушное формование) Mt = толщина материала BA = припуск на изгиб BD = вычет изгиба OSSB = внешний отступ 0,017453 = π / 180 0,0078 = коэффициент K × π / 180 коэффициент K = 0. 446
446 Примечание. Формула OSSB может иметь включенный или дополнительный угол изгиба, в зависимости от того, как вы выполняете расчеты плоской заготовки. Подробнее об этом см. «Основы применения функций гибки» на сайте www.thefabricator.com.
Онлайн-калькулятор луча | Калькулятор изгибающего момента и силы сдвига выступающей балки
NEWS | ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ | ЛИСТ
Бесплатный онлайн-калькулятор предназначен для расчета величины поперечной силы и изгибающего момента в точке свисающей балки, несущей равномерно распределенную нагрузку (UDL), или точечной нагрузки в любой точке по длине.
Он даже обеспечивает количество наивысшего изгибающего момента, в котором его местоположение появляется. Калькуляторы соответствуют установленным формулам для поперечной силы и изгибающего момента нависающей балки и предложены преподавателями колледжа.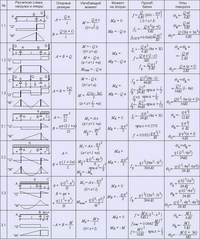
В случае объединения нагрузок можно реализовать закон суперпозиции для вычисления результирующих величин.
Примеры нагрузок для нависающей балки: калькулятор предлагает результаты для поперечной силы и изгибающего момента на части нависающей балки, вероятно, в направлении точечной нагрузки на пролет.Вычисленные величины можно использовать для схематического изображения изгибающего момента и поперечной силы.
Калькулятор также можно использовать для определения ординат диаграммы линий влияния для зданий.
Равномерная нагрузка на балку: калькулятор предлагает результаты для поперечной силы и изгибающего момента на части выступающей балки, вероятно, по отношению к равномерно распределенной нагрузке на участке пролета. Пожалуйста, сделайте ссылку на представление и введите количество нагрузки и пролеты в форме, представленной ниже, а затем нажмите «Рассчитать».
Предполагается, что все восходящие рабочие нагрузки положительны, а нисходящие — отрицательны.

 В маркировке после номера присутствует буква «У». Норматив предусматривает производство изделий с высотой стенки 50-400 мм, шириной полки 32-115 мм, толщиной стенки 4,4-8,0 мм, толщиной полки 7,0-13,5 мм. Если в обозначении между номером профиля и буквой «У» присутствует буква «а», это означает, что изделие имеет увеличенную ширину и толщину полок. Основная область применения этого вида швеллера – строительство. Благодаря некоторому утолщению во внутренних углах, профиль обладает повышенными прочностными характеристиками. Такая металлопродукция используется в каркасном строительстве, для устройства перекрытий, сооружения ферм, лестниц, малых архитектурных форм, металлических конструкций различного назначения.
В маркировке после номера присутствует буква «У». Норматив предусматривает производство изделий с высотой стенки 50-400 мм, шириной полки 32-115 мм, толщиной стенки 4,4-8,0 мм, толщиной полки 7,0-13,5 мм. Если в обозначении между номером профиля и буквой «У» присутствует буква «а», это означает, что изделие имеет увеличенную ширину и толщину полок. Основная область применения этого вида швеллера – строительство. Благодаря некоторому утолщению во внутренних углах, профиль обладает повышенными прочностными характеристиками. Такая металлопродукция используется в каркасном строительстве, для устройства перекрытий, сооружения ферм, лестниц, малых архитектурных форм, металлических конструкций различного назначения.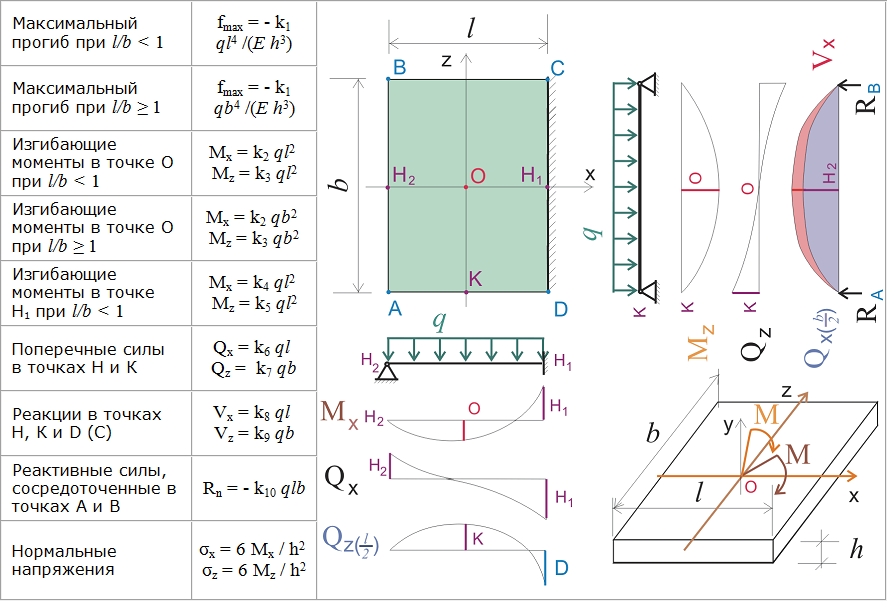

 Временные перегородки из ГКЛ, стационарное оборудование, складируемые материалы, а также как результат изменения влажности или усадки.
Временные перегородки из ГКЛ, стационарное оборудование, складируемые материалы, а также как результат изменения влажности или усадки. ГОСТ 8639-82 (для изделий квадратного сечения) и ГОСТ 8645-68 (прямоугольного) регламентированы: момент инерции трубы (I), длину пролета (L), нагрузку (Q), модуль упругости в соответствии СНиП. Схемы вычислений индивидуальные и для каждого случая подбирается формула.
ГОСТ 8639-82 (для изделий квадратного сечения) и ГОСТ 8645-68 (прямоугольного) регламентированы: момент инерции трубы (I), длину пролета (L), нагрузку (Q), модуль упругости в соответствии СНиП. Схемы вычислений индивидуальные и для каждого случая подбирается формула. Тавр укладывается на один пролет. Целый двутавровый профиль – на один или несколько пролетов. Эти металлоизделия очень массивны. Плюсом их использования является возможность использования в качестве самостоятельного элемента без применения усиливающих деталей.
Тавр укладывается на один пролет. Целый двутавровый профиль – на один или несколько пролетов. Эти металлоизделия очень массивны. Плюсом их использования является возможность использования в качестве самостоятельного элемента без применения усиливающих деталей.
 5.
5. включили проверку стоек по значению гибкости.
включили проверку стоек по значению гибкости.
 Это тот случай, когда высота поперечного сечения значительно меньше длины балки (в 10 и более раз), а также поперечное сечение не является многослойным (не сечение сэндвич-типа).
Это тот случай, когда высота поперечного сечения значительно меньше длины балки (в 10 и более раз), а также поперечное сечение не является многослойным (не сечение сэндвич-типа).