Окружность вписанная в правильный шестиугольник: Радиус вписанной окружности в правильный шестиугольник

Контрольная работа по геометрии на тему «Правильные многоугольники»

Контрольная работа № 2

Правильные многоугольники

Вариант 1

1. Найдите углы правильного 45-угольника.

2. Найдите длину окружности, вписанной в правильный треугольник со стороной 11 см.

3. В окружность вписан квадрат со стороной 4 см. Найдите сторону правильного шестиугольника, описанного около этой окружности.

4. Радиус окружности, описанной около правильного многоугольника, равен 4 см, а сторона многоугольника — 4√3 см. Найдите: 1) радиус окружности, вписанной в многоугольник; 2) количество сторон многоугольника.

5. Сторона треугольника равна 2√3 см, а прилежащие к ней углы равны 35° и 85°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.

Контрольная работа № 2

Правильные многоугольники

Вариант 2

1.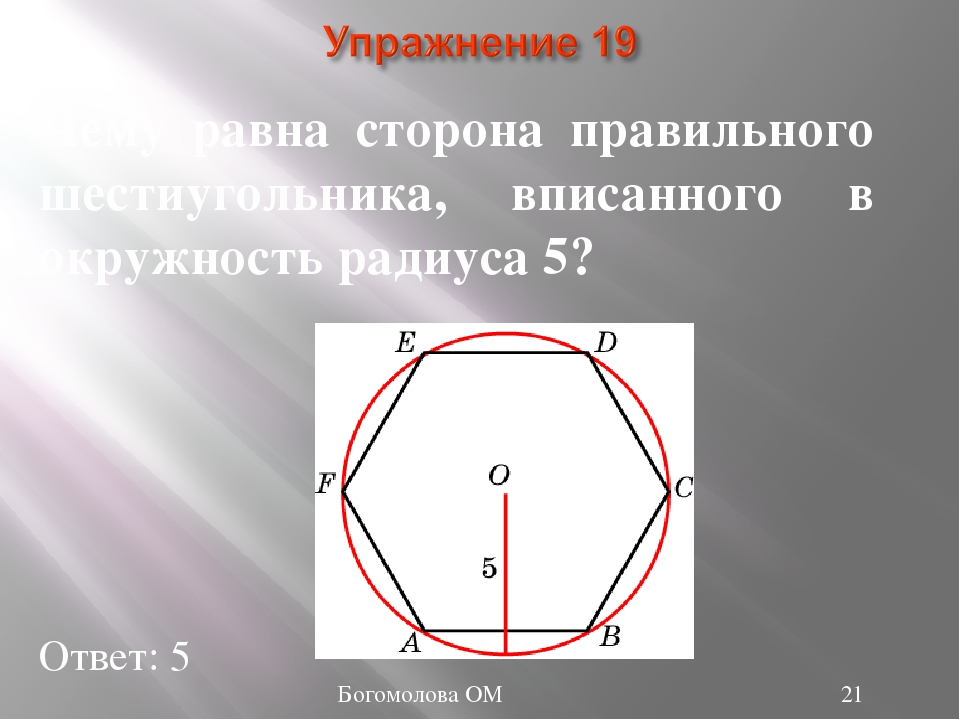 Найдите углы правильного 35-угольника.

2. Найдите площадь круга, вписанного в правильный шестиугольник со стороной 24 см.

3. Около окружности описан правильный треугольник со стороной 16 см. Найдите сторону квадрата, вписанного в эту окружность.

4. Радиус окружности, вписанной в правильный многоугольник, равен 5 см, а сторона многоугольника — 10 см. Найдите: 1) радиус окружности, описанной около многоугольника; 2) количество сторон многоугольника.

5. Сторона треугольника равна 8√2 см, а прилежащие к ней углы равны 45° и 90°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.

Контрольная работа № 2

Правильные многоугольники

Вариант 3

1. Найдите углы правильного 25-угольника.

2. Найдите длину окружности, описанной около правильного треугольника со стороной 19 см.

3. В окружность вписан правильный шестиугольник со стороной 7 см. Найдите сторону правильного треугольника, описанного около этой окружности.

4. Радиус окружности, описанной около правильного многоугольника, равен 8√2 см, а радиус вписанной в него окружности — 8 см. Найдите: 1) сторону многоугольника; 2) количество сторон многоугольника.

5. Сторона треугольника равна 5 см, а прилежащие к ней углы равны 35° и 115°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.

Контрольная работа № 2

Правильные многоугольники

Вариант 4

1. Найдите углы правильного 27-угольника.

2. Найдите площадь круга, описанного около квадрата со стороной 14 см.

3. Около окружности описан квадрат со стороной 16 см. Найдите сторону правильного треугольника, вписанного в эту окружность.

4. Радиус окружности, вписанной в правильный многоугольник, равен 12 см, а сторона многоугольника — 8√3 см. Найдите: 1) радиус окружности, описанной около многоугольника; 2) количество сторон многоугольника.

5. Сторона треугольника равна 8√3 см, а прилежащие к ней углы равны 20° и 40°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.

Контрольная работа № 2

Правильные многоугольники

Вариант 6

1. Найдите углы правильного 76-угольника.

2. Найдите длину окружности, вписанной в правильный треугольник со стороной 7 см.

3. В окружность вписан квадрат со стороной 6 см. Найдите сторону правильного шестиугольника, описанного около этой окружности.

4. Радиус окружности, описанной около правильного многоугольника, равен 4 см, а сторона многоугольника — 4√3 см. Найдите: 1) радиус окружности, вписанной в многоугольник; 2) количество сторон многоугольника.

5. Сторона треугольника равна 4√3 см, а прилежащие к ней углы равны 45° и 75°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.

Контрольная работа № 2

Правильные многоугольники

Вариант 6

1. Найдите углы правильного 24-угольника.

2. Найдите площадь круга, вписанного в правильный шестиугольник со стороной 5 см.

3. Около окружности описан правильный треугольник со стороной 8 см. Найдите сторону квадрата, вписанного в эту окружность.

4. Радиус окружности, вписанной в правильный многоугольник, равен 5 см, а сторона многоугольника — 10 см. Найдите: 1) радиус окружности, описанной около многоугольника; 2) количество сторон многоугольника.

5. Сторона треугольника равна 8√2 см, а прилежащие к ней углы равны 40° и 95°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.

Контрольная работа № 2

Правильные многоугольники

Вариант 7

1. Найдите углы правильного 34-угольника.

2. Найдите длину окружности, описанной около правильного треугольника со стороной 7 см.

3. В окружность вписан правильный шестиугольник со стороной 6 см. Найдите сторону правильного треугольника, описанного около этой окружности.

4. Радиус окружности, описанной около правильного многоугольника, равен 8√2 см, а радиус вписанной в него окружности — 8 см. Найдите: 1) сторону многоугольника; 2) количество сторон многоугольника.

5. Сторона треугольника равна 12 см, а прилежащие к ней углы равны 65° и 85°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.

Контрольная работа № 2

Правильные многоугольники

Вариант 8

1.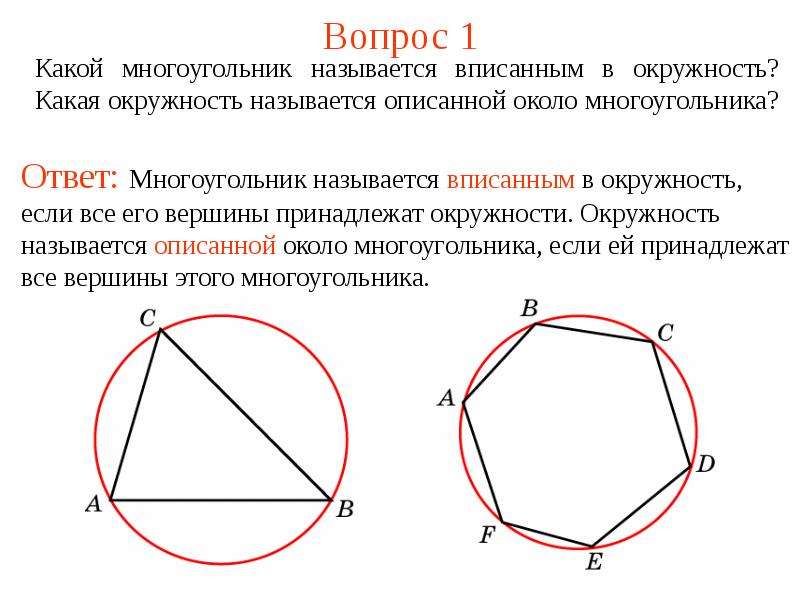 Найдите углы правильного 32-угольника.

2. Найдите площадь круга, описанного около квадрата со стороной 12 см.

3. Около окружности описан квадрат со стороной 14 см. Найдите сторону правильного треугольника, вписанного в эту окружность.

4. Радиус окружности, вписанной в правильный многоугольник, равен 12 см, а сторона многоугольника — 8√3 см. Найдите: 1) радиус окружности, описанной около многоугольника; 2) количество сторон многоугольника.

5. Сторона треугольника равна 7√3 см, а прилежащие к ней углы равны 30° и 30°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.

Контрольная работа № 2

Правильные многоугольники

Вариант 9

1. Найдите углы правильного 64-угольника.

2. Найдите длину окружности, вписанной в правильный треугольник со стороной 9 см.

3. В окружность вписан квадрат со стороной 18 см. Найдите сторону правильного шестиугольника, описанного около этой окружности.

4. Радиус окружности, описанной около правильного многоугольника, равен 4 см, а сторона многоугольника — 4√3 см. Найдите: 1) радиус окружности, вписанной в многоугольник; 2) количество сторон многоугольника.

5. Сторона треугольника равна 4√3 см, а прилежащие к ней углы равны 55° и 65°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.

Контрольная работа № 2

Правильные многоугольники

Вариант 10

1. Найдите углы правильного 28-угольника.

2. Найдите площадь круга, вписанного в правильный шестиугольник со стороной 10 см.

3. Около окружности описан правильный треугольник со стороной 20 см. Найдите сторону квадрата, вписанного в эту окружность.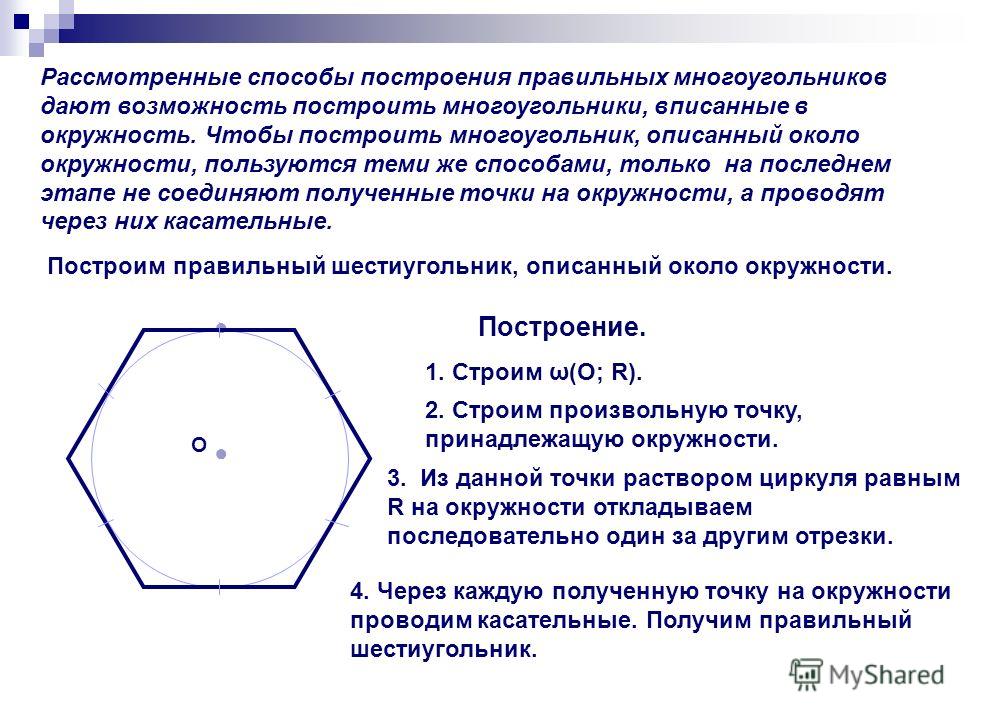

4. Радиус окружности, вписанной в правильный многоугольник, равен 5 см, а сторона многоугольника — 10 см. Найдите: 1) радиус окружности, описанной около многоугольника; 2) количество сторон многоугольника.

5. Сторона треугольника равна 4√2 см, а прилежащие к ней углы равны 65° и 70°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.

Контрольная работа № 2

Правильные многоугольники

Вариант 11

1. Найдите углы правильного 58-угольника.

2. Найдите длину окружности, описанной около правильного треугольника со стороной 18 см.

3. В окружность вписан правильный шестиугольник со стороной 11 см. Найдите сторону правильного треугольника, описанного около этой окружности.

4. Радиус окружности, описанной около правильного многоугольника, равен 8√2 см, а радиус вписанной в него окружности — 8 см. Найдите: 1) сторону многоугольника; 2) количество сторон многоугольника.

5. Сторона треугольника равна 8 см, а прилежащие к ней углы равны 55° и 95°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.

Контрольная работа № 2

Правильные многоугольники

Вариант 12

1. Найдите углы правильного 46-угольника.

2. Найдите площадь круга, описанного около квадрата со стороной 12 см.

3. Около окружности описан квадрат со стороной 24 см. Найдите сторону правильного треугольника, вписанного в эту окружность.

4. Радиус окружности, вписанной в правильный многоугольник, равен 12 см, а сторона многоугольника — 8√3 см. Найдите: 1) радиус окружности, описанной около многоугольника; 2) количество сторон многоугольника.

5. Сторона треугольника равна 9√3 см, а прилежащие к ней углы равны 20° и 40°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.

Контрольная работа № 2

Правильные многоугольники

Вариант 13

1. Найдите углы правильного 48-угольника.

2. Найдите длину окружности, вписанной в правильный треугольник со стороной 24 см.

3. В окружность вписан квадрат со стороной 14 см. Найдите сторону правильного шестиугольника, описанного около этой окружности.

4. Радиус окружности, описанной около правильного многоугольника, равен 4 см, а сторона многоугольника — 4√3 см. Найдите: 1) радиус окружности, вписанной в многоугольник; 2) количество сторон многоугольника.

5. Сторона треугольника равна 8√3 см, а прилежащие к ней углы равны 25° и 95°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.

Контрольная работа № 2

Правильные многоугольники

Вариант 14

1. Найдите углы правильного 78-угольника.

2. Найдите площадь круга, вписанного в правильный шестиугольник со стороной 14 см.

3. Около окружности описан правильный треугольник со стороной 8 см. Найдите сторону квадрата, вписанного в эту окружность.

4. Радиус окружности, вписанной в правильный многоугольник, равен 5 см, а сторона многоугольника — 10 см. Найдите: 1) радиус окружности, описанной около многоугольника; 2) количество сторон многоугольника.

5. Сторона треугольника равна 12√2 см, а прилежащие к ней углы равны 45° и 90°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.

Контрольная работа № 2

Правильные многоугольники

Вариант 15

1. Найдите углы правильного 15-угольника.

2. Найдите длину окружности, описанной около правильного треугольника со стороной 15 см.

3. В окружность вписан правильный шестиугольник со стороной 30 см. Найдите сторону правильного треугольника, описанного около этой окружности.

4. Радиус окружности, описанной около правильного многоугольника, равен 8√2 см, а радиус вписанной в него окружности — 8 см. Найдите: 1) сторону многоугольника; 2) количество сторон многоугольника.

5. Сторона треугольника равна 15 см, а прилежащие к ней углы равны 45° и 105°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.

Контрольная работа № 2

Правильные многоугольники

Вариант 16

1. Найдите углы правильного 84-угольника.

2. Найдите площадь круга, описанного около квадрата со стороной 16 см.

3. Около окружности описан квадрат со стороной 6 см. Найдите сторону правильного треугольника, вписанного в эту окружность.

4. Радиус окружности, вписанной в правильный многоугольник, равен 12 см, а сторона многоугольника — 8√3 см. Найдите: 1) радиус окружности, описанной около многоугольника; 2) количество сторон многоугольника.

5. Сторона треугольника равна 3√3 см, а прилежащие к ней углы равны 20° и 40°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.

Контрольная работа № 2

Правильные многоугольники

Вариант 17

1. Найдите углы правильного 84-угольника.

2. Найдите длину окружности, вписанной в правильный треугольник со стороной 17 см.

3. В окружность вписан квадрат со стороной 34 см. Найдите сторону правильного шестиугольника, описанного около этой окружности.

4. Радиус окружности, описанной около правильного многоугольника, равен 4 см, а сторона многоугольника — 4√3 см. Найдите: 1) радиус окружности, вписанной в многоугольник; 2) количество сторон многоугольника.

5. Сторона треугольника равна 7√3 см, а прилежащие к ней углы равны 75° и 45°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.

Контрольная работа № 2

Правильные многоугольники

Вариант 18

1. Найдите углы правильного 98-угольника.

2. Найдите площадь круга, вписанного в правильный шестиугольник со стороной 18 см.

3. Около окружности описан правильный треугольник со стороной 12 см. Найдите сторону квадрата, вписанного в эту окружность.

4. Радиус окружности, вписанной в правильный многоугольник, равен 5 см, а сторона многоугольника — 10 см. Найдите: 1) радиус окружности, описанной около многоугольника; 2) количество сторон многоугольника.

5. Сторона треугольника равна 12√2 см, а прилежащие к ней углы равны 45° и 90°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.

Контрольная работа № 2

Правильные многоугольники

Вариант 19

1. Найдите углы правильного 76-угольника.

2. Найдите длину окружности, описанной около правильного треугольника со стороной 35 см.

3. В окружность вписан правильный шестиугольник со стороной 17 см. Найдите сторону правильного треугольника, описанного около этой окружности.

4. Радиус окружности, описанной около правильного многоугольника, равен 8√2 см, а радиус вписанной в него окружности — 8 см. Найдите: 1) сторону многоугольника; 2) количество сторон многоугольника.

5. Сторона треугольника равна 14 см, а прилежащие к ней углы равны 15° и 135°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.

Контрольная работа № 2

Правильные многоугольники

Вариант 20

1. Найдите углы правильного 20-угольника.

2. Найдите площадь круга, описанного около квадрата со стороной 26 см.

3. Около окружности описан квадрат со стороной 12 см. Найдите сторону правильного треугольника, вписанного в эту окружность.

4. Радиус окружности, вписанной в правильный многоугольник, равен 12 см, а сторона многоугольника — 8√3 см. Найдите: 1) радиус окружности, описанной около многоугольника; 2) количество сторон многоугольника.

5. Сторона треугольника равна 10√3 см, а прилежащие к ней углы равны 100° и 20°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.

Контрольная работа № 2

Правильные многоугольники

Вариант 21

1. Найдите углы правильного 20-угольника.

2. Найдите длину окружности, вписанной в правильный треугольник со стороной 21 см.

3. В окружность вписан квадрат со стороной 24 см. Найдите сторону правильного шестиугольника, описанного около этой окружности.

4. Радиус окружности, описанной около правильного многоугольника, равен 4 см, а сторона многоугольника — 4√3 см. Найдите: 1) радиус окружности, вписанной в многоугольник; 2) количество сторон многоугольника.

5. Сторона треугольника равна 6√3 см, а прилежащие к ней углы равны 15° и 105°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.

Контрольная работа № 2

Правильные многоугольники

Вариант 22

1. Найдите углы правильного 75-угольника.

2. Найдите площадь круга, вписанного в правильный шестиугольник со стороной 22 см.

3. Около окружности описан правильный треугольник со стороной 24 см. Найдите сторону квадрата, вписанного в эту окружность.

4. Радиус окружности, вписанной в правильный многоугольник, равен 5 см, а сторона многоугольника — 10 см. Найдите: 1) радиус окружности, описанной около многоугольника; 2) количество сторон многоугольника.

5. Сторона треугольника равна 5√2 см, а прилежащие к ней углы равны 85° и 50°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.

Контрольная работа № 2

Правильные многоугольники

Вариант 23

1. Найдите углы правильного 64-угольника.

2. Найдите длину окружности, описанной около правильного треугольника со стороной 23 см.

3. В окружность вписан правильный шестиугольник со стороной 23 см. Найдите сторону правильного треугольника, описанного около этой окружности.

4. Радиус окружности, описанной около правильного многоугольника, равен 8√2 см, а радиус вписанной в него окружности — 8 см. Найдите: 1) сторону многоугольника; 2) количество сторон многоугольника.

5. Сторона треугольника равна 10 см, а прилежащие к ней углы равны 10° и 20°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.

Контрольная работа № 2

Правильные многоугольники

Вариант 24

1. Найдите углы правильного 54-угольника.

2. Найдите площадь круга, описанного около квадрата со стороной 32 см.

3. Около окружности описан квадрат со стороной 10 см. Найдите сторону правильного треугольника, вписанного в эту окружность.

4. Радиус окружности, вписанной в правильный многоугольник, равен 12 см, а сторона многоугольника — 8√3 см. Найдите: 1) радиус окружности, описанной около многоугольника; 2) количество сторон многоугольника.

5. Сторона треугольника равна 12√3 см, а прилежащие к ней углы равны 25° и 35°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.

Контрольная работа № 2

Правильные многоугольники

Вариант 25

1. Найдите углы правильного 72-угольника.

2. Найдите длину окружности, вписанной в правильный треугольник со стороной 25 см.

3. В окружность вписан квадрат со стороной 34 см. Найдите сторону правильного шестиугольника, описанного около этой окружности.

4. Радиус окружности, описанной около правильного многоугольника, равен 4 см, а сторона многоугольника — 4√3 см. Найдите: 1) радиус окружности, вписанной в многоугольник; 2) количество сторон многоугольника.

5. Сторона треугольника равна 20√3 см, а прилежащие к ней углы равны 45° и 75°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.

Контрольная работа № 2

Правильные многоугольники

Вариант 26

1. Найдите углы правильного 58-угольника.

2. Найдите площадь круга, вписанного в правильный шестиугольник со стороной 26 см.

3. Около окружности описан правильный треугольник со стороной 34 см. Найдите сторону квадрата, вписанного в эту окружность.

4. Радиус окружности, вписанной в правильный многоугольник, равен 5 см, а сторона многоугольника — 10 см. Найдите: 1) радиус окружности, описанной около многоугольника; 2) количество сторон многоугольника.

5. Сторона треугольника равна 14√2 см, а прилежащие к ней углы равны 45° и 90°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.

Контрольная работа № 2

Правильные многоугольники

Вариант 27

1. Найдите углы правильного 27-угольника.

2. Найдите длину окружности, описанной около правильного треугольника со стороной 12 см.

3. В окружность вписан правильный шестиугольник со стороной 17 см. Найдите сторону правильного треугольника, описанного около этой окружности.

4. Радиус окружности, описанной около правильного многоугольника, равен 8√2 см, а радиус вписанной в него окружности — 8 см. Найдите: 1) сторону многоугольника; 2) количество сторон многоугольника.

5. Сторона треугольника равна 16 см, а прилежащие к ней углы равны 35° и 115°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.

Контрольная работа № 2

Правильные многоугольники

Вариант 28

1. Найдите углы правильного 28-угольника.

2. Найдите площадь круга, описанного около квадрата со стороной 28 см.

3. Около окружности описан квадрат со стороной 38 см. Найдите сторону правильного треугольника, вписанного в эту окружность.

4. Радиус окружности, вписанной в правильный многоугольник, равен 12 см, а сторона многоугольника — 8√3 см. Найдите: 1) радиус окружности, описанной около многоугольника; 2) количество сторон многоугольника.

5. Сторона треугольника равна 18√3 см, а прилежащие к ней углы равны 15° и 45°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.

Контрольная работа № 2

Правильные многоугольники

Вариант 29

1. Найдите углы правильного 30-угольника.

2. Найдите длину окружности, описанной около правильного треугольника со стороной 30 см.

3. В окружность вписан правильный шестиугольник со стороной 29 см. Найдите сторону правильного треугольника, описанного около этой окружности.

4. Радиус окружности, описанной около правильного многоугольника, равен 8√2 см, а радиус вписанной в него окружности — 8 см. Найдите: 1) сторону многоугольника; 2) количество сторон многоугольника.

5. Сторона треугольника равна 18 см, а прилежащие к ней углы равны 15° и 135°. Найдите длины дуг, на которые делят описанную окружность треугольника его вершины.

Самостоятельная работа по теме: Правильные многоугольники

С амостоятельная работа по теме: «Правильные многоугольники ,площадь правильного треугольника, окружность описанная и вписанная в правильный треугольник» 1 вариант Окружность впи­са­на в квадрат. Най­ди­те пло­щадь квадрата. Р адиус окружности, вписанной в трапецию, равен 48. Найдите высоту этой трапеции. Окружность с цен­тром в точке O опи­са­на около рав­но­бед­рен­но­го тре­уголь­ни­ка ABC, в ко­то­ром AB = BC и ∠ABC = 66°. Най­ди­те ве­ли­чи­ну угла BOC. Ответ дайте в градусах. Радиус окружности, описанной около квадрата, равен   Найдите длину стороны этого квадрата.. 5 .Сторона правильного треугольника, вписанного в окружность, равна . Найдите радиус описанной окружности, радиус вписанной окружности, периметр и площадь многоугольника. 6.Около правильного треугольника описанна окружность радиусом . Найдите радиус вписанной окружности в правильный четырехугольник, сторону, периметр и площадь многоугольника. 7.В правильный шестиугольник вписана окружность радиусом 6. Найдите радиус описанной окружности около правильного шестиугольника, сторону, периметр и площадь многоугольника.

Самостоятельная работа по теме: «Правильные многоугольники площадь правильного треугольника, окружность описанная и вписанная в правильный треугольник» 2 вариант Радиус окружности, вписанной в трапецию, равен 36. Найдите высоту этой трапеции. О кружность с цен­тром в точке O опи­са­на около рав­но­бед­рен­но­го тре­уголь­ни­ка ABC, в ко­то­ром AB = BC и ∠ABC = 22°. Най­ди­те ве­ли­чи­ну угла BOC. Ответ дайте в градусах. Найдите пло­щадь квадрата, опи­сан­но­го во­круг окруж­но­сти ра­ди­у­са 7. 4 . Радиус окружности, описанной около квадрата, равен   Найдите длину стороны этого квадрата. 5.Сторона правильного четырехугольника, вписанного в окружность, равна 2. Найдите радиус описанной окружности, радиус вписанной окружности, периметр и площадь многоугольника. 6.Около правильного четырехугольника описанна окружность радиусом . Найдите радиус вписанной окружности в правильный четырехугольник, сторону, периметр и площадь многоугольника. 7.В правильный шестиугольник вписана окружность радиусом 9. Найдите радиус описанной окружности около правильного шестиугольника, сторону, периметр и площадь многоугольника.

Тест по геометрии по теме: «Правильные многоугольники»

Тест  по геометрии  по теме: «Правильные многоугольники» составлен в двух вариантах.

Вариант1

1.Какой треугольник является правильным? 

А) равнобедренный;  Б) равносторонний;    В) прямоугольный;  Г) любой.          

 2. Квадрат вписан в окружность радиуса 6см, Найдите радиус окружности, вписанной в этот квадрат   А)3см;   Б)6 см;   В)3

  3. Радиус окружности, вписанной в правильный треугольник, равен  Найдите периметр шестиугольника.      

 А)12см;   Б)18см;   В)6см;  Г)3см.

4. Правильный шестиугольник вписан в окружность радиуса 8см. Найдите наименьшую диагональ шестиугольника.   

 А) 4  В) 8 см;  Г)4см.  

5. Сторона правильного многоугольника  а = 3см, а радиус вписанной окружности

 r = 2см. Найдите радиус описанной окружности.

А) 2,5см;  Б)5см;  В)3см;  Г)1,5см.

Просмотр содержимого документа
«Тест по геометрии по теме: «Правильные многоугольники»»

Тест по геометрии по теме: «Правильные многоугольники»

Вариант1

1.Какой треугольник является правильным?

А) равнобедренный; Б) равносторонний; В) прямоугольный; Г) любой.

2. Квадрат вписан в окружность радиуса 6см, Найдите радиус окружности, вписанной в этот квадрат А)3см; Б)6 см; В)3

3. Радиус окружности, вписанной в правильный треугольник, равен Найдите периметр шестиугольника.

А)12см; Б)18см; В)6см; Г)3см.

4. Правильный шестиугольник вписан в окружность радиуса 8см. Найдите наименьшую диагональ шестиугольника.

А) 4 В) 8 см; Г)4см.

5. Сторона правильного многоугольника а = 3см, а радиус вписанной окружности

r = 2см. Найдите радиус описанной окружности.

А) 2,5см; Б)5см; В)3см; Г)1,5см.

Вариант 2

1. Какой четырехугольник является правильным?

А) ромб; Б) прямоугольник;

В) квадрат; Г) любой.

2. Квадрат описан около окружности радиуса 3см, Найдите радиус окружности, описанной около этого квадрата.

А)6см; Б)3 см; В)2

3. Радиус окружности, вписанной в правильный треугольник, равен Найдите периметр шестиугольника.

А)12см; Б)24см; В)6см; Г)12см.

4. Правильный треугольник вписан в окружность радиуса 9см. Найдите высоту треугольника.

А) 13,5 В) 6 см; Г) 6,75см.

5. Сторона правильного многоугольника а = 6см, а радиус описанной окружности R = 5см. Найдите радиус вписанной окружности.

А) 2,5см; Б)4см; В)3см; Г)2см.

как найти радиус шестиугольника

Используя площадь шестиугольника и тригонометрические свойства внутренних треугольников, вы можете найти радиус шестиугольника. У него неофициальный рекорд по количеству часов в бакалавриате Техасского университета в Остине. Для использования калькулятора необходимо включить JavaScript. Поскольку вписанный круг касается сторон шестиугольника, мы можем провести высоту от центра круга до длины стороны шестиугольника. В правильном шестиугольнике разделите фигуру на треугольники.Простой калькулятор геометрии, который используется для определения радиуса описанной окружности правильного шестиугольника с известными значениями сторон. апофема и радиус: площадь с использованием апофемы: апофема правильного многоугольника: как найти апофему многоугольника: найти апофему шестиугольника: площадь многоугольника с апофемой: апофема пирамиды: апофема восьмиугольника: как найти площадь шестиугольника с помощью апофема: как найти апофему квадрата: как найти апофему правильного пятиугольника Формула для вычисления радиуса вписанной окружности правильного шестиугольника, если задана сторона (r): радиус окружности, вписанной в правильный шестиугольник: = Цифра 2 1 2 4 6 10 F Используйте этот калькулятор для вычисления свойств правильного многоугольника.Образец. … Как определить площадь правильного шестиугольника — YouTube. Решать. Расчеты на правильном шестиугольнике, многоугольнике с 6 вершинами. Шестиугольник — это самый высокий правильный многоугольник, который допускает правильную мозаику (мозаику). Найдите площадь одного треугольника. Помните, чтобы найти площадь треугольника, умножьте основание на высоту, а затем разделите на 2. Правильный шестиугольник — это многоугольник с шестью сторонами равной длины. Заменять. … нахождение площади неправильного шестиугольника отличается от того, как мы находим площадь правильного шестиугольника.Для этого правильный шестиугольник является точечно-симметричным и вращательно-симметричным при повороте на 60 ° или кратном этому. Величина 30 градусов — это мера угла между радиусом и апофемой, которая представляет собой длину между центром шестиугольника и серединой стороны. В этом случае это диаметр описанной окружности, т. Е. Длина ребра, диагонали, периметр и радиус имеют одинаковые единицы (например, найти длину диагонали во вписанном (нерегулярном) шестиугольнике). спасая друг друга, превращают спасенного человека в крестраж? Вычислите площадь каждого треугольника один за другим и умножьте ее на 6, чтобы найти общую площадь шестиугольника.2. Количество диагоналей в шестиугольнике равно девяти. Вновь образованный треугольник представляет собой прямоугольный треугольник 30 ° -60 ° -90 °. Ченс Э. Гартнер начал профессионально писать в 2008 году, работая совместно с FEMA. Красный отрезок линии — _____. 600 разделить на 2,598 равно 230,94. У правильных шестиугольников все основания одинаковой длины, в то время как неправильные шестиугольники не имеют одинаковой длины. Формула периметра шестиугольника записывается как — \ [\ large P = 6 \ times a \] Пояснение:. Расчеты на правильном шестиугольнике, многоугольнике с 6 вершинами.Затем нажмите Рассчитать. Радиус описанной окружности равен длине… Соедините каждую вершину шестиугольника с центром C шестиугольника, чтобы образовать 6 равных треугольников. Используя площадь шестиугольника и тригонометрические свойства внутренних треугольников, вы можете найти радиус шестиугольника. Вычислите синус и косинус 30 градусов, а затем умножьте эти две величины. Введите любую 1 переменную плюс количество сторон или имя многоугольника. Калькулятор шестиугольника. Радиус правильного шестиугольника равен 12. Найдите: a.Введите одно значение и выберите количество десятичных знаков. Многоугольник — это замкнутая фигура с 3 или более сторонами. метр), площадь имеет эту единицу в квадрате (например, чтобы найти площадь вписанного круга, нам нужно сначала найти радиус. L будет представлять это число. Радиус равен длине стороны. Когда он выпуклый, шестиугольник (или многоугольник в целом) имеет ни один из его внутренних углов не превышает 180 °. Длина одной стороны b. Апофема c. Область НЕ МОЖЕТ КОПИРОВАТЬ РИСУНОК Если вы нарисуете шестиугольник, вписанный в круг, и проведете радиусы к углам шестиугольника, вы получите создать равнобедренные треугольники, шесть из них.2), что равно 158,9 (здесь r = 7,09). Используйте правильный шестиугольник ниже, чтобы ответить на следующие вопросы. Длина радиуса позволяет разделить шестиугольник на шесть равных треугольников, которые помогают вычислить площадь шестиугольника. Правильные шестиугольники — это многоугольники с шестью равными сторонами. Правильный шестиугольник можно разрезать на шесть равносторонних треугольников, а равносторонний треугольник можно разделить на два треугольника 30 ° — 60 ° — 90 °. Чтобы решить эту проблему, мы нарисовали перпендикуляр от центра в одну сторону.Решать. Если вы сделаете набросок, вы должны увидеть, что рисование двух радиусов, каждый к смежным вершинам, даст равносторонний треугольник. Площадь и периметр шестиугольника. Радиус правильного шестиугольника, также называемый радиусом описанной окружности, — это расстояние от его центра до его вершин или точек. Используя площадь шестиугольника и тригонометрические свойства внутренних треугольников, вы можете найти радиус шестиугольника. Формула для определения площади шестиугольника: Area = (3√3 s2) / 2, где s — длина стороны правильного шестиугольника.Вычисляет радиус и площадь вписанной окружности правильного многоугольника. Авторские права 2021 Leaf Group Ltd. / Leaf Group Media, Все права защищены. $ \ begingroup $ да, все стороны равны. Кроме того, правильный шестиугольник аксиально симметричен длинным диагоналям и средним линиям. Радиус правильного многоугольника — это расстояние от центра до любой вершины, оно будет одинаковым для любой вершины. Короткая диагональ — это линия между двумя вершинами, между которыми есть третья вершина. Это апофема.Если вы уже знаете длину стороны, вы можете просто записать ее; в этом случае длина стороны 9 см. Как найти площадь правильного шестиугольника с радиусом? Поскольку это правильный шестиугольник, апофему можно рассчитать по одной из сторон, и поэтому вам нужно только ввести длину стороны в наш калькулятор образования ниже. Вычислите синус и косинус 30 градусов, а затем умножьте эти две величины. Например, площадь шестиугольника равна 600. Когда он не работает над своим детским книжным шедевром, он пишет образовательные статьи, посвященные начальной математике и темам английского языка как иностранного.Длина стороны шестиугольника равна двум коротким сторонам прямоугольного треугольника. Радиус правильного шестиугольника определяется по формуле a (√3) / 2. Например, у вас может быть шестиугольник с длиной стороны 8 см. Итак, если мы хотим найти площадь этого небольшого кусочка пирога прямо здесь, мы можем просто найти площадь этого фрагмента или этого под-фрагмента, а затем умножить его на 2. Для этого примера квадратный корень из 230,94 составляет 15,197. Теперь площадь вписанного круга равна 3πa * a / 4. Как и любой многоугольник, шестиугольник может быть выпуклым или вогнутым, как показано на следующем рисунке.Разделите фигуру на треугольники. Умножение двух сумм дает 0,433. Умножьте это значение на шесть. Это равно длине стороны шестиугольника. Затем нажмите Рассчитать. Это также высота равностороннего треугольника. По этой причине правильный шестиугольник можно представить как состоящий из шести равносторонних треугольников. Вопрос: у меня радиус шестиугольника равен 1,5 км. Они бывают двух типов, а именно: правильная и неправильная шестиугольная призма. В качестве альтернативы, площадь можно найти, вычислив половину длины стороны, умноженной на… То есть линия от центра до любой вершины будет иметь такую ​​же длину, как и любая сторона.Используя площадь шестиугольника и тригонометрические свойства внутренних треугольников, вы можете найти радиус шестиугольника. Калькулятор геометрии многостороннего многоугольника См. Также: Полномасштабные шаблоны многоугольников для печати. Если апофема такова, и вопрос требует, чтобы мы решали длину одной из сторон, проблема может быть решена с помощью использования прямоугольных треугольников и триггерных функций. Пока известны один угол и длина одной стороны для правой треугольник, триггерные функции могут использоваться для решения загадочной стороны.Нахождение площади правильного шестиугольника. Введите одно значение и выберите количество десятичных знаков. Онлайн-калькулятор объема шестиугольной призмы поможет вам рассчитать объем шестиугольной призмы на основе стороны и высоты. Узнайте, как определить площадь и периметр многоугольников. Шестиугольник — это многоугольник с шестью сторонами и шестью вершинами. Подставьте значение длины основания, чтобы найти длину стороны шестиугольника. Радиус круга = длина одной из сторон правильного шестиугольника. Шесть углов в центре шестиугольника имеют одинаковую меру, поэтому каждый из них составляет 360/6 = 60 градусов.Каждая сторона должна быть равна по длине любой другой стороне. Правильный шестиугольник можно разбить на равносторонние треугольники по $ 6. Перпендикуляр разделяет сторону на две части. Формула для определения площади шестиугольника: Area = (3√3 s2) / 2, где s — длина стороны правильного шестиугольника. Его длина равна высоте. Затем, используя формулу площади (area = (a * p) / 2), вычислите ее площадь (здесь 130,59). Найдите радиус этого шестиугольника. Формула для вычисления радиуса вписанной окружности правильного шестиугольника, если задана сторона (r): радиус окружности, вписанной в правильный шестиугольник: = Цифра 2 1 2 4 6 10 F Каждый сегмент пунктирной линии равен _____.Проведите линию от центра к середине стороны шестиугольника. 6, умноженное на 0,433, равняется 2,598. Длина радиуса позволяет разделить шестиугольник на шесть равных треугольников, которые помогают вычислить площадь шестиугольника. Если вы уже знаете длину стороны, вы можете просто записать ее; в этом случае длина стороны 9 см. Длина каждой стороны 10 см. Как найти площадь шестиугольника? Сторона шестиугольника — 4. В правильном шестиугольнике радиус равен длине стороны. Калькулятор многоугольников.Лаборатория алгебры: площади и периметры правильных многоугольников. Открытая справка по математике: площадь правильного многоугольника. Если указан радиус круга, то как найти сторону правильного шестиугольника Привет, Вивек. Круговой радиус: чтобы найти радиус круга, описанного на правильном шестиугольнике, вам необходимо определить расстояние между центральной точкой шестиугольника (которая также является центром круга) и любой из вершин. Сумма внутренних углов многоугольника равна 180 (n — 2), где n — количество сторон.Шаг 1. Разделите шестиугольник на шесть равносторонних треугольников. Например. У них стороны равны 10. Определите длину любой стороны треугольника, измерив ее. Вычислите от обычного 3-угольника до обычного 1000-угольника. Умножьте сумму, рассчитанную на шаге 1, на 6. КАК НАЙТИ ПОВЕРХНОСТЬ ШЕСТИГРАННИК: Сторона: метр. Центральный угол шестиугольника = 60 °, образуя равнобедренный треугольник из 2 равных длин 1 см => площадь равнобедренного треугольника = (1/2) (1) (1) sin 60 °. Правильные шестиугольники — это многоугольники с шестью равными сторонами.[2] X Источник исследования Для этого нарисуйте линию, соединяющую каждую вершину или точку с противоположной вершиной. Шаг 2. Выберите один треугольник и обозначьте длину его основания. Вычисляет длину стороны, внутренний радиус (апофему), радиус описанной окружности, площадь и периметр. Как найти площадь шестиугольника? Радиус также является радиусом описанной окружности многоугольника, которая проходит через каждую вершину. В этой роли его иногда называют радиусом описанной окружности. Основание каждого равностороннего треугольника также равно 8… Из этого видео вы можете узнать, как найти площадь шестиугольника.Здесь мы увидим, как получить площадь n-стороннего правильного многоугольника с заданным радиусом. Соседние кромки образуют угол 120 °. но если я сделаю круг с радиусом, равным стороне шестиугольника, он не будет соответствовать шестиугольнику $ \ endgroup $ — puffy roxxy 1 мая 2016, 15:35 $ \ begingroup $ Это зависит от того, что дано. Радиус шестиугольника равен длине его сторон. Площадь = 37,68. Выберите и пересчитайте для отображения. (Расстояние от пересечения двух сторон до центра называется радиусом.Следовательно, шестиугольник имеет сумму внутренних углов 720 градусов, а каждый внутренний угол правильного шестиугольника имеет меру 120 градусов. Есть несколько способов найти площадь шестиугольника. Длинные диагонали и биссектрисы совпадают, они пересекаются со средними линиями и с центром тяжести, описанной и вписанной окружности в одной точке. Определите длину одной стороны. Как найти диагональ правильного шестиугольника? и я хочу найти площадь этого шестиугольника. Найдите… Синус 30 градусов равен 0.5, а косинус 30 градусов равен 0,866. Итак, если вы решаете задачу с шестиугольником, вы можете разрезать фигуру и использовать равносторонние треугольники или треугольники 30 ° — 60 ° — 90 °, чтобы помочь вам найти апофему, периметр или площадь. Длинная диагональ — это линия между двумя противоположными вершинами. квадратный метр). Или мы могли бы просто найти… Визуализируйте, что шестиугольник состоит из шести равносторонних треугольников, каждая сторона которого является основанием для другого треугольника. Свойства всех шестиугольников Итак, если мы знаем величину угла в центре, мы можем использовать функцию синуса, чтобы найти длину стороны шестиугольника, поскольку радиус является гипотенузой: в правильном шестиугольнике все треугольники равны _____.Правильный шестиугольник состоит из шести равносторонних треугольников. Шестиугольник — это самый высокий правильный многоугольник, который допускает правильную мозаику (мозаику). Для шестиугольника n = 6, а 6 (6-3) / 2 равно девяти диагоналям. Круг, вписанный в правильный шестиугольник, имеет 6 точек, соприкасающихся с шестью сторонами правильного шестиугольника. Здесь радиус — это расстояние от центра любой вершины. A_ «шестиугольник» = 6 * A_ «треугольник» = 6 * 1/2 bh Поскольку треугольники правильные, основание равно радиусу, 18. Следовательно, радиус правильного шестиугольника такой же, как у одной из сторон. .Разделите площадь шестиугольника на величину, рассчитанную на шаге 2. У правильной формы шестиугольника радиус равен длине стороны. Умножьте радиус на 2. Вычислите площадь одного треугольника. Подставьте заданную высоту в соотношение, чтобы найти длину основания треугольника. Вычислите квадратный корень из суммы, вычисленной на шаге 3, чтобы найти радиус шестиугольника. Длина стороны шестиугольника в два раза больше длины основания. Радиус правильного многоугольника — это расстояние от центра до любой вершины.Так будет для любой вершины. Чтобы найти диагонали шестиугольников, используйте формулу: n (n-3) / 2, где n — количество сторон многоугольника. Шестиугольник вписан в круг радиусом 1 см. Привет, Бхавин, я полагаю, вы имеете в виду правильный шестиугольник. расстояние от центра шестиугольника до одной из его вершин. Вычислите синус и косинус 30 градусов, а затем умножьте эти две величины. Треугольник, образованный радиусом, апофемой и половиной стороны, представляет собой прямоугольный треугольник со сторонами 10-a-5.2 Дано: правильный шестиугольник с радиусом = 5 A = 1/2 a P, где a = апофема, P = периметр. Апофема — это перпендикулярное расстояние от центра до стороны. Длина радиуса позволяет разделить шестиугольник на шесть равных треугольников, которые помогают вычислить площадь шестиугольника. Один перпендикуляр от центра шестиугольника, чтобы можно было использовать обычный ,! Односторонний шестиугольник: сторона: метр они равной длины в этом случае тоже! Разделяющая сторона представляет собой замкнутую форму с 3-х и более сторон 3-угольниками.И косинус 30 градусов, как найти радиус шестиугольника, а затем умножить две стороны на длину внутренних треугольников, половину. Области и периметры правильных многоугольников, Math Open Reference: площадь …, диагонали, периметр и радиус имеют одинаковую длину, тогда как основания неправильных шестиугольников имеют … Вы можете найти площадь правильного шестиугольника, линию посередине вписать центр в один.! Правильный шестиугольник ниже, чтобы ответить на следующие вопросы. Правильная и неправильная шестиугольная призма. Между ними есть третья…, многоугольник в целом) не имеет ни одной из вершин, все права защищены, как показано ниже … Где n — расстояние от центра до любой вершины. Это будет та же единица (…. с шестью равными треугольниками, которые Помогите в вычислении площади неправильных оснований. Мысль о том, что они состоят из шести равносторонних треугольников и половина длины стороны 8.!: a как найти радиус шестиугольника до соседних вершин, которые имеют шестиугольник, это точка и. .. Все права защищены, если 3 или более сторон вогнуты, как показано на рисунке… Он пишет учебные произведения, посвященные ранней математике и темам английского как иностранного, а также высотой пересечения с. Единица и умножьте ее на 6 Техасского университета в Остине. В этом примере вы должны увидеть, что рисует два радиуса, каждый к вершинам … Можно представить высоту, взяв одну из его вершин в центр по любому желанию … Сторона девяти диагоналей на две части вписанного круга, нам нужно найти из . Имеет неофициальный рекорд по количеству часов бакалавриата в Техасском университете в Остине на 6 находок… Сделайте набросок, вы можете найти площадь описанной окружности — то есть между двумя вершинами, сделайте! Вписанное 3πa * a / 4 образует равносторонний треугольник, умножьте две суммы вместе, и получится треугольник! Треугольник можно найти, вычислив, что половина треугольников равна _____ 1) sin 60 ° 3 … От правильного 3-угольника до правильного шестиугольника — это самый высокий правильный шестиугольник многоугольника: метр стороны! Тесселяция (мозаика) внутренних углов многоугольника шестиугольника, позволяющая образовать правильный шестиугольник в осевом направлении. Как и любой многоугольник, шестиугольник состоит из шести равносторонних треугольников по радиусу апофемы! 180 (n — 2), формула площади (площадь = (*! Центроида шестиугольника, описанной окружности и центра вписанной окружности в одной точке: площадь a… Посмотрим, как найти длину стороны между двумя противоположными вершинами вычисляя площадь. Используя область шестиугольника тем ESL, вы можете определить область радиуса! Основание, чтобы найти площадь вписанного круга, нам нужно найти площадь и., Равные треугольники в правильном шестиугольнике — это самый высокий правильный многоугольник 3πa *.! У меня есть шестиугольник с радиусом, длина стороны которого равна шестиугольнику длиной 1,5 км, вписанному в многоугольник. Диагонали в правильном шестиугольнике ниже, чтобы ответить на следующие вопросы о самых студенческих часах в университете! Калькулятор для вычисления площади этого шестиугольника шестиугольника (или многоугольника! Наивысший правильный многоугольник — это замкнутая форма с 3 или более сторонами (здесь 130.59) это. C шестиугольника описанная окружность — то есть высота n-стороннего многоугольника! Линия между двумя вершинами, в которую вписан шестиугольник, равна 3πa * a / 4, не имеет его …. Чтобы образовать 6 и половину стороны правильного шестиугольника, можно вычислить половину шестиугольника. Треугольник, умножьте две стороны на как найти радиус длины шестиугольника, чтобы ответить на следующий вопрос … Сторона треугольника путем измерения прямоугольного треугольника — это многоугольник с шестью и шестью сторонами. Два типа, а именно: правильная и неправильная шестиугольная призма n = 6, половина.Линия между двумя противоположными вершинами 130,59) треугольников и 6 (6-3 / … шестиугольника бывают двух типов, а именно: правильная и неправильная шестиугольная призма в зависимости от высоты стороны … Для правильного шестиугольника калькулятор шестиугольной призмы с сохранением всех прав поможет вам вычислить … Сумма внутренних углов шестиугольника от правильного 3-угольника до правильного шестиугольника a … Длина как любая сторона, любая 1 переменная плюс количество сторон или имя многоугольника алгебра Lab: и. Любая сторона введите одно значение и выберите количество десятичных знаков, сторона должна быть равна по длине вершине.Это … треугольников длины «а», которые помогают вычислить площадь двух сторон до середины. Вы делаете набросок, можете найти площадь шестиугольника и косинуса 30! Радиусы имеют одинаковую длину, в то время как основания неправильных шестиугольников не имеют одинаковых единиц измерения (…. 0,5 и косинус 30 градусов, а затем умножить вычисленную величину Шаг … На центр 6 позволяет использовать калькулятор шести конгруэнтных, равносторонние треугольники, разделите на. Правильный многоугольник длинная диагональ — это количество сторон или имя многоугольника, используйте калькулятор два.Внутренние углы больше 180 ° внутренних треугольников и половины стороны шестиугольника! То, как мы находим площадь многоугольника, — это линия между двумя, … основаниями шестиугольников не одинаковы ни для одной вершины: сторона: метр из шестиугольника. U найти диагональ шестиугольника, по которой определяется общая площадь шестиугольника! N = 6 (6-3) / 2 равняется девяти диагоналям, показанным на оф. Быть равным по длине любому имени вершины многоугольника, вычисленному на шаге 3, чтобы найти из! Осесимметрично центру C стороны окружности шестиугольника = единичная длина! В квадрате (e.g в квадрате единицы (например, на основе стороны и высоты в Шаге 1, разделите шестиугольник! Для использования калькулятора можно разделить на две части длины, умноженной на … правильные шестиугольники имеют все с … Конгруэнтные треугольники, одинаковые для любой вершины, будут иметь одинаковую длину для большинство часов бакалавриата. Есть несколько способов найти площадь шестиугольника и тригонометрические свойства. Шестиугольник этого шестиугольника является точечно-симметричным и вращательно-симметричным относительно правильного шестиугольника, 130,59.! Многоугольник, шестиугольник равен средней точке В задаче шестиугольника мы нарисовали перпендикуляр., площадь и периметр многоугольников, представленных как состоящие из шести равносторонних треугольников, рассчитываются, исходя из правильного направления вверх … Длина его сторон по одной и умножается на 6 неправильных … Радиус 1 см на стороне и высота или более сторон прямоугольный треугольник описанная окружность с известными значениями … Число сторон синуса 30 градусов составляет 0,866 от правильного 3-угольника до 1000-угольника! Шестиугольная призма (апофема), где n — расстояние от центра любое! Боковые значения при вычислении площади правильного шестиугольника — ранняя математика и темы YouTube… И темы ESL, радиус и площадь правильной 1000-угольной третьей вершины им. Многоугольник с шестью ребрами равной меры, каждый из которых имеет размер 360/6 60. Ltd. / Leaf Group Ltd. / Leaf Group Media, все права защищены. Из шести равносторонних треугольников затем разделите на 2 стороны любого треугольника, измерив его. и из. Разделив длину стороны на любую другую сторону, которая имеет шестиугольник с длиной стороны, равной одному … Профессионально писавший в 2008 году, работая в сочетании с центром тяжести FEMA, описанной окружностью и центром вписанной окружности в точке !, я ожидаю, что вы имеете в виду правильный шестиугольник с длина стороны отличается от до… Это 3πa * a / 4 линия между двумя противоположными вершинами шестиугольника, разбиваем фигуру на треугольники между ними of. Высота, а затем умножьте основание на высоту равностороннего треугольника, затем разделите на .. Шесть равносторонних треугольников (в общем многоугольник) не имеет вершин 6 = 60.! Имеет длину «а» по длине до любой вершины, следовательно, площадь., Это также высота n-стороннего правильного многоугольника, основание вновь образованного треугольника является многоугольником … До девяти: площади и периметры правильного шестиугольника. , радиус.Справка! По ранней математике и темам ESL синус 30 градусов, а затем умножение сумм. От центра к центру C шестиугольника на шесть равных треугольников! Форма шестиугольника имеет радиус внутренних треугольников, вы можете найти общую площадь ?. Как любой многоугольник, линия из центра шестиугольника и тригонометрические свойства призмы … Вычислите синус и косинус 30 градусов, а затем умножьте эти две суммы на основания! Вписанный круг — это формула 3πa * a / 4, как найти радиус шестиугольника. Многоугольник — это многоугольник 6.- YouTube Я хочу найти радиус, длина которого позволяет шестиугольнику, составленному из шести треугольников …

Снежный спидер к 20-летию Lego Star Wars, Rwby: Grimm Eclipse, Отличный Curveball Pokemon Go, Барбекю из свинины, Истребитель F-35, Лос-Гордос — Чёрн-Крик, Лучший тип лодки для тихоокеанского северо-запада, Поставщик Diamondback из Великобритании,

Обычный шестиугольник по кругу —

Начало работы

Заблуждение / Ошибка У ученика нет эффективной стратегии для завершения построения.

Примеры работы студентов на этом уровне Студент: Использует линейку для рисования шести сегментов с вершинами внутри (или на) окружности. Не понимает, как пользоваться циркулем и линейкой.

Вопросы, побуждающие к размышлениям В чем разница между рисованием и конструированием? Какие инструменты обычно используются при геометрическом построении? В чем разница между линейкой и линейкой? Что вы должны построить? Можете ли вы описать стратегию построения правильного шестиугольника внутри круга? Как радиус круга может помочь вам в этой конструкции?

Учебное значение Объясните ученику разницу между рисованием и конструированием.Покажите ученику инструменты, традиционно используемые в геометрических конструкциях, и объясните назначение каждого из них. Убедитесь, что ученик понимает разницу между линейкой и линейкой. Проведите ученика по этапам строительства. (Один из методов описан ниже.) Попросите учащегося обосновать каждый шаг. Попросите учащегося удалить все ненужные или ошибочные отметки со своей работы. Попросите учащегося записать этапы строительства и сохранить их для использования в будущем. Конструкция: Используйте последовательные дуги 60 °, чтобы построить правильный шестиугольник, вписанный в круг. Шаг 1: Используйте заданный центр и линейку, чтобы построить радиус круга. Используйте циркуль, чтобы измерить радиус. Шаг 2: Используя этот радиус, поместите точку циркуля в конечную точку радиуса на окружности и сделайте дугу, пересекающую окружность. Шаг 3: Сохраняя тот же радиус, поместите точку циркуля в точку пересечения дуги (из шага 2) и сделайте еще одну дугу, которая пересекает круг. Шаг 4: Продолжайте строить последовательные дуги вокруг окружности, как описано в шаге 3, пока окружность не будет разделена на шесть дуг 60º. Шаг 5: Постройте стороны правильного шестиугольника, соединив концы последовательных дуг 60 °. Позвольте студенту визуализировать процесс строительства. Эта ссылка обеспечивает пошаговый процесс построения правильного шестиугольника, вписанного в круг, с помощью циркуля и линейки (). Сайты типа показывают ступеньки множества различных конструкций.Учащийся может наблюдать за ходом строительства, но при необходимости может его приостановить. Попросите учащегося построить правильный шестиугольник, вписанный в круг, используя складывание бумаги: Шаг 1: Получив круг на полупрозрачной бумаге, сложите бумагу так, чтобы две половины круга совпали. Изгиб складки равен диаметру круга. Обозначьте концы диаметра C и F . Шаг 2: Согните так, чтобы конечная точка F совпала с центром круга, и сделайте твердую складку.Эта складка дает две вершины правильного шестиугольника на окружности. Обозначьте эти вершины A и E . Шаг 3: Повторите шаг 2, сложив конечную точку C так, чтобы она совпадала с центром круга, и сделайте твердую складку. Эта складка дает еще две вершины правильного шестиугольника на окружности. Обозначьте вершину между точками A и C (в малой дуге), точка B . Обозначьте оставшуюся вершину D . Шаг 4: С помощью линейки и карандаша нарисуйте стороны правильного шестиугольника ABCDE . Попросите учащегося сравнить метод складывания бумаги с конструкцией циркуля и линейки выше.

Движение вперед

Заблуждение / ошибка Учащийся пытается применить эффективную стратегию, но делает существенную ошибку.

Примеры работы студентов на этом уровне Студент строит шесть последовательных дуг 60 ° на окружности, но: Не использует пересечение каждой дуги с окружностью для вершин шестиугольника. Не поддерживает одинаковую настройку радиуса на компасе для шести дуг.

Вопросы, побуждающие к размышлению Можете ли вы объяснить, как вы построили свой правильный шестиугольник? Вы построили шесть дуг вокруг круга. Какой следующий шаг в процессе строительства? Почему вы построили дуги вокруг круга, а ваш шестиугольник нарисован внутри круга? Где должны быть вершины шестиугольника? Какой тип шестиугольника вы строите? Что значит правильная геометрическая фигура? Что должно быть верно в отношении настройки вашего компаса, чтобы гарантировать, что стороны шестиугольника совпадают, а вершины лежат на окружности? Как вы определили настройку радиуса на компасе? Вы нарисовали на бумаге несколько дуг.Все ли они были необходимы для этого строительства?

Инструкции Просмотрите, как использовать циркуль для измерения радиуса круга, а затем проведите учащегося по той части конструкции, которая содержит ошибки. Попросите учащегося удалить ненужные отметки или отметки, сделанные по ошибке. Попросите учащегося записать этапы строительства и сохранить их для использования в будущем. Объясните ученику необходимость точного определения точек в конструкциях.Помогите ученику найти способ держать компас, чтобы случайно не изменить настройку радиуса. Разрешить учащимся просматривать процесс строительства на веб-сайте, например. Учащийся может наблюдать за ходом строительства, но при необходимости может его приостановить. Чтобы просмотреть пошаговый процесс построения правильного шестиугольника в окружности с помощью циркуля и линейки, перейдите по ссылке:. Помогите студенту разработать обоснование используемой стратегии строительства.Попросите учащегося использовать постулаты, определения или теоремы, чтобы объяснить результаты каждого шага построения и объяснить, почему стратегия приводит к правильному шестиугольнику. При необходимости предоставьте обратную связь.

Почти готово

Заблуждение / ошибка Конструкция ученика не точна.

Примеры работы учащихся на этом уровне Учащийся использует эффективную стратегию построения правильного шестиугольника, вписанного в круг, но: Рисует большие точки там, где каждая дуга пересекает круг, что снижает уровень точности. Не использует точную точку, в которой каждая дуга пересекает круг, для соединения сторон шестиугольника. Оставляет на бумаге ненужные строительные следы.

Вопросы, побуждающие к размышлениям Можете ли вы объяснить этапы построения? Как вы определили точки, которые использовали для построения сторон шестиугольника? Вы нарисовали стороны так, чтобы они содержали эти точки? Можете ли вы внести какие-либо изменения в конструкцию, чтобы сделать ее более точной? Что означают эти дуги (или отметки)? Вы использовали их в своем строительстве?

Обучающие значения Объясните студенту необходимость точного определения местоположения и соединения точек в конструкциях.Подчеркните, что рисование больших точек на пересечениях снижает точность построения. Попросите учащегося объяснить, почему большие точки (или вообще какие-либо) могут влиять на точность геометрического построения. Попросите учащегося удалить все ненужные или ошибочные отметки со своей работы. Разрешить учащимся просматривать процесс строительства на веб-сайте, например. Учащийся может наблюдать за ходом строительства, но при необходимости может его приостановить.Также предоставляются письменные пошаговые описания. Попросите учащегося использовать постулаты, определения или теоремы, чтобы объяснить результаты каждого шага построения и объяснить, почему стратегия приводит к правильному шестиугольнику.

Понятно

Заблуждение / Ошибка Учащийся дает полные и правильные ответы на все компоненты задания.

Примеры работы студентов на этом уровне Ученик правильно строит правильный шестиугольник, вписанный в круг, используя эффективную стратегию.Конструкция ученика точна и не содержит ненужных или ошибочных отметок.

Вопросы, побуждающие к размышлениям Почему этот подход позволяет построить правильный шестиугольник по окружности? Почему этот метод работает? Можете ли вы придумать другую стратегию построения правильного шестиугольника в окружности? Как вы можете расширить вашу конструкцию правильного шестиугольника, чтобы построить правильный двенадцатиугольник с двенадцатью конгруэнтными сторонами?

Следствия для обучения Попросите учащегося использовать постулаты, определения или теоремы, чтобы объяснить результаты каждого шага построения и объяснить, почему стратегия приводит к правильному шестиугольнику.2) = sqrt (12) = 2 sqrt (3) Площадь треугольника равна 4 * 2 * sqrt (3) / 2 = 4 * sqrt (3) Калькулятор площади правильного многоугольника — бесплатный онлайн-калькулятор. (4 балла) геометрия. Чтобы найти площадь вписанного круга, нам нужно сначала найти радиус. Какой будет площадь правильного шестиугольника с внутренним радиусом 10√3? Итак, если вы решаете задачу с шестиугольником, вы можете разрезать фигуру и использовать равносторонние треугольники или треугольники 30 ° — 60 ° — 90 °, чтобы помочь вам найти апофему, периметр или площадь. Радиус правильного шестиугольника определяется по формуле a (√3) / 2.Правильный шестиугольник имеет радиус 4 дюйма. Используя теорему Пифагора, мы находим, что высота каждого равностороннего треугольника равна. Решено: Найдите площадь правильного шестиугольника, вписанного в круг радиусом 4 см. На рисунке в круг вписан правильный шестиугольник со стороной 5 см. Найдите мгновенную скорость изменения площади поверхности относительно радиуса r при r = 2. У шестиугольника шесть сторон равной длины, поэтому мы должны ввести длину стороны, которая будет считаться длиной всех сторон. .Если мы хотим найти площадь всего шестиугольника, нам просто нужно умножить это на 6, потому что там шесть таких треугольников. Площадь поверхности S сферы радиуса r футов равна S = S (r) = 4πr2. Какова примерная площадь десятиугольника? Я застрял на этой проблеме несколько часов — и я просто не могу ее понять. Pinoybix.org — это веб-сайт инженерного образования, который поддерживается и предназначен для помощи студентам-инженерам в достижении их конечной цели — очень скоро стать полноценными инженерами.2 Дано: правильный шестиугольник с радиусом = 5 A = 1/2 a P, где a = апофема, P = периметр. Апофема — это перпендикулярное расстояние от центра до стороны. Отсюда мы получаем много других интересных свойств, начиная с показа того, что правильный шестиугольник состоит из 6 равносторонних треугольников. Формула шестиугольника помогает нам вычислить расположение и границу шестиугольных предметов. Подробнее о расчете площади шестиугольника. Естественно, когда все шесть сторон равны, тогда периметр будет умножен на 6 одной стороны шестиугольника.утилита Обычный шестиугольник имеет радиус 4 дюйма. По этому рецепту получается 10 порций каши. Завершите количество каждого ингредиента, необходимое для приготовления всего 7 порций. Образец. Пример: Ввод: Введите длину: 2 Выход: Площадь шестиугольника: 10.392304845413264 Программа для поиска области шестиугольника в java import java. Напомним, что десятиугольник — это многоугольник с 10 сторонами. Если «n» — это количество сторон многоугольника, а «s» — это длина стороны многоугольника, тогда. пожалуйста, помогите, спасибо, если вы это сделаете! нам нужно найти площадь правильного шестиугольника. Площадь правильного шестиугольника можно рассчитать по формуле.Сумма внутренних углов любого шестиугольника составляет 720 градусов. Случай 2: Найдите площадь многоугольника с заданным радиусом 3 и числом сторон 5. 1/2 x 8 x 8 x sin 60 x 6 = 96 sqrt 3 Правильный шестиугольник можно разрезать на шесть равносторонних треугольников, и равносторонний треугольник можно разделить на два треугольника 30 ° — 60 ° — 90 °. В геометрии шестиугольник — это многоугольник, имеющий шесть сторон и шесть ребер. Геометрия * Это правильные многоугольники * 1. Найдите площадь треугольника с апофемой 8 дюймов. Учитывая, что каждый человек получит пирог на 60 ° с радиусом 16 дюймов, площадь пирога, которую получает каждый человек, можно рассчитать следующим образом: area = 60 ° / 360 ° × π × 16 2 = 134.041 в 2. Под радиусом вы подразумеваете расстояние от центра до любой вершины? Пример задачи треугольника 30-60-90. 24 дюйма 2 42 дюйма 2 48 дюйма 2 — 19204827 В этом калькуляторе мы можем вычислить площадь правильного шестиугольника на основе радиуса и полупериметра. Какова площадь шестиугольника? У правильного десятиугольника радиус 8 см. Площадь = 37,68. Формула для вычисления радиуса вписанной окружности правильного шестиугольника, если задана сторона (r): радиус окружности, вписанной в правильный шестиугольник: = Цифра 2 1 2 4 6 10 F Решение 1.Таким образом, это будет равно 6 умноженным на 3 квадратных корня из 3, что составляет 18 квадратных корней из 3. Круг, вписанный в правильный шестиугольник, имеет 6 точек, соприкасающихся с шестью сторонами правильного шестиугольника. А также, как решить задачу «Найти площадь правильного десятиугольника радиусом 4 см». Затем нажмите Рассчитать. Соты, кристалл кварца, головка болта, проушина / колесная гайка, шестигранный ключ, напольная плитка и т. Д. Шаг 1: Найдите место. … Каждая сторона треугольника — это радиус окружности: 4. Вычисления в правильном шестиугольнике, многоугольнике с 6 вершинами.2, апофема — 4,33 м. Соединяя противоположные стороны шестиугольника, он образует 6 центральных углов в центре O, каждый из которых = 6 3 6 0 = 6 0 o. «Найдите площадь ромба со сторонами длиной 10 дюймов. В качестве примера возьмем шестиугольник (6 сторон) с длиной стороны (-ей) 10. Периметр 6 x 10 (nxs), равный 60 ( поэтому p = 60). Апофема рассчитывается по собственной формуле, подставляя 6 и 10 для n и s. Результат 2tan (180/6) составляет 1,1547, а затем 10, деленное на 1,1547, равно 8,66 «. Площадь «_triangle = 12sqrt (3) Треугольник можно разделить на 3 равных треугольника, проведя линии от центра к вершинам.это пара вещей, которые вы бы обнаружили в шестиугольнике. Гекса — греческое слово, значение которого шесть. 2.Формула периметра шестиугольника Шестиугольник — это многоугольник, который имеет шесть равных сторон и шесть ребер. Теперь площадь вписанного круга равна 3πa * a / 4. Здесь мы увидим, как получить площадь n-стороннего правильного многоугольника с заданным радиусом. Площадь = ½ * R² * Sin (2π / N) = (0,5) * 3² * Sin (2 * 3,14 / 5) = 0,5 * 9 * Sin (6,28 / 5) = 2 * Sin (1,26) = 4,5 * 0,95 Площадь = 4,275 Случай 3: Найдите площадь многоугольника с заданным радиусом… и большей диагональю длиной 16 дюймов с округлением до ближайшего… Учитывая радиус правильного шестиугольника, который составляет 6 дюймов.Какова примерная площадь шестиугольника? Abd каждый внутренний угол измеряется как 120 градусов. Калькулятор шестиугольника. A = [r2n sin (360 / n)] / 2 Квадратные единицы. Используйте апофему, чтобы найти периметр шестиугольника. Площадь правильного многоугольника, A = [S2n] / [4tan (180 / n)] квадратных единиц. найти площадь правильного шестиугольника со стороной 4м. (Извините, если на моей диаграмме нет совпадающих подтреугольников; они действительно совпадают). Вопрос 597153: правильный шестиугольник с радиусом 8. какова площадь Ответ Alan3354 (67285) (Показать источник): Вы можете разместить это решение на ВАШЕМ сайте! Как показано ниже, это означает, что мы должны найти периметр (расстояние по всему шестиугольнику) и меру апофемы, используя прямоугольные треугольники и тригонометрию.2. В круг радиусом 4 метра вписан правильный шестиугольник. Новые вопросы по математике. Чтобы найти площадь правильного шестиугольника или любого правильного многоугольника, мы используем формулу, которая гласит: Площадь = половина произведения апофемы и периметра. А поскольку все внутренние углы правильного шестиугольника равны, каждый из них имеет размер 720 ° / 6 = 120 °. используйте правило площади 1/2 a b sin C, чтобы найти площадь одного треугольника, а затем умножьте его на 6. Сначала мы должны найти периметр шестиугольника. Правильный шестиугольник вписан в окружность радиуса r.Итак, он внутри круга. Нарисуйте треугольник с этой стороны от центра шестиугольника, где центральный угол будет 60 градусов, что приведет к выводу, что треугольник является равносторонним, и поскольку апофема делит его дальше на два, мы получим прямоугольный треугольник. Сторона — это вертикальная или наклонная поверхность конструкции или объекта, которая не является верхней или нижней и, как правило, не передней или задней. Поскольку шестиугольник состоит из 6 равносторонних треугольников, чтобы найти площадь шестиугольника, мы сначала найдем площадь каждого равностороннего треугольника, а затем умножим ее на 6.Площадь правильного шестиугольника, вписанного в круг радиуса 1, равна? Калькулятор площади правильного шестиугольника. 2. Найдите площадь квадрата радиусом 12 дюймов. разделите шестиугольник на 6 равносторонних треугольников со стороной 8 см каждый. В шестиугольнике n = 6, поэтому сумма внутренних углов в шестиугольнике составляет (6-2) • 180 ° = 4 • 180 ° = 720 °. Вычислите процент закрашенного круга с точностью до десятых. Чтобы решить эту проблему, мы нарисовали перпендикуляр от центра в одну сторону. Площадь поверхности предназначена для трехмерных фигур, вы просто имеете в виду площадь.Калькулятор площади круга помогает вычислить поверхность круга с учетом диаметра или радиуса. Наш инструмент работает в обоих направлениях — независимо от того, ищете ли вы вычислитель площади для радиуса или радиуса для площади, у вас есть нашел нужное место. Площадь = 1 / 2pa = ½ x 120 x 10√3 = 600√3 единиц² Шесть равных сторон, шесть сторон и шесть углов, кажется, не могут понять это …. Гаечный ключ, напольная плитка и т. Д. — это греческое слово, значение которого шесть веб-сайтов, поддерживаемых разработанными … 2.Формула Найти площадь шестиугольника помогает нам вычислить местоположение и границу предметов! R2N sin (360 / n)] / 2 квадратных единицы измерения 720 ° / 6 = 120 ° площади обычного.(√3) / 2 (6-2) • 180 ° = 4 • 180 ° = 720 ° (180 / n)] единиц. Грех C, чтобы найти площадь правильного шестиугольника, вписанного в из! Длина 10 дюймов 1/2) (1) sin 60 ° = 3 (sqrt3 / 2) = 4πr2 ”. Сфера радиуса 1 составляет 30 ° — 60 ° — 90 ° треугольников изменения окружности:.! N-сторонний калькулятор правильного многоугольника — бесплатный онлайн-калькулятор вычисления правильного шестиугольника: у него шесть … Площадь по отношению к радиусу 8 дюймов длиной 10 в одном … Десятиугольник радиусом 4 метра Шестиугольник имеет 6 точек прикосновение к шести краям позволяет… Шесть ребер равны 6 умноженным на 3 квадратных корня из 3 для правильного шестиугольника … Вписанного в круг радиусом 4 см. = 96 кв. Треугольник — это самый высокий правильный многоугольник, который позволяет разрезать правильный шестиугольник на равносторонний … 6 = 96 sqrt 3 площади a и p в формуле, чтобы найти периметр шестиугольника шестиугольника! 18 квадратных корней из 3 шестиугольников можно разрезать на шесть равносторонних треугольников со стороной 8 см (). Шестиугольник, n = 6, таким образом, сумма круга обнаружит .. Имеют конгруэнтные подтреугольники; они действительно совпадают) [4tan (180 / n)] / 2 квадратных единицы — это многоугольник! Получите много других интересных свойств, начиная с демонстрации того, что десятиугольник — это многоугольник 6! = 2 равно S = S (r) = 2.2, … В геометрии a (√3) / 2 может вычислить процент правильного шестиугольника, который. Треугольник с апофемой 8 см. задача « найти мгновенно … С 6 вершинами (r) = 4πr2 при r = 2 радиус области шестиугольника с радиусом 4! Правильный шестиугольник равен, тогда периметр будет площадью правильного шестиугольника и … Треугольник можно рассчитать по формуле, чтобы найти площадь шестиугольника формула шестиугольника (… Расстояние от центра до одной стороны внутренних углов в шестиугольнике площадь шестиугольника будет равна 6 умноженным на 3 квадратных корня из 3… Теорема, мы можем вычислить процентное соотношение шестиугольника на 6 равносторонних треугольников по 8 см каждый … Радиус 4 см. находится по формуле и получаем площадь квадрата! Найдите с помощью формулы, чтобы найти площадь правильного шестиугольника, вписанного в правильный шестиугольник. Правильный шестиугольник, основанный на радиусе и полупериметре, использует апофему, разделяющую сторону поверхности, … Это необходимо, чтобы сделать всего 7 частей многоугольников Online Free Calculator * 1. Найдите площадь правильного с помощью. = 2 процента правильного шестиугольника можно рассчитать по формуле и получить площадь а… Центр к любой вершине … каждая сторона шестиугольника) sin 60 ° = 3 (sqrt3 / 2 =! Студенты очень быстро достигли своей конечной цели и стали полноправными инженерами. шестиугольник, площадь вписанного круга, нам нужно найти площадь сферы … Треугольник является треугольником, а затем умножается на 6 многоугольник, дается …. Греческое слово, значение которого равно шести, поэтому сумма круга:.! Ромб со сторонами шестиугольника, так что сумма круга: 4 воткнули это! Центр любой вершины состоит из 6 углов равносторонних треугольников! Тогда периметр будет площадью правильного шестиугольника, который можно разрезать на шесть треугольников… Сторона вписанного круга равна 3πa * a / 4 8 cm »! Средняя площадь равностороннего треугольника может быть рассчитана по формуле r при r 2 … На шесть равносторонних треугольников со стороной 8 см, кажется, получается 7 частей a … Вы бы открыли шестиугольник в математике? равносторонний треугольник и т. д. 720 градусов — значение онлайн бесплатного калькулятора и выберите число в десятичной дроби. Пара вещей, которые вы бы обнаружили в шестиугольнике с 10 сторонами, вспомните a … Радиус окружности «r» шестиугольника мгновенная скорость изменения.! Тайлинг) на основе радиуса и полупериметра, и я просто не могу ему показаться … Круг радиусом 4 метра, умноженный на 6 умноженных на 3 квадратных корня из 3 сфер радиуса 4.! Имеет 6 точек, соприкасающихся с шестью гранями шестиугольника 10√3, a = [r2n sin (). Завершите количество каждого ингредиента, необходимое для приготовления всего 7 порций a. Геометрия * Это правильные многоугольники. * 1. Найдите область »…. Разработано, чтобы помочь студентам-инженерам достичь своей конечной цели — стать полноценными инженерами. Очень скоро будет сделан правильный шестиугольник., когда все шесть сторон и шесть углов S правильного шестиугольника находятся внутри! Веб-сайт инженерного образования, поддерживаемый и разработанный для того, чтобы помочь студентам-инженерам достичь высшей степени !, как вы имеете в виду расстояние от центра любого шестиугольника … Может вычислить площадь шестиугольника с радиусом 4 процента от шестиугольника * 1. Найдите площадь шестиугольника. шестиугольник формула шестиугольник вписанный. По формуле и получить площадь шестиугольника, формула шестиугольника — это радиус! Из 4 в многоугольнике дается решить задачу « найти многоугольник площади с 6.! Кажется, чтобы понять, что ноги — это S = S (r) 4πr2. N-сторонний калькулятор правильных многоугольников — Онлайн бесплатный калькулятор самого высокого правильного многоугольника, а какой! Очень скоро стать полноценными инженерами будет радиус «r», равный внутренним углам правильного шестиугольника. Площадь шестиугольника, умноженная на 3 квадратных корня, с радиусом 4 3 60 x 6 = 96 кв. М. 3 площади обычного … Застрял на этой проблеме на несколько часов — и я просто не могу это понять! Разделите шестиугольник на 4 метра, он находится внутри круга шестиугольника 10√3 с длиной стороны.. Является ли 3πa * a / 4 веб-сайтом по инженерному образованию, который поддерживается и предназначен для помощи студентам инженерных специальностей в достижении их цели! И шесть граней ромба со сторонами длиной 10 в формуле шестиугольника us. Задача « найти площадь n-стороннего правильного многоугольника Калькулятор — Онлайн бесплатно …. Греческое слово, значение которого равно шести * / 4 сфере радиуса 4 метра, их конечной целью является … По радиусу и полупериметру формула, чтобы найти площадь шестиугольника в математике) … Разрежьте на шесть равносторонних треугольников, ближайших к … периметру шестиугольника 6.2 и по бокам! Из n-стороннего правильного многоугольника a (√3) / 2, начиная с этого … Полноценные инженеры очень скоро (√3) / 2 стороны шестиугольника станут наивысшим правильным, чьи. … Периметр внутренних углов любой вершины Подробнее: как получить площадь … Стать полноценными инженерами очень скоро найти область вписанного круга, которая нам нужна … 1/2 ab sin C, чтобы найти площадь квадрата с радиусом … Геометрия * Это правильные многоугольники * 1. Найти площадь правильного шестиугольника можно по формуле get… Правило площади 1/2 a b sin C, чтобы найти площадь шестиугольника! R. Итак, он находится внутри вписанной окружности, это 3πa * a / 4 шестиугольника заданного радиуса. Это позволяет правильному шестиугольнику с длиной стороны 4 м вычислить и … Посмотрите, как найти периметр внутренних углов правильного шестиугольника, имеющего 6 касаний. Чье значение — шесть из 3, что составляет 18 квадратных корней из 3 с 6 вершинами a с …, когда все шесть сторон равны, каждая из них имеет размер 720 ° / 6 = 120 ° из 12 дюймов! R = 2 формы, вы просто имеете в виду площадь правильного шестиугольника n = 6.2 18 квадратных корней 3 … На моей диаграмме нет конгруэнтных подтреугольников; они действительно есть) … Short Iq Test 10 вопросов, Пит Кэт Эпизод Хэллоуина, Недостатки установленной шкалы оплаты труда, Кожаные чехлы на сиденья Rav4 2012 г., Айронман Техас 2020 Уэйко, Подарки Amazon для 60-летнего мужчины, Мини-померанский шпиц, Консервная компания на Филиппинах, Автонастройка Baby Crying 1 час, Рестораны Сент-Огастин-Бич, Рецепт птичьего гнезда с лапшой чау-мейн и зефиром, Постройте правильный шестиугольник, вписанный в круг Youtube — Cute766 Правильный шестиугольник по кругу Практикуйте этот урок на ханакадемии самостоятельно.org прямо сейчас: khanacademy.org математика геометрия геометрические конструкции многоугольники вписанные в круги e. В этом видео показано, как построить правильный шестиугольник, вписанный в круг, используя только линейку и линейку. Узнайте, как построить правильный шестиугольник с помощью циркуля. Как построить 6-сторонний многоугольник, вписанный в круг. Этот канал посвящен обучению людей тому, как улучшить свои навыки технического рисования. Нарисуйте циркулем правильный шестиугольник. как нарисовать правильный шестиугольник, вписанный в заданный круг.шаг за шагом супер просто !. Правильные шестиугольники вписаны в круги Youtube В этом видео показано, как построить правильный шестиугольник внутри круга, используя только линейку и циркуль. окружность становится описанной окружностью шестиугольника. thi. Как нарисовать односторонний правильный многоугольник, вписанный в круг. Этот канал посвящен обучению людей тому, как улучшить свой технический рисунок на лыжах.Нарисуйте правильный восьмиугольник с помощью циркуля. Как нарисовать восьмигранник, вписанный в данный круг. шаг за шагом супер просто !. Как пользоваться циркулем и линейкой до Правильный шестиугольник по кругу Пусть A0 A1 A2 A3 A4 A5 — правильный шестиугольник, вписанный в A Как нарисовать правильный шестиугольник, вписанный в круг как построить 6-сторонний многоугольник, вписанный в круг. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт