Измерение модуля упругости
Приложение:
Измерение модуля продольной упругости, модуля сдвига и коэффициента Пуассона (поперечной деформации) в недисперсионных изотропных конструкционных материалах.
Общие сведения:
Модуль Юнга (модуль продольной упругости) определяется как отношение напряжения (сила на единицу площади) к деформации сжатия.
Модуль сдвига определяется как отношение напряжения сдвига к деформации сдвига.
Коэффициент Пуассона отношение относительного поперечного сжатия к относительному продольному растяжению.
Эти основные свойства материалов обязательно учитываются в производстве и в различных научных исследованиях, и определяются с помощью измеренных значений скорости звука и плотности материала. Скорость распространения звука легко вычисляется путем ультразвукового контроля в режиме импульс-эхо с использованием соответствующего оборудования. Представленная ниже процедура действительна для любого однородного, изотропного, недисперсионного материала (скорость звука не изменяется с частотой).
Каучук не может быть измерен ультразвуковым методом по причине высокой степени дисперсии и нелинейно упругих свойств. Мягкие пластики точно так же показывают высокую степень затухания в режиме сдвиговых волн, и обычно не могут быть измерены. В случае анизотропных материалов, упругость варьируется в зависимости от направления, так же как и скорость распространения продольных волн и/или сдвиговых волн. Для генерации полной матрицы модуля упругости в анизотропных образцах обычно требуется шесть серий ультразвуковых измерений. Пористость или зернистость материала может влиять на точность измерения модуля упругости, поскольку вызывает колебания скорости звука исходя из размера и ориентации зерен или размера и распределения пор, вне зависимости от упругости материала.
Оборудование:
Для измерения скорости звука при расчете упругости обычно используются прецизионные толщиномеры 38DL PLUS или 45MG с ПО для одноэлементных ПЭП, или дефектоскопы с функцией измерения скорости звука (например, серии EPOCH). Генераторы/приемники модели 5072PR или 5077PR в комбинации с осциллографом или дискретизатором сигналов также могут использоваться для измерения времени распространения волн. Для данного теста потребуется два преобразователя, подходящих для эхо-импульсного измерения скорости звука в материале продольными и поперечными волнами. Среди наиболее используемых ПЭП: широкополосный преобразователь продольных волн M112 или V112 (10 МГц) и преобразователь поперечных волн с нормальным углом падения V156 (5 МГц). Они подходят для измерения наиболее распространенных металлов и обожженных керамических образцов. Для измерения очень толстых и очень тонких материалов или образцов с высоким затуханием ультразвука требуются специальные преобразователи.
Тестовый образец может быть любой формы, позволяющей выполнять эхо-импульсное измерение времени прохождения ультразвука через материал. Обычно, это образец толщиной 12,5 мм с ровными параллельными поверхностями, ширина или диаметр которого больше диаметра используемого преобразователя. Необходимо проявлять крайнюю осторожность при измерении узких образцов по причине возможных пограничных эффектов, которые могут повлиять на измеренное время прохождения импульса. При использовании сильно тонких образцов, разрешение будет ограничено из-за небольших колебаний во времени прохождения импульса через короткий УЗ-путь. Мы рекомендуем брать образцы толщиной минимум 5 мм, но желательно толще. Во всех случаях толщина тестового образца должна быть точно известна.
Процедура:
Измерьте скорость распространения продольных и сдвиговых волн тестового образца с использованием подходящих ПЭП и настроек прибора. Для измерения скорости сдвиговых волн потребуется специальная контактная жидкость высокой вязкости, как например SWC. Толщиномеры 38DL PLUS и 45MG могут напрямую измерять скорость звука в материале на основе введенной толщины образца, а дефектоскопы серии EPOCH измеряют скорость звука в ходе калибровки скорости звука. В обоих случаях, следуйте рекомендуемой процедуре измерения скорости звука, представленной в руководстве по эксплуатации прибора. При использовании генератора/приемника, зафиксируйте время прохождения сигнала туда и обратно через участок известной толщины с помощью преобразователей продольных и поперечных волн, и рассчитайте:
При необходимости, переведите единицы измерения скорости звука в дюйм/с или см/с. (Время обычно измеряется в микросекундах; для получения измерений в дюйм/с или см/с умножьте дюйм/мкс или см/мкс на 106. ) Полученные значения скорости звука могут использоваться в следующих формулах.
) Полученные значения скорости звука могут использоваться в следующих формулах.
Примечание: Если скорость звука выражена в см/с, а плотность – в г/см3, модуль упругости будет выражен в дин/см2

Для определения модуля сдвига умножьте квадрат скорости распространения поперечной волны на плотность.
Опять же, используйте единицы измерения см/с и г/см 3 для получения модуля упругости в дин/см2 или английскую систему мер (дюйм/с и фунт/дюйм3) и умножьте результат на коэффициент пересчета масса/сила.
Библиография
Подробнее об измерении модулей упругости ультразвуковым методом см. в представленных ниже источниках:
2. Krautkramer, J., H. Krautkramer, Ultrasonic Testing of Materials, Berlin, Heidelberg, New York 1990 (Fourth Edition), pp. 13-14, 533-534.
Модуль (коэффициент) упругости бетона: формула для расчета
Определение упругости и единицы измерения
Изделия и конструкции из бетона подвергаются большим нагрузкам, причем этот процесс происходит постоянно. Технологи нашли возможность придать бетону упругость, т. е. способность упруго деформироваться при воздействии давления и силы, направленной на сжатие и расширение. Величина, которая характеризует этот показатель, называется модулем упругости бетона и по определению вычисляется с помощью формулы соотношения напряжения и упругой деформации образца: данные занесены в специальную таблицу.
Технологи нашли возможность придать бетону упругость, т. е. способность упруго деформироваться при воздействии давления и силы, направленной на сжатие и расширение. Величина, которая характеризует этот показатель, называется модулем упругости бетона и по определению вычисляется с помощью формулы соотношения напряжения и упругой деформации образца: данные занесены в специальную таблицу.
Нормативные сведения также включают данные о:
- классе материала,
- его видах (тяжелый, мелкозернистый, легкий, пористый бетон и т. д:.),
- технологии производства, в частности способах твердения (естественное, автоклавная или тепловая обработка).
В связи с этим модуль упругости бетона В30 может быть различным и определяться исходя из других характеристик. Если взять в качестве примера тяжелые и ячеистые бетоны одного и того же класса прочности, их модули будут иметь абсолютно разные значения.
Таблица утверждена СНиП и составлена на основе результатов опытных исследований.
Таблица начальных модулей упругости E (МПа*10-3) при сжатии и растяжении бетонов с различными эксплуатационными характеристиками
|
Классы по прочности на сжатие |
В3,5 |
В5 |
В7,5 |
В10 |
В12,5 |
В15 |
В20 |
В25 |
В30 |
В35 |
В40 |
В45 |
В50 |
В55 |
В60 |
|
Характеристики бетона |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тяжелые бетоны |
|||||||||||||||
|
Естественное твердение |
9,5 |
13 |
16 |
18 |
21 |
23 |
27 |
30 |
32,5 |
34,5 |
36 |
37,5 |
39 |
39,5 |
40 |
|
Тепловая обработка при атмосферном давлении |
8,5 |
11,5 |
14,5 |
16 |
19 |
20,5 |
24 |
27 |
29 |
31 |
32,5 |
34 |
35 |
35,5 |
36 |
|
Автоклавная обработка |
7 |
10 |
12 |
13,5 |
16 |
17 |
20 |
22,5 |
24,5 |
26 |
27 |
28 |
29 |
29,5 |
30 |
|
Мелкозернистые |
|||||||||||||||
|
Естественное твердение, А-группа |
7 |
10 |
13,5 |
15,5 |
17,5 |
19,5 |
22 |
24 |
26 |
27,5 |
28,5 |
— |
— |
— |
— |
|
Тепловая обработка при атмосферном давлении |
6,5 |
9 |
12,5 |
14 |
15,5 |
17 |
20 |
21,5 |
23 |
— |
— |
— |
— |
— |
— |
|
Естественное твердение, Б-группа |
6,5 |
9 |
12,5 |
14 |
15,5 |
17 |
20 |
21,5 |
23 |
— |
— |
— |
— |
— |
— |
|
Автоклавная теплообработка |
5,5 |
8 |
11,5 |
13 |
14,5 |
15,5 |
17,5 |
19 |
20,5 |
— |
— |
— |
— |
— |
— |
|
Автоклавное твердение, В-группа |
— |
— |
— |
— |
— |
16,5 |
18 |
19,5 |
21 |
21 |
22 |
23 |
24 |
24,5 |
25 |
|
Легкие и поризованные |
|||||||||||||||
|
Марка средней плотности, D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
800 |
4,5 |
5,0 |
5,5 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
|
1000 |
5,5 |
6,3 |
7,2 |
8 |
8,4 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
|
1200 |
6,7 |
7,6 |
8,7 |
9,5 |
10 |
10,5 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
|
1400 |
7,8 |
8,8 |
10 |
11 |
11,7 |
12,5 |
13,5 |
14,5 |
15,5 |
— |
— |
— |
— |
— |
— |
|
1600 |
9 |
10 |
11,5 |
12,5 |
13,2 |
14 |
15,5 |
16,5 |
17,5 |
18 |
— |
— |
— |
— |
— |
|
1800 |
— |
11,2 |
13 |
14 |
14,7 |
15,5 |
17 |
18,5 |
19,5 |
20,5 |
21 |
— |
— |
— |
— |
|
2000 |
— |
— |
14,5 |
16 |
17 |
18 |
19,5 |
21 |
22 |
23 |
23,5 |
— |
— |
— |
— |
|
Ячеистые автоклавного твердения |
|||||||||||||||
|
Марка средней плотности, D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
700 |
2,9 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
|
800 |
3,4 |
4 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
|
900 |
3,8 |
4,5 |
5,5 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
|
1000 |
— |
6 |
7 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
|
1100 |
— |
6,8 |
7,9 |
8,3 |
8,6 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
|
1200 |
— |
|
8,4 |
8,8 |
9,3 |
— |
— |
— |
— |
— |
— |
— |
— |
— |
— |
От чего зависит упругость бетона
1. Состав
Состав
Бетон с более высоким модулем упругости подвергается меньшей относительной деформации.
Значительную роль в этом играет качество цементного камня и наполнителя – двух компонентов, из которых и состоит бетон. И раствор, и заполнитель берут на себя всю нагрузку. При анализе зависимости модуля упругости бетона от модуля упругости его составляющих, исследователи выяснили, что прочность заполнителя не всегда задействуется для улучшения характеристик готового материала, а вот показатель упругости оказывает значительное влияние.
2. Класс
Начальный модуль упругости бетона при сжатии и расширении зависит от класса изделия по прочности на сжатие.
Эта зависимость устанавливается путем применения эмпирических формул, поэтому для практических целей проще всего получать информацию из готовой таблицы. Даже без сложных математических расчетов можно заметить, что модуль упругости увеличивается пропорционально прочности материала. Другими словами, чем выше класс, тем больше модуль упругости бетона, т.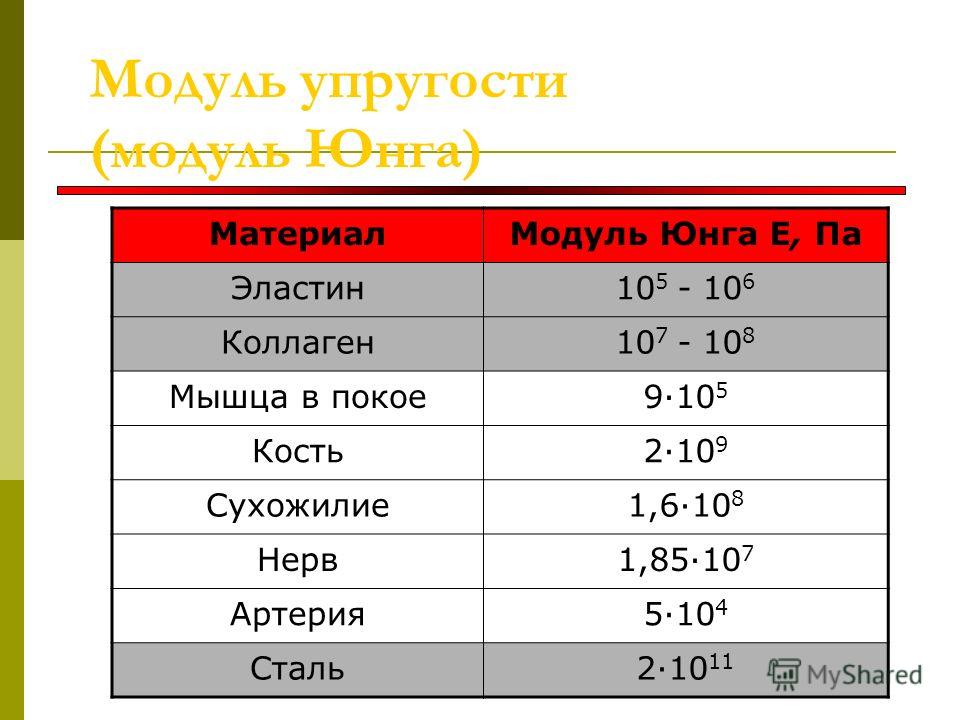 е. материал класса В25 является более устойчивым к относительным деформациям по сравнению с В20.
е. материал класса В25 является более устойчивым к относительным деформациям по сравнению с В20.
Расчет модуля упругости в лабораторных условиях
Когда речь идет о модуле упругости, принимают во внимание оба его варианта – динамический и статический. У первого значение выше и определяется в ходе вибрации образца.
Статический модуль, помимо основной информации, предоставляет данные о такой характеристике, как ползучесть бетона – динамика образования деформаций при постоянной нагрузке.
При расчетах учитывают тождество модулей упругости материала как на растяжение, так и на сжатие. Замечено, что если напряжение составляет 0,2 и более максимальной прочности бетона, происходят остаточные деформации. Это приводит к тому, что при сцеплении раствора и наполнителей возникают микротрещины, а это становится причиной крошения и в конечном итоге разрушения.
Во время эксперимента образец подвергают непрерывной нагрузке, имеющей тенденцию к возрастанию, до полного разрушения. Для этого используют особое оборудование – нагружающие установки. В диаграмму вносят данные, показывающие влияние нагрузок на степень деформаций. На завершающем этапе производится расчет среднего модуля упругости всех образцов.
Для этого используют особое оборудование – нагружающие установки. В диаграмму вносят данные, показывающие влияние нагрузок на степень деформаций. На завершающем этапе производится расчет среднего модуля упругости всех образцов.
Модуль упругости разных материалов, включая сталь
Перед тем, как использовать какой-либо материал в строительных работах, следует ознакомиться с его физическими характеристиками для того, чтобы знать как с ним обращаться, какое механическое воздействие будет для него приемлемым, и так далее. Одной из важных характеристик, на которые очень часто обращают внимание, является модуль упругости.
Ниже рассмотрим само понятие, а также эту величину по отношению к одному из самых популярных в строительстве и ремонтных работах материалу — стали. Также будут рассмотрены эти показатели у других материалов, ради примера.
Блок: 1/3 | Кол-во символов: 563
Источник: https://stanok.guru/stal/modul-uprugosti-raznyh-materialov-vklyuchaya-stal.html
Связь с другими модулями упругости
В случае изотропного тела модуль Юнга связан с модулем сдвига и модулем объёмной упругости соотношениями
и
где — коэффициент Пуассона.
Блок: 2/8 | Кол-во символов: 176
Источник: https://ru.wikipedia.org/wiki/%D0%9C%D0%BE%D0%B4%D1%83%D0%BB%D1%8C_%D0%AE%D0%BD%D0%B3%D0%B0
Модуль упругости — что это?
Модулем упругости какого-либо материала называют совокупность физических величин, которые характеризуют способность какого-либо твёрдого тела упруго деформироваться в условиях приложения к нему силы. Выражается она буквой Е. Так она будет упомянута во всех таблицах, которые будут идти далее в статье.
Невозможно утверждать, что существует только один способ выявления значения упругости. Различные подходы к изучению этой величины привели к тому, что существует сразу несколько разных подходов. Ниже будут приведены три основных способа расчёта показателей этой характеристики для разных материалов:
- Модуль Юнга (Е) описывает сопротивление материала любому растяжению или сжатию при упругой деформации. Определяется вариант Юнга отношением напряжения к деформации сжатия.
 Обычно именно его называют просто модулем упругости.
Обычно именно его называют просто модулем упругости. - Модуль сдвига (G), называемый также модулем жёсткости. Этот способ выявляет способность материала оказывать сопротивление любому изменению формы, но в условиях сохранения им своей нормы. Модуль сдвига выражается отношением напряжения сдвига к деформации сдвига, которая определяется в виде изменения прямого угла между имеющимися плоскостями, подвергающимися воздействию касательных напряжений. Модуль сдвига, кстати, является одной из составляющих такого явления, как вязкость.
- Модуль объёмной упругости (К), которые также именуется модулем объёмного сжатия. Данный вариант обозначает способность объекта из какого-либо материала изменять свой объём в случае воздействия на него всестороннего нормального напряжения, являющимся одинаковым по всем своим направлениям. Выражается этот вариант отношением величины объёмного напряжения к величине относительного объёмного сжатия.

- Существуют также и другие показатели упругости, которые измеряются в других величинах и выражаются другими отношениями. Другими ещё очень известными и популярными вариантами показателей упругости являются параметры Ламе или же коэффициент Пуассона.
Блок: 2/3 | Кол-во символов: 1976
Источник: https://stanok.guru/stal/modul-uprugosti-raznyh-materialov-vklyuchaya-stal.html
Температурная зависимость модуля Юнга
Температурная зависимость модуля упругости простых кристаллических материалов объясняется исходя из того, что модуль упругости определяется как вторая производная от внутренней энергии по соответствующей деформации . Поэтому при температурах ( — температура Дебая) температурная зависимость модуля упругости определяется простым соотношением
где — адиабатический модуль упругости идеального кристалла при ; — дефект модуля, обусловленный тепловыми фононами; — дефект модуля, обусловленный тепловым движением электронов проводимости
Блок: 3/8 | Кол-во символов: 578
Источник: https://ru.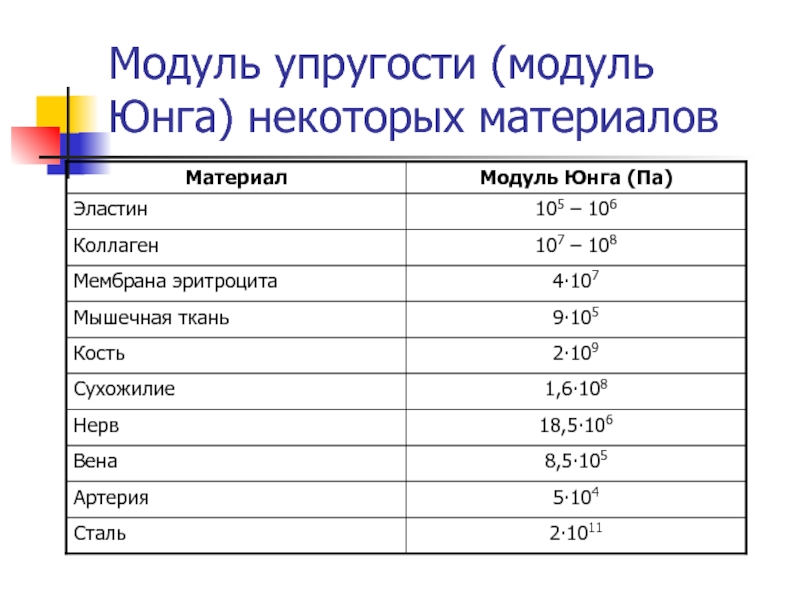 wikipedia.org/wiki/%D0%9C%D0%BE%D0%B4%D1%83%D0%BB%D1%8C_%D0%AE%D0%BD%D0%B3%D0%B0
wikipedia.org/wiki/%D0%9C%D0%BE%D0%B4%D1%83%D0%BB%D1%8C_%D0%AE%D0%BD%D0%B3%D0%B0
Механические свойства
Только при работе на растяжение или сжатие модуль (Юнга) упругости помогает угадать поведение того или иного материала. А вот при изгибе, срезе, смятии и прочих нагрузках потребуется ввести дополнительные параметры:
- Жёсткостью называют произведение поперечного сечения профиля на модуль упругости. По этой величине можно судить о пластичности узла конструкции в целом, а не о материале отдельно. Единицей измерения являются килограммы силы.
- Продольное относительное удлинение — это отношение абсолютного удлинения материала-образца к его общей длине. К примеру, на стержень, длина которого равна 200 миллиметров, приложили некоторую силу. В результате он стал короче на 5 миллиметров. В результате относительное удлинение будет равняться 0,05. Эта величина безразмерная. Для более удобного восприятия иногда её переводят в проценты.
- Поперечное относительное удлинение рассчитывается точно так же, как и продольное относительное удлинение, но вместо длины берут диаметр стержня.
 Опытным путём было установлено, что для большего количества материала поперечное меньше продольного удлинения приблизительно в 4 раза.
Опытным путём было установлено, что для большего количества материала поперечное меньше продольного удлинения приблизительно в 4 раза. - Коэффициент Пуассона. Это отношения относительной продольной к относительной поперечной деформации. При помощи этой величины можно полностью описать под воздействием нагрузки изменения формы.
- Модуль сдвига описывает упругие свойства под воздействием касательных свойств на образец. Иными словами, когда вектор силы направляется к поверхности тела под 90 градусов. Примером подобных нагрузок служит работа гвоздей на смятие, заклёпок на срез и пр. Этот параметр связан с вязкостью материала.
- Модуль упругости объёмной характеризует изменение объёма образца для разностороннего равномерного приложения нагрузки. Эта величина является отношением давления объёмного к деформации сжатия объёмной. Как пример можно рассматривать опущенный в воду материал, на который воздействует давление жидкости по всей его площади.
youtube.com/embed/1dPNbX-KW3o»/>
Кроме всего вышесказанного стоит упомянуть, что у некоторых материалов в зависимости от направления нагрузки разные механические свойства. Подобные материалы называются анизотропными. Примерами подобного является ткани, некоторые виды камня, слоистые пластмассы, древесина и прочее.
У материалов изотропных механические свойства и деформация упругая в любом направлении одинаковы. К таким материалам относятся металлы: алюминий, медь, чугун, сталь и прочее, а также каучук, бетон, естественные камни, пластмассы неслоистые.
Блок: 3/4 | Кол-во символов: 2487
Источник: https://tokar.guru/metally/stal/modul-deformacii-stali-i-ee-uprugosti.html
Таблица показателей упругости материалов
Перед тем, как перейти непосредственно к этой характеристике стали, рассмотрим для начала, в качестве примера и дополнительной информации, таблицу, содержащую данные об этой величине по отношению к другим материалам. 2 .
2 .
Это общие данные, приведённые для видов стали и стальных изделий. Каждая величина была высчитано согласно всем физическим правилам и с учётом всех имеющихся отношений, которые используются для выведения величин этой характеристики.
Ниже будет приведена вся общая информация об этой характеристике стали. Значения будут даваться как по модулю Юнга, так и по модулю сдвига, как в одних единицах измерения (МПа), так и в других (кг/см2, ньютон*м2).
Сталь и несколько разных её марок
Значения показателей упругости стали разнятся, так как существуют сразу несколько модулей, которые исчисляются и высчитываются по-разному. Можно заметить тот факт, что в принципе сильно показатели не разнятся, что свидетельствует в пользу разных исследований упругости различных материалов. Но сильно углубляться во все вычисления, формулы и значения не стоит, так как достаточно выбрать определённое значение упругости, чтобы уже в дальнейшем ориентироваться на него. 2.
2.
Данная информация поможет разобраться с самим понятием модуля упругости, а также ознакомиться с основными значения данной характеристики для стали, стальных изделий, а также для нескольких других материалов.
Следует помнить, что показатели модуля упругости разные для различных сплавов стали и для различных стальных конструкций, которые содержат в своём составе и другие соединения. Но даже в таких условиях, можно заметить тот факт, что различаются показатели ненамного. Величина модуля упругости стали практически зависит от структуры. а также от содержания углерода. Способ горячей или холодной обработки стали также не может сильно повлиять на этот показатель.
Блок: 3/3 | Кол-во символов: 3589
Источник: https://stanok.guru/stal/modul-uprugosti-raznyh-materialov-vklyuchaya-stal.html
Модуль упругости для разных марок стали
Металлурги разработали несколько сотен марок сталей. Им свойственны разные значения прочности. В таблице 2 показаны характеристики для наиболее распространенных сталей.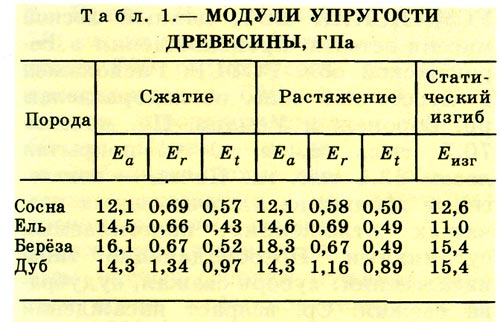
Таблица 2: Упругость сталей
| Наименование стали | Значение модуля упругости, 10¹²·Па |
| Сталь низкоуглеродистая | 165…180 |
| Сталь 3 | 179…189 |
| Сталь 30 | 194…205 |
| Сталь 45 | 211…223 |
| Сталь 40Х | 240…260 |
| 65Г | 235…275 |
| Х12МФ | 310…320 |
| 9ХС, ХВГ | 275…302 |
| 4Х5МФС | 305…315 |
| 3Х3М3Ф | 285…310 |
| Р6М5 | 305…320 |
| Р9 | 320…330 |
| Р18 | 325…340 |
| Р12МФ5 | 297…310 |
| У7, У8 | 302…315 |
| У9, У10 | 320…330 |
| У11 | 325…340 |
| У12, У13 | 310…315 |
Видео: закон Гука, модуль упругости.
Блок: 4/5 | Кол-во символов: 686
Источник: https://metmastanki.ru/modul-uprugosti-stali-i-metallov
Модули прочности
Кроме нормального нагружения, существуют и иные силовые воздействия на материалы.
Модуль сдвига G определяет жесткость. Эта характеристика показывает предельное значение нагрузки изменению формы предмета.
Модуль объемной упругости К определяет упругие свойства материала изменить объем. При любой деформации происходит изменение формы предмета.
Коэффициент Пуассона μ определяет изменения отношение величины относительного сжатия к растяжению. Эта величина зависит только от свойств материала.
Для разных сталей значения указанных модулей приведены в таблице 3.
Таблица 3: Модули прочности для сталей
| Наименование стали | Модуль упругости Юнга, 10¹²·Па | Модуль сдвига G, 10¹²·Па | Модуль объемной упругости, 10¹²·Па | Коэффициент Пуассона, 10¹²·Па |
| Сталь низкоуглеродистая | 165…180 | 87…91 | 45…49 | 154…168 |
| Сталь 3 | 179…189 | 93…102 | 49…52 | 164…172 |
| Сталь 30 | 194…205 | 105…108 | 72…77 | 182…184 |
| Сталь 45 | 211…223 | 115…130 | 76…81 | 192…197 |
| Сталь 40Х | 240…260 | 118…125 | 84…87 | 210…218 |
| 65Г | 235…275 | 112…124 | 81…85 | 208…214 |
| Х12МФ | 310…320 | 143…150 | 94…98 | 285…290 |
| 9ХС, ХВГ | 275…302 | 135…145 | 87…92 | 264…270 |
| 4Х5МФС | 305…315 | 147…160 | 96…100 | 291…295 |
| 3Х3М3Ф | 285…310 | 135…150 | 92…97 | 268…273 |
| Р6М5 | 305…320 | 147…151 | 98…102 | 294…300 |
| Р9 | 320…330 | 155…162 | 104…110 | 301…312 |
| Р18 | 325…340 | 140…149 | 105…108 | 308…318 |
| Р12МФ5 | 297…310 | 147…152 | 98…102 | 276…280 |
| У7, У8 | 302…315 | 154…160 | 100…106 | 286…294 |
| У9, У10 | 320…330 | 160…165 | 104…112 | 305…311 |
| У11 | 325…340 | 162…170 | 98…104 | 306…314 |
| У12, У13 | 310…315 | 155…160 | 99…106 | 298…304 |
Для других материалов значения прочностных характеристик указывают в специальной литературе. Однако, в некоторых случаях проводят индивидуальные исследования. Особенно актуальны подобные исследования для строительных материалов. На предприятиях, где выпускают железобетонные изделия, регулярно проводят испытания по определению предельных значений.
Однако, в некоторых случаях проводят индивидуальные исследования. Особенно актуальны подобные исследования для строительных материалов. На предприятиях, где выпускают железобетонные изделия, регулярно проводят испытания по определению предельных значений.
Блок: 5/5 | Кол-во символов: 1940
Источник: https://metmastanki.ru/modul-uprugosti-stali-i-metallov
Литература
- Модули упругости // Большая Советская энциклопедия (в 30 т.) / А. М. Прохоров (гл. ред.). — 3-е изд. — М.: Сов. энциклопедия, 1974. — Т. XVI. — С. 406. — 616 с.
- G. Mavko, T. Mukerji, J. Dvorkin. The Rock Physics Handbook. Cambridge University Press 2003 (paperback). ISBN 0-521-54344-4
Эта страница в последний раз была отредактирована 21 февраля 2019 в 15:38.
Блок: 4/4 | Кол-во символов: 427
Источник: https://wiki2.org/ru/%D0%9C%D0%BE%D0%B4%D1%83%D0%BB%D1%8C_%D1%83%D0%BF%D1%80%D1%83%D0%B3%D0%BE%D1%81%D1%82%D0%B8
Количество использованных доноров: 5
Информация по каждому донору:
- https://ru.
 wikipedia.org/wiki/%D0%9C%D0%BE%D0%B4%D1%83%D0%BB%D1%8C_%D0%AE%D0%BD%D0%B3%D0%B0: использовано 2 блоков из 8, кол-во символов 754 (5%)
wikipedia.org/wiki/%D0%9C%D0%BE%D0%B4%D1%83%D0%BB%D1%8C_%D0%AE%D0%BD%D0%B3%D0%B0: использовано 2 блоков из 8, кол-во символов 754 (5%) - https://wiki2.org/ru/%D0%9C%D0%BE%D0%B4%D1%83%D0%BB%D1%8C_%D1%83%D0%BF%D1%80%D1%83%D0%B3%D0%BE%D1%81%D1%82%D0%B8: использовано 1 блоков из 4, кол-во символов 427 (3%)
- https://metmastanki.ru/modul-uprugosti-stali-i-metallov: использовано 3 блоков из 5, кол-во символов 4379 (28%)
- https://tokar.guru/metally/stal/modul-deformacii-stali-i-ee-uprugosti.html: использовано 2 блоков из 4, кол-во символов 3756 (24%)
- https://stanok.guru/stal/modul-uprugosti-raznyh-materialov-vklyuchaya-stal.html: использовано 3 блоков из 3, кол-во символов 6128 (40%)
Модуль упругости первого рода — Энциклопедия по машиностроению XXL
Коэффициент пропорциональности Е называется модулем продольной упругости или модулем упругости первого рода, он имеет размерность напряжений (даН/см или даН/мм ) и характеризует способность материала сопротивляться упругой деформации при растяжении и сжатии. Величину модуля продольной упругости для различных материалов определяют экспериментально. Для стали = (2,0- 2,15) 10 даН/см , для алюминия = (0,7н-0,8) 10 даН/см , для бронзы = 1,15-10 даН/см , для дерева вдоль волокон = 1-10 даН/см , для стеклопластиков = (0,18-ь н-0,4) 10 даН/см
[c.130]
Величину модуля продольной упругости для различных материалов определяют экспериментально. Для стали = (2,0- 2,15) 10 даН/см , для алюминия = (0,7н-0,8) 10 даН/см , для бронзы = 1,15-10 даН/см , для дерева вдоль волокон = 1-10 даН/см , для стеклопластиков = (0,18-ь н-0,4) 10 даН/см
[c.130] Приведенный модуль упругости первого рода, [c.249]
В формуле (11.3) Е — коэффициент, зависящий от материала и называемый модулем продольной упругости или модулем упругости первого рода. Он характеризует жесткость материала, т. е. его способность сопротивляться деформированию. [c.24]
Отсюда найдем зависимость между модулем сдвига G и модулем упругости первого рода [c.86]
Примечание. Обозначения Д — натяг создаваемый при посадке, см Е . Е, — модули упругости первого рода материалов сопрягаемых деталей, кгс/см д , — коэффициенты Пуассона материалов деталей г — радиус посадки, см г , -= соответственно внутренний радиус внутренней детали и наружный радиус наружной детали, см.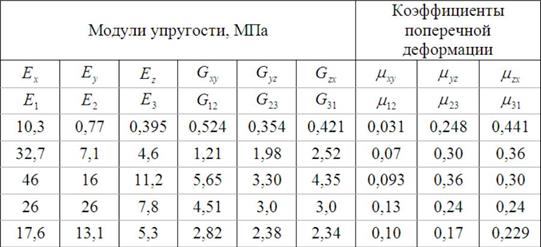 [c.239]
[c.239]
Коэффициент пропорциональности Е в формуле (2.2) называется модулем продольной упругости (иногда его называют модулем упругости первого рода, или модулем Юнга). Модуль характеризует ж ест к ос т ь материала при растяжении и сжатии. [c.213]
Коэффициент пропорциональности Е в формуле (2.2) называется модулем продольной упругости (иногда его называют модулем упругости первого рода, или модулем Юнга). [c.189]
Принятое соотношение (Х.З) приближенно, так как не всегда совпадает с экспериментальными данными при малых деформациях и дает ошибочные результаты при определении модуля упругости первого рода. [c.118]
Коэффициент пропорциональности Е характеризует жесткость материала, т. е. его способность сопротивляться упругим деформациям растяжения или сжатия, и называется модулем продольной упругости или модулем упругости первого рода. [c.190]
Коэффициент Пуассона, как и модуль упругости первого рода, зависит только от материала и характеризует его упругие свойства. При растяжении и сжатии коэффициент Пуассона полагают одинаковым.
[c.192]
При растяжении и сжатии коэффициент Пуассона полагают одинаковым.
[c.192]
С помощью диаграммы растяжения в координатах (о, е) определяем модуль упругости первого рода [c.194]
Е, О—модули упругости первого рода (модуль Юнга) и второго рода (модуль сдвига) х — коэффициент Пуассона [c.12]
В этих уравнениях Е — модуль упругости первого рода J — момент инерции поперечного сечения балки относительно оси [c.93]
Сделаем некоторые замечания по поводу терминологии. Мы приняли термин моду,ль продольной упругости как рекомендованный Комитетом по технической терминологии Академии наук. Наряду с ним применяют термины модуль нормальной упругости , модуль Юнга , модуль упругости первого рода . Полагаем, что предпочтителен термин, официально рекомендованный для краткости речи можно говорить просто модуль упругости . [c.67]
В табл.
 3.2.1 приведены диапазоны модулей упругости первого рода Е и коэффициента Пуассона ц для различных материалов.
[c.40]
3.2.1 приведены диапазоны модулей упругости первого рода Е и коэффициента Пуассона ц для различных материалов.
[c.40]Модуль упругости первого рода, Е, МПа [c.40]
Е, G —модуля упругости первого рода (модуль Юнга) и второго рода (модуль сдвига) [c.10]
Величина Е называется модулем упругости первого рода (сокращенно—модулем упругости) . Это физи- [c.31]
Коэффициент пропорциональности в (11.9) Е называется модулем продольной упругости (модулем упругости при растяжении-сжатии, модулем упругости первого рода). Для каждого материала Е определяется экспериментально и имеет размерность напряжения Е вторая константа, вместе с х полностью определяющая упругие свойства материала. [c.42]
Между модулем сдвига G, модулем упругости первого рода Е и коэффициентом Пуассона существует следующая зависимость [c.108]
Величина Е, которая входит в формулу, выражающую закон Гука, является одной из важнейших физических постоянных материала. Она характеризует его жесткость, т. е. способность сопротивляться упругому деформированию. Эта величина называется модулем продольной упругости (также модулем упругости первого рода, или модулем Юнга).
[c.78]
Она характеризует его жесткость, т. е. способность сопротивляться упругому деформированию. Эта величина называется модулем продольной упругости (также модулем упругости первого рода, или модулем Юнга).
[c.78]
Основные свойства материалов. При проверке прочности и проектировочных расчетах механизмов и их деталей необходимо знать основные механические свойства материалов прочность, упругость (характеризуемую модулем упругости первого рода и коэффициентом Пуассона V),твердость (способность данного тела препятствовать проникновению в него другого тела путем упругого или пластического деформирования, либо путем разрушения части поверхности тела), пластичность (характеризуемую способностью материала давать остаточную деформацию). [c.135]
В общем виде соотношение между модулем упругости второго рода и модулем упругости первого рода выражается формулой [c.139]
Е — модуль упругости первого рода материала пружины. [c.372]
[c.372]
Т. е. числовая величина модуля упругости первого рода может быть определена в масштабе диаграммы как тангенс угла наклона прямолинейного участка ОА к оси абсцисс. [c.34]
Что характеризует модуль упругости первого рода [c.48]
Модуль G с модулем упругости первого рода Е связан следующим соотношением [c.69]
Здесь X — длина движущейся трещины — внешние силы In — линейные размеры Е — модуль упругости первого рода р, /упруго-вязкой среды 7 — удельная поверхностная энергия материала t — время. [c.179]
Модуль упругости первого рода Ес, модуль упругости второго рода G и коэффициент Пуассона V для рассматриваемого композита можно записать в виде [c.29]
Рис. 2.7. Изменение модуля упругости первого рода в зависимости от направления растяжения. Примечание. На рисунке справа изображена часть слоистой пластины, состоящей из стеклоткани 143 и эпоксидной смолы (параллельное расположение слоев) слева — то же самое, но с перпендикулярным расположением слоев. Структура стеклоткани 143 переплетение атласное, на 25,4 мм приходятся 49 продольных и 30 поперечных Структура стеклоткани 143 переплетение атласное, на 25,4 мм приходятся 49 продольных и 30 поперечных
|
На рис. 2.12 приведены результаты определения модуля упругости первого рода для композита, составленного из кобальта и карбида вольфрама. Эти результаты получены на основании изложенной выше методики, которую можно распространить и на случай композитов, состоящих из п фаз. Для этого случая можно установить, что [c.38]
Величина Е представляет собой коэффициент пропорциональности, называемый модулем упругости первого рода. Модуль упругости является физической константой материала и определяется экспериментально. Величина Е измеряется в тех же единицах, что и а, т.е. в мегапаскалях. Вместе с тем, поскольку модуль упругости может иметь довольно большие числовые значения, его предпочтительнее измерять не в мега-, а в гигапаскалях 1 ГПа= 1000 МПа. [c.42]
[c.42]
Величина Е представляет собой ко эффициент пропор- ональности, называемый модулем продольной упруго-ч (модуль упругости первого рода, модуль Юнта). Мо-1Ь упругости имеет ту же размерность, что и напря-ffle. [c.23]
К — коэффициент жесткости пружины, — коэффициент жесткости эквивалентной пружины, Яв — коэффициент крутильной жесткости вала, т — масса груза, J — момент инерции диска относительно оси вращения, — момент инерции эквивалентного диска относительно оси вращения, д — ускорение свободного падения, — статический прогиб упругого звена под действием силы веса, Е — модуль упругости первого рода упругого звена, О — модуль упругости второго рода упругого звена, 2 — жесткость балки при изгибе, — площадь поперечного сечения стержня, ддцна стержня. [c.102]
Епоа — модули упругости первого рода материала конуса и подшипника [c.458]
Коэффициент Е, входящий в формулу (6), называется, модулем упругости- первого рода или модулем Юнга, по имени ученого, введшего его в науку. Из формулы (6) видно, что размерность модуля упругости Е такая же, как и напряжения, так как е —величина отвлеченная, т. е. Е выражается в кГ1см . При одном и том же напряжении относительная деформация будет меньше у того материала, для которого Е будет больше. Следовательно, модуль упругости характеризует жесткость материала, т. е. способность сопротивляться деформации, что и
[c.24]
Из формулы (6) видно, что размерность модуля упругости Е такая же, как и напряжения, так как е —величина отвлеченная, т. е. Е выражается в кГ1см . При одном и том же напряжении относительная деформация будет меньше у того материала, для которого Е будет больше. Следовательно, модуль упругости характеризует жесткость материала, т. е. способность сопротивляться деформации, что и
[c.24]
Ej и Em — модули упругости первого рода соответственно для волокна и матрицы Ес и Стс — модуль упругости первого рода и разрушающее напряжение для композита Ofu — разрушающее напряжение для волокна ( Tm)efu — напряжение в матрице, соответствующее разрушающей деформации волокна а и р — коэффициенты, зависящие от расположения волокна (при однонаправленном упрочнении равны 1,0, при ортогональном упрочнении примерно равны 0,5, при случайном расположении волокон примерно равны 3/8). [c.26]
Определение модуля упругости — ВВС-инжиниринг
LOADTRAC II-RM
Установка по определению модуля упругости «LoadTrac-II» производства «Geocomp» полностью автоматизирует испытания по определению модуля упругости материалов основания, подстилающего слоя, земляного полотна. «LoadTrac II» удовлетворяет или превосходит все требования для испытаний по определению модуля упругости материалов основания, подстилающего слоя, земляного полотна, установленные спецификациями Американской Ассоциации Руководителей Дорожных и Транспортных служб Штатов (AASHTO) T-294/T-307 и Программы Стратегических Исследований в области автомобильных дорог (SHRP), Протокол P46. Она минимизирует рабочее время в течение испытаний и предлагает гибкий механизм для выполнения дополнительных геотехнических испытаний.
«LoadTrac II» удовлетворяет или превосходит все требования для испытаний по определению модуля упругости материалов основания, подстилающего слоя, земляного полотна, установленные спецификациями Американской Ассоциации Руководителей Дорожных и Транспортных служб Штатов (AASHTO) T-294/T-307 и Программы Стратегических Исследований в области автомобильных дорог (SHRP), Протокол P46. Она минимизирует рабочее время в течение испытаний и предлагает гибкий механизм для выполнения дополнительных геотехнических испытаний.
ОСОБЕННОСТИ И ПРЕИМУЩЕСТВА ДЛЯ ПОЛЬЗОВАТЕЛЯ
ВОЗМОЖНОСТЬ ДОПОЛНИТЕЛЬНЫХ ИСПЫТАНИЙ
Силовая рама производства «Geocomp» выполняет не только испытания по определению модуля упругости. С помощью программного обеспечения и аксессуаров, также могут быть проведены следующие испытания:
• Определение несущей способности грунта калифорнийским методом
• Испытание на сжатие слабых пород и цементных смесей
• Испытание на деформацию при уплотнении при постоянной скорости деформации
• Циклические испытания на трехосное сжатие
• Ступенчатая консолидация
• Испытание асфальта по методу Маршалла
• Испытание на трехосное сжатие
• Испытание на неограниченное сжатие.
ПОЛНАЯ АВТОМАТИЗАЦИЯ ПРИ МИНИМАЛЬНОМ ВМЕШАТЕЛЬСТВЕ ОПЕРАТОРА
«LoadTrac-II» проводит испытания по удельной работе деформации от начала до конца в соответствии с самыми последними стандартами AASHTO, без вмешательство оператора.
ПРИЛОЖЕНИЕ ТОЧНОЙ НАГРУЗКИ В ТЕЧЕНИЕ ИСПЫТАНИЯ
Испытание по определению модуля упругости — это сложное испытание, в котором при приложении нагрузки изменяется жесткость образца. Так как производительность системы циклического нагружения зависит от жесткости образца, большинство систем не могут прилагать надлежащую нагрузку на всем протяжении испытания. В системе LOADTRAC II-RM применяется настройка пропорционально-интегрально-дифференциального регулятора в реальном времени, чтобы корректировать параметры управления системы, когда меняется жесткость образца. Эта особенность позволяет системе прилагать точную нагрузку от начала и до окончания испытания.
Cистема удовлетворяет всем строгим спецификациям AASHTO относительно точности графика нагрузки в форме гаверсинуса.
ПРОСТАЯ РАБОТА В СРЕДЕ WINDOWS ®
Время на обучение невелико, так как большинство людей знакомы с операционной средой Windows. Пользователи могут конфигурировать разнообразные экраны графических представлений для отображения результатов испытания, включая табличное и графическое отображение значений во времени, графическое отображение напряжений, деформаций, смещений и значений удельной работы деформации.
РЕЗУЛЬТАТЫ ИСПЫТАНИЙ В ЛЮБОЙ ФОРМЕ
Система формирует данные в различных форматах, таким образом пользователи могут извлечь из данных наибольшую пользу.
Дополнительные возможности:
• Полный итоговый протокол испытания со всеми соответствующими вычислениями и базовыми соотношениями, основанный на публикации №FHWA-RD-97-083
• Текстовый файл с необработанными данными и текстовый файл данных в технических единицах.
Данные также могут быть с легкостью загружены в электронную таблицу для дальнейшего анализа.
Включено полное программное обеспечение для формирования отчетов. Это программное обеспечение обрабатывает результаты испытания, которые выводятся на печать в табличной или графической форме сразу после испытания. Результаты доступны в любых единицах измерения, независимо от того, какие единицы измерения использовались во время испытания.
Система по определению модуля упругости от «Geocomp» эффективна и надежна. Многие компоненты испытательной камеры, измерительной аппаратуры и системы нагрузок были оптимизированы нами при тестировании на разнообразных материалах, с применением более чем 15-летнего опыта в области исследований и разработок. Система непрерывно совершенствуется на основе новых технологий и опыта потребителей.
ТЕХНИЧЕСКАЯ СПЕЦИФИКАЦИЯ
| Давление в камере | Прилагается автоматические, поддерживается и увеличивается с помощью электропневматического регулятора давления |
| Тип циклического нагружения | Гаверсинусоидальный импульс |
| Циклическая скорость | 0,1 секунда на импульс, 1 импульс в секунду и любая более медленная скорость, заданная пользователем |
| Привод циклической нагрузки | Высокопроизводительный заказной линейный исполнительный механизм |
| 2,8 кВт максимум, малоинерционная система с сервоприводом, с малым временем реакции | |
| Система обратной связи с высоким разрешением для точного и безошибочного управления нагрузкой и скоростью | |
| Непрерывная нагрузка 22 кН (5000 фунт-сила) при скоростях более 200 мм (8″) /сек | |
| Автономный и не требующий обслуживания | |
| Однофазный переменный ток 208 В, 60 Гц (США) / переменный ток 220 В, 50 Гц (международный) | |
| Варианты завершения испытания | Максимальное количество циклов |
| Максимальная деформация | |
| Варианты отчетов | Напряжение сдвига по отношению к числу импульсов; Осевая деформация по отношению к числу импульсов; Модуль упругости по отношению к числу импульсов; Модуль упругости по отношению к девиаторному напряжению; Модуль упругости по отношению к эффективному давлению при исследовании керна; Автоматическое или заданное пользователем масштабирование любого из вышеназванных графиков; Вывод графика на монитор, принтер, плоттер или в файл |
| Испытательная камера | Модифицированная камера трехосного сжатия с принадлежностями для подготовки образцов |
| Системы единиц | СИ, метрическая, США, английская, изменяема в любое время до, во время и после испытания |
| Диаметр образца | 70, 100, and 150 мм (2,8/4/6 дюймов) |
Заказные размеры — по спец. заказу заказу | |
| Датчики | • Силы: 2, 5,10 кН (500, 1000, 2500 фунт-сила) |
| • Смещения: интервал 0.5 дюйма, +25.4 мм (+1,00 дюйм) | |
| • Давления в камере: 0-500 кПа (0-70 фунтов на квадратный дюйм) | |
| СИСТЕМНЫЕ ТРЕБОВАНИЯ | Система поставляется укомплектованной для выполнения испытаний, хранения данных, обработки данных и вывода результатов испытаний. Сразу после установки система будет откалибрована и готова к проведению испытания. |
| ДОКУМЕНТАЦИЯ | Предоставляются полная документация и руководства пользователя. В программе в любом месте доступны экраны с подсказками |
Для просмотра форм отчета и интерфейса управляющей программы щелкните мышью на соответствующей миниатюре.
ⓘ Энциклопедия — Модуль упругости
ⓘ Модуль упругости
Модуль упругости — общее название нескольких физических величин, характеризующих способность твёрдого тела упруго деформироваться при приложении к нему силы. В области упругой деформации модуль упругости тела в общем случае зависит от напряжения и определяется производной зависимости напряжения от деформации, то есть тангенсом угла наклона начального линейного участка диаграммы напряжений-деформаций:
В области упругой деформации модуль упругости тела в общем случае зависит от напряжения и определяется производной зависимости напряжения от деформации, то есть тангенсом угла наклона начального линейного участка диаграммы напряжений-деформаций:
где:
- σ {\displaystyle \sigma } — напряжение, вызываемое в образце действующей силой равно силе, делённой на площадь приложения силы;
- E — модуль упругости;
- ε {\displaystyle \varepsilon } — упругая деформация образца, вызванная напряжением равна отношению изменения размера образца после деформации к его первоначальному размеру.
В наиболее распространенном случае зависимость напряжения и деформации линейная закон Гука:
E = σ ε {\displaystyle E={\frac {\sigma }{\varepsilon }}}. Если напряжение измеряется в паскалях, то, поскольку деформация является безразмерной величиной, единицей измерения Е также будет паскаль. Альтернативным определением является определение, что модуль упругости — это напряжение, достаточное для того, чтобы вызвать увеличение длины образца в два раза. Такое определение не является точным для большинства материалов, потому что это значение намного больше чем предел текучести материала или значения, при котором удлинение становится нелинейным, однако оно может оказаться более интуитивным.
Альтернативным определением является определение, что модуль упругости — это напряжение, достаточное для того, чтобы вызвать увеличение длины образца в два раза. Такое определение не является точным для большинства материалов, потому что это значение намного больше чем предел текучести материала или значения, при котором удлинение становится нелинейным, однако оно может оказаться более интуитивным.
Разнообразие способов, которыми могут быть изменены напряжения и деформации, включая различные направления действия силы, позволяют определить множество типов модулей упругости. Здесь даны три основных модуля:
- Модуль Юнга E характеризует сопротивление материала растяжению/сжатию при упругой деформации, или свойство объекта деформироваться вдоль оси при воздействии силы вдоль этой оси; определяется как отношение напряжения к деформации сжатия удлинения. Часто модуль Юнга называют просто модулем упругости.
- Модуль объёмной упругости или Модуль объёмного сжатия K характеризует способность объекта изменять свой объём под воздействием всестороннего нормального напряжения объёмного напряжения, одинакового по всем направлениям.
 Он равен отношению величины объёмного напряжения к величине относительного объёмного сжатия. В отличие от двух предыдущих величин, модуль объёмной упругости невязкой жидкости отличен от нуля для несжимаемой жидкости — бесконечен.
Он равен отношению величины объёмного напряжения к величине относительного объёмного сжатия. В отличие от двух предыдущих величин, модуль объёмной упругости невязкой жидкости отличен от нуля для несжимаемой жидкости — бесконечен. - Модуль сдвига или модуль жесткости G или μ {\displaystyle \mu } характеризует способность материала сопротивляться изменению формы при сохранении его объёма; он определяется как отношение напряжения сдвига к деформации сдвига, определяемой как изменение прямого угла между плоскостями, по которым действуют касательные напряжения. Модуль сдвига является одной из составляющих явления вязкости.
Существуют и другие модули упругости: коэффициент Пуассона, параметры Ламе.
Гомогенные и изотропные материалы твердые, обладающие линейными упругими свойствами, полностью описываются двумя модулями упругости, представляющими собой пару любых модулей. Если дана пара модулей упругости, все другие модули могут быть получены по формулам, представленным в таблице ниже.
В невязких течениях не существует сдвигового напряжения, поэтому сдвиговый модуль всегда равен нулю. Это влечёт также и равенство нулю модуля Юнга.
Модули упругости Е для некоторых веществ:
Модули упругости материалов — Справочник химика 21
Из уравнения (5.33) видно, что ЪТ не зависит от среднего уровня нагрузок, тем не менее, недавние исследования показали, что константа термоупругости зависит от нагрузок это объясняется зависимостью модуля упругости материалов от температуры [78]. [c.169] Данные, приведенные в упомянутых таблицах, свидетельствуют о непосредственной связи собственных частот с размерами образца, а также с характеристиками упругости и плотностью материала. Поэтому широко применяют определение модуля упругости материалов по резонансным частотам стержня, изготовленного из исследуемого Материала. Чаще всего, возбуждая продольные резонансные колебания, определяют модуль упругости Е в соответствии с формулой [c. 152]
152]
Формулы для определения усилий и напряжений приведены для стыка рассматриваемых элементов. Чтобы найти усилия и напряжения в произвольном сечении элемента, следует использовать соответствующие выражения для данного элемента, суммируя алгебраически их значения от нагружения внутренним давлением и краевыми силами и моментами Мд, полученными для данной составной конструкции, причем для сферического сегмента в качестве Яд следует принимать разность (Яд — Я), учитывающую наличие распорной силы. Формулы приведены при условии, что модули упругости материалов сопрягаемых элементов конструкции одинаковы [c.270]
Е и Е1—модули упругости материалов цилиндра и поршня (А И —коэффициенты Пуассона для материалов цилиндра и поршня. [c.130]
Для ряда конструкций определяющим являются не столько абсолютные значения прочности и модуля упругости материалов, сколько их удельные значения — отношение прочности и модуля упругости к плотности материала — ар/р и /р. Удельная прочность стекловолокнитов намного превосходит удельную прочность, а удельный модуль упругости соизмерим с удельным модулем упругости металлических конструкционных материалов (табл. 1У.12). [c.151]
Удельная прочность стекловолокнитов намного превосходит удельную прочность, а удельный модуль упругости соизмерим с удельным модулем упругости металлических конструкционных материалов (табл. 1У.12). [c.151]Предел прочности и модуль упругости материалов [c.371]
Жесткость элемента выбирается такой, чтобы его деформация при ударе была пренебрежимо мала по сравнению с деформацией призмы, что достигается соблюдением соотношений при выборе его материала и толщины Н йкл, где Е и р — модули упругости материалов элемента и призмы и ккл — толщины накладки и клеевого слоя. [c.110]
Среди различных факторов, оказывающих влияние на термические напряжения в покрытиях, можно выделить первичные и вторичные. К первичным следует отнести различия в значениях к. т. р. и модулях упругости материалов покрытия и металла геометрические размеры образцов ползучесть материала покрытия и металлов предел текучести металлов , интервалы размягчения покрытия, когда теряются упругие свойства материала покрытия. Эти факторы оказывают непосредственное влияние на величину напряжений в покрытиях и могут быть учтены количественно с помощью теории. термоупругости, термопластичности и т. д. [c.24]
Эти факторы оказывают непосредственное влияние на величину напряжений в покрытиях и могут быть учтены количественно с помощью теории. термоупругости, термопластичности и т. д. [c.24]
Зависимость величины прогиба от соотношения модулей упругости можно вычислить по формуле (I. 54) и при неизвестных абсолютных величинах модулей упругости. Для определения же напряжений необходимо знать абсолютные величины модулей упругости материалов. Однако анализ деформаций позволяет получить зависимость их от соотношения модулей упругости для прогибающейся полосы [c.30]
Здесь Еб, Е, и Е — модули упругости материалов болта и частей шатуна Рб, я — плош,ади сечений болта и соединяемых частей шатуна 6, /1 и /2 —длины болта и соединяемых деталей. [c.258]
Расчет цилиндров высокого давления и их втулок производят по формулам для толстостенных цилиндров, учитывая напряжения при посадке втулки и различие модулей упругости материалов цилиндра и втулки. Ввиду пульсирующей нагрузки, при выборе запаса прочности принимают во внимание усталостную характеристику. материала. [c.135]
Ввиду пульсирующей нагрузки, при выборе запаса прочности принимают во внимание усталостную характеристику. материала. [c.135]
На рис. 48 показана диаграмма усилий, построенная в предположении, что модуль упругости материалов деталей не изменяется. Это допущение может быть принято при условии, что температура деталей при проведении процессов не превышает 200° С. [c.83]
Давление уплотнения /о должно быть достаточным для того, чтобы материал прокладки заполнил бы неровности от обработки уплотняемых поверхностей. Величина /о или отвечающее ему е может быть найдена экспериментально. Уравнение (8.12) по заданным параметрам и модулям упругости материалов деталей конструкций и величине затяга Q позволяет найти ркр- [c.216]
Уравнение (13.15) по заданным параметрам и модулям упругости материалов деталей конструкций и величине затяга О позволяет найти Ркр. [c.396]
Епр — приведенный модуль упругости материалов шестерни и колеса в кГ/см -, [c. 129]
129]
Контактное давление зависит от величины натяга, модулей упругости материалов сопрягаемых деталей Е1 и и коэффициентов, учитывающих соотношение наружного и внутреннего диаметров подщипника. [c.58]
Ех, — модули упругости материалов при растяжении. [c.93]
Поскольку прочностные характеристики и модули упругости материалов, из которых изготовлены элементы конструкций колонных аппаратов, изменяются при повышении температуры, для каждого расчетного сечения (см. разд. 12.6.5) необходимо знать температуру (обычно в условиях эксплуатации, так как в условиях монтажа и испытаний температура равна температуре окружающей среды). Температура внутри корпуса задается условиями технологического процесса н обычно считается постоянной по времени и высоте корпуса. Однако в опорной обечайке в верхней ее части температура равна температуре корпуса, а в нижней — значительно ниже, поскольку нижняя часть охлаждается фундаментом. Для элементов нижнего опорного узла опорной обечайки, приваренной к корпусу колонны и теплоизолированной, расчетную температуру в рабочих условиях определяют по формуле [c. 211]
211]
Е и модули упругости материалов отверстия и вала. [c.19]
Жесткость проклад ки и болтов (С р и Се) определяются площадью прокладки и поперечного сечения болта (Fnp, Fe), толщиной прокладки и рабочей длиной болта (Л, Ц), а также модулями упругости материалов ( пр. Еб) [c.16]
Теория образования анизотропной фазы также распространена на случай, в котором раствор или расплав, содержащий жесткоцепные или полужесткоцепные макромолекулы, подвергается воздействию продольного гидродинамического поля (гл. IV). Особый интерес представляют растворы полужесткоцепных макромолекул. В этом случае образование межмолекулярных зацеплений в системе может наложиться на переход в анизотропную фазу под воздействием продольного гидродинамического поля. Явления такого типа могут происходить даже при воздействии сдвигового поля, что, по-видимому, может объяснять высокие значения модулей упругости материалов, сформованных из растворов полужесткоцепных макромолекул, неспособных образовывать анизотропные фазы в состоянии покоя (гл. VII). [c.11]
VII). [c.11]
Выражая отношение напряжений как отношение модулей упругости материалов текстофаолита [c.187]
В рабочем диапазоне температур все исследованные материалы переходят из стеклообразного в высокоэластическое состояние. Модуль упругости материалов в стеклообразном состоянии практически не зависит от температуры. При переходе в высокоэластическое состояние вследствие нагрева до рабочей температуры он уменьша.ется на один-два порядка. [c.52]
Модули упругости — обзор
Модуль упругости
Модуль упругости бетона также является важным механическим свойством, которое используется для определения твердости бетона и его сопротивления истиранию. В общем, модуль упругости бетона тесно связан с его прочностью на сжатие. Модуль упругости бетона увеличивается с увеличением его прочности на сжатие. Тем не менее, в большинстве литературных источников показано отрицательное влияние POFA на модуль упругости бетона, хотя прочность на сжатие была улучшена (Awal and Hussin, 2011; Sata et al . , 2004; Ислам и др. ., 2016). С другой стороны, некоторые исследования доказали, что POFA обладает положительным эффектом для улучшения модуля упругости бетона (Tangchirapat and Jaturapitakkul, 2010; Hussin et al ., 2010; Alsubari et al ., 2018). Фактически, заполнитель будет в основном вносить вклад в модуль упругости бетона, в то время как введение POFA может изменить свойства сцепления заполнителя и цементной пасты.
, 2004; Ислам и др. ., 2016). С другой стороны, некоторые исследования доказали, что POFA обладает положительным эффектом для улучшения модуля упругости бетона (Tangchirapat and Jaturapitakkul, 2010; Hussin et al ., 2010; Alsubari et al ., 2018). Фактически, заполнитель будет в основном вносить вклад в модуль упругости бетона, в то время как введение POFA может изменить свойства сцепления заполнителя и цементной пасты.
Исследования, проведенные Sata et al .(2004) указали, что содержание G-POFA до 30% оказало незначительное влияние на модуль упругости бетона. Было также высказано предположение, что уменьшение крупного заполнителя бетона в результате включения G-POFA вызвало небольшое снижение модуля упругости. Кроме того, статическая эластичность бетона, содержащего 30% POFA, и бетона без POFA были измерены Авалом и Хусином (2011). Результаты показали, что бетон POFA имеет более низкий модуль упругости, чем обычный бетон.Пуццолановый продукт, содержащий 30% POFA, показал более низкую прочность, чем гидратация OPC.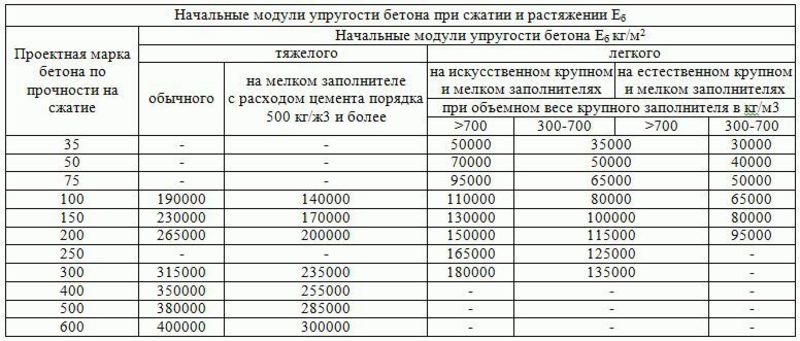 Кроме того, модули упругости бетона, состоящего с различным содержанием POFA и отвержденного в условиях воздуха (AC) и полной воды (WC), были определены Исламом и др. . (2016). По результатам исследования, модуль упругости бетона постепенно уменьшался с увеличением содержания POFA (от 0% до 25% POFA). В литературе объясняется, что POFA имеет ограниченное влияние на улучшение межфазной зоны бетона.Тем не менее, уменьшение модуля упругости было минимальным, например, модуль упругости уменьшился на 15%, когда содержание POFA увеличилось с 0% до 25%. Между тем, модуль упругости водоотверждаемого бетона был примерно на 10–23% выше, чем у соответствующего воздушного бетона.
Кроме того, модули упругости бетона, состоящего с различным содержанием POFA и отвержденного в условиях воздуха (AC) и полной воды (WC), были определены Исламом и др. . (2016). По результатам исследования, модуль упругости бетона постепенно уменьшался с увеличением содержания POFA (от 0% до 25% POFA). В литературе объясняется, что POFA имеет ограниченное влияние на улучшение межфазной зоны бетона.Тем не менее, уменьшение модуля упругости было минимальным, например, модуль упругости уменьшился на 15%, когда содержание POFA увеличилось с 0% до 25%. Между тем, модуль упругости водоотверждаемого бетона был примерно на 10–23% выше, чем у соответствующего воздушного бетона.
Хуссин и др. . (2010) провели исследование на образцах простого газобетона и обнаружили, что пенобетон POFA обладает более высоким значением жесткости и, следовательно, имеет более высокий модуль упругости, чем контрольный бетон.Частичная замена цемента на POFA позволила протекать пуццолановой реакции, в результате которой образовался дополнительный гель C-S-H, что привело к уплотнению внутренней структуры легкого бетона, что сделало ее более жесткой. Кроме того, Tangchirapat и Jaturapitakkul (2010) пришли к выводу, что использование грубого POFA (CP) и мелкого POFA (FP) незначительно влияет на изменение модуля упругости бетона по сравнению с бетоном OPC. Фактически, прочность, обеспечиваемая крупными заполнителями, больше влияет на определение модуля упругости бетона, чем прочность цементной пасты.
Кроме того, Tangchirapat и Jaturapitakkul (2010) пришли к выводу, что использование грубого POFA (CP) и мелкого POFA (FP) незначительно влияет на изменение модуля упругости бетона по сравнению с бетоном OPC. Фактически, прочность, обеспечиваемая крупными заполнителями, больше влияет на определение модуля упругости бетона, чем прочность цементной пасты.
Кроме того, Alsubari et al . (2018) включили модифицированный обработанный POFA (MT-POFA) в создание SCC. Было показано, что модули упругости незначительно увеличиваются при увеличении содержания MT-POFA с 0% до 30% для бетонов в возрасте 28 и 56 дней. Это произошло из-за пуццолановых свойств MT-POFA, которые улучшили сцепление между цементным тестом и заполнителем. Тем не менее, модули упругости значительно снизились для последующего увеличения POFA на 50% и 70%. На модуль упругости бетона в первую очередь влияет содержание крупного заполнителя.Таким образом, снижение модулей упругости для бетонов на 50% и 70% было связано с уменьшением отношения заполнителя к пасте, где содержание заполнителя уменьшилось. Кроме того, Lau et al . (2018) включили POFA и обработанный известью осадок сточных вод для создания легкого заполнителя и получили название Posslite LWA. В ходе исследования для производства бетона использовался Posslite LWA. Было обнаружено, что модуль упругости бетона, изготовленного из Posslite LWA, был немного ниже, чем у контрольного бетона, но все же был сравним с контрольным бетоном.Точно так же снижение модуля упругости было связано с более слабой межфазной переходной зоной бетона, содержащего Posslite LWA.
Кроме того, Lau et al . (2018) включили POFA и обработанный известью осадок сточных вод для создания легкого заполнителя и получили название Posslite LWA. В ходе исследования для производства бетона использовался Posslite LWA. Было обнаружено, что модуль упругости бетона, изготовленного из Posslite LWA, был немного ниже, чем у контрольного бетона, но все же был сравним с контрольным бетоном.Точно так же снижение модуля упругости было связано с более слабой межфазной переходной зоной бетона, содержащего Posslite LWA.
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie.Вам необходимо сбросить настройки браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.

- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, используйте кнопку «Назад» и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie.Чтобы исправить это, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или уточнить у системного администратора.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie
потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Чтобы предоставить доступ без файлов cookie
потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файлах cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в файле cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
Elasticity — The Physics Hypertextbook
Обсуждение
основы
Эластичность — это свойство твердых материалов возвращаться к своей исходной форме и размеру после устранения деформирующих их сил. Вспомните закон Гука — впервые официально сформулированный Робертом Гук в Истинная теория упругости или упругости (1676)…
Вспомните закон Гука — впервые официально сформулированный Робертом Гук в Истинная теория упругости или упругости (1676)…
uttensio, sic vis
, что буквально можно перевести как…
Как расширение, так и сила.
или официально переведен на…
Вытяжка прямо пропорциональна силе.
Скорее всего, мы заменим слово «расширение» символом (∆ x ), «сила» — символом ( F ), а «прямо пропорционально» — знаком равенства (=) и константа пропорциональности ( k ), тогда, чтобы показать, что упругий объект пытается вернуться в исходное состояние, мы добавили бы знак минус (-). Другими словами, мы бы записали уравнение…
F = — k ∆ x
Это закон Гука для пружины — простого объекта, который по существу одномерный.Закон Гука можно обобщить до…
Напряжение пропорционально деформации.
, где деформация относится к изменению некоторого пространственного измерения (длины, угла или объема) по сравнению с его исходным значением, а напряжение относится к причине изменения (сила, приложенная к поверхности).
Коэффициент, который связывает конкретный тип напряжения с возникающей деформацией, называется модулем упругости (во множественном числе, модули). Модули упругости — это свойства материалов, а не объектов.Существует три основных типа напряжения и три связанных модуля.
| модуль (символы) | напряжение (символ) | штамм (символ) | конфигурация изменение |
|---|---|---|---|
| Янг ( E или Y ) | по нормали к противоположным граням (σ) | длина ε = ∆ℓ / ℓ 0 | длиннее и тоньше или короче и толще |
| ножницы ( G или S ) | по касательной к противоположным граням (τ) | касательная γ = ∆ x / y | прямоугольников превращаются в параллелограмма |
| навалом ( K или B ) | нормально ко всем сторонам, давление ( P ) | объем θ = ∆ V / V 0 | объем изменяется , но форма не изменяется |
Международные стандартные символы для модулей являются производными от соответствующих неанглийских слов — E для élasticité (французское слово «эластичность»), G для glissement (французский язык для скольжения) и K для компрессии. (немецкое для сжатия).Некоторые американские учебники решили порвать с традициями и использовать первую букву каждого модуля на английском языке — Y для Юнга, S для сдвига и B для пухлости.
(немецкое для сжатия).Некоторые американские учебники решили порвать с традициями и использовать первую букву каждого модуля на английском языке — Y для Юнга, S для сдвига и B для пухлости.
Напряжения в твердых телах всегда описываются как сила, деленная на площадь. Направление сил может измениться, а единицы — нет. Единицей измерения напряжения в системе СИ является ньютон на квадратный метр , которому присвоено особое название паскаль в честь Блеза Паскаля (1623–1662), французского математика (треугольник Паскаля), физика (принцип Паскаля), изобретателя (принцип Паскаля). калькулятор) и философ (пари Паскаля).
| ⎡ ⎢ ⎣ | Па = | N | ⎤ ⎥ ⎦ |
| м 2 |
Штаммы всегда безразмерны.
| вид штамма | наименование символа | определение | шт. |
|---|---|---|---|
| линейный | эпсилон | ε = ∆ℓ / ℓ 0 | м / м = 1 |
| ножницы | гамма | γ = ∆ x / y | м / м = 1 |
| объем | тета | θ = ∆ В / В 0 | м 3 / м 3 = 1 |
Это означает, что паскаль также является единицей СИ для всех трех модулей.
| напряжение | = | модуль | × | штамм | ||
| [ | Па | = | Па | × | 1 | ] |
отказ — вариант
- Предел упругости, предел текучести
- предел прочности, предел прочности
- Прочность материала — это мера его способности выдерживать нагрузку без разрушения.

- Banerjee, et al. показывают, что когда иглы монокристаллического алмаза в наномасштабе упруго деформируются, они выходят из строя при максимальной локальной прочности на разрыв от ~ 89 до 98 ГПа.
- Экспериментальные результаты и расчеты ab initio показывают, что модуль упругости углеродных нанотрубок и графена приблизительно равен 1 ТПа.
- Напротив, заявленная прочность на разрыв объемного кубического алмаза составляет <10 ГПа
Модуль Юнга
Представьте себе кусок теста.Растяните это. Он становится длиннее и тоньше. Раздавите это. Он становится короче и толще. А теперь представьте кусок гранита. Проведите тот же мысленный эксперимент. Изменение формы обязательно должно произойти, но невооруженным глазом незаметно. Некоторые материалы довольно легко растягиваются и сжимаются. Некоторые этого не делают.
Величина, описывающая реакцию материала на напряжения, приложенные перпендикулярно противоположным граням, называется модулем Юнга в честь английского ученого Томаса Янга (1773–1829).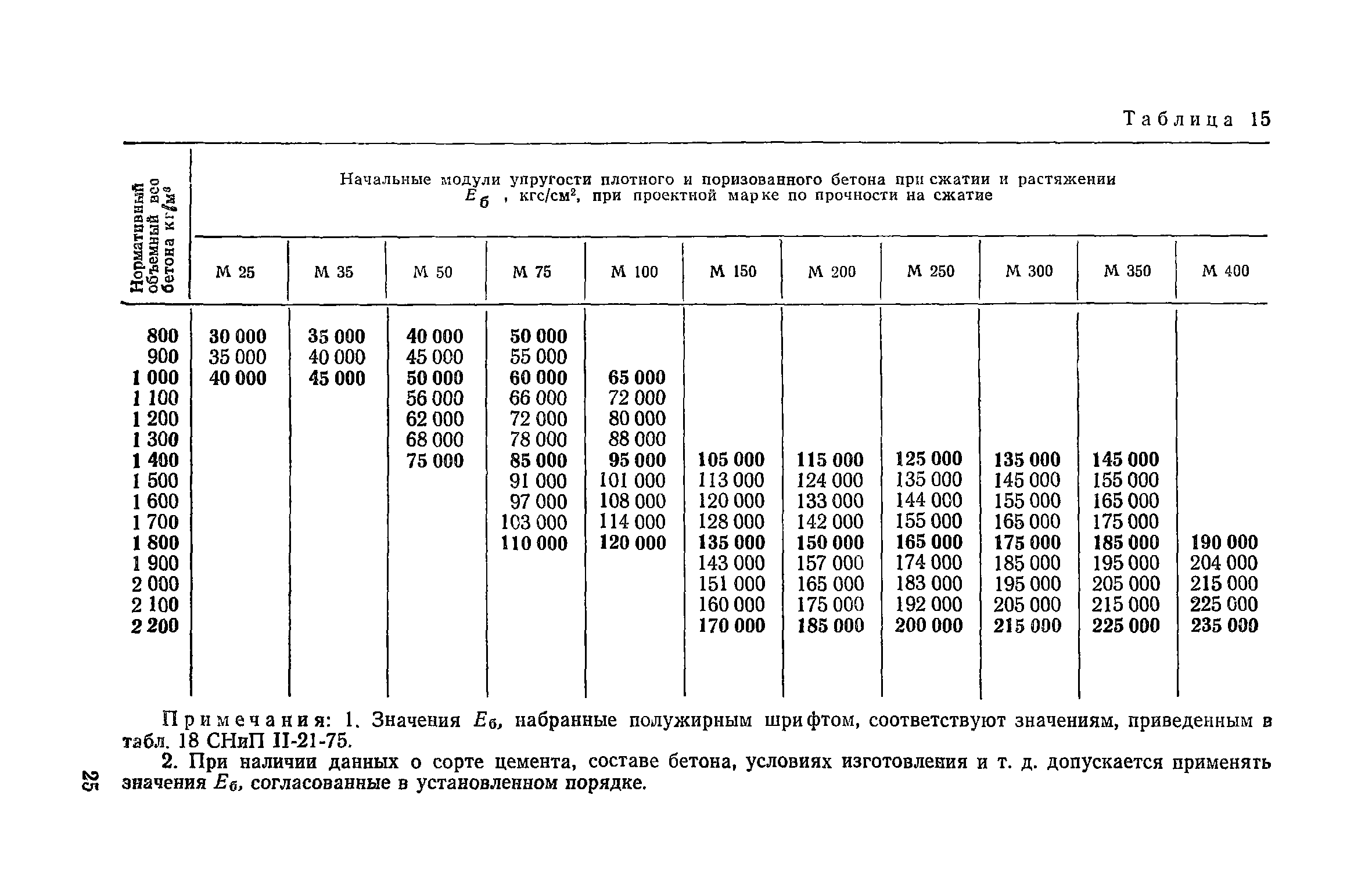 Янг был первым, кто определил работу как продукт смещения силы, первым использовал слово энергия в его современном смысле и первым показал, что свет — это волна.Он не был первым, кто количественно оценил сопротивление материалов растяжению и сжатию, но он стал самым известным ранним сторонником модуля, который теперь носит его имя. Янг не назвал модуль в честь себя. Он назвал это модулем упругости . Символ модуля Юнга обычно E от французского слова élasticité (эластичность), но некоторые предпочитают Y в честь ученого.
Янг был первым, кто определил работу как продукт смещения силы, первым использовал слово энергия в его современном смысле и первым показал, что свет — это волна.Он не был первым, кто количественно оценил сопротивление материалов растяжению и сжатию, но он стал самым известным ранним сторонником модуля, который теперь носит его имя. Янг не назвал модуль в честь себя. Он назвал это модулем упругости . Символ модуля Юнга обычно E от французского слова élasticité (эластичность), но некоторые предпочитают Y в честь ученого.
определяется для всех форм и размеров по одному и тому же правилу, но для удобства представим, что стержень длиной 0 и площадью поперечного сечения A растягивается силой F до новой длины ℓ 0 + ∆ℓ.
Растягивающее напряжение — это внешняя нормальная сила на площадь (σ = F / A ), а деформация растяжения — частичное увеличение длины стержня (ε = ∆ℓ / ℓ 0 ). Константа пропорциональности, которая связывает эти две величины вместе, представляет собой отношение растягивающего напряжения к растягивающей деформации — модуль Юнга .
Константа пропорциональности, которая связывает эти две величины вместе, представляет собой отношение растягивающего напряжения к растягивающей деформации — модуль Юнга .
То же соотношение справедливо и для сил в противоположном направлении; то есть напряжение, которое пытается сократить объект.
Заменить прилагательное «растяжение» на «сжатие». Нормальная сила, приходящаяся на площадь, направленную внутрь (σ = F / A ), называется напряжением сжатия , а частичное уменьшение длины (ε = ∆ℓ / ℓ 0 ) называется деформацией сжатия . Это делает модуль Юнга отношением сжимающего напряжения к сжимающей деформации. Прилагательное могло быть изменено, но математическое описание — нет.
Единицы измерения модуля Юнга в системе СИ — паскаль [Па]…
| ⎡ ⎢ ⎣ | N | = Па | м | ⎤ ⎥ ⎦ |
| А | м |
, но для большинства материалов более подходящим является значение гигапаскаль [ГПа].
1 ГПа = 10 9 Па
Коэффициент Пуассона
Растяжение и сжатие — противоположные типы линейной деформации. Продлить — значит стать длиннее. Сокращение означает стать короче. Когда материал растягивается или сжимается под действием линейного напряжения в одном направлении (называемом осью x ), обратная деформация обычно имеет место в перпендикулярных направлениях (оси y и z ). Направление линейного напряжения называется осевым направлением .Все направления, которые перпендикулярны этому, называются поперечными направлениями .
Осевое разгибание обычно сопровождается поперечным сокращением. Растягивание теста делает его тоньше и длиннее. Так делают китайскую лапшу, вытянутую вручную (拉面, la mian ). Точно так же осевое сокращение обычно сопровождается поперечным растяжением. Если кусок теста сплющить, он станет шире, длиннее и тоньше. Так делают итальянскую свежую пасту ( pasta fresca ).
Отношение поперечной деформации к осевой деформации известно как коэффициент Пуассона (ν) в честь его изобретателя, французского математика и физика Симеона Пуассона (1781–1840). Отрицательный знак необходим, чтобы показать, что изменения обычно противоположного типа (+ растяжение против — сужение). Если придерживаться традиции, согласно которой x — это осевое направление, а y и z — поперечные направления, то коэффициент Пуассона можно записать как…
| ν = — | ∆ y / y 0 | = — | ∆ z / z 0 |
| ∆ x / x 0 | ∆ x / x 0 |
Символ, который, к сожалению, похож на латинскую букву v (vee), на самом деле является греческой буквой ν (nu), которая связана с латинской буквой n (en).
| в | ν | n |
| Латинское «vee» скорость | Греческое «nu» Коэффициент Пуассона | Латинское «en» число |
Типичные значения коэффициента Пуассона находятся в диапазоне от 0,0 до 0,5. Пробка — это пример материала с низким коэффициентом Пуассона (почти нулевым). Когда в винную бутылку вставляют пробку, она становится короче, но не толще.(Есть некоторая осевая деформация, но практически отсутствует поперечная.) Резина, с другой стороны, имеет высокий коэффициент Пуассона (почти 0,5). Когда резиновую пробку вставляют в колбу для химикатов, она становится короче на определенную величину и шире почти вдвое. (Осевая деформация сопровождается большой поперечной деформацией.) Пробки можно толкать в бутылки с помощью молотка. Забить резиновую пробку в стеклянную колбу молотком, скорее всего, закончится катастрофой.
Как ни странно, возможны и отрицательные коэффициенты Пуассона.Такие материалы называются ауксетическими . Они увеличиваются в поперечном направлении при растяжении и уменьшаются при сжатии. Большинство ауксетических материалов представляют собой полимеры с мятой пенистой структурой. Вытягивание пены заставляет складки разворачиваться, и вся сеть расширяется в поперечном направлении.
| материал | модуль Юнга | на сжатие прочность | растяжение прочность |
|---|---|---|---|
| алюминий | 70 | 0.040 | |
| морковь, свежая | 0,00136 | 0,000504 | |
| морковь, хранится 1 неделя | 0,00103 | 0,000507 | |
| бетон | 17 | 0,021 | 0,0021 |
| бетон высокой прочности | 30 | 0. 040 040 | |
| медь | 130 | 0,22 | |
| кость компактная | 18 | 0,17 | 0,12 |
| кость губчатая | 76 | 0,0022 | |
| латунь | 110 | 0,25 | |
| алмаз | 1100 | ||
| стекло | 50–90 | 0.050 | |
| гранит | 52 | 0,145 | 0,0048 |
| золото | 74 | ||
| утюг | 210 | ||
| мрамор | 0,015 | ||
| зефир | 0. 000029 000029 | ||
| никель | 170 | ||
| нейлон | 2–4 | 0,075 | |
| дуб | 11 | 0,059 | 0,12 |
| пластик, ♳ ПЭТ | 2,0–2,7 | 0,055 | |
| пластик, ♴ HDPE | 0.80 | 0,015 | |
| пластик, ♵ ПВХ | |||
| пластик, ♶ LDPE | |||
| пластик, ♷ PP | 1,5–2,0 | 0,040 | |
| пластик, ♸ PS | 3,0–3,5 | 0,040 | |
| плутоний | 97 | ||
| фарфор | 0. 55 55 | 0,0055 | |
| кремний | 110 | ||
| карбид кремния | 450 | ||
| сталь, нержавеющая | 0,86 | ||
| сталь конструкционная | 200 | 0,40 | 0,83 |
| сталь высокопрочная | 0.76 | ||
| резина | 0,01–0,10 | 0,0021 | |
| банка | 47 | ||
| титан | 120 | ||
| вольфрам | 410 | ||
| карбид вольфрама | 500 | ||
| уран | 170 |
Модуль сдвига
Сила, приложенная тангенциально (или поперечно, или сбоку) к поверхности объекта, называется напряжением сдвига. Возникающая в результате деформация называется деформацией сдвига. Приложение напряжения сдвига к одной грани прямоугольного ящика сдвигает эту сторону в направлении, параллельном противоположной грани, и изменяет прилегающие грани с прямоугольников на параллелограммы.
Возникающая в результате деформация называется деформацией сдвига. Приложение напряжения сдвига к одной грани прямоугольного ящика сдвигает эту сторону в направлении, параллельном противоположной грани, и изменяет прилегающие грани с прямоугольников на параллелограммы.
Коэффициент, который связывает напряжение сдвига (τ = F / A ) к деформации сдвига (γ = ∆ x / y ), называется модулем сдвига , модулем жесткости , или Кулоновский модуль .Обычно он обозначается символом G от французского слова glissement (скользящий), хотя некоторые предпочитают использовать вместо него S от английского слова shear.
Жидкости (жидкости, газы и плазма) не могут противостоять напряжению сдвига. Они скорее текут, чем деформируются. Величина, которая описывает, как текучие среды текут в ответ на напряжения сдвига, называется вязкостью и рассматривается в другом месте этой книги.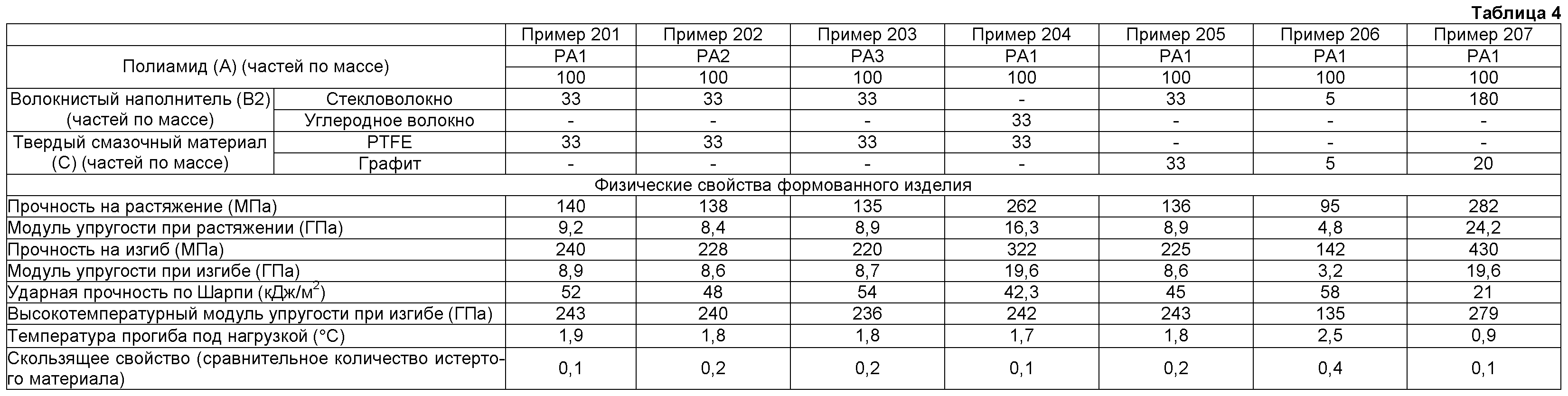
Невозможность сдвига также означает, что жидкости непрозрачны для поперечных волн, таких как вторичные волны землетрясения (также известные как поперечные волны или s волны ).Жидкое внешнее ядро Земли было обнаружено по тенью s-волны, которую она отбрасывала на сети сейсмометров. Типы волн обсуждаются в других разделах этой книги.
Жидкости могут противостоять нормальному стрессу. Это означает, что жидкости и газы прозрачны для первичных волн землетрясения (также известных как волны давления или волны p ). Твердое внутреннее ядро Земли было обнаружено в сигналах p-волны, которые прошли весь путь от одной стороны Земли через жидкое внешнее ядро к другой стороне.Также слышны зубцы P. Вы можете услышать их, когда они передаются в воздух.
Сопротивление материала нормальному напряжению описывается модулем объемного сжатия, который является следующей темой в этом разделе.
| материал | сдвиг модуль | сдвиг прочность |
|---|---|---|
| алюминий | ||
| бетон | ||
| бетон высокой прочности | ||
| медь | ||
| кость компактная | ||
| кость губчатая | ||
| латунь | ||
| алмаз | ||
| стекло | ||
| гранит | ||
| золото | ||
| утюг | ||
| мрамор | ||
| зефир | ||
| никель | ||
| нейлон | ||
| дуб | ||
| пластик, ♳ ПЭТ | ||
| пластик, ♴ HDPE | ||
| пластик, ♵ ПВХ | ||
| пластик, ♶ LDPE | ||
| пластик, ♷ PP | ||
| пластик, ♸ PS | ||
| плутоний | ||
| фарфор | ||
| кремний | ||
| карбид кремния | ||
| сталь, нержавеющая | ||
| сталь конструкционная | ||
| сталь высокопрочная | ||
| резина | ||
| банка | ||
| титан | ||
| вольфрам | ||
| карбид вольфрама | ||
| уран |
Модуль объемной упругости
Сила, приложенная равномерно к поверхности объекта, будет равномерно сжимать его. Это изменяет объем объекта без изменения его формы.
Это изменяет объем объекта без изменения его формы.
Напряжение в этом случае просто описывается как давление ( P = F / A ). Результирующая объемная деформация измеряется по частичному изменению объема (θ = ∆ V / V 0 ). Коэффициент, который связывает напряжение с деформацией при равномерном сжатии, известен как модуль объемной упругости или модуль сжатия .Его традиционный символ — K от немецкого слова kompression (сжатие), но некоторым нравится использовать B от английского слова bulk, которое является другим словом для обозначения объема.
Модуль объемной упругости — это свойство материалов в любой фазе, но чаще обсуждают модуль объемной упругости для твердых тел, чем для других материалов. У газов есть объемный модуль, который изменяется в зависимости от начального давления, что делает его более важным для термодинамики, в частности, для газовых законов.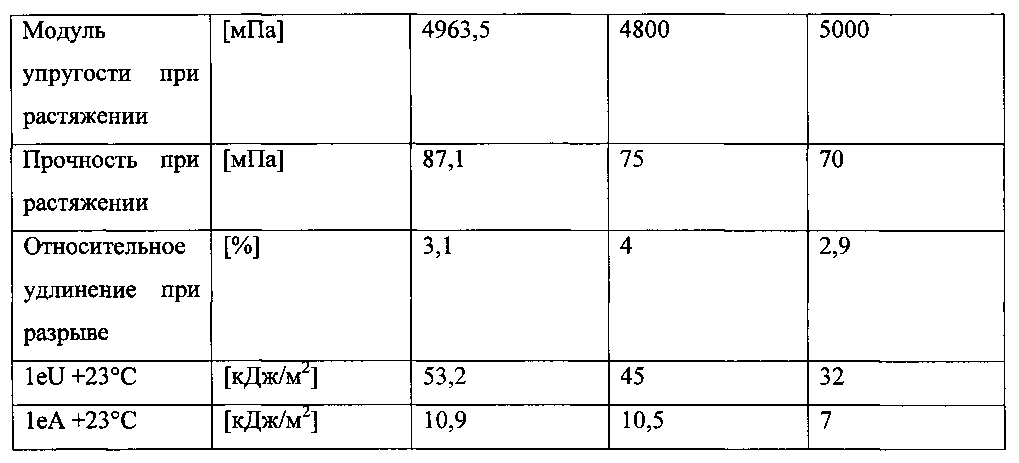
Обратный модуль объемного сжатия называется сжимаемостью .Его символ обычно β (бета), но некоторые люди предпочитают κ (каппа). Материал с высокой сжимаемостью испытывает большое изменение объема при приложении давления.
Единица сжимаемости в системе СИ — это обратный паскаль [Па -1 ].
| материал | объем модуль | материал | объем модуль |
|---|---|---|---|
| алюминий | пластик, ♳ ПЭТ | ||
| морковь, свежая | пластик, ♴ HDPE | ||
| морковь, хранится 1 неделя | пластик, ♵ ПВХ | ||
| бетон | пластик, ♶ ПВД | ||
| бетон высокой прочности | пластик, ♷ PP | ||
| медь | пластик, ♸ PS | ||
| кость компактная | плутоний | ||
| кость губчатая | фарфор | ||
| латунь | кремний | ||
| алмаз | карбид кремния | ||
| стекло | сталь, нержавеющая | ||
| гранит | сталь конструкционная | ||
| золото | Сталь | , высокопрочная | |
| утюг | каучук | ||
| мрамор | банка | ||
| зефир | титан | ||
| никель | вольфрам | ||
| нейлон | карбид вольфрама | ||
| дуб | уран |
масштабирование
- без гигантских животных
- площадь поверхности пропорциональна длине 2
- масса и объем пропорциональны длине 3
- BMR пропорционален массе 3/4
- напряжение пропорционально длине (закон Гука)
- давление пропорционально длине 2 (растяжение желудка, мочевого пузыря)
поверхностное натяжение
| материал | поверхностное натяжение (мкН / м) |
|---|---|
| спирт этиловый (зерновой) | 223. 2 2 |
| спирт изопропиловый (15 ° C) | 217,9 |
| спирт метиловый (дерево) | 225,5 |
| молоко сырое | 1000–2000 |
| молоко гомогенизированное | 3000–4000 |
| вода чистая | 728 |
| вода мыльная | 250–450 |
Капиллярность
- Средний диаметр капилляров составляет около 20 мкм, хотя некоторые из них имеют диаметр всего 5 мкм.На 1 кг мышцы приходится около 190 км капилляров, площадь поверхности капилляров на 1 кг мышцы составляет около 12 м 2 .
Модуль упругости — интерактивное покрытие
Модуль упругости иногда называют модулем Юнга в честь Томаса Янга, который опубликовал эту концепцию еще в 1807 году. Модуль упругости (E) может быть определен для любого твердого материала и представляет собой постоянное соотношение напряжения и деформации (жесткость):
Материал является эластичным, если он может вернуться к своей первоначальной форме или размеру сразу после растяжения или сжатия.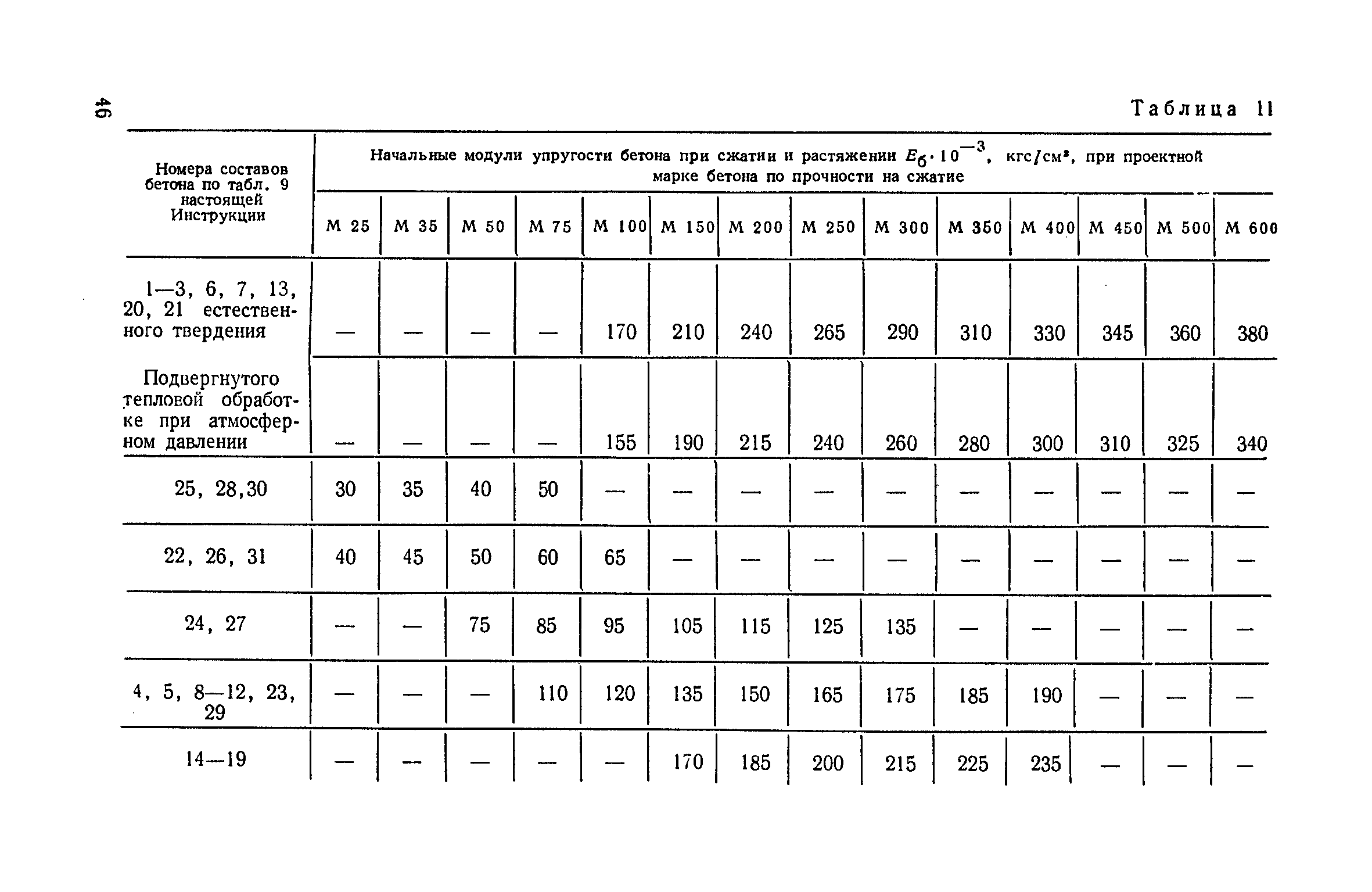 Почти все материалы в той или иной степени эластичны, если приложенная нагрузка не вызывает их постоянной деформации. Таким образом, «гибкость» любого объекта или конструкции зависит от его модуля упругости и геометрической формы.
Почти все материалы в той или иной степени эластичны, если приложенная нагрузка не вызывает их постоянной деформации. Таким образом, «гибкость» любого объекта или конструкции зависит от его модуля упругости и геометрической формы.
Модуль упругости материала — это, по сути, наклон его графика зависимости напряжения от деформации в пределах диапазона упругости (как показано на рисунке 1). На рисунке 2 показана кривая зависимости напряжения от деформации для стали. Начальная прямолинейная часть кривой — это диапазон упругости стали.Если в этой части кривой материал нагружен до любого значения напряжения, он вернется к своей исходной форме. Таким образом, модуль упругости представляет собой наклон этой части кривой и равен примерно 207 000 МПа (30 000 000 фунтов на квадратный дюйм) для стали. Важно помнить, что показатель модуля упругости материала не является показателем прочности . Прочность — это напряжение, необходимое для разрыва или разрыва материала (как показано на рисунке 1), тогда как эластичность — это мера того, насколько хорошо материал возвращается к своей первоначальной форме и размеру.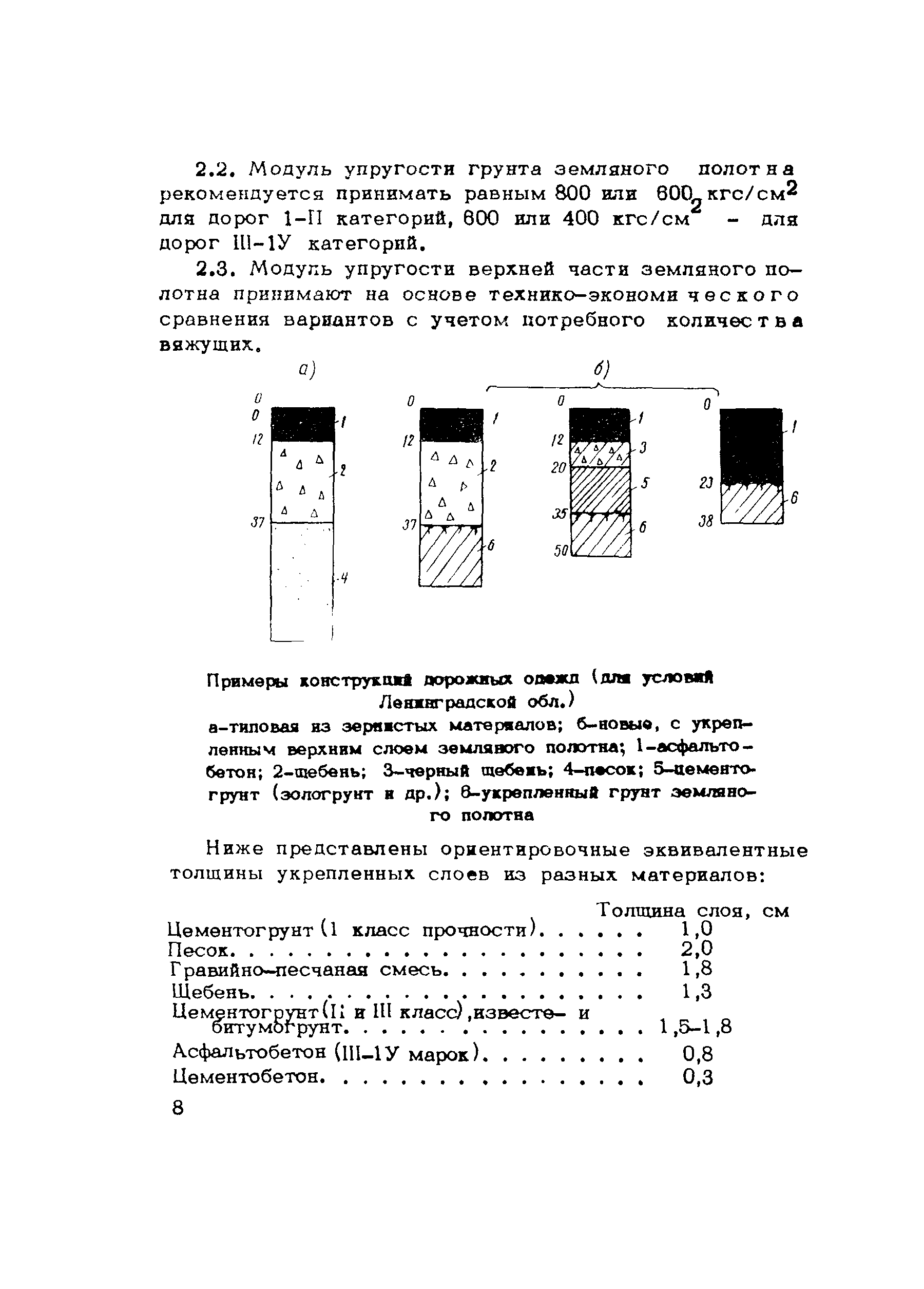
Номенклатура и условные обозначения
Номенклатура и символы из Руководства AASHTO 1993 г. обычно используются для обозначения модулей дорожного покрытия. Например:
- E AC = модуль упругости асфальтобетона
- E BS = модуль упругости основного слоя
- E SB = модуль упругости основного слоя
- M R (или E SG ) = модуль упругости грунта (земляного полотна) дорожного полотна (используются взаимозаменяемо)
Чувствительность модулей
к напряжениюИзменения напряжения могут иметь большое влияние на модуль упругости.«Типичные» отношения показаны на рисунках 3 и 4.
Рисунок 3. Модуль упругости в зависимости от объемного напряжения для нестабилизированных крупнозернистых материалов. Рисунок 4. Модуль упругости в зависимости от девиаторного напряжения для нестабилизированных мелкозернистых материалов.
Рисунок 4. Модуль упругости в зависимости от девиаторного напряжения для нестабилизированных мелкозернистых материалов.Типичные значения
В таблице 2 приведены типичные значения модуля упругости для различных материалов.
Таблица 2. Типичные значения модуля упругости для различных материалов
| Материал | Модуль упругости | |
| МПа | фунтов на кв. Дюйм | |
| Алмаз | 1,200,000 | 170 000 000 |
| Сталь | 200 000 | 30 000 000 |
| Стекловолокно | 71 000 | 10,600,000 |
| Алюминий | 70 000 | 10 000 000 |
| Дерево | 7 000–14 000 | 1 000 000–2 000 000 |
| Щебень | 150-300 | 20 000–40 000 |
| илистые почвы | 35–150 | 5 000–20 000 |
| Глинистые почвы | 35–100 | 5 000–15 000 |
| Резина | 7 | 1 000 |
модулей упругости углеродных нанорогов
Углеродные нанотрубки — это особый случай углеродных нанорогов или углеродных наноконусов с нулевым углом при вершине.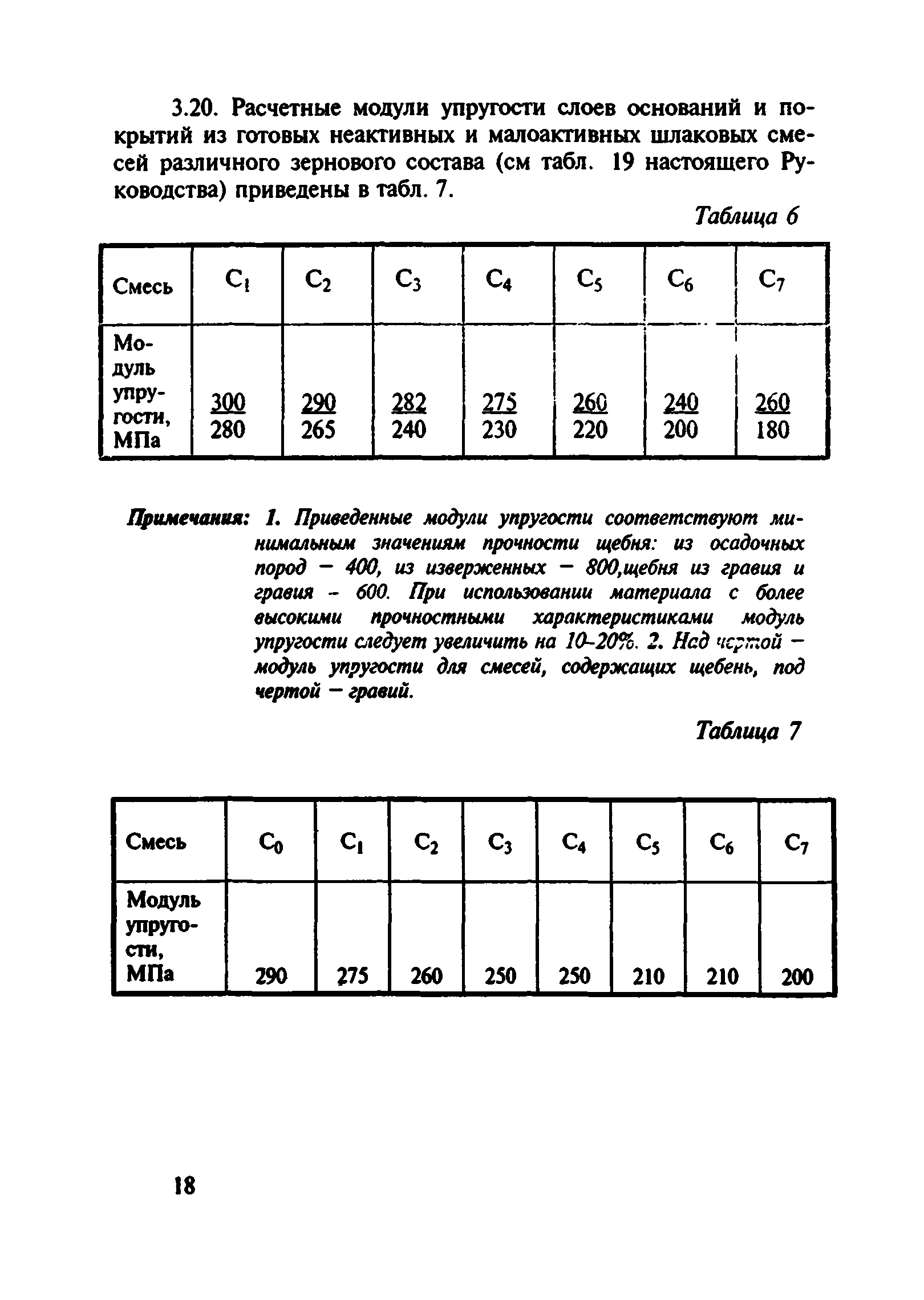 Исследования углеродных нанорогов начались почти одновременно с открытием нанотрубок в 1991 году. Большинство исследователей сосредоточились на изучении нанотрубок, а исследование нанорогов не привлекло особого внимания. Для моделирования углеродных нанорогов мы используем более надежный реактивный эмпирический эмпирический потенциал порядка связей второго поколения Бреннера с соавторами. Мы исследовали модули упругости и пришли к выводу, что эти нанороги одинаково прочны и требуют более глубокого изучения. Значения модулей Юнга и сдвига уменьшаются с увеличением угла при вершине.
Исследования углеродных нанорогов начались почти одновременно с открытием нанотрубок в 1991 году. Большинство исследователей сосредоточились на изучении нанотрубок, а исследование нанорогов не привлекло особого внимания. Для моделирования углеродных нанорогов мы используем более надежный реактивный эмпирический эмпирический потенциал порядка связей второго поколения Бреннера с соавторами. Мы исследовали модули упругости и пришли к выводу, что эти нанороги одинаково прочны и требуют более глубокого изучения. Значения модулей Юнга и сдвига уменьшаются с увеличением угла при вершине.
1. Введение
С момента открытия углеродных нанотрубок (УНТ) в начале 1990-х годов [1] в этой области было проведено много исследований. В ряде отчетов было обнаружено, что УНТ обладают низкой плотностью, но высокой жесткостью и высокой прочностью, а также превосходными электронными свойствами. Сочетание структурного совершенства и этих желаемых свойств делает УНТ популярным материалом для изучения, и ожидается, что они найдут широкий спектр применения в электронике, батареях и суперконденсаторах, хранении водорода, армировании композитов, наносенсорах и зондах, а также эмиссии электронов. Исследования наноматериалов также показали, что углерод — гибкий материал, который может образовывать самые разные структуры. Помимо УНТ и фуллеренов, он может существовать в форме углеродных луковиц [2], углеродных боксов [3], нанокапсул [4] и углеродных нанорогов (CNH) или наноконусов (CNC) [5, 6]. УНТ с нулевым углом при вершине можно рассматривать как частный случай ЧПУ.
Исследования наноматериалов также показали, что углерод — гибкий материал, который может образовывать самые разные структуры. Помимо УНТ и фуллеренов, он может существовать в форме углеродных луковиц [2], углеродных боксов [3], нанокапсул [4] и углеродных нанорогов (CNH) или наноконусов (CNC) [5, 6]. УНТ с нулевым углом при вершине можно рассматривать как частный случай ЧПУ.
Исследования ЧПУ начались почти одновременно с открытием УНТ в 1991 году. Официальный отчет об открытии изолированных ЧПУ был сделан в 1993 году, когда Ге и Саттлер [5] из Гавайского университета сообщили о своих наблюдениях за углеродом. шишки смешиваются с трубочками на плоской графитовой поверхности.Продукты были получены путем закалки горячего углеродного пара на подложке. Ge и Sattler также предсказали, что пять углов при вершине, 19,2 °, 38,9 °, 60 °, 83,6 ° и 112,9 °, могут использоваться для различения ЧПУ. Однако в углах раскрытия их образцов обнаружен только угол 19,2 °. Наблюдаемые конусы имели длину до 24 нм и диаметр основания 8 нм.
В то время большинство исследователей сосредоточилось на изучении УНТ, а исследование ЧПУ не привлекло особого внимания.Открытия Ге и Саттлера были в значительной степени забыты, пока Кришнан и др. [6] подтвердили существование пяти типов конусов, которые они образовали в результате пролиза углеводородов в угольной дуге. Эти результаты показали, что кривизна углеродных структур почти всегда определяется на стадии зародышеобразования, и в своих экспериментах они продемонстрировали, что добавлением пятиугольника ЧПУ с углом раскрытия 19,2 ° может превратиться в УНТ.
Построение одностенного ЧПУ может быть выполнено с использованием стратегии, аналогичной той, которая использовалась для построения CNT.Прежде всего, аксиальное и поперечное направления определяются заданием поступательного и кирального векторов на листе графена. Затем лист графена прокатывается в желаемом направлении, и открытые края соединяются для получения ЧПУ.
Цель этой стратегии состоит в том, чтобы сформировать конус, используя ту же процедуру катания сектора листа графена вокруг вершины и соединения открытых сторон.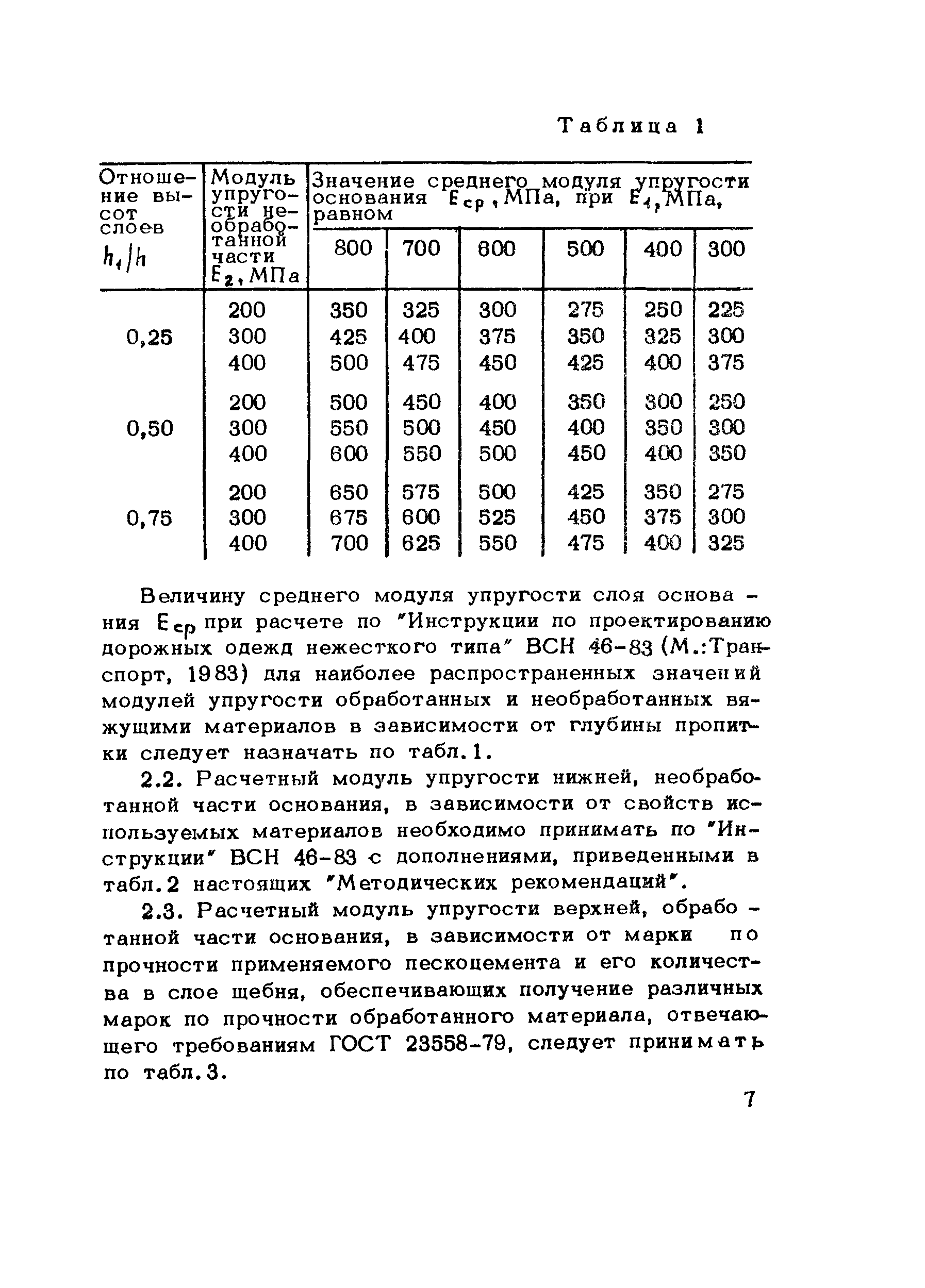 При прокатке простого листа можно получить любой угол конуса, но это не так с листом графена, в котором точки решетки располагаются периодически, и необходимо учитывать сотовую текстуру графена.Для закрытия двух открытых сторон конструкция должна совпадать по линии стыка.
При прокатке простого листа можно получить любой угол конуса, но это не так с листом графена, в котором точки решетки располагаются периодически, и необходимо учитывать сотовую текстуру графена.Для закрытия двух открытых сторон конструкция должна совпадать по линии стыка.
Углы при вершинах конусов, образованных таким образом, также могут быть заданы как 2arcsin (1 − 𝑛 / 6) или 2arcsin (1 − 𝜃 / 360), где 𝑛 — количество пятиугольников в конструкции, а 𝜃 — угол дисклинации в градусах. Принимая 𝑛 от 1 до 5, углы при вершине замкнутых конусов составляют 19,2 °, 38,9 °, 60 °, 83,6 ° и 112,9 °. В случае конструкции с открытым конусом всего шесть пятиугольников дают трубку с нулевым углом при вершине.
Существуют разные подходы к изучению механических свойств УНТ. Большое количество работ посвящено определению модуля Юнга УНТ, например, с использованием эмпирических методов МД [7–11], сильной связи [12–14] или ab initio [15–17], а также конечных значений на атомистической основе.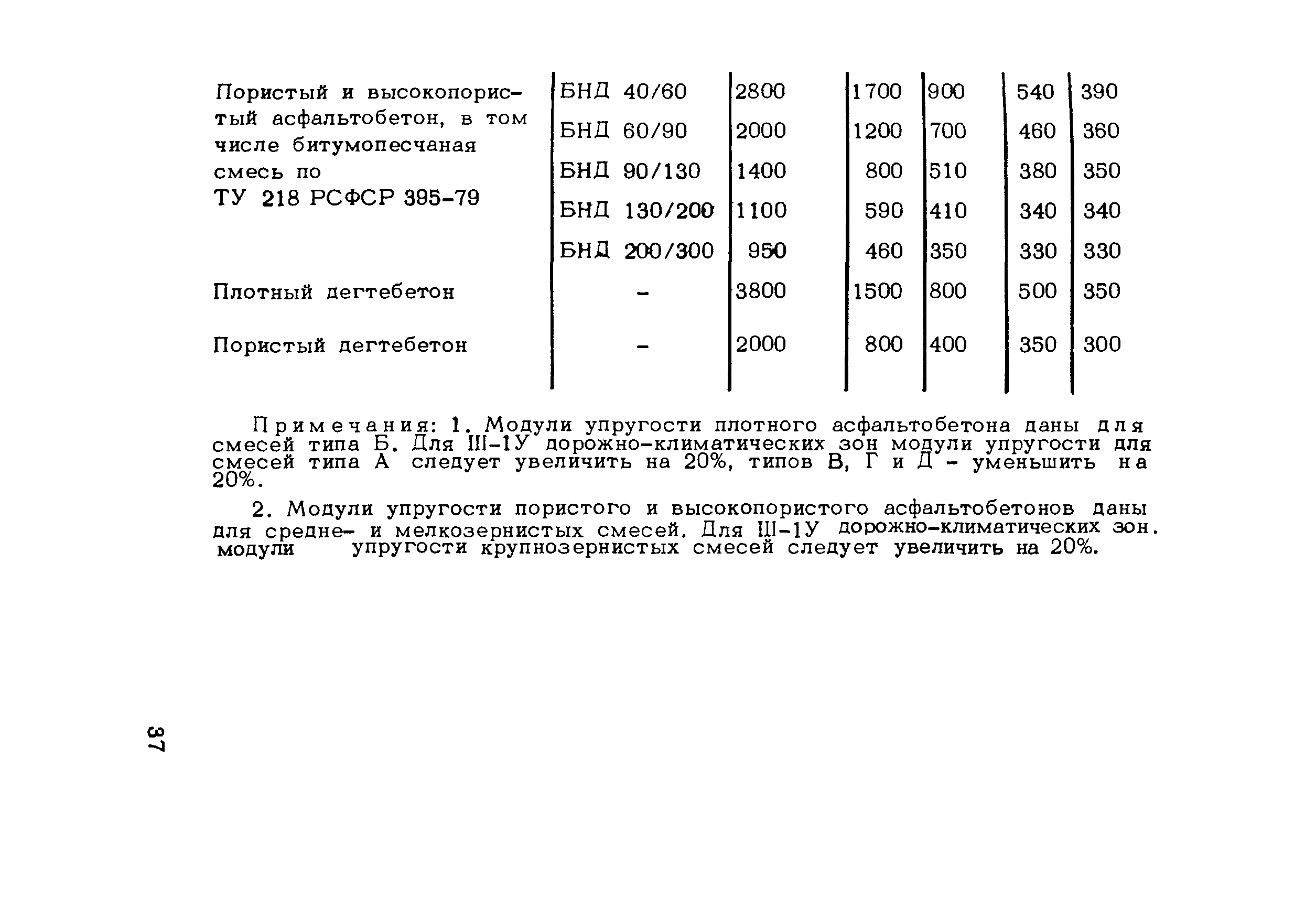 теория деформационных оболочек однослойных УНТ [18]. Оболочечная теория углеродных нанотрубок основана на межатомном потенциале и атомной структуре [19]. С другой стороны, было проведено очень мало теоретических работ по структуре CNH, и исследователи все еще изо всех сил пытаются установить общепринятые подходы для определения структуры и механизма роста CNH.Данная работа представляет собой попытку изучения структуры и модулей упругости CNH с использованием потенциала REBO второго поколения [20]. Некоторые параметры были изменены нами [21] для учета длины связи и энергии когезии для углеродных систем. Мы сообщаем здесь модули упругости углеродных нанорогов.
теория деформационных оболочек однослойных УНТ [18]. Оболочечная теория углеродных нанотрубок основана на межатомном потенциале и атомной структуре [19]. С другой стороны, было проведено очень мало теоретических работ по структуре CNH, и исследователи все еще изо всех сил пытаются установить общепринятые подходы для определения структуры и механизма роста CNH.Данная работа представляет собой попытку изучения структуры и модулей упругости CNH с использованием потенциала REBO второго поколения [20]. Некоторые параметры были изменены нами [21] для учета длины связи и энергии когезии для углеродных систем. Мы сообщаем здесь модули упругости углеродных нанорогов.
2. Потенциал модели
2.1. Реактивный эмпирический потенциал связи второго поколения
Энергия системы — это сумма энергии каждой связи C – C, состоящей из отталкивающей части и части притяжения [20].В этой работе мы использовали улучшенную форму потенциала «второго поколения», и подробности этого выражения потенциальной энергии приведены ниже 𝑉𝑅 (𝑟) = 𝑓𝑐𝑄 (r) 1 + 𝑟𝐴𝑒 − 𝛼𝑟𝑉, (1 ) 𝐴 (𝑟) = 𝑓𝑐 (r) 𝑛 = 1,3𝐵𝑛𝑒 − 𝛽𝑛𝑟. (2)
Выражения (1) и (2) используются для парных членов отталкивания и притяжения соответственно. Нижний индекс 𝑛 относится к сумме в (2), а 𝑟 — скалярное расстояние между атомами. Экранированная кулоновская функция, используемая для парного отталкивающего взаимодействия, стремится к бесконечности, когда межатомные расстояния приближаются к нулю.Функция 𝑓𝑐 (𝑟) ограничивает диапазон ковалентных взаимодействий и принимает значение единицы для 𝑓𝑐 (𝑟) для ближайших соседей и нуля для межатомных расстояний более 2,1, а значение около 𝑅 задается как 1 (𝑟) = 1, 𝑟 <(𝑅 − 𝐷), 2−121sin2𝜋 (𝑟 − 𝑅) 𝐷, (𝑅 − 𝐷) <𝑟 <(𝑅 + 𝐷), 0, 𝑟> (𝑅 + 𝐷 ). (3)
Чтобы воспроизвести длину связи и энергию когезии, мы модифицируем некоторые параметры потенциала второго поколения Бреннер с соавторами. Исходные параметры соответствуют минимумам при 1,32 Å для связи углерод-углерод, но модифицированные параметры дают минимумы при 1.42 Å. Эти модифицированные параметры используются для изучения углеродных наноструктур (см. Таблицу 1).
(2)
Выражения (1) и (2) используются для парных членов отталкивания и притяжения соответственно. Нижний индекс 𝑛 относится к сумме в (2), а 𝑟 — скалярное расстояние между атомами. Экранированная кулоновская функция, используемая для парного отталкивающего взаимодействия, стремится к бесконечности, когда межатомные расстояния приближаются к нулю.Функция 𝑓𝑐 (𝑟) ограничивает диапазон ковалентных взаимодействий и принимает значение единицы для 𝑓𝑐 (𝑟) для ближайших соседей и нуля для межатомных расстояний более 2,1, а значение около 𝑅 задается как 1 (𝑟) = 1, 𝑟 <(𝑅 − 𝐷), 2−121sin2𝜋 (𝑟 − 𝑅) 𝐷, (𝑅 − 𝐷) <𝑟 <(𝑅 + 𝐷), 0, 𝑟> (𝑅 + 𝐷 ). (3)
Чтобы воспроизвести длину связи и энергию когезии, мы модифицируем некоторые параметры потенциала второго поколения Бреннер с соавторами. Исходные параметры соответствуют минимумам при 1,32 Å для связи углерод-углерод, но модифицированные параметры дают минимумы при 1.42 Å. Эти модифицированные параметры используются для изучения углеродных наноструктур (см. Таблицу 1).
| |||||||||||||||||||||||||||||||||||||||
| . | |||||||||||||||||||||||||||||||||||||||
3. Вычислительный метод
CNT можно рассматривать как частный случай CNH с нулевым коническим углом. Конфигурации нескольких однослойных CNH и CNT с одинаковой высотой и верхним радиусом, но с разными нижними радиусами или, альтернативно, с разными коническими углами представлены на рисунке 1.Шесть расчетных случаев демонстрируют постепенное изменение угла при вершине от 112,9 ° до 0 °, что соответствует углу дисклинации от 60 ° до 360 ° на листе графена. Размеры CNH тщательно подобраны, чтобы их можно было сравнить с (10,10) CNT (/ 𝐷 = 9,0) [21].
Координаты атомов углерода генерируются для углеродных рогов, и с использованием потенциала Бреннера и его сотрудников вычисляется энергия системы. Затем система расслабляется, чтобы получить конфигурацию с минимальной энергией.Для получения модулей упругости мы прикладываем к системе напряжение или скручивание и получаем вторую производную энергии, которая, в свою очередь, используется для вычисления модулей, как описано в следующем разделе. Нанороги имеют переменный радиус по высоте, поэтому распределение напряжений в них неоднородно, а зависит от высоты.
Затем система расслабляется, чтобы получить конфигурацию с минимальной энергией.Для получения модулей упругости мы прикладываем к системе напряжение или скручивание и получаем вторую производную энергии, которая, в свою очередь, используется для вычисления модулей, как описано в следующем разделе. Нанороги имеют переменный радиус по высоте, поэтому распределение напряжений в них неоднородно, а зависит от высоты.
Когда CNH находится в равновесии, верхний уровень должен иметь наибольшее напряжение, а нижний уровень наименьшее, и поэтому обычные кривые напряжение-деформация неприменимы.Моделирование в CNH выполняется путем приложения осевого напряжения на верхнем (наименьший радиус) конце открытого CNH, в то же время удерживая другой конец неподвижным. На протяжении всего процесса ни один из концов CNH не подвергается воздействию межатомных сил. В результате верхние атомы перемещаются наружу вдоль оси, а внутренние атомы расслабляются, а концевые атомы фиксируются. Таким образом, вся структура CNH растягивается небольшими шагами.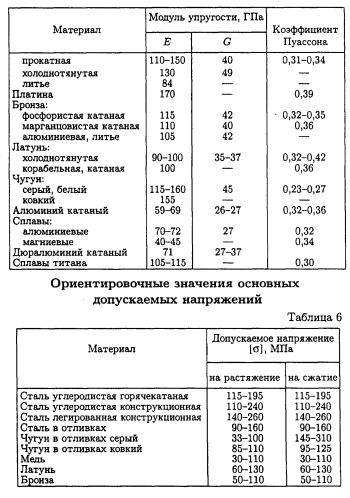 Модуль Юнга однооболочечных углеродных нанорогов изменяется прямо пропорционально cos4 equivalent эквивалентной одностенной углеродной нанотрубки.
Модуль Юнга однооболочечных углеродных нанорогов изменяется прямо пропорционально cos4 equivalent эквивалентной одностенной углеродной нанотрубки.
4. Модуль Юнга
Модуль Юнга (𝑌) конусообразной наноструктуры может быть определен с помощью второй производной энергии деформации относительно энергии деформации. осевая деформация axis = 𝑑2𝐸𝑉𝑑𝜀2, (4) где 𝑉 — общий объем оболочки конуса 𝑉 = sin (𝜃 / 2) 2𝑏 − 𝑅2𝑎. (5)
Толщина стенки принята равной 𝑡 = 3,4 Å. На рисунках 2–4 показано изменение модуля Юнга с радиусом вершины для трех типов конусов с углом при вершине 19,2 °, 38,9 ° и 60 °. Модуль Юнга, который часто используется для измерения прочности материалов, уменьшается с увеличением угла при вершине.
5. Коэффициент Пуассона
Для нанорога с одной оболочкой, находящегося под напряжением вдоль оси конуса, координаты определены таким образом, что 𝑋 и 𝑌 расположены вдоль радиальных направлений, а, — вдоль оси конуса, при этом соответствующие деформации как 𝜀𝑥, 𝜀𝑦 и. Поскольку связи C – C на наклонной плоскости графена принимают действительную нагрузку, осевая деформация, длина конуса и ее изменение вдоль плоскости графена вводятся как 𝜀𝑧, ||, 𝐿 || и 𝛿𝐿 ||, соответственно. , как показано на рисунке 5.
Поскольку связи C – C на наклонной плоскости графена принимают действительную нагрузку, осевая деформация, длина конуса и ее изменение вдоль плоскости графена вводятся как 𝜀𝑧, ||, 𝐿 || и 𝛿𝐿 ||, соответственно. , как показано на рисунке 5.
Геометрические соображения показывают, что 𝐿 || + 𝛿𝐿 || = √ (𝐿tan𝜃) 2+ (𝐿 + 𝛿𝐿) 2, где 𝛾 = −𝜀𝑥, 𝑦 / 𝜀𝑧 — коэффициент Пуассона, а 𝛿𝐿 — изменение длины 𝐿 по оси. Связь между 𝜀 и 𝜀 || таким образом может быть выражено как 𝜀𝑧, || = 𝛿𝐿 || 𝐿 || = cos2𝜃 − 𝛾sin2𝜃𝜀𝑧𝜀 + 𝑂2𝑧. (6) Опуская члены высшего порядка в 𝜀, соответствующее соотношение для коэффициента Пуассона вдоль плоскости графена может быть выражено как 𝛾 || = −𝜀𝑟 / 𝜀𝑧, || = −𝜀𝑥, 𝑦 / 𝜀𝑧, || = 𝛾 / (cos2𝜃 −𝛾sin2𝜃), где 𝜀𝑟 — деформация в радиальном направлении.Пренебрегая членами высшего порядка в, коэффициент Пуассона далее записывается как = 𝛾 || cos2𝜃. (7)
Поскольку энергия деформации 𝐸 = (1/2) 𝑘𝜀2 может быть эквивалентно выражена как функция от 𝜀𝑧 или 𝜀𝑧, ||, соответствующее соотношение для силовой постоянной 𝑘 и его аналог 𝑘 || в плоскости графена можно записать как 𝑘 = 𝑘 || cos4𝜃 (1 − 𝛾 || sin2𝜃) 2.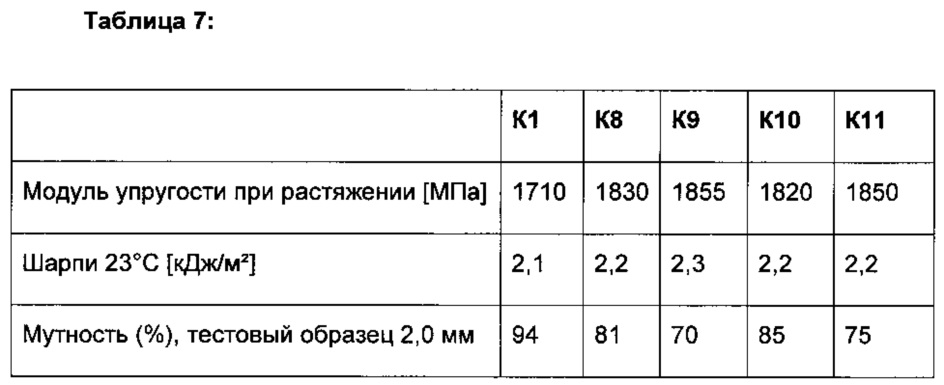 Модуль Юнга однослойного наноконуса, таким образом, выражается как 𝑌cone = 𝑌SWNTcos4𝜃1 − 𝛾 || sin2𝜃2, (8)
где 𝑌SWNT — модуль Юнга УНТ, а толщина стенок конуса и УНТ принимается такой же, как ℎ0.
Модуль Юнга однослойного наноконуса, таким образом, выражается как 𝑌cone = 𝑌SWNTcos4𝜃1 − 𝛾 || sin2𝜃2, (8)
где 𝑌SWNT — модуль Юнга УНТ, а толщина стенок конуса и УНТ принимается такой же, как ℎ0.
Для широкоугольного наноконуса 𝜃 = 30∘, 𝑅1∼15 Å, 2∼3 Å и ∼20 Å применялись осевые деформации до 5%. Если пренебречь изменением радиусов из-за эффекта коэффициента Пуассона, то силовая постоянная для наноконуса оказывается равной 25,70 эВ / атом. Аналогичным образом, с использованием REBO, для прямых УНТ было установлено, что оно составляет 45,70 эВ / атом, и это значение не сильно зависит от радиуса и хиральности при> 3,5 Å. Используя эти силовые постоянные в соотношении 𝑌cone≈𝑌SWNTcos4𝜃 (с 𝛾 = 0) в (8), получается значение 𝜃 = 30,01∘, которое отлично согласуется с = 30∘ из геометрии, показанной на рисунке 5.Точно так же смоделированный методом МД 𝛾≈0,25 для наноконуса отлично согласуется с 𝛾≈0,23, как предсказано (6) для 𝛾 || ≈0,30, смоделированным для УНТ большого диаметра. Таким образом, наши результаты подтверждают (7) и [8] для однооболочечных нанорогов.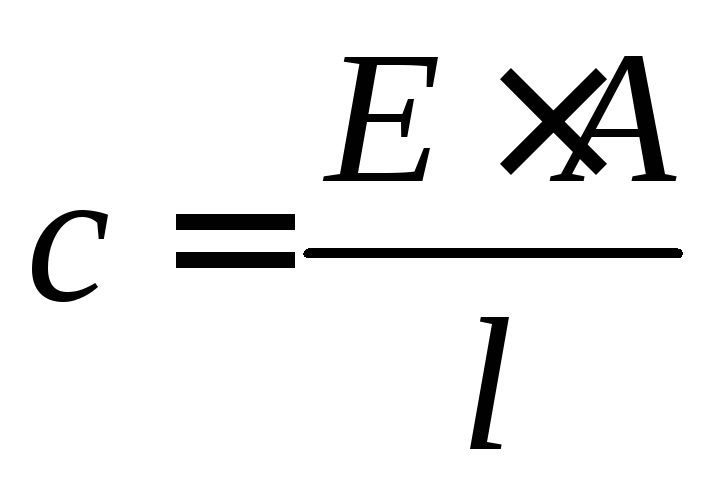
6. Модуль сдвига
Боковое усилие в форме скручивания прикладывается к конусу заданного радиуса вершины и высоты, при этом один из его концов остается неподвижным. Общее кручение, которое должно быть придано конусу, было распределено равномерно по всей длине конуса, и снова были получены координаты конуса в конфигурации с минимальной энергией.
На основе теории упругости модуль сдвига в макроскопическом масштабе определяется выражением = 𝑇𝑙𝑜𝜃𝐽 (𝑡), (9) где 𝑇, 𝑙𝑜, 𝜃 и 𝐽 (𝑡) обозначают крутящий момент, действующий на конце CNH, длину конуса, полный угол кручения, приложенный к конусу, и полярный момент инерции в поперечном сечении. наноконуса соответственно 𝜋𝐽 (𝑡) = 2𝑅𝑎 + 𝑡24 − 𝑅𝑎 − 𝑡24. (10) Модуль сдвига для трех различных конусов показан на рисунках 6–8. Тенденции такие же, как и для модуля Юнга.
7. Обсуждение и заключение
Для углеродных наноконусов значение модуля Юнга находится в диапазоне от 0,24 до 0,73 МПа, а модуль сдвига варьируется от 0,10 до 0,29 МПа в зависимости от верхний радиус уменьшен. Оба модуля уменьшаются с увеличением радиуса или высоты ЧПУ. При фиксированном отношении высоты к верхнему радиусу обнаруживается, что модули достигают своего предела, когда верхний радиус приближается к определенному уровню. Для УНТ значение модуля Юнга составляет около 1 ТПа, а модуль сдвига — порядка 300 ГПа [22].Значение коэффициента Пуассона для нанорогов составляет 0,23, а для УНТ — около 0,15 [22]. Мы попытались понять эти структуры, используя модельный потенциал Бреннера и его сотрудников, и пришли к выводу, что нанороги одинаково сильны по сравнению с углеродными нанотрубками. Их необходимо исследовать экспериментально, а также теоретически на предмет их потенциального применения.
Оба модуля уменьшаются с увеличением радиуса или высоты ЧПУ. При фиксированном отношении высоты к верхнему радиусу обнаруживается, что модули достигают своего предела, когда верхний радиус приближается к определенному уровню. Для УНТ значение модуля Юнга составляет около 1 ТПа, а модуль сдвига — порядка 300 ГПа [22].Значение коэффициента Пуассона для нанорогов составляет 0,23, а для УНТ — около 0,15 [22]. Мы попытались понять эти структуры, используя модельный потенциал Бреннера и его сотрудников, и пришли к выводу, что нанороги одинаково сильны по сравнению с углеродными нанотрубками. Их необходимо исследовать экспериментально, а также теоретически на предмет их потенциального применения.
Механически регулируемые проводящие гидрогели с взаимопроникающей сеткой, которые имитируют модули упругости биологической ткани
Синтез и характеристика гидрогелей PEDOT: PSS
Для синтеза C-IPN гидрогели PEDOT: PSS были сначала сформированы из коммерческих водных дисперсий PEDOT: PSS с низкое содержание полимера примерно 1. 1 мас.% (11 мг / мл -1 ). Недавно Leaf и Muthukumar 28 предложили, что водный раствор PEDOT: PSS состоит из больших частиц микрогеля, которые внутренне напоминают полуразбавленную полиэлектролитную сетку и имеют низкую концентрацию перекрытия 1 мг / мл -1 . Авторы обнаружили, что увеличение ионной силы может вызвать фазовый переход раствора PEDOT: PSS в твердоподобный гель, что приводит к кардинальным изменениям реологических свойств без изменения профиля внутреннего рассеяния микрогелей.Поскольку было обнаружено, что первичное взаимодействие между частицами микрогеля носит электростатический характер, авторы пришли к выводу, что повышенная ионная сила помогает экранировать электростатическое отталкивание между частицами и, таким образом, позволяет им образовывать физические поперечные связи между собой посредством π – π укладки PEDOT. Когда между частицами образуется достаточное количество физических поперечных связей, получается макроскопически связанный гель 28 .
1 мас.% (11 мг / мл -1 ). Недавно Leaf и Muthukumar 28 предложили, что водный раствор PEDOT: PSS состоит из больших частиц микрогеля, которые внутренне напоминают полуразбавленную полиэлектролитную сетку и имеют низкую концентрацию перекрытия 1 мг / мл -1 . Авторы обнаружили, что увеличение ионной силы может вызвать фазовый переход раствора PEDOT: PSS в твердоподобный гель, что приводит к кардинальным изменениям реологических свойств без изменения профиля внутреннего рассеяния микрогелей.Поскольку было обнаружено, что первичное взаимодействие между частицами микрогеля носит электростатический характер, авторы пришли к выводу, что повышенная ионная сила помогает экранировать электростатическое отталкивание между частицами и, таким образом, позволяет им образовывать физические поперечные связи между собой посредством π – π укладки PEDOT. Когда между частицами образуется достаточное количество физических поперечных связей, получается макроскопически связанный гель 28 .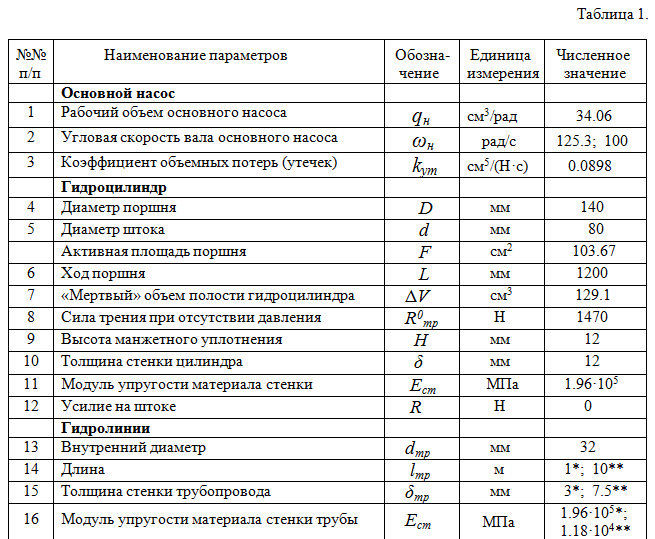 Основываясь на этих выводах, мы предположили, что макроскопически связанные частицы микрогеля приведут к увеличению количества связанных путей, доступных для проводимости заряда, и, таким образом, должны быть способом формирования высокопроводящих гидрогелей PEDOT: PSS при относительно низкой концентрации.
Основываясь на этих выводах, мы предположили, что макроскопически связанные частицы микрогеля приведут к увеличению количества связанных путей, доступных для проводимости заряда, и, таким образом, должны быть способом формирования высокопроводящих гидрогелей PEDOT: PSS при относительно низкой концентрации.
Для получения гелей PEDOT: PSS мы увеличили ионную силу раствора с помощью ионной жидкости трифлата 4- (3-бутил-1-имидазолио) -1-бутансульфоновой кислоты. В предыдущей публикации нашей группы было обнаружено, что эта ионная жидкость является отличной присадкой для тонких пленок PEDOT: PSS и что она достаточно сильно взаимодействует с PEDOT: PSS, чтобы вызвать значительное изменение морфологии тонких пленок 29 . Основываясь на этих наблюдениях, мы предположили, что та же самая ионная жидкость также должна в достаточной степени электростатически взаимодействовать с PEDOT: PSS, чтобы вытолкнуть раствор за границу его гелевой фазы.Действительно, смешивание ионной жидкости с PEDOT: PSS привело к образованию твердого геля, на что указывает тот факт, что накопительный модуль геля ( G ‘) превышает его модуль потерь ( G ”) в диапазоне частот 0,1 –100 Гц (рис.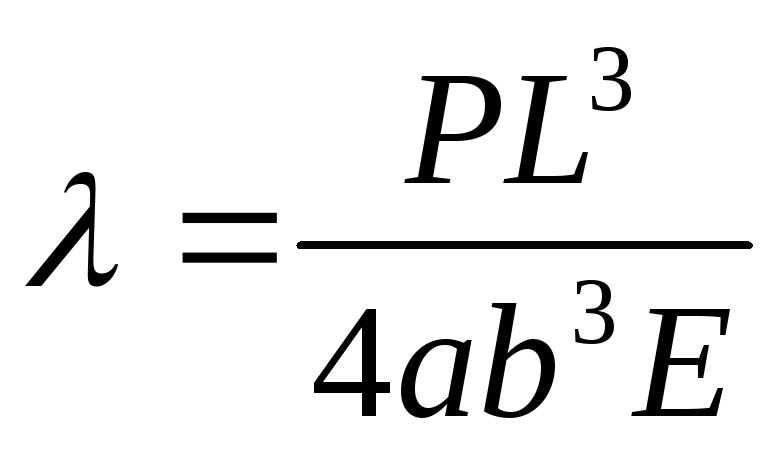 2а). Кроме того, жесткость геля, определяемая G ’, увеличивалась с увеличением ионной силы (фиг. 2b), что согласуется с предложенным механизмом, в котором электростатическое экранирование вызывает физическое сшивание. В этом каучуковом режиме G ’слегка увеличивался с частотой, отражая динамический характер физических поперечных связей, присутствующих в геле (рис.2б). Эти реологические свойства согласуются с теми, которые наблюдали Leaf и Muthukumar 28 , которые использовали как небольшие соли, так и более крупные ионные жидкости, такие как тетрацианоборат 1-этил-3-метилимидазолия (EMIM: TCB), чтобы вызвать гелеобразование PEDOT: PSS.
2а). Кроме того, жесткость геля, определяемая G ’, увеличивалась с увеличением ионной силы (фиг. 2b), что согласуется с предложенным механизмом, в котором электростатическое экранирование вызывает физическое сшивание. В этом каучуковом режиме G ’слегка увеличивался с частотой, отражая динамический характер физических поперечных связей, присутствующих в геле (рис.2б). Эти реологические свойства согласуются с теми, которые наблюдали Leaf и Muthukumar 28 , которые использовали как небольшие соли, так и более крупные ионные жидкости, такие как тетрацианоборат 1-этил-3-метилимидазолия (EMIM: TCB), чтобы вызвать гелеобразование PEDOT: PSS.
Гелеобразование PEDOT: PSS. a , b PEDOT: PSS образует гель a после смешивания его с ионной жидкостью. Прочность геля, определяемая модулем накопления ( G ’), увеличивается с увеличением ионной силы b . c Смешивание PEDOT: PSS либо с ионной жидкостью, либо с CuCl 2 приведет к превращению раствора в гель, хотя гелеобразование происходит гораздо быстрее с CuCl 2 . В случае ионной жидкости смесь PEDOT: PSS начинает становиться более твердой ( G ’> G ”) только через 13 минут. В отличие от этого, смесь с CuCl 2 гелируется так быстро, что G ‘уже превышает G ”к началу измерения реологии
В случае ионной жидкости смесь PEDOT: PSS начинает становиться более твердой ( G ’> G ”) только через 13 минут. В отличие от этого, смесь с CuCl 2 гелируется так быстро, что G ‘уже превышает G ”к началу измерения реологии
Интересно, что мы обнаружили, что скорость гелеобразования, которая является важным фактором технологичности, можно настроить подбором молекулярной добавки.Чтобы исследовать это, мы смешали PEDOT: PSS как с нашей ионной жидкостью, так и с более мелкой солью металла (CuCl 2 ) с одинаковой общей ионной силой и загрузили смесь на реометр с параллельными пластинами, колеблющийся с постоянной скоростью деформации 1%. и частотой 1 Гц. Для смеси ионных жидкостей точка перехода, при которой G ’> G ”, наступает через 15 минут, до которых смесь может легко течь. Для сравнения, смешивание PEDOT: PSS с CuCl 2 с эквивалентной ионной силой привело к почти немедленному гелеобразованию: к тому времени, когда раствор был загружен в реометр, значение G ’уже превышало G » (рис. 2в). Расширенное окно жидкоподобных свойств смеси PEDOT: PSS / ионная жидкость позволяет нам более легко обрабатывать ее в различных формах (рис. 1b). Мы могли даже переработать его в пирамидальные структуры с разрешением 10 мкм, залив смесь в готовые силиконовые формы (рис. 1c, d). Насколько нам известно, это первое обсуждение кинетики гелеобразования растворов PEDOT: PSS.
2в). Расширенное окно жидкоподобных свойств смеси PEDOT: PSS / ионная жидкость позволяет нам более легко обрабатывать ее в различных формах (рис. 1b). Мы могли даже переработать его в пирамидальные структуры с разрешением 10 мкм, залив смесь в готовые силиконовые формы (рис. 1c, d). Насколько нам известно, это первое обсуждение кинетики гелеобразования растворов PEDOT: PSS.
Синтез и характеристика гелей C-IPN
Хотя гидрогели PEDOT: PSS ведут себя аналогично твердым веществам, они также очень хрупкие.Для улучшения механических свойств мы выбрали полиакриловую кислоту (PAAc) в качестве вторичной полимерной сетки из-за ее биосовместимости 30,31 и высокой концентрации водородных связей, которые, как мы предположили, могут дополнительно механически усилить C-IPN. Кроме того, было показано, что водный раствор PEDOT: PSS образует гель при воздействии сильных кислот, и мы предположили, что инфильтрация гидрогеля PEDOT: PSS кислотными мономерами приведет к дополнительному усилению матрицы PEDOT: PSS 12 . Наконец, гидрогели PAAc можно легко настроить, варьируя концентрацию мономеров в воде и соотношение бисакриламида к акриловой кислоте, которое контролирует степень ковалентного сшивания (дополнительный рисунок 1).
Наконец, гидрогели PAAc можно легко настроить, варьируя концентрацию мономеров в воде и соотношение бисакриламида к акриловой кислоте, которое контролирует степень ковалентного сшивания (дополнительный рисунок 1).
Чтобы пропитать гели PEDOT: PSS мономерами PAAc, гели замачивали в водном растворе акриловой кислоты, бисакриламида и инициатора термической радикальной полимеризации, который активируется при температуре выше 60 ° C. Как и ожидалось, кислотность акриловой кислоты вызвала небольшую усадку гелей PEDOT: PSS во время процесса обмена (дополнительный рисунок 2b), что качественно усилило композит PEDOT: PSS / акриловая кислота еще до того, как акриловая кислота была полимеризована.Наконец, сетка акриловой кислоты была полимеризована в геле PEDOT: PSS путем помещения геля в герметичный контейнер в печь при 70 ° C на 30 мин. Термический инициатор был выбран вместо УФ-инициатора из-за его относительно быстрой кинетики и нечувствительности к кислороду, а также из-за того, что он позволяет полимеризовать акриловую кислоту в объеме геля PEDOT: PSS, который непрозрачен из-за своей электронопроводящей природы.
Чтобы подтвердить наличие вторичной сети внутри C-IPN, была проведена инфракрасная спектроскопия с преобразованием Фурье на C-IPN и проведено сравнение с гидрогелями PEDOT: PSS и PAAc (рис.1е). Пики, приписываемые карбоновой кислоте и водородным связям между группами карбоновых кислот, могут быть идентифицированы как в образцах PAAc, так и в C-IPN, что указывает на успешное включение PAAc. Кроме того, изображение с помощью сканирующей электронной микроскопии (SEM) поперечного сечения лиофилизированного образца C-IPN подтверждает, что гель является гомогенным и пористым (рис. 1e). Наконец, измерения рентгеновской фотоэлектронной спектроскопии (XPS) на PEDOT: PSS и C-IPN показывают, что на сеть PEDOT: PSS химически не влияет присутствие PAAc.В XPS-спектрах PEDOT: PSS два пика S2p соответствуют присутствию серы в PEDOT и PSS соответственно. Относительный размер этих двух пиков пропорционален отношению PEDOT к PSS, тогда как положения пиков соответствуют энергии связи серы в ее двух соответствующих химических средах 29,32 .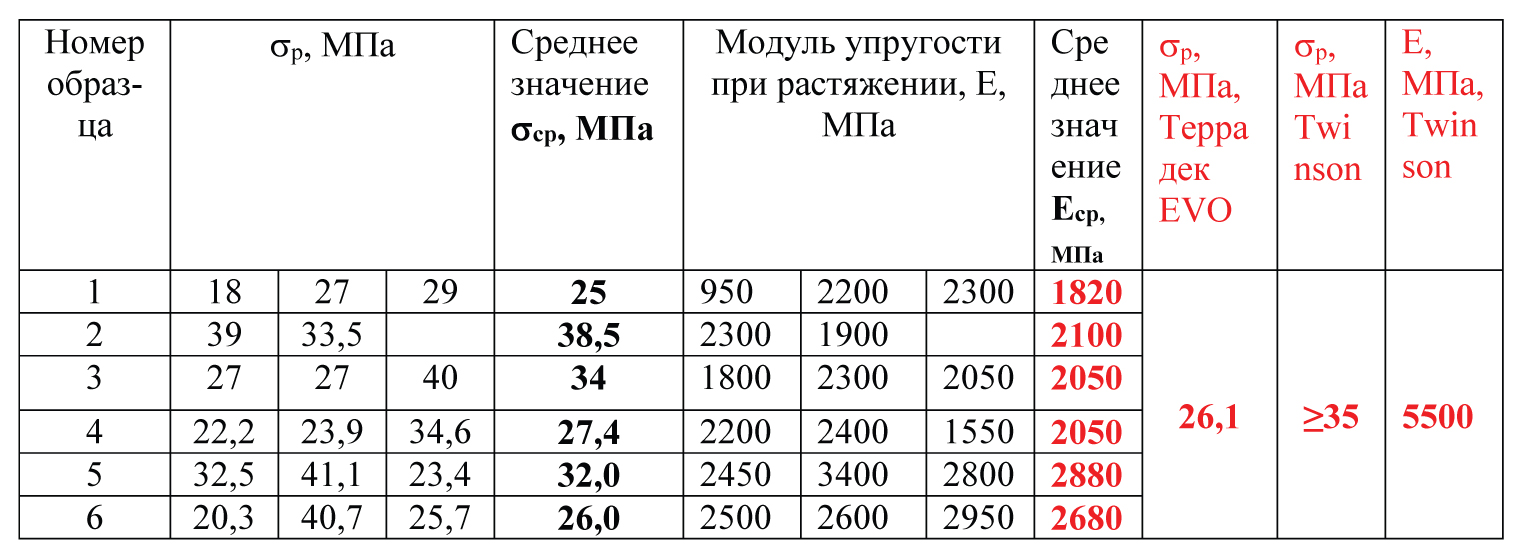 После введения PAAc не наблюдалось значительных изменений в площади или положении пика в PEDOT: PSS (дополнительный рисунок 2a).
После введения PAAc не наблюдалось значительных изменений в площади или положении пика в PEDOT: PSS (дополнительный рисунок 2a).
Хотя ионная жидкость используется для индукции гелеобразования PEDOT: PSS, мы хотели удалить ее из конечного геля C-IPN из-за ее цитотоксичности.Чтобы облегчить диффузию ионной жидкости из геля, мы замочили гели PEDOT: PSS в деионизированной (DI) воде и несколько раз заменили воду перед пропиткой PEDOT: PSS акриловой кислотой. Для нашей системы фтор является уникальным маркером анионного компонента ионной жидкости, однако фтор не может быть обнаружен с помощью XPS на C-IPN. Чтобы подтвердить, что катионный компонент также удаляется, мы также выполнили 1 H-спектроскопию ядерного магнитного резонанса (ЯМР) раствора, полученного при промывании гелей PEDOT: PSS деионизированной водой, и сравнили его со спектром чистой ионной жидкости. (Дополнительный рисунок 3).Катион явно присутствует в промывочном растворе. Широкие пики около 6.5–7.5 p.pm. соответствуют ароматическим кольцам, которые являются уникальными для PSS, что позволяет предположить, что часть PSS также удаляется из промывочного геля. Небольшие сдвиги в пике при 6,2 м.д., который приписывается гидроксилу катиона, могут быть связаны с присутствием PSS, поскольку скорость протонного обмена между гидроксильной группой и растворителем сильно зависит от кислой среды. Взятые вместе, данные XPS и ЯМР предполагают, что ионную жидкость можно легко удалить после промывки, что ожидается с учетом высокопористой природы гидрогеля.
соответствуют ароматическим кольцам, которые являются уникальными для PSS, что позволяет предположить, что часть PSS также удаляется из промывочного геля. Небольшие сдвиги в пике при 6,2 м.д., который приписывается гидроксилу катиона, могут быть связаны с присутствием PSS, поскольку скорость протонного обмена между гидроксильной группой и растворителем сильно зависит от кислой среды. Взятые вместе, данные XPS и ЯМР предполагают, что ионную жидкость можно легко удалить после промывки, что ожидается с учетом высокопористой природы гидрогеля.
Готовые гели C-IPN продолжают набухать при погружении в воду, достигая конечного веса, который зависит от состава геля. Состав с самым высоким содержанием твердого вещества (C-IPN 1) набухает примерно в два раза по сравнению с исходным весом, тогда как состав с самым низким содержанием твердого вещества (C-IPN 5) набухает почти в семь раз по сравнению с исходным весом (дополнительная фигура 8a). Гели также можно сушить и снова набухать в воде.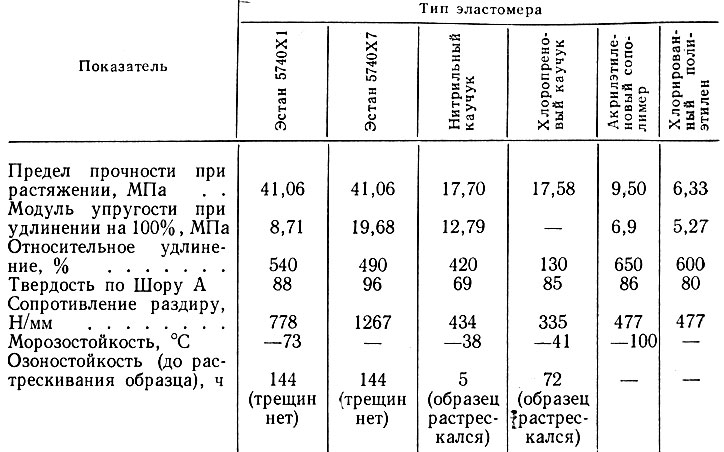 Интересно отметить, что конечный вес гелей после повторного набухания превышает равновесный вес синтезированных гелей C-IPN, погруженных в воду, причем весовое соотношение повторно набухших веществ также зависит от состава геля.Состав с самым высоким содержанием твердого вещества (C-IPN 1) имеет конечный вес повторного набухания, который в 1,3 раза превышает его равновесный вес в набухшем состоянии перед сушкой, тогда как состав с самым низким содержанием твердого вещества (C-IPN 5) имеет окончательное набухание. вес, который почти в 6 раз превышает равновесный набухший вес (дополнительный рисунок 8а). Это наблюдение предполагает, что сушка гидрогелей C-IPN приводит к изменению морфологии полимера, что изменяет его способность к набуханию. Сушка гидрогелей может стимулировать π – π-взаимодействия между PEDOT: PSS, которые разрушают проводящую полимерную сеть на агрегаты, оставляя более крупные непрерывные пустые фракции для проникновения воды во время процесса повторного набухания.Эта гипотеза подтверждается тем фактом, что гидрогели, содержащие только PEDOT: PSS, полученные непосредственно в результате смешивания с ионной жидкостью, также повторно набухают до 1,8 ± 0,5 от своего первоначального веса после сушки.
Интересно отметить, что конечный вес гелей после повторного набухания превышает равновесный вес синтезированных гелей C-IPN, погруженных в воду, причем весовое соотношение повторно набухших веществ также зависит от состава геля.Состав с самым высоким содержанием твердого вещества (C-IPN 1) имеет конечный вес повторного набухания, который в 1,3 раза превышает его равновесный вес в набухшем состоянии перед сушкой, тогда как состав с самым низким содержанием твердого вещества (C-IPN 5) имеет окончательное набухание. вес, который почти в 6 раз превышает равновесный набухший вес (дополнительный рисунок 8а). Это наблюдение предполагает, что сушка гидрогелей C-IPN приводит к изменению морфологии полимера, что изменяет его способность к набуханию. Сушка гидрогелей может стимулировать π – π-взаимодействия между PEDOT: PSS, которые разрушают проводящую полимерную сеть на агрегаты, оставляя более крупные непрерывные пустые фракции для проникновения воды во время процесса повторного набухания.Эта гипотеза подтверждается тем фактом, что гидрогели, содержащие только PEDOT: PSS, полученные непосредственно в результате смешивания с ионной жидкостью, также повторно набухают до 1,8 ± 0,5 от своего первоначального веса после сушки.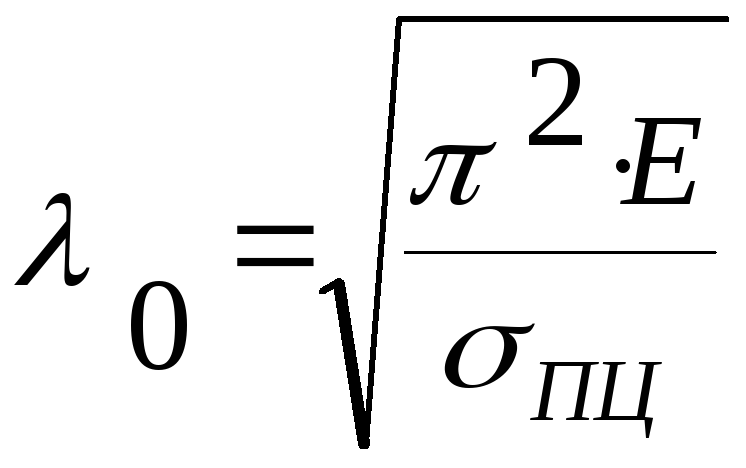 Важно отметить, что повторно набухшие гели сохраняют ту же высокую растяжимость и низкий модуль упругости, что и гели в исходном состоянии (дополнительный рисунок 8b).
Важно отметить, что повторно набухшие гели сохраняют ту же высокую растяжимость и низкий модуль упругости, что и гели в исходном состоянии (дополнительный рисунок 8b).
Чтобы охарактеризовать механические свойства гидрогелей C-IPN, измерения напряжения и деформации были записаны при удлинении при растяжении. Исходя из состава, гидрогели C-IPN имеют широкий диапазон модулей упругости от 8 кПа до почти 400 кПа (Таблица 1).Несмотря на такой широкий диапазон жесткости, все составы C-IPN можно было растянуть до более чем 100% деформации перед разрушением (рис. 3a, b). Одной из причин превосходной растяжимости может быть высокое содержание воды, которое обеспечивает много степеней свободы для полимерных цепей в C-IPN для переориентации в ответ на механическую деформацию. Кроме того, наличие водородных связей в сети PAAc может обеспечивать жертвенные динамические связи, которые могут разрушаться, чтобы рассеять напряжение от механической деформации, устраняя необходимость рассеивания энергии из разрыва 33,34 .
Механические и зависимые от деформации свойства гидрогелей C-IPN. a Кривые удлинения при растяжении различных составов C-IPN, показывающие, что все составы могут быть растянуты более чем на 100%, несмотря на большие различия в модулях упругости, которые задаются начальным наклоном кривой напряжения / деформации. b Изображение геля C-IPN 4, растягивающегося до 250%. c Данные циклического напряжения / деформации при растяжении для C-IPN 2 демонстрируют минимальный гистерезис, отражающий его превосходные эластичные свойства. d Изменение сопротивления, выраженное как соотношение между сопротивлением ( R ) и начальным сопротивлением ( R o ) в геле C-IPN 2, поскольку он обратимо циклически меняется от 0 до 100% деформации в течение 10 циклы. Несмотря на большие изменения деформации при растяжении, сопротивление остается довольно постоянным вблизи своего начального значения. e Из-за в значительной степени независимой от деформации проводимости гелей он может поддерживать световой индикатор даже после растяжения до 50% деформации
e Из-за в значительной степени независимой от деформации проводимости гелей он может поддерживать световой индикатор даже после растяжения до 50% деформации
Этим методом также можно изготавливать высокоэластичные проводящие гели (рис.3в). Это особенно примечательно, поскольку свойство эластичности было сложной задачей для включения в растяжимые проводящие полимерные материалы. Например, пластификаторы использовались в литературе для повышения растяжимости сухого PEDOT: PSS, но эти материалы по-прежнему деформируются при относительно низких деформациях <20%, что потенциально ограничивает их применимость в качестве растягиваемых проводников в приложениях с высокой деформацией 29 . Например, по сравнению с хорошо растяжимым проводником PEDOT: PSS / ионная жидкость, разработанным в нашей группе (дополнительный рисунок 4), гели C-IPN демонстрируют значительно меньший гистерезис при циклическом изменении деформации в тех же условиях.Таким образом, возможность ортогонального управления механическими свойствами с использованием сети PAAc позволяет нам использовать преимущества эластичности определенных составов гидрогелей PAAc для придания эластичности проводящему композиту.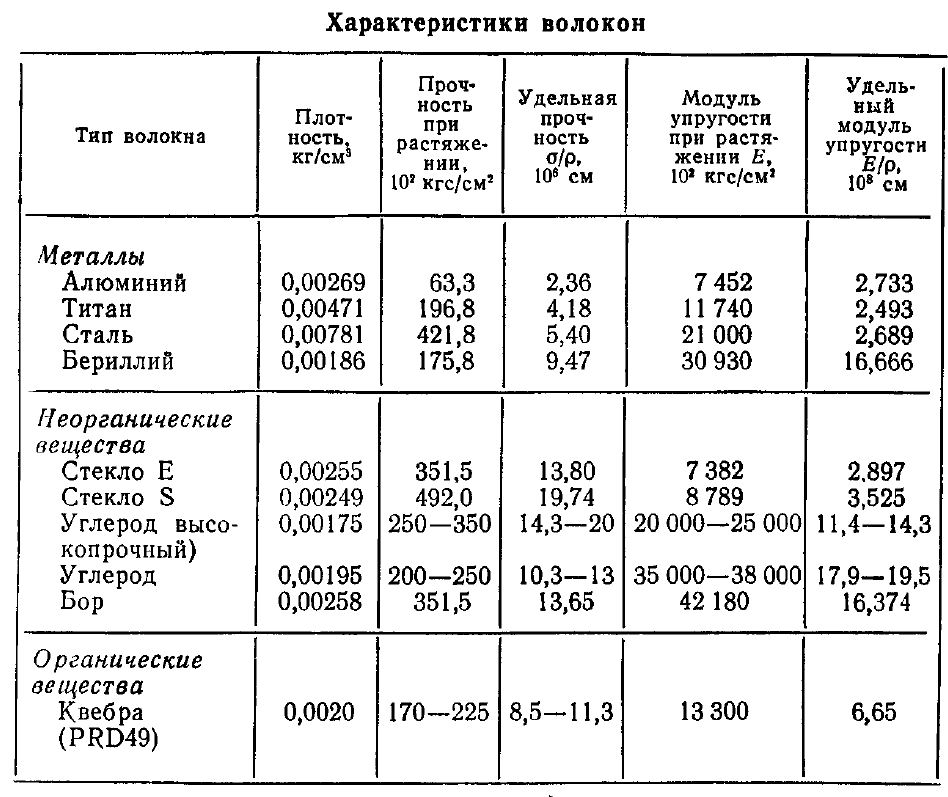
Электропроводность гелей C-IPN рассчитывалась путем измерения сопротивления гелей с использованием метода четырехточечного зонда. Для всех составов проводимость была больше 10 См · м -1 . Наивысшая проводимость составляла 23 ± 5,6 См · м -1 , и проводимость имела тенденцию к снижению в зависимости от концентрации акриловой кислоты в растворе предшественника гидрогеля PAAc (таблица 1).Тот факт, что удельная электропроводность может поддерживаться на уровне выше 10 См · м -1 , несмотря на большие вариации модулей упругости, вероятно, обусловлен способностью водных растворов PEDOT: PSS образовывать связанные CP-сети с низкой массовой концентрацией по сравнению с акриловой кислотой. Действительно, массовый процент PEDOT: PSS в конечном геле значительно ниже, чем сообщалось ранее, растяжимых гидрогелей PEDOT: PSS (дополнительная таблица 1). Хотя возможность соединения проводящих доменов имеет решающее значение для достижения высокой электропроводности 35 , механические свойства композитов, такие как модуль упругости, в значительной степени определяются относительным количеством каждого компонента 36,37 .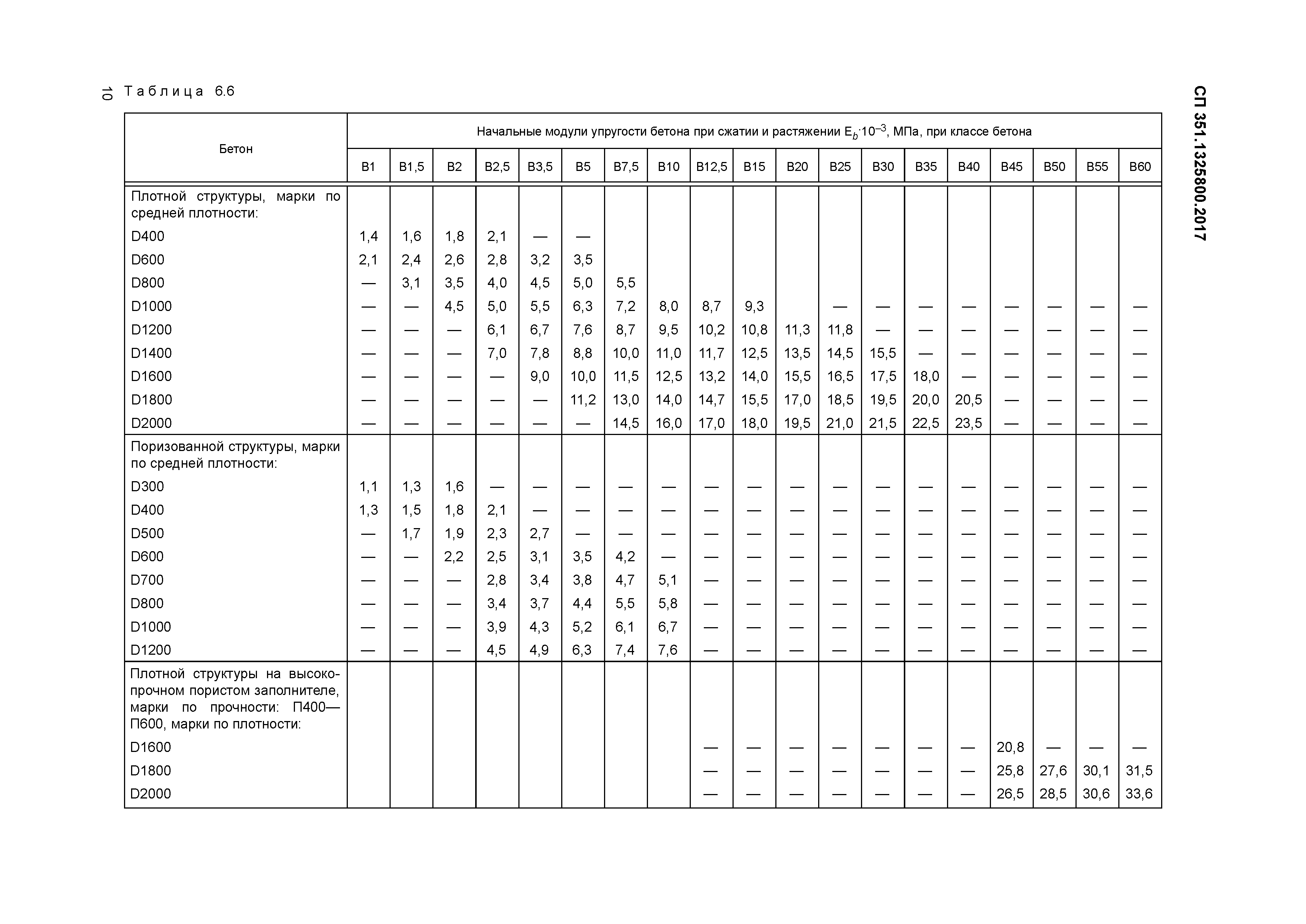 Таким образом, композитный материал, состоящий преимущественно из мягкого материала, будет мягким, даже если он содержит небольшое количество жестких доменов. Аналогичным образом, из-за разбавленной микрогелевой структуры PEDOT: PSS в водных растворах, относительно небольшое количество PEDOT: PSS, необходимое для формирования связного проводящего пути в C-IPN, позволяет почти ортогонально контролировать его механические свойства непроводящим PAAc. сеть. Это представляет собой явное преимущество перед другими проводящими растягиваемыми гидрогелями, которые были синтезированы путем полимеризации EDOT в электрически инертной гидрогелевой матрице, где приличная проводимость достигается только при концентрациях до 30 мас.%.
Таким образом, композитный материал, состоящий преимущественно из мягкого материала, будет мягким, даже если он содержит небольшое количество жестких доменов. Аналогичным образом, из-за разбавленной микрогелевой структуры PEDOT: PSS в водных растворах, относительно небольшое количество PEDOT: PSS, необходимое для формирования связного проводящего пути в C-IPN, позволяет почти ортогонально контролировать его механические свойства непроводящим PAAc. сеть. Это представляет собой явное преимущество перед другими проводящими растягиваемыми гидрогелями, которые были синтезированы путем полимеризации EDOT в электрически инертной гидрогелевой матрице, где приличная проводимость достигается только при концентрациях до 30 мас.%.
Хотя проводимость C-IPN остается в пределах того же порядка величины, несмотря на значительно разные модули упругости, небольшие различия в проводимости можно отнести к разнице в концентрации акриловой кислоты, что согласуется с разной степенью усадки, визуально наблюдаемой во время PAAc. шаг инфильтрации. Тот факт, что проводимость существенно не меняется, предполагает, что эти различия в прочности геля PEDOT: PSS невелики по сравнению с увеличением проводимости, которое происходит за счет образования связанной проводящей сети.Этот вывод имеет смысл, учитывая, что в проводящих композитах наиболее резкое увеличение проводимости обычно происходит при пороге перколяции 38,39 .
шаг инфильтрации. Тот факт, что проводимость существенно не меняется, предполагает, что эти различия в прочности геля PEDOT: PSS невелики по сравнению с увеличением проводимости, которое происходит за счет образования связанной проводящей сети.Этот вывод имеет смысл, учитывая, что в проводящих композитах наиболее резкое увеличение проводимости обычно происходит при пороге перколяции 38,39 .
Учитывая, что кислотные мономеры, очевидно, взаимодействуют с PEDOT: PSS, наш метод инфильтрации необходим для их эффективного проникновения через гель PEDOT: PSS в однородную смесь. Напротив, прямое смешивание PEDOT: PSS с акриловой кислотой привело к быстрому разделению фаз, вероятно, из-за кислотности мономеров (дополнительный рисунок 6а).Хотя смесь может быть полимеризована с образованием мягкого геля с умеренной растяжимостью (дополнительный рисунок 6b), проводимость смеси была значительно ниже, при 0,21 См -1 . Как и ожидалось, это значение находится в том же диапазоне проводимостей, что и в недавней работе Wu et al.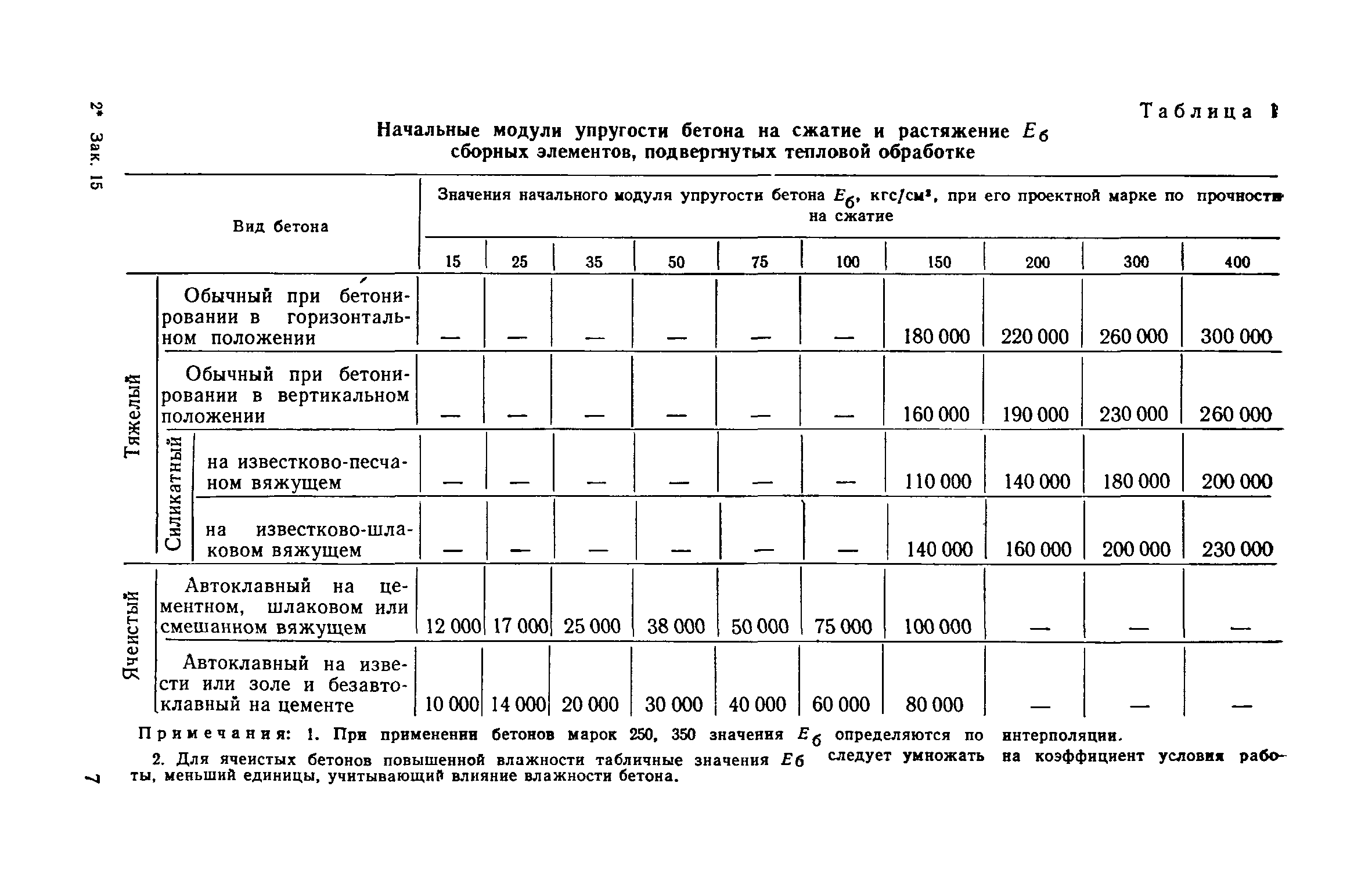 15 , который непосредственно смешал PEDOT: PSS с мономерами, используемыми для создания механически армирующих инертных вторичных сетей (0,2–2,2 См –1 ) 15 . Кроме того, модуль и деформация при разрыве гидрогелей PEDOT: PSS / PAAc, полученных смешиванием, были ниже, чем для гидрогелей, изготовленных только с PAAc, вероятно, потому что значительное количество мономера теряется, когда он разрушается с PEDOT: PSS при смешивании (дополнительная информация Рисунок 6c).Таким образом, мы считаем, что наш метод инфильтрации позволяет в большей степени ортогонально контролировать выбор двух взаимопроникающих сетей в проводящем геле. Эта функция также позволяет нам включать альтернативные вторичные сети, помимо PAAc, в C-IPN. Например, композитные гидрогели, полученные путем инфильтрации гелей PEDOT: PSS с предшественниками полиакриламида (PAAm), проявляли механические свойства, которые очень напоминали гели, полученные только с PAAm (дополнительный рисунок 7).
15 , который непосредственно смешал PEDOT: PSS с мономерами, используемыми для создания механически армирующих инертных вторичных сетей (0,2–2,2 См –1 ) 15 . Кроме того, модуль и деформация при разрыве гидрогелей PEDOT: PSS / PAAc, полученных смешиванием, были ниже, чем для гидрогелей, изготовленных только с PAAc, вероятно, потому что значительное количество мономера теряется, когда он разрушается с PEDOT: PSS при смешивании (дополнительная информация Рисунок 6c).Таким образом, мы считаем, что наш метод инфильтрации позволяет в большей степени ортогонально контролировать выбор двух взаимопроникающих сетей в проводящем геле. Эта функция также позволяет нам включать альтернативные вторичные сети, помимо PAAc, в C-IPN. Например, композитные гидрогели, полученные путем инфильтрации гелей PEDOT: PSS с предшественниками полиакриламида (PAAm), проявляли механические свойства, которые очень напоминали гели, полученные только с PAAm (дополнительный рисунок 7).
Затем мы охарактеризовали изменение электрического поведения при механической деформации, измерив сопротивление через C-IPN при циклическом переключении между 0 и 50% деформации (рис.3д). Электрические свойства геля были на удивление устойчивыми в этой области, при этом сопротивление оставалось примерно на своем начальном значении на протяжении всех 10 циклов. Чтобы убедиться, что высокое контактное сопротивление не маскирует изменение сопротивления от двухточечного испытания, измерения сопротивления по четырем точкам также были выполнены на C-IPN после растяжения вручную до нескольких деформаций. Несмотря на очевидный вклад контактного сопротивления в 17 Ом при измерении по двум точкам, измерение растяжения по четырем точкам подтвердило, что сопротивление гелей практически не изменилось даже при больших деформациях, превышающих 60% (дополнительный рисунок 5).Устойчивая проводимость может быть объяснена как связанной природой геля PEDOT: PSS, так и способностью C-IPN реагировать на деформацию путем переориентации в среде с высоким содержанием воды или разрыва водородных связей в сети PAAc.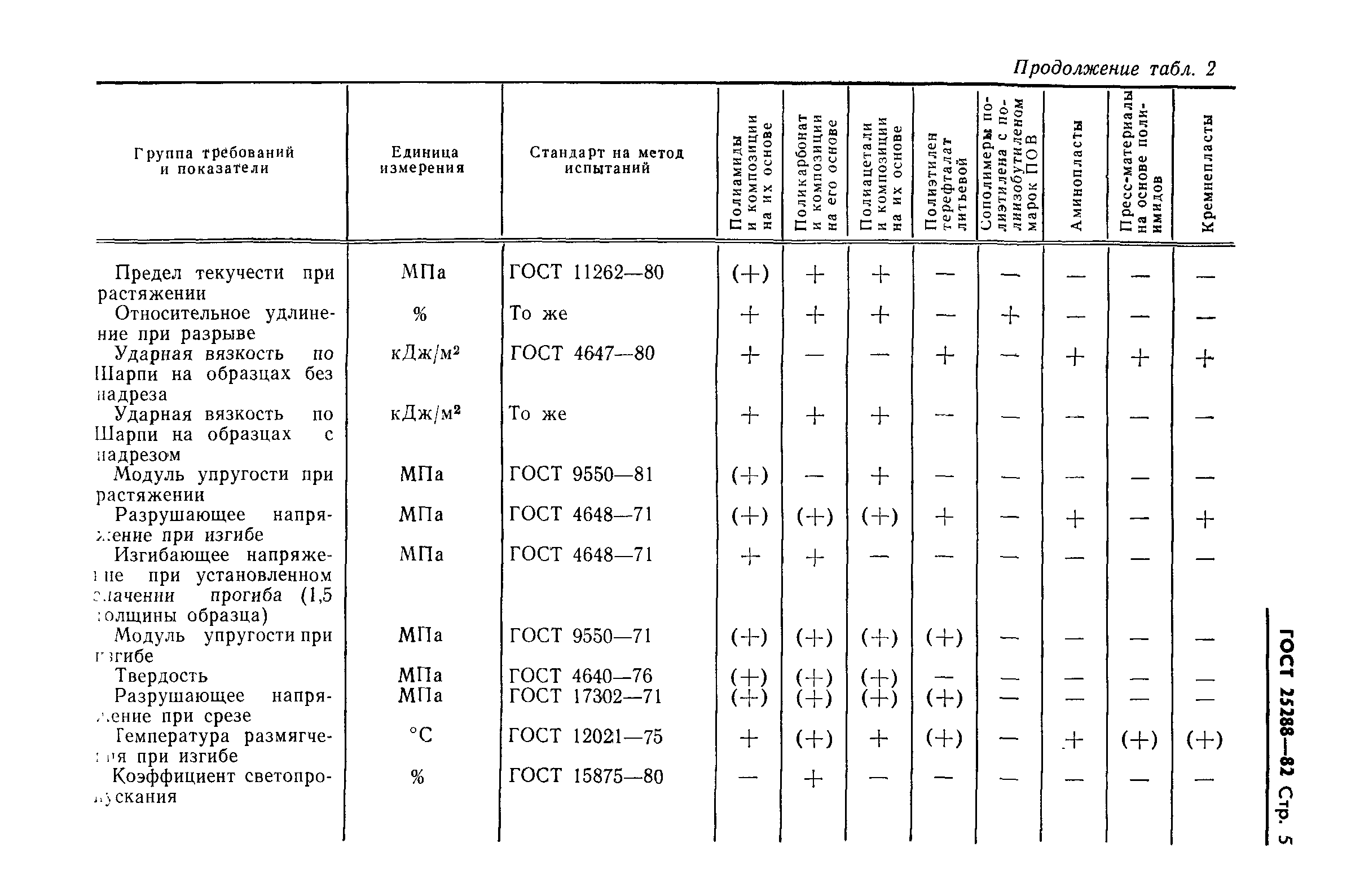 Эти альтернативные механизмы рассеивания могут позволить запутанной коллоидной сетке PEDOT: PSS оставаться нетронутой, а не нарушать перколяцию.
Эти альтернативные механизмы рассеивания могут позволить запутанной коллоидной сетке PEDOT: PSS оставаться нетронутой, а не нарушать перколяцию.
Для приложений биоинтерфейса присутствие ионов в физиологическом растворе может дополнительно влиять на проводимость электродов C-IPN, особенно с учетом высокого содержания жидкости в гидрогелях.Чтобы разделить ионную и электронную проводимость, мы насыщали гели C-IPN в 1 × фосфатно-солевом растворе (PBS) и характеризовали их импеданс с помощью спектроскопии электрохимического импеданса (EIS). Данные соответствовали модели эквивалентной схемы, изображенной на рис. 4a, где R c представляет омическое сопротивление сборки элемента, R e представляет электронное сопротивление, R i представляет ионное сопротивление, и CPE dl и CPE g представляют собой элементы с постоянной фазой, соответствующие емкости двойного слоя, возникающей из-за ионной проводимости, и геометрической емкости геля, соответственно 40,41,42,43 .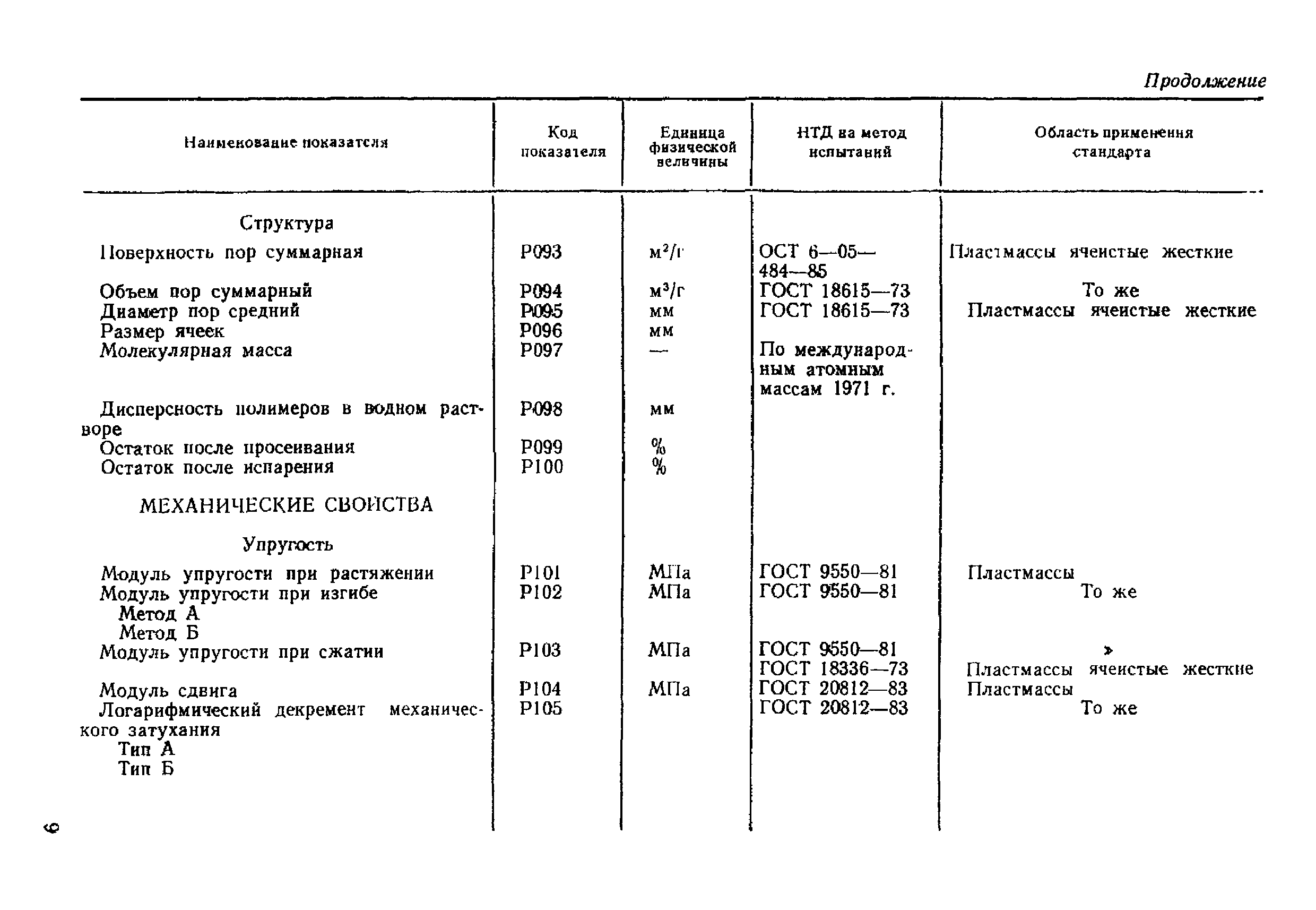 Искаженная полукруглая форма графика Найквиста предполагает наличие сопоставимых ионной и электронной проводимости (рис. 4b, d) 44 . Параметры, извлеченные из подгонки данных к модели эквивалентной схемы, подтверждают, что ионное и электронное сопротивления находятся в пределах одного порядка величины (рис. 4e). Чтобы проверить эту модель, мы измерили постоянное напряжение как функцию времени для постоянного приложенного тока 5 мА на образце C-IPN 2 (рис. 4c) 45 . Значение плато напряжения, 0.0247 В соответствует только электронному вкладу в сопротивление, а значение R e , экстраполированное этим методом (4,94 Ом), сравнимо со значением, полученным при подгонке данных переменного тока (4,97 Ом) с погрешностью <1%. . Наконец, мы охарактеризовали влияние различных составов C-IPN на смешанную проводимость, выполнив измерение EIS на трех составах различной плотности, при этом C-IPN 1 является наиболее плотным, а C-IPN 3 - наименее плотным (рис. 4d).
Искаженная полукруглая форма графика Найквиста предполагает наличие сопоставимых ионной и электронной проводимости (рис. 4b, d) 44 . Параметры, извлеченные из подгонки данных к модели эквивалентной схемы, подтверждают, что ионное и электронное сопротивления находятся в пределах одного порядка величины (рис. 4e). Чтобы проверить эту модель, мы измерили постоянное напряжение как функцию времени для постоянного приложенного тока 5 мА на образце C-IPN 2 (рис. 4c) 45 . Значение плато напряжения, 0.0247 В соответствует только электронному вкладу в сопротивление, а значение R e , экстраполированное этим методом (4,94 Ом), сравнимо со значением, полученным при подгонке данных переменного тока (4,97 Ом) с погрешностью <1%. . Наконец, мы охарактеризовали влияние различных составов C-IPN на смешанную проводимость, выполнив измерение EIS на трех составах различной плотности, при этом C-IPN 1 является наиболее плотным, а C-IPN 3 - наименее плотным (рис. 4d).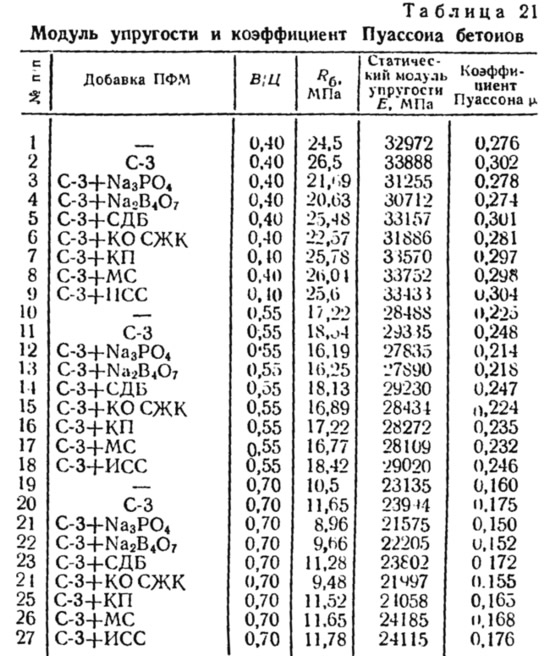 . По мере уменьшения плотности гелей относительный вклад ионного сопротивления в общий импеданс также уменьшается (рис.4д). Это разумно, учитывая, что плотность гидрогеля прямо пропорциональна электронной проводимости (таблица 1), тогда как она обратно пропорциональна общему объему электролита, который способствует переносу ионов в гидрогеле.
. По мере уменьшения плотности гелей относительный вклад ионного сопротивления в общий импеданс также уменьшается (рис.4д). Это разумно, учитывая, что плотность гидрогеля прямо пропорциональна электронной проводимости (таблица 1), тогда как она обратно пропорциональна общему объему электролита, который способствует переносу ионов в гидрогеле.
Характеристика двойной ионной и электронной проводимости. a Эквивалентная модель схемы, представляющая объемный гидрогель C-IPN. R e представляет собой электронное сопротивление, R i представляет ионное сопротивление, CPE dl представляет собой двухслойный емкостный фазовый элемент (CPE), тогда как CPE g представляет собой геометрический CPE.Элементы CPE используются для учета неоднородной или несовершенной емкости и представлены параметрами Q и α , где Q — значение псевдоемкости, а α — его отклонение от идеального емкостного поведения. Истинная емкость ( C ) может быть рассчитана из этих параметров по соотношению C = Q ω max α-1 , где ω max представляет частоту, на которой мнимая составляющая достигает максимума 43 . R c представляет собой полное омическое сопротивление сборки элементов. b График Найквиста, полученный при выполнении спектроскопии электрохимического импеданса (EIS) через объемный гель C-IPN 2, наложенный на график, предсказанный на основе модели эквивалентной схемы. Импеданс измерялся в диапазоне от 500 до 7 МГц, при этом более высокие реальные составляющие импеданса были получены на более низких частотах. c Когда через гель C-IPN 2 подается постоянный постоянный ток 5 мА, напряжение на плато геля достигает значения 0.0247 В. Это значение можно использовать для расчета электронного сопротивления, которое сопоставимо со значением R e , извлеченным из модели.
Истинная емкость ( C ) может быть рассчитана из этих параметров по соотношению C = Q ω max α-1 , где ω max представляет частоту, на которой мнимая составляющая достигает максимума 43 . R c представляет собой полное омическое сопротивление сборки элементов. b График Найквиста, полученный при выполнении спектроскопии электрохимического импеданса (EIS) через объемный гель C-IPN 2, наложенный на график, предсказанный на основе модели эквивалентной схемы. Импеданс измерялся в диапазоне от 500 до 7 МГц, при этом более высокие реальные составляющие импеданса были получены на более низких частотах. c Когда через гель C-IPN 2 подается постоянный постоянный ток 5 мА, напряжение на плато геля достигает значения 0.0247 В. Это значение можно использовать для расчета электронного сопротивления, которое сопоставимо со значением R e , извлеченным из модели.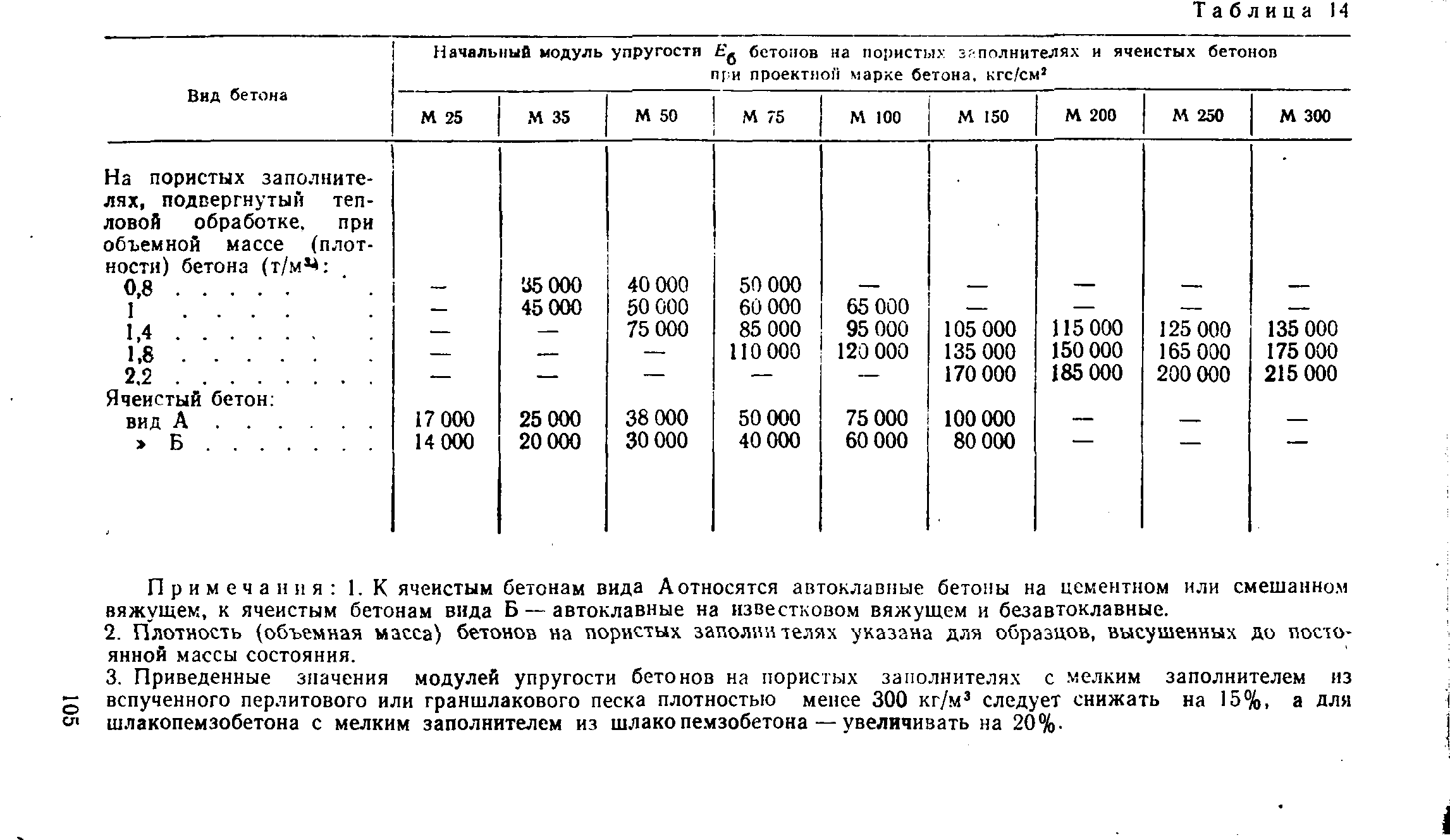 d Наложение графиков Найквиста, полученных для трех составов C-IPN, где C-IPN 1 — самый жесткий и самый плотный, а C-IPN 3 — самый мягкий и наименее плотный. Импеданс измерялся в диапазоне от 500 до 7 МГц, при этом более высокие реальные составляющие импеданса были получены на более низких частотах. e Значения всех релевантных параметров, извлеченных для трех составов C-IPN путем подгонки их данных EIS с моделью эквивалентной схемы.По мере увеличения жесткости и плотности геля относительное ионное сопротивление внутри геля также увеличивается.
d Наложение графиков Найквиста, полученных для трех составов C-IPN, где C-IPN 1 — самый жесткий и самый плотный, а C-IPN 3 — самый мягкий и наименее плотный. Импеданс измерялся в диапазоне от 500 до 7 МГц, при этом более высокие реальные составляющие импеданса были получены на более низких частотах. e Значения всех релевантных параметров, извлеченных для трех составов C-IPN путем подгонки их данных EIS с моделью эквивалентной схемы.По мере увеличения жесткости и плотности геля относительное ионное сопротивление внутри геля также увеличивается.
Модуль упругости — Instron
Что такое модуль упругости?
Модуль упругости, также известный как модуль упругости или просто модуль упругости, является мерой упругости материала. Модуль упругости количественно определяет сопротивление материала непостоянной или упругой деформации. Находясь под напряжением, материалы сначала проявляют упругие свойства: напряжение заставляет их деформироваться, но материал вернется в свое предыдущее состояние после снятия напряжения.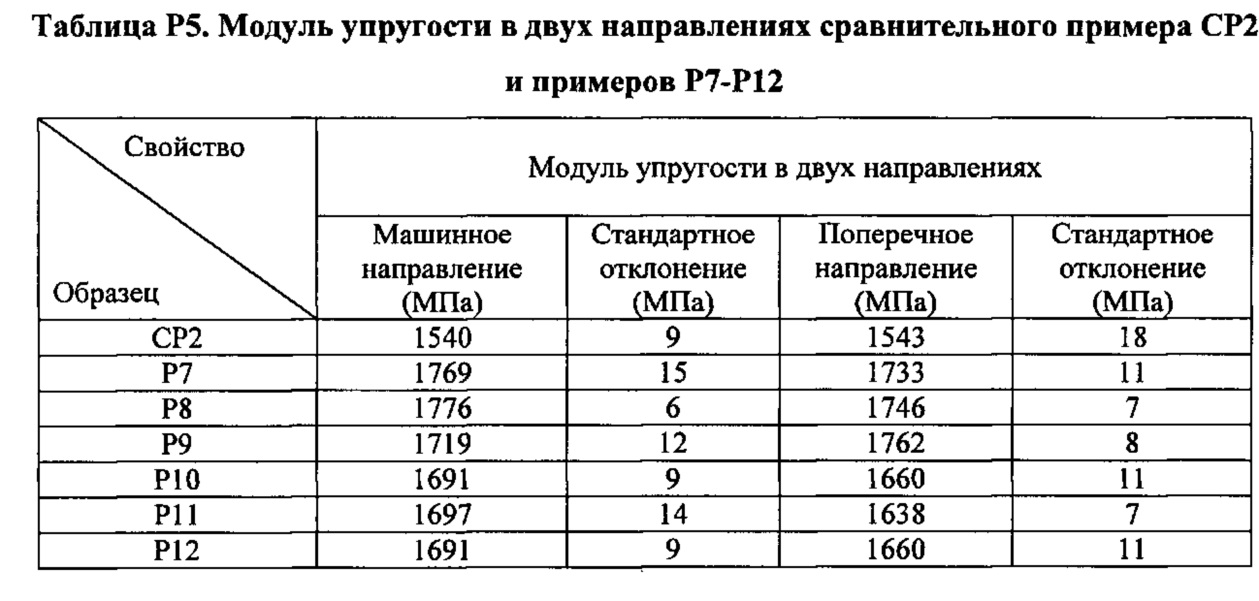 Пройдя через упругую область и достигнув предела текучести, материалы попадают в пластическую область, где они демонстрируют остаточную деформацию даже после снятия растягивающего напряжения.
Пройдя через упругую область и достигнув предела текучести, материалы попадают в пластическую область, где они демонстрируют остаточную деформацию даже после снятия растягивающего напряжения.
Модуль определяется как наклон прямолинейной части кривой напряжения (σ) деформации (ε). Сосредоточившись на упругой области, если наклон взят между двумя точками напряжения-деформации, модуль представляет собой изменение напряжения, деленное на изменение деформации. Модуль = (σ2 — σ1) / (ε2 — ε1) , где напряжение (σ) — это сила, деленная на площадь поперечного сечения образца, а деформация (ε) — это изменение длины материала, деленное на исходную калибровочную длину материала. .Поскольку как напряжение, так и деформация являются нормализованными измерениями, модуль упругости является неизменным свойством материала, которое можно сравнивать между образцами разных размеров. Большой стальной образец будет иметь тот же модуль упругости, что и маленький стальной образец, хотя для большого образца потребуется более высокая максимальная сила для деформации материала. Хрупкие материалы, такие как металлы, пластмассы и композиты, будут иметь более крутой наклон и более высокое значение модуля, чем пластичные материалы, такие как резина.
Хрупкие материалы, такие как металлы, пластмассы и композиты, будут иметь более крутой наклон и более высокое значение модуля, чем пластичные материалы, такие как резина.
Модуль эластомеров
В отличие от хрупких материалов, таких как пластмассы и металлы, эластомерные материалы не имеют предела текучести и продолжают упруго деформироваться до разрыва.В этом случае модуль просто указывается как мера силы при заданном удлинении. Например, на приведенном ниже графике модуль представлен как напряжение при деформации 100, 200 и 300%.
Хотя модуль упругости чаще всего сообщается во время испытаний на растяжение, модуль упругости также может быть указан как модуль упругости при сжатии для испытаний на сжатие, модуль упругости при изгибе для испытаний на изгиб, модуль упругости при сдвиге для испытаний на сдвиг или модуль упругости при кручении. тесты.Модуль упругости также можно определить с помощью динамических испытаний, где он может быть получен из комплексного модуля.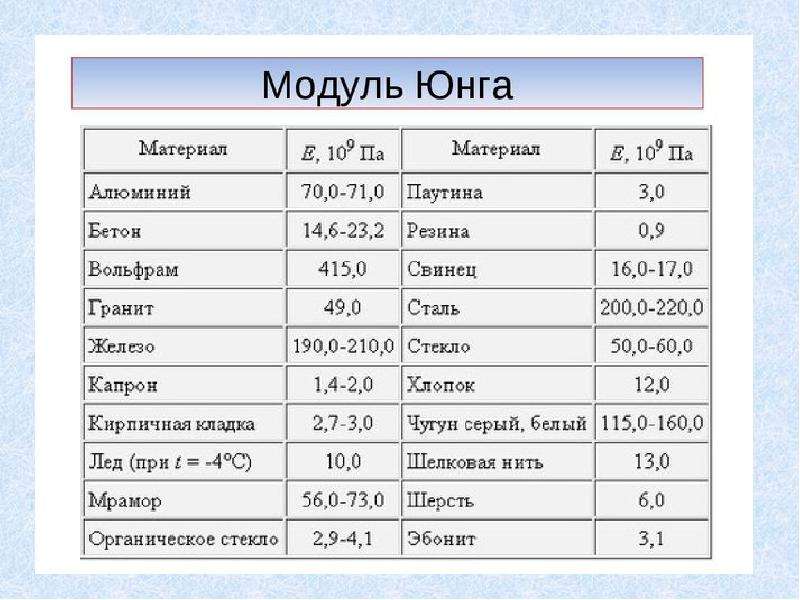
Расчет различных типов модуля упругости
Пользователи, регистрирующие модуль упругости, должны знать, что существует множество различных способов вычисления наклона начального линейного участка кривой напряжения / деформации. Например, программное обеспечение Instron Bluehill® Universal предлагает более восьми различных способов расчета модуля упругости. При сравнении результатов модуля упругости для данного материала в разных лабораториях очень важно знать, какой тип расчета модуля был выбран.
Модуль Юнга
Наклоны рассчитываются на начальном линейном участке кривой с использованием метода наименьших квадратов для данных испытаний. Самый крутой наклон указывается как модуль.
Хордовый модуль
Пользователь выбирает начальную точку деформации и конечную точку деформации. Между двумя точками проводится линия, и наклон этой линии записывается как модуль.
Секущий модуль
Использует нулевую точку напряжения / деформации как начальное значение и выбранную пользователем точку деформации как конечное значение.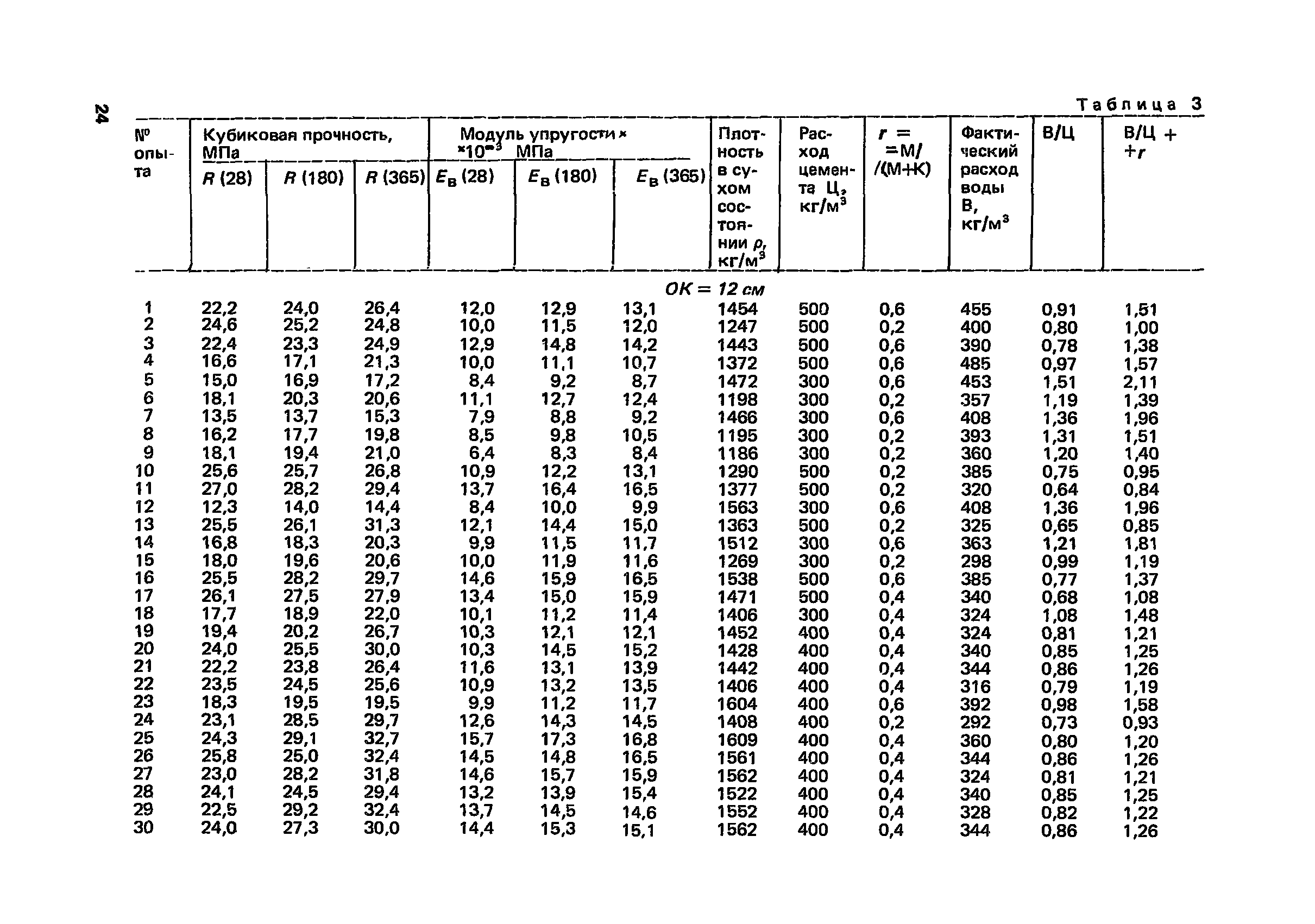 Между двумя точками проводится линия, и наклон этой линии записывается как модуль.
Между двумя точками проводится линия, и наклон этой линии записывается как модуль.
Модуль упругости сегмента
Пользователь выбирает начальную точку деформации и конечную точку деформации. Используя метод наименьших квадратов для всех точек между начальной и конечной точками, строится линия. Наклон наиболее подходящей линии указывается как модуль.
Модуль упругости
Пользователь выбирает точку касания на кривой напряжения / деформации. Наклон касательной обозначается как модуль.
Модуль упругости E
Модуль упругости определяется с помощью стандартной методики линейной регрессии. Часть кривой, которая будет использоваться для расчета, выбирается автоматически и исключает начальную и конечную части упругой деформации, где кривая напряжения-деформации является нелинейной.
Модуль гистерезиса
Модуль упругости определяется петлей гистерезиса, создаваемой секцией загрузки и перезагрузки.

 Обычно именно его называют просто модулем упругости.
Обычно именно его называют просто модулем упругости.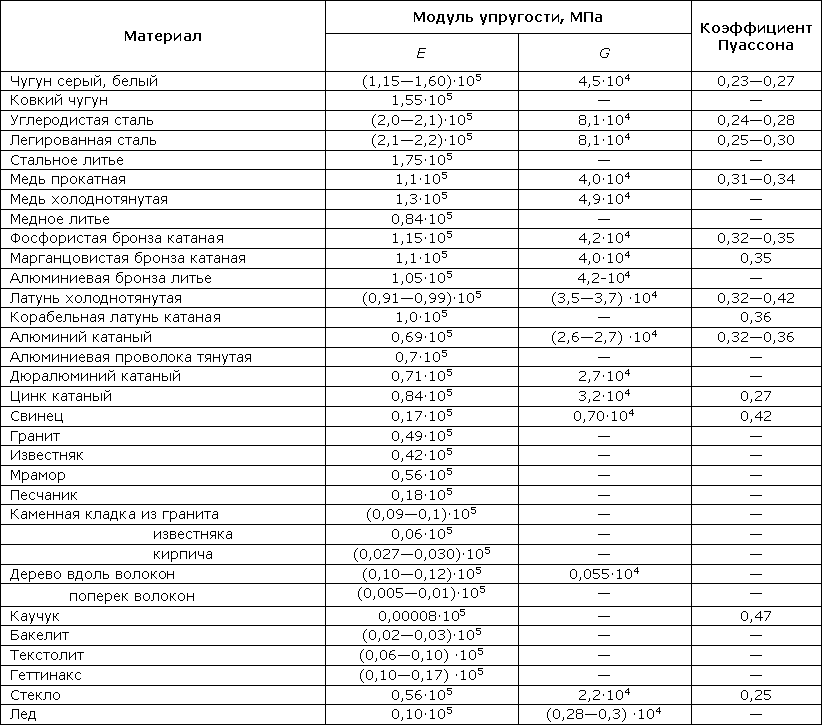
 Опытным путём было установлено, что для большего количества материала поперечное меньше продольного удлинения приблизительно в 4 раза.
Опытным путём было установлено, что для большего количества материала поперечное меньше продольного удлинения приблизительно в 4 раза. wikipedia.org/wiki/%D0%9C%D0%BE%D0%B4%D1%83%D0%BB%D1%8C_%D0%AE%D0%BD%D0%B3%D0%B0: использовано 2 блоков из 8, кол-во символов 754 (5%)
wikipedia.org/wiki/%D0%9C%D0%BE%D0%B4%D1%83%D0%BB%D1%8C_%D0%AE%D0%BD%D0%B3%D0%B0: использовано 2 блоков из 8, кол-во символов 754 (5%) Он равен отношению величины объёмного напряжения к величине относительного объёмного сжатия. В отличие от двух предыдущих величин, модуль объёмной упругости невязкой жидкости отличен от нуля для несжимаемой жидкости — бесконечен.
Он равен отношению величины объёмного напряжения к величине относительного объёмного сжатия. В отличие от двух предыдущих величин, модуль объёмной упругости невязкой жидкости отличен от нуля для несжимаемой жидкости — бесконечен.


 3826
3826