Модуль продольной упругости: Модуль продольной упругости — Справочник химика 21 — Лазерная резка металла от "ТМК" Ярославль (Тутаев)

Содержание

Модуль продольной упругости — Справочник химика 21

Модуль упругости. Расчетное значение модуля продольной упругости для углеродистых и легированных сталей аустенитного класса в зависимости от температуры приведено в табл. 4.4. [c.155]

Наиболее важными характеристиками механических свойств при выборе материалов являются предел прочности или временное сопротивление а , предел текучести а , относительное удлинение б, относительное сужение 1 1, модуль упругости при растяжении Е (модуль продольной упругости), коэффициент Пуассона л, ударная вязкость а . [c.5]

Стали Модуль продольной упругости Е-10 МПа при температуре, °С [c.442]

Модуль продольной упругости (модуль Юнга) Сосредоточенная сила воздействие вообще Модуль упругости при сдвиге постоянная нагрузка (вес) [c.375]

Е Б — модуль продольной упругости материала болтов, Е б = 1,67-10 МПа аф, ав — коэффициенты температурного расширения для материалов фланцев и болтов, выбираем по таблице 3.

7.21, аф = 13,0-10 1/V, ав = 14,7-10 1/°С. [c.77]

Е — модуль продольной упругости материала аппарата при расчетной температуре, МПа [c.365]

Модуль продольной упругости ( 10 5, МПа) сталей [c.285]

Модуль продольной упругости [c.442]

Расчетные значения модуля продольной упругости Е в зависимости от температуры для углеродистых и легированных сталей, алюминиевых, медных и титановых сплавов приведены в приложении, табл. VII—X. [c.10]

Расчетные значения модуля продольной упругости (ГОСТ 14249—80)

[c.14]

Е — модуль продольной упругости, Па, МПа f —сила, Н, МН [c.7]

Исходные данные. Скорость вращения ш == 16,75 рад/с, масса мешалки т = 25 кг, модуль продольной упругости материала вала = 2-10 М1а, его плотность р = 7800 кг/м . Валы отличаются только схемами крепления (рис. 3.20). [c.181]

Расчетные значения модуля продольной упругости Е в зависимости от температуры приведены в приложении (табл. VII). [c.227]

Модуль продольной упругости ( 10 5, МПа) алюминия и его сплавов

[c.285]

ГОСТ 14249—80 Сосуды и аппараты. Нормы и методы расчета на прочность , СТ СЭВ 596—77 и СТ СЭВ 597—77 устанавливают нормы и методы расчета на прочность цилиндрических обечаек, конических элементов, днищ и крышек сосудов и аппаратов из углеродистых и легированных сталей, применяемых в химической, нефтеперерабатывающей и смежных отраслях промышленности и работающих в условиях одтюкратных и многократных статических нагрузок под внутренним избыточным давлением, вакуумом или наружным избыточным давлением и под действием осевых, поперечных, силий и изгибающих моментов. Указанные стандарты уста-навлгвают также значения допускаемых напряжений, модулей продольной упругости и коэффициентов прочности сварных швов. Нормы и методы расчета на прочность применимы при соблюдении правил устройства и безопасной эксплуатации сосудов, работающих под давлением, утвержденных Госгортехнадзором СССР, и нри условии, что отклонения от геометрической формы и неточности изготовления рассчитываемых элементов сосудов и аппаратов не превышают допусков, установленных нормативно-технической документацией.

[c.117]

Модуль упругости, в пределах применимости закона Гука, равен отношению напряжения а в материале к величине, соответствующей упругой деформации 8. В данном случае речь идет о модуле продольной упругости (при линейном растяжении), называемом иначе модулем Юнга. Модуль упругости тем больше, чем меньше относительное удлинение при данном напряжении.

[c.574]

Кристаллические твердые вещества обладают модулем продольной упругости (модулем Юнга) порядка 10 —10 дин1см и очень малым конечным удлинением. Если такое тело растянуто до постоянной длины и температура понижается при сохранении той же длины тела, то напряжение непрерывно возрастает. По ур. (XVII, 3) это означает, что изменение внутренней энергии, связан- [c.576]

Для измельчения материала необходимо выполнение условия дробления ход щеки 5 в точке контакта с куском должен обеспечить такую его деформацию, которая вызывает разрушение куска, т. е. S > гd , где г = S mJE — относительная деформация сжатия (Стс предел прочности при сжатии, Е—модуль продольной упругости).

[c.164]

Уп — л/(яОл срЬаЕл), где Ец — модуль продольной упругости материала прокладки. [c.269]

О = 1600 мм, длина цилиндрической обечайки I = 2500 мм, толщина стеики = = 10 мм, расстояние между опорами Lon 1600 мм, коэффициент трения в опорах /=0,4, масса аппарата та = 1670 кг. Материал — сталь 12Х18Н10Т (ГОСТ 5632—72 ), прибавка к расчетной толщине с = 2 мм допускаемое напряжение и модуль продольной упругости при рабочей температуре [о] = 152 МПа, =2-10 МПа, плотность обрабатываемой среды ро = 1117 кг/м , остаточное давление рост = 0.01 МПа.

[c.45]

Исходные данные. Остаточное давление рост = 0,01 МПа, внутрен, ний диаметр О = 1600 мм, длина обечайки I = 2665 мм, толщина стенки = 6 мм-прибавка к расчетной толщине стенки с = 2 мм, материал — листовой прокат из стали 12Х18НЮТ, допускаемое напряжение и модуль продольной упругости при рабочей температуре /= 100 °С [о] = 152 МПа, Е = 2-10 МПа, масса крышки с приводом т = 1000 кг.

[c.47]

Принимаем решение расположить кольца жесткости с внешней стороны обечайки, не подвергающейся коррозионному воздействию обрабатываемой среды, и изготовить их из низколегированной стали 16ГС (прокат). Тогда в рабочих условиях допускаемое напряжение и модуль продольной упругости кольца будут иметь [c.48]

Расчетное значение модуля продольной упругости при заданной температуре ( =50°С) для стали 10Х17Н13М2Т =2-10 МПа. [c.66]

Исходные данные. Внутреннее давление рр = 1 МПа, внутренний диаметр аппарата О = 2000 мм, расчетная температура стенок аппарата t = 100 °С, материал — листовой прокат из стали 08Х22Н6Т, сопрягаемые элементы цилиндрическая оболочка толщиной 8=8 мм, эллиптическое днище толщиной Зэ = 8 мм, прибавка к расчетной толщине стенки с = 1 мм коэффициент прочности сварных швов ф = 1 допускаемое напряжение и модуль продольной упругости при рабочей температуре [о] = 146 МПа, Е— 1,99.10 МПа.

[c. 69]

Модуль продольной упругости (Юнга) — Энциклопедия по машиностроению XXL

Модуль сдвига, кгс/м Модуль продольной упругости (Юнга), кгс/м 2 5-10 7,1-10 [c.378]

Для идеально упругой среды наличие зависимости Гр и от приложенной нагрузки свидетельствует о том, что связь между деформациями и напряжением нелинейная, в противном случае (т. е. при соблюдении закона Гука) модуль продольной упругости (Юнга) Е представлял бы собой постоянную величину и, соответственно, скорости упругих волн не зависели бы от давления.

[c.31]

Модуль продольной упругости (модуль Юнга) Сосредоточенная сила воздействие вообще Модуль упругости при сдвиге постоянная нагрузка (вес) [c.32]

Математически он выражается так с = Ег, где Е — коэффициент пропорциональности, называемый модулем продольной упругости или модулем Юнга. [c.36]

Модуль продольной упругости Е называется также модулем Юнга в честь Томаса Юнга ( 11Ъ-М29) — английского ученого, физика и механика, который впервые ввел эту величину.

[c.37]

Е Модуль продольной упругости (модуль Юнга) [c.246]

Коэффициент пропорциональности Е в формуле (2.2) называется модулем продольной упругости (иногда его называют модулем упругости первого рода, или модулем Юнга). Модуль характеризует ж ест к ос т ь материала при растяжении и сжатии. [c.213]

Коэффициент пропорциональности Е в формуле (2.2) называется модулем продольной упругости (иногда его называют модулем упругости первого рода, или модулем Юнга). [c.189]

Величина Е называется модулем продольной упругости или моду-мм Юнга (1773—1829), а v — коэффициентом поперечной деформации или коэффициентом Пуассона (1781—1840).

[c.63]

Величина Е, которая входит в формулу, выражающую закон Гука, является одной из важнейших физических постоянных материала. Она характеризует его жесткость, т. е. способность сопротивляться упругому деформированию. Эта величина называется модулем продольной упругости (также модулем упругости первого рода, или модулем Юнга). [c.78]

Модуль продольной упругости (модуль Юнга). Если твердый образец подвергнуть одностороннему растяжению или сжатию, он деформируется (растягивается или сжимается), причем его деформация подчиняется (в некоторых пределах) закону Гука

[c.168]

В этой формуле Д/ — деформация, 1 — первоначальная длина, Р — деформирующая сила, 5 — площадь поперечного сечения образца. Стоящий в знаменателе коэффициент носит название модуля продольной упругости или модуля Юнга. [c.168]

Здесь Е — коэффициент пропорциональности, носящий название модуля продольной упругости или модуля Юнга ), —характеризует жесткость материала чем больше Е, тем жестче материал, т. е. меньше относительные линейные продольные деформации [c.130]

Модуль Юнга Е модуль продольной упругости) — отношение величины напряжения ст к вызванной им относительной деформации е (только в области упругих деформаций) Е = а/е. [c. 90]

Модуль Юнга (модуль продольной упругости), согласно закону Гука, равен отношению величин приложенного напряжения к вызванной им относительной деформации (только в области упругих деформаций) [c.87]

Как видно из диаграммы состояния железо—углерод (см. рис. 4.1), феррит составляет основную фазу стали. Наличие в феррите растворенного в нем марганца, усиливает металлическую связь в его кристаллической решетке, вследствие чего возрастают значения модуля Юнга (модуля продольной упругости) и модуля сдвига. [c.78]

Е — модуль продольной упругости (модуль Юнга) [c.6]

Коэффициент пропорциональности Е называется модулем продольной упругости, или модулем Юнга, р. — коэффициент Пуассона, С — модуль сдвига. Эти коэффициенты связаны соотношением [c.406]

В упругой области нагружения, где имеется прямая пропорциональность между удлинением образца и соответствующей нагрузкой (участок О—Рпц, см. рис. 11.3), основной характеристикой является модуль продольной упругости (модуль первого рода, или модуль Юнга) [c.192]

Нормальное и касательное напряжения о, ат, модуль продольной упругости (модуль Юнга) =о/Ео, модуль сдвига О=0т/д, модуль объемного сжатия — все эти величины имеют ту же размерность, что и давление, и выражаются в паскалях (вп — относительное удлинение, 0 — угол сдвига). [c.31]

Упругое поведение всякого изотропного тела характеризуется модулем продольной упругости Е (модуль Юнга), модулем сдвига G, модулем всестороннего сжатия К (модуль объемной упругости) и коэффициентом Пуассона р. Величины Е, G ч К являю гся коэффициентами пропорциональности между напряжениями и деформациями при растяжении, сдвиге и всестороннем сжатии [c.68]

Разумеется, эта величина, которая имеет размерность длины, также не зависит от формы и размеров тела. Как будет видно из дальнейшего, величина h является в точности тем, что 32 годами позже Юнг назвал высотой модуля .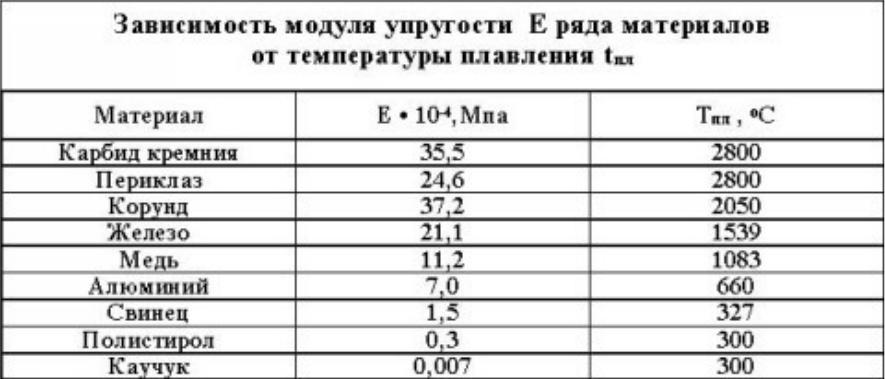 В современной терминологии Е — это модуль продольной упругости, обычно называемый модулем Юнга ), однако сам Юнг никогда не вводил такого понятия. Его высота модуля зависела от плотности материала, а вес модуля — от размеров образца. Как одна, так и другая величина не являются константами материала в собственном смысле слова, и поэтому их употребление нежелательно, хотя высота модуля и не зависит от [c.220]

Модуль Юнга модуль продольной упругости). Для случая продольной деформации (линейного растяжения или [c.42]

Модуль продольной упругости (модуль Юнга), модуль сдвига Жесткость [c.226]

Коэффициент пропорциональности Е называют модулем продольной упругости (другие названия модуль нормальной упругости модуль упругости модуль упругости 1-го рода модуль Юнга). Очевидно, Е имеет ту же размерность, что и напряжение, т. е. выражается в Па или МПа. [c.33]

Величину Е называют модулем Юнга, модулем продольной упругости или просто модулем упругости. Если предел упругости не перейдён, то для данного материала модуль упругости Е представляет собой постоянную величину — это характерная величина, определяющая упругие свойства данного материала ). Твёрдые тела, в особенности металлы, очень сильно сопротивляются изменению своей длины, поэтому модуль Юнга Е, который в технике обычно выражают в килограммах на квадратный миллиметр, представляет собой очень большое число. Так, для стали =22 000 для железа — 20 790 кГ/мм , [c.353]

Величину Е называют модулем Юнга, модулем продольной упругости или просто модулем упругости. Если предел упругости не перейден, то для данного материала модуль упругости Е представляет собой постоянную величину — это характерная величина, определяющая упругие свойства данного материала ). Твердые тела, в особенности металлы, [c.432]

Адсорбционные слои, сформированные из вертикально ориентированных молекул, отличаются выдающимися механическими свойствами при сжатии.

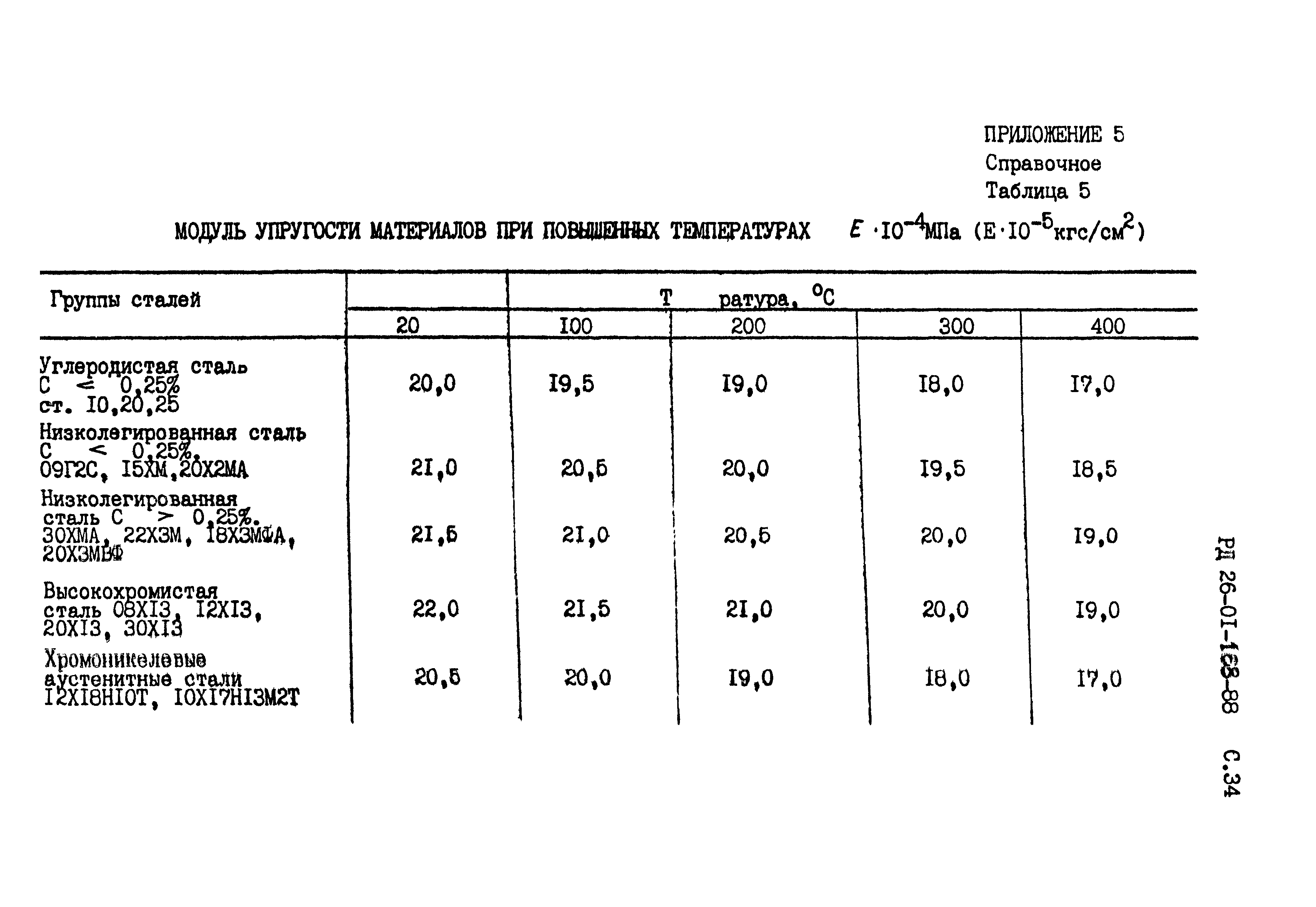Они могут выдерживать нормальные давления порядка многих тысяч кПсм . Модуль продольной упругости (Юнга) метиленовых цепей одиночных молекул открытого строения равен (3,5—5)-10 кГ см [3], т. е. вдвое выше, чем у стали. Однако механические свойства мультимолекулярных слоев сильно зависят от общей толщины слоя и приложенного давления. [c.128]

Модуль продольной упругости введен Л. Эйлером (1707—1783) в 1727 г. н его следовало бы называть модулем Эйлера. В учебной и научной лнтеоа-туре модуль Е часто несправедливо называют модулем Юнга (1773—1829), хотя последний никогда его не вводил. [c.34]

Модуль продольной упругости (модуль Юнга) Е—величина, равная отношению нормального напряжения о к относител П1эму удлинению (или укорочению) е==А/// [c.67]

Модуль продольной упругости Е (модуль Юнга), кгс/мм — отношение нор-ма.льпого напряжения к соответствующему ему относительному удлинению при растяжении в пределах применимости закона Гука. [c.6]

МОДУЛЬ [продольной упругости определяется отношением нормального напряжения в поперечном сечении цилиндрического образца к относительному удлинению при его растяжении сдвига измеряется отношением касательного напряжения в поперечном сечении трубчатого тонкостенного образца к деформации сдвига при его кручении Юнга равен нормальному напряжению, при котором линейный размер тела изменяется в два раза] МОДУЛЯЦИЯ [есть изменение по заданному во времени величин, характеризующих какой-либо регулярный физический процесс колебаний определенному закону какого-либо из параметров периодических колебаний, осуществляемое за время, значительно большее, чем период колебаний амплитудная выражается в изменении амплитуды фазовая указывает на изменение их фазы частотная состоит в изменении их частоты) пространственная заключается в изменении в пространстве характеристик постоянного во времени колебательного процесса] МОЛЕКУЛА [есть наименьшая устойчивая частица данного вещества, обладающая его химическими свойствами атомная (гомеополярная) возникает в результате взаимного притяжения нейтральных атомов ионная (гетерополярная) образуется в результате превращения взаимодействующих атомов в противоположно электрически заряженные и взаимно притягивающиеся ионы эксимерная является корот-коживущим соединением атомов инертных газов друг с другом, с галогенами или кислородом, существующим только в возбужденном состоянии и входящим в состав активной среды лазеров некоторых типов МОЛНИЯ электрический разряд между облаками или между облаками и землей линейная является гигантским электрическим искровым разрядом в атмосфере с диаметром канала от 10 до 25 см и длиной до нескольких километров при максимальной силе тока до ЮОкА) [c. 250]

Для упругой области нагружения характерна прямая пропорциональная зависимость между Р и I (участок ОРцц на рис. 15.4). Основной характеристикой прочности в этой области является модуль продольной упругости Е (модуль первого рода или модуль Юнга ), определяемый тангенсом угла наклона упругой Рц,2 линии диаграммы растяжения— зависимости Р — А/ (о — е). [c.213]

Юнг Томас (Young Т., 1773-1829) —английский ученый, в честь которого назван модуль продольной упругости, впервые введенный Л. Эйлером в 1727 г. [c.43]

Модуль Юнга (модуль продольной упругости) — отношение механического напряжения к соответствующей линейной деформации в пределах упругого участка растяжения единицы измерения н1м (в СИ и МКС), дин1с.и (в СГС) и кГ/м (в МКГСС). [c.93]

Модуль продольной упругости — Энциклопедия по машиностроению XXL

Е — модуль продольной упругости материала аппарата при расчетной температуре, МПа (см.

приложение 11, табл. 7) [c.22]

Модуль продольной упругости [c.99]

Стали Модуль продольной упругости Е-10 МПа, при температуре, С [c.99]

П — модуль продольной упругости [c.5]

Модуль продольной упругости = 2,0- 10 Мн/м , Предел пропорциональности = 270 Мн/м . Подставив значения, получим [c.99]

Е — модуль продольной упругости, Е = 2, — О МПа. [c.31]

Пользуясь принципом Гамильтона — Остроградского, составить дифференциальное уравнение продольных колебаний тонкого стержня, заделанного на одном конце и с массой т на другом конце, и получить граничные условия. Плотность материала стержня р, модуль продольной упругости Е, площадь поперечного сечения Р, длина I, [c. 377]

Коэффициент пропорциональности Е называется модулем продольной упругости или модулем упругости первого рода, он имеет размерность напряжений (даН/см или даН/мм ) и характеризует способность материала сопротивляться упругой деформации при растяжении и сжатии. Величину модуля продольной упругости для различных материалов определяют экспериментально. Для стали = (2,0- 2,15) 10 даН/см , для алюминия = (0,7н-0,8) 10 даН/см , для бронзы = 1,15-10 даН/см , для дерева вдоль волокон = 1-10 даН/см , для стеклопластиков = (0,18-ь н-0,4) 10 даН/см [c.130]

В формуле (11.3) Е — коэффициент, зависящий от материала и называемый модулем продольной упругости или модулем упругости первого рода. Он характеризует жесткость материала, т. е. его способность сопротивляться деформированию. [c.24]

Модуль продольной упругости Е называется также модулем Юнга в честь Томаса Юнга ( 11Ъ-М29) — английского ученого, физика и механика, который впервые ввел эту величину. [c.37]

Е Модуль продольной упругости (модуль Юнга) [c.246]

В формулах (23.1)… (23.3) Е ц О — модули продольной упругости и сдвига материала / —длина звена А — площадь его поперечного сечения Jр — полярный момент инерции сечения J — момент инерции сечения, [c.294]

Пользуясь выражением для удельной потенциальной энергии упругого тела, доказать, что модуль сдвига G связан с модулем продольной упругости Е и коэффициентом Пуассона зависимостью G = /[2(l4-p.)]. [c.130]

Приводим значения модуля продольной упругости для некоторых материалов [c.213]

Следовательно, абсолютное удлинение бруса прямо пропорционально величине продольной силы, возникающей в его поперечных сечениях, и длине бруса и обратно пропорционально площади поперечного сечения и модулю продольной упругости. [c.213]

Задача 2.6. Стальная тяга длиной 1=2 м, площадью поперечного сечения К=6 см под действием растягивающей нагрузки получила абсолютное удлинение Д/=0,8 мм. Определить величину нагрузки Р и напряжение а, если известно, что модуль продольной упругости материала тяги Я=2,0-10 н/мм . [c.240]

Задача 2.7. Пруток диаметром =13 мм, длиной 1=3 м под действием нагрузки Р=90 кн получает абсолютное удлинение Д1= 10 Л1Л . Определить величину модуля продольной упругости материала прутка. [c.240]

Задача 2. 31. Определить предельную гибкость для хромомолибденовой стали, если предел пропорциональности 0 ц=54О н/жж и модуль продольной упругости =2,15-105 [c.319]

Не останавливаясь на доказательстве, укажем, что между тремя упругими постоянными материала — модулями продольной упругости Е и сдвига G и коэффициентом Пуассона х — существует следующая зависимость [c.228]

Пользуясь принципом Гамильтона — Остроградского, составить дифференциальное уравнение поперечных колебаний шарнирно опертой балки, а также получить граничные условия. Плотность материала балки р, модуль продольной упругости Е, площадь поперечного сечения Е, момент ииерцип поперечного сечения У, длина балки I. [c.378]

Пользуясь принципом Гам [ль-топа — Остроградского, составить уравнения малых колебаний системы, состоя-птей из консольной балки длины / и груза массы т, прикрепленного к балке и к основанию пружинами жесткости с. Плотность материа.яа балки р, модуль продольной упругости Е, площадь поперечного сечения Е, момент инерции поперечного сечения У. [c.378]

Иапменогшние и марка Плотность, Предел прочности при растяжении р, МПа Предел прочности при сжатии МПа Предел прочности при изги-Д.и, МПа Модуль продольной упругости , МПа [c.165]

Определите размеры поперечного сечения стержня, удовлетворяющие условиям прочности и жесткости, если допускаемое напряжение материала [о] = 80 МПа, а перемещение свободного конца не должно превыщать величины [8] = 0,0001/, F = 800kH, модуль продольной упругости Е = 200 ГПа. [c.117]

Следует помнить, что для валов, размеры которых устанавливают в зависимости от требований жесткости, использование дорогих легированных сталей неоправдано, так как модуль продольной упругости для всех сталей примерно одинаков и применение стали повышенного качества не способствует уменьшению диаметра вала. [c.376]

Сопротивление материалов (1988) — [ c.0 ]

Единицы физических величин и их размерности Изд.3 (1988) — [ c.168 , c.356 , c.374 ]

Теплоэнергетика и теплотехника Общие вопросы Книга1 (2000) — [ c.406 ]

Машиностроение Энциклопедия Т I-3 Кн 2 (1995) — [ c.36 , c.38 ]

Сопротивление материалов Издание 3 (1969) — [ c.30 ]

Волны напряжения в твердых телах (1955) — [ c.17 , c.178 , c.182 ]

Теория упругости Изд4 (1959) — [ c. 69 ]

Теория пограничного слоя (1974) — [ c.21 ]

Сопротивление материалов (1964) — [ c.27 ]

Справочник машиностроителя Том 6 Издание 2 (0) — [ c.3 , c.6 , c.6 , c.13 , c.22 ]

Машиностроение Энциклопедический справочник Раздел 1 Том 1 (1947) — [ c.165 ]

Определение эффективного модуля упругости для металлической сетки Текст научной статьи по специальности «Физика»

УДК 539.3

ОПРЕДЕЛЕНИЕ ЭФФЕКТИВНОГО МОДУЛЯ УПРУГОСТИ ДЛЯ МЕТАЛЛИЧЕСКОЙ СЕТКИ

И. К. Архипов, В.И. Абрамова

Рассматривается упругое равновесие регулярной симметричной относительно горизонтальной оси сетевой металлической структуры. Для определения эффективного модуля Юнга при растяжении построена модель, которая заменяет сеть одним стержнем с продольным растяжением. Получены зависимости эффективного модуля такого стержня от геометрических параметров сети, показана анизотропия модуля упругости в зависимости от направления нагружения.

Ключевые слова: эффективный модуль Юнга, регулярная структура композита, металлическая сеть из регулярных структур.

Фрагменты регулярной симметрической сетевой конструкции, составленной из стержней одинакового поперечного сечения Бь представленной на рис. 1.

Рис. 1. Фрагмент регулярной сетевой конструкции

Учитывая симметрию, выделим представительный элемент, нагруженный продольной силой N2, усилия растяжения в стержнях, составляющих этот элемент, обозначим через N1 (рис. cos aE*

E1F1 cos2 a EF cos2 a

Учитывая, что левая часть уравнения равна N2, имеем:

2 N1E* Ei cosa

Подставляем в соотношение (5) условие равновесия (1)

2N1 cos a _

Отсюда имеем:

2 N1E* Ei cosa

E 2 2 — _ cos a или E* _E1cos a

Ei 1

(4)

(5)

(6)

Таким образом, эффективный модуль продольной упругости металлической сетки зависит от модуля стержней, составляющих сеть и от угла между этими стержнями.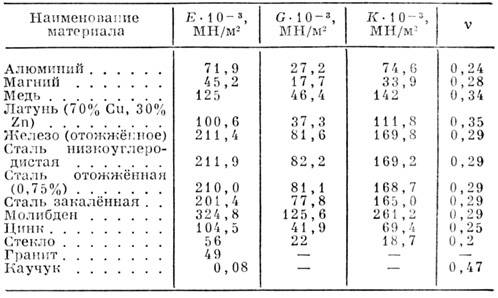 2.

Заметим, что при растяжении сети в поперечном направлении, аналогичные выводы приводят к утверждению об анизотропии механических свойств, т.к. эффективный модуль при поперечном растяжении определя-

ется из формулы (7), где угол oq , т.е.

E*i = Ei cos2 (p — a) = Ei sin2 a.

(8)

Отношение продольного эффективного модуля к поперечному определяется формулой:

E*ii

cos a 2

—= ctg a

sin a

(9)

В случае а = 0, конструкция сети преобразуется в один стержень, сечением 2Б1 и модулем продольной упругости Е* = Е1 .

200 ISO 130 170 160 150 140 130 120 110 100 50 SO 70 «0 50 40 JO 20 10 , Е*

\ \

0 1 2. 3 3 44 5 71

Рис. 3. Зависимость продольного модуля упругости для стальной (а) и алюминиевой (б) сети от угла а.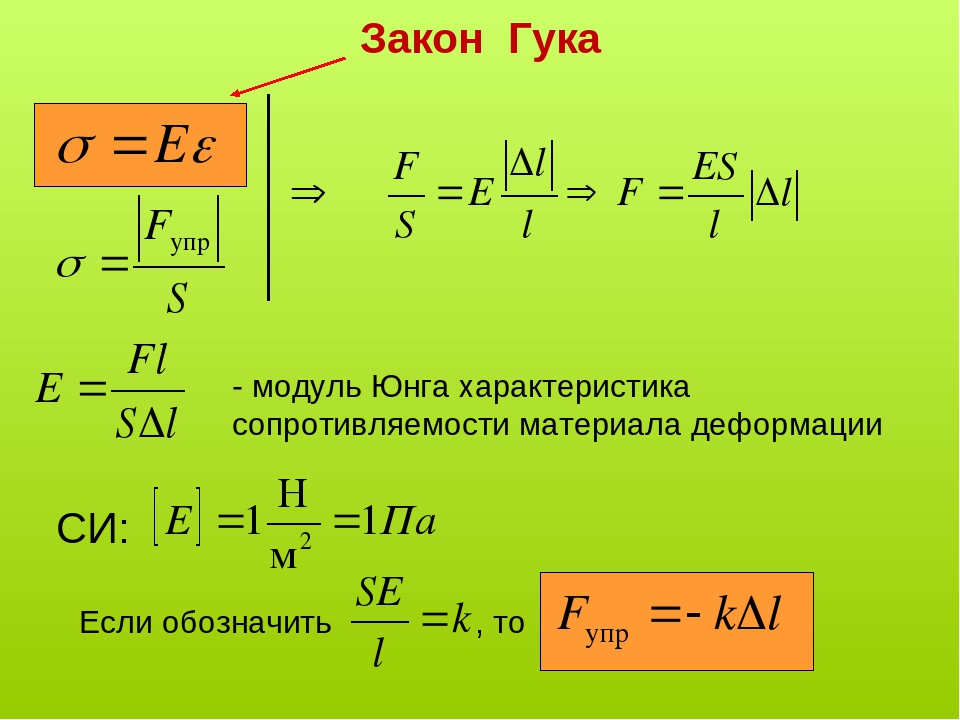 —— зависимость Е* = f не является корректной и следует ограничить интервал значений а в конструкции модели.

Список литературы

1. Прочность, устойчивость, колебания: справочник. М: Машиностроение, 1968. 831с.

Архипов Игорь Константинович, д-р техн. наук, проф., [email protected], Россия, Тула, Российский экономический университет им. Г.В. Плеханова. Тульский филиал,

Абрамова Влада Игоревна, канд. техн. наук, доц., [email protected], Россия, Тула, Тульский государственный педагогический университет им. Л.Н.Толстого

DETERMINA TION OF EFFECTIVE MOD UL US OF ELASTICITY FOR METAL MESH

I.K. Arkhipov, V.I. Abramova

We consider the elastic equilibrium of a regular symmetrical about the horizontal axis of the metal network structure. To determine the effective young’s modulus in tension of the model, which replaces the network with one rod with a longitudinal tension. The obtained dependence of the effective modulus of such a core from the geometric parameters of the network shown anisotropy of the elastic modulus depending on the direction of loading.

Key words: effective Young’s modulus, regular composite structure, a metal network of regular structures.

Arkhipov Igor Konstantinovich, doctor of technical science, professor, [email protected], Russia, Tula, Plekhanov Russian University of Economics. Tula branch,

Abramova Vlada Igorevna, candidate of technical science, docent, gwoz-dew. alexandr2 013@yandex. ru, Russia, Tula, Tula Leo Tolstoy State Pedagogical University

УДК 681.513

ОПТИМАЛЬНЫЕ ПО КРИТЕРИЯМ ТОЧНОСТИ СИСТЕМЫ УПРАВЛЕНИЯ ЭЛЕКТРОМЕХАНИЧЕСКИМИ ОБЪЕКТАМИ

М. Е. Прокофьев, Б.В. Сухинин, В.В. Сурков

Рассматривается ««физический» подход к решению задачи точности на основе функций переключения. Показывается, что для нелинейных систем оптимальное по точности управление в общем случае состоит из n интервалов управлений, которые могут быть найдены один за другим по мере сжатия — расширения фазового пространства в процессе функционирования системы.

Ключевые слова: аналитическое конструирование оптимальных по точности регуляторов, количество интервалов управлений.

Достаточно большой класс электромеханических объектов (например, промышленно-выпускаемые частотно-регулируемые асинхронные электроприводы с короткозамкнутым ротором с векторным или скалярным управлением, синхронные электроприводы) с достаточной точностью можно описать обыкновенным векторным нелинейным дифференциальным уравнением возмущенного движения (по терминологии А. М. Ляпунова):

DX = A(DX) + B(DX) • u (t), (1)

242

Модуль упругости

★ Модуль упругости

Модуль упругости-общее название нескольких физических величин, характеризующих способность твердого тела упруго деформироваться под действием сил. В области упругой деформации модуль упругости тела в общем случае зависит от напряжения и определяется производной зависимости напряжения от деформации, то есть тангенс угла наклона начального линейного участка инженерных напряжение-деформация:

E = def d (Е = защ) σ d ε {\displaystyle E\ {\stackrel {\text{def}}{=}}\ {\frac {d\sigma }{d\varepsilon }}}

где:

E — модуль упругости.
Ε {\свойства стиль отображения значение \Попова закон нуля или единицы } — упругая деформация образца, вызванная напряжением равна отношению изменения размера образца после деформации к его первоначальному размеру.
Σ {\свойства стиль отображения значение \Сигма } (σ {\the style property display the value of \Sigma }) — напряжение вызвало в образце действующая сила равна силе, деленной на площадь приложения силы.

В самом общем случае, зависимость напряжения и деформации закон Гука линейной:

E = σ ε {\displaystyle E={\frac {\sigma }{\varepsilon }}}.

Если напряжение измеряется в Паскалях, то, поскольку деформация является безразмерной величиной, единицы Е будет Паскаль. альтернативным определением является определение, что модуль упругости-это напряжение достаточно, чтобы вызвать увеличение длины образца в два раза. это определение не является точным для большинства материалов, потому что стоимость значительно превышает предел текучести материала. или в месте удлинения становится нелинейной, но это может быть более интуитивно понятным.

Разнообразие способов, которыми могут быть изменены напряжения и деформации, включая различные направления действия силы могут быть использованы для выявления многих типов модулей упругости. вот три основных модуля:

Модуль объемной упругости или модуль объемного сжатия K характеризует способность объекта изменять свой объем под воздействием всестороннего нормального напряжения объемной деформации, одинакова во всех направлениях. это равное величине объемного напряжения на объемном величина относительного обжатия. В отличие от двух предыдущих значений, модуль объемной упругости невязкой жидкости отличен от нуля для несжимаемой жидкости бесконечной.
Модуль сдвига или модуль жесткости G или μ {\свойства стиль отображения значение \му } характеризует способность материала сопротивляться изменению формы при сохранении его объема, определяется как отношение напряжения сдвига к деформации сдвига, определяемой как изменение прямого угла между плоскостями, которые касательных напряжений. модуля сдвига-это одна из составляющих явления вязкости.
Модуль Юнга E характеризует сопротивление материала на растяжение / сжатие упругой деформации, или свойство объекта деформироваться вдоль оси при воздействии силы вдоль этой оси определяется как отношение напряжения к деформации удлинения. часто модуль Юнга называют модулем упругости.

Существуют и другие модули упругости: коэффициент Пуассона, параметры Ламе.

Однородного и изотропного твердого материала, имеющего линейные упругие свойства полностью описываются двумя модулями упругости, который представляет собой пару любых модулей. если дана пара модулей упругости, все другие модули могут быть получены по формулам, представленным в таблице ниже.

В потоках невязкого отсутствуют касательные напряжения, поэтому модуль сдвига всегда ноль. это подразумевает также равенство нулю модуля Юнга.

Модули упругости Е для некоторых веществ:

Определение модуля упругости и коэффициента Пуассона

0. ВВЕДЕНИЕ

В методических указаниях к лабораторной работе N 3 «Определение модуля упругости и коэффициента Пуассона» указывается цель работы, приводится характеристика испытуемого образца и даётся методика проведения испытаний.

Для лучшего усвоения материала по темам: «Растяжение и сжатие» и «Упруго – механические свойства материалов» приводятся основные теоретические положения, позволяющие квалифицированно провести испытания, экспериментально определить по одному испытанию образца величины упругих постоянных (Е и μ) и проанализировать полученные результаты.

Завершаются методические указания перечнем возможных вопросов при защите отчета по этой лабораторной работе.

2. ЦЕЛЬ РАБОТЫ

Определить опытным путем величину модуля упругости Ε и коэффициент Пуассона μ и сравнить полученные результаты со справочными данными.

3. ОБОРУДОВАНИЕ, ПРИБОРЫ И ИНСТРУМЕНТЫ

Испытательная машина – МР-0,5. Тензометрическая станция – ЦТМ-5. Штангенциркуль.

4. ХАРАКТЕРИСТИКА ОБРАЗЦОВ

Вид образца, имеющего прямоугольное поперечное сечение, представлен на рис.1. На больших сторонах поперечного сечения образца наклеены по одному тензодатчику в продольном направлении и по одному в поперечном. Каждый тензодатчик подключен к отдельному каналу тензометрической станции ЦТМ-5.

Рис. 1. Вид обра о тензо датчиками

5. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

При деформациях подавляющего большинства материалов в упругой стадии справедлив закон Гука, который устанавливает прямую пропорциональную зависимость между напряжениями и деформациями:

σ = Ε·ε (1)

Величина Ε представляет собой коэффициент пропорциональности и называется модулем упругости первого рода.). Поперечную деформацию обозначим:

абсолютную – ДЬ (Ab = bi – b),

относительную – ε1 (ε1 = Ab / b). Как показывает опыт ε’= – μ · ε,

где μ – безразмерный коэффициент пропорциональности, называемый коэффициентом Пуассона, величина которого зависит только от материала и характеризует его свойства. Знак » – » указывает, что продольная и поперечная деформации всегда противоположны по знаку. Коэффициент Пуассона принято считать положительной величиной, поэтому относительные линейные деформации берутся по абсолютной величине (μ= ε11 /1 ε |).

6. ПОРЯДОК ПРОВЕДЕНИЯ ИСПЫТАНИЙ

1. Перед испытанием студентам необходимо ознакомиться с устройством машины МР-0,5 ( первое занятие ) и правилами поведения в лаборатории при проведении испытаний (вводный инструктаж ).

2. Измеряют штангенциркулем характерные линейные размеры испытуемого образца.

3. Убеждаются в подключении тензодатчиков к тензометрической станции ЦТМ-5.

4. Наблюдают за включением машины, процессом нагружения образца начальной нагрузкой (0 – 100 Η ), которая задается преподавателем.

5. Путем последовательного переключения соответствующих каналов тензометрической станции снимают показания каждого из тензометров. Эти данные заносятся в журнал наблюдений. В отчете по лабораторной работе в разделе «Результаты испытаний» предварительно готовится таблица..

6. Наблюдают за последующими двумя ступенями нагружения (100 – 200 Η каждая по указанию преподавателя ) образца, снимают показания тензодатчиков и заносят их в таблицу.

7. В процессе проведения испытаний внимательно следят за комментариями преподавателя и при завершении испытаний по его указанию приступают к обработке результатов испытания.

7. ОБРАБОТКА РЕЗУЛЬТАТОВ ИСПЫТАНИЯ

В журнале наблюдений ( табл. ) подсчитываются приращения соответствующих отсчетов и определяются их средние значения (АсрР, АсрАь АсрА2, ДсрВь АсрВ2). Затем подсчитываются средние приращения по тензометрам в продольном (АсрА) и поперечном (АсрВ) направлениях.

По найденным АсрА и АсрВ находятся значения относительной линейной деформации соответственно в продольном и поперечном направлениях:

ε = АсрА · с , ε1 = АсрВ · с ,

где с – коэффициент чувствительности тензодатчика, который определяется тарировкой и сообщается преподавателем.

Определяются значение нормального напряжеия, средин для каждой ступени нагружения образца:

σ = АсрР / F, где F – площадь поперечного сечения образца ( F = b · d).

Исходя из закона Гука при растяжении – сжатии (σ= Ε-ε) находится модуль упругости материала образца:

Ε = σ/ε.

По найденным значениям относительных деформаций в продольном и поперечном направлениях определяется величина коэффициента Пуассона:

μ=Η/Ιε|.

Для любого материала величина коэффициента Пуассона должна находиться в пределах от 0 до 0,5.

Найденные значения модуля упругости Ε и коэффициента Пуассона μ следует сравнить с соответствующими величинами, приведенными в справочной литературе и сделать выводы.

Модуль упругости древесины при изгибе вдоль волокон

Упругость древесины – способность к восстановлению исходной формы после прекращения действия нагрузки. Это механическая характеристика, присущая строительным материалам, в том числе, дереву. Характеристика математически выражается модулем упругости – соотношением между нормальными напряжениями и относительными деформациями.

Несмотря на развитие технологий, появления большого разнообразия строительных материалов, дерево было и остается тем материалом, которому отдают предпочтение многие профессиональные строители и заказчики. Дерево как строительный материал используется с незапамятных времен. Сейчас внешний вид, конструкция построек из него значительно изменились. Пролеты деревянных построек могут достигать 120 м! Проектируя подобные строения, обязательно определяют внутренние усилия от действия внешних сил, в том числе с учетом деформированного состояния. В программах для подобных расчетов одной из исходных характеристик является модуль упругости. Рассчитывая этот показатель, определяют, какую нагрузку будет испытывать доска или брус без необратимой деформации, то есть не ломаясь. Чем больше значение характеристики, тем жестче материал.

Параметры, от которых зависит упругость древесины

Модуль упругости древесины — параметр изменяющийся, на его значение влияют:

Влажность. Упругость древесины находится в обратной зависимости от влажности. То есть при высокой влажности дерева, его способность возвращаться к исходной форме будет минимальной.
Прямослойность. Если волокна расположены извилисто, беспорядочно, то способность восстанавливать форму у неё будет заметно ниже, чем у прямослойной.
Плотность. Дерево с низкой плотностью не так упруго, как более плотное.
Возраст дерева. Древесина старого дерева более упруга, чем молодого.
Природные особенности дерева. Хвойные деревья имеют однорядные мелкие сердцевинные лучи, поэтому их древесина более упругая, хотя удельный вес у таких пород не велик.
Возраст самой древесины. Более молодые слои ствола дерева называют заболонью, те, что располагаются ближе к центру, и, соответственно, старее – ядром. Заболонь более упругая, чем ядро.

Нормативная документация

Упругость строительных материалов, древесины в частности, в значительной мере влияет на уровень безопасности для людей зданий и сооружений, а так же сохранности материальных ценностей в них находящихся. Поэтому разрабатываются и утверждаются нормативные документы, определяющие методологию определения параметра упругости а так же расчетов и проектирования конструкций из клееной и цельной древесины.

СНиП II-25-80. Свод правил. Деревянные конструкции. Этот документ определяет методологию расчета и проектирования зданий, сооружений и конструкций из древесины (цельной и клееной). В том числе в СНиП определенно что конструкции из древесины должны:

соответствовать требованиям расчетов по деформациям и по несущей способности;
проектироваться с учетом условий эксплуатации, монтажа, перевозки;
быть долговечными, что обеспечивается конструктивными решениями, защитной обработкой.

ГОСТ 16483.9-73. Межгосударственный стандарт. Древесина. Методы определения модуля упругости при статическом изгибе. В данном ГОСТе:

установлены методы определения модуля упругости при статическом изгибе;
описан процесс определения данного показателя при статическом изгибе кондиционированных и не кондиционированных образцов;
даны образцы протоколов определения модулей упругости.

Модуль упругости дерева

Древесина считается упругой, если она после устранения действия силы изгибающей её, принимает исходную форму. У упругости есть предел. Он достигается, когда при изгибе деревянная детальили изделие сохранит конечную форму.Попросту говоря, предел упругости доски достигается в тот момент, когда она ломается. Свойства упругости и гибкости не идентичны. Гибкость – способность менять форму под действием внешних воздействий. Упругость – возможность возвращать утраченную форму. Дерево с высоким модулем необходимо для того, чтобы делать спортивные снаряды, мебель. Наиболее упруга древесина таких пород как ясень, бук, кария, лиственница.

Вместо термина упругость часто употребляют понятия жесткость или деформативность.

Чтобы описать способность к возвращению исходной формы, используют следующие физические величины:

модуль упругости Е;
коэффициент деформации µ;
модуль сдвига G.

В общем, можно говорить о том, что при приложении силы вдоль древесных волокон, модуль упругости в 20-25 раз выше, чем если та же сила действует поперек волокон. Если сила действует перпендикулярно направлению волокон и направлена радиально, то этот показатель на 20-50 % больше, чем при действии той же силы в тангенциальном направлении.

Ниже рассмотрим более подробно эти физические величины, определяющие способность дерева возвращать исходную форму при снятии деформирующего усилия.

Модуль упругости древесины основных пород

Модуль упругости в физике рассматривается как единое наименование комплекса физических величин, характеризующих способность твердого тела (в нашем случае – дерева) упруго деформироваться, если к нему будет приложена какая-то сила.

Модуль упругости древесины (Е) – соотношение между нормальными напряжениями и относительными деформациями. Он измеряется в Мпа либо в кГс/см² (1Мпа=10.197 кГс/см²) Выделяют несколько видов:

вдоль волокон Е_а.
поперек волокон (тангенциальный) Е_t.
поперек волокон (радиальный) Е_r.
модуль упругости при изгибе Е_изг.

Таблица. Сведения по наиболее часто используемым породам.*

Коэффициенты поперечной деформации основных пород дерева

Во время приложения нагрузки, кроме продольной деформации вдоль волокон так же появляется поперечная при изгибе.

Коэффициенты этого типа деформации приведены в таблице:

Модуль сдвига основных пород древесины

Модуль сдвига – коэффициент пропорциональности между касательными напряжениями и угловыми деформациями древесины.

Данные по модулю сдвига для основных пород приведены ниже:

Пластичность древесины

Дерево способно под давлением менять без разрушения свою форму, сохранять её после того, как давление будет снято. Такое свойство называется пластичностью. Пластичность зависит от тех же критериев, что упругость, только в обратном направлении. Например, чем выше влажность древесины, тем она более пластична, при этом менее упруга.

Пластичность дерева повышают с помощью специальной обработки. Пропаривая или проваривая его в воде, получаем более пластичный материал, которую затем используют для изготовления мебели, полозьев саней. Наивысшая пластичность у бука, вяза, ясеня, дуба. Это свойство обусловлено строением проводящей системы данных пород. У бука, например, много крупных сердцевинных лучей, изгибающих волокна древесины. Сосуды, расположенные группами в годовых слоях вяза, дуба, ясеня, сильно сдавлены более плотной поздней древесиной, поэтому пластичность этих пород высока.

Коэффициент Пуассона

При приложении нагрузки к стержню, кроме продольной деформации ε, появляется поперечная деформация ε1. Коэффициентом поперечной деформации, или коэффициентом Пуассона μ, называется отношение ε1 к ε.

Коэффициент Пуассона древесины определяют путем сжатия прямоугольных призматических образцов сечением 40х40 мм, высотой 150 мм. Чтобы измерить деформацию на образце устанавливается шесть тензометров с базой 20 мм, передаточным числом около 1000. Из этих тензометров два регистрируют продольную деформацию (деформация в направлении действия силы сжатия), остальные четыре измеряют поперечные деформации в двух взаимно перпендикулярных направлениях. Каждый из образцов шестикратно нагружают до 400 и 1600 кг при сжатии вдоль волокон, до 40 и 160 кг при сжатии поперек волокон.

Для древесины сосны, ели коэффициент Пуассона при усилии, направленном вдоль волокон v₀=0,5.

Модуль упругости фанеры

Фанера – строительный материал, производимый путем склеивания нескольких слоев деревянного шпона. Она очень популяренна, и неспроста. Кроме эстетической ценности, фанера обладает рядом значений параметров, выделяющих её в ряду материалов для строительства. Проходя обработку, фанера приобретает прочность, упругость, влагостойкость.

На характеристики фанеры влияют многие факторы:

порода дерева, используемого для шпона;
исходное состояние сырья;
влажность самой фанеры;
тип и состав клея, которым соединяются слои шпона;
технология предварительной обработки.

Для фанеры так же рассчитывается модуль упругости и все соответствующие коэффициенты.

Важно то, что модуль упругости фанеры и другие показатели выше, чем у древесины, из которой она была изготовлена.

Модуль упругости древесины рассчитывают обязательно перед постройкой кровельных, стропильных систем. Знание внутренних усилий, появляющихся в строительных материалах, важно для безопасности, долговечности постройки. Способность возвращать утраченную форму значимо при выборе материала рукояток ударных инструментов, оружейных лож.

Модуль упругости

— обзор

Измерения нанотвердости

Существуют основные технологические и методологические различия между испытанием объемной твердости и наноиндентированием из-за крайней степени миниатюризации и дополнительных свойств материалов, например Модуль Юнга, измеренный на этом наноуровне. Тестеры наноиндентирования предназначены для измерения твердости тонких поверхностных покрытий, например, полученных ионной имплантацией [78,79], физическим осаждением из паровой фазы [80], термообработкой [e.грамм. 81], полимерные покрытия [например, 82] и тонкие поверхностные пленки [например, 70,83-89]. Испытания на наноиндентирование позволяют определять широкий спектр механических свойств поверхностных пленок без удаления пленки с подложки. Из-за чрезвычайно малого размера отпечатка вмятины эти измерения позволяют исследовать поверхность в различных точках и наносить на карту ее механические свойства в пространстве.

В отличие от обычных испытаний на микротвердость, наноинденторы не только позволяют измерять твердость очень тонких пленок, но также могут использоваться для определения модуля упругости.При обычных испытаниях на микротвердость невозможно измерить модуль упругости, в то время как твердость очень тонких пленок в лучшем случае измерить трудно. Причина этой трудности заключается в том, что для того, чтобы убедиться, что подложка не влияет на измерения, размер отпечатка должен быть небольшим по сравнению с толщиной пленки. Консервативное правило состоит в том, что глубина отпечатка должна быть менее 10% толщины пленки [90,91]. Однако также сообщалось, что для некоторых материалов микротвердость не изменилась, когда эта глубина составляла до 25% толщины пленки [91-94].

При наноиндентировании минимальная глубина, на которой могут быть получены значения нанотвердости, может быть уменьшена до 100 [нм] [95]. Однако кажется, что ниже 25 [нм] упругая деформация как индентора, так и материала вдавления может помешать точной оценке твердости [96]. При масштабе вдавливания, сравнимом с размером атомов, оценка глубины вдавливания должна учитывать расстояние туннелирования электронов, а также упругую и пластическую деформацию образца и индентора [96].Чрезвычайно малые смещения при наноиндентировании серьезно ограничивают методы, которые можно использовать для точного определения области оттиска. Например, для поверхностной пленки толщиной 1 [ мкм м] глубина вдавливания составляет около 100 [нм], а площадь отпечатка слишком мала, чтобы ее можно было точно определить с помощью оптических микроскопов. При наноиндентировании эту трудность преодолевают путем точного измерения характеристик смещения нагрузки.

Основной принцип работы наноинденторов заключается в способности создавать и измерять очень малые нагрузки и смещения.Механические свойства материала определяются простым измерением нагрузки, смещения и времени. Нагрузки обычно прикладываются через узел катушки и магнита или с помощью пьезоэлектрических приводов. В первом случае нагрузка определяется непосредственно по току, протекающему в катушке, а во втором используются специально разработанные датчики нагрузки. Смещение почти всегда измеряется с помощью емкостных датчиков. При вдавливании индентора в пленку возникают как упругие, так и пластические деформации. Во время пластической деформации отпечаток постоянной твердости, соответствующий форме индентора, образуется на некоторой глубине контакта « h _c », в то время как упругая деформация создает дополнительную составляющую « h _s » смещения.Это схематично показано на рис. 6.14.

Рисунок 6.14. Схематическое изображение процесса наноиндентирования на примере типичных данных «нагрузка-смещение» при вдавливании, где « h _c » — это глубина проникновения (глубина контакта), а « h _s » — упругое смещение.

(адаптировано из [91])

Основными проблемами, связанными с техникой наноиндентирования, являются: чрезвычайная восприимчивость к вибрации, сложность управления движением компонентов с очень малыми допусками и более высокая вероятность сильных адгезионных сил, препятствующих втягиванию индентор после разгрузки.Для получения надежных данных без помех от вибрации и т. Д. Наноинденторы устанавливаются на систему без вибрации, а движение индентора контролируется пьезоэлектрическими преобразователями, способными перемещать индентор со скоростью от 1 до 10 [нм / с] с минимальной обнаруживаемой силой 1 [ мкм Н] [87,97]. Однако также было достигнуто разрешение по нагрузке и смещению лучше, чем 0,01 [ мкм, Н] и 0,1 [нм] [91]. Радиусы алмазного наконечника обычно находятся в диапазоне от 0,1 от до 1 [ мкм м] и апикальный угол 80 ° обычно используются для индентора [87,91].Значения этих радиусов необходимо учитывать, чтобы получить точные результаты; это особенно верно для небольших вдавливаний [91].

Еще одним серьезным недостатком этого метода является эффект «скопления» или «втягивания» материала вокруг отпечатка на измеренную глубину вдавливания [77]. Этот эффект можно исправить, и с помощью этих приборов можно получить воспроизводимые измерения нанотвердости [например, 70,77,91,92,98,99]. Кроме того, этот метод также позволяет определить модуль Юнга, который может быть непосредственно измерен по наклону кривой напряжения-деформации в упругом режиме, полученном во время цикла разгрузки [e.грамм. 77,91,99,100].

Наиболее распространенный метод измерения твердости и модуля упругости тонкой пленки заключается в создании небольших углублений в пленке, обычно с помощью индентора Берковича, при непрерывной регистрации нагрузки на вдавливание « P » и смещения « h», в течение один полный цикл погрузки и разгрузки [91,98,99,101]. Индентор Берковича имеет идеальную трехстороннюю пирамидальную геометрию с тем же соотношением глубины и площади, что и индентор Виккерса [102,103].Эта особая форма индентора, то есть трехсторонняя, намного проще в изготовлении, чем четырехсторонний индентор, такой как индентор Виккерса. Довольно сложно отшлифовать четырехсторонний индентор Виккерса до точки. Недостатком остроконечных инденторов является то, что они создают отпечатки почти постоянной пластической деформации, и возникают трудности с оценкой модуля упругости по непрерывно изменяющейся кривой разгрузки. Эти проблемы устраняются с помощью сферических инденторов, поскольку переход от упругого к пластическому поведению может быть легко определен и, следовательно, найден предел текучести [104].Однако заостренные инденторы очень полезны при исследовании тонких пленок, требующих неглубокого вдавливания, и, следовательно, игла Берковича чаще всего используется для оценки наномеханических свойств материалов. Также были разработаны экспериментальные процедуры для компенсации формы острия [71].

Во время теста наноиндентирования измеряемыми величинами являются пиковая нагрузка ‘ P _max‘, смещение при пиковой нагрузке ‘ h _max‘, начальная жесткость контакта разгрузки S = dP / dh, и.е. наклон начального участка кривой разгрузки и смещение, найденное путем линейной экстраполяции начального участка кривой разгрузки на нулевую нагрузку « ч ₀». Типичные данные «нагрузка-смещение» показаны на рис. 6.14 [91].

Когда индентор извлекается, данные нагрузки-смещения записываются, а данные упругой разгрузки используются для соотнесения экспериментально измеренных величин с предполагаемой площадью контакта и эффективным модулем упругости [69,91,105,106].Например, приведенный модуль упругости пленки « E _r » определяется из значения разгрузочной контактной жесткости « S », то есть:

(6.1) S = dPdh = 2πErA

где:

S	— контактная жесткость [Н / м];
P	— нагрузка [Н];
ч	— водоизмещение [м];
A	— площадь контакта [м ²];
E _r	— приведенный модуль упругости [Па], т.е.e .:

1Er = 121 − υf2Ef + 1 − υi2Ei

, где:

E _f	— модуль упругости пленки [Па];
υ _f	— коэффициент Пуассона пленки;
E _i	— модуль упругости индентора [Па];
υ _i	— коэффициент Пуассона индентора, т.е.грамм. для алмаза E _i = 1141 [ГПа] и υ _i = 0,07 [107].

Твердость пленки определяется по ее нормальному определению, т.е.

(6.2) H = PmaxA

Площадь контакта при пиковой нагрузке оценивается по глубине контакта ‘ h _c ‘, то есть A = f (h _c) и зависит от формы индентора. Глубина контакта рассчитывается по следующей формуле [99]:

(6.3) hc = h0 + 0.25hmax ‐ h0 = hmax ‐ 0,75Pmax / S

где:

h ₀	находится путем линейной экстраполяции начальной доли кривой разгрузки [м], показанной на рисунке 6.14, до нуля. нагрузка [91];
h _max	— смещение при пиковой нагрузке ‘ P _max ’ [м];
P _max	— максимальная нагрузка [Н].

Более совершенные инструменты позволяют непрерывно измерять контактную жесткость « S » во время теста наноиндентирования [91,108,109].При использовании в сочетании с уравнением (6.1) полученные данные предоставляют информацию об изменениях модуля упругости или площади контакта. Метод непрерывного измерения жесткости предлагает способ непрерывного измерения контактных площадей контактов нанометрового размера во время теста наноиндентирования [91, 110].

На крошечный отпечаток вмятины, создаваемый наноиндентором, легко повлиять шероховатость поверхности, поэтому необходимо соблюдать осторожность, чтобы найти отпечаток вдавливания на плоской части поверхности. Испытания на нанотвердость часто проводят с помощью микроскопа, чтобы облегчить точный контроль индентора и обеспечить одновременное наблюдение микроскопических особенностей поверхности вместе с вариациями нанотвердости и механических свойств пленки.Оптический микроскоп не обеспечивает достаточного разрешения для вмятин размером примерно 0,1 [ мкм м], поэтому для получения изображения области вдавливания обычно используется АСМ (атомно-силовой микроскоп). Для этой цели также можно использовать другие специализированные микроскопы с большим увеличением, описанные в главе 8. Аппарат для испытания на нанотвердость (наноиндентор) схематично показан на рисунке 6.15.

Рисунок 6.15. Схематическое изображение наноиндентора.

Процедура вдавливания может незначительно отличаться в зависимости от типа используемого индентора, но основные шаги одинаковы для всех инденторов. Сначала опускают индентор с постоянной нагрузкой на подвесные пружины, пока не установится контакт с образцом. После того, как исследуемый участок был определен, нагрузка на индентор постепенно увеличивается, и поддерживается либо постоянная нагрузка, либо постоянная скорость смещения. Нагрузка и глубина вдавливания контролируются во время циклов загрузки и разгрузки.Сила сопротивления подвешиваемых пружин и смещение, связанное с измеренной податливостью прибора, компенсируются [77].

В одной из ранних разработок смещение определялось по измерениям интенсивности света, отраженного от зеркала на тарелке для образцов, как схематично показано на рис. 6.16 [87].

Рисунок 6.16. Схематическое изображение прибора для измерения нанотвердости (наноиндентора).

(адаптировано из [87])

Свет попадал на зеркало через оптоволокно, а при его возвращении измерялся фотодетектором.После установления контакта между образцом и индентором расстояние между оптоволокном и зеркалом регулировалось микрометрическим винтом [87]. Затем фиброоптическое положение фиксировалось винтом, и нагрузка прикладывалась к индентору через пьезоэлектрический привод. Во время фазы нагрузки напряжение на пьезоэлектрическом приводе увеличивалось, заставляя индентор проникать в образец, а во время разгрузки это напряжение снижалось. Сообщается, что для этого прибора разрешение смещения составляет 4 [нм] [87].

Технологические разработки в этой области происходят быстро, и время от времени появляются новые улучшенные конструкции наноинденторов. Несмотря на то, что принципы работы этих инструментов остаются неизменными, разработки в области электроники позволяют повысить точность управления и улучшить разрешение по перемещению и нагрузке.

Используемые датчики перемещения различаются в зависимости от конструкции прибора и производителя. К датчикам перемещения относятся: поляризационные интерферометры [77,111,112] (глубина вдавливания измеряется с разрешением 0.2 [нм] [77]), индуктивные преобразователи смещения [например, 113] (разрешение 5 [нм]) или емкостные преобразователи [например, 70,114-116]. Сообщалось, что для емкостных преобразователей разрешение смещения достигает 0,015 [нм] [76,116] и даже выше [117].

Также доступны наноинденторы, которые позволяют проводить измерения трения, износа, сопротивления наноцарапинам, вязкости разрушения, модуля упругости и т. Д. [Например, 77,117].

ГЛАВА II — Свойства США

ВЗАИМОСВЯЗЬ МЕЖДУ УЛЬТРАЗВУКОВОЙ СКОРОСТЬЮ И УПРУГОЙ МОДУЛЯМИ

МОЛОДЕЖНЫЙ МОДУЛЬ

В силу симметрии соотношение скоростей ультразвука к касательному модулю найден для изотропных однородных материалов путем упрощения 36 возможных упругих постоянных, полученных для анизотропных материалов.Формулы для изотропных однородных материалы показаны ниже. Продольная скорость определяется выражением

когда длина волны распространяющегося ультразвука больше, чем в пять раз больше диаметра стержня или стержня. Эффективная жесткость модуль Y L такого ограниченного ¹ сечения будет выше, чем модуль Юнга Y o для свободного стержня. где формула для Y o учитывает сдерживающий силы для C L: , с пределом b = 1, когда п = 0.5. Модуль жесткости — это комплексное число с мнимой частью. соответствующий коэффициенту потерь. Когда коэффициент потерь мал, его обычно игнорируют, и модуль жесткости записывается как номер скейлера.

Уравнение (4)

где K = модуль объемной упругости, G = модуль сдвига и

Уравнение (5)

¹ Ультразвук, распространяющийся по длине стержня, будет заставляют поперечные размеры изменяться динамически в соответствии с к положению волны давления внутри бара.Материал с бесконечным поперечным размером не ограничивает поперечный края продольной волны напряжений.

где n = коэффициент Пуассона. Когда n равно 1/2, C L не определено.

Однако модуль Юнга эквивалентен

E = 3K (1-2n)

Уравнение (6)

Теперь, подставив уравнение. (6) в уравнение. (5) условие может быть установлено, что справедливо для идеальной простой жидкости, т. е. жидкость без вязкости.Сначала позвольте

3 (1 — 2n) (1 — n) / [(1 + n) (1 — 2n)] = 1 Уравнение (7)

Решение уравнения. (7) дает

3 (1-2n) = 1 + n

2 = 4n
n = 1/2

Следовательно, поскольку n = 1/2, материал соответствует требованиям к жидкости, и замена скорости может быть завершена для идеального жидкое состояние

CF = (K /) ¹ / ² Уравнение (8)

который описывает скорость звука во многих жидкостях и газы.Скорость сдвига находится в материалах, которые выдерживают сдвиг. силы, такие как большинство твердых тел и многие вязкие жидкости. Сдвиг скорость звука определяется выражением

Cs = (G /) ¹ / ² Уравнение (9)

Теперь можно ошибочно комбинировать уравнение. (8) и (9) и заменить результат обратно в формулу. (4), что тогда дало бы

Уравнение (10)

Однако более раннее требование наложено на справедливость уравнения. (8) будет нарушено, если требование справедливости для уравнения.(9) остается существующий, то есть материал не может быть идеальной жидкостью и поддерживать усилия сдвига. Читателю остается предположить, Уравнение (10) может преобладать сразу после детонации высокого взрывчатого вещества в твердый материал, в результате чего этот материал становится совершенно жидкий на мгновение. Однако маловероятно, что материал мог выдержать силы сдвига в этот момент во время. Есть еще одна продольная скорость звука, которая встречается в материалах, способных выдерживать силу сдвига.Эта продольная скорость называется продольной, стержневой или скорость тонкого стержня. Стержни, стержни или проволока, которые подвергаются волна сжатия с длиной волны более пяти раз размер поперечного сечения стержня позволяет волне распространяться при пониженной скорости по сравнению с объемным образцом продольной волна. Эта скорость, C o, связана с модулем Юнга формулой. (11).

Co = (E /) ¹ / ² Уравнение (11)

и рассчитывается либо из C, L и C s или измерено специально разработанные образцы и преобразователи.Решая уравнение. (9) для модуль сдвига,

G = C²s уравнение (12)

и подставив это уравнение в уравнение. (4) модуль объемной упругости рассчитывается:

[K + (4/3) C²s] / Уравнение (13)

а также

K = [C²L — (4/3) C²s]

Отношение модуля Юнга к объему и модулю сдвига является

E = 9 кг / (G + 3 K) уравнение (14)

Если уравнение(13) заменяется K, и уравнение. (12) заменяется для G в уравнении. (14) модуль Юнга принимает вид

E = C²s (3 C²L — 4 C²s) / (C²L — C²s) Уравнение (15)

и подставив уравнение. (15) в уравнение. (11) скорость расширения становится

Зависимость скорости растяжения от скорости сдвига очевиден и согласуется с концепцией, что материалы которые не могут поддерживать силы сдвига, например жидкости с нулевым вязкость, не может распространяться со скоростью растяжения.Экстенсиональный скорость может быть визуализирована как волна давления сжатия, которая проявляет эффект маниска на стенках образца при распространении волны по оси стержня.

КОЭФФИЦИЕНТ ПУАССОНА

То, что все упругие постоянные взаимосвязаны, является аксиомой. Следовательно, как только изотропные модули установлены, пуассоновский Соотношение может быть рассчитано. Коэффициент Пуассона также является функцией соотношение продольной и поперечной скоростей,

v = [1-2 (Cs / CL) ²] / [2-2 (Cs / CL) ²] Ур.(17)

а набор кривых приведен в Справочнике по неразрушающему контролю. ²¹, обозначающее соотношение любых двух из четырех скоростей ультразвука как функция коэффициента Пуассона.

ХРАМНЫЕ КОНСТАНТЫ

Имеются две упругие постоянные Ламе, рассчитанные на основе скоростей ультразвука. Одна из постоянных Ламе задана как модуль сдвига. Другой иногда называют модулем Хромости. Хромой модуль ¹ ° является определяющим фактором как для продольного, так и для продольного скорости сдвига:

C²L = (+ 2 G) / Ур.(18)

и, изменив формулу, модуль Ламе равен

= (C²L — 2 C²s) Уравнение (19)

Модуль Хромости, возможно, заинтересует тех, кто работает с пластмассовые материалы. По мере увеличения коэффициента Пуассона модуль Хромости численно приблизится к модулю объемной упругости. Модуль сдвига исчезнет, когда вязкость жидкости приблизится к нулю. Это можно увидеть из признания уравнения для объемный модуль: К = + [2 µ / 3], где сдвиг приближается к нулю для жидкостей и одновременно пуассоновский отношение приближается к 0.5. Скорость сжатия жидкостей равна пропорциональна модулю объемной упругости, как показано в уравнении (8)

ТЕМПЕРАТУРА ДЕБИ

Механизмы тепловых потерь (температурная зависимость) материалов. наиболее подходящим образом описывается в терминах температуры Дебая, . Температуру Дебая можно рассчитать с помощью бесконечная среда, сдвиговые и продольные скорости. Значение интегральная скорость 5 рассчитана для изотропного материала а затем введен в уравнение, содержащее постоянную Планка, Больцмана константа, число Авогадро, средний атомный вес и плотность материала.Средняя интегральная скорость C M определяется выражением

CM = [3 (Cs CL) ³ / (2 C³L + C³s)] ¹ / ³ Уравнение (20)

а температура Дебая

(Градусы Кельвина)

Где:
ч / к = постоянная Планка / постоянная Больцмана = 47,99216 ° K с [1 / 10¹²],
P = Число атомов в молекуле,
N = число Авогадро (602,2167 x 10 ²¹ x [1 / кмоль])
M = Средний атомный вес.

АДИАБАТИЧЕСКИЙ МОДУЛЬ В ОТНОШЕНИИ ИЗОТЕРМИЧЕСКОЙ МОЛОДЕЖИ

Ультразвуковые измерения скорости при испытании материалов не позволяют время, достаточное для термодиффузии. Следовательно, модуль Юнга, рассчитанный по скоростям ультразвука, является адиабатическим модуль упругости, который немного выше изотермического модуля. Связь между адиабатическим и изотермическим коэффициентами Юнга. модуль определяется по формуле:

EA / Ei = 1 + a²T (EA / CP) Ур.(22)

Ei / EA / [1 + {a²T (EA / CP)}]

EA = Ei CP / (CP — Ei a² T)

Где:

a = коэффициент теплового расширения, м / м / ° K
Cp = удельная теплоемкость при постоянном напряжении, Дж / кг ° K
T = абсолютная температура
r = плотность
EA = адиабатический модуль Юнга
Ei = изотермический модуль Юнга

Вы можете продолжить с Главы III и начать с:
ЧТО ЕЩЕ? ПОСМОТРЕТЬ НЕКОТОРЫЕ ДРУГИЕ ТЕХНИКИ

Рольф Дидерихс 22.Ноябрь 1995 г., [email protected]

/ DB: Артикул / AU: Brown_A_E / CN: US / CT: UT / ED: 1996-03

КОМПОЗИЦИОННЫЕ МАТЕРИАЛЫ И КОНСТРУКЦИИ

ГЛАВА — 4

СВОЙСТВА КОМПОЗИТОВ — МИКРОМЕХАНИКА

4.1 ВВЕДЕНИЕ

4.2 ОДНОНАПРАВЛЕННЫЕ КОМПОЗИТЫ

4.2.1 Упругие свойства (Инженерные константы)

4.2.2 Прочностные характеристики Однонаправленные композиты

4.2.3 Гигротермические свойства

4.3 КОМПОЗИТЫ ЧАСТИЦ И КОРОТКОГО ВОЛОКНА

4.3.1 Композиты из твердых частиц

4.3.2 Композиты с короткими волокнами

4.4 БИБЛИОГРАФИЯ

4,5 УПРАЖНЕНИЯ

4,1 ВВЕДЕНИЕ

Механические и гигротермические свойства композитов: первостепенное значение при проектировании и анализе композитных конструкций.В механические свойства — это прежде всего модули и прочностные характеристики. Гигротермические свойства: коэффициент расширения за счет влаги (β), коэффициент диффузии тумана (d), коэффициент теплового расширения (α), тепловое проводимость (k) и теплоемкость (c). Микромеханический анализ касается теоретическое предсказание этих свойств составляющих волокон и матрицы, а также ряд других параметров, таких как форма, размер и распределение волокон, несовпадение волокон, свойства поверхности раздела волокно-матрица, пустотное содержимое, разрыв волокна, растрескивание матрицы и т. д.Исследования в микромеханика использует микромодели, поскольку диаметры волокон обычно варьируются в зависимости от микроскопический масштаб от 5 до 140 м. Микромодели должны имитировать микроструктура реалистичного композита, но это обычно делает модели очень сложный. Проблемы, связанные с такими сложными моделями, обычно решаются использование передовых аналитических методов, а также численного анализа техники (методы конечных элементов и конечных разностей). Даже в случае сложная модель, упрощенная идеализация с достаточно хорошим приближением желателен настоящий композит, иначе он ни к чему не приведет.Нет в этой главе представлена полная теоретическая основа различных микромодели, используемые для аналитического прогнозирования всех свойств композита. В изложение ограничено лишь несколькими более простыми случаями, чтобы познакомить читателя фона развития в этой области. Дополнительная микромеханика отношения для однонаправленных композитов, которые могут найти применение в дизайне приложения, перечислены в таблице 4.1. Типичные свойства некоторых распространенных волокна и матрицы перечислены в таблицах 4.2 и 4.3 соответственно. В составные свойства нескольких составных систем, полученных с использованием некоторых из отношения, представленные в этой главе, перечислены в Таблице 4.4. Таблицы с 4.1 по 4.4 включены в конце этой главы.

4.2 ОДНОНАПРАВЛЕННЫЕ КОМПОЗИТЫ

4.2.1 Упругие свойства (инженерные константы)

Соотношение напряжение-деформация обеспечивает базовый интерфейс между материал и структура.Для одномерного изотропного упругого тела Закон Гука σ = E определяет поведение напряжения и деформации. Здесь E — материал постоянная и обычно обозначается как постоянная упругости (инженерная постоянная) или Модуль для младших. Помимо E, другая обычная инженерная константа для двумерным или трехмерным изотропным телом является коэффициент Пуассона ν. Модуль сдвига G не является независимым, но связан с E и ν как

G = E / 2 (1+ ν ).Композиционный материал существенно неоднороден по природы, поэтому технические константы, определенные выше, для изотропного материал не действителен. Здесь мы рассматриваем трехмерный блок однонаправленный композит (рис. 4.1), в котором волокна выровнены по оси x ‘₁ ось. Упругое поведение для такого трехмерного тела

ортотропна, а инженерные константы равны « (Три модуля Юнга по трем основным осям материала x ‘₁, x ‘₂, x’ ₃ ), ν ‘₁₂, ν ‘ ₁₃, ν ‘₂₃, ν ‘ ₂₁, ν ‘₃₁, ν ‘ ₃₂, (шесть коэффициентов Пуассона) и G ‘₁₂, G’ ₁₃, G ‘₂₃, (три модуля сдвига).Из них первые девять инженерных констант, т. Е. Три Модули Юнга и шесть коэффициентов Пуассона не являются независимыми. Благодаря симметрии соответствия (см. уравнение 6.18) они связаны согласно

(4,1)

Обратите внимание, что

(4,2)

Здесь ν ‘₁₂ и ν ‘ ₁₃ обычно называются основными коэффициентами Пуассона.

«Механика материаловедения» _{обеспечивает удобный
средство для определения упругих свойств композита. Предполагается, что
композит без пустот, соединение волокна с матрицей идеальное, волокна
одинакового размера и формы и равномерно распределены, а поведение материала
линейный и эластичный.}

Рассмотрим двумерную однонаправленную пластину (рис. 4.2), в который мы определяем как небольшой элемент объема, который представляет не только микроуровень структурные детали, а также общее поведение композита.Просто элемент представительного объема состоит из изотропного волокна, заключенного в изотропная матрица (рис. 4.2б). Этот элемент объема дополнительно упрощен, как показано на рисунке. на рис. 4.2c, на котором предполагается, что волокно имеет прямоугольное поперечное сечение той же толщины, что и матрица. Соотношение ширины выбрано одинаковым как объемная доля волокна в самом композите. Цель состоит в том, чтобы получить свойства композита (E ‘₁₁, E’ ₂₂, ν ‘₁₂, G ₁₂) по модулям, коэффициентам Пуассона и объемным долям волокно и матрица.

Модуль продольной упругости, E ‘₁₁

Микромодель (рис. 4.2c) подвергается одноосное растягивающее напряжение σ` ₁₁, как показано на рис. 4.3. Предполагается, что плоские сечения остаются плоскими после деформации. Следовательно,

‘₁₁ =’ _11f = ‘_{11 м} = ΔL / L

и σ ‘_11f = E’ _11f ‘₁₁, σ’ _11m = E ‘_11m‘ ₁₁, σ ‘₁₁ = E’ ₁₁ ‘₁₁ (4.3)

Теперь σ ‘₁₁ Вт = σ ‘₁₁ _f Вт _f + Σ ‘₁₁ _м Вт _м (4,4)

Подставляя уравнение. (4.3) в уравнение. (4.4) и переставляя, получаем

E ‘₁₁ = E’ _11f W _f / W + E ‘_{11 м} W _м / Вт (4.5)

Учитывая, что объемные доли волокна и матрицы равны

V _f = W _f / W и V _м = W _м / W соответственно, уравнение. 4.5 снижается до

E ‘₁₁ = E’ _11f V _f + E ‘_11м V _м (4.6)

Уравнение 4.6 определяет составное свойство как «взвешенную» сумму составляющих свойства и часто называют «правилом смешения».

Поперечный модуль, E ‘₂₂

Растягивающее напряжение σ ‘₂₂ приложено вдоль направление x ‘₂ (рис. 4.4), и предполагается, что одно и то же действует как на волокно и матрица. Напряжение на волокне и матрице

‘_{22 f} = σ’ ₂₂ / E ‘_22f и ‘_{22 м} = σ’ ₂₂ / E ‘_{22 м} (4.7)

также ‘₂₂ = ΔW / W

и ΔW _{= ‘_22f (V _f W) +
‘_{22 м} (В _м Вт)}

Итак, ‘₂₂ = ΔW / W = ‘_{22 f} V _f + ‘_{22 м} В _м

или,

или же, (4.8)

Главный коэффициент Пуассона, ν ‘₁₂

Микромодель подчеркнута, как и в случае определения E` ₁₁ (рис. 4.3). Поперечное сжатие обозначается как ΔW и вносится как волокном, так и матрицей. Таким образом,

ΔW = (ΔW) _f + (ΔW) _м

или, ΔW = W V _f ν ‘_12f‘ ₁₁ + W V _m ν ‘_12m‘ ₁₁ (4.9)

Сейчас , (4.10)

и ‘₂₂ = — ΔW / W (4.11)

Комбинируя уравнения. С 4.9 по 4.11 получается

или, ν ‘₁₂ = V _f ν ‘ ₁₂ _f + V _м ν ‘₁₂ _м (4.12)

Модуль сдвига в плоскости, G ‘₁₂

На микромодель теперь действует напряжение сдвига σ ‘₁₂ как показано на рис. 4.5, и предполагается, что и волокно, и матрица испытывают такое же напряжение сдвига.

‘_12f = σ’ ₁₂ / G ‘_12f и ‘_{12 м} = σ’ ₁₂ / G ‘_{12 м} (4.13)

Теперь Δ = ‘₁₂ W = W V _f ‘_12f + W V _м‘ _{12 м}

или, ‘₁₂ = V _f ‘_12f + V _м‘ _{12 м} (4.14)

также, (4.15)

Подставляя уравнения. 4.13 и 4.15 в формулу. 4.14 и исключив σ ‘₁₂ с двух сторон, получаем

или же, (4,16)

Отметим, что для изотропного волокна

E ‘_11f = E’ _22f = E _f, ν ‘_12f = ν _f

и (4.17)

а для изотропной матрицы

E ‘_{11 м} = E’ _{22 м} = E _м, ν ‘_{12 м} = ν _м

и (4,18)

Уравнения 4.6 и 4.12 дают достаточно точную оценку продольного модуль E ₁₁ и ν ₁₂ соответственно.Однако поперечный модуль упругости E ₂₂ и модуль сдвига G ₁₂, оценивается по формулам. 4.8 и 4.16, не так точны в основном по причине что напряжения как в волокне, так и в матрице считаются одинаковыми. Элемент объема, рассмотренный в вышеупомянутом подходе механики материалов, действительно неадекватно представляют микроструктуру композита. Передовой аналитические методы используют лучшие микромодели наряду с реалистичным материалом поведение и граничные условия.Аналитический метод с использованием самосогласованного полевая модель обеспечивает лучшую оценку свойств композита по сравнению с к механике материалов подход. Модель предполагает, что композит концентрический цилиндр (рис. 4.6), в котором расположена трансверсально изотропная матрица. Хотя предполагаемая микромодель проста, она позволяет сформулировать задача, основанная на теории упругости, так что можно достичь вариации напряжений и деформаций в реалистичной манере, а также соотношения для Затем выводятся эффективные составные свойства.Эти свойства выражаются следующим образом:

(4,19)

(4.20)

(4,21)

(4,22)

(4,23)

где K ‘- модуль объемной упругости при плоской деформации.

(4.24)

в котором K ‘, G’ ₂₃, ν ‘₁₂ ² и E’ ₁₁ являются определены в уравнениях. С 4.19 по 4.23.

(4,25)

с E ‘₁₁, E’ ₂₂, K ‘и ν’ ₁₂, определенными в выше отношения.

Обратите внимание, что для изотропных волокон и матриц

;

и (4.26)

4.2.2 Прочностные характеристики однонаправленных композитов

Прочность материала определяется как уровень напряжения при котором происходит сбой. Прочность — это материальная константа. Большинство из изотропные конструкционные материалы обладают только одной константой — одноосным предел прочности. Прочность на сдвиг обычно связана с растяжением. сила. Хрупкий изотропный материал может иметь разные значения прочности в растяжение и сжатие и может быть назван двухпостоянным материалом.В Напротив, композит — это многопостоянный материал. Ссылаясь на рис. 4.1, он Можно сказать, что однонаправленный композит может обладать тремя нормальными значениями прочности X ‘₁₁, X’ ₂₂, X ‘₃₃ и три значения прочности на сдвиг X’ ₁₂, X ‘₁₃, X’ ₂₃. Нормальная сила может иметь разные значения при растяжении и сжатии, поскольку сжимающая сила обычно вызывает преждевременный выход из строя из-за коробления волокон с очень высоким коэффициент стройности.Итак, всего существует девять независимых силовых констант. X ‘₁₁ ^т, X’ ₂₂ ^т, X ‘₃₃ ^т, X ‘₁₁ ^c, X’ ₂₂ ^c, X ‘₃₃ ^c, X ‘₁₂, X’ _13, X ‘₂₃.

Попытки с помощью микромеханического анализа определить эти константы прочности, с небольшим успехом. Это в первую очередь связано с причиной что микромодели, используемые в этих анализах, в высшей степени нереалистичны.По факту, смоделировать реалистичную композицию крайне сложно, так как начальный микроструктура постоянно изменяется с увеличением приложенного напряжения и распространение разрушения в виде разрушения волокна, растрескивания матрицы, волокна-матрицы дебонд и т. д. в нескольких точках, случайно расположенных внутри композита. В хрупкость волокна и матрицы усугубляет ситуацию. Это проиллюстрировано на рис. 4.7. Обратите внимание, что l _c — это неэффективная длина. В Наличие единственного поверхностного дефекта в хрупком волокне приводит к его растрескиванию. трещина в точке A (рис.4.7а). Это вызывает высокие напряжения сдвига и приводит к тому, что волокнистая матрица дебонд вдоль направления волокна (рис. 4.7b). Также при разрыве волокна перераспределение напряжений в окрестности приводит к разрушению при растяжении соседнее волокно из-за концентрации напряжений. Этот процесс приводит к распространение трещины в направлении, поперечном распространению трещина в направлении, поперечном волокнам (рис. 4.7в). Фактически, финальный разрушение композита происходит из-за совокупного ущерба, вызванного несколько сбоев на микро- и макроуровне.

Предел прочности при продольном растяжении, X ‘₁₁ ^т

Простое отношение может быть рассчитано для прочности композита на продольное растяжение X ‘₁₁ ^т с использованием «правила смесей» и выражается как

X ‘₁₁ ^t = X’ _11f V _f + X ‘_{11 м} В _м (4.27)

Здесь предполагается, что при определенном уровне напряжения все волокна ломаются на в то же время и отказ происходит в одной плоскости. Эта идеализация в высшей степени нереалистично, как уже было сказано в предыдущем абзаце.

Теперь давайте проверим справедливость уравнения. 4,27 для двух составных системы: (i) композит углерода / эпоксидной смолы, в котором деформация разрушения волокна меньше чем деформация разрушения матрицы, т. е. ‘_11fu < '_11mu (рис.4.8a) и (ii) углерод / углеродный композит когда ‘_11fu> ‘_11mu (рис. 4.8b). В этих случаях как волокна, так и матрицы хрупкие. В случае углеродно-эпоксидного композита, когда V _f намного выше, чем V _м, прочность композита в первую очередь контролируется изломом волокна. Как только волокна выходят из строя, очень мало сопротивления предлагается матрицей. Итак, прочность композита составляет

.
X ‘₁₁ ^t = X’ _11f V ‘_f + σ ‘_{11 м} В _м (4.28)
где σ ‘_11m — уровень напряжений в матрице когда волокна ломаются. С другой стороны, при низком V _f является достаточным количеством матрицы, чтобы выдержать нагрузку после разрушения волокон. В этом случае
X ‘₁₁ ^т = X’ _{11 м} ^т _{V _м (4,29)}
Поэтому очевидно, что существует предельное значение V _f при при котором окончательный отказ переходит из режима отказа волокна в матрицу режим отказа.Подобным образом можно рассуждать, чтобы определить возможный сбой. механизмы в случае углерод / углеродного композита также (рис. 4.8b), а также в случаях других композитов, в которых либо волокна, либо матрицы, либо и то, и другое являются пластичный. Но факт остается фактом: не существует единого отношения, которое могло бы определить прочность на одноосное растяжение реалистичного композита.
Однако модель совокупного ущерба Розена, основанная на Распределение Вейбулла зависимости силы от длины дает несколько лучшая оценка X ‘₁₁ ^t, когда волокна и матрица проявляют хрупкое поведение.Эта модель предполагает, что композит состоит из N волокна исходной длины L, а более слабые волокна ломаются из-за нанесенного растягивающее напряжение (рис. 4.9). Затем исходная длина делится на M сегментов, где каждый сегмент (связка или звено) имеет длину 1 _c. Таким образом композит образует цепочку из M связок (звеньев). Когда количество волокон очень большой (высокий V _f) прочность каждого пучка или звена цепи предполагает то же значение, т.е. прочность композита становится равной звену сила.Это выражается как
.
(4,30)
где α и β — материальные постоянные, которые могут быть определены экспериментально. В Затем определяют предел прочности композита с использованием
(4,31)
Обратите внимание, что l _c называется неэффективной длиной или критическим волокном. длина и определяется с использованием напряжения сдвига.Выдается
(4,32)
где X ‘_f — прочность волокна на разрыв при растяжении, d — диаметр волокна, а X _i — межфазный сдвиг волокно-матрица сила.
Прочность на сжатие в продольном направлении X ‘₁₁ ^c на однонаправленный композит в первую очередь влияет коробление волокон.В В упрощенной модели волокна рассматриваются как изотропные тонкие пластинки, лежащие в x ‘₁ x’ ₂ плоскости (рис. 4.10) и поддерживаются на изотерпическом эластичная среда (матрица). Волокна могут изгибаться двумя способами: растяжением и сдвигом. В
режим растяжения, матрица по длине волокна испытывает попеременное расширение и сжатие, тогда как матрица подвергается сдвигу деформация в режиме сдвига. Затем определяется прочность на сжатие. с использованием метода энергии деформации.Для расширенного режима
(4,33)
или же, (4.34)
а для режима сдвига
(4,35)
Свойства поперечной прочности обычно зависят от матрицы характеристики.Поперечная прочность на растяжение X ‘₂₂ ^т также может зависят от прочности границы раздела волокно-матрица, как показано на рис. 4.11. В экспериментальные данные для некоторых композитов подтверждают, что поперечное растяжение прочность повышается с улучшением связи на границе раздела волокно-матрица. В реальная траектория разрушения, однако, представляет собой смесь волоконно-матричного дебонд, волокно расщепление и растрескивание матрицы. Реалистичная модель должна основываться на вариация статистических данных для всех этих видов отказов.Два простых отношения, для прогноза поперечной прочности на разрыв X ‘₂₂ ^т и поперечной прочности на сжатие X ‘₂₂ ^c a однонаправленные составные, представлены следующим образом:
(4,36)
(4,37)
Эти соотношения предполагают, что поперечная прочность композита в первую очередь зависит от прочности матрицы.
4.2.3 Гигротермические свойства
Транспортные свойства
Оценка транспортных свойств, таких как коэффициент диффузии влаги, теплопроводность, электропроводность, диэлектрическая проницаемость и магнитная проницаемость однонаправленного композита следует аналогичной процедуре, когда один использует самосогласованную модель поля. Таким образом, результирующие отношения таковы: идентичен по всем транспортным свойствам. Таким образом, процедура проиллюстрирована рассматривая только один случай диффузии влаги через однонаправленный композитный.Рассмотрим концентрическую цилиндрическую модель, показанную на рис. 4.6. Оба предполагается, что волокно и матрица проницаемы для влаги. Например, арамидные волокна и полимерные матрицы проницаемы для влаги. Для распространения влажность вдоль направления волокна (ось x ‘₁), диффузия влаги уравнение принимает вид
(4,38)
где C — концентрация влаги в единице объема, t — время и d ‘ ₁₁ — продольный коэффициент диффузии влаги композита.
Предполагая, что граничные условия (рис. 4.6) равны
x ‘₁ = 0, C = 0 и x’ ₁ = L, C = C ₀ (4,40)
решение получается как
(4,41)
что удовлетворяет уравнениям.4.39 и 4.40.
Направление диффузии влаги на единицу площади параллельно оси x ‘_{1
Направление} определяется как
(4,42)
Суммарная скорость диффузии влаги через поперечное сечение концентрический цилиндр равен
(4,43)
Обратите внимание, что
а также (4.44)
где d ‘_11f и d’ _11m — продольная влажность коэффициенты диффузии для волокна и матрицы соответственно. Подставляя уравнения. 4,42 и 4,44 в уравнении. 4.43 и отмечая, что
R _f ² / R ² = V _f и (R ² — R _f ²) / R ² = V _м получается
d ‘₁₁ = d’ _11f V _f + d ‘_{11 м} V _м (4.45)
когда волокна (например, стекло, углерод и т. д.) непроницаемы для влаги
d ‘₁₁ = d’ _{11 м} V _м (4,46)
Коэффициент поперечной диффузии влаги d ‘₂₂ может также определяется с использованием аналогичной модели самосогласованного поля и задается как
(4.47)
Когда волокна непроницаемы для влаги, уравнение. 4.47 уменьшается до
(4,48)
Продольная и поперечная теплопроводности k ‘₁₁ и k ‘₂₂ однонаправленного композитного материала можно определить по формуле замена «d» на «k» в уравнениях 4.45 и 4.47 соответственно. Обратите внимание, что в этом В этом случае теплопроводность происходит как через волокно, так и через матрицу.В другие транспортные свойства также могут быть получены аналогичным образом, используя уравнения. 4,45 и 4.47.
Деформация расширения
Деформации продольного расширения (из-за температуры или влажность) однонаправленного композита можно определить с помощью простого «подход механики материалов», как обсуждалось ранее. Рассмотрим Микромодель на рис. 4.3. Суммарные продольные деформации с учетом механическая деформация и деформация расширения даны как
а также и также (4.49)
Решение уравнений. (4.49) получается
и (4.50)
Предполагая свободное расширение ‘₁₁ =’ ₁₁ ^e, первое соотношение уравнений 4,50 дает
σ ‘₁₁ = 0 (4.51)
Следовательно,
σ ‘₁₁ W = σ’ ₁₁ _е W _f + σ ‘₁₁ _м Вт _м = 0
или же, (4.52)
Деление уравнения. (4.52) через W и отмечая, что и и
V _м = W _м / W получается
(4.53)
Наблюдая, что деформация теплового расширения образец длиной L из-за повышения температуры ΔT определяется выражением ^e = LαΔT, продольное тепловое расширение коэффициент α ‘₁₁ однонаправленного композита получается из уравнения.4.53 следующим образом:
(4.54)
Аналогичным образом, коэффициент продольного расширения влажности β ‘₁₁ однонаправленный композит получается из уравнения. 4.54 замена «α» на «β».
Для деформации поперечного расширения ‘₂₂ ^e, «модель самосогласованного поля» однако подход является предпочтительным. Выражение для ‘₂₂ ^e может быть получено как
(4.55)
Затем вычисляется коэффициент поперечного теплового расширения α ‘₂₂ из уравнения 4.55 аналогичным образом
(4.56)
Коэффициент поперечного расширения по влаге β ‘₂₂ получается из Уравнение (4.56) заменой «α» на «β».
4.3 КОМПОЗИТЫ ЧАСТИЦ И КОРОТКОГО ВОЛОКНА
Однонаправленный композит обеспечивает некоторую регулярность в микроструктуре, так как волокна непрерывны и выровнены в одну направление.Это помогает создать простую микромодель с постоянной деформацией или поле напряжений и использовать подход «механики материалов» для определения композитные свойства. Такое простое аналитическое лечение с постоянным стрессом или постоянное поле деформации не подходит для твердых частиц и коротких волокон композиты. Микроструктура композитной среды неоднородна. В точечные вариации микроструктуры весьма значительны во многих ситуации из-за больших различий в форме, размере и свойствах наполнителей и подкрепления, их ориентация и распределение в матричной фазе.Прерывистый характер некоторых из этих подкреплений добавляет больше сложности. Существует бесчисленное множество зон высокого напряжения вокруг неправильной формы. армирующие частицы и на концах коротких волокон. Предположение о постоянные поля напряжений и деформаций больше не действуют. Возникают дальнейшие осложнения из-за анизотропии, вызванной совмещением коротких волокон и чешуек твердые частицы.
Все это препятствует общему решению проблемы. Один Составная микромодель никоим образом не может представить все композиты данной категории.Для композитов с разным армированием могут потребоваться разные микромодели и аналитические процедуры. Вероятно, это основная причина, по которой микромеханика анализу этого класса композитов не уделялось особого внимания со стороны исследователи. Есть еще одна важная причина нехватки информация в районе. По сравнению с мелким и коротким волокном композиты, однонаправленные композиты находят широкое применение в конструкционных компоненты в нескольких инженерных дисциплинах. Это создало больше осведомленности и, в свою очередь, способствовали росту знаний в области микромеханики однонаправленные композиты, а понимание микромеханических поведение композита из твердых частиц и коротких волокон по-прежнему остается на уровне его зарождающийся этап.
4.3.1 Композиты из твердых частиц
В простейшем подходе к механике материалов используется классический подход Фойгта. (постоянная деформация) и Рейсса (постоянное напряжение) для оценки упругой свойства изотропного композита. В модели Фойгта объемный модуль упругости k а модуль сдвига G равен
P = V _f P _f + V _м P _м,
где P = K, G
и E = 9 кг / (3K + G)
ν = (3К-2Г) / (6K + 2G) (4.58)
а с моделью Ройсса отношения равны
(4.59)
Свойства, предсказанные моделью Фойгта (наивысший) и модель Ройсса (самый низкий), следующие: две крайности к реальным значениям. Известно несколько улучшенных аналитических моделей. существуют, но не поддаются простому дизайну. Модель Халпин-Цай, который основан на полуэмпирическом подходе, популярен и обеспечивает как верхнюю и нижние границы, попадающие в пределы Фойгта и Ройсса.Простые отношения которые разработаны на основе улучшенного правила комбинирования, как выяснилось, обеспечивают достаточно хорошая оценка свойств изотропного композита (P _f> P _м и 0 <ν _f <0,5).
Они представлены следующим образом:
(4.60)
с P = K, G.
Для модуля объемной упругости
а для модуля сдвига G: (4.61)
Модуль Юнга E и коэффициент Пуассона ν затем определяются из Уравнения 4.60 и 4.61 с использованием уравнений 4.58.
Коэффициент теплового расширения α равен
.
(4,62)
где K получается с использованием формул 4.60 и 4.61.
4.3.2 Композиты с короткими волокнами
Простая модель предполагает случайную ориентацию короткого волокна. композит в виде квазиизотропного микроламина, в котором каждая пластина состоит из группа коротких волокон, ориентированных в определенном направлении.P определяется используя модифицированное соотношение Халпина-Цая, как указано в
(4,63)
где для
E ‘₁₁, модуль продольной упругости, ξ = 2l / D
E ‘₂₂, поперечный модуль, ξ = 2
G ‘₁₂, модуль сдвига в плоскости, ξ = 1
G ‘₂₃, модуль поперечного сдвига, ξ = (3 4 ν _м) ^-1
Обратите внимание, что l и d — длина и диаметр короткого волокна, соответственно.И матрица, и волокно изотропны по своей природе. Пуассон Отношение ν ‘₁₂ оценивается с помощью простого правила смеси.
Прочность на продольное растяжение зависит от критического волокна. длина l _c (уравнение 4.32) и определяется как
где σ ‘_м — напряжение на матрице при волокно обрывается.
Таблица 4.1 Дополнительные соотношения микромеханики для однонаправленных композиты
Объемные доли:
V _f + V _м + V _v = 1 (1)
Для композита без пустот V _v = 0; V _f + V _м = 1
Массовые доли
M _f + M _м = 1 (2)
Объемная доля пустот ρ
V _v = 1 — ρ [(M _f / ρ _f) + (M _м / ρ _м) ] (3)
Плотность композита
ρ = ρ _f V _f + ρ _м V _м (4)
Объемная доля волокна
(5)
Объемная доля матрицы
(6)
7.Поперечный модуль
(7)
8. Модуль сдвига
(8a)
(8b)
9. Коэффициент Пуассона
(9)
10. Прочность на продольное сжатие
(волокно дробление) (10a)
(микровыступ) (10b)
(10c)
11.Поперечная теплопроводность
(11а)
(11b)
где K _mf = 2 (K _m / K _f-1) для цилиндрическое волокно.
(для MMC) (11c)
12. Поперечный коэффициент диффузии влаги
(12а)
)
(12b)
где d _mf = 2 (d _m / d _f-1) для цилиндрической волокно.
13. Коэффициенты теплового расширения
(13а)
(13b)
(13c)
(для MMC)
(13д)
14.Коэффициенты поперечного расширения по влаге
(14)
15. Тепловая мощность
(15)
Таблица 4.2 : Типичные свойства некоторых распространенных волокон
С. N0.
Недвижимость
Бор
Карбон (T300)
Кельвар-49
S-стекло
Электронное стекло
Вискоза (T50)
1.
Волокно диаметр, д м
140
8
12
9
9
8
2.
Плотность, ρ _ф г / см ³
2.63
1,77
1,47
2,49
2,49
1,94
3.
Модуль упругости в продольном направлении, E ‘_11f ГПа
400
220
150
85
75
380
4.
Поперечный Модуль, E ‘_22f ГПа
400
14
4,2
85
75
6,2
5.
Модуль продольного сдвига, G ‘_12f ГПа
170
9
2.9
36
30
7,6
6.
Поперечный Модуль сдвига, G ‘_23f ГПа
170
4,6
1,5
36
30
4.8
7.
Продольный коэффициент Пуассона, ν ‘_12f
0,2
0,2
0,35
0,2
0,2
0,2
8.
Поперечный Коэффициент Пуассона, ν ‘_23f
0.2
0,25
0,35
0,2
0,22
0,25
9.
Тепло мощность, C _f кДж / (кг · л)
1,30
0,92
1.05
0,71
0,71
0,84
10.
Продольная теплопроводность k ‘_11f Вт / (мк)
38,0
1003,0
2,94
36,30
13.0
1003,0
11.
Поперечный Теплопроводность k ‘_22f Вт / (мк)
38,0
100,3
2,94
36,30
13,0
100,3
12.
Коэффициент продольного теплового расширения, α ‘_11f 10 ^-6 м / м / К
5,0
1.0
-4,0
5,0
5,0
7,7
13.
Поперечный коэффициент теплового расширения, α ‘_22f 10 ^-6 м / м / К
5.0
10,1
54
5,0
5,0
10,1
С. N0.
Недвижимость
Бор
Карбон (T300)
Кельвар-49
S-стекло
Электронное стекло
Вискоза (T50)
14.
Прочность при продольном сжатии, X ‘_11f ^т МПа
4140
2415
2760
4140
2760
1730
15.
Прочность при продольном сжатии, X ‘_11f ^c МПа
4830
1800
500
3450
2400
1380
16.
Сдвиг прочность, X ‘_12f МПа
700
550
400
1050
690
350
Таблица 4.3 : Типичные свойства некоторых распространенных матриц
S Нет.
Недвижимость
Полиимид
Эпоксидная
Фенолик
Полиэфир
Нейлон
6061 Al
Никель
Титан
1.
Плотность, ρ _м г / см ³
1,22
1,3
1,2
1,2
1,14
2,8
8,9
4,4
2.
Модуль Юнга, E _м ГПа
3,45
3,45
11
3
3,45
70
210
110
3.
Модуль сдвига, G _м ГПа
1,28
1,28
4,07
1.11
1,28
26.12
81,40
44
4.
Коэффициент Пуассона, ν _м
0,35
0,35
0,35
0,35
0,35
0,34
0,29
0,25
5.
Теплоемкость, C _м кДж / (кгк)
1.05
0,96
1,30
1,15
1,67
0,96
0,46
0,39
6.
Теплопроводность, к _м Вт / (мк)
2,16
0,18
0,21
0,25
0,19
171
62,0
7,0
7.
Коэффициент теплового расширения, α _м 10 ^-6 м / м / к
36,0
64,3
80,0
80,0
46,0
23,4
13,3
9,5
8.
Коэффициент диффузии влаги, d _м 10 ^-13 м ² / с
0,39
1,637
1,20
1,80
1,10
0,0
0,0
0,0
9.
Коэффициент расширения по влаге, β _м м / м / С
0,33
0,38
0,38
0,50
0,45
0,0
0,0
0,0
10.
Предел прочности, X _т ^м МПа
120
90
60
60
81,4
310
760
1170
11.
Прочность на сжатие, X _c ^м МПа
210
130
200
140
60,7
310
760
1170
12.
Прочность на сдвиг, X _с ^м МПа
90
60
80
50
66,2
180
440
675
Таблица 4.4 : Термоупругие свойства трех однонаправленных композитов (V _f = 0,6)
С. №
Недвижимость
Кельвар / Эпоксидная смола
T300 / эпоксидная
Бор / полиимид
Fomulae б / у
1.
Плотность, ρ гм / см ³
1.40
1,58
2,07
Ур.4 ^*
2.
Модуль продольной упругости, E ‘₁₁ ГПа
91,38
133,38
241,38
Уравнение 4.6 ^*
3.
Поперечный модуль, E ‘₂₂ ГПа
4,00
8,29
14,87
Ур.7 ^*
4.
Пуассона отношение, ν ‘₁₂ = ν’ ₁₃
0,35
0.26
0,26
Уравнение 4.12 ^*
5.
Пуассона отношение, ν ‘₂₃
0,484
0,424
0,394
Ур.9 ^*
6.
В самолете модуль сдвига, G ‘₁₂ = G’ ₁₃ ГПа
2,26
3,81
5,53
Ур. 8a ^*
7.
Поперечный модуль сдвига, G ‘₂₃ ГПа
1.44
2,90
5,53
Ур. 8b ^*
8.
Продольная проводимость, к ‘₁₁ Вт / (мк)
1,836
601,87
23,66
Уравнение4,45 ^*
9.
Поперечный электропроводность, к ‘₂₂ Вт / (мк)
0,57
0,72
6,95
Ур. 11b ^*
10.
Тепло мощность, ц кДж / (кгк)
1.017
0,933
5,28
Уравнение 15 ^*
11.
Коэффициент продольного теплового расширения, α ‘₁₁ (x10 ^-6) м / м / к
-2,48
1,99
5,28
Уравнение4,54 ^*
12.
Поперечный коэффициент теплового расширения, α ‘₂₂ (x10 ^-6) м / м / к
61,32
2,73
1,48
Уравнение 13b ^*
* Ур. Таблицы 4.1

4.4 БИБЛИОГРАФИЯ
1. J.M. Whitney и R.L. McCromechanical Materials Modeling, Delware Composites. Энциклопедия дизайна, том 2, Technomic Publishing Co., Inc., Ланкастер, 1990.
2. J.W. Уитон, Д. Петерс и К. Томас (ред.), Руководство инженера по Композиционные материалы, Американское общество металлов, Металл Парк, Огайо, 1987.
3. Г.С. Спрингер, С.В. Цай, Теплопроводность однонаправленных Материал, J.Composotie Materials, 1,1967,166.
4.М. Тайя, Р. Арсено, Металлический матричный композит. Пергамон, Оксфорд, 1989.
5. Р.А. Шапери, Коэффициент теплового расширения композиционных материалов на основе Принципы энергии, J. Composite Materials, 2, 1968, 157.
6. Р.М. Джонс, Механика композитных материалов, McGraw Hill Book Companym New Йорк, 1975.
7. С.В. Цай и Х. Хан, Введение в композиционные материалы, Technomic Publishing co., Inc., Ланкастер, 1980.
8. Б.Д. Агарвал и Л.Дж. Браутман, Анализ и характеристики волокнистых композитов, Wiley-Interscience, Нью-Йорк, 1980.
9. J.C. Halpin, Primer on Composite Materials: Analysis, Technomic Publishing. Co. Inc., Ланкастер, 1984.
10. З. Хашин, Теория армированных волокном материалов, НАСА CR-1974, 1972 г.

4,5 УПРАЖНЕНИЯ
(Используйте свойства материала и формулы, приведенные в этой главе, для численного результатов)
1.Используя простые правила смешивания, выведите выражения для E ‘₁₁, E’ ₂₂, ν ‘₁₂ и G’ ₁₂.
2. Какой должен быть вес волокон для матрицы заданного веса, чтобы Объемная доля волокна в композите составляет 0,7, т. е. V _f = 0,7.
3. Для композита бор / полиимид (V _f = 0,7) определите значения из E ‘₂₂ и G’ ₂₂ с использованием различных формул и Сравнительный анализ.
4. Для композита углерод / алюминий (V _f = 0,5) определите значения из E ‘₁₁, E’ ₂₂, ν ‘₁₂ и G’ ₁₂.
5. Определите d ‘₁₁ и d’ ₂₂ для угля / эпоксидной смолы. композитов (V _f = 0,7) и для кевлара / эпоксидного композита (V _f = 0,6 и d _f = 5 d _м).
6. Определите k ‘₁₁ и k’ ₂₂ для полиимида углерода и композиты бор / полиимид (V _f = 0.7).
7. Определите α ‘₁₁ и α’ ₂₂ для бора / алюминия. композитный (V _f = 0,5).
8. Определите β ‘₁₁ и β’ ₂₂ для кевларового / эпоксидного композита. (V _f = 0,7). Предположим, β ‘_f = 0,5 β’ _m.

Что такое коэффициент Пуассона?
Определение коэффициента Пуассона
Коэффициент Пуассона — это отношение деформации поперечного сжатия к деформации продольного растяжения в направлении силы растяжения.Деформация растяжения считается положительной, а деформация сжатия — отрицательной. Определение коэффициента Пуассона содержит знак минус, так что нормальные материалы имеют положительное отношение. Коэффициент Пуассона, также называемый коэффициентом Пуассона или коэффициентом Пуассона, или коэффициентом де Пуассона, обычно представляется в виде греческого nu, n в нижнем регистре.
Если ваш браузер неправильно интерпретирует шрифт Symbol, греческий nu, n может вместо этого выглядеть жирным лицевая латиница n . Альтернативную страницу можно найти здесь.
n = — e _транс / e _{продольный}

Деформация e определяется в элементарной форме как изменение длины, деленное на исходную длину.
Коэффициент Пуассона: почему обычно положительный
Практически все распространенные материалы, такие как синяя резинка справа, сужаются в поперечном сечении при растяжении. Причина, по которой, с точки зрения континуума, заключается в том, что большинство материалов сопротивляются изменению объема, определяемому модулем объемного сжатия K (также называемым B), больше, чем они сопротивляются изменению формы, определяемому модулем сдвига G.
Со структурной точки зрения причина обычного положительного коэффициента Пуассона в том, что межатомные связи перестраиваются с деформацией. Растяжение желтых сот под действием вертикальных сил, показанное справа, иллюстрирует эту концепцию. Отрицательный коэффициент Пуассона в разработанных материалах и в некоторых анизотропных материалах к настоящему времени хорошо известен.
Коэффициент Пуассона: отношение к модулям упругости в изотропных твердых телах
Коэффициент Пуассона связан с модулем упругости K (также называемым B), модулем объемной упругости; G — модуль сдвига; и E, модуль Юнга, следующим образом (для изотропных твердых тел, свойства которых не зависят от направления).Модули упругости являются мерой жесткости. Это соотношение напряжения к напряжению. Напряжение — это сила на единицу площади с указанием направления силы и площади. См. Sokolnikoff Ref. [1]; также дальнейшие подробности.
n = (3K — 2G) / (6K + 2G)
E = 2G (1 + п)
E = 3K (1-2 п)
Дальнейшие взаимосвязи между упругими постоянными для изотропных твердых тел заключаются в следующем. B — объемный модуль.

Теория изотропной линейной упругости допускает коэффициенты Пуассона в диапазоне от -1 до 1/2 для объекта со свободными поверхностями без каких-либо ограничений.Физическая причина в том, что для того, чтобы материал был устойчивым, жесткость должна быть положительной; объемная жесткость и жесткость на сдвиг взаимосвязаны формулами, включающими коэффициент Пуассона. Объекты, ограниченные поверхностью, могут иметь коэффициент Пуассона за пределами указанного диапазона и быть стабильными.
Коэффициент Пуассона в различных материалах: таблица коэффициента Пуассона
Коэффициент Пуассона элементов, если не указано иное, приводится через веб-элементы, в которых приводятся ссылки [2-4]. В большом наборе свойств поликристаллических материалов [5] большинство из них имеет коэффициент Пуассона около 1/3.Некоторые эксперименты, например. грамм. резонансные ультразвуковые исследования в [9] обеспечивают перекрестную проверку; сравнение нескольких частот мод колебаний подтверждает, что модуль и коэффициент Пуассона соответствуют линейной изотропной упругости.
Материал
Верхний предел изотропии [1]
Резина [6]
Индий [11]
золота [4]
Свинец [4]
Медь [7]
Алюминий [4]
Медь [4]
Полистирол [6]
Латунь [1]
Лед [8]
Пенополистирол [6]
Нержавеющая сталь [7]
Сталь [1]
Вольфрам [4]
Вольфрам
Цинк [5]
Уран [4]
Плавленый кварц [9]
Европий
Бор [12]
Бериллий [4]
Входящая пена [10]
Нижний предел изотропии [1] Коэффициент Пуассона
0.5
0,48- ~ 0,5
0,45
0,42
0,44
0,37
0,34
0,35
0,34
0,33
0,33
0,3
0,30
0,29
0,30
0,28
0,25
0,23
0,17
0,15
0,08
0,03
-0,7
-1 Список литературы
[1] Сокольников И. С. Математическая теория упругости. Кригер, Малабар Флорида, второе издание, 1983.
[2] А. М. Джеймс и М. П. Лорд в «Химических и физических данных Макмиллана», Макмиллан, Лондон, Великобритания, 1992.
[3] G.W.C. Кэй и Т. Лаби в таблицах физических и химических констант, Лонгман, Лондон, Великобритания, 15-е издание, 1993.
[4] Г.В. Самсонова (ред.) В Справочнике по физико-химическим свойствам элементов, IFI-Plenum, Нью-Йорк, США, 1968.
[5] Г. Симмонс, Х. Ван, Монокристаллическая эластичность. константы и рассчитанные совокупные свойства: справочник, MIT Press, Кембридж, 2-е изд., 1971.
[6] Дж. А. Ринде, Коэффициент Пуассона для жестких пенопластов, J. Applied Polymer Science, 14, 1913-1926, 1970.
[7] Д. Э. Грей, Справочник Американского института физики, 3-е изд., Глава 3, Макгроу-Хилл, Нью-Йорк, 1973.
[8] Э. М. Шульсон, Структура и механическое поведение льда, JOM, 51 (2) стр. 21-27, 1999. ссылка на статью
[9] Х. Х. Демарест, мл., Кубический резонансный метод для определения упругих постоянных твердых тел, J. Acoust. Soc. Являюсь. 49, 768-775 (1971).
[10] Р. С. Лейкс, Пенные структуры с отрицательным коэффициентом Пуассона, Science, 235 1038-1040, 1987.
[11] Д. Ли, Т.М. Яглински, Д. С. Стоун и Р. С. Лейкс, Нечувствительные к температуре отрицательные коэффициенты Пуассона в изотропных сплавах вблизи морфотропной границы раздела фаз, Прикл. Phys. Lett, 101, 251903, декабрь (2012).
[12] К. А. Гшнайднер, мл., Физические свойства и взаимосвязи металлических и полуметаллических элементов, Физика твердого тела, 16, 275-426, 1964
Дальнейшее подтверждение устойчивости низкого коэффициента Пуассона (0,05) бериллия было предоставлено в работах A. Migliori, H. Ledbetter, D.Дж. Тома и Т. В. Дарлинг, «Константы упругости монокристаллов и поликристаллов бериллия», J. Applied Physics 95, 2436-2440 (2004). Бериллий имеет самый низкий коэффициент Пуассона для любого поликристаллического металла. Константы упругости были измерены как для монокристаллов, так и для поликристаллических образцов. Бериллий не подчиняется соотношению Коши, поэтому предполагались нецентральные силы между атомами.
Коэффициент Пуассона при изгибе.
Согните брус или пластину. Коэффициент Пуассона определяет кривизну в направлении, перпендикулярном направлению изгиба.Эту «антикластическую кривизну» легко увидеть при изгибе резинового ластика. Здесь показан изгиб с помощью момента, приложенного к противоположным краям, соты с шестиугольными ячейками. Если сотовые ячейки представляют собой правильные шестиугольники, коэффициент Пуассона может приближаться к +1. Поскольку соты анизотропны, коэффициент Пуассона не обязательно должен находиться в указанном выше диапазоне.
Коэффициент Пуассона и анизотропия.
В анизотропных твердых телах, включая монокристаллы, соты и волокнистые композиты, физические свойства, включая коэффициент Пуассона и модули упругости, зависят от направления.Коэффициент Пуассона может иметь положительные или отрицательные значения сколь угодно большой величины в анизотропных материалах.
Для ортотропных материалов коэффициент Пуассона ограничен отношением модулей Юнга E следующим образом.
| n ₁₂ | 1 / E ₂) ^1/2
B. M. Lempriere «Коэффициент Пуассона в ортотропных материалах» AIAA Journal, 6, No. 11, 2226-2227 (1968)
Максимальные и минимальные значения коэффициента Пуассона получены с точки зрения упругой податливости материалов с кубической симметрией.
Хейс М., Шувалов А. «Об экстремальных значениях модуля Юнга, модуля сдвига и коэффициента Пуассона для кубических материалов», ASME J. Appl. Mech., 65, 786-787, (1998).
Коэффициент Пуассона в вязкоупругих материалах
Коэффициент Пуассона в вязкоупругом материале зависит от времени в контексте переходных испытаний, таких как ползучесть и релаксация напряжений. Если деформация синусоидальна во времени, коэффициент Пуассона может зависеть от частоты и может иметь связанный фазовый угол.В частности, поперечная деформация может быть не в фазе с продольной деформацией в вязкоупругом твердом теле. Получите pdf-файл с исследовательской статьей по этому поводу. Для полимеров в стеклообразном режиме коэффициент Пуассона составляет порядка 1/3. При более высокой температуре (или при более длительном времени или более низкой частоте), достаточной для эластичности, жесткость значительно уменьшается, и коэффициент Пуассона приближается к 1/2.
Коэффициент Пуассона и фазовые преобразования
Коэффициент Пуассона может существенно изменяться вблизи фазового превращения.Обычно модуль объемной упругости размягчается вблизи фазового превращения, но модуль сдвига не сильно изменяется. Затем коэффициент Пуассона уменьшается вблизи фазового превращения и может достигать отрицательных значений. Фазовые превращения обсуждаются далее на связанной странице.
Коэффициент Пуассона, волны и деформация
Коэффициент Пуассона материала влияет на скорость распространения и отражения волн напряжения. В геологических приложениях соотношение скорости продольной и поперечной волны важно для определения природы горной породы глубоко в недрах Земли.Этот коэффициент скорости волны зависит от коэффициента Пуассона. Коэффициент Пуассона также влияет на спад напряжения с расстоянием в соответствии с принципом Сен-Венана и на распределение напряжения вокруг отверстий и трещин.
Пример. Анализ влияния коэффициента Пуассона на сжатие слоя.
Как насчет влияния коэффициента Пуассона на ограниченный сжатие в направлении 1 (или x)? Ограниченное сжатие означает, что эффект Пуассона не возникает.Это можно было бы сделать с помощью боковых стенок в эксперименте. Кроме того, эффективно сдерживается сжатие тонкого слоя жесткими поверхностями. Более того, при ультразвуковом контроле длина волны ультразвука обычно намного меньше размеров образца. В этом случае также не возникает эффекта Пуассона.
По закону Гука (с тензор модуля упругости как C _ijkl суммируем по k и l, но из-за ограничения только компонент деформации, который не равен нулю, равен e ₁₁.
s _ij = C _ijkl e _kl = C ₁₁₁₁ e ₁₁ + C ₁₁₂₂ e ₂₂ + C ₁₁₃₃ e ₃₃ = C ₁₁₁₁ e ₁₁ ,
, поэтому эффективная жесткость при ограниченном сжатии это C ₁₁₁₁.
Найдем физический смысл этого элемента тензора в терминах инженерные константы.
Можно также работать с элементарной изотропной формой закона Гука.
e _xx = (1 / E) {s _xx — ns _yy -ns _zz}
e _yy = (1 / E) {s _yy — ns _xx -ns _zz}
e _zz = (1 / E) {s _zz — ns _xx -ns _yy}
Для простого растяжения или сжатия в направлении x, эффект Пуассона может возникнуть. Напряжение существует только в одном направлении, но напряжение может быть в трех направлениях. s _xx ≠ 0, не равное нулю, s _yy = 0, с _zz = 0.Затем
So Young’s Модуль E — это жесткость при простом растяжении, при котором может возникнуть эффект Пуассона.
Считать ограниченным сжатие , при этом e _yy = 0, e _zz = 0. Тогда
s _yy = ns _xx + ns _zz.
s _zz = нс _хх + нс _гг.
Подстановка,
s _yy = s _zz = s _xx (n (1+ n) / (1- n ²)).
Итак, подставляя в Закон Гука, отношение напряжения к деформации для сжатого сжатия, которое по определению является связанным модулем C ₁₁₁₁, это
(s _xx / e _xx) = C ₁₁₁₁ = E ((1 — n) / (1 + n) (1-2n)).

Физический смысл C ₁₁₁₁ — жесткость на растяжение или сжатие в x (или 1) направление, когда деформация в направлениях y и z ограничена нулем. Причина в том, что для такого ограничения сумма в тензорном уравнении закона Гука сворачивается в один член, содержащий только C ₁₁₁₁. Ограничение может быть применено с помощью жесткой формы, или если материал сжимается тонким слоем. между жесткими плитами.C ₁₁₁₁ также регулирует распространение продольных волн в протяженной среде, поскольку волны испытывают аналогичное ограничение на поперечное смещение.
Резиновые материалы имеют коэффициенты Пуассона, очень близкие к 1/2, модули сдвига порядка МПа и объемные модули порядка ГПа. Следовательно, ограниченный модуль упругости C ₁₁₁₁ сравним с модулем объемной упругости и намного больше, чем сдвиг или модуль Юнга резины.
Практический пример — пробка в бутылке.
Примером практического применения определенного значения коэффициента Пуассона является пробка винной бутылки. Пробка должна легко вставляться и извлекаться, но при этом она должна выдерживать давление изнутри бутылки. Резину с коэффициентом Пуассона 0,5 для этой цели использовать нельзя, потому что она расширяется при сжатии в горлышко бутылки и заедает. Пробка, напротив, с почти нулевым коэффициентом Пуассона идеально подходит для этого применения.
Практический пример — конструкция резиновых буферов.
Как трехмерная деформация влияет на использование вязкоупругой резины в таких областях, как стельки для обуви для уменьшения силы удара при беге или маты для борьбы для уменьшения силы удара при падениях?
Решение
Обратитесь к приведенному выше анализу, в котором анализируется деформация под действием поперечного ограничения. Резиновые материалы намного жестче при сжатии в геометрии тонкого слоя, чем при сдвиге или простом растяжении; они слишком жесткие, чтобы выполнять функцию уменьшения удара.Податливые слои могут быть сформированы путем гофрирования резины для обеспечения пространства для бокового расширения или использования эластомерной пены, которая обычно имеет коэффициент Пуассона около 0,3, в отличие от резины, для которой коэффициент Пуассона может превышать 0,49. Гофрированный каучук используется в стельках обуви (кроссовок) и в виброизоляторах машин. Пена используется в обуви и борцовских матах.
Практический пример — авиационные сэндвич-панели.
Соты, показанные выше, используются в композитных сэндвич-панелях для самолетов.Сота — это стержень между лицевыми панелями из графит-эпоксидного композита. Такие панели обычно бывают плоскими. Если желательны изогнутые панели, форма сотовых ячеек должна быть изменена от обычной правильной формы шестиугольника, в противном случае ячейки будут раздавлены во время изгиба. Известно несколько альтернативных форм ячеек, включая те, которые приводят к отрицательному коэффициенту Пуассона.
Практический пример — Интерпретация испытаний на сжатие блоков из гибкого материала.
Материал удерживается на контактных поверхностях сжимающим устройством, поэтому эффект Пуассона не может возникать свободно.Выпуклость возникает посередине, как показано на изображении справа. Эксперимент не дает модуля Юнга E. Определение модуля Юнга E предполагает свободу от поперечного ограничения, но блок достаточно короткий, чтобы ограничение контактными поверхностями было уместным. Определение модуля упругости E включает использование корректирующих формул, которые зависят от коэффициента Пуассона.
Обзорная статья с акцентом на материаловедение:
Гривз, Г.Н., Грир А. Л., Лейкс Р. С. и Руссель Т., «Коэффициент Пуассона и современные материалы», Nature Materials , 10 , 823-837 ноябрь (2011). При сравнении сопротивления материала деформации под действием механической нагрузки, а не изменению объема, коэффициент Пуассона представляет собой фундаментальную метрику, с помощью которой можно сравнивать характеристики любого материала при упругом растяжении. Числовые пределы установлены 1/2 и -1, между которыми находятся все стабильные изотропные материалы. С помощью новых экспериментов, вычислительных методов и способов синтеза материалов мы оцениваем, что означает коэффициент Пуассона в современном понимании механических характеристик современных материалов.В центре этих последних достижений мы подчеркиваем важность взаимосвязей за пределами предела упругости между коэффициентом Пуассона и уплотнением, связностью, пластичностью и вязкостью твердых тел; и их связь с динамическими свойствами жидкостей, из которых они были конденсированы и в которых они плавятся. получить pdf.
Закладка Google
Род Лейкс возвращение домой
Отрицательный коэффициент Пуассона Фазовые преобразования
Включения отрицательной жесткости
Вершина
Модуль упругости композитов и коэффициент Пуассона
В таблицах ниже показаны значения модуля Юнга (модуля упругости) и коэффициента Пуассона при комнатной температуре для нескольких композитов, используемых в технике.Свойства материала выражаются в средних значениях или в диапазонах, которые могут значительно варьироваться в зависимости от обработки и качества материала или от возможного присутствия минеральных наполнителей. Точные значения могут быть измерены с помощью неразрушающего тестирования систем Sonelastic ^® при комнатной температуре, а также при низких и высоких температурах и / или времени отверждения.
Композиционные материалы
Материал Модуль упругости Коэффициент Пуассона
ГПа 10 ⁶ фунтов на кв. Дюйм
Композиционные материалы
Арамидные волокна-эпоксидная матрица: 0.34
Продольный: 76 11 –
Поперечный: 5,5 0,8 –
Высокомодульное углеродное волокно-эпоксидная смола: 0,25
Продольный: 220 32 –
Поперечный: 6,9 1.0 –
Стекловолокно Е-эпоксидная матрица: 0,19
Продольный: 45 6,5 –
Поперечный: 12 1,8 —
Значения только для справки. Для получения точных значений охарактеризуйте материал с помощью систем Sonelastic ^®.
Модули упругости (модуль Юнга, модуль сдвига и коэффициент Пуассона) и демпфирование композитов можно точно охарактеризовать с помощью неразрушающего испытания систем Sonelastic ^® при комнатной температуре, а также при низких и высоких температурах, и / или время отверждения.Знание точных значений жизненно важно для оптимизации использования материала и надежности моделирования с помощью конечных элементов. Модули упругости и характеристики демпфирования также используются при разработке новых вариантов этих материалов.

Список литературы
Современная пластиковая энциклопедия´96, McGraw-Hill Companies, Нью-Йорк, Нью-Йорк; Р. Ф. Флорал и С. Т. Петерс.

Откройте для себя системы Sonelastic
^®: Система Sonelastic ^® для малых образцов
Система Sonelastic ^® для средних образцов
Система Sonelastic ^® для больших образцов
Специальная система Sonelastic ^® и предложение
База данных рассеяния Бриллюэна
Изотропная эластичность: продольный модуль и модуль Юнга
Интересное обозначение упругой постоянной возникло в последние годы в рассеянии Бриллюэна, названное «продольный модуль».Ниже приводится объяснение того, как это соотносится с модулем Юнга в изотропной системе. В предположении изотропной упругой системы тензор жесткости определяется выражением: \ [ \ begin {eqnarray} c_ {ij} = \ left [\ begin {array} {cccccc} c_ {11} & c_ {12} & c_ {12} & 0 & 0 & 0 \\ c_ {12} & c_ {11} & c_ {12} & 0 & 0 & 0 \\ c_ {12} & c_ {12} & c_ {11} & 0 & 0 & 0 \\ 0 & 0 & 0 & c_ {44} & 0 & 0 \\ 0 & 0 & 0 & 0 & c_ {44} & 0 \\ 0 & 0 & 0 & 0 & 0 & c_ {44} \ end {array} \ right] знак равно \ left [\ begin {array} {cccccc} c_ {11} & c_ {12} & c_ {12} & 0 & 0 & 0 \\ c_ {12} & c_ {11} & c_ {12} & 0 & 0 & 0 \\ c_ {12} & c_ {12} & c_ {11} & 0 & 0 & 0 \\ 0 & 0 & 0 & \ frac {c_ {11} -c_ {12}} {2} & 0 & 0 \\ 0 & 0 & 0 & 0 & \ frac {c_ {11} -c_ {12}} {2} & 0 \\ 0 & 0 & 0 & 0 & 0 & \ frac {c_ {11} -c_ {12}} {2} \ end {array} \ right] \ end {eqnarray} \] где \ (c_ {44} = \ frac {1} {2} \ left (c_ {11} -c_ {12} \ right) \) Следовательно, изотропные системы имеют только две жесткости: \ (c_ {11} \) и \ (c_ {12} \). Продольный модуль (\ (LM \)), как упоминается в эксперименте по рассеянию Бриллюэна, является измерением жесткости от продольной акустической моды.В изотропной системе это просто один элемент тензора жесткости: \ (c_ {11} \) \ [ LM = c_ {11} \] Чтобы получить \ (c_ {12} \), необходимо измерить поперечную моду и получить поперечный модуль \ (c_ {44} \). В эксперименте по обратному рассеянию, в котором большинство современных экспериментов Бриллюэна преимущественно проводится из-за использования микроскопа, симметрия запрещает появление поперечных пиков. Таким образом, поперечные моды должны быть измерены с использованием другой геометрии рассеяния. Опять же, эта поперечная мода соответствует \ (c_ {44} \), которая может быть связана с \ (c_ {12} \) с помощью приведенных выше уравнений.Скорость звука связана с жесткостью (где ij равно 11 или 44 в изотропном случае) и плотностью \ (\ rho \) через уравнение Ньютона: \ [ V = \ sqrt {\ frac {c_ {ij}} {\ rho}} \] Бриллюэн дает сдвиг частоты (\ (\ nu \)), который можно преобразовать в скорость звука с помощью уравнения: \ [ V = \ pm \ frac {n \ Delta \ nu} {\ lambda_o} \ sin \ left (\ frac {\ Theta} {2} \ right) \] Скорость звука равна скорости звука, поэтому это означает, что рассеяние Бриллюэна напрямую измеряет жесткость, если плотность известна.
Как это связано с модулем Юнга
В литературе по Бриллюэну возникает проблема с использованием «продольного модуля» и модуля Юнга. Продольный модуль — это жесткость. Связь с модулем Юнга (\ (E \)), модулем сдвига (\ (G \)) или объемным модулем (\ (B \)) осуществляется через комбинации другого элемента жесткости или, скорее, поперечного модуля, как он будет называться в соответствии с этим обозначением. Итак, если вы измеряете \ (c_ {11} \) или \ (c_ {12} \), как это связано с модулем Юнга \ (Y \) и коэффициентом Пуассона \ (\ sigma \)? \ [ c_ {11} = LM = \ frac {Y (1- \ sigma)} {(1+ \ sigma) (1-2 \ sigma)} \] \ [ c_ {12} = \ frac {\ sigma Y} {(1+ \ sigma) (1-2 \ sigma)} \] \ [ c_ {44} = G = \ frac {Y} {2 (1+ \ sigma)} \] Обратите внимание, что продольный модуль не является модулем Юнга, а представляет собой некоторую комбинацию модуля Юнга и коэффициента Пуассона.2} {c_ {12} + c_ {44}} = \ frac {(c_ {11} -c_ {12}) (c_ {11} + 2c_ {12})} {c_ {11} + c_ {12} } \] Из определяющих соотношений модуль Юнга представляет собой комбинацию \ (c_ {11} \) и \ (c_ {12} \). Это не просто \ (c_ {11} \) и не просто продольный модуль. Именно здесь в литературе Бриллюэна делается много ошибок. Остальные механические постоянные можно рассчитать по жесткости следующим образом: Модуль сдвига: \ [ G = c_ {44} \] Объемный модуль: \ [ B = \ frac {1} {3} \ left (c_ {11} + 2c_ {12} \ right) \] Коэффициент Пуассона: \ [ \ sigma = \ frac {c_ {12}} {c_ {11} + c_ {12}} \] Отсюда следует, что модуль Юнга связан с объемным модулем соотношением \ [ Y = \ frac {9BG} {(3B + G)} \] Очень странные дебаты, по-видимому, возникли в спектроскопии Бриллюэна, где утверждается, что содержание воды, а не жесткость, определяет рассеяние Бриллюэна.Это странная дихотомия. Состав смеси определяет жесткость; кого волнует, что в смеси. Упругие изотропные системы лучше всего демонстрируются Правилами смесей, как показано на рисунке ниже. Правила смесей заключаются в том, что при добавлении одного компонента, чтобы сделать материал более жестким или мягким, жесткость должна вести себя приблизительно линейно (конечно, с последствиями для реального мира, которые всегда искривляют кривую). Этот тип правил пригодится при смешивании цементов, добавлении воды в желе (как все эти биологические фантомы), добавлении свинца в стекло и т. Д… Есть, конечно, исключения из правила смесей, но в изотропной линейно-упругой системе, с которыми не следует сталкиваться. Если это так, то более вероятно, что система не является линейно-упругой.
Заключительные соображения
Механическое рассмотрение: Бриллюэн бесконтактен и дает незначительное смещение. Он линейный и эластичный. Механическое возмущение нелинейно и неупруго. Различия возникают преимущественно в механике, которая имеет: Механические проблемы, не обнаруженные в рассеянии Бриллюэна
1.Нелинейность напряжения
2. Нелинейность деформации
3. Вязкопластичность
Чтобы точно сравнить измерения рассеяния Бриллюэна с механическими измерениями, необходимо учитывать деформацию твердого тела или рассматриваемых материалов. Термодинамическое рассмотрение:
Рассеяние Бриллюэна изоэнтропическое. Механическое возмущение изотермическое.
Теоретическое и экспериментальное определение механических свойств сверхпроводящего композитного провода.[Nb Ti / C] (Технический отчет)
Грей, В. Х. и Сан, К. Т. Теоретическое и экспериментальное определение механических свойств сверхпроводящего композитного провода. [Nb Ti / C] . США: Н. П., 1976. Интернет. DOI: 10,2172 / 7355113.
Грей, В. Х. и Сан, К. Т. Теоретическое и экспериментальное определение механических свойств сверхпроводящего композитного провода.[Nb Ti / C] . Соединенные Штаты. https://doi.org/10.2172/7355113
Грей, В. Х., и Сан, К. Т. Чт. «Теоретическое и экспериментальное определение механических свойств сверхпроводящего композитного провода. [Nb Ti / C]». Соединенные Штаты. https://doi.org/10.2172/7355113. https://www.osti.gov/servlets/purl/7355113.
@article {osti_7355113, title = {Теоретическое и экспериментальное определение механических свойств сверхпроводящего композитного провода.[Nb Ti / C]}, author = {Грей, У. Х. и Сан, К. Т.}, abstractNote = {Механические свойства композитного сверхпроводящего (NbTi / Cu) провода характеризуются с точки зрения механических свойств каждого составляющего материала. Для конкретного композитного сверхпроводящего провода были экспериментально определены и теоретически рассчитаны пять констант упругого материала. Поскольку коэффициенты Пуассона для волокна и материала матрицы были очень близки, не было практически никакой (менее 1 процента) разницы между всеми теоретическими предсказаниями для любой индивидуальной механической постоянной.Из-за дороговизны и сложности получения данных об упругих константах с точностью до 0,1% и, следовательно, окончательного определения того, какая теория является наилучшей, дальнейшие эксперименты не проводились.
No related posts.

Модуль продольной упругости — Справочник химика 21

Модуль продольной упругости (Юнга) — Энциклопедия по машиностроению XXL

Модуль продольной упругости — Энциклопедия по машиностроению XXL

Определение эффективного модуля упругости для металлической сетки Текст научной статьи по специальности «Физика»

Модуль упругости

★ Модуль упругости

Оп­ределение модуля упругости и коэффициента Пуассона

Модуль упругости древесины при изгибе вдоль волокон

Параметры, от которых зависит упругость древесины

Нормативная документация

Модуль упругости дерева

Модуль упругости древесины основных пород

Модуль сдвига основных пород древесины

Пластичность древесины

Коэффициент Пуассона

Модуль упругости фанеры

— обзор

Измерения нанотвердости

ГЛАВА II — Свойства США

ВЗАИМОСВЯЗЬ МЕЖДУ УЛЬТРАЗВУКОВОЙ СКОРОСТЬЮ И УПРУГОЙ МОДУЛЯМИ

МОЛОДЕЖНЫЙ МОДУЛЬ

E = 3K (1-2n)

3 (1-2n) = 1 + n

КОЭФФИЦИЕНТ ПУАССОНА

ХРАМНЫЕ КОНСТАНТЫ

ТЕМПЕРАТУРА ДЕБИ

АДИАБАТИЧЕСКИЙ МОДУЛЬ В ОТНОШЕНИИ ИЗОТЕРМИЧЕСКОЙ МОЛОДЕЖИ

КОМПОЗИЦИОННЫЕ МАТЕРИАЛЫ И КОНСТРУКЦИИ

Что такое коэффициент Пуассона?

Модуль упругости композитов и коэффициент Пуассона

Композиционные материалы

Список литературы

Откройте для себя системы Sonelastic

База данных рассеяния Бриллюэна

Изотропная эластичность: продольный модуль и модуль Юнга

Как это связано с модулем Юнга

Заключительные соображения

Теоретическое и экспериментальное определение механических свойств сверхпроводящего композитного провода.[Nb Ti / C] (Технический отчет)

Добавить комментарий Отменить ответ

Определение модуля упругости и коэффициента Пуассона

`Добавить комментарий Отменить ответ`