Картинка правильный шестиугольник: %d0%bf%d1%80%d0%b0%d0%b2%d0%b8%d0%bb%d1%8c%d0%bd%d1%8b%d0%b9 %d1%88%d0%b5%d1%81%d1%82%d0%b8%d1%83%d0%b3%d0%be%d0%bb%d1%8c%d0%bd%d0%b8%d0%ba PNG, векторы, PSD и пнг для бесплатной загрузки

%d0%bf%d1%80%d0%b0%d0%b2%d0%b8%d0%bb%d1%8c%d0%bd%d1%8b%d0%b9 %d1%88%d0%b5%d1%81%d1%82%d0%b8%d1%83%d0%b3%d0%be%d0%bb%d1%8c%d0%bd%d0%b8%d0%ba PNG, векторы, PSD и пнг для бесплатной загрузки

Мемфис дизайн геометрические фигуры узоры мода 80 90 х годов

4167*4167

поп арт 80 х патч стикер

3508*2480

естественный цвет bb крем цвета

1200*1200

аудиокассета изолированные вектор старая музыка ретро плеер ретро музыка аудиокассета 80 х пустой микс

5000*5000

схема бд электронный компонент технологии принципиальная схема технологическая линия

2000*2000

Мемфис шаблон 80 х 90 х годов стилей фона векторные иллюстрации

4167*4167

поп арт 80 х патч стикер

3508*2480

green environmental protection pattern garbage can be recycled green clean

2000*2000

набор векторных иконок реалистичные погоды изолированных на прозрачной ба

800*800

Мемфис бесшовные модели 80 х 90 х стилей

4167*4167

диско дизайн в стиле ретро 80 х неон

5556*5556

поп арт 80 х патч стикер

3508*2480

80 летний юбилей дизайн шаблона векторные иллюстрации

4083*4083

поп арт 80 х патч стикер

2292*2293

вектор поп арт иллюстрацией черная женщина шопинг

800*800

мемфис бесшовной схеме 80s 90 все стили

4167*4167

пентаграмма наклейки 80 х мультик звезд мультика стикер

2003*2003

поп арт 80 х патч стикер

3508*2480

поп арт 80 х патч стикер

3508*2480

80 основных форм силуэта

5000*5000

80 е брызги краски дизайн текста

1200*1200

поп арт 80 х патч стикер

3508*2480

аэрозольный баллончик увлажняющий лосьон bb cream парфюм для рук

3072*4107

blue series frame color can be changed text box streamer

1024*1369

рисованной радио 80 х

1200*1200

80 летия золотой шар векторный дизайн шаблона иллюстрация

4083*4083

но логотип компании вектор дизайн шаблона иллюстрация

4083*4083

3d модель надувной подушки bb cream

2500*2500

Воздушная подушка cc крем косметика косметика по уходу за кожей плакат пресная Воздушная подушка bb крем cc

3240*4320

чат комментарий образование синий значок на абстрактных облако сообщение

5556*5556

мемфис образца 80 s 90 стилей на белом фоневектор иллюстрация

4167*4167

в первоначальном письме вв логотипа

1200*1200

в первоначальном письме bd логотипа

1200*1200

поп арт 80 х патч стикер

2292*2293

мега распродажа 80

1200*1200

поп арт 80 х патч стикер

2292*2293

bb крем ню макияж косметика косметика

1200*1500

в первоначальном письме вв логотип шаблон векторный дизайн

1200*1200

80 х годов ретро слово градиент цвета искусства

1200*1200

Элементы рок н ролла 80 х

1200*1200

Ретро ТВ игра 80 х годов в стиле арт дизайн

1200*1200

bd письмо 3d круг логотип

1200*1200

буква bf фитнес логотип дизайн коллекции

3334*3334

в эти выходные только мега продажи баннер скидки до 80 с

10418*10418

80 летия векторный дизайн шаблона иллюстрация

4083*4083

Рождество 80 х годов ретро пиксель

9449*5315

Тенденция персонажа мультфильма 80 х годов

2000*2000

в первоначальном письме ба логотипа

1200*1200

витамин b3 ниацин вектор витамин золото масло таблетки значок органический витамин золото таблетки значок медицина капсула золотое вещество для красоты косметическое здоровье промо реклама дизайн 3d комплекс витаминов иллюстрация

5000*5000

Мода цвет 80 х годов ретро вечеринка слово искусства

1200*1200

★ Шестиугольник — cтатьи по математике .

. Информация

Пользователи также искали:

неправильный шестиугольник, периметр шестиугольника, площадь шестиугольника, правильный шестиугольник формулы, радиус шестиугольника, шестиугольник вписанный в окружность, сторона правильного шестиугольника вписанного в окружность, выпуклый шестиугольник, шестиугольника, Шестиугольник, шестиугольник, окружность, радиус, площадь шестиугольника, периметр шестиугольника, шестиугольник вписанный в окружность, выпуклый шестиугольник, радиус шестиугольника, правильный шестиугольник формулы, правильный, площадь, периметр, вписанный, сторона, правильного, вписанного, выпуклый, формулы, неправильный, неправильный шестиугольник, сторона правильного шестиугольника вписанного в окружность, cтатьи по математике.

шестиугольник,

Технические рисунки правильных многоугольников и круга

Технические рисунки правильных многоугольников и круга, лежащих в плоскостях П₁ и П₂. Обычно технические рисунки выполняют на основе изометрической проекции, так как в этом случае не надо сокращать размеры по оси у. Поэтому в дальнейшем главное место будет отведено объяснениям выполнения таких рисунков. На фиг. 602 показаны приемы выполнения технических рисунков правильных многоугольников и круга : I₁ II₁ III₁ IV₁ и V₁ на основе кабинетной проекции; I

2 II₂, III₂, IV₂ и V₂ а также I₃, II₃, III₃, IV₃, V₃ на основе изометрической проекции. Объяснения выполнения рисунков даны общие.

Правильный треугольник.

1. Правильный треугольник, а₃ = АВ (фиг. 602, I).
а) По направлению оси х’ проводят сторону АВ, из середины (точки К) которой проводят вверх по направлению оси z’ (а для I₃ по направлению оси у’) прямую; затем отрезок АК делят на глаз на три равные части и полученную

1/₃ АК откладывают на этой прямой вверх от точки К пять раз; получают точку С.
б) Соединив точку С с точками A и B, получают технические рисунки треугольника. Для нахождения центра О одну из сторон, например AС, делят пополам и полученную точку М соединяют прямой с точкой В.

Правильный четырехугольник.

2. Правильный четырехугольник, а₄ = АВ (фиг. 602, II).
а) По направлению данных осей проводят две взаимно пересекающиеся в точке О прямые; от точки О откладывают на них отрезки, равные A В|₂; получают точки 1, 2, 3 и 4.
б) Через эти точки проводят прямые, параллельные данным осям; получают технические рисунки квадрата.

Правильный пятиугольник.

3. Правильный пятиугольник, а₅ = АВ (фиг. 602, III).
а) По направлению оси х’ проводят сторону AB, из середины М которой проводят прямую по направлению оси z’ (а для III₃ — по направлению оси y’) и откладывают на ней от точки М три раза отрезок АМ = ¹/₂ АВ, получают точку D. Средний отрезок делят пополам, верхнюю его половину — еще раз пополам и полученную верхнюю четвертую часть — еще раз пополам, получают точку К. Затем отрезок АВ делят на глаз на три равные части AB ÷ 3 т. е. АN.

б) На продолжении (в обе стороны) отрезка АВ откладывают по АN и проводят вверх вертикальные линии (а для III₃ по направлению оси у’) до пересечения с прямой, проведенной через точку  К  (AM ÷ 8) параллельно   основанию АВ; получают точки С и Е. Соединив точки С и Е с точкой D и с точками А и B, получают технические рисунки правильного пятиугольника.

Правильный шестиугольник.

4. Правильный шестиугольник, а₆ = АВ (фиг. 602, IV).
а) По направлению оси х’ проводят сторону AВ, из концов которой проводят прямые по направлению оси z’ (а для IV

3 — по направлению оси у’).
Сторону АВ делят на глаз на три равные части; ¹/₃ АВ откладывают на линии, проведенной из точки A, пять раз, из полученной точки С проводят луч параллельно АВ. Внутри получившегося четырехугольника АВСD проводят диагонали; находят центр О.
б) Через центр О проводят линию параллельно AВ; она пересечет отрезок АС в точке М. На внешних концах проведенной линии откладывают отрезки по ОМ; получают точки Е и F. Соединяя точку Е с точками A и С, а точку F с точками D и В, получают технические рисунки правильного шестиугольника.

Круг.

5. Круг

(фиг. 602, V).
а) Согласно фиг. 602, II выполняют технический рисунок квадрата, сторона которого равна диаметру D круга. Отрезки А1 и А2 делят пополам — получают точки К и L отрезок L2 делят пополам — получают точку N. Линия, соединяющая точки К и N, пересечет диагональ в точке М.
б) Из точки М проводят лучи параллельно данным осям — получают на другой диагонали точки 5 и 6; точку 7 получают путем откладывания от центра О отрезка ОМ. Последовательно соединив точки 1, М, 2, 5, 3, 7, 4, 6 и 1 плавной кривой линией, получают технические рисунки круга.
Приемы выполнения технических рисунков правильных многоугольников на основе диметрической проекции отличаются от предыдущих построений технических рисунков только тем, что ось х’ проводят под углом 7°, а ось у’ — под углом 41° (см. фиг. 601, д); размеры линий, направленных по оси у, сокращают вдвое.
Форма овалов (точнее эллипсов) на технических рисунках круга, выполненных на основе диметрических проекций, во многом отличается от показанных на фиг. 602, V. Поэтому на фигуре №603 показаны приемы выполнения таких рисунков; как видно из чертежа, последовательность приемов остается такая же, как и на фиг.

602, V.

Плоская фигура произвольного очертания.

6. Плоская фигура произвольного очертания, лежащая в плоскостях П1 или П2, или П3 (согласно данной ортогональной проекции). Дана ортогональная проекция фигуры, лежащей в плоскости П1 или П2, или П3, пользуясь которой надо выполнить рисунки этой фигуры (на основе изометрической проекции) (фиг. 604, а). Через произвольно намеченную точку К’ проводят по направлению аксонометрических осей данной проекции ось симметрии и сторону основания фигуры (фиг. 604, б — г). Пользуясь размерами h⁴, l¹ и l², находят аксонометрические проекции точек Е и D; пользуясь размерами h³

и l³, находят аксонометрическую проекцию точки С и т. д.
Аксонометрические проекции точек Т, Р, М, L, H и G находят как симметричные точкам A, В, С, D, Е и F. Последовательно соединяя найденные точки соответствующими линиями, получают рисунки данной фигуры.
Примечание. Если фигура несим-метрична, то за начало осей координат принимают вершину какого-либо угла фигуры, например точку A, и через нее проводят соответствующие оси координат, от которых откладывают размеры l¹, l², l³ и т. д. и h¹, h², h³ и т. д.

Смотри далее не менее интересные материалы: Технические рисунки геометрических тел и определение технического рисунка.



Рисунок правильной пирамиды

Чертеж — первый и очень важный шаг в решении геометрической задачи. Каким должен быть рисунок правильной пирамиды?

Сначала вспомним свойства параллельного проектирования:

— параллельные отрезки фигуры изображаются параллельными отрезками;

— сохраняется отношение длин отрезков параллельных прямых и отрезков одной прямой.

Рисунок правильной треугольной пирамиды

Сначала изображаем основание. Поскольку при параллельном проектировании углы и отношения длин не параллельных отрезков не сохраняются, правильный треугольник в основании пирамиды изображается произвольным треугольником.

Центр правильного треугольника — точка пересечения медиан треугольника. Поскольку медианы в точке пересечения делятся в отношении 2:1, считая от вершины, мысленно соединяем вершину основания с серединой противолежащей стороны, приблизительно делим ее на три части, и на расстоянии 2 частей от вершины ставим точку. Из этой точки вверх проводим перпендикуляр. Это — высота пирамиды. Перпендикуляр рисуем такой длины, чтобы боковое ребро не закрывало изображение высоты.

Рисунок правильной четырехугольной пирамиды

Рисунок правильной четырехугольной пирамиды также начинаем с основания. Поскольку параллельность отрезков сохраняется, а величины углов — нет, то квадрат в основании изображается параллелограммом.  Желательно острый угол этого параллелограмма делать поменьше, тогда боковые грани получаются больше. Центр квадрата — точка пересечения его диагоналей. Проводим диагонали, из точки пересечения восстанавливаем перпендикуляр. Этот перпендикуляр — высота пирамиды. Выбираем длину перпендикуляра таким образом, чтобы боковые ребра не сливались между собой.

Рисунок правильной шестиугольной пирамиды

Поскольку при параллельном проектировании параллельность отрезков сохраняется, основание правильной шестиугольной пирамиды — правильный шестиугольник — изображаем шестиугольником, у которого противолежащие стороны параллельны и равны. Центр правильного шестиугольника — точка пересечения его диагоналей. Чтобы не загромождать рисунок, диагонали не проводим, а находим эту точку приблизительно. Из нее восстанавливаем перпендикуляр — высоту пирамиды — так, чтобы боковые ребра не сливались между собой.

Занимательная математика. Правильный шестиугольник

Не знаю уж в силу чего, но у меня иногда возникает навязчивая идея решить ту или иную задачу из школьного/институтского курсов по математике или программированию. Обычно (пока что) это что-то достаточно простое. Интересен сам процесс получения результата на основе тех знаний, которые есть в голове на данный момент.  

Как-то раз зашел разговор о сотах, пчелиных сотах. Раньше я не особо задумывался о том, что сота представляет собой правильный шестиугольник. Не то что не знал, а просто не думал о том, как эти маленькие создания сами(!) создают такую структуру, состоящую из абсолютно правильных шестиугольников… Задачка пришла сама собой — нарисовать правильный шестиугольник, как водится, только с использованием циркуля и линейки.

Шаг 1. Рисуем окружность, в которую будет вписан наш шестиугольник

Шаг 1

Шаг 2. Докажем, что сторона правильного шестиугольника равна радиусу окружности, в которую он вписан.

Шаг 2

Док-во: Исходя из условий (и признаков рав-ва треугольников), понимаем, что все три треугольники в верхней части рисунка — равны между собой.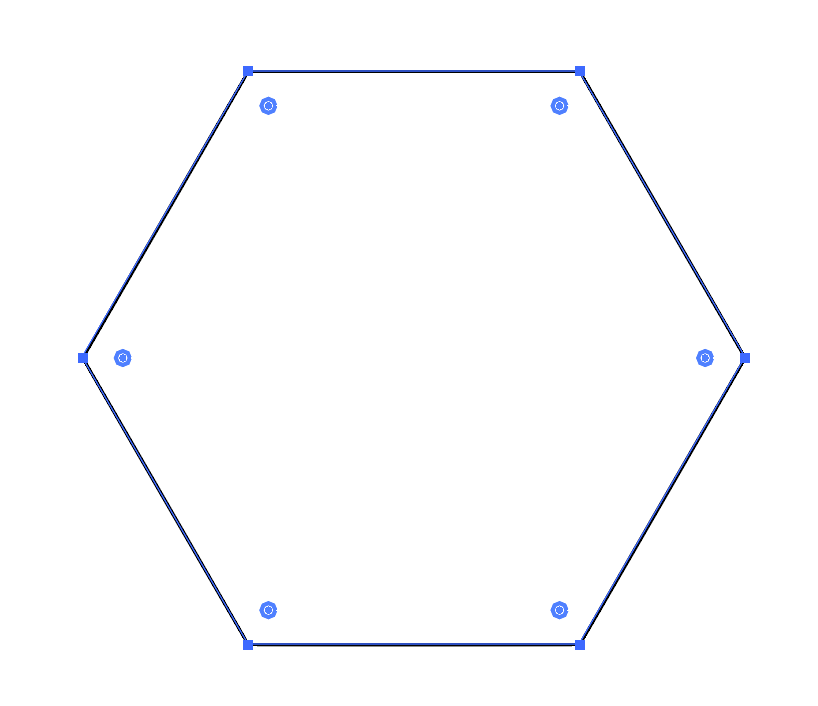 Соотв. угол Альфа = 60° (180 / 3), а это значит, что треугольник равносторонний (на остальные углы в треугольнике приходится по 120° и они так же равны между собой, как прилежащие к равным сторонам треугольника) и, соотв. сторона шестиугольника равна радиусу.

Шаг 3

Шаг 3. Строим шестиугольник: ставим циркуль в произвольное место на окружности, откладываем радиус на окружности, переносим циркуль в только что поставленную метку, делаем засечку дальше и так еще 4 раза, пока не придем в исходную точку. При помощи линейки соединяем полученные точки. Вуаля.

P.S. Иллюстрации сделаны на планшете, поэтому не придирайтесь  картинка с сотами взята из инета (google.com, поиск: пчелиные соты)

Контакты:

Площадь основания правильной шестиугольной призмы. Формулы площади правильного шестиугольника

В школьном курсе геометрии изучаются свойства различных видов призм, включая шестиугольную. Последняя часто встречается при рассмотрении кристаллических решеток металлов, поэтому знание ее характеристик важно при определении свойств этого класса материалов. Данная статья посвящена вопросу площади основания правильной шестиугольной призмы.

Объемная фигура — призма

В геометрии под призмой понимают такую фигуру, которая образована двумя одинаковыми многоугольниками, расположенными параллельно друг другу, и некоторым числом параллелограммов, соединяющих вершины названных многоугольников. Если основание образовано многоугольником с n вершинами, то количество параллелограммов также будет равно n.

Призмы характеризуются по типу многоугольника в основании (правильные и неправильные треугольные, четырехугольные и так далее), который может быть вогнутым и выпуклым, и по углу между боковыми гранями (параллелограммами) и основанием (прямоугольные и косоугольные).

Основными элементами любой призмы являются ее грани (Г), ребра (Р) и вершины (В). На рисунке выше приведена для примера треугольная призма.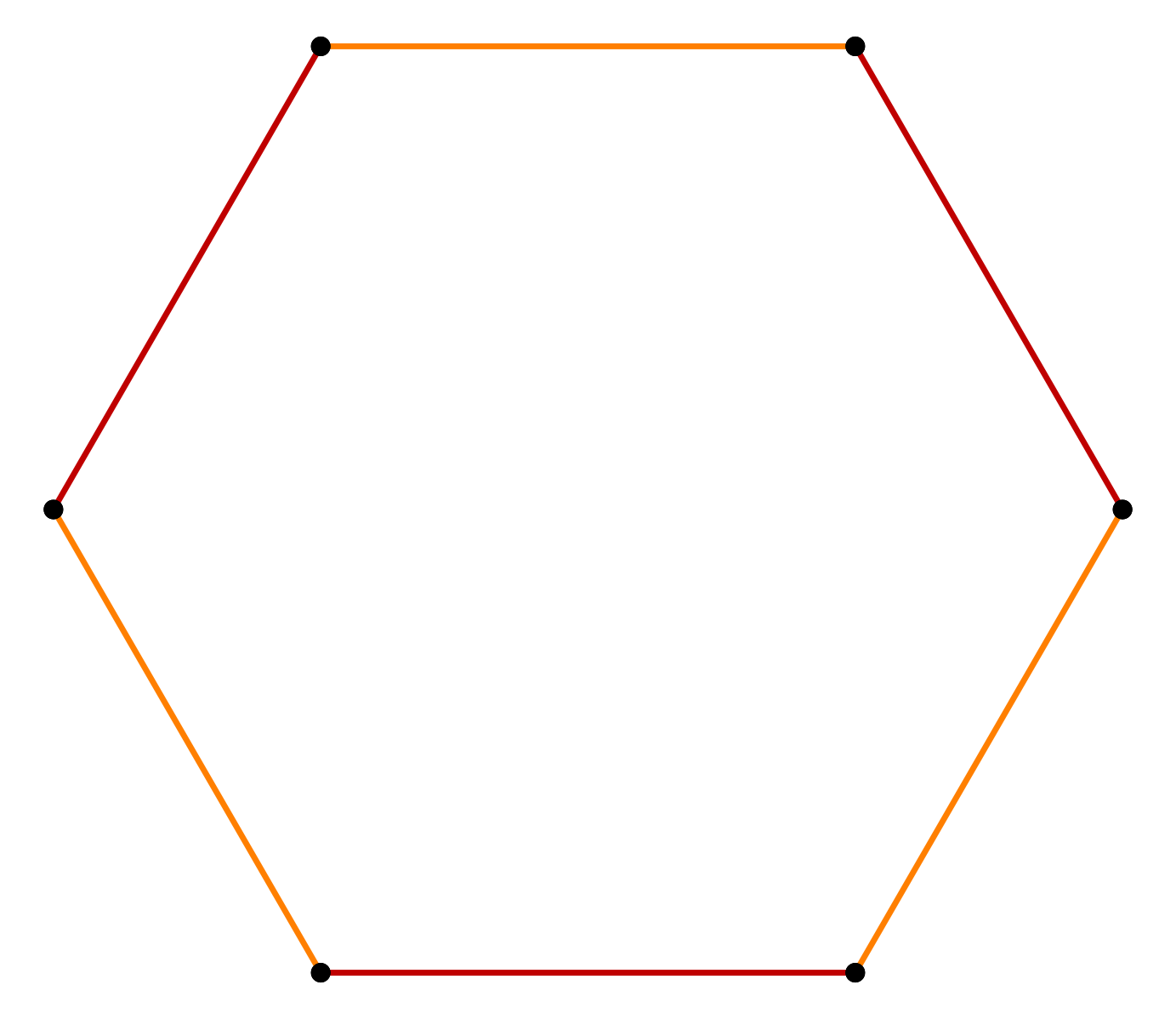 Как видно, она имеет 6 вершин (по 3 для каждого основания). Ниже приведена развертка этой призмы. Рисунок показывает, что она состоит из 5 граней: 2 треугольника и 3 прямоугольника.

Чтобы посчитать число ребер рассматриваемой фигуры, следует применить теорему Эйлера:

Р = В + Г — 2

Это выражение дает число ребер для этой призмы, равное 9. Действительно, если обратиться к трехмерному изображению призмы выше, то можно увидеть, что 6 ребер образуют основания фигуры, и еще 3 ребра являются результатом пересечения прямоугольников.

Призма шестиугольная

Перед рассмотрением вопроса площади основания правильной шестиугольной призмы, сначала познакомимся с этой фигурой. Из названия и приведенной выше классификации призм понятно, что речь пойдет о фигуре, в основании которой лежит шестиугольник. Это означает, что число сторон в такой призме будет равно 8 (два основания и шесть параллелограммов), а число вершин составит 12 (6 + 6). Тогда количество ребер будет равно:

Р = 12 + 8 — 2 = 18

Из этих 18-ти ребер основаниям принадлежат 12.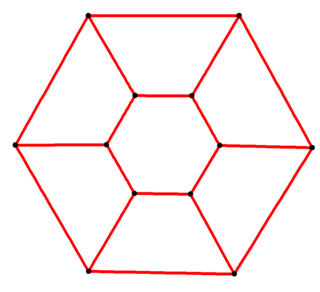

Если в основании находится правильный шестиугольник, а углы между боковыми сторонами (параллелограммами) и основаниями равны 90^o, то такая фигура будет называться прямоугольной призмой с правильным шестиугольником в основании, или просто правильной шестиугольной призмой. Ее схематическое изображение приводится ниже.

В правильной шестиугольной призме все ребра равны только в том случае, если c = a, где c — высота (длина бокового ребра) и a — длина стороны шестиугольника. В общем случае c ≠ a.

Далее приведем формулы для расчета площади поверхности и объема рассматриваемой призмы. Чтобы это сделать, необходимо знать площадь основания правильной шестиугольной призмы.

Площадь шестиугольника

Получим формулу площади правильного шестиугольника. Для этого рассмотрим эту плоскую фигуру, которая изображена на рисунке ниже.

Видно, что многоугольник состоит из шести одинаковых сторон, которые образуют угол 120^o. Поскольку этих углов шесть, то их сумма составит 720^o.

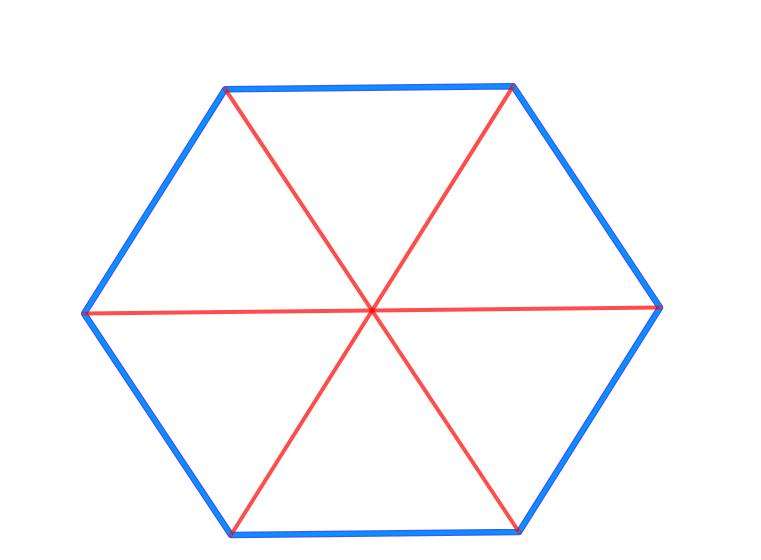
Рисунок также показывает, что правильный шестиугольник гармонично вписывается в окружность. Если соединить центр окружности с каждой вершиной фигуры, то получим 6 одинаковых треугольников. Поскольку угловая мера всей окружности составляет 360^o, то соответствующие углы треугольника равны 60^o (360^o/6). Они обозначены на рисунке. Поскольку каждый серый отрезок делит угол шестиугольника пополам, то оставшиеся два треугольника также равны по 60^o. Это означает, что изображенные 6 треугольников являются равносторонними. Длина каждой из их сторон равна стороне шестиугольника, обозначим ее буквой a.

Из курса геометрии известно, что площадь S₃ любого треугольника равна произведению его высоты h на сторону a, к которой она проведена, деленному пополам, то есть:

S₃ = h*a/2

Длину h легко вычислить, используя понятие о тригонометрической функции. Она равна:

h = a*cos(30^o) = a*√3/2

Тогда площадь всего треугольника равна:

S₃ = √3*a²/4

Умножая эту площадь на 6, получаем формулу площади правильного шестиугольника:

S₆ = 6*S₃ = 3*√3*a²/2

Для полноты информации следует отметить, что существует формула площади правильного многоугольника с произвольным количеством сторон n. Ниже приведено соответствующее выражение:

S_n = n/ a²*ctg(pi/n)

Если подставить в это выражение значение n = 6, то мы получим формулу площади основания правильной шестиугольной призмы, которая совпадет с приведенной выше.

Заметим, что деление шестиугольника на 6 равносторонних треугольников означает, что шестиугольная призма состоит из 6 правильных треугольных призм.

Площадь поверхности

Полная площадь поверхности любой призмы может быть получена, если сложить соответствующие площади S_o для двух оснований и для боковой поверхности S_b, представленной параллелограммами:

S = 2*S_o + S_b

Изучим развертку рассматриваемого вида призмы, которая приведена на рисунке ниже.

Мы видим, что призма состоит из двух одинаковых шестиугольников и 6 прямоугольников. Обозначим сторону основания буквой a, а стороны прямоугольников буквами a и c (сторона a является общей для шестиугольника и прямоугольника). В таком случае площадь полной поверхности шестиугольной призмы будет составлять:

S = 2*3*√3*a²/2 + 6*a*c = 3*a*(√3*a + 2*c)

Объем призмы

Эта важная величина для любого реального объекта в случае призмы находится просто: необходимо лишь умножить площадь основания на высоту фигуры, то есть:

V = S_o*h

Поскольку мы рассматриваем прямоугольную призму, то ее высота равна длине бокового ребра, то есть h = c. Тогда формула для объема правильной шестиугольной призмы запишется в виде:

V = 3*√3*a²*c/2

Таким образом, для определения площади и объема рассматриваемой фигуры необходимо знать длину ее ребра в основании и на боковой поверхности.

Для чего нужно знать свойства шестиугольной призмы?

Как было сказано во введении, эти призмы встречаются в природе в металлах. В частности, кристаллическая атомная упаковка титана, цинка, циркония, магния и некоторых других металлов имеет форму шестиугольной призмы, в основании которой лежат 7 атомов (6 в вершинах и 1 в центре). От соотношения длины ребра этой фигуры к длине стороны основания зависят многие механические свойства этих металлов (деформационные и упругие характеристики).

Выше приведен пример этой упаковки атомов, который носит сокращенное название ГПУ (гексагональная плотная упаковка).

пошаговое строительство с фото и видео

Интересная форма шестигранной беседки вызывает удивление и восхищение. Классические «квадраты» и «прямоугольники» всем уже порядком надоели, хочется чего-то нового и эстетичного. Именно сооружение с шестью гранями в данной ситуации оказывается в центре внимания.

Идея деревянной шестигранной беседки

Больше фотографий вы сможете найти в публикации про идеи дачных шестигранных беседок.

В этой статье мы сделаем упор на тонкости строительства, а также приведём подробную инструкцию из 13 шагов

В сооружении шестигранной формы нет абсолютно ничего сложно. Даже установка крыши не отличается особой сложностью, хотя некоторые особенности присутствуют.

В данной статье мы поэтапно покажем процесс строительства беседки шестиугольной формы.

Подготовка к работе

Выбор строительного материала

На данном этапе вам нужно определиться со строительным материалом. Наиболее популярными вариантами являются дерево и металл (профильная труба). В случае с деревом можно использовать брус 100 на 100 мм, а металлом — трубу с сечением 60 на 40 мм.

Из дерева

Из металла

Если вы предпочитаете надежный кирпич, тогда вся технология воздвижения будет заметно отличаться. Необходимо будет заливать надежный фундамент (ленточного или монолитного типа), а затем заниматься кирпичной кладкой. Каких-то конструктивных особенной здесь нет, достаточно будет выложить стены в шесть граней.

Из кирпича и камня

Чертежи с размерами и пояснениями

Если вы не до конца понимаете устройство шестигранной беседки, тогда предлагаю изучить чертежи ниже.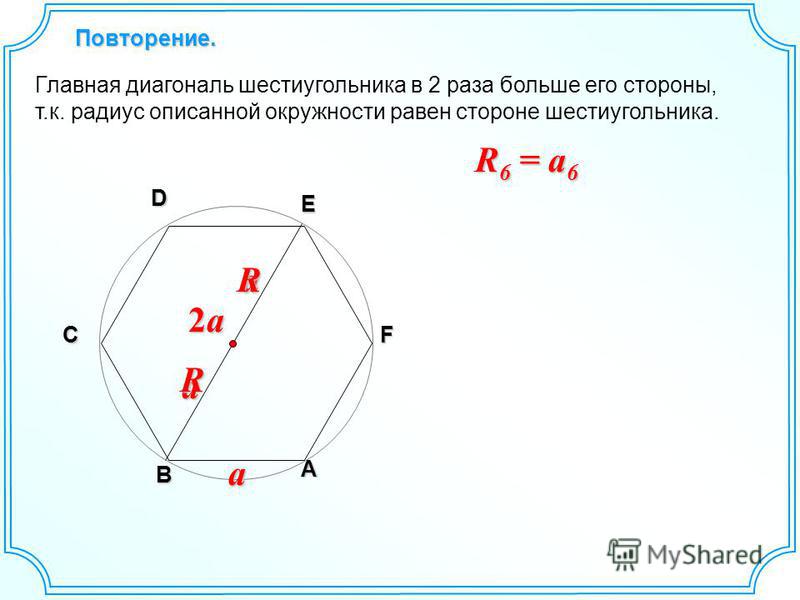 На них отчётливо показаны размеры потенциальных строений, площадь, размеры стропильной системы, соединения в стыках названия составных частей.

Приведенных проектов достаточно, чтобы у вас сложилось определенно мнение о подобной форме. На рисунках разве что не показана обшивка крыши, которая делается для укладки мягкой черепицы, об этом мы будем говорить позже.

Строительство своими силами

Разметка шестигранной формы основания

Беседка с площадью 6 кв/м. Длина одного бруска обвязки — 1,5 м.

Первая задача, которую необходимо будет решить, это определиться с размерами беседки и сделать разметку правильного шестиугольника (гексагон). Для этого нам понадобится рулетка, колышки и шесть одинаковых брусков нижней обвязки.

1. Изготавливаем 6 брусков строго одинакового размера.
2. Выкладываем их на заранее расчищенную от мусора поверхность в форме шестиугольника (рисунок ниже).
3. В местах стыков забиваем колышки.
4. Убираем бруски и готовимся к закладыванию фундамента.

Обвязка в форме правильного шестиугольника

Фундамент

Для основания дешевле всего использовать фундаментные блоки, которые можно купить в магазине или изготовить самостоятельно. Если уж вообще работать «на совесть», то имеется более дорогой, но очень надёжный вариант фундамента с буронабивными сваями.

Основная задача состоит в создании ровной (по уровню) плоскости, поверх которой пойдёт нижняя обвязка.

Основание из блоков 20 на 20 на 40 см

Соединения в нижней обвязке

Для крепления нижней обвязки можно использовать два способа:

1. В половину дерева (на конце каждого бруса отрезаем половину сечения и кладём друг на друга).
2. С помощью металлических уголков.

Уголков в большинстве случаев достаточно, чтобы плотно зафиксировать брус. Но если вы хотите всё сделать «на века», тогда можно заняться выпиливанием и добавить дополнительное крепление. На фотографии выше, где показано основание из блоков, данное соединение представлено во всей красе.

Соединение в полдерева

Установка столбов

Необходимо установить шесть вертикальных столбов и зафиксировать их под углом 90 градусов. Удобнее всего работать с напарником, который будет придерживать столб, пока вы его будете крепить к нижней обвязке.

По аналогии с обвязкой, используем металлические уголки и саморезы. На фотографии ниже вы можете наглядно увидеть готовый результат.

Если вам недостаточно металлических уголков, то для дополнительной надежности можно использовать соединение с помощью шипа и гнезда. работы заметно прибавиться, но устойчивость столба возрастет в разы.

Шиповое соединение

Крепление столба к нижней обвязке на уголки

 Пол

Для пола можно использовать любой вид досок, который выдержит людей и мебель внутри. Классическим вариантом является сороковая обрезная доска из сосны. Более дорогой вариант — лиственница. Способов укладки пола имеется несколько:

• Сплошняком, параллельно одной из граней.
• В каждой из шести секций пола отдельно.

Сплошняком

Устройство пола

С красивым полом

Возведение крыши

Сразу же небольшой секрет: стропильную систему лучше всего собирать на земле. Это гораздо проще и надежнее. Затем её необходимо будет поднять на вертикальные столбы и зафиксировать. Эта техника используется повсеместно, поэтому рекомендую и вам её тоже.

Стропильная система состоит из шести брусков (чаще всего используется брус 150 на 50 мм), которые крепятся в центре друг с другом с помощью деревянного шпиля и металлического фартука, а также в каждом угле отдельно к верхней обвязке.

Собранная на земле крыша (без обрешётки)

Стропильная система (вид сверху)

Стропильная система (вид снизу)

Выбор и укладка кровли

При выборе кровли необходимо исходить из того, готовы ли вы заниматься обшивкой крыши ОСП плитами.

Установив стропильную систему и обрешётку, вы можете уложить, например, профнастил или металлочерепицу. Если же вы хотите уложить мягкую черепицу (типа Шинглас), то необходимо дополнительно обшить крышу плитами, поверх которых уже и будет укладываться кровля.

мягкая черепица

Ондулин

Шестискатная

Пошаговая инструкция с фото

Ниже приведено строительство шестигранной беседки в 13 шагов. Каждая фотографии подписана и описывает процесс, который происходил. В следующем пункте будет показано видео, в котором данный процесс показан ещё нагляднее.

Шаг 1. Основание — фундаметные блоки из бетона вокруг лавочки

Шаг 2. Снятие опалубки блоков

Шаг 3. Установка вертикальных столбов

Шаг 4. Установка верхней обвязки

Шаг 5. Готовая нижняя обвязка и перила

Шаг 6. Изготовление деревянного шпиля

Шаг 7. Возведение стропильной системы

Шаг 8. Обшивка стен

Шаг 9. Обшивка крыши

Шаг 10. Обшитая крыша

Шаг 11. Укладка мягкой черепицы

Шаг 12. Изготовление водоотлива

Шаг 13. Готовая постройка

Видеоинструкция

Интересное видео по строительству представил канал на Youtube под названием «Вся наша жизнь!». С помощью фотографий, авторы видеоролика показывают свои шаги от момента возведения фундамента до укладки мягкой черепицы на крышу.

Как найти диагональ шестиугольника

Обновлено 14 февраля 2020 г.

Розанн Козловски

Рецензент: Lana Bandoim, B.S.

Диагонали шестиугольников можно рассчитать, понимая структуру шестиугольника и соотнося сторону шестиугольника с его радиусом. Продолжайте читать, чтобы узнать, как делать математику.

Свойства правильных шестиугольников

Шестиугольник — это шестиугольник или шестиугольник. Слово шестиугольник происходит от греческого hex, означающего шесть, и gonia, что означает угол или угол.

Свойства правильных шестиугольников:

• внутренние углы 120 градусов
• сумма внутренних углов шестиугольника составляет 720 градусов
• с каждой стороны, а внутренние углы равны друг другу
• нет изогнутых сторон
• : все линии соединяются, образуя замкнутую форму.

Неправильный шестиугольник имеет шесть неравных сторон. У выпуклого шестиугольника нет углов, направленных внутрь. Угол вогнутого шестиугольника больше 180 градусов (направлен внутрь).

Диагонали шестиугольников

Чтобы найти диагонали шестиугольников, используйте формулу:

n (n-3) / 2 , где n — количество сторон многоугольника.

Для шестиугольника n = 6 и 6 (6-3) / 2 равно девяти диагоналям.

У правильного шестиугольника радиус равен длине стороны. Это создает шесть треугольников. Напомним, что радиус шестиугольника — это центральная точка шестиугольника по отношению к одному из его углов.

Также напомним, что диагональ — это линия, соединяющая два противоположных угла прямой формы.Для правильных шестиугольников девять диагоналей образуют шесть равносторонних треугольников.

Определение длины диагоналей в шестиугольниках

Поскольку девять диагоналей образуют шесть равносторонних треугольников, а радиус равен длине стороны, это упрощает определение длины каждой диагональной линии. Если одна сторона шестиугольника известна, тогда известны все стороны, и диагонали рассчитываются с использованием следующих основных шагов:

Шаг 1: Определите длину одной стороны шестиугольника

Все стороны равны в правильном шестиугольник.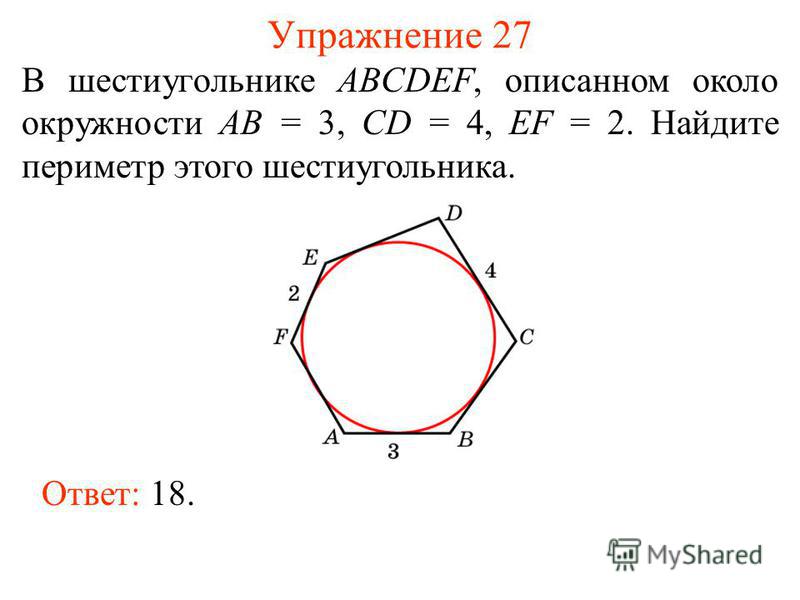 Если известна длина одной стороны, то известны все. Известное или данное обозначается буквой «g» (заданная сторона).

Шаг 2: Расчет диагонали шестиугольника

Запишите уравнение для нахождения диагонали правильного шестиугольника:

d (диагональ) = 2g (заданная сторона)

Умножьте известную или заданную сторону шестиугольника на два . Изделие представляет собой длину диагонали правильного шестиугольника.

Например, если заданная сторона равна 10 метрам, то диагональ будет: 2 (10 метров) или 20 метров.

Диагонали неправильного шестиугольника

Стандартной формулы для определения диагоналей неправильного шестиугольника не существует.

Хотя вы можете рассчитать количество диагоналей неправильного шестиугольника, для определения диагонали неправильного шестиугольника потребуется разбить шестиугольник на треугольники. Однако, если это не прямоугольные треугольники, не существует формата для определения длины внутренней стороны, диагонали. Теорема Пифагора применима только к прямоугольным треугольникам.

Если бы каждая сторона и угол были заданы вместе с площадью, то можно было бы определить диагонали; однако маловероятно, что в задаче будет указано так много переменных.

Шестиугольник в природе

Улей — одна из самых легко узнаваемых шестиугольных структур в природе. В улье есть соединенные между собой шестиугольники, и эта структура оказалась хорошей для упаковки, так как не оставляет пустого пространства внутри улья. По той же причине мыльные пузыри, выстраиваясь в линию, образуют шестиугольные формы.

Когда вода вращается с большой скоростью, она принимает форму шестиугольника. Точно так же на северном полюсе Сатурна есть постоянное грозовое облако в форме шестиугольника.

Углеродное кольцо представляет собой шестиугольник с графитом на каждом углу. Глаза стрекозы имеют шестиугольную форму, как и узор на панцире черепахи.

Cool math .com — онлайн-словарь по математике

Простые для понимания математические определения для математики K-Algebra
Просто прокрутите вниз или щелкните нужное слово, и я прокручу вниз для вас!

Полусфера Полусфера — это половина сферы. На нашей планете верхняя половина называется Северным полушарием, а нижняя половина — Южным полушарием.

Гептагон Семигранник — это семиугольник. Семиугольник на картинке справа — правильный семиугольник, потому что все стороны и углы одинаковы (совпадают). Для получения дополнительной информации о семиугольниках посетите мою страницу свойств семиугольников.

Шестиугольник Шестиугольник — это шестиугольный многоугольник. Шестиугольник на картинке справа — правильный шестиугольник, потому что все стороны и углы одинаковы (совпадают). Для получения дополнительной информации о шестиугольниках посетите мою страницу свойств шестиугольников.

Шестигранник Шестигранник — это шестигранная трехмерная геометрическая фигура (многогранник). Правильный шестигранник — это куб, потому что все грани одинакового размера (конгруэнтны).

Горизонтально Горизонтальная линия — это линия, проходящая вдоль горизонта.

полигональных изображений

Мы получили множество отличных решений этой проблемы, поэтому спасибо Питеру из Даремской школы Джонстона в Дареме, Тому, Ронану, Карми, Нардиа, Брин, Джастину, Вивеку, Прие, Адену, Тегану и Люси от Школа Святого Стефана Каррамар в Австралии, Алекс из Межобщинной школы Цюриха в Швейцарии, Махди из Международной школы Махатмы Ганди в Индии и Беркли из начальной школы Мэри Хоган в США за то, что прислали нам свои решения. \ circ $.

Махди прислал нам это подробное и ясное объяснение того, как найти все углы на диаграмме пятиугольника.

Как сделать шестиугольные изображения для Instagram — Hexagon Project

Можете ли вы помочь обеспечить ТВОРЧЕСКИЙ поток ПОДКЛЮЧЕНИЯ и СВЯЗИ в такое время DIS-connected?

Проект «Гексагон взаимозависимости» обращается ко всем, кто считает, что мы должны оставаться на связи. В такие времена человеческая связь может расцветать по-разному.Что с помощью нашего Искусства мы можем рассказать выразительную, прогрессивную историю того, кто мы есть и как мы справляемся. Мы называем это «Искусство в действии». Действие в искусстве ». Что с помощью нашего Искусства мы можем посылать вдохновляющие визуальные послания сочувствия, надежды и сострадания тем, кто в любом случае болен, находится под угрозой или уязвим. Открыт для всех возрастов.

Используйте следующие хэштеги, и мы поделимся ими в нашем Instagram @interdependencehexagonproject

# hexagonproject2020 #hexagonproject #hexagonproject

Традиционный путь:

1. Загрузите шаблон шестиугольника с нашего веб-сайта в разделе «Формы» и распечатайте или создайте свой собственный шестиугольник.
2. Создайте свой шестиугольник на шаблоне или другой опоре, используя любые художественные материалы, включая коллажные фотографии из газет, журналов или свои собственные фотографии и трехмерные материалы.
3. Фотография на контрастном фоне и пост! Если хотите, укажите, где вы живете.

в цифровом формате:

Чтобы обрезать изображения до шестиугольника (и многого другого), вы можете использовать Canva в веб-браузерах Chrome, Firefox или Edge.

При регистрации выберите «Пропустить», когда приложение пытается зарегистрировать вас на платный план, бесплатная версия отлично подходит для наших целей.

1. Создайте изображение с помощью шаблона Instagram для квадратного изображения 1080 x 1080 пикселей или создайте пользовательские размеры 1260 x 1080 для широкого изображения (шестиугольник указывает слева и справа) или 1080 x 1260 для высокого изображения (шестиугольник указывает на Верх и низ).
2. Выберите «Элементы» в меню вдоль левого края интерфейса, а затем «Рамки» (не формы!) И прокрутите вниз, чтобы найти шестиугольную рамку.
3. Выберите шестигранную рамку и расположите, поверните и измените размер в соответствии с вашими предпочтениями.
4. Затем выберите «Загрузки» в меню слева, чтобы загрузить свое изображение. Щелкните свое изображение (вы можете повернуть и обрезать его), затем перетащите его, чтобы закрепить в шестиугольной рамке. Дважды щелкните шестиугольник / изображение, чтобы отредактировать его (вы можете переместить изображение и изменить его размер внутри рамки.
5. При желании вы можете добавить фон из меню вдоль левого края.
6. Загрузите изображение в формате jpeg. Выберите «Загрузить» из меню «Опубликовать» в правом верхнем углу.

Другой цифровой ресурс:

https: // fotorus.en.uptodown.com/android

или https://apps.apple.com/us/app/fotorus-camera-photo-editor/id457517348

фигур для детей — правильные многоугольники

Добро пожаловать в Math Salamanders Shapes для детей.

Здесь вы найдете широкий спектр бесплатных печатных форм правильных многоугольников.

У Math Salamanders есть большой банк бесплатных картинок для печати.

Каждый из листов фигур для печати доступен в цветном или черно-белом цвете.

Использование этого клипарт с фигурами поможет вашему ребенку научиться распознавать фигуры и учиться. о различных свойствах фигур.

На листах разной формы мы показали формы разного размера и ориентации, чтобы Ваш ребенок будет распознавать вариации одной и той же формы и замечать свойства, которые имеют все одинаковые формы.

Листы можно использовать как часть математического дисплея, как карточки или как раскраски для печати.

Здесь вы найдете наш ассортимент бесплатных 2D-листов с правильными многоугольниками.

Следующие распечатки содержат изображения правильных многоугольников, от равносторонних треугольников (3-сторонних многоугольников) до додекагонов (12-сторонних многоугольников). что ваш ребенок должен знать.

Их можно использовать для информации или как часть дисплея.

Использование этих листов поможет вашему ребенку:

• распознавать и называть различные типы правильных многоугольников.

Взгляните на еще несколько наших рабочих листов, похожих на эти.

Если вы ищете дополнительную информацию о правильных формах или хотите несколько изображений групп правильных форм на одном листе, затем попробуйте страницу ниже.

На странице «Обычные формы» вы найдете множество фактов о правильных формах, рабочих листов и печатных материалов.

Здесь вы найдете подборку листов 2D-формы, разработанных чтобы помочь вашему ребенку выучить свои имена и свойства двумерных фигур.

Использование этих листов поможет вашему ребенку:

• распознают ряд 2D-форм;
• распознает, что квадрат также является членом семейства прямоугольников;
• распознает формы в разных ориентациях и размерах.

Все бесплатные листы фигур для печати в этом разделе поддерживают Тесты по элементарной математике.

Здесь вы найдете подборку листов для печати в формате 2d и 3d.

Каждый лист доступен в цветном или черно-белом цвете, с маркировкой или без нее.

Использование этих листов поможет вашему ребенку:

• распознает и назовет ряд двух- и трехмерных фигур;
• распознает правильные и неправильные формы.

Здесь вы найдете подборку листов 3D-форм, предназначенных для помогите своему ребенку узнать свои имена и свойства трехмерных фигур.

Использование этих листов поможет вашему ребенку:

• распознают ряд трехмерных форм;
• знает некоторые свойства различных 3D-форм;
• распознает трехмерные формы в разных ориентациях и размерах.

Все бесплатные листы фигур для печати в этом разделе поддерживают Тесты по элементарной математике.

Саламандры-математики надеются, что вам понравятся эти бесплатные распечатываемые рабочие листы по математике. и все другие наши математические игры и ресурсы.

Мы приветствуем любые комментарии о нашем сайте или рабочие листы в поле для комментариев Facebook внизу каждой страницы.

Шестиугольник — Энциклопедия Нового Света

В геометрии шестиугольник — это многоугольник с шестью ребрами и шестью вершинами. У правильного шестиугольника есть символ Шлефли {6}.

Шестигранник правильный

Внутренние углы правильного шестиугольника (у которого все стороны и все углы равны) равны 120 °, а шестиугольник — 720 градусов.Он имеет шесть линий симметрии. Подобно квадратам и равносторонним треугольникам, правильные шестиугольники подходят друг к другу без каких-либо зазоров, чтобы укладывал плоскость (три шестиугольника, пересекающиеся в каждой вершине), и поэтому они полезны для построения мозаики.

Ячейки сотового улья шестиугольные по этой причине, а также потому, что форма позволяет эффективно использовать пространство и строительные материалы. Диаграмма Вороного правильной треугольной решетки представляет собой сотовую мозаику шестиугольников.

Площадь правильного шестиугольника со стороной t {\ displaystyle t \, \!} Определяется выражением А = 332т2≃2.{2}.}

Периметр правильного шестиугольника со стороной t {\ displaystyle t \, \!}, Конечно же, 6t {\ displaystyle 6t \, \!}, Его максимальный диаметр 2t {\ displaystyle 2t \, \!} , и его минимальный диаметр t3 {\ displaystyle t {\ sqrt {3}} \, \!}.

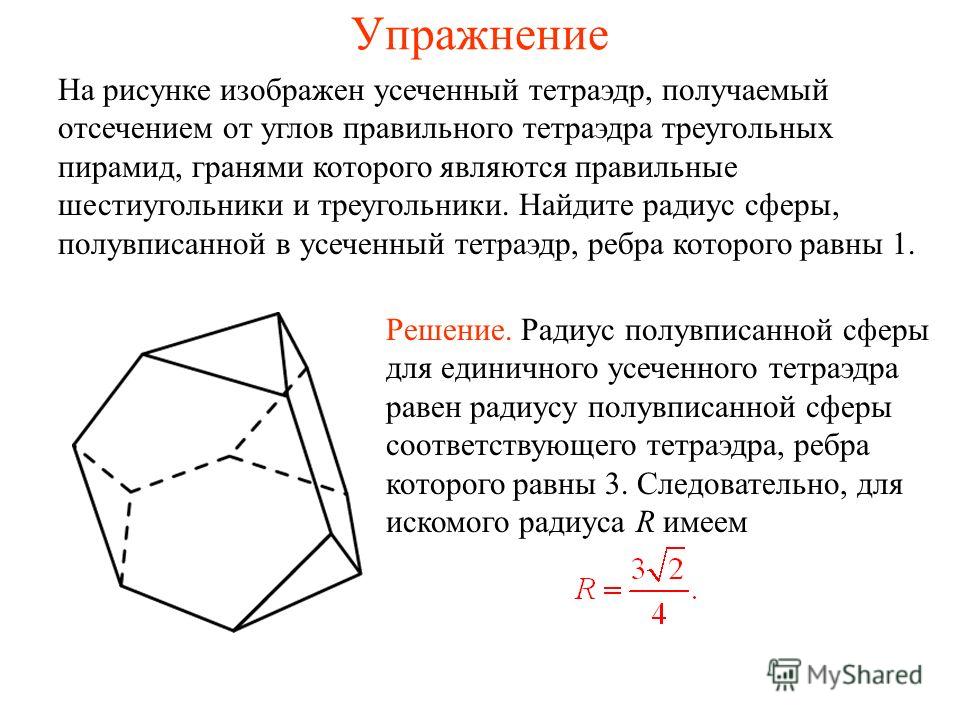
Платоновы тела не состоят из правильных шестиугольников. Архимедовы тела с несколькими шестиугольными гранями — это усеченный тетраэдр, усеченный октаэдр, усеченный икосаэдр (футбольного мяча и фуллеренов), усеченный кубооктаэдр и усеченный икосододекаэдр.

Шестиугольники натуральные и искусственные

• Щитки панциря черепахи

• Гексагональное облако северной полярности на Сатурне, обнаруженное космическим аппаратом «Вояджер-1» и подтвержденное в 2006 году Кассини [1] [2] [3]

• Микрофотография снежинки

• Кристаллическая структура молекулярного шестиугольника, состоящего из гексагональных ароматических колец, описана Müllen и соавторами в Chem. Евро. Дж., 2000, 1834-1839 гг.

• Естественно сформированные базальтовые колонны с Дороги гигантов в Ирландии; большие массы должны медленно остывать, чтобы образовался полигональный узор изломов

• Вид с воздуха на Форт Джефферсон в национальном парке Драй Тортугас

• Зеркало космического телескопа Джеймса Уэбба состоит из 18 шестиугольных сегментов.

См. Также

Список литературы

• Арноне, Венди. 2001. Геометрия для чайников .Хобокен, Нью-Джерси: Для чайников (Wiley). ISBN 0764553240
• Хартсхорн, Робин. 2002. Геометрия: Евклид и за его пределами . Тексты для бакалавриата по математике. Нью-Йорк, штат Нью-Йорк: Спрингер. ISBN 0387986502
• Лефф, Лоуренс С. 1997. Простая геометрия . Хауппог, Нью-Йорк: Образовательная серия Бэррона. ISBN 0764101102
• Стиллвелл, Джон. 2005. Четыре столпа геометрии . Тексты для бакалавриата по математике. Нью-Йорк, штат Нью-Йорк: Спрингер. ISBN 0387255303

Внешние ссылки

Все ссылки получены 24 декабря 2017 г.

Полигоны
Треугольник • Четырёхугольник • Пентагон • Шестиугольник • Гептагон • Восьмиугольник • Эннеагон (Нонагон) • Десятиугольник • Шестиугольник • Додекагон • Трискаидакагон • Пентадекагон • Шестиугольник • Гептадекагон • Эннеадекагон • Икозагон • Хилиагон • Мириагон

Кредиты

Энциклопедия Нового Света Писатели и редакторы переписали и завершили статью Википедия в соответствии со стандартами New World Encyclopedia .Эта статья соответствует условиям лицензии Creative Commons CC-by-sa 3.0 (CC-by-sa), которая может использоваться и распространяться с указанием авторства. Кредит предоставляется в соответствии с условиями этой лицензии, которая может ссылаться как на участников Энциклопедии Нового Света, участников, так и на самоотверженных добровольцев Фонда Викимедиа. Чтобы процитировать эту статью, щелкните здесь, чтобы просмотреть список допустимых форматов цитирования. История более ранних публикаций википедистов доступна исследователям здесь:

История этой статьи с момента ее импорта в энциклопедию Нового Света :

Примечание. Некоторые ограничения могут применяться к использованию отдельных изображений, на которые распространяется отдельная лицензия.

Файл: Regular hexagon.svg — Wikimedia Commons

Щелкните дату / время, чтобы просмотреть файл в том виде, в каком он был в тот момент.

900L (Официальный) talk | contribs)

	Дата / время	Миниатюра	Размеры	Пользователь	Комментарий
текущий	03:39, 9 мая 2020 г.		400 × 400 (443 байта)	Удалена повторяющаяся вершина
	00:07, 7 апреля 2006 г.		400 × 400 (482 байта)	Густавб (обсуждение | вклад)	Правильный шестиугольник == Источник = = Создано Gustavb с использованием пользователя: Gustavb / regular_polygon. пл. == Лицензирование == {{self2 | GFDL | cc-by-2.5}} Категория: Полигоны

Вы не можете перезаписать этот файл.

Этот файл используется на следующих 2 страницах:

• В свободном доступе: наборы изображений
• Категория: Правильные шестиугольники

Этот файл используют следующие другие вики:

• Использование на ar.wikipedia.org
• Использование на ba.wikipedia.org
• Использование на bn.wikipedia.org
• Использование на en.wikipedia.org
• Использование на en.wiktionary.org
• Использование на es.wikipedia.org
• Использование на eu.wikipedia.org
• Использование на fa.wikipedia.org
• Использование на fi.wikipedia.org
• Использование на fr.wikipedia.org
• Использование на gv.wikipedia.org
• Использование на hi.wikipedia.org
• Использование на hy.wikipedia.org
• Использование на id.

  No related posts.