Онлайн калькулятор: Длина стороны правильного многоугольника
РаботаИнженерные
Определение длины стороны правильного многоугольника по радиусу вписанной окружности
От нашего нового пользователя поступил вот такой запрос:
«Калькулятор должен вычислять длину стороны правильного многоугольника (шестиугольник, пятигольник) по указанному диаметру (или радиусу) описанной окружности».
Удовлетворяем запрос оперативно. Заметим, что для решения задачи нужно найти длину третьей стороны треугольника, исходящего из центра описанной окружности и опирающегося на две соседние вершины правильного многоугольника. Про этот треугольник известно многое: длины двух сторон — это радиусы описанной окружности, и угол, как нетрудно заметить, — это 360, деленное на число вершин правильного многоугольника. Далее используется соотношение из теоремы синусов — две стороны относятся друг к другу также как и синусы противолежащих им углов. Поскольку треугольник равнобедренный и сумма углов в треугольнике равна 180 градусам, угол, противолежащий радиусу вычисляется тривиально. Результат — ниже.
Результат — ниже.
Определение длины стороны правильного многоугольника по радиусу описанной окружности
Радиус описанной окружности
Число сторон
Число сторон правильного многоугольника
Точность вычисления
Знаков после запятой: 2
Длина стороны правильного многоугольника
P.S. В комментариях некто Александр поинтересовался, а как же найти длину стороны по радиусу вписанной окружности?
Отвечаю — с вписанной окружностью все гораздо проще. Надо рассмотреть треугольник, образованный перпендикуляром к точке касания окружности и многоугольника, половиной стороны многоугольника и линией от центра окружности до ближайшей к перпендикуляру вершины многоугольника. Этот треугольник перпендикулярный, и острый угол его равен 360, деленное на число вершин правильного многоугольника и еще пополам. Половина длины стороны находится легко — это радиус (прилежащий катет), умноженный на тангенс острого угла.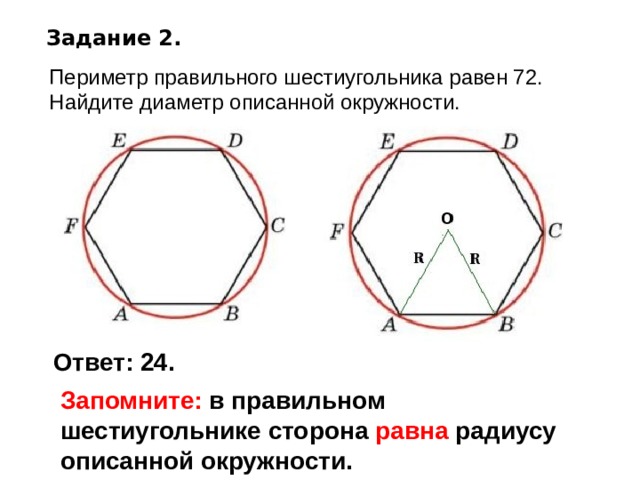 Домножаем затем на два — получаем искомую длину стороны. Результат — ниже.
Домножаем затем на два — получаем искомую длину стороны. Результат — ниже.
Определение длины стороны правильного многоугольника по радиусу вписанной окружности
Радиус вписанной окружности
Число сторон
Число сторон правильного многоугольника
Точность вычисления
Знаков после запятой: 2
Длина стороны правильного многоугольника
Ссылка скопирована в буфер обмена
Похожие калькуляторы
- • Правильный многоугольник. Описанная и вписанная окружность
- • Определение параметров правильного многоугольника по радиусам вписанной и описанной окружности
- • Треугольник. Вписанная окружность
- • Треугольник. Описанная окружность
- • Площадь правильного многоугольника
- • Раздел: Инженерные ( 100 калькуляторов )
вписанная окружность Инженерные многоугольники описанная окружность
PLANETCALC, Длина стороны правильного многоугольника
Timur2020-11-03 14:19:27
Правильный многоугольник.
 Формулы, признаки и свойства правильного многоугольника
Формулы, признаки и свойства правильного многоугольникаНавигация по странице: Определение правильного многоугольника Признаки правильного многоугольника Основные свойства правильного многоугольника Правильный n-угольник — формулы — длина стороны — радиус вписанной окружности — радиус описанной окружности — площадь — периметр — угол между сторонами Правильный треугольник Правильный четырехугольник Правильный шестиугольник Правильный восьмиугольник
Определение. Правильный многоугольник — это многоугольник, у которого все стороны и углы одинаковые.
Многоугольником называется часть площади, которая ограничена замкнутой ломаной линией, не пересекающей сама себя.
Многоугольники отличаются между собой количеством сторон и углов.
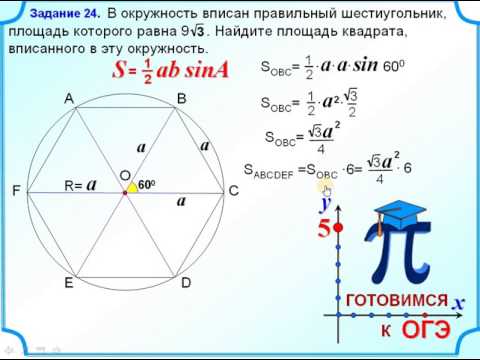 1 1 |
Рис.2 |
Признаки правильного многоугольника
Многоугольник будет правильным, если выполняется следующее условие:
Все стороны и углы одинаковы:
a1 = a2 = a3 = … = an-1 = an
α1 = α2 = α3 = … = αn-1 = αn
Основные свойства правильного многоугольника
1. Все стороны равны:
2. Все углы равны:
3. Центр вписанной окружности Oв совпадает з центром описанной окружности Oо, что и образуют центр многоугольника O
4. Сумма всех углов n-угольника равна:
180° · (n — 2)
5. Сумма всех внешних углов n-угольника равна 360°:
Сумма всех внешних углов n-угольника равна 360°:
β1 + β2 + β3 + … + βn-1 + βn = 360°
6. Количество диагоналей (Dn) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины:
| Dn = | n · (n — 3) |
| 2 |
7. В любой многоугольник можно вписать окружность и описать круг при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника:
| S = | π | a2 |
| 4 |
8. Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O
Правильный n-угольник — формулы
Формулы длины стороны правильного n-угольника
1. Формула стороны правильного n-угольника через радиус вписанной окружности:
| a = 2r · tg | 180° |
| n |
| a = 2r · tg | π |
| n |
2. Формула стороны правильного n-угольника через радиус описанной окружности:
Формула стороны правильного n-угольника через радиус описанной окружности:
| a = 2 R · sin | 180° |
| n |
| a = 2 R · sin | π |
| n |
Формула радиуса вписанной окружности правильного n-угольника
Формула радиуса вписанной окружности n-угольника через длину стороны:
| r = a : (2tg | 180° | ) |
| n |
| r = a : (2tg | π | ) |
| n |
Формула радиуса описанной окружности правильного n-угольника
Формула радиуса описанной окружности n-угольника через длину стороны:
| R = a : (2sin | 180° | ) |
| n |
| R = a : (2sin | π | ) |
| n |
Формулы площади правильного n-угольника
1. Формула площади n-угольника через длину стороны:
Формула площади n-угольника через длину стороны:
| S = | na2 | · ctg | 180° |
| 4 | n |
2. Формула площади n-угольника через радиус вписанной окружности:
| S = | nr2 · tg | 180° |
| n |
3. Формула площади n-угольника через радиус описанной окружности:
| S = | nR2 | · sin | 360° |
| 2 | n |
Формула периметра правильного многоугольника:
Формула периметра правильного n-угольника:
P = na
Формула определения угла между сторонами правильного многоугольника:
Формула угла между сторонами правильного n-угольника:
| αn = | n — 2 | · 180° |
| n |
Рис. 3 3 |
Правильный треугольник
Формулы правильного треугольника:
1. Формула стороны правильного треугольника через радиус вписанной окружности:
a = 2r √3
2. Формула стороны правильного треугольника через радиус описанной окружности:
a = R√3
| r = | a√3 |
| 6 |
4. Формула радиуса описанной окружности правильного треугольника через длину стороны:
| R = | a√3 |
| 3 |
5. Формула площади правильного треугольника через длину стороны:
| S = | a2√3 |
| 4 |
6. Формула площади правильного треугольника через радиус вписанной окружности:
S = r2 3√3
7.
| S = | R2 3√3 |
| 4 |
8. Угол между сторонами правильного треугольника:
α = 60°
| Рис.4 |
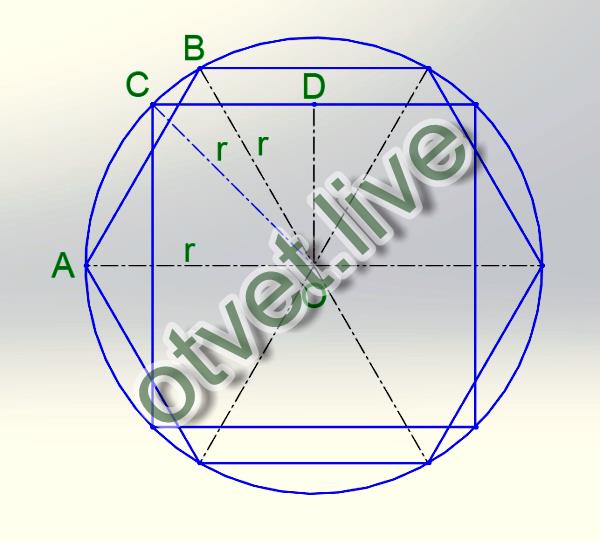
Правильный четырехугольник
Правильный четырехугольнику — квадрат.
Формулы правильного четырехугольника:
1. Формула стороны правильного четырехугольника через радиус вписанной окружности:
a = 2r
2. Формула стороны правильного четырехугольника через радиус описанной окружности:
a = R√2
3. Формула радиуса вписанной окружности правильного четырехугольника через длину стороны:
| r = | a |
| 2 |
4. Формула радиуса описанной окружности правильного четырехугольника через длину стороны:
Формула радиуса описанной окружности правильного четырехугольника через длину стороны:
| R = | a√2 |
| 2 |
5. Формула площади правильного четырехугольника через длину стороны:
S = a2
6. Формула площади правильного четырехугольника через радиус вписанной окружности:
S = 4 r2
7. Формула площади правильного четырехугольника через радиус описанной окружности:
S = 2 R2
8. Угол между сторонами правильного четырехугольника:
α = 90°
Смотрите также формулы и свойства квадрата
Правильный шестиугольник
Формулы правильного шестиугольника:
1. Формула стороны правильного шестиугольника через радиус вписанной окружности:
| a = | 2√3 | r |
| 3 |
2.
a = R
3. Формула радиуса вписанной окружности правильного шестиугольника через длину стороны:
| r = | a√3 |
| 2 |
4. Формула радиуса описанной окружности правильного шестиугольника через длину стороны:
R = a
5. Формула площади правильного шестиугольника через длину стороны:
| S = | a2 3√3 |
| 2 |
6. Формула площади правильного шестиугольника через радиус вписанной окружности:
S = r2 2√3
7. Формула площади правильного шестиугольника через радиус описанной окружности:
| S = | R2 3√3 |
| 2 |
8. Угол между сторонами правильного шестиугольника:
α = 120°
Правильный восьмиугольник
Формулы правильного восьмиугольника:
1.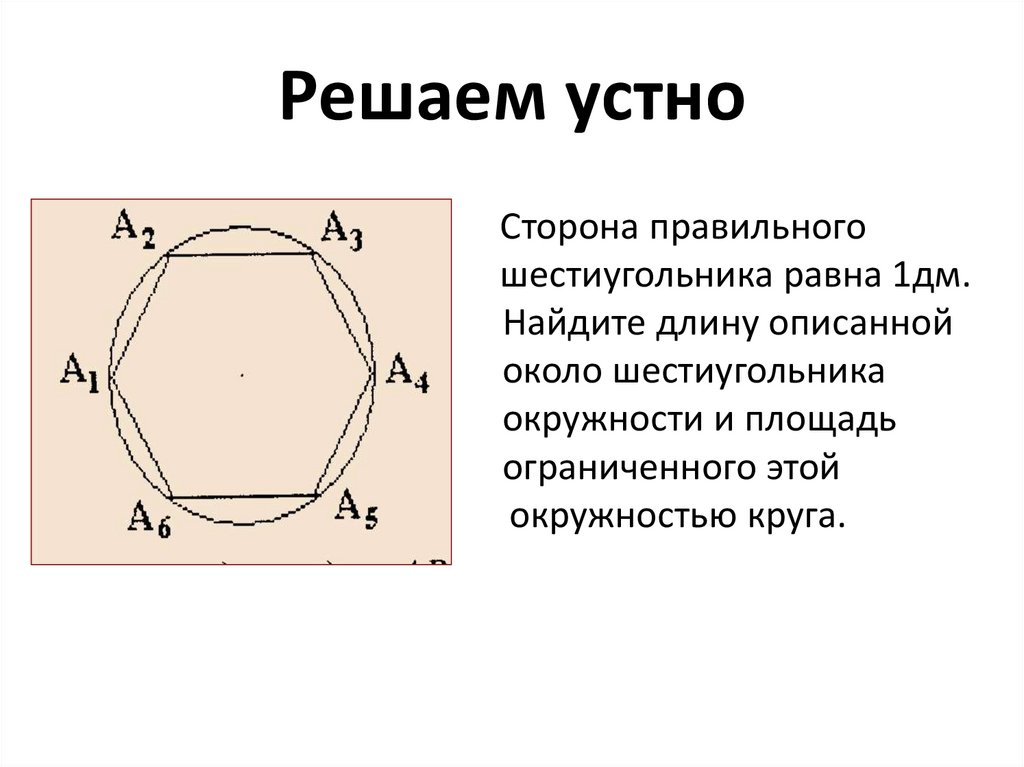 Формула стороны правильного восьмиугольника через радиус вписанной окружности:
Формула стороны правильного восьмиугольника через радиус вписанной окружности:
a = 2r · (√2 — 1)
2. Формула стороны правильного восьмиугольника через радиус описанной окружности:
a = R√2 — √2
3. Формула радиуса вписанной окружности правильного восьмиугольника через длину стороны:
| r = | a(√2 + 1) |
| 2 |
4. Формула радиуса описанной окружности правильного восьмиугольника через длину стороны:
| R = | a√4 + 2√2 |
| 2 |
5. Формула площади правильного восьмиугольника через длину стороны:
S = a2 2(√2 + 1)
6. Формула площади правильного восьмиугольника через радиус вписанной окружности:
S = r2 8(√2 — 1)
7. Формула площади правильного восьмиугольника через радиус описанной окружности:
S = R2 2√2
8. Угол между сторонами правильного восьмиугольника:
Угол между сторонами правильного восьмиугольника:
α = 135°
Все таблицы и формулы
Видео-вопрос: Нахождение площадей кругов и шестиугольников
Стенограмма видео
На рисунке показана окружность внутри правильного шестиугольника. Найдите площадь заштрихованных областей, давая ответ с точностью до десятых.
В этом вопросе нам дают цифру. И на этом рисунке у нас есть круг, который находится внутри правильного шестиугольника. Нам нужно использовать нашу фигуру, чтобы определить площадь всех заштрихованных областей, сложенных вместе. И нам нужно дать наш ответ с точностью до десятых.
Итак, чтобы ответить на этот вопрос, давайте начнем с заштрихованной области на нашем рисунке. Мы видим, что заштрихованная область является частью области между нашим шестиугольником и нашим кругом. Мы бы знали, как вычислить всю площадь между нашим кругом и нашим шестиугольником. Нам нужно найти площадь нашего шестиугольника, а затем вычесть площадь круга. Но тогда, поскольку это правильный шестиугольник, а наша окружность вписана внутрь нашего шестиугольника, каждый из этих сегментов будет иметь одинаковую площадь. Итак, поскольку три из шести областей заштрихованы, нам нужно умножить это на половину. Следовательно, площадь заштрихованной области равна половине площади шестиугольника минус площадь круга.
Но тогда, поскольку это правильный шестиугольник, а наша окружность вписана внутрь нашего шестиугольника, каждый из этих сегментов будет иметь одинаковую площадь. Итак, поскольку три из шести областей заштрихованы, нам нужно умножить это на половину. Следовательно, площадь заштрихованной области равна половине площади шестиугольника минус площадь круга.
Итак, чтобы найти площадь заштрихованной области, нам нужно найти две вещи. Нам нужно найти площадь шестиугольника и площадь нашего круга. Начнем с нахождения площади нашего шестиугольника. Есть несколько способов сделать это. Воспользуемся формулой нахождения площади правильного многоугольника. Напомним, что площадь правильного 𝑛-стороннего многоугольника с длиной стороны 𝑥 равна 𝑛𝑥 в квадрате над четырьмя, умноженному на койку 180, деленную на 𝑛 градусов.
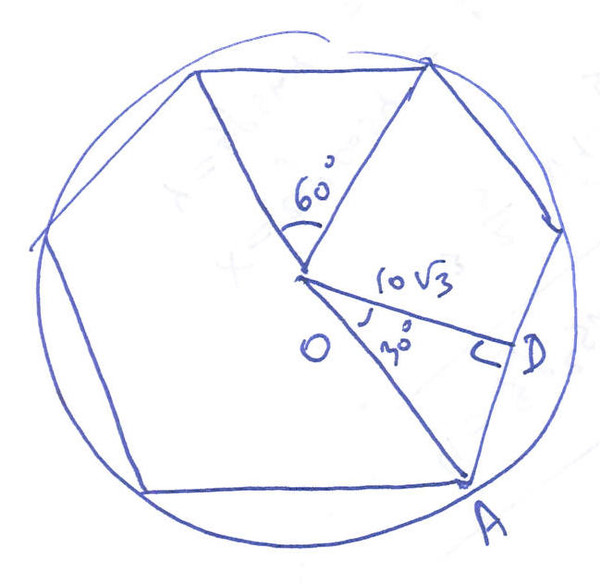
Итак, чтобы найти площадь нашего шестиугольника, нам нужно найти значение 𝑛 и значение 𝑥. Конечно, значение 𝑛 — это количество сторон, а любой шестиугольник имеет шесть сторон.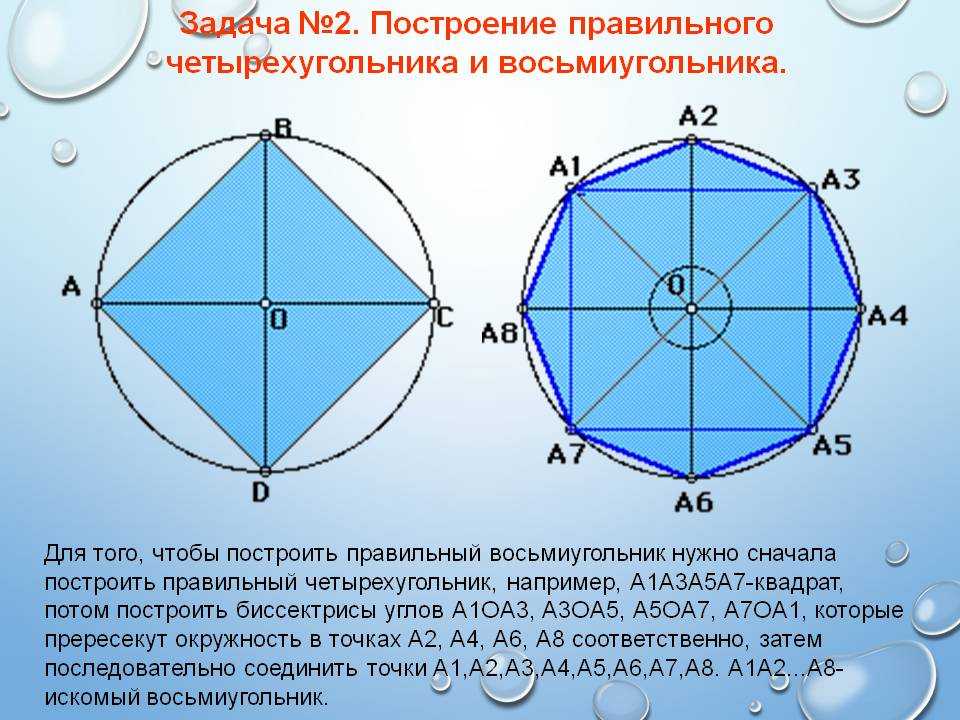 Итак, наше значение 𝑛 равно шести. Однако на нашей диаграмме нам не дана ни одна из длин сторон нашего шестиугольника. Так что нам нужно найти их. И есть несколько разных способов сделать это. Проще всего это сделать, зная, что внутренний угол правильного шестиугольника равен 120 градусам. Если мы затем разделим это пополам следующей строкой, мы получим кое-что интересное.
Итак, наше значение 𝑛 равно шести. Однако на нашей диаграмме нам не дана ни одна из длин сторон нашего шестиугольника. Так что нам нужно найти их. И есть несколько разных способов сделать это. Проще всего это сделать, зная, что внутренний угол правильного шестиугольника равен 120 градусам. Если мы затем разделим это пополам следующей строкой, мы получим кое-что интересное.
Так как мы разделили угол в 120 градусов пополам, здесь угол равен 60 градусам. То же самое и с другой стороны. Мы разбиваем внутренний угол правильного шестиугольника. Угол здесь тоже 60 градусов. Следовательно, все внутренние углы этого треугольника равны 60 градусов. Это должен быть равносторонний треугольник. А в равностороннем треугольнике все длины равны. Таким образом, длина стороны нашего шестиугольника должна быть 14. Следовательно, в нашей формуле площади шестиугольника наше значение 𝑥 равно 14,9.0005
Стоит отметить, что это был не единственный способ рассчитать это значение. Если бы мы не знали, что внутренний угол правильного шестиугольника равен 120 градусам, мы могли бы построить тот же треугольник, и мы знали бы, что две длины равны 14.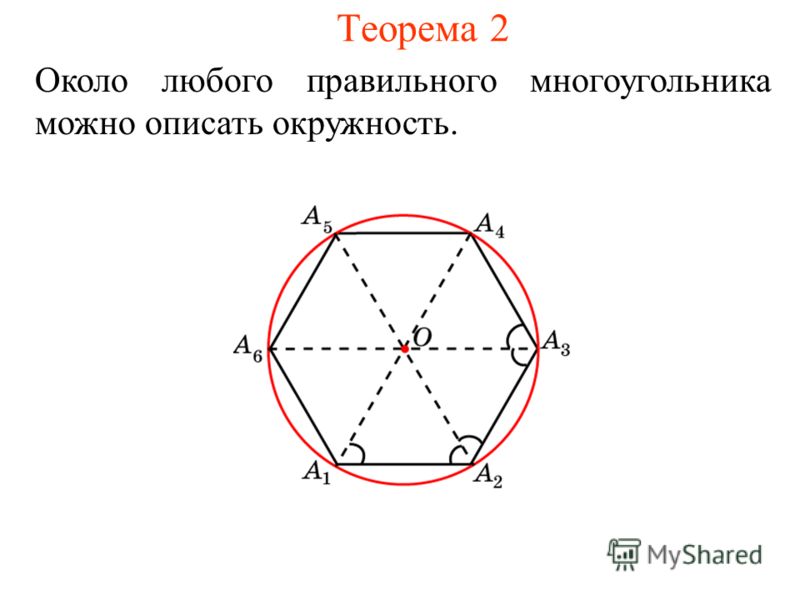 Тогда мы можем построить следующие шесть конгруэнтных треугольников. Затем мы видим, что разбиваем угол в 360 градусов на шесть равных сегментов. Таким образом, мы можем найти, что угол между двумя нашими длинами 14 равен 60 градусам.
Тогда мы можем построить следующие шесть конгруэнтных треугольников. Затем мы видим, что разбиваем угол в 360 градусов на шесть равных сегментов. Таким образом, мы можем найти, что угол между двумя нашими длинами 14 равен 60 градусам.
Итак, в этом треугольнике мы знали бы две длины и угол между ними. Затем мы можем использовать закон косинусов, чтобы найти другую длину нашего треугольника. Это также дало бы нам ответ 14. Однако этот метод более сложен.
Теперь мы готовы найти площадь нашего шестиугольника. Наше значение 𝑛 равно шести, а наше значение 𝑥 равно 14. Поэтому мы подставляем их. Площадь нашего шестиугольника равна шести, умноженным на 14 в квадрате на четыре, умноженным на койку 180, деленную на шесть градусов. И мы можем это оценить. Во-первых, шесть умножить на 14 в квадрате на четыре равно 294, а 180 разделить на шесть равно 30. Таким образом, это упрощает, чтобы получить 294, умноженное на 30 градусов. И чтобы оценить это, нам нужно вспомнить, что умножение на котангенс угла равносильно делению на тангенс этого угла.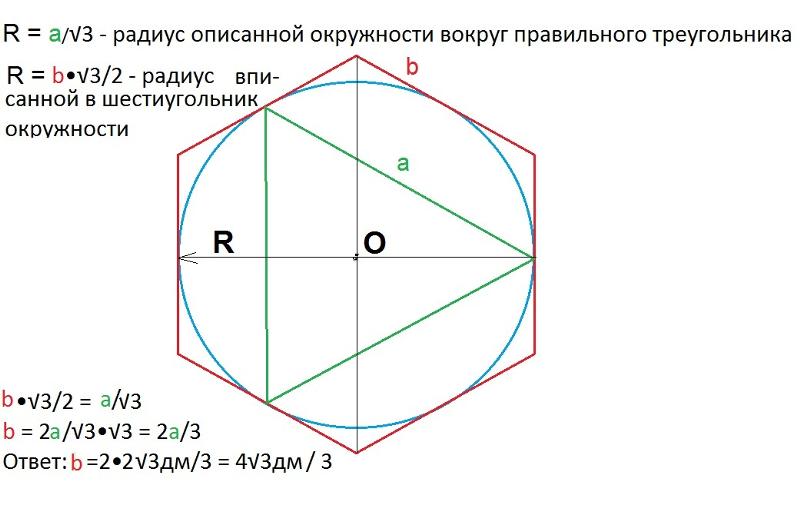 Таким образом, мы можем упростить это, чтобы дать нам 294 разделить на тангенс 30 градусов.
Таким образом, мы можем упростить это, чтобы дать нам 294 разделить на тангенс 30 градусов.
Но 30 градусов — это один из наших стандартных углов. Мы знаем, что тангенс 30 градусов будет равен единице, деленной на квадратный корень из трех. И, конечно же, деление на один квадратного корня из трех равносильно умножению на квадратный корень из трех. Таким образом, мы можем точно найти площадь нашего шестиугольника. Это 294 корня из трех квадратных единиц.
Теперь, чтобы найти площадь заштрихованной области, нам нужно найти площадь нашего круга. И чтобы найти это, вспомним, что площадь круга радиуса 𝑟 равна 𝜋𝑟 в квадрате. Итак, чтобы найти площадь нашего круга, нам нужно найти длину его радиуса. Самый простой способ сделать это — нарисовать следующий радиус на нашей диаграмме. Это называется апофема, и у него есть несколько очень полезных свойств.
Во-первых, угол, который он образует со сторонами нашего шестиугольника, будет прямым. Будет 90 градусов. Затем он разделит пополам угол в центре нашего круга. Так как это было 60 градусов, у нас есть 60 на два, это 30 градусов. И хотя на этот вопрос отвечать не обязательно, апофема также будет делить пополам стороны нашего шестиугольника. Мы хотим использовать эту информацию, чтобы найти значение нашего радиуса 𝑟.
Так как это было 60 градусов, у нас есть 60 на два, это 30 градусов. И хотя на этот вопрос отвечать не обязательно, апофема также будет делить пополам стороны нашего шестиугольника. Мы хотим использовать эту информацию, чтобы найти значение нашего радиуса 𝑟.
Мы видим, что 𝑟 находится в прямоугольном треугольнике. Мы знаем гипотенузу нашего прямоугольного треугольника и знаем угол между гипотенузой и 𝑟. Таким образом, мы можем найти значение 𝑟 с помощью тригонометрии. Мы знаем, что косинус угла в прямоугольном треугольнике равен длине стороны, прилежащей к этому углу, деленной на длину нашей гипотенузы. Итак, в нашем треугольнике cos 30 градусов равен 𝑟, деленному на 14. Мы можем найти значение 𝑟, умножив обе части этого уравнения на 14. И еще раз, 30 градусов — это стандартный угол. Итак, мы знаем, что cos 30 градусов — это квадратный корень из трех, разделенный на два. Таким образом, мы можем точно найти значение 𝑟. 𝑟 — это 14, умноженное на корень три из двух. И 14 над двумя семь.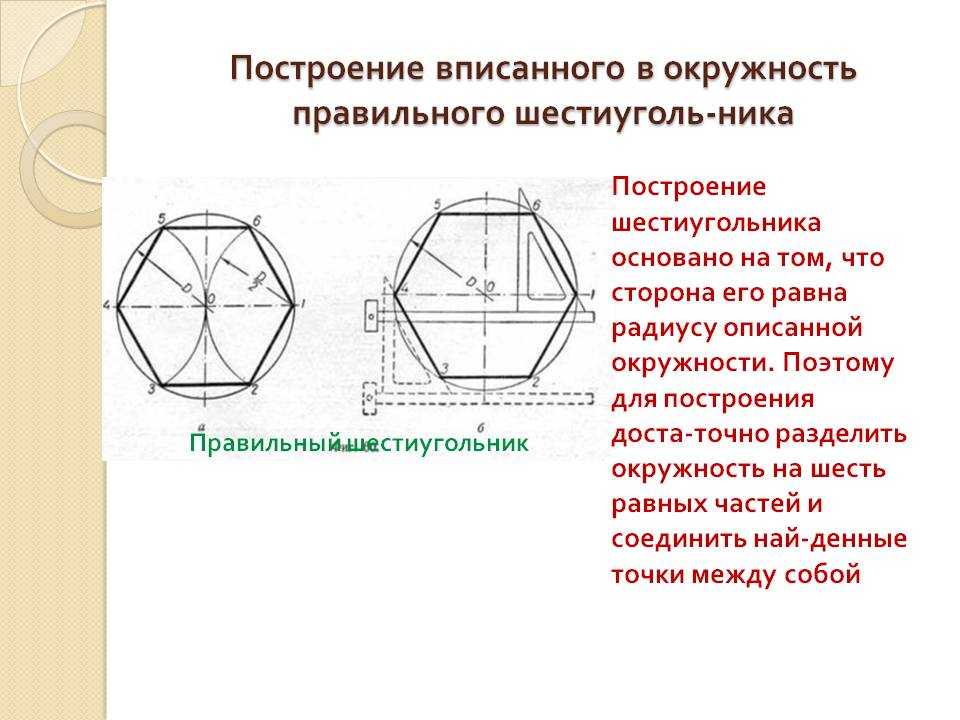 Итак, 𝑟 равно семи корням из трех.
Итак, 𝑟 равно семи корням из трех.
Теперь, когда мы нашли длину радиуса нашего круга, мы можем использовать его, чтобы найти площадь нашего круга. Это равно 𝜋𝑟 в квадрате, что в данном случае равно 𝜋, умноженному на семь, корень из трех, все в квадрате. Опять же, мы можем точно найти площадь круга. Мы начнем с распределения квадрата по скобкам. Это дает нам 𝜋, умноженное на семь в квадрате, умноженное на корень из трех в квадрате. Можем еще упростить. Семь в квадрате равно 49, а корень три в квадрате равен трем. Таким образом, мы получаем 𝜋 умноженное на 49.раза три. А 49 умножить на три равно 147. Значит площадь нашего круга 147𝜋 квадратных единиц.
Теперь, когда мы нашли площадь нашего шестиугольника и нашего круга, мы можем найти площадь заштрихованной области. Помните, что это половина, умноженная на площадь шестиугольника минус площадь круга. Подставляя в наши выражения площадь шестиугольника и площадь круга, получаем половину, умноженную на корень из трех 294 минус 147𝜋. И если мы посчитаем это, мы получим 23,704, и это расширение продолжается в квадратных единицах.
И если мы посчитаем это, мы получим 23,704, и это расширение продолжается в квадратных единицах.
Но помните, вопрос требует, чтобы мы давали ответ с точностью до десятых. Так что нам нужно это округлить. Ближайшая десятая до ближайшего десятичного знака. Нам нужно проверить наше второе десятичное место. Второй десятичный знак в этом расширении равен нулю. Значит, нам нужно округлить. Это дает нам 23,7. И хотя в этом нет необходимости, потому что это представляет собой площадь, полезно указать здесь единицу измерения. Мы запишем их как квадратные единицы.
Таким образом, в этом вопросе мы смогли найти заштрихованную область, которая была частью области между кругом, вписанным внутрь правильного шестиугольника. Для этого нам нужно было использовать тригонометрию и нашу формулу для нахождения площади правильного шестиугольника и площади круга. Нам удалось показать, что площадь этого региона с точностью до десятых составляет 23,7 кв.
Свойства шестигранного и обычного калькулятора шестигранника
СОДЕРЖАНИЕ
-Определения
-Свойства регулярных шестигранных гексагонов
-Симметрия
-Угол и центральный угол
-Окружение и окружение
—
— Ограничивающая рамка
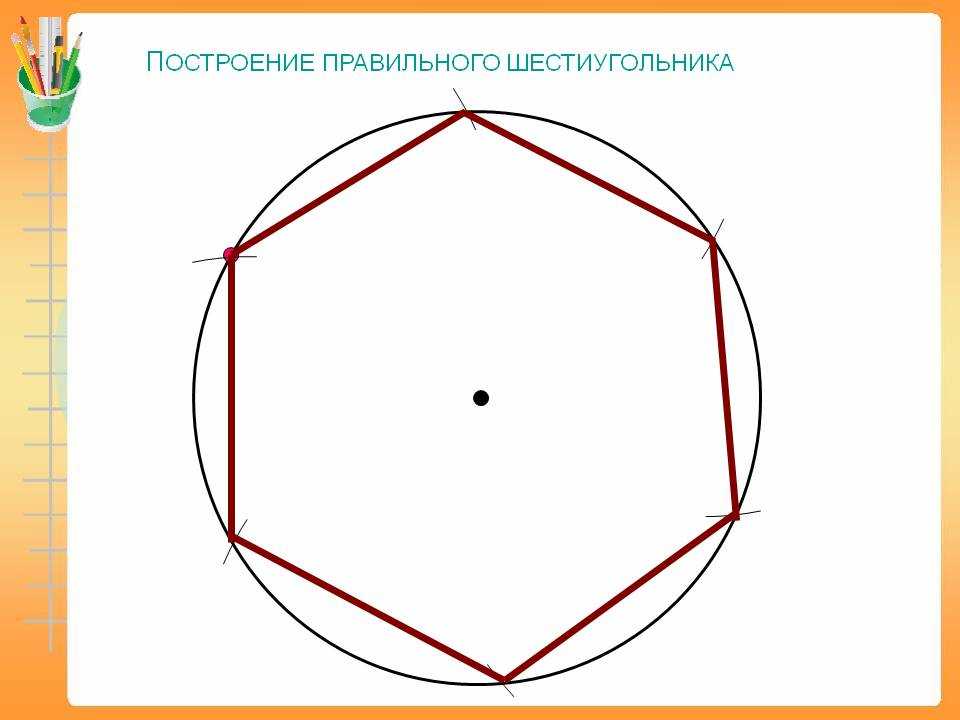
— Как нарисовать правильный шестиугольник
— Примеры
— Шпаргалка по правильному шестиугольнику
— См. также
также
Определения
Шестиугольник — это многоугольник с шестью сторонами и шестью вершинами. Как и любой многоугольник, шестиугольник может быть выпуклым или вогнутым, как показано на следующем рисунке. В выпуклом состоянии шестиугольник (или вообще многоугольник) не имеет внутренних углов, превышающих 180°. Напротив, вогнутый шестиугольник (или многоугольник) имеет один или несколько внутренних углов больше 180°. Шестиугольник называется правильным, если все его стороны и внутренние углы равны . В отличие от треугольника, наличие равных сторон не означает, что внутренние углы также равны, поскольку шестиугольник может быть вогнутым. Как показано на рисунке ниже, можно определить множество возможных вогнутых шестиугольников с равными сторонами, но неравными внутренними углами (они называются равносторонними). Любой шестиугольник, который не является правильным, называется неправильным.
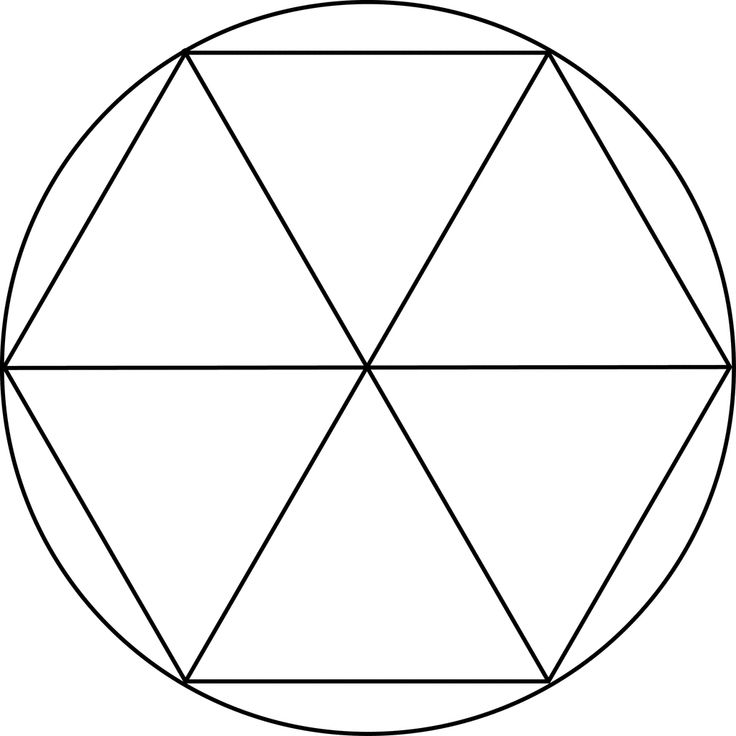
Типы шестиугольников Сумма внутренних углов любого шестиугольника, выпуклого или вогнутого, всегда равна 720°.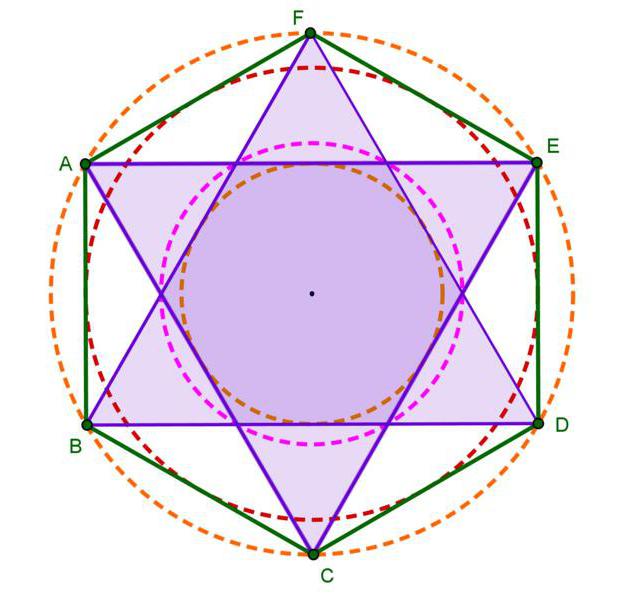 В этом легко убедиться, подсчитав количество треугольников, умещающихся внутри шестиугольника, соединив его вершины (избегая пересечений). Действительно, треугольников 4. Поскольку сумма внутренних углов в одном треугольнике равна 180°, 4 треугольника, расположенные рядом, должны иметь размеры до 4×180=720°.
В этом легко убедиться, подсчитав количество треугольников, умещающихся внутри шестиугольника, соединив его вершины (избегая пересечений). Действительно, треугольников 4. Поскольку сумма внутренних углов в одном треугольнике равна 180°, 4 треугольника, расположенные рядом, должны иметь размеры до 4×180=720°.
Свойства правильных шестиугольников
Симметрия
Правильный шестиугольник имеет шесть осей симметрии. Половина из них проходит через диагонально противоположные вершины, а остальные — через середины противоположных ребер.
Оси симметрии правильного шестиугольникаРЕКЛАМА
Внутренний угол и центральный угол
Правильные многоугольники имеют равные внутренние углы по определению. Так как всего их шесть, то можно сделать вывод, что каждый внутренний угол правильного шестиугольника равен: 9\circ
Остальные два угла треугольника также равны 60°. На самом деле это \varphi/2, потому что диагонали шестиугольника (линии, соединяющие противоположные вершины) также являются осями симметрии, таким образом делящие пополам внутренний угол \varphi (который равен 120°). Следовательно, все шесть треугольников, имеющих центр шестиугольника в качестве одной из своих вершин, являются одинаковыми равносторонними треугольниками.
Следовательно, все шесть треугольников, имеющих центр шестиугольника в качестве одной из своих вершин, являются одинаковыми равносторонними треугольниками.
Внутренний и центральный углы также являются дополнительными, так как их сумма равна 180°:
\varphi+\theta=120°+60°=180°
Окружность и вписанность
Как и в случае с любым правильным многоугольником, можно нарисовать окружность, проходящую через все шесть вершин шестиугольника. Это описанная окружность или описанная окружность многоугольника. Центр этого круга является центром шестиугольника. Точно так же диагонали шестиугольника являются диаметрами описанной окружности. Радиус описанной окружности R_c обычно называют радиусом описанной окружности.
Можно также нарисовать еще одну окружность, проходящую через середины сторон шестиугольника. Этот круг называется вписанным кругом или обведите . Он касается всех шести сторон, а его центр совпадает с центром описанной окружности.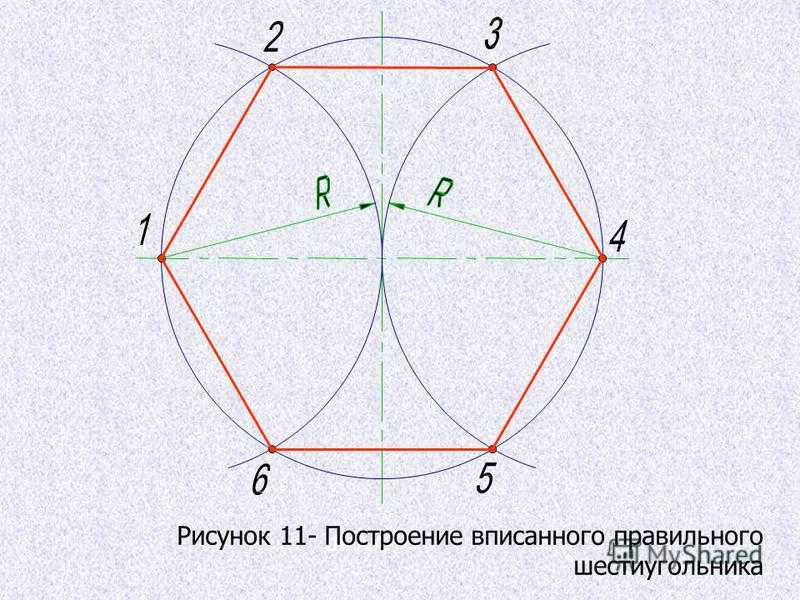 Радиус вписанной окружности R_i обычно называют внутренним радиусом.
Радиус вписанной окружности R_i обычно называют внутренним радиусом.
Радиусы описанной окружности R_c и вписанной окружности R_i связаны с длиной стороны \alpha, а также между собой. Эти отношения можно обнаружить, используя свойства прямоугольного треугольника, сторонами которого являются: радиус описанной окружности, внутренний радиус и половина стороны шестиугольника, как показано на рисунке ниже. Используя базовую тригонометрию, мы находим:
\begin{split} R_c & = \frac{a}{2 \sin{\frac{\theta}{2}}} \\ R_i & = \frac{a}{2 \tan{\frac{\ theta}{2}}} \\ R_i & = R_c \cos{\frac{\theta}{2}} \end{split}
, где \theta — центральный угол, а \alpha — длина стороны. Оказывается, эти выражения справедливы для любого правильного многоугольника, а не только для шестиугольника. Мы можем получить конкретное выражение для правильного шестиугольника, установив θ = 60°. Вот эти выражения:
\begin{split} R_c & = \frac{a}{2 \sin{30^{\circ}}} = a \\ R_i & = \frac{a}{2 \tan{30 ^{\circ}}} \приблизительно 0,866 a \\ \\ R_i & = R_c \cos{30^{\circ}} \приблизительно 0,866 R_c \end{split}.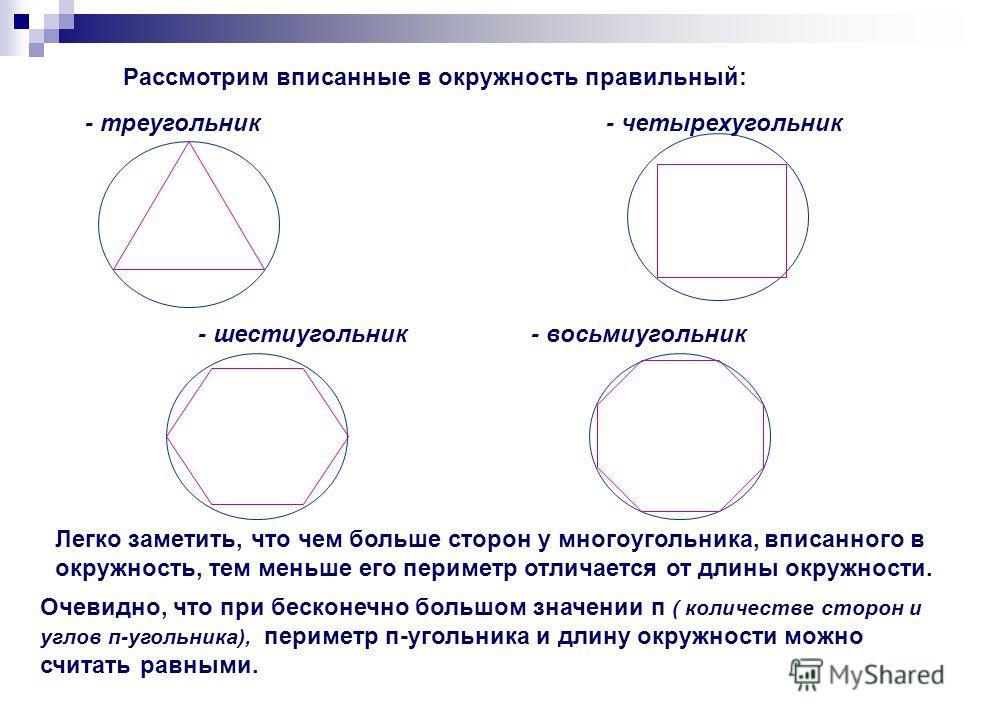 92
92
Периметр любого N-стороннего правильного многоугольника представляет собой просто сумму длин всех сторон: P = N a . Следовательно, для правильного шестиугольника:
P = 6a
Ограничивающая рамка
Ограничивающая рамка плоской формы — это наименьший прямоугольник, полностью охватывающий фигуру. Размеры этого прямоугольника определяются высотой h и шириной w правильного шестиугольника.
Высота
Высота h правильного шестиугольника — это расстояние между двумя противоположными сторонами. Это равно удвоенному радиусу R_i: 9\circ}
, что приблизительно равно:
h\приблизительно 1,732 R_c
h\приблизительно 1,732 a
Ширина
Ширина w — это расстояние между двумя противоположными вершинами правильного шестиугольника (длина его диагонали) . Это равно удвоенному радиусу описанной окружности R_c:
w=2R_c
Поскольку R_c=a, мы могли бы написать также:
w=2a
Как нарисовать правильный шестиугольник
Вы можете нарисовать правильный шестиугольник заданной длины стороны \альфа, используя только линейку и циркуль.
- Сначала просто нарисуйте линейный сегмент, длина которого равна желаемой длине стороны шестиугольника \alpha.
- Затем постройте окружность с центром на одном конце линейного отрезка и радиусом, равным длине отрезка.
- Не изменяя радиуса, постройте вторую окружность с центром на другом конце линейного отрезка. Определяются две точки, в которых эта окружность пересекается с первой.
- Используя тот же радиус, поместите кончик компаса в одну из последних определенных точек и постройте новую окружность. Новая точка определяется на пересечении с первой окружностью.
- Повторите ту же процедуру еще два раза. Поместите кончик компаса в последнюю точку и постройте новый круг. Новая точка определяется на пересечении с первой окружностью.
- Шесть точек были определены вокруг первого круга. Это вершины шестиугольника. Нарисуйте линейные сегменты между ними, и теперь правильный шестиугольник готов. Начальная окружность — это описанная окружность шестиугольника.