Как вписать шестиугольник в окружность с помощью циркуля: а) правильный шестиугольник; б) правильный треугольник; в) квадрат; г) правильный восьмиугольник. — Лазерная резка металла от "ТМК" Ярославль (Тутаев)

Содержание

Как построить восьмиугольник в окружности

Основы черчения

Строительное

Машиностроительное

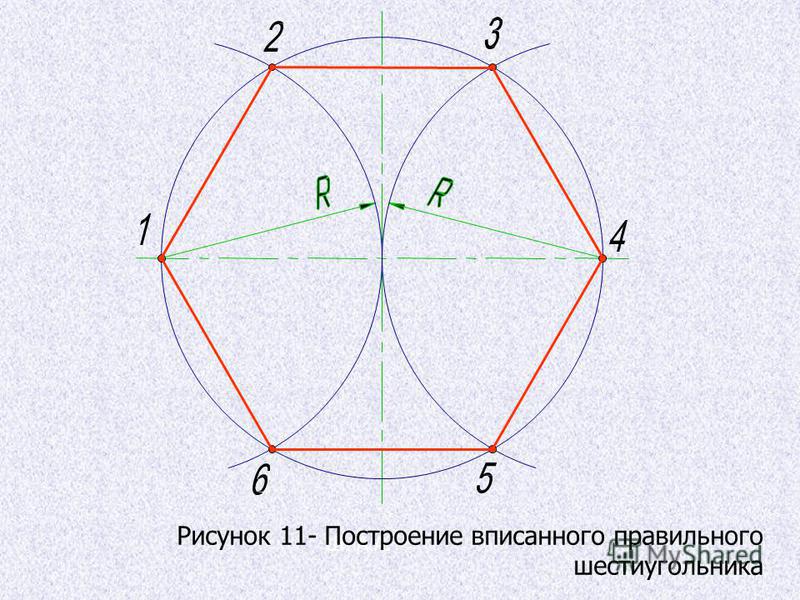
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего проводим стороны 5—6 и 3—2.

Построение вписанного в окружность равностороннего треугольника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.

Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.

1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.

Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.

Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4.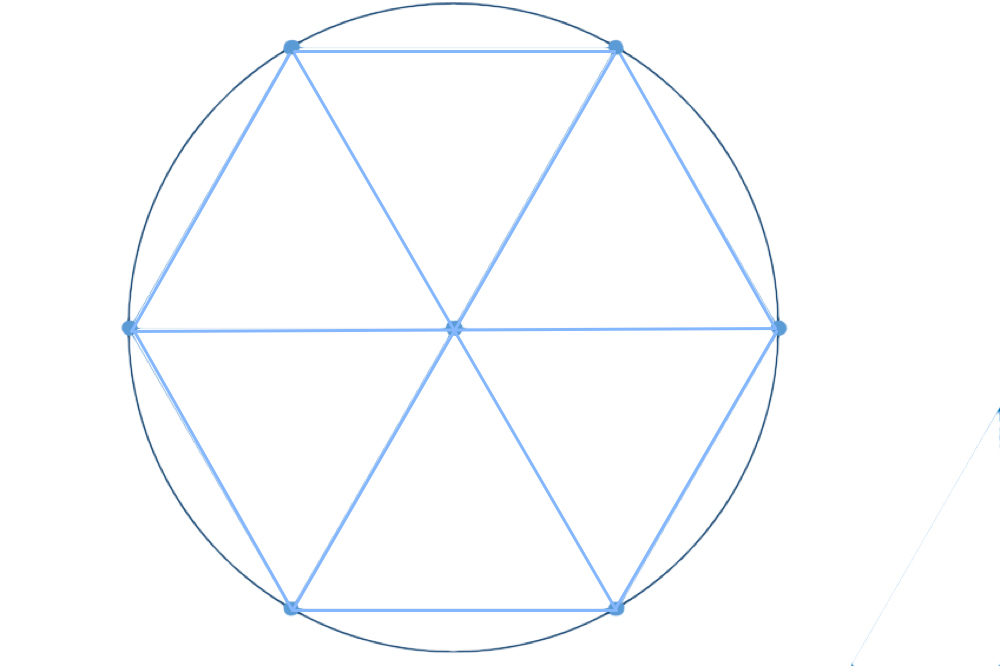 Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.

Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля.

Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.

Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.

Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.

Построение вписанного в окружность правильного пятиугольника.

Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.

Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5.

Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.

Построение правильного пятиугольника по данной его стороне.

Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.

Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.

Построение вписанного в окружность правильного семиугольника.

Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг.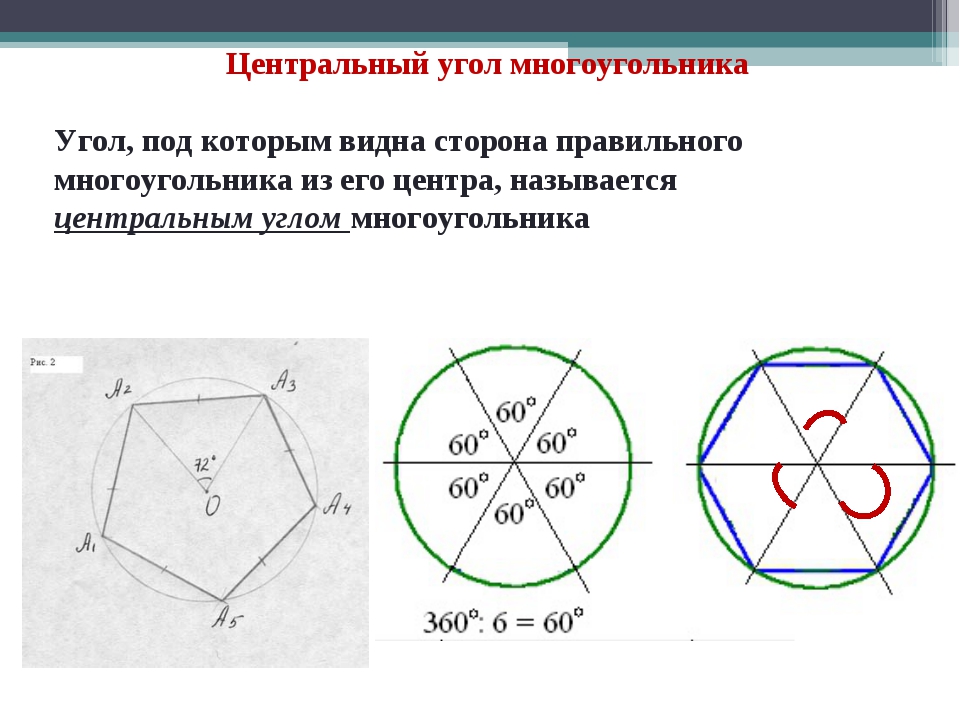 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.

Приведённый способ годен для построения правильных многоугольников с любым числом сторон.

Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.

В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты.

Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.

Деление окружности на равные части и построение правильных вписанных многоугольников можно выполнить как циркулем, так и с помощью угольников и рейсшины.

Деление окружности на четыре равные части и построение правильного вписанного четырехугольника. Две взаимно перпендикулярные центровые линии делят окружность на четыре равные части (рис. 115, а). Соединив точки пересечения этих линий с окружностью прямыми, получают правильный вписанный четырехугольник.

Деление окружности на восемь равных частей и построение правильного вписанного восьмиугольника. Две взаимно перпендикулярные линии, проведенные под углом 45° к центровым линиям с помощью угольника с углами 45, 45 и 90° и рейсшины (рис. 115, б), вместе с центровыми линиями разделят окружность на восемь равных частей.

Деление окружности на восемь равных частей можно выполнить циркулем. Для этого из точек 1 и 3 (точки пересечения центровых линий с окружностью) произвольным радиусом делаются засечки до взаимного пересечения, тем же радиусом делают две засечки из точек 3 и 5 (рис. 115, в). Через точки пересечения засечек и центр окружности проводят прямые линии до пересечения с окружностью в точках 2, 4, 6, 8.

Если полученные восемь точек соединить последовательно прямыми линиями, то получится правильный вписанный восьмиугольник (рис. 115, в).

Деление окружности на три равные части и построение правильного вписанного треугольника выполняют с помощью циркуля или угольника с углами 30, 60 и 90° и рейсшины.

При делении окружности циркулем на три равные части из любой точки окружности, например из точки Л пересечения центровых линий с окружностью (рис. 116, а и б), проводят дугу радиусом R, равным радиусу данной окружности, получают точки 1 и 2.

Третья точка деления (точка 3) будет находиться на противоположном конце диаметра, проходящего через точку Л. Последовательно соединив точки 1, 2 и 3, получают правильный вписанный треугольник. При построении правильного вписанного треугольника, если задана одна из его вершин, например точка 1, находят точку А. Для этого через заданную точку 1 проводят диаметр (рис. 116, в). Точка А будет находиться на противоположном конце этого диаметра. Затем проводят дугу радиусом R равным радиусу данной окружности, получают точки 2 и 3.

При делении окружности на три равные части с помощью угольника и рейсшины через точку 1 под углом 60° проводят две прямые линии до пересечения с окружностью в точках 2 и 3 (рис. 117, а, б), точки 2 и 3 соединяют и получают правильный вписанный треугольник (рис. 117, в).

Деление окружности на шесть равных частей и построение правильного вписанного шестиугольника выполняют с помощью угольника с углами 30, 60 и 90° и рейсшины или циркуля. При делении окружности на шесть равных частей циркулем из двух концов одного диаметра радиусом, равным радиусу данной окружности, проводят дуги до пересечения с окружностью в точках 2, 6 и 3, 5 (рис.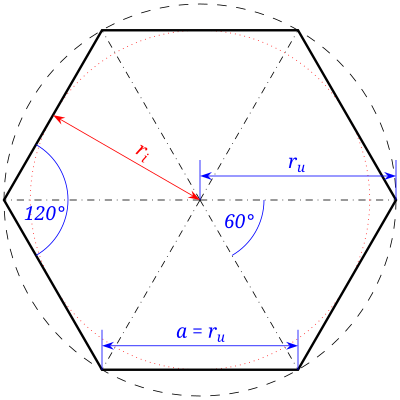 118). Последовательно соединив полученные точки, получают правильный вписанный шестиугольник. Деление окружности на шесть равных час-1ен и построение правильного вписанного шестиугольника с помощью угольника и рейсшины показано на рис. 119 и 120. Деление окружности на двенадцать равных частей и построение правильного вписанного двенадцатиугольника выполняют с помощью угольника с углами 30, 60 и 90° и рейсшины или циркуля.

При делении окружности циркулем из четырех концов двух взаимно перпендикулярных диаметров окружности проводят радиусом, равным радиусу данной окружности, дуги до пересечения с окружностью (рис. 121). Соединив полученные точки, получают двенадцатиугольник.

При построении двенадцатиугольника с помощью угольника и рейсшины точки деления строят, как показано на рис.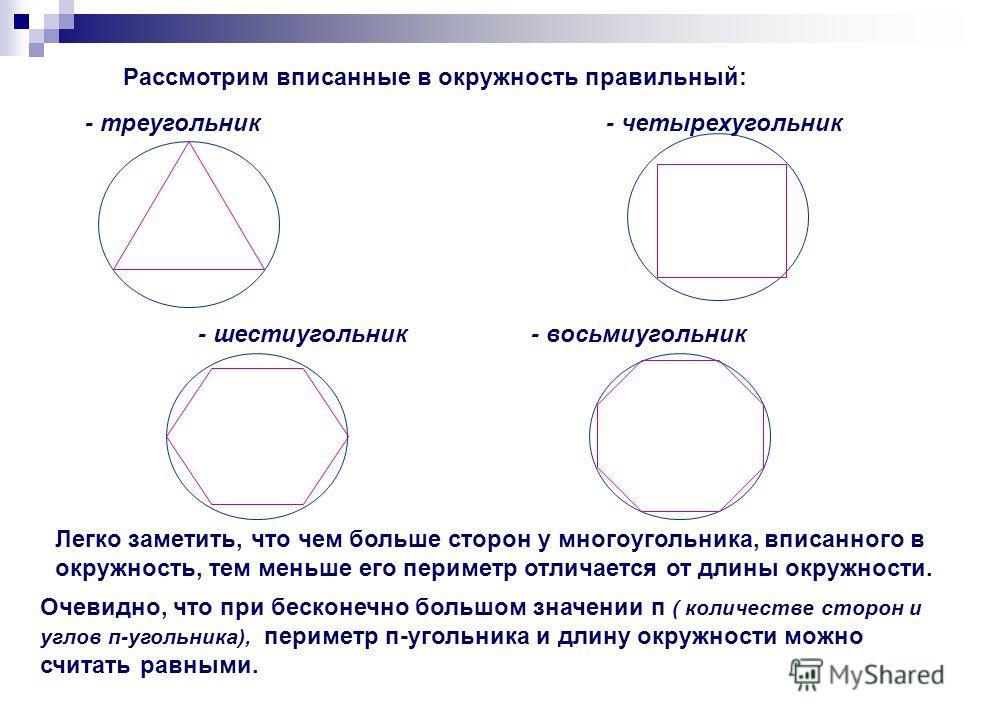 119 и 120.

Деление окружности на пять и десять равных частей и построение правильного вписанного пятиугольника и десятиугольника показано на рис. 122.

Половину любого диаметра (радиус) делят пополам (рис. 122, а), получают точку А. Из точки А, как из центра, проводят дугу радиусом, равным расстоянию от точки А до точки 1, до пересечения со второй половиной этого диаметра, в точке В (рис. 122, б). Отрезок 1В равен хорде, стягивающей дугу, длина которой равна 1 /₅ длины окружности. Делая засечки на окружности (рис. 122, в) радиусом R, равным отрезку 1В, делят окружность на пять равных частей. Начальную точку 1 выбирают в зависимости от расположения пятиугольника. Из точки / строят точки 2 и 5 (рис. 122, в), затем из точки 2 строят точку 3, а из точки 5 строят точку 4. Расстояние от точки 3 до точки 4 проверяют циркулем; если расстояние между точками 3 и 4 равно отрезку 1В, то построения были выполнены точно. Нельзя выполнять засечки последовательно, в одну сторону, так как происходит набегание ошибок и последняя сторона пятиугольника получается перекошенной. Последовательно соединив найденные точки, получают пятиугольник (рис. 122, г).

Деление окружности на десять равных частей выполняют аналогично делению окружности на пять равных частей (рис. 122), но сначала делят окружность на пять частей, начиная построение из точки /, а затем из точки 6, находящейся на противоположном конце диаметра (рис. 123, а). Соединив последовательно все точки, получают правильный вписанный десятиугольник (рис. 123, б).

Деление окружности на семь и четырнадцать равных частей и построение правильного вписанного семиугольника и четырнадцатиугольника показано на рис. 124 и 125.

Из любой точки окружности, например точки Л, радиусом заданной окружности проводят дугу (рис. 124, а) до пересечения с окружностью в точках В и D. Соединим точки В и D прямой. Половина полученного отрезка (в данном случае отрезок ВС) будет равна хорде, которая стягивает дугу, составляющую 1 /₇ длины окружности.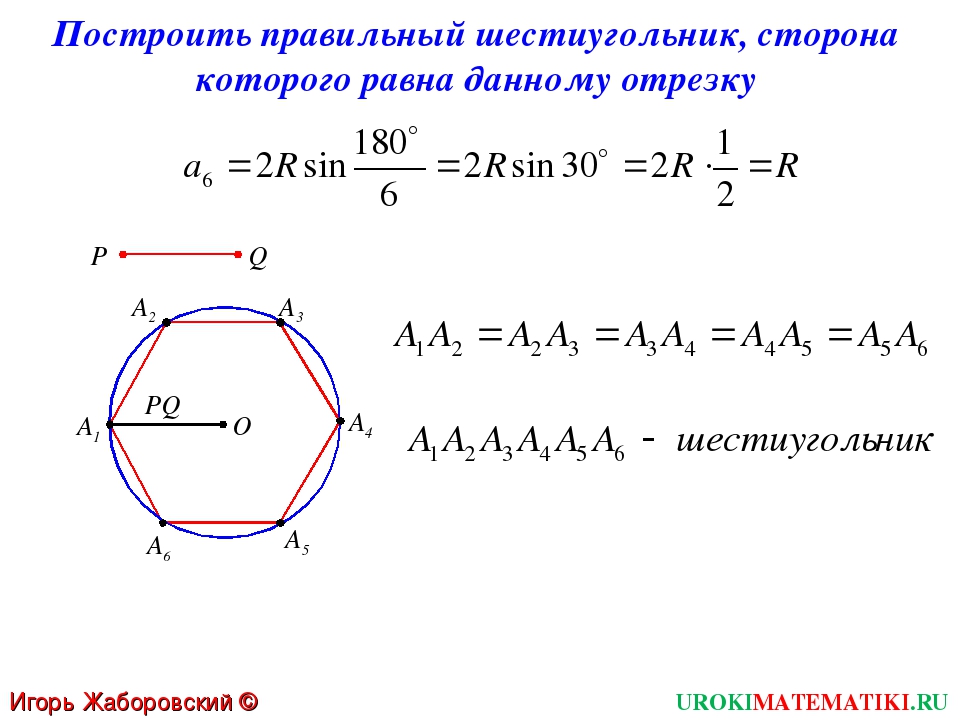 Радиусом, равным отрезку ВС, делают засечки на окружности в последовательности, показанной на рис. 124, б. Соединив последовательно все точки, получают правильный вписанный семиугольник (рис. 124, в).

Деление окружности на четырнадцать равных частей выполняется делением окружности на семь равных частей два раза от двух точек (рис. 125, а).

Сначала окружность делится на семь равных частей от точки /, затем то же построение выполняется от точки 8. Построенные точки соединяют последовательно прямыми линиями и получают правильный вписанный четырна-дцатиугольник (рис. 125, б).

СОПРЯЖЕНИЯ

Рассматривая детали, видим, что в их конструкции часто одна поверхность переходит в другую. Обычно эти переходы делают плавными, что повышает прочность деталей и делает их более удобными в работе. На чертеже поверхности изображаются линиями, которые также плавно переходят одна в другую.

На рис. 126, а изображена деталь, в которой плавные переходы одних плоскостей в другие представляют собой цилиндрические поверхности.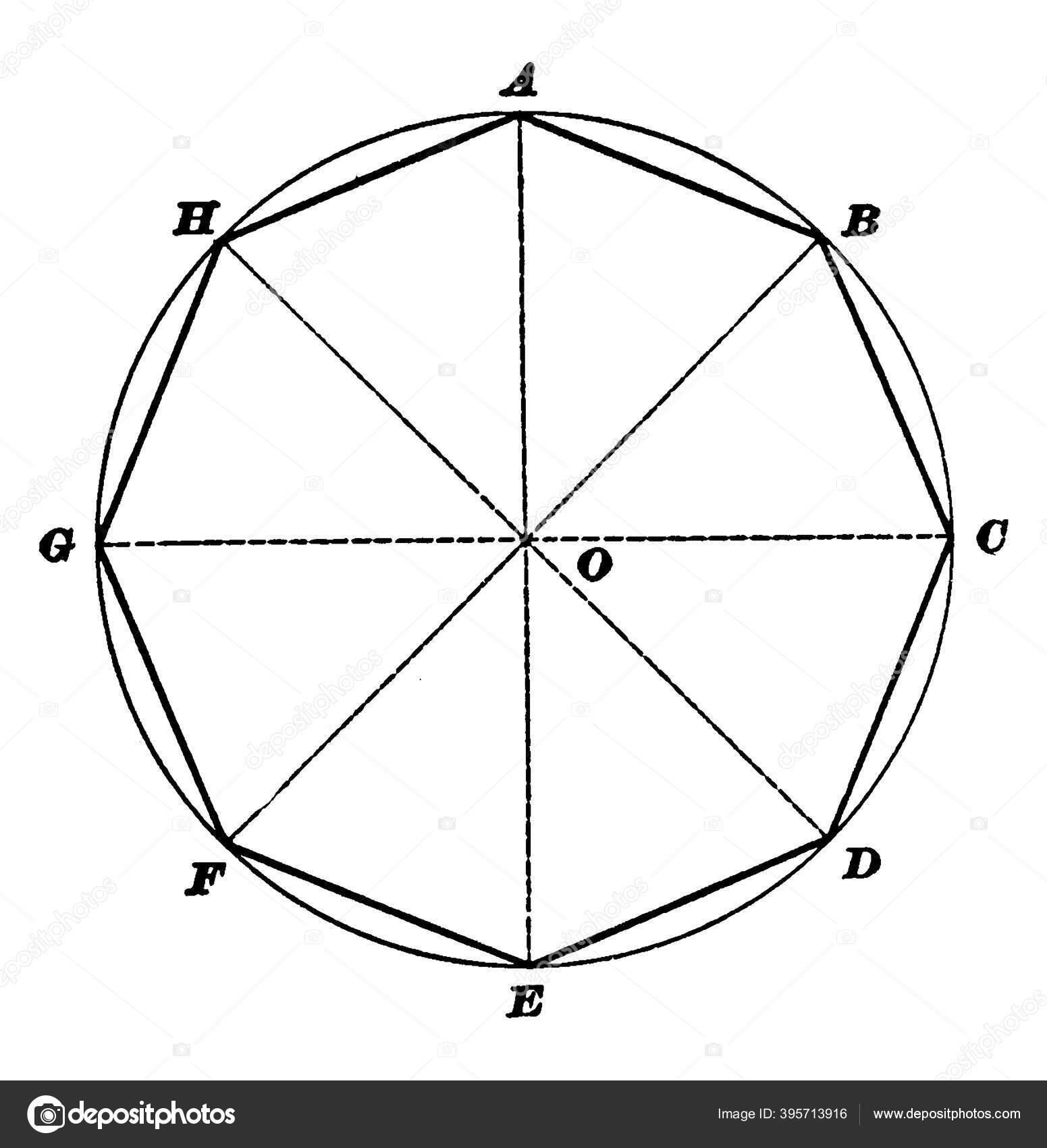 На чертеже (рис. 126, б) эти плоскости изображены прямыми линиями, а цилиндрические поверхности — дугами окружностей. Плавные переходы от одной прямой к другой в этих случаях выполняются дугой заданного радиуса.

Плавный переход одной цилиндрической поверхности в другую может являться цилиндрической поверхностью (рис. 127, а). На чертеже эти цилиндрические поверхности изображены дугами окружностей, (рис. 127, б). В этом случае плавный переход одной дуги окружности в другую осуществляется дугой окружности заданного радиуса.

На рис. 126, а и 127, а рассмотрены простейшие примеры плавных переходов поверхностей. В чертежах более сложных деталей плавные переходы между поверхностями изображаются различными сочетаниями прямых, окружностей и их дуг. Вариантов таких сочетаний может быть много, но их объединяет одно — плавность перехода. Такой плавный переход одной линии (поверхности) в другую линию (поверхность) называют сопряжением. При построении сопряжения необходимо определить границу, где кончается одна линия и начинается другая, т.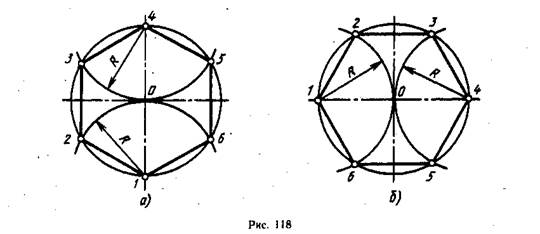 е. найти на чертеже точку перехода, которая называется точкой сопряжения или точкой касания.

Задачи на сопряжения условно можно разделить на три группы.

Первая группа задачвключает в себя задачи на построение сопряжений, где участвуют прямые линии. Это может быть непосредственное касание прямой и окружности, сопряжение двух прямых дугой заданного радиуса, а также проведение касательной прямой к двум окружностям.

Построение окружности, касательной к прямой, связано с нахождением точки касания и центра окружности.

Задана горизонтальная прямая АВ, требуется построить окружность радиусом R, касательную к данной прямой (рис. 128). Точка касания выбирается произвольно. Так как точка касания не задана, то окружность радиуса R может коснуться данной прямой в любой точке. Таких окружностей можно провести множество. Центры этих окружностей (O₁, О₂и т. д.) будут находиться на одинаковом расстоянии от заданной прямой, т.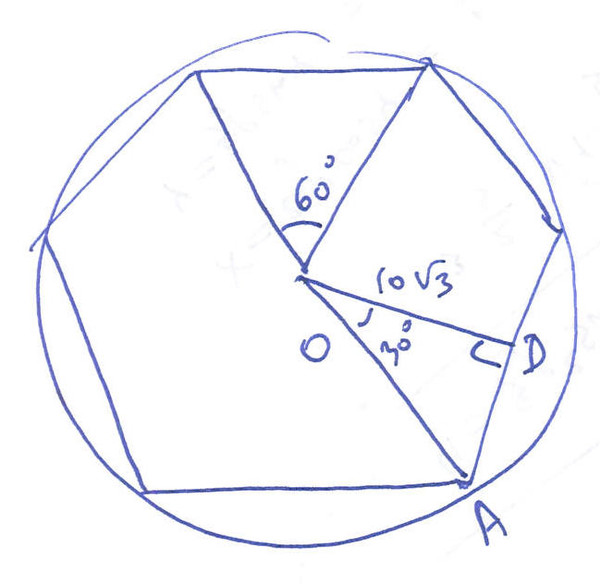 е. на линии, расположенной параллельно заданной прямой АВ на расстоянии, равном радиусу заданной окружности (рис. 128). Назовем эту линию линией центров. Проведем линию центров параллельно прямой АВ на расстоянии R. Так как центр касательной окружности не задан, возьмем любую точку на линии центров, например точку О. Прежде чем проводить касательную окружность, следует определить точку касания. Точка касания будет лежать на перпендикуляре, опущенном из точки О на прямую АВ. В пересечении перпендикуляра с прямой АВ получим точку К, которая будет точкой касания. Из центра О радиусом R от точки К проведем окружность. Задача решена.

В детали, которая изображена на рис. 129, а, пластина плавно переходит в цилиндр. При выполнении чертежа этой детали необходимо построить плавный переход прямой в окружность.

Задача аналогична предыдущей, но дополнена условием, что точка касания задана, так как задан размер А (рис. 129, б), который определяет величину прямолинейного участка.

Отложив размер Л, находят точку касания (точку /С), затем из точки К восставляют перпендикуляр, на котором откладывают радиус R заданной окружности, и находят центр окружности (точку О). При обводке сначала от точки касания проводится дуга заданного радиуса, а потом — прямая.

Из сказанного следует:

1) центр окружности, касательной к прямой, лежит на прямой (линия центров), проведенной параллельно заданной прямой, на расстоянии, равном радиусу данной окружности;

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Сдача сессии и защита диплома – страшная бессонница, которая потом кажется страшным сном. 8801 – | 7160 – или читать все.

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены.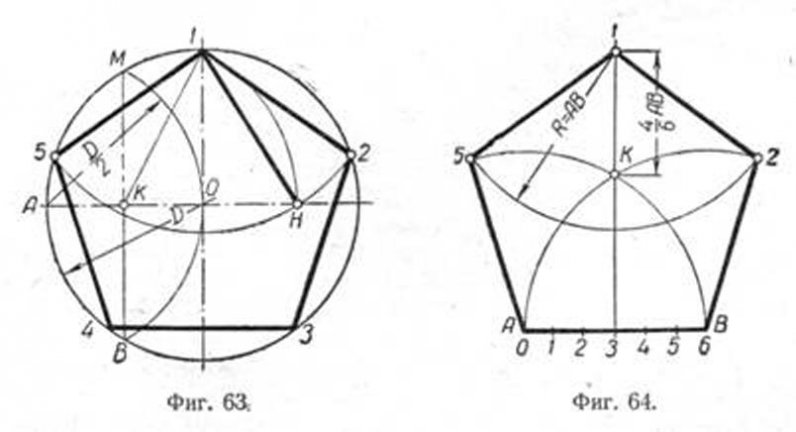 2)/(4 tan⁡〖(180°)/n〗 )

В правильный многоугольник можно вписать окружность и описать окружность вокруг него. Радиусы внутренней и внешней окружности всецело зависят от длины стороны и их количества. Чтобы найти радиус вписанной окружности правильного многоугольника, зная сторону, нужно разделить ее на два тангенса угла, полученного делением 180 градусов на количество сторон. Радиус описанной окружности, в свою очередь, равен стороне, деленной еа два синуса того же угла. r=a/(2 tan⁡〖(180°)/n〗 ) R=a/(2 sin⁡〖(180°)/n〗 )

Угол правильного многоугольника зависит только от количества сторон и рассчитывается как 180 градусов, деленные на количество сторон, и умноженные на разность количества сторон и двух. α=(n-2) (180°)/n

Как построить правильный шестиугольник с помощью циркуля

Урок 35. Геометрия 9 класс

Конспект урока «Построение правильных многоугольников»

На этом уроке мы рассмотрим способы построения некоторых правильных многоугольников с помощью циркуля и линейки. А также изобразим правильный многоугольник графически.

Для начала давайте вспомним определение правильного многоугольника. Итак, правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.

Для выполнения построений мы используем циркуль и линейку.

– построить дугу окружности,

– отложить на прямой отрезок, равный данному.

– построить прямую линию,

– построить отрезок, соединяющий две точки,

– найти точку пересечения двух прямых.

Ранее мы с вами уже рассматривали построения правильного треугольника и четырехугольника, т.е. квадрата.

Давайте рассмотрим, каким образом можно с помощью циркуля и линейки построить правильный треугольник и правильный четырехугольник, вписанные в окружность.

Задача 1. Вписать в заданную окружность правильный треугольник

Построение. Пусть задана окружность с центром О. Проведем произвольный диаметр BD окружности. Построим прямую l, являющуюся серединным перпендикуляром к радиусу OD. Середину радиуса ОD обозначим точкой К. Отметим точки А и C – пересечения прямой l с окружностью. И построим отрезки BA и BC. Треугольник ABC – правильный.

В Тогда Отсюда, .

Значит,

Задача 2. Вписать в заданную окружность правильный четырехугольник.

Построение. Пусть задана окружность с центром О. Построим диаметр AC. Затем построим диаметр BD перпендикулярный диаметру AC. Точки А, C и B, D – точки пересечения диаметров с окружностью. И построим отрезки АB, BC, CD и АD. Четырехугольник ABCD – правильный.

Т.к. Т.к. Т.к. Т.к. Следовательно, – квадрат.

Значит, – правильный четырехугольник.

Теперь давайте рассмотрим построения правильных n-угольников при n>4. Обычно для построения таких n-угольников используется окружность, описанная около многоугольника.

Задача 3. Построить правильный шестиугольник, сторона которого равна данному отрезку.

Построение. Так как в правильном шестиугольнике сторона а равна радиусу, то достаточно последовательно отложить от одной точки окружности 6 радиусов-хорд.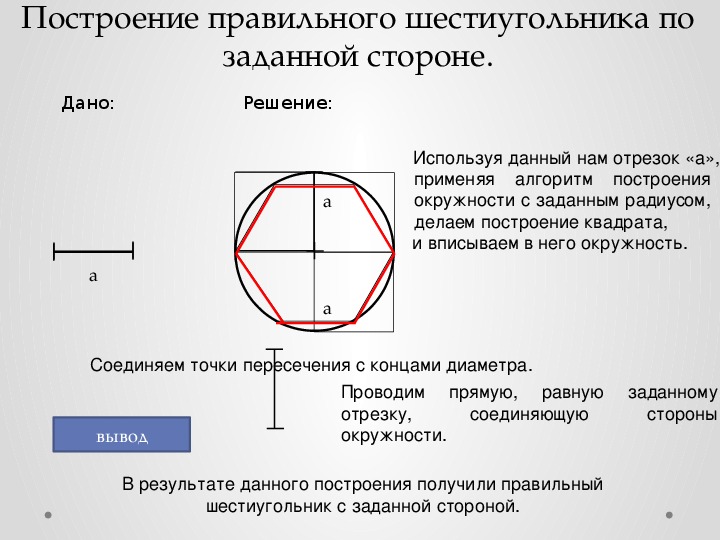 Пусть МN – заданный отрезок. Построим окружность с произвольным центром О и радиуса MN. Отметим на этой окружности произвольную точку А. Затем, не меняя раствора циркуля, последовательно от этой точки А будем делать на окружности засечки, пока последняя засечка не совпадет с взятой первоначально точкой А. Отметим точки B, C, D, Е и F. Теперь соединим последовательно построенные точки отрезками. Получим искомый правильный шестиугольник ABCD.

Равные хорды стягивают равные дуги.

Все углы шестиугольника будут равны, так как опираются на дуги, состоящие из четырех равных меньших дуг.

Для построения правильных многоугольников часто используется следующая задача: дан правильный n-угольник. Построить правильный 2n-угольник.

Задача 4. Дан правильный шестиугольник. Построить правильный двенадцатиугольник.

Пусть ABCDEF – данный правильный шестиугольник. Опишем около него окружность.

1. 2. Окружность .

3. – серединные

перпендикуляры к .

5. – правильный двенадцатиугольник.

Применяя указанный способ, можно с помощью циркуля и линейки построить целый ряд правильных многоугольников, если построен один из них. Например, построив правильный четырехугольник, т.е. квадрат, и пользуясь задачей 4, можно построить правильный восьмиугольник, затем правильный шестнадцати-угольник и вообще правильный 2 k угольник, где k – любое целое число, большее 2.

Замечание. Рассмотренные примеры показывают, что многие правильные многоугольники могут быть построены с помощью циркуля и линейки. Но важно заметить, что не все правильные многоугольники могут быть построены таким образом.

С давних времен построению правильных многоугольников математики уделяли большое внимание. Древние греки умели строить правильные треугольники, четырехугольники, пятиугольники. А также многоугольники, получаемые удвоением их сторон, шестиугольники, восьмиугольники, десятиугольники и т.д. Далее дело зашло в тупик. И только 2000 лет спустя великий немецкий математик 17 века Карл Гаусс, которого называли «королем математики», решил эту математическую проблему. Будучи девятнадцати летним юношей, он доказал, что можно построить правильный семнадцати-угольник, а вот семиугольник, девятиугольник, одиннадцатиугольник, тринадцати-угольник циркулем и линейкой построить нельзя. Задача о построении правильного семнадцати-угольника была самым первым его научным открытием.

Подведем итоги урока.

Сегодня мы рассмотрели способы построения некоторых правильных многоугольников с помощью циркуля и линейки. Научились строить правильные треугольник и четырехугольник, вписанные в окружность. А также выполнили задачу на построение правильного многоугольника по заданному отрезку, и задачу на построение правильного 2n-угольника по заданному n-угольнику.

Есть ли поблизости от Вас карандаш? Взгляните-ка на его сечение – оно представляет собой правильный шестиугольник или, как его еще называют, гексагон. Такую форму имеет также сечение гайки, поле гексагональных шахмат, кристаллическая решетка некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты. Гигантский правильный шестиугольник был недавно обнаружен в атмосфере Сатурна. Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим эту фигуру поподробнее.

Длина его сторон соответствует радиусу описанной окружности. Из всех геометрических фигур это свойство имеет лишь правильный шестиугольник.
Углы равны между собой, и величина каждого составляет 120°.
Периметр гексагона можно найти по формуле Р=6*R, если известен радиус описанной вокруг него окружности, или Р=4*√(3)*r, если окружность в него вписана. R и r – радиусы описанной и вписанной окружности.
Площадь, которую занимает правильный шестиугольник, определяется следующим образом: S=(3*√(3)*R 2 )/2. Если радиус неизвестен, вместо него подставляем длину одной из сторон – как известно, она соответствует длине радиуса описанной окружности.

Теперь рассмотрим построение правильного шестиугольника. Есть несколько способов, самый простой из которых предполагает использование циркуля, карандаша и линейки. Вначале рисуем циркулем произвольную окружность, затем в произвольном месте на этой окружности делаем точку. Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек. Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.

Построение шестигранника может производиться несколькими способами. Удобнее всего использовать стандартный набор чертежных инструментов: циркуль, линейку. Однако, в отсутствие циркуля, фигура этого типа может быть начерчена с помощью рейсшины, угольника заводского изготовления с углами 90/60/30°.

Шестигранники применяются для откручивания и закручивания болтов при ремонте и сборке мебели.

В обоих случаях особенностью построения является элементарное знание основ геометрии.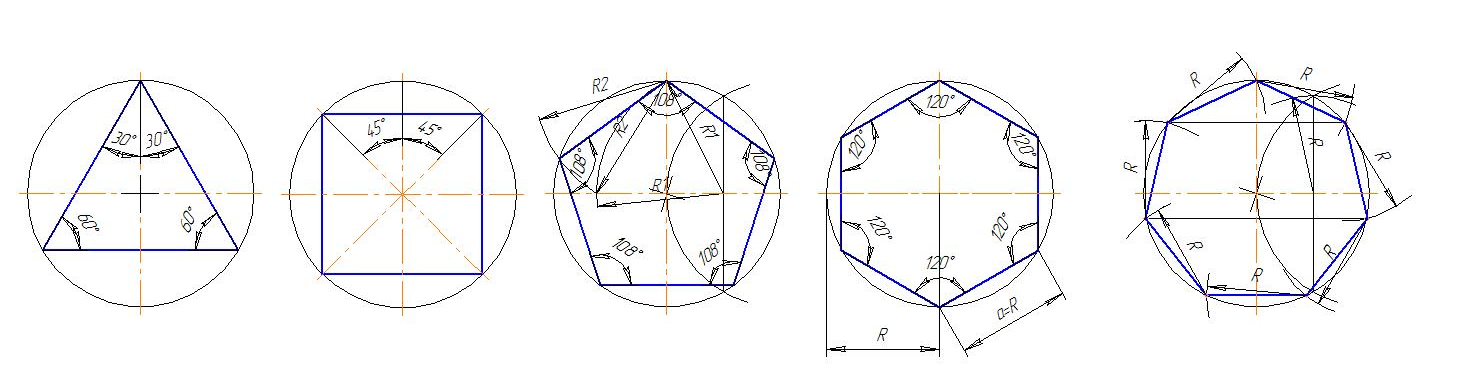 В правильном шестиугольнике длина его стороны всегда равна радиусу окружности, описанной вокруг него, противоположные стороны параллельны, грани сопрягаются под углом 60°.

Способ вычерчивания шестиугольника циркулем, линейкой

Чтобы построить шестигранник при наличии циркуля, достаточно вычертить окружность, найти на ее дуге 6 точек, соединив их отрезками. Для этого достаточно настроить циркуль один раз, отложив на нем значение стороны многогранника. Линейка потребуется для строительства вспомогательных, основных линий.

Метод выглядит следующим образом:

Первый способ вычерчивания шестиугольника циркулем: 1,2,3,4,5,6 — углы, 0 — центр, D — радиус шестигранника.

циркулем вычерчивается окружность — радиус является размером стороны;
по линейке проводится радиус — точки пересечения этого отрезка будут углами многоугольника;
находятся два угла многоугольника — циркуль переставляется в одну из точек пересечения отрезка (проведенный на предыдущем этапе диаметр), на дуге делаются отметки;
находятся оставшиеся два угла — циркуль перемещается в противоположную точку пересечения отрезка с дугой окружности, создаются отметки пересечения на второй стороне окружности.

Построение правильного шестигранника завершается соединением получившихся углов по линейке. Это самый точный способ, требующий минимального количества чертежного инструмента. При значительном размере сторон (например, крой листового металла, деревянных заготовок) можно использовать шнур с карандашом. Один край шнура крепится к карандашу/маркеру, второй неподвижно фиксируется в центре окружности, затем в точках пересечения диаметра с дугой окружности.

Построение занимает минимальное количество времени, точность целиком зависит от заточки карандаша, наличия фиксатора на циркуле.

Способ вычерчивания шестиугольника без циркуля

Построение правильного шестигранника без циркуля требует обязательного наличия рейсшины — специального инструмента в виде линейки, внутри корпуса которой расположен массивный вал с резиновыми элементами, препятствующими проскальзыванию. Он создан для быстрого изготовления параллельных прямых, обеспечивая высокую точность построений. Качество вычерчивания в данном методе полностью зависит от точности угла 60° в угольнике заводского изготовления, градуирования шкалы линейки.

Способ построения выглядит следующим образом:

Второй способ вычерчивания шестиугольника циркулем: 1,2,3,4,5,6 — углы, 0 — центр, D — радиус шестигранника.

к одной стороне отрезка прикладывается угольник — короткая сторона совмещена с линией, угол 60° примыкает к концу отрезка изнутри, по гипотенузе угольника проводится линия произвольного размера, который корректируется впоследствии по шкале линейки;
на листе/заготовке вычерчивается линия — длина ее равна двум размерам стороны многоугольника, края автоматически становятся центрами многогранника;
операция повторяется при развороте угольника — угол 60° перемещается к противоположной стороне отрезка, центром вращения является длинный катет угольника;
разворот угольника — теперь центром вращения становится короткий катет угольника, вычерчиваются еще две грани;
уточнение размеров сторон — на четырех получившихся сторонах многоугольника по линейке откладывается их точный размер;
строительство двух оставшихся сторон — они расположены параллельно линии, с которой было начато черчение, проводятся по линейке, затем уточняется их размер;
контроль параллельности — шкала рейсшины совмещается с линией, от которой началось построение фигуры, затем инструмент перемещается вверх/вниз для удостоверения параллельности двух противоположных граней между собой, с этим отрезком

Шестигранник в этом случае вычерчивается дольше, чем в первом способе. Однако так можно построить необходимую фигуру, в отсутствие циркуля, угольником. Технология основана на параллельности противоположных сторон правильного шестиугольника, одинаковых внутренних углах 60°.

Промышленность выпускает угольники как с острыми углами, удобными для данного метода, так и со скругленными.

Третий способ вычерчивания шестиугольника циркулем: a — диаметр, b — сторона шестигранника.

В последнем случае удобнее несколько изменить технологию:

после вычерчивания центрального отрезка по нему выравнивается рейсшина;
инструмент откатывается вниз на произвольную величину;
короткая гипотенуза угольника совмещается с линейкой рейсшины, а не с центральным отрезком;
скругленный край инструмента не участвует в построении, линия проводится по цельной части гипотенузы.

Операция повторяется с противоположной стороны отрезка, после чего рейсшина разворачивается на 180°, опять совмещается с центральной линией, откатывается вверх для построения двух других сторон многогранника.

Это стандартные способы вычерчивания равностороннего многоугольника с шестью углами, гранями. Они удобны для кроя заготовок любых размеров из разных материалов, в стандартном черчении на ватмане. Обе методики имеют исключительно прикладное значение, так как в профессиональных графических редакторах (AutoCAD, Компас-3D) подобные фигуры создаются автоматически заданием нужных параметров.

Как вписать двенадцатиугольник в окружность

Являющиеся одной из неотъемлемых частей школьной программы, геометрические задачи на построение правильных многоугольников достаточно тривиальны. Как правило, построение ведется путем вписывания многоугольника в окружность, которая вычерчивается первой. Но что делать, если окружность задана, а фигура весьма сложна?Вам понадобится

К имеющейся окружности постройте хорду. Вычертите произвольный отрезок прямой так, чтобы он имел две точки пересечения с ю. Определите эти точки как A и B.

Постройте отрезок прямой, перпендикулярной AB и разделяющий его в точке пересечения на две равные части. Поставьте иглу циркуля в точку A. Поставьте ножку с грифелем в точку B, либо в любую точку отрезка, которая находится ближе к B чем к A. Начертите окружность. Не меняя раствор ножек циркуля установите его иглу в точку B. Начертите еще одну окружность.Вычерченные окружности пересекутся в двух точках. Проведите через них отрезок прямой. Обозначьте точку пересечения данного отрезка с отрезком AB как C. Обозначьте точки пересечения этого отрезка с первоначальной окружностью как D и E.

Постройте перпендикуляр к отрезку DE, делящий его пополам. Произведите действия, аналогичные тем, что были описаны в предыдущем шаге, по отношению к отрезку DE. Пусть вычерченный отрезок пересекает DE в точке O. Данная точка будет являться центром окружности. Также обозначьте точки пересечения построенного перпендикуляра с первоначальной окружностью как F и G.

Установите раствор ножек циркуля таким образом, чтобы расстояние между их концами было равно радиусу первоначальной окружности. Для этого поместите иглу циркуля в одну из точек A, B, D, E, F или G. Конец ножки с грифелем поместите в точку O.

Постройте правильный шестиугольник. Установите иглу циркуля в любую точку линии окружности. Обозначьте эту точку H. В направлении движения по часовой стрелке сделайте циркулем дугообразную засечку так, чтобы она пересекала линию окружности. Обозначьте эту точку I. Переместите иглу циркуля в точку I. Снова сделайте засечку на окружности и обозначьте полученную точку J. Аналогичным образом постройте точки K, L, M. Последовательно попарно соедините точки H, I, J, K, L, M, H. Полученная фигура является правильным шестиугольником, вписанным в заданную окружность.

Найдите недостающие точки вершин углов двенадцатиугольника. К отрезкам HI, IJ, JK постройте делящие их пополам перпендикуляры так, чтобы построенные отрезки пересекали окружность O в двух точках. Обозначьте полученные точки буквами N, O, P, Q, R, S, начиная с той, что находится за точкой H на окружности по направлению движения часовой стрелки.

Постройте правильный двенадцатиугольник, вписанный в окружность. Попарно соедините точки H, N, I, O, J, P, K, Q, L, R, M, S, H отрезками. Многоугольник HNIOJPKQLRMS является искомым двенадцатиугольником.

необходимый минимум информации. Получение с помощью полоски бумаги

Если под руками нет циркуля, то можно нарисовать простую звезду с пятью лучами затем просто соединить эти лучи. как видим на картинке ниже получается абсолютно правильный пятиугольник.

Математика сложная наука и у нее много своих секретиков, некоторые из них весьма забавны. Если вы увлекаетесь такими вещами советую найти книгу Забавная математика.

Окружность можно нарисовать не только при помощи циркуля. Можно, например, использовать карандаш и нитку. Отмеряем нужный диаметр на нитке. Один конец плотно зажимаем на листе бумаги, где будем чертить окружность. А на другой конец нитки устанавливаемые карандаш и одержим. Теперь действует как с циркулем: натягиваем нить и по окружности слегка надавливая карандашом чкртим окружность.

Внутри окружности рисуем крестьян от центра: вертикальная линия и горизонтальная линия. Точка пересечения вертикальной линии и окружности будет вершиной пятиугольника (точка 1). Теперь правую половину горизонтальной линии делим пополам (точка 2). Измеряем расстояние от этой точки до вершины пятиугольника и этот отрезок откладывает влево от точки 2 (точка 3). При помощи нитки и карандаша проводим от точки 1 радиусом до точки 3 дугу, пересекающую первую окружность слева и справа — точки пересечения будут вершинами пятиугольника. Обозначим их точка 4 и 5.

Теперь от точки 4 делаем дугу, пересекающую окружность в нижней части, радиусом равной длине от точки 1 до 4 — это будет точкой 6. Точно так же и от точки 5 — обозначим точкой 7.

Остатся соединить наш пятиугольник с вершинами 1, 5, 7, 6, 4.

Я знаю как построить простой пятиугольник с помощью циркуля: Строим окружность, отмечаем пять точек, соединяем их. Можно построить пятиугольник с равными сторонами, для этого нам еще понадобится транспортир. Просто те же самые 5 точек ставим по транспортиру. Для этого отмечаем углы по 72 градуса. После чего также соединяем отрезками и получаем нужную нам фигуру.

Зеленую окружность можно чертить произвольным радиусом. В эту окружность будем вписывать правильный пятиугольник. Без циркуля начертить точно окружность нельзя, но это не обязательно. Окружность и все дальнейшие построения можно выполнять от руки. Далее через центр окружности О нужно провести две взаимно перпендикулярные прямые и одну из точек пересечения прямой с окружностью обозначить А. Точка А будет вершиной пятиугольника. Радиус ОВ разделим пополам и поставим точку С. Из точки С проводим вторую окружность радиусом АС. Из точки А проводим третью окружность радиусом АD. Точки пересечения третьей окружности с первой (Е и F)будут также вершинами пятиугольника. Из точек Е и F радиусом АЕ делаем засечки на первой окружности и получаем остальные вершины пятиугольника G и H.

Адептам черного искусства: что бы просто, красиво и быстро нарисовать пятиугольник, следует начертить правильную, гармоничную основу для пентаграммы (пятиконечная звезда) и соединить окончания лучей этой звезды посредством прямых, ровных линий. Если все было сделано верно — соединительная черта вокруг основы и будет искомым пятиугольником.

(на рисунке — завершенная, но незаполненная пентаграмма)

Для тех, кто неуверен в правильности начертания пентаграммы: возьмите за основу витрувианского человека Да Винчи (см. ниже)

Если нужен пятиугольник — тыкаете произвольным образом 5 точке и их внешний контур будет пятиугольником.

Если нужен правильный пятиугольник, то без математического циркуля это построение совершить невозможно, поскольку без него нельзя провести два одинаковых, но не параллельных отрезка. Любой другой инструмент, который позволяет провести два одинаковых, но не параллельных отрезка эквивалентен математическому циркулю.

Сначала надо надо начертить круг, потом направляющие, потом второй пунктирный круг, находим верхнюю точку, потом отмеряем два угла верхние, от них чертим нижние. Заметьте, радиус циркуля один и тот же при всем построении.

Вс зависит от того, какой пятиугольник вам необходим. Если любой, то ставите пять точек и соединяете их между собой(естествено точки ставим не по прямой линии). А если нужен пятиугольник правильно формы, возьмите любые пять по длине(полосок бумаги, спичек, карандашей и т.п), выложите пятиугольник и обчертите его.

Пятиугольник можно начертить, к примеру, из звезды. Если умеете чертить звезду, но не умеете пятиугольник, начертите звезду карандашом, затем соедините между собой соседние концы звезды, а саму звезду потом сотрите.

Второй способ. Вырежьте полосочку из бумаги, длиной, равной желаемой стороне пятиугольника, а шириной узкой, допустим 0.5 — 1 см. Как по шаблону, вырежьте по этой полосочке ещ четыре таких же полосочки, чтобы их получилось всего 5.

Затем положите лист бумаги (лучше его закрепить на столе при помощи четырх кнопок или иголочек). Затем наложите эти 5 полосочек на листок так, чтобы они образовали пятиугольник. Приколите эти 5 полосочек к листку бумаги кнопками или иголочками, чтобы они оставались неподвижными. Затем обведите полученный пятиугольник и снимите эти полосочки с листка.

Если нет циркуля и нужно построить пятиугольник, то я могу посоветовать следующее. Я и сама так строила. Можно начертить правильную пятиконечную звезду. И после этого, чтобы получить пятиугольник, просто нужно соединить все вершины звезды. Вот так и получится пятиугольник. Вот что мы получим

Ровными чрными линии мы соединили вершины звезды и получили пятиугольник.

Уровень сложности: Несложно

1 шаг

Сначала, выбирайте, где разместить центр окружности. Там нужно поставить начальную точку, пусть она называется О. С помощью циркуля вычерчиваем вокруг нее окружность заданного диаметра или радиуса.

2 шаг

Затем проводим две оси через точку О, центр окружности, одна горизонтальная, другая под 90 градусов по отношению к ней – вертикальная. Точки пересечения по горизонтали назовем слева на право А и В, по вертикали, сверху вниз – М и Н. Радиус, который лежит на любой оси, например, на горизонтальной в правой части, делим пополам. Это можно сделать так: циркуль с радиусом известной нам окружности устанавливаем острием в точку пересечения горизонтальной оси и окружности – В, отчеркиваем пересечения с окружностью, полученные точки называем, соответственно сверху вниз – С и Р, соединяем их отрезком, который будет пересекать ось ОВ, точку пересечения называем К.

3 шаг

Соединяем точки К и М и получаем отрезок КМ, устанавливаем циркуль в точку М, задаем на нем расстояние до точки К и очерчиваем метки на радиусе ОА, эту точку называем Е, далее ведем циркуль до пересечения с левой верхней частью окружности ОМ. Эту точку пересечения называем F. Расстояние равное отрезку МЕ является искомой стороной равностороннего пятиугольника. При этом точка М будет являться одной вершиной встраиваемого в окружность пятиугольника, а точка F – другой.

4 шаг

Далее из полученных точек по всей окружности отчерчиваем циркулем расстояния, равные отрезку МЕ, всего точек должно получиться 5. Соединяем все точки отрезками – получаем пятиугольник, вписанный в окружность.

При черчении будьте аккуратны в измерениях расстояний, не допускайте погрешностей, чтобы пятиугольник действительно полчился равносторонним

Правильный пятиугольник представляет собой геометрическую фигуру, которая образовывается пересечением пяти прямых, создающих пять одинаковых углов. Такая фигура носит название — пентагон. С пятиугольником тесно связана работа художников — их рисунки строятся на основе правильных геометрических фигур. Для этого необходимо знать то, как быстро построить пентагон.

Чем интересна эта фигура? Форму пентагона имеет здание Министерства обороны Соединенных Штатов Америки . Это можно увидеть на фото, сделанных с высоты полета. В природе не существует кристаллов и камней, форма которых напоминала бы пентагон. Только в этой фигуре количество граней совпадает с числом диагоналей.

Параметры правильного пятиугольника

Прямоугольный пятиугольник, как и каждая фигура в геометрии, имеет свои параметры. Зная необходимые формулы, можно рассчитать эти параметры, что облегчит процесс построения пентагона. Способы и формулы расчетов:

сумма всех углов в многоугольниках равна 360 градусам. В правильном пятиугольнике все углы равны, соответственно, центральный угол находится таким способом: 360/5 = 72 градуса;
внутренний угол находится таким образом: 180*(n -2)/ n = 180*(5−2)/5 = 108 градусов. Сумма всех внутренних углов: 108*5 = 540 градусов.

Сторона пентагона находится с помощью параметров, которые уже даны в условии задачи:

если вокруг пятиугольника описана окружность и известен ее радиус, сторона находится по такой формуле: a = 2*R*sin (α/2) = 2*R*sin (72/2) = 1,1756*R.
Если известен радиус вписанной в пентагон окружности, то формула расчета стороны многоугольника: 2*r*tg (α/2) = 2*r*tg (α/2) = 1,453*r.
При известной величине диагонали пентагона его сторона рассчитывается таким образом: а = D/1,618.

Площадь пентагона так же , как и его сторона, зависит от уже найденных параметров:

с помощью известного радиуса вписанной окружности площадь находится так: S = (n*a*r)/2 = 2,5*a*r.
описанная вокруг пятиугольника окружность позволяет найти площадь по такой формуле: S = (n*R2*sin α)/2 = 2,3776*R2.
в зависимости от стороны пентагона: S = (5*a2*tg 54°)/4 = 1,7205* a2.

Построение пентагона

Построить правильный пятиугольник можно с помощью линейки и циркуля, на основе вписанной в него окружности или одной из сторон.

Как начертить пятиугольник на основе вписанной окружности? Для этого необходимо запастись циркулем и линейкой и сделать такие шаги:

Сначала необходимо начертить окружность с центром О, после чего на ней выбрать точку, А — вершину пентагона. От центра к вершине проводится отрезок.
Затем строится перпендикулярная прямой ОА отрезок, который также проходит через О — центр окружности. Его пересечение с окружностью обозначается точкой В. Отрезок О. В. делится пополам точкой С.
Точка С станет центром новой окружности, проходящей через А. Точка D — это ее пересечение с прямой ОВ в границах первой фигуры.
После этого проводится третья окружность через D, центром которой является точка А. Она пересекается с первой фигурой в двух точках, их необходимо обозначить буквами Е и F.
Следующая окружность имеет центр в точке Е и проходит через А, а ее пересечение с первоначальной находится в новой точке G.
Последняя окружность в этом рисунке проводится через точку, А с центром F. На ее пересечении с начальной ставится точка Н.
На первой окружности после всех проделанных шагов появились пять точек, которые необходимо соединить отрезками. Таким образом получился правильный пятиугольник АЕ G Н F.

Как построить правильный пятиугольник иным способом? С помощью линейки и циркуля пентагон можно построить немного быстрее. Для этого необходимо:

Cначала необходимо с помощью циркуля нарисовать окружность, центр которой — точка О.
Чертится радиус ОА — отрезок, который откладывается на окружность. Его делят пополам точкой В.
Перпендикулярно радиусу ОА начерчивается отрезок ОС, точки В и С соединяются прямой.
Следующим шагом является отложение длины отрезка ВС с помощью циркуля на диаметральной линии. Перпендикулярно отрезку ОА появляется точка D. Точки В и D соединяются, образуя новый отрезок.
Для того, чтобы получить величину стороны пентагона, необходимо соединить точки С и D.
D с помощью циркуля переносится на окружность и обозначается точкой Е. Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.

В пятиугольнике с одинаковыми сторонами диагонали равны и образуют пятиконечную звезду, которая называется пентаграммой. Золотое сечение — это отношение величины диагонали к стороне пентагона.

Пентагон непригоден для полного заполнения плоскости. Использование любого материала в этой форме оставляет промежутки или образует наложения. Хотя природных кристаллов этой формы не существует в природе, но при образовании льда на поверхности гладких медных изделий возникают молекулы в виде пентагона, которые соединены в цепочки.

Наиболее простой способ получить правильный пятиугольник из полоски бумаги — завязать ее узлом и немного придавить. Этот способ полезен для родителей детей-дошкольников, которые хотят научить своих малышей распознавать геометрические фигуры.

Видео

Посмотрите, как можно быстро начертить пятиугольник.

Задача построения верного пятиугольника сводится к задаче деления окружности на пять равных частей. От того что верный пятиугольник – это одна из фигур, содержащая в себе пропорции золотого сечения, его построением издавна интересовались живописцы и математики. Сейчас обнаружены несколько методов построения верного многоугольника, вписанного в заданную окружность.

Вам понадобится

– линейка
– циркуль

Инструкция

1. Видимо, что если возвести верный десятиугольник, а после этого объединить его вершины через одну, то получим пятиугольник. Для построения десятиугольника начертите окружность заданного радиуса. Обозначьте ее центр буквой O. Проведите два перпендикулярных друг друга радиуса, на рисунке они обозначены как OA1 и OB. Радиус OB поделите напополам с подмогой линейки либо способом деления отрезка напополам с подмогой циркуля. Постройте маленькую окружность с центром C в середине отрезка OB радиусом, равным половине OB.Объедините точку C с точкой A1 на начальной окружности по линейке. Отрезок CA1 пересекает вспомогательную окружность в точке D. Отрезок DA1 равен стороне верного десятиугольника, вписанного в данную окружность. Циркулем подметьте данный отрезок на окружности, после этого объедините точки пересечения через одну и вы получите положительный пятиугольник.

2. Еще один метод обнаружил немецкий художник Альбрехт Дюрер. Дабы возвести пятиугольник по его методу, начните вновь с построения окружности. Вновь подметьте ее центр O и проведите два перпендикулярных радиуса OA и OB. Радиус OA поделите напополам и середину подметьте буквой C. Установите иглу циркуля в точку C и раскройте его до точки B. Проведите окружность радиуса BC до пересечения с диаметром начальной окружности, на котором лежит радиус OA. Точку пересечения обозначьте D. Отрезок BD – сторона положительного пятиугольника. Отложите данный отрезок пять раз на начальной окружности и объедините точки пересечения.

3. Если же требуется возвести пятиугольник по его заданной стороне, то вам надобен 3-й метод. Начертите по линейке сторону пятиугольника, обозначьте данный отрезок буквами A и B. Поделите его на 6 равных частей. Из середины отрезка AB проведите луч, перпендикулярный отрезку. Постройте две окружности радиусом AB и центрами в A и B, как если бы вы собирались разделять отрезок напополам. Эти окружности пересекаются в точке С. Точка C при этом лежит на луче, исходящем перпендикулярно вверх из середины AB. Отложите от C вверх по этому лучу расстояние, равное 4/6 от длины AB, обозначьте эту точку D. Постройте окружность радиуса AB с центром в точке D. Пересечение этой окружности с двумя вспомогательными построенными ранее даст последние две вершины пятиугольника.

Тема деления окружности на равные части с целью построения верных вписанных многоугольников издавна занимала умы древних ученых. Эти тезисы построения с использованием циркуля и линейки были высказаны еще в эвклидовых «Началах». Впрочем лишь через два тысячелетия эта задача была всецело решена не только графически, но и математически.

Инструкция

1. Приближенное построение положительного пятиугольника методом А. Дюрера, с подмогой циркуля и линейки (через две окружности с всеобщим радиусом, равным стороне пятиугольника ).

2. Построение верного пятиугольника на основе положительного десятиугольника, вписанного в окружность (объединив вершины десятиугольника через одну).

3. Графическое построение через вычисленный внутренний угол пятиугольника с поддержкой транспортира и линейки (сумма углов выпуклого n-угольника равна Sn=180°(n – 2), т.к. у положительного многоугольника все углы равны). При n=5, S5=5400, тогда величина угла 1080.А так же с поддержкой окружности и 2-х лучей, выходящих из ее центра, при условии, что угол между ними равен 720, т.к. (36005=720). Их пересечение с окружностью даст отрезок, равный стороне пятиугольника .

4. Еще один легкой графический метод: поделить диаметр заданной окружности AB на три части (AC=CD=DE). Из точки D опустить перпендикуляр до пересечения с окружность в точках E, F.Проведя прямые через отрезки EC и FC до пересечения с окружностью, получим точки G, H.Точки G,E,B,F,H – вершины положительного пятиугольника .

5. Построение с поддержкой приема Биона (дозволяющего возвести верный вписанный в окружность многоугольник с любым числом сторон n по заданному соотношению).Скажем: для n=5. Возведем положительный треугольник ABC, где AB – диаметр заданной окружности. Обнаружим на AB точку D, по дальнейшему соотношению: AD: AB = 2: n. При n=5, AD=25*AB. Проведем прямую через CD до пересечения с окружностью в точке E. Отрезок AE – сторона верного вписанного пятиугольника .При n=5,7,9,10 погрешность построения не превышает 1%. С возрастанием n, погрешность приближения растёт, но остаётся поменьше 10,3%.

6. Построение по заданной стороне по способу Л. Да Винчи (применяя соотношение между стороной многоугольника (аn) и апофемой (ha): аn/2: ha =3/(n-1), которое дозволено выразить так: tg180°/n =3/(n-1)).

7. Всеобщий метод построения положительных многоугольников по заданной стороне по способу Ф. Коваржика (1888 г.), на основе правила Л. да Винчи.Цельный метод построения положительного n-угольника на основании теоремы Фалеса.Дозволено добавить только, что приближенные способы построения многоугольников подлинны, примитивны и прекрасны.

Существуют два основных метода построения верного многоугольника с пятью сторонами. Оба они полагают применение циркуля, линейки и карандаша. 1-й метод представляет собой вписывание пятиугольника в окружность, а 2-й метод базируется на заданной длине стороны вашей грядущей геометрической фигуры.

Вам понадобится

Циркуль, линейка, карандаш

Инструкция

1. 1-й метод построения пятиугольника считается больше «типичным». Для начала постройте окружность и как-либо обозначьте ее центр (обычно для этого применяется буква О). После этого проведите диаметр этой окружности (назовем его АВ) и поделите один из 2-х полученных радиусов (скажем, ОА) ровно напополам. Середину этого радиуса обозначим буквой С.

2. Из точки О (центра начальной окружности) проведите еще один радиус (ОD), тот, что будет сурово перпендикулярен проведенному ранее диаметру (АВ). После этого возьмите циркуль, поставьте его в точку С и отмерьте расстояние до пересечения нового радиуса с окружностью (СD). Это же расстояние отложите на диаметре АВ. Вы получите новую точку (назовем ее Е). Отмерьте циркулем расстояние от точки D до точки Е – оно будет равно длине стороны вашего грядущего пятиугольника .

3. Поставьте циркуль в точку D и отложите на окружности расстояние, равное отрезку DЕ. Повторите эту процедуру еще 3 раза, а после этого объедините точку D и 4 новые точки на начальной окружности. Получившаяся в итоге построения фигура будет верным пятиугольником.

4. Дабы возвести пятиугольник иным методом, для начала начертите отрезок. Скажем, это будет отрезок АВ длиной 9 см. Дальше поделите ваш отрезок на 6 равных частей. В нашем случае длина всякой части будет составлять 1,5 см. Сейчас возьмите циркуль, поставьте его в один из концов отрезка и проведите окружность либо дугу с радиусом, равным длине отрезка (АВ). После этого переставьте циркуль в иной конец и повторите операцию. Полученные окружности (либо дуги) пересекутся в одной точке. Назовем ее C.

5. Сейчас возьмите линейку и проведите прямую через точку С и центр отрезка AB. После этого начиная от точки С отложите на этой прямой отрезок, составляющий 4/6 отрезка AB. 2-й конец отрезка обозначим буквой D. Точка D будет являться одной из вершин грядущего пятиугольника . Из этой точки проведите окружность либо дугу с радиусом, равным АВ. Эта окружность (дуга) пересечет ранее построенные вами окружности (дуги) в точках, являющихся двумя недостающими вершинами пятиугольника . Объедините эти точки с вершинами D, А и В, и построение положительного пятиугольника будет закончено.

Видео по теме

Луч — это прямая линия, проведенная из точки и не имеющая конца. Существуют и другие определения луча: скажем, «…это прямая, ограниченная точкой с одной стороны». Как положительно начертить луч и какие принадлежности для черчения вам потребуются?

Вам понадобится

Лист бумаги, карандаш и линейка.

Инструкция

1. Возьмите лист бумаги и подметьте в произвольном месте точку. После этого приложите линейку и проведите линию, начиная с указанной точки и до бесконечности. Эта нарисованная линия и именуется лучом. Сейчас подметьте на луче еще одну точку, к примеру, буквой C. Линия от исходной и до точки C будет именоваться отрезком. Если вы примитивно начертите линию и не подметите правда бы одну точку, то эта прямая не будет являться лучом.

2. Нарисовать луч в любом графическом редакторе либо в том же MSOffice не труднее, чем вручную. Для примера возьмите программу Microsoft Office 2010. Зайдите в раздел «Вставка» и выберите элемент «Фигуры». В выпадающем списке выберите фигуру «Линия». Дальше курсор примет вид крестика. Дабы начертить ровную линию, нажмите клавишу «Shift»и проведите линию требуемой длины. Сразу позже начертания откроется вкладка «Формат». Теперь у вас нарисована примитивно прямая линия и отсутствует фиксированная точка, а исходя из определения, луч должен быть лимитирован точкой с одной стороны.

3. Дабы сделать точку в начале линии, сделайте следующее: выделите нарисованную линию и вызовите контекстное меню, нажав правую кнопку мыши.

4. Выберите пункт «Формат фигуры». В меню слева выберите пункт «Тип линии». Дальше обнаружьте заголовок «Параметры линий» и выберите «Тип начала» в виде кружочка. Там же вы можете настроить толщину линий начала и конца.

5. Уберите выделение с линии и увидите, что в начале линии возникла точка. Для создания надписи нажмите кнопку «Нарисовать надпись» и сделайте поле, где будет находиться надпись. Позже написания надписи кликните на свободное место и она активируется.

6. Луч благополучно нарисован и заняло это каждого несколько минут. Рисование луча в иных редакторах осуществляется по такому же тезису. При нажатой клавише «Shift» неизменно будут рисоваться пропорциональные фигуры. Славного пользования.

Видео по теме

Обратите внимание!
Отношение диагонали верного пятиугольника к его стороне составляет золотое сечение (иррациональное число (1+√5)/2).Весь из пяти внутренних углов пятиугольника равен 108°.

Полезный совет
Если объединить вершины верного пятиугольника диагоналями, то получится пентаграмма.

Построение вписанного в окружность правильного шестиугольника.

Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой.

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4, строим стороны 1 — 6, 4 — 3, 4 — 5 и 7 — 2, после чего проводим стороны 5 — 6 и 3 — 2.

Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля. Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.

Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0 — 1 — 2 равен 30°, то для нахождения стороны 1 — 2 достаточно построить по точке 1 и стороне 0 — 1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1 — 2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2 — 3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.

Для построения треугольника намечаем на диаметре вершину точку 1 и проводим диаметральную линию 1 — 4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.

Это построение можно выполнить при помощи угольника и циркуля.

Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4 — 1 и 3 -2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1 — 2 и 4 — 3.

Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра. Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.

Построение вписанного в окружность правильного пятиугольника.

Чтобы вписать в окружность правильный пятиугольник, производим следующие построения. Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.

Построение правильного пятиугольника по данной его стороне.

Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую. Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB. Получим точку 1 -вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.

Построение вписанного в окружность правильного семиугольника.

Приведённый способ годен для построения правильных многоугольников с любым числом сторон.

Длины сторон правильных вписанных многоугольников.

В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй — коэффициенты. Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.

Как сделать правильный пятиугольник. Как построить пятиугольник с помощью циркуля

Толковый словарь Ожегова гласит, что пятиугольник представляет собой ограниченную пятью пересекающимися прямыми, образующими пять внутренних углов, а также любой предмет подобной формы. Если у данного многоугольника все стороны и углы одинаковые, то он называется правильным (пентагоном).

Чем интересен правильный пятиугольник?

Именно в такой форме было построено всем известное здание Минобороны Соединенных Штатов. Из объемных правильных многогранников лишь додекаэдр имеет грани в форме пентагона. А в природе напрочь отсутствуют кристаллы, грани которых напоминали бы собой правильный пятиугольник. Кроме того, эта фигура является многоугольником с минимальным количеством углов, которым невозможно замостить площадь. Только у пятиугольника количество диагоналей совпадает с количеством его сторон. Согласитесь, это интересно!

Основные свойства и формулы

Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон.

Центральный угол α = 360 / n = 360/5 =72°.
Внутренний угол β = 180° * (n-2)/n = 180° * 3/5 = 108°. Соответственно, сумма внутренних углов составляет 540°.
Отношение диагонали к боковой стороне равно (1+√5) /2, то есть (примерно 1,618).
Длина стороны, которую имеет правильный пятиугольник, может быть рассчитана по одной из трех формул, в зависимости от того, какой параметр уже известен:

если вокруг него описана окружность и известен ее радиус R, то а = 2*R*sin (α/2) = 2*R*sin(72°/2) ≈1,1756*R;
в случае, когда окружность c радиусом r вписана в правильный пятиугольник, а = 2*r*tg(α/2) = 2*r*tg(α/2) ≈ 1,453*r;
бывает так, что вместо радиусов известна величина диагонали D, тогда сторону определяют следующим образом: а ≈ D/1,618.

Площадь правильного пятиугольника определяется, опять-таки, в зависимости от того, какой параметр нам известен:
если имеется вписанная или описанная окружность, то используется одна из двух формул:

S = (n*a*r)/2 = 2,5*a*r либо S = (n*R 2 *sin α)/2 ≈ 2,3776*R 2 ;

площадь можно также определить, зная лишь длину боковой стороны а:

S = (5*a 2 *tg54°)/4 ≈ 1,7205* a 2 .

Правильный пятиугольник: построение

Данную геометрическую фигуру можно построить по-разному. Например, вписать его в окружность с заданным радиусом либо построить на базе заданной боковой стороны. Последовательность действий была описана еще в «Началах» Евклида примерно 300 лет до н.э. В любом случае, нам понадобятся циркуль и линейка. Рассмотрим способ построения с помощью заданной окружности.

1. Выберите произвольный радиус и начертите окружность, обозначив ее центр точкой O.

2. На линии окружности выберите точку, которая будет служить одной из вершин нашего пятиугольника. Пусть это будет точка А. Соедините точки О и А прямым отрезком.

3. Проведите прямую через точку О перпендикулярно к прямой ОА. Место пересечения этой прямой с линией окружности обозначьте, как точку В.

4. На середине расстояния между точками О и В постройте точку С.

5. Теперь начертите окружность, центр которой будет в точке С и которая будет проходить через точку А. Место ее пересечения с прямой OB (оно окажется внутри самой первой окружности) будет точкой D.

6. Постройте окружность, проходящую через D, центр которой будет в А. Места ее пересечения с первоначальной окружностью нужно обозначить точками Е и F.

7. Теперь постройте окружность, центр которой будет в Е. Сделать это надо так, чтобы она проходила через А. Ее другое место пересечения оригинальной окружности нужно обозначить

8. Наконец, постройте окружность через А с центром в точке F. Обозначьте другое место пересечения оригинальной окружности точкой H.

9. Теперь осталось только соединить вершины A, E, G, H, F. Наш правильный пятиугольник будет готов!

Уровень сложности: Несложно

1 шаг

2 шаг

3 шаг

4 шаг

При черчении будьте аккуратны в измерениях расстояний, не допускайте погрешностей, чтобы пятиугольник действительно полчился равносторонним

8 июня 2011

Первый способ — по данной стороне S с помощью транспортира.

Проводим прямую и откладываем на ней AB = S; принимаем эту линию за радиус и этим радиусом из точек A и В описываем дуги: далее с помощью транспортира строим в этих точках углы в 108°, стороны которых пересекутся с дугами в точках С и D; из этих точек радиусом АВ = 5 описываем дуги, которые пересекутся в Е, и прямыми линиями соединяем точки Л, С, Е, D, В.

Полученный пятиугольник — искомый.

Второй способ. Проведем окружность радиусом r. Из точки А циркулем проводим дугу радиуса AM до пересечения в точках В и С с окружностью. Соединяем В и С линией, которая пересечет горизонтальную ось в точке Е.

Затем из точки Е проводим дугу, которая пересечет горизонтальную линию в точке О. Описываем, наконец, из точки F дугу, которая пересечет окружность в точках Н и К. Отложив по окружности расстояние FO = FH = FK пять раз и соединив точки деления линиями, получим правильный пятиугольник.

Третий способ. В данный круг вписать правильный пятиугольник. Проводим два взаимно перпендикулярных диаметра АВ и МС. Делим радиус АО точкой Е пополам. Из точки Е, как из центра, проводим дугу окружности радиуса ЕМ и засекаем ею диаметр АВ в точке F. Отрезок MF равен стороне искомого правильного пятиугольника. Раствором циркуля, равным MF, делаем засечки N 1 , Р 1 , Q 1 , К 1 и соединяем их прямыми.

На рисунке построен шестиугольник по данной стороне.

Прямой АВ = 5, как радиусом, из точек А и В описываем дуги, которые пересекутся в С; из этой точки тем же радиусом описываем окружность, на которой сторона А В отложится 6 раз.

Шестиугольник ADEFGB — искомый.

«Отделка комнат при ремонте»,
Н.П.Краснов

Первый способ построения. Проводим горизонтальную (АВ) и вертикальную (CD) оси и из точки их пересечения М откладываем в соответствующем масштабе полуоси. Наносим малую полуось от точки М на большой оси до точки Е. Эллипс, первый способ построения Делим BE на 2 части и одну наносим от точки М на большой оси (до F или H)…

Основанием для нанесения росписи служат полностью законченные окраской поверхности стен, потолков и других конструкций; роспись делается по высококачественным клеевым и масляным окраскам, сделанным под торцовку или флейц. Приступая к разработке эскиза отделки, мастер должен ясно представить себе всю композицию в бытовой обстановке и отчетливо осознать творческий замысел. Только при соблюдении этого основного условия можно правильно…

Обмер выполненных работ, за исключением особо оговоренных случаев, производится по площади действительно обработанной поверхности с учетом ее рельефа и за вычетом необработанных мест. Для определения действительно обработанных поверхностей при малярных работах следует пользоваться переводными коэффициентами, приведенными в таблицах. А. Деревянные оконные устройства (обмер производится по площади проемов по наружному обводу коробок) Наименование устройств Коэффициент при…

Вам понадобится

– линейка
– циркуль

Инструкция

Вам понадобится

Циркуль, линейка, карандаш

Инструкция

Видео по теме

Вам понадобится

Лист бумаги, карандаш и линейка.

Инструкция

Видео по теме

Полезный совет
Если объединить вершины верного пятиугольника диагоналями, то получится пентаграмма.

Построение вписанного в окружность правильного шестиугольника.

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4, строим стороны 1 — 6, 4 — 3, 4 — 5 и 7 — 2, после чего проводим стороны 5 — 6 и 3 — 2.

Это построение можно выполнить при помощи угольника и циркуля.

Построение вписанного в окружность правильного пятиугольника.

Построение правильного пятиугольника по данной его стороне.

Построение вписанного в окружность правильного семиугольника.

Приведённый способ годен для построения правильных многоугольников с любым числом сторон.

Длины сторон правильных вписанных многоугольников.

Презентация по геометрии на тему «Построение правильных многоугольников с помощью циркуля и линейки» 9 класс

МБОУ «Специализированная школа № 2 им. Д.И. Ульянова с углублённым изучением английского языка г. Феодосии Республики Крым»

Подготовила и провела учитель математики

Покрищук Ж.В.

Феодосия

2018 г

Урок – практикум:

Построение правильных многоугольников, вписанных в окружность и описанных около неё.

Цель: проверить знания учащимися определений и свойств правильных многоугольников; умения решать задачи на нахождение внутренних, внешних и центральных углов, а также кол-ва сторон правильного многоугольника, формировать навыки использования формул по известной стороне; показать алгоритм построения правильных многоугольников с помощью циркуля и линейки; подготовить к выполнению практической работы.

Ход урока.

1. Орг. момент: сообщение темы и целей урока; проверка готовности к уроку.

2. Актуализация знаний учащихся: Опрос

Какой многоугольник называется правильным?
Является ли правильным треугольник, у которого все стороны равны? А четырехугольник?
Чему равна сумма внутренних углов многоугольника?
Чему равен внутренний угол правильного многоугольника?
Чему равна сумма внешних углов многоугольника?
Чему равен внешний угол правильного многоугольника?
Когда окружность называется описанной около многоугольника? Где лежит центр такой окружности?
Когда окружность называется вписанной в многоугольник? Где лежит центр такой окружности?
Что называется центром правильного многоугольника?
По каким формулам вычисляются для правильных многоугольников?

3.Решение задач:

№1. Около правильного треугольника описана окружность. Найти радиус этой окружности, сторону треугольника и его площадь, если радиус окружности вписанной в него равен

№2. Найти площадь квадрата, вписанного в окружность, если площадь правильного шестиугольника, описанного около этой окружности равна

4.Изучение нового материала.

Сегодня на уроке мы покажем как с помощью циркуля можно построить правильные многоугольники, вписанные в окружность и описанные около окружности.

Задача №1. Построить правильный треугольник, в который вписана окружность и около которого описана окружность.

Начинаем построение с правильного шестиугольника. Используя формулы для радиуса описанной около правильного шестиугольника окружности имеем: .Значит проведем окр (О;R), выберем на ней произвольную точку и от этой точки отложим отрезки равные радиусу. Соединим полученные точки отрезками – построили правильный шестиугольник, соединили эти точки через одну – правильный треугольник.

Задача №2. Построить квадрат с помощью циркуля и линейки.

Проводим окружность. Строим в ней два взаимно перпендикулярных диаметра. Соединяем концы диаметров. Полученная фигура – квадрат.

Задача №3. В данный круг вписать правильный пятиугольник. Проводим два взаимно перпендикулярных диаметра АВ и МС. Делим радиус АО точкой Е пополам. Из точки Е, как из центра, проводим дугу окружности радиуса ЕМ и засекаем ею диаметр АВ в точке F. Отрезок MF равен стороне искомого правильного пятиугольника. Раствором циркуля, равным MF, делаем засечки N₁, Р₁, Q₁, К₁ и соединяем их прямыми.

Чтобы построить многоугольники с количеством сторон, большим в 2 раза, надо в уже построенных многоугольниках разделить каждую сторону пополам и провести серединные перпендикуляры к сторонам до пересечения с окружностью.

4. Итоги урока:

Домашнее задание : построить на альбомном листе правильные многоугольники , вписать в них окружность и описать около них окружность

Как начертить квадрат в окружности

Построе́ния с по́мощью ци́ркуля и лине́йки — раздел евклидовой геометрии, известный с античных времён.

В задачах на построение циркуль и линейка предполагаются идеальными инструментами, в частности:

Линейка не имеет делений и имеет сторону бесконечной длины, но только одну.
Циркуль может иметь какой угодно большой или малый раствор (то есть может чертить окружность произвольного радиуса).

Содержание

Примеры [ править | править код ]

Задача на бисекцию. С помощью циркуля и линейки разбить данный отрезок AB на две равные части. Одно из решений показано на рисунке:

Циркулем проводим окружности с центром в точках A и B радиусом AB.
Находим точки пересечения P и Q двух построенных окружностей (дуг).
По линейке проводим отрезок или линию, проходящую через точки P и Q.
Находим искомую середину отрезка AB — точку пересечения AB и PQ.

Формальное определение [ править | править код ]

В задачах на построение рассматривается множество следующих объектов: все точки плоскости, все прямые плоскости и все окружности плоскости. В условиях задачи изначально задается (считается построенными) некоторое множество объектов. К множеству построенных объектов разрешается добавлять (строить):

произвольную точку;
произвольную точку на заданной прямой;
произвольную точку на заданной окружности;
точку пересечения двух заданных прямых;
точки пересечения/касания заданной прямой и заданной окружности;
точки пересечения/касания двух заданных окружностей;
произвольную прямую, проходящую через заданную точку;
прямую, проходящую через две заданные точки;
произвольную окружность с центром в заданной точке;
произвольную окружность с радиусом, равным расстоянию между двумя заданными точками;
окружность с центром в заданной точке и с радиусом, равным расстоянию между двумя заданными точками.

Требуется с помощью конечного количества этих операций построить другое множество объектов, находящееся в заданном соотношении с исходным множеством.

Решение задачи на построение содержит в себе три существенные части:

Описание способа построения заданного множества.
Доказательство того, что множество, построенное описанным способом, действительно находится в заданном соотношении с исходным множеством. Обычно доказательство построения производится как обычное доказательство теоремы, опирающееся на аксиомы и другие доказанные теоремы.
Анализ описанного способа построения на предмет его применимости к разным вариантам начальных условий, а также на предмет единственности или неединственности решения, получаемого описанным способом.

Известные задачи [ править | править код ]

Задача Аполлония о построении окружности, касающейся трех заданных окружностей. Если ни одна из заданных окружностей не лежит внутри другой, то эта задача имеет 8 существенно различных решений.
Задача Брахмагупты о построении вписанного четырехугольника по четырем его сторонам.

Построение правильных многоугольников [ править | править код ]

Античным геометрам были известны способы построения правильных n-угольников для n = 2 k <displaystyle n=2^> , n = 3 ⋅ 2 k <displaystyle n=3cdot 2^> , n = 5 ⋅ 2 k <displaystyle n=5cdot 2^> и n = 3 ⋅ 5 ⋅ 2 k <displaystyle n=3cdot 5cdot 2^> .cdot p_<1>cdots p_> , где p i <displaystyle p_> — различные простые числа Ферма. В 1836 году Ванцель доказал, что других правильных многоугольников, которые можно построить циркулем и линейкой, не существует.

Неразрешимые задачи [ править | править код ]

Следующие три задачи на построение были поставлены ещё древними греками:

трисекция угла — разбить произвольный угол на три равные части;
удвоение куба — построить ребро куба вдвое большего по объёму, чем данный куб;
квадратура круга — построить квадрат, равный по площади данному кругу.

Лишь в XIX веке было строго доказано, что все эти три задачи неразрешимы при использовании только циркуля и линейки. Доказательство неразрешимости этих задач построения было достигнуто с помощью алгебраических методов, основанными на теории Галуа [1] . В частности, невозможность построения квадратуры круга следует из трансцендентности числа π.

Другая известная и неразрешимая с помощью циркуля и линейки задача — построение треугольника по трём заданным длинам биссектрис [2] . Эта задача остаётся неразрешимой даже при наличии инструмента, выполняющего трисекцию угла, например томагавка. [3]

Допустимые отрезки для построения с помощью циркуля и линейки [ править | править код ]

С помощью этих инструментов возможно построение отрезка, который по длине:

равен сумме длин нескольких отрезков;
равен разности длин двух отрезков;
численно равен произведению длин двух отрезков;
численно равен частному от деления длин двух отрезков;
численно равен квадратному корню из длины заданного отрезка (следует из возможности построения среднего геометрического двух отрезков, см. иллюстрацию). [4]

Для построения отрезка с длиной численно равной произведению, частному и квадратному корню из длин заданных отрезков необходимо задание на плоскости построения единичного отрезка (то есть отрезка длины 1), иначе задача неразрешима из-за отсутствия масштаба. Извлечение корней из отрезков с иными натуральными степенями, не являющимися степенью числа 2, невозможны с помощью циркуля и линейки. Так, например, невозможно при помощи циркуля и линейки из единичного отрезка построить отрезок длиной 2 3 <displaystyle <sqrt[<3>]<2>>> . Из этого факта, в частности, следует неразрешимость задачи об удвоении куба. [5]

Возможные и невозможные построения [ править | править код ]

С формальной точки зрения, решение любой задачи на построение сводится к графическому решению некоторого алгебраического уравнения, причем коэффициенты этого уравнения связаны с длинами заданных отрезков. Поэтому можно сказать, что задача на построение сводится к отысканию действительных корней некоторого алгебраического уравнения.

Поэтому удобно говорить о построении числа — графического решения уравнения определенного типа.

Исходя из возможных построений отрезков возможны следующие построения:

Построение решений линейных уравнений.
Построение решений уравнений, сводящихся к решениям квадратных уравнений.

Иначе говоря, возможно строить лишь отрезки, равные арифметическим выражениям с использованием квадратного корня из исходных чисел (заданных длин отрезков).<3>-2=0,> связанное со знаменитой задачей на удвоение куба, сводящаяся к этому кубическому уравнению. Как было сказано выше, решение этого уравнения ( 2 3 <displaystyle <sqrt[<3>]<2>>> ) невозможно построить циркулем и линейкой.

Возможность построить правильный 17-угольник следует из выражения для косинуса центрального угла его стороны:

cos ⁡ ( 2 π 17 ) = − 1 16 + 1 16 17 + 1 16 34 − 2 17 + <displaystyle cos <left(<frac <2pi ><17>>
ight)>=-<frac <1><16>>;+;<frac <1><16>><sqrt <17>>;+;<frac <1><16>><sqrt <34-2<sqrt <17>>>>;+;> + 1 8 17 + 3 17 − 34 − 2 17 − 2 34 + 2 17 , <displaystyle +<frac <1><8>><sqrt <17+3<sqrt <17>>-<sqrt <34-2<sqrt <17>>>>-2<sqrt <34+2<sqrt <17>>>>>>,> что, в свою очередь, следует из возможности сведения уравнения вида x F n − 1 = 0 , <displaystyle x^>-1=0,> где F n <displaystyle F_> — любое простое число Ферма, с помощью замены переменной к квадратному уравнению.

Основы черчения

Строительное

Машиностроительное

Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.

Построение вписанного в окружность правильного пятиугольника.

Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.

Построение правильного пятиугольника по данной его стороне.

Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.

Построение вписанного в окружность правильного семиугольника.

Приведённый способ годен для построения правильных многоугольников с любым числом сторон.

Анализируя различные положения квадрата и окружности относительно точки зрения и линии горизонта а также правила их изображения в перспективе легко обнаружить общие закономерности. Геометрическая связь этих фигур определяется тем, что вокруг любой окружности можно описать квадрат, а также в любой квадрат можно вписать окружность.

Как вписать окружность в квадрат?

Рассмотрите рисунок 48. Квадрат и вписанная в него окружность имеют общий центр — точку пересечения диагоналей квадрата. Окружность касается сторон квадрата в точках 1,2,3,4.Точки касания делят стороны квадрата пополам. Для того чтобы изобразить вписанную в квадрат окружность (в перспективном рисунке — эллипс) необходимо определить положение осей эллипса и найти точки, задающие его размеры (точки 1 — 4).

Горизонтальный квадрат.

Найдите точки касания на перспективном рисунке горизонтально расположенного квадрата (рис.49): для этого через точку пересечения диагоналей проведите прямые, параллельные сторонам квадрата и уходящие с ними в одну точку схода.

Окружность, лежащая в горизонтальной плоскости, изображается в виде эллипса с вертикальной и горизонтальной осями. Проведите через точку пересечения диагоналей вертикальную линию — малую ось эллипса. Большая ось эллипса перпендикулярна малой оси и проходит через точку, смещенную от пересечения диагоналей квадрата (центра окружности) ближе к зрителю (рис.50). Таким образом, мы получили две оси эллипса и четыре точки, определяющие его габариты. Продолжите рисунок: сначала легкими движениями карандаша наметьте эллипс, затем уточните линию, добиваясь того, чтобы она действительно касалась сторон квадрата в точках 1,2,3,4. Проверьте симметричность полученного эллипса относительно его осей (рис. 51).

перспективный рисунок простых геометрических тел

Вертикальный квадрат.

При вертикальном положении квадрата точки 1,2,3,4найдите, как и в предыдущем примере: проведите через точку пересечения диагоналей квадрата прямые, параллельные его сторонам (рис.52). Несколько сложнее определить направление осей эллипса. Для решения этой задачи представьте, что изображаемый нами эллипс является основанием цилиндра, лежащего на горизонтальной плоскости (рис. 53). Ось цилиндра всегда перпендикулярна большой оси эллипса основания и совпадает с его малой осью. Проведите ось цилиндра через точку пересечения диагоналей квадрата. Ее направление можно найти, опираясь на знание и опыт рисования куба, или взять с натуры, если таковая имеется. Таким образом, мы определили положение малой оси эллипса. А большая ось будет ей перпендикулярна и пройдет через точку, смещенную от пересечения диагоналей — центра окружности — ближе к зрителю (рис.54). На двух осях и по четырем точкам сначала наметьте эллипс легкими линиями, а затем уточните рисунок (рис.55).

Заметим, что эллипс, вписанный в квадрат, часто получается несимметричным относительно осей, а потому его приходится уточнять и, как следствие, изменять очертания квадрата. В этом случае работа идет как бы методом последовательных приближений и исправлений, что трудно и долго. Часто на рисунках остаются не вполне правильные квадраты и не вполне правильные эллипсы, а лишь фигуры, близкие к ним. Правильный эллипс нарисовать легче, чем построить правильный квадрат в перспективе, поэтому задачу грамотного изображения квадрата современная методика рисования предлагает решать с помощью эллипса, вокруг которого описывается квадрат.

Построение правильных шестиугольников, вписанных в круги по материалам Walch Education.

Презентация на тему: «Построение правильных шестиугольников, вписанных в круги по материалам Walch Education» — стенограмма презентации:

ins [data-ad-slot = «4502451947»] {display: none! important;}} @media (max-width: 800px) {# place_14> ins: not ([data-ad-slot = «4502451947»]) {display: none! important;}} @media (max-width: 800px) {# place_14 {width: 250px;}} @media (max-width: 500 пикселей) {# place_14 {width: 120px;}} ]]>

2 Построение правильных шестиугольников, вписанных в круги, адаптированные из Walch Education

3 Ключевые концепции У правильных шестиугольников шесть равных сторон и шесть углов, каждый размером 120.Процесс вписывания правильного шестиугольника в круг аналогичен вписанию равносторонних треугольников и квадратов в круг. Построение правильного шестиугольника — это результат построения двух равносторонних треугольников, вписанных в круг. 1.3.3: Построение правильных шестиугольников, вписанных в круги2

4 3 Метод 1. Построение правильного шестиугольника, вписанного в круг, с помощью циркуля 1.Чтобы построить правильный шестиугольник, вписанный в круг, сначала отметьте положение центральной точки круга. Обозначьте точку X. 2. Постройте круг с острием циркуля в центре. 3. Обозначьте точку на окружности A. 4. С помощью линейки соедините точку A и точку X. Протяните линию через окружность, создав диаметр окружности. Обозначьте вторую точку пересечения D. (продолжение)

5 1.3.3: Построение правильных шестиугольников, вписанных в круги4 5. Не меняя настройки компаса, поместите острие циркуля на A. Нарисуйте дугу, чтобы пересечь круг в двух точках. Обозначьте точки B и F. 6. Поместите острие циркуля на D. Не меняя настройки циркуля, нарисуйте дугу, чтобы пересечь круг в двух точках. Отметьте точки C и E. 7. С помощью линейки соедините точки A и B, B и C, C и D, D и E, E и F, F и A. Не стирайте свои отметки.Шестиугольник ABCDEF правильный и вписан в круг X.

6 Ключевые концепции После того, как круг построен, его можно разделить на шесть равных частей. Сделайте это, выбрав начальную точку на круге и перемещая циркуль по кругу, делая отметки равными длине радиуса. Соединение каждой точки пересечения приводит к правильному шестиугольнику. 1.3.3: Построение правильных шестиугольников, вписанных в круги5

7 6 Метод 2: построение правильного шестиугольника, вписанного в круг, с помощью циркуля 1.Чтобы построить правильный шестиугольник, вписанный в круг, сначала отметьте положение центральной точки круга. Обозначьте точку X. 2. Постройте круг с острием циркуля в центре. 3. Отметьте точку на окружности A. 4. Не меняя настройки компаса, поместите острие компаса на A. Нарисуйте дугу, чтобы пересечь окружность в одной точке. Обозначьте точку пересечения B. (продолжение)

8 1.3.3: Построение правильных шестиугольников, вписанных в круги7 5. Поместите острие циркуля в точку B. Не меняя настройки циркуля, нарисуйте дугу, чтобы пересечь круг в одной точке. Обозначьте точку пересечения C. 6. Продолжайте движение по кругу, отмечая точки D, E и F. Убедитесь, что не изменили настройку компаса. 7. С помощью линейки соедините точки A и B, B и C, C и D, D и E, E и F, F и A. Не стирайте свои отметки. Шестиугольник ABCDEF правильный и вписан в круг X.

9 Спасибо за просмотр! Г-жа дамбревиль

Что нужно сделать, чтобы с помощью циркуля и линейки построить правильный шестиугольник, вписанный в круг? перетащите ступеньки и отпустите

Чтобы создать правильный шестиугольник, обычный метод — создать круг с помощью циркуля, а затем, не меняя его настроек, выбрать точку на окружности и нарисовать 2 дуги. Это определит 3 точки: точку, в которой вы устанавливаете циркуль, и точки пересечения двух дуг с кругом.Затем вы помещаете точку циркуля на одно из пересечений и рисуете другую дугу. Продолжайте до тех пор, пока не получите 6 точек, необходимых для шестиугольника, и, наконец, нарисуйте линии шестиугольника. Имея это в виду, давайте посмотрим на доступные шаги. «Construct и JMâŽŻâŽŻâŽŻâŽŻâ, MOââŽŻâŽŻâŽŻâŽŻââŽŻ, OKââŽŻâŽŻâŽŻâŽŻâŽŻâŽŻ, KPâŽŻâŽŻâŽŻâŽŻâŽŻ, PNââŽŻâŽŻâŽŻâŽŻ, и NJââŽŻââŽŻââ для завершения регулярного шестиугольника». ** Очевидно, что это последний шаг. Он также сообщает мне названия всех точек шестиугольника.«Постройте круг с центром в точке H.» ** Поскольку H не является точкой шестиугольника и вам нужно сначала построить круг, это хороший первый шаг. «Постройте круг с центром в точке J и радиусом HJ. Постройте круг с центром в точке K и радиусом HJ». ** Это выглядит хорошо, за исключением того, что у нас нет точки с меткой J или точки с меткой K. Давайте поищем что-то, что создает эти метки. «Обозначьте точку пересечения окружности и прямой l слева от точки H, точки J, и отметьте точку пересечения окружности и прямой l справа от точки H, точки K.» ** Ага! Теперь у нас есть ярлыки. Но где та строка, о которой говорится в инструкции? Давайте посмотрим еще немного и посмотрим, сможем ли мы его найти. «Постройте горизонтальную линию l и точку H на прямой l». ** Похоже на то. Пересечение линии с построенным кругом также определило бы 2 точки на шестиугольнике. И у нас есть достаточно информации, чтобы выполнить этот шаг. Так что это выглядит как второй разумный шаг. Кроме того, обозначение точек J и K, упомянутых выше, становится тогда разумным третьим шагом.Затем можно построить два упомянутых круга с их центрами в точках J и K, так что это четвертый шаг. «Обозначьте точку пересечения окружностей H и J, которая находится выше прямой l, точку M, и точку их пересечения, которая находится ниже прямой l, точки N. Обозначьте точку пересечения окружностей H и K, которая находится выше прямой l. , точка O, и точка их пересечения, лежащая ниже прямой l, точка P. » ** Пора впадать в безумие навешивания ярлыков. И это вполне подходящий пятый шаг.Итак, 6 шагов по порядку таковы: 1. Постройте окружность с центром в точке H. 2. Постройте горизонтальную прямую l и точку H на прямой l. 3. Обозначьте точку пересечения окружности и прямой l слева от точки H, точки J, и отметьте точку пересечения окружности и прямой l справа от точки H, точки K. 4. Постройте окружность с центром в точке J и радиусом HJ. Постройте окружность с центром в точке K и радиусом HJ. 5. Обозначьте точку пересечения окружностей H и J, которая находится выше прямой l, точки M, и точку их пересечения, которая находится ниже прямой l, точки N.Обозначьте точку пересечения окружностей H и K, которая находится выше прямой l, точки O, и точку их пересечения, которая находится ниже прямой l, точки P. 6. Construct и JMââŽŻâŽŻâŽŻâŽŻ, MOâŽŻâŽŻâŽŻâŽŻâŽŻââŽŻ, OKââŽŻâŽŻââââŽŻ, KPââŽŻâŽŻâŽŻâŽŻ, PNââŽŻâŽŻâŽŻâŽŻ, и NJââââŽŻâŽŻâ, чтобы заполнить обычный шестиугольник. Примечание. Шаги 1 и 2 можно поменять местами. На самом деле не имеет значения, построите ли вы сначала круг или сначала построите линию. Любой порядок будет работать.

открытых учебников | Сиявула

Математика

Наука

- Читать онлайн
- Учебники
  - Английский
    - Класс 7A
    - Марка 7Б
    - Оценка 7 (вместе A и B)
  - Африкаанс
    - Граад 7А
    - Граад 7Б
    - Граад 7 (A en B saam)
- Пособия для учителя
- Читать онлайн
- Учебники
  - Английский
    - класс 8A
    - Марка 8Б
    - Оценка 8 (вместе A и B)
  - Африкаанс
    - Граад 8А
    - Граад 8Б
    - Граад 8 (A en B saam)
- Пособия для учителя
- Читать онлайн
- Учебники
  - Английский
    - Марка 9А
    - Марка 9Б
    - 9 класс (A и B вместе)
  - Африкаанс
    - Граад 9А
    - Граад 9Б
    - Граад 9 (A en B saam)
- Пособия для учителя
- Читать онлайн
- Учебники
  - Английский
    - Класс 4A
    - Класс 4Б
    - Класс 4 (вместе A и B)
  - Африкаанс
    - Граад 4А
    - Граад 4Б
    - Граад 4 (A en B saam)
- Пособия для учителя
- Читать онлайн
- Учебники
  - Английский
    - Марка 5А
    - Марка 5Б
    - Оценка 5 (вместе A и B)
  - Африкаанс
    - Граад 5А
    - Граад 5Б
    - Граад 5 (A en B saam)
- Пособия для учителя
- Читать онлайн
- Учебники
  - Английский
    - Класс 6A
    - класс 6Б
    - 6 класс (A и B вместе)
  - Африкаанс
    - Граад 6А
    - Граад 6Б
    - Граад 6 (A en B saam)
- Пособия для учителя

Наша книга лицензионная

Эти книги не просто бесплатные, они также имеют открытую лицензию! Один и тот же контент, но разные версии (брендированные или нет) имеют разные лицензии, как объяснено:

CC-BY-ND (фирменные версии)

Вам разрешается и поощряется свободное копирование этих версий.Вы можете делать ксерокопии, распечатывать и распространять их сколько угодно раз. Вы можете скачать их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственным ограничением является то, что вы не можете адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, спонсорские логотипы и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный.

Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.

CC-BY (безымянные версии)

Эти небрендированные версии одного и того же контента доступны для вас, чтобы вы могли делиться ими, адаптировать, трансформировать, модифицировать или дополнять их любым способом, с единственным требованием — дать соответствующую оценку Siyavula. Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.

Конструкции линейки и циркуля

Вы можете следить за этапами построения, нажимая на кнопки. Reset показывает указанные объекты.

1.		Серединный перпендикуляр данного отрезка.
2.		Линия, перпендикулярная данной линии, проходит через данную точку не на данной линии.
3.		Прямой угол в данной точке на данной прямой.
4.		Квадрат с заданным сегментом в качестве стороны.
5.		Равносторонний треугольник с заданным отрезком стороной.
6.		Шестиугольник с данным сегментом сбоку.
7.		Скопируйте заданный угол в заданный сегмент.
8.		Прямая, параллельная данной прямой, проходит через точку не на данной прямой.
9.		Разделение данного отрезка на N равных частей.
10.		Деление пополам заданного угла.
11.		Построить угол 30 градусов на данном сегменте.
12.		Найдите центр круга через три заданные точки.
13.		Найдите описанную окружность данного треугольника.
14.		Найдите вписанную окружность данного треугольника.
15.		Постройте прямоугольник с двумя заданными длинами сторон.
16.		Постройте треугольник, подобный заданному на заданном отрезке.
17.		Дана точка P на отрезке QR, найдите точку C, которая делит данный отрезок AB. в таком же соотношении.
18А.		Постройте медианы заданного треугольника.
18Б.		Постройте высоту заданного треугольника.
19.		Постройте золотой прямоугольник.
20.		Постройте квадрат, площадь которого в два раза больше данного квадрата.
21.		Постройте круг, площадь которого в два раза больше данного круга.
22.		Постройте линию, параллельную заданной линии, на заданном расстоянии от нее.
23.		Постройте окружность заданного радиуса по касательной к двум линиям, проходящим через точку.
24.		Постройте квадрат той же площади, что и заданный прямоугольник.
25.		Дана точка на одной стороне линии, найдите ее зеркальное отображение относительно линии.
26.		Даны две точки на одной стороне прямой, найдите путь луча свет между точками, который отражается от линии.
27.		Дана точка за пределами круга, найдите две прямые, проходящие через точку касательная к окружности.
28.		Из двух окружностей постройте окружность заданного радиуса, касательную к два круга.
29.		Постройте линию на полпути между двумя заданными параллельными линиями.
30.		Из четырех произвольных точек постройте квадрат, каждая из которых расширена. стороны проходят через одну из указанных точек.
31А.		Из двух окружностей постройте внешние касательные к окружностям.
31Б.		Из двух окружностей постройте внутренние касательные к окружностям.
32.		Из двух параллельных прямых и окружности постройте окружность, касательную ко всем три.
33.		Учитывая угол и окружность, центр которой находится на биссектрисе угла, построить окружности, касательные к сторонам угла и окружности.
34.		Учитывая угол и точку внутри угла, постройте точка, касательная к сторонам угла и проходящая через точку.
35.		По заданному углу и произвольной окружности построить касательные окружности. к кругу и двум сторонам угла.
36.		Учитывая прямую и две точки с одной стороны от нее, постройте обведите точки и касайтесь линии.
37.		Дан прямая, окружность и точка, постройте окружность через точку и касательную к прямой и окружности.
38.		Дан отрезок и две окружности, постройте окружности, касательные ко всем трем.
39.		Из трех произвольных окружностей постройте окружности, касательные ко всем трем. (Проблема Аполлония)
40.		Постройте правильный пятиугольник. (Теорема Гаусса-Вантцеля: правильный N-угольник конструктивно, если множители N являются разными простыми числами среди 2,3,5,17,257,65537, …)
41.		Постройте правильный 17-угольник.
42.		Постройте правильный 257-угольник и правильный 65537-угольник.

Рисование шестиугольников в EQ7 на рабочем столе Pieced PatchDraw 13 мая / 13 июня

Рисование шестиугольников в EQ7 на рабочем столе PatchDraw

Традиционный способ нарисовать шестиугольник на бумаге — написать его в круге с помощью циркуля и линейки.Мы можем нарисовать шестиугольник почти так же, используя сетку Circle на рабочем столе Pieced PatchDraw в Electric Quilt 7 (EQ7).

В рабочей таблице блоков щелкните БЛОК> Новый блок> Блок PatchDraw . По умолчанию вы будете на вкладке «Сложенные» рабочего стола.
Если полоса точности не отображается на экране, нажмите ПРОСМОТР> Полоса точности , чтобы поставить галочку рядом с ней.
На панели точности введите следующие настройки:
Ширина блока: 12
Высота блока: 12
Сетка: Круг
Кольца: 5 Спицы: 12
Графическая бумага: Переключено выкл.
Ваша доска для рисования будет выглядеть так:
Щелкните и удерживайте инструмент Polydraw на левой панели инструментов, чтобы появилось всплывающее окно, и выберите инструмент PolyLine .
Мы впишем шестиугольник в самый большой полный круг на чертежной доске. Каждая из шести точек шестиугольника будет на пересечении направляющих.
Используя иллюстрацию ниже в качестве ориентира, щелкните точку №1, перейдите к перекрестку №2 и щелкните, перейдите к перекрестку №3 и щелкните, и так далее. Дважды щелкните в той же точке, где вы начали заканчивать форму. Форма изменится на сплошной кремовый цвет, указывая на то, что она закрыта.
Нажмите Добавить в Sketchbook , и у вас есть основной шестиугольник, готовый к использованию! Но давайте посмотрим, как легко оживить базовую форму шестиугольника…
Щелкните инструмент Pick на левой панели инструментов, а затем щелкните шестиугольник, чтобы выбрать его.Щелкните правой кнопкой мыши шестиугольник и выберите « Преобразовать в направляющие » в появившемся контекстном меню.
Это руководство по шестиугольнику поможет нам сохранить наш новый рисунок в пределах формы.
Щелкните на инструменте Полилиния . Давайте нарисуем три фигуры, чтобы получился более сложный шестиугольник.
Используйте приведенные ниже иллюстрации в качестве руководства при рисовании фигур. Форма 1:

Форма 2:

Форма 3:
Нажмите Ctrl + A на клавиатуре, чтобы выбрать все формы.
Щелкните инструмент Clone , чтобы создать еще один набор фигур. Затем дважды щелкните инструмент Повернуть .
Поместите курсор на перекрестие в середине выбранных фигур и щелкните, удерживайте и перетащите фигуры, чтобы поместить их слева от исходного набора фигур. Они защелкнутся на сетке.
Продолжайте клонировать и дважды повернуть , пока не заполните шестиугольник.
Щелкните вкладку Color внизу экрана и раскрасьте новый блок.
Нажмите Добавить в альбом .
Круговая сетка с щелчком мыши позволяет быстро и легко рисовать вариации шестиугольника! Используйте макет лоскутного одеяла Custom Set, чтобы создать лоскутное одеяло с образцом шестиугольника. Попробуйте нарисовать несколько блоков шестиугольника в лоскутном одеяле ниже или сделайте свой собственный!

Построение правильных многоугольников — Бесплатные задания по математике

Мы знаем, что — правильный многоугольник — это многоугольник, у которого все стороны равны, а все внутренние углы равны.В этом уроке мы узнаем, как построить их с помощью циркуля и линейки.

Равносторонний треугольник

Начнем с построения первого правильного многоугольника, равностороннего треугольника.

Пример. Постройте треугольник, если нам известна длина стороны $ a $.

Сначала создаем эскиз. Он не обязательно должен быть точным, но он даст нам представление, с чего начать.

Нарисуем луч с конечной точкой $ A $, который будет первой вершиной треугольника.Берем линейку и устанавливаем ширину циркуля равной длине заданной стороны $ a $. Затем введите стрелку компаса в точку $ A $ и нарисуйте дугу. Убедитесь, что дуга пересекается с ранее нарисованным лучом. Точка пересечения дуги и луча — это наша вторая вершина, $ B $. Не меняя ширину циркуля, повторяем предыдущий шаг. Единственная разница в том, что мы наводим стрелку циркуля на точку $ B $ и делаем дугу, которая пересекается с первой. Мы видим, что дуги пересекаются в двух точках, что дает нам две последние вершины, $ C $ и $ C ’$.Теперь у нас есть два треугольника: $ \ bigtriangleup ABC $ и $ \ bigtriangleup ABC ’$. Треугольники конгруэнтны из-за теоремы SSS, поэтому мы говорим, что у нас есть только одно решение.

Продвинутый:

Мы использовали луч, чтобы получить точки $ A $ и $ B $, но если бы мы использовали прямую, мы получили бы еще одну вершину $ B ’$ по другую сторону от $ A $. Выполнив шаги, описанные выше, мы получим еще два треугольника, всего четыре. Все четыре из них совпадают, и мы рассматриваем их как одно решение проблемы.

Пример. Постройте треугольник, если мы знаем радиус описанной окружности.

Сначала мы делаем окружность $ c (O, r) $ и один диаметр $ \ overline {AA ’} $. Затем мы делаем круг $ c (A ’, | OA’ |) $. Точки пересечения окружностей $ c (O, r) $ и $ c (A ’, | OA’ |) $ — это $ B $ и $ C $, две оставшиеся вершины нашего треугольника.

Квадрат

Пример. Постройте квадрат, если нам известна сторона $ a $.

Сначала мы делаем набросок, чтобы узнать расположение точек и сторон.{\ circ} $.

Теперь у нас есть перпендикулярная линия, и мы знаем, что вершина $ C $ будет на ней. Возьмите длину стороны $ a $ в ширину циркуля и сделайте дугу, которая пересекается с перпендикулярной линией — это пересечение и есть наша вершина $ C $. Осталось построить вершину $ D $. Мы делаем это, создавая две дуги окружностей $ c (A, a) $ и $ c (C, a) $. Их пересечение является последней вершиной, вершиной $ D $.

* Здесь мы построили только один квадрат, но мы могли бы построить четыре из них, следуя тому же процессу, что и при построении равностороннего треугольника.

Пример. Как построить квадрат, если мы знаем радиус описанной окружности?

Сначала мы рисуем точку $ O $ и окружность $ c (O, r) $. Выберите начальную точку $ A $ в любом месте круга. Теперь давайте нарисуем диаметр от $ A $ до $ O $. Пусть точка пересечения диаметра и окружности будет точкой $ C $. Прямая $ AB $ — это одна диагональ квадрата, который мы хотим построить. Как получить другой? Мы знаем, что диагонали в квадрате перпендикулярны, поэтому мы создаем перпендикулярную линию к диаметру $ AC $.Убедитесь, что точкой пересечения является точка $ O $. Теперь точки пересечения перпендикуляра и окружности $ c (O, r) $ — это точки $ B $ и $ C $, две наши последние вершины.

Правильный пятиугольник

Сначала рисуем эскиз от руки. Он не обязательно должен быть идеальным, поскольку это не наша окончательная конструкция, мы просто воспользуемся им для строгания.

Пример. Постройте правильный пятиугольник, если нам известна сторона $ a $.

Создайте луч, конечной точкой которого является $ B $, а затем постройте точку $ A $ так, чтобы $ | AB | = a $.Мы хотим построить биссектрису $ | AB | $. Возьмите циркуль и убедитесь, что его ширина равна длине стороны $ a $ (ВАЖНО!). Поставьте иглу на $ B $ и сделайте две дуги окружности $ c (B, a) $. Повторите шаг для дуг из $ c (A, a) $. Дуги пересекаются в точках $ K $ и $ L $. Присоединяйтесь к ним, чтобы получить среднюю точку между $ A $ и $ B $, точку $ M $. Опять же, сохраните радиус циркуля равным $ a $, поместите стрелку циркуля на $ M $ и сделайте дугу, пересекающуюся с биссектрисой, образуя точку $ N $. Теперь отрегулируйте компас до длины $ AN $.Поместите иглу в $ A $ и сделайте дугу, которая пересекается с лучом, который мы сделали в начале, что даст нам точку $ P $.

Расстояние от $ M $ до $ P $ — очень важное расстояние — оно даст нам остальные вершины. Сделайте радиус компаса равным расстоянию между $ M $ и $ P $. Поставьте иглу на $ B $ и сделайте дугу, которая пересекается с одной из дуг, которые мы сделали, чтобы получить среднюю точку. Сделайте вторую дугу, которая пересекается с биссектрисой. Пересечения будут точками $ E $ и $ D $ соответственно.Чтобы получить вершину $ C $, мы поместим иглу в $ A $ и повторим процесс.

Пример. Постройте правильный пятиугольник, если мы знаем радиус описанной окружности.

Постройте окружность $ c (O, r) $ и два перпендикулярных диаметра: $ \ overline {AA ’} $ и $ \ overline {PP’} $. Теперь построим биссектрису отрезка $ \ overline {OP} $, пересечение будет точкой $ M $. По ширине циркуля возьмите длину между $ A $ и $ M $ и поместите стрелку циркуля на $ M $, чтобы создать дугу, пересекающуюся с $ \ overline {PP ’} $.Пересечение $ N $.

Расстояние от $ A $ до $ N $ — это длина стороны $ a $ правильного пятиугольника. Теперь, когда мы знаем длину $ a $, нам нужно построить вершины. Пусть $ D $ — наша первая вершина.

Во-первых, мы открываем циркуль на длину $ a $ и наводим стрелку циркуля на $ A $. Теперь создайте дугу, которая пересекается с окружностью $ c (O, r |) $, что дает нам вершину $ B $. Не меняя ширины циркуля, мы помещаем стрелку на $ B $ и проделываем тот же процесс, чтобы получить вершину $ A $, и так далее.Этот процесс даст нам оставшиеся $ 4 $ вершины.

Шестигранник правильный

Пример. Постройте правильный шестиугольник, если нам известна сторона $ a $.

Мы можем разбить правильный шестиугольник на равносторонние треугольники по $ 6 $ со стороной $ a $. Вершина $ O $ является центром вписанной и описанной окружностей, а $ | AO | = | BO | = | CO | = | DO | = | EO | = | FO | $. Сначала мы построим $ \ bigtriangleup ABO $, следуя процессу, который мы использовали при построении равностороннего треугольника.Нарисуем $ c (O, | AO |) $. Поскольку $ O $ — центр описанной окружности, мы знаем, что вершины шестиугольника будут на окружности. Теперь мы просто берем длину $ a $ в ширину циркуля и делаем на окружности дуги в $ 4 $.

Не меняя ширины циркуля, мы помещаем стрелку циркуля на $ B $, make и дугу, которая пересекается с окружностью $ c (O, | AO |) $, дающей нам вершину $ C $. Затем мы кладем иглу на $ C $ и проделываем тот же процесс, чтобы получить вершину $ D $, и так далее. Этот процесс даст нам последние $ 4 $ вершины.Неважно, начнем ли мы с $ A $ и сделаем это по часовой стрелке или с $ B $, как здесь, результат будет таким же.

Важно помнить: В правильном шестиугольнике $ \ bigtriangleup ABO $ — это равносторонний треугольник, что означает, что длина радиуса описанной окружности и длина стороны всегда равны.

Пример. Постройте правильный шестиугольник, если мы знаем радиус описанной окружности.

Это еще проще.Мы просто рисуем круг $ c (O, r) $ и выбираем на нем начальную точку, пусть это будет точка $ A $. В правильном шестиугольнике мы знаем, что радиус описанной окружности равен стороне многоугольника, то есть $ r = | AO | = | AB | $. Теперь, когда у нас есть сторона правильного шестиугольника, мы строим оставшиеся $ 5 $ вершин, как в предыдущем примере.

Правильный восьмиугольник

Пример. Как построить правильный восьмиугольник, если мы знаем радиус описанной окружности?

Сначала мы строим квадрат внутри данного круга с его диагоналями, следуя процессу, описанному выше.Затем мы строим биссектрисы углов $ \ измеренный угол AOB, \ измеренный угол BOC, \ измеренный угол COD $ и $ \ измеренный угол DOA $. Биссектрисы пересекаются с описанными окружностями, что дает нам $ 4 $ новых точек: $ E, F, G $ и $ H $. Эти точки — оставшиеся вершины восьмиугольника.

Правильный десятиугольник

Пример. Как построить правильный десятиугольник, если мы знаем радиус описанной окружности?

Сначала мы строим правильный пятиугольник внутри данного круга, следуя процессу, описанному при построении пятиугольника.Затем мы соединяем каждую вершину с центром описанной окружности, чтобы разделить пятиугольник на $ 5 $ конгруэнтных треугольников. Следующим шагом является построение биссектрис построения углов $ \ measureangle AOB, \ measureangle BOC, \ measureangle COD, \ measureangle DOE $ и $ \ measureangle EOA $.

Биссектрисы пересекаются с описанными окружностями, давая нам $ 5 $ новых точек, $ F, G, H, I $ и $ J $. Эти точки — оставшиеся вершины десятиугольника.

Правильный двенадцатигранник

Пример. Как построить правильный двенадцатиугольник, если мы знаем радиус описанной окружности?

Как и в последних двух примерах, мы можем построить правильный двенадцатиугольник из правильного шестиугольника. Биссектрисы центральных углов шестиугольника дают нам оставшиеся вершины двенадцатиугольника.

Построить вписанные фигуры (равносторонние треугольники, квадраты, правильные шестиугольники) — Common Core: High School

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее то информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

.
No related posts.

Как построить восьмиугольник в окружности

Popular

Основы черчения

Строительное

Машиностроительное

Как построить правильный шестиугольник с помощью циркуля

Урок 35. Геометрия 9 класс

Конспект урока «Построение правильных многоугольников»

Способ вычерчивания шестиугольника циркулем, линейкой

Способ вычерчивания шестиугольника без циркуля

Как вписать двенадцатиугольник в окружность

необходимый минимум информации. Получение с помощью полоски бумаги

1 шаг

2 шаг

3 шаг

4 шаг

Параметры правильного пятиугольника

Построение пентагона

Видео

Инструкция

Инструкция

Инструкция

Инструкция

Как сделать правильный пятиугольник. Как построить пятиугольник с помощью циркуля

1 шаг

2 шаг

3 шаг

4 шаг

Инструкция

Инструкция

Инструкция

Инструкция

Презентация по геометрии на тему «Построение правильных многоугольников с помощью циркуля и линейки» 9 класс

Как начертить квадрат в окружности

Содержание

Примеры [ править | править код ]

Формальное определение [ править | править код ]

Известные задачи [ править | править код ]

Построение правильных многоугольников [ править | править код ]

Неразрешимые задачи [ править | править код ]

Допустимые отрезки для построения с помощью циркуля и линейки [ править | править код ]

Возможные и невозможные построения [ править | править код ]

Popular

Основы черчения

Строительное

Машиностроительное

Построение правильных шестиугольников, вписанных в круги по материалам Walch Education.

Презентация на тему: «Построение правильных шестиугольников, вписанных в круги по материалам Walch Education» — стенограмма презентации:

Что нужно сделать, чтобы с помощью циркуля и линейки построить правильный шестиугольник, вписанный в круг? перетащите ступеньки и отпустите

открытых учебников | Сиявула

Математика

Наука

Наша книга лицензионная

CC-BY-ND (фирменные версии)

CC-BY (безымянные версии)

Конструкции линейки и циркуля

Рисование шестиугольников в EQ7 на рабочем столе Pieced PatchDraw 13 мая / 13 июня

Построение правильных многоугольников — Бесплатные задания по математике

Равносторонний треугольник

Квадрат

Правильный пятиугольник

Шестигранник правильный

Правильный восьмиугольник

Правильный десятиугольник

Правильный двенадцатигранник

Построить вписанные фигуры (равносторонние треугольники, квадраты, правильные шестиугольники) — Common Core: High School

Добавить комментарий Отменить ответ