Правильный пятиугольник — построение, свойства и формулы
Бывают задачи на построение и нахождение некоторых геометрических параметров правильного пятиугольника. Построить фигуру непросто. Для этого математики рекомендуют несколько методик, позволяющих выполнить операцию более точно или за короткий промежуток времени. У фигуры есть свойства, а также формулы, позволяющие найти ее геометрические характеристики.
Точное построение фигуры
Специалисты рекомендуют некоторую последовательность действий, по которым построить правильный пятиугольник очень просто. Для операции необходимы обыкновенная тетрадь в клеточку, циркуль, карандаш, резинка и линейка. Следует выполнить некоторые шаги:


Если все пункты алгоритма выполнены правильно, то должен получиться пентагон, изображенный на рисунке 1:
Этот способ следует применять для точных построений и чертежей деталей. Однако для решения задач, в которых необходимо схематически изобразить пятиугольник, этот вариант не подойдет.
Алгоритм Биона
Прием Биона является менее точным методом, чем первый. Он позволяет построить любой правильный многоугольник, вписанный в произвольный круг. Для операции необходимо воспользоваться алгоритмом (шаблоном) Биона, имеющим такой вид:
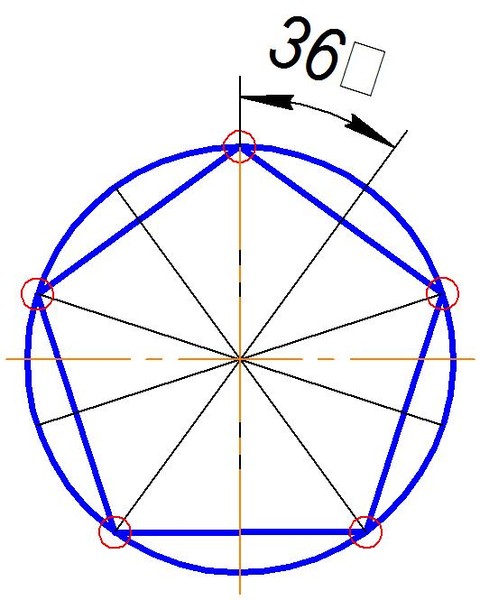
Погрешность построения многоугольника с 5, 7, 9 и 10 сторонами при использовании алгоритма довольно маленькая. Ее значения равно 3,2%. Однако при n>10 погрешность составляет не более 11%.
Приближенные методы
Существует несколько методов, позволяющих приближенно изобразить фигуру. Однако оптимальным является построение пентагона (рис. 2), используя две окружности (описанную и вписанную).
Метод известного математика А.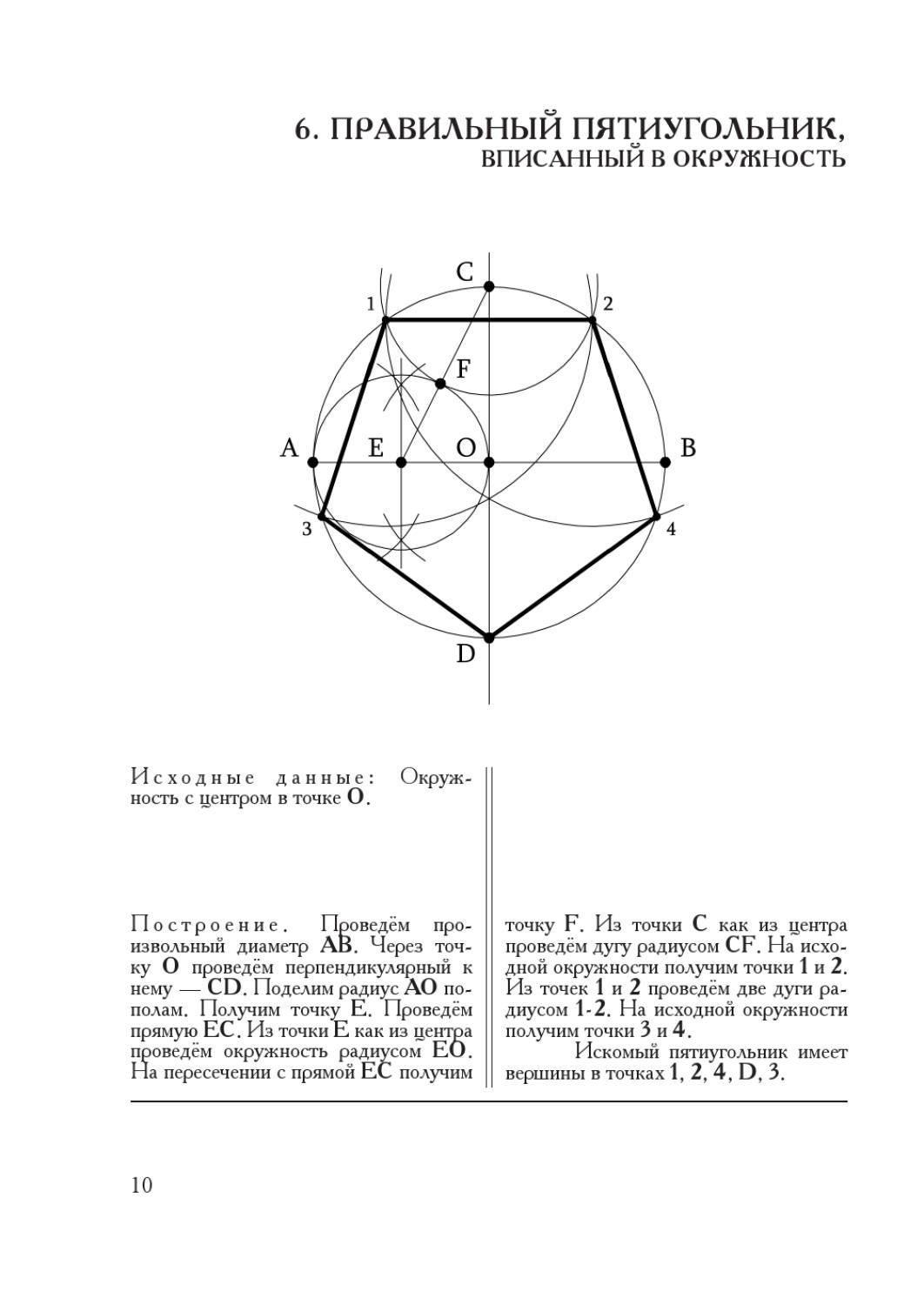 Дюрера является оптимальным среди остальных, поскольку на построение затрачивается минимальное количество времени
Дюрера является оптимальным среди остальных, поскольку на построение затрачивается минимальное количество времени
Существует еще один метод — построение пятиугольника из десятиугольника, который вписан в окружность. Для этого следует соединить его вершины через одну. Однако способ рекомендуется применять только в том случае, когда исходная фигура уже имеется. Кстати, его следует строить также методом А. Дюрера.
Однако способ рекомендуется применять только в том случае, когда исходная фигура уже имеется. Кстати, его следует строить также методом А. Дюрера.
Математики рекомендуют еще один простой способ. Для его реализации необходимо начертить окружность с диаметром АD. После этого его нужно поделить на 3 равные части, то есть AB = BC = CD. Затем из точки С следует опустить перпендикуляры на окружность. Обозначить места пересечения точками E и F. Проделать такую же процедуру с точкой B, обозначив пересечения точками G и H. Остается лишь соединить все точки отрезками.
Признаки и свойства
Не всегда получается верно идентифицировать пятиугольник. Для этого математики предлагают признаки, которые применимы только к правильной фигуре. К ним можно отнести следующие:
 (1/2)] / 2.
(1/2)] / 2.Однако свойств недостаточно при решении задач, поскольку существуют некоторые формулы и соотношения для нахождения основных параметров пентагона.
Расчет параметров
С помощью соотношений можно легко найти необходимые характеристики любой фигуры. Однако в некоторых источниках не указаны условные обозначения известного параметра пентагона. Это существенно затрудняет понимание формулы, а также ее дальнейшее использование. Перед изучением следует нарисовать фигуру и обозначить некоторые величины, которыми могут быть диагонали, стороны, апофемы и радиусы.
Рекомендуется использовать различные литеры или буквенные обозначения. Недопустимо пронумеровывать вершины, поскольку при вычислениях можно ошибиться. Нельзя использовать вместо букв цифры при обозначениях. Например, пентагон ABCDE является правильной записью. Допускается применение чисел в индексах, а именно, в пятиугольнике правильного типа ABCDE при пересечении его диагоналей образовался пентагон A1B1C1D1E1.
Математики рекомендуют обозначать только промежуточные фигуры или их проекции литерами с индексами. Для каждой новой фигуры следует вводить другие обозначения. Не следует использовать зарезервированные переменные. Например, центр окружности в точке P является недопустимой записью, поскольку такой буквой обозначается периметр.
Условные обозначения
Для нахождения основных величин пентагона следует обозначить некоторые его параметры. Фигура имеет следующие обозначения:
Значения сторон равны между собой. Площадь правильного пятиугольника — характеристика двумерной фигуры, которая показывает ее размерность.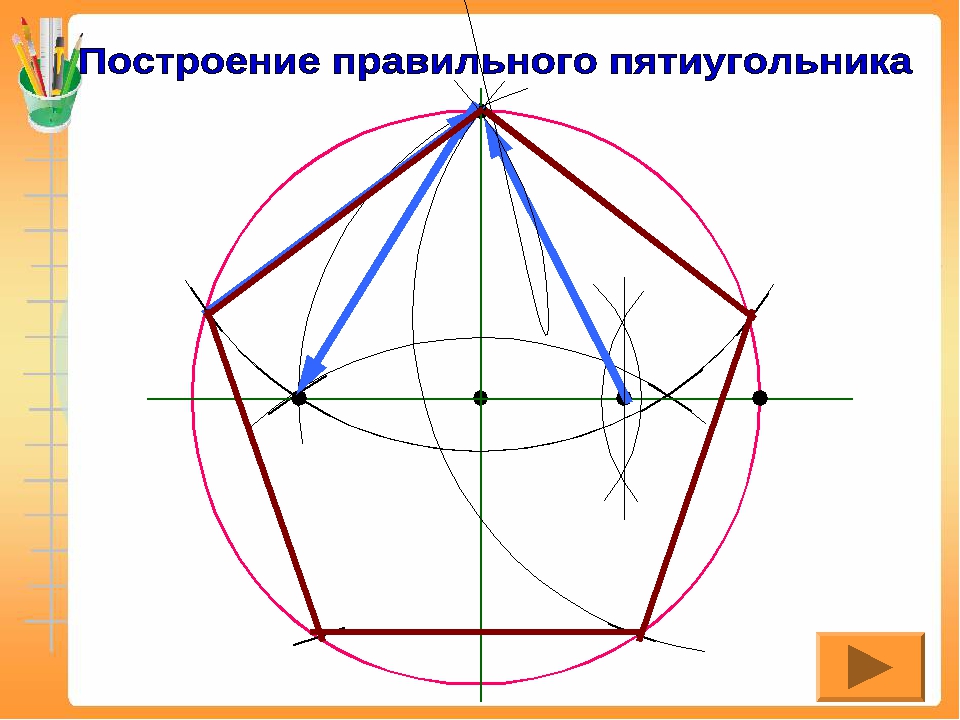 (1/2).
(1/2).
Таким образом, при решении задач необходимо знать основные признаки, свойства, соотношения и формулы для нахождения основных характеристик пентагона. Практика обязательна, поскольку теоретические знания без практического применения бесполезны.
ПредыдущаяГеометрияСвойства диагоналей ромба — основные формулы и доказательство теоремы
СледующаяГеометрияДодекаэдр — свойства, вид и структура двенадцатигранника
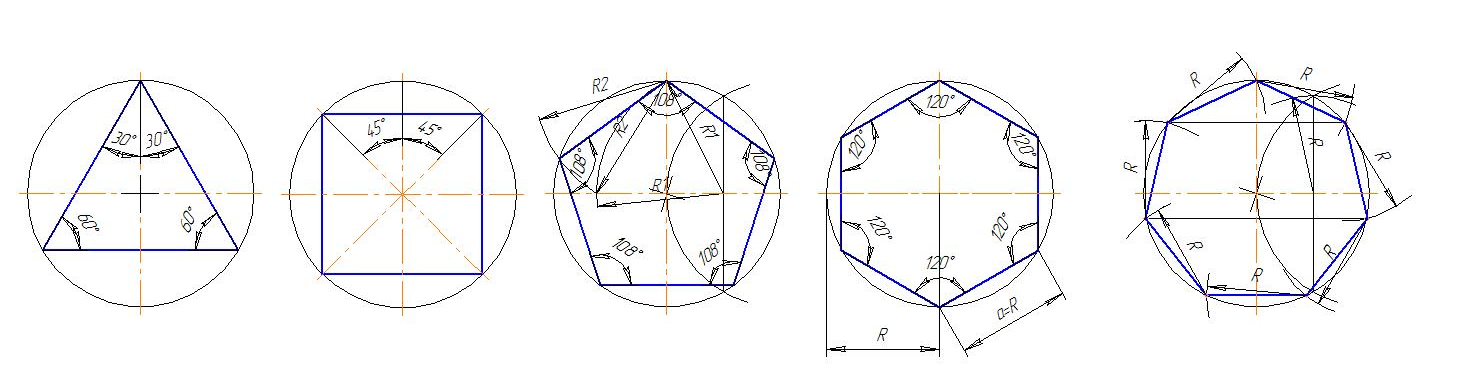
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а). Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего проводим стороны 5—6 и 3—2. Построение вписанного в окружность равностороннего треугольника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля. Рассмотрим два способа построения вписанного в окружность равностороннего треугольника. Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны 1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника. Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля. Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.
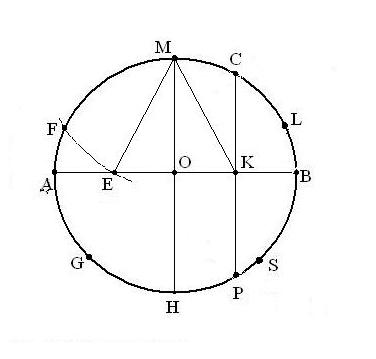
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою. Построение вписанного в окружность правильного пятиугольника. Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения. Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1.
Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой. Построение правильного пятиугольника по данной его стороне. Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую. Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB. Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Построение вписанного в окружность правильного семиугольника. Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника.
Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра. Приведённый способ годен для построения правильных многоугольников с любым числом сторон. Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
|
Правильный пятиугольник — это… Что такое Правильный пятиугольник?
Правильный пятиугольникПравильный пятиугольник (греч. πενταγωνον) — геометрическая фигура, правильный многоугольник с пятью сторонами.
Свойства
Построение правильного пятиугольника- Площадь правильного пятиугольника рассчитывается по любой из формул:
- ,
где — радиус описанной окружности, — радиус вписанной окружности, — диагональ, — сторона.
- Высота правильного пятиугольника:
- Диагонали правильного пятиугольника являются трисектрисами его внутренних углов.
- Отношение диагонали правильного пятиугольника к стороне равно золотому сечению, то есть числу .
Поэтому радиус вписанной окружности, радиус описанной окружности, высоту и площадь правильного пятиугольника можно вычислить и без использования тригонометрических функций:
- Радиус вписанной окружности:
- Радиус описанной окружности:
- Правильным пятиугольником невозможно заполнить плоскость без промежутков (см. также Паркет)
- Отношение площадей правильного пятиугольника и другого правильного пятиугольника, образованного пересечением диагоналей исходного
- ,
- где — отношение золотого сечения.
Построение
Построение правильного пятиугольникаПостроение правильного пятиугольника
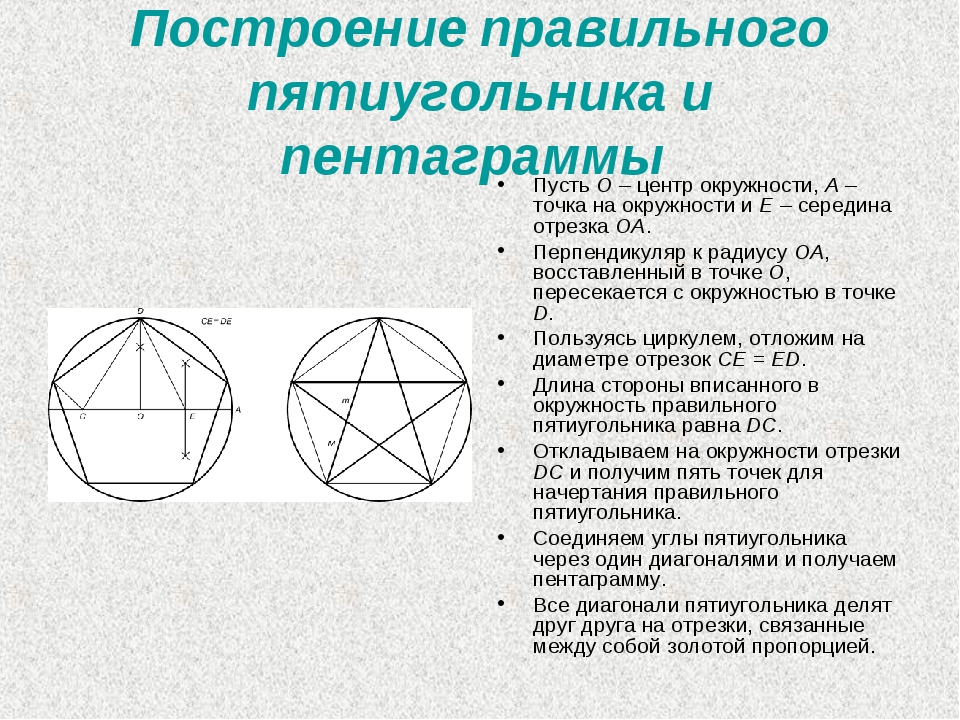
Правильный пятиугольник может быть построен с помощью циркуля и линейки, или вписыванием его в заданную окружность, или построением на основе заданной стороны. Этот процесс описан Евклидом в его «Началах» около 300 года до н. э.
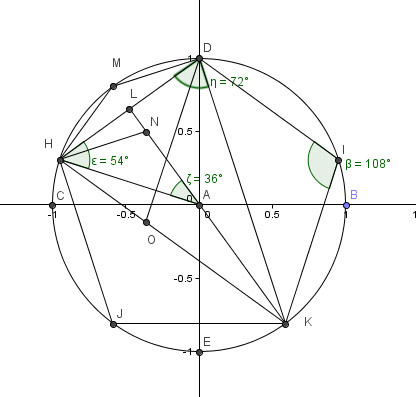
Вот один из методов построения правильного пятиугольника в заданной окружности:
- Постройте окружность, в которую будет вписан пятиугольник и обозначьте её центр как O. (Это зелёная окружность на схеме справа).
- Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
- Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью, как точку B.
- Постройте точку C посередине между O и B.
- Проведите окружность с центром в C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
- Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F.
- Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.
- Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.
- Постройте правильный пятиугольник AEGHF.
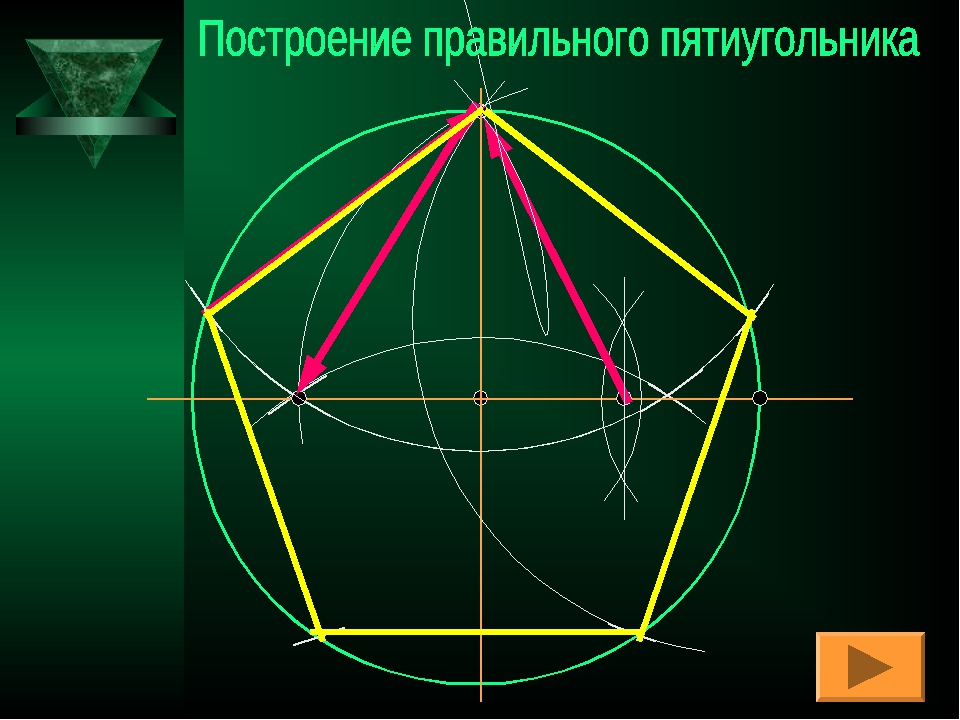
Альтернативный метод построения правильного многоугольника с помощью линейки и циркуля
Получение с помощью полоски бумаги
Правильный пятиугольник можно получить, завязав узлом полоску бумаги.
Overhand knot of a paper stripВ природе
Исследования формирования водяного льда на ровной поверхности меди при температурах 100—140 K показали, что сначала на поверхности возникают цепочки молекул шириной около 1 нм не гексагональной, а пентагональной структуры.[1]
Интересные факты
Пентагон- Додекаэдр — единственный из правильных многогранников, грани которого представляют собой правильные пятиугольники.
- Пентагон — здание Министерства обороны США имеет форму правильного пятиугольника.
- Правильный пятиугольник — правильный многоугольник с наименьшим количеством углов из тех, которыми нельзя замостить плоскость.
- В природе не существует кристаллов с гранями в форме правильного пятиугольника.
См. также
Примечания
Как вписать шестигранник в окружность
Popular
Основы черчения
Строительное
Машиностроительное
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего проводим стороны 5—6 и 3—2.
Построение вписанного в окружность равностороннего треугольника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны
1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.
Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты.
Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.
Есть ли поблизости от Вас карандаш? Взгляните-ка на его сечение – оно представляет собой правильный шестиугольник или, как его еще называют, гексагон. Такую форму имеет также сечение гайки, поле гексагональных шахмат, кристаллическая решетка некоторых сложных молекул углерода (к примеру, графит), снежинка, пчелиные соты и другие объекты. Гигантский правильный шестиугольник был недавно обнаружен в атмосфере Сатурна. Не кажется ли странным столь частое использование природой для своих творений конструкций именно этой формы? Давайте рассмотрим эту фигуру поподробнее.
- Длина его сторон соответствует радиусу описанной окружности. Из всех геометрических фигур это свойство имеет лишь правильный шестиугольник.
- Углы равны между собой, и величина каждого составляет 120°.
- Периметр гексагона можно найти по формуле Р=6*R, если известен радиус описанной вокруг него окружности, или Р=4*√(3)*r, если окружность в него вписана. R и r – радиусы описанной и вписанной окружности.
- Площадь, которую занимает правильный шестиугольник, определяется следующим образом: S=(3*√(3)*R 2 )/2. Если радиус неизвестен, вместо него подставляем длину одной из сторон – как известно, она соответствует длине радиуса описанной окружности.
Теперь рассмотрим построение правильного шестиугольника. Есть несколько способов, самый простой из которых предполагает использование циркуля, карандаша и линейки. Вначале рисуем циркулем произвольную окружность, затем в произвольном месте на этой окружности делаем точку. Не меняя раствора циркуля, ставим острие в эту точку, отмечаем на окружности следующую насечку, продолжаем так до тех пор, пока не получим все 6 точек. Теперь остается лишь соединить их между собой прямыми отрезками, и получится искомая фигура.
В широком смысле шестиугольник — это многоугольник с шестью углами. У правильного же шестиугольника углы и стороны равны. Нарисовать такой шестиугольник можно при помощи рулетки и транспортира, грубый шестиугольник — при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи интуиции и карандаша. Если вы хотите знать, как нарисовать шестиугольник различными способами, просто читайте далее.
Геометрические построения являются одной из главных частей обучения. Они формируют пространственное и логическое мышление, а также разрешают понять примитивные и натуральные геометрические обоснованности. Построения производятся на плоскости при помощи циркуля и линейки. Этими инструментами дозволено возвести крупное число геометрических фигур. При этом многие фигуры, кажущиеся довольно трудными, строятся с использованием простейших правил. Скажем, то, как возвести верный шестиугольник, дозволено описать каждого в нескольких словах.
Вам понадобится
- Циркуль, линейка, карандаш, лист бумаги.
Инструкция
1. Нарисуйте окружность. Установите некоторое расстояние между ножками циркуля. Это расстояние будет являться радиусом окружности. Выберите радиус таким образом, дабы вычерчивание окружности было довольно комфортным. Окружность должна всецело помещаться на листе бумаги. Слишком огромное либо слишком маленькое расстояние между ножками циркуля может привести к его изменению во время черчения. Оптимальным будет расстояние, при котором угол между ножками циркуля равен 15-30 градусов.
2. Постройте точки вершин углов верного шестиугольника. Установите ножку циркуля, в которой закреплена игла, в всякую точку окружности. Игла должна проткнуть начерченную линию. Чем вернее будет установлен циркуль, тем вернее будет построение. Проведите дугу окружности так, дабы она пересекла начерченную ранее окружность. Переставьте иглу циркуля в точку пересечения только что начерченной дуги с окружностью. Начертите еще одну дугу, пересекающую окружность. Вновь переставьте иглу циркуля в точку пересечения дуги и окружности и вновь начертите дугу. Произведите данное действие еще три раза, перемещаясь в одном направлении по окружности. Каждого должно получиться шесть дуг и шесть точек пересечения.
3. Постройте положительный шестиугольник. Ступенчато объедините все шесть точек пересечения дуг с изначально начерченной окружностью. Соединяйте точки прямыми, вычерчиваемыми при помощи линейки и карандаша. Позже произведенных действий будет получен верный шестиугольник, вписанный в окружность.
Шестиугольником считается многоугольник, владеющий шестью углами и шестью сторонами. Многоугольники бывают как выпуклыми, так и вогнутыми. У выпуклого шестиугольника все внутренние углы тупые, у вогнутого один либо больше угол является острым. Шестиугольник довольно легко возвести. Это делается в пару шагов.
Вам понадобится
- Карандаш, лист бумаги, линейка
Инструкция
1. Берется лист бумаги и на нем отмечается 6 точек приблизительно так, как это показано на рис. 1.
2. Позже того, как были подмечены точки, берется линейка, карандаш и с их подмогой ступенчато, друг за ином соединяются точки так, как это выглядит на рис. 2.
Видео по теме
Обратите внимание!
Сумма всех внутренних углов шестиугольника равна 720 градусам.
Шестиугольник – это многоугольник, тот, что владеет шестью углами. Для того, дабы начертить произвольный шестиугольник, надобно проделать каждого 2 действия.
Вам понадобится
- Карандаш, линейка, лист бумаги.
Инструкция
1. Нужно взять в руку карандаш и разметить на листе 6 произвольных точек. В дальнейшем эти точки будут исполнять роль углов в шестиугольнике. (рис.1)
2. Взять линейку и начертить по данным точкам 6 отрезков, которые бы соединялись друг с ином по начерченным ранее точкам (рис.2)
Видео по теме
Обратите внимание!
Специальным типом шестиугольника является положительный шестиугольник. Он именуется таковым потому, что все его стороны и углы равны между собой. Вокруг такого шестиугольника дозволено описать либо вписать окружность. Стоит подметить, что в точках, которые получились путем касания вписанной окружности и сторон шестиугольника, стороны положительного шестиугольника делятся напополам.
Полезный совет
В природе положительные шестиугольники владеют крупный популярностью. К примеру, вся пчелиная сота владеет положительной шестиугольной формой. Либо кристаллическая решетка графена (модификация углерода) тоже владеет формой положительного шестиугольника.
Как возвести тот либо другой угол – крупной вопрос. Но для некоторых углов задача невидимо упрощается. Одним из таких углов является угол в 30 градусов. Он равен ?/6, то есть число 30 является делителем 180. Плюс к этому его синус вестим. Это и помогает при его построении.
Вам понадобится
- транспортир, угольник, циркуль, линейка
Инструкция
1. Для начала разглядим особенно примитивную обстановку, когда у вас на руках есть транспортир. Тогда прямую под углом 30 градусов к данной дозволено легко отложить с поддержкой него.
2. Помимо транспортира существуют и угол ьники, один из углов которых равен 30 градусам. Тогда иной угол угол ьника будет равен 60 градусам, то есть вам необходим визуально меньший угол для построения требуемой прямой.
3. Перейдем сейчас к нетривиальным способам построения угла 30 градусов. Как вестимо, синус угла 30 градусов равен 1/2. Для его построения нам надобно возвести прямоугол ьный треугол ьник. Возможен, мы можем возвести две перпендикулярные прямые. Но тангенс 30 градусов – иррациональное число, следственно соотношение между катетами мы можем посчитать лишь примерно (исключительно, если нет калькулятора), а, значит, и возвести угол в 30 градусов примерно.
4. В этом случае дозволено сделать и точное построение. Возведем вновь две перпендикулярные прямые, на которых будут располагаться катеты прямоугол ьного треугол ьника. Отложим по одной прямой катет BC какой-нибудь длины с поддержкой циркуля (B – прямой угол ). После этого увеличим длину между ножками циркуля в 2 раза, что элементарно. Проводя окружность с центром в точке C с радиусом этой длины, обнаружим точку пересечения окружности с иной прямой. Эта точка и будет точкой A прямоугол ьного треугол ьника ABC, а угол A будет равен 30 градусам.
5. Возвести угол в 30 градусов дозволено и с поддержкой окружности, применяя то, что он равен ?/6. Возведем окружность с радиусом OB. Разглядим в теории треугол ьник, где OA = OB = R – радиус окружности, где угол OAB = 30 градусов. Пускай OE – высота этого равнобедренного треугол ьника, а, следственно, и его биссектриса и медиана. Тогда угол AOE = 15 градусов, и, по формуле половинного угла, sin(15o) = (sqrt(3)-1)/(2*sqrt(2)).Следственно, AE = R*sin(15o). Отсель, AB = 2AE = 2R*sin(15o). Строя окружность радиусом BA с центром в точке B, обнаружим точку пересечения A этой окружности с начальной. Угол AOB будет равен 30 градусам.
6. Если мы можем определять длину дуг каким-нибудь образом, то, отложив дугу длиной ?*R/6, мы также получим угол в 30 градусов.
Обратите внимание!
Нужно помнить, что в 5 пункте мы можем возвести угол лишь приближенно, потому что в вычислениях будут фигурировать иррациональные числа.
Шестиугольником называют частный случай полигона – фигуры, образованной большинством точек плоскости, ограниченным замкнутой полилинией. Положительный шестиугольник (гексагон), в свою очередь, также является частным случаем – это полигон с шестью равными сторонами и равными углами. Эта фигура знаменательна тем, что длина всей из ее сторон равна радиусу описанной вокруг фигуры окружности.
Вам понадобится
Инструкция
1. Выберите длину стороны шестиугольника. Возьмите циркуль и установите расстояние между концом иглы, расположенной на одной из его ножек, и концом грифеля, расположенным на иной ножке, равным длине стороны вычерчиваемой фигуры. Для этого дозволено воспользоваться линейкой либо предпочесть случайное расстояние, если данный момент несущественен. Зафиксируйте ножки циркуля винтом, если есть такая вероятность.
2. Нарисуйте окружность при помощи циркуля. Выбранное расстояние между ножками будет являться радиусом окружности.
3. Разбейте окружность точками на шесть равных частей. Эти точки будут являться вершинами углов шестиугольника и, соответственно, окончаниями отрезков, представляющих его стороны.
4. Ножку циркуля с иглой установите в произвольную точку, находящуюся на линии очерченной окружности. Игла должна верно проткнуть линию. От точности установки циркуля напрямую зависит точность построений. Очертите циркулем дугу так, дабы она пересекла в 2-х точках окружность, начерченную первой.
5. Переставьте ножку циркуля с иглой в одну из точек пересечения начерченной дуги с изначальной окружностью. Вычертите еще одну дугу, также пересекающую окружность в 2-х точках (одна из них совпадет с точкой предыдущего расположения иглы циркуля).
6. Сходственным же образом переставляйте иглу циркуля и вычерчивайте дуги еще четыре раза. Перемещайте ножку циркуля с иглой в одном направлении по окружности (неизменно по либо вопреки часовой стрелки). В итоге обязаны быть выявлены шесть точек пересечения дуг с изначально построенной окружностью.
7. Нарисуйте положительный шестиугольник. Ступенчато попарно объедините отрезками полученные на предыдущем шаге шесть точек. Вычерчивайте отрезки при помощи карандаша и линейки. В итоге будет получен верный шестиугольник. Позже осуществления построения дозволено стереть вспомогательные элементы (дуги и окружность).
Обратите внимание!
Имеет толк выбирать такое расстояние между ножками циркуля, дабы угол между ними был равен 15-30 градусов, напротив при осуществлении построений данное расстояние может легко сбиться.
При строительстве либо разработке домашних дизайн-планов зачастую требуется возвести угол , равный теснее имеющемуся. На поддержка приходят образцы и школьные умения геометрии.
Инструкция
1. Угол образуют две прямые, исходящие из одной точки. Эта точка будет именоваться вершиной угла, а линии будут являться сторонами угла.
2. Для обозначения углов используйте три буквы: одна у вершины, две у сторон. Называют угол , начиная с той буквы, которая стоит у одной стороны, дальше называют букву, стоящую у вершины, и после этого букву у иной стороны. Используйте и другие методы для обозначения углов, если вам комфортнее напротив. Изредка называют только одну букву, которая стоит у вершины. А дозволено обозначать углы греческими буквами, скажем, α, β, γ.
3. Встречаются обстановки, когда нужно начертить угол , дабы он был равен теснее данному углу. Если при построении чертежа применять транспортир вероятности нет, дозволено обойтись только линейкой и циркулем. Возможен, на прямой, обозначенной на чертеже буквами MN, надобно возвести угол у точки К, так, дабы он был равен углу В. То есть из точки K нужно провести прямую, образующую с линией MN угол , тот, что будет равен углу В.
4. В начале подметьте по точке на всей стороне данного угла, скажем, точки А и С, дальше объедините точки С и А прямой линией. Получите треугол ьник АВС.
5. Теперь постройте на прямой MN такой же треугол ьник, дабы его вершина В находилась на линии в точке К. Используйте правило построения треугол ьника по трем сторонам. Отложите от точки К отрезок KL. Он должен быть равен отрезку ВС. Получите точку L.
6. Из точки K вычертите окружность радиусом равным отрезку ВА. Из L вычертите окружность радиусом СА. Полученную точку (Р) пересечения 2-х окружностей объедините с К. Получите треугол ьник КPL, тот, что будет равен треугол ьнику ABC. Так вы получите угол К. Он и будет равен углу В. Дабы это построение сделать комфортнее и стремительней, от вершины В отложите равные отрезки, применяя один раствор циркуля, не сдвигая ножек, опишите этим же радиусом из точки К окружность.
Видео по теме
Обратите внимание!
Избегайте случайного метаморфозы расстояния между ножками циркуля. В этом случае шестиугольник может получиться неправильным.
Полезный совет
Имеет толк изготавливать построения при помощи циркуля с отлично заточенным грифелем. Так построения будут особенно точны.
Построение шестигранника может производиться несколькими способами. Удобнее всего использовать стандартный набор чертежных инструментов: циркуль, линейку. Однако, в отсутствие циркуля, фигура этого типа может быть начерчена с помощью рейсшины, угольника заводского изготовления с углами 90/60/30°.
Шестигранники применяются для откручивания и закручивания болтов при ремонте и сборке мебели.
В обоих случаях особенностью построения является элементарное знание основ геометрии. В правильном шестиугольнике длина его стороны всегда равна радиусу окружности, описанной вокруг него, противоположные стороны параллельны, грани сопрягаются под углом 60°.
Способ вычерчивания шестиугольника циркулем, линейкой
Чтобы построить шестигранник при наличии циркуля, достаточно вычертить окружность, найти на ее дуге 6 точек, соединив их отрезками. Для этого достаточно настроить циркуль один раз, отложив на нем значение стороны многогранника. Линейка потребуется для строительства вспомогательных, основных линий.
Метод выглядит следующим образом:
Первый способ вычерчивания шестиугольника циркулем: 1,2,3,4,5,6 — углы, 0 — центр, D — радиус шестигранника.
- циркулем вычерчивается окружность — радиус является размером стороны;
- по линейке проводится радиус — точки пересечения этого отрезка будут углами многоугольника;
- находятся два угла многоугольника — циркуль переставляется в одну из точек пересечения отрезка (проведенный на предыдущем этапе диаметр), на дуге делаются отметки;
- находятся оставшиеся два угла — циркуль перемещается в противоположную точку пересечения отрезка с дугой окружности, создаются отметки пересечения на второй стороне окружности.
Построение правильного шестигранника завершается соединением получившихся углов по линейке. Это самый точный способ, требующий минимального количества чертежного инструмента. При значительном размере сторон (например, крой листового металла, деревянных заготовок) можно использовать шнур с карандашом. Один край шнура крепится к карандашу/маркеру, второй неподвижно фиксируется в центре окружности, затем в точках пересечения диаметра с дугой окружности.
Построение занимает минимальное количество времени, точность целиком зависит от заточки карандаша, наличия фиксатора на циркуле.
Способ вычерчивания шестиугольника без циркуля
Построение правильного шестигранника без циркуля требует обязательного наличия рейсшины — специального инструмента в виде линейки, внутри корпуса которой расположен массивный вал с резиновыми элементами, препятствующими проскальзыванию. Он создан для быстрого изготовления параллельных прямых, обеспечивая высокую точность построений. Качество вычерчивания в данном методе полностью зависит от точности угла 60° в угольнике заводского изготовления, градуирования шкалы линейки.
Способ построения выглядит следующим образом:
Второй способ вычерчивания шестиугольника циркулем: 1,2,3,4,5,6 — углы, 0 — центр, D — радиус шестигранника.
- к одной стороне отрезка прикладывается угольник — короткая сторона совмещена с линией, угол 60° примыкает к концу отрезка изнутри, по гипотенузе угольника проводится линия произвольного размера, который корректируется впоследствии по шкале линейки;
- на листе/заготовке вычерчивается линия — длина ее равна двум размерам стороны многоугольника, края автоматически становятся центрами многогранника;
- операция повторяется при развороте угольника — угол 60° перемещается к противоположной стороне отрезка, центром вращения является длинный катет угольника;
- разворот угольника — теперь центром вращения становится короткий катет угольника, вычерчиваются еще две грани;
- уточнение размеров сторон — на четырех получившихся сторонах многоугольника по линейке откладывается их точный размер;
- строительство двух оставшихся сторон — они расположены параллельно линии, с которой было начато черчение, проводятся по линейке, затем уточняется их размер;
- контроль параллельности — шкала рейсшины совмещается с линией, от которой началось построение фигуры, затем инструмент перемещается вверх/вниз для удостоверения параллельности двух противоположных граней между собой, с этим отрезком
Шестигранник в этом случае вычерчивается дольше, чем в первом способе. Однако так можно построить необходимую фигуру, в отсутствие циркуля, угольником. Технология основана на параллельности противоположных сторон правильного шестиугольника, одинаковых внутренних углах 60°.
Промышленность выпускает угольники как с острыми углами, удобными для данного метода, так и со скругленными.
Третий способ вычерчивания шестиугольника циркулем: a — диаметр, b — сторона шестигранника.
В последнем случае удобнее несколько изменить технологию:
- после вычерчивания центрального отрезка по нему выравнивается рейсшина;
- инструмент откатывается вниз на произвольную величину;
- короткая гипотенуза угольника совмещается с линейкой рейсшины, а не с центральным отрезком;
- скругленный край инструмента не участвует в построении, линия проводится по цельной части гипотенузы.
Операция повторяется с противоположной стороны отрезка, после чего рейсшина разворачивается на 180°, опять совмещается с центральной линией, откатывается вверх для построения двух других сторон многогранника.
Это стандартные способы вычерчивания равностороннего многоугольника с шестью углами, гранями. Они удобны для кроя заготовок любых размеров из разных материалов, в стандартном черчении на ватмане. Обе методики имеют исключительно прикладное значение, так как в профессиональных графических редакторах (AutoCAD, Компас-3D) подобные фигуры создаются автоматически заданием нужных параметров.
В широком смысле шестиугольник — это многоугольник с шестью углами. У правильного же шестиугольника углы и стороны равны. Нарисовать такой шестиугольник можно при помощи рулетки и транспортира, грубый шестиугольник — при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи интуиции и карандаша. Если вы хотите знать, как нарисовать шестиугольник различными способами, просто читайте далее.
Правильный шестиугольник – это многоугольник, состоящий из шести равных сторон. Все соседние стороны образуют угол 120°.
Формулы
- P – периметр
- S – площадь
- R – радиус K
- r – радиус k
- S’ – центр
- a – сторона
- K – окружность описанная
- k – окружность вписанная
При предоставлении услуг веб-сайт «Calculat.org» использует файлы куки.
Вы не любите рекламу? Мы ее тоже не любим, тем не менее доходы от рекламы предоставляют возможность функционирования нашего веб-сайта и бесплатного обслуживания наших посетителей. Пожалуйста, подумайте, не стоит ли отменить блокировку рекламы на этом веб-сайте. Спасибо.
| Обратная связь ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса — ваш вокал Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими Целительная привычка Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Тренинг уверенности в себе Вкуснейший «Салат из свеклы с чесноком» Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Как слышать голос Бога Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека — Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д. Отёска стен и прирубка косяков — Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) — В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. | Построение правильных многоугольников Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а). Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего проводим стороны 5—6 и 3—2. Построение вписанного в окружность равностороннего треугольника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля. Рассмотрим два способа построения вписанного в окружность равностороннего треугольника. Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны 1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника. Второй способ основан на том, что, если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник. Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника. Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля. Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3. Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения. Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою. Построение вписанного в окружность правильного пятиугольника. Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения. Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой. |
Упаковка кругов в круг
Следующий код пытается упаковать заранее определенное количество меньших кругов (со случайными радиусами между двумя заданными пределами) в больший.
Алгоритм просто выбирает случайный набор радиусов, сортирует их в порядке убывания (так, чтобы сначала располагались большие круги), и отслеживает, где был размещен каждый круг. Пытаясь разместить следующий круг, он выбирает равномерно случайную точку внутри содержащего круга в качестве своего центра и проверяет, не будет ли он перекрывать другие.Если будет, выбирается другая точка (до некоторого разумного предела попыток, после чего мы отказываемся от попыток разместить кружок и переходим к следующему, меньшему).
Размеры изображения, цветовую палитру, размер внешнего круга, диапазон размеров внутреннего круга и количество внутренних кругов можно настроить в конструкторе для класса Circles .
импортировать numpy как np
класс Круг:
"" "Маленький класс, представляющий круг SVG." ""
def __init __ (self, cx, cy, r, icolour = None):
"" "Инициализируйте круг с его центром (cx, cy) и радиусом r.icolour - это индекс цвета круга.
"" "
self.cx, self.cy, self.r = cx, cy, r
self.icolour = icolour
def overlap_with (self, cx, cy, r):
"" "Перекрывается ли круг с другим радиусом r в точке (cx, cy)?" ""
d = np.hypot (cx-self.cx, cy-self.cy)
вернуть d Печатать текст по кругу / по кругу
Создание кружков слов или круглых текстов - это разновидность художественного текста. Дизайнеры то и дело сталкиваются с необходимостью создавать изогнутые тексты.
В этом руководстве мы узнаем, как вводить текст по кругу в Affinity Designer от Serif.
1) Запустите Affinity Designer и создайте новый документ ( ⌘ + N ). Чтобы работать с прозрачным фоном, отметьте Прозрачный фон в разделе Цвет диалогового окна, которое только что появилось.
2) Выберите инструмент Ellipse Tool .
3) Обведите эллипс и нажмите SHIFT , пока начертите его; это создаст идеальный круг. Залейте фон каким-нибудь цветом. Выберите инструмент Move Tool и щелкните кружок, чтобы выбрать его.
4) Затем выберите инструмент Artistic Text Tool , чтобы написать несколько слов вокруг только что созданного круга.
5) Наведите указатель мыши на край круга.Курсор изменится на букву « T » с небольшой волной под ней. Или вы можете просто выбрать Layer > Convert to Text Path , чтобы добиться того же.
6) Щелкните левой кнопкой мыши, удерживайте ее и немного перетащите в правый нижний угол. Буква « A » появится прямо над курсором. Отпустите мышь.
7) Два маленьких зеленого и оранжевого треугольника появляются на краю круга, отмечая начальную и конечную точки для текста, который нужно напечатать в направлении.Курсор мигает на зеленом треугольнике. Теперь мы готовы ввести текст.
8) Набираем несколько слов, скажем, «РАЗВЕДКА ЗВЕЗДНОГО ФЛОТА». Помните, что вы можете выбрать Font , который вам нравится, выбрать соответствующий цвет, а также установить желаемый размер шрифта. Зеленый треугольник можно перетащить по окружности круга до точки, в которой должен начинаться текст. Ваш напечатанный текст может доходить до оранжевого треугольника, за которым он переворачивается внутрь круга.Оранжевый треугольник также можно перетаскивать, поэтому установите метки по своему усмотрению.
9) Теперь нам нужно добавить еще несколько слов после «ИНТЕЛЛЕКТ». Нажмите пробел и начните вводить новые слова - «UNITED ...». Ой! Когда он закрывает оранжевую метку, новый текст автоматически переворачивает положение внутрь круга, начиная с исходной зеленой начальной точки, но переворачивая и в направлении против часовой стрелки. Другой набор треугольников - один зеленый (более темный) и один красноватый - автоматически вставляется на окружность.
10) Нам нужно заполнить текст «ОБЪЕДИНЕННАЯ ФЕДЕРАЦИЯ ПЛАНЕТ» внутри круга, и он должен уместиться между начальной и конечной точками. Для этого мы можем либо уменьшить размер шрифта, либо уменьшить расстояние между ними (хотя это маловероятно), либо расширить область обведенного круга.
Теперь есть две вещи относительно изменения размера области:
- Если вы перетащите любой угловой маркер выделения, высота и ширина изменятся одновременно, без изменения размера текста на пути.
- Из нижнего правого угла выделенной области выходит дополнительная точка, известная как ручка шкалы . Если вы перетащите его, текст также масштабируется вместе с высотой и шириной объекта.
Выберите любой подход (или и то, и другое), внесите необходимые изменения и разместите добавленный текст.
11) Отметим, что на внутренней стороне окружности написан текст «ЕДИНАЯ ФЕДЕРАЦИЯ ПЛАНЕТ».Чтобы разместить его по внешнему контуру окружности, увеличьте ползунок Baseline . Здесь мы увеличиваем его до 80%.
Ниже представлен круговой текст, который мы только что создали. Кстати, надеюсь, вы не внутри клингонского сосуда 😉
Банкноты
- Чтобы создать текст в виде круга, мы также можем выбрать круг и в меню Layer просто выбрать Convert to Text Path . Курсор изменится на букву « T » с небольшой волной под ней.
- Таким же образом художественные тексты контуров могут быть созданы из любой линии, кривой или контура фигуры.
Калькулятор калорий - ежедневная потребность в калориях
Сколько калорий мне нужно съесть?
Универсальные рекомендации по потреблению калорий не работают . Они должны быть адаптированы к каждому человеку.
Чтобы точно определить суточное количество калорий, указанное выше, введите в калькулятор свой текущий вес, возраст, рост и пол. Максимально оцените, сколько упражнений вы будете делать .
Результаты покажут, сколько калорий вы можете съесть, чтобы поддерживать или терять вес. Вам не нужно регулировать это в зависимости от частоты тренировок - это учитывается в уравнении. Стоимость обслуживания такая же, как и то, что некоторые люди называют общим дневным расходом энергии (TDEE).
По мере того, как вы худеете на , вам нужно будет пересчитать на основе вашего нового веса.
калорий для сжигания жира
Наука говорит нам, что 1 фунт жира равен 3500 калориям, поэтому ежедневный дефицит в 500 калорий должен привести к потере 1 фунта жира в неделю.
На самом деле все работает не так эффективно!
Как правило, расход энергии человека уменьшается по мере того, как он становится легче, а это означает, что вы неизбежно выйдете на плато. Количество потребляемой пищи, которое когда-то приводило к потере веса, теперь будет поддерживать только 2 .
Нужна помощь с основами похудания? Прочтите наше простое руководство.
Предупреждение!
Всегда старайтесь стремиться к дневному уровню калорийности «Снижение жира».
«Экстремальная потеря жира» - это минимальный уровень калорийности . Не пытайтесь сразу же снизить количество калорий до этого уровня в надежде на быстрое решение. В конечном итоге это может иметь неприятные последствия.
Уровень экстремальной потери жира указывает на минимальное количество калорий
, которое можно считать . Это следует рассматривать как исключение, а не правило.
Действительно лучше сжигать жир, чем морить его голодом.
Плато для похудания
Зачем использовать 7-дневный цикл калорий (зигзагообразный)?
Со временем наш организм приспосабливается к пониженному уровню калорий.
Наше тело становится более эффективным в использовании энергии (снижается метаболизм) и, следовательно, сжигает меньше жира.
Вот почему большинство из нас достигают плато потери веса.
На данный момент единственный вариант - ускорить метаболизм :
- увеличение кардио,
- силовые тренировки,
- «чит-обедов» (т. Е. Периодических высококалорийных блюд),
- калорий при циклическом (или зигзагообразном) движении,
калорий- , даже изменение соотношения макронутриентов может помочь в этом (не забывайте о достаточном сне и гидратации).
Вы часто обнаруживаете, что чем ближе вы подходите к своему целевому весу (или процентному содержанию жира в организме), тем сложнее становится!
Постоянное снижение калорийности способствует еще большему снижению метаболизма - как только вы вернетесь к «нормальному» питанию, вес снова вернется. 7-дневный зигзаг дает рекомендации по ежедневному потреблению калорий, которые заставят ваше тело гадать и увеличат ваши шансы на постоянную потерю веса.
Нужна помощь с выбором продуктов? Минимальное дневное потребление калорий
Трудно установить абсолютный минимальный уровень калорий, потому что у всех разный состав тела и уровень активности.
Органы здравоохранения устанавливают некоторые базовые уровни - это 1200 калорий в день для женщин и 1800 калорий в день для мужчин.
Эти абсолютные правила не имеют смысла - вы ведете сидячий образ жизни с небольшой мышечной массой? Или кто-то высокий, мускулистый и много тренируется? Абсолютные уровни не работают, но дают нам отправную точку.
При снижении калорийности:
Старайтесь не снижать потребление калорий более чем на 500 калорий ниже нормы .
Это может вызвать реакцию организма на голод, что может привести к эффекту диеты йо-йо.
Постарайтесь постепенно снизить калорий. Внезапное падение (например, на 500 калорий и более) может замедлить ваш метаболизм.
Научитесь есть медленно - исследования показывают, что люди, которые быстрее едят, тяжелее 1 .
Что происходит, когда калорий слишком мало?
- Мышечная масса расщепляется на энергию (катаболизм).
- Скорость метаболизма начинает падать (обычно) через 3 дня очень низкого потребления калорий - это связано с потерей мышечной массы и усугубляется ею.
- При очень низком уровне калорий вы рискуете вялостью, недостатком питательных веществ, усталостью и часто раздражительностью.
Вы полностью настроены на набор жира, если внезапно вернетесь к своему прежнему режиму питания.
Уровень упражнения
Поскольку ваш уровень упражнений уже учтен в уравнении, НЕ ТРЕБУЕТСЯ вычитать калории, сожженные во время упражнений.
Очень трудно обобщить нагрузку из упражнений.
Для простоты мы определяем здесь тренировку как 20 минут учащенного пульса.
Итак, 3 раза в неделю - это 20 минут повышенного пульса 3 раза в неделю. Для вас это может означать быструю прогулку, для других - медленную пробежку.
Интенсивные упражнения можно определить как час повышенного пульса (однако интенсивные тренировки, такие как серия упражнений с собственным весом (или с тяжелыми весами) с небольшими перерывами или без них, считаются интенсивными, даже если их продолжительность меньше).
Поиграйте с нашим инструментом для сжигания калорий, чтобы сравнить разные упражнения.
Мы рекомендуем включить физические упражнения в свой образ жизни: они помогают поддерживать мышцы при дефиците калорий, а также полезны для сердца и психического состояния.
Подсчет макросов
Подсчет макросов - популярный способ похудения на основе калорий, потому что он очень персонализированный и неограниченный. Он учит людей, сидящих на диете, рассчитывать свои потребности в калориях (как это делает наш калькулятор выше), а также сколько граммов углеводов, жиров и белков (макросов) им следует съедать каждый день для похудения.
Нет запрещенных продуктов, если они соответствуют вашему дневному количеству макро.
ПОПУЛЯРНОЕ Макрорешение от Теда Каллмайера - отличное место для начала. Это стало популярным выбором в последние годы из-за политики запрета на еду. Нет запрещенных продуктов - при условии, что они соответствуют вашим ежедневным или еженедельным целям. Похудеть и нарастить мышцы?
Большинство людей теряют мышечную массу при ограничении калорий. Для поддержания мышечного тонуса требуются огромные усилия, а нарастить мышечную массу при одновременной потере жира еще сложнее.
Для этого есть отличные ресурсы.
- ПОПУЛЯРНЫЙ Old School New Body от Стива Холмана - отличная программа , которая фокусируется на более коротких тренировках (максимум 90 минут в неделю), при этом сжигая жир и наращивая мышцы. Возраст здесь не оправдание, так как автору уже за 50!
Самое простое решение
Если у вас есть бюджет, доставка еды с контролируемой калорийностью - самый эффективный способ получить правильное питание и добиться потери веса.
- ПОПУЛЯРНЫЙ Diet-to-go - одна из лучших программ доставки в США. Если ваш дневной калорийность, указанная на калькуляторе, находится в диапазоне 1200-1500, тогда вам может подойти план «Диета на вынос». Обратите внимание, что цены составляют около 18-24 долларов в день.
«Я просто хотел сообщить вам, насколько ваш сайт помог мне за последние 6 месяцев…… Я использовал этот калькулятор, чтобы похудеть. Всего я похудел на 50 фунтов, я перешел с 14-го размера на 6-8-й… »
Список литературы
Этот калькулятор был разработан с использованием наиболее точных методологий из рецензируемых исследований.Полное объяснение см. В Руководстве по потреблению калорий.
- [1] Более высокая скорость приема пищи, по оценке самих специалистов, связана с более высоким индексом массы тела в общенациональном опросе женщин среднего возраста. Сук Линг Леонг, Клара Мэдден, Эндрю Грей, Дебра Уотерс, Кэролайн Хорват Журнал Американской диетической ассоциации 1 августа 2011 г. (том 111, выпуск 8, страницы 1192-1197 DOI: 10.1016 / j.jada.2011.05.012)
- [2] Моделирование поддержания потери веса для предотвращения восстановления веса.Кевин Д. Холл и Питер Н. Джордан, Американский журнал клинического питания, декабрь 2008 г. (Том 88, № 6, 1495-1503doi: 10.3945 / ajcn.2008.26333)
Ссылка
- MD Mifflin, ST St Jeor, et al. Новое уравнение для прогнозирования расхода энергии в состоянии покоя у здоровых людей.
J Am Diet Assoc 2005: 51: 241-247. Ссылка - Frankenfield DC, et al. Сравнение прогнозных уравнений для скорости метаболизма в покое у здоровых взрослых без ожирения и с ожирением: систематический обзор.J Am Diet Assoc. 2005; 105: 775-789. Ссылка
- Frankenfield DC, et al. Исследования Харриса-Бенедикта основного метаболизма человека: история и ограничения. J Am Diet Assoc. 1998; 98: 439-445.
- Манини, Т. М., Эверхарт, Дж. Э., Патель, К. В., Шоллер, Д. А., Кольбер, Л. Х., Виссер, М.,… и Харрис, Т. Б. (2006). Ежедневный расход энергии и смертность среди пожилых людей. Джама , 296 (2), 171-179.




 Однако точное деление окружности путем геометрического построения возможно лишь на 3, 4, 5 и 15 равных частей, а также при делении на число частей, получаемое последовательным удвоением этих чисел. В остальных случаях приходится…
Однако точное деление окружности путем геометрического построения возможно лишь на 3, 4, 5 и 15 равных частей, а также при делении на число частей, получаемое последовательным удвоением этих чисел. В остальных случаях приходится… От этого зависит ваш авторитет художника, а значит и заказы.
От этого зависит ваш авторитет художника, а значит и заказы.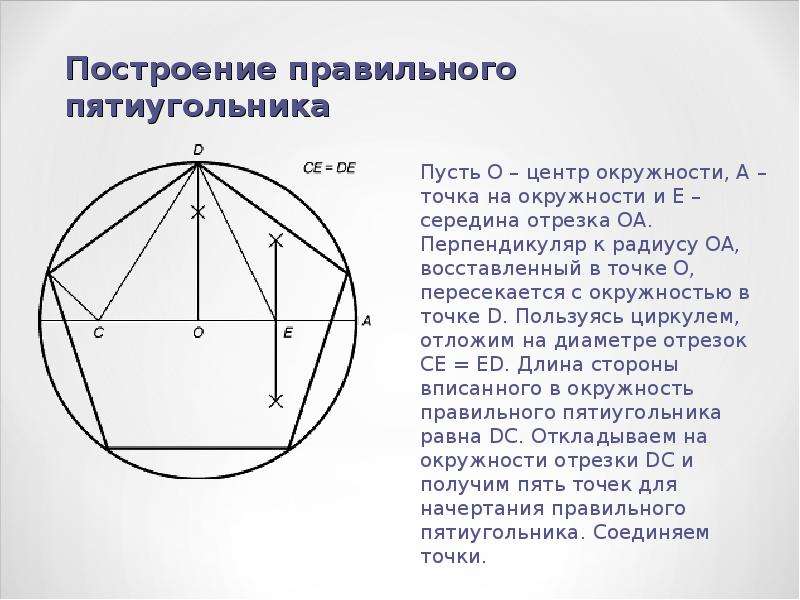
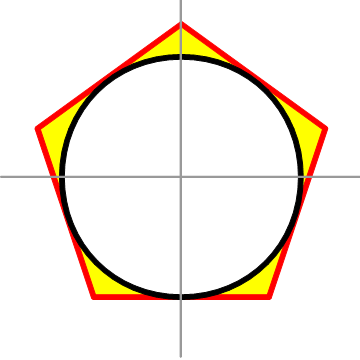 Смотрим картинку.
Смотрим картинку.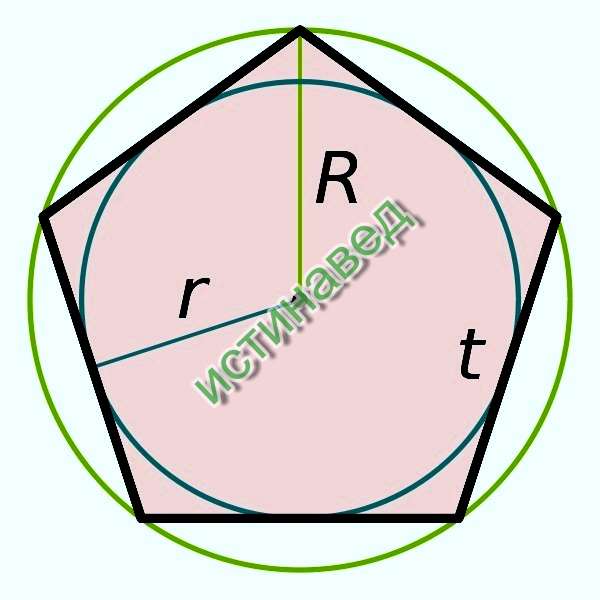 Дан правильный многоугольник, число сторон которого представляет собой произведение натуральных чисел k и m, где m>2. Как построить правильный m-угольник? Гаусс показал также возможность построения правильного 257-угольника с помощью циркуля и линейки.
Дан правильный многоугольник, число сторон которого представляет собой произведение натуральных чисел k и m, где m>2. Как построить правильный m-угольник? Гаусс показал также возможность построения правильного 257-угольника с помощью циркуля и линейки. Полученный пятиугольник — искомый.
Полученный пятиугольник — искомый. ru
ru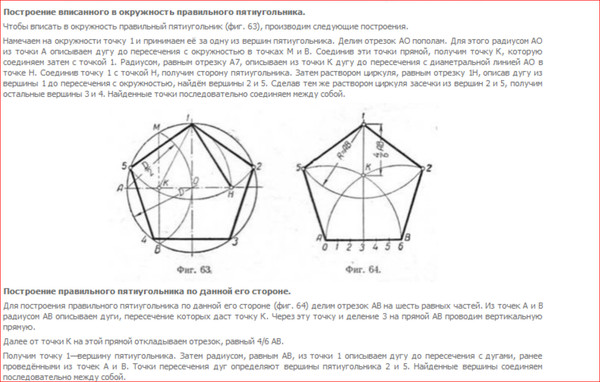 Казалось бы, нет ничего проще. Взял карандаш да и нарисовал круг.
Казалось бы, нет ничего проще. Взял карандаш да и нарисовал круг.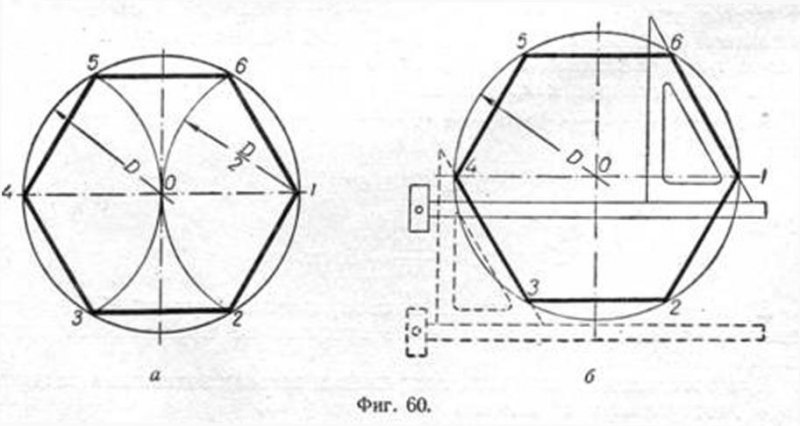 Если у данного многоугольника все стороны и углы одинаковые, то он называется правильным (пентагоном).
Если у данного многоугольника все стороны и углы одинаковые, то он называется правильным (пентагоном).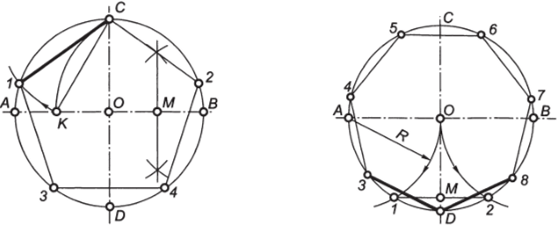

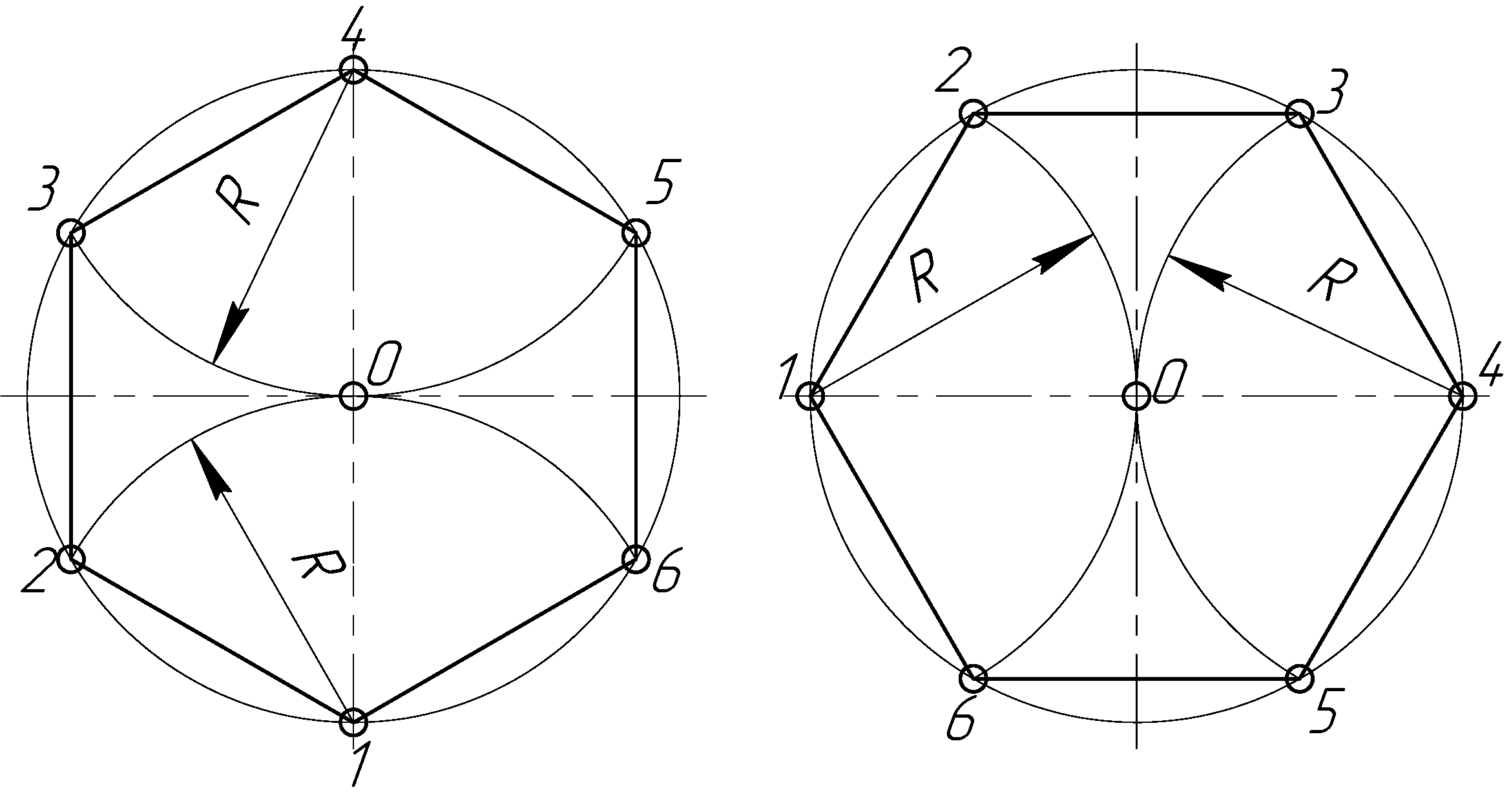 Первым…
Первым…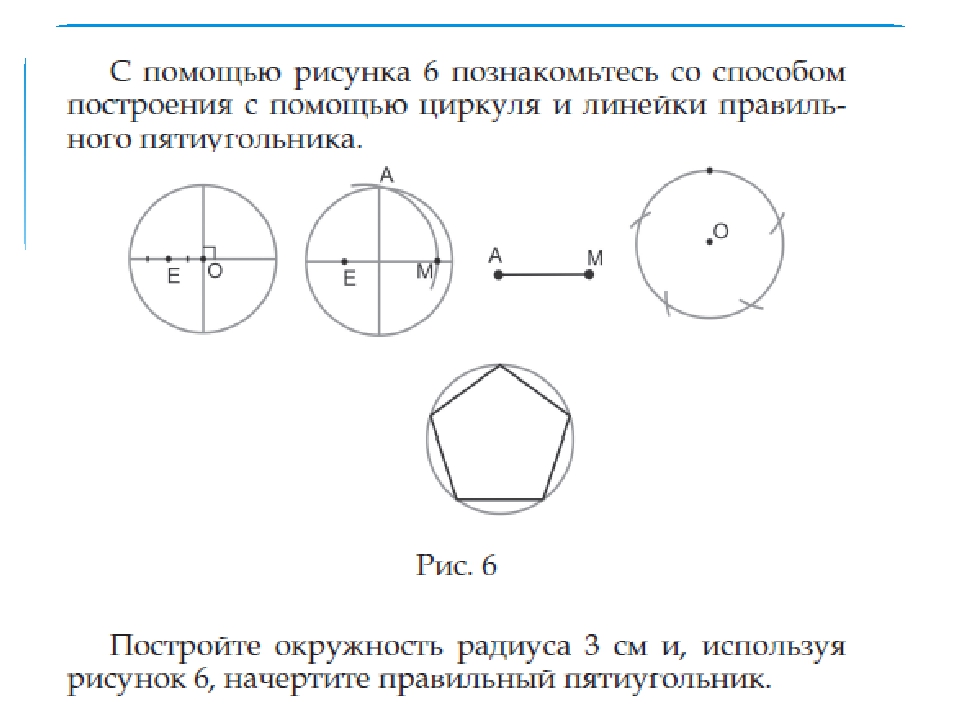
 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.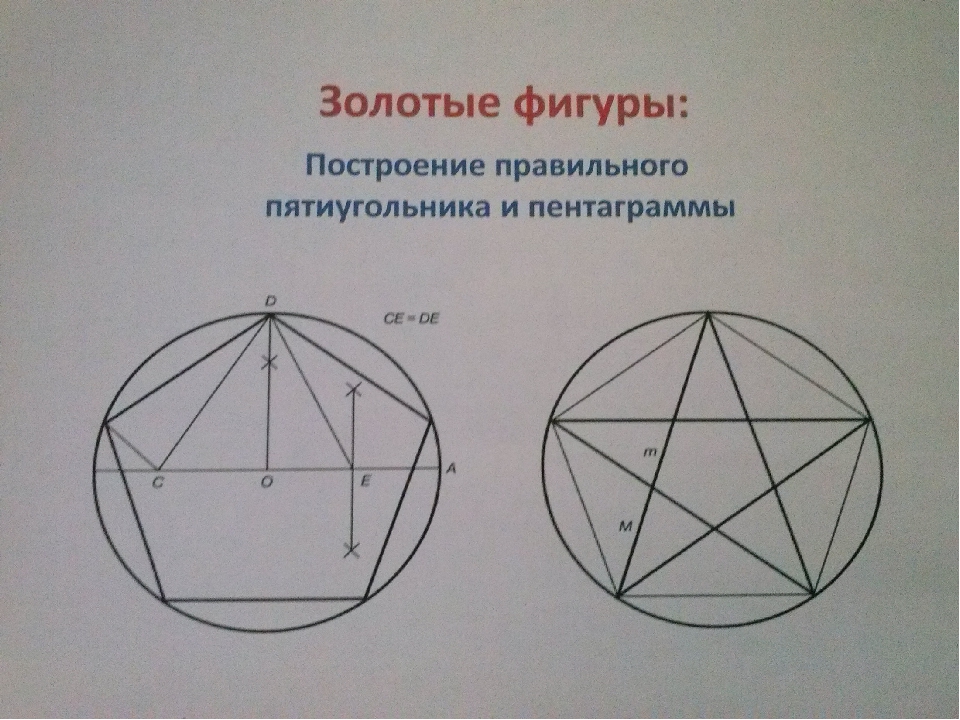 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5.
Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5.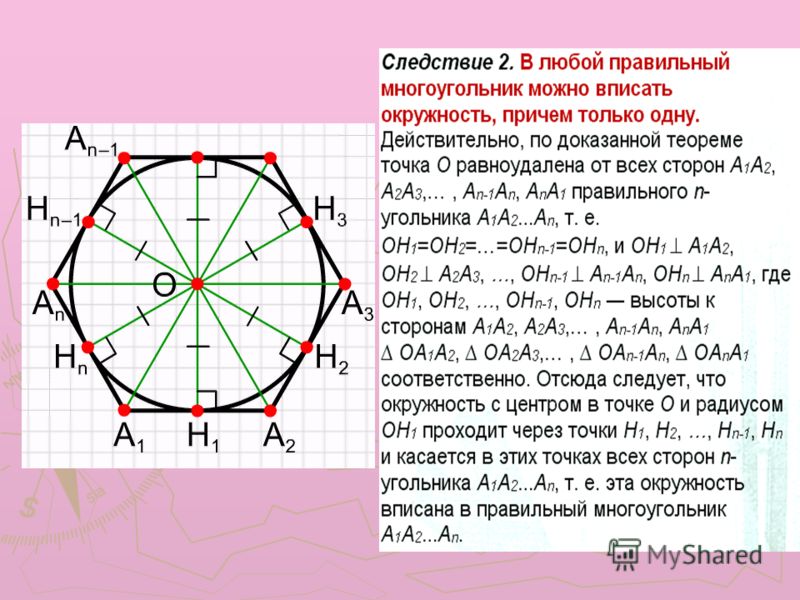 Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.

 Эта точка называется центром правильного многоугольника. Вписанной в многоугольник окружностью называется окружность, касающаяся его сторон. Если многоугольник взят произвольно, то в него нельзя вписать и около него нельзя описать окружность.
Эта точка называется центром правильного многоугольника. Вписанной в многоугольник окружностью называется окружность, касающаяся его сторон. Если многоугольник взят произвольно, то в него нельзя вписать и около него нельзя описать окружность. Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон.
Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон.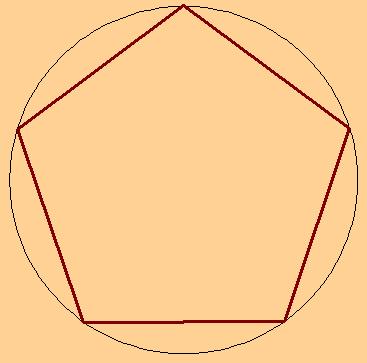 Правильный пятиугольник можно получить, завязав узлом полоску бумаги.
Правильный пятиугольник можно получить, завязав узлом полоску бумаги.
 65). Делим вертикальный диаметр окружности на семь равных частей.
65). Делим вертикальный диаметр окружности на семь равных частей.