Как сделать пятиугольник в окружности: Построение пятиугольника подробно. — Чертежик

Построение пятиугольника подробно. — Чертежик

Построение пятиугольника рассмотрим подробно:

1. Чертим необходимую окружность;
2. Строим вспомогательную окружность такого же размера;
3. Соединяем точки пересечения прямой линией, полученные при построении вспомогательной окружности;
4. Соединяем пересечение прямой линии с осью первоначальной окружности;
5. От полученной точки ведем отрезок к верхней точки пересечения окружности и оси;
6. Полученный отрезок есть ни что иное как радиус 2-й вспомогательной окружности;
7. Соединяем прямой линией от верхней точки пересечения с осью к точки пересечения вспомогательной окружности с горизонтальной осью. Полученная прямая и есть необходимый нам радиус для построения пятиугольника;
8. Строим «засечки» с первоначальной окружностью;
9. Соединяем полученные точки пересечения.

Вы можете посмотреть построение пятиугольника в видео:

Посмотрите примеры чертежей

Как построить и нарисовать правильный пятиугольник по окружности

Правильный пятиугольник представляет собой геометрическую фигуру, которая образовывается пересечением пяти прямых, создающих пять одинаковых углов. Такая фигура носит название — пентагон. С пятиугольником тесно связана работа художников — их рисунки строятся на основе правильных геометрических фигур. Для этого необходимо знать то, как быстро построить пентагон.

Чем интересна эта фигура? Форму пентагона имеет здание Министерства обороны Соединенных Штатов Америки. Это можно увидеть на фото, сделанных с высоты полета. В природе не существует кристаллов и камней, форма которых напоминала бы пентагон. Только в этой фигуре количество граней совпадает с числом диагоналей.

Параметры правильного пятиугольника

Прямоугольный пятиугольник, как и каждая фигура в геометрии, имеет свои параметры. Зная необходимые формулы, можно рассчитать эти параметры, что облегчит процесс построения пентагона. Способы и формулы расчетов:

• сумма всех углов в многоугольниках равна 360 градусам. В правильном пятиугольнике все углы равны, соответственно, центральный угол находится таким способом: 360/5 = 72 градуса;
• внутренний угол находится таким образом: 180*(n -2)/ n = 180*(5−2)/5 = 108 градусов. Сумма всех внутренних углов: 108*5 = 540 градусов.

Сторона пентагона находится с помощью параметров, которые уже даны в условии задачи:

• если вокруг пятиугольника описана окружность и известен ее радиус, сторона находится по такой формуле: a = 2*R*sin (α/2) = 2*R*sin (72/2) = 1,1756*R.
• Если известен радиус вписанной в пентагон окружности, то формула расчета стороны многоугольника: 2*r*tg (α/2) = 2*r*tg (α/2) = 1,453*r.
• При известной величине диагонали пентагона его сторона рассчитывается таким образом: а = D/1,618.

Площадь пентагона так же, как и его сторона, зависит от уже найденных параметров:

• с помощью известного радиуса вписанной окружности площадь находится так: S = (n*a*r)/2 = 2,5*a*r.
• описанная вокруг пятиугольника окружность позволяет найти площадь по такой формуле: S = (n*R2*sin α)/2 = 2,3776*R2.
• в зависимости от стороны пентагона: S = (5*a2*tg 54°)/4 = 1,7205* a2.

Построение пентагона

Построить правильный пятиугольник можно с помощью линейки и циркуля, на основе вписанной в него окружности или одной из сторон.

Как начертить пятиугольник на основе вписанной окружности? Для этого необходимо запастись циркулем и линейкой и сделать такие шаги:

1. Сначала необходимо начертить окружность с центром О, после чего на ней выбрать точку, А — вершину пентагона. От центра к вершине проводится отрезок.
2. Затем строится перпендикулярная прямой ОА отрезок, который также проходит через О — центр окружности. Его пересечение с окружностью обозначается точкой В. Отрезок О. В. делится пополам точкой С.
3. Точка С станет центром новой окружности, проходящей через А. Точка D — это ее пересечение с прямой ОВ в границах первой фигуры.
4. После этого проводится третья окружность через D, центром которой является точка А. Она пересекается с первой фигурой в двух точках, их необходимо обозначить буквами Е и F.
5. Следующая окружность имеет центр в точке Е и проходит через А, а ее пересечение с первоначальной находится в новой точке G.
6. Последняя окружность в этом рисунке проводится через точку, А с центром F. На ее пересечении с начальной ставится точка Н.
7. На первой окружности после всех проделанных шагов появились пять точек, которые необходимо соединить отрезками. Таким образом получился правильный пятиугольник АЕ G Н F.

Как построить правильный пятиугольник иным способом? С помощью линейки и циркуля пентагон можно построить немного быстрее. Для этого необходимо:

1. Cначала необходимо с помощью циркуля нарисовать окружность, центр которой — точка О.
2. Чертится радиус ОА — отрезок, который откладывается на окружность. Его делят пополам точкой В.
3. Перпендикулярно радиусу ОА начерчивается отрезок ОС, точки В и С соединяются прямой.
4. Следующим шагом является отложение длины отрезка ВС с помощью циркуля на диаметральной линии. Перпендикулярно отрезку ОА появляется точка D. Точки В и D соединяются, образуя новый отрезок.
5. Для того, чтобы получить величину стороны пентагона, необходимо соединить точки С и D.
6. D с помощью циркуля переносится на окружность и обозначается точкой Е. Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.

Интересные факты

В пятиугольнике с одинаковыми сторонами диагонали равны и образуют пятиконечную звезду, которая называется пентаграммой. Золотое сечение — это отношение величины диагонали к стороне пентагона.

Пентагон непригоден для полного заполнения плоскости. Использование любого материала в этой форме оставляет промежутки или образует наложения. Хотя природных кристаллов этой формы не существует в природе, но при образовании льда на поверхности гладких медных изделий возникают молекулы в виде пентагона, которые соединены в цепочки.

Наиболее простой способ получить правильный пятиугольник из полоски бумаги — завязать ее узлом и немного придавить. Этот способ полезен для родителей детей-дошкольников, которые хотят научить своих малышей распознавать геометрические фигуры.

Видео

Посмотрите, как можно быстро начертить пятиугольник.

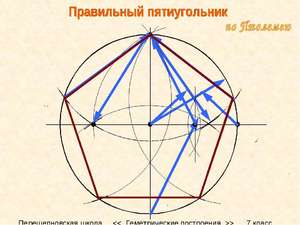
Правильный пятиугольник

Построение правильного пятиугольника — Сведения, необходимые при выполнении росписи

Первый способ — по данной стороне S с помощью транспортира.

Проводим прямую и откладываем на ней AB = S; принимаем эту линию за радиус и этим радиусом из точек A и В описываем дуги: далее с помощью транспортира строим в этих точках углы в 108°, стороны которых пересекутся с дугами в точках С и D; из этих точек радиусом АВ = 5 описываем дуги, которые пересекутся в Е, и прямыми линиями соединяем точки Л, С, Е, D, В.

Полученный пятиугольник — искомый.

---

Первый способ построения пятиугольника

 

---

Второй способ. Проведем окружность радиусом r. Из точки А циркулем проводим дугу радиуса AM до пересечения в точках В и С с окружностью. Соединяем В и С линией, которая пересечет горизонтальную ось в точке Е.

Затем из точки Е проводим дугу, которая пересечет горизонтальную линию в точке О. Описываем, наконец, из точки F дугу, которая пересечет окружность в точках Н и К. Отложив по окружности расстояние FO = FH = FK пять раз и соединив точки деления линиями, получим правильный пятиугольник.

---

Второй способ построения пятиугольника

---

Третий способ. В данный круг вписать правильный пятиугольник. Проводим два взаимно перпендикулярных диаметра АВ и МС. Делим радиус АО точкой Е пополам. Из точки Е, как из центра, проводим дугу окружности радиуса ЕМ и засекаем ею диаметр АВ в точке F. Отрезок MF равен стороне искомого правильного пятиугольника. Раствором циркуля, равным MF, делаем засечки N₁, Р₁, Q₁, К₁ и соединяем их прямыми.

---

Третий способ построения пятиугольника

---

На рисунке построен шестиугольник по данной стороне.

---

Построение шестиугольника

---

Прямой АВ = 5, как радиусом, из точек А и В описываем дуги, которые пересекутся в С; из этой точки тем же радиусом описываем окружность, на которой сторона А В отложится 6 раз.

Шестиугольник ADEFGB — искомый. 

«Отделка комнат при ремонте»,
Н.П.Краснов

Пятиугольник — Картины и живопись художников. Графика и галереи.

Здравствуйте коллеги.
Сегодня построим правильный пятиугольник в окружности, попробуем начертить циркулем и линейкой фигуру.

Рисунки художников очень тесно связаны с черчением и геометрией. Если мы задумали какую-то композицию, а в ней есть геометрические фигуры, то нам необходимо знать, как изобразить предмет, что бы он не выглядел смешно, и что бы вы не выглядели дилетантом и смогли нарисовать пятиконечную звезду циркулем или в фотошопе. От этого зависит ваш авторитет художника, а значит и заказы.

Построение правильного пятиугольника не так часто встречается в рисунке, но все же есть моменты, когда нам это необходимо.

Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Это посмотрите в другом уроке.

Мы попробуем нарисовать звезду в фотошопе фронтально. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Всего лишь с помощью таких инструментов:

1. Циркуль
2. Карандаш
3. Линейка
4. Резинка

Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь. Количество углов не четное, поэтому просто разделить окружность на равные части циркулем или линейкой не получится.

Что бы вписанный пятиугольник в окружность был пропорциональный, нам необходимо точно вычислить одну из сторон, а затем отложить этот отрезок пять раз на теле овала.

 

Как выглядит пятиугольник и звезда

Внизу на фото разберем, как нарисовать звезду поэтапно.
Для начала рисуем окружность с центром О.

 

Дальше отложим отрезок OA равный радиусу и разделим его пополам точкой B, как показано на фото внизу.

Теперь от точки В до точки С проведем прямую.

 

Отложим расстояние отрезка ВС на диаметральной линии окружности. Для этого можно воспользоваться циркулем. Таким образом у нас появилась точка D.

И отрезок DB. Картинка внизу.

 

Дальше, проведя линию от точки D к точке С, Мы получи длину равную стороне пятиугольника.

Дальше этот отрезок можно отложить на окружности. У нас появилась точка Е. Смотрим фото ниже.

Итак, одна из сторон пятиугольника у нас есть, это линия ЕС.

 

Такие же отрезки наносим на всей части круга. Смотрим картинку.

На этом построение правильного пятиугольника можно закончить. Что бы нарисовать звезду нужно просто соединить углы через один.

 

Нарисовать пятиконечную звезду циркулем можно так же, как и на нашем уроке в программе Photoshop, весь процесс такой же, только вместо программы графического редактора используем инструменты для черчения.

Так же можно посмотреть уроки построения шестиугольника,  разделение на восемь частей, деление круга на семь частей, десять равных частей.

 

Пятиугольник, виды, свойства и формулы

Пятиугольник, виды, свойства и формулы.

 

 

Пятиугольник – это многоугольник, общее количество углов (вершин) которого равно пяти.

 

Пятиугольник, выпуклый и невыпуклый пятиугольник

Правильный многоугольник

Свойства правильного пятиугольника

Построение правильного пятиугольника

Формулы правильного пятиугольника

Правильный пятиугольник в природе, технике и культуре

Пятиугольник, шестиугольник, семиугольник, восьмиугольник

 

Пятиугольник, выпуклый и невыпуклый пятиугольник:

Пятиугольник – это многоугольник, общее количество углов (вершин) которого равно пяти.

Пятиугольник – фигура, состоящая из пяти углов (вершин), которые образуются пятью отрезками (сторонами).

Пятиугольник может быть выпуклым и невыпуклым.

Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.

Соответственно выпуклый пятиугольник – это пятиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

Рис. 1. Выпуклый пятиугольник

Сумма внутренних углов любого выпуклого шестиугольника равна 540°.

Невыпуклый пятиугольник – это пятиугольник, у которого одна часть его точек лежат по одну сторону, а другая часть – по другую от любой прямой, проходящей через две его соседние вершины.

Рис. 2. Невыпуклый пятиугольник

Звёздчатый пятиугольник (пентаграмма) – пятиугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного семиугольника многоугольника. Стороны звёздчатого пятиугольника могут пересекаться между собой.

 

Правильный многоугольник:

Правильный пятиугольник (пентагон) – это правильный многоугольник с пятью сторонами.

В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.

Правильный пятиугольник – это пятиугольник, у которого все стороны равны, а все внутренние углы равны 108°.

Рис. 3. Правильный пятиугольник

Правильный пятиугольник имеет 5 сторон, 5 углов и 5 вершин.

Углы правильного семиугольника образуют семь равнобедренных треугольников.

Правильный пятиугольник может быть построен с помощью циркуля и линейки или вписыванием его в заданную окружность, или построением на основе заданной стороны.

 

Свойства правильного пятиугольника:

1. Все стороны правильного пятиугольника равны между собой.

a₁ = a₂ = a₃ = a₄= a₅.

2. Все углы равны между собой и каждый угол равен 108°.

α₁ = α₂ = α₃ = α₄ = α₅ = 108°.

Рис. 4. Правильный пятиугольник

3. Сумма внутренних углов правильного пятиугольника равна 540°.

4. Все биссектрисы углов между сторонами равны и проходят через центр правильного пятиугольника O.

Рис. 5. Правильный пятиугольник

5. Количество диагоналей правильного пятиугольника равно 5.

Рис. 6. Правильный пятиугольник

6. Центр вписанной окружности O₁ совпадает с центром описанной окружности O₂, что и образуют центр пятиугольника O.

Рис. 7. Правильный пятиугольник

7. Диагонали правильного пятиугольника являются трисектрисами его внутренних углов.

Рис. 8. Правильный пятиугольник

8. Отношение диагонали правильного пятиугольника к стороне равно золотому сечению.

a / c ≈ 5 / 8 ≈ 0,618.

Рис. 9. Правильный пятиугольник

 

Построение правильного пятиугольника:

Метод построения правильного пятиугольника вписыванием его в заданную окружность:

1. Постройте окружность, в которую будет вписан пятиугольник, и обозначьте её центр как O.

2. Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.

3. Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью как точку B.

4. Постройте точку C посередине между O и B.

5. Проведите окружность с центром в точке C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.

6. Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F.

7. Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.

8. Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.

9. Постройте правильный пятиугольник AEGHF.

 

Формулы правильного пятиугольника:

Пусть a – сторона пятиугольника, r – радиус окружности, вписанной в пятиугольник, R – радиус описанной окружности пятиугольника, S – площадь пятиугольника, h – высота пятиугольника, d – диагональ пятиугольника, Ф – отношение золотого сечения.

Формулы площади правильного пятиугольника:

Формулы высоты правильного пятиугольника:

Формулы стороны правильного пятиугольника:

Формулы диагонали правильного пятиугольника:

Формулы радиуса окружности, вписанной в правильный пятиугольник:

Формулы радиуса окружности, описанной вокруг правильного пятиугольника:

 

Правильный пятиугольник в природе, технике и культуре:

Пентасимметрию можно наблюдать в некоторых фруктах (например, у мушмулы германской), у иглокожих (например, у морских звёзд) и у некоторых растений.

Исследования формирования водяного льда на ровной поверхности меди при температурах 100-140 K показали, что сначала на поверхности возникают цепочки молекул шириной около 1 нм не гексагональной, а пентагональной структуры.

Пентагон — здание Министерства обороны США — имеет форму правильного пятиугольника.

Паркет, тротуарная плитка, мозайки и т.п. может выкладываться элементами, которые имеют вид пятиугольников.

Государственный знак качества СССР имеет форму пятиугольника с выпуклыми сторонами.

 

Прямоугольник

Прямоугольный треугольник

Равнобедренный треугольник

Равносторонний треугольник

Пятиугольник

Шестиугольник

Семиугольник

Восьмиугольник

 

Примечание: © Фото https://www.pexels.com, https://pixabay.com

 

карта сайта

 

Коэффициент востребованности 485

Построение на плоскости | Журнал Ярмарки Мастеров

Наверняка каждому из нас приходилось сталкиваться с тем, что нужно срочно что-то начертить, точный угол или многоугольник, а транспортира как нарочно под рукой нет, или Вы вообще никогда раньше ничего не чертили. Сегодня я хочу поделиться с Вами простыми схемами построения фигур на плоскости. Думаю, этот навык пригодится всем. Продолжение статьи:
http://www.livemaster.ru/topic/383001-postroenie-na-ploskosti-chast-2?inside=1&wf=&cp=1&vr=1

Нам понадобятся: карандаш, линейка, циркуль.

Построение угла в 60

1. Проведём прямую и отметим на ней точку А.

2. Из точки А проведём дугу произвольного радиуса и получим точку В.

3. Из точки В проведём дугу радиуса АВ, чтобы она пересекла ранее начерченную дугу.

4. Проведённая через точку пересечения (С) и точку А прямая будет второй стороной требуемого угла.

Построение угла в 45

1. Построим угол 60, кака описано выше.

2. Разделим полученный угол пополам.

3. Угол между лучами 60 и 30 разделим пополам. В результате получим угол в 45.

Построение угла в 75

1. Построим угол в 60, как описано выше, и разделим его пополам.

2. В ходе дальнейшего деления надвое получим угол в 15.

3. Отразим угол в 15 через луч 60 и так получим угол в 75.

Построение угла в 90

1. Построим угол в 60, как описано выше, и разделим его пополам.

2. Получившийся угол в 30 через луч 60 и так получим угол точно в 90.

Разделение отрезка на равные части.

1. Проведём прямую и отметим на ней отрезок АВ.

2. Из точки А проведём вспомогательную прямую и разделим её на столько одинаковых частей, на сколько требуется разделить отрезок АВ. Делить будем при помощи циркуля. Последнюю точку обозначим буквой С.

3. Последнюю точка (С) соединим с концом отрезка АВ. Построим рад параллельных отрезку СВ прямых по всей длине отрезка АВ. Точки пересечения параллельных прямых с отрезком АВ и будут точками раздела отрезка на несколько равных частей.

Построение правильного пятиугольника.

1. Проведём окружность радиусом 50 мм. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.

2. Разделим пополам расстояние ОВ. Разведём ножки циркуля на расстояние FC. Из точки F проведём дугу через С. Дуга пересечёт горизонтальную линию в точке G.

3. Расстояние CG будет длиной стороны пятиугольника. Из вершины С отложим пять раз расстояние CG.

Построение правильного шестиугольника.

1. Проведём окружность радиусом 50 мм.

2. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.

3. Из точки А на линии окружности отложим шесть раз радиус нашей окружности. Соединив прямыми точки пересечения, получим шестиугольник.

Построение правильного семиугольника.

1. Проведём окружность заданного радиуса. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.

2. Из точки D проведём дугу радиусом равным радиусу окружности.

3. Дуга пересечёт окружность в точках E и G.

4. Длина отрезка EF на хорде EG равна длине стороны семиугольника. Из вершины С семь раз отложим расстояние EF.

Общий метод построения многоугольников.

1. Проведём окружность радиусом 50 мм. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии. Продолжим горизонтальную лини. За точки А и В.

2. Из точки D проведём дугу радиусом, равным радиусу окружности так, чтобы дуга пересекла горизонтальную линию.

3. При помощи вспомогательной прямой разделим вертикальную линию на столько равных частей, сколько сторон многоугольника требуется получить. Для примера показано построение одиннадцатиугольника.

4. Из точки Е проведём прямые через нечётные точки раздела вертикальной линии так, чтобы эти прямые пересекли окружность. Такую же операцию проведём из точки G. Полученные лучи пересекают окружность в точках, соединив которые прямыми получаем одиннадцатиугольник.

❶ Как построить правильный десятиугольник 🚩 Математика

Вам понадобится

• — бумага;
• — циркуль;
• — линейка;
• — карандаш.

Постройте окружность произвольного радиуса с известным центром. Обозначьте на поверхности точку O, которая будет являться центром. Выберите оптимальный раствор ножек циркуля. Установите иглу циркуля в точку O. Вычертите окружность.

Постройте отрезок прямой, проходящей через центр окружности и пересекающий ее в двух точках. При помощи линейки вычертите отрезок, проходящий через точку O таким образом, чтобы он дважды пересекал линию окружности. Одну из точек пересечения построенного отрезка и окружности обозначьте A, другую — P1. Постройте отрезок прямой, проходящий через точку O и перпендикулярный отрезку OA. Установите иглу циркуля в точку A установите ножку циркуля с грифелем в точку P1. Вычертите окружность. Не меняя раствора ножек, установите иглу циркуля в точку P1. Вычертите окружность. Постройте отрезок прямой, проходящий через точки пересечения начерченных окружностей. Он пройдет также и через точку O. Обозначьте точки пересечения данного отрезка с окружностью O как B и P2. Найдите точку, принадлежащую отрезку OB и равноудаленную от его концов. Для этого произведите действия, аналогичные тем, что были описаны в третьем шаге, для построения перпендикуляра к OB, делящего его на две равные части. Обозначьте найденную точку C.

Вычертите окружность с центром в точке C и радиусом CA. Установите иглу циркуля в точку C. Установите ножку циркуля с грифелем в точку A. Постройте окружность. Обозначьте точку пересечения этой окружности с отрезком OP2 как D.

Постройте правильный пятиугольник. Установите ножку с иглой циркуля в точку A. Установите ножку с грифелем циркуля в точку D. Теперь длина между концами ножек циркуля равна стороне правильного пятиугольника, вписанного в окружность с центром O.Сделайте циркулем засечку на окружности O в направлении движения по часовой стрелке (игла циркуля находится в точке A). Обозначьте полученную точку E. Не меняя раствора ножек, переместите иглу в точку E. Сделайте еще одну засечку. Обозначьте току как F. Действуя подобным образом, последовательно постройте точки G и H. Попарно соедините точки A, E, F, G, H отрезками. Фигура AEFGH является правильным пятиугольником.

Постройте правильный десятиугольник. К отрезкам AE, EF, FG, GH, HA постройте перпендикуляры, делящие их на две равные части. Произведите действия, аналогичные тем, что были описаны в третьем шаге, для построения делящего перпендикуляра к каждому отрезку.Стройте перпендикуляры так, чтобы они пересекали окружность с центром в точке O. Пусть точки пересечения перпендикуляров к отрезкам AE, EF, FG, GH, HA с окружностью O будут I, J, K, L, и M соответственно.Постройте отрезки AI, IE, EJ, JF, FK, KG, GL, LH, HM, MA. Многоугольник AEJFKGLHM будет являться правильным десятиугольником.

Печатные инструкции по построению пятиугольника, вписанного в заданный круг.

(C) Открытый справочник по математике, 2011 г.
Все права защищены.

После этого	Ваша работа должна выглядеть так
Начинаем с данного круга, центр О. Примечание: Если вам не дали центр, вы можете найти его, используя метод, показанный на Нахождение центра круга с помощью циркуля и линейки.
1. Проведите диаметр круга через центральную точку и отметьте его конечные точки C и M. Он не обязательно должен быть вертикальным.
2. Постройте перпендикуляр к CM в точке O. Для получения дополнительной информации см. Построение перпендикуляра в точке на линии.
3. Отметьте точку S, где она пересекает круг.
4. Найдите середину L отрезка SO, построив его серединный перпендикуляр. Для получения дополнительной информации см. Построение серединного перпендикуляра отрезка прямой.
5. Установите циркуль на L, отрегулируйте его ширину на S или O и нарисуйте круг.
6. Проведите линию от M через L так, чтобы она пересекала маленький кружок в двух местах.Обозначьте их N и P.
7. Установите циркуль на M и отрегулируйте его ширину на P.
8. Нарисуйте широкую дугу, пересекающую заданный круг в двух местах. Обозначьте их A и E.
9. Установите циркуль на M и отрегулируйте его ширину на N.
10. Нарисуйте широкую дугу, пересекающую заданный круг в двух местах. Обозначьте их B и D.
11. Проведите линию от A к B, затем от B к C и т. Д., Пока не проведете все пять сторон пятиугольника.
Готово. ABCDE — правильный пятиугольник, вписанный в данную окружность.

.

Как нарисовать идеальный пятиугольник

Используя несколько простых математических и геометрических инструментов, мы покажем вам , как нарисовать идеальный пятиугольник . Не нужно сходить с ума или тратить два ластика целиком. Получение пятиугольника , где каждая сторона равна с углами, которые соприкасаются, возможно, как мы объясним ниже.

Следующие шаги:

1

Первый шаг к нарисуйте идеальный пятиугольник — это отметить точку в центре вашего листа.Поместите компас в точку и нарисуйте идеальный круг. Если у вас есть время, вот и другие способы нарисовать круг.

2

Используя центральную точку и транспортир, разделите круг на 5 точек. В круге 360 °, а 360/5 = 72 °. Итак, вы должны отмечать точку через каждые 72º. Чтобы получить правильное измерение, используйте транспортир, чтобы получить идеальное измерение для вашего пятиугольника .

3

Подключите каждую соседнюю точку. Теперь у вас есть пятиугольник.

Если вы хотите нарисовать пентаграмму вместо пятиугольника: вместо того, чтобы соединять соседние точки вместе, вы должны соединить каждую точку с двумя противоположными точками.

Сотрите круг, если он вам больше не нужен.

4

Вы также можете нарисовать пятиугольник с помощью циркуля и линейки, если дан круг. Это будет полезно для определенных упражнений, а также может применяться, когда вам не нужно иметь определенный размер для боков.

1. Нарисуйте круг с радиусом циркуля A и центром A B.
2. Нарисуйте второй круг с тем же радиусом с центром на A.
3. Пересечение, где встречаются оба круга, будет C.
4. Проведите линейкой прямую линию через A и C.
5. Нарисуйте еще одну прямую линию через B и C.
6. Эта вторая линия даст вам пересечение с первым кругом, который будет D.
7. Нарисуйте прямую линию от A до D.
8. Это создаст третье пересечение между второй окружностью и этой последней линией. Это будет пересечение E.
9. Установите компас на расстоянии между C и E и нарисуйте круг с центром в B.
10. Этот третий круг будет пересекать первую прямую линию. Это пересечение будет F.
11. Нарисуйте исходный круг еще раз.
12. Установите компас на расстояние между E и F. Это даст вам длину края идеального пятиугольника.
13. С помощью циркуля нарисуйте линии заданной длины.
14. Объедините каждую отметку, которую вы создали с помощью компаса. Теперь у вас есть пятиугольник.

Этот метод может быть более сложным, но он дает 100% точность и даст вам идеальный пятиугольник.

Если вы хотите прочитать статьи, похожие на Как нарисовать идеальный пятиугольник , мы рекомендуем вам посетить нашу категорию «Ремесла и досуг».

,