Как нарисовать пятиугольник с помощью окружности
Последние события
Раскраски к Хеллоуину для мальчиков
В России – празднование Хэллоуина ни с чем не связано. Это, скорее всего дань моде, чем традиции предков. Интересное яркое шоу, о значении и первоисточнике которого многие даже не догадываются.
Коллекция раскрасок к Хеллоуину
Скоро Хеллоуин. Праздник страшилка, праздник пугалка. Не зря его так любят дети всех стран.
На сайте я уже как-то выкладывала подборку раскрасок к Хеллоуину.
Осень. Деревья и листья
Как выглядят деревья осенью? Рассмотрите картинки и раскрасьте осенние листики.
Кто такие мишки Гамми?
Посмотрите с детьми этот мультсериал про мишек Гамми, затем скачайте раскраски и раскрасьте героев.
Несколько раскрасок для самых маленьких
Совсем простенькие раскраски с крупными деталями для самых маленьких художников.
Осеннее настроение. Раскраски
В разгаре золотая осень. В этом году она в наших краях как никогда поздняя и ослепительно красивая.
В этом году она в наших краях как никогда поздняя и ослепительно красивая.
Рассказы про осень. Читаем и раскрашиваем картинки
Что такое осень? Какая осенью погода? Что делают птицы осенью? Задайте эти и другие вопросы про осень своему малышу.
Популярное
Архив
Как нарисовать правильную звездочку? Как нарисовать правильный пятиугольник? Как разделить круг на пять равных частей? На все эти вопросы вы сможете найти ответ, если проделаете вслед за мной эти шаги.
Как нарисовать правильную звездочку?
Как нарисовать правильный пятиугольник?
Как разделить круг на пять равных частей?
На все эти вопросы вы сможете найти ответ, если проделаете вслед за мной вот эти шаги.
Конечно же, нам понадобится циркуль с карандашом и линейка.
Для начала нарисуйте циркулем круг.
Разделите его на четыре части линиями сверху вниз и справа налево.
Можно сразу объяснить ребенку, что отрезок, соединяющий две точки на окружности и проходящий через ее центр, называется диаметр.
А отрезок, соединяющий центр и точку на окружности, называется радиус.
С помощью линейки измерьте и разделите пополам один из радиусов.
У меня это отрезок слева от центра.
Серединку радиуса я обозначила
Нам понадобится точка сверху окружности.
Ее я обозначила цифрой 0.
Устанавливаем иголку циркуля
в точку 1, а карандашик в точку 0.
Рисуем дугу до пересечения с горизонтальным диаметром.
Обозначаем точку пересечения
Сейчас устанавливаем иголку циркуля
в точку 0, а карандашик в точку 2.
И рисуем дугу до пересечения с окружностью, причем с двух сторон.
Точки пересечения помечены
Не меняя ширину циркуля, устанавливаем иголку
в точку 3 и отмеряем кусочек окружности.
Точку 6 можно отмерить и от
точки 5 и от точки 4.
Главное, не изменять ширину (раствор) ножек циркуля.
Вот, практически и все.
Если соединим точки, получим правильный пятиугольник.
Здравствуйте коллеги.
Сегодня построим правильный пятиугольник в окружности, попробуем начертить циркулем и линейкой фигуру.
Рисунки художников очень тесно связаны с черчением и геометрией. Если мы задумали какую-то композицию, а в ней есть геометрические фигуры, то нам необходимо знать, как изобразить предмет, что бы он не выглядел смешно, и что бы вы не выглядели дилетантом и смогли нарисовать пятиконечную звезду циркулем или в фотошопе. От этого зависит ваш авторитет художника, а значит и заказы.
Построение правильного пятиугольника не так часто встречается в рисунке, но все же есть моменты, когда нам это необходимо.
Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Это посмотрите в другом уроке.
Мы попробуем нарисовать звезду в фотошопе фронтально. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Всего лишь с помощью таких инструментов:
Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь. Количество углов не четное, поэтому просто разделить окружность на равные части циркулем или линейкой не получится.
Количество углов не четное, поэтому просто разделить окружность на равные части циркулем или линейкой не получится.
Что бы вписанный пятиугольник в окружность был пропорциональный, нам необходимо точно вычислить одну из сторон, а затем отложить этот отрезок пять раз на теле овала.
Как выглядит пятиугольник и звезда
Внизу на фото разберем, как нарисовать звезду поэтапно.
Для начала рисуем окружность с центром О.
Дальше отложим отрезок OA равный радиусу и разделим его пополам точкой B, как показано на фото внизу.
Теперь от точки В до точки С проведем прямую.
Отложим расстояние отрезка ВС на диаметральной линии окружности. Для этого можно воспользоваться циркулем. Таким образом у нас появилась точка D.
И отрезок DB. Картинка внизу.
Дальше, проведя линию от точки D к точке С, Мы получи длину равную стороне пятиугольника.
Дальше этот отрезок можно отложить на окружности. У нас появилась точка Е. Смотрим фото ниже.
Смотрим фото ниже.
Итак, одна из сторон пятиугольника у нас есть, это линия ЕС.
Такие же отрезки наносим на всей части круга. Смотрим картинку.
На этом построение правильного пятиугольника можно закончить. Что бы нарисовать звезду нужно просто соединить углы через один.
Нарисовать пятиконечную звезду циркулем можно так же, как и на нашем уроке в программе Photoshop, весь процесс такой же, только вместо программы графического редактора используем инструменты для черчения.
Так же можно посмотреть уроки построения шестиугольника, разделение на восемь частей, деление круга на семь частей, десять равных частей.
Правильный пятиугольник представляет собой геометрическую фигуру, которая образовывается пересечением пяти прямых, создающих пять одинаковых углов. Такая фигура носит название — пентагон. С пятиугольником тесно связана работа художников — их рисунки строятся на основе правильных геометрических фигур. Для этого необходимо знать то, как быстро построить пентагон.
Чем интересна эта фигура? Форму пентагона имеет здание Министерства обороны Соединенных Штатов Америки. Это можно увидеть на фото, сделанных с высоты полета. В природе не существует кристаллов и камней, форма которых напоминала бы пентагон. Только в этой фигуре количество граней совпадает с числом диагоналей.
Параметры правильного пятиугольника
Прямоугольный пятиугольник, как и каждая фигура в геометрии, имеет свои параметры. Зная необходимые формулы, можно рассчитать эти параметры, что облегчит процесс построения пентагона. Способы и формулы расчетов:
- сумма всех углов в многоугольниках равна 360 градусам. В правильном пятиугольнике все углы равны, соответственно, центральный угол находится таким способом: 360/5 = 72 градуса;
- внутренний угол находится таким образом: 180*(n -2)/ n = 180*(5−2)/5 = 108 градусов. Сумма всех внутренних углов: 108*5 = 540 градусов.
Сторона пентагона находится с помощью параметров, которые уже даны в условии задачи:
- если вокруг пятиугольника описана окружность и известен ее радиус, сторона находится по такой формуле: a = 2*R*sin (α/2) = 2*R*sin (72/2) = 1,1756*R.

- Если известен радиус вписанной в пентагон окружности, то формула расчета стороны многоугольника: 2*r*tg (α/2) = 2*r*tg (α/2) = 1,453*r.
- При известной величине диагонали пентагона его сторона рассчитывается таким образом: а = D/1,618.
Площадь пентагона так же, как и его сторона, зависит от уже найденных параметров:
- с помощью известного радиуса вписанной окружности площадь находится так: S = (n*a*r)/2 = 2,5*a*r.
- описанная вокруг пятиугольника окружность позволяет найти площадь по такой формуле: S = (n*R2*sin α)/2 = 2,3776*R2.
- в зависимости от стороны пентагона: S = (5*a2*tg 54°)/4 = 1,7205* a2.
Построение пентагона
Построить правильный пятиугольник можно с помощью линейки и циркуля, на основе вписанной в него окружности или одной из сторон.
Как начертить пятиугольник на основе вписанной окружности? Для этого необходимо запастись циркулем и линейкой и сделать такие шаги:
- Сначала необходимо начертить окружность с центром О, после чего на ней выбрать точку, А — вершину пентагона.
 От центра к вершине проводится отрезок.
От центра к вершине проводится отрезок. - Затем строится перпендикулярная прямой ОА отрезок, который также проходит через О — центр окружности. Его пересечение с окружностью обозначается точкой В. Отрезок О. В. делится пополам точкой С.
- Точка С станет центром новой окружности, проходящей через А. Точка D — это ее пересечение с прямой ОВ в границах первой фигуры.
- После этого проводится третья окружность через D, центром которой является точка А. Она пересекается с первой фигурой в двух точках, их необходимо обозначить буквами Е и F.
- Следующая окружность имеет центр в точке Е и проходит через А, а ее пересечение с первоначальной находится в новой точке G.
- Последняя окружность в этом рисунке проводится через точку, А с центром F. На ее пересечении с начальной ставится точка Н.
- На первой окружности после всех проделанных шагов появились пять точек, которые необходимо соединить отрезками. Таким образом получился правильный пятиугольник АЕ G Н F.

Как построить правильный пятиугольник иным способом? С помощью линейки и циркуля пентагон можно построить немного быстрее. Для этого необходимо:
- Cначала необходимо с помощью циркуля нарисовать окружность, центр которой — точка О.
- Чертится радиус ОА — отрезок, который откладывается на окружность. Его делят пополам точкой В.
- Перпендикулярно радиусу ОА начерчивается отрезок ОС, точки В и С соединяются прямой.
- Следующим шагом является отложение длины отрезка ВС с помощью циркуля на диаметральной линии. Перпендикулярно отрезку ОА появляется точка D. Точки В и D соединяются, образуя новый отрезок.
- Для того, чтобы получить величину стороны пентагона, необходимо соединить точки С и D.
- D с помощью циркуля переносится на окружность и обозначается точкой Е. Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.

Интересные факты
В пятиугольнике с одинаковыми сторонами диагонали равны и образуют пятиконечную звезду, которая называется пентаграммой. Золотое сечение — это отношение величины диагонали к стороне пентагона.
Пентагон непригоден для полного заполнения плоскости. Использование любого материала в этой форме оставляет промежутки или образует наложения. Хотя природных кристаллов этой формы не существует в природе, но при образовании льда на поверхности гладких медных изделий возникают молекулы в виде пентагона, которые соединены в цепочки.
Наиболее простой способ получить правильный пятиугольник из полоски бумаги — завязать ее узлом и немного придавить. Этот способ полезен для родителей детей-дошкольников, которые хотят научить своих малышей распознавать геометрические фигуры.
Видео
Посмотрите, как можно быстро начертить пятиугольник.
Как построить равносторонний пятиугольник с помощью циркуля. Правильный пятиугольник: необходимый минимум информации
Уровень сложности: Несложно
1 шаг
Сначала, выбирайте, где разместить центр окружности.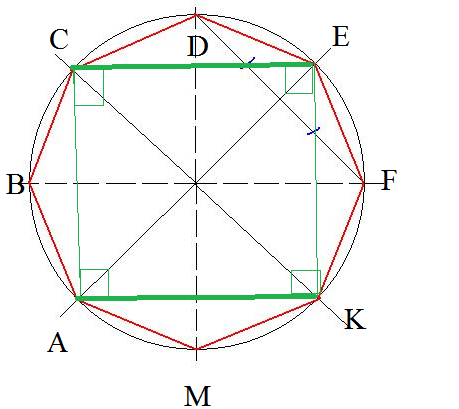 Там нужно поставить начальную точку, пусть она называется О. С помощью циркуля вычерчиваем вокруг нее окружность заданного диаметра или радиуса.
Там нужно поставить начальную точку, пусть она называется О. С помощью циркуля вычерчиваем вокруг нее окружность заданного диаметра или радиуса.
2 шаг
Затем проводим две оси через точку О, центр окружности, одна горизонтальная, другая под 90 градусов по отношению к ней – вертикальная. Точки пересечения по горизонтали назовем слева на право А и В, по вертикали, сверху вниз – М и Н. Радиус, который лежит на любой оси, например, на горизонтальной в правой части, делим пополам. Это можно сделать так: циркуль с радиусом известной нам окружности устанавливаем острием в точку пересечения горизонтальной оси и окружности – В, отчеркиваем пересечения с окружностью, полученные точки называем, соответственно сверху вниз – С и Р, соединяем их отрезком, который будет пересекать ось ОВ, точку пересечения называем К.
3 шаг
Соединяем точки К и М и получаем отрезок КМ, устанавливаем циркуль в точку М, задаем на нем расстояние до точки К и очерчиваем метки на радиусе ОА, эту точку называем Е, далее ведем циркуль до пересечения с левой верхней частью окружности ОМ. Эту точку пересечения называем F. Расстояние равное отрезку МЕ является искомой стороной равностороннего пятиугольника. При этом точка М будет являться одной вершиной встраиваемого в окружность пятиугольника, а точка F – другой.
Эту точку пересечения называем F. Расстояние равное отрезку МЕ является искомой стороной равностороннего пятиугольника. При этом точка М будет являться одной вершиной встраиваемого в окружность пятиугольника, а точка F – другой.
4 шаг
Далее из полученных точек по всей окружности отчерчиваем циркулем расстояния, равные отрезку МЕ, всего точек должно получиться 5. Соединяем все точки отрезками – получаем пятиугольник, вписанный в окружность.
- При черчении будьте аккуратны в измерениях расстояний, не допускайте погрешностей, чтобы пятиугольник действительно полчился равносторонним
Правильный пятиугольник представляет собой геометрическую фигуру, которая образовывается пересечением пяти прямых, создающих пять одинаковых углов. Такая фигура носит название — пентагон. С пятиугольником тесно связана работа художников — их рисунки строятся на основе правильных геометрических фигур. Для этого необходимо знать то, как быстро построить пентагон.
Чем интересна эта фигура? Форму пентагона имеет здание Министерства обороны Соединенных Штатов Америки
 Это можно увидеть на фото, сделанных с высоты полета. В природе не существует кристаллов и камней, форма которых напоминала бы пентагон. Только в этой фигуре количество граней совпадает с числом диагоналей.
Это можно увидеть на фото, сделанных с высоты полета. В природе не существует кристаллов и камней, форма которых напоминала бы пентагон. Только в этой фигуре количество граней совпадает с числом диагоналей. Параметры правильного пятиугольника
Прямоугольный пятиугольник, как и каждая фигура в геометрии, имеет свои параметры. Зная необходимые формулы, можно рассчитать эти параметры, что облегчит процесс построения пентагона. Способы и формулы расчетов:
- сумма всех углов в многоугольниках равна 360 градусам. В правильном пятиугольнике все углы равны, соответственно, центральный угол находится таким способом: 360/5 = 72 градуса;
- внутренний угол находится таким образом: 180*(n -2)/ n = 180*(5−2)/5 = 108 градусов. Сумма всех внутренних углов: 108*5 = 540 градусов.
Сторона пентагона находится с помощью параметров, которые уже даны в условии задачи:
- если вокруг пятиугольника описана окружность и известен ее радиус, сторона находится по такой формуле: a = 2*R*sin (α/2) = 2*R*sin (72/2) = 1,1756*R.

- Если известен радиус вписанной в пентагон окружности, то формула расчета стороны многоугольника: 2*r*tg (α/2) = 2*r*tg (α/2) = 1,453*r.
- При известной величине диагонали пентагона его сторона рассчитывается таким образом: а = D/1,618.
Площадь пентагона так же , как и его сторона, зависит от уже найденных параметров:
- с помощью известного радиуса вписанной окружности площадь находится так: S = (n*a*r)/2 = 2,5*a*r.
- описанная вокруг пятиугольника окружность позволяет найти площадь по такой формуле: S = (n*R2*sin α)/2 = 2,3776*R2.
- в зависимости от стороны пентагона: S = (5*a2*tg 54°)/4 = 1,7205* a2.
Построение пентагона
Построить правильный пятиугольник можно с помощью линейки и циркуля, на основе вписанной в него окружности или одной из сторон.
Как начертить пятиугольник на основе вписанной окружности? Для этого необходимо запастись циркулем и линейкой и сделать такие шаги:
- Сначала необходимо начертить окружность с центром О, после чего на ней выбрать точку, А — вершину пентагона.
 От центра к вершине проводится отрезок.
От центра к вершине проводится отрезок. - Затем строится перпендикулярная прямой ОА отрезок, который также проходит через О — центр окружности. Его пересечение с окружностью обозначается точкой В. Отрезок О. В. делится пополам точкой С.
- Точка С станет центром новой окружности, проходящей через А. Точка D — это ее пересечение с прямой ОВ в границах первой фигуры.
- После этого проводится третья окружность через D, центром которой является точка А. Она пересекается с первой фигурой в двух точках, их необходимо обозначить буквами Е и F.
- Следующая окружность имеет центр в точке Е и проходит через А, а ее пересечение с первоначальной находится в новой точке G.
- Последняя окружность в этом рисунке проводится через точку, А с центром F. На ее пересечении с начальной ставится точка Н.
- На первой окружности после всех проделанных шагов появились пять точек, которые необходимо соединить отрезками. Таким образом получился правильный пятиугольник АЕ G Н F.

Как построить правильный пятиугольник иным способом? С помощью линейки и циркуля пентагон можно построить немного быстрее. Для этого необходимо:
- Cначала необходимо с помощью циркуля нарисовать окружность, центр которой — точка О.
- Чертится радиус ОА — отрезок, который откладывается на окружность. Его делят пополам точкой В.
- Перпендикулярно радиусу ОА начерчивается отрезок ОС, точки В и С соединяются прямой.
- Следующим шагом является отложение длины отрезка ВС с помощью циркуля на диаметральной линии. Перпендикулярно отрезку ОА появляется точка D. Точки В и D соединяются, образуя новый отрезок.
- Для того, чтобы получить величину стороны пентагона, необходимо соединить точки С и D.
- D с помощью циркуля переносится на окружность и обозначается точкой Е. Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.

В пятиугольнике с одинаковыми сторонами диагонали равны и образуют пятиконечную звезду, которая называется пентаграммой. Золотое сечение — это отношение величины диагонали к стороне пентагона.
Пентагон непригоден для полного заполнения плоскости. Использование любого материала в этой форме оставляет промежутки или образует наложения. Хотя природных кристаллов этой формы не существует в природе, но при образовании льда на поверхности гладких медных изделий возникают молекулы в виде пентагона, которые соединены в цепочки.
Наиболее простой способ получить правильный пятиугольник из полоски бумаги — завязать ее узлом и немного придавить. Этот способ полезен для родителей детей-дошкольников, которые хотят научить своих малышей распознавать геометрические фигуры.
Видео
Посмотрите, как можно быстро начертить пятиугольник.
Если под руками нет циркуля, то можно нарисовать простую звезду с пятью лучами затем просто соединить эти лучи.
Математика сложная наука и у нее много своих секретиков, некоторые из них весьма забавны. Если вы увлекаетесь такими вещами советую найти книгу Забавная математика.
Окружность можно нарисовать не только при помощи циркуля. Можно, например, использовать карандаш и нитку. Отмеряем нужный диаметр на нитке. Один конец плотно зажимаем на листе бумаги, где будем чертить окружность. А на другой конец нитки устанавливаемые карандаш и одержим. Теперь действует как с циркулем: натягиваем нить и по окружности слегка надавливая карандашом чкртим окружность.
Внутри окружности рисуем крестьян от центра: вертикальная линия и горизонтальная линия. Точка пересечения вертикальной линии и окружности будет вершиной пятиугольника (точка 1). Теперь правую половину горизонтальной линии делим пополам (точка 2). Измеряем расстояние от этой точки до вершины пятиугольника и этот отрезок откладывает влево от точки 2 (точка 3).
Теперь от точки 4 делаем дугу, пересекающую окружность в нижней части, радиусом равной длине от точки 1 до 4 — это будет точкой 6. Точно так же и от точки 5 — обозначим точкой 7.
Остатся соединить наш пятиугольник с вершинами 1, 5, 7, 6, 4.
Я знаю как построить простой пятиугольник с помощью циркуля: Строим окружность, отмечаем пять точек, соединяем их. Можно построить пятиугольник с равными сторонами, для этого нам еще понадобится транспортир. Просто те же самые 5 точек ставим по транспортиру. Для этого отмечаем углы по 72 градуса. После чего также соединяем отрезками и получаем нужную нам фигуру.
Зеленую окружность можно чертить произвольным радиусом. В эту окружность будем вписывать правильный пятиугольник. Без циркуля начертить точно окружность нельзя, но это не обязательно. Окружность и все дальнейшие построения можно выполнять от руки. Далее через центр окружности О нужно провести две взаимно перпендикулярные прямые и одну из точек пересечения прямой с окружностью обозначить А. Точка А будет вершиной пятиугольника. Радиус ОВ разделим пополам и поставим точку С. Из точки С проводим вторую окружность радиусом АС. Из точки А проводим третью окружность радиусом АD. Точки пересечения третьей окружности с первой (Е и F)будут также вершинами пятиугольника. Из точек Е и F радиусом АЕ делаем засечки на первой окружности и получаем остальные вершины пятиугольника G и H.
Окружность и все дальнейшие построения можно выполнять от руки. Далее через центр окружности О нужно провести две взаимно перпендикулярные прямые и одну из точек пересечения прямой с окружностью обозначить А. Точка А будет вершиной пятиугольника. Радиус ОВ разделим пополам и поставим точку С. Из точки С проводим вторую окружность радиусом АС. Из точки А проводим третью окружность радиусом АD. Точки пересечения третьей окружности с первой (Е и F)будут также вершинами пятиугольника. Из точек Е и F радиусом АЕ делаем засечки на первой окружности и получаем остальные вершины пятиугольника G и H.
Адептам черного искусства: что бы просто, красиво и быстро нарисовать пятиугольник, следует начертить правильную, гармоничную основу для пентаграммы (пятиконечная звезда) и соединить окончания лучей этой звезды посредством прямых, ровных линий. Если все было сделано верно — соединительная черта вокруг основы и будет искомым пятиугольником.
(на рисунке — завершенная, но незаполненная пентаграмма)
Для тех, кто неуверен в правильности начертания пентаграммы: возьмите за основу витрувианского человека Да Винчи (см. ниже)
ниже)
Если нужен пятиугольник — тыкаете произвольным образом 5 точке и их внешний контур будет пятиугольником.
Если нужен правильный пятиугольник, то без математического циркуля это построение совершить невозможно, поскольку без него нельзя провести два одинаковых, но не параллельных отрезка. Любой другой инструмент, который позволяет провести два одинаковых, но не параллельных отрезка эквивалентен математическому циркулю.
Сначала надо надо начертить круг, потом направляющие, потом второй пунктирный круг, находим верхнюю точку, потом отмеряем два угла верхние, от них чертим нижние. Заметьте, радиус циркуля один и тот же при всем построении.
Вс зависит от того, какой пятиугольник вам необходим. Если любой, то ставите пять точек и соединяете их между собой(естествено точки ставим не по прямой линии). А если нужен пятиугольник правильно формы, возьмите любые пять по длине(полосок бумаги, спичек, карандашей и т.п), выложите пятиугольник и обчертите его.
Пятиугольник можно начертить, к примеру, из звезды. Если умеете чертить звезду, но не умеете пятиугольник, начертите звезду карандашом, затем соедините между собой соседние концы звезды, а саму звезду потом сотрите.
Второй способ. Вырежьте полосочку из бумаги, длиной, равной желаемой стороне пятиугольника, а шириной узкой, допустим 0.5 — 1 см. Как по шаблону, вырежьте по этой полосочке ещ четыре таких же полосочки, чтобы их получилось всего 5.
Затем положите лист бумаги (лучше его закрепить на столе при помощи четырх кнопок или иголочек). Затем наложите эти 5 полосочек на листок так, чтобы они образовали пятиугольник. Приколите эти 5 полосочек к листку бумаги кнопками или иголочками, чтобы они оставались неподвижными. Затем обведите полученный пятиугольник и снимите эти полосочки с листка.
Если нет циркуля и нужно построить пятиугольник, то я могу посоветовать следующее. Я и сама так строила. Можно начертить правильную пятиконечную звезду. И после этого, чтобы получить пятиугольник, просто нужно соединить все вершины звезды. Вот так и получится пятиугольник. Вот что мы получим
Вот так и получится пятиугольник. Вот что мы получим
Ровными чрными линии мы соединили вершины звезды и получили пятиугольник.
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего проводим стороны 5-6 и 3-2.
Построение вписанного в окружность равностороннего треугольника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны
1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
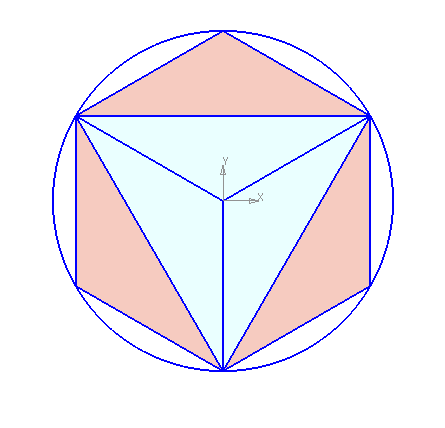
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
Эта фигура является многоугольником с минимальным количеством углов, которым невозможно замостить площадь. Только у пятиугольника количество диагоналей совпадает с количеством его сторон.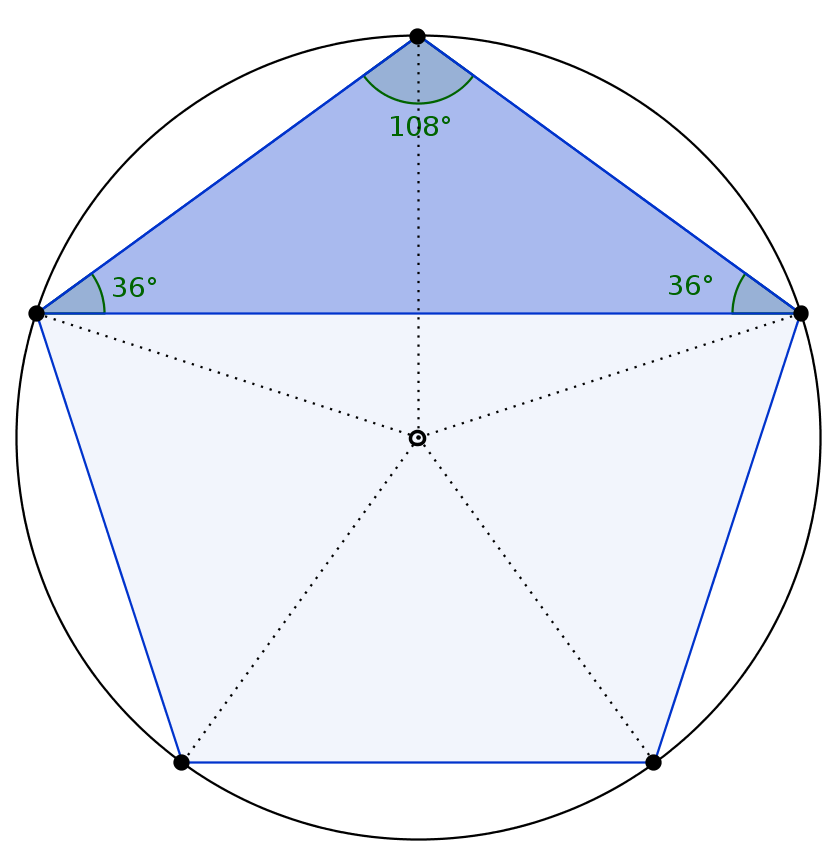 Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон. Например, вписать его в окружность с заданным радиусом либо построить на базе заданной боковой стороны.
Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон. Например, вписать его в окружность с заданным радиусом либо построить на базе заданной боковой стороны.
Как правильно начертить луч и какие принадлежности для черчения вам понадобятся? Возьмите листок бумаги и отметьте в произвольном месте точку. Затем приложите линейку и проведите линию, начиная с указанной точки и до бесконечности. Чтобы начертить ровную линию, нажмите клавишу «Shift»и проведите линию нужной длины. Сразу после начертания откроется вкладка «Формат». Уберите выделение с линии и увидите, что в начале линии появилась точка. Для создания надписи нажмите кнопку «Нарисовать надпись» и создайте поле, где будет находиться надпись.
Первый способ построения пятиугольника считается более «классическим». Получившаяся в результате построения фигура будет правильным пятиугольником. Двенадцатиугольник не является исключением, поэтому его построение будет невозможным без применения циркуля.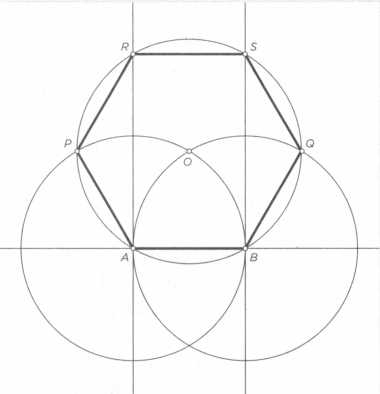 Задача построения правильного пятиугольника сводится к задаче деления окружности на пять равных частей. Начертить пентаграмму можно с использованием простейших инструментов.
Задача построения правильного пятиугольника сводится к задаче деления окружности на пять равных частей. Начертить пентаграмму можно с использованием простейших инструментов.
Я долго бился пытаясь этого добиться и самостоятельно найти пропорции и зависимости, но мне этого не удалось. Оказалось, что есть несколько различных вариантов построения правильного пятиугольника, разработанных известными математиками. Инересным моментов является то, что арифметически эту задачу решить только приблизительно точно, поскольку придется использовать иррациональные числа. Зато ее можно решить геометрически.
Деление окружностей. Точки пересечения этих линий с окружностью и являются вершинами квадрата. В окружности радиуса R (Шаг 1) следует провести вертикальный диаметр. В точке сопряжения N прямой и окружности прямая является касательной к окружности.
Получение с помощью полоски бумаги
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника. Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника. Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
А на другой конец нитки устанавливаемые карандаш и одержим. Если умеете чертить звезду, но не умеете пятиугольник, начертите звезду карандашом, затем соедините между собой соседние концы звезды, а саму звезду потом сотрите. Затем положите лист бумаги (лучше его закрепить на столе при помощи четырёх кнопок или иголочек). Приколите эти 5 полосочек к листку бумаги кнопками или иголочками, чтобы они оставались неподвижными. Затем обведите полученный пятиугольник и снимите эти полосочки с листка.
Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь.
С центра опусти на окружность 2 луча, чтоб угол между ними был 72 градуса (транспортиром). Деление круга на пять частей осуществляется с помощью обычного циркуля или транспортира. Поскольку правильный пятиугольник — это одна из фигур, содержащая в себе пропорции золотого сечения, его построением издавна интересовались живописцы и математики. Эти принципы построения с применением циркуля и линейки были изложены еще в эвклидовых «Началах».
\frac{{t^2 \sqrt {25 + 10\sqrt 5 } }}{4} = | ||||||||||||||||||||||||||||||
| ||||||||||||||||||||||
| ||||||||||||||||||||||||||||||
Отрывок, характеризующий Правильный пятиугольник
Петя не знал, как долго это продолжалось: он наслаждался, все время удивлялся своему наслаждению и жалел, что некому сообщить его. Его разбудил ласковый голос Лихачева.
Его разбудил ласковый голос Лихачева.– Готово, ваше благородие, надвое хранцуза распластаете.
Петя очнулся.
– Уж светает, право, светает! – вскрикнул он.
Невидные прежде лошади стали видны до хвостов, и сквозь оголенные ветки виднелся водянистый свет. Петя встряхнулся, вскочил, достал из кармана целковый и дал Лихачеву, махнув, попробовал шашку и положил ее в ножны. Казаки отвязывали лошадей и подтягивали подпруги.
– Вот и командир, – сказал Лихачев. Из караулки вышел Денисов и, окликнув Петю, приказал собираться.
Быстро в полутьме разобрали лошадей, подтянули подпруги и разобрались по командам. Денисов стоял у караулки, отдавая последние приказания. Пехота партии, шлепая сотней ног, прошла вперед по дороге и быстро скрылась между деревьев в предрассветном тумане. Эсаул что то приказывал казакам. Петя держал свою лошадь в поводу, с нетерпением ожидая приказания садиться. Обмытое холодной водой, лицо его, в особенности глаза горели огнем, озноб пробегал по спине, и во всем теле что то быстро и равномерно дрожало.
– Ну, готово у вас все? – сказал Денисов. – Давай лошадей.
Лошадей подали. Денисов рассердился на казака за то, что подпруги были слабы, и, разбранив его, сел. Петя взялся за стремя. Лошадь, по привычке, хотела куснуть его за ногу, но Петя, не чувствуя своей тяжести, быстро вскочил в седло и, оглядываясь на тронувшихся сзади в темноте гусар, подъехал к Денисову.
– Василий Федорович, вы мне поручите что нибудь? Пожалуйста… ради бога… – сказал он. Денисов, казалось, забыл про существование Пети. Он оглянулся на него.
– Об одном тебя пг»ошу, – сказал он строго, – слушаться меня и никуда не соваться.
Во все время переезда Денисов ни слова не говорил больше с Петей и ехал молча. Когда подъехали к опушке леса, в поле заметно уже стало светлеть. Денисов поговорил что то шепотом с эсаулом, и казаки стали проезжать мимо Пети и Денисова. Когда они все проехали, Денисов тронул свою лошадь и поехал под гору. Садясь на зады и скользя, лошади спускались с своими седоками в лощину.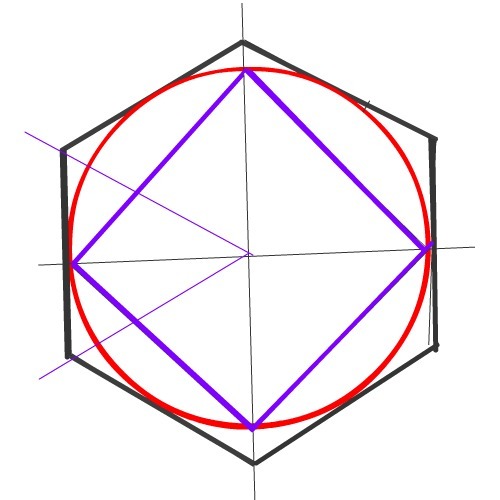 Петя ехал рядом с Денисовым. Дрожь во всем его теле все усиливалась. Становилось все светлее и светлее, только туман скрывал отдаленные предметы. Съехав вниз и оглянувшись назад, Денисов кивнул головой казаку, стоявшему подле него.
Петя ехал рядом с Денисовым. Дрожь во всем его теле все усиливалась. Становилось все светлее и светлее, только туман скрывал отдаленные предметы. Съехав вниз и оглянувшись назад, Денисов кивнул головой казаку, стоявшему подле него.
– Сигнал! – проговорил он.
Казак поднял руку, раздался выстрел. И в то же мгновение послышался топот впереди поскакавших лошадей, крики с разных сторон и еще выстрелы.
В то же мгновение, как раздались первые звуки топота и крика, Петя, ударив свою лошадь и выпустив поводья, не слушая Денисова, кричавшего на него, поскакал вперед. Пете показалось, что вдруг совершенно, как середь дня, ярко рассвело в ту минуту, как послышался выстрел. Он подскакал к мосту. Впереди по дороге скакали казаки. На мосту он столкнулся с отставшим казаком и поскакал дальше. Впереди какие то люди, – должно быть, это были французы, – бежали с правой стороны дороги на левую. Один упал в грязь под ногами Петиной лошади.
У одной избы столпились казаки, что то делая. Из середины толпы послышался страшный крик. Петя подскакал к этой толпе, и первое, что он увидал, было бледное, с трясущейся нижней челюстью лицо француза, державшегося за древко направленной на него пики.
Петя подскакал к этой толпе, и первое, что он увидал, было бледное, с трясущейся нижней челюстью лицо француза, державшегося за древко направленной на него пики.
– Ура!.. Ребята… наши… – прокричал Петя и, дав поводья разгорячившейся лошади, поскакал вперед по улице.
Впереди слышны были выстрелы. Казаки, гусары и русские оборванные пленные, бежавшие с обеих сторон дороги, все громко и нескладно кричали что то. Молодцеватый, без шапки, с красным нахмуренным лицом, француз в синей шинели отбивался штыком от гусаров. Когда Петя подскакал, француз уже упал. Опять опоздал, мелькнуло в голове Пети, и он поскакал туда, откуда слышались частые выстрелы. Выстрелы раздавались на дворе того барского дома, на котором он был вчера ночью с Долоховым. Французы засели там за плетнем в густом, заросшем кустами саду и стреляли по казакам, столпившимся у ворот. Подъезжая к воротам, Петя в пороховом дыму увидал Долохова с бледным, зеленоватым лицом, кричавшего что то людям. «В объезд! Пехоту подождать!» – кричал он, в то время как Петя подъехал к нему.
– Подождать?.. Ураааа!.. – закричал Петя и, не медля ни одной минуты, поскакал к тому месту, откуда слышались выстрелы и где гуще был пороховой дым. Послышался залп, провизжали пустые и во что то шлепнувшие пули. Казаки и Долохов вскакали вслед за Петей в ворота дома. Французы в колеблющемся густом дыме одни бросали оружие и выбегали из кустов навстречу казакам, другие бежали под гору к пруду. Петя скакал на своей лошади вдоль по барскому двору и, вместо того чтобы держать поводья, странно и быстро махал обеими руками и все дальше и дальше сбивался с седла на одну сторону. Лошадь, набежав на тлевший в утреннем свето костер, уперлась, и Петя тяжело упал на мокрую землю. Казаки видели, как быстро задергались его руки и ноги, несмотря на то, что голова его не шевелилась. Пуля пробила ему голову.
Переговоривши с старшим французским офицером, который вышел к нему из за дома с платком на шпаге и объявил, что они сдаются, Долохов слез с лошади и подошел к неподвижно, с раскинутыми руками, лежавшему Пете.
– Готов, – сказал он, нахмурившись, и пошел в ворота навстречу ехавшему к нему Денисову.
– Убит?! – вскрикнул Денисов, увидав еще издалека то знакомое ему, несомненно безжизненное положение, в котором лежало тело Пети.
– Готов, – повторил Долохов, как будто выговаривание этого слова доставляло ему удовольствие, и быстро пошел к пленным, которых окружили спешившиеся казаки. – Брать не будем! – крикнул он Денисову.
Эта фигура является многоугольником с минимальным количеством углов, которым невозможно замостить площадь. Только у пятиугольника количество диагоналей совпадает с количеством его сторон. Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон. Например, вписать его в окружность с заданным радиусом либо построить на базе заданной боковой стороны.
Как правильно начертить луч и какие принадлежности для черчения вам понадобятся? Возьмите листок бумаги и отметьте в произвольном месте точку. Затем приложите линейку и проведите линию, начиная с указанной точки и до бесконечности. Чтобы начертить ровную линию, нажмите клавишу «Shift»и проведите линию нужной длины. Сразу после начертания откроется вкладка «Формат». Уберите выделение с линии и увидите, что в начале линии появилась точка. Для создания надписи нажмите кнопку «Нарисовать надпись» и создайте поле, где будет находиться надпись.
Затем приложите линейку и проведите линию, начиная с указанной точки и до бесконечности. Чтобы начертить ровную линию, нажмите клавишу «Shift»и проведите линию нужной длины. Сразу после начертания откроется вкладка «Формат». Уберите выделение с линии и увидите, что в начале линии появилась точка. Для создания надписи нажмите кнопку «Нарисовать надпись» и создайте поле, где будет находиться надпись.
Первый способ построения пятиугольника считается более «классическим». Получившаяся в результате построения фигура будет правильным пятиугольником. Двенадцатиугольник не является исключением, поэтому его построение будет невозможным без применения циркуля. Задача построения правильного пятиугольника сводится к задаче деления окружности на пять равных частей. Начертить пентаграмму можно с использованием простейших инструментов.
Я долго бился пытаясь этого добиться и самостоятельно найти пропорции и зависимости, но мне этого не удалось. Оказалось, что есть несколько различных вариантов построения правильного пятиугольника, разработанных известными математиками. Инересным моментов является то, что арифметически эту задачу решить только приблизительно точно, поскольку придется использовать иррациональные числа. Зато ее можно решить геометрически.
Инересным моментов является то, что арифметически эту задачу решить только приблизительно точно, поскольку придется использовать иррациональные числа. Зато ее можно решить геометрически.
Деление окружностей. Точки пересечения этих линий с окружностью и являются вершинами квадрата. В окружности радиуса R (Шаг 1) следует провести вертикальный диаметр. В точке сопряжения N прямой и окружности прямая является касательной к окружности.
Получение с помощью полоски бумаги
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника. Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
А на другой конец нитки устанавливаемые карандаш и одержим. Если умеете чертить звезду, но не умеете пятиугольник, начертите звезду карандашом, затем соедините между собой соседние концы звезды, а саму звезду потом сотрите. Затем положите лист бумаги (лучше его закрепить на столе при помощи четырёх кнопок или иголочек). Приколите эти 5 полосочек к листку бумаги кнопками или иголочками, чтобы они оставались неподвижными. Затем обведите полученный пятиугольник и снимите эти полосочки с листка.
Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь.
С центра опусти на окружность 2 луча, чтоб угол между ними был 72 градуса (транспортиром). Деление круга на пять частей осуществляется с помощью обычного циркуля или транспортира. Поскольку правильный пятиугольник — это одна из фигур, содержащая в себе пропорции золотого сечения, его построением издавна интересовались живописцы и математики. Эти принципы построения с применением циркуля и линейки были изложены еще в эвклидовых «Началах».
Деление круга на пять частей осуществляется с помощью обычного циркуля или транспортира. Поскольку правильный пятиугольник — это одна из фигур, содержащая в себе пропорции золотого сечения, его построением издавна интересовались живописцы и математики. Эти принципы построения с применением циркуля и линейки были изложены еще в эвклидовых «Началах».
Если под руками нет циркуля, то можно нарисовать простую звезду с пятью лучами затем просто соединить эти лучи. как видим на картинке ниже получается абсолютно правильный пятиугольник.
Математика сложная наука и у нее много своих секретиков, некоторые из них весьма забавны. Если вы увлекаетесь такими вещами советую найти книгу Забавная математика.
Окружность можно нарисовать не только при помощи циркуля. Можно, например, использовать карандаш и нитку. Отмеряем нужный диаметр на нитке. Один конец плотно зажимаем на листе бумаги, где будем чертить окружность. А на другой конец нитки устанавливаемые карандаш и одержим. Теперь действует как с циркулем: натягиваем нить и по окружности слегка надавливая карандашом чкртим окружность.
Внутри окружности рисуем крестьян от центра: вертикальная линия и горизонтальная линия. Точка пересечения вертикальной линии и окружности будет вершиной пятиугольника (точка 1). Теперь правую половину горизонтальной линии делим пополам (точка 2). Измеряем расстояние от этой точки до вершины пятиугольника и этот отрезок откладывает влево от точки 2 (точка 3). При помощи нитки и карандаша проводим от точки 1 радиусом до точки 3 дугу, пересекающую первую окружность слева и справа — точки пересечения будут вершинами пятиугольника. Обозначим их точка 4 и 5.
Теперь от точки 4 делаем дугу, пересекающую окружность в нижней части, радиусом равной длине от точки 1 до 4 — это будет точкой 6. Точно так же и от точки 5 — обозначим точкой 7.
Остатся соединить наш пятиугольник с вершинами 1, 5, 7, 6, 4.
Я знаю как построить простой пятиугольник с помощью циркуля: Строим окружность, отмечаем пять точек, соединяем их. Можно построить пятиугольник с равными сторонами, для этого нам еще понадобится транспортир. Просто те же самые 5 точек ставим по транспортиру. Для этого отмечаем углы по 72 градуса. После чего также соединяем отрезками и получаем нужную нам фигуру.
Зеленую окружность можно чертить произвольным радиусом. В эту окружность будем вписывать правильный пятиугольник. Без циркуля начертить точно окружность нельзя, но это не обязательно. Окружность и все дальнейшие построения можно выполнять от руки. Далее через центр окружности О нужно провести две взаимно перпендикулярные прямые и одну из точек пересечения прямой с окружностью обозначить А. Точка А будет вершиной пятиугольника. Радиус ОВ разделим пополам и поставим точку С. Из точки С проводим вторую окружность радиусом АС. Из точки А проводим третью окружность радиусом АD. Точки пересечения третьей окружности с первой (Е и F)будут также вершинами пятиугольника. Из точек Е и F радиусом АЕ делаем засечки на первой окружности и получаем остальные вершины пятиугольника G и H.
Адептам черного искусства: что бы просто, красиво и быстро нарисовать пятиугольник, следует начертить правильную, гармоничную основу для пентаграммы (пятиконечная звезда) и соединить окончания лучей этой звезды посредством прямых, ровных линий. Если все было сделано верно — соединительная черта вокруг основы и будет искомым пятиугольником.
(на рисунке — завершенная, но незаполненная пентаграмма)
Для тех, кто неуверен в правильности начертания пентаграммы: возьмите за основу витрувианского человека Да Винчи (см. ниже)
Если нужен пятиугольник — тыкаете произвольным образом 5 точке и их внешний контур будет пятиугольником.
Если нужен правильный пятиугольник, то без математического циркуля это построение совершить невозможно, поскольку без него нельзя провести два одинаковых, но не параллельных отрезка. Любой другой инструмент, который позволяет провести два одинаковых, но не параллельных отрезка эквивалентен математическому циркулю.
Сначала надо надо начертить круг, потом направляющие, потом второй пунктирный круг, находим верхнюю точку, потом отмеряем два угла верхние, от них чертим нижние. Заметьте, радиус циркуля один и тот же при всем построении.
Вс зависит от того, какой пятиугольник вам необходим. Если любой, то ставите пять точек и соединяете их между собой(естествено точки ставим не по прямой линии). А если нужен пятиугольник правильно формы, возьмите любые пять по длине(полосок бумаги, спичек, карандашей и т.п), выложите пятиугольник и обчертите его.
Пятиугольник можно начертить, к примеру, из звезды. Если умеете чертить звезду, но не умеете пятиугольник, начертите звезду карандашом, затем соедините между собой соседние концы звезды, а саму звезду потом сотрите.
Второй способ. Вырежьте полосочку из бумаги, длиной, равной желаемой стороне пятиугольника, а шириной узкой, допустим 0.5 — 1 см. Как по шаблону, вырежьте по этой полосочке ещ четыре таких же полосочки, чтобы их получилось всего 5.
Затем положите лист бумаги (лучше его закрепить на столе при помощи четырх кнопок или иголочек). Затем наложите эти 5 полосочек на листок так, чтобы они образовали пятиугольник. Приколите эти 5 полосочек к листку бумаги кнопками или иголочками, чтобы они оставались неподвижными. Затем обведите полученный пятиугольник и снимите эти полосочки с листка.
Если нет циркуля и нужно построить пятиугольник, то я могу посоветовать следующее. Я и сама так строила. Можно начертить правильную пятиконечную звезду. И после этого, чтобы получить пятиугольник, просто нужно соединить все вершины звезды. Вот так и получится пятиугольник. Вот что мы получим
Ровными чрными линии мы соединили вершины звезды и получили пятиугольник.
Правильный пятиугольник представляет собой геометрическую фигуру, которая образовывается пересечением пяти прямых, создающих пять одинаковых углов. Такая фигура носит название — пентагон. С пятиугольником тесно связана работа художников — их рисунки строятся на основе правильных геометрических фигур. Для этого необходимо знать то, как быстро построить пентагон.
Чем интересна эта фигура? Форму пентагона имеет здание Министерства обороны Соединенных Штатов Америки . Это можно увидеть на фото, сделанных с высоты полета. В природе не существует кристаллов и камней, форма которых напоминала бы пентагон. Только в этой фигуре количество граней совпадает с числом диагоналей.
Параметры правильного пятиугольника
Прямоугольный пятиугольник, как и каждая фигура в геометрии, имеет свои параметры. Зная необходимые формулы, можно рассчитать эти параметры, что облегчит процесс построения пентагона. Способы и формулы расчетов:
- сумма всех углов в многоугольниках равна 360 градусам. В правильном пятиугольнике все углы равны, соответственно, центральный угол находится таким способом: 360/5 = 72 градуса;
- внутренний угол находится таким образом: 180*(n -2)/ n = 180*(5−2)/5 = 108 градусов. Сумма всех внутренних углов: 108*5 = 540 градусов.
Сторона пентагона находится с помощью параметров, которые уже даны в условии задачи:
- если вокруг пятиугольника описана окружность и известен ее радиус, сторона находится по такой формуле: a = 2*R*sin (α/2) = 2*R*sin (72/2) = 1,1756*R.
- Если известен радиус вписанной в пентагон окружности, то формула расчета стороны многоугольника: 2*r*tg (α/2) = 2*r*tg (α/2) = 1,453*r.
- При известной величине диагонали пентагона его сторона рассчитывается таким образом: а = D/1,618.
Площадь пентагона так же , как и его сторона, зависит от уже найденных параметров:
- с помощью известного радиуса вписанной окружности площадь находится так: S = (n*a*r)/2 = 2,5*a*r.
- описанная вокруг пятиугольника окружность позволяет найти площадь по такой формуле: S = (n*R2*sin α)/2 = 2,3776*R2.
- в зависимости от стороны пентагона: S = (5*a2*tg 54°)/4 = 1,7205* a2.
Построение пентагона
Построить правильный пятиугольник можно с помощью линейки и циркуля, на основе вписанной в него окружности или одной из сторон.
Как начертить пятиугольник на основе вписанной окружности? Для этого необходимо запастись циркулем и линейкой и сделать такие шаги:
- Сначала необходимо начертить окружность с центром О, после чего на ней выбрать точку, А — вершину пентагона. От центра к вершине проводится отрезок.
- Затем строится перпендикулярная прямой ОА отрезок, который также проходит через О — центр окружности. Его пересечение с окружностью обозначается точкой В. Отрезок О. В. делится пополам точкой С.
- Точка С станет центром новой окружности, проходящей через А. Точка D — это ее пересечение с прямой ОВ в границах первой фигуры.
- После этого проводится третья окружность через D, центром которой является точка А. Она пересекается с первой фигурой в двух точках, их необходимо обозначить буквами Е и F.
- Следующая окружность имеет центр в точке Е и проходит через А, а ее пересечение с первоначальной находится в новой точке G.
- Последняя окружность в этом рисунке проводится через точку, А с центром F. На ее пересечении с начальной ставится точка Н.
- На первой окружности после всех проделанных шагов появились пять точек, которые необходимо соединить отрезками. Таким образом получился правильный пятиугольник АЕ G Н F.
Как построить правильный пятиугольник иным способом? С помощью линейки и циркуля пентагон можно построить немного быстрее. Для этого необходимо:
- Cначала необходимо с помощью циркуля нарисовать окружность, центр которой — точка О.
- Чертится радиус ОА — отрезок, который откладывается на окружность. Его делят пополам точкой В.
- Перпендикулярно радиусу ОА начерчивается отрезок ОС, точки В и С соединяются прямой.
- Следующим шагом является отложение длины отрезка ВС с помощью циркуля на диаметральной линии. Перпендикулярно отрезку ОА появляется точка D. Точки В и D соединяются, образуя новый отрезок.
- Для того, чтобы получить величину стороны пентагона, необходимо соединить точки С и D.
- D с помощью циркуля переносится на окружность и обозначается точкой Е. Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.
В пятиугольнике с одинаковыми сторонами диагонали равны и образуют пятиконечную звезду, которая называется пентаграммой. Золотое сечение — это отношение величины диагонали к стороне пентагона.
Пентагон непригоден для полного заполнения плоскости. Использование любого материала в этой форме оставляет промежутки или образует наложения. Хотя природных кристаллов этой формы не существует в природе, но при образовании льда на поверхности гладких медных изделий возникают молекулы в виде пентагона, которые соединены в цепочки.
Наиболее простой способ получить правильный пятиугольник из полоски бумаги — завязать ее узлом и немного придавить. Этот способ полезен для родителей детей-дошкольников, которые хотят научить своих малышей распознавать геометрические фигуры.
Видео
Посмотрите, как можно быстро начертить пятиугольник.
Правильный пятиугольник — построение, свойства и формулы
Бывают задачи на построение и нахождение некоторых геометрических параметров правильного пятиугольника. Построить фигуру непросто. Для этого математики рекомендуют несколько методик, позволяющих выполнить операцию более точно или за короткий промежуток времени. У фигуры есть свойства, а также формулы, позволяющие найти ее геометрические характеристики.
Точное построение фигуры
Специалисты рекомендуют некоторую последовательность действий, по которым построить правильный пятиугольник очень просто. Для операции необходимы обыкновенная тетрадь в клеточку, циркуль, карандаш, резинка и линейка. Следует выполнить некоторые шаги:
Если все пункты алгоритма выполнены правильно, то должен получиться пентагон, изображенный на рисунке 1:
Этот способ следует применять для точных построений и чертежей деталей. Однако для решения задач, в которых необходимо схематически изобразить пятиугольник, этот вариант не подойдет.
Алгоритм Биона
Прием Биона является менее точным методом, чем первый. Он позволяет построить любой правильный многоугольник, вписанный в произвольный круг. Для операции необходимо воспользоваться алгоритмом (шаблоном) Биона, имеющим такой вид:
Погрешность построения многоугольника с 5, 7, 9 и 10 сторонами при использовании алгоритма довольно маленькая. Ее значения равно 3,2%. Однако при n>10 погрешность составляет не более 11%.
Приближенные методы
Существует несколько методов, позволяющих приближенно изобразить фигуру. Однако оптимальным является построение пентагона (рис. 2), используя две окружности (описанную и вписанную).
Метод известного математика А. Дюрера является оптимальным среди остальных, поскольку на построение затрачивается минимальное количество времени. Для его реализации следует выполнить определенные шаги алгоритма Дюрера:
Существует еще один метод — построение пятиугольника из десятиугольника, который вписан в окружность. Для этого следует соединить его вершины через одну. Однако способ рекомендуется применять только в том случае, когда исходная фигура уже имеется. Кстати, его следует строить также методом А. Дюрера.
Математики рекомендуют еще один простой способ. Для его реализации необходимо начертить окружность с диаметром АD. После этого его нужно поделить на 3 равные части, то есть AB = BC = CD. Затем из точки С следует опустить перпендикуляры на окружность. Обозначить места пересечения точками E и F. Проделать такую же процедуру с точкой B, обозначив пересечения точками G и H. Остается лишь соединить все точки отрезками.
Признаки и свойства
Не всегда получается верно идентифицировать пятиугольник. Для этого математики предлагают признаки, которые применимы только к правильной фигуре. К ним можно отнести следующие:
Следует отметить, что признаки справедливы для любого правильного многогранника. Пять осей симметрии имеет правильный пятиугольник (сколько сторон, столько и осей). Пентагон обладает некоторыми свойствами, которые будут очень полезны при решении задач. К ним можно отнести следующие:
Однако свойств недостаточно при решении задач, поскольку существуют некоторые формулы и соотношения для нахождения основных параметров пентагона.
Расчет параметров
С помощью соотношений можно легко найти необходимые характеристики любой фигуры. Однако в некоторых источниках не указаны условные обозначения известного параметра пентагона. Это существенно затрудняет понимание формулы, а также ее дальнейшее использование. Перед изучением следует нарисовать фигуру и обозначить некоторые величины, которыми могут быть диагонали, стороны, апофемы и радиусы.
Рекомендуется использовать различные литеры или буквенные обозначения. Недопустимо пронумеровывать вершины, поскольку при вычислениях можно ошибиться. Нельзя использовать вместо букв цифры при обозначениях. Например, пентагон ABCDE является правильной записью. Допускается применение чисел в индексах, а именно, в пятиугольнике правильного типа ABCDE при пересечении его диагоналей образовался пентагон A1B1C1D1E1.
Математики рекомендуют обозначать только промежуточные фигуры или их проекции литерами с индексами. Для каждой новой фигуры следует вводить другие обозначения. Не следует использовать зарезервированные переменные. Например, центр окружности в точке P является недопустимой записью, поскольку такой буквой обозначается периметр.
Условные обозначения
Для нахождения основных величин пентагона следует обозначить некоторые его параметры. Фигура имеет следующие обозначения:
Значения сторон равны между собой. Площадь правильного пятиугольника — характеристика двумерной фигуры, которая показывает ее размерность. Периметром называется сумма всех 5 сторон.(1/2).
Таким образом, при решении задач необходимо знать основные признаки, свойства, соотношения и формулы для нахождения основных характеристик пентагона. Практика обязательна, поскольку теоретические знания без практического применения бесполезны.
ПредыдущаяГеометрияСвойства диагоналей ромба — основные формулы и доказательство теоремы
СледующаяГеометрияДодекаэдр — свойства, вид и структура двенадцатигранника
Персональный сайт учителя Низамутдиновой З.И.
Правильный пятиугольник
Правилый пятиугольник
Правильный пятиугольник или пентагон — геометрическая фигура, правильный многоугольник с пятью сторонами.
Свойства
Построение правильного пятиугольника
У правильного пятиугольника угол равен
Площадь правильного пятиугольника с длиной стороны t рассчитывается по формуле:
или
,
где R — радиус описанной окружности, r — радиус вписанной окружности.
Отношение диагонали правильного пятиугольника к стороне равно золотому сечению, то есть числу.
Поэтому радиус вписанной окружности, радиус описанной окружности, высоту и площадь правильного пятиугольника можно вычислить и без использования тригонометрических функций:
Сторона правильного пятиугольника:
Высота правильного пятиугольника:
Площадь правильного пятиугольника:
Радиус вписанной окружности правильного пятиугольника:
Радиус описанной окружности правильного пятиугольника:
Пятиугольником невозможно заполнить плоскость без промежутков.
Построение
Правильный пятиугольник может быть построен с помощью циркуля и линейки, или вписыванием его в заданную окружность, или построением на основе заданной стороны. Этот процесс описан Евклидом в его «Началах» около 300 года до н. э.
Вот один из методов построения правильного пятиугольника в заданной окружности:
By Aldoaldoz — Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=10023658
- Постройте окружность, в которую будет вписан пятиугольник и обозначьте её центр как O. (Это зелёная окружность на схеме справа).
- Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
- Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью как точку B.
- Постройте точку C посередине между O и B.
- Проведите окружность с центром в C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
- Проведите окружность с центром в A через точку D. Обозначьте её пересечения с оригинальной (зелёной окружностью) как точки E и F.
- Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.
- Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.
- Постройте правильный пятиугольник AEGHF.
Альтернативный метод построения правильного многоугольника с помощью линейки и циркуля
Правильный шестиугольник
Правильный шестиугольник
Правильный шестиугольник (гексагон) — это правильный многоугольник с шестью сторонами.
Свойства
Особенность правильного шестиугольника — равенство его стороны и радиуса описанной окружности .
Все углы равны 120°.
Радиус вписанной окружности равен:
Периметр правильного шестиугольника равен:
Площадь правильного шестиугольника рассчитывается по формулам:
Шестиугольники замощают плоскость (то есть могут заполнять плоскость без пробелов и наложений).
Правильный шестиугольник со стороной является универсальной покрышкой, то есть всякое множество диаметра 1 можно покрыть правильным шестиугольником со стороной (лемма Пала).
Построение
Правильный шестиугольник можно построить с помощью циркуля и линейки. Ниже приведён метод построения, предложенный Евклидом в «Началах», книга IV, теорема 15.
Правильный семиугольник
Правильный семиугольник
Правильный семиугольник — это правильный многоугольник с семью сторонами.
Свойства
Пусть t — сторона семиугольника, R — радиус описанной окружности, r — радиус вписанной окружности.
Периметр правильного семиугольника равен
Площадь правильного семиугольника рассчитывается по формулам:
Построение
Приближённое построение правильного семиугольника
Точное
Согласно теореме Гаусса — Ванцеля, правильный семиугольник невозможно построить с помощью циркуля и линейки, но можно построить с помощью циркуля и размеченной линейки то есть линейки, на которой можно делать отметки и с помощью которой можно проводить прямые, проходящие через какую-нибудь точку, причём отмеченные на линейке точки будут принадлежать данным линиям (прямым или окружностям).
Приближённое
Приближённое (но с достаточной для практики точностью — 0,2 %) построение семиугольника показано на рисунке. Из точки A на окружности радиусом, равным радиусу окружности, проводим дугу BOC. Отрезок и даст искомое приближение.
Семиугольные звезды
Семиугольная звезда 7/2
Семиугольная звезда 7/3
Существует два звёздчатых семиугольника (гептаграммы): 7/2 и 7/3. Методы их построения аналогичны построению обычного семиугольника, только вершины нужно соединять через одну (7/2) или через две (7/3).
Правильный восьмиугольник
Правильный восьмиугольник
Правильный восьмиугольник (октагон) — геометрическая фигура из группы правильных многоугольников. У него восемь сторон и восемь углов и все углы и стороны равны между собой.
Свойства
Построение правильного восьмиугольника
Восьмиугольник можно построить, проведя к сторонам квадрата серединные перпендикуляры и соединив точки их пересечения с описанной окружностью квадрата с его сторонами.
Сумма всех внутренних углов правильного восьмиугольника составляет 1080°.
Угол правильного восьмиугольника составляет 135°
Формулы расчёта параметров правильного восьмиугольника
Примем:
* t — длина стороны восьмиугольника
* r — радиус вписанной окружности
* R — радиус описанной окружности
* S — площадь восьмиугольника
Так как правильный восьмиугольник можно получить соответствующим отсечением углов квадрата со стороной , радиус вписанной окружности, радиус описанной окружности и площадь правильного восьмиугольника можно вычислить и без использования тригонометрических функций:
* Радиус вписанной окружности правильного восьмиугольника:
* Радиус описанной окружности правильного восьмиугольника:
* Площадь правильного восьмиугольника:
Правильный девятиугольник
Правильный девятиугольник
Правильный девятиугольник — это правильный многоугольник с девятью сторонами.
Свойства
Правильный девятиугольник имеет внутренние углы, равные 140°. Площадь правильного девятиугольника со стороной A определяется выражением
Построение
Хотя правильный девятиугольник и невозможно построить с помощью циркуля и линейки, существуют методы построения достаточно точных приближений.
Девятиугольные звёзды
Существует три звёздчатых девятиугольника: {9/2}, {9/3} и {9/4}, причём звезда {9/3} состоит из трёх равносторонних треугольников:
Правильный семнадцатиугольник
Правильный семнадцатиугольник
Правильный семнадцатиугольник — геометрическая фигура, принадлежащая к группе правильных многоугольников. Он имеет семнадцать сторон и семнадцать углов, все его углы и стороны равны между собой, все вершины лежат на одной окружности.
Свойства
Центральный угол a равен
Отношение длины стороны к радиусу описанной окружности составляет
Правильный семнадцатиугольник можно построить при помощи циркуля и линейки, что было доказано Гауссом в 1796 году.
Факты
* Гаусс был настолько воодушевлён своим открытием, что в конце жизни завещал, чтобы правильный семнадцатиугольник высекли на его могиле. Скульптор отказался это сделать, утверждая, что построение будет настолько сложным, что результат нельзя будет отличить от окружности.
* В 1825 году Йоханнес Эрхингер впервые опубликовал подробное описание построения правильного семнадцатиугольника в 64 шагах. Ниже приводится это построение.
Примерное построение
1. Ставим на плоскости точку M, строим вокруг неё окружность k и проводим её диаметр AB;
2. Делим пополам радиус AM три раза по очереди по направлению к центру (точки C, D и E).
3. Делим пополам отрезок EB (точка F).
4. строим перпендикуляр к AB в точке F.
* Вкратце: строим перпендикуляр к диаметру на расстоянии 9/16 диаметра от B.
Точки пересечения последнего перпендикуляра с окружностью являются хорошим приближением для точек P3 и P14.
При этом построении получается относительная ошибка в 0,83%. Углы и стороны получаются таким образом немного больше, чем нужно. При радиусе 332,4 мм сторона получается длиннее на 1 мм.
Построение семнадцатиугольника циркулем и линейкой в 64 шага по Йоханнесу Эрхингеру
| ||||||||||||||||||||||
| ||||||||||||||||||||||||||||||
Отрывок, характеризующий Правильный пятиугольник
Петя не знал, как долго это продолжалось: он наслаждался, все время удивлялся своему наслаждению и жалел, что некому сообщить его. Его разбудил ласковый голос Лихачева.– Готово, ваше благородие, надвое хранцуза распластаете.
Петя очнулся.
– Уж светает, право, светает! – вскрикнул он.
Невидные прежде лошади стали видны до хвостов, и сквозь оголенные ветки виднелся водянистый свет. Петя встряхнулся, вскочил, достал из кармана целковый и дал Лихачеву, махнув, попробовал шашку и положил ее в ножны. Казаки отвязывали лошадей и подтягивали подпруги.
– Вот и командир, – сказал Лихачев. Из караулки вышел Денисов и, окликнув Петю, приказал собираться.
Быстро в полутьме разобрали лошадей, подтянули подпруги и разобрались по командам. Денисов стоял у караулки, отдавая последние приказания. Пехота партии, шлепая сотней ног, прошла вперед по дороге и быстро скрылась между деревьев в предрассветном тумане. Эсаул что то приказывал казакам. Петя держал свою лошадь в поводу, с нетерпением ожидая приказания садиться. Обмытое холодной водой, лицо его, в особенности глаза горели огнем, озноб пробегал по спине, и во всем теле что то быстро и равномерно дрожало.
– Ну, готово у вас все? – сказал Денисов. – Давай лошадей.
Лошадей подали. Денисов рассердился на казака за то, что подпруги были слабы, и, разбранив его, сел. Петя взялся за стремя. Лошадь, по привычке, хотела куснуть его за ногу, но Петя, не чувствуя своей тяжести, быстро вскочил в седло и, оглядываясь на тронувшихся сзади в темноте гусар, подъехал к Денисову.
– Василий Федорович, вы мне поручите что нибудь? Пожалуйста… ради бога… – сказал он. Денисов, казалось, забыл про существование Пети. Он оглянулся на него.
– Об одном тебя пг»ошу, – сказал он строго, – слушаться меня и никуда не соваться.
Во все время переезда Денисов ни слова не говорил больше с Петей и ехал молча. Когда подъехали к опушке леса, в поле заметно уже стало светлеть. Денисов поговорил что то шепотом с эсаулом, и казаки стали проезжать мимо Пети и Денисова. Когда они все проехали, Денисов тронул свою лошадь и поехал под гору. Садясь на зады и скользя, лошади спускались с своими седоками в лощину. Петя ехал рядом с Денисовым. Дрожь во всем его теле все усиливалась. Становилось все светлее и светлее, только туман скрывал отдаленные предметы. Съехав вниз и оглянувшись назад, Денисов кивнул головой казаку, стоявшему подле него.
– Сигнал! – проговорил он.
Казак поднял руку, раздался выстрел. И в то же мгновение послышался топот впереди поскакавших лошадей, крики с разных сторон и еще выстрелы.
В то же мгновение, как раздались первые звуки топота и крика, Петя, ударив свою лошадь и выпустив поводья, не слушая Денисова, кричавшего на него, поскакал вперед. Пете показалось, что вдруг совершенно, как середь дня, ярко рассвело в ту минуту, как послышался выстрел. Он подскакал к мосту. Впереди по дороге скакали казаки. На мосту он столкнулся с отставшим казаком и поскакал дальше. Впереди какие то люди, – должно быть, это были французы, – бежали с правой стороны дороги на левую. Один упал в грязь под ногами Петиной лошади.
У одной избы столпились казаки, что то делая. Из середины толпы послышался страшный крик. Петя подскакал к этой толпе, и первое, что он увидал, было бледное, с трясущейся нижней челюстью лицо француза, державшегося за древко направленной на него пики.
– Ура!.. Ребята… наши… – прокричал Петя и, дав поводья разгорячившейся лошади, поскакал вперед по улице.
Впереди слышны были выстрелы. Казаки, гусары и русские оборванные пленные, бежавшие с обеих сторон дороги, все громко и нескладно кричали что то. Молодцеватый, без шапки, с красным нахмуренным лицом, француз в синей шинели отбивался штыком от гусаров. Когда Петя подскакал, француз уже упал. Опять опоздал, мелькнуло в голове Пети, и он поскакал туда, откуда слышались частые выстрелы. Выстрелы раздавались на дворе того барского дома, на котором он был вчера ночью с Долоховым. Французы засели там за плетнем в густом, заросшем кустами саду и стреляли по казакам, столпившимся у ворот. Подъезжая к воротам, Петя в пороховом дыму увидал Долохова с бледным, зеленоватым лицом, кричавшего что то людям. «В объезд! Пехоту подождать!» – кричал он, в то время как Петя подъехал к нему.
– Подождать?.. Ураааа!.. – закричал Петя и, не медля ни одной минуты, поскакал к тому месту, откуда слышались выстрелы и где гуще был пороховой дым. Послышался залп, провизжали пустые и во что то шлепнувшие пули. Казаки и Долохов вскакали вслед за Петей в ворота дома. Французы в колеблющемся густом дыме одни бросали оружие и выбегали из кустов навстречу казакам, другие бежали под гору к пруду. Петя скакал на своей лошади вдоль по барскому двору и, вместо того чтобы держать поводья, странно и быстро махал обеими руками и все дальше и дальше сбивался с седла на одну сторону. Лошадь, набежав на тлевший в утреннем свето костер, уперлась, и Петя тяжело упал на мокрую землю. Казаки видели, как быстро задергались его руки и ноги, несмотря на то, что голова его не шевелилась. Пуля пробила ему голову.
Переговоривши с старшим французским офицером, который вышел к нему из за дома с платком на шпаге и объявил, что они сдаются, Долохов слез с лошади и подошел к неподвижно, с раскинутыми руками, лежавшему Пете.
– Готов, – сказал он, нахмурившись, и пошел в ворота навстречу ехавшему к нему Денисову.
– Убит?! – вскрикнул Денисов, увидав еще издалека то знакомое ему, несомненно безжизненное положение, в котором лежало тело Пети.
– Готов, – повторил Долохов, как будто выговаривание этого слова доставляло ему удовольствие, и быстро пошел к пленным, которых окружили спешившиеся казаки. – Брать не будем! – крикнул он Денисову.
Первый способ — по данной стороне S с помощью транспортира.
Проводим прямую и откладываем на ней AB = S; принимаем эту линию за радиус и этим радиусом из точек A и В описываем дуги: далее с помощью транспортира строим в этих точках углы в 108°, стороны которых пересекутся с дугами в точках С и D; из этих точек радиусом АВ = 5 описываем дуги, которые пересекутся в Е, и прямыми линиями соединяем точки Л, С, Е, D, В.
Полученный пятиугольник — искомый.
Второй способ. Проведем окружность радиусом r. Из точки А циркулем проводим дугу радиуса AM до пересечения в точках В и С с окружностью. Соединяем В и С линией, которая пересечет горизонтальную ось в точке Е.
Затем из точки Е проводим дугу, которая пересечет горизонтальную линию в точке О. Описываем, наконец, из точки F дугу, которая пересечет окружность в точках Н и К. Отложив по окружности расстояние FO = FH = FK пять раз и соединив точки деления линиями, получим правильный пятиугольник.
Третий способ. В данный круг вписать правильный пятиугольник. Проводим два взаимно перпендикулярных диаметра АВ и МС. Делим радиус АО точкой Е пополам. Из точки Е, как из центра, проводим дугу окружности радиуса ЕМ и засекаем ею диаметр АВ в точке F. Отрезок MF равен стороне искомого правильного пятиугольника. Раствором циркуля, равным MF, делаем засечки N 1 , Р 1 , Q 1 , К 1 и соединяем их прямыми.
На рисунке построен шестиугольник по данной стороне.
Прямой АВ = 5, как радиусом, из точек А и В описываем дуги, которые пересекутся в С; из этой точки тем же радиусом описываем окружность, на которой сторона А В отложится 6 раз.
Шестиугольник ADEFGB — искомый.
«Отделка комнат при ремонте»,
Н.П.Краснов
Первый способ построения. Проводим горизонтальную (АВ) и вертикальную (CD) оси и из точки их пересечения М откладываем в соответствующем масштабе полуоси. Наносим малую полуось от точки М на большой оси до точки Е. Эллипс, первый способ построения Делим BE на 2 части и одну наносим от точки М на большой оси (до F или H)…
Основанием для нанесения росписи служат полностью законченные окраской поверхности стен, потолков и других конструкций; роспись делается по высококачественным клеевым и масляным окраскам, сделанным под торцовку или флейц. Приступая к разработке эскиза отделки, мастер должен ясно представить себе всю композицию в бытовой обстановке и отчетливо осознать творческий замысел. Только при соблюдении этого основного условия можно правильно…
Обмер выполненных работ, за исключением особо оговоренных случаев, производится по площади действительно обработанной поверхности с учетом ее рельефа и за вычетом необработанных мест. Для определения действительно обработанных поверхностей при малярных работах следует пользоваться переводными коэффициентами, приведенными в таблицах. А. Деревянные оконные устройства (обмер производится по площади проемов по наружному обводу коробок) Наименование устройств Коэффициент при…
Положительный пятиугольник – это многоугольник, у которого все пять сторон и все пять углов равны между собой. Вокруг него легко описать окружность. Возвести пятиугольник и поможет именно эта окружность.
Инструкция
1. В первую очередь нужно возвести циркулем окружность. Центр окружности пускай совпадает с точкой O. Проведите оси симметрии перпендикулярные друг другу. В точке пересечения одной из этих осей с окружностью поставьте точку V. Эта точка будет вершиной грядущего пятиугольник а. В точке пересечения иной оси с окружностью расположите точку D.
2. На отрезке OD обнаружьте середину и подметьте в ней точку А. Позже этого надобно возвести циркулем окружность с центром в этой точке. Помимо того, она должна проходить через точку V, то есть, радиусом CV. Точку пересечения оси симметрии и этой окружности обозначьте за В.
3. Позже этого при помощи циркуля проведите окружность такого же радиуса, поставив иголку в точку V. Пересечение этой окружности с изначальной обозначьте как точку F. Эта точка станет 2-й вершиной грядущего верного пятиугольник а.
4. Сейчас необходимо провести такую же окружность через точку Е, но с центром в F. Пересечение только что проведенной окружности с изначальной обозначьте как точку G. Эта точка так же станет еще одной из вершин пятиугольник а. Аналогичным образом нужно возвести еще один круг. Центр его в G. Точка пересечения его с изначальной окружностью пускай будет H. Это последняя вершина верного многоугольника.
5. У вас должно получиться пять вершин. Остается их легко объединить по линейке. В итоге всех этих операций вы получите вписанный в окружность положительный пятиугольник .
Построение положительных пятиугольников дозволено с поддержкой циркуля и линейки. Правда, процесс это довольно долгий, как, однако, и построение всякого положительного многоугльника с нечетным числом сторон. Современные компьютерные программы разрешают сделать это за несколько секунд.
Вам понадобится
- – компьютер с программой AutoCAD.
Инструкция
1. Обнаружьте в программе AutoCAD верхнее меню, а в нем — вкладку «Основная». Нажмите на нее левой клавишей мыши. Появится панель «Рисование». Появятся различные типы линий. Выберите замкнутую полилинию. Она и представляет собой многоугольник, остается только ввести параметры. AutoCAD. Дозволяет рисовать самые различные правильне многоугольники. Число сторон может добиваться 1024. Дозволено применять и командную строку, в зависимости от версии набрав « _polygon» либо «мн.-угол».
2. Вне зависимости от того, пользуетесь ли вы командной строкой либо контекстными меню, на экране у вас появится окошко, в которое предлагается ввести число сторон. Введите туда цифру «5» и нажмите Enter. Вам будет предложено определить центр пятиугольника. Вбейте в появившееся окошко координаты. Дозволено обозначить их как (0,0), но могут быть и всякие другие данные.
3. Выберите необходимый метод построения. . AutoCAD предлагает три варианта. Пятиугольник может быть описанным вокруг окружности либо вписанным в нее, но дозволено возвести его и по заданному размеру стороны. Выберите надобный вариант и нажмите на ввод. В случае необходимости задайте радиус окружности и тоже нажмите enter.
4. Пятиугольник по заданной стороне вначале строится верно так же. Выберите «Рисование», замкнутую полилинию и введите число сторон. Правой клавишей мыши вызовите контекстное меню. Нажмите команду «edge” либо «сторона”. В командной строке наберите координаты исходной и финальной точек одной из сторон пятиугольника. Позже этого пятиугольник появится на экране.
5. Все операции дозволено исполнять с поддержкой командной строки. Скажем, для построения пятиугольника по стороне в русскоязычной версии программы введите букву «с». В англоязычной версии это будет «_e”. Дабы возвести вписанный либо описанный пятиугольник, введите позже определения числа сторон буквы «о» либо «в» (либо же английские “_с” либо “_i”)
Видео по теме
Видео по теме
Полезный совет
Таким нехитрым методом дозволено возвести не только пятиугольник. Для того дабы возвести треугольник, нужно разведите ножки циркуля на расстояние, равное радиусу окружности. После этого в всякую точку установите иглу. Проведите тонкую вспомогательную окружность. Две точки пересечения окружностей, а так же точка, в которой была ножка циркуля образуют три вершины положительного треугольника.
необходимый минимум информации. Построение правильных многоугольников по заданной стороне
Без изучения техники этого процесса не обойтись. Существует несколько вариантов выполнения работы. Как нарисовать звезду с помощью линейки, помогут понять самые известные методы этого процесса.
Разновидности звезд
Существует множество вариантов внешнего вида такой фигуры, как звезда.
Еще с древних времен пятиконечная ее разновидность использовалась для начертания пентаграмм. Это объясняется ее свойством, которое позволяет сделать рисунок, не отрывая ручки от бумаги.
Существуют также шестиконечные, хвостатые кометы.
Пять вершин традиционно имеет морская звезда. Такой же формы нередко встречаются изображения рождественского варианта.
В любом случае, чтобы нарисовать пятиконечную звезду поэтапно, необходимо прибегнуть к помощи специальных инструментов, так как изображение от руки вряд ли будет выглядеть симметрично и красиво.
Выполнение чертежа
Чтобы понять, как нарисовать ровную звезду, следует осознать суть этой фигуры.
Основой для ее начертания является ломаная линия, концы которой сходятся в начальной точке. Она образовывает правильный пятиугольник — пентагон.
Отличительными свойствами такой фигуры являются возможности вписания ее в окружность, а также окружности в этот многоугольник.
Все стороны пентагона равны между собой. Понимая, как правильно выполнить чертеж, можно осознать суть процесса построения всех фигур, а также разнообразных схем деталей, узлов.
Для достижения такой цели, как нарисовать звезду с помощью линейки, необходимо владеть знаниями о простейших математических формулах, являющихся основополагающими в геометрии. А также потребуется умение считать на калькуляторе. Но самое главное — это логическое мышление.
Работа не является сложной, но она потребует точности и скрупулезности. Потраченные усилия будут вознаграждены хорошим симметричным, а потому и красивым изображением пятиконечной звезды.
Классическая техника
Самый известный способ того, как нарисовать звезду при помощи циркуля, линейки и транспортира, является достаточно несложным.
Для этой методики понадобится несколько инструментов: циркуль или транспортир, линейка, простой карандаш, ластик и лист белой бумаги.
Чтобы понять, как красиво нарисовать звезду, действовать следует последовательно, этап за этапом.
Можно в работе воспользоваться специальными вычислениями.
Расчет фигуры
На этом этапе рисования правильной звезды проступают контуры готовой фигуры.
Если все сделано правильно, полученное изображение будет ровным. Это можно проверить визуально, вращая лист бумаги и оценивая форму. Она будет неизменной при каждом повороте.
Основные контуры наводятся при помощи линейки и простого карандаша более четко. Все вспомогательные линии убираются.
Чтобы понять, как нарисовать звезду поэтапно, следует проводить все действия вдумчиво. В случае ошибки можно подправить рисунок ластиком или провести все манипуляции заново.
Оформление работы
Готовую форму можно украсить самыми разнообразными способами. Главное — не нужно бояться экспериментировать. Фантазия подскажет оригинальный и красивый образ.
Можно разукрасить нарисованную ровную звезду простым карандашом или использовать самые разнообразные цвета и оттенки.
Чтобы разобраться в том, как нарисовать правильную звезду, необходимо придерживаться идеальных линий во всем. Поэтому самый популярный вариант оформления заключается в разделении каждого луча фигуры на две равные части линией, исходящей от вершины до центра.
Можно не разделять стороны звезды линиями. Допускается просто закрасить каждый луч фигуры более темным оттенком с одного бока.
Такой вариант также будет ответом на вопрос о том, как нарисовать правильную звезду, ведь все ее линии будут симметричны.
По желанию при эстетическом оформлении фигуры можно добавить орнамент или другие всевозможные элементы. Добавив кружочки к вершинам, можно получить звезду шерифа. Применив плавную растушевку теневых сторон, можно получить морскую звезду.
Эта техника является самой распространенной, так как без особых усилий позволяет понять, как нарисовать пятиконечную звезду поэтапно. Не прибегая к сложным математическим вычислениям, возможно получить правильное, красивое изображение.
Рассмотрев все способы того, как нарисовать звезду с помощью линейки, можно выбрать для себя более подходящий. Наиболее популярным является геометрический поэтапный метод. Он достаточно несложный и эффективный. Применив фантазию и воображение, можно из полученной правильной, красивой формы создать оригинальную композицию. Вариантов оформления рисунка существует великое множество. Но ведь всегда можно придумать свой собственный, самый необычный и запоминающийся сюжет. Главное — не стоит бояться экспериментировать!
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего проводим стороны 5-6 и 3-2.
Построение вписанного в окружность равностороннего треугольника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны
1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
Уровень сложности: Несложно
1 шаг
Сначала, выбирайте, где разместить центр окружности. Там нужно поставить начальную точку, пусть она называется О. С помощью циркуля вычерчиваем вокруг нее окружность заданного диаметра или радиуса.
2 шаг
Затем проводим две оси через точку О, центр окружности, одна горизонтальная, другая под 90 градусов по отношению к ней – вертикальная. Точки пересечения по горизонтали назовем слева на право А и В, по вертикали, сверху вниз – М и Н. Радиус, который лежит на любой оси, например, на горизонтальной в правой части, делим пополам. Это можно сделать так: циркуль с радиусом известной нам окружности устанавливаем острием в точку пересечения горизонтальной оси и окружности – В, отчеркиваем пересечения с окружностью, полученные точки называем, соответственно сверху вниз – С и Р, соединяем их отрезком, который будет пересекать ось ОВ, точку пересечения называем К.
3 шаг
Соединяем точки К и М и получаем отрезок КМ, устанавливаем циркуль в точку М, задаем на нем расстояние до точки К и очерчиваем метки на радиусе ОА, эту точку называем Е, далее ведем циркуль до пересечения с левой верхней частью окружности ОМ. Эту точку пересечения называем F. Расстояние равное отрезку МЕ является искомой стороной равностороннего пятиугольника. При этом точка М будет являться одной вершиной встраиваемого в окружность пятиугольника, а точка F – другой.
4 шаг
Далее из полученных точек по всей окружности отчерчиваем циркулем расстояния, равные отрезку МЕ, всего точек должно получиться 5. Соединяем все точки отрезками – получаем пятиугольник, вписанный в окружность.
- При черчении будьте аккуратны в измерениях расстояний, не допускайте погрешностей, чтобы пятиугольник действительно полчился равносторонним
Правильный пятиугольник представляет собой геометрическую фигуру, которая образовывается пересечением пяти прямых, создающих пять одинаковых углов. Такая фигура носит название — пентагон. С пятиугольником тесно связана работа художников — их рисунки строятся на основе правильных геометрических фигур. Для этого необходимо знать то, как быстро построить пентагон.
Чем интересна эта фигура? Форму пентагона имеет здание Министерства обороны Соединенных Штатов Америки . Это можно увидеть на фото, сделанных с высоты полета. В природе не существует кристаллов и камней, форма которых напоминала бы пентагон. Только в этой фигуре количество граней совпадает с числом диагоналей.
Параметры правильного пятиугольника
Прямоугольный пятиугольник, как и каждая фигура в геометрии, имеет свои параметры. Зная необходимые формулы, можно рассчитать эти параметры, что облегчит процесс построения пентагона. Способы и формулы расчетов:
- сумма всех углов в многоугольниках равна 360 градусам. В правильном пятиугольнике все углы равны, соответственно, центральный угол находится таким способом: 360/5 = 72 градуса;
- внутренний угол находится таким образом: 180*(n -2)/ n = 180*(5−2)/5 = 108 градусов. Сумма всех внутренних углов: 108*5 = 540 градусов.
Сторона пентагона находится с помощью параметров, которые уже даны в условии задачи:
- если вокруг пятиугольника описана окружность и известен ее радиус, сторона находится по такой формуле: a = 2*R*sin (α/2) = 2*R*sin (72/2) = 1,1756*R.
- Если известен радиус вписанной в пентагон окружности, то формула расчета стороны многоугольника: 2*r*tg (α/2) = 2*r*tg (α/2) = 1,453*r.
- При известной величине диагонали пентагона его сторона рассчитывается таким образом: а = D/1,618.
Площадь пентагона так же , как и его сторона, зависит от уже найденных параметров:
- с помощью известного радиуса вписанной окружности площадь находится так: S = (n*a*r)/2 = 2,5*a*r.
- описанная вокруг пятиугольника окружность позволяет найти площадь по такой формуле: S = (n*R2*sin α)/2 = 2,3776*R2.
- в зависимости от стороны пентагона: S = (5*a2*tg 54°)/4 = 1,7205* a2.
Построение пентагона
Построить правильный пятиугольник можно с помощью линейки и циркуля, на основе вписанной в него окружности или одной из сторон.
Как начертить пятиугольник на основе вписанной окружности? Для этого необходимо запастись циркулем и линейкой и сделать такие шаги:
- Сначала необходимо начертить окружность с центром О, после чего на ней выбрать точку, А — вершину пентагона. От центра к вершине проводится отрезок.
- Затем строится перпендикулярная прямой ОА отрезок, который также проходит через О — центр окружности. Его пересечение с окружностью обозначается точкой В. Отрезок О. В. делится пополам точкой С.
- Точка С станет центром новой окружности, проходящей через А. Точка D — это ее пересечение с прямой ОВ в границах первой фигуры.
- После этого проводится третья окружность через D, центром которой является точка А. Она пересекается с первой фигурой в двух точках, их необходимо обозначить буквами Е и F.
- Следующая окружность имеет центр в точке Е и проходит через А, а ее пересечение с первоначальной находится в новой точке G.
- Последняя окружность в этом рисунке проводится через точку, А с центром F. На ее пересечении с начальной ставится точка Н.
- На первой окружности после всех проделанных шагов появились пять точек, которые необходимо соединить отрезками. Таким образом получился правильный пятиугольник АЕ G Н F.
Как построить правильный пятиугольник иным способом? С помощью линейки и циркуля пентагон можно построить немного быстрее. Для этого необходимо:
- Cначала необходимо с помощью циркуля нарисовать окружность, центр которой — точка О.
- Чертится радиус ОА — отрезок, который откладывается на окружность. Его делят пополам точкой В.
- Перпендикулярно радиусу ОА начерчивается отрезок ОС, точки В и С соединяются прямой.
- Следующим шагом является отложение длины отрезка ВС с помощью циркуля на диаметральной линии. Перпендикулярно отрезку ОА появляется точка D. Точки В и D соединяются, образуя новый отрезок.
- Для того, чтобы получить величину стороны пентагона, необходимо соединить точки С и D.
- D с помощью циркуля переносится на окружность и обозначается точкой Е. Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.
В пятиугольнике с одинаковыми сторонами диагонали равны и образуют пятиконечную звезду, которая называется пентаграммой. Золотое сечение — это отношение величины диагонали к стороне пентагона.
Пентагон непригоден для полного заполнения плоскости. Использование любого материала в этой форме оставляет промежутки или образует наложения. Хотя природных кристаллов этой формы не существует в природе, но при образовании льда на поверхности гладких медных изделий возникают молекулы в виде пентагона, которые соединены в цепочки.
Наиболее простой способ получить правильный пятиугольник из полоски бумаги — завязать ее узлом и немного придавить. Этот способ полезен для родителей детей-дошкольников, которые хотят научить своих малышей распознавать геометрические фигуры.
Видео
Посмотрите, как можно быстро начертить пятиугольник.
Толковый словарь Ожегова гласит, что пятиугольник представляет собой ограниченную пятью пересекающимися прямыми, образующими пять внутренних углов, а также любой предмет подобной формы. Если у данного многоугольника все стороны и углы одинаковые, то он называется правильным (пентагоном).
Чем интересен правильный пятиугольник?
Именно в такой форме было построено всем известное здание Минобороны Соединенных Штатов. Из объемных правильных многогранников лишь додекаэдр имеет грани в форме пентагона. А в природе напрочь отсутствуют кристаллы, грани которых напоминали бы собой правильный пятиугольник. Кроме того, эта фигура является многоугольником с минимальным количеством углов, которым невозможно замостить площадь. Только у пятиугольника количество диагоналей совпадает с количеством его сторон. Согласитесь, это интересно!
Основные свойства и формулы
Воспользовавшись формулами для произвольного правильного многоугольника, можно определить все необходимые параметры, которые имеет пентагон.
- Центральный угол α = 360 / n = 360/5 =72°.
- Внутренний угол β = 180° * (n-2)/n = 180° * 3/5 = 108°. Соответственно, сумма внутренних углов составляет 540°.
- Отношение диагонали к боковой стороне равно (1+√5) /2, то есть (примерно 1,618).
- Длина стороны, которую имеет правильный пятиугольник, может быть рассчитана по одной из трех формул, в зависимости от того, какой параметр уже известен:
- если вокруг него описана окружность и известен ее радиус R, то а = 2*R*sin (α/2) = 2*R*sin(72°/2) ≈1,1756*R;
- в случае, когда окружность c радиусом r вписана в правильный пятиугольник, а = 2*r*tg(α/2) = 2*r*tg(α/2) ≈ 1,453*r;
- бывает так, что вместо радиусов известна величина диагонали D, тогда сторону определяют следующим образом: а ≈ D/1,618.
- Площадь правильного пятиугольника определяется, опять-таки, в зависимости от того, какой параметр нам известен:
- если имеется вписанная или описанная окружность, то используется одна из двух формул:
S = (n*a*r)/2 = 2,5*a*r либо S = (n*R 2 *sin α)/2 ≈ 2,3776*R 2 ;
- площадь можно также определить, зная лишь длину боковой стороны а:
S = (5*a 2 *tg54°)/4 ≈ 1,7205* a 2 .
Правильный пятиугольник: построение
Данную геометрическую фигуру можно построить по-разному. Например, вписать его в окружность с заданным радиусом либо построить на базе заданной боковой стороны. Последовательность действий была описана еще в «Началах» Евклида примерно 300 лет до н.э. В любом случае, нам понадобятся циркуль и линейка. Рассмотрим способ построения с помощью заданной окружности.
1. Выберите произвольный радиус и начертите окружность, обозначив ее центр точкой O.
2. На линии окружности выберите точку, которая будет служить одной из вершин нашего пятиугольника. Пусть это будет точка А. Соедините точки О и А прямым отрезком.
3. Проведите прямую через точку О перпендикулярно к прямой ОА. Место пересечения этой прямой с линией окружности обозначьте, как точку В.
4. На середине расстояния между точками О и В постройте точку С.
5. Теперь начертите окружность, центр которой будет в точке С и которая будет проходить через точку А. Место ее пересечения с прямой OB (оно окажется внутри самой первой окружности) будет точкой D.
6. Постройте окружность, проходящую через D, центр которой будет в А. Места ее пересечения с первоначальной окружностью нужно обозначить точками Е и F.
7. Теперь постройте окружность, центр которой будет в Е. Сделать это надо так, чтобы она проходила через А. Ее другое место пересечения оригинальной окружности нужно обозначить
8. Наконец, постройте окружность через А с центром в точке F. Обозначьте другое место пересечения оригинальной окружности точкой H.
9. Теперь осталось только соединить вершины A, E, G, H, F. Наш правильный пятиугольник будет готов!
Как нарисовать пятиугольник с помощью компаса
Пятиугольник — это пятиугольник, стороны которого равны по длине. Это может быть полезная форма при изготовлении реквизита; он также может служить основой для пятигранной звезды. Может быть сложно разметить с помощью стандартных инструментов для рисования, но с помощью метода, описанного ниже, вы можете нарисовать его только с помощью циркуля и линейки.
Начните с круга, размер которого идеально подходит для вашего пятиугольника; то есть каждый угол вашего пятиугольника будет касаться внешней стороны вашего круга.
Рисунок 1В моем круге я нарисовал две перпендикулярные линии, проходящие через центральную точку O. Там, где они пересекают круг, я пометил A, X, Y и Z (A будет верхней точкой пятиугольника, поэтому поместите это соответственно).
Я разделил линию OY пополам, чтобы найти точку M; то есть M находится точно на полпути между O и Y.
Рисунок 2Поместите циркуль на M и вытяните его так, чтобы карандаш касался A. Нарисуйте дугу, пересекающую линию XO; мы назовем это пересечение «R».
Рисунок 3Переместите точку циркуля на A и вытяните его так, чтобы карандаш касался R. Теперь радиус вашего циркуля равен длине сторон вашей пентаграммы. Когда вы рисуете дугу от R до вашего круга, вы найдете точку «B».
Рис. 4Когда вы перемещаете компас для поворота на B и рисуете дугу, он пересекает круг в двух точках: A и в новой точке «C».
Рис. 5Вернув компас к точке А, нарисуйте дугу, пересекающую правую сторону круга, чтобы найти букву «Е».
Рисунок 6Переместите циркуль в положение E и нарисуйте дугу, чтобы найти «D». На картинке выше я нарисовал дугу так, чтобы она дважды пересекала круг, в точке D и снова в точке A. На самом деле этого делать не нужно.
Чтобы проверить, что у вашего пятиугольника пять равных сторон, вы можете поставить точку циркуля на D. Карандаш должен коснуться C.
Рис. 7A, B, C, D и E — углы вашего пятиугольника. Осталось только соединить их линейкой. Престо! Идеальные пятиугольники!
Эссе 2: Построение правильных многоугольников
Шона Д.Broderick
Правильные многоугольники — это замкнутые плоские фигуры, состоящие из ребер равной длины и вершин равного размера. Самый простой правильный многоугольник — это равносторонний треугольник, который состоит из трех ребер равной длины и трех углов между каждой парой ребер, составляющих 60 градусов. Три ребра — это наименьшее количество ребер для построения многоугольника, потому что два ребра образуют угол, а одно ребро — сегмент. Полигоны — это замкнутые фигуры. Правильный многоугольник с четырьмя ребрами и есть квадрат. Пять ребер составляют пятиугольник, а шесть — шестиугольник.
Мы исследуем, как построить правильные многоугольники, используя циркуль и линейку, в сравнении с программой динамической геометрии, такой как Sketchpad Geometer.
Сначала рассмотрим построение равностороннего треугольника с помощью линейки и циркуля. Это простейший правильный многоугольник на плоскости. Он состоит из трех сторон.
1. Мы начинаем с рисования произвольной точки A.
2. Затем мы открываем наш компас на фиксированное расстояние и делаем небольшую отметку справа от нашей точки A.Это то место, где в конечном итоге будет наша точка B.
3. Не отрывая стрелки циркуля от бумаги, перемещаем конец карандаша вверх и к середине и делаем еще одну отметку. Это будет то место, куда в конечном итоге попадет точка C.
4. Теперь мы помечаем нашу точку B в любом месте отметки. (Почему мы можем отметить его где-нибудь на линии и при этом сохранить определенную длину?)
5. Теперь поместите конец циркуля в точку B и сделайте отметку вверх и до середины, пересекая место, куда пойдет точка C.
6. Отметьте пересечение как точку C.
7. Используя линейку, проведите первую сторону треугольника от A до B.
8. Снова, используя линейку, проведите вторую сторону треугольника от B по C.
9. Нарисуйте последнюю сторону. На этом мы закончили построение равностороннего треугольника.
Теперь мы сравним этот процесс с процессом, который можно использовать для построения равностороннего треугольника в GSP:
1. Начнем с рисования отрезка произвольной длины.Это будет одна из сторон нашего треугольника.
2. Обозначим точки A для левой точки и B для правой точки.
3. Теперь мы построим круг, используя точку B в качестве центра и точку A в качестве края.
4. Затем мы делаем еще один круг, используя точку A в качестве центра и точку B в качестве края.
5. Строим их пересечение и маркируем его точкой C.
6. Строим отрезок AC.
7. Строим отрезок ВС.
8. Если мы скроем наши круги, у нас теперь есть равносторонний треугольник.
1. Почему эти конструкции работают?
2. Что делает этот треугольник равносторонним в любой из сред?
3. Теряем ли мы что-нибудь или получаем что-нибудь, если учим студентов делать это, используя один, другой или оба средства?
1 (и часть 2). В классе мы обсуждали, что эти равносторонние треугольники работают, потому что две окружности, которые построены, или отметки из двух окружностей, мы увидим, что сегменты треугольника являются радиусами окружностей. Если круги одинакового размера, то радиусы одинакового размера и их положение таково, что они пересекаются в трех точках (центры кругов и их пересечение).Вот диаграмма, которая может помочь:
Мы начали с одного круга и построили два радиуса. Затем мы отразили круг поперек линии, чтобы получилось два круга.
Мы выберем один круг и объединим его с другим, чтобы показать, как радиусы образуют равносторонний треугольник.
По мере приближения мы видим, что радиусы образуют треугольник.
Поскольку круги слились и теперь имеют общие радиусы, образующие основу, мы можем видеть, что, поскольку все радиусы равны, если они перекрываются, образуя основание, а два других соединяются наверху, у нас должен быть равносторонний треугольник.
Остальные части 2. Мы видели, что составляет равносторонний треугольник в GSP, но что касается конструкции из карандаша и бумаги, мы видим, что они такие же, но вместо того, чтобы использовать круги, чтобы показать конгруэнтность радиусов, компас (открытость которого остается постоянной) используется для создания конгруэнтных радиусов.
3. Мы можем немного потерять конструкцию из карандаша и бумаги, потому что круги полностью проиллюстрированы в GSP, а с карандашом и бумагой мы видим только дуги кругов, а равномерное расстояние, созданное компасом, скрыто.Однако я считаю, что оба типа конструкций полезны для того, чтобы у учащихся было более полное представление о конструкциях.
Давайте посмотрим, как построить квадрат. Снова начнем с построения с помощью циркуля и линейки:
1. Мы отмечаем точку A, устанавливаем наш циркуль на определенную длину и делаем отметку. Нам нужно сохранить эту длину, поэтому не теряйте ее.
2. Мы отмечаем точку на отметке компаса, B.
3. Затем мы проводим прямую линию через точку A и точку B.
4. Используя циркуль при текущей настройке, сделайте отметку слева от точки A и справа от точки B.
5. Если мы хотим сделать квадрат, нам нужно построить перпендикулярные линии, идущие вверх от точек A и B. Итак, для этого нам нужно немного удлинить циркуль от нашей произвольной длины. Затем мы размещаем точку на самом левом пересечении и делаем дугу, как показано выше. Затем мы помещаем конец циркуля в точку B и делаем еще одну дугу вокруг точки A, чтобы они пересекались, как показано на рисунке.Повторите этот процесс, чтобы сделать аналогичные дуги вокруг точки B. Начните с точки циркуля на точке A и сделайте дугу вокруг B. Затем поместите точку циркуля на крайнее правое пересечение и сделайте дугу, соединяющуюся с другим. , охватывающую точку B.
6. Сначала сделайте две отметки над точками A и B, используя исходный циркуль произвольной длины. Это будет означать высоту квадрата. Он будет точно такой же длины, как и от A до B, поэтому он будет квадратным.Далее нам нужно выяснить, где будет вершина квадрата. Вот почему мы сделали дуги. Используя линейку, проведите линию от A вверх через две дуги вокруг A и пересеките ее с отметкой сверху. На иллюстрации показано, как это могло теперь выглядеть.
7. Теперь мы закончим построение, проведя перпендикулярную линию вверх от B до отметки и обозначив эту точку пересечения C. Наконец, мы соединяем точку D и точку C, чтобы закончить квадрат.
Теперь проиллюстрируем, как можно построить квадрат, используя GSP:
1.Постройте отрезок произвольной длины.
2. Постройте круг, используя A как центр и B как край. В верхней части круга мы отметили расстояние, такое же, как и от A до B.
3. Итак, теперь мы строим перпендикулярную линию через A к отрезку AB. Пересечение этой линии через вершину круга мы обозначим точкой D.
4. Построим перпендикулярную линию через точку D к прямой AD.
5. Затем мы строим еще одну перпендикулярную линию, на этот раз через точку B к прямой AB.
6. Мы обозначаем эту точку, C.
7.Если мы скроем объекты, которые помогли нам в строительстве, мы получим построенный квадрат ABCD.
Комментарий:
Кажется, что причина, по которой это работает, аналогична объяснению равностороннего треугольника. Вот несколько эскизов:
Здесь мы имеем тот же тип конструкции, что и у треугольника. Теперь наши радиусы перпендикулярны и одинаковой длины. Это похоже на атрибуты квадрата.
Теперь мы выделяем две точки на одном круге и объединяем их с другим.
Как только они объединятся, мы увидим квадрат. Просто соединяем верхние точки и у нас будет наш квадрат.
Теперь обратим наше внимание на построение пятиугольника с помощью циркуля и линейки. Сначала я понятия не имел, как это сделать, поэтому мне пришлось использовать Интернет. Есть много разных способов построить пятиугольник. Основное внимание в этом эссе уделяется тому, чтобы показать, как это сделать, и обсудить, почему этот подход работает.Что за математика стоит за этим?
1. Пятиугольник состоит из круга. Каждая из вершин будет пересекаться с краем круга. Итак, сначала строим круг с помощью циркуля. Далее мы проводим линию по центру круга, разделяя его пополам.
2. Нам нужно построить еще одну линию, разделяющую левую половину круга пополам. На рисунке мы сделали это, разделив пополам угол 180 градусов, идущий вниз по середине круга.Для этого выставляем компас на определенную точку открытия. Мы помещаем конец циркуля в центр круга и делаем отметки на обоих лучах на произвольном расстоянии. Затем мы помещаем конец циркуля в сделанные отметки и делаем еще одну отметку в области, где будет проходить деление угла пополам. Создает X, пересечение которого — это то место, где должен пройти луч круга. Проведите линейкой биссектрису угла.
3.Следующая цель — построить середину отрезка, который мы только что нарисовали. Для этого мы открываем компас на произвольное расстояние, которое чуть больше, чем приблизительная средняя точка сегмента. Помещаем конец циркуля в центр круга и делаем отметку дуги как на картинке. Затем мы сохраняем измерение компаса как есть и помещаем точку компаса на пересечение сегмента и края круга и делаем аналогичную отметку. Если компас открыт достаточно далеко, дуги должны пересекаться, как показано.Если эти новые пересечения соединены, пересечение обоих сегментов является средней точкой сегмента.
4. Затем соедините середину найденного сегмента с вершиной круга и с пересечением разделительной линии и края круга. Наша следующая цель — разделить пополам угол, образованный отрезком, от центра к краю и средней точки к краю, как показано на рисунке. Используем те же методы, что и в начале.Раскрываем циркуль на произвольную длину, которая меньше длины отрезков угла. Поместив острие циркуля в вершину угла, делаем отметки на отрезках угла. Затем мы немного закрываем циркуль и помещаем его конец на сделанные нами отметки и делаем новые отметки в направлении центра угла. Эти отметки должны пересекаться под биссектрисой угла. Проведена линия биссектрисы угла от вершины угла через точку X до линии, разделяющей круг на две равные части.(На самом деле, как показано на следующем рисунке, вам нужно продлить биссектрису угла за вертикальную линию.)
5. Следующая цель — построить линию, параллельную горизонтальному сегменту, в точке пересечения вертикального сегмента и биссектрисы угла. Это делается путем размещения точки циркуля в вершине угла, разделенного пополам, и разметки угла дугой, как показано. Там, где биссектриса угла пересекает вертикальный сегмент, поместите точку циркуля и нарисуйте еще одну дугу, как и раньше.Затем мы открываем компас ровно настолько, чтобы переходить от углового сегмента к угловому сегменту на сделанной вами отметке. Затем сделайте еще одну отметку вниз от дуги, которую вы делаете выше, и это пересечение является точкой, где параллельная линия может быть проведена через пересечение биссектрисы угла и вертикальной линии. Давай, сделай так.
6. Соедините точку пересечения нового сегмента и края круга с верхним пересечением вертикальной линии и края круга, и мы построили первую сторону нашего пятиугольника.
7. Теперь нам нужно повторить весь этот процесс, чтобы построить еще три стороны. Четвертую сторону можно соединить с пятой, не делая конструкции. Однако мы все равно делаем его, чтобы убедиться, что фигура построена правильно. Теперь нам просто нужно определиться, с чего начать. Поскольку мы построили сторону, начинающуюся сверху и наклоненную вниз влево, мы делаем наш сегмент, проходящий через центр круга, начиная с последней точки, которую мы только что построили.
8. Повторим этот процесс в другой раз.
9. Повторяем этот процесс еще раз.
10. Теперь мы закончим построением последней стороны, хотя в этом нет необходимости. Теперь у нас есть пятиугольник ABCDE.
Мне также любопытно, что есть математические побочные продукты построения пятиугольника, которые можно наблюдать.Это большой круг на внешней стороне конструкции, прежде чем мы его скроем. Кроме того, внутри пятиугольника есть маленький кружок, если дуги, определяющие середину сегмента, были немного более согласованными. Внутри большого тоже есть маленький пятиугольник. Однако регулярно ли это? Это пропорционально большому пятиугольнику? Если бы конструкция была нарисована идеально, был бы маленький пятиугольник правильным? Означает ли это, что большой пятиугольник не совсем правильный?
Теперь мы покажем этот же процесс с помощью GSP:
1.Строим круг произвольной длины. Затем мы проводим линию по центру круга.
2. Затем мы строим перпендикулярную линию к вертикальной линии, проходящей через центр круга. Мы делаем отрезок с линией, которую только что создали, от центра к левому краю. Затем мы строим середину этого отрезка.
3. Оттуда мы проводим линию, соединяющую среднюю точку с вершиной круга.Это создает угол, а затем мы строим биссектрису угла.
4. Мы строим линию, параллельную предыдущей горизонтальной линии, и пересечение новой линии с краем круга является точкой для создания первой стороны нашего пятиугольника. Теперь рисуем эту сторону. Этот процесс будет повторяться с разными цветами, начиная с боковой точки, которую мы только что построили.
5.Теперь повторяем этот процесс для второй стороны бордового цвета.
6. Повторяем этот процесс еще раз с оранжевым.
7. Мы повторяем этот процесс с розовым или темно-синим цветом, каким бы он ни был. На этом этапе мы можем просто соединить последние две стороны, но, поскольку меня интересовала внутренняя геометрия, я повторил процесс еще раз, чтобы посмотреть, поможет ли точность GSP.
8. Кажется, что в середине этого сооружения происходит много всего. Однако пятиугольник, который, как я думал, находится прямо внутри, не так идеально расположен, как я думал.
9. Если мы скроем все тонкие линии, мы увидим наш пятиугольник.
Вопрос:
Почему это работает?
Ответ:
В классе мы обсуждали использование золотого сечения.В пятиугольнике,
отношение длины красной диагонали к длине стороны равно специальному числу.
Мы будем использовать эту демонстрацию, чтобы показать, как конструкция выше представляет собой пятиугольник. Теперь сделаем круг радиуса с одной стороной единицы длины:
.Затем мы наклеили несколько ярлыков, чтобы облегчить обсуждение:
Сначала мы замечаем, что треугольник ABF похож на треугольник AEB .На основании этого можно сделать вывод, что:
Тогда через подстановку получаем:
Что дает:
Мы знаем, что фи — это золотое сечение. Таким образом, мы имеем утверждение, что отношение длины диагонали правильного пятиугольника к длине его стороны есть золотое сечение. Теперь посмотрим на нашу конструкцию:
Чтобы обсудить, почему эта конструкция представляет собой пятиугольник, мы используем вышеуказанные метки.Наша цель — доказать, что отношение диагонали пятиугольника (EF) к стороне (AE) равно фи или золотому сечению, тогда фигура оказывается пятиугольником. Изображенная выше конструкция является той же конструкцией, которую мы использовали, за исключением того, что я построил сегмент EO, чтобы облегчить вычисление EF.
Я начинаю с того, что нам дано, что отрезки AO, BO и EO имеют длину 2 единицы. Сегменты BC и CO имеют длину одну единицу, потому что C является средней точкой BO. Если AO равно 2, а CO равно 1, то AC:
Теперь мы можем найти угол ACO с помощью тригонометрии.Следовательно, угол ACO равен:
Таким образом, угол DCO равен половине этого, по определению:
Сегмент DO / 1 равен:
Поскольку мы знаем, что EO равно 2, мы используем теорему Пифагора, чтобы найти ED. Таким образом, ED 2 + DO 2 = EO 2 . Итак, имеем:
Следовательно, ED =
Мы умножаем это выражение на 2, чтобы получить длину EF.Итак, EF =
Мы на полпути к нашей цели. Помните, что мы рассчитываем соотношение длины стороны нашей фигуры к длине диагонали. У нас есть диагональ EF. Теперь мы ищем длину стороны, скажем AE. Мы планируем использовать теорему Пифагора, чтобы найти AE. Мы будем использовать уравнение AE 2 = ED 2 + AD 2 . Мы знаем ED и можем найти AD с выражением 2 — DO. Следовательно, решаем:
Когда мы находим AE и используем наш калькулятор для десятичного приближения, мы получаем AE = 2.35114100917. Десятичное приближение для EF = 3,80422606518. Тогда EF / AE = 1,61803398875. Десятичное приближение для золотого сечения — это то же самое, что и мое приближение для EF / AE. Следовательно, эта конструкция дает правильный многоугольник.
Теперь перейдем к разделу о построении шестиугольника с линейкой и циркулем:
1. Начнем с построения круга произвольного размера.
2. Делаем отметку на краю круга с правой стороны.Сохраняя исходный произвольный размер компаса, мы помещаем точку циркуля на эту отметку и отмечаем пересечения круга сверху и снизу.
3. Теперь мы рисуем диаметр круга от верхнего пересечения кругов через центр и продолжаем через противоположный край внизу с помощью нашей линейки.
4. Проделываем то же самое на противоположном перекрестке.
5.Теперь мы можем приступить к построению сторон шестиугольника. Наша первая сторона идет от отмеченной нами правой точки до верхнего пересечения круга.
6. Наша вторая сторона соединяет верхние перекрестки. Но подождите, куда пойдет наша третья сторона?
7. Делаем нашу третью сторону, строя линию, соединяющую отметки центров наших двух кругов. Если мы продолжим эту линию через другую сторону, у нас будет пересечение слева, которое отмечает точку, где наша третья сторона закончится.Теперь мы можем построить эту третью сторону.
8. Мы рисуем четвертую сторону, начиная с только что созданного пересечения и заканчивая левым нижним пересечением.
9. Наша пятая сторона построена путем соединения нижних перекрестков.
10. Мы закончили конструирование сторон шестиугольника, соединив точки пересечения от правого нижнего до крайней правой отметки.
11.У нас есть шестиугольник!
Хм … Похоже, верх немного криво … Не знаю, почему так получилось. Мы снова спрашиваем, как эта конструкция дает шестиугольник. Связано ли это с умением создавать внутренние или дополнительные углы?
Мы выполняем этот процесс в GSP:
1. Сначала строим круг произвольного размера.
2. Затем мы строим горизонтальную линию от центра круга до края.
3. Затем мы строим еще один круг, используя край первого в качестве центра и центр первого в качестве края.
4. Затем мы строим линию через центр первого круга и верхнее пересечение обоих кругов.
5. Затем мы строим еще одну линию через центр первого круга, которая проходит через нижнее пересечение кругов.
6.Теперь мы готовы нарисовать стороны нашего шестиугольника. Первая сторона начинается от нижнего пересечения обоих кругов и идет к центру второго круга.
7. Вторая сторона идет от нижнего пересечения двух кругов до нижнего пересечения первой линии, которую мы нарисовали, и первого круга.
8. Третья сторона идет от нижнего пересечения первой окружности и первой линии до левого пересечения горизонтальной линии и первой окружности.
9. Четвертая сторона идет от пересечения первой окружности и горизонтальной линии до верхнего пересечения первой окружности и второй линии.
10. Пятая сторона идет от верхнего пересечения первого круга и второй линии до верхнего пересечения обоих кругов.
11. Шестая сторона соединяет пятую сторону с первой стороной, и у нас есть шестиугольник.
12.Когда мы скрываем линии и помечаем вершины, мы получаем чистое изображение нашего построенного шестиугольника.
Теперь мы подошли к вопросу о том, как построить семиугольник. Невозможно построить идеально правильный семиугольник, используя только линейку и циркуль, как мы делали раньше. Итак, мой вопрос: почему это так?
Поскольку это невозможно, я считаю, что сейчас самое время закончить это эссе.
Эссе 2: Построение правильных многоугольников
Шона Д.Broderick
Правильные многоугольники — это замкнутые плоские фигуры, состоящие из ребер равной длины и вершин равного размера. Самый простой правильный многоугольник — это равносторонний треугольник, который состоит из трех ребер равной длины и трех углов между каждой парой ребер, составляющих 60 градусов. Три ребра — это наименьшее количество ребер для построения многоугольника, потому что два ребра образуют угол, а одно ребро — сегмент. Полигоны — это замкнутые фигуры. Правильный многоугольник с четырьмя ребрами и есть квадрат. Пять ребер составляют пятиугольник, а шесть — шестиугольник.
Мы исследуем, как построить правильные многоугольники, используя циркуль и линейку, в сравнении с программой динамической геометрии, такой как Sketchpad Geometer.
Сначала рассмотрим построение равностороннего треугольника с помощью линейки и циркуля. Это простейший правильный многоугольник на плоскости. Он состоит из трех сторон.
1. Мы начинаем с рисования произвольной точки A.
2. Затем мы открываем наш компас на фиксированное расстояние и делаем небольшую отметку справа от нашей точки A.Это то место, где в конечном итоге будет наша точка B.
3. Не отрывая стрелки циркуля от бумаги, перемещаем конец карандаша вверх и к середине и делаем еще одну отметку. Это будет то место, куда в конечном итоге попадет точка C.
4. Теперь мы помечаем нашу точку B в любом месте отметки. (Почему мы можем отметить его где-нибудь на линии и при этом сохранить определенную длину?)
5. Теперь поместите конец циркуля в точку B и сделайте отметку вверх и до середины, пересекая место, куда пойдет точка C.
6. Отметьте пересечение как точку C.
7. Используя линейку, проведите первую сторону треугольника от A до B.
8. Снова, используя линейку, проведите вторую сторону треугольника от B по C.
9. Нарисуйте последнюю сторону. На этом мы закончили построение равностороннего треугольника.
Теперь мы сравним этот процесс с процессом, который можно использовать для построения равностороннего треугольника в GSP:
1. Начнем с рисования отрезка произвольной длины.Это будет одна из сторон нашего треугольника.
2. Обозначим точки A для левой точки и B для правой точки.
3. Теперь мы построим круг, используя точку B в качестве центра и точку A в качестве края.
4. Затем мы делаем еще один круг, используя точку A в качестве центра и точку B в качестве края.
5. Строим их пересечение и маркируем его точкой C.
6. Строим отрезок AC.
7. Строим отрезок ВС.
8. Если мы скроем наши круги, у нас теперь есть равносторонний треугольник.
1. Почему эти конструкции работают?
2. Что делает этот треугольник равносторонним в любой из сред?
3. Теряем ли мы что-нибудь или получаем что-нибудь, если учим студентов делать это, используя один, другой или оба средства?
1 (и часть 2). В классе мы обсуждали, что эти равносторонние треугольники работают, потому что две окружности, которые построены, или отметки из двух окружностей, мы увидим, что сегменты треугольника являются радиусами окружностей. Если круги одинакового размера, то радиусы одинакового размера и их положение таково, что они пересекаются в трех точках (центры кругов и их пересечение).Вот диаграмма, которая может помочь:
Мы начали с одного круга и построили два радиуса. Затем мы отразили круг поперек линии, чтобы получилось два круга.
Мы выберем один круг и объединим его с другим, чтобы показать, как радиусы образуют равносторонний треугольник.
По мере приближения мы видим, что радиусы образуют треугольник.
Поскольку круги слились и теперь имеют общие радиусы, образующие основу, мы можем видеть, что, поскольку все радиусы равны, если они перекрываются, образуя основание, а два других соединяются наверху, у нас должен быть равносторонний треугольник.
Остальные части 2. Мы видели, что составляет равносторонний треугольник в GSP, но что касается конструкции из карандаша и бумаги, мы видим, что они такие же, но вместо того, чтобы использовать круги, чтобы показать конгруэнтность радиусов, компас (открытость которого остается постоянной) используется для создания конгруэнтных радиусов.
3. Мы можем немного потерять конструкцию из карандаша и бумаги, потому что круги полностью проиллюстрированы в GSP, а с карандашом и бумагой мы видим только дуги кругов, а равномерное расстояние, созданное компасом, скрыто.Однако я считаю, что оба типа конструкций полезны для того, чтобы у учащихся было более полное представление о конструкциях.
Давайте посмотрим, как построить квадрат. Снова начнем с построения с помощью циркуля и линейки:
1. Мы отмечаем точку A, устанавливаем наш циркуль на определенную длину и делаем отметку. Нам нужно сохранить эту длину, поэтому не теряйте ее.
2. Мы отмечаем точку на отметке компаса, B.
3. Затем мы проводим прямую линию через точку A и точку B.
4. Используя циркуль при текущей настройке, сделайте отметку слева от точки A и справа от точки B.
5. Если мы хотим сделать квадрат, нам нужно построить перпендикулярные линии, идущие вверх от точек A и B. Итак, для этого нам нужно немного удлинить циркуль от нашей произвольной длины. Затем мы размещаем точку на самом левом пересечении и делаем дугу, как показано выше. Затем мы помещаем конец циркуля в точку B и делаем еще одну дугу вокруг точки A, чтобы они пересекались, как показано на рисунке.Повторите этот процесс, чтобы сделать аналогичные дуги вокруг точки B. Начните с точки циркуля на точке A и сделайте дугу вокруг B. Затем поместите точку циркуля на крайнее правое пересечение и сделайте дугу, соединяющуюся с другим. , охватывающую точку B.
6. Сначала сделайте две отметки над точками A и B, используя исходный циркуль произвольной длины. Это будет означать высоту квадрата. Он будет точно такой же длины, как и от A до B, поэтому он будет квадратным.Далее нам нужно выяснить, где будет вершина квадрата. Вот почему мы сделали дуги. Используя линейку, проведите линию от A вверх через две дуги вокруг A и пересеките ее с отметкой сверху. На иллюстрации показано, как это могло теперь выглядеть.
7. Теперь мы закончим построение, проведя перпендикулярную линию вверх от B до отметки и обозначив эту точку пересечения C. Наконец, мы соединяем точку D и точку C, чтобы закончить квадрат.
Теперь проиллюстрируем, как можно построить квадрат, используя GSP:
1.Постройте отрезок произвольной длины.
2. Постройте круг, используя A как центр и B как край. В верхней части круга мы отметили расстояние, такое же, как и от A до B.
3. Итак, теперь мы строим перпендикулярную линию через A к отрезку AB. Пересечение этой линии через вершину круга мы обозначим точкой D.
4. Построим перпендикулярную линию через точку D к прямой AD.
5. Затем мы строим еще одну перпендикулярную линию, на этот раз через точку B к прямой AB.
6. Мы обозначаем эту точку, C.
7.Если мы скроем объекты, которые помогли нам в строительстве, мы получим построенный квадрат ABCD.
Комментарий:
Кажется, что причина, по которой это работает, аналогична объяснению равностороннего треугольника. Вот несколько эскизов:
Здесь мы имеем тот же тип конструкции, что и у треугольника. Теперь наши радиусы перпендикулярны и одинаковой длины. Это похоже на атрибуты квадрата.
Теперь мы выделяем две точки на одном круге и объединяем их с другим.
Как только они объединятся, мы увидим квадрат. Просто соединяем верхние точки и у нас будет наш квадрат.
Теперь обратим наше внимание на построение пятиугольника с помощью циркуля и линейки. Сначала я понятия не имел, как это сделать, поэтому мне пришлось использовать Интернет. Есть много разных способов построить пятиугольник. Основное внимание в этом эссе уделяется тому, чтобы показать, как это сделать, и обсудить, почему этот подход работает.Что за математика стоит за этим?
1. Пятиугольник состоит из круга. Каждая из вершин будет пересекаться с краем круга. Итак, сначала строим круг с помощью циркуля. Далее мы проводим линию по центру круга, разделяя его пополам.
2. Нам нужно построить еще одну линию, разделяющую левую половину круга пополам. На рисунке мы сделали это, разделив пополам угол 180 градусов, идущий вниз по середине круга.Для этого выставляем компас на определенную точку открытия. Мы помещаем конец циркуля в центр круга и делаем отметки на обоих лучах на произвольном расстоянии. Затем мы помещаем конец циркуля в сделанные отметки и делаем еще одну отметку в области, где будет проходить деление угла пополам. Создает X, пересечение которого — это то место, где должен пройти луч круга. Проведите линейкой биссектрису угла.
3.Следующая цель — построить середину отрезка, который мы только что нарисовали. Для этого мы открываем компас на произвольное расстояние, которое чуть больше, чем приблизительная средняя точка сегмента. Помещаем конец циркуля в центр круга и делаем отметку дуги как на картинке. Затем мы сохраняем измерение компаса как есть и помещаем точку компаса на пересечение сегмента и края круга и делаем аналогичную отметку. Если компас открыт достаточно далеко, дуги должны пересекаться, как показано.Если эти новые пересечения соединены, пересечение обоих сегментов является средней точкой сегмента.
4. Затем соедините середину найденного сегмента с вершиной круга и с пересечением разделительной линии и края круга. Наша следующая цель — разделить пополам угол, образованный отрезком, от центра к краю и средней точки к краю, как показано на рисунке. Используем те же методы, что и в начале.Раскрываем циркуль на произвольную длину, которая меньше длины отрезков угла. Поместив острие циркуля в вершину угла, делаем отметки на отрезках угла. Затем мы немного закрываем циркуль и помещаем его конец на сделанные нами отметки и делаем новые отметки в направлении центра угла. Эти отметки должны пересекаться под биссектрисой угла. Проведена линия биссектрисы угла от вершины угла через точку X до линии, разделяющей круг на две равные части.(На самом деле, как показано на следующем рисунке, вам нужно продлить биссектрису угла за вертикальную линию.)
5. Следующая цель — построить линию, параллельную горизонтальному сегменту, в точке пересечения вертикального сегмента и биссектрисы угла. Это делается путем размещения точки циркуля в вершине угла, разделенного пополам, и разметки угла дугой, как показано. Там, где биссектриса угла пересекает вертикальный сегмент, поместите точку циркуля и нарисуйте еще одну дугу, как и раньше.Затем мы открываем компас ровно настолько, чтобы переходить от углового сегмента к угловому сегменту на сделанной вами отметке. Затем сделайте еще одну отметку вниз от дуги, которую вы делаете выше, и это пересечение является точкой, где параллельная линия может быть проведена через пересечение биссектрисы угла и вертикальной линии. Давай, сделай так.
6. Соедините точку пересечения нового сегмента и края круга с верхним пересечением вертикальной линии и края круга, и мы построили первую сторону нашего пятиугольника.
7. Теперь нам нужно повторить весь этот процесс, чтобы построить еще три стороны. Четвертую сторону можно соединить с пятой, не делая конструкции. Однако мы все равно делаем его, чтобы убедиться, что фигура построена правильно. Теперь нам просто нужно определиться, с чего начать. Поскольку мы построили сторону, начинающуюся сверху и наклоненную вниз влево, мы делаем наш сегмент, проходящий через центр круга, начиная с последней точки, которую мы только что построили.
8. Повторим этот процесс в другой раз.
9. Повторяем этот процесс еще раз.
10. Теперь мы закончим построением последней стороны, хотя в этом нет необходимости. Теперь у нас есть пятиугольник ABCDE.
Мне также любопытно, что есть математические побочные продукты построения пятиугольника, которые можно наблюдать.Это большой круг на внешней стороне конструкции, прежде чем мы его скроем. Кроме того, внутри пятиугольника есть маленький кружок, если дуги, определяющие середину сегмента, были немного более согласованными. Внутри большого тоже есть маленький пятиугольник. Однако регулярно ли это? Это пропорционально большому пятиугольнику? Если бы конструкция была нарисована идеально, был бы маленький пятиугольник правильным? Означает ли это, что большой пятиугольник не совсем правильный?
Теперь мы покажем этот же процесс с помощью GSP:
1.Строим круг произвольной длины. Затем мы проводим линию по центру круга.
2. Затем мы строим перпендикулярную линию к вертикальной линии, проходящей через центр круга. Мы делаем отрезок с линией, которую только что создали, от центра к левому краю. Затем мы строим середину этого отрезка.
3. Оттуда мы проводим линию, соединяющую среднюю точку с вершиной круга.Это создает угол, а затем мы строим биссектрису угла.
4. Мы строим линию, параллельную предыдущей горизонтальной линии, и пересечение новой линии с краем круга является точкой для создания первой стороны нашего пятиугольника. Теперь рисуем эту сторону. Этот процесс будет повторяться с разными цветами, начиная с боковой точки, которую мы только что построили.
5.Теперь повторяем этот процесс для второй стороны бордового цвета.
6. Повторяем этот процесс еще раз с оранжевым.
7. Мы повторяем этот процесс с розовым или темно-синим цветом, каким бы он ни был. На этом этапе мы можем просто соединить последние две стороны, но, поскольку меня интересовала внутренняя геометрия, я повторил процесс еще раз, чтобы посмотреть, поможет ли точность GSP.
8. Кажется, что в середине этого сооружения происходит много всего. Однако пятиугольник, который, как я думал, находится прямо внутри, не так идеально расположен, как я думал.
9. Если мы скроем все тонкие линии, мы увидим наш пятиугольник.
Вопрос:
Почему это работает?
Ответ:
В классе мы обсуждали использование золотого сечения.В пятиугольнике,
отношение длины красной диагонали к длине стороны равно специальному числу.
Мы будем использовать эту демонстрацию, чтобы показать, как конструкция выше представляет собой пятиугольник. Теперь сделаем круг радиуса с одной стороной единицы длины:
.Затем мы наклеили несколько ярлыков, чтобы облегчить обсуждение:
Сначала мы замечаем, что треугольник ABF похож на треугольник AEB .На основании этого можно сделать вывод, что:
Тогда через подстановку получаем:
Что дает:
Мы знаем, что фи — это золотое сечение. Таким образом, мы имеем утверждение, что отношение длины диагонали правильного пятиугольника к длине его стороны есть золотое сечение. Теперь посмотрим на нашу конструкцию:
Чтобы обсудить, почему эта конструкция представляет собой пятиугольник, мы используем вышеуказанные метки.Наша цель — доказать, что отношение диагонали пятиугольника (EF) к стороне (AE) равно фи или золотому сечению, тогда фигура оказывается пятиугольником. Изображенная выше конструкция является той же конструкцией, которую мы использовали, за исключением того, что я построил сегмент EO, чтобы облегчить вычисление EF.
Я начинаю с того, что нам дано, что отрезки AO, BO и EO имеют длину 2 единицы. Сегменты BC и CO имеют длину одну единицу, потому что C является средней точкой BO. Если AO равно 2, а CO равно 1, то AC:
Теперь мы можем найти угол ACO с помощью тригонометрии.Следовательно, угол ACO равен:
Таким образом, угол DCO равен половине этого, по определению:
Сегмент DO / 1 равен:
Поскольку мы знаем, что EO равно 2, мы используем теорему Пифагора, чтобы найти ED. Таким образом, ED 2 + DO 2 = EO 2 . Итак, имеем:
Следовательно, ED =
Мы умножаем это выражение на 2, чтобы получить длину EF.Итак, EF =
Мы на полпути к нашей цели. Помните, что мы рассчитываем соотношение длины стороны нашей фигуры к длине диагонали. У нас есть диагональ EF. Теперь мы ищем длину стороны, скажем AE. Мы планируем использовать теорему Пифагора, чтобы найти AE. Мы будем использовать уравнение AE 2 = ED 2 + AD 2 . Мы знаем ED и можем найти AD с выражением 2 — DO. Следовательно, решаем:
Когда мы находим AE и используем наш калькулятор для десятичного приближения, мы получаем AE = 2.35114100917. Десятичное приближение для EF = 3,80422606518. Тогда EF / AE = 1,61803398875. Десятичное приближение для золотого сечения — это то же самое, что и мое приближение для EF / AE. Следовательно, эта конструкция дает правильный многоугольник.
Теперь перейдем к разделу о построении шестиугольника с линейкой и циркулем:
1. Начнем с построения круга произвольного размера.
2. Делаем отметку на краю круга с правой стороны.Сохраняя исходный произвольный размер компаса, мы помещаем точку циркуля на эту отметку и отмечаем пересечения круга сверху и снизу.
3. Теперь мы рисуем диаметр круга от верхнего пересечения кругов через центр и продолжаем через противоположный край внизу с помощью нашей линейки.
4. Проделываем то же самое на противоположном перекрестке.
5.Теперь мы можем приступить к построению сторон шестиугольника. Наша первая сторона идет от отмеченной нами правой точки до верхнего пересечения круга.
6. Наша вторая сторона соединяет верхние перекрестки. Но подождите, куда пойдет наша третья сторона?
7. Делаем нашу третью сторону, строя линию, соединяющую отметки центров наших двух кругов. Если мы продолжим эту линию через другую сторону, у нас будет пересечение слева, которое отмечает точку, где наша третья сторона закончится.Теперь мы можем построить эту третью сторону.
8. Мы рисуем четвертую сторону, начиная с только что созданного пересечения и заканчивая левым нижним пересечением.
9. Наша пятая сторона построена путем соединения нижних перекрестков.
10. Мы закончили конструирование сторон шестиугольника, соединив точки пересечения от правого нижнего до крайней правой отметки.
11.У нас есть шестиугольник!
Хм … Похоже, верх немного криво … Не знаю, почему так получилось. Мы снова спрашиваем, как эта конструкция дает шестиугольник. Связано ли это с умением создавать внутренние или дополнительные углы?
Мы выполняем этот процесс в GSP:
1. Сначала строим круг произвольного размера.
2. Затем мы строим горизонтальную линию от центра круга до края.
3. Затем мы строим еще один круг, используя край первого в качестве центра и центр первого в качестве края.
4. Затем мы строим линию через центр первого круга и верхнее пересечение обоих кругов.
5. Затем мы строим еще одну линию через центр первого круга, которая проходит через нижнее пересечение кругов.
6.Теперь мы готовы нарисовать стороны нашего шестиугольника. Первая сторона начинается от нижнего пересечения обоих кругов и идет к центру второго круга.
7. Вторая сторона идет от нижнего пересечения двух кругов до нижнего пересечения первой линии, которую мы нарисовали, и первого круга.
8. Третья сторона идет от нижнего пересечения первой окружности и первой линии до левого пересечения горизонтальной линии и первой окружности.
9. Четвертая сторона идет от пересечения первой окружности и горизонтальной линии до верхнего пересечения первой окружности и второй линии.
10. Пятая сторона идет от верхнего пересечения первого круга и второй линии до верхнего пересечения обоих кругов.
11. Шестая сторона соединяет пятую сторону с первой стороной, и у нас есть шестиугольник.
12.Когда мы скрываем линии и помечаем вершины, мы получаем чистое изображение нашего построенного шестиугольника.
Теперь мы подошли к вопросу о том, как построить семиугольник. Невозможно построить идеально правильный семиугольник, используя только линейку и циркуль, как мы делали раньше. Итак, мой вопрос: почему это так?
Поскольку это невозможно, я считаю, что сейчас самое время закончить это эссе.
Построение правильных многоугольников
«ВОЗВРАЩАТЬСЯ» Copyright 2001 & nbsp & nbsp & nbsp 1728 Программные системы |
Геометрические свойства пятиугольника | calcresource
Теоретические основы
Содержание
Определения
Пентагон — это многоугольник с пятью сторонами и пятью вершинами. Пятиугольник может быть выпуклым или вогнутым , как показано на следующем рисунке. В выпуклом состоянии пятиугольник (или любой замкнутый многоугольник в этом отношении) имеет все внутренние углы ниже 180 °.Напротив, вогнутый многоугольник имеет один или несколько внутренних углов больше 180 °. Пятиугольник — это обычный , когда все его стороны и внутренние углы равны. Недостаточно иметь равные только стороны, потому что пятиугольник может быть вогнутым с равными сторонами. В этом случае пятиугольник называется равносторонним . На следующем рисунке показана классификация пятиугольников, а также равносторонние вогнутые. Любой пятиугольник, который не является правильным, называется неправильным .
Типы пятиугольникаСумма внутренних углов пятиугольника постоянна и равна 540 °. Это верно как для правильных, так и для неправильных пятиугольников, выпуклых или вогнутых. Это легко доказать, разложив пятиугольник на отдельные непересекающиеся треугольники. Если мы попытаемся провести прямые линии между всеми вершинами, избегая любых пересечений, мы разделим пятиугольник на три отдельных треугольника. Есть много разных способов провести линии между вершинами, в результате чего получаются разные треугольники, однако их количество всегда равно трем.В одном треугольнике сумма внутренних углов составляет 180 °, поэтому для трех треугольников, расположенных бок о бок, внутренние углы должны составлять до 3×180 ° = 540 °.
Пятиугольник можно разделить на три треугольникаСвойства правильных пятиугольников
Симметрия
Правильный пятиугольник имеет пять осей симметрии. Каждый из них проходит через вершину пятиугольника и середину противоположного ребра, как показано на следующем рисунке. Все оси симметрии пересекаются в общей точке — центре правильного пятиугольника.\ circ
Другими словами \ varphi и \ theta являются дополнительными.
Внутренний и центральный угол правильного пятиугольникаПравильный пятиугольник разделен на пять одинаковых равнобедренных треугольников, имеющих общую вершину — центр многоугольника.
Окружность и вписанная окружность
Можно нарисовать окружность, проходящую через все пять вершин правильного пятиугольника. Это так называемая окружность с описанием круга или описанная окружность правильного пятиугольника (действительно, это общая характеристика всех правильных многоугольников).Центр этого круга также является центром пятиугольника, где также пересекаются все оси симметрии. Радиус описанной окружности, R_c, обычно называют описанным радиусом .
Также можно нарисовать еще одну окружность, касающуюся всех пяти ребер правильного пятиугольника в серединах (также общая характеристика всех правильных многоугольников). Это так называемый вписанный круг или вписанный круг . Его центр совпадает с центром описанной окружности и касается всех пяти сторон правильного пятиугольника.Радиус вписанной окружности R_i обычно обозначается как inradius .
На следующем рисунке изображены описанная окружность правильного пятиугольника и вписанная окружность.
Окружность и вписанная окружность правильного пятиугольникаМы попытаемся найти отношения между длиной стороны a правильного пятиугольника и его радиусом описанной окружности R_c и внутренним радиусом R_i. С этой целью мы исследуем треугольник со сторонами, равными радиусу описанной окружности, внутреннему радиусу и половина края пятиугольника, как показано на рисунке ниже.Это прямоугольный треугольник, поскольку по определению вписанная окружность касается всех сторон многоугольника.
Используя базовую тригонометрию, находим:
\ begin {split} R_c & = \ frac {a} {2 \ sin {\ frac {\ theta} {2}}} \\ R_i & = \ frac {a} { 2 \ tan {\ frac {\ theta} {2}}} \\ R_i & = R_c \ cos {\ frac {\ theta} {2}} \ end {split}
, где \ theta — центральный угол, а длина стороны. Оказывается, эти выражения действительны для любого правильного многоугольника, а не только для пятиугольника. Мы можем получить конкретное выражение для правильного пятиугольника, установив θ = 72 °.{\ circ}} \ приблизительно 0.809 R_c \ end {split}
Площадь и периметр
Чтобы найти площадь правильного пятиугольника, мы должны принять во внимание, что его общая площадь разделена на пять одинаковых равнобедренных треугольников. Все. у этого треугольника есть одна сторона a и две стороны R_c, а их высота, отброшенная из вершины, лежащей в центре пятиугольника, равна R_i (помните, что вписанная окружность тангенциальна ко всем сторонам пятиугольника, касающимся их в их серединах). Тогда площадь каждого треугольника равна: \ frac {1} {2} a R_i.2
Периметр любого N-стороннего правильного многоугольника — это просто сумма длин всех сторон: P = N a. Следовательно, для правильного пятиугольника:
P = 5a
Ограничивающая рамка
Ограничивающая рамка плоской формы — это наименьший прямоугольник, который полностью охватывает форму. Для правильного пятиугольника ограничивающая рамка может быть нарисована интуитивно, как показано на следующем рисунке, но ее точные размеры требуют некоторых расчетов.
Высота
Высота h правильного пятиугольника — это расстояние от одной из его вершин до противоположного края.Он действительно перпендикулярен противоположному краю и проходит через центр пятиугольника. Хотя по определению расстояние от центра до вершины — это радиус описанной окружности R_c пятиугольника, а расстояние от центра до края — это внутренний радиус R_i. Таким образом, получается следующее выражение:
h = R_c + R_i
Высоту h можно выразить через окружной радиус R_c, внутренний радиус R_i или длину стороны a, используя соответствующие аналитические выражения для этих величин.\ circ.
Подставляя значение \ theta в последние выражения, мы получаем следующие приближения:
h \ приблизительно 1,809 R_c
h \ приблизительно 2,236 R_i
h \ приблизительно 1,539 a
Ширина
Ширина w — это расстояние между двумя противоположными вершинами правильного пятиугольника (длина его диагонали). Чтобы найти это расстояние, мы воспользуемся прямоугольным треугольником, выделенным пунктирной линией на рисунке выше. Гипотенуза треугольника — это длина стороны пятиугольника, равная a.Кроме того, один из углов треугольника является дополнительным к прилегающему внутреннему углу \ varphi пятиугольника. Однако ранее объяснялось, что дополнительным элементом \ varphi действительно является центральный угол \ theta. Следовательно, мы можем найти длину w_1 стороны треугольника:
w_1 = a \ cos \ theta
Наконец, мы можем определить общую ширину w, прибавив удвоенную длину w_1 к длине стороны a (из-за симметрии треугольника справа от пятиугольника идентичен рассмотренному).\ circ мы получаем аппроксимацию последней формулы:
w = 1.618a
Диагональ правильного пятиугольника связана золотым сечением со стороной
Как нарисовать правильный пятиугольник
Вы можете нарисовать правильный пятиугольник учитывая длину стороны a, используя простые инструменты для рисования. Выполните шаги, описанные ниже:
- Сначала нарисуйте линейный сегмент с длиной a, равной желаемой длине стороны пятиугольника.
- Увеличьте линейный сегмент влево.
- Постройте дугу окружности с центром на правом конце линейного сегмента и радиусом, равным длине сегмента.
- Повторите последний шаг, изменив центральную точку на левом конце линейного сегмента. Радиус такой же.
- Нарисуйте линию, перпендикулярную отрезку a, проходящую через точку пересечения двух дуг. Он пересекает линейный сегмент в его середине.
- Также нарисуйте линию, перпендикулярную линейному сегменту, проходящую через левый конец линейного сегмента a.Отметьте точку пересечения дугой окружности (нарисованной на шаге 4)
- Нарисуйте еще одну дугу окружности, поместив одну стрелку циркуля в середину линейного сегмента a (найденного на шаге 5) и начертите рисунок кончик на пересечении, отмеченном на шаге 6. Поверните циркуль, пока он не пересечет продолжение линейного сегмента, нарисованного на шаге 2. Отметьте и это новое пересечение.
- Нарисуйте еще одну дугу окружности, поместив одну стрелку циркуля на правый конец линейного сегмента a, а кончик рисования на пересечение, отмеченное на шаге 7.Поверните компас по часовой стрелке. Отметьте два пересечения, одно с дугой, нарисованной на шаге 4, а другое с линией, нарисованной на шаге 5. Это две вершины пятиугольника.
- Поместив стрелку циркуля на пересечение 2 и , а кончик для рисования на 1 -й (оба пересечения отмечены на последнем шаге) нарисуйте дугу окружности, пока она не пересечет дугу, нарисованную на шаге 3. Отметьте это новое пересечение, которое является вершиной пятиугольника.
- Два конца линейного сегмента a, а также три пересечения, отмеченные на шагах 8 и 9, являются пятью вершинами правильного пятиугольника.Нарисуйте между ними линейные отрезки, чтобы построить окончательную форму.
На следующем рисунке шаг за шагом показана процедура рисования.
Рисование правильного пятиугольника с учетом длины его стороны a.Обратите внимание, что описанная процедура не является построением строго по принципу «линейка и циркуль». На шагах 5 и 6 треугольник использовался для проведения перпендикулярных линий из точек другой линии. Это было выбрано для простоты и для того, чтобы сократить количество необходимых шагов. Рисование перпендикулярной линии — это простая геометрическая конструкция с использованием только линейки и циркуля, и можно заменить использование треугольника в шагах 5 и 6, если требуется строгий геометрический рисунок «линейкой и циркулем».2
Пример 2
Каков диаметр самого большого правильного пятиугольника, который может быть помещен внутри:
- круга диаметром 25 дюймов
- квадрата со стороной 25 дюймов
1. Установка правильный пятиугольник в круге
Самый большой правильный пятиугольник, помещающийся внутри круга, должен касаться круга всеми его вершинами. Другими словами, окружность должна быть описанной окружностью пятиугольника, и в результате ее радиус должен быть радиусом описанной окружности:
R_c = \ frac {25 »} {2} = 12.\ circ} {2}} = 14,69 »
2. Подгонка правильного пятиугольника к квадрату
Высота h и ширина w правильного многоугольника аппроксимируются следующими выражениями:
h \ приблизительно 1,539 a
w \ около 1,618 a
Из этих приближений очевидно, что ширина на самом деле является наибольшим из двух измерений. Следовательно, самый большой правильный пятиугольник, помещающийся внутри квадрата, должен быть ограничен только его шириной. Другими словами, ширина пятиугольника должна быть равна стороне квадрата:
w = 25 »
Однако ширина правильного пятиугольника связана с длиной стороны a по формуле:
w = a + 2a \ cos \ theta
Следовательно:
a = \ frac {w} {1 + 2 \ cos \ theta}
Из последнего уравнения мы можем вычислить требуемую длину стороны a, если подставить значения w = 25 » и \ theta = 72 ^ \ circ:
a = \ frac {25 »} {1 + 2 \ cos72 ^ \ circ} \ приблизительно 15.2
См. Также
Рисование фигур
Рисование фигурTOTAL Sketch обеспечивает доступ к различным заранее заданным формам линий области, которые вы можете можно добавить к вашему эскизу в качестве отправной точки для областей, которые вы создаете.
- На эскизе щелкните вниз
стрелку рядом с кнопкой Draw на панели инструментов или выберите Нарисуйте панель в правой части экрана и выберите нужную
форма. Формы включают:
- прямоугольник
- Круг
- Пентагон
- восьмиугольник
Если вы рисуете многоугольник, отличный от прямоугольника, пятиугольника или восьмиугольник, сначала щелкните Нарисуйте и выберите Площадь. линия .Затем щелкните сетку в том месте, где вы хотите разместить многоугольник. размещен. Введите количество сторон многоугольника, до 20 сторон, используя цифры 0‑9 на клавиатуре. Затем введите символ @ ( Shift + 2 ), а затем длина стен. Пример: 12 @ 5 создает 12-сторонний многоугольник длиной 5 футов. стены.
- После того, как вы выбрали форму (и скорректировали количество сторон, если необходимо), наведите курсор на желаемую начальную точку для форма.Для кругов этой начальной точкой является центр круга. Для всех Для других фигур отправной точкой является одно из пересечений фигуры.
- Щелкните, чтобы разместить начальную точку, и, удерживая нажатой кнопку мыши, перетащите наведите курсор на любое направление, чтобы увеличить фигуру. Когда форма достигает желаемого размера, отпустите кнопку мыши.
- При необходимости вы можете повернуть фигуру или отрегулировать длину отдельных линий
внутри.Просто нажмите Изменить на главной панели инструментов и выполните одно
из следующих:
- Щелкните, чтобы выбрать фигуру, а затем щелкните зеленый кружок над ней и перетащите его, чтобы повернуть фигуру.
- Щелкните и перетащите конечную точку внутри фигуры, чтобы отрегулировать длину линии. и / или углы.
Кажется, мы не можем найти эту страницу
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}} *
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}} / 500 {{l10n_strings.TAGS}} {{$ item}} {{l10n_strings.ПРОДУКТЫ}} {{l10n_strings.DRAG_TEXT}}{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.LANGUAGE}} {{$ select.selected.display}}{{article.content_lang.display}}
{{l10n_strings.AUTHOR}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$ select.selected.display}} {{l10n_strings.

 От центра к вершине проводится отрезок.
От центра к вершине проводится отрезок.


 От центра к вершине проводится отрезок.
От центра к вершине проводится отрезок.

 Дан правильный многоугольник, число сторон которого представляет собой произведение натуральных чисел k и m, где m>2. Как построить правильный m-угольник? Гаусс показал также возможность построения правильного 257-угольника с помощью циркуля и линейки.
Дан правильный многоугольник, число сторон которого представляет собой произведение натуральных чисел k и m, где m>2. Как построить правильный m-угольник? Гаусс показал также возможность построения правильного 257-угольника с помощью циркуля и линейки.
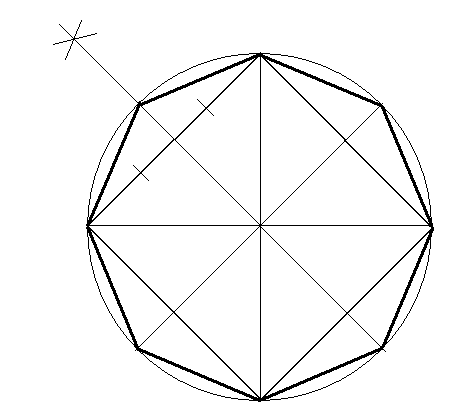 Восьмиугольник — это геометрическая фигура с восемью углами. Правильный восьмиугольник – это восьмиугольник, у которого все стороны (и углы) равны. Эта статья расскажет вам, как сделать восьмиугольник.
Восьмиугольник — это геометрическая фигура с восемью углами. Правильный восьмиугольник – это восьмиугольник, у которого все стороны (и углы) равны. Эта статья расскажет вам, как сделать восьмиугольник. У вас получится «глаз» в середине окружности. Нарисуйте две дуги, пересекающие внутреннюю окружность.
У вас получится «глаз» в середине окружности. Нарисуйте две дуги, пересекающие внутреннюю окружность. Практическая задача построения таких многоугольников с помощью циркуля и линейки имеет давнюю историю.
Практическая задача построения таких многоугольников с помощью циркуля и линейки имеет давнюю историю. πενταγωνον ) — геометрическая фигура , правильный многоугольник с пятью сторонами.
πενταγωνον ) — геометрическая фигура , правильный многоугольник с пятью сторонами.