Как определить модуль упругости: Определение модуля упругости I рода (Юнга)

Определение модуля упругости I рода (Юнга)

Лабораторная работа №3. Экспериментальное определение модуля упругости I рода (Юнга)

Цель работы – опытная проверка справедливости закона Гука при растяжении и определение модуля упругости I рода.

Основные сведения

Экспериментальные исследования на растяжение (сжатие) стандартных образцов показывают, что абсолютные удлинения, получающиеся в начальной стадии растяжения (сжатия), остаются прямопропорциональными растягивающей (сжимающей) силе и зависят от первоначальной длины образца l₀ и площади поперечного сечения А:

Величина ЕА называется жесткостью стержня при растяжении и сжатии.

Коэффициент Е носит название модуля упругости I рода (используют также название «модуль Юнга» или «модуль продольной упругости«) и является основной физической постоянной, характеризующей упругие свойства (жесткость) материала при линейной деформации.

Чем больше значение Е, тем меньше при прочих равных условиях продольная деформация. Из формулы (3.1) следует, что модуль упругости

имеет размерность, что и напряжение, — в [Па] или кратных единицах — [кПа], [МПа], а для экспериментального определения его потребуется замерить величины: F, A, l, Δl.

Испытания проводятся на испытательной машине типа Р-5.

Испытывается образец квадратного сечения. Влияние возможной неточности изготовления образца на центральное приложение нагрузки устраняется за счет установки двух тензометров на противоположных продольных гранях образца.

В качестве тензодатчиков используются тензометры Аистова. Среднее удлинение, получаемое из  показания двух тензодатчиков, принимают равным удлинению оси образца.

Диапазон нагрузок зависит от состояния и класса точности установки и предела пропорциональности материала образца. Минимальная загрузка зависит от жесткости самой установки (выборка лифтов, затяжка клиньев и т.п.) и определяется опытным путем. Максимальная загрузка рассчитывается по формуле

Зная диапазон нагрузок, определяют количество и величину ступеней нагружения ΔF.

Порядок выполнения и обработка результатов

Перед началом выполнения лабораторной работы необходимо ознакомиться с устройством машины Р-5 и рычажным тензометром Аистова.

Образец с закрепленными на нем тензодатчиками устанавливают в захватах машины и приводят в рабочее состояние.

Производят предварительное (минимальное) нагружение образца начальной нагрузкой и при этой нагрузке снимают показания приборов.

Далее нагрузку увеличивают плавно равными ступенями ΔF (5-6 ступеней) и производят соответственно снятие показаний с тензометров.

Доводить нагрузку до очередного значения нужно плавно, не «перескакивая» нужное значение. После осуществления загрузки последней ступени следует разгрузить образец до нагрузки, соответствующей минимальной.

При очередной ступени загрузки результаты опыта заносят в таблицу. Каждому приращению ΔF будет соответствовать приращение ΔП_1i и ΔП_2i, по которым подсчитывают среднее значение

ΔП_ср = (ΔП_1i + ΔП_2i)/2.

Истинное значение удлинения образца находим как

Δl_срi = ΔП_срiК,

где К = 10^-3 мм – цена 1 деления тензометра Аистова.

По значениям нагрузки F и суммарному нарастанию удлинения оси образца строят график диаграммы растяжения образца в координатах F : Δl, по которому проверяют линейность зависимости (справедливость закона Гука).

Для среднего приращения нагрузки (ступени нагружения) определяют среднюю продольную абсолютную деформацию

где П – число ступеней нагружения.

Модуль продольной упругости

где l – база тензометра Аистова.

Полученное в опыте значение модуля упругости Е_оп сравнивают с табличным Е_Т = 2·10¹¹ Па и определяют погрешность опыта.

В заключение работы делают выводы.

Контрольные вопросы

1. Как формулируется закон Гука для линейного напряженного состояния? Как ограничить верхнюю максимальную нагрузку?
2. Каковы границы применения закона Гука?
3. Что характеризует модуль упругости Е, от чего он зависит и какова его размерность?
4. По какому геометрическому выражению с использованием диаграммы напряжений можно определить Е?
5. Почему при определении деформаций растянутого образца используют два тензометра?

Определение коэффициента Пуассона >
Другие лабораторные работы >

Сохранить или поделиться с друзьями

Вы находитесь тут:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:

✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Подробнее

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

---

НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ

На нашем сайте можно бесплатно скачать:

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Сохранить или поделиться с друзьями

Помощь с решением

---

ВЫБЕРИТЕ РАЗДЕЛ МЕХАНИКИ

• Техническая механика (техмех)
• Теоретическая механика (теормех)
• Сопротивление материалов (сопромат)
• Строительная механика (строймех)
• Теория механизмов и машин (ТММ)
• Детали машин и ОК (ДМ)

Поиск формул и решений задач
Поддержать сайт

Модуль Юнга (модуль упругости): что это, таблица и формулы

Модуль Юнга (модуль упругости) — это физическая величина, которая характеризует свойства какого-либо материала сгибаться или растягиваться под воздействием силы; по сути именно от этого зависит жёсткость тела.

Это свойство любого материала, и оно зависит от температуры и оказываемого давления.

В физике упругость — это свойство твёрдых материалов возвращаться в свою первоначальную форму и размер после устранения сил, которые применялись при деформации.

Другими словами: когда тело деформируется, то появляется сила, которая стремится восстановить первоначальную форму и размер тела. Сила упругости является этой проявляющейся силой. Также она представляет собой следствие электромагнитного взаимодействия между частицами.

Низкое значение

модуля Юнга означает, что изучаемое твёрдое тело является эластичным.

Высокое значение модуля Юнга означает, что изучаемое твёрдое тело является неэластичным или жёстким.

Примеры значений модуля Юнга (упругости) для:

• (т.е. для резины он в 5 раз меньше стали)

Таблица

Большинство материалов имеют значение E очень высокого порядка, поэтому они записываются при помощи «гигапаскалей» ([ГПа]; ).

Материал	Модуль Юнга E, [ГПа]
Алмаз	1220
Алюминий	69
Дерево	10
Кадмий	50
Латунь	97
Медь	110
Никель	207
Резина	0,9 (≈ 1 МПа, мегапаскаль)
Сталь	200
Титан	107

Единица измерения и формулы

Единица измерения модуля Юнга в СИ — Ньютон на метр в квадрате (Н/м²), т.е. Паскаль (Па).

Формулы

Существует несколько формул, из которых можно вычислить модуль Юнга. Например, закон Гука.

Закон Гука

Можно вычислить модуль Юнга через эти формулы (мы это и сделаем на примере). Из-за этого закона существуют несколько интересных равенств, которые могут быть полезны для расчётов.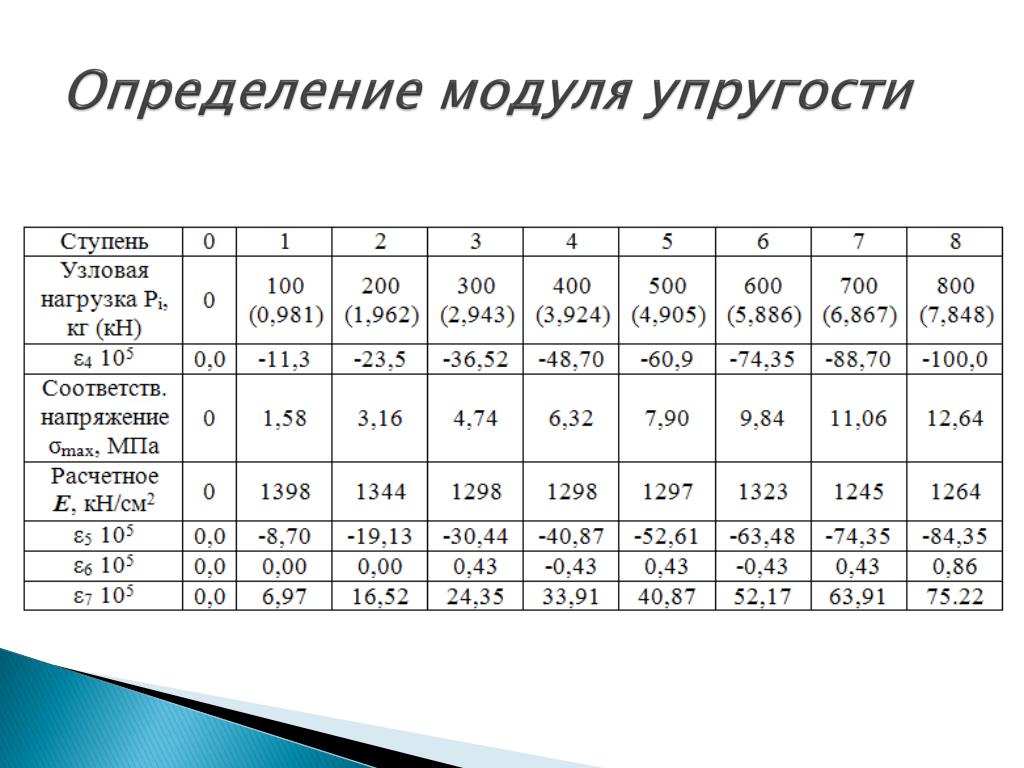

Закон Гука (этот описывает явления в теле, в дифференциальной форме):

Где:

• σ — механическое напряжение
• E — модуль Юнга (модуль упругости)
• ε — относительное удлинение

Закон Гука (этот описывает явления в теле)

Где:

• Fупр — сила упругости
• k × Δl — удлинение тела

Где:

• Fупр — сила упругости
• E — модуль Юнга (модуль упругости)
• S — площадь поперечного сечения
• l — первоначальная длина тела
• Δl — удлинение тела

Где:

• Fупр/S — механическое напряжение, обозначается как σ
• Δl/l — относительное удлинение, обозначается как ε

Следует заметить, что этот закон действует до той точки, когда материал необратимо деформируется и уже не возвращается в свою первоначальную форму. В какой точке это происходит, уже зависит от материала. Если материал очень жёсткий (значит высокое показание модуля упругости), то эта точка может совпадать с разрывом/деформацией.

Другие формулы вычисления модуля Юнга (модуля упругости)

Где:

• E — модуль Юнга (модуль упругости)
• k — жёсткость тела
• l — первоначальная длина стержня
• S — площадь поперечного сечения

Либо можно выразить k (жёсткость тела):

Где:

• k — жёсткость тела
• E — модуль Юнга (модуль упругости)
• S — площадь поперечного сечения
• l — первоначальная длина стержня/тела

Пример решения задачи (через закон Гука):

Проволока длиной 2,5 метра и площадью поперечного сечения 2,5 миллиметра² удлинилась на 1 миллиметр под действием силы 50 ньютонов. Определить модуль Юнга.

Дано:

• l = 2,5 м
• F = 50 H
• E = ?

Будем искать через закон Гука (σ = E × ε).

Помним из закона Гука:

σ = F / S (помните, что Fупр/S — механическое напряжение, обозначается как σ)

ε = Δl/l (а это относительное удлинение, обозначается как ε)

Подставляем в формулу (σ = E × ε):

Например, в нашей таблице такой модуль Юнга имеет кадмий.

Узнайте также про:

• Напряжённость электрического поля
• Законы Ньютона
• Закон сохранения энергии

Дата обновления 22/06/2021.

---

---

Другие значения и понятия, которые могут вас заинтересовать

• Закон сохранения энергии
• Напряженность электрического поля
• Сила Архимеда
• Сансара
• Гипербола в математике
• Законы Ньютона
• Ускорение свободного падения
• Теория относительности
• Уравнения Максвелла
• Теория вероятностей

Узнай Что Такое: узнайте значения, понятия и определения.

ПоследниеПопулярныеКонтактыПолитика КонфиденциальностиО нас

2018 — 2022 © 7Graus

Как рассчитать модуль упругости

Обновлено 28 декабря 2020 г.

Автор: H.L.M. Lee

Если вы сдвинете концы резинового стержня друг к другу, вы приложите ​ сжимающую ​ силу и сможете немного укоротить стержень. Если потянуть за концы друг от друга, сила называется натяжением, и можно растянуть стержень вдоль. Если вы потянете один конец к себе, а другой конец от себя, используя так называемую сдвиговую силу, стержень растянется по диагонали.

Модуль упругости (​ E ​) является мерой жесткости материала при сжатии или растяжении, хотя существует также эквивалентный модуль сдвига. Это свойство материала и не зависит от формы или размера объекта.

Небольшой кусок резины имеет тот же модуль упругости, что и большой кусок резины.​ Модуль упругости ​, также известный как модуль Юнга, названный в честь британского ученого Томаса Янга, связывает силу сжатия или растяжения объекта с результирующим изменением длины.

Что такое стресс и напряжение?

​ Напряжение ​ (​ σ ​) представляет собой сжатие или растяжение на единицу площади и определяется как:

\sigma=\frac{F}{A}

площадь поперечного сечения, к которому приложена сила. В метрической системе напряжение обычно выражается в паскалях (Па), ньютонах на квадратный метр (Н/м ² ) или ньютонах на квадратный миллиметр (Н/мм ² ).

Когда к объекту прикладывается напряжение, изменение формы называется штамм. ​ В ответ на сжатие или растяжение ​ нормальная деформация ​ (​ ε ​) определяется пропорцией:

\epsilon=\frac{\Delta L}{L}

В этом случае Δ​ L ​ – изменение длины, ​ L ​ – исходная длина. Нормальная деформация, или просто деформация , безразмерна.

Разница между упругой и пластической деформацией

Пока деформация не слишком велика, такой материал, как резина, может растягиваться, а затем возвращаться к исходной форме и размеру при снятии силы; резина испытала упругая деформация, представляющая собой обратимое изменение формы. Большинство материалов могут выдерживать некоторую упругую деформацию, хотя она может быть незначительной в прочном металле, таком как сталь.

Однако, если напряжение слишком велико, материал будет подвергаться пластической деформации и необратимому изменению формы. Напряжение может даже увеличиться до такой степени, что материал порвется, например, когда вы тянете резиновую ленту, пока она не разорвется на две части.

Использование формулы модуля упругости

Уравнение модуля упругости используется только в условиях упругой деформации от сжатия или растяжения. Модуль упругости представляет собой просто напряжение, деленное на деформацию:

E=\frac{\sigma}{\epsilon}

в паскалях (Па), ньютонах на квадратный метр (Н/м ² ) или ньютонах на квадратный миллиметр (Н/мм ² ). Для большинства материалов модуль упругости настолько велик, что обычно выражается в мегапаскалях (МПа) или гигапаскалях (ГПа).

Для проверки прочности материалов инструмент тянет за концы образца с большей и большей силой и измеряет результирующее изменение длины, иногда до тех пор, пока образец не сломается. Площадь поперечного сечения образца должна быть определена и известна, чтобы можно было рассчитать напряжение от приложенной силы. Данные испытания мягкой стали, например, могут быть построены в виде кривой напряжения-деформации, которую затем можно использовать для определения модуля упругости стали.

Модуль упругости по кривой напряжения-деформации

Упругая деформация возникает при малых деформациях и пропорциональна напряжению. На кривой напряжение-деформация это поведение видно как прямолинейный участок для деформаций менее примерно 1 процента. Итак, 1 процент — это предел упругости или предел обратимой деформации.

Например, чтобы определить модуль упругости стали, сначала определите область упругой деформации на кривой напряжение-деформация, которая, как вы теперь видите, относится к деформации менее примерно 1 процента, или 92

Калькулятор модуля Юнга

Создано Лучано Мино

Рассмотрено Войцехом Сас, доктором философии и Аденой Бенн

Последнее обновление: 28 сентября 2022 г.

Содержание:

• Что такое модуль упругости?
• Уравнение модуля Юнга
• Как рассчитать модуль Юнга?
• Пример использования формулы модуля упругости
• Как рассчитать модуль Юнга по кривой напряжения-деформации
• Часто задаваемые вопросы

С помощью этого калькулятора модуля Юнга вы можете рассчитать модуль упругости материала, учитывая деформацию, вызванную известным напряжением растяжения/сжатия .

Мы также объясним, как автоматически рассчитать модуль Юнга по кривой напряжения-деформации с помощью этого инструмента или специального программного обеспечения для построения графиков.

Продолжайте читать, чтобы узнать больше о:

• Что такое модуль упругости;
• Как рассчитать модуль Юнга по формуле модуля упругости;
• Что такое модуль Юнга?
• Какой материал имеет самый высокий модуль Юнга; и более.

Что такое модуль упругости?

Модуль Юнга или модуль упругости — это свойство материала, которое говорит нам, насколько трудно растянуть или сжать материал по заданной оси.

Это говорит нам о том, что зависимость между продольной деформацией и вызывающим ее напряжением является линейной. Следовательно, мы можем записать его как частное обоих членов.

💡 Узнайте больше о деформации и напряжении в нашем калькуляторе истинной деформации и калькуляторе напряжения!

Однако эта линейная зависимость прекращается, когда мы прикладываем к материалу достаточное напряжение. Область, в которой пропорциональность деформации остается постоянной, называется упругой областью .

Если снять напряжение после растяжения/сжатия в этой области, материал вернется к своей первоначальной длине .

Из-за этого мы можем рассчитать модуль Юнга только в этой упругой области, где мы знаем соотношение между растягивающим напряжением и продольной деформацией.

🙋 Если вы хотите узнать, как растяжение и сжатие материала по заданной оси влияет на другие его размеры, воспользуйтесь нашим калькулятором коэффициента Пуассона!

Уравнение модуля Юнга

Прежде чем перейти к формуле модуля упругости, давайте определим продольную деформацию ϵ\epsilonϵ:

ϵ=L−L0L0,\epsilon =\frac{L — L_{0}}{L_{0 }},ϵ=L0​L−L0​​,

где:

• L0L_{0}L0​ — начальная длина материала; и
• LLL — это длина при растягивающем напряжении.

И растягивающее напряжение σ\sigmaσ как:

σ=FA,\sigma = \frac{F}{A},σ=AF​,

где:

• FFF сила, вызывающая растяжение/сжатие ; и
• AAA — это область, к которой прикладывается сила.

Таким образом, уравнение модуля Юнга дает следующее:

E=σϵE = \frac{\sigma}{\epsilon}E=ϵσ

растягивающее напряжение (паскали или Па в единицах СИ).

Как рассчитать модуль Юнга?

Чтобы рассчитать модуль упругости E материала, выполните следующие действия:

1. Измерьте его начальную длину, L₀ без приложения к материалу напряжения.
2. Измерить площадь поперечного сечения A .
3. Приложите известную силу F к площади поперечного сечения и измерьте длину материала во время приложения этой силы. это будет Л .
4. Рассчитайте деформацию ϵ , ощущаемую материалом, используя формулу продольной деформации: ϵ = (L - L₀) / L₀ .
5. Рассчитайте приложенное растягивающее напряжение, используя формулу напряжения: σ = F / A .
6. Разделите растягивающее напряжение на продольную деформацию, чтобы получить модуль Юнга: E = σ / ϵ .

Пример использования формулы модуля упругости

Допустим, у нас есть тонкая проволока из неизвестного материала, и мы хотим получить ее модуль упругости.

Предположим, что мы измерили стороны поперечного сечения, получив площадь A = 0,5×0,4 мм . Затем измеряем его длину и получаем L₀ = 0,500 м .

Теперь приложим известную силу, например, F = 100 Н , и снова измерим ее длину, в результате чего L = 0,502 м .

Перед вычислением напряжения нам нужно преобразовать площадь в метры:

A = 0,5×0,4 мм = 0,0005×0,0004 м

С этими значениями мы теперь готовы вычислить напряжение σ = 100/(0,0005×0,0004) = 5·10⁸ Па и деформация ϵ = (0,502 - 0,500) / 0,500 = 0,004 .

Наконец, если мы разделим напряжение на деформацию в соответствии с уравнением модуля Юнга, мы получим: E = 5·10⁸ Па / 0,004 = 1,25·10¹¹ Па или E = 125 ГПа , что действительно близко к модуль упругости меди ( 130 ГПа ). Следовательно, наш провод, скорее всего, сделан из меди!

Как рассчитать модуль Юнга по кривой напряжения-деформации

Наш калькулятор модуля Юнга также позволяет рассчитать модуль Юнга по графику напряжения-деформации !

Чтобы построить кривую напряжения-деформации, нам сначала нужно знать исходную длину материала , L0L_{0}L0​. Затем мы применяем набор известных растягивающих напряжений и записываем его новую длину , LLL, для каждого значения напряжения.

Наконец, мы вычисляем деформацию (независимо для каждого значения напряжения), используя формулу деформации, и строим график каждые напряжение-деформация 9Пара значений 0126 с использованием оси YYY и оси XXX соответственно.

Анализ диаграммы напряжения-деформации

Диаграмма напряжения-деформации. Черные линии представляют собой конец эластичной области.

Как видно из диаграммы выше, напряжение пропорционально (линейно) деформации до определенного значения . Это упругая область, и после пересечения этого участка материал не вернется в исходное состояние при отсутствии напряжения.

Поскольку модуль упругости представляет собой пропорцию между растягивающим напряжением и деформацией, градиент этой линейной области будет численно равен модулю Юнга материала.

Затем мы можем использовать линейную регрессию для точек внутри этой линейной области, чтобы быстро получить модуль Юнга из графика напряжение-деформация.

Наш калькулятор модуля Юнга автоматически идентифицирует эту линейную область и выводит для вас модуль упругости . Попробуйте!

Часто задаваемые вопросы

Жесткость совпадает с модулем Юнга?

Нет, но они похожи . Жесткость определяется как способность данного объекта противостоять деформации под действием внешней силы и зависит от физических компонентов и структуры объекта. Модуль Юнга — это интенсивное свойство, связанное с материалом, из которого вместо этого сделан объект.

Совпадает ли модуль упругости с модулем Юнга?

Да . Модуль упругости — это другое название модуля Юнга, модуля упругости или модуля упругости материала. Он связывает деформацию, возникающую в материале, с напряжением, необходимым для ее создания.

Какой материал имеет самый высокий модуль Юнга?

Алмазы имеют самый высокий модуль Юнга или модуль упругости около ~1200 ГПа . Алмазы — самые твердые из известных природных веществ, и они образуются при экстремальных давлениях и температурах внутри мантии Земли.

Является ли модуль упругости постоянным?

Да . Поскольку модуль упругости является интенсивным свойством материала, которое связывает растягивающее напряжение, приложенное к материалу, и вызываемую им продольную деформацию, его численное значение является постоянным.

No related posts.