Как найти площадь равностороннего шестиугольника. Что такое правильный шестиугольник и какие задачи с ним могут быть связаны? Как узнать площадь многоугольника
Математические свойства
Особенность правильного шестиугольника — равенство его стороны и радиуса описанной окружности , поскольку
Все углы равны 120°.
Радиус вписанной окружности равен:
Периметр правильного шестиугольника равен:
Площадь правильного шестиугольника рассчитывается по формулам:
Шестиугольники замощают плоскость, то есть могут заполнять плоскость без пробелов и наложений, образуя так называемый паркет.
Шестиугольный паркет (шестиугольный паркетаж) — замощение плоскости равными правильными шестиугольниками, расположенными сторона к стороне.
Шестиугольный паркет является двойственным треугольному паркету: если соединить центры смежных шестиугольников, то проведённые отрезки дадут треугольный паркетаж. Символ Шлефли шестиугольного паркета — {6,3}, что означает, что в каждой вершине паркета сходятся три шестиугольника.
Шестиугольный паркет является наиболее плотной упаковкой кругов на плоскости. В двумерном евклидовом пространстве наилучшим заполнением является размещение центров кругов в вершинах паркета, образованного правильными шестиугольниками, в котором каждый круг окружен шестью другими. Плотность данной упаковки равна . В 1940 году было доказано, что данная упаковка является самой плотной.
Правильный шестиугольник со стороной является универсальной покрышкой, то есть всякое множество диаметра можно покрыть правильным шестиугольником со стороной (лемма Пала).
Правильный шестиугольник можно построить с помощью циркуля и линейки. Ниже приведён метод построения, предложенный Евклидом в «Началах», книга IV, теорема 15.
Правильный шестиугольник в природе, технике и культуре
показывают разбиение плоскости на правильные шестиугольники. Шестиугольная форма больше остальных позволяет сэкономить на стенках, то есть на соты с такими ячейками уйдёт меньше воска.
Некоторые сложные кристаллы и молекулы
, например графит, имеют гексагональную кристаллическую решётку.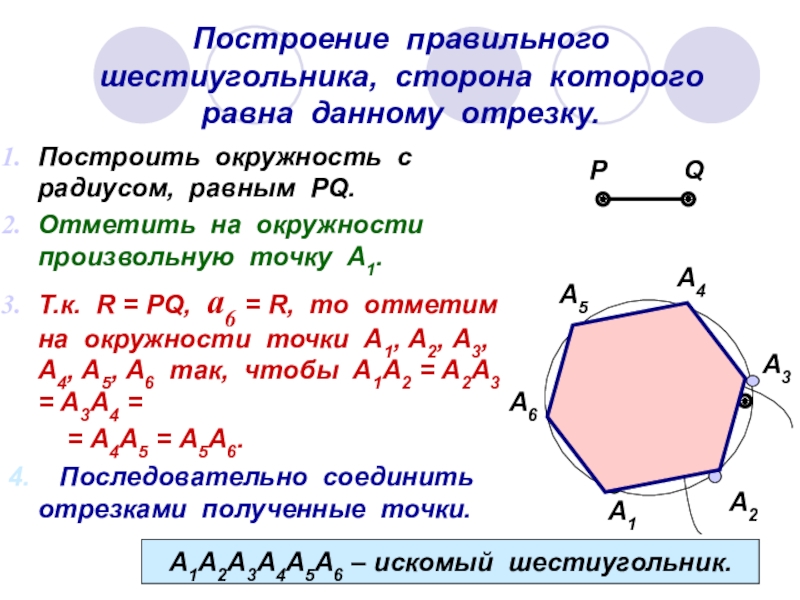
Образуется, когда микроскопические капли воды в облаках притягиваются к пылевым частицам и замерзают. Появляющиеся при этом кристаллы льда, не превышающие поначалу 0,1 мм в диаметре, падают вниз и растут в результате конденсации на них влаги из воздуха. При этом образуются шестиконечные кристаллические формы. Из-за структуры молекул воды между лучами кристалла возможны углы лишь в 60° и 120°. Основной кристалл воды имеет в плоскости форму правильного шестиугольника. На вершинах такого шестиугольника затем осаждаются новые кристаллы, на них — новые, и так получаются разнообразные формы звёздочек-снежинок.
Учёные из Оксфордского университета смогли в лабораторных условиях смоделировать возникновение подобного гексагона. Чтобы выяснить, как возникает такое образование, исследователи поставили на вертящийся стол 30-литровый баллон с водой. Она моделировала атмосферу Сатурна и её обычное вращение. Внутри учёные поместили маленькие кольца, вращающиеся быстрее ёмкости. Это генерировало миниатюрные вихри и струи, которые экспериментаторы визуализировали при помощи зелёной краски.
Памятник природы из примерно 40 000 соединённых между собой базальтовых (реже андезитовых) колонн, образовавшихся в результате древнего извержения вулкана. Расположен на северо-востоке Северной Ирландии в 3 км к северу от города Бушмилса.
Верхушки колонн образуют подобие трамплина, который начинается у подножья скалы и исчезает под поверхностью моря. Большинство колонн шестиугольные, хотя у некоторых четыре, пять, семь и восемь углов. Самая высокая колонна высотой около 12 м.
Около 50-60 миллионов лет назад, во время палеогенового периода, месторасположение Антрим подвергалось интенсивной вулканической активности, когда расплавленный базальт проникал через отложения, формируя обширные лавовые плато. По мере быстрого охлаждения происходило сокращение объёма вещества (подобное наблюдается при высыхании грязи).
Сечение гайки имеет вид правильного шестиугольника.
Шестиугольник или гексагон — это правильный многоугольник, у которого стороны равны между собой, а каждый угол равен строго 120 градусов. Гексагон иногда встречается в человеческой повседневности, поэтому вам может понадобиться вычислить его площадь не только в школьных задачах, но и в реальной жизни.
Выпуклый шестиугольник
Гескагон — это правильный выпуклый многоугольник, соответственно, все его углы равны, все стороны равны, а если провести отрезок через две соседние вершины, то вся фигура окажется по одну сторону от этого отрезка. Как и в любой правильный n-угольник, вокруг гексагона можно описать окружность или вписать ее вовнутрь. Главная особенность шестиугольника заключается в том, что длина радиуса описанной окружности совпадает с длиной стороны многоугольника. Благодаря этому свойству можно легко найти площадь гексагона по формуле:
S = 2,59 R 2 = 2,59 a 2 .
Кроме того, радиус вписанной окружности соотносится со стороной фигуры как:
Из этого следует, что вычислить площадь шестиугольника можно, оперируя одной из трех переменных на выбор.
Гексаграмма
Звездчатый правильный шестиугольник предстает перед нами в виде шестиконечной звезды. Такая фигура образуется путем наложения друг на друга двух равносторонних треугольников. Самой известной реальной гексаграммой является Звезда Давида — символ еврейского народа.
Шестиугольные числа
В теории чисел существуют фигурные числа, связанные с определенными геометрическими фигурами. Наибольшее применение находят треугольные и квадратные, а также тетраэдрические и пирамидальные числа, используя которые легко выкладывать геометрические фигуры при помощи реальных предметов. Например, пирамидальные числа подскажут вам, как сложить пушечные ядра в устойчивую пирамиду. Существуют также и шестиугольные числа, которые определяют число точек, необходимое для построения гексагона.
Шестиугольник в реальности
Гексагоны часто встречаются в реальной жизни. К примеру, сечения гаек или карандашей имеют шестиугольную форму, благодаря чему обеспечивается удобный обхват предмета. Шестиугольник — это эффективная геометрическая фигура, способная замостить плоскость без пробелов и наложений. Именно поэтому шестиугольную форму часто имеют декоративные отделочные материалы, например, кафельная и тротуарная плитка или гипсокартонные панели.
Эффективность гексагона делает его популярным и в природе. Пчелиные соты обладают именно шестиугольной формой, благодаря которой пространство улья заполняется без пробелов. Еще одним примером гексагонального замощения плоскости является Тропа Великанов — памятник живой природы, сформированный во время извержения вулкана. Вулканический пепел был спрессован в шестиугольные колонны, которые замостили поверхность побережья Северной Ирландии.
Упаковка кругов на плоскости
И еще немного об эффективности гексагона. Упаковка шаров — классическая задача комбинаторной геометрии, которая требует найти оптимальный способ укладки непересекающихся шаров. На практике такая задача превращается в логистическую проблему упаковки апельсинов, яблок, пушечных ядер или любых других шарообразных объектов, которые требуется уложить максимально плотно. Гескагон — решение данной проблемы.
Упаковка шаров — классическая задача комбинаторной геометрии, которая требует найти оптимальный способ укладки непересекающихся шаров. На практике такая задача превращается в логистическую проблему упаковки апельсинов, яблок, пушечных ядер или любых других шарообразных объектов, которые требуется уложить максимально плотно. Гескагон — решение данной проблемы.
Известно, что наиболее эффективным расположением кругов в двухмерном пространстве является размещение центров окружностей на вершинах шестиугольников, которые заполняют плоскость без пробелов. В трехмерной реальности задача размещения шаров решается путем гексагональной укладки объектов.
При помощи нашего калькулятора вы можете вычислить площадь правильного шестиугольника, зная его сторону или радиусы соответствующих окружностей. Давайте попробуем вычислить площади гексагонов на реальных примерах.
Примеры из реальной жизни
Гигантский гексагон
Гигантский гексагон — уникальное атмосферное явление на Сатуре, которое выглядит как грандиозный вихрь в форме правильного шестиугольника.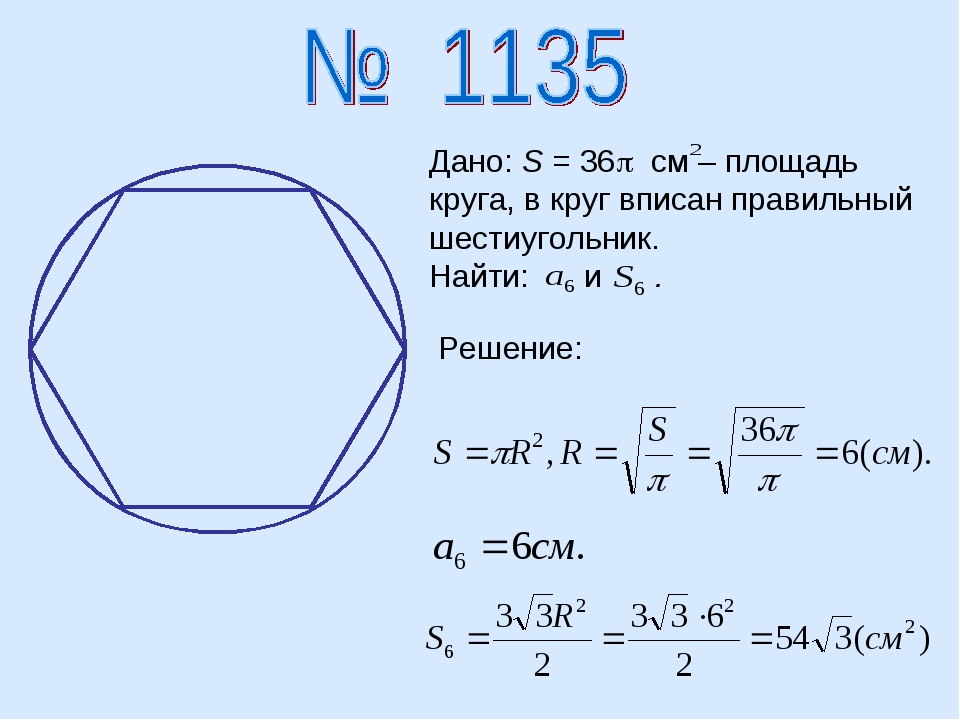 Известно, что сторона гигантского гексагона составляет 13 800 км, благодаря чему мы можем определить площадь «облака». Для этого достаточно ввести значение стороны в форму калькулятора и получить результат:
Известно, что сторона гигантского гексагона составляет 13 800 км, благодаря чему мы можем определить площадь «облака». Для этого достаточно ввести значение стороны в форму калькулятора и получить результат:
Таким образом, площадь атмосферного вихря на Сатурне приблизительно составляет 494 777 633 квадратных километров. Поистине впечатляет.
Гексагональные шахматы
Мы все привыкли к шахматному полю, разделенному на 64 квадратные ячейки. Однако существуют и гексагональные шахматы, игровое поле которых разделено на 91 правильный шестиугольник. Давайте определим площадь игровой доски для гексагональной версии известной игры. Пусть сторона ячейки составляет 2 сантиметра. Площадь одной игровой клетки составит:
Тогда площадь всей доски будет равна 91 × 10,39 = 945,49 квадратных сантиметров.
Заключение
Шестиугольник часто встречается в реальности, хотя мы и не замечаем этого. Используйте наш онлайн-калькулятор для расчета площадей гексагонов при решении повседневных или школьных задач.
Сторон. Р = а1+а2+а3+а4+а5+а6,где P – периметр шестиугольника , а а1, а2 … а6 – длины его сторон.Единицы измерения каждой из сторон приведите к одному виду – в этом случае достаточно будет сложить только числовые значения длин сторон. Единица измерения периметра шестиугольника будет совпадать с единицей измерения сторон.
Примеры из реальной жизни
Геометрия — это отрасль математики, которая занимается изучением форм различных измерений и анализом их свойств. В этом исследовании форм многоугольное семейство является одной из наиболее часто изучаемых фигур. Многоугольники закрыты 2-мерными плоскими объектами, которые имеют прямые стороны. Многоугольник, состоящий из 6 сторон и 6 углов, известен как шестиугольник. Любая замкнутая плоская двумерная структура с 6 прямыми сторонами будет называться шестиугольником. Слово «шестнадцатеричный» означает 6, а «угол» относится к углу.
Пример.Имеется шестиугольник с длинами сторон 1 см, 2 мм, 3 мм, 4 мм, 5 мм, 6 мм. Требуется найти его периметр.Решение.1. Единица измерения первой стороны (см) отличается от единиц измерения длин остальных сторон (мм). Поэтому, переведите: 1 см = 10 мм.2. 10+2+3+4+5+6=30 (мм).
Требуется найти его периметр.Решение.1. Единица измерения первой стороны (см) отличается от единиц измерения длин остальных сторон (мм). Поэтому, переведите: 1 см = 10 мм.2. 10+2+3+4+5+6=30 (мм).
Если шестиугольник правильный, то чтобы найти его периметр, умножьте длину его стороны на шесть:Р = а * 6,где а – длина стороны правильного
Как показано на диаграмме ниже, шестиугольник имеет 6 сторон или края, 6 углов и 6 вершин. Площадь шестиугольника — это пространство, занимаемое в границах шестиугольника. Используя измерения стороны и угла, мы можем найти область шестиугольника. Шестиугольники можно наблюдать в разных формах в нашей красивой природе . На приведенном ниже рисунке показана заштрихованная часть внутри границ шестиугольника, которая называется зоной шестиугольника.
Этот тип шестиугольника также не имеет 6 равных углов. Если вершины нерегулярного шестиугольника направлены наружу, то он известен как выпуклый нерегулярный шестиугольник, а если вершины шестиугольника направлены внутрь, то он известен как вогнутый нерегулярный шестиугольник, как показано на рисунке ниже.
Правильный шестиугольник обладает уникальным свойством: радиус описанной вокруг такого
Область регулярного шестиугольника: правильный шестиугольник имеет все 6 сторон и 6 углов, равных по мере. Когда тянутся диагонали, проходящие через центр шестиугольника, образуются 6 равносторонних треугольников одинакового размера. Если рассчитывается площадь одного равностороннего треугольника, то мы можем легко вычислить площадь данного правильного шестиугольника. Следовательно, все его стороны также равны.
Теперь правильный шестиугольник состоит из 6 таких конгруэнтных равносторонних треугольников.
Пример.Рассчитать периметр правильного шестиугольника , писанного в окружность диаметром 20 см.Решение. Радиус описанной окружности будет равен: 20/2=10 (см).Следовательно, периметр шестиугольника : 10 * 6 = 60 (см).
Пример: найдите область нерегулярного шестиугольника, показанного на рисунке ниже. Шестиугольные сетки используются в некоторых играх, но они не так просты или распространены как квадратные сетки. Многие части этой страницы являются интерактивными; выбор типа сетки будет обновлять диаграммы, код и текст для соответствия. Образцы кода на этой странице написаны в псевдокоде; они предназначены для легкого чтения и понимания, чтобы вы могли написать свою собственную реализацию.
Шестиугольники — это шестигранные многоугольники. Обычные шестиугольники имеют все стороны одинаковой длины. Типичные ориентации для гексарифмических сеток являются горизонтальными и вертикальными. Каждое ребро разделяется двумя шестиугольниками. Каждый угол разделяется тремя шестиугольниками. В моей статье о частях сетки. В правильном шестиугольнике внутренние углы 120 °. Есть шесть «клиньев», каждый из которых равносторонний треугольник с углами 60 ° внутри.
Типичные ориентации для гексарифмических сеток являются горизонтальными и вертикальными. Каждое ребро разделяется двумя шестиугольниками. Каждый угол разделяется тремя шестиугольниками. В моей статье о частях сетки. В правильном шестиугольнике внутренние углы 120 °. Есть шесть «клиньев», каждый из которых равносторонний треугольник с углами 60 ° внутри.
Если по условиям задачи задан радиус вписанной окружности, то примените формулу:P = 4 * √3 * r,где r – радиус вписанной в правильный шестиугольник окружности.
Если известна площадь правильного шестиугольника , то для расчета периметра используйте следующее соотношение:S = 3/2 * √3 * а²,где S – площадь правильного шестиугольника . Отсюда можно найти а = √(2/3 * S / √3), следовательно:Р = 6 * а = 6 * √(2/3 * S / √3) = √(24 * S / √3) = √(8 * √3 * S) = 2√(2S√3).
Учитывая гексагон, который 6 гексов соседствуют с ним? Как и следовало ожидать, ответ прост с координатами куба, все еще довольно простой с осевыми координатами и немного сложнее с координатами смещения. Мы могли бы также захотеть рассчитать 6 диагональных гексов.
Мы могли бы также захотеть рассчитать 6 диагональных гексов.
Учитывая местоположение и расстояние, что видно из этого места, а не заблокировано препятствиями? Самый простой способ сделать это — нарисовать линию для каждого гексагонального диапазона. Если линия не ударяет по стенам, вы можете увидеть гекс. Мышь над шестнадцатеричным, чтобы увидеть, как линия тянется к этому гексу, и к каким стенам он попадает.
По определению из планиметрии правильным многоугольником называется выпуклый многоугольник, у которого стороны равны между собой и углы так же равны между собой. Правильный шестиугольник является правильным многоугольником, с числом сторон равным шести. Существует несколько формул для расчета площади правильного многоугольника.
- Выпуклый семиугольник — это тот, у которого нет тупых внутренних углов.
- Вогнутая спираль — одна с тупым внутренним углом.

где а – длина стороны правильного шестиугольника.
Пример.
Найти периметр правильного шестиугольника с длиной стороны равной 10 см.
Решение: 10 * 6 = 60 (см).
Правильный шестиугольник обладает уникальным свойством: радиус описанной вокруг такого шестиугольника окружности равен длине его стороны. Поэтому, если известен радиус описанной окружности, до воспользуйтесь формулой:
где R – радиус описанной окружности.
Пример.
Рассчитать периметр правильного шестиугольника, писанного в окружность диаметром 20 см.
Решение.
Радиус описанной окружности будет равен: 20/2=10 (см).
Следовательно, периметр шестиугольника: 10 * 6 = 60 (см).
Если по условиям задачи задан радиус вписанной окружности, то примените формулу:
где r – радиус вписанной в правильный шестиугольник окружности.
Если известна площадь правильного шестиугольника, то для расчета периметра используйте следующее соотношение:
S = 3/2 * v3 * а?,
где S – площадь правильного шестиугольника.
Отсюда можно найти а = v(2/3 * S / v3), следовательно:
Р = 6 * а = 6 * v(2/3 * S / v3) = v(24 * S / v3) = v(8 * v3 * S) = 2v(2Sv3).
Как просто
С вопросом: «Как найти площадь шестиугольника?» , можно столкнуться не только на экзамене по геометрии и т.п., эти знания пригодятся и в быту, например, для правильного и точного вычисления площади помещения в процессе ремонта. Подставив в формулу требуемые значения, получится определить нужное количество рулонов обоев, плитки в ванную или на кухню и т.д.
Немного фактов из истории
Геометрия использовалась еще в древнем Вавилоне и прочих государствах, существовавших в одно время с ним. Вычисления помогали при возведении значительных сооружений, так как благодаря ей зодчие знали как выдержать вертикаль, правильно составить план, определить высоту.
Эстетика тоже имела большое значение, и здесь снова шла в ход геометрия. Сегодня этой науки нужны строителю, закройщику, архитектору, да и не специалисту тоже.
Поэтому лучше уметь рассчитывать S фигур, понимать, что формулы могут пригодиться на практике.
Площадь правильного 6-угольника
Итак, у нас шестиугольная фигура с равными сторонами и углами . В повседневности мы часто имеем возможность встретить предметы правильной шестиугольной формы.
К примеру:
- гайка;
- пчелиные соты;
- снежинка.
Шестиугольная фигура наиболее экономично заполняет пространство на плоскости. Взгляните на тротуарную плитку, одна подогнана к другой так, что зазоров не остается.
Каждый угол равен 120˚. Сторона фигуры равна радиусу описанной окружности .
Расчет
Требуемое значение можно вычислить, разбив фигуру на шесть треугольников с равными сторонами.
Вычислив S одного из треугольников, нетрудно определить и общую. Простая формула, так как правильный шестиугольник, по сути, является шестью равными треугольниками. Таким образом, для ее расчета найденную площадь одного треугольника умножают на 6.
Если от центра шестиугольника к любой его стороне провести перпендикуляр, получается отрезок – апофема .
Посмотрим, как находить S шестиугольника, если апофема известна:
- S =1/2×периметр×апофема.
- Возьмем апофему равную 5√3 см.
- Находим периметр, используя апофему: так как апофема перпендикулярно к стороне 6-угольника, углы треугольника, образованного с помощью апофемы, равняются 30˚-60˚-90˚. Каждая сторона треугольника соответствует: x-x√3-2x, где короткая, против угла 30˚,- это x; длинная сторона против угла 60˚- x√3, а гипотенуза — 2x.
- Апофему x√3 можно подставить в формулу a=x√3. Если апофема равна 5√3, подставив данную величину, получим: 5√3см=x√3, или x=5см.
- Короткая сторона треугольника составляет 5см, так как эта величина – половина длины стороны 6-угольника. Умножив 5 на 2, получим 10см, что есть значение длиной стороны.
- Полученную величину умножим на 6 и получим значение периметра – 60см.
Подставляем полученные результаты в формулу: S=1/2×периметр×апофема
S=½×60 см× 5√3
Считаем:
Упрощаем полученный ответ, чтоб избавиться от корней.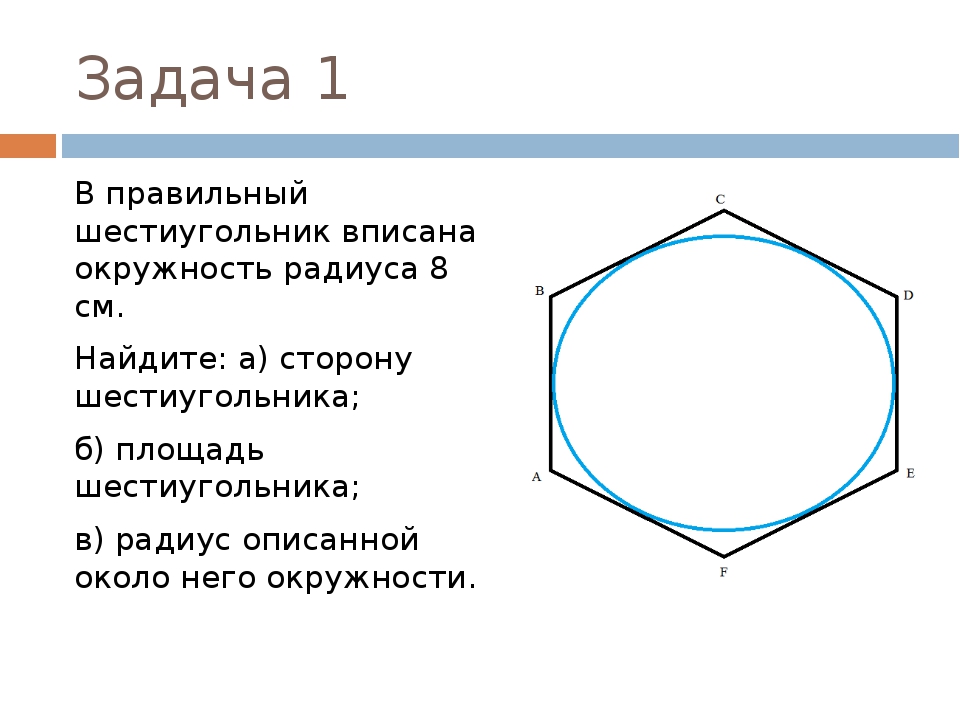 Результат будет выражен в квадратных сантиметрах: ½×60см×5√3см=30×5√3см=150 √3см=259,8с м².
Результат будет выражен в квадратных сантиметрах: ½×60см×5√3см=30×5√3см=150 √3см=259,8с м².
Как находить площадь неправильного шестиугольника
Есть несколько вариантов:
- Разбивка 6-угольника на другие фигуры.
- Метод трапеции.
- Расчет S неправильных многоугольников с помощью осей координат.
Выбор способа диктуется исходными данными.
Метод трапецииШестиугольник делится на отдельные трапеции, после чего вычисляется площадь каждой полученной фигуры.
Использование осей координатИспользуем координаты вершин многоугольника:
- В таблицу записываем координаты вершин x и y . Последовательно выбираем вершины, «двигаясь» против часовой стрелки, завершая список повторной записью координат первой вершины.
- Умножаем значения координаты x 1-й вершины на значение y 2-й вершины, и продолжаем так умножать. Складываем полученные результаты.
- Значения координат y1-й вершины умножаем на значения координат x 2-й вершины.
 Складываем результаты.
Складываем результаты. - Вычитаем сумму, полученную на 4-м этапе из суммы, полученной на третьем этапе.
- Делим результат, полученный на предыдущем этапе, и находим, что искали.
Разбивка шестиугольника на другие фигуры
Многоугольники разбиваются на другие фигуры: трапеции, треугольники, прямоугольники. Пользуясь формулами вычисления площадей перечисленных фигур, требуемые значения вычисляются и складываются.
Неправильный шестиугольник может состоять из двух параллелограммов. Чтоб вычислить площадь параллелограмма, его длина умножается на его ширину, а далее уже известные две площади складываются.
Площадь равностороннего шестиугольника
У правильного шестиугольника шесть равных сторон. Площадь равносторонней фигуры равна 6S треугольников, на которые разбит правильный шестиугольник. Каждый треугольник в правильном шестиугольнике равен, поэтому для вычисления площади такой фигуры довольно знать площадь хотя б одного треугольника.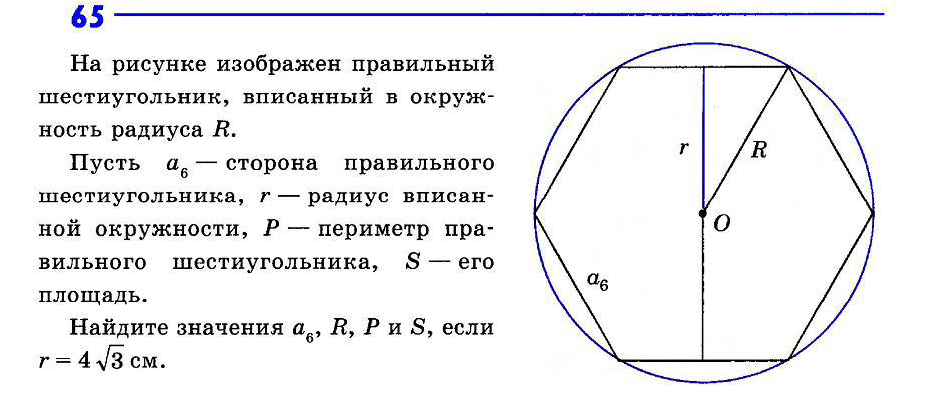
Чтоб найти искомое значение пользуются формулой площади правильной фигуры, описанной выше.
Тему многоугольников проходят в школьной программе, но не уделяют ей достаточного внимания. А между тем она интересна, и особенно это касается правильного шестиугольника или гексагона — ведь эту форму имеют многие природные объекты. К ним относятся пчелиные соты и многое другое. Эта форма очень хорошо применяется на практике.
Определение и построение
Правильным шестиугольником называется плоскостная фигура, имеющая шесть равных по длине сторон и столько же равных углов.
Если вспомнить формулу суммы углов многоугольника
то получается, что в этой фигуре она равна 720°. Ну а поскольку все углы фигуры равны, нетрудно посчитать, что каждый из них равен 120°.
Начертить шестиугольник очень просто, для этого достаточно циркуля и линейки.
Пошаговая инструкция будет выглядеть так:
При желании можно обойтись и без линии, начертив пять равных по радиусу окружностей.
Полученная таким образом фигура будет правильным шестиугольником, и это можно доказать ниже.
Свойства простые и интересные
Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:
Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:
- диаметр описанной окружности;
- диаметр вписанной окружности;
- площадь;
- периметр.
Описанная окружность и возможность построения
Вокруг гексагона можно описать окружность, и притом только одну. Поскольку фигура эта правильная, то можно поступить довольно просто: от двух соседних углов провести внутрь биссектрисы. Они пересекутся в точке О, и образуют вместе со стороной между ними треугольник.
Углы между стороной гексагона и биссектрисами будут по 60°, поэтому можно определенно сказать, что треугольник, к примеру, АОВ — равнобедренный. А поскольку третий угол тоже будет равен 60°, то он еще и равносторонний. Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.
Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.
После этого можно перейти к следующей стороне, и из угла при точке С тоже вывести биссектрису. Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность. Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:
Именно поэтому и возможно построение этой фигуры с помощью циркуля и линейки.
Ну а площадь этой окружности будет стандартная:
Вписанная окружность
Центр описанной окружности совпадет с центром вписанной. Чтобы в этом убедиться, можно провести из точки О перпендикуляры к сторонам шестиугольника. Они будут являться высотами тех треугольников, из которых составлен гексагон. А в равнобедренном треугольнике высота является медианой по отношению к стороне, на которую она опирается. Таким образом, эта высота не что иное, как серединный перпендикуляр, являющийся радиусом вписанной окружности.
Таким образом, эта высота не что иное, как серединный перпендикуляр, являющийся радиусом вписанной окружности.
Высота равностороннего треугольника вычисляется просто:
h²=а²-(а/2)²= а²3/4, h=а(√3)/2
А поскольку R=a и r=h, то получается, что
r=R(√3)/2 .
Таким образом, вписанная окружность проходит через центры сторон правильного шестиугольника.
Ее площадь будет составлять:
S=3πa²/4 ,
то есть три четверти от описанной.
Периметр и площадь
С периметром все ясно, это сумма длин сторон:
P=6а , или P=6R
А вот площадь будет равна сумме всех шести треугольников, на которые можно разбить гексагон. Поскольку площадь треугольника вычисляется как половина произведения основания на высоту, то:
S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 или
S=3R²(√3)/2
Желающим вычислять эту площадь через радиус вписанной окружности можно сделать и так:
S=3(2r/√3)²(√3)/2=r²(2√3)
Занимательные построения
В гексагон можно вписать треугольник, стороны которого будут соединять вершины через одну:
Всего их получится два, и их наложение друг на друга даст звезду Давида. Каждый из этих треугольников — равносторонний. В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:
Каждый из этих треугольников — равносторонний. В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:
- Высота АВС из вершины В будет равна половине стороны шестиугольника, поскольку sin30°=1/2. Желающим убедиться в этом можно посоветовать пересчитать по теореме Пифагора, она здесь подходит как нельзя лучше.
- Сторона АС будет равна двум радиусам вписанной окружности, что опять-таки вычисляется по той же теореме. То есть АС=2(a(√3)/2)=а(√3).
- Треугольники АВС, СДЕ и АЕF равны по двум сторонам и углу между ними, и отсюда вытекает равенство сторон АС, СЕ и ЕА.
Пересекаясь друг с другом, треугольники образуют новый гексагон, и он тоже правильный. Доказывается это просто:
Таким образом, фигура отвечает признакам правильного шестиугольника — у нее шесть равных сторон и углов. Из равенства треугольников при вершинах легко вывести длину стороны нового гексагона:
Из равенства треугольников при вершинах легко вывести длину стороны нового гексагона:
d=а(√3)/3
Она же будет радиусом описанной вокруг него окружности. Радиус вписанной будет вдвое меньше стороны большого шестиугольника, что было доказано при рассмотрении треугольника АВС. Его высота составляет как раз половину стороны, следовательно, вторая половина — это радиус вписанной в маленький гексагон окружности:
r₂=а/2
S=(3(√3)/2)(а(√3)/3)²=а(√3)/2
Получается, что площадь гексагона внутри звезды Давида в три раза меньше, чем у большого, в который вписана звезда.
От теории к практике
Свойства шестиугольника очень активно используются как в природе, так и в различных областях деятельности человека. В первую очередь это касается болтов и гаек — шляпки первых и вторые представляют собой ничто иное, как правильный шестигранник, если не брать в расчет фаски. Размер гаечных ключей соответствует диаметру вписанной окружности — то есть расстоянию между противоположными гранями.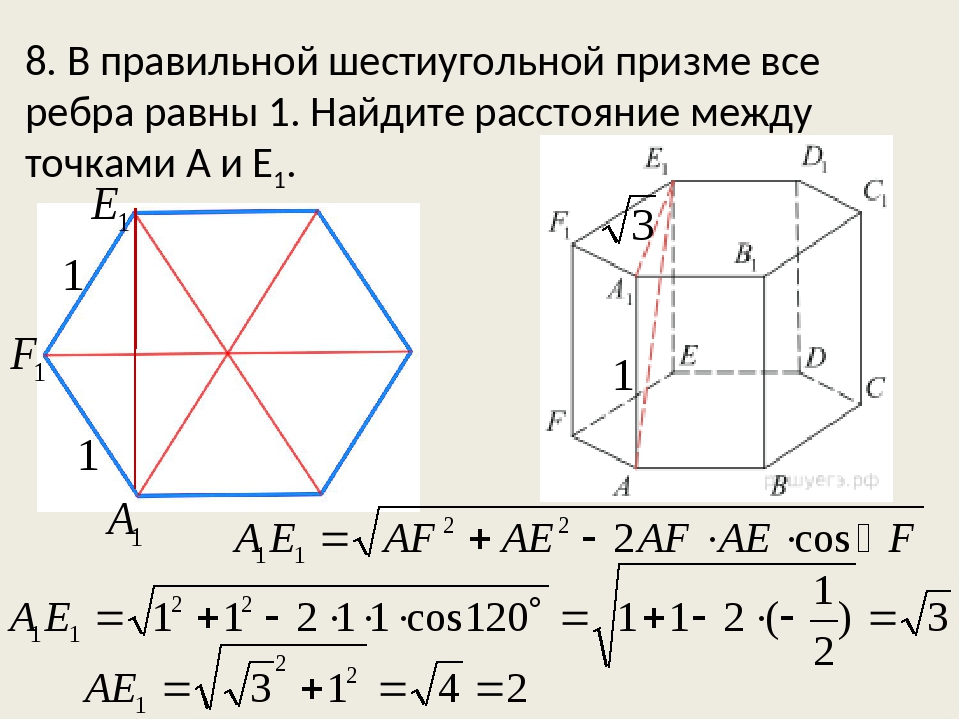
Нашла свое применение и гексагональная плитка. Она распространена куда меньше четырехугольной, но класть ее удобнее: в одной точке смыкаются три плитки, а не четыре. Композиции могут получаться очень интересные:
Выпускается и бетонная плитка для мощения.
Распространенность гексагона в природе объясняется просто. Таким образом, проще всего плотно уместить круги и шары на плоскости, если у них одинаковый диаметр. Из-за этого у пчелиных сот такая форма.
Площадь шестиугольной пирамиды — формула, пример расчета
Пирамида, в основании которой лежит правильный шестиугольник, а боковые стороны образуются правильными треугольниками, называется шестиугольной.
Этот многогранник отличается множеством свойств:
- Все стороны и углы основания равны между собой;
- Все ребра и двугранные угля пирамиды также равны между собой;
- Треугольники, образующие боковые стороны одинаковы, соответственно, у них одинаковые площади, стороны и высоты.

Для расчета площади правильной шестиугольной пирамиды применяется стандартная формула площади боковой поверхности шестиугольной пирамиды:
где P – периметр основания, a – длина апофемы пирамиды. В большинстве случаев можно рассчитать боковую площадь по этой формуле, однако иногда можно воспользоваться и другим методом. Так как боковые грани пирамиды образованы равными треугольниками, можно найти площадь одного треугольника, а потом умножить его на количество боковых сторон. В шестиугольной пирамиде их 6. Но этот способ можно применять и при расчете площади треугольной пирамиды.Рассмотрим пример расчета площади боковой поверхности шестиугольной пирамиды.
Пусть дана правильная шестиугольная пирамида, в которой апофема равна a = 7 см, сторона основания b = 3 см. Рассчитайте площадь боковой поверхности многогранника.Для начала найдем периметр основания. Так как пирамида правильная – в ее основании лежит правильный шестиугольник. Значит, все его стороны равны, а периметр рассчитывается по формуле:
Подставляем данные в формулу:
Теперь можем легко найти площадь боковой поверхности, подставив найденное значение в основную формулу:
Также немаловажным моментом является поиск площади основания. Формула площади основания шестиугольной пирамиды выводится из свойств правильного шестиугольника:
Формула площади основания шестиугольной пирамиды выводится из свойств правильного шестиугольника:
Формула площади шестиугольной пирамиды представляет собой сумму площади основания и боковой развертки:
Рассмотрим пример расчета площади шестиугольной пирамиды.
Площадь правильного многоугольника | Треугольники
Найдём площадь правильного многоугольника через радиусы вписанной и описанной окружностей и через его сторону.
Любой правильный многоугольник вписан в окружность и описан около окружности. Центры вписанной и описанной окружностей совпадают и называются центром правильного многоугольника.
Соединив центр правильного n-угольника
со всеми его вершинами, получим n равнобедренных треугольников.
Основание каждого такого треугольника равно стороне многоугольника, боковые стороны равны радиусу описанной около многоугольника окружности угол при вершине — центральному углу правильного многоугольника
Так как площадь треугольника равна половине произведения его сторон на синус угла между ними,
Отсюда
Поскольку многоугольник состоит из n таких треугольников, формула площади правильного многоугольника через радиус описанной окружности:
Проведём в треугольнике A1OA2 высоту OF. Её длина равна радиусу вписанной в правильный n-угольник окружности:
Её длина равна радиусу вписанной в правильный n-угольник окружности:
По свойству равнобедренного треугольника OF является также его биссектрисой и медианой:
Из прямоугольного треугольника A1OF по определению тангенса
откуда
Так как площадь треугольника равна половине произведения стороны на высоту, проведённую к этой стороне,
Площадь
равна сумме n таких площадей.
Таким образом, формула площади правильного многоугольника через радиус вписанной окружности:
Из треугольника A1OF
Следовательно,
Поскольку многоугольник состоит из n равных треугольников, формула площади правильного многоугольника через его сторону:
Площадь правильного шестиугольника со стороной 1. Что такое правильный шестиугольник и какие задачи с ним могут быть связаны? Чем он отличается от неправильного
Шестиугольник или гексагон — это правильный многоугольник, у которого стороны равны между собой, а каждый угол равен строго 120 градусов. Гексагон иногда встречается в человеческой повседневности, поэтому вам может понадобиться вычислить его площадь не только в школьных задачах, но и в реальной жизни.
Гексагон иногда встречается в человеческой повседневности, поэтому вам может понадобиться вычислить его площадь не только в школьных задачах, но и в реальной жизни.
Выпуклый шестиугольник
Гескагон — это правильный выпуклый многоугольник, соответственно, все его углы равны, все стороны равны, а если провести отрезок через две соседние вершины, то вся фигура окажется по одну сторону от этого отрезка. Как и в любой правильный n-угольник, вокруг гексагона можно описать окружность или вписать ее вовнутрь. Главная особенность шестиугольника заключается в том, что длина радиуса описанной окружности совпадает с длиной стороны многоугольника. Благодаря этому свойству можно легко найти площадь гексагона по формуле:
S = 2,59 R 2 = 2,59 a 2 .
Кроме того, радиус вписанной окружности соотносится со стороной фигуры как:
Из этого следует, что вычислить площадь шестиугольника можно, оперируя одной из трех переменных на выбор.
Гексаграмма
Звездчатый правильный шестиугольник предстает перед нами в виде шестиконечной звезды. Такая фигура образуется путем наложения друг на друга двух равносторонних треугольников. Самой известной реальной гексаграммой является Звезда Давида — символ еврейского народа.
Такая фигура образуется путем наложения друг на друга двух равносторонних треугольников. Самой известной реальной гексаграммой является Звезда Давида — символ еврейского народа.
Шестиугольные числа
В теории чисел существуют фигурные числа, связанные с определенными геометрическими фигурами. Наибольшее применение находят треугольные и квадратные, а также тетраэдрические и пирамидальные числа, используя которые легко выкладывать геометрические фигуры при помощи реальных предметов. Например, пирамидальные числа подскажут вам, как сложить пушечные ядра в устойчивую пирамиду. Существуют также и шестиугольные числа, которые определяют число точек, необходимое для построения гексагона.
Шестиугольник в реальности
Гексагоны часто встречаются в реальной жизни. К примеру, сечения гаек или карандашей имеют шестиугольную форму, благодаря чему обеспечивается удобный обхват предмета. Шестиугольник — это эффективная геометрическая фигура, способная замостить плоскость без пробелов и наложений. Именно поэтому шестиугольную форму часто имеют декоративные отделочные материалы, например, кафельная и тротуарная плитка или гипсокартонные панели.
Именно поэтому шестиугольную форму часто имеют декоративные отделочные материалы, например, кафельная и тротуарная плитка или гипсокартонные панели.
Эффективность гексагона делает его популярным и в природе. Пчелиные соты обладают именно шестиугольной формой, благодаря которой пространство улья заполняется без пробелов. Еще одним примером гексагонального замощения плоскости является Тропа Великанов — памятник живой природы, сформированный во время извержения вулкана. Вулканический пепел был спрессован в шестиугольные колонны, которые замостили поверхность побережья Северной Ирландии.
Упаковка кругов на плоскости
И еще немного об эффективности гексагона. Упаковка шаров — классическая задача комбинаторной геометрии, которая требует найти оптимальный способ укладки непересекающихся шаров. На практике такая задача превращается в логистическую проблему упаковки апельсинов, яблок, пушечных ядер или любых других шарообразных объектов, которые требуется уложить максимально плотно. Гескагон — решение данной проблемы.
Гескагон — решение данной проблемы.
Известно, что наиболее эффективным расположением кругов в двухмерном пространстве является размещение центров окружностей на вершинах шестиугольников, которые заполняют плоскость без пробелов. В трехмерной реальности задача размещения шаров решается путем гексагональной укладки объектов.
При помощи нашего калькулятора вы можете вычислить площадь правильного шестиугольника, зная его сторону или радиусы соответствующих окружностей. Давайте попробуем вычислить площади гексагонов на реальных примерах.
Примеры из реальной жизни
Гигантский гексагон
Гигантский гексагон — уникальное атмосферное явление на Сатуре, которое выглядит как грандиозный вихрь в форме правильного шестиугольника. Известно, что сторона гигантского гексагона составляет 13 800 км, благодаря чему мы можем определить площадь «облака». Для этого достаточно ввести значение стороны в форму калькулятора и получить результат:
Таким образом, площадь атмосферного вихря на Сатурне приблизительно составляет 494 777 633 квадратных километров.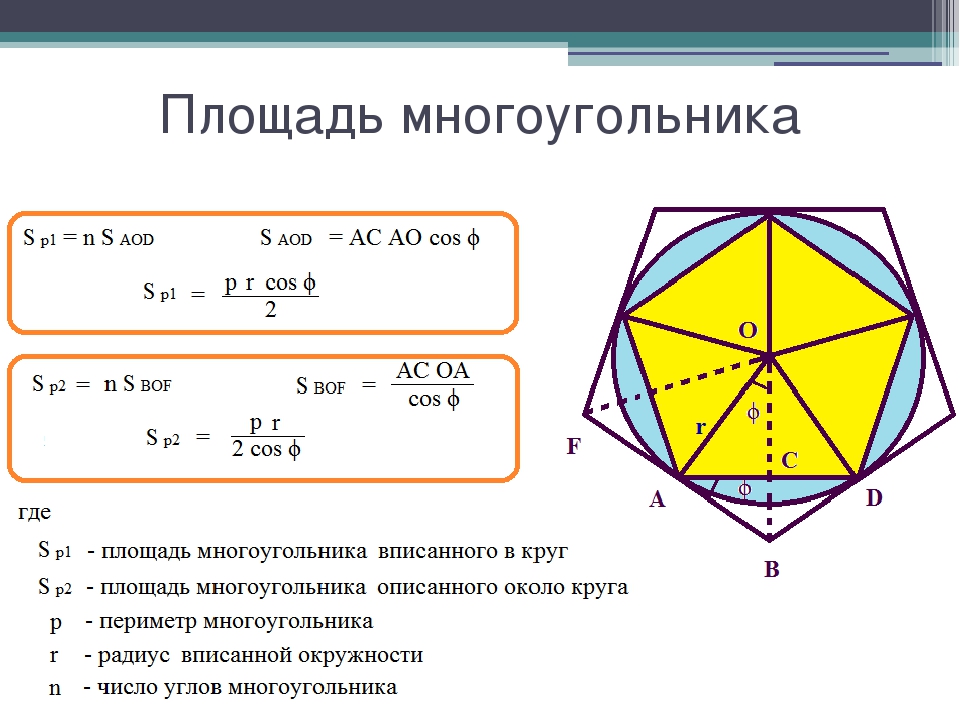 Поистине впечатляет.
Поистине впечатляет.
Гексагональные шахматы
Мы все привыкли к шахматному полю, разделенному на 64 квадратные ячейки. Однако существуют и гексагональные шахматы, игровое поле которых разделено на 91 правильный шестиугольник. Давайте определим площадь игровой доски для гексагональной версии известной игры. Пусть сторона ячейки составляет 2 сантиметра. Площадь одной игровой клетки составит:
Тогда площадь всей доски будет равна 91 × 10,39 = 945,49 квадратных сантиметров.
Заключение
Шестиугольник часто встречается в реальности, хотя мы и не замечаем этого. Используйте наш онлайн-калькулятор для расчета площадей гексагонов при решении повседневных или школьных задач.
Самая известная фигура, у которой больше четырех углов — это правильный шестиугольник. В геометрии он часто используется в задачах. А в жизни именно такой вид имеют соты на срезе.
Чем он отличается от неправильного?
Во-первых, шестиугольником является фигура с 6 вершинами. Во-вторых, он может быть выпуклым или вогнутым.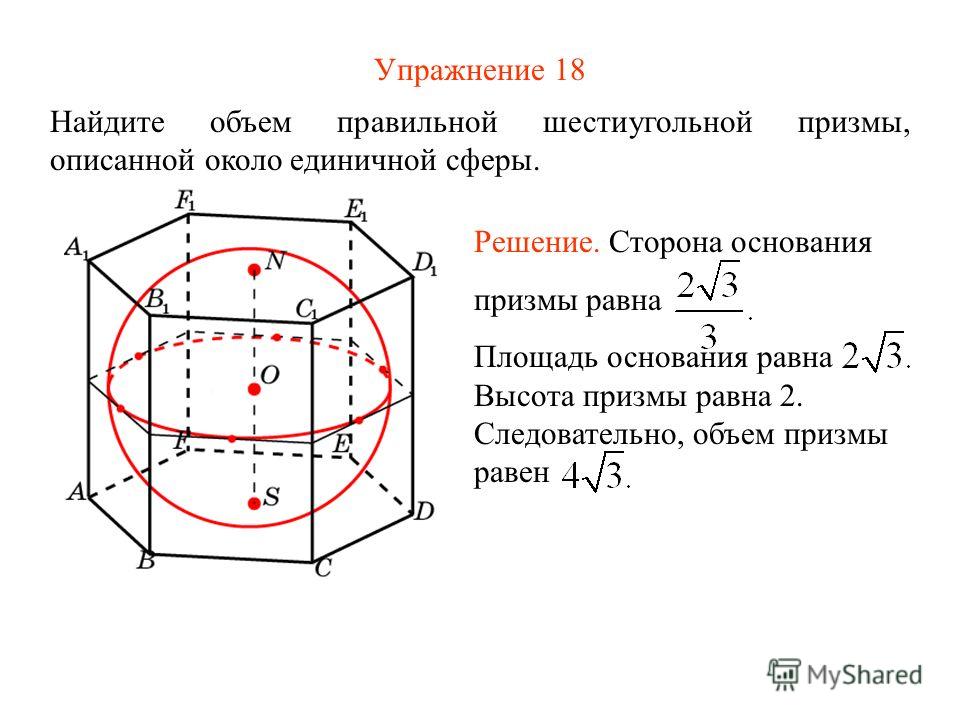 Первый отличается тем, что четыре вершины лежат по одну сторону от прямой, проведенной через две другие.
Первый отличается тем, что четыре вершины лежат по одну сторону от прямой, проведенной через две другие.
В-третьих, правильный шестиугольник характеризуется тем, что все его стороны равны. Причем каждый угол фигуры тоже имеет одинаковое значение. Чтобы определить сумму всех его углов, потребуется воспользоваться формулой: 180º * (n — 2). Здесь n — число вершин фигуры, то есть 6. Простой расчет дает значение в 720º. То есть каждый угол равен 120 градусам.
В повседневной деятельности правильный шестиугольник встречается в снежинке и гайке. Химики видят ее даже в молекуле бензола.
Какие свойства требуется знать при решении задач?
К тому, что указано выше, следует добавить:
- диагонали фигуры, проведенные через центр, делят ее на шесть треугольников, которые являются равносторонними;
- сторона правильного шестиугольника имеет значение, которое совпадает с радиусом описанной около него окружности;
- используя такую фигуру, есть возможность заполнить плоскость, причем между ними не получится пропусков и не будет наложений.

Введенные обозначения
Традиционно сторона правильной геометрической фигуры обозначается латинской буквой «а». Для решения задач требуются еще площадь и периметр, это S и P соответственно. В правильный шестиугольник бывает вписана окружность или описана около него. Тогда вводятся значения для их радиусов. Обозначаются они соответственно буквами r и R.
В некоторых формулах фигурируют внутренний угол, полупериметр и апофема (являющаяся перпендикуляром к середине любой стороны из центра многоугольника). Для них используются буквы: α, р, m.
Формулы, которые описывают фигуру
Для расчета радиуса вписанной окружности потребуется такая: r = (a * √3) / 2, причем r = m. То есть такая же формула будет и для апофемы.
Поскольку периметр шестиугольника — это сумма всех сторон, то он определится так: P = 6 * a. С учетом того, что сторона равна радиусу описанной окружности, для периметра существует такая формула правильного шестиугольника: P = 6 * R.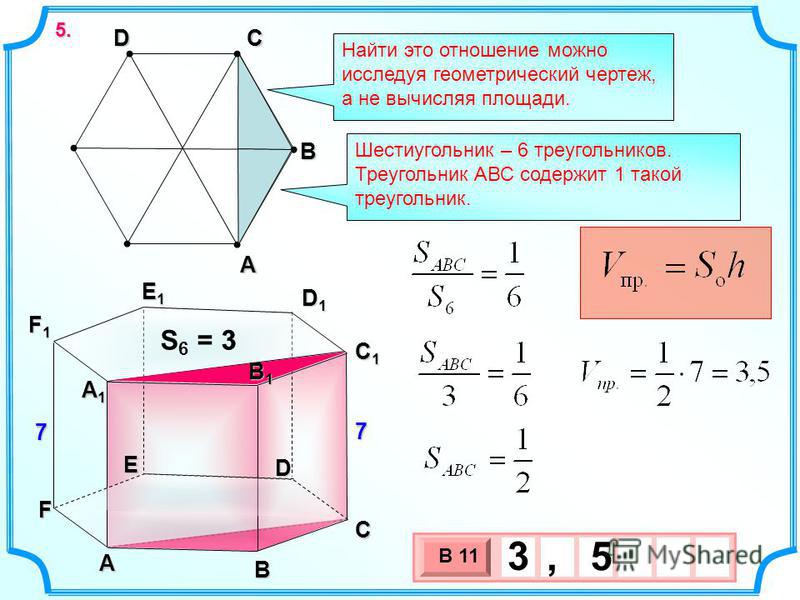 Из той, что приведена для радиуса вписанной окружности, выводится зависимость между а и r. Тогда формула принимает такой вид: Р = 4 r * √3.
Из той, что приведена для радиуса вписанной окружности, выводится зависимость между а и r. Тогда формула принимает такой вид: Р = 4 r * √3.
Для площади правильного шестиугольника может пригодиться такая: S = p * r = (a 2 * 3 √3) / 2.
Задачи
№ 1. Условие. Имеется правильная шестиугольная призма, каждое ребро которой равно 4 см. В нее вписан цилиндр, объем которого необходимо узнать.
Решение. Объем цилиндра определяется как произведение площади основания на высоту. Последняя совпадает с ребром призмы. А она равна стороне правильного шестиугольника. То есть высота цилиндра — тоже 4 см.
Чтобы узнать площадь его основания, потребуется вычислить радиус вписанной в шестиугольник окружности. Формула для этого указана выше. Значит, r = 2√3 (см). Тогда площадь круга: S = π * r 2 = 3,14 * (2√3) 2 = 37,68 (см 2).
Ответ . V = 150,72 см 3 .
№ 2. Условие. Вычислить радиус окружности, которая вписана в правильный шестиугольник. Известно, что его сторона равна √3 см. Чему будет равен его периметр?
Известно, что его сторона равна √3 см. Чему будет равен его периметр?
Решение. Эта задача требует использования двух из указанных формул. Причем их необходимо применять, даже не видоизменяя, просто подставить значение стороны и вычислить.
Таким образом, радиус вписанной окружности получается равным 1,5 см. Для периметра оказывается верным такое значение: 6√3 см.
Ответ. r = 1,5 см, Р = 6√3 см.
№ 3. Условие. Радиус описанной окружности равен 6 см. Какое значение в этом случае будет у стороны правильного шестиугольника?
Решение. Из формулы для радиуса вписанной в шестиугольник окружности легко получается та, по которой нужно вычислять сторону. Ясно, что радиус умножается на два и делится на корень из трех. Необходимо избавиться от иррациональности в знаменателе. Поэтому результат действий принимает такой вид: (12 √3) / (√3 * √3), то есть 4√3.
Ответ. а = 4√3 см.
Шестиугольник – это многоугольник, имеющий 6 сторон и 6 углов.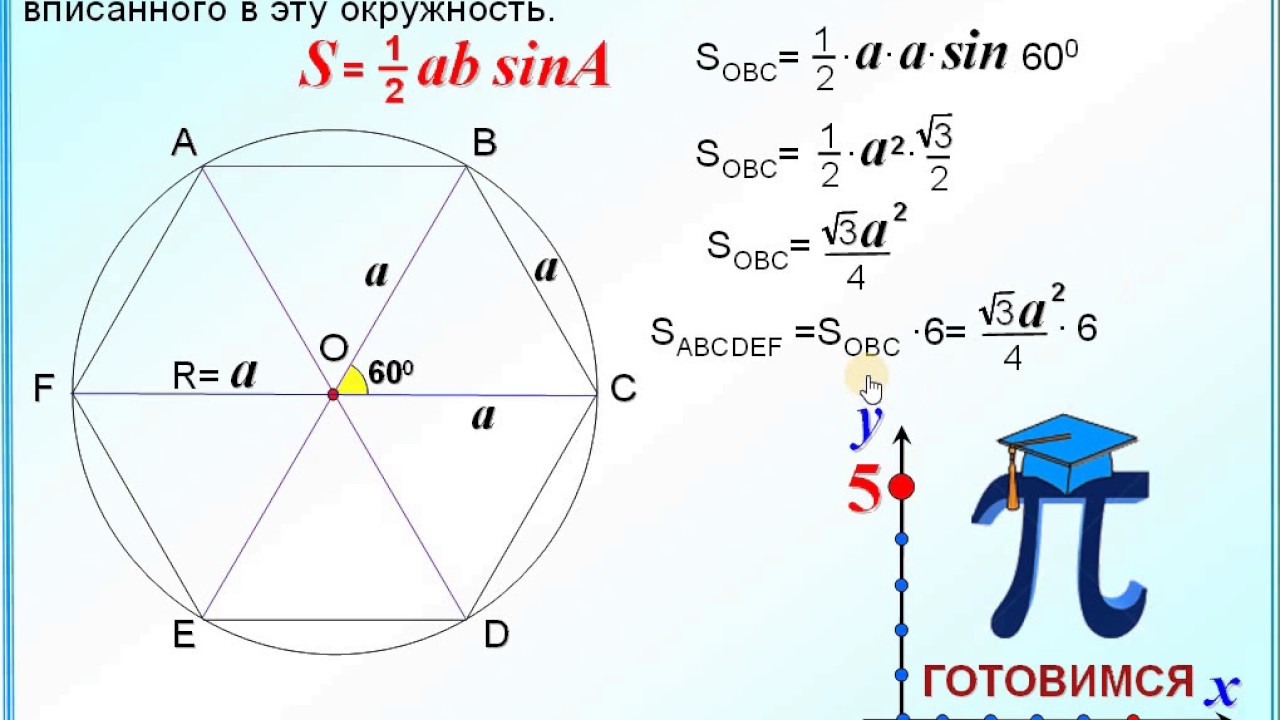 В зависимости от того, правильный шестиугольник или нет, существует несколько методов нахождения его площади. Мы рассмотрим все.
В зависимости от того, правильный шестиугольник или нет, существует несколько методов нахождения его площади. Мы рассмотрим все.
Как найти площадь правильного шестиугольника
Формулы для вычисления площади правильного шестиугольника – выпуклого многоугольника с шестью одинаковыми сторонами.
Дана длина стороны:
- Формула площади: S = (3√3*a²)/2
- Если длина стороны a известна, то подставив её в формулу, мы легко найдём площадь фигуры.
- В противном случае длину стороны можно найти через периметр и апофему.
- Если задан периметр, то мы просто делим его на 6 и получаем длину одной стороны. Например, если периметр равен 24, то длина стороны будет равняться 24/6 = 4.
- Апофема – перпендикуляр, проведённый из центра к одной из сторон. Чтобы найти длину одной стороны, подставляем длину апофемы в формулу а = 2*m/√3. То есть, если апофема m = 2√3, то длина стороны а = 2*2√3/√3 = 4.
Дана апофема:
- Формула площади: S = 1/2*p*m, где p – периметр, m – апофема.

- Найдём через апофему периметр шестиугольника. В предыдущем пункте мы научились находить длину одной стороны через апофему: а = 2*m/√3. Осталось только этот результат умножить на 6. Получаем формулу периметра: p = 12*m/√3.
Дан радиус описанной окружности:
- Радиус описанной вокруг правильного шестиугольника окружности равен стороне этого шестиугольника.
Формула площади: S = (3√3*a²)/2
Дан радиус вписанной окружности:
- Формула площади: S = 3√3*r², где r = √3*a/2 (a – одна из сторон многоугольника).
Как найти площадь неправильного шестиугольника
Формулы для вычисления площади неправильного шестиугольника – многоугольника, стороны которого не равны между собой.
Метод трапеции:
- Делим шестиугольник на произвольные трапеции, вычисляем площадь каждой из них и складываем.
- Основные формулы площади трапеции: S = 1/2*(a + b)*h, где a и b – основания трапеции, h – высота.

S = h*m, где h – высота, m – средняя линия.
Известны координаты вершин шестиугольника:
- Для начала запишем координаты точек, причём, располагая их не в хаотичном порядке, а последовательно друг за другом. Например:
A: (-3, -2)
B: (-1, 4)
C: (6, 1)
D: (3, 10)
E: (-4, 9)
F: (-5, 6) - Далее, внимательно, умножаем координату x каждой точки на координату y следующей точки:
-3*4 = -12
-1*1 = -1
6*10 = 60
3*9 = 27
-4*6 = -24
-5*(-2) = 10
Результаты складываем:
-12 – 1 + 60 + 27 – 24 + 10 = 60
Далее умножаем координату y каждой точки на координату x следующей точки.
-2*(-1) = 2
4*6 = 24
1*3 = 3
10*(-4) = -40
9*(-5) = -45
6*(-3) = -18
Результаты складываем:
2 + 24 + 3 – 40 – 45 – 18 = -74
Из первого результата вычитаем второй:
60 -(-74) = 60 + 74 = 134
Полученное число делим на два:
134/2 = 67
Ответ: 67 квадратных единиц.
- Также для нахождения площади шестиугольника вы можете разбить его на треугольники, квадраты, прямоугольники, параллелограммы и так далее.
 Найти площади составляющих его фигур и сложить.
Найти площади составляющих его фигур и сложить.
Итак, методы нахождения площади шестиугольника на все случаи жизни изучены. Теперь вперёд, применять полученные знания! Удачи!
Знаете ли вы, как выглядит правильный шестиугольник?
Этот вопрос задан не случайно. Большинство учащихся 11 класса не знают на него ответа.
Правильный шестиугольник — такой, у которого все стороны равны и все углы тоже равны .
Железная гайка. Снежинка. Ячейка сот, в которых живут пчелы. Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.
Многие школьники теряются, видя задачи на правильный шестиугольник, и считают, что для их решения нужны какие-то особые формулы. Так ли это?
Проведем диагонали правильного шестиугольника. Мы получили шесть равносторонних треугольников.
Мы знаем, что площадь правильного треугольника: .
Тогда площадь правильного шестиугольника — в шесть раз больше.
Где — сторона правильного шестиугольника.
Обратите внимание, что в правильном шестиугольнике расстояние от его центра до любой из вершин одинаково и равно стороне правильного шестиугольник.
Значит, радиус окружности, описанной вокруг правильного шестиугольника, равен его стороне .
Радиус окружности, вписанной в правильный шестиугольник, нетрудно найти.
Он равен .
Теперь вы легко решите любые задачи ЕГЭ, в которых фигурирует правильный шестиугольник.
Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .
Радиус такой окружности равен .
Ответ: .
Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
С вопросом: «Как найти площадь шестиугольника?» , можно столкнуться не только на экзамене по геометрии и т.п., эти знания пригодятся и в быту, например, для правильного и точного вычисления площади помещения в процессе ремонта.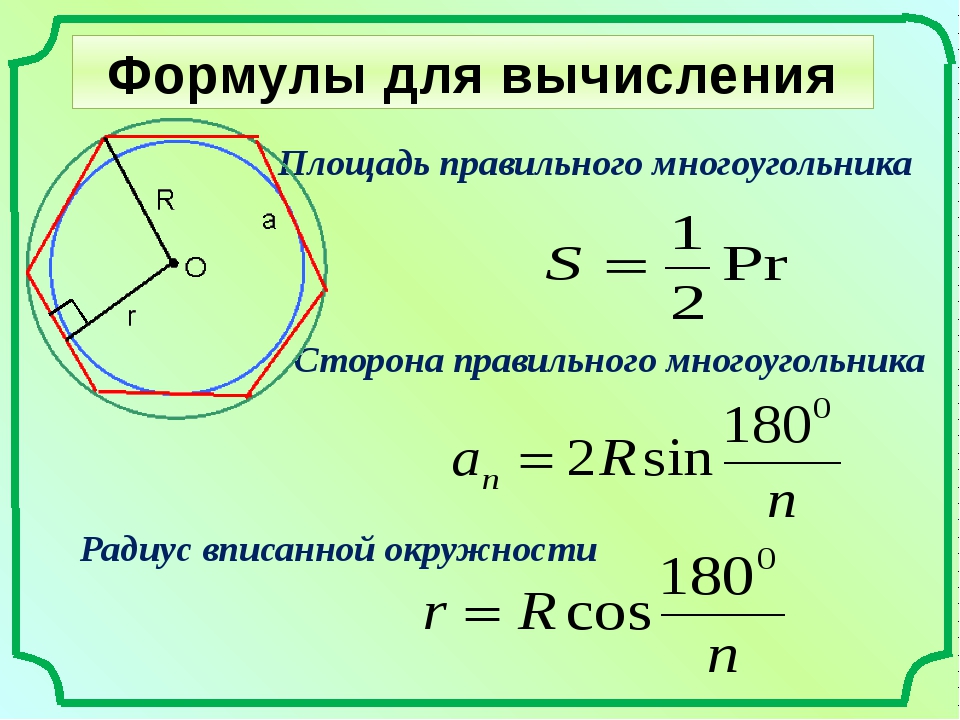 Подставив в формулу требуемые значения, получится определить нужное количество рулонов обоев, плитки в ванную или на кухню и т.д.
Подставив в формулу требуемые значения, получится определить нужное количество рулонов обоев, плитки в ванную или на кухню и т.д.
Немного фактов из истории
Геометрия использовалась еще в древнем Вавилоне и прочих государствах, существовавших в одно время с ним. Вычисления помогали при возведении значительных сооружений, так как благодаря ей зодчие знали как выдержать вертикаль, правильно составить план, определить высоту.
Эстетика тоже имела большое значение, и здесь снова шла в ход геометрия. Сегодня этой науки нужны строителю, закройщику, архитектору, да и не специалисту тоже.
Поэтому лучше уметь рассчитывать S фигур, понимать, что формулы могут пригодиться на практике.
Площадь правильного 6-угольника
Итак, у нас шестиугольная фигура с равными сторонами и углами . В повседневности мы часто имеем возможность встретить предметы правильной шестиугольной формы.
К примеру:
- гайка;
- пчелиные соты;
- снежинка.

Шестиугольная фигура наиболее экономично заполняет пространство на плоскости. Взгляните на тротуарную плитку, одна подогнана к другой так, что зазоров не остается.
Каждый угол равен 120˚. Сторона фигуры равна радиусу описанной окружности .
Расчет
Требуемое значение можно вычислить, разбив фигуру на шесть треугольников с равными сторонами.
Вычислив S одного из треугольников, нетрудно определить и общую. Простая формула, так как правильный шестиугольник, по сути, является шестью равными треугольниками. Таким образом, для ее расчета найденную площадь одного треугольника умножают на 6.
Если от центра шестиугольника к любой его стороне провести перпендикуляр, получается отрезок – апофема .
Посмотрим, как находить S шестиугольника, если апофема известна:
- S =1/2×периметр×апофема.
- Возьмем апофему равную 5√3 см.
- Находим периметр, используя апофему: так как апофема перпендикулярно к стороне 6-угольника, углы треугольника, образованного с помощью апофемы, равняются 30˚-60˚-90˚.
 Каждая сторона треугольника соответствует: x-x√3-2x, где короткая, против угла 30˚,- это x; длинная сторона против угла 60˚- x√3, а гипотенуза — 2x.
Каждая сторона треугольника соответствует: x-x√3-2x, где короткая, против угла 30˚,- это x; длинная сторона против угла 60˚- x√3, а гипотенуза — 2x. - Апофему x√3 можно подставить в формулу a=x√3. Если апофема равна 5√3, подставив данную величину, получим: 5√3см=x√3, или x=5см.
- Короткая сторона треугольника составляет 5см, так как эта величина – половина длины стороны 6-угольника. Умножив 5 на 2, получим 10см, что есть значение длиной стороны.
- Полученную величину умножим на 6 и получим значение периметра – 60см.
Подставляем полученные результаты в формулу: S=1/2×периметр×апофема
S=½×60 см× 5√3
Считаем:
Упрощаем полученный ответ, чтоб избавиться от корней. Результат будет выражен в квадратных сантиметрах: ½×60см×5√3см=30×5√3см=150 √3см=259,8с м².
Как находить площадь неправильного шестиугольника
Есть несколько вариантов:
- Разбивка 6-угольника на другие фигуры.
- Метод трапеции.
- Расчет S неправильных многоугольников с помощью осей координат.

Выбор способа диктуется исходными данными.
Метод трапецииШестиугольник делится на отдельные трапеции, после чего вычисляется площадь каждой полученной фигуры.
Использование осей координатИспользуем координаты вершин многоугольника:
- В таблицу записываем координаты вершин x и y . Последовательно выбираем вершины, «двигаясь» против часовой стрелки, завершая список повторной записью координат первой вершины.
- Умножаем значения координаты x 1-й вершины на значение y 2-й вершины, и продолжаем так умножать. Складываем полученные результаты.
- Значения координат y1-й вершины умножаем на значения координат x 2-й вершины. Складываем результаты.
- Вычитаем сумму, полученную на 4-м этапе из суммы, полученной на третьем этапе.
- Делим результат, полученный на предыдущем этапе, и находим, что искали.
Разбивка шестиугольника на другие фигуры
Многоугольники разбиваются на другие фигуры: трапеции, треугольники, прямоугольники. Пользуясь формулами вычисления площадей перечисленных фигур, требуемые значения вычисляются и складываются.
Пользуясь формулами вычисления площадей перечисленных фигур, требуемые значения вычисляются и складываются.
Неправильный шестиугольник может состоять из двух параллелограммов. Чтоб вычислить площадь параллелограмма, его длина умножается на его ширину, а далее уже известные две площади складываются.
Площадь равностороннего шестиугольника
У правильного шестиугольника шесть равных сторон. Площадь равносторонней фигуры равна 6S треугольников, на которые разбит правильный шестиугольник. Каждый треугольник в правильном шестиугольнике равен, поэтому для вычисления площади такой фигуры довольно знать площадь хотя б одного треугольника.
Чтоб найти искомое значение пользуются формулой площади правильной фигуры, описанной выше.
Кирпич. Облицовка камнем. Мокрый фасад. Фасадные панели. Дизайн и декор
Шестигранник вписанный в окружность формулы. Как найти площадь шестиугольника по формуле? Как узнать площадь многоугольника
Шестиугольник или гексагон — это правильный многоугольник, у которого стороны равны между собой, а каждый угол равен строго 120 градусов. Гексагон иногда встречается в человеческой повседневности, поэтому вам может понадобиться вычислить его площадь не только в школьных задачах, но и в реальной жизни.
Гексагон иногда встречается в человеческой повседневности, поэтому вам может понадобиться вычислить его площадь не только в школьных задачах, но и в реальной жизни.
Выпуклый шестиугольник
Гескагон — это правильный выпуклый многоугольник, соответственно, все его углы равны, все стороны равны, а если провести отрезок через две соседние вершины, то вся фигура окажется по одну сторону от этого отрезка. Как и в любой правильный n-угольник, вокруг гексагона можно описать окружность или вписать ее вовнутрь. Главная особенность шестиугольника заключается в том, что длина радиуса описанной окружности совпадает с длиной стороны многоугольника. Благодаря этому свойству можно легко найти площадь гексагона по формуле:
S = 2,59 R 2 = 2,59 a 2 .
Кроме того, радиус вписанной окружности соотносится со стороной фигуры как:
Из этого следует, что вычислить площадь шестиугольника можно, оперируя одной из трех переменных на выбор.
Гексаграмма
Звездчатый правильный шестиугольник предстает перед нами в виде шестиконечной звезды. Такая фигура образуется путем наложения друг на друга двух равносторонних треугольников. Самой известной реальной гексаграммой является Звезда Давида — символ еврейского народа.
Такая фигура образуется путем наложения друг на друга двух равносторонних треугольников. Самой известной реальной гексаграммой является Звезда Давида — символ еврейского народа.
Шестиугольные числа
В теории чисел существуют фигурные числа, связанные с определенными геометрическими фигурами. Наибольшее применение находят треугольные и квадратные, а также тетраэдрические и пирамидальные числа, используя которые легко выкладывать геометрические фигуры при помощи реальных предметов. Например, пирамидальные числа подскажут вам, как сложить пушечные ядра в устойчивую пирамиду. Существуют также и шестиугольные числа, которые определяют число точек, необходимое для построения гексагона.
Шестиугольник в реальности
Гексагоны часто встречаются в реальной жизни. К примеру, сечения гаек или карандашей имеют шестиугольную форму, благодаря чему обеспечивается удобный обхват предмета. Шестиугольник — это эффективная геометрическая фигура, способная замостить плоскость без пробелов и наложений. Именно поэтому шестиугольную форму часто имеют декоративные отделочные материалы, например, кафельная и тротуарная плитка или гипсокартонные панели.
Именно поэтому шестиугольную форму часто имеют декоративные отделочные материалы, например, кафельная и тротуарная плитка или гипсокартонные панели.
Эффективность гексагона делает его популярным и в природе. Пчелиные соты обладают именно шестиугольной формой, благодаря которой пространство улья заполняется без пробелов. Еще одним примером гексагонального замощения плоскости является Тропа Великанов — памятник живой природы, сформированный во время извержения вулкана. Вулканический пепел был спрессован в шестиугольные колонны, которые замостили поверхность побережья Северной Ирландии.
Упаковка кругов на плоскости
И еще немного об эффективности гексагона. Упаковка шаров — классическая задача комбинаторной геометрии, которая требует найти оптимальный способ укладки непересекающихся шаров. На практике такая задача превращается в логистическую проблему упаковки апельсинов, яблок, пушечных ядер или любых других шарообразных объектов, которые требуется уложить максимально плотно. Гескагон — решение данной проблемы.
Гескагон — решение данной проблемы.
Известно, что наиболее эффективным расположением кругов в двухмерном пространстве является размещение центров окружностей на вершинах шестиугольников, которые заполняют плоскость без пробелов. В трехмерной реальности задача размещения шаров решается путем гексагональной укладки объектов.
При помощи нашего калькулятора вы можете вычислить площадь правильного шестиугольника, зная его сторону или радиусы соответствующих окружностей. Давайте попробуем вычислить площади гексагонов на реальных примерах.
Примеры из реальной жизни
Гигантский гексагон
Гигантский гексагон — уникальное атмосферное явление на Сатуре, которое выглядит как грандиозный вихрь в форме правильного шестиугольника. Известно, что сторона гигантского гексагона составляет 13 800 км, благодаря чему мы можем определить площадь «облака». Для этого достаточно ввести значение стороны в форму калькулятора и получить результат:
Таким образом, площадь атмосферного вихря на Сатурне приблизительно составляет 494 777 633 квадратных километров. Поистине впечатляет.
Поистине впечатляет.
Гексагональные шахматы
Мы все привыкли к шахматному полю, разделенному на 64 квадратные ячейки. Однако существуют и гексагональные шахматы, игровое поле которых разделено на 91 правильный шестиугольник. Давайте определим площадь игровой доски для гексагональной версии известной игры. Пусть сторона ячейки составляет 2 сантиметра. Площадь одной игровой клетки составит:
Тогда площадь всей доски будет равна 91 × 10,39 = 945,49 квадратных сантиметров.
Заключение
Шестиугольник часто встречается в реальности, хотя мы и не замечаем этого. Используйте наш онлайн-калькулятор для расчета площадей гексагонов при решении повседневных или школьных задач.
Шестиугольник – это многоугольник, имеющий 6 сторон и 6 углов. В зависимости от того, правильный шестиугольник или нет, существует несколько методов нахождения его площади. Мы рассмотрим все.
Как найти площадь правильного шестиугольника
Формулы для вычисления площади правильного шестиугольника – выпуклого многоугольника с шестью одинаковыми сторонами.
Дана длина стороны:
- Формула площади: S = (3√3*a²)/2
- Если длина стороны a известна, то подставив её в формулу, мы легко найдём площадь фигуры.
- В противном случае длину стороны можно найти через периметр и апофему.
- Если задан периметр, то мы просто делим его на 6 и получаем длину одной стороны. Например, если периметр равен 24, то длина стороны будет равняться 24/6 = 4.
- Апофема – перпендикуляр, проведённый из центра к одной из сторон. Чтобы найти длину одной стороны, подставляем длину апофемы в формулу а = 2*m/√3. То есть, если апофема m = 2√3, то длина стороны а = 2*2√3/√3 = 4.
Дана апофема:
- Формула площади: S = 1/2*p*m, где p – периметр, m – апофема.
- Найдём через апофему периметр шестиугольника. В предыдущем пункте мы научились находить длину одной стороны через апофему: а = 2*m/√3. Осталось только этот результат умножить на 6. Получаем формулу периметра: p = 12*m/√3.
Дан радиус описанной окружности:
- Радиус описанной вокруг правильного шестиугольника окружности равен стороне этого шестиугольника.

Формула площади: S = (3√3*a²)/2
Дан радиус вписанной окружности:
- Формула площади: S = 3√3*r², где r = √3*a/2 (a – одна из сторон многоугольника).
Как найти площадь неправильного шестиугольника
Формулы для вычисления площади неправильного шестиугольника – многоугольника, стороны которого не равны между собой.
Метод трапеции:
- Делим шестиугольник на произвольные трапеции, вычисляем площадь каждой из них и складываем.
- Основные формулы площади трапеции: S = 1/2*(a + b)*h, где a и b – основания трапеции, h – высота.
S = h*m, где h – высота, m – средняя линия.
Известны координаты вершин шестиугольника:
- Для начала запишем координаты точек, причём, располагая их не в хаотичном порядке, а последовательно друг за другом. Например:
A: (-3, -2)
B: (-1, 4)
C: (6, 1)
D: (3, 10)
E: (-4, 9)
F: (-5, 6) - Далее, внимательно, умножаем координату x каждой точки на координату y следующей точки:
-3*4 = -12
-1*1 = -1
6*10 = 60
3*9 = 27
-4*6 = -24
-5*(-2) = 10
Результаты складываем:
-12 – 1 + 60 + 27 – 24 + 10 = 60
Далее умножаем координату y каждой точки на координату x следующей точки.
-2*(-1) = 2
4*6 = 24
1*3 = 3
10*(-4) = -40
9*(-5) = -45
6*(-3) = -18
Результаты складываем:
2 + 24 + 3 – 40 – 45 – 18 = -74
Из первого результата вычитаем второй:
60 -(-74) = 60 + 74 = 134
Полученное число делим на два:
134/2 = 67
Ответ: 67 квадратных единиц.
- Также для нахождения площади шестиугольника вы можете разбить его на треугольники, квадраты, прямоугольники, параллелограммы и так далее. Найти площади составляющих его фигур и сложить.
Итак, методы нахождения площади шестиугольника на все случаи жизни изучены. Теперь вперёд, применять полученные знания! Удачи!
С вопросом: «Как найти площадь шестиугольника?» , можно столкнуться не только на экзамене по геометрии и т.п., эти знания пригодятся и в быту, например, для правильного и точного вычисления площади помещения в процессе ремонта. Подставив в формулу требуемые значения, получится определить нужное количество рулонов обоев, плитки в ванную или на кухню и т. д.
д.
Немного фактов из истории
Геометрия использовалась еще в древнем Вавилоне и прочих государствах, существовавших в одно время с ним. Вычисления помогали при возведении значительных сооружений, так как благодаря ей зодчие знали как выдержать вертикаль, правильно составить план, определить высоту.
Эстетика тоже имела большое значение, и здесь снова шла в ход геометрия. Сегодня этой науки нужны строителю, закройщику, архитектору, да и не специалисту тоже.
Поэтому лучше уметь рассчитывать S фигур, понимать, что формулы могут пригодиться на практике.
Площадь правильного 6-угольника
Итак, у нас шестиугольная фигура с равными сторонами и углами . В повседневности мы часто имеем возможность встретить предметы правильной шестиугольной формы.
К примеру:
- гайка;
- пчелиные соты;
- снежинка.
Шестиугольная фигура наиболее экономично заполняет пространство на плоскости. Взгляните на тротуарную плитку, одна подогнана к другой так, что зазоров не остается.
Каждый угол равен 120˚. Сторона фигуры равна радиусу описанной окружности .
Расчет
Требуемое значение можно вычислить, разбив фигуру на шесть треугольников с равными сторонами.
Вычислив S одного из треугольников, нетрудно определить и общую. Простая формула, так как правильный шестиугольник, по сути, является шестью равными треугольниками. Таким образом, для ее расчета найденную площадь одного треугольника умножают на 6.
Если от центра шестиугольника к любой его стороне провести перпендикуляр, получается отрезок – апофема .
Посмотрим, как находить S шестиугольника, если апофема известна:
- S =1/2×периметр×апофема.
- Возьмем апофему равную 5√3 см.
- Находим периметр, используя апофему: так как апофема перпендикулярно к стороне 6-угольника, углы треугольника, образованного с помощью апофемы, равняются 30˚-60˚-90˚. Каждая сторона треугольника соответствует: x-x√3-2x, где короткая, против угла 30˚,- это x; длинная сторона против угла 60˚- x√3, а гипотенуза — 2x.

- Апофему x√3 можно подставить в формулу a=x√3. Если апофема равна 5√3, подставив данную величину, получим: 5√3см=x√3, или x=5см.
- Короткая сторона треугольника составляет 5см, так как эта величина – половина длины стороны 6-угольника. Умножив 5 на 2, получим 10см, что есть значение длиной стороны.
- Полученную величину умножим на 6 и получим значение периметра – 60см.
Подставляем полученные результаты в формулу: S=1/2×периметр×апофема
S=½×60 см× 5√3
Считаем:
Упрощаем полученный ответ, чтоб избавиться от корней. Результат будет выражен в квадратных сантиметрах: ½×60см×5√3см=30×5√3см=150 √3см=259,8с м².
Как находить площадь неправильного шестиугольника
Есть несколько вариантов:
- Разбивка 6-угольника на другие фигуры.
- Метод трапеции.
- Расчет S неправильных многоугольников с помощью осей координат.
Выбор способа диктуется исходными данными.
Метод трапецииШестиугольник делится на отдельные трапеции, после чего вычисляется площадь каждой полученной фигуры.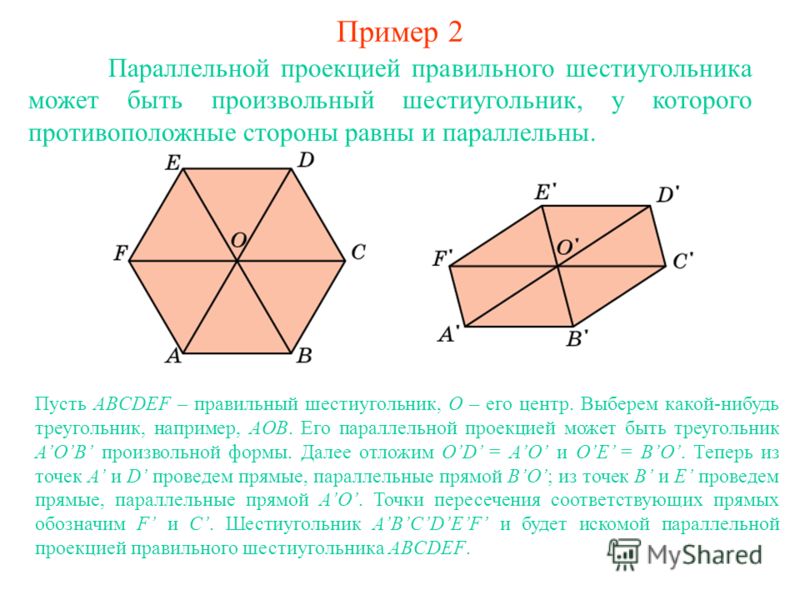
Используем координаты вершин многоугольника:
- В таблицу записываем координаты вершин x и y . Последовательно выбираем вершины, «двигаясь» против часовой стрелки, завершая список повторной записью координат первой вершины.
- Умножаем значения координаты x 1-й вершины на значение y 2-й вершины, и продолжаем так умножать. Складываем полученные результаты.
- Значения координат y1-й вершины умножаем на значения координат x 2-й вершины. Складываем результаты.
- Вычитаем сумму, полученную на 4-м этапе из суммы, полученной на третьем этапе.
- Делим результат, полученный на предыдущем этапе, и находим, что искали.
Разбивка шестиугольника на другие фигуры
Многоугольники разбиваются на другие фигуры: трапеции, треугольники, прямоугольники. Пользуясь формулами вычисления площадей перечисленных фигур, требуемые значения вычисляются и складываются.
Неправильный шестиугольник может состоять из двух параллелограммов. Чтоб вычислить площадь параллелограмма, его длина умножается на его ширину, а далее уже известные две площади складываются.
Чтоб вычислить площадь параллелограмма, его длина умножается на его ширину, а далее уже известные две площади складываются.
Площадь равностороннего шестиугольника
У правильного шестиугольника шесть равных сторон. Площадь равносторонней фигуры равна 6S треугольников, на которые разбит правильный шестиугольник. Каждый треугольник в правильном шестиугольнике равен, поэтому для вычисления площади такой фигуры довольно знать площадь хотя б одного треугольника.
Чтоб найти искомое значение пользуются формулой площади правильной фигуры, описанной выше.
Знаете ли вы, как выглядит правильный шестиугольник?
Этот вопрос задан не случайно. Большинство учащихся 11 класса не знают на него ответа.
Правильный шестиугольник — такой, у которого все стороны равны и все углы тоже равны .
Железная гайка. Снежинка. Ячейка сот, в которых живут пчелы. Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.
Многие школьники теряются, видя задачи на правильный шестиугольник, и считают, что для их решения нужны какие-то особые формулы. Так ли это?
Проведем диагонали правильного шестиугольника. Мы получили шесть равносторонних треугольников.
Мы знаем, что площадь правильного треугольника: .
Тогда площадь правильного шестиугольника — в шесть раз больше.
Где — сторона правильного шестиугольника.
Обратите внимание, что в правильном шестиугольнике расстояние от его центра до любой из вершин одинаково и равно стороне правильного шестиугольник.
Значит, радиус окружности, описанной вокруг правильного шестиугольника, равен его стороне .
Радиус окружности, вписанной в правильный шестиугольник, нетрудно найти.
Он равен .
Теперь вы легко решите любые задачи ЕГЭ, в которых фигурирует правильный шестиугольник.
Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .
Радиус такой окружности равен .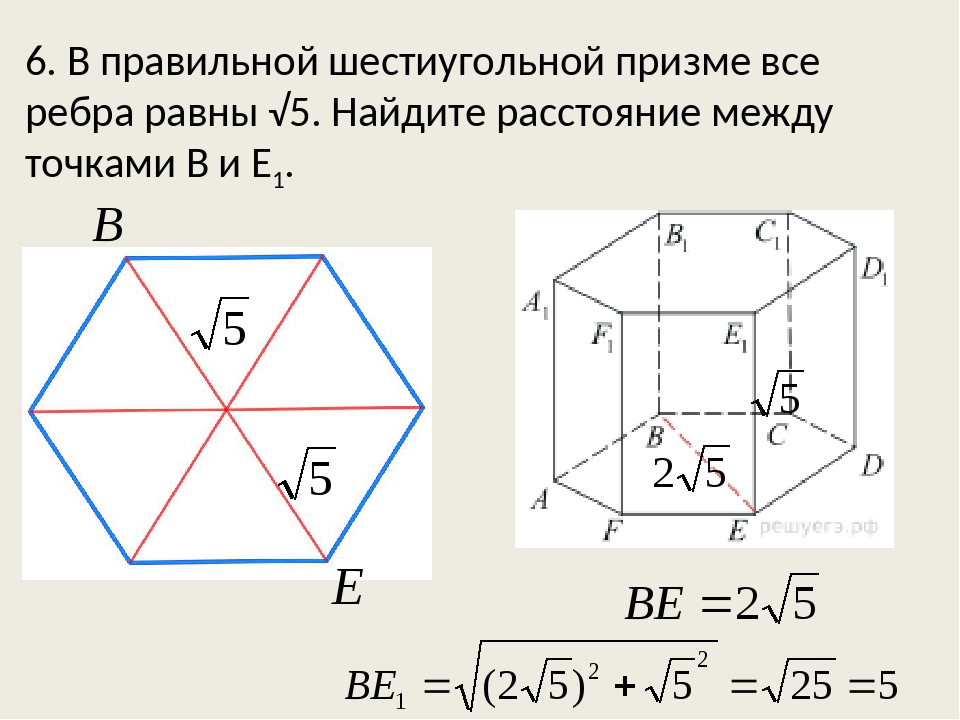
Ответ: .
Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
Самая известная фигура, у которой больше четырех углов — это правильный шестиугольник. В геометрии он часто используется в задачах. А в жизни именно такой вид имеют соты на срезе.
Чем он отличается от неправильного?
Во-первых, шестиугольником является фигура с 6 вершинами. Во-вторых, он может быть выпуклым или вогнутым. Первый отличается тем, что четыре вершины лежат по одну сторону от прямой, проведенной через две другие.
В-третьих, правильный шестиугольник характеризуется тем, что все его стороны равны. Причем каждый угол фигуры тоже имеет одинаковое значение. Чтобы определить сумму всех его углов, потребуется воспользоваться формулой: 180º * (n — 2). Здесь n — число вершин фигуры, то есть 6. Простой расчет дает значение в 720º. То есть каждый угол равен 120 градусам.
В повседневной деятельности правильный шестиугольник встречается в снежинке и гайке. Химики видят ее даже в молекуле бензола.
Какие свойства требуется знать при решении задач?
К тому, что указано выше, следует добавить:
- диагонали фигуры, проведенные через центр, делят ее на шесть треугольников, которые являются равносторонними;
- сторона правильного шестиугольника имеет значение, которое совпадает с радиусом описанной около него окружности;
- используя такую фигуру, есть возможность заполнить плоскость, причем между ними не получится пропусков и не будет наложений.
Введенные обозначения
Традиционно сторона правильной геометрической фигуры обозначается латинской буквой «а». Для решения задач требуются еще площадь и периметр, это S и P соответственно. В правильный шестиугольник бывает вписана окружность или описана около него. Тогда вводятся значения для их радиусов. Обозначаются они соответственно буквами r и R.
В некоторых формулах фигурируют внутренний угол, полупериметр и апофема (являющаяся перпендикуляром к середине любой стороны из центра многоугольника). Для них используются буквы: α, р, m.
Для них используются буквы: α, р, m.
Формулы, которые описывают фигуру
Для расчета радиуса вписанной окружности потребуется такая: r = (a * √3) / 2, причем r = m. То есть такая же формула будет и для апофемы.
Поскольку периметр шестиугольника — это сумма всех сторон, то он определится так: P = 6 * a. С учетом того, что сторона равна радиусу описанной окружности, для периметра существует такая формула правильного шестиугольника: P = 6 * R. Из той, что приведена для радиуса вписанной окружности, выводится зависимость между а и r. Тогда формула принимает такой вид: Р = 4 r * √3.
Для площади правильного шестиугольника может пригодиться такая: S = p * r = (a 2 * 3 √3) / 2.
Задачи
№ 1. Условие. Имеется правильная шестиугольная призма, каждое ребро которой равно 4 см. В нее вписан цилиндр, объем которого необходимо узнать.
Решение. Объем цилиндра определяется как произведение площади основания на высоту. Последняя совпадает с ребром призмы.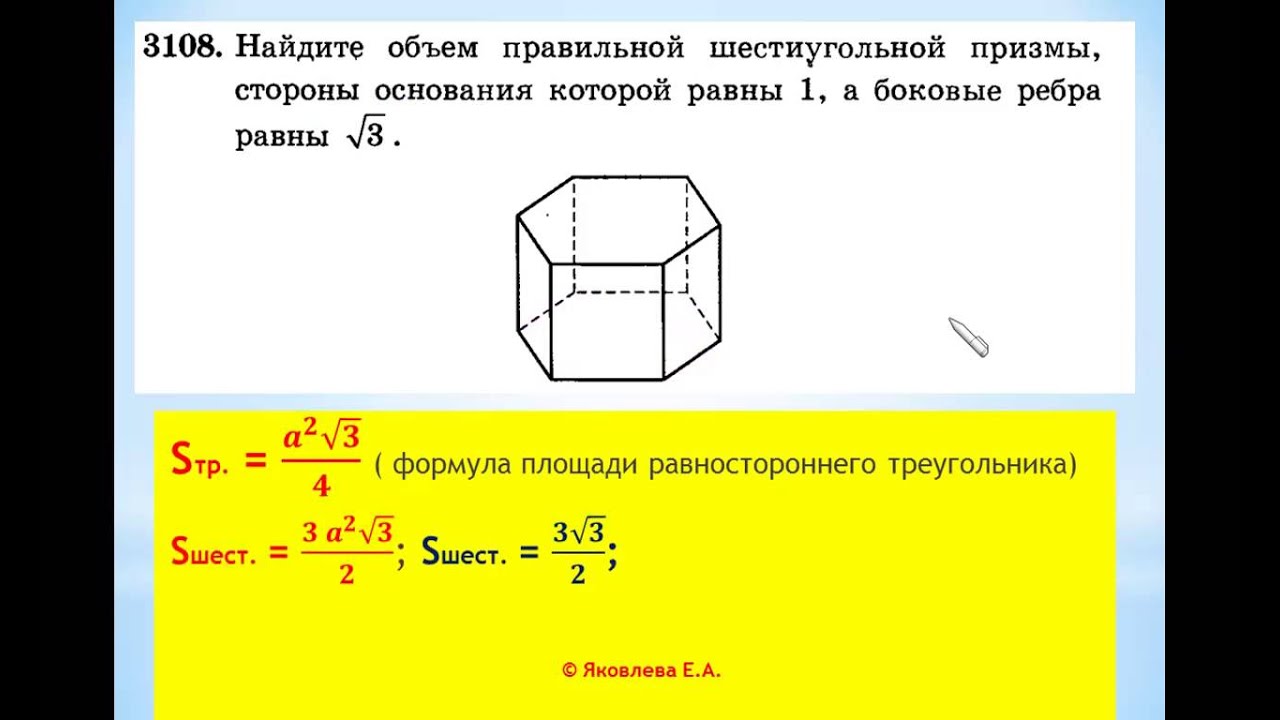 А она равна стороне правильного шестиугольника. То есть высота цилиндра — тоже 4 см.
А она равна стороне правильного шестиугольника. То есть высота цилиндра — тоже 4 см.
Чтобы узнать площадь его основания, потребуется вычислить радиус вписанной в шестиугольник окружности. Формула для этого указана выше. Значит, r = 2√3 (см). Тогда площадь круга: S = π * r 2 = 3,14 * (2√3) 2 = 37,68 (см 2).
Ответ . V = 150,72 см 3 .
№ 2. Условие. Вычислить радиус окружности, которая вписана в правильный шестиугольник. Известно, что его сторона равна √3 см. Чему будет равен его периметр?
Решение. Эта задача требует использования двух из указанных формул. Причем их необходимо применять, даже не видоизменяя, просто подставить значение стороны и вычислить.
Таким образом, радиус вписанной окружности получается равным 1,5 см. Для периметра оказывается верным такое значение: 6√3 см.
Ответ. r = 1,5 см, Р = 6√3 см.
№ 3. Условие. Радиус описанной окружности равен 6 см. Какое значение в этом случае будет у стороны правильного шестиугольника?
Решение. Из формулы для радиуса вписанной в шестиугольник окружности легко получается та, по которой нужно вычислять сторону. Ясно, что радиус умножается на два и делится на корень из трех. Необходимо избавиться от иррациональности в знаменателе. Поэтому результат действий принимает такой вид: (12 √3) / (√3 * √3), то есть 4√3.
Из формулы для радиуса вписанной в шестиугольник окружности легко получается та, по которой нужно вычислять сторону. Ясно, что радиус умножается на два и делится на корень из трех. Необходимо избавиться от иррациональности в знаменателе. Поэтому результат действий принимает такой вид: (12 √3) / (√3 * √3), то есть 4√3.
Ответ. а = 4√3 см.
Площадь многоугольника
Площадь многоугольника. Друзья! К вашему вниманию пару задачек с многоугольником и вписанной в него окружностью. Существует формула, которой связывается радиус указанной окружности и периметр с площадью такого многоугольника. Вот она:
Как выводится эта формула? Просто!
Имеем многоугольник и вписанную окружность. *Рассмотрим вывод на примере пятиугольника. Разобьём его на треугольники (соединим центр окружности и вершины отрезками). Получается, что у каждого треугольника основание является стороной многоугольника, а высоты образованных треугольников равны радиусу вписанной окружности:
Используя формулу площади треугольника можем записать:
Вынесем общие множители:
Уверен, сам принцип вам понятен.
*При выводе формулы количество сторон взятого многоугольника не имеет значения. В общем виде вывод формулы выглядел бы так:
*Дополнительная информация!
Известна формула радиуса окружности вписанной в треугольник
Не трудно заметить, что она исходит из полученной нами формулы, посмотрите (a,b,c – это стороны треугольника):
27640. Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 20. Найдите его площадь.
Вычисляем:
Ответ: 30
Ещё пара задач с многоугольниками.
27930. Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 540. Найдите n.
Если угол между радиусом окружности и стороной многоугольника равен 540, то угол между сторонами многоугольника будет равен 1080. Тут необходимо вспомнить формулу угла правильного многоугольника:
Остаётся подставить в формулу значение угла и вычислить n:
Ответ: 5
27595. Периметры двух подобных многоугольников относятся как 2:7. Площадь меньшего многоугольника равна 28. Найдите площадь большего многоугольника.
Периметры двух подобных многоугольников относятся как 2:7. Площадь меньшего многоугольника равна 28. Найдите площадь большего многоугольника.
Здесь нужно вспомнить о том, что если линейные размеры фигуры увеличивается в k раз, то площадь фигуры увеличивается в k2 раз. *Свойство подобия фигур.
Периметр большего многоугольника больше периметра меньшего в 7/2 раза, значит площадь увеличилась в (7/2)2 раза. Таким образом, площадь большего многоугольника равна:
Ответ: 343
27639. Около окружности, радиус которой равен 3, описан многоугольник, площадь которого равна 33. Найдите его периметр.
Посмотреть решение
27641. Около окружности описан многоугольник, площадь которого равна 5. Его периметр равен 10. Найдите радиус этой окружности.
Посмотреть решение
27595. Периметры двух подобных многоугольников относятся как 3:5. Площадь меньшего многоугольника равна 18. Найдите площадь большего многоугольника.
Ответ: 50
Всего доброго! Учитесь с удовольствием!
С уважением, Александр.
| С4Дан параллелограмм $ABCD$, сторона которого $AB=13$. В7Найдите, если $\operatorname{tg}\alpha=-4$ [посмотреть решение] |
Как найти площадь шестиугольника
Объяснение:Есть несколько способов найти площадь шестиугольника.
- Разделите фигуру правильным шестиугольником на треугольники.
- Найдите площадь одного треугольника.
- Умножьте это значение на шесть.
В качестве альтернативы площадь можно найти, вычислив половину длины стороны, умноженную на апофему.
Правильные шестиугольники:
Правильные шестиугольники — это интересные многоугольники.Шестиугольники представляют собой шестигранные фигуры и имеют следующую форму:
В правильном шестиугольнике все стороны равны по длине, а все внутренние углы имеют одинаковую меру; следовательно, мы можем написать следующее выражение.
Один из самых простых способов найти площадь многоугольника — разбить фигуру на треугольники. Начнем с разделения шестиугольника на шесть треугольников.
На этом рисунке центральная точка находится на равном расстоянии от всех вершин.В результате шесть пунктирных линий внутри шестиугольника имеют одинаковую длину. Точно так же все треугольники внутри шестиугольника конгруэнтны по правилу стороны-стороны-стороны: каждый из треугольников имеет две стороны внутри шестиугольника, а также основную сторону, которая составляет периметр шестиугольника. Подобным образом у всех треугольников одинаковые углы. Они находятся в круге, а шестиугольник на нашем изображении разделил его на шесть равных частей; следовательно, мы можем написать следующее:
Нам также известно следующее:
Теперь давайте посмотрим на каждый из треугольников шестиугольника. Мы знаем, что у каждого треугольника две стороны равны; следовательно, каждый из углов основания каждого треугольника должен быть одинаковым. Мы знаем, что у треугольника есть, и можем вычислить два основных угла каждого треугольника, используя эту информацию.
Мы знаем, что у каждого треугольника две стороны равны; следовательно, каждый из углов основания каждого треугольника должен быть одинаковым. Мы знаем, что у треугольника есть, и можем вычислить два основных угла каждого треугольника, используя эту информацию.
Каждый угол в треугольнике равен. Теперь мы знаем, что все треугольники равносторонние и равносторонние: каждый треугольник имеет три равные длины сторон и три равных угла. Теперь мы можем использовать эту важную информацию для определения площади шестиугольника.Если мы найдем площадь одного из треугольников, то мы можем умножить ее на шесть, чтобы вычислить площадь всей фигуры. Начнем с анализа. Если мы проведем через треугольник высоту, то получим два треугольника.
Давайте решим длину этого треугольника. Помните, что в треугольниках длина сторон треугольников определяется следующим соотношением:
Теперь мы можем проанализировать, используя заменяющую переменную для длины стороны,.
Нам известны размеры основания и высоты, и мы можем вычислить их площадь.
Теперь нам нужно умножить это на шесть, чтобы найти площадь всего шестиугольника.
Мы решили для площади правильного шестиугольника с длиной стороны,. Если мы знаем длину стороны правильного шестиугольника, мы можем найти площадь.
Если нам не дан правильный шестиугольник, то мы вычисляем площадь шестиугольника, используя длину стороны (т.е.е. ) И апофема (то есть), которая представляет собой длину линии, проведенной от центра многоугольника до прямого угла любой стороны. Это обозначено переменной на следующем рисунке:
Альтернативный метод:
Если нам даны переменные и, то мы можем найти площадь шестиугольника по следующей формуле:
В этом уравнении площадь, периметр и апофема. Мы должны рассчитать периметр, используя длину стороны и уравнение, где — длина стороны.
Мы должны рассчитать периметр, используя длину стороны и уравнение, где — длина стороны.
Решение:
В задаче сказано, что соты два сантиметра в диаметре. Чтобы решить задачу, нам нужно разделить диаметр на два. Это потому, что радиус этого диаметра равен длине внутренней стороны равносторонних треугольников в соте. Давайте найдем длину стороны правильного шестиугольника / соты.
Подставить и решить.
Нам известна следующая информация.
В результате мы можем написать следующее:
Давайте подставим это значение в формулу площади правильного шестиугольника и решим.
Упростить.
Решить.
Округлите до ближайшей десятой доли сантиметра.
Площадь шестиугольника
Площадь шестиугольника — это пространство внутри его периметра. Серое пространство — это область шестиугольника на рисунке ниже.
Формула площади правильного шестиугольника
Есть много разных типов шестиугольников. Самый распространенный тип — это правильный шестиугольник, который представляет собой шестиугольник со сторонами равной длины и равными углами.
Площадь A правильного шестиугольника может быть определена только по длине его стороны s по формуле:
Пример:
Найдите площадь правильного шестиугольника с периметром 72.
Учитывая, что периметр равен 72, длину каждой стороны правильного шестиугольника можно найти, разделив периметр на 6, получив длину каждой стороны 12.
Подставляем длину стороны в формулу площади:
Иногда в реальной жизни легче измерить расстояние между противоположными сторонами правильного шестиугольника. В этом случае площадь шестиугольника составляет:
В этом случае площадь шестиугольника составляет:
Апофема a правильного шестиугольника равна половине расстояния между противоположными сторонами шестиугольника. Формула площади с использованием апофемы:
Нахождение участка по сетке
Другой способ найти площадь шестиугольника — это определить, сколько единичных квадратов нужно, чтобы покрыть его поверхность.Ниже представлен единичный квадрат со стороной 1 см.
При определении площади шестиугольника можно использовать сетку из единичных квадратов.
Сетка выше содержит единичные квадраты площадью 1 см 2 каждый. Правильный шестиугольник слева содержит 6 полных квадратов и 10 частичных квадратов, поэтому его площадь составляет примерно
.Правильный шестиугольник справа содержит 17 полных квадратов и 10 частичных квадратов, поэтому его площадь составляет приблизительно:
С помощью этого метода можно найти площадь любой формы; это не ограничивается правильными шестиугольниками. Однако это лишь приблизительная стоимость площади. Чем меньше используемый единичный квадрат, тем выше точность приближения. Использование сетки из квадратов 1 мм в 10 раз точнее, чем использование сетки из квадратов 1 см.
Однако это лишь приблизительная стоимость площади. Чем меньше используемый единичный квадрат, тем выше точность приближения. Использование сетки из квадратов 1 мм в 10 раз точнее, чем использование сетки из квадратов 1 см.
Вывод формулы площади
Разделите правильный шестиугольник на шесть равносторонних треугольников, проведя отрезки прямых к противоположным вершинам. Каждый треугольник имеет длину стороны s и высоту (также апофему правильного шестиугольника). Площадь A одного из равносторонних треугольников, нарисованных синим цветом, может быть найдена с помощью:
Так как равносторонних треугольников шесть, площадь правильного шестиугольника равна:
Шестиугольник
ШестиугольникПлощадь и периметр правильных многоугольников
ШестигранникЦель содержания:
Студенты узнают, как найти периметр правильных шестиугольников.
Студенты откроют для себя два разных метода
для нахождения площади правильных шестиугольников относительно правильных
треугольники и апофема.
Материалы:
Линейки парные шестигранные рабочий лист периметра, рабочий лист шестиугольника
Процедура:
Периметр
1. Снова напомним коллективно определение периметра, указанного в день проверки и для правильных треугольников и квадраты. Попросите учащихся разделиться на пары и распределить шестиугольник. лист периметра.После того, как рабочий лист будет заполнен и студенты получат сравнили их ответы, задайте всем классу следующие вопросов:
Что вы заметили по поводу длины сторон? нашего шестиугольника? Вы этого ожидали?
Что происходит с периметром, когда сбоку длины меняются?
Есть ли способ найти периметр правильный шестиугольник без измерения всех шести сторон?
Вспоминая общие выражения для периметр из правильных треугольников и квадратов.Вы замечаете закономерность? Чего мы можем ожидать, когда обнаруживаем периметр шестиугольника?
2. Продемонстрируйте с помощью Sketchpad Geometer
свойства длин сторон правильного шестиугольника. кликните сюда
использовать файл GSP и наблюдать за анимацией изменения периметра.
Продемонстрируйте с помощью Sketchpad Geometer
свойства длин сторон правильного шестиугольника. кликните сюда
использовать файл GSP и наблюдать за анимацией изменения периметра.
Площадь
Мы покажем два способа нахождения области правильный шестиугольник. Первый метод использует предыдущие знание равносторонних треугольников.
МЕТОД 1:
Начните с показа приведенных ниже цифр и спросите следующие вопросы:
Нажмите здесь, чтобы использовать эскиз этих изображений GSP.
Во-первых, как мы можем разбить эту цифру в знакомые формы? Какого особого свойства обладают эти шестерки треугольники есть? Учитывая, что сторона нашего шестиугольника — это длина s, какова длина стороны каждого из треугольников? Напомним метод поиска местности. правильного треугольника. Какова площадь ОДНОГО из треугольников в нашем шестиугольнике? Как быстро найти район на весь шестиугольник?Итак, мы открыли общую формулу для площадь, используя меньшие треугольники внутри шестиугольника!
Пример 1:
Используйте выражение площади выше, чтобы вычислить площадь шестиугольника с длиной стороны s = 3.
00см и высота h = 2,60 см для сравнения с методом 2 позже.
МЕТОД 2:
Напомним формулу периметра нашей регулярной шестиугольник. Как мы можем упростить найденное выражение для площади?
Назовем периметр р . Итак, теперь у нас естьТеперь мы можем взглянуть на общий метод для нахождение площади правильного многоугольника. Определите апофему для студентов чтобы начать второй метод определения площади правильного шестиугольника.
Apothem — расстояние отрезка линии от центра правильного многоугольника, перпендикулярного стороне (т.е. когда правильный многоугольник разбит на треугольники, апофема — высота один из треугольников, основание которого является стороной правильного многоугольника).
Обсудить концепцию апофемы со студентами и задайте следующие вопросы:
Что означает апофема правильного шестиугольника выглядит как?
Как апофема связана с высотой, которую мы найдено в правильных шестиугольниках выше?
Сколько апофем у правильного шестиугольника? У всех апофемы одинаковой длины?
Как мы можем переписать нашу формулу для площади, используя апофема для правильного шестиугольника вместо высоты х правильного треугольника?
Пример 2:
Теперь мы можем заполнить значения для p и a чтобы найти площадь этого правильного шестиугольника.
Опять же, пусть s = 3,00 см. и пусть a = 2,60 см. Какой район?
МЕТОДЫ СРАВНЕНИЯ:
Обсудите со студентами два разных метода для определения площади правильного шестиугольника.
Обсудите в классе преимущества и недостатки по каждому из методов и задайте следующие вопросы:
Какой метод сформулировать проще?
Будут ли эти методы когда-либо давать разные ответы?
Наконец, распределяем шестиугольник рабочий лист и попросите учащихся заполнить группы, используя любой метод.Затем с классом сравните ответы и обсудите методы поиска решений.
Продемонстрируйте с помощью Sketchpad Geometer свойства длин сторон и длин апофем регулярных шестиугольники. Нажмите здесь, чтобы использовать GSP и наблюдайте за анимацией изменяющейся области.
Вернуться к учебному блоку
Площадь шестиугольника
Площадь шестиугольника
Геометрия — это раздел математики, который занимается изучением форм различных размеров и анализом их свойств. В этом исследовании форм семейство многоугольников — одна из наиболее часто изучаемых фигур. Многоугольники — это замкнутые двумерные плоские объекты с прямыми сторонами. Многоугольник, состоящий из 6 сторон и 6 углов, известен как Шестиугольник. Любая закрытая плоская двумерная конструкция с 6 прямыми сторонами будет называться Шестиугольником. Слово «шестигранник» означает 6, а «гон» означает угол. Как показано на схеме ниже, шестиугольник имеет 6 сторон или ребер, 6 углов и 6 вершин.
В этом исследовании форм семейство многоугольников — одна из наиболее часто изучаемых фигур. Многоугольники — это замкнутые двумерные плоские объекты с прямыми сторонами. Многоугольник, состоящий из 6 сторон и 6 углов, известен как Шестиугольник. Любая закрытая плоская двумерная конструкция с 6 прямыми сторонами будет называться Шестиугольником. Слово «шестигранник» означает 6, а «гон» означает угол. Как показано на схеме ниже, шестиугольник имеет 6 сторон или ребер, 6 углов и 6 вершин. Площадь шестиугольника — это пространство, занимаемое в границах (или сторонах) шестиугольника.Используя измерения сторон и углов, мы можем найти площадь шестиугольника. Шестиугольники обычно можно наблюдать в различных формах в нашей красивой природе вокруг. На рисунке ниже показана заштрихованная часть внутри границ шестиугольника, которая называется площадью шестиугольника.
Типы шестиугольников:
Шестиугольники делятся в основном на 2 типа: правильные шестиугольники и неправильные шестиугольники.
1) Обычный шестиугольник: Шестиугольник, у которого все 6 сторон равны по размеру, известен как правильный шестиугольник.Наряду с 6 равными сторонами, у него также есть все 6 углов равных размеров. Поэтому, когда правильный шестиугольник делится на треугольники путем соединения его диагоналей, образуются 6 равносторонних треугольников, как показано на рисунке ниже.
(Примечание: диагональ — это отрезок прямой, образованный путем соединения любых двух несмежных вершин, как показано на рисунке справа). Площадь правильного шестиугольника легко вычислить, рассмотрев 6 равносторонних треугольников, образованных внутри.
2) Неправильный шестиугольник: Шестиугольник, у которого нет 6 равных сторон, известен как неправильный шестиугольник.У этого типа шестиугольника тоже нет 6 равных углов. Если вершины неправильного шестиугольника направлены наружу, то он известен как выпуклый неправильный шестиугольник, а если вершины шестиугольника (или хотя бы одна вершина) направлены внутрь, то он известен как вогнутый неправильный шестиугольник, как показано на рисунке ниже. . Поскольку размеры сторон и углов неодинаковы, мы должны использовать разные стратегии, чтобы найти площадь неправильного шестиугольника.
. Поскольку размеры сторон и углов неодинаковы, мы должны использовать разные стратегии, чтобы найти площадь неправильного шестиугольника.
Площадь шестиугольника:
Площадь шестиугольника — это пространство, занимаемое сторонами шестиугольника.Метод вычисления площади правильного шестиугольника отличается от метода вычисления площади неправильного шестиугольника.Площадь правильного шестиугольника:
У правильного шестиугольника все 6 сторон и 6 углов равны по размеру. При рисовании диагоналей, проходящих через центр шестиугольника, образуются 6 равносторонних треугольников равного размера (как показано на рисунке ниже). Если вычислить площадь одного равностороннего треугольника, то мы можем легко вычислить площадь данного правильного шестиугольника.
Если у выпуклого правильного многоугольника есть n сторон, то сумма всех его внутренних углов S = (n — 2) * 180 °
Следовательно, сумма всех внутренних углов выпуклого правильного шестиугольника S = (6-2) * 180 ° = 720 °
Если выпуклый правильный многоугольник имеет n сторон, то каждый внутренний угол = (n — 2 ) / п * 180 °
Следовательно, каждый внутренний угол выпуклого правильного шестиугольника = (6-2) / 6 * 180 ° = 120 °
Дан правильный выпуклый шестиугольник, как показано на рисунке выше, где точка «C» — центр шестиугольника.
Треугольник ABC — это равносторонний треугольник, так как все углы внутри треугольника ABC равны 60 ° (половина внутреннего угла 120 °). Следовательно, все его стороны также равны.
Поэтому пусть стороны AB = BC = CA = s
CM — перпендикуляр, проведенный к стороне AB. Пусть CM = h
Поскольку «M» становится серединой стороны AB, следовательно, MB = s / 2 (половина длины стороны AB).
Теперь в треугольнике CMB мы можем применить теорему Пифагора, чтобы получить связь между высотой треугольника h и длиной стороны s.
Следовательно, h 2 + (s / 2) 2 = s 2 . Отсюда следует, что h 2 + s 2 /4 = s 2 . Это дает h 2 = s 2 — s 2 /4
Итак, h 2 = 3s 2 /4 ==> h = √ (3s 2 /4). Следовательно, высота треугольника ABC, h = s * √3 / 2
Теперь площадь треугольника ABC = 1/2 * основание * высота.
Это означает, что Область A = 1/2 * s * h ==> A = 1/2 * s * (s * √3 / 2) ==> A = s 2 * √3 / 4
Следовательно, площадь треугольника ABC = s 2 * √3 / 4.

Теперь правильный шестиугольник состоит из 6 таких равносторонних равносторонних треугольников.
Следовательно, площадь правильного шестиугольника = 6 * с 2 * √3 / 4, что можно упростить следующим образом:
Площадь правильного шестиугольника = 3/2 * с 2 * √3
Пример 1 : Какова площадь правильного шестиугольника с длиной стороны 8 см?
Учитывая, что длина стороны, s = 8 см
Площадь правильного шестиугольника, A = 3/2 * s 2 * √3
Следовательно, Площадь = 3/2 * 8 2 * √3 = 96 √3, что равно 166.3 см 2 (приблизительно)
Пример 2: Если площадь правильного шестиугольника составляет √12 квадратных футов, то какова длина стороны шестиугольника?
Заданная площадь правильного шестиугольника, A = √12 квадратных футов, и это можно упростить до 2√3 футов 2 .
Площадь правильного шестиугольника, A = 3/2 * s 2 * √3.
Следовательно, 3/2 * s 2 * √3 = √12. Отсюда следует s 2 = 2/3 * √12 / √3.
Это дает: s 2 = 2/3 * 2√3 / √3 (12√3 также можно записать как 2√3).
Следовательно, s 2 = 4/3. Это означает, что s = √ (4/3) = 2 / √3 = 1,15 (приблизительно)
Следовательно, длина стороны правильного шестиугольника составляет 1,15 фута (приблизительно)
Площадь неправильного шестиугольника:
Найти площадь неправильного шестиугольника — это не то же самое, что найти площадь правильного шестиугольника. Площадь правильного шестиугольника можно легко вычислить по формуле, приведенной выше, но для неправильного шестиугольника мы используем различные методы в соответствии с предоставленной информацией, чтобы найти его площадь.Давайте посмотрим на пример ниже, где информация представлена на рисунке.
Пример: Найдите площадь неправильного шестиугольника, показанного на рисунке ниже.
На данном рисунке мы видим, что указаны длины сторон и длины диагоналей.

Мы видим, что неправильный шестиугольник разделен на 4 треугольника A, B, C и D.
Поскольку длины сторон каждого треугольника указаны, мы можем использовать формулу Герона.
Формула Герона:
Если треугольник имеет длину сторон как ‘a’, ‘b’ и ‘c’, тогда s = (a + b + c) / 2
Тогда Площадь треугольника = √ [ с * (са) * (сбн) * (сбн)]
Треугольник A:
s = (10+ 6 + 10) / 2 ==> s = 13
Теперь Площадь треугольника A = √ [s (s-a) (s-b) (s-c)] = √ [(13 * (13 -10) * (13 — 6) * (13-10)]
Площадь треугольника A = √ (13 * 3 * 7 * 3) = 28.6 мес. 2
Треугольник B:
s = (10 + 11 + 7) / 2 = 14
Площадь треугольника B = √ [(14 * (14 — 10) * (14 — 7) * (14 — 11)] = √ (14 * 4 * 7 * 3) = 34,3 м 2
Аналогично, используя формулу Герона, как показано выше, мы также получаем площади треугольников C и D.
Площадь треугольника C = 16,9 м 2 и площадь треугольника D = 19,9 м 2
Итак, площадь неправильного шестиугольника = площадь треугольника A + площадь треугольника B + площадь треугольника C + площадь треугольника D
.
 Площадь шестиугольника = 28.6 + 34,3 + 16,9 + 19,9 = 99,7 млн 2
Площадь шестиугольника = 28.6 + 34,3 + 16,9 + 19,9 = 99,7 млн 2 Периметр шестиугольника:
Периметр шестиугольника (правильного или неправильного) можно легко рассчитать, сложив все длины сторон данного шестиугольника.Периметр правильного шестиугольника равен сумме длин всех его сторон.
Следовательно, периметр правильного шестиугольника с длиной стороны «s» (как показано на рисунке справа) = s + s + s + s + s + s
Это дает нам Периметр правильного шестиугольника = 6s
Периметр неправильного шестиугольника также равен сумме длин всех его сторон.
Если ‘a’, ‘b’, ‘c’, ‘d’, ‘e’ и ‘f’ являются длинами сторон неправильного шестиугольника (как показано на рисунке справа), тогда периметр неправильного шестиугольника = a + b + c + d + e + f
Видео с вопросом: Определение площади правильного шестиугольника с учетом его длины стороны
Стенограмма видео
Найдите площадь правильного шестиугольника
со стороной 35 сантиметров, дающей ответ с двумя десятичными знаками.
Итак, давайте взглянем на шестиугольник. Итак, вот я нарисовал обычный шестиугольник. И каждой из сторон по 35 сантиметры. И мы знаем это, потому что регулярный Шестиугольник — это шестиугольник, у которого все стороны одинаковой длины. Но в нем также есть все внутренние углы такие же. Итак, теперь то, что я сделал, я разделил наш шестиугольник на шесть равных треугольников. И каждый угол, сделанный эти треугольники в центре круга будут такими же, потому что, как мы знаете, каждый из этих треугольников будет идентичным, потому что у нас есть обычный шестиугольник.
С тех пор, как выяснилось, что такое 𝑥 или
Каждый из этих углов мы разделим 360 на шесть. И это потому, что это делает
полный круг в центре. А это 60 градусов. Итак, мы знаем, что каждый из этих
углы будут 60 градусов. Но что мы также знаем о каждом из
наши треугольники — это две линии, которые являются внутренними частями наших треугольников, поэтому
линии от края к центру будут одинаковой длины. И потому что они все одинаковые
length, то два основных угла наших треугольников также должны быть равны.
И потому что они все одинаковые
length, то два основных угла наших треугольников также должны быть равны.
И чтобы разобраться, что мы собираюсь сделать 180, потому что это углы в треугольнике минус 60, потому что это верхний угол, затем деленный на два, потому что есть два основных угла. Это даст нам больше 120 два. А 120 больше двух равно 60 градусов. Итак, теперь мы можем сказать, что каждый из наших треугольников, составляющих наш правильный шестиугольник, будет равносторонним треугольники, потому что у нас есть 60, 60, 60 в качестве их внутренних углов.Итак, если мы хотим найти определить, какой будет площадь нашего правильного шестиугольника, тогда все, что нам нужно сделать, это найдите площадь одного из наших треугольников, а затем умножьте ее на шесть, потому что они все идентично.
Что ж, если мы посмотрим на
треугольник, который у нас есть, хорошо, если мы хотим найти площадь треугольника, что нам нужно
do — это умножение основания на высоту перпендикуляра.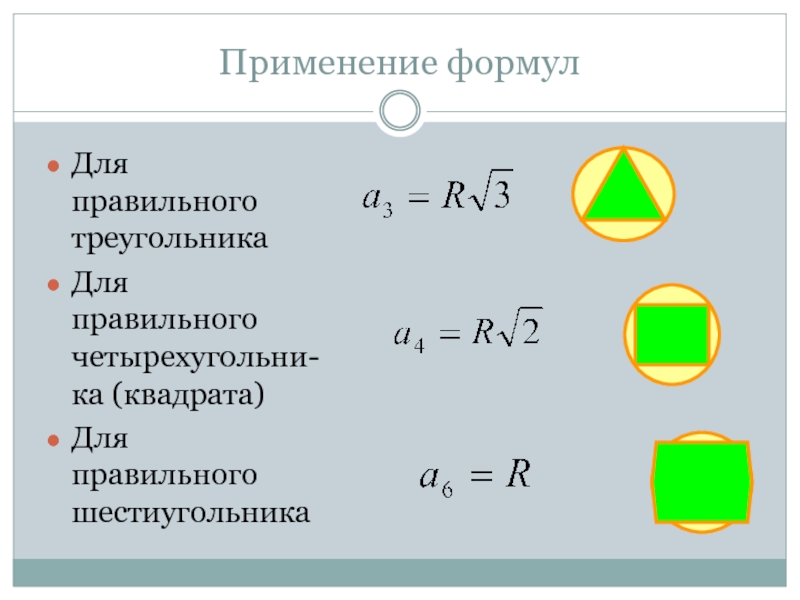 Итак, теперь, если мы посмотрим на
треугольник, который у нас есть, ну, если мы хотим найти площадь треугольника, ну, это
будет равно половине, умноженной на базу, умноженную на высоту.А высота перпендикулярная
высоту, и я отмечу это здесь оранжевой пунктирной линией. И мы видим этот перпендикуляр
высота, потому что у нас есть прямой угол внизу.
Итак, теперь, если мы посмотрим на
треугольник, который у нас есть, ну, если мы хотим найти площадь треугольника, ну, это
будет равно половине, умноженной на базу, умноженную на высоту.А высота перпендикулярная
высоту, и я отмечу это здесь оранжевой пунктирной линией. И мы видим этот перпендикуляр
высота, потому что у нас есть прямой угол внизу.
Хорошо, а как нам разобраться, что является? Ну, как мы могли это работать это потому, что когда мы смотрим на треугольник, который был разделен на две части, то у нас есть два прямоугольных треугольника. Мы посмотрим на правую треугольник.Это треугольник с высота, или перпендикулярная высота, ℎ. У нас есть гипотенуза, которая равна 35 сантиметры. У нас есть база — 17,5 сантиметры — это половина 35 сантиметров.
Так как это прямоугольный треугольник,
мы можем использовать теорему Пифагора, которая говорит нам, что в квадрате плюс 𝑏 в квадрате
равно 𝑐 в квадрате.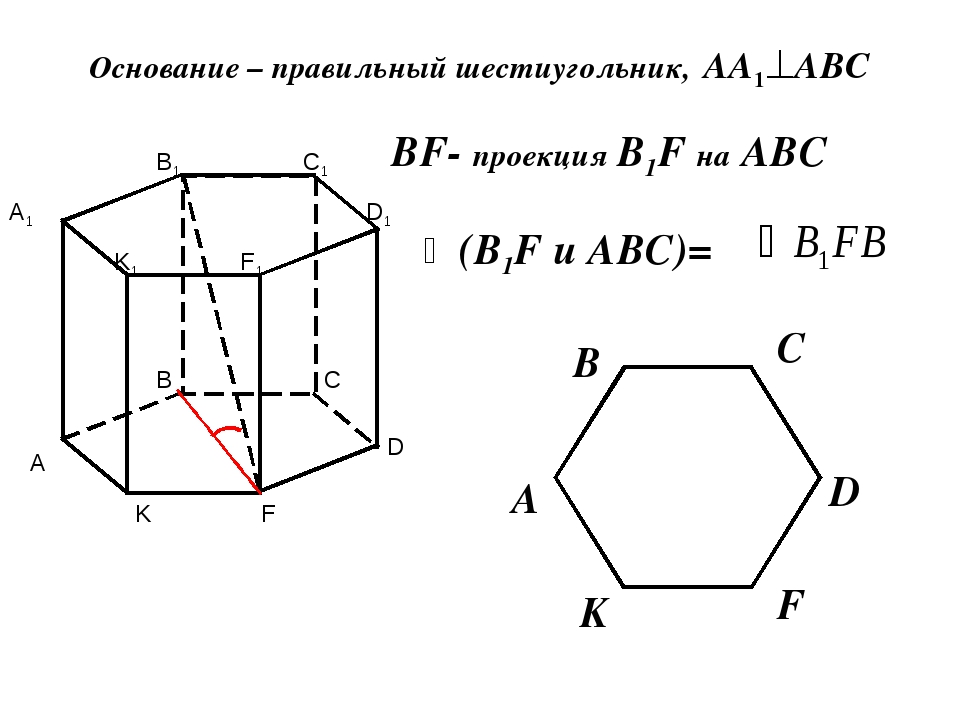 Итак, сумма двух меньших
Квадрат сторон равен большему квадрату гипотенузы.Хорошо, если мы переставим это, чтобы найти
одной из коротких сторон, то можно сказать, что квадрат короткой стороны равен
квадрат гипотенузы минус квадрат другой короткой стороны.
Итак, сумма двух меньших
Квадрат сторон равен большему квадрату гипотенузы.Хорошо, если мы переставим это, чтобы найти
одной из коротких сторон, то можно сказать, что квадрат короткой стороны равен
квадрат гипотенузы минус квадрат другой короткой стороны.
Итак, получаем в квадрате равно 35 в квадрате минус 17,5 в квадрате. Таким образом, в квадрате равно 918,75. Итак, если мы возьмем квадрат корень обеих частей нашего уравнения, мы получим, что ℎ равно 30,31, et так далее.И это наша ℎ, это наша перпендикулярная высота. На данный момент мы не будем округлять потому что мы хотим сохранить точность.
Итак, теперь мы можем работать
площадь нашего треугольника. И мы можем решить это, потому что это
половина, умноженная на основание, умноженная на высоту. Итак, это будет увеличено вдвое
на 35 умноженное на 30,31 продолжение, что даст нам 530,440 продолжения. Опять же, на данном этапе не округление
Потому что мы хотим сохранить точность.
Опять же, на данном этапе не округление
Потому что мы хотим сохранить точность.
Как мы говорим, высота было бы в сантиметрах, а эта область была бы в сантиметрах в квадрате, но Я надену их в конце, когда мы проработаем финальную часть. Итак, теперь выясним, что за площадь шестиугольника, что мы делаем, мы умножаем площадь нашего треугольника, который составляет 530,440, продолжение на шесть. И это потому, что у нас шесть одинаковые треугольники, составляющие наш шестиугольник.
Итак, когда мы вычислим это,
мы получаем 3182,64 сантиметра в квадрате с двумя десятичными знаками. Итак, это область наших регулярных
шестиугольник. Что ж, мы можем
проверьте наш ответ. Мы можем это сделать, потому что в
Фактически, формула, которую вы могли бы встретить для площади правильного шестиугольника. То есть площадь равна трем
корень три из двух, умноженный на в квадрате, где 𝑎 — длина одного из
стороны.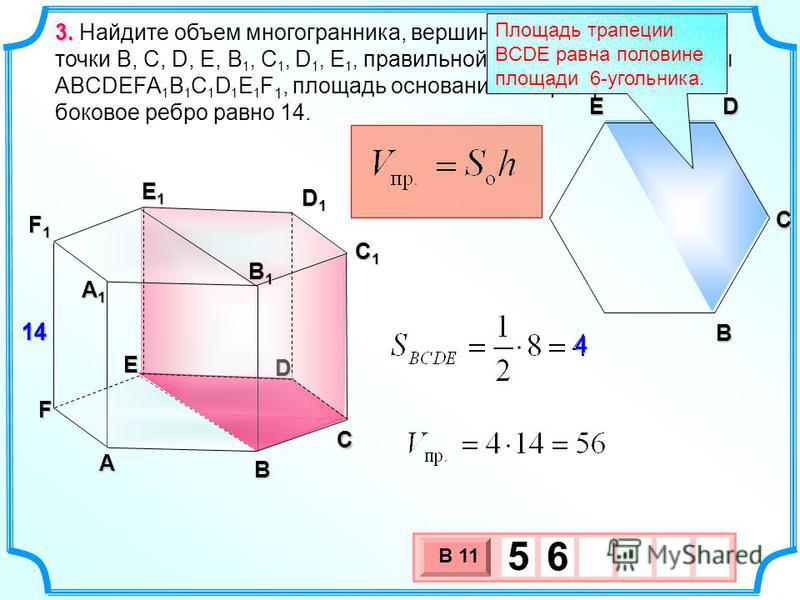
Таким образом, мы можем сказать, что площадь шестиугольника будет равна корню три из трех над двумя, умноженным на 35 в квадрате с 𝑎, равным 35, что снова даст нам 3182,64. Итак, мы можем однозначно сказать да, это правильная область для нашего шестиугольника.
| 1D линия
2D правильные многоугольники: равносторонний треугольник, квадрат, пятиугольник, шестиугольник, семиугольник, восьмиугольник, нонагон, десятиугольник, шестиугольник, двенадцатигранник, шестиугольник, N-угольник, многоугольник кольцо другие многоугольники: 90 202 круглые формы: тетраэдр, куб, октаэдр, додекаэдр, икосаэдр архимедова Solids: Каталонских Сухой остаток: Твердые тела Джонсона: Другие многогранники: 000, большой додекаэдр Круглые формы: | Anzeige Расчеты в правильном шестиугольнике, многоугольнике с 6 вершинами. Формулы: Длина кромки, диагонали, периметр и радиус имеют одинаковые единицы (например,грамм. метр), площадь имеет квадрат (например, квадратный метр). Anzeige Короткая диагональ — это линия между двумя вершинами, между которыми есть третья вершина. Его длина равна высоте. Длинная диагональ — это линия между двумя противоположными вершинами. Длинные диагонали и биссектрисы совпадают, они пересекаются со средними линиями и с центром тяжести, описанной и вписанной окружности в одной точке. Для этого правильный шестиугольник является точечно-симметричным и вращательно-симметричным при повороте на 60 ° или кратном этому.
© Jumk.de Webprojects Anzeige |
Формула площади правильного многоугольника — Math Open Reference
Формула площади правильного многоугольника — Math Open ReferenceКоличество квадратных единиц, необходимое для полного заполнения правильного многоугольника.Даны четыре различных способа вычисления площади с формулой для каждого.
Попробуйте это Перетащите оранжевые точки на каждую вершину чтобы изменить размер многоугольника. Измените количество сторон. Площадь будет постоянно рассчитываться. Приведенные ниже формулы дают площадь правильного многоугольника.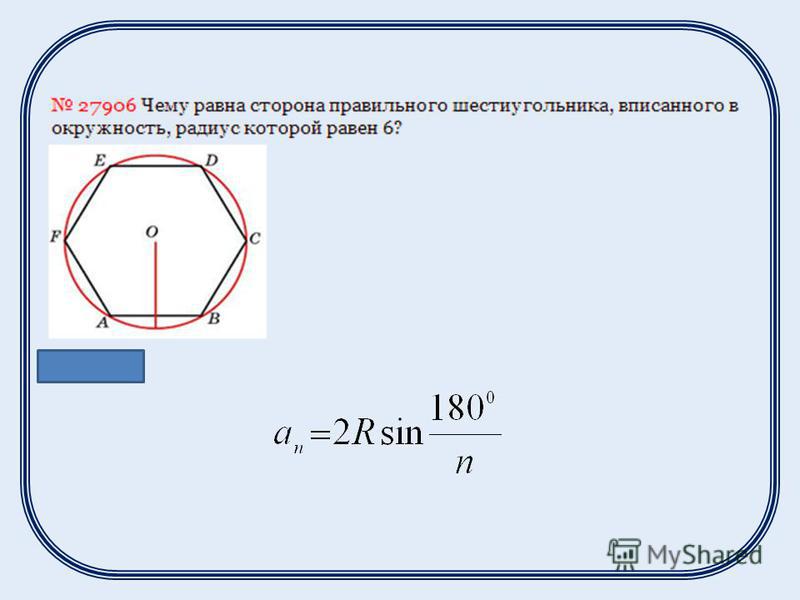 Для начала используйте тот, который соответствует тому, что вам дано.
Они предполагают, что вы знаете, сколько сторон у многоугольника. Большинство из них требуют определенных знаний тригонометрии (не рассматриваются в этом томе,
но см. Обзор тригонометрии).
Для начала используйте тот, который соответствует тому, что вам дано.
Они предполагают, что вы знаете, сколько сторон у многоугольника. Большинство из них требуют определенных знаний тригонометрии (не рассматриваются в этом томе,
но см. Обзор тригонометрии).
1. Учитывая длину стороны.
По определению, все стороны правильного многоугольника равны по длине. Если вам известна длина одной из сторон, площадь определяется по формуле: гдеs — длина любой стороны
n — количество сторон
tan — функция тангенса, вычисленная в градусах
(см. Обзор тригонометрии)
Чтобы узнать, как выводится это уравнение, см. Выведение формулы площади правильного многоугольника.
2. Заданный радиус (описанный радиус)
Если вы знаете радиус (расстояние от центра до вершины, см. Рисунок выше): гдеr — радиус (окружной радиус)
n — количество сторон
sin — функция синуса, вычисленная в градусах
(см.
 Обзор тригонометрии)
Обзор тригонометрии)Чтобы узнать, как выводится это уравнение, см. Выведение формулы площади правильного многоугольника.
3. Учитывая апофему (inradius)
Если вы знаете апофема, или inradius, (перпендикулярное расстояние от центра до стороны.См. Рисунок выше), площадь определяется как: гдеa — длина апофемы (inradius)
n — количество сторон
tan — функция тангенса, вычисленная в градусах (см. Обзор тригонометрии).
Чтобы узнать, как выводится это уравнение, см. Выведение формулы площади правильного многоугольника.
Неправильные многоугольники
Найти площадь неправильного многоугольника сложнее, так как нет простых формул. Видеть Площадь неправильного многоугольникаДругие полигоны
Общий
Типы многоугольника
Площадь различных типов полигонов
Периметр различных типов многоугольников
Углы, связанные с многоугольниками
Именованные многоугольники
(C) Открытый справочник по математике, 2011 г.

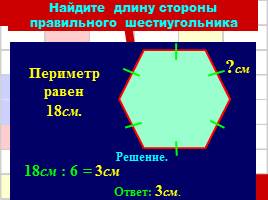 Складываем результаты.
Складываем результаты.
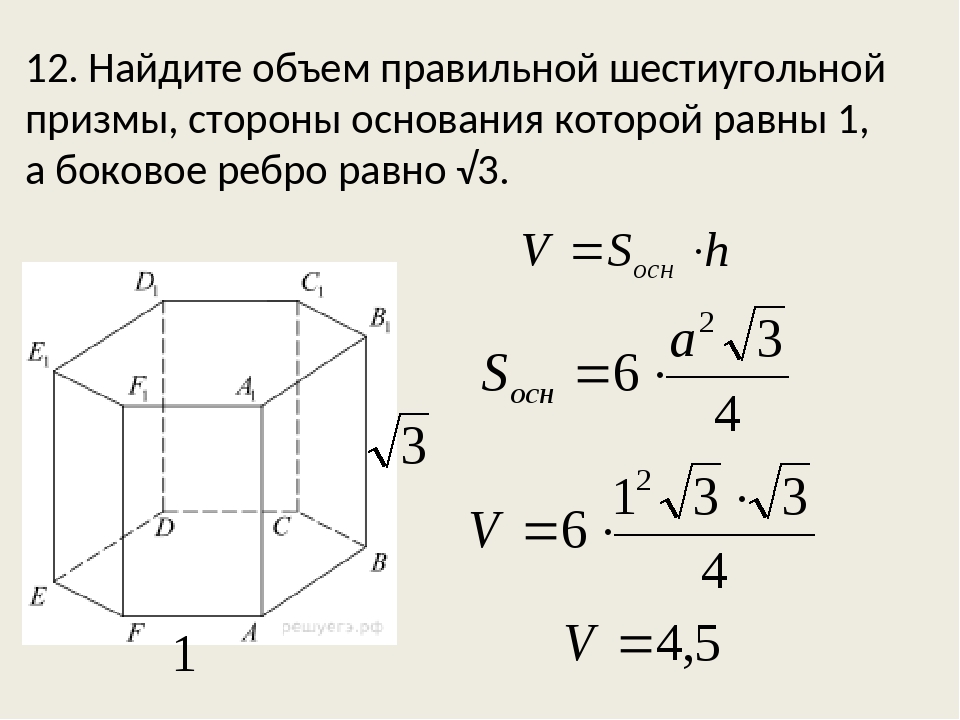


 Найти площади составляющих его фигур и сложить.
Найти площади составляющих его фигур и сложить.
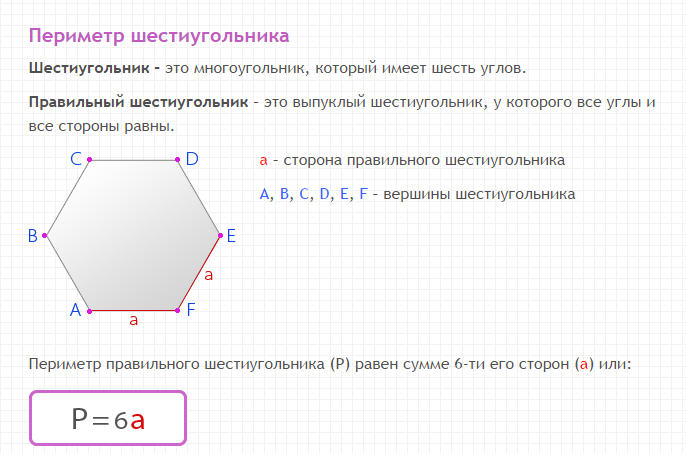 Каждая сторона треугольника соответствует: x-x√3-2x, где короткая, против угла 30˚,- это x; длинная сторона против угла 60˚- x√3, а гипотенуза — 2x.
Каждая сторона треугольника соответствует: x-x√3-2x, где короткая, против угла 30˚,- это x; длинная сторона против угла 60˚- x√3, а гипотенуза — 2x.

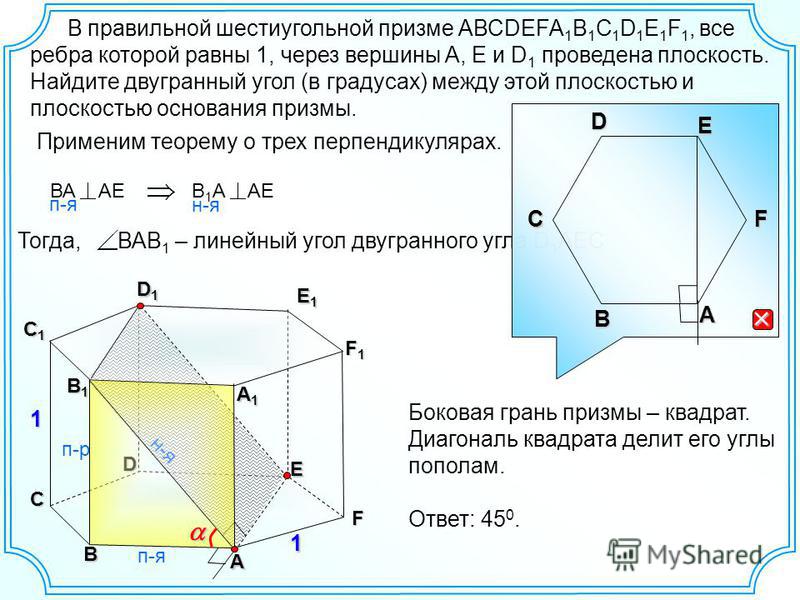
 Формулы с этого форума показываются в браузере при помощи технологии MathML, которую на текущий момент поддерживают только Firefox и Opera. Мы рекомендуем просматривать этот форум именно через браузер Firefox, потому что отображение в нем MathML-формул самое лучшее.
Формулы с этого форума показываются в браузере при помощи технологии MathML, которую на текущий момент поддерживают только Firefox и Opera. Мы рекомендуем просматривать этот форум именно через браузер Firefox, потому что отображение в нем MathML-формул самое лучшее. {\circ}$ больше вписанного угла ACB, опирающегося на ту же дугу. Ответ дайте в градусах. [посмотреть решение]
{\circ}$ больше вписанного угла ACB, опирающегося на ту же дугу. Ответ дайте в градусах. [посмотреть решение] 00см и высота
h = 2,60 см для сравнения с методом 2 позже.
00см и высота
h = 2,60 см для сравнения с методом 2 позже. Опять же, пусть s = 3,00 см.
и пусть a = 2,60 см. Какой район?
Опять же, пусть s = 3,00 см.
и пусть a = 2,60 см. Какой район? Спираль, Треугольник Рело, Циклоида, Двойная циклоида, Астроид, Гипоциклоида, Кардиоида, Эпициклоида, Параболический сегмент, Сердце, Треугольник, Межугловой треугольник, Круговой треугольник дуги, Четырехугольник Interarc, Межкруговый четырехугольник, Круговой четырехугольник дуги, Круговой дуговый многоугольник, Коготь, Коготь -Янг, Арбелос, Салинон, Выпуклость, Луна, Три круга, Поликруг, Многоугольник с закругленными краями, Роза, Шестеренка, Овал, Профиль яйца, Лемниската, Сквикул, Круглый квадрат, Дигон, Сферический треугольник
Спираль, Треугольник Рело, Циклоида, Двойная циклоида, Астроид, Гипоциклоида, Кардиоида, Эпициклоида, Параболический сегмент, Сердце, Треугольник, Межугловой треугольник, Круговой треугольник дуги, Четырехугольник Interarc, Межкруговый четырехугольник, Круговой четырехугольник дуги, Круговой дуговый многоугольник, Коготь, Коготь -Янг, Арбелос, Салинон, Выпуклость, Луна, Три круга, Поликруг, Многоугольник с закругленными краями, Роза, Шестеренка, Овал, Профиль яйца, Лемниската, Сквикул, Круглый квадрат, Дигон, Сферический треугольник  Шестиугольник — это самый высокий правильный многоугольник, который допускает правильную мозаику (мозаику). Введите одно значение и выберите количество десятичных знаков. Затем нажмите Рассчитать.
Шестиугольник — это самый высокий правильный многоугольник, который допускает правильную мозаику (мозаику). Введите одно значение и выберите количество десятичных знаков. Затем нажмите Рассчитать. Кроме того, правильный шестиугольник аксиально симметричен длинным диагоналям и средним линиям.
Кроме того, правильный шестиугольник аксиально симметричен длинным диагоналям и средним линиям.