Как найти площадь через диаметр в физике: Формулы, как найти площадь круга

Площадь круга все формулы и примеры расчета

Главная » Геометрия » Как рассчитать площадь круга — все формулы

Геометрия

Автор Ольга Андрющенко На чтение 3 мин. Просмотров 13.9k. Опубликовано 29 июня 2020

Площадь круга часто требуется рассчитать в различных задачах и это не только задачи по геометрии, иногда знать как рассчитывается площадь круга важно знать и в некоторых текстовых задачах алгебры. Итак, давайте разбираться.

Содержание

Что такое площадь круга

Площадь круга — это мера заполненности области внутри окружности, являющейся границей круга, выраженная в квадратных единицах (м², см², кв.ед.). В математике эти единицы могут разными, в физике же если вы определяете площадь круга — вы должны указать единицы в системе СИ, а это м².

Визуально, площадь круга это величина закрашенной области на рисунке:

Как можно найти площадь круга

Если дан радиус круга

Здесь все зависит от того, какие вам величины даны в самом начале. Если вам дан радиус круга, то площадь круга определяется по формуле:

 — число . Число пи является одним из наиболее важных констант в математике, определяется как постоянное отношение длины окружности к ее диаметру в евклидовой плоскости. Другими словами:

π = длина окружности круга/диаметр этого круга.

Таким образом, приблизительное значение , наиболее известное, как: 3,14.

Это приблизительное значение, потому что число π — это то, что мы называем иррациональным числом. Оно не может быть записано как отношение двух целых чисел. Сегодня мы знаем более 12 000 миллиардов знаков после запятой. Однако до сих пор нет определенной модели, которая давала бы все эти значения.

Найти площадь круга можно и с помощью нашего онлайн калькулятора.

Найти площадь круга, зная его радиус. Онлайн калькулятор.

Введите радиус:

Площадь круга:

Площадь круга в π:

Если дан диаметр круга

Если известен диаметр круга, то площадь круга можно найти по формуле:

Найти площадь круга через диаметр онлайн

Введите диаметр круга:

Площадь круга:

Площадь круга в π:

Если дана длина окружности

Так как длина окружности определяется по формуле: , то можно выразить радиус круга: . Тогда площадь: .

Найти площадь круга через длину окружности — онлайн калькулятор

Длина окружности круга (введите число):

Площадь круга:

Площадь круга в π:

Примеры расчета

Пример 1.

Рассчитать площадь круга, если известен радиус круга .

Решение: По формуле (1) находим .

Пример 2.

Найдите площадь, если дан диаметр круга .

Решение: По формуле (2) находим .

Вы видите, что находить площадь круга совсем не сложно, если  известны все формулы и даны все необходимые для расчета величины.

( 10 оценок, среднее 4.5 из 5 )

Площадь круга — формулы, примеры расчетов

Круг – это плоская фигура, которая представляет собой множество точек равноудаленных от центра. Все они находятся на одинаковом расстоянии и образуют собой окружность.

Отрезок, который соединяет центр круга с точками его окружности, называется радиусом. В каждой окружности все радиусы равны между собой. Прямая, соединяющая две точки на окружности и проходящая через центр называется диаметром. Формула площади круга рассчитывается с помощью математической константы – числа π..

Это интересно: Число π. представляет собой соотношение длины окружности к длине ее диаметра и является постоянной величиной. Значение π = 3,1415926 получило применение после работ Л. Эйлера в 1737 г.

Площадь окружности можно вычислить через константу π. и радиус окружности. Формула площади круга через радиус выглядит так:

Рассмотрим пример расчета площади круга через радиус. Пусть дана окружность с радиусом R = 4 см. Найдем площадь фигуры.

Площадь нашей окружности будет равна 50,24 кв. см.

Существует формула площади круга через диаметр. Она также широко применяется для вычисления необходимых параметров. Данные формулы можно использовать для нахождения площади треугольника по площади описанной окружности.

Рассмотрим пример расчета площади круга через диаметр, зная его радиус. Пусть дана окружность с радиусом R = 4 см. Для начала найдем диаметр, который, как известно, в два раза больше радиуса.


Теперь используем данные для примера расчета площади круга по приведенной выше формуле:

Как видим, в результате получаем тот же ответ, что и при первых расчетах.

Знания стандартных формул расчета площади круга помогут в дальнейшем легко определять площадь секторов и легко находить недостающие величины.

Мы уже знаем, что формула площади круга рассчитывается через произведение постоянной величины π на квадрат радиуса окружности. Радиус можно выразить через длину окружности и подставить выражение в формулу площади круга через длину окружности:
Теперь подставим это равенство в формулу расчета площади круга и получим формулу нахождения площади круга, через длину окружности

Рассмотрим пример расчета площади круга через длину окружности.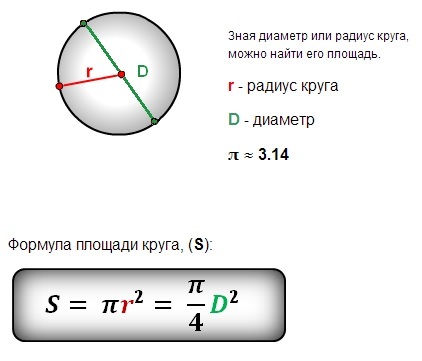 Пусть дана окружность с длиной l = 8 см. Подставим значение в выведенную формулу:

Итого площадь круга будет равна 5 кв. см.

Очень легко можно найти площадь круга описанного вокруг квадрата.

Для этого потребуется только сторона квадрата и знание простых формул. Диагональ квадрата будет равна диагонали описанной окружности. Зная сторону a ее можно найти по теореме Пифагора: отсюда .
После того, как найдем диагональ – мы сможем рассчитать радиус: .
И после подставим все в основную формулу площади круга описанного вокруг квадрата:

Рассмотрим пример расчета площади круга, описанного вокруг квадрата.
Задача: дан квадрат, вписанный в круг. Его сторона a = 4 см. Найдите площадь окружности.
Для начала рассчитаем длину диагонали d.


Теперь подставляем данные в формулу

Зная несколько простых правил и теорему Пифагора, мы смогли рассчитать площадь описанной вокруг квадрата окружности.

Как вычислить площадь круга с диаметром

••• mr. suphachai praserdumrongchai/iStock/GettyImages

Обновлено 16 ноября 2020 г. , но изучение математических понятий диаметра и площади иногда может показаться сложным. Независимо от того, измеряете ли вы размер круглого ковра, который вам нужно купить, или определяете пространство, необходимое для строительства круглого сада или патио, знание того, как рассчитать площадь круга по его диаметру, является ценным навыком.

TL;DR (слишком длинно, не читал)

Площадь круга — это площадь, которую занимает круг. Формула для вычисления площади круга: A = π r ² , где число пи (π) равно 3,14, а радиус ( r ) равен половине диаметра.

Первым шагом для вычисления площади круга по его диаметру является определение этого диаметра. В то время как математические задачи часто указывают это значение, в реальном мире вы должны найти диаметр самостоятельно. Диаметр — это длина линии, которая начинается на краю круга, проходит через центр круга и заканчивается на противоположном краю круга. Для измерения вам понадобится линейка для маленьких кругов или рулетка для больших кругов.

Зная диаметр (​ d ​) окружности, вы можете найти радиус (​ r ​), используя уравнение ​ d ​=2​ r ​. Радиус круга — это расстояние от центра круга до любой точки на краю круга. Радиус также равен половине диаметра. Если ваш диаметр представляет собой простое число, вы, вероятно, можете вычислить радиус в уме. Если нет, измените уравнение, чтобы найти ​ r ​

r = \frac{d}{2} 92

Пи (π) — неалгебраическое число, представляющее отношение расстояния по окружности (окружности) к ее диаметру, обычно оцениваемое как 3,14. Чтобы найти площадь, возведите радиус в квадрат (радиус умножить на радиус), а затем умножьте на 3,14.

Поскольку площадь является мерой двух измерений, вы всегда указываете площадь в квадратных единицах, таких как квадратные дюймы (в ² ) или квадратные футы (футы ² ). Это особенно важно при расчете площади круга для задания, поскольку ответ без правильно сообщенных единиц измерения, скорее всего, будет неверным или неполным.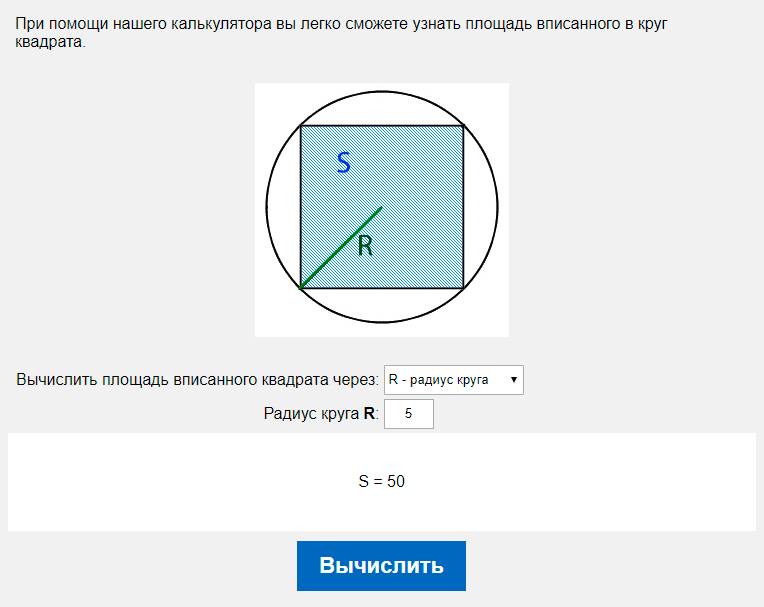

_{^{Каждый раз, когда вам нужно определить пространство внутри круга или количество пространства, покрываемого кругом, вы можете использовать уравнение для площади круга. Особенно для реальных приложений этого навыка измерение диаметра часто является самым простым способом начать.}}

Статьи по теме

Ссылки

• Академия Хана: площадь и периметр
• Забавная математика: площадь круга

Ресурсы

• Живая наука: что такое число Пи?

Об авторе

Мелисса Майер — разноплановый научный писатель с опытом работы в области молекулярной биологии, протеомики, геномики, микробиологии, биобанкинга и пищевой науки. В нише науки и медицинских текстов ее работа включает пять лет работы с Thermo Scientific (ускорение научных блогов), SomaLogic, Mental Floss, Society for Neuroscience и Healthline. Она также работала временным заместителем редактора глянцевого торгового журнала Clinical Lab Products, который читают патологоанатомы, и написала научно-популярную книгу для подростков (Как справиться с изнасилованием на свидании и изнасилованием по знакомству). Она готовит две книги, посвященные неврологии психического здоровья.

Площадь кругов: формула, уравнение и диаметр

Круг — одна из самых распространенных форм. Если вы посмотрите на линии орбит планет в Солнечной системе, на простое, но эффективное функционирование колес или даже на молекулы на молекулярном уровне, круг продолжает появляться!

Окружность — это форма, в которой все точки, составляющие границу, равноудалены от одной точки, расположенной в центре.

Элементы круга

Прежде чем мы обсудим площадь кругов, давайте рассмотрим уникальные характеристики, определяющие форму круга. На рисунке ниже изображен круг с центром O. Напомним из определения, что все точки, расположенные на границе окружности, равноудалены (равноудалены) от этой центральной точки O . Расстояние от центра круга до его границы называется радиусом , R .

Диаметр , D , это расстояние от одной конечной точки окружности до другой, проходящей через центр окружности . Диаметр всегда в два раза больше длины радиуса, так что если мы знаем одно из этих измерений, то мы знаем и другое! А хорда — это расстояние от одной конечной точки до другой на окружности, которая, в отличие от диаметра, , а не должна проходить через центральную точку.

Иллюстрация круга, StudySmarter Original

Площадь кругов: формула / уравнение

Теперь, когда мы рассмотрели элементы круга, давайте начнем с обсуждения площади круга. Во-первых, мы начнем с определения.

Площадь круга — это пространство, занимаемое кругом на поверхности или плоскости. Измерения площади записываются в квадратных единицах, например, фут 9.0015 2 и м ² .

Чтобы вычислить площадь круга, мы можем использовать формулу:

Для этой формулы важно знать, что равно числу пи. Что такое пи? Это константа, представленная греческой буквой, и ее значение приблизительно равно 3,14159.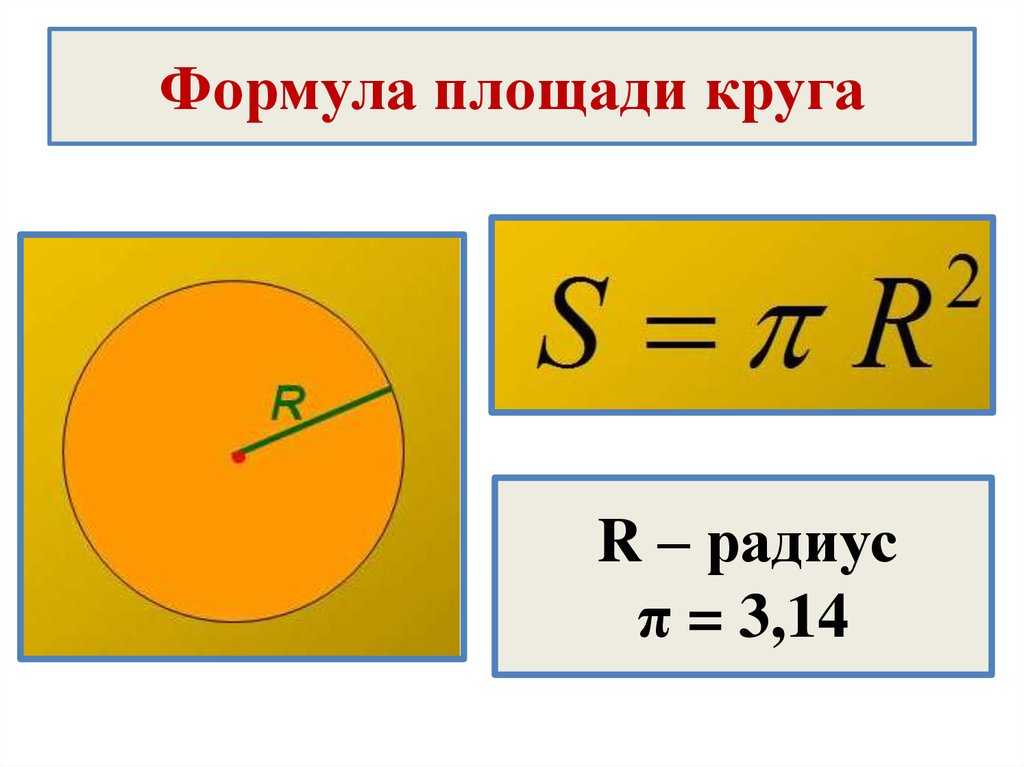

Пи равно математической константе, которая определяется как отношение длины окружности к диаметру круга.

Вам не нужно запоминать число пи, потому что в большинстве калькуляторов есть клавиша для быстрого ввода, показанная как . Давайте используем формулу площади в примере, чтобы увидеть, как мы можем применить этот расчет на практике.

Радиус круга 8 м. Вычислите его площадь.

Решение:

Сначала подставим значение радиуса в формулу площади круга.

Затем мы возводим значение радиуса в квадрат и умножаем его на число пи, чтобы найти площадь в квадратных единицах. Имейте в виду, что это не равно , а скорее равно .

Расчет площади круга диаметром

Мы видели формулу площади круга, в которой используется радиус . Однако мы также можем найти площадь круга, используя его диаметр . Для этого мы делим длину диаметра на 2, что дает нам значение радиуса для ввода в нашу формулу. (Напомним, что диаметр окружности в два раза больше длины ее радиуса.) Давайте рассмотрим пример, использующий этот метод.

Круг имеет диаметр 12 метров. Найдите площадь круга.

Решение:

Начнем с формулы площади круга:

Из формулы видно, что нам нужно значение радиуса. Чтобы найти радиус круга, мы делим диаметр на 2, например:

Теперь мы можем ввести значение радиуса 6 метров в формулу для определения площади:

Вычисление площади круги с окружностью

Помимо площади круга, другой распространенной и полезной мерой является его длина окружности.

Окружность круга — это периметр или охватывающая граница формы. Он измеряется в длине, что означает, что единицами являются метры, футы, дюймы и т. д.

Давайте посмотрим на некоторые формулы, связывающие длину окружности с радиусом и диаметром окружности:

Приведенные выше формулы показывают, что мы можем умножить на диаметр круга, чтобы вычислить его длину окружности. Поскольку диаметр в два раза больше длины радиуса, мы можем заменить его на , если нам нужно изменить уравнение окружности.

Вас могут попросить найти площадь круга, используя его длину окружности. Давайте поработаем на примере.

Длина окружности 10 м. Вычислите площадь круга.

Решение:

Сначала воспользуемся формулой длины окружности для определения радиуса круга:

Теперь, когда мы знаем радиус, мы можем использовать его для нахождения площади круга:

Итак, площадь круга с длиной окружности 10 м равна 7,95 м ² .

Площадь полукругов и четвертей кругов с примерами

Мы также можем проанализировать форму круга с точки зрения половин или четвертей . В этом разделе мы обсудим площадь полукругов (кругов, разрезанных пополам) и четвертей кругов (кругов, разрезанных на четверти).

Площадь и длина окружности полукруга

Полукруг представляет собой полукруг. Он образуется путем деления круга на две равные половины, разрезанные по его диаметру. Площадь полукруга можно записать как:

Где r радиус полукруга

Чтобы найти длину окружности полукруга , мы сначала делим длину всей окружности пополам, затем добавляем дополнительную длину, равную диаметр d . Это связано с тем, что периметр или граница полукруга должны включать диаметр, чтобы замкнуть дугу. Формула длины окружности полукруга:

Вычислите площадь и длину окружности полукруга диаметром 8 см.

Решение:

Поскольку диаметр равен 8 см, радиус равен 4 см. Мы знаем это, потому что диаметр любого круга в два раза больше его радиуса. Используя формулу площади полукруга, получаем:

Для длины окружности вводим значение диаметра в формулу:

Площадь и длина окружности четверти круга

Окружность можно разделить на четыре равные четверти, что дает четыре четверти круга.