| 1. | Определение длины окружности по диаметру | 1 вид — рецептивный | лёгкое | 1 Б. | Необходимо определить длину окружности, если дан диаметр окружности. |
| 2. | Определение длины окружности по радиусу | 1 вид — рецептивный | лёгкое |
1 Б.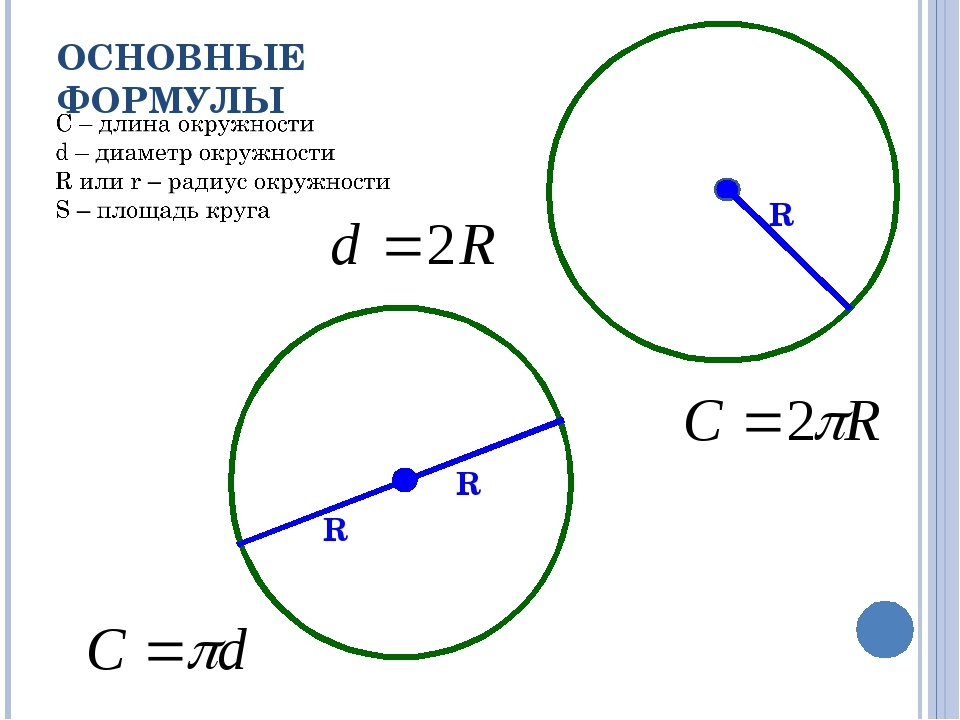
|
Необходимо определить длину окружности, если дан радиус окружности. |
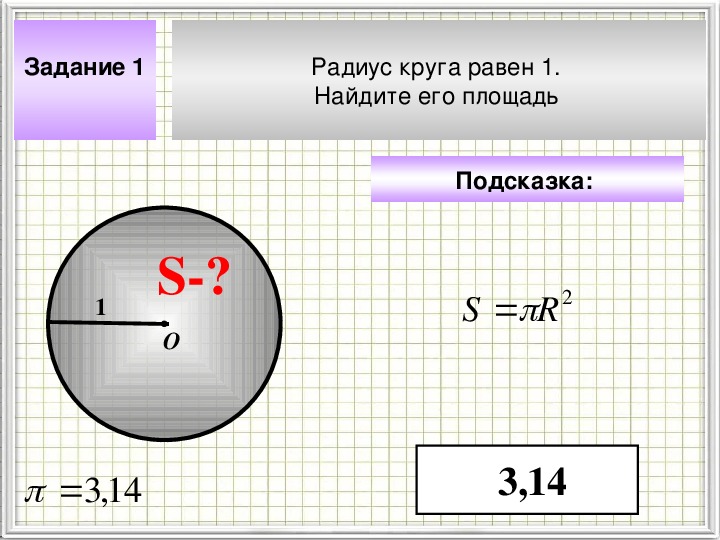
| 3. | 1 вид — рецептивный | лёгкое | 1 Б. | Необходимо определить площадь круга, если дан радиус. | |
4. |
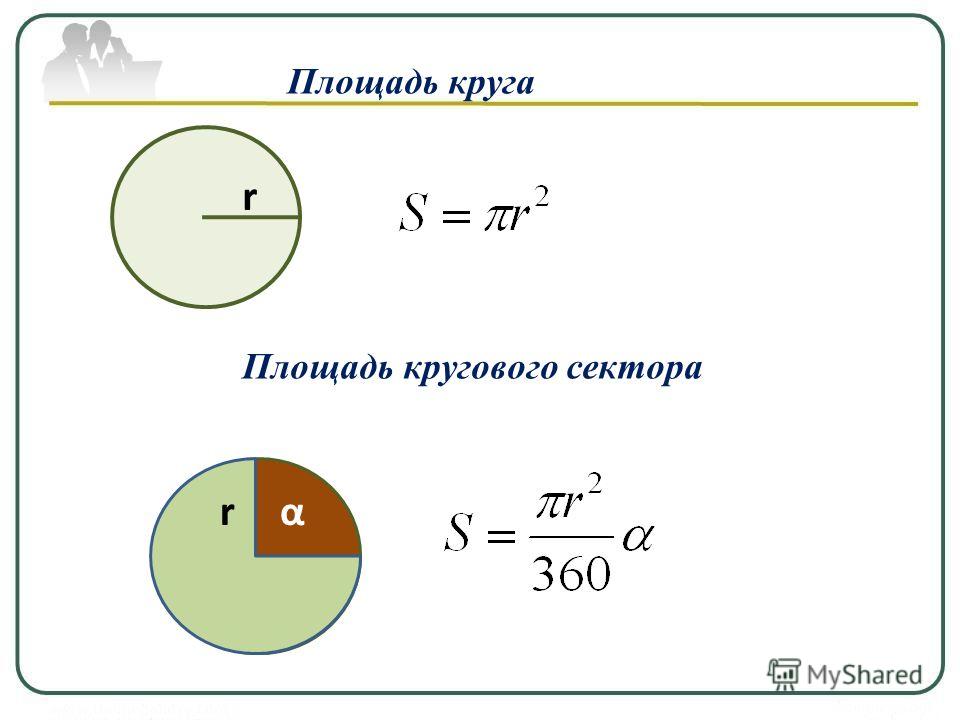
Определение площади круга по данному диаметру | 1 вид — рецептивный | среднее | 1 Б. | Необходимо вычислить площадь круга, если дан диаметр. |
| 5. | Определение диаметра окружности | 1 вид — рецептивный | среднее |
1 Б.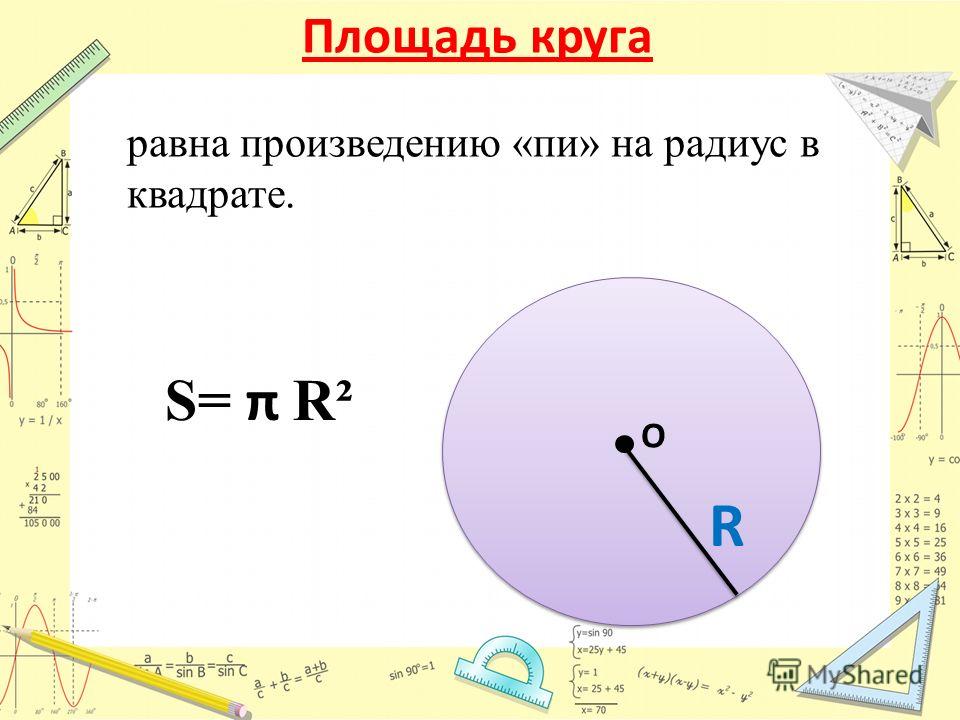
|
Необходимо определить диаметр окружности, если известна длина окружности. |
| 6. | Радиус круга | 2 вид — интерпретация | среднее | 1 Б. | Необходимо определить радиус круга, если дана площадь круга. |
7.
|
Круги с общим центром | 2 вид — интерпретация | сложное | 3 Б. | Необходимо определить площадь одного круга, если дана площадь другого круга. |
| 8. | Площадь цветочной клумбы | 3 вид — анализ | сложное |
3 Б. |
Необходимо вычислить площадь, образованную из квадрата и полукругов. |
Окружность, радиус, диаметр, число Пи, сектор, касательная
Окружность — геометрическое место точек плоскости, расстояние от которых до центра окружности равно.
Центр окръжности
Радиус: расстояние от центра окружности до его границы.
Диаметр: наибольшее расстояние от одной границы окружности до другой. Диаметр равен двум радиусам.
$d = 2\cdot r$
Периметр (длина окружности): длина границы окружности.
Длина окружности $= \pi \cdot$ диаметр $= 2 \cdot \pi \cdot$ радиус
Длина окружности $= \pi \cdot d = 2 \cdot \pi \cdot r$
$\pi$ — pi: число, равное 3,141592… или $\approx \frac{22}{7}$, то есть отношение $\frac{\text{длины окружности}}{\text{диаметр}}$ любого окружности. \circ$
\circ$
Хорды
Если две хорды пересекаются внутри окружности, как на рисунке выше, тогда:
$AX \cdot XB = CX \cdot XD$
Длина окружности и площадь круга • Популярные калькуляторы • Онлайн-конвертеры единиц измерения
Определения и формулы
В геометрии окружностью называется совокупность точек на плоскости, которые находятся на одном расстоянии от точки, называемой центром окружности. Иными словами, окружность — это геометрическое место точек, находящихся в одной плоскости и равноудаленных от точки, называемой центром. Расстояние между любой точкой окружности до центра этой окружности называется радиусом. Мы привыкли видеть окружность в форме круглой линии или круга. Однако так окружность выглядит только в евклидовой геометрии. В некоторых метрических пространствах, например, в чебышевском или манхэттенском пространстве окружности выглядят скорее квадратными.
Диаметр круга — это наибольший отрезок, соединяющий две точки на окружности. Или, точнее, это отрезок, соединяющий две точки окружности и проходящий через ее центр. Диаметр окружности равен ее удвоенному радиусу. Любой диаметр разделяет окружность, а точнее, круг, на две равные половины.
Или, точнее, это отрезок, соединяющий две точки окружности и проходящий через ее центр. Диаметр окружности равен ее удвоенному радиусу. Любой диаметр разделяет окружность, а точнее, круг, на две равные половины.
Говоря точным языком, окружность — это линия или замкнутая кривая, которая окружает часть плоскости, называемую кругом.
Длина окружности
Длина C окружности — это длина замкнутой плоской кривой, ограничивающей круг, то есть это расстояние, равное длине границы круга. Она измеряется в единицах длины. Если разделить длину любой окружности на ее диаметр D, получится число 3.14159265359… Это число — одна из самых важных констант в математике, которое обозначается греческой буквой пи (π):
где R — радиус окружности. Если решить это уравнение для длины окружности, мы получим формулу, которая всем нам знакома с детства:
Математическая константа π широко используется в многих формулах в математике, технике, архитектуре и строительстве. Несмотря на то, что число π известно с древних времен, греческой буквой пи его стали обозначать совсем недавно — с середины XVIII века. π — иррациональное и трансцендентное число. Это означает, что его нельзя точно представить в виде простой дроби и оно не является корнем любого многочлена с рациональными коэффициентами. Есть много чисел, которые являются иррациональными, но не являются трансцендентными. Например, √2 — иррациональное, но не трансцендентное число, так как оно является корнем уравнения x² — 2 = 0. Интересно отметить, что поскольку точное значение π определить невозможно, значит невозможно найти и точное значение длины окружности или площади любого круга.
Несмотря на то, что число π известно с древних времен, греческой буквой пи его стали обозначать совсем недавно — с середины XVIII века. π — иррациональное и трансцендентное число. Это означает, что его нельзя точно представить в виде простой дроби и оно не является корнем любого многочлена с рациональными коэффициентами. Есть много чисел, которые являются иррациональными, но не являются трансцендентными. Например, √2 — иррациональное, но не трансцендентное число, так как оно является корнем уравнения x² — 2 = 0. Интересно отметить, что поскольку точное значение π определить невозможно, значит невозможно найти и точное значение длины окружности или площади любого круга.
Площадь круга
Поскольку TranslatorsCafe.com — сайт для переводчиков, в том числе с английского языка, вначале отметим, что в английском языке площадь круга не совсем корректно называется area of a circle, что буквально означает «площадь окружности», то есть площадь кривой линии (окружность — это кривая!), а, как известно, у линии не может быть площади.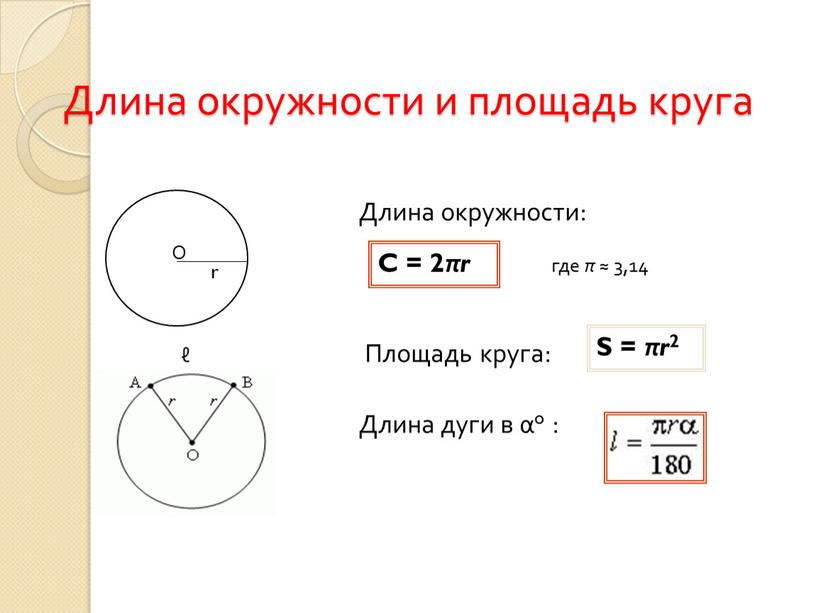 Но ничего, так уж сложилось и англоговорящие люди привыкли к этой неточности.
Но ничего, так уж сложилось и англоговорящие люди привыкли к этой неточности.
Итак, площадь A круга, то есть части плоскости, лежащей внутри окружности радиуса R, равна произведению числа π на квадрат радиуса:
Во многих других языках, в том числе и в русском, такой путаницы в терминах «круг» и «окружность» нет. Впрочем, она есть в других терминах. Площадь круга можно также описать как число единичных квадратов, которые покрывают круг, лежащий внутри окружности.
Окружности в архитектуре
Окружность — весьма совершенная форма, потому что каждая точка окружности находится на одном и том же расстоянии от ее центра. Как и другие совершенные формы, окружность часто используют архитекторы. Круг и окружность широко применяются в архитектуре, и это при том, что круглые здания строить труднее, чем здания прямоугольной формы. Поэтому для постройки круглых зданий всегда была нужна особая мотивация. Возможно, что самая серьезная мотивация была религиозной. Окружности и сферы можно найти практически в любой культуре, религии или системе верований в качестве магических знаков или символов. Многие культовые здания и сооружения являются окружностями в плане — например, буддийские ступы в форме полусферы или Стоунхендж.
Окружности и сферы можно найти практически в любой культуре, религии или системе верований в качестве магических знаков или символов. Многие культовые здания и сооружения являются окружностями в плане — например, буддийские ступы в форме полусферы или Стоунхендж.
Тысячи лет люди наблюдали Солнце и Луну, и первые строители использовали их форму в конструкциях жилищ и поселений, потому что ведь на земле легко было разметить окружность — все, что для этого требовалось — это веревка из кожи или другого материала, да пара колышков.
Среди наиболее известных деталей собора Парижской Богоматери — три огромных окна-розетки с витражами. На фотографии показана западная роза над главным порталом собора
Северное окно-розетка с витражом в парижском Нотр-Даме
Архитекторы считают окружность и сферу самыми совершенными из всех геометрических форм. Покрытия зданий в форме верхней части сферы, то есть купола, широко применяются в архитектуре и бывают различных форм и размеров. Они могут быть полусферическими или заостренной на вершине формы, или с конусным верхом, который можно увидеть в исламской архитектуре. Они могут иметь совершенную сферическую форму, как римские и византийские купола или могут плавно заостряться на вершине, и тогда купол становится похожим на луковицу, как в православных храмах или в архитектурных стилях Великих Моголов.
Они могут иметь совершенную сферическую форму, как римские и византийские купола или могут плавно заостряться на вершине, и тогда купол становится похожим на луковицу, как в православных храмах или в архитектурных стилях Великих Моголов.
Позолоченный купол Исаакиевского собора в Сант-Петербурге имеет почти полусферическую форму
Тадж-Махал в индийском городе Агре — знаменитый пример архитектуры стиля моголов с пятью луковичными куполами
Сферические купола часто используются в архитектуре индуистских храмов, как например, в этом беломраморном индуистском храме Шри Сварминараян Мандир в канадском городе Торонто
Полукруглые арки известны со второго тысячелетия до нашей эры. Древнеримские архитекторы систематически использовали их в своих сооружениях. На снимке показан арочный мост Турнель над р. Сеной в Париже
Окружность в технике
Невозможно представить себе технику без колес и других деталей в форме окружности. Некоторые из них (например, шасси самолетов и колеса автомобилей) хорошо видны. Другие спрятаны в компьютерах, стиральных и посудомоечных машинах, холодильниках, турбинах и другом оборудовании.
Другие спрятаны в компьютерах, стиральных и посудомоечных машинах, холодильниках, турбинах и другом оборудовании.
Сферические радиопрозрачные купола антенн часто используются для защиты механизмов поворота антенн и электронного оборудования радиолокационных станций
Люки в космических кораблях, такие как этот люк в спускаемом аппарате корабля Союз ТМА-А, часто делаются круглой формы, так как такая конструкция без углов позволяет сильно уменьшить механические напряжения, а также облегчает их герметизацию
В машинном отделении в музее Тауэрского моста в Лондоне можно увидеть старые работающие механизмы подъема моста
Сколько колес можно насчитать на этой фотографии, сделанной на первом этаже Музея науки и техники в Лондоне?
Окружности в сельском хозяйстве
Пролетая над пустынями, в которых ничего не растет, мы часто видим зеленые круги. Это поля, которые имеют такую форму из-за того, что фермеры используют системы кругового орошения с центральной осью, вокруг которой вращается оросительное устройство.
Круглые поля с системами кругового орошения в пустыне Мохаве в штате Невада можно наблюдать, пролетая из Торонто в Сан-Франциско; радиус окружности обычно равен ¼ мили или 400 м, длина окружности 2,5 км, а площадь такого поля составляет 125 акров или чуть более 50 гектаров
Калькулятор расчета сечения кабеля по диаметру
Правильный выбор электрического кабеля для питания электрооборудования – залог длительной и стабильной работы установок. Использование неподходящего провода влечет за собой серьезные негативные последствия.
Физика процесса порчи электрической линии вследствие использования неподходящего провода такова: из-за
недостатка места в кабельной жиле для свободного передвижения электронов повышается плотность тока; это
приводит к избыточному выделению энергии и повышению температуры металла. Когда температура становится
слишком высокой, оплавляется изоляционная оболочка линии, что может стать причиной пожара.
Чтобы избежать неприятностей, необходимо использовать кабель с жилами подходящей толщины. Один из способов определить площадь сечения кабеля – отталкиваться от диаметра его жил.
Калькулятор расчета сечения по диаметру
Для простоты вычислений разработан калькулятор расчета сечения кабеля по диаметру. В его основе лежат формулы, по которым можно найти площадь сечения одножильных и многожильных проводов.
Измерять сечение нужно измеряя жилу без изоляции иначе нечего не получится.
Когда речь идет о вычислении десятков и сотен значений, онлайн-калькулятор способен существенно упростить жизнь электрикам и проектировщикам электрических сетей за счет удобства и повышения скорости расчетов. Достаточно ввести значение диаметра жилы, а при необходимости указать количество проволок, если кабель многожильный, и сервис покажет искомое сечение провода.
Формула расчета
Вычислить площадь сечения электрического провода можно разными способами в зависимости от его типа.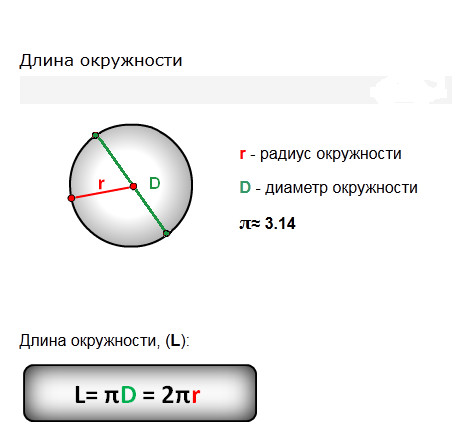 Для всех
случаев применяется единая формула расчета сечения кабеля по диаметру. Она имеет следующий вид:
Для всех
случаев применяется единая формула расчета сечения кабеля по диаметру. Она имеет следующий вид:
D – диаметр жилы.
Диаметр жилы обычно указывается на оплетке провода или на общем ярлыке с другими техническими характеристиками. При необходимости определить это значение можно двумя способами: с применением штангенциркуля и вручную.
Первым способом измерить диаметр жилы очень просто. Для этого ее необходимо очистить от изоляционной оболочки, после чего воспользоваться штангенциркулем. Значение, которое он покажет, и есть диаметр жилы.
Если провод многожильный, необходимо распустить пучок, пересчитать проволоки и измерить штангенциркулем только одну из них. Определять диаметр пучка целиком смысла нет – такой результат будет некорректным из-за наличия пустот. В этом случае формула расчета сечения будет иметь вид:
D – диаметр жилы;
а – количество проволок в жиле.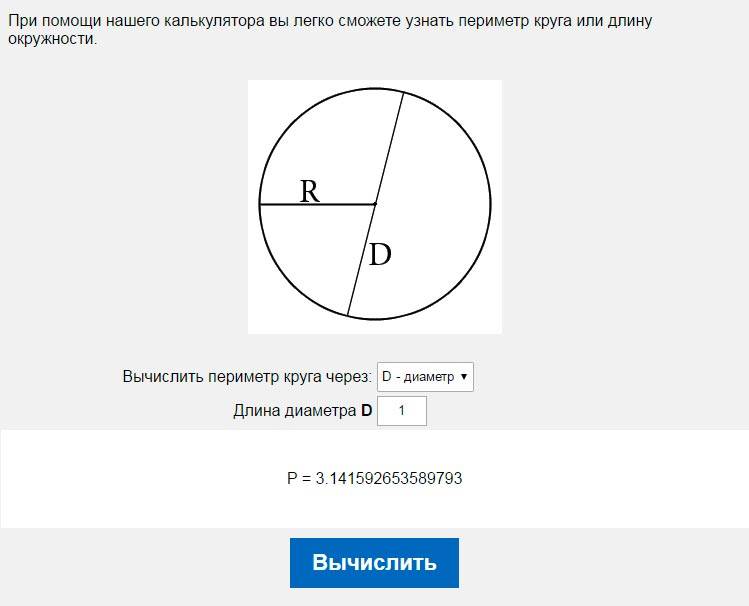
При отсутствии штангенциркуля диаметр жилы можно определить вручную. Для этого ее небольшой отрезок необходимо освободить от изоляционной оболочки и намотать на тонкий цилиндрический предмет, например, на карандаш. Витки должны плотно прилегать друг к другу. В этом случае формула вычисления диаметра жилы провода выглядит так:
L – длина намотки проволоки;
N – число полных витков.
Чем больше длина намотки жилы, тем точнее получится результат.
Выбор по таблице
Зная диаметр провода, можно определить его сечение по готовой таблице зависимости. Таблица расчета сечения кабеля по диаметру жилы выглядит таким образом:
| Диаметр проводника, мм | Сечение проводника, мм2 |
| 0.8 | 0. 5 5 |
| 1 | 0.75 |
| 1.1 | 1 |
| 1.2 | 1.2 |
| 1.4 | 1.5 |
| 1.6 | 2 |
| 1.8 | 2.5 |
| 2 | 3 |
| 2.3 | 4 |
| 2.5 | 5 |
2. 8 8 | 6 |
| 3.2 | 8 |
| 3.6 | 10 |
| 4.5 | 16 |
Когда сечение известно, можно определить значения допустимых мощности и тока для медного или алюминиевого провода. Таким образом удастся выяснить, на какие параметры нагрузки рассчитана токопроводящая жила. Для этого понадобится таблица зависимости сечения от максимального тока и мощности.
| В воздухе (лотки, короба,пустоты,каналы) | Сечение,кв. мм мм | В земле | |||||||||
| Медные жилы | Алюминиевые жилы | Медные жилы | Алюминиевые жилы | ||||||||
| Ток. А | Мощность, кВт | Тон. А | Мощность, кВт | Ток, А | Мощность, кВт | Ток. А | Мощность,кВт | ||||
| 220 (В) | 380 (В) | 220(В) | 380 (В) | 220(В) | 380 (В) | 220(В) | |||||
| 19 | 4. 1 1 | 17.5 | 1,5 | 77 | 5.9 | 17.7 | |||||
| 35 | 5.5 | 16.4 | 19 | 4.1 | 17.5 | 7,5 | 38 | 8. 3 3 | 75 | 79 | 6.3 |
| 35 | 7.7 | 73 | 77 | 5.9 | 17.7 | 4 | 49 | 10.7 | 33.S | 38 | 8.4 |
| *2 | 9.7 | 77.6 | 37 | 7 | 71 | 6 | 60 | 13. 3 3 | 39.5 | 46 | 10.1 |
| 55 | 17.1 | 36.7 | 47 | 9.7 | 77.6 | 10 | 90 | 19.8 | S9.7 | 70 | 15.4 |
| 75 | 16.5 | 49.3 | 60 | 13.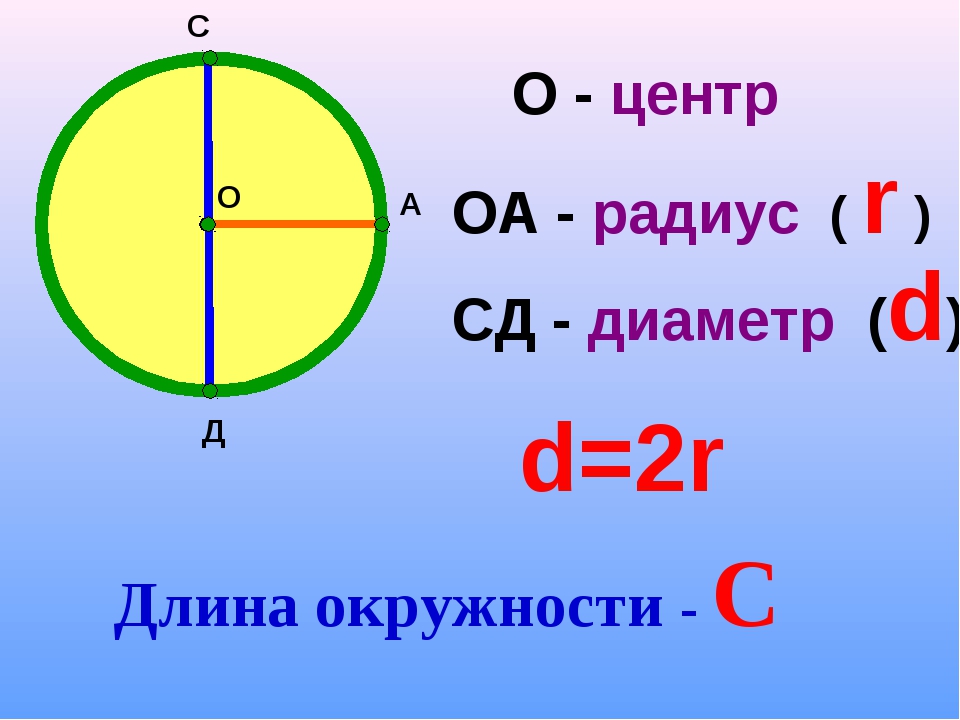 7 7 | 39.5 | 16 | 115 | 753 | 75.7 | 90 | 19,8 |
| 95 | 70,9 | 67.5 | 75 | 16.5 | 49.3 | 75 | 150 | 33 | 98.7 | 115 | 75.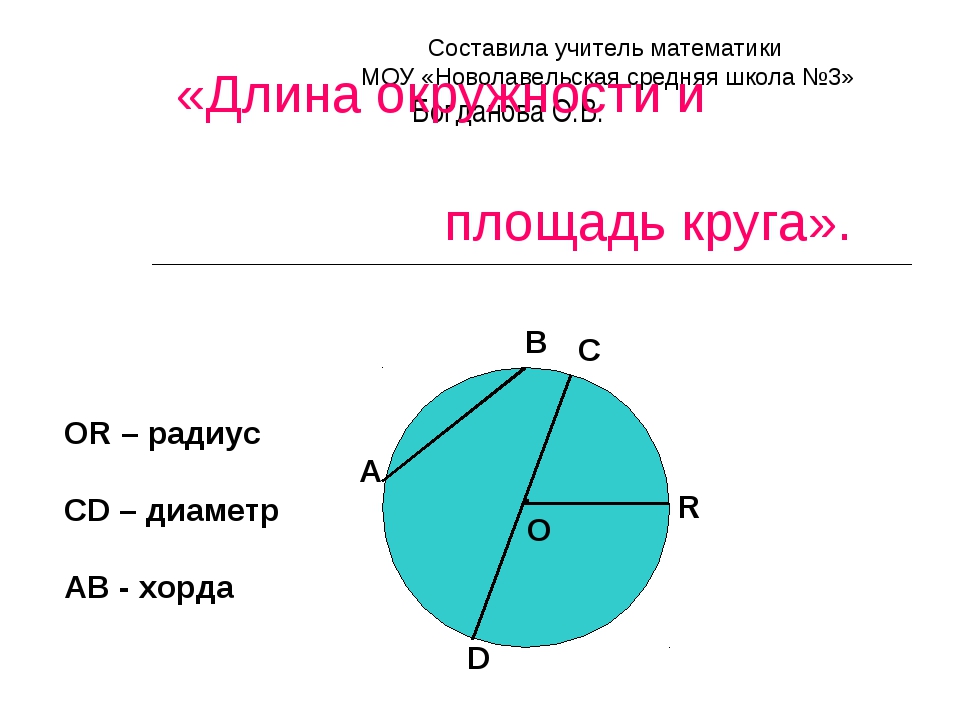 3 3 |
| 170 | 76.4 | 78.9 | 90 | 19.8 | 59.7 | 35 | 180 | 39.6 | 118.5 | 140 | 30.8 |
| 145 | 31.9 | 95.4 | 110 | 74.7 | 77.4 | 50 | 775 | 493 | 148 | 175 | 38. 5 5 |
| ISO | 39.6 | 118.4 | 140 | 30.8 | 97.1 | 70 | 775 | 60.5 | 181 | 710 | 46.7 |
| 770 | 48.4 | 144.8 | 170 | 37.4 | 111.9 | 95 | 310 | 77. 6 6 | 717.7 | 755 | 56.1 |
| 760 | 57,7 | 171.1 | 700 | 44 | 131,6 | 170 | 385 | 84.7 | 753.4 | 795 | 6S |
| 305 | 67.1 | 700.7 | 735 | 51.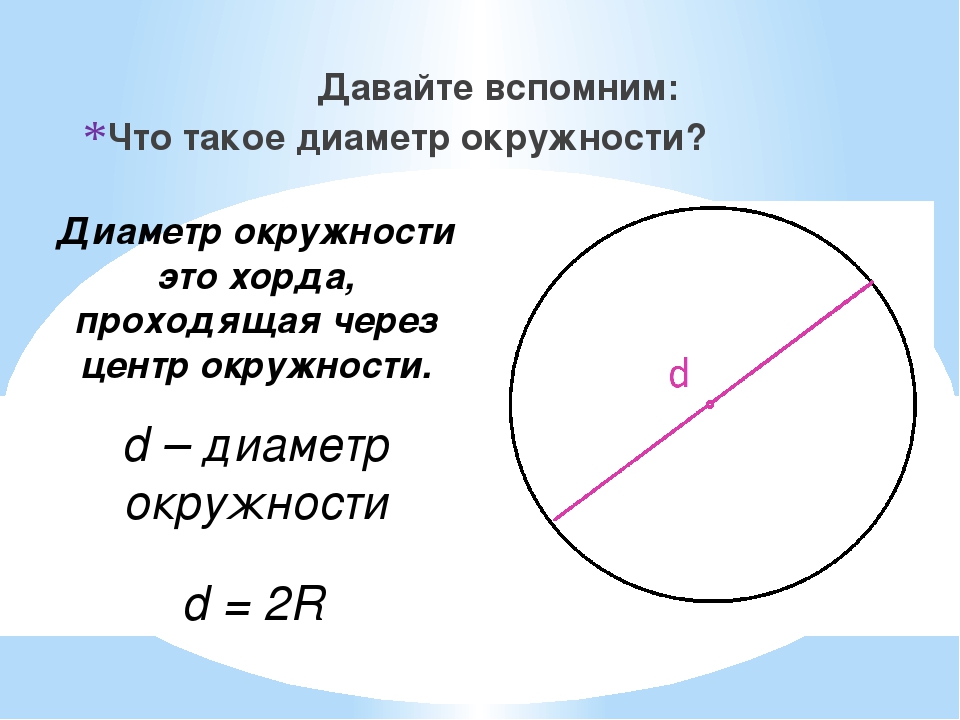 7 7 | 154.6 | 150 | 435 | 95.7 | 786.3 | 335 | 73.7 |
| 350 | 77 | 730.3 | 770 | 59.4 | 177.7 | 185 | 500 | 110 | 379 | 385 | 84. 7 7 |
Перевод ватт в киловатты
Чтобы правильно воспользоваться таблицей зависимости сечения провода от мощности, важно правильно перевести ватты в киловатты.
1 киловатт = 1000 ватт. Соответственно, чтобы получить значение в киловаттах, мощность в ваттах необходимо разделить на 1000. Например, 4300 Вт = 4,3 кВт.
Примеры
Пример 1. Необходимо определить значения допустимых тока и мощности для медного провода с диаметром жилы 2,3 мм. Напряжение питания – 220 В.
В первую очередь следует определить площадь сечения жилы. Сделать это можно по таблице или по формуле. В первом случае получается значение 4 мм2, во втором – 4,15 мм2.
Расчетное значение всегда более точное, чем табличное.
С помощью таблицы зависимости сечения кабеля от мощности и тока, можно выяснить, что для сечения медной жилы
площадью 4,15 мм2 допустима мощность 7,7 кВт и ток 35 А.
Пример 2. Необходимо вычислить значения тока и мощности для алюминиевого многожильного провода. Диаметр жилы – 0,2 мм, число проволок – 36, напряжение – 220 В.
В случае с многожильным проводом пользоваться табличными значениями нецелесообразно, лучше применить формулу расчета площади сечения:
Теперь можно определить значения мощности и тока для многожильного алюминиевого провода сечением 2,26 мм2. Мощность – 4,1 кВт, ток – 19 А.
понятие, площадь, формула и таблица соответствия диаметру
Содержание статьи:
Для правильного выбора и организации электролинии необходимо учитывать параметры и нагрузку проводников. Они представляют собой металлическую нить из меди, алюминия, стали, цинка, титана, никеля и обеспечивают передачу тока от его источника до потребителя. У проводников есть поперечное сечение – это фигура, образованная от их рассечения плоскостью поперечного направления. Если его подобрать неправильно, линия выйдет из строя или загорится при скачках напряжения.
Если его подобрать неправильно, линия выйдет из строя или загорится при скачках напряжения.
Площадь поперечного сечения как электротехническая величина
От поперечного сечения зависит токопроводимость провода
В качестве примера сечения можно рассмотреть распил изделия под углом 90 градусов относительно поперечной оси. Контур фигуры, получившейся в результате, определяется конфигурацией объекта. Кабель имеет вид небольшой трубы, поэтому при распиле выйдет фигура в виде двух окружностей определенной толщины. При поперечном рассечении круглого металлического прута получится форма круга.
В электротехнике площадь ПС будет значить прямоугольное сечение проводника в отношении к его продольной части. Сечение жил всегда будет круглым. Измерение параметра осуществляется в мм2.
Начинающие электрики могут перепутать диаметр и сечение элементов. Чтобы определить, какая площадь сечения у жилы, понадобиться учесть его круглую форму и воспользоваться формулой:
S = πхR2, где:
- S – площадь круга;
- π – постоянная величина 3,14;
- R – радиус круга.

Если известен показатель площади, легко найти удельное сопротивление материала изготовления и длину провода. Далее вычисляется сопротивление тока.
Для удобства расчетов начальная формула преобразуется:
- Радиус – это ½ диаметра.
- Для вычисления площади π умножается на D (диаметр), разделенный на 4, или 0,8 умножается на 2 диаметра.
При вычислениях используют показатель диаметра, поскольку его неправильный подбор может вызвать перегрев и воспламенение кабеля.
Цели расчета
Поперечное сечение проводов для освещения
Рассчитывать параметры площади сечения проводника необходимо с несколькими целями:
- получение необходимого количества электричества для запитки бытовых приборов;
- исключение переплат за неиспользуемый энергоноситель;
- безопасность проводки и предотвращение возгораний;
- возможность подключения высокомощной техники к сети;
- предотвращение оплавления изоляционного слоя и коротких замыканий;
- правильная организация осветительной системы.

Оптимальное сечение провода для освещения – 1,5 мм2 для линии, 4-6 мм2 на вводе.
Соотношение диаметра кабеля с площадью его сечения
Определение посредством формулы площади поперечного сечения проводников занимает длительное время. В некоторых случаях уместно использовать данные из таблицы. Поскольку для организации современной проводки применяется медный кабель, в таблицу вносятся параметры:
- диаметр;
- сечение в соответствии с показателем диаметра;
- предельная мощность нагрузки проводников в сетях с напряжением 220 и 380 В.
| Диаметр жилы, мм | Параметры сечения, мм2 | Сила тока, А | Мощность медного проводника, кВт | |
| Сеть 220 В | Сеть 380 В | |||
| 1,12 | 1 | 14 | 3 | 5,3 |
| 1,38 | 1,5 | 15 | 3,3 | 5,7 |
| 1,59 | 2 | 19 | 4,1 | 7,2 |
| 1,78 | 2,5 | 21 | 4,6 | 7,9 |
| 2,26 | 4 | 27 | 5,9 | 10 |
| 2,76 | 6 | 34 | 7,7 | 12 |
| 3,57 | 10 | 50 | 11 | 19 |
Посмотрев данные в соответствующих колонках, можно узнать нужные параметры для электролинии жилого здания или производственного объекта.
Расчет сечения многожильного проводника
Многожильный провод представляет собой несколько отдельных жил. Расчет его сечения осуществляется следующим образом:
- Находится показатель площади сечения у одной жилы.
- Пересчитываются кабельные жилы.
- Количество умножается на поперечное сечение одной жилы.
При подключении многожильного проводника его концы обжимаются специальной гильзой с использованием обжимных клещей.
Особенности самостоятельного расчета
Самостоятельное вычисление продольного сечения выполняется на жиле без изоляционного покрытия. Кусочек изоляции можно отодвинуть или снять на отрезке, приобретенном специально для тестирования. Вначале понадобится определить диаметр и по нему найти сечение. Для работ используется несколько методик.
При помощи штангенциркуля
Способ оправдан, если будут измеряться параметры усеченного, или бракованного кабеля. К примеру, ВВГ может обозначаться как 3х2,5, но фактически быть 3х21.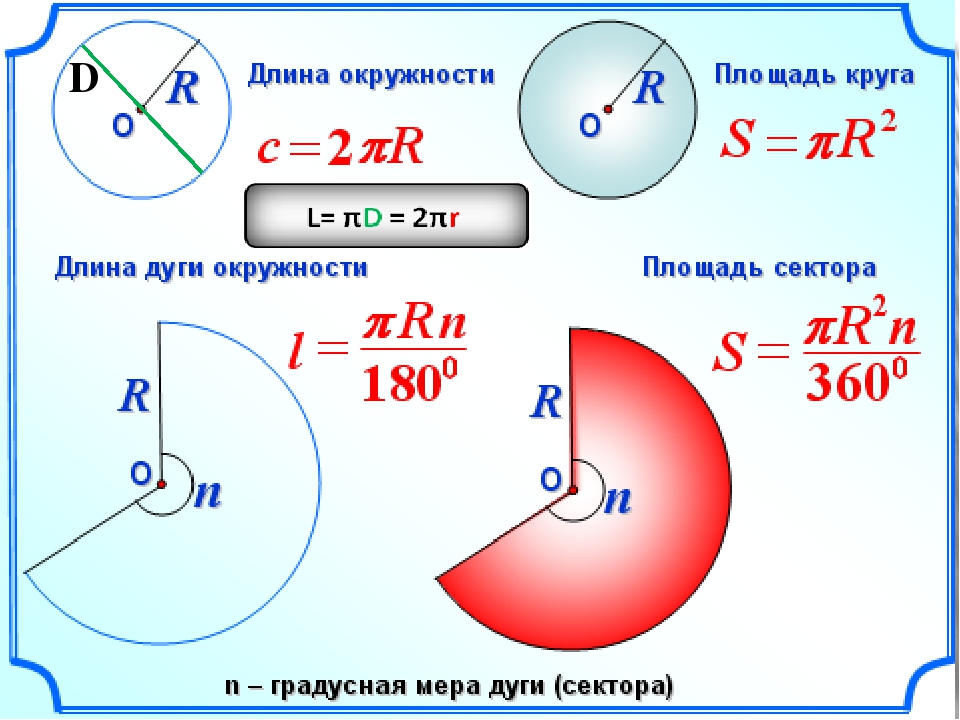 Вычисления производятся так:
Вычисления производятся так:
- С проводника снимается изоляционное покрытие.
- Диаметр замеряется штангенциркулем. Понадобится расположить провод между ножками инструмента и посмотреть на обозначения шкалы. Целая величина находится сверху, десятичная – снизу.
- На основании формулы поиска площади круга S = π (D/2)2 или ее упрощенного варианта S = 0,8 D² определяется поперечное сечение.
- Диаметр равен 1,78 мм. Подставляя величину в выражение и округлив результат до сотых, получается 2,79 мм2.
Для бытовых целей понадобятся проводники с сечением 0,75; 1,5; 2,5 и 4 мм2.
С использованием линейки и карандаша
Вычисление ПС с помощью линейки и карандаша
При отсутствии специального измерителя можно воспользоваться карандашом и линейкой. Операции выполняются с тестовым образом:
- Зачищается от изоляционного слоя участок, равный 5-10 см.
- Получившаяся проволока наматывается на карандаш. Полные витки укладываются плотно, пространства между ними быть не должно, «хвостики» направляются вверх или вниз.

- В конечном итоге должно получиться определенное число витков, их требуется посчитать.
- Намотка прикладывается к линейке так, чтобы нулевое деление совпадало с первой намоткой.
- Замеряется длина отрезка и делится на количество витков. Получившаяся величина – диаметр.
- Например, получилось 11 витков, которые занимают 7,5 мм. При делении 7,5 на 11 выходит 0,68 мм – диаметр кабеля. Сечение можно найти по формуле.
Точность вычислений определяется плотностью и длиной намотки.
Таблица соответствия диаметра проводов и площади их сечения
Если нет возможности пройти тестирование диаметра или сделать вычисление при покупке, допускается использовать таблицу. Данные можно сфотографировать, распечатать или переписать, а затем применять, чтобы найти нормативный или популярный размер жилы.
| Диаметр кабеля, мм | Сечение проводника, мм2 |
| 0,8 | 0,5 |
| 0,98 | 0,75 |
| 1,13 | 1 |
| 1,38 | 1,5 |
| 1,6 | 2 |
| 1,78 | 2,5 |
| 2,26 | 4 |
| 2,76 | 6 |
| 3,57 | 10 |
При покупке электрокабеля понадобится посмотреть параметры на этикетке. К примеру, используется ВВНГ 2х4. Количество жил – величина после «х». То есть, изделие состоит из двух элементов с поперечным сечением 4 мм2. На основании таблицы можно проверить точность информации.
К примеру, используется ВВНГ 2х4. Количество жил – величина после «х». То есть, изделие состоит из двух элементов с поперечным сечением 4 мм2. На основании таблицы можно проверить точность информации.
Чаще всего диаметр кабеля меньше, чем заявлен на упаковке. У пользователя два варианта – применять другой или выбрать с большей площадью сечения кабель по диаметру. Выбрав второй, понадобится проверить изоляцию. Если она не сплошная, тонкая, разная по толщине, остановитесь на продукции другого изготовителя.
Определение сечения проводника на вводе
Уточнить номинальные показатели можно в компании Энергосбыта или документации к товару. К примеру, номинал автомата на вводе составляет 25 А, мощность потребления – 5 кВт, сеть однофазная, на 220 В.
Подбор сечения осуществляется так, чтобы допустимый ток жил за длительный период был больше номинала автомата. Например, в доме на ввод пущен медный трехжильный проводник ВВГнг, уложенный открытым способом. Оптимальное сечение – 4 мм2, поэтому понадобится материал ВВГнг 3х4.
Оптимальное сечение – 4 мм2, поэтому понадобится материал ВВГнг 3х4.
После этого высчитывается показатель условного тока отключения для автомата с номиналом 25 А: 1,45х25=36,25 А. У кабеля с площадью сечения 4 мм2 параметры длительно допустимого тока 35 А, условного – 36,25 А. В данном случае лучше взять вводный проводник из меди сечением 6 мм2 и допустимым предельным током 42 А.
Вычисление сечения провода для линии розеток
Сечение кабелей для домашних электроустановок
Каждый электроприбор имеет показатели собственной мощности. Они замеряются в Ваттах и указываются в паспорте либо на наклейке на корпусе. Примером поиска сечения будет линия запитки для стиральной машины мощностью 2,4 кВт. При расчетах учитывается:
- материал провода и способ укладки – трехжильный ВВГнг-кабель из меди, спрятанный в стене;
- особенности сечения – оптимальная величина составляет 1,5 мм2, т.е. понадобится кабель 3х1,5;
- использование розетки. Если подключается только машинка-автомат, характеристик будет достаточно;
- система защиты – автомат, номинальный ток которого 10 А.

Для двойных розеток применяется кабель из меди с сечением 2,5 мм2 и автомат номиналом 16 А.
Подбор сечения для трехфазной линии 380 В с несколькими приборами
Подключение нескольких видов бытовой техники к трехфазной линии предусматривает протекание потребляемого тока по трем жилам. В каждом из них будет меньшая величина, чем в двухжильном. На основании данного явления в трехфазной сети допускается применять кабель с меньшим сечением.
К примеру, в доме устанавливается генератор с мощностью 20 кВт и суммарной мощностью по трем фазам 52 А. На основании значений таблицы выйдет, что оптимальное сечение кабеля – 8,4 мм2. На основании формулы высчитывается фактическое сечение: 8,4/1,75=4,8 мм2. Чтобы подсоединить генератор мощностью 20 кВт на трехфазную сеть 380 В необходим медный проводник, сечение каждой жилы которого 4,8 мм2.
Сечение проводов в домах старой застройки и предельная нагрузка
В многоэтажках советского периода используется алюминиевая проводка. С учетом правильного соединения узлов в распредкоробе, качества изоляции и надежности контактов соединения она прослужит от 10 до 30 лет.
С учетом правильного соединения узлов в распредкоробе, качества изоляции и надежности контактов соединения она прослужит от 10 до 30 лет.
При необходимости подключения техники с большой энергоемкостью в домах с проводкой из алюминия на основе мощности потребления подбирается сечение и диаметр жил. Все данные указаны в таблице.
| Ток, А | Максимальная мощность, ВА | Диаметр кабеля, мм | Сечение кабеля, мм2 |
| 14 | 3000 | 1,6 | 2 |
| 16 | 3500 | 1,8 | 2,5 |
| 18 | 4000 | 2 | 3 |
| 21 | 4600 | 2,3 | 4 |
| 24 | 5300 | 2,5 | 5 |
| 26 | 5700 | 2,7 | 6 |
| 31 | 6800 | 3,2 | 8 |
| 38 | 8400 | 3,6 | 10 |
Какой кабель выбрать для квартирной проводки
Несмотря на дешевизну алюминиевых проводников, от их применения лучше отказаться. Причина – низкая надежность контактов, через которые будут проходить токи. Второй повод – несоответствие сечения провода мощности современной бытовой техники. Кабель из меди отличается надежностью, длительным сроком эксплуатации.
Причина – низкая надежность контактов, через которые будут проходить токи. Второй повод – несоответствие сечения провода мощности современной бытовой техники. Кабель из меди отличается надежностью, длительным сроком эксплуатации.
В квартирах и домах допускается использовать провод с маркировкой:
- ПУНП – плоский проводник с медными жилами в ПВХ-оболочке. Рассчитан на напряжение номиналом 250 В при частоте 50 Гц.
- ВВГ/ВВГнг – плоские кабели из меди с двойным ПВХ-покрытием. Применяются внутри и снаружи сооружений, не подвержены возгоранию. Бывают с 2-мя, 3-мя и 4-мя жилами.
- NYM – провод из меди для внутренней одиночной линии. Имеет изоляционную ПВХ-оболочку и наружное покрытие, жилы с заземлением и без него.
При выборе количества жил понадобится учесть способность токопроводимости на единицу сечения. В данном случае квартирную сеть лучше сделать из одножильного провода, толщина которого больше. Многожильные элементы можно изгибать многократно, подсоединять на них электроприборы. Качественным будет только кабель с тонкими жилами.
Качественным будет только кабель с тонкими жилами.
Правильное сечение проводников, учет мощности оборудования и типа сети – важные факторы при организации электролинии. Диаметр кабеля можно несколькими способами вычислить самостоятельно. Основываясь на этих показаниях, легко определить сечение жил по формулам или с помощью таблицы.
Сечение арматуры — площадь сечения, таблица для расчета
Горячекатаная арматурная сталь – вид металлопродукции, используемый практически на всех строительных объектах. Назначение арматурных стержней, плоских сеток и объемных каркасов, – повышение устойчивости бетона к нагрузкам различных видов. Эта металлопродукция необходима при возведении фундамента, монолитных стен, производстве железобетонных изделий. Для того чтобы определить прочность арматуры, составить смету, рассчитать массу партии проката, необходим такой показатель, как площадь поперечного сечения. Арматурные стержни имеют поверхность – гладкую или периодического профиля. В обозначении прутов с гладкой поверхностью указывается их наружный диаметр, периодического профиля – номинальный диаметр, который равен наружному диаметру гладкого стержня с равновеликой площадью сечения.
Для того чтобы определить прочность арматуры, составить смету, рассчитать массу партии проката, необходим такой показатель, как площадь поперечного сечения. Арматурные стержни имеют поверхность – гладкую или периодического профиля. В обозначении прутов с гладкой поверхностью указывается их наружный диаметр, периодического профиля – номинальный диаметр, который равен наружному диаметру гладкого стержня с равновеликой площадью сечения.
Расчет площади сечения арматурных стержней с гладкой поверхностью
Площадь сечения арматурной стали можно просто определить по таблице ГОСТа 5781-82. Однако если при покупке арматуры иногда возникает необходимость узнать эту величину, а таблицы нет под рукой, то можно самостоятельно произвести несложные расчеты. Для них понадобятся штангенциркуль и калькулятор.
С помощью штангенциркуля определим наружный диаметр в миллиметрах. Расчет площади поперечного сечения арматуры производится по формуле:
S = π*dн2/4,
в которой:
- S – площадь сечения, мм2;
- π – постоянная величина, равная 3,14;
- dн – наружный диаметр, мм.

Расчеты для стержней периодического профиля
Арматурная сталь периодического профиля обеспечивает хорошее сцепление с бетоном, поэтому именно она используется в качестве рабочей арматуры, воспринимающей и распределяющей основные нагрузки на бетонную конструкцию.
Для определения номинального диаметра производят два измерения с помощью штангенциркуля – по вершинам ребер и по углублениям. Номинальный диаметр равен среднему арифметическому значению этих двух величин. Их суммируют и делят пополам. Площадь сечения определяется по той же формуле, что и в случае стержней с гладкой поверхностью, но вместо наружного значения мы подставляем в формулу значение номинального диаметра.
Вам не понадобится производить расчеты, если под рукой у вас будет таблица площади поперечного сечения стержней арматуры.
| Dном, мм | S, см2 | Dном, мм | S, см2 |
| 6 | 0,283 | 18 | 2,64 |
| 7 | 0,385 | 20 | 3,14 |
| 8 | 0,503 | 22 | 3,8 |
| 10 | 0,785 | 25 | 4,91 |
| 12 | 1,131 | 28 | 6,16 |
| 14 | 1,54 | 36 | 10,18 |
| 16 | 2,01 | 40 | 12,58 |
Как найти площадь, если известен диаметр
Зная лишь длину диаметра окружности, можно вычислить не только площадь круга, но и площади некоторых других геометрических фигур. Это вытекает из того, что диаметры вписанных или описанных вокруг таких фигур окружностей совпадают с длинами их сторон либо диагоналей.
Это вытекает из того, что диаметры вписанных или описанных вокруг таких фигур окружностей совпадают с длинами их сторон либо диагоналей.Если надо найти площадь круга (S) по известной длине его диаметра (D), умножайте число пи (π) на возведенную в квадрат длину диаметра, а результат делите на четыре: S=π ²*D²/4. Например, если диаметр круга равен двадцати сантиметрам, то его площадь можно вычислить так: 3,14² * 20² / 4 = 9,86 * 400 / 4 = 986 квадратных сантиметров.
Если надо найти площадь квадрата (S) по диаметру описанной вокруг него окружности (D), возводите длину диаметра в квадрат, а результат разделите пополам: S=D²/2. Например, если диаметр описанной окружности равен двадцати сантиметрам, то площадь квадрата можно вычислить так: 20² / 2 = 400 / 2 = 200 квадратных сантиметров.
Если площадь квадрата (S) нужно найти по диаметру вписанной в него окружности (D), достаточно возвести длину диаметра в квадрат: S=D². Например, если диаметр вписанной окружности равен двадцати сантиметрам, то площадь квадрата можно вычислить так: 20² = 400 квадратных сантиметров. 2 / 4 + 20*10/2», а затем нажать клавишу Enter.
2 / 4 + 20*10/2», а затем нажать клавишу Enter.
Площадь круга | Формула для радиуса, диаметра и окружности
Содержание
- Какова площадь круга?
- Как найти площадь круга
Какова площадь круга?
Круг — это не квадрат, а площадь круга (количество внутреннего пространства, заключенного в круг) измеряется в квадратных единицах. Найти площадь квадрата просто: длина умножена на ширину.
У круга, однако, есть только диаметр или расстояние в поперечнике. У него нет четко видимой длины и ширины, поскольку круг (по определению) — это набор всех точек, равноудаленных от данной точки в центре.
Тем не менее, имея только диаметр или половину диаметра (радиус ), или даже только длину окружности (расстояние вокруг), вы можете вычислить площадь любого круга.
Как найти площадь круга
Напомним, что отношение между длиной окружности и ее диаметром всегда одинаковое, 3. 14159265, пи или π. Это число, π, умноженное на квадрат радиуса круга, дает вам площадь внутри круга в квадратных единицах.
14159265, пи или π. Это число, π, умноженное на квадрат радиуса круга, дает вам площадь внутри круга в квадратных единицах.
Формула площади круга
Если вам известен радиус r в любых единицах измерения (мм, см, м, дюймы, футы и т. Д.), Используйте формулу π r 2 , чтобы найти площадь, A:
Ответом будут квадратные единицы линейных единиц, такие как мм2, см2, м2, квадратные дюймы, квадратные футы и так далее.
Вот круг радиусом 7 метров. Какова его площадь?
[вставить чертеж круга шириной 14 м с обозначенным радиусом 7 м]
А = π · r2
А = π × 72
А = π × 49
A = 153,9380 м2
Площадь круга с использованием диаметра
Если вам известен диаметр d в любых единицах измерения, возьмите половину диаметра, чтобы получить радиус r в тех же единицах.
Вот проект недвижимости Сан-Сити, штат Аризона, круглого города диаметром 1. 07 километров. Какой район Сан-Сити?
07 километров. Какой район Сан-Сити?
Сначала найдите половину заданного диаметра, чтобы получить радиус:
1,072 = 0,535 км = 535 м
Подставьте радиус в нашу формулу:
А = π · r2
А = π × 5352
А = π × 286,225
A = 899 202,3572 м2
Чтобы преобразовать квадратные метры, м2, в квадратные километры, км2, разделите на 1000000:
A = 0,8992 км2
Самый западный круглый жилой комплекс Сан-Сити имеет площадь почти 1 квадратный километр!
Как рассчитать площадь круга
Попробуйте эти вычисления площади для четырех разных кругов.Будь осторожен; некоторые указывают радиус r, а некоторые — диаметр d.
Не забудьте взять половину диаметра, чтобы найти радиус, прежде чем возводить радиус в квадрат и умножать на π.
Проблемы
- Велосипедное колесо диаметром 406 мм
- Колесо обозрения «Лондонский глаз», радиус 60 метров
- Велосипедное колесо диаметром 26 дюймов
- Самая большая пицца в мире имела радиус 61 фут 4 дюйма (736 дюймов)
Не заглядывайте в ответы, пока не произведете расчеты!
Ответы
- Велосипедное колесо диаметром 406 мм имеет радиус r 203 мм:
- Колесо обозрения «Лондонский глаз», радиус 60 метров:
- Велосипедное колесо диаметром 26 дюймов имеет радиус r 13 дюймов:
- Самая большая пицца в мире с радиусом 736 дюймов:
А = πr2
A = π × 203 мм2
А = 637. 7433 мм2
7433 мм2
А = πr2
A = π × 60 м2
A = 188,4955 м2
А = πr2
A = π × 13 дюймов2
A = 530,9291 дюйм2
А = πr2
A = π × 736 дюйм2
A = 1 701 788,17 дюйм2
То есть 11817.97 квадратных футов пиццы! Ням! В любом случае, как вы справились с четырьмя задачами?
Площадь круга по окружности
Если вы не знаете, что такое радиус или диаметр, но знаете длину окружности C, вы можете по-прежнему найти площадь.
Формула площади и окружности
Окружность (расстояние по окружности) находится по следующей формуле:
С = 2πr
Это означает, что мы можем взять формулу окружности и «решить для r», что даст нам:
г = C2π
Мы можем заменить r в нашей исходной формуле этим новым выражением:
А = π C2π2
Это выражение упрощается до следующего:
Эта формула работает каждый раз!
Как найти площадь по окружности
Вот красивая пицца разумного размера , которую вы можете разделить с тремя друзьями. Вы знаете, что окружность вашей пиццы составляет 50,2655 дюйма, но вы не знаете ее общую площадь. Вы хотите знать, сколько квадратных дюймов пиццы вам понравится.
Вы знаете, что окружность вашей пиццы составляет 50,2655 дюйма, но вы не знаете ее общую площадь. Вы хотите знать, сколько квадратных дюймов пиццы вам понравится.
[вставить мультяшный рисунок типичной 16-дюймовой пиццы, но не указывать диаметр]
Замените C в формуле на 50,2655 дюйма:
А = 50,265524π
А = 2,526,62044π
A = 201,0620 дюйм2
Поровну разделите эту общую площадь для полноразмерной пиццы между четырьмя друзьями, и каждый получит 50.2655 дюйм2 пиццы! Это примерно треть квадратного фута на каждого из вас! Ням ням!
Следующий урок:
Площадь сектора круга
Калькулятор площади круга
- Цель использования
- Чтобы найти силу натяжения ремня цепи печи, в котором используются воздушные цилиндры
[1] 2021/02/07 11:37 Мужчина / Уровень 50 лет / Инженер / Очень /
- Цель использования
- Немедленно получаю ответ ОК
- Комментарий / запрос
- Я могу найти такие единицы, как см.
 Дюйм, метр, мм.
Дюйм, метр, мм.
Можете ли вы прояснить, все в порядке, цифровой ответ в порядке, хорошо
[2] 2021.01.10 00:03 Мужчина / Уровень 50 / Инженер / Немного /
- Цель использования
- определение базовой поверхности голландских духовок, чтобы решить, нужно ли мне увеличивать время приготовления, когда я удваиваю рецепт
[3] 2020/12/17 02:13 Мужчина / 60 лет и старше / Самостоятельно занятые лица / Очень /
- Цель использования
- круги и геометрия
- Комментарий / запрос
- я люблю чито! Еще я люблю завязывать шнурки! пойти по магазинам с моим старым папой он еще жив! а я люблю стирать одежду
[4] 2020/12/10 07:02 Мужчина / 60 лет и старше / Инженер / Совсем нет /
- Цель использования
- Проверить, можете ли вы назвать больше, чем просто эти цифры числа Пи.
- Комментарий / запрос
- Это больше, чем я могу.
 Спасибо!
Спасибо!
[5] 2020/10/27 07:16 Мужчина / До 20 лет / Начальная школа / Ученик неполной средней школы / Очень /
- Цель использования
- Для расчета внутренней площади геодомовой теплицы.
- Комментарий / запрос
- Очень полезный сайт — большое спасибо!
[6] 2020/10/24 23:38 Женский / Уровень 20 лет / Старшая школа / Университет / Аспирант / Очень /
- Цель использования
- Помог мне найти области круга.
[7] 2020/10/08 18:09 Мужчина / До 20 лет / Начальная школа / Ученик неполной средней школы / Полезно /
- Цель использования
- определение площади деревянного шнура
[8] 2020/09/16 02:24 Женщины / 60 лет и старше / Самозанятые / Полезные /
- Цель использования
- сравнивает площадь круглой водопропускной трубы с площадью прямоугольной водопропускной трубы и предоставляет распечатку заинтересованному землевладельцу.
[9] 2020/08/26 00:40 Мужчина / 60 лет и старше / Офисный работник / Государственный служащий / Очень /
- Комментарий / запрос
- Это было действительно полезно, мой учитель был поражен, увидев, что я могу делать это на калькуляторе
[10] 2020/08/06 23:23 Женский / До 20 лет / Начальная школа / Младшая средняя школа / — /
какова площадь круга диаметром 15 дюймов?
Вот ответ на такие вопросы, как: как найти площадь круга диаметром 15 дюймов?
Калькулятор кругов
Площадь Окружность
Площадь круга диаметром 15 равна 176. | |
Изображение Circler = 7.5d = 15C = 47.1 | A = πr 2 = π (d2) 2 А = С 2 4π π = 3,1415A = площадь C = окружность или периметр r = радиус , d = диаметр |
Площадь круга через радиус
:Площадь = π · r 2 = 3.14 · 7,5 2 = 176,7 квадратных дюймов (*)
Площадь круга по диаметру
:Площадь = π · (d2) 2 = 3,14 · (152) 2 = 3,14 · (7,5) 2 = 176,7 квадратных дюймов (*)
Площадь круга через длину окружности
: Площадь
= С 2 4π
= 47,12 2 4π
= 2220,29 (4 · 3,14)
= 2220,2912,56
= 176. 7 квадратных дюймов (*)
7 квадратных дюймов (*)
(*) 176,71458676443 дюймов, точно или ограничено точностью этого калькулятора (13 знаков после запятой).
Примечание: для простоты приведенные выше операции были округлены до 2 десятичных знаков, а число π было округлено до 3,14.
Окружность с радиусом = 7,5 или диаметром = 15 или длиной окружности = 47,12 дюйма имеет площадь:
- 1.14 × 10 -7 квадратных километров (км²)
- 0,114 квадратных метров (м²)
- 1140 квадратных сантиметров (см²)
- 1,14 × 10 5 квадратных миллиметров (мм²)
- 4,40156 × 10 -8 квадратные мили (mi²)
- 0,136343 квадратного ярда (ярд²)
- 1,22708 квадратных футов (фут²)
- 176,7 квадратных дюймов (дюйм²)
Используйте калькулятор площади круга ниже, чтобы найти площадь круга с учетом его диаметра или других параметров. Чтобы рассчитать площадь, вам просто нужно ввести положительное числовое значение в одно из 3-х полей калькулятора. Вы также можете увидеть пошаговое решение в нижней части калькулятора.
Чтобы рассчитать площадь, вам просто нужно ввести положительное числовое значение в одно из 3-х полей калькулятора. Вы также можете увидеть пошаговое решение в нижней части калькулятора.
Формула площади круга
Вот три способа найти площадь круга (формулы):
Формула площади круга через радиус
А = πr 2
Формула площади круга через диаметр
А = π (d2) 2
Формула площади круга через длину окружности
А = С 2 4π
См. Ниже некоторые определения, относящиеся к формулам:
Окружность
Окружность — это линейное расстояние по краю круга.
Радиус
Радиус круга — это любой из отрезков прямой от центра до периметра. Радиус равен половине диаметра или r = d2.
Диаметр
Диаметр круга — это любой отрезок прямой, который проходит через центр круга и концы которого лежат на окружности. Диаметр в два раза больше радиуса или d = 2 · r.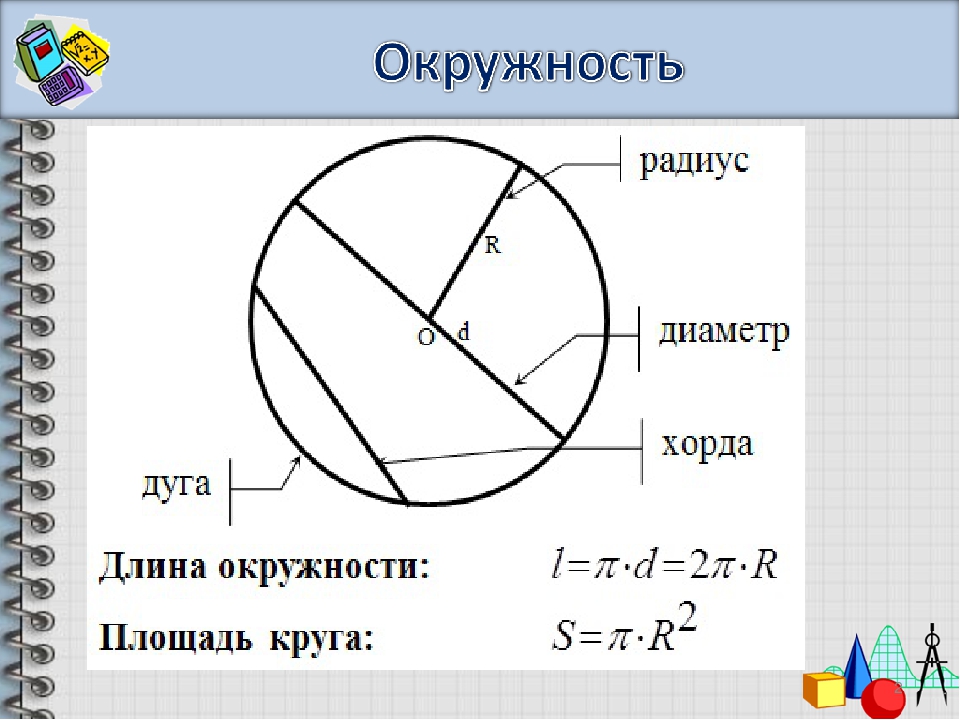
Греческая буква π
π представляет собой число Pi, которое определяется как отношение длины окружности к ее диаметру или π = Cd .Для простоты можно использовать Pi = 3,14 или Pi = 3,1415. Пи — иррациональное число. Первые 100 цифр числа Пи: 3,1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 …
Примечание:
Если вы введете радиус в сантиметрах, вы получите ответ в квадратных сантиметрах (см²), если в дюймах, получите ответ в квадратных дюймах (in²) и так далее …
Окружность часто ошибочно обозначается как окружность.
Пример расчета площади круга
Заявление об ограничении ответственности
Несмотря на то, что прилагаются все усилия для обеспечения точности информации, представленной на этом веб-сайте, ни этот веб-сайт, ни его авторы не несут ответственности за какие-либо ошибки или упущения или за результаты, полученные в результате использования этой информации. Вся информация на этом сайте предоставляется «как есть», без каких-либо гарантий полноты, точности, своевременности или результатов, полученных в результате использования этой информации.
Вся информация на этом сайте предоставляется «как есть», без каких-либо гарантий полноты, точности, своевременности или результатов, полученных в результате использования этой информации.
Рабочий лист упражнений на «Площадь круга по диаметру»
Вот три случайно выбранных вопроса из более крупного упражнения, которые можно отредактировать , и отправить по электронной почте студентам или напечатать для создания рабочих листов упражнений.от
по
Определение площади круга по диаметру (Урок)
Площадь круга определяется по формуле:
В этой формуле d — диаметр окружности.На изображении ниже показано, что мы подразумеваем под диаметром:
Интерактивный виджет
Используйте этот интерактивный виджет , чтобы нарисовать круг, а затем вычислить его площадь по диаметру. Начните с нажатия на заштрихованную область.
Ой, сломано!
Переверните телефон на бок, чтобы использовать этот виджет.
Как найти площадь круга по диаметру
Найти площадь круга по диаметру легко.
Какова площадь круга диаметром 10 см, как показано ниже?
Пошаговая инструкция:
Начните с формулы:
Не забывайте: π — это пи (≈ 3,14) и d 2 = d × d (d в квадрате) и / означает ÷.
Подставьте диаметр в формулу. В нашем примере d = 10.
Площадь = π × 10 2 ⁄4
Площадь = π × 10 × 10 ÷ 4
Площадь = π × 100 ÷ 4
Площадь = π × 25
Площадь = 3.14 × 25
Площадь = 78,5 см 2
Ответ:
Площадь круга диаметром 10 см составляет 78,5 см. 2 .
Слайдер
Ползунок ниже показывает еще один реальный пример того, как найти площадь круга по диаметру.
Как найти площадь круга по радиусу
Площадь круга можно определить по радиусу, а не по диаметру.
Площадь круга с учетом радиуса определяется по формуле:
В формуле r — радиус окружности. На изображении ниже показано, что мы подразумеваем под радиусом:
Подробнее о том, как найти площадь круга с помощью радиуса
Помогите нам улучшить математику Монстр- Вы не согласны с чем-то на этой странице?
- Заметили опечатку?
См. Также
Что такое круг? Что такое пи? Какой диаметр? Найдите площадь круга, используя радиус Как найти радиус по диаметру Показатель степени, где основание — дробь Что такое числитель? Что такое знаменатель? Калькулятор площади круга— вычисление радиуса, диаметра и окружности
Ниже представлен калькулятор площади круга , который вычислит радиус, диаметр и длину окружности линейных размеров, если вы знаете площадь круга.
Знаете ли вы другое измерение? Вместо этого попробуйте один из других калькуляторов размеров круга:
Калькулятор радиуса
Что такое площадь круга?
Область круга — это пространство, заключенное в его границах, как определено выше.
Если вы нарисовали идеальный круг с помощью маркера, затем поменяли цвета и полностью залили круг — цвет, на который вы переключились, будет областью круга.
Размеры круга
Площадь, как определено выше, — это все пространство, содержащееся внутри круга.Вычислить площадь (или наоборот) из любого из линейных размеров, приведенных ниже, просто, но вот как найти радиус из площади круга:
r = \ sqrt {(a / \ pi)}
Размеры круга : O — начало координат, R — радиус, D — диаметр, C — длина окружности (Викимедиа)Чаще всего используются три длины:
- Радиус — расстояние от центра или начала круга до края
- диаметр — расстояние от края до края круга, проходящего через его начало или центр.
 2
2Использование калькулятора площади круга
Вы можете ввести площадь, а затем вычислить длину, диаметр и окружность в мил, дюймах, футах, ярдах, милях, миллиметрах, сантиметрах, метрах и километрах .
Мы разрешим ввод площади в тоннах единиц. Выберите: квадратных милов, квадратных дюймов, квадратных футов, квадратных ярдов, квадратных миль, акров, гектаров, квадратных миллиметров, квадратных сантиметров, квадратных метров и квадратных километров.
Чтобы запустить вычисления, нажмите кнопку «Вычислить размеры круга», когда вы ввели известный радиус.
Нравится? Посетите другие наши калькуляторы и инструменты.
Площадь 10-сантиметрового круга
Какова площадь круга с ДИАМЕТРОМ 10 см (радиус 5 см)?
Площадь круга диаметром 10 см



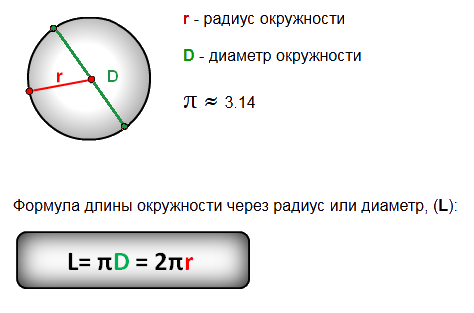


 Дюйм, метр, мм.
Дюйм, метр, мм.  Спасибо!
Спасибо!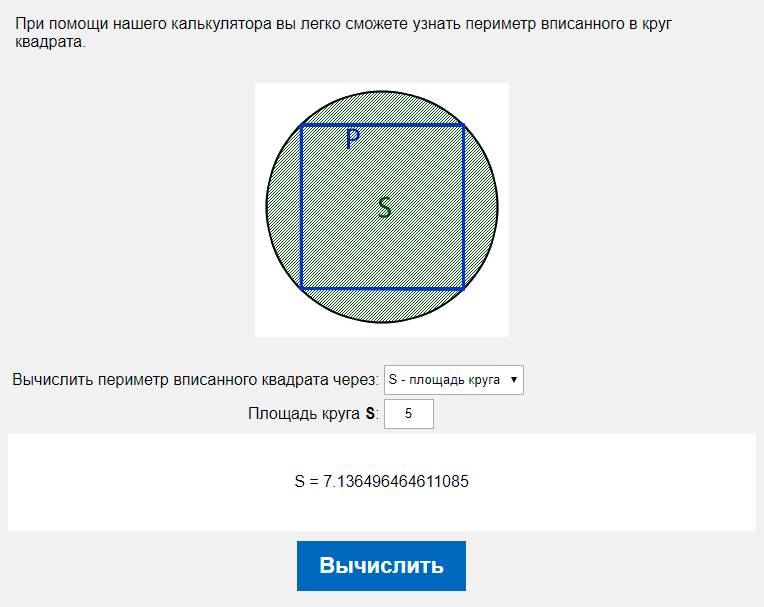 7
7  2
2 0078540
0078540 1 см
1 см 1138
1138 01327
01327 6 см
6 см π = 3,14159265359 ……..
π = 3,14159265359 ……..