Как найти площадь правильного шестиугольника вписанного в окружность: формула
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Нахождение площади правильного шестиугольника: формула и примеры
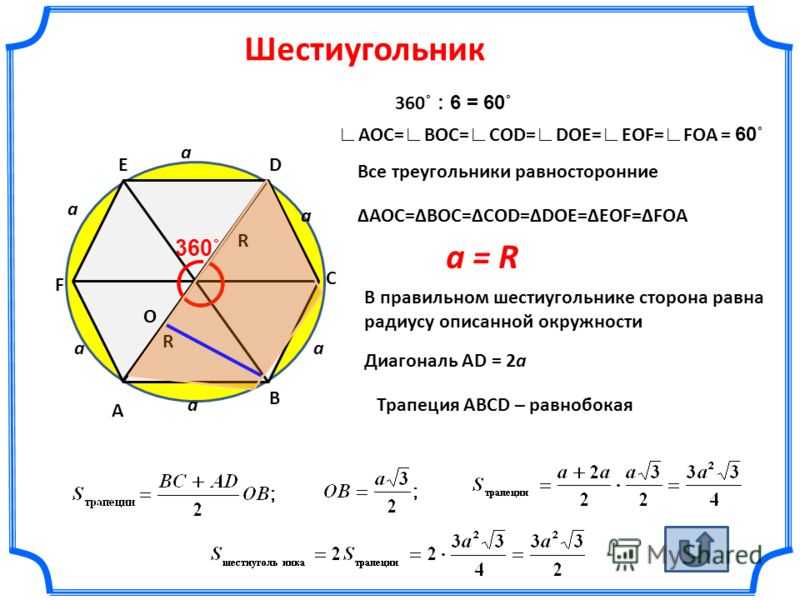
Правильный шестиугольник – это геометрическая фигура; правильный многоугольник с 6 равными углами и сторонами.
- Общая формула вычисления площади
- Площадь правильного шестиугольника, вписанного в окружность
- Примеры задач
Общая формула вычисления площади
Площадь (S) правильного шестиугольника вычисляется по формуле ниже, где a – длина его стороны:
Формула получена следующим образом:
Правильный шестиугольник состоит из шести равных равносторонних треугольников. Площадь каждого рассчитывается так:
Следовательно, площадь правильного шестиугольника равна:
Площадь правильного шестиугольника, вписанного в окружность
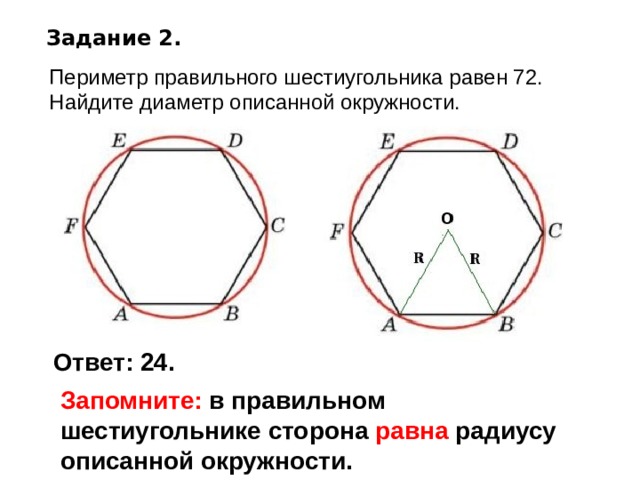
Сторона правильного шестиугольника равняется радиусу окружности, описанной вокруг него (a=r).
Это значит, что формула площади может быть представлена в таком виде (а заменяем на r):
Примеры задач
Задание 1
Сторона правильного шестиугольника равна 8 см. Найдите его площадь.
Решение:
Используем первую формулу, в которой задействована длина стороны:
Задание 2
Вычислите площадь правильного шестиугольника, ели радиус описанной вокруг нее окружности равен 15 см.
Решение:
Воспользуемся второй формулой (через радиус окружности):
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Треугольник вписанный в окружность — формулы, свойства, примеры
Главная » геометрия
Обновлено
Содержание
- Определение
- Формулы
- Радиус вписанной окружности в треугольник
- Радиус описанной окружности около треугольника
- Площадь треугольника
- Периметр треугольника
- Сторона треугольника
- Средняя линия треугольника
- Высота треугольника
- Свойства
- Доказательство
Определение
Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.
На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.
ВD = FC = AE — не диаметры описанной около треугольника окружности.
O — центр вписанной в треугольник окружности.
Формулы
Радиус вписанной окружности в треугольник
r — радиус вписанной окружности.
- Радиус вписанной окружности в треугольник,
если известна площадь и все стороны:\[ r = \frac{S}{(a+b+c)/2} \]
- Радиус вписанной окружности в треугольник,
если известны площадь и периметр:\[ r = \frac{S}{\frac{1}{2}P} \]
- Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:\[ r = \sqrt{\frac{(p-a)(p-b)(p-c)}{p}} \]
Радиус описанной окружности около треугольника
R — радиус описанной окружности.
- Радиус описанной окружности около треугольника,
если известна одна из сторон и синус противолежащего стороне угла:\[ R = \frac{AC}{2 \sin \angle B} \]
- Радиус описанной окружности около треугольника,
\[ R = \frac{abc}{4S} \]
- Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:\[ R = \frac{abc}{4\sqrt{p(p-a)(p-b)(p-c)}} \]
Площадь треугольника
S — площадь треугольника.
2}{2\cdot (sin(α)⋅sin(β)) : sin(180 — (α + β))} \]
Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:\[ S = \frac{1}{2}ab \cdot \sin \angle C \] Периметр треугольника
P — периметр треугольника.
- Периметр треугольника вписанного в окружность,
если известны все стороны:\[ P = a + b + c \]
- Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:\[ P = \frac{2S}{r} \]
- Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:\[ P = \sqrt{ b2 + с2 — 2 * b * с * cosα} + (b + с) \]
Сторона треугольника
a — сторона треугольника.
Высота треугольника
h — высота треугольника.
- Высота треугольника вписанного в окружность,
если известна площадь и основание:\[ h = \frac{2S}{a} \]
- Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:\[ h = b \cdot \sin \alpha \] - Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:\[ h = \frac{bc}{2R} \]
Свойства
- Центр вписанной в треугольник окружности
находится на пересечении биссектрис.- В треугольник, вписанный в окружность,
можно вписать окружность, причем только одну.- Для треугольника, вписанного в окружность,
справедлива Теорема Синусов, Теорема Косинусов
и Теорема Пифагора.- Центр описанной около треугольника окружности
находится на пересечении серединных перпендикуляров. - Все вершины треугольника, вписанного
в окружность, лежат на окружности.- Сумма всех углов треугольника — 180 градусов.
- Площадь треугольника вокруг которого описана окружность, и
треугольника, в который вписана окружность, можно найти по
формуле Герона.Доказательство
Около любого треугольника, можно
описать окружность притом только одну.Дано: окружность и треугольник,
которые изображены на рисунке 2.Доказать: окружность описана
около треугольника.Доказательство:
- Проведем серединные
перпендикуляры — HO, FO, EO.- O — точка пересечения серединных
перпендикуляров равноудалена от
всех вершин треугольника.- Центр окружности — точка пересечения
серединных перпендикуляров — около
треугольника описана окружность — O,
от центра окружности к вершинам можно
провести равные отрезки — радиусы — OB, OA, OC.
Следовательно: окружность описана около треугольника,
что и требовалось доказать.Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
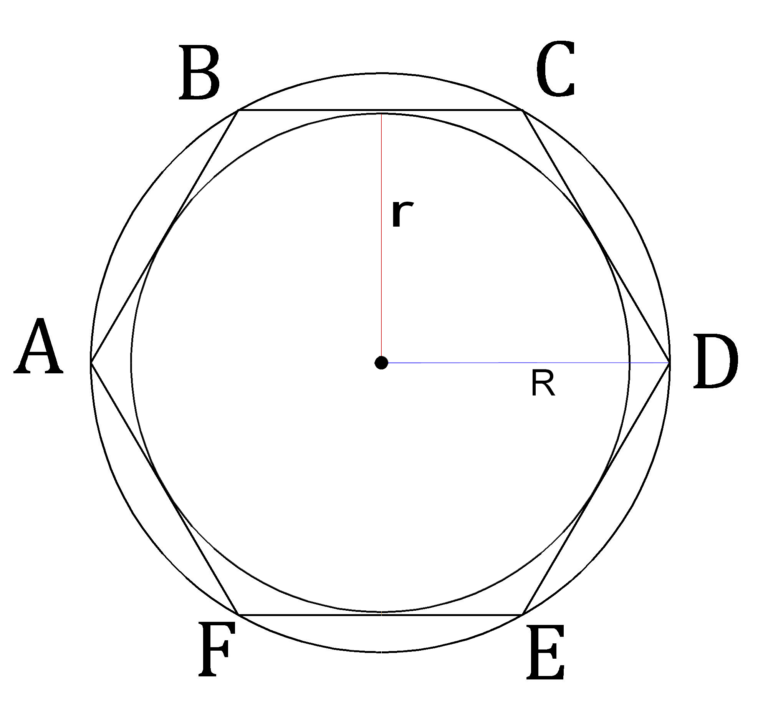
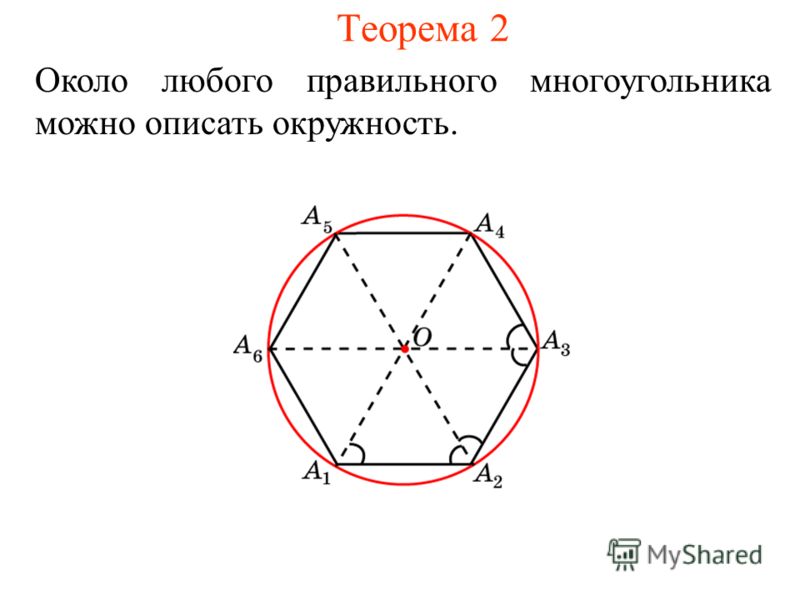
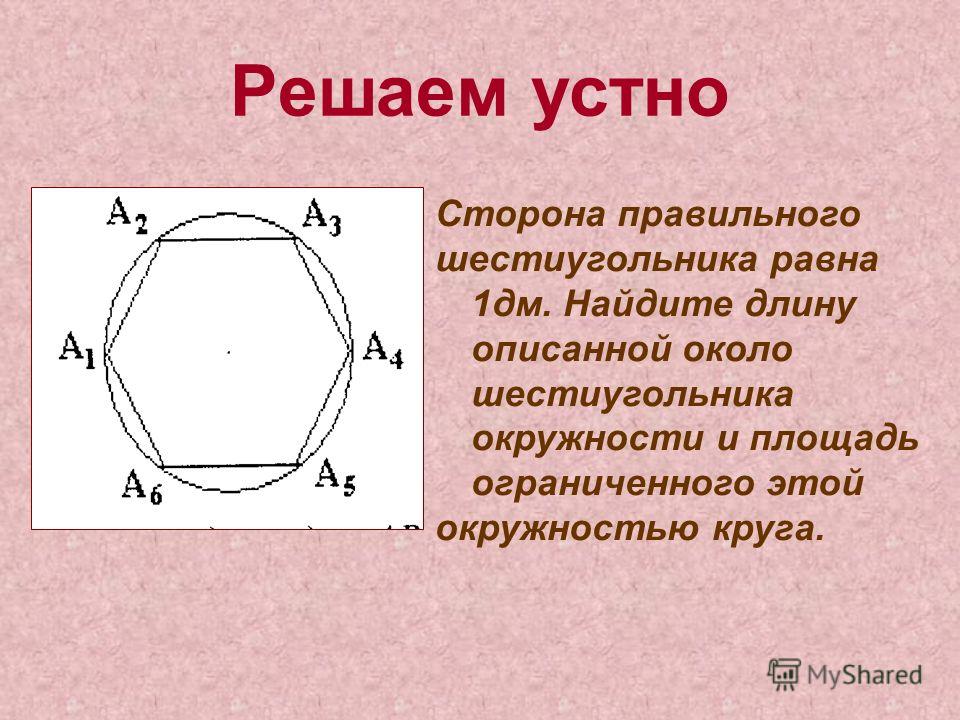
равноудалена от всех вершин треугольника.Если правильный шестиугольник вписан в круг радиуса 10 класса по математике CBSE
Ответ
Подтверждено
254.7k+ просмотров
— Подсказка: данный правильный шестиугольник вписан в круг радиуса r. Попробуйте доказать, что шестиугольник состоит из шести равносторонних треугольников, соединив противоположные стороны шестиугольника.
После этого вы заметите, что стороны каждого равностороннего треугольника равны r, равным радиусу окружности. Теперь вы можете легко найти периметр шестиугольника. 9\circ $
\[\следовательно \] Треугольники являются равносторонними треугольниками.
Это дает, все стороны равны.
Вы можете наблюдать это на рисунке ниже.
\[\следовательно \] Все стороны каждого треугольника равны r.
Следовательно,
Периметр правильного шестиугольника $=6\times\ стороны\ равностороннего\ треугольника$
$\begin{align}
& =6\times r \\
& =6r \\
\end{align}$
Значит, вариант Б правильный.Примечание: Этот вопрос можно легко решить следующим образом — (Вы можете ответить на этот вопрос, наблюдая и размышляя таким образом).
Правильный шестиугольник — это многоугольник, у которого все стороны равны, и он состоит из шести равносторонних треугольников.
Теперь, если правильный шестиугольник вписан в окружность, то его сторона равна радиусу окружности.
Следовательно, периметр правильного шестиугольника = 6r.Недавно обновленные страницы.0003
Имеет ли нихром высокое сопротивление 12 класса по физике CBSE
Если альфа и бета альфа и гамма альфа и дельта относятся к 10 классу математики JEE_Main
Значение p, для которого оба корня уравнения 10 класса математики JEE_Main
Электроотрицательность Паулингса значения для элементов: химия 11 класса CBSE
Для частицы, совершающей простое гармоническое движение, физика 11 класса CBSE
Дальнозоркий человек, потерявший очки, читает физику 10 класса JEE_Main
Имеет ли нихром высокое сопротивление 12 классу физики CBSE
Если альфа и бета альфа и гамма альфа и дельта относятся к 10 классу математики JEE_Main
Значение p для которого оба корня уравнения 10 класса математики JEE_Main
0
Сомнения в тренде
Как построить правильный шестиугольник, вписанный в окружность, с помощью циркуля и линейки или линейки
На этой странице показано, как построить (нарисовать) правильный шестиугольник вписанный в круг с помощью циркуля и линейки или линейки.
Печатные пошаговые инструкции
Вышеупомянутая анимация доступна как распечатанная пошаговая инструкция, которую можно использовать для изготовления раздаточных материалов или когда компьютер недоступен.
Объяснение метода
Как видно из определения шестиугольника, каждая сторона правильного шестиугольника равна расстоянию от центра до любой вершины. Эта конструкция просто устанавливает ширину компаса на этот радиус, а затем уменьшает эту длину по кругу. чтобы создать шесть вершин шестиугольника.
Доказательство
Изображение ниже является окончательным рисунком из приведенной выше анимации, но с помеченными вершинами.
Аргумент Причина 1 A, B, C, D, E, F лежат на окружности O По конструкции. 2 АВ = ВС = CD = DE = EF Все они были нарисованы с одинаковой шириной компаса. Из (2) видно, что пять сторон равны по длине, но последняя сторона FA циркулем не проведена. Это было «лишнее» пространство, когда мы обошли круг и остановились на F. Итак, мы должны доказать, что оно конгруэнтно остальным пяти сторонам. 3 OAB представляет собой равносторонний треугольник AB было нарисовано с шириной компаса, установленной на OA,
и OA = OB (оба радиуса круга).4 м∠AOB = 60° Все внутренние углы равностороннего треугольника равны 60°. 5 м∠AOF = 60° Как и в (4), m∠BOC, m∠COD, m∠DOE, m∠EOF равны &60deg; Поскольку сумма всех центральных углов равна 360°,
м∠AOF = 360 — 5(60)6 Треугольники BOA и AOF конгруэнтны SAS См. Тест на конгруэнтность, сторона-угол-сторона. 7 АФ = АВ CPCTC — Соответствующие части конгруэнтных треугольников конгруэнтны Итак, теперь у нас есть все части, чтобы доказать конструкцию .8 ABCDEF — правильный шестиугольник, вписанный в данную окружность
- Из (1) все вершины лежат на окружности
- Из (20), (7), все стороны имеют одинаковую длину
- Многоугольник имеет шесть сторон.
— Q.E.D
Попробуйте сами
Нажмите здесь, чтобы распечатать рабочий лист, содержащий две задачи, которые можно попробовать.
Другие страницы по конструкциям на этом сайте
- Список рабочих листов по конструкциям для печати
Линии
- Введение в конструкции
- Скопируйте сегмент линии
- Сумма n отрезков
- Разница двух отрезков
- Биссектриса отрезка прямой
- Перпендикуляр в точке на линии
- Перпендикуляр от прямой через точку
- Перпендикулярно от конечной точки луча
- Разделить отрезок на n равных частей
- Параллельная линия через точку (угловая копия)
- Параллельная линия через точку (ромб)
- Параллельная линия через точку (перемещение)
Углы
- Разделение угла пополам
- Скопируйте угол
- Построить угол 30°
- Построить угол 45°
- Построить угол 60°
- Построить угол 90° (прямой угол)
- Сумма n углов
- Разность двух углов
- Дополнительный уголок
- Дополнительный уголок
- Построение углов 75° 105° 120° 135° 150° и более
Треугольники
- Копирование треугольника
- Равнобедренный треугольник с основанием и стороной
- Равнобедренный треугольник с основанием и высотой
- Равнобедренный треугольник с катетом и углом при вершине
- Равносторонний треугольник
- Треугольник 30-60-90 по гипотенузе
- Треугольник по трем сторонам (sss)
- Треугольник по одной стороне и прилежащим углам (asa)
- Треугольник с двумя углами и не включенной стороной (aas)
- Треугольник по двум сторонам и углу между ними (sas)
- Медианы треугольника
- Средняя часть треугольника
- Высота треугольника
- Высота треугольника (вне корпуса)
Прямоугольные треугольники
- Прямоугольный треугольник с одним катетом и гипотенузой (HL)
- Прямоугольный треугольник с учетом обеих сторон (LL)
- Прямоугольный треугольник по гипотенузе и одному углу (HA)
- Прямоугольный треугольник по одному катету и одному углу (LA)
Центры треугольников
- Центры треугольников
- Центр окружности треугольника
- Ортоцентр треугольника
- Центр тяжести треугольника
Окружности, дуги и эллипсы
- Нахождение центра окружности
- Круг с 3 очками
- Касательная в точке окружности
- Касательные через внешнюю точку
- Касательные к двум окружностям (внешние)
- Касательные к двум окружностям (внутренние)
- Вписанная окружность треугольника
- Точки фокусировки данного эллипса
- Окружность треугольника
Многоугольники
- Квадрат с одной стороной
- Квадрат, вписанный в круг
- Шестигранник с одной стороной
- Шестиугольник, вписанный в данную окружность
- Пятиугольник вписан в заданный круг
Неевклидовы конструкции
- Построение эллипса с помощью нити и булавок
- Найдите центр круга с любым прямоугольным объектом
(C) 2011 Copyright Math Open Reference.
2}{2\cdot (sin(α)⋅sin(β)) : sin(180 — (α + β))} \]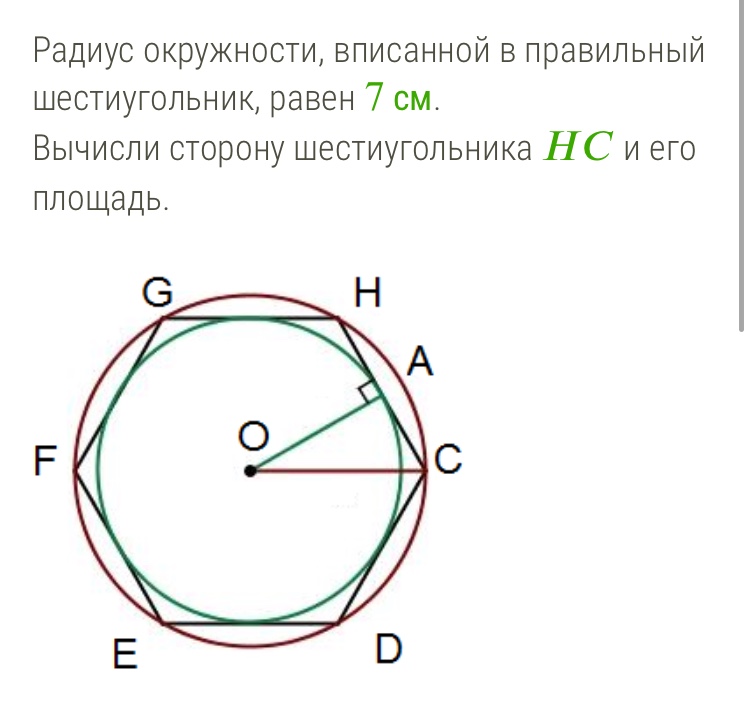
2-2bc \cdot \cos \alpha}}{2} \]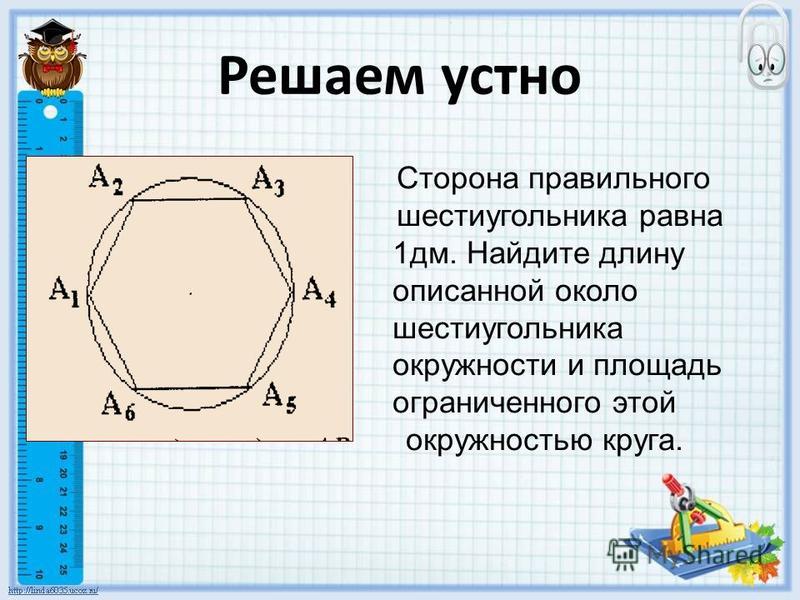
Это самый большой шестиугольник, который поместится в круг, с каждым
вершина
касаясь круга. В правильном шестиугольнике длина стороны равна расстоянию от центра до вершины, поэтому мы используем этот факт, чтобы установить циркуль на правильную длину стороны, а затем шагаем по кругу, отмечая вершины.
Когда вы попадете на страницу, используйте команду печати браузера, чтобы распечатать столько, сколько хотите. Распечатанный результат не защищен авторским правом.