Мощность электрического тока — Основы электроники
Обычно электрический ток сравнивают с течением жидкости по трубке, а напряжение или разность потенциалов — с разностью уровней жидкости.
В этом случае поток воды, падающий сверху вниз, несет с собой определенное количество энергии. В условиях свободного падения эта энергия растрачивается бесполезно для человека. Если же направить падающий поток воды на лопасти турбины, то последняя начнет вращаться и сможет производить полезную работу.
Работа, производимая потоком воды в течение определенного промежутка времени, например, в течение одной секунды, будет тем больше, чем с большей высоты падает поток и чем больше масса падающей воды.
Точно так же и электрический ток, протекая по цепи от высшего потенциала к низшему, совершает работу. В каждую данную секунду времени будет совершаться тем больше работы, чем больше разность потенциалов и чем большее количество электричества ежесекундно проходит через поперечное сечение цепи.
Мощность электрического тока это количество работы, совершаемой за одну секунду времени, или скорость совершения работы.
Количество электричества, проходящего через поперечное сечение цепи в течение одной секунды, есть не что иное, как сила тока в цепи. Следовательно, мощность электрического тока будет прямо пропорциональна разности потенциалов (напряжению) и силе тока в цепи.
Для измерения мощности электрического тока принята единица, называемая ватт (Вт).
Мощностью в 1 Вт обладает ток силой в 1 А при разности потенциалов, равной 1 В.
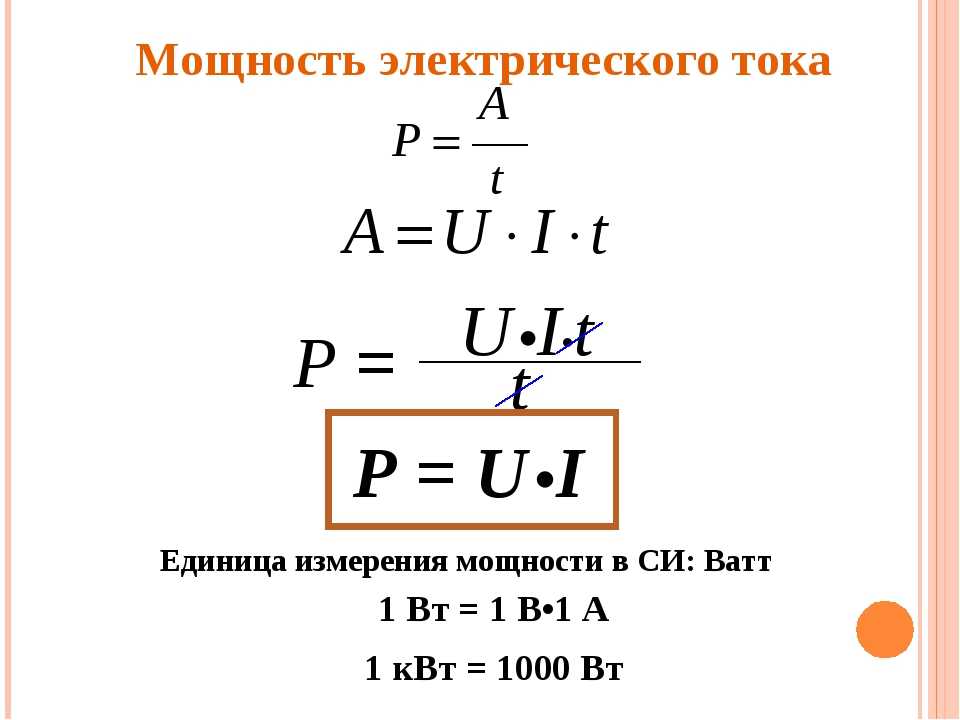
Для вычисления мощности постоянного тока в ваттах нужно силу тока в амперах умножить на напряжение в вольтах.
Если обозначить мощность электрического тока буквой P, то приведенное выше правило можно записать в виде формулы
P = I*U. (1)
Воспользуемся этой формулой для решения числового примера. Требуется определить, какая мощность электрического тока необходима для накала нити радиолампы, если напряжение накала равно 4 в, а ток накала 75 мА
Определим мощность электрического тока, поглощаемую нитью лампы:
Р= 0,075 А*4 В = 0,3 Вт.
Мощность электрического тока можно вычислить и другим путем. Предположим, что нам известны сила тока в цепи и сопротивление цепи, а напряжение неизвестно.
В этом случае мы воспользуемся знакомым нам соотношением из закона Ома:
U=IR
и подставим правую часть этого равенства (IR) в формулу (1) вместо напряжения U.
Тогда формула (1) примет вид:
P = I*U =I*IR
или
Р = I2*R. (2)
Например, требуется узнать, какая мощность теряется в реостате сопротивлением в 5 Ом, если через него проходит ток, силой 0,5 А. Пользуясь формулой (2), найдем:
P= I2*R = (0,5)2*5 =0,25*5 = 1,25 Вт.
Наконец, мощность электрического тока может быть вычислена и в том случае, когда известны напряжение и сопротивление, а сила тока неизвестна. Для этого вместо силы тока I в формулу (1) подставляется известное из закона Ома отношение U/R и тогда формула (1) приобретает следующий вид:
Р = I*U=U2/R (3)
Например, при 2,5 В падения напряжения на реостате сопротивлением в 5 Ом поглощаемая реостатом мощность будет равна:
Р = U2/R=(2,5)2/5=1,25 Вт
Таким образом, для вычисления мощности требуется знать любые две из величин, входящих в формулу закона Ома.
Мощность электрического тока равна работе электрического тока, производимой в течение одной секунды.
P = A/t
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Мощность тока?. Формула мощности ? электрического тока. Как найти мощность?
Автор Даниил Леонидович На чтение 6 мин. Просмотров 40.9k. Опубликовано Обновлено
Благосостояние и комфорт современного общества зависит всецело от высокотехнологичных гаджетов. Люди уже не представляют жизни без «умных» устройств. Микроэлектроника поглотила наш быт дома и на работе. Функционирует оборудование исключительно от электричества. Такие устройства обладают рядом преимуществ, как и недостатков — чувствительность к перепадам эл. напряжения.
напряжения.
Если в офисе компании эту проблему способен устранить штат квалифицированных сотрудников, то дома часто приходится рассчитывать исключительно на собственные силы. Покупая новое оборудование в дом, необходимо учитывать технические характеристики устройства. Производитель указывает такую информацию для покупателей на шильдике, расположенном на задней стенке гаджета.
Формула мощности представляет собой произведение силы тока на напряжение. Если знать этот параметр, то для пользователя складывается четкое представление, сколько электричество девайс будет потреблять и не вызовет ли проблем с электроснабжением.
Содержание
- Что такое мощность в электричестве: просто о сложном
- Как рассчитать электрическую мощность в быту
- Как измерить электрическую мощность дома
- Почему реактивное сопротивление схемы влияет на мощность переменного тока
- Формулы расчета мощности для однофазной и трехфазной схемы питания
- Как работает схема трехфазного электроснабжения
- Как узнать ток, зная мощность и напряжение
- Как узнать напряжение, зная силу тока
- Как рассчитать мощность, зная силу тока и напряжение
- Интересная инфа по теме
- Заключение
Что такое мощность в электричестве: просто о сложном
Механическая мощность как физическая величина равна отношению выполненной работы к некоторому промежутку времени. Поскольку понятие работы определяется количеством затраченной энергии, то и мощность допустимо представить как скорость преобразования энергий.
Поскольку понятие работы определяется количеством затраченной энергии, то и мощность допустимо представить как скорость преобразования энергий.
Разобрав составляющие механической мощности, рассмотрим из чего складывается электрическая. Напряжение — выполняемая работа по перемещению одного кулона электрического заряда, а ток — количество проходящих кулонов за одну секунду. Произведение напряжения на ток показывает полный объем работы, выполненной за одну секунду.
Проанализировав полученную формулу, можно заключить, что силовой показатель зависит одинаково от тока и напряжения. То есть, одно и тоже значение возможно получить при низком напряжении и большом тока, или при высоком напряжении и низком токе.
Пользуясь зависимостью мощности от напряжения и силы тока, инженеры научились передавать электричество на большие расстояния путем преобразования энергии на понижающих и повышающих трансформаторных подстанциях.
Наука подразделяет электрическую мощность на:
- активную.
 Подразумевает преобразование мощности в тепловую, механическую и другие виды энергии. Показатель выражают в Ваттах и вычисляют по формуле U*I;
Подразумевает преобразование мощности в тепловую, механическую и другие виды энергии. Показатель выражают в Ваттах и вычисляют по формуле U*I; - реактивную. Эта величина характеризует электрические нагрузки, создаваемые в устройствах колебаниями энергии электромагнитного поля. Показатель выражается как вольт-ампер реактивный и представляет собой произведение напряжения на силу тука и угол сдвига.
Для простоты понимания смысла активной и реактивной мощности, обратимся к нагревательному оборудованию, где электрическая энергия преобразуется в тепловую.
Как рассчитать электрическую мощность в быту
Теоретическая электротехника рассматривает показатели как мгновенные величины, которые зафиксированы в некоторый временной отрезок. Если мгновенная мощность постоянной сети остается неизменной в любой точке цепи и во всех интервалах времени, то для переменной этот показатель будет всегда неодинаковым.
Отсюда получим формулы для расчета мощности (P):
- U*I;
- I2*R;
- U*I*cos(фи).

В интернете сейчас есть онлайн-калькуляторы, которые сами посчитают и выдадут результат. Пользователю нужно лишь подставить значения характеристик, которые находятся на шильдике устройства.
Как измерить электрическую мощность дома
Знать силовые характеристики бытового оборудования необходимо всегда. Это требуется для расчета сечения проводки, учета расхода электроэнергии или электрофикации дома. До начала монтажных работ такую информацию можно получить только путем сложения показателей мощности каждого отдельного устройства, добавив 10% запаса.
Определить потребляемую нагрузку дома поможет счетчик. Прибор показывает сколько киловатт было потрачено за один час работы оборудования. И для того чтобы убедиться в правильности показаний, владелец квартиры может проверить точность устройства с помощью электронных средств измерения. Сюда относится амперметр, вольтметр или мультиметр.
Также существуют ваттметры и варметры, которые показывают результаты измерений в ваттах.
Во время снятия показания включенной оставить только активную нагрузку как лампочки и нагреватели. Далее померить токовое напряжение. В конце сверить показания счетчика с полученным результатом вычислений.
Почему реактивное сопротивление схемы влияет на мощность переменного тока
Потеря энергии в переменной цепи обусловлена наличием реактивного сопротивления, которое подразделяют на индуктивное и емкостное. В процессе работы оборудования часть энергии передается формируемым электрическим или магнитным полям.
Это приводит к уменьшению полезной работы, потере электроэнергии и превышению силовых нагрузок устройств.
Формулы расчета мощности для однофазной и трехфазной схемы питания
Выше уже была представлена формула для одной фазы: P=U*I*cos(фи).
Отсюда следует, что в трехфазной сети показатель равен тройной мощности однофазной, соединенной в треугольник: P=3*U*I*cos(фи). На практике же инженеры пользуются формулой P=1,73*U*I*cos(фи).
Как работает схема трехфазного электроснабжения
Принцип работы трехфазной схемы электроснабжения заключается в одновременном задействовании четырех питающих кабелей, один из которых нулевой. Ток одинаковой частоты вырабатывается одним генератором и сдвинут по отношению друг к другу по времени на фазовый угол равный 120 градусам.
Как узнать ток, зная мощность и напряжение
Для вычисления тока электросети по мощности и напряжению используют формулы:
- I=P/U – постоянный ток;
- I=P/(U*cos(фи)) — однофазная сеть;
- I=P/(1,73*U*cos(фи)) — трехфазная сеть.
Для простоты расчетов значение фи принимают равной 0,95.
Как узнать напряжение, зная силу тока
Для расчета напряжения используют формулы:
U=P/I – постоянный ток;
U=P/(I*cos(фи)) — однофазная сеть;
U=P/(1,73*I*cos(фи)) — трехфазная сеть.
Из выражения видно, что напряжение прямо пропорционально напряжению и обратно пропорционально силе тока.
Как рассчитать мощность, зная силу тока и напряжение
Силовую характеристику электроустановок рассчитывают по формуле:
P=U*I — постоянный ток;
P=U*I*cos(фи) – переменный ток однофазной сети.
P=1,73*U*I*cos(фи) — трехфазная сеть.
В статье приведены упрощенные формулы расчета активной мощности электросети, которые дают приблизительные результаты.
Для получения точных результатов, необходимо учитывать также реактивное и обычное сопротивление, а также потери.
Интересная инфа по теме
Трехфазную схему электроснабжения используют в производстве. Суммарный вольтаж такой сети равен 380 В. Также такую проводку устанавливают на многоэтажные дома, а затем раздают по квартирам. Но есть один нюанс, который влияет на конечное напряжение в сети — соединение жилы под напряжение в результате дает 220 В. Трехфазная в отличие от однофазной не дает перекосы при подключении силового оборудования, так как нагрузка распределяется в щитке.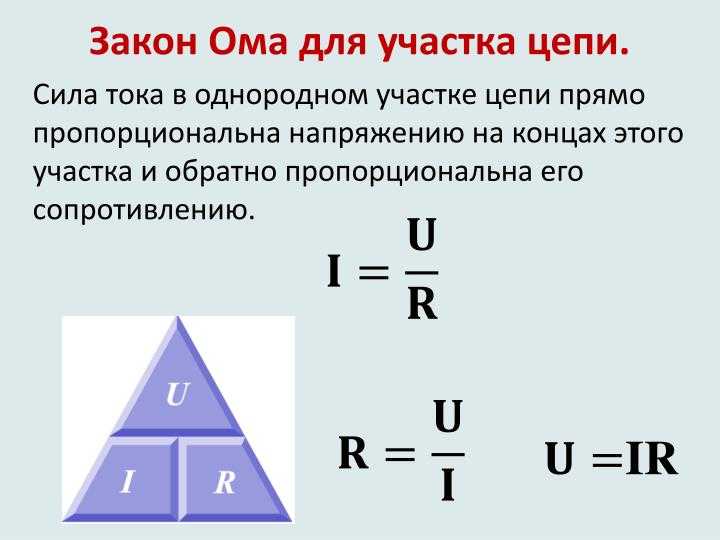 Но для подведения трехфазной сети к частному дому требуется специальное разрешение, поэтому широко распространена схема с двумя жилами, одна их которых нулевая.
Но для подведения трехфазной сети к частному дому требуется специальное разрешение, поэтому широко распространена схема с двумя жилами, одна их которых нулевая.
Заключение
Мощность электрического тока — один из важных параметров, который обязан знать каждый человек. Такая необходимость обусловлена безопасностью электросети (лимит на одновременное подключение нескольких приборов). Во время работы оборудования происходит нагрев не только внутренней схемы, но и проводки. Зная предельные возможности сети, всегда можно избежать неприятных ситуаций, связанных с ее перегревом и возможным коротким замыканием.
Сопротивление току напряжения и электрическая мощность Общие основные электрические формулы Математические расчеты Формула калькулятора для расчета мощности Уравнение работы энергии Закон мощности Понимание ватт Общая электрическая круговая диаграмма Расчет электричества ЭДС напряжение Формула мощности уравнение два разных уравнения для расчета мощности Общий закон Ома аудио физика электричество электроника формула колесо формулы амперы ватты вольты омы уравнение косинуса аудиотехника круговая диаграмма заряд физика мощность звукозапись расчет электротехника формула мощность математика пи физика отношение отношение
Напряжение, ток, сопротивление и электрическая мощность, общие основные электрические формулы, математические расчеты, формула калькулятора для расчета мощности, энергия, работа, уравнение, мощность, закон, ватты, понимание, общая электрическая круговая диаграмма, расчет электричества, электрическая ЭДС, напряжение, формула мощности, уравнение, два разных уравнения для расчета мощности, общий закон Ома, аудиофизика, электричество, электроника.
| Немецкая версия |
Electric Current , Electric Power , Electrical Voltage
Electricity and Electric Charge
The most common general formulas used in electrical engineering
● Основные формулы and Calculations ●
Relationship of the physical and electrical quantities (parameters)
Electric voltage V , amperage I , resistivity R ,
Вольт В , Ампер А,
8 сопротивление
Импеданс Ом ω и WATT W. Номинальный импеданс Z = 4, 8, и 16 Ом (Loudspeakers) часто используются в Aspakers). Р . Номинальный импеданс Z = 4, 8, и 16 Ом (Loudspeakers) часто используются в Aspakers). Р . Уравнение закона Ома (формула): В = I × R и уравнение степенного закона (формула): P = мощность, I или J = латиница: influare, международный ампер или интенсивность и R = сопротивление. В = напряжение, разность электрических потенциалов Δ В или E = электродвижущая сила (ЭДС = напряжение). |
| Введите два любых известных значения и нажмите «Рассчитать», чтобы решить для двух других. Пожалуйста, введите только два значения. |
Используемый браузер, к сожалению, не поддерживает Javascript.  |
| В происходит от «напряжение», а E от «электродвижущая сила (ЭДС)». E означает также энергия , поэтому мы выбираем V . Энергия = напряжение × заряд. Е = В × Q . Некоторым лучше придерживаться |
| 12 самых важных формул: Напряжение V = I × R = P / I = √ ( P × R ) в Volts V Current I 9 = ). = P / В = √( P / R ) в амперах A Сопротивление R = V / I = P / I 2 = V 2 / P в 2 / P в OHM × I = R × I 2 = В |
 также: Колесо формулы акустики (аудио)
также: Колесо формулы акустики (аудио) | The Big Power Formulas Расчет электрической и механической мощности (сила) |
|
| Андр-Мари Ампре был французским физиком и математиком. Его именем названа единица измерения электрического тока в системе СИ ампер . Алессандро Джузеппе Антонио Анастасио Вольта был итальянским физиком. В его честь была названа единица измерения электрического напряжения в системе СИ вольт . Георг Симон Ом — немецкий физик и математик. Его именем названа единица измерения электрического сопротивления в системе СИ, равная Ом Ом. Джеймс Уатт был шотландским изобретателем и инженером-механиком. Его именем названа единица измерения электрической мощности (мощности) в системе СИ ватт . |
| Мощность, как и все размеры энергии, в первую очередь является расчетным значением.  |
| Слово «усилитель мощности» используется неправильно, особенно в аудиотехнике. Напряжение и ток могут быть усилены. Странный термин «усилитель мощности» стал пониматься как усилитель, предназначенный для управления нагрузкой например громкоговоритель. Мы называем произведение усиления по току и усиления по напряжению «усилением мощности». |
Пожалуйста, введите два значения , будет рассчитано третье значение.
Пожалуйста, введите два значений, будет рассчитано третье значение.

С помощью магического треугольника можно легко вычислить все формулы. Вы прячетесь с
пальцем вычисляемое значение. Два других значения показывают, как производить вычисления.
Расчеты: закон Ома — магический треугольник Ома
Измерение входного и выходного импеданса
ПЕРЕМЕННЫЙ ТОК (AC) ~
В l = линейное напряжение (вольт), В p = фазное напряжение (вольт), I l = линейный ток (ампер), ампер)
Z = импеданс (Ом), P = мощность (ватт), φ = угол коэффициента мощности, VAR = вольт-ампер (реактивный)
| Ток (одна фаза): I = P / В p × cos φ | Current (3 phases): I = P / √3 V l ×cos φ or I = P / 3 V p ×cos φ |
| Мощность (одна фаза): P = В p × I p ×cos φ | Мощность (3 фазы): P = √3 В л × I l × cos φ или P = √3 V p × I p × cos 1 0 × cos 90 90 9060 60 |
 Для чисто резистивной цепи PF = 1 (идеально).
Для чисто резистивной цепи PF = 1 (идеально). Полная мощность S рассчитана по Пифагору, активная мощность P и реактивная мощность Q . S = √( P 2 + Q 2 )
| Формулы мощности постоянного тока Напряжение В дюйм (В) расчет по току I дюйм (А) и сопротивлению R дюйм (Ом): В (В) = I (А) R (Ом) Мощность P в (Вт) расчет от напряжения V в (V) и ток I в (A): P (W) = В (V) × I (A) 666 × I (A) 9066 = 60. . (a) 66 × . (V) / R (Ω) = I 2 (A) R (Ω) AC power formulas Напряжение В в вольтах (В) равно силе тока I в амперах (А), умноженной на импеданс Z в омах (Ом): В (В) = I (А) Z ((Ом) = (| 1 0 Z) | 0 | и ( θ I + θ Z ) Полная мощность S в вольт-амперах (ВА) равна напряжению В в вольтах (В), умноженному на ток I в амперах (А): S (ВА) = В (В) И (А) = (| В | × | I |) и ( θ В − θ I ) Реальная мощность P в ваттах (Вт) равна напряжению В в вольтах (В), умноженному на ток I в амперах (А), умноженному на коэффициент мощности (cos φ ): P (Вт) = В (В) × I (A) × 000 1 φ Реактивная мощность Ом в вольт-амперах реактивной (ВАР) равно напряжению В в вольтах (В) умноженному на ток I в амперах (А) умноженному на синус комплексного фазового угла мощности ( φ ): Q (ВАР) = В (В) × I (А) × sin φ Коэффициент мощности (FP) равен абсолютному значению косинуса комплексного фазового угла мощности ( φ ): ПФ = | cos φ | |
| Количество | Имя | Определение |
| частота f | герц (Гц) | 1/с |
| усилие F | ньютон (Н) | кг · м/с² |
| давление р | паскаль (Па) = Н/м² | кг/м · с² |
| энергия Е | рабочий джоуль (Дж) = Н · м | кг · м²/с² |
| мощность Р | ватт (Вт) = | Дж/скг · м²/с³ |
| электрический заряд Q | кулон (К) = A · с | А · с |
| напряжение В | вольт (В) = Вт/А | кг · м²/А · с³ |
| текущий I | ампер (А) = Q/s | А |
| емкость Кл | фарад (Ф) = C/V = A · с/В = с/Ом | A² · s 4 /кг · м² |
| индуктивность л | Генри (H) = Wb/A = V · с/A | кг · м²/А² · с² |
| сопротивление R | Ом (Ом) = В/А | кг · м²A² · с³ |
| проводимость Г | Сименс (С) = А/В | A² · с³/кг · м² |
| магнитный поток Φ | Вебер (Wb) = V · с | кг · м²/А · с² |
| плотность потока B | тесла (T) = Втб/м² = В · с/м² | кг/А · с² |
Поток электрического заряда Q обозначается как электрический ток I. Количество заряда в единицу времени Количество заряда в единицу времени это изменение электрического тока. Ток течет с постоянной величиной I. за время t , он переносит заряд Q = I × t . Для постоянной во времени мощности соотношение между зарядом и током: I = Q/t или Q = I×t. Благодаря этому соотношению основные единицы ампер и секунда кулон в Установлена международная система единиц. Кулоновскую единицу можно представить как 1 C = 1 A × s. Зарядка Q , (единица измерения в ампер-часах Ач), ток разряда I , (единица измерения в амперах А), время t , (единица измерения в часах ч). |
В акустике у нас есть » Акустический эквивалент закона Ома »
Соотношения акустических величин, связанных с плоскими прогрессивными звуковыми волнами
Преобразование многих единиц, таких как мощность и энергия
префиксы | длина | площадь | объем | вес | давление | температура | время | энергия | сила | плотность | скорость | ускорение | сила
[начало страницы]
| задняя часть | Поисковая система | дом |
Калькулятор электрической мощности
Автор Miłosz Panfil, PhD
Отзыв от Małgorzata Koperska, MD.
Этот Калькулятор электроэнергии поможет вам рассчитать мощность, потребляемую электрическими устройствами. Хотите знать, как рассчитать электрическую мощность? Вы задаетесь вопросом: что такое коэффициент мощности? Просто прочитайте текст ниже, чтобы узнать.
Как рассчитать электрическую мощность
Электрическая мощность, как и механическая, представляет собой количество работы, выполняемой в единицу времени. В электрических цепях работа совершается электрическим током. Мощность зависит от «количества рабочих, имеющихся в единицу времени» — тока I и энергии «одного рабочего» — напряжения V . В цепи постоянного тока мощность равна
P=IV,P = IV,P=IV,
, где
-
I [A]это текущий, -
В [В]— напряжение, -
P [Вт]— мощность.
В цепях переменного тока используется уравнение
P=I∗V∗PF,P = I * V * PF,P=I∗V∗PF,
, где новый символ PF означает коэффициент мощности .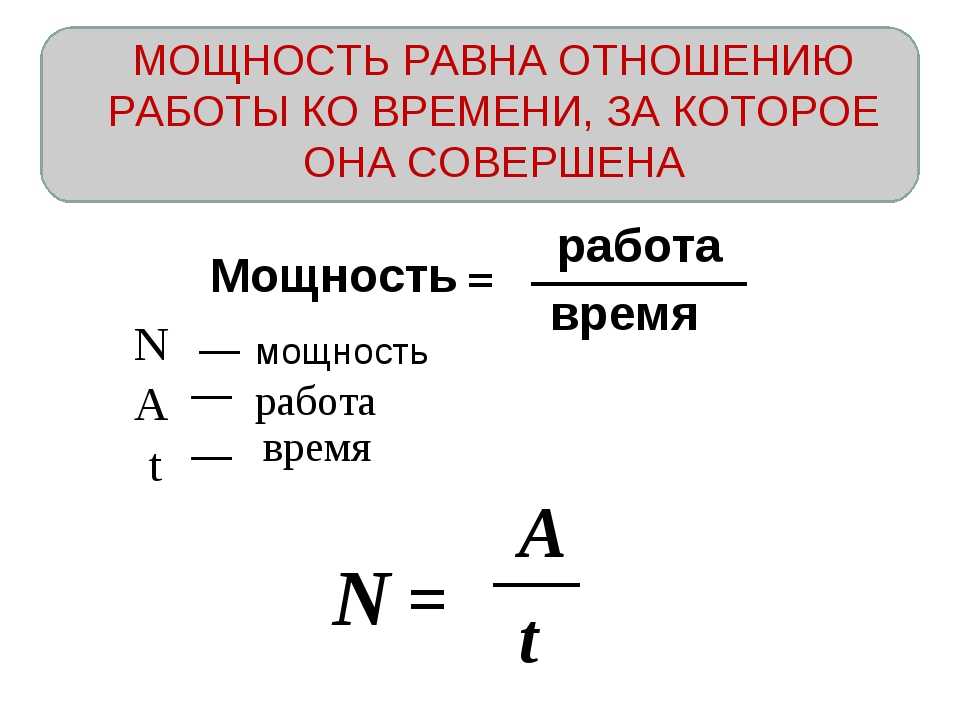 .
.
Что такое коэффициент мощности
В токах переменного тока ток и напряжение периодически изменяются во времени. Значения I или V соответствуют среднеквадратичному значению (RMS). RMS — это квадратный корень из среднего квадрата чисел; обратитесь к калькулятору среднего квадрата корня, чтобы узнать больше. Обычно упоминаемое напряжение электрических розеток ( 230 В в ЕС и Австралии, 110 В в США и Канаде, 100 В в Японии) — среднеквадратичное значение напряжения. В цепях переменного тока ток и напряжение могут не совпадать по фазе. Максимальное значение тока может опережать или отставать от максимального значения напряжения. Это делает передачу власти менее эффективной. В худшем случае, когда ток и напряжение полностью не синхронизированы, передаваемая мощность равна нулю.
Коэффициент мощности говорит нам, насколько ток синхронизирован с напряжением. Если они синхронизированы, коэффициент мощности равен 9. 1304 1 . В противном случае он меньше единицы и достигает нуля в случае полной рассинхронизации. Коэффициент мощности зависит от устройства. Для чисто резистивного устройства, такого как электрический чайник или электронагреватель, коэффициент мощности равен
1304 1 . В противном случае он меньше единицы и достигает нуля в случае полной рассинхронизации. Коэффициент мощности зависит от устройства. Для чисто резистивного устройства, такого как электрический чайник или электронагреватель, коэффициент мощности равен 1 . Устройство с индуктивными или емкостными элементами выводит ток и напряжение не по фазе. Это делает его коэффициент мощности меньше 1. Проверьте калькулятор коэффициента мощности, чтобы узнать больше.
Калькулятор электрической мощности
Для расчета электрической мощности необходимо указать ток, напряжение и коэффициент мощности. Для устройств, подключенных к электрическим розеткам, напряжение — это просто напряжение бытовой электросети. Ток, потребляемый устройством, обычно можно найти либо на вилке, либо где-то на устройстве. Коэффициент мощности найти немного сложнее, если только у вас нет под рукой анализатора качества электроэнергии. Проверьте этот список для коэффициентов мощности нескольких типичных бытовых устройств:
- лампы со стандартной колбой:
ПФ = 1, - люминесцентные лампы:
PF = 0,93, - обычный асинхронный двигатель при половинной нагрузке:
PF = 0,73, при полной нагрузке:PF = 0,85, - электрическая духовка (с резистивным нагревательным элементом):
PF = 1,0, - индукционная печь:
PF = 0,85.

 Подразумевает преобразование мощности в тепловую, механическую и другие виды энергии. Показатель выражают в Ваттах и вычисляют по формуле U*I;
Подразумевает преобразование мощности в тепловую, механическую и другие виды энергии. Показатель выражают в Ваттах и вычисляют по формуле U*I;


 : Звуковое давление и звуковая мощность − следствие и причина
важно эффективность громкоговорителей. Сюда входит типичный вопрос:
: Звуковое давление и звуковая мощность − следствие и причина
важно эффективность громкоговорителей. Сюда входит типичный вопрос: 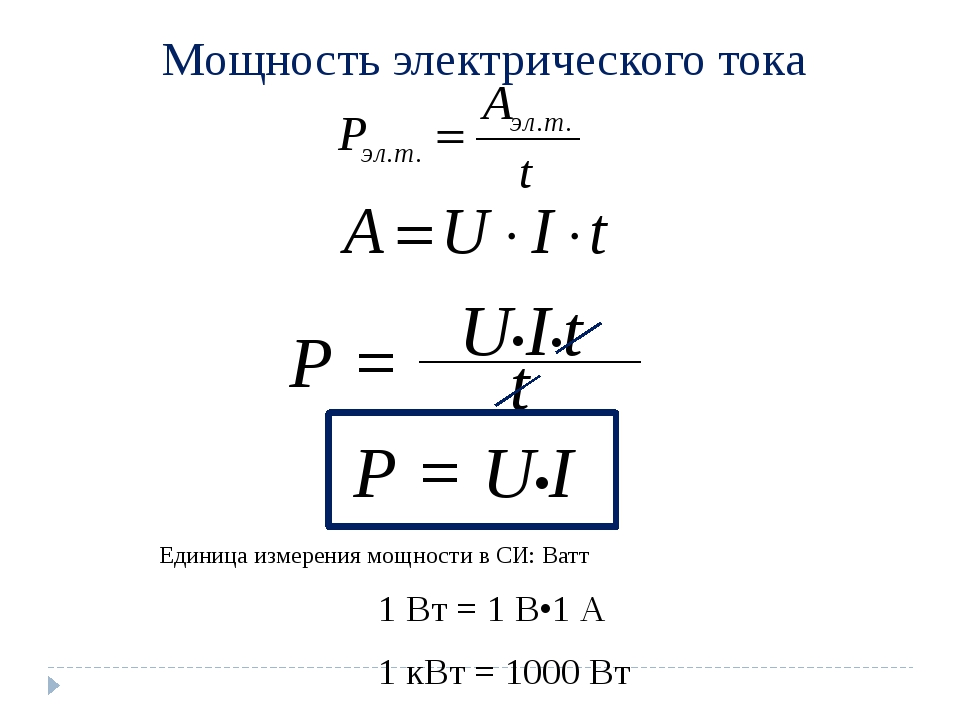 Ожидайте платить больше, когда
Ожидайте платить больше, когда 