Единицы измерения жесткости, или модуля Юнга |
Вспомним, что деформация нашей веревки под действием веса кирпича составляла0,5%, или 0,005, при напряжении 24,5 МН/м Поэтому модуль ЮнгаверевкиE = s/e = 24,5/0,005 = 4900 МН/м= ~ 5·10 кгс/см.
Единицы измерения жесткости, или модуля Юнга
Поскольку модуль Юнга представляет собой отношение напряжения к безразмернойвеличине, то размерность его та же, что и у напряжения, например МН/мили кгс/см. Формально модуль Юнга можно рассматривать как напряжение,требуемое для 100%-ного удлинения материала (если с материалом при этомничего не произойдет), вследствие чего его численные значения настольковелики, что их трудно себе представить.
Фактические значения модуля Юнга
Значения модуля Юнга для многих органических веществ и инженерных материаловпредставлены в табл. 1. Они расположены в порядке возрастания — от модуляЮнга мягкого покрова взрослой самки саранчи (отнюдь не самого мягкого биологическогоматериала; кстати, покров самцов и молодых самок саранчи не многим жестче)до алмаза.
Таблица 1. Значения модуля Юнга для различных материалов
Материал/Модуль Юнга (E), МН/м
Мягкий покров взрослой самки саранчи 0,2
Резина 7
Пленка скорлупы яйца 8
Хрящ человека 24
Сухожилие человека 600
Штукатурка 1400
Неармированный пластик, полиэтилен, нейлон 1400
Фанера 7000
Дерево (вдоль волокон) 14000
Свежая кость 21000
Магний 42000
Обычное стекло 70000
Алюминиевые сплавы 70000
Латунь и бронза 120000
Железо и сталь 210000
Окись алюминия (сапфир) 420000
Алмаз 1200000
Следует отметить, что многие очень мягкие биологические материалы отсутствуютв таблице. Дело в том, что их упругие свойства даже приближенно не описываютсязаконом Гука, а потому для них невозможно ввести модуль Юнга — во всякомслучае, в том виде, как обсуждалось выше.
К упругим свойствам таких материаловмы вернемся позже.
В настоящее время модуль Юнга считается фундаментальным понятием — оногосподствует в инженерном деле, в материаловедении и начинает вторгатьсяв биологию. Однако должна была пройти вся первая половина XIX столетия,прежде чем модуль Юнга завоевал умы инженеров.
Элементы теории упругости | Мир сварки
Введение
Под воздействием внешних сил всякое твердое тело изменяет свою форму – деформируется. Деформация, исчезающая с прекращением действия сил, называется упругой.
При упругой деформации тела возникают внутренние силы упругости, стремящиеся вернуть телу первоначальную форму. Величина этих сил пропорциональна деформации тела.
Деформация растяжения и сжатия
Возникающее удлинение образца (Δl) под действием внешней силы (F) пропорционально величине действующей силы, первоначальной длине (l) и обратно пропорционально площади поперечного сечения (
| 1) |
где
| 1/E | — | коэффициент пропорциональности. |
Величина E называется модулем упругости первого рода или модулем Юнга и характеризует упругие свойства материала. Величина F/S = p называется напряжением.
Деформация стержней любых длин и сечений (образцов) характеризуется величиной, называемой относительной продольной деформацией, ε = Δ
Закон Гука для образцов любых форм:
| 2) |
Модуль Юнга численно равен напряжению, увеличивающему длину образцов в два раза. Однако разрыв образца наступает при значительно меньших напряжениях. На рис.1 графически изображена экспериментальная зависимость p от ε, где pмакс – предел прочности, т.е. напряжение, при котором на стержне получается местное сужение (шейка), pтек – предел текучести, т.е. напряжение, при котором появляется текучесть (т.е. увеличение деформации без увеличения деформирующей силы), pупр – предел упругости, т.
Рис.1. Зависимость напряжения от относительной продольной деформации: Кривая I относится к пластичному материалу, а кривая II – к хрупкому. Точки О характеризуют разрушение материала |
Материалы разделяются на хрупкие и пластичные. Хрупкие вещества разрушаются при очень малых относительных удлинениях. Хрупкие материалы обычно выдерживают, не разрушаясь, большее сжатие, чем растяжение.
Совместно с деформацией растяжения наблюдается уменьшение диаметра образца. Если Δd – изменение диаметра образца, то ε1 = Δ
Абсолютная величина μ = |ε1/ε| носит название коэффициент поперечной деформации или коэффициента Пуассона.
Деформация сдвига
Сдвигом называют деформацию, при которой все слои тела, параллельные некоторой плоскости, смещаются друг относительно друга.
При сдвиге объем деформируемого образца не меняется. Отрезок АА1 (рис.2), на который сместилась одна плоскость относительно другой, называют абсолютным сдвигом. При малых углах сдвига угол α ≈ tg α =
Рис.2. Деформация сдвига |
Закон Гука для деформации сдвига может быть записан в виде
| 3) |
где коэффициент G называется модуль сдвига.
Сжимаемость вещества
Всестороннее сжатие тела приводит к уменьшению объема тела на ΔV и возникновению упругих сил, стремящихся вернуть телу первоначальный объем. Сжимаемостью (β) называется величина, численно равная относительному изменению объема тела ΔV/V при изменении действующего по нормали к поверхности напряжения (
Величина, обратная сжимаемости, носит название модуля объемной упругости (K).
Изменение объема тела ΔV при всестороннем увеличении давления на ΔP вычисляется по формуле
| 4) |
где
| V | — | первоначальный объем тела. |
Соотношения между упругими постоянными
Модуль Юнга, коэффициент Пуассона, модуль объемной упругости и модуль сдвига связаны между собой уравнениями:
которые по двум известным упругим характеристикам позволяют, в первом приближении, рассчитать остальные.
Потенциальная энергия упругой деформации определяется по формуле
| 5) |
где
| F | — | сила упругости; |
| Δl | — | величина деформации. |
Единицы измерения модулей упругости: Н/м2 (СИ), дин/см2 (СГС), кгс/м2 (МКГСС) и кгс/мм
Приложение
Рис.3. Зависимость предела прочности от температуры: 1 – вольфрам, 2 – никелевая сталь, 3 – кобальтовая сталь, 4 – сталь N-155, 5 – Mo 0,5 Ti, 6 – Ti 36Al |
| Материал | Предел прочности | |
|---|---|---|
| при растяжении | при сжатии | |
| Аминопласты слоистые | 8 | 20 |
| Бакелит | 2–3 | 8–10 |
| Бетон | — | 0,5–3,5 |
| Винипласт | 4 | 8 |
| Гетинакс | 15–17 | 15–18 |
| Гранит | 0,3 | 15–26 |
| Графит | 0,5–1,0 | 1,6–3,8 |
| Дуб (при 15% влажности) вдоль волокон | 9,5 | 5 |
| Дуб (при 15% влажности) поперек волокон | — | 1,5 |
| Кирпич | — | 0,74–3 |
| Латунь, бронза | 22–50 | — |
| Лед (0 °С) | 0,1 | 0,1–0,2 |
| Пенопласт плиточный | 0,06 | — |
| Полиакрилат (оргстекло) | 5 | 7 |
| Полистирол | 4 | 10 |
| Сосна (при 15% влажности) вдоль волокон | 8 | 4 |
| Сосна (при 15% влажности) поперек волокон | — | 0,5 |
| Сталь для конструкций | 38–42 | — |
| Сталь кремнехромомарганцовистая | 155 | — |
| Сталь углеродистая | 32–80 | — |
| Сталь рельсовая | 70–80 | — |
| Текстолит ПТК | 10 | 15–25 |
| Фенопласт текстолитовый | 8–10 | 10–26 |
| Фторопласт-4 | 2 | — |
| Целлон | 4 | 16 |
| Целлулоид | 5–7 | — |
| Чугун белый | — | до 175 |
| Чугун серый мелкозернистый | 21–25 | до 140 |
| Чугун серый обыкновенный | 14–18 | 60–100 |
| Наименование материала | Модуль Юнга E, 107 Н/м2 | Модуль сдвига G, 107 Н/м2 | Коэффициент Пуассона μ |
|---|---|---|---|
| Алюминий | 6300–7000 | 2500–2600 | 0,32–0,36 |
| Бетон | 1500–4000 | 700–1700 | 0,1–0,15 |
| Висмут | 3200 | 1200 | 0,33 |
| Бронза алюминиевая, литье | 10300 | 4100 | 0,25 |
| Бронза фосфористая катаная | 11300 | 4100 | 0,32–0,35 |
| Гранит, мрамор | 3500–5000 | 1400–4400 | 0,1–0,15 |
| Дюралюминий катаный | 7000 | 2600 | 0,31 |
| Известняк плотный | 3500 | 1500 | 0,2 |
| Инвар | 13500 | 5500 | 0,25 |
| Кадмий | 5000 | 1900 | 0,3 |
| Каучук | 0,79 | 0,27 | 0,46 |
| Кварцевая нить (плавленая) | 7300 | 3100 | 0,17 |
| Константан | 16000 | 6100 | 0,33 |
| Латунь корабельная катаная | 9800 | 3600 | 0,36 |
| Манганин | 12300 | 4600 | 0,33 |
| Медь прокатанная | 10800 | 3900 | 0,31–0,34 |
| Медь холоднотянутая | 12700 | 4800 | 0,33 |
| Никель | 20400 | 7900 | 0,28 |
| Плексиглас | 525 | 148 | 0,35 |
| Резина мягкая вулканизированная | 0,15–0,5 | 0,05–0,15 | 0,46–0,49 |
| Серебро | 8270 | 3030 | 0,37 |
| Стали легированные | 20600 | 8000 | 0,25–0,30 |
| Стали углеродистые | 19500–20500 | 800 | 0,24–0,28 |
| Стекло | 4900–7800 | 1750–2900 | 0,2–0,3 |
| Титан | 11600 | 4400 | 0,32 |
| Целлулоид | 170–190 | 65 | 0,39 |
| Цинк катаный | 8200 | 3100 | 0,27 |
| Чугун белый, серый | 11300–11600 | 4400 | 0,23–0,27 |
| Вещество | Температура, °С | В интервале давлений, атм | Сжимаемость β, 10-6 атм-1 |
|---|---|---|---|
| Ацетон | 14,2 | 9–36 | 111 |
| 0 | 100–500 | 82 | |
| 0 | 500–1000 | 59 | |
| 0 | 1000–1500 | 47 | |
| 0 | 1500–2000 | 40 | |
| Бензол | 16 | 8–37 | 90 |
| 20 | 99–296 | 78,7 | |
| 20 | 296–494 | 67,5 | |
| Вода | 20 | 1–2 | 46 |
| Глицерин | 14,8 | 1–10 | 22,1 |
| Касторовое масло | 14,8 | 1–10 | 47,2 |
| Керосин | 1 | 1–15 | 67,91 |
| 16,1 | 1–15 | 76,77 | |
| 35,1 | 1–15 | 82,83 | |
| 52,2 | 1–15 | 92,21 | |
| 72,1 | 1–15 | 100,16 | |
| 94 | 1–15 | 108,8 | |
| Кислота серная | 0 | 1–16 | 302,5 |
| Кислота уксусная | 25 | 92,5 | 81,4 |
| Керосин | 10 | 1–5,25 | 74 |
| 100 | 1–5,25 | 132 | |
| Нитробензол | 25 | 192 | 43,0 |
| Оливковое масло | 14,8 | 1–10 | 56,3 |
| 20,5 | 1–10 | 63,3 | |
| Парафин (с температурой плавления 55 °С) | 64 | 20–100 | 83 |
| 100 | 20–400 | 24 | |
| 185 | 20–400 | 137 | |
| Ртуть | 20 | 1–10 | 3,91 |
| Спирт этиловый | 20 | 1–50 | 112 |
| 20 | 50–100 | 102 | |
| 20 | 100–200 | 95 | |
| 20 | 200–300 | 86 | |
| 20 | 300–400 | 80 | |
| 100 | 900–1000 | 73 | |
| Толуол | 10 | 1–5,25 | 79 |
| 20 | 1–2 | 91,5 |
Модуль упругости — Энциклопедия по машиностроению XXL
Случайный характер других механических характеристик, например модуля упругости Е, можно учесть, используя формулу полной вероятности.
Пусть модуль упругости случаен и закон распределения его/s Е) известен. Принимая значение модуля Е равным фиксированной величиной , определим по формуле полной вероятности/ (vv)
[c.7]Таким образом, как динамическая вязкость, так и динамическая жесткость (или модуль упругости) представляют собой величины, зависящие от частоты. Динамическая вязкость монотонно убывает до нуля с увеличением частоты. Значение, соответствующее (0 = 0, должно совпадать с вискозиметрической вязкостью при нулевой скорости сдвига [c.220]
Если исследовать в общем виде задачу о распространении волн в простых жидкостях с исчезающей памятью, то скорость распространения оказывается равной корню квадратному из отношения модуля упругости и плотности. Модуль упругости должен оцениваться локально величиной ц/Л он определяется только при распространении волны в покоящейся среде. Волны ускорения (т. е.
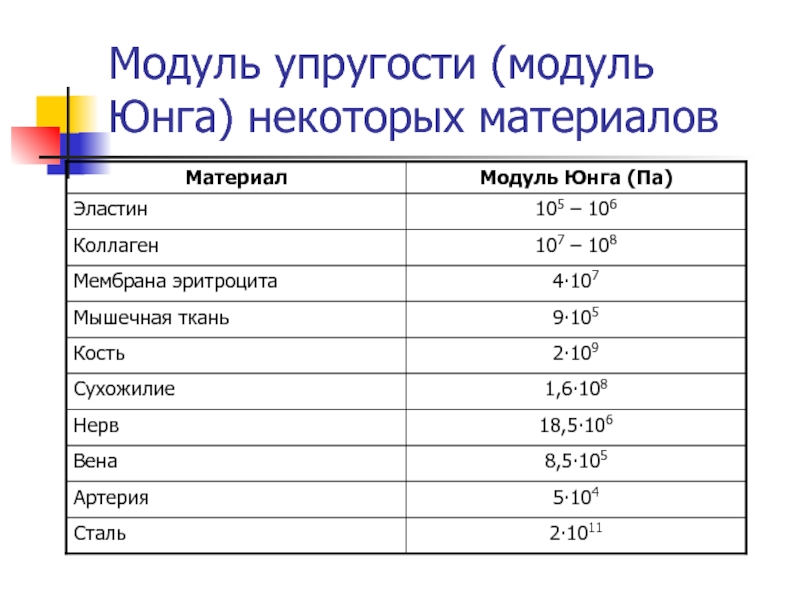разрывы ускорения, соответствующие разрывам скорости деформации) могут затухать в процессе их распространения, но могут также и возрастать по амплитуде, перерождаясь в ударные волны (разрывы скорости) за конечное время. Последняя ситуация возникает при условии, что начальная амплитуда волны достаточно велика, и при условии, что уравнение состояния в достаточной степени нелинейно. Интересно, что волна, распростра-
[c.296]Трусделла 75 Модуль упругости 218, 220 Момент наблюдения 92 [c.304]
Величина, обратная коэффициенту Рр, представляет собой объем-пын модуль упругости К. [c.9]
Определять напряжения в стержнях системы после нагрева среднего стержня на 65°С. Вертикальный стержень дюралюминиевый с площадью поперечного сечения >1э 3 см и модулем упругости Ej [c.16]
Модуль продольной упругости (модуль Юнга) Сосредоточенная сила воздействие вообще Модуль упругости при сдвиге постоянная нагрузка (вес)
[c.
32]
Материал Модули упругости, ГПа Температурный коэффициент, а, 10 Коэффи- циент Пуассона V Плотность р, кг/м [c.53]
Модуль упругости, модуль сдвига, модуль объемного сжатия тс 1 р НЬЮТОН на квадратный метр н1м N/m [c.11]
Распространение продольных волн выражается аналогичным уравнением, если функцию рассматривать как плотность среды. В этом случае модуль упругости Е заменяет натяжение струны т, масса единицы объема заменяет массу единицы длины р и скорость распространения волны будет иметь вид [c.73]
Если распространение звуковых волн в идеальном газе происходит изотермически, то модулем упругости будет давление р и скорость звука будет равна [c.73]
В действительности распространение звуковых волн в воздухе по существу является адиабатным процессом и модуль упругости ближе всего к величине kp, где k — отношение теплоемкости при постоянном давлении к теплоемкости при постоянном
[c.
73]
По диаграмме деформации определяют только прочностные характеристики аи и 00,2- На этой диаграмме модуль нормальной упругости (тангенс на-клена кривой О А) значительно меньше действительного, так как диаграммный аппарат фиксирует и упругую деформацию частей машины. Чтобы определить модуль упругости, на испытуемый образец навешивают тензометры, позволяющие определить малые величины деформаций, и тем самым точно построить участок ОА. Деформационные характеристики — 6 и tp по той же причине определяют также не по диаграмме, а измерением образца до и после испытания. [c.64]
Вместе с тем повышение температуры, изменяющее (увеличивающее) межатомные расстояния, изменяет (снижает) модуль упругости. [c.65]
Все остальные механические характеристики, кроме модуля упругости, являются структурно чувствительными и изменяются в завнснмости от обработки (структуры) в весьма широких пределах, о чем подробно будет сказано ниже при рассмотрении свойств различных металлов.
[c.65]
Принято делить свойства (характеристики) на структурно чувствительные и структурно нечувствительные, т. е. зависящие и не зависящие от структуры. Такое деление условно, так как все свойства зависят, от структуры (в том числе и модуль упругости), вопрос лишь в какой степени. К структурно нечувствительным свойствам относят такие, которые практически не зависят от структуры, для н.х изменения не следует применять термическую обработку. [c.65]
Твердость и прочность стали могут быть увеличены в результате термической обработки в три — пять раз (есл И сравнивать с отожженным состоянием, медленно охлажденным), а модули упругости при этом изменяются менее чем на 5%. [c.180]
СПЛАВЫ С ПОСТОЯННЫМ МОДУЛЕМ УПРУГОСТИ [c.539]
Состав конкретных марок элинваров и других промышленных сплавов с низким температурным коэффициентом модуля упругости приведен в табл. 103. [c.539]
Состав сплавов (%) с низким температурным коэффициентом модуля упругости
[c.
539]
Бериллий и особенно его сплав обладают при малой плотности (1,8 г/см- ) высокими модулем упругости и прочностью, размерной стабильностью, хорошей коррозионной стойкостью в ряде сред . [c.600]
А1 и 0,5—1,5 % Zn, а также 0,15—0,5 % Мп, имеют невысокий модуль упругости (Е = 43 ООО МПа) и вследствие этого хорошие демпфирующие свойства (гасят колебания конструкции). Однако эти сплавы обладают невысокой коррозионной стойкостью, и для ее повышения отливки оксидируют, покрывают лаками. [c.18]
При снятии внешних сил, вызывающих изгиб заготовки, растянутые слои стремятся сжаться, а сжатые слои — удлиниться. Благодаря этому при разгрузке изменяются углы между полками (пружи-нение при гибке). Угол между полками при разгрузке изменяется в зависимости от механических свойств (отношения предела текучести к модулю упругости), от rIS и угла а, и увеличивается с увеличением этих параметров. [c.106]
В связи с большой величиной коэффициента линейного расширения ы низки.
м модулем упругости сплав имеет повышенную склонность к короблению. Поэтому 1Шобходимо прибегать к жесткому закреплению листов с помощью грузов, а такгке ннев-мо- или гидравлических прижимов на специальных стендах для сварки полотнищ и секций из этих сплавов. Ввиду высокой теплопроводности алюминия приспособления следует изготовлять из материалов с низкой теплопроводностью (легированР1ые стали и т. п.).
[c.354]
Различают адиабатный и изотермический модуль упругости. Первый больше второго ггрцблизнтельио в 1,5 рааа и проявляется при быстротечных процессах сжатия жидкости беа теплообме][а. Приведенные выше значения К являются значениями изотермического модуля. [c.10]
Для бруса из материала с постоянным модулем упругости осерые перемещения можно определить по формуле [c.9]
При изменении нагрузки на 100 кН разность отсчетов тензометра, поставленного на деталь с поперечным сечением А 10 см , оказалась равной Л = 25 мм.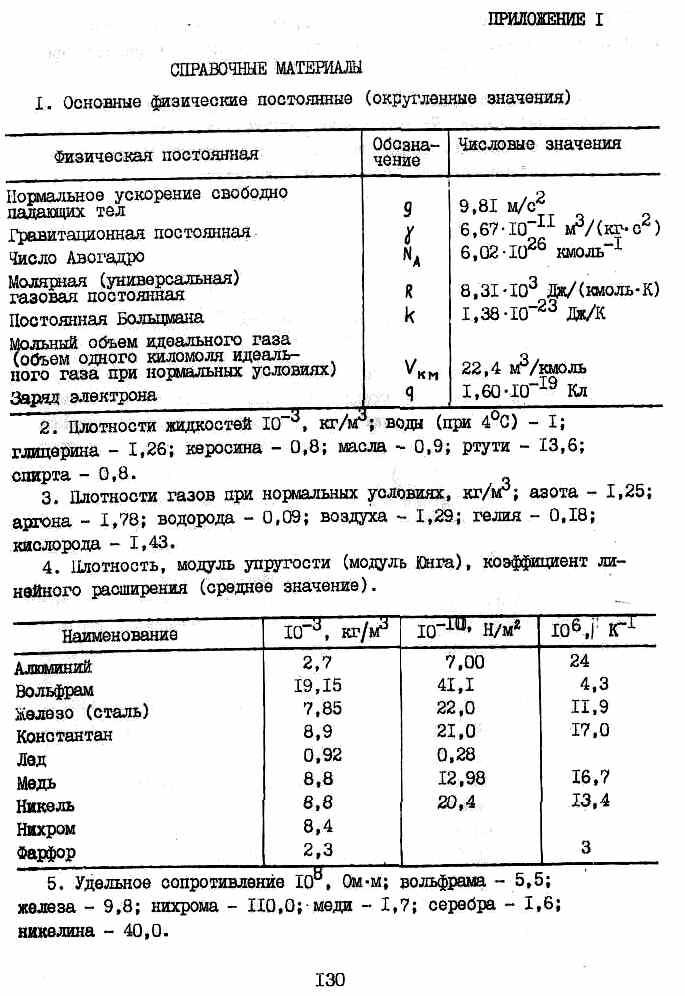
База тензометра S = 100 мы, а его увеличение К 500. Чецу равен модуль упругости материала детали
[c.4]
J.20.0п еделить наибольшие сжимающие напряжения и полное укорочение бетонной колонны постоянного сечения высотой 10 м, если один кубический метр бетона весит 24 а его модуль упругости равен 20 ГПа. [c.5]
Значение модулей упругости определяется силами межатомного взаимодействия и являются константами материала. Так, например, модуль нормальной упругости для алюмшния 0,8Х >механическая характеристика структурно нечувствительна, т. е. термическая обработка или другие способы изменения структуры металла практически не изменяют модуля упругости. [c.65]
Почти для всех промышленных сплавов удельный модуль упругости — У = 2,7ч-2,9-10 , тогда как для бериллия он 16,5-10 , т. с, в 6 раз больше. Если бы в расчет входила только упругая константа (модуль упругости), то иримснепие бериллия позволило бы сократить массу изделия во много раз.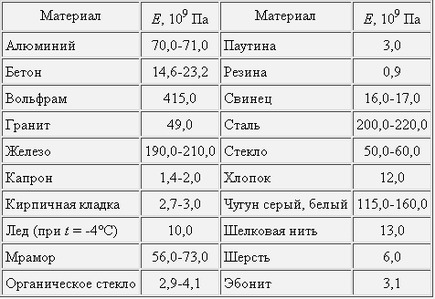
Это было бы возможно, если бы бериллий не был так дорог.
[c.600]
Влияние графита на механические характеристики серого чугуна проявляется в уменьшении временного сопротивления, пластичности, модуля упругости и тем больше, чем большее количество графита выделяется при кристаллизации чугуна, чем крупнее его включения и чем неравномернее он распределен по сече1гию стенки отливки. [c.158]
Деформация деталей. Вал сплошной т/ =0, с = = 48 мм. Зубчатое колесо выполнено без ступицы в виде диска. Принимаем, ориентируясь на делительный диаметр колеса, т/2 174мм. Модули упругости =/ , = = 2.1 10 Н/мм , коэффициенты ц, =Ц2 = (),3 (см. с. 95). Тогда [c.216]
Основы гидромеханики неньютоновских жидкостей (1978) — [ c.218 , c.220 ]
Сопротивление материалов (1970) — [ c.33 ]
Теоретическая механика
(1976) — [
c.
240
]
Физика. Справочные материалы (1991) — [ c.91 ]
Курс теоретической механики. Т.2 (1977) — [ c.512 ]
Физические основы механики и акустики (1981) — [ c.158 ]
Основы теории упругости и пластичности (1990) — [ c.37 ]
Гидравлика и аэродинамика (1975) — [ c.11 ]
Термодинамика (1991) — [ c.45 , c.46 ]
Термодинамика и статистическая физика (1986) — [ c.38 , c.39 ]
Сопротивление материалов усталостному и хрупкому разрушению
(1975) — [
c.
8
,
c.154
]
Прикладная механика (1985) — [ c.148 ]
Лабораторный практикум по сопротивлению материалов (1975) — [ c.16 , c.22 ]
Прикладная механика твердого деформируемого тела Том 1 (1975) — [ c.173 , c.195 , c.230 ]
Машиностроительные материалы Краткий справочник Изд.2 (1969) — [ c.4 ]
Демпфирование колебаний (1988) — [ c.113 , c.115 ]
Справочник строителя тепловых сетей (1967) — [ c.11 ]
Материалы ядерных энергетических установок
(1979) — [
c.
36
]
Теплоэнергетика и теплотехника Общие вопросы (1987) — [ c.35 , c.278 , c.309 , c.358 ]
Теплотехнический справочник (0) — [ c.54 ]
Моделирование конструкций в среде MSC.visual NASTRAN для Windows (2004) — [ c.211 ]
Материаловедение Учебник для высших технических учебных заведений (1990) — [ c.89 ]
Сопротивление материалов (1976) — [ c.32 , c.34 ]
Теплофикационные паровые турбины и турбоустановки (2002) — [ c.62 ]
Вибрации в технике Справочник Том 1
(1978) — [
c.
138
]
Металловедение и термическая обработка Издание 6 (1965) — [ c.63 ]
Лабораторный практикум по испытанию лакокрасочных материалов и покрытий (1977) — [ c.126 , c.128 ]
Промышленные полимерные композиционные материалы (1980) — [ c.78 , c.151 , c.154 , c.158 , c.187 , c.249 ]
Ползучесть в обработке металлов (БР) (1986) — [ c.73 ]
Металлы и сплавы Справочник (2003) — [ c.39 , c.40 ]
Ротационные приборы Измерение вязкости и физико-механических характеристик материалов
(1968) — [
c.
16
]
Механика сплошных сред (2000) — [ c.118 ]
Словарь-справочник по механизмам (1981) — [ c.187 ]
Наука и искусство проектирования (1973) — [ c.86 ]
Металловедение и термическая обработка стали Справочник Том1 Изд4 (1991) — [ c.2 , c.213 ]
Пластинки и оболочки (1966) — [ c.15 , c.360 , c.361 ]
Справочник по гидравлике (1977) — [ c.67 ]
Механика материалов (1976) — [ c.19 ]
Краткий курс сопротивления материалов Издание 2
(1977) — [
c.
29
,
c.30
,
c.53
]
Справочник машиностроителя Том 3 (1951) — [ c.17 ]
Теплотехнический справочник Том 1 (1957) — [ c.54 ]
Проектирование деталей из пластмасс Издание 2 (1977) — [ c.104 , c.108 ]
Примеры расчетов по гидравлики (1976) — [ c.6 , c.230 ]
Расчет на прочность деталей машин Издание 3 (1979) — [ c.7 ]
Механические свойства металлов Издание 3 (1974) — [ c.88 , c.330 , c.352 ]
Теоретическая механика
(2002) — [
c.
344
]
Трехмерные задачи математической теории упругости и термоупругости Изд2 (1976) — [ c.24 ]
Курс теоретической механики для физиков Изд3 (1978) — [ c.546 ]
Уравнения и краевые задачи теории пластичности и ползучести (1981) — [ c.92 ]
Сопротивление материалов Издание 13 (1962) — [ c.35 , c.36 , c.57 ]
Конструкции и механический расчет линий электропередачи (1979) — [ c.40 ]
Технология металлов и конструкционные материалы Издание 2 (1989) — [ c.27 ]
Расчёты и конструирование резиновых изделий Издание 2
(1977) — [
c.
14
,
c.15
]
Основы прогнозирования механического поведения каучуков и резин (1975) — [ c.32 ]
Сопротивление материалов (1962) — [ c.17 ]
Металловедение и технология металлов (1988) — [ c.86 ]
Методы статических испытаний армированных пластиков Издание 2 (1975) — [ c.27 , c.47 , c.74 ]
Основы технологии автостроения и ремонт автомобилей (1976) — [ c.99 , c.411 , c.422 ]
Примеры и расчеты металлических конструкций Изд3 (2006) — [ c.0 ]
Теория сварочных процессов Издание 2
(1976) — [
c.
33
]
Справочник механика заводов цветной металлургии (1981) — [ c.28 , c.29 ]
Металловедение и термическая обработка стали Том 1, 2 Издание 2 (1961) — [ c.72 , c.241 , c.363 ]
Пневматические приводы (1969) — [ c.150 ]
Металловедение Издание 4 1963 (1963) — [ c.40 ]
Металловедение Издание 4 1966 (1966) — [ c.44 ]
Техническая энциклопедия Т 10 (1931) — [ c.371 ]
Метрология, специальные общетехнические вопросы Кн 1
(1962) — [
c.9
,
c.
776
]
Машиностроение энциклопедия ТомIII-7 Измерения контроль испытания и диагностика РазделIII Технология производства машин (2001) — [ c.145 ]
Технический справочник железнодорожника Том 1 (1951) — [ c.405 ]
Внедрение Международной системы единиц (1986) — [ c.32 , c.76 ]
Компьютерное материаловедение полимеров Т.1 (1999) — [ c.102 , c.111 , c.252 , c.275 ]
Проектирование деталей из пластмасс Издание 2 (1977) — [ c.104 , c.108 ]
Колебания и волны Введение в акустику, радиофизику и оптику Изд.
2
(1959) — [
c.185
]
Справочное руководство по физике (0) — [ c.170 ]
Накопители энергии (1991) — [ c.0 ]
Сопротивление материалов (1962) — [ c.27 , c.122 , c.123 , c.129 , c.155 , c.310 ]
Гидравлика и гидропривод горных машин (1979) — [ c.61 ]
Ультразвук и его применение в науке и технике Изд.2 (1957) — [ c.45 , c.343 ]
Справочник по Международной системе единиц Изд.3
(1980) — [
c.
30
]
Машиностроение Энциклопедический справочник Раздел 2 Том 3 (1948) — [ c.21 , c.23 , c.51 ]
Техническая энциклопедия Том 1 (0) — [ c.394 ]
Техническая энциклопедия Т 9 (1938) — [ c.371 ]
Модуль юнга для стали и других материалов
ПОИСК
Е — приведенный модуль Юнга, принятый равным модулю упругости стали [c.71]
Деформационные свойства. Модуль Р. (Е) при небольшом растяжении на 4—5 десятичных порядков ниже модуля Юнга для стали [соответственно 0,5— [c.158]
МОДУЛЬ ЮНГА УГЛЕРОДИСТОЙ И ЛЕГИРОВАННОЙ СТАЛЕЙ ПРИ РАЗНЫХ ТЕМПЕРАТУРАХ [c.16]
Следует отметить, что высокая эластичность каучука совершенно отлична от упругих деформаций кристаллических веществ или металлов, составляющих всего несколько процентов от исходных размеров, тогда как каучук можно растягивать в 10 раз.
Резко различаются также необходимые для деформации напряжения.
Модуль упругости (или модуль Юнга) Е, характеризующий отношение между приложенным напряжением и относительным удлинением образца, составляет для стали около 20000 кг/мм , для стекла около 6000 кг/мм , а для каучука лишь около [c.228]
При конструировании важно установить распределение деформаций конструкции, возникающих в процессе эксплуатации под влиянием приложенных напряжений. Напряжения могут возникать из-за давления, создаваемого жидкостью или газом, течением жидкости или неоднородным температурным расширением при изменениях температуры. Упругие свойства часто считают не зависящими от структуры, но существуют ситуации, когда такое утверждение становится неверным. Отдельные зерна металлических кристаллов в отношении упругих свойств анизотропны. Таким образом, упругие постоянные зависят от ориентации зерна по отношению к ориентации приложенных напряжений. В процессе производства деталей может возникнуть преимущественная ориентация отдельных зерен, что и создает упругую анизотропию.
Весьма вероятно, что различные степени преимущественной ориентации приводят к довольно широкому разбросу данных по упругим свойствам металлов и сплавов. Вследствие того что этот разброс может вызывать появление погрешности, достигающей в некоторых случаях при расчетах деформаций 20 %, эта тема детально рассматривается в настоящем параграфе. Таблица 3, 4.5,8 — лишь пример того типа информации, которая встречается в литературе. Можно полагать, например, что стали с 5—9 %-ным содержанием хрома должны иметь примерно те же значения модуля Юнга, что и стали, содержание хрома в которых близко к указанному. [c.196]
Прочность сталей значительно изменяется при переходе к высоким температурам. Так, предел прочности при растяжении хромоникелевой стали типа 18-8 падает с 7000 до 4000 кгс/см при 700 °С до 2000 кгс/см при 800 °С. Модуль Юнга углеродистой и легированной сталей уменьшается при нагревании от 20 до 500 °С на 30%. [c.19]
Иногда для повышения прочности между двумя пьезоэлементами помещают металлическую пластину [318].
Собственная частота преобразователя может быть повышена расположением двух пассивных (например, стальных) пластин по обе стороны от биморфного преобразователя из двух пьезопластин.
Это объясняется тем, что модуль Юнга стали много больше, чем у пьезокерамики, а изгибная жесткость конструкции определяется в основном ее [c.70]
Твердость вещества можно оценить при помощи модуля Юнга, представляющего собой отношение приложенного напряжения (или силы, отнесенной к единице площади) и соответствующей ему деформации или удлинения.
Типичные значения модуля Юнга для различных материалов представлены на рис. 7.1. На одном конце шкалы расположены неорганические кристаллические материалы, такие, как алмаз, кварц, сталь и т. д., модули которых [c.
131]
Еще большее впечатление производит различие в силе, необходимой для осуществления деформации.
Для удлинения стальной проволоки диаметром 1 мм на 1% требуется нагрузка в 1600 Н (двукратный средний вес человека), а для удлинения каучуковой нити того же диаметра на ту же величину необходима нагрузка меньше Ю Н.
Так называемый модуль Юнга (отношение напряжения к удлинению) для стали в 100 000 раз больше, чем для каучука. [c.45]
Характеристика сталей и сплавов при комнатной температуре и частоте колебаний 20 кгц (р — плотность Е — модуль Юнга Спр — скорость звука рс — волновое сопротивление [c.115]
Следует отметить, что для коммуникаций часто применяют титан неоправданно большой толщины, что не вызывается ни прочностными, ни коррозионными требованиями. Часто на титан как конструкционный материал переносятся представления, сложившиеся в результате многолетней работы со сталью.
Так, при замене коммуникаций из стали на титановые используют титан той же толщины, что и сталь. Большой расход титана именно на коммуникации объясняется в некоторой степени и этой причиной.
Например, коллекторы влажного хлора на заводах делают из листов титана толщиной 3—5 мм (только на двух предприятиях эти коллекторы сделаны из листов толщиной 2 мм, но и это значительная толщина).
За рубежом для данных целей используют титан толщиной 0,8—1,0 мм.
В связи с тем, что модуль Юнга у титана незначителен, при расчетах следует обращать внимание на возможный прогиб труб, а при монтаже — на крепление трубопроводов. [c.156]
Любопытные наблюдения публикует Фирс-Виккерс, утверждая, что нержавеющие аустенитовые стали (хромовые и хромоникелевые) дают падение модуля Юнга приблизительно на 1% на каждые 30° повыщения температуры. В случае особенно тяжелых условий работы лучше всего обратиться за информацией к поставщикам стали. [c.670]
Вулканизованный каучук способен испытывать обратимые деформации на сотни процентов при весьма малом значении модуля упругости. (Модуль Юнга для стали 20 000—22 000 кг/см , для каучука [c.10]
Следует отметить, что высокая эластичность каучука совершенно отличается от упругих деформаций кристаллических веществ или металлов, которые составляют всего несколько процентов от исходных размеров, тогда как каучук можно растягивать до десятикратных удлинений.
Резко различаются также необходимые для деформации напряжения.
Модуль упругости (или модуль Юнга) Е, характеризующий отношение между приложенным напряжением и относительным удлинением образца, составляет для стали около 20 ООО кг/мм”, для стекла—около 6000 кг/мм , а для каучука—лишь около 0,1 кг/мм”. Эти различия объясняются тем, что нри упругой деформации кристаллов происходят лишь небольшие изменения средних расстояний между молекулами и валентных расстояний между атомами, связанные со значительными изменениями внутренней энергии напротив, при чистой высоко-эластической деформации большие удлинения происходят без изменения валентных расстояний нри постоянстве внутренней энергии. [c.272]
На практике все большее применение стали получать ОВ с двуслойным покрытием, в которых первый слой выполнен мягким (буферным) с низким (1—2 МПа) модулем Юнга, а второй—с высоким модулем Юнга от 0,1 до 4 ГПа [52] [c.101]
В формуле (П1.
2
влияющие факторы и методы определения
Для характеристики эксплуатационных и физико-механических свойств материалов используются различные показатели. Широкое распространение получил модуль упругости бетона, характеризующий способность упруго деформироваться в результате воздействия внешней силы и давления. Чтобы разобраться в свойствах готового бетонного раствора, стоит узнать, что это такое, от чего зависит и каким образом определяется.
Читайте в статье
Понятие модуля упругости бетона и единицы измерения
В процессе эксплуатации твёрдые тела подвергаются нагружению и начинают деформироваться. Сначала протекающие деформационные изменения являются обратимыми, а их величина от прикладываемого усилия является линейной. Как только нагрузка снимается, изделие полностью восстанавливает первоначальную форму. Для описания протекающих процессов используется закон Гука, согласно которому в качестве коэффициента пропорциональности между абсолютным сжатием либо удлинением и прикладываемым усилием используется модуль упругости.
Определение данного показателя звучит следующим образом: модуль упругости – коэффициент пропорциональности между нормальным напряжением и соответствующей ему относительной продольной деформацией. Измеряется в кгс/см² (Н/м², Па). Называют модулем Юнга.
Как только нагрузка превысит определённый уровень, начинается фаза необратимых изменений. Деформативность становится неупругой. Сдвиг увеличивается без дальнейшего приложения нагрузки. В зоне ползучести внутренние связи начинают разрушаться, и бетонная конструкция теряет прочность.
ФОТО: gidrocor.ruПри превышении определённого значения бетонная конструкция начинает разрушатьсяФакторы, влияющие на модуль упругости бетона
Значение модуля упругости может существенно отличаться. На него влияет множество факторов. Чтобы получить желаемый результат, стоит с ними познакомиться заранее.
Качество и объёмное содержание заполнителей
Бетон представляет собой смесь, состоящую из некоторого количества цемента и заполнителей. Качество и концентрация последних оказывают непосредственное влияние на значение модуля упругости. Если структура является неоднородной, вероятность возникновения сложного напряжённого состояния существенно возрастает. Основная нагрузка приходится на жёсткие частицы. Зоны с пустотами и порами испытывают поперечное растяжение.
ФОТО: house-keys.ruСоотношение компонентов может отличатьсяВнимание! Введение в состав крупного заполнителя способствует увеличению упругих свойств железобетона.
Класс бетона
Класс бетона оказывает непосредственное влияние на модель упругости. Чем выше класс, тем большей прочностью на сжатие и плотностью будет обладать состав и будет лучше сопротивляться воздействующей нагрузке. Самое высокое значение – у бетона В60 – численно равно 39,5 МПа×10-3. Наименьшее значение у В10 и соответствует 19 МПа×10-3.
ФОТО: cemmix.ruКласс бетона – важный критерийТемпература воздуха и влажность среды
При повышении температуры деформация в бетоне увеличивается, а упругие свойства снижаются. Это способствует повышению внутренней энергии смеси, а также линейному расширению материала, траекторий движения молекул и увеличению пластичности.
ФОТО: static.tildacdn.comТемпература определяет скорость набора прочности и количество деформацийВнимание! Температурные колебания учитывают только, если их диапазон превышает 20 °С.
Влажность влияет на упругость материала. В расчётах используется коэффициент ползучести. Чем выше процентное содержание водяного пара, тем ниже будут пластические деформации.
ФОТО: wallpapertag.comУровень влажности бетона влияет на пластичностьВремя воздействия нагрузки и условия твердения смеси
Продолжительность действия нагрузки на бетонную конструкцию также влияет на модуль упругости. Если нагружение осуществляется, мгновенно деформация конструкции увеличивается пропорционально приложенным внешним силам. Длительное напряжение приводит к уменьшению величины модуля. Зависимость носит нелинейный характер. Пластическая и упругая деформация складываются.
ФОТО: static.tildacdn.comХарактер прикладываемой нагрузки может отличатьсяУсловия, в которых бетон набирает свою прочность, могут отличаться. В естественных условиях значение всегда выше. Если материал обрабатывается в автоклавной установке либо осуществляется пропаривание в условия атмосферных давлений, значение несколько снизится. Причиной этого является образование большого числа пустот и пор благодаря неравномерному температурному расширению объёма, понижению качества гидратации зёрен цемента.
ФОТО: beton-house.comТвердение в естественных условиях предпочтительнейВозраст бетона и армирование конструкции
Для набора прочности свежезалитому бетону достаточно четырёх недель. По истечении указанного периода смесь будет обладать упругими свойствами и достаточной пластичностью. Максимальная твёрдость будет достигнута только через 200-250 дней. Именно в это время модуль упругости достигнет максимального значения, соответствующего марочной прочности.
ФОТО: cemmix.ruДля набора прочности требуется времяДля того чтобы монтируемая конструкция прослужила подольше, её обязательно армируют. В качестве армирующих элементов берётся сетка либо каркас, для изготовления которого использовалась арматура, относящаяся к классам АI, AIII, А500С, Ат800, древесина и композиты. Все эти элементы в процессе эксплуатации воспринимают растягивающие и сжимающие нагрузки, воздействующие на бутон.
Благодаря армированию удается повысить упругость и прочностные характеристики конструкции. Уменьшается вероятность образования трещин деформационного и усадочного типа.
ФОТО: a-plus-enterprises.comАрмирование повышает упругостьМодуль упругости бетона (Еб): способы определения значения
Порядок определения Еб может несколько отличаться. Каждый способ имеет свои отличительные особенности. Стоит ознакомиться с нюансами каждого метода, чтобы не допустить ошибок в момент определения значения.
Механическое испытание
При проведении механических испытаний образец подвергается разрушению. Исследование производится с учётом требований ГОСТ 24452, устанавливающих требования к используемым образцам и порядку проведения исследований.
ФОТО: nilstroi.ruДля проведения испытания требуется специальное оборудованиеМатериалы и инструменты
Для проведения исследований используются образцы, имеющие форму круга либо квадрата. Соотношение высоты и поперечного сечения принимают равным четырём. Образцы высверливаются, выбуриваются либо выпиливаются из готового изделия. До начала испытаний их держат под влажной тканью.
Для получения искомого значения образцы помещают на пресс, оснащённый специальными базами, позволяющими измерить деформацию. Приборы располагаются под разными углами к грани образца. Для фиксации индикаторов используются стальные рамки. В некоторых случаях индикаторы приклеиваются к опорным вставкам.
ФОТО: beton-house.comОбразец помещается под прессВнимание! Если конструкция работает в условиях повышенной влажности, требуется специальная подготовка по ГОСТ 24452-80.
Схема испытания образцов
Испытания выполняются в следующей последовательности:
- Образцы подготавливаются и с индикаторами помещаются под пресс, добиваясь совмещения осей образца и центра плиты. Назначают разрушающую нагрузку в т/м2. Величина зависит от марочной прочности бетона.
- Производят ступенчатое увеличение нагрузки с шагом 10 % от разрушающей и интервалом 4-5 минут.
- Доводят значение до 40-45 % от максимального. При отсутствии дополнительных требований приборы снимают, а дальнейшее нагружение выполняют с постоянной скоростью.
- Результаты для каждого образца обрабатывают, когда нагрузка составляет 30 % от разрушающей. Данные отображаются в журнале испытаний.
По проведенным исследованиям определяют начальный модуль упругости Еб. Нормативные значения для каждого класса содержатся в таблицах со строительными нормами и маркировке изделия. Для В15, В20, В25, В30, полученного в условиях естественного твердения, коэффициент равен 23, 27, 30, 32,5 МПа×10-3 соответственно, в условиях термической обработки – 25, 24,5, 27, 29.
ФОТО: studfile.netНагрузка повышается ступенчатоНеразрушающий ультразвуковой способ
Механический способ предполагает выемку образца из уже готовой конструкции. Это не всегда удобно и сопряжено с рядом трудностей. Ультразвуковой способ позволяет обойтись без локального разрушения. В условиях повышенной влажности погрешность составляет 15 -75 % из-за более высокой скорости распространения ультразвуковых волн в водной среде. Существует метод, позволяющий найти значение при различной влажности материала. Испытания проводятся на образцах, имеющих различную водонасыщенность.
Для нахождения нормативных и расчётных значений используют корректирующие коэффициенты, учитывая соответствующие значения. Методика приведена в СП 63.13330.2012.
Делитесь в комментариях, какому методу определения модуля упругости бетона вы доверяете больше всего и каким приходилось пользоваться.
ПОНРАВИЛАСЬ СТАТЬЯ? Поддержите нас и поделитесь с друзьями
Таблица. Значения модулей продольных упругостей Е, модулей сдвигов G и коэффициентов Пуассона µ (при температуре 20oC).
| |||
Модуль упругости
Модуль упругости или модуль упругости — это математическое описание тенденции объекта или вещества к упругой деформации (т. Е. Непостоянно) при приложении к нему силы. Модуль упругости объекта определяется как наклон его кривой напряжения-деформации в области упругой деформации: [1] Таким образом, более жесткий материал будет иметь более высокий модуль упругости.
где лямбда ( λ ) — модуль упругости; напряжение — это восстанавливающая сила, вызванная деформацией, деленная на площадь, к которой приложена сила; и деформация — отношение изменения, вызванного напряжением, к исходному состоянию объекта.Если напряжение измеряется в паскалях, поскольку деформация является безразмерной величиной, то единицы λ также являются паскалями. [2]
Поскольку знаменатель становится равным единице, если длина удваивается, модуль упругости становится напряжением, индуцированным в материале, когда образец материала поворачивается в два раза больше своей исходной длины при приложении внешней силы. Хотя эта конечная точка нереальна, потому что большинство материалов выйдет из строя до ее достижения, она практична, поскольку небольшие доли определяющей нагрузки будут работать в точно таком же соотношении.Таким образом, для стали с модулем Юнга 30 миллионов фунтов на квадратный дюйм нагрузка в 30 тысяч фунтов на квадратный дюйм удлинит 1-дюймовый стержень на одну тысячную дюйма; аналогично для метрических единиц, где тысячная часть модуля в гигапаскалях изменит метр на миллиметр.
Указание способа измерения напряжения и деформации, включая направления, позволяет определять многие типы модулей упругости. Три основных:
- Модуль Юнга ( E ) описывает упругость при растяжении или тенденцию объекта к деформации вдоль оси, когда вдоль этой оси действуют противоположные силы; он определяется как отношение напряжения растяжения к деформации растяжения.Его часто называют просто модулем упругости .
- Модуль сдвига или модуль жесткости ( G или) описывает тенденцию объекта к сдвигу (деформация формы при постоянном объеме) под действием противодействующих сил; он определяется как напряжение сдвига по сравнению с деформацией сдвига. Модуль сдвига является частью определения вязкости.
- Модуль объемной упругости ( K ) описывает объемную упругость или тенденцию объекта к деформации во всех направлениях при равномерной нагрузке во всех направлениях; она определяется как объемное напряжение по сравнению с объемной деформацией и является обратной величиной сжимаемости.Объемный модуль — это расширение модуля Юнга до трех измерений.
Три других модуля упругости — это коэффициент Пуассона, первый параметр Ламе и модуль продольной волны.
Однородные и изотропные (похожие во всех направлениях) материалы (твердые тела) имеют свои (линейные) упругие свойства, полностью описываемые двумя модулями упругости, и можно выбрать любую пару. Учитывая пару модулей упругости, все остальные модули упругости можно рассчитать по формулам, приведенным в таблице ниже в конце страницы.
Невязкие жидкости отличаются тем, что они не выдерживают напряжения сдвига, а это означает, что модуль сдвига всегда равен нулю. Это также означает, что модуль Юнга всегда равен нулю.
См. Также
Список литературы
Дополнительная литература
- Hartsuijker, C .; Веллеман, Дж. (2001). Инженерная механика . 2 . Springer. ISBN 978-1-4020-4123-5.
Измерение модуля упругости
Применение:
Измерение модуля Юнга, модуля упругости при сдвиге и коэффициента Пуассона в недисперсных изотропных технических материалах.
Задний план:
Модуль упругости Юнга определяется как отношение напряжения (силы на единицу площади) к соответствующей деформации (деформации) в материале при растяжении или сжатии.
Модуль упругости при сдвиге аналогичен отношению напряжения к деформации в материале, подверженном напряжению сдвига.
Коэффициент Пуассона — это отношение поперечной деформации к соответствующей осевой деформации материала, напряженного вдоль одной оси.
Эти основные свойства материала, которые представляют интерес для многих производственных и исследовательских приложений, могут быть определены с помощью расчетов на основе измеренных скоростей звука и плотности материала. Скорость звука можно легко измерить с помощью ультразвуковых эхо-импульсных методов с соответствующим оборудованием. Общая процедура, описанная ниже, действительна для любого однородного, изотропного, недисперсного материала (скорость не меняется с частотой). Сюда входят наиболее распространенные металлы, промышленная керамика и стекло, если размеры поперечного сечения не близки к длине волны тестовой частоты.Жесткие пластмассы, такие как полистирол и акрил, также могут быть измерены, хотя это сложнее из-за более высокого затухания звука.
Резина не может быть охарактеризована ультразвуком из-за ее высокой дисперсии и нелинейных упругих свойств. Мягкие пластмассы также демонстрируют очень высокое затухание в режиме сдвига и на практике обычно не могут быть протестированы. В случае анизотропных материалов упругие свойства меняются в зависимости от направления, а также скорость звука продольной и / или поперечной волны.Для создания полной матрицы модулей упругости в анизотропных образцах обычно требуется шесть различных наборов ультразвуковых измерений. Пористость или крупная зернистость материала могут повлиять на точность измерения модуля ультразвука, так как эти условия могут вызывать изменения скорости звука в зависимости от размера и ориентации зерен или размера и распределения пористости, независимо от эластичности материала.
Оборудование:
Измерения скорости для расчета модуля обычно выполняются с помощью прецизионных толщиномеров, таких как модели 38DL PLUS и 45MG с программным обеспечением Single Element, или дефектоскопа с возможностью измерения скорости, такого как приборы серии EPOCH.Импульсный генератор / приемник, например модель 5072PR или 5077PR, также можно использовать с осциллографом или оцифровщиком сигналов для измерения времени прохождения. Для этого испытания также требуются два преобразователя, соответствующие испытуемому материалу, для измерения скорости звука в режиме эхо-импульса в продольном и поперечном режимах. Обычно используемые преобразователи включают широкополосный преобразователь продольной волны M112 или V112 (10 МГц) и преобразователь поперечной волны нормального падения V156 (5 МГц). Они подходят для многих обычных образцов металла и обожженной керамики.Для очень толстых, очень тонких или сильно ослабляющих образцов потребуются разные преобразователи. В некоторых случаях может также потребоваться использование методов сквозной передачи, когда пары преобразователей расположены на противоположных сторонах детали. Во всех случаях рекомендуется, чтобы пользователь консультировался с Olympus для получения конкретных рекомендаций по датчику и помощи в настройке прибора.
Испытуемый образец может иметь любую геометрию, которая позволяет точно измерять импульс / эхо времени прохождения звука через сечение по толщине.В идеале это должен быть образец толщиной не менее 0,5 дюйма (12,5 мм) с гладкими параллельными поверхностями и шириной или диаметром больше диаметра используемого преобразователя. Следует соблюдать осторожность при испытании узких образцов из-за возможных краевых эффектов, которые могут повлиять на измеренное время прохождения импульса. При использовании очень тонких образцов разрешение будет ограничено из-за небольших изменений времени прохождения импульса по коротким звуковым путям. По этой причине мы рекомендуем, чтобы образцы были не менее 0,2 дюйма.(5 мм) толщиной, желательно толще. Во всех случаях необходимо точно знать толщину испытуемого образца.
Процедура:
Измерьте скорость звука продольной и поперечной волны в испытуемом образце, используя соответствующие преобразователи и настройку прибора. Измерение поперечной волны потребует использования специального связующего вещества с высокой вязкостью, такого как SWC. Модель 38DL PLUS, толщиномер 45MG может обеспечивать прямое считывание скорости материала на основе введенной толщины образца, а дефектоскоп серии EPOCH может измерять скорость с помощью процедуры калибровки скорости.В любом случае следуйте рекомендуемой процедуре измерения скорости, как описано в руководстве по эксплуатации прибора. При использовании генератора / приемника просто запишите время прохождения в оба конца через область известной толщины с помощью датчиков продольных и поперечных волн и вычислите:
Преобразуйте единицы, если необходимо, чтобы получить скорости, выраженные в дюймах в секунду или сантиметрах в секунду. (Время обычно измеряется в микросекундах, поэтому умножьте единицы / мкс или см / мкс на 10 6 , чтобы получить дюйм / см или см / с.Полученные таким образом скорости можно подставить в следующие уравнения.
Примечание к единицам измерения: если скорость звука выражена в см / с, а плотность — в г / см 3 , то модуль Юнга будет выражен в единицах дин / см 2 . Если для вычисления модуля в фунтах на квадратный дюйм (PSI) используются английские единицы дюйм / с и фунт / дюйм 3 , помните о различии между «фунтом» как единицей силы и единицей массы. Поскольку модуль выражается как сила на единицу площади, при вычислении в английских единицах необходимо умножить решение вышеуказанного уравнения на константу преобразования массы / силы (1 / Ускорение силы тяжести), чтобы получить модуль в фунтах на квадратный дюйм.В качестве альтернативы, если первоначальный расчет выполняется в метрических единицах, используйте коэффициент преобразования 1 фунт / кв. Дюйм = 6,89 x 10 4 дин / см 2 . Другой вариант — ввести скорость в дюймах / с, плотность в г / см 3 и разделить на коэффициент преобразования 1,07 x 10 4 , чтобы получить модуль упругости в фунтах на квадратный дюйм.
Для определения модуля сдвига просто умножьте квадрат скорости поперечной волны на плотность.
Опять же, используйте единицы см / С и г / см 3 , чтобы получить модуль в дин / см 2 или английские единицы дюйм / с и фунт / дюйм 3 и умножьте результат на преобразование массы / силы. постоянный.
Библиография
Для получения дополнительной информации об ультразвуковом измерении модуля упругости обратитесь к следующему:
1. Мур, П. (ред.), Справочник по неразрушающему контролю, Том 7, Американское общество неразрушающего контроля, 2007, стр. 319-321.
2. Крауткрамер, Дж., Х. Крауткрамер, Ультразвуковой контроль материалов , Берлин, Гейдельберг, Нью-Йорк 1990 (четвертое издание), стр. 13-14, 533-534.
15. МОДУЛЬ УПРУГОСТИ — Скачать PDF бесплатно
Стресс-деформационные отношения
Взаимоотношения напряжений и деформаций Испытания на растяжение Одним из основных ингредиентов в изучении механики деформируемых тел являются резистивные свойства материалов.Эти свойства относятся к напряжениям
Дополнительная информацияДАТЧИК ДАВЛЕНИЯ ДАТЧИКА
ДАТЧИК ДАТЧИКА ДАВЛЕНИЯ ДАТЧИКА ДАВЛЕНИЯ В датчиках давления используются различные чувствительные устройства, обеспечивающие электрический выходной сигнал, пропорциональный приложенному давлению. Чувствительное устройство, используемое в преобразователях
Дополнительная информацияЛаборатория испытаний на растяжение
Лаборатория испытаний на растяжение Стефан Фавилла 0723668 ME 354 AC Дата представления лабораторного отчета: 11 февраля 2010 г. Дата лабораторных испытаний: 28 января 2010 г. 1 Краткое содержание Испытания на растяжение являются фундаментальными
Дополнительная информацияЗатвердевший бетон.Лекция № 14
Лекция по затвердевшему бетону № 14 Прочность бетона Прочность бетона обычно считается его наиболее ценным свойством, хотя во многих практических случаях и другие характеристики, такие как долговечность
Дополнительная информацияМАТЕРИАЛЫ И МЕХАНИКА ГИБКИ
ГЛАВА Проектирование железобетона Пятое издание МАТЕРИАЛЫ И МЕХАНИЗМЫ ИЗГИБА Школа инженерии А. Дж. Ларка, инженерная и экологическая инженерия, Часть I, Проектирование и анализ бетона b ОСЕНЬ
Дополнительная информацияВведение в балки
ГЛАВА Расчет конструкционной стали Метод LRFD ВВЕДЕНИЕ В БАЛКИ Третье издание A.Инженерная школа Дж. Кларка Департамент гражданского и экологического строительства Часть II Проектирование и анализ металлоконструкций
Дополнительная информацияСВОЙСТВА МАТЕРИАЛОВ
1 СВОЙСТВА МАТЕРИАЛОВ 1.1 СВОЙСТВА МАТЕРИАЛОВ Различные материалы обладают разными свойствами в разной степени и, следовательно, ведут себя по-разному в данных условиях. Эти объекты
Дополнительная информацияКЕРАМИКА: Свойства 2
КЕРАМИКА: Свойства 2 (Анализ хрупкого разрушения) S.К. БЕЙН, 1 J.Y. Томпсон 2 1 Школа стоматологии Мичиганского университета, Анн-Арбор, Мичиган, 48109-1078 [email protected] 2 Юго-восточный стоматологический колледж Нова
Дополнительная информацияИспытание стали на растяжение
C 265 Лаборатория № 2: Испытание стали на растяжение См. Типичный формат отчета на веб-сайте, включая: TITL PAG, ABSTRACT, TABL OF CONTNTS, LIST OF TABL, LIST OF FIGURS 1.0 — INTRODUCTION See General Lab Report Format
Дополнительная информацияσ y (ε f, σ f) (ε f
Типичные кривые напряжение-деформация для мягкой стали и алюминиевого сплава по результатам испытаний на растяжение LL (1 + ε) A = — A uu 0 1 E l Излом мягкой стали u (ε f, f) (ε f, f) ε 0 ε 0.2 = 0,002 излом алюминиевого сплава
Дополнительная информацияОБЪЯСНЕНИЕ СОВМЕСТНЫХ ДИАГРАММ
ОБЪЯСНЕНИЕ СХЕМ СОЕДИНЕНИЙ Когда болтовые соединения подвергаются внешним растягивающим нагрузкам, какие силы и упругая деформация действительно существуют? Большинство инженеров в производстве крепежа
Дополнительная информацияСвойства материалов
ГЛАВА 1 Свойства материалов ВВЕДЕНИЕ Материалы являются движущей силой технологических революций и ключевыми ингредиентами производства.Материалы повсюду вокруг нас, и
Дополнительная информацияПРАКТИЧЕСКИЕ ИСПЫТАНИЯ НА РАСТЯЖЕНИЕ
ПРАКТИЧЕСКИЕ ИСПЫТАНИЯ НА РАСТЯЖЕНИЕ MTK 2B — Наука о материалах Ts epo Mputsoe 215024596 Резюме Материалы обладают различными свойствами, от механических до химических. Особый интерес к
Дополнительная информацияДолговременные характеристики полимеров
1.0 Введение Долговременные характеристики полимеров Полимерные материалы показывают поведение в зависимости от времени. Напряжение и деформация, возникающие при приложении нагрузки, зависят от времени. В самом общем виде
Дополнительная информацияПОДХОД STRAIN-LIFE (e -N)
ПОДХОД ЦИКЛИЧЕСКОЙ ДЕФОРМАЦИИ И ДЕФОРМАЦИИ (e -N) ИСПЫТАНИЕ НА МОНОТОННОЕ НАПРЯЖЕНИЕ И МЕТОДЫ ИСПЫТАНИЙ НА ДЕФОРМАЦИЮ С УПРАВЛЕНИЕМ НА ДЕФОРМАЦИЮ ЦИКЛИЧЕСКУЮ ДЕФОРМАЦИЮ И НАПРЯЖЕНИЕ-ДЕФОРМАЦИЮ НА ОСНОВЕ НАПРЯЖЕНИЯ ПОДХОД К
Дополнительная информацияТехнология измерения веса
Kistler-Morse (KM) представила системы измерения веса на болтах три десятилетия назад.В этих устройствах использовалось изобретение Уолтера Кистлера — Microcell. За прошедшие годы в Microcell
было внесено множество улучшений. Дополнительная информацияСверхминиатюрный тензодатчик модели 8417
w Техническая информация о продукте Сверхминиатюрный датчик веса 1. Введение … 2 2. Подготовка к использованию … 2 2.1 Распаковка … 2 2.2 Первое включение прибора … 2 2.3 Заземление и подключение потенциала …
Дополнительная информацияAPE T углепластик Аслан 500
Полимерная лента, армированная углеродным волокном (CFRP), используется для структурного усиления бетона, кирпичной кладки или деревянных элементов с использованием техники, известной как укрепление на поверхности или NSM.Использование CFRP
Дополнительная информацияИзгибающее напряжение в балках
936-73-600 Напряжение изгиба в балке Вывести зависимость для напряжения изгиба в балке: Основные допущения :. Прогибы очень малы по сравнению с глубиной балки. Плоские разрезы перед гибкой
Дополнительная информацияАнализ структурной целостности
Анализ структурной целостности 1.КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ Игорь Кокчаров 1.1 НАПРЯЖЕНИЯ И КОНЦЕНТРАТОРЫ 1.1.1 Напряжение Приложенная внешняя сила F вызывает внутренние силы в несущей конструкции. Внутренние силы
Дополнительная информацияРешение для домашнего задания №1
Решение домашнего задания № 1 Глава 2: вопросы с несколькими вариантами ответа (2.5, 2.6, 2.8, 2.11) 2.5 Какие из следующих типов облигаций классифицируются как первичные облигации (более одной)? (а) ковалентная связь, (б) водород
Дополнительная информация8.2 Энергия упругой деформации
Раздел 8. 8. Энергия упругой деформации. Энергия деформации, запасенная в упругом материале при деформации, рассчитывается ниже для ряда различных геометрических форм и условий нагружения. Эти выражения для
Дополнительная информацияTSL профессиональные услуги
Отчет для: Лаборатория №: 402876-05 5375 Эджуэй Драйв, АЛЛЕНДЕЙЛ, Мичиган, США Дата отчета: 21 декабря 2005 г. 49401 Дата получения: 3 ноября 2005 г. Телефон: 616 875 7725 Факс: 616 875 6009 Заказчик П.О. #: COD
Дополнительная информацияМодуль упругости — Infogalactic: ядро планетарных знаний
Модуль упругости (также известный как модуль упругости , модуль упругости при растяжении или модуль Юнга ) — это число, которое измеряет величину объекта или вещества. сопротивление упругой деформации (т. е. непостоянно) при приложении к нему силы. Модуль упругости объекта определяется как наклон его кривой напряжение – деформация в области упругой деформации: [1] Более жесткий материал будет иметь более высокий модуль упругости.Модуль упругости имеет вид.
, где напряжение — это сила, вызывающая деформацию, деленная на площадь, к которой приложена сила, а деформация — это отношение изменения некоторого параметра длины, вызванного деформацией, к исходному значению параметра длины. Если напряжение измеряется в паскалях, то, поскольку деформация является безразмерной величиной, единицы λ также будут паскалями. [2] Антоним эластичности — «Соответствие».
Поскольку деформация равна единице для объекта, длина которого увеличилась вдвое, модуль упругости равен напряжению, вызванному в материале удвоением длины. Хотя этот сценарий, как правило, нереалистичен, поскольку большинство материалов выйдет из строя, не дойдя до него, он дает эвристические рекомендации, поскольку небольшие доли определяющей нагрузки будут работать в точно таком же соотношении. Таким образом, для стали с модулем Юнга 30 миллионов фунтов на квадратный дюйм нагрузка в 30 тысяч фунтов на квадратный дюйм удлинит 1-дюймовый стержень на одну тысячную дюйма; аналогично, для метрических единиц нагрузка в одну тысячную модуля (теперь измеряется в гигапаскалях) изменит длину метрового стержня на миллиметр.
В общем описании, поскольку и напряжение, и деформация описываются тензорами второго ранга, включая компоненты растяжения и сдвига, тензор упругости является тензором четвертого ранга с до 21 независимой константой.
Указание способа измерения напряжения и деформации, включая направления, позволяет определять многие типы модулей упругости. Три основных:
- Модуль Юнга ( E ) описывает упругость при растяжении или тенденцию объекта к деформации вдоль оси, когда вдоль этой оси действуют противоположные силы; он определяется как отношение напряжения растяжения к деформации растяжения.Его часто называют просто модулем упругости .
- Модуль сдвига или модуль жесткости ( G или) описывает тенденцию объекта к сдвигу (деформация формы при постоянном объеме) под действием противодействующих сил; он определяется как напряжение сдвига по сравнению с деформацией сдвига. Модуль сдвига является частью определения вязкости.
- Модуль объемной упругости ( K ) описывает объемную упругость или тенденцию объекта к деформации во всех направлениях при равномерной нагрузке во всех направлениях; она определяется как объемное напряжение по сравнению с объемной деформацией и является обратной величиной сжимаемости.Объемный модуль — это расширение модуля Юнга до трех измерений.
Три других модуля упругости — это осевой модуль, первый параметр Ламе и модуль продольной волны.
Однородные и изотропные (похожие во всех направлениях) материалы (твердые тела) имеют свои (линейные) упругие свойства, полностью описываемые двумя модулями упругости, и можно выбрать любую пару. Учитывая пару модулей упругости, все остальные модули упругости можно рассчитать по формулам, приведенным в таблице ниже в конце страницы.
Невязкие жидкости отличаются тем, что они не выдерживают напряжения сдвига, а это означает, что модуль сдвига всегда равен нулю. Это также означает, что модуль Юнга всегда равен нулю.
В некоторых текстах на английском языке описанная здесь величина называется постоянной упругости , а обратная величина обозначается как модуль упругости .
См. Также
Список литературы
- ↑ Askeland, Donald R .; Фуле, Прадип П. (2006). Материаловедение и инженерия (5-е изд.). Cengage Learning. п. 198. ISBN 978-0-534-55396-8 .
- ↑ Beer, Ferdinand P .; Джонстон, Э. Рассел; Девольф, Джон; Мазурек, Дэвид (2009). Механика материалов . Макгроу Хилл. п. 56. ISBN 978-0-07-015389-9 .
Дополнительная литература
- Hartsuijker, C.; Веллеман, Дж. У. (2001). Инженерная механика . Том 2. Спрингер. ISBN 978-1-4020-4123-5 .
- Де Йонг, Маартен; Чен, Вэй (2015). «Схема полных упругих свойств неорганических кристаллических соединений». Научные данные . 2 : 150009. DOI: 10.1038 / sdata.2015.9.
Модуль упругости бетона — определение и важность при проектировании
Модуль упругости бетона (Ec) определяется как отношение приложенного напряжения к соответствующей деформации.Он не только демонстрирует способность бетона противостоять деформации из-за приложенного напряжения, но и его жесткость. Другими словами, он отражает способность бетона упруго отклоняться. Модуль упругости бетона зависит от пропорций заполнителя и смеси бетона.
При проектировании бетонных конструкций очень важен модуль упругости, который требует определения. Линейный расчет элементов, основанный на теории упругости, используется в некоторых случаях для удовлетворения требований предельного состояния по прочности и пригодности к эксплуатации, например, при проектировании предварительно напряженных бетонных конструкций.
Общие применимые нормы по всему миру, такие как Кодекс ACI, Европейский Кодекс, Британские стандарты, Канадская ассоциация стандартов и Индийский стандарт, предоставили формулу для расчета модуля упругости бетона.
Расчет модуля упругости бетона
Расчет модуля упругости бетона с использованием уравнений различных кодов представлен ниже:
1. Модуль упругости на основе ACI 318-14
Согласно ACI 318-14 раздел 19.2.2 модуль упругости бетона оценивается следующим образом:
Для бетона удельный вес (wc) колеблется от 1440 до 2560 кг на кубический метр.
Для бетона с нормальным весом:
2. Модуль упругости на основе CSA
Модуль упругости для бетона с нормальным весом согласно Канадской ассоциации стандартов (CSA A23.3):
Для высокопрочного бетона:
3. Модуль упругости согласно EC
.Модуль упругости бетона по Еврокоду можно оценить с помощью следующего выражения:
Где,
Ecm: средний модуль упругости
фут · см: средняя прочность бетона на сжатие через 28 дней в соответствии с таблицей 3.1 BS EN 1992-1-1: 2004
4. Модуль упругости согласно британскому стандарту
Значение модуля упругости при 28-дневном возрасте бетона приведено в BS 8110: Часть II 1985:
.Где:
ko: составляет 20 кН на квадратный миллиметр для нормального бетона
fcu, 28: прочность бетона на сжатие через 28 дней.
5. Модуль упругости согласно IS 456
Модуль упругости бетона по индийскому стандарту можно рассчитать с помощью следующего выражения:
Важность проектирования бетонных конструкций
Очень важно определить модуль упругости бетона при проектировании бетонной конструкции.Линейный анализ элементов, основанный на теории упругости, используется для удовлетворения требований как к пределу прочности, так и к предельному состоянию по пригодности к эксплуатации, например, в случае предварительно напряженного бетона, который демонстрирует сечение без трещин вплоть до разрушения.
В дополнение к расчету прогибов, которые должны быть ограничены в соответствии с требованиями эксплуатационной пригодности для всех конструкций. Наконец, знание модуля упругости высокопрочного бетона очень важно для предотвращения чрезмерной деформации, обеспечения удовлетворительной эксплуатационной пригодности и избегания наиболее экономичных конструкций.
Испытания пластмасс на растяжение
Испытания пластмасс на растяжение
Предел прочности на разрыв
Способность противостоять разрушению при растягивающем напряжении — одно из наиболее важных и широко измеряемых свойств материалов, используемых в конструкциях. Сила на единицу площади (МПа или фунт / кв. Дюйм), необходимая для разрушения материала таким образом, составляет предел прочности на разрыв или предел прочности на разрыв .Скорость, с которой образец разрывается в испытании, может варьироваться от 0,2 до 20 дюймов в минуту и будет влиять на результаты. Аналогичным испытанием для измерения свойств на растяжение в системе ISO является ISO 527. Значения, указанные в испытаниях ASTM D638 и ISO 527, в целом существенно не различаются, и любое испытание даст хорошие результаты на ранних этапах процесса выбора материала. Для полимерных пленок (ASTM D882 или ISO 1184) и эластомеров (ASTM D412 или ISO 37) обычно применяются отдельные методы испытаний на растяжение.
На приведенном ниже рисунке из компании Quadrant Engineering Plastic Products показана геометрия испытания.
ASTM D638:Для этого испытания образцы пластика либо обрабатываются механической обработкой из заготовок, либо отливаются под давлением. Машина для испытания на растяжение вытягивает образец с обоих концов и измеряет усилие, необходимое для разрыва образца, а также степень растяжения образца перед разрушением.
Относительное удлинение при растяжении
Предельное удлинение инженерного материала — это процентное увеличение длины, которое происходит до того, как он разорвется при растяжении.Предельные значения удлинения в несколько сотен процентов являются обычными для эластомеров и полиолефинов пленки / упаковки. Жесткие пластмассы, особенно армированные волокном, часто имеют значения менее 5%. Сочетание высокого предела прочности на разрыв и большого удлинения позволяет получать материалы с высокой вязкостью.
Модуль упругости при растяжении
Модуль упругости — это отношение напряжения к упругой деформации при растяжении. Высокий модуль упругости означает, что материал жесткий — требуется большее напряжение для создания заданной величины деформации.В полимерах модуль упругости при растяжении и модуль сжатия могут быть близкими или широко варьироваться. Это изменение может составлять 50% или более, в зависимости от типа смолы, армирующих агентов и методов обработки. Модули растяжения и сжатия металлов часто очень близки.
В таблице ниже приведены значения среднего предела прочности на разрыв, удлинения при разрыве и модулей растяжения для некоторых наполненных и ненаполненных полимеров.