Чем отличается вес от массы
В современной науке вес и масса — разные понятия. Вес — сила, с которой тело действует на горизонтальную опору или вертикальный подвес. Масса же — мера инертности тела.
Масса измеряется в килограммах, а вес в ньютонах. Вес — это произведение массы на ускорение свободного падения (P = mg). Значение веса (при неизменной массе тела) пропорционально ускорению свободного падения, которое зависит от высоты над земной (или другой планеты) поверхностью. А если, еще точнее, то вес — это частное определение 2-го закона Ньютона — сила равна произведению массы на ускорение (F=ma). Поэтому его и вычисляют в Ньютонах, как все силы.
Масса — вещь постоянная, а вес, строго говоря, зависит, например, от высоты, на которой тело находится. Известно, что с увеличением высоты ускорение свободного падения падает, соответственно уменьшается и вес тела, при одних и тех же условиях измерения.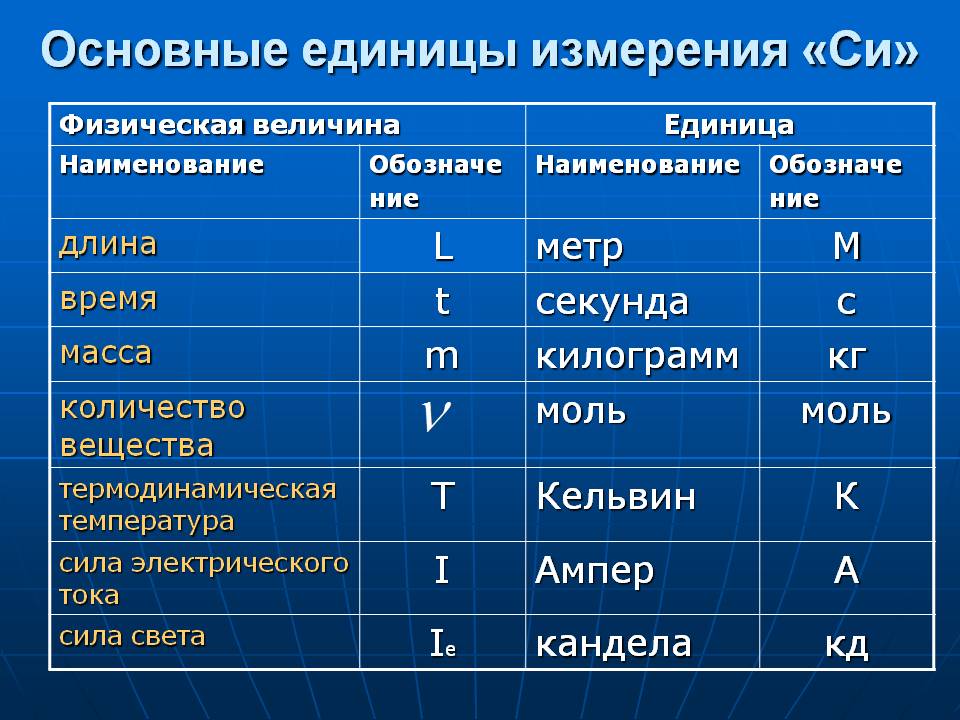
Например, в условиях невесомости у всех тел вес равен нулю, а масса у каждого тела своя. И если в состоянии покоя тела показания весов будут нулевыми, то при ударе по весам тел с одинаковыми скоростями воздействие будет разным.
Интересно, что в результате суточного вращения Земли существует широтное уменьшение веса: на экваторе примерно на 0,3 % меньше, чем на полюсах.
И все же строгое различение понятий веса и массы принято в основном в физике, а во многих повседневных ситуациях слово «вес» продолжает использоваться, когда фактически речь идет о «массе». Кстати видя на товаре надписи: «масса нетто» и «масса брутто» не пугайтесь, НЕТТО — чистая масса продукта, а БРУТТО — масса с упаковкой.
Строго говоря, при походе на рынок, обращаясь к продавцу, следовало бы говорить: «Взвесьте, пожалуйста, килограммчик»…» или «Дайте ка 2 ньютона докторской колбасы». Конечно, термин «вес» уже прижился, как синоним термина «масса», но это не избавляет от необходимости понимать, что это вовсе не одно и то же.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Что такое килограмм
Килограмм — единица массы, одна из основных единиц системы СИ
Килограмм обозначается как кг
Килограм это то масса международного образца (валик высотой 39 мм, выполненный из сплава 90 % платины и 10 % иридия), хранящийся в Международном бюро мер в Севре, около Парижа. Образец килограмма был установлен Первой генеральной конференцией мер в 1889 году. Первоначально образец был приравнен к одному литру воды температурой 4 градуса Цельсия, при нормальном давлении.
В ежедневном использовании, масса объекта, заданного в килограммах, часто упоминается как его вес, который является мерой силы тяжести. Вес в килограммах технически не входит в список единиц СИ, а единица измерения для веса известна как килограмм-сила. Эквивалентной единицей измерения силы тяжести является фунт-сила. В строгом научном контексте, сила, как правило, измеряется единицей СИ ньютон.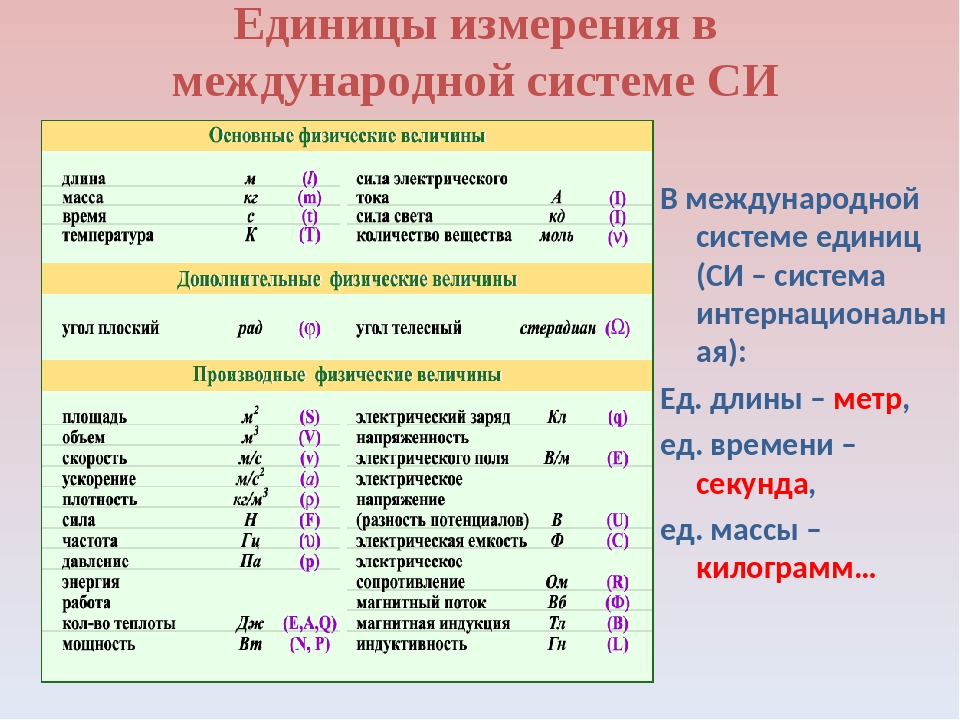
Килограмм является единственной базовой единицей СИ с приставкой в рамках своего имени. Кроме того, это единственная единица СИ, которая до сих пор непосредственно определяется артефактом, а не фундаментальными физическими свойствами, которые могут быть изучены в разных лабораториях. Четыре из семи базовых величин в системе СИ определяются по отношению к килограмму, поэтому её полная стабильность очень важна.
1 килограмм = 1000 грамм
Кратные и дольные единицы
По историческим причинам, название «килограмм» уже содержит десятичную приставку «кило», поэтому кратные и дольные единицы образуют, присоединяя стандартные приставки СИ к названию или обозначению единицы измерения «грамм» (которая в системе СИ сама является дольной: 1 г = 10−3 кг).
Вместо мегаграмма (1000 кг), как правило, используют единицу измерения «тонна».
В определениях мощности атомных бомб в тротиловом эквиваленте вместо гигаграмма применяется килотонна, вместо тераграмма — мегатонна.
| Кратные | Дольные | ||||||
|---|---|---|---|---|---|---|---|
| величина | название | обозначение | величина | название | обозначение | ||
| 101 г | декаграмм | даг | dag | 10−1 г | дециграмм | дг | dg |
| 102 г | гектограмм | гг | hg | 10 |
сантиграмм | сг | cg |
| 103 г | килограмм | кг | kg | 10−3 г | миллиграмм | мг | mg |
| 106 г | мегаграмм | Мг | Mg | 10−6 г | микрограмм | мкг | µg |
| 109 г | гигаграмм | Гг | Gg | 10−9 г | нанограмм | нг | ng |
| 1012 г | тераграмм | Тг | Tg | 10−12 г | пикограмм | пг | pg |
| 1015 г | петаграмм | Пг | Pg | 10−15 г | фемтограмм | фг | fg |
| 1018 г | эксаграмм | Эг | Eg | 10−18 г | аттограмм | аг | ag |
| 1021 г | зеттаграмм | Зг | Zg | 10−21 г | зептограмм | зг | zg |
| 1024 г | иоттаграмм | Иг | Yg | 10−24 г | иоктограмм | иг | yg |
| применять не рекомендуется не применяются или редко применяются на практике | |||||||

Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Вес тела 🐲 СПАДИЛО.РУ
ОпределениеВес тела — сила, с которой тело вследствие притяжения к Земле давит на опору или растягивает подвес.
Вес тела имеет электромагнитную природу (не путать с силой тяжести — она возникает между двумя телами и имеет гравитационную природу!). Обозначается P. Измеряется динамометром. Единица измерения — Н (Ньютон).
Вес имеет направление, противоположное силе реакции опоры или силе натяжения нити. Точкой приложения веса является точка опоры или подвеса: P↑↓N или P↑↓T.
Согласно III закону Ньютона модуль веса тела определяется одной из следующих формул:
P = T; P = N; P = Fупр.
Если тело и опора или подвес неподвижны, то модули силы реакции опоры, силы натяжения подвеса, а также силы упругости равны модулю силы тяжести. Поэтому в неподвижной системе модуль веса неподвижного тела тоже равен модулю силы тяжести:
P0 = Fтяж = mg
Если тело находится в состоянии невесомости, его вес равен нулю: P = 0. Это значит, что это тело не оказывает никакого действия ни на подвес, ни на опору.
Это значит, что это тело не оказывает никакого действия ни на подвес, ни на опору.
Пример №1. Гиря массой 1 пуд стоит на полу. Определить вес гири.
Так как гиря покоится, ее вес будет равен модулю силы тяжести. 1 пуд = 16,38 кг. Следовательно:
P = mg = 16,38∙10 = 163,8 (Н)
Перегрузка
Перегрузка — отношение абсолютной величины линейного ускорения, вызванного негравитационными силами, к стандартному ускорению свободного падения на поверхности.
Перегрузка определяется отношением:
Перегрузка возникает, когда система, в которой находится тело, движется с ускорением.
Вес тела в движущейся равноускоренно системеВес тела в движущейся системе может быть больше или меньше веса того же тела в системе, которая находится в состоянии покоя:
- Если система движется равноускоренно в направлении ускорения свободного падения, вес тела меньше веса тела в неподвижной системе: при a↑↑g — P < P0.

- Если система движется равноускоренно в направлении, противоположном ускорению свободного падения, вес тела больше веса тела в неподвижной системе: при a↑↓g — P > P0.
- Если система движется с равномерной скоростью (ускорение равно нулю) в любом направлении по отношению к ускорению свободного падения, вес тела равен весу тела в неподвижной системе: при a = 0 — P = P0.
Применение законов Ньютона для определения веса тела
Опора или подвес неподвижны | |
| Второй закон Ньютона в векторной форме: N + mg = ma или T + mg = ma Проекция на ось ОУ:N – mg = 0 или T — mg = 0 | |
Ускорение опоры направлено вверх | |
| Второй закон Ньютона в векторной форме: N + mg = ma Проекция на ось ОУ:N – mg = ma Вес тела:P = N = ma + mg = m(a + g) | |
Ускорение опоры направлено вниз | |
| Второй закон Ньютона в векторной форме: N + mg = ma Проекция на ось ОУ:mg – N = ma Вес тела:P = N = mg – ma = m(g – a) | |
Вершина выпуклого моста | |
| Второй закон Ньютона в векторной форме: N + mg = maц. mg – N = m aц.с. Вес тела:P = N = mg – m aц.с. = m(g – aц.с.) | |
Нижняя точка вогнутого моста | |
| Второй закон Ньютона в векторной форме: N + mg = maц.с. Проекция на ось ОУ:N – mg = maц.с. Вес тела:P = N = maц.с. + mg = m(aц.с. + g) | |
Полный оборот на подвесе | |
| Второй закон Ньютона в векторной форме: T + mg = ma Проекция на ось ОУ в точке А:T + mg = maц.с. Вес тела в точке А:P = T = maц.с. – mg = m (aц.с. – g) Проекция на ось ОУ в точке В:T – mg = maц.с. Вес тела в точке В:P = T = maц.с. + mg = m (aц.с. + g) Важно! Центростремительное ускорение всегда направлено к центру окружности. | |
Пример №2. Автомобиль массой 1000 кг едет по выпуклому мосту с радиусом кривизны 40 м. Какую скорость должен иметь автомобиль в верхней точке моста, чтобы пассажиры в этой точке почувствовали невесомость?
Вес тела в верхней точке выпуклого моста равен:
P = m(g – aц.с.)
Чтобы пассажиры почувствовали состояние невесомости, вес тела должен быть равен 0:
m(g – aц.с.) = 0
Масса не может быть нулевой, поэтому:
g – aц.с. = 0
g = aц.с
Значит, пассажиры в верхней точке моста почувствуют невесомость, если центростремительное ускорение будет равно ускорению свободного падения. Центростремительное ускорение определяется формулой:
Отсюда скорость автомобиля в верхней точке моста должна быть равна:
Вес — это… Что такое Вес?
Вес — сила воздействия тела на опору (или подвес или другой вид крепления), препятствующую падению, возникающая в поле сил тяжести[1]. (В случае нескольких опор под весом понимается суммарная сила, действующая на все опоры; впрочем, для жидких и газообразных опор в случае погружения тела в них часто делается исключение, т. е. тогда силы воздействия тела на них исключают из веса и включают в силу Архимеда). Единица измерения веса в Международной системе единиц (СИ) — ньютон, иногда используется единица СГС — дина.
(В случае нескольких опор под весом понимается суммарная сила, действующая на все опоры; впрочем, для жидких и газообразных опор в случае погружения тела в них часто делается исключение, т. е. тогда силы воздействия тела на них исключают из веса и включают в силу Архимеда). Единица измерения веса в Международной системе единиц (СИ) — ньютон, иногда используется единица СГС — дина.
Вес P тела, покоящегося в инерциальной системе отсчёта , совпадает с силой тяжести, действующей на тело, и пропорционален массе и ускорению свободного падения в данной точке:
Значение веса (при неизменной массе тела) пропорционально ускорению свободного падения, которое зависит от высоты над земной поверхностью (или поверхностью другой планеты, если тело находится вблизи нее, а не Земли, и массы и размеров этой планеты), и, ввиду несферичности Земли, а также ввиду ее вращения (см. ниже), от географических координат точки измерения. Другим фактором, влияющим на ускорение свободного падения и, соответственно, вес тела, являются гравитационные аномалии, обусловленные особенностями строения земной поверхности и недр в окрестностях точки измерения.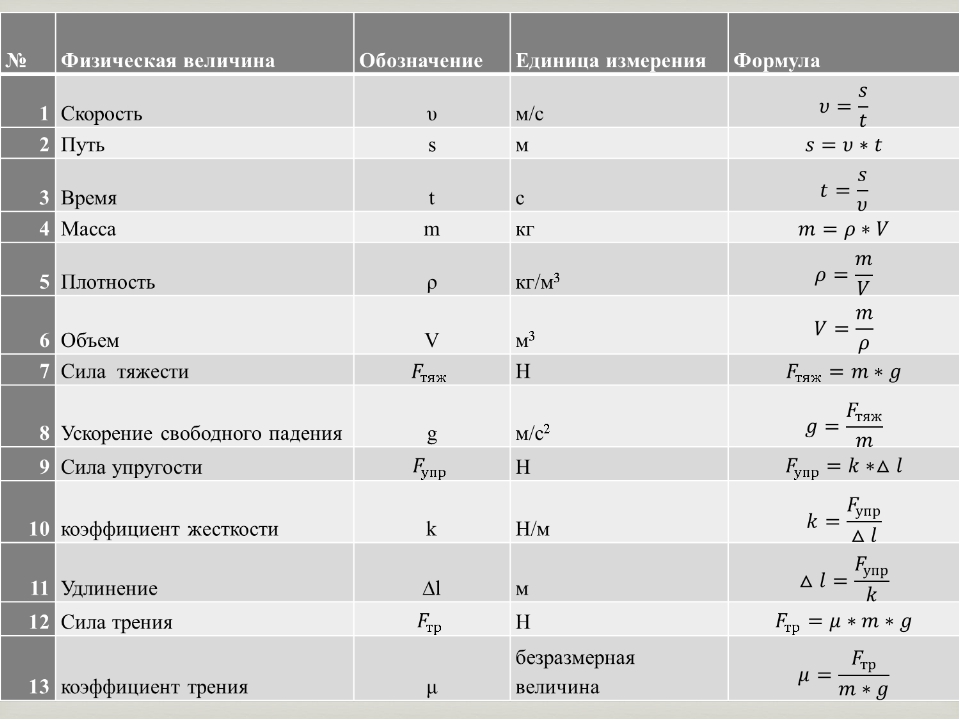
При движении системы тело — опора (или подвес) относительно инерциальной системы отсчёта c ускорением вес перестаёт совпадать с силой тяжести:
В результате суточного вращения Земли существует широтное уменьшение веса: на экваторе примерно на 0,3 % меньше, чем на полюсах.
Широтное уменьшение веса.Вес можно измерять с помощью пружинных весов, которые могут служить и для косвенного измерения массы, если их соответствующим образом проградуировать; рычажные весы в такой градуировке не нуждаются, так как в этом случае сравниваются массы, на которые действует одинаковое ускорение свободного падения или сумма ускорений в неинерциальных системах отсчёта. При взвешивании с помощью технических пружинных весов вариациями ускорения свободного падения обычно пренебрегают, так как влияние этих вариаций обычно меньше практически необходимой точности взвешивания.
На вес тела в жидкой или газообразной среде влияет также сила Архимеда, таким образом, вес тела, погружённого в среду, уменьшается на вес вытесненного объёма среды; в случае, если плотность тела меньше плотности среды, вес становится отрицательным (то есть на тело действует выталкивающая сила). Сила Архимеда может оказать влияние и на взвешивание с помощью рычажных весов, если сравниваются тела с различной плотностью.
Сила Архимеда может оказать влияние и на взвешивание с помощью рычажных весов, если сравниваются тела с различной плотностью.
Состояние отсутствия веса (невесомость) наступает при удалении тела от притягивающего объекта, либо когда тело находится в свободном падении, то есть .
Вес и масса
В современной науке вес и масса — разные понятия. Вес — сила, с которой тело действует на горизонтальную опору или вертикальный подвес. Масса же не является силовым фактором; масса — мера инертности тела. Например, в условиях невесомости у всех тел вес равен нулю, а масса у каждого тела своя. И если в состоянии покоя тела показания весов будут нулевыми, то при ударе по весам тел с одинаковыми скоростями воздействие будет разным (см. закон сохранения импульса, закон сохранения энергии).
Вместе с тем строгое различение понятий веса и массы принято в основном в физике, а во многих повседневных ситуациях слово «вес» продолжает использоваться, когда фактически речь идет о «массе».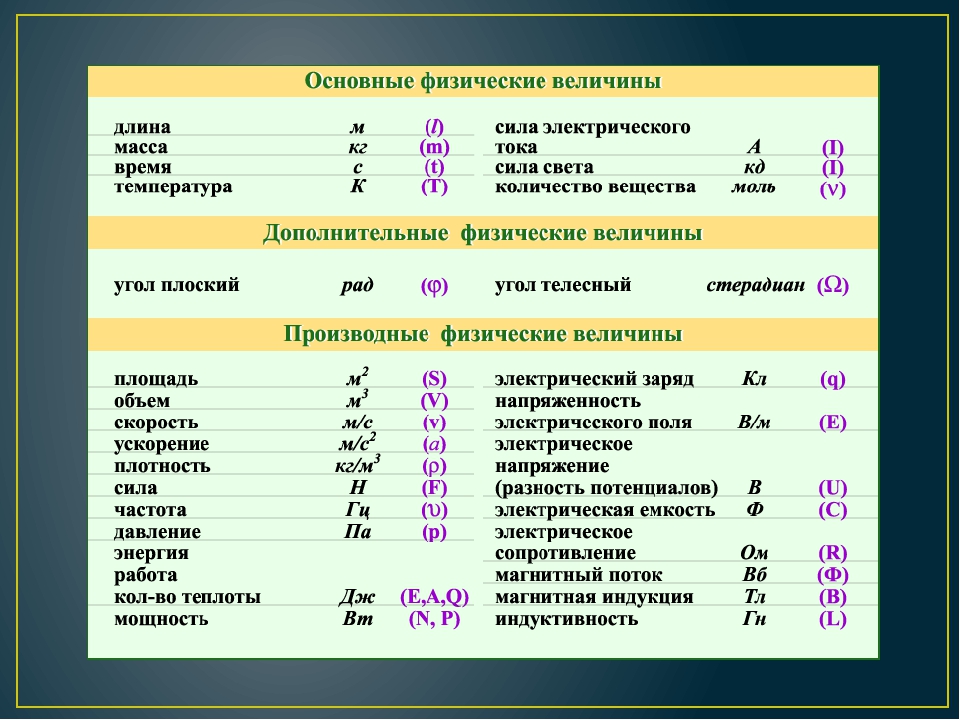 Например, мы говорим, что какой-то объект «весит один килограмм», несмотря на то, что килограмм представляет собой единицу массы. Кроме того, термин «вес» в значении «масса» традиционно используется в цикле наук о человеке — в сочетании «вес тела человека»[2][3][4].
Например, мы говорим, что какой-то объект «весит один килограмм», несмотря на то, что килограмм представляет собой единицу массы. Кроме того, термин «вес» в значении «масса» традиционно используется в цикле наук о человеке — в сочетании «вес тела человека»[2][3][4].
Примечания
См. также
Силы, действующие на самолёт
Единицы измерения массы — это… Что такое Единицы измерения массы?
Исторически многие меры веса были кратны эталону — массе зерна (семени) различных растений: пшеницы, ячменя, некоторых бобовых, риса, просо, горчицы, некоторых кактусов (в Америке)[1].
Метрическая система
- Грамм — изначально определялся как масса 1 см³ воды при температуре 4 °C и давлении в 1 атмосферу. В настоящее время грамм определяется как 1/1000 килограмма. Килограмм определяется как масса эталонного килограмма, хранящегося в Палате мер и весов около Парижа. Прототип килограмма изготовлен из платиноиридиевого сплава (Pt 90%, Ir 10%) в виде цилиндрической гири диаметром и высотой 39 мм.
 Старое определение обладало следующими недостатками:
Старое определение обладало следующими недостатками:- Определение паскаля зависит от определения килограмма, таким образом, определение было рекурсивным.
- Определение паскаля зависит от определения метра и секунды, таким образом, неточность в измерении длины и времени приводила к неточному измерению массы.
В настоящее время
- Тонна — 106 (1 000 000) граммов, или 1000 килограммов.
- Центнер — 105 (100 000) граммов, или 100 килограммов.
- Карат — 0,2 грамма.
Меры массы в науке
- Атомная единица массы (а.е.м., дальтон) = 1,660 538 921(73)·10−27 кг = 1,660 538 921(73)·10−24 г [2](в химии высокомолекулярных соединений и биохимии применяются также кратные единицы килодальтон, мегадальтон).
- Солнечная масса M☉ = 1,988 92(25)·1030 кг[3].
- Электронвольт, 1 эВ = 1,782 661 845(39)·10−36 кг[4]; применяются также кратные (килоэлектронвольт, кэВ; мегаэлектронвольт, МэВ, гигаэлектронвольт, ГэВ; тераэлектронвольт, ТэВ) и дольные (миллиэлектронвольт, мэВ) единицы.

- Масса электрона me = 9,109 382 91(40)·10−31 кг[5].
- Масса протона mp = 1,672 621 777(74)·10−27кг[6].
- Планковская единица массы MPl = 2,176 51(13)·10−8 кг[7].
(Порманиузиум)100000 пор.=100000000кг.
Американская система (см. Английская система мер)
- Стоун — 14 фунтов, или 6,35029318 кг
- фунт — 453,59237 г (точное и официальное значение)
- Унция — 1/16 фунта, или 1/224 стоуна, или 28,349523125 г
- Драхма (единица измерения массы, США) — 1/16 унции, или 1/256 фунта, или 1/3584 стоуна, или 1,7718451953125 г
- Гран — 1/98000 стоуна ,или 1/7000 фунта, или 1/437,5 унции , или 1/27,34375 драхмы , или 64,79891 мг
- Короткая тонна = 20 коротких хандредвейтов = 2000 фунтов = 0,90718474 т
- Короткий хандредвейт = 100 фунтов = 45,359237 кг
Британская аптечная система (см. Английская система мер)
Английская система мер)
- Тройский фунт (единица измерения), или аптечный фунт = 373,2417216 граммов
- Тройская унция = 1/12 тройского фунта, или 31,1034768 граммов
- Драхма (единица измерения массы, Великобритания) = 1/8 тройской унции, или 1/96 тройского фунта, или 3,8879346 граммов
- Скрупул = 1/3 драхмы, или 1/288 тройского фунта, или 1,2959782 граммов
- Гран = 1/20 скрупула, или 0,06479891 г
Русская система мер
- Берковец = 164 килограммов
- Пуд = 1/10 берковца = 40 фунтам = 1280 лотам = 3840 золотникам = 368 640 долям = 16,3804815 кг
- Фунт = 491,4 граммов
- Лот = 1/32 фунта = 3 золотникам = 288 долям = 12,797 251 191 395 300 граммам
- Золотник = 1/96 фунта = 4,26575417 г
- Доля = 1/96 золотника = 44,435 миллиграммов
Европейские меры массы (см. Английская система мер)
Английская система мер)
- Аса — Германия, Голландия = 0,048063 г
- Английская тонна (или длинная) = 1,016 т
- Тод — Англия = 12 торговых фунтов = 5,44310844 кг
- Феркин — Англия = 56 фунтов = 25,40117272кг или = 64 фунтов = 29,02991168 кг
- Хандредвейт — Англия = 112 торговых фунтов = 50,80234544 кг
- Хогсхед — Англия = 1000 фунтов = 453,6 кг
Античная
В странах Юго-Восточной Азии
Древнееврейские
Арабские
Примечания
Ссылки
| Производные величины | Символ | Описание | Единица СИ | Примечания |
|---|---|---|---|---|
| Площадь | S | Протяженность объекта в двух измерениях. | м2 | |
| Объём | V | Протяжённость объекта в трёх измерениях. | м3 | экстенсивная величина |
| Скорость | v | Быстрота изменения координат тела. | м/с | вектор |
| Ускорение | a | Быстрота изменения скорости объекта. | м/с² | вектор |
| Импульс | p | Произведение массы и скорости тела. | кг·м/с | экстенсивная, сохраняющаяся величина |
| Сила | F | Действующая на объект внешняя причина ускорения. | кг·м/с2 (ньютон, Н) | вектор |
| Механическая работа | A | Скалярное произведение силы и перемещения. | кг·м2/с2 (джоуль, Дж) | скаляр |
| Энергия | E | Способность тела или системы совершать работу. | кг·м2/с2 (джоуль, Дж) | экстенсивная, сохраняющаяся величина, скаляр |
| Мощность | P | Скорость изменения энергии. | кг·м2/с3 (ватт, Вт) | |
| Давление | p | Сила, приходящаяся на единицу площади. | кг/(м·с2) (паскаль, Па) | интенсивная величина |
| Плотность | ρ | Масса на единицу объёма. | кг/м3 | интенсивная величина |
| Поверхностная плотность | ρA | Масса на единицу площади. | кг/м2 | |
| Линейная плотность | ρl | Масса на единицу длины. | кг/м | |
| Количество теплоты | Q | Энергия, передаваемая от одного тела к другому немеханическим путём | кг·м2/с2 (джоуль, Дж) | скаляр |
| Электрический заряд | q | А·с (кулон, Кл) | экстенсивная, сохраняющаяся величина | |
| Напряжение | U | Изменение потенциальной энергии, приходящееся на единицу заряда. | м2·кг/(с3·А) (вольт, В) | скаляр |
| Электрическое сопротивление | R | сопротивление объекта прохождению электрического тока | м2·кг/(с3·А2) (ом, Ом) | скаляр |
| Магнитный поток | Φ | Величина, учитывающая интенсивность магнитного поля и занимаемую им область. | кг/(с2·А) (вебер, Вб) | |
| Частота | ν | Число повторений события за единицу времени. | с−1 (герц, Гц) | |
| Угол | α | Величина изменения направления. | радиан (рад) | |
| Угловая скорость | ω | Скорость изменения угла. | с−1 (радиан в секунду) | |
| Угловое ускорение | ε | Быстрота изменения угловой скорости | с−2 (радиан на секунду в квадрате) | |
| Момент инерции | I | Мера инертности объекта при вращении. | кг·м2 | тензорная величина |
| Момент импульса | L | Мера вращения объекта. | кг·м2/c | сохраняющаяся величина |
| Момент силы | M | Произведение силы на длину перпендикуляра, опущенного из точки на линию действия силы. | кг·м2/с2 | вектор |
| Телесный угол | Ω | стерадиан (ср) |
Как преобразовать единицы измерения в физике
- Образование
- Наука
- Физика
- Как преобразовать единицы измерения в физике
Стивен Хольцнер
В задачах физики часто просят преобразовать разные единицы измерения измерение. Например, вы можете измерить количество футов, которое ваша игрушечная машинка проходит за три минуты, и, таким образом, сможете рассчитать скорость автомобиля в футах в минуту, но это не стандартная единица измерения, поэтому вам нужно преобразовать футы в минуту. до миль в час или метров в секунду.
до миль в час или метров в секунду.
В качестве другого примера предположим, что у вас есть 180 секунд — сколько это в минутах? Вы знаете, что в минуте 60 секунд, поэтому 180 секунд равны трем минутам. Вот некоторые распространенные преобразования единиц:
1 м = 100 см = 1000 мм (миллиметры)
1 км (километр) = 1000 м
1 кг (килограмм) = 1000 г (граммы)
1 Н (ньютон) = 10 5 дин
1 Дж (джоуль) = 10 7 эрг
1 P (паскаль) = 10 Ba
1 А (ампер) = 0.1 Bi
1 Тл (тесла) = 10 4 Гс (гаусс)
1 C (кулон) = 2,9979 x 10 9 Fr
Преобразование между CGS и MKS почти всегда включает только множитель 10, поэтому преобразование между ними просто. Но как насчет преобразования в ИФП и другие системы измерения и обратно? Вот несколько удобных преобразований, к которым вы можете вернуться при необходимости:
Длина:
Масса:
Сила:
1 фунт (фунт) = 4.
 448 N
448 N1 N = 10 5 дин
1 Н = 0,2248 фунта
Энергия:
1 Дж = 10 7 эрг
1 Дж = 0,7376 фут-фунт
1 BTU (британская тепловая единица) = 1055 Дж
1 кВтч (киловатт-час) = 3.600 x 10 6 Дж
1 эВ (электрон-вольт) = 1,602 x 10 –19 Дж
Мощность:
Поскольку преобразования являются такой важной частью физических задач, и поскольку вы должны очень тщательно отслеживать их, существует систематический способ обработки преобразований: вы умножаете на константу преобразования, равную 1, так что единицы, которые вы не используете не хочу отменить.
Пример вопроса
Мяч падает с 5 метров. На сколько сантиметров он упал?
Правильный ответ — 500 сантиметров.
 Чтобы выполнить преобразование, необходимо выполнить следующий расчет:
Чтобы выполнить преобразование, необходимо выполнить следующий расчет:Обратите внимание, что 100 сантиметров, разделенных на 1 метр, равны 1, потому что в метре 100 сантиметров. В расчетах отменяются единицы, которые вам не нужны — метры.
Практические вопросы
Сколько сантиметров в 2.35 метров?
Сколько секунд в 1,25 минутах?
Сколько дюймов в 2,0 метра?
Сколько граммов в 3,25 кг?
Ниже приведены ответы на вопросы практики:
235 см
Преобразование 2,35 метра в сантиметр:
75 сек
Преобразование 1,25 минуты в секунды:
79 в
Конвертировать 2.0 метров в дюймах:
3250 г
Перевести 3,25 килограмма в граммы:
Об авторе книги
Стивен Хольцнер, доктор философии, был преподавателем и редактором журнала PC Magazine .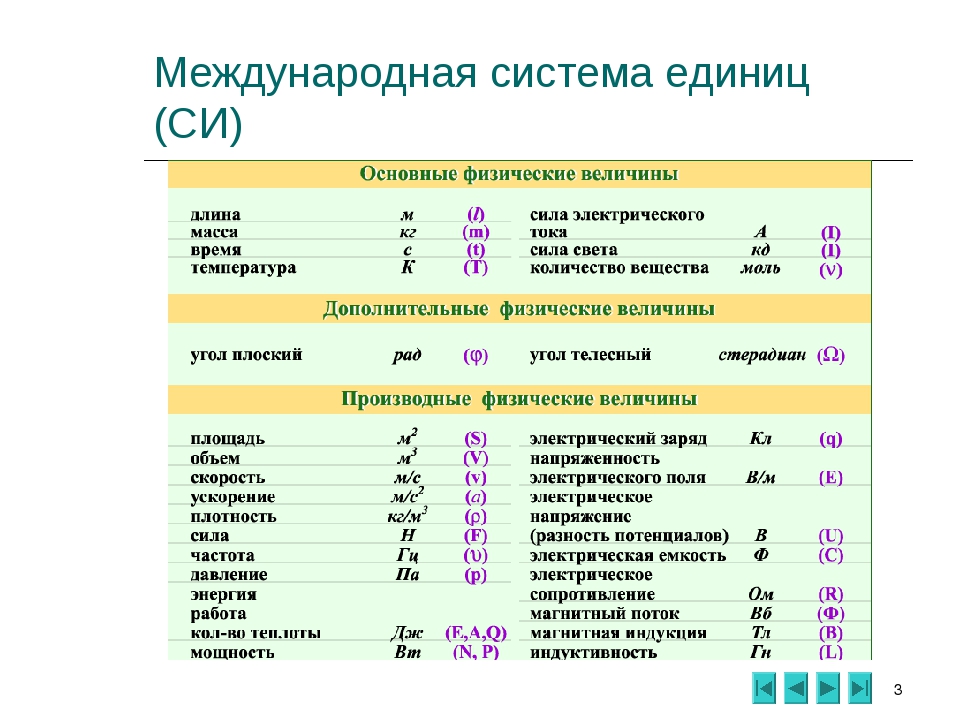
: Путаница в единицах массы и веса, Рон Куртус
SfC Home> Физика> Гравитация>
, автор: Рон Куртус (от 18 июня 2020 г.)
Может возникнуть путаница с единицами массы и веса , используемыми в научных измерениях, а также в повседневной жизни.Например, килограммы и фунты обычно называют весом. Однако с технической точки зрения они обе фактически являются единицами массы.
В определениях системы СИ или метрической системы указано, что килограмм является единицей массы, а ньютон — единицей силы или веса. Кроме того, в британских или американских стандартах фунт экирдупуа является единицей массы, а фунт также может использоваться в качестве веса.
Как изучающий естественные науки, вы должны быть уверены, что понимаете определения, используемые для массы и веса, особенно при преобразовании между системами.
Вопросы, которые могут у вас возникнуть:
- Что за путаница с килограммами?
- Что за путаница с фунтами?
- А как насчет преобразования между системами?
Этот урок ответит на эти вопросы. Полезный инструмент: Преобразование единиц
Путаница с килограммами
килограмм определяется как система СИ или метрическая единица массы . К сожалению, многие люди — и даже некоторые учебники — указывают вес в килограммах.Это может вызвать путаницу при проведении научных расчетов.
Официальная метрическая единица силы — ньютон ( Н ), которая представляет собой силу, необходимую для ускорения 1 кг массы до 1 метра на секунду в квадрате. Тогда вес является результирующей силой, когда масса ускоряется под действием силы тяжести, как указано в ньютонах.
Однако большинство людей не используют ньютоны для измерения веса в повседневных измерениях. Когда они говорят «объект весит килограмм», они на самом деле имеют в виду килограмм-силу ( кг — ), что составляет около 9.Масса в 8 раз больше килограмма.
Хотя это неудобно, в научной работе наиболее безопасным подходом следует называть объект килограммовой массой ( кг, ) и килограммовой массой ( кг-f ).
Обратите внимание на , что обозначение килограмм-массы как кг-м может привести к путанице с кг-м .
Отношение массы к массе
Соотношение между весом объекта и его массой в метрической системе составляет:
Вт = мг
где
- W — вес в ньютонах ( N ) или килограммах-силах ( кгс )
- м — масса в килограммах ( кг )
- г — ускорение свободного падения; на Земле г = 9.8 м / с 2
Таким образом, если объект имеет массу 50 кг, его вес будет 490 Н или 490 кгс-сила:
Вт = мг
490 кгс = (50 кг ) * (9,8 м / с 2 )
Путаница относительно фунтов
Фунт эвердупуа ( фунт ) юридически определен как мера массы в британской имперской системе измерения, а также в системе единиц Соединенных Штатов.
Однако в обычном использовании люди часто указывают вес в фунтах. Кроме того, в некоторых учебниках физики говорится, что фунт — это единица веса или силы, например фут-фунт для крутящего момента.
Это может привести к путанице при расчетах. Называя массу объекта фунтовой массой, можно облегчить эту путаницу.
Отношение массы к массе
Соотношение между весом объекта и его массой в англо-американской системе составляет:
Вт = мг
где
- Вт — вес в фунт-силах ( фунт-сила )
- м — масса в фунтах ( фунт )
- г — ускорение свободного падения; на Земле г = 32 фут / с 2 .
Таким образом, если объект весит 64 фунта, его масса составляет 2 фунта-масса:
Вт = мг
64 фунт-сила = (2 фунта) * (32 фут / с 2 )
Преобразование между системами
При переводе из британской / американской системы в метрическую систему необходимо внимательно следить за тем, какие определения веса и массы используются для преобразования.
- Один килограмм-сила составляет примерно 2.2 фунта силы
- Международный фунт экирдупуа определяется как масса около 0,45 кг.
Таблицы преобразования:
Фунт в Килограмм
Фунт в Килограмм
Резюме
Важно указывать единицы массы и веса таким образом, чтобы не было путаницы в расчетах.
В метрической системе единицей массы является килограмм. Вес указывается в ньютонах, килограммах-силе или килограммах-весе, , а не просто килограммах.
В американской системе единицей массы является фунт-масса. Обычно используются фунты как вес, но на самом деле это фунт-сила.
Как изучающий естественные науки, вы должны быть осторожны в том, что вы называете вещами.
Используйте точные слова в научной работе
Ресурсы и ссылки
Полномочия Рона Куртуса
Сайтов
Обычные единицы США — Википедия
Масса и вес — Набор инструментов для проектирования
Фунт (масса) — Википедия
Фунт (сила) — Википедия
Пуля (единица) — Википедия
Гравитационные ресурсы
Книги
Книги с самым высоким рейтингом по простой науке о гравитации
Книги с самым высоким рейтингом по продвинутой физике гравитации
Вопросы и комментарии
У вас есть вопросы, комментарии или мнения по этой теме? Если это так, отправьте свой отзыв по электронной почте.Я постараюсь вернуться к вам как можно скорее.
Поделиться страницей
Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:
Студенты и исследователи
Веб-адрес этой страницы:
www.school-for-champions.com/science/
gravity_mass_weight_confusion.htm
Пожалуйста, включите его в качестве ссылки на свой веб-сайт или в качестве ссылки в своем отчете, документе или диссертации.
Авторские права © Ограничения
Где ты сейчас?
Школа чемпионов
Гравитационные темы
Мини-викторина: путаница в единицах массы и веса
1.3 Язык физики: физические величины и единицы
Точность, прецизионность и значащие числа
Наука основана на экспериментах, требующих точных измерений.Достоверность измерения можно описать с точки зрения его точности и точности (см. Рисунок 1.19 и рисунок 1.20). Точность — это насколько измерение близко к правильному значению для этого измерения. Например, предположим, что вы измеряете длину стандартного листа бумаги для принтера. На упаковке, в которой вы приобрели бумагу, указано, что она имеет длину 11 дюймов, и предположим, что указанное значение верное. Вы трижды измеряете длину бумаги и получаете следующие размеры: 11.1 дюйм, 11,2 дюйма и 10,9 дюйма. Эти измерения довольно точны, потому что они очень близки к правильному значению 11,0 дюймов. Напротив, если бы вы получили размер в 12 дюймов, ваше измерение не было бы очень точным. Вот почему измерительные приборы калибруются на основе известного измерения. Если прибор постоянно возвращает правильное значение известного измерения, его можно безопасно использовать для поиска неизвестных значений.
Рис. 1.19. Механические весы с двумя чашами используются для сравнения различных масс.Обычно объект неизвестной массы помещается в одну чашу, а объекты известной массы — в другую. Когда стержень, соединяющий две посуды, расположен горизонтально, массы в обеих посуде равны. Известные массы обычно представляют собой металлические цилиндры стандартной массы, например 1 грамм, 10 грамм и 100 грамм. (Серж Мелки)
Рис. 1.20. В то время как механические весы могут считывать массу объекта только с точностью до десятых долей грамма, некоторые цифровые весы могут измерять массу объекта с точностью до ближайшей тысячной доли грамма.Как и в других измерительных приборах, точность шкалы ограничивается последними измеренными цифрами. Это сотые доли шкалы, изображенной здесь. (Splarka, Wikimedia Commons)
«Точность» указывает, насколько хорошо повторяющиеся измерения чего-либо дают одинаковые или похожие результаты. Следовательно, точность измерений означает, насколько близки друг к другу измерения, когда вы измеряете одно и то же несколько раз. Один из способов анализа точности измерений — определение диапазона или разницы между самым низким и самым высоким измеренными значениями.В случае размеров бумаги для принтера наименьшее значение было 10,9 дюйма, а наибольшее — 11,2 дюйма. Таким образом, измеренные значения отклонялись друг от друга не более чем на 0,3 дюйма. Эти измерения были достаточно точными, потому что они варьировались всего на долю дюйма. Однако, если бы измеренные значения были 10,9 дюймов, 11,1 дюймов и 11,9 дюймов, тогда измерения не были бы очень точными, потому что есть много различий от одного измерения к другому.
Измерения в бумажном примере точны и точны, но в некоторых случаях измерения точны, но не точны, или они точны, но неточны.Давайте рассмотрим систему GPS, которая пытается определить местоположение ресторана в городе. Представьте, что ресторан находится в центре мишени в яблочко. Затем представьте, что каждая попытка GPS определить местонахождение ресторана — это черная точка в яблочко.
На рисунке 1.21 вы можете видеть, что измерения GPS далеко разнесены друг от друга, но все они относительно близки к фактическому местоположению ресторана в центре цели. Это указывает на низкую точность и высокую точность измерительной системы.Однако на Рисунке 1.22 измерения GPS сосредоточены довольно близко друг к другу, но они находятся далеко от места назначения. Это указывает на высокую точность измерительной системы с низкой точностью. Наконец, на рис. 1.23 GPS является точным и точным, что позволяет определить местонахождение ресторана.
Рис. 1.21. Система GPS пытается определить местонахождение ресторана в центре мишени. Черные точки обозначают каждую попытку определить местонахождение ресторана. Точки расположены довольно далеко друг от друга, что указывает на низкую точность, но каждая из них находится довольно близко к фактическому местоположению ресторана, что указывает на высокую точность.(Темное зло)
Рис. 1.22 На этом рисунке точки сосредоточены близко друг к другу, что указывает на высокую точность, но они находятся довольно далеко от фактического местоположения ресторана, что указывает на низкую точность. (Темное зло)
Рис. 1.23 На этом рисунке точки сосредоточены близко друг к другу, что указывает на высокую точность, и они находятся близко к фактическому местоположению ресторана, что указывает на высокую точность. (Темное зло)
Неопределенность
Точность и прецизионность измерительной системы определяют неопределенность ее измерений.Неопределенность — это способ описать, насколько ваше измеренное значение отклоняется от фактического значения, которое имеет объект. Если ваши измерения не очень точны или точны, то неопределенность ваших значений будет очень высокой. В более общем плане неопределенность можно рассматривать как отказ от ответственности за ваши измеренные значения. Например, если кто-то попросил вас указать пробег вашего автомобиля, вы можете сказать, что это 45 000 миль, плюс-минус 500 миль. Сумма плюс или минус — это неопределенность в вашей стоимости.То есть вы указываете, что фактический пробег вашего автомобиля может составлять от 44 500 миль до 45 500 миль или где-то посередине. Все измерения содержат некоторую неопределенность. В нашем примере измерения длины бумаги мы могли бы сказать, что длина бумаги составляет 11 дюймов плюс-минус 0,2 дюйма или 11,0 ± 0,2 дюйма. Неопределенность измерения, A , часто обозначается как δA («дельта A »),
Факторы, способствующие неопределенности измерения, включают следующее:
- Ограничения измерительного прибора
- Навыки человека, производящего измерение
- Неровности в измеряемом объекте
- Любые другие факторы, влияющие на результат (в значительной степени зависящие от ситуации)
В примере с бумагой для принтера неточность может быть вызвана: тем фактом, что наименьшее деление на линейке равно 0.1 дюйм, человек, использующий линейку, имеет плохое зрение или неуверенность, вызванную бумагорезательной машиной (например, одна сторона бумаги немного длиннее другой). Хорошей практикой является тщательное рассмотрение всех возможных источников неопределенности в измерение и уменьшение или устранение их,
Процент неопределенности
Один из методов выражения неопределенности — это процент от измеренного значения. Если измерение A выражается с неопределенностью δ A , неопределенность в процентах составляет
1.2% неопределенность = δAA × 100%.% Неопределенность = δAA × 100%.Рабочий пример
Расчет процентной погрешности: мешок яблок
В продуктовом магазине продаются 5-фунтовые пакеты с яблоками. Вы покупаете четыре пакета в течение месяца и каждый раз взвешиваете яблоки. Вы получите следующие размеры:
- Неделя 1 Вес: 4,8 фунта 4,8 фунта
- Неделя 2 Вес: 5,3 фунта 5,3 фунта
- Неделя 3 Вес: 4,9 фунта 4,9 фунта
- Неделя 4 вес: 5.4 фунта 5,4 фунта
Вы определили, что вес мешка 5 фунтов имеет погрешность ± 0,4 фунта. Какова погрешность в процентах от веса мешка?
Стратегия
Во-первых, заметьте, что ожидаемое значение веса мешка, AA, составляет 5 фунтов. Неопределенность этого значения, δAδA, составляет 0,4 фунта. Мы можем использовать следующее уравнение для определения процентной погрешности веса.
% Неопределенности = δAA × 100%.% Неопределенности = δAA × 100%.Решение
Подставьте известные значения в уравнение
% Неопределенности = 0.4 фунта5 фунтов × 100% = 8%.% Погрешности = 0,4 фунта5 фунтов × 100% = 8%.Обсуждение
Можно сделать вывод, что вес мешка с яблоками составляет 5 фунтов ± 8 процентов. Подумайте, как изменился бы этот процент неопределенности, если бы мешок с яблоками был вдвое меньше, но неопределенность в весе осталась бы прежней. Совет для будущих расчетов: при вычислении процентной погрешности всегда помните, что вы должны умножить дробь на 100 процентов. Если вы этого не сделаете, у вас будет десятичное число, а не процентное значение.
Неопределенность в расчетах
Есть неопределенность в любом вычислении измеренных величин. Например, площадь пола, рассчитанная на основе измерений его длины и ширины, имеет неопределенность, поскольку и длина, и ширина имеют неопределенности. Насколько велика неопределенность в том, что вы вычисляете умножением или делением? Если измерения в расчетах имеют небольшие погрешности (несколько процентов или меньше), то можно использовать метод сложения процентов.В этом методе говорится, что процент неопределенности в величине, вычисленной путем умножения или деления, представляет собой сумму процентных погрешностей в элементах, используемых для выполнения расчета. Например, если пол имеет длину 4,00 м и ширину 3,00 м с погрешностями 2 процента и 1 процент соответственно, то площадь пола составляет 12,0 м 2 и имеет погрешность 3 процента ( выраженная как площадь, это 0,36 м ( 2 ), которую мы округляем до 0,4 м ( 2 , поскольку площадь пола дается с точностью до одной десятой квадратного метра).
Чтобы быстро продемонстрировать точность, прецизионность и неопределенность измерений в зависимости от единиц измерения, попробуйте это моделирование. У вас будет возможность измерить длину и вес стола в миллиметрах по сравнению с сантиметрами. Как вы думаете, что обеспечит большую точность, точность и неопределенность при измерении стола и блокнота в симуляции? Подумайте, как природа гипотезы или вопроса исследования может повлиять на точность измерительного инструмента, необходимого для сбора данных.
Точность измерительных инструментов и значимых фигур
Важным фактором точности и точности измерений является точность измерительного инструмента. В общем, точный измерительный инструмент — это инструмент, который может измерять значения с очень маленькими приращениями. Например, рассмотрите возможность измерения толщины монеты. Стандартная линейка может измерять толщину с точностью до миллиметра, а микрометр может измерять толщину с точностью до 0,005 миллиметра. Микрометр — более точный измерительный инструмент, поскольку он может измерять очень небольшие различия в толщине.Чем точнее измерительный инструмент, тем точнее и точнее могут быть измерения.
Когда мы выражаем измеренные значения, мы можем перечислить только столько цифр, сколько мы первоначально измерили с помощью нашего измерительного инструмента (например, линейки, показанные на рисунке 1.24). Например, если вы используете стандартную линейку для измерения длины палки, вы можете измерить ее дециметровой линейкой как 3,6 см. Вы не можете выразить это значение как 3,65 см, потому что ваш измерительный инструмент не был достаточно точным, чтобы измерить сотую долю сантиметра.Следует отметить, что последняя цифра в измеренном значении была определена каким-то образом лицом, выполняющим измерение. Например, человек, измеряющий длину палки линейкой, замечает, что длина палки находится где-то между 36 и 37 мм. Он или она должны оценить значение последней цифры. Правило состоит в том, что последняя цифра, записанная в измерении, является первой цифрой с некоторой погрешностью. Например, последнее измеренное значение 36,5 мм состоит из трех цифр или трех значащих цифр.Количество значащих цифр в измерении указывает на точность измерительного инструмента. Чем точнее инструмент измерения, тем большее количество значащих цифр он может сообщить.
Рисунок 1.24 Показаны три метрические линейки. Первая линейка измеряется в дециметрах и может измерять до трех дециметров. Вторая линейка имеет длину в сантиметрах и может измерять три целых шесть десятых сантиметра. Последняя линейка в миллиметрах и может измерять тридцать шесть целых пять десятых миллиметра.
Нули
Особое внимание уделяется нулям при подсчете значащих цифр.Например, нули в 0,053 не имеют значения, потому что они всего лишь заполнители, устанавливающие десятичную точку. В 0,053 есть две значащие цифры — 5 и 3. Однако, если ноль встречается между другими значащими цифрами, нули имеют значение. Например, оба нуля в 10.053 значимы, поскольку эти нули были фактически измерены. Следовательно, заполнитель 10.053 содержит пять значащих цифр. Нули в 1300 могут иметь значение, а могут и не иметь значения, в зависимости от стиля написания чисел.Они могут означать, что число известно до последнего нуля, или нули могут быть заполнителями. Таким образом, 1300 может иметь две, три или четыре значащих цифры. Чтобы избежать этой двусмысленности, запишите 1300 в экспоненциальном формате как 1,3 × 10 3 . Только значащие цифры приведены в множителе x для числа в экспоненциальном представлении (в форме x × 10yx × 10y). Поэтому мы знаем, что 1 и 3 — единственные значащие цифры в этом числе. Таким образом, нули имеют значение, кроме случаев, когда они служат только в качестве заполнителей.В таблице 1.4 приведены примеры количества значащих цифр в различных числах.
| Номер | Значимые цифры | Обоснование |
|---|---|---|
| 1,657 | 4 | Нет нулей, и все ненулевые числа всегда значимы. |
| 0,4578 | 4 | Первый ноль — это всего лишь место для десятичной запятой. |
| 0.000458 | 3 | Первые четыре нуля — это заполнители, необходимые для представления данных с точностью до десятитысячных. |
| 2000,56 | 6 | Три нуля здесь значимы, потому что они находятся между другими значащими цифрами. |
| 45 600 | 3 | Без подчеркивания или научного обозначения мы предполагаем, что последние два нуля являются заполнителями и не имеют значения. |
| 15895 00 0 | 7 | Два подчеркнутых нуля значимы, а последний ноль — нет, поскольку он не подчеркнут. |
| 5,457 × 10 13 | 4 | В экспоненциальном представлении все числа перед знаком умножения являются значащими |
| 6.520 × 10 –23 | 4 | В экспоненциальном представлении все числа, указанные перед знаком умножения, значимы, включая нули. |
Таблица 1.4
Значимые цифры в расчетах
При объединении измерений с разной степенью точности и точности количество значащих цифр в окончательном ответе не может быть больше количества значащих цифр в наименее точном измеренном значении.Существует два разных правила: одно для умножения и деления, а другое — для сложения и вычитания, как описано ниже.
Для умножения и деления: Ответ должен содержать такое же количество значащих цифр, что и начальное значение с наименьшим количеством значащих цифр. Например, площадь круга можно вычислить по его радиусу, используя A = πr2A = πr2. Посмотрим, сколько значащих цифр будет у площади, если в радиусе всего две значащие цифры, например, r = 2.0 мин. Тогда, используя калькулятор, который хранит восемь значащих цифр, вы получите
A = πr2 = (3,1415927 …) × (2,0 м) 2 = 4,5238934 м2. A = πr2 = (3,1415927 …) × (2,0 м) 2 = 4,5238934 м2.Но поскольку радиус состоит только из двух значащих цифр, вычисленная площадь имеет смысл только до двух значащих цифр или
, даже если значение ππ имеет значение не менее восьми цифр.
Для сложения и вычитания : ответ должен иметь одинаковые числовые разряды (например,грамм. разряда десятков, разряда единиц, разряда десятых и т. д.) как наименее точное начальное значение. Предположим, вы купили в продуктовом магазине 7,56 кг картофеля, измеренного по шкале с точностью 0,01 кг. Затем вы кладете в лабораторию 6,052 кг картофеля, измеренного по шкале с точностью до 0,001 кг. Наконец, вы идете домой и добавляете 13,7 кг картофеля, измеренное на весах с точностью до 0,1 кг. Сколько у вас сейчас килограммов картофеля и сколько значащих цифр уместно в ответе? Масса находится простым сложением и вычитанием:
7.56 кг − 6,052 кг + 13,7 кг_ 15,208 кг 7,56 кг − 6,052 кг + 13,7 кг_ 15,208 кгНаименьшее точное измерение — 13,7 кг. Это измерение выражается с точностью до 0,1 десятичного знака, поэтому наш окончательный ответ также должен быть выражен с точностью до 0,1. Таким образом, ответ следует округлить до десятых, получая 15,2 кг. То же самое и с недесятичными числами. Например,
6527,23 + 2 = 6528,23 = 6528,6527,23 + 2 = 6528,23 = 6528.Мы не можем указать десятичные разряды в ответе, потому что 2 не имеет значимых десятичных знаков.Следовательно, мы можем отчитаться только до одного места.
Рекомендуется оставлять лишние значащие цифры при вычислении и округлять до правильного числа значащих цифр только в окончательных ответах. Причина в том, что небольшие ошибки из-за округления при вычислении иногда могут приводить к значительным ошибкам в окончательном ответе. В качестве примера попробуйте вычислить 5,098– (5.000) × (1010) 5,098– (5.000) × (1010), чтобы получить окончательный ответ только на две значащие цифры. Удерживая все значимое при вычислении, получаем 48.Округление до двух значащих цифр в середине вычисления изменяет его до 5,100 — (5.000) × (1000) = 100, 5,100 — (5.000) × (1000) = 100, что далеко. Точно так же вы могли бы избежать округления в середине вычислений при подсчете и ведении бухгалтерского учета, когда нужно аккуратно сложить и вычесть много маленьких чисел, чтобы получить, возможно, гораздо большие окончательные числа.
Значимые цифры в этом тексте
В этом учебнике предполагается, что большинство чисел состоит из трех значащих цифр.Более того, во всех рабочих примерах используется постоянное количество значащих цифр. Вы заметите, что ответ, данный для трех цифр, основан на правильности ввода как минимум трех цифр. Если на входе меньше значащих цифр, ответ также будет содержать меньше значащих цифр. Также необходимо следить за тем, чтобы количество значащих цифр соответствовало создаваемой ситуации. В некоторых темах, таких как оптика, будет использоваться более трех значащих цифр. Наконец, если число является точным, например, 2 в формуле, c = 2πrc = 2πr, оно не влияет на количество значащих цифр в вычислении.
Рабочий пример
Приближение огромных чисел: триллион долларов
Федеральный дефицит США в 2008 финансовом году был немногим больше 10 триллионов долларов. Большинство из нас не имеют представления о том, сколько на самом деле стоит даже один триллион. Предположим, вам дали триллион долларов банкнотами по 100 долларов. Если вы составили стопки по 100 купюр, как показано на рис. 1.25, и использовали их для равномерного покрытия футбольного поля (между концевыми зонами), сделайте приблизительное представление о том, насколько высокой станет стопка денег.(Здесь мы будем использовать футы / дюймы, а не метры, потому что футбольные поля измеряются в ярдах.) Один из ваших друзей говорит, что 3 дюйма, а другой говорит, что 10 футов. Что вы думаете?
Рисунок 1.25. Банковская пачка содержит сто банкнот по 100 долларов и стоит 10 000 долларов. Сколько банковских стеков составляет триллион долларов? (Эндрю Мэджилл)
Стратегия
Когда вы представляете себе ситуацию, вы, вероятно, представляете тысячи маленьких стопок по 100 завернутых банкнот по 100 долларов, которые вы могли бы увидеть в фильмах или в банке.Поскольку это величина, которую легко оценить, давайте начнем с нее. Мы можем найти объем стопки из 100 купюр, узнать, сколько стопок составляют один триллион долларов, а затем установить этот объем равным площади футбольного поля, умноженной на неизвестную высоту.
Решение
- Рассчитайте объем стопки из 100 купюр. Размеры одной банкноты составляют примерно 3 на 6 дюймов. Пачка из 100 таких банкнот имеет толщину примерно 0,5 дюйма. Таким образом, общий объем стопки из 100 купюр равен объем стопки = длина × ширина × высота, объем стопки = 6 дюймов× 3 дюйма × 0,5 дюйма, объем стопки = 9 дюймов. 3. объем стопки = длина × ширина × высота, объем стопки = 6 дюймов × 3 дюйма × 0,5 дюйма, объем стопки = 9 дюймов .3.
Подсчитайте количество стопок. Обратите внимание, что триллион долларов равен 1 × 1012 $ 1 × 1012, а стопка из ста 100-долларовых банкнот равна 10000, 10000 долларов или 1 × 104 доллара 1 × 104. Количество стопок у вас будет
1,3 $ 1 × 1012 (триллион долларов) / 1 × 104 доллара на стек = 1 × 108 стеков. 1 доллар × 1012 (триллион долларов) / 1 × 104 доллара на стек = 1 × 108 стеков.Вычислите площадь футбольного поля в квадратных дюймах. Площадь футбольного поля составляет 100 ярдов × 50 ярдов 100 ярдов × 50 ярдов, что дает 5 000 ярдов 25 000 ярдов2. Поскольку мы работаем в дюймах, нам нужно преобразовать квадратные ярды в квадратные дюймы
Площадь = 5000 ярдов2 × 3 фут1 ярд × 3 фут1 ярд × 12 дюймов 1 фут × 12 дюймов 1 фут = 6 480000 дюймов 2, Площадь ≈6 × 106 дюймов 2 Площадь = 5000 ярдов2 × 3 фут1 ярд × 3 фут1 ярд × 12 дюймов 0,1 фут × 12 дюймов 1 фут = 6 480000 дюймов 2, Площадь ≈6 × 106 дюймов 2.Это преобразование дает нам 6 × 106 дюймов.26 × 106 дюймов 2 для площади поля. (Обратите внимание, что в этих расчетах мы используем только одну значащую цифру.)
- Рассчитайте общий объем купюр. Объем всех стопок банкнот по 100 долларов составляет 9 дюймов 3 / стопку × 108 стопок = 9 × 108 дюймов 39 дюймов / стопку × 108 стопок = 9 × 108 дюймов 3
- Рассчитайте высоту. Чтобы определить высоту купюр, используйте следующее уравнение
объем купюр = площадь поля × высота денег Высота денег = объем купюр Площадь поля Высота денег = 9 × 108 дюймов.36 × 106 дюймов 2 = 1,33 × 102 дюйма Высота денег = 1 × 102 дюйма = 100 дюймов Объем купюр = площадь поля × высота денег Высота денег = объем купюр площадь поля Высота денег = 9 × 108 дюйм 36 × 106 дюймов 2 = 1,33 × 102 дюйма Высота = 1 × 102 дюйма = 100 дюймов
Высота денег будет около 100 дюймов. Преобразование этого значения в футы дает
100 дюймов × 1 фут 12 дюймов = 8,33 футов ≈ 8 футов 100 дюймов × 1 фут 12 дюймов = 8,33 футов ≈ 8 футов
Обсуждение
Окончательное приблизительное значение намного выше, чем ранняя оценка 3 дюйма., но другая ранняя оценка 10 футов (120 дюймов) была примерно правильной. Насколько это приближение соответствует вашему первому предположению? Что может сказать вам это упражнение с точки зрения приблизительных оценок , и тщательно рассчитанных приближений?
В приведенном выше примере окончательное приблизительное значение намного выше, чем ранняя оценка первого друга в 3 дюйма. Однако ранняя оценка другого друга в 10 футов (120 дюймов) была примерно правильной. Насколько это приближение соответствует вашему первому предположению? Что это упражнение может предложить о значении приблизительных приблизительных оценок по сравнению с тщательно рассчитанными приближениями?
Преобразование единиц веса и массы
Наиболее часто используемое преобразование единиц измерения
- карат в грамм конвертер единиц
- 1 карат (метрическая система) равен 0.2 грамм (г) используйте этот конвертер
- конвертер граммов в караты
- 1 грамм (г) равен 5 карат (метрическая система) использовать этот преобразователь
- конвертер грамм в зерно
- 1 грамм (г) равен 15.432358352941 зерно (гр) использовать этот преобразователь
- конвертер граммов в граммы
- 1 гран (гр) равен 0,064798
0002 грамм (г) используйте этот конвертер - конвертер единиц зерна в ньютон
- 1 гран (гр) равен 0.00063546023075152 ньютон (Земля) использовать этот преобразователь
- преобразователь ньютон в зерно
- 1 ньютон (Земля) равен 1573,662 6016979 гран (гр) используйте этот преобразователь
- фунт в тонна конвертер единиц
- 1 фунт (фунт) равен 0,00045359237 тонна (т) использовать этот преобразователь
- конвертер единиц тонна в фунт
- 1 тонна (т) равна 2204,6226218488 фунт (фунт) использовать этот преобразователь
Определение
Вес — сила, с которой земля или любое другое астральное тело, создающее гравитацию, притягивает объекты, это векторная величина.В обычном использовании вес часто путают с массой.
Единицы измерения
единица атомной массы (а.е.м.), карат (метрическая), центаль, сантиграмма, декаграмма, драм (dr), зерно (гр), грамм (г), центнер (Великобритания), килограмм (кг), микрограмм (мкг), миллиграмм ( мг), ньютон (Земля), унция (oz), пеннивейт (dwt), фунт (фунт), четверть, стоун, тонна (Великобритания, длинная), тонна (США, короткая), тонна (т), тройская унция
Об инструменте преобразования единиц веса и массы.
Мы используем округление в unit-conversion.info. Это означает, что некоторые результаты будут округлены, чтобы числа не становились слишком длинными. Хотя часто округление работает до определенного десятичного знака, мы решили, что ограничение длины результата 13 цифрами будет более благоприятным для сохранения согласованности результатов. Конвертеры принимают научную нотацию и немедленно преобразуют.
Перевести килограммы в ньютоны | Кг в Н Преобразование
Нажмите здесь, чтобы увидеть наш онлайн-калькулятор, переводящий килограммы в ньютоны! Этот конвертер веса точно преобразует любое количество. Доступно больше конвертеров.
Конвертер Ньютонов в КилограммыНьютон — это единица измерения, наиболее часто используемая в физике. Она названа в честь сэра Исаака Ньютона из-за его работы. килограмм — это единица измерения веса в метрической системе.Этот преобразователь веса кг — N поможет вам в преобразовании единиц измерения. Посмотрите остальные наши калькуляторы весовых конвертеров, чтобы увидеть больше примеров.
Как преобразовать из кг в Н?
Введите количество килограммов, которое вы хотите преобразовать в ньютоны, в поле выше и нажмите кнопку «преобразовать», чтобы получить точное преобразование единиц в . Чтобы преобразовать те же единицы веса в в обратном порядке, воспользуйтесь нашим преобразованием Ньютонов в килограммы. Наш калькулятор килограмм — ньютон прост в использовании для изменения измерений.
Формула для перевода килограммов — ньютонов
Для изменения этих двух единиц измерения используется формула кг x 9,807 = N , что является тем же самым преобразованием, которое автоматически используется калькулятором преобразования кг в N. Например, 2 кг = 19,6 Н и 5 кг = 49 Н.
Измерения в килограммах
Единица массы, кг, , используется для измерения взвешенных предметов, которые могут быть подняты людьми. Например, вес тела иногда измеряется в килограмм, килограммов, а также продукты питания и предметы повседневного обихода, такие как книги.Преобразователь кг в N поможет вам в этом.
Измерения в ньютонах
Ньютоны — это единица силы , которая в основном используется в физике в отношении веса и массы. Это измерение используется, чтобы увидеть, сколько силы прилагает определенная масса (например, ваше тело или яблоко). Теперь вы можете легко преобразовать ньютоны с помощью этого конвертера для килограммов в ньютонов.
Килограммы Ньютонов 1 кг 9.81 ньютон 2 кг 19,61 ньютона 3 кг 29,42 ньютона 4 кг 39,23 ньютона 5 кг 49,04 ньютона 10 кг 98,07 ньютона 15 кг 147,11 ньютон 20 кг 196,14 ньютона 25 кг 245,18 ньютона 30 кг 294.21 ньютон Сколько это 1 килограмм в ньютонах?
1 килограмм равен 9,81 ньютона
(1 кг = 9,81 Н)Сколько 2 Килограмма в Ньютонах?
2 Килограмма равны 19,61 Ньютона
(2 кг = 19,61 Н)Сколько 3 Килограмма в Ньютонах?
3 килограмма равны 29.42 Ньютона
(3 кг = 29,42 Н)Сколько 4 Килограммы в Ньютонах?
4 Килограмма равны 39,23 Ньютона
(4 кг = 39,23 Н)Сколько 5 Килограмм в Ньютонах?
5 Килограммов равны 49,04 Ньютона
(5 кг = 49,04 Н)Сколько 10 Килограмм в Ньютонах?
10 килограммов равны 98.07 Ньютонов
(10 кг = 98,07 Н)Сколько 15 Килограмм в Ньютонах?
15 Килограммов равны 147,11 Ньютона
(15 кг = 147,11 Н)Сколько 20 Килограмм в Ньютонах?
20 Килограммов равны 196,14 Ньютона
(20 кг = 196,14 Н)Сколько 25 Килограмм в Ньютонах?
25 килограммов равны 245.18 Ньютонов
(25 кг = 245,18 Н)Сколько 30 Килограмм в Ньютонах?
30 Килограммов равны 294,21 Ньютон
(30 кг = 294,21 Н)Сколько 50 Килограмм в Ньютонах?
50 Килограммов равны 490,35 Ньютона
(50 кг = 490,35 Н)Сколько 100 Килограмм в Ньютонах?
100 килограммов равны 980.7 Ньютонов
(100 кг = 980,7 Н)Сколько 200 Килограмм в Ньютонах?
200 Килограммов равны 1961,4 Ньютона
(200 кг = 1961,4 Н)Сколько 500 Килограмм в Ньютонах?
500 Килограммов равны 4903,5 Ньютона
(500 кг = 4903,5 Н)Сколько 1000 Килограмм в Ньютонах?
1000 Килограмм равняются 9807 Ньютонам
(1000 кг = 9807N)Pon este converor en tu web
Калькулятор преобразования единицДлина
1 из = 2.54 см = 0,0254 м 1 фут = 30,48 см = 0,3048 м 1 ярд = 91,44 см = 0,9144 м 1 миля = 1.6093 км = 1609,3 м
Площадь
1 дюйм 2 = 6,4516 см 2 1 фут 2 = 0,0929 м 2 1 акр = 0.4047 га = 4047 м 2
Объем
1 дюйм 3 = 16,387 см 3 1 фут 3 = 0,0283 м 3 1 us f.oz = 29.574 мл 1 имп. Унц. = 28,41 мл 1 галлон США = 3,7854 л 1 имп гал = 4.546 л Используйте инженерные единицы. Например: 5.23e-7 От: кубометры литры у.е. сантиметры куб ярдов Cu ноги у.е. дюймов бочки (брит.) баррели (нефть США) бушели (брит.) бушели (США) галлоны (брит.) галлоны (США, сухие) галлоны (США, liq) унции (брит, грипп) унции (США, грипп) пинты (брит.) пинты (США, сухие) пинты (США, liq) кварты (брит.) кварты (США, сухие) кварты (США, жидкие) чашки столовые ложки чайные ложки Кому: кубометры литры у.е. сантиметры куб. ярды Cu ноги у.е. дюймов бочки (брит.) баррели (нефть США) бушели (брит.) бушели (США) галлоны (брит.) галлоны (США, сухие) галлоны (США, liq) унции (брит, грипп) унции (США, грипп) пинты (брит.) пинты (США, сухие) пинты (США, liq) кварты (брит.) кварты (США, сухие) кварты (США, жидкие) чашки столовые ложки чайные ложки Масса
1 унция = 28.35 г 1 фунт = 0,4536 кг = 453,6 г 1 имп. Тонна = 1016 кг
Температура
o F = o C * 1,8 + 32 o С = ( o F — 32) / 1.8 o R = o Факс + 459.


 с.
с. Старое определение обладало следующими недостатками:
Старое определение обладало следующими недостатками: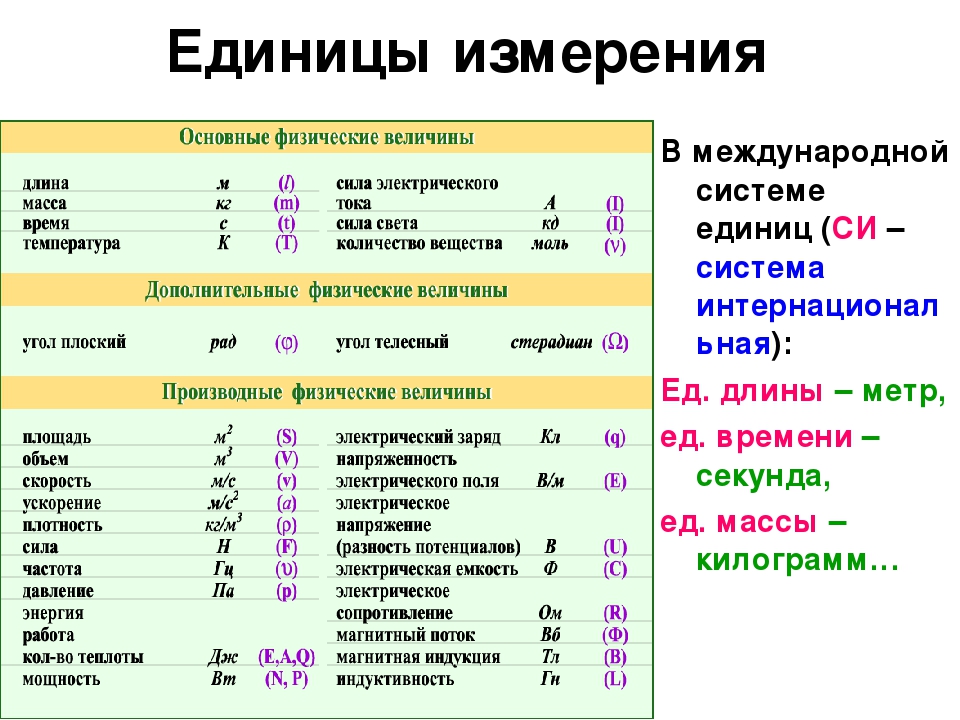
 Английская система мер)
Английская система мер) Английская система мер)
Английская система мер) 448 N
448 N Чтобы выполнить преобразование, необходимо выполнить следующий расчет:
Чтобы выполнить преобразование, необходимо выполнить следующий расчет: