Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Определение многоугольника
Рассмотрим n отрезков
| [A1 A2], [A2 A3], … , [An An +1] | (1) |
причём таких, что два любых отрезка, имеющих общий конец, не лежат на одной прямой (рис.1).
Рис. 1
Определение 1. Ломаной линией с n звеньями называют фигуру L, составленную из отрезков (1), то есть фигуру, заданную равенством
L = [A1 A2] U [A2 A3] U …
… U [An An +1]
В случае, когда точки A1 и An +1 совпадают, ломаную линию называют замкнутой ломаной линией (рис.
Рис. 2
Определение 2. Многоугольником называют часть плоскости, ограниченную замкнутой ломаной линией без самопересечений (рис. 3). Отрезки, составляющие ломаную линию (звенья), называют сторонами многоугольника. Концы отрезков называют вершинами многоугольника.
Рис. 3
Определение 3. Многоугольник называют n – угольником, если он имеет n сторон.
Таким образом, многоугольник, имеющий 3 стороны, называют треугольником, многоугольник, имеющий 4 стороны, называют четырёхугольником и т.д.
Определение 4 . Периметром многоугольника называют сумму длин всех сторон многоугольника.
Величину, равную половине периметра, называют полупериметром.
Диагонали n — угольника
| Фигура | Рисунок | Описание |
| Диагональ многоугольника | Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника | |
| Диагонали n – угольника, выходящие из одной вершины | Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника | |
| Все диагонали n – угольника | Число диагоналей n – угольника равно |
| Диагональ многоугольника |
Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника |
| Диагонали n – угольника, выходящие из одной вершины |
Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n |
| Все диагонали n – угольника |
Число диагоналей n – угольника равно |
Внешний угол многоугольника
Определение 5 . Два угла называют смежными, если они имеют общую сторону, и их сумма равна 180° (рис.1).
Два угла называют смежными, если они имеют общую сторону, и их сумма равна 180° (рис.1).
Рис.1
Определение 6 . Внешним углом многоугольника называют угол, смежный с внутренним углом многоугольника (рис.2).
Замечание. Мы рассматриваем только выпуклые многоугольникивыпуклые многоугольники.
Свойства углов треугольника
| Фигура | Рисунок | Формулировка теоремы |
| Углы треугольника | Сумма углов треугольника равна 180° α + β + γ = 180° Посмотреть доказательство | |
| Внешний угол треугольника | Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним δ = α + β Посмотреть доказательство |
Свойства углов многоугольника
Свойства углов правильного n – угольника
Доказательства свойств углов многоугольника
Теорема 1. В любом треугольнике сумма углов равна 180°.
В любом треугольнике сумма углов равна 180°.
Доказательство. Проведем, например, через вершину B произвольного треугольника ABC прямую DE, параллельную прямой AC, и рассмотрим полученные углы с вершиной в точке B (рис. 3).
Углы ABD и BAC равны как внутренние накрест лежащие. По той же причине равны углы ACB и CBE. Поскольку углы ABD, ABC и CBE в сумме составляют развёрнутый угол, то и сумма углов треугольника ABC равна 180°. Теорема доказана.
Теорема 2. Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
Доказательство. Проведём через вершину C прямую CE, параллельную прямой AB, и продолжим отрезок AC за точку C (рис.4).
Рис.4
Углы ABC и BCE равны как внутренние накрест лежащие. Углы BAC и ECD равны как соответственные равны как соответственные.
Замечание. Теорема 1 является следствием теоремы 2.
Теорема 3. Сумма углов n – угольника равна
Доказательство. Выберем внутри n – угольника произвольную точку O и соединим её со всеми вершинами n – угольника (рис. 5).
Рис.5
Получим n треугольников:
OA1A2, OA2A
Сумма углов всех этих треугольников равна сумме всех внутренних углов n – угольника плюс сумма всех углов с вершиной в точке O. Поэтому сумма всех углов n – угольника равна
что и требовалось доказать.
Теорема 4. Сумма внешних углов n – угольника, взятых по одному у каждой вершины, равна 360°.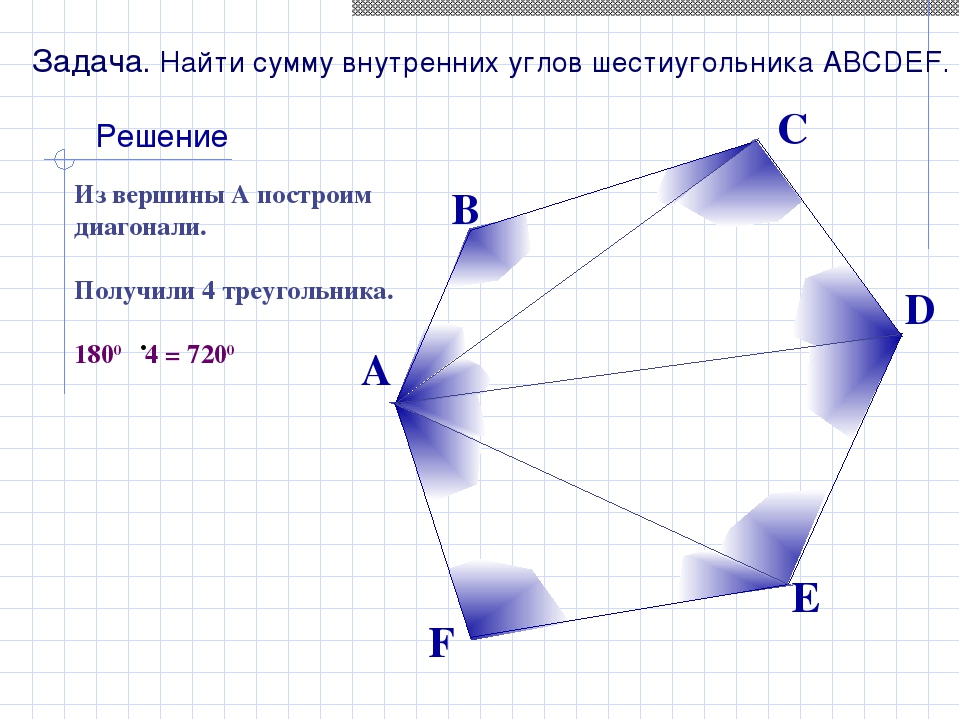
Доказательство. Рассмотрим рисунок 6.
Рис.6
В соответствии рисунком 6 справедливы равенства
Теорема доказана.
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Что такое правильный шестиугольник — Морской флот
/
/
Что такое правильный шестиугольник
Правильный шестиугольник — это такой шестиугольник у которого все шесть сторон равны и его шесть углов равны.
Центр правильного шестиугольника — на рисунке точка O равноудалена от вершин.
Светлая линия обозначающая высоту треугольника AOB : h называется — апофемой.
Отрезки OA , OB — радиусы правильного шестиугольника.
Обозначения на рисунке для правильного шестиугольника
| n=6 | число сторон и вершин правильного шестиугольника, | шт |
|---|---|---|
| α | центральный угол правильного шестиугольника, | радианы, ° |
| β | половина внутреннего угла правильного шестиугольника, | радианы, ° |
| γ | внутренний угол правильного шестиугольника, | радианы, ° |
| a | сторона правильного шестиугольника, | м |
| R | радиусы правильного шестиугольника, | м |
| p | полупериметр правильного шестиугольника, | м |
| L | периметр правильного шестиугольника, | м |
| h | апофемы правильного шестиугольника, | м |
Основные формулы для правильного шестиугольника
Периметр правильного шестиугольника
Полупериметр правильного шестиугольника
Центральный угол правильного шестиугольника в радианах
Центральный угол правильного шестиугольника в градусах
Половина внутреннего угла правильного шестиугольника в радианах
Половина внутреннего угла правильного шестиугольника в градусах
Внутренний угол правильного шестиугольника в радианах
Внутренний угол правильного шестиугольника в градусах
Площадь правильного шестиугольника
Отсюда получим апофему правильного шестиугольника
Содержание
- Особенность правильного шестиугольника — равенство его стороны и радиуса описанной окружности ( R = t <displaystyle R=t>), поскольку 2 sin π 6 = 1 <displaystyle 2sin <frac <pi ><6>>=1> .
 circ)
circ)Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
(m = alargefrac<<sqrt 3 >><2>
ormalsize)Радиус вписанной окружности правильного шестиугольника равен апофеме:
(r = m = alargefrac<<sqrt 3 >><2>
ormalsize)Радиус описанной окружности равен стороне правильного шестиугольника:
(R = a)Периметр правильного шестиугольника
(P = 6a)Площадь правильного шестиугольника
(S = pr = largefrac<<3sqrt 3 >><2>
ormalsize),
где (p) − полупериметр шестиугольника.Сколько сторон имеет правильный многоугольник
ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ
Составила: Шатрабаева Тамара Захаровна
1 УРОВЕНЬ
Найдите углы правильного двенадцатиугольника.
Сколько сторон имеет правильный многоугольник, если каждый его угол равен 144°?
Найдите внешний угол правильного пятнадцатиугольника.

2 УРОВЕНЬ
Сколько сторон имеет правильный многоугольник, если его внешний угол в два раза меньше внутреннего?
Докажите, что четыре вершины правильного восьмиугольника, взятые через одну, служат вершинами квадрата.
Площадь правильного треугольника равна 4. Найдите его периметр.
3 УРОВЕНЬ
Докажите, что в правильном шестиугольнике ABCDEF диагональ AC делит его на две фигуры, площади которых пропорциональны числам 1 и 5.
Три вершины правильного шестиугольника, взятые через одну, служат вершинами треугольника. Найдите отношение периметров данного шестиугольника и получившегося треуголбника.
Можно ли покрыть плоскость правильными треугольниками и правильными шестиугольниками без просветов? Ответ обоснуйте.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ:
Найдите углы правильного шестнадцатиугольника.

Каждый угол правильного многоугольника равен 162°. Найдите число его сторон.
Чему равен внешний угол правильного восемнадцатиугольника?
Внешний угол правильного многоугольника равен 15°. Найдите число его сторон.
Является ли равнобедренный треугольник с углом при вершине в 60° правильным?
Ответ обоснуйте.Диагональ AD делит шестиугольник ABCDEF на две равновеликие трапеции. Является ли шестиугольник ABCDEF правильным? Ответ обоснуйте.
В правильном шестиугольнике ABCDEF проведены диагонали AC,AD,AE. Найдите площади получившихся треугольников, если площадь шестиугольника равна 42.
Как найти углы правильного многоугольника
Правильные многоугольники встречаются в жизни каждый день, например, квадрат, треугольник или шестиугольник, в форме которого сделаны все пчелиные соты. Чтобы построить правильный многоугольник самостоятельно, необходимо знать его углы.
Чтобы построить правильный многоугольник самостоятельно, необходимо знать его углы.Сначала по формуле S= 180⁰(n-2) рассчитайте сумму внутренних углов вашего многоугольника. Например, если вам нужно найти углы правильного многоугольника с 15 сторонами, подставьте n=15 в уравнение. У вас получится S=180⁰(15-2), S=180⁰х13, S=2340⁰.
Далее разделите полученную сумму внутренних углов на их количество. Например, в примере с многоугольником количество углов равно количеству сторон, то есть 15. Таким образом, вы получите, что угол равен 2340⁰/15=156⁰. Каждый внутренний угол многоугольника равен 156⁰.
Если вам удобнее рассчитать углы многоугольника в радианах, действуйте следующим образом. Вычтите из количества сторон число 2 и умножьте полученную разность на число П (Пи). Затем разделите произведение на количество углов в многоугольнике. Например, если вам нужно рассчитать углы правильного 15-угольника, действуйте так: П*(15-2)/15=13/15П, или 0,87П, или 2,72 (но, как правило, число П остается в неизменном виде).
 Либо просто разделите размер угла в градусах на 57,3 — именно столько градусов содержится в одном радиане.
Либо просто разделите размер угла в градусах на 57,3 — именно столько градусов содержится в одном радиане.Также можете попробовать рассчитать углы правильного многоугольника в градах. Для этого вычтите из количества сторон число 2, разделите полученное число на количество сторон и умножьте результат на 200. Эта единица измерения углов сегодня почти не используется, но если вы решили посчитать углы в градах, не забудьте, что град разбивается на метрические секунды и минуты (по 100 секунд в минуте).
Возможно, вам необходимо рассчитать внешний угол правильного многоугольника, в этом случае поступайте так. Вычтите из 180⁰ внутренний угол – в результате вы получите значение смежного, то есть внешнего угла. Он может принимать значение от -180⁰ до +180⁰.
Задание 1. Правильный многоугольник | Уроки математики и физики для школьников и родителей
Прежде чем приступить к решению примеров и задач, обязательно ознакомьтесь с теоретической частью урока
1. Укажите номера верных утверждений.
1) Вписанный угол равен половине центрального, опирающегося на ту же дугу.2) Сумма углов треугольника равна 360°.
3) Катет всегда больше гипотенузы.
4) Все равнобедренные треугольники равны.
5) Все углы правильного шестиугольника равны 135°.
а) 2, 5;
б) 4;
в) 1, 3;
г) 1. 2. Найдите сумму внутренних углов правильного пятиугольника. а) 540°;
б) 360°;
в) 450°;
г) 720°. 3. Найдите количество сторон правильного многоугольника, если сумма его внутренних углов равна 1080°. а) 6;
б) 9;
в) 8;
г) 7. 4. Выразите через радиус R описанной окружности апофему правильного треугольника. а) 0,25R;
б) 0,5R;
в) 2R;
г) R. 5. Найдите количество сторон правильного
многоугольника, внешний угол которого равен
60°. а) 5;
5. Найдите количество сторон правильного
многоугольника, внешний угол которого равен
60°. а) 5;
б) 8;
в) 6;
г) 7. 6. Центральный угол правильного многоугольника равен 30°. Определите количество сторон многоугольника. а) 12;
б) 18;
в) 6;
г) 10. 7. Найдите градусную меру внутреннего угла правильного шестиугольника. а) 150°;
б) 90°;
в) 100°;
г) 120°. 8. Шаблон для гаек имеет углы, равные
90°, 120° и 135°.
Для каких правильных многоугольников можно использовать этот шаблон ? а) 4, 5, 8;
б) 5, 6, 8;
в) 4, 6, 8;
г) 3, 6, 9. 9. Сколько сторон имеет правильный многоугольник, угол которого равен 140° ? а) 9;
б) 8;
в) 7;
г) 10. 10. Укажите
неправильное утверждение. а) если стороны четырёхугольника равны, то его углы равны;
10. Укажите
неправильное утверждение. а) если стороны четырёхугольника равны, то его углы равны;б) если вокруг четырёхугольника можно описать окружность, то суммы его противоположных углов равны;
в) любой правильный п – угольник имеет ось симметрии;г) в любой правильный п – угольник можно вписать окружность.
11. Найдите углы треугольника, вершины которого находятся на серединах сторон правильного шестиугольника. а) 40°, 60°, 80⁰;
б) 45⁰, 45°, 90°;в) 60°, 90°, 30°;
12. Найдите внутренний угол правильного десятиугольника.
г) 60°, 60°, 60°.а) 36°;
б) 144°;
в) 90°;
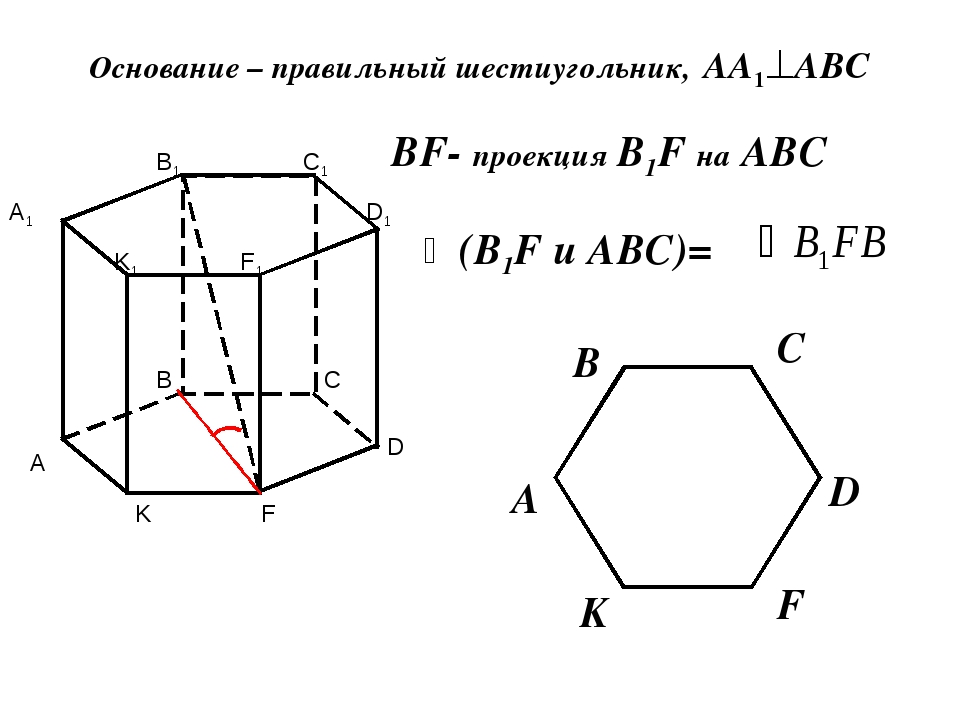
г) 120°.Угол в правильной шестиугольной призме
На сайте уже были рассмотрены некоторые типы задач по стереометрии, которые входят в единый банк заданий экзамена по математике.
 Например, задания про составные многогранники .
Например, задания про составные многогранники .Призма называется правильной если её боковые перпендикулярны основаниям и в основаниях лежит правильный многоугольник. То есть правильная призма – это прямая призма, у которой в основании правильный многоугольник.
Правильная шестиугольная призма – в основании правильный шестиугольник, боковые грани – прямоугольники.
В этой статье для вас задачи на решение призмы, в основании которой лежит правильный шестиугольник . Особенностей и сложностей в решении нет никаких. В чём суть? Дана правильная шестиугольная призма, требуется вычислить расстояние между двумя вершинами или найти заданный угол. Задачи на самом деле простые, в итоге решение сводится к нахождению элемента в прямоугольном треугольнике.
Используется теорема Пифагора и теорема косинусов . Необходимо знание определений тригонометрических функций в прямоугольном треугольнике.
Обязательно посмотрите информацию о правильном шестиугольнике в этой статье (пункт 6) .
 Ещё вам пригодится навык извлечения квадратного корня их большого числа. Можете посмотреть статью на решение многогранников, там тоже вычисляли расстояние между вершинами и углы.
Ещё вам пригодится навык извлечения квадратного корня их большого числа. Можете посмотреть статью на решение многогранников, там тоже вычисляли расстояние между вершинами и углы.Кратко: что представляет собой правильный шестиугольник?
Известно, что в правильном шестиугольнике стороны равны. Кроме этого, углы между сторонами тоже равны .
*Противолежащие стороны параллельны.
Радиус окружности описанной около правильного шестиугольника равен его стороне. *Это подтверждается очень просто: если мы соединим противоположные вершины шестиугольника, то получим шесть равных равносторонних треугольников. Почему равносторонних?
У каждого треугольника угол при его вершине лежащей в центре равен 60 0 (360:6=60). Так как у треугольника две стороны имеющие общую вершину в центре равны (это радиусы описанной окружности), то каждый угол при основании такого равнобедренного треугольника так же равен 60 градусам.
То есть правильный шестиугольник, образно говоря, состоит как бы из шести равных равносторонних треугольников.

Какой полезный для решения задач факт ещё следует отметить? Угол при вершине шестиугольника (угол между его соседними сторонами) равен 120 градусам.
*Умышленно не коснулись формул правильного N-угольника. Данные формулы мы подробно рассмотрим в будущем, здесь они просто не нужны.
272533. В правильной шестиугольной призме ABCDEFA 1B 1C 1D 1E 1F 1 все ребра равны 48. Найдите расстояние между точками A и E1.
Рассмотрим прямоугольный треугольник AA 1 E 1 . По теореме Пифагора:
*Угол между сторонами правильного шестиугольника равен 120 градусам.
Отрезок АЕ 1 является гипотенузой, АА 1 и А 1 Е 1 катеты. Ребро АА 1 нам известно. Катет А 1 Е 1 мы можем найти используя используя теорему косинусов.
Теорема: Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними.

По теореме Пифагора:
*Обратите внимание, что 48 возводить в квадрат совсем не обязательно.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 35. Найдите расстояние между точками B и E.
Рассмотрим правильный шестиугольник:
Сказано, что все рёбра равны 35, то есть сторона шестиугольника лежащего в основании равна 35. А так же, как уже сказано, радиус описанной около него окружности равен этому же числу.
273353. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны сорока корням из пяти. Найдите расстояние между точками B и E1.
Рассмотрим прямоугольный треугольник BB 1 E 1 . По теореме Пифагора:
Отрезок B 1 E 1 равен двум радиусам описанной около правильного шестиугольника окружности, а её радиус равен стороне шестиугольника, то есть
273683.
 В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 45. Найдите тангенс угла AD1D.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 45. Найдите тангенс угла AD1D.Рассмотрим прямоугольный треугольник ADD1, в котором AD равно диаметру окружности, описанной вокруг основания. Известно, что радиус окружности, описанной вокруг правильного шестиугольника равен его стороне.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 23. Найдите угол DAB. Ответ дайте в градусах.
Рассмотрим правильный шестиугольник:
В нём углы между сторонами равны 120°. Значит,
Сама длина ребра не имеет значения, на величину угла она не влияет.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 10. Найдите угол AC1C.
 Ответ дайте в градусах.
Ответ дайте в градусах.Рассмотрим прямоугольный треугольник AC1C:
Найдём AC . В правильном шестиугольнике углы между его сторонами равны 120 градусам, тогда по теореме косинусов для треугольника АВС :
Значит, угол AC 1 C равен 60 градусам.
274453. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 10. Найдите угол AC1C. Ответ дайте в градусах.
Рассмотрим треугольник AС 1 С, он прямоугольный. Вычислим тангенс указанного в условии угла и определим угол. Известно, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему, то есть
Катет С1С = 10. Отрезок АС вычислим по теореме косинусов (это мы уже делали в первой задаче, запишем ещё раз):
В правильном шестиугольнике углы при вершинах равны 120 градусам, то есть
245364.
 В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками А и Е1.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками А и Е1.245365. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками В и Е.
245366. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1все ребра равны корню из пяти. Найдите расстояние между точками В и Е1.
245367. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите тангенс угла AD1D.
245368. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите угол DAB. Ответ дайте в градусах.

245369. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите угол AC1C. Ответ дайте в градусах.
На этом всё! Успеха Вам!
В состав ЕГЭ включены и другие задачи по стереометрии, и они довольно разнообразны. Обязательно будем их рассматривать, не пропустите! Успехов вам!
Что ты хочешь узнать?
Ответ
Проверено экспертом
Найдите угол DAB – угол правильного шестиугольника ( основания призмы)
Сумма углов многоугольника находится по формуле
180(n-2)
180*(6-2)=720°
Величина одного угла правильного шестиугольника
720:6=120°Вопрос задан полностью? Иначе призма и ее ребра здесь как будто ни при чем.
Изучением призм занимается пространственная геометрия. Важными их характеристиками являются заключенный в них объем, площадь поверхности и число составляющих элементов.
 В статье рассмотрим все эти свойства для шестиугольной призмы.
В статье рассмотрим все эти свойства для шестиугольной призмы.О какой призме пойдет речь?
Призма шестиугольная – это фигура, образованная двумя многоугольниками, имеющими шесть сторон и шесть углов, и шестью параллелограммами, соединяющими отмеченные шестиугольники в единое геометрическое образование.
На рисунке изображен пример этой призмы.
Отмеченный красным цветом шестиугольник называется основанием фигуры. Очевидно, что число ее оснований равно двум, причем оба они идентичны. Желто-зеленоватые грани призмы называются ее боковыми сторонами. На рисунке они представлены квадратами, но в общем случае они являются параллелограммами.
Шестиугольная призма может быть наклонной и прямой. В первом случае углы между основанием и боковыми сторонами не являются прямыми, во втором они равны 90 o . Также эта призма может быть правильной и неправильной. Правильная шестиугольная призма обязательно должна быть прямой и иметь правильный шестиугольник в основании.
 Приведенная выше призма на рисунке этим требованиям удовлетворяет, поэтому она называется правильной. Далее в статье будем изучать только ее свойства, как общий случай.
Приведенная выше призма на рисунке этим требованиям удовлетворяет, поэтому она называется правильной. Далее в статье будем изучать только ее свойства, как общий случай.Элементы
Для любой призмы главными ее элементами являются ребра, грани и вершины. Шестиугольная призма не является исключением. Приведенный выше рисунок позволяет посчитать количество этих элементов. Так, граней или сторон мы получаем 8 (два основания и шесть боковых параллелограммов), число вершин составляет 12 (по 6 вершин для каждого основания), количество ребер шестиугольной призмы равно 18 (шесть боковых и 12 для оснований).
В 1750-е годы Леонард Эйлер (швейцарский математик) установил для всех полиэдров, к которым относится призма, математическую связь между числами указанных элементов. Эта связь имеет вид:
число ребер = число граней + число вершин – 2.
Указанные выше цифры удовлетворяют этой формуле.
Диагонали призмы
Все диагонали шестиугольной призмы можно разделить на два типа:
- те, которые лежат в плоскостях ее граней;
- те, которые принадлежат всему объему фигуры.

Рисунок ниже показывает все эти диагонали.
Видно, что D1 – это диагональ боковой стороны, D2 и D3 – диагонали всей призмы, D4 и D5 – диагонали основания.
Длины диагоналей боковых сторон между собой равны. Вычислить их легко, используя всем известную теорему Пифагора. Обозначим символом a длину стороны шестиугольника, символом b – длину бокового ребра. Тогда диагональ имеет длину:
Диагональ D4 также легко определяется. Если вспомнить, что правильный шестиугольник вписывается в окружность радиусом a, то D4 является диаметром этой окружности, то есть получим следующую формулу:
Диагональ D5 основания найти несколько сложнее. Для этого следует рассмотреть равносторонний треугольник ABC (см. рис.). Для него AB = BC = a, угол ABC равен 120 o . Если из этого угла опустить высоту (она же будет биссектрисой и медианой), тогда половина основания AC будет равно:
Сторона AC является диагональю D5, поэтому получаем:
Теперь остается найти диагонали D2 и D3 правильной шестиугольной призмы.
 Для этого нужно увидеть, что они являются гипотенузами соответствующих прямоугольных треугольников. Воспользовавшись теоремой Пифагора, получаем:
Для этого нужно увидеть, что они являются гипотенузами соответствующих прямоугольных треугольников. Воспользовавшись теоремой Пифагора, получаем:Таким образом, самой большой диагональю для любых значений a и b является D2.
Площадь поверхности
Чтобы понять, о чем идет речь, проще всего рассмотреть развертку этой призмы. Она показана на рисунке.
Видно, что для определения площади всех сторон рассматриваемой фигуры необходимо рассчитать отдельно площадь четырехугольника и площадь шестиугольника, затем умножить их на соответствующие целые числа, равные количеству каждого n-угольника в призме, и сложить полученные результаты. Шестиугольников 2, прямоугольников 6.
Для площади прямоугольника получаем:
Тогда площадь боковой поверхности равна:
Для определения площади шестиугольника проще всего воспользоваться соответствующей формулой, которая имеет вид:
Подставляя в это выражение число n равное 6, получаем площадь одного шестиугольника:
Это выражение следует умножить на два, чтобы получить площадь оснований призмы:
Остается сложить Sos и S2, чтобы получить полную площадь поверхности фигуры:
Объем призмы
После того как была получена формула для площади шестиугольного основания, вычислить объем, заключенный в рассматриваемую призму, проще простого.
 Для этого следует лишь умножить площадь одного основания (шестиугольника) на высоту фигуры, длина которой равна длине бокового ребра. Получаем формулу:
Для этого следует лишь умножить площадь одного основания (шестиугольника) на высоту фигуры, длина которой равна длине бокового ребра. Получаем формулу:Отметим, что произведение основания на высоту дает значение объема абсолютно любой призмы, включая наклонную. Однако в последнем случае расчет высоты осложняется, поскольку она уже не будет равна длине бокового ребра. Что касается шестиугольной правильной призмы, то значение ее объема является функцией двух переменных: сторон a и b.
“>
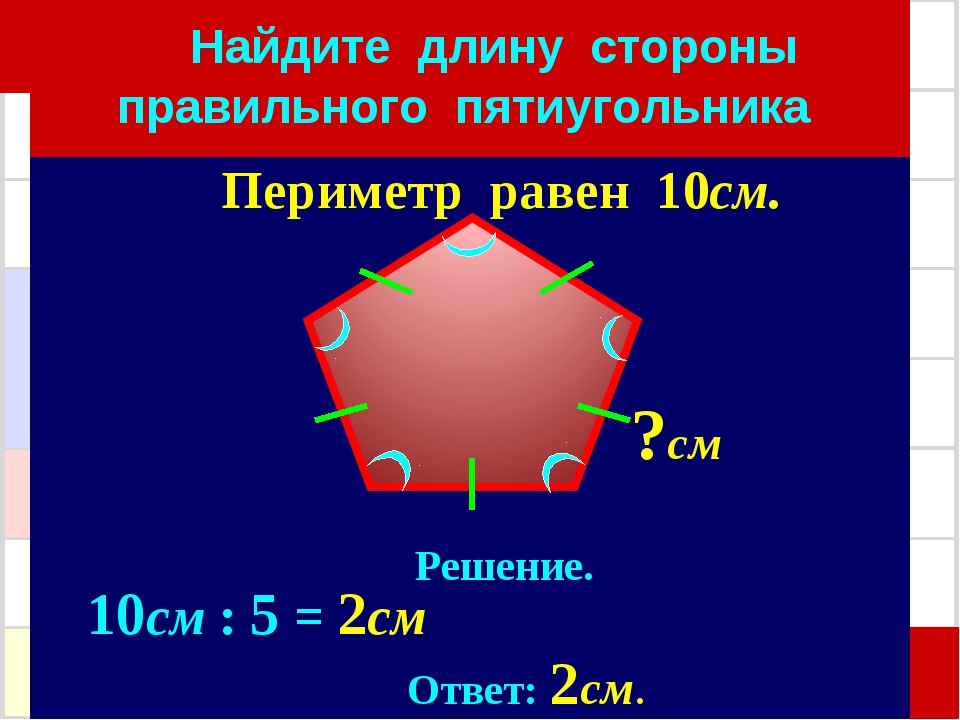
Онлайн калькулятор: Длина стороны правильного многоугольника
От нашего нового пользователя поступил вот такой запрос:
«Калькулятор должен вычислять длину стороны правильного многоугольника (шестиугольник, пятигольник) по указанному диаметру (или радиусу) описанной окружности».Удовлетворяем запрос оперативно. Заметим, что для решения задачи нужно найти длину третьей стороны треугольника, исходящего из центра описанной окружности и опирающегося на две соседние вершины правильного многоугольника. Про этот треугольник известно многое: длины двух сторон — это радиусы описанной окружности, и угол, как нетрудно заметить, — это 360, деленное на число вершин правильного многоугольника. Далее используется соотношение из теоремы синусов — две стороны относятся друг к другу также как и синусы противолежащих им углов. Поскольку треугольник равнобедренный и сумма углов в треугольнике равна 180 градусам, угол, противолежащий радиусу вычисляется тривиально. Результат — ниже.
Определение длины стороны правильного многоугольника по радиусу описанной окружности
Число сторон правильного многоугольника
Точность вычисленияЗнаков после запятой: 2
Длина стороны правильного многоугольника
content_copy Ссылка save Сохранить extension Виджет
P.S. В комментариях некто Александр поинтересовался, а как же найти длину стороны по радиусу вписанной окружности?
Отвечаю — с вписанной окружностью все гораздо проще. Надо рассмотреть треугольник, образованный перпендикуляром к точке касания окружности и многоугольника, половиной стороны многоугольника и линией от центра окружности до ближайшей к перпендикуляру вершины многоугольника. Этот треугольник перпендикулярный, и острый угол его равен 360, деленное на число вершин правильного многоугольника и еще пополам. Половина длины стороны находится легко — это радиус (прилежащий катет), умноженный на тангенс острого угла. Домножаем затем на два — получаем искомую длину стороны. Результат — ниже.
Определение длины стороны правильного многоугольника по радиусу вписанной окружности
Число сторон правильного многоугольника
Точность вычисленияЗнаков после запятой: 2
Длина стороны правильного многоугольника
content_copy Ссылка save Сохранить extension Виджет
Как найти угол в шестиугольнике
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105Или заполните форму ниже:
Как найти угол в шестиугольнике
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105Или заполните форму ниже:
Внутренние углы полигонов
Внутренний угол — это угол внутри формы
Другой пример:
Треугольники
Суммарные внутренние углы треугольника составляют 180 °
Давайте попробуем треугольник:
90 ° + 60 ° + 30 ° = 180 °Это работает для этого треугольника
Теперь наклоните линию на 10 °:
80 ° + 70 ° + 30 ° = 180 °Еще работает!
Один угол пошел на вверх, на на 10 °,
, а другой на вниз на на 10 °Четырехугольники (квадраты и т. Д.)
(У четырехугольника 4 прямые стороны)
Попробуем квадрат:
90 ° + 90 ° + 90 ° + 90 ° = 360 °Квадрат в сумме дает 360 °
Теперь наклоните линию на 10 °:
80 ° + 100 ° + 90 ° + 90 ° = 360 °В сумме все равно 360 °
Внутренние углы четырехугольника в сумме составляют 360 °
Потому что в квадрате 2 треугольника…
Сумма внутренних углов в треугольнике составляет 180 ° …
… а для квадрата они составляют 360 ° …
… потому что квадрат можно составить из двух треугольников!
Пентагон
У пятиугольника 5 сторон, и его можно составить из трех треугольников , так что вы знаете, что …
… его внутренние углы в сумме составляют 3 × 180 ° = 540 °
А когда это обычный (все углы одинаковые), то каждый угол будет 540 ° /5 = 108 °
(Упражнение: убедитесь, что каждый треугольник здесь составляет 180 °, и убедитесь, что внутренние углы пятиугольника составляют в сумме 540 °)
Внутренние углы пятиугольника в сумме составляют 540 °
Общие правила
Каждый раз, когда мы добавляем сторону (треугольник к четырехугольнику, четырехугольник к пятиугольнику и т. Д.), Мы добавляем еще на 180 °, к общей сумме:
Итак, общее правило:
Сумма внутренних углов = ( n −2) × 180 °
Каждый угол (правильного многоугольника) = ( n −2) × 180 ° / n
Возможно, поможет пример:
Пример: А как насчет правильного десятиугольника (10 сторон)?
Сумма внутренних углов = ( n −2) × 180 °
= ( 10 −2) × 180 °
= 8 × 180 °
= 1440 °
А для обычного десятиугольника:
Каждый внутренний угол = 1440 ° /10 = 144 °
Примечание: внутренние углы иногда называют «внутренними углами»
Обычный шестигранник | Справка по геометрии
В этом посте мы более подробно рассмотрим правильный шестиугольник — шестиугольник, у которого все стороны равны.Мы посмотрим на его углы и найдем формулы для его периметра и площади, используя его сторону или радиус.
Что такое правильный шестиугольник?
Правильный многоугольник — это двумерная выпуклая форма, стороны и внутренние углы которой равны. У правильного шестиугольника шесть равных сторон и шесть равных внутренних углов.
Внутренние углы правильного шестиугольника
Для любого многоугольника сумма внутренних углов равна S = (n-2) • 180 °, где n — количество сторон многоугольника.В шестиугольнике n = 6, поэтому сумма внутренних углов в шестиугольнике составляет (6-2) • 180 ° = 4 • 180 ° = 720 °. И поскольку все внутренние углы правильного шестиугольника равны, каждый из них имеет размер 720 ° / 6 = 120 °. Отсюда мы получаем много других интересных свойств, начиная с показа того, что правильный шестиугольник состоит из 6 равносторонних треугольников.
Правильный шестиугольник состоит из шести равносторонних треугольников
Многие из «доказательств», которые я видел, которые показывают, что правильный шестиугольник состоит из шести равносторонних треугольников, начинаются с таких вещей, как «Нарисуйте круг, проходящий через вершины правильного шестиугольника. «- но они не доказывают, что такой круг действительно можно нарисовать (это, конечно, можно, но довольно сложно).Итак, давайте формально докажем этот интуитивный результат.
Нарисуем биссектрисы двух смежных внутренних углов и назовем их точку пересечения O:
. Легко видеть, что ΔOAB равносторонний — m∠BAF = m∠ABC = 120 °, как внутренние углы правильного угла. шестиугольник. Биссектрисы образуют два половинных угла размером 60 °: m∠OAB = m∠OBA = 60 °. И из суммы углов в треугольнике, ∠AOB также является углом 60 °, а ΔOAB — равносторонним треугольником.
Теперь давайте соединим O с вершиной C и сравним треугольники ΔOAB и ΔOCB
OB = OB как общую сторону
AB = BC как равные стороны правильного шестиугольника
m∠ABO = m∠CBO = 60 ° как BO биссектриса угла
∠ABO≅∠CBO (определение конгруэнтных углов)
Таким образом, ΔOAB и ΔOCB являются конгруэнтными треугольниками согласно постулату «сторона-угол-сторона», а ΔOCB — равносторонний треугольник, идентичный ΔOAB.Мы можем продолжить и сделать это для остальных сторон, соединив точку O с вершинами D, E и F, чтобы достичь желаемого результата — шесть одинаковых равносторонних треугольников составляют шестиугольник, все они встречаются в его центре, O.Площадь и периметр
Поскольку мы показали, что шесть равносторонних треугольников образуют правильный шестиугольник, легко найти формулу для его площади — она в 6 раз больше площади одного из равносторонних треугольников. Мы показали, как вывести формулу площади равностороннего треугольника из длины его стороны: Площадь ΔРавносторонний = (s 2 * √3) / 4, где s — длина стороны.
[Быстрое напоминание о том, как мы это сделали: если мы возьмем высоту за основание любого из этих треугольников, мы получим прямоугольный треугольник 30 ° -60 ° -90 ° с гипотенузой, равной s, катет, равный к s / 2, а другой катет равен s / 2 · √3. Площадь такого треугольника равна (ножка · ножка) / 2 или (s / 2 · s / 2 · √3) / 2. Два одинаковых треугольника 30-60-90 составляют равносторонний треугольник, поэтому его площадь равна 2 * (s / 2 * s / 2 · √3) / 2 = (s 2 * √3) / 4]
Итак Площадь ⬡hex = 6 • (s 2 * √3) / 4 = 3 • √3 • s 2 /2.
Периметр любого многоугольника — это просто сумма его сторон. В правильном шестиугольнике все стороны равны, поэтому P ⬡hex = 6s.
Радиус
Радиус правильного многоугольника — это расстояние от его центра до любой из его вершин. По симметрии это расстояние одинаково для всех вершин. Так что же это за радиус в правильном шестиугольнике? Мы уже видели, что центр правильного шестиугольника образует равносторонний треугольник со сторонами, поэтому его радиус (R) равен длине каждой из сторон.Это также показывает, что мы можем вписать правильный шестиугольник в круг с радиусом R
Шестиугольник
Шестиугольник — это многоугольник с 6 сторонами и 6 углами (шестиугольник означает шесть). На рисунке ниже представлены 3 различных типа шестиугольников.
Шестиугольник — это форма, которая обычно встречается в повседневной жизни. Формы, из которых состоят соты, гайка и болты, — все это примеры реальных объектов в форме шестиугольника.
Классификация шестиугольника
Как и другие многоугольники, шестиугольник можно разделить на правильный и неправильный.Если все стороны и внутренние углы шестиугольника равны, это правильный шестиугольник. В противном случае это неправильный шестиугольник.
Правильный шестигранник Неправильный шестигранник Все стороны и внутренние углы равны Не все стороны и углы равны Шестиугольники и другие многоугольники также можно разделить на выпуклые и вогнутые. Если все внутренние углы шестиугольника или многоугольника меньше 180 °, он выпуклый.Если один или несколько внутренних углов больше 180 °, он вогнутый. Правильный шестиугольник — это всегда выпуклый шестиугольник.
Выпуклый шестигранник Вогнутый шестигранник Все внутренние углы <180 ° Один или несколько внутренних углов> 180 ° Диагонали шестигранника
Диагональ — это отрезок прямой, соединяющий две непоследовательные вершины. Из каждой вершины можно провести по три диагонали.Всего для шестиугольника можно нарисовать девять диагоналей. Следующий рисунок является примером.
Внутренние углы шестигранника
Сумма внутренних углов шестиугольника равна 720 °.
Как показано на рисунке выше, можно нарисовать три диагонали, чтобы разделить шестиугольник на четыре треугольника. Синие линии выше показывают только один способ разделить шестиугольник на треугольники; есть и другие. Сумма внутренних углов четырех треугольников равна сумме внутренних углов шестиугольника.Поскольку сумма внутренних углов треугольника равна 180 °, сумма внутренних углов шестиугольника составляет 4 × 180 ° = 720 °.
Шестигранник правильный
Правильный шестиугольник — это шестиугольник, все стороны которого равны по длине, а все внутренние углы имеют одинаковую меру.
Углы и стороны правильного шестиугольника
Поскольку каждый из шести внутренних углов в правильном шестиугольнике равны по размеру, каждый внутренний угол составляет 720 ° / 6 = 120 °, как показано ниже.
Каждый внешний угол правильного шестиугольника равен 60 °.
Стороны правильного шестиугольника равны по длине, а противоположные стороны параллельны.
AB = BC = CD = DE = EF = FA и AB // DE, BC // EF, CD // FA
Симметрия правильного шестиугольника
Правильный шестиугольник имеет 6 линий симметрии и вращательную симметрию порядка 6, что означает, что его можно повернуть таким образом, чтобы он 6 раз выглядел так же, как исходная форма на 360 °.
Линии симметрии Вращательная симметрия 6 линий симметрии Шесть углов поворота по 60 ° Площадь правильного шестиугольника
Площадь правильного шестиугольника со стороной s составляет:
От центра правильный шестиугольник можно разделить на шесть равносторонних треугольников, у каждого из которых есть длина стороны s, как показано ниже.
Площадь T одного из равносторонних треугольников, нарисованных синим цветом, может быть найдена с помощью, где апофема — это высота треугольника. Поскольку имеется шесть равносторонних треугольников, площадь правильного шестиугольника равна.
Пример:
Найдите площадь правильного шестиугольника с длиной стороны 8.
Использование:
Что такое шестиугольник? — Определение, площадь и ракурсы — Видео и стенограмма урока
Правильные шестиугольники
Шестиугольник — это пример многоугольника или многосторонней формы. Hex — это греческий префикс, означающий «шесть». У правильного шестиугольника шесть сторон, которые равны или равны по размеру. Правильный шестиугольник — это выпуклый , что означает, что все точки шестиугольника направлены наружу. Все углы правильного шестиугольника равны и составляют 120 градусов. Это означает, что углы правильного шестиугольника в сумме составляют 720 градусов, или 6 умноженных на 120.
Неправильные шестиугольники
Неправильные шестиугольники могут выглядеть совершенно иначе.Неправильный шестиугольник также имеет шесть сторон, но они не одинаковой длины. Концы неправильных шестиугольников могут указывать внутрь или наружу. Когда точки шестиугольника направлены внутрь, даже если только одна точка направлена внутрь, шестиугольник считается вогнутым шестиугольником .
Область поиска
Как и у всех правильных форм, есть простая формула, которую мы можем использовать для вычисления площади шестиугольника. Формула площади правильного шестиугольника выглядит так:
Где s — длина одной из сторон шестиугольника.Просто подставив длину одной из сторон в уравнение и введя ее в калькулятор, вы получите площадь шестиугольника.
Так, например, если у вас есть правильный шестиугольник, каждая сторона которого имеет длину 5 сантиметров, вы должны умножить три корня из трех на пять в квадрате и разделить ответ на два. Это даст вам 65 сантиметров в квадрате. Если вы использовали другую единицу измерения длины стороны, например, метры, ответ был бы в метрах в квадрате. Вот и все.
Краткое содержание урока
Шестиугольник — это многоугольник с 6 прямыми сторонами. Это обычно встречается в природе, потому что это особенно эффективная форма. Правильный шестиугольник имеет стороны, равные , и углы, равные 120 градусам. Это означает, что углы правильного шестиугольника в сумме составляют 720 градусов. Вы можете найти площадь шестиугольника, используя измерение одной из сторон и формулу площади:
Шестигранник неправильной формы имеет стороны, размеры которых не совпадают, и точки могут быть обращены как внутрь, так и наружу.Шестиугольник с даже одной внутренней точкой считается вогнутым шестиугольником .
Калькулятор свойств шестиугольника и правильного шестиугольника
Теоретические основы
Оглавление
Определения
Шестиугольник — это многоугольник с шестью сторонами и шестью вершинами. Как и любой многоугольник, шестиугольник может быть выпуклым или вогнутым, как показано на следующем рисунке. В выпуклом состоянии шестиугольник (или многоугольник в целом) не имеет внутренних углов больше 180 °.Напротив, вогнутый шестиугольник (или многоугольник) имеет один или несколько внутренних углов больше 180 °. Шестиугольник называется правильным, если все его стороны и внутренние углы равны . В отличие от треугольника, наличие равных сторон не означает, что внутренние углы также равны, поскольку шестиугольник может быть вогнутым. Как показано на рисунке ниже, можно определить множество возможных вогнутых шестиугольников с равными сторонами, но с разными внутренними углами (они называются равносторонними). Неправильный шестиугольник называется неправильным.
Типы шестиугольниковСумма внутренних углов любого шестиугольника, выпуклого или вогнутого, всегда равна 720 °. Это легко сделать, посчитав количество треугольников, помещающихся внутри шестиугольника, соединив его вершины (избегая пересечений). Действительно, есть 4 треугольника. Так как сумма внутренних углов в одном треугольнике равна 180 °, четыре треугольника, расположенные рядом, должны иметь размер 4×180 = 720 °.
Диагонали шестиугольника разделяют его внутреннюю часть на 4 треугольникаСвойства правильных шестиугольников
Симметрия
Правильный шестиугольник имеет шесть осей симметрии.\ circ
Два оставшихся угла в треугольнике также равны 60 °. На самом деле это \ varphi / 2, потому что диагонали шестиугольника (линии, соединяющие противоположные вершины) также являются осями симметрии, таким образом разделяя внутренний угол \ varphi пополам (который составляет 120 °). Следовательно, все шесть треугольников, у которых центр шестиугольника является одной из вершин, являются идентичными равносторонними треугольниками.
Внутренний и центральный углы также являются дополнительными, поскольку их сумма равна 180 °:
\ varphi + \ theta = 120 ° + 60 ° = 180 °
Правильный шестиугольник состоит из шести одинаковых равносторонних треугольников, имеющих общую вершину, центр многоугольника.
Окружность и вписанная окружность
Как и любой правильный многоугольник, можно нарисовать круг, проходящий через все шесть вершин шестиугольника. Это окружность, описанная выше, или описанная окружность многоугольника. Центр этого круга — центр шестиугольника. Точно так же диагонали шестиугольника — это диаметры описанной окружности. Радиус описанной окружности R_c обычно называют радиусом описанной окружности.
Можно также нарисовать еще один круг, проходящий через середины сторон шестиугольника.Этот круг называется вписанным кругом или вписанным кругом . Он касается всех шести сторон, а его центр совпадает с центром описанной окружности. Радиус вписанной окружности R_i обычно называют внутренним радиусом.
Описанные и вписанные окружности правильного шестиугольникаРадиусы описанной окружности R_c и вписанной окружности R_i связаны с длиной стороны \ alpha, а также между собой. Эти отношения могут быть обнаружены с помощью свойств прямоугольного треугольника, стороны которого: радиус описанной окружности, внутренний радиус и половина стороны шестиугольника, как показано на рисунке ниже.Используя базовую тригонометрию, мы находим:
\ begin {split} R_c & = \ frac {a} {2 \ sin {\ frac {\ theta} {2}}} \\ R_i & = \ frac {a} {2 \ tan {\ frac {\ theta} {2}}} \\ R_i & = R_c \ cos {\ frac {\ theta} {2}} \ end {split}
, где \ theta — центральный угол, а \ alpha — сторона длина. {\ circ}}}
Аппроксимация последнего уравнения:
A \ приблизительно 2.2
Периметр любого N-стороннего правильного многоугольника — это просто сумма длин всех сторон: P = N a. Следовательно, для правильного шестиугольника:
P = 6a
Ограничивающая рамка
Ограничивающая рамка плоской формы — это наименьший прямоугольник, который полностью охватывает форму. Размеры этого прямоугольника определяются высотой h и t шириной w правильного шестиугольника.
Высота
Высота h правильного шестиугольника — это расстояние между двумя противоположными краями.\ circ}
, что приблизительно равно:
h \ приблизительно 1,732 R_c
h \ приблизительно 1,732 a
Ширина
Ширина w — это расстояние между двумя противоположными вершинами правильного шестиугольника (длина его диагонали) . Это равно удвоенному радиусу описанной окружности R_c:
w = 2R_c
Поскольку R_c = a, мы могли бы также написать:
w = 2a
Как нарисовать правильный шестиугольник
Вы можете нарисовать правильный шестиугольник заданная длина стороны \ alpha, используя только линейку и циркуль.Выполните шаги, описанные ниже:
- Сначала просто нарисуйте линейный сегмент, длина которого равна желаемой длине стороны шестиугольника \ alpha.
- Затем постройте окружность, имеющую центр на одном конце линейного сегмента и радиус, равный длине сегмента.
- Не меняя радиуса, постройте вторую окружность с центром на другом конце линейного сегмента. Определены две точки, где этот круг пересекается с первым.
- Используя тот же радиус, поместите кончик циркуля в любую из последних определенных точек и постройте новый круг.Новая точка определяется на пересечении с первым кругом.
- Повторите ту же процедуру еще два раза. Поместите кончик циркуля в последнюю точку и постройте новый круг. Новая точка определяется на пересечении с первым кругом.
- На данный момент определено шесть точек вокруг первого круга. Это вершины шестиугольника. Нарисуйте между ними линейные отрезки, и правильный шестиугольник теперь готов. Начальная окружность — это описанная окружность шестиугольника. {\ circ}}} \ end {split}.2
Ключевой особенностью правильного шестиугольника является его способность размещать мозаику на плоскости, не оставляя зазоров. Это свойство позволяет предположить, что ни одно пространство в рамке улья не остается незанятым. Другими словами, мы можем найти количество ячеек в рамке улья, N, разделив общую площадь рамки на площадь ячеек:
N = \ frac {A_f} {A}
Путем подстановки и преобразования из квадратных дюймов до мм 2 (т.е. 1 » = 25,4 мм) получаем:
N \ приблизительно \ frac {171 \ \ left (25.2} \ Rightarrow
N \ приблизительно 5825
Почти шесть тысяч ячеек. Это число могло бы быть немного меньше, если учесть, что рядом с границами кадра формирование правильных шестиугольников невозможно. Если предположить, что один вертикальный и один горизонтальный столбцы ячеек потрачены впустую, по этой причине количество ячеек будет меньше примерно на 140 ячеек. Также имейте в виду, что размер ячеек может варьироваться.

 circ)
circ)

 Чтобы построить правильный многоугольник самостоятельно, необходимо знать его углы.
Чтобы построить правильный многоугольник самостоятельно, необходимо знать его углы. Либо просто разделите размер угла в градусах на 57,3 — именно столько градусов содержится в одном радиане.
Либо просто разделите размер угла в градусах на 57,3 — именно столько градусов содержится в одном радиане.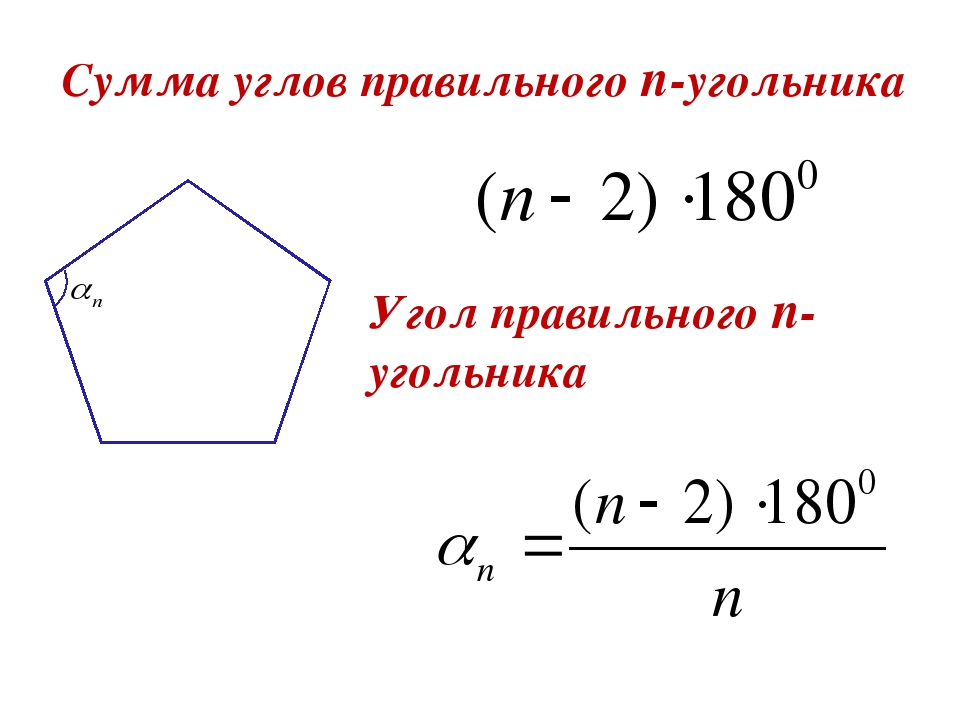
 5. Найдите количество сторон правильного
многоугольника, внешний угол которого равен
60°. а) 5;
5. Найдите количество сторон правильного
многоугольника, внешний угол которого равен
60°. а) 5;  10. Укажите
неправильное утверждение. а) если стороны четырёхугольника равны, то его углы равны;
10. Укажите
неправильное утверждение. а) если стороны четырёхугольника равны, то его углы равны; Например, задания про составные многогранники .
Например, задания про составные многогранники .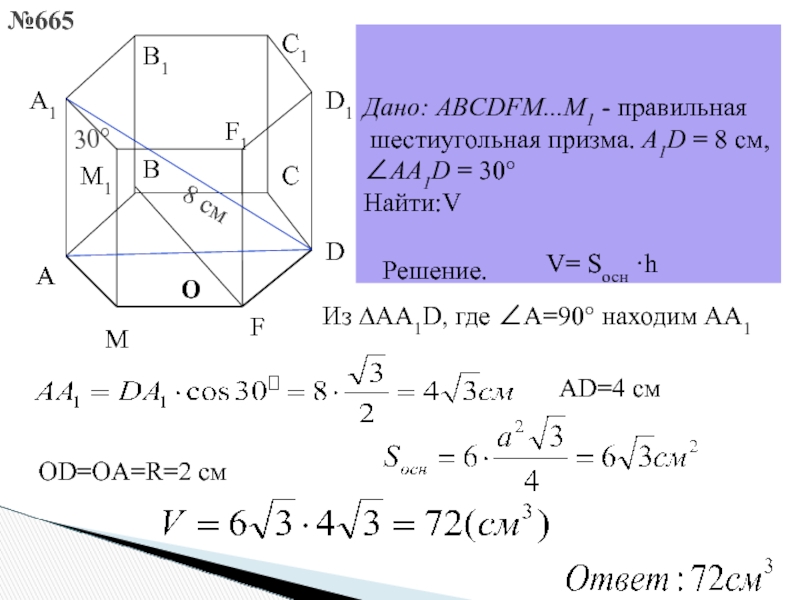 Ещё вам пригодится навык извлечения квадратного корня их большого числа. Можете посмотреть статью на решение многогранников, там тоже вычисляли расстояние между вершинами и углы.
Ещё вам пригодится навык извлечения квадратного корня их большого числа. Можете посмотреть статью на решение многогранников, там тоже вычисляли расстояние между вершинами и углы.

 В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 45. Найдите тангенс угла AD1D.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 45. Найдите тангенс угла AD1D.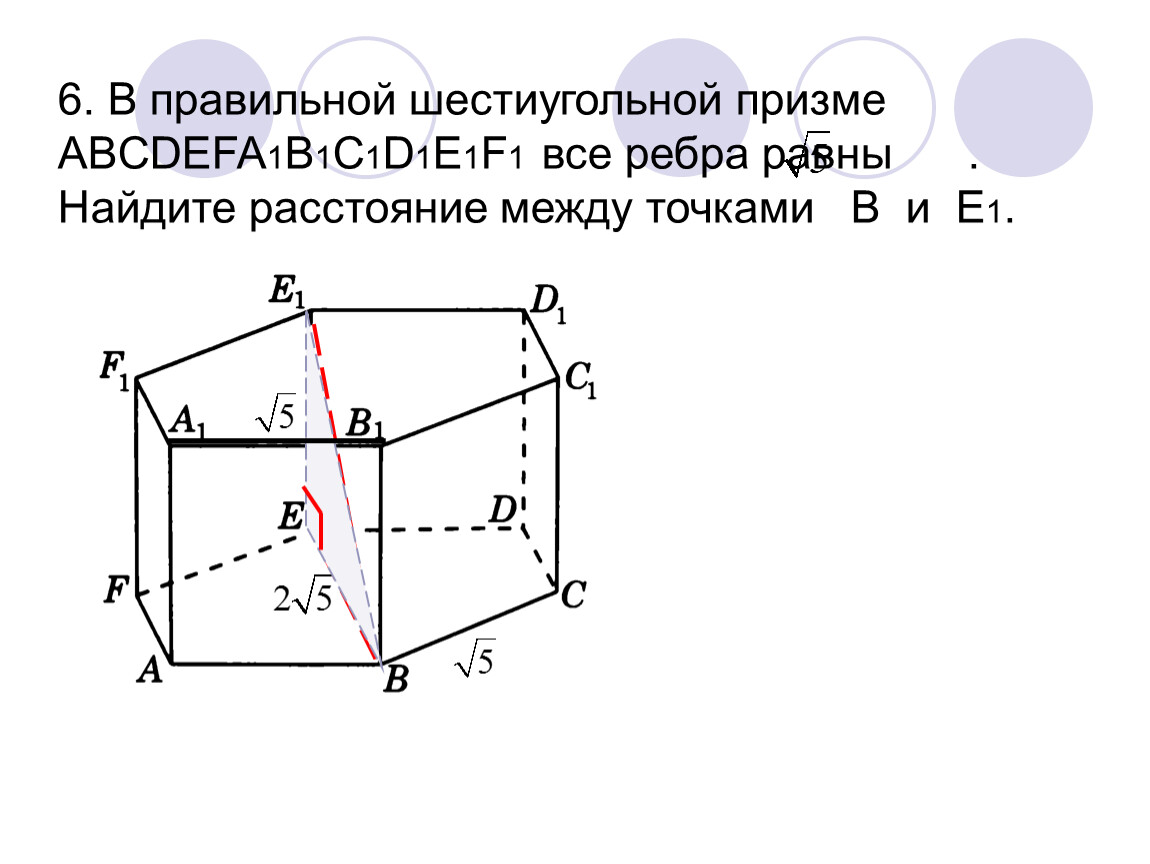 Ответ дайте в градусах.
Ответ дайте в градусах. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками А и Е1.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками А и Е1.
 В статье рассмотрим все эти свойства для шестиугольной призмы.
В статье рассмотрим все эти свойства для шестиугольной призмы. Приведенная выше призма на рисунке этим требованиям удовлетворяет, поэтому она называется правильной. Далее в статье будем изучать только ее свойства, как общий случай.
Приведенная выше призма на рисунке этим требованиям удовлетворяет, поэтому она называется правильной. Далее в статье будем изучать только ее свойства, как общий случай.
 Для этого нужно увидеть, что они являются гипотенузами соответствующих прямоугольных треугольников. Воспользовавшись теоремой Пифагора, получаем:
Для этого нужно увидеть, что они являются гипотенузами соответствующих прямоугольных треугольников. Воспользовавшись теоремой Пифагора, получаем: Для этого следует лишь умножить площадь одного основания (шестиугольника) на высоту фигуры, длина которой равна длине бокового ребра. Получаем формулу:
Для этого следует лишь умножить площадь одного основания (шестиугольника) на высоту фигуры, длина которой равна длине бокового ребра. Получаем формулу: