Правильный шестиугольник и его свойства
Определение
Выпуклый многоугольник называется правильным, если все его стороны равны и все его углы равны.
Замечание
Т.к. сумма всех углов \(n\)–угольника равна \(180^\circ(n-2)\), то каждый угол правильного \(n\)–угольника равен \[\alpha_n=\dfrac{n-2}n \cdot 180^\circ\]
Пример
Каждый угол правильного четырехугольника (т.е. квадрата) равен \(\dfrac {4-2}4\cdot 180^\circ=90^\circ\);
каждый угол правильного шестиугольника равен \(\dfrac{6-2}6\cdot 180^\circ=120^\circ\).
Теоремы
1. Около любого правильного многоугольника можно описать окружность, и притом только одну.
2. В любой правильный многоугольник можно вписать окружность, и притом только одну.
Следствия
1. Окружность, вписанная в правильный многоугольник, касается всех его сторон в серединах.
2. Центры вписанной и описанной окружности у правильного многоугольника совпадают.
Теорема
Если \(a\) – сторона правильного \(n\)–угольника, \(R\) и \(r\) – радиусы описанной и вписанной окружностей соответственно, то верны следующие формулы: \[\begin{aligned} S&=\dfrac n2ar\\ a&=2R\cdot \sin\dfrac{180^\circ}n\\ r&=R\cdot \cos\dfrac{180^\circ}n \end{aligned}\]
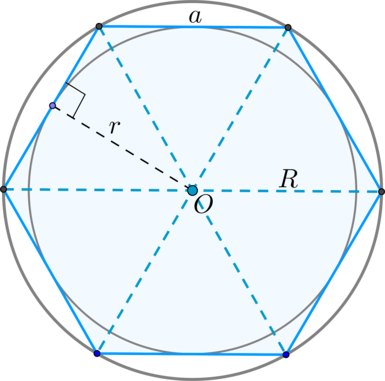
Свойства правильного шестиугольника
1. Сторона равна радиусу описанной окружности: \(a=R\).
2. Радиус описанной окружности является биссектрисой угла правильного шестиугольника.
3. Все углы правильного шестиугольника равны \(120^\circ\).
4. Площадь правильного шестиугольника со стороной \(a\) равна \(\dfrac{3\sqrt{3}}{2}a^2\).
5. Диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу \(r\) вписанной в правильный шестиугольник окружности.
6. Инвариантен относительно поворота плоскости на угол, кратный \(60^\circ\) относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями).
Замечание
В общем случае правильный \(n\)-угольник инвариантен относительно поворота на угол \(\dfrac{360^\circ}{n}\).
Гексагон
фывафыва
Гексагон — правильный выпуклый многоугольник с шестью сторонами или шестиугольник.
Шестиугольник — это многоугольник, имеющий шесть сторон и шесть углов. В правильном шестиугольнике все стороны равны, а углы образуют шесть равносторонних треугольников.
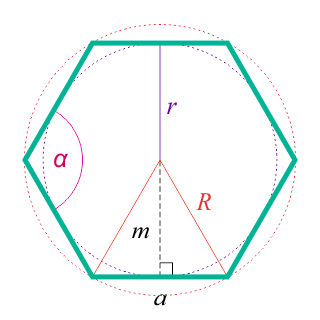
Выпуклый шестиугольник — это многоугольник, с общим количеством вершин, равным шести, при этом все точки такого шестиугольника лежат по одну сторону от прямой, которая проведена между двумя любыми соседними его вершинами.
Правильный шестиугольник — это шестиугольник, все стороны которого равны между собой.
Сумма углов выпуклого шестиугольника определяется по общей формуле 180°(n-2) и равна 180 ( 6 — 2 ) = 720 градусов.
При решении задач для нахождения площади произвольного (неправильного) шестиугольника используют метод трапеций, который заключается в разбиении фигуры на отдельные трапеции, площадь каждой из которых можно найти по известным всем формулам.
Свойства правильного шестиугольника
- все внутренние углы равны между собой
- каждый внутренний угол правильного шестиугольника равен 120 градусам
- все стороны равны между собой
- сторона правильного шестиугольника равна радиусу описанной окружности
- большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам
- меньшая диагональ правильного шестиугольника в \( \sqrt{3} \)раз больше его стороны.
- vеньшая диагональ правильного шестиугольника перпендикулярна его стороне
- правильный шестиугольник заполняет плоскость без пробелов и наложений
- диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу вписанной в правильный шестиугольник окружности. 6.
- инвариантен относительно поворота плоскости на угол, кратный относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями)
- nреугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60°.
Внутренние углы Внутренние углы в правильном шестиугольнике равны \(120^\circ\):
\(\alpha = 120^\circ\)
Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
\(m = a\large\frac{{\sqrt 3 }}{2}\normalsize\)
Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
\(m = a\large\frac{{\sqrt 3 }}{2}\normalsize\)
Радиус вписанной окружности правильного шестиугольника равен апофеме:
\(r = m = a\large\frac{{\sqrt 3 }}{2}\normalsize\)
Радиус описанной окружности равен стороне правильного шестиугольника:
\(R = a\)
Периметр правильного шестиугольника
\(P = 6a\)
Площадь правильного шестиугольника Формула площади правильного шестиугольника через длину стороны
\(S = pr = {a^2}\large\frac{{3\sqrt 3 }}{2}\normalsize\),
где \(p\) − полупериметр шестиугольника.
Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус вписанной окружности
\( S = r^{2}\cdot 2\sqrt{3} \)
Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус описанной окружности
\( S = \frac{R^{2}\cdot 3\sqrt{3}}{2} \)
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Правильный шестиугольник | Формулы и расчеты онлайн
Правильный шестиугольник — это такой шестиугольник у которого все шесть сторон равны и его шесть углов равны.
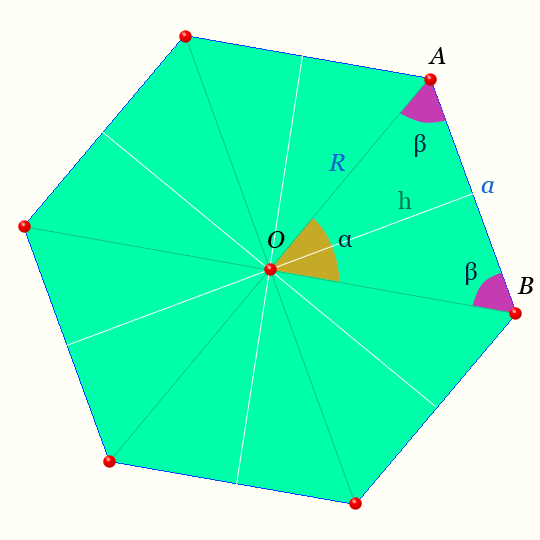
Правильный шестиугольник
Центр правильного шестиугольника — на рисунке точка O равноудалена от вершин.
Светлая линия обозначающая высоту треугольника AOB : h называется — апофемой.
Отрезки OA, OB — радиусы правильного шестиугольника.
Обозначения на рисунке для правильного шестиугольника
| n=6 | число сторон и вершин правильного шестиугольника, | шт |
|---|---|---|
| α | центральный угол правильного шестиугольника, | радианы, ° |
| β | половина внутреннего угла правильного шестиугольника, | радианы, ° |
| γ | внутренний угол правильного шестиугольника, | радианы, ° |
| a | сторона правильного шестиугольника, | м |
| R | радиусы правильного шестиугольника, | м |
| p | полупериметр правильного шестиугольника, | м |
| L | периметр правильного шестиугольника, | м |
| h | апофемы правильного шестиугольника, | м |
Основные формулы для правильного шестиугольника
Периметр правильного шестиугольника
\[ L = 6a \]
Полупериметр правильного шестиугольника
\[ p = 3a \]
Центральный угол правильного шестиугольника в радианах
\[ α = \frac{π}{3} \]
Центральный угол правильного шестиугольника в градусах
\[ α = \frac{180°}{3} = 60° \]
Половина внутреннего угла правильного шестиугольника в радианах
\[ β = \frac{π}{3} \]
Половина внутреннего угла правильного шестиугольника в градусах
\[ β = \frac{180°}{3} = 60° \]
Внутренний угол правильного шестиугольника в радианах
\[ γ = 2β = \frac{2}{3}π \]
Внутренний угол правильного шестиугольника в градусах
\[ γ = \frac{2}{3}180° = 120° \]
Площадь правильного шестиугольника
\[ S = ph = 3ha \]
Или учитывая формулу Площади правильного шестиугольника получим
\[ S = \frac{3\sqrt{3}}{2}a^2 \]
Отсюда получим апофему правильного шестиугольника
\[ h = \frac{\sqrt{3}}{2}a \]
В помощь студенту
Правильный шестиугольник |
стр. 269 |
|---|
Шестиугольник, виды, свойства и формулы
Шестиугольник, виды, свойства и формулы.
Шестиугольник – это многоугольник, общее количество углов (вершин) которого равно шести.
Шестиугольник, выпуклый и невыпуклый шестиугольник
Правильный шестиугольник (понятие и определение)
Свойства правильного шестиугольника
Формулы правильного шестиугольника
Правильный шестиугольник в природе, технике и культуре
Звездчатый шестиугольник
Восьмиугольник
Шестиугольник, выпуклый и невыпуклый шестиугольник:
Шестиугольник – это многоугольник с шестью углами.
Шестиугольник – это многоугольник, общее количество углов (вершин) которого равно шести.
Шестиугольник может быть выпуклым и невыпуклым.
Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.
Соответственно выпуклый шестиугольник – это шестиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

Рис. 1. Выпуклый шестиугольник
 Рис. 2. Невыпуклый шестиугольник
Рис. 2. Невыпуклый шестиугольник
Сумма внутренних углов любого выпуклого шестиугольника равна 720°.
 .
.
Правильный шестиугольник (понятие и определение):
Правильный шестиугольник (гексагон) – это правильный многоугольник с шестью сторонами.
В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.
Правильный шестиугольник – это шестиугольник, у которого все стороны равны, а все внутренние углы равны 120°.

Рис. 3. Правильный шестиугольник
Правильный шестиугольник имеет 6 сторон, 6 углов и 6 вершин.
Углы правильного шестиугольника образуют шесть равносторонних треугольников.
Правильный шестиугольник можно построить с помощью циркуля и линейки.
Свойства правильного шестиугольника:
1. Все стороны правильного шестиугольника равны между собой.
a1 = a2 = a3 = a4= a5 = a6.
2. Все углы равны между собой и составляют 120°.
α1 = α2 = α3 = α4 = α5 = α6 = 120°.

Рис. 4. Правильный шестиугольник
3. Сумма внутренних углов любого правильного шестиугольника равна 720°.
4. Все биссектрисы углов между сторонами равны и проходят через центр правильного шестиугольника O.

Рис. 5. Правильный шестиугольник
5. Количество диагоналей правильного шестиугольника равно 9.

Рис. 6. Правильный шестиугольник
6. Центр вписанной окружности O

Рис. 7. Правильный шестиугольник
7. Правильные шестиугольники замощают плоскость (то есть могут заполнять плоскость без пробелов и наложений).
8. Радиус описанной окружности правильного шестиугольника и его сторона равны.

Рис. 8. Правильный шестиугольник
R = a
Правильный шестиугольник в природе, технике и культуре:
Пчелиные соты имеют форму правильного шестиугольника.
Графит, графен имеют гексагональную кристаллическую решетку.
Гигантский гексагон – атмосферное явление на Сатурне – имеет форму правильного шестиугольника.

Рис. 9. Гигантский гексагон на Сатурне
Сечение гайки и многих карандашей имеет вид правильного шестиугольника.
Игровое поле гексагональных шахмат составляют шестиугольники, в отличие от квадратов традиционной шахматной доски.
Панцирь черепахи состоит из шестиугольников.
Гексагоном иногда называют материковую часть Франции, потому что её географические очертания напоминают данную геометрическую фигуру.

Рис. 10. Материковая часть Франции
Формулы правильного шестиугольника:
Пусть a – сторона шестиугольника, r
Формулы периметра правильного шестиугольника:

Формулы площади правильного шестиугольника:

Формула радиуса окружности, вписанной в правильный шестиугольник:

Формула радиуса окружности, описанной вокруг правильного шестиугольника:
R = a
Звездчатый шестиугольник:
Звездчатый шестиугольник
Гексаграмма (др.-греч. ἕξ – «шесть» и γραμμή – «черта, линия») – это звезда с шестью углами, которая образуется из двух наложенных друг на друга равносторонних треугольников.
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Шестиугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
карта сайта
Коэффициент востребованности 1 485
Правильный шестиугольник ≪ Scisne?
Правильный шестиугольник (гексагон) — это правильный многоугольник с шестью сторонами. Правильный шестиугольник |
Математические свойства
Особенность правильного шестиугольника — равенство его стороны и радиуса описанной окружности , поскольку .
Все углы равны 120°.
Радиус вписанной окружности равен:
.Периметр правильного шестиугольника равен:
Площадь правильного шестиугольника рассчитывается по формулам:,
.
Шестиугольники замощают плоскость, то есть могут заполнять плоскость без пробелов и наложений, образуя так называемый паркет.
 Шахматная раскраска шестиугольного паркета |
Шестиугольный паркет является двойственным треугольному паркету: если соединить центры смежных шестиугольников, то проведённые отрезки дадут треугольный паркетаж. Символ Шлефли шестиугольного паркета — {6,3}, что означает, что в каждой вершине паркета сходятся три шестиугольника.
Наиболее плотная упаковка кругов на плоскости |
Правильный шестиугольник со стороной является универсальной покрышкой, то есть всякое множество диаметра можно покрыть правильным шестиугольником со стороной (лемма Пала).
Правильный шестиугольник можно построить с помощью циркуля и линейки. Ниже приведён метод построения, предложенный Евклидом в «Началах», книга IV, теорема 15.
 Построение правильного шестиугольника с помощью циркуля и линейки |
Правильный шестиугольник в природе, технике и культуре
Пчелиные соты показывают разбиение плоскости на правильные шестиугольники. Шестиугольная форма больше остальных позволяет сэкономить на стенках, то есть на соты с такими ячейками уйдёт меньше воска.
 Пчелиные соты |
Некоторые сложные кристаллы и молекулы, например графит, имеют гексагональную кристаллическую решётку.
 Кристаллическая решетка графита |
Снежинки образуется, когда микроскопические капли воды в облаках притягиваются к пылевым частицам и замерзают. Появляющиеся при этом кристаллы льда, не превышающие поначалу 0,1 мм в диаметре, падают вниз и растут в результате конденсации на них влаги из воздуха. При этом образуются шестиконечные кристаллические формы. Из-за структуры молекул воды между лучами кристалла возможны углы лишь в 60° и 120°. Основной кристалл воды имеет в плоскости форму правильного шестиугольника. На вершинах такого шестиугольника затем осаждаются новые кристаллы, на них — новые, и так получаются разнообразные формы звёздочек-снежинок.
 Снежинки |
Гигантский гексагон — атмосферное явление на Сатурне.
 Гигантский гексагон — устойчивое атмосферное образование на северном полюсе Сатурна, открытое аппаратом Вояджер-1 и наблюдаемое снова в 2006 году аппаратом Кассини-Гюйгенс. |
Учёные из Оксфордского университета смогли в лабораторных условиях смоделировать возникновение подобного гексагона. Чтобы выяснить, как возникает такое образование, исследователи поставили на вертящийся стол 30-литровый баллон с водой. Она моделировала атмосферу Сатурна и её обычное вращение. Внутри учёные поместили маленькие кольца, вращающиеся быстрее ёмкости. Это генерировало миниатюрные вихри и струи, которые экспериментаторы визуализировали при помощи зелёной краски. Чем быстрее вращалось кольцо, тем больше становились вихри, заставляя близлежащий поток отклоняться от круговой формы. Таким образом авторам опыта удалось получить различные фигуры — овалы, треугольники, квадраты и, конечно, искомый шестиугольник.
 Вращение гексагона на северном полюсе Сатурна |
Дорога гигантов — памятник природы из примерно 40 000 соединённых между собой базальтовых (реже андезитовых) колонн, образовавшихся в результате древнего извержения вулкана. Расположен на северо-востоке Северной Ирландии в 3 км к северу от города Бушмилса.
Верхушки колонн образуют подобие трамплина, который начинается у подножья скалы и исчезает под поверхностью моря. Большинство колонн шестиугольные, хотя у некоторых четыре, пять, семь и восемь углов. Самая высокая колонна высотой около 12 м.
Около 50-60 миллионов лет назад, во время палеогенового периода, месторасположение Антрим подвергалось интенсивной вулканической активности, когда расплавленный базальт проникал через отложения, формируя обширные лавовые плато. По мере быстрого охлаждения происходило сокращение объёма вещества (подобное наблюдается при высыхании грязи). Горизонтальное сжатие приводило к характерной структуре шестигранных столбов.
 Дорога гигантов |
Игровое поле зачастую составляют шестиугольники. Замощение плоскости правильными шестиугольниками является основой для гекса, гексагональных шахмат и других игр на клетчатом поле, полигексов, вариантов модели «Жизнь» и других двумерных клеточных автоматов, кольцевых флексагонов и т.п.
 Гексагональные шахматы Глинского. Начальное положение фигур. |
Сечение гайки имеет вид правильного шестиугольника.
 Гайки |
Звезда Давида (гексаграмма) — шестиконечная звезда, образованная двумя правильными треугольниками, символ иудаизма.
 Звезда Давида |
Правильный шестиугольник — это… Что такое Правильный шестиугольник?
Шестиугольник — Правильный шестиугольник Шестиугольник многоугольник с шестью углами. Также шестиугольником называют всякий предмет такой формы. Сумма внутренних углов выпуклого шестиугольника р … Википедия
Шестиугольник Сатурна — Гексагональное устойчивое атмосферное образование на северном полюсе Сатурна, открытое аппаратом Вояджер 1 и наблюдаемое снова в 2006 году а … Википедия
Правильный многоугольник — Правильный семиугольник Правильный многоугольник это выпуклый многоугольник, у которого все стороны и углы равны . Определение правильного многоугольника может зависеть от определения … Википедия
Правильный семиугольник — Правильный семиугольник это правильный многоугольник с семью сторонами. Содержание … Википедия
Правильный треугольник — Правильный треугольник. Правильный (или равносторонний) треугольник это правильный многоугольник с тремя сторонами, первый из правильных многоугольников. Все стороны … Википедия
Правильный девятиугольник — это правильный многоугольник с девятью сторонами. Свойства Правиль … Википедия
Правильный 17-угольник — Правильный семнадцатиугольник геометрическая фигура, принадлежащая к группе правильных многоугольников. Он имеет семнадцать сторон и семнадцать углов, все его углы и стороны равны между собой, все вершины лежат на одной окружности. Содержание 1… … Википедия
Правильный семнадцатиугольник — геометрическая фигура, принадлежащая к группе правильных многоугольников. Он имеет семнадцать сторон и семнадцать углов, все его углы и стороны равны между собой, все вершины лежат на одной окружности. Содержание … Википедия
Правильный восьмиугольник — (октагон) геометрическая фигура из группы правильных многоугольников. У него восемь сторон и восемь углов и все углы и стороны равны между собой … Википедия
Правильный 65537-угольник — 65537 угольник или окружность? Правильный 65537 угольник (шестѝдесятипятиты̀сячпятисо̀ттридцатисемиугольник) геометрическая фигура из группы правильных многоугольников, состоящая из 65537 … Википедия
Правильный шестиугольник, площадь правильного шестиугольника
Знаете ли вы, как выглядит правильный шестиугольник?
Этот вопрос задан не случайно. Большинство учащихся 11 класса не знают на него ответа.
Правильный шестиугольник — такой, у которого все стороны равны и все углы тоже равны.
Железная гайка. Снежинка. Ячейка сот, в которых живут пчелы. Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.

Многие школьники теряются, видя задачи на правильный шестиугольник, и считают, что для их решения нужны какие-то особые формулы. Так ли это?
Проведем диагонали правильного шестиугольника. Мы получили шесть равносторонних треугольников.
Мы знаем, что площадь правильного треугольника: .
Тогда площадь правильного шестиугольника — в шесть раз больше.
, где — сторона правильного шестиугольника.
Обратите внимание, что в правильном шестиугольнике расстояние от его центра до любой из вершин одинаково и равно стороне правильного шестиугольник.
Значит, радиус окружности, описанной вокруг правильного шестиугольника, равен его стороне.
Радиус окружности, вписанной в правильный шестиугольник, нетрудно найти.
Он равен .
Теперь вы легко решите любые задачи ЕГЭ, в которых фигурирует правильный шестиугольник.
Ты нашел то, что искал? Поделись с друзьями!
. Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .

Радиус такой окружности равен .
Ответ: .
. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?

Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
Ответ: .
правильных многоугольников — свойства
Многоугольник
Многоугольник — это плоская форма (двумерная) с прямыми сторонами. Примеры включают треугольники, четырехугольники, пятиугольники, шестиугольники и так далее.
Обычный
«Правильный многоугольник» содержит: В противном случае это неправильный . |
|
Здесь мы смотрим только на правильных многоугольников .
Недвижимость
Итак, что мы можем знать о правильных многоугольниках? Прежде всего, мы можем проработать углы.
Внешний угол Внешний угол — это угол между любой стороной формы, |
Все внешние углы многоугольника в сумме составляют 360 °, поэтому:
Каждый внешний угол должен составлять 360 ° / n
(где n — количество сторон)
Нажмите кнопку воспроизведения, чтобы увидеть.
Внешний угол
(правильного восьмиугольника)
Пример: Каков внешний угол правильного восьмиугольника?
У восьмиугольника 8 сторон, поэтому:
Внешний угол = 360 ° / n
= 360 ° / 8
= 45 °
Внутренние углыВнутренний угол и Внешний угол измеряются от одной линии, поэтому в сумме получается 180 ° . |
Внутренний угол = 180 ° — Внешний угол
Мы знаем Внешний угол = 360 ° / n , поэтому:
Внутренний угол = 180 ° — 360 ° / n
Что можно переставить так:
Внутренний угол = 180 ° — 360 ° / n
= (п × 180 ° / п) — (2 × 180 ° / п)
= (п − 2) × 180 ° / п
Итак, у нас также есть это:
Внутренний угол = (n − 2) × 180 ° / n
Пример: Каков внутренний угол правильного восьмиугольника?
У правильного восьмиугольника 8 сторон, поэтому:
Внешний угол = 360 ° /8 = 45 °
Внутренний угол = 180 ° — 45 ° = 135 °
Внутренний угол
(правильного восьмиугольника)
Или мы могли бы использовать:
Внутренний угол = (n − 2) × 180 ° / n
= (8−2) × 180 ° / 8
= 6 × 180 ° / 8
= 135 °
Пример: Каковы внутренние и внешние углы правильного шестиугольника?
У правильного шестиугольника 6 сторон, поэтому:
Внешний угол = 360 ° /6 = 60 °
Внутренний угол = 180 ° — 60 ° = 120 °
А теперь несколько имен:
«Окружность, вписанная окружность, радиус и апофема… «
Звучит довольно музыкально, если повторить это несколько раз, но это просто названия «внешних» и «внутренних» кругов (и каждого радиуса), которые можно нарисовать на многоугольнике следующим образом:
«Внешний» круг называется описанной окружностью , и он соединяет все вершины (угловые точки) многоугольника.
Радиус описанной окружности также равен радиусу многоугольника.
«Внутренний» круг называется вписанной окружностью , и он просто касается каждой стороны многоугольника в его средней точке.
Радиус вписанной окружности равен апофемой многоугольника.
(Не все многоугольники обладают этими свойствами, но треугольники и правильные многоугольники обладают).
Разбиение на треугольники
Мы можем многое узнать о правильных многоугольниках, разбив их на треугольники следующим образом:
Обратите внимание, что:
- «основание» треугольника — это одна сторона многоугольника.
- «высота» треугольника — это «апофема» многоугольника
Итак, площадь треугольника равна половине основания, умноженной на высоту, поэтому:
Площадь одного треугольника = основание × высота / 2 = сторона × апофема / 2
Чтобы получить площадь всего многоугольника, просто сложите площади всех маленьких треугольников («n» из них):
Площадь многоугольника = n × сторона × апофема / 2
А так как периметр равен всем сторонам = n × сторона, получаем:
Площадь многоугольника = периметр × апофема / 2
Маленький треугольник
Разрезав треугольник пополам, получим:
(Примечание: углы указаны в радианах, а не в градусах)
Маленький треугольник является прямоугольным, поэтому мы можем использовать синус, косинус и тангенс, чтобы найти, как связаны между собой сторона , радиус , апофема и n (количество сторон):
| sin (π / n) = (Сторона / 2) / Радиус | Сторона = 2 × Радиус × sin (π / n) | |
| cos (π / n) = Апофема / Радиус | Апофема = Радиус × cos (π / n) | |
| загар (π / n) = (Сторона / 2) / Апофема | Сторона = 2 × Апофема × загар (π / n) |
Подобных отношений гораздо больше (большинство из них просто «перестановки»), но пока они подойдут.
Другие формулы площади
Мы можем использовать это для расчета площади, когда мы знаем только Апофему:
Площадь малого треугольника = ½ × Апофема × (Сторона / 2)
И мы знаем (из формулы «загар» выше), что:
Сторона = 2 × Апофема × загар (π / n)
Итак:
Площадь малого треугольника = ½ × Апофема × (Апофема × тангенс (π / n))
= ½ × Апофема 2 × tan (π / n)
И таких треугольников по 2 на каждую сторону, или 2n для всего полигона :
Площадь многоугольника = n × Апофема 2 × tan (π / n)
Когда мы не знаем Апофему, мы можем использовать ту же формулу, но переработанную для Радиуса или Стороны:
Площадь многоугольника = ½ × n × радиус 2 × sin (2 × π / n)
Площадь многоугольника = ¼ × n × сторона 2 / tan (π / n)
Таблица значений
А вот таблица сторон, апофем и площадей по сравнению с радиусом «1» с использованием разработанных нами формул:
График
А вот график из таблицы выше, но с числом сторон («n») от 3 до 30.
Обратите внимание, что по мере увеличения «n» Апофема стремится к 1 (равному радиусу), а Площадь стремится к π = 3,14159 …, как круг.
К чему стремится длина стороны?
,Hexagon — математическое определение слова
Шестиугольник — определение слова в математике — Открытый справочник по математике Попробуй это Отрегулируйте шестиугольник ниже, перетащив любую оранжевую точку. Вы можете переключаться между регулярные и неправильный шестиугольник с помощью флажка «обычный».Поскольку у шестиугольника четное число сторон, правильный шестиугольник, противоположные стороны параллельны друг другу.
Свойства правильных шестиугольников
| Внутренний угол | 120 ° | Как и любой правильный многоугольник, чтобы найти внутренний угол, мы используем формулу (180n-360) / п.Для шестиугольника n = 6. См. Внутренние углы многоугольника |
| Внешний угол | 60 ° | Чтобы найти внешний угол правильного шестиугольника, мы используем тот факт, что внешний угол образует линейная пара с внутренним углом, поэтому в целом он определяется формулой 180-внутренний угол. См. Внешние углы многоугольника |
| Площадь | 2,598 с 2 приблизительно | Где S — длина стороны.Чтобы найти точную площадь шестиугольника или любого многоугольника различными способами, см. Площадь правильного многоугольника и Площадь неправильного многоугольника |
Радиус равен длине стороны


В правильном шестиугольнике радиус равен длине стороны. То есть линия от центра до любой вершины будет такой же длины, как и любая сторона.
Поэтому можно представить себе правильный шестиугольник, состоящий из шести равносторонние треугольники.
Свойства всех шестиугольников
| Количество диагоналей | 9 | Количество различных диагоналей, возможных для всех вершин. (Обычно ½n (n – 3)). На рисунке выше нажмите «показать диагонали», чтобы увидеть их. См. Диагонали многоугольника |
| Количество треугольников | 4 | Количество треугольников, созданных путем рисования диагоналей из заданной вершины. (В общем n – 2). На рисунке выше нажмите «показать треугольники», чтобы увидеть их.Увидеть треугольники многоугольника |
| Сумма внутренних углов | 720 ° | Обычно 180 (n – 2) градусов. См. Внутренние углы многоугольника |
Болты и гайки шестигранников
 Большинство гаек и головок болтов имеют форму шестигранника. Поскольку шестигранник имеет три пары параллельных граней, можно установить гаечный ключ.
по любой паре.
Большинство гаек и головок болтов имеют форму шестигранника. Поскольку шестигранник имеет три пары параллельных граней, можно установить гаечный ключ.
по любой паре.
В ограниченном пространстве ключ можно повернуть на 60 ° (внешний угол шестиугольника), а затем ключ переставляется на следующую пару сторон.Повторение этого действия приведет к затяжке гайки.
Таким образом, вам не понадобится место для поворота всего гаечного ключа на полный круг.
Другие полигоны
Общие
Типы многоугольника
Площадь различных типов полигонов
Периметр различных типов полигонов
Углы, связанные с многоугольниками
Именованные полигоны
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Полигоны — Шестиугольники
Свойства шестиугольников, внутренние углы шестиугольников
| Полигоны: Свойства шестиугольников | ||||||||||||||||
| ||||||||||||||||
| ||||||||||||||||
Внутренние углы шестиугольника: | ||||||||||||||||
| ||||||||||||||||
| ||||||||||||||||
| Обычные шестиугольники: | ||||||||||||||||
| Свойства правильных шестиугольников: | ||||||||||||||||
Чтобы найти меру внутренних углов, мы знаем, что сумма всех углов составляет 720 градусов (сверху) … И есть шесть углов … Итак, мера внутренний угол правильного шестиугольника составляет 120 градусов. | ||||||||||||||||
| ||||||||||||||||
| Мера центральных углов правильного шестиугольника: | |
| Найти меру центрального угла правильный шестиугольник, сделайте круг посередине… Окружность составляет 360 градусов вокруг … Разделите ее на шесть углов … Итак, центральный угол правильного шестиугольника равен 60 градусам. Правильный шестиугольник состоит из 6 равносторонних треугольников! |
| 6-сторонний многоугольник
Сотовый узор — почему 6-сторонняя форма так распространена в природе
Сотовый узор состоит из правильных шестиугольников, расположенных рядом . Они полностью заполняют всю покрываемую ими поверхность, поэтому между ними нет дыр. Этот сотовый узор встречается не только в сотах (сюрприз!), Но и в многих других местах в природе . Фактически, он настолько популярен, что можно сказать, что это форма по умолчанию, когда действуют конфликтующие силы, а сферы невозможны из-за характера проблемы.
От пчел «ульев» до трещин в горных породах через органическую химию (даже в строительных блоках жизни: белках) правильные шестиугольники являются наиболее распространенной многоугольной формой, существующей в природе. И тому есть причина: углы шестиугольника. Угол 120º является наиболее механически устойчивым из всех, и по совпадению это также угол , под которым стороны встречаются в вершинах , когда мы выстраиваем шестиугольники бок о бок. Для полного описания важности и преимуществ правильных шестиугольников рекомендуем посмотреть видео выше.Тем, кто заядлый читатель, читайте дальше (вы можете проверить, насколько быстро вы читаете, с помощью калькулятора скорости чтения).
То, как углы 120º распределяют силы (и, в свою очередь, напряжения) между двумя сторонами шестиугольника, делает его очень стабильной и механически эффективной геометрией. Это значительное преимущество шестиугольников. Еще одним важным свойством правильных шестиугольников является то, что они могут заполнять поверхность без промежутков между ними (вместе с правильными треугольниками и квадратами). Вдобавок ко всему, у обычной 6-сторонней формы наименьший периметр при наибольшей площади среди этих заполняющих поверхность многоугольников, что, очевидно, делает ее очень эффективной.

Очень интересный пример на видео выше — это мыльных пузырей . Когда вы создаете пузырь, используя воду, мыло и немного собственного дыхания, он всегда имеет сферическую форму. Это потому, что объем сферы является самым большим из любого другого объекта для данной площади поверхности.
Однако, когда мы кладем пузыри вместе на плоскую поверхность, сфера теряет свое преимущество в эффективности , поскольку сечение сферы не может полностью покрыть двумерное пространство.Следующая лучшая форма с точки зрения объема и площади поверхности также лучше всего уравновешивает межпузырьковое натяжение, которое создается на поверхности пузырьков. Мы, конечно, говорим о нашем всемогущем шестиугольнике .
Пузыри представляют интересный способ визуализации преимуществ шестиугольника над другими формами, но это не единственный способ. В природе, как мы уже упоминали, существует примеров гексагональных образований , в основном из-за напряжений и напряжений в материале.К сожалению, мы не можем подробно остановиться на них. Тем не менее, можно назвать несколькими местами, где в природе можно встретить правильные шестиугольные узоры :
- Соты
- Органические соединения
- Стеки пузырей
- Скальные образования (например, Дорога гигантов)
- Глаза насекомых
- …
Богна Хапонюк и Альваро Диес
.







