разница с точки зрения науки — OneKu
Содержание статьи:Современным юным физикам и не только часто приходится сталкиваться с различными понятиями. Нередко возникает вопрос, в чем разница между массой и весом. Действительно, многие их путают и неверно употребляют в предложениях, хотя они обозначают не совсем одно и то же. Эти слова в некотором смысле являются синонимами. Так в чем разница веса и массы тела?
Общие понятия
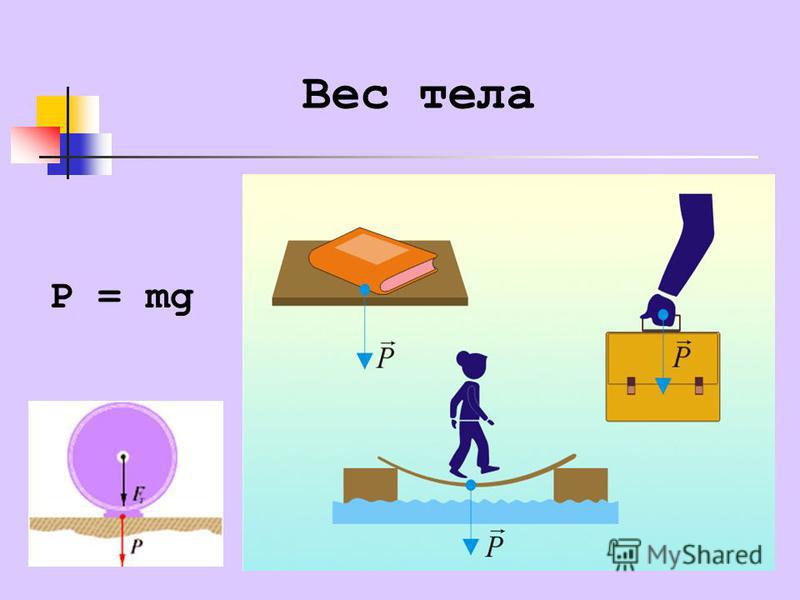
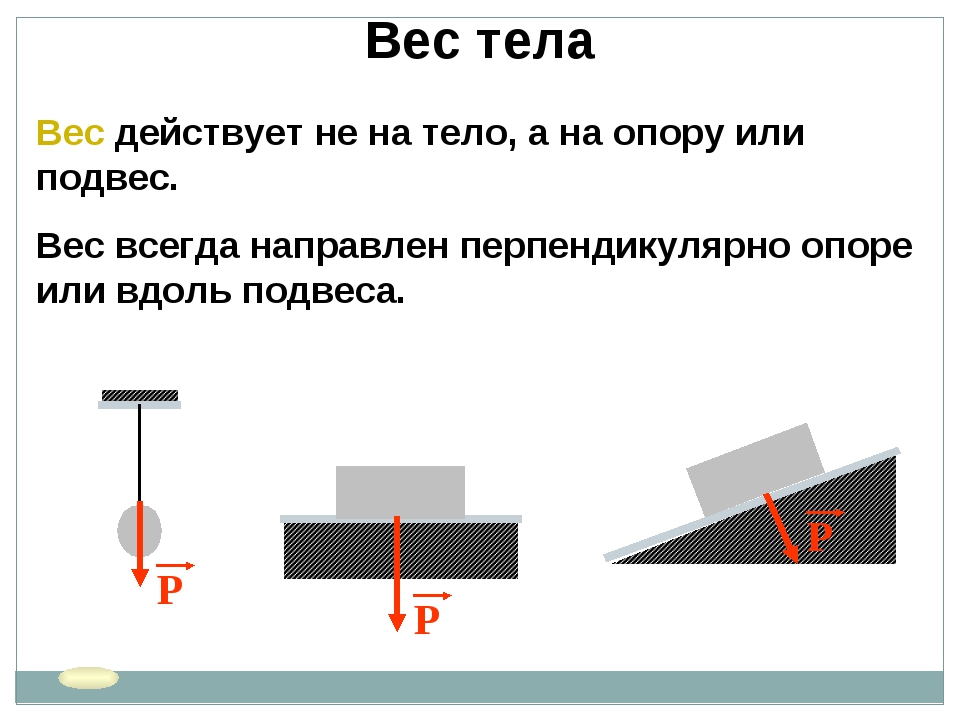
Следует начать с определений интересующих нас слов. С точки зрения науки, вес – сила, с которой тело действует на опору, если она в горизонтальном положении, или подвес, если положение вертикальное. Масса же – физическая величина, измеряющая гравитационные и инертные свойства тел. Первая разница веса и массы в том, что вес измеряется в Ньютонах, а масса в килограммах, согласно международной системе единиц.
Вам будет интересно:Вопрошающий – это просьба или унижение?
В качестве примера, который поможет увидеть разницу двух понятий, можно привести даже человеческое тело.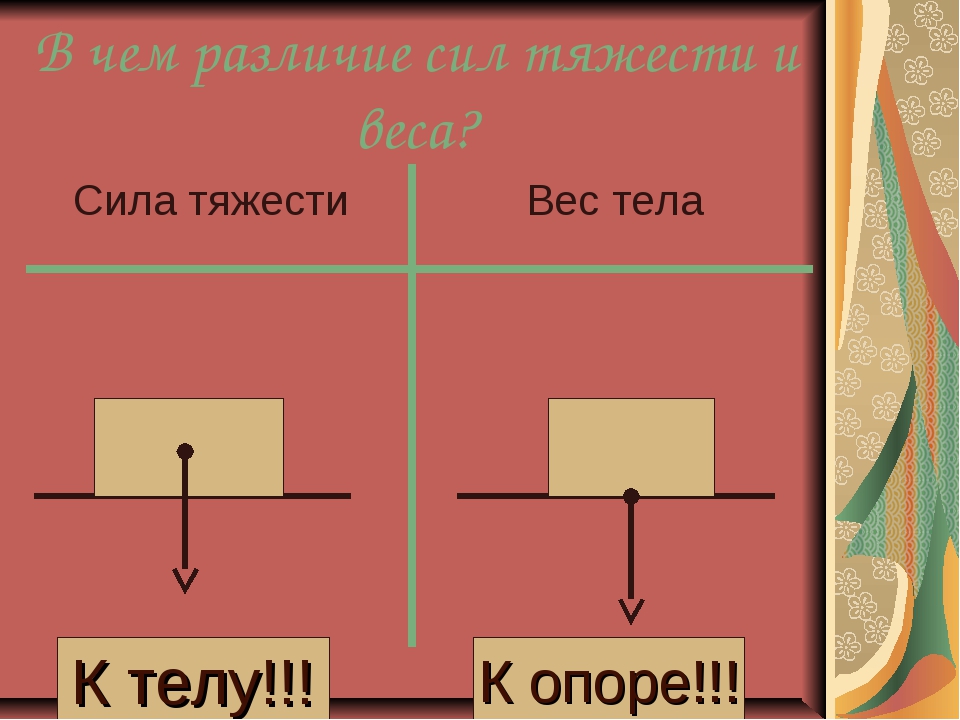
Или же, например, вес космонавта на Земле был один, на Луне он бы уменьшился почти в 6 раз, а на других планетах увеличился в десятки раз. Но все это время его масса бы ни на грамм не изменилась.
Еще разница веса и массы в том, что первое понятие зависит от движения (скорости), а второе – нет.
Математическое выражение
Существует даже формула зависимости этих двух понятий, с помощью которой вес можно найти через массу и наоборот:
P = mg,
где P – вес, m – масса тела, g – ускорение свободного падения.
Также существует закон сохранения массы, который гласит, что какие бы процессы ни происходили, какие бы силы к телам ни прикладывались, их масса всегда остается постоянной.
Более того, так как вес является силой, то он имеет направление. Масса же – величина количественная, и ни о каком направлении здесь речи быть не может.
Разница массы и веса
Существенное отличие между этими понятиями заключается в том, что масса объекта остается постоянной, а вот вес может изменяться в зависимости от условий, например, он может зависеть от высоты, с которой тело падает вниз.
Также в состоянии невесомости вес предметов может быть равен нулю, в то время как их масса вовсе не нулевая и даже у каждого своя.
Интересно, что из-за повседневного вращения Земли вокруг своей оси в некоторых местах наблюдается уменьшение широтного веса.
Наше время
Сейчас люди практически не видят разницу массы и веса. Типичным примером этого является любая покупка в магазине, когда покупатель спрашивает у продавца информацию о весе продукта. С точки зрения науки, правильно было бы поинтересоваться его массой. Тем не менее на упаковках производитель указывает все как нужно.
Мы можем увидеть там такие надписи, как «масса нетто» (то есть масса чистого продукта) и «масса брутто» (масса продукта вместе с упаковкой). В результате этого масса и вес стали практически синонимами в потребительской сфере, и большинство людей искренне удивляются, когда кто-то пытается им доказать, что есть разница в массе и весе.
В настоящее время нет особых требований в том, чтобы каждый человек умел различать данные понятия. Скорее, это больше необходимо тем, кто занимается научной деятельностью.
Источник
Что такое масса? Чем масса отличается от веса?
Однако с точки зрения науки физики в таком подходе кроется ошибка. Масса и вес не равны друг другу, измеряются в разных единицах и означают совершенно разные вещи.
Масса и вес не равны друг другу, измеряются в разных единицах и означают совершенно разные вещи.
Две характеристики предмета — неизменная и легко изменяемая
На языке науки масса — это постоянное свойство, которое не меняется и остается прежним в любых условиях. Если объяснять простыми словами, это количественное понятие, говорящее о том, сколько вещества содержится во взятом объекте — камне, бруске дерева, капле воды и так далее. Понятно, что на Земле, в открытом пространстве космоса или на любой из планет этот показатель будет оставаться одним и тем же.
Почти все, что есть во Вселенной, обладает хоть какой-то, пусть даже очень малой, массой. Не относится это только к фотонам и еще гравитонам — частицам, которые до сих пор не зафиксированы официально. Массы, уходящей «в минус», фактически не бывает — хотя здесь можно отметить, что ее наличие допускают умозрительные математические выкладки.
При этом вес – величина нестабильная
 Согласно формулировке, это сила давления тела на существующую опору. Поэтому на показатель влияет в первую очередь притяжение. Взятое для изучения тело будет весить неодинаково на разных планетах, поскольку гравитация небесных тел притягивает предметы с разной силой. А в открытом космосе, в удалении от всех планет, термин и вовсе теряет свой смысл.
Согласно формулировке, это сила давления тела на существующую опору. Поэтому на показатель влияет в первую очередь притяжение. Взятое для изучения тело будет весить неодинаково на разных планетах, поскольку гравитация небесных тел притягивает предметы с разной силой. А в открытом космосе, в удалении от всех планет, термин и вовсе теряет свой смысл.Для записи двух понятий применяются разные системы. Так, основной единицей массы является один килограмм. А вот вес исчисляется в ньютонах по специальной формуле — для того, чтобы узнать его, требуется найти произведение уже известной массы и значения гравитации.
Различие между двумя понятиями можно объяснить и другими словами — в противоположность массе, вес всегда куда-то направлен, он имеет вектор, в котором действует взятый объект.
Конечно, в разговорной речи люди редко обращают внимание на подобные нюансы. Если допустить ошибку и использовать один термин вместо другого в обычной беседе, никакого недопонимания не возникнет. Но важно понимать, что означают эти физические понятия на самом деле. Во многих случаях, произнося слово «вес», мы рассуждаем о массе — так же, как и наоборот.
Но важно понимать, что означают эти физические понятия на самом деле. Во многих случаях, произнося слово «вес», мы рассуждаем о массе — так же, как и наоборот.
Похожие статьи
Вес — Википедия. Что такое Вес
Вес — сила воздействия тела на опору (или подвес, или другой вид крепления), препятствующую падению, возникающая в поле сил тяжести[1][2]. Единица измерения веса в Международной системе единиц (СИ) — ньютон, иногда используется единица СГС — дина.
Свойства
Вес P{\displaystyle \mathbf {P} } тела, покоящегося в инерциальной системе отсчёта, равен силе тяжести, действующей на тело, и пропорционален массе m{\displaystyle m} и ускорению свободного падения g{\displaystyle \mathbf {g} } в данной точке:
- P=mg{\displaystyle \mathbf {P} =m\mathbf {g} }.
Ускорение свободного падения зависит от высоты над земной поверхностью и — ввиду несферичности Земли, а также ввиду её вращения — от географических координат точки измерения. В результате суточного вращения Земли существует широтное уменьшение веса: на экваторе вес примерно на 0,3 % меньше, чем на полюсах. Другим фактором, влияющим на значение g{\displaystyle \mathbf {g} } и, соответственно, вес тела, являются гравитационные аномалии, обусловленные особенностями строения земной поверхности и недр в окрестностях точки измерения. Если тело находится вблизи другой планеты, а не Земли, то ускорение свободного падения будет определяться массой и размерами этой планеты, наряду с расстоянием между её поверхностью и телом.
В результате суточного вращения Земли существует широтное уменьшение веса: на экваторе вес примерно на 0,3 % меньше, чем на полюсах. Другим фактором, влияющим на значение g{\displaystyle \mathbf {g} } и, соответственно, вес тела, являются гравитационные аномалии, обусловленные особенностями строения земной поверхности и недр в окрестностях точки измерения. Если тело находится вблизи другой планеты, а не Земли, то ускорение свободного падения будет определяться массой и размерами этой планеты, наряду с расстоянием между её поверхностью и телом.
При движении системы «тело» — «опора или подвес» относительно инерциальной системы отсчёта с ускорением w{\displaystyle \mathbf {w} } вес перестаёт совпадать с силой тяжести:
- P=m(g−w){\displaystyle \mathbf {P} =m(\mathbf {g} -\mathbf {w} )}.
Например, если ускорение (независимо от скорости) лифта направлено вверх, то вес находящегося в нём груза увеличивается, а если вниз, то уменьшается. Ускорение за счёт вращения Земли не входит в w{\displaystyle \mathbf {w} }, оно уже учтено в g{\displaystyle \mathbf {g} }.
Комментарий
Тело массой m{\displaystyle m}, вес которого анализируется, может стать субъектом приложения дополнительных сил, косвенно обусловленных присутствием гравитационного поля, в том числе силы Архимеда и трения. При этом воздействие изучаемого тела на опоры и подвесы будет опосредовано наличием указанных привходящих факторов.[прояснить]
В официальном определении, приведённом в преамбуле, отсутствует конкретизация, должны ли учитываться подобные факторы. Не оговорено также, обязательно ли роль опоры-подвеса должно играть упругое твёрдое тело и что если опор несколько. Кроме того, в публикациях встречаются и неэквивалентные дефиниции веса [источник не указан 205 дней]
[источник не указан 205 дней]
Так, при учёте только вклада силы тяжести покоящемуся на наклонной поверхности телу приписывается направленный по нормали к опоре вес mgcosα{\displaystyle mg\cos \alpha }, где α{\displaystyle \alpha } — угол наклона[4]. Но если учесть ещё и силу трения покоя (а она, по третьему закону Ньютона, приложена и к телу, и к опоре), то вектор веса станет равным mg{\displaystyle m\mathbf {g} }[3]. Аналогично с силой Архимеда: в жидкости или газе с плотностью ρ{\displaystyle \rho } на тело действует подъёмная сила FA=−ρgV{\displaystyle \mathbf {F} _{A}=-\rho \mathbf {g} V} (где V{\displaystyle V} — объём тела), из-за которой, скажем, воздействие тела на неровное[6] дно водоёма ослабляется. Трактуя эту ситуацию, можно либо заявить, что вес тела снижается на вес вытесненного объёма воды, либо считать, что вес по-прежнему составляет mg{\displaystyle m\mathbf {g} } и есть ещё подлежащая отдельному анализу архимедова сила.
Сила веса, формулы
Определение 1
Вес представляет силу влияния тела на опору (подвес, или иную разновидность крепления), препятствующую падению, и возникающую в поле действия сил тяжести. Единицей измерения веса в СИ принят ньютон.
Понятие веса тела
Понятие «вес» как таковое в физике не считается необходимым. Так, больше говорится о массе или о силе тела. Более содержательной величиной считается сила воздействия на опору, знание которой может помочь, например, при оценке способности конструкции удержать исследуемое тело в заданных условиях.
Вес возможно измерить с помощью пружинных весов, служащих также для косвенного измерения массы при их соответствующем градуировании. В то же время, рычажные весы в этом не нуждаются, поскольку в такой ситуации сравнению подлежат массы, на которые воздействует равное ускорение свободного падения либо сумма ускорений в неинерциальных системах отсчета.
При взвешивании за счет технических пружинных весов, вариации ускорения свободного падения обычно не учитываются, поскольку из влияние зачастую оказывается меньше того, что требуется на практике в отношении точности взвешивания. В некоторой степени, на результатах измерений может отражаться сила Архимеда, при условии взвешивания на рычажных весах тел различной плотности и их сравнительных показателей.
В некоторой степени, на результатах измерений может отражаться сила Архимеда, при условии взвешивания на рычажных весах тел различной плотности и их сравнительных показателей.
Готовые работы на аналогичную тему
Вес и масса в физике представляют различные понятия. Так, вес считается векторной величиной, с которой тело будет непосредственно воздействовать на горизонтальную опору либо вертикальный подвес. Масса в то же время представляет скалярную величину, меру инертности тела (инертную массу) или заряд гравитационного поля (гравитационную массу). У таких величин будут отличаться и единицы измерения (в СИ масса обозначена в килограммах, а вес— в ньютонах).
Возможны также ситуации с нулевым весом и также ненулевой массой (когда речь идет об одном и том же теле, к примеру, при невесомости вес каждого тела будет равным нулевому значению, а вот масса у всех окажется разной).
Важные формулы для расчета веса тела
Вес тела ($P$), которое покоится в инерциальной системе отсчёта, равнозначен силе тяжести, воздействующей на него, и пропорционален массе $m$, а также ускорению свободного падения $g$ в данной точке.
$P = mg$
Замечание 1
Ускорение свободного падения будет зависимым от высоты над земной поверхностью, а также от географических координат точки измерения.
Результатом суточного вращения Земли является широтное уменьшение веса. Так, на экваторе вес окажется меньшим, в сравнении с полюсами.
Другим фактором, влияющим на значение $g$, можно считать гравитационные аномалии, которые обусловлены особенностями строения земной поверхности. При местонахождении тела вблизи другой планеты (не Земли), ускорение свободного падения зачастую определяется за счет массы и размеров этой планеты.
Состояние отсутствия веса (невесомости) наступит в условиях отдаленности тела от притягивающего объекта или его пребывании в свободном падении, то есть в ситуации, когда
${g – w} = 0$.
Тело массой $m$, чей вес анализируется, может оказаться субъектом приложения определенных дополнительных сил, косвенно обусловленных фактом присутствия гравитационного поля, в частности, силы Архимеда и силы трения.
Отличие силы веса тела от силы тяжести
Замечание 2
Сила тяжести и вес представляют собой два различных понятия, участвующих непосредственно в теории гравитационного поля физики. Эти два совершенно разных понятия зачастую истолковывают неверно, используя их в неверном контексте.
Такая ситуация усугубляется еще и тем, что в стандартном понимании понятия массы (имеется в виду свойство материи) и веса также будут восприниматься как тождественные. Именно по этой причине правильное понимание тяжести и веса считается очень важным для научной среды.
Зачастую эти две практически аналогичные концепции применяются в формате взаимозаменяемых. Сила, которая направляется на объект со стороны Земли или другой планеты в нашей Вселенной (в более широком понимании — любого астрономического тела) будет представлять силу тяжести:
$Fт = mg$
Сила, с которой тело оказывает непосредственное воздействие на опору или вертикальный подвес и будет считаться весом тела, обозначаемым как $W$ и представляющим собой векторно направленную величину.
Атомы (молекулы) тела будут отталкиваться от частиц основания. Следствием такого процесса становится:
- осуществление частичной деформации не только опоры, но и также объекта;
- возникновение сил упругости;
- изменение в определенных ситуациях (в незначительной степени) формы тела и опоры, что будет происходить на макроуровне;
- возникновение силы реакции опоры при параллельном на поверхности тела возникновении силы упругости, что становится ответной реакцией на опору (это и будет представлять вес).
ЕДИНИЦ ИЗМЕРЕНИЙ — Тематические тексты
Главная → ЕДИНИЦЫ ИЗМЕРЕНИЙ — Тематические текстыТекст 1
Любые измерения — например, температуры, расстояния, времени или веса — основаны на единицах измерения. Единица — это фиксированная величина. В древности для измерения длины использовали части тела. (Греки использовали палец как основную единицу длины, 16 пальцев равнялись одной ноге). Изначально измерение веса основывалось на том, сколько человек может поднять. Эти неточные измерения превратились в систему общих единиц.
Эти неточные измерения превратились в систему общих единиц.
Текст 2
Связанные движения Земли, Луны и Солнца дают нам отметки времени. Полный день и ночь (24 часа) — это время, за которое Земля совершает один оборот вокруг своей оси. Время, необходимое для обращения Луны по орбите (кругу) вокруг Земли, составляет один месяц. Наши календарные месяцы варьируются от 28 до 31 дня, но лунный (лунный) месяц составляет ровно 29 ½ дней. Двенадцать календарных месяцев составляют один год или 365 дней, примерно столько же времени требуется Земле, чтобы вращаться вокруг Солнца.Каждый четвертый год является високосным, у него есть дополнительный день.
Текст 3
Примерно 5000 лет назад египтяне были первыми, кто измерил время. Они разделили свои дни на два периода по двенадцать равных часов, как мы это делаем сегодня. Первые часы включали солнечные часы и другие формы часов, которые измеряли изменения уровня воды или песка. Они были неточными, и только в 1600-х годах более надежные маятниковые часы были изобретены голландским ученым Кристианом Гюйгенсом (1629–1695).
Текст 4
Ваш вес — это сила, которую вы прилагаете к Земле. Это результат действия силы тяжести на ваше тело. Вес отличается от массы: ваша масса постоянна независимо от силы тяжести. Ученые измеряют массу в килограммах (кг). Это указывает на количество вещества в вашем теле. Ученые измеряют вес в ньютонах (Н), а 1 кг равен силе 9. 81 Н. На Луне ваш вес будет намного меньше, чем на Земле, из-за меньшей силы тяжести.
Текст 5
Толчок или тяга, которые приводят в движение объект, — это сила.Силы не только заставляют вещи двигаться, они также могут ускорять или замедлять движущийся объект, заставлять его менять направление или даже искажать его форму. Как правило, чем сильнее сила, тем сильнее она влияет на объект.
Текст 6
Вы давите на что-то, когда прикладываете к этому силу. Величина давления зависит от двух вещей: размера силы и, что более важно, размера области, на которую она действует. Чем меньше площадь, тем больше давление. Этот принцип объясняет, почему тонкие туфли на шпильке проваливаются в деревянные полы и повреждают их. Это также объясняет, почему большие плоские лапы верблюда не позволяют ему погрузиться в песок в пустыне.
Этот принцип объясняет, почему тонкие туфли на шпильке проваливаются в деревянные полы и повреждают их. Это также объясняет, почему большие плоские лапы верблюда не позволяют ему погрузиться в песок в пустыне.
Текст 7
Все в мире движется. Некоторые формы движения мы можем ясно видеть, например, полет самолета. Но даже объекты, которые кажутся неподвижными, такие как камни и здания, содержат атомы (крошечные частицы), которые мгновенно движутся или вибрируют. Сама Земля движется вокруг Солнца, и вся Вселенная расширяется.Любое движение требует силы для начала, изменения скорости или направления или остановки.
расчет моментов расчет силы поворота решение задач механического преимущества приложения равновесия шестерни рычаги уравновешивающие силы igcse / gcse 9-1 Physics revision notes
СИЛЫ 5. Расчет крутящих сил и моментов
от гаечных ключей до тачек и ситуаций равновесия
Редакция Доктора Брауна по физике Банкноты
Подходит для курсов GCSE / IGCSE Physics / Science или их эквивалент
Эта страница поможет вам ответить на такие вопросы, как как:
Что такое момент? Что такое механический преимущество? Как вы рассчитываете эффект поворота силы? Почему поворачивающие эффекты силы так важно? Где мы применяем преимущества поворачивающий эффект силы?
Субиндекс этой страницы
(а) An введение моментам и механическим силам вращения
(б) Несколько простых расчетов моментов
(в) Расчет моментов и балансирующая ситуация (равновесие)
(г) Более сложные вычисления моментов и равновесия
(д) Некоторые простые приложения поворачивающего воздействия сил с рычагами
(ж) Шестерни и винтик колеса — средство передачи вращательных воздействий
Смотрите также Масса — действие на нее силы тяжести — вес, (упоминание о проделанной работе, ГПД и круговом движении)
а) An i nпроизводство моментам и механическим силам вращения
Силы могут вызвать вращение объекта и эффект поворота силы называется
момент .
Если на объект действует равнодействующая сила около фиксированной точки поворота (точка поворота , точка поворота ) это приведет к тому, что объект будет повернуть например поворот гайки гаечным ключом, использование отвертки, открытие двери фиксируется на петлях. Поворот можно также назвать точка опоры .
Эффект вращения или поворота, момент, легко имеет величину рассчитывается по формуле:
M = F x d , где M = момент силы ( Нм, ), F = приложенная сила ( Н, )
и d ( м ) — это перпендикулярное расстояние от точки поворота до линии действия сила.
Вы получить максимальный момент, нажав / потянув ключ под прямым углом (при 90 o ) к линии (d) между точкой поворота и линией действия, где приложена сила.
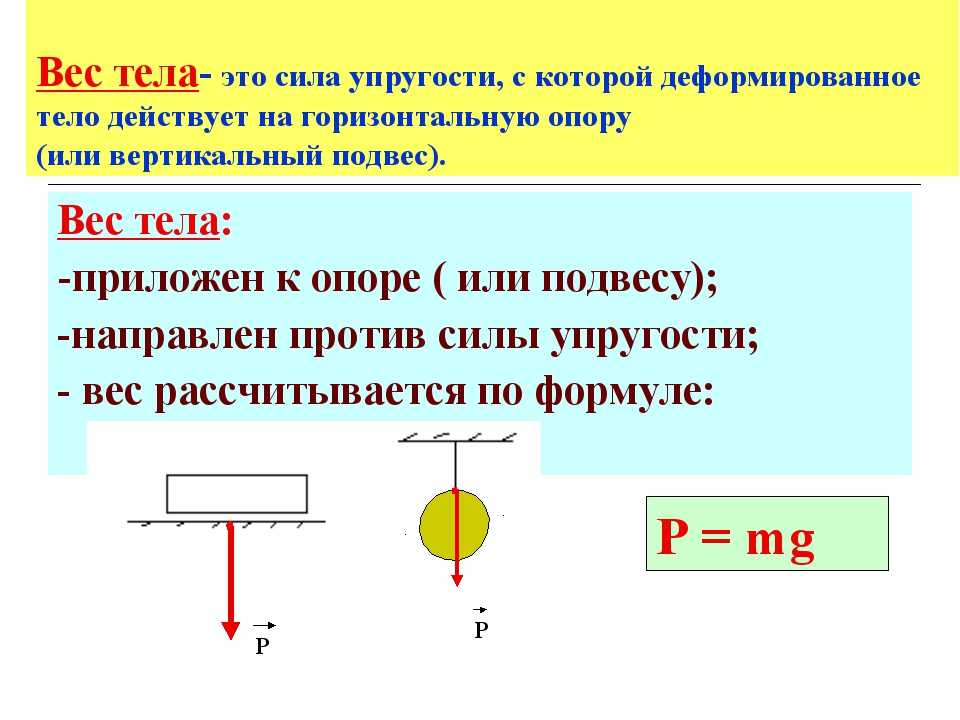
Закручивание или откручивание гайки на болте
Это проиллюстрировано простой схемой гаечного ключа выше.
Поворот усилие F x d .
Точка поворота — центральная ось болт, на котором гайка поворачивается гаечным ключом.
Чтобы затянуть или ослабить гайку, используйте усилие, в лучшем случае, под углом 90 o к самому гаечному ключу.
Приложение силы под любым другим углом менее 90 o уменьшает d и, таким образом, уменьшает эффективный момент сила.
Вы определяете силу F по тому, насколько сильно вы толкать / тянуть конец гаечного ключа, но d — фиксированное расстояние для гаечный ключ.
Это одна из многих ситуаций, когда вы прикладывают силу для усиления эффекта мышц руки .
Размер момента увеличивается с увеличением увеличение расстояния d или приложенной силы F.
Чем длиннее гаечный ключ, тем больше d, следовательно, чем больше создаваемое усилие поворота — тем больше механическое преимущество рычажная система.
Подробнее о физике откручивания туго орех!
Гаечный ключ «ситуации» от A до D
Относительные комментарии к трем «моментным» ситуациям от A до C
Ситуация A
С более длинным ключом и сила, перпендикулярная (под углом 90 o ) к линии от точки приложения силы (конец «ручки») к точке поворота (центр гайки или болта), вы создаете максимальный момент (F x d).
Перпендикулярное расстояние d — это кратчайшее расстояние между шарнирами. и линия действия силы
Ситуация B
Если применить силу к любому другому угол, чем под углом 90 o к перпендикулярной линии расстояния (d), d всегда будет короче и, следовательно, меньший момент генерируется применяя ту же силу, что и в ситуации А.
Обратите внимание, что когда линия действия сила приложена к «спине» гаечного ключа, d равно нулю, а момент равно нулю.
Это показано синей силой стрелка в положении D .
Ситуации A и B и верховая езда велосипед
Вы получаете ситуацию B при нажатии педали a велосипед, когда ваша нога и педаль находятся в верхней или нижней части цикл кривошипа — точка поворота — ось кривошипа.Если вы нажмете вниз вы создаете минимальный момент — минимальную движущую силу вперед.
В верхней части «педального цикла», если направление силы вниз через кривошип, вращающая сила, момент, очень мал.
НО, наверху педаль цикл ‘, вы скоро научитесь толкать вперед , чтобы использовать максимальный момент и генерировать максимальное силы, чтобы вы имитировали ситуацию A, в которой вы генерируете силу под углом 90 o к поворотной оси и линии действия сила — максимальный момент = F x d на диаграмме выше .
Вы получаете максимальную силу передается, когда кривошип и педаль параллельны земле и вы прикладываете максимальную направленную вниз силу под углом 90 o к точка поворота (ось) и линия действия силы.
Ситуация C
С более коротким ключом, несмотря на приложение силы под углом 90 o (перпендикулярно), d меньше и вы не можете создать такой большой момент, как в ситуации А.
Итак, при той же приложенной силе, момент меньше для гаечного ключа меньшей длины.
Центр масс и устойчивость отдельно стоящего объекта
Центр масс — одна точка в объекте, через который считается, что весь вес объекта действовать.
Его довольно легко представить, где он для правильной формы e.
грамм. прямоугольный блок — показан в профиль в диаграмму ниже. Это совпадает с тем, что называют центром . гравитации ‘объекта.
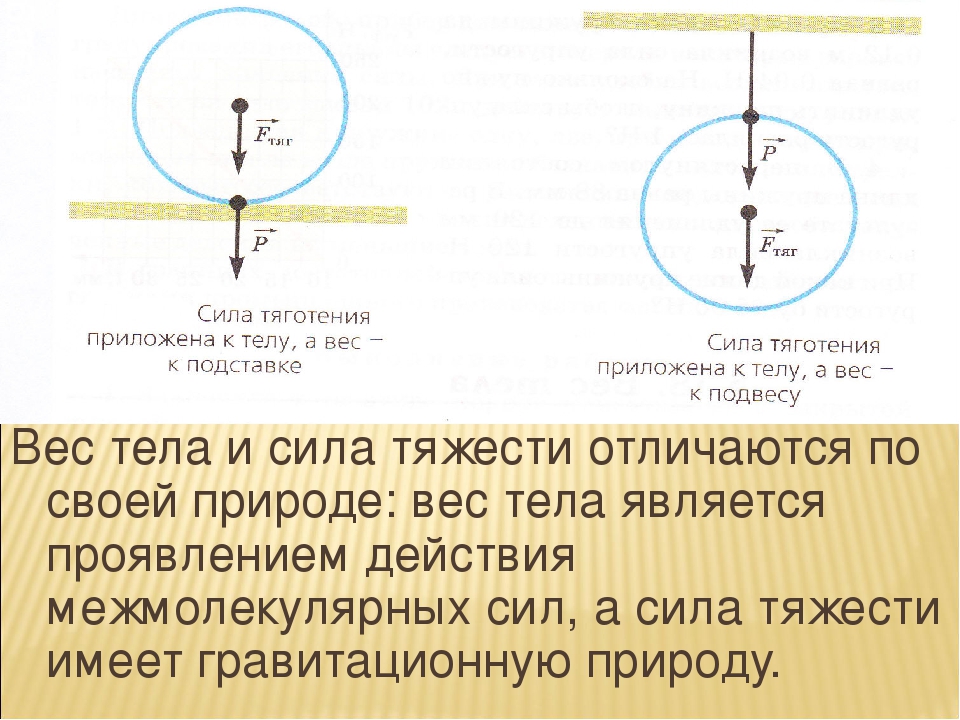
Стоящий объект становится неустойчивым когда вертикальная линия, проходящая через его центр масс, выходит за пределы его база, которая эффективно действует как база — это происходит, если она наклоняется на одну кромку, создавая момент — вращающую силу .
В этих условиях вес объекта вызывает эффект поворота вокруг стержневой базы.
Идея иллюстрируется приведенная ниже диаграмма блока правильной формы, показанного в профиль и наклоненного под разными углами (но это может быть автобус за углом!).
1. Вертикальная линия от центра массы проходит прямо через центр основания блока.
Объект полностью устойчива — момент (вращающее усилие) не создается.
2. Вертикальная линия от центра массы все еще проходит через основание, но не через его центр, а блок неустойчив, поэтому он будет немного покачиваться из стороны в сторону и в конечном итоге устойчивое вертикальное положение как в 1.
Край блока, касающийся поверхность действует как точка поворота.
Вес блока создает момент против часовой стрелки (сила поворота), заставляющий блок снова упасть против часовой стрелки, но этого недостаточно, чтобы опрокинуть блок на его длинной стороне.
3. Вертикальная линия от центра массы проходит за пределы основания блока. Блок даже не будет колебаться, он очень нестабилен и может просто опрокинуться длинной стороной (чтобы стать стабильным!).
Опять край блока прикосновение к поверхности действует как точка поворота.
Опять же вес блока создает момент по часовой стрелке (вращающее усилие), заставляющий блок падать по часовой стрелке и достаточно, чтобы опрокинуть блок на его более длинную сторону.
Испытания на устойчивость по центр масс важны, например дорожные транспортные средства, такие как автобусы, безопасны проверено, чтобы увидеть максимально допустимый угол при наклоне без перевернуться в результате аварии.
НАЧАЛО СТРАНИЦЫ и субиндекс
(б) Несколько простых расчетов моментов
1 квартал
Рассчитайте момент, если сила 5.0 с.ш. прилагается к гаечному ключу длиной 15 см.
F = 5, d = 15/100 = 0,15 м
момент M = F x d = 5 x 0,15 = 0,75 Нм
2 квартал К двери прилагается сила 20 Н, создающая момент 5 Нм.
Рассчитайте расстояние в см от ось шарнира до точки на двери, к которой прикладывалась сила.
момент M = F x d, поэтому d = M / F = 5/20 = 0.25 м, поэтому d = 0,25 x 100 = 25 см
3 квартал Какое усилие необходимо приложить к гаечному ключу длиной 30 см, чтобы создать момент 6,0 Нм?
момент M = F x d, поэтому F = M / d , d = 30 см = 30/100 = 0,30 м
F = M / d = 6,0 / 0,30 = 20 Н
Q4 —
НАЧАЛО СТРАНИЦЫ и субиндекс
(c) Расчет моментов и состояние равновесия (равновесие)
Левая диаграмма иллюстрирует сбалансированную ситуацию (равновесие), когда линейка повернуты посередине, а два груза w1 и w2 расположены на расстояниях d1 и d2 от точки поворота.Помните, что вес = сила в ньютонах.
Гири висят вертикально, поэтому сила тяжести действующий перпендикулярно (под углом 90 o ) к линейке
Чтобы линейка находилась в идеальном горизонтальном положении
две вращающие силы должны быть равны.
Здесь мы используем термины , момент по часовой стрелке и . Момент против часовой стрелки для двух вращающих воздействий задействованных сил.
момент против часовой стрелки = w1 x d1 (левая сторона оси), Момент по часовой стрелке = w2 x d2 (правая сторона оси)
так когда w1d1 = w2d2
линейка уравновешена горизонтально , при равновесие, когда поворачивающие эффекты сил равны.
Эта ситуация соответствует принципу моментов которые
заявляет, что когда общая сумма против часовой стрелки
моменты это
равна общей сумме поворотов по часовой стрелке
моменты система находится в равновесии и объект (система) НЕ повернется на . Когда система стабильна (нет движения) или сбалансирована, говорят, что она
равновесие, поскольку все силы, действующие на систему, нейтрализуют друг друга.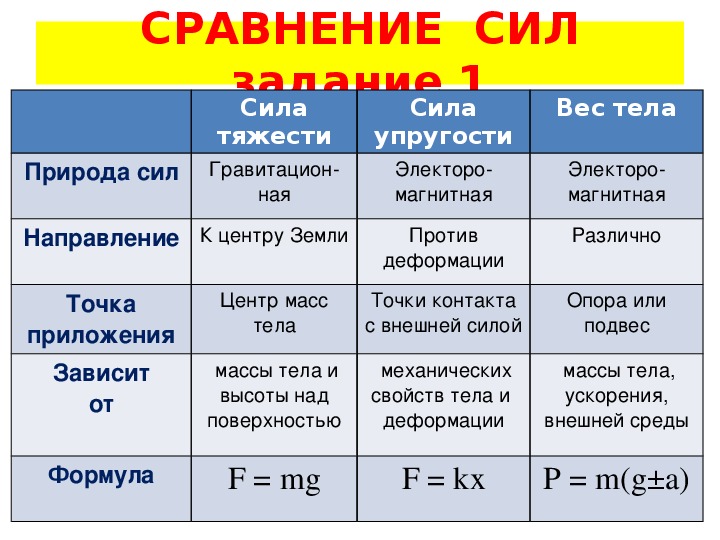
Вы убедитесь в этом, если проведете простой эксперимент, балансируя правило на карандаше и положив по обе стороны небольшие гири до равновесия.
Точно так же, когда гайка болта затягивается, наступает момент, когда момент, когда вы применяете, уравновешивается противодействующим моментом болта и гайку, и гайку больше нельзя затянуть.
В середина качелей — это точка поворота.Если два человека равного веса сидеть на обоих концах, качели сбалансированы горизонтально — моменты по часовой стрелке и против часовой стрелки равны. Если два человека отличаются вес, качели упадут на сторону самого тяжелого человека, потому что моменты по часовой стрелке и против часовой стрелки не равны.
Направление вращения, т.е. по часовой стрелке или против часовой стрелки, будет определились с относительными весами (силами) на каждом конце качелей.Один конец будет падать в направлении наибольшего момента
Пример использования принципа моменты — старинные кухонные весы
Луч весов должен быть горизонтальным.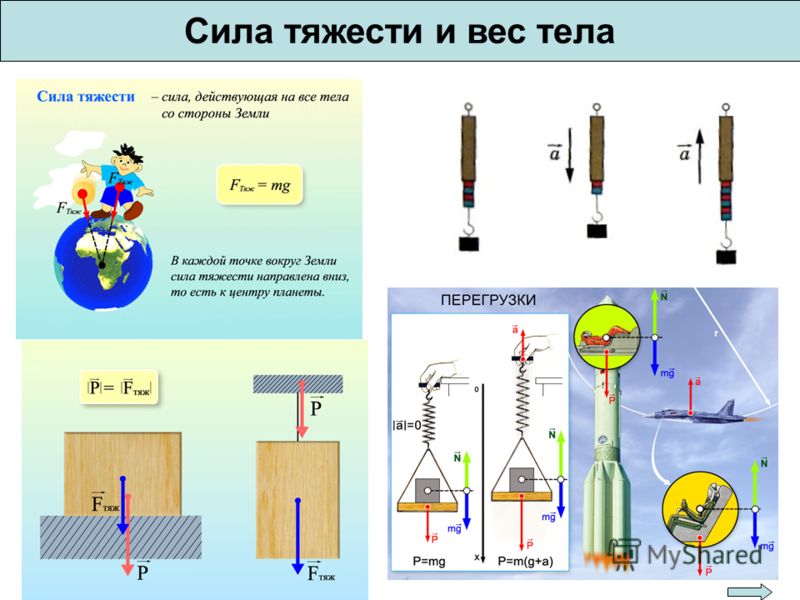 когда чаша и тарелка с грузами пусты (d1 = d2, w1 = w2).
когда чаша и тарелка с грузами пусты (d1 = d2, w1 = w2).
Когда взвешиваемый объект помещается в блюдо, весы наклоняются против часовой стрелки вниз слева.
Затем вы добавляете веса, пока балка не станет снова горизонтально сбалансировать, таким образом давая вес материала, например, порошок в миске.
Примеры простых вычислений с использованием вышеперечисленных ситуаций
Предскажите, что произойдет в следующих ситуациях с Q1 (a) по (c)
1 кг = 1000 г и 100 см = 1 м и для простота предположим г = 10 Н / кг (вес = масса x сила тяжести)
Q1 (a) Предположим, что d1 = 20 см, w1 = масса 25 г, d2 = 10 см, w2 = масса 50 г
но сбалансировано ли это?
момент против часовой стрелки = d1w1 = (20/100) x (10 х 25/1000) = 0.
05 Нм
момент по часовой стрелке = d2w2 = (10/100) x (10 x 50/1000) = 0,05 Нм
В данном случае момент против часовой стрелки = момент по часовой стрелке, поэтому линейка сбалансирована по горизонтали.
однояйцевые близнецы на качелях уравновесятся !!
НО, применяя дополнительную попеременную силу поворота мышц, вы можете получить отличный весело !!!
Q1 (b) Предположим, что d1 составляет 14 см, w1 = масса 52 г, d2 = 12 см, w2 = масса 60 г
но сбалансировано ли это?
момент против часовой стрелки = d1w1 = (14/100) x (10 х 52/1000) = 0.073 Нм
момент по часовой стрелке = d2w2 = (12/100) x (10 x 60/1000) = 0,072 Нм
В данном случае момент против часовой стрелки > момент по часовой стрелке, поэтому линейка будет вращаться против часовой стрелки .
Q1 (c) Предположим, что d1 составляет 2,5 м, w1 = масса 55 кг, d2 = 3,0 m, w2 = масса 50 кг
но сбалансировано ли это?
момент против часовой стрелки = d1w1 = 2,5 x (10 x 55) = 1375 Нм
момент по часовой стрелке = d2w2 = 3.0 х (10 х 50) = 1500 Нм
В данном случае момент по часовой стрелке> по часовой стрелке, поэтому линейка будет вращаться по часовой стрелке.
НАЧАЛО СТРАНИЦЫ и субиндекс
(г) Более сложные расчеты моментов и равновесия
2 квартал
Если w1 составляет 12,5 Н и 3,5 м от оси поворота точка, какой вес w2 требуется, если поставить на 2.5 м от оси до баланса луч?
момент против часовой стрелки = 12,5 x 3,5 = 43,75 Нм
момент по часовой стрелке = w2 x 2,5
Для баланса моменты должны быть равны так:
w2 x 2,5 = 43,75, поэтому w2 = 43,75 / 2,5 = 17,5 N
3 квартал
Балка равномерно размещена на точке поворота
(точка опоры).
С одной стороны груз 10 Н размещается на расстоянии 2 м от точку поворота и груз 40 Н на расстоянии 4 м от точки поворота.
На каком расстоянии от точки поворота должен находиться центр силы тяжести 80 Н для идеальной балансировки балки горизонтально?
Принцип моментов гласит, что сумма моментов по часовой стрелке должны равняться сумме моментов против часовой стрелки достичь равновесия. Момент (Нм) = F (Н) x d (м)
Сумма моментов по часовой стрелке = (10 x 2) + (40 x {2 + 4}) = 20 + 240 = 260 Нм
Чтобы уравновесить это, момент против часовой стрелки должен = 240 Нм, 240 = 80 x d, d = 260/80 = 3.25
Следовательно, необходимо разместить груз 80 Н слева 3,25 м от точки поворота.
4 квартал Этот расчет — это то, что должны делать инженеры-строители и архитекторы.
учитывать при строительстве «современных» зданий.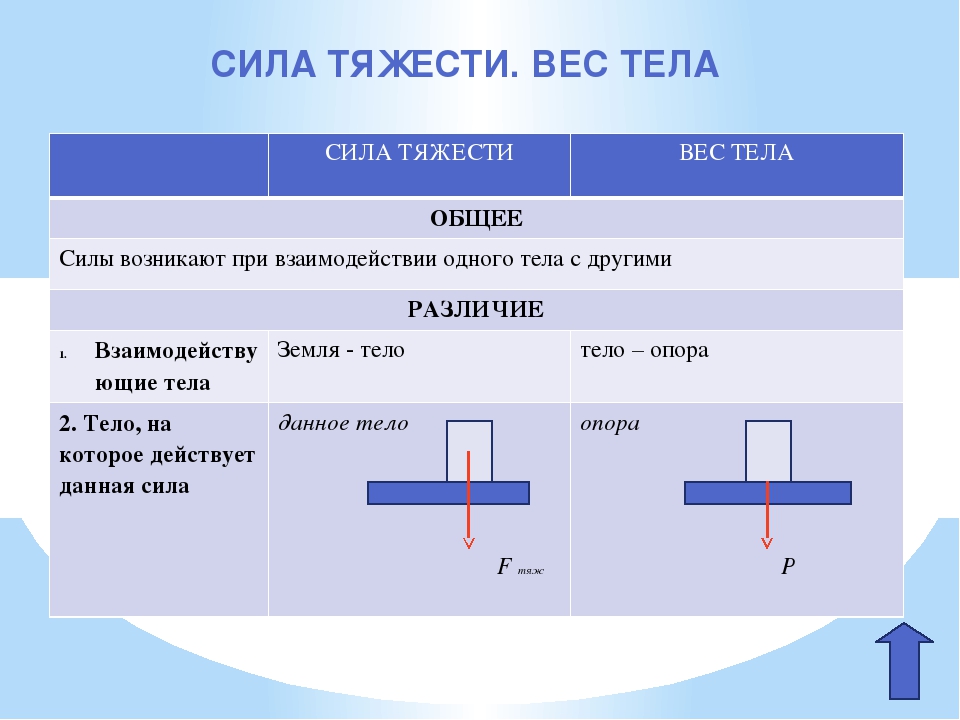
Алюминиевая балка 5,0 м подвешена на стальной трос от бетонной балки и длиной 3,0 м опирается на стальную опору.
Предполагая, что сила гравитационного поля равна 9.8 Н / кг, вычисляют Т , напряжение в ньютонах на опорной стальной трос.
Вес алюминиевой балки = 9,8 х 200 = 1960 Н.
момент = сила x перпендикулярное расстояние от поворотный момент.
Вы учитываете вес алюминиевой балки действовать через его центр масс на расстоянии 2,5 м с обоих концов, но на расстоянии 0,5 м от стальной стержень, который фактически является точкой поворота, на которой вы основываете свой момент расчеты.
Фактически такая же ситуация, как и тачка описана дальше вниз по странице!
момент против часовой стрелки = вес балки x расстояние от стальной опоры до центра масс алюминиевой балки = 1960 x 0,5 = 980 Нм
момент по часовой стрелке = натяжение стального троса x расстояние от стального троса до стальной опоры = T x 3,0
в состоянии равновесия, т. е.е. сбалансированный, по часовой стрелке
момент = момент против часовой стрелки
е.е. сбалансированный, по часовой стрелке
момент = момент против часовой стрелки
поэтому: T x 3,0 = 980, поэтому T = 980/3 = 327 N (3 SF)
Q5 На диаграмме справа показаны направленные вниз силы (4000 Н и 6000 Н), действующие на бетонная балка, удерживаемая стеной на P — эффективно действовать в качестве точки поворота.
Другая вторая несущая стена должна быть возведен в X.
Рассчитайте усилие F , которое 2-я стена должна быть способной выдержать, чтобы обеспечить конструктивную устойчивость. состояние сбалансированного равновесия.
Момент по часовой стрелке = 6000 x (40 + 20) = 360 000 N
Моменты против часовой стрелки = (4000 x 32) + (40 х F)
360 000 = 128 000 + (40 x F)
232 000 = 40F
F = 232 000/40 = 5800 Н
НАЧАЛО СТРАНИЦЫ и субиндекс
(е) Некоторые простые применения поворачивающих воздействий сил, включая рычаги
Многие из описанных ниже примеров включают
рычаг , который является средством увеличения вращательного действия силы.
Вы нажимаете на один конец рычага, и вращение вокруг точки поворота может привести к тому, что другой конец поднимется с большей сила.
На схеме ниже показан принцип рычага, чтобы получить механическое преимущество — все дело в соотношении d1 / d2.
F — задействованная сила (Н) и d (м) — (кратчайшее) перпендикулярное расстояние от точки поворота до точки, в которой сила прикладывается ИЛИ генерируется.
F1 = приложенная входная сила, d1 = расстояние от оси до перпендикулярного приложения силы F1
F2 = выходное усилие, d2 = расстояние от оси до места, где перпендикулярно создается сила F2
В сбалансированном состоянии, т.е. непосредственно перед тем, как что-то ‘рычаги’ и заставили двигаться
входной момент = F1 x d1 = выходной момент = F2 x d2
Из F1 x d1 = F2 x d2 перестановка дает F2 = F1 x d1 / d2
Следовательно, сделав d1 намного больше, чем d2
вы можете произвести гораздо большую выходную силу по сравнению с исходным входом
сила.
Вообще говоря, вы делаете расстояние d1 намного больше, чем расстояние d2 — вы можете увидеть это с помощью ножниц, подняв крышку с банки, и это очень похожая ситуация при использовании вилки для подъема на глубину извлечение твердых корней из почвы или перемещение тяжелого камня шестом.
Итак, рычаги очень полезны, потому что они значительно упростить подъем и перемещение предметов за счет уменьшения входной силы необходимо для выполнения задачи.
Пример рычага вопрос
Предположим, что для тяжелой крышки люка требуется усилие 160Н, чтобы открыть его.Представьте, что у вас повернут стальной стержень длиной 1 метр. на расстоянии 0,1 м (10 см) от конца, чтобы рычагом открыть тяжелую крышку люка.
Если надавить с силой 20 Н, Достаточно ли создаваемой вами восходящей силы, чтобы поднять крышку люка?
ссылаясь снова на диаграмму
входной момент = F1 x d1 = 20 x 0,9 = 18 Нм
выходной момент = F2 x d2 = F2 x 0,1 Нм
Поскольку F1 x d1 = F2 x d2
F2 = (F1 x d1) / d2 = 18/0.
1 = 180 Н
В выходное усилие 180 Н превышает требуемое усилие 160 Н, поэтому крышка люка можно поднять.
Дырокол некоторого описания
Этот станок может пробивать отверстия в материале. Точка поворота (точка поворота) находится слева.
Мы можем проанализировать эту ситуацию с точки зрения поворачивающие силы.
Применение принципа моментов: F1 x d1 = F2 x d2
Перестановка уравнений дает: F1 = F2 x d2 / d1
Следовательно, сделав d2 «длинным» и d1 «коротким» вы значительно увеличиваете силу F1 по сравнению с F2.
Таким образом, вы можете легко пробивать отверстия в прочный материал, например лист металла.
Например, предположим, что d2 составляет 0,5 м (50 см). и d1 0,05 м (5 см)
F1 = F2 x 0.
5 / 0,05, поэтому F1 = 10 x F2
Итак, сила, которую вы прикладываете вручную, умножается на 10 раз десять, неплохо за небольшое усилие!
Другими словами, чтобы получить в тот же момент.
Ножницы
Когда вы сжимаете руки-ножницы вместе, вы создаете мощное вращающее усилие. эффект близко к точке поворота.
F1 x d1 = F2 x d2, перестановка дает F2 = F1 х d1 / d2
Итак, сделав d1 >> d2, вы создадите много большее усилие F2, достаточное для резкого прорезания бумаги или карты.
Вот почему вы применяете лезвия ко всему вы режете как можно ближе к точке поворота.
Нельзя резать ножницами
лезвия, где вы получаете небольшое механическое преимущество, т. е. без значительного увеличения силы
вы подаете заявку. Это тот же принцип, что и для всей дыропробивной машины
описано в пункте (а) выше.
Это тот же принцип, что и для всей дыропробивной машины
описано в пункте (а) выше.
Крышка банки откидная
Вы можете использовать отвертку с широким лезвием, чтобы крышка от банки с краской. Точка поворота — это край банки.
Длина отвертки до шкворня острие (d2) намного больше, чем острие отвертки за обод (d1).
F1 x d1 = F2 x d2, F1 = F2 x d2 / d1, поэтому если d2 намного больше, чем d1, вы получаете большое увеличение силы, которую вы прилагаете (F2), чтобы придать гораздо большую поднимающую силу (F1), чтобы оторвать крышку.
Еще один пример того, что для получения в тот же момент, чтобы открыть банку.
Относительно длинная ручка гаечного ключа
Гаечные ключи имеют длинные ручки для надежного
эффект силы поворота.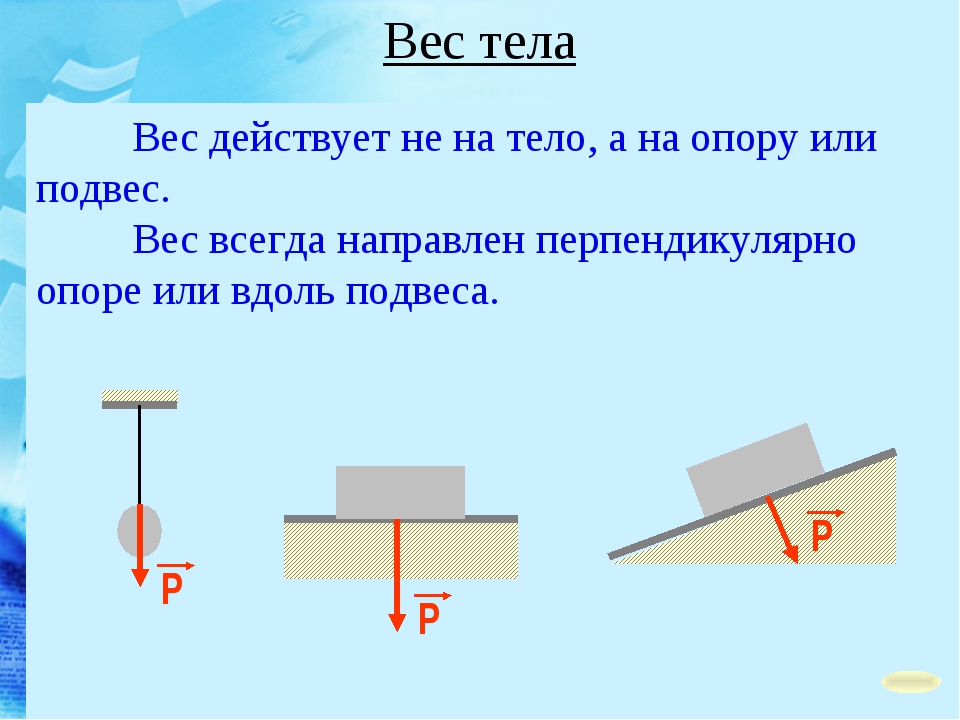
Вообще говоря, чем крупнее должна быть гайка затянут, тем длиннее гаечный ключ.
Гаечные ключиподробно обсуждались на начало страницы.
Винт пробковый
Радиус ручки намного больше чем буровой стержень. Большая разница в радиусе дает гораздо больший крутящий момент (эффект поворачивающей силы), чтобы просверлить пробку винной бутылки.
Отвертка
Аргумент для отвертки такой же, как и для штопора над. Чем больше диаметр ручки отвертки по сравнению с диаметр головки винта, тем больше усилие (крутящий момент) вы может применяться для вбивания шурупа в дерево.
Тачка
Ручки тачки расположены намного дальше от оси колеса, чем центр тяжести полной тачки.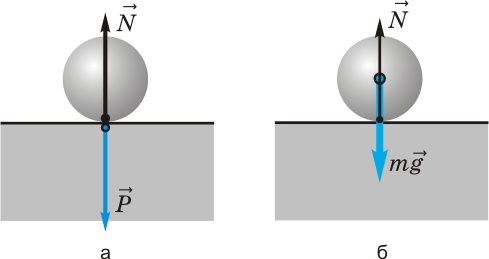 (показано
желтая капля!).Ось колеса — это точка поворота, относительно которой вы рассчитываете
вовлечены два момента.
(показано
желтая капля!).Ось колеса — это точка поворота, относительно которой вы рассчитываете
вовлечены два момента.
F1 — масса загруженной тачки, действующей от его центр масс (центр тяжести).
F2 — сила, которую вы прикладываете для подъема загруженного тачка.
Вот два момента:
«Весовой» момент F1 x d1 — небольшой момент для управлять весом тачки.
(F1 действует вниз от центра масс / тяжести)
Однако «подъемный» момент равен F2 x d2, поэтому a требуется меньшая сила F2, действующая на большем перпендикулярном расстоянии d2, чтобы поднять тачку и ее груз.
F1 x d1 = F2 x d2, поэтому F2 = F1 x d1 / d2
Итак, F2 равно << F1
Величина подъемной силы F2 очень велика. меньше веса груза, поэтому вы можете поднимать тачку и перемещать ее вдоль. Еще один пример того, что нужно меньше сил, чтобы получить тот же момент для выполнения работа по подъему колесной тележки для ее перемещения.
Обратите внимание, что, поскольку Работа = сила x расстояние, вы можете думать об этом как о выполняющем работу против Гравитационное поле Земли.
В случае моментов подъема объектов вертикально , каждый момент = прирост в GPE = mgh ,
GPE = гравитационная потенциальная энергия (Дж), m = масса (кг), g = 9,8 Н / кг, h = высота подъема в м, и больше по GPE
см. Масса и влияние на него силы тяжести — вес, (упоминание о проделанной работе и GPE)
Решающий экспериментальный результат — шестилетняя внучка Ниам едва ли может поднимать тачка оторвана от земли (всего несколько см), но у бабушки Молли нет проблемы с подъемом тележки, чтобы ее переместить!
Загар в более раннем возрасте Ниам не так интересовался наукой!
НАЧАЛО СТРАНИЦЫ и субиндекс
(f) Шестерни и шестерни колеса — средство передачи силы вращения
Некоторые простые вычисления включены в конец раздела (f)
Зубчатые колеса
круглые диски с зубьями и компоненты многих машин на транспорте и
промышленность.
Они являются средством передачи вращательного эффекта сила от одной части к другой части механического устройства, например промышленный машина, автомобиль или велосипед.
Когда несколько из них соединены вместе (связаны в контакте через зубья ) вращательное усилие может передаваться при установке в контакте друг с другом. Зубчатые колеса / шестерни при прямом контакте будут вращаться противоположные направления.
Благодаря блокировке одно зубчатое колесо может вращать другое в противоположное направление т.е. если одна шестерня идет по часовой стрелке, шестерня колесо в контакте с ним будет вращаться против часовой стрелки, независимо от того, сколько передач колеса соединены между собой.
При использовании зубчатых колес разного размера, различающихся количеством зубьев, вы можете увеличить или уменьшить силу, создаваемую эффектом поворота шестерен.
От передаточного числа можно работать обороты одной шестерни относительно соседнего колеса e.грамм.
на схеме шестерня 1 имеет 12 зубья и шестерня 2 имеет 18 зубьев.
Если меньшее колесо 1 один оборот, колесо 2 оборота 2/3 трети оборота, соотношение зубьев 12/18 = 2/3 (0,66).
Если большее колесо делает два оборота один раз, колесо 1 оборачивается 1,5 оборота, передаточное число зубьев 18/12 = 3/2 = 1,5.
Соотношение зубьев дает вам передаточное число.
Сила, приложенная к меньшей шестерне создает небольшой момент
— меньшее расстояние от зубьев до оси цапфы точка.
Сила, приложенная к шестерне большего размера создает больший момент
— большее расстояние от зубьев до оси цапфы точка.

Поскольку момент = сила x расстояние, соотношение двух моментов ушей равно отношению радиусов шестерни что равняется соотношению зубьев.
Если вы передаете усилие от большего зубчатого колеса (шестерни с большим количеством зубьев) на меньшее зубчатое колесо (шестерня с меньшим количеством зубьев) вы уменьшаете момент 2-го , так как вы уменьшили расстояние от приложенная сила к точке поворота оси.
Нет механического преимущества — вы не увеличили выходное усилие меньшего зубчатого колеса.
Меньшее зубчатое колесо будет сделано для поворачивается быстрее, чем зубчатое колесо большего размера.
Это способ увеличения вращательного скорости в машинах.
Если у первого зубчатого колеса 20 зубьев и второе зубчатое колесо 5 зубьев, один оборот первого колеса вызывает колесо меньшего размера должно вращаться в 20/5 раз = в 4 раза больше — передаточное число 1: 4.
Если бы было наоборот, и вы сначала повернул 2-е зубчатое колесо меньшего размера, один его оборот поверните большее зубчатое колесо на 1/4 (5/20) оборота — передаточное число 4 : 1, уменьшая скорость вращения.
Если вы передаете усилие от меньшего зубчатого колеса (шестерня колесо с меньшим количеством зубьев) на зубчатое колесо большего размера (зубчатое колесо с большим количеством зубьев) вы увеличить момент по мере увеличения расстояния от применяемого усилие на точку поворота оси.
Получено механическое преимущество — вы увеличили выходное усилие большего зубчатого колеса.
Используя набор блокирующих шестерен, становиться все больше и больше можно умножить момент первой малой передачи.
Чем больше зубчатое колесо, тем больше крутится медленнее, чем меньший.
Это способ относительно маломощного машину можно заставить поднимать тяжелые грузы.
Если у первого зубчатого колеса 8 зубьев и второе колесо 56 зубьев, первое колесо нужно повернуть 56/8 = 7 раз чтобы полностью повернуть второе колесо.
Примеры зубчатого колеса (зубчатого колеса) заявки
Старинная ручная дрель
Большое зубчатое колесо поворачивает меньшее зубчатое колесо с гораздо большей скорость со старомодной силой мускулов!
Усилие передается от одного зубчатого колеса к другому.
Так как большее зубчатое колесо с большим количеством зубьев приводит в движение меньшее зубчатое колесо колесо с меньшим количеством зубьев, на выходе получается высокая скорость вращения дрели.
Зубчатая передача в системах мельничных колес
Сложные машины, такие как старые мукомольные и текстильные фабрики, использование шестерни, чтобы использовать мощность, например, водяное колесо, чтобы передать силу для движения техника с необходимой скоростью и мощностью.
Медленно вращающееся водяное колесо, приводящее в движение систему зубчатых колес (a зубчатая передача ) может обеспечивать высокую скорость вращения для привода прядильной машины — важный механическая особенность в промышленной революции с 18 по 19 гг. век.
Часы
Часы используют шестерни для передачи потенциальную энергию пружины и двигайте руками в правильная скорость, чтобы указать правильное время.
Шестерни разных размеров необходимо управлять минутной и часовой стрелками.
Минутная стрелка должна идти в 60 раз быстрее, чем часовая стрелка, поэтому передаточные числа будут принимать это в учетную запись.
Шестерни на велосипеды
Шестерни (зубчатые колеса) используются в велосипеды для передачи усилия от педалирования передних передач на шестерни на задних колесах.
Шестерни не контактируют с друг с другом, но винтики соединены непрерывным цепным механизмом.
Сила вашей стопы, приложенная к педаль
Физика Задачи: динамика: вес, сила тяжести
Задача 1.
Если объект весит 30 Н на Земле, сколько он будет весить на Луне?
Решение
Проблема 2.
Ребенок бросает мяч вниз с высокого здания. Обратите внимание, что мяч бросается, а не падает, и не обращайте внимания на сопротивление воздуха. Каково ускорение мяча сразу после того, как он покинет руку ребенка?
Решение
Задача 7.
На рисунке показаны три частицы, расположенные далеко от любых других объектов на прямой линии. Массы этих частиц составляют: частиц A = 400 кг, частиц B = 500 кг и частиц C = 100 кг.Найдите величину и направление чистой гравитационной силы, действующей на каждую из трех частиц (направление вправо положительное).
Массы этих частиц составляют: частиц A = 400 кг, частиц B = 500 кг и частиц C = 100 кг.Найдите величину и направление чистой гравитационной силы, действующей на каждую из трех частиц (направление вправо положительное).
Решение
Задача 13.
Самое высокое место на Земле — гора. Эверест, который находится на высоте 8857 м над уровнем моря. Если радиус Земли до уровня моря составляет 6369 км, насколько величина g изменяется между уровнем моря и вершиной горы.Эверест?
Решение
Задача 14.
Величина g на поверхности Земли составляет 9,78 Н / кг, а на поверхности Венеры величина g составляет 8,6 Н / кг. Космонавт имеет массу 60 кг на поверхности земли. Каким будет ее вес на поверхности Венеры?
Решение
Проблема 24.
Сила тяготения, которую Солнце оказывает на Луну, перпендикулярна силе, которую Земля оказывает на Луну.
Массы: Масса Солнца, Масса Земли: ,, Масса Луны:. Расстояние между солнцем и луной равно, а между луной и землей.
Определите величину чистой гравитационной силы на Луне.
Решение
Задача 29.
Космический шаттл движется по орбите вокруг Земли на расстоянии около 300 км от ее поверхности. На таком расстоянии гравитационное ускорение почти такое же, как и на поверхности. Сколько времени нужно, чтобы шаттл совершил один оборот вокруг Земли? Предположим, что орбита круговая.
Сопротивление воздуха не учитывать.
Решение
Задача 33.
Когда падающий объект находится на расстоянии от поверхности Земли, в 4 раза превышающем радиус Земли, каково его ускорение свободного падения из-за действующей на него гравитационной силы Земли?
Решение
Задача 49.
Если масса вещества 5 граммов, каков его вес?
Решение
Задача 58.
Ящик размещается на крыше под углом 35 градусов к горизонту. Чтобы ящик не повредил черепицу, составляющая силы тяжести ящика, перпендикулярная крыше, не может превышать 425 Н. Каков максимально допустимый вес ящика?
Решение
Задача 61.
Вычислите давление, которое оказывает девушка, если ее масса составляет 70 кг, а площадь ступни 1 равна и ступни 2.
Решение
Задача 81.
Том массой 70 кг в лифте спускается со скоростью 10 м / с. Лифт останавливается на первом этаже за 4,0 с. Каков кажущийся вес Тома при торможении лифта?
Решение
Задача 82.
Джим массой 70 кг находится в лифте, движущемся вверх со скоростью 10 м / с.Лифт останавливается на пятом этаже за 4,0 с. Каков кажущийся вес Джима во время торможения лифта?
Решение
Задача 85.
Студент весом 70 кг стоит на пружине лифта, ускоряющегося вверх. Жесткость пружины составляет 3000 Н / м. Насколько сжимается пружина?
Решение
Найдите свою проблему в базе данных решенных физических задач (БЕСПЛАТНО) |
19 продуктов для быстрого и безопасного набора веса
Следующие продукты, богатые питательными веществами, могут помочь человеку безопасно и эффективно набрать вес.
1. Молоко
Поделиться на PinterestПротеиновые коктейли помогают людям легко набирать вес и наиболее эффективны, если их выпить вскоре после тренировки.Молоко содержит смесь жиров, углеводов и белков.
Это также отличный источник витаминов и минералов, включая кальций.
Содержание белка в молоке делает его хорошим выбором для людей, стремящихся нарастить мышцы.
Одно исследование показало, что после тренировки с отягощениями употребление обезжиренного молока помогает нарастить мышцы более эффективно, чем продукты на основе сои.
Аналогичное исследование с участием женщин, занимающихся силовыми тренировками, показало улучшение результатов у тех, кто пил молоко после тренировки.
Для всех, кто хочет набрать вес, в течение дня можно добавлять молоко в рацион.
2. Протеиновые коктейли
Протеиновые коктейли могут помочь человеку легко и эффективно набрать вес. Шейк наиболее эффективен для наращивания мышечной массы, если его выпить вскоре после тренировки.
Однако важно отметить, что готовые коктейли часто содержат дополнительный сахар и другие добавки, которых следует избегать.Внимательно проверяйте этикетки.
3. Рис
Стакан риса содержит около 200 калорий, а также является хорошим источником углеводов, которые способствуют увеличению веса. Многие люди легко добавляют рис в блюда, содержащие белки и овощи.
4. Красное мясо
Было доказано, что употребление красного мяса помогает нарастить мышцы и набрать вес.
Стейк содержит лейцин и креатин, питательные вещества, которые играют важную роль в увеличении мышечной массы.Стейк и другое красное мясо содержат как белок, так и жир, которые способствуют увеличению веса.
Хотя человеку рекомендуется ограничить потребление, более постные куски красного мяса полезнее для сердца, чем более жирные куски.
Одно исследование показало, что добавление постного красного мяса в рацион 100 женщин в возрасте 60–90 лет помогло им набрать вес и увеличить силу на 18 процентов во время тренировок с отягощениями.
5. Орехи и ореховая паста
Регулярное употребление орехов может помочь человеку безопасно набрать вес.Орехи — отличная закуска, их можно добавлять во многие блюда, в том числе в салаты. Наибольшую пользу для здоровья имеют сырые или сушеные жареные орехи.
Ореховое масло, приготовленное без добавления сахара или гидрогенизированных масел, также может помочь. Единственным ингредиентом этих масел должны быть сами орехи.
Поделиться на Pinterest Цельнозерновой хлеб содержит сложные углеводы и семена, которые могут способствовать увеличению веса.6. Цельнозерновой хлеб
Этот хлеб содержит сложные углеводы, которые могут способствовать увеличению веса.Некоторые также содержат семена, которые обеспечивают дополнительные преимущества.
7. Прочие крахмалы
Крахмалы помогают некоторым из уже перечисленных продуктов ускорить рост мышц и прибавку в весе. Они увеличивают объем пищи и увеличивают количество потребляемых калорий.
К другим продуктам, богатым крахмалом, относятся:
- картофель
- кукуруза
- киноа
- гречка
- фасоль
- тыква
- овес
- бобовые
- цельные корнеплоды
- зерновые злаки
- цельнозерновой хлеб
- зерновые батончики
Крахмалы не только добавляют калорий, но и дают энергию в виде глюкозы.Глюкоза хранится в организме в виде гликогена. Исследования показывают, что гликоген может улучшить производительность и энергию во время упражнений.
8. Протеиновые добавки
Спортсмены, стремящиеся набрать вес, часто используют протеиновые добавки для увеличения мышечной массы в сочетании с тренировками с отягощениями.
Протеиновые добавки можно приобрести в Интернете. Они могут быть недорогим способом потреблять больше калорий и набирать вес.
9. Лосось
Шесть унций лосося содержат около 240 калорий, и лосось также богат полезными жирами, что делает его хорошим выбором для тех, кто хочет набрать вес.
Он также содержит множество питательных веществ, включая омега-3 и белок.
10. Сухофрукты
Сухофрукты богаты питательными веществами и калориями, четверть стакана сушеной клюквы содержит около 130 калорий.
Многие люди предпочитают сушеный ананас, вишню или яблоки. Сушеные фрукты широко доступны в Интернете, или человек может сушить свежие фрукты дома.
11. Авокадо
Авокадо богат калориями и жирами, а также некоторыми витаминами и минералами.
12. Темный шоколад
Темный шоколад — это высококалорийный продукт с высоким содержанием жира. Он также содержит антиоксиданты.
Человек, желающий набрать вес, должен выбрать шоколад с содержанием какао не менее 70 процентов.
13. Зерновые батончики
Зерновые батончики могут предложить витаминный и минеральный состав злаков в более удобной форме.
Человек должен искать батончики, содержащие цельнозерновые, орехи и фрукты.
Избегайте тех, которые содержат чрезмерное количество сахара.
14. Цельнозерновые злаки
Многие злаки обогащены витаминами и минералами.
Однако некоторые из них содержат много сахара и мало сложных углеводов. Этого следует избегать.
Вместо этого выберите злаки, содержащие цельнозерновые и орехи. Они содержат здоровый уровень углеводов и калорий, а также питательные вещества, такие как клетчатка и антиоксиданты.
15. Яйца
Яйца — хороший источник белка, полезных жиров и других питательных веществ.Большинство питательных веществ содержится в желтке.
16. Жиры и масла
Масла, например, полученные из оливок и авокадо, обеспечивают калорийность и полезные для сердца ненасыщенные жиры. Столовая ложка оливкового масла будет содержать около 120 калорий.
17. Сыр
Сыр является хорошим источником жира, белка, кальция и калорий. Человек, желающий набрать вес, должен выбирать полножирные сыры.

 Поворот усилие F x d .
Поворот усилие F x d .

 грамм. прямоугольный блок — показан в профиль в
диаграмму ниже. Это совпадает с тем, что называют центром .
гравитации ‘объекта.
грамм. прямоугольный блок — показан в профиль в
диаграмму ниже. Это совпадает с тем, что называют центром .
гравитации ‘объекта.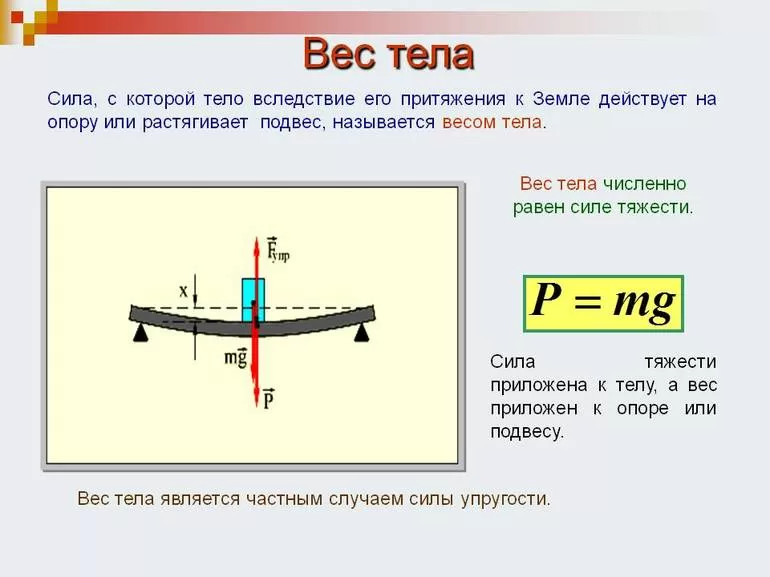

 05 Нм
05 Нм
 1 = 180 Н
1 = 180 Н  5 / 0,05, поэтому F1 = 10 x F2
5 / 0,05, поэтому F1 = 10 x F2