Рисунок Пентагона, шестиугольника в Pygame
Я пытаюсь создать функции, которые могут рисовать пятиугольник, шестиугольник и т. д. Беспокоясь об алгоритме, должен ли я сравнивать строки с pygame.draw.line ? Похоже, что слишком много работы вокруг определения координат линий. Есть ли простой способ нарисовать их? Кроме того, я не знаю другой библиотеки, которая могла бы нарисовать эти вещи. Я знаю только Pygame, есть ли еще один ?
Поделиться Источник GLHF 15 марта 2015 в 18:05
2 ответа
- Как создать форму Пентагона для изображения Аватара?
Я не могу понять, как создать форму Пентагона для изображения аватара пользователя (или .svg). Ищу форму, которая указывает вниз, а не сверху. Я нашел примеры здесь http://css-tricks.com/examples/ShapesOfCSS/ , но не знаю, как заполнить изображение в такой форме.

- Обрезать UIImage в форме шестиугольника?
Итак, я видел решения для того, как обрезать UIImages в определенные формы, но как насчет шестиугольника ? Мысль: подкласс UIImage, изменить метод drawRect, чтобы рисовать только определенные разделы? EDIT: если быть более точным, я надеюсь сохранить границы изображения одинаковыми, но сделать…
6
Вы можете нарисовать его с помощью lines . Вам нужно только сгенерировать список вершин с помощью простой тригонометрии.
Что-то вроде этого (если я не ошибся):
def draw_ngon(Surface, color, n, radius, position):
pi2 = 2 * 3.14
for i in range(0, n):
pygame.draw.line(Surface, color, position, (cos(i / n * pi2) * radius + position[0], sin(i / n * pi2) * radius + position[1]))
return pygame.draw.lines(Surface,
color,
True,
[(cos(i / n * pi2) * radius + position[0], sin(i / n * pi2) * radius + position[1]) for i in range(0, n)])
Поделиться ciechowoj 15 марта 2015 в 18:15
0
Вы можете использовать 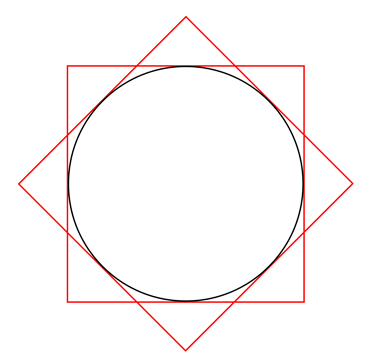 draw.polygon(surface, color, point_list)
draw.polygon(surface, color, point_list)point_list . Вот функция, которая рисует любой правильный многоугольник, имеющий vertex_count вершин:
def draw_regular_polygon(surface, color, vertex_count, radius, position): n, r = vertex_count, radius x, y = position pygame.draw.polygon(surface, color, [ (x + r * cos(2 * pi * i / n), y + r * sin(2 * pi * i / n)) for i in range(n) ])
Вы можете запустить эту демонстрацию и увидеть эту функцию в действии, изменив количество вершин с помощью клавиш со стрелками UP / DOWN.
Поделиться Arthur Khazbs 24 августа 2019 в 14:47
Похожие вопросы:
Pygame рисунок не отображается в окне Pygame
Итак, я тестировал pygame и хотел нарисовать простой прямоугольник.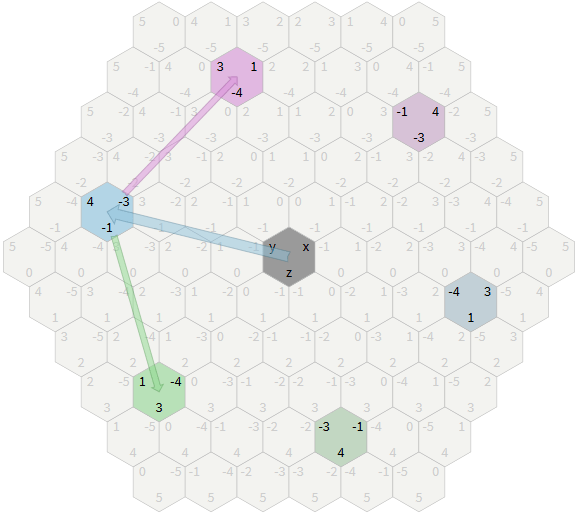 Когда я запускаю код, нет никаких сообщений об ошибках, но прямоугольник не появляется в окне. То, что я вижу, — это пустое белое…
Когда я запускаю код, нет никаких сообщений об ошибках, но прямоугольник не появляется в окне. То, что я вижу, — это пустое белое…
Проект Пентагона в c++
Су… я пишу проект Пентагона для своего класса c++, и, честно говоря, сейчас я не очень хорошо справляюсь с работой и другими классами. Итак… нам нужно сделать программу Пентагона, которая будет…
Проект Пентагона в c++ с классами
Итак, мне нужно создать проект Пентагона, и я немного запутался. Я имею в виду, что он отлично работает, но мне не хватает одного класса, в котором должен быть какой-то код. Назначение есть:…
Как создать форму Пентагона для изображения Аватара?
Я не могу понять, как создать форму Пентагона для изображения аватара пользователя (или .svg). Ищу форму, которая указывает вниз, а не сверху. Я нашел примеры здесь…
Обрезать UIImage в форме шестиугольника?
Итак, я видел решения для того, как обрезать UIImages в определенные формы, но как насчет шестиугольника ? Мысль: подкласс UIImage, изменить метод drawRect, чтобы рисовать только определенные.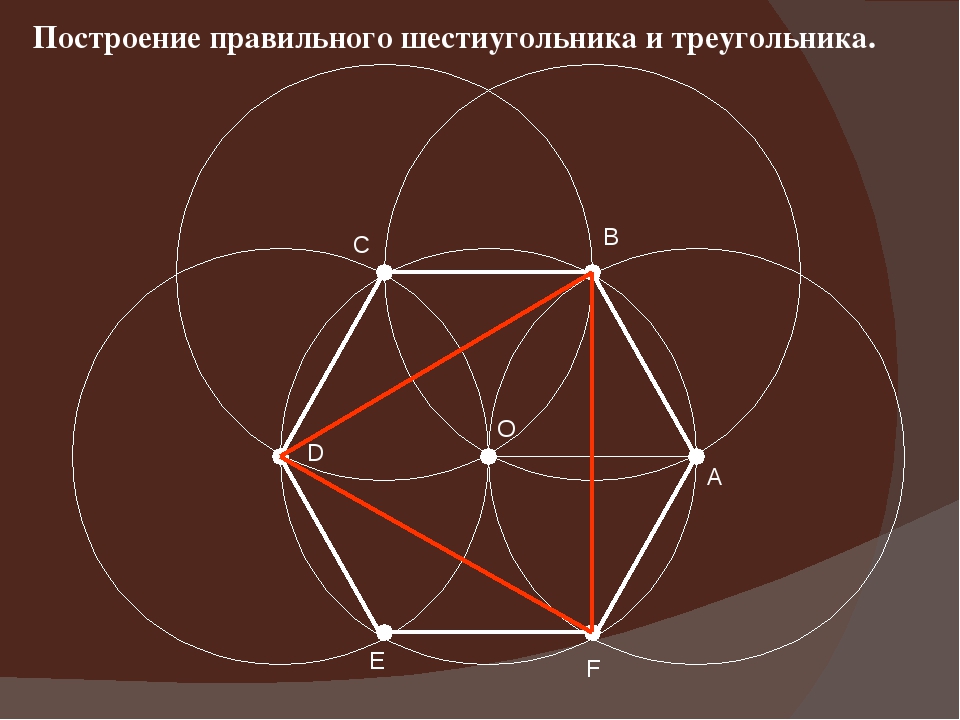 ..
..
Площадь шестиугольника вне окружности
Пусть будет круг радиусом r. Я хочу узнать площадь шестиугольника, нарисованного вокруг круга. Дополнено образцовое изображение, за исключением того, что мне нужно, чтобы все были шестиугольника, а…
Рисование шестиугольника
Нахождение положения Пентагона внутри круга
Я пытаюсь нарисовать маленькие круги над углами Пентагона внутри круга. Мне известна следующая информация. Радиус окружности равен 50. Центр окружности равен x = 100, y = 100 Как я могу получить…
Просмотреть изображение шестиугольника в NS
Как я могу создать такой компонент, как NS? Как придать форму шестиугольника ImageView Я хочу создать компонент изображения, который имеет вид шестиугольника, но я не могу понять, как правильно.
Pygame Рисунок (На Пасху)
Мне было интересно, как нарисовать cloud на pygame. Единственное, что я умею делать, — это делать правильные круги и эллипсы. Кроме того, Пожалуйста, скажите мне, как нарисовать кролика или…
CorelDRAW Graphics Suite — Учебные пособия
Автор: Анна Мария Лопес Лопес (Anna María López López)
Этот урок был опубликован одним из первых на сайте www.CORELCLUB.org, который в 1996 году был известен как «Anna’s CorelClub Spain».
Благодаря своему успеху среди пользователей продуктов Corel этот урок был впоследствии включен в несколько моих книг. Кроме того, я преподавала эту технику на курсах и семинарах, посвященных CorelDRAW.
Пришла пора сдуть пыль с этого учебного пособия и сделать его широко доступным.
Этот несложный прием позволяет добиться интересных творческих результатов с помощью трех простых инструментов CorelDRAW: Многоугольник, Указатель и Форма.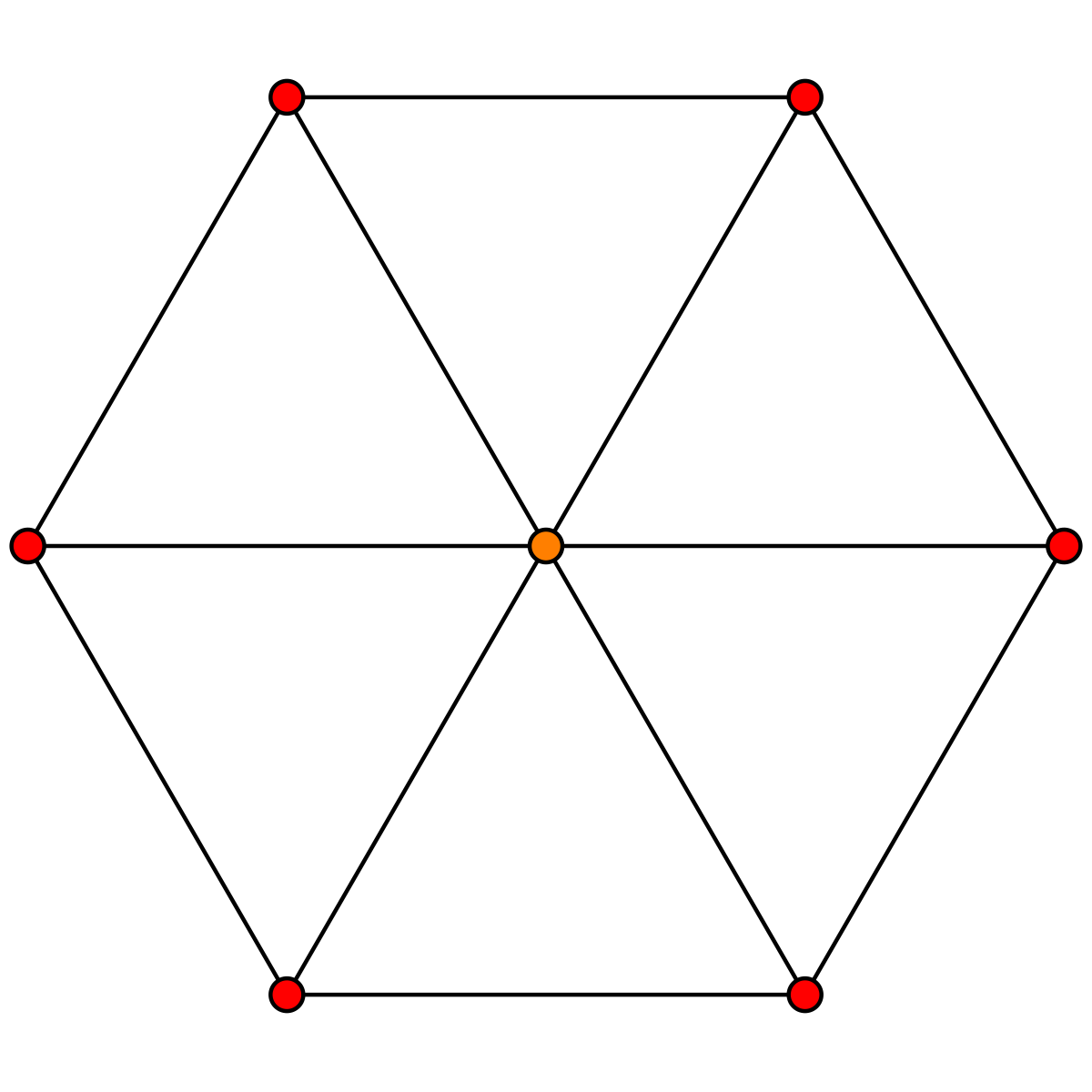
Процесс создания многоугольников в CorelDRAW интуитивно понятен. Когда в версии 6 впервые был представлен инструмент Многоугольник, постоянные пользователи CorelDRAW по достоинству оценили его универсальность и интерактивность.
На первый взгляд этот инструмент не создает впечатление креативного инструмента с широкими возможностями, ведь он предназначен для создания многосторонних многоугольников. Этот урок убедит вас в обратном.
Для начала нам нужно начертить простой многоугольник. Для этого щелкните инструмент «Многоугольник» и протащите курсор в окне рисования, пока многоугольник не достигнет желаемых размеров.
Совет: для создания симметричного многоугольника (многоугольника с равными сторонами) удерживайте клавишу Ctrl, а для создания многоугольника от центра наружу — клавишу Shift.
После того, как многоугольник создан, выделите его с помощью инструмента Указатель. Количество сторон многоугольника может быть изменено в любой момент. Для этого в поле Точки или стороны на панели свойств нужно ввести число сторон. Помните, что для внесения изменений в объект его нужно выделить с помощью инструмента Указатель.
Количество сторон многоугольника может быть изменено в любой момент. Для этого в поле Точки или стороны на панели свойств нужно ввести число сторон. Помните, что для внесения изменений в объект его нужно выделить с помощью инструмента Указатель.
У нашего многоугольника 8 восемь сторон (восьмиугольник).
После того, как многоугольник создан, щелкните инструмент Форма и нарисуйте окно вокруг многоугольника.
Будут выделены два узла, а на панели свойств отобразятся параметры редактирования узлов. Нажмите значок
На первый взгляд изменения не будут заметны. Однако, щелкнув один из узлов или путь многоугольника с помощью инструмента Форма и протащив курсор внутрь или наружу, вы заметите, что стороны многоугольника искривляются. Это позволяет создавать разнообразные формы. Посмотрите:
Вы можете продолжать изменять форму многоугольника.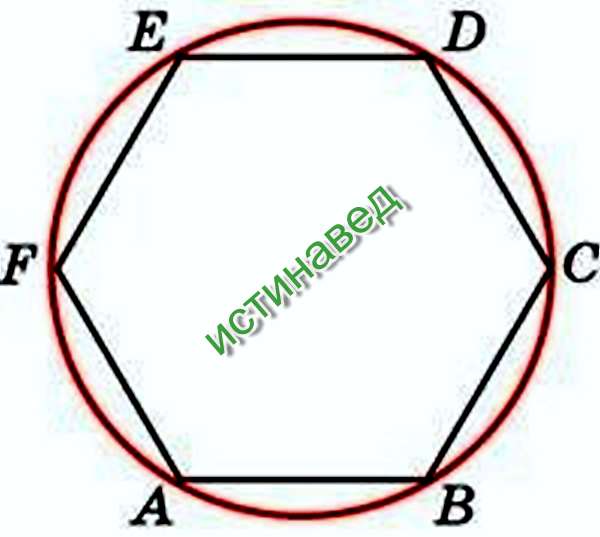 Для этого нужно щелкнуть и перетащить узлы и опорные маркеры.
Для этого нужно щелкнуть и перетащить узлы и опорные маркеры.
Кроме того, к многоугольнику можно применить заливку цветом. Как видите, здесь я залила многоугольник черным цветом, щелкнув нужный образец цвета на цветовой палитре.
Замечательная особенность состоит в том, что в течение всего процесса исходный многоугольник можно модифицировать — изменять количество сторон многоугольника можно столько раз, сколько нужно.
Каждый раз при изменении количества сторон многоугольника будет создаваться новая фигура.
Попробуйте: выделите многоугольник и измените количество сторон. Для этого в поле Точки или стороны на панели свойств введите нужное число. Как и в этом примере, ваш многоугольник будет автоматически преобразован в новую форму.
Это может показаться удивительным, но все формы на изображении ниже были созданы с помощью этой техники. Щелкнув изображение*, вы можете загрузить исходный файл (http://www. corelclub.org/tutoriales/practicas/ejercicio-tutorial-poligonos-corelclub.cdr).
corelclub.org/tutoriales/practicas/ejercicio-tutorial-poligonos-corelclub.cdr).
*Объем этого .cdr файла — 31 КБ. Чтобы сохранить его на своем компьютере, щелкните ссылку правой кнопкой мыши и выберите «Сохранить ссылку как». Затем файл можно будет открыть в CorelDRAW.
Вы сможете взаимодействовать с каждым многоугольником в этом файле и убедиться в универсальности и огромных возможностях инструмента CorelDRAW Многоугольник.
—————
Этот урок разработала Анна Мария Лопес Лопес (Anna María López López) — многопрофильный дизайнер, основатель www.corelclub.org и автор многочисленных книг по цифровому дизайну, таких как www.cursodisenografico.net.
Источник: http://www.corelclub.org/tutorial-poligonos-coreldraw/
чем он интересен и как его построить
Сетки из шестиугольников (гексагональные сетки) используются в некоторых играх, но они не так просты и распространены, как сетки прямоугольников. Я коллекционирую ресурсы о сетках шестиугольников уже почти 20 лет, и написал это руководство по самым элегантным подходам, реализуемым в простейшем коде. В статье часто используются руководства Чарльза Фу (Charles Fu) и Кларка Вербрюгге (Clark Verbrugge). Я опишу различные способы создания сеток шестиугольников, их взаимосвязь, а также самые общие алгоритмы. Многие части этой статьи интерактивны: выбор типа сетки изменяет соответствующие схемы, код и тексты. (Прим. пер.: это относится только к оригиналу, советую его изучить. В переводе вся информация оригинала сохранена, но без интерактивности.) .
Я коллекционирую ресурсы о сетках шестиугольников уже почти 20 лет, и написал это руководство по самым элегантным подходам, реализуемым в простейшем коде. В статье часто используются руководства Чарльза Фу (Charles Fu) и Кларка Вербрюгге (Clark Verbrugge). Я опишу различные способы создания сеток шестиугольников, их взаимосвязь, а также самые общие алгоритмы. Многие части этой статьи интерактивны: выбор типа сетки изменяет соответствующие схемы, код и тексты. (Прим. пер.: это относится только к оригиналу, советую его изучить. В переводе вся информация оригинала сохранена, но без интерактивности.) .
Примеры кода в статье написаны псевдокодом, так их легче читать и понимать, чтобы написать свою реализацию.
Геометрия
Шестиугольники — это шестигранные многоугольники. У правильных шестиугольников все стороны (грани) имеют одинаковую длину. Мы будем работать только с правильными шестиугольниками. Обычно в сетках шестиугольников используются горизонтальная (с острым верхом) и вертикальная (с плоским верхом) ориентации.
Шестиугольники с плоским (слева) и острым (справа) верхом
У шестиугольников по 6 граней. Каждая грань общая для двух шестиугольников. У шестиугольников по 6 угловых точек. Каждая угловая точка общая для трёх шестиугольников. Подробнее о центрах, гранях и угловых точках можно прочитать в моей статье о частях сеток (квадратах, шестиугольниках и треугольниках).
Углы
В правильном шестиугольнике внутренние углы равны 120°. Есть шесть «клиньев», каждый из которых является равносторонним треугольником с внутренними углами 60°. Угловая точка i находится на расстоянии (60° * i) + 30° , на size единиц от центра center . В коде:Function hex_corner(center, size, i):
var angle_deg = 60 * i + 30
var angle_rad = PI / 180 * angle_deg
return Point(center.x + size * cos(angle_rad), center.y + size * sin(angle_rad))
Для заполнения шестиугольника нужно получить вершины многоугольника с hex_corner(…, 0) по hex_corner(…, 5) . Для отрисовки контура шестиугольника нужно использовать эти вершины, а затем нарисовать линию снова в hex_corner(…, 0) .
Разница между двумя ориентациями в том, что x и y меняются местами, что приводит к изменению углов: углы шестиугольников с плоским верхом равны 0°, 60°, 120°, 180°, 240°, 300°, а с острым верхом — 30°, 90°, 150°, 210°, 270°, 330°.
Углы шестиугольников с плоским и острым верхом
Размер и расположение
Теперь мы хотим расположить несколько шестиугольников вместе. В горизонтальной ориентации высота шестиугольника height = size * 2 . Вертикальное расстояние между соседними шестиугольниками vert = height * 3/4 .Ширина шестиугольника width = sqrt(3)/2 * height . Горизонтальное расстояние между соседними шестиугольниками horiz = width .
В некоторых играх для шестиугольников используется пиксель-арт, который не точно соответствует правильным шестиугольникам. Формулы углов и расположений, описанные в этом разделе, не будут совпадать с размерами таких шестиугольников. Остальная часть статьи, описывающая алгоритмы сеток шестиугольников, применима даже если шестиугольники немного растянуты или сжаты.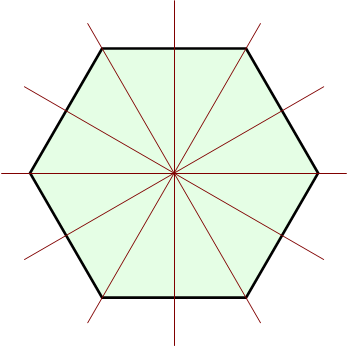
Системы координат
Давайте приступим к сборке шестиугольников в сетку. В случае сеток квадратов существует только один очевидный способ сборки. Для шестиугольников же есть множество подходов. Я рекомендую использовать в качестве первичного представления кубические координаты. Осевые координаты или координаты смещений следует использовать для хранения карт и отображения координат для пользователя.Координаты смещений
Наиболее частый подход — смещение каждого последующего столбца или строки. Столбцы обозначаются col или q . Строки обозначаются row или r . Можно смещать нечётные или чётные столбцы/строки, поэтому у горизонтальных и вертикальных шестиугольников есть по два варианта.
Горизонтальное расположение «нечет-r»
Горизонтальное расположение «чёт-r»
Вертикальное расположение «нечет-q»
Вертикальное расположение «чёт-q»
Кубические координаты
Ещё один способ рассмотрения сеток шестиугольников — видеть в них три основные оси, а не две , как в сетках квадратов.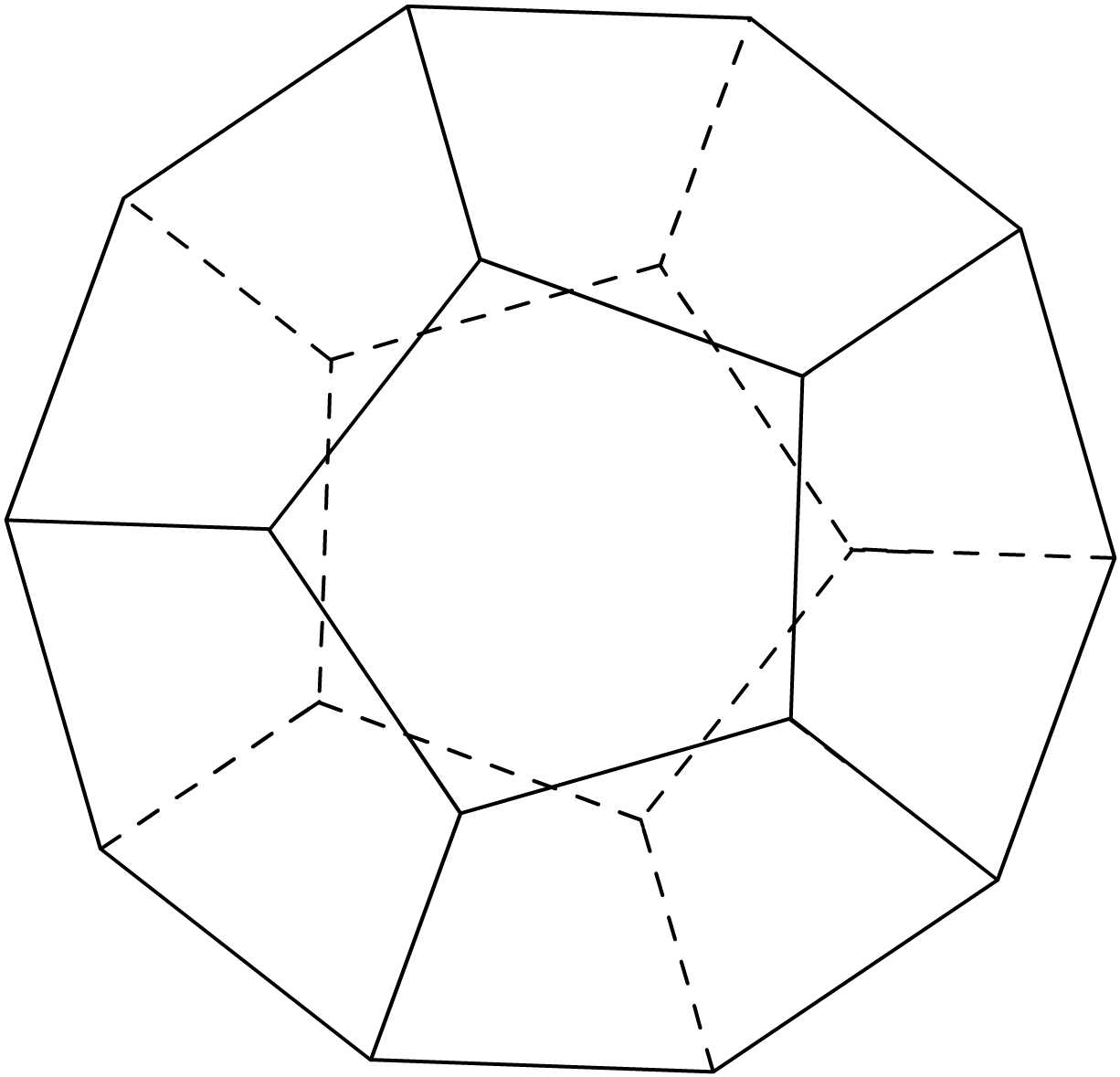 В них проявляется элегантная симметрия.
В них проявляется элегантная симметрия.Возьмём сетку кубов и вырежем диагональную плоскость в x + y + z = 0 . Это странная мысль, но она поможет нам упростить алгоритмы сеток шестиугольников. В частности, мы сможем воспользоваться стандартными операциями из декартовых координат: суммированием и вычитанием координат, умножением и делением на скалярную величину, а также расстояниями.
Заметьте три основные оси на сетке кубов и их соотношение с шестью диагональными направлениями сетки шестиугольников. Диагональные оси сетки соответствуют основному направлению сетки шестиугольников.
Шестиугольники
Кубы
Поскольку у нас уже есть алгоритмы для сеток квадратов и кубов, использование кубических координат позволяет нам адаптировать эти алгоритмы под сетки шестиугольников. я буду использовать эту систему для большинства алгоритмов статьи. Для использования алгоритмов с другой системой координат я преобразую кубические координаты, выполню алгоритм, а затем преобразую их обратно.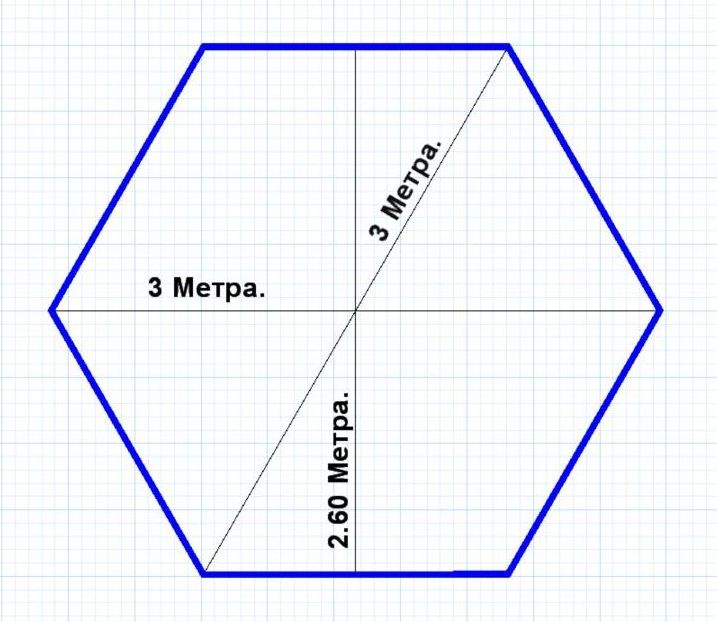
Изучите, как кубические координаты работают для сетки шестиугольников. При выборе шестиугольников выделяются кубические координаты, соответствующие трём осям.
- Каждое направление сетки кубов соответствует линии на сетке шестиугольников. Попробуйте выделить шестиугольник с z , равным 0, 1, 2, 3, чтобы увидеть связь. Строка отмечена синим. Попробуйте то же самое для x (зелёный) и y (сиреневый).
- Каждое направление сетки шестиугольника — это сочетание двух направлений сетки кубов. Например, «север» сетки шестиугольников лежит между +y и -z , поэтому каждый шаг на «север» увеличивает y на 1 и уменьшает z на 1.
Существует множество различных систем координат для кубов и шестиугольников.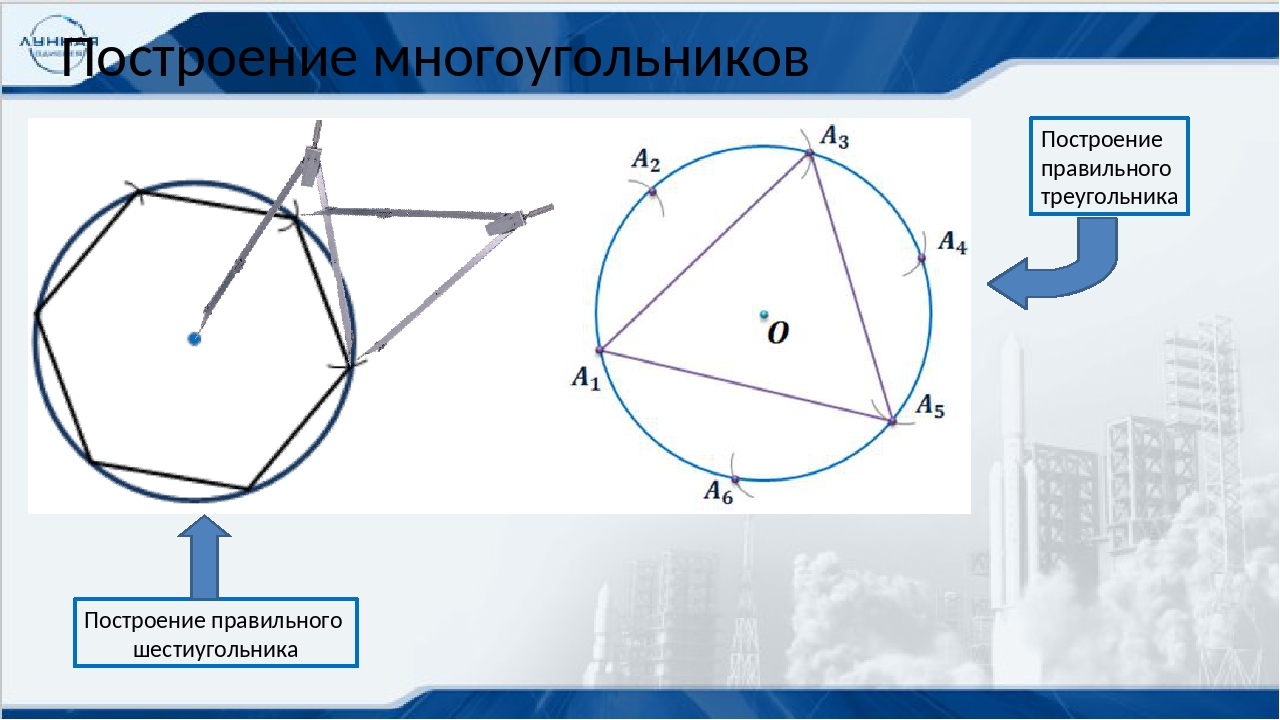 В некоторых из них условие отличается от x + y + z = 0 . Я показал только одну из множества систем. Можно также создать кубические координаты с x-y , y-z , z-x , у которых будет свой набор интересных свойств, но я не буду их здесь рассматривать.
В некоторых из них условие отличается от x + y + z = 0 . Я показал только одну из множества систем. Можно также создать кубические координаты с x-y , y-z , z-x , у которых будет свой набор интересных свойств, но я не буду их здесь рассматривать.
Но вы можете возразить, что не хотите хранить 3 числа для координат, потому что не знаете, как хранить карту в таком виде.
Осевые координаты
Осевая система координат, иногда называемая «трапецеидальной», строится на основе двух или трёх координат из кубической системы координат. Поскольку у нас есть условие x + y + z = 0 , третья координата не нужна. Осевые координаты полезны для хранения карт и отображения координат пользователю. Как и в случае с кубическими координатами, с ними можно использовать стандартные операции суммирования, вычитания, умножения и деления декартовых координат.Существует множество кубических систем координат и множество осевых. В этом руководстве я не буду рассматривать все сочетания. Я выберу две переменные, q (столбец) и r (строка). В схемах этой статьи q соответствует x , а r соответствует z , но такое соответствие произвольно, потому что можно вращать и поворачивать схемы, получая различные соответствия.
В схемах этой статьи q соответствует x , а r соответствует z , но такое соответствие произвольно, потому что можно вращать и поворачивать схемы, получая различные соответствия.
Преимущество этой системы перед сетками смещений в большей понятности алгоритмов. Недостатком системы является то, что хранение прямоугольной карты выполняется немного странно; см. раздел о сохранении карт. Некоторые алгоритмы ещё понятнее в кубических координатах, но поскольку у нас есть условие x + y + z = 0 , мы можем вычислить третью подразумеваемую координату и использовать её в этих алгоритмах. В своих проектах я называю оси q , r , s , поэтому условие выглядит как q + r + s = 0 , и я, когда нужно, могу вычислить s = -q — r .
Оси
Координаты смещения — это первое, о чём думает большинство людей, потому что они совпадают со стандартными декартовыми координатами, используемыми для сеток квадратов. К сожалению, одна из двух осей должна проходить «против шерсти», и это в результате всё усложняет. Кубическая и осевая система идут «по шерсти» и у них более простые алгоритмы, но хранение карт немного более сложное. Существует ещё одна система, называемая «чередуемой» или «двойной», но здесь мы не будем её рассматривать; некоторые считают, что с ней проще работать, чем с кубической или осевой.Координаты смещения, кубические и осевые
Ось — это направление, в котором соответствующая координата увеличивается. Перпендикуляр к оси — это линия, на которой координата остаётся постоянной. На схемах сеток выше показаны линии перпендикуляров.
Преобразование координат
Вероятно, что вы будете использовать в своём проекте осевые координаты или координаты смещения, но многие алгоритмы проще выражаются в кубических координатах. Поэтому нам нужно уметь преобразовывать координаты между системами.Осевые координаты близко связаны с кубическими, поэтому преобразование делается просто:
# преобразование кубических в осевые координаты
q = x
r = z
# преобразование осевых в кубические координаты
x = q
z = r
y = -x-z
В коде эти две функции могут быть записаны следующим образом:
Function cube_to_hex(h): # осевая
var q = h.x
var r = h.z
return Hex(q, r)
function hex_to_cube(h): # кубическая
var x = h.q
var z = h.r
var y = -x-z
return Cube(x, y, z)
Координаты смещения совсем немного сложнее:
Соседние шестиугольники
Дан один шестиугольник, с какими шестью шестиугольниками он находится рядом? Как и можно ожидать, легче всего дать ответ в кубических координатах, довольно просто в осевых координатах, и немного сложнее в координатах смещения. Также может потребоваться рассчитать шесть «диагональных» шестиугольников.Кубические координаты
Перемещение на одно пространство в координатах шестиугольников приводит к изменению одной из трёх кубических координат на +1 и другой на -1 (сумма должна оставаться равной 0). На +1 могут изменяться три возможных координаты, а на -1 — оставшиеся две. Это даёт нам шесть возможных изменений. Каждое соответствует одному из направлений шестиугольника. Простейший и быстрейший способ — предварительно вычислить изменения и поместить их в таблицу кубических координат Cube(dx, dy, dz) во время компиляции:Var directions = [
Cube(+1, -1, 0), Cube(+1, 0, -1), Cube(0, +1, -1),
Cube(-1, +1, 0), Cube(-1, 0, +1), Cube(0, -1, +1)
]
function cube_direction(direction):
return directions
function cube_neighbor(hex, direction):
return cube_add(hex, cube_direction(direction))
Осевые координаты
Как и раньше, мы используем для начала кубическую систему. Возьмём таблицу Cube(dx, dy, dz) и преобразуем в таблицу Hex(dq, dr) :Var directions = [
Hex(+1, 0), Hex(+1, -1), Hex(0, -1),
Hex(-1, 0), Hex(-1, +1), Hex(0, +1)
]
function hex_direction(direction):
return directions
function hex_neighbor(hex, direction):
var dir = hex_direction(direction)
return Hex(hex.q + dir.q, hex.r + dir.r)
Координаты смещения
В осевых координатах мы вносим изменения в зависимости от того, в каком месте сетки находимся. Если мы в столбце/строке смещения, то правило отличается от случая столбца/строки без смещения.Как и раньше, мы создаём таблицу чисел, которые нужно прибавить к col and row . Однако на этот раз у нас будет два массива, один для нечётных столбцов/строк, а другой — для чётных. Посмотрите на (1,1) на рисунке карты сетки выше и заметьте, как меняются col и row меняются при перемещении в каждом из шести направлений. Теперь повторим процесс для (2,2) . Таблицы и код будут разными для каждого из четырёх типов сеток смещений, приводим соответствующий код для каждого типа сетки.
Нечет-r
var directions = [
[ Hex(+1, 0), Hex(0, -1), Hex(-1, -1),
Hex(-1, 0), Hex(-1, +1), Hex(0, +1) ],
[ Hex(+1, 0), Hex(+1, -1), Hex(0, -1),
Hex(-1, 0), Hex(0, +1), Hex(+1, +1) ]
]
function offset_neighbor(hex, direction):
var parity = hex.row & 1
var dir = directions
return Hex(hex.col + dir.col, hex.row + dir.row)
Чёт-r
var directions = [
[ Hex(+1, 0), Hex(+1, -1), Hex(0, -1),
Hex(-1, 0), Hex(0, +1), Hex(+1, +1) ],
[ Hex(+1, 0), Hex(0, -1), Hex(-1, -1),
Hex(-1, 0), Hex(-1, +1), Hex(0, +1) ]
]
function offset_neighbor(hex, direction):
var parity = hex.row & 1
var dir = directions
return Hex(hex.col + dir.col, hex.row + dir.row)
Сетка для чётной (EVEN) и нечётной (ODD) строк
Нечет-q
var directions = [
[ Hex(+1, 0), Hex(+1, -1), Hex(0, -1),
Hex(-1, -1), Hex(-1, 0), Hex(0, +1) ],
[ Hex(+1, +1), Hex(+1, 0), Hex(0, -1),
Hex(-1, 0), Hex(-1, +1), Hex(0, +1) ]
]
function offset_neighbor(hex, direction):
var parity = hex.col & 1
var dir = directions
return Hex(hex.col + dir.col, hex.row + dir.row)
Чёт-q
var directions = [
[ Hex(+1, +1), Hex(+1, 0), Hex(0, -1),
Hex(-1, 0), Hex(-1, +1), Hex(0, +1) ],
[ Hex(+1, 0), Hex(+1, -1), Hex(0, -1),
Hex(-1, -1), Hex(-1, 0), Hex(0, +1) ]
]
function offset_neighbor(hex, direction):
var parity = hex.col & 1
var dir = directions
return Hex(hex.col + dir.col, hex.row + dir.row)
Сетка для чётного (EVEN) и нечётного (ODD) столбцов
Диагонали
Перемещение в «диагональном» пространстве в координатах шестиугольников изменяет одну из трёх кубических координат на ±2 и две другие на ∓1 (сумма должна оставаться равной 0).Var diagonals = [
Cube(+2, -1, -1), Cube(+1, +1, -2), Cube(-1, +2, -1),
Cube(-2, +1, +1), Cube(-1, -1, +2), Cube(+1, -2, +1)
]
function cube_diagonal_neighbor(hex, direction):
return cube_add(hex, diagonals)
Как и раньше, мы можем преобразовать эти координаты в осевые, откинув одну из трёх координат, или преобразовать в координаты смещения, предварительно вычислив результаты.
Расстояния
Кубические координаты
В кубической системе координат каждый шестиугольник является кубом в трёхмерном пространстве. Соседние шестиугольники находятся в сетке шестиугольников на расстоянии 1 друг от друга, но на расстоянии 2 в сетке кубов. Это делает расчёт расстояний простым. В сетке квадратов манхэттенские расстояния равны abs(dx) + abs(dy) . В сетке кубов манхэттенские расстояния равны abs(dx) + abs(dy) + abs(dz) . Расстояние в сетке шестиугольников равно их половине:Function cube_distance(a, b):
return (abs(a.x — b.x) + abs(a.y — b.y) + abs(a.z — b.z)) / 2
Эквивалентом этой записи будет выражение того, что одна из трёх координат должна быть суммой двух других, а затем получение её в качестве расстояния. Можно выбрать форму деления пополам или форму максимального значения, приведённую ниже, но они дают одинаковый результат:
Function cube_distance(a, b):
return max(abs(a.x — b.x), abs(a.y — b.y), abs(a.z — b.z))
На рисунке максимальные значения выделены цветом. Заметьте также, что каждый цвет обозначает одно из шести «диагональных» направлений.
GIF
Осевые координаты
В осевой системе третья координата выражена неявно. Давайте преобразуем из осевой в кубическую систему для расчёта расстояния:Function hex_distance(a, b):
var ac = hex_to_cube(a)
var bc = hex_to_cube(b)
return cube_distance(ac, bc)
Если компилятор в вашем случае встраивает (inline) hex_to_cube и cube_distance , то он сгенерирует такой код:
Function hex_distance(a, b):
return (abs(a.q — b.q)
+ abs(a.q + a.r — b.q — b.r)
+ abs(a.r — b.r)) / 2
Существует множество различных способов записи расстояний между шестиугольниками в осевых координатах, но вне зависимости от способа записи расстояние между шестиугольниками в осевой системе извлекается из манхэттенского расстояния в кубической системе . Например, описанная «разность разностей» получается из записи a.q + a.r — b.q — b.r как a.q — b.q + a.r — b.r и с использованием формы максимального значения вместо формы деления пополам cube_distance . Все они аналогичны, если увидеть связь с кубическими координатами.
Координаты смещения
Как и в случае с осевыми координатами, мы преобразуем координаты смещения в кубические координаты, а затем используем расстояние кубической системы.Function offset_distance(a, b):
var ac = offset_to_cube(a)
var bc = offset_to_cube(b)
return cube_distance(ac, bc)
Мы будем использовать тот же шаблон для многих алгоритмов: преобразуем из шестиугольников в кубы, выполняем кубическую версию алгоритма и преобразуем кубические результаты в координаты шестиугольников (осевые или координаты смещения).
Отрисовка линий
Как нарисовать линию от одного шестиугольника до другого? Я использую линейную интерполяцию для рисования линий . Линия равномерно сэмплируется в N+1 точках и вычисляется, в каких шестиугольниках находятся эти сэмплы.GIF
- Сначала мы вычисляем N , которое будет расстоянием в шестиугольниках между конечными точками.
- Затем равномерно сэмплируем N+1 точек между точками A и B. С помощью линейной интерполяции определяем, что для значений i от 0 до N , включая их, каждая точка будет A + (B — A) * 1.0/N * i . На рисунке эти контрольные точки показаны синим. В результате получаются координаты с плавающей запятой.
- Преобразуем каждую контрольную точку (float) обратно в шестиугольники (int). Алгоритм называется cube_round (см. ниже).
Function lerp(a, b, t): // для float
return a + (b — a) * t
function cube_lerp(a, b, t): // для шестиугольников
return Cube(lerp(a.x, b.x, t),
lerp(a.y, b.y, t),
lerp(a.z, b.z, t))
function cube_linedraw(a, b):
var N = cube_distance(a, b)
var results =
for each 0 ≤ i ≤ N:
results.append(cube_round(cube_lerp(a, b, 1.0/N * i)))
return results
Примечания:
- Бывают случаи, когда cube_lerp возвращает точку, находящуюся точно на грани между двумя шестиугольниками. Затем cube_round сдвигает её в ту или иную сторону. Линии выглядят лучше, если их сдвигают в одном направлении. Это можно сделать, добавив «эпсилон»-шестиугольный Cube(1e-6, 1e-6, -2e-6) к одной или обеим конечным точкам перед началом цикла. Это «подтолкнёт» линию в одном направлении, чтобы она не попадала на границы граней.
- Алгоритм DDA-линии в сетках квадратов приравнивает N к максимуму расстояния по каждой из осей. Мы делаем то же самое в кубическом пространстве, что аналогично расстоянию в сетке шестиугольников.
- Функция cube_lerp должна возвращать куб с координатами в float. Если вы программируете на языке со статической типизацией, то не сможете использовать тип Cube . Вместо него можно определить тип FloatCube или встроить (inline) функцию в код отрисовки линий, если вы не хотите определять ещё один тип.
- Можно оптимизировать код, встроив (inline) cube_lerp , а затем рассчитав B.x-A.x , B.x-A.y и 1.0/N за пределами цикла. Умножение можно преобразовать в повторяющееся суммирование. В результате получится что-то вроде алгоритма DDA-линии.
- Для отрисовки линий я использую осевые или кубические координаты, но если вы хотите работать с координатами смещения, то изучите .
- Существует много вариантов отрисовки линий. Иногда требуется «сверхпокрытие» . Мне прислали код отрисовки линий с сверхпокрытием в шестиугольниках, но я пока не изучал его.
Диапазон перемещения
Диапазон координат
Для заданного центра шестиугольника и диапазона N какие шестиугольники находятся в пределах N шагов от него?Мы можем произвести обратную работу из формулы расстояния между шестиугольниками distance = max(abs(dx), abs(dy), abs(dz)) . Чтобы найти все шестиугольники в пределах N , нам нужны max(abs(dx), abs(dy), abs(dz)) ≤ N . Это значит, что нужны все три значения: abs(dx) ≤ N и abs(dy) ≤ N и abs(dz) ≤ N . Убрав абсолютное значение, мы получим -N ≤ dx ≤ N и -N ≤ dy ≤ N и -N ≤ dz ≤ N . В коде это будет вложенный цикл:
Var results =
for each -N ≤ dx ≤ N:
for each -N ≤ dy ≤ N:
for each -N ≤ dz ≤ N:
if dx + dy + dz = 0:
results.append(cube_add(center, Cube(dx, dy, dz)))
Этот цикл сработает, но будет довольно неэффективным. Из всех значений dz , которые мы перебираем в цикле, только одно действительно удовлетворяет условию кубов dx + dy + dz = 0 . Вместо этого мы напрямую вычислим значение dz , удовлетворяющее условию:
Var results =
for each -N ≤ dx ≤ N:
for each max(-N, -dx-N) ≤ dy ≤ min(N, -dx+N):
var dz = -dx-dy
results.append(cube_add(center, Cube(dx, dy, dz)))
Этот цикл проходит только по нужным координатам. На рисунке каждый диапазон является парой линий. Каждая линия — это неравенство. Мы берём все шестиугольники, удовлетворяющие шести неравенствам.
GIF
Пересекающиеся диапазоны
Если нужно найти шестиугольники, находящиеся в нескольких диапазонах, то перед генерированием списка шестиугольников можно пересечь диапазоны.Можно подойти к этой проблеме с точки зрения алгебры или геометрии. Алгебраически каждая область выражается как условия неравенств в форме -N ≤ dx ≤ N , и нам нужно найти пересечение этих условий. Геометрически каждая область является кубом в трёхмерном пространстве, и мы пересечём два куба в трёхмерном пространстве для получения прямоугольного параллелепипеда в трёхмерном пространстве. Затем мы проецируем его обратно на плоскость x + y + z = 0 , чтобы получить шестиугольники. Я буду решать эту задачу алгебраически.
Во-первых, мы перепишем условие -N ≤ dx ≤ N в более общей форме x min ≤ x ≤ x max , и примем x min = center.x — N и x max = center.x + N . Сделаем то же самое для y и z , в результате получив общий вид кода из предыдущего раздела:
Var results =
for each xmin ≤ x ≤ xmax:
for each max(ymin, -x-zmax) ≤ y ≤ min(ymax, -x-zmin):
var z = -x-y
results.append(Cube(x, y, z))
Пересечением двух диапазонов a ≤ x ≤ b и c ≤ x ≤ d является max(a, c) ≤ x ≤ min(b, d) . Поскольку область шестиугольников выражена как диапазоны над x , y , z , мы можем отдельно пересечь каждый из диапазонов x , y , z , а затем использовать вложенный цикл для генерирования списка шестиугольников в пересечении. Для одной области шестиугольников мы принимаем x min = H.x — N and x max = H.x + N , аналогично для y и z . Для пересечения двух областей шестиугольников мы принимаем x min = max(h2.x — N, h3.x — N) и x max = min(h2.x + N, h3.x + N), аналогично для y и z . Тот же шаблон работает для пересечения трёх или более областей.
GIF
Препятствия
При наличии препятствий проще всего выполнить заливку с ограничением по расстоянию (поиск в ширину). На рисунке ниже мы ограничиваемся четырьмя ходами. В коде fringes[k] — это массив всех шестиугольников, которых можно достичь за k шагов. При каждом проходе по основному циклу мы расширяем уровень k-1 на уровень k .Function cube_reachable(start, movement): var visited = set() add start to visited var fringes = fringes.append() for each 1
Повороты
Для заданного вектора шестиугольника (разницу между двумя шестиугольниками) нам может понадобиться повернуть его, чтобы он указывал на другой шестиугольник. Это просто сделать, имея кубические координаты, если придерживаться поворота на 1/6 окружности.Поворот на 60° вправо сдвигает каждую координату на одну позицию вправо:
[ x, y, z]
to [-z, -x, -y]
Поворот на 60° влево сдвигает каждую координату на одну позицию влево:
[ x, y, z]
to [-y, -z, -x]
«Поиграв» [в оригинале статьи] со схемой, можно заметить, что каждый поворот на 60° меняет знаки и физически «поворачивает» координаты. После поворота на 120° знаки снова становятся теми же. Поворот на 180° меняет знаки, но координаты поворачиваются в своё изначальное положение.
Вот полная последовательность поворота положения P вокруг центрального положения C, приводящего к новому положению R:
- Преобразование положений P и C в кубические координаты.
- Вычисление вектора вычитанием центра: P_from_C = P — C = Cube(P.x — C.x, P.y — C.y, P.z — C.z) .
- Поворот вектора P_from_C как описано выше и присваивание итоговому вектору обозначения R_from_C .
- Преобразование вектора обратно в положение прибавлением центра: R = R_from_C + C = Cube(R_from_C.x + C.x, R_from_C.y + C.y, R_from_C.z + C.z) .
- Преобразование кубического положения R обратно в нужную систему координат.
Кольца
Простое кольцо
Чтобы выяснить, принадлежит ли заданный шестиугольник к кольцу заданного радиуса radius , нужно вычислить расстояние от этого шестиугольника до центра, и узнать, равно ли оно radius . Для получения списка всех таких шестиугольников нужно сделать radius шагов от центра, а затем следовать за поворачиваемыми векторами по пути вдоль кольца.Function cube_ring(center, radius): var results = # этот код не работает для radius == 0; вы понимаете, почему? var cube = cube_add(center, cube_scale(cube_direction(4), radius)) for each 0 ≤ i В этом коде cube начинается на кольце, показанном большой стрелкой от центра к углу схемы. Я выбрал для начала угол 4, потому что он соответствует пути, в котором двигаются мои числа направлений. Вам может понадобиться другой начальный угол. На каждом этапе внутреннего цикла cube двигается на один шестиугольник по кольцу. Через 6 * radius шагов он завершает там, где начал.
Спиральные кольца
Проходя по кольцам по спиральному паттерну, мы можем заполнить внутренние части колец:Function cube_spiral(center, radius):
var results =
for each 1 ≤ k ≤ radius:
results = results + cube_ring(center, k)
return results
Площадь большого шестиугольника равна сумме всех окружностей плюс 1 для центра. Для вычисления площади используйте эту формулу .
Обход шестиугольников таким способом можно также использовать для вычисления диапазона перемещения (см. выше).
Область видимости
Что видимо из заданного положения с заданным расстоянием, и не перекрывается препятствиями? Простейший способ определить это — нарисовать линию к каждому шестиугольнику в заданном диапазоне. Если линия не встречается со стенами, то вы видите шестиугольник. Перемещайте мышь по шестиугольникам [на схеме в оригинале статьи], чтобы увидеть отрисовку линий к этим шестиугольникам и стены, с которыми линии встречаются.Этот алгоритм может быть медленным на больших площадях, но его легко реализовать, поэтому рекомендую начать с него.
GIF
Существует много разных определений видимости. Хотите ли вы видеть центр другого шестиугольника из центра начального? Хотите ли вы видеть любую часть другого шестиугольника из центра начального? Может быть, любую часть другого шестиугольника из любой точки начального? Мешающие взгляду препятствия меньше полного шестиугольника? Область видимости — это более хитрое и разнообразное понятие, чем кажется на первый взгляд. Начнём с простейшего алгоритма, но ждите, что он обязательно правильно вычислит ответ в вашем проекте. Бывают даже случаи, когда простой алгоритм даёт нелогичные результаты.
Я хочу в дальнейшем расширять это руководство. У меня есть
Построение вписанного в окружность правильного шестиугольника. Построение правильного пятиугольника по данной его стороне. Переставьте иглу циркуля в точку пересечения только что начерченной дуги с окружностью. Это построение можно выполнить при помощи угольника и циркуля. Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Постройте точки вершин углов правильного шестиугольника.
Построение вписанного в окружность равностороннего треугольника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Метод 1 из 3: Рисуем идеальный шестиугольник при помощи циркуля
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника.
Именно на умении строить биссектрисы углов и серединные перпендикуляры отрезков и основывается методика построения правильных многоугольников
В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй-коэффициенты. Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.
Тема этого видеоурока – «Построение правильных многоугольников». Также еще раз дадим определение правильному многоугольнику, изобразим его графически, после чего еще раз убедимся, что центры вписанной и описанной окружностей вокруг такой фигуры будут совпадать. В этот многоугольник всегда можно вписать окружность и около него всегда можно описать окружность. В ходе предыдущих уроков мы выяснили, что базовую роль для описания свойств многоугольников играют биссектрисы его углов и серединные перпендикуляры к его сторонам.
4. Получили искомый правильный треугольник АВС. Задача решена. 3. Поместив одну ножку циркуля в произвольную точки А1 на окружности, при помощи второй ножки отметим на той же окружности точку А2 и соединим ее с точкой А1. Получим первую сторону шестиугольника. 3. При помощи серединных перпендикуляров к сторонам многоугольника, опущенным из точки О, разделим все его стороны и все дуги окружности, заключенные между его соседними вершинами, пополам.
Геометрические построения являются одной из важных частей обучения. Игла должна проткнуть начерченную линию. Чем точнее будет установлен циркуль, тем точнее будет построение. Начертите еще одну дугу, пересекающую окружность. Последовательно соедините все шесть точек пересечения дуг с первоначально начерченной окружностью. В этом случае шестиугольник может получиться неправильным.
Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые
Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра. Центры обеих окружностей совпадают (точка О на Рис. 1). Также на рисунке приведены радиусы описанной (R) и вписанной (r) окружностей.
Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. На данном занятии мы рассмотрим способы построения правильных многоугольников с помощью циркуля и линейки. Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник. Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего проводим стороны 5-6 и 3-2.
Построение вписанного в окружность равностороннего треугольника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны
1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
Содержимое:
Обычный шестиугольник, также называемый идеальным шестиугольником, имеет шесть равных сторон и шесть равных углов. Вы можете нарисовать шестиугольник при помощи рулетки и транспортира, грубый шестиугольник – при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи только карандаша и немного интуиции. Если вы хотите знать, как нарисовать шестиугольник различными способами – просто читайте далее.
Шаги
1 Рисуем идеальный шестиугольник при помощи циркуля
- 1 При помощи циркуля рисуем круг. Вставьте карандаш в циркуль. Расширьте циркуль на желаемую ширину радиуса вашего круга. Радиус может быть от пары до десятка сантиметров шириной. Далее поставьте циркуль с карандашом на бумагу и нарисуйте круг.
- Иногда легче сначала нарисовать пол круга, а затем вторую половину.
- 2 Передвиньте иглу циркуля к краю круга. Поставьте его на вершину круга. Не меняйте угол и расположение циркуля.
- 3 Сделайте небольшую отметку карандашом на краю круга. Сделайте ее отчетливой, но не слишком темной, так как позже вы ее сотрете. Не забудьте сохранять угол, который вы установили для циркуля.
- 4 Передвиньте иглу циркуля на ту отметку, которую вы только что сделали. Поставьте иглу прямо на отметку.
- 5 Сделайте еще одну отметку карандашом на краю круга. Таким образом, вы сделаете вторую отметку на определенной дистанции от первой отметки. Продолжайте двигаться в одном направлении.
- 6 Тем же способом сделайте еще четыре отметки. Вы должны вернуться назад на первоначальную отметку. Если нет, тогда, скорее всего, угол, под которым вы держали циркуль и делали отметки, изменился. Возможно, это случилось из-за того, что вы сжали его слишком сильно или наоборот, немного ослабили.
- 7 Соедините отметки при помощи линейки. Шесть мест, где ваши отметки пересекаются с краем круга, — это шесть вершин шестиугольника. При помощи линейки и карандаша нарисуйте прямые линии, соединяя соседние отметки.
- 8 Сотрите и круг, и отметки на краях круга, и другие метки, которые вы сделали. После того, как вы стерли все свои вспомогательные линии, ваш идеальный шестиугольник должен быть готов.
2 Рисуем грубый шестиугольник при помощи круглого предмета и линейки
- 1 Обведите ободок стакана карандашом. Таким образом, вы нарисуете круг. Очень важно рисовать именно карандашом, так как позже вам нужно будет стереть все вспомогательные линии. Вы также можете обвести перевернутый стакан, банку или что-то еще, что имеет круглую основу.
- 2 Нарисуйте горизонтальные линии через центр вашего круга. Можете воспользоваться линейкой, книгой — чем угодно с прямым краем. Если у вас все же есть линейка, вы можете отметить середину, рассчитав вертикальную длину круга и разделив его пополам.
- 3 Нарисуйте «Х» над половиной круга, разделяя его на шесть равных секций. Так как вы уже провели линию через середину круга, Х должен быть больше в ширину, чем в высоту, чтобы части были равны. Представьте, что вы делите пиццу на шесть частей.
- 4 Сделайте из каждой секции треугольники. Чтобы это сделать, при помощи линейки нарисуйте прямую линию под изогнутой частью каждой секции, соединяя ее с другими двумя линиями, образовывая треугольник. Сделайте это с оставшимися пятью секциями. Думайте об этом, как об изготовлении корочки вокруг ваших кусков пиццы.
- 5 Сотрите все вспомогательные линии. К вспомогательным линиям относятся ваш круг, три линии, которые разделили ваш круг на секции и другие отметки, которые вы делали в процессе.
3 Рисуем грубый шестиугольник при помощи одного карандаша
- 1 Нарисуйте горизонтальную линию. Чтобы нарисовать прямую линию без линейки, просто нарисуйте начальную и конечную точку вашей горизонтальной линии. Затем поместите карандаш в начальную точку и протягивайте линию к концу. Длина этой линии может быть всего пара сантиметров.
- 2 Нарисуйте две диагональные линии с концов горизонтальной. Диагональная линия с левой стороны должна быть направлена наружу так же, как и диагональная линия справа. Вы можете представить, что эти линии формируют угол в 120 градусов по отношению к горизонтальной линии.
- 3 Нарисуйте еще две горизонтальные линии, исходящие из первых горизонтальных прямых, нарисованных вовнутрь. Таким образом, будет создано зеркальное отображение первых двух диагональных линий. Нижняя левая линия должна быть отражением верхней левой линии, а нижняя правая — отражением верхней правой линии. В то время как верхние горизонтальные линии должны смотреть наружу, нижние должны смотреть вовнутрь основания.
- 4 Нарисуйте еще одну горизонтальную линию, соединяя нижние две диагональные линии. Таким образом, вы нарисуете основу для своего шестиугольника. В идеале эта линия должна быть параллельной к верхней горизонтальной линии. Вот вы и завершили свой шестиугольник.
- Карандаш и циркуль должны быть острыми, чтобы минимизировать ошибки от слишком широких отметок.
- Если при использовании метода с циркулем вы соединили каждую отметку вместо всех шести, то получите равносторонний треугольник.
Предупреждения
- Циркуль — довольно острый предмет, будьте с ним очень аккуратны.
Принцип работы
- Каждый метод поможет нарисовать шестиугольник, образованный шестью равносторонними треугольниками с радиусом, равным длине всех сторон. Шесть нарисованных радиусов одинаковой длины и все линии для создания шестиугольника тоже одной длины, так как ширина циркуля не менялась. Благодаря тому, что шесть треугольников равносторонние, углы между их вершинами равны 60 градусов.
Что вам понадобится
- Бумага
- Карандаш
- Линейка
- Пара циркулей
- Что-то, что можно подложить под бумагу, чтобы игла циркуля не соскальзывала.
- Ластик
Геометрические узоры весьма популярны в последнее время. В сегодняшнем уроке мы научимся создавать один из таких узоров. Используя переход, оформление и модные цвета мы создадим паттерн, который вы сможете использовать в веб и полиграфическом дизайне.
Результат
Шаг 2
Нарисуйте еще один шестиугольник, на этот раз меньше — выберите радиус в 20pt .
2. Переход между шестиугольниками
Шаг 1
Выделите оба шестиугольника и выровняйте их по центру (вертикально и горизонтально). Используя инструмент Blend/Переход (W) , выделите оба шестиугольника и укажите им переход в 6 шагов (Steps) . Чтобы было лучше видно, измените перед переходом цвет фигур.
3. Делим на секции
Шаг 1
Инструментом Line Segment/Отрезок линии (\) нарисуйте линию, пересекающую шестиугольники по центру от самого левого угла к самому правому. Нарисуйте еще две линии, пересекающие шестиугольники по центру от противоположных углов.
4. Закрашиваем секции
Шаг 1
Перед тем как начать закрашивать секции, давайте определимся с палитрой. Вот какова палитра из примера:
- Синий: C 65 M 23 Y 35 K 0
- Бежевый: C 13 M 13 Y 30 K 0
- Персиковый: C 0 M 32 Y 54 K 0
- Светло-розовый: C 0 M 64 Y 42 K 0
- Темно-розовый: C 30 M 79 Y 36 K 4
В примере сразу использовался режим CMYK, чтобы можно было распечатать узор без изменений.
5. Последние штрихи и узор
Шаг 1
Сгруппируйте (Control-G) все секции и шестиугольники, после того как закончите с их окраской. Копируйте (Control-C) и Вставьте (Control-V) группу из шестиугольников. Назовем оригинальную группу Hexagon A, а ее копию Hexagon B . Выровняйте группы.
Шаг 2
Примените Linear Gradient/Линейный градиент к группе Hexagon B. В палитре Gradient/Градиент укажите заливку от фиолетового (C60 M86 Y45 K42 ) к кремовому цвету (C0 M13 Y57 K0 ).
python — Рисование пятиугольника, шестиугольника в пигаме
Я пытаюсь создать функции, которые могут рисовать шестиугольник пятиугольника и т. Д. Обеспокоены алгоритмом, мне сравнить строки с pygame.draw.line? Похоже, слишком много работы по определению координат линий. Есть ли простой способ их нарисовать? Также я не знаю другой библиотеки, которая может рисовать эти вещи. Я знаю только Pygame, есть еще один?
3
GLHF 15 Мар 2015 в 21:05
2 ответа
Лучший ответ
Вы можете нарисовать его, используя lines. Вам нужно только создать список вершин с простой тригонометрией.
Примерно так (если я не ошибся):
def draw_ngon(Surface, color, n, radius, position):
pi2 = 2 * 3.14
for i in range(0, n):
pygame.draw.line(Surface, color, position, (cos(i / n * pi2) * radius + position[0], sin(i / n * pi2) * radius + position[1]))
return pygame.draw.lines(Surface,
color,
True,
[(cos(i / n * pi2) * radius + position[0], sin(i / n * pi2) * radius + position[1]) for i in range(0, n)])
5
mloskot 28 Янв 2019 в 01:51
Вы можете использовать pygame.draw.polygon(surface, color, point_list), чтобы нарисовать многоугольник. В этом случае вы можете использовать тригонометрию для генерации списка вершин и передачи его в качестве параметра point_list. Вот функция, которая рисует любой правильный многоугольник, имеющий vertex_count вершины:
def draw_regular_polygon(surface, color, vertex_count, radius, position):
n, r = vertex_count, radius
x, y = position
pygame.draw.polygon(surface, color, [
(x + r * cos(2 * pi * i / n), y + r * sin(2 * pi * i / n))
for i in range(n)
])
Вы можете запустить эту демонстрацию и увидеть эту функцию в действии, изменяя количество вершин с помощью кнопок UP / DOWN. клавиши со стрелками.
0
Arthur Khazbs 24 Авг 2019 в 14:47
Как сделать шестигранник в компасе — MOREREMONTA
Для построения правильных многоугольников служит команда «Многоугольник».
Для вызова команды, нажимаем кнопку «Многоугольник» в компактной панели
Или в верхнем меню последовательно нажимаем команды «Инструменты» — «Геометрия» — «Многоугольник».
Мы можем производить построения, как по описанной окружности, так и по вписанной, для указания способа построения служат два переключателя на панели свойств. По умолчанию активен переключатель «По вписанной окружности».
Первое, что мы должны сделать — это ввести на панели свойств число вершин многоугольника, допустим восемь, затем указываем центр многоугольника, укажем координаты «0;0». Само собой центр можно указывать в любом месте чертежа при помощи курсора и мышки.
Теперь осталось указать координаты второй точки, для построений по описанной окружности — это будет одна из вершин, для построений по вписанной окружности — это будет середина одной из сторон. Многоугольник построен.
Также можно построить многоугольник введением на панели свойств значений радиуса или диаметра (на панели имеются соответствующие переключатели, по умолчанию активен диаметр).
Кроме того, можно задавать угол наклона многоугольника, если он известен, введем для примера угол 35°.
Углом наклона будет считаться угол между осью абсцисс и радиус-вектором, проведенным из центра многоугольника к его вершине (при построении по описанной окружности) или к середине стороны (при построении по вписанной окружности). Для многоугольника с четным количеством углов доступна автоматическая отрисовка осевых линий, соответствующий переключатель находится на панели свойств.
Это все что хотелось сказать про построение многоугольников, на следующем уроке приступим к изучению лекальных кривых.
Урок №19. Построение многоугольников в Компас 3D.
Для построения правильных многоугольников служит команда «Многоугольник».
Для вызова команды, нажимаем кнопку «Многоугольник» в компактной панели
Или в верхнем меню последовательно нажимаем команды «Инструменты» — «Геометрия» — «Многоугольник».
Мы можем производить построения, как по описанной окружности, так и по вписанной, для указания способа построения служат два переключателя на панели свойств. По умолчанию активен переключатель «По вписанной окружности».
Первое, что мы должны сделать — это ввести на панели свойств число вершин многоугольника, допустим восемь, затем указываем центр многоугольника, укажем координаты «0;0». Само собой центр можно указывать в любом месте чертежа при помощи курсора и мышки.
Теперь осталось указать координаты второй точки, для построений по описанной окружности — это будет одна из вершин, для построений по вписанной окружности — это будет середина одной из сторон. Многоугольник построен.
Также можно построить многоугольник введением на панели свойств значений радиуса или диаметра (на панели имеются соответствующие переключатели, по умолчанию активен диаметр).
Кроме того, можно задавать угол наклона многоугольника, если он известен, введем для примера угол 35°.
Углом наклона будет считаться угол между осью абсцисс и радиус-вектором, проведенным из центра многоугольника к его вершине (при построении по описанной окружности) или к середине стороны (при построении по вписанной окружности). Для многоугольника с четным количеством углов доступна автоматическая отрисовка осевых линий, соответствующий переключатель находится на панели свойств.
Это все что хотелось сказать про построение многоугольников, на следующем уроке приступим к изучению лекальных кривых.
Если у Вас есть вопросы можно задать их ЗДЕСЬ.
Список последних уроков по программе Компас-3D
Автор: Саляхутдинов Роман
«БОСК 8.0»
Познай Все Cекреты КОМПАС-3D
- Более 100 наглядных видеоуроков;
- Возможность быстрее стать опытным специалистом КОМПАС-3D;
- Умение проектировать 3D изделия (деталей и сборок) любой степени сложности;
- Гарантии доставки и возврата.
>> Читать Полное Описание
Автор: Саляхутдинов Роман
«БОСК 5.0»
Новый Видеокурс. «Твердотельное и Поверхностное Моделирование в КОМПАС-3D»
- Большая свобода в обращении с поверхностями;
- Возможность формирования таких форм, которые при твердотельном моделировании представить невозможно;
- Новый уровень моделирования;
- Гарантии доставки и возврата.
>> Читать Полное Описание
Автор: Саляхутдинов Роман
«Эффективная работа в SolidWorks»
Видеокурс. «Эффективная работа в SolidWorks» поможет Вам:
- Многократно сократить временя на освоение программы;
- Научит проектировать 3D изделия (деталей и сборок) любой степени сложности; создавать конструкторскую документацию; проводить инженерный анализ.
- Поможет быстрее стать грамотным специалистом;
- Гарантии доставки и возврата.
>> Читать Полное Описание
Автор: Дмитрий Родин
«AutoCAD ЭКСПЕРТ»
Видео самоучитель По AutoCAD
- 60 наглядных видеоуроков;
- Более 15 часов только AutoCAD;
- Создание проектов с нуля прямо у Вас на глазах;
- 365-дневная гарантия
Рассмотрим, как можно создать в шестигранник в Компас 3D. Шестигранник — под ключ. Файл прилагается. В качестве примера, смоделировал переходник. Шестигранник делается параметризованный. Изменяя параметр размера под ключ и ширину, можно получать разные шестигранники.
Шестигранник в Компас 3D
Скачать
Аббревиатура «2Ф2КО» означает 2 фаски и два контровочных отверстия.
Шестигранник в Компас 3D: Описание
Включите вкладку «Переменные» в панели управления (то место, где дерево сборки или детали). Для включения этой вкладки, надо выбрать в главном меню команду: Настройка — Панели — Переменные. Сделайте активной эту вкладку. На рисунке ниже показан вид дерева.
Вкладка Переменные включена. Для редактирования выбрана переменная с комментарием «Под ключ».
Размер под ключ задается в переменной v28. Ширина шестигранной части задается в переменной v21. В верхней части панели «Переменные» если строка поиска нужной переменной.
Пример применения
Шестигранник и резьбовые части штуцеров добавлены как локальные детали (деталь-заготовка). Резьбы пришлось перестроить, иначе они не отображались на чертеже.
Локальные детали перемещены в деталь и объединены булевыми операциями. При таком раскладе, упрощенная резьба у меня потерялась и я создал резьбы снова.
Следует отметить, что Компас работал неустойчиво при редактировании эскизов в локальных деталях.
Добавить комментарий
Отменить ответЭтот сайт использует Akismet для борьбы со спамом. Узнайте как обрабатываются ваши данные комментариев.
-> Компас 3D
Автор: Александр Соловьев (все работы автора)
Если мы не успеваем посмотреть интересное кино по телевидению, то на помощь нам приходят DVD диски. В магазине klivlend.com.ua каждый может найти интересный фильм и купить сериал. Продажа DVD осуществляется в России и в Украине..
Для изучения уроков компас 3d, в первую очередь необходимо скачать Компас 3d бесплатно на официальном сайте Аскон. Так же для понимания, что означают сокращения в моём тексте, прошу перейти по ссылке и ознакомиться с вводным уроком, благодарю за понимание.
Шестиугольник — многоугольник с шестью углами. Также шестиугольником называют всякий предмет такой формы. В машиностроении примером классического шестиугольника являются головки болтов.
Как начертить шестиугольник в трехмерной проекции. Мы несколько усложним задачу, я составлю шестиугольник и треугольников, это будет сделано для понимания на простом примере некоторых моментов сборки узла их деталей. Для начала создадим деталь, для сборки правильного шестиугольника нам потребуется шесть равносторонних треугольника, так как радиус описанной окружности равняется стороне шестиугольника.
увеличить
Начнем работать в документе Деталь. Для того, чтобы начать чертить, нам необходимо выбрать плоскость. В данном случае нам не принципиально, после чего начинаем чертить необходимую деталь в формате 2d. Для того, чтобы построить равносторонний треугольник, откладываем основание необходимой нам длины, и от середины чертим перпендикуляр. От любого конца основания откладываем отрезок, под углом 60 градусов к нему и получаем точку пересечения с перпендикуляром. Соединяем оставшиеся две точки. Производим операцию выдавливания, и получаем 3d модель нашего треугольника. Сохраняем эту деталь и переходим на документ Сборка чтобы начертить шестиугольник.
Как вы помните, нам необходимо 6 треугольников для сборки. Но это не значит что придется копировать файл, программа позволяет вставить одну и ту же деталь сколько угодно раз, но не забывайте! При изменении файла в исходнике, изменятся все детали на сборке. Для соединения всех деталей в одно целое нам понадобятся два инструмента – Совпадение объектов и На расстоянии. С помощью этих двух элементов, легко и просто мы получим шестиугольник из треугольников.
увеличить
Для того чтобы перенести нашу 3d деталь или узел на лист, создадим чертеж и воспользуемся кнопкой Стандартные виды, откроется диалоговое окно, выбираем нужный файл, и определяем виды, которые хотим спроектировать. Часто бывают моменты, когда простую деталь проще начертить в 3-d, а потом перенести на лист, чем сидеть и представлять, как она будет выглядеть, в данном случае мы начертили шестиугольник.
Еще полезно почитать по теме Компас 3D следующее:
| Требуемые действия и комментарии | Иллюстрации |
| Создать трехмерную модель детали Плита нижняя | |
| Выберите из меню кнопки Создать пункт Деталь | |
| В окне Дерева моделивыберите ПлоскостьZХ | |
| Нажмите кнопку Эскиз на Панели текущего состояния | |
| В рабочей области выполните построение эскиза как показано на образце. На панели Геометрия нажмите кнопку Прямоугольник по центру и вершине, введите в поля значение высоты 90 мм и ширины – 90 мм. На панели Геометрия нажмите кнопку Окружностьивыполните построения крепежного отверстия D=20 мм. Для простановки линейных размеров нажмите кнопку Линейный размерна панели Размеры. Установите в соответствии с образцом нужные размеры высоты, ширины и межцентровых расстояний. Снимите фаски с длинами катетов 5 мм. | |
| Для завершения построения эскиза наПанели Текущее состояние нажмите кнопку Эскиз. Пиктограмма эскиза с порядковым номером отобразится в Дереве модели | |
| На панели Редактирование детали нажмите кнопку Операция выдавливания для создания детали в виде элемента выдавливания | |
| На вкладке Параметры на Панели свойств из списка Направлениевыберите опцию Прямое направление. В поле Расстояние 1установитезначение 10,остальные параметры примите по умолчанию. Примечание. Значение параметров модели (диаметра отверстия, расстояния, на которое выдавливается модель) устанавливаются в соответствии с индивидуальным вариантом задания | |
| Нажмите кнопку Создать объектдля построения элемента. Система построит модель детали | |
| Для изменения свойств детали в щелкните правой кнопкой мыши Дереве модели на имени Деталь и выберите из контекстного меню команду Свойства модели. На Панели свойств в соответствующие поля введите наименование детали – Плита нижняя, обозначение чертежа, измените цвет детали в соответствии с выбранным материалом. Для подтверждения выполненных действий нажмите кнопку Создать объект | |
| В Дереве модели отобразится наименование и обозначение детали Плита нижняя, а цвет модели будет соответствовать выбранному цвету | |
| Данные свойств модели будут передаваться в спецификацию сборки, связанную с моделью. Для этого выполните команду меню Сервис/Добавить объект. В окне диалога выберите пункт Деталь. Введите в строку спецификации обозначение детали и ее наименование, нажмите кнопку ОК. Сохраните файл в папке под именем Плита нижняя | |
| Для создания второй детали отредактируйте толщину детали, например, введите значение толщины детали – 20 мм. Измените свойства детали: введите наименование детали Плита верхняя, обозначение – КИГ 003.0ХХ.002, измените цвет детали в соответствии с выбранным материалом. Создайте объект спецификации. Для сохранения детали Плита верхняявыполните команду Сохранить как…для файла Плита нижняя. В окне диалога в поле Имя файла ведите имя Плита верхняя, нажмите кнопку Сохранить. | |
| Для создания сборки в меню кнопки Создать выберите пункт Сборка | |
| На панели Редактирование сборки выберите команду Добавить из файла. В окне диалога выберите файл Плита нижняя и зафиксируйте щелчком мышью положение детали в Начале координат. | |
| В Дереве модели в списке Компоненты отобразится первая деталь сборочной единицы | |
| Для вставки второй детали на панели Редактирование сборки выберите команду Добавить из файла. В окне диалога выберите файл Плита верхняя и зафиксируйте щелчком мышью в любом месте окна модели | |
| На панели Сопряжения выберите сопряжение Совпадение объектов, укажите совпадаемые поверхности, после чего выполните сопряжение Соосность. Для выполнения сопряжения выберите крепежное отверстие | |
| Для вставки болтового соединения выполните команду Библиотеки/Стандартные изделия/Вставить элемент. В окне диалога последовательно раскройте разделы Крепежные изделия/Болты/Болты с шестигранной головкой/Болт ГОСТ 7798-70 (исп.1). Установите параметры болта: диаметр резьбы, длину стержня болта, остальные параметры болта примите по умолчанию. Подтвердите выполненные действия. | |
| В окне модели укажите последовательно поверхности для вставки болтового соединения: Плита верхняя, затем Плита верхняя. После вставки болта в отверстие автоматически создается объект спецификации. Нажмите кнопку Создать объект | |
| Для выбора шайбы выполните команду Шайбы/Шайба класса А ГОСТ 11371-78 (исп.1). В окне диалога выберите шайбу, установите диаметр крепежной детали 20 мм. В окне диалога модели выберите последовательно поверхности для выполнения сопряжений. Система выполнит вставку элемента –шайба | |
| Аналогичным образом выполните вставку гайки шестигранной по ГОСТ 5915 (исп. 1). После выбора в библиотеке гайки, задайте ее параметры и установите гайку по месту крепления | |
| В Дереве модели присвойте имя сборке – Опора, обозначение – КИГ –3.0ХХ. Сохраните файл сборки под именем Опора. Указанные данные будут передаваться в спецификацию, связанную со сборочной единицей | |
| Для создания бланка спецификации выполните команду из меню кнопки Создать Для подключения спецификации к модели сборки выполните команду Сервис/Управление сборкой…. В окне диалога выберите файл модели сборки Опора,в окне диалога нажмите кнопку Подключить документ и кнопку Выход. Данные объектов спецификации будут переданы в файл спецификации. Для заполнения основной надписи спецификации перейдите в режим разметки страницы. |
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Увлечёшься девушкой-вырастут хвосты, займёшься учебой-вырастут рога 9837 — | 7697 — или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Решение задач по теме «Правильный многоугольник»
1. Решение задач по теме «ПРАВИЛЬНЫЙ МНОГОУГОЛЬНИК».
МОУ СОШ № 8 г. Аткарск9 класс.
2. Контроль знаний.
п3
4
6
1800
1800
ап 2 R sin
r R cos
n
n
R 3
R 2
R
1
R
2
2
R
2
3
R
2
1
S Pr
2
3 3 2
R
4
2R
2
3 3 2
R
2
3. Построение правильного шестиугольника, сторона которого равна данному отрезку.
Какая зависимость существует междустороной правильного шестиугольника и
радиусом описанной около него окружности?
Ответ: a6 = R
Пусть РQ – заданный отрезок, равный
стороне правильного шестиугольника,
который нам необходимо построить. Чему
равен радиус описанной около этого
шестиугольника окружности?
Ответ: PQ.
Составьте план построения правильного
шестиугольника со стороной РQ.
4. Построение правильного шестиугольника, сторона которого равна данному отрезку.
1.2.
3.
4.
Построить окружность с
радиусом, равным PQ.
Отметить на окружности
произвольную точку А1.
P
А5
Т.к. R = PQ, а6 = R, то
отметим на окружности
точки А1, А2, А3, А4, А5, А6 так,
А6
чтобы А1А2 = А2А3 = А3А4 =
= А4А5 = А5А6.
Последовательно соединить
А1
отрезками полученные точки.
Q
А4
А3
А2
А1А2А3А4А5А6 – искомый шестиугольник.
5. Задача. Как, используя правильный шестиугольник построить правильный треугольник?
1) Построим правильныйшестиугольник.
2) Соединим точки через
одну: А1, А3, А5.
3) А1А3А5 – искомый
А6
правильный
треугольник.
А5
А4
А3
А1
А2
6. Задача. Как, используя правильный шестиугольник построить правильный двенадцатиугольник?
Провести высотытреугольников до пересечения
с окружностью.
Разделить дуги пополам
А5
точками В1, В2, В3, В4, В5, В6.
В4
А4
В5
А1В1А2В2А3В3А4В4А5В5А6В6 –
искомый
двенадцатиугольник.
В3
А6
А3
В6
А1
В1
А2
В2
План построения правильного
2п-угольника из имеющегося п-угольника.
1. Провести биссектрисы
углов правильного п-угольника.
Точка пересечения биссектрис О
будет являться центром
А2
описанной окружности.
Построить эту окружность.
Н2
2. Из точки О провести
О
перпендикуляры к сторонам
Ап
А1
Н
1
правильного п-угольника до
пересечения с окружностью.
3. Соединить последовательно вершины правильного
п-угольника с полученными точками пересечения.
Полученный многоугольник – искомый правильный
2п-угольник.
8. Домашнее задание:
П.109, №№ 1094;1100 ( в, г )
Линейно-конструктивный рисунок шестигранной призмы | СПЛАЙН
ЦЕЛЬ ЗАДАНИЯ. Научиться изображать шестигранную призму в различных положениях.
ПОСТАНОВКА ЗАДАНИЯ. Изучите различные способы построения правильного шестиугольника, сделайте рисунки шестиугольников, проверьте правильность их построения. На основе шестиугольников постройте шестигранные призмы.
РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ.
Рассмотрите шестигранную призму на рис. 3.52 и ее ортогональные проекции на рис. 3.53. В основании шестигранной призмы (шестигранника) лежат правильные шестиугольники, боковые грани — одинаковые прямоугольники. Для того, чтобы правильно изобразить шестигранник в перспективе, необходимо сначала научиться грамотно изображать в перспективе его основание (рис. 3.54). В шестиугольнике на рис. 3.55 вершины обозначены цифрами от одного до шести.
Если соединить точки 1 и 3, 4 и 6 вертикальными прямыми, можно заметить, что эти прямые вместе с точкой центра окружности делят диаметр 5— 2 на четыре равных отрезка (эти отрезки обозначены дугами). Противоположные стороны шестиугольника параллельны друг другу и прямой, проходящей через его центр и соединяющей две вершины (например, стороны 6— 1 и 4— 3 параллельны прямой 5— 2). Эти наблюдения помогут вам построить шестиугольник в перспективе, а также проверить правильность этого построения.
Построить правильный шестиугольник по представлению можно двумя способами: на основе описанной окружности и на основе квадрата.
На основе описанной окружности. Рассмотрите рис. 3.56. Все вершины правильного шестиугольника принадлежат описанной окружности, радиус которой равен стороне шестиугольника.
Горизонтальный шестиугольник
Изобразите горизонтальный эллипс произвольного раскрытия, т.е. описанную окружность в перспективе. Теперь необходимо найти на ней шесть точек, являющихся вершинами шестиугольника. Проведите любой диаметр данной окружности через ее центр (рис. 3.57).
Крайние точки диаметра — 5 и 2, лежащие на эллипсе, являются вершинами шестиугольника. Для нахождения остальных вершин необходимо разделить этот диаметр на четыре одинаковых отрезка. Диаметр уже разделен точкой центра окружности на два радиуса, остается разделить каждый радиус пополам. На перспективном рисунке все четыре отрезка равномерно сокращаются при удалении от зрителя (рис. 3.58). Теперь проведите через середины радиусов — точки А и В — прямые, перпендикулярные прямой 5— 2. Найти их направление можно при помощи касательных к эллипсу в точках 5 и 2 (рис. 3.59). Эти касательные будут перпендикулярны диаметру 5— 2, а прямые, проведенные через точки А и В параллельно этим касательным, будут также перпендикулярны прямой 5— 2. Обозначьте точки, полученные на пересечении этих прямых с эллипсом, как 1, 3, 4, 6 (рис. 3.60). Соедините все шесть вершин прямыми линиями (рис. 3.61).
Проверьте правильность вашего построения разными способами. Если построение верно, то линии, соединяющие противоположные вершины шестиугольника, пересекаются в центре окружности (рис. 3.62), а противоположные стороны шестиугольника параллельны соответствующим диаметрам (рис. 3.63). Еще один способ проверки показан на рис. 3.64.
Вертикальный шестиугольник
В таком шестиугольнике прямые, соединяющие точки 1 и 3, 6 и 4, а также касательные к описанной окружности в точках 5 и 2, имеют вертикальное направление и сохраняют его на перспективном рисунке. Таким образом, проведя две вертикальные касательные к эллипсу, найдем точки 5 и 2 (точки касания). Соедините их прямой линией, а затем разделите полученный диаметр 5— 2 на 4 равных отрезка, учитывая их перспективные сокращения (рис. 3.65). Проведите вертикальные прямые через точки А и В, а на их пересечении с эллипсом найдите точки 7, 3, 6 и 4. Затем последовательно соедините точки 1— 6 прямыми (рис. 3.66). Правильность построения шестиугольника проверьте аналогично предыдущему примеру.
Описанный способ построения шестиугольника позволяет получить эту фигуру на основе окружности, изобразить которую в перспективе проще, чем
квадрат заданных пропорций. Поэтому данный способ построения шестиугольника представляется наиболее точным и универсальным. Способ постро
ения на основе квадрата позволяет легко изобразить шестигранник в том случае, когда на рисунке уже есть куб, иными словами, когда пропорции квадрата и направление его сторон определены.
На основе квадрата. Рассмотрите рис. 3.67. Вписанный в квадрат шестиугольник по горизонтальному направлению 5— 2 равен стороне квадрата, а по вертикали — меньше ее длины.
Вертикальный шестиугольник
Нарисуйте вертикальный квадрат в перспективе. Проведите через пересечение диагоналей прямую, параллельную его горизонтальным сторонам. Разделите полученный отрезок 5— 2 на четыре равные части и проведите через точки А и В вертикальные прямые (рис. 3.68).
Линии, ограничивающие шестиугольник сверху и снизу, не совпадают со сторонами квадрата. Изобразите их на некотором расстоянии (1/14 а) от горизонтальных сторон квадрата и параллельно им. Соединив найденные таким образом точки 1 и 3 с точкой 2, а точки 6 и 4 — с точкой 5, получим шестиугольник (рис. 3.69).
Гэризонтальный шестиугольник строится в той же последовательности (рис. 3.70 и 3.71).
Этот способ построения уместен только для шестиугольников с достаточным раскрытием. В случае, если раскрытие шестиугольника незначительно, лучше воспользоваться способом на основе описанной окружности. Для проверки шестиугольника, построенного через квадрат, можно использовать уже известные вам методы.
Кроме того существует еще один — описать вокруг полученного шестиугольника окружность (на вашем рисунке — эллипс). Все вершины шестиугольника должны принадлежать этому эллипсу.
Овладев навыками изображения шестиугольника, вы свободно перейдете к изображению шестигранной призмы. Внимательно рассмотрите схему
на рис. 3.72, а также схемы построения шестигранных призм на основе описанной окружности (рис. 3.73; 3.74 и 3.75) и на основе квадрата (рис. 3.76; 3.77 и 3.78).
Изобразите вертикальные и горизонтальные шестигранники различными способами. На рисунке вертикального шестигранника длинные стороны боковых граней будут параллельными друг другу вертикальными прямыми, а шестиугольник
основания будет тем больше раскрыт, чем дальше он находится от линии горизонта. На рисунке горизонтального шестигранника длинные стороны боковых граней будут сходиться в точке схода на горизонте, а раскрытие шестиугольника основания будет тем больше, чем дальше от зрителя он находится. Изображая шестигранник, следите также за тем, чтобы параллельные грани обоих оснований сходились в перспективе (рис. 3.79; 3.80).
% PDF-1.5 % 43 0 obj> эндобдж xref 43 212 0000000016 00000 н. 0000004974 00000 н. 0000004536 00000 н. 0000005036 00000 н. 0000005215 00000 н. 0000005569 00000 н. 0000005743 00000 н. 0000005912 00000 н. 0000005946 00000 н. 0000006164 00000 н. 0000006545 00000 н. 0000006758 00000 н. 0000007655 00000 н. 0000008757 00000 н. 0000009813 00000 п. 0000010839 00000 п. 0000011978 00000 п. 0000013099 00000 н. 0000014162 00000 п. 0000015281 00000 п. 0000016343 00000 п. 0000017141 00000 п. 0000054032 00000 п. 0000078448 00000 п. 0000078607 00000 п. 0000078916 00000 п. 0000085105 00000 п. 0000085317 00000 п. 0000085346 00000 п. 00000
00000 п. 00000
Расчет углов и длин сторон многоугольника
Многоугольник — это любая фигура на замкнутой плоскости. Оно происходит от латинского poly , что означает «много», и gōnia, , что означает «угол». «Замкнутый» в этом контексте означает, что стороны образуют замкнутый контур. Это определение не исключает такие формы, как песочные часы или звезда, стороны которых пересекаются друг с другом. Когда стороны не пересекаются, мы называем их «простыми многоугольниками». В этой статье мы будем использовать только простые многоугольники.
Многоугольники должны иметь как минимум три стороны, так как двусторонняя фигура не может быть закрыта. Точка, где встречаются две стороны, называется «вершиной» (множественное число: «вершины»). Когда вы рисуете отрезок линии, соединяющий одну вершину с другой, это называется «диагональю».
Многоугольник является «выпуклым», если любая диагональ проведена снаружи многоугольника. Логотип Красного Креста выпуклый, потому что диагональ от одного угла до другого находится снаружи. «Углы» многоугольника — это все внутренние углы.Таким образом, четыре угла стыка поперечин составляют 270 °, а не 90 °.
Именование полигонов
Именование многоугольников обычно основано на количестве сторон или углов. Например, «равносторонний» треугольник имеет три равные стороны, а «равносторонний» треугольник — три равных угла. (Конечно, они такие же.) Однако обычно имена относятся к количеству сторон многоугольника. Шестиугольник имеет шесть сторон, восьмиугольник — восемь и т. Д. Общее название « n -угольник» — это многоугольник с n сторонами.Итак, шестиугольник — это 6-угольник.
Когда стороны многоугольника имеют одинаковую длину и углы равны одинаковому градусу, мы называем его «правильным» многоугольником. Квадрат правильный. Все стороны и все углы равны. Пентагон в Вашингтоне, округ Колумбия, представляет собой обычный 5-угольник. Вырез большинства карандашей представляет собой правильный шестиугольник, а знаки остановки обычно представляют собой правильные восьмиугольники. Прямоугольник имеет четыре равных угла (90 °), а ромб — четыре равные стороны, но они не являются «правильными».
Угловые измерения
Сумма всех углов
Сумма углов любого треугольника всегда будет равна 180 °, независимо от его размера.
Вы можете разделить большие многоугольники на треугольники, нарисовав диагонали между вершинами, четырехугольники (4-сторонние многоугольники) на два треугольника, пятиугольники (5-сторонние многоугольники) на три треугольника и т. Д. Вы можете разделить любой n -угольник на n -2 треугольника. Сумма каждого треугольника равна 180 °.
Таким образом, сумма углов любого многоугольника равна:
S = ( n — 2) * 180
Например, сумма всех восьми углов восьмиугольника равна: S = (8-2) * 180 = 1080 °.
Эта формула работает независимо от того, является ли многоугольник правильным, и даже работает, если многоугольник выпуклый. Символ Красного Креста — выпуклый 12-угольник. Он имеет четыре угла 270 ° в месте пересечения поперечин и восемь углов 90 ° на внешних углах.
4 (270) + 8 (90) = 1800 °.
Используя нашу формулу многоугольника, (12-2) * 180 = 1800 °. Разве это не потрясающе?
Индивидуальные уголки
Эту формулу можно использовать для нахождения отдельных углов, если многоугольник правильный. Для правильного восьмиугольника, такого как знак остановки, сумма всех восьми углов составляет 1080 °, поэтому каждый угол должен быть 1080/8 = 135 °.Каждый угол в правильном шестиугольнике равен (6-2) * 180/6 = 120 °.
Для неправильных многоугольников, если вы знаете все углы, кроме одного, вы можете найти недостающий угол.
У садовника есть проходы, которые образуют почти пятиугольник — почти потому, что один из углов покрыт прудом. Форма имеет два прямых угла, а два других он измеряет на 65 ° и 58 °. Сумма известных углов составляет 303 °. Сумма всех углов пятиугольника составляет 540 °, поэтому угол под прудом составляет 540 — 303 = 237 °.Этот внутренний угол больше 180 °. Скорее всего, садовнику нужен внешний угол, который составляет 237 — 180 = 57 °.
Длина стороны
Правил для определения длин сторон многоугольника не так уж и много, но обычно это не проблема. Длину сторон намного легче измерить, чем углы, особенно если вы работаете с правильным многоугольником. На правильных многоугольниках все стороны равны. Если вы измеряете одну сторону, вы узнаете длину остальных. У прямоугольников противоположные стороны равны.
Теорема ПифагораОдин из способов вычислить стороны прямоугольного треугольника — использовать теорему Пифагора. Прямоугольный треугольник — это треугольник с прямым углом (90 °), образованным двумя ножками. «Гипотенуза» — это сторона, лежащая напротив прямого угла. Если возвести в квадрат (умножить число на себя) длину двух катетов, а затем сложить суммы вместе, вы получите результат возведения в квадрат гипотенузы. Если длины участков представлены как a и b, , а длина гипотенузы равна c , то уравнение имеет вид a2 + b2 = c2
.Вот простой пример.Обычный лист фанеры имеет ширину 4 фута и длину 8 футов. Какова длина диагонали от одного угла до противоположного?
42 + 82 = c2
16 + 64 = с2
80 = c2
√ (80) = c ≈ 8,94
Вы могли бы выразить это в математике плотника как: 0,94 фута = 0,94 x 12 дюймов / фут = 11,28 дюйма. Длина диагонали составляет примерно 8 футов 11 дюймов.
Тригонометрические отношенияТригонометрические соотношения полезны для соотношений прямоугольного треугольника.Они основаны на наблюдении схожих треугольников (одинаковой формы, но не одинакового размера). Если два треугольника имеют одинаковые три угла, то отношение двух сторон первого треугольника будет равно отношению соответствующих сторон второго треугольника.
Вот как работают триггерные функции. Рассмотрим треугольник с прямым углом в одном углу и углом 31 ° в другом углу. Третий угол должен быть 180 — 90 — 31 = 59 °. Все треугольники 31-59-90 подобны, и отношение двух сторон одного будет равно отношению соответствующих сторон всех остальных.
Помните, стороны, образующие прямой угол, называются «ножками» (обычно обозначаются a и b ), а сторона, противоположная прямому углу, называется «гипотенузой» (обычно обозначается c ). Более конкретно, сторона, противоположная обозначенному углу (в данном случае 31 °), равна a, , а сторона, прилегающая к нему, равна b , а размеры угла равны α и β соответственно.
Отношение a / b или противоположное / смежное называется «касательной».«Вы можете определить значение тангенса, измерив a и b , а затем разделив его. Но поскольку оно будет одинаковым для каждого треугольника 31-59-90, вы можете найти значение, используя триггерные таблицы или научные или калькуляторы онлайн.
Теорема Пифагора и триггерные функции применимы только к прямоугольным треугольникам, но очень часто вы можете разбить более сложные многоугольники на несколько прямоугольных треугольников. Затем вы можете использовать известные значения для вычисления неизвестных.
Оставьте первый комментарий ниже.
Полигоны
Многоугольник — это замкнутая плоская фигура, образованная соединением трех или более прямые линии. Правильный многоугольник — это многоугольник с равными сторонами и равными внутренние углы.
Правильные многоугольники | |||
Стороны | Имя | Интерьер Уголки | Внешний Уголки |
|---|---|---|---|
3 | Треугольник | 60.00 ° | 120,00 ° |
4 | Четырехугольник | 90,00 ° | 90,00 ° |
5 | Пентагон | 108,00 ° | 72,00 ° |
6 | Шестигранник | 120.00 ° | 60,00 ° |
7 | Гептагон | 128,57 ° | 51,43 ° |
8 | восьмиугольник | 135,00 ° | 45,00 ° |
9 | Nonagon | 140.00 ° | 40,00 ° |
10 | Десятиугольник | 144,00 ° | 36,00 ° |
11 | Hendecagon | 147,27 ° | 32,73 ° |
12 | Додекагон | 150.00 ° | 30,00 ° |
13 | Triskaidecagon | 152,31 ° | 27,69 ° |
14 | Tetrakaidecagon | 154,29 ° | 25,71 ° |
15 | Pendecagon | 156.00 ° | 24,00 ° |
16 | Шестигранник | 157,50 ° | 22,50 ° |
17 | Heptdecagon | 158,82 ° | 21,18 ° |
18 | Восьмиугольник | 160.00 ° | 20,00 ° |
19 | Enneadecagon | 161,05 ° | 18.95 ° |
20 | Икосагон | 162,00 ° | 18.00 ° |
30 | Триаконтагон | 168.00 ° | 12,00 ° |
40 | Тетрактагон | 171,00 ° | 9,00 ° |
50 | Пентаконтагон | 172,80 ° | 7.20 ° |
60 | Шестигранник | 174.00 ° | 6,00 ° |
70 | Гептаконтагон | 174,86 ° | 5,14 ° |
80 | Octacontagon | 175,50 ° | 4,50 ° |
90 | Эннеаконтагон | 176.00 ° | 4,00 ° |
100 | Гектогон | 176,40 ° | 3,60 ° |
1,000 | Чилигон | 179,64 ° | 0,36 ° |
10 000 | Мириагон | 179.96 ° | 0,04 ° |
Примечание. После шести сторон математики обычно обращаются к
эти многоугольники как
n-угольников, поэтому 23-сторонний многоугольник будет называться 23-угольником.
Сумма углов выпуклого многоугольника со сторонами n равна ( n — 2) 180.
Углы в многоугольниках — объяснения и примеры
Многоугольник касается не только сторон.Возможны сценарии, когда у вас есть несколько фигур с одинаковым количеством сторон.
Как же тогда их различать?
УГЛОВ!
Самый простой пример — прямоугольник и параллелограмм имеют 4 стороны каждая, причем противоположные стороны параллельны и равны по длине. Разница заключается в углах: у прямоугольника со всех четырех сторон углы составляют 90 градусов, а у параллелограмма — противоположные углы равной меры.
Из этой статьи вы узнаете:
- Как найти угол многоугольника?
- Внутренние углы многоугольника.
- Внешние углы многоугольника.
- Как рассчитать размер каждого внутреннего и внешнего угла правильного многоугольника.
Как найти углы многоугольника?
Мы знаем, что многоугольник — это двухмерная многосторонняя фигура, составленная из отрезков прямой линии . Сумма углов многоугольника — это сумма всех внутренних углов многоугольника.
Так как все углы внутри многоугольников одинаковые.Таким образом, формула для определения углов правильного многоугольника имеет вид;
Сумма внутренних углов = 180 ° * (n — 2)
Где n = количество сторон многоугольника.
Примеры
треугольник имеет 3 стороны, следовательно,
n = 3
Подставьте n = 3 в формулу нахождения углов многоугольника.
Сумма внутренних углов = 180 ° * (n — 2)
= 180 ° * (3 — 2)
= 180 ° * 1
= 180 °
- Углы четырехугольника:
A четырехугольник — это четырехугольник, поэтому
n = 4.
Путем подстановки
сумма углов = 180 ° * (n — 2)
= 180 ° * (4-2)
= 180 ° * 2
= 360 °
Пятиугольник равен 5 — двусторонний многоугольник.
n = 5
Заменитель.
Сумма внутренних углов = 180 ° * (n — 2)
= 180 ° * (5-2)
= 180 ° * 3
= 540 °
Восьмиугольник — это 8-сторонний многоугольник
n = 8
При замене
Сумма внутренних углов = 180 ° * (n — 2)
= 180 ° * (8-2)
= 180 ° * 6
= 1080 °
Углы a Hectagon:
a Hectagon — это 100-сторонний многоугольник.
n = 100.
Заменитель.
Сумма внутренних углов = 180 ° * (n — 2)
= 180 ° * (100-2)
= 180 ° * 98
= 17640 °
Внутренний угол многоугольников
Внутренний угол равен угол, образованный внутри многоугольника, между двумя сторонами многоугольника.
Количество сторон в многоугольнике равно количеству углов, образованных в конкретном многоугольнике. Размер каждого внутреннего угла многоугольника определяется выражением;
Измерение каждого внутреннего угла = 180 ° * (n — 2) / n
, где n = количество сторон.
Примеры
- Размер внутреннего угла десятиугольника.
Десятиугольник — это 10-сторонний многоугольник.
n = 10
Измерение каждого внутреннего угла = 180 ° * (n — 2) / n
Замена.
= 180 ° * (10-2) / 10
= 180 ° * 8/10
= 18 ° * 8
= 144 °
- Внутренний угол шестигранника.
Шестигранник имеет 6 сторон. Следовательно, n = 6
Заменитель.
Измерение каждого внутреннего угла = 180 ° * (n — 2) / n
= 180 ° * (6-2) / 6
= 180 ° * 4/6
= 60 ° * 2
= 120 °
- Внутренний угол прямоугольника
Прямоугольник является примером четырехугольника (4 стороны)
n = 4
Измерение каждого внутреннего угла = 180 ° * (n — 2) / n
= 180 ° * (4-2) / 4
= 180 ° * 1/2
= 90 °
- Внутренний угол пятиугольника.
Пятиугольник состоит из 5 сторон.
n = 5
Размер каждого внутреннего угла = 180 ° * (5-2) / 5
= 180 ° * 3/5
= 108 °
Внешний угол многоугольников
Внешний угол равен угол, образованный вне многоугольника между одной стороной и расширенной стороной. Мера каждого внешнего угла правильного многоугольника определяется выражением;
Размер каждого внешнего угла = 360 ° / n, где n = количество сторон многоугольника.
Одним из важных свойств внешних углов правильного многоугольника является то, что сумма размеров внешних углов многоугольника всегда равна 360 °.
Примеры
- Внешний угол треугольника:
Для треугольника n = 3
Заменить.
Измерение каждого внешнего угла = 360 ° / n
= 360 ° / 3
= 120 °
- Внешний угол пятиугольника:
n = 5
Измерение каждого внешнего угла = 360 ° / n
= 360 ° / 5
= 72 °
ПРИМЕЧАНИЕ: Формулы внутреннего и внешнего углов работают только для правильных многоугольников.Неправильные многоугольники имеют разные внутренние и внешние размеры углов.
Давайте рассмотрим другие примеры задач о внутренних и внешних углах многоугольников.
Пример 1
Внутренние углы неправильного 6-стороннего многоугольника равны; 80 °, 130 °, 102 °, 36 °, x ° и 146 °.
Вычислить размер угла x в многоугольнике.
Решение
Для многоугольника с 6 сторонами n = 6
сумма внутренних углов = 180 ° * (n — 2)
= 180 ° * (6-2)
= 180 ° * 4
= 720 °
Следовательно, 80 ° + 130 ° + 102 ° + 36 ° + x ° + 146 ° = 720 °
Упростить.
494 ° + x = 720 °
Вычтем 494 ° с обеих сторон.
494 ° — 494 ° + x = 720 ° — 494 °
x = 226 °
Пример 2
Найдите внешний угол правильного многоугольника с 11 сторонами.
Решение
n = 11
Измерение каждого внешнего угла = 360 ° / n
= 360 ° / 11
≈ 32,73 °
Пример 3:
Внешние углы многоугольник; 7x °, 5x °, x °, 4x ° и x °.Определите значение x.
Решение
Сумма экстерьера = 360 °
7x ° + 5x ° + x ° + 4x ° + x ° = 360 °
Упростите.
18x = 360 °
Разделите обе стороны на 18.
x = 360 ° / 18
x = 20 °
Следовательно, значение x равно 20 °.
Пример 4
Как называется многоугольник, каждый внутренний угол которого равен 140 °?
Решение
Размер каждого внутреннего угла = 180 ° * (n — 2) / n
Следовательно, 140 ° = 180 ° * (n — 2) / n
Умножьте обе стороны на n
140 ° n = 180 ° (n — 2)
140 ° n = 180 ° n — 360 °
Вычтем обе стороны на 180 ° n.
140 ° n — 180 ° n = 180 ° n — 180 ° n — 360 °
-40 ° n = -360 °
Разделите обе стороны на -40 °
n = -360 ° / -40 °
= 9.
Следовательно, количество сторон равно 9 (неугольник).
Практические вопросы- Первые четыре внутренних угла пятиугольника — это все, а пятый угол равен 140 °. Найдите размер четырех углов.
- Найдите размер восьми углов многоугольника, если первые семь углов равны 132 ° каждый.
- Вычислите углы многоугольника, которые задаются как; (x — 70) °, x °, (x — 5) °, (3x — 44) ° и (x + 15) °.
- Отношение углов шестиугольника равно; 1: 2: 3: 4: 6: 8. Вычислите величину углов.
- Как называется многоугольник, каждый внутренний угол которого равен 135 °?
Диагонали многоугольника: многоугольники
Диагональ — это отрезок прямой, соединяющий две несмежные вершины многоугольника.
Почему мы указываем несмежные? Потому что, если вы соедините две соседние вершины, это будет просто сторона многоугольника, а не диагональ!
Можем ли мы вычислить, сколько диагоналей имеет многоугольник? Конечно можем. Давайте начнем с конкретного примера, а затем воспользуемся им, чтобы разработать формулу.
Давайте возьмем шестигранник ниже. Сколько у него диагоналей?
Чтобы начать разбираться, давайте выберем вершину и проведем все диагонали от этой вершины ко всем остальным вершинам.Сколько их там? Ну, мы не можем провести диагональ от вершины к самой себе, и мы не можем провести диагональ ни к одной из двух соседних вершин, так что это три вершины, к которым мы не можем провести диагонали. Так как всего 9 вершин, получается 9 — 3 = 6 диагоналей, которые мы можем нарисовать:
Поскольку у нас девять вершин, мы сможем сделать это девять раз, верно? Здесь зеленые линии представляют диагонали, проведенные из другой вершины.
Но подождите минутку! Вы заметили, что мы нарисовали диагональ дважды ? Есть одна диагональ, которая нарисована как красным , так и зеленым (на картинке она выглядит сероватой)!
Получается, что если мы проведем диагонали из каждой вершины, мы посчитаем каждую диагональ дважды .Но это не проблема — мы можем взять нашу сумму и разделить ее на два, чтобы получить результат.
Итак, из каждой вершины мы можем нарисовать 6 диагоналей, и мы можем сделать это из всех 9 вершин, всего 54 диагонали. Но поскольку мы посчитали каждую по два раза, на самом деле получается 54, разделенные на 2, или 27 .
Обобщение для n-угольника
Если вы посмотрите на наш пример для 9-сторонней фигуры, вы увидите, как мы использовали число 9 в нашем рисунке, и мы можем просто заменить его на , чтобы найти количество диагоналей в n-угольнике:
d = 1 / 2 n ( n -3)
2D многоугольников — факты о пятиугольниках, шестиугольниках, восьмиугольниках и многом другом
Многоугольник — это плоская (двумерная) фигура, у которой есть как минимум 3 прямые стороны и углы.
У правильного многоугольника есть стороны одинаковой длины и одинаковые углы. Примеры правильных многоугольников включают равносторонний треугольник и квадрат.
Треугольник — это трехсторонний многоугольник с внутренними углами, составляющими в сумме 180 градусов.
Квадрат — это четырехсторонний многоугольник с внутренними углами, составляющими в сумме 360 градусов. Квадрат — это тоже разновидность четырехугольника.
Пятиугольник — это 5-сторонний многоугольник с внутренними углами, составляющими в сумме 540 градусов.
Правильные пятиугольники имеют равные стороны и внутренние углы 108 градусов.
Штаб-квартира Министерства обороны США называется «Пентагон».
Съедобное растение окра имеет форму пятиугольника.
Шестиугольник — это 6-сторонний многоугольник с внутренними углами, составляющими 720 градусов.
У правильных шестиугольников равные стороны и внутренние углы равны 120 градусам.
Улья шестиугольные.
Семиугольник — это 7-сторонний многоугольник с внутренними углами, составляющими в сумме 900 градусов.
Правильные семиугольники имеют равные стороны и внутренние углы 128.57 градусов.
Британские монеты номиналом 50 и 20 пенсов представляют собой изогнутые семиугольники.
Восьмиугольник — это 8-сторонний многоугольник с внутренними углами, которые в сумме составляют 1080 градусов.
У правильных восьмиугольников стороны одинаковой длины и внутренние углы 135 градусов.
Нонагон — это 9-сторонний многоугольник с внутренними углами, составляющими в сумме 1260 градусов.
Обычные неагоны имеют равную длину сторон и внутренний угол 140 градусов.
Десятиугольник — это 10-сторонний многоугольник с внутренними углами, составляющими в сумме 1440 градусов.
У правильных декагонов стороны одинаковой длины и внутренние углы равны 144 градусам.
Пятиугольник — это 15-сторонний многоугольник с внутренними углами, составляющими в сумме 2340 градусов.
Икозагон — это 20-сторонний многоугольник с внутренними углами, составляющими в сумме 3240 градусов.
Посмотрите наши фотографии фигур.
Геометрия многоугольника: пятиугольники, шестиугольники и додекагоны
Немногие геометрические фигуры столь же разнообразны, как многоугольники.Они включают знакомые треугольник, квадрат и пятиугольник, но это только начало.
В геометрии многоугольник — это любая двумерная форма, которая удовлетворяет следующим условиям:
- Состоит из трех или более прямых
- Закрытый без отверстий и разрывов по форме
- Имеет пары линий, соединяющихся в углах или вершинах, образующих углы
- Имеет одинаковое количество сторон и внутренних углов
Двумерный означает плоский, как лист бумаги.Кубы не являются многоугольниками, потому что они трехмерны. Круги не являются многоугольниками, потому что они не содержат прямых линий.
Особый вид многоугольника может иметь разные углы. В данном случае это называется неправильным многоугольником .
О полигонах
Де Агостини / А. Дагли Орти / Getty Images
Название многоугольник происходит от двух греческих слов:
- Poly , , что означает много
- Гон , , что означает угол
Фигуры, которые представляют собой многоугольники
- Тригон (треугольник): 3 стороны
- Тетрагон (квадрат): 4 стороны
- Пентагоны: 5 сторон
- Шестиугольник: 6 сторон
- семиугольник: 7 сторон
- восьмиугольники: 8 сторон
- Nonagon: 9 сторон
- Десятиугольник: 10 сторон
- Undecagon: 11 сторон
- Додекагоны: 12 сторон
Как называются многоугольники
Lifewire / Тед Френч
Имена отдельных многоугольников основаны на количестве сторон или углов фигуры.У многоугольников одинаковое количество сторон и углов.
Обычное название для большинства многоугольников — это греческий префикс для «сторон», присоединенный к греческому слову «угол» (гон).
Примеры этого для пяти- и шестигранных правильных многоугольников:
- Пента (греческое означает пять) + гон = пятиугольник
- Hexa (греческое означает шесть) + гон = шестиугольник
Из этой схемы именования есть исключения.В частности, слова, которые чаще используются для обозначения некоторых многоугольников:
- Треугольник: Используется греческий префикс Tri , но вместо греческого угольника , используется латинский угол . Trigon — правильное геометрическое имя, но используется редко.
- Четырехугольник : Производный от латинского префикса quadri, , означающий четыре, присоединенный к слову боковой, , которое является другим латинским словом, означающим сторона .
- Квадрат : Иногда четырехугольник (квадрат) называется четырехугольником или четырехугольником .
N-угольники
Многоугольники с более чем 10 сторонами встречаются нечасто, но следуют тому же греческому соглашению об именах. Итак, 100-сторонний многоугольник называется гектогоном .
Однако в математике пятиугольники иногда удобнее называть n-угольниками :
- 11-угольник: Hendecagon
- 12-угольник: Додекагон
- 20-угольник: Icosagon
- 50-угольник: Pentecontagon
- 1000-угольник: Chiliagon
- 1000000-угольник: Мегагон
В математике n-угольники и их аналоги с греческими именами используются как синонимы.
Предел полигона
Теоретически у многоугольника нет ограничений на количество сторон.
По мере того, как размер внутренних углов многоугольника увеличивается, а длина его сторон становится короче, многоугольник приближается к кругу, но никогда не достигает его.
Классифицирующие многоугольники
Lifewire / Тед Френч
Правильные и неправильные многоугольники
Полигоны классифицируются в зависимости от того, равны ли все углы или стороны.
- Обычный многоугольник : Все углы имеют одинаковый размер, и все стороны равны по длине.
- Нерегулярный многоугольник : не имеет равных углов или сторон равной длины.
Выпуклые и вогнутые многоугольники
Второй способ классификации полигонов — по размеру их внутренних углов.
- Выпуклые многоугольники : Не имеют внутренних углов больше 180 °.
- Вогнутые многоугольники : иметь хотя бы один внутренний угол больше 180 °.
Простые и сложные многоугольники
Другой способ классификации многоугольников — это способ пересечения линий, образующих многоугольник.
- Простые многоугольники : линии соединяются или пересекаются только один раз — в вершинах.
- Сложные многоугольники : линии пересекаются более одного раза.
Имена сложных многоугольников иногда отличаются от названий простых многоугольников с тем же числом сторон.
Например:
- Шестиугольник правильной формы — это простой шестигранный многоугольник.
- Гексаграмма в форме звезды. — это шестигранный сложный многоугольник, образованный наложением двух равносторонних треугольников.
Правило суммы внутренних углов
Ян Лишман / Getty Images
Как правило, каждый раз, когда к многоугольнику добавляется сторона, например:
- От треугольника к четырехугольнику (от трех до четырех сторон)
- От пятиугольника к шестиугольнику (пять-шесть сторон)
еще 180 ° добавляется к сумме внутренних углов.
Это правило можно записать в виде формулы:
(п — 2) × 180 °
где n равно количеству сторон многоугольника.
Таким образом, сумму внутренних углов шестиугольника можно найти по формуле:
(6 — 2) × 180 ° = 720 °
Сколько треугольников в этом многоугольнике?
Приведенная выше формула внутреннего угла получается путем деления многоугольника на треугольники, и это число можно найти с помощью вычисления:
п — 2
В этой формуле n равно количеству сторон многоугольника.
Шестиугольник (шесть сторон) можно разделить на четыре треугольника (6–2), а двенадцатигранник — на 10 треугольников (12–2).
Размер угла для правильных многоугольников
Для правильных многоугольников, в которых все углы имеют одинаковый размер, а стороны имеют одинаковую длину, размер каждого угла в многоугольнике может быть вычислен путем деления общего размера углов (в градусах) на общее количество сторон.
Для правильного шестигранного шестиугольника каждый угол равен:
720 ° ÷ 6 = 120 °
Некоторые хорошо известные полигоны
Скотт Каннингем / Getty Images
К хорошо известным полигонам относятся:
Фермы
Фермы крыши часто имеют треугольную форму.В зависимости от ширины и наклона крыши ферма может включать равносторонние или равнобедренные треугольники. Из-за большой прочности треугольники используются при строительстве мостов и велосипедных рам. Они выделяются на Эйфелевой башне.
Пентагон
Пентагон — штаб-квартира Министерства обороны США — получил свое название от формы. Здание представляет собой пятиугольник правильной формы.
Домашняя плита
Еще один хорошо известный пятигранный правильный пятиугольник — это домашняя пластина на бейсбольном ромбе.
Поддельный Пентагон
Гигантский торговый центр недалеко от Шанхая, Китай, построен в форме правильного пятиугольника и иногда его называют Фальшивым Пентагоном.
Снежинки
Каждая снежинка начинается с шестиугольника, но температура и влажность добавляют ветки и усики, так что каждая из них выглядит по-разному.
Пчелы и осы
К естественным шестиугольникам также относятся ульи, где каждая ячейка соты, которую пчелы строят для хранения меда, имеет шестиугольную форму.Гнезда бумажных ос также содержат шестиугольные клетки, в которых они выращивают своих детенышей.
Дорога гигантов
Шестиугольники также можно найти на Дороге гигантов, расположенной на северо-востоке Ирландии. Это естественное горное образование, состоящее из примерно 40 000 взаимосвязанных базальтовых колонн, которые образовались как лава в результате медленно остывшего извержения древнего вулкана.
Октагон
Октагон — название, данное кольцу или клетке, используемым в боях Ultimate Fighting Championship (UFC), — получил свое название от своей формы.Это правильный восьмиугольник с восемью гранями.

