Модули упругости: Модуль Юнга (упругости) для стали и других материалов: определение, смысл

Модуль Юнга (упругости) для стали и других материалов: определение, смысл

Все твердые тела, как кристаллические, так и аморфные, имеют свойство изменять свою форму под воздействие приложенной к ним силы. Другими словами, они подвергаются деформации. Если тело возвращается к исходным размерам и форме после того, как внешнее усилие прекращает свое воздействие, то его называют упругим, а его деформацию считают упругой. Для любого тела существует предел приложенного усилия, после которого деформация перестает быть упругой, тело не возвращается в исходную форму и к исходным размерам, а остается в деформированном состоянии или разрушается. Теория упругих деформаций тел была создана в конце 17 века британским ученым Р. Гуком и развита в трудах его соотечественника Томаса Юнга. В их честь Гука и Юнга были названы соответственно закон и коэффициент, определяющий степень упругости тел. Он активно применяется в инженерном деле в ходе расчетов прочности конструкций и изделий.

Модуль Юнга

Основные сведения

Модуль Юнга, (называемый также модулем продольной упругости и модулем упругости первого рода) это важная механическая характеристика вещества. Он является мерой сопротивляемости продольным деформациям и определяет степень жесткости. Он обозначается как E; измеряется н/м² или в Па.

Это важный коэффициент применяют при расчетах жесткости заготовок, узлов и конструкций, в определении их устойчивости к продольным деформациям. Вещества, применяемые для изготовления промышленных и строительных конструкций, имеют, как правило, весьма большие значения E. И поэтому на практике значения Е для них приводят в гигаПаскалях (10¹²Па)

Величину E для стержней поддается расчету, у более сложных конструкций она измеряется в ходе опытов.

Приближенные величины E возможно узнать из графика, построенного в ходе тестов на растяжение.

График теста на растяжение

E- это частное от деления нормальных напряжений σ на относительное удлинение ε.

E=α/ε

Закон Гука также можно сформулировать и с использованием модуля Юнга.

Физический смысл модуля Юнга

Во время принудительного изменения формы предметов внутри них порождаются силы, сопротивляющиеся такому изменению, и стремящиеся к восстановлению исходной формы и размеров упругих тел.

Если же тело не оказывает сопротивления изменению формы и по окончании воздействия остается в деформированном виде, то такое тело называют абсолютно неупругим, или пластичным. Характерным примером пластичного тела является брусок пластилина.

Виды деформации

Р. Гук исследовал удлинение стрежней из различных веществ, под воздействием подвешенных к свободному концу гирь. Количественным выражением степени изменения формы считают относительное удлинение, равное отношению абсолютного удлинения и исходной длины.

В результате серии опытов было установлено, что абсолютное удлинение пропорционально с коэффициентом упругости исходной длине стрежня  и деформирующей силе F и обратно пропорционально площади сечения этого стержня S:

Δl = α * (lF) / S

Величину, обратную α, и называют модулем Юнга:

1/α = E

Относительная деформация:

ε = (Δl) / l = α * (F/S)

Отношение растягивающей силы F к S называют упругим напряжением σ:

ε=α σ

Закон Гука, записанный с использованием модуля Юнга, выглядит так:

σ = ε/α = E ε

Теперь можно сформулировать физический смысл модуля Юнга: он соответствует напряжению, вызываемому растягиванием стержнеобразного образца вдвое, при условии сохранения целостности.

В реальности подавляющее большинство образцов разрушаются до того, как растянутся вдвое от первоначальной длины. Значение E вычисляют с помощью косвенного метода на малых деформациях.

Коэффициент жёсткости при упругой деформации стержня вдоль его оси k = (ES) / l

Модуль Юнга определяет величину потенциальной энергии тел или сред, подвергшихся упругой деформации.

Значения модуля юнга для некоторых материалов

В таблице показаны значения E ряда распространенных веществ.

Материал	модуль Юнга E, ГПа
Алюминий	70
Бронза	75-125
Вольфрам	350
Графен	1000
Латунь	95
Лёд	3
Медь	110
Свинец	18
Серебро	80
Серый чугун	110
Сталь	200/210
Стекло	70

Модуль продольной упругости стали вдвое больше модуля Юнга меди или чугуна. Модуль Юнга широко применяется в формулах прочностных расчетов элементов конструкций и изделий в целом.

Предел прочности материала

Это предел возникающего напряжения, после которого образец начинает разрушаться.

Статический предел прочности измеряется при продолжительном приложении деформирующего усилия, динамический — при кратковременном, ударном характере такого усилия. Для большинства веществ динамический предел больше, чем статический.

Инструмент для определения предела прочности

Кроме того, существуют пределы прочности на сжатие материала и на растяжение. Они определяются на испытательных стенда опытным путем, при растягивании или сжатии образцов мощными гидравлическим машинами, снабженными точными динамометрами и измерителями давления. В случае невозможности достижения требуемого давления гидравлическим способом иногда применяют направленный взрыв в герметичной капсуле.

Допускаемое механическое напряжение в некоторых материалах при растяжении

Из жизненного опыта известно, что разные материалы по-разному сопротивляются изменению формы. Прочностные характеристики кристаллических и других твердых тел определяются силами межатомного взаимодействия. По мере роста межатомных расстояний возрастают и силы, притягивающие атомы друг к другу. Эти силы достигают максимума при определенной величине напряжения, равной приблизительно одной десятой от модуля Юнга.

Испытание на растяжение

Эту величину называют теоретической прочностью, при ее превышении начинается разрушение материала. В реальности разрушение начинается при меньших значениях, поскольку строение реальных образцов неоднородно. Это вызывает неравномерное распределение напряжений, и разрушение начинается с тех участков, где напряжения максимальны.

Значения σ_раст в МПа:

Материалы	σраст
Бор	5700	0,083
Графит	2390	0,023
Сапфир	1495	0,030
Стальная проволока	415	0,01
Стекловолокно	350	0,034
Конструкционная сталь	60	0,003
Нейлон	48	0,0025

Эти цифры учитываются конструкторами при выборе материала деталей будущего изделия. С их использованием также проводятся прочностные расчеты. Так, например, тросы, используемые для подъемно- транспортных работ, должны иметь десятикратный запас по прочности. Периодически их проверяют, подвешивая груз в десять раз больше, чем паспортная грузоподъемность троса.

Запасы прочности, закладываемые в ответственные конструкции, также многократны.

Коэффициент запаса прочности

Для количественного выражения запаса прочности при конструировании применяют коэффициент запаса прочности. Он характеризует способность изделия к перегрузкам выше номинальных. Для бытовых изделий он невелик, но для ответственных узлов и деталей, могущих при разрушении представлять опасность для жизни и здоровья человека, его делают многократным.

Запас прочности

Точный расчет прочностных характеристик позволяет создать достаточный для безопасности запас прочности и одновременно не перетяжелить конструкцию, ухудшая ее эксплуатационные характеристики. Для таких расчетов используются сложные математические методы и совершенное программное обеспечение. Наиболее важные конструкции обсчитывают на суперкомпьютерах.

Связь с другими модулями упругости

Модуль Юнга связан с модулем сдвига, определяющим способность образца к сопротивлению против деформации сдвига, следующим соотношением:

E связан также и с модулем объёмной упругости, определяющим способность образца к сопротивлению против одновременного сжатия со всех сторон.

Модуль упругости — что это такое? Определение модуля упругости для материалов

Модуль упругости — это физическая величина, которая характеризует упругое поведение материала при приложении к нему внешней силы в конкретном направлении. Под упругим поведением материала подразумевается его деформация в упругой области.

История исследования упругости материалов

Физическая теория упругих тел и их поведения при действии внешних сил была подробно рассмотрена и изучена английским ученым XIX века Томасом Юнгом. Однако сама концепция упругости была развита еще в 1727 году швейцарским математиком, физиком и философом Леонардом Эйлером, а первые эксперименты, связанные с модулем упругости, провел в 1782 году, то есть за 25 лет до работ Томаса Юнга, венецианский математик и философ Якопо Рикатти.

Заслуга Томаса Юнга заключается в том, что он придал теории упругости стройный современный вид, который впоследствии был оформлен в виде простого, а затем и обобщенного закона Гука.

Физическая природа упругости

Любое тело состоит из атомов, между которыми действуют силы притяжения и отталкивания. Равновесие этих сил обуславливает состояние и параметры вещества при данных условиях. Атомы твердого тела при приложении к ним незначительных внешних сил растяжения или сжатия начинают смещаться, создавая противоположную по направлению и равную по модулю силу, которая стремится вернуть атомы в начальное состояние.

В процессе такого смещения атомов энергия всей системы увеличивается. Эксперименты показывают, что при малых деформациях энергия пропорциональна квадрату величины этих деформаций. Это означает, что сила, будучи производной по энергии, оказывается пропорциональной первой степени величины деформации, то есть зависит от нее линейно. Отвечая на вопрос, что такое модуль упругости, можно сказать, что это коэффициент пропорциональности между силой, действующей на атом, и деформацией, которую эта сила вызывает. Размерность модуля Юнга совпадает с размерностью давления (Паскаль).

Предел упругости

Согласно определению, модуль упругости показывает, какое напряжение нужно приложить к твердому телу, чтобы его деформация составила 100 %. Однако все твердые тела обладают пределом упругости, который равен 1 % деформации. Это означает, что если приложить соответствующее усилие и деформировать тело на величину, меньшую 1 %, тогда после прекращения действия этого усилия тело точно восстанавливает свою первоначальную форму и размеры. При приложении слишком большого усилия, при котором величина деформации превышает 1 %, после прекращения действия внешней силы тело уже не восстановит первоначальные размеры. В последнем случае говорят о существовании остаточной деформации, которая является свидетельством превышения упругого предела данного материала.

Модуль Юнга в действии

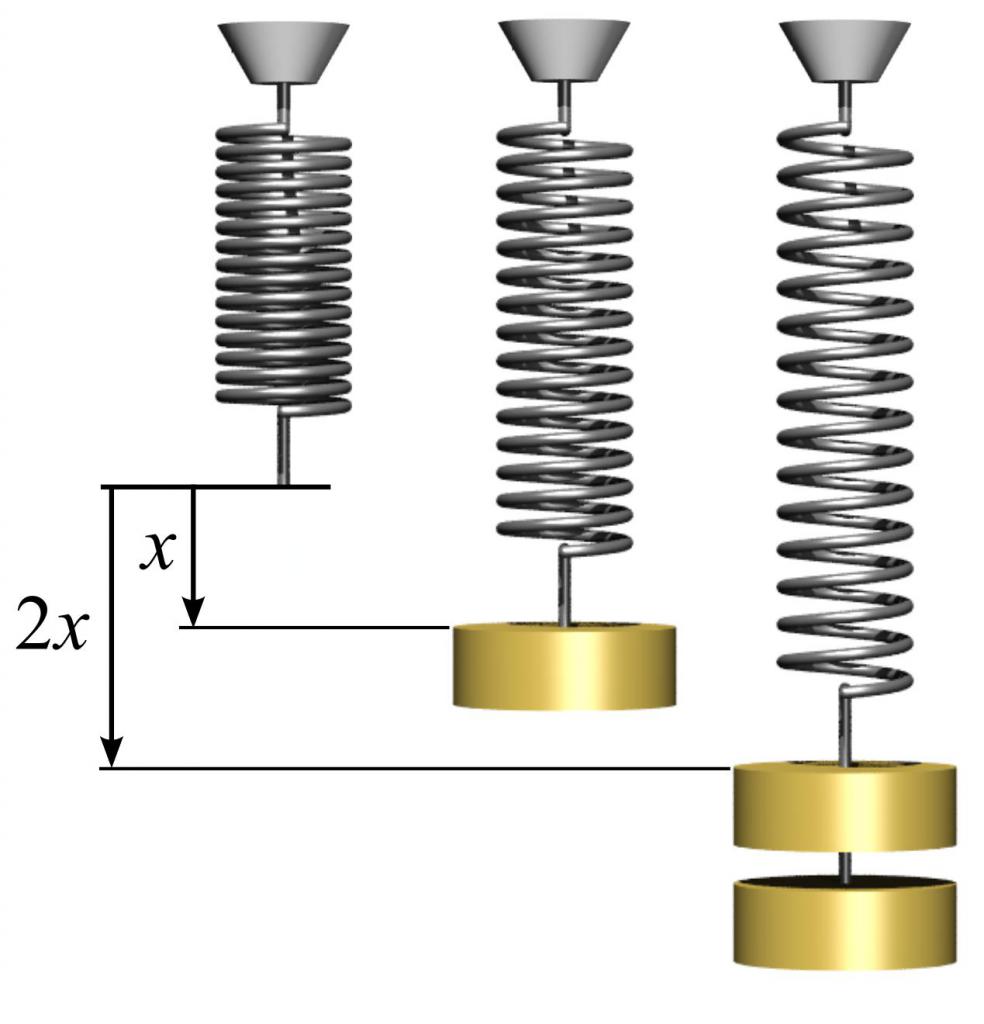
Для определения модуля упругости, а также для понимания, как им пользоваться, можно привести простой пример с пружиной. Для этого необходимо взять металлическую пружину и измерить площадь круга, который образуют ее витки. Это делается по простой формуле S = πr², где п — число пи, равное 3,14, а r — радиус витка пружины.

Далее следует замерить длину пружины l₀ без нагрузки. Если повесить какой-либо груз массой m₁ на пружину, тогда она увеличит свою длину до некоторой величины l₁. Модуль упругости E можно вычислить, исходя из знания закона Гука по формуле: E = m₁gl₀/(S(l₁-l₀)), где g — ускорение свободного падения. В данном случае отметим, что величина деформации пружины в упругой области может намного превышать 1 %.

Знание модуля Юнга позволяет предсказывать величину деформации при действии конкретного напряжения. В данном случае, если повесить на пружину другую массу m₂, получим следующую величину относительной деформации: d = m₂g/(SE), где d — относительная деформация в упругой области.

Изотропия и анизотропия

Модуль упругости является характеристикой материала, которая описывает силу связи между его атомами и молекулами, однако конкретный материал может иметь несколько различных модулей Юнга.

Дело в том, что свойства каждого твердого тела зависят от его внутренней структуры. Если свойства одинаковы во всех пространственных направлениях, то речь идет об изотропном материале. Такие вещества имеют однородное строение, поэтому действие внешней силы в различных направлениях на них вызывает одинаковую реакцию со стороны материала. Все аморфные материалы обладают изотропией, например, резина или стекло.

Анизотропия — явление, которое характеризуется зависимостью физических свойств твердого тела или жидкости от направления. Все металлы и сплавы на их основе обладают той или иной кристаллической решеткой, то есть упорядоченным, а не хаотичным расположением ионных остовов. Для таких материалов модуль упругости меняется в зависимости от оси действия внешнего напряжения. Например, металлы с кубической симметрией, к которым относятся алюминий, медь, серебро, тугоплавкие металлы и другие, обладают тремя различными модулями Юнга.

Модуль сдвига

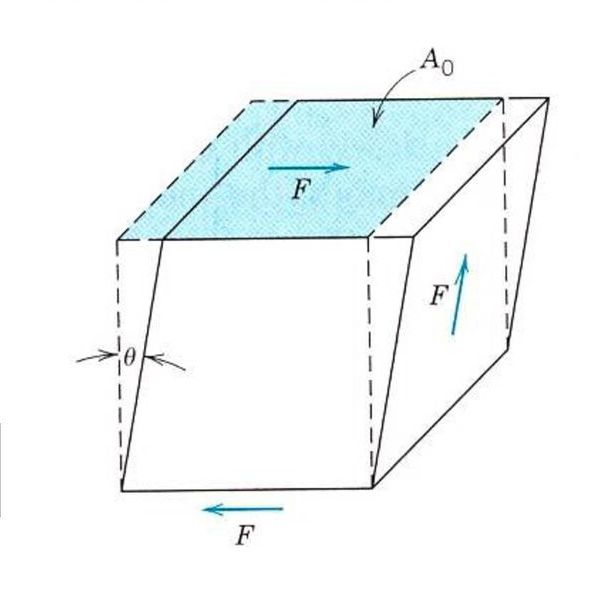
Описание упругих свойств даже изотропного материала не обходится знанием одного модуля Юнга. Поскольку, помимо растяжения и сжатия, на материал можно подействовать сдвиговыми напряжениями или напряжениями кручения. В этом случае он будет реагировать на внешнее усилие иначе. Для описания упругой деформации сдвига вводят аналог модуля Юнга, модуль сдвига или модуль упругости второго рода.

Все материалы слабее сопротивляются сдвиговым напряжениям, чем растяжению или сжатию, поэтому значение модуля сдвига для них в 2-3 раза меньше, чем значения модуля Юнга. Так, для титана, модуль Юнга которого равен 107 ГПа, модуль сдвига составляет всего лишь 40 ГПа, для стали эти цифры имеют значения 210 ГПа и 80 ГПа, соответственно.

Модуль упругости дерева

Дерево относится к анизотропным материалам, поскольку древесные волокна ориентированы вдоль конкретного направления. Именно вдоль волокон измеряют модуль упругости древесины, поскольку поперек волокон он меньше на 1-2 порядка. Знание модуля Юнга для дерева играет важную роль и учитывается при проектировании конструкций из деревянных панелей.

Значения модуля упругости древесины для некоторых видов деревьев приведены в таблице ниже.

Вид дерева	Модуль Юнга в ГПа
Лавровое дерево	14
Эвкалипт	18
Кедр	8
Ель	11
Сосна	10
Дуб	12

Следует отметить, что приведенные значения могут отличаться на величину порядка 1 ГПа для конкретного дерева, поскольку на его модуль Юнга влияет плотность древесины и условия произрастания.

Модули сдвига для различных пород деревьев находятся в пределах 1-2 ГПа, например, для сосны это 1,21 ГПа, а для дуба 1,38 ГПа, то есть древесина практически не сопротивляется сдвиговым напряжениям. Данный факт должен учитываться при изготовлении деревянных несущих конструкций, которые проектируют так, чтобы они работали только на растяжение или сжатие.

Характеристики упругости металлов

Если сравнивать с модулем Юнга древесины, то средние значения этой величины для металлов и сплавов на порядок больше, что показано в следующей таблице.

Металл	Модуль Юнга в ГПа
Бронза	120
Медь	110
Сталь	210
Титан	107
Никель	204

Упругие свойства металлов, которые имеют кубическую сингонию, описываются тремя упругими постоянными. К таким металлам относятся медь, никель, алюминий, железо. Если металл имеет гексагональную сингонию, тогда для описания его упругих характеристик уже необходимо шесть постоянных.

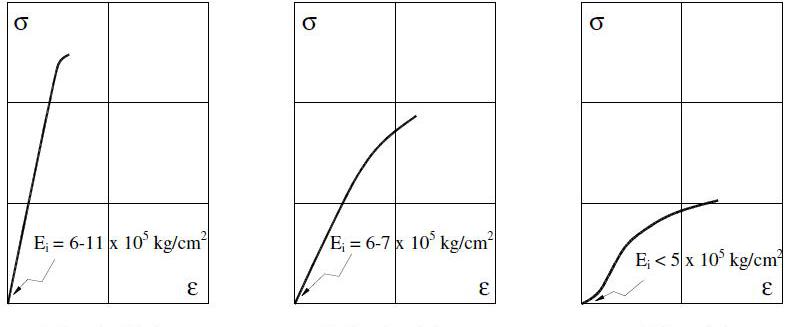
Для металлических систем модуль Юнга измеряют в пределах 0,2 % деформации, поскольку большие значения могут происходить уже в неупругой области.

Модуль упругости стали: терминология + основные формулы

Модуль упругости стали: терминология + формула расчета + предел прочности и допускаемое механическое напряжение + 6 вспомогательных физических величин для инженерных расчетов упругости металлов + инструкция расчета модуля упругости стали на онлайн-калькуляторе.

Вспомните школьное время, когда вопрос «Где это нам пригодится в жизни?» звучал чуть ли не на каждом занятии. Для людей, связавших собственную жизнь напрямую/косвенно с металлургией, физика стала неотъемлемой частью практики.

Чтобы качественно выполнить сооружение конструкции, базовых основ может быть недостаточно, и придется протаптывать более тонкие пути направления. Модуль упругости стали – один из моментов, который пригодится инженерам проектирования.

Что именно из себя представляет термин, его расчеты в отношении стали и прочие нюансы вопроса будут рассмотрены далее.

Что такое модуль упругости стали: определение + назначение

Предположим, инженер производит сооружение массивной конструкции. Выбор материала крайне важен, ибо от результата принятого решения будет зависеть прочность всего проекта. Тип материала и сечение профиля выбирается на основании показателя модуля упругости. Задача человека – подобрать оптимальный размер элемента, параметры которого смогут сдержать статическую/динамическую нагрузку + не выгребут из кармана застройщика последние деньги.

1) Модуль упругости: что это такое?

В природе 100% физических тел имеют свойство менять форму при использовании на них силы давления. Вопрос в том, насколько сильно тело восстановит свою форму после изначальной деформации, и случится ли это вообще.

Калькулятор веса стального круга

А) Терминология по модулю упругости

Давайте обратимся к повседневным объектам. Нажмите на буханку мягкого хлеба с качественной муки, и вы увидите близкое к полному восстановление формы. Другой пример – антистресс игрушка на основании полиуретана. Сжимайте ее, как пожелаете, за 30-60 секунд игрушка полностью вернет свою формы к изначальной. В сравнение, брусок пластилина считается полностью неупругим телом.

Важно: у каждого тела имеется точка невозврата деформации, когда приложенные усилия достигают своего предела. В таком случае искажается кристаллическая структура материала, и оно либо разрушается, либо остается в деформированной форме навсегда.

Впервые о модуле упругости завели речь еще в 17 веке. Труды шли от имени, известного в научных кругах физиков, ученого – Юнги. Помощником в разработке теории был Гук. Именно связка данных двух личностей привела к возникновению взаимосвязанных понятий – Закон Гука и модуль Юнга. Применяемость оговоренных законов крайне широка в инженерном деле, при определении прочности конструкции/изделия.

Модуль упругости стали (модуль Юнга) – характеристика металлического элемента. В основе меры лежит сопротивляемость деформации растяжения. По-простому, цифра дает понять на сколько металл перед глазами инженера пластичен.

Обозначается модуль Юнги через латинскую букву «Е». Единица измерения – ньютоны на метры в квадрате или Паскали. В инженерной практике больше устоялся именно второй вариант размерности. Для расчета модуля упругости используется обобщенная формула, которую можете лицезреть на рисунке ниже.

Физический смысл модуля упругости – напряжение, что вызывается при вытягивании исследуемого образца на длину, в два раза большую от первоначальной. В процессе эксперимента, предмет исследования обязан оставаться целым, но из-за сложности выполнения данного условия, модуль Юнга рассчитывают косвенным путем, через применение малых деформаций.

Б) Предел прочности и допускаемое механическое напряжение

Предел прочности – неотъемлемая часть модуля Юнга. Расчет данного показателя производится на специализированных устройствах опытным путем. Как правило, машины-разрушители работают на гидравлике + в их комплектации идет встроенный динамометр и измеритель давления.

Выделяют два типа предела прочности:

• статический. На объект анализа производится длительное усилие с постепенно усиливающимся показателем давления;
• динамический. Точечное резкое приложение силы. Чаще всего, — это удар.

Таблица веса квадрата стального

Для 85% веществ в природе значение динамического предела выше, нежели значение статического. Если классические гидравлические машины не в состоянии определить предел прочности образца металла или прочего вещества, на помощь приходят направленные взрывы в герметичной капсуле.

Различные вещества имеют свои особенности сопротивления деформациям. Для твёрдых тел важную роль отыгрывает прочность межатомных связей. При усилиях в сторону растяжения, расстояние между атомами внутри стали и других веществ увеличивается. Пропорционально возрастает и сопротивление прилагаемым усилиям.

Обратите внимание: существует так называемая теоретическая прочность стали – 1/10 от модуля упругости тестируемого вещества. Актуально для всех твердых веществ на основе железа. При достижении оговоренного значения, межатомные связи начинают разрушаться.

В реальных условиях сталь имеет неоднородную структуру, из-за чего разрывы распределяются по всей длине элемента неравномерно. Первым рушатся те участки, где межатомное напряжение выше всего.

В связи с оговоренным выше, в строительстве введено такое понятие как «запас прочности». То бишь, если человек занимается производством стальных тросов, он обязан вкладывать по ГОСТу не менее десятикратного запаса прочности от максимально допустимого теоретического предела. Если речь идет о каркасе здания, необходимо закладывать еще больший запас прочности от минимального.

Все расчеты по запасу прочности в промышленных масштабах производятся на специализированном оборудовании при использовании сложных математических формул. Для домашнего просчета имеются более доступные способы расчета показателей. К примеру, онлайн-калькуляторы инженерного типа.

В) Связь модуля упругости с другими физическими величинами

В инженерном деле одного лишь модуля упругости стали будет недостаточно. На конструкцию действует множество других сил. Соответственно, обеспечить полную безопасность проекта можно лишь при учете всех возможных рисков возведения сооружения. Давайте детальнее взглянем на вспомогательные показатели, используемые в строительной практике.

10 самых крепких металлов в мире

Параметр	Описание	Значимость (из 5 ★)
Жесткость	По сути, — это перемножение модуля Юнги на поперечное сечение объекта. Результатом подсчета станет общий показатель пластичности узлового элемента конструкции, а не ее отдельной детали. Жесткость измеряется в килограммах силы	★★★★
Продольное относительное удлинение	Высчитывается как результат деления абсолютного значения удлинения стали и общей длины. Например, имеется брусок стали с показателем длины в 10 сантиметров. Прилагая усилия на сжатие, длина бруска уменьшилась на 2 миллиметра. Тогда продольное относительное удлинение будет 2/10*10=0.02. У параметра не имеется определенной размерности, потому для удобства его измеряют в процентах.	★★★★
Поперечное относительное удлинение	Значение рассчитывается аналогично вышеописанному, только вместо длины объект берётся его поперечка по сечению. За десятки лет опытных расчетов было установлено, что коэффициент разницы между продольным и поперечным составляет ¼.	★★★★
Значение Пуассона	Высчитывается как деление продольной и поперечной относительной деформации объекта. Благодаря оговоренному показателю, человек может спрогнозировать возможность изменения формы стального элемента под воздействием статической и динамической нагрузок.	★★★
Модуль по сдвигу	Значение описывает взаимосвязь вязкости и деформации. Для определения значения на предмет исследования опускается движущая сила под прямым углом. Простым примером проверки модуля по сдвигу может служить удар молотком по шляпке гвоздя. Переломный момент наступает при сгибании стержня.	★★★★
Объемный модуль упругости	Привносит характеристику смены объема предмета исследования, при равномерном давлении со всех сторон. Простым примером может служить помещение пластичного материала на большую глубину. Что происходит с объектом в таких случаях большинство знает из художественных фильмов.	★★★

Выделяют и менее значимые показатели деформации объектов. Пример таких — параметры Ламе, которые являются константами материального типа, отображающие характеристики по упругим деформациям твердых тел. Кроме того, существуют изотропные и анизотропные материалы. Первые меняют механические свойства в зависимости от прилагаемой нагрузки, а вторые остаются неизменными. Сталь и прочие металлические сплавы относятся к изотропным материалам.

2) Пару слов о стали

Рассказа столько о модуле упругости, было бы неправильно обойти стороной сам материал. Профаны в металлургии часто путают сталь с железом. Следует понимать, что сталь – это сплав из железа+ углерода с процентным содержанием второго до 2.2%. Углерод является неотъемлемой частью стальных сплав, хоть его содержание бывает и крайне мало.

Важно: рост доли углерода в сплаве стали приводит к повышению характеристик прочности материала в строительстве, но у данного момента имеется и отрицательная сторона – снижение пластичности (сталь становится хрупкой) и меньшая восприимчивость к сварочным работам.

Обращаясь к практической стороне вопроса, среднее содержание углерода в 85%+ марок стали находится в пределах 1% (колебания в пару десятых). В зависимости от вспомогательных добавок цветных металлов и прочих веществ, вхождение чистого железа может падать до 45% от общего объема.

Добавки в промышленности именуются легирующими компонентами, и чем больше их имеет сталь, тем сильнее меняются физические/химические свойства материала.

Картинка выше отображает распространенные маркировки конструкционных типов стали в зависимости от количества добавок в сплаве и соответствию ГОСТам. В основе маркировки лежит один из двух признаков – химический состав сплава или перечисление уровней базовых свойств. По территории нашего государства большее распространение приобрела именно первая разновидность классификации.

2 подразделения удельной теплоемкости стали с учетом марок

Базовые показатели стальных сплавов:

• прочность – на сколько сталь устойчива к образованию дефектов/разрушений. Часто приравнивают к пластичности стального сплава;
• плотность – удельный вес, иными словами. Качественная сталь имеет значения в промежутке между 7.6-7.9;
• твёрдость – на сколько сталь может сопротивляться внешним нагрузкам без существенного изменения формы. Единица измерения – ножи по шкале Роквелла;
• износостойкость – на сколько хорошо сталь сохраняет форму при трении и в процессе эксплуатации в общем;
• коррозийная стойкость – на сколько хорошо марка стали может противостоять воздействию внешней среды в отношении окисления. Высоколегированные марки стали с цинком и другими антикоррозийными элементами могут служить от 50+ лет без существенных изменений во внешнем виде;
• упругость – то, о чем речь в сегодняшней статье.

В зависимости от количества вредных примесей в стальном сплаве, те классифицируют по степени чистоты на обыкновенно качественные, качественные, высококачественные и особовысококачественные. Основными «вредными» добавками здесь выступают фосфор и сера. Детальнее о классификациях марок стали по их свойствам, методам изготовления и прочим параметрам можно прочитать в ГОСТах РФ.

Разъяснение понятия о модуле упругости, как физической величине:

Как посчитать модуль упругости стали?

Важно понимать, что модуль упругости Юнга не относится к постоянным величинам. Даже одна и та же марка стали может менять значения в зависимости от точечного применения силы на предмет (колебания незначительные, но они все же есть). Если говорить о более-менее точных показателях, то ими в мире металлов может похвастаться только алюминий, сталь и медь.

Пример выше для строительных материалов взят из справочника, но цифры на бумаге не всегда отображают на 100% верные данные. Куда правильнее будет обратиться к онлайн-расчётам, или воспользоваться специализированным софтом.

Как узнать модуль упругости стали:

1. Онлайн-калькуляторов для расчета найти не проблема в сети. Наш выбор пал на сайт из первой десятки поисковика. Переходим по ссылке — http://www.stresscalc.ru/ex.php и сразу попадаем на вкладку инженерного калькулятора для просчета модуля упругости для разнообразных марок стали. Если этого не произошло, то клацаем на главную страницу, а уже оттуда выбираем кнопку, выделенную на скрине ниже.



2. Чтобы изучить весь ассортимент по маркам, можно нажать ссылку «марка стали».



3. Пользователя перенаправит на страницу, где расписаны все имеющиеся марки стали по ГОСТам РФ порядком на 2020 год. Информация обновляется каждые полгода, потому, здесь можно найти даже недавно разработанные сплавы на основе железа и легирующих добавок.



4. Чтобы добавить необходимую марку стали в окно ввода данных, потребуется выбрать смежную гиперссылку, расположенную в скобках.



5. При наведении на марку стали, она будет подсвечиваться красным цветом. Выбираем нужное наименование и просто нажимаем.



6. Далее, потребуется ввести температуру, в которой будет эксплуатироваться материал.



7. После ввода всех сопутствующих данных и нажатия кнопки «Определить», перед глазами появится полоска с синей заливкой, в которой будет указан модуль упругости («Е»), выбранной марки стали при оговорённой температуре.

Здесь же можно прочесть условные обозначения. Все физические характеристики материалов приняты по ПНАЭ Г-7-002-86, а промежуточные значения расчетных данных модуля упругости стали определяются методом линейной интерполяции.

Перед непосредственным использованием полученной информации на практике, следует провести сверку с ГОСТами. Неофициальные источники информации могут использоваться лишь для прикидочных расчетов и домашнем строительстве.

При возведении масштабных объектов, модуль Юнга нужно проверять по несколько раз, ведь от выбранных элементов будет зависеть крепость конструкции в целом.

Модуль упругости стали и других материалов

Развитие металлургии и других сопутствующих направлений по изготовлению предметов из металла обязано созданию оружия. Сначала научились выплавлять цветные металлы, но прочность изделий была относительно невысокой. Только с появлением железа и его сплавов началось изучение их свойств.

Первые мечи для придания им твердости и прочности делали довольно тяжелыми. Воинам приходилось брать их в обе руки, чтобы управляться с ними. Со временем появились новые сплавы, разрабатывались технологии производства. Легкие сабли и шпаги пришли на замену тяжеловесному оружию. Параллельно создавались орудия труда. С повышением прочностных характеристик совершенствовались инструменты и способы производства.

Виды нагрузок

При использовании металлов прилагаются разные нагрузки статического и динамического воздействия. В теории прочности принято определять нагружения следующих видов.

• Сжатие – действующая сила сдавливает предмет, вызывая уменьшение длины вдоль направления приложения нагрузки. Такую деформацию ощущают станины, опорные поверхности, стойки и ряд других конструкций, выдерживающих определённый вес. Мосты и переправы, рамы автомобилей и тракторов, фундаменты и арматура, – все эти конструктивные элементы находятся при постоянном сжатии.

• Растяжение – нагрузка стремится удлинить тело в определенном направлении. Подъемно-транспортные машины и механизмы испытывают подобные нагружения при подъеме и переноске грузов.

• Сдвиг и срез – такое нагружение наблюдается в случае действия сил, направленных вдоль одной оси навстречу друг другу. Соединительные элементы (болты, винты, заклепки и другие метизы) испытывают нагрузку подобного вида. В конструкции корпусов, металлокаркасов, редукторов и других узлов механизмов и машин обязательно имеются соединительные детали. От их прочности зависит работоспособность устройств.

• Кручение – если на предмет действует пара сил, находящихся на определенном расстоянии друг от друга, то возникает крутящий момент. Эти усилия стремятся произвести скручивающую деформацию. Подобные нагружения наблюдаются в коробках передач, валы испытывают именно такую нагрузку. Она чаще всего непостоянная по значению. В течение времени величина действующих сил меняется.

• Изгиб – нагрузка, которая изменяет кривизну предметов, считается изгибающей. Мосты, перекладины, консоли, подъемно-транспортные механизмы и другие детали испытывают подобное нагружение.

Понятие о модуле упругости

В середине XVII века одновременно в нескольких странах начались исследования материалов. Предлагались самые разные методики по определению прочностных характеристик. Английский исследователь Роберт Гук (1660 г.) сформулировал основные положения закона по удлинению упругих тел в результате приложения нагрузки (закона Гука). Введены и понятия:

1. Напряжения σ, которое в механике  измеряется в виде нагрузки, приложенной к определенной площади (кгс/см², Н/м², Па).
2. Модуля упругости Е, который определяет способность твердого тела деформироваться под действием нагружения (приложения силы в заданном направлении). Единицы измерения также определяются в кгс/см² (Н/м², Па).

Формула по закону Гука записывается в виде ε = σz/E, где:

• ε – относительное удлинение;
• σz – нормальное напряжение.

Демонстрация закона Гука для упругих тел:

Из приведенной зависимости выводится значение Е для определенного материала опытным путем, Е = σz/ε.

Модуль упругости – это постоянная величина, характеризующая сопротивление тела и его конструкционного материала при нормальной растягивающей или сжимающей нагрузке.

В теории прочности принято понятие модуль упругости Юнга. Это английский исследователь дал более конкретное описание способам изменения прочностных показателей при нормальных нагружениях.

Значения модуля упругости для некоторых материалов приведены в таблице 1.

Таблица 1: Модуль упругости для металлов и сплавов

Наименование материала	Значение модуля упругости, 10¹²·Па
Алюминий	65…72
Дюралюминий	69…76
Железо, содержание углерода менее 0,08 %	165…186
Латунь	88…99
Медь (Cu, 99 %)	107…110
Никель	200…210
Олово	32…38
Свинец	14…19
Серебро	78…84
Серый чугун	110…130
Сталь	190…210
Стекло	65…72
Титан	112…120
Хром	300…310

Модуль упругости для разных марок стали

Металлурги разработали несколько сотен марок сталей. Им свойственны разные значения прочности. В таблице 2 показаны характеристики для наиболее распространенных сталей.

Таблица 2: Упругость сталей

Наименование стали	Значение модуля упругости, 10¹²·Па
Сталь низкоуглеродистая	165…180
Сталь 3	179…189
Сталь 30	194…205
Сталь 45	211…223
Сталь 40Х	240…260
65Г	235…275
Х12МФ	310…320
9ХС, ХВГ	275…302
4Х5МФС	305…315
3Х3М3Ф	285…310
Р6М5	305…320
Р9	320…330
Р18	325…340
Р12МФ5	297…310
У7, У8	302…315
У9, У10	320…330
У11	325…340
У12, У13	310…315

Видео: закон Гука, модуль упругости.

Модули прочности

Кроме нормального нагружения, существуют и иные силовые воздействия на материалы.

Модуль сдвига G определяет жесткость. Эта характеристика показывает предельное значение нагрузки изменению формы предмета.

Модуль объемной упругости К определяет упругие свойства материала изменить объем. При любой деформации происходит изменение формы предмета.

Коэффициент Пуассона μ определяет изменения отношение величины относительного сжатия к растяжению. Эта величина зависит только от свойств материала.

Для разных сталей значения указанных модулей приведены в таблице 3.

Таблица 3: Модули прочности для сталей

Наименование стали	Модуль упругости Юнга, 10¹²·Па	Модуль сдвига G, 10¹²·Па	Модуль объемной упругости, 10¹²·Па	Коэффициент Пуассона, 10¹²·Па
Сталь низкоуглеродистая	165…180	87…91	45…49	154…168
Сталь 3	179…189	93…102	49…52	164…172
Сталь 30	194…205	105…108	72…77	182…184
Сталь 45	211…223	115…130	76…81	192…197
Сталь 40Х	240…260	118…125	84…87	210…218
65Г	235…275	112…124	81…85	208…214
Х12МФ	310…320	143…150	94…98	285…290
9ХС, ХВГ	275…302	135…145	87…92	264…270
4Х5МФС	305…315	147…160	96…100	291…295
3Х3М3Ф	285…310	135…150	92…97	268…273
Р6М5	305…320	147…151	98…102	294…300
Р9	320…330	155…162	104…110	301…312
Р18	325…340	140…149	105…108	308…318
Р12МФ5	297…310	147…152	98…102	276…280
У7, У8	302…315	154…160	100…106	286…294
У9, У10	320…330	160…165	104…112	305…311
У11	325…340	162…170	98…104	306…314
У12, У13	310…315	155…160	99…106	298…304

Для других материалов значения прочностных характеристик указывают в специальной литературе. Однако, в некоторых случаях проводят индивидуальные исследования. Особенно актуальны подобные исследования для строительных материалов. На предприятиях, где выпускают железобетонные изделия, регулярно проводят испытания по определению предельных значений.

Модуль упругости для стали, а также для других материалов

Перед тем, как использовать какой-либо материал в строительных работах, следует ознакомиться с его физическими характеристиками для того, чтобы знать как с ним обращаться, какое механическое воздействие будет для него приемлемым, и так далее. Одной из важных характеристик, на которые очень часто обращают внимание, является модуль упругости.

Ниже рассмотрим само понятие, а также эту величину по отношению к одному из самых популярных в строительстве и ремонтных работах материалу — стали. Также будут рассмотрены эти показатели у других материалов, ради примера.

Модуль упругости — что это?

Модулем упругости какого-либо материала называют совокупность физических величин, которые характеризуют способность какого-либо твёрдого тела упруго деформироваться в условиях приложения к нему силы. Выражается она буквой Е. Так она будет упомянута во всех таблицах, которые будут идти далее в статье.

Невозможно утверждать, что существует только один способ выявления значения упругости. Различные подходы к изучению этой величины привели к тому, что существует сразу несколько разных подходов. Ниже будут приведены три основных способа расчёта показателей этой характеристики для разных материалов:

• Модуль Юнга (Е) описывает сопротивление материала любому растяжению или сжатию при упругой деформации. Определяется вариант Юнга отношением напряжения к деформации сжатия. Обычно именно его называют просто модулем упругости.
• Модуль сдвига (G), называемый также модулем жёсткости. Этот способ выявляет способность материала оказывать сопротивление любому изменению формы, но в условиях сохранения им своей нормы. Модуль сдвига выражается отношением напряжения сдвига к деформации сдвига, которая определяется в виде изменения прямого угла между имеющимися плоскостями, подвергающимися воздействию касательных напряжений. Модуль сдвига, кстати, является одной из составляющих такого явления, как вязкость.
• Модуль объёмной упругости (К), которые также именуется модулем объёмного сжатия. Данный вариант обозначает способность объекта из какого-либо материала изменять свой объём в случае воздействия на него всестороннего нормального напряжения, являющимся одинаковым по всем своим направлениям. Выражается этот вариант отношением величины объёмного напряжения к величине относительного объёмного сжатия.
• Существуют также и другие показатели упругости, которые измеряются в других величинах и выражаются другими отношениями. Другими ещё очень известными и популярными вариантами показателей упругости являются параметры Ламе или же коэффициент Пуассона.

Таблица показателей упругости материалов

Перед тем, как перейти непосредственно к этой характеристике стали, рассмотрим для начала, в качестве примера и дополнительной информации, таблицу, содержащую данные об этой величине по отношению к другим материалам. Данные измеряются в МПа.

Модуль упругости различных материалов

Как можно заметить из представленной выше таблицы, это значение является разным для разных материалов, к тому же показателя разнятся, если учитывать тот или иной вариант вычисления этого показателя. Каждый волен выбирать именно тот вариант изучения показателей, который больше подойдёт ему. Предпочтительнее, возможно, считать модуль Юнга, так как он чаще применяется именно для характеристики того или иного материала в этом отношении.

После того как мы кратко ознакомились с данными этой характеристики других материалов, перейдём непосредственно к характеристике отдельно стали.

Для начала обратимся к сухим цифрам и выведем различные показатели этой характеристики для разных видов сталей и стальных конструкций:

• Модуль упругости (Е) для литья, горячекатанной арматуры из сталей марок, именуемых Ст.3 и Ст. 5 равняется 2,1*106 кг/см^2.
• Для таких сталей как 25Г2С и 30ХГ2С это значение равно 2*106 кг/см^2.
• Для проволоки периодического профиля и холоднотянутой круглой проволоки, существует такое значение упругости, равняющееся 1,8*106 кг/см^2. Для холодно-сплющенной арматуры показатели аналогичны.
• Для прядей и пучков высокопрочной проволоки значение равняется 2·10 6 кГ/см^2
• Для стальных спиральных канатов и канатов с металлическим сердечником значение равняется 1,5·10 4 кГ/см^2, в то время как для тросов с сердечником органическим это значение не превышает1,3·10 6 кГ/см^2 .
• Модуль сдвига (G) для прокатной стали равен 8,4·10 6 кГ/см^2 .
• И напоследок коэффициент Пуассона для стали равен значению 0,3

Это общие данные, приведённые для видов стали и стальных изделий. Каждая величина была высчитано согласно всем физическим правилам и с учётом всех имеющихся отношений, которые используются для выведения величин этой характеристики.

Ниже будет приведена вся общая информация об этой характеристике стали. Значения будут даваться как по модулю Юнга, так и по модулю сдвига, как в одних единицах измерения (МПа), так и в других (кг/см2, ньютон*м2).

Сталь и несколько разных её марок

Материал	Показатели модуля упругости (Е, G; Н*м2, кг/см^2, МПа)
Сталь	20,6*10^10 ньютон*метр^2
Сталь углеродистая	Е=(2,0…2,1)*10^5 МПа; G=(8,0…8,1)*10^4 МПа
Сталь 45	Е=2,0*10^5 МПа; G=0,8*10^5 МПа
Сталь 3	Е=2,1*10^5 МПа; G=0,8*10^5 МПа
Сталь легированная	Е=(2,1…2,2)*10^5 МПа; G=(8,0…8,1)*10^4 МПа

Значения показателей упругости стали разнятся, так как существуют сразу несколько модулей, которые исчисляются и высчитываются по-разному. Можно заметить тот факт, что в принципе сильно показатели не разнятся, что свидетельствует в пользу разных исследований упругости различных материалов. Но сильно углубляться во все вычисления, формулы и значения не стоит, так как достаточно выбрать определённое значение упругости, чтобы уже в дальнейшем ориентироваться на него.

Кстати, если не выражать все значения числовыми отношениями, а взять сразу и посчитать полностью, то эта характеристика стали будет равна: Е=200000 МПа или Е=2 039 000 кг/см^2.

Данная информация поможет разобраться с самим понятием модуля упругости, а также ознакомиться с основными значения данной характеристики для стали, стальных изделий, а также для нескольких других материалов.

Следует помнить, что показатели модуля упругости разные для различных сплавов стали и для различных стальных конструкций, которые содержат в своём составе и другие соединения. Но даже в таких условиях, можно заметить тот факт, что различаются показатели ненамного. Величина модуля упругости стали практически зависит от структуры. а также от содержания углерода. Способ горячей или холодной обработки стали также не может сильно повлиять на этот показатель.

Оцените статью: Поделитесь с друзьями!

Модуль нормальной упругости (Модуль Юнга) для различных марок сталей и сплавов

Ст2пс	198	183	175	167	158	—	—	—	—	—
Ст2сп	198	183	175	167	158	—	—	—	—	—
Ст3кп	213	208	202	195	187	176	167	153	—	—
Ст3пс	213	208	202	195	187	176	167	153	—	—
Ст3сп	194	192	187	183	178	167	159	146	120	99
Ст4пс	196	183	174	167	158	—	—	—	—	—
Ст5пс	198	196	186	175	167	—	—	—	—	—
Ст5сп	198	196	191	185	164	—	—	—	—	—
Ст6пс	197	197	186	175	168	—	—	—	—	—
Ст6сп	197	197	186	175	168	—	—	—	—	—
08	203	207	182	153	141	—	—	—	—	—
08кп	203	207	182	153	141	—	—	—	—	—
10	206	190	195	186	178	169	157	—	—	—
10кп	186	—	—	—	—	—	—	—	—	—
15	198	183	—	166	154	—	—	—	—	—
15кп	201	192	185	172	156	—	—	—	—	—
20 [3]	210	203	199	190	182	172	160	—	—	—
20кп	212	208	203	197	189	177	163	140	—	—
25	198	196	191	185	164	—	—	—	—	—
30	200	196	191	185	—	—	163	—	—	—
35	206	197	183	176	167	—	—	—	—	—
40	209	206	—	196	—	—	—	—	—	—
45	200	—	191	190	172	—	—	—	—	—
50	216	211	—	216	—	177	—	—	—	—
55	210	—	—	—	—	—	—	—	—	—
60	204	—	208	189	175	—	—	—	—	—
75	191	—	—	—	—	—	—	—	—	—
85	191	—	—	—	—	—	—	—	—	—
20К	200	196	191	184	177	—	—	—	—	—
22К	207	205	201	194	188	—	—	—	—	—
А12	198	183	—	167	154	—	—	—	—	—
15Г	—	186	183	—	—	—	—	—	—	—
20Г	204	—	—	—	—	—	—	—	—	—
30Г	204	—	—	—	—	—	—	—	—	—
40Г	200	—	—	—	—	—	—	—	—	—
50Г	216	213	208	199	185	174	160	142	130	—
35Г2	204	—	—	—	—	—	—	—	—	—
40Г2	212	—	—	—	—	—	—	—	—	—
45Г2	204	—	—	—	—	—	—	—	—	—
09Г2С	—	—	—	—	179	169	145	91	80	59
20Х	216	213	198	193	181	171	165	143	133	—
30Х	208	211	—	197	—	175	—	—	—	—
35Х	214	—	—	—	—	—	—	—	—	—
38ХА	196	—	—	—	—	—	—	—	—	—
40Х	214	211	—	197	—	—	—	—	—	—
45Х	206	—	—	—	—	—	—	—	—	—
50Х	—	—	—	206	—	207	—	—	—	—
10ГН2МФА, 10ГН2МФА-ВД, 10ГН2МФА-Ш	210	205	198	191	182	—	—	—	—	—
12МХ	212	106	201	195	189	179	170	160	—	—
15ХМ	204	—	—	—	169	—	—	—	—	—
30ХМ, 30ХМА	209	—	204	197	188	—	—	—	—	—
35ХМ	209	—	204	197	188	—	—	—	—	—
33ХС	214	206	196	186	176	168	157	137	127	—
38ХС	219	—	—	—	—	—	—	—	—	—
40ХС	219	—	—	—	—	—	—	—	—	—
15ХФ	206	—	—	—	—	—	—	—	—	—
14ХГС	200	—	—	—	—	—	—	—	—	—
25ХГСА	213	206	194	187	175	168	163	143	130	—
30ХГСА	194	—	174	169	156	—	—	—	—	—
18ХГТ	211	205	197	191	176	168	155	136	129	—
30ХГТ	212	202	195	189	174	169	157	138	132	—
12Х1МФ (ЭИ 575)	209	206	202	197	189	179	166	—	—	—
13Х1МФ (14Х1ГМФ, ЦТ 1)	214	211	205	198	185	179	170	155	—	—
15Х1М1Ф	210	204	197	190	182	174	166	157	—	—
25Х1МФ (ЭИ 10)	213	207	202	194	187	177	163	—	—	—
25Х1М1Ф (Р2, Р2МА)	216	214	210	205	197	186	171	—	—	—
20Х1М1Ф1ТР (ЭП 182)	211	208	204	198	190	179	167	150	—	—
20Х1М1Ф1БР (ЭП 44)	213	207	201	192	184	177	164	149	—	—
40ХН	200	—	—	—	—	—	—	—	—	—
30ХН2МА	204	201	194	186	182	171	159	—	—	—
12ХН3А	200	—	—	—	—	—	—	—	—	—
20ХН3А	212	204	194	188	169	169	153	138	132	—
30ХН3А	215	207	195	187	175	171	—	—	—	—
25Х2М1Ф (ЭИ 723)	219	214	209	203	196	188	179	172	—	—
10Х2МФБ (ЭИ 531), 12Х2МФБ (ЭИ 531)	220	—	—	—	—	181	173	—	—	—
38Х2МЮА (38ХМЮА)	209	202	194	190	181	174	162	147	137	—
15Х2НМФА, 15Х2НМФА-А, 15Х2НМФА класс 1	214	210	205	198	190	—	—	—	—	—
20Х3МВФ (ЭИ 415, ЭИ 579)	201	—	200	179	171	153	119	118	—	—
15Х5М (12Х5МА, Х5М)	211	—	—	—	178	145	102	—	—	—
65Г	207	—	—	—	—	—	—	—	—	—
40ХФА	203	—	—	—	—	—	—	—	—	—
50ХФА	196	—	—	—	—	—	—	—	—	—
55С2	196	—	—	—	—	—	—	—	—	—
60С2, 60С2А	245	—	—	—	—	—	—	—	—	—
ШХ15	201	—	—	—	—	—	—	—	—	—
95Х18 (9Х18, ЭИ 229)	205	—	—	—	—	—	—	—	—	—
12Х8ВФ (1Х8ВФ)	218	—	—	164	153	—	—	—	—	—
10Х9МФБ (ДИ 82)	220	215	210	200	190	180	170	—	—	—
10Х9В2МФБР-Ш	191	184	184	173	—	152	98	—	—	—
40Х10С2М (4Х10С2М, ЭИ 107)	214	211	205	202	196	187	172	151	129	—
15Х11МФ (1Х11МФ)	224	218	209	201	189	177	—	—	—	—
12Х11В2МФ (типа ЭИ 756)	208	204	199	191	182	170	161	148	—	—
18Х11МНФБ (2Х11МФБН, ЭП 291)	224	177	209	201	189	177	—	—	—	—
03Х11Н10М2Т	196	—	—	—	—	—	—	—	—	—
10Х11Н20Т3Р (ЭИ 696)	160	—	—	—	140	135	132	115	113	90
10Х11Н23Т3МР (10Х12Н22Т3МР, ЭП 33, ЭИ 696М)	160	—	—	—	142	138	132	115	—	—
18Х12ВМБФР-Ш (ЭИ 993-Ш)	224	—	211	205	191	184	170	152	—	—
20Х12ВНМФ (ЭП 428)	212	—	—	196	190	180	163	—	—	—
06Х12Н3Д	212	211	205	198	187	—	—	—	—	—
10Х12Н3М2ФА (Ш), 10Х12Н3М2ФА-А (Ш)	217	212	207	199	189	176	167	—	—	—
37Х12Н8Г8МФБ (ЭИ 481)	171	—	157	147	140	133	126	115	—	—
08Х13 (0Х13, ЭИ 496)	217	212	206	198	189	180	—	—	—	—
12Х13 (1Х13)	217	212	206	198	189	180	—	—	—	—
20Х13 (2Х13)	218	214	208	200	189	181	169	—	—	—
30Х13 (3Х13)	216	212	206	196	187	177	166	—	—	—
40Х13 (4Х13)	214	208	202	194	185	173	160	—	—	—
12Х13Г12АС2Н2 (ДИ 50)	188	—	185	—	159	—	142	—	—	—
10Х13Г12БС2Н2Д2Б (ДИ 59)	195	192	185	77	166	160	150	141	137	—
03Х13Н8Д2ТМ (ЭП 699)	195	191	187	182	171	—	—	—	—	—
08Х14МФ	222	219	213	203	195	183	175	—	—	—
10Х14Г14Н4Т (Х14Г14Н3Т, ЭИ 711)	194	189	181	170	164	159	161	—	—	—
1Х14Н14В2М (ЭИ 257)	198	—	—	—	—	168	160	—	—	—
45Х14Н14В2М (ЭИ 69) [3]	212	200	194	185	176	169	160	152	144	—
09Х14Н19В2БР (ЭИ 695Р) [5]	207	—	—	—	—	—	158	151	147	—
09Х14Н19В2БР1 (ЭИ 726)	198	195	189	182	175	166	157	149	—	—
08Х15Н2В4ТР (ЭП 164) [5]	223	215	209	200	191	182	173	165	156	—
07Х16Н6 (Х16Н6, ЭП 288)	199	—	—	—	—	—	—	—	—	—
08Х16Н9М2 (Х16Н9М2)	210	198	188	80	172	157	153	143	138	—
08Х16Н13М2Б (ЭИ 405, ЭИ 680)	202	196	188	180	171	164	155	147	—	—
10Х16Н14В2БР (1Х16Н14В2БР, ЭП 17)	188	181	174	166	158	151	145	136	—	—
08Х17Т (0Х17Т, ЭИ 645)	206	—	—	—	—	—	—	—	—	—
12Х17 (Х17, ЭЖ 17)	232	227	219	211	201	192	182	165	148	—
14Х17Н2 (1Х17Н2, ЭИ 268)	193	—	—	164	—	148	133	—	—	—
02Х17Н11М2	200	—	—	—	170	—	150	—	135	—
08Х17Н13М2Т (0Х17Н13М2Т)	206	—	186	177	177	167	157	147	—	—
10Х17Н13М2Т (Х17Н13М2Т, ЭИ 448)	206	—	186	177	177	167	157	147	—	—
10Х17Н13М3Т (Х17Н13М3Т, ЭИ 432)	206	—	186	177	177	167	157	147	—	—
03Х17Н14М3 (000Х17Н13М2)	195	—	—	190	—	—	—	—	—	—
08Х17Н15М3Т (ЭИ 580)	203	—	—	—	—	—	—	—	—	—
015Х18М2Б-ВИ (ЭП 882-ВИ)	216	12	206	198	185	179	163	144	—	—
12Х18Н9 (Х18Н9)	199	—	—	—	—	—	—	—	—	—
12Х18Н9Т (Х18Н9Т)	195	189	182	175	167	160	153	143	135	—
17Х18Н9 (2Х18Н9)	199	—	—	—	—	—	—	—	—	—
08Х18Н10 (0Х18Н10)	196	—	—	—	—	—	—	—	—	—
08Х18Н10Т (0Х18Н10Т, ЭИ 914) [4]	196	—	—	—	158	128	127	117	108	102
12Х18Н10Т [4]	198	194	189	181	174	166	157	147	—	—
12Х18Н12Т (Х18Н12Т)	210	198	193	186	177	170	157	147	—	—
10Х18Н18Ю4Д (ЭП 841)	186	182	178	171	165	161	156	146	38	127
36Х18Н25С2 (4Х18Н25С2, ЭЯ 3С)	200	—	—	191	186	178	171	162	154	147
01Х19Ю3БЧ-ВИ (02Х18Ю3Б-ВИ, ЭП 904-ВИ)	220	216	210	200	192	183	167	152	—	—
31Х19Н9МВБТ (ЭИ 572)	201	—	—	186	181	176	167	157	—	—
08Х21Н6М2Т (0Х21Н6М2Т, ЭП 54)	196	196	185	178	169	164	—	—	—	—
02Х22Н5АМ3	200	194	186	180	—	—	—	—	—	—
08Х22Н6Т (0Х22Н5Т, ЭП 53)	203	201	193	181	165	162	154	141	139	—
20Х23Н13 (Х23Н13, ЭИ 319)	207	—	—	—	—	—	—	—	—	—
20Х23Н18 (Х23Н18, ЭИ 417)	200	—	—	182	176	170	160	150	141	—
03Х24Н6АМ3 (ЗИ 130)	200	196	185	180	171	—	—	—	—	—
15Х25Т (Х25Т, ЭИ 439)	204	200	197	189	176	164	140	124	119	109
12Х25Н16Г7АР (ЭИ 835)	193	186	178	171	163	156	147	138	131	127
20Х25Н20С2 (Х25Н20С2, ЭИ 283)	195	192	186	185	180	175	150	140	130	120
03Н18К9М5Т	185	—	—	—	—	—	—	—	—	—
У8, У8А	209	205	199	192	185	175	166	—	—	—
У9, У9А	209	—	—	—	—	—	—	—	—	—
У12, У12А	209	205	200	193	185	178	166	—	—	—
9ХС	190	—	—	—	—	—	—	—	—	—
Р9	220	—	—	—	—	—	—	—	—	—
Р12	223	—	—	—	—	—	—	—	—	—
20Л	201	196	188	183	173	165	152	132	120	—
35Л	212	206	201	192	176	163	151	131	118	—
50Л	219	214	208	196	178	170	155	136	122	—
20ГЛ	204	—	—	—	—	—	—	—	—	—
110Г13Л	204	—	—	—	—	—	—	—	—	—
08ГДНФЛ	212	206	201	189	177	167	155	137	127	—
32Х06Л	216	211	207	195	178	174	166	141	131	—
40ХЛ	219	216	210	204	185	176	164	143	132	—
20ХМФЛ	197	192	187	182	178	171	163	155	—	—
35ХМЛ	215	212	207	203	192	179	166	141	130	—
35ХГСЛ	215	211	203	196	184	174	164	143	125	—
20Х5МЛ	211	—	—	—	178	145	102	—	—	—
15Х11МФБЛ (1Х11МФБЛ, Х11ЛА)	210	—	202	195	187	178	162	—	—	—
10Х12НДЛ	217	216	212	204	198	188	179	164	—	—
20Х12ВНМФЛ (15Х12ВНМФЛ, Х11ЛБ, ЭИ 802Л)	210	—	202	195	187	178	162	—	—	—
20Х13Л [4]	222	216	211	203	196	184	167	149	140	—
10Х13Н3М1Л	215	—	—	—	—	—	—	—	—	—
10Х18Н9Л	170	143	135	127	120	—	—	—	—	—
12Х18Н9ТЛ [4]	194	189	176	165	149	138	133	125	112	—
06ХН28МДТ (0Х23Н28М3Д3Т, ЭИ 943)	—	191	186	179	171	161	156	151	145	—
ХН32Т (ЭП 670)	205	—	—	—	—	—	—	—	—	—
ХН35ВТ (ЭИ 612), ХН35ВТ-ВД	198	195	190	186	179	177	166	158	—	—
ХН35ВТК (ЭИ 612К)	198	184	175	—	171	164	159	141	—	—
ХН35ВТЮ (ЭИ 787)	214	207	199	195	189	181	170	163	149	—
ХН35ВТР (ЭИ 725)	206	—	186	—	177	167	167	157	157	—
36НХТЮ8М	210	—	—	—	—	—	—	—	—	—
ХН45Ю (ЭП 747)	207	201	192	187	178	171	156	148	124	120
06ХН46Б (Х20Н46Б, ЭП 350)	—	175	173	168	164	157	151	147	—	—
05ХН46МВБЧ (ДИ 65)	207	203	196	190	183	177	170	163	154	144
ХН55ВМТКЮ (ЭИ 929), ХН55ВМТКЮ-ВД (ЭИ 929-ВД)	218	—	—	—	—	—	—	181	172	163
ХН59ВГ-ИД (ЭК 82-ИД)	217	214	208	203	196	191	189	180	172	166
ХН60Ю (ЭИ 559А)	210	—	—	—	—	—	—	—	169	—
ХН60ВТ (ЭИ 868)	218	—	—	—	204	198	192	184	176	160
ХН62МБВЮ (ЭП 709)	226	—	—	—	—	197	189	—	—	—
ХН62МВКЮ (ЭИ 867)	228	—	—	—	—	—	—	191	179	140
ХН65ВМТЮ (ЭИ 893)	219	—	206	201	196	193	183	176	162	—
ХН65КМВЮБ-ВД (ЭП 800-ВД)	230	227	222	217	211	204	200	188	181	171
ХН65МВУ (ЭП 760)	200	—	—	—	—	—	—	—	—	—
ХН67МВТЮ (ЭП 202, ЭИ 445Р)	212	208	203	197	192	185	178	170	161	139
ХН70БДТ (ЭК 59)	219	214	208	201	198	—	—	—	—	—
ХН70ВМЮТ (ЭИ 765)	222	217	211	205	199	193	186	179	—	—
ХН70ВМТЮ (ЭИ 617)	196	—	—	—	—	—	162	147	142	127
ХН70ВМТЮФ (ЭИ 826), ХН70ВМТЮФ-ВД, (ЭИ 826-ВД)	196	—	—	—	—	167	162	152	142	127
ХН73МБТЮ (ЭИ 698)	203	—	—	—	—	177	177	160	150	—
ХН75ВМЮ (ЭИ 827)	240	236	231	225	218	215	204	195	187	178
ХН77ТЮР (ЭИ 437Б)	210	—	—	—	—	—	163	153	130	115 (850°C)
ХН78Т (ЭИ 435)	210	—	—	—	—	—	—	169	—	—
ХН80ТБЮ (ЭИ 607)	216	216	211	206	200	196	186	177	—	—
ХН80ТБЮА (ЭИ 607А)	218	—	—	—	—	191	184	176	—	—
Н70МФВ-ВИ (ЭП 814А-ВИ)	155	—	—	—	—	—	—	—	—	—
ХН58ВКМТЮБЛ (ЦНК 8МП)	211	—	—	—	—	—	—	—	—	—
ХН60КВМЮТЛ (ЦНК 7П)	210	207	203	198	192	185	178	171	164	—
ХН64ВМКЮТЛ (ЗМИ 3)	225	222	219	214	209	201	193	186	177	168
ХН65ВМТЮЛ (ЭИ 893Л)	222	214	210	202	195	190	184	174	165	160
ХН65КМВЮТЛ (ЖС 6К)	210	207	203	198	192	185	178	171	164	—
ХН65ВКМБЮТЛ (ЭИ 539ЛМУ)	213	211	207	203	197	190	183	175	167	158
АД, АД00, АД0, АД1 [6]	71	—	—	—	—	—	—	—	—	—
АМг2 [6]	—	59	—	—	—	—	—	—	—	—
АМг2	69	—	—	—	—	—	—	—	—	—
АМг3	68	—	—	—	—	—	—	—	—	—
АМг5	69	—	—	—	—	—	—	—	—	—
АМг6	69	—	—	—	—	—	—	—	—	—
ЛС59-1	105	—	—	—	—	—	—	—	—	—
ЛЖМц59-1-1	106	—	—	—	—	—	—	—	—	—
ЛАМш77-2-0,05	102	—	—	—	—	—	—	—	—	—
БрА10Ж3Мц2 (БрАЖМц10-3-1,5)	102	—	—	—	—	—	—	—	—	—
БрБ2	123	—	—	—	—	—	—	—	—	—
БрО5Ц5С5 (БрОЦС5-5-5)	90	—	—	—	—	—	—	—	—	—
БрО10Ф1 (БрОФ10-1)	103	—	—	—	—	—	—	—	—	—
Б83	48	—	—	—	—	—	—	—	—	—
ВТ1-0	103	—	—	—	—	—	—	—	—	—
ВТ1-00	103	—	—	—	—	—	—	—	—	—
ВТ5-1	115,7	—	—	—	—	—	—	—	—	—
ОТ4	107,9	—	—	—	—	—	—	—	—	—
ОТ4-0	112,8	—	—	—	—	—	—	—	—	—
ОТ4-1	107,9	—	—	—	—	—	—	—	—	—

УПРУГОСТЬ, МОДУЛЬ УПРУГОСТИ, ЗАКОН ГУКА

УПРУГОСТЬ, МОДУЛЬ УПРУГОСТИ, ЗАКОН ГУКА. Упругость – свойство тела деформироваться под действием нагрузки и восстанавливать первоначальную форму и размеры после ее снятия. Проявление упругости лучше всего проследить, проведя простой опыт с пружинными весами – динамометром, схема которого показана на рис.1.

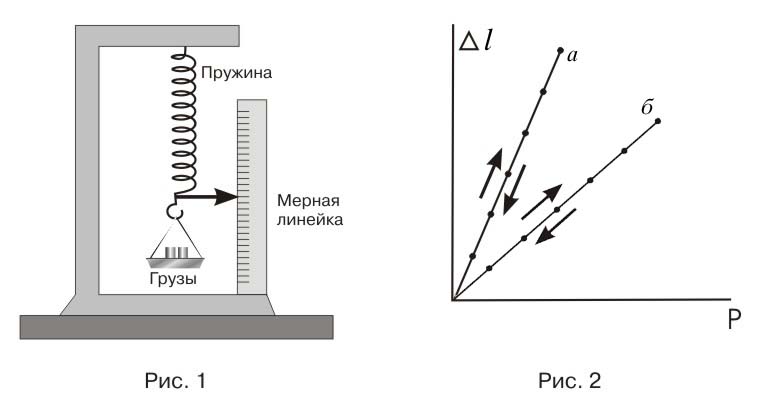
При нагрузке в 1 кг стрелка-индикатор сместится на 1 деление, при 2 кг – на два деления, и так далее. Если нагрузки последовательно снимать, процесс идет в обратную сторону. Пружина динамометра – упругое тело, ее удлинение Dl, во-первых, пропорционально нагрузке P и, во-вторых полностью исчезает при полном снятии нагрузки. Если построить график, отложить по вертикали оси величины нагрузки, а по горизонтальной – удлинение пружины, то получаются точки, лежащие на прямой, проходящей через начало координат, рис.2. Это справедливо как для точек, изображающих процесс нагружения так и для точек, соответствующих нагрузке.

Угол наклона прямой характеризует способность пружины сопротивляться действию нагрузки: ясно, что «слабая» пружина (рис.3). Эти графики называются характеристиками пружины.

Тангенс угла наклона характеристики называется жесткостью пружины С. Теперь можно записать уравнение деформирования пружины Dl = P / C

Жесткость пружины С имеет размерность кг / см\up122 и зависит от материала пружины (например, сталь или бронза) и ее размеров – длины пружины, диаметра ее витка и толщины проволоки, из которой она сделана.

В той или иной мере все тела, которые можно считать твердыми, обладают свойством упругости, но заметить это обстоятельство можно далеко не всегда: упругие деформации обычно очень малы и наблюдать их без специальных приборов удается практически только при деформировании пластинок, струн, пружин, гибких стержней.

Прямым следствием упругих деформаций являются упругие колебания конструкций и природных объектов. Можно легко обнаружить дрожание стального моста, по которому идет поезд;иногда можно услышать, как звенит посуда, когда на улице проезжает тяжелый грузовик; все струнные музыкальные инструменты так или иначе преобразуют упругие колебания струн в колебания частичек воздуха;в ударных инструментах тоже упругие колебания (например, мембраны барабана) преобразуются в звук.

При землетрясении происходят упругие колебания поверхности земной коры; при сильном землетрясении кроме упругих деформаций возникают пластические (которые остаются после катаклизма как изменения микрорельефа), а иногда появляются трещины. Эти явления не относятся к упругости: можно сказать, что в процессе деформирования твердого тела сначала всегда появляются упругие деформации, потом пластические, и, наконец, образуются микротрещины. Упругие деформации очень малы – не больше 1%, а пластические могут достигнуть 5–10% и более, поэтому обычное представление о деформациях относится к пластическим деформациям – например, пластилин или медная проволока. Однако, несмотря на свою малость, упругие деформации играют важнейшую роль в технике: расчет на прочность авиалайнеров, подводных лодок, танкеров, мостов, туннелей, космических ракет – это, в первую очередь, научный анализ малых упругих деформаций, возникающих в перечисленных объектах под действием эксплуатационных нагрузок.

Еще в неолите наши предки изобрели первое дальнобойное оружие – лук и стрелы, используя упругость изогнутой ветки дерева; потом катапульты и баллисты, построенные для метания больших камней, использовали упругость канатов, свитых из растительных волокон или даже из женских длинных волос. Эти примеры доказывают, что проявление упругих свойств было давно известно и давно использовалось людьми. Но понимание того, что любое твердое тело под действием даже небольших нагрузок обязательно деформируется, хотя и на очень малую величину, впервые появилось в 1660 у Роберта Гука, современника и коллеги великого Ньютона. Гук был выдающимся ученым, инженером и архитектором. В 1676 он сформулировал свое открытие очень кратко, в виде латинского афоризма: «Ut tensio sic vis», смысл которого состоит в том, что «какова сила, таково и удлинение». Но опубликовал Гук не этот тезис, а только его анаграмму: «ceiiinosssttuu». (Таким образом тогда обеспечивали приоритет, не раскрывая сути открытия.)

Вероятно, в это время Гук уже понимал, что упругость – универсальное свойство твердых тел, но считал необходимым подтвердить свою уверенность экспериментально. В 1678 вышла книга Гука, посвященная упругости, где описывались опыты, из которых следует, что упругость есть свойство «металлов, дерева, каменных пород, кирпича, волос, рога, шелка, кости, мышцы, стекла и т.п.» Там же была расшифрована анаграмма. Исследования Роберта Гука привели не только к открытию фундаментального закона упругости, но и к изобретению пружинных хронометров (до того были только маятниковые). Изучая различные упругие тела (пружины, стержни, луки), Гук установил, что «коэффициент пропорциональности» (в частности, жесткость пружины) сильно зависит от формы и размеров упругого тела, хотя материал играет решающую роль.

Прошло более ста лет, в течение которых опыты с упругими материалами проводили Бойль, Кулон, Навье и некоторые другие, менее известные физики. Одним из основных опытов стало растяжение пробного стержня из изучаемого материала. Для сравнения результатов, полученных в разных лабораториях, нужно было либо использовать всегда одинаковые образцы, либо научиться исключать слияние размеров образца. И в 1807 появилась книга Томаса Юнга, в которой был введен модуль упругости – величина, описывающая свойство упругости материала независимо от формы и размеров образца, который использовался в опыте. Для этого нужно силу P, приложенную к образцу, разделить на площадь сечения F, а произошедшее при этом удлинение Dl разделить на первоначальную длину образца l. Соответствующие отношения – это напряжение s и деформация e.

Теперь закон Гука о пропорциональности можно записать в виде:

s = Еe

Коэффициент пропорциональности Е называется модулем Юнга, имеет размерность, как у напряжения (МПа), а обозначение его есть первая буква латинского слова elasticitat – упругость.

Модуль упругости Е – это характеристика материала того же типа, как его плотность или теплопроводность.

В обычных условиях, чтобы продеформировать твердое тело, требуется значительная сила. Это означает, что модуль Е должен быть большой величиной – по сравнению с предельными напряжениями, после которых упругие деформации сменяются пластическими и форма тела заметно искажается.

Если измерять величину модуля Е в мегапаскалях (МПа), получатся такие средние значения:

Сталь	20·104
Медь	10·104
Алюминий	7·104
Стекло	7·104
Кость	3·104
Дерево	1·104
Резина*	0,001·104

Физическая природа упругости связана с электромагнитным взаимодействием (в том числе с силами Ван-дер-Ваальса в решетке кристалла). Можно считать, что упругие деформации связаны с изменением расстояния между атомами.

Упругий стержень имеет еще одно фундаментальное свойство – утоньшаться при растяжении. То, что канаты при растяжении становятся тоньше, было известно давно, но специально поставленные опыты показали, что при растяжении упругого стержня всегда имеет место закономерность: если измерить поперечную деформацию e’, т.е. уменьшение ширины стержня db , деленное на первоначальную ширину b, т.е.

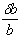
и разделить ее на продольную деформацию e, то это отношение остается постоянным при всех значениях растягивающей силы P, то есть

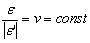
(Полагают, что e’< 0 ; поэтому используется абсолютная величина). Константа v называется коэффициентом Пуассона (по имени французского математика и механика Симона Дени Пуассона) и зависит только от материала стержня, но не зависит от его размеров и формы сечения. Величина коэффициента Пуассона для разных материалов изменяется от 0 (у пробки) до 0,5 (у резины). В последнем случае объем образца в процессе растяжения не изменяется (такие материалы называются несжимаемыми). Для металлов значения различны, но близки к 0,3.

Модуль упругости E и коэффициент Пуассона вместе образуют пару величин, которые полностью характеризуют упругие свойства любого конкретного материала (имеются в виду изотропные материалы, т.е. такие, у которых свойства не зависят от направления; пример древесины показывает, что это не всегда так – ее свойства вдоль волокон и поперек волокон сильно различаются. Это – анизотропный материал. Анизотропными материалами являются монокристаллы, многие композиционные материалы (композиты) типа стеклопластика. Такие материалы тоже в известных пределах обладают упругостью, но само явление оказывается значительно более сложным).

Если от рассмотрения растяжения стержня перейти к рассмотрению некоторого упругого тела, подверженного действию заданных сил, то следует выбрать некоторую точку M и перейти к рассмотрению ее малой окрестности в виде параллелепипеда с ребрами, параллельными координатным осям XYZ. Как известно (см. ДЕФОРМАЦИЯ), на гранях параллелепипеда действуют напряжения, которые задаются тензором s, что приводит к деформациям, которые задаются тензором e.

В общем случае закон Гука устанавливает связь между компонентами этих тензоров, которую можно записать в виде:

,

,

,

, ,

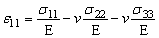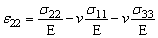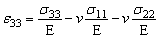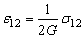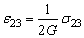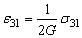
В последние три уравнения входит величина G, которая называется модулем сдвига и выражается через E и v по формуле:

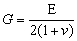
Модуль сдвига можно непосредственно определить из опыта на кручение круглого образца.

В физике для идеального газа вводится уравнение состояния (уравнение Клапейрона – Менделеева). Можно сказать, что закон Гука – это уравнение состояния для идеально упругого тела.

Владимир Кузнецов

Модуль Юнга — предел текучести и растяжения для обычных материалов

Модуль упругости — или модуль Юнга alt. Модуль упругости — это показатель жесткости эластичного материала. Он используется для описания упругих свойств таких объектов, как проволока, стержни или колонны, когда они растягиваются или сжимаются.

Модуль упругости при растяжении определяется как

«отношение напряжения (силы на единицу площади) вдоль оси к деформации (отношение деформации к начальной длине) вдоль этой оси»

Его можно использовать для прогнозирования удлинения или сжатие объекта до тех пор, пока напряжение меньше предела текучести материала.Подробнее об определениях под таблицей.

900 18 58 170 9001 8 Нейлон-6 900 18

АБС-пластик	1,4 — 3,1	40
A53 Стандартная сварная и бесшовная стальная труба — марка A		331	207
A53 Бесшовная и сварная стандартная сталь Труба — класс B		414	241
A106 Бесшовная труба из углеродистой стали — класс A		400	248
A106 Бесшовная труба из углеродистой стали A106 — класс B		483	345
Бесшовная труба из углеродистой стали A106 — класс C		483	276
Стальная труба A252 свайная — сорт 1		345	207
Стальная труба A252 свай — сорт 2		414	241
A252 Стальная труба для забивки свай — Gr ade 3		455	310
A501 Конструкционные трубы из углеродистой стали горячей штамповки — класс A		400	248
A501 Конструкционные трубы из горячеформованной углеродистой стали — класс B		483	345
A523 Стальные трубы для кабельных цепей — класс A		331	207
A523 Стальные трубы для кабельных цепей — класс B		414	241
A618 горячеформованные высокопрочные Низколегированные конструкционные трубы — классы Ia и Ib		483	345
A618 Горячеформованные высокопрочные низколегированные конструкционные трубы — класс II		414	345
A618 Hot- Формованные высокопрочные низколегированные конструкционные трубы — класс III		448	345
Линейная труба API 5L		310 — 1145	175 — 1048
Ацетали	2.8	65
Акрил	3,2	70
Алюминий бронза	120
Алюминий	69	110	95
Алюминиевые сплавы	70
Сурьма	78
Арамид	70-112
Бериллий (Be)	287
Бериллий Медь	124
Висмут	32
Кость компактная	18	170 (компрессионная)
Кость губчатая	76
Bo ron			3100
Латунь	102-125	250
Латунь, морской	100
Бронза	96-120
CAB	0.8
Кадмий	32
Пластик, армированный углеродным волокном	150
Углеродная нанотрубка, одностенная	1000
Чугун 4.5 % C, ASTM A-48		170
Целлюлоза, хлопок, древесная масса и регенерированная		80-240
Ацетат целлюлозы, формованный		12-58
Ацетат целлюлозы, лист		30-52
Нитрат целлюлозы, целлулоид		50
Хлорированный полиэфир	1.1	39
Хлорированный ПВХ (ХПВХ)	2,9
Хром	248
Кобальт	207
Бетон 17
Бетон, высокая прочность (сжатие)	30	40 (сжатие)
Медь	117	220	70
Алмаз (C)	1220
Древесина пихты Дугласа	13	50 (сжатие)
Эпоксидные смолы	3-2	26-85
Древесноволокнистая плита средней плотности	4
Льняное волокно
Стекло	50-90	50 (сжатие)
Стеклоармированная полиэфирная матрица	17
Золото	74
Гранит	52
Графен	1000
Серый чугун	130
Конопляное волокно	35
Инконель	214
Иридий	517
Железо	210
Свинец	13.8
Магний металлический (Mg)	45
Марганец	159
Мрамор		15
МДФ — средней плотности ДВП	4
Ртуть
Молибден (Мо)	329
Монель Металл	179
Никель
Никель-серебро	128
Никелевая сталь	200
Ниобий (колумбий)	103
2-4	45-90	45
Нейлон-66		60-80
Дуб (вдоль волокон)	11
Осмий (Os)	550
Фенольные литые смолы		33-59
Формовочные смеси фенолформальдегида		45-52
Фосфорная бронза	116
Сосновая древесина (вдоль волокон)	9	40
Платина	147
Плутоний	97
Полиакрилонитрил, волокна		200
Полибенз оксазол	3.5
Поликарбонаты	2,6	52-62
Полиэтилен HDPE (высокая плотность)	0,8	15
Полиэтилентерефталат, ПЭТ	2 — 2,7	55
Полиамид	2,5	85
Полиизопрен, твердая резина		39
Полиметилметакрилат (ПММА)	2.4 — 3,4
Полиимидные ароматические углеводороды	3,1	68
Полипропилен, PP	1,5 — 2	28-36
Полистирол, PS	3 — 3,5	30-100
Полиэтилен, LDPE (низкая плотность)	0,11 — 0,45
Политетрафторэтилен (PTFE)	0,4
Жидкий полиуретановый литой		10-20
Полиуретановый эластомер		29-55
Поливинилхлорид (ПВХ)	2.4 — 4,1
Калий
Родий	290
Резина, малая деформация	0,01 — 0,1
Сапфир	435
Селен	58
Кремний	130-185
Карбид кремния	450		3440
Серебро	72
Натрий
Сталь, высокопрочный сплав ASTM A-514		760	690
Сталь нержавеющая AISI 302	180	860	502
Сталь, конструкционная ASTM-A36	200	400	250
Тантал	186
Торий	59
Олово	47
Титан
Титановый сплав	105-120	900	730
Эмаль для зуба	83
Вольфрам (Вт)	400-410
Карбид вольфрама (WC)	450-650
Уран	170
Ванадий	131
Кованое железо	190-210
Дерево
Цинк	83

• 1 Па (Н / м ² ) = 1×10 ^-6 Н / мм ² = 1.4504×10 ^-4 psi
• 1 МПа = 10 ⁶ Па (Н / м ² ) = 0,145×10 ³ psi (фунт _f / дюйм ² ) = 0,145 тыс. фунтов на квадратный дюйм
• 1 ГПа = 10 ⁹ Н / м ² = 10 ⁶ Н / см ² = 10 ^{3 2 Н / мм} 0,145×10 ⁶ фунтов на кв. Дюйм (фунт _на / дюйм ² )
• 1 МПа = 10 ⁶ фунтов на квадратный дюйм = 10 ³ тысяч фунтов на квадратный дюйм
  
47 фунтов на квадратный дюйм 1 2 ) = 0.001 тыс. Фунтов на квадратный дюйм = 144 фунта / кв. Дюйм (фунт _на / фут ² ) = 6 894,8 Па (Н / м ² ) = 6,895×10 ^-3 Н / мм ²

Примечание! — этот онлайн-преобразователь давления может использоваться для преобразования единиц модуля упругости при растяжении.

Деформация — ε

Деформация — это «деформация твердого тела под действием напряжения» — изменение размера, деленное на исходное значение размера — и может быть выражено как

ε = dL / L (1)

где

ε = деформация (м / м, дюйм / дюйм)

дл = удлинение или сжатие (смещение) объекта (м , дюйм)

L = длина объекта (м, дюйм)

Напряжение — σ

Напряжение — это сила на единицу площади и может быть выражена как

σ = F / A (2)

где

σ = напряжение (Н / м ² , фунт / дюйм ² , psi)

F = приложенная сила (Н, фунт)

A = площадь напряжения объекта (м ² , в ² )

• растягивающее напряжение — напряжение, которое стремится к растяжение или удлинение материала — действует нормально по отношению к напряженной области
• сжимаемое напряжение — напряжение, которое имеет тенденцию сжимать или укорачивать материал — действует нормально по отношению к напряженной области
• напряжение сдвига — напряжение, которое имеет тенденцию к сдвигу материала — действует в плоскости напряженной области под прямым углом к ​​напряжению сжатия или растяжения

Модуль Юнга — Модуль упругости при растяжении, Модуль упругости — E

Модуль Юнга можно выразить как

E = напряжение / деформация

= σ / ε

= (F / A) / (dL / L) (3)

, где

E = Модуль упругости Юнга (Па, Н / м ² , фунт / дюйм ² , фунт / кв. Дюйм)

• , названный в честь XVIII века Английский врач и физик Томас Янг

Эластичность

Эластичность — это свойство объекта или материала, указывающее, как он восстановит его первоначальную форму после искажения.

Пружина — это пример упругого объекта: при растяжении она создает восстанавливающую силу, которая стремится вернуть его к исходной длине. Эта восстанавливающая сила в целом пропорциональна растяжению, описанному законом Гука.

Закон Гука

Чтобы растянуть пружину вдвое дальше, требуется примерно вдвое больше силы. Эта линейная зависимость смещения от силы растяжения называется законом Гука и может быть выражена как

F _s = -k dL (4)

, где

F _s = усилие в пружине (Н)

k = жесткость пружины (Н / м)

dL = удлинение пружины (м)

Обратите внимание, что можно также применить закон Гука к материалам, испытывающим трехмерное напряжение (трехосное нагружение).

Предел текучести — σ _y

Предел текучести определяется в инженерии как величина напряжения (предел текучести), которому может подвергаться материал перед переходом от упругой деформации к пластической деформации.

• Предел текучести — материал постоянно деформируется

Предел текучести для низко- или среднеуглеродистой стали представляет собой напряжение, при котором происходит заметное увеличение деформации без увеличения нагрузки. В других сталях и цветных металлах этого явления не наблюдается.

Предел прочности на разрыв — σ _u

Предел прочности на разрыв — UTS — материала — это предельное напряжение, при котором материал фактически разрывается с внезапным высвобождением накопленной упругой энергии.

.

модулей упругости — это … Что такое модули упругости?

Модуль упругости — Модуль упругости или модуль упругости — это математическое описание тенденции объекта или вещества к упругой деформации (т. Е. Непостоянно) при приложении к нему силы. Модуль упругости объекта определяется как…… Wikipedia

Moduli — Модуль упругости, n .; пл. {Модули}. [Л., малая мера. См. {Module}, n.] (Math., Mech., & Physics) Величина или коэффициент, или константа, которая выражает меру некоторой указанной силы, свойства или качества, например эластичности, прочности,…… The Collaborative International Dictionary of English

квазиупругий метод — Метод анализа напряжений для нелинейных и / или зависящих от времени материалов, особенно полимеров, в котором модули упругости в уравнениях упругости заменяются значениями соответствующего секущего модуля или модуля ползучести при необходимый…… Словарь автомобильных терминов

твердое тело, механика — ▪ физика Введение в науку о напряжении (напряжении), деформации (деформации и текучести) и разрушении твердых материалов и конструкций.Что же такое твердое тело? Любой материал, жидкий или твердый, может выдерживать нормальные силы.…… Universalium

Закон Гука — моделирует свойства пружин при малых изменениях длины Проф. Уолтер Левин объясняет закон Гука в… Wikipedia

Модуль сдвига — Символ СИ: G Единица СИ: гигапаскаль Получение других величин: G = τ / γ… Википедия

Контактная механика — Механика сплошной среды… Википедия

Объемный модуль — сюда перенаправляется несжимаемость.По теме гидродинамики см. Сжимаемость. Иллюстрация равномерного сжатия Объемный модуль (K) вещества измеряет сопротивление вещества однородному сжатию. Он определяется как…… Wikipedia

Линейная эластичность — Механика сплошной среды… Википедия

Поперечная изотропия — Трансверсально изотропный материал симметричен относительно оси, перпендикулярной плоскости изотропии. Эта поперечная плоскость имеет бесконечное количество плоскостей симметрии, и, следовательно, в этой плоскости свойства материала одинаковы во всех направлениях.С этим…… Википедия

Модуль упругости продольной волны — При линейной упругости модуль упругости продольной волны M, также известный как продольный модуль, является одним из модулей упругости, доступных для описания изотропных однородных материалов. Он определяется как отношение осевого напряжения к осевой деформации в одноосном…… Wikipedia

.

Эластичность, упругие свойства

Объемные упругие свойства материала определяют, насколько он будет сжиматься при заданной величине внешнего давления. Отношение изменения давления к дробному объему сжатия называется объемным модулем материала.

Репрезентативная стоимость для большого количества модуль упругости по стали , а для воды — Величина, обратная модулю объемного сжатия, называется сжимаемостью вещества.Величина сжатия твердых тел и жидкостей кажется очень маленьким.

Модуль объемной упругости твердого тела влияет на скорость звука и других механических волн в материале. Это также фактор количества энергии, хранящейся в твердом материале земной коры. Это накопление упругой энергии может резко высвободиться при землетрясении, поэтому знание модулей объемной массы для материалов земной коры является важной частью изучения землетрясений.Объемный модуль упругости является фактором скорости сейсмических волн от землетрясений.

Распространено утверждение, что вода — несжимаемая жидкость. Это не совсем так, о чем свидетельствует его конечный модуль объемной упругости, но степень сжатия очень мала. На дне Тихого океана на глубине около 4000 метров давление около 4 x 10 ⁷ Н / м ² . Даже при таком огромном давлении относительное объемное сжатие составляет всего около 1,8%, а для стали — всего около 0.025%. Так что будет справедливо сказать, что вода почти несжимаема. Ссылка: Холлидей, Резник, Уокер, 5-е изд. Расширенный.

Джон Херманс указывает, что для более точной картины сжимаемости воды необходимо учитывать температуру. Причина, по которой сжатие 1,8% может быть указано выше, заключается в том, что сжимаемость воды при 20 ° C на поверхности примерно такая же, как сжимаемость на глубине 4000 м, если температура на дне составляет 5 ° C.Сжимаемость при таком давлении и глубине имеет более высокое значение из-за более низкой температуры, чем было бы при 20 ° C. Используя подробные данные о сжимаемости воды из компиляции Fine & Millero, можно увидеть, что если бы нижняя температура была 5 ° C, сжатие было бы примерно 1,82%, но если бы оно было 20 ° C, степень сжатия была бы примерно 1,66 %.

Температура ° C	Давление Атм	Сжимаемость на мбар	% Сжатие при 400 бар
20 ° C	0	45.895	…
5 ° C	400	45,498	1,82%
20 ° C	400	41,492	1,66%

Другой способ заявить, что если температура на дне составляет 5 ° C, сжимаемость уменьшится только на 0,9% от поверхности к глубине, тогда как если температура на дне будет также 20 ° C, сжимаемость снизится примерно на 9,6%.

Интерес Hermance к этой подробной картине сжимаемости исходит из приложения к сжимаемости подземных вод в недрах Земли.Эти грунтовые воды могут иметь более высокую температуру, и изменение сжимаемости имеет большое значение для понимания процессов хранения и выпуска грунтовых вод из трещин и пор в породе, а также последствий гидроразрыва пласта, землетрясений и т. Д. В верхняя кора Земли.

Ссылка: Fine, R. A. и Millero, F. J., 1973. «Сжимаемость воды как функция температуры и давления», Journal of Chemical Physics 59 (10): 5529-5536. DOI: 10.1063 / 1.1679903.

.

Модули упругости | Статья о модулях упругости от The Free Dictionary

Также обсуждались влияние ZnO на его модули упругости и сравнение модулей упругости, полученных экспериментально, и модулей упругости, полученных теоретически. Таким образом, СП также имеют самые высокие модули упругости: 86,27 ГПа, 35,20 ГПа, 99,31 ГПа и 52,38 ГПа для LB4 E , G, L и K, соответственно. Модули упругости, построенные на основе теоретической модели на рисунке 3, демонстрируют тенденцию, аналогичную экспериментальным результатам.Кромп, «Новый метод резонансного пучка для определения модулей упругости в зависимости от ориентации и температуры до 2000 [градусов] C», Review of Scientific Instruments, том. После отжига ни одноосно растянутые, ни магнитно ориентированные пленки не показали заметных увеличение модулей упругости, измеренных при комнатной температуре. Модуль упругости магнитно-ориентированных пленок был ниже, чем у механически ориентированных пленок той же степени ориентации, но был сравним с модулями упругости механически ориентированных пленок или даже превышал их. более низкие степени ориентации.Таким образом, мы заключаем, что схемы последовательной и параллельной связи агрегированной модели могут только обеспечивать границы, и неоправданно использовать любую схему для получения точных значений модулей упругости. Таблица 1. Wu, «О параметризации модулей упругости двухфазных материалов», Журнал прикладной механики, том (2). Модули упругости распределенного по направлению SFRC, заданные теорией композитных материалов и полуэмпирическими формулами. отличаются от экспериментальных значений.Поскольку для пористого материала модули упругости являются функцией пористости [15, 16], скорость ультразвука в однородном материале будет зависеть от пористости. Родригес, Кейрос, Эспиноза и Зандонади (2006) определили модули упругости стеблей кофе, рассматривая стебли как консольные балки с сосредоточенной массой на свободном конце. Кривые были построены с использованием Microsoft Excel для каждого материала для сравнения. Результаты показали, что модули упругости постоянно увеличивались в следующем порядке; Cavex Cream Alginate (r)> Tulip (r)> Cavex Color Change (r)> TOL (r)> Cavex CA37 (r), и скорость увеличения была выше в конце рабочего времени, а затем снизилась..

No related posts.